Heuristika i generalizacija Heronove formule u dva smjera
|
|
|
- Brian Hill
- 5 years ago
- Views:
Transcription
1 MAT-KOL (Banja Luka) XXIII ()(07), DOI: 0.75/МК70049S ISSN (o) ISSN (o) Heurstka generalzacja Heronove formule u dva smjera Petar Svrčevć Zagreb, Hrvatska e-mal:petar.svrcevc@zg.t-com.hr Sažetak. U ovome članku ćemo pomoću heurstčke metode zvest, a onda strogo dokazat sljedeće formule: Heronova formula kao funkcja duljna stranca trokuta, Heronova formula kao funkcja duljna vsna trokuta Heronova formula kao funkcja duljna težšnca trokuta. Nakon toga ćemo sve tr formule kumulrat u jednu, koja ćemo zvat Kumulatvna formula za površnu trokuta, to b bla generalzacja u prvom smjeru. Još ćemo zvest Heronovu formulu kao funkcja duljna polumjera trokutu prpsanh kružnca, koja je slčna prethodnm Heronovm formulama, al se s njma ne može kumulrat. Nadalje, generalzacjom u drugom smjeru ćemo heurstčk zvest Kumulatvnu formulu za površnu tetvnoga polgona, pokazat ćemo, da ona općento vrjed samo za trokut tetvn četverokut. Ključne rječ: kumulatvna formula, površna trokuta, površna tetvnog polgona Heurstcs and The Generalzaton of Heron's Formula n two Drectons Abstract. In ths artcle we wll be usng heurstc methods to construct, and then rgorously prove the followng formula: Heron's formula as a functon of the length of the sdes of the trangle, Heron's formula as a functon of the length of the alttudes of the trangle and Heron's formula as a functon of the length of the medans of the trangle. All three formulas we wll cumulate nto a sngle one, whch we call the cumulatve formula for the area of a trangle, and t would be a generalzaton n the frst drecton. We wll also formulate Heron s formula as a functon of the length of
2 MAT-KOL, XXIII ()(07) P.Svrčevć the raduses of the trangle assgned to the crcle, whch s "smlar" to the prevous Heron's formula, but cannot be cumulated wth them. Furthermore, by generalzaton nto another drecton we wll heurstcally formulate the Cumulatve formula for the surface of the tendon polygon, and we wll show that t generally apples only to a trangle and a tendon quadrlateral. Keywords: cumulatve formula, the surface of a trangle, the surface of the tendon polygon. Napomena. Praktčno je, da se za svaku velčnu a, koja predstavlja broj duljnskh jednca uvedemo oznaku a D = L, čtamo ''dmenzja od a je L'', a to je duljna; dakle ne preczramo da l se rad o: m (metru), cm (centmetru), mm (mlmetru),... Slčno ćemo za velčnu P, koja predstavlja broj površnskh jednca, psat da joj je dmenzja jednaka L ; dakle P D = L, ovdje ne preczramo, da l se rad o: m, cm, mm,...; broj volumnh jednca defnramo da je V D = L 3, Jasno je, da je λ D = L 0 =, gdje je λ nemenovan broj, tj. λ R +. a) Generalzacja u smjeru Kumulatvne formule za površnu trokuta Ako su a,b,c, duljne stranca ABC, tada vrjed dobro poznatu Heronova formula P = s(s a)(s b)(s c), () gdje je a + b + c s = poluopseg trokuta. No, () se može psat u oblku P = 4 (a + b + c)(b + c a)(c + a b)(a + b c), () koj lako transformramo u modfcran oblk P = 4 (a + b + c ) (a 4 + b 4 + c 4 ), (3) a on je praktčan za prmjenu, ako su duljne stranca npr.: a = 9, b =, c = 3. Nadalje, ćemo reć, da trokut postoj ako samo ako je P > 0. Dakle P R +, jer P uzmamo kao broj nemenovanh kvadratnh jednca; dok su: a, b, c, s brojev stovrsnh nemenovanh duljnskh jednca, pa je: a, b, c, s R +. Prema tome je funkcja P: (R + ) 3 R +. Iz () sljed ekvvalencja (P > 0) ((b + c > a) (c + a > b) (a + b > c)), (4) a to znač da trokut postoj onda samo onda ako su spunjene sve tr nejednakost. Nadalje vrjed ekvvalencja (P = 0) ((b + c = a) (c + a = b) (a + b = c)), (5) dakle to je realan, al degenerran, slučaj; jer je trokut degenerrao u dužnu. I na kraju mamo slučaj, kada površna nema realnu vrjednost, name (P R) ((b + c < a) (c + a < b) (a + b < c)), (6) 50
3 MAT-KOL, XXIII ()(07) P.Svrčevć Sada ćemo heurstčk doć do formule (). Jasno je, da je nužn uvjet za postojanje trokuta valjanost nejednakost: (b + c > a) (a + b + c > a) a + b + c a = s a > 0 (s a > 0). Na osnov toga, po zakonu analogje stovremeno vrjede ove tr nejednakost: s a > 0, s b > 0, s c > 0 ; koje su sada nužan dovoljan uvjet za postojanje trokuta. Naslućujemo, da će velčne: s a, s b, s c ; tvort formulu za površnu trokuta, odnosno bt će zastupljen njhov produkt, jer su one međusobno ravnopravne. No, ((s a)(s b)(s c)) D = L 3, a to znač da b trebal ubact još jedan neutraln varjabln faktor, tako da korjenovanjem toga zraza dobjemo dmenzju površne. Za očekvat je, da b taj faktor mogao bt poluopseg s. Na osnov znesenog naslućujemo, da je formula za površnu trokuta dana u oblku P = k s(s a)(s b)(s c), (7) gdje je k konstanta koju moramo odredt. No, ona se najjednostavnje određuje, da se zvrš specjalzacja za jednakostrančn trokut, za koj je: P = a 3, a = b = c, s = 3a. Ako te vrjednost uvrstmo u (7), tada sljed da je k =, dakle naslućujemo da je () točno. No, ovu formulu pak nećemo strogo zvodt, jer ona spada u standardno srednjoškolsko gradvo, može se zvest na vše načna. Napomenmo, da smo m mogl naslutt da formula za površnu trokuta zgleda npr. ovako P = k (s a) 4 + (s b) 4 +(s c) 4 ). No, to nje točno, jer b već za dva posebna slučaja kod određvanja konstante k vjerojatno dobl razlčte vrjednost, a to b bla kontradkcja, dakle ova formula općento nema smsla. Svakako, da b mogl sptat, da l postoje specjaln slučajev za ovaj oblk formule. Izvedmo sada formulu za površnu trokuta kao funkcju duljna vsna. Ako je a duljna vsne na strancu duljne a, td.,..., tada je P = a a = b b = c c, a odatle sljed a = P, b = P, c = P. (8) a b c Vdmo, da nam ove zadnje jednakost sugerraju uz uvažavanje (), da b formula za površnu trokuta pomoću duljna vsna mogla bt u oblku P = k ( a + b + c )( b + c a )( c + a b )( a + b c ). (9) Ako opet uzmemo, da je a = b = c, onda je P = a a = b = c = a 3. Uvrstmo l te vrjednost u (9), tada dobvamo da je k =, dakle sada naslućujemo da je točna ova formula P = ( a + b + c )( b + c a )( c + a b )( a + b c ). (0) A sada dokažmo (0). Name, ako (8) uvrstmo u (), tada dobvamo da je (0) točno. Nadalje, vdmo da vrjede nejednakost b + c > a, c + a > b, a + b > c, koje baš nsu evdentne bez sljedeće analze. 5
4 MAT-KOL, XXIII ()(07) P.Svrčevć Name, uvedmo velčnu s čja je recpročna vrjednost jednaka poluzbroju recpročnh vrjednost duljna vsna, tj. s = ( a + b + c ), () tada pomoću (0) () dobvamo vezu P = 4 s (s a )(s b )(s c ), () a odatle se lako dobje modfcran oblk P = ( a + b + c ) ( a 4 + b 4 + c 4 ). (3) Analogon relacjama: od (4) do (6), osm (5); sada za duljne vsna vrjede ekvvalencje: (P > 0) (( b + c > a ) ( c + a > b ) ( a + b > c )), (P = 0) (( a = 0) ( b = 0) ( c = 0)), (4) (P R) (( b + c < a ) ( c + a < b ) ( a + b < c )). Dakle, evvalencja (P = 0) (( b + c = a ) ( c + a = b ) ( a + b = c )), ako formalno gledamo, b trebala odgovarat ekvvalencj (5). No, to nje stna, jer b tada z (5) sljedlo da je P =, a mora bt P = 0. Prema tome je jasno, da duljna blo koje vsne mora bt jednaka nul, da b trokut degenerrao u dužnu, tako da mu je površna jednaka nul, dakle (4) je točno. Konačno, zvedmo formulu za površnu trokuta kao funkcju duljna njegovh težšnca uz uobčajene oznake. Name, ako pogledamo (3) (3), tada je logčno da očekujemo, da tražena formula ma oblk P = k (t a + t b + t c ) (t 4 a + t 4 b + t 4 c ). (5) Svakako, da ćemo ovdje zvršt specjalzacju a = b = c, pa dobvamo da je t a = t b = t c = a 3 P = a 3, a pomoću th vrjednost z (5) dobvamo k = / Dakle, heurstčkom metodom dobvamo da je P = (t 3 a + t b + t c ) (t 4 a + t 4 b + t 4 c ). (6) Da b (6) strogo dokazal, tada se moramo prsjett, kako pomoću kosnusovog poučka možemo dobt, da su kvadrat duljna težšnca: t a = 4 (b + c a ), t b = 4 (c + a b ), t c = 4 (a + b c ). (7) Iz th relacja dobvamo, da je: a = 4 (t 9 b + t c t a ), b = 4 (t 9 c + t a t b ), c = 4 (t 9 a + t b t c ). (8) Sumramo l jednakost (8), tada dobvamo da je a + b + c = 4 (t 3 a + t b + t c ). (9) A ako te ste jednakost kvadrramo zbrojmo, tada nakon sređvanja (sps je malo duž) sljed a 4 + b 4 + c 4 = 6 (t 9 a 4 + t 4 b + t 4 c ). (0) Uvrstmo l (9) (0) u (3), tada dobvamo (6). Jasno je, do po analogj () (3) z (6) sljed 5
5 MAT-KOL, XXIII ()(07) P.Svrčevć P = 3 (t a + t b + t c )(t b + t c t a )(t c + t a t b )(t a + t b t c ). () Nadalje, ako sa s t označmo poluzbroj duljna težšnca, dakle s t = (t a + t b + t c ), ako to uvrstmo u () dobvamo formulu P = 4 3 s t(s t t a )(s t t b )(s t t c ). () Vdljvo je, da z () sljede nejednakost t b + t c > t a, t c + t a > t b, t a + t b > t c. Za ovaj slučaj vrjede analogne ekvvalencje kao (4), (5), (6). Sada ćemo kumulrat formule: (), (), () u jednu, koja ćemo zvat Kumulatvna formula za površnu trokuta. Analogno ćemo napravt s modfcranm formulama: (3), (3), (6). No, da b do navedenog došl moramo prje dat jednu defncju o oznakama velčna trokuta defnrat još tr funkcje. Defncja. Neka su A, B, C vrhov ABC; a, b, c duljne stranca nasuprot tm vrhovma; a, b, c duljne vsna z th vrhova, konačno a 3, b 3, c 3 su duljne težšnca z th vrhova. Defnrajmo jednu dobro poznatu još dvje nove funkcje: Defncja., x < 0 sng: R,0, ; sng(x) = 0, x = 0., x > 0 Defncja 3. ε:,,3, ; ε = ( ) + ; ( =,,3). Defncja 4. K:,,3, 4, 4 3 ; K = 4 3 sng ( ) ( ) sng ( ), ( =,,3). Kumulatvna formula za površnu trokuta može se napsat u oblku ε ε P = K s ε (s ε a ε )(s ε b ε )(s ε c ), (3) ε gdje je s = (a ε ε + b ε + c ), l u modfcranom oblku P = ε K ε 4 ε (a ε + b ε + c ) 4ε (a 4ε + b 4ε + c ) ; (4) dakle površna je funkcja: duljna stranca za =, duljna vsna za =, duljna težšnca za = 3. Prmjenmo zvedene formule na tr problema. Problem. Izračunajmo P, t a, t b, t c, a, b, c ; ako je a = 5, b = 0, c = 3. Rješenje. Iz (3) sljed 53
6 MAT-KOL, XXIII ()(07) P.Svrčevć P = 4 (a + b + c ) (a 4 + b 4 + c 4 ) = = 4, a z (7) je, t a = 4 (b + c a ) =...4, tj. t a = 4. Analogno dobvamo, da je t b = 6 t c = 7. Nadalje je a = P a = = 4 5, odnosno b = 4 0 c = 4 3. Problem. Izračunajmo P, ako je t a = 4, t b = 6 t c = 7. Rješenje. P = (t 3 a + t b + t c ) (t 4 a + t 4 b + t 4 c ) =...=4, što smo očekval zbog P. Problem 3. Izračunajmo P, ako je a = 4 5, b = 4 0 c = 4 3. Rješenje. Iz (3) sljed P = ( a + b + c ) ( a 4 + b 4 + c 4 ) = 5 = = = 4, 4 a to smo očekval. Sada dolazmo do još jedne formule, koja je slčna Heronovm formulama. Name, ako je trokut zadan s duljnama polumjera njemu prpsanh kružnca, tada je površna trokuta dana s formulom P = r b + r c + r c + r a + r a + r b r b + r c 4 + r c + r a 4 + r a + r b (5) Da b dokazal (5) korstmo dobro poznate formule: r = P, r s a = P, r s a b = P, r s b c = P, (6) s c gdje je r duljna polumjera trokutu upsane kružnce, dok su: r a, r b, r c duljne polumjera trokutu prpsanh kružnca. Dalje, pomoću navedenh formula lagano dobvamo, da je r = r a + r a + r a P = rr a r b r c, a pomoću njh dolazmo do tražene formule. Problem 4. Ako su duljne polumjera prpsanh kružnca trokutu dane s: 4 r a =, r b =, r c = ; (7) tada trebamo nać površnu P. Rješenje. Ako te vrjednost supstturamo u (5) dobvamo da je P = 4. No, to je stna, jer pomoću: a = 5, b = 0 c = 3 ; smo već dobl P = 4, a također možemo dobt (7), ako prmjenmo (6). Napomena. Razmatranje b mogl prošrt tako, da s a 4, b 4, c 4 označmo duljne smetrala kutova trokuta. Znamo da vrjede formule a 4 = b c b +c a, b b +c 4 = c a c +a b, c c +a 4 = a b a +b c a +b.
7 MAT-KOL, XXIII ()(07) P.Svrčevć Možemo dokazat da formule tpa (3) (4) za duljne smetrala kutova trokuta ne vrjede. Name, ako je = 4, tada možemo pokazat da za ε 4 = ± velčna K 4 nje konstanta. To je najjednostavnje napravt, tako da najprje uzmemo posebn slučaj a = b = c (trokut je jednakostrančan) za koj nađemo K 4, zatm uzmemo drug slučaj a + b = c (trokut je pravokutan), te za njega nađemo K 4. Vdjet ćemo, da ta konstanta u ova dva slučaja nema stu vrjednost, dakle formule tpa (3) (4) nje moguće općento prošrt na duljne smetrala kuta. Nakon ovh razmatranja možemo postavt dvje, čn se baš ne jednostavne, hpoteze, koje b se mogle razmatrat. Hpoteza. Ako su a 4, b 4, c 4 duljne smetrala kutova trokuta, tada ne postoj formula P = 4 K 4 (a 4 p + b 4 p + c 4 p ) (a 4 4p + b 4 4p + c 4 4p ) gdje je K 4 = const pq = za p, q Q. Hpoteza. Ako su a 5, b 5, c 5 duljne polumjera trokutu prpsanh kružnca, tada ne postoj formula P = 4 K 5 (a 5 p + b 5 p + c 5 p ) (a 5 4p + b 5 4p + c 5 4p ) gdje je K 5 = const pq = za p, q Q. q q b) Generalzacja u smjeru Kumulatvne formule za površnu tetvnoga polgona Sada ćemo napravt poopćenje Heronove formule u drugom smjeru pomoću heurstčke metode za opć tetvn polgon. Strog dokaz te formule se odnos samo na trokut tetvn četverokut, onda dokazujemo, da ona općento ne vrjed za ostale tetvne polgone. Konačno ćemo formulrat naš problem, doć do vjerodostojne hpoteze, koju ćemo onda dokazat matematčkom ndukcjom. Hpoteza o površn općeg tetvnog polgona. Neka je zadan tetvn n-terokut (n 3), čj su vrhov desno orjentran nalaze se u točkama: A, A,, A n. Njegove duljne stranca su a = A A + ; =,,, n ; a n = A n A ; te je poluopseg s n = (a + a + + a n ), (8) tada je površna toga polgona dana formulom P n = ctg 80 n nn s n n n 4 n (s n a ) (s n a n ). (9) Napomena 3. Formulu (9) ćemo zvat Kumulatvna formula za površnu tetvnog polgona, ako je n 3,4 ; koju možemo još psat u oblcma P 3 = 4 (a + a + a 3 ) (a 4 + a 4 + a 3 4 ), P 4 = 4 (a + a + a 3 + a 4 ) (a 4 + a 4 + a a 4 4 ) + 8a a a 3 a 4, (30) 55
8 MAT-KOL, XXIII ()(07) P.Svrčevć zavsno o tome da l se rad o trokutu l tetvnom četverokutu. Pokazat ćemo da za slučajeve n > 4 ta formula općento ne vrjed, dakle nje heronskog tpa. Napomena 4. Pravokutnk je tetvn četverokut, ako su mu duljne stranca a b, pa mu je tada površna P = ab. No, tu formulu možemo dobl, ako u (30) uvrstmo da je a = a 3 = a a = a 4 = b. dana s Izvod hpoteze. Polazmo najprje od pravlnog n-terokuta, čja je površna P n = na 80 ctg, (3) 4 n gdje je a = a; =,,, n. Pokušajmo sada nać još koj posebn slučaj. Neka to bude, kada polgon degenerra u dužnu; a to znač da mu duljna polumjera opsane kružnce tež u beskonačnost; name, neka je a + a a n = a, a odatle je, jer smo uvažl (8), s n a = 0. Zbog toga posebnog slučaja površna polgona je P n = 0, pa očekujemo da se u formul pojav razlka s n a = 0 kao faktor. Buduć, da formula ne zavs o tome, kako smo označl duljne stranca, onda to povlač, da ona sadrž faktore s n a, s n a 3,, s n a n, a odatle zaključujemo da naša formula sadrž produkt p n = (s n a )(s n a ) (s n a n ). (3) Uvažmo l napomenu o dmenzonranju, onda je jasno da je dmenzja od p n dana s p n D = L n, no znamo da mora bt P n D = L (33) Malo se podsjetmo Heronove formule za površnu trokuta, sada u novoj oznac, P 3 = s 3 (s 3 a )(s 3 a )(s 3 a 3 ), (34) gdje je s 3 = (a + a + a 3 ) formule za površnu tetvnog četverokuta dane u oblku P 4 = (s 4 a )(s 4 a )(s 4 a 3 )(s 4 a 4 ), (35) gdje je s 4 = (a + a + a 3 + a 4 ). Evdentno je, da se (34) može dobt z (35), to tako da trokut shvatmo kao degenerran četverokut, kada mu je duljna jedne strance jednaka nul (npr. a 4 = 0). U formulama (34) (35) se pojavljuje drug korjen, pa pretpostavljamo da naša formula mora bt u oblku P n = f(a, a,, a n )p n, (36) gdje je f(a, a,, a n ) homogena smetrčna funkcja, al takva da je f(a, a,, a n ) D = L 4 n, jer tada važ (33). Naslućujemo da je f(a, a,, a n ) = ks n 4 n, (k = const. ) te z (36) sljed da je P n = ks n 4 n p n. (37) Dakle, u (37) trebamo još odredt konstantu k. Da b nju dobl napravmo specjalzacju a = a = a = = a n, prema tome rad se o pravlnom n-terokutu, kod kojega je 56
9 MAT-KOL, XXIII ()(07) P.Svrčevć s n = na, p n = (n )n n a n, (38) dakle vrjed (3). Ako (38) (3) supstturamo u (9) dobvamo da je a odatle je k = ctg 80 0 na 80 ctg 4 n nn = k na 4 n (n ) n n a n n (n ) n, pa (37) poprma oblk (9), jer smo uvažl (3). Prema tome došl smo do vjerodostojne Hpoteze o površn općeg tetvnog polgona. Pokazat ćemo da ona općento ne vrjed. Sada ćemo najprje dat dvje posljedce dane hpoteze. Napomena 5. Ako je n = 3, tada z (9) sljed Heronova formula (34), jer smo uvažl da je ctg60 0 = 3/3. Napomena 6. Za n = 4 z (9) sljed formula za površnu tetvnog četverokuta (35), jer smo uvažl da je ctg45 0 =. Napomena 7. Ako je n = 5, tada z (9) sljed P 5 = (ctg36 0 ) 53 s (s 5 a )(s 5 a )(s 5 a 3 )(s 5 a 4 )(s 5 a 5 ). (39) Moramo pokazat da ova formula općento nje točna za opć tetvn peterokut, no u nekm slučajevma ona je dobra aproksmacja, što možemo provjert upotrebom programa GSP l nekog drugog (Maple V, Mahtematca,...). Dokaz da hpoteza ne vrjed za n = 5. Navedenu formulu ne znamo zvest, al ćemo je provjert za tetvn peterokut A A 5 koj je prkazan na slc., gdje je a = a = a 3 =, a 4 = a 5, (40), Slka. a četverokut A A A 3 A 4 je kvadrat. Nađmo a 4. Iz slke se vd, da je. A S = A 5 S =. Dalje dobvamo da je a 4 = A 4 A 5 = + l 57
10 MAT-KOL, XXIII ()(07) P.Svrčevć. a 4 = a 5 = 4 = (4) Iz (40) (4) dobvamo s 5 = =.0496 (4) Supstturamo l (40),(4) (4) u (39) sljed P 5 =.03. (43) Na drug načn dobjemo P 5 drektno z slke, dakle potpuno točno l prblžno; ako zvršmo korjenovanje; rezultat ovom metodom je P 5 = + = 3+ = (44) 4 Lako provjermo, da se rezultat (43) (44) razlkuju za (relatvna greška je oko 0.%) a to nje čudo jer smo korstl formulu (39) gdje je realzrano 7 všh operacja, koje su mogle napravt navedenu grešku, pa b dalje mogl vjerovat da je upotrebljena formula možda potpuno točna, jer je nsmo strogo dokazal. Sada ćemo jednom strožom analzom to negrat. Ako se bavmo sa zlatnm rezom konstrukcjom pravlnog peterokuta, tada dolazmo do relacje sn36 = 4 0 5, a odatle je ctg36 = (45) Supstturamo l sada vrjednost: a = a = a 3 =, a 4 = a 5 = 4, P 5 = 3+ (45); 4 u (39) vdmo da formula nje točna, jer ljeva strana te jednakost ne sadrž 5, a desna ga sadrž (postoj barem jedna kontradkcja), dakle formula (39) samo prblžno zračunava površnu. Dokaz da hpoteza ne vrjed za n > 5. Znamo, da je mplkacja stnta, ako z stne sljed stna. Nadalje, nestna je da z stne sljed nestna, stna je da z nestne može sljedt stna l nestna. Analzrajmo sada formulu (9). Name, dokazal smo da je ona nestnta za n = 5. Pretpostavmo sada, da (9) vrjed za n = 6. No, polgon za n = 6 može degenerrat tako da duljna jedne stranca bude jednaka nula, a to znač da b (9) trebala vrjedt za n = 5 što nje stna. I na osnovu ovh razmatranja možemo matematčkom ndukcjom pokazat da (9) ne vrjed za n > 5, pa b tme hpoteza bla u potpunost dokazana. Iz mnemotehnčkh razloga, sada na kraju spšmo sve formule heronskog tpa:. Heronova formula kao funkcja duljna stranca trokuta; P = s(s a)(s b)(s c), (46) gdja su: a,b,c, duljne stranca trokuta a s = a+b+c. (46) se može psat u oblku P = 4 (a + b + c ) (a 4 + b 4 + c 4 ). 58
11 MAT-KOL, XXIII ()(07) P.Svrčevć. Heronova formula kao funkcja duljna vsna trokuta; P = 4 s (s a )(s b )(s c ), (47) gdje su: a, b, c, duljne vsna trokuta; a s = ( a + b + c ). (47) se može psat u oblku P = ( a + a + a ) ( a 4 + a 4 + a 4 ). 3. Heronova formula kao funkcja duljna težšnca trokuta; P = 4 3 s t(s t t a )(s t t b )(s t t c ), (48) gdje su: t a, t b, t c ; duljne težšnca trokuta; a s t = (t a + t b + t c ). (48) se može psat u oblku P = 3 (t a + t b + t c ) (t a 4 + t b 4 + t c 4 ) 4. Kumulatvna formula za površnu trokuta gdje je: s ε = (a P = K s ε (s ε a ε )(s ε b ε )(s ε c ε ). ε, (49) ε + b ε + c ε ); = rad se o duljn stranca, = rad se o duljn vsna, = 3 rad se o duljn težšnca; gdje je ε = ( ) +, K = 4 3 sng ( ) ( ) sng ( ). (49) se pše u oblku P = 4 ε K (a ε + b ε + c ε ) (a 4ε + b 4ε + c 4ε ) 5. Formula kao funkcja duljna polumjera trokutu prpsanh kružnca; P = r b + r c + r c + r a + r a + r b r b + r c 4 + ε. r c + r a 4 + r a + r b 4, (50) gdje su: r a, r b, r c duljne polumjera prpsanh kružnca. Ta formula nje formula heronskog tpa, premda je njoj slčna. I na kraju napomenmo, kada je u ptanju trokut, da (50), ako uvažmo vezu r = r a + r b + r c, možemo psat u oblku P = r a + r b + r c r a r b r c 6. Kumulatvna formula za površnu tetvnog polgona za n 3,4 P n = ctg 80 n 59. nn s n n n 4 n (s n a ) (s n a n ), (5) gdje su: a, a,, a n duljne stranca s n = (a + + a n ). (5) se može psat u oblku:
12 MAT-KOL, XXIII ()(07) P.Svrčevć P 3 = 4 (a + a + a 3 ) (a 4 + a 4 + a 3 4 ). P 4 = 4 (a + a + a 3 +a 4 ) (a 4 + a 4 + a a 4 4 ) + 8a a a 3 a 4. Zaključak. Svrha ovoga članka je, da se prezentra heurstka (grč., nauka o metodama stražvanja novh spoznaja) l ars nvenend (lat., umjeće naslućvanja), koja ma velku važnost u matematc, al u drugm naukama (fzka, kemja, bologja,...). No, u matematc zakon dobven heurstčkom metodom moraju bt potvrđen još strogm teorjskm dokazom, koj drektno l ndrektno sljed z postavljenh aksoma za konkretnu matematčku granu. Međutm, uvjetno rečeno, u drugm naukama zakon dobven tom metodom se prhvaćaju kao pravovaljan nakon konačnog broja emprjakh provjera, osm u onm djelovma fzke koj su aksomatsk zgrađen (klasčna mehanka, mehanka neba, specjalna teorja relatvnost,...). Lteratura G. L. Alexanderson, The random walks of George Pólya, Washngton, DC, 000. B. Pavkovć, Metoda posebnh slučajeva, HMD, Zbornk radova, Šest susret nastavnka matematke; Zagreb, srpnja P. Svrčevć, Kumulatvna formula za površnu trokuta, Matematčko-fzčk lst, br. 3, Zagreb, 008/09. 4 P. Svrčevć, Heurstka kumulatvna formula za površnu tetvnog polgona, Matematčko-fzčk lst, br., Zagreb, 0/3. 5 П. Свирчевић, Заједничка анализа три тврђења о троуглу, Настава математике, LIX - / 04., 6 H.Taylor and L.Taylor, George Pólya - Master of Dscovery, Palo Alto, CA,
ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA. Šefket Arslanagić, Sarajevo, BiH
 MAT-KOL (Banja Luka) XXIII ()(7), -7 http://wwwimviblorg/dmbl/dmblhtm DOI: 75/МК7A ISSN 5-6969 (o) ISSN 986-588 (o) ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA Šefket Arslanagić,
MAT-KOL (Banja Luka) XXIII ()(7), -7 http://wwwimviblorg/dmbl/dmblhtm DOI: 75/МК7A ISSN 5-6969 (o) ISSN 986-588 (o) ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA Šefket Arslanagić,
PRILOG O PROŠIRIVANJU I UOPŠTAVANJU ZADATAKA IZ GEOMETRIJE TROUGLA
 MAT-KOL (Banja Luka) XX(3)(2014) 145--151 http://wwwmvblorg/dmbl/dmblhtm ISSN 0354-6969 (o) ISSN 1986-5828 (o) PRILOG O PROŠIRIVANJU I UOPŠTAVANJU ZADATAKA IZ GEOMETRIJE TROUGLA (Some attachment on the
MAT-KOL (Banja Luka) XX(3)(2014) 145--151 http://wwwmvblorg/dmbl/dmblhtm ISSN 0354-6969 (o) ISSN 1986-5828 (o) PRILOG O PROŠIRIVANJU I UOPŠTAVANJU ZADATAKA IZ GEOMETRIJE TROUGLA (Some attachment on the
O homomorfizam-homogenim geometrijama ranga 2
 UNIVERZITET U NOVOM SADU PRIRODN0-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Eva Jungael O homomorfzam-homogenm geometrjama ranga 2 -završn rad- Nov Sad, oktoar 2009 Predgovor Za strukturu
UNIVERZITET U NOVOM SADU PRIRODN0-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Eva Jungael O homomorfzam-homogenm geometrjama ranga 2 -završn rad- Nov Sad, oktoar 2009 Predgovor Za strukturu
Red veze za benzen. Slika 1.
 Red veze za benzen Benzen C 6 H 6 je aromatično ciklično jedinjenje. Njegove dve rezonantne forme (ili Kekuléove structure), prema teoriji valentne veze (VB) prikazuju se uobičajeno kao na slici 1 a),
Red veze za benzen Benzen C 6 H 6 je aromatično ciklično jedinjenje. Njegove dve rezonantne forme (ili Kekuléove structure), prema teoriji valentne veze (VB) prikazuju se uobičajeno kao na slici 1 a),
TEORIJA SKUPOVA Zadaci
 TEORIJA SKUPOVA Zadai LOGIKA 1 I. godina 1. Zapišite simbolima: ( x nije element skupa S (b) d je član skupa S () F je podskup slupa S (d) Skup S sadrži skup R 2. Neka je S { x;2x 6} = = i neka je b =
TEORIJA SKUPOVA Zadai LOGIKA 1 I. godina 1. Zapišite simbolima: ( x nije element skupa S (b) d je član skupa S () F je podskup slupa S (d) Skup S sadrži skup R 2. Neka je S { x;2x 6} = = i neka je b =
HRVATSKA MATEMATIČKA OLIMPIJADA
 HRVATSKA MATEMATIČKA OLIMPIJADA prvi dan 5. svibnja 01. Zadatak 1. Dani su pozitivni realni brojevi x, y i z takvi da je x + y + z = 18xyz. nejednakost x x + yz + 1 + y y + xz + 1 + z z + xy + 1 1. Dokaži
HRVATSKA MATEMATIČKA OLIMPIJADA prvi dan 5. svibnja 01. Zadatak 1. Dani su pozitivni realni brojevi x, y i z takvi da je x + y + z = 18xyz. nejednakost x x + yz + 1 + y y + xz + 1 + z z + xy + 1 1. Dokaži
Projektovanje paralelnih algoritama II
 Projektovanje paralelnih algoritama II Primeri paralelnih algoritama, I deo Paralelni algoritmi za množenje matrica 1 Algoritmi za množenje matrica Ovde su data tri paralelna algoritma: Direktan algoritam
Projektovanje paralelnih algoritama II Primeri paralelnih algoritama, I deo Paralelni algoritmi za množenje matrica 1 Algoritmi za množenje matrica Ovde su data tri paralelna algoritma: Direktan algoritam
PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU
 MAT KOL Banja Luka) ISSN 0354 6969 p) ISSN 1986 58 o) Vol. XXI )015) 105 115 http://www.imvibl.org/dmbl/dmbl.htm PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU Bernadin Ibrahimpašić 1 Senka Ibrahimpašić
MAT KOL Banja Luka) ISSN 0354 6969 p) ISSN 1986 58 o) Vol. XXI )015) 105 115 http://www.imvibl.org/dmbl/dmbl.htm PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU Bernadin Ibrahimpašić 1 Senka Ibrahimpašić
SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE
 SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE Vuko Vukčevć, Mhael Lobrovć Teorjsko numerčk prstup problemu lamnarnog grančnog sloja oko ravne ploče Zagreb, 2011. Ovaj rad zrađen je na Katedr
SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE Vuko Vukčevć, Mhael Lobrovć Teorjsko numerčk prstup problemu lamnarnog grančnog sloja oko ravne ploče Zagreb, 2011. Ovaj rad zrađen je na Katedr
Algoritam za množenje ulančanih matrica. Alen Kosanović Prirodoslovno-matematički fakultet Matematički odsjek
 Algoritam za množenje ulančanih matrica Alen Kosanović Prirodoslovno-matematički fakultet Matematički odsjek O problemu (1) Neka je A 1, A 2,, A n niz ulančanih matrica duljine n N, gdje su dimenzije matrice
Algoritam za množenje ulančanih matrica Alen Kosanović Prirodoslovno-matematički fakultet Matematički odsjek O problemu (1) Neka je A 1, A 2,, A n niz ulančanih matrica duljine n N, gdje su dimenzije matrice
Strojno učenje 7 Linearne metode & SVM. Tomislav Šmuc
 Srojno učenje 7 Lnearne meode & Tomslav Šmuc Leraura Lnearne meode The Elemens of Sascal Learnng Hase, Tbshran, Fredman s ed - ch. 4 The Elemens of Sascal Learnng Hase, Tbshran, Fredman s ed - ch. A Tuoral
Srojno učenje 7 Lnearne meode & Tomslav Šmuc Leraura Lnearne meode The Elemens of Sascal Learnng Hase, Tbshran, Fredman s ed - ch. 4 The Elemens of Sascal Learnng Hase, Tbshran, Fredman s ed - ch. A Tuoral
Erdös-Mordellova nejednakost
 Sveu ili²te J. J. Strossmayera u Osijeku Odjel za matematiku Dino Duman i Erdös-Mordellova nejednakost Diplomski rad Osijek, 015. Sveu ili²te J. J. Strossmayera u Osijeku Odjel za matematiku Dino Duman
Sveu ili²te J. J. Strossmayera u Osijeku Odjel za matematiku Dino Duman i Erdös-Mordellova nejednakost Diplomski rad Osijek, 015. Sveu ili²te J. J. Strossmayera u Osijeku Odjel za matematiku Dino Duman
Pitagorine trojke. Uvod
 Pitagorine trojke Uvod Ivan Soldo 1, Ivana Vuksanović 2 Pitagora, grčki filozof i znanstvenik, često se prikazuje kao prvi pravi matematičar. Ro - den je na grčkom otoku Samosu, kao sin bogatog i zaslužnog
Pitagorine trojke Uvod Ivan Soldo 1, Ivana Vuksanović 2 Pitagora, grčki filozof i znanstvenik, često se prikazuje kao prvi pravi matematičar. Ro - den je na grčkom otoku Samosu, kao sin bogatog i zaslužnog
Miroslav Josipović. Množenje vektora i struktura 3D euklidskog prostora
 Mroslav Jospovć Množenje vektora struktura D eukldskog prostora I naljut se Bog na ljudsk rod dade m da govore razlčtm jezcma da jedn druge ne razumju Vrus Svjetska zdravstvena organzacja je objavla postojanje
Mroslav Jospovć Množenje vektora struktura D eukldskog prostora I naljut se Bog na ljudsk rod dade m da govore razlčtm jezcma da jedn druge ne razumju Vrus Svjetska zdravstvena organzacja je objavla postojanje
Osobine metode rezolucije: zaustavlja se, pouzdanost i kompletnost. Iskazna logika 4
 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Rezolucija 1 Metod rezolucije je postupak za dokazivanje da li je neka iskazna (ili
Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Rezolucija 1 Metod rezolucije je postupak za dokazivanje da li je neka iskazna (ili
FIZIKALNA KOZMOLOGIJA VII. VRLO RANI SVEMIR & INFLACIJA
 FIZIKALNA KOZMOLOGIJA VII. VRLO RANI SVEMIR & INFLACIJA KOZMIČKI SAT ranog svemira Ekstra zračenje u mjerenju CMB Usporedba s rezultatima LEP-a Usporedba CMB i neutrina Vj.: Pozadinsko zračenje neutrina
FIZIKALNA KOZMOLOGIJA VII. VRLO RANI SVEMIR & INFLACIJA KOZMIČKI SAT ranog svemira Ekstra zračenje u mjerenju CMB Usporedba s rezultatima LEP-a Usporedba CMB i neutrina Vj.: Pozadinsko zračenje neutrina
Geometrijski smisao rješenja sustava od tri linearne jednadžbe s tri nepoznanice
 Osječki matematički list 6(2006), 79 84 79 Geometrijski smisao rješenja sustava od tri linearne jednadžbe s tri nepoznanice Zlatko Udovičić Sažetak. Geometrijski smisao rješenja sustava od dvije linearne
Osječki matematički list 6(2006), 79 84 79 Geometrijski smisao rješenja sustava od tri linearne jednadžbe s tri nepoznanice Zlatko Udovičić Sažetak. Geometrijski smisao rješenja sustava od dvije linearne
Metode izračunavanja determinanti matrica n-tog reda
 Osječki matematički list 10(2010), 31 42 31 STUDENTSKA RUBRIKA Metode izračunavanja determinanti matrica n-tog reda Damira Keček Sažetak U članku su opisane metode izračunavanja determinanti matrica n-tog
Osječki matematički list 10(2010), 31 42 31 STUDENTSKA RUBRIKA Metode izračunavanja determinanti matrica n-tog reda Damira Keček Sažetak U članku su opisane metode izračunavanja determinanti matrica n-tog
Mathcad sa algoritmima
 P R I M J E R I P R I M J E R I Mathcad sa algoritmima NAREDBE - elementarne obrade - sekvence Primjer 1 Napraviti algoritam za sabiranje dva broja. NAREDBE - elementarne obrade - sekvence Primjer 1 POČETAK
P R I M J E R I P R I M J E R I Mathcad sa algoritmima NAREDBE - elementarne obrade - sekvence Primjer 1 Napraviti algoritam za sabiranje dva broja. NAREDBE - elementarne obrade - sekvence Primjer 1 POČETAK
Zanimljive rekurzije
 Zanimljive rekurzije Dragana Jankov Maširević i Jelena Jankov Riječ dvije o rekurzijama Rekurzija je metoda definiranja funkcije na način da se najprije definira nekoliko jednostavnih, osnovnih slučajeva,
Zanimljive rekurzije Dragana Jankov Maširević i Jelena Jankov Riječ dvije o rekurzijama Rekurzija je metoda definiranja funkcije na način da se najprije definira nekoliko jednostavnih, osnovnih slučajeva,
Ash Wednesday. First Introit thing. * Dómi- nos. di- di- nos, tú- ré- spi- Ps. ne. Dó- mi- Sál- vum. intra-vé-runt. Gló- ri-
 sh Wdsdy 7 gn mult- tú- st Frst Intrt thng X-áud m. ns ní- m-sr-cór- Ps. -qu Ptr - m- Sál- vum m * usqu 1 d fc á-rum sp- m-sr-t- ó- num Gló- r- Fí- l- Sp-rí- : quó-n- m ntr-vé-runt á- n-mm c * m- quó-n-
sh Wdsdy 7 gn mult- tú- st Frst Intrt thng X-áud m. ns ní- m-sr-cór- Ps. -qu Ptr - m- Sál- vum m * usqu 1 d fc á-rum sp- m-sr-t- ó- num Gló- r- Fí- l- Sp-rí- : quó-n- m ntr-vé-runt á- n-mm c * m- quó-n-
Upravljački prometni sustavi
 Upravljačk prometn sustav Predvđanje prometnh parametara Izv. prof. dr. sc. Nko Jelušć Doc. dr. sc. Edouard Ivanjko Upravljačk prometn sustav :: Predvđanje prometnh parametara 2017 Ivanjko, Jelušć Sadržaj
Upravljačk prometn sustav Predvđanje prometnh parametara Izv. prof. dr. sc. Nko Jelušć Doc. dr. sc. Edouard Ivanjko Upravljačk prometn sustav :: Predvđanje prometnh parametara 2017 Ivanjko, Jelušć Sadržaj
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
KLASIFIKACIJA NAIVNI BAJES. NIKOLA MILIKIĆ URL:
 KLASIFIKACIJA NAIVNI BAJES NIKOLA MILIKIĆ EMAIL: nikola.milikic@fon.bg.ac.rs URL: http://nikola.milikic.info ŠTA JE KLASIFIKACIJA? Zadatak određivanja klase kojoj neka instanca pripada instanca je opisana
KLASIFIKACIJA NAIVNI BAJES NIKOLA MILIKIĆ EMAIL: nikola.milikic@fon.bg.ac.rs URL: http://nikola.milikic.info ŠTA JE KLASIFIKACIJA? Zadatak određivanja klase kojoj neka instanca pripada instanca je opisana
Fibonaccijev brojevni sustav
 Fibonaccijev brojevni sustav Ljerka Jukić asistentica Odjela za matematiku Sveučilišta u Osijeku, ljukic@mathos.hr Helena Velić studentica Odjela za matematiku Sveučilišta u Osijeku, hvelic@mathos.hr Sažetak
Fibonaccijev brojevni sustav Ljerka Jukić asistentica Odjela za matematiku Sveučilišta u Osijeku, ljukic@mathos.hr Helena Velić studentica Odjela za matematiku Sveučilišta u Osijeku, hvelic@mathos.hr Sažetak
Slika 1. Slika 2. Da ne bismo stalno izbacivali elemente iz skupa, mi ćemo napraviti još jedan niz markirano, gde će
 Permutacije Zadatak. U vreći se nalazi n loptica različitih boja. Iz vreće izvlačimo redom jednu po jednu lopticu i stavljamo jednu pored druge. Koliko različitih redosleda boja možemo da dobijemo? Primer
Permutacije Zadatak. U vreći se nalazi n loptica različitih boja. Iz vreće izvlačimo redom jednu po jednu lopticu i stavljamo jednu pored druge. Koliko različitih redosleda boja možemo da dobijemo? Primer
Formule za udaljenost točke do pravca u ravnini, u smislu lp - udaljenosti math.e Vol 28.
 1 math.e Hrvatski matematički elektronički časopis Formule za udaljenost točke do pravca u ravnini, u smislu lp - udaljenosti Banachovi prostori Funkcija udaljenosti obrada podataka optimizacija Aleksandra
1 math.e Hrvatski matematički elektronički časopis Formule za udaljenost točke do pravca u ravnini, u smislu lp - udaljenosti Banachovi prostori Funkcija udaljenosti obrada podataka optimizacija Aleksandra
Decepcijski i teški optimizacijski problemi za genetske algoritme
 Decepcjsk tešk optmzacjsk problem za genetske algortme Stjepan Pcek Rng Datacom d.o.o. Trg J. J. Strossmayera 5, Zagreb 10000 stjepan@rng.hr Sažetak Genetsk algortm (GA) predstavljaju robusnu adaptvnu
Decepcjsk tešk optmzacjsk problem za genetske algortme Stjepan Pcek Rng Datacom d.o.o. Trg J. J. Strossmayera 5, Zagreb 10000 stjepan@rng.hr Sažetak Genetsk algortm (GA) predstavljaju robusnu adaptvnu
2008/2009. Fakultet prometnih znanosti Sveučilište u Zagrebu ELEKTROTEHNIKA
 008/009 Fakultet proetnh znanost Sveučlšte u Zagrebu ZMJENČNE SJE EEKOEHNKA ZMJENČNE SJE zjenčne struje su vreensk projenljve struje koja se pored jakost jenja sjer strujanja naboja. renutna vrjednost
008/009 Fakultet proetnh znanost Sveučlšte u Zagrebu ZMJENČNE SJE EEKOEHNKA ZMJENČNE SJE zjenčne struje su vreensk projenljve struje koja se pored jakost jenja sjer strujanja naboja. renutna vrjednost
Afine transformacije ravnine
 1/ 7 Hrvatski matematički elektronski časopis mathe Broj 12 http://emathhr/ Afine transformacije ravnine Harun Šiljak Sadržaj: 1 Uvod 2 Primjeri riješenih zadataka 3 Zadaci za samostalan rad Literatura
1/ 7 Hrvatski matematički elektronski časopis mathe Broj 12 http://emathhr/ Afine transformacije ravnine Harun Šiljak Sadržaj: 1 Uvod 2 Primjeri riješenih zadataka 3 Zadaci za samostalan rad Literatura
This model contains two bonds per unit cell (one along the x-direction and the other along y). So we can rewrite the Hamiltonian as:
 1 Problem set #1 1.1. A one-band model on a square lattce Fg. 1 Consder a square lattce wth only nearest-neghbor hoppngs (as shown n the fgure above): H t, j a a j (1.1) where,j stands for nearest neghbors
1 Problem set #1 1.1. A one-band model on a square lattce Fg. 1 Consder a square lattce wth only nearest-neghbor hoppngs (as shown n the fgure above): H t, j a a j (1.1) where,j stands for nearest neghbors
Sveučilište J.J.Strossmayera u Osijeku Odjel za matematiku. Sveučilišni preddiplomski studij matematike
 Sveučilište J.J.Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Lorena Škalac Fermatova metoda beskonačnog spusta Završni rad Osijek, 014. Sveučilište J.J.Strossmayera
Sveučilište J.J.Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Lorena Škalac Fermatova metoda beskonačnog spusta Završni rad Osijek, 014. Sveučilište J.J.Strossmayera
Teorem o reziduumima i primjene. Završni rad
 Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Matej Petrinović Teorem o reziduumima i primjene Završni rad Osijek, 207. Sveučilište J. J. Strossmayera
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Matej Petrinović Teorem o reziduumima i primjene Završni rad Osijek, 207. Sveučilište J. J. Strossmayera
Iskazna logika 1. Matematička logika u računarstvu. oktobar 2012
 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia oktobar 2012 Iskazi, istinitost, veznici Intuitivno, iskaz je rečenica koja je ima tačno jednu jednu
Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia oktobar 2012 Iskazi, istinitost, veznici Intuitivno, iskaz je rečenica koja je ima tačno jednu jednu
Ariana Trstenjak Kvadratne forme
 Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Ariana Trstenjak Kvadratne forme Završni rad Osijek, 014. Sveučilište Josipa Jurja Strossmayera
Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Ariana Trstenjak Kvadratne forme Završni rad Osijek, 014. Sveučilište Josipa Jurja Strossmayera
TEORIJE IZBORA U UVJETIMA NEIZVJESNOSTI
 Perca Vojnć, mag. Asstentca Odjel za ekonomju poslovnu ekonomju Sveučlšte u Dubrovnku E-mal: perca.vojnc@undu.hr TEORIJE IZBORA U UVJETIMA NEIZVJESNOSTI UDK / UDC: 330.131.7 JEL klasfkacja / JEL classfcaton:
Perca Vojnć, mag. Asstentca Odjel za ekonomju poslovnu ekonomju Sveučlšte u Dubrovnku E-mal: perca.vojnc@undu.hr TEORIJE IZBORA U UVJETIMA NEIZVJESNOSTI UDK / UDC: 330.131.7 JEL klasfkacja / JEL classfcaton:
Rješavanje simultanih jednadžbi kao ekonometrijskog modela pomoću programskog paketa EViews
 Rješavanje smultanh jednadžb kao ekonometrjskog modela pomoću programskog paketa EVews Sažetak - U ovom radu se analzra rješavanje sustava smultanh jednadžb kao ekonometrjskog modela. Između razlčh mogućnost
Rješavanje smultanh jednadžb kao ekonometrjskog modela pomoću programskog paketa EVews Sažetak - U ovom radu se analzra rješavanje sustava smultanh jednadžb kao ekonometrjskog modela. Između razlčh mogućnost
NAPREDNI FIZIČKI PRAKTIKUM 1 studij Matematika i fizika; smjer nastavnički MJERENJE MALIH OTPORA
 NAPREDNI FIZIČKI PRAKTIKUM 1 studij Matematika i fizika; smjer nastavnički MJERENJE MALIH OTPORA studij Matematika i fizika; smjer nastavnički NFP 1 1 ZADACI 1. Mjerenjem geometrijskih dimenzija i otpora
NAPREDNI FIZIČKI PRAKTIKUM 1 studij Matematika i fizika; smjer nastavnički MJERENJE MALIH OTPORA studij Matematika i fizika; smjer nastavnički NFP 1 1 ZADACI 1. Mjerenjem geometrijskih dimenzija i otpora
Položaj nultočaka polinoma
 Osječki matematički list 4 (204), 05-6 Položaj nultočaka polinoma Mandalena Pranjić Rajna Rajić Sažetak Prema Rolleovom teoremu, bilo koji segment čiji su krajevi međusobno različite realne nultočke polinoma
Osječki matematički list 4 (204), 05-6 Položaj nultočaka polinoma Mandalena Pranjić Rajna Rajić Sažetak Prema Rolleovom teoremu, bilo koji segment čiji su krajevi međusobno različite realne nultočke polinoma
Matrice traga nula math.e Vol. 26. math.e. Hrvatski matematički elektronički časopis. Matrice traga nula. komutator linearna algebra. Sažetak.
 1 math.e Hrvatski matematički elektronički časopis komutator linearna algebra Marijana Kožul i Rajna Rajić Matrice traga nula marijana55@gmail.com, rajna.rajic@rgn.hr Rudarsko-geološko-naftni fakultet,
1 math.e Hrvatski matematički elektronički časopis komutator linearna algebra Marijana Kožul i Rajna Rajić Matrice traga nula marijana55@gmail.com, rajna.rajic@rgn.hr Rudarsko-geološko-naftni fakultet,
Cyclical Surfaces Created by a Conical Helix
 Professional paper Accepted 23.11.2007. TATIANA OLEJNÍKOVÁ Cyclical Surfaces Created by a Conical Helix Cyclical Surfaces Created by a Conical Helix ABSTRACT The paper describes cyclical surfaces created
Professional paper Accepted 23.11.2007. TATIANA OLEJNÍKOVÁ Cyclical Surfaces Created by a Conical Helix Cyclical Surfaces Created by a Conical Helix ABSTRACT The paper describes cyclical surfaces created
FEUERBACHOVA TOČKA. Maja Mihalic PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK. Diplomski rad. Voditelj rada: doc. dr. sc.
 SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Maja Mihalic FEUERBACHOVA TOČKA Diplomski rad Voditelj rada: doc. dr. sc. Mea Bombardelli Zagreb, srpanj, 2015. Ovaj diplomski
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Maja Mihalic FEUERBACHOVA TOČKA Diplomski rad Voditelj rada: doc. dr. sc. Mea Bombardelli Zagreb, srpanj, 2015. Ovaj diplomski
On the relation between Zenkevich and Wiener indices of alkanes
 J.Serb.Chem.Soc. 69(4)265 271(2004) UDC 547.21:54 12+539.6 JSCS 3152 Original scientific paper On the relation between Zenkevich and Wiener indices of alkanes IVAN GUTMAN a*, BORIS FURTULA a, BILJANA ARSI]
J.Serb.Chem.Soc. 69(4)265 271(2004) UDC 547.21:54 12+539.6 JSCS 3152 Original scientific paper On the relation between Zenkevich and Wiener indices of alkanes IVAN GUTMAN a*, BORIS FURTULA a, BILJANA ARSI]
Zadatci sa ciklusima. Zadatak1: Sastaviti progra koji određuje z ir prvih prirod ih rojeva.
 Zadatci sa ciklusima Zadatak1: Sastaviti progra koji određuje z ir prvih prirod ih rojeva. StrToIntDef(tekst,broj) - funkcija kojom se tekst pretvara u ceo broj s tim da je uvedena automatska kontrola
Zadatci sa ciklusima Zadatak1: Sastaviti progra koji određuje z ir prvih prirod ih rojeva. StrToIntDef(tekst,broj) - funkcija kojom se tekst pretvara u ceo broj s tim da je uvedena automatska kontrola
Harmonijski brojevi. Uvod
 MATEMATIKA Harmonijski brojevi Darko Žubrinić, Zagreb Beskonačno! Niti koje drugo pitanje nije nikada toliko duboko dirnulo duh čovjeka. David Hilbert (862. 943.) Uvod U ovom članku opisat ćemo jedan pomalo
MATEMATIKA Harmonijski brojevi Darko Žubrinić, Zagreb Beskonačno! Niti koje drugo pitanje nije nikada toliko duboko dirnulo duh čovjeka. David Hilbert (862. 943.) Uvod U ovom članku opisat ćemo jedan pomalo
Karakteri konačnih Abelovih grupa
 Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Matija Klarić Karakteri konačnih Abelovih grupa Završni rad Osijek, 2015. Sveučilište J. J. Strossmayera
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Matija Klarić Karakteri konačnih Abelovih grupa Završni rad Osijek, 2015. Sveučilište J. J. Strossmayera
Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku
 Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Valentina Volmut Ortogonalni polinomi Diplomski rad Osijek, 2016. Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku
Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Valentina Volmut Ortogonalni polinomi Diplomski rad Osijek, 2016. Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku
SLIČNOST I HOMOTETIJA. Ivana Major Šomodi PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK. Diplomski rad
 SVEUČILIŠTE U ZGREU PRIRODOSLOVNO MTEMTIČKI FKULTET MTEMTIČKI ODSJEK Ivana Major Šomodi SLIČNOST I HOMOTETIJ Diplomski rad Voditelj rada: prof. dr. sc Sanja Varošanec Zagreb, srpanj, 2015. Ovaj diplomski
SVEUČILIŠTE U ZGREU PRIRODOSLOVNO MTEMTIČKI FKULTET MTEMTIČKI ODSJEK Ivana Major Šomodi SLIČNOST I HOMOTETIJ Diplomski rad Voditelj rada: prof. dr. sc Sanja Varošanec Zagreb, srpanj, 2015. Ovaj diplomski
Matrice u Maple-u. Upisivanje matrica
 Matrice u Maple-u Tvrtko Tadić U prošlom broju upoznali ste se s matricama, a u ovom broju vidjeli ste neke njihove primjene. Mnoge je vjerojatno prepalo računanje s matricama. Pa tko će raditi svo to
Matrice u Maple-u Tvrtko Tadić U prošlom broju upoznali ste se s matricama, a u ovom broju vidjeli ste neke njihove primjene. Mnoge je vjerojatno prepalo računanje s matricama. Pa tko će raditi svo to
SPH SIMULACIJA POISEULLEOVOG STRUJANJA PRI NISKIM REYNOLDSOVIM BROJEVIMA
 Vuko, VUKČEVIĆ, Sveučlšte u Zagrebu, Fakultet strojarstva brodogradnje, Zagreb Andreja, WERER, Sveučlšte u Zagrebu, Fakultet strojarstva brodogradnje, Zagreb asta, DEGIULI, Sveučlšte u Zagrebu, Fakultet
Vuko, VUKČEVIĆ, Sveučlšte u Zagrebu, Fakultet strojarstva brodogradnje, Zagreb Andreja, WERER, Sveučlšte u Zagrebu, Fakultet strojarstva brodogradnje, Zagreb asta, DEGIULI, Sveučlšte u Zagrebu, Fakultet
Scripture quotations marked cev are from the Contemporary English Version, Copyright 1991, 1992, 1995 by American Bible Society. Used by permission.
 N Ra: E K B Da a a B a a, a-a- a aa, a a. T, a a. 2009 Ba P, I. ISBN 978-1-60260-296-0. N a a a a a, a,. C a a a Ba P, a 500 a a aa a. W, : F K B Da, Ba P, I. U. S a a a a K Ja V B. S a a a a N K Ja V.
N Ra: E K B Da a a B a a, a-a- a aa, a a. T, a a. 2009 Ba P, I. ISBN 978-1-60260-296-0. N a a a a a, a,. C a a a Ba P, a 500 a a aa a. W, : F K B Da, Ba P, I. U. S a a a a K Ja V B. S a a a a N K Ja V.
Funkcijske jednadºbe
 MEMO pripreme 2015. Marin Petkovi, 9. 6. 2015. Funkcijske jednadºbe Uvod i osnovne ideje U ovom predavanju obradit emo neke poznate funkcijske jednadºbe i osnovne ideje rje²avanja takvih jednadºbi. Uobi
MEMO pripreme 2015. Marin Petkovi, 9. 6. 2015. Funkcijske jednadºbe Uvod i osnovne ideje U ovom predavanju obradit emo neke poznate funkcijske jednadºbe i osnovne ideje rje²avanja takvih jednadºbi. Uobi
NIZOVI I REDOVI FUNKCIJA
 SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Danijela Piškor NIZOVI I REDOVI FUNKCIJA Diplomski rad Voditelj rada: izv. prof. dr. sc. Ljiljana Arambašić Zagreb, rujan 206.
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Danijela Piškor NIZOVI I REDOVI FUNKCIJA Diplomski rad Voditelj rada: izv. prof. dr. sc. Ljiljana Arambašić Zagreb, rujan 206.
Modified Zagreb M 2 Index Comparison with the Randi} Connectivity Index for Benzenoid Systems
 CROATICA CHEMICA ACTA CCACAA 7 (2) 83 87 (2003) ISSN-00-3 CCA-2870 Note Modified Zagreb M 2 Index Comparison with the Randi} Connectivity Index for Benzenoid Systems Damir Vuki~evi} a, * and Nenad Trinajsti}
CROATICA CHEMICA ACTA CCACAA 7 (2) 83 87 (2003) ISSN-00-3 CCA-2870 Note Modified Zagreb M 2 Index Comparison with the Randi} Connectivity Index for Benzenoid Systems Damir Vuki~evi} a, * and Nenad Trinajsti}
Lecture 10: May 6, 2013
 TTIC/CMSC 31150 Mathematcal Toolkt Sprng 013 Madhur Tulsan Lecture 10: May 6, 013 Scrbe: Wenje Luo In today s lecture, we manly talked about random walk on graphs and ntroduce the concept of graph expander,
TTIC/CMSC 31150 Mathematcal Toolkt Sprng 013 Madhur Tulsan Lecture 10: May 6, 013 Scrbe: Wenje Luo In today s lecture, we manly talked about random walk on graphs and ntroduce the concept of graph expander,
Section 8.1 Exercises
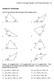 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
- Prefixes 'mono', 'uni', 'bi' and 'du' - Why are there no asprins in the jungle? Because the parrots ate them all.
 - Prfs '', '', 'b' a '' - Na: Wrsar 27 Dat: W ar tr asrs t? Bas t arrts at t a. At t btt f t a s a st f wrs. Ts wrs ar t. T wrs av b a rta (ra arss), vrta (ra w) r aa (fr rr t rr). W f a wr, raw a at r
- Prfs '', '', 'b' a '' - Na: Wrsar 27 Dat: W ar tr asrs t? Bas t arrts at t a. At t btt f t a s a st f wrs. Ts wrs ar t. T wrs av b a rta (ra arss), vrta (ra w) r aa (fr rr t rr). W f a wr, raw a at r
SELECTED PROOFS. DeMorgan s formulas: The first one is clear from Venn diagram, or the following truth table:
 SELECTED PROOFS DeMorgan s formulas: The frst one s clear from Venn dagram, or the followng truth table: A B A B A B Ā B Ā B T T T F F F F T F T F F T F F T T F T F F F F F T T T T The second one can be
SELECTED PROOFS DeMorgan s formulas: The frst one s clear from Venn dagram, or the followng truth table: A B A B A B Ā B Ā B T T T F F F F T F T F F T F F T T F T F F F F F T T T T The second one can be
Kvaternioni i kvaternionsko rješenje kvadratne jednadžbe
 Kvaternioni i kvaternionsko rješenje 1 Uvod Kvaternioni i kvaternionsko rješenje kvadratne jednadžbe Željko Zrno 1 i Neven Jurić Što je matematika? Na što prvo čovjeka asocira riječ matematika? Matematika
Kvaternioni i kvaternionsko rješenje 1 Uvod Kvaternioni i kvaternionsko rješenje kvadratne jednadžbe Željko Zrno 1 i Neven Jurić Što je matematika? Na što prvo čovjeka asocira riječ matematika? Matematika
DETEKCIJA I RASPOZNAVANJE PROMETNIH ZNAKOVA U VIDEO SNIMCI
 SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Igor Bonač Ivan Kovaček Ivan Kusalć DETEKCIJA I RASPOZNAVANJE PROMETNIH ZNAKOVA U VIDEO SNIMCI Zagreb, 2010 Ovaj rad zrađen je u Zavodu za elektronku,
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Igor Bonač Ivan Kovaček Ivan Kusalć DETEKCIJA I RASPOZNAVANJE PROMETNIH ZNAKOVA U VIDEO SNIMCI Zagreb, 2010 Ovaj rad zrađen je u Zavodu za elektronku,
MUSICAL COMPOSITION AND ELEMENTARY EXCITATIONS OF THE ENVIRONMENT
 Interdisciplinary Description of Complex Systems (-2), 22-28, 2003 MUSICAL COMPOSITION AND ELEMENTARY EXCITATIONS OF THE ENVIRONMENT Mirna Grgec-Pajić, Josip Stepanić 2 and Damir Pajić 3, * c/o Institute
Interdisciplinary Description of Complex Systems (-2), 22-28, 2003 MUSICAL COMPOSITION AND ELEMENTARY EXCITATIONS OF THE ENVIRONMENT Mirna Grgec-Pajić, Josip Stepanić 2 and Damir Pajić 3, * c/o Institute
Matematika (PITUP) Prof.dr.sc. Blaženka Divjak. Matematika (PITUP) FOI, Varaždin
 Matematika (PITUP) FOI, Varaždin Dio II Bez obzira kako nam se neki teorem činio korektnim, ne možemo biti sigurni da ne krije neku nesavršenost sve dok se nam ne čini prekrasnim G. Boole The moving power
Matematika (PITUP) FOI, Varaždin Dio II Bez obzira kako nam se neki teorem činio korektnim, ne možemo biti sigurni da ne krije neku nesavršenost sve dok se nam ne čini prekrasnim G. Boole The moving power
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Cauchy-Schwarz-Buniakowskyjeva nejednakost
 Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Neda Krička Cauchy-Schwarz-Buniakowskyjeva nejednakost Diplomski rad Osijek, 2012. Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Neda Krička Cauchy-Schwarz-Buniakowskyjeva nejednakost Diplomski rad Osijek, 2012. Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku
An Algorithm for Computation of Bond Contributions of the Wiener Index
 CROATICA CHEMICA ACTA CCACAA68 (1) 99-103 (1995) ISSN 0011-1643 CCA-2215 Original Scientific Paper An Algorithm for Computation of Bond Contributions of the Wiener Index Istvan Lukouits Central Research
CROATICA CHEMICA ACTA CCACAA68 (1) 99-103 (1995) ISSN 0011-1643 CCA-2215 Original Scientific Paper An Algorithm for Computation of Bond Contributions of the Wiener Index Istvan Lukouits Central Research
STATISTICAL ANALYSIS OF WET AND DRY SPELLS IN CROATIA BY THE BINARY DARMA (1,1) MODEL
 Hrvatski meteoroloπki Ëasopis Croatian Meteorological Journal, 4, 2006., 43 5. UDK: 55.577.22 Stručni rad STATISTICAL ANALYSIS OF WET AND DRY SPELLS IN CROATIA BY THE BINARY DARMA (,) MODEL Statistička
Hrvatski meteoroloπki Ëasopis Croatian Meteorological Journal, 4, 2006., 43 5. UDK: 55.577.22 Stručni rad STATISTICAL ANALYSIS OF WET AND DRY SPELLS IN CROATIA BY THE BINARY DARMA (,) MODEL Statistička
Dynamic analysis of 2-D and 3-D quasi-brittle solids and structures by D/BEM
 THEORETICAL AND APPLIED MECHANICS vol. 27, pp. 39-48, 2002 Dynamic analysis of 2-D and 3-D quasi-brittle solids and structures by D/BEM George D.Hatzigeorgiou and Dimitri E.Beskos Submitted 12 February,
THEORETICAL AND APPLIED MECHANICS vol. 27, pp. 39-48, 2002 Dynamic analysis of 2-D and 3-D quasi-brittle solids and structures by D/BEM George D.Hatzigeorgiou and Dimitri E.Beskos Submitted 12 February,
Konstrukcije ravnalom i šestarom
 Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Emanuela Vrban Konstrukcije ravnalom i šestarom Diplomski rad Osijek, 2013. Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za
Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Emanuela Vrban Konstrukcije ravnalom i šestarom Diplomski rad Osijek, 2013. Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za
DISTRIBUIRANI ALGORITMI I SISTEMI
 Postavka 7: međusobno isključivanje sa read/write promenljivama 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch Read/Write deljene promenljive
Postavka 7: međusobno isključivanje sa read/write promenljivama 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch Read/Write deljene promenljive
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
BROJEVNE KONGRUENCIJE
 UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Vojko Nestorović BROJEVNE KONGRUENCIJE - MASTER RAD - Mentor, dr Siniša Crvenković Novi Sad, 2011. Sadržaj Predgovor...............................
UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Vojko Nestorović BROJEVNE KONGRUENCIJE - MASTER RAD - Mentor, dr Siniša Crvenković Novi Sad, 2011. Sadržaj Predgovor...............................
Harmoniteti. Matija Bucić, Domagoj Ćevid. 20. lipnja 2016.
 Harmoniteti Matija Bucić, Domagoj Ćevid 20. lipnja 2016. 1 Uvod Harmoniteti su jedan od veoma korisnih alata koje jedan olimpijac treba znati. To je posebna konfiguracija točaka ili pravaca koja se pojavljuje
Harmoniteti Matija Bucić, Domagoj Ćevid 20. lipnja 2016. 1 Uvod Harmoniteti su jedan od veoma korisnih alata koje jedan olimpijac treba znati. To je posebna konfiguracija točaka ili pravaca koja se pojavljuje
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Preddiplomski sveučilišni studij matematike. Završni rad. Tema : Vedska matematika
 Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Preddiplomski sveučilišni studij matematike Završni rad Tema : Vedska matematika Student : Vedrana Babić Broj indeksa: 919 Osijek, 2016. 1 Sveučilište
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Preddiplomski sveučilišni studij matematike Završni rad Tema : Vedska matematika Student : Vedrana Babić Broj indeksa: 919 Osijek, 2016. 1 Sveučilište
ANALYSIS OF THE RELIABILITY OF THE "ALTERNATOR- ALTERNATOR BELT" SYSTEM
 I. Mavrin, D. Kovacevic, B. Makovic: Analysis of the Reliability of the "Alternator- Alternator Belt" System IVAN MAVRIN, D.Sc. DRAZEN KOVACEVIC, B.Eng. BRANKO MAKOVIC, B.Eng. Fakultet prometnih znanosti,
I. Mavrin, D. Kovacevic, B. Makovic: Analysis of the Reliability of the "Alternator- Alternator Belt" System IVAN MAVRIN, D.Sc. DRAZEN KOVACEVIC, B.Eng. BRANKO MAKOVIC, B.Eng. Fakultet prometnih znanosti,
Krivulja središta i krivulja fokusa u pramenu konika. konika zadanom pomoću dviju dvostrukih točaka u izotropnoj ravnini
 Stručni rad Prihvaćeno 18.02.2002. MILJENKO LAPAINE Krivulja središta i krivulja fokusa u pramenu konika zadanom pomoću dviju dvostrukih točaka u izotropnoj ravnini Krivulja središta i krivulja fokusa
Stručni rad Prihvaćeno 18.02.2002. MILJENKO LAPAINE Krivulja središta i krivulja fokusa u pramenu konika zadanom pomoću dviju dvostrukih točaka u izotropnoj ravnini Krivulja središta i krivulja fokusa
Prsten cijelih brojeva
 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ODJEL ZA MATEMATIKU Marijana Pravdić Prsten cijelih brojeva Diplomski rad Osijek, 2017. SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ODJEL ZA MATEMATIKU
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ODJEL ZA MATEMATIKU Marijana Pravdić Prsten cijelih brojeva Diplomski rad Osijek, 2017. SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ODJEL ZA MATEMATIKU
The interpretability logic ILF
 Mathematical Communications 2(1997), 205-210 205 The interpretability logic ILF Mladen Vuković Abstract.In this paper we determine a characteristic class of IL set - frames for the principle F. Then we
Mathematical Communications 2(1997), 205-210 205 The interpretability logic ILF Mladen Vuković Abstract.In this paper we determine a characteristic class of IL set - frames for the principle F. Then we
Deni Vlašić Numerički alat za preliminarni projekt brodskog vijka
 SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE Den Vlašć Numerčk alat za prelmnarn projekt brodskog vjka Zagreb, 2017. Ovaj rad zrađen je na Zavodu za brodogradnju pomorsku tehnku na Fakultetu
SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE Den Vlašć Numerčk alat za prelmnarn projekt brodskog vjka Zagreb, 2017. Ovaj rad zrađen je na Zavodu za brodogradnju pomorsku tehnku na Fakultetu
International Mathematical Olympiad. Preliminary Selection Contest 2012 Hong Kong. Outline of Solutions
 Internatonal Mathematcal Olympad Prelmnary Selecton ontest Hong Kong Outlne of Solutons nswers: 7 4 7 4 6 5 9 6 99 7 6 6 9 5544 49 5 7 4 6765 5 6 6 7 6 944 9 Solutons: Snce n s a two-dgt number, we have
Internatonal Mathematcal Olympad Prelmnary Selecton ontest Hong Kong Outlne of Solutons nswers: 7 4 7 4 6 5 9 6 99 7 6 6 9 5544 49 5 7 4 6765 5 6 6 7 6 944 9 Solutons: Snce n s a two-dgt number, we have
Standard Parallel and Secant Parallel in Azimuthal Projections
 Original Scientific Paper Received: 24-1 1-201 7 Accepted: 06-01 -201 8 Standard Parallel and Secant Parallel in Azimuthal Projections Miljenko LAPAI NE University of Zagreb, Faculty of Geodesy, Kačićeva
Original Scientific Paper Received: 24-1 1-201 7 Accepted: 06-01 -201 8 Standard Parallel and Secant Parallel in Azimuthal Projections Miljenko LAPAI NE University of Zagreb, Faculty of Geodesy, Kačićeva
Keywords: anticline, numerical integration, trapezoidal rule, Simpson s rule
 Application of Simpson s and trapezoidal formulas for volume calculation of subsurface structures - recommendations 2 nd Croatian congress on geomathematics and geological terminology, 28 Original scientific
Application of Simpson s and trapezoidal formulas for volume calculation of subsurface structures - recommendations 2 nd Croatian congress on geomathematics and geological terminology, 28 Original scientific
Sveučilište J.J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike. Ivana Oreški REKURZIJE.
 Sveučilište J.J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Ivana Oreški REKURZIJE Završni rad Osijek, 2011. Sveučilište J.J. Strossmayera u Osijeku Odjel za
Sveučilište J.J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Ivana Oreški REKURZIJE Završni rad Osijek, 2011. Sveučilište J.J. Strossmayera u Osijeku Odjel za
ANALYTICAL AND NUMERICAL PREDICTION OF SPRINGBACK IN SHEET METAL BENDING
 ANALYTICAL AND NUMERICAL PREDICTION OF SPRINGBACK IN SHEET METAL BENDING Slota Ján, Jurčišin Miroslav Department of Technologies and Materials, Faculty of Mechanical Engineering, Technical University of
ANALYTICAL AND NUMERICAL PREDICTION OF SPRINGBACK IN SHEET METAL BENDING Slota Ján, Jurčišin Miroslav Department of Technologies and Materials, Faculty of Mechanical Engineering, Technical University of
MOUNT SAINT JOSEPH MILPERRA
 Student Name : MOUNT SAINT JOSEPH MILPERRA MOUNT SAINT JOSEPH I YEAR 8 MATHEMATICS 17th November 2006 70 MINUTES (plus 5 mnutes readng tme)... :... INSTRUCTIONS: > WRITE IN BLUE OR BLACK PEN ONLY > ALL
Student Name : MOUNT SAINT JOSEPH MILPERRA MOUNT SAINT JOSEPH I YEAR 8 MATHEMATICS 17th November 2006 70 MINUTES (plus 5 mnutes readng tme)... :... INSTRUCTIONS: > WRITE IN BLUE OR BLACK PEN ONLY > ALL
Metoda parcijalnih najmanjih kvadrata: Regresijski model
 Sveučilište u Zagrebu Prirodoslovno-matematički fakultet Matematički odsjek Tamara Sente Metoda parcijalnih najmanjih kvadrata: Regresijski model Diplomski rad Voditelj rada: Izv.prof.dr.sc. Miljenko Huzak
Sveučilište u Zagrebu Prirodoslovno-matematički fakultet Matematički odsjek Tamara Sente Metoda parcijalnih najmanjih kvadrata: Regresijski model Diplomski rad Voditelj rada: Izv.prof.dr.sc. Miljenko Huzak
Kleinova boca... Zanimljiva matematika. ...i kako se u vruće ljetne dane rashladiti hladnim pićem... Sandra Gračan, Zagreb. Korak po korak: ::
 Zanmljva matematka Klenova boca...... kako se u vruće ljetne dane rasladt ladnm pćem... Sandra Gračan, Zagreb Upšete l u tražlcu na Webu pojam Klen s-bottle, rezultat pretrage bt će stotnjak web stranca.
Zanmljva matematka Klenova boca...... kako se u vruće ljetne dane rasladt ladnm pćem... Sandra Gračan, Zagreb Upšete l u tražlcu na Webu pojam Klen s-bottle, rezultat pretrage bt će stotnjak web stranca.
Math 702 Midterm Exam Solutions
 Math 702 Mdterm xam Solutons The terms measurable, measure, ntegrable, and almost everywhere (a.e.) n a ucldean space always refer to Lebesgue measure m. Problem. [6 pts] In each case, prove the statement
Math 702 Mdterm xam Solutons The terms measurable, measure, ntegrable, and almost everywhere (a.e.) n a ucldean space always refer to Lebesgue measure m. Problem. [6 pts] In each case, prove the statement
Uvod u numericku matematiku
 Uvod u numericku matematiku M. Klaricić Bakula Oujak, 2009. Uvod u numericku matematiku 2 1 Uvod Jedan od osnovnih problema numericke matematike je rješavanje linearnih sustava jednadbi. U ovom poglavlju
Uvod u numericku matematiku M. Klaricić Bakula Oujak, 2009. Uvod u numericku matematiku 2 1 Uvod Jedan od osnovnih problema numericke matematike je rješavanje linearnih sustava jednadbi. U ovom poglavlju
Problem Set 9 Solutions
 Desgn and Analyss of Algorthms May 4, 2015 Massachusetts Insttute of Technology 6.046J/18.410J Profs. Erk Demane, Srn Devadas, and Nancy Lynch Problem Set 9 Solutons Problem Set 9 Solutons Ths problem
Desgn and Analyss of Algorthms May 4, 2015 Massachusetts Insttute of Technology 6.046J/18.410J Profs. Erk Demane, Srn Devadas, and Nancy Lynch Problem Set 9 Solutons Problem Set 9 Solutons Ths problem
Konstrukcija i analiza algoritama
 Konstrukcija i analiza algoritama 27. februar 2017 1 Pravila zaključivanja i tehnike dokazivanja u iskaznoj i predikatskoj logici 1 1.1 Iskazna logika Pravila zaključivanja za iskaznu logiku: 1. DODAVANJE
Konstrukcija i analiza algoritama 27. februar 2017 1 Pravila zaključivanja i tehnike dokazivanja u iskaznoj i predikatskoj logici 1 1.1 Iskazna logika Pravila zaključivanja za iskaznu logiku: 1. DODAVANJE
A B A B. Logičke operacije koje još često upotrebljavamo su implikacija ( ) i ekvivalencija A B A B A B
 1 MATEMATIČKI SUDOVI Jedan od osnovnih oblika mišljenja su pojmovi. Oni ne dolaze odvojeno, nego se na odredeni način vezuju i tvore sudove. Sud (izjava, izreka, iskaz) je suvisla deklarativna rečenica
1 MATEMATIČKI SUDOVI Jedan od osnovnih oblika mišljenja su pojmovi. Oni ne dolaze odvojeno, nego se na odredeni način vezuju i tvore sudove. Sud (izjava, izreka, iskaz) je suvisla deklarativna rečenica
AKSIOM IZBORA I EKVIVALENCIJE
 Sveučilište J.J. Strossmayera Odjel za matematiku Preddiplomski sveučilišni studij matematike Igor Sušić AKSIOM IZBORA I EKVIVALENCIJE Završni rad Osijek, 2013. Sveučilište J.J. Strossmayera Odjel za matematiku
Sveučilište J.J. Strossmayera Odjel za matematiku Preddiplomski sveučilišni studij matematike Igor Sušić AKSIOM IZBORA I EKVIVALENCIJE Završni rad Osijek, 2013. Sveučilište J.J. Strossmayera Odjel za matematiku
Predlog za određivanje promene entropije poluidealnog gasa primenom srednjih vrednosti temperaturnih funkcija
 Predlog a određvanje romene entroje oludealnog gasa rmenom srednjh vrednost temeraturnh funkcja Branko B. Pejovć, Vladan M. Mćć, Mtar D. Perušć, Goran S. adć, Ljubca C. Vasljevć, Slavko N. Smljanć ehnološk
Predlog a određvanje romene entroje oludealnog gasa rmenom srednjh vrednost temeraturnh funkcja Branko B. Pejovć, Vladan M. Mćć, Mtar D. Perušć, Goran S. adć, Ljubca C. Vasljevć, Slavko N. Smljanć ehnološk
i;\-'i frz q > R>? >tr E*+ [S I z> N g> F 'x sa :r> >,9 T F >= = = I Y E H H>tr iir- g-i I * s I!,i --' - = a trx - H tnz rqx o >.F g< s Ire tr () -s
 5 C /? >9 T > ; '. ; J ' ' J. \ ;\' \.> ). L; c\ u ( (J ) \ 1 ) : C ) (... >\ > 9 e!) T C). '1!\ /_ \ '\ ' > 9 C > 9.' \( T Z > 9 > 5 P + 9 9 ) :> : + (. \ z : ) z cf C : u 9 ( :!z! Z c (! $ f 1 :.1 f.
5 C /? >9 T > ; '. ; J ' ' J. \ ;\' \.> ). L; c\ u ( (J ) \ 1 ) : C ) (... >\ > 9 e!) T C). '1!\ /_ \ '\ ' > 9 C > 9.' \( T Z > 9 > 5 P + 9 9 ) :> : + (. \ z : ) z cf C : u 9 ( :!z! Z c (! $ f 1 :.1 f.
Linearno programiranje i primjene
 Sveučilište J.J.Strossmayera u Osijeku Odjel za matematiku Rebeka Čordaš Linearno programiranje i primjene Diplomski rad Osijek, 2014. Sveučilište J.J.Strossmayera u Osijeku Odjel za matematiku Rebeka
Sveučilište J.J.Strossmayera u Osijeku Odjel za matematiku Rebeka Čordaš Linearno programiranje i primjene Diplomski rad Osijek, 2014. Sveučilište J.J.Strossmayera u Osijeku Odjel za matematiku Rebeka
Vedska matematika. Marija Miloloža
 Osječki matematički list 8(2008), 19 28 19 Vedska matematika Marija Miloloža Sažetak. Ovimčlankom, koji je gradivom i pristupom prilagod en prvim razredima srednjih škola prikazuju se drugačiji načini
Osječki matematički list 8(2008), 19 28 19 Vedska matematika Marija Miloloža Sažetak. Ovimčlankom, koji je gradivom i pristupom prilagod en prvim razredima srednjih škola prikazuju se drugačiji načini
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni nastavnički studij matematike i informatike. Mirjana Mikec.
 Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni nastavnički studij matematike i informatike Mirjana Mikec Broj e Diplomski rad Osijek, 20. Sveučilište J. J. Strossmayera u Osijeku
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni nastavnički studij matematike i informatike Mirjana Mikec Broj e Diplomski rad Osijek, 20. Sveučilište J. J. Strossmayera u Osijeku
KRITERIJI KOMPLEKSNOSTI ZA K-MEANS ALGORITAM
 SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Stela Šeperić KRITERIJI KOMPLEKSNOSTI ZA K-MEANS ALGORITAM Diplomski rad Voditelj rada: doc.dr.sc. Pavle Goldstein Zagreb, Srpanj
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Stela Šeperić KRITERIJI KOMPLEKSNOSTI ZA K-MEANS ALGORITAM Diplomski rad Voditelj rada: doc.dr.sc. Pavle Goldstein Zagreb, Srpanj
Use precise language and domain-specific vocabulary to inform about or explain the topic. CCSS.ELA-LITERACY.WHST D
 Lesson eight What are characteristics of chemical reactions? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading
Lesson eight What are characteristics of chemical reactions? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading
