Logică și structuri discrete. Marius Minea 25 septembrie 2017
|
|
|
- Brianne Jacobs
- 5 years ago
- Views:
Transcription
1 Logică și structuri discrete Funcții Marius Minea 25 septembrie 2017
2 Ce cuprinde domeniul informaticii? Imagine:
3 The Joint Task Force on Computing Curricula Association for Computing Machinery (ACM) IEEE Computer Society Ce se învață în universități? Computer Science Curricula 2013 Curriculum Guidelines for Undergraduate Degree Programs in Computer Science A Cooperative Project of December 20, 2013 The Joint Task Force on Computing Curricula Association for Computing Machinery (ACM) IEEE Computer Society
4 An overview of the number of core hours (both Tier-1 and Tier-2) by KA in the CS2013 Body of Knowledge is provided below. For comparison, the number of core hours from both the Informatica e mult mai mult decât programare! previous CS2008 and CC2001 reports are provided as well. CS2013 CS2008 CC2001 Knowledge Area Tier1 Tier2 Core Core AL-Algorithms and Complexity AR-Architecture and Organization CN-Computational Science DS-Discrete Structures GV-Graphics and Visualization HCI-Human-Computer Interaction IAS-Information Assurance and Security IM-Information Management IS-Intelligent Systems NC-Networking and Communication OS-Operating Systems PBD-Platform-based Development PD-Parallel and Distributed Computing PL-Programming Languages SDF-Software Development Fundamentals SE-Software Engineering SF-Systems Fundamentals SP-Social Issues and Professional Practice Total Core Hours All Tier1 + All Tier2 Total 308
5 Ce învățăm la acest curs?
6 Funcții, mulțimi, relații INPUT x funcții: modulul de bază pentru calcule FUNCTION f: OUTPUT f(x) relații: grafuri, rețele (sociale), planificare (relații de precedență), programare concurentă/paralelă (relații de dependență),... liste, mulțimi, dicționare: lucrul cu colecții de obiecte Imagine:
7 Recursivitate: fundamentală în programare recursivitate: cum definim simplu prelucrări complexe și rezolvăm probleme prin subprobleme mai mici C k n = C k n 1 + C k 1 n 1 0 < k < n expresie: întreg expresie + expresie expresie - expresie expresie * expresie expresie / expresie Fractalul lui Koch
8 Logică matematică p q = p q (a b) = a b xp(x) = x P(x) cum exprimăm precis afirmații pentru definiții riguroase, specificații în software,... cum demonstrăm afirmații pentru a arăta că un algoritm e corect cum prelucrăm formule logice pentru a găsi soluții la probleme (ex. programare logică)
9 Limbaje și automate automate: sisteme cu logică de control simplă b a a, b a b a expresii regulate: prelucrări simple de text (a b) * aba(a b) * gramatici: sintaxa limbajelor de programare IfStmt ::= if ( Expr ) Stmt else Stmt b
10 Arbori și grafuri * arbori: reprezentări / prelucrări de expresii + arbori de căutare, etc grafuri: vizualizarea relațiilor parcurgeri, drumuri minime,... Imagine:
11 Discret vs. continuu Nu studiem domeniul continuu numere reale, infinitezimale, limite, ecuații diferențiale vezi: analiză matematică Studiem noțiuni/obiecte care iau valori distincte, discrete (întregi, valori logice, relații, arbori, grafuri, etc.)
12 Logică și structuri discrete, sau... Matematici discrete cu aplicații folosind programare funcțională Bazele informaticii noțiunile de bază din știința calculatoarelor unde și cum se aplică, mai ales în limbajele de programare cum să programăm mai bine
13 Programare funcțională în ML Vom lucra cu un limbaj în care noțiunea fundamentală e funcția ilustrează concepte de matematici discrete (liste, mulțimi, etc.) concis (în câteva linii de cod se pot face multe) fundamentat riguros ajută să evităm erori Cursul e complementar celui de programare imperativă (în C) vom discuta ce e comun, și ce e diferit (și de ce) Limbajul ML: dezvoltat la Univ. Edinburgh (anii 70) împreună cu un demonstrator de teoreme (logică matematică)
14 E relevantă programarea funcțională? Conceptele din programarea funcțională au influențat alte limbaje: JavaScript, Python, Scala; F# (.NET) e foarte similar cu ML Exemplu: adoptarea funcțiilor anonime (lambda-expresii) 1930 λ-calcul (Alonzo Church) pur teoretic 1958: LISP (John McCarthy) 1973: ML (Robin Milner) 2007: C# v : C : Java 8 A language that doesn t affect the way you think about programming, is not worth knowing. Alan Perlis Caml: un dialect de ML, cu interpretorul și compilatorul OCaml
15 Unde se predă programare funcțională?
16 Funcții Fiind date mulțimile A și B, o funcție f : A B e o asociere prin care fiecărui element din A îi corespunde un singur element din B. A B a d b c Imagine:
17 O funcție e definită prin trei componente 1. domeniul de definiție A domeniul de valori (codomeniul) 3. asocierea/corespondența propriu-zisă (legea, regula de asociere) B a d b c d c f : Z Z, f (x) = x + 1 și f : R R, f (x) = x + 1 sunt funcții distincte! În limbajele de programare, domeniul de definiție și de valori corespund tipurilor de date (întregi, reali, booleni, enumerare,...)
18 Exemple care NU sunt funcții A B a d b c A B a d b c nu asociază o valoare fiecărui element asociază mai multe valori unui element Imagine:
19 Funcții: aspectul computațional În limbajele de programare, o funcție exprimă un calcul: primește o valoare (argumentul) și produce ca rezultat altă valoare INPUT x FUNCTION f: OUTPUT f(x) Imagine:
20 Funcții în OCaml Cel mai simplu, definim funcții astfel: let f x = x + 1 fie funcția f de argument x, cu valoarea x + 1 Putem defini și identificatori cu alte valori (de ex. numerice): let y = 3 definește identificatorul y cu valoarea 3 (un întreg) În general let nume = expresie leagă (asociază) identificatorul nume cu valoarea expresiei date
21 Funcțiile sunt și ele valori În diagrame, funcțiile nu au neapărat nume: funcția care asociază 1 lui 0, etc. Putem scrie și în OCaml: fun x -> x + 1 o expresie reprezentând o funcție anonimă Ca la orice expresie, putem asocia un nume cu valoarea expresiei: let f = fun x -> x + 1 e la fel ca let f x = x + 1 Ultima scriere e mai concisă și apropiată celei din matematică. Prima scriere ne arată că o funcție e și ea o valoare (ca și întregii, realii, etc.) și poate fi folosită la fel cu alte valori.
22 Apelul de funcție Dacă am definit o funcție: let f x = x + 3 o apelăm (calculăm valoarea) scriind funcția, apoi argumentul: f 2 Interpretorul răspunde: - : int = 5 avem o valoare fără nume ( ), care e un întreg, și are valoarea 5 În ML, funcțiile se apelează fără paranteze! În matematică, folosim paranteze: ca să grupăm calcule care se fac întâi: (2 + 3) (7 3) ca să identificăm argumentele funcțiilor: f(2) În ML, folosim paranteze doar pentru a grupa (sub)expresii. Putem scrie f(2), la fel ca ((2))+(3), dar e inutil și derutant. Diverse limbaje au reguli de scris diferite (sintaxa). Putem apela direct și o funcție anonimă: (fun x -> x + 3) 2 (cu paranteze pentru a grupa expresia funcției anonime)
23 Tipuri de date Dacă definim let f x = x + 1 interpretorul OCaml evaluează definiția și răspunde: val f : int -> int = <fun> Matematic: f e o funcție de la întregi la întregi În program: f e o funcție cu argument de tip întreg (int) și rezultat de tip întreg (domeniul și codomeniul devin tipuri) În programare, un tip de date e o mulțime de valori, împreună cu niște operații definite pe astfel de valori. int -> int e tot un tip, al funcțiilor de argument întreg cu valoare întreagă. În ML, tipurile pot fi deduse automat (inferență de tip): pentru că la x se aplică +, compilatorul deduce că x e întreg Pentru reali, am scrie let f x = x cu punct zecimal pentru reali, și în operatori: +., *. etc.
24 Funcții definite pe cazuri Fie abs : Z Z abs(x) = { x dacă x 0 x altfel (x < 0) Valoarea funcției nu e dată de o singură expresie, ci de una din două expresii diferite (x sau -x), depinzând de o condiție (x 0). let abs x = if x >= 0 then x else - x if expr 1 then expr 2 else expr 3 e o expresie condițională Dacă evaluarea lui expr 1 dă valoarea true (adevărat) valoarea expresiei e valoarea lui expr 2, altfel e valoarea lui expr 3. expr 2 și expr 3 trebuie să aibe același tip (ambele întregi, reale,...) În alte limbaje (C, Java, etc.) if și ramurile lui sunt instrucțiuni. În ML, if e o expresie. ML nu are instrucțiuni, ci doar expresii (care sunt evaluate), și definiții (let) care dau nume unor valori. Vom lucra mai târziu și cu definiții de tipuri și de module.
25 Funcții injective Def.: O funcție f : A B e injectivă dacă asociază valori diferite la argumente diferite. Riguros: pentru orice x 1, x 2 A, x 1 x 2 f (x 1 ) f (x 2 ) Exemple: funcție injectivă A B și neinjectivă A B 1 d 1 d 2 b 2 b 3 c 3 c a 4 Imagine:
26 Funcții injective (cont.) În locul condiției x 1, x 2 A, x 1 x 2 f (x 1 ) f (x 2 ) putem scrie echivalent: f (x 1 ) = f (x 2 ) x 1 = x 2 dacă valorile sunt egale, atunci argumentele sunt egale contrapozitiva afirmației de mai sus: negăm premisa și concluzia, și le inversăm: P Q Q P În logică, faptul că o afirmație e echivalentă cu contrapozitiva ei ne permite demonstrația prin reducere la absurd. presupunem concluzia falsă arătăm că atunci premisa e falsă, absurd (știm că e adevărată) deci concluzia nu poate fi falsă, e adevărată E la fel să scriem x 1, x 2 A, x 1 = x 2 f (x 1 ) = f (x 2 )? Nu! Oricare ar fi funcția, dând același argument ia aceeași valoare! (e o proprietate de bază a egalității și substituției).
27 Proprietăți ale funcțiilor injective Dacă mulțimile A și B sunt finite, și f e injectivă, atunci A B. Nu neapărat invers!! (oricum ar fi A > 1 putem construi f să ducă două elemente din A în aceeași valoare din B). Demonstrăm prin inducție după n că dacă A > B = n, f : A B nu poate fi injectivă. Cazul de bază: n = 1, B = {b 1 }. Cum A are cel puțin 2 elemente, avem f (a 1 ) = f (a 2 ) = b 1 (unica posibilitate), deci f nu e injectivă. Cazul inductiv: fie B = n + 1 și b n+1 B. Dacă pentru cel puțin 2 elemente din A, f ia valoarea b n+1, f nu e injectivă. Altfel, eliminăm din A aceste elemente (cel mult 1), și codomeniul devine B =B \ {b n+1 }. Rămânem cu A > B = n. Din ipoteza inductivă, cel puțin două elemente din A au valori egale pentru f. Similar, principiul lui Dirichlet: dacă împărțim n + 1 obiecte în n categorii există cel puțin o categorie cu mai mult de un obiect.
28 Funcții surjective Def.: O funcție f : A B e surjectivă dacă pentru fiecare y B există un x A cu f (x) = y. Exemple: funcție surjectivă și nesurjectivă A B A B 1 d 1 d 2 b 2 b 3 c 3 c 4 a Imagine: Imagine:
29 Funcții surjective: discuție Dacă A și B sunt finite și f : A B e surjectivă, atunci A B. Nu neapărat invers! (construim f să nu ia ca valoare un element anume din B, dacă B > 1). Putem transforma o funcție ne-surjectivă într-una surjectivă prin restrângerea domeniului de valori: f 1 : R R, f 1 (x) = x 2 nu e surjectivă, dar f 2 : R [0, ) (restrânsă la valori nenegative) este. În programare, e util să definim funcția cu tipul rezultatului cât mai precis (dacă e posibil, surjectivă). Astfel, când citim un program, știm deja din tipul funcției ce valori poate returna, fără a trebui să-i examinăm codul.
30 Funcții bijective Def.: O funcție care e injectivă și surjectivă se numește bijectivă. O funcție bijectivă f : A B pune în corespondență unu la unu elementele lui A cu cele ale lui B. A B d b c a Pentru orice funcție, din definiție, la fiecare x A corespunde un unic y B cu f (x) = y Pentru o funcție bijectivă, și invers: la fiecare y B corespunde un unic x A cu f (x) = y Dacă mulțimile A și B sunt finite, și f e bijectivă, atunci A = B. Imagine:
31 Câte funcții există de la A la B? Dacă A și B sunt mulțimi finite există B A funcții de la A la B. Notație: A = cardinalul lui A (numărul de elemente) Demonstrație: prin inducție matematică după A Principiul inducției matematice Dacă o propoziție P(n) depinde de un număr natural n, și 1) (cazul de bază) P(0) e adevărată 2) (pasul inductiv) pentru orice n 0, P(n) P(n + 1) atunci P(n) e adevărată pentru orice n. Mulțimea funcțiilor f : A B se notează uneori B A Notația ne amintește că numărul acestor funcții e B A.
32 Compunerea funcțiilor Fie functiile f : A B și g : B C. Compunerea lor este funcția g f : A C, (g f )(x) = g(f (x)). Putem compune g f doar când codomeniul lui f = domeniul lui g! b A f g B C a d c #!! Imagine:
33 Compunerea funcțiilor - ilustrare computațională INPUT x=3 FUNCTION f: OUTPUT f(x)=9 INPUT FUNCTION g: Rezultatul funcției f devine argument pentru funcția g Prin compunere, construim funcții complexe din funcții mai simple. OUTPUT g(f(x))=10 Imagine:
34 Proprietăți ale compunerii funcțiilor Compunerea a două funcții e asociativă: (f g) h = f (g h) Demonstrație: fie x oarecare din domeniul lui h. Atunci: ((f g) h)(x) = rescriem = (f g)(h(x)) rescriem = f (g(h(x))) (f (g h))(x) = rescriem = f ((g h)(x)) rescriem = f (g(h(x))) Prelucrăm formulele atent, rescriindu-le conform definiției. Compunerea a două funcții nu e neapărat comutativă Puteți da un exemplu pentru care f g g f?
35 Funcții cu mai multe argumente Matematic, scriem de ex. f : Z Z Z, f (x, y) = 2x + y 1 În ML, enumerăm doar argumentele (fără paranteze, făra virgule): let f x y = 2*x + y - 1 iar interpretorul răspunde val f : int -> int -> int = <fun> f e o funcție care ia un întreg și încă un întreg și dă un întreg. Să fixăm primul argument, de ex. x = 2. Obținem: f (2, y) = y 1 Am obținut o funcție de un argument (y), singurul rămas nelegat. În ML, evaluând f 2 (fixând x = 2), interpretorul răspunde: - : int -> int = <fun>. Deci, f e de fapt o funcție cu un argument x, care returnează o funcție. Aceasta ia argumentul y și returnează rezultatul numeric.
36 Compunerea funcțiilor în ML Definim o funcție comp care compune două funcții: let comp f g x = f (g x) Echivalent, puteam scrie: let comp f g = fun x -> f (g x) adică comp f g e funcția care primind argumentul x returnează f (g(x)) Interpretorul indică val comp : ( a -> b) -> ( c -> a) -> c -> b = <fun> Tipurile a, b, c pot fi oarecare. Argument cu argument: c e tipul lui x c -> a e tipul lui g: duce pe x în tipul a a -> b e tipul lui f: duce tipul a în tipul b (codomeniul lui g e domeniul lui f) b e tipul rezultatului Putem apela comp (fun x -> 2*x) (fun x -> x + 1) 3 care dă 2 * (x + 1) pentru x = 3, adică 8.
37 Operatorii sunt funcții Operatorii (ex. matematici, +, *, etc.) sunt tot niște funcții: ei calculează un rezultat din valorile operanzilor (argumentelor). Diferența e doar de sintaxă: scriem operatorii între operanzi (infix), iar numele funcției înaintea argumentelor (prefix). Putem scrie în ML operatorii și prefix: (+) 3 4 paranteza deosebește de operatorul + unar let add1 = (+) 1 add1 3 la fel ca: (+) 1 3 add1 e funcția care adaugă 1 la argument, deci fun x -> x + 1
38 Funcții inversabile Pe orice mulțime A definim funcția identitate id A : A A, id A (x) = x (notată adeseori și 1 A ) Def.: O funcție f : A B e inversabilă dacă există o funcție f 1 : B A astfel încât f 1 f = id A și f f 1 = id B. O funcție e inversabilă dacă și numai dacă e bijectivă. Demonstrăm: Dacă f e inversabilă: pentru y B oarecare, fie x = f 1 (y). Atunci f (x) = f (f 1 (y)) = y, deci f e surjectivă dacă f (x 1 )=f (x 2 ), atunci f 1 (f (x 1 ))=f 1 (f (x 2 )), deci x 1 =x 2 Reciproc, dacă f e bijectivă: f e surjectivă pentru orice y B există x A cu f (x) = y f fiind injectivă, dacă f (x 1 ) = y = f (x 2 ), atunci x 1 = x 2. Deci f 1 : B A, f 1 (y) = acel x astfel încât f (x) = y e o funcție bine definită, f 1 (f (x)) = x, și f (f 1 (y)) = y.
39 Imagine și preimagine Fie f : A B. Dacă S A, mulțimea elementelor f (x) cu x S se numește imaginea lui S prin f, notată f (S). Dacă T B, mulțimea elementelor x cu f (x) T se numește preimaginea lui T prin f, notată f 1 (T ). În general, f 1 (f (S)) S aplicând întâi funcția și apoi preimaginea (încercând să aflăm din ce argument a provenit) se pierde precizie (în general, nu orice calcul e reversibil).
40 Nu orice inversă e ușor calculabilă Pentru o funcție inversabilă, inversa nu e neapărat ușor calculabilă. Fie mulțimea Z p a resturilor nenule modulo p, cu p prim. Ea formează un grup multiplicativ cu operația de înmulțire mod p. Teorema lui Fermat: a p 1 = 1 mod p pentru orice a Z p. Se mai știe că dacă p e prim, grupul Z p are cel puțin un generator, adică un element g astfel încăt șirul g, g 2, g 3,..., g p 1 parcurge toată mulțimea Z p. De exemplu, 3 e generator în Z 7 : șirul 3k mod 7 e 3, 2, 6, 4, 5, 1 Înseamnă că funcția f : Z p Z p, f (x) = g x (și inversabilă). mod p e o bijecție Nu se cunoaște însă un mod eficient de a o inversa când p e mare (problema logaritmului discret) e folosită în criptografie.
41 Rezumat Prin funcții exprimăm calcule în programare. Operatorii sunt cazuri particulare de funcții. Domeniile de definiție și valori corespund tipurilor din programare. Cănd scriem/compunem funcții, tipurile trebuie să se potrivească. În limbajele funcționale, funcțiile pot fi manipulate ca orice valori. Funcțiile pot fi argumente și rezultate de funcții. Funcțiile de mai multe argumente (sau de tuple) pot fi rescrise ca funcții de un singur argument care returnează funcții.
42 De știut Să raționăm despre funcții injective, surjective, bijective, inversabile Să construim funcții cu anumite proprietăți Să numărăm funcțiile definite pe mulțimi finite (cu proprietăți date) Să compunem funcții simple pentru a rezolva probleme Să identificăm tipul unei funcții
Sisteme cu logica fuzzy
 Sisteme cu logica fuzzy 1/15 Sisteme cu logica fuzzy Mamdani Fie un sistem cu logică fuzzy Mamdani două intrări x şi y ieşire z x y SLF Structura z 2/15 Sisteme cu logica fuzzy Mamdani Baza de reguli R
Sisteme cu logica fuzzy 1/15 Sisteme cu logica fuzzy Mamdani Fie un sistem cu logică fuzzy Mamdani două intrări x şi y ieşire z x y SLF Structura z 2/15 Sisteme cu logica fuzzy Mamdani Baza de reguli R
Divizibilitate în mulțimea numerelor naturale/întregi
 Divizibilitate în mulțimea numerelor naturale/întregi Teorema îmărţirii cu rest în mulțimea numerelor naturale Fie a, b, b 0. Atunci există q, r astfel încât a=bq+r, cu 0 r < b. În lus, q şi r sunt unic
Divizibilitate în mulțimea numerelor naturale/întregi Teorema îmărţirii cu rest în mulțimea numerelor naturale Fie a, b, b 0. Atunci există q, r astfel încât a=bq+r, cu 0 r < b. În lus, q şi r sunt unic
FORMULELE LUI STIRLING, WALLIS, GAUSS ŞI APLICAŢII
 DIDACTICA MATHEMATICA, Vol. 34), pp. 53 67 FORMULELE LUI STIRLING, WALLIS, GAUSS ŞI APLICAŢII Eugenia Duca, Emilia Copaciu şi Dorel I. Duca Abstract. In this paper are presented the Wallis, Stirling, Gauss
DIDACTICA MATHEMATICA, Vol. 34), pp. 53 67 FORMULELE LUI STIRLING, WALLIS, GAUSS ŞI APLICAŢII Eugenia Duca, Emilia Copaciu şi Dorel I. Duca Abstract. In this paper are presented the Wallis, Stirling, Gauss
Despre AGC cuasigrupuri V. Izbaș
 Despre AGC cuasigrupuri V Izbaș 1 Introducere Se ştie că grupurile au apărut în matematică ca grupuri de automorfisme Rolul automorfismelor este remarcabil şi bine cunoscut La studierea diverselor structuri
Despre AGC cuasigrupuri V Izbaș 1 Introducere Se ştie că grupurile au apărut în matematică ca grupuri de automorfisme Rolul automorfismelor este remarcabil şi bine cunoscut La studierea diverselor structuri
Soluţii juniori., unde 1, 2
 Soluţii juniori Problema 1 Se consideră suma S x1x x3x4... x015 x016 Este posibil să avem S 016? Răspuns: Da., unde 1,,..., 016 3, 3 Termenii sumei sunt de forma 3 3 1, x x x. 3 5 6 sau Cristian Lazăr
Soluţii juniori Problema 1 Se consideră suma S x1x x3x4... x015 x016 Este posibil să avem S 016? Răspuns: Da., unde 1,,..., 016 3, 3 Termenii sumei sunt de forma 3 3 1, x x x. 3 5 6 sau Cristian Lazăr
1.3. OPERAŢII CU NUMERE NEZECIMALE
 1.3. OPERAŢII CU NUMERE NEZECIMALE 1.3.1 OPERAŢII CU NUMERE BINARE A. ADUNAREA NUMERELOR BINARE Reguli de bază: 0 + 0 = 0 transport 0 0 + 1 = 1 transport 0 1 + 0 = 1 transport 0 1 + 1 = 0 transport 1 Pentru
1.3. OPERAŢII CU NUMERE NEZECIMALE 1.3.1 OPERAŢII CU NUMERE BINARE A. ADUNAREA NUMERELOR BINARE Reguli de bază: 0 + 0 = 0 transport 0 0 + 1 = 1 transport 0 1 + 0 = 1 transport 0 1 + 1 = 0 transport 1 Pentru
Teorema Reziduurilor şi Bucuria Integralelor Reale Prezentare de Alexandru Negrescu
 Teorema Reiduurilor şi Bucuria Integralelor Reale Preentare de Alexandru Negrescu Integrale cu funcţii raţionale ce depind de sint şi cost u notaţia e it, avem: cost sint i ( + ( dt d i, iar integrarea
Teorema Reiduurilor şi Bucuria Integralelor Reale Preentare de Alexandru Negrescu Integrale cu funcţii raţionale ce depind de sint şi cost u notaţia e it, avem: cost sint i ( + ( dt d i, iar integrarea
ON THE QUATERNARY QUADRATIC DIOPHANTINE EQUATIONS (II) NICOLAE BRATU 1 ADINA CRETAN 2
 ON THE QUATERNARY QUADRATIC DIOPHANTINE EQUATIONS (II) NICOLAE BRATU 1 ADINA CRETAN ABSTRACT This paper has been updated and completed thanks to suggestions and critics coming from Dr. Mike Hirschhorn,
ON THE QUATERNARY QUADRATIC DIOPHANTINE EQUATIONS (II) NICOLAE BRATU 1 ADINA CRETAN ABSTRACT This paper has been updated and completed thanks to suggestions and critics coming from Dr. Mike Hirschhorn,
Barem de notare clasa a V-a
 Barem de notare clasa a V-a Problema1. Determinați mulțimile A și B, formate din numere naturale, știind că îndeplinesc simultan condițiile: a) A B,5,6 ; b) B A 0,7 ; c) card AB 3; d) suma elementelor
Barem de notare clasa a V-a Problema1. Determinați mulțimile A și B, formate din numere naturale, știind că îndeplinesc simultan condițiile: a) A B,5,6 ; b) B A 0,7 ; c) card AB 3; d) suma elementelor
UNITATEA DE ÎNVĂȚARE 3 Analiza algoritmilor
 UNITATEA DE ÎNVĂȚARE 3 Analiza algoritmilor Obiective urmărite: La sfârşitul parcurgerii acestei UI, studenţii vor 1.1 cunoaște conceptul de eficienta a unui algoritm vor cunoaste si inţelege modalitatile
UNITATEA DE ÎNVĂȚARE 3 Analiza algoritmilor Obiective urmărite: La sfârşitul parcurgerii acestei UI, studenţii vor 1.1 cunoaște conceptul de eficienta a unui algoritm vor cunoaste si inţelege modalitatile
Gradul de comutativitate al grupurilor finite 1
 Gradul de comutativitate al grupurilor finite Marius TĂRNĂUCEANU Abstract The commutativity degree of a group is one of the most important probabilistic aspects of finite group theory In this survey we
Gradul de comutativitate al grupurilor finite Marius TĂRNĂUCEANU Abstract The commutativity degree of a group is one of the most important probabilistic aspects of finite group theory In this survey we
Teoreme de Analiză Matematică - I (teorema Weierstrass-Bolzano) 1
 Educaţia Matematică Vol. 3, Nr. 1-2 (2007), 79-84 Teoreme de Analiză Matematică - I (teorema Weierstrass-Bolzano) 1 Silviu Crăciunaş, Petrică Dicu, Mioara Boncuţ Abstract In this paper we propose a Weierstrass
Educaţia Matematică Vol. 3, Nr. 1-2 (2007), 79-84 Teoreme de Analiză Matematică - I (teorema Weierstrass-Bolzano) 1 Silviu Crăciunaş, Petrică Dicu, Mioara Boncuţ Abstract In this paper we propose a Weierstrass
Ecuatii si inecuatii de gradul al doilea si reductibile la gradul al doilea. Ecuatii de gradul al doilea
 Ecuatii si inecuatii de gradul al doilea si reductibile la gradul al doilea Ecuatia de forma Ecuatii de gradul al doilea a + b + c = 0, (1) unde a, b, c R, a 0, - variabila, se numeste ecuatie de gradul
Ecuatii si inecuatii de gradul al doilea si reductibile la gradul al doilea Ecuatia de forma Ecuatii de gradul al doilea a + b + c = 0, (1) unde a, b, c R, a 0, - variabila, se numeste ecuatie de gradul
O V E R V I E W. This study suggests grouping of numbers that do not divide the number
 MSCN(2010) : 11A99 Author : Barar Stelian Liviu Adress : Israel e-mail : stelibarar@yahoo.com O V E R V I E W This study suggests grouping of numbers that do not divide the number 3 and/or 5 in eight collumns.
MSCN(2010) : 11A99 Author : Barar Stelian Liviu Adress : Israel e-mail : stelibarar@yahoo.com O V E R V I E W This study suggests grouping of numbers that do not divide the number 3 and/or 5 in eight collumns.
Pentru clasa a X-a Ştiinţele naturii-sem II
 Pentru clasa a X-a Ştiinţele naturii-sem II Reprezentarea algoritmilor. Pseudocod. Principiile programării structurate. Structuri de bază: structura liniară structura alternativă structura repetitivă Algoritmi
Pentru clasa a X-a Ştiinţele naturii-sem II Reprezentarea algoritmilor. Pseudocod. Principiile programării structurate. Structuri de bază: structura liniară structura alternativă structura repetitivă Algoritmi
Teoria Modelelor Master Anul I, Semestrul II 2016
 Ce este logica? Teoria Modelelor Master Anul I, Semestrul II 2016 Laurenţiu Leuştean Pagina web: http:unibuc.ro/~lleustean/ În această prezentare sunt folosite parţial slideurile Ioanei Leuştean din Semestrul
Ce este logica? Teoria Modelelor Master Anul I, Semestrul II 2016 Laurenţiu Leuştean Pagina web: http:unibuc.ro/~lleustean/ În această prezentare sunt folosite parţial slideurile Ioanei Leuştean din Semestrul
Procedeu de demonstrare a unor inegalităţi bazat pe inegalitatea lui Schur
 Procedeu de demonstrare a unor inegalităţi bazat pe inegalitatea lui Schur Andi Gabriel BROJBEANU Abstract. A method for establishing certain inequalities is proposed and applied. It is based upon inequalities
Procedeu de demonstrare a unor inegalităţi bazat pe inegalitatea lui Schur Andi Gabriel BROJBEANU Abstract. A method for establishing certain inequalities is proposed and applied. It is based upon inequalities
Câteva rezultate de algebră comutativă
 Facultatea de Matematică Anul II Master, Geometrie Algebrică Câteva rezultate de algebră comutativă Aceste note conţin noţiuni şi rezultate de algebră comutativă care sunt utilizate pe parcursul cursului.
Facultatea de Matematică Anul II Master, Geometrie Algebrică Câteva rezultate de algebră comutativă Aceste note conţin noţiuni şi rezultate de algebră comutativă care sunt utilizate pe parcursul cursului.
Cristalul cu N atomi = un sistem de N oscilatori de amplitudini mici;
 Curs 8 Caldura specifica a retelei Cristalul cu N atomi = un sistem de N oscilatori de amplitudini mici; pentru tratarea cuantica, se inlocuieste tratamentul clasic al oscilatorilor cuplati, cu cel cuantic
Curs 8 Caldura specifica a retelei Cristalul cu N atomi = un sistem de N oscilatori de amplitudini mici; pentru tratarea cuantica, se inlocuieste tratamentul clasic al oscilatorilor cuplati, cu cel cuantic
Avem 6 tipuri de simboluri in logica predicatelor:
 Semantica Avem 6 tipuri de simboluri in logica predicatelor: Predicate: p, q, r,, p1, q2 etc. Constante: a, b, c,, z, a1, b4,, ion, mihai, labus etc. Variabile: x, y, z, x1, y1, z4 etc. Conective:,,,,
Semantica Avem 6 tipuri de simboluri in logica predicatelor: Predicate: p, q, r,, p1, q2 etc. Constante: a, b, c,, z, a1, b4,, ion, mihai, labus etc. Variabile: x, y, z, x1, y1, z4 etc. Conective:,,,,
Utilizarea limbajului SQL pentru cereri OLAP. Mihaela Muntean 2015
 Utilizarea limbajului SQL pentru cereri OLAP Mihaela Muntean 2015 Cuprins Implementarea operatiilor OLAP de baza in SQL -traditional: Rollup Slice Dice Pivotare SQL-2008 Optiunea ROLLUP Optiunea CUBE,
Utilizarea limbajului SQL pentru cereri OLAP Mihaela Muntean 2015 Cuprins Implementarea operatiilor OLAP de baza in SQL -traditional: Rollup Slice Dice Pivotare SQL-2008 Optiunea ROLLUP Optiunea CUBE,
Liste. Stive. Cozi SD 2017/2018
 Liste. Stive. Cozi SD 2017/2018 Conţinut Tipurile abstracte LLin, LLinOrd, Stiva, Coada Liste liniare Implementarea cu tablouri Implementarea cu liste simplu înlănțuite Liste liniare ordonate Stive Cozi
Liste. Stive. Cozi SD 2017/2018 Conţinut Tipurile abstracte LLin, LLinOrd, Stiva, Coada Liste liniare Implementarea cu tablouri Implementarea cu liste simplu înlănțuite Liste liniare ordonate Stive Cozi
Ce este logica? Aristotel (IV î.e.n.) Gottfried Wilhelm Leibniz ( ) Visul lui Leibniz. raţionament
 Ce este logica? Logică Matematică şi Computaţională Anul I, Semestrul I 2017/2018 Laurenţiu Leuştean Pagina web: http://unibuc.ro/~lleustean/ În prezentarea acestui curs sunt folosite parţial slideurile
Ce este logica? Logică Matematică şi Computaţională Anul I, Semestrul I 2017/2018 Laurenţiu Leuştean Pagina web: http://unibuc.ro/~lleustean/ În prezentarea acestui curs sunt folosite parţial slideurile
Anul I, Semestrul I 2017/2018
 Logică Matematică şi Computaţională Anul I, Semestrul I 2017/2018 Laurenţiu Leuştean Pagina web: http://unibuc.ro/~lleustean/ În prezentarea acestui curs sunt folosite parţial slideurile Ioanei Leuştean
Logică Matematică şi Computaţională Anul I, Semestrul I 2017/2018 Laurenţiu Leuştean Pagina web: http://unibuc.ro/~lleustean/ În prezentarea acestui curs sunt folosite parţial slideurile Ioanei Leuştean
Inteligenta Artificiala
 Inteligenta Artificiala Universitatea Politehnica Bucuresti Anul universitar 2010-2011 Adina Magda Florea http://turing.cs.pub.ro/ia_10 si curs.cs.pub.ro 1 Curs nr. 4 Cautare cu actiuni nedeterministe
Inteligenta Artificiala Universitatea Politehnica Bucuresti Anul universitar 2010-2011 Adina Magda Florea http://turing.cs.pub.ro/ia_10 si curs.cs.pub.ro 1 Curs nr. 4 Cautare cu actiuni nedeterministe
Programarea Dinamica. (si alte chestii adiacente) Andrei Olariu
 Programarea Dinamica (si alte chestii adiacente) Andrei Olariu andrei@olariu.org Despre mine - Absolvent FMI UniBuc - Doctorand in prelucrarea limbajului natural, in special in mediul online (Twitter)
Programarea Dinamica (si alte chestii adiacente) Andrei Olariu andrei@olariu.org Despre mine - Absolvent FMI UniBuc - Doctorand in prelucrarea limbajului natural, in special in mediul online (Twitter)
INEGALITĂŢI DE TIP HARNACK ŞI SOLUŢII POZITIVE MULTIPLE PENTRU PROBLEME NELINIARE
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA ŞCOALA DOCTORALĂ DE MATEMATICĂ ŞI INFORMATICĂ INEGALITĂŢI DE TIP HARNACK ŞI SOLUŢII POZITIVE MULTIPLE PENTRU PROBLEME NELINIARE Rezumatul tezei de doctorat Doctorand:
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA ŞCOALA DOCTORALĂ DE MATEMATICĂ ŞI INFORMATICĂ INEGALITĂŢI DE TIP HARNACK ŞI SOLUŢII POZITIVE MULTIPLE PENTRU PROBLEME NELINIARE Rezumatul tezei de doctorat Doctorand:
APLICAŢII ALE FORMULELOR LUI NEWTON PENTRU POLINOAME SIMETRICE
 DIDACTICA MATHEMATICA, Vol. 33(2015), pp. 27 37 APLICAŢII ALE FORMULELOR LUI NEWTON PENTRU POLINOAME SIMETRICE Cristina-Aida Coman Abstract. In this paper we present some applications of Newton s formulae
DIDACTICA MATHEMATICA, Vol. 33(2015), pp. 27 37 APLICAŢII ALE FORMULELOR LUI NEWTON PENTRU POLINOAME SIMETRICE Cristina-Aida Coman Abstract. In this paper we present some applications of Newton s formulae
Legi de distribuţie (principalele distribuţii de probabilitate) Tudor Drugan
 Legi de distribuţie (principalele distribuţii de probabilitate) Tudor Drugan Introducere In general distribuţiile variabilelor aleatoare definite pe o populaţie, care face obiectul unui studiu, nu se cunosc.
Legi de distribuţie (principalele distribuţii de probabilitate) Tudor Drugan Introducere In general distribuţiile variabilelor aleatoare definite pe o populaţie, care face obiectul unui studiu, nu se cunosc.
Cercet¼ari operaţionale
 Cercet¼ari operaţionale B¼arb¼acioru Iuliana Carmen CURSUL 9 Cursul 9 Cuprins Programare liniar¼a 5.1 Modelul matematic al unei probleme de programare liniar¼a.................... 5. Forme de prezentare
Cercet¼ari operaţionale B¼arb¼acioru Iuliana Carmen CURSUL 9 Cursul 9 Cuprins Programare liniar¼a 5.1 Modelul matematic al unei probleme de programare liniar¼a.................... 5. Forme de prezentare
Rădăcina pătrată a unei matrici reale de ordinul 2
 Rădăcina pătrată a unei matrici reale de ordinul Mircea Crasmareanu Mai 19, 017 ( a c Actorii acestei poveşti: matricile A = M b d (R. PROBLEMA STUDIATĂ: Există B M (R aşa încât: B = A? O astfel de matrice
Rădăcina pătrată a unei matrici reale de ordinul Mircea Crasmareanu Mai 19, 017 ( a c Actorii acestei poveşti: matricile A = M b d (R. PROBLEMA STUDIATĂ: Există B M (R aşa încât: B = A? O astfel de matrice
COMPARATIVE DISCUSSION ABOUT THE DETERMINING METHODS OF THE STRESSES IN PLANE SLABS
 74 COMPARATIVE DISCUSSION ABOUT THE DETERMINING METHODS OF THE STRESSES IN PLANE SLABS Codrin PRECUPANU 3, Dan PRECUPANU,, Ștefan OPREA Correspondent Member of Technical Sciences Academy Gh. Asachi Technical
74 COMPARATIVE DISCUSSION ABOUT THE DETERMINING METHODS OF THE STRESSES IN PLANE SLABS Codrin PRECUPANU 3, Dan PRECUPANU,, Ștefan OPREA Correspondent Member of Technical Sciences Academy Gh. Asachi Technical
Subiecte geometrie licenta matematica-informatica 4 ani
 Class: Date: Subiecte geometrie licenta matematica-informatica 4 ani Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. 1. Complementara unui subspatiu
Class: Date: Subiecte geometrie licenta matematica-informatica 4 ani Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. 1. Complementara unui subspatiu
PROBLEME DIVERSE lecţie susţinută la lotul de 13 de Andrei ECKSTEIN Bucureşti, 25 mai 2015
 PROBLEME DIVERSE lecţie susţinută la lotul de 13 de Andrei ECKSTEIN Bucureşti, 5 mai 015 I. SUBSTITUŢIA TAIWANEZĂ 1. Fie a, b, c > 0 astfel încât a bc, b ca şi c ab. Determinaţi valoarea maximă a expresiei
PROBLEME DIVERSE lecţie susţinută la lotul de 13 de Andrei ECKSTEIN Bucureşti, 5 mai 015 I. SUBSTITUŢIA TAIWANEZĂ 1. Fie a, b, c > 0 astfel încât a bc, b ca şi c ab. Determinaţi valoarea maximă a expresiei
PRELUCRARI PE IMAGINI BINARE (ALB/NEGRU)
 PRELUCRRI PE IMGINI BINRE (LB/NEGRU) Imagine binara? 2 nuante: alb ( 0 ) pixelii de fond ( I(x,y)= 255 pt. imagini indexate cu 8 biti/pixel ) negru ( 1 ) pixelii apartinand obiectelor ( I(x,y)= 0 pt. imagini
PRELUCRRI PE IMGINI BINRE (LB/NEGRU) Imagine binara? 2 nuante: alb ( 0 ) pixelii de fond ( I(x,y)= 255 pt. imagini indexate cu 8 biti/pixel ) negru ( 1 ) pixelii apartinand obiectelor ( I(x,y)= 0 pt. imagini
INCLUZIUNI OPERATORIALE PRIN TEHNICA PUNCTULUI FIX ÎN SPAŢII METRICE VECTORIALE
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ INCLUZIUNI OPERATORIALE PRIN TEHNICA PUNCTULUI FIX ÎN SPAŢII METRICE VECTORIALE REZUMATUL TEZEI DE DOCTORAT Coordonator ştiinţific
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ INCLUZIUNI OPERATORIALE PRIN TEHNICA PUNCTULUI FIX ÎN SPAŢII METRICE VECTORIALE REZUMATUL TEZEI DE DOCTORAT Coordonator ştiinţific
Laborator 5. Instructiuni de control logic : FOR, IF, WHILE. - Staţii de lucru care au instalat Orcad9.2. si MatLab 7.1
 Laborator 5. Instructiuni de control logic : FOR, IF, WHILE. Scopul lucrarii: Scopul acestei lucrari este de a invata si intelege instructiunile de control logic, pe care, le vom folosi in realizarea unui
Laborator 5. Instructiuni de control logic : FOR, IF, WHILE. Scopul lucrarii: Scopul acestei lucrari este de a invata si intelege instructiunile de control logic, pe care, le vom folosi in realizarea unui
Habilitation Thesis. Periodic solutions of differential systems: existence, stability and bifurcations
 UNIVERSITATEA BABEŞ BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Habilitation Thesis Mathematics presented by Adriana Buică Periodic solutions of differential systems: existence, stability
UNIVERSITATEA BABEŞ BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Habilitation Thesis Mathematics presented by Adriana Buică Periodic solutions of differential systems: existence, stability
Graduări pe algebre de matrice
 UNIVERSITATEA DIN BUCUREŞTI FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ ŞCOALA DOCTORALĂ DE MATEMATICĂ Graduări pe algebre de matrice TEZĂ DE DOCTORAT REZUMAT Coordonator ştiinţific: Prof.univ.dr. Sorin Dăscălescu
UNIVERSITATEA DIN BUCUREŞTI FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ ŞCOALA DOCTORALĂ DE MATEMATICĂ Graduări pe algebre de matrice TEZĂ DE DOCTORAT REZUMAT Coordonator ştiinţific: Prof.univ.dr. Sorin Dăscălescu
ȘIRURI (TABLOURI UNIDIMENSIONALE)
 Problema 1 Enunț ȘIRURI (TABLOURI UNIDIMENSIONALE) Se citesc mai multe numere naturale, până la introducerea numărului 0 şi se memorează într-un şir. Să se găsească toate numerele perfecte din şir. Un
Problema 1 Enunț ȘIRURI (TABLOURI UNIDIMENSIONALE) Se citesc mai multe numere naturale, până la introducerea numărului 0 şi se memorează într-un şir. Să se găsească toate numerele perfecte din şir. Un
PLANIFICAREA TEMELOR LA GRUPELE DE EXCELENȚĂ DISCIPLINA MATEMATICĂ AN ȘCOLAR
 PLANIFICAREA TEMELOR LA GRUPELE DE EXCELENȚĂ DISCIPLINA MATEMATICĂ AN ȘCOLAR 0-0 Grupa V. Matematică Profesor coordonator: Aldescu Alina.0.0 Operatii in N-Teorema impartirii cu rest 0..0 Patrate perfecte,cuburi
PLANIFICAREA TEMELOR LA GRUPELE DE EXCELENȚĂ DISCIPLINA MATEMATICĂ AN ȘCOLAR 0-0 Grupa V. Matematică Profesor coordonator: Aldescu Alina.0.0 Operatii in N-Teorema impartirii cu rest 0..0 Patrate perfecte,cuburi
PROPRIETĂŢI GEOMETRICE ŞI ANALITICE ALE UNOR CLASE DE FUNCŢII UNIVALENTE
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ GABRIELA ROXANA ŞENDRUŢIU PROPRIETĂŢI GEOMETRICE ŞI ANALITICE ALE UNOR CLASE DE FUNCŢII UNIVALENTE Rezumatul tezei de doctorat
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ GABRIELA ROXANA ŞENDRUŢIU PROPRIETĂŢI GEOMETRICE ŞI ANALITICE ALE UNOR CLASE DE FUNCŢII UNIVALENTE Rezumatul tezei de doctorat
Arhitectura sistemelor de calcul
 Arhitectura sistemelor de calcul - Prelegerea 1 - Evoluția sistemelor de calcul Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Istoricul evolutiei calculatoarelor
Arhitectura sistemelor de calcul - Prelegerea 1 - Evoluția sistemelor de calcul Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Istoricul evolutiei calculatoarelor
Rezultate în Teoria Punctului Fix şi Procese Iterative cu Aplicaţii
 Rezultate în Teoria Punctului Fix şi Procese Iterative cu Aplicaţii Asist. drd. Adrian Sorinel Ghiura Departamentul de Matematică & Informatică Universitatea Politehnica din Bucureşti REZUMATUL TEZEI DE
Rezultate în Teoria Punctului Fix şi Procese Iterative cu Aplicaţii Asist. drd. Adrian Sorinel Ghiura Departamentul de Matematică & Informatică Universitatea Politehnica din Bucureşti REZUMATUL TEZEI DE
Logică avansată pentru informatică Master Anul I, Semestrul I
 Logică avansată pentru informatică Master Anul I, Semestrul I 2017-2018 Laurenţiu Leuştean Pagina web: http:unibuc.ro/~lleustean/ În prezentarea acestui curs sunt folosite parţial slideurile Ioanei Leuştean
Logică avansată pentru informatică Master Anul I, Semestrul I 2017-2018 Laurenţiu Leuştean Pagina web: http:unibuc.ro/~lleustean/ În prezentarea acestui curs sunt folosite parţial slideurile Ioanei Leuştean
Sisteme cu logica fuzzy cu mai multe intrari (MISO)
 Sisteme cu logica fuzzy cu mai multe intrari (MISO) Structura unui sistem cu logică fuzzy MISO Structura unui SLF cu 2 intrari Fie un sistem cu logică fuzzy Mamdani două intrări x şi y ieşire z x y SLF
Sisteme cu logica fuzzy cu mai multe intrari (MISO) Structura unui sistem cu logică fuzzy MISO Structura unui SLF cu 2 intrari Fie un sistem cu logică fuzzy Mamdani două intrări x şi y ieşire z x y SLF
SIMULAREA DECIZIEI FINANCIARE
 SIMULAREA DECIZIEI FINANCIARE Conf. univ. dr. Nicolae BÂRSAN-PIPU T5.1 TEMA 5 DISTRIBUŢII DISCRETE T5. Cuprins T5.3 5.1 Variabile aleatoare discrete 5. Distribuţia de probabilitate a unei variabile aleatoare
SIMULAREA DECIZIEI FINANCIARE Conf. univ. dr. Nicolae BÂRSAN-PIPU T5.1 TEMA 5 DISTRIBUŢII DISCRETE T5. Cuprins T5.3 5.1 Variabile aleatoare discrete 5. Distribuţia de probabilitate a unei variabile aleatoare
TEOREME DE PUNCT FIX PENTRU OPERATORI CE NU INVARIAZĂ DOMENIUL DE DEFINIŢIE ŞI
 Universitatea Babeş-Bolyai, Cluj-Napoca Facultatea de Matematică şi Informatică Tania Angelica Lazăr TEOREME DE PUNCT FIX PENTRU OPERATORI CE NU INVARIAZĂ DOMENIUL DE DEFINIŢIE ŞI APLICAŢII Coordonator
Universitatea Babeş-Bolyai, Cluj-Napoca Facultatea de Matematică şi Informatică Tania Angelica Lazăr TEOREME DE PUNCT FIX PENTRU OPERATORI CE NU INVARIAZĂ DOMENIUL DE DEFINIŢIE ŞI APLICAŢII Coordonator
Definiţie. Pr(X a) - probabilitatea ca X să ia valoarea a ; Pr(a X b) - probabilitatea ca X să ia o valoare în intervalul a,b.
 Variabile aleatoare Definiţie Se numeşte variabilă aleatoare pe un spaţiu fundamental E şi se notează prin X, o funcţie definită pe E cu valori în mulţimea numerelor reale. Unei variabile aleatoare X i
Variabile aleatoare Definiţie Se numeşte variabilă aleatoare pe un spaţiu fundamental E şi se notează prin X, o funcţie definită pe E cu valori în mulţimea numerelor reale. Unei variabile aleatoare X i
Mugur Acu OPERATORUL INTEGRAL LIBERA-PASCU ŞI PROPRIETĂŢILE ACESTUIA CU PRIVIRE LA FUNCŢIILE UNIFORM STELATE, CONVEXE, APROAPE CONVEXE ŞI
 Mugur Acu OPERATORUL INTEGRAL LIBERA-PASCU ŞI PROPRIETĂŢILE ACESTUIA CU PRIVIRE LA FUNCŢIILE UNIFORM STELATE, CONVEXE, APROAPE CONVEXE ŞI α-uniform CONVEXE Editura Universităţii Lucian Blaga din Sibiu
Mugur Acu OPERATORUL INTEGRAL LIBERA-PASCU ŞI PROPRIETĂŢILE ACESTUIA CU PRIVIRE LA FUNCŢIILE UNIFORM STELATE, CONVEXE, APROAPE CONVEXE ŞI α-uniform CONVEXE Editura Universităţii Lucian Blaga din Sibiu
Rezolvarea ecuaţiilor şi sistemelor de ecuaţii diferenţiale ordinare (II)
 Rezolvarea ecuaţiilor şi sistemelor de ecuaţii diferenţiale ordinare (II) Metode multipas Prof.dr.ing. Universitatea "Politehnica" Bucureşti, Facultatea de Inginerie Electrică Suport didactic pentru disciplina
Rezolvarea ecuaţiilor şi sistemelor de ecuaţii diferenţiale ordinare (II) Metode multipas Prof.dr.ing. Universitatea "Politehnica" Bucureşti, Facultatea de Inginerie Electrică Suport didactic pentru disciplina
Sem. I, Ioana Leustean FMI, UB
 LOGICA MATEMATICĂ ŞI COMPUTAŢIONALĂ Sem. I, 2017-2018 Ioana Leustean FMI, UB Ce este logica? logike tekhne = ştiinţa raţionamentelor logos = cuvînt, raţionament A deduction is speech (logos) in which,
LOGICA MATEMATICĂ ŞI COMPUTAŢIONALĂ Sem. I, 2017-2018 Ioana Leustean FMI, UB Ce este logica? logike tekhne = ştiinţa raţionamentelor logos = cuvînt, raţionament A deduction is speech (logos) in which,
Teoreme de compresie-extensie de tip Krasnoselskii şi aplicaţii (Rezumatul tezei de doctorat)
 Teoreme de compresie-extensie de tip Krasnoselskii şi aplicaţii (Rezumatul tezei de doctorat) Sorin Monel Budişan Coordonator ştiinţi c: Prof. dr. Radu Precup Cuprins Introducere 1 1 Generaliz¼ari ale
Teoreme de compresie-extensie de tip Krasnoselskii şi aplicaţii (Rezumatul tezei de doctorat) Sorin Monel Budişan Coordonator ştiinţi c: Prof. dr. Radu Precup Cuprins Introducere 1 1 Generaliz¼ari ale
GENERATOARE DE SEMNAL DIGITALE
 Technical University of Iasi, Romania Faculty of Electronics and Telecommunications Signals, Circuits and Systems laboratory Prof. Victor Grigoras Cuprins Clasificarea generatoarelor Filtre reursive la
Technical University of Iasi, Romania Faculty of Electronics and Telecommunications Signals, Circuits and Systems laboratory Prof. Victor Grigoras Cuprins Clasificarea generatoarelor Filtre reursive la
Utilizarea claselor de echivalenta in analiza asistata de calculator a sistemelor cu evenimente discrete
 72 Utilizarea claselor de echivalenta in analiza asistata de calculator a sistemelor cu evenimente discrete Conf.dr. Alexandru TERTISCO, ing. Alexandru BOICEA Facultatea de Automatica si Calculatoare,
72 Utilizarea claselor de echivalenta in analiza asistata de calculator a sistemelor cu evenimente discrete Conf.dr. Alexandru TERTISCO, ing. Alexandru BOICEA Facultatea de Automatica si Calculatoare,
REZUMATUL TEZEI DE DOCTORAT
 UNIVERSITATEA BABEŞ-BOLYAI FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ CERCETĂRI DE TEORIE MORSE DISCRETĂ ŞI APLICAŢII REZUMATUL TEZEI DE DOCTORAT Conducător ştiinţific: Prof. univ. dr. DORIN ANDRICA Doctorand:
UNIVERSITATEA BABEŞ-BOLYAI FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ CERCETĂRI DE TEORIE MORSE DISCRETĂ ŞI APLICAŢII REZUMATUL TEZEI DE DOCTORAT Conducător ştiinţific: Prof. univ. dr. DORIN ANDRICA Doctorand:
Metode clasice. Camelia Chira.
 Metode clasice Camelia Chira http://users.utcluj.ro/~cchira camelia.chira@cs.utcluj.ro Am vazut deja ca... Probleme de optimizare pot fi foarte complexe SAT, TSP, NLP, etc Spatiul de cautare Clase de complexitate
Metode clasice Camelia Chira http://users.utcluj.ro/~cchira camelia.chira@cs.utcluj.ro Am vazut deja ca... Probleme de optimizare pot fi foarte complexe SAT, TSP, NLP, etc Spatiul de cautare Clase de complexitate
Alte rezultate din teoria codurilor
 Prelegerea 20 Alte rezultate din teoria codurilor 20.1 Coduri aritmetice Construcţiile oferite de teoria codurilor pot fi utilizate şi în alte domenii decât în cele clasice, de transmitere şi recepţie
Prelegerea 20 Alte rezultate din teoria codurilor 20.1 Coduri aritmetice Construcţiile oferite de teoria codurilor pot fi utilizate şi în alte domenii decât în cele clasice, de transmitere şi recepţie
array a[0..n-1] a[0] = v0,..., a[n-1] = vn-1
![array a[0..n-1] a[0] = v0,..., a[n-1] = vn-1 array a[0..n-1] a[0] = v0,..., a[n-1] = vn-1](/thumbs/76/73793144.jpg) Curs 5 - Agenda sortare interna buble sort sortare prin insertie sortare pri selectie naiva sistematica ( heap sort ) sortare prin interclasare ( merge sort ) sortare rapida ( quick sort ) cautare in liste
Curs 5 - Agenda sortare interna buble sort sortare prin insertie sortare pri selectie naiva sistematica ( heap sort ) sortare prin interclasare ( merge sort ) sortare rapida ( quick sort ) cautare in liste
Laborator 3. Backtracking iterativ
 Programare Delphi Laborator 3 Backtracking iterativ Metoda backtracking este o strategie generală de căutare din aproape în aproape a unei soluţii dintr-o mulţime finită de posibilităţi. Problema trebuie
Programare Delphi Laborator 3 Backtracking iterativ Metoda backtracking este o strategie generală de căutare din aproape în aproape a unei soluţii dintr-o mulţime finită de posibilităţi. Problema trebuie
ECUAŢII CU DERIVATE PARŢIALE ŞI EVALUAREA OPŢIUNILOR CU VOLATILITATE STOHASTICĂ
 Universitatea Babeş-Bolyai, Cluj-Napoca Facultatea de Matematică şi Informatică Vasile Lucian Lazăr ECUAŢII CU DERIVATE PARŢIALE ŞI EVALUAREA OPŢIUNILOR CU VOLATILITATE STOHASTICĂ Coordonator ştiinţific
Universitatea Babeş-Bolyai, Cluj-Napoca Facultatea de Matematică şi Informatică Vasile Lucian Lazăr ECUAŢII CU DERIVATE PARŢIALE ŞI EVALUAREA OPŢIUNILOR CU VOLATILITATE STOHASTICĂ Coordonator ştiinţific
Test de Departajare pentru MofM 2014 (Bucureşti) Enunţuri & Soluţii
 Test de Departajare petru MofM 04 Bucureşti Euţuri & Soluţii Problem. Give + distict real umbers i the iterval [0,], prove there exist two of them a b, such that ab a b < Solutio. Idex the umbers 0 a 0
Test de Departajare petru MofM 04 Bucureşti Euţuri & Soluţii Problem. Give + distict real umbers i the iterval [0,], prove there exist two of them a b, such that ab a b < Solutio. Idex the umbers 0 a 0
Reactoare chimice cu curgere piston (ideala) cu amestecare completa de tip batch (autoclava)
 Reactoare chimice cu curgere piston (ideala) cu amestecare completa de tip batch (autoclava) Reactorul cu curgere ideala Toate particulele se deplaseaza intr-o directie de-a lungul reactorului, precum
Reactoare chimice cu curgere piston (ideala) cu amestecare completa de tip batch (autoclava) Reactorul cu curgere ideala Toate particulele se deplaseaza intr-o directie de-a lungul reactorului, precum
Self-Small Abelian Groups and Related Problems. (Abstract)
 UNIVERSITATEA BABEŞ-BOLYAI, CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Habilitation Thesis Self-Small Abelian Groups and Related Problems (Abstract) Author: Simion BREAZ 2013 Abstract Let R be
UNIVERSITATEA BABEŞ-BOLYAI, CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Habilitation Thesis Self-Small Abelian Groups and Related Problems (Abstract) Author: Simion BREAZ 2013 Abstract Let R be
Manual Limba Germana
 Manual Limba Germana If you are searched for the book Manual limba germana in pdf format, in that case you come on to loyal site. We furnish utter variation of this ebook in txt, doc, epub, DjVu, PDF formats.
Manual Limba Germana If you are searched for the book Manual limba germana in pdf format, in that case you come on to loyal site. We furnish utter variation of this ebook in txt, doc, epub, DjVu, PDF formats.
Universitatea Politehnica Bucureşti Facultatea de Automatică şi Calculatoare Departamentul de Automatică şi Ingineria Sistemelor
 Universitatea Politehnica Bucureşti Facultatea de Automatică şi Calculatoare Departamentul de Automatică şi Ingineria Sistemelor TEZĂ DE ABILITARE Metode de Descreştere pe Coordonate pentru Optimizare
Universitatea Politehnica Bucureşti Facultatea de Automatică şi Calculatoare Departamentul de Automatică şi Ingineria Sistemelor TEZĂ DE ABILITARE Metode de Descreştere pe Coordonate pentru Optimizare
Ordin. pentru aprobarea structurii informaţiilor înscrise pe cardul naţional de asigurări sociale de sănătate
 CASA NATIONALA DE ASIGURARI DE SANATATE Ordin pentru aprobarea structurii informaţiilor înscrise pe cardul naţional de asigurări sociale de sănătate Având în vedere: Act publicat in Monitorul Oficial al
CASA NATIONALA DE ASIGURARI DE SANATATE Ordin pentru aprobarea structurii informaţiilor înscrise pe cardul naţional de asigurări sociale de sănătate Având în vedere: Act publicat in Monitorul Oficial al
METODE NUMERICE: Laborator #4 Eliminare gaussiană cu pivotare totală şi scalare. Algoritmul Thomas pentru rezolvarea sistemului 3-diagonal
 METODE NUMERICE: Laborator #4 Eliminare gaussiană cu pivotare totală şi scalare. Algoritmul Thomas pentru rezolvarea sistemului 3-diagonal Titulari curs: Florin Pop, George-Pantelimon Popescu Responsabil
METODE NUMERICE: Laborator #4 Eliminare gaussiană cu pivotare totală şi scalare. Algoritmul Thomas pentru rezolvarea sistemului 3-diagonal Titulari curs: Florin Pop, George-Pantelimon Popescu Responsabil
Teoria probabilit¼aţilor şi statistic¼a matematic¼a
 Teoria probabilit¼aţilor şi statistic¼a matematic¼a B¼arb¼acioru Iuliaa Carme CURSUL 7 Cursul 7 2 Cupris 1 Legea umerelor mari 5 1.1 Geeralit¼aţi............................... 5 1.2 Iegalitatea lui Cebîşev........................
Teoria probabilit¼aţilor şi statistic¼a matematic¼a B¼arb¼acioru Iuliaa Carme CURSUL 7 Cursul 7 2 Cupris 1 Legea umerelor mari 5 1.1 Geeralit¼aţi............................... 5 1.2 Iegalitatea lui Cebîşev........................
PENTRU CERCURILE DE ELEVI
 M.Opincariu, M.Stroe, Despre matrice şi determinanţi de ordinul doi 559 Demonstraţie. Aplicăm Propoziţia 3.5. pentru funcţia: g :[a 1,a ] (0, ), g(x) =1. Bibliografie [1]R.P.BoasJr.,M.B.Marcus,Generalizations
M.Opincariu, M.Stroe, Despre matrice şi determinanţi de ordinul doi 559 Demonstraţie. Aplicăm Propoziţia 3.5. pentru funcţia: g :[a 1,a ] (0, ), g(x) =1. Bibliografie [1]R.P.BoasJr.,M.B.Marcus,Generalizations
ALGORITMI DE OPTIMIZARE IN INGINERIE ELECTRICA. Sef lucrari ing. Alin-Iulian DOLAN
 ALGORITMI DE OPTIMIZARE IN INGINERIE ELECTRICA Sef lucrari ing. Alin-Iulian DOLAN PROBLEME DE OPTIMIZARE OPTIMIZAREA gasirea celei mai bune solutii ale unei probleme, constand in minimizarea (maximizarea)
ALGORITMI DE OPTIMIZARE IN INGINERIE ELECTRICA Sef lucrari ing. Alin-Iulian DOLAN PROBLEME DE OPTIMIZARE OPTIMIZAREA gasirea celei mai bune solutii ale unei probleme, constand in minimizarea (maximizarea)
2D AND 3D PROCESSING OF THE INTERDEPENDENCE BETWEEN THE COMFORT MAIN INDICATORS
 BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LVII (LXI), Fasc. 1, 2011 SecŃia TEXTILE. PIELĂRIE 2D AND 3D PROCESSING OF THE INTERDEPENDENCE
BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LVII (LXI), Fasc. 1, 2011 SecŃia TEXTILE. PIELĂRIE 2D AND 3D PROCESSING OF THE INTERDEPENDENCE
Probleme actuale în studiul funcţiei zeta Igusa
 Probleme actuale în studiul funcţiei zeta Igusa Denis Ibadula 1 1 This paper is supported by the Sectorial Operational Programme Human Resources Development (SOP HRD), financed from the European Social
Probleme actuale în studiul funcţiei zeta Igusa Denis Ibadula 1 1 This paper is supported by the Sectorial Operational Programme Human Resources Development (SOP HRD), financed from the European Social
CURS 11: Programare dinamică - II - Algoritmica - Curs 12 1
 CURS 11: Programare dinamică - II - Algoritmica - Curs 12 1 Structura Ce este programarea dinamică? Aplicație: problema discretă a rucsacului Funcții de memorie (memoizare) Aplicație: înmulțirea optimală
CURS 11: Programare dinamică - II - Algoritmica - Curs 12 1 Structura Ce este programarea dinamică? Aplicație: problema discretă a rucsacului Funcții de memorie (memoizare) Aplicație: înmulțirea optimală
MATEMATICĂ 3 PROBLEME DE REFLECŢIE
 Recapitulare din liceu MATEMATIĂ 3 ANALIZĂ OMPLEXĂ PROBLEME DE REFLEŢIE. Scrieţi numerele următoare sub forma a + bi, unde a, b R: a) 3i + i ; b) i + i ;. Reolvaţi în ecuaţiile: ( + i)( i) c) ( + i)(4
Recapitulare din liceu MATEMATIĂ 3 ANALIZĂ OMPLEXĂ PROBLEME DE REFLEŢIE. Scrieţi numerele următoare sub forma a + bi, unde a, b R: a) 3i + i ; b) i + i ;. Reolvaţi în ecuaţiile: ( + i)( i) c) ( + i)(4
A GENERALIZATION OF A CLASSICAL MONTE CARLO ALGORITHM TO ESTIMATE π
 U.P.B. Sci. Bull., Series A, Vol. 68, No., 6 A GENERALIZATION OF A CLASSICAL MONTE CARLO ALGORITHM TO ESTIMATE π S.C. ŞTEFĂNESCU Algoritmul Monte Carlo clasic A1 estimeazează valoarea numărului π bazându-se
U.P.B. Sci. Bull., Series A, Vol. 68, No., 6 A GENERALIZATION OF A CLASSICAL MONTE CARLO ALGORITHM TO ESTIMATE π S.C. ŞTEFĂNESCU Algoritmul Monte Carlo clasic A1 estimeazează valoarea numărului π bazându-se
ARTIFICIAL INTELLIGENCE
 BABEŞ-BOLYAI UNIVERSITY Faculty of Computer Science and Mathematics ARTIFICIAL INTELLIGENCE Intelligent systems Rule-based systems uncertainty 2 Topics A. Short introduction in Artificial Intelligence
BABEŞ-BOLYAI UNIVERSITY Faculty of Computer Science and Mathematics ARTIFICIAL INTELLIGENCE Intelligent systems Rule-based systems uncertainty 2 Topics A. Short introduction in Artificial Intelligence
AN APPROACH TO THE NONLINEAR LOCAL PROBLEMS IN MECHANICAL STRUCTURES
 U.P.B. Sci. Bull., Series D, Vol. 74, Iss. 3, 2012 ISSN 1454-2358 AN APPROACH TO THE NONLINEAR LOCAL PROBLEMS IN MECHANICAL STRUCTURES Marius-Alexandru GROZEA 1, Anton HADĂR 2 Acest articol prezintă o
U.P.B. Sci. Bull., Series D, Vol. 74, Iss. 3, 2012 ISSN 1454-2358 AN APPROACH TO THE NONLINEAR LOCAL PROBLEMS IN MECHANICAL STRUCTURES Marius-Alexandru GROZEA 1, Anton HADĂR 2 Acest articol prezintă o
9. Logica de ordinul intai. First-order logic. December 8, 2015
 9. Logica de ordinul intai. First-order logic December 8, 2015 Outline First order logic Sintaxa FOL Adevarul in FOL Propozitii atomice Propozitii complexe Cuantificatorul universal Cuantificatorul existential
9. Logica de ordinul intai. First-order logic December 8, 2015 Outline First order logic Sintaxa FOL Adevarul in FOL Propozitii atomice Propozitii complexe Cuantificatorul universal Cuantificatorul existential
HABILITATION THESIS. Semisimple Hopf algebras and fusion categories
 Institute of Mathematics,,Simion Stoilow of the Romanian Academy HABILITATION THESIS Semisimple Hopf algebras and fusion categories Sebastian Marius Burciu Specialization: Mathematics Bucharest, 2013 To
Institute of Mathematics,,Simion Stoilow of the Romanian Academy HABILITATION THESIS Semisimple Hopf algebras and fusion categories Sebastian Marius Burciu Specialization: Mathematics Bucharest, 2013 To
Sisteme de Recunoastere a Formelor Lab 12 Clasificare cu Support Vector Machine
 Sisteme de Recunoastere a Formelor Lab 12 Clasificare cu Support Vector Machine 1. Obiective In aceasta lucrare se va implementa clasificatorul SVM liniar si se va studia mecanismele de clasificare bazate
Sisteme de Recunoastere a Formelor Lab 12 Clasificare cu Support Vector Machine 1. Obiective In aceasta lucrare se va implementa clasificatorul SVM liniar si se va studia mecanismele de clasificare bazate
Matematici speciale Integrarea functiilor complexe
 Matematii speiale Integrarea funtiilor omplexe Martie 18 ii Be yourself, everyone else is already taken. Osar Wilde 5 Integrarea funtiilor omplexe Integrala Riemann a unei funtii u valori omplexe se defineste
Matematii speiale Integrarea funtiilor omplexe Martie 18 ii Be yourself, everyone else is already taken. Osar Wilde 5 Integrarea funtiilor omplexe Integrala Riemann a unei funtii u valori omplexe se defineste
STRUCTURAL PARASITIC CAPACITANCE REDUCTION TECHNIQUES IN PLANAR MAGNETIC INTEGRATED STRUCTURES
 STRUCTURAL PARASITIC CAPACITANCE REDUCTION TECHNIQUES IN PLANAR MAGNETIC INTEGRATED STRUCTURES STRUCTURAL PARASITIC CAPACITANCE REDUCTION TECHNIQUES IN PLANAR MAGNETIC INTEGRATED STRUCTURES Lecturer Eng.
STRUCTURAL PARASITIC CAPACITANCE REDUCTION TECHNIQUES IN PLANAR MAGNETIC INTEGRATED STRUCTURES STRUCTURAL PARASITIC CAPACITANCE REDUCTION TECHNIQUES IN PLANAR MAGNETIC INTEGRATED STRUCTURES Lecturer Eng.
Matematici speciale Variabile aleatoare discrete
 Matematici speciale Variabile aleatoare discrete Aprilie 208 ii Expose yourself to as much randomness as possible. Ben Casnocha 9 Variabile aleatoare discrete Texas Holdem Poker: In Texas Hold em Poker
Matematici speciale Variabile aleatoare discrete Aprilie 208 ii Expose yourself to as much randomness as possible. Ben Casnocha 9 Variabile aleatoare discrete Texas Holdem Poker: In Texas Hold em Poker
4/68. Mini-comutatoare cu came. Prezentare generalã a sistemului. Întreruptoare Pornit-Oprit TM. Comutatoare de comandã TM.
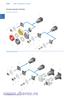 / Mini-comutatoare cu came Prezentare generalã a sistemului Întreruptoare Pornit-Oprit Comutatoare de comandã HA ND AU TO HPL-de-DE O Mini-comutatoare cu came / Montaj pe ușã (.../E) Frontal IP Montaj
/ Mini-comutatoare cu came Prezentare generalã a sistemului Întreruptoare Pornit-Oprit Comutatoare de comandã HA ND AU TO HPL-de-DE O Mini-comutatoare cu came / Montaj pe ușã (.../E) Frontal IP Montaj
Controlul predictiv bazat pe modele intare-stare-iesire. Cuprins. 2. Modele intrare-stare-iesire :01
 Modelare si control predictiv - proiect - Controlul predictiv bazat pe modele intrare-stare-iesire Asist. ing. Constantin Florin Caruntu 23:01 Cuprins Controlul predictiv bazat pe modele intare-stare-iesire
Modelare si control predictiv - proiect - Controlul predictiv bazat pe modele intrare-stare-iesire Asist. ing. Constantin Florin Caruntu 23:01 Cuprins Controlul predictiv bazat pe modele intare-stare-iesire
ELEMENTE DE DINAMICĂ ŞI GEOMETRIE PE SPAŢII VECTORIALE POISSON
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ ELEMENTE DE DINAMICĂ ŞI GEOMETRIE PE SPAŢII VECTORIALE POISSON REZUMATUL TEZEI DE DOCTORAT Conducător ştiinţific: Prof. univ.
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ ELEMENTE DE DINAMICĂ ŞI GEOMETRIE PE SPAŢII VECTORIALE POISSON REZUMATUL TEZEI DE DOCTORAT Conducător ştiinţific: Prof. univ.
FUNCŢII SPECIALE CU APLICAŢII ÎN ANALIZA NUMERICĂ
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ ELENA-IULIA STOICA FUNCŢII SPECIALE CU APLICAŢII ÎN ANALIZA NUMERICĂ REZUMATUL TEZEI DE DOCTORAT CONDUCĂTOR ŞTIINŢIFIC PROF.
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ ELENA-IULIA STOICA FUNCŢII SPECIALE CU APLICAŢII ÎN ANALIZA NUMERICĂ REZUMATUL TEZEI DE DOCTORAT CONDUCĂTOR ŞTIINŢIFIC PROF.
Probleme extremale pentru grafuri si retele de transport
 Revista Inormatica Economica nr 4 (4)/00 9 Proleme extremale pentru grauri si retele de transport Drd Rodica MIRONENCO A variety o prolems can e constructed using Ford-Fulkerson s maximum-low minimumcut
Revista Inormatica Economica nr 4 (4)/00 9 Proleme extremale pentru grauri si retele de transport Drd Rodica MIRONENCO A variety o prolems can e constructed using Ford-Fulkerson s maximum-low minimumcut
XI International Zhautykov Olympiad in Sciences Almaty Kazakhstan, January 11-17, 2015 Presentation of the Mathematics Section by Dan Schwarz
 XI International Zhautykov Olympiad in Sciences Almaty Kazakhstan, January 11-17, 015 Presentation of the Mathematics Section by Dan Schwarz First Day January 13, 015) Problems Problem 1. Each point with
XI International Zhautykov Olympiad in Sciences Almaty Kazakhstan, January 11-17, 015 Presentation of the Mathematics Section by Dan Schwarz First Day January 13, 015) Problems Problem 1. Each point with
Proiectarea Algoritmilor
 Proiectarea Algoritmilor Ștefan Trăușan-Matu stefan.trausan@cs.pub.ro Obiectivele cursului Discutarea relaţiei dintre caracteristicile problemelor, modul de rezolvare şi calitatea soluţiilor. Obiectivele
Proiectarea Algoritmilor Ștefan Trăușan-Matu stefan.trausan@cs.pub.ro Obiectivele cursului Discutarea relaţiei dintre caracteristicile problemelor, modul de rezolvare şi calitatea soluţiilor. Obiectivele
Arhivele Electronice Los Alamos arxiv:physics/ v2 [physics.ed-ph] 30 Apr 2000
![Arhivele Electronice Los Alamos arxiv:physics/ v2 [physics.ed-ph] 30 Apr 2000 Arhivele Electronice Los Alamos arxiv:physics/ v2 [physics.ed-ph] 30 Apr 2000](/thumbs/79/79555034.jpg) arxiv:physics/0003106v2 [physics.ed-ph] 30 Apr 2000 Arhivele Electronice Los Alamos http://xxx.lanl.gov/physics/0003106 ELEMENTE DE MECANICĂ CUANTICĂ HARET C. ROSU e-mail: rosu@ifug3.ugto.mx fax: 0052-47187611
arxiv:physics/0003106v2 [physics.ed-ph] 30 Apr 2000 Arhivele Electronice Los Alamos http://xxx.lanl.gov/physics/0003106 ELEMENTE DE MECANICĂ CUANTICĂ HARET C. ROSU e-mail: rosu@ifug3.ugto.mx fax: 0052-47187611
Curs 5 ELEMENTE STRUCTURALE SOLICITATE LA RASUCIRE
 Curs 5 ELEENTE STRUCTURALE SOLICITATE LA RASUCIRE Rasucirea (torsiunea), ca stare de solicitare nu apare in mod independent, ci in combinatie cu alte solicitari (ex. incovoiere cu rasucire, compresiune
Curs 5 ELEENTE STRUCTURALE SOLICITATE LA RASUCIRE Rasucirea (torsiunea), ca stare de solicitare nu apare in mod independent, ci in combinatie cu alte solicitari (ex. incovoiere cu rasucire, compresiune
BOOST CIRCUIT CONTROL IN TRANSIENT CONDITIONS
 U.P.B. Sci. Bull., Series C, Vol. 68, No. 4, 2006 BOOST CIRCUIT CONTROL IN TRANSIENT CONDITIONS D. OLARU * Lucrarea îşi propune să abordeze câteva aspecte legate de modelarea şi comanda circuitului boost.
U.P.B. Sci. Bull., Series C, Vol. 68, No. 4, 2006 BOOST CIRCUIT CONTROL IN TRANSIENT CONDITIONS D. OLARU * Lucrarea îşi propune să abordeze câteva aspecte legate de modelarea şi comanda circuitului boost.
Structura matematicii (II)
 Structura matematicii (II) Oana Constantinescu Contents 1 Notiuni - denitii 1 2 Propozitii adevarate: axiome si teoreme 5 2.1 Elemente de logica.......................... 5 2.2 Teoreme................................
Structura matematicii (II) Oana Constantinescu Contents 1 Notiuni - denitii 1 2 Propozitii adevarate: axiome si teoreme 5 2.1 Elemente de logica.......................... 5 2.2 Teoreme................................
GAZETA MATEMATICĂ SERIA A. ANUL XXXVI (CXV) Nr. 1 2/ 2018 ARTICOLE. Computing exponential and trigonometric functions of matrices in M 2 (C)
 GAZETA MATEMATICĂ SERIA A ANUL XXXVI CXV) Nr. 1 / 18 ARTICOLE Computing exponential and trigonometric functions of matrices in M C) Ovidiu Furdui 1) Abstract. In this paper we give a new technique for
GAZETA MATEMATICĂ SERIA A ANUL XXXVI CXV) Nr. 1 / 18 ARTICOLE Computing exponential and trigonometric functions of matrices in M C) Ovidiu Furdui 1) Abstract. In this paper we give a new technique for
DanielaMANEA. x n +a 1. EdituraParalela45
 DanielaMANEA REZOLVAREA ECUAŢILORALGEBRICE DEGRAD SUPERIOR n +a n- + +a n =0 EdituraParalela45 Daniela Manea REZOLVAREA ECUAŢIILOR ALGEBRICE DE GRAD SUPERIOR Referent ştiinţific: lectunivdr Eduard Asadurian
DanielaMANEA REZOLVAREA ECUAŢILORALGEBRICE DEGRAD SUPERIOR n +a n- + +a n =0 EdituraParalela45 Daniela Manea REZOLVAREA ECUAŢIILOR ALGEBRICE DE GRAD SUPERIOR Referent ştiinţific: lectunivdr Eduard Asadurian
TEZĂ DE ABILITARE. Subvarietăți de curbură medie paralelă și subvarietăți biarmonice în varietăți riemanniene
 ACADEMIA ROMÂNĂ SCOSAAR TEZĂ DE ABILITARE Subvarietăți de curbură medie paralelă și subvarietăți biarmonice în varietăți riemanniene Dorel Fetcu Domeniul fundamental Matematică și științe ale naturii Domeniul
ACADEMIA ROMÂNĂ SCOSAAR TEZĂ DE ABILITARE Subvarietăți de curbură medie paralelă și subvarietăți biarmonice în varietăți riemanniene Dorel Fetcu Domeniul fundamental Matematică și științe ale naturii Domeniul
Metode numerice de aproximare. a zerourilor unor operatori. şi de rezolvare a inegalităţilor variaţionale. cu aplicaţii
 Facultatea de Matematică şi Informatică Universitatea Babeş-Bolyai Erika Nagy Metode numerice de aproximare a zerourilor unor operatori şi de rezolvare a inegalităţilor variaţionale cu aplicaţii Rezumatul
Facultatea de Matematică şi Informatică Universitatea Babeş-Bolyai Erika Nagy Metode numerice de aproximare a zerourilor unor operatori şi de rezolvare a inegalităţilor variaţionale cu aplicaţii Rezumatul
