1.3. OPERAŢII CU NUMERE NEZECIMALE
|
|
|
- Kristin Walker
- 6 years ago
- Views:
Transcription
1 1.3. OPERAŢII CU NUMERE NEZECIMALE OPERAŢII CU NUMERE BINARE A. ADUNAREA NUMERELOR BINARE Reguli de bază: = 0 transport = 1 transport = 1 transport = 0 transport 1 Pentru a aduna două numere binare se adună între ei biţii numerelor (începând de la dreapta la stânga) iar la acest rezultat se adaugă transportul (care poate fi 0 sau 1) conform regulilor de mai sus. Exemple de adunări cu numere binare Transport A B A+B Algoritmul de realizare a adunării de mai sus: Se adună biţii de pe prima coloană din dreapta. Rezultatul se trece sub coloană iar transportul deasupra celei de-a doua coloane din dreapta. Se adună biţii de pe a doua coloană din dreapta. Rezultatul se adună cu transportul de deasupra coloanei apoi se trece rezultatul obţinut sub coloană iar transportul se trece deasupra celei de-a treia coloane din dreapta. Se continuă adunarea după acest algoritm până se ajunge la prima coloana din stânga = 0 transport 0 la rezultatul adunării se adună transportul = = 1 transport 0 la rezultatul adunării se adună transportul = = 0 transport 0 la rezultatul adunării se adună transportul = = 1 transport 1 la rezultatul adunării se adună transportul = = 1 transport 1 la rezultatul adunării se adună transportul = = 1 transport 1 la rezultatul adunării se adună transportul = = 0 transport 1 la rezultatul adunării se adună transportul = = 1 transport 0 la rezultatul adunării se adună transportul = = 0 transport 0 la rezultatul adunării se adună transportul = = 0 transport 1 la rezultatul adunării se adună transportul = 1 la rezultatul adunării se adună transportul = 1
2 Transport A B A + B Transport A B A + B B. SCĂDEREA NUMERELOR BINARE Reguli de bază: 0-0 = 0 împrumut = 1 împrumut = 0 împrumut = 1 împrumut 1 Pentru a scade două numere binare se scad între ei biţii numerelor (începând de la dreapta la stânga) iar din acest rezultat se scade împrumutul (care poate fi 0 sau 1) conform regulilor de mai sus. Exemple de scăderi cu numere binare Transport A B A - B Algoritmul de realizare a scăderii de mai sus: Se scad din biţii numărului A biţii numărului B de pe prima coloană din dreapta. Rezultatul se trece sub coloană iar împrumutul deasupra celei de-a doua coloane din dreapta. Se scad biţii de pe a doua coloană din dreapta. Din rezultat se scade împrumutul de deasupra coloanei apoi se trece rezultatul obţinut sub coloană iar împrumutul se trece deasupra celei de-a treia coloane din dreapta. Se continuă scăderea după acest algoritm până se ajunge la prima coloana din stânga.
3 Împrumut A B A - B Împrumut A B A - B Împrumut A B A - B Împrumut A B A + B
4 C. ÎNMULŢIREA NUMERELOR BINARE Reguli de bază: 0 x 0 = 0 1 x 0 = 0 0 x 1 = 0 1 x 1 = 1 Pentru a înmulţii două numere binare A (deînmulţit) şi B(înmulţitor) se procedează exact ca la înmulţirea a două numere zecimale: Se înmulţeşte pe rând fiecare cifră a înmulţitorului cu cifrele deînmulţitului Se scriu rezultatele obţinute unul sub altul decalându-le cu o unitate spre stânga Se adună pe verticală cifrele rezultatelor fiecărei înmulţiri respectând regulile de adunare a numerelor binare Exemple de înmulţiri a numerelor binare deînmulţit x 13 x înmulţitor produse parţiale care se adună PRODUS deînmulţit x 24 x înmulţitor produse parţiale care se adună
5 D. ÎMPĂRŢIREA NUMERELOR BINARE Algoritmul de împărţire a două numere binare are la bază metoda împărţirii a două numere întregi. Fiind dat deîmpărţitul D şi împărţitorul Î, pentru operaţia de împărţire trebuie să se determine câtul C şi restul R, astfel încât să fie satisfăcută relaţie: D = Î x C + R Operaţia de împărţire în cazul numerelor binare, se va reduce la o serie de scăderi ale împărţitorului din restul parţial ţinând cont de următoarele reguli: Dacă restul este mai mare decât împărţitorul câtul este 1 Dacă restul este mai mic decât împărţitorul câtul este 0 La efectuarea scăderilor se respectă regulile de scăderea a numerelor binare. Exemple de împărţire a numerelor binare CÂT CÂT REST REST Algoritmul împărţirii deîmpărţitului la împărţitorul 1011: Deoarece împărţitorul 1011 este mai mare decât primii 4 biţi ai deîmpărţitului 1001 împărţitorul se va împărţii la primi 5 biţi ai deîmpărţitului Deoarece este mai mare decât 1011 primul bit al câtului este 1 Înmulţim câtul 1 cu împărţitorul 1011 şi trecem rezultatul în stânga sub primi 5 biţi ai deîmpărţitului Scădem 1011 din (respectând regulile scăderii în binar) şi obţinem restul 111 Coborâm bitul deîmpărţitului, care este 0 (vezi săgeata) şi obţinem restul 1110 Deoarece restul 1110 este mai mare decât împărţitorul 1011 câtul este 1. Deci al doilea bit al câtului este 1. Înmulţim câtul 1 cu împărţitorul 1011 şi trecem rezultatul în stânga sub restul 1110 Scădem 1011 din 1110 (respectând regulile scăderii în binar) şi obţinem restul 11 Coborâm bitul deîmpărţitului, care este 1 (vezi săgeata) şi obţinem restul 111 Deoarece restul 111 este mai mic decât împărţitorul 1011 câtul este 0. Deci al treilea bit al câtului este 0 Coborâm bitul deîmpărţitului, care este 1 (vezi săgeata) şi obţinem restul 1111 Deoarece restul 1111 este mai mare decât împărţitorul 1011 câtul este 1 Deci al patrulea bit al câtului este 1 Înmulţim câtul 1 cu împărţitorul 1011 şi trecem rezultatul în stânga sub restul 1111 Scădem 1011 din 1111 (respectând regulile scăderii în binar) şi obţinem restul 100.
6 CÂT CÂT REST REST Algoritmul împărţirii deîmpărţitului la împărţitorul 1011: Deoarece numărul format din primi 4 biţi ai deîmpărţitului 1101 este mai mare decât 1011 primul bit al câtului este 1 Înmulţim câtul 1 cu împărţitorul 1011 şi trecem rezultatul în stânga sub primi 4 biţi ai deîmpărţitului Scădem 1011 din 1101 (respectând regulile scăderii în binar) şi obţinem restul 10 Coborâm bitul deîmpărţitului, care este 1 (vezi săgeata) şi obţinem restul 101 Deoarece restul 101 este mai mic decât împărţitorul 1011 câtul este 0. Deci al doilea bit al câtului este 0 Coborâm bitul deîmpărţitului, care este 0 (vezi săgeata) şi obţinem restul 1010 Deoarece restul 1010 este mai mic decât împărţitorul 1011 câtul este 0. Deci al treilea bit al câtului este 0 Coborâm bitul deîmpărţitului, care este 0 (vezi săgeata) şi obţinem restul Deoarece restul este mai mare decât împărţitorul 1011 câtul este 1 Deci al patrulea bit al câtului este 1 Înmulţim câtul 1 cu împărţitorul 1011 şi trecem rezultatul în stânga sub restul Scădem 1011 din (respectând regulile scăderii) şi obţinem restul 1001 Coborâm bitul deîmpărţitului, care este 1 (vezi săgeata) şi obţinem restul Deoarece restul este mai mare decât împărţitorul 1011 câtul este 1 Deci al cincilea bit al câtului este 1 Înmulţim câtul 1 cu împărţitorul 1011 şi trecem rezultatul în stânga sub restul Scădem 1011 din (respectând regulile scăderii) şi obţinem restul 1000.
7 1.3.2 OPERAŢII CU NUMERE OCTALE ŞI HEXAZECIMALE A. ADUNAREA NUMERELOR OCTALE Reguli: Adunarea se face ca în sistemul zecimal, prin scrierea numerelor unul sub altul Dacă prin adunarea caracterelor de pe o coloana se depăşeşte valoarea 7 numărul obţinut se scrie ca o sumă de 2 numere (un număr reprezintă baza sistemului adică 8 iar celălalt reprezintă valoarea cu care s-a depăşit baza) astfel: 8 = ; 9 = ; 10 = ; = Numărul care reprezintă baza (care are valoarea în octal 1) se transportă deasupra următoarei coloane din stânga. Suma cifrelor de pe coloana respectivă se adună cu transportorul de deasupra coloanei care ATENŢIE! are valoarea 1. Numărul care reprezintă valoarea cu care s-a depăşit baza este rezultatul adunării de pe coloana respectivă în cazul în care suma numerelor de pe coloana respectivă este mai mare decât 7. Dacă suma numerelor de pe o coloană este mai mică sau egală cu 7, rezultatul obţinut reprezintă rezultatul adunării de pe coloana respectivă. Exemple de adunare a două numere octale = (5+0) (8+3) (8+0) (5+0) = 5 transport 0 prima cifră (din dreapta) este = 8 = = 0 transport 1 a doua cifră este = 11 = = 3 transport 1 a treia cifră este = 5 transport 0 a patra cifră este
8 B. SCĂDEREA NUMERELOR OCTALE Reguli: Scăderea se face ca în sistemul zecimal, prin scrierea numerelor unul sub altul Dacă prin scăderea caracterelor de pe o coloana rezultatul obţinut este negativ (numărul de sus este mai mic decât numărul de jos), se împrumută de pe următoarea coloană din stânga o unitate în octal care înseamnă opt unităţi în zecimal. Se face suma algebrică dintre împrumut şi numerele de pe coloana respectivă iar în urma calculului se obţine cifra corespunzătoare rezultatului de pe acea coloană. Unitatea (1) împrumutată de pe o coloană se scade din cifra de sus a coloanei de unde a fost împrumutată. Exemple de adunare a două numere octale = (4-1-2=1) ( =6) (8+3-4=7) Scad numerele de pe coloana din dreapta 3 4 < 0 împrumut o unitate octală de pe coloana din mijloc. Adun împrumutul la diferenţa numerelor de pe coloană 8+3-4=7 prima cifră 7 Scad din diferenţa numerelor de pe coloana din mijloc împrumutul < 0 împrumut o unitate octală de pe coloana din stânga. Adun împrumutul la diferenţa numerelor de pe coloană =6 a doua cifră 6 Din diferenţa numerelor de pe coloana din stânga scad unitatea împrumutată = 1 a treia cifră
9 C. ADUNAREA NUMERELOR HEXAZECIMALE Reguli: Adunarea se face ca în sistemul zecimal, prin scrierea numerelor unul sub altul Înainte de a efectua adunările, caracterele alfabetice (A, B,C,D,E,F) se înlocuiesc cu valorile lor în zecimal (10,11,12,13,14,15) vezi tabelul 1.3 din secţiunea 1.1. Dacă prin adunarea caracterelor de pe o coloana se depăşeşte valoarea 15 numărul obţinut se scrie ca o sumă de 2 numere (un număr reprezintă baza sistemului adică 16 iar celălalt reprezintă valoarea cu care s-a depăşit baza) astfel: 16 = ; 17 = ; 18 = ; = Numărul care reprezintă baza (care are valoarea în hexazecimal 1) se transportă deasupra următoarei coloane din stânga. Suma cifrelor de pe coloana respectivă se adună cu transportorul de deasupra coloanei care ATENŢIE! are valoarea 1. Rezultatul adunării se transformă în hexazecimal (conform tabelului 1.1 din secţiunea 3) şi reprezintă rezultatul adunării de pe coloana respectivă. Exemple de adunare a două numere hexazecimale D 8 A D 8 A E 4 C E 4 C (16+1) (16+6) A 1 6 E F A = 10 = A 16 transport 0 prima cifră (din dreapta) este A = 15 = F transport 0 a doua cifră este F = 14 = E transport 0 a treia cifră este E = 22 = = 6 transport 1 a patra cifră este = 17 = = 1 transport 1 a cincea cifră este = 10 = A transport 0 a şasea cifră este A A 3 D A B C F E B B C 7 E B F E 1 9 F 16
10 D. SCĂDEREA NUMERELOR HEXAZECIMALE Reguli: Scăderea se face ca în sistemul zecimal, prin scrierea numerelor unul sub altul Înainte de a efectua scăderile, caracterele alfabetice (A, B,C,D,E,F) se înlocuiesc cu valorile lor în zecimal (10,11,12,13,14,15) vezi tabelul 1.3 din secţiunea 1.1. Dacă prin scăderea caracterelor de pe o coloana rezultatul obţinut este negativ (numărul de sus este mai mic decât numărul de jos), se împrumută de pe următoarea coloană din stânga o unitate în hexazecimal care înseamnă 16 unităţi în zecimal. Se face suma algebrică dintre împrumut şi numerele de pe coloana respectivă iar în urma calculului se obţine cifra corespunzătoare rezultatului de pe acea coloană. Unitatea (1) împrumutată de pe o coloană se scade din cifra de sus a coloanei de unde a fost împrumutată. Exemple de scădere a două numere hexazecimale C 2 B A C F C 16 (5-3=2) ( =1) ( =5) ( =12=C) C 8 Scad numerele de pe coloana din dreapta < 0 împrumut o unitate hexazecimală de pe coloana din mijloc. Adun împrumutul la diferenţa numerelor de pe coloană = 12 = C Fac suma algebrică a numerelor de pe următoarea coloană din stânga < 0 împrumut o unitate hexazecimală de pe următoarea coloană. Adun împrumutul la diferenţa numerelor de pe coloană = 5 Fac suma algebrică a numerelor de pe următoarea coloană din stânga = 1 Fac suma algebrică a numerelor de pe următoarea coloană din stânga 5 3 = A 3 D 4 16 C E D 0 16 F 2 C B 16-1 F 0 C 16-9 D 6 E 16 2 E B 9 16 B F C
O V E R V I E W. This study suggests grouping of numbers that do not divide the number
 MSCN(2010) : 11A99 Author : Barar Stelian Liviu Adress : Israel e-mail : stelibarar@yahoo.com O V E R V I E W This study suggests grouping of numbers that do not divide the number 3 and/or 5 in eight collumns.
MSCN(2010) : 11A99 Author : Barar Stelian Liviu Adress : Israel e-mail : stelibarar@yahoo.com O V E R V I E W This study suggests grouping of numbers that do not divide the number 3 and/or 5 in eight collumns.
Divizibilitate în mulțimea numerelor naturale/întregi
 Divizibilitate în mulțimea numerelor naturale/întregi Teorema îmărţirii cu rest în mulțimea numerelor naturale Fie a, b, b 0. Atunci există q, r astfel încât a=bq+r, cu 0 r < b. În lus, q şi r sunt unic
Divizibilitate în mulțimea numerelor naturale/întregi Teorema îmărţirii cu rest în mulțimea numerelor naturale Fie a, b, b 0. Atunci există q, r astfel încât a=bq+r, cu 0 r < b. În lus, q şi r sunt unic
Soluţii juniori., unde 1, 2
 Soluţii juniori Problema 1 Se consideră suma S x1x x3x4... x015 x016 Este posibil să avem S 016? Răspuns: Da., unde 1,,..., 016 3, 3 Termenii sumei sunt de forma 3 3 1, x x x. 3 5 6 sau Cristian Lazăr
Soluţii juniori Problema 1 Se consideră suma S x1x x3x4... x015 x016 Este posibil să avem S 016? Răspuns: Da., unde 1,,..., 016 3, 3 Termenii sumei sunt de forma 3 3 1, x x x. 3 5 6 sau Cristian Lazăr
Barem de notare clasa a V-a
 Barem de notare clasa a V-a Problema1. Determinați mulțimile A și B, formate din numere naturale, știind că îndeplinesc simultan condițiile: a) A B,5,6 ; b) B A 0,7 ; c) card AB 3; d) suma elementelor
Barem de notare clasa a V-a Problema1. Determinați mulțimile A și B, formate din numere naturale, știind că îndeplinesc simultan condițiile: a) A B,5,6 ; b) B A 0,7 ; c) card AB 3; d) suma elementelor
Teorema Reziduurilor şi Bucuria Integralelor Reale Prezentare de Alexandru Negrescu
 Teorema Reiduurilor şi Bucuria Integralelor Reale Preentare de Alexandru Negrescu Integrale cu funcţii raţionale ce depind de sint şi cost u notaţia e it, avem: cost sint i ( + ( dt d i, iar integrarea
Teorema Reiduurilor şi Bucuria Integralelor Reale Preentare de Alexandru Negrescu Integrale cu funcţii raţionale ce depind de sint şi cost u notaţia e it, avem: cost sint i ( + ( dt d i, iar integrarea
Sisteme cu logica fuzzy
 Sisteme cu logica fuzzy 1/15 Sisteme cu logica fuzzy Mamdani Fie un sistem cu logică fuzzy Mamdani două intrări x şi y ieşire z x y SLF Structura z 2/15 Sisteme cu logica fuzzy Mamdani Baza de reguli R
Sisteme cu logica fuzzy 1/15 Sisteme cu logica fuzzy Mamdani Fie un sistem cu logică fuzzy Mamdani două intrări x şi y ieşire z x y SLF Structura z 2/15 Sisteme cu logica fuzzy Mamdani Baza de reguli R
ON THE QUATERNARY QUADRATIC DIOPHANTINE EQUATIONS (II) NICOLAE BRATU 1 ADINA CRETAN 2
 ON THE QUATERNARY QUADRATIC DIOPHANTINE EQUATIONS (II) NICOLAE BRATU 1 ADINA CRETAN ABSTRACT This paper has been updated and completed thanks to suggestions and critics coming from Dr. Mike Hirschhorn,
ON THE QUATERNARY QUADRATIC DIOPHANTINE EQUATIONS (II) NICOLAE BRATU 1 ADINA CRETAN ABSTRACT This paper has been updated and completed thanks to suggestions and critics coming from Dr. Mike Hirschhorn,
Ecuatii si inecuatii de gradul al doilea si reductibile la gradul al doilea. Ecuatii de gradul al doilea
 Ecuatii si inecuatii de gradul al doilea si reductibile la gradul al doilea Ecuatia de forma Ecuatii de gradul al doilea a + b + c = 0, (1) unde a, b, c R, a 0, - variabila, se numeste ecuatie de gradul
Ecuatii si inecuatii de gradul al doilea si reductibile la gradul al doilea Ecuatia de forma Ecuatii de gradul al doilea a + b + c = 0, (1) unde a, b, c R, a 0, - variabila, se numeste ecuatie de gradul
ȘIRURI (TABLOURI UNIDIMENSIONALE)
 Problema 1 Enunț ȘIRURI (TABLOURI UNIDIMENSIONALE) Se citesc mai multe numere naturale, până la introducerea numărului 0 şi se memorează într-un şir. Să se găsească toate numerele perfecte din şir. Un
Problema 1 Enunț ȘIRURI (TABLOURI UNIDIMENSIONALE) Se citesc mai multe numere naturale, până la introducerea numărului 0 şi se memorează într-un şir. Să se găsească toate numerele perfecte din şir. Un
7. OPERATIILE ARITMETICE
 7. OPERATIILE ARITMETICE 1. Procesorul Aritmetic. Un procesor aritmetic reprezinta un dispozitiv capabil sa efectueze operatii simple sau complexe asupra unor operanzi furnizati in formate corespunzatoare.
7. OPERATIILE ARITMETICE 1. Procesorul Aritmetic. Un procesor aritmetic reprezinta un dispozitiv capabil sa efectueze operatii simple sau complexe asupra unor operanzi furnizati in formate corespunzatoare.
Cercet¼ari operaţionale
 Cercet¼ari operaţionale B¼arb¼acioru Iuliana Carmen CURSUL 9 Cursul 9 Cuprins Programare liniar¼a 5.1 Modelul matematic al unei probleme de programare liniar¼a.................... 5. Forme de prezentare
Cercet¼ari operaţionale B¼arb¼acioru Iuliana Carmen CURSUL 9 Cursul 9 Cuprins Programare liniar¼a 5.1 Modelul matematic al unei probleme de programare liniar¼a.................... 5. Forme de prezentare
UNITATEA DE ÎNVĂȚARE 3 Analiza algoritmilor
 UNITATEA DE ÎNVĂȚARE 3 Analiza algoritmilor Obiective urmărite: La sfârşitul parcurgerii acestei UI, studenţii vor 1.1 cunoaște conceptul de eficienta a unui algoritm vor cunoaste si inţelege modalitatile
UNITATEA DE ÎNVĂȚARE 3 Analiza algoritmilor Obiective urmărite: La sfârşitul parcurgerii acestei UI, studenţii vor 1.1 cunoaște conceptul de eficienta a unui algoritm vor cunoaste si inţelege modalitatile
A GENERALIZATION OF A CLASSICAL MONTE CARLO ALGORITHM TO ESTIMATE π
 U.P.B. Sci. Bull., Series A, Vol. 68, No., 6 A GENERALIZATION OF A CLASSICAL MONTE CARLO ALGORITHM TO ESTIMATE π S.C. ŞTEFĂNESCU Algoritmul Monte Carlo clasic A1 estimeazează valoarea numărului π bazându-se
U.P.B. Sci. Bull., Series A, Vol. 68, No., 6 A GENERALIZATION OF A CLASSICAL MONTE CARLO ALGORITHM TO ESTIMATE π S.C. ŞTEFĂNESCU Algoritmul Monte Carlo clasic A1 estimeazează valoarea numărului π bazându-se
METODE NUMERICE: Laborator #4 Eliminare gaussiană cu pivotare totală şi scalare. Algoritmul Thomas pentru rezolvarea sistemului 3-diagonal
 METODE NUMERICE: Laborator #4 Eliminare gaussiană cu pivotare totală şi scalare. Algoritmul Thomas pentru rezolvarea sistemului 3-diagonal Titulari curs: Florin Pop, George-Pantelimon Popescu Responsabil
METODE NUMERICE: Laborator #4 Eliminare gaussiană cu pivotare totală şi scalare. Algoritmul Thomas pentru rezolvarea sistemului 3-diagonal Titulari curs: Florin Pop, George-Pantelimon Popescu Responsabil
Arhitectura sistemelor de calcul
 Arhitectura sistemelor de calcul - Prelegerea 1 - Evoluția sistemelor de calcul Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Istoricul evolutiei calculatoarelor
Arhitectura sistemelor de calcul - Prelegerea 1 - Evoluția sistemelor de calcul Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Istoricul evolutiei calculatoarelor
SIMULAREA DECIZIEI FINANCIARE
 SIMULAREA DECIZIEI FINANCIARE Conf. univ. dr. Nicolae BÂRSAN-PIPU T5.1 TEMA 5 DISTRIBUŢII DISCRETE T5. Cuprins T5.3 5.1 Variabile aleatoare discrete 5. Distribuţia de probabilitate a unei variabile aleatoare
SIMULAREA DECIZIEI FINANCIARE Conf. univ. dr. Nicolae BÂRSAN-PIPU T5.1 TEMA 5 DISTRIBUŢII DISCRETE T5. Cuprins T5.3 5.1 Variabile aleatoare discrete 5. Distribuţia de probabilitate a unei variabile aleatoare
The 2017 Danube Competition in Mathematics, October 28 th. Problema 1. Să se găsească toate polinoamele P, cu coeficienţi întregi, care
 The 017 Dnube Competition in Mthemtics, October 8 th Problem 1. ă se găsescă tote polinomele P, cu coeficienţi întregi, cre verifică relţi + b c P () + P (b) P (c), pentru orice numere întregi, b, c. Problem.
The 017 Dnube Competition in Mthemtics, October 8 th Problem 1. ă se găsescă tote polinomele P, cu coeficienţi întregi, cre verifică relţi + b c P () + P (b) P (c), pentru orice numere întregi, b, c. Problem.
Reactoare chimice cu curgere piston (ideala) (Plug Flow Reactor PFR) cu amestecare completa (Mixed Flow Reactor MFR) de tip batch (autoclava)
 Reactoare chimice cu curgere piston (ideala) (Plug Flow Reactor PFR) cu amestecare completa (Mied Flow Reactor MFR) de tip batch (autoclava) Reactorul cu curgere ideala Toate particulele se deplaseaza
Reactoare chimice cu curgere piston (ideala) (Plug Flow Reactor PFR) cu amestecare completa (Mied Flow Reactor MFR) de tip batch (autoclava) Reactorul cu curgere ideala Toate particulele se deplaseaza
Pentru clasa a X-a Ştiinţele naturii-sem II
 Pentru clasa a X-a Ştiinţele naturii-sem II Reprezentarea algoritmilor. Pseudocod. Principiile programării structurate. Structuri de bază: structura liniară structura alternativă structura repetitivă Algoritmi
Pentru clasa a X-a Ştiinţele naturii-sem II Reprezentarea algoritmilor. Pseudocod. Principiile programării structurate. Structuri de bază: structura liniară structura alternativă structura repetitivă Algoritmi
FORMULELE LUI STIRLING, WALLIS, GAUSS ŞI APLICAŢII
 DIDACTICA MATHEMATICA, Vol. 34), pp. 53 67 FORMULELE LUI STIRLING, WALLIS, GAUSS ŞI APLICAŢII Eugenia Duca, Emilia Copaciu şi Dorel I. Duca Abstract. In this paper are presented the Wallis, Stirling, Gauss
DIDACTICA MATHEMATICA, Vol. 34), pp. 53 67 FORMULELE LUI STIRLING, WALLIS, GAUSS ŞI APLICAŢII Eugenia Duca, Emilia Copaciu şi Dorel I. Duca Abstract. In this paper are presented the Wallis, Stirling, Gauss
Utilizarea limbajului SQL pentru cereri OLAP. Mihaela Muntean 2015
 Utilizarea limbajului SQL pentru cereri OLAP Mihaela Muntean 2015 Cuprins Implementarea operatiilor OLAP de baza in SQL -traditional: Rollup Slice Dice Pivotare SQL-2008 Optiunea ROLLUP Optiunea CUBE,
Utilizarea limbajului SQL pentru cereri OLAP Mihaela Muntean 2015 Cuprins Implementarea operatiilor OLAP de baza in SQL -traditional: Rollup Slice Dice Pivotare SQL-2008 Optiunea ROLLUP Optiunea CUBE,
Cristalul cu N atomi = un sistem de N oscilatori de amplitudini mici;
 Curs 8 Caldura specifica a retelei Cristalul cu N atomi = un sistem de N oscilatori de amplitudini mici; pentru tratarea cuantica, se inlocuieste tratamentul clasic al oscilatorilor cuplati, cu cel cuantic
Curs 8 Caldura specifica a retelei Cristalul cu N atomi = un sistem de N oscilatori de amplitudini mici; pentru tratarea cuantica, se inlocuieste tratamentul clasic al oscilatorilor cuplati, cu cel cuantic
Procedeu de demonstrare a unor inegalităţi bazat pe inegalitatea lui Schur
 Procedeu de demonstrare a unor inegalităţi bazat pe inegalitatea lui Schur Andi Gabriel BROJBEANU Abstract. A method for establishing certain inequalities is proposed and applied. It is based upon inequalities
Procedeu de demonstrare a unor inegalităţi bazat pe inegalitatea lui Schur Andi Gabriel BROJBEANU Abstract. A method for establishing certain inequalities is proposed and applied. It is based upon inequalities
PROBLEME DIVERSE lecţie susţinută la lotul de 13 de Andrei ECKSTEIN Bucureşti, 25 mai 2015
 PROBLEME DIVERSE lecţie susţinută la lotul de 13 de Andrei ECKSTEIN Bucureşti, 5 mai 015 I. SUBSTITUŢIA TAIWANEZĂ 1. Fie a, b, c > 0 astfel încât a bc, b ca şi c ab. Determinaţi valoarea maximă a expresiei
PROBLEME DIVERSE lecţie susţinută la lotul de 13 de Andrei ECKSTEIN Bucureşti, 5 mai 015 I. SUBSTITUŢIA TAIWANEZĂ 1. Fie a, b, c > 0 astfel încât a bc, b ca şi c ab. Determinaţi valoarea maximă a expresiei
Reactoare chimice cu curgere piston (ideala) cu amestecare completa de tip batch (autoclava)
 Reactoare chimice cu curgere piston (ideala) cu amestecare completa de tip batch (autoclava) Reactorul cu curgere ideala Toate particulele se deplaseaza intr-o directie de-a lungul reactorului, precum
Reactoare chimice cu curgere piston (ideala) cu amestecare completa de tip batch (autoclava) Reactorul cu curgere ideala Toate particulele se deplaseaza intr-o directie de-a lungul reactorului, precum
Sisteme cu logica fuzzy cu mai multe intrari (MISO)
 Sisteme cu logica fuzzy cu mai multe intrari (MISO) Structura unui sistem cu logică fuzzy MISO Structura unui SLF cu 2 intrari Fie un sistem cu logică fuzzy Mamdani două intrări x şi y ieşire z x y SLF
Sisteme cu logica fuzzy cu mai multe intrari (MISO) Structura unui sistem cu logică fuzzy MISO Structura unui SLF cu 2 intrari Fie un sistem cu logică fuzzy Mamdani două intrări x şi y ieşire z x y SLF
Prelegerea 7. Sistemul de criptare AES. 7.1 Istoric
 Prelegerea 7 Sistemul de criptare AES 7.1 Istoric La sfârşitul anilor 90 se decide înlocuirea sistemului de criptare DES. Motivele sunt multiple, dar menţionăm numai două: În iulie 1998 sistemul DES pe
Prelegerea 7 Sistemul de criptare AES 7.1 Istoric La sfârşitul anilor 90 se decide înlocuirea sistemului de criptare DES. Motivele sunt multiple, dar menţionăm numai două: În iulie 1998 sistemul DES pe
Numere prime. O selecţie de probleme pentru gimnaziu
 Numere prime O selecţie de probleme petru gimaziu Adria Zaoschi Colegiul Natioal "Costache Negruzzi" Iasi (Clasa a V-a) Determiați submulțimea B a mulțimii A 0,,,, 49, 50, formată di toate elemetele lui
Numere prime O selecţie de probleme petru gimaziu Adria Zaoschi Colegiul Natioal "Costache Negruzzi" Iasi (Clasa a V-a) Determiați submulțimea B a mulțimii A 0,,,, 49, 50, formată di toate elemetele lui
2D AND 3D PROCESSING OF THE INTERDEPENDENCE BETWEEN THE COMFORT MAIN INDICATORS
 BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LVII (LXI), Fasc. 1, 2011 SecŃia TEXTILE. PIELĂRIE 2D AND 3D PROCESSING OF THE INTERDEPENDENCE
BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LVII (LXI), Fasc. 1, 2011 SecŃia TEXTILE. PIELĂRIE 2D AND 3D PROCESSING OF THE INTERDEPENDENCE
APLICAŢII ALE FORMULELOR LUI NEWTON PENTRU POLINOAME SIMETRICE
 DIDACTICA MATHEMATICA, Vol. 33(2015), pp. 27 37 APLICAŢII ALE FORMULELOR LUI NEWTON PENTRU POLINOAME SIMETRICE Cristina-Aida Coman Abstract. In this paper we present some applications of Newton s formulae
DIDACTICA MATHEMATICA, Vol. 33(2015), pp. 27 37 APLICAŢII ALE FORMULELOR LUI NEWTON PENTRU POLINOAME SIMETRICE Cristina-Aida Coman Abstract. In this paper we present some applications of Newton s formulae
Inteligenta Artificiala
 Inteligenta Artificiala Universitatea Politehnica Bucuresti Anul universitar 2010-2011 Adina Magda Florea http://turing.cs.pub.ro/ia_10 si curs.cs.pub.ro 1 Curs nr. 4 Cautare cu actiuni nedeterministe
Inteligenta Artificiala Universitatea Politehnica Bucuresti Anul universitar 2010-2011 Adina Magda Florea http://turing.cs.pub.ro/ia_10 si curs.cs.pub.ro 1 Curs nr. 4 Cautare cu actiuni nedeterministe
Utilizarea claselor de echivalenta in analiza asistata de calculator a sistemelor cu evenimente discrete
 72 Utilizarea claselor de echivalenta in analiza asistata de calculator a sistemelor cu evenimente discrete Conf.dr. Alexandru TERTISCO, ing. Alexandru BOICEA Facultatea de Automatica si Calculatoare,
72 Utilizarea claselor de echivalenta in analiza asistata de calculator a sistemelor cu evenimente discrete Conf.dr. Alexandru TERTISCO, ing. Alexandru BOICEA Facultatea de Automatica si Calculatoare,
LIGHTNING MVP System
 LIGHTNING MVP System Lightning MVP System Control (HACCP+SSOP) Swab-uri pentru lichide si pentru Suprafete Accesorii ph Temperatura Condutivitate Monitorizare ATP Prin Bioluminescenta Cel mai complet si
LIGHTNING MVP System Lightning MVP System Control (HACCP+SSOP) Swab-uri pentru lichide si pentru Suprafete Accesorii ph Temperatura Condutivitate Monitorizare ATP Prin Bioluminescenta Cel mai complet si
array a[0..n-1] a[0] = v0,..., a[n-1] = vn-1
![array a[0..n-1] a[0] = v0,..., a[n-1] = vn-1 array a[0..n-1] a[0] = v0,..., a[n-1] = vn-1](/thumbs/76/73793144.jpg) Curs 5 - Agenda sortare interna buble sort sortare prin insertie sortare pri selectie naiva sistematica ( heap sort ) sortare prin interclasare ( merge sort ) sortare rapida ( quick sort ) cautare in liste
Curs 5 - Agenda sortare interna buble sort sortare prin insertie sortare pri selectie naiva sistematica ( heap sort ) sortare prin interclasare ( merge sort ) sortare rapida ( quick sort ) cautare in liste
FLORENTIN SMARANDACHE Asupra unor conjecturi si probleme nerezolvate referitoare la o functie in Teoria Numerelor
 FLORENTIN SMARANDACHE Asupra unor conjecturi si probleme nerezolvate referitoare la o functie in Teoria Numerelor In Florentin Smarandache: Collected Papers, vol. II. Chisinau (Moldova): Universitatea
FLORENTIN SMARANDACHE Asupra unor conjecturi si probleme nerezolvate referitoare la o functie in Teoria Numerelor In Florentin Smarandache: Collected Papers, vol. II. Chisinau (Moldova): Universitatea
CURS 11: Programare dinamică - II - Algoritmica - Curs 12 1
 CURS 11: Programare dinamică - II - Algoritmica - Curs 12 1 Structura Ce este programarea dinamică? Aplicație: problema discretă a rucsacului Funcții de memorie (memoizare) Aplicație: înmulțirea optimală
CURS 11: Programare dinamică - II - Algoritmica - Curs 12 1 Structura Ce este programarea dinamică? Aplicație: problema discretă a rucsacului Funcții de memorie (memoizare) Aplicație: înmulțirea optimală
Câteva rezultate de algebră comutativă
 Facultatea de Matematică Anul II Master, Geometrie Algebrică Câteva rezultate de algebră comutativă Aceste note conţin noţiuni şi rezultate de algebră comutativă care sunt utilizate pe parcursul cursului.
Facultatea de Matematică Anul II Master, Geometrie Algebrică Câteva rezultate de algebră comutativă Aceste note conţin noţiuni şi rezultate de algebră comutativă care sunt utilizate pe parcursul cursului.
THE BEHAVIOUR OF ELASTOMERIC BEARINGS UNDER LOAD COMBINATIONS
 BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LX (LXIV), Fasc. 3, 2014 Secţia CONSTRUCŢII. ARHITECTURĂ THE BEHAVIOUR OF ELASTOMERIC BEARINGS
BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LX (LXIV), Fasc. 3, 2014 Secţia CONSTRUCŢII. ARHITECTURĂ THE BEHAVIOUR OF ELASTOMERIC BEARINGS
MATEMATICĂ 3 PROBLEME DE REFLECŢIE
 Recapitulare din liceu MATEMATIĂ 3 ANALIZĂ OMPLEXĂ PROBLEME DE REFLEŢIE. Scrieţi numerele următoare sub forma a + bi, unde a, b R: a) 3i + i ; b) i + i ;. Reolvaţi în ecuaţiile: ( + i)( i) c) ( + i)(4
Recapitulare din liceu MATEMATIĂ 3 ANALIZĂ OMPLEXĂ PROBLEME DE REFLEŢIE. Scrieţi numerele următoare sub forma a + bi, unde a, b R: a) 3i + i ; b) i + i ;. Reolvaţi în ecuaţiile: ( + i)( i) c) ( + i)(4
Despre AGC cuasigrupuri V. Izbaș
 Despre AGC cuasigrupuri V Izbaș 1 Introducere Se ştie că grupurile au apărut în matematică ca grupuri de automorfisme Rolul automorfismelor este remarcabil şi bine cunoscut La studierea diverselor structuri
Despre AGC cuasigrupuri V Izbaș 1 Introducere Se ştie că grupurile au apărut în matematică ca grupuri de automorfisme Rolul automorfismelor este remarcabil şi bine cunoscut La studierea diverselor structuri
Definiţie. Pr(X a) - probabilitatea ca X să ia valoarea a ; Pr(a X b) - probabilitatea ca X să ia o valoare în intervalul a,b.
 Variabile aleatoare Definiţie Se numeşte variabilă aleatoare pe un spaţiu fundamental E şi se notează prin X, o funcţie definită pe E cu valori în mulţimea numerelor reale. Unei variabile aleatoare X i
Variabile aleatoare Definiţie Se numeşte variabilă aleatoare pe un spaţiu fundamental E şi se notează prin X, o funcţie definită pe E cu valori în mulţimea numerelor reale. Unei variabile aleatoare X i
"IIITO-TEC 'NIKI" & EQUIPME
 LIGHTING "IIITO-TEC 'NIKI" & EQUIPME T FOR CITIES 6 MAKEDONOMAHON STR.,ZIPCaDE:67009,KALO ORI,THESSALONIKI, GREECE TEL / FAX: 0030 2310761824/751626,8 mall: hito@otenet.qi' Webslte:www.hlto..techkl.gr
LIGHTING "IIITO-TEC 'NIKI" & EQUIPME T FOR CITIES 6 MAKEDONOMAHON STR.,ZIPCaDE:67009,KALO ORI,THESSALONIKI, GREECE TEL / FAX: 0030 2310761824/751626,8 mall: hito@otenet.qi' Webslte:www.hlto..techkl.gr
GENERATOARE DE SEMNAL DIGITALE
 Technical University of Iasi, Romania Faculty of Electronics and Telecommunications Signals, Circuits and Systems laboratory Prof. Victor Grigoras Cuprins Clasificarea generatoarelor Filtre reursive la
Technical University of Iasi, Romania Faculty of Electronics and Telecommunications Signals, Circuits and Systems laboratory Prof. Victor Grigoras Cuprins Clasificarea generatoarelor Filtre reursive la
Alte rezultate din teoria codurilor
 Prelegerea 20 Alte rezultate din teoria codurilor 20.1 Coduri aritmetice Construcţiile oferite de teoria codurilor pot fi utilizate şi în alte domenii decât în cele clasice, de transmitere şi recepţie
Prelegerea 20 Alte rezultate din teoria codurilor 20.1 Coduri aritmetice Construcţiile oferite de teoria codurilor pot fi utilizate şi în alte domenii decât în cele clasice, de transmitere şi recepţie
Graduări pe algebre de matrice
 UNIVERSITATEA DIN BUCUREŞTI FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ ŞCOALA DOCTORALĂ DE MATEMATICĂ Graduări pe algebre de matrice TEZĂ DE DOCTORAT REZUMAT Coordonator ştiinţific: Prof.univ.dr. Sorin Dăscălescu
UNIVERSITATEA DIN BUCUREŞTI FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ ŞCOALA DOCTORALĂ DE MATEMATICĂ Graduări pe algebre de matrice TEZĂ DE DOCTORAT REZUMAT Coordonator ştiinţific: Prof.univ.dr. Sorin Dăscălescu
IMAR Problema 1. Fie P un punct situat în interiorul unui triunghi ABC. Dreapta AP intersectează
 IMAR 017 Problema 1 Fie P u puct situat î iteriorul uui triughi ABC Dreapta AP itersectează latura BC î puctul D ; dreapta BP itersectează latura CA î puctul E ; iar dreapta CP itersectează latura AB î
IMAR 017 Problema 1 Fie P u puct situat î iteriorul uui triughi ABC Dreapta AP itersectează latura BC î puctul D ; dreapta BP itersectează latura CA î puctul E ; iar dreapta CP itersectează latura AB î
Laborator 3. Backtracking iterativ
 Programare Delphi Laborator 3 Backtracking iterativ Metoda backtracking este o strategie generală de căutare din aproape în aproape a unei soluţii dintr-o mulţime finită de posibilităţi. Problema trebuie
Programare Delphi Laborator 3 Backtracking iterativ Metoda backtracking este o strategie generală de căutare din aproape în aproape a unei soluţii dintr-o mulţime finită de posibilităţi. Problema trebuie
Rezolvarea ecuaţiilor şi sistemelor de ecuaţii diferenţiale ordinare (II)
 Rezolvarea ecuaţiilor şi sistemelor de ecuaţii diferenţiale ordinare (II) Metode multipas Prof.dr.ing. Universitatea "Politehnica" Bucureşti, Facultatea de Inginerie Electrică Suport didactic pentru disciplina
Rezolvarea ecuaţiilor şi sistemelor de ecuaţii diferenţiale ordinare (II) Metode multipas Prof.dr.ing. Universitatea "Politehnica" Bucureşti, Facultatea de Inginerie Electrică Suport didactic pentru disciplina
Legi de distribuţie (principalele distribuţii de probabilitate) Tudor Drugan
 Legi de distribuţie (principalele distribuţii de probabilitate) Tudor Drugan Introducere In general distribuţiile variabilelor aleatoare definite pe o populaţie, care face obiectul unui studiu, nu se cunosc.
Legi de distribuţie (principalele distribuţii de probabilitate) Tudor Drugan Introducere In general distribuţiile variabilelor aleatoare definite pe o populaţie, care face obiectul unui studiu, nu se cunosc.
COMPARATIVE DISCUSSION ABOUT THE DETERMINING METHODS OF THE STRESSES IN PLANE SLABS
 74 COMPARATIVE DISCUSSION ABOUT THE DETERMINING METHODS OF THE STRESSES IN PLANE SLABS Codrin PRECUPANU 3, Dan PRECUPANU,, Ștefan OPREA Correspondent Member of Technical Sciences Academy Gh. Asachi Technical
74 COMPARATIVE DISCUSSION ABOUT THE DETERMINING METHODS OF THE STRESSES IN PLANE SLABS Codrin PRECUPANU 3, Dan PRECUPANU,, Ștefan OPREA Correspondent Member of Technical Sciences Academy Gh. Asachi Technical
Modelling the Steady State Characteristic of ph Neutralization Process: a Neuro-Fuzzy Approach
 BULETINUL Universităţii Petrol Gaze din Ploieşti Vol. LXVII No. 2/2015 79 84 Seria Tehnică Modelling the Steady State Characteristic of ph Neutralization Process: a Neuro-Fuzzy Approach Gabriel Rădulescu
BULETINUL Universităţii Petrol Gaze din Ploieşti Vol. LXVII No. 2/2015 79 84 Seria Tehnică Modelling the Steady State Characteristic of ph Neutralization Process: a Neuro-Fuzzy Approach Gabriel Rădulescu
Laborator 5. Instructiuni de control logic : FOR, IF, WHILE. - Staţii de lucru care au instalat Orcad9.2. si MatLab 7.1
 Laborator 5. Instructiuni de control logic : FOR, IF, WHILE. Scopul lucrarii: Scopul acestei lucrari este de a invata si intelege instructiunile de control logic, pe care, le vom folosi in realizarea unui
Laborator 5. Instructiuni de control logic : FOR, IF, WHILE. Scopul lucrarii: Scopul acestei lucrari este de a invata si intelege instructiunile de control logic, pe care, le vom folosi in realizarea unui
Habilitation Thesis. Periodic solutions of differential systems: existence, stability and bifurcations
 UNIVERSITATEA BABEŞ BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Habilitation Thesis Mathematics presented by Adriana Buică Periodic solutions of differential systems: existence, stability
UNIVERSITATEA BABEŞ BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Habilitation Thesis Mathematics presented by Adriana Buică Periodic solutions of differential systems: existence, stability
Subiecte geometrie licenta matematica-informatica 4 ani
 Class: Date: Subiecte geometrie licenta matematica-informatica 4 ani Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. 1. Complementara unui subspatiu
Class: Date: Subiecte geometrie licenta matematica-informatica 4 ani Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. 1. Complementara unui subspatiu
Rezultate în Teoria Punctului Fix şi Procese Iterative cu Aplicaţii
 Rezultate în Teoria Punctului Fix şi Procese Iterative cu Aplicaţii Asist. drd. Adrian Sorinel Ghiura Departamentul de Matematică & Informatică Universitatea Politehnica din Bucureşti REZUMATUL TEZEI DE
Rezultate în Teoria Punctului Fix şi Procese Iterative cu Aplicaţii Asist. drd. Adrian Sorinel Ghiura Departamentul de Matematică & Informatică Universitatea Politehnica din Bucureşti REZUMATUL TEZEI DE
REZUMATUL TEZEI DE DOCTORAT
 UNIVERSITATEA BABEŞ-BOLYAI FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ CERCETĂRI DE TEORIE MORSE DISCRETĂ ŞI APLICAŢII REZUMATUL TEZEI DE DOCTORAT Conducător ştiinţific: Prof. univ. dr. DORIN ANDRICA Doctorand:
UNIVERSITATEA BABEŞ-BOLYAI FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ CERCETĂRI DE TEORIE MORSE DISCRETĂ ŞI APLICAŢII REZUMATUL TEZEI DE DOCTORAT Conducător ştiinţific: Prof. univ. dr. DORIN ANDRICA Doctorand:
Gradul de comutativitate al grupurilor finite 1
 Gradul de comutativitate al grupurilor finite Marius TĂRNĂUCEANU Abstract The commutativity degree of a group is one of the most important probabilistic aspects of finite group theory In this survey we
Gradul de comutativitate al grupurilor finite Marius TĂRNĂUCEANU Abstract The commutativity degree of a group is one of the most important probabilistic aspects of finite group theory In this survey we
Rădăcina pătrată a unei matrici reale de ordinul 2
 Rădăcina pătrată a unei matrici reale de ordinul Mircea Crasmareanu Mai 19, 017 ( a c Actorii acestei poveşti: matricile A = M b d (R. PROBLEMA STUDIATĂ: Există B M (R aşa încât: B = A? O astfel de matrice
Rădăcina pătrată a unei matrici reale de ordinul Mircea Crasmareanu Mai 19, 017 ( a c Actorii acestei poveşti: matricile A = M b d (R. PROBLEMA STUDIATĂ: Există B M (R aşa încât: B = A? O astfel de matrice
Liste. Stive. Cozi SD 2017/2018
 Liste. Stive. Cozi SD 2017/2018 Conţinut Tipurile abstracte LLin, LLinOrd, Stiva, Coada Liste liniare Implementarea cu tablouri Implementarea cu liste simplu înlănțuite Liste liniare ordonate Stive Cozi
Liste. Stive. Cozi SD 2017/2018 Conţinut Tipurile abstracte LLin, LLinOrd, Stiva, Coada Liste liniare Implementarea cu tablouri Implementarea cu liste simplu înlănțuite Liste liniare ordonate Stive Cozi
PLANIFICAREA TEMELOR LA GRUPELE DE EXCELENȚĂ DISCIPLINA MATEMATICĂ AN ȘCOLAR
 PLANIFICAREA TEMELOR LA GRUPELE DE EXCELENȚĂ DISCIPLINA MATEMATICĂ AN ȘCOLAR 0-0 Grupa V. Matematică Profesor coordonator: Aldescu Alina.0.0 Operatii in N-Teorema impartirii cu rest 0..0 Patrate perfecte,cuburi
PLANIFICAREA TEMELOR LA GRUPELE DE EXCELENȚĂ DISCIPLINA MATEMATICĂ AN ȘCOLAR 0-0 Grupa V. Matematică Profesor coordonator: Aldescu Alina.0.0 Operatii in N-Teorema impartirii cu rest 0..0 Patrate perfecte,cuburi
ARTICOLE ŞI NOTE MATEMATICE
 S. Rădulescu, M. Drăgan, I. V. Maftei, On W. J. Blundon s inequality 3 ARTICOLE ŞI NOTE MATEMATICE SOME CONSEQUENCES OF W.J.BLUNDON S INEQUALITY Sorin Rădulescu 1), Marius Drăgan 2), I.V.Maftei 3) Abstract.
S. Rădulescu, M. Drăgan, I. V. Maftei, On W. J. Blundon s inequality 3 ARTICOLE ŞI NOTE MATEMATICE SOME CONSEQUENCES OF W.J.BLUNDON S INEQUALITY Sorin Rădulescu 1), Marius Drăgan 2), I.V.Maftei 3) Abstract.
PRELUCRARI PE IMAGINI BINARE (ALB/NEGRU)
 PRELUCRRI PE IMGINI BINRE (LB/NEGRU) Imagine binara? 2 nuante: alb ( 0 ) pixelii de fond ( I(x,y)= 255 pt. imagini indexate cu 8 biti/pixel ) negru ( 1 ) pixelii apartinand obiectelor ( I(x,y)= 0 pt. imagini
PRELUCRRI PE IMGINI BINRE (LB/NEGRU) Imagine binara? 2 nuante: alb ( 0 ) pixelii de fond ( I(x,y)= 255 pt. imagini indexate cu 8 biti/pixel ) negru ( 1 ) pixelii apartinand obiectelor ( I(x,y)= 0 pt. imagini
Probleme actuale în studiul funcţiei zeta Igusa
 Probleme actuale în studiul funcţiei zeta Igusa Denis Ibadula 1 1 This paper is supported by the Sectorial Operational Programme Human Resources Development (SOP HRD), financed from the European Social
Probleme actuale în studiul funcţiei zeta Igusa Denis Ibadula 1 1 This paper is supported by the Sectorial Operational Programme Human Resources Development (SOP HRD), financed from the European Social
4/68. Mini-comutatoare cu came. Prezentare generalã a sistemului. Întreruptoare Pornit-Oprit TM. Comutatoare de comandã TM.
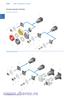 / Mini-comutatoare cu came Prezentare generalã a sistemului Întreruptoare Pornit-Oprit Comutatoare de comandã HA ND AU TO HPL-de-DE O Mini-comutatoare cu came / Montaj pe ușã (.../E) Frontal IP Montaj
/ Mini-comutatoare cu came Prezentare generalã a sistemului Întreruptoare Pornit-Oprit Comutatoare de comandã HA ND AU TO HPL-de-DE O Mini-comutatoare cu came / Montaj pe ușã (.../E) Frontal IP Montaj
Equations P $UnitSystem K kpa. F luid$ = Air (1) Input data for fluid. $If Fluid$= Air. C P = [kj/kg K] ; k = 1.
![Equations P $UnitSystem K kpa. F luid$ = Air (1) Input data for fluid. $If Fluid$= Air. C P = [kj/kg K] ; k = 1. Equations P $UnitSystem K kpa. F luid$ = Air (1) Input data for fluid. $If Fluid$= Air. C P = [kj/kg K] ; k = 1.](/thumbs/94/119197129.jpg) P09-169 Equations Thermodynamics - An Engineering Approach (5th Ed) - Cengel, Boles - Mcgraw-Hill (2006) - pg. 549 Ciclul Brayton cu regenerare (aer, heliu) cu comprimare si destindere in trepte, c p =ct.
P09-169 Equations Thermodynamics - An Engineering Approach (5th Ed) - Cengel, Boles - Mcgraw-Hill (2006) - pg. 549 Ciclul Brayton cu regenerare (aer, heliu) cu comprimare si destindere in trepte, c p =ct.
Decision Trees Some exercises
 Decision Trees Some exercises 0. . Exemplifying how to compute information gains and how to work with decision stumps CMU, 03 fall, W. Cohen E. Xing, Sample questions, pr. 4 . Timmy wants to know how to
Decision Trees Some exercises 0. . Exemplifying how to compute information gains and how to work with decision stumps CMU, 03 fall, W. Cohen E. Xing, Sample questions, pr. 4 . Timmy wants to know how to
Teoreme de Analiză Matematică - I (teorema Weierstrass-Bolzano) 1
 Educaţia Matematică Vol. 3, Nr. 1-2 (2007), 79-84 Teoreme de Analiză Matematică - I (teorema Weierstrass-Bolzano) 1 Silviu Crăciunaş, Petrică Dicu, Mioara Boncuţ Abstract In this paper we propose a Weierstrass
Educaţia Matematică Vol. 3, Nr. 1-2 (2007), 79-84 Teoreme de Analiză Matematică - I (teorema Weierstrass-Bolzano) 1 Silviu Crăciunaş, Petrică Dicu, Mioara Boncuţ Abstract In this paper we propose a Weierstrass
Testarea ipotezelor statistice
 Testarea ipotezelor statistice Formularea de ipoteze statistice este una din cele mai importante aspecte ale cercetarii stiintifice. O ipoteza noua trebuie verificata! Pentru verificarea unor ipoteze statistice
Testarea ipotezelor statistice Formularea de ipoteze statistice este una din cele mai importante aspecte ale cercetarii stiintifice. O ipoteza noua trebuie verificata! Pentru verificarea unor ipoteze statistice
Programarea Dinamica. (si alte chestii adiacente) Andrei Olariu
 Programarea Dinamica (si alte chestii adiacente) Andrei Olariu andrei@olariu.org Despre mine - Absolvent FMI UniBuc - Doctorand in prelucrarea limbajului natural, in special in mediul online (Twitter)
Programarea Dinamica (si alte chestii adiacente) Andrei Olariu andrei@olariu.org Despre mine - Absolvent FMI UniBuc - Doctorand in prelucrarea limbajului natural, in special in mediul online (Twitter)
$IfNot ParametricTable= P_ratio_gas. P ratio,gas = 14; Raport comprimare compresor aer - Pressure ratio for gas compressor (2) $EndIf
 P10-078 Equations Thermodynamics - An Engineering Approach (5th Ed) - Cengel, Boles - Mcgraw-Hill (2006) - pg. 598 Centrala cu cicluri combinate Se considera o centrala electrica cu ciclu combinat gaze-abur
P10-078 Equations Thermodynamics - An Engineering Approach (5th Ed) - Cengel, Boles - Mcgraw-Hill (2006) - pg. 598 Centrala cu cicluri combinate Se considera o centrala electrica cu ciclu combinat gaze-abur
Ordin. pentru aprobarea structurii informaţiilor înscrise pe cardul naţional de asigurări sociale de sănătate
 CASA NATIONALA DE ASIGURARI DE SANATATE Ordin pentru aprobarea structurii informaţiilor înscrise pe cardul naţional de asigurări sociale de sănătate Având în vedere: Act publicat in Monitorul Oficial al
CASA NATIONALA DE ASIGURARI DE SANATATE Ordin pentru aprobarea structurii informaţiilor înscrise pe cardul naţional de asigurări sociale de sănătate Având în vedere: Act publicat in Monitorul Oficial al
Mugur Acu OPERATORUL INTEGRAL LIBERA-PASCU ŞI PROPRIETĂŢILE ACESTUIA CU PRIVIRE LA FUNCŢIILE UNIFORM STELATE, CONVEXE, APROAPE CONVEXE ŞI
 Mugur Acu OPERATORUL INTEGRAL LIBERA-PASCU ŞI PROPRIETĂŢILE ACESTUIA CU PRIVIRE LA FUNCŢIILE UNIFORM STELATE, CONVEXE, APROAPE CONVEXE ŞI α-uniform CONVEXE Editura Universităţii Lucian Blaga din Sibiu
Mugur Acu OPERATORUL INTEGRAL LIBERA-PASCU ŞI PROPRIETĂŢILE ACESTUIA CU PRIVIRE LA FUNCŢIILE UNIFORM STELATE, CONVEXE, APROAPE CONVEXE ŞI α-uniform CONVEXE Editura Universităţii Lucian Blaga din Sibiu
QUASI-ANALYTIC SOLUTIONS OF FIRST-ORDER PARTIAL DIFFERENTIAL EQUATIONS USING THE ACCURATE ELEMENT METHOD
 U.P.B. Sci. Bull., Series A, Vol. 7, Iss., 010 ISSN 13-707 QUASI-ANALYTIC SOLUTIONS OF FIRST-ORDER PARTIAL DIFFERENTIAL EQUATIONS USING THE ACCURATE ELEMENT METHOD Maty BLUMENFELD 1 O ecuaţie diferenţială
U.P.B. Sci. Bull., Series A, Vol. 7, Iss., 010 ISSN 13-707 QUASI-ANALYTIC SOLUTIONS OF FIRST-ORDER PARTIAL DIFFERENTIAL EQUATIONS USING THE ACCURATE ELEMENT METHOD Maty BLUMENFELD 1 O ecuaţie diferenţială
ROMANIAN MATHEMATICAL SOCIETY
 ROMANIAN MATHEMATICAL SOCIETY Mehedinți Branch ROMANIAN MATHEMATICAL MAGAZINE R.M.M. Nr.20-2018 1 ROMANIAN MATHEMATICAL MAGAZINE NR. 20 ROMANIAN MATHEMATICAL SOCIETY Mehedinți Branch DANIEL SITARU-ROMANIA
ROMANIAN MATHEMATICAL SOCIETY Mehedinți Branch ROMANIAN MATHEMATICAL MAGAZINE R.M.M. Nr.20-2018 1 ROMANIAN MATHEMATICAL MAGAZINE NR. 20 ROMANIAN MATHEMATICAL SOCIETY Mehedinți Branch DANIEL SITARU-ROMANIA
Clasa a 10-a. Review of preview
 1 of 12 2/1/2016 11:10 AM PHI 2016 You are logged in as Admin User (Logout) edesc PHI2016 Quizzes Clasa a 10-a Review of preview Info Results Preview Edit Clasa a 10-a Review of preview Started on Monday,
1 of 12 2/1/2016 11:10 AM PHI 2016 You are logged in as Admin User (Logout) edesc PHI2016 Quizzes Clasa a 10-a Review of preview Info Results Preview Edit Clasa a 10-a Review of preview Started on Monday,
Matematici speciale Variabile aleatoare discrete
 Matematici speciale Variabile aleatoare discrete Aprilie 208 ii Expose yourself to as much randomness as possible. Ben Casnocha 9 Variabile aleatoare discrete Texas Holdem Poker: In Texas Hold em Poker
Matematici speciale Variabile aleatoare discrete Aprilie 208 ii Expose yourself to as much randomness as possible. Ben Casnocha 9 Variabile aleatoare discrete Texas Holdem Poker: In Texas Hold em Poker
Logică și structuri discrete. Marius Minea 25 septembrie 2017
 Logică și structuri discrete Funcții Marius Minea marius@cs.upt.ro http://cs.upt.ro/~marius/curs/lsd/ 25 septembrie 2017 Ce cuprinde domeniul informaticii? Imagine: https://hkn.eecs.berkeley.edu/courseguides
Logică și structuri discrete Funcții Marius Minea marius@cs.upt.ro http://cs.upt.ro/~marius/curs/lsd/ 25 septembrie 2017 Ce cuprinde domeniul informaticii? Imagine: https://hkn.eecs.berkeley.edu/courseguides
7 ECUAŢII ALGEBRICE ŞI TRANSCENDENTE
 7 ECUAŢII ALGEBRICE ŞI TRANSCENDENTE 7 Separarea rădăcnlor Ecuaţe algebrcă dacă ( este polnom Ecuaţa transcendentă în caz contrar ( = Rădăcnă apromatvă valoare ξ apropată de valoarea eactă ξ Denţ neechvalente:
7 ECUAŢII ALGEBRICE ŞI TRANSCENDENTE 7 Separarea rădăcnlor Ecuaţe algebrcă dacă ( este polnom Ecuaţa transcendentă în caz contrar ( = Rădăcnă apromatvă valoare ξ apropată de valoarea eactă ξ Denţ neechvalente:
HABILITATION THESIS. Semisimple Hopf algebras and fusion categories
 Institute of Mathematics,,Simion Stoilow of the Romanian Academy HABILITATION THESIS Semisimple Hopf algebras and fusion categories Sebastian Marius Burciu Specialization: Mathematics Bucharest, 2013 To
Institute of Mathematics,,Simion Stoilow of the Romanian Academy HABILITATION THESIS Semisimple Hopf algebras and fusion categories Sebastian Marius Burciu Specialization: Mathematics Bucharest, 2013 To
RECREAŢ II MATEMATICE REVISTĂ DE MATEMATICĂ PENTRU ELEVI Ş I PROFESORI
 Anul IX, Nr. Iulie Decembrie 007 RECREAŢ II MATEMATICE REVISTĂ DE MATEMATICĂ PENTRU ELEVI Ş I PROFESORI e iπ = 1 Asociaţia Recreaţii Matematice IAŞI - 007 Semnificaţia formulei de pe copertă: iπ Într-o
Anul IX, Nr. Iulie Decembrie 007 RECREAŢ II MATEMATICE REVISTĂ DE MATEMATICĂ PENTRU ELEVI Ş I PROFESORI e iπ = 1 Asociaţia Recreaţii Matematice IAŞI - 007 Semnificaţia formulei de pe copertă: iπ Într-o
Universitatea Politehnica Bucureşti Facultatea de Automatică şi Calculatoare Departamentul de Automatică şi Ingineria Sistemelor
 Universitatea Politehnica Bucureşti Facultatea de Automatică şi Calculatoare Departamentul de Automatică şi Ingineria Sistemelor TEZĂ DE ABILITARE Metode de Descreştere pe Coordonate pentru Optimizare
Universitatea Politehnica Bucureşti Facultatea de Automatică şi Calculatoare Departamentul de Automatică şi Ingineria Sistemelor TEZĂ DE ABILITARE Metode de Descreştere pe Coordonate pentru Optimizare
THE INFLUENCE OF SOME CHARACTERISTICS OF RANITIDINE HYDROCHLORIDE ON THE FORMING AND PREPARATION OF THE TABLETS
 FARMACIA, 2012, Vol. 60, 4 517 THE INFLUENCE OF SOME CHARACTERISTICS OF RANITIDINE HYDROCHLORIDE ON THE FORMING AND PREPARATION OF THE TABLETS POSTOLACHE LILIANA* 1,2, ONUŢĂ ALEXANDRU-EVLAMPIE 2,3 1 Faculty
FARMACIA, 2012, Vol. 60, 4 517 THE INFLUENCE OF SOME CHARACTERISTICS OF RANITIDINE HYDROCHLORIDE ON THE FORMING AND PREPARATION OF THE TABLETS POSTOLACHE LILIANA* 1,2, ONUŢĂ ALEXANDRU-EVLAMPIE 2,3 1 Faculty
Laborator 4. Rezolvarea ecuaţiilor diferenţiale în Matlab
 Laborator 4. Rezolvarea ecuaţiilor difereţiale î Matlab Bibliografie. G. Aastassiou, I. Iata, Itelliget Routies: Solvig Mathematical Aalsis with Matlab, Mathcad, Mathematica ad Maple, Spriger, 03.. I.
Laborator 4. Rezolvarea ecuaţiilor difereţiale î Matlab Bibliografie. G. Aastassiou, I. Iata, Itelliget Routies: Solvig Mathematical Aalsis with Matlab, Mathcad, Mathematica ad Maple, Spriger, 03.. I.
ELABORATION AND VALIDATION OF AN HPLC METHOD FOR THE QUANTITATIVE ASSAY OF 5-FLUOROURACIL
 526 ELABORATION AND VALIDATION OF AN HPLC METHOD FOR THE QUANTITATIVE ASSAY OF 5-FLUOROURACIL LAURA PALADE, IULIANA POPOVICI, GRATIELA POPA, ILEANA COJOCARU * Pharmaceutical Technology Department, Faculty
526 ELABORATION AND VALIDATION OF AN HPLC METHOD FOR THE QUANTITATIVE ASSAY OF 5-FLUOROURACIL LAURA PALADE, IULIANA POPOVICI, GRATIELA POPA, ILEANA COJOCARU * Pharmaceutical Technology Department, Faculty
ASPECTS REGARDING NUMERICAL MODELING OF INDUCTIVE HEATING PROCESS FOR LOW VOLTAGE ELECTRICAL CABLES
 U.P.B. Sci. Bull., Series C, Vol. 72, Iss. 3, 2010 ISSN 1454-234x ASPECTS REGARDING NUMERICAL MODELING OF INDUCTIVE HEATING PROCESS FOR LOW VOLTAGE ELECTRICAL CABLES Costel PĂUN 1 În această lucrare se
U.P.B. Sci. Bull., Series C, Vol. 72, Iss. 3, 2010 ISSN 1454-234x ASPECTS REGARDING NUMERICAL MODELING OF INDUCTIVE HEATING PROCESS FOR LOW VOLTAGE ELECTRICAL CABLES Costel PĂUN 1 În această lucrare se
Aplicaţie SCADA. Simularea procesului de incalzire a unei pompe de caldura
 UNIVERSITATEA PETRU MAIOR TARGU-MURES FACULTATEA DE INGINERIE SPECIALIZAREA: SISTEME AUTOMATE DE CONDUCERE A PROCESELOR INDUSTRIALE Aplicaţie SCADA Simularea procesului de incalzire a unei pompe de caldura
UNIVERSITATEA PETRU MAIOR TARGU-MURES FACULTATEA DE INGINERIE SPECIALIZAREA: SISTEME AUTOMATE DE CONDUCERE A PROCESELOR INDUSTRIALE Aplicaţie SCADA Simularea procesului de incalzire a unei pompe de caldura
Probleme extremale pentru grafuri si retele de transport
 Revista Inormatica Economica nr 4 (4)/00 9 Proleme extremale pentru grauri si retele de transport Drd Rodica MIRONENCO A variety o prolems can e constructed using Ford-Fulkerson s maximum-low minimumcut
Revista Inormatica Economica nr 4 (4)/00 9 Proleme extremale pentru grauri si retele de transport Drd Rodica MIRONENCO A variety o prolems can e constructed using Ford-Fulkerson s maximum-low minimumcut
Agricultural Engineering
 THE DETERMINATION OF QUALITY CHARACTERISTICS FOR THE WORKING PROCESS OF INDENTED CYLINDER SEPARATORS AS FUNCTIONS OF PROCESS PARAMETERS OF THESE EQUIPMENTS / DETERMINAREA CARACTERISTICILOR CALITATIVE ALE
THE DETERMINATION OF QUALITY CHARACTERISTICS FOR THE WORKING PROCESS OF INDENTED CYLINDER SEPARATORS AS FUNCTIONS OF PROCESS PARAMETERS OF THESE EQUIPMENTS / DETERMINAREA CARACTERISTICILOR CALITATIVE ALE
Curs 6. Discrete Event Simulation
 Curs 6 Discrete Event Simulation C6 ~ 12.04.2017 1/43 In discrete-event simulation, the operation of a system is represented as a chronological sequence of events. Each event occurs at an instant in time
Curs 6 Discrete Event Simulation C6 ~ 12.04.2017 1/43 In discrete-event simulation, the operation of a system is represented as a chronological sequence of events. Each event occurs at an instant in time
BOOST CIRCUIT CONTROL IN TRANSIENT CONDITIONS
 U.P.B. Sci. Bull., Series C, Vol. 68, No. 4, 2006 BOOST CIRCUIT CONTROL IN TRANSIENT CONDITIONS D. OLARU * Lucrarea îşi propune să abordeze câteva aspecte legate de modelarea şi comanda circuitului boost.
U.P.B. Sci. Bull., Series C, Vol. 68, No. 4, 2006 BOOST CIRCUIT CONTROL IN TRANSIENT CONDITIONS D. OLARU * Lucrarea îşi propune să abordeze câteva aspecte legate de modelarea şi comanda circuitului boost.
Metode clasice. Camelia Chira.
 Metode clasice Camelia Chira http://users.utcluj.ro/~cchira camelia.chira@cs.utcluj.ro Am vazut deja ca... Probleme de optimizare pot fi foarte complexe SAT, TSP, NLP, etc Spatiul de cautare Clase de complexitate
Metode clasice Camelia Chira http://users.utcluj.ro/~cchira camelia.chira@cs.utcluj.ro Am vazut deja ca... Probleme de optimizare pot fi foarte complexe SAT, TSP, NLP, etc Spatiul de cautare Clase de complexitate
Exemplifying the application of hierarchical agglomerative clustering (single-, complete- and average-linkage)
 Clustering 0. 1. Exemplifying the application of hierarchical agglomerative clustering (single-, complete- and average-linkage) CMU, 2012 fall, Tom Mitchell, Ziv Bar-Joseph, HW4, pr. 2.a extended by Liviu
Clustering 0. 1. Exemplifying the application of hierarchical agglomerative clustering (single-, complete- and average-linkage) CMU, 2012 fall, Tom Mitchell, Ziv Bar-Joseph, HW4, pr. 2.a extended by Liviu
Tablouri bidimensionale(matrici)
 Tablouri bidimensionale(matrici) ianta în Pascal Problema 1: Secvență de matrici Enunț Scrieţi un program care citeşte de la tastatură două numere naturale n și m ( 2
Tablouri bidimensionale(matrici) ianta în Pascal Problema 1: Secvență de matrici Enunț Scrieţi un program care citeşte de la tastatură două numere naturale n și m ( 2
THERMAL CONDUCTIVITY MEASUREMENT OF CONSTRUCTION MATERIALS USING THE THERMAL PROBE METHOD
 BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LVIII (LXII), Fasc. 2, 2012 Secţia CONSTRUCŢII. ARHITECTURĂ THERMAL CONDUCTIVITY MEASUREMENT
BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LVIII (LXII), Fasc. 2, 2012 Secţia CONSTRUCŢII. ARHITECTURĂ THERMAL CONDUCTIVITY MEASUREMENT
AN APPROACH TO THE NONLINEAR LOCAL PROBLEMS IN MECHANICAL STRUCTURES
 U.P.B. Sci. Bull., Series D, Vol. 74, Iss. 3, 2012 ISSN 1454-2358 AN APPROACH TO THE NONLINEAR LOCAL PROBLEMS IN MECHANICAL STRUCTURES Marius-Alexandru GROZEA 1, Anton HADĂR 2 Acest articol prezintă o
U.P.B. Sci. Bull., Series D, Vol. 74, Iss. 3, 2012 ISSN 1454-2358 AN APPROACH TO THE NONLINEAR LOCAL PROBLEMS IN MECHANICAL STRUCTURES Marius-Alexandru GROZEA 1, Anton HADĂR 2 Acest articol prezintă o
Test de Departajare pentru MofM 2014 (Bucureşti) Enunţuri & Soluţii
 Test de Departajare petru MofM 04 Bucureşti Euţuri & Soluţii Problem. Give + distict real umbers i the iterval [0,], prove there exist two of them a b, such that ab a b < Solutio. Idex the umbers 0 a 0
Test de Departajare petru MofM 04 Bucureşti Euţuri & Soluţii Problem. Give + distict real umbers i the iterval [0,], prove there exist two of them a b, such that ab a b < Solutio. Idex the umbers 0 a 0
TEZĂ DE ABILITARE. Subvarietăți de curbură medie paralelă și subvarietăți biarmonice în varietăți riemanniene
 ACADEMIA ROMÂNĂ SCOSAAR TEZĂ DE ABILITARE Subvarietăți de curbură medie paralelă și subvarietăți biarmonice în varietăți riemanniene Dorel Fetcu Domeniul fundamental Matematică și științe ale naturii Domeniul
ACADEMIA ROMÂNĂ SCOSAAR TEZĂ DE ABILITARE Subvarietăți de curbură medie paralelă și subvarietăți biarmonice în varietăți riemanniene Dorel Fetcu Domeniul fundamental Matematică și științe ale naturii Domeniul
FINDING THE TRACES OF A GIVEN PLANE: ANALYTICALLY AND THROUGH GRAPHICAL CONSTRUCTIONS
 BULETINUL INSTITUTULUI POLITEHNI DIN IŞI Publicat de Universitatea Tehnică Gheorghe sachi din Iaşi Tomul LVII (LXI), Fasc. 3, 20 Secţia ONSTRUŢII DE MŞINI FINDING THE TRES OF GIVEN PLNE: NLYTILLY ND THROUGH
BULETINUL INSTITUTULUI POLITEHNI DIN IŞI Publicat de Universitatea Tehnică Gheorghe sachi din Iaşi Tomul LVII (LXI), Fasc. 3, 20 Secţia ONSTRUŢII DE MŞINI FINDING THE TRES OF GIVEN PLNE: NLYTILLY ND THROUGH
OPTIMAL OBSERVABILITY OF PMU'S USING ANALYTIC HIERARCHY PROCESS (AHP) METHOD
 U.P.B. Sci. Bull., Series C, Vol. 73, Iss. 4, 2011 ISSN 1454-234x OPTIMAL OBSERVABILITY OF PMU'S USING ANALYTIC HIERARCHY PROCESS (AHP) METHOD Sebastian ANGHELESCU 1, Gianfranco CHICCO 2 Lucrarea propune
U.P.B. Sci. Bull., Series C, Vol. 73, Iss. 4, 2011 ISSN 1454-234x OPTIMAL OBSERVABILITY OF PMU'S USING ANALYTIC HIERARCHY PROCESS (AHP) METHOD Sebastian ANGHELESCU 1, Gianfranco CHICCO 2 Lucrarea propune
Curs II Dinamica spaţiului disponibil al sedimentării -noţiuni de stratigrafie secvenţială- modele diferite
 Curs II Dinamica spaţiului disponibil al sedimentării -noţiuni de stratigrafie secvenţială- modele diferite Lect. Dr. R. D. Roban STRATIGRAFIA SECVENŢIALĂ, o derivată a stratigrafiei seismice, (Vail et
Curs II Dinamica spaţiului disponibil al sedimentării -noţiuni de stratigrafie secvenţială- modele diferite Lect. Dr. R. D. Roban STRATIGRAFIA SECVENŢIALĂ, o derivată a stratigrafiei seismice, (Vail et
