Ecuatii si inecuatii de gradul al doilea si reductibile la gradul al doilea. Ecuatii de gradul al doilea
|
|
|
- Marcus Glenn
- 6 years ago
- Views:
Transcription
1 Ecuatii si inecuatii de gradul al doilea si reductibile la gradul al doilea Ecuatia de forma Ecuatii de gradul al doilea a + b + c = 0, (1) unde a, b, c R, a 0, - variabila, se numeste ecuatie de gradul al doilea (ecuatia patrata). Numerele a, b si c din (1) se numesc coeficienti ai ecuatiei de gradul al doilea, iar numarul = b 4ac se numeste discriminant al ecuatiei de gradul al doilea. Eemplul 1. Ecuatiile ce urmeaza sunt ecuatii de gradul al doilea: a) = 0, cu a = 6, b = 5, c = 1 si = = 1; b) = 0, cu a = 9, b = 1, c = 4 si = ( 1) = 0; c) = 0, cu a = 1, b = 1, c = si = ( 1) 4 1 ( ) = 9; d) = 0, cu a = 1, b = 3, c = 4 si = ( ( 3) 4 1 ) ( 4) = 5. Ecuatiile de gradul al doilea pot fi rezolvate conform urmatoarei afirmatii: Afirmatia 1. Daca a) discriminantul ecuatiei (1) este pozitiv, atunci ecuatia (1) are doua radacini distincte: 1 = b a si = b + ; () a b) discriminantul ecuatiei (1) este egal cu zero, atunci ecuatia (1) are doua radacini egale (o radacina de multiplicitatea doi): 1 = = b a ; (3) c) discriminantul ecuatiei (1) este negativ, atunci ecuatia (1) nu are radacini reale. Asadar, (a se vedea eemplul 1): 1. ecuatia a) are doua radacini distincte 1 = 1 si = 1 3 ;. ecuatia b) are doua radacini egale 1 = = 3 ; 3. ecuatia c) are doua radacini distincte 1 = 1 si = ; 4. ecuatia d) nu are radacini reale. 1
2 Ecuatia de gradul al doilea cu a = 1 se numeste ecuatie patrata redusa si se noteaza de regula + p + q = 0 (4) si formulele () si (3) de calcul ale radacinilor devin 1, = p ± (p ) q, ( > 0) (5) Ecuatiile de forma 1 = = p, ( = 0). (6) a + b = 0, (7) a + c = 0. (8) se numesc ecuatii de gradul al doilea incomplete. Ecuatiile (7), (8) pot fi rezolvate cu ajutorul afirmatiei 1 altfel, mai simplu: a + b = 0 (a + b) = 0 a + c = 0 = c a Eemplul. Sa se rezolve ecuatiile 1 = 0; = b a. 1, = ± c a, ac 0, {, ac > 0. a) 7 = 0; b) 9 5 = 0; c) + 3 = 0. Rezolvare. a) 7 = 0 ( 7) = 0 1 = 0, = 7 ; b) 9 5 = 0 9 = 5 = 5 9 1, = ± 5 3 ; c) + 3 = 0 = 3, de unde rezulta ca ecuatia nu are radacini (membrul din stanga egalitatii este nenegativ, iar cel din dreapta - negativ). In continuare vom analiza cateva eemple de ecuatii ce se reduc la rezolvarea ecuatiilor de gradul al doilea.
3 Ecuatii bipatrate. Ecuatia de forma a 4 + b + c = 0 (9) unde a, b, c R, a 0, - variabila, se numeste ecuatie bipatrata. Prin substitutia = t (atunci 4 = t ) ecuatia bipatrata se reduce la o ecuatie de gradul al doilea. Eemplul 3. Sa se rezolve ecuatiile a) = 0; b) = 0; c) = 0. Rezolvare. a) Se noteaza = t, atunci 4 = t si se obtine o ecuatie de gradul al doilea in t: t 9t = 0 cu solutiile t 1 = 4 si t = 5. Astfel se obtine totalitatea de ecuatii [ = 4, = 5, de unde rezulta solutiile = ± si = ±5. b) Se procedeaza similar eemplului precedent si se obtine ecuatia patrata t + t 6 = 0 cu solutiile t = 3 si t =. Cum t = 0, ramane t = =, de unde = ±. c) Se utilizeaza substitutia t =, si se obtine ecuatia de gradul al doilea in t, t 3t+4 = 0 care nu are solutii reale. Prin urmare, si ecuatia enuntata nu are solutii reale. Ecuatii simetrice de gradul patru. Ecuatiile de forma a 4 + b 3 + c + b + a = 0 (10) unde a, b, c R, a 0 se numesc ecuatii simetrice de gradul patru. Prin intermediul substitutiei t = + 1 acest tip de ecuatii se reduce la ecuatii de gradul al doilea. In adevar, cum = 0 nu este solutie a ecuatiei (10) (a 0), multiplicand cu 1 ambii membri ai ecuatiei, se obtine ecuatia echivalenta a + b + c + b + a = 0 a ( + 1 ) ( + b + 1 ) + c = 0. Se noteaza + 1 = t atunci t si cum + 1 ( = + 1 = t ), ecuatia devine a(t ) + bt + c = 0, 3
4 adica o ecuatie de gradul al doilea, rezolvarea careia nu prezinta greutati. Nota. Ecuatia a 4 b 3 ± c ± b + a = 0 se reduce la o ecuatie utilizand substitutia t = 1. Eemplul 4. Sa se rezolve ecuatiile a) = 0, b) = 0. Rezolvare. a) Ecuatia data este o ecuatie simetrica de gradul patru. Cum = 0 nu e solutie, ecuatia este echivalenta cu ecuatia (se divide la 0 si se grupeaza convenabil) + 1 ( ) + = 0. Se noteaza t = + 1, t, atunci + 1 = t si ecuatia devine t + 5t + = 0 t + 5t = 0, cu solutiile t 1 = 5, t = 0 (nu se verifica conditia t ). Prin urmare, + 1 = 5, de unde rezulta ecuatia patrata = 0 cu solutiile 1 = 5 1 si = b) Cum = 0 nu este solutie a ecuatiei date, se divide cu si se obtine ecuatia ( + 1 ) ( ) 4 = 0. Se noteaza t = 1, atunci + 1 = ( 1 ) + = t + si se obtine ecuatia patrata (t + ) + 3t 4 = 0 t + 3t = 0, cu solutiile t 1 = 0 si t = 3. Prin urmare 1 = 0, 1 = 3. Din prima ecuatie a sistemului se obtine 1 = 1 si = 1, iar din a doua 3 = si 4 = 1. Ecuatii reversibile 4
5 Ecuatia a 4 + b 3 + c + d + e = 0, (11) unde {a, b, c, d} R, a 0, b 0 si e a = ( d b ) se numeste ecuatie reversibila de gradul patru. Acest tip de ecuatii se reduc la ecuatii de gradul al doilea utilizand substitutia t = + d b. Eemplul 5. Sa se rezolve ecuatia = 0. ( ( ) 4 Rezolvare. Se observa ca = si prin urmare ecuatia este o ecuatie reversibila 1) 1 de gradul patru. Cum = 0 nu este soltuie, se divide la (si nu se pierd solutii), si se obtine ecuatia = 0. Se noteaza t =, atunci t = + 4 4, de unde + 4 = t + 4 si se obtine ecuatia de gradul al doilea t t 6 = 0 t + t = 0 cu solutiile t 1 = si t = 1. Astfel se obtine totalitatea =, = 1,, echivalent ( 0) [ + = 0, = 0, de unde se obtin solutiile = 1 ± 3, = 1 si =. Ecuatii de forma Se utilizeaza substitutia t = + a + b Eemplul 6. Sa se rezolve ecuatia ( + a) 4 + ( + b) 4 = c. (1) si se reduce la o ecuatie bipatrata in raport cu t. ( + 3) 4 + ( 1) 4 = 8. Rezolvare. Se utileaza substitutia t = ( 1) = +1 si se obtine ecuatia echivalenta in t: (t + ) 4 + (t ) 4 = 8 5
6 t 4 + 8t 3 + 4t + 3t t 4 8t 3 + 4t 3t = 0 de unde rezulta ecuatia bipatrata t 4 + 4t 5 = 0 cu solutia t = 1, de unde t = ±1 si + 1 = ±1 conduce la solutiile = si = 0. Ecuatia de forma ( + a)( + b)( + c)( + d) = m (13) unde a + b = c + d. Acest tip de ecuatii se reduce la ecuatii de gradul doi utilizand esential conditia a+b = c+d. In adevar, ( + a)( + b) = + (a + b) + ab ( + c)( + d) = + (c + d) + cd = + (a + b) + cd si notand +(a+b) = t ( +(a+b)+ab = t) se obtine ecuatia patrata (t+ab)(t+cd) = m (respectiv t(t + cd ab) = m). Eemplul 7. Sa se rezolve ecuatia ( )( + 1)( + 4)( + 7) = 19. Rezolvare. Se observa ca + 7 = 1 + 4, se grupeaza convenabil si se deschid parantezele rotunde [( )( + 7)] [( + 1)( + 4)] = 19 [ ][ ] = 19. Se noteaza t = , atunci = t + 18 si ecuatia devine t(t + 18) = 19 t + 18t 19 = 0 cu solutiile t = 19 si t = 1. Asadar, se obtine totalitatea de ecuatii = 19, = 1, cu solutiile 1, = 5 ± 5 si 3,4 = 5 ± 85. Ecuatii fractionar-rationale 6
7 Eemplul 8. Sa se rezolve ecuatiile: a) = 0; b) c) 1 ( )( 3) = 0; = 0; d) = { Rezolvare. a) DVA al ecuatiei este R \ 3; 4 }. In DVA ecuatia este echivalenta cu 5 ecuatia (se multiplica ambii membri ai ecuatiei cu (5 4)( + 3)): (3 + 4)( + 3) ( 1)(5 4) = 0 de unde, deschizand parantezele, se obtine ecuatia patrata = 0 cu solutiile 1 = 7 si = 4. Ambele solutii verifica DVA. b) DVA al ecuatiei este R \ {; 3}. Se multiplica ambii membri ai ecuatiei cu ( )( 3) (in DVA acest produs este diferit de zero) si se obtine ecuatia 1 + ( )( 3) + 3 = = 0 cu solutiile 1 = 1 si =. Cum ultima radacina nu verifica DVA ramane = 1. c) DVA al ecuatiei este R \ {3; 4; 5; 6}. Se grupeaza convenabil ( ) ( ) = 0 5 si se aduce la numitor comun in fiecare paranteza 9 ( 6)( 3) + 9 ( 4)( 5) = 0. Se multiplica cu ( 6)( 3)( 4)( 5) ( 0 pe DVA) si se obtine ecuatia ( 9)( 4)( 5) + ( 9)( 6)( 3) = 0 ( 9)[( 4)( 5) + ( 6)( 3)] = 0, 7
8 de unde rezulta totalitatea de ecuatii 9 = 0, = 0 cu solutiile = 9, = 9 ± 5. d) DVA al ecuatiei este R \ {1; 3; 4; 5}. Se evidentiaza partea intreaga a fiecarui termen al ecuatiei: = = de unde = = Se aduce in fiecare membru la numitor comun si se obtine de unde rezulta totalitatea de ecuatii ( 1)( 3) = ( 4)( 5) ( 4)( 5) ( 1)( 3) = 0, = 0, = 0, cu solutiile 1 = 0 si,3 = 7 ± 3 (toate solutiile sunt din DVA). Ecuatii de forma p a + b + c + q a + d + c = r, (r 0). (14) Acest tip de ecuatii se reduc la ecuatii patrate utilizand substitutia t = a + c. Eemplul 9. Sa se rezolve ecuatia Rezolvare. DVA al ecuatiei este R \ ecuatia se scrie { 1; = 6. }. Cum = 0 nu este solutie a acestei ecuatii, = 6 8
9 (numaratorul si numitorul fractiilor din membrul stang al ecuatiei se divid cu ). Se noteaza t = + 3 si ecuatia devine t t + 1 = 6 (t + 1) + 13(t 5) = 6(t 5)(t + 1), de unde rezulta ecuatia patrata 6t 39t + 33 = 0 t 13t + 11 = 0 cu solutiile t 1 = 1 si t = 11 (ambele solutii verifica restrictiile t 5 si t 1). Prin urmare, se obtine totalitatea de ecuatii + 3 = 1, + 3 = = 0,, = 0 cu solutiile 1 = 3 4 si =. Ecuatiile de forma Ecuatii ce contin epresii reciproc inverse a f() g() + b g() + c = 0 (ab 0), (15) f() se reduc la ecuatii patrate prin substitutia t = f() g(), atunci g() f() = 1 t at + ct + b = 0. Eemplul 10. Sa se rezolve ecuatiile a) ( + 1 = 5, b) { 1 } ; 0 Rezolvare. a) DVA al ecuatiei este R \ ) 5 si ecuatia (15) se scrie ( ) = 0.. Se noteaza t = + 1, atunci = 4 1 t si ecuatia devine t + 4 t = 5 de unde rezulta ecuatia t 5t + 4 = 0 cu solutiile t 1 = 1 si t = 4. Astfel se obtine totalitatea de ecuatii de gradul intai = 1, = 4,
10 cu solutiile = 1 si = 1 (ambele solutii verifica DVA). b) DVA al ecuatiei este R \ {±1}. Se observa, ca = ± nu verifica ecuatia data si prin urmare multiplicand ecuatia cu 1 se obtine ecuatia echivalenta 4 Se noteaza t = ( )( 1) ( + 1)( + ) ( )( 1) + )( + 1) 0 5( + 48 = 0. ( + 1)( + ) ( 1)( ) si ecuatia devine 0t 5 t + 48 = 0 0t + 48t 5 = 0 cu solutiile t 1 = 1 10 si t = 5. Astfel se obtine totalitatea de ecuatii ( )( 1) ( + 1)( + ) = 1 10, ( )( 1) ( + 1)( + ) = 5, cu solutiile 1 = 3, = (ambele solutii sunt din DVA). 3 In unele cazuri este comod de separat un patrat complet. Eemplul 11. Sa se rezolve ecuatiile = 0, = 0, a) = 0; b) + Rezolvare. a) Se separa un patrat complet ( ) = = 0, ( ) ( ) + 1 = 0. Se noteaza t = si se obtine ecuatia patrata t t + 1 = 0 de unde t = 1, 1 = 0, cu solutiile = 1 ± 5. { 1 b) DVA al ecuatiei este R \. Se aduna in ambii membri ai ecuatiei epresia } 1 10
11 si se obtine ( + de unde rezulta ecuatia ( Se noteaza t = 1 ( ) = si ecuatia devine ) = ) 1 = 0. t t = 0. Solutiile acestei ecuatii sunt t = 1 si t =, prin urmare se obtine totalitatea de ecuatii 1 = 1, 1 =, + 1 = 0, + 1 = 0, cu solutiile 1, = 1 ± 3 si 3 = 1. Inecuatii de gradul doi si inecuatii reductibile la cele se gradul doi Prin inecuatie de gradul al doilea se intelege una din urmatoarele inecuatii a + b + c > 0, (16) unde a, b, c R, a 0. a + b + c 0, (17) a + b + c < 0, (18) a + b + c 0, (19) Inecuatiile de gradul al doilea se rezolva utilizand urmatoarele afirmatii. 11
12 Afirmatia. Daca a > 0 si discriminantul trinomului a + b + este pozitiv, atunci: 1. inecuatia (16) are solutiile ( ; 1 ) ( ; + );. inecuatia (17) are solutiile ( ; 1 ] [ ; + ); 3. inecuatia (18) are solutiile ( 1, ); 4. inecuatia (19) are solutiile [ 1, ] unde 1 si ( 1 < ) sunt radacinile trinomului a + b + c. Afirmatia 3. Daca a > 0 si discriminantul trinomului a + b + c este egal cu zero, atunci 1. inecuatia (16) are solutiile R \ { 1 };. inecuatia (17) are solutiile R; 3. inecuatia (18) nu are solutii; 4. inecuatia (18) are o solutie unica: = 1, unde 1 este radacina dubla a trinomului a + b + c. Afirmatia 4. Daca a > 0 si dscriminantul trinomului a + b + c este negativ, atunci 1. inecuatiile (16) si (17) au solutiile R;. inecuatiile (18) si (19) nu au solutii. Daca a < 0 inecuatile (16)-(19) se multiplica prin (-1) si schimband semnul inecuatiei in opusul lui se obtine o inecuatie cu a > 0 si se aplica afirmatiile -4. Eemplul 1. Sa se rezolve inecuatiile a) 90 > 0; d) + > 0; b) ; e) ; c) 6 < 0; f) Rezolvare. a) Cum radacinile trinomului 90 sunt 1 = 9 si = 10, a = 1 > 0, solutiile inecuatiei 90 > 0 sunt ( ; 9) (10; + ). b) Cum discriminatul trinomului este egal cu zero, a = 4 > 0, unica solutie a inecuatiei este = 3. c) Radacinile trinomului 6 sunt 1 = 0 si = 6. Cum a = 1 > 0, solutiile inecuatiei 6 < 0 sunt (0; 6). d) Discriminantul trinomului + este negativ, a = 1 > 0, prin urmare, orice numar real este solutie a inecuatiei + > 0. 1
13 e) Se multiplica ambii membri ai inecuatiei cu 1 si se obtine inecuatia cu solutiile ( ; 1 3 ] [ 1 ; + ). f) Inecuatia data nu are solutii. Metodele de reducere ale ecuatiilor de grad superior la ecuatii de gradul al doilea raman valabile si in cazul inecuatiilor. In unele cazuri se utilizeaza in plus metoda intervalelor (a se vedea [1]-[4]). Eemplul 13. Sa se rezolve inecuatiile a) ; b) ( )( 4)( 6) 9; c) < 0; d) < 0; e) ; f) > 1; g) ( + 5) 4 + ( + 3) 4 < 7. Rezolvare. a) Se rezolva ecuatia (a se vedea (10)) = 0 si se determina zerourile membrului din stanga inecuatiei: = 0 6 ( + 1 ) ( ) 38 = 0 [ ( ) ( ] ) 6t + 5t 50 = 0, 38 = 0 t = + 1, t 1 = 10 3, t = 5, t = + 1, + 1 = 10 3, + 1 = 5, = 0, 5 + = 0, 1 = 3, = 1 3, 3 = 1, 4 =. Prin urmare ( + 3) 13 ( + 1 ) ( 1 ) ( ) 0 3
14 de unde, utilizand metoda intervalelor, se obtine multime solutiilor inecuatiei initiale [ 3; 1 3] [ 1 ; ]. b) Se tine seama de metoda de rezolvare a ecuatiilor de tip (13) si se obtine ( )( 4)( 6) 9 ( 6)( )( 4) 9 0 { t(t + 8) 9 0, ( 6)( 6 + 8) 9 0 t = 6, [ { t + 8t 9 0, t 9, [ 6 9, t 1 t = 6, 6 1, t = 6, [ [ , = 3, 6 1 0, ( ; 3 10] [3 + 10; + ), c) Se separa un patrat complet, ( ; 3 10] {3} [3 + 10; + ) < 0 ( ) < 0 { t { 4t + 3 < 0, 1 < t < 3, ( ) 4( ) + 3 < 0 t =, t =, { { 1 < < 3, < 3, 3 < 0, [ > 1 +, > 1, 1 > 0, < 1, d) Se utilizeaza metoda intervalelor ( 1; 1 ) (1 + ; 3). ( )( 1) ( 3) 8 ( 3)( 1) < 0 < 0 5 ( 3)( 1) (0; 1) (3; 5). < 0 ( 5) ( 3)( 1) < 0 e) Se rezolva ecuatia (a se vedea (11)) = 0 si se determina zerourile membrului din stanga inecuatiei (se tine seama ca = 0 este solutie 14
15 a inecuatiei) = 0 (5 + 1 ) [ ( ) ( 10] ) + 74 = 0 Prin urmare t = 6, t = 9, t = 5 + 1, = 6, = 9, ( ) + 74 = 0 t = 0, t = 5 + 1, [ = 0, = 0, = 1 5, = 1, = 1, = 5. ( 1 ) ( ( 1) 1 ) ( ) Se utilizeaza metoda intervalelor si se obtine ( ; 1] [ ; 1 ] [1; + ). 5 5 f) Cum = 0 nu este solutie a inecuatiei (0 > 1) inecuatia enuntata este echivalenta cu inecuatia > 1. Se noteaza t = , atunci + ( = + 7 ) = t si inecuatia devine t t 10 > 1. Se rezolva cu ajutorul metodei intervalelor si se obtine (t 10) + 3(t 4) (t 10)(t 4) > 0 t 5t + 7 (t 4)(t 10) (t )(t 10) < 0 ( t 9 ) (t 8) (t 4)(t 10) < 0 t (4; 9 ) (5; 8). Prin urmare 4 < + 7 < 9, 5 < + 7 de unde < 8, > 0, < 0, > 0, < 0, 15
16 { > 0, < 0, > 0, [ < 0, 1 < < 7, [, (1; 7), (1; 7). g) Se grupeaza t = , t = + 4 (a se vedea (1)) si inecuatia devine de unde rezulta (t + 1) 4 + (t 1) 4 < 7 t 4 + 6t 135 < 0 (t 9)(t + 15) < 0 t < 3. Prin urmare + 4 < 3. Se utilizeaza proprietatile modulului si se obtine I. Sa se rezolve ecuatiile 1. ( + 1)( + )( + 3) = 4.. (1 )( )( + 3)( + 3) = ( + ) = < 3 3 < + 4 < 3 7 < < 1. Eercitii pentru autoevaluare 4. ( + 5 4) 5 ( + 5 4) = ( ) ( ) + = = = 13 5 ( + 3 ) ( = ) = = ( 1)( + 3) = 0. 16
17 1. 3 ( + )( 1) = 1 ( 1) + 3 ( 3). 13. ( + + 1)( + + ) = = = 0. II. Sa se rezolve inecuatiile < > < < < < ( 1)( )( + 3)( + 4) ( 1) 4 + ( + 1) ( ) ( ) + 1. Bibliografie 1. P.Cojuhari. Ecuatii si inecuatii. Teorie si practica. Chisinau, Universitas, P.Cojuhari, A.Corlat. Ecuatii si inecuatii algebrice. Mica biblioteca a elevului. Chisinau, Editura ASRM, F.Iavemciuk, P.Rudenko. Alghebra i elementarnii funktii. Kiev, Naukova Dumka, 1987 (ucr.). 4. Gh.Andrei si altii. Eercitii si probleme de algebra pentru concursuri si olimpiade scolare. Partea I, Constanta,
ON THE QUATERNARY QUADRATIC DIOPHANTINE EQUATIONS (II) NICOLAE BRATU 1 ADINA CRETAN 2
 ON THE QUATERNARY QUADRATIC DIOPHANTINE EQUATIONS (II) NICOLAE BRATU 1 ADINA CRETAN ABSTRACT This paper has been updated and completed thanks to suggestions and critics coming from Dr. Mike Hirschhorn,
ON THE QUATERNARY QUADRATIC DIOPHANTINE EQUATIONS (II) NICOLAE BRATU 1 ADINA CRETAN ABSTRACT This paper has been updated and completed thanks to suggestions and critics coming from Dr. Mike Hirschhorn,
Soluţii juniori., unde 1, 2
 Soluţii juniori Problema 1 Se consideră suma S x1x x3x4... x015 x016 Este posibil să avem S 016? Răspuns: Da., unde 1,,..., 016 3, 3 Termenii sumei sunt de forma 3 3 1, x x x. 3 5 6 sau Cristian Lazăr
Soluţii juniori Problema 1 Se consideră suma S x1x x3x4... x015 x016 Este posibil să avem S 016? Răspuns: Da., unde 1,,..., 016 3, 3 Termenii sumei sunt de forma 3 3 1, x x x. 3 5 6 sau Cristian Lazăr
FORMULELE LUI STIRLING, WALLIS, GAUSS ŞI APLICAŢII
 DIDACTICA MATHEMATICA, Vol. 34), pp. 53 67 FORMULELE LUI STIRLING, WALLIS, GAUSS ŞI APLICAŢII Eugenia Duca, Emilia Copaciu şi Dorel I. Duca Abstract. In this paper are presented the Wallis, Stirling, Gauss
DIDACTICA MATHEMATICA, Vol. 34), pp. 53 67 FORMULELE LUI STIRLING, WALLIS, GAUSS ŞI APLICAŢII Eugenia Duca, Emilia Copaciu şi Dorel I. Duca Abstract. In this paper are presented the Wallis, Stirling, Gauss
Laborator 4. Rezolvarea ecuaţiilor diferenţiale în Matlab
 Laborator 4. Rezolvarea ecuaţiilor difereţiale î Matlab Bibliografie. G. Aastassiou, I. Iata, Itelliget Routies: Solvig Mathematical Aalsis with Matlab, Mathcad, Mathematica ad Maple, Spriger, 03.. I.
Laborator 4. Rezolvarea ecuaţiilor difereţiale î Matlab Bibliografie. G. Aastassiou, I. Iata, Itelliget Routies: Solvig Mathematical Aalsis with Matlab, Mathcad, Mathematica ad Maple, Spriger, 03.. I.
Teorema Reziduurilor şi Bucuria Integralelor Reale Prezentare de Alexandru Negrescu
 Teorema Reiduurilor şi Bucuria Integralelor Reale Preentare de Alexandru Negrescu Integrale cu funcţii raţionale ce depind de sint şi cost u notaţia e it, avem: cost sint i ( + ( dt d i, iar integrarea
Teorema Reiduurilor şi Bucuria Integralelor Reale Preentare de Alexandru Negrescu Integrale cu funcţii raţionale ce depind de sint şi cost u notaţia e it, avem: cost sint i ( + ( dt d i, iar integrarea
Barem de notare clasa a V-a
 Barem de notare clasa a V-a Problema1. Determinați mulțimile A și B, formate din numere naturale, știind că îndeplinesc simultan condițiile: a) A B,5,6 ; b) B A 0,7 ; c) card AB 3; d) suma elementelor
Barem de notare clasa a V-a Problema1. Determinați mulțimile A și B, formate din numere naturale, știind că îndeplinesc simultan condițiile: a) A B,5,6 ; b) B A 0,7 ; c) card AB 3; d) suma elementelor
DanielaMANEA. x n +a 1. EdituraParalela45
 DanielaMANEA REZOLVAREA ECUAŢILORALGEBRICE DEGRAD SUPERIOR n +a n- + +a n =0 EdituraParalela45 Daniela Manea REZOLVAREA ECUAŢIILOR ALGEBRICE DE GRAD SUPERIOR Referent ştiinţific: lectunivdr Eduard Asadurian
DanielaMANEA REZOLVAREA ECUAŢILORALGEBRICE DEGRAD SUPERIOR n +a n- + +a n =0 EdituraParalela45 Daniela Manea REZOLVAREA ECUAŢIILOR ALGEBRICE DE GRAD SUPERIOR Referent ştiinţific: lectunivdr Eduard Asadurian
Divizibilitate în mulțimea numerelor naturale/întregi
 Divizibilitate în mulțimea numerelor naturale/întregi Teorema îmărţirii cu rest în mulțimea numerelor naturale Fie a, b, b 0. Atunci există q, r astfel încât a=bq+r, cu 0 r < b. În lus, q şi r sunt unic
Divizibilitate în mulțimea numerelor naturale/întregi Teorema îmărţirii cu rest în mulțimea numerelor naturale Fie a, b, b 0. Atunci există q, r astfel încât a=bq+r, cu 0 r < b. În lus, q şi r sunt unic
Procedeu de demonstrare a unor inegalităţi bazat pe inegalitatea lui Schur
 Procedeu de demonstrare a unor inegalităţi bazat pe inegalitatea lui Schur Andi Gabriel BROJBEANU Abstract. A method for establishing certain inequalities is proposed and applied. It is based upon inequalities
Procedeu de demonstrare a unor inegalităţi bazat pe inegalitatea lui Schur Andi Gabriel BROJBEANU Abstract. A method for establishing certain inequalities is proposed and applied. It is based upon inequalities
Rădăcina pătrată a unei matrici reale de ordinul 2
 Rădăcina pătrată a unei matrici reale de ordinul Mircea Crasmareanu Mai 19, 017 ( a c Actorii acestei poveşti: matricile A = M b d (R. PROBLEMA STUDIATĂ: Există B M (R aşa încât: B = A? O astfel de matrice
Rădăcina pătrată a unei matrici reale de ordinul Mircea Crasmareanu Mai 19, 017 ( a c Actorii acestei poveşti: matricile A = M b d (R. PROBLEMA STUDIATĂ: Există B M (R aşa încât: B = A? O astfel de matrice
Sisteme cu logica fuzzy
 Sisteme cu logica fuzzy 1/15 Sisteme cu logica fuzzy Mamdani Fie un sistem cu logică fuzzy Mamdani două intrări x şi y ieşire z x y SLF Structura z 2/15 Sisteme cu logica fuzzy Mamdani Baza de reguli R
Sisteme cu logica fuzzy 1/15 Sisteme cu logica fuzzy Mamdani Fie un sistem cu logică fuzzy Mamdani două intrări x şi y ieşire z x y SLF Structura z 2/15 Sisteme cu logica fuzzy Mamdani Baza de reguli R
1.3. OPERAŢII CU NUMERE NEZECIMALE
 1.3. OPERAŢII CU NUMERE NEZECIMALE 1.3.1 OPERAŢII CU NUMERE BINARE A. ADUNAREA NUMERELOR BINARE Reguli de bază: 0 + 0 = 0 transport 0 0 + 1 = 1 transport 0 1 + 0 = 1 transport 0 1 + 1 = 0 transport 1 Pentru
1.3. OPERAŢII CU NUMERE NEZECIMALE 1.3.1 OPERAŢII CU NUMERE BINARE A. ADUNAREA NUMERELOR BINARE Reguli de bază: 0 + 0 = 0 transport 0 0 + 1 = 1 transport 0 1 + 0 = 1 transport 0 1 + 1 = 0 transport 1 Pentru
Rezolvarea ecuaţiilor şi sistemelor de ecuaţii diferenţiale ordinare (II)
 Rezolvarea ecuaţiilor şi sistemelor de ecuaţii diferenţiale ordinare (II) Metode multipas Prof.dr.ing. Universitatea "Politehnica" Bucureşti, Facultatea de Inginerie Electrică Suport didactic pentru disciplina
Rezolvarea ecuaţiilor şi sistemelor de ecuaţii diferenţiale ordinare (II) Metode multipas Prof.dr.ing. Universitatea "Politehnica" Bucureşti, Facultatea de Inginerie Electrică Suport didactic pentru disciplina
APLICAŢII ALE FORMULELOR LUI NEWTON PENTRU POLINOAME SIMETRICE
 DIDACTICA MATHEMATICA, Vol. 33(2015), pp. 27 37 APLICAŢII ALE FORMULELOR LUI NEWTON PENTRU POLINOAME SIMETRICE Cristina-Aida Coman Abstract. In this paper we present some applications of Newton s formulae
DIDACTICA MATHEMATICA, Vol. 33(2015), pp. 27 37 APLICAŢII ALE FORMULELOR LUI NEWTON PENTRU POLINOAME SIMETRICE Cristina-Aida Coman Abstract. In this paper we present some applications of Newton s formulae
O V E R V I E W. This study suggests grouping of numbers that do not divide the number
 MSCN(2010) : 11A99 Author : Barar Stelian Liviu Adress : Israel e-mail : stelibarar@yahoo.com O V E R V I E W This study suggests grouping of numbers that do not divide the number 3 and/or 5 in eight collumns.
MSCN(2010) : 11A99 Author : Barar Stelian Liviu Adress : Israel e-mail : stelibarar@yahoo.com O V E R V I E W This study suggests grouping of numbers that do not divide the number 3 and/or 5 in eight collumns.
Cristalul cu N atomi = un sistem de N oscilatori de amplitudini mici;
 Curs 8 Caldura specifica a retelei Cristalul cu N atomi = un sistem de N oscilatori de amplitudini mici; pentru tratarea cuantica, se inlocuieste tratamentul clasic al oscilatorilor cuplati, cu cel cuantic
Curs 8 Caldura specifica a retelei Cristalul cu N atomi = un sistem de N oscilatori de amplitudini mici; pentru tratarea cuantica, se inlocuieste tratamentul clasic al oscilatorilor cuplati, cu cel cuantic
Despre AGC cuasigrupuri V. Izbaș
 Despre AGC cuasigrupuri V Izbaș 1 Introducere Se ştie că grupurile au apărut în matematică ca grupuri de automorfisme Rolul automorfismelor este remarcabil şi bine cunoscut La studierea diverselor structuri
Despre AGC cuasigrupuri V Izbaș 1 Introducere Se ştie că grupurile au apărut în matematică ca grupuri de automorfisme Rolul automorfismelor este remarcabil şi bine cunoscut La studierea diverselor structuri
MATEMATICĂ 3 PROBLEME DE REFLECŢIE
 Recapitulare din liceu MATEMATIĂ 3 ANALIZĂ OMPLEXĂ PROBLEME DE REFLEŢIE. Scrieţi numerele următoare sub forma a + bi, unde a, b R: a) 3i + i ; b) i + i ;. Reolvaţi în ecuaţiile: ( + i)( i) c) ( + i)(4
Recapitulare din liceu MATEMATIĂ 3 ANALIZĂ OMPLEXĂ PROBLEME DE REFLEŢIE. Scrieţi numerele următoare sub forma a + bi, unde a, b R: a) 3i + i ; b) i + i ;. Reolvaţi în ecuaţiile: ( + i)( i) c) ( + i)(4
Câteva rezultate de algebră comutativă
 Facultatea de Matematică Anul II Master, Geometrie Algebrică Câteva rezultate de algebră comutativă Aceste note conţin noţiuni şi rezultate de algebră comutativă care sunt utilizate pe parcursul cursului.
Facultatea de Matematică Anul II Master, Geometrie Algebrică Câteva rezultate de algebră comutativă Aceste note conţin noţiuni şi rezultate de algebră comutativă care sunt utilizate pe parcursul cursului.
TWO BOUNDARY ELEMENT APPROACHES FOR THE COMPRESSIBLE FLUID FLOW AROUND A NON-LIFTING BODY
 U.P.B. Sci. Bull., Series A, Vol. 7, Iss., 9 ISSN 3-77 TWO BOUNDARY ELEMENT APPROACHES FOR THE COMPRESSIBLE FLUID FLOW AROUND A NON-LIFTING BODY Luminiţa GRECU, Gabriela DEMIAN, Mihai DEMIAN 3 În lucrare
U.P.B. Sci. Bull., Series A, Vol. 7, Iss., 9 ISSN 3-77 TWO BOUNDARY ELEMENT APPROACHES FOR THE COMPRESSIBLE FLUID FLOW AROUND A NON-LIFTING BODY Luminiţa GRECU, Gabriela DEMIAN, Mihai DEMIAN 3 În lucrare
Gradul de comutativitate al grupurilor finite 1
 Gradul de comutativitate al grupurilor finite Marius TĂRNĂUCEANU Abstract The commutativity degree of a group is one of the most important probabilistic aspects of finite group theory In this survey we
Gradul de comutativitate al grupurilor finite Marius TĂRNĂUCEANU Abstract The commutativity degree of a group is one of the most important probabilistic aspects of finite group theory In this survey we
Cercet¼ari operaţionale
 Cercet¼ari operaţionale B¼arb¼acioru Iuliana Carmen CURSUL 9 Cursul 9 Cuprins Programare liniar¼a 5.1 Modelul matematic al unei probleme de programare liniar¼a.................... 5. Forme de prezentare
Cercet¼ari operaţionale B¼arb¼acioru Iuliana Carmen CURSUL 9 Cursul 9 Cuprins Programare liniar¼a 5.1 Modelul matematic al unei probleme de programare liniar¼a.................... 5. Forme de prezentare
COMPARATIVE DISCUSSION ABOUT THE DETERMINING METHODS OF THE STRESSES IN PLANE SLABS
 74 COMPARATIVE DISCUSSION ABOUT THE DETERMINING METHODS OF THE STRESSES IN PLANE SLABS Codrin PRECUPANU 3, Dan PRECUPANU,, Ștefan OPREA Correspondent Member of Technical Sciences Academy Gh. Asachi Technical
74 COMPARATIVE DISCUSSION ABOUT THE DETERMINING METHODS OF THE STRESSES IN PLANE SLABS Codrin PRECUPANU 3, Dan PRECUPANU,, Ștefan OPREA Correspondent Member of Technical Sciences Academy Gh. Asachi Technical
QUASI-ANALYTIC SOLUTIONS OF FIRST-ORDER PARTIAL DIFFERENTIAL EQUATIONS USING THE ACCURATE ELEMENT METHOD
 U.P.B. Sci. Bull., Series A, Vol. 7, Iss., 010 ISSN 13-707 QUASI-ANALYTIC SOLUTIONS OF FIRST-ORDER PARTIAL DIFFERENTIAL EQUATIONS USING THE ACCURATE ELEMENT METHOD Maty BLUMENFELD 1 O ecuaţie diferenţială
U.P.B. Sci. Bull., Series A, Vol. 7, Iss., 010 ISSN 13-707 QUASI-ANALYTIC SOLUTIONS OF FIRST-ORDER PARTIAL DIFFERENTIAL EQUATIONS USING THE ACCURATE ELEMENT METHOD Maty BLUMENFELD 1 O ecuaţie diferenţială
INEGALITĂŢI DE TIP HARNACK ŞI SOLUŢII POZITIVE MULTIPLE PENTRU PROBLEME NELINIARE
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA ŞCOALA DOCTORALĂ DE MATEMATICĂ ŞI INFORMATICĂ INEGALITĂŢI DE TIP HARNACK ŞI SOLUŢII POZITIVE MULTIPLE PENTRU PROBLEME NELINIARE Rezumatul tezei de doctorat Doctorand:
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA ŞCOALA DOCTORALĂ DE MATEMATICĂ ŞI INFORMATICĂ INEGALITĂŢI DE TIP HARNACK ŞI SOLUŢII POZITIVE MULTIPLE PENTRU PROBLEME NELINIARE Rezumatul tezei de doctorat Doctorand:
Teoreme de Analiză Matematică - I (teorema Weierstrass-Bolzano) 1
 Educaţia Matematică Vol. 3, Nr. 1-2 (2007), 79-84 Teoreme de Analiză Matematică - I (teorema Weierstrass-Bolzano) 1 Silviu Crăciunaş, Petrică Dicu, Mioara Boncuţ Abstract In this paper we propose a Weierstrass
Educaţia Matematică Vol. 3, Nr. 1-2 (2007), 79-84 Teoreme de Analiză Matematică - I (teorema Weierstrass-Bolzano) 1 Silviu Crăciunaş, Petrică Dicu, Mioara Boncuţ Abstract In this paper we propose a Weierstrass
PENTRU CERCURILE DE ELEVI
 M.Opincariu, M.Stroe, Despre matrice şi determinanţi de ordinul doi 559 Demonstraţie. Aplicăm Propoziţia 3.5. pentru funcţia: g :[a 1,a ] (0, ), g(x) =1. Bibliografie [1]R.P.BoasJr.,M.B.Marcus,Generalizations
M.Opincariu, M.Stroe, Despre matrice şi determinanţi de ordinul doi 559 Demonstraţie. Aplicăm Propoziţia 3.5. pentru funcţia: g :[a 1,a ] (0, ), g(x) =1. Bibliografie [1]R.P.BoasJr.,M.B.Marcus,Generalizations
Subiecte geometrie licenta matematica-informatica 4 ani
 Class: Date: Subiecte geometrie licenta matematica-informatica 4 ani Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. 1. Complementara unui subspatiu
Class: Date: Subiecte geometrie licenta matematica-informatica 4 ani Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. 1. Complementara unui subspatiu
Rezultate în Teoria Punctului Fix şi Procese Iterative cu Aplicaţii
 Rezultate în Teoria Punctului Fix şi Procese Iterative cu Aplicaţii Asist. drd. Adrian Sorinel Ghiura Departamentul de Matematică & Informatică Universitatea Politehnica din Bucureşti REZUMATUL TEZEI DE
Rezultate în Teoria Punctului Fix şi Procese Iterative cu Aplicaţii Asist. drd. Adrian Sorinel Ghiura Departamentul de Matematică & Informatică Universitatea Politehnica din Bucureşti REZUMATUL TEZEI DE
Nonlinear Vibrations of Elastic Beams
 Acta Technica Napocensis: Civil Engineering & Architecture Vol. 56, No. 1, (2013) Journal homepage: http://constructii.utcluj.ro/actacivileng Nonlinear Vibrations of Elastic Beams Iacob Borş 1, Tudor Milchiş
Acta Technica Napocensis: Civil Engineering & Architecture Vol. 56, No. 1, (2013) Journal homepage: http://constructii.utcluj.ro/actacivileng Nonlinear Vibrations of Elastic Beams Iacob Borş 1, Tudor Milchiş
Habilitation Thesis. Periodic solutions of differential systems: existence, stability and bifurcations
 UNIVERSITATEA BABEŞ BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Habilitation Thesis Mathematics presented by Adriana Buică Periodic solutions of differential systems: existence, stability
UNIVERSITATEA BABEŞ BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Habilitation Thesis Mathematics presented by Adriana Buică Periodic solutions of differential systems: existence, stability
Numere prime. O selecţie de probleme pentru gimnaziu
 Numere prime O selecţie de probleme petru gimaziu Adria Zaoschi Colegiul Natioal "Costache Negruzzi" Iasi (Clasa a V-a) Determiați submulțimea B a mulțimii A 0,,,, 49, 50, formată di toate elemetele lui
Numere prime O selecţie de probleme petru gimaziu Adria Zaoschi Colegiul Natioal "Costache Negruzzi" Iasi (Clasa a V-a) Determiați submulțimea B a mulțimii A 0,,,, 49, 50, formată di toate elemetele lui
Legi de distribuţie (principalele distribuţii de probabilitate) Tudor Drugan
 Legi de distribuţie (principalele distribuţii de probabilitate) Tudor Drugan Introducere In general distribuţiile variabilelor aleatoare definite pe o populaţie, care face obiectul unui studiu, nu se cunosc.
Legi de distribuţie (principalele distribuţii de probabilitate) Tudor Drugan Introducere In general distribuţiile variabilelor aleatoare definite pe o populaţie, care face obiectul unui studiu, nu se cunosc.
Dynamic Response of Beams on Elastic Foundation with Axial Load
 Acta Technica Napocensis: Civil Engineering & Architecture Vol. 56, No. 1, (2013) Journal homepage: http://constructii.utcluj.ro/actacivileng Dynamic Response of Beams on Elastic Foundation with Axial
Acta Technica Napocensis: Civil Engineering & Architecture Vol. 56, No. 1, (2013) Journal homepage: http://constructii.utcluj.ro/actacivileng Dynamic Response of Beams on Elastic Foundation with Axial
PROBLEME DIVERSE lecţie susţinută la lotul de 13 de Andrei ECKSTEIN Bucureşti, 25 mai 2015
 PROBLEME DIVERSE lecţie susţinută la lotul de 13 de Andrei ECKSTEIN Bucureşti, 5 mai 015 I. SUBSTITUŢIA TAIWANEZĂ 1. Fie a, b, c > 0 astfel încât a bc, b ca şi c ab. Determinaţi valoarea maximă a expresiei
PROBLEME DIVERSE lecţie susţinută la lotul de 13 de Andrei ECKSTEIN Bucureşti, 5 mai 015 I. SUBSTITUŢIA TAIWANEZĂ 1. Fie a, b, c > 0 astfel încât a bc, b ca şi c ab. Determinaţi valoarea maximă a expresiei
Reactoare chimice cu curgere piston (ideala) (Plug Flow Reactor PFR) cu amestecare completa (Mixed Flow Reactor MFR) de tip batch (autoclava)
 Reactoare chimice cu curgere piston (ideala) (Plug Flow Reactor PFR) cu amestecare completa (Mied Flow Reactor MFR) de tip batch (autoclava) Reactorul cu curgere ideala Toate particulele se deplaseaza
Reactoare chimice cu curgere piston (ideala) (Plug Flow Reactor PFR) cu amestecare completa (Mied Flow Reactor MFR) de tip batch (autoclava) Reactorul cu curgere ideala Toate particulele se deplaseaza
PLANIFICAREA TEMELOR LA GRUPELE DE EXCELENȚĂ DISCIPLINA MATEMATICĂ AN ȘCOLAR
 PLANIFICAREA TEMELOR LA GRUPELE DE EXCELENȚĂ DISCIPLINA MATEMATICĂ AN ȘCOLAR 0-0 Grupa V. Matematică Profesor coordonator: Aldescu Alina.0.0 Operatii in N-Teorema impartirii cu rest 0..0 Patrate perfecte,cuburi
PLANIFICAREA TEMELOR LA GRUPELE DE EXCELENȚĂ DISCIPLINA MATEMATICĂ AN ȘCOLAR 0-0 Grupa V. Matematică Profesor coordonator: Aldescu Alina.0.0 Operatii in N-Teorema impartirii cu rest 0..0 Patrate perfecte,cuburi
Teoreme de compresie-extensie de tip Krasnoselskii şi aplicaţii (Rezumatul tezei de doctorat)
 Teoreme de compresie-extensie de tip Krasnoselskii şi aplicaţii (Rezumatul tezei de doctorat) Sorin Monel Budişan Coordonator ştiinţi c: Prof. dr. Radu Precup Cuprins Introducere 1 1 Generaliz¼ari ale
Teoreme de compresie-extensie de tip Krasnoselskii şi aplicaţii (Rezumatul tezei de doctorat) Sorin Monel Budişan Coordonator ştiinţi c: Prof. dr. Radu Precup Cuprins Introducere 1 1 Generaliz¼ari ale
Acta Technica Napocensis: Civil Engineering & Architecture Vol. 54 No.1 (2011)
 1 Technical University of Cluj-Napoca, Faculty of Civil Engineering. 15 C Daicoviciu Str., 400020, Cluj-Napoca, Romania Received 25 July 2011; Accepted 1 September 2011 The Generalised Beam Theory (GBT)
1 Technical University of Cluj-Napoca, Faculty of Civil Engineering. 15 C Daicoviciu Str., 400020, Cluj-Napoca, Romania Received 25 July 2011; Accepted 1 September 2011 The Generalised Beam Theory (GBT)
Programarea Dinamica. (si alte chestii adiacente) Andrei Olariu
 Programarea Dinamica (si alte chestii adiacente) Andrei Olariu andrei@olariu.org Despre mine - Absolvent FMI UniBuc - Doctorand in prelucrarea limbajului natural, in special in mediul online (Twitter)
Programarea Dinamica (si alte chestii adiacente) Andrei Olariu andrei@olariu.org Despre mine - Absolvent FMI UniBuc - Doctorand in prelucrarea limbajului natural, in special in mediul online (Twitter)
GAZETA MATEMATICĂ SERIA A. ANUL XXXVI (CXV) Nr. 1 2/ 2018 ARTICOLE. Computing exponential and trigonometric functions of matrices in M 2 (C)
 GAZETA MATEMATICĂ SERIA A ANUL XXXVI CXV) Nr. 1 / 18 ARTICOLE Computing exponential and trigonometric functions of matrices in M C) Ovidiu Furdui 1) Abstract. In this paper we give a new technique for
GAZETA MATEMATICĂ SERIA A ANUL XXXVI CXV) Nr. 1 / 18 ARTICOLE Computing exponential and trigonometric functions of matrices in M C) Ovidiu Furdui 1) Abstract. In this paper we give a new technique for
UNITATEA DE ÎNVĂȚARE 3 Analiza algoritmilor
 UNITATEA DE ÎNVĂȚARE 3 Analiza algoritmilor Obiective urmărite: La sfârşitul parcurgerii acestei UI, studenţii vor 1.1 cunoaște conceptul de eficienta a unui algoritm vor cunoaste si inţelege modalitatile
UNITATEA DE ÎNVĂȚARE 3 Analiza algoritmilor Obiective urmărite: La sfârşitul parcurgerii acestei UI, studenţii vor 1.1 cunoaște conceptul de eficienta a unui algoritm vor cunoaste si inţelege modalitatile
ECUAŢII CU DERIVATE PARŢIALE ŞI EVALUAREA OPŢIUNILOR CU VOLATILITATE STOHASTICĂ
 Universitatea Babeş-Bolyai, Cluj-Napoca Facultatea de Matematică şi Informatică Vasile Lucian Lazăr ECUAŢII CU DERIVATE PARŢIALE ŞI EVALUAREA OPŢIUNILOR CU VOLATILITATE STOHASTICĂ Coordonator ştiinţific
Universitatea Babeş-Bolyai, Cluj-Napoca Facultatea de Matematică şi Informatică Vasile Lucian Lazăr ECUAŢII CU DERIVATE PARŢIALE ŞI EVALUAREA OPŢIUNILOR CU VOLATILITATE STOHASTICĂ Coordonator ştiinţific
SIMULAREA DECIZIEI FINANCIARE
 SIMULAREA DECIZIEI FINANCIARE Conf. univ. dr. Nicolae BÂRSAN-PIPU T5.1 TEMA 5 DISTRIBUŢII DISCRETE T5. Cuprins T5.3 5.1 Variabile aleatoare discrete 5. Distribuţia de probabilitate a unei variabile aleatoare
SIMULAREA DECIZIEI FINANCIARE Conf. univ. dr. Nicolae BÂRSAN-PIPU T5.1 TEMA 5 DISTRIBUŢII DISCRETE T5. Cuprins T5.3 5.1 Variabile aleatoare discrete 5. Distribuţia de probabilitate a unei variabile aleatoare
Reactoare chimice cu curgere piston (ideala) cu amestecare completa de tip batch (autoclava)
 Reactoare chimice cu curgere piston (ideala) cu amestecare completa de tip batch (autoclava) Reactorul cu curgere ideala Toate particulele se deplaseaza intr-o directie de-a lungul reactorului, precum
Reactoare chimice cu curgere piston (ideala) cu amestecare completa de tip batch (autoclava) Reactorul cu curgere ideala Toate particulele se deplaseaza intr-o directie de-a lungul reactorului, precum
Avem 6 tipuri de simboluri in logica predicatelor:
 Semantica Avem 6 tipuri de simboluri in logica predicatelor: Predicate: p, q, r,, p1, q2 etc. Constante: a, b, c,, z, a1, b4,, ion, mihai, labus etc. Variabile: x, y, z, x1, y1, z4 etc. Conective:,,,,
Semantica Avem 6 tipuri de simboluri in logica predicatelor: Predicate: p, q, r,, p1, q2 etc. Constante: a, b, c,, z, a1, b4,, ion, mihai, labus etc. Variabile: x, y, z, x1, y1, z4 etc. Conective:,,,,
METODE NUMERICE: Laborator #4 Eliminare gaussiană cu pivotare totală şi scalare. Algoritmul Thomas pentru rezolvarea sistemului 3-diagonal
 METODE NUMERICE: Laborator #4 Eliminare gaussiană cu pivotare totală şi scalare. Algoritmul Thomas pentru rezolvarea sistemului 3-diagonal Titulari curs: Florin Pop, George-Pantelimon Popescu Responsabil
METODE NUMERICE: Laborator #4 Eliminare gaussiană cu pivotare totală şi scalare. Algoritmul Thomas pentru rezolvarea sistemului 3-diagonal Titulari curs: Florin Pop, George-Pantelimon Popescu Responsabil
HABILITATION THESIS. Qualitative analysis of some differential equations
 Institute of Mathematics,,Simion Stoilow of the Romanian Academy HABILITATION THESIS Qualitative analysis of some differential equations Ioan Liviu Ignat Specialization: Mathematics Bucharest, 212 To
Institute of Mathematics,,Simion Stoilow of the Romanian Academy HABILITATION THESIS Qualitative analysis of some differential equations Ioan Liviu Ignat Specialization: Mathematics Bucharest, 212 To
Autor: Instituţia: Coordonator
 Aplicaţii ale numerelor complexe în geometrie, utilizând Geogebra Mathematics consists in proving the most obvious thing in the least obvious way George Polya Autor: Instituţia: Coordonator ştiinţific:
Aplicaţii ale numerelor complexe în geometrie, utilizând Geogebra Mathematics consists in proving the most obvious thing in the least obvious way George Polya Autor: Instituţia: Coordonator ştiinţific:
Inteligenta Artificiala
 Inteligenta Artificiala Universitatea Politehnica Bucuresti Anul universitar 2010-2011 Adina Magda Florea http://turing.cs.pub.ro/ia_10 si curs.cs.pub.ro 1 Curs nr. 4 Cautare cu actiuni nedeterministe
Inteligenta Artificiala Universitatea Politehnica Bucuresti Anul universitar 2010-2011 Adina Magda Florea http://turing.cs.pub.ro/ia_10 si curs.cs.pub.ro 1 Curs nr. 4 Cautare cu actiuni nedeterministe
Test de Departajare pentru MofM 2014 (Bucureşti) Enunţuri & Soluţii
 Test de Departajare petru MofM 04 Bucureşti Euţuri & Soluţii Problem. Give + distict real umbers i the iterval [0,], prove there exist two of them a b, such that ab a b < Solutio. Idex the umbers 0 a 0
Test de Departajare petru MofM 04 Bucureşti Euţuri & Soluţii Problem. Give + distict real umbers i the iterval [0,], prove there exist two of them a b, such that ab a b < Solutio. Idex the umbers 0 a 0
2. Finite Impulse Response Filters (FIR)
 ..3.3aximum error minimizing method. Finite Imule Reone Filter (FIR)..3 aximum error minimizing method he zero hae tranfer function N H a' n con tye n N H b n con n tye ' the lat relation can be exreed
..3.3aximum error minimizing method. Finite Imule Reone Filter (FIR)..3 aximum error minimizing method he zero hae tranfer function N H a' n con tye n N H b n con n tye ' the lat relation can be exreed
Logică și structuri discrete. Marius Minea 25 septembrie 2017
 Logică și structuri discrete Funcții Marius Minea marius@cs.upt.ro http://cs.upt.ro/~marius/curs/lsd/ 25 septembrie 2017 Ce cuprinde domeniul informaticii? Imagine: https://hkn.eecs.berkeley.edu/courseguides
Logică și structuri discrete Funcții Marius Minea marius@cs.upt.ro http://cs.upt.ro/~marius/curs/lsd/ 25 septembrie 2017 Ce cuprinde domeniul informaticii? Imagine: https://hkn.eecs.berkeley.edu/courseguides
Utilizarea claselor de echivalenta in analiza asistata de calculator a sistemelor cu evenimente discrete
 72 Utilizarea claselor de echivalenta in analiza asistata de calculator a sistemelor cu evenimente discrete Conf.dr. Alexandru TERTISCO, ing. Alexandru BOICEA Facultatea de Automatica si Calculatoare,
72 Utilizarea claselor de echivalenta in analiza asistata de calculator a sistemelor cu evenimente discrete Conf.dr. Alexandru TERTISCO, ing. Alexandru BOICEA Facultatea de Automatica si Calculatoare,
TEZA DE DOCTORAT. probleme de optimizare infinit dimensionale
 Academia Română Institutul de matematică Simion Stoilow TEZA DE DOCTORAT rezumat Aplicaţii ale dualităţii în unele probleme de optimizare infinit dimensionale Coordonator ştiinţific: CS I dr. Dan Tiba
Academia Română Institutul de matematică Simion Stoilow TEZA DE DOCTORAT rezumat Aplicaţii ale dualităţii în unele probleme de optimizare infinit dimensionale Coordonator ştiinţific: CS I dr. Dan Tiba
GAZETA MATEMATICĂ SERIA A. ANUL XXXI(CX) Nr. 1 2/ 2013 ANIVERSĂRI. Profesorul Ioan Tomescu la a 70-a aniversare
 GAZETA MATEMATICĂ SERIA A ANUL XXXI(CX) Nr. / 03 ANIVERSĂRI Profesorul Ioan Tomescu la a 70-a aniversare La 5 noiembrie 0 domnul profesor universitar Ioan Tomescu, membru corespondent al Academiei Române,
GAZETA MATEMATICĂ SERIA A ANUL XXXI(CX) Nr. / 03 ANIVERSĂRI Profesorul Ioan Tomescu la a 70-a aniversare La 5 noiembrie 0 domnul profesor universitar Ioan Tomescu, membru corespondent al Academiei Române,
Pentru clasa a X-a Ştiinţele naturii-sem II
 Pentru clasa a X-a Ştiinţele naturii-sem II Reprezentarea algoritmilor. Pseudocod. Principiile programării structurate. Structuri de bază: structura liniară structura alternativă structura repetitivă Algoritmi
Pentru clasa a X-a Ştiinţele naturii-sem II Reprezentarea algoritmilor. Pseudocod. Principiile programării structurate. Structuri de bază: structura liniară structura alternativă structura repetitivă Algoritmi
Mugur Acu OPERATORUL INTEGRAL LIBERA-PASCU ŞI PROPRIETĂŢILE ACESTUIA CU PRIVIRE LA FUNCŢIILE UNIFORM STELATE, CONVEXE, APROAPE CONVEXE ŞI
 Mugur Acu OPERATORUL INTEGRAL LIBERA-PASCU ŞI PROPRIETĂŢILE ACESTUIA CU PRIVIRE LA FUNCŢIILE UNIFORM STELATE, CONVEXE, APROAPE CONVEXE ŞI α-uniform CONVEXE Editura Universităţii Lucian Blaga din Sibiu
Mugur Acu OPERATORUL INTEGRAL LIBERA-PASCU ŞI PROPRIETĂŢILE ACESTUIA CU PRIVIRE LA FUNCŢIILE UNIFORM STELATE, CONVEXE, APROAPE CONVEXE ŞI α-uniform CONVEXE Editura Universităţii Lucian Blaga din Sibiu
Graduări pe algebre de matrice
 UNIVERSITATEA DIN BUCUREŞTI FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ ŞCOALA DOCTORALĂ DE MATEMATICĂ Graduări pe algebre de matrice TEZĂ DE DOCTORAT REZUMAT Coordonator ştiinţific: Prof.univ.dr. Sorin Dăscălescu
UNIVERSITATEA DIN BUCUREŞTI FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ ŞCOALA DOCTORALĂ DE MATEMATICĂ Graduări pe algebre de matrice TEZĂ DE DOCTORAT REZUMAT Coordonator ştiinţific: Prof.univ.dr. Sorin Dăscălescu
Matematici speciale Integrarea functiilor complexe
 Matematii speiale Integrarea funtiilor omplexe Martie 18 ii Be yourself, everyone else is already taken. Osar Wilde 5 Integrarea funtiilor omplexe Integrala Riemann a unei funtii u valori omplexe se defineste
Matematii speiale Integrarea funtiilor omplexe Martie 18 ii Be yourself, everyone else is already taken. Osar Wilde 5 Integrarea funtiilor omplexe Integrala Riemann a unei funtii u valori omplexe se defineste
Definiţie. Pr(X a) - probabilitatea ca X să ia valoarea a ; Pr(a X b) - probabilitatea ca X să ia o valoare în intervalul a,b.
 Variabile aleatoare Definiţie Se numeşte variabilă aleatoare pe un spaţiu fundamental E şi se notează prin X, o funcţie definită pe E cu valori în mulţimea numerelor reale. Unei variabile aleatoare X i
Variabile aleatoare Definiţie Se numeşte variabilă aleatoare pe un spaţiu fundamental E şi se notează prin X, o funcţie definită pe E cu valori în mulţimea numerelor reale. Unei variabile aleatoare X i
Probleme extremale pentru grafuri si retele de transport
 Revista Inormatica Economica nr 4 (4)/00 9 Proleme extremale pentru grauri si retele de transport Drd Rodica MIRONENCO A variety o prolems can e constructed using Ford-Fulkerson s maximum-low minimumcut
Revista Inormatica Economica nr 4 (4)/00 9 Proleme extremale pentru grauri si retele de transport Drd Rodica MIRONENCO A variety o prolems can e constructed using Ford-Fulkerson s maximum-low minimumcut
Lucrarea de laborator nr. 8
 Metode Numerice Lucrarea de laborator r. 8 I. Scopul lucrării Metoda Newto II. Coţiutul lucrării 1. Metoda tagetei 2. Metoda Newto cazul m-dimesioal III. Prezetarea lucrării III.1. Metoda tagetei Metoda
Metode Numerice Lucrarea de laborator r. 8 I. Scopul lucrării Metoda Newto II. Coţiutul lucrării 1. Metoda tagetei 2. Metoda Newto cazul m-dimesioal III. Prezetarea lucrării III.1. Metoda tagetei Metoda
array a[0..n-1] a[0] = v0,..., a[n-1] = vn-1
![array a[0..n-1] a[0] = v0,..., a[n-1] = vn-1 array a[0..n-1] a[0] = v0,..., a[n-1] = vn-1](/thumbs/76/73793144.jpg) Curs 5 - Agenda sortare interna buble sort sortare prin insertie sortare pri selectie naiva sistematica ( heap sort ) sortare prin interclasare ( merge sort ) sortare rapida ( quick sort ) cautare in liste
Curs 5 - Agenda sortare interna buble sort sortare prin insertie sortare pri selectie naiva sistematica ( heap sort ) sortare prin interclasare ( merge sort ) sortare rapida ( quick sort ) cautare in liste
FINDING THE TRACES OF A GIVEN PLANE: ANALYTICALLY AND THROUGH GRAPHICAL CONSTRUCTIONS
 BULETINUL INSTITUTULUI POLITEHNI DIN IŞI Publicat de Universitatea Tehnică Gheorghe sachi din Iaşi Tomul LVII (LXI), Fasc. 3, 20 Secţia ONSTRUŢII DE MŞINI FINDING THE TRES OF GIVEN PLNE: NLYTILLY ND THROUGH
BULETINUL INSTITUTULUI POLITEHNI DIN IŞI Publicat de Universitatea Tehnică Gheorghe sachi din Iaşi Tomul LVII (LXI), Fasc. 3, 20 Secţia ONSTRUŢII DE MŞINI FINDING THE TRES OF GIVEN PLNE: NLYTILLY ND THROUGH
QUASIGRUPURI AUTOORTOGONALE: CONEXIUNI CU PARATOPIILE UNOR SISTEME ORTOGONALE
 INSTITUTUL DE MATEMATICĂ ŞI INFORMATICĂ AL ACADEMIEI DE ŞTIINŢE A MOLDOVEI Cu titlu de manuscris C.Z.U.: 512.548 CEBAN DINA QUASIGRUPURI AUTOORTOGONALE: CONEXIUNI CU PARATOPIILE UNOR SISTEME ORTOGONALE
INSTITUTUL DE MATEMATICĂ ŞI INFORMATICĂ AL ACADEMIEI DE ŞTIINŢE A MOLDOVEI Cu titlu de manuscris C.Z.U.: 512.548 CEBAN DINA QUASIGRUPURI AUTOORTOGONALE: CONEXIUNI CU PARATOPIILE UNOR SISTEME ORTOGONALE
Laborator 3. Backtracking iterativ
 Programare Delphi Laborator 3 Backtracking iterativ Metoda backtracking este o strategie generală de căutare din aproape în aproape a unei soluţii dintr-o mulţime finită de posibilităţi. Problema trebuie
Programare Delphi Laborator 3 Backtracking iterativ Metoda backtracking este o strategie generală de căutare din aproape în aproape a unei soluţii dintr-o mulţime finită de posibilităţi. Problema trebuie
ELEMENTE DE DINAMICĂ ŞI GEOMETRIE PE SPAŢII VECTORIALE POISSON
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ ELEMENTE DE DINAMICĂ ŞI GEOMETRIE PE SPAŢII VECTORIALE POISSON REZUMATUL TEZEI DE DOCTORAT Conducător ştiinţific: Prof. univ.
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ ELEMENTE DE DINAMICĂ ŞI GEOMETRIE PE SPAŢII VECTORIALE POISSON REZUMATUL TEZEI DE DOCTORAT Conducător ştiinţific: Prof. univ.
Modelling the Steady State Characteristic of ph Neutralization Process: a Neuro-Fuzzy Approach
 BULETINUL Universităţii Petrol Gaze din Ploieşti Vol. LXVII No. 2/2015 79 84 Seria Tehnică Modelling the Steady State Characteristic of ph Neutralization Process: a Neuro-Fuzzy Approach Gabriel Rădulescu
BULETINUL Universităţii Petrol Gaze din Ploieşti Vol. LXVII No. 2/2015 79 84 Seria Tehnică Modelling the Steady State Characteristic of ph Neutralization Process: a Neuro-Fuzzy Approach Gabriel Rădulescu
THE BEHAVIOUR OF ELASTOMERIC BEARINGS UNDER LOAD COMBINATIONS
 BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LX (LXIV), Fasc. 3, 2014 Secţia CONSTRUCŢII. ARHITECTURĂ THE BEHAVIOUR OF ELASTOMERIC BEARINGS
BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LX (LXIV), Fasc. 3, 2014 Secţia CONSTRUCŢII. ARHITECTURĂ THE BEHAVIOUR OF ELASTOMERIC BEARINGS
Curs de Geometrie. Andrei-Dan Halanay
 Curs de Geometrie Andrei-Dan Halanay Cuprins 1 Introducere. Curbe în plan şi spaţiu 3 1.1 Introducere.................................... 3 1.2 Curbe. Noţiuni propedeutice şi exemple....................
Curs de Geometrie Andrei-Dan Halanay Cuprins 1 Introducere. Curbe în plan şi spaţiu 3 1.1 Introducere.................................... 3 1.2 Curbe. Noţiuni propedeutice şi exemple....................
A GENERALIZATION OF A CLASSICAL MONTE CARLO ALGORITHM TO ESTIMATE π
 U.P.B. Sci. Bull., Series A, Vol. 68, No., 6 A GENERALIZATION OF A CLASSICAL MONTE CARLO ALGORITHM TO ESTIMATE π S.C. ŞTEFĂNESCU Algoritmul Monte Carlo clasic A1 estimeazează valoarea numărului π bazându-se
U.P.B. Sci. Bull., Series A, Vol. 68, No., 6 A GENERALIZATION OF A CLASSICAL MONTE CARLO ALGORITHM TO ESTIMATE π S.C. ŞTEFĂNESCU Algoritmul Monte Carlo clasic A1 estimeazează valoarea numărului π bazându-se
Alte rezultate din teoria codurilor
 Prelegerea 20 Alte rezultate din teoria codurilor 20.1 Coduri aritmetice Construcţiile oferite de teoria codurilor pot fi utilizate şi în alte domenii decât în cele clasice, de transmitere şi recepţie
Prelegerea 20 Alte rezultate din teoria codurilor 20.1 Coduri aritmetice Construcţiile oferite de teoria codurilor pot fi utilizate şi în alte domenii decât în cele clasice, de transmitere şi recepţie
Arhivele Electronice Los Alamos arxiv:physics/ v2 [physics.ed-ph] 30 Apr 2000
![Arhivele Electronice Los Alamos arxiv:physics/ v2 [physics.ed-ph] 30 Apr 2000 Arhivele Electronice Los Alamos arxiv:physics/ v2 [physics.ed-ph] 30 Apr 2000](/thumbs/79/79555034.jpg) arxiv:physics/0003106v2 [physics.ed-ph] 30 Apr 2000 Arhivele Electronice Los Alamos http://xxx.lanl.gov/physics/0003106 ELEMENTE DE MECANICĂ CUANTICĂ HARET C. ROSU e-mail: rosu@ifug3.ugto.mx fax: 0052-47187611
arxiv:physics/0003106v2 [physics.ed-ph] 30 Apr 2000 Arhivele Electronice Los Alamos http://xxx.lanl.gov/physics/0003106 ELEMENTE DE MECANICĂ CUANTICĂ HARET C. ROSU e-mail: rosu@ifug3.ugto.mx fax: 0052-47187611
Prof univ dr. Sever Spânulescu - LUCRARI DE LABORATOR
 UNIVERSITATEA HYPERION Facultatea de Stiițe Exacte și Igierești Prof uiv dr. Sever Spâulescu CALCUL NUMERIC - LUCRARI DE LABORATOR Lucrarea de laborator. Rezolvarea sistemelor de ecuatii liiare pri metode
UNIVERSITATEA HYPERION Facultatea de Stiițe Exacte și Igierești Prof uiv dr. Sever Spâulescu CALCUL NUMERIC - LUCRARI DE LABORATOR Lucrarea de laborator. Rezolvarea sistemelor de ecuatii liiare pri metode
RECREAŢ II MATEMATICE REVISTĂ DE MATEMATICĂ PENTRU ELEVI Ş I PROFESORI
 Anul IX, Nr. Iulie Decembrie 007 RECREAŢ II MATEMATICE REVISTĂ DE MATEMATICĂ PENTRU ELEVI Ş I PROFESORI e iπ = 1 Asociaţia Recreaţii Matematice IAŞI - 007 Semnificaţia formulei de pe copertă: iπ Într-o
Anul IX, Nr. Iulie Decembrie 007 RECREAŢ II MATEMATICE REVISTĂ DE MATEMATICĂ PENTRU ELEVI Ş I PROFESORI e iπ = 1 Asociaţia Recreaţii Matematice IAŞI - 007 Semnificaţia formulei de pe copertă: iπ Într-o
3-D FINITE ELEMENT ANALYSIS OF A SINGLE-PHASE SINGLE-POLE AXIAL FLUX VARIABLE RELUCTANCE MOTOR
 BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LIX (LXIII), Fasc. 1, 2013 Secţia ELECTROTEHNICĂ. ENERGETICĂ. ELECTRONICĂ 3-D FINITE ELEMENT
BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LIX (LXIII), Fasc. 1, 2013 Secţia ELECTROTEHNICĂ. ENERGETICĂ. ELECTRONICĂ 3-D FINITE ELEMENT
Metode numerice de aproximare. a zerourilor unor operatori. şi de rezolvare a inegalităţilor variaţionale. cu aplicaţii
 Facultatea de Matematică şi Informatică Universitatea Babeş-Bolyai Erika Nagy Metode numerice de aproximare a zerourilor unor operatori şi de rezolvare a inegalităţilor variaţionale cu aplicaţii Rezumatul
Facultatea de Matematică şi Informatică Universitatea Babeş-Bolyai Erika Nagy Metode numerice de aproximare a zerourilor unor operatori şi de rezolvare a inegalităţilor variaţionale cu aplicaţii Rezumatul
4/68. Mini-comutatoare cu came. Prezentare generalã a sistemului. Întreruptoare Pornit-Oprit TM. Comutatoare de comandã TM.
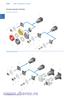 / Mini-comutatoare cu came Prezentare generalã a sistemului Întreruptoare Pornit-Oprit Comutatoare de comandã HA ND AU TO HPL-de-DE O Mini-comutatoare cu came / Montaj pe ușã (.../E) Frontal IP Montaj
/ Mini-comutatoare cu came Prezentare generalã a sistemului Întreruptoare Pornit-Oprit Comutatoare de comandã HA ND AU TO HPL-de-DE O Mini-comutatoare cu came / Montaj pe ușã (.../E) Frontal IP Montaj
ARTICOLE ŞI NOTE MATEMATICE
 S. Rădulescu, M. Drăgan, I. V. Maftei, On W. J. Blundon s inequality 3 ARTICOLE ŞI NOTE MATEMATICE SOME CONSEQUENCES OF W.J.BLUNDON S INEQUALITY Sorin Rădulescu 1), Marius Drăgan 2), I.V.Maftei 3) Abstract.
S. Rădulescu, M. Drăgan, I. V. Maftei, On W. J. Blundon s inequality 3 ARTICOLE ŞI NOTE MATEMATICE SOME CONSEQUENCES OF W.J.BLUNDON S INEQUALITY Sorin Rădulescu 1), Marius Drăgan 2), I.V.Maftei 3) Abstract.
Metode clasice. Camelia Chira.
 Metode clasice Camelia Chira http://users.utcluj.ro/~cchira camelia.chira@cs.utcluj.ro Am vazut deja ca... Probleme de optimizare pot fi foarte complexe SAT, TSP, NLP, etc Spatiul de cautare Clase de complexitate
Metode clasice Camelia Chira http://users.utcluj.ro/~cchira camelia.chira@cs.utcluj.ro Am vazut deja ca... Probleme de optimizare pot fi foarte complexe SAT, TSP, NLP, etc Spatiul de cautare Clase de complexitate
ALGORITMI DE OPTIMIZARE IN INGINERIE ELECTRICA. Sef lucrari ing. Alin-Iulian DOLAN
 ALGORITMI DE OPTIMIZARE IN INGINERIE ELECTRICA Sef lucrari ing. Alin-Iulian DOLAN PROBLEME DE OPTIMIZARE OPTIMIZAREA gasirea celei mai bune solutii ale unei probleme, constand in minimizarea (maximizarea)
ALGORITMI DE OPTIMIZARE IN INGINERIE ELECTRICA Sef lucrari ing. Alin-Iulian DOLAN PROBLEME DE OPTIMIZARE OPTIMIZAREA gasirea celei mai bune solutii ale unei probleme, constand in minimizarea (maximizarea)
INCLUZIUNI OPERATORIALE PRIN TEHNICA PUNCTULUI FIX ÎN SPAŢII METRICE VECTORIALE
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ INCLUZIUNI OPERATORIALE PRIN TEHNICA PUNCTULUI FIX ÎN SPAŢII METRICE VECTORIALE REZUMATUL TEZEI DE DOCTORAT Coordonator ştiinţific
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ INCLUZIUNI OPERATORIALE PRIN TEHNICA PUNCTULUI FIX ÎN SPAŢII METRICE VECTORIALE REZUMATUL TEZEI DE DOCTORAT Coordonator ştiinţific
ROMANIAN MATHEMATICAL SOCIETY
 ROMANIAN MATHEMATICAL SOCIETY Mehedinți Branch ROMANIAN MATHEMATICAL MAGAZINE R.M.M. Nr.20-2018 1 ROMANIAN MATHEMATICAL MAGAZINE NR. 20 ROMANIAN MATHEMATICAL SOCIETY Mehedinți Branch DANIEL SITARU-ROMANIA
ROMANIAN MATHEMATICAL SOCIETY Mehedinți Branch ROMANIAN MATHEMATICAL MAGAZINE R.M.M. Nr.20-2018 1 ROMANIAN MATHEMATICAL MAGAZINE NR. 20 ROMANIAN MATHEMATICAL SOCIETY Mehedinți Branch DANIEL SITARU-ROMANIA
The 2017 Danube Competition in Mathematics, October 28 th. Problema 1. Să se găsească toate polinoamele P, cu coeficienţi întregi, care
 The 017 Dnube Competition in Mthemtics, October 8 th Problem 1. ă se găsescă tote polinomele P, cu coeficienţi întregi, cre verifică relţi + b c P () + P (b) P (c), pentru orice numere întregi, b, c. Problem.
The 017 Dnube Competition in Mthemtics, October 8 th Problem 1. ă se găsescă tote polinomele P, cu coeficienţi întregi, cre verifică relţi + b c P () + P (b) P (c), pentru orice numere întregi, b, c. Problem.
TEOREME DE PUNCT FIX PENTRU OPERATORI CE NU INVARIAZĂ DOMENIUL DE DEFINIŢIE ŞI
 Universitatea Babeş-Bolyai, Cluj-Napoca Facultatea de Matematică şi Informatică Tania Angelica Lazăr TEOREME DE PUNCT FIX PENTRU OPERATORI CE NU INVARIAZĂ DOMENIUL DE DEFINIŢIE ŞI APLICAŢII Coordonator
Universitatea Babeş-Bolyai, Cluj-Napoca Facultatea de Matematică şi Informatică Tania Angelica Lazăr TEOREME DE PUNCT FIX PENTRU OPERATORI CE NU INVARIAZĂ DOMENIUL DE DEFINIŢIE ŞI APLICAŢII Coordonator
FLORENTIN SMARANDACHE Asupra unor conjecturi si probleme nerezolvate referitoare la o functie in Teoria Numerelor
 FLORENTIN SMARANDACHE Asupra unor conjecturi si probleme nerezolvate referitoare la o functie in Teoria Numerelor In Florentin Smarandache: Collected Papers, vol. II. Chisinau (Moldova): Universitatea
FLORENTIN SMARANDACHE Asupra unor conjecturi si probleme nerezolvate referitoare la o functie in Teoria Numerelor In Florentin Smarandache: Collected Papers, vol. II. Chisinau (Moldova): Universitatea
7 ECUAŢII ALGEBRICE ŞI TRANSCENDENTE
 7 ECUAŢII ALGEBRICE ŞI TRANSCENDENTE 7 Separarea rădăcnlor Ecuaţe algebrcă dacă ( este polnom Ecuaţa transcendentă în caz contrar ( = Rădăcnă apromatvă valoare ξ apropată de valoarea eactă ξ Denţ neechvalente:
7 ECUAŢII ALGEBRICE ŞI TRANSCENDENTE 7 Separarea rădăcnlor Ecuaţe algebrcă dacă ( este polnom Ecuaţa transcendentă în caz contrar ( = Rădăcnă apromatvă valoare ξ apropată de valoarea eactă ξ Denţ neechvalente:
Matematici speciale Variabile aleatoare discrete
 Matematici speciale Variabile aleatoare discrete Aprilie 208 ii Expose yourself to as much randomness as possible. Ben Casnocha 9 Variabile aleatoare discrete Texas Holdem Poker: In Texas Hold em Poker
Matematici speciale Variabile aleatoare discrete Aprilie 208 ii Expose yourself to as much randomness as possible. Ben Casnocha 9 Variabile aleatoare discrete Texas Holdem Poker: In Texas Hold em Poker
PROPRIETĂŢI GEOMETRICE ŞI ANALITICE ALE UNOR CLASE DE FUNCŢII UNIVALENTE
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ GABRIELA ROXANA ŞENDRUŢIU PROPRIETĂŢI GEOMETRICE ŞI ANALITICE ALE UNOR CLASE DE FUNCŢII UNIVALENTE Rezumatul tezei de doctorat
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ GABRIELA ROXANA ŞENDRUŢIU PROPRIETĂŢI GEOMETRICE ŞI ANALITICE ALE UNOR CLASE DE FUNCŢII UNIVALENTE Rezumatul tezei de doctorat
2D AND 3D PROCESSING OF THE INTERDEPENDENCE BETWEEN THE COMFORT MAIN INDICATORS
 BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LVII (LXI), Fasc. 1, 2011 SecŃia TEXTILE. PIELĂRIE 2D AND 3D PROCESSING OF THE INTERDEPENDENCE
BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LVII (LXI), Fasc. 1, 2011 SecŃia TEXTILE. PIELĂRIE 2D AND 3D PROCESSING OF THE INTERDEPENDENCE
Utilizarea limbajului SQL pentru cereri OLAP. Mihaela Muntean 2015
 Utilizarea limbajului SQL pentru cereri OLAP Mihaela Muntean 2015 Cuprins Implementarea operatiilor OLAP de baza in SQL -traditional: Rollup Slice Dice Pivotare SQL-2008 Optiunea ROLLUP Optiunea CUBE,
Utilizarea limbajului SQL pentru cereri OLAP Mihaela Muntean 2015 Cuprins Implementarea operatiilor OLAP de baza in SQL -traditional: Rollup Slice Dice Pivotare SQL-2008 Optiunea ROLLUP Optiunea CUBE,
AN APPROACH TO THE NONLINEAR LOCAL PROBLEMS IN MECHANICAL STRUCTURES
 U.P.B. Sci. Bull., Series D, Vol. 74, Iss. 3, 2012 ISSN 1454-2358 AN APPROACH TO THE NONLINEAR LOCAL PROBLEMS IN MECHANICAL STRUCTURES Marius-Alexandru GROZEA 1, Anton HADĂR 2 Acest articol prezintă o
U.P.B. Sci. Bull., Series D, Vol. 74, Iss. 3, 2012 ISSN 1454-2358 AN APPROACH TO THE NONLINEAR LOCAL PROBLEMS IN MECHANICAL STRUCTURES Marius-Alexandru GROZEA 1, Anton HADĂR 2 Acest articol prezintă o
KINEMATIC ANALYSIS OF BEVEL PLANETARY GEARS BY USING THE INSTANTANEOUS AXIS OF ROTATION
 U.P.B. Sci. Bull. Series D Vol. 70 No. 008 ISSN 454-58 KINEMATIC ANALYSIS OF BEVEL PLANETARY GEARS BY USING THE INSTANTANEOUS AXIS OF ROTATION Victor MOISE Iulian Alexandru TABĂRĂ În lucrare se preintă
U.P.B. Sci. Bull. Series D Vol. 70 No. 008 ISSN 454-58 KINEMATIC ANALYSIS OF BEVEL PLANETARY GEARS BY USING THE INSTANTANEOUS AXIS OF ROTATION Victor MOISE Iulian Alexandru TABĂRĂ În lucrare se preintă
Counties of Romania List
 O P A Romanian PSK Award eria de diplome Romanian PSK Award a fost conceputa de clubul European de PSK (EPC) la data de 22 mai 009. Scopul fiind de a stimula activitatea PSK cu statii de radioamatori din
O P A Romanian PSK Award eria de diplome Romanian PSK Award a fost conceputa de clubul European de PSK (EPC) la data de 22 mai 009. Scopul fiind de a stimula activitatea PSK cu statii de radioamatori din
ASPECTS REGARDING NUMERICAL MODELING OF INDUCTIVE HEATING PROCESS FOR LOW VOLTAGE ELECTRICAL CABLES
 U.P.B. Sci. Bull., Series C, Vol. 72, Iss. 3, 2010 ISSN 1454-234x ASPECTS REGARDING NUMERICAL MODELING OF INDUCTIVE HEATING PROCESS FOR LOW VOLTAGE ELECTRICAL CABLES Costel PĂUN 1 În această lucrare se
U.P.B. Sci. Bull., Series C, Vol. 72, Iss. 3, 2010 ISSN 1454-234x ASPECTS REGARDING NUMERICAL MODELING OF INDUCTIVE HEATING PROCESS FOR LOW VOLTAGE ELECTRICAL CABLES Costel PĂUN 1 În această lucrare se
Solution by Nicuşor Zlota, Traian Vuia Technical College, Focşani, Romania
 Revista Virtuala Ifo MateTehic ISSN 069-7988 ISSN-L 069-7988 Probleme rouse sre rezolvare Nicusor Zlota, Focsai 08.Prove that C, j N,where the fiboacci, F F F 0 F F, F 0, F + = + + = = = 0 + j + j 09.Let
Revista Virtuala Ifo MateTehic ISSN 069-7988 ISSN-L 069-7988 Probleme rouse sre rezolvare Nicusor Zlota, Focsai 08.Prove that C, j N,where the fiboacci, F F F 0 F F, F 0, F + = + + = = = 0 + j + j 09.Let
Decision Trees Some exercises
 Decision Trees Some exercises 0. . Exemplifying how to compute information gains and how to work with decision stumps CMU, 03 fall, W. Cohen E. Xing, Sample questions, pr. 4 . Timmy wants to know how to
Decision Trees Some exercises 0. . Exemplifying how to compute information gains and how to work with decision stumps CMU, 03 fall, W. Cohen E. Xing, Sample questions, pr. 4 . Timmy wants to know how to
1 Generarea suprafeţelor
 Motto: Cu vesele glasuri de tinere firi, Cuprinşi de-amintirea străbunei măriri, Spre soare ni-e gândul şi mergem spre el, Lumina ni-e ţinta şi binele ţel - Traiască-ne ţara şi neamul! Coşbuc - Imnul studenţilor
Motto: Cu vesele glasuri de tinere firi, Cuprinşi de-amintirea străbunei măriri, Spre soare ni-e gândul şi mergem spre el, Lumina ni-e ţinta şi binele ţel - Traiască-ne ţara şi neamul! Coşbuc - Imnul studenţilor
FINITE ELEMENT ANALYSIS OF FRICTIONAL CONTACTS
 BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LIV (LVIII), Fasc. 3, 2011 Secţia CONSTRUCŢII. ARHITECTURĂ FINITE ELEMENT ANALYSIS OF FRICTIONAL
BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LIV (LVIII), Fasc. 3, 2011 Secţia CONSTRUCŢII. ARHITECTURĂ FINITE ELEMENT ANALYSIS OF FRICTIONAL
