OSNOVE AUTOMATIZACIJE. Prof.dr.sc. Joško Petrić Mihael Cipek, dipl.inž.
|
|
|
- Philip Harvey
- 6 years ago
- Views:
Transcription
1 Uvoda riječ OSNOVE AUTOMATIZACIJE Proizvodo ižejersvo, 4. semesar Predavaja poedjeljak -4 h; (dvoraa II) Vježbe uorak - h; (dvoraa I) Prof.dr.sc. Joško Perić Mihael Cipek, dipl.iž. Cilj kolegija Uvod ciljevi kolegija razumijevaje zašo je auomaizacija, odoso auomaska regulacija korisa ižejeru srojarsva ključe ideje, pojmovi i kocepi upozavaje emelje eorijske podloge (maemaičke) mogućos rješavaja jedosavih problema upozavaje s osovim račuarskim alaima (Malab/Simulik) Pohađaje asave i ispii Za popis: 7 % predavaja ili vježbi Kolokviji: kolokvija amijejeo oima koji redovio pohađaju predavaja i vježbe; Prolaz: 4% od oba kolokvija, prolaz zamjejuje pismei + usmei ije predviđe rezervi rok za kolokvije. kolokvij: uvje izlaska a. kolokvij je pohađaje barem 7 % prehode asave.. kolokvij: uvje izlaska a. kolokvij je pohađaje barem 7 % prehode asave i rješeje 5 %. kolokvija. Redovii ispi pismei i usmei, prolaz pismeog 5 %, pismei vrijedi za dva usmea; ( 45 % pismei vrijedi jeda usmei) Sadržaj kolegija Uvod šo je auomaizacija? Osove defiicije i pojmovi Primjeri iz primjee Povijes Maemaički prikaz diamike ehičkih susava Aaliički modeli (mehaički, elekriči i elekromehaički susav) Prijeosa fukcija Meoda prosora saja Liearizacija, eksperimeala ideifikacija Aaliza susava u vremeskom području Sadarde pobude fukcije Rješeje dif. jedadžbe Začajke diamičkog susava Osovi diamički člaovi Zahjevi kod vremeskog odziva
2 Osova ačela povrae veze Djelovaje povrae veze Regulaori Sabilos i očos Aaliza susava u frekvecijskom području Grafički prikaz Frekvecijski odziv osovih člaova Začajke susava u frekvecijskom području Elemei regulacijskog kruga Mjeri, izvrši i upravljački člaovi Lieraura T.Šuria Auomaska regulacija, Šk. kjiga Zagreb 98. hp:// Maerijali s predavaja, obavijesi a: UVOD Šo je auomaizacija? Auomaizacija eorija i ehika koja proces čii auomaskim, samogibajućim ili samoupravljivim Auomaizacija je proces kojim se ešo pravi auomaskim, a akođer je saje koje je rezula og isog procesa. Auomaizacija je asavak procesa mehaizacije, zao jer se auomaskim može učiii samo oaj proces koji je u dovoljoj mjeri mehaizira. Auomaizacija u širem smislu obuhvaća sve mjere i procese kojima se smajuje udio ljudskog rada, opažaja i odlučivaja. Auomaska regulacija po defiiciji je auomasko održavaje željeog saja ekog procesa ili mijejaje og saja po određeom zakou, bez obzira a djelovaje vajskih i uuarjih poremećaja. To se posiže pomoću povrae veze, koja omogućava usporedbu izmjeree vrijedosi eke veličie reguliraog procesa sa jeom željeom vrijedosi (referecijom), e se a emelju razlike ih dviju veličia odlučuje kako proces usmjerii. Srce svakog susava auomaske regulacije jes ideja povrae veze (A.Isidori) Ideja p.v.? Usporedii akueli rezula sa željeim i djelovai a emelju jihove razlike! p.v. je jedosavi pricip koji pokriva sve pricipe regulacije u prirodi (pr. ras živih orgaizama, jelesa emperaura, lak, zaim ravoeža, gibaje, odziv a sres,...)
3 Regulacijska pelja ili zavorei krug Proces se usmjerava upravljajem okom eergije ili vari. Skica avedeoga zavoreog kruga ili regulacijske pelje daa je a slici: Pridjev auomasko, j. auomaika? Razi uređaji su zadužei za mjereje, uspoređivaje, odlučivaje i izvršeje upravljačke odluke. U lacu regulacije može bii i čovjek koji će ešo od oga (ili sve o) radii, o akva regulacija ije auomaska. Varijable podlože auomaskom vođeju? U mehaici? Čovjek? Državo gospodarsvo? Kibereika je zaos o općim zakoiosima procesa vođeja, reguliraja, dobivaja, pohrajivaja, prevorbe i prijeosa iformacija u susavima, eoviso o jihovoj fizikaloj prirodi. Auomaska regulacija jeda je od brojih ograaka kibereike, o susav s povraom vezom smara se ajvažijim oblikom osovog susava za kibereiku i za auomaizaciju. Porebo je aglasii da susav s povraom vezom ije užo ehički, ego je svojsve i biološkim, ekoomskim, socijalim, poliičkim, psihološkim, i iim susavima. Dakle regulacija ije samo posupak u ehici, ego prije svega je prirodi zako. Pojmovi upravljaja i regulacije Povraa veza (feedback) emelji je pojam auomaske regulacije. Upravljaje vs. regulacija Varijabla koju se želi regulirai mjeri se, i šalje se azad u uređaj amijeje vođeju. Pri om se uspoređuje željea i svara vrijedos, a emelju jihove razlike djeluje eki regulacijski zako, koji šalje aredbu izvršom uređaju da bi se smajila razlika između željee i svare vrijedosi. To zovemo regulacijom. Napomea: regulaciju dijelimo a čvrsu i slijedu. 3
4 Pojmovi upravljaja i regulacije Upravljaje je posupak pri kojem jeda ili više ulazih veličia uječu a jedu ili više izlazih veličia ekog procesa prema zakoiosima svojsveim upravljaom procesu. Pri om se upravljaje odvija u ovoreom krugu. To zači da, za razliku od regulacije, kod upravljaja ema povrae veze koja će omogučii usporedbu željee i svare vrijedosi, ii će se proces usmjeravai a emelju jihove razlike. Soga ema mogućosi popravljaja upravljačke odluke a emelju promaraja odvijaja procesa. Upravljaje Ovorei krug plairaje Nije robuso a pogreške modela Nema rizika esabilosi (kada su svi elemei sabili) Regulacija Zavorei krug povraa veza Reagiraje po događaju Robuso a pogreške u ekom području Rizik esabilosi Vođeje procesa općeiiji je pojam koji obuhvaća i upravljaje i regulaciju U pravilu je vođeje povezao uz upravljaje i regulaciju složeijih susava pomoću račuala. U ovom kolegiju pojam vođeje se korisi kada je obuhvaćeo upravljaje i regulacija, ali i kada ije izričio određeo a koji se od a dva posupka misli. Dakle, vođeje se može smarai hrvaskim pojmom općeiog egleskog pojma corol. (prof. Božićević) Zašo je povraa veza egaiva? Veličie u krugu: Izlaz = reguliraa veličia Željea vrijedos = referea veličia, vodeća v. (slijeda), aziva v. (čvrsa) Regulacijska pogreška ili odsupaje Posava veličia Poremećaja veličia Moderi susav regulacije Poopćei osovi blok dijagram auomaske regulacije šum vajski poremećaji šum izlaz željea vrijedos r( referea veličia, ili referecija (aziva veličia - čvrsa regulacija; vodeća veličia - slijeda regulacija. Referea veličia (referece ipu je vajski sigal primjeje a susavu auomaske regulacije a komparaoru. y( reguliraa veličia. Česo se kaže samo izlaz. Reguliraa veličia (corolled variable ili corolled oupu, ili ajčešće samo oupu predsavlja izlazu veličiu reguliraog procesa. e( regulacijsko odsupaje, ili regulacijska pogreška. Regulacijsko odsupaje (acuaig sigal, ili error sigal) je razlika između referee i regulirae veličie, koja ulazi u regulacijski uređaj i poiče jegovo djelovaje. u( posava veličia. Posava veličia (corol sigal ili maipulaed variable) je sigal koji predsavlja izlaz iz regulacijskog uređaja, i ulaz u proces. d( poremećaja veličia. Poremećaja veličia (disurbace) je ulazi sigal koji ima eželjei ujecaj a regulirau veličiu. 4
5 Osovi blok dijagram auomaske regulacije s posavim i mjerim člaom Regulacijski uređaj (coroller) dio susava auomaske regulacije koji geerira posavu veličiu koja će djelovai a regulirai proces. Regulacijski uređaj ili regulaor običo sadrži pojačalo, ekakvo vremesko djelovaje, e komparaor. U širem smislu regulaor uz o može obuhvaii i geeraor referee veličie, e raze elemee za obradbu sigala (pr. filere, aalogo-digialu i digialo-aalogu koverziju, id.). Objek regulacije ili proces (process, pla obuhvaća susav, podsusav ili proces čija veličia (ili veličie) je predme regulacije. Negaiva povraa veza i komparaor (comparaor) osova fukcija povrae veze, usporedba željee i svare vrijedosi veličie koju se želi regulirai obavlja se komparaorom. Prirodo je soga da povraa veza ima egaivu vrijedos. Izvrši čla - sasoji se od posavog pogoa, (pr. elekromoor) i posavog člaa (pr. veil) Mjeri čla sasoji se od mjerog osjeila i prevarača ( mjeri šum Jedovarijabili susavi (SISO) Mulivarijabili susavi (MIMO) Osovi zahjevi pri regulaciji su: sabilos očos brzia (kvaliea) odziva (robusos Susav: kombiacija kompoei koje djeluju zajedo da bi osvarili fukciju koja se e može osvarii pojediačim djelovajem Sigal je fizikala veličia koja se mijeja s vremeom. Aaliza susava bavi se odosima među sigalima koji mogu bii bilo kakve fizikale veličie koje se mijejaju s vremeom. Da bi vodili (ili regulirali) eki susav, šo je porebo? (Osim uređaja s kojima ćemo se poslužii) Kako se formalizira zaje o ekom ehičkom susavu (kako ga opisujemo?) Proces je općeio skup akivosi kojima se ulazi elemei rasformiraju u izlaze elemee sa specifičim svojsvima, a sama rasformacija određea je paramerima i ograičejima. Promaraje odosa ulaza i izlaza, odoso pobude i odziva, odoso uzroka i posljedice (kauzalos bia je ema ovog kolegija Ovaj kolegij bavi se upozavajem osovih elemeaa auomaskog vođeja, upozavajem susava i ačia jihovog opisa, e ciljevima i zahjevima pri upravljaju susava, e ačiu posizavaja ih ciljeva i zahjeva. 5
6 Uvod asaak i povijes Kyberees, grčka riječ za kormilara odoso avigaora, povezaa s Laiskim guberaorom (goveror). U Plaoovoj Republici (3-4. s. B.C.) upravljaje (vođeje) brodom uspoređuje se s upravljajem (vođejem) drušvom. A.M.Ampere (fr. fizičar iz 8-9. s.) auka o upravljaju (vođeju) rebala bi se zvai kibereika iz Essai sur la philosophie des sciece. N. Wieer Cybereics or corol ad commuicaio i he aimal ad he machie MIT Press 948 Eimologija: do riječi kibereike došlo se proučavajući eimologiju egleske riječi goveror (regulaor, upravielj), odoso laiske guberare, odoso origiale grčke κυβερνάν (kormilar) Dakle, auomasko upravljaje ije ehički izum već prirodi zako. Auomasko upravljaje s povraom vezom jedo je od osovih ačela a kojima počiva kibereika. U ehici (a zapadu pogoovo) pojam kibereike zamjejuje se upravljajem, regulacijom, vođejem (corol, feedback corol, feedforward corol, Regelug, Seuerug) Povijes auomaizacije (kraki osvr Povijes auomaizacije (kraki osvr Raa faza Počeci (do II svj. raa) pari srojevi, mliovi, avioi, brodovi, procesa idusrija, elekomuikacije II svjeski ra aglo šireje u idusriju, obrazovaje, orgaizacije (okupljaje ljudi iz razih područja, e iz eorije i prakse! počeak susavog mišljeja) 6-e zahjeve primjee (svemirska israživaja, i sve osalo), počije era digialog račuala Nova faza ugrađeo (embedded) vođeje, mreže, biologija, fizika auoomija i disribucija, eksplozija primjea Kesibios, Grk iz Aleksadrije, 5. g.p..e., smara se ocem auomaike (vodei sa s regulaorom prooka (uz o i vodee orgulje, kaapul, pumpa, id.) Philo, Bizaiac, ešo mlađi od Kesibiosa (ulja lampa, akođer regulaor prooka) Hero, Grk, I s p..e. (kjiga Peumaica s opisom različiih regulaora prooka) Mehaizam upravljaja ivoom ekućie s plovkom (sezor i akuaor) Vodei saovi (9.-.s., Arapi, Kia,) 6
7 Povijes auomaizacije (kraki osvr Sai mehaizam Prijašja koiuiraos u mjereju vremea (pijesak, voda, problem koiuiea) promijejea je razbijajući vrijeme mehaizmom ( verge-ad-foilo mechaism ) u iervale, koji se broje. Krua je pogojea ereom, a svaki udarac ležaja u zubac krue reuo uspori brziu roacije, i jihovo međusobo djelovaje predsavlja povrau vezu. Iače, svaka zasebo kompoea bi se vrila epresao, a povraom vezom dobiva se koača, raja brzia krue, kojom mjerimo proicaje vremea. Povijes auomaizacije (kraki osvr Regulacija emperaure (ikubaor) sa sakleom cijevi ispujeom alkoholom i živom kojom se regulira plame (Drebbel, 6. g.) Cerifugali regulaor brzie parog sroja (James Wa 788. g.) Povijes auomaizacije (kraki osvr Povijes auomaizacije (kraki osvr 8. i 9. soljeće Razvoj eorije au.reg., Maxwellova rasprava o regulaorima iz 868. g. Nasavak, Rouh, Hourwiz, Lyapuov (89.),.. Zrakoplovsvo (Braća Wrigh, Kiy Hawk, NC, ) Žiroskopi, Sperry je kosruirao auomaski pilo za zrakoplove a bazi sigala iz žiroskopa (el.sigal slačei zrak krilca) 99.g. 7
8 Povijes auomaizacije (kraki osvr W. Wrigh a Weser Sociey of Egieers 9: Me already kow how o cosruc wigs or airplaes, which whe drive hrough he air a sufficie speed, will o oly susai he weigh of he wigs hemselves, bu also ha of he egie, ad of he egieer as well. Me also kow how o build egies ad screws of sufficie lighess ad power o drive hese plaes a susaiig speed... Iabiliy o balace ad seer sill cofros sudes of he flyig problem.... Whe his oe feaure has bee worked ou, he age of flyig will have arrived, for all oher difficulies are of mior imporace. Telekomuikacije ako I svj.raa. (Bellovi laboraoriji, SAD) operacijsko pojačalo s povraom vezom (H. Black 97 g.) PID regulaor, između dva raa Nako II svj. raa, zrakoplova i svemirska ehika Wrigh was righ! Povijes auomaizacije (kraki osvr Povijes auomaizacije (kraki osvr Osvr a auomobilske moore 5-godie modera eorija au. Upravljaja mulivarijabili susavi, kocep prosora saja mikroprocesori (969-7 g. Iel, 44, 4 bii) i mikrokoroleri idusrijska elekroika (frekv. prevarači) Daašje doba! Budućos auomaizacije Everyhig will, i some sese, be smar; ha is, every produc, every service, ad every bi of ifrasrucure will be aued o he eeds of he humas i serves ad will adap is behavior o hose eeds. Sesig, acuaio, ad corol USA Naioal Academy of Egieerig, The Egieer of Fligh Ieraioal, Aug 5, Corol sciece ops lis of USAF sciece ad echology prioriies By Sephe Trimble If he chief scieis of he US Air Force is correc, he key echology challege for airpower over he ex wo decades is o direced eergy, cruise missile defece or eve saellie-killig weapos. I a sweepig ew 53-page repor Techology Horizos, USAF chief scieis Werer Dahm isead ideifies advaces i "corol sciece", a obscure iche of he sofware idusry, as poeially he mos impora breakhrough for airpower bewee ow ad 3. 8
9 Primjee Proizvodja i disribucija eergije Komuikacije Traspor Idusrijski procesi Pojediača proizvodja Meharoika Precizi isrumei Porošačka elekroika Ekoomija Biologija Medicia Primjeri ( ) Auomobilski susavi Upravljaje radom moora (Powers, Ford u g. Auomobili su x čišći i x učikoviiji zahvaljujući poajviše disribued microprocessor based corol sysem ) Pogoi (4x4, auomaski mjejači, dual cluch mjejači, AD i TVD) Tempoma, adapivi empoma TCS, ESP Pomoć držaja voze rake Vožja u koloi Poluakivi i akivi ovjesi Primjeri Tempoma (regulaor brzie vozila) Tempoma? Segway? Chrysler cruise corol, Chrysler Imperial 958. Segway Šo omogućava povraa veza (eka zadivljujuća svojsva): Akuaori - dva isosmjera servomoora bez čekica koji su smješei uuar koača s prijeosom preko redukora. Baerije Li-Io Sezori 5 žiroskopa (mjere promjeu orijeacije koriseći Coriolisov efek, izvedei su kao MEMS-ovi (micro elecro-mechaical sysem) sa vibrirajućim prseom (vibraig rig rae-gyroscope)) Upravljaje više umrežeih mikroprocesora z skreaje Susav može bii eosjeljiv a poremećaje i promjee svojih elemeaa (op-amp, H.Black 97.g.) Može apravii dobar susav od loših elemeaa (primjer e- zaklopka) Sabilizirai esabila susav (Segway, eki zrakoplovi) Svorii eko poželjo poašaje susava (pr. liearo poašaje susava iz eliearih kompoei) agijaje valjaje x y 9
10 Koji je osovi problem s povraom vezom? Zašo bi ižejeri srojarsva rebali učii (i zai ešo) o vođeju? Može uijei esabilos pojavljuje se svugdje daje dodau slobodu projekau ehičkih susava (pr. MB A) iegralo projekraje srojarskog susava i vođeja posaje sve važije (prožimaje, siergija, ideja meharoike!) kocepi i alai su široko primjeljivi Povraa veza Povraa veza Dobar susav od loših elemeaa: primjeri e-zaklopka, poluakivi ovjes,... Susav može bii eosjeljiv a poremećaje i promjee svojih elemeaa Osjeljivos predsavlja omjer posoe promjee eke mjere svojsava susava (šo može bii odziv Y() i posoe promjee ekog paramera susava ai. Šo se odziv maje mijeja kao posljedica promjee koeficijeaa susava, o je maje osjeljiv. Za male promjee koeficijea ai od počee vrijedosi a može se pisai da je osjeljivos S: a) S Y a Y ( / Y ( ai / a R GR Go Y S Y G = b) R - GR Go Y S Y = G + GR GO ( Povraa veza Povraa veza Djelovaje vajskog poremećaja D: a) D R Y GR Go Ya ( = GO ( D( Može sabilizirai esabila susav: m θ I & θ m g l siθ = τ Liearizacija, polovi su: p = g / l / ± b) R - GR D Go Y G ( Y ( O b = D( + GR ( GO ( l, l, I τ τ τ = K & θ K θ m g l siθ D Zako vođeja: P V Dobiva se: Opasos (i ograičeje): šum V!!! Ne samo sabila, ego i lieara! Umjea opruga i prigušivač! I && θ + K & D θ + K θ = P
11 Povraa veza Povraa veza Dalje: τ = & θ m g l siθ K D τ Može svorii eko poželjo poašaje susava: pr. liearo od eliearog (prehodi primjer, ali i primjeri sa samog počeka auomaike vodei sa l, I dobiva se... I && θ + K & D θ + m g l si θ = m θ jihalo (s viskozim prigušejem)! Opasos povrae veze: duboko mijeja susav, i od sabilog susava može posai esabila (kašjeja; šum sezora ili vodeće veličie sa derivacijskim ili čak proporcioalim djelovajem regulaora mogu bii jako poecirae; preveliko ražeje od ograičeih akuaora (iegraor widup), prevelika pojačaja, id.) Povraa veza Povraa veza Temelja ograičeja svojsava koja se mogu posići povraom vezom: piaje smješaja polova i ula, odoso piaje sabilosi (fazaemiimalos piaje kosrukcije Ako se o primjei a prehodi primjer iverzog jihala: [ π g / Ω] Ω l S = π g / l Smi = exp l / Bodeov iegral predsavlja zako održaja (čega?) određea količia (vrijedos iegrala logarima ampliude fukcije osjeljivosi) je sačuvaa djelovajem povrae veze, odoso ukupa vrijedos je uvijek jedaka. Oa je jedaka uli za sabile polove/ule, ili je jedaka ekoj poziivoj vrijedosi za esabile polove/ule: l T ( jω) dω = π ω l S( jω) dω = π p k= m i= k z i Smi OM=7.5 OM= OM=5 Ako se uzme u obzir ograičeja upravljačkog hardvera, šo je vrlo važo, oda posaje: Ω l [m] kvaliea vođeja ovisi o dužii jihala i ograičeju hardvera Uvod MATEMATIČKI PRIKAZ DINAMIKE TEHNIČKIH SUSTAVA Prof.dr.sc. Joško Perić Pozavaje susava preduvje upravljaja Pozavaje susava predsavljeo je modelom Model maemaički, ali i kvaliaivi, e saisički Model diamike susava amijeje upravljaju: opisuje vezu između uzroka i posljedica promjea saja susava u vremeu Model omogućava aalizu i siezu upravljaja Corol orieed model kompaki Lieari vremeski ivarijai susavi opisuju se liearim D.J. s kosaim koeficijeima
12 Aaliički modeli Mehaički susav (raslaori) Modeliraje dobiveo eoreskim ili aaliičkim puem (jedadžbe održaja mase, eergije i impulsa, e fizikali ili kemijski zakoi) Eksperimealim puem Kombiacije (verifikacija, parameriraje) 3. Newoov zako (suma primjejeih sila jedaka je silama koje im se suprosavljaju) f( A x A ( K B x B ( M D Mehaički susav (raslaori) Mehaički susav (raslaori) Iz ravoeže sila: Točka A f = fk = K ( xa xb ) f ozačava vajsku silu koja djeluje a očku A; f K, f M i f D su sile opružog djelovaja, sila iercije i sila prigušeja; sa x su ozačei pomaci u očkama A i B; a K, M i D ozačavaju kosau kruosi opruge, masu i kosau viskozog prigušeja amorizera. Točka B d x dx f f f M B D B K = M + D = + Ovaj susav je drugog reda, sa dva spremika eergije, gdje masa u gibaju čuva kieičku eergiju, a opruga poecijalu. Tijekom gibaja, poakuim vajskom silom f ili pohrajeom eergijom uuar susava (a šo ukazuju počei uvjei u modelu), eergija prelazi iz jedog oblika u drugi, gubeći se prigušejem. Omjeri mase, elasičosi i prigušeja određuju kakav će bii oblik ih prijelaza. Mehaički susav izraže pomoću prijeose fukcije (prijeosih fukcija) iegraor, spremik eergije, kašjeje Primjer: hidr.cilidar v=q/a Kako je cilj modela diamike susava dobii apsraka opis veza između posljedica ekih promjea (izlaze veličie) sa pobudama koje su ih uzrokovale, ovdje se ameću ri akva para: x a i f, x b i x a, e koačo x b i f. Parovi će se dai pomoću prijeosih fukcija. x = v
13 Mehaički susav izraže pomoću prijeose fukcije (prijeosih fukcija) f ( = K ( xa( xb ( ) d x dx f M B ( ) D B ( ) ( ) = + Trasformacijom se dobiva : F( = K ( X A ( X B ( ) F( = M s X B ( + D s X B ( Iz prve jed. može se izlučii izraz za X B i uvrsii u drugu, pa se sređivajem dobiva veza između sile F( kao ulaze varijable i X A ( kao izlaze: ( M s + D s + K) F( = ( M s + D X A( K Napomea: velikim slovima ozačavaju se varijable u s-području, a malim u vremeskom ( području U drugoj jedadžbi izražea je veza između F( kao ulaze varijable i X B ( kao izlaze: Nameće se još ražeje veze između gibaja u čvoru A kao ulaza (pobude) i gibaja u čvoru B kao izlaza (posljedice). Ta veza lako se dobije izjedačavajem prve i druge jedadžbe gibaja meh. susava: F( = ( M s + D s ) X B ( K X ( ) ( A s = M s + D s + K ) X B ( Iz prehode 3 jedadžbe mogu se dobii 3 prijeose fukcije: X s M s D s K G s A( ) + + ( ) = = F( ( M s + D K X s K G s B ( ) ( ) = = X A( M s + D s + K X s G s B ( ) ( ) = = F( M s + D s Prehode prijeose fukcije možemo prikazai slijedećim blok dijagramima: F F G XA G G XB XB 3
14 Prijeosa fukcija Prijeosa fukcija (rasfer fucio) jeda je od ekoliko osovih pojmova svojsveih auomaizaciji, i općeio eoriji susava. Prijeosa fukcija povezuje ulaz i izlaz ekog susava ili elemea, odoso uzrok i posljedicu promjea, e ako predsavlja diamičko poašaje susava ili ekog pojediog elemea. Prijeosa fukcija zamjejuje klasičo rješavaje diferecijale jedadžbe. Iako je maemaička eorija a kojoj se emelji prijeosa fukcija dosa složea, jeo korišeje je razmjero jedosavo, i ije uvjeovao pozavajem e eorije. To je svakako jeda od razloga jee široke primjee i popularosi. Ipak, porebo je pozavai jea ograičeja odoso jeo područje primjee. Prijeosa fukcija ačelo je povezaa uz područje liearih vremeski ivarijaih susava. Oa se emelji a operaorskom račuu, odoso preslikavaju fukcije a fukciju. Na aj ači je egleski fizičar Heaviside krajem 9. soljeća pojedosavio rješavaje liearih diferecijalih jedadžbi, ali bez čvrsih maemaičkih dokaza. Kasije je a emelju Laplaceove rasformacije a meoda maemaički dokazaa, e se za ju i korisi aj aziv Laplaceova rasformacija. Daa je lieara diferecijala jedadžba s kosaim koeficijeima u slijedećem obliku: d y( d y( dy( a + a... a a y( = m m d x( d x( dx( = bm + bm b + b x( m m y( je izlaza veličia, x( je ulaza veličia, dok su a k i b k pripadajući koeficijei, preposavka je da su reali brojevi. Susav je da povezaošću između ulaze i izlaze veličie opisae diferecijalom jedadžbom. Gorja D.J. je -og reda, pa se i za susav kojeg oa predsavlja kaže da je -og reda. U pravilu je m (ali može bii izimaka). Uvodi se rasformacija, ako da fukcija x( posaje X(, odoso y( posaje Y(. Derivacija se zamjejuje operaorom s, odoso iegracija se zamjejuje sa / s. Napomea: Operaor preslikava fukciju a fukciju, dok fukcija preslikava brojeve a brojeve. dx( s X ( x ( X ( s d x( s X ( ( ) ( ) x X s s d x( s X ( Prehoda D.J. rasformirajem posaje: a s Y( + a s Y( a sy( + ay ( = = b s m X ( b s m m + m X ( b s X ( + ax ( Dakle, diferecijala jedadžba posala je algebarska jedadžba, šo jeo rješavaje čii zao lakšim. Međuim, važo je uočii da rješeje alg. j. eće bii fukcija vremea, odoso eće bii u vremeskom području ego u području operaora s. Operaor s je kompleksa varijabla, ili kompleksa frekvecija, soga je rješeje u području komplekse varijable. (Dakle, frekvecijsko područje). Prijelaz u vremesko područje poovo zahijeva rasformaciju koja se zove obruom ili iverzom Laplaceovom rasformacijom. 4
15 Defiicija prijeose fukcije Prehodu algebarsku jedadžbu u s području možemo izrazii kao omjer izlaze (Y) i ulaze (X) veličie: ( ) b s m b s m Y s... b s b G( m + m = = X ( a s a s a s + a Gorji izraz predsavlja prijeosu fukciju susava, koja se običo ozačava sa G( (poegdje akođer H(). Dakle, prijeosa fukcija G( ekog susava jes rasformirai omjer izlaze i ulaze fukcije uz počee uvjee jedake uli: G( = Y( / X( Iz pojma rasformirai uočava se da je prijeosa fukcija povezaa uz područje komplekse varijable s. Osim oga, može se uočii da prijeosa fukcija opisuje diamiku susav samo povezujući ujecaj pobude a izlazu veličiu, a isključuje ujecaj pohrajee eergije u susavu, pošo su počei uvjei po defiiciji jedaki uli. Red prijeose fukcije je red polioma jeog azivika. Člaovi u aziviku predsavljaju kašjeja u susavu (broj iegracija), dok člaovi u brojiku predsavljaju poašaje susava s obzirom a pobudu. U pravilu je red polioma azivika prijeose fukcije veći ili jedak redu polioma jeog brojika ( m), uz moguće izimke. Karakerisiča jedadžba, polovi i ule m ( s zi ) G( = K i= ( s pi ) i= Vrijedosi s = p i za koje je poliom azivika prijeose fukcije jedak uli zovu se polovi prijeose fukcije, ili polovi susava kojeg prijeosa fukcija predsavlja. Za e vrijedosi komplekse varijable, ili komplekse frekvecije s prijeosa fukcija poprima beskoače izose (dijeljeje ulom). Vrijedosi s = z i za koje je poliom brojika prijeose fukcije jedak uli zovu se ule prijeose fukcije. Za e vrijedosi komplekse varijable s prijeosa fukcija bii će jedaka uli. Drugim riječima, za e vrijedosi s izlaz iz susava bii će jedak uli, bez obzira kakva pobuda djeluje a ulazu. K je omjer b / a i predsavlja pojačaje prijeose fukcije. Kako je o pojačaje pri kompleksoj frekveciji s =, česo se aziva DC gai (direc curre. Dakle, polovi prijeose fukcije rješeja su jedadžbe koja asaje kada se azivik prijeose fukcije iz (3.) izjedači sa ulom. Takva jedadžba aziva se karakerisiča jedadžba: a s + a s a s + a = To je isa karakerisiča jedadžba koju reba riješii kada se raži opće rješeje homogee diferecijale jedadžbe koja opisuje susav uz pobudu jedaku uli. Njeo rješeje, odoso korijeovi odgovaraju polovima (klasičo rješeje diferecijale jedadžbe aalizira se kasije). Karakerisiča jedadžba, odoso polovi i ule vrlo su važi pojmovi u auomaizaciji. Pozavajući broj i smješaj polova, e ula (prikazaih u Gaussovoj ravii) može se zai mogo o svojsvima liearog vremeski ivarijaog susava, popu sabilosi i brzie odziva. Laplaceova rasformacija Operacija Laplaceove rasformacije vremeske fukcije daa je epravim iegralom: F( = f ( e s gdje je s kompleksa varijabla (ili kompleksa frekvecija): s = σ + jω σ predsavlja reali dio a ω imagiari dio komplekse varijable. Simbolička ozaka Laplaceove rasformacije: operaor L, dok je iverza rasformacija L-. Laplaceova rasformacija Sve fukcije e mogu se rasformirai. f( će imai Laplaceovu rasformaciju ako je ekspoecijalog reda, odoso ako je epravi iegral apsoluo kovergea. To je oda kada reala vrijedos Sigma je veća od reale poziive vrijedosi Sigma_a koja zadovoljava ejedadžbu: Primjer fukcije koja se e može rasformirai: (jer rase brže ego šo prigušeje eˆ(-s pada s vremeom) f e σ a ( ) < σ > σ a e 5
16 Laplaceova rasformacija Laplaceova resformacija (aokolo je lakše) Obrua Laplaceova rasformacija prijeose fukcije predsavlja ežisku fukciju g(, odoso odziv susava a pobudu u obliku impulse fukcije σ + j = e s f ( F ( s ) ds πj σ j Nap: Dealji prikaz eorije Laplaceove rasformacije, jea svojsva i eoremi, usporedbe sa Fourierovom rasformacijom, e ablice rasformacije fukcija u kjizi (prof. Šuria) Laplaceova rasformacija: Trasformacija operacija Derivacije Iegracije Teoremi: Teorem liearosi Teorem prigušeja Teorem pomaka Teorem počee vrijedosi Teorem koače vrijedosi Teorem kovolucije Blok dijagrami Raširei oblik prikazivaja modela susava su blok dijagrami. Pojedii elemei, ili dijelovi susava povezuju se međusobo i prikazuju a slikovii ači. Ako blokovi predsavljaju prijeose fukcije dijelova susava, e ako se ok sigala ozači odgovarajućom varijablom, oda je riječ o srukurom blok dijagramu, koji čii model susava. Pri sasavljaju sveukupog modela pošuju se pravila operacija među blokovima. X G Y Fukcioali odosi među elemeima ekog susava akođer se česo prikazuju grafički pomoću blokova, o oi se običo craju ležerije, bez srogih maemaičkih pravila. Takvi blok dijagrami zovu se fukcioali. 6
17 Algebra blokova Točke račvaja i zbrajaja sigala Algebra blokova: Serijska veza Paralela veza Povraa veza (jediiča pov. veza) Meoda prosora saja Meoda prosora saja ači je prikaza i aalize maemaičkog modela susava u vremeskom području. Prijeosa fukcija (ili je grafički prikaz pomoću srukurog blok dijagrama) alazi se u području komplekse varijable, odoso komplekse frekvecije. Broja ograičeja koja se pojavljuju uslijed eizrave aalize dif.jedadžbi kod prijeose fkc. moguće je prevladai meodom prosora saja. Npr. mulivarijabili susavi, elieari susavi ili susavi s vremeski promjeljivim paramerima. Opimale meode odabira parameara regulaora priklade su opisu susava meodom prosora saja. Meoda prosora saja korisi zapis diferecijale jedadžbe -og reda kao diferecijalih jedadžbi. reda, odoso pišu se kao akozvai ormali susavi prvog reda. Iso ako ako posoji simulae diferecijale jedadžbe koje su ukupo -og reda, zapisuju se kao diferecijalih jedadžbi. reda. Korisi se sadardi oblik upisivaja parameara u marice, e se s jima račua pravilima maričog račua. Razvoj i primjea meode prosora saja aročio poakua sve širom uporabom račuala u drugom dijelu prošlog soljeća, pa se uz u meodu česo vezuje pridjev modera, iako i jea eorijska osova poječe iz 9. soljeća. Upozavaje sa meodom prosora saja zahijeva pozavaje osovih operacija maričog račua (zbrajaje i možeje marica) Opis susava meodom prosora saja Mariči blok dijagram meode prosora saja Odabirom akozvaih varijabli saja, kojih ima, model se prevara u diferecijalih jedadžbi prvog reda. Varijable saja upisuju se u vekor saja x, ulaze varijable upisuju se u vekor ulaza u, dok se izlaze varijable upisuju u vekor izlaza y. Marice koeficijeaa susava, ulaza, izlaza i prijeosa, koje se ozačavaju sa A, B, C i D povezuju avedee vekore i vore zapis maemaičkog modela u obliku prosora saja: u B dx D x C y x& ( = A x( + Bu( y( = Cx( + Du( x( vekor saja, dimezija [] u( vekor ulaza, dimezija [m] y( vekor izlaza, dimezija [p] A marica susava, dimezija [ x ] B marica ulaza, dimezija [ x m] C marica izlaza, dimezija [p x ] D marica prijeosa, dimezija [p x m] A Veze između blokova su dae širokom liijom zbog oga šo predsavljaju vekore. Uočava se uloga marice prijeosa D, koja direko povezuje ulaze i izlaze varijable, odoso povezuje ih bez kašjeja, koje predsavlja iegraor. U većii primjera marica D će bii ul-marica, dakle ema direke veze ulaza i izlaza. Primjer kada posoji eki koeficije uuar D marice različi od ule, jes primjer čisog pojačaja (P diamičkog člaa) 7
18 Pojmovi i defiicije meode prosora saja Saje susava - predsavlja maemaički oblik koji sadržava skup od varijabli x (, x (,..., x i (,...,x (, azvaih varijable saja, a aj oblik je akav da su počee vrijedosi x i ( ) oga skupa uz varijable ulaza u j ( dovolji da jedozačo opišu odziv susava u ekom budućem reuku >. Vekor saja skup varijabli saja x i ( predsavlja -dimezioali vekor saja x(. Prosor saja jes dimezioali prosor gdje varijable saja predsavljaju jegove koordiae osi. Trajekorija saja defiiraa je kao puaja u prosoru saja proizvedea od vekora saja x( kako se o mijeja sa vremeom. Varijable saja oe mogu imai eko fizikalo začeje ali mogu bii i apsrake maemaičke veličie bez ekog određeog fizikalog začeja. Odabir varijabli saja običo je prvi korak u opisivaju susava meodom varijabli saja. Varijable saja Tri su vrse varijabli saja: fizikale, faze i kaoske. Fizikale varijable saja odabiru se jedosavo svojim fizikalim začejem u modelu, kao pr. pu, brzia, apo, sila, lak, prook, emperaura, id. Faze varijable saja odabiru se ako da marica susava A čii zv. Frobeiusovu maricu, koja ima jediice izad glave dijagoale, a koeficijei azivika prijeose fukcije su elemei posljedjeg reda. U om slučaju može se razvii blok dijagram susava razmjero lako, meodički, šo se česo korisi prilikom formiraja modela u Malab/Simuliku. Kaoske varijable saja, marica susava A posaje dijagoala (ozačava se sa Λ), gdje su u glavoj dijagoali korijei karakerisiče jedadžbe, o jes vlasie vrijedosi marice. Karakerisika je akvog odabira varijabli saja da je susav raspregu, bez međusobih ujecaja varijabli saja. Važo je uočii da odabir varijabli saja e mora bii uvijek jedozača. Također, varijable saja mogu se maričim operacijama rasformirai iz jedog oblika u drugi. Primjer: elekromehaički susav (DC moor) + u ( - R L i( Umjeso korišeja zakoa moora i geeraora koji povezuju magesku gusoću i geomerijske karakerisike moora, mome razvije moorom T da je pomoću kosae moora K m i sruje armaure i, dok je suprosavljajući apo e svore gibajem u mageskom polju (elekromoora sila) da pomoću kosae geeraora K g i brzie gibaja (kua brzia roora): + e( - J T = Km i e = K & g θ Kosaa moora K m i geeraora K g jedake i ozačee su sa K. D θ( Iz Newoovih zakoa za mehaički dio i Kirchoffovih zakoa za elekriči krug, mogu se dobii jedadžbe koje opisuju gibaje isosmjerog moora: J && θ + D & θ = K i di L + Ri = u K & θ J je mome romosi roora i povezaih operećeja, D koeficije viskozog reja. L je idukivie, R opor armaure, u je apo izvora (ulaza varijabla) Elekromehaički susav, prijeosa fukcija Elekromehaički susav, meoda prosora saja Trasformacijom pomoću operaora s prehode diferecijale jedadžbe posaju: J s θ ( + D sθ ( = K I( L s I ( + R s I ( = U ( K sθ ( Nako uvršavaja I( dobiveog iz gorje u doju alg. jed., e ako poešo sređivaja, dobiva se: 3 ( ) ( J L s + D L + J R s + D R + K ) s θ ( = U( K K K Odale se može apisai prijeosa fukcija između apoa izvora kao ulaze varijable i zakrea osovie moora kao izlaze varijable: ( K G( = θ = U( s ( JL s + ( DL + JR) s + ( DR + K )) Kako je ukupa red modela ri, bii će i ri varijable saja. Odabir varijabli ulaza, saja i izlaza je slijedeći: u( = u( x( = θ ( x( = & θ ( = x& ( x& ( = && θ ( x3( = i( x& 3( = di( / y( = uc ( = x( Da bi se model upisao u mariči oblik meode prosora saja, izrazii će se druga derivacija zakrea (kuo ubrzaje), e prvu derivaciju sruje po vremeu: && D K θ ( = & θ ( + i( J J di( R K = i( & θ ( + u ( L L L 8
19 Maemaički model u Simuliku, Prehode jedadžbe upisuju se u oblik meode prosora saja pošujući pravila maričog možeja i zbrajaja, pa model isosmjerog elekromoora u prosoru saja izgleda a slijedeći ači: x& x& = x& 3 y = D / J K / L x x3 [ ] x + u x K / J x + u R / L x3 / L Maemaički model prikaza grafički Malab/Simulikom svara se koriseći ačela daa u prehodim primjerima. Kao osova grafičkog modela u Simuliku može se korisii izražavaje ajviše derivacije (iso vrijedi i za modele dae meodom prosora saja sa fazim varijablama saja) U prošlosi se isa meoda korisila kod simulacija aalogim račualima pod azivom direko programiraje. Maemaički model u Simuliku, primjer elekromehaičkog susava K/J hea_dodo hea_do hea s s Pojacaje Iegraor Iegraor i Pojacaje D/J Pojacaje4 K/L Odziv Liearizacija Liearizacijom se maemaički opisuje zamisao da će se elieari susav poašai približo kao jegova lieara aproksimacija u okolom području svoga ravoežog saja. Susav običo radi u okolii ekog od svojih ravoežih saja. U im očkama odziv susava je bez promjee, odoso sacioara, pa se akve očke mogu i azvai radim. Tražeje ravoežih saja susava, e piaja sabilosi susava (asimposka ili ekspoecijala, lokala ili globala) vezao je uz Lyapuovu eoriju sabilosi. Liearizacija se može provesi razvojem fukcije u Taylorov red u okolii rade očke, e odbacivajem člaova čiji red je viši od dva. Odskoca fkc. u /L Pojacaje3 i_do i s Iegraor Pojacaje R/L Nehomogei susav (pobuda ) da je eliearom diferecijalom jedadžbom: dy = f ( y, x) gdje je y je izlaza varijabla, a x ulaza. Razvojem fukcije u Taylorov red dobiva se: dy f y y f x x f ( y, x) + + +L y RT! x RT! RT - ravoeža očka Člaovi čiji red je viši od dva se odbacuju. Uz preposavku da je u ravoežoj očki (po defiiciji), zaim uz uvođeje ovih varijabli y' i x' koje predsavljaju male pomake oko ul očke, e zamjejujući dy/ sa dy'/, dobiva se lieari izraz. Parcijale derivacije predsavljaju različie koeficijee, koji su agibi fukcija u ravoežoj očki. dy' f f = y' + x' y RT x RT ANALIZA SUSTAVA U VREMENSKOM PODRUČJU Prof.dr.sc. Joško Perić 9
20 STANDARDNE POBUDNE FUNKCIJE Za porebe aalize susava važo je imai osovicu za usporedbu različiih susava. Jeda vrlo prihvaće ači usporedbe je promaraje odziva diamičkih susava a ulaze pobude koje su sadarde. Sadarde pobude fukcije su odskoča fukcija, agiba fukcija, parabola fukcija i impulsa fukcija. Iako su sadarde pobude fukcije ekoiuirae u ishodišu, pa soga isu aaliičke fukcije, ipak se s jima formalo izvode sve maemaičke operacije kao i s aaliičkim fukcijama (još se i azivaju sigulare fukcije (sigulariy fucio) Kao sadarde pobude fukcije u širem smislu može se avesi općeio red poecija koji se korisi poekad za aaliički izraču ekih odziva, e siusa fukcija koja se kao pobuda korisi za aalizu u frekvecijskom području posoji iz drugih fukcija koje se mogu korisii kao pobude, ali su prisuije u drugim područjima popu pr. eorije sigala, pa se ovdje posebo e spomiju. Odskoča fukcija Odskoča fukcija (sep fucio) ili jediiči odskok (ui sep fucio): ajčešće se ozačava sa u(, a prema O. Heavisideu koji ju je česo korisio aziva se poekad i Heavisideova fukcija. u( f ( = u( za < za Laplaceova rasformacija odskoče fkc. odgovara rasformaciji iegracije: L { u ( } = U ( s Nagiba fukcija Odziv susava a pobudu u obliku jediiče odskoče fukcije zove se prijelaza fukcija, a česo se ozačava sa h(. Napomije se da kod prakiče, eksperimeale primjee odskoče fukcije, ije moguće osvarii je ideali, eoreski oblik. No, važo je da skok bude dovoljo brz, šo zači da je skok fukcije zao kraći od promjea susava a koji se odskoča fukcija primjejuje. Mjera brzie promjee ekog susava jes jegova vremeska kosaa (ili vremeske kosae). Odskoča fukcija bi rebala dosići jediiču vrijedos u vremeu barem 5 pua kraćem od vremeske kosae ispiivaog susava. Isa apomea važi i za eksperimealu primjeu impulse fukcije. Nagiba fukcija (ramp fucio): predsavlja umožak varijable vremea i jediiče odskoče fukcije u(, pa se može azvai i jediičim agibom: u( f( 45 za < f ( za Laplaceova rasformacija agibe fukcije: s L { f ( } = F( Parabola fukcija Parabola fukcija, ili jediiča parabola, daa je umoškom agibe fukcije i vremeske varijable: u(. f( f ( za < za Impulsa fukcija Derivacijom odskoče fukcije dobiva se impulsa fukcija (impulse fucio), koja prema ome ima vrijedos u svakom reuku, osim u reuku =, kada je jea ampliuda beskoača. Impulsa fukcija ili jediiči impuls još se aziva i Diracova dela fukcija, prema P. Diracu koji je uveo u eorijsku fiziku, a ozačava se sa δ(. Laplaceova rasformacija: L { f ( } = F( s 3 δ ( f ( = δ ( za za = za
21 U defiiciju impulse fukcije δ( uključe je podaak da impuls zavara jediiču površiu, šo se može pokazai krećući iz izraza za derivaciju odskoče fukcije u(: du( δ ( = ε ε δ ( = du( = u( = = ε ε Impulsa fukcija δ( može se defiirai i a druge ačie. Prakičije defiiraje impulse fukcije jes da oa asaje kao razlika dviju odskočih fukcija u( koje imaju ampliudu /a (dakle isu jediiče), od kojih druga kasi za vremeski ierval a. Kako a eži k uli, ako i avedea razlika dviju odskočih fukcija posaje impulsa fukcija: u( a, = u( u( a) a a δ ( = lim u( a, a Impulsa fukcija sa slike može se prakičo primijeii, vodeći račua da je a dovoljo kraak u odosu a vremeske kosae susava a koji se primjejuje kao pobuda. u(a, /a u( u(-a) u(a, RJEŠENJE DIFERENCIJALNIH JEDNADŽBI Impulsa fukcija alazi veliku primjeu u aalizi razih susava. Kako je primijejei impuls vrlo kraak, dobivei odzivi odgovaraju prakički odzivima a pohrajeu uuarju eergiju u susavu (dakle a počee uvjee). Laplaceova rasformacija impulse fukcije izosi jeda: δ L { ( } = ( Imajući a umu defiiciju prijeose fukcije, odakle slijedi da je odziv u području komplekse varijable Y( = G( X(. Kako je u slučaju impulse fukcije kao pobude X( =, može se zaključii da odziv a pobudu u obliku impulse fukcije u vremeskom području odgovara prijeosoj fukciji u području komplekse varijable s. Odziv a pobudu u obliku impulse fukcije aziva se ežiska fukcija, i običo se ozačava sa g(. Oa a eki ači određuje ežiu kojom pojedii impuls pridoosi vrijedosi odziva. Diferecijale jedadžbe dobivee modelirajem opisuju diamički susav. No odosi ulaza i izlaza susava ada su opisai implicio, o jes ulaz i izlaz međusobo su povezai diferecijalom jedadžbom. Aaliza jedog susava u pravilu raži jeo eksplicio rješeje, odoso da varijabla izlaza bude izražea samo kao fukcija ulaze i vremeske varijable. D.j. se rješavaju egzakim aaliičkim meodama ili umeričkim meodama. Pozavaje egzakih aaliičkih meoda rješavaja diferecijalih jedadžbi u pravilu ije užo za rješavaje ehičkih problema u auomaizaciji. Međuim, važo je za dublje razumijevaje aalize i sieze diamičkih susava koje se različiim meodama rabe u auomaizaciji, jer o je usko povezao sa ključim pojmovima u auomaizaciji. Također, poašaje različiih fizikalih susava prikazuje se uuar uiverzalog maemaičkog okvira. Klasičo rješeje Klasičo rješeje običe lieare diferecijale jedadžbe s kosaim koeficijeima sasoji se od komplemeare fukcije i parikularog iegrala. Opće rješeje diferecijale jedadžbe uz pobudu jedaku uli aziva se komplemeara fukcija. Općeio diferecijala jedadžba daa je u obliku: d y( d y( dy( a + a... a a y( x( = gdje u okvirima auomaizacije začeje y( jes odziv susava ili izlaz, a x( pobuda ili ulaz. Ako se uvede operaor difereciraja D, a pobuda x( je jedaka uli, dobiva se homogea jedadžba: ( a D + a D ad + a ) y( = Do koačog rješeja dolazi se preposavkom rješeja (3.) u obliku ekspoecijale fukcije: y ( = K e r y( uvršava se u homogeu j. Kako ekspoecijala fukcija ije ula čiavo vrijeme (osim u rivijalom slučaju), da bi se zadovoljila homogea jedadžba, slijedi da je je poliom jedak uli: a r + a r ar + a = Gorja algebarska jedadžba aziva se karakerisiča jedadžba, a jeo rješeje su korijei susava r i, ili vlasie vrijedosi. Tako se opće rješeje homogee diferecijale jedadžbe, odoso komplemeara fukcija ri sasoji od izraza Ki e ako su korijei reali i različii. Također, korijei se mogu poavljai ili mogu bii kompleksi brojevi.
22 Primjer klasičog rješeja mehaički susav Komplemeara fukcija ekada se aziva i prijelazim odzivom (rasie respose) diferecijale jedadžbe. Ovisi samo o susavu samome, a e i o pobudi (pobuda = ). To će se moći povezai s aalizom sabilosi liearog susava, koja se odosi akođer a sami susav, e vodeći račua o pobudi. Parikulari iegral je posebo rješeje ehomogee diferecijale jedadžbe (dakle, pobuda ). Oo predsavlja bilo koje rješeje koje zadovoljava kompleu diferecijalu jedadžbu, a ije sadržao u komplemearoj fukciji. Dok za komplemearu fukciju posoje razrađee meode, o ije ako za parikulari iegral, koji ovisi i o pobudoj fukciji koje mogu poprimii mogo različiih oblika. Posoje meode za rješavaje ehomogee diferecijale jedadžbe popu Cauchyevom meodom ili meodom varijacije kosai, e operaorske meode. Parikulari iegral aziva se i sacioarim rješejem (seady sae) diferecijale jedadžbe, koje ovisi i o pobudi i o susavu. Aaliza očosi susava, odoso aaliza sacioare pogreške, akođer propiuje i pobudu i susav f( A x A ( K B x B ( M Porebo je izračuai gibaje x B (, ako je pobuda (gibaje x A () u obliku jediiče odkoče fukcije u(. Rješeje se sasoji od komplemeare fukcije koje određuje prijelazi odziv i parikularog iegrala koje određuje sacioaro saje: D x B = xb, kf + xb, pi d xb dx M + D B + K xb = K xa Najprije se može odredii rješeje koje će se odosii a sacioaro saje. Pošo je pobuda kosaa, odziv x B će dosići eku fiksu sacioaru vrijedos (za sabila susav). Ako je x B kosaa, oda će brzia i ubrzaje bii jedaki uli. Uvršavajući ubrzaje i brziu ula u d.j. susava, slijedi da je parikulari iegral: K xb = K xa xb, pi = xa = u = Prijelazi odziv rješava se ako se preposavi rješeje homogee jedadžbe u obliku ekspoecijale fukcije. Karakerisiča jedadžba ada izgleda slijedeće: M r + D r + K = Radi jasijeg prikaza, koeficijei iz kvadrae jedadžba česo se pišu izražei pomoću eprigušee vlasie frekvecije ω i supja prigušeja ζ, pa kvadraa jedadžba posaje: r + ζ ω + r ω = Korijei r i r susava dobivaju se rješavajem kvadrae jedadžbe: r, = ζ ω ± ω ζ Prijelazi odziv ovisi o ome da li je supaj prigušeja ζ veći od (slučaj a), jedak (slučaj b), ili maji od (slučaj c). Oviso o ome korijei r, su reali ili kompleksi brojevi. a) ζ >, korijei su reali i različii: r r B, kf = K e + K e x Ukupo rješeje suma je komplemeare fukcije i parikularog iegrala. Kako je parikulari iegral jedak jediici, rješeje je: x B = + x B, kf b) ζ =, korijei su reali i jedaki (r = r = -ζω ): xb, kf ζω ζω = K e + K e c) ζ <, korijei su kojugirao-kompleksi par: ζω xb, kf = Ke si( ω ζ K ) + šo se može apisai i kao: ζω xb, kf = Ke si( ωd + φ) gdje komplemeara fukcija poprima jeda od oblika daa u slučaju a), b) ili c). Za jedozačo rješeje porebo je, osim pobude, pozavai i reuačo saje susava, odoso počee uvjee. Kosae iegracije K i K određuju se iz počeih uvjea, i o ako da se počei pomak x B ( = ) uvrsi u prehodi izraz, odoso počea brzia dx B / ( = ) se uvrsi u derivaciju prehodog izraza. Primjer cjelokupog rješeja za slučaj c), kada je ζ <, je slijedeći: ζω e x si( ω ζ cos B = + ζ ) ζ Uvršavajem brojčaih podaaka za eprigušeu vlasiu frekveciju ω i supaj prigušeja ζ može se odredii pomak x B u očki B u svakom reuku.
23 ZNAČAJKE DINAMIČKOG SUSTAVA Oscilacijski prijelazi odziv Supaj prigušeja Defiiraje supja prigušeja i eprigušee vlasie frekvecije može se vidjei a primjeru mehaičkog susava sa masom, prigušejem i oprugom, čija karakerisiča jedadžba je: M r + D r + K = Rješeje karakerisiče jedadžbe može bii kojugirao-kompleksi par: r, = D M 4MK D ± j = σ ± jωd 4M K e σ Prijelazi odziv u slučaju rješeja sa kojugirao-kompleksim parom jes oscilacijski: σ xb, kf = Ke si( ωd + φ) -. σ K e si( ω + ϕ) Reali dio da je sa σ (sigma) i predsavlja ekspoe od e. Vlasia prigušea frekvecija ω d (damped aural frequecy) je frekvecija oscilaorog dijela koji proizlazi iz kojugirao-kompleksog para. D predsavlja kosau prigušeja (viskozog) u susavu. U slučaju kada su rješeja karakerisiče jedadžbe r i r jedaka (kada je brojik pod korijeom = ) kaže se da kosaa prigušeja ima kriiču vrijedos D kr : D kr = M K Supaj prigušejaζ(zea, dampig raio) defiira je kao omjer akuale i kriiče kosae prigušeja: ζ = D = Dkr D M K Prijelazi odzivi prema supju prigušeja mogu se podijelii a: < ζ < korijei su kojugirao-kompleksi parovi, odziv je prigušeo oscilacijski, j. odziv je prigušea siusoida (uderdamped) ζ > korijei su reali, odziv je aperiodski (overdamped) ζ = korijei su jedaki i reali, odziv je graičo aperiodski ζ = odziv su eprigušee oscilacije ζ < odziv su raspiree oscilacije (susav je esabila) Prikazi ekoliko ormaliziraih odziva (kao fukcija ω a pobudu u obliku jediiče odskoče fukcije za različie supjeve prigušeja: Neprigušea vlasia frekvecija X B ς = ς =.3 ς =.5 ς =.75 ς = ς = ω Karakerisiča jedadžba iz prehodog može se podijelii sa koeficijeom K, a zaim apisai u akozvaom sadardom obliku kvadrae jedadžbe pomoću ω i ζ (umjeso koeficijeaa ozačeih sa pr. M, K i D): M D ζ r + r + = r + r + = r + ζ ω r + ω K K ω ω Neprigušea vlasia frekvecijaω (udamped aural frequecy) defiiraa je kao frekvecija koiuiraih oscilacija odziva ako je kosaa prigušeja D jedaka uli: ω = K M Slučaj kada je D =, odoso supaj prigušeja ζ =, zači da prijelazi odziv rajo oscilira (siusoida kosae ampliude). 3
24 ω Vremeska kosaa Rješeja karakerisiče jedadžbe mogu se apisai kao: r, = σ ± jωd = ζω ± jω ζ Prijelazi odziv za prigušeo oscilacijski slučaj da pomoću ω i ζ posaje: σ ζω K si( ) si( e ωd + φ = Ke ω ζ + φ) Iz gorjeg izraza može se uočii da povećaje umoška ω i ζ (j. σ) ubrzava smirivaje oscilacija. Susav prvog reda uz pobudu jedaku uli da je homogeom d.j.: dy( τ + y( = Koeficije τ u ovom slučaju može se azvai vremeskom kosaom, a imai će jediicu vremea (pr. sekude). Klasičim rješejem d.j. korije karakerisiče jedadžbe je r = - / τ, a prijelazi odziv prehode d.j. u obliku je ekspoecijale fukcije: y( = K e τ Prijelazi odziv susava prikaza je a slici uz počeu vrijedos K (koja je u ovom slučaju jedaka ): y(,368 r = τ Im Re Za vrijeme jedog iervala vremeske kosae τ, odziv se smajuje a.368 pua maju vrijedos od počee, pošo je e - =.368. Tako bi se, a primjer, za 5 vremeskih kosai odziv smajio a svoje počee vrijedosi, odoso imao bi.68 % počee vrijedosi. Bio bi dakle, prakički ula (soga se česo uzima 5 vremeskih kosai kao mjera dovoljo bržeg, odoso sporijeg susava kada je o porebo). Teoreski, odziv ikada eće dosići ulu, o o ema prakiče važosi. Može se i drugim rječima defiirai: vrijedos vremea kada se ekspoe izad e izjedači sa zove se vremeska kosaa susava. ako se promara odziv a jediiču odskoču fukciju, ada je vremeska kosaa vrijeme porebo da odziv susava poprimi.63 pua koače vrijedosi (a vrijedos dobiva se iz - e - ). U slučaju prigušeo oscilacijskog slučaja odziva vremeska kosaa odgovara realom dijelu odziva σ, odoso umošku ω i ζ: τ = = σ ζ ω τ τ 3τ Važo je uočii da šo je korije (pol) udaljeiji od ishodiša, o je vremeska kosaa kraća, a odziv susava je brži. Začajke susava prikazae u Gaussovoj ravii Prehodo defiirai supaj prigušeja ζ i eprigušea vlasia frekvecija ω začajke su koje određuju poašaje diamičkog susava. Te se začajke mogu pokazai u Gaussovoj ravii (kompleksa ravia). Točke u ravii predsavljaju korijee karakerisiče jedadžbe, odoso polove prijeose fukcije, pa kompleksa ravia dobiva aziv i s-ravia (po operaoru Ovisos odziva o smješaju polova susava β σ ω d σ ζ = = cos β ω 4
25 OSNOVNI DINAMIČKI ČLANOVI Proporcioali čla ulog reda - P Složeiji diamički susavi u pravilu se daju rasavii a jedosavije elemee, odoso člaove, šo olakšava jihovo proučavaje. Osovi diamički člaovi svrsavaju se prema ome kako pobuda djeluje a jih, pa posoje proporcioali, iegrali i derivacijski člaovi, i ozačavaju se kao P, I i D. Osim oga, člaovi se dijele i prema kašjeju, odoso broju iegracija koje reba provesi da bi se dobila izlaza veličia. To odgovara broju spremika eergije, pa su osovi člaovi ulog, prvog ili drugog reda (pr. proporcioali čla P, P ili P ). Uz o se pojavljuje čla sa mrvim vremeom, koji se e može svrsai po prehodim krierijima. Taj čla aziva se i rasporim člaom. Složeiji člaovi, ili oi višeg reda, mogu se prikazai kao kombiacije osovih člaova. Dodaje se da je svrsavaje po člaovim svojsveije jemačkoj lierauri, uz ešo drugačije ozačavaje (pr. P ozačava se sa PT gleid), dok se u američkoj e susreće ako česo. b x( a Y ( G ( = = K P X ( y( b y( = x( = KP x( a x(, y( y Kp x Proporcioali čla prvog reda - P f( A x A ( K B x B ( D Odziv P člaa e može imai oscilacije, pošo ema izmjea eergije među spremicima, kojih ima samo jeda. U ovom primjeru o je opruga. Sa slike se vidi da odziv kasi, a kašjeje ovisi o karakerisici opruge, e o oporu koji pruža prigušik. Prijeosa fukcija P člaa općeio se može dai sa: D dxb ( + xb ( = xa( K.5 Xa(, Xb( Xa Y ( K G( = = P X ( τ s + x ( ) ( )( ( K / D) B = xa e ).63.5 Xb Primjeri P člaa su elekriči krug sa serijski spojeim oporikom i kodezaorom (RC), zaim jedosava susav prijelaza oplie sa usredoočeim paramerima. D/K Proporcioali čla drugog reda - P Primjeri su mehaički susav s masom, prigušejem i oprugom, prikaza, e elekriči sa oporikom, svikom i kodezaorom (RLC), koji su opisai u poglavlju o maemaičkom prikazu ehičkih susava. Susavi su opisai diferecijalom jedadžbom. reda. Odzivi akvog susava mogu bii oscilacijski ili aperiodski, oviso o supju prigušeja susava. Odzivi a pobudu u obliku jediiče odskoče fukcije: Prijeosa fukcija P člaa općeio se može dai sa: Y( K G( = = P X ( s + ζ ω s + ω XB Supaj prigušeja ζ i eprigušea vlasia frekvecija ω ovise o omjerima parameara susava. ς = ς =. 3 ς =.5 ς =.7 5 ς = ς = ω 5
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
TEORIJA SKUPOVA Zadaci
 TEORIJA SKUPOVA Zadai LOGIKA 1 I. godina 1. Zapišite simbolima: ( x nije element skupa S (b) d je član skupa S () F je podskup slupa S (d) Skup S sadrži skup R 2. Neka je S { x;2x 6} = = i neka je b =
TEORIJA SKUPOVA Zadai LOGIKA 1 I. godina 1. Zapišite simbolima: ( x nije element skupa S (b) d je član skupa S () F je podskup slupa S (d) Skup S sadrži skup R 2. Neka je S { x;2x 6} = = i neka je b =
OPTIMIRANJE SLIJEDNOG SUSTAVA S ISTOSMJERNIM MOTOROM S PERMANENTNIM MAGNETIMA TE REFERENTNIM MODELOM I SIGNALNOM ADAPTACIJOM
 SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA DIPLOMSKI RAD br 4 OPTIMIRANJE SLIJEDNOG SUSTAVA S ISTOSMJERNIM MOTOROM S PERMANENTNIM MAGNETIMA TE REFERENTNIM MODELOM I SIGNALNOM ADAPTACIJOM
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA DIPLOMSKI RAD br 4 OPTIMIRANJE SLIJEDNOG SUSTAVA S ISTOSMJERNIM MOTOROM S PERMANENTNIM MAGNETIMA TE REFERENTNIM MODELOM I SIGNALNOM ADAPTACIJOM
Gabrijel Kolar, Žana Nevjestić MATEMATIČKI MODEL NTC TERMISTORA
 Sveučilište u Zagrebu Fakultet elektrotehike i račuarstva Fakultet kemijskog ižejerstva i tehologije Gabrijel Kolar, Žaa Nevjestić MATEMATIČKI MODEL NTC TERMISTORA Zagreb, 2017 Ovaj rad izrađe je a Fakultetu
Sveučilište u Zagrebu Fakultet elektrotehike i račuarstva Fakultet kemijskog ižejerstva i tehologije Gabrijel Kolar, Žaa Nevjestić MATEMATIČKI MODEL NTC TERMISTORA Zagreb, 2017 Ovaj rad izrađe je a Fakultetu
Red veze za benzen. Slika 1.
 Red veze za benzen Benzen C 6 H 6 je aromatično ciklično jedinjenje. Njegove dve rezonantne forme (ili Kekuléove structure), prema teoriji valentne veze (VB) prikazuju se uobičajeno kao na slici 1 a),
Red veze za benzen Benzen C 6 H 6 je aromatično ciklično jedinjenje. Njegove dve rezonantne forme (ili Kekuléove structure), prema teoriji valentne veze (VB) prikazuju se uobičajeno kao na slici 1 a),
Solutions Manual 4.1. nonlinear. 4.2 The Fourier Series is: and the fundamental frequency is ω 2π
 Soluios Maual. (a) (b) (c) (d) (e) (f) (g) liear oliear liear liear oliear oliear liear. The Fourier Series is: F () 5si( ) ad he fudameal frequecy is ω f ----- H z.3 Sice V rms V ad f 6Hz, he Fourier
Soluios Maual. (a) (b) (c) (d) (e) (f) (g) liear oliear liear liear oliear oliear liear. The Fourier Series is: F () 5si( ) ad he fudameal frequecy is ω f ----- H z.3 Sice V rms V ad f 6Hz, he Fourier
The Eigen Function of Linear Systems
 1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
P a g e 3 6 of R e p o r t P B 4 / 0 9
 P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA. Šefket Arslanagić, Sarajevo, BiH
 MAT-KOL (Banja Luka) XXIII ()(7), -7 http://wwwimviblorg/dmbl/dmblhtm DOI: 75/МК7A ISSN 5-6969 (o) ISSN 986-588 (o) ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA Šefket Arslanagić,
MAT-KOL (Banja Luka) XXIII ()(7), -7 http://wwwimviblorg/dmbl/dmblhtm DOI: 75/МК7A ISSN 5-6969 (o) ISSN 986-588 (o) ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA Šefket Arslanagić,
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
Zadatci sa ciklusima. Zadatak1: Sastaviti progra koji određuje z ir prvih prirod ih rojeva.
 Zadatci sa ciklusima Zadatak1: Sastaviti progra koji određuje z ir prvih prirod ih rojeva. StrToIntDef(tekst,broj) - funkcija kojom se tekst pretvara u ceo broj s tim da je uvedena automatska kontrola
Zadatci sa ciklusima Zadatak1: Sastaviti progra koji određuje z ir prvih prirod ih rojeva. StrToIntDef(tekst,broj) - funkcija kojom se tekst pretvara u ceo broj s tim da je uvedena automatska kontrola
Ideal Amplifier/Attenuator. Memoryless. where k is some real constant. Integrator. System with memory
 Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
176 5 t h Fl oo r. 337 P o ly me r Ma te ri al s
 A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o
 I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
Mathcad sa algoritmima
 P R I M J E R I P R I M J E R I Mathcad sa algoritmima NAREDBE - elementarne obrade - sekvence Primjer 1 Napraviti algoritam za sabiranje dva broja. NAREDBE - elementarne obrade - sekvence Primjer 1 POČETAK
P R I M J E R I P R I M J E R I Mathcad sa algoritmima NAREDBE - elementarne obrade - sekvence Primjer 1 Napraviti algoritam za sabiranje dva broja. NAREDBE - elementarne obrade - sekvence Primjer 1 POČETAK
Šime Šuljić. Funkcije. Zadavanje funkcije i područje definicije. š2004š 1
 Šime Šuljić Funkcije Zadavanje funkcije i područje definicije š2004š 1 Iz povijesti Dvojica Francuza, Pierre de Fermat i Rene Descartes, posebno su zadužila matematiku unijevši ideju koordinatne metode
Šime Šuljić Funkcije Zadavanje funkcije i područje definicije š2004š 1 Iz povijesti Dvojica Francuza, Pierre de Fermat i Rene Descartes, posebno su zadužila matematiku unijevši ideju koordinatne metode
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
Analiza svojstava konveksnosti obveznica bez primjene diferencijalnog računa
 Trg J. F. Keedya 6 10000 Zagreb, Croaia Tel +385(0)1 38 3333 www.efzg.hr/wps wps@efzg.hr EFZG WORKING PAPER SERIES E FZ G SERIJA Č LANAKA U NAS TA JANJU U D K 3 3 : 6 5 Br. 15-01 Vedra Kojić Aaliza svojsava
Trg J. F. Keedya 6 10000 Zagreb, Croaia Tel +385(0)1 38 3333 www.efzg.hr/wps wps@efzg.hr EFZG WORKING PAPER SERIES E FZ G SERIJA Č LANAKA U NAS TA JANJU U D K 3 3 : 6 5 Br. 15-01 Vedra Kojić Aaliza svojsava
Electrical Engineering Department Network Lab.
 Par:- Elecrical Egieerig Deparme Nework Lab. Deermiaio of differe parameers of -por eworks ad verificaio of heir ierrelaio ships. Objecive: - To deermie Y, ad ABD parameers of sigle ad cascaded wo Por
Par:- Elecrical Egieerig Deparme Nework Lab. Deermiaio of differe parameers of -por eworks ad verificaio of heir ierrelaio ships. Objecive: - To deermie Y, ad ABD parameers of sigle ad cascaded wo Por
Harmonic excitation (damped)
 Harmoic eciaio damped k m cos EOM: m&& c& k cos c && ζ & f cos The respose soluio ca be separaed io par;. Homogeeous soluio h. Paricular soluio p h p & ζ & && ζ & f cos Homogeeous soluio Homogeeous soluio
Harmoic eciaio damped k m cos EOM: m&& c& k cos c && ζ & f cos The respose soluio ca be separaed io par;. Homogeeous soluio h. Paricular soluio p h p & ζ & && ζ & f cos Homogeeous soluio Homogeeous soluio
Geometrijsko mesto korena
 Geometrijsko mesto korea U dosadašjem delu kursa su, između ostalog, bile razmatrae karakteristike SAU i povezaost tih karakteristika sa položajem polova sistema u kompleksoj ravi. Uočea je direkta zavisost
Geometrijsko mesto korea U dosadašjem delu kursa su, između ostalog, bile razmatrae karakteristike SAU i povezaost tih karakteristika sa položajem polova sistema u kompleksoj ravi. Uočea je direkta zavisost
University of California at Berkeley College of Engineering Department of Electrical Engineering and Computer Sciences
 A Uiversity of Califoria at Berkeley College of Egieerig Departmet of Electrical Egieerig ad Computer Scieces U N I V E R S T H E I T Y O F LE T TH E R E B E LI G H T C A L I F O R N 8 6 8 I A EECS : Sigals
A Uiversity of Califoria at Berkeley College of Egieerig Departmet of Electrical Egieerig ad Computer Scieces U N I V E R S T H E I T Y O F LE T TH E R E B E LI G H T C A L I F O R N 8 6 8 I A EECS : Sigals
Section 8 Convolution and Deconvolution
 APPLICATIONS IN SIGNAL PROCESSING Secio 8 Covoluio ad Decovoluio This docume illusraes several echiques for carryig ou covoluio ad decovoluio i Mahcad. There are several operaors available for hese fucios:
APPLICATIONS IN SIGNAL PROCESSING Secio 8 Covoluio ad Decovoluio This docume illusraes several echiques for carryig ou covoluio ad decovoluio i Mahcad. There are several operaors available for hese fucios:
ECE-314 Fall 2012 Review Questions
 ECE-34 Fall 0 Review Quesios. A liear ime-ivaria sysem has he ipu-oupu characerisics show i he firs row of he diagram below. Deermie he oupu for he ipu show o he secod row of he diagram. Jusify your aswer.
ECE-34 Fall 0 Review Quesios. A liear ime-ivaria sysem has he ipu-oupu characerisics show i he firs row of he diagram below. Deermie he oupu for he ipu show o he secod row of he diagram. Jusify your aswer.
Projektovanje paralelnih algoritama II
 Projektovanje paralelnih algoritama II Primeri paralelnih algoritama, I deo Paralelni algoritmi za množenje matrica 1 Algoritmi za množenje matrica Ovde su data tri paralelna algoritma: Direktan algoritam
Projektovanje paralelnih algoritama II Primeri paralelnih algoritama, I deo Paralelni algoritmi za množenje matrica 1 Algoritmi za množenje matrica Ovde su data tri paralelna algoritma: Direktan algoritam
Uvod u relacione baze podataka
 Uvod u relacione baze podataka Ana Spasić 2. čas 1 Mala studentska baza dosije (indeks, ime, prezime, datum rodjenja, mesto rodjenja, datum upisa) predmet (id predmeta, sifra, naziv, bodovi) ispitni rok
Uvod u relacione baze podataka Ana Spasić 2. čas 1 Mala studentska baza dosije (indeks, ime, prezime, datum rodjenja, mesto rodjenja, datum upisa) predmet (id predmeta, sifra, naziv, bodovi) ispitni rok
CHE302 LECTURE VI DYNAMIC BEHAVIORS OF REPRESENTATIVE PROCESSES. Professor Dae Ryook Yang
 CHE30 LECTURE VI DYNAMIC BEHAVIORS OF REPRESENTATIVE PROCESSES Professor Dae Ryook Yang Fall 00 Dep. of Chemical and Biological Engineering orea Universiy CHE30 Process Dynamics and Conrol orea Universiy
CHE30 LECTURE VI DYNAMIC BEHAVIORS OF REPRESENTATIVE PROCESSES Professor Dae Ryook Yang Fall 00 Dep. of Chemical and Biological Engineering orea Universiy CHE30 Process Dynamics and Conrol orea Universiy
Provjera znanja 17. veljače godine. 1.) Maksimalna površina pravokutnika kojemu su dva vrha na osi x, a dva na krivulji y=1-x 2 iznosi.
 Provjera zaja 7. veljače 00. godie Matematika.) Maksimala površia pravokutika kojemu su dva vrha a osi x, a dva a krivulji y=-x izosi 4 9.) Površia lika određeog ejedadžbama (x-) y - x- izosi 4 9 5 7 Matematika.)
Provjera zaja 7. veljače 00. godie Matematika.) Maksimala površia pravokutika kojemu su dva vrha a osi x, a dva a krivulji y=-x izosi 4 9.) Površia lika određeog ejedadžbama (x-) y - x- izosi 4 9 5 7 Matematika.)
Sampling. AD Conversion (Additional Material) Sampling: Band limited signal. Sampling. Sampling function (sampling comb) III(x) Shah.
 AD Coversio (Addiioal Maerial Samplig Samplig Properies of real ADCs wo Sep Flash ADC Pipelie ADC Iegraig ADCs: Sigle Slope, Dual Slope DA Coverer Samplig fucio (samplig comb III(x Shah III III ( x = δ
AD Coversio (Addiioal Maerial Samplig Samplig Properies of real ADCs wo Sep Flash ADC Pipelie ADC Iegraig ADCs: Sigle Slope, Dual Slope DA Coverer Samplig fucio (samplig comb III(x Shah III III ( x = δ
ODREĐIVANJE DINAMIČKOG ODZIVA MEHANIČKOG SUSTAVA METODOM RUNGE-KUTTA
 Sveučilište u Zagrebu GraĎevinski faklultet Kolegij: Primjenjena matematika ODREĐIVANJE DINAMIČKOG ODZIVA MEHANIČKOG SUSTAVA METODOM RUNGE-KUTTA Seminarski rad Student: Marija Nikolić Mentor: prof.dr.sc.
Sveučilište u Zagrebu GraĎevinski faklultet Kolegij: Primjenjena matematika ODREĐIVANJE DINAMIČKOG ODZIVA MEHANIČKOG SUSTAVA METODOM RUNGE-KUTTA Seminarski rad Student: Marija Nikolić Mentor: prof.dr.sc.
Fourier transform. Continuous-time Fourier transform (CTFT) ω ω
 Fourier rasform Coiuous-ime Fourier rasform (CTFT P. Deoe ( he Fourier rasform of he sigal x(. Deermie he followig values, wihou compuig (. a (0 b ( d c ( si d ( d d e iverse Fourier rasform for Re { (
Fourier rasform Coiuous-ime Fourier rasform (CTFT P. Deoe ( he Fourier rasform of he sigal x(. Deermie he followig values, wihou compuig (. a (0 b ( d c ( si d ( d d e iverse Fourier rasform for Re { (
Let s express the absorption of radiation by dipoles as a dipole correlation function.
 MIT Deparme of Chemisry 5.74, Sprig 004: Iroducory Quaum Mechaics II Isrucor: Prof. Adrei Tokmakoff p. 81 Time-Correlaio Fucio Descripio of Absorpio Lieshape Le s express he absorpio of radiaio by dipoles
MIT Deparme of Chemisry 5.74, Sprig 004: Iroducory Quaum Mechaics II Isrucor: Prof. Adrei Tokmakoff p. 81 Time-Correlaio Fucio Descripio of Absorpio Lieshape Le s express he absorpio of radiaio by dipoles
Mechatronics. Time Response & Frequency Response 2 nd -Order Dynamic System 2-Pole, Low-Pass, Active Filter
 Time Respose & Frequecy Respose d -Order Dyamic System -Pole, Low-Pass, Active Filter R 4 R 7 C 5 e i R 1 C R 3 - + R 6 - + e out Assigmet: Perform a Complete Dyamic System Ivestigatio of the Two-Pole,
Time Respose & Frequecy Respose d -Order Dyamic System -Pole, Low-Pass, Active Filter R 4 R 7 C 5 e i R 1 C R 3 - + R 6 - + e out Assigmet: Perform a Complete Dyamic System Ivestigatio of the Two-Pole,
PI3B V, 16-Bit to 32-Bit FET Mux/DeMux NanoSwitch. Features. Description. Pin Configuration. Block Diagram.
 33V, 6-Bi o 32-Bi FET Mux/DeMux NaoSwich Feaures -ohm Swich Coecio Bewee Two Pors Near-Zero Propagaio Delay Fas Swichig Speed: 4s (max) Ulra -Low Quiesce Power (02mA yp) Ideal for oebook applicaios Idusrial
33V, 6-Bi o 32-Bi FET Mux/DeMux NaoSwich Feaures -ohm Swich Coecio Bewee Two Pors Near-Zero Propagaio Delay Fas Swichig Speed: 4s (max) Ulra -Low Quiesce Power (02mA yp) Ideal for oebook applicaios Idusrial
Algoritam za množenje ulančanih matrica. Alen Kosanović Prirodoslovno-matematički fakultet Matematički odsjek
 Algoritam za množenje ulančanih matrica Alen Kosanović Prirodoslovno-matematički fakultet Matematički odsjek O problemu (1) Neka je A 1, A 2,, A n niz ulančanih matrica duljine n N, gdje su dimenzije matrice
Algoritam za množenje ulančanih matrica Alen Kosanović Prirodoslovno-matematički fakultet Matematički odsjek O problemu (1) Neka je A 1, A 2,, A n niz ulančanih matrica duljine n N, gdje su dimenzije matrice
Linear Time Invariant Systems
 1 Liear Time Ivaria Sysems Oulie We will show ha he oupu equals he covoluio bewee he ipu ad he ui impulse respose: sysem for a discree-ime, for a coiuous-ime sysdem, y x h y x h 2 Discree Time LTI Sysems
1 Liear Time Ivaria Sysems Oulie We will show ha he oupu equals he covoluio bewee he ipu ad he ui impulse respose: sysem for a discree-ime, for a coiuous-ime sysdem, y x h y x h 2 Discree Time LTI Sysems
EGR 544 Communication Theory
 EGR 544 Commuicaio heory 7. Represeaio of Digially Modulaed Sigals II Z. Aliyazicioglu Elecrical ad Compuer Egieerig Deparme Cal Poly Pomoa Represeaio of Digial Modulaio wih Memory Liear Digial Modulaio
EGR 544 Commuicaio heory 7. Represeaio of Digially Modulaed Sigals II Z. Aliyazicioglu Elecrical ad Compuer Egieerig Deparme Cal Poly Pomoa Represeaio of Digial Modulaio wih Memory Liear Digial Modulaio
10.3 Autocorrelation Function of Ergodic RP 10.4 Power Spectral Density of Ergodic RP 10.5 Normal RP (Gaussian RP)
 ENGG450 Probabiliy ad Saisics for Egieers Iroducio 3 Probabiliy 4 Probabiliy disribuios 5 Probabiliy Desiies Orgaizaio ad descripio of daa 6 Samplig disribuios 7 Ifereces cocerig a mea 8 Comparig wo reames
ENGG450 Probabiliy ad Saisics for Egieers Iroducio 3 Probabiliy 4 Probabiliy disribuios 5 Probabiliy Desiies Orgaizaio ad descripio of daa 6 Samplig disribuios 7 Ifereces cocerig a mea 8 Comparig wo reames
F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mathematics
![F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mathematics F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mathematics](/thumbs/89/97771684.jpg) F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mahemaics Prelim Quesio Paper Soluio Q. Aemp ay FIVE of he followig : [0] Q.(a) Defie Eve ad odd fucios. [] As.: A fucio f() is said o be eve fucio if
F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mahemaics Prelim Quesio Paper Soluio Q. Aemp ay FIVE of he followig : [0] Q.(a) Defie Eve ad odd fucios. [] As.: A fucio f() is said o be eve fucio if
STK4080/9080 Survival and event history analysis
 STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
Moment Generating Function
 1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A. Ήχος Πα. to os se e e na aș te e e slă ă ă vi i i i i
 CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
Vrednovanje opcija polisa osiguranja za katastrofe
 Uiverzie u Novom Sadu Prirodo-maemaički fakule Deparma za maemaiku i iformaiku Jasa Mirović Vredovaje opcija polisa osiguraja za kaasrofe Maser rad Novi Sad, 3 Vredovaje opcija polisa osiguraja za kaasrofe
Uiverzie u Novom Sadu Prirodo-maemaički fakule Deparma za maemaiku i iformaiku Jasa Mirović Vredovaje opcija polisa osiguraja za kaasrofe Maser rad Novi Sad, 3 Vredovaje opcija polisa osiguraja za kaasrofe
Termodinamika. FIZIKA PSS-GRAD 29. studenog Copyright 2015 John Wiley & Sons, Inc. All rights reserved.
 Termodinamika FIZIKA PSS-GRAD 29. studenog 2017. 15.1 Thermodynamic Systems and Their Surroundings Thermodynamics is the branch of physics that is built upon the fundamental laws that heat and work obey.
Termodinamika FIZIKA PSS-GRAD 29. studenog 2017. 15.1 Thermodynamic Systems and Their Surroundings Thermodynamics is the branch of physics that is built upon the fundamental laws that heat and work obey.
PI3B
 234789023478902347890223478902347890234789022347890234789023478902234789023478902347890223478902 Feaures Near-Zero propagaio delay -ohm swiches coec ipus o oupus Fas Swichig Speed - 4s max Permis Ho Iserio
234789023478902347890223478902347890234789022347890234789023478902234789023478902347890223478902 Feaures Near-Zero propagaio delay -ohm swiches coec ipus o oupus Fas Swichig Speed - 4s max Permis Ho Iserio
PROGRAMSKO PRONALAŽENJE RJEŠENJA MBCP PROBLEMA PROGRAMMATICALLY SOLUTION FOR MBCP PROBLEMS
 PROGRAMSKO PRONALAŽENJE RJEŠENJA MBCP PROBLEMA mr. sc. Ato Vrdoljak, prof. matematike Građeviski fakultet Sveučilišta u Mostaru Sažetak: U radu je da osvrt a programsko rješavaje problema vezaog za particioiraje
PROGRAMSKO PRONALAŽENJE RJEŠENJA MBCP PROBLEMA mr. sc. Ato Vrdoljak, prof. matematike Građeviski fakultet Sveučilišta u Mostaru Sažetak: U radu je da osvrt a programsko rješavaje problema vezaog za particioiraje
FIZIKALNA KOZMOLOGIJA VII. VRLO RANI SVEMIR & INFLACIJA
 FIZIKALNA KOZMOLOGIJA VII. VRLO RANI SVEMIR & INFLACIJA KOZMIČKI SAT ranog svemira Ekstra zračenje u mjerenju CMB Usporedba s rezultatima LEP-a Usporedba CMB i neutrina Vj.: Pozadinsko zračenje neutrina
FIZIKALNA KOZMOLOGIJA VII. VRLO RANI SVEMIR & INFLACIJA KOZMIČKI SAT ranog svemira Ekstra zračenje u mjerenju CMB Usporedba s rezultatima LEP-a Usporedba CMB i neutrina Vj.: Pozadinsko zračenje neutrina
Solution. The straightforward approach is surprisingly difficult because one has to be careful about the limits.
 ose ad Varably Homewor # (8), aswers Q: Power spera of some smple oses A Posso ose A Posso ose () s a sequee of dela-fuo pulses, eah ourrg depedely, a some rae r (More formally, s a sum of pulses of wdh
ose ad Varably Homewor # (8), aswers Q: Power spera of some smple oses A Posso ose A Posso ose () s a sequee of dela-fuo pulses, eah ourrg depedely, a some rae r (More formally, s a sum of pulses of wdh
Communication Systems Lecture 25. Dong In Kim School of Info/Comm Engineering Sungkyunkwan University
 Commuiaio Sysems Leure 5 Dog I Kim Shool o Io/Comm Egieerig Sugkyukwa Uiversiy 1 Oulie Noise i Agle Modulaio Phase deviaio Large SNR Small SNR Oupu SNR PM FM Review o Agle Modulaio Geeral orm o agle modulaed
Commuiaio Sysems Leure 5 Dog I Kim Shool o Io/Comm Egieerig Sugkyukwa Uiversiy 1 Oulie Noise i Agle Modulaio Phase deviaio Large SNR Small SNR Oupu SNR PM FM Review o Agle Modulaio Geeral orm o agle modulaed
NAPREDNI FIZIČKI PRAKTIKUM 1 studij Matematika i fizika; smjer nastavnički MJERENJE MALIH OTPORA
 NAPREDNI FIZIČKI PRAKTIKUM 1 studij Matematika i fizika; smjer nastavnički MJERENJE MALIH OTPORA studij Matematika i fizika; smjer nastavnički NFP 1 1 ZADACI 1. Mjerenjem geometrijskih dimenzija i otpora
NAPREDNI FIZIČKI PRAKTIKUM 1 studij Matematika i fizika; smjer nastavnički MJERENJE MALIH OTPORA studij Matematika i fizika; smjer nastavnički NFP 1 1 ZADACI 1. Mjerenjem geometrijskih dimenzija i otpora
EXPERIMENTAL ANALYSIS OF THE STRENGTH OF A POLYMER PRODUCED FROM RECYCLED MATERIAL
 A. Jurić et al. EXPERIMENTAL ANALYSIS OF THE STRENGTH OF A POLYMER PRODUCED FROM RECYCLED MATERIAL Aleksandar Jurić, Tihomir Štefić, Zlatko Arbanas ISSN 10-651 UDC/UDK 60.17.1/.:678.74..017 Preliminary
A. Jurić et al. EXPERIMENTAL ANALYSIS OF THE STRENGTH OF A POLYMER PRODUCED FROM RECYCLED MATERIAL Aleksandar Jurić, Tihomir Štefić, Zlatko Arbanas ISSN 10-651 UDC/UDK 60.17.1/.:678.74..017 Preliminary
Beechwood Music Department Staff
 Beechwood Music Department Staff MRS SARAH KERSHAW - HEAD OF MUSIC S a ra h K e rs h a w t r a i n e d a t t h e R oy a l We ls h C o l le g e of M u s i c a n d D ra m a w h e re s h e ob t a i n e d
Beechwood Music Department Staff MRS SARAH KERSHAW - HEAD OF MUSIC S a ra h K e rs h a w t r a i n e d a t t h e R oy a l We ls h C o l le g e of M u s i c a n d D ra m a w h e re s h e ob t a i n e d
O & M Cost O & M Cost
 5/5/008 Turbie Reliabiliy, Maieace ad Faul Deecio Zhe Sog, Adrew Kusiak 39 Seamas Ceer Iowa Ciy, Iowa 54-57 adrew-kusiak@uiowa.edu Tel: 39-335-5934 Fax: 39-335-5669 hp://www.icae.uiowa.edu/~akusiak Oulie
5/5/008 Turbie Reliabiliy, Maieace ad Faul Deecio Zhe Sog, Adrew Kusiak 39 Seamas Ceer Iowa Ciy, Iowa 54-57 adrew-kusiak@uiowa.edu Tel: 39-335-5934 Fax: 39-335-5669 hp://www.icae.uiowa.edu/~akusiak Oulie
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 4 9/16/2013. Applications of the large deviation technique
 MASSACHUSETTS ISTITUTE OF TECHOLOGY 6.265/5.070J Fall 203 Lecure 4 9/6/203 Applicaios of he large deviaio echique Coe.. Isurace problem 2. Queueig problem 3. Buffer overflow probabiliy Safey capial for
MASSACHUSETTS ISTITUTE OF TECHOLOGY 6.265/5.070J Fall 203 Lecure 4 9/6/203 Applicaios of he large deviaio echique Coe.. Isurace problem 2. Queueig problem 3. Buffer overflow probabiliy Safey capial for
CS623: Introduction to Computing with Neural Nets (lecture-10) Pushpak Bhattacharyya Computer Science and Engineering Department IIT Bombay
 CS6: Iroducio o Compuig ih Neural Nes lecure- Pushpak Bhaacharyya Compuer Sciece ad Egieerig Deparme IIT Bombay Tilig Algorihm repea A kid of divide ad coquer sraegy Give he classes i he daa, ru he percepro
CS6: Iroducio o Compuig ih Neural Nes lecure- Pushpak Bhaacharyya Compuer Sciece ad Egieerig Deparme IIT Bombay Tilig Algorihm repea A kid of divide ad coquer sraegy Give he classes i he daa, ru he percepro
Dynamic Response of Linear Systems
 Dyamic Respose of Liear Systems Liear System Respose Superpositio Priciple Resposes to Specific Iputs Dyamic Respose of st Order Systems Characteristic Equatio - Free Respose Stable st Order System Respose
Dyamic Respose of Liear Systems Liear System Respose Superpositio Priciple Resposes to Specific Iputs Dyamic Respose of st Order Systems Characteristic Equatio - Free Respose Stable st Order System Respose
Lecture 15: Three-tank Mixing and Lead Poisoning
 Lecure 15: Three-ak Miig ad Lead Poisoig Eigevalues ad eigevecors will be used o fid he soluio of a sysem for ukow fucios ha saisfy differeial equaios The ukow fucios will be wrie as a 1 colum vecor [
Lecure 15: Three-ak Miig ad Lead Poisoig Eigevalues ad eigevecors will be used o fid he soluio of a sysem for ukow fucios ha saisfy differeial equaios The ukow fucios will be wrie as a 1 colum vecor [
K3 p K2 p Kp 0 p 2 p 3 p
 Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
Source-Free RC Circuit
 First Order Circuits Source-Free RC Circuit Initial charge on capacitor q = Cv(0) so that voltage at time 0 is v(0). What is v(t)? Prof Carruthers (ECE @ BU) EK307 Notes Summer 2018 150 / 264 First Order
First Order Circuits Source-Free RC Circuit Initial charge on capacitor q = Cv(0) so that voltage at time 0 is v(0). What is v(t)? Prof Carruthers (ECE @ BU) EK307 Notes Summer 2018 150 / 264 First Order
6.003: Signals and Systems
 6.003: Sigals ad Sysems Lecure 8 March 2, 2010 6.003: Sigals ad Sysems Mid-erm Examiaio #1 Tomorrow, Wedesday, March 3, 7:30-9:30pm. No reciaios omorrow. Coverage: Represeaios of CT ad DT Sysems Lecures
6.003: Sigals ad Sysems Lecure 8 March 2, 2010 6.003: Sigals ad Sysems Mid-erm Examiaio #1 Tomorrow, Wedesday, March 3, 7:30-9:30pm. No reciaios omorrow. Coverage: Represeaios of CT ad DT Sysems Lecures
Le classeur à tampons
 Le classeur à tampons P a s à pa s Le matériel 1 gr a n d cla s s e u r 3 pa pi e r s co o r d o n n é s. P o u r le m o d è l e pr é s e n t é P a p i e r ble u D ai s y D s, pa pi e r bor d e a u x,
Le classeur à tampons P a s à pa s Le matériel 1 gr a n d cla s s e u r 3 pa pi e r s co o r d o n n é s. P o u r le m o d è l e pr é s e n t é P a p i e r ble u D ai s y D s, pa pi e r bor d e a u x,
The universal vector. Open Access Journal of Mathematical and Theoretical Physics [ ] Introduction [ ] ( 1)
![The universal vector. Open Access Journal of Mathematical and Theoretical Physics [ ] Introduction [ ] ( 1) The universal vector. Open Access Journal of Mathematical and Theoretical Physics [ ] Introduction [ ] ( 1)](/thumbs/85/92727336.jpg) Ope Access Joural of Mahemaical ad Theoreical Physics Mii Review The uiversal vecor Ope Access Absrac This paper akes Asroheology mahemaics ad pus some of i i erms of liear algebra. All of physics ca be
Ope Access Joural of Mahemaical ad Theoreical Physics Mii Review The uiversal vecor Ope Access Absrac This paper akes Asroheology mahemaics ad pus some of i i erms of liear algebra. All of physics ca be
MODERN CONTROL SYSTEMS
 MODERN CONTROL SYSTEMS Lecure 9, Sae Space Repreeaio Emam Fahy Deparme of Elecrical ad Corol Egieerig email: emfmz@aa.edu hp://www.aa.edu/cv.php?dip_ui=346&er=6855 Trafer Fucio Limiaio TF = O/P I/P ZIC
MODERN CONTROL SYSTEMS Lecure 9, Sae Space Repreeaio Emam Fahy Deparme of Elecrical ad Corol Egieerig email: emfmz@aa.edu hp://www.aa.edu/cv.php?dip_ui=346&er=6855 Trafer Fucio Limiaio TF = O/P I/P ZIC
Software Process Models there are many process model s in th e li t e ra t u re, s om e a r e prescriptions and some are descriptions you need to mode
 Unit 2 : Software Process O b j ec t i ve This unit introduces software systems engineering through a discussion of software processes and their principal characteristics. In order to achieve the desireable
Unit 2 : Software Process O b j ec t i ve This unit introduces software systems engineering through a discussion of software processes and their principal characteristics. In order to achieve the desireable
5 th INTERNATIONAL CONFERENCE Contemporary achievements in civil engineering 21. April Subotica, SERBIA
 5 th INTERNATIONAL CONFERENCE Contemporary achievements in civil engineering 21. April 2017. Subotica, SERBIA COMPUTER SIMULATION OF THE ORDER FREQUENCIES AMPLITUDES EXCITATION ON RESPONSE DYNAMIC 1D MODELS
5 th INTERNATIONAL CONFERENCE Contemporary achievements in civil engineering 21. April 2017. Subotica, SERBIA COMPUTER SIMULATION OF THE ORDER FREQUENCIES AMPLITUDES EXCITATION ON RESPONSE DYNAMIC 1D MODELS
Economics 8723 Macroeconomic Theory Problem Set 2 Professor Sanjay Chugh Spring 2017
 Deparme of Ecoomics The Ohio Sae Uiversiy Ecoomics 8723 Macroecoomic Theory Problem Se 2 Professor Sajay Chugh Sprig 207 Labor Icome Taxes, Nash-Bargaied Wages, ad Proporioally-Bargaied Wages. I a ecoomy
Deparme of Ecoomics The Ohio Sae Uiversiy Ecoomics 8723 Macroecoomic Theory Problem Se 2 Professor Sajay Chugh Sprig 207 Labor Icome Taxes, Nash-Bargaied Wages, ad Proporioally-Bargaied Wages. I a ecoomy
Lecture 10 - Model Identification
 Lecure - odel Idenificaion Wha is ssem idenificaion? Direc impulse response idenificaion Linear regression Regularizaion Parameric model ID nonlinear LS Conrol Engineering - Wha is Ssem Idenificaion? Experimen
Lecure - odel Idenificaion Wha is ssem idenificaion? Direc impulse response idenificaion Linear regression Regularizaion Parameric model ID nonlinear LS Conrol Engineering - Wha is Ssem Idenificaion? Experimen
University of California at Berkeley College of Engineering Department of Electrical Engineering and Computer Sciences
 A Uiversity of Califoria at Berkeley College of Egieerig Departmet of Electrical Egieerig ad Computer Scieces U N I V E R S T H E I T Y O F LE T TH E R E B E LI G H T C A L I F O R N 8 6 8 I A EECS : Sigals
A Uiversity of Califoria at Berkeley College of Egieerig Departmet of Electrical Egieerig ad Computer Scieces U N I V E R S T H E I T Y O F LE T TH E R E B E LI G H T C A L I F O R N 8 6 8 I A EECS : Sigals
Big O Notation for Time Complexity of Algorithms
 BRONX COMMUNITY COLLEGE of he Ciy Uiversiy of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI 33 Secio E01 Hadou 1 Fall 2014 Sepember 3, 2014 Big O Noaio for Time Complexiy of Algorihms Time
BRONX COMMUNITY COLLEGE of he Ciy Uiversiy of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI 33 Secio E01 Hadou 1 Fall 2014 Sepember 3, 2014 Big O Noaio for Time Complexiy of Algorihms Time
KLASIFIKACIJA NAIVNI BAJES. NIKOLA MILIKIĆ URL:
 KLASIFIKACIJA NAIVNI BAJES NIKOLA MILIKIĆ EMAIL: nikola.milikic@fon.bg.ac.rs URL: http://nikola.milikic.info ŠTA JE KLASIFIKACIJA? Zadatak određivanja klase kojoj neka instanca pripada instanca je opisana
KLASIFIKACIJA NAIVNI BAJES NIKOLA MILIKIĆ EMAIL: nikola.milikic@fon.bg.ac.rs URL: http://nikola.milikic.info ŠTA JE KLASIFIKACIJA? Zadatak određivanja klase kojoj neka instanca pripada instanca je opisana
ANALYSIS OF THE RELIABILITY OF THE "ALTERNATOR- ALTERNATOR BELT" SYSTEM
 I. Mavrin, D. Kovacevic, B. Makovic: Analysis of the Reliability of the "Alternator- Alternator Belt" System IVAN MAVRIN, D.Sc. DRAZEN KOVACEVIC, B.Eng. BRANKO MAKOVIC, B.Eng. Fakultet prometnih znanosti,
I. Mavrin, D. Kovacevic, B. Makovic: Analysis of the Reliability of the "Alternator- Alternator Belt" System IVAN MAVRIN, D.Sc. DRAZEN KOVACEVIC, B.Eng. BRANKO MAKOVIC, B.Eng. Fakultet prometnih znanosti,
Review Answers for E&CE 700T02
 Review Aswers for E&CE 700T0 . Deermie he curre soluio, all possible direcios, ad sepsizes wheher improvig or o for he simple able below: 4 b ma c 0 0 0-4 6 0 - B N B N ^0 0 0 curre sol =, = Ch for - -
Review Aswers for E&CE 700T0 . Deermie he curre soluio, all possible direcios, ad sepsizes wheher improvig or o for he simple able below: 4 b ma c 0 0 0-4 6 0 - B N B N ^0 0 0 curre sol =, = Ch for - -
Use precise language and domain-specific vocabulary to inform about or explain the topic. CCSS.ELA-LITERACY.WHST D
 Lesson eight What are characteristics of chemical reactions? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading
Lesson eight What are characteristics of chemical reactions? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading
The analysis of the method on the one variable function s limit Ke Wu
 Ieraioal Coferece o Advaces i Mechaical Egieerig ad Idusrial Iformaics (AMEII 5) The aalysis of he mehod o he oe variable fucio s i Ke Wu Deparme of Mahemaics ad Saisics Zaozhuag Uiversiy Zaozhuag 776
Ieraioal Coferece o Advaces i Mechaical Egieerig ad Idusrial Iformaics (AMEII 5) The aalysis of he mehod o he oe variable fucio s i Ke Wu Deparme of Mahemaics ad Saisics Zaozhuag Uiversiy Zaozhuag 776
Chemical Engineering 374
 Chemical Egieerig 374 Fluid Mechaics NoNeoia Fluids Oulie 2 Types ad properies of o-neoia Fluids Pipe flos for o-neoia fluids Velociy profile / flo rae Pressure op Fricio facor Pump poer Rheological Parameers
Chemical Egieerig 374 Fluid Mechaics NoNeoia Fluids Oulie 2 Types ad properies of o-neoia Fluids Pipe flos for o-neoia fluids Velociy profile / flo rae Pressure op Fricio facor Pump poer Rheological Parameers
Chapter 15: Fourier Series
 Chapter 5: Fourier Series Ex. 5.3- Ex. 5.3- Ex. 5.- f(t) K is a Fourier Series. he coefficiets are a K; a b for. f(t) AcosZ t is a Fourier Series. a A ad all other coefficiets are zero. Set origi at t,
Chapter 5: Fourier Series Ex. 5.3- Ex. 5.3- Ex. 5.- f(t) K is a Fourier Series. he coefficiets are a K; a b for. f(t) AcosZ t is a Fourier Series. a A ad all other coefficiets are zero. Set origi at t,
ECE 340 Lecture 19 : Steady State Carrier Injection Class Outline:
 ECE 340 ecure 19 : Seady Sae Carrier Ijecio Class Oulie: iffusio ad Recombiaio Seady Sae Carrier Ijecio Thigs you should kow whe you leave Key Quesios Wha are he major mechaisms of recombiaio? How do we
ECE 340 ecure 19 : Seady Sae Carrier Ijecio Class Oulie: iffusio ad Recombiaio Seady Sae Carrier Ijecio Thigs you should kow whe you leave Key Quesios Wha are he major mechaisms of recombiaio? How do we
Comparison between Fourier and Corrected Fourier Series Methods
 Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
I N A C O M P L E X W O R L D
 IS L A M I C E C O N O M I C S I N A C O M P L E X W O R L D E x p l o r a t i o n s i n A g-b eanste d S i m u l a t i o n S a m i A l-s u w a i l e m 1 4 2 9 H 2 0 0 8 I s l a m i c D e v e l o p m e
IS L A M I C E C O N O M I C S I N A C O M P L E X W O R L D E x p l o r a t i o n s i n A g-b eanste d S i m u l a t i o n S a m i A l-s u w a i l e m 1 4 2 9 H 2 0 0 8 I s l a m i c D e v e l o p m e
Modified Zagreb M 2 Index Comparison with the Randi} Connectivity Index for Benzenoid Systems
 CROATICA CHEMICA ACTA CCACAA 7 (2) 83 87 (2003) ISSN-00-3 CCA-2870 Note Modified Zagreb M 2 Index Comparison with the Randi} Connectivity Index for Benzenoid Systems Damir Vuki~evi} a, * and Nenad Trinajsti}
CROATICA CHEMICA ACTA CCACAA 7 (2) 83 87 (2003) ISSN-00-3 CCA-2870 Note Modified Zagreb M 2 Index Comparison with the Randi} Connectivity Index for Benzenoid Systems Damir Vuki~evi} a, * and Nenad Trinajsti}
Linear System Theory
 Naioal Tsig Hua Uiversiy Dearme of Power Mechaical Egieerig Mid-Term Eamiaio 3 November 11.5 Hours Liear Sysem Theory (Secio B o Secio E) [11PME 51] This aer coais eigh quesios You may aswer he quesios
Naioal Tsig Hua Uiversiy Dearme of Power Mechaical Egieerig Mid-Term Eamiaio 3 November 11.5 Hours Liear Sysem Theory (Secio B o Secio E) [11PME 51] This aer coais eigh quesios You may aswer he quesios
A Note on Random k-sat for Moderately Growing k
 A Noe o Radom k-sat for Moderaely Growig k Ju Liu LMIB ad School of Mahemaics ad Sysems Sciece, Beihag Uiversiy, Beijig, 100191, P.R. Chia juliu@smss.buaa.edu.c Zogsheg Gao LMIB ad School of Mahemaics
A Noe o Radom k-sat for Moderaely Growig k Ju Liu LMIB ad School of Mahemaics ad Sysems Sciece, Beihag Uiversiy, Beijig, 100191, P.R. Chia juliu@smss.buaa.edu.c Zogsheg Gao LMIB ad School of Mahemaics
RAHAMA I NTEGRATED FARMS LI MI TED RC
 RAHAMA I NTEGRATED FARMS LI MI TED RC 1 0 6 2 6 3 1 CORPORATE PROFI LE ---------------------------------------------------------------------------------------- ---------------------------- Registered Name
RAHAMA I NTEGRATED FARMS LI MI TED RC 1 0 6 2 6 3 1 CORPORATE PROFI LE ---------------------------------------------------------------------------------------- ---------------------------- Registered Name
Executive Committee and Officers ( )
 Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
Chapter 2: Time-Domain Representations of Linear Time-Invariant Systems. Chih-Wei Liu
 Caper : Time-Domai Represeaios of Liear Time-Ivaria Sysems Ci-Wei Liu Oulie Iroucio Te Covoluio Sum Covoluio Sum Evaluaio Proceure Te Covoluio Iegral Covoluio Iegral Evaluaio Proceure Iercoecios of LTI
Caper : Time-Domai Represeaios of Liear Time-Ivaria Sysems Ci-Wei Liu Oulie Iroucio Te Covoluio Sum Covoluio Sum Evaluaio Proceure Te Covoluio Iegral Covoluio Iegral Evaluaio Proceure Iercoecios of LTI
Vibration damping of the cantilever beam with the use of the parametric excitation
 The s Ieraioal Cogress o Soud ad Vibraio 3-7 Jul, 4, Beijig/Chia Vibraio dampig of he cailever beam wih he use of he parameric exciaio Jiří TŮMA, Pavel ŠURÁNE, Miroslav MAHDA VSB Techical Uiversi of Osrava
The s Ieraioal Cogress o Soud ad Vibraio 3-7 Jul, 4, Beijig/Chia Vibraio dampig of he cailever beam wih he use of he parameric exciaio Jiří TŮMA, Pavel ŠURÁNE, Miroslav MAHDA VSB Techical Uiversi of Osrava
THIS PAGE DECLASSIFIED IAW E
 THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
DISTRIBUIRANI ALGORITMI I SISTEMI
 Postavka 7: međusobno isključivanje sa read/write promenljivama 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch Read/Write deljene promenljive
Postavka 7: međusobno isključivanje sa read/write promenljivama 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch Read/Write deljene promenljive
EE/ME/AE324: Dynamical Systems. Chapter 8: Transfer Function Analysis
 EE/ME/AE34: Dynamical Sytem Chapter 8: Tranfer Function Analyi The Sytem Tranfer Function Conider the ytem decribed by the nth-order I/O eqn.: ( n) ( n 1) ( m) y + a y + + a y = b u + + bu n 1 0 m 0 Taking
EE/ME/AE34: Dynamical Sytem Chapter 8: Tranfer Function Analyi The Sytem Tranfer Function Conider the ytem decribed by the nth-order I/O eqn.: ( n) ( n 1) ( m) y + a y + + a y = b u + + bu n 1 0 m 0 Taking
PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU
 MAT KOL Banja Luka) ISSN 0354 6969 p) ISSN 1986 58 o) Vol. XXI )015) 105 115 http://www.imvibl.org/dmbl/dmbl.htm PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU Bernadin Ibrahimpašić 1 Senka Ibrahimpašić
MAT KOL Banja Luka) ISSN 0354 6969 p) ISSN 1986 58 o) Vol. XXI )015) 105 115 http://www.imvibl.org/dmbl/dmbl.htm PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU Bernadin Ibrahimpašić 1 Senka Ibrahimpašić
Introduction to Control Systems
 Itroductio to Cotrol Sytem CLASSIFICATION OF MATHEMATICAL MODELS Icreaig Eae of Aalyi Static Icreaig Realim Dyamic Determiitic Stochatic Lumped Parameter Ditributed Parameter Liear Noliear Cotat Coefficiet
Itroductio to Cotrol Sytem CLASSIFICATION OF MATHEMATICAL MODELS Icreaig Eae of Aalyi Static Icreaig Realim Dyamic Determiitic Stochatic Lumped Parameter Ditributed Parameter Liear Noliear Cotat Coefficiet
Last 4 Digits of USC ID:
 Chemistry 05 B Practice Exam Dr. Jessica Parr First Letter of last Name PLEASE PRINT YOUR NAME IN BLOCK LETTERS Name: Last 4 Digits of USC ID: Lab TA s Name: Question Points Score Grader 8 2 4 3 9 4 0
Chemistry 05 B Practice Exam Dr. Jessica Parr First Letter of last Name PLEASE PRINT YOUR NAME IN BLOCK LETTERS Name: Last 4 Digits of USC ID: Lab TA s Name: Question Points Score Grader 8 2 4 3 9 4 0
Chapter 6 - Work and Energy
 Caper 6 - Work ad Eergy Rosedo Pysics 1-B Eploraory Aciviy Usig your book or e iere aswer e ollowig quesios: How is work doe? Deie work, joule, eergy, poeial ad kieic eergy. How does e work doe o a objec
Caper 6 - Work ad Eergy Rosedo Pysics 1-B Eploraory Aciviy Usig your book or e iere aswer e ollowig quesios: How is work doe? Deie work, joule, eergy, poeial ad kieic eergy. How does e work doe o a objec
C(p, ) 13 N. Nuclear reactions generate energy create new isotopes and elements. Notation for stellar rates: p 12
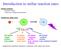 Iroducio o sellar reacio raes Nuclear reacios geerae eergy creae ew isoopes ad elemes Noaio for sellar raes: p C 3 N C(p,) 3 N The heavier arge ucleus (Lab: arge) he ligher icomig projecile (Lab: beam)
Iroducio o sellar reacio raes Nuclear reacios geerae eergy creae ew isoopes ad elemes Noaio for sellar raes: p C 3 N C(p,) 3 N The heavier arge ucleus (Lab: arge) he ligher icomig projecile (Lab: beam)
Rešenja zadataka za vežbu na relacionoj algebri i relacionom računu
 Rešenja zadataka za vežbu na relacionoj algebri i relacionom računu 1. Izdvojiti ime i prezime studenata koji su rođeni u Beogradu. (DOSIJE WHERE MESTO_RODJENJA='Beograd')[IME, PREZIME] where mesto_rodjenja='beograd'
Rešenja zadataka za vežbu na relacionoj algebri i relacionom računu 1. Izdvojiti ime i prezime studenata koji su rođeni u Beogradu. (DOSIJE WHERE MESTO_RODJENJA='Beograd')[IME, PREZIME] where mesto_rodjenja='beograd'
Sinusoidal Steady-state Analysis
 Siusoidal Steady-state Aalysis Complex umber reviews Phasors ad ordiary differetial equatios Complete respose ad siusoidal steady-state respose Cocepts of impedace ad admittace Siusoidal steady-state aalysis
Siusoidal Steady-state Aalysis Complex umber reviews Phasors ad ordiary differetial equatios Complete respose ad siusoidal steady-state respose Cocepts of impedace ad admittace Siusoidal steady-state aalysis
Linear Systems Analysis in the Time Domain
 Liar Sysms Aalysis i h Tim Domai Firs Ordr Sysms di vl = L, vr = Ri, d di L + Ri = () d R x= i, x& = x+ ( ) L L X() s I() s = = = U() s E() s Ls+ R R L s + R u () = () =, i() = L i () = R R Firs Ordr Sysms
Liar Sysms Aalysis i h Tim Domai Firs Ordr Sysms di vl = L, vr = Ri, d di L + Ri = () d R x= i, x& = x+ ( ) L L X() s I() s = = = U() s E() s Ls+ R R L s + R u () = () =, i() = L i () = R R Firs Ordr Sysms
Clock Skew and Signal Representation
 Clock Skew ad Sigal Represeaio Ch. 7 IBM Power 4 Chip 0/7/004 08 frequecy domai Program Iroducio ad moivaio Sequeial circuis, clock imig, Basic ools for frequecy domai aalysis Fourier series sigal represeaio
Clock Skew ad Sigal Represeaio Ch. 7 IBM Power 4 Chip 0/7/004 08 frequecy domai Program Iroducio ad moivaio Sequeial circuis, clock imig, Basic ools for frequecy domai aalysis Fourier series sigal represeaio
