Fourier transform. Continuous-time Fourier transform (CTFT) ω ω
|
|
|
- Nora Russell
- 5 years ago
- Views:
Transcription
1 Fourier rasform Coiuous-ime Fourier rasform (CTFT P. Deoe ( he Fourier rasform of he sigal x(. Deermie he followig values, wihou compuig (. a (0 b ( d c ( si d ( d d e iverse Fourier rasform for Re { ( } a From he defiiio ( ( b ( d x( = 0 = 4 0 = x d = 9 = 0 j x( = ( e d x( 0 4 = = si d = Y d = y 0 Y = c ( ( ( We deoe ( ( si We kow ha: siτ pt p ( = (from he able pairs sigal-fourier rasform ( ( F ( Y = p y = x p = x( τ p ( τ dτ
2 + y ( = x( τ dτ 9 y ( 0 = ( x τ dτ = 4 si 9 9 ( d = Y ( d y ( 0 = = = 4 d ( d - homework Apply ( d x d = Ad from he skeched sigal, we have he values of x(: 0, <, < 0,0 x = + < 4, <, < 3 0, > 3 e The iverse rasform of { ( } Re is x p ( + ( x x = - homework P. For a liear ivaria ime (LTI sysem S wih ipu sigal x( ad oupu sigal y( 3 4 ( = + σ ( ; ( y = e e σ x e e a deermie he frequecy respose of he sysem b deermie he impulse respose of he sysem c deermie he differeial equaio ; impleme he sysem usig iegraors, adders ad mulipliers Soluio. a H ( =? Y ( H ( = ( ( ( ( 3 j x = e e σ ( + + = + = + j 3+ j + j 3+ j
3 4 6 y = e e σ Y ( = = + j 4 + j + j 4 + j ( H = 3( 3 + j ( 4 + j ( + j b h? H ( 3( 3 + ( ( j A B = = = j + j 4 + j + j ( + j ( + j A = H ( ( 4 + j = = j= 4 ( + j ( + j j = B = H ( ( + j = = j= 4 j = 3 3 H = h e e + = j + j 4 ( ( σ ( 3( 3 + j j Y ( c H ( = = = ( 4 + j ( + j j + ( j ( 9 ( + 3 j ( = 8Y ( + 6 jy ( + ( j Y ( We have as propery of Fourier rasform: ( j ( ( ( ( ( ( 9x + 3x = 8y + 6y + y ( ( ( d x ( ( ( ( ( 9 x d d + 3 x d = 8 y d d + 6 y d + y d Caoical form I 3
4 Caoical form II x = + is coeced o he ipu of he sysem wih he P3. The sigal ( cos cos3 followig impulse respose (hree cases: si ( si ( si ( 4 = ; h = ; h ( ( si cos 4 ha b c = a Deermie he frequecy respose of he sysem i he hree cases. Skech he correspodig magiude specra. b Deermie he respose of he hree sysems o x( c If x( would has a useful compoe ad a oisy compoe, which of he hree sysems would you pick, assumig he disurbace is cos( cos( 3? Soluio H, H, H =? a ( ( ( a b c From he able pairs sigals-fourier rasform we have, si ( F, o < 0 p ( = 0 0, > 0 ( si F ha = p = H ( ( ( ( si si 4 hb = p p4 = p p4 = H a ( ( ( ( ( b? Wha if i s 4
5 ( ( ( ( si cos 4 si 6 si hc = = si a cos b = si ( a + b + si ( a b si ( 6 si ( hc = Hc ( = p6 ( p ( y, y, y =? b ( ( ( a b c 0, < 6 6, 6 + < Hb ( c = 4, < 6, < 6 0, 6 ( For x( = cos ( 0 y ( = H ( 0 cos 0 + arg{ H ( 0 } ( = cos + cos 3 ( ( { ( } x ( ( ( { ( } y = H cos + arg H + H 3 cos 3 + arg H 3 5
6 For H a (, we have he oupu sigal ( ( { ( } ( ( ( { ( } y = H cos + arg H + H 3 cos 3 + arg H 3 a a a a a ya = cos ( I he same maer, we have y = 4 cos + 3 cos 3 b ( ( ( yc ( = cos( 3 Discree-ime Fourier rasform (DTFT A aperiodic discree-ime sigal ca be decomposed i x[ ] = ( e d Ω Ω The Fourier rasform ( Ω = x[ ] e = P. Deermie he fourier rasform for he followig discree-ime sigals c x [ ] = σ [ + ] 3 4 6
7 Soluio. By defiiio, he DTFT is ( Ω = x[ ] e a ( = ( e e e e Ω = = = Ω Ω Ω e j j j e e e e Ω ( j ( Ω 3 j j si Ω 3 si Ω ( Ω = e = e Ω Ω j si si e e e ( Ω = si ( Ω Ω si b ( Ω = e + e + e + e + e + e + 3 ( Ω = cos( 3Ω + cos( Ω + cos Ω + ( = Ω Ω + Ω + Ω + 3 4cos 3cos cos 3cos 3 ( ( Ω = 4cos Ω + 4cos Ω = 4cos Ω cos Ω + 7
8 Ω Ω ( Ω = 4 cos Ω cos = 8cos Ω cos Secod mehod: Noice ha 3 y + = x [ ] [ ] si Ω ( Ω = e Y ( Ω = e e shifig Ω si si Ω ( Ω = Ω si We ca verify ha he wo resuls are he same: Ω Ω 8cos Ω cos si Ω cos Ω si Ω si Ω 8cos Ω cos = = = Ω Ω Ω si si si c x3 4 Direc compuaio [ ] = σ [ + ] x e ( Ω = [ ] 3 3 = ( 8
9 ( Ω = e + e + + e + e + e ( Ω = e + e + e e 6 = e = 4 e e 4 4 From he able Pairs sigals- Fourier rasform a σ [ ] ae y x3 4 4 Y ( Ω = 6 = e 3 ( Ω e 4 [ ] = [ ] = σ [ ] = 6 σ [ ] 6e 3 ( Ω = e Y ( Ω = e ( Ω = = 7 cos si cos Ω Ω + Ω P. We have he sigal x( a (0 arg Ω { } b ( c ( Ω 9
10 d ( e ( Ω f d ( Ω { } g iverse Fourier rasform for Re ( Ω Soluio. a ( x[ ] e ( x[ ] Ω = 0 = = 6 = { } = b arg ( Ω Le y[ ] = x[ + ] - symmerical eve sigal Y ( Bu ( Ω = e Y ( Ω arg{ ( Ω } = Ω + arg{ Y ( Ω } = Ω I d c = ( Ω Ω =? x[ ] = ( Ω e [ ] I = x 0 = 4 Ω R d ( [ ] j Ω Ω = x e ( = x[ ] e j =, because e j = ( = = e I = ( Ω = ( because we have x[ ] = f ( Ω d -homework Properies: x[ ] j d ( Ω ( Ω d ( x[ ] = d Ω g The iverse Fourier rasform of Re{ ( Ω } is xp [ ] [ ] + [ ] I x x = -homework 0
Ideal Amplifier/Attenuator. Memoryless. where k is some real constant. Integrator. System with memory
Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
ECE-314 Fall 2012 Review Questions
ECE-34 Fall 0 Review Quesios. A liear ime-ivaria sysem has he ipu-oupu characerisics show i he firs row of he diagram below. Deermie he oupu for he ipu show o he secod row of he diagram. Jusify your aswer.
6.003: Signals and Systems Lecture 20 April 22, 2010
6.003: Sigals ad Sysems Lecure 0 April, 00 6.003: Sigals ad Sysems Relaios amog Fourier Represeaios Mid-erm Examiaio #3 Wedesday, April 8, 7:30-9:30pm. No reciaios o he day of he exam. Coverage: Lecures
Linear Time Invariant Systems
1 Liear Time Ivaria Sysems Oulie We will show ha he oupu equals he covoluio bewee he ipu ad he ui impulse respose: sysem for a discree-ime, for a coiuous-ime sysdem, y x h y x h 2 Discree Time LTI Sysems
Notes 03 largely plagiarized by %khc
1 1 Discree-Time Covoluio Noes 03 largely plagiarized by %khc Le s begi our discussio of covoluio i discree-ime, sice life is somewha easier i ha domai. We sar wih a sigal x[] ha will be he ipu io our
Section 8 Convolution and Deconvolution
APPLICATIONS IN SIGNAL PROCESSING Secio 8 Covoluio ad Decovoluio This docume illusraes several echiques for carryig ou covoluio ad decovoluio i Mahcad. There are several operaors available for hese fucios:
Solutions - Midterm Exam
DEPARTMENT OF ELECTRICAL AND COMPUTER ENGINEERING, THE UNIVERITY OF NEW MEXICO ECE-34: ignals and ysems ummer 203 PROBLEM (5 PT) Given he following LTI sysem: oluions - Miderm Exam a) kech he impulse response
UNIT 6 Signals and Systems
UNIT 6 ONE MARK MCQ 6. dy dy The differeial equaio y x( ) d d + describes a sysem wih a ipu x () ad a oupu y. () The sysem, which is iiially relaxed, is excied by a ui sep ipu. The oupu y^h ca be represeed
Sampling Example. ( ) δ ( f 1) (1/2)cos(12πt), T 0 = 1
Samplig Example Le x = cos( 4π)cos( π). The fudameal frequecy of cos 4π fudameal frequecy of cos π is Hz. The ( f ) = ( / ) δ ( f 7) + δ ( f + 7) / δ ( f ) + δ ( f + ). ( f ) = ( / 4) δ ( f 8) + δ ( f
The Eigen Function of Linear Systems
1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
Chapter 2: Time-Domain Representations of Linear Time-Invariant Systems. Chih-Wei Liu
Caper : Time-Domai Represeaios of Liear Time-Ivaria Sysems Ci-Wei Liu Oulie Iroucio Te Covoluio Sum Covoluio Sum Evaluaio Proceure Te Covoluio Iegral Covoluio Iegral Evaluaio Proceure Iercoecios of LTI
Linear System Theory
Naioal Tsig Hua Uiversiy Dearme of Power Mechaical Egieerig Mid-Term Eamiaio 3 November 11.5 Hours Liear Sysem Theory (Secio B o Secio E) [11PME 51] This aer coais eigh quesios You may aswer he quesios
6.003: Signals and Systems
6.003: Sigals ad Sysems Lecure 8 March 2, 2010 6.003: Sigals ad Sysems Mid-erm Examiaio #1 Tomorrow, Wedesday, March 3, 7:30-9:30pm. No reciaios omorrow. Coverage: Represeaios of CT ad DT Sysems Lecures
Solutions Manual 4.1. nonlinear. 4.2 The Fourier Series is: and the fundamental frequency is ω 2π
Soluios Maual. (a) (b) (c) (d) (e) (f) (g) liear oliear liear liear oliear oliear liear. The Fourier Series is: F () 5si( ) ad he fudameal frequecy is ω f ----- H z.3 Sice V rms V ad f 6Hz, he Fourier
e 2t u(t) e 2t u(t) =?
EE : Signals, Sysems, and Transforms Fall 7. Skech he convoluion of he following wo signals. Tes No noes, closed book. f() Show your work. Simplify your answers. g(). Using he convoluion inegral, find
Ch3 Discrete Time Fourier Transform
Ch3 Discrete Time Fourier Trasform 3. Show that the DTFT of [] is give by ( k). e k 3. Determie the DTFT of the two sided sigal y [ ],. 3.3 Determie the DTFT of the causal sequece x[ ] A cos( 0 ) [ ],
Clock Skew and Signal Representation
Clock Skew ad Sigal Represeaio Ch. 7 IBM Power 4 Chip 0/7/004 08 frequecy domai Program Iroducio ad moivaio Sequeial circuis, clock imig, Basic ools for frequecy domai aalysis Fourier series sigal represeaio
Electrical Engineering Department Network Lab.
Par:- Elecrical Egieerig Deparme Nework Lab. Deermiaio of differe parameers of -por eworks ad verificaio of heir ierrelaio ships. Objecive: - To deermie Y, ad ABD parameers of sigle ad cascaded wo Por
MODERN CONTROL SYSTEMS
MODERN CONTROL SYSTEMS Lecure 9, Sae Space Repreeaio Emam Fahy Deparme of Elecrical ad Corol Egieerig email: emfmz@aa.edu hp://www.aa.edu/cv.php?dip_ui=346&er=6855 Trafer Fucio Limiaio TF = O/P I/P ZIC
1. Solve by the method of undetermined coefficients and by the method of variation of parameters. (4)
7 Differeial equaios Review Solve by he mehod of udeermied coefficies ad by he mehod of variaio of parameers (4) y y = si Soluio; we firs solve he homogeeous equaio (4) y y = 4 The correspodig characerisic
φ ( t ) = φ ( t ). The notation denotes a norm that is usually
7h Europea Sigal Processig Coferece (EUSIPCO 9) Glasgo, Scolad, Augus -8, 9 DESIG OF DIGITAL IIR ITEGRATOR USIG RADIAL BASIS FUCTIO ITERPOLATIO METOD Chie-Cheg Tseg ad Su-Lig Lee Depar of Compuer ad Commuicaio
State-Space Model. In general, the dynamic equations of a lumped-parameter continuous system may be represented by
Sae-Space Model I geeral, he dyaic equaio of a luped-paraeer coiuou ye ay be repreeed by x & f x, u, y g x, u, ae equaio oupu equaio where f ad g are oliear vecor-valued fucio Uig a liearized echique,
EGR 544 Communication Theory
EGR 544 Commuicaio heory 7. Represeaio of Digially Modulaed Sigals II Z. Aliyazicioglu Elecrical ad Compuer Egieerig Deparme Cal Poly Pomoa Represeaio of Digial Modulaio wih Memory Liear Digial Modulaio
10.3 Autocorrelation Function of Ergodic RP 10.4 Power Spectral Density of Ergodic RP 10.5 Normal RP (Gaussian RP)
ENGG450 Probabiliy ad Saisics for Egieers Iroducio 3 Probabiliy 4 Probabiliy disribuios 5 Probabiliy Desiies Orgaizaio ad descripio of daa 6 Samplig disribuios 7 Ifereces cocerig a mea 8 Comparig wo reames
Principles of Communications Lecture 1: Signals and Systems. Chih-Wei Liu 劉志尉 National Chiao Tung University
Priciples of Commuicaios Lecure : Sigals ad Sysems Chih-Wei Liu 劉志尉 Naioal Chiao ug Uiversiy cwliu@wis.ee.cu.edu.w Oulies Sigal Models & Classificaios Sigal Space & Orhogoal Basis Fourier Series &rasform
Sampling. AD Conversion (Additional Material) Sampling: Band limited signal. Sampling. Sampling function (sampling comb) III(x) Shah.
AD Coversio (Addiioal Maerial Samplig Samplig Properies of real ADCs wo Sep Flash ADC Pipelie ADC Iegraig ADCs: Sigle Slope, Dual Slope DA Coverer Samplig fucio (samplig comb III(x Shah III III ( x = δ
ECE 350 Matlab-Based Project #3
ECE 350 Malab-Based Projec #3 Due Dae: Nov. 26, 2008 Read he aached Malab uorial ad read he help files abou fucio i, subs, sem, bar, sum, aa2. he wrie a sigle Malab M file o complee he followig ask for
Comparison between Fourier and Corrected Fourier Series Methods
Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
ODEs II, Supplement to Lectures 6 & 7: The Jordan Normal Form: Solving Autonomous, Homogeneous Linear Systems. April 2, 2003
ODEs II, Suppleme o Lecures 6 & 7: The Jorda Normal Form: Solvig Auoomous, Homogeeous Liear Sysems April 2, 23 I his oe, we describe he Jorda ormal form of a marix ad use i o solve a geeral homogeeous
6.003: Signals and Systems. Relations among Fourier Representations
6.003: Signals and Sysems Relaions among Fourier Represenaions April 22, 200 Mid-erm Examinaion #3 W ednesday, April 28, 7:30-9:30pm. No reciaions on he day of he exam. Coverage: Lecures 20 Reciaions 20
ELEG3503 Introduction to Digital Signal Processing
ELEG3503 Itroductio to Digital Sigal Processig 1 Itroductio 2 Basics of Sigals ad Systems 3 Fourier aalysis 4 Samplig 5 Liear time-ivariat (LTI) systems 6 z-trasform 7 System Aalysis 8 System Realizatio
6.01: Introduction to EECS I Lecture 3 February 15, 2011
6.01: Iroducio o EECS I Lecure 3 February 15, 2011 6.01: Iroducio o EECS I Sigals ad Sysems Module 1 Summary: Sofware Egieerig Focused o absracio ad modulariy i sofware egieerig. Topics: procedures, daa
6/10/2014. Definition. Time series Data. Time series Graph. Components of time series. Time series Seasonal. Time series Trend
6//4 Defiiio Time series Daa A ime series Measures he same pheomeo a equal iervals of ime Time series Graph Compoes of ime series 5 5 5-5 7 Q 7 Q 7 Q 3 7 Q 4 8 Q 8 Q 8 Q 3 8 Q 4 9 Q 9 Q 9 Q 3 9 Q 4 Q Q
6.003: Signals and Systems
6.003: Signals and Sysems Relaions among Fourier Represenaions November 5, 20 Mid-erm Examinaion #3 Wednesday, November 6, 7:30-9:30pm, No reciaions on he day of he exam. Coverage: Lecures 8 Reciaions
King Fahd University of Petroleum & Minerals Computer Engineering g Dept
Kig Fahd Uiversiy of Peroleum & Mierals Compuer Egieerig g Dep COE 4 Daa ad Compuer Commuicaios erm Dr. shraf S. Hasa Mahmoud Rm -4 Ex. 74 Email: ashraf@kfupm.edu.sa 9/8/ Dr. shraf S. Hasa Mahmoud Lecure
EE 224 Signals and Systems I Complex numbers sinusodal signals Complex exponentials e jωt phasor addition
EE 224 Signals and Sysems I Complex numbers sinusodal signals Complex exponenials e jω phasor addiion 1/28 Complex Numbers Recangular Polar y z r z θ x Good for addiion/subracion Good for muliplicaion/division
6.003 Homework #5 Solutions
6. Homework #5 Soluios Problems. DT covoluio Le y represe he DT sigal ha resuls whe f is covolved wih g, i.e., y[] = (f g)[] which is someimes wrie as y[] = f[] g[]. Deermie closed-form expressios for
EECE 301 Signals & Systems Prof. Mark Fowler
EECE 3 Signals & Sysems Prof. Mark Fowler Noe Se #2 Wha are Coninuous-Time Signals??? Reading Assignmen: Secion. of Kamen and Heck /22 Course Flow Diagram The arrows here show concepual flow beween ideas.
K3 p K2 p Kp 0 p 2 p 3 p
Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science. Fall Problem Set 11 Solutions.
Massachusetts Istitute of Techology Departmet of Electrical Egieerig ad Computer Sciece Issued: Thursday, December 8, 005 6.341: Discrete-Time Sigal Processig Fall 005 Problem Set 11 Solutios Problem 11.1
Lecture 15: Three-tank Mixing and Lead Poisoning
Lecure 15: Three-ak Miig ad Lead Poisoig Eigevalues ad eigevecors will be used o fid he soluio of a sysem for ukow fucios ha saisfy differeial equaios The ukow fucios will be wrie as a 1 colum vecor [
11. Adaptive Control in the Presence of Bounded Disturbances Consider MIMO systems in the form,
Lecure 6. Adapive Corol i he Presece of Bouded Disurbaces Cosider MIMO sysems i he form, x Aref xbu x Bref ycmd (.) y Cref x operaig i he presece of a bouded ime-depede disurbace R. All he assumpios ad
2 f(x) dx = 1, 0. 2f(x 1) dx d) 1 4t t6 t. t 2 dt i)
Mah PracTes Be sure o review Lab (ad all labs) There are los of good quesios o i a) Sae he Mea Value Theorem ad draw a graph ha illusraes b) Name a impora heorem where he Mea Value Theorem was used i he
12 Getting Started With Fourier Analysis
Commuicaios Egieerig MSc - Prelimiary Readig Geig Sared Wih Fourier Aalysis Fourier aalysis is cocered wih he represeaio of sigals i erms of he sums of sie, cosie or complex oscillaio waveforms. We ll
Clock Skew and Signal Representation. Program. Timing Engineering
lock Skew ad Sigal epreseaio h. 7 IBM Power 4 hip Iroducio ad moivaio Sequeial circuis, clock imig, Basic ools for frequecy domai aalysis Fourier series sigal represeaio Periodic sigals ca be represeed
EECS20n, Solution to Midterm 2, 11/17/00
EECS20n, Soluion o Miderm 2, /7/00. 0 poins Wrie he following in Caresian coordinaes (i.e. in he form x + jy) (a) 2 poins j 3 j 2 + j += j ++j +=2 (b) 2 poins ( j)/( + j) = j (c) 2 poins cos π/4+jsin π/4
Signals and Systems Profs. Byron Yu and Pulkit Grover Fall Midterm 1 Solutions
8-90 Signals and Sysems Profs. Byron Yu and Pulki Grover Fall 07 Miderm Soluions Name: Andrew ID: Problem Score Max 0 8 4 6 5 0 6 0 7 8 9 0 6 Toal 00 Miderm Soluions. (0 poins) Deermine wheher he following
6.302 Feedback Systems Recitation 4: Complex Variables and the s-plane Prof. Joel L. Dawson
Number 1 quesion: Why deal wih imaginary and complex numbers a all? One answer is ha, as an analyical echnique, hey make our lives easier. Consider passing a cosine hrough an LTI filer wih impulse response
Q1) [20 points] answer for the following questions (ON THIS SHEET):
![Q1) [20 points] answer for the following questions (ON THIS SHEET):](/thumbs/87/96063197.jpg "Q1) [20 points] answer for the following questions (ON THIS SHEET):")
Dr. Anas Al Tarabsheh The Hashemie Universiy Elecrical and Compuer Engineering Deparmen (Makeup Exam) Signals and Sysems Firs Semeser 011/01 Final Exam Dae: 1/06/01 Exam Duraion: hours Noe: means convoluion
6.003 Homework #8 Solutions
6.003 Homework #8 Soluions Problems. Fourier Series Deermine he Fourier series coefficiens a k for x () shown below. x ()= x ( + 0) 0 a 0 = 0 a k = e /0 sin(/0) for k 0 a k = π x()e k d = 0 0 π e 0 k d
Problems and Solutions for Section 3.2 (3.15 through 3.25)
3-7 Problems ad Soluios for Secio 3 35 hrough 35 35 Calculae he respose of a overdamped sigle-degree-of-freedom sysem o a arbirary o-periodic exciaio Soluio: From Equaio 3: x = # F! h "! d! For a overdamped
λiv Av = 0 or ( λi Av ) = 0. In order for a vector v to be an eigenvector, it must be in the kernel of λi
Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
Finite-length Discrete Transforms. Chapter 5, Sections
Fiite-legth Discrete Trasforms Chapter 5, Sectios 5.2-50 5.0 Dr. Iyad djafar Outlie The Discrete Fourier Trasform (DFT) Matrix Represetatio of DFT Fiite-legth Sequeces Circular Covolutio DFT Symmetry Properties
2D DSP Basics: 2D Systems
- Digital Image Processig ad Compressio D DSP Basics: D Systems D Systems T[ ] y = T [ ] Liearity Additivity: If T y = T [ ] The + T y = y + y Homogeeity: If The T y = T [ ] a T y = ay = at [ ] Liearity
th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)
![th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)](/thumbs/80/81319353.jpg "th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)")
1 Trasform Techiques h m m m m mome : E[ ] x f ( x) dx h m m m m ceral mome : E[( ) ] ( ) ( x) f ( x) dx A coveie wa of fidig he momes of a radom variable is he mome geeraig fucio (MGF). Oher rasform echiques
Stochastic Processes Adopted From p Chapter 9 Probability, Random Variables and Stochastic Processes, 4th Edition A. Papoulis and S.
Sochasic Processes Adoped From p Chaper 9 Probabiliy, adom Variables ad Sochasic Processes, 4h Ediio A. Papoulis ad S. Pillai 9. Sochasic Processes Iroducio Le deoe he radom oucome of a experime. To every
Moment Generating Function
1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
What is a Communications System?
Wha is a ommuiaios Sysem? Aual Real Life Messae Real Life Messae Replia Ipu Sial Oupu Sial Ipu rasduer Oupu rasduer Eleroi Sial rasmier rasmied Sial hael Reeived Sial Reeiver Eleroi Sial Noise ad Disorio
ONE RANDOM VARIABLE F ( ) [ ] x P X x x x 3
![ONE RANDOM VARIABLE F ( ) [ ] x P X x x x 3](/thumbs/87/96063720.jpg "ONE RANDOM VARIABLE F ( ) [ ] x P X x x x 3")
The Cumulive Disribuio Fucio (cd) ONE RANDOM VARIABLE cd is deied s he probbiliy o he eve { x}: F ( ) [ ] x P x x - Applies o discree s well s coiuous RV. Exmple: hree osses o coi x 8 3 x 8 8 F 3 3 7 x
Samuel Sindayigaya 1, Nyongesa L. Kennedy 2, Adu A.M. Wasike 3
Ieraioal Joural of Saisics ad Aalysis. ISSN 48-9959 Volume 6, Number (6, pp. -8 Research Idia Publicaios hp://www.ripublicaio.com The Populaio Mea ad is Variace i he Presece of Geocide for a Simple Birh-Deah-
Manipulations involving the signal amplitude (dependent variable).
Oulie Maipulaio of discree ime sigals: Maipulaios ivolvig he idepede variable : Shifed i ime Operaios. Foldig, reflecio or ime reversal. Time Scalig. Maipulaios ivolvig he sigal ampliude (depede variable).
DEPARTMENT OF ELECTRICAL AND ELECTRONIC ENGINEERING EXAMINATIONS 2008
[E5] IMPERIAL COLLEGE LONDON DEPARTMENT OF ELECTRICAL AND ELECTRONIC ENGINEERING EXAMINATIONS 008 EEE/ISE PART II MEng BEng and ACGI SIGNALS AND LINEAR SYSTEMS Time allowed: :00 hours There are FOUR quesions
Frequency Response of FIR Filters
EEL335: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we itroduce the idea of the frequecy respose of LTI systems, ad focus specifically o the frequecy respose of FIR filters.. Steady-state
6.003 Homework #9 Solutions
6.003 Homework #9 Soluions Problems. Fourier varieies a. Deermine he Fourier series coefficiens of he following signal, which is periodic in 0. x () 0 3 0 a 0 5 a k a k 0 πk j3 e 0 e j πk 0 jπk πk e 0
Pure Math 30: Explained!
ure Mah : Explaied! www.puremah.com 6 Logarihms Lesso ar Basic Expoeial Applicaios Expoeial Growh & Decay: Siuaios followig his ype of chage ca be modeled usig he formula: (b) A = Fuure Amou A o = iial
Part II Converter Dynamics and Control
Par II overer Dyamics ad orol haper 7. A Equivale ircui Modelig 7. A equivale circui modelig 8. overer rasfer fucios 9. oroller desig. Ac ad dc equivale circui modelig of he discoiuous coducio mode. urre
Signals and Systems Linear Time-Invariant (LTI) Systems
Signals and Sysems Linear Time-Invarian (LTI) Sysems Chang-Su Kim Discree-Time LTI Sysems Represening Signals in Terms of Impulses Sifing propery 0 x[ n] x[ k] [ n k] k x[ 2] [ n 2] x[ 1] [ n1] x[0] [
STK4080/9080 Survival and event history analysis
STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
Supplement for SADAGRAD: Strongly Adaptive Stochastic Gradient Methods"
Suppleme for SADAGRAD: Srogly Adapive Sochasic Gradie Mehods" Zaiyi Che * 1 Yi Xu * Ehog Che 1 iabao Yag 1. Proof of Proposiio 1 Proposiio 1. Le ɛ > 0 be fixed, H 0 γi, γ g, EF (w 1 ) F (w ) ɛ 0 ad ieraio
Harmonic excitation (damped)
Harmoic eciaio damped k m cos EOM: m&& c& k cos c && ζ & f cos The respose soluio ca be separaed io par;. Homogeeous soluio h. Paricular soluio p h p & ζ & && ζ & f cos Homogeeous soluio Homogeeous soluio
A Two-Level Quantum Analysis of ERP Data for Mock-Interrogation Trials. Michael Schillaci Jennifer Vendemia Robert Buzan Eric Green
A Two-Level Quaum Aalysis of ERP Daa for Mock-Ierrogaio Trials Michael Schillaci Jeifer Vedemia Rober Buza Eric Gree Oulie Experimeal Paradigm 4 Low Workload; Sigle Sessio; 39 8 High Workload; Muliple
6.003 Homework #9 Solutions
6.00 Homework #9 Soluions Problems. Fourier varieies a. Deermine he Fourier series coefficiens of he following signal, which is periodic in 0. x () 0 0 a 0 5 a k sin πk 5 sin πk 5 πk for k 0 a k 0 πk j
Boundary-to-Displacement Asymptotic Gains for Wave Systems With Kelvin-Voigt Damping
Boudary-o-Displaceme Asympoic Gais for Wave Sysems Wih Kelvi-Voig Dampig Iasso Karafyllis *, Maria Kooriaki ** ad Miroslav Krsic *** * Dep. of Mahemaics, Naioal Techical Uiversiy of Ahes, Zografou Campus,
Guest Lectures for Dr. MacFarlane s EE3350 Part Deux
Gues Lecures for Dr. MacFarlane s EE3350 Par Deux Michael Plane Mon., 08-30-2010 Wrie name in corner. Poin ou his is a review, so I will go faser. Remind hem o go lisen o online lecure abou geing an A
Using Linnik's Identity to Approximate the Prime Counting Function with the Logarithmic Integral
Usig Lii's Ideiy o Approimae he Prime Couig Fucio wih he Logarihmic Iegral Naha McKezie /26/2 aha@icecreambreafas.com Summary:This paper will show ha summig Lii's ideiy from 2 o ad arragig erms i a cerai
Discrete-Time Signals and Systems. Introduction to Digital Signal Processing. Independent Variable. What is a Signal? What is a System?
Discree-Time Sigals ad Sysems Iroducio o Digial Sigal Processig Professor Deepa Kudur Uiversiy of Toroo Referece: Secios. -.4 of Joh G. Proakis ad Dimiris G. Maolakis, Digial Sigal Processig: Priciples,
5. Response of Linear Time-Invariant Systems to Random Inputs
Sysem: 5. Response of inear ime-invarian Sysems o Random Inpus 5.. Discree-ime linear ime-invarian (IV) sysems 5... Discree-ime IV sysem IV sysem xn ( ) yn ( ) [ xn ( )] Inpu Signal Sysem S Oupu Signal
FIR Filter Design: Part II
EEL335: Discrete-Time Sigals ad Systems. Itroductio I this set of otes, we cosider how we might go about desigig FIR filters with arbitrary frequecy resposes, through compositio of multiple sigle-peak
International Association of Scientific Innovation and Research (IASIR) (An Association Unifying the Sciences, Engineering, and Applied Research)
Ieraioal Associaio of Scieific Iovaio ad Research (IASIR (A Associaio Uifyig he Scieces, Egieerig, ad Applied Research ISSN (Pri: 79- ISSN (Olie: 79-39 Ieraioal Joural of Egieerig, Busiess ad Eerprise
Signal Processing in Mechatronics. Lecture 3, Convolution, Fourier Series and Fourier Transform
Sigal Processig i Mechatroics Summer semester, 1 Lecture 3, Covolutio, Fourier Series ad Fourier rasform Dr. Zhu K.P. AIS, UM 1 1. Covolutio Covolutio Descriptio of LI Systems he mai premise is that the
Available online at J. Math. Comput. Sci. 4 (2014), No. 4, ISSN:
Available olie a hp://sci.org J. Mah. Compu. Sci. 4 (2014), No. 4, 716-727 ISSN: 1927-5307 ON ITERATIVE TECHNIQUES FOR NUMERICAL SOLUTIONS OF LINEAR AND NONLINEAR DIFFERENTIAL EQUATIONS S.O. EDEKI *, A.A.
APPROXIMATE SOLUTION OF FRACTIONAL DIFFERENTIAL EQUATIONS WITH UNCERTAINTY
APPROXIMATE SOLUTION OF FRACTIONAL DIFFERENTIAL EQUATIONS WITH UNCERTAINTY ZHEN-GUO DENG ad GUO-CHENG WU 2, 3 * School of Mahemaics ad Iformaio Sciece, Guagi Uiversiy, Naig 534, PR Chia 2 Key Laboraory
Calculus Limits. Limit of a function.. 1. One-Sided Limits...1. Infinite limits 2. Vertical Asymptotes...3. Calculating Limits Using the Limit Laws.
Limi of a fucio.. Oe-Sided..... Ifiie limis Verical Asympoes... Calculaig Usig he Limi Laws.5 The Squeeze Theorem.6 The Precise Defiiio of a Limi......7 Coiuiy.8 Iermediae Value Theorem..9 Refereces..
Approximating Solutions for Ginzburg Landau Equation by HPM and ADM
Available a hp://pvamu.edu/aam Appl. Appl. Mah. ISSN: 193-9466 Vol. 5, No. Issue (December 1), pp. 575 584 (Previously, Vol. 5, Issue 1, pp. 167 1681) Applicaios ad Applied Mahemaics: A Ieraioal Joural
Problem Set 11(Practice Problems) Spring 2014
Issued: Wednesday April, ECE Signals and Sysems I Problem Se (Pracice Problems) Spring Due: For pracice only. No due. Reading in Oppenheim/Willsky/Nawab /9/ Secions 6.-6. // Secions 6.-6. See revised schedule
SHOCK AND VIBRATION RESPONSE SPECTRA COURSE Unit 21 Base Excitation Shock: Classical Pulse
SHOCK AND VIBRAION RESPONSE SPECRA COURSE Ui 1 Base Exciaio Shock: Classical Pulse By om Irvie Email: omirvie@aol.com Iroucio Cosier a srucure subjece o a base exciaio shock pulse. Base exciaio is also
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science. BACKGROUND EXAM September 30, 2004.
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Departmet of Electrical Egieerig ad Computer Sciece 6.34 Discrete Time Sigal Processig Fall 24 BACKGROUND EXAM September 3, 24. Full Name: Note: This exam is closed
Laplace transfom: t-translation rule , Haynes Miller and Jeremy Orloff
Laplace ransfom: -ranslaion rule 8.03, Haynes Miller and Jeremy Orloff Inroducory example Consider he sysem ẋ + 3x = f(, where f is he inpu and x he response. We know is uni impulse response is 0 for
COMPARISON OF ALGORITHMS FOR ELLIPTIC CURVE CRYPTOGRAPHY OVER FINITE FIELDS OF GF(2 m )
COMPARISON OF ALGORITHMS FOR ELLIPTIC CURVE CRYPTOGRAPHY OVER FINITE FIELDS OF GF( m ) Mahias Schmalisch Dirk Timmerma Uiversiy of Rosock Isiue of Applied Microelecroics ad Compuer Sciece Richard-Wager-Sr
Notes 04 largely plagiarized by %khc
Noes 04 largely plagiarized by %khc Convoluion Recap Some ricks: x() () =x() x() (, 0 )=x(, 0 ) R ț x() u() = x( )d x() () =ẋ() This hen ells us ha an inegraor has impulse response h() =u(), and ha a differeniaor
Dynamic h-index: the Hirsch index in function of time
Dyamic h-idex: he Hirsch idex i fucio of ime by L. Egghe Uiversiei Hassel (UHassel), Campus Diepebeek, Agoralaa, B-3590 Diepebeek, Belgium ad Uiversiei Awerpe (UA), Campus Drie Eike, Uiversieisplei, B-260
Transform Techniques
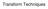Trasform Techiques (a)maually derived leas square fi Se of pois smooheed by a had draw curve ad by liear leas square fi. (Show i Fig.4.) Poi X Y Y P -. -.8 -.8 P -.9 -. -.9 P3 -.6.4 -.7 P4 -. -.9 -.6 P5..5
EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D. S. Palimkar
Ieraioal Joural of Scieific ad Research Publicaios, Volue 2, Issue 7, July 22 ISSN 225-353 EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D S Palikar Depare of Maheaics, Vasarao Naik College, Naded
The analysis of the method on the one variable function s limit Ke Wu
Ieraioal Coferece o Advaces i Mechaical Egieerig ad Idusrial Iformaics (AMEII 5) The aalysis of he mehod o he oe variable fucio s i Ke Wu Deparme of Mahemaics ad Saisics Zaozhuag Uiversiy Zaozhuag 776
5.74 Introductory Quantum Mechanics II
MIT OpeCourseWare hp://ocw.mi.edu 5.74 Iroducory Quaum Mechaics II Sprig 009 For iformaio aou ciig hese maerials or our Terms of Use, visi: hp://ocw.mi.edu/erms. drei Tokmakoff, MIT Deparme of Chemisry,
Vibration damping of the cantilever beam with the use of the parametric excitation
The s Ieraioal Cogress o Soud ad Vibraio 3-7 Jul, 4, Beijig/Chia Vibraio dampig of he cailever beam wih he use of he parameric exciaio Jiří TŮMA, Pavel ŠURÁNE, Miroslav MAHDA VSB Techical Uiversi of Osrava
ME 3210 Mechatronics II Laboratory Lab 6: Second-Order Dynamic Response
Iroucio ME 30 Mecharoics II Laboraory Lab 6: Seco-Orer Dyamic Respose Seco orer iffereial equaios approimae he yamic respose of may sysems. I his lab you will moel a alumium bar as a seco orer Mass-Sprig-Damper
Part B: Transform Methods. Professor E. Ambikairajah UNSW, Australia
Par B: rasform Mhods Profssor E. Ambikairaah UNSW, Ausralia Chapr : Fourir Rprsaio of Sigal. Fourir Sris. Fourir rasform.3 Ivrs Fourir rasform.4 Propris.4. Frqucy Shif.4. im Shif.4.3 Scalig.4.4 Diffriaio
Review Exercises for Chapter 9
0_090R.qd //0 : PM Page 88 88 CHAPTER 9 Ifiie Series I Eercises ad, wrie a epressio for he h erm of he sequece..,., 5, 0,,,, 0,... 7,... I Eercises, mach he sequece wih is graph. [The graphs are labeled
F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mathematics
![F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mathematics](/thumbs/89/97771684.jpg "F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mathematics")
F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mahemaics Prelim Quesio Paper Soluio Q. Aemp ay FIVE of he followig : [0] Q.(a) Defie Eve ad odd fucios. [] As.: A fucio f() is said o be eve fucio if