CARACTERIZAREA BAZATA PE CUNOASTERE A CAPACITATII DE AMORTIZARE A NANOCOMPOZITELOR DIN MATERIALE AUXETICE SI NANOTUBURI DE CARBON LUCRARE
|
|
|
- Oswald Spencer
- 6 years ago
- Views:
Transcription
1 CARACTERIZAREA BAZATA PE CUNOASTERE A CAPACITATII DE AMORTIZARE A NANOCOMPOZITELOR DIN MATERIALE AUXETICE SI NANOTUBURI DE CARBON LUCRARE Colectv Dr. mat. Lga Munteanu drector de program cercetator stntfc grad Dr. mat. Vetura Chrou cercetator stntfc grad Dr. ng. Dan Dumtru cercetator stntfc Dr. mat. Mruna Beldman cercetator stnctfc Dr. ng. Crstan Rugna cercetator stntfc grad II Drd. Ing. Cornel Secara cercetator stntfc Drd. Ing. Danel Baldovn cercetator stntfc Drd. mat. Ana Mara Ntu cercetator stntfc Drd. mat. Valerca Mosnegutu cercetator stntfc Rezumat Nanocompoztele cu materale auxetce s nanotubur de carbon sunt materale no, de mare performanta n controlul vbratlor s al zgomotulu. Materalele auxetce admt un coefcent Posson negatv (metale cubce moleculare s spume), s au un comportament bzar deoarece expandeaza atunc cand sunt ntnse. Nanotuburle de carbon au avantajul alunecar la nterfetele nanotub-nanotub s nanotub-polmer, mbunatatnd amortzarea structurala fara alterarea propretatlor mecance sau a ntegrtat structurale. Caracterzarea nanocompoztelor este esentala pentru cercetator s producator de nanomateral, n partcular pentru IMM-ur, prn punerea la dspozte a une cunoaster avansate n caracterzarea nanomateralelor. Lmtarle nstrumentate s a metodelor exstente (nanondentarea) sunt : calculul modululu de elastctate s a durtat se realzeaza numa pentru materale zotrope s lnare, fara sa se obtna nformat prvnd propretatle elasto-vascoase s de amortzare. Caracterzarea amortzar este o problema deschsa fnd lmtata de o ntelegere ncompleta a propretatlor la nanoscara. Metodele exstente esueaza la acest nvel s nu pot prezce amortzarea, deoarece nu sunt luate n consderate fenomene precum energa dscontnua de legatura adezva, hsterezs, dfuze, fluaj, dslocat, forfecarea atomca, curgere plastca, relaxare, gradent de temperatura. Acest proect este capabl sa depaseasca aceste lmtar prn avansarea une de no prvnd nanonstrumentata s modelarea amortzar la dferte scar metrce. Proectul este conceput pe 3 an, cu accent pe: ) Auxetctate- dee noua pentru nanocompozte; ) Nanotubur de carbon-materale cu mare capactate de amortzare; 3) Nanocompozte cu
2 ncluzun auxetce s nanotubur de carbon; 4) Concept nou pentru testarea prn nanondentare, 5) Stud de caz: Nanocompozte, Nanopanour acustce. Scopul proectulu Proectul se focalzeaza pe: () dezvoltarea une teor no de caracterzare a amortzar compoztelor nanostructurate s de asemenea, a propretatlor lor elastce s vascoelastce, bazate pe teor nelocale s teora soltonlor. Aceasta teore va sta la baza dezvoltar une no tehnc de nanondentare s masurare care sa conduca la dezvoltarea une nstrumentat no de nanondentare adecvate pentru masurarea capactat de amortzare la nanoscara; ()arhtecturarea s avansarea unor no nanocompozte s materale nanostructurate bazate pe materale auxetce s nanotubur de carbon cu propretat crote la cerere, cu aplcat la reducerea s controlul vbratlor s zgomotulu. Ca stud de caz: cresterea capactat de amortzare a structurlor ngnerest prn utlzarea materalelor auxetce s a nanotuburlor de carbon, controlul vbratlor s a zgomotulu, nanocompozte, panour sonce. Cuprnsul lucrar Prefata. O noua cunoastere s concept prvnd corelata dntre propretat s nanostructura materalelor, n detalu, prn combnata dntre snteza, masurator ale propretatlor mecance, examnarea nanostructur s modelare... Identfcarea parametrlor nano- structural s construrea leglor consttutve nelocale de tp elastc s vasco-elastc.. Analza conceptelor de nanostructurare a sstemelor compozte alcatute dn materale dferte. Dezvoltarea capabltatlor tehnologce ale metode nelocale Presach-Tztzeca ca baza pentru caracterzarea amortzar prn nanondentare.. Defnrea une probleme nverse pentru determnarea parametrlor nanostructural dn analza datelor expermentale.. Cuplarea analze nelocale de tp Erngen cu metoda Presach de analza a hsterzsulu s cu teora pseudosuprafetelor Tztzeca cu curbura negatva. Modele de caracterzare a propretatlor elastce s vasco-elastce ale materalelor prn nanondentare 3. Metoda noua de caracterzare a amortzar prn nanondentare. Realzarea vrtuala a nstrumentulu de nanondentare (etapa I-metoda) 3.. Descrerea metode. Studul capactat de amortzare a materalelor la dferte scar metrce. Metode macroscopce de caracterzare a amortzar. 3.. Analza capactat de amortzare a nanotuburlor de carbon. Caracterzarea amortzar une frangh alcatute dn nanotubur de carbon 3.3. Adaptarea metode nelocale Presach-Tteca la caracterzarea amortzar prn nanondentare. 4. O dee noua: auxetctatea aplcata nanocompoztelor n scopul crester capactat de amortzare. 4.. Modelarea materalelor auxetce. Leg consttutve nelocale 4.. Analza capactat de amortzare a materalelor auxetce 5. Nanocompozte pe baza de nanotubur de carbon 6. Fol nanocompozte cu ncluzun de materale auxetce s nanotubur de carbon (fol nanosonce)
3 3 6.. Materal cu arhtectura noua cu materale auxetce s nanotubur de carbon. Modele de fol nanocompozte cu ncluzun de materale auxetce s nanotubur de carbon 6.. Studul propretatlor elastce s vasco-elastce ale materalelor auxetce s nanotuburlor de carbon 7. Un nou concept prvnd nanondentarea capabl sa masoare propretat elastce, vasco-elastce s amortzare 7.. Modelarea nanocontactelor s a fenomenulu de nanondentare cu ndentere avand forme dferte 7.. Includerea n teore a frecar care nsoteste nanondentarea la dferte scar metrce 7.3. Teor cuplate atomstc-contnue de smulare a nanondentar 7.4. Metode de rezolvare a ecuatlor nelnare (metoda cnodala) 8. Integrare s desgn tehnologc a nanonstrumentate vrtuale pentru masurarea propretatlor elastce s vasco-elastce ale materalelor 8.. O problema nversa de dentfcare a propretatlor elastce, vasco-elastce s de amortzare a unu materal nanostructurat 8.. Expermente de nanondentare smulate realst pe computer (I. Model) Bblografe Prefata O parte substantala dn paragrafele s a fost realzata n cadrul deplasarlor efectuate n 7 la Laboratory for Machne Tools and Manufacturng Engneerng, Department of Mechancal Engneerng, Arstoteles Unversty, Thessalonk, Greca (drd.c.secara s drd.d.baldovn) s la Laboratore de Mécanque et Modélsaton des Matéraux et Structures du Géne Cvl, Egletons, Unversté de Lmoges, Franţa (dr. D.Dumtru). Problemele nverse rezolvate n paragrafele 3-5 au utlzat datele expermentale achztonate n cadrul deplasarlor efectuate n 8 la Unverstatea dn Bremen (dr.v.chrou, dr.l.munteanu), Hafa, Israel Insttute of Technology, Dynamcs Lab., Faculty of Mechancs Engneerng Technon (drd.a.m. Mtu, drd.d.baldovn), Hafa, Israel Insttute of Technology Bomechancs Lab. of Technon (drd.v.mosnegutu), Unverstatea Tehnca a Moldove (dr. V.Chrou, dr. D.Dumtru), Torno, Poltecnco d Torno (dr. V.Chrou s dr. L.Munteanu), Heraklon Unversty of Crete Heraklon Creta (dr.v.chrou), Unversty of Thessalonk, Lab. For Machne Tools and Manufacturng (drd. C.Secara) s Faculty of Cvl Constructon Management Unv. Unon Belgrad Serba (dr.d.dumtru, drd.d.baldovn s dr.c.rugna). In paragrafele 5-8 s-au utlzat datele expermentale achztonate n anul 9, n cadrul deplsarlor efectuate la Centre for Advanced Materals, Faculty of Engneerng, The Brtsh Unversty of Egypt (dr.v.chrou, drd.a.m.mtu, drd. V.Mosnegutu), la Gdansk Unversty of Technology, Faculty of Mechancal Engneerng dn Gdansk s Poltecnco d Torno, dp.d Fsca (dr. L.Munteanu, dr.v.chrou s drd.a.m.mtu).. O noua cunoastere s concept prvnd corelata dntre propretat s nanostructura materalelor, n detalu, prn combnata dntre snteza, masurator ale propretatlor mecance, examnarea nanostructur s modelare Noua cunoastere s concept are la baza natura, care ne furnzează modele nteresante pentru structur cu o largă gamă de utlzare. De exemplu, caracatţa nu-ş încurcă ncodată tentaculele char ş atunc când se află în mşcare, pentru că are, la nvelul fecăru braţ, câte un mn-creer responsabl cu coordonarea. Mn-sau nano-creerul este un sstem nervos perferc ndependent
4 4 de sstemul nervos central, care reglementează actvtatea fecăre tentacule. Sstemul nervos al tentaculelor este responsabl de mşcărle fecărua dntre braţe, ş consttue un model perfect pentru controlul braţelor-robot care ar putea f utlzate în cadrul operaţlor chrurgcale sau pentru dverse alte aplcaţ în ndustrle de mare fneţe. Tabel... Componente macroscopce ş componente moleculare (Drexler). Technolog e Funcţe Exemple moleculare Transmt forţe, menţn Bare, grnz pozţ Pereţ celular, mcrotubur Cablur Transmt tensune Colagen Adezv Conectează părţ Forţe ntermoleculare Solenoz, actuator Deplasează corpur Muşch Motoare Transmt mşcare Motor flagelar Arbor Transmt torsune Bactera flagella Reazeme Suport corpur în mşcare Legătură Capete de prndere Manpulează pese Legătur enzmatce Instrumente Modfcă pese Enzme, molecule reactve Ln de producţe Control Sstem enzmatc, rbozom Ssteme de Memorează ş cteşte control programe numerc Sstem genetc Astfel de exemple abundă în natură, ş nanotehnologa s nanomecanca caută să înţeleagă cum sunt construte ş cum funcţonează aceste ssteme, pentru a le putea reconstru sntetc pentru dferte aplcaţ în medcnă, ştnţa calculatoarelor, explorarea spaţulu, etc. (Forrest 995). Exemplul rbozonulu demonstrează faptul că dspoztvele mecance moleculare specalzate lucrează asemenea sstemelor blogce. O comparaţe a componentelor ş funcţlor bomoleculare cu cele macrodmensonale este prezentată în tabelul. (Drexler 98). Un exemplu natural îl consttue mcroscopul electronc de transmse descopert în bactera magnetotactcă. Bacterle conţn o busolă care le permt să se mşte într-o drecţe magnetcă partculară. Busola este compusă dntr-o sere de nanopartcule magnetce (5 nm) care se alnază după câmpul magnetc terestru (Alvsatos, în Whtesdes ş Alvsatos, 999).
5 5 Fg... Model computatonal pentru o nanostructura. Pentru a descre corelata dntre propretat s structura, pentru nanomaterale, un model computatonal pentru o nanostructura este prezentat schematc n fg.. Modelul este aplcat n cazul a ma multor nanostructur s nanocompozte. Am nceput cu nanotubul de carbon, unul dntre cele ma promţătoare nanostructur cu propretăţ mecance, electronce ş magnetce neaşteptate (Srvastava, Menon ş Cho 999, Gao, Cagn ş Goddard 998) (vez paragraf.). Un prm element esental n corelata dntre propretat s structura este cunoasterea suprafaţe materale ca nterfaţă dntre două med sau faze materale, care nu este contnuă ş netedă la scara atomcă ş moleculară. Arhtectura atomcă a suprafeţelor este caracterzată de prezenţa aspertăţlor de dferte dmensun, forme, unghur de contact ş denstăţ. Dscutăm acum câteva modele ale suprafetelor n contact la scara contnua macroscopca, tnand seama de legăturle de tp adezv pentru contactul sold. Pentru a separa două suprafeţe trebue nvnse legăturle care exstă între aceste suprafeţe prntr-o forţă negatvă, numtă forţă adezvă. Natura aceste forţe de suprafaţă este nanoscopcă. Prmul model pentru forţa adezvă este dat de Johnson, Kendall s Roberts (JKR) în anul 97. În acest model se presupune că adezunea se datoreşte unor forţe atractve cu rază nfntă de acţune ş care acţonează în ara de contact, fnd nulă în afara aceste ar. Forţa necesară pentru desprnderea suprafeţelor este
6 6 unde energa adezvă de suprafaţă are forma relate Dupré: 3 F = πr γ, (.) γ = γ + γ γ, (.) unde γ este energa de suprafaţă a prmulu sold, γ este energa de suprafaţă a celu de al dolea sold, ar γ este energa de nterfaţă. În acest model se presupune că forţele de întndere acţonează pe margnle are de contact ş forţele de compresune acţonează în centrul are, ş că exstă o are fnta de contact pentru sarcn aplcate nule. Un model nelocal este dezvoltat de Derjagun, Muller ş Toporov (DMT) (975). Acest model este ma realst decât modelul JKR ş presupune că forţele atractve de suprafaţă au un domenu fnt de acţune ş sunt exersate ş în afara are de contact. In acest model forţa care rupe contactul este F = πr γ. (.3) In ambele modele exstă o are crculară de contact la ncarcare nula, cu raza de contact a data de unde 3 a = ( R γ R) (.4) K cu ν, ν, k s k sunt coefcent lu Posson s modul lu Young pentru cele doua materale. Prezentăm în contnuare modelul nelocal lu Derjagun, Muller ş Toporov. Acest model se referă la nfluenţa recprocă dntre deformaţle de contact ş forţele moleculare de atracţe pentru Eball contactul dntre o sferă elastcă de rază R ş un suprafaţă rgdă cu <<, unde E ball ş E surf Esurf sunt modulele de elastctate a sfere s a suprafeţe. Autor au arătat ca în pofda faptulu că forţele Van der Waals fac să crească ara elastcă de contact dntre sferă ş plan, forţa necesară pentru a nvnge forţele moleculare în cazul ruper contactulu nu creşte. Aceste rezultat pare bzar. De fapt, forţa ramâne egală cu valoarea forţe de atracţe determnată în cazul une sfere nedeformate cu contact punctual pe un plan. In absenţa componente electrostatce, forţa de adezune este proporţonală cu puterea întâa a raze sfere ş cu lucrul mecanc pe untatea de are. Potrvt cu teora lu Hertz, dstrbuţa presun normale pe ara crculara de contact, pentru o forta normală P este Pz ( ρ ) = a (.5) / 3F ρ, (.6) π unde ρ este dstanţa de la centrul cerculu de contact la punctul consderat, a este raza cerculu de contact (fg..), α este deplasarea centrulu sfere sub acţunea forţe F a
7 7 Fg... Modelul orgnal al lu Derjagun, Muller ş Toporov (975). Componenta normală a deformaţe sfere este σ Pz dω d wr ( ) =, (.7) πe R cu Pz dω sarcna concentrată normală, ş R dstanţa de la punctul de aplcaţe a sarcn până la punctul în care se consderă deformaţa. E este modulul de elastctate al sfere, σ este coefcentul lu Posson, ş dω este elementul are de contact. Deformaţa normală se obţne prn înlocurea exprese (.7) în (.6) ş ntegrând pe ara de contact. Consderând un punct de pe sferă de coordonate ( rz,, ) componenta normală a deformaţe este unde a π σ P ( ) wr ( ) z ρ = ρρϕ d d πe, (.8) R = ( ρ ) + = ρcosϕ+ ρ +. (.9) R r z r r z Când calculăm deformaţa în puncte pe suprafaţa sfere lângă permetrul are de contact, negljăm z în (.9). Dacă luăm z = în (.9) obţnem 3θF w() r = T, (.) π a Unde T = a π a ρρρϕ d d. ρ + ρ cosϕ r r ρ ρ Pentru ρ r obţnem ntegrala elptcă completă de ordnul întâ de modul, K r r :
8 8 π dϕ ρ = K ρ + r ρrcosϕ r r. (.) Scrnd a ρ x =, y =, valoarea lu T dn (.) devne r a ( ) ρ a a T K a d K xy y d y T a a = ρ ρ ρ= = r r r r, (.) ş unde π ( ) ( n ) n n K xy = C x y, (.3) n (n )!! Cn =. n (.4) n! Substtund valoarea lu K ( xy ) dn (.3) în (.) avem ( ) π n π n = = y yd y = ( Cn) anx, (.5) n T K xy yd y ( Cn ) x n 3 Γ ( n + ) 3 Γ n+ n n! an = y yd y B( n, ) = + = =, (.6) 5 (n + 3)!! Γ n + unde Γ ş B sunt funcţle Eulerene. Dn (.4) ş (.6) avem n Substtund n+ n! (n )!! n( n) = = n a C an( C n) în (.5) avem Cn (n+ 3)!! n! (n+ 3)(n+ ). n Cx n T =π. (.7) n= (n+ 3)(n+ ) Avem în contnuare dn (.4): n Cx n =. (.8) x n= cu x avem Înmulţnd la stânga ş la dreapta expresa (.8) cu 4 x ş ntegrând de două or în raport n+ Cx n = { x ( x ) ( x )arccos( x )}. (n+ 3)(n+ ) 8 n=
9 9 Impărţnd la x 3/, determnăm pe T : π T = 3/ { x ( x ) ( x )arccos( x ). (.9) 8 x Dn (.9), (.) ş (.) obţnem deformaţa în drecţa axe z în afara are de contact, adcă pentru r a: 3θF a wr ( ) = a r a ( a r )arccos +. (.) πa r Pentru r = a avem 3πθF wa ( ) =. (.) 8a Deformaţa în orgnea coordonatelor r = z= se determnă dn (.8) 3πθF w() = = wa ( ). (.) 4a Daca z este coordonata unu punct de pe sferă înante de deformate, pentru orce punct de pe suprafaţa deformată este valablă relaţa cu z = z + w α, (.3) r z =. (.4) R De ac apare că, în orgnea coordonatelor z = z =, avem w () =α, adcă în tmp ce pe permetrul are de contact avem r α (.), wa ( ) =, ş găsm dn (.3) relaţa cunoscută 3πθF α=, (.5) 4a = a, z = ş z a =. Se observă că, potrvt cu R a α a + α= α=. (.6) R R 3θ F Comparând (.5) cu (.6) avem 3 =, ş după substturea aceste expres în 4a π R (.) avem wr a r a a r ( ) = + ( )arccos πr r Acum, substtund în (.3) pe z, α ş w dn (.4), (.6) ş (.7) găsm a. (.7)
10 r zr ( ) = a r a ( a r)arctan. (.8) πr a Formula (.8) defneşte forma suprafeţe deformate a sfere depnzând de α (sau a valor forţe elastce) în combnaţe cu (.5) ş (.6). Formula (.8) determnă dstanţa între punctele opuse ale sfere ş plan. Aproape de ara de contact, dstanţa dntre aceste puncte nu este zero, deoarece trebue sa adăugăm o valoare ε cu ordnul de mărme 3-4Å, necesară pentru a calcula componenta forţe de nteracţune moleculară care acţonează între plan s suprafaţa une sfere deformate, în afara are de contact. Prn urmare formula fnală pentru zr () este r z a r a a r πr a = ( )arctan +ε. (.9) Dn (.9) putem calcula dec componenta forţe de nteracţune moleculară care acţonează între plan ş suprafaţa une sfere deformate, în afara are de contact. Conceptul se materalzeaza sub forma unu algortm de calcul pentru calculul propretatlor unu nananomateral. Conceptul s-a aplcat pentru pramda Ge (Ge pyramd) de atom de germanu pe o suprafaţă de slcon, cu latura baze de nm ş înălţmea de,5 nm, este realzată prn autoasamblare în câteva secunde (Wllams, R. S. în Whtesdes ş Alvsatos, 999). În cazul coralulu cuantc, 48 atom de fer, aşezaţ într-un cerc de rază 7,3 nm pe un strat de cupru, sunt pozţonaţ ndvdual cu ajutorul unu mcroscop (Egler, D. în Whtesdes ş Alvsatos, 999). Polmer nanstructuraţ formaţ prn autoasamblarea unor structur polmerce, au dverse aplcaţ în ndustra avatcă, ca lubrfanţ în mcroelectroncă (Stupp n Whtesdes ş Alvsatos, 999). În paralel, tehnca bottom-up, care constă în controlul nanostructurlor complexe începând de la nvelul molecular, se dezvoltă ca un nstrument deosebt de efcent pentru nanomanufactură. Sublnem mportanţa majoră în dezvoltarea nano-manufactur a nventăr mcroscoapelor de scanare (scannng probe mcroscopy SPM ş scannng tunnelng mcroscopy STM) de către Bnng ş Rohrer în anul 98, urmate de nventarea mcroscopulu atomc (atomc force mcroscope AFM) în anul 986 de către Bnng, Quate ş Gerber (Chrou, Ştucă, Munteanu s Donescu 5)... Identfcarea parametrlor nano-structural s construrea leglor consttutve nelocale de tp elastc s vasco-elastc Nanostructurle au o dmensune ntermedară între structurle moleculare (dmensunea 7 une molecule m ) ş structurle mcroscopce măsurate în mcron ( m ), adcă de la. nm. Ele conţn un număr foarte mare de atom. Prvte ca molecule, nanostructurle sunt prea mar pentru a putea f modelate cu metodele mecanc cuantce. Prvte ca materale, sunt mult prea mc ş prezntă caracterstc care nu sunt observable la structurle macroscopce (char în jur de,µm ). Noţunea de nanostructură combnă concepte dferte: dmensune mcă, organzare complexă, raport dntre are (nterfeţe) ş volum, mare, denstate mare ş nteracţun electromecance puternce. Caracterstcle electronce ş magnetce ale acestor structur sunt domnate de un comportament cuantc. La dmensun mc, materalele au propretăţ dferte de cele la scară macroscopcă. De exemplu, la scară nanometrcă materalele au o rezstenţă mecancă ma mare decât probele macroscopce ale aceluaş materal. Abltatea unu materal de a se deforma (întndere, compresune, încovoere, torsune) fără să se rupă depnde de legăturle chmce care ţn atom împreună. În prncpu, legăturle chmce sunt aceleaş atât în scara nanometrcă cât ş în scara macroscopcă. Dar probele macroscopce nclud multe defecte,
11 cavtăţ, atom lpsă, etc., care lmtează propretăţle mecance. Denstatea acestor defecte poate f mult ma mcă la scară nanometrcă, ş ca rezultat nanomateralele devn ma rezstente. Cercetător au în vedere exploatarea propretăţlor superoare ale matere la scară nanometrcă ş combnarea unor pese sau blocur nanometrce în construrea unor materale nanostructurate, care pot f consderate ca fnd compuse dn blocur nanometrce (Jackson 4, (Chrou, Ştucă, Munteanu s Donescu 5). Tradţonal, rezstenţa mecancă σ a unu materal crstaln depnde de dmensunea d granule (conform leg lu Hall-Petch σ=σ + kd / ). Dar, cu cât scara structurală se reduce, rezstenţa mecancă depnde ş de alţ factor, s că exstă o lmtă pentru descrerea e convenţonală (Msra et al. 998). O valoare rdcată a raportulu volum/nterfaţă poate nfluenţa substanţal procesele de mobltate, frecare nternă, hsterezs, plastctate dn materalul nanostucturat. Un studu recent pe compozte Cu/Nb ş Cu/Ag a pus n evdenţă reducerea fragltăţ s înlăturarea completă a ruper frelor încercate la întndere la temperatura helulu lchd (Han et al.999), deş metalele bcc. (cum este Nb) sunt cunoscute ca având o rupere fraglă la 4. K. Materalul nanostructurat Cu/Nb prezntă o combnaţe nteresantă de rezstenţă ş ductbltate până la rupere ( GPa ş deformaţe %). Aceasta arată că prn reducerea scăr structurale la nvel nanometrc relaţa rezstenţă-ductbltate poate f extnsă dncolo de lmtele ngnereşt actuale (Kung ş Lowe, în Whtesdes ş Alvsatos, 999). De exemplu, pentru o nanobara cu sectune crculara dn slcon (raza 5nm, lungme 6nm), s-au determnat lungmle de unda caracterstce, λ =67nm, λ =75nm. In fg... se preznta varata tensun n raport cu lungmea pentru nanobara de slcon. Fg.... Campul de tensune versus lungme pentru o nanobara dn slcon cu sectune crculara.. Pentru a descre corelata dntre propretat s structura, pentru nanomaterale, consderam ca obect de studu nanotubul de carbon. În urma descoperr C 6 de către Curl, Kroto ş Smalley (premul Nobel pe anul 996), a fost înteleasă ş formarea nanotuburlor de carbon, care au fost descoperte în anul 99 de către Ijma. Forţele de legătură covalente reprezntă o metodă de formare a nanostructurlor mar ş unforme. Nanotuburle de carbon sunt rezstente dn punct de vedere mecanc, au conductvtate excelentă ş sunt în mnatură, exemple de fre utlzate în fabrcarea compoztelor ş a nanocalculatoarelor. Nanotuburle de carbon sunt clndr lung ş subţr de carbon, formate dn macromolecule mar, de fapt o foae de graft (reţea hexagonală de carbon) răsuctă sub forma unu clndru (Fg..).Se cunosc patru structur alotropce de carbon: carbon amorf, graft, damant ş nanotubur de carbon. Nanotubul de carbon poate f consderat o structură cvas-undmensonală deoarece
12 raportul lungme/dametru este foarte mare (dametrul este de aproxmatv câţva nanometr, ar lungmea de până 5 mcron). Nanotubul este de de or ma subţre decât frul de păr uman, rezstenţa la întndere este de or ma mare decât a oţelulu ş denstatea sa este de or ma mcă decât a alumnulu. Nanotuburle de carbon sunt utlzate ca fre atomce. Fbrele care nclud în compozţe fre moleculare dn nanotubur de carbon au rezstenţă mare, cântăresc de 5 or ma puţn, ş au conductvtatea de 5 or ma mare decât a argntulu ş transmt căldura ma bne decât damantul (Chrou s Chrou 3, Teodorescu, Dumtru s Chrou 6) al. 3). Fg.... O secţune prntr-un tub de carbon (zgzag) văzută dntr-o parte (Ruoff et Nanotubul de carbon poate avea o structură cu un sngur perete sau cu ma mulţ pereţ. Pentru dentfcarea structur tubulu de carbon, ntroducem un parametru geometrc asocat procesulu răsucr fo de graft, notat cu r, care este o combnaţe lnară de baza reţele a ş b, cu ( n, m ) o pereche partculară de întreg (Fg...3) r = na + mb. (..) Fg...3. Defnţa parametrulu geometrc r.. Pentru m =, avem forma zgzag, pentru n= m, forma armchar, ş pentru restul forma chral. Un nanotub de carbon cu capete închse este stabl atunc când dametrul său este ma mare decât a tuburlor (5,5) ş (9,). Aplcabltatea nanotuburlor de carbon este largă. Propretăţlor lor mecance încluzând rezstenţa înaltă, rgdtate mare, denstate redusă ş structură perfectă fac ca ele să fe deale pentru aplcaţ medcale ş ndustrale: frângh nanometrce, nanosenzor, polmer armaţ cu nanotubur de carbon, nanotubur de carbon mplute cu dferţ atom, cu aplcaţ în NEMS. Pe de altă parte, adăugarea de nanotubur într-un materal tradţonal creşte aprecabl propretăţle mecance ale nanocompoztulu în comparaţe cu acelea unu polmer nearmat. De exemplu, un adaus de % de nantubur cu pereţ multpl rdcă rezstenţa la întndere a polstrenulu cu peste 5%.Curgerea fludulu prntr-un nanotub de carbon este granulară în sensul că ş pereţ se mşcă odată cu fludul, ar comportarea fludulu în nanotub depnde de rgdtatea tubulu. Gazele sau lchdele ntroduse în volume foarte mc sunt mportante în nanotehnologe. De exemplu, ele servesc ca flude hdraulce în actuarea mecancă, la pstoane, sau pot conduce moleculele în camere de reacţe.
13 3 Fg...4. Curgerea unu flud prntr-un nanotub. Nanotuburle de carbon au aplcaţ dverse. Se pot fabrca semconductoare de putere, comutatoare ce pot controla LED-ur sau motoare electrce, tranzstoare pentru chp-ur de computer pentru a stoca ş procesa nformaţa. Nanotuburle de carbon sunt foarte flexble ş pot suporta deformaţ mar datortă rezstenţe mar pe care o au la întndere, compresune, răsucre ş încovoere. Ijma (99), Ijma ş Ichhash (993) au arătat expermental că nanotubul de carbon se poate încovoa semnfcatv până la un ungh crtc de aproxmatv de 7,8, pentru un tub cu un sngur perete cu raza de 6 A. La acest ungh, tubul se flambează local ş apare un comportament postcrtc de tp deformaţe elastcă knk. S-a observat că pereţ tubulu se pot apropa unul de altul până la o dstanţă de echlbru de aproxmatv 3,5 A, pentru care forţele van der Waals de nteracţune se transformă dn forţe atractve, în forţe puternc repulsve. Nanotubul poate suporta unghur de încovoere de până la, cu deformaţ complet reversble, astfel încât după înlăturarea sarcnlor exteroare, tubul revne la forma nţală. Pentru un ungh de, legăturle atomce se rup ş deformaţle devn reversble. Un fenomen nteresant care poate f studat prn nanondentare este nuclearea (generarea s formarea de nuclee) s cresterea flmelor la nvel de nanoscara pe stratur s nterfete suport (Raf-Tabar ). Acest proces repreznta o tranzte de faza vapor-sold, n care o stare ntala de atom s molecule este urmata de dfuza, coalescenta s eventual cresterea n substructur stratfcate. Atom s molecule zolate aflate n faza gazoasa s care nu sunt ntal n echlbru termc ajung la ntefata unu materal, condenseaza pe aceasta dupa complcate mscar colectve sau ndvduale, apo mgreaza prn aceasta nterfata, se pot rentoarce la faza de gaz prun desorbte, sau pot f captat n materal prn ntermedul defectelor sau dslocatlor prn absorbte. Condensarea ntala este o compette dntre aceste doua fenomene adsorbte s desorbte (Bethune et al. 993, Sato et al. 998). Exemple de adsorbte: () adsorbta moleculelor C6 de o suprafata S(), () adsorbta atomlor de Ag n graft, (3) adsorbta gazelor n nanotubur de carbon.. C6 este o noua faza a carbonulu condensat, localzat ntre clusterele mc de carbon cum este C3 s faza solda de carbo. In cazul unu sstem de nanotubur de carbon, adsorpta gazelor poate aparea n locur dstncte (fg...5): () n nterorul tuburlor, () n spatle ntersttale dntre 3 tubur, (3) n spatle externe dntre tubur adacente. Fenomenul de nteractune multcorp dntre atom s moleculele adsorbte, este foarte mportant n cunoasterea termodnamc sstemulu. Este nteresant de stut ca fenomenul adsorbte poate f controlat s drjat pentru obtnerea de no structur cu propretat controlate, ca de exemplu cresterea frelor de Ag n graft.
14 4 Fg...5. Locurle n care pot f captat vapor de gaz ntr-o structura de nanotubur de carbon. Pentru ntelegerea acestor fenomene s pentru a putea modela deformata s evoluta nanotuburlor de carbon supuse la dfererte ncarcar, dferte tpur de potentale pot f consderate. Modelarea ş smularea propretăţlor matere sunt legate de determnarea scăr de reprezentare. Metodele de calcul ale nanomecanc au la bază cuplarea metodelor atomstce ş contnue. Un element mportant al acestor metode cuplate îl conttue determnarea energe potenţale totale a unu sstem mecanc sau nanomecanc ca o funcţe de gradele de lbertate ale acestu sstem. Aceste grade de lbertate pot f atom sau pozţle nodale descrse în metoda elementulu fnt (FEM). Starea de echlbru statc se obţne prn mnmzarea energe totale, sau, echvalent, dn determnarea pozţlor de forţă nulă pentru fecare grad de lbertate. Forţa asocată unu grad de lbertate este dervata energe totale în raport cu coordonata gradulu de lbertate. În smulărle mecanc moleculare, se utlzează legea a doua a lu Newton. Soldele care au structură crstalnă sunt caracterzate prntr-un aranjament perodc al atomlor. O reţea Bravas este reprezentată prntr-un aranjament geometrc trdmensonal de paralelppede dentce cu atom dentc dstrbut la varfur. Paralppedele nterstţale cu un atom la fecare vârf se numesc celule elementare. Într-o astfel de celulă elementară sau untate, exstă un sngur atom [38]. Dacă înlocum atom cu molecule orentate se obţne o reţea generală, în care fecare celulă untate conţne numărul de atom dn moleculă. Ac termenul de moleculă nu se referă la o moleculă reală, c descre un aranjament geometrc de atom. Pentru a deven o moleculă reală trebue defnte tpul de legătur chmce între atom ş molecule. Descrem ma întâ reţelele cele ma smple, care sunt caracterstce pentru cele ma multe dntre metale ş pentru forma soldă a gazelor nerte. Ele sunt reţelele cubce ce pot apare în tre forme: cubcă smplă (SC), cubcă cu volum centrat ntern (BCC) ş cubcă cu feţe centrate (FCC). Sstemul de vector untar se notează cu a,a,a 3. Pentru SC (NaCl) avem a = ( a,,), a a a a a a a a a a = (, a,) ş a 3 = (,, a) ; pentru BCC, a = (,, ), a = (,, ) ş a 3 = (,, ) ; a a a a a a pentru FCC (Na Cl, damant, ZnS) a = (,, ), a = (,, ) ş a 3 = (,,). Fg...6 reprezntă căteva tpur de crstale SC, BCC ş FCC.
15 5 Fg...6. Crstale SC, BCC ş FCC. Ordonarea atomlor sferc în reţeaua crstalnă se poate face hexagonal, sau cu stratur deplasate orzontal obţnându-se o smetre hexagonală. Unele metale ca argntul ş cuprul sunt crstale cubce cu feţe centrate ntern, altele ca berlul ş magnezul formeaza crstale hexagonale. Exstă şapte tpur de crstale: cubc, tetragonal, ortorombc, hexagonal, trgonal, monoclnc, ş trclnc. Crstalele se pot clasfca după tpul de forţă atomcă : crstale once, crstale van der Waals sau moleculare, crstale covalente ş metale. Valenţa este puterea unu atom de a se combna cu alţ atom, ş se măsoară prn numărul de electron pe care un atom î poate ceda, capta sau împărţ pentru a forma un compus chmc. Sngurele elemente cu valenţă nulă sunt gazele noble. Legătura covalentă este cea ma puterncă legătură atomcă. Această legătură apare atunc când do atom împart electron. Ion sunt atom care perd electron ş care posedă o sarcnă electrcă datortă lpse de blanţ între numărul de proton ş electron. Ionul care câştgă electron se numeşte anon ş este încărcat negatv. Ionul care perde electron este un caton ş este încărcat poztv. Caton ş anon sunt atraş un de celalţ prn forţele coulombene dntre sarcna negatvă ş cea poztvă. Această atracţe se numeşte oncă ş este ma slabă decât legătura covalentă. Crstalele once (NaCl, sare) sunt crstalele în care atom ndvdual nu au legătur covalente, e fnd mentnuţ împreună datortă forţelor electrostatce. Aceste crstale sunt rezstente ş au un punct de topre relatv înalt. Crstalele moleculare (zahăr) conţn molecule care pot f recunoscute ş care sunt menţnute împreună prn nteracţ necovalente, aşa cum este legătura de hdrogen. Aceste crstale sunt fragle ş au punctul de topre scăzut. Un crstal covalent (damant, ZnS) este o moleculă mare, având punctul de topre înalt. Crstalele metalce sunt compuse dn atom metalc, ş electron care se mşcă lber în reţea, au punctul de topre înalt ş denstăţ mar. Modelarea numercă la scară nanometrcă se realzează cu metodele de dnamcă moleculară, care analzează mşcarea atomlor ndvdual dntr-o structură care conţne N atom, pe baza leg lu Newton sau a leg stocastce a lu Langevn, în poteza că pozţa ş vteza lor se cunoaşte la momentul nţal. Dn cauza numărulu foarte mare de atom care se află într-o structură, se alege de obce un volum fnt care conţne N atom, de exemplu, ca celulă prmară de calcul, ş se ntroduc condţ perodce pe fronteră pentru a putea replca celula în tot spaţul prn generarea de magn perodce ale aceste celule ş a înlătura efectele nedorte ale nterfeţelor artfcale asocate cu dmensunea fntă a sstemulu care se smulează. Teora se bazează pe potenţalul nteratomc H ( rj ) dn care se determnă forţele newtonene care acţonează asupra atomlor F = rhr ( ) j, (..) j> unde j r este dstanţa dntre atom ş j. Se face poteza că fecare atom nteracţonează cu atom dn vecnătate sa, să zcem o sferă cu rază specfcată. Se obţne un număr de 3N ecuaţ
16 6 dferenţale de mşcare, cuplate, pentru 3N grade de lbertate care reprezntă pozţle spaţale ale celor N atom. O metodă de rezolvare a acestu sstem de ecuaţ este algortmul Verlet, potrvt cărua pozţle r ş vtezele v ale atomlor de masă m sunt calculate la fecare pas de tmp conform relaţlor F () t r( t+ d t) = r( t) + v(t)dt+ dt m F () t v( t+ d t) = v( t) + dt, (..) m F ( t + d t) v( t+ d t) = v( t+ d t) + dt m În problemele de termodnamcă, se ntroduce temperatura ca un parametru de control, ş se efectueaza efectuează smularea moleculară a sstemulu pentru o temperatură constantă. Pentru a menţne o temperatură de refernţă, se folosesc metode constrânse care restrcţonează energa cnetcă totală a sstemulu, sau metode stocastce de tp Langevn. O altă metodă este metoda sstemelor extnse a lu Nosé ş Hoover, care se bazează pe ansamblul canonc reprezentatv. În mecanca statstcă ansamblul canonc reprezentatv se poate constru consderând un număr mare de ssteme, care sunt replca mentală a unor ssteme fzce (fecare având un volum V cu N atom), ş aranjându-le împreună pentru a forma un bloc trdmensonal. Acest bloc se scufundă apo într-o bae caldă aflată la temperatura T. Presupunând că suprafeţele care separă elementele dn bloc sunt permeable la schmbăr de energe, atunc toate elementele dn bloc vor atnge după un tmp aceeaş temperatură T. Un astfel de bloc zolat termc formează un ansamblu canonc. Potrvt cu această metodă, sstemul ş baa caldă sunt cuplate ş formează un sstem compozt, cu o dnamcă contnuă determnstă. Teora se bazează pe extensa spaţulu varablelor dnamce ale sstemulu, dncolo de coordonatele ş mpulsurle partculelor reale, pentru a nclude o coordonată fantomă adţonală s ş mpulsul său conjugat p s, care acţonează ca o bae caldă pentru partculele reale. Prn această metodă se poate selecta un Hamltonan pentru sstemul extns ş, smultan, varablele sstemulu fzc real se pot lega de cele ale unu sstem vrtual, astfel încât funcţa de partţe mcrocanoncă a sstemulu vrtual extns să fe proporţonală cu funcţa de partţe canoncă a sstemulu fzc real. Avem prn urmare sstemul real ( r, p ), sstemul vrtual ( r, p ), sstemul real extns ( r, p, s, ps) ş sstemul vrtual extns ( r, p, s, p s). Hamltonanul sstemulu vrtual extns este defnt astfel: N * s H = + Hr ( ) ln j + + gkt B s = ms Q p p, (..3) unde g este numărul gradelor de lbertate, k B constanta lu Boltzmann, Q este un parametru care se comportă ca o masă asocată mşcăr coordonate s, ar r, p, r ş p sunt coordonatele ş mpulsurle canonce ale tuturor partculelor reale ş vrtuale. Deoarece Hamltonanul H este energa potenţală pentru ambele ssteme, real ş vrtual, prm do termen dn (..3) reprezntă energa cnetcă ş energa potenţală a sstemulu fzc, ar următor do termen reprezntă energa cnetcă ş energa potenţală asocate gradelor de lbertate adţonale. Coordonatele vrtuale ş tmpul, sunt legate de coordonatele fzce reale prn relaţle
17 7 r = r, p = p, dt = dt. (..4) s s * Dn Hamltonanul H rezultă ecuaţle de mşcare pentru sstemul fzc, ecuaţ care se ma numesc ecuaţle termostat ale lu Nosé-Hoover: dr dt p =, dp m dt dη p = F η p, = gkbt, (..5) dt Q m unde η este numt coefcentul de frecare al bă deoarece caracterzează frecarea dn nterorul bă. Acest coefcent nu este o constantă ş poate avea atât valor poztve cât ş negatve, fnd legat de un mecansm negatv de feedback. Ultma ecuaţe (..5) controlează funcţonarea bă calde. Dn această ecuaţe observăm că dacă energa cnetcă totală este ma mare decât gkbt, atunc d η ş dec η sunt poztve. Acest fapt produce frecare în nterorul bă ş ca urmare dt mşcarea atomlor este decelerată ş energa cnetcă a bă scade. Dacă energa cnetcă totală este ma mcă decât gkbt, atunc d η ş dec η sunt negatve, ş ca rezultat baa se încălzeşte ş dt mşcarea atomlor este accelerată. Ecuaţle de mşcare (..) pentru ansamblul canonc, se pot reformula în sprtul metode Verlet: F () t r( t+ d t) = r( t) + v(t)dt+ d t η( t) v( t) m F () t v( t+ d) t = v() t + d t η() t v() t m N η ( t + d t) =η ( t) + d t mv ( t) gkbt Q (..6) = N η ( t + d) t =η ( t+ d) t + d t mv ( t d) t gkbt Q + = F ( t+ d) t v( t+ d t) = v( t+ d t) + dt +η ( t+ d t)dt m O parametrzare partculară a lu Q se poate defn astfel: Q = gkbtτ, (..7) unde τ este tmpul de relaxare al bă, care are acelaş ordn de mărme cu pasul de tmp dt, ş care controlează fluctuaţle în temperatură ale bă. Numărul gradelor de lbertate este g = 3( N ). În contnuare prezentăm pe scurt expresle potenţallor nteratomc utlzaţ în dnamca moleculară ş care au fost descrş pentru dferţ atom metalc sau pentru atom cu legătur covalente. Pentru potenţal atomlor metalc avem (Chrou et al. 5):
18 8 Potenţal dn metoda atomulu nclus (EAM) Conform metode atomulu nclus, energa necesară pentru a nclude un atom într-un nod al une reţele atomce este funcţe de denstatea electroncă a acelu nod. Denstatea electroncă totală a reţele se poate exprma ca o superpozţe lnară a denstăţlor electronce a atomlor ndvdual. Prn urmare, în fecare pozţe atomcă sau nod, denstatea electroncă este defntă ca o contrbuţe atât a atomulu luat în consderaţe cât ş a celorlalţ atom dn reţea. Energa necesară ncluder unu atom în reţea este suma energlor asocate denstăţ electronce a nodulu ş o energe constantă asocată celorlalţ atom dn reţea. Energa totală a sstemulu se scre sub forma [ ] ( ), (..8) ( EAM ) H = F ρ h, + φj rj j unde ρh, este denstatea electroncă a atomulu datortă contrbuţe celorlalţ atom dn reţea, F [ ] ρ este energa necesară ncluder atomulu în nodul de denstatea electroncă ρ, ş φj este potenţalul central al perech de atom ş j, separaţ prn dstanţa r j, ş care reprezntă nteracţunea repulsvă nucleu-nucleu. Denstatea electroncă ρh, este suma contrbuţlor ndvduale: * ρ h, = ρ j( rj), (..9) j * unde ρ este denstatea electroncă a atomulu j. Acest potenţal a fost construt pentru calculul energe ş relaxăr de suprafaţă pentru o varetate de metale FCC (N, Pd, alaje N-Cu), ş pentru calculul constantelor elastce ş a modurlor de vbraţe pentru N 3 Al ş pentru alte alaje. Potenţal Fnns ş Snclar (FS) Energa totală a unu sstem de N atom se exprmă astfel: N FS H = V( r ) c ρ, (..) j = j unde V ( r j ) este nteracţunea repulsvă a pereche de atom ş j, aflaţ la dstanţa r j, c fnd o constantă poztvă, ş ρ = φ( rj), (..) j unde φ j este potenţalul de coezune de tp corpur. Cel de al dolea termen reprezntă contrbuţa coezvă de tp multe corpur la energa totală. Forma de radcal este motvată de analoga cu modelul legătur atomce de tp radcal, în care energa de coezune este de acelaş ordn de mărme cu rădăcna pătrată dn numărul atomc. Expresa (..) este smlară cu (..8), dar nterpretarea este dfertă. Potenţal FS au fost obţnuţ dn modelul legătur atomce de tp radcal, ş de aceea partea de nteracţune de tp mult-corp care corespunde funcţonale F [ ρ h, ] dn potenţalul EAM are ac forma unu termen de rădăcnă pătrată. Acest potenţal necestă o converse de la metale pure la alajele lor, ma greoae decât potenţalul EAM. Poenţalul FS a fost construt pentru câteva alaje de metale noble Au, Ag, Cu, etc.
19 9 Potenţal cu rază mare de acţune Sutto ş Chen (SC) Acest potenţal a fost construt dn descrerea energetcă a metale elementare cu faţă cubc centrată (FCC). Energa totală a unu sstem de N atom se exprmă la fel ca în (..): N SC H =ε V( rj) c ρ = j, (..) a V( rj ) = r j m m, (..3) a ρ =, (..4) j r j unde ε este un parametru cu dmensune de energe, a constanta reţele atomce cu dmensune de lungme, m ş n sunt întreg poztv n> m. Forma de putere a termenlor a fost adoptată pentru a constru un model untar care să combne nteracţunle cu rază mcă de acţune (prmul termen dn partea dreaptă a (..), care este utl pentru descrerea fenomenulu de relaxare a suprafeţe), cu forţele van der Waals care dau o ma bună descrere a nteracţunlor cu rază mare de acţune. În tabelul.. sunt prezentaţ parametr potenţalulu Sutton-Chen, determnaţ dn date expermentale prvnd energa coezvă. Tabel... Parametr potenţalulu Sutton-Chen (Raf-Tabar ). element m n ε [ev] c N 6 9,577 39,43 Cu 6 9,38 3 Rh 6 4,937 3 Pd 7 4,79 3 Ag 6,545 3 Ir 6 4,4489 Pt Au 8,793 3 Pb 7 5,5765 Al 6 7 3,347 39,43 44,4 8,7 44,4 334,94 34,48 34,48 45,778 6,399 Potenţal cu rază mare de acţune Sutto ş Chen (SC) Potenţalul SC a fost generalzat pentru a modela nteracţunle atomce în alaje metalce bnare cu fată cubc centrată. Ecuaţle (..) (..4) au fost rescrse pentru alaje bnare A-B: unde N RST AA A BB B = ( j ) ˆ ρ ˆ ( ˆ ) ρ = j, (..5) H V r d p d p p AA BB AB V ( r ) ˆ ˆ ( ) ( ˆ )( ˆ ) ( ) [ ˆ ( ˆ ) ˆ ( ˆ j = p pjv rj + p pj V rj + p pj + pj p )] V ( rj ), (..6)
20 ρ A = φ A ( r ) = [ pˆ φ AA ( r ) + ( pˆ ) φ AB ( r )], j j j j j j j ρ B B ( ) [( ˆ ) BB ( ) ˆ AB = φ rj = pj φ rj + pjφ ( rj )], (..7) j unde operator p ˆ sunt defnţ astfel: Funcţle V µν ş Constantele AA d ş µν φ j, atomul A ocupa pozta, pˆ = (..8), atomul B ocupa pozta. sunt defnte astfel BB d se determnă dn d µν µν µν a V () r =ε r µν µν a φ ( r) = r =ε c, d AA AA AA µν m µν n BB BB BB, (..9). (..) =ε c. (..) Parametr ε, c, a, m ş n pentru AA ş BB sunt parametr potenţalulu SC pentru elementele pure A ş B lstate în tabelul... Parametr mxt AB se obţn după legea mxtur AB AA BB AB AA BB φ = φ φ, V = V V, (..) care conduce la AB ( AA BB m = m + m ), AB ( AA BB n = n + n ), AB AA BB a = a a, AB AA BB a = a a. (..3) Potenţalul (..5) a fost utlzat pentru a calcula constantele elastce ş termce pentru o sere de alaje metalce FC ş pentru a modela formarea flmelor ultrasubţr Pd pe o suprafaţă Cu() (Raf-Tabar 4). Potenţal de nteracţune unghulară, Morarty (MO) Metalele de tranzţe începând cu T, Zr ş Hf ş termnând cu N, Pd ş Pt, corespund la acoperrea orbtelor 3d, 4d ş, respectv, 5d. Interacţunle dntre orbte dau naştere unor forţe unghulare care joacă un rol mportant în energetca acestor metale. Pentru metalele BCC, energa coezvă totală este defntă astfel: H MO = H ( Ω ) + vol ( ) ( ) N V j + 6 V jk + V4 ( jkl), (..4) 3 j N j k, j 4N j k, jl, j, k unde Ω este volumul atomc, N este numărul de on, V 3 ş V 4 sunt potenţal unghular de nteracţune pentru 3 ş respectv pentru 4 on, ar H vol nclude toate contrbuţle de nteracţune oncă nteratomce. Avem
21 V j V r j ( ) (, Ω ), V3( jk) V3( r, r, r, Ω ), V4( jkl) V4( r, r, r, r, r, r, Ω ), (..5) j jk k j jk kl l k lj unde r j este dstanţa dntre on ş j. Cu ajutorul acestu potenţal s-au determnat constante elastce, de asemenea frecvenţa fononlor pentru o sere de metale de tranzţe. Pentru atom cu legătur covalente se utlzează următor potenţal: unde Potenţal Tersoff de tp mult-corp C-C, S-S ş C-S Energa totală de legătură este defntă astfel: TR H = E = V( rj ), (..6) j E este energa atomulu ş V j energa de nteracţune dntre atom ş j dată de R A V ( r ) = f ( r )[ V ( r ) + bv ( r )]. (..7) j c j j j j R Funcţa V ( r j ) reprezntă potenţalul repulsv al perech de atom ş j, cum ar f A nteracţunea nucleu-nucleu, ar funcţa V ( r j ) este potenţalul de legătură datortă valenţe electronlor. Termenul b j caracterzează ordnul legătur ş natura nteracţun de tp multcorp. Aceşt potenţal au următoarea formă analtcă: R V ( rj) = Ajexp( λ jrj), V A ( rj) = Bj exp( µ jrj), (), rj < Rj, () π( rj Rj ) () () fc( rj) = + cos, R, () () j < rj < Rj Rj Rj (), rj > Rj, n n ( /) n =χ ( +β ζ ) b j j ζ = f ( r ) ω g( θ ) j c k k jk k, j c c g( θ jk ) = + d [ d + ( h cos θjk) ] ( λ +λ j ) ( µ + µ j ) λ j = µ j = A () () () = AA, Bj = BB j, Rj = R Rj, R = R R j j ω = µ r r. 3 3 k exp[ k ( j k ) ] () () () j j (..8) unde ndc, j ş k se referă la atom dn legătura jk, r j ş r k se referă la lungmea legătur j ş, respectv, a legătur k, al căru ungh este θ jk. Parametr cu un sngur ndce λ ş n se referă la un sngur tp de atom, de exemplu C sau S. Parametr pentru C C, S S ş S C sunt lstaţ în tabelul...
22 Tabel... Parametr potenţalulu Tersoff pentru C ş S (Raf-Tabar ). C S A[eV] 3,3936 3,838 B[eV] 3,467 4,78 λ [Å - ] 3,4879,4799 µ [Å - ],9,73 β 7,574 6, n 7,75 7,8734 c 4 3,849 5,39 d 4,384 6,7 h -,5758 -,5985 () R [Å],8,7 () R [Å], 3 χ χ( C S),9776 Å Potenţalul Brenner Tersoff Acest tp de potenţal modelează legătura atomcă pentru molecule mc de hdrocarbon, ş dă o descrere realstă pentru C C, cu legătur smple, duble ş trple, pentru graft ş damant, însă pentru stuaţ ntermedare între legătură smplă ş dublă se obţne un model nerealst. În acest potenţal, (..6) ş (..7) se scru sub forma H Br = V( rj ), (..9) j R A V ( r ) = f ( r )[ V ( r ) + bv ( r )]. (..3) j c j j j j unde D V r = S β r R R j ( e) ( j ) exp( j j ( j j ) Sj DS V r = β r R A j j ( e) ( j ) exp( j ( j j ) Sj Sj ( b + b ) b = + F N N N j j () t () t conj j j (, j, j ) b = + G + H N N ( H) ( C) δ j [ j j (, )] c Gc ( θ ) = a + d d + (+ cos θ) c (..3) Canttăţle ( C ) ( t) ( C) ( H) ( ) G = f r G θ α r R r R. ( e) ( e) j c ( k ) ( jk )exp[ jk (( j j ) ( k k ))] k, j N ş N reprezntă numărul de atom C ş H legaţ de atomul, ( H ) N = N + N este numărul total al atomlor dn vecnătatea atomulu, ş de asemenea
23 3 determnă dacă legătura este parte a unu sstem conjugat. De exemplu, dacă atomul de carbon formează o legătură conjugată cu atom de carbon vecn, N < 4, atunc N depnde de faptul dacă o legătură de carbon j est parte a unu sstem conjugat. Aceste canttăţ sunt defnte astfel: () t conj j atom hdrogen atom carbon ( H ) ( C ) N = fc ( rl ), N = fc ( rk ), l, j k, j atom carbon atom carbon conj j = + c k k + c jl jl k, j l, j N f ( r ) F( x ) f ( r ) F( x ), xk, F( xk ) = + cos[ π( xk )], < xk < 3,, xk 3, x = N f ( r ). (..3) () t k k c k conj Pentru N j =, legătura dntre perechea de atom ş j nu este parte a unu sstem conj conjugat, în tmp ce, pentru Nj, este parte a unu sstem conjugat. Potenţalul (..9) poate f rescrs sub o formă care nclude funcţ analtce pentru nteracţunle ntramoleculare p π =π +π rc dh j j j Q R j V ( rj ) = fc ( rj ) + Aj exp( αjrj ) rj A V ( r ) = f ( r ) B exp( β r ) j c j jn jn j n=,3 σπ σπ ( pj + pj ) π bj = + pj G = f ( r ) G (cos θ )exp[ λ ( r r )] j c k jk jk j k k, j () () π rc ( t, t, conj j = Fj N Nj Nj ) atom carbon atom carbon conj j = + c( k ) ( k ) + c( jl ) ( jl ) k, j l, j N f r F x f r F x () () π hd ( t, t, conj j = Tj N N j Nj ) ( cos ωjkl ) fc ( rk ) fc ( rjl ) k, jl, j ω = e e. (..33) cos jkl jk jl Q j este potenţalul Coulomb care tnde către nfnt atunc când dstanţa tnde către zero. rc Termenul π j reprezntă nfluenţa radcallor ş a legătur conjugate π, ş valoarea sa depnde de faptul dacă legătura dntre atom ş j are caracter radcal sau este parte a unu sstem conjugat. Valoarea termenulu rc πj depnde de unghul dedru pentru legătura dublă C C. Funcţle Hj sunt parametrzate prn funcţ splne bdmensonale P j, ş prn funcţ splne trdmensonale F j ş
24 4 T j. Funcţle e jk sunt versor asocaţ produsulu vectoral R j R k, unde R sunt vector nteratomc. Funcţa G (cos θ jk ) reprezntă contrbuţa la b j a atomlor dn vecnătatea atomulu, ş a fost determnată pentru θ= 9,47 damant ş foaa de graft, ş pentru θ= 9 ş respectv θ=, pentru unghul de legătură în ş respectv θ= 8, pentru unghul de legătură întro reţea cubcă smplă. Reţeaua FCC conţne unghur de 6º, 9º, º ş 8º. S-a calculat ş valoarea G (cos 6 ). Pentru θ între º ş 9º, pentru un atom de carbon, se utlzează funcţa unghulară t g = G (cos θ ) + Q( N )[ γ (cos θ) G (cos θ )], (..34) c c c c unde γ (cos θ) este o funcţe splne determnată pentru unghur ma mc decât 9,47º. Funcţa c Q( N t ) este t, N 3, t t π( N 3,) t QN ( ) = + cos, 3,< N < 3,7 (3,7 3,) t, N 3,7. (..35) Potenţal Lennard-Jones Interacţunle care nu sunt de tpul legăturlor atomce se pot modela prn potenţalul Lennard-Jones care descre nteracţunle ntermoleculare în reţeaua atomcă de graft sau în moleculele C 6. Potenţalul de nteracţune total între atom de carbon în două molecule C 6, sau dntre două plane de graft se scre sub forma H LJ 6 IJ σ σ ( rj ) = 4ε IJ IJ, j> r j r (..36) j IJ unde I ş J reprezntă două molecule sau două plane, r j este dstanţa dntre atomul dn molecula (planul) I ş atomul j dn molecula (planul) J. Parametr acestu potenţal sunt ε=,47 ev, σ= 3,4 Å. Potenţalul 6-exp Acest potenţal descre nteracţunea dntre atom de carbon în două molecule C 6 : A H ( r ) = + Bexp( αr ). (..37) DJ IJ IJ j IJ 6 j j> ( rj ) Parametr dn acest potenţal sunt lstaţ în tabelul..3. Valoarea măsurată a parametrulu a pentru C 6 este a = 4,4 Å la T = K, ar valoarea calculată în cazul, este a = 3, Å, ar în cazul, a = 4,3 Å.
25 5 Tabel..3. Parametr potenţalulu 6-exp pentru C (Raf-Tabar ). A [kcal Å 6 /mol] B [kcal/mol] α [Å - Cazul Cazul , ,6 ] Potenţal Ruoff-Hckman Acest potenţal descre nteracţunea une molecule C 6 cu un substrat de graft. Aceste două ssteme se modelează ca suprafeţe contnue. Sumele se înlocuesc cu ntegrale care se evaluează analtc. Molecula C 6 este modelată ca o sferă goală cu raza b = 3,55 Å, ş nteracţunea C C se consderă de forma Lennard-Jones H ( rj ) c r c r =, (..38) 6 6 unde c 6 = 9,97 evå 6 ş c = 348 evå. Potenţalul de nteracţune dntre C 6 ş un sngur atom de carbon al substratulu de graft aflat la o dstanţă z> b de centrul sfere, se scre unde V ( z) = V ( z) V ( z), (..39) 6 c N V ( z) = ( n ) bz ( z b) ( z+ b) n n n n, (..4) cu N numărul de atom pe sferă ( N = 6 în cazul acesta) ş n = ş 6. Energa totală de nteracţune între C6 ş planul de graft se obţne prn ntegrarea funcţe V() z pe domenul atomlor dn plan: H ( R) = E ( R) E ( R), (..4) 6 unde R este dstanţa vertcală de la centrul sfere la plan, ş E c N 4( n )( n 3) b ( R b) ( R+ b) n n ( R) = 3 n 3 n 3. (..4) Potenţal metal-carbon În modelarea creşter flmelor metalce pe substratur sem-metalce cum este graftul, un rol mportant îl are nterfaţa metal-carbon, deoarece ea controlează umezrea nţală a substratulu, dfuza ş alnerea fnală a atomlor. Un potenţal care descre nteracţunea unu atom metalc FCC (M) cu C, se poate constru prn regula mxtur. Se consderă un potenţal generalzat de tp Morse cu parametr necunoscuţ MC H ( rj ) = EMC [exp( Nα( rj rw )) Nexp( α( rj rw ))], (..43) j> un potenţal Morse cunoscut, care descre nteracţunea C C
26 6 CC H ( r ) = E [exp( α ( r r )) exp( α ( r r ))], (..44) j C j d j d j> ş un potenţal generalzat Morse cunoscut, care descre nteracţunea M M MM H ( r ) = E [exp( mα ( r r )) mexp( α ( r r ))], (..45) j M j j j> O lege mxtă poate f de forma E = EE, rw = rdr, α= αα, N = m. (..46) MC C M În felul acesta se obţne MC H ( r ) = E [exp( Nα( r r )) Nexp( α( r r ))] j MC j w j w j> E [exp( Nα( r r )) Nexp( α( r r )) MC c w c w EMC Nα [ exp( η( rj rc ))][exp( Nα( rc rw )) exp( α( rc rw ))], η unde r c este valoarea la care potenţalul este nul, η fnd o constantă care este egală cu. Parametr acestu potenţal pentru M Ag sunt lstaţ în tabelul..4. (..47) Tabel..4. Parametr potenţalulu Ag-C (Raf-Tabar ). α 4,959 Å - α,375 Å - 3, ev E C E,84875 ev Ag m 6 r r d 4,44476 Å,49 Å Prmul scop al lucrar este de a constru o clasa de leg consttutve pentru nanotuburle de carbon, bazate pe date expermentale. Aceasta clasa de leg se construeste prn consderarea une problemed de deformate unaxala a unu nanotub de carbon cu un sngur perete. Se aplca metoda reducer pseudosferce a probleme de deformate (Teodorescu, Chrou s Munteanu 5 a,b,c,d, Rogers s Schef 997). Pentru ntelegerea aceste probleme, consderam ecuatle de mscare ntr-un sstem de coordonate Lagrangean, sub forma ε t = vx, ρ vt =σ X. (..48) Ecuata consttutva unaxala este data de σ=σ( ε, X ). (..49)
27 7 ρ Ac, σ s ρ sunt tensunea unaxala s respectv, denstatea materalulu, ar ε= este ρ alungrea, ρ este denstatea materalulu n stare nedeformata, s v( X, t ) este vteza. Intr-un sstem ce coordonate Euleran x = xxt (, ), avem d x = ( ε+ )dx = vdt, (..5) astfel ncat ρ dx = ρdx ρ vdt. (..5) In (..5), X corespunde functe partcula ψ n formularea lu Martn. Varablele ndependente sunt σ s ψ, cu ρ =. In acest caz, se obtne ecuata Monge Ampère (Munteanu s Donescu, 4) ξσσξψψ ξ σψ =ε σ, (..5) t = ξ σ, v = ξ ψ, d x = ξξ ψ σσ + ( ξξ ψ σψ +ε)dψ, (..53) < ξσσε<. Daca soluta ξ( σ, ψ ) ecuate (..5) se cunoaste, atunc traectora partuculelor se calculeaza dn x = [ ξξ ψ σσ + ( ξξ ψ σψ +ε)d ψ], t = ξ p, (..54) n functe de σ, pentru ψ = const. Rezolvand (.), se obtne soluta σ( ψ, t), ar soluta orgnala a ecuatlor (..48),(..49) se determna parametrc sub forma (Rogers s Schef 997) x = x( ψ, t), v = v( ψ, t), σ=σ( ψ, t). (..55) Pentru a arata conexunea geometrca a aceste probleme, consderam o suprafata Σ n scrsa sub forma parametrca Monge 3 3 R, r = xe + ye + z( x, y) e, (..56) unde r = rxyz (,, ) eset vectorul de pozte a unu punct P de pe suprafata Prmele doua forme fundamentale se defnesc astfel I = Edx + Fdxdy+ Gd y = ( + zx)dx + zxzydxd y+ ( + zy)d y, Curbura Gaussana a suprafete Σ este eg f z z z Κ= = EG F + z + z xx yy xy ( x y). (..57) Daca Σ este o suprafata hperbolca, atunc curbura totala este negatva s lnle asmptotce pe Σ pot f consderate curbe parametrce. Introducem no varable ndependente σ s ψ, astfel s varabla dependenta ξ Avem σ= z x, zy ψ =, (..58) ξ = x, ξ = y. (..59) σ ψ
28 8 zyy ξ σσ = zxxzyy zxy Curbura Gaussana (..57) devne z xx xy, ξ ψψ =, ξ σψ = zxxzyy zxy zxxzyy zxy z. (..6) K =. (..6) ( +σ +ψ ) ( ξσσξψψ ξσψ ) Curbura Gaussana se poate pune n corespondenta bunvoca cu ecuata Monge Ampère (..5) prn ε σ =, (..6) Κ ( +σ +ψ ) s A Κ=. (..63) ( +σ + X ) unde A urmare screm σ =, cu A vteza de unda Lagrangeana. Suprafata Σ este pseudosferca, prn ε X K =, a = const. (..64) a In acest caz, relata (..63) devne ε Integrand (..65), avem σ σ = ( +σ + X ) σ X > X a ε, σ>. (..65) a σ σ + X ε= [arctan( ) + ] +α( X ), (..66) 3/ ( + X ) + X +σ + X unde α ( X ) se determna dn date expermentale cu ajutorul unor probleme nverse. Pentru σ ε= =, rezulta α ( X ) =. Relata (..66) repreznta o clasa de ecuat consttutve pentru nanotubur de carbon, pentru care ecuata de mscare (..48) este asocata une suprafete pseudosferce Σ. Legle consttutve s potental atomc sunt n masura sa dentfce parametr nanostructural pentru materalele elastce s vasco-elastce. O extense a reducer pseudo sferce se paote face s pentru materalele vascoelastce prn cuplarea cu un model nelocal. Un domenu fzc în care teora nelocală este aplcablă constă în descrerea fenomenelor de ndentare în materale mcro ş nanostructurate. Toate materalele au o mcrostructură fnd alcătute dn subcorpur (atom, molecule, granule, etc) care se atrag între ele prn forţe nteratomce. Pentru un corp dat, scărle de lungme macro-, mcro ş nanometrcă sunt asocate une lungm caracterstce λ. Această lungme caracterstcă poate f o dstanţă atomcă sau o dstanţă granulară depnzând de natura fenomenulu studat. Scara de tmp τ sau de frecvenţă ω poate f tmpul mnm de transmtere a unu semnal sau a une frecvenţe asocate de la un subcorp la altul. Domenul de aplcabltate a teore corpurlor deformable depnde de raportul ( λ/, l τ/ τ ) sau ( λ/, l ω / ω )..
29 9 Valorle mărmlor de stare care caracterzează fenomenul într-un punct al medulu, la un moment de tmp, depnd nu numa de valorle pe care le au aceste mărm în acelaş punct într-un moment anteror, c ş de valorle pe care le aveau mărmle în acel moment în puncte ale medulu stuate la depărtăr comparable cu lungmea de undă a propagăr fenomenulu. În teora atomcă a latcelor, exstenţa forţelor coezve cu un domenu larg de acţune este recunoscută ş efectul lor asupra dsperse undelor elastce a fost stablt de expermentator. Interacţunea dntre domen ale căror dmensun sunt de acelaş ordn de mărme cu lungmea de undă a propagăr fenomenulu, este o problemă care a preocupat pe mulţ dntre matematcen ş fzcen. Teora elastctăţ se bazează pe deea că forţele de răspuns au o rază de acţune practc nulă. Aceasta mplcă o anumtă lmtare în aplcaţ deoarece forţele de coezune în materalele reale au un domenu de acţune fnt dar nenul. Domenul de acţune al forţelor nterne ş contnutatea matere sunt două concepte dferte. Împreună pot conduce la o teore nelocală a elastctăţ, adcă la o teore a conţnutulu care a în consderaţe un domenu fnt de acţune al forţelor coezve. Trăsăturle care fac dstncte teorle nelocale ş teorle clasce sunt postulatele prvnd întregul corp ş aparţa în ecuaţle locale a unor termen numţ de Erngen rezduur de localzare. Erngen a obţnut dn legle globale de bază formele nelocale ale leglor de blanţ ş ale negaltăţ entrope, prn ncluderea rezduurlor de localzare a căror contrbuţe totală în legle globale este nulă. Rezduurle de localzare sunt sufcente pentru a lua în consderaţe nteracţunea tuturor părţlor corpulu cu starea orcăru punct materal dn corp. Stablm acum ecuaţle nelocale de blanţ ş legle consttutve pentru un sold elastc cu mcrostructură, conducător de căldură, alcătut dn n consttuenţ (granule solde sau flude vâscoase, compresble, conducătoare de căldură). Se consderă două ssteme de coordonate, unul spaţal ş altul materal, având vector de pozţe x, respectv X. Spaţul de refernţă, în raport cu care se descre fenomenul de nteracţune sold-flud este un spaţu eucldean trdmensonal E al punctelor x, ale căror k coordonate spaţale se notează cu x, k =,,3. Soldul ş consttuenţ sunt suprapuş în aşa fel încât orce punct spaţal x este ocupat smultan de către o partculă a fecăru consttuent. Tmpul de refernţă, în raport cu care se descre fenomenul de nteracţune dntre fazele sold-flud este un spaţu eucldean undmensonal al punctelor t, numte momente de tmp. Conform lu Truesdell p prn mxtură contnuă se înţelege o famle de varetăţ trdmensonale B ξ de clasă C, p ale punctelor X ξ. Punctele X ξ reprezntă partculele consttuenţlor ξ a mxtur. Este greu să se stablească o corespondenţă bunvocă între partculele X ξ ale mxtur contnue defnte ma sus ş partculele elementare solde sau flude care formează mxtura soldă propru-zsă. Varetăţle B ξ se raportează la un sstem cartezan ortogonal de coordonate ş astfel se k poate stabl o corespondenţă bunvocă între partculele X ξ ş trpletele de numere reale X ξ, k =,,3 X = X X X X. (..67) 3 ξ ξ( ξ, ξ, ξ) k Numerele X ξ, k =,,3 se numesc coordonatele materale ale partculelor X ξ ale consttuentulu ξ. Se presupune că structura nternă a une partcule solde sau flude X ξ este caracterzată de un câmp tensoral χ ξ care determnă starea nternă a partculelor. Corespondenţa bunvocă dntre varetatea B ξ ş un domenu E al spaţulu eucldean trdmensonal stableşte o k corespondenţă bunvocă între coordonatele materale X ξ ş valorle câmpulu χ ξ
30 3 x = χ ( X, t).. (..68) ξ ξ Câmpul tensoral χξ descre mşcarea consttuentulu ξ la momentul t. Punctul spaţal x la momentul t este ocupat smultan conform leg (..68) de către o partculă materală a fecăru k consttuent. Se presupune că (..68) este bunvocă ş contnuu dferenţablă în raport cu X ξ ş t. Vteza fecăru consttuent materal este defntă prn χξ vξ = X. (..69) ξ t Notând denstatea de masă a consttuentulu ξ cu ρ ξ, denstatea de masă a medulu este dată de formula ρ = ρξ. (..7) Dervata materală a funcţe tensorale ψ relatv la consttuentul ξ este Dψ dψ ψ ξ = = + v ψ Dt dt t ξ k X ξ x ξ, k unde ψ,k reprezntă dervata parţală a funcţe ψ în raport cu, (..7) k x. Înante de a trece la legle de blanţ se dau două formule fundamentale utlzate în stablrea ecuaţlor nelocale de blanţ. Dervata în raport cu tmpul a ntegrale funcţe tensorale ψ consderată pe volumul V ξ asocat consttuentulu ξ poate f scrsă sub forma d dt Vξ ψ ψ d V = [ + ( ψ v ) ]d V + ψ ( v u ) nkdσ t, (..7) * Vξ k k k ξ, k ξ σ * unde V ξ reprezntă partea dn V ξ care nu conţne vecnătăţ ale suprafeţe de dscontnutate σ, n vectorul untar normal la σ în drecţa propagăr dscontnutăţ, u vteza cu care se propagă suprafaţa de dscontnutate σ, ş parantezele duble saltul valor canttăţ respectve de-a lungul suprafeţe de dscontnutate în drecţa de propagare. Interfaţa dntre consttuent o putem defn ca o astfel de suprafaţă de dscontnutate. A doua formulă este dată de teorema generalzată Green-Gauss pentru o funcţe vectorală A pe suprafaţa S ξ a lu V ξ A nds= AdV+ A ndσ. k k k k, k k S * ξ V σ ξ (..73) În cele ce urmează nu se au în consderaţe fenomenele electro-magnetce, relatvste sau cuantce. Legle de blanţ, în cazul medulu nelocal, nclud legle de blanţ ale mase, energe, mpulsulu, momentulu cnetc ş negaltatea lu Clausus-Duhem.. Conservarea mase. Dervata în raport cu tmpul a ntegrale denstăţ de masă pentru consttuentul ξ, consderată pe volumul de materal V ξ trebue să fe nulă d ρ ξdv = t. (..74) d V ξ
31 3 Utlzând (..7) ecuaţa nelocală a denstăţ de masă poate f scrsă pentru fecare consttuent în parte astfel ρ ξ + k ( ρ v ), ˆ ξ ξ k = ρ ξ, (..75) t ρ ˆ ξdv =, Vξ (..76) k k ρ ( v u ) n ˆ ξ ξ k = Rξ, (..77) ˆ Rξd σ=. (..78) σ În ecuaţle de ma sus au apărut nşte câmpur scalare, arbtrareρ ˆ ξ ş ˆR * ξ defnte pe V ξ, respectv σ, care îndeplnesc (..76) ş (..78). Astfel de leg de blanţ sunt famlare reacţlor chmce unde canttăţle notate cu ^ reprezntă varaţ ale canttăţ respectve în V ξ datortă nteracţunlor cu restul corpulu, ele fnd o consecnţă drectă a nteracţunlor nterne nelocale. * În (..75) ρ ˆ ξ caracterzează varaţa de masă a consttuentulu ξ în volumul V ξ, datortă reacţlor chmce. Câmpul scalar ˆR ξ poate f nterpretat ca fnd varaţa de masă a consttuentulu ξ de-a lungul suprafeţe de dscontnutate σ. În cazul absenţe reacţlor chmce, atât ρ ˆ ξ cât ş ˆR ξ se anulează. Condţle (..76) ş (..78) caracterzează faptul că nu exstă creştere netă de masă în corp. Deoarece aceşt termen apar în procesul de localzare a leglor globale de blanţ, e se numesc, potrvt cu Erngen, rezduur de localzare. Înlocund în (..4) ψ cu ρψ ξ ş ţnând seama de (..75), formula (..7) devne d dt Vξ ψ ρψ d V = [ ρ + ρ v ψ + ψρ ]d V + ρψ ( v u ) nkdσ. (..79) k k k ˆ ξ ξ ξ ξ, k ξ ξ ξ * t V σ ξ Sub această formă, formula (..79) va f utlzată ma departe în obţnerea leglor nelocale de blanţ. Cum se va vedea, fecare lege de blanţ acompanată de condţa de salt, va conţne un * rezduu de localzare de volum ş un rezduu de localzare de suprafată, defnte pe V ξ ş respectv * pe σ, completate de condţa ca ntegralele pe V ξ ş σ ale acestor rezduur să fe nule.. Blanţul mpulsulu. Presupunând că exstă un tensor al tensun t ξ pentru fecare consttuent ş o fortă de volum f ξ pentru fecare consttuent, ecuaţa de blanţ al mpulsulu se scre sub forma d dt k jk k ρ ξvξdv = tξnjds + ρξfξdv. (..8) Vξ Sξ Aplcând (..73) ş (..79) se obţne ecuaţa nelocală de blanţ al mpulsulu pentru fecare consttuent în parte Vξ k dv jk k ξ k ˆ ˆ k tξ, j +ρξ( fξ ) = vξρ ξ +ρ ξfξ, (..8) dt
32 3 ˆ fξ d V =, * Vξ (..8) jk k j j ( ) ˆ k tξ ρξvξ vξ u nj =ρξfξ, (..83) ˆ Fdσ=. ξ (..84) σ În (..8)-(..84) ˆf ξ ş ˆF ξ reprezntă rezduurle de localzare ale forţelor de volum * defnte pe V ξ ş respectv pe σ. Câmpul vectoral ˆF ξ poate f nterpretat ca reprezentând efectele nelocale pe suprafaţa σ ntroduse de varaţa forţe de volum ce acţonează asupra consttuentulu ξ de-a lungul suprafeţe de dscontnutate σ. 3. Blanţul momentulu cnetc. Forma ntegrală a ecuaţe de blanţ a momentulu cnetc pentru fecare consttuent este d dt j k j k j k ejk p ρ ξvξdv = ejk p tξnds + ejk p ρξfξdv, (..85) Vξ unde e jk sunt componentele tensorulu alternatv, ar Sξ Vξ j p componenetle vectorulu de pozţe. Făcând uz de (..73) ş (..79) ş de condţa de blanţ a mpulsulu, ecuaţa nelocală de blanţ a momentulu cnetc devne e [ t jk + ρ p j fˆ k ] = ρ lˆ, (..86) jk ξ ξ ξ ξ ξ ˆ ldv ξ =, * Vξ (..87) e pf j ˆ k = Lˆ, (..88) jk ξ ξ ˆ Ldσ=. ξ (..89) σ În formulele de ma sus ˆl ξ ş ˆL ξ reprezntă rezduurle de localzare ale cuplelor de volum * defnte pe V ξ ş respectv pe σ. Ele caracterzează efectul nelocal ntrodus de varaţa cuplelor de volum pe untatea de masă. În cele ce urmează se consderă că termen. ˆl ξ ş ˆL ξ se pot elmna atâta vreme cât nu sunt consderate în ecuaţa (..85) cuplele de tensun, de suprafată ş de volum. Prn urmare se consderă lˆ ξ =, Lˆ ξ =. (..9) 4. Blanţul energe. Presupunând că exstă pentru fecare consttuent energa nternă specfcă ε ξ, vectorul flux de cădură q ξ îndreptat spre nterorul volumulu matere ş sursa de căldură h ξ, ecuaţa conservăr totale a energe se scre astfel
33 33 d [ k ]d jk k ρ ξvξvξk + ρξεξ V tξvξ knjds ρξfξvξ k d V dt ξ V ξ ξ S ξ ξ k qnds ρ hdv= ξ Sξ ξ k ξ ξ ξ Vξ Vξ (..9) Utlzând (..73) ş (..79), precum ş ecuaţle de blanţ a mpulsulu, ş a momentulu cnetc, ecuaţa nelocală de conservare a energe devne k k qξ dεξ v jk ξ ˆ k k ρ t h v ˆ ˆ ˆ k ξ + ξ +ρ j ξ ξ ρ ξ ξk fξ + ρξεξ ρ ξvξkvξ = ρξhξ, (..9) x dt x ˆ ρ ξhξ d V =, * Vξ (..93) k j j jk j ρ ( v )( ) ˆ ξ ξk +εξ vξ u tξ vξ k q ξ nj =ρξhξ, (..94) ˆ Hξd σ=. (..95) σ unde ĥξ ş Ĥ * ξ reprezntă rezduurle de localzare defnte pe V ξ ş respectv pe σ, caracterzând varaţa energe nelocale pe untatea de masă respectv efectul de suprafaţă corespunzător.
34 34.. Analza conceptelor de nanostructurare a sstemelor compozte alcatute dn materale dferte Nuzzo ş Allara au raportat prmul studu al mono-straturlor auto-asamblate în 983. De atunc acest domenu de actvtate se dezvoltă rapd, în specal mono-straturle pe substrat de aur, chemoabsorbte dn soluţ sau gaze. Posbltatea de a fabrca flme mono-moleculare omogene cu propretăţ controlate a captat substanţal atenţa cercetătorlor în domenu în ultm an. Autoasamblarea mono-straturlor SAMs de sulf pe substrat de aur este un procedeu uşor de a forma fre omogene. Procesul de absorbţe are do paş. În prmul pas, moleculele sunt fzc absorbte (prn absorbţe zotermă Langmur) ş aranjate aproape paralel, în lne cu suprafaţa. În pasul al dolea, moleculele se reorentează ş-ş organzează lanţurle alchl prn chemobsorbţe într-un monostrat omogen cu propretăţ controlate. Crstalele se pot aranja în dferte forme ordonate, ş se pot utlza ca flme ant-îngheţ pentru avoane, stratur lubrfante în mcroelectroncă, agenţ ant-trombotc pentru artere, etc. In lucrare s-a studat o colecţe de nanopartcule de aur de aproxmatv 5nm dametru, aranjate în crcute moleculare ntr- matrce de cupru, sunt prezentate în fg.... Fg... Crcute moleculare dn nanopartcule de aur n matrce de cupru. Pentru obtnerea unor propretat superoare de rezstenta s amortzare, se utlzeaza compozte cu materale dferte. Implementand n crcutele moleculare cu nanopartcule de aur, nanopartcule dntr-un materal auxetc, propretatle de amortzare a nanocompoztulu cresc. IN lucrare se studaza materalele auxetce s materalele cu rgdtate negatva (sau a materalelor auxetce cu coefcent Posson negatv n scopul arhtecturar a no nanocompozte cu propretat superoare sau la cerere (Chrou, Munteanu, Dumtru, Beldman s Secara 7, Chrou, Dumtru, Munteanu 7). Motvata pentru studul materalelor cu rgdtate negatva este data de rezultatele expermentale estrem de promtatoare dn ultm an, care au demonstrat ca mecansmul rgdtate negatvă exerctă o forţă opusă care anulează rgdtatea resortulu elastc. Acest mecansm amortzează vbraţle de la două or la tre or ma bne dacật orce mecansm actv sau sem-actv de reducere a vbraţlor (Chrou, Munteanu, Dumtru, Beldman s Secara, 8). Rezultatul esental pe care se bazeaza aceasta lucrare este demonstrarea atat expermentala (Lakes, Lakes, Lee, Berse s Wang ) cat s teoretca (Teodorescu, Badea, Munteanu ş Onşoru 5, Teodorescu, Munteanu s Chrou 5) exstenţa materalelor cu constante elastce de materal avậnd valor negatve. În cazul cuprulu se arată că acest materal poate avea constante elastce negatve pentru deformaţ nţale mar poztve sau negatve. Idea prncpală a lucrar constă în aceea că, înglobate într-o matrce de materal cu rgdtate poztvă, ncluzunle dn materal cu rgdtate negatvă actvează în tmpul vbraţlor mecansmul rgdtate negatvă prn care dezvoltă deformaţ ma mar în ncluzun ş în vecnatatea lor, decật în restul matrc. Datortă acestor deformaţ mar, mşcarea globală a
35 35 compoztulu este amortzată. Deş materalul de rgdtate negatvă este nstabl, ncluzunle pot f stablzate prn matrcea în care sunt ncorporate. Mecansmul rgdtate negatvă are ca efect reducerea deformaţlor une structur nanostructurate. O lege consttutva tpc pentru astfel de materale cu rgdtate negatva este reprezentata n fg.... C klmn Fg.... Lege consttutve n care nstabltatea materala apare dn cauza nmuer. In cele ce urmeaza vom folos urmatoarele notat: u k, k =,,3 vector deplasare; σ, k, l =,,3 tensor tensune; kl t tensune de tractune; ( n) k m kl tensor tensun cuplate (or moment pe untatea de are); m cuple de suprafata; ( nk ) n l normala exteroara la frontera; e = /( u + u ) tensorul Lagrange al macrodeformatlor; kl k, l l, k ϕ k vector de mcrorotate; ν = ϕ vector vteza de mcrorotate (vectorul grate); k k ε = u +ϕ tensor mcrodeformate; kl k, l k, l ε klm ( ε 3 =ε 3 = ε 3 = ε 3 = ε 3 = ε 3 =, altfel ε klm = ) smbol de permutare; r = /ε u vector macrorotate; k klm m, l λ, µ constante elastce Lamé ; B klmn ( ε=ε= C ε) constante Cosserat gradent de rotate; C C b = + 3 ( C jkl C Y C C B constanta Cosserat de rotate; jkl ) constante chrale elastce; jkl A energa specfca ; L energe electrostatca Coulomb (energe Madelung ); d energe free-electron, care depnde de volumul crstalulu; b energa de banda structurala;
36 36 ( x, y, z) energe repulsva on-core (Born-Mayer) ; l parametru a energe repulsve; α volumul celule elementare.. Ecuatle consttutve pentru un materal sotrop centrosmetrc de tp Cosserat sunt (Lakes 98, Chrou, Munteanu s Dumtru 8) σ kl =λerrδ kl + ( µ +κ ) ekl +κεklm( rm ϕ m), m kl =αϕr, rδ kl +βϕ k, l + γϕ l, k, (..) In (..) sase constante elastce ndpendente descru comportarea soldulu sotrop centrosmetrc Coserat. Pentru un corp sotrop non-centrosymmetrc de tp Cosserat, energa de deformate s tensorul deformate se scru sub forma s = ε ε + ϕ ϕ + ε ϕ, (..) V Cklmn kl mn Bklmn k, l m, n Aklmn kl m, n ε = e +ε ( r ϕ ). (..3) kl kl klm m m Tensunle s cuplele de tensun se obtn dn V σ =, ε kl kl m kl V =. (..4) ϕ Dn (..3) s (..4) obtnem ecuatle consttutve pentru un corp sotropc noncentrosmetrc de tp Cosserat sau σ kl = Cklmnε mn + Aklmnϕ m, n, mkl Bklmn m, n Aklmn mn l, k = ϕ + ε. (..5) σ = ε δ + ε + ε + ϕ δ + ϕ + ϕ (..6) kl C rr kl C kl C3 lk A r, r kl A k, l A3 l, k, unde m = Bϕ δ + B ϕ + B ϕ + Aε δ + A ε + Aε, (..7) kl r, r kl l, k 3 k, l rr kl lk 3 kl C =λ, C = µ, C 3 =κ, B =α, B = β, B 3 = γ, A = C, A = C, A3 = C3, Ecuatle consttutve (..6) s (..7) conduc la σ =λe δ + ( µ +κ ) e +κε ( r ϕ ) + Cϕ δ + C ϕ + C ϕ, (..8) kl rr kl kl klm m m r, r kl k, l 3 l, k m =αϕ δ +βϕ + γϕ + C e δ + ( C + C ) e + ( C C ) ε ( r ϕ ). (..9) kl r, r kl k, l l, k rr kl 3 kl 3 klm m m Ecuatle (..9) repreznta ecuatle consttutve pentru un corp de tp Cosserat care se comporta sotropc n raport cu o rotate a sstemulu de refernta dar nu n raport cu o nverse. Constantele chrale C, =,,3 caracterzeaza noncentrosmetra. Pentru C = se reobtn ecuatle elastctat sotrope mcropolare. Pentru α=β = γ =κ=, ecuatle (..8) and (..9) se reduc la ecuatle consttutve ale teore elastctat lnare sotrope. Condtle pe frontera sunt date de σ lknl = t( n) k, mn lk l m( n) k Legea de mscare este ndependenta de smetra materala. Avem =. (..)
37 37 σ ρ =, m, +ε σ ρϕ j =. (..) kl, k ul rk r klr lr k Pentru a calcula constantele elastce de ordn superor adoptam modelul materal al lu Jankowsk and Tsakalakos (985) (Chrou, Munteanu s Dumtru 8). Energa totala a crstalulu se scre sub forma Calculele arata ca Avem E = Ees + Efe + Ebs + Er, (..) E r repreznta termenul predomnant n calculul constantelor elastce. E exp( R), (..3) r = α β R cu α, β parametr energetc care se determna expermental pentru fecare materal n parte. Constantele elastce se determna dn V V V E C =, B =, A =, V =. (..4) ε ε ϕ ϕ ε ϕ Ω jkl j kl jkl, j k, l unde V este denstatea energe de deformate, Ω este volumul celule elementare s ε j tensorul Lagrange de deformate. Formula de calcul este jkl j k, l = ( X + X j ). (..5) ε x x j j In (..5) X sunt coordonatele Lagrange corespunzatoare star ntale care poate f supusa une deformat fnte ntale, x sunt coordonatele fnale Euler, care dfera de X prntr-o deformate nfntezmala. Dervatele une funct dferentable f () r se calculeaza conform cu formula unde f() r = [ Rf ( R) f ( R)] Y ( ) 3 jkl + f R Z εkl εj R 4R r= R jkl, Y = XXX X, Zjkl = XXkδ jl + XXlδ jk + X jxlδ k + X jxkδ l, jkl j k l R = X + X + X. 3 Dn (..)-(..4) rezulta cu Cjkl = ajkl bjkl, (..6) ( n) ( n) ( n) ( n) ( n) ( n) ( n) ( n) βr ajkl = f Yjkl, bjkl = g Zjkl, f = f( R ) = 4 g [ + ], ( n) n n ( R ) ( n) ( ( n) ) K exp( ( n) g = g R = β R ), K αβ =, ( n) R 8 Ω unde Ω este volumul celule elementare. Consderam acum un crstal FCC caracterzat de 3 constante ndependente, care este defomat n drecta [] (fg...3).
38 38 Fg...3. Reprezentarea sstemelor de axe ( x, y, z) s ( X, YZ, ). Ultmul este utlzat pentru a studa deformata baxala a crstalulu, Ecuatle de transformare dn sstemul ( x, y, z ) n ( X, YZ, ) sunt x + y + z x+ y X =, Y =, 3 Dn (..7) se obtn coordonatele atomlor dupa deformare la ma X =, Y =, 3 8 x y + z Z =. ( na Z =, (..8) 4 cu l, m, n numere ntreg. Celula untara a crstalulu este reprezentata n fg,..4, n fg...5 se arata aranjamentul latce obtnut dn (..8) ar n fg...6 locata atomlor n cele doua ssteme de coordonate deformat s nedeformat. Deformata baxala n drecta [] este descrsa de unde X = X ( +ε ), X = Y( +ε ), X3 = Z( +ε ), (..9) X sunt coordonatele dupa deformate.
39 39 Fg...4. Celula untara a crstalulu FCC. Fg...5. Reprezentarea latce n sstemul de refernta deformat ( X, YZ, )..
40 4 Fg...6. Reprezentarea atomlor (a) n sstemul nedeformat ( x, y, z ), s b) n sstemul deformat ( X, YZ, ). Dupa deformata baxala, constantele elastce dferte de zero au expresle cu A f C = A B, C = C33 = A B, C44 = ( C ) C3, C55 = C66 = A3 B55, C = C3 = A3, C3 = A, C5 = C46 = A5, C35 = A5, 3 4 = η, 3 c A (9 f f ) 6 4 = a + c η, A f 3 = η η, 6 c = η η, c 3 A5 f (..) B g = 8 c η, B (6g g ) = a + c η, [3 ( 4 a c )] B55 = g η + g η + η, Ra f a = f( R ), f = f( R ), g = gr ( ), g = gr ( ), a = η a, c R a 3 6 c c = η + η, a a c η = +ε, η = +ε. c (..)
41 4 Se utlzeaza conventa de notate a lu Vogt,,33 3,3 4,3 5, 6. Defnm modulul baxal Yb σ = ε, s σ =σ 3 =σ, σ =σ 4 =σ 5 =σ 6 =, ε =ε 3 =ε. ε =ε = ( S + S ) σ, 3 3 Y b = S + S 3. (..) In (..) S j sunt complantele SC j jk =δ k. Avem ε=ε= ε, C C C Yb = C + C3. C. Consderam o placa de lungme L, latme d s grosme b, alcatuta dntr-un materal celular de tp tabla de sah (fg...7) (Chrou, Munteanu s Dumtru 8). Notam cu WC setul de puncte ( x, y, z ) care apartne cuburlor albe s cu BC, setul de puncte care apartne cuburlor negre. Cubul untare are lungmea l, cu unghul ntre doua latur α, α=π /4. Celulele sunt alcatute duntr-un materala auxetc cu coefcentul Posson negatv. Fg...7. O structura celulara - tabla de sah. In urma deformate baxale n drecta [], materalul dn celulele BC se transforma ntrun materal cu rgdtate negatva (admte cel putn o constanta elastca negatva) s n mod normal ar deven nstabl. Prezenta celulelor albe nsa reduce aceasta nstabltate s n fnal materalul compozt se stablzeaza. Se obtne astfel un materal compozt n care materalul auxetc dn celulele negre este caracterzat de o rgdtate negatva (fg...9). Prntre avantajele prezente materalulu auxetc cu rgdtate negatvaa n nanocompozte, specfcam o mare capactate de amortzare, greutatea redusa s rezstenta mecanca mare la ntndere s compresune.
42 4 Fg...8. Orentarea structur, b) Sngulartatle n coltur la celulele BC. Fg...9. Celulele BC de rgdtate negatve ncluse n matrcea de materal auxetc.. Dezvoltarea capabltatlor tehnologce ale metode nelocale Presach-Tteca ca baza pentru caracterzarea amortzar prn nanondentare In această secţune este prezentat un model cu frecare (FCM) pentru contactul dntre două untat (granule) vbrator în sprtul lu Yang, Chu and Menq (998) care permte cuplarea modelelor Presach s Tteca pentru caracterzarea amortzar. Granulele au dmensun n domenul mezzo-mcro s nanoscopc. Acest model este prezentat schematc n fg.. ş reprezntă nterfaţa dntre două granule cu o încărcare nţală n = kve, modelate ca elemnte elastce fără masă caracterzate de două arcur lnare de lungm l u and respectv l v, ş modul ku and respectv k v (ce contorzează proprtaţle de forfecare s ntndere). Deasemenea punctul de contact respectă legea de frecare a lu Coulomb cu coefcentul de frecare µ.
43 43 Am notat cu u deplasarea relatvă tangenţală, v este deplasarea relatvă normală ş w este deplasarea tangentală (de alunecare) a punctulu de contact faţă de granula. Când partculele sunt în contact este posbl să apară o mşcare tangenţală (de lpre alunecare), ar când deplasarea relatvă normală v devne mare poate avea loc un fenomen de separare a partculelor (fg..). Fg.. Model pentru nterfaţa dntre două granule. Fg... Fazele de alunecare ş separare ale nterfeţe.
44 44 Incarcarea normală ş forţa de frecare sund date prn relaţle: n + kv v, pentru v -n / kv n =, pentru v < -n / kv (.) f = k ( u w) (.) u Când deplasărle sunt mc cele două granule sunt în contact fără alunecare, ar forţa de frecare este proporţonală cu u în tmp ce w este nul. Forţa de frecare îş păstrează lmtele între valorle ±µ n. Când forţa de frecare tnde să depăşescă valoarea poztvă µ n, cele două partcule încep să alunece una faţă de cealaltă în drecţa poztvă a lu u. Forţa de frecare rămâne egală cu încărcarea de alunecare varablă până când nterfaţa dntre cele două granule prezntă un contact fără alunecare. Tranzţa între fazele nterfeţe de alunecare ş lpre depnde de deplasarea tangenţală relatvă u ş de încărcarea normală. Momentul în care nterfaţa ajunge dn nou în fază de lpre fără alunecare nu corespunde cu schmbarea drecţe deplasăr tangenţale u. In tmpul une mşcăr cclce încărcarea normală se poate anula ceea ce duce la faza de separare a nterfeţe dntre cele doua granulere. In fg..3 este prezentat cel ma smplu model de frecare pentru nterfaţă în care încărcarea normală este constantă. Interfaţa este supusă une mşcăr relatve cclce de forma u = Acosθ, θ=ω t, ω fnd frecvenţa de osclare ş t tmpul. In acest caz curba de hsterezs constă dn două regun smetrce în faza de lpre a nterfeţe ş dn alte două regun smetrce în faza de alunecare a nterfeţe. In cazul une nterfeţe cu o încărcare normală varablă regunle de alunecare devn ln înclnate (fg..4), încărcarea varablă având expresa n + γ k d u, unde γ este o constantă ş kd = ku / kv. Tranzţa lpre alunecare are loc totdeauna în momentul când mşcarea relatvă îş schmbă drecţa ( θ= sau θ= 8 ). In ambele stuaţ curba de hsterezs a fazelor nterfeţe de lpre alunecare poate f uşor obţnută.
45 45 Fg..3. (a) Modelul de frecare pentru nterfaţă, (b) curba de hsterezs pentru o nterfaţă supusă la o încărcare normală constantă. Intorcându-ne la modelul prezentat în fg.. condţa de lpre alunecare este caracterzată de forţa de frecare f ş vteza de alunecare w, a caror expres trebuesc formulate n termen de deplasărle relatve de ntrare. Dn (.) ş (.) avem: ku ( u u) + f, pentru w = (lpre) f = µ n=µ n +µ kvv, pentru w > (alunecare poztva) µ n = µ n µ kvv, pentru w < (alunecare negatva) (.3) unde u ş f sunt valorle ntale pentru u ş f la începutul stăr de lpre t =, u() = u, f () = f. Fg..4 (a) Modelul de frecare pentru nterfaţa, (b) curba de hsterezs pentru o nterfaţă supusă la o încărcare normală varablă cos θ = ( µ n/ kd A µγ + ) /( µγ ) ş cos θ = ( µ n / k A µγ ) /( µγ ) Dervând (.)-(.3) în raport cu tmpul obţnem: d
46 46, pentru lpre µ kv w = u v, pentru alunecare poztva ku µ kv u + v, pentru alunecare negatva ku (.4) In tebelul. sunt prezentate crterle de tranzţe între cele patru stăr dstncte ale nterfeţe: lpre, alunecare în sens poztv, alunecare în sens negatv ş separare. Aceste condţ au fost obţnute fără nc un fel de presupunere asupra deplasărlor relatve de ntrare. Tabel. Crterle de tranzţe tranzţa crterul lpre alunecare poztvă f µ n=, f µ n > sau folosnd (.), (.3) ku u µ kv v + ( f µ n ku u ) =, ku u µ kv v > lpre alunecare negatvă f + µ n=, f + µ n > sau folosnd (.), (.3) ku u + µ kv v + ( f +µ n ku u ) =, ku u + µ kv v < lpre separare n =, n < sau folosnd (.) n + kvv =, v < alunecare poztvă - lpre w =, w < sau folosnd (.4) µ kv µ kv u v =, u v < ku ku alunecare negatvă - lpre w =, w > sau folosnd (.4) µ kv µ kv u + v =, u + v > ku ku alunecare poztvă separare n =, n < sau folosnd (.) n + kvv =, v < alunecare negatvă separare n =, n > sau folosnd (.) n + kvv =, v > separare lpre µ n < f <µ n, w = sau folosnd n = kvv, f = ku ( u w ) µ kv µ kv v < u < v ku ku separare alunecare poztvă µ kv u > v ku separare alunecare negatvă µ kv u < v k u Menţonăm că starea de alunecarea în sens poztv nu poate f urmată de alunecare în sens negatv. Aceste crter sunt foloste pentru a obţne unghurle de tranzţe în tmpul une peroade a mşcăr. Presupunem că avem o mşcare cclcă de tp snusodal
47 47 u = asn θ, v= bsn( θ+ϕ ). (.5) Caracterstcle de amortzare ş rgdtate ale nterfeţe sunt ndependente de frecvenţa mşcăr, unghul de tranzţe putând f nterpretat ca tmpul admensonal ω t. Incărcarea varablă normală este descrsă prn: n + kb v sn( θ+ϕ), pentru sn( θ+ϕ) n / kb v n =, pentru sn( θ+ϕ ) < n / kvb (.6) Unghurle de tranzţe sunt exprmate prn ntermedul a tre varable admensonale: n = µ n k a, b =µ kb/ ka ş ϕ, (.7) / u Dn relaţa (.4), forţa de frecare pentru regunea stăr de lpre a nterfeţe de la θ 8 la θ este: v 8 8 u f = k ( u u( θ )) + f( θ ). (.8) u Cum f( θ 8) = µ n( θ8) ş folosnd (.5) ş (.6) avem: Folosnd notaţle f = k a(sn( θ) sn( θ )) µ ( n + k bsn( θ +ϕ )). (.9) u 8 v 8 l = + b b ϕ, cos l = + b + b ϕ (.) cos ş aplcând crterle descrse în tabelul., se pot formula 8 unghur de tranzţe pentru a caracterza trecerea de la o stare la alta în tmpul une mşcăr cclce. Defnţa acestor unghur este dată în tabelul. Tabelul. Defnţa unghurlor de tranzţe Starle anteroară curentă Unghurle de tranzţe următoare alunecare negatvă lpre θ =π+θ 7 + cos [( l n )/ l] alunecare poztvă alunecare poztvă lpre θ =π+θ 8 + cos [( l n )/ l] alunecare negatvă separare lpre alunecare θ 3 =π+θ 7 + cos [( sn θ6 n ) / l] poztvă separare lpre alunecare θ 4 =π+θ 7 + cos [(sn θ7 n ) / l] negatvă lpre (sau alunecare θ 5 =π ϕ+ sn ( n / b ) poztvă sau alunecare negatvă) separare separare lpre (sau θ 6 = ϕ sn ( n / b ) alunecare poztvă sau alunecare negatvă) alunecare poztvă lpre θ 7 =π tan [( b cos ϕ) /( b sn ϕ)]
48 48 alunecare negatvă lpre θ 8 =π+ tan [( + b cos ϕ) /( b sn ϕ)] Cu aceste unghur stablte putem să obţnem acum curba de hsterezs. S-au gast posble secvenţe ale regunlor lpre/alunecare separare datorate mşcăr snusodale. Aceste secvenţe sunt prezentate în tabelul.3 Tabelul.3 Secvenţele posble în curba de hsterezs cazul Secvenţa regune de lpre (fară alunecare) alunecare fără separare stck negatve slp stck postve slp θ θ θ θ θ postve negatve postve separaton slp stck slp stck slp θ θ θ θ θ θ θ separaton postve slp θ θ θ separaton postve slp stck negatve slp θ θ θ θ θ negatve postve negatve separaton slp stck slp stck slp θ θ θ θ θ θ θ separaton negatve slp stck postve slp θ θ θ θ θ separaton negatve slp θ θ θ postve separaton stck slp stck negatve slp θ θ θ θ θ θ postve separaton stck slp θ θ θ θ negatve separaton stck slp stck negatve slp θ θ θ θ θ θ separaton stck negatve slp θ θ θ θ Pentru prma secvenţa deplasarea relatvă este mcă, ar nterfaţa se găseşte mereu în starea de lpre. Acest caz are loc când: ( cos cos ) n > + b b ϕ + + b + b ϕ (.)
49 49 Pentru al dolea caz, forma curbe de hsterezs se schmbă odată cu unghul de fază ϕ dntre u ş v. Acest caz are loc când: ( + b b cos ϕ + + b + b cos ϕ ) > n > b (.) Pentru studul fenomenulu de hsterezs la scara mezo-mcro s nano utlzam o teore cuplata Presach-Tteca. Ideea modelulu Presach este de a exprma o functe de eşre f () t în raport cu o funcţe de ntrare ut () sub forma une ntegrale: f( t) = P( α, β) Gαβu( t)dαdβ (.3) α β unde G αβ este operatorul hsterezs elementar având o formă rectangulară prezentată în fg..5. Numerele α ş β corespund schmbăr în sus ş jos a valorlor de ntrare, + ş fnd cele doua valor de eşre posble. Modelul (.3) descre operatorul hsterezs cu memore nelocală (globală). Atunc când ut () este monoton crescătoare se urmează curba ascendentă abcde. In cazul cnd funcţa de ntrare este descrescătoare va f trasată curba descendentă. Funcţa P( α, β ) este funcţa lu Presach, o funcţe ce caracterzează nelnartăţle hsteretce. In cele ce urmează vom presupune că α β, ceea ce este char natural dn punct de vedere fzc. Asfel, domenul de ntegrare în (.3) este un trungh dreptunghc în planul ( α, β ), cu potenuza reprezentată de dreapta α=β ş unghul drept reprezentat de punctul ( α, β = α ). Valoarea α > este defntă prn maxmul global al funcţe de ntrare ut (). Fg..5. Operatorul hsterezs elementar Exstă o corespondenţa bunvocă între operatorul G αβ ş punctele ( α, β ) ale trunghulu. Acest trungh (fg..6) este numt trungh lmtă, fnd suport al funcţe Presach, dn moment ce funcţa Presach P( α, β ) este presupusă nulă n exterorul acestu trungh. Interfaţa dntre cele două părţ ale trunghulu este o funcţe de tp treaptă Lt (). Vârfurle aceste ln au coordonatele
50 5 ( α, β ) corespunzătoare punctelor de maxm ş mnm local ale funcţe de ntrare calculate la momentele de tmp anteroare. Dacă funcţa de ntrare este crescătoare atunc Lt () este orzontală, ar dacă funcţa de ntrare este descrescătoare atunc lna este vertcală. La orce moment de tmp trunghul este + împărţt în doua submulţm: o parte A () t corespunzătoare punctelor ( α, β ) pentru care Gαβ u( t) =, ş una A () t corespunzătoare punctelor ( α, β ) pentru care Gαβ u( t) =, separate de Lt (). Astfel, ecuaţa (.3) poate f scrsă sub forma:. (.4) f( t) = P( α, β)dαd β P( α, β)dαdβ + A () t A () t Fg..6. Trunghul lmtă cu nterfaţa Lt () Se poate arăta că acest model are următoarea propretate: fecare punct de maxm local al funcţe de ntrare elmna vârfurle lu Lt () a caror coordonate α sunt ma mc decăt acest maxm, ar fecare mnm local elmnă vârfurle de coordonate β ma mar decât acest mnm. Cu alte cuvnte, modelul Presach nregstrează serle alternante ale punctelor de extrem domnante, în tmp ce celelalte celelalte puncte de extrem sunt elmnate (fg..7). Elmnarea acestor vârfur este echvalentă cu ştergerea store asocată acestor puncte. O altă propretate a modelulu este lulstrată în fg..8: toate curbele de hsterezs corespunzătoare aceluaş punct de extrem al funcţe de ntrare sunt congruente. Funcţa Presach P( α, β ) poate f determnată astfel. Pornm dn starea de saturaţe negatvă ş creştem funcţa de ntrare la o anumtă valoare α. Funcţa de eşre urmează partea ascendentă a curbe prncpale ş pentru u =α va avea valoarea f α. Dacă deşcreştem funcţa de
51 5 ntrare la o anumtă valoare β, funcţa de eşre urmează curba de întoarcere (tranzţe), ca n fg Notănd valoarea funcţe de eşre la u = β prn f αβ, obţnem: s după dervarea în raport cu β ş α, avem: F( α, β) P( αβ, ) = α β α α F( α, β ) = fαβ fα = [ P( α, β )d α ]dβ, (.5) β β, P( α, β ) = P( α, β ). (.6) Dec, putem concluzona că datele expermentale pentru o curbă de tranzţe de ordnul întâ ne permt determnarea funcţe Presach P( α, β ). Propretăţle macroscopce ale materalulu sunt descrse prn ntermedul unu ansamblu de untaţ hsteretce mezoscopce ca în fg..5. Fg..7. Modelul Presach nregstrează serle alternante ale punctelor de extrem domnante.
52 5 Fg..8. Propretatea de congruenta. Fg..9. Curba de tranzţe de ordnul I obţnută prn nversarea valor funcţe de ntrare de la u =α la u = β. Vom face următoarele notat: ku ( lu + lv) kk k =, kh = l k + k, kv ( lu lv) k + =. (.7) l u v
53 53 Untatea elementara hsteretca este reprezentata n fg..9. Pentru un materal compus dntr-un nfnt de granule sferce, se adoptă o conexune în paralel de un număr nfnt de astfel de untăţ (fg..). Untaţle au aceeaş coefcenţ de elastctate ş de încarcare, dar coefcenţ de frecare sunt presupuş dferţ µ mn µ µ max. Presupunem că în materal exstă o dstrbuţe unformă de coefcenţ de frecare µ max µ mn = constant. Fecare untate poate f gândtă ca o granulă ndvduală într-un materal polcrstaln. Granulele cele ma predspuse către stărle de alunecare ş separare corespund elementelor ma slabe. Fg..9. Untate elementară. Fg... Conexune în paralel dntr-un nr. nfnt de untăţ elementare. negatve slp postve slp Curba de hsterezs în cazul dn tabelul.3 : ( θ7 θ θ8 θ θ 7) este prezentată în fg... pentru ϕ= 9, k = k =, a = b =, µ =.4, n =.. Forma curbe se u v stck stck
54 54 schmbă odată cu unghul de fază ϕ dntre u ş v. Pentru alte secvenţe curba este mult ma complcată, fnd împărţtă în regun corespunzătoare fazelor de lpre, alunecare poztvă, alunecare negatvă ş separare. Modelul lu Presach facltează obţnerea curbe de hsterezs pentru fecare secvenţă n parte s de ac, pentru întreg materalul. Funcţa Presach poate f constrută pentru a caracterza nelnartăţle hsteretce. In tabelul.3 este prezentată funcţa Presach P( α, β ) pentru două modele foarte smple: o conexune în paralel a unu element de alunecatre (Sant-Venant) cu un element elastc (Hooke) ş un element de alunecare legat în sere cu un element elastc. Tabelul.4. Funcţa Presach P( α, β ) model P( α, β ) nput f () t output ut () nput ut () output f () t f = αβ ( n) k β + µ, f β f µ n fαβ β + µ n α, fαβ = fα, = H ( α β µ n) β k P( α, β ) = δ( α β µ n) k f u( t) = Gαα, µ n f( t) dα k ( µ n) f f = µ αβ n k( α β ), µ α n β α k β + µ n α, f = µ n f β α and αβ fαβ = µ n f µ β α n k fαβ µ n = kh [ ( α β) H( α β ) β k k P( αβ, ) = [ δα β ( ) δα β ( µ n/ k) u u k f( t) = [ G u() t dα G u() t dα] αα, αα, µ n/ k u ( µ n/ k) u In tabelul.4, H este funcţa Heavsde ş δ este funcţa Drac. Sa consderă curba de hsterezs prezentată n fg... Pentru o untate elementară, când valorle de ntrare sunt date de deplasărle relatve u ş v, ar forţa de frecare reprezntă funcţa de eşre, funcţa Presach are suportul determnat de dreptele α β = ş α β = µ n ş este dată de: k µ n P( α, β ) = δ( α β) ( k kh ) δ( α β ) (.8) k unde n are expresa (.6). Forţa de frecare în funcţe de deplasărle de ntrare are forma: u u k f( t) = [ Gαβutd () ( k kh) Gα, α ( µ n/ k) utd () ] α α (.9) u ( µ n/ k) u
55 55 Fg... Curba de hsterezs în cazul (tabelul.3) pentru ϕ= 9. Pentru un sstem format dntr-un număr nfnt de astfel de untăţ elementare, conectate în paralel ş având o dstrbuţe unformă de coefcenţ de frecare forţa de frecare se scre sub forma: u k f( t) = [ G u( t)d α ( k k ) G u( t)dαd β] ( ), (.) u αβ h α, α ( µ n/ k) n µ max µ mn A unde domenul de ntegrare A este ara dn trungh cuprnsă între dreptele n µ α β=. kmax n µ k mn α β= şo
56 56 Fg... Bucla hsteretca pentru modelul dn fg..9. Metoda de evaluare a amortzar, propusa de no, pe baza teorlor nelocale de tp Erngen s a suprafetelor cu curbura negatva Tteca, prn reducerea pseudosferca a problem3 dnamce, este prezentata n paragraful.... Defnrea une probleme nverse pentru determnarea parametrlor nanostructural dn analza datelor expermentale In acest paragraf s au utlzat datele expermentale achztonate dn deplasarle anulu 8. O metoda practca de nvestgare a propretatlor mecance de rezstenta s amortzare ale materalelor este ndentarea sau stantarea materalu consderat. Problema contactulu elastc are la baza ntelegerea mecansmulu de transmtere a fortelor. Problema a fost abordata pentru prma data de catre H. Hertz (88). Soluta probleme stante cu baza plana elptca, precum s sugesta de a folos aceasta solute n problema contactulu fara frecare, au fost obtnute concomtent de J. Boussnesq (885). Ideea de baza consta n asmlarea corpurlor n contact cu nste semspat. In felul acesta se poate utlza
57 57 problema lu Neumann pentru semspatul elastc. Corpurle n contact se presupun perfect luc, adca separate de un strat de lubrfant. Componentele tangentale ale tensun la lmta n zona de contact sunt nule, transmtandu-se numa sarcnle normale pe un domenu de contact necunoscut. Problema contactulu 3D fara frecare a doua corpur elastce perfect luc, n cazul mclor deformat, este tratata extensv de Solomon (964, 968, 969), Jonhson (985), Solomon s Zamfrescu (963). Alte lucrăr valoroase în domenu aparţn lu Olver ş Pharr (99, 4), Hay, Bolshakov s Pharr (999). Hertz a dezvoltat un model care descre campul tensunlor s al deformatlor la contactul a doua corpur sferce (fg...). Deplasarea totala este notată cu δ ş reprezntă suma dntre deplasărle celor două suprafeţe δ ş δ. Ara de contact are raza a. Raza de curbură relatvă R se determnă dn relata /R=/R +/R, unde R ş R sunt razele de curbură ale celor două sfere. Modelul lu Hertz se aplca doar n cazul contactulu elastc ş este bazat pe următoarele poteze:. Suprafeţele sunt elastce, netede, contnue,. Deformaţle sunt mc a<<r, 3. Fecare sold se modelează ca un semspaţu a<<r,, 4. Suprafeţele sunt fără frecare, nu se transferă prn urmare sarcn tangenţale c doar normale. Hertz a observat că deformaţa în tmpul contactulu se poate modela ca două resortur elastce legate n sere. Hertz a defnt ş ntrodus modulul de elastctate redus E red ( ν ) ( ν ) = +. Ered E E (..) Ac, ν ş E ( =, ) sunt coefcentul lu Posson ş respectv modulul de elastctate al lu Young pentru cele două corpur. In cazul stantelor de revoluţe, sferce ş parabolce, soluţa lu Hertz pentru forţa aplcată este 4 P E Rδ 3/ =. (..) 3 red Modelul lu Hertz nu este valabl pentru suprafete rugoase ş alte geometr ale stante. Sneddon (965) a rezolvat problema pentru dferte geometr ale stante. De exemplu, pentru un contact conc a obţnut formula P E ϕ δ π unde φ este semunghul conulu. Durtatea se calculează cu formula Pmax H =, (..4) A = red tan( ), (..3) unde P max este forţa corespunzătoare adâncm maxme de ndentare, ş A c este ara de contact care în acest caz este crculară A π a Raza de contact a se determnă, în cazurle sferc ş parabolc, dn relatle c =. (..5) a 9P δ = =, (..6) R 6REred
58 58 Pentru cazul stante conce, a se determna dn a = Rδ. (..7) a = tan( ϕ) δ. (..8) Olver ş Pharr [9], [] au analzat ndentarea cvasstatcă bazata doar pe un sngur cclu de încărcare-descărcare. Ideea mportanta este ca la ncarcare solctarea poate contne s deformat nelastce sau plastce, reversble, nsa la descarcare curba caracterstca este pur elastca. Aceasta curba este elementul esental n determnarea caracterstclor de materal, de exemplu a modulu de elastctate al lu Young. Olver ş Pharr au numt aceasta metoda Analza Mecancă în domenul Dnamc (DMA). O curbă tpc cvasstatcă forţă-deplasare pentru ndentare este reprezentată în fg... Rgdtatea la descărcare este notată cu S, deplasarea stante s-a notat cu h, ar adâncmea fnală după descărcare cu h f. Fg..3 prezntă secţunea transversală a ndentăr. Deplasarea vertcală de la suprafata lberă s-a notat cu h s, ar cu h c s-a notat adâncmea de contact sau dstanţa până la contact. Olver ş Pharr dau următoarea relaţe pentru h c : h P ε S max c = hmax. (..9) Fg.... Contactul a două sfere (Johnson 985).
59 59 Ac, ε este determnat emprc în funcţe de geometra stante. Pentru un ndenter conc avem ε =,7, ar pentru un ndenter parabolod de revolute ε =,75. Pentru sferă, formula (..9) devne h h h max f c =. (..) Fg.... Dagrama forţă-deplasare. Fg...3. Schema secţun transversale a ndentăr. Olver ş Pharr au ajuns la concluza că rezultatele lu Hertz ş Sneddon pentru relaţa forţădeplasare pot f generalzate pentru stante cu dferte geometr, astfel P = α( h h ) m f. (..) unde α ş m sunt constante. Parametrul m depnde de geometra stante. De exemplu, pentru m = 3/ obtnem ecuata (..), ar pentru m =, se obtne ecuata (..3). Olver ş Pharr (99) obtn următoarele relaţ pentru rgdtatea la descarcare S : dp S = Ered Ac dh = π, (..) S = β Ered Ac. (..3) π
60 6 Ecuaţa (..) se poate aplca doar n cazul mclor deformaţ ale materalelor solctate cu stante rgde smetrce. Factorul β este utlzat pentru a corecta soluta n cazul unor geometr dverse, nesmetrce s necrculare, sau n cazul unor deformaţ mar sau a une comportar elastoplastce. Ecuata (..) este valablă numa pentru un ndenter rgd axal smetrc. De aceea, cazul β = poate conduce la eror. Pentru alte stuaţ, s-au determnat alte valor pentru β, ş anume,55 sau,85. Hay, Bolshakov s Pharr (999) au demonstrat următoarea legătură între β ş coefcentul lu Posson ν : (..4) unde ϕ este unghul conulu la ndentarea semspaţulu cu un varf rgd conc. În fg...4 este reprezentată geometra utlzata de Sneddon pentru analza ndentăr unu semspaţu cu un ndenter rgd conc. Deplasarea radală în cazul modelulu dn fg...4. este calculată de Sneddon (..5) Pentru coefcentul lu Posson ν =,5 (materal ncompresbl) ş ϕ = 9º (stanta plana) rezultă u =. Pentru alte tpur de materal, u este negatv ş ara reală de deformaţe este reprezentată în Fg...4 (jos). Raza efectvă de contact este dată de aefectv ş dn (..3) expresa are de contact se poate scre astfel: = β a, (..6) (..7) Fg...4. Geometra utlzată de Sneddon pentru analza ndentăr unu semspaţu cu un ndenter rgd conc. Revennd la (..), în mod normal S se determnă dn prma parte a curbe de descărcare (fg...), ş se calculeaxă astfel:
61 6 dp S =. (..8) dh Dacă ara de contact A c este cunoscută atunc E red se poate determna usor. Durtatea H se determnă dn (..4). Dec, pentru a determna modulul lu Young ş durtatea materalulu supus ndentar, trebue să cunoaştem ara de contact A c. Pentru contactul crcular cu un ndenter de rază a, ara de contact este Ac = π a. Pentru alte stuaţ ara de contact rămâne necunoscută. Modelul DMA se referă la ndentarea dnamcă. In aceasta metoda, se consderă sstemul dnamc al unu ndenter (fg...5), cu m masa ndenterulu, C f complanţa (nversul rgdtăţ) cadrulu de încărcare, K f rgdtatea cadrulu de încărcare, S rgdtatea de contact, D amortzarea sstemulu ş K s rgdtatea suportulu. Prn aplcarea une sarcn osclante Pos = snωt, de frecvenţă ω, asupra cadrulu de încărcare, se obţne următorul răspuns pentru ampltudne ş respectv fază Pos h( ω) (( ) ) f s ω = s + C + K m + ω D (..9) (..) unde h este ampltudnea osclaţe ş θ unghul de fază dntre forţă ş deplasare. Ampltudnea ş faza pot f măsurate expermental. În aceste formule S este necunoscută. La exctaţe lberă S =, ş dn ecuaţle (..9) ş (..) se pot determna K s ş D. Fg...5. Modelul dnamc al ndentăr (Olver s Pharr 99). Ara de contact se poate determna dn formula (..) unde coefcenţ C,..., C 8 se pot determna prntr-o metodă de calbrare. Presupunem că cunoaştem modulul de elastctate E al materalulu. Măsurând S, P max, h max ş ntroducând aceste canttăţ în (..) obţnem A c pentru anumte valor h c. Incepem cu modelarea locală a contactulu cu frecare. Consderăm un punct materal P constrâns să se mşte pe o suprafaţă de ecuaţe g( x, x, x 3) =. Notăm forţa normală de constrângere cu N = λ grad g, unde λ este o constantă. Dacă suprafaţa este rugoasă atunc constrângerea nu ma este deală, ar forţa de constrângere R nu ma este normală la suprafaţă.
62 6 Apare o componentă T a aceste forţe care se află în planul tangent la suprafaţă în punctul P, ş are drecţa opusă faţă de rezultanta forţelor care acţonează asupra punctulu. Conform teore lu Coulomb, modulul forţe de frecare la alunecare verfcă relaţa T f N, (..) egaltatea având loc la echlbru. Coefcentul f, care depnde numa de starea suprafeţe, ş nu de vteza v a punctulu, se numeşte coefcent statc de frecare (coefcentul dnamc de frecare este de forma f = f() v ). Dacă notăm cu ϕ unghul de frecare, coefcentul statc de frecare este f = tanϕ (..3) Dn relaţa T = tan µ tanϕ, obţnem µ ϕ. N Dacă punctul P este constrâns să se mşte pe o curbă contnuă C, de ecuaţe g ( x, x, x 3) =, =,, forţa de constrângere N = λ grad g + λgrad g, se află în planul normal la curbă în P, ar λ, λ sunt constante. Dacă curba este rugoasă, forta de frecare la alunecare T are forma (..), de-a lungul tangente la curbă în P. La echlbru, este sufcent ca unghul dntre suportul forţe de constrângere R ş tangenta la curbă să fe ma mare sau egal decât π / ϕ. Dacă frecarea are loc între o partculă ş un flud, frecarea este vâscoasă, ş coefcentul de frecare se numeşte coefcent de vâscoztate, ar forţa de constrângere este o fortă de rezstenţă. Legle expermentale ale frecăr de alunecare ş de rostogolre au fost stablte de C.A. Coulomb (736-86). Frecarea este un fenomen complex, care este greu de modelat dn punct de vedere teoretc, ş care este esenţal în înţelegerea comportăr sstemelor electromecance. Frecarea clască Coulomb este reprezentată prntr-o forţă de frecare în cazul mşcăr de translaţe, sau prntr-un moment de frecare în cazul mscăr de rotaţe, care se opun mşcăr ş îş schmbă semnul odată cu drecţa de mşcare (Lyshevsk, Chrou s Chrou 3): dx FC = kfcsgn( v) = kfcsgn( ), (..4a) dt dθ MC = kmcsgn( ω) = kmcsgn( ), (..4b) dt dx dθ unde x este deplasarea lnară, θ deplasarea unghulară, v = vteza lnară, ω = vteza dt dt unghulară, ar k Fc ş k Mc sunt coefcenţ de frecare Coulomb. Ampltudnle forţe sau momentulu de frecare sunt constante. Frecarea vâscoasă este reprezentată de o forţă sau moment care sunt funcţ lnare de vteza lnară în cazul mşcăr de translaţe, ş de vteza unghulară în cazul mşcăr de rotaţe: dx FV = kfvv= kfv, (..5a) dt dθ MV = kmvω = kmv, (..5b) dt unde k Fv ş kmv sunt coefcenţ de frecare vâscoasă. Frecarea statcă exstă numa când corpul nu se mşcă, ea opunându-se mşcăr nţale ş anulându-se atunc când corpul începe să se mşte.
63 63 Fg...6. Reprezentarea frecăr: a) frecare Coulomb, b) frecare vâscoasă, c) frecare statcă Frecarea statcă este reprezentată de o forţă sau moment cu următoarele expres: FS =± F S v =, (..6a) MS =± MS ω=. (..6b) În fg...6 sunt reprezentate forţele ş momentele de frecare coulombană, vâscoasă ş statcă. În general, forţa sau momentul de frecare statcă sunt forţe nelnare care se modelează utlzând memora frecăr, condţle nţale de alunecare, etc. Se utlzează de multe or formule emprce, ca de exemplu F = ( k k exp( k v ) + k v )sgn( v), (..7a) S 3 S = ( exp( ω ) + 3 ω ) sgn( ω), (..7b) M k k k k unde k, k, k 3 ş k sunt coefcenţ care se determnă expermental. Acest tp de frecare statcă este reprezentată în Fg...7. Fg...7. Forţa ş momentul de frecare sunt funcţ de vteza lnară ş unghulară
64 64 Consderăm două corpur S ş Σ aflate în contact, smplu rezemate în P. În realtate soldele se deformează în vecnătatea lu P, astfel încât contactul este obţnut pe o suprafată mcă pe care apar forţe de constrângere (Fg...8a). Reducând sstemul de forţe în punctul P, obţnem torsorul (forţa de constrângere R ş momentul de constrângere M), reprezentând acţunea lu Σ asupra corpulu S (Fg...8b). In Fg...8c se pun în evdenţă forţa normală de constrângere N, forţa tangenţală T corespunzătoare frecăr la alunecare, conţnută în planul tangent, momentul M p normal la planul tangent, corespunzător frecăr de pvotare, care se opune rotaţe în jurul normale, ş momentul M r conţnut în planul tangent, corespunzător frecăr de tp rollng care se opune rotaţe în jurul une axe dn planul tangent care trece prn P. Fg...8. Zona de contact ntre două corpur S ş Σ (a). Forţa de constrângere R ş momentul de constrângere M (b) ş componentele lor (c). Coefcentul de frecare la alunecare nu depnde în general de vteza relatvă de alunecare dntre două corpur sau de magntudnea suprafeţe de contact, c numa de natura materalelor aflate în contact. Valorle numerce ale acestu coefcent f sunt date în tabelul... Un exemplu de dependenţă de vteză este dat n tabelul.. pentru metal/metal. Tabelul... Coefcentul de frecare pentru dferte materale lemn pe lemn, uscat...,5-,5 pele pe metal, uscat..,56 lemn pe lemn, sapun., pele pe metal, umed.,36 metal pe stejar,5-,6 pele pe metal, grăsme,3 uscat... metal pe stejar, umed.,4-,6 pele pe metal, ule...,5 metal pe stejar, grasme..., oţel pe agat, uscat..., metal pe ulm, uscat..,-,5 oţel pe agat, ule...,7 cânepă pe stejar, uscat..,53 fer pe patră.,3-,7 cânepă pe stejar, umed...,33 lemn pe patră...,4 pele pe stejar.,7-,38 pământ pe pământ.,5-, metal pe metal, uscat.,3 arglă pe arglă...,3 metal pe metal, umed,5-, metal pe,-
65 65... ghaţă..,3 suprafeţe netede,3- suprafeţe netede,,7-...,36 grăsme..,8 Tabelul... Dependenţa de vteză pentru metal/metal. v (km/h),93,8 43,5 65,8 87,6 96,48 f,4,88,7,7,57,38,7 Suprafaţa materală, ca nterfaţă dntre două med sau faze materale, nu este contnuă ş netedă la scara atomcă ş moleculară. Arhtectura atomcă a suprafeţelor este caracterzată de prezenţa aspertăţlor de dferte dmensun, forme, unghur de contact ş denstăţ. Dscutăm acum câteva modele ale suprafetelor n contact la scara contnua macroscopca, tnand seama de legăturle de tp adezv pentru contactul sold. Pentru a separa două suprafeţe trebue nvnse legăturle care exstă între aceste suprafeţe prntr-o forţă negatvă, numtă forţă adezvă. Natura aceste forţe de suprafaţă este nanoscopcă. In contnuare ne bazam pe teora prezentata n acest paragraf s n paragraful. Pe baza rezultatelor expermentale de nanondentare, construm cateva probleme nverse, pentru determnarea parametrlor nanostructural s a propretatlor unor nano compozte. Se consdera un sstem cu frecare D prezentat n fg...9. Fg...9. Sstem cu frecare In fg...9, mt () este unu ndentaer (varf de damant) care aluneca pe un strat de Cu, s care varaza ca rezultat al adezun atomlor de Cu, k x este rgddatea elastca n drecta x - - ( Nm ), k z este rgdtatea elastca n drecta z ( Nm ), V este vteza de alunecare, xt () este deplasarea n drecta orzontala, zt () deplasarea n drecta vertcala; Fx () t s Fz () t sunt fortele care actoneaza asupra mase care aluneca n drecta x s respectv, z. Valorle specfcate rezulta dn calcule de dnamca moleculara. Alegem potentalul atomc generalzat de tp Morse dat de..43, cu parametr necunoscuţ, MC H ( r ) = E [exp( Nα( r r )) Nexp( α( r r ))] j MC j w j w j>
66 66 Problema nversa propusa este de a determna mt (), EMC N, r w s α dn masurator expermentale prvnd pozta varfulu de damant n raport cu tmpul. Indenterul are o mscare de tp stck-slp. Cu un algortm genetc se obtne mt ( ) =.34t.6, E = 3.59eV, N = 5.3, r w =,4A s α=,35a. N =,56. Fg... preznta varata traectore x a ndenterulu n functe de constanta. MC F x, pentru F z Fg... Traectora ndenterulu n drecta x n raport cu forta pe drecta orzontala [N]. Consderam acum o nanostructura alcatuta dn stratur perodce dn alumnu s un materal auxetc (fg...). Pentru predcta propretatlor mecance ale nanocompoztulu, exstenta defectelor (dslocat, frontere dntre granule, etc.) joaca un rol mportant. Pentru a analza comportarea defectelor, le-am studat dn punct de vedere al elastctat s al caracterstclor lor energetce, prn metoda nelocala Presach-Tteca. In materale nanostructurate, propretatle elastce ale defectelor se modfca puternc dn cauza nteractun cu nterfetele. Fg... preznta schematc tre tpur de nterfete: coerenta, semcoerenta s ncoerenta. In lucrare se analzeaza toate tpurle de nterfete. De asemenea, se studaza modul n care modulul de elastctate al lu Young creste pentru un materal auxetc fata de un materal neauxetc avand acelas coefcent Possson n valoare absoluta. In tabelul.. sunt prezentate propretatle materalulu auxetc s a unu materal neauxetc avand acelas coefcent Possson n valoare absoluta pentru valor dferte ale fractun θ de alumnu dn compozt, obtnute dntr-o problema nversa dn date expermentale. Comportamentul hsteretc al plac compozte pentru nterfete coerente s materal auxetc este prezentat n fg...3.
67 67 Fg.... Placa compozta. Fg...3. Structura nterfetelor: (a) coerenta, (b) semcoerenta, (c) ncoerenta.
68 68 neauxetc. Tabel... Modulul lu Young pentru un materal auxetc s un materal Young s modulus [GPa] ν θ Young s modulus [GPa] ν θ Fg...4. Comportamentul hsteretc al plac compozte pentru nterfete coerente s materal auxetc.
69 69.. Cuplarea analze nelocale de tp Erngen cu metoda Presach de analza a hsterzsulu s cu teora pseudosuprafetelor Tztzeca cu curbura negatva In contnuare prezentam modelul cuplat de evaluare a capactat de amortzare Presach- Tteca. Nanostructurle s materalele nanostructurate cu propretat foarte bune de amortzare, au atras atenta specalstlor doar n ultm 5 an. Dsparea energe sta la baza controlulu ntelgent de tp actv sau semactv al vbratlor mecance. Tradtonal, rezstenta mecanca σ s propretatea de dspare a energe ( tanδ - faza dntre tensune s deformate) pentru un materal crstaln pot f controlate la nvelul dmensun d a une granule (prn legea / lu Hall-Petch σ=σ + kd ). Dar, s-a observat n ultm an ca, atunc cand scara structurala se reduce, tnzand catre dmensunea nanometrca, aceste propretat depnd semnfcatv de scara, s ca exsta o lmta pentru descrerea conventonala a acestor propretat (Msra et al. 998). O valoare rdcata a raportulu volum-nterfata poate nfluenta radcal procesele de mobltate, frecare nterna, hsterezs, plastctate, ar controlul capactat de dspare a energe, s a rezstente mecance, ar trebu sa tna seama de aceste elemente. Un studu recent pe compozte Cu/Nb a pus n evdenta reducerea fragltat s cresterea amortzar la temperatura Helulu lchd (Han et al.998), des metalele bcc (cum este Nb) preznta o rupere fragla la 4. K. Pentru materalele nanostructurate Cu/Nb s-a pus n evdenta o combnate nteresanta de rezstenta s ductbltate pana la tensunea de rupere ~ GPa. Damantul s ntrda boronca cubca (cbn) sunt cele ma dure substante cunoscute de om. Se pune ntrebarea: este posbl sa obtnem materale cu propretat superoare acestora? Teoretc, raspunsul este afrmatv. Iar expermentele la scara nanometrca au reust sa creeze un materal stratfcat damant-cbn mult ma rezstent s care are o buna amnortzare decat orcare dn aceste doua substante. Rezstenta mare se explca prn dslocatle la nterfetele fazce. Aceste rezultate arata ca, prn reducerea scar structurale la nvel nanometrc, propretatle fzce s mecance ale materalelor pot depas cu mult grantele ngnerest cunoscute pana n present. Prn cunoasterea completa a fenomenelor de amortzare s deformate plastca la nvel nanometrc se pot produce materale no care combna perfect propretat ca dsparea de energe, ductbltate, rezstenta, nu prn schmbarea compozte chmce cum se procedeaza n prezent, c prn controlul atomc al dmensunlor, locate s al forme consttuentlor. Controlul acestor fenomene sta la baza stratege de control optmal al dspar energe, pentru obtnerea de materale cu o capactate nalta de amortzare, combnata cu propretat mecance foarte bune. Comportarea mecanca a nanostructurlor se poate smula pe supercomputere, s aceste smular pot avea o relevanta deosebta n aprofundarea cunostntelor n stntele fundamentale s n tehnologle aplcate, cu perspectve certe de mplementare ndustrala. Aplcat ale nanotehnologe sunt deja evdente n programele tehnologce exstente: materale magnetorezstente, materale nanostructurate pe baza de nanotubur de carbon, polmer, nanossteme DNA cu relevanta n proectul genomulu uman, procesoare bazate pe prncple mecanc cuantce, aerogel, etc. Obectvele cercetar nanostntfce s nanotehnologce n urmator 5- an cuprnd ntelegerea propretatlor nanostructurlor zolate, cunoasterea precsa la nvel atomc a structurlor arbtrare, smularea producer acestor structur n numar mare, eftn s rapd, crearea de no structur cu propretat dorte s controlate, smularea producer lor, s n fnal tehnologzarea lor. In prezent se pot realza smular de dnamca moleculara 3D pana la mloane de atom prn dferte metode, s aceasta realzare deschde posbltat fara precedent n compararea teore cu expermentul s n ntelegerea fenomenelor fzce aflate la lmta teoretca. Dsparea energe (amortzarea) contrbue la reducerea nvelulu ampltudnlor de rezonanta sau zgomot n structur s materale, mbunatatnd astfel ntegrtatea s durata lor de vata. La scara macrometrca, se poate obtne o amortzare semnfcatva prn echpamente
70 7 externe. La scara mcrometrca nvelul de amortzare este ma mc, ar la scara nanometrca s ma mc. La scara nanometrca, nsa, putem controla fenomenul dspar energe prn exploatarea s controlul propretatlor s fenomenelor caracterstce acestor dmensun (Teodorescu, Chrou s Munteanu 5a,b). Domenul de nteres sunt nanostructurle s materalele nanostructurate cu caracterstc foarte bune de amortzare, prn controlul matere s a mecansmelor de dspare a energe n gama (- nm). La scara nanometrca sunt accesble no mecansme de dspare a energe cum sunt: vascoztate s hsterezs atomc, dependenta frecar nterne de ampltudnea deformatlor, nteractunea spn-orbta, varata conductvtat, mobltatea nterfetelor deformate ntal, chraltate, generare de unde spn, magnon, fracton s phonon, generarea dlatonlor energetc, etc. Prn cunoasterea completa a fenomenelor de amortzare la nvel nanometrc se pot produce materale no care combna perfect propretat ca dsparea de energe, ductbltatea s rezstenta, nu prn schmbarea compozte chmce cum se procedeaza n prezent, c prn controlul dmensun, a forme consttuentor s a unu aranjament precs al atomlor n materal Metale ca alumnul, alajele de ttan s otel au o capactate de dspare a energe extrem de redusa (n jurul a 3 ). Vbratle pot nfluenta sguranta, rezstenta s durata de vata a structurlor alcatute dn aceste materale. Doua trem dn erorle descoperte la rachete s satelt sunt legate de vbrat s zgomot. Aceleas materale nsa, combnate prn tehnc nanometrce pot avea alte caracterstc de amortzare. In aceasta lucrare, s-a smulat la nvel molecular producerea une fol stratfcate perodce Cu-N, 66% Cu. Aceasta fole manfesta propretat stuate n afara lmtelor ngnerest obtnute prn smpla regula a mxtur. De exemplu, fola raporteaza un modul de elastctate Y[] de 8.9 TPa (Y[] pentru un alaj omogen Cu-N cu aceeas compozte este.4 TPa) s o capactate de dspare a energe de 75 or ma mare decat a structur omogene. De asemenea, nanostructurle feromagnetce pot avea propretat extrem de dferte fata de propretatle materalelor consttuente, ar capactatea de amortzare poate f mbunatatta substantal prn control la scara nanometrca (Olkhovets ). Nanostructurle au o dmensune ntermedară între structurle moleculare (dmensunea 7 une molecule m ) ş structurle mcroscopce măsurate în mcron ( m ), adcă de la. nm. Ele conţn un număr foarte mare de atom. Prvte ca molecule, nanostructurle sunt prea mar pentru a putea f modelate cu metodele mecanc cuantce. Prvte ca materale, sunt mult prea mc ş prezntă caracterstc care nu sunt observable la structurle macroscopce (char în jur de,µm ). Noţunea de nanostructură combnă concepte dferte: dmensune mcă, organzare complexă, raport dntre are (nterfeţe) ş volum, mare, denstate mare ş nteracţun electromecance puternce. Caracterstcle electronce ş magnetce ale acestor structur sunt domnate de un comportament cuantc. O posblă defnţe a unu materal nanostructurat, bazată pe observaţle asupra unu număr mare de fenomene fzce ş mecance a fost propus de Krshna, Prasad ş Srnvasan (4). Aceşt autor sugerează că înafară de stărle matere soldă, lchdă ş gazoasă, nanofaza poate f consderată ca o stare dstnctă a matere. Pentru valor ale raportulu dntre volumul V al materalulu ş volumul celule untare V c 5 6 (blocul reprezentatv constructv al matere) ma mc decât sau, materalul se comportă ca o nanostructură. Sau, putem spune, pentru valor ale raportulu dntre numărul de partcule N ale materalulu ş numărul de partcule dn celula untară N ma mc decât 5 sau 6, materalul se comportă ca o nanostructură. Ac, V ş N tnd către nfnt, ar raportul N V este fnt. Faza nanometrcă poate f obţnută prn transformăr dn faza soldă, lchdă sau gazoasă ş trebue studată ca atare cu ajutorul mecanc cuantce ca o fază dstnctă a matere. c
71 7 Dmensunea este un factor mportant, ş prn urmare raportul dntre are ş volum creşte /3 V pentru ssteme de dmensune mcă, asta însemnând că = devne mc ş ma mc pe / 3 V V măsură ce V creşte. Ca rezultat, efectele de suprafată domnă faza nanometrcă spre deosebre de faza macrometrca ă matere. Expermente recente efectuate pe apă în domenul nanometrc arată că de la K la 3 K, deplasarea în mede pătratcă a hdrogenulu (parametrul fzc utlzat în experment) nu suferă schmbăr majore, în tmp ce în domenul macrometrc în procesul de transformare al gheţ în apă, acest parametru suferă varaţ puternce (Krshna, Prasad and V Srnvasan 4). Dacă V este ma mare decât 5 6 or, faza nanometrcă se poate transforma c în orcare altă fază în funcţe de temperatură. Potenţalul chmc µˆ este nul pentru faza nanometrcă ş dfert de zero pentru faza macrometrcă. Energa lberă a lu Gbbs are varaţ V puternce atunc când V este ma mare decât 6. Această valoare pare să capete o mportanţă c deosebtă ş de aceea poate f asocată une mulţm canonce crtce. Energa lberă a lu Gbbs este în general o funcţe de de temperatură T, presune P ş numărul mwdu de partcule N. Potenţalul chmc µˆ, per partculă nu este zero pentru mulţmea canoncă crtcă. Pentru o nanostructură descrsă numa de mecanca cuantcă, µˆ este nul. Prn urmare, consderente termodnamce pun în evdenţă o varaţe puterncă a funcţe lu Gbbs în raport cu N, atunc când N c creşte. Un fenomen fzc poate f examnat la dferte scăr de lungme ş scăr de tmp. De exemplu, mşcarea undelor în ocean poate f observată cu ochul lber sau vzualzând cu och mnţ mşcarea moleculelor de apă. Depnzând de scara care nteresează, modelarea are nevoe de analze dferte, în cazul acesta dnamca fludulu contnuu pentru a descre propagarea undelor ş dnamca moleculară pentru a descre mşcarea moleculelor. La dmensun mc, materalele au propretăţ dferte de cele la scară macroscopcă. De exemplu, la scară nanometrcă materalele au o rezstenţă mecancă ma mare decât probele macroscopce ale aceluaş materal. Abltatea unu materal de a se deforma (întndere, compresune, încovoere, torsune) fără să se rupă depnde de legăturle chmce care ţn atom împreună. În prncpu, legăturle chmce sunt aceleaş atât în scara nanometrcă cât ş în scara macroscopcă. Dar probele macroscopce nclud multe defecte, cavtăţ, atom lpsă, etc., care lmtează propretăţle mecance. Denstatea acestor defecte poate f mult ma mcă la scară nanometrcă, ş ca rezultat nanomateralele devn ma rezstente. Cercetător au în vedere exploatarea propretăţlor superoare ale matere la scară nanometrcă ş combnarea unor pese sau blocur nanometrce în construrea unor materale nanostructurate, care pot f consderate ca fnd compuse dn blocur nanometrce (Jackson 4, Chrou, Munteanu s Stuca 5). Modelarea ş smularea propretăţlor matere sunt legate de determnarea scăr de reprezentare. Această determnare trebue realzată bdmensonal. Axa spaţală are un nterval de la dmensunea unu atom ( A) la dmensunea une nanopartcule ( µm ). Axa temporală este lnară în raport cu numărul de partcule. Mşcarea atomcă este mult prea rapdă decât multe procese macrospcopce, fnd caracterzată de ntervale temporale de ordnul fsec, ceace înseamnă că avem nevoe de 5 ordne de mărme pentru a atnge o secundă. Mcroscopa electroncă este capablă să vzualzeze atom ndvdual dn nanonstructur cu precze angstromală. În cazul fasccolulu de electron vzualzarea se obţne dn nformaţ prvnd energa perdută de electron, sau dn măsurător de emse de raze X. Pentru fasccolul de on avem o rezoluţe de nm, ar pentru fasccol de foton în jur de un mcron. În general, putem vorb de patru scăr de lungme, propr unor fenomene fzce dstncte. 8 Cea la mcă lungme de nteres practc este de ordnul a câţva amgstrom ( cm ) ş se asocază
72 7 electronlor ndvdual dn atom. Sstemul este reprezentat prntr-o colecţe de atom (nuclee sau on), ş electron, ar metodele de calcul potrvte sunt dn mecanca cuantcă. Următoarea scară, ncluzând sute de angstrom, este scara atomcă. Ac sstemul este reprezentat prntr-o colecţe de atom, ş analza se realzează cu dnamca moleculară ş metoda Monte-Carlo. Aceste metode necestă de asemenea cunoaşterea funcţe potenţal atomc U ( r, r,..., r n ), pentru determnarea cărea se folosesc metodele nverse bazate pe date expermentale ş pe metode de optmzare cu funcţ mult-obctv ş algortm genetc (Chrou ş Chrou 4). Smularea atomcă este ma smplă decât smularea electroncă, deoarece structura 9 electroncă este gnorată. Ac putem modela un număr ma mare de partcule (în jur de ). Evaluarea amortzar s a energe dspate se realzeaza cu ajutorul teore nelnare a propagar undelor n materale cu dmensune mca (< mcron). Se utlzeaza metoda lu Rogers s Schef (997) de reducere pseudosferca a probleme de deformare. Pentru ntelegerea teore, pentru un caz smplu undmensonal, deformata unaxala a unu medu elastc nelnar, Τntr-un sstem de coordonate lagrangan ( Xteste, ) descrsa de ecuatle (Munteanu s Donescu, 4) ε t = vx, ρ vt =σ X, (..) cu legea consttutva σ=σ( ε, X ). (..) ρ unde σ, ρ sunt tensunea s respectv denstatea materalulu, ε= deformata unaxala, ρ ρ denstatea medulu n starea nedeformata, v( X, t ) vteza materala. Indc t s X repreznta dervate partale, reducerea peseudosfercă repreznta asocerea ecuate de mscare Lagrange la o suprafata pseudosferca (suprafata Tteca) parametrzata n raport cu coordonatele asmptotce. Se determna apo reprezentarea parametrca a leg consttutve. Pe baza aceste leg, s tnanduse seama de faptul ca curbura Gaussana a suprafete Σ este un nvarant, rezulta ( +σ ) Xv σxσv ( + X ) σt cot ω= a. (..3) 3/ ( +σ + X ) Pe aceasta exprese se bazeaza rezultatul mportant conform carua energa dspata este proportonala cu cot ω, s prn urmare cu curbura Gaussana a suprafete Tteca asocata modelulu de deformare. Metoda se poate generalza pentru orce fel de problema, ar suprafata pseudosferca de multe or este o suprafata Tteca. Astfel, suprafata Tteca asocata probleme de deformate are o varate n spatu s tmp s repreznta o masura a capactat de amortzare a structur (energa dspata pe cclu). Functa Tteca contne un numar varabl de parametr de control, care caracterzeaza structura nterna a materalulu (pozta s dmensunle atomlor), numarul de stratur s propretatle nterfetelor. Construrea functe Tteca se bazeaza pe studul amortzar la dferte scar metrce: ) metodele tradtonale de ntroducere a amortzar n structura, ) conceptul de strat gradent care se refera la acoperrea structur cu un strat cu propretat care varaza n raport cu grosmea, 3) spume polmerce auxetce, 4) conceptul de proemnenta atomca (ntroducerea n reteaua crstalna de atom cu dmensune ma mar, cub de gana (atom de dmensune ma mca), s ruptura atomca (lpsa de atom). Ca urmare a modelăr complexe a fenomenulu de amortzare, a fost luat în consderaţe şî fenomenul relaxăr tensunlor. Mecansmul de relaxare cu comportament vâscoelastc, poate f explcat prn varaţa câmpulu de tensune în materal (Mhalescu s Chrou 4, Chrou, Donescu s Munteanu 5). Prn aplcarea une forţe exteroare, energa sstemulu creşte. Dacă sstemul poate depăş potenţalul bareră, atunc este posblă tranzţa de la prma stare la starea a doua, ş sstemul se
73 73 relaxează deoarece dferenţa dntre energle celor două stăr se perde (Iordache et al. 998, Iordache, Scalerand s Iordache, Zener 947, 949). Pentru a descre matematc fenomenul de relaxare a tensunlor utlzăm modelele reologce. În fg... sunt reprezentate câteva modele reologce, ş anume un element elastc Hooke care descre comportarea elastcă (fg...a), un element Newton pentru a descre comportarea vâscoasă (fg...b), un element St. Venant pentru descrerea amortzăr coulombene (fg...c), ş un element Zener pentru descrerea relaxăr tensunlor (fg...d). Elementul Zener constă dntr-un element Hooke legat în paralel cu un element Newton, ş un element adţonal Hooke legat în sere (Chrou, Stuca, Munteanu s Donescu 5). Fg.... Modele reologce, a) element Hooke; b) element Newton ; c) element St. Venant; d) element Zener. Fg.... Dependenţa caltatvă a rapoartelor ş E Q E, de temperatură. În fg... se reprezntă grafc dependenţa rapoartelor Q ş E, de temperatură E (Duemlng ). Relaxarea termoelastcă care a fost confrmată expermental de câtre Zener, a fost luată ş ea în consderare. Analza capactat de dspare a energe s propretatle de amortzare sunt descrse de functa Tteca, care depnde de curbura Gaussana a suprafete Tteca asocata modelulu de
74 74 defomate. Dn aceasta functe putem determna cu usurnta s alt evaluator a amortzar precum: energa dspata pe cclu, energa dspata pe untatea de greutate, energa potentala maxma, factorul de perdere, rgdtatea secanta s amortzarea vascoasa echvalenta. Energa dspata pe cclu este evaluata ca ara mede a bucle hsteretce pentru aceeas ampltudne. Energa dspata pe untatea de greutate se obtne mpartnd energa dspata pe cclu la greutatea probe. Ea exprma efcenta probe n ceeace prveste capactatea de amortzare. Energa potentala maxma pentru un materal lnar vascoelastc este U = εmaxσmax unde σ max s ε max repreznta tensune s deformata maxma. Pentru un materal nelnar, o defnte ma precsa este data de U = W W unde W este energa potentala de deformate maxma la ε max, s W este energa dspata pana la acest punct. Factorul de perdere este defnt prn relata W η=. Valoarea de la numtor se justfca prn faptul ca la ncarcarea cclca energa π U dspata total este de doua or energa dspata doar la ntndere. Rgdtatea secanta se calculeaza dn Ks = ( Fmax Fmn )/( δmax δmn ), unde F ax s F n sunt fortele corespunzatoare deplasarlor cclce maxme δ ax s δ n. Amortzarea vascoasa echvalenta caracterzeaza efcenta n amortzarea vbratlor. Ea se calculeaza dn ζ eq = WD )( πksδ ), unde W D este energa dspata pe cclu s δ este deplasarea maxma cclca. Parametr de control care apoar n smulare se rezolva cu probleme nverse s algortm genetc (Chrou s Chrou 3) Nanostructurle sunt gândte ca ssteme materale care prezntă abltatea de a-s adapta propra functonaltate. Aceste structur realzează acest concept prn ntegrarea n sstem a nanoactuatorlor, nanosenzorlor s a nanocontrolelor, confectonate dn materale functonale. Pentru a reduce vbratle une structur, parametr structural sunt modfcat prn actvtat s actun de control. Structurle actve s semactve (adaptve) sunt ma efcente decât structurle pasve deoarece pot controla varaţ ale structur prn acţun feedback (Chrou, Munteanu s Rugna 3, Chrou, Mhalescu s Munteanu 6). Studle noastre teoretce pe nanofre (nanotubur de carbon) la ncarcar cclce au avut drept scop studul nfluente vteze de deformate a ncarcar, a deformate, a temperatur, a tensun crtce care nduce trasformarea de faza s nvers, a nterfetelor, a frecvente de ncarcare, a numarulu de ccl de ncarcare asupra raspunsulu hsteretc al materalulu, asupra energe dspate, asupra factorulu de perdere, asupra canttat de deformate rezduala, asupra deformate care se poate recupera dupa elmnarea ncarcar exteroare, asupra rezstente materalulu, etc. Rezultatele noastre prncpale se refera la faptul ca, la.incarcar cclce ntndere-compresune pentru nanotubur de carbon cu un sngur perete de dametru de catva nm, cu deformate maxma prescrsa, apare un efect puternc de ecrusare, deformatle rezduale se acumuleaza s energa hsteretca creste progresv dupa mult ccl de ncarcare. Amortzarea este o functe de ampltudnea deformate s tnde sa se stablzeze la deformat mar. Pentru tre nvele de deformate,3 s 4%, cresterea temperatur cauzeaza o crestere a buclelor hsteretce ale tensun. Pentru frecvente mc s o valoare fxa a deformate de 4%, se produce o crestere a buclelor hsteretce ale tensun s dec a energe dspate. La frecvente ma mar buclele hsterezs se reduc. Frecventa nteractoneaza cu ampltudnea deformate. In partcular, la o deformate de % exsta o varate usoara a energe dspate cu frecventa, n tmp ce pentru o deformate de 4%, varata este ma mportanta. Pentru valor ma mar ale frecvente, energa dspata descreste. Factorul de perdere descreste cu cresterea temperatur, care orcum nu are un efecet semnfcatv asupra energe dsspate. Deformata rezduala descreste cu numarul de ccl.. Controlul ntelgent al amortzar n nanostructur se bazeaza pe functa Tteca. Parametr de control caracterzeaza structura nterna a materalulu (pozta s dmensunle atomlor),
75 75 numarul de stratur s propretatle nterfetelor. Functa Tteca caracterzeaza n termen geometrc structura nterna a materalulu, ar curbura sa Gaussana, capactatea de amortzare (energa dspata). Astfel, functa Tteca asocata probleme de deformate sta la baza controlulu ntelgent al amortzar prn alegerea optma a parametrlor de control, astfel ncat dsparea de energe sa fe maxma. Dn functa Tteca putem determna cu usurnta s alt evaluator a amortzar precum: energa dspata pe cclu, energa dspata pe untatea de greutate, energa potentala maxma, factorul de perdere, rgdtatea secanta s amortzarea vascoasa echvalenta. Metale ca alumnul, alajele de ttan s otel au o capactate de dspare a energe extrem de 3 redusa (n jurul a ). Vbratle pot nfluenta sguranta, rezstenta s durata de vata a structurlor alcatute dn aceste materale. Doua trem dn erorle descoperte la rachete s satelt sunt legate de vbrat s zgomot. Aceleas materale nsa, combnate prn tehnc nanometrce pot avea alte caracterstc de amortzare. Am smulat la nvel molecular producerea unor fol metalce bstratfcate perodce (Au- N, Cu-Pd, Cu-N, Ag-Pd) (Chrou 999) de grosme h = Nλ. Parametr de control sunt raportul r al razelor celor doua tpur de atom, dstanta d dntre atom, lungmea de unda λ a modular s ampltudnea A a modular (fg...3). Fg...3.Geometra fole bstratfcate. Aceste fol se pot arhtectura astfel ncat sa manfeste propretat stuate n afara lmtelor ngnerest obtnute prn smpla regula a mxtur. De exemplu, pentru o lege de modulare πz Asn( ), fola Cu-N cu 66% Cu, de grosme h=.5µm, λ = 7.nm, s A =,, raporteaza λ
76 76 la o solctare baxala n drecta [] un modul de elastctate Y[] de.3tpa (Y[] pentru un alaj omogen Cu-N cu aceeas compozte este.4 TPa) s o capactate de dspare a energe de 75 or ma mare decat a structur omogene. De asemenea, nanostructurle feromagnetce pot avea propretat extrem de dferte fata de propretatle materalelor consttuente, ar capactatea de amortzare poate f mbunatatta substantal prn control la scara nanometrca. Am analzat functa Tteca pentru aceste fol bstratfcate perodc. Varata functe Tteca asocata probleme de deformate baxala n drecta [,,] este reprezentata n fg..6 pentru fol Cu-N, n fg..7 pentru fol Au-N, n raport cu lungmea de unda λ a modular s ampltudnea A a modular. Functa repreznta o masura a capactat de amortzare a structur (energa dspata pe cclu), n sensul ca putem alege acest parametr astfel oncat functa Tteca sa fe maxma.. Pentru fre dntr-un alaj cu memora forme (N-T) functa Tteca este reprezentata n fg..7. Fg...4. Varata Tteca asocata probleme de deformate baxala [] pentru fol Cu- N.
77 77 Fg...5. Varata functe Tteca asocata probleme de deformate baxala [] pentru fol Au-N. Fg...6. Varata functe Tteca asocata probleme de deformate baxala [] pentru fre dntr-un alaj cu memora forme SMA (N-T). In tabelul... sunt prezentate propratatle mecance ale fole Au-N, cu A=.3 s λ =,9nm ( σ m tensunea lmta la rupere s ε m deformata la rupere). Tabel... Propretat mecance ale fole Au-N (% N) h( µ m) λ (nm) σ m (GPa) ε m (%) 5, 7,,65,65 5,7 6,7,69,68 64,99 4,3,64,79 5,9,54,59,48 55,6,4,75,6 59,3,34,79,7 59,3,37,8,77 56,75,,78,6 6,6,7,.97,37 6,3,84,64,36 65,68,5,6,56 S-au analzat pe baza metode de reducere pseudosferca, o sere de nanostructur (Munteanu s Chrou 5). De exemplu s-a consderat o nanobara alcatuta dn 3 stratur alumnu-spuma auxetca-alumnu (fg...7 sus) s o nanobara n care stratul dn mjloc este un crstal cu proemnente atomce dstrbute aaleator (fg...7 jos).
78 78 Fg...7. Bara compozta alumnu-spuma auxetca. Structurle sunt solctate la ncovoere. Reducerea ampltudnlor vbratlor capatulu bare n raport cu tmpul este reprezentata n fg...8 pentru ambele structur.se observa ca proemnentele atomce ntroduse n structura crstalna a materalulu ntroduce o canttate semnfcatva de amortzare. Fg...8. Varata ampltudn n raport cu tmpul pentru structurle dn fg Rezonator se caracterzează prntr-un factor de caltate foarte mare (de aproxmatv ), pentru a putea reduce cât se poate de mult semnalele de nterferenţă. Pentru a modela astfel de
79 79 rezonator trebue înţelese mecansmele de dspare a energe ş de relaxare a tensunlor la scară nanometrcă. Structurle mcro-electromecance (MEMS) se utlzează în ndustra senzorlor ş în comuncaţle fără fr. Ltografa electroncă permte reducerea dmensunlor acestor structur până la nm, ş fabrcarea de ssteme nano-electromecance (NEMS), care consumă foarte puţnă energe. Prn analoge cu bosstemele, oamen au construt o sere de structur electromecance la scară nanometrcă, cum ar f rezonator (Chrou, Stuca, Munteanu s Donescu 5). Reducerea dmensun unu rezonator creşte frecvenţa sa de rezonanţă în domenul GHz. Sstemele nano-electromecance se caracterzează prntr-un factor de caltate foarte înalt. Cele ma multe stud prvnd mecansmele de dspare a energe au fost realzate pe ssteme osclante cu dmensun mar, ş la frecvenţă mcă de aproxmatv Hz. Pentru a rdca factorul de caltate a NEMS înspre valoarea 7, trebue să înţelegem cum funcţonează cele ma mportante mecansme de dspare a energe la scară nanometrcă. Inversul factorulu de caltate Q este prn defnţe raportul dntre energa dspată pe cclu W c ş energa elastcă totală W e Wc =. (..) Q π We De exemplu, în cazul amortzăr coulombene, ntroducem un modul de elastctate complex. Presupunând că tensunea este de forma σ=σ exp( t) ω, (..) datortă modululu complex, deformaţa se scre la fel ε=ε exp( t ) ω +φ. (..3) Energa elastcă a osclatorulu, ş respectv, energa dspată pe cclu devn W = Eσ, W =πeησ. (..4) Factorul de caltate (..) se exprmă astfel W = = tan φ =η, (..5) Q πw unde η, care este capactatea specfcă de amortzare pe radan ş pe cclu de mşcare, se numeşte ş factor de perdere. Sub altă formă, factorul de caltate se ma scre ş sub forma Im( ω) = Q Re( ω ). (..6) Ca un exemplu, factorul de perdere a valor în ntervalul 5 3 pentru alumnu, în ntervalul,,6 pentru beton,,, pentru stclă, ş în ntervalul,,pentru oţel. În general, dfertele mecansme de dspare a energe contrbue împreună la descrerea factorulu de caltate. În consecnţă, putem spune că factorul de caltate total este suma factorlor de caltate ndvdual =. (..7) Qtot Q este aproxmatv aceeaş ca cea a unu oscllator neamortzat.
80 8 De4 exemplu, un rezonator nanomecanc poate f paleta rezonantă, care prezntă două modur fundamentale de rezonanţă, unul la mşcarea de translaţe ş celălalt la mşcarea de torsune. Geometra rezonatorulu ş cele două modur de rezonanţă sunt reprezentate în fg...9. Grosmea palete este notată cu θ (, t) = Osclator torsonal mcromecanc pot detecta deformaţ foarte mc, fapt pentru care sunt deal pentru studul propretăţlor electromagnetce ale materalelor. Pentru mşcarea de translaţe, se poate consdera un model smplfcat în care se presupune că paleta rămâne nedeformată în tmpul mşcăr, datortă rgdtăţ sale relatv mar (Olkhovets ). Fecare bară poate f consderată încastrată la ambele capete. Datortă smetre, secţunea dn mjlocul fecăre bare nu suferă deformaţ de încovoere. Modelul lu Olkhovets pentru mşcarea de translaţe al palete este reprezentat în fg.... Expermental, acest model prezntă o comportare nelnară la vbraţ. De aceea, în ecuaţa care descre mşcarea acestu sstem se ntroduce o forţă elastcă nelnară. Fg...9. Geometra palete rezonante.
81 8 Fg.... Model pentru mşcarea de translaţe a palete. Fg.... Modelul pentru mşcarea de torsune a palete. Revennd la paletă, notăm momentul de nerţe cu I p, ş presupunem că barele suport sunt modelate ca resoarte elastce fără masă, de constantă elastcă κ b. Pentru modelul dn fg..., putem aplca aceeas teore daca adaugam un termen de amortzare ş un moment de torsune exteror τθ (, t).
82 8 Fg.... Modelul pentru mşcarea de torsune a palete. Fg...3. Frecvenţa de rezonanţă la mşcarea de translaţe. Pentru o paletă (fg...) cu dmensunle a = nm, b = 75nm, L =,5µm, w = µm, 3 d = 3,5µm, modulul lu Young pentru slcon E =5GPa, denstatea ρ= 33kg/m ş coefcentul Posson ν =,7, se obţne pentru prma frecvenţă de rezonanţă valoarea,35 MHz, aşa cum se observă dn fg...3. Pentru aceleaş dmensun ale palete, se obţne frecvenţa de rezonanţă la mşcarea de torsune, egală cu 3,34 MHz. Descrem în contnuare un motor celular cu două stăr (ataşat ş detaşat) (fg...4). O masă lberă este ancorată pe o magstrală ca un pendul, ş magstrala este ataşată une că moleculare cu o vteză de ataşare t. Deplasarea mase se descre cu ajutorul unu potenţal d
83 83 kξ armonc U ( ξ ) =, unde ξ este deplasarea relatvă a mase, ş k o constantă elastcă. Masa se detaşează la tmpul t d, ş trece într-o nouă stare la tmpul t a, când se ataşează dn nou. În acest moment ea se deplasează ş generează forţă între cale ş magstrală. După un tmp masa se detaşează, ş cclul se repetă. Acest model se poate generalza la N mase ndependente, rgde, pozţonate pe o magstrală care se poate ataşa une că moleculare (fg...5). Notăm cu x pozţa mase care poate f lberă sau legată, ş cu y pozţa capătulu pendululu pe magstrală. Deplasarea mase este ξ = y x. Aceste deplasăr se pot descre cu ajutorul unu potenţal armonc Η= U ( ξ ξ d ), kξ cu U ( ξ ) =. După ataşare sau detaşare are loc o devaţe a potenţalulu cu dstanţa d, adcă ξ d = în starea ataşată ş ξ d = d în starea detaşată. Aparţa aceste asmetr spaţale consttue baza mecansmulu de generare a mşcăr drecţonale. Presupunem că tranzţa dntre stăr apare stocastc cu tmp caracterstc t d ş t a, ş cu vteza de ataşare a mase t constantă. Exstă tre scenar mcroscopce posble de ataşare a d mase la calea mcroscopcă. În prmele două, se presupune că are loc o reacţe de întârzere înante ca masa să se ataşeze (fg...6). Masa are o mşcare aleatoare trdmensonală înante de ataşare. În prmul scenaru, tendnţa mase de a se ataşa creşte gradat (fg...6a). În al dolea scenaru, masa se ataşează parţal la început, are o mşcare aleatoare undmensonală ş apo se ataşează total. În al trelea scenaru, ataşarea are loc medat. Alegem prmul scenaru care este propru motorulu actn-mosn dn muşch. Conform cu Svoboda ş Schmdt (993) se obţne pentru a două valor, a = 5,5nm pentru actn ş a = 8nm, pentru mcrotubur. Fner, Mehta ş. Spudch (995) au determnat expermental valorle k =,4pN/nm, d = nm. Fg...4. Dagrama unu motor molecular cu două stăr.
84 84 Fg...5. Dagrama unu motor molecular cu masa care se deplasează pe o cale moleculară.. Fg...6. Tre scenar de ataşare a mase la calea moleculară.. Până acum am vorbt de magstrale ş că rgde. O cuplare elastcă a motoarelor moleculare se poate realza consderând că magstrala sau calea moleculară este elastcă. În contnuare consderăm că magstrala este elastcă, fnd modelată ca un resort elastc de complanţă γ pe untatea de lungme. Presupunem că tmp de ataşare t a ş respectv, de detaşare t d sunt constanţ. Un număr de N motoare (motorul este un pendul cu masă ataşată la capăt) sunt fxate echdstant pe magstrala elastcă, la dstanţă L (fg...7). Pozţa nţală la t = a capătulu pendululu pe magstrala nedeformată este z, ar pozţa sa la tmpul t este y () t, relatv cu z. Pozţa nţală a mase relatv cu capătul pendululu este d (fg..9), ar pozţa sa la momentul t este este x () t (fg...8).
85 85 Fg...7. Model cu magstrală elastcă. Fg...8. Modelul mşcăr magstrale elastce. Generalzând acest motor celular, problema construr unu nanomotor cu rezoluţe atomcă fără sstem de amortzare a vbraţlor, cu dmensun de aproxmatv 5nm (de 3 de or ma mc decât grosmea unu fr de păr uman), utlzând un rotor de aur montat pe un arbore alcătut dntr-un sngur nanotub de carbon de grosme în jur de la 5 la nm, nu a fost greu de rezolvat (Nod ş Sumpter, Stuca, Chrou s Ncolescu 4). Arborele de carbon încărcat electrc se roteşte sub acţunea unu câmp osclant generat de un laser. Cu ma puţn de 5V aplcat statorulu, nanomotorul se poate rot m de ccl fără degradare. Funcţonarea motorulu este modelată cu metode ntelgente de tp neuronal. Nanomotorul este sufcent de mc pentru a putea f montat în cordul uman pentru contracţa actvă a muşchulu cardac, sau într-un dspoztv care să agte lchdul într-un echpament mcrofludc, sau poate funcţona ca un întrerupător optc de redrecţonare a lumn, sau poate f montat în cel ma mc mcroscop (scannng tunnelng mcroscop SMT) care exstă în prezent. Acest mnmcroscop se poate folos de exemplu, pentru nscrţonarea unor structur pe un superconductor aflat la temperatură mare. In cadrul proectulu s-a realzat controlul amortzăr în cateva nanostructur, cu aplcaţ la reducerea vbraţlor (Chrou et al., Chrou, Stuca, Munteanu s Donescu 5) dntre care: Mecansm de amortzare cu nanostratur vâscoelastce (fg...9) Fg...9. Mecansm de amortzare cu nanostratur vâscoelastce. Mecansm de acţune cu elemente PZT la întndere ş alunecare (fg...).
86 86 Fg.... Mecansme de acţune PZT la întndere ş alunecare (dmensun n nm). 3. Nanobară stratfcată alcătută dn materale vâscoelastce (fg...). Fg.... Bară stratfcată dn materale vâscoelastce. 4. Placă sandwch alcătută dn nanostratur vâscoelastce supusă la solctăr complexe fg..34 sunt reprezentate câteva modur de deformaţe controlate. Functa Tteca admensonala pentru prmele tre modur controlate ale plăc sandwch sunt prezentate n fg....
87 Fg.... Functa Tteca admensonala pentru prmele tre modur controlate ale plăc sandwch 87
88 55 3. Metoda noua de caracterzare a amortzar prn nanondentare. Realzarea vrtuala a nstrumentulu de nanondentare (etapa I-metoda) Metodele clasce cunoscute nu sunt adecvate la scara nano, amortzarea nu se poate estma cu aceste tehnc. Evaluarea amortzar la nvel nano este o problema deschsa. Apar aspecte neelucdate legate de efecte cuantce (zgomot Johnson datorta temperatur, forta Casmr), legate de trbologe (orgnea frecar, ara reala de contact, adezune moleculara, efecte electronce, superlubrctate), s alte fenomene precum energa dscontnua de legatura adezva, hsterezs, dfuze, fluaj, dslocat, forfecarea atomca, curgere plastca, relaxare, gradent termc. Prn urmare, lmtarle metodelor s a nstrumentate exstente (nanondentare) se refera la calculul modululu de elastctate care se face doar pentru materale zotrope s lnare, fara sa se obtna nformat prvnd propretatle elasto-vascoase s de amortzare. In present, dn analza dnamca se obtn nformat lmtate prvnd amortzarea pentru materalele cu amortzare redusa. Un rezultat ncorect prvnd capactatea de amortzare a materalelor poate cauza schmbar de desgn cu reducer nedorte ale rezstente s rgdtat. Noul concept propus de no consta ntr-un nou experment. Acest experment este justfcat prn teora pe care am construt-o s care evdentaza capabltatle acestu experment. Este vorba de construrea une ln de ndentere care se msca cu vteza v, unele dn ele actonand pe o parte a suprafate probe, altele pe cealalta suprafata n aceeas drecte sau drect opuse. Indenterele pot actona pe o parte a probe, cealalata parte fnd ncastrata. In fg.3. este prezentat schematc acest ndenter multplu. In acest fel este posbla evaluarea nu numa a propretatlor elastce dar s a capactat de amortzare, lbere de efectul de substrat. Prncpalele rezultate ale echpe de cercetare care stau la baza prezente cercetar sunt: (Teodorescu, Munteanu, Chrou, Dumtru s.beldman 8, Chrou, Munteanu, D.Dumtru, Beldman s.secara 8, Munteanu, Chrou, Dumtru, s Beldman 8, Chrou 8, Munteanu, Dumtru, Donescu s.chrou 8). : Modelarea locala a contactulu fara frecare Modelarea locala a contactulu cu frecare Modelarea nelocala a contactulu fara frecare Modelarea relocala a contactulu cu frecare Dezvoltarea de modele ale suprafetelor n contact la scara contnua macroscopca. Modelul Derjagun, Muller s Toporov, Teora nelocala de tp Erngen, Modelarea nelocala a contactulu elastc, Problema lu Boussnesq. Soluta lu Sneddon, Ecuatle ntegrale duale ale lu Sneddon. Solut exacte ale stante plane de forma arbtrara Dezvoltarea de modele la scara mezoscopca s la scara nanoscopca Teor cuplate atomstc-contnue. Potental atomc Analza fenomenulu de adsorbte Rezolvarea numerca a probleme ndentar cu ajutorul elementelor fnte. Scopul lucrar este de a constru o teore adecvata pentru un procedeu de nanondentare prezentat n fg.3.3..
89 56 Fg. 3.. Reprezentarea schematca a conceptulu a doua nedentere care se msca cu aceeas vteza n aceeas drecte pe suprafata probe. Construrea relatlor consttutve pentru star de tensune multaxale s complexe se bazeaza pe studul geometre dferenţale afne, care a fost nţat de Ţţeca în 9, cu o lucrare remarcablă asupra une clase partculare de suprafeţe hperbolce nvarante la o transformare Bächlund. Suprafeţele sale sunt cunoscute sub numele de sfere afne (Affnsphäaren), deoarece ele sunt analogul sferelor dn geometra dferenţală afnă. Dn aceasta teore cuplata cu o metoda de optmzare s rezultate expermentale, se construesc teor consttutve care se verfca expermental pentru materalele nanostructurate (Munteanu s Donescu, 4). Dezvoltarea teore optmzar a condus la aparta une teor a dualtat s la o multtudne de metode de rezolvare. Optmzarea matematca are doua surse prncpale, prma consttuta de teora echlbrulu economc al lu Edgeworth (88) s teora bunastar a lu Pareto (96), s a doua consttută de fundamentele matematce ale teore spatlor ordonate ale lu Cantor (897) s Hausdorf (96). Acest domenu ncepe sa se dezvolte n peroada 9-93 odata cu ncercarle de rezolvare a une probleme economce fundamentale, s anume alocarea optma a unor resurse lmtate. Lucrarea de baza este cea a lu Kantorovc (939). Pentru optmzarea matematca o mare mportanta au avut-o teora jocurlor ntata de Borel (9) s von Neumann (96) s teora producte al lu Koopmans (95). Optmzarea matematca a fost recunoscuta ca dscplna aba dupa publcarea lucrar lu Kuhn s Tucker (95) care stableste condt de optmaltate pentru probleme de optmzare nelnara cu restrct negaltat. Problema determnar relatlor consttutve dn rezultate expermentale a condus la generalzarea s extnderea rezultatelor dn analza convexa. Asa au luat nastere domen no ale matematc cum ar f convextatea generalzata ş analza convexa abstracta. Consderăm o suprafată Σ scrsă parametrc sub forma Monge
90 57 r = xe + ye + z( x, y) e. (3.) 3 Se şte că prma ş a doua formă fudamentală sunt date de I = + z dx + z z dxdy+ + z dy ( x) x y ( y), II = z dx + z dxdy + z dy + z + ( xx xy yy ). x zy (3.) Ac, ndc xy, reprezntă dervate parţale gaussană a suprafeţe Σ se scru sub forma z = z x x etc. Curbura mede ş curbura Η= + z z z z z + + z z ( x ) yy x y xy ( y ) xx 3/ ( + zx + zy), (3.3a) z z z Κ= ( ) xx yy xy + zx + zy. (3.3b) Introducem varablele ndependente p ş ψ p= z x, ψ = zy, (3.4) ş varabla dependentă ξ ξ = x, ξ p = y. (3.5) p ψ Avem ξ σσ = z z z yy xx yy zxy ξ = xx, ψψ zxxzyy zxy z ξ = xy, pψ zxxzyy zxy z. (3.6) Dn (3.3b) obţnem ξppξψψ ξ pψ =. (3.7) Κ ( + p +ψ ) Mşcarea gazulu într-un sstem de coordonate lagrangan ( Xt, ) este descrsă de ecuaţle împreună cu legea consttutvă ε =, (3.8a) t vx ρ vt =σ X, (3.8b) σ= p = p( ρ, X). ρ În ecuaţle de ma sus, p, ρ sunt presunea ş respectv denstatea materalulu, ε= ρ deformaţa unaxală, ρ denstatea medulu în starea nedeformată, v( X, t ) vteza materală. Indc t ş X reprezntă dervate parţale. Dacă ataşăm sstemulu lagrangan (3.8) o lege consttutvă care descre deformaţa unaxală a unu medu elastc nelnear
91 58 σ=σ( ε, X ), (3.9) obţnem o problemă de propagare a undelor într-un medu elastc nelnar ş neomogen. Dacă ntroducem coordonatele eulerene x = x( X, t) dx = ( ε+ ) dx = vdt, (3.) astfel încât obţnem ecuaţa Monge-Ampère ρ dx = ρ dx ρ vdt, (3.) ξ ξ ξ =ε, (3.) pp ψψ pψ p unde t = ξ p, v = ξ ψ, dx = ξξ ψ pp + ( ξξ ψ pψ +ε) dψ, < ξ ppε<. (3.3) Traectorle partculelor se determnă parametrc dn x = [ ξξ ψ pp + ( ξξ ψ pψ +ε) dψ], t = ξ p, (3.4) în funcţe de presunea p, pentru ψ = const. Izobarele se obţn parametrc în raport cu ψ, pentru p = const. în (3.4). Dacă rezolvăm (3.4) obţnem p = p( ψ, t), ş soluţa sstemulu orgnal de ecuaţ (3.8) se poate scre parametrc în raport cu varablele Lagrange ş x = x( ψ, t), v = v( ψ, t), p = p( ψ, t). (3.5) Dn ecuaţa Monge-Ampère (3.) ş (3.7) se obţne expresa curbur gaussene ε p =, (3.6) Κ ( + p +ψ ) ρλ Κ= ( + p +ψ ), (3.7) unde p λ = ρ ψ ş λ este vteza locală a sunetulu în gaz. În contextul elastctăţ nelnare avem A Κ= ( +σ + X ), (3.8) unde A σ =, A fnd vteza lagrangană de undă. În contnuare presupunem că ε X În acest caz relaţa (3.8) devne K =, a= const. (3.9) a σ σ = ( +σ + X ) σ X > X a ε ε, σ>. (3.)
92 59 Integrând (3.6) cu p σ ş ψ X avem a σ σ + X ε= [arctan( ) + ] +α( X ), (3.) 3/ ( + X ) + X +σ + X cu α( X ) arbtrar. Dacă mpunerm condţa σ ε= =, rezultă α ( X ) =. Relaţa (3.8) descre comportarea unu materal elastc nelnar ş neomogen. Pentru smplfcare, ntroducem în (3.) Obţnem + X σ= + X tan[ ( c c )]. (3.) a a c c + X ε= [ + ]sn( ( c c ))]. (3.3) ( + X ) a + X a Relaţle (3.) s (3.3) sunt o reprezentare parametrcă a leg consttutve pentru care ecuaţle de mşcare Lagrange sunt asocate cu o suprafată pseudosfercă. Aceste ecuaţ conduc la σ =ε, (3.4) XX sau prn utlzarea relaţe (3.6) σ = [ a σ ]. (3.5) XX ( +σ + X ) t t Se poate arăta că ecuaţa (3.5) admte soluţ de tp solton, fnd legată de ecuaţa sne- Gordon. Curbura mede Η a suprafeţe Σ a căru exprese este un nvarant, de unde rezultă expresa ( +σ ) Xv σxσv ( + X ) σt cot ω= a. (3.6) 3/ ( +σ + X ) tt Întroducând transformarea ( Xt,) ( X = vt, t), < v X <, (3.7) avem t = vx t t, X = v t X t + v, (3.8) X v t v t sau Dn (.6) obţnem t= t, v v X X t vt X = + t v X t v t X X t +σ σxσx ( + X )( σtvx vtσx) 3/ a cot ω= a v ( +σ + X ) Ecuaţle gaussene r = rtv (, ) ale suprafeţe Σ devn X r = ze, r = ze = σ e = Xe, tt tt 3 tv tv 3 v 3 t 3 vv vv 3 v 3. (3.9). (3.3) r = z e = X e, (3.3)
93 6 la care atasăm condţa de compatbltate Dacă utlzăm relaţle σ =. (3.3) v X t vt X σ X t= vx t σ v t, Xt v=, (3.33) v ş < v X <, ecuaţa (3.3) este o altă formă a ecuate de mşcare cu ρ =. Dacă v ş t sunt varable ndependente, ecuaţa de conservare a mase se scre sub forma Expresa curbur gaussene devne X t ( X, ε ) =. (3.34) (,) vt de unde rezultă σ txv + σ vxt = Κ ( + σ + X ), (3.35) ( X, ε) σ = Κ ( +σ + X ) (,) vt ε X. (3.36) Transformata Bäcklund pentru suprafeţele pseudosferce cu curbură gaussană Κ=, cu a r pozţa unu vector pe o astfel de suprafaţă Σ, presupune că r r = an n, n n = cosζ. (3.37) Transformarea (3.37) determnă pozţa vectorulu r al une no suprafeţe pseudosferce Σ cu aceeaş curbură gaussană. În (3.37) ζ este unghul dntre normalele untare n ş n la Σ ş respectv Σ, ş este constant. În acealaş paragraf am văzut că ecuaţa sne-gordon asocată une suprafeţe pseudosferce Σ, parametrzată în raport cu coordonatele asmptotce α ş β se scre sub forma ω ω µ ω+ω = sn, a α ω αβ = sn ω, (3.38) a ω+ω ω ω = sn, µ a β unde ω ş ω sunt două perech de soluţ ale ecuaţe sne-gordon (3.38). În raport cu varablele fzce, transformata (3.37) se scre acos ζ( X X ) acos ζ( σ σ ) t t =, v v =, +σσ + XX +σσ + XX acos ζ( σ X σx ) z z = = σ( t t) + X( v v), +σσ + XX +σσ + XX +σ + X +σ + X = cosζ, (3.39)
94 6 unde dz = σ dt + Xdv, dz = σ dt + X dv. Transformata Bäcklund (3.39) lasă prn construcţe nvarantă ecuaţa Monge-Ampère ztt zvv ztv = ( + zt + zv ). (3.4) a Menţonăm că transformata Bäcklund (3.39) admte o nterpretare mportantă în raport cu ecuaţle caracterstce ale ecuaţe Monge-Ampère (3.4), ş anume ax ax α β tα =, t β =, +σ + X +σ + X aσ aσ α β vα =, v β =, (3.4) +σ + X +σ + X z +σt Xv = α α α. Dacă ( t, vzxσ,,, ) este o soluţe a acestu sstem de ecuaţ, atunc o soluţe a ecuaţe Monge-Ampère (3.4) este dată de dn care rezultă că Jacobanul ( t, v) αβ (, ) z = z( α (, t v), β (, t v)), nu se anulează. Transformata Bäcklund (.39) reprezntă o dscretzare ntegrablă a ecuaţlor caracterstce nelnare (.4) ale ecuaţe Monge-Ampère. Utlzăm acelaş procedeu de a constru ecuaţ dscrete ntegrable sugerat ma sus pentru ecuaţa sne-gordon. Aşa încât ntroducem varablele contnue ˆα ş ˆβ α=ε ˆ n, β ˆ =ε n, pentru ε, =, sufcent de mc ca să putem aplca dezvoltarea în sere Taylor ω =ω+ε ω + O( ε ), αˆ ω =ω+ε ω + O( ε ), βˆ ω =ω+εω +εω +εεω + O( ε, ε ). ˆ αˆ βˆ αβˆ Dacă ntroducem ş dezvoltarea µ εε = + O( ε, ε ), (.4) µ 4aˆ avem la lmtă ( ε ) la ecuaţa sne-gordon ω ˆ ˆ = αβ sn ω. â
95 6 ş Transformata Bäcklund nduce următoarele ecuaţ dscrete în varable fzce a cos ζ( X X) t t = +σσ + XX acos ζ( σ σ) v v= +σσ + XX a cos ζ ( X X),, t t = +σσ + XX a cos ζ ( σ σ),, v v= +σσ + XX z z == σ( t t) + X( v v), z z == σ( t t) + X( v v), (3.43) +σσ + XX +σ + X +σ + X = cosζ +σσ + XX, +σ + X +σ + X = cosζ. Dezvoltărle ζ =εκ + O( ε ), ζ =π+ε κ + O( ε ), sunt consstente cu (3.4) deoarece µ = tan( ζ ). Char dacă parametr transformăr ζ ş ζ sunt constanţ în raport cu α ş β, e trebue prvţ ca funcţ de n ş respectv n. Astfel, ecuaţle dscrete (3.43) se scru sub forma t αˆ ax ax = = +σ + X +σ + X αˆ βˆ, t βˆ, s v αˆ aσ aσ = = +σ + X +σ + X αˆ αˆ αˆ αˆ βˆ, v βˆ z +σt Xv =, zˆ +σtˆ Xvˆ =. β β β. In fnal avem σ + X + ( σx Xσ ) αˆ αˆ αˆ αˆ ( +σ + X ) =κ ( αˆ ), σ + X + ( σx Xσ ) βˆ βˆ βˆ βˆ ( +σ + X ) =κ ( βˆ ). Parametr necunoscut dn aceste ecuat se determna prun probleme nverse cu ajutorul algortmlor genetc, utlzand date expermentale. Prn urmare, ecuaţle (3.43) pot f prvte ca dscretzarea ntegrablă a ecuaţlor caracterstce (3.4). Incheem paragraful cu exemple de leg consttutve determnate aplcând aceasta teore (fg.3. pulbere carbune, fg. 3. roc Kayenta, fg.3.3 cment ranforsat cu fbre de poletlenă).
96 63 Fg. 3.. Lege consttutva pentru roc Berea. Fg. 3.. Lege consttutva pentru 3 tpur de roca Kayenta..
97 64 Fg Lege consttutva pentru doua tpur de cment ranforsat cu fbre de poletlenă. 3.. Descrerea metode. Studul capactat de amortzare a materalelor la dferte scar metrce. Metode macroscopce de caracterzare a amortzar Pentru a descre un experment vrtual prn ndentare utlzand echpamentul dn fg. 3., consderam ca exemplu un flm subtre de materal s o pereche de ndentere care patrund n materal pana la o adancme ht () s se deplaseaza pe dstanta d zgarnd suprafata flmulu, cu vteza vt () n ntervalul de tmp t [, t] (fg.3..) Fg.3... Cazul unu ndenter sferc. Consderam doua cazur : () un ndenter actoneaza pe o parte a flmulu ar celalalt ndenter pe partea opusa, deplasandu-se n drect opuse, () ambele ndentere actoneaza pe o sngura parte a flmulu, celalata parte a flmulu fnd ncastrata. Fe Oxyz un system rectangular de coordnate, s w( xyt,, ) componenta transversala a deplasar. Lungmea flmulu este foarte mare comparatv cu grosmea sa H, astfel ncat se poate consdera nfnta
98 65 Ecuata de mscare a flmulu este < x <, H < y < H, t [, t]. (3..) w, xx + w, yy = w, tt, V V µ = ρ, (3..) unde V este vteza de propagare a unde de forfecare, µ este modulul de forfecare s ρ denstatea materalulu. Indenterele se msca cu vteza vt () pe suprafata flmulu v= 4v Facem schmbarea de varabla exp( kt) ( + exp( kt)). ξ = x v t, ρv y η=, t = t. µ Vteza ndenterelor ndeplneste condta v < V. Inlocund schmbarea de varabla n (3..) s (3..), obtnem < ξ <, ρ H <η< v ρv H µ µ, (3..3) w, ξξ w, ηη + =. (3..4) In cadrul probeme (), presunea p( ξ ) cu care ndenterul apasa suprafeta flmulu n ξ < a, este ntrodusa n condtle pe frontera. Asadar, problema () a ndentar consta n determnarea une solut a ecuate (3..4) cu condtle pe frontera w( ξ,) = p( ξ ), ξ < a, (3..5a) σηz ( ξ,) =, ξ > a. (3..5b) In cadrul probleme (), presunle f ( ξ ) s g( ξ ) cu care ndenterele actoneaza asupra suprafete flmulu n a< ξ < b s b<ξ < a, sunt ntroduse n condtle pe frontera. Problema () a ndentar consta n determnarea une solut a ecuate (3..4) cu condtle pe frontera w( ξ,) = f ( ξ ), a< ξ < b, w( ξ,) = g( ξ ), b<ξ < a, (3..6a) Transformarea σηz ( ξ,) =, ξ < a, ξ > b. (3..6b) ρv ω=ξ+ η= tanh ζπ/ H, ζ = ξ +η, µ (3..7)
99 66 reduc problemele (3..4), (3..5) s respectve (3..4)-(3..6) la probleme specfce pentru semplanul η>, s anume la problema determnar une funct armonce n semplanul superor care satsface anumte condt. Astfel, condtle (3..5) s (3..6) devn w( ξ,) =, ξ >, (3..8a) w, η (,) ξ =, <ξ < α, α<ξ <, ρv α= tanh aπ/ H µ, (3..8b) s w( ξ,) = pˆ ( ξ ), ξ >α, (3..8c) w( ξ,) =, ξ >, (3..9a) w, η (,) ξ =, ξ >α, <ξ < β, β < ξ <, ρv β= tanh bπ/ H, µ w( ξ,) = fˆ ( ξ ), α<ξ < β, w( ξ,) = gˆ ( ξ ), β < ξ < α. Problemele )) s () se pot rezolva analtc. In cazul probleme (), o solute margnta pentru (3..4) s (3..8) este data de (3..9b) (3..9c) cu α α R( ω) Ωω ( ) =χ + w= pˆ () τ Q(, τ ω)dτ C Q(, τ ω)dτ C Q(, τ ω)d τ, π α α (3..) ρv α= tanh aπ/ H µ, (3..a) Q(, τω ) = ( τ ω ) R( τ ), R( τ ) = ( τ )( τ α ), (3..b) S S C =, λ λ C S S == +, λ λ (3..c) S α α τ pˆ ()d τ τ = ( τ )( τ α ), τdτ λ = ( τ )( τ α ), =,,... α α (3..d) Tensunea σ pentru ξ < a, are expresa ηz
100 67 s a AC( ξ) Ct () p, t () t B( a) B() t σ ηz = dt D π B ( a) B ( ξ) Bt () B( ξ) a ρv A= µπ/ H µ, (3..) (3..3a) ρv C( ξ ) = sech ξπ/ H µ ρv B( θ ) = tanh θπ/ H µ,, (3..3b) (3..3c) S S D λ λ = λ Formula (3..) rezulta dervand (3..) α pˆ, τ() τ R() τ Ω, ω = dτ+ D πr( ω), τ ω α. (3..3d) s trecand la lmta η pentru ξ < a. Pentru p= p, expresa tensun (3..) se reduce la Deoarece AC( ξ) σ ηz =, ξ < a. π B ( a) B ( ξ ) rezulta p ξ w( ξ,) = χ dξ, =, η α D dξ = π ( ξ )( ξ α ), s constanta D devne cu K( k) s K( k ) ntegrale elptce D = πp, K [ Ba ( )]
101 68 Kk ( ) = π du, K ( k) K( k ) k sn u =, k + k =. In cadrul probleme (), o solute margnta pentru (.4) s (.9) este data de α β β R( ω) Ωω ( ) =χ + w= gˆ () τq(, τω)d τ+ fˆ () τq(, τω)dτ C Q(, τω)dτ π β α (3..4) α - C Q( τω, )dτ- C3 Q( τω, )dτ α β cu α s Q(, τω) date de (3..a) s (3..b), ar R() τ are expresa ρv β= tanh bπ/ H µ, (3..5a) R( τ ) = ( τ )( τ α )( τ β ), (3..5b) C + C C = ( G F ) 3 λ C + C = ( G F),, 3 λ π C + C ( ) C = ( G F ), 3 λ λ (3..5c) G α τ gˆ( τ)dτ =, =,,... ( τ )( β τ )( τ α ) β (3..5d) F β τ fˆ( τ )d τ =, =,,... ( τ )( β τ )( τ α ) α (3..5e) τdτ λ =, =,,... ( τ )( τ α )( τ β ) β (3..5f) Pentru α β, determnantul ecuatlor (3..5c) este dfert de zero. Pentru se obtne cu F dat de C C C f ( ) = 3 =, λ ( ξ ) =, ξ = p, g p F C λ F F, = π λ λ
102 69 Tensunea F β τ pdτ =, =,,... ( τ )( β τ )( τ α ) α σ ηξ pentru a< ξ < b are expresa EAC( ξ) σ ηξ = (3..6) π B ( b) B ( ξ ) B ( ξ ) B ( a) cu A, C( ξ ) s B date de (3..3a), (3..3b) s respectv (3..3c).Constanta E are expresa cu E π p cosh( ) cosh( ) snh( ac ) snh( bc) snh( bc) = K ρv c= π/ H µ. Formula (3..6) rezulta prn dervarea solute (3..4) β α gˆ ˆ, τ() τ R() τ f, τ() τ R() τ Ω, ω = dτ+ dτ+ D + D3ω πr( ω) τ ω τ ω β α, s trecand la lmta η pentru ξ < a. Constantele D s D au expresle α 4 τ dτ D = ( G4 F4 ( C+ C3) λ 4 + C, ( τ )( β τ )( α τ ) Dn (3..9) avem α ( ) D = G F + ( C C λ E R, ω (3..7) (3..8) (3..9) = π ( ωω ) ( ω ), (3..) unde Ω este data de (3..4) ar R se calculeaza dn (3..5b). Deoarece urmeaza ξ w( ξ,) = χ dξ, =, η p β E dτ = π, ( τ )( τ β )( τ α ) s dn (.) se obtne (.7). Forta cu care actoneaza ndenterul asupra suprafete de contact Γ se scre astfel
103 7 Ft ( ) = σηξdξdη. Γ (3..) Energa potentala de deformate maxma W pmax este Wpmax = Wp + Wamort, (3..) unde W p este energa potentala ar W amort energa de amortzare. Factorul de perdere este defnt prn Wamort η=. (3..3) π W pmax Flmele DLC sunt polcrstalne n natura lor, avand grosm n jurul a -3nm, s au propretat asemanatoare damantulu. Flmul suporta tensun de compresune mar, are coefcent de frecare redusa s rezstenta mare la uzura. In tabelul 3.. se preznta cateva propretat ale flmulu DCL obtnute cu noua metoda de ndentare. Tabel.3... Propretat: damant, graft s flm DCL Materal Denstate [gm cm -3 ] Durtate [GPa] Modul Young [GPa] damant flm DCL.6. 3 Fenomenele de avalansa ale dscontnutatlor energe de contact, comportamentul hsteretc s dfuza atomca locala sunt consecnte ale faptulu ca frecarea dntre suprafete depnde de vteza relatva, tmp, ncarcare, admte memore s comportament de tp stck-slp. Componenta adezvă a frecăr se datorează forţelor de legătură între suprafeţele aflate în contact. Rezstenţa la alunecare (forfecare) a une legătur adezve, care depnde de fapt de ara reală de contact, determnă forţa de frecare. Forţa de frecare este astfel proporţonală cu ara reală de contact. Mşcarea relatvă apare atunc când forţele externe sunt sufcent de mar ca să depăşească rezstenţa de adezune a suprafeţelor. O teore ma groseră a frecăr presupune că forţa de frecare apare datortă soldarzăr aspertăţlor care oferă rezstenţă la mşcarea relatvă. Mşcarea relatvă apare atunc când aspertăţle cedează. Acest lucru este lustrat în fg.3.. (Kondepud 3). Potrvt cu teora deformăr, forţa de frecare rezultă dn săparea aspertăţ ma moale a une suprafeţe de către aspertatea ma dură a celelalte suprafeţe, aşa cum rezultă dn fg Componenta domnantă a frecăr depnde de propretăţle materale ale suprafeţelor în contact.
104 7 Fg Suprafeţe aflate în contact. Fg Componenta de deformare a frecăr. Ca urmare a componentelor frecăr, coefcentul de frecare se poate scre ca o sumă dntre tre termen S yy tanα µ= + tan θ+. (3..4) H π In (3..4) yy S ş H sunt rezstenţa la rupere ş ecrusarea materalulu ma slab, θ unghul aspertăţ ş α unghul aspertăţ conce. Tolsto, Borsova s Grgorova (97) au găst că tranzţa de la lpre la alunecare este însoţtă de o mşcare cu un sngur grad de lbertate. Oden s Martns (985) au analzat această problemă consderând ş gradele de lberate ale mşcăr normale, tangenţale ş de torsune. Deterch (978) ş Rce, Runa (983) au obţnut leg de frecare varable care permt ntroducerea memore frecăr. Feen ş Guran (998) au pus în evdenţă haosul în fenomenul stck-slp în ssteme osclator smple cu nelnartate dată de
105 7 frecarea uscată. Un model de frecare cu 7 parametr a fost ntrodus de Armstrong et al. (994). Ce ma mportanţ parametr care nfluenţează frecarea sunt vteza de alunecare, tmpul ş încărcarea. Detal prvnd efectul acestor parametr asupra frecăr ş asupra comportăr sstemelor dnamce se vor da în paragrafele următoare ş pot f găste în Ibrahm (99). In lteratura de specaltate au fost propuse dferte modele în care forţa de frecare este o funcţe exponenţală de vteza de alunecare V rel = V X, unde V ş X sunt vtezele suprafeţelor care alunecă una în raport cu cealaltă. Dependenţa frecăr de vteza relatvă este unul dn factor care cauzează mşcarea stck-slp. Panta negatvă a curbe forţă de frecare - vteză relatvă cauzează vbraţ (fg.3..4). Acest fenomen se manfestă ca o amortzare vâscoasă negatvă. Relaţa dntre forţa de frecare ş vteză a fost observat expermental de mulţ autor dntre care amntm Sampson et al (943). Frecarea poate avea ma mult decât o sngură valoare pentru aceeaş vteză relatvă, depnzând dacă vteza creşte sau descreşte. Aceasta înseamnă că frecarea depnde de acceleraţe sau de deceleraţe. Natura nebjectva a frecăr a fost observată prma data de Sampson et al. n 943. Alţ autor au contnuat expermentărle pe o varetate largă de materale ngnereşt, cu dferte condţ de lubrfere, punând în evdenţă acest fenomen (fg.3..5). Partea de sus a curbe corespunde acceleraţe, ar cea de jos deceleraţe. Acest efect poate f explcat prn răspunsul întârzat în tmp al frecăr la schmbarea vteze, fnd cunoscut sub numele de memore a frecăr. Fg Dependenţa de vteză a frecăr arătând o pantă negatvă.
106 73 Fg Varaţa coefcentulu de frecare în raport cu vteza relatvă. Strbeck (9) a propus un alt model pentru suprafeţe lubrfate (fg.3..6). In grafc apar patru regun: (a) frecare statcă, (b) condţe de lubrfcare, (c) lubrfcare parţală cu flud, ş (d) lubrfcare totală cu flud. Prma regune (frecare statcă (a)) nu depnde de vteză. Aceste regun sunt mportante n dnamca structurlor care sunt accelerate pornnd de la o vteză nulă. Blok (94) a arătat că descreşterea valor coefcentulu de frecare în curba Strbeck nu înseamnă că forţa de frecare descreşte de asemenea, dacă apar fluctuaţ de încărcare. Potrvt cu Berger (), panta negatvă în curba frecăr este necesară dar nu sufcentă pentru aparţa nstabltăţlor în comportarea unu sstem dnamc. Dependenţa coefcentulu statc de frecare de tmp a fost observată de Deterch (978) s Berger (). S-a observat că µ s creşte cu tmpul pentru un contact staţonar (fg.3..7). Când se nţază lprea (stck), coefcentul statc de frecare este echvalent cu coefcentul dnamc (sau cnetc) de frecare. Coefcentul statc de frecare creşte în raport cu tmpul la lpre datortă creşter are reale de contact prn deformaţ vâscoplastce ale aspertăţlor s a fluajulu. Factor responsabl pentru acest efect sunt:. Ara reală a contactulu dntre suprafeţe poate creşte datortă unu fluaj localzat, care rezultă dn reducerea rezstenţe suprafeţe în tmp.. Creşterea rezstenţe la forfecare a legăturlor datortă exstenţe efectulu de sudare la rece.
107 74 Fg Curba Strbeck cu 4 regun. Dependenţa coefcentulu statc de frecare de încărcare este complcată căc depnde de tpul suprafeţelor în contact ş de natura materalelor. Valoarea coefcentulu statc de frecare depnde de varaţa forţe tangenţale. In general această valoare descreşte cu creşterea forţe tangenţale (Courtney-Pratt ş Esner 957). Coefcentul statc de frecare descreşte cu creşterea forţe normale (Bowden ş Tabor 95). Deş µ s descreşte, forţa de frecare încă creşte datortă creşter forţe normale. Dependenţa frecăr statce de încărcare are nfluenţă asupra frecăr dnamce. Aceasta datortă schmbăr coefcentulu cnetc în prezenţa osclaţlor normale. Coefcentul cnetc descreşte când coefcentul statc descreşte cu forţa normală. Coefcentul de frecare al nterfeţe nu depnde explct de vteza de alunecare, ş dferenţa dntre coefcentul statc ş coefcentul cnetc este o consecnţă a vbraţlor normale care acompanază alunecarea cu frecare.
108 75 Fg Varaţa coefcentulu statc de frecare în raport cu tmpul. D Souza s Dweb (99) au efectuat experenţe pe dscur ş au găst că forţa de frecare depnde de încărcarea normală pentru o vteză constantă de alunecare. Au fost puse în evdenţă patru regmur dferte (fg.3..8):. regune staţonară de frecare unde forţa de frecare creşte lnar cu încărcarea normală.. regune de frecare nelnară în care forţa creşte nelnar cu forţa normală ş coefcentul de frecare nu ma este constant dar creşte cu încărcarea normală. 3. regune de tranzţe, în care forţa de frecare creşte ş descreşte ntermtent fără nc o exctaţe externă. 4. regune de autovbraţ în care forţa de frecare mede capătă o valoare foarte scăzută ş este însoţtă de autovbraţ perodce cu ampltudn mar. Rce ş Runa (983) au dezvoltat un model în care frecarea depnde nu numa de vteza de alunecare dar ş de stora alunecăr. Modelele clasce în care frecarea nduce vbraţ consderă un element masă-resort care alunecă pe o curea moblă, pe un dsc care se roteşte, lame de turbnă, lagăre lubrfate cu apă, ssteme roată-cale rulantă, frâne auto. Vbraţle stck-slp apar datortă energe care ntră în sstem. De exemplu, pentru un sstem cu un sngur grad de lbertate condţa necesară este panta negatvă în curba frecare-vteză, care este responsablă pentru furnzarea de energe care provoacă vbraţ. Fenomenul stck-slp apare pe două că - suprafeţele se lpesc ş aspertăţle se deformează elastc, sau suprafeţele alunecă una în raport cu alta ş deformaţle sunt plastce. Acest fenomen a fost observat prma dată de Wells în 99 în tmp ce încerca să determne coefcentul dnamc de frecare. Alte lucrăr nteresante care analzează acest fenomen sunt Kato ş Matsubayash (978), Chrou s Chrou (3), Badea ş Ncolescu (3), Donescu ş Munteanu (, 4).
109 76 Fg Dependenţa forţe de frecare de încărcarea normală. Raspunsul unu materal cu nanostructura, care contne defecte, mcrofsur, golur s care este solctat atat termc cat s mecanc, se masoara n raport cu tensorul macroscopc al rate deformate D s tensorul tensun σ. Prezentam la nceput modelarea matematca a contactulu elasto-plastc. Ecuata de mscare s ecuata caldur sunt date de dvσ = ρv, (3..5) s p, (3..6) v ρ c T = k T +σd unde v = u este vteza, u,ρ,cv s k noteaza vectorul deplasar, denstatea de masa, caldura p specfca s respectv conductvtatea termca. D reprezntra partea plastca a tensorulu de deformate D. D este defnt ca partea smetrca a gradentulu vteze de deformate Dj = ( v, j + vj, ). (3..7) e In comportarea elasto-vscoplastca, D se descompune ntr-o parte elastca D s o parte p plastca D D + e p = D D. (3..8) Spnul asocat W este defnt ca partea antsmetrca a gradentulu vtezelor, ntr-un mod analog cu vartejul n mecanca fludelor
110 77 Wj = ( v, j vj, ). (3..9) e p W se descompune, ntr-un mod asemanator, ntr-o parte elastca W s alta plastca W W + e p = W W. (3..3) Este utl sa screm s tensorul deformate ε j = ( u, j + u j, ) ca o suma dntre o parte elastca e p ε s una plastca ε. Pentru cele ma multe materale raspunsul elastc este lnar, putand f exprmat prn legea lu Hooke scrsa sub forma ncrementala, pentru deformat mar T, (3..3) e σ= C D γ unde γ este coefcentul termc al tensun la deformate constanta, σ este tensorul rate al tensunlor Cauchy σ, s C tensorul constantelor elastce. Exsta cateva aleger pentru σ. Cea ma des utlzata este tensorul Jaumann de tp rate al tensunlor Cauchy scrs sub forma σ=σ+ω σ σ ω, (3..3) unde ω este spnul defnt ca dferenta dntre spnul de materal W s spnul plastc W ω= W W p. (3..33) Combnand (3..3) cu (3..8) avem σ= C( D D p ) γ T. (3..34) p p Avem nevoe de leg consttutve pentru D s W. Deformata macroplastca s spnul plastc sunt produse de mscarea dslocatlor. Aceste leg se bazeaza pe cunoasterea mcrostructur s a propretatlor mecance ale materalulu. Ne ntereseaza modul n care putem determna aceste propretat prn teste de ndentare s de nanondentare. Tensunea ndusa de o dslocate arbtrara de tp loop ntr-un punct arbtrar P( x ) se poate calcula cu ecuata Peach-Koehler µ µ σ αβ( P) = bmεm α Rdx β bmεm β Rdx α 8π x 8π x C C (3..35) 3 µ R bmεmk( δ αβ R) dx k 4 π( ν) x x x x C unde b este vectorul lu Burgers, ε jk este tensorul de permutare, µ este modulul de forfecare, ν este coefcentul lu Posson s R = x x este raza defnta ca o norma dntre punctul P s curba dslocate. Aceasta ntegrala se poate calcula numerc. O metoda de ntegrare consta n dvzarea curbe n puncte nodale s ntegrarea pe portun lnare m j+ j+ µ µ σ αβ( P) = [ bkεkα Rdx β bkεkβ Rdx α all loops j = 8π x 8π x j j (3..36) j+ 3 µ R bkεkl( δ αβ R) dx l] 4 π( ν) x x x x j α unde m este numarul total de puncte nodale. Integrala pe ntervalul de la j la j+ se poate evalua explct. Astfel, (3..36) se reduce la β α β p
111 78 N P j, j+ j= σ ( ) = σ, (3..37) unde N este numarul total de nodur pentru toate dslocatle s σ j, j+ =σj+ σ j. Utlzand (3..37), putem calcula forta Peach-Kohler pe nodul N a = [ σ j, j+ ( ) +σ ( )] ξ j= F P P b, (3..38) unde ξ ndca sensul. Consderam ca un numar de N nodur ale dslocatlor ( N grade de lbertate) se msca smultan prn alunecare. Ecuatle de mscare sunt mv + v = F, =,... N, (3..39) M unde v sunt vtezele de alunecare, m este masa efectva pe untatea de dslocat s M este mobltatea dslocate. In (3..39), F este data de (3..38). Pentru m avem formula pentru o dslocate de tp screw W m = ( + ) (3..4) v 3 γ γ s pentru o dslocate de tp edge unde P Wv m = ( 6γ γ+ + ), (3..4) P 4 l v γl γl γ γ γ v v γ l =, γ=, v P este vteza longtudnala s v S vteza transversala a undelor, v v S ar W este energa n stare de echlbru pentru dslocata screw. Cand un ndenter (stanta) este presat pe suprafata une probe aflata la o anumta temperatura, atunc el patrunde n materal s deformata depnde de temperatura s de fluaj. Presupunem n contnuare ca legea consttutva este data de n q c b Qc ε = A σ ( ) ( ) exp E d RT, n q F b Qc u = Au ( ) ( ) exp Eu d RT, c unde ε este rata deformate efectve la fluaj, u este vteza ndenterulu, A, A sunt constante, σ este tensunea de curgere von Mses, u este deplasarea ndenterulu, F forta de apasare a ndenterulu, E modulul lu Young la temperatura probe, b magntudnea vectorulu lu Burgers, d dmensunea granulelor materalulu, R constanta gazelor s T temperatura (Mukherjee et al. 969, Cadek 988). Atunc cand T s d sunt constante n tmpul ndentar pentru o forta F data, exponentul n s K sunt dat de (Fujwara s Otsuka 999) sau (ln u ) n = (ln u) Td,, K = Eu ( ) F n u u
112 79 q b Qc ( ) K = A exp d RT. Pentru d constant, energa de actvare la fluaj este (ln K ) Qc = R (/ T ). d Daca notam cu A ara de contact, ea este proportonala cu u. La echlbru presunea de ndentare p este p = F (durtate Meyer). Atunc cand frecarea dntre ndenter s materal este A foarte mca s poate f negljata, tensunea de curgere reprezentatva σ poate f aproxmata n zona plastca prn (Tabor 95, Johnson 97, Bolshakov s Pharr 998) p σ α F. 3 u In fnal avem n q u d(ln u) b Qc ε nd = = = A σ 3 ( ) ( ) exp u dt E d RT, (ln ε nd ) n = [ln( / E)], σ T, d unde σ este masura tensunlor von Mses n zona plastca, ε nd este rata deformate la ndentare, A 3 este o constanta s n masoara senzvtatea la tensune a rate deformate de ndentare ε nd. Takag s Dao (3) au testat expermental la ndentare un alaj Al 5.3 mol% Mg, la temperatura K, cu un ndenter conc de naltme mm (fg.3..9) cu forta de ndentare F =.39 N s tmpul total de ndentare s. Fg Indenter conc. Aplcand teora descrsa ma sus, Takag s Dao (3) au modelat comportamentul materalulu sub stanta la fluaj. Fg. 3.. reprezenta atat rezultatele expermentale (lne solda) cat s valorle corespunzatoare ale deplasarlor (lne ntrerupta, valor calculate la temperatura T = 773K, cu ajutorul metode elementelor fnte). Conturul tensunlor prncpale maxme n tmpul ndentar la dfert tmp, este reprezentat n fg.3... Rezultatele expermentale arata ca fluajul este controlat de propagarea vascoasa a dslocatlor n materal pentru n = 3, s energa de - actvare Q = 3kJmol. c
113 8 Fg Rezultate expermentale s calculate pentru varata n tmp a deplasarlor pentru un alaj Al 5.3 mol%mg. Mecansmul de relaxare în solde cu comportament vâscoelastc poate f explcat prn varaţa câmpulu de tensune în materal. Consderăm două stăr ale unu sstem mecanc, caracterzate prn două valor dferte ale energe, separate prntr-un potenţal bareră sau energe de actvare, de ampltudne H (fg.3..). În fgură, α este coefcentul de expansune termcă ş T temperatura absolută. Înante de aplcarea forţe exteroare, sstemul se află în starea sa de energe mnmă. Prn aplcarea une forţe exteroare, energa sstemulu creşte. Dacă sstemul poate depăş potenţalul bareră, atunc este posblă tranzţa de la prma stare la starea a doua, ş sstemul se relaxează deoarece dferenţa dntre energle celor două stăr se perde.
114 8 Fg Conturul tensunlor prncpale maxme n tmpul ndentar la dferte valor de tmp. Fg Influenţa une forţe exteroare asupra energe unu sstem mecanc. Pentru a descre matematc fenomenul de relaxare a tensunlor utlzăm modelele reologce prezentate n fg.... In aceasta fgyra sunt prezentate un element elastc Hooke care descre comportarea elastcă, un element Newton pentru a descre comportarea vâscoasă, un element St. Venant pentru descrerea amortzăr coulombene, ş un element Zener pentru descrerea relaxăr tensunlor). Elementul Zener constă dntr-un element Hooke legat în paralel cu un element Newton, ş un element adţonal Hooke legat în sere. Ecuaţa consttutvă a modelulu lu Zener este
115 8 ηd d σ() t EE s p Epηd d() ε t σ () t + = ε () t +, (3..4) E + E dt E + E E + E dt s p s p s p sau într-o formă ma smplă d σ() t d() ε t aσ () t + b = cε () t + d. (3..4) dt dt Semnfcaţa fzcă a constantelor dn (3..4) se poate obţne analzând fenomenele de relaxare ş de fluaj. La o deformaţe constantă ε la t =, ecuaţa consttutvă (3..4) devne d σ( t) aσ () t + b = cε, (3..4) dt cu soluţa c c a σ () t = ε + σ ε exp t a a b. (3..43) c Tensunea atnge o valoare de echlbru constantă σ= ε. Se pot ntroduce un modul de a c b elastctate Young relaxat E R =, ş un tmp de relaxare τ σ =. Pentru t =τ σ, tensunea se a a reduce la 36% dn valoarea sa nţală. La o tensune constantă σ la t =, ecuaţa consttutvă (3..4) se scre sub forma cu soluţa d d ε( t) σ = ERε () t + ER, (3..44) c d t c ε () t = σ + ε σ exp t. (3..45) ER ER d Deformaţa atnge o valoare de echlbru constantă ε= σ. Tmpul de fluaj devne c τ ε =. Dacă σ ( t) =σ exp( ω t), modulul de elastctate în starea nerelaxată se defneşte astfel d E u R E R τσ = E. (3..46) τ ε Negljând dferenţa de fază, avem pentru deformaţe expresa ε ( t) =ε exp( ω t), ş ecuaţa consttutvă (3..4) devne (+ωτ ) σ = (+ωτ ) ε. (3..47) ε E R σ Dn (3..47) se poate determna modulul complex de elastctate Ê +ω τ τ + ( τ τ ) R +ω τε Eˆ σ ε σ ε = E. (3..48)
116 83 Partea magnară a modululu elastc Ê este echvalenta cu factorul de amortzare, ş prn urmare ωτ ( σ τε) Eu ER ωτ ωτ =η= = = η max Q +ω τ τ E +ω τ +ω τ, (3..49) unde η max este coefcentul maxm de amortzare ş σ ε τ= τστ ε, E = EE. (3..5) Se observă că amortzarea este maxmă pentru ωτ =. Dacă peroada de vbraţe este mult ma mare decât tmpul de relaxare ( ω<< ), sstemul mecanc se află în echlbru ş nu se dspă τ prea multă energe. Dacă peroada de vbraţe este mult ma mcă decât tmpul de relaxare ( ω>> ), sstemul mecanc nu are tmp să se relaxeze ş nu se dspă prea multă energe. τ Dn (3..49) rezstenţa la relaxare E se defneşte astfel E E σ ε u R E =. (3..5) E Partea reală a modululu de elastctate complex Ê depnde de frecvenţă ş de tmpul de relaxare la deformaţe +ω τστε Eu ER Eu ER E = ER = E u = η max +ωτ +ωτ +ωτ +ωτ. (3..5) ε De multe or se consderă τε τ. Pentru varaţa modululu de elastctate avem E = η max E +ω τ. (3..53) ε Dependenţa caltatvă a nversulu factorulu de caltate Q (dependenţa relaxăr Debye de frecarea nternă) în raport cu ωτ, ş respectv dependenţa caltatvă a modululu de elastctate E în raport cu ωτ, sunt reprezentate grafc în fg E
117 84 Fg Dependenţa caltatvă a rapoartelor Q ş E E de ωτ. Pentru cele ma multe fenomene de relaxare, tmpul de relaxare este o funcţe exponenţală de temperatură ş poate f descrs de legea lu Arrhenus ( T ) exp H kt, (3..54) τ =τ unde H este energa de actvare ş τ conţne dependenţa lu H de temperatură. În fg.3..4 se reprezntă grafc dependenţa rapoartelor Q ş E de temperatură. E Fg Dependenţa caltatvă a rapoartelor Q ş E E de temperatură. Relaxarea termoelastcă a fost confrmată expermental de câtre Zener în 937. Pornnd de la această lucrare, Lfshtz ş Roukes au dezvoltat un model de relaxare termoelastcă pentru bara Euler-Bernoull (). Prezentăm în contnuare acest model. Legea consttutvă a bare se consderă de forma ν ε z = σ z +α T, ε x =ε y = σ x +α T, (3..55) E E unde α este coefcentul de expansune termcă, E modulul de elastctate a lu Young, ν coefcentul lu Posson ş T temperatura absolută. Ecuaţa de mşcare devne unde nerţa termcă I T este defntă astfel u u ρ A + EI + Eα I = t z z x x y T, I T = x Tdxdy. A
118 85 Ecuaţa de transfer termc în prezenţa cuplăr termoelastce în drecţa y se scre +ν E T T + u E = Dth + y, ν t x α x unde E este rezstenţa la relaxare Eα T E =, CP unde C P este capactatea calorcă pe untatea de volum la presune constantă, D th constanta de dfuze dependentă de temperatură ş T temperatura nţală. Presupunem că transferul termc se realzează fără tmp de întârzere. Frecvenţa devne ω=ω + E ( + f ( ω )), unde ω este frecvenţa de rezonanţă a bare fără perder termoelastce, ar f ( ω ) este dat de unde h este grosmea bare ş 4 hk hk f ( ω ) = tan 3 3 hk, ω k = ( + ). D Constanta de dfuze D th este defntă astfel H Dth = D exp kt. Relaţa de dsperse cu negljarea termenlor superor devne th Factorul de caltate a forma E ω=ω + ( + f ( ω)). cu Im( ) E T 6 6 snh sn = = 3 Q ω α ξ + ξ Re( ω) C ξ ξ cosh ξ+ cosξ, ω ξ= h. D th Se observă că factorul de caltate depnde puternc de grosmea bare. Pornnd de la ecuaţa (3..55) Zener a calculat factorul de caltate pentru bara cu secţune dreptunghulară cu Ead E ωτ Eα T ωτ = Q E +ω τ c σ +ω τ,
119 86 a τ=. π D Cavtăţle, mpurtăţle, granulele cu orentăr dferte, dslocaţle, ntroduc o stare neunformă de tensune în materal, char în absenţa forţelor exteroare. Această stare neunformă de tensune creşte perderle termoelastce. Însă, dacă lungmea bare este ma mcă decât pasul lber al fotonulu termal, conceptul de relaxare termcă nu ma este valabl. În cazul crstalulu cu defecte, putem asoca o smetre fecăru defect. Dacă smetra defectulu este ma slabă decât a crstalulu, apare un dpol elastc care va nteracţona cu câmpul de tensune. Dacă se atnge valoarea energe de actvare, se obţne o rearanjare a dpollor, ş ca urmare apare o relaxare a tensunlor în crstal. Granulele produc dspare de energe datortă mşcăr lor relatve. Granulele actonează ca untăţ rgde sau elastce, în tmp ce nterfeţele dntre granule formează un sstem de nterfeţe care controlează comportarea dnamcă a materalulu. Aceste nterfeţe sunt heterogene ca formă, sunt nano- sau mezoscopce ca dmensune, ş reprezntă o fabrcă de defecte, fsur, dslocaţ, golur, etc. care partcpă la răspunsul temoelastc al materalulu. Aceste nterfeţe absorb energe ş, în anumte condţ, sunt apte să formeze dlaton. Conceptul de dlaton a fost utlzat de Zhurkov s Petrov în 983 pentru a explca ruperea dnamcă a materalelor. Acelaş concept a fost utlzat de Engelbrecht ş Khamdulln în 988, ş apo de Engelbrecht în 99, pentru a explca fenomenul de amplfcare a undelor sesmce observat expermental. Ipotezele de lucru ale modelulu lu Engelbrecht sunt următoarele: dlaton absorb sau genereaza energe; energa maxmă a unu dlaton este fntă; procesul prn care dlatonul absoarbe sau generează energe este controlat de ntenstatea undelor care se propagă în medu; undele cedează o parte dn energa lor dlatonlor ş ca rezultat apare atenuarea undelor. Când energa dlatonulu este maxmă, dlatonul se rupe elberând energe ş ca rezultat apare amplfcarea undelor. La nvel nanometrc acest dlaton se numeşte nanodlaton ş este responsabl de ruperea materalulu. Dlatonul se poate defn ca o fluctuaţe localzată a denstăţ energe nterne datorată slăbr unor legătur structurale dntre atom. th
120 Analza capactat de amortzare a nanotuburlor de carbon. Caracterzarea amortzar une frangh alcatute dn nanotubur de carbon Inante de a analza capactatea de amortzare a compoztelor pe baza de nanotubur, prezentam o metoda mbunatatta a grnzlor cu zabrele pentru modelarea nanotuburlor de carbon. Energa potenţală a câmpulu de forţe care exstă între atom ndvdual dn nanostructura unu materal se poate descre ca o contrbuţe adtvă a ma multor energ (Odegard et al. ) m ρ θ τ ω νdw el E = E + E + E + E + E + E, (3..) ρ θ τ unde E, E, E ş E ω sunt energle potenţale de legătură atomcă asocate deformaţe de alungre, a varaţe unghulu, a torsun ş respectv a nverse. dw Energle care nu sunt de tp legătură atomcă sunt energa Van der Waals, E ν ş energa el electrostatcă E. Expresle acestor energ depnd de materal ş de condţle de încărcare. Pentru determnarea parametrlor câmpulu de forţe atomce se utlzează atât date expermentale cât ş metodele mecanc cuantce. Pentru reprezentarea expreslor termenlor dn (3..) se poate utlza modelul grnzlor cu zăbrele, în care fecare bară dn reţea reprezntă forţa dntre do atom. Modelul grnzlor cu zăbrele poate descre comportarea mecancă a unu nanosstem mecanc în raport cu deplasărle atomlor, ş poate serv ca un pas ntermedar dntre potenţalul de vbraţe ş modelul echvalenţe contnue. În acest model fecare bară corespunde une legătur chmce sau une nteracţun de alt tp. Potenţalul elastc al deformaţe la întndere sau compresune corespunde întnder sau compresun elementulu corespunzător dn grnda cu zăbrele. Atom dntr-o reţea atomcă pot f prvţ, tradţonal. ca mase concentrate asupra cărora acţonează forţe atomce reprezentate prn resort elastc (Born ş Huang 954). De aceea, elementele dn grndă care sunt supuse încovoer nu trebue să smuleze legătur chmce, ş nodurle de legătură dntre barele grnz cu zăbrele sunt îmbnăr care nu sunt fxe. Presupunem că grnda cu zăbrele are un număr de celule ş fecare celulă conţne ma multe bare. Energa potenţală de deformaţe t a une grnz cu zăbrele este dată de AE r R j j t j j ( ), (3..) j j R = j j unde A ş E sunt ara secţun transversale ş modulul elastc al lu Young al bare dn j j celula j. Termenul ( r R ) reprezntă întnderea sau compresunea bare dn celula j, j j unde R ş r sunt lungmle nedeformate ş respectv, lungmle deformate ale grnz. Menţonăm că în (3..) nu se utlzează convenţa sumăr ndclor care se repetă. Prn compararea ecuaţlor (3..) ş (3..), se observă că (3..) conţne numa termen de tp deformaţe de alungre, ar (3..) conţne ş termen de varaţe a unghulu ş termen de torsune. Totuş, prn egalarea acestor ecuaţ se poate obţne un model rudmentar pentru descrerea legăturlor chmce ale nanostructur, căc fecare atom are ma multe grade de lbertate pentru a descre alungrea, varaţa unghulu, etc. În anumte condţ, modelul grnz cu zăbrele se poate dezvolta sub forma unu model echvalent contnuu (Noor et al. 978, Sun ş Lebbe 99, Lee 994). Pentru aceasta, ntroducem noţunea de element de volum reprezentatv (celula dn grnda cu zăbrele), n sprtul metode elementelor fnte FEM. Notăm acest element de volum reprezentatv cu RVE (Fg. 3..). RVE permte ca fecare grad de lbertate a atomulu de carbon să poată f modelat cu metoda grnzlor cu zăbrele ş metoda elementulu fnt, în care gradele de
121 88 lbertate sunt deplasărle nodale. RVE permte defnrea une corespondenţe bunvoce între deplasărle reţele chmce ş modelul contnuu. Condţle de încărcare macroscopce aplcate asupra fo de graft contnuă, se pot reduce la condţ pe fronteră perodce aplcate volumulu RVE. Modelul grnz cu zăbrele cu nodur de tp îmbnare se poate înlocu cu un model echvalent de placă contnuă bazat pe teora clască a medulu contnuu (Erngen 967), dacă se îndeplnesc următoarele condţ :. Modelele au aceleaş grade de lbertate.. Deplasărle asocate volumulu RVE sunt dentce pentru cele două modele pentru aceleaş condţ statce de încărcare. 3. Energa de deformaţe termoelastcă asocată celor două modele trebue să fe aceeaş pentru aceleaş condţ statce de încărcare. Fg.3... Elementul de volum reprezentatv (REV) pentru foaa de graft Modelarea fo de graft Acest paragraf utlzează valorle constantelor pentru câmpul de forţe date de Allnger et al. 989, L ş Allnger (989) ş Odegard et al. (). În cazul mclor deformaţ putem neglja torsunea, nversa ş nteracţunle care nu sunt de tp legătură chmcă. Energa cnetcă a fo de graft cu legătură de tp carbon-carbon se poate reprezenta ca o sumă de funcţ armonce, (3..3) g E = K ( ρ P) + K ( θ Θ ) ρ θ unde ρ ş θ sunt dstanţele ş unghurle după deformaţe ale legătur chmce, P ş Θ, sunt dstanţele nteratomce nedeformate ale legătur chmce ş respectv ale unghulu nedeformat, ar K ρ ş K θ sunt forţele constante asocate defomaţe de alungre ş deformaţe unghurlor t legătur chmce. Este destul de complcat să exprmăm energa potenţală de deformaţe pentru grnda cu zăbrele, în funcţe de ( θ Θ ). Pentru smpltate, se pot consdera doar grade de lbertate de tp alungre, prn încorporarea în RVE a două tpur de bare elastce, bare de tp a ş bare de tp b pentru a reprezenta nteracţunea dntre atom de carbon (fg. 3..). Scopul nostru este de a lega modelul molecular de modelul contnuu. Pentru aceasta trebue să dscutăm condţle pe care trebue să le îndeplnm pentru a înlocu modelul grnz cu zăbrele
122 89 cu o placă contnuă echvalentă. Va trebu să determnăm ş să egalăm expresle energle potenţale de deformaţe ale grnz ş ale plăc pentru o încărcare exteroară dată. Conform cu Allnger et al. (989), L ş Allnger (989), Odegard et al. () avem următoarele constante în cazul fo de graft K ρ K θ = = = 63 kcal/(mole rad ) = 4.38 nj/(ungh nm ) kcal/(mole nm ) 3.7 nj/(legatura nm ) P =.4nm Fg Elementul de volum semnfcatv (REV) pentru modelul chmc, modelul grnz cu zăbrele ş modelul contnuu). Energa potenţală de deformaţe se obţne dn (3..3) ş este de forma AE AE = + a a b b t a a b b ( r R ) ( r R ) a b R R, (3..4) unde ndc a ş b se referă la barele de tp a ş b. Comparând între ele expresle (3..3) ş (3..4), se observă că termenul de alungre dn (4.4.) se poate lega de prmul termen dn (3..4) pentru barele de tp a a a A E K ρ =, (3..5) a R a a unde se presupune că ρ = r ş P = R. Orcum, cel de-al dolea termen dn (3..3) ş dn (4.4.) nu pot f legaţ drect. Varaţa unghulu dn legătura chmcă poate f exprmat în raport cu alungrea elastcă a barelor de tp b. Se poate presupune că încărcarea se poate prescre astfel încât să avem numa mc deformaţ. În acest caz putem exprma modulul elastc al lu Young al bare de tp b în funcţe de unghul de legătură constant (fg.3..3). Pentru deformaţ mc ale RVE, varaţle unghurlor
123 9 sunt mc. În acest caz, putem presupune că r (3..4). Avem a = R în termen secunz dn ecuaţle (3..3) ş b b r R θ Θ= a R (3..6) Substtund (3..6) în (3..3) ş (3..4), rezultă b b b K = RAE. 3 (3..7) Ca urmare, modulul lu Young pentru cele două bare, devne ρ a θ a K R b 3K E =, E a = b b A R A. (3..8) Expresa (3..4) energe potenţale a grnz se poate scre sub forma θ t ρ a a 3K b b = K ( r R ) + ( r ) b R. 4( R ) (3..9) Pentru înlocurea modelulu grnz cu zăbrele cu modelul une plăc contnue, avem nevoe c de expresa energe potenţale a plăc contnue echvalente în funcţe de deplasăr, ceeace este dfcl de obţnut. O soluţe ar f aplcarea metode elementelor fnte (FEM) pentru a determna energa potenţală asocată celor două modele, pentru un set dat de condţ de încărcare. a Fg Schema deformaţe volumulu REV (Odegard et al.). Modelul grnz cu zăbrele se poate înlocu cu un model echvalent de placă contnuă dacă se îndeplnesc condţle expuse în secţunea 4.3. Pentru aceasta se presupune că placa echvalentă poate f modelată utlzând elemente fnte de tp placă. Presupunem că nodurle corespunzătoare celor două modele sunt pozţonate în aceleaş puncte ş avem aceleaş grade de lbertate (fg. 3..). Orgnea sstemulu de coordonate se află în centrul volumulu RVE. Nodurle pot avea o mşcare de translaţe numa în drecţle x ş x. Gradele de lbertate ale celor două modele sunt dentce. Ne stuăm în cazul une teor lnare în care gradenţ deplasărlor sunt lnar. Cele
124 9 două modele de element fnt sunt supuse la condţ dentce de încărcare ş energa de deformaţe este calculată în raport cu deplasărle nodale. Grosmea plăc echvalente este consderată a f g g grosmea efectvă a fo de graft. Valorle modululu lu Young E ş coefcentul lu Posson ν pentru foaa de graft sunt măsurate mcroscopc (Kelly 98, Harrs 999) g g E = 3GPa ν =,7. Pentru a determna grosmea efectvă a plăc, grnda cu zăbrele ş placa contnuă sunt încărcate cu tre setur de încărcăr exteroare aplcate une fo de graft macroscopce, cu dmensun la scară macroscopcă, ş anume întndere axală în drecţa axe x, întndere axală în drecţa axe x, ş forfecare pură. Datortă dmensun macroscopce a fo de graft, vom avea un număr foarte mare de volume RVE conţnute în structură. Condţle în deplasăr perodce pentru RVE sunt ( α) ( α) ( α) ( α) uˆ k k ( m + m ) = k ( m) + l l u x d u x d, k, lm=,,, (3..) x ( ) unde u α ( ) k sunt deplasărle une feţe a RVE, d α () k este vectorul de perodctate ( dk este paralel cu (3) a, dk este paralel cu a ), u ˆk sunt deplasărle macroscopce medate pe volum, x l sunt coordonatele centrulu volumulu RVE. Indcele α este faţa volumulu RVE. Repetarea unu ndce înseamnă sumare după acel ndce. Vectorul de perodctate este orce vector care leagă două puncte echvalente într-o reţea perodcă ş este reprezentat în fg Vector de perodctate pentru fecare faţă sunt defnţ în raport cu coordonatele x k a a a a () R 3 3R, () R 3 3R dk =,, () a d k =, d k = ( R 3,). (3..) Substtund (3..) în (3..) obţnem constrângerle care reprezntă condţle perodce pe fronteră pentru fecare grup de feţe opuse ale RVE a a () R 3 3R uk 3 x, x + = a a () a R 3 3R = u ( 3 3, ) ˆ ˆ k x R x + uk, + uk,, a a () R 3 3R uk 3 x +, x + = a a () a R 3 3R = u ( 3 3, ) ˆ ˆ k x + R x uk, + uk,, R 3 R 3 u x u x R u a a (3) (3) a k, = k, + 3ˆk, (3..)
125 9 Fg Vector de perodctate pentru volumul RVE. Consderăm prmul caz de încărcare ş anume, condţa de încărcare unaxală în drecţa ( n,), reprezentată în fg Presupunem că se prescre o deplasare axală pe latura de sus, în tmp ce partea nferoară este fxată. Deplasarea este relatv mcă ş placa de dmensun h w este perfect elastcă. Dacă se presupune că deplasărle û ş û varază lnar în raport cu coordonatele globale ˆx ş ˆx, atunc aceste deplasăr se pot scre astfel uˆ ( xˆ ˆ k ) = Bx+ B, uˆ ( xˆ ˆ k ) = B3x + B4, (3..3) unde B, =,, 3, 4, sunt constante care depnd de geometra elementulu ş de tpul încărcăr. Condţle pe fronteră devn uˆ h xˆ, = h ˆ ˆ, =, u x, ˆ ( ˆ ) u, x =. (3..4) Ecuaţle consttutve care leagă deformaţle ε ş ε de tensunle ο, σ sunt date de ε = g uˆ =,ˆ ( ) g E σ ν σ, g ε = uˆ = ( σ, ˆ ν σ ). (3..5) g E Substtund (3..4) ş (3..5) în (3..3) ş rezolvând sstemul pentru determnarea g ν constantelor B, =,, 3, 4, obţnem B =, B =, B3 =, B4 =. h h Prn urmare, (3..3) se reduce la g ν uˆ ˆ ˆ ( xk ) = x, uˆ ˆ ˆ ( xk ) = x +. (3..6) h h Legătura dntre coordonatele globale ş coordonatele RVE este dată de xˆk = x k + f k, (3..7)
126 93 unde f k este un vector care ndcă pozţa relatvă a sstemulu de două coordonate, unul în raport cu celălalt. Dn (3..), (3..6) ş (3..7), rezultă condţle pe fronteră în deplasăr pentru volumul RVE a a g a () R 3 3R () a ν R 3 u 3 x, x + = u ( 3x 3 R, x), h a a a () R 3 3R () a 3R u 3 x, x + = u ( 3x 3 R, x) +, h, a a g a () R 3 3R () a ν R 3 u 3 x +, x + = u ( 3x + 3 R, x) + h a a a () R 3 3R () a 3R u 3 x +, x + = u ( 3x + 3 R, x) +, (3..8) h a a g a (3) R 3 (3) R 3 ν R 3 u, x = u, x h. a a (3) R 3 (3) R 3 u, x = u, x, Fg Prmul caz de încărcare. Consderăm în contnuare cel de-al dolea caz de încărcare ş anume condţa de încărcare unaxală în drecţa (, n ), reprezentată în fg Condţle pe fronteră sunt
127 94 w w uˆ ˆ, x =, uˆ ˆ, x =, uˆ( x ˆ,) =. (3..9) Dn (3..3), (3..5) ş (3..9), rezultă deplasărle globale g ν uˆ ˆ ˆ ( xk ) = x +, uˆ ˆ ˆ ( xk ) = x. (3..) w w Utlzând (4.4.), (4.4.5), ş (4.4.8), condţle pe fronteră în deplasăr pentru volumul RVE, devn a a a () R 3 3R () a R 3 u 3 x, x + = u ( 3x 3 R, x) +, w a a g a () R 3 3R () a 3ν R u 3 x, x + = u ( 3x 3 R, x), w, a a a () R 3 3R () a R 3 u 3 x +, x + = u ( 3x + 3 R, x) w a a h a () R 3 3R () a 3ν R u 3 x +, x + = u ( 3x + 3 R, x), (3..) w a a a (3) R 3 (3) R 3 R 3 u, x = u, x + w. a a (3) R 3 (3) R 3 u, x = u, x,
128 95 Fg Al dolea caz de încărcare. Cazul de încărcare forfecare pură este reprezentat în fg Deplasărle sunt mc ş placa de dmensun h w este perfect elastcă. Se presupune că deplasărle globale û ş û varază lnar în raport cu coordonatele globale ˆx ş ˆx. Aceste deplasăr se pot scre astfel uˆ ( xˆ ˆ ˆ k ) = B5x+ B6x+ B7, uˆ ( xˆ ˆ ˆ k ) = B8x+ B9x+ B, (3..) Condţle pe fronteră în deplasăr pentru volumul RVE, sunt w w u ˆ, x = u ˆ, x = w u ˆ, x = w, ˆ =, (3..3), u x h h u ˆ ˆ x, = u x,. h h u ˆ ˆ x, = u x, Substtund (3..3) în (3..) avem uˆ ˆ ( x k ) =, uˆ ˆ ˆ ( xk ) = x+. (3..4) w Dn (3..), (3..7) ş (3..4) deplasărle pe fronteră pentru RVE sunt date de a a () R 3 3R () a u 3 x, x + = u ( 3x 3 R, x )
129 96 a a a () R 3 3R () a 3R u 3 x, x + = u ( 3x 3 R, x) +, w, R 3 3R u x x u x R x a ( ) a a () () 3 +, + = 3 + 3, a a a () R 3 3R () a 3R u 3 x +, x + = u ( 3x + 3 R, x), (3..5) w, a a (3) R 3 (3) R 3 u, x = u, x. a a a (3) R 3 (3) R 3 3R u, x = u, x + w Pentru smplfcare, presupunem fără a perde generaltatea uˆ x + d = uˆ x. (3..6) ( α) k ( m m ) k( m) Fg Al trelea caz de încărcare. Pentru a aplca FEM folosm un element de tp grndă cu două grade de lbertate pe fecare nod (deplasărle paralele drecţlor x ş x ). Presupunem că barele de tp a ş b au aceeaş secţune transversală, dar au modul de elastctate Young dferţ. Volumulu RVE se poate asoca o are a secţun transversale de tpul bare a împărţtă la, deoarece aceste bare au în comun cu RVE ara lor totală. Elementul echvalent de placă RVE se poate modela cu elemente dreptunghulare cu 4 nodur, având o varaţe lnară a deplasărlor pe latur (fg. 3..). Condţle pe fronteră descrse ma sus se 6 6 aplcă fecăru nod al fo de graft macroscopce de înălţme nm, lăţme nm ş
130 97 deplasare nm (corespunzătoare une deformaţ globale unaxale ş de forfecare,% ). S- au calculat pentru ambele modele, valorle energlor de deformaţe pentru fecare element, pentru condţle pe fronteră consderate, apo s-au însumat energle rezultate pentru a se obţne energa totală pentru volumul RVE. S-a utlzat o varaţe sstematcă a grosm pentru a calcula energa de deformaţe a plăc echvalente ş un algortm genetc pentru a determna grosmea efectvă a peretelu h ef (cu o precze de,nm) dn condţa ca dferenţa dntre energa grnz ş energa plăc să fe mnmă ( t c j j) mn. (3..7) j F = Pentru cazurle de încărcare I ş II, după 3 teraţ s-a obţnut h ef =.8nm. Pentru cazul III de încărcare s-a obţnut h ef =.4nm, după 34 teraţ. Aceste valor sunt apropate între ele ş sunt ma mc decât valoarea acceptată,.34nm care reprezntă spaţul nteratomc, ş sunt ma mar decât valoarea.66 nm, sugerată de Yakobson et al. Fg reprezntă legea tensunedeformaţe a fo de graft întnsă conform cazulu I de încărcare. Pentru deformaţ mc această nt lege este lnară, aşa ca putem scre σ= E ε, unde σ este tensunea normală în drecţa de întndere ş ε este deformaţa corespunzătoare. Acest rezultat obţnut în urma apolcăr algortmulu genetc este apropat de rezultatul expermental obţnut de Loure ş Wagner (998) prn metoda spectroscopcă mcro- Raman, pentru acelaş tp de încărcare. Fg Legea consttutvă corespunzătoare prmulu caz de încărcare. Se presupune că modulul lu Young pentru nanotubul de carbon se calculează dn nt E = nt A, (3..8) nt unde A este ara secţun transversale a unu clndru contnuu, gol, cu o rază a planulu medan constantă r. Raza nteroară r ş raza exteroară r a tubulu sunt date de
131 98 t t r = r, r = r +, (3..9) unde t este grosmea peretelu. Ara secţun transversale a clndrulu gol este nt A = π tr. (3..3) În tabelul 3.. sunt prezentate grosmea plăc echvalente, ara secţun transversale ş valorle modululu elastc E nt lu Young pentru tre cazur de încărcare. Rezultatele arată că valorle măsurate ş calculate ale propretăţlor fzce ş mecance ale nanotuburlor de carbon sunt dependente de dmensunle tubulu contnuu ş pot dfer semnfcatv în raport cu geometra consderată. Tabel 3... Valorle grosm peretelu, a are secţun transversale ş a modululu lu Young. Cazur de încărcare I ş II Cazul de încărcare III Spaţu nteratomc Grosmea efectvă a Ara secţun Modulul lu peretelu h ef [nm] transversale Young [TPa] [ nm ],8,76 r 3,388,4,5 r 3,976,34,4 r,8 Nanotuburle de carbonncorporate n compozte rdca capactatea de amortzare a materalulu compozt. De exemplu, am studat expermental capactatea de amortzare a unu compozt alcatut dn nanotubur de carbon cu ma mult peret ncorporate ntr-o matrce de 4Al, pentru frecvente de,5; ; 5; ; 3 Hz, s la temperature de 5 4 C. rezultatele au aratat ca pentru o temperature ma mare decat 3 C, frecventa nfluenteaza semnfcatv capactatea de amortzare (Chrou, Munteanu s Dumtru 8, Chrou, Munteanu s Beldman 8, Dumtru, Pop s Baldovn 8, Donescu, Chrou s Munteanu 8).. Capactatea de amortzare a compoztulu la o frecventa de.5 Hz atnge 975 3, s modulul storage de elastctate atnge valoarea 8.3 GPa la o temperatura de 4 C. Acest fapt arata ca nanotuburle de carbon pot arma matrc de metal s se pot obtne astfel propretat de amortzare superoare la temperature mar fara sa se parda rezstenta mecanca a structur composte. Pentru a studa capactatea de amortzare a unu materal nanostructurat, consderam o franghe alcatuta dn nanotubur de carbon cu un sngur perete. Frangha contne ma multe grupur de nanotubur ncorporate ntr-o matrce polmerca. Fecare grup, un anumt numar de nanotubur cu dferte chraltat s raze (fg.3..9).
132 99 Fg Structura nanofranghe. La scara macroscopca, nanotubul de carbon este modelat ca o bara de lungme l, cu sectunea transversala crculara avand raza mult ma mca decat lungmea tubulu r<< l. Capetele bare sunt fxate prn forte. Bara este supusa la torsune. Pentru a parametrza regunea ocupata de corp x [ r, r], s [, l], pentru un nterval de tmp t [, T ], trecem de la x [ r, r] la x [,]. Pentru orce functe ntegrabla A( x, s ), x [,], s [, l], t [, T ], avem dezvoltarea n sere ( k) * A( xst,, ) = A ( stu, ) k ( x), x [,], s [, l], t [, T ], (3..3) k= ( k unde A ) ( s, t ) este cel de al k coefcent al functe A( xst,, ) n raport cu polnoamele * ortonormale Chebyshev de ordnal do { Uk ( x)} k=. Polnoamele ortonormale Chebyshev de ordnal do pe ntervalul [,] sunt n + U n( x) = [/( n+ )] T ( x), x, n Ν. Ac, Tn ( x) = cos( narccos x) sunt polnoamele de prmul ordn s Ν un set de numere naturale. Polnoamle Chebyshev modfcate sunt defnte astfel Functle U * ( t) = U (t ) = {/[ t( t)]}sn[( n+ )arccos(t )]. n n * F rt r rt (,) = /[ + ) 4 ], h * ( x) = ( t), cu r, t, sunt funct generatoare pentru aceste polnoame. Relatle de recurenta sunt date de Integrala 4 tu () t = U () t + U () t + U () t, * * * * n n n n+ tu () t = nu () t + U () t + U () t, n, * * * * n n n n U ( t) = 4 nu ( t) + U ( t), n * * * n n n I ( A) AxstU (,, ) ( xhx ) ( )dx ( k) * = k este egala cu cel de al k coefcent n sera (3..3) k Ν s [, l], (3..3),
133 I ( A) AxstU (,, ) ( xhx ) ( )d x A ( st, ) ( k) * ( k) = k =, (3) cu k Ν. (3..33) a In modelarea atomstca, energa totala atomca E se scre ca suma energlor ndvduale ale atomlor. Energa unu atom este a E = F( ρ ) + αvj( rj), (3..34) j unde F este energa electronca dependenta de denstatea electronulu, V j potentalul nteratomc care depnde de dstanta nteratomca r j, s α constante. Denstatea ρ a atomulu, se scre ca o suma a contrbutlor atomlor dn vecnatate ρ = ρ ( r ). Forta van der Waals j j j ntre atom s j se exprma sub forma potentalulu Lennard-Jones de tp 6-6 d Vj ( rj ) = A 6, (3..35) rj r j 79 6 a unde A = 4.3 Jm s d =.383nm. Pentru E ( x, s ) se consdera dezvoltarea de forma (3..3) E xs E su x, (3..36) a a( k) * (, ) = ( ) k ( ) k = ak ( unde xa [,], sa [, l] repreznta regunea modelata atomstc. In (3..6), E ) () s se calculeaza cu (3). Parametrzarea regun de tranzte xtr [,], str [, l] se construeste astfel ncat. tr Energa E ( x, s ) dn regunea de tranzte ndeplneste condtle s unde cu xtr [,], str [, l]. tr( k Coefcent E ) () s se calculeaza astfel tr c E ( xs, ) E( xs, ) pentru xtr xc, str sc, (3..37) tr a E ( xs, ) E( xs, ) pentru xtr xa, str sa, (3..38) E xs E su x, (3..39) tr tr( k ) * (, ) = ( ) k ( ) k= s E ( s) E ( x, s) U ( x) h ( x)dx ( k) tr a * k E ( s) E ( x, s) U ( x) h ( x)dx ( k) tr c * k c a, k Ν, pentru xtr xa, str sa, (3..4), k Ν, pentru xtr xc, str sc, (3..4) cu functle necunoscute ha ( x ) s hc ( x) determnate dntr-o problema nversa, astfel ncat (3..37) s (3..38) sa fe verfcate. Energa potentala totala pentru modelul cuplat atomstc-contnuubtne prn sumarea energlor asocate regunlor atomstce, contnue s de tranzte
134 Energa totala de deformateu c a tr E( xs, ) = E( x, s) + E ( x, s) + E ( x, s ), (3..4) c c a a tr tr ( x, s ) I, ( x, s ) I, ( x, s ) I c c c a a a tr tr tr Ic Ia Itr = [,] [, l], I I j = O,, j = a, c, tr. def, energa dspata U s factorul de perdere sunt dat de Udef = j jdv σ ε, U = 4 πτ rl ( ε ε ), arcsn U η=, (3..43) V πu dss unde σ j este tensorul tensune, ε j tensorul defromate, r raza nanofranghe, l lungmea nanofranghe, ε deformata dn matrcea de materal, τ tensunea de legatura s ε deformata de lagatura suntre nanotubur s matrce, data de τl G ε =, A E eq AB = E ln( R/ r), B= eq l / ( βl z ) ( βl ) snh / ) d z, (3..44) snh / unde R este raza volumulu reprezentatv al compoztulu, G modulul de forfecare al polmerulu s E modulul echvalent Young, s eq β= πgr V ϕe ln( R/ r) eq, cu V volumul matrc de materal s ϕ fractunea volumca a nanotuburlor. S-a consderat 5 r = -5nm, l = nm, τ=.4mpa, V = 9%, ϕ = 65wt%, s G = MPa pentru polmer. Raza nanotuburlor este nm cu grosmea peretelu.34nm. Fg. 4 repreznta varata modululu efectv Young a nanofranghe n raport cu raza r a nanofranghe. Fg Varata modululu efectv Young a nanofranghe n raport cu raza r a franghe. Pentru E eq = 5MPa s G eq = 4.MPa, varata factorulu de perdere n raport cu raza nanofranghe este prezentata n fg.3... Factorul de perdere este maxm pentru r = nm s r = nm.
135 Fg Varata factorulu de perdere a nanofranghe n raport cu raza r a franghe. Varata factorulu de perdere n raport cu frecventa este prezentata n fg.3.., pentru o tensune de forfecare de.8 MPa ntre nanotub s matrce. Rezulta o energe nterfacala mare care este utlzata ca energe de dspare, s astfel avand un factor de perdere mare. Rezultatele demonstreaza o crestere de pana la % a amortzar structurale s cu 3% a rgdtat. Fg Varata factorulu de perdere n raport cu frecventa. Fg Sarcna transferata ca functe de unghul de rasucre.
136 3 Pentru a cuantfca magntudbea rasucr defnm unghul de rasucre ca rasucrea relatve ntre capetele franghe. Sarcna transferata este defnta ca forta axala dn centrul nanofranghe. Fg.3..3 arata varata sarcn ca functe de unghul de rasucre. Observam ca unghurle mc au un effect redus. Pentru (nu e rasucre) forta este de.8 9 J/A, ar pentru. sarcna transferata creste la J/A, aproape de de or ma mult. Acest calcul ndca ca se poate obtne un transfer ma bun de sarcna ncadrandu-ne ntre anumte lmte ale unghulu de rasucre. Matrcea de materal este alcatuta dn ceramca, ntrucat acest materal are propretat superoare de rezstenta la rupere (Chrou, Munteanu s Dumtru 8, Chrou, Munteanu s Beldman 8, Dumtru, Pop s Baldovn 8, Donescu, Chrou s Munteanu 8).. Fg (stanga) tensunea mede de contact [GPa] n raport cu forta de ndentare [N], (dreapta) dametrul are de contact [nm] ca o functe de forta de ndentare [N] n domenul elastc pentru un contact de ceramca-nanotub de carbon. Pentru o sfera neteda elastca de raza R, n contact cu o suprafata une nanofrangh nfnte, nesolctate, putem calcula forta necesara pentru separarea nanotuburlor de carbon de ceramca 3 F = πr γ, (3..45) unde energa de adezune γ este data de relata Dupré γ = γ + γ γ, (3..46) cu γ, γ, γ energle de suprafata ale nanotubulu de carbon, ale ceramc, precum s energa nterfete. Daca consderam cazul unu ndenter de dametru 5-nm, el poate genera presun n suprafata ndentata de crca zec de GPa, fara sa depaseasca lmta elastca s fara separarea suprafetelor. Fg.3..4 preznta tensunea mede de contact [GPa] n raport cu forta de ndentare [N] (stanga) s dametrul are de contact [nm] ca o functe de forta de ndentare [N] n domenul elastc (dreapta) pentru un contact de ceramca-nanotub de carbon, cu E = 85GPa, s ν =.4. Indenterul damant e caracterzat prn E = 6GPa, s ν =.7. Separarea suprafelor apare, n forma ncpenta, pentru o forta de ndentare de cca N Adaptarea metode nelocale Presach-Tteca la caracterzarea amortzar prn nanondentare
137 4 Prn construrea de compozte de ceramca n care s-au ncorporat nanotubur de carbon, rezstenta la rupere creste de la 3 la 5 or. In compozte, suprafetele materale au un rol semnfcatv. O suprafata materala este o nterfata ntre doua sau ma multe corpur sau faze, s are o structura mult ma bogata decat o suprafata geometrca. Daca prvm cu ajutorul unu mcroscop suprafata unu sold, aceasta este ma rugoasa la nvel atomc sau molecular, cu dverse neregulartat n toate drectle. Rugoztatea pare sa fe generata aleator ca o fluctuate cu lungme de unda mca, ar arhtectura atomca a suprafete este caracterzata prn prezenta la scara atomca a unu relef varat de forme, dmensune, unghur de contact s denstat. Este o structura localzata, stochastca cu dmensune nanoscopca, s este compusa dn sute de atom sau molecule. Aspertatle nanoscopce se formeaza pe suprafata metalelor, a ceramcelor s a materalelor pe baza de carbon. Dstrbuta lor poate f drectonata sau omogena n toate drectle, depnzand de natura suprafete. Dn perspectva nanoscopca, putem spune ca suprafetele solde, n partcular a metalelor, pot avea o morfologe complexa alcatuta dntr-o multtudne de clustere. Atrbutele fzce ale acestor suprafete sunt, prn urmare mult ma bogate decat cele mplcate de o topografe smpla s contnua. Cand suprafetele solde cu astfel de propretat la nanoscara formeaza o suprafata solda, de contact, sub aplcarea une forte, atunc ara aparenta de contact este consderabl dferta de ara reala de contact. Ara reala de contact se determna dn caracterstcle raspunsulu puternc localzat al aspertatlor la sarcn exteroare. Pentru cele ma multe materale, campul de tensune este sufcent pentru a determna campul deformatlor elastce. Daca forta aplcata este sufcent de mare, pot apare deformat plastce s curgerea plastca n regunea ma putn coezva a aspertatlor materalulu, transformand formele conce n suprafete plane s creand astfel jonctun nterfacale. In portunle unde aspertatle sufera curgere plastca, se dezvolta dslocat care se pot multplca s creste n raport cu forta aplcata. Evdentele expermentale au aratat ca la ssteme precum lthum fluorde, dslocatle de la suprafata s n regunle de langa suprafata se pot propaga n nteror s coalescenta lor localzata poate produce zone slabte n materal, unde pot nuclea s multplca fsur s golur. Aceste fsur se pot propaga ar spre suprafata, transformand aspertatle n partcule slabe. Pe de alta parte, daca, sub o forta aplcata, o aspertate dura ca cea de tungsten (W) ntra n contact sold cu o suprafata moale s plata cum ar f plumbul (Pb), materalul se afla n echlbru numa daca ara de contact suporta sarcna aplcata. In aceste condt, daca aspertatea se msca tangental, apare fenomenul de forfecare n zonele de slaba coezune, n tmp ce aspertatea dura n contact cu o suprafata dura produce fsur de suprafata Aplcand, pentru frangha dn fg...9, metoda reducer pseudosferce (paragraf. s 3), obtnem urmatoarele rezultate:. coefcent de amortzare.35,. modul Young GPa. Fg preznta functa Tteca n raport cu raza franghe s unghul de rasucre. Se observa ca maxmle apar pentru raze mar s pentru unghur de rasucre mc. Aceste maxme sunt proprotonale cu capactatea de amortzare a franghe.
138 5 Fg Functa lu Tteca. 4. O dee noua: auxetctatea aplcata nanocompoztelor n scopul crester capactat de amortzare Evans a numt aceste materale "auxetce" dn cuvantul grec auxetos, care înseamnă creştere. Prmul materal auxetc sntetc a fost fabrcat în anul 987 de Roderck Lakes de la Unverstatea dn Iowa. Roderck Lakes a fabrcat spume poluretane ordnare, care constau dn celule de tp fagure de mere de formă hexagonală, umplute cu aer ş având dmensunea în jur de mm (fg.4.). De cele ma multe or un coefcent Posson negatv conduce la constante elastce ş rgdtăţ negatve, în acest ultm caz materulul fnd nstabl. Coefcentul lu Posson poate f negatv ar constantele elastce pot să fe totuş poztve. Acesta este cazul consderat în această parte a lucrăr. În laboratul lu Ken Evans de la Unverstatea dn Exeter a fost descopert în anul un alt materal auxetc cu mcrostructură care se gaseşte sub formă comercală ş anume un polmer polytetrafluorethylene (PTFE). Anumţ polmer sntetc foarte bne cunoscuţ sunt de asemenea auxetc. Oamen de ştnţă cunosc acest materal de peste de an, dar nu -au dat atenţe, consderându-l ca un accdent sau o curoztate. Acest materal exstă în mod natural: ugerul vac, anumte roc ş mnerale, polmer, spume, oase ale anmalelor ş ale omulu. Pentru un materal zotrop, coefcentul lu Posson a valor de la -. la +.5, conform consderaţlor termodnamce asupra energe de deformaţe dn teora elastctăţ. Love a prezentat în 96 un exemplu de crstal cubc de prtă cu coefcentul lu Posson negatv -.4 (fg. 4.). Comportamentul dnamc al materalulu auxetc se dstnge de comportamentul unu materal tradţonal prn aceea că la întndere el expandează în loc să se subţeze. Comparatv cu materalele tradţonale, materalul auxetc este ma rezstent, are capactate de amortzare ma mare (Rosaks, Runa ş Lakes 993), Munteanu et al. (7a).
139 6. Fg. 4.. Un materal auxetc compus dn celule de tp hexagon sau sferă. Fg.4.. Materalul auxetc se înconvoae în două drecţ fără ca ntegrtatea structur să fe afectată (Lakes 99). Fg.4.3. Prezentarea schematcă a materalulu neauxetc ş a materalulu auxetc (Lakes 987).
140 7 Materalul auxetc se poate deforma prn încovoere în două drecţ, având forme cu curbură dublă de mare nteres în aeronautcă, autovehcule ş construcţ (fg.4.). În dagrama 4.3 se prezntă schematc o bandă elastcă neauxetcă cu coefcentul Posson poztv, care se subţază la întndere. În schmb, banda auxetcă cu structură fagure de mere sau sold celular expandează lateral la întndere. Propretatle mecance ale spumelor se pot descre n prma aproxmate prn prsma propretatlor soldelor celulare.eralel auxetce termoplastce PU PE se obtn dn spume 3 polyurethane cu celule deschse avand 3 35 pores/n. s denstatea.7 gr/cm (Bezaz s Scarpa 7). Fgs se preznta mcrostructura dfertelor tpur de spume. Fotografle au fost facute cu un mcroscop optc (Torno 8). Spuma conventonala (fg. 4.3) are por cu un dametru de crca 9 µ m. Procedeul tehnologc prn care o spuma neauxetca poate f transformata n spuma auxetca, se bazeaza pe reducerea dmensunlor porlor (a celulelor) prn compresune n dferte drect. Se poate obtne astfel o spuma cu aceeas denstate (fg.4.4). Versunea auxetca a spume este prezentata n fg.4.5. Varata coefcentulu Posson n raport cu deformata la compresunepentru spumele analzate este prezentata n fg Spuma conventonala are un coefcent Posson egal cu.5, pentru o deformate la compresune de %. Coefcentul Posson descreste rapd cu cresterea deformate la compresune de la 6% la 8%, ajungand negatv. Spuma cu aceeas denstate are un coefcent Posson aproape nul pentru o deformate de crca 8%. La randul e, spuma auxetca admte un coefcent Posson negatv egal cu -.85 pentru o deformate de la % la 5%, s admte un un coefcent Posson aproape nul pentru o deformate de 55%, s un coefcent Posson poztv egal cu.33 pentru o deformate de 8%. Curbele consttutve pentru spumele analzate sunt prezentate n fg. 4.7 (Chrou, Munteanu s Dumtru 8, Chrou, Munteanu s Beldman 8, Dumtru, Pop s Baldovn 8, Donescu, Chrou s Munteanu 8).. Fg Spuma conventonala.
141 8 Fg Spuma cu aceeas denstate. Fg Spuma auxetca.
142 9 Fg.4.6. Varata coefcentulu Posson n raport cu deformata la compresunepentru spumele analzate. Fg Curbele consttutve pentru spumele analzate.
143 4.. Modelarea materalelor auxetce. Leg consttutve nelocale Analzam comportarea materalelor auxetce cu ajutorul teore elastctat de tp Cosserat (paragraf.) care ntroduce grade de lbertate care nu exsta n teora clasca a elastctat, s anume rotatle partculelor s cuplele de tensune pe untatea de are. Scopul nostru este se a evalua modulul de elastctate al lu Young pentru o placa sandwch de tp fgure de mere realzat dntr-un materal auxetc (Munteanu 6, Munteanu s Mosnegutu 6). Consderam o placa sandwch cu mez fgure de mere alcatut dntr-un materal auxetc supus la ntndere s compresune, avand modulul lu Young.55 GPa, denstare = 837 kg/m 3, s coefcentul Posson = -.5. Matrcea este dn alumnu cu modulul de elastctate 9 GPa, denstate = 7 kg/m3, s coefcent Posson.34 (fg.4..). Materalul auxetc este are o structura de tp network consttuta dn celule re-entrant sau hexagoane auxetce (fg.4..). Teora clasca a elastctat nu permte analza deformate unu materal auxetc. Materalul auxetc este un materalc chral (noncentrosmetrc) care se comporta zotrop la o rotate a axelor de coordonate dar nu s n raport cu o nverse. De aceea, aceste materale se comporta caltatv dfert n comparate cu soldele zotrope (Chrou, Munteanu s Dumtru 8, Chrou, Munteanu s Beldman 8, Dumtru, Pop s Baldovn 8, Donescu, Chrou s Munteanu 8).. Fg. 4...Placa sandwch de tp facure de mere cu mez auxetc. Fg.4... Structura auxetca.
144 Efectele chrale nu se pot modela n cadrul elastctat clasce deoarece tensorul constantelor elastce care este de ordnul patru nu se schmba la o converse. Legle consttutve ale unu materal anzotrop non-centrosmetrc Cosserat sunt date de (..8) and (..9) σ = λe δ + ( µ + κ) e + κε ( r ϕ ) + Cϕ δ + C ϕ + Cϕ, (4..) kl rr kl kl klm m m r, r kl k, l 3 l, k m = αϕ δ + βϕ + γϕ + Ce δ + ( C + C ) e + ( C C ) ε ( r ϕ ), (4..) kl r, r kl k, l l, k rr kl 3 kl 3 klm m m unde ekl = ( uk. l + ul, k ) este vectorul macrodeformate, λ s µ sunt constantele elastce ale lu Lamé, κ este modulul de rotate Cosserat, α, βγ,, modul gradent de rotate Cosserat, s C, =,,3 sunt constantele chrale asocate cu non-centrosmetra. Pentru C = se regasec ecuatle elastctat mcropolare zotrope. Pentru α = β = γ = κ =, (4.) se reduce la ecuatle consttutve ale elastctat lnare sotrope.dn consderente termomecance avem restrctle 3λ + µ + κ, µ + κ, κ, 3α + β + γ, γ β γ, γ, sc, C, C 3 negatce sau poztve. In (4.) σ kl este tensorul tensune, m kl este tensorul cuple de tensune, u este vectorul deplasare, ϕ k este vectorul de mcrorotate, care n elastctatea Cosserat este cnematc dstnct de vectorul macrorotate rk = ε klmum, l, s ε klm este smbolul de permutare. Reamntm ca ϕ k se refera la rotata punctelor, ar r k la rotata punctelor nvecnate. Legea de mscare este (..) σ ρ =, m, +ε σ ρϕ j =, (4..3) kl, k ul unde ρ este denstatea s j mcronerta. Condtle ntale sunt date de (,,,) (,, ) rk r klr lr k u xyz = u xyz, ϕ ( xyz,,,) =, =,,3, mj ( x, y, z,) =, σ j ( xyz,,,) =, = j 3. (4..4) Fara a perde generaltatea, analzam cazul D n care toate canttatle depnd doar de x s z. Fe F = { σkl, mkl, uk, ϕ k, k, l =,,3} un set de tensor asmetrc σ kl, m kl, e kl, k, l =,,3, s vector u k, ϕ k. Numm F stare elastodnamca care satsface (4..) (4..4). Se poate demonstra urmatoarea teorema (fara demonstrate) (.Teodorescu, Badea,.Munteanu s. Onsoru 5): TEOREMA. Legea bunvoca cu uˆ = K ( u + u u ), 3 K 3 ϕ ˆ = ( ϕ + ϕ ϕ ), K uˆ = K ( u + u u ), uˆ = K ( u + u u ), 3 K K 3 ϕ ˆ = ( ϕ + ϕ ϕ ), ϕ ˆ = ( ϕ + ϕ ϕ ), ( C + C ) ( C C ) 4( µ +κ)( γ β ), 3 = 4( µ +κ)( β + γ ), 3 K = (3 C + C + C3) K = 4(3λ+ µ +κ)(3 α+β + γ ), transforma starea elastodnamca F n alta stare elastodnamca
145 ˆF = { σˆ, ˆ, ˆ, ˆ kl mkl uk ϕ k, k, l =,,3}, compusa dn tensor smetrc σ ˆ kl, m ˆ kl, e ˆkl, k, l =,,3, s vector u ˆk, ϕ ˆ k, care satsfac acelas set de ecuat. Starea ˆF se poate descompune n Fˆ = Fˆ ˆ + F, unde F ˆ = { σˆ, σˆ ˆ ˆ ˆ ˆ ˆ 3, σ33, m, u, u3, ϕ}, F ˆ = { σˆ, mˆ ˆ ˆ ˆ ˆ ˆ, m3, m33, u, ϕ, ϕ3}. Dupa o aranjare potrvta a termenlor n ecuatle de mscare se obtn urmatoarele ecuat n uˆ = ( uˆ ˆ ˆ, u, u3) s ϕ ˆ = ( ϕˆ ˆ ˆ, ϕ, ϕ 3) ( λ+ µ +κ) uˆ ( µ +κ) K uˆ +κ( K ) ϕ = ρu ˆ, ˆ ( α+β + γ) ϕˆ γk ϕ ˆ +κ( K ) uˆ κ( K ) ϕ ˆ = ρϕ j ˆ, (4..5) cu un coefcent de cuplare K defnt astfel ( C + C + C3) K = +. (4..6) ( λ+ µ +κ)( α+β + γ ) Observam ca (4..5) se pot descompune n doua setur de ecuat fecare pentru ˆF, s respectv ˆF. Acum ne concentram asupra setulu de ecuat pentru ˆF. Introducem canttatle admensonale (Teodorescu,.Munteanu s.chrou 5) unde ω ω ω x = x, z = z, v ˆ = u, =,, c c c c κ( K ) m ˆ j = m j ω = γω K ρj Ecuatle (4..5) devn λ+µ K = ρc s v + ( a ) v + a v s φ = v, *, xx 3, xz, zz 4, z s + s v + ( a ) v + a v + s φ = v, * 3, zz, xz 3, xx 4, x 3 s + s, xx, zz Kω ( v, z v3, x ) ωγ s4 µ K ˆ φ = ϕ *, t =ω t, σ j = σ ˆ j, ρω j µ K λ+ µ +κ c =, j =,3 ρ c µ φ + φ φ + = φ, (4..7) s κ( K ) +µ K = ρc κj( K ) ω * 3 = µ Kc c κ K ω = ωγk s s γk 4 = ρ jc s * s3 ( ) a =, s4 =, K. s + s s + s Condtle ntale (4..4) devn v ( xy,,) = v, =, 3, φ ( xy,,) =. (4..8) Pentru a rezolva (4..7) s (4..8) aplcam tehnca transformarlor Laplace s Fourer.
146 3 Astfel avem { v( xzp,, ), φ ( xzp,, )} = { v( xzt,, ), φ ( xzt,, )}exp( pt)d t, =,3, { v ( ξ, z, p), φ ( ξ, z, p)} = { v ( x, z, p), φ ( x, z, p)}exp( ξ x)d x, =,3. p ξ( a ) s v v v, * 4 = [ ξ + ] φ a s + s a a p v a v s a v, * 3 = [ ξ + ] 3 + ξ 4φ + ξ( ) s+ s c c φ = µ v ξ µ v 3 +Γφ, ωγ ωγ c κ( K ) µ p Γ=ξ + + ωγk s4. (4..9) Problema de valor propr se obtne consderand solutle ecuatlor (4..(9) sub forma W ( ξ, zp, ) = X( ξ, p)exp( qz), (4..) W( ξ, z, p) = { v, v, φ }. Obtnem ecuata caracterstca cu 3 cu q λ q +λ q+λ =, (4..) 3 3 p c µ s λ = ξ + +, * 4 ps Kω a s4 ωγa * p cµ s4 λ = ξ + Kω + ps + + ξ ( ps + ξ ) + ( p )( ), s +ξ ps + a ξ s4 a ωγa a * p s4 cµ p λ 3 = ( ξ + ps )( ps + a ξ ) +ξ + Kω ( ps +ξ ) ξ, ps =. a s4 a ωγ s + s Radacnle aceste ecuat (4..), q, =,,3, sunt reale s poztve. Vectorul propru X ( ξ, p) este dat de aq aq X (, ) ξ p = b, X (, ) ξ p = bq ξ ξq * c µ s4ξ a =ξ( a )( Kξ q ) ω γ, =,,3,
147 4 ( ξ) b = ( ξ + ps) Kξ + a q q K * cµ s4q ( ξ + ps) q +, ωγ p Kξ =ξ + Kω +, s4 c µ = ( q ( )) ξ + ps ωγ Astfel, (4..) devne 3 =, =,,3. (4..) W ( ξ, z, p) = BX( ξ, p)exp( q( ξ, p) z), (4..3) unde B, =,,3 sunt constante arbtrare. Dn (4..3) rezulta campul transformat al deplasarlor, mcrorotatlor s tensunlor v ( ξ, z, p) = aqbexp( q) z) + aqbexp( qz) + aqbexp( qz), (4..4) v ( ξ, z, p) = bb exp( q ) z) + b B exp( q z) + b B exp( q z)}, (4..5) φ ( ξ, z, p) = ξ { B exp( q z) + B exp( q z) + B exp( q z)}. (4..6) 3 3 Pentru a obtne necunoscutele B, =,,3, aplcam transformarle Laplace s Fourer ecuatlor (4..8). Functle transformate depend de z, s de parametr p s ξ, avand forma f( ξ, z, p). Pentru a obtne acesata functe f( x, z, t ), se aplca transformarea Fourer nversa f ( x, z, p) = exp( ξx) f ( ξ, z, p)d ξ = {cos( ξx) fe sn( ξx) f}d ξ, π π (4..7) unde f e s f sunt partle pare s mpare ale functe f( ξ, z, p) f ( x, z, p) poate f prvta ca transformata Laplace ( ) C + C. Pentru valor fxate ξ, x s z, g p a une funct gt (), defnta astfel g( t) = exp( pt) g( p)dp π, unde C este un numar real arbtrar, ma mare decat toate partle reale ale sngulartatlor functe g( p ). Pentru p = C + y avem exp( Ct) g t ty g C y y π. ( ) = exp( ) ( + )d Pentru modulul de elastctate al lu Young avem formula clasca pentru un materal zotrop. Suntem nteresat sa cunoastem nfluenta celor 4 constante Cosserat (modul de rotate, 3 modul gradent de rotate) s a celor 3 constante elastce chrale aupra valor modululu lu Young. Pentru aceasta utlzam cunoscutul prncpu varatonal al lu Hashn s Shtrkman (96). Placa este un materal ortotrop fnd caracterzat de doua module de elastctate E x n drecta x s E y n drecta y, de do coefcent Posson ν xy s ν yx, n drecta celu de al dolea ndce la o ntndere unaxala n drecta prmulu ndce Exν xy = Eyν yx.
148 5 Pentru a confrma teora consderam, ma nta, o bara cu sectune crculara, de dametru d = 3 m, lungme l = 5 m, alcatuta dntr-un materal auxetc (fg. 4..). Constantele utlzate sunt: 9 3 Denstate ρ=.5 kg/m, Coefcent Posson ν =.. Relata dntre constantele de materal s ν, este extrasa dn valorle expermentale prvnd modulul lu Young s modulul de forfecare (modul Young E = 59.93MPa, modul forfecare µ = 49.96MPa ). Introducem, modul de materal redus K K =, K K K =, K K K =, (4..8) K unde K, K s K sunt dat de K ( C + C ) = 4( µ +κ)( β + γ ), 3 K K ( C C ) = 4( µ +κ)( γ β ), 3 (3 C + C + C ) = 4(3λ+ µ +κ)(3 α+β + γ ). 3 Dependenta modullor redus de materal de coefcenul Posson ν, este reprezentata n fg Pentru o valoare data ν, este posbl sa determnam un set de valor permsble pentru constantele de materal., negatve sau postve. Fecare set de constante poate reprezenta o posbla structura cu propretat auxetce demonstrable {capactate de amortzare s rezsternta). Intrebarea care se pune cum anume pot f aceste matreale sntetzate. Fg Varata modullor redus n raport cu coefcentul Posson.
149 6 Coefcentul lu Posson depnde de deformate. Varata coefcentulu ν n raport cu deformata axala la ntndere s compresune este reprezentata n fg Lnle solde sunt consstente cu rezultatele expermentale. Lnle ntrerupte se refera la cazul classc zotrop s lnar ( α=β = γ =κ=, C = C = C3 = ) s respectve soldulu zotrop mcropolar ( C = C = C3 = ). Varata deplasar v ( x ) s a tensun 3 σ ( x) 33 pentru t = s z = sunt reprezentate n fg.4..6, s respectv fg.4..7, pentru ν =.. Fgs s 4..7, reporteaza un rezultat surprnzator. Foecare unda este compusa dn doua unde care se propaga cu vteze dferte. Unda rapda este unda uzuala dn teora mcropolara theory. A doua unda este ma lenta. Astfel de unde au fost rarortate expermental (Lake 983). Fg Dependenta coefcentulu Posson n raport cu deformata axala.
150 7 Fg Varata deplasr v 3 n raport cu x. Fg Varata tensun σ33 n raport cu x. In contnuare determnam modlul lu Young, utlzand aceeas teore pentru structura reprezentata n fg Ca rezultat obtnem valorle maxme s mnme ale modululu lu Young
151 8 E = F( λ, µ, λ, µ ) + E, E = F( λ, µ, λ, µ ) + E, (4..9) x a a p p x y a a p p y cu λ a s x(max) ( ) E = + p Ex, E x(mn) = ( q + p ) Ex, (4..) 6 6 λ, µ constantele Lamé ale materalulu auxetc. Functa µ a constantele Lamé, s p p F( λ a, µ a, λ p, µ p) se determna numa numerc. Valorle maxme s mnme ale modululu lu Young sunt prezentate n fg Lna ( x x) repreznta valoarea maxma a lu E x (3 GPa), lna ( y y ) repreznta valoarea maxma a lu E y (3 GPa)), lna 3 ( x x) este valoarea mnma a lu E x (3.5 GPa), lna 4 ( y y ) repreznta valoarea mnma a lu E y (3.4 GPa), lna 5 ( E maxma a modululu E pentru alumnu (9 GPa), ar lna 6 ( E modululu de elastctate pentru materalul auxetc (.55 GPa). E) este valoarea E) este valoarea mnma a Fg Valorle lmta ale modululu lu Young pentru placa sandwch. Se observa performantele unu astfel de compozt bazat pe un materal auxetc- rezstenta mare la ntndere s compresune. Valorle mnme ale modululu de elastctate sunt ma mar decat valoarea modululu materalulu auxetc, ar valorle maxme depasesc valoarea modululu pentru alumnu. Astfel de compozte pot f utlzae n dferte aplcat ngnerest precum ndustra aerospatala s avatca, ssteme mcroelectromecance (MEMS) s steme nanoelectro mecance (NEMS), datorta reztente mar s a greutat lor reduse (Chrou, Munteanu s Dumtru 8, Chrou, Munteanu s Beldman 8, Dumtru, Pop s Baldovn 8, Donescu, Chrou s Munteanu 8).
152 9 4.. Analza capactat de amortzare a materalelor auxetce Geometrle deale pentru structura auxetca cu mare capactate de amortzare sunt prezentate n fg Aceste structur suporta deformat mar s au o mare capactate de dspare a energe de deformate (Teodorescu, Munteanu, Chrou, Dumtru s.beldman 8, Chrou, Munteanu, D.Dumtru, Beldman s.secara 8, Munteanu, Chrou, Dumtru, s Beldman 8, Chrou 8, Munteanu, Dumtru, Donescu s.chrou 8). Asa cum s-a dscutat n paragraful 4., coefcentul lu Posson depnde de deformate. Varata coefcentulu ν n raport cu deformata axala la ntndere s compresune a fost reprezentata n fg Lnle solde sunt consstente cu rezultatele expermentale. Lnle ntrerupte se refera la cazul classc zotrop s lnar ( α=β = γ =κ=, C = C = C3 = ) s respectve soldulu zotrop mcropolar ( C = C = C3 = ). In tmpul deformatlor suprafata probe spume auxetce se deformeaza neregulat n sensul ca anumte ar se deformeaza ma mult decat altele, cum reese dn fg. 4.. (Smth, Grma s Evans ). In fg.4..3 sunt prezentate dstorsonar ale structur deformate prn torsune. Fg.4... Geometr deale pentru structura auxetca. Fg Sectune prn suprafata une materal auxetc, cu deformat neregulate.
153 Fg Sectune prn suprafata une materal auxetc cu deformat neregulate. Am studat probe conventonale neauxetce cu sectune transversala patrata de dmensun 5 mm pe 5 mm, s lungme 75 mm. Probele auxetce au dmensunle 35 mm pe 35 mm s 5 mm lungme. Aceste probe au fost supuse la compresune 8,6 % n fecare drecte pana s-au obtnut dmensunle 5mmpe 5mm s lungme 75mm. S-au ncalzt apo probele la C tmp de mn ntr-un cuptor, apo s-au ract s framantat cu mana cateva momente, dupa care s-au ncalzt dn nou n cuptor tmp de mn. Proba s-a ract s apo a fost ncalzta dn nou la C tmp de o ora (conform procedeulu tehnologc Chan s Evans 997). Spuma a fost examnata cu un mcroscop stereo. Ambele probe conventonala s auxetca, au aceleas dmensun. Au fost supuse la teste pe o masna unversala de ncercar (Shmadzu AGS-kN D). Toate probele au aratat un comportament vscoelastc. Deformatle au fost masurate cu un extensometer vdeo (Vdeoextensometer, Messphysk GmbH, Austra). S-au studat aceste probe teoretc, conform teorlor prezentate nante (materalele au fost modelate cu teora noncentrosmetrca de tp Cosserat) (Chrou, Munteanu s Dumtru 8, Chrou, Munteanu s Beldman 8, Dumtru, Pop s Baldovn 8, Donescu, Chrou s Munteanu 8). Rezultatele sunt prezentate n fg Se observa o buna concordanta ntre teore s experment. La ncarcar cclce de ntndere s compresune se obtne o comportare hsteretca, asa cum reese dn fg Se observa cresterea capacta de amortzare la materalul auxetc, fata de cel conventonal. O analza a capactat de amortzare a nanocompoztelor arata ca atat nanotuburle de carbon cat s materalele auxetce, nglobate n matrcea de materal, conduc la o crestere semnfcatva a amortzar. Aceste compozte au mare aplcabltate n controlul vbratlor s a zgomotulu.
154 Fg Curba tensune-deformate pentru proba conventonala s auxetca (teore s exeperment). Fg Comportarea hsteretca a probelor conventonala s auxetca.
155 5. Nanocompozte pe baza de nanotubur de carbon În acest paragraf prezentăm o metodă cuas-contnuă QC-GFG (secţunea 3.4) pentru determnarea unor leg consttutve pentru compoztele cu nanotuburle de carbon (Munteanu ş Chrou 5). Ne oprm asupra nanotuburlor de carbon, cu secţune perfect crculară ş cu un sngur perete de grosme,34nm. Presupunem că nanotubul este supus la întndere. Aplcăm o metodă nversă în încercarea de a lega nanoscara metrcă de scara macroscopcă a corpulu contnuu, cu ajutorul FEM ş a unu algortm genetc. La scară atomcă, comportarea nanotubulu de ccarbon este descrsă de mecanca cuantcă (Wang, Tomanek and Bertsch 99, Curtn ş Mller 3). Energa totală este o funcţe de coordonatele atomlor care reprezntă gradele de lbertate electronce. Funcţonala energe este mnmzată în raport cu aceste grade de lbertate pentru coordonate fxate. a Consderăm că energa totală atomcă E se exprmă ca în teora Stllnger Weber SW (Stllnger ş Weber (985), ca o sumă a energlor tuturor atomlor, care într-o formulare a nteracţunlor dntre ş 3 corpur este dată de (3.3.4) a E = E = w V( rj) + w V3( rj, rk,cos θjk) j 6, (5.) j, k (, j) unde w ş w sunt ponder necunoscute, r j este dstanţa dntre atom ş j, ar θ jk este unghul defnt de trpleta de atom, j ş k. Forţele corespunzătoare fecăru atom, în absenţa a forţelor externe, sunt date de f = E, r. Canttăţle necunoscute w ş w se determnă ma târsu dn rezultate expermentale. a Energa de deformaţe W se obţne prn normalzarea funcţe E în raport cu volumul atomc Ω W a = E. (5.) Ω Presupunem că regunle contnue dn materal nu conţn deformaţ mar ş nc efecte nelastce. De asemenea, presupunem că exstă o funcţe denstate de energe de deformaţe W, astfel încât în volumul dv care înconjoară un punct materal X, este dată de W ( X )dv. În consecnţă, energa potenţală a materalulu se calculează ca o ntegrală pe volumul Ω corpulu este dată de Gradentul deformaţe devne c E = W( X)dV. (5.3) Ω dx F( X) = = I+ u( X), (5.4) dx unde este calculat în raport cu X. Deformaţa lagrangană deformaţlor nfntezmale devne ( T e = F F I ), în cazul ( ( ) T ε= u + u ). (5.5) Pentru a determna starea de deformaţe ş de deplasare a nanotubulu de carbon, în condţ de încărcare cu forţe exteroare, mnmzăm energa E c, cu ajutorul metode elementelor fnte
156 3 (FEM). Elementele fnte (FE) se bazează pe ntroducerea unu set de puncte X j (nodur j ) în care se calculează deplasărle U j = ux ( j). Deplasărle în alte pozţ ale corpulu decât în aceste nodur, se calculează prn nterpolarea deplasărlor nodale în pozţle dorte. Dacă gradele de lbertate sunt deplasărle nodale, FEM mpune o constrângere cnematcă a deformaţe materalulu. Energa totală în regunea contnuă a materalulu se scre ca o sumă a energlor elementelor µ, cu N numărul de elemente dn regunea Ω µ e N e c E WV d E µ, Eµ = W( X)dV, W ( X) = W( F( X)), (5.6) = = cu W date de (5.3). Deplasărle elementelor se pot scre sub forma Ω µ N u( X) = U S ( X), j= j j Ωµ N F( X) = I + U j Sj( X). (5.7) c E unde S j ( X ) sunt funcţle de formă. Forţa dn nodul se calculează dn. U În metoda QC, ca ş în alte metode cuplate, se face o descrere atomstcă pentru anumte regun dn materal ş o descrere contnuă pentru alte regun dn materal. Regunea de tranzţe sau frontera dntre regunea atomcă ş regunea contnuă (nterfaţa tampon, sau pad) necestă o atenţe deosebtă. Această nterfaţă este modelată în aşa fel încât nteracţunle nelocale dntre atom să fe luate în consderaţe. O astfel de nterfaţă tampon este reprezentată în fg. 5. (Curtn ş Mller). Atom gr dn partea dreaptă a nterfeţe dn fgură concd cu un set de nodur FE dn zona contnuă. Atom dn nterfaţa atomcă formează o zonă care desparte regunea atomcă de cea contnuă. Se poate ca o parte dn aceşt atom să concdă cu nodurle dn reţeaua FE. În contnuare folosm ndc A, I ş P pentru a desemna atom dn zona atomstcă, dn nterfaţa atom-nod ş dn nterfaţa pad. Energa potenţală totală E este obţnută prn sumarea energlor corespunzătoare regun atomstce, padulu ş domenulu contnuu, conform formule (5.5) cu contrbuţa separată a nteracţunlor dntre ş 3 corpur () (3) A I P A I P µ µ, (5.8) η ( AI, ) η ( AI, ) µ j= E = E ( r, r, r ) + E ( r, r, r ) + w E unde < w µ < este funcţa pondere care este egală cu untatea pentru toate elementele care nu sunt legate de nterfaţă. Pentru elemente trnghulare, avem w µ =, pentru un element cu două 3 nodur pe nterfaţă, şî w µ =, pentru elemente cu un sngur nod pe nterfaţă. 3
157 4 Fg. 5. Interfata tampon ntre zona contnua s zona atomca (Curtn ş Mller). Energa potenţală QC conduce la un rezultat cu caracter nefzc în regunea de tranzţe. Orgnea acestor forţe fantomă stă în presupunerea de localtate în zona contnuă ş de nepotrvrea conceptelor local/nelocal în zona de tranzţe. Pentru a remeda această stuaţe, utlzăm modelul QC-GFC, în care se ntroduc nşte încărcăr moarte care sunt aplcate nodurlor ş atomlor dn sstem, pentru a anula forţele fantomă g. Modelul QC-GFC consderă următoarea exprese pentru energa totală în domenul atomstc = 3 g E E w g u, (5.9) unde ultmul termen este lucrul mecanc al acestor sarcn moarte în tmpul deformaţe, ş w 3 o pondere necunoscută. Menţonăm că forţele fantomă g, se pot calcula pentru starea nţală de refernţă a sstemulu. În cazul încărcărlor unforme, numărul atomlor reprezentatv nu este unc. De acest număr depnde totuş reducerea gradelor de lbertate ale sstemulu, fără deterorarea rezultatelor probleme. Astfel, ne propunem să determnăm numărul optm de atom reprezentatv R, ale h căror pozţ vor consttut gradele de lbertate. Pozţle x unu atom arbtrar pot f obţnute prn nterpolare h x = N ( X ) x, (5.) unde Nα ( X ) sunt funcţle de formă centrate în atomul reprezentatv α, care este un nod fnt ataşat pozţe nedeformate X a atomulu. Energa potenţală E este calculată dn (4.6.9), care depnde numa de pozţle atomlor reprezentatv. Echlbrul statc se obţne prn mnmzarea energe totale α α α
158 5 N R α α, (5.) = α= E = E = n E cu n α ponder necunoscute, care pot f nterpretate ca fnd numărul de atom reprezentat de atomul reprezentatv α. Desgur, prn problema nversă pe care vrem să o construm dorm să determnăn ş ponderle necunoscute w, w, w 3 ş n α, α=,...,r. În consecnţă, necunoscutele probleme sunt numărul atomlor reprezentatv R, ş ponderle necunoscute n α, α=,...,r, w, =,,3. Aceste necunoscute sunt determnate dn condţa ca dferenţa dntre rezultatele teoretce ş rezultatele smlare, expermentale, să fe mnmă. Acest mnm este determnat cu un algortm genetc. Notăm cu p = { Rn,, n,..., nr, w, w, w3} necunoscutele în număr de (4 + R). Dscretzăm aceste necunoscute cu valorle R, n,..., nr, w,..., w3. Setul de parametr pentru o soluţe arbtrară p= { R, n,, n,..., n, w,... w }, (5.),,, R, R, j 3, j3 este caracterzat de numărul (Tanaka and Nakamura 994) M = ( ) I... I J J J + ( ) I... I J J J j, (5.3)... R R 3 R 3 3 unde I, I,... sunt numărul total de valor dscrete corspunzător fecăru parametru. Acest număr este calculat pornnd de la un set de parametr nţal p= p. Ca funcţe obectv alegem suma dferenţelor dntre rezultatele măsurate dn curba expermentală tensune-deformaţe pentru câteva exemple de nanotubur de carbon cu un sngur perete, cu dferte raze ş chraltate W M m m ( ), (5.4) m= = σ σ m unde σ este deformaţa măsurată expermental în punctul m dn dagrama expermentală σ ε, m ş σ este deformaţa calculată în acelaş punct m. M este numărul de puncte dn dagrama σ ε. Funcţa ftness F este defntă sub forma unde W F =, (5.5) W W M m ( ). (5.6) m= = σ Crterul de convergenţă este defnt prn expresa admensonală Z W Z = log. (5.7) W Presupunem că grosmea nanotubulu este h =,34nm, ş numărul de atom pe lungmea L este N = πρlr, unde R este raza tubulu ş ρ denstatea. Utlzăm rezultatele expermentale date de Qan, Wagner ş Lu (), Yu et al. (), ş Shenoy (998, 3).
159 6 Pentru toate exemplele, numărul populaţlor este 5, coefcentul de reproducere, numărul de puncte crossovers, probabltatea de mutaţe,5, ş numărul maxm de generaţ 3. Calculăm energa de deformaţe pe atom de carbon în raport cu raza forme sale crculare relatv la graft, pentru o structură stablă pentru formele armchar (,), chral (,6), ş zgzag (7,), care au dametrul secţunlor transversale comparable. Rezultatele sunt arătate în Fg.5.a,b,c, pentru tubul chral (,6), tubul zgzag (7,), ş respectve pentru tubul armchar (,). Rezultatele expermentale sunt prezentate în aceste fgur prn pătrăţele. Observăm dn fgur o bună potrvre dntre rezultatele teoretce, obţnute în urma aplcăr algortmulu genetc ş rezultatele expermentale date de Qan, Wagner ş Lu (), Yu et al. (), ş Gao, Cagn ş Goddard (998). Legle consttutve la întndere sunt prezentate în Fg. 4.6.a,b,c, pentru tuburle zgzag (7,), b) armchar (,), ş respectv, chral (,6). Rezultatele expermentale sunt prezentate în aceste fgur prn cerculeţe. Observăm, de asemenea, o bună potrvre dntre rezultatele teoretce ş rezultatele expermentale date de Qan, Wagner ş Lu, ş Yu et al. Pentru tubul armchar s-a consderat a = 6,78A 3, denstatea ρ=.34g/cm, pentru tubul chral a = 6,5A ş 3 ρ=,4g/cm, ş pentru tubul zg-zag a = 6,5A 3, şρ=,34g/cm (Gao, Cagn and Goddard). Curbele consttutve obţnute sunt foarte apropate de rezultatele expermentale. Pentru modul elastc Young, în drecţa axe tuburlor, calculaţ dn dervata a doua a energe potenţale conform cu relaţa (3..), se obţn valorle E (,) = 65,33GPa, E (,6) = 688,37GPa ş E (7,) = 65,43GPa, pentru cele tre exemple consderate.
160 7 Fg. 5.. Energa pe atom de carbon pentru nanotuburle a) chral (, 6), b) zgzag (7,), s c) armchar (,). In paragraful 3. s-a studat nanofrangha alcatuta dn nanotubur de carbon. Matrcea de materal este alcatuta dn ceramca, ntrucat acest materal are propretat superoare de rezstenta la rupere. Varata factorulu de perdere n raport cu frecventa este prezentata n fg.3.., pentru o tensune de forfecare de.8 MPa ntre nanotub s matrce. Rezulta o energe nterfacala mare care este utlzata ca energe de dspare, s astfel avand un factor de perdere mare. Rezultatele demonstreaza o crestere de pana la % a amortzar structurale s cu 3% a rgdtat (Teodorescu, Munteanu, Chrou, Dumtru s.beldman 8, Chrou, Munteanu, D.Dumtru, Beldman s.secara 8, Munteanu, Chrou, Dumtru, s Beldman 8, Chrou 8, Munteanu, Dumtru, Donescu s.chrou 8). Prn construrea de compozte de ceramca n care s-au ncorporat nanotubur de carbon, rezstenta la rupere creste de la 3 la 5 or. In compozte, suprafetele materale au un rol semnfcatv. O suprafata materala este o nterfata ntre doua sau ma multe corpur sau faze, s are o structura mult ma bogata decat o suprafata geometrca. Dstrbuta nanotuburlor de carbon n matrcea de ceramca poate f aleatoare (fg. 5.) sau perodca (fg.5.). Cu alb s negru s-au notat nanotubur de carbon cu un sngur perete s respectve, cu peret multpl.
161 8 Interacţunle care nu sunt de tpul legăturlor atomce se pot modela prn potenţalul Lennard-Jones care descre nteracţunle ntermoleculare în reţeaua atomcă de graft sau în moleculele C 6. Potenţalul de nteracţune total între atom de carbon în două molecule C 6, sau dntre două plane de graft este datcde (..36) H LJ 6 IJ σ σ ( rj ) = 4ε IJ IJ j> r j r j, unde I ş J reprezntă două molecule sau două plane, r IJ j este dstanţa dntre atomul dn molecula (planul) I ş atomul j dn molecula (planul) J. Parametr acestu potenţal sunt ε=,47 ev, σ= 3,4 Å. Fg Nanotubur de carbon ntr-o matrce de ceramca. Fg.5.4. Dstrbute perodca a nanotuburlor de carbon n matrcea de ceramca. Tnandu-se seama de faptul ca curbura Gaussana a suprafete Σ este un nvarant, rezulta dn (..3) expresa
162 9 cot ω= a ( +σ ) Xv σxσv ( + X ) σt 3/ ( +σ + X ). conform carea energa dspata este proportonala cu cot ω, s prn urmare cu curbura Gaussana a suprafete Tteca asocata modelulu de deformare. Capactatea de amortzare este rdcata la ambele tpur de structura. In fg. 5.5 este reprezentata functa lu Tteca pentru structura dn fg Fg Functa lu Tteca pentru structura perodca dn fg In contnuare studem dn punct de vedere atomstc ruperea nanotuburlor de carbon în sprtul lucrăr lu Belytschko et al. (). Nanotuburle de carbon sunt alcătute dn molecule în care atom sunt legaţ prn legătur atomce dentce. Dn această cauză, utlzăm un potenţal nteratomc de tp Brenner Tersoff pentru hdrocarbon (paragraf. formulele..9 s (..3), pe care îl screm sub forma unde Ej = VR( rj) BjVA( rj)], (5.8) j= B j este o funcţe de unghul legătur atomce (legătură este dstanţa dntre nuclee), ş e VR( rj) = f( rj) D exp( Sβ( r re)) S e, VA( rj) = f( rj) DS exp( β( r re)), (5.9) S S Constantele acestu model sunt - β=, m, S =,, r =,7 m ş, r < r, π( r r) f r = + r < r< r, r > r, ( ) cos,, r r r =,457 m, r = m. (5.) 9 D e = 9,648 Nm,
163 3 Pentru comparaţe consderăm ş un potenţal de tp Morse (..43), care ac este exprmat ca o sumă dntre o energe E a legăturlor atomce la întndere ş o energe E a legăturlor atomce unghulare la încovoere unde E = D β r r, e [( exp( ( )) ] E = E + E, (5.) 4 E = kθ( θ θ )[ + k s ( θ θ )], (5.) unde r este lungmea legătur, θ unghul legătur adacente. Utlzăm următor parametr corespunzător une energ de dsocaţe (separare) de 4kcal/mole (5,6eV/atom) r =,39 m D e = 9 6,35 Nm - β=,65 m θ =,94rad k =,9 θ Nm/rad 8 k =,754rad În fg. 5.6 se prezntă varaţa energe Brenner ş Morse în raport cu deformaţa n cazul ntnder, ar n fg. 5.7 se preznta varata forte Brenner s Morse n raport cu deformata n cazul întnder (Belytschko et al.). l l Deformaţa este ε=, unde l este lungmea nţală a legătur atomce ş l, lungmea l legătur după deformaţe. În potenţalul Brenner, funcţa f( r j ) ntroduce o creştere semnfcatvă a forţe nteratomce pentru r = r, după cum se vede în fg. 5.7, pentru o deformaţe de aproxmatv,3. Acesată comportare se datorează funcţe f( r j ). s -4 Fg Varaţa energe Brenner ş Morse în raport cu deformaţa în cazul întnder (Belytschko et al.).
164 3 Fg Varaţa forţe Brenner ş Morse în raport cu deformaţa în cazul întnder (Belytschko et al.). Modulul lu Young medu ş coefcentul lu Posson pentru potenţalul Morse în ntervalul de deformaţe de la la, este,94 TPa, ş respectv,,9. Pentru potenţalul Brenner aceste valor sunt de,7tpa ş respectv,,9. Energa de dsocaţe este pentru potenţalul Morse de 4kcal/mol. Prezentăm smularea comportăr la rupere prn ntndere, a unu nanotub de carbon armchar (,), ş a unu nanotub chral (6,8) de lungme,8 µm ş dametru 3nm (Belytschko et al.). In smulare s-au consderat 84 atom. Se utlzează potenţalul Morse cu o energe de separare de 4kcal/mol. Evoluţa fsur este prezentată în fg Tensunea de rupere la nanotubul armchar este de GPa corespunzător une deformaţ de,87. Nanotubul chral este ma puţn rezstent decât nanotubul armchar, tensunea lu de rupere fnd de 6 GPa la o deformaţe de,7. La încovoere, smulăm comportarea unu nanotub zgzag (,) de rază 6,6 A, cu un sngur perete de grosme,67 A, având un modul Young echvalent de 4,88 TPa, ş un coeffcent Posson ν =,9. Evoluţa fsur este prezentată în fg Tensunea de rupere este de 96 GPa la o deformaţe de,47. Fg Evoluţa une fsur într-un nanotub la întndere: dreapta nanotub armchar {,}, stanga nanotub chral (6,8) (Belytschko et al.).
165 3 Fg Evoluţa une fsur într-un nanotub zgzag (,) la încovoere. 6. Fol nanocompozte cu ncluzun de materale auxetce s nanotubur de carbon (fol nanosonce) Dnamca follor subtr cu geometre constransa a fost studata cu dferte metode de smulare. S-au consderat fol alcatute dn materale anzotrope granulare, cu structura nterna. Structurle stratfcate perodc în care două plane atomce formează un strat care se repetă, au un aranjament de tpul AABBAABB... Atom A ş B dferă ca dmensune. Presupunem că atomul A are dmensun ma mar decât atomul B. Interfaţa A/B este deformată deoarece atom A sunt supuş la compresune ar atom B la întndere (fg...3). Efectul deformaţe asupra constantelor elastce într-o astfel de structură a fost studat de către Jankowsk, Tsakalakos (985) ş de Jankowsk (988). Pentru a explca creşterea valorlor constantelor elastce observată expermental, autor au studat dependenţa constantelor elastce de deformaţa elastcă nţală. Rezultatele au ndcat creşter mar ale valorlor constantelor elastce C, C ş C 66 precum ş a valor modululu baxal Y[]=C + C C3/ C33 pentru un sngur strat de Cu, Ag ş Au supus la tensune baxală. Rezultate smlare au fost raportate ş pentru Au N, Cu Pd ş Ag Pd. De exemplu, pentru o superlatce Cu N cu 66 % Cu se obţne Y []=,3 TPa. Această valoare depăşeşte cu 5 % valoarea modululu elastc al unu alaj Cu N cu aceeaş concentraţe de Cu pentru care Y []=,4 TPa (Chrou s Chrou 3). Delsanto, Provenzano ş Uberall (99) au studat cazul structurlor deformate baxal în planul (), utlzând aceeaş metodă de calcul. E au pus în evdenţă sensbltatea modululu baxal Y[] în raport cu semnul deformaţe nţale. Astfel, pentru o structură deală având propretăţ medate care să caracterzeze metalele Cu, Au ş Ag, modulul baxal Y[] creşte cu 65 % pentru ε =.3, ar pentru ε =,3 modulul baxal descreşte cu 4 %. De asemenea, s-a observat că valoarea maxmă a modululu baxal se obţne pentru o grosme a stratulu de,8, nm ş pentru o lungme de undă a compozţe modulate de,66,5 mm. Efectul acusto-elastc defneşte dependenţa de tensune a vtezelor de propagare ale sunetulu într-un medu elastc deformat. Prn măsurarea varaţlor produse în vtezele de propagare ale undelor se pot evalua tensunle nţale dn materal. Benson ş Raelson au descrs acest fenomen în anul 959 (Toupn ş Bernsten 96) ş au prezentat o metodă de determnare a tensunlor într-un materal elastc zotrop utlzând polarzarea transversală a undelor sonore. Danels ş Smth au determnat în anul 958 (Toupn ş Bernsten 96) efectul presun hdrostatce asupra vteze sunetulu în crstale ş alte materale. Alţ autor au măsurat efectul tensun unaxale asupra vteze sunetulu în materale elastce zotrope, ş au arătat că valorle constantelor elastce de ordnul tre se pot determna dn aceste date.
166 33 Condţle de compatbltate necesare ş sufcente pentru ca datele prvnd propagarea undelor sonore în materale elastce să fe compatble cu teora clască a elastctăţ au fost obţnute de Toupn ş Bernsten (96). Autor au studat propagarea undelor plane cu ampltudne mcă într-un materal elastc deformat nţal ş au arătat modul în care măsurarea efectulu acusto-elastc poate f utlzat pentru determnarea constantelor elastce de ordnul tre într-un materal zotrop. Pentru astfel de materale se aplca teora mclor deformat elastce suprapuse peste o deformate elastca fnta. Pentru a scre ecuaţle aceste teor trebue să ntroducem tre confguraţ dstncte pentru punctele materale { P } care alcătuesc corpul B (Toupn ş Bernsten 96): - confguraţa naturală sau lberă de tensun C, - confguraţa nţală sau deformată (în echlbru) C, - confguraţa curentă Ct (). În aceste confguraţ pozţa partculelor materale { P } este descrsă de coordonatele naturale (materale sau lagrangene) ξµ ( P ), coordonatele nţale X A ( P ) ş coordonatele curente (eulerene) x ( P ). Sstemele de coordonate ( µ ), (A) ş () sunt ssteme nedeformate, nerţale ş staţonare. Descrerea deformaţlor fnte dferă de descrerea deformaţlor mc sau nfntezmale. Datortă deformaţlor mar, coordonatele în confguraţa nedeformată nu se pot nlocu cu coordonatele fnale în confguraţa deformată. De asemenea, expresa energe specfce de deformaţe se schmbă. Deformaţle elastce fnte pot f tratate dn două puncte de vedere. În formularea lagrangană deformaţa este descrsă în confguraţa naturală, ş coordonatele ξ µ sunt luate ca varable ndependente. În formularea eulerană deformaţa este descrsă în confguraţa curentă ş coordonatele x sunt luate ca varable ndependente. Pentru smplfcare presupunem că sstemele de coordonate ( µ ), (A) ş () sunt reprezentate într-un sstem cartezan unc () pe care îl numm sstem comun de coordonate (SCC). Vom specfca atunc când ecuaţle se vor scre în SCC. () Folosm notaţle ( ); µ, ( ); A s () ; pentru dervatele care se reduc la ξ, () () ş în X x SCC. Mşcarea unu corp materal este reprezentată de o famle de funcţ care depnd de tmp x = x ( ξ, t), ξ = ξ ( x, t). (6.) µ µ Aceste relaţ reprezntă o legătură bunvocă între coordonatele curente ş coordonatele naturale ale fecăru punct materal. Vom consdera numa mşcărle pentru care (6.) este de clasă C. Confguraţa nţală este confguraţa curentă la un moment t, astfel încât dacă cunoaştem relaţa dntre sstemele de coordonate (A) ş () putem deduce dn (6.) relaţ de forma X ( ) A = X A ξ, ξ = ξ ( X ), x = x( X,t), X A = X A( x, t). (6.) µ µ Ecuaţle ş defnţle teore mşcăr unu materal omogen perfect elastc dn care se vor deduce prn aproxmaţe ecuaţle teore mclor deformaţ suprapuse peste o deformaţe nţală fntă sunt date de t j; j = ρ x, (6.3)
167 34 t j x W ( E) x x j = tj = ξ Eµν ξµ ξν, (6.4) tj = dac E µν =, (6.5) x x( ξ,t) x = + x ; jx j, x =, (6.6) t t x x j ( Eµν = gj gµν ), (6.7) ξ ξ µ ν x ρ=ρ, ρ = const., (6.8) ξ x x det ξ ξ µ. (6.9) În (6.3)-(6.9) am folost următoarele notaţ: t tensorul Cauchy al tensun în Ct (), ρ denstatea în pozţa curentă, ρ denstatea în confguraţa naturală, x vteza, x acceleraţa, x ξµ gradentul de deformaţe corespunzător mşcăr (6.) a confguraţe curente în raport cu confguraţa naturală, E µν tensorul de deformaţe fntă a confguraţe Ct () relatv la C care se anulează numa dacă mşcarea de la C la Ct () este rgdă (6.5), W energa specfcă de deformaţe sau energa elastcă raportată la untatea de volum sau ma pe scurt potenţalul elastc, g j componentele tensorulu metrc în sstemul de coordonate (), g µν componentele tensorulu metrc în sstemul de coordonate ( µ ). Atât g j cât ş g µν se reduc la δ j în SCC. Ecuaţa (6.3) reprezntă ecuaţa de mşcare cu negljarea forţelor de volum, (6.4) legea consttutvă ş (6.7) legatura geometrcă dntre deformaţ ş deplasăr. Presupunem că potenţalul elastc W ( E ) este un polnom în deformaţle fnte W( E ) = Cµνλς EµνEλς + Cµνλςρτ EµνEλςEρτ +..., (6.) 6 unde C µνλς ş C µνλςρτ sunt constantele elastce de ordnul do ş de ordnul tre ale materalulu. Pentru un materal cu un sngur grup de smetre reprezentat prn transformarea dentcă (datortă smetre tensorlor t j ş E µν ), avem C k 5+ k constante ndependente de ordnul k. Dacă sstemul de coordonate () este rectangular, atunc forţa rezultantă pe orce porţune v a corpulu (negljăm forţele de volum) este dată de
168 35 F = t ds, (6.) j j s unde s este frontera lu v ş elementul dferenţal ds este dat de xl xk ds =± ejk dpdp, (6.) p p unde e[ jk ] = ejk este tensorul axal antsmetrc cu e 3 = în orce sstem de coordonate, ş xk ( p, p, t ) ecuaţa parametrcă a lu s. Forţa rezultantă F (v) poate f exprmată ca o ntegrală pe magnea σ a lu s în confguraţa naturală C, sau pe magnea S a lu s în confguraţa nţală C cu F = τ µ dσµ, F TAdSA σ S =, (6.3) unde x X A x dσ µ = ξ x ds, ds ξ µ A x = ξ x X A ds, (6.4) este gradentul de deformaţe corespunzător mşcăr (6.) a confguraţe actuale în raport cu confguraţa nţală. Tensor tensune de tp mxt care apar în (6.3) au fost ntroduş de Pola în 833 ş Krchhoff în anul 85, ş sunt defnţ astfel unde ξ µ x j este nversa lu x j ξ, ş µ x ξ ξ x τ µ = X A x j µ j t T x X = A j, A j ξ x j este nversa lu x j X A t, (6.5). Prmul tensor nesmetrc Pola- Krchhoff τ µ este convenabl în anumte prvnţe, ş anume dacă exprmăm potenţalul elastc ca x o funcţe W( gj, gµν, ) = W( E ), ceea ce este posbl deoarece E este determnat de ξ ş x ξ µ. Avem µ W τ µ = x ξ µ g j, g µν, (6.6) conform ecuaţlor consttutve (relaţa tensune-deformaţe). Utlzând denttatea x ξ x j ξµ ecuaţa de mşcare (6.3) se poate scre sub o forma echvalentă ; j =, (6.7)
169 36 x ( ξ, t) τ µµ ; =ρ. (6.8) t În mod smlar, ecuaţa (6.3) se poate scre sub altă formă echvalentă T x ( X, t), (6.9) t A; A =ρ x unde ρ este denstatea în confguraţa nţală deformată ρ=ρ. X Doua modele de fole cu ncluzun de nanotubur de carbon s materal auxetce sunt reprezentate n fg. 6. s respectv fg. 6.. Grosmea fole este de catva mlmetr, ar celelate doua dmensun sunt de ordnul macroscopc. Aceste fol au fost studate pentru reducerea zgomotulu n domenul audbl de frecvente. In fg.6.. nabotuburle de carbon au o dstrbute aleatoare, nsa n fg. 6. nanotuburle de carbon sunt aranjate perodc n raport cu raza, n drecte perpendculara pe planul fole. grosm. Aceste fol se numesc fol sonce deoarece au aceasta propreatate de a reduce zgomotul. Fg. 6.. Model compozt de fole cu ncluzun aleatoare de nanotubur de carbon s materal auxetc.
170 37 Fg. 6.. Model compozt de fole cu ncluzun perodce de nanotubur de carbon s materal auxetc 6.. Materal cu arhtectura noua cu materale auxetce s nanotubur de carbon. Modele de fol nanocompozte cu ncluzun de materale auxetce s nanotubur de carbon Expermental, a fost demonstrata cresterea capactat de amortzare a unu compozt prn ncorporarea nanotuburlor de carbon (Koratkar, Lass, We s Ajayan 3). Fg Mcrostructura compoztulu armat cu nanotubur de carbon, flmata cu 5X s 85X (nsertata).
171 38 In aceasta lucrare am reust sa explcam s teoretc aceste propretat atat pentru ncorporarea n compozt a nanotuburlor de carbon cat s a materalelor auxetce (Teodorescu, Munteanu, Chrou, Dumtru s.beldman 8, Chrou, Munteanu, D.Dumtru, Beldman s.secara 8, Munteanu, Chrou, Dumtru, s Beldman 8, Chrou 8, Munteanu, Dumtru, Donescu s.chrou 8). Amortzarea n fol subtr armate cu nanotubur de carbon este guvernata de frecarea care apare la nvel atomc, de nterfetele dntre nanotubur de carbon s nterfetele dntre matrce s nanotubur de carbon. Am utlzat expermente dnamce de forfecare n domenul -5Hz, realzate pe Slan Elastomer (aflat pe pata comercala 3M-ISD-). In fg. 6.. este prezentata mcrostructura compoztulu armat cu nanotubur de carbon, flmata cu 5X s 85X (nsertata). Rezultatele expermentale la testele de ncovoere sunt prezentate n fg Rezulattele teoretce obtnute de no sunt prezentate n fg Fg Rezultate expermentale ale testelor de ncovoere. Slane este un materal cu un nalt factor de perdere. Renforsarea cu nanotubur de carbon cu peret multpl mbunatateste mult capactatea de amortzare a compoztulu, asa cum reese dn fg, 6..4.
172 39 Fg Rezultate teoretce ale testelor de ncovoere Fg Caracterzarea capactat de amortzare a Slanulu narmat cu nanotubur de carbon cu peret multpl.
173 4 In contnuare analzam propretatle sonce ale unu materal alcatut dntr-un array de scatere sau rezonator acustc local (sfere goale dn materal pezoelectrc PZ) ncorporate ntr-o matrce de epoxna (ER) (Beldman, Munteanu s Chrou 9) (fg.6..5). Rezonator sunt alcatut dn materale functonale de tp graded, cu polarzare radala, s care verfca legea Reddy s legea cosnus. Pentru aceasta structura am arata anteror ca exsta doua clase de vbrat (Chrou and Munteanu 7). Placa are un numar de 7 resonator local de dametru a. Consderam un sstem de axe rectangular Ox x x3. Orgnea este localzata n partea stanga a plac, n mjlocul planulu medan, cu axa Ox n plan s Ox 3 normala pe plan. Lungmea plac este l, latmea d s grosmea este egala cu dametrul sfere goale a. In cazul crstalelor sonce uzuale, la care atenuarea sunetulu rezulta dn superpozta multplelor unde reflectate, este esental sa calculam un numar mare de peroade pentru undele transmse, pentru a se obtne un coefcent de transmse corect. In cazul crstalelor sonce alcatute dn rezonator local, putem reduce pas de tmp n smulare, deoarece atenuarea se datoreaza n prmul rand rezonatorlor. Pentru a evta reflexle undelor (care nu au caracter fzc) de la margnle probe, e necesar sa mplementam condt absorbante de frontera n drecta x, pentru x = s x = l. Un transducer s un recever (observator) sunt localzate la x = b s x = l b. Rolul transducerulu este de a njecta n placa unde plane monochromatce care se propaga n drecta x. Deplasarle sunt nregstrate pe ambele capete ale plac. Coefcentul de atenuare a sunetulu se obtne dn raportul dntre deplasarle de la recever s transducer. Orcum dureaza pana cand osclatle devn statonare. Prn urmare calculam pentru fecare frecventa n jur de peroade pentru unda transmsa. Fg Schema plac sonce. Ecuatle consttutve ale sfere pezoelectrce sunt (Chen, Wang and Lu, Mhalescu s Chrou 4, Chrou s Munteanu 7) rσ = C S + C S + C S + f rφ θθ θθ ϕϕ 3 rr 3 rσ = C S + C S + C S + f rφ ϕϕ θθ ϕϕ 3 rr 3, r rσ = C S + C S + C S + f rφ r C S f rr 3 θθ 3 ϕϕ 33 rr 33, r σ rθ = 44 rθ + 5 φ, θ, r rϕ C44Srϕ f5 csc, ϕ r r σ = + θφ, (6..) σ θϕ = C66Sθϕ rdθ = C5Srθ ζ φ, θ
174 4 unde rd = f S r ζ cscθφ ϕ 5 ϕ, ϕ rd = f S + f S + f S ζ rφ r 3 θθ 3 ϕϕ 33 rr 33, r σ j este tensorul tensune, φ este potentalul electrc, D este vectorul deplasar electrce, C j sunt constantele elastce, s C66 = ( C C )/, f j sunt constantele pezoelectrce, ζ j sunt constantele delectrce, s = r, θ, ϕ. Constantele elastce, pezoelectrce s delectrce sunt funct arbtrare care depnd de coordonata radala r. Notand cu ε j tensorul de deformate, u, = r, θ, ϕ, deplasarle, canttatle S j care sunt legate de ε j, se defnesc astfel S = rε = ru Sθθ = rε θθ = uθ, θ + ur rr rr r, r Sϕϕ = rε ϕϕ = cscθ uϕ, ϕ + ur + uθ cot θ Sr = rε r = ur, + ru, r u θ θ θ θ θ Srϕ = rε rϕ = cscθ ur, ϕ + ruϕ, r uϕ Sθϕ = rε θϕ = cscθ uθ, ϕ + uϕ, θ uϕ cot θ (6..) Notand cu ρ denstatea materalulu, care este o functe arbtrara de r, ecuata de mscare devne rσ + θσ +Σ + Σ + Σ Σ θ=ρ rθ, r csc ϕθ, ϕ θθ, θ rθ ( θθ ϕϕ)cot r uθ rσ + θσ +Σ + Σ + Σ θ=ρ, (6..3) rϕ, r csc ϕϕ, ϕ θϕ, θ rϕ θϕ cot ruϕ rσ + cscθσ +Σ +Σ Σ Σ +Σ cot θ=ρr u rr, r rϕϕ, rθθ, rr θθ ϕϕ rθ r Ecuata de ncarcare electrostatca este r rr, r θ, θ ϕ, ϕ Λ+Λ+ csc θ( Λsn θ ) + cscθλ =. (6..4) Functle Chen F, G s w, precum s functle tensune Σ s Σ uθ = cscθf, ϕ G, θ, uϕ = F, θ cscθ G, ϕ, ur = w, (6..5) Σ rθ = cscθσ, ϕ Σ, θ, rϕ, θ csc, ϕ Σ =Σ θσ. (6..6) sunt utlzate pentru a smplfca (6..) (6..4). Ca urmare, aceste ecuat pot f separate n doua setur de ecuat ndependente ra,r = MA, rb,r = PB, unde prmul set de ecuat se leaga de doua varable de stare Σ s F, ar cel de al dolea de sase varable de stare ra,r = MA, rb,r = PB, A =Σ [, F] T, B=Σ [,,,,, ] T rr Σ G w Λr φ, (6..7) M C ( + ) + ρ = t C r = + θ + θ θ θ ϕ cot csc P = β P = P = k 3 P = k + r ρ t 4 P5 = P5 = P64 = γ P = β P = P = k C + r ρ t 3 66
175 4 P 44 = β unde P = k, 4 P =α f P α= C ζ + f =, P33 = P34 = P55 =, 3 C P = C f P = k 56 3 β=α C3ζ 33 + f3f33 ( ) P P = C f, =α f 6 33 γ=α P 4 33 P = γ 63 =α ζ, ( C f C f ) P P 43 = β, = α (6..8) C k = ( C3β+ f3γ) ( C + C ), k =.5k C66, k3 =ζ + f5c 44. (6..9) Consderam acum doua sfere goale pezoceramce cu raportul dntre raza nteroara s cea exteroara ξ =.3 s ξ =.5. Propretatle de tp graded a materalelor functonale sunt defnte de legea lu Reddy (Reddy 987, Reddy s Lu 987, Reddy, Wang s Ktporncha 999) λ λ M = M µ + M ( µ ), (6..) p z cu µ = ( b r)/( b a), λ este un parametru de beomogebtate sau ndex gradent (Chen, Wang s Lu ), M p s M z sunt constantele de materal ale celor doua materale, s anume PZT-4 s ZnO (Deulesant s Royer 98, Tang s Xu 994). Cazul λ= corespunde une sfere omogene PZT-4 s λ, une sferea omogene ZnO. A doua lege este data de M = M cos µ + M ( cos µ ). (6..) p z Materalel sonce sunt confectonate prn ncorporarea rezonatorlor acustc ntr-o matrce omogena de epoxna, cu mpendante dferte. Ecuatle consttutve pentru epoxna sunt t j e = λ ε unde t j este tensorul tensuner, ε j este tensorul deformate, kk δ j + e e e e µ εj + A ε lε jl + 3B ε kkεj + C ε kkδj, (6..) e λ s ar e e e A, B s C sunt constante elastce de ordnal do. The moton equatons are e ρ u = j. j e µ constantele elastce Lamé, t, (6..3) e unde ρ este denstatea epoxne s u vectorul deplasare. La nterfetele dntre sfere s matrce se pun condt de contnutate ale deplasarlor s tractunlor. Aplcam, metoda cnodala pentru gasrea solutlor. ecuatlor (6..7)-(6..9) s (6..3). Introducem condt de frontera absorbanta cu rezstvtatea σ e, pentru x = s x = l. Reflecta se reduce atunc cand rezstvtatea este mare, nsa grosmea stratulu poros absorbant trebue sa fe mc deoarece undele se amortzeaza repede ntr-un strat cu rezstvtate mare. Cand rezstvtatea este redusa, reflecta se reduce de asemenea, nsa grosmea stratulu absorbent trebue sa fe mare pentru a amortza unda. Altfel unda se reflecta la stratul absorbant s se ntoarce napo n medu. Selectarea rezstvtat σ e trebue facuta n asa fel ncat sa reduca reflexa undelor la capete. Aratam ca modelarea frnterelor absorbante coexsta cu dferte comportar dnamce ncluzand haosul. Rezultatele numerce au fost obtnute pentru PZT-4 C = 3.9 N/m C 33 =.5 N/m C = 7.8 N/m C 44 =.56 N/m C 3 = 7.4 N/m f 5 =.7C/m f 3 = 5.C/m
176 43 f 33 = 5.C/m ζ = 65 F/m ζ = F/m 3 ρ=75kg/m for ZnO C =.97 N/m, C 33 =.9 N/m f 33 =.4C/m C =. N/m, C 44 = 4.5 N/m ζ = 7.38 F/m ζ = C 3 =.5 N/m, f 5 =.59C/m F/m f 3 =.6C/m 3 ρ=5676kg/m e 9 e 9 e 9 e s pentru epoxna λ =4.3 N/m, µ = 3.76 N/m, A =.8 N/m, B = 9 e 9 e N/m, C = 5.7 N/m, ρ = 7 kg/m. Seturle ndependente de ecuat (6..7) conduc la doua setur de vbrat lbere. Pe masura ce λ creste, frecventele naturale pentru toate modurle cresc. Pentru λ varata frecventelor naturale n raport cu λ nu este semnfcatva. Fgs s 6..7 preznta transmterea sunetulu prn compoztul sonc pentru o sfera de dametru a = 3.7mm, pentru legea lu Reddy (6..) s respectve pentru legea cosnus (6..). Condtle pe frontera absorbanta se calculeaza pentru <σ e < 3. Se obtn doua benz s respectve tre benz de atenuare puternca n domenul audbl la frecvente de.8 khz, 8.5 khz, s respectve, de.8 khz, 4.kHz and 7.8 khz, cu o atenuare relatve de 5dB. Fg Transmterea sunetulu prn compoztul sonc pentru a = 3.7mm, s legea lu Reddy.
177 44 Fg Transmterea sunetulu prn compoztul sonc pentru a = 3.7mm, s legea cosnus. Fg Portret de faza stabl pentru <σ e < 3 n cazul leg lu Reddy. Pentru <σ e < 3, compoztul sonc admte solut stable. Portretul de faza vteza- u - pozte x pentru a = 3.7mm s legea lu Reddy law, este reprezentat n fg Se obtn do atractor stran pentru σe s 3 σe 4.5, asa cum apare n fg
178 45 Fg Portret de faza pentru σe s 3 σe 4.5 n cazul leg lu Reddy. 6.. Studul propretatlor elastce s vasco-elastce ale materalelor auxetce s nanotuburlor de carbon Modelarea matematca a contactulu elasto-plastc a fost prezentata n paragraful 3.. O metodă efcentă de determnare a propretăţlor mecance de rezstenţă ş amortzare ale materalelor constă în ndentarea une suprafeţe-eşanton cu un ndenter de geometre cunoscută (Chrou, Munteanu s Dumtru 8, Chrou, Munteanu s Beldman 8, Dumtru, Pop s Baldovn 8, Donescu, Chrou s Munteanu 8). În cele ce urmează, prezentăm rezolvarea numercă a ndentăr unu semspaţu elastc zotrop cu un ndenter rgd cu bază plană, problemă cunoscută ş sub numele de problema ştanţe cu bază plană (Dumtru s Chrou 8). Consderăm că ndenterul acţonează asupra semspaţulu cu o forţă normală centrată. Pentru moment ne stuăm cu studul probleme la scară macroscopcă, extensle la scară nanometrcă urmând a f efectuate în următoarea etapă pe baza elementelor teoretce enunţate în captolele anteroare (spre exemplu, aplcarea teore nelocale a lu Erngen. Pentru o ştanţă cu bază plană elptcă ce acţonează cu o forţă normală asupra unu semspaţu elastc, Solomon a obţnut prn calcul analtc soluţ exacte pentru presunle de contact ş pentru adâncmea de pătrundere. Soluţle numerce obţnute folosnd elementele fnte vor f comparate cu aceste soluţ exacte pentru problema ştanţe cu bază plană elptcă. Prn calcul analtc, s-a reuşt obţnerea unor soluţ exacte ale ştanţe plane de formă arbtrară, folosnd ecuaţle ntegrale duale ale lu Sneddon. Reconsderam problema stante (fg. 6..) cu bază plană elptcă, acţonată cu o forţă normală centrată P. Domenul de contact D este dec o elpsă având semaxele a ş b. Notăm cu D frontera domenulu de contact ş cu δ adâncmea de pătrundere. Semspaţul elastc zotrop este caracterzat de modulul de elastctate E ş de coefcentul Posson ν.
179 46 Fg.6... Indentarea unu semspaţu elastc cu un ndenter cu bază plană. Soluţle exacte ale probleme ştanţe cu bază plană elptcă sunt date de (Solomon 967) P ξ η π ab p( ξη, ) = a b pentru ( ξη, ) D (6..) pe D s pentru ( ξη, ) D ν K( e) δ = P, (6..) π E a unde p( ξ, η ) este presunea de contact în punctul ( ξ, η ) al domenulu de contact (stuat în planul x-y), b dϕ e = reprezntă excentrctatea elpse de contact ş K( e) = a. e sn ϕ Plecând de la expresa potenţalulu de smplu strat, Solomon a redus problema ştanţe cu bază plană acţonată de o forţă normală la rezolvarea următoare ecuaţ ntegrale: π/ ν p( ξ, η) δ = dξ dη π E pentru orce ( x, y) D, ( x ξ) + ( y η) D (6...3) la care trebue adăugată următoarea condţe de echlbru: P= p( ξ, η)dξ dη. D (6..4) Problema de rezolvat se rezumă astfel: cunoscând P, E ş ν, să se determne presunle de contact p( ξ, η ) ş adâncmea de pătrundere δ. Exprmată sub forma ecuaţlor ntegrale (6..3) ş a condţe de echlbru (6..4), problema ştanţe cu bază plană elptcă a fost rezolvată numerc folosnd elementele fnte, codul de calcul fnd scrs în lmbajul C. Fg. 6.. lustrează dvzarea în elemente fnte a domenulu elptc de contact D, după coordonatele polare r ş θ j : D = Dj, unde =,..., Nr ş j =,..., N θ. Am notat cu N r numărul, j
180 47 de dvzun elementare radale ş cu N θ numărul de dvzun elementare unghulare. Rezultatele prezentate ma jos au fost obţnute pentru N r = 5 ş N θ = 36. Numărul total de domen elementare D j consderate este dec N = NN r θ. Fg Secţune plană a domenulu de contact D, lustrând dvzarea lu D în elemente fnte. Presunea de contact pe fecare domenu elementar D j este consderată constantă ş egală cu p( ξj, η j), pentru j =,..., N. Coordonatele cartezene ξ j ş η j ale centrulu lu D j ş ara elementară A Dj a lu D j se calculează uşor cunoscând coordonatele polare r ş θ j. Ecuaţle ntegrale (9.3) ş condţa de echlbru (9.4) pot f aproxmate după cum urmează: ν p( ξ, η ) A δ + = pentru orce ( xj, yj ) D, πe x + y N j j Dj j= ( j ξj ) ( j ηj ) N j= (6..5) p( ξj, ηj ) AD = P. (6..6) j Necunoscutele probleme sunt cele N presun de contact p( ξj, η j) plus adâncmea de pătrundere δ, dec avem un total de N+ necunoscute. Pentru a rezolva problema, N+ ecuaţ sunt necesare, adcă avem nevoe de N ecuaţ (6..5), la care se adaugă ecuaţa (6..6). După cum se observă în fg. 6.., cele N puncte ( xj, y j) sunt consderate câte unul în fecare domenu elementar D j, dar de fecare dată dferte de centrul lu D j, adcă ( xj, yj) ( ξj, ηj) pentru a evta numtor nul în (6..5). Avem dec N+ ecuaţ lnare, cu N+ necunoscute. Rezolvarea acestu sstem algebrc este faclă, char dacă N este destul de mare. În practcă, problema fnd smetrcă, rezolvarea poate f redusă la un sfert dn domenul de contact elptc D. Smularea numercă a fost obtnuta pentru: P = [kn], a =.5 [mm], b =.5 [mm], E = 5 [GPa] (GPa = kn/mm ), ν =.7. Dacă analzăm cu atenţe soluţa exactă (6..), putem remarca smetra radală a presun de contact, adcă presunea de contact este constantă pe fecare dsc elptc elementar D a lu D (cf. fg. 6..):
181 48 not.,, =,, =,3,3 = =, Nθ, Nθ = = p( ξ, η ) p( ξ, η ) p( ξ, η ) p( ξ, η ) ct. p( a ), unde a = a este semaxa mare a dsculu elementar elptc D. În consecnţă, este sufcent să Nr reprezentăm doar evoluţa presun de contact pe segmentul OM, notată cu p( a ), pentru =,..., N r = 5. Pe lângă rezolvarea propusă ma sus bazată pe elemente fnte, am folost ca termen de comparaţe ş rezolvarea probleme ştanţe folosnd programul de elemente fnte ANSYS. Smularea comparatvă folosnd ANSYS a fost realzată de către colegul nostru de la IMS, Drd. Ing. Justn Onşoru. Fg. 6.. prezntă soluţa exactă de cele două soluţ numerce: soluţa formularea (6..5) ş (6..6) a lu Solomon, respectv soluţa p exact ( a ) dată de (6..) pentru presunea de contact, lătur p Solomon ( a ) obţnută rezolvând prn elemente fnte p ANSYS ( a ) obţnută cu ANSYS. Presunle de contact, n [GPa] Soluta exacta Soluta formular Solomon Soluta ANSYS semaxa mare a [mm] Fg Compararea soluţe exacte cu cele două soluţ numerce pentru p(a ). În fg se observă că soluţlor numerce obţnute concd practc cu soluţa exactă. De asemenea, se observă că presunle de contact tnd spre nfnt în medata vecnătate a frontere D. Studle expermentale ş alte stud teoretce ndcă însă valor fnte pentru câmpul de tensune (ş mplct presunle de contact) în vecnătatea sau pe frontera domenulu de contact. Teora nelocală este cea care permte obţnerea prn calcul a unor presun de contact ce admt un maxm care nu apare pe fronteră c în medata vecnătate a frontere. Teora nelocală de tp Erngen a fost prezentata n paragrafele anteroare. În faza următoare, aplcarea acestor formulăr teoretce ne va permte să obţnem rezultate în acord cu studle expermentale ş să explcăm fenomenele ş comportărle la dferte scar metrce. Fg compară erorle relatve obţnute folosnd cele două rezolvăr numerce (rezolvarea formulăr (6..5) ş (6..6) a lu Solomon versus rezolvarea folosnd ANSYS), adcă Solomon exact ANSYS exact p ( a ) ( ) Solomon p a p ( a ANSYS ) p ( a ) ε = ş ε exact = (exprmate în %). exact p ( a ) p ( a )
182 49 Erorle relatve pentru presunle de contact, n [%] % eroare rezolv. formular Solomon % eroare ANSYS semaxa mare a [mm] Fg Erorle relatve ε Solomon (a ) ş ε ANSYS (a ), în %. Erorle relatve obţnute sunt acceptable pentru rezolvăr folosnd elemente fnte, fnd ma bune pentru rezolvarea formulăr Solomon, cea propusă de no ca bază de plecare macroscopcă pentru abordăr nanometrce. Pe de altă parte am vrut să demonstrăm că, pentru anumte probleme specfce, de cercetare, folosrea unor mc programe orgnale poate da rezultate ma bune decât programe foarte cunoscute, dar poate prea generale în abordare, precum ANSYS-ul. În prvnţa adâncm de pătrundere δ, soluţa numercă obţnută prn rezolvarea formulăr Solomon este [mm], în tmp ce soluţa exactă este.577 [mm]. Eroarea relatvă este de.6%, dec foarte mcă. Deş ma sus am studat numerc doar problema ştanţe cu bază plană elptcă, folosrea elementelor fnte permte rezolvarea probleme ştanţe cu formă arbtrară, ceea ce este foarte dfcl de realzat analtc. În concluze, la scară nanometrcă teora nelocală a lu Erngen descre ma bne decât teora locală nteracţunle la dstanţă dntre partculele unu materal, nelmtându-se sa consdere doar nteracţunea cu atomul vecn. Vom contnua dec modelzarea nanocontactelor ş a ndentăr folosnd această teore nelocală, ca parte a unor no metode cuplate atomstc-contnue. Consderam acum nanotuburle de carbon cu un sngur perete cu dferte raze ş forme (armchar ( n, n ), chral ( n, n ), ş zgzag ( n,) ) având secţunea crculară. Studem vbraţle transversale ale acestor tubur. Presupunem că grosmea peretelu nanotubulu este h =,34nm, ş numărul de atom de carbon pe lungmea L este N = πρ LR, unde R este raza tubulu ş ρ denstatea. Deoarece dametrul tubulu de carbon este de câteva or ma mare decât ordnul de mărme al legătur dntre atom de carbon, putem utlza modele contnue pentru a descre comportarea mecancă a nanotubulu. Cele ma smple modele contnue pentru studul mecanc nanotubulu de carbon consderat ca un medu omogen ş zotrop, sunt teora bare elastce cu deformaţ mc ş teora plăc subţr pentru deformaţ mar (Qan et al. ). Presupunem că legea lu Hooke care leagă tensunea σ de deformaţa ε, este lnară σ= Eε. Pe drecţa perpendculară axe sale, bara este supusă une contracţ dată de relaţa
183 5 ε p = νε, cu ν coefcentul lu Posson. În cazul de tensune trdmensonală, legea lu Hooke este dată de σ j =λεllδ j + µε j,, j, l =,,3, (6..7) u u j unde ε j = + este tensorul deformaţe, u x j x vectorul deplasare, σ j este tensorul tensune, ε =ε +ε +ε33 evaluează dlatarea de volum, ar λ ş µ sunt constantele lu Lamé. În locul constantelor lu Lamé se pot folos modulul lu Young E, constanta lu Coulomb µ = G ş coefcentul lu Posson ν (Solomon 968) E µ= G = ( +ν ), νe λ= ( +ν)( ν ). (6..8) Dn sumarea tensunlor normale se obţne dn (6..7) σ kk = (3λ+ µ ) ε kk = 3Ke, (6..9) unde K este modulul de compresbltate. Lucrul mecanc de deformaţe raportat la untatea de volum este (Nowack 969) du Φ= = σε, (6..) dv unde U este lucrul mecanc de deformaţe corespunzător întregulu corp de volum V. Studem în contnuare vbraţle transversale ale nanotubulu de carbon modelat ca o bară elastcă de lungme l n drecţa axe x, ara secţun transversale A, ρ denstatea, I = r A momentul de nerţe al secţun transversale în raport cu axa neutră de încovoere care se află în planul prncpal al bare (Novack 969). Notăm cu w deplasarea transversală a bare. Aplcând prncpul lu Hamlton avem t t, (6..a) δ ( U K)dt = δfdt t t unde U este lucrul mecanc de deformaţe, K energa cnetcă ş δ F este lucrul mecanc al forţelor exteroare. Dacă încărcarea exteroară este conservatvă, atunc exstă o funcţe potenţal Π= U F care reprezntă energa totală a sstemulu, astfel încật să avem t t. (6..b) δ ( U K F)d t =δ ( Π K)dt = t t Dn w ε= z, σ= Eε, rezultă x d w U = Ez dv x Prn ntegrare pe lungmea bare ş pe secţunea transversală se obţne, dv = dda x. (6..)
184 5 l l x x E w EI w U = dx z da = dx. (6..3) Energa cnetcă K este compusă dn energa mşcăr de translaţe ş energa mşcăr de rotaţe a secţun transversale l w t w K = ρ A [ r ]dx +, (6..4) t x unde w este vteza mşcăr de translaţe. t Dacă încărcarea pe untatea de lungme a bare este Q avem Prncpul lu Hamlton (6..a) conduce la l δ F = Qwx δ d. (6..5) t l t l EI w ρ A w w δ dt r + dx= dt Qdxδw t x t x t. (6..6) Calculând varaţle ş ţnând seama că pentru t = t ş t = t avem δ w =, obţnem t l 4 4 EI w w w dt ρ 4 I + ρ Q dx w δ = x x t t, ρ = ρ A. (6..7) t Dn condţa ca (6..6) să fe satsfăcută pentru orce valoare δ w, se obţne ecuaţa vbraţlor transversale ale bare 4 4 EI w w w 4 I ρ + ρ = Q. (6..8) x x t t Studle lu Rayleygh au arătat că nfluenţa exprese ρ Iw,xx asupra deplasăr w este mcă pentru frecvenţe mc ş deformaţ mc, aşa încât ecuaţa (6..7) se smplfcă (Novack 969) 4 w EI w ρ + = 4 Q, (6..9) t x sau 4 w w EI Q c + = q, c =, q =. (6..a) 4 x t ρ ρ Ecuaţe (4.5.) î asocem condţle nţale pentru t = w w( x,) = f( x), ( x,) = g ( x ), (6..) t ceace arată că la momentul nţal bara este încovoată potrvt cu funcţa f ( x ) ş avem o vteză nţală gx. ( ) Pentru o bară smplu rezemată la capătul x = condţle la lmtă sunt
185 5 Dacă bara este este încastrată la capătul x = w(, t ) =, avem w (, t ) =. (6..) x w w(, t ) =, (, t) =, (6..3) x Sa analzăm acum vbraţle lbere ale une bare de lungme l ale căre capete sunt lbere sau smplu rezemate sau încastrate. Presupunem că soluţa ecuaţe de mşcare (6..8a) este de forma unde ω este frecvenţa unghulară. Ecuaţa (6..8a) cu q = devne w( xt, ) = ux ( )exp( ω t), (6..4) 4 u ku=, 4 x Aplcând transformata Laplace u( p) = u( x)exp( px)dx k ω =. (6..5) c ecuaţe (6..3), obţnem Transformata nversă Laplace aplcată ecuaţe (6..4) conduce la soluţa 3 3 u u u 4 3 u( p) = [ p u() + p () + p () + ()]. (6..6) p k x x x u( x) = u( p)exp( px)dp 3 u u u u( x) = u() S( kx) + () T ( kx) + () U ( kx) + () V ( kx), (6..7) 3 3 λ x λ x λ x 3 u u unde constantele u (), (), x x () u ş () reprezntă deplasarea, rotrea secţun 3 x transversale a bare, o mărme proporţonală cu momentul încovoetor ş o mărme proporţonală cu forţa tăetoare în secţunea transversală x =, dacă ţnem seama că momentul încovoetor ş forţa tăetoare sunt date de w M( x, t) = EI x Funcţle care apar în (6..5) sunt S( λ x) = (cosh λ x+ cos λx) 3 u T( x, t) = EI 3 x T( λ x) = (snh kx+ sn kx)
186 53 x = l U ( λ x) = (cosh λx cos λ x), V ( λ x) = (snhkλx sn kx). (6..8) Presupunem că bara este încastrată în secţunea x = ş smplu rezemată în secţunea u u u () =, () =, ul ( ) =, x ( l x ) =. (6..9) 3 u u Calculând dervatele ( x ), x ( x x ) u ş ( ) 3 x dn (6..5) ş ntroducând expresle x obnute în (6..7) obţnem sstemul de două ecuaţ 3 u u ul ( ) = () Ukl ( ) + () Vkl ( ) = 3 3 λ x λ x 3 3 u u u ( l) = () S( kl) + () T( kl) = 3 3 x x λ x Condţa ca determnatul acestu sstem de ecuaţ să fe nul conduce la ecuaţa Prmele tre rădăcn ale aceste ecuaţ transcendente sunt β = 3,97 β = 7,69 β 3 =, Celelalte rădăcn se pot calcula aproxmatv dn π β r = (4r + ) r > 5 4 Frecvenţele unghulare propr se calculează dn formula cβr βr EI EI ω r = = = l l tanhβ tanβ =, β = kl. (6..3) kr ρ ρ, A ρ = ρ, r =,,...,, (6..3) unde k r este numărul de undă unghular corespunzător frecvenţe propr r. Modurle propr corespunzătoare frecvenţelor propr se calculează dn (6..5). Dacă bara este încastrată la ambele capete, condţle la lmtă devn În mod analog se obţne ecuaţa u u u () =, () =, ul ( ) =, ( l ) =. (6..3) x x ale căre prmele tre rădăcn sunt β = 4,73 β = 7,853 β 3 =,996 coshβcosβ =, β = kl, (6..33) Celelalte rădăcn sunt date de (6..8). Pentru o bară încastrată în x = ş lberă în x= l avem condţle la lmtă u () =, u () =, u ( l) =, u ( l) =. (6..34)
187 54 Ecuaţa transcendentă este dată de coshβcosβ+ =, β = kl, (6..35) ale căre prmele tre rădăcn sunt β =,875 β = 4,694 β 3 = 7,855 Celelalte rădăcn sunt date de (6..8). Modurle vbraţonale reprezntă de fapt unde staţonare în bară. Expresa generală a unde staţonare este dată de (6..). Toate punctele bare vbrează cu o mşcare armoncă având aceeaş frecvenţă unghulară ω. Numărul de undă unghular k (nversul lungm de undă π k = ) se măsoară în radan pe metru sau metru la puterea ş reprezntă pentru λ vbraţle în spaţu mărmea analogă frecvenţe unghulare ω dn cazul vbraţlor în tmp. Legătura dntre frecvenţa ş numărul de undă a modurlor vbraţonale este dată de (6..8). Masurătorle expermentale ale frecvenţelor propr ale nanotuburlor de carbon se pot utlza pentru detemnarea modululu lu Young. Astfel, Treacy et al. (996) a determnat modulul lu Young pentru nanotubur cu pereţ multpl ş a obţnut valor cuprnse între,4 TPa ş 4,5 TPa, cu o valoare mede de E =,8TPa, pentru un nanotub de grosme,34nm. Stud smlare au fost făcute pe 7 tubur cu un sngur perete de către Krshnan et al. (998), care a obţnut o valoare mede E =,3TPa. Loure ş Wagner (998) utlzând metoda spectroscopcă mcro-raman au măsurat modulul lu Young pentru un nanotub cu un sngur perete, prn deformaţe la compresune într-o matrce de epoxnă. Au obţnut valor între,8 3,6 TPa. Pentru nanotubur cu pereţ multpl au obţnut valor între,7,4 TPa. Studul expermental al modurlor vbraţonale ale nanotuburlor de carbon au pus în 3 evdenţa tre tpur de vbraţ propr: modul Helmholtz pentru k 3 m, modul forfecare 4 4 pentru k m ş modul cclop pentru k m (Gao, Cagn ş Goddard 998). Problema nversă este un subect mportant în nanomecana ca ş în alte domen. Problemele nverse se întâlnesc în multe ramur ale matematc ş ngnere mecance: bomecancă, evaluarea nedstructvă, caracterzarea materalelor ş a structurlor prn metode ultrasonce, raze X, termografe, probleme de dentfcare ale propretăţlor necunoscute ale materalelor (constante elastce, propretăţ de dspare a energe, etc.), a geometre ş a forme, a surselor sau a condţlor pe fronteră nespecfcate, a dentfcăr defectelor în materale ş structur, a metodelor expermentale, etc. În contnuare, revenm la problema nţală ş prezentăm o problemă nversă de determnare a modululu lu Young pentru tre nanotubur de carbon cu un sngur perete ş anume forma armchar (,), chral (,6) ş zg-zag (7,) pentru care cunoaştem determnăr expermentale ale modurlor vbraţonale (Gao, Cagn ş Goddard 998). Ca funcţe obectv pentru algormul genetc ntroducem suma dferenţelor pătratce dntre modurle vbraţonale măsurate ş modurle corespunzătoare calculate N n n ( ), (6..36) n= W = M M n unde M, n=,... N, sunt modurlemăsurate, ş calculate. Defnm funcţa ftness F astfel M, n=,... N, sunt modurle corespunzătoare n W F =, (6..37) W
188 55 cu W N n = ( M ). (6..38) n= Necunoscutele sunt N parametr p= { M, M,..., M N } reprezentând modurle vbraţonale. Valorle acestor parametr sunt dscretzate într-un şr de valor cu paş M, M,..., MN. Setul de parametr pentru o problemă arbtrară p= { M, M,..., M }, (6..39),, N, N este exprmat sub forma unu număr (Tanaka ş Nakamura 994) M = ( ) I... I + ( ) I... I + ( ) I... I +...( ) I +, (6..4) cu... R R R 3 R R R R I, I,..., I N numărul total de valor dscrete pentru fecare parametru p. Acest număr este contorzat începând cu p= { M,, M,,..., M N,}. (6..4) Utlzăm datele expermentale raportate de Gao, Cagn ş Goddard în 998. Ma jos se prezntă rezultatele algortmulu genetc. Utlzând valorle expermentale ale modurlor de vbraţe (Gao, Cagn ş Goddard 998), se obţn în urma aplcăr algortmulu genetc, următoarele valor ale modululu lu Young pentru un tub de grosme,34nm: 3,8 TPa pentru armchar (,), 3,86 TPa pentru tubul chral (,6) ş 3,83 pentru tubul zg-zag (7,), valor care sunt ma mar decât valoarea mede care apare în tabelul 6... În tabelele sunt prezentate modurle de vbraţe pentru aceste nanotubur, determnate expermental (Gao, Cagn ş Goddard 998) ş teoretc, pentru o grosme de,34nm. Tabel 6... Modur de vbraţ calculate ş măsurate pentru un nanotub armchar (,) mod Helmholtz Teore m Helmholtz Măsurat m Forfecare Teore m Forfecare Măsurat m Cclop Teore m Cclop Măsurat m
189 56 Tabel 6... Modur de vbraţ calculate ş măsurate pentru un nanotub chral (,6) mod Helmholtz Teore m Helmholtz Măsurat m Forfecare Teore m Forfecare Măsurat m Cclop Teore m Cclop Măsurat m Tabel Modur de vbraţ calculate ş măsurate pentru un nanotub zg-zag (7,) mod Helmholtz Teore m Helmholtz Măsurat m Forfecare Teore m Forfecare Măsurat m Cclop Teore m Cclop Măsurat m
190 57 7. Un nou concept prvnd nanondentarea capabl sa masoare propretat elastce, vascoelastce s amortzare Metoda noua de caracterzare a amortzar prn nanondentare pentru realzarea vrtuala a nstrumentulu de nanondentare (etapa I-metoda) a fost descrsa n paragraful 3 (Teodorescu, Munteanu, Chrou, Dumtru s.beldman 8, Chrou, Munteanu, D.Dumtru, Beldman s.secara 8, Munteanu, Chrou, Dumtru, s Beldman 8, Chrou 8, Munteanu, Dumtru, Donescu s.chrou 8). Evaluarea amortzar la nvel nano este o problema deschsa. Multe aspecte legate de efecte cuantce, trbologe, adezune moleculara, efecte electronce, superlubrctate, s alte fenomene precum energa dscontnua de legatura adezva, hsterezs, dfuze, fluaj, dslocat, forfecarea atomca, curgere plastca, relaxare, gradent termc, nu sunt nca elucdate.. Lmtarle metodelor s a nstrumentate exstente de nanondentare se refera la calculul modululu de elastctate (care se face doar pentru materale zotrope s lnare), fara sa se obtna nformat prvnd propretatle elasto-vascoase s de amortzare. Prn urmare, metodele clasce cunoscute nu sunt adecvate la scara nano, amortzarea nu se poate estma cu aceste tehnc. Un rezultat ncorect prvnd capactatea de amortzare a materalelor poate cauza schmbar de desgn cu reducer nedorte ale rezstente s rgdtat. Pentru a propune o noua nstrumentate de nanondentare este necesara ma nta elaborarea metodelor s a modelelor, pe baza carora s-ar constru softul afferent. Noul concept propus de no consta ntr-un nou experment. Acest experment este justfcat prn teora pe care am construt-o s care evdentaza capabltatle acestu experment Este vorba de construrea une ln de ndentere care se msca cu vteza v, unele dn ele actonand pe o parte a suprafate probe, altele pe cealalta suprafata n aceeas drecte sau drect opuse. Indenterele pot actona pe o parte a probe, cealalata parte fnd ncastrata. In fg.3. este prezentat schematc acest ndenter multplu. In acest fel este posbla evaluarea nu numa a propretatlor elastce dar s a capactat de amortzare. Conceptul no metodolog se bazeaza pe o sere de rezultate (fg.7.):. Dezvoltarea de modele ale suprafetelor n contact, la scara nano-, mcro- s macroscopca.. Modelarea nelocala a contactulu cu s fara frecare 3. Modelarea nelocala a campulu de tensun s de deformat dn ara de contact 4. Teor cuplate atomstc-contnue pentru modelarea comportar mecance a nanostructurlor, 5. Modele de reducere pseudosferca pentru determnarea leglor consttutve ale materalelor nanostructurate pe baza datelor expermentale, 6. Modele de caracterzare a capactat de amortzare pe baza metodelor cuplate Presach- Tteca. 7. Introducerea functe lu Tteca pentru caracterzarea capactat de amortzare prn prsma suprafetelor cu curbura negatva. Acest concept, noua tehnca de masurare s metoda vor face obectul unu brevet de nvente
191 58 Fg. 7.. Schema concept. Prezentam n contnuare un model n care amortzarea este adaugata prn elemente exteroare atasate. Consderam bara dn fg.7., de lungme L, la care s-a atasat un numar de k p amortzoare nelocale externe de grosme h p. Aceste elemente sunt atasate n ( x, x + x), ( x, x + x)... ( xk, xk + xk), x x + x, x, x + x =,..., k,. Ecuata care descre mscarea unu sstem D lnar s cu amortzare este (Le, Frswell and Adhkar 6) ρ ( x) uxt (, ) + M uxt (, ) = x Ω, t [, T], (7.) t t unde u( x, t) este vectorul deplasar, x Operatorul M este defnt de Ω este varabla spatala, t este tmpul, ρ ( x ) este denstatea. t M u( x,) t = C(, x ξ, t τ) u(, ξ τ)dd, τ ξ t (7.) t cu Cx (, ξ, t τ ) nucleul de amortzare pentru amortzarea externa, s care este functe de deplasare. Pentru Cx (, ξ, t τ ) se poate scre forma Cx (, ξ, t τ ) = Hxcx ( ) ( ξ) gt ( τ ). (7.3)
192 59 Fg. 7.. Bara cu elemente de amortzare. Expresa (7.3) repreznta forma generala a modelulu de amortzare vscoelastca nelocala. Functa H( x ) noteaza prezenta amotzar nelocale. Avem H ( x) = H (constant) daca x se gaseste n elementul atasat, s H( x ) = altfel. Un caz partcular pentru (7.3) este modelul amortzar nelocale vscoase (hsterezs spatal), unde nucleul este o functe delta n tmp. In acest caz, forta depnde numa de valoarea nstantanee a vteze sau de rata deformate gt ( τ ) =δ( t τ ), (7.4) s poate depnde s de dstrbuta spatala a vtezelor. Prn (7.4), vtezele dn dferte locat ale corpulu pot nfluenta forta de amortzare ntr-un punct dat. Nucleul spatal cx ( ξ ) se normalzeaza pentru a satsface condta cx ( )dx =, s poate f ales astfel α cx ( ξ ) = exp( α x ξ ), (7.5a) α cx ( ξ ) = exp α ( x ξ). π Ac, α este un parametru caracterstc pentru amortzarea materalulu. Pentru α rezulta cx ( ξ). Alte forme pentru cx ( ξ ) pot f l cx ( ξ ) = pentru x ξ, s altfel, l x ξ cx ( ξ ) = pentru l l x ξ l, s altfel, (7.5b) unde l este un parametru de dstanta. Rezulta cx ( ξ) pentru x ξ > l. Alta forma pentru cx ( ξ ) poate f functa delta Drac δ( x ξ ), care reflecta caracterul reactv al forte de amortzare cx ( ξ ) =δ( x ξ ). (7.6) In cazul (7.6), avem doua posbltat pentru of Cx (, ξ, t τ ) : () amortzare vscoelastca (hsteress temporal) cu nucleu care depnde de stora n tmp Cx (, ξ, t τ ) = Hx ( ) δ( x ξ) gt ( τ ). (7.7) () amortzare vscoasa cu forta depnzand numa de valoarea nstantanee a vteze sau de rata deformate Cx (, ξ, t τ ) = Hx ( ) δ( x ξ) δ( t τ ). (7.8) Modelul (7.8) repreznta cunoscutul model de amortzare vscoasa. Pentru gt τ ( ), avem
193 6 gt ( τ ) = gµ exp( µ ( t τ )), (7.9) cu µ constanta de relaxare s g o constanta. Parametr de desgn sunt: numarul de elemente k p, coordonatele x j, s lungmle elementelor atasate x j, j =,,..., k p, supuzse condtlor x x + x, x, x + x =,..., k p. In problema drecta acest parametr sunt cunoscut. Ecuata de mscare a bare este wxt (, ) wxt (, ) EI ( x) A( x), + ρ +ϒ= (7.) x x t unde EI ( x) este rgdtatea la ncovoere ( E este modulul lu Young s I( x) momentul de nerte), ρax ( ) este masa pe untatea de lungme ( ρ denstatea s A( x ) ara sectun transversale), w( x, t ) este deplasarea transversala. Al trelea termen repreznta amortzarea nelocala defnta pe ( x, x + x ), =,,..., k, astfel x + x t k w(,) ξ τ ϒ = Cx (, ξ, t τ) dτd ξ. t (7.) = x Ac, Cx (, ξ, t τ ) este dat de (7.4). Alegem pentru cx ( ξ ) forma exponentala s functa eroare date de (.5a), precum s forma hat s forma trungh (7.5b) s functa Drac delta δ( x ξ ), cu ambele forme pentru Cx (, ξ, t τ ), s anume (7.7) s (7.8). Condtle ntale se scru w( x,) ( ), w( xt,) v(). x t = w x t= = (7.) Condtle pe frontera se scru pentru dferte forme de prndere: bara ncastrata, smplu rezemata, cu un capat lber wxt (,) =, wxt (, ) = for x x =, x = L, (7.3a) wxt (, ) wxt (,) =, = for x =, x = L, (7.3b) x wxt (, ) wxt (, ) =, EI( x) for = x =, x= L. (7.3c) x x x Problema de valor propr (7.)-(7.3) este caracterzata de ecuata ntegro-dferentala (7.), care poate f rezolvata analtc cu metoda cnodala (Munteanu s Donescu, 4, Chrou s Chrou 3). Soluta generala se poate cauta sub forma N (,) = jcn( η j ) j= w xt A m, η = kx ω t +ϕ (7.4) unde N este numarul functlor cnodale (funct Jacobene elptce, A j sunt constante necunoscute, k numarul de unda, ω frecventa s ϕ faza. Functa Jacobana elptca cn( η m) = cnη, este defnta astfel η= ϕ dθ, m -msn θ,
194 6 cu snη= snϕ, cnη= cosϕ, dn msn η = ϕ. Pentru m =, se obtne snη= snη, cnη = cosη, dnη =, s pentru m =, snη= tanhη, cnη= sechη, dnη= sechη. Notand η m j =η j s ntroducand (7.4) n (7.) obtnem cu N N ( ) EI x Ajcn η j + ρa( x) A jcn η j +ϒ=, x x j= t j= (7.5) ϒ = ξ τ ζ τ ξ k x+ x t N Cx (,, t ) Ajcn j d d. = t x j=, j k j j j ζ = ξ ω τ+ϕ. (7.6) Avantajul metode consta n modul smplu de determnare a constantelor A j, j =,,..., N dn condtle (7.4). Valorle propr se determna prn rezolvarea probleme (7.5), (7.6) s (7.), (7.3). Presupunem bara are sectune crculara cu dametru varabl x d( x) = d a = d( bx). Pentru b =, bara are un dametru d. Ara sectun L πd ( x) πd transversale este A( x) = = A ( bx) cu A =, s momentul de nerte este πd ( x) 4 πd I ( x) = = I ( bx) cu I = In urma calculelor avem N N 4 Ajcn η j = k ( mj + Aj(3mj )cn ηj Ajmjcn ηj), x j= j= N N 4 Ajcn η j = ω ( mj + Aj(3mj )cn ηj Ajmjcn ηj) t j= j=, N N Ajcn η j = ω Ajcnηjsnηjdnηj t j= j=, cn j sn j Problema de valor propr se reduce la η + η =, dn η + msn η =, N ( Pj + ρω Qj +ω Rj +ϒ j) = j= unde P, Q, R sunt polnoame n cn, sn s dn k x+ x t j j, (7.7), j ϒ = ωa C( x, ξ, t τ)(cnη snη dn η )dτd ξ. j j j j j = x η =η m = kξ ωτ+ϕ. (7.8) Egaland termen cu aceeas putere n cn, sn s dn, se obtne dn (7.7) un numar de K ecuat j
195 6 λ ( A, m, k, ϕ ) =ω, j j λ ( A, m, k, ϕ ) =ω, j j (7.9) λ ( A, m, k, ϕ ) =ω. K j j K Numarul necunoscutelor pm = { Aj, mj, k, ϕ, ω, j =,..., kp}, M = k p + 3, este ma mare decat numarul de ecuat K < M. Introducem functle rezduale λ ( A, m, k, ϕ) ω = r, l =,,..., K. (7.) l j j l l Problema se transforma n determnarea necunoscutelor Functa obectv este defnte astfel p M dn mnmzarea rezduurlor. K N 6 - j l j n j j j l= n= = j=, (7.) I ( p ) = K r ( p ) + (4 N ) δ ( p ) + δ ( p ) unde δ n( pj ), =,, n =,,..., N, sunt do ndcator de control pentru verfcarea condtlor ntale (7.) n punctele x,,,..., n n= N δ n = w( xn,) w( xn), δ n = w( xn,) v( xn). (7.) t Verfcarea condtlor pe frontera (7.3) este controlata de ndcator pentru o bara smplu rezemata lbera sau ncastrata δ 3 = w(,), δ 4 = w( L,), δ 5 = δ 3 = w(,), δ 4 = w( L,), w(,) x w( L,) δ =, (7.3a) x, 6 w(,) wl (,) δ 5 =, δ 6 =. (7.3b) x x w(, ) w( L,) w(,) δ 3 =, δ 4 =, δ 5 = EI (), x x x x (7.3c) wl (,) δ 5 = EI ( L). x x Necunoscutele pm = { Aj, mj, k, ϕ, ω, j =,..., kp}, M = k p + 3, se determna dntr-un algortm genetc. Exemplul 7.. Consderam o bara de alumnu smplu rezemata de lungme L = m, cu 3 dametrul d =.5 m. Alte date : modulul lu Young E = 7GPa, denstatea ρ = 7 kg/m, k p =, x =.m s x =.m, grosmea h p =.3m. Avem doua cazur: amortzare vscoelastca µ = or g( t) = exp( t), s amortzare vscoasa µ = or g( t) =δ ( t) ). Sunt luate n seama modelele: (model) exponental (7.5a), (model) functa eroare (7.5a), (model3) functa hat (7.5b) s (model 4) functa trungh (7.5b). Luam α= 5 s l =.8. Numarul N este 4. Pentru N > 4, cresterea acuratete rezultatelor nu este semnfcatva. Tabel 7.. Amortzare vscoelastca: prmele 5 valor propr pentru o bara cu un element atasat.
196 63 Mode l Mod Mod Mod 3 Mod 4 Mod ± ± ± ± ± ±. -.9 ± ± ± ± ± ± ± ± ± ± ± ± ± ± Tabel 7.. Amortzare vscoasa: prmele 5 valor propr pentru o bara cu un element atasat. Model Mod Mod Mod 3 Mod 4 Mod ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± Tabelul 7. preznta estmarle nferoare a prmelor 5 valor propr pentru baracu amortzare vscoelastca. Tabelul 7. preznta estmarle nferoare a prmelor 5 valor propr pentru bara cu amortzare vscoasa. In ambele cazur se observa ca modelul are cea ma mare amortzare, ar modelul 4are cea ma mca amortzare. Exemplul 7.. Consderam aceeas bara ca n exemplul anteror cu k =, x =.m, x =.m, x =.6m s x =.m. Tabelul 7. preznta estmarle nferoare a prmelor 5 valor propr pentru bara cu amortzare vscoelastca s cu doua elemente atasate. Exemplul 7.3. Consderam aceeas bara ca n exemplul anteror cu k =, x =.m, x =.m, x =.6m s x =.m. Tabelul 7.3 preznta estmarle nferoare a prmelor 5 valor propr pentru bara cu amortzare vscoasa s cu doua elemente atasate. Tabel 7.3. Amortzare vscoelastca: prmele 5 valor propr pentru o bara cu doua elemente atasate. Model Mod Mod Mod 3 Mod 4 Mod ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± 43.3 Tabelul 7.4 preznta estmarle nferoare a prmelor 5 valor propr pentru bara cu amortzare vscoasa s cu doua elemente. Amortzarea pentru modurle s este ma mare decat n exemplul 7. pentru toare cazurle. Modelul are cea ma mare amortzarear modelul 4 cea ma mca. Table 7.4. Amortzare vscoasa: prmele 5 valor propr pentru o bara cu doua elemente atasate. Model Mod Mod Mod 3 Mod 4 Mod ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± ± 43.3
197 64 Problema nversa consta n determnarea necunoscutelor x j, x j, j =,,..., k p, astfel ncat toate valorle propr sa fe deasupra une constante complexe date C + C Sa se determne x j, x j, j =,,..., k p, dn: max C, C condt : Re ω C, Im ω C N ( Pj + ρω Qj +ω Rj +ϒ j) = j= k x+ x t,, ϒ = ωa C( x, ξ, t τ)(cnη snη dn η )dτd ξ. j j j j j = x η =η m = kξ ωτ+ϕ. j cu P, Q, R polnoame n cn, sn s dn. Daca vrem sa maxmzam dferenta ntre doua valor propr consecutve problema devne Sa se determne x j, j x j, j =,,..., k p, dn: max Re C4 C3, Im C4 C3 condt : Re ω Re C, Re ω + Re C3, Im ω Im C, Im ω+ Im C3 N ( Pj + ρω Qj +ω Rj +ϒ j) =, j= k x+ x t, ϒ = ωa C( x, ξ, t τ)(cnη snη dn η )dτd ξ. j j j j j = x η =η m = kξ ωτ+ϕ. j j (7.4) ω s + ω, (7.5) Exemplul 7.5. Consderam bara dn exemplul 7., k =, de locate x [m] necunoscuta, x =.m, h p =.3m, µ = s µ =. Se rezolva problema nversa (7.4) cu C + C =.5 ± pentru cazul, s C + C =.59 ± pentru cel de al dolea caz. Tabel 7.7. Caz : locate element vscoelastc (model ) s prmele valor propr Mod Mod Mod 3 Mod 4 Mod ± ± ± ± ± x.46 s.34.3 s.49. s.58 Tabel 7.8. Caz : locate element vscos (model ) s prmele valor propr. Mod Mod Mod 3 Mod 4 Mod 5 -. ± ± ± ± ± x.9 sd.6.33 s.47. s.68
198 65 S-a studat s cazul n care elementele atasate sunt alcatute dn materal auxetc. In acest caz amortzarea bare este ma buna decat a materalelor tradtonale elastovscoase s vscoase. Prn ndentare se pot determna drect aceste propretat. 7.. Modelarea nanocontactelor s a fenomenulu de nanondentare cu ndentere avand forme dferte Asa cum s-a atratat n paragrafele anteroare, teora nelocala de caracterzare a nanocontactelor s a nanondentar este capabla sa descre tehnca de ndentare cu ndentere avand forme dferte. Metoda se bazeaza pe urmatoarele teoreme (Dumtru s Chrou 7a, Rauchs, s Dumtru 9, Donescu, Chrou s Munteanu 9): TEOREMA (Erngen 97). Pentru o teore lnara nelocala a unu corp, a care stare naturala este lbera de efecte nelocale, forta de volum nelocala este nula,.e. f ˆ k =. TEOREMA (Erngen 97). Ecuatle consttutve pentru un corp elastc lnar zotrop s omogen s rezduurle de localzare nu voleaza negaltatea globala a entrope ρh ρη q ρ bˆ + ρη ˆ n V σ, θ unde η este denstatea de entrope, θ este temperature absoluta s ˆb este rezduul entrope care verfca condta ρ bˆd v=. daca s numa daca, au urmatoarea forma V t =λe δ + µ e + ( λ e δ + µ e )dv, (7..) kl rr kl kl rr kl kl V σ Σ=Σ + λ ( e ) +µ ed + ( λ ee +µ ee )dv, ρ ˆ =, f ˆ k =, (7..) kk kl kl kk ll kl kl V σ unde λ, µ sunt constantele elastce clasce Lamé, λ s µ sunt functle elastce nelocale Lamé care depnd de x x, Σ este o functonala care depnde de x (care a valor n ntreg corpul), defnte de ρψ=σ ( x, x, k ), cu ψ =ε θη functonala energe lbere, Σ se refera la valoarea n starea naturala, s ρeste denstatea n starea naturala, δ kl este smbolul lu Kronecher, e kl este tensorul de deformate n teora lnara ekl = ( uk, l + ul, k ). (7..3) s u k componentele vectorulu deplasare. Semnul prm ndca faptul ca aceste canttat depend de x s t t, unde x a valor n ntreg corpul, s t este orce tmp aprorc tmpulu prezent t. Condtle ρ ˆ =, f ˆ k = arata ca nu exsta producte neta de masa s forta nelocala n corp. Functle elastce nelocale Lamé λ ( x x ) s µ ( x x ) sunt funct de nfluenta, care sunt postve s descrescatoare s depend de x x. Alta forma a relatlor (7..) s (7..) se obtne prn ncluderea modullor λ s µ n λ s µ
199 66 tkl = [ λ ( x x ) e rr ( x ) δ kl + µ ( x x ) e kl ( x )]d v ( x ), (7..4) V σ Σ=Σ + [ λ ( x x ) ekk ( x) e ll ( x ) +µ ( x x ) ekl ( x) e kl ( x )]d v ( x ). (7..5) V σ Nanondentarea este o tehnca de detremnare a propretatlor mecance a materalelor la scar reduse (mcro s nanoscara). Propretat ca modulul de elastctate, durtatea se determna prntr-o smpla analza a curbe forta-deplasare (Kelchner, Plmpton and Hamlton 998, Bhushan 995). Consderam ac un strat de grosme h s lungme L asezat pe un plan orzontal. Stratul este solctat de un ndenter cu baza orzontala de latme a (fg.7..). Contavtul este fara frecare s nu se pot transmte prn nterfata tensun de tractune. Stratul este solctat la forte vertcale datorta gravtate. Notam cu V volumul stratulu s cu S suprafta de contact. Fg Schema ndentar. Raspunsul orcaru punct dn V depnde de starea dn ntreg volumul. Aceasta dependenta poate f descrsa de legle consttutve (7..4) care devn t = [ λ ( x x ) e ( x ) δ + µ ( x x ) e ( x )]d v ( x ), kl rr kl kl V Constantele Lamé se au de forma (7..6) λ ( x x ) =α( x x ) λ, µ ( x x ) =α( x x ) µ, (7..7) unde λ s µ sunt constantele Lamé pentru cazul nelocal, s α( x x ) este functa nucleu nelocal care masoara efectul tensun n x asupra tensun n x. Erngen () a aratat ca t kl = α( x x ) σkl ( x )d v ( x ), (7..8) V
200 67 unde σ ( x ) este campul local de tensune. Pentru functa nucleu folosm reprezentarea lu Artan (996, 997, ) kl x x B, x x < d, α( x x ) = d (7..9), x x > d, 7 cu B= / d, unde d este o dstanta atomca. Pentru probleme de ndentare d = 4 cm. Campul local de tensune este dat de (Cvelek, Erdogan and Cakroglu 978, Solomon 969) σ ( x) = ρgh a L exp( u)[( + u)exp( u) + u ] u + σ( t) cos[( t x) ]dud t, π h exp(4 u) + 4uexp( u) h a L a (7..) σ ()d t t = P. (7..) a Tensunea nelocala n ara de contact se calculeaza dn (7..6) x+ d x x t( x) = σ( x)dx d, (7..) x d unde σ ( x) este data de (7..) s (7..). Trecand la canttat admensonale t x σ( as) s =, q =, f() s =, (7..3) a L ρ gh ecuatle (7..), (7..) se scru sub forma σ( x) = ρgh al exp( ql)[( + ql)exp( ql) + ql ] ql + f( s) cos[( as x) ]dqd s, π h exp(4 ql) + 4qLexp( ql) h (7..4) a h P f()d s s=. ρ gh (7..5) Tensunle de contact se calculeaza pentrur a/ h=.5, L/ h= 5, utlzand formula de ntegrare Gauss. Se obtn urmatoarele rezultate. Langa frontera domenulu de contact x/ a, n teora locala tensunea tnde catre nfnt. In cazul teore nelocale aceasta tensune este fnta. Tensunle nelocale sunt aceleas ca tensunle locale n nterorul are de contact dar nu s la frontera e. Fgs.7.. s 7..3 arata dferentele dntre rezultatele teore locale s a teore nelocale n campul de tensune pentru a/ h=.5 s respectv a/ h=.3. Ambele fgur arata ca, daca punctele sunt stuate n vecnatatea frontere x/ a>.95 pentru prmul caz, s x/ a>.965 pentru cea deal dolea, sau pe frontera domenulu de contact x/ a=, atunc dferenta dntre teor nu ma poate f gnorata. Tensunle nelocale sunt fnte n toate punctele de frontera a domenulu de contact.
201 68 Fg Tensun locale s nelocale la frontera de contact (prmul caz). Fg Tensun locale s nelocale pe frontera de contact (al dolea caz). Tensunea nelocala admte un maxm, nsa acset maxm nu se gaseste pe frontera domenulu de contact. Tensunle locale s nelocale sunt practce constante n zona de sub contact pentru x/ a.95 n prmul caz, s x/ a.965 n al dolea, dare le dfera la frontera x/ a>.95, s respectv x/ a>.965. Pentru x/ a>.95 s respectv x/ a>.965 ambele solut depnd de a/ h.
202 69 In contnuare obtnem, utlzand ecuatle ntegrale duale ale lu Sneddon, solut exacte ale stante plane de forma arbtrara. Comparam acum aceste rezultate aplcand soluta lu Soluta lu Sneddon (965) descre ndentarea unu semspatu elastc cu un con drept crcular rgd (fg. 7.. sus), propusa pentru prma data de Boussnesq n 885. Sneddon obtne pentru forma are reale de contact urmatoarea formula scrsa n coordonate clndrce r - coordonata radala s z - coordonata axala : (7..6) unde ν este coefcentul lu Posson. Axa z concde cu axa de smetre a ndenterulu. Suprafata lbera a semspatulu are ecuata z =. Jumatate dn unghul conulu ndenterulu este notat cu φ. Raza cerculu de contact este notata cu a. Pentru deducerea formule (7..6), ncepem cu a= h c tan φ. (7..7) Adancmea de penetrare este h data de (7..8) de unde rezulta (7..9) Expresa pentru sarcna este (7..) Condtle pe frontera ale lu Sneddon sunt (7..) Sneddon obtne urmatoarea formula foarte mportanta pentru deplasarea radala a punctelor de pe cercul de contact u r ( ν) r r/ a ( r/ a) = ln 4( ) tan + ( r/ a) ( / ) ν φ r a. (7..)
203 7 Fg Indentarea semspatulu cu un con rgd. Problema lu Sneddon. Se vede dn (7..) ca deplasarea radala este negatva s se anuleaza pentru coefcentul lu Posson,5 (materal ncompresbl), sau cand unghul ndenterulu conc este φ = 9. Pentru cazurle de nteres practc φ < 9 s ν <,5, deplasarea este fnta. Rezulta ca forma are de contact n problema lu Sneddon nu este conca c este ma complcata (fg. 7..4). Pentru determnarea are reale de contact folosm formula (7..) s condta pe frontera (7..) 3. Punctele care ntal se aflau pe semspatu r = r, z = se muta n pozta data de r = r + ur, (7..3) (7..4) cu u r data de (7..). De ac se obtne formula (7..6). Problema contactulu elastc pentru o stanta plana se reduce la ntegrarea ecuatlor p(, ξ η) δ=θ dξdη n D, (7..5) ( x ξ ) + ( y η) s a condte de echlbru D Relata de contnutate este P= p( ξ, η)dξdη. (7..6) D p( ξ, η ) = pe D, (7..7) unde θ= ν este o caracterstca de materal, D este domenul de contact, D frontera lu D, πµ p( ξ, η ) este presunea n D (tensunea normala exerctata de stanta n D ), δ este adancmea de patrundere n semspatu, P este forta normala aplcata, µ este constanta elastca a lu Coulomb, ν este coefcentul lu Posson. Pentru P, µ s ν cunoscute, problema se reduce la determnarea p( ξ, η ), δ s D.
204 7 Un mod de rezolvare a probleme este de a exprma presunea p( ξ, η ) dn (7.) ca o functe de δ s de alt parametr geometrc care caracterzeaza domenul D, apo de a determna acest parametr δ s D dn (7.) s (7.3). In fnal, se determna presunea p( ξ, η ). Pentru domen de contact crculare s elptce, problema a fost rezolvata. Pe de alta parte, problema contactulu se poate reduce la problema stante parabolce. Pentru o stanta parabolca cu raze de curbura ρ s ρ, pot f calculate semaxele a s b ale elpse de contact s deplasarea vertcala δ, cu formulele 3πθ P E( k) a = 4 H π( k ) /3 / 3, /3 /3 3πθ P E( k) b = k 4 H π( k ), (7..8) unde H = + ρ ρ π / ( ) -k sn d Ek = ψ ψ s /3 4( k ) 3 /3 δ= πθ P H K( k), (7..9) π Ek ( ) 4 este curbura mede, Kk ( ) = k = b excentrtatea elpse de contact, ar a dψ a doua, s respectv de prma speta. Presunea maxma sub stanta π\ sunt ntegralele elptce complete de speta -k sn ψ /3 π 6H P max 5 /3 p max este data de / 6 p = p(,) = ( k ) Ek ( ) πθ. (7..3) Pentru baze neelptce nu exsta formule exacte c doar aproxmatve. Solomon (964) a ncercat sa construasca o teore unversala pentru stanta plana. Teora sa este exacta pentru cerc s rezonabla pentru un polgon regulat, dar devne falsa pentru o elpsa cu excentrtate mare. Fabrkant (986) a plecat de la urmatoarea exprese parametrca pentru frontera D a are de contact: ρ = a( ϕ ), (7..3) s, dn poteza ca dstrbuta de presun sub stanta, datorta une sarcn P aplcate central, este p( ρϕ, ) = unde c este o constanta care se determna dn (7..6) π a( ϕ) π ca( ϕ) d d ( )d a ( ϕ) ρ ca( ϕ), (7..3) a ( ϕ) ρ ϕ ρ ρ= c a ϕ ϕ= Ac= P, (7..33) cu A ara baze, obtne Pa( ϕ) p( ρϕ, ) = A a ( ϕ) ρ. (7..34) Dn (7..34) s dn reprezentarea nversulu dstante dntre doua puncte
205 7 x λ ρρ, ϕ ϕ dx mn( ρ, ρ) = cos( ) π, ( x )( x ) ρ +ρ ρρ ϕ ϕ ρ ρ (7..35) cu Fabrkant a obtnut formula u λ ( uv, ) =, (7..36) + u u cosv θpπ r δ= a, (7..37) A unde r a este raza mede n raport cu centrul de masa. Dumtru s Chrou (8) au rezolvat problema (7..5)-(7..7) utlzand ecuatle ntegrale ale lu Sneddon. Prncpalul rezultat obtnut n aceasta lucrare consta n obtnerea de formule exacte pentru presune s adancmea de patrundere, care s-au dovedt a f exacte pentru stantele parabolce, crculare, elptce s patratce. Avantajele acestor solut constau n: () soluta p( ξ, η ) a ecuate (7.) este contnua s margnta n D ; () n vecnatatea orcaru punct regulat ( ξ, η ) langa frontera D, se obtne p( ξ, η), unde ( ξ, η ) D. In contnuare ( ξη, ) ( ξη, ) prezentam pe scurt aceste rezultate. Consderam semspatul z a caru suprafata z = este solctata de o stanta rgda de forma data. Aceasta problema a fost analzata pentru prma data de catre Boussnesq n 885. Consderam cazul condtlor mxte pe frontera n care corpul elastc B este solctat pe o parte S a frontere sale cu un set de deplasar normale, n tmp ce pe alta parte S a suprafete tensunle aplcate sunt nule. Problema consta n determnarea une funct barmonce n B care sa ndeplneasca condtle L ϕ ( r) = f( r), r S, s L ϕ ( r) =, r S, unde L s L sunt operator dferental cunoscut, ar functa f () r este data. Analza unor astfel de probleme conduce la ecuat ntegrale duale. Utlzam teora transformate Hankel Fm ( k ) a une funct f () t Fm( k ) = f( t) J ( ) d m kt t t, (7..38) unde J m este functa Bessel de prma speta s de ordn m, cu m /. Transformata nversa a lu Hankel F ( k ) este m f( t) = F ( ) ( ) d m k Jm kt k k. (7..39) Dn (7..38), soluta ( uρ, uθ, u z ) a ecuatlor de echlbru n coordonate clndrce ( ρ, θ, z) se poate exprma, cu ajutorul solutlor G ( t, z ) ale ecuate sub aceasta forma m ( ) D t G m =, d D = dz, (7..4)
206 73 u = [ U ( ρ, z) U ( ρ, z)]cosmθ, (7..4a) ρ m+ m m= u = [ U ( ρ, z) + U ( ρ, z)]snmθ, (7..4b) θ m+ m m= cos [( ) ( ) ] ( )d z = θ ν m ν m m ρ m=, (7..4c) u m t D G t G J t t unde ν este coefcentul lu Posson, ar U ( ρ, z) este m m( ρ, ) = ( )d m m ρ U z t DG J t t. (7..4) Componentele tensun se exprma astfel cos [( ) 3 ( ) ] ( )d zz m m m m=, (7..43a) σ = µ mθ t ν D G ν t DG J ρt t sn [ ( ) ][ ( ) ( )]d θz m m m m+ m=, (7..43b) σ =µ mθ t ν D G + ν t G J ρ t + J ρt t cos [ ( ) ][ ( ) ( )]d ρ z m m m+ m m=. (7..43c) σ = µ mθ t ν D G + ν t G J ρt J ρt t In cazul axal smetrc n raport cu axa z, campul deplasarlor este dat de uρ = tdgtzj (, ) ( ρt)dt, (7..44a) u θ =, (7...44b) [( ) ( ) ] ( )d uz = t ν D G ν t G J ρt t, (7..44c) unde G este soluta ecuate (7..4). Pentru tensun avem relatle 3 [( ) ( ) ] ( )d σ zz = µ t ν DG ν t DGJ ρt t, (7..45a) σ =, (7..45b) θz [ ( ) ] ( )d σ ρz = µ t ν DG+ ν tgj ρt t. (7..45c) Consderam acum ca ara de contact este un domenu convex necunoscut D, descrs de o superelpsa (sau curba Lamé) n n x y + =, n >, (7..45) a b unde a s b sunt razele forme ovale. Cazul n = /3 corespunde unu astrod turtt, n = corespunde unu damant turtt, n = une elpse, s n corespunde unu dreptungh. Reprezentarea parametrca este data de / x( θ ) = acos n / θ, y( θ ) = bsn n θ. (7..46)
207 74 Calculam s ara superelpse / / n n a n 4 ab πγ+ x n A= 4b dx =, (7..47) a Γ + n z nn! unde Γ este functa Gamma Γ () z = lm, ( z,,,...). n z ( z+ )...( z+ n ) In coordonate polare x= rcosθ, y= rsn θ, superelpsa se exprma astfel n cosθ r( θ ) = + a sn θ b n / n π, θ<, (7..48) / n r unde r =, r, ( n n r = a + b ) max( a, b) n, lm r = max( ab, ). Consderam ca n deformatle n D sunt axal smetrce. Condtle pe frontera z = sunt urmatoarele π σ rz =σ θz =, r, θ<, (7..49a) π u z =δ, r <, θ<, (7..49b) prθ (, ) =σ zz =, r, π θ<. (7..49c) Condta (7..49c) asgura anularea presun pe D. Componentele tensunlor s ale deplasarlor trebue sa se anuleze atunc cand dstanta tnde catre. Rezulta G( tz, ) = At ( )( ν+ tz)exp( tz), t, (7..5) 4 t unde At () este o functe necunoscuta. Se observa ca (7..49a) sunt satsfacute automat. Dn (7..44c), (7..45a) s z =, rezulta Avem z ( ) ( ) ( )d u = ν t A t J rt t, (7..5) p( r( θ )) =σ = µ A( t) J ( rt)dt. (7..5) zz t δ A() t J ( rt)dt =. (7..53) ( ν) Restul condtlor (7..59b) s (7..49c) sunt satsfacute daca s numa daca At () verfca ecuatle t δ A() t J ( rt)dt =, r <, (7..54a) ( ν)
208 75 A tj rt t ( ) ( )d =, r. (7..54b) Aceste relat (7..54) se numesc ecuatle ntegrale duale ale lu Sneddon. Introducem operator L s L astfel Ecuatle (7..54) devn L ( rt,) At () = AtJ () ( rt)dt, L ( rt,) At () = t AtJ () ( rt)dt. (7..55) L (,) rt At () = w, r <, (7..56a) L ( r,) t A () t =, r, δ unde w = ( ν ). Presupunem ca L admte un operator nvers unc satsface relata Forma operatorlor L s L se alege astfel (7..56b) A( t) = L ( r, t) w care L ( r,) t L (,) r t w =. (7..57) s s s, s= L ( rt,)() = sr t F ( ϕ, kr)() s s s s= L ( rt,)() = + r t E( ϕ, kr)(), (7..58) F( ϕ, kr) = ϕ dψ, k r sn ψ ϕ (, ) sn d E ϕ kr = k r ψ ψ, (7..59) ( ) / n n π nr b unde ϕ = arcsn( r), ϕ, k =, a = max( ab, ). F( ϕ, kr), E( ϕ, kr) sunt a ntegralele elptce de prma speta, s respectv de a doua speta. Aplcam acum operatorul L( rtl,) (,) rt unu polnom Pr () 3 3 P( r) = w r wr + wr w3. Avem n ( ) C k r F kr Pr ( ) = E( ϕ, kr) 3 ( ϕ, ) unde C este o constanta. Sa presupunem ca Pr () este o constanta s r ( ) /3, (7..6) π ϕ=. Rezulta C k K( k) w =, (7..6) /3 E ( k) unde F( π /, k) = K( k) s E( π /, k) = E( k) sunt ntegralele elptce complete de prma speta, s respectv de speta a doua. Dn (7..56a) s (7..59) rezulta ( ) = + s s ( ϕ, ), r s= A t r t E kr w <. (7..6)
209 76 Pentru presune se obtne dn (7..53) formula sau ( ( )) ( ) ( )d ( ) s p r θ = µ A t J rt t = µ J rt + r t s E s ( ϕ, k ) w dt s=, (7..63) /3 pr (()) C θ = E( ϕ, rk) rk ( ) / 6, (7..64) 3 ( ν) C = P H 4πµ / 3, / 3 3PH C µ = ( ν), (7..65) n n x y unde H = + este curbura mede a superparabolodulu z = +, s ρ, ρ sunt n ρ ρ n ρ ρ razele de curbura n orgne. Valoarea maxma a presun pr () se determna scrnd r π ϕ= /3 max () = = ( ). Se obtne E( π/, k) Rezultatele obtnute se raporteaza sub forma a doua teoreme: / 6. (7..66) TEOREMA 7... Soluta pr () a ecuate (7..5) este o functe contnua s margnta n orce punct nteror al domenulu D Valoarea maxma a presun este data de In plus, presunea se anuleaza pe D. /3 /3 3PH µ pr (()) θ = ( ν) E( ϕ, rk) /3 /3 3PH µ ( rk ) pmax = p() = k ( ν) E( π/, k) / 6 ( ) TEOREMA 7.. Adancmea δ sub stanta se calculeaza dn formula. (7..67) / 6. (7..68) ( k ) /3 /3 ν PH /3 3 ( ) Kk ( ) δ=. 4 πµ E ( k) (7..69) Aceste formule se verfca pentru cazul stante elptce ( n =, k = k). De asemenea se verfca s pentru cazul unu patrat de latura l ( n = 4, k = ) pentru care se obtne r a π /4 4 l 4l = dθ= c π, cosθ π /3 Hµ A = d P 3( ν) / 3, (7..7)
210 77 cu constantele c s d date de 3 c = π ln tg 8 In fnal, se observa ca avem, / 3 Γ + πp 4 = Γ + 4 /4 d 4 c l /3 H 3( ν) P δ= 4 µ /3,. (7..7) sau P( ν) δ=π ra, (7..7) 4πµ A care este dentca cu formula (7..37). In concluze, s-au obtnut solut exacte pentru problema semspatulu z a caru frontera z = este solctata de o stanta rgda plana cu forma data. Aceste solut sunt exacte pentru cazul stantelor parabolce, crculare, elptce s patratce, s aproxmatve pentru alte tpur. In fg. 7..5, se preznta dstrbuta tensunlor de forfecare de suprafata s nterne la adancmea de 4.5 nm pentru o probas de alumnu. In stanga sunt rezultatele masurate (Ma s Levne 7) s n dreapta rezultatele calculate (Munteanu 9). Fg Dstrbuta tensunlor de forfecare pe o proba de alumnu (stanga: rezultate masurate dreapta: calculate)
211 Includerea n teore a frecar care nsoteste nanondentarea la dferte scar metrce S-a studat comportamentul hsteretc la nvel nanometrc s s-a evaluat forta de frecare la nvel mcro s nanometrc. S-a aratat ca alura bucle de hsterezs depnde de efectele vascoase, char atunc cand acestea sunt foarte mc. Pentru descrerea hsteretca a nanocontactulu, s-a defnt un nanotraductor HT prezentat schemetc n fg. 7., de ecuate t W ut ( ) = ut ( ) sau W ut ( ) = xt ( ) + ut ( )ds. t Fg Nanotraductor. Pentru clarfcarea comportar stck-slp la scara atomca, consderam un sstem cu frecare D la scara atomca, compus dntr-un ndenter rgd de damant cu o structura crstalna perfecta, care aluneca cu vteza V pe o suprafata unu nanotub de carbon modelat ca o bara Euler-Bernoull (fg.7..). Modelul dn fg. 7.. este bazat pe modelul unu sstem cu frecare prezentat n fg...9. Suprafaţa materală, ca nterfaţă dntre două med sau faze materale, nu este contnuă ş netedă la scara atomcă ş moleculară. Arhtectura atomcă a suprafeţelor este caracterzată de prezenţa aspertăţlor de dferte dmensun, forme, unghur de contact ş denstăţ. Dscutăm acum câteva modele ale suprafetelor n contact la scara contnua macroscopca, tnand seama de legăturle de tp adezv pentru contactul sold Modelarea dnamca permte smularea comportar unu sstem cu N grade de lbertate, ar rezolvarea smultana a sstemulu rezultant de N ecuat dferentale de mscare cuplate se poate rezolva prn algortmul Verlet. Fg.7... Sstem ndenter-nanotub de carbon. Ecuatle de mscare a modelulu dn fg.7.. sunt m( txt ) ( ) = Fx( t) + kx( Vt xt ( )), m( tzt ) ( ) = Fz( t) + kzt z ( ), unde mt () este masa ndenterulu mobl care varaza ca rezultat al adezun partculelor, k x este constanta elastca a resortulu n drecta x ( Nm ), k z este constanta elastca a resortulu n drecta z ( Nm ), V este vteza ndenterulu mobl, t tmpul, xt () este pozta n drecta orzontala, zt () este pozta n drecta vertcala, F () t s F () t sunt x z
212 79 fortele exerctate de ndenterul mobl n drectle x s respectv z. Modelul pentru nterfata dntre ndenter s nanotub este prezentat n fg.7..3 (bazat pe modelul de nterfata dntre doua granule (fg..), n care nanotraductorul apare n partea dreapta a fgur... Fg Model pentru nterfata dntre ndenter s nanotub, pe baza de nanotraductor. In fg.6 este reprezentata forta de nteractune [N] ntre atom de carbon n raport cu dstanta [A]. Fg Forta de nteractune C-C [N] n functe de dstanta [A]. Nu folosm ecuatle dnamc moleculare c un model de frecare dntre ndenter s nanotub care se va prezenta n contnuare. Acest model este prezentat schematc n fg.. ş reprezntă nterfaţa (desenata exagerat) dntre ndenter s nanotub, cu o încărcare nţală n = kve. Indenterul s nanotubul sunt modelate ca elemente elastce fără masă caracterzate de două resortur lnare de lungm l u and respectv l v, ş modul k u = k x and respectv k v = k z (ce contorzează propretaţle de forfecare s ntndere). De asemenea punctul de contact respectă legea de frecare a lu Coulomb cu coefcentul de frecare µ. Fg.7..5 lustreaza fenomenul tpc de stck-slp n absenta deformatlor nanotubulu de carbon. Se repreznta pozta denterulu n * E raport cu pas de tmp. S-a utlzat o varabla admensonala de tmp dt = dt, E energa mr de coezune a atomlor de carbon, r o dstanta de refernta.
213 8 Fg Varata pozte ndenterulu n raport cu pas de tmp. Forta de frecare exerctata n drecta x (fara deformarea nanotubulu) este prezentata n fg Varata este aproape snusodala. Fg Varata forte de frecare n drecta x n raport cu pas de tmp. Datortă facltăţ de realzare/prelucrare, am ales acest tp de cap de ndentare, ş anume cel sferc, în detrmentul unora pramdale (Berkovch, Vckers, etc). Prezentăm ma jos rezolvarea probleme ndentăr unu semspaţu elastc cu un ndenter având cap sferc (fg. 7..7). Fg Indentarea unu semspaţu elastc cu un ndenter având cap sferc. Indenterul cu cap sferc acţonează asupra semspaţulu elastc cu o forţă P, producând o adâncme de pătrundere la vărful capulu sferc δ varf =δ x= y=. Materalul elastc studat, zotrop, este caracterzat de modulul lu Young E mat ş de coefcentul Posson ν mat.
214 8 Abordares numercă consta n determnarea presunlor de contact p( xy, ) ş a adâncm de pătrundere δ varf a vârfulu, pentru o forţă de apăsare dată P ş pentru un materal cunoscut caracterzat de E mat ş ν mat. Plecând de la expresa potenţalulu de smplu strat (Solomon 969), această problemă se reduce la rezolvarea următoare ecuaţ ntegrale: p( ξ, η) δ ( xy, ) = dξdη πe ( x ξ ) + ( y η) pentru orce ( x, y) la care trebue adăugată următoarea condţe de echlbru D D, P= p( ξ, η)dξ dη. Ecuaţle ntegrale de ma sus se rezolvă numerc prn dscretzarea domenulu de contact D în element fnte de fronteră. Rezultatele obţnute sunt prezentate în fg. 6, comparându-se soluţa analtcă cu soluţa numercă. Exemplul prezentat se referă la ndentarea unu semspaţu dn plexglas ( E plexglas = 38 [MPa], ν plexglas =.35 ) cu o forţă P = 5 [N] ş pentru un cap sferc al ndenterulu cu raza R = 3 [mm]. D Fg Presunle de contact la ndentarea unu semspaţu elastc cu un ndenter având cap sferc. Compararea soluţe numerce cu cea analtcă. Rezultatele obţnute numerc sunt satsfăcătoare, ele putând f înbunătăţte prntr-o ma bună dsctretzare în elemente fnte de fronteră a domenulu de contact D. În cazul ndentăr une plăc dn plexglas, am obţnut ş unele rezultate expermentale, ele fnd obţnute în colaborare cu Laboratore de Mécanque et Modélsaton des Matéraux et Structures du Géne Cvl, Egletons, Unversté de Lmoges, Franţa. Protocolul testelor expermentale efectuate la laboratorul dn Egletons este următorul: - încercărle au fost realzate pe o maşnă de încercăr Zwck cu o capactate de [kn]; - deplasărle sunt măsurate cu ajutorul unu captor LVDT (marca HBM); - maşna de încercăr Zwck este plotată în deplasare, vteza de încărcare fnd de. [mm/s]; - pentru încercăr s-au folost ble dn oţel noxdabl (ble de rulment) cu dametrele de 8.7 [mm], 7.44 [mm] ş respectv 5.38 [mm] ; - placa supusă testăr este dn plexglas, cu dmensunle [mm 3 ]. Fg prezntă o lustrare grafcă testelor de ndentare efectuate cu maşna de încercăr Zwck.
215 8 Fg Indentarea une plăc dn plexglas, folosnd o maşnă de încercăr Zwck. Curbele forţă-deplasare obţnute prn încercărle de ndentare ale plăc dn plexglas consderate sunt prezentate în fg.8, pentru tre dametre dferte ale ble sferce cu care s-a efectuat ndentarea: 8.7 [mm], 7.44 [mm] ş 5.38 [mm]. Fg Curbele forţă de apăsare-adâncme de pătrundere corespunzătoare ndentăr plăc de plexglas consderate. Pentru a aborda ş expermental ndentarea prn mpact, ma precs pentru realzarea în bune condţ a unu pendul de mpact ( mpact hammer ), a fost în prealabl nevoe de o estmare a nvelulu de acceleraţ ş forţe pe care le vom avea de măsurat, pentru a folos accelerometre ş traductoare de forţă cât ma adaptate. Acest calcul este prezentat ma jos, menţonând că s-au folost poteze smplfcatoare nu foarte exacte, însă sufcente pentru efectuarea une estmăr în ln mar. Cele patru relaţ pe care s-a bazat estmarea nvelulu de acceleraţ la mpact sunt:
216 83 4 3/ P = E δ 3 R, (7..) F,ext = mg P = m δ, (7..) F,ext v v + t m (7..3) F,ext δ + =δ + v t + ( t), m (7..4) unde m este masa ble ş a pendululu ce lovesc placa ndentată prn mpact, F,ext reprezntă forţele (exteroare) ce acţonează asupra ansamblulu blă-pendul la momentul de tmp t, t = t+ t este pasul de tmp consderat, v este vteza la momentul t a ansamblulu blăpendul, ar δ =δ varf, este adâncmea de pătrundere a vârfulu ble la momentul t. Ipotezele smplfcatoare consderate pentru a descre evoluţa procesulu de mpact sunt următoarele: - Relaţa (7..) corespunde une ndentăr cvasstatce a unu semspaţu elastc, ş nu une ndentăr prn mpact, mpactul fnd un fenomen dnamc foarte accelerat ş necestând relaţ de calcul ma elaborate. Am consderat însă că, pentru estmarea în ln mar a nvelulu de acceleraţ (pentru stablrea accelerometrelor de care este nevoe), putem folos relaţa (7..), cu toate nexacttăţle e în descrerea unu fenomen de mpact. - Relaţa (7..) reprezntă prncpul fundamental al dnamc newtonene. - v v+ v Relaţa (7..3) aproxmează acceleraţa la tmpul t ca fnd egală cu =, în t t F,ext t fne relaţa (7..4) provne dn aproxmaţa δ + =δ + v t +, cu v = v +. + m La tmpul t se cunosc δ ş v ş se doresc a se calcula δ + ş v + la tmpul t +, fapt posbl prn rezolvarea sstemulu format de ecuaţle (7..)-(7..4). Am smulat această estmare nu foarte exactă a fenomenulu de mpact cu ajutorul unu mc program realzat în Matlab/Smulnk. Datele exemplulu consderat sunt următoarele: masa ansamblulu blă-pendul m = [kg], materalul ndentat consderat este oţelul ( E otel = [MPa] ş ν otel =.3 ), raza ble de ndentare rgde R = [mm], vteza ansamblulu blă-pendul medat înante de mpact v = ghcadere [m/s]. Fg.7.. prezntă evoluţa acceleraţlor δ în cazul unu mpact corespunzător acestu exemplu.
217 84 Fg.7... Evoluţa acceleraţe în tmpul mpactulu pentru exemplul consderat. Nvelul maxm de acceleraţe obţnut este de crca 3 m 3g, tmpul de mpact estmat s este tmpact.54 [ms], ar adâncmea maxmă de pătrundere a vârfulu ble este δvarf, MAX.8 [mm]. În condţle acestor estmăr prelmnare, am decs achzţonarea unu accelerometru de şoc Brüel&Kjaer având capactatea de a măsura până la un nvel de acceleraţ de 5g, arhsufcent char ş în cazul unor eror mar ntroduse în calculul nostru estmatv de folosrea unor formule cvasstatce smple. Intorcandu-ne la nanotubul de carbon, Ijma (99), Ijma ş Ichhash (993) au arătat expermental că nanotubul de carbon se poate încovoa semnfcatv până la un ungh crtc de aproxmatv de 7,8, pentru un tub cu un sngur perete cu raza de 6 A. La acest ungh, tubul se flambează local ş apare un comportament post crtc de tp knk, cu un model de deformaţe numt knk. Între pereţ tubulu apare un spaţu de 3,5 A, pentru care forţa van der Waals de nteracţune devne puternc repulsvă. Nanotuburle de carbon pot suporta unghur de până la, ş prn înlăturarea sarcn exteroare, deformaţle nanotubulu sunt complet reversble, tubul revennd la forma nţală. Pentru un ungh de, legăturle atomce se rup ş deformaţle devn reversble. Mamals et al. (989) au observat expermental un mod de rupere plastcă a macrotuburlor crculare supuse la încovoere, ş anume au observat forme în V, numte ş forme knk, cu regun trunghulare în peretele comprmat. Acest mecansm de deformaţe a fost asocat cu deformaţa plastcă. În cazul nanotuburlor de carbon, mecansmul de deformaţe knk este asocat cu deformaţa elastcă, ş el explcă rezstenţa mare pe care o au la încovoere. Fg Geometra nanotubulu.
218 85 În acest paragraf modelăm încovoerea elastcă a nanotuburlor de carbon, bazându-ne pe lucrarea autorlor Vodentcharova, ş Zhang (4), ş constrund un model cuplat contnuu/atomstc pentru deformaţa nanotubulu, în raport cu valoarea unghulu crtc de încovoere. Pentru valor ma mc decât unghul crtc, aplcăm metoda contnuă Brazer, ar pentru valor ma mar ale unghulu de încovoere, o teore atomstcă. Consderăm un nanotub de carbon cu un sngur perete de tp zgzag (,), supus la un moment de încovoere exteror M (Fg. 7..). Negljăm deformaţa crcumferenţală ş ne bazăm pe teora Brazer a încovoer elastce a macrotuburlor, pe care o prezentăm pe scurt în contnuare. Pentru un tub de grosme h, rază R, lungme L, modulul lu Young E, ş coefcentul Posson ν, curbura axe în drecţa longtudnală x este dată de unde c este curbura admensonală defntă prn C = R ch ν 3 ( ), (7..5) 3ζ c =, (7..6) ş ζ, coefcentul de deformare a secţun transversale, unde R este raza secţun nedeformate, ş R c, raza secţun deformate, care depnde de unghul de încovoere ψ R R ζ= c. (7..7) R Energa de deformaţe Π pe untatea de lungme este egală cu suma dntre energa de întndere longtudnală ş energa de încovoere crcumferenţală ˆ πEhh ζ Π= πrhce ζ+ ζ +, ˆ h h = 8 8R ν. (7..8) Energa totală a tubulu ş respectv, momentul încovoetor sunt date de dπt Π t =Π L, M =. d ψ (7..9) Notăm cu N forţa axală. Tensunea crtcă la compresune axală ş respectv, momentul crtc de încovoere pentru flambajul local, sunt N σ cr = = h EhR 3( ) ν, M cr πerhhˆ =. (7..) 3 În expresa momentulu M r nu se ţne seama de efectul deformăr secţun. Deformarea secţun face să descrească valoarea acestu moment crtc, astfel M = mm cr, m = c( c ). (7..) Pentru valor mc ale lu ζ, putem calcula raza curbur locale în punctul unde tensunea de compresune este maxmă R ρ=. (7..) 3 ζ
219 86 Tensunea maxmă poate f exprmată ca o fracţune dn tensunea de compresune crtcă σ= sσ, (7..3) unde s este tensunea admensonală a fbre extreme. Presupunem că tensunea de compresune la flambaj local depnde de curbura locală cr cr R s =. (7..4) ρ Deformaţa de compresune se poate scre sub forma ε= CR( ζ ). (7..5) Formulele de ma sus sunt valable atâta tmp cât tubul nu flambează la sarcna crtcă. La flambaj, apar deformaţ de tp knk, care transformă nanotubul într-un mecansm mecanc. Ş anume, o porţune a peretelu se deformează, formând două plăc trnghulare ACF ş ACE, care se rotesc în jurul lne AC, numtă lne knk. Acest mecansm knk este schţat în Fg. 7..3, cu o magne laterală prezentată în fg. 7..4, ş o magne de sus, în fg Partea care rămâne dn nanotub se păstrează crculară char dacă tubul se deformeză în contnuare, ş curbura descreşte. Frontera dntre zona trunghulară ş zona crculară este descrsă de lnle AE, CE, AF ş CF. Nanotubul contnuă să se deformeze elastc, char după aparţa deformaţlor knk. Dn fg. 7,, se obţn deplasărle normale ş tangenţale sub forma w= Rζ cosθ, v= Rζsn θ. (7..6) Când tensunea de compresune atnge valoarea crtcă corespunzătoare unghulu crtc de încovoere, tubul se va flamba, ş valoarea lu ζ pentru flambajul local este în jur de,4. Fg Schţa mecansmululu de deformaţe knk.
220 87 Fg Imagnea laterală a schţe dn fg Fg Imagnea de sus a schţe dn fg Secţunea transversală se deformează astfel încât arcul crcular A C, defnt de unghul φ se deformează ş produce lna knk AC (fg ş fg. 7..7). Această condţe devne AC = A C = Rφ. (7..7) Menţonăm că pentru macrotubur avem altă condţe, ş anume AC = Rφ. Se observă ca avem unde R este raza arculu ADC dn fg AC = AB = R snφ, (7..8)
221 88 Fg Secţunea transversală I-I dn fg Fg Secţunea transversală II-II dn fg Ecuaţle (7..7) ş (7..8) devn Rφ = R sn φ, (7..9) de unde rezultă R sn φ R În contnuare, avem pentru arcul AGC AGC = R ( π φ ). (7..) sau Dn condţa C + AGC = π R, rezultă φ =. (7..) Rφ + R ( π φ ) = π R, (7..a)
222 89 Rsn φ + R ( π φ ) = π R, (7..b) Parametr R ş φ se pot lega de deformaţa dn drecţa longtudnală prn parametrul δ (Fg. 7..6) R + R cosφ = R δ. (7..3) Dn (7..a) avem πr R = sn φ +π φ. (7..4) Coordonatele punctulu A sunt xa = l ya = Rcosλ Rsn λ(l Rsn λ) za = R sn φ Lungmea forme knk este l, ş se presupune că este egală cu R. În acest caz parametrul δ devne De asemenea, avem ş pentru lungmea lnlor AE, CE, AT, CF, obţnem δ=. (7..5) R yb R α= asn l sn λ l, (7..6) l l AB h = +. (7..7) Nu utăm că tubul se deformează elastc. Partea clndrcă dn forma knk în pozţa nedeformată are o curbură în drecţa crcumferenţală,. După flambaj, această parte se R deformează în zonele trunghulare ACF ş ACE, având o curbură. Prn urmare, momentul de R încovoere în drecţa crcumferenţală θ, este dat de 3 Eh M = θθ, (7..8) R ( ν ) Calculăm în contnuare energa de deformaţe corespunzătoare W = 4M Rφ. (7..9) θθ În mod smlar, partea nferoară a zone crculare, nţal cu o curbură în drecţa crcumferenţală R, se deformează într-un arc de curbură. Prn urmare, momentul de R încovoere M în drecţa crcumferenţală ş energa de deformaţe corespunzătoare, sunt date de M θθ 3 Eh = R R ν ( ), (7..3) W = 4 M R ( π φ )( φ φ ). (7..3) Părţle trangulare ale forme knk se rotesc în jurul lne knk AC cu un ungh relatv de rotaţe π α. Momentul de încovoere elastc M, în tmpul aceste rotaţ, are drecţa x. xx
223 9 Pentru a calcula această canttate, ma întâ evaluăm curbura ρ (fg. 7..4). Pentru π α= care corespunde tubulu nedeformat, avem =. Datortă aparţe deformaţe knk, curbura ρ locală creşte, ar FB ş FE (Fg ) nu se pot apropa ma mult decât dstanţa de echlbru d eq = 3,4A. Pentru α= (deformaţe maxmă), dstanţa dntre pereţ este egală cu dstanţa de echlbru, formându-se un arc de curbură = 3,4 A. Într-o prmă aproxmaţe, varaţa curbur locale în ρ raport cu α, se poate consdera lnară de la π la. Avem 3 π α Eh M xx =, (7..3) d eq π ( ν ) cu energa de deformaţe corespunzătoare W3 = Mxx ( π α ) AC. (7..33) Momentul de încovoere elastc în drecţa perpendculară pe AE, CE. AF ş CF, se obţne sub forma Mnn = M xxcos ε x + M θθ sn ε x, (7..34) unde ε x este unghul dntre normala la aceste ln ş drecţa longtudnală x l ε x = a tan AB. (7..35) Energa de deformaţe în fecare lne AE, CE. AF ş CF, este M nn l h φ W4 =. (7..36) l În consecnţă, energa totală de deformaţe, în procesul de încovoere datortă momentulu mecanc exteror, este suma celor patru energ calculate, fnd o funcţe de unghul de încovoere ψ 4 W ( ψ ) = W. (7..37) Momentul de încovoere extern se calculează dn d d W ψ. În cazul nanotubulu, în analza atracţe dntre pereţ care se aprope în tmpul deformaţe, trebue să ţnem seama de forţa de nteracţune van der Waals. Mărmea forţe depnde de dstanţa dntre atom. Pentru dstanţe mar, forţa van der Waals este atractvă, dar când dstanţa dntre atom este ma mcă decât dstanţa de echlbru 3,4A, ea devne puternc repulsvă. În cazul nanotubulu, forţa van der Waals acţonează atunc când apare deformaţa knk. Pe măsură ce unghul de încovoere creşte, partea superoară ş partea nferoară a forme knk se aprope una de alta, până când se atnge dstanţa de echlbru. Această dstanţă rămâne neschmbată, char =
224 9 dacă procesul de încovoere contnuă, pentru că nu exstă forţe normale exteroare care să acţoneze asupra pereţlor ca să anhleze forţa van der Waals. Forţa van der Waals dntre atom ş j se poate exprma sub forma potenţalulu Lennard- Jones 6 σ σ Uj ( rj ) = 4ε 6, (7..38) rj r j 9 unde ε= 4,7483 Nmm, σ= 3,47A, ş r j este dstanţa dntre atom. Energa potenţală de deformaţe este suma energlor tuturor atomlor. Lucrul mecanc al forţe van der Waals pentru fecare atom, este produsul dntre forţă ş deplasarea atomulu în tmpul deformaţe knk. Aplcăm această teore ma întâ pentru un nanotub zgzag (,) de rază 6,6 A, cu un sngur perete de grosme,67 A, având un modul Young echvalent de 4,88 TPa, ş un coefcent Posson ν =,9. Teora Brazer este valablă numa pentru valor al unghulu de încovoere până la ψ= 5,58, pentru care energa are o varaţe nelnară. În fg este reprezentată energa totală a nanotubulu, cu ş fără forţa van der Waals (vdw). Fg Energa totală de deformaţe a nanotubulu. Varaţa momentulu de încovoere M ( ψ ) este reprezentată în fg Se observă că până la ψ=, momentul creşte aproape lnar (ecuaţa (7..9). Momentul de încovoere corespunzător lnlor AC, AE, CE, AF ş CF, după aparţa forme knk este reprezentat în fg Se vede că momentul M xx asocat lne knk AC este domnant deoarece curbura ac este mare.
225 9 Fg Momentul de încovoere a nanotubulu. Pentru a calcula lucrul mecanc al forţe van der Waals trebue să cunoaştem pozţle nţale ş curente ale pozţlor atomlor de carbon. În raport cu un sstem de coordonate aşezat în centrul secţun transversale a unua dn capetele tubulu, înante de deformaţe, atom de pe crcumfernţă au coordonata y fxă,4 3A, ar coordonata x are valor de la,7a la,4a. În tmpul deformaţe tubul rămâne în acelaş plan ( xy ). Secţunea longtudnală prntr-o formă knk pentru un ungh de încovoere de 5,4 este reprezentată în fg. 7.., ar câteva nele atomce deformate în palnul (yz) a secţun transversale a nanotubulu în punctul de maxmă curbură (nele atomce), pentru acelaş ungh de încovoere, sunt reprezentate în fg Deformaţa nţală a secţunlor x = ş x= l se poate lua în consderare pentru flambajul local, dar calculele au arătat că aceste condţ au o nfluenţă negljablă. În tmpul deformaţe se ajunge repede la dstanţa de echlbru 3,4A, care rămâne neschmbată char dacă deformaţa creşte în contnuare. În Fg sunt reprezentate energle dspate în mecansmul knk, cu W, energa dspată totală, W, energa de deformaţe în regunea trnghulară, W, energa de deformaţe în zona crculară, W 3, energa de rotaţe corespunzătoare lne knk AC, W 4, energa de deformaţe de rotaţe corespunzătoare lnlor AE, CE, AF ş CE, ar W vdw, energa van der Waals..
226 93 Fg Momente de încovoere după aparţa deformaţe knk. Fg Secţune longtudnală prntr-o formă knk pentru un ungh de încovoere de 5,4. Fg Deformaţ ale secţun transversale (yz) a nnaotubulu în punctul de maxmă curbură (nele atomce), pentru un ungh de încovoere de 5,4. Lucrul mecanc al forţe van der Waals este negatv, ş era de aşteptat acest lucru (fg. 7..3) deoarece această forţă acţonează ma degrabă ca o forţă exteroară, care se adună la lucrul mecanc al momentulu de încovoere exteror M ( ψ ). În calculul forţe van der Waals se
227 94 consderă numa nteracţounea dntre pereţ forme knk, cu o dstanţă mnmă de 3A. Se negljează nteracţunea dntre părţle aflate la un ungh α una în raport cu cealaltă (fg. 7..4). Fg Energ dspate în mecansmul knk. Fg Câteva forme ale secţun transversale pentru dferte valor ale parametrulu de deformaţe.
228 95 În fnal, fg prezntă câteva forme ale secţun transversale deformate a nanotubulu de carbon, pentru dferte valor ale parametrulu ζ, în dferte stad de deformaţe. În plus, a fost pusă în evdenţă urme de ondulaţ (încreţre) a părţ nferoare a tubulu, aşa cum se observă dn fg. 7..5, înante de aparţa deformaţlor knk. Fg Urme de încreţre a parţ nferoare a nanotubulu, înante de aparţa deformaţlor knk.
229 Teor cuplate atomstc-contnue de smulare a nanondentar În modelele cuplate atomstc-contnue, nterfeţele care despart regunle modelate atomstc de cele modelate contnuu se analzează în mod specal. Fe V volumul regun ocupate de un corp deformabl B în confguraţa de refernţă lagrangană. Mecanca medulu contnuu presupune că pentru un materal dat exstă o funcţonală a denstăţ energe de deformaţe. Notăm cu W ( X ) denstatea energe de deformaţe pe untatea de volum dn confguraţa de refernţă, astfel încât energa asocată unu element de volum dv să fe W( X )dv. Orgnea aceste funcţonale de energe ş dependenţa sa de deformaţa materalulu reprezentă date de c ntrare pentru mecanca medulu contnuu. Energa potenţală a materalulu E se poate scre ca o ntegrală pe volumul V al corpulu c E = W ( X )dv. (7.3.) V În metodele cuplate se utlzează de multe or presupunerea că regunle contnue dn materal nu conţn deformaţ mar ş nc efecte nelastce. De aceea în astfel de regun denstatea energe de deformaţe W este energa defntă de teora lnară a elastctăţ Wln( X) = Cjklεj ( X) εkl ( X ), (7.3.) unde C jkl este tensorul de ordnul patru al constantelor elastce ale materalulu ş ε j sunt componentele tensorulu de deformaţe în punctul X. Pentru a determna starea de deformaţe ş de deplasare a corpulu, în condţ de încărcare c cu forţe exteroare, mnmzăm energa E. Această mnmzare se realzează cel ma smplu cu ajutorul metode elementelor fnte (FEM). Elementele fnte (FE) se bazează pe ntroducerea unu set de puncte X j (nodur j ) în care se calculează deplasărle U j = ux ( j). Deplasărle în alte pozţ ale corpulu decât în aceste nodur, se calculează prn nterpolarea deplasărlor nodale în pozţle dorte (nterpolare predetermnaţă sau cu funcţ de formă). Dacă gradele de lbertate sunt deplasărle nodale, FEM mpune o constrângere cnematcă a deformaţe materalulu. Energa totală în regunea contnuă a materalulu se scre ca o sumă a energlor elementelor µ, cu N numărul de elemente dn regunea V µ e N e c E WV d E µ, E = µ W ( X )dv, W( X) = W( F( X )), (7.3.3) = = V µ Vµ unde F este gradentul deformaţe. Dscretzarea ş nterpolarea stau la baza calcululu deplasărlor elementelor N u( X) = U jsj( X ), j= N F( X) = I+ U S ( X ), (7.3.4) j= j j unde N este numărul de nodur dn regunea consderată, este produsul tensoral ş S j funcţle de formă asocate nodulu j. Un rezultat mportant este specfcat de Curtn ş Mller (3): pentru materale perfect crstalne fără defecte, propretatea de localtate a energe potenţale W ( X ) mplcă faptul că energa în punctul X este egală cu energa pe untatea de volum a unu crstal nfnt ş perfect, deformat omogen cu un gradent de deformaţe FX ( ).
230 97 Energa de deformaţe pe untatea de volum a unu crstal nfnt se calculează cu ajutorul potenţalulu nteratomc. Ş anume, având gradentul deformaţe FX ( ), se aplcă legea Cauchy- Born (Tadmor, Ortz ş Phllps 996): celula untate deformată se obţne prn transformarea vectorlor latce Bravas prmtve nedeformate A, =,,3, în vector ataşaţ structur deformate a = FA, unde a, =,,3, sunt pozţle no ale nodurlor dn reţeaua crstalulu. Vector de pozţe R ş r ale nodurlor reţele nedeformate ş respectv deformate sunt daţ de R = la + ma + na 3, = l + m + n 3 r a a a. (7.3.5) Pentru reţele Bravas smple cu un sngur atom în celulă, se calculează destul de greu o celulă untate deformată. Dar pentru crstale complexe, cu ma mulţ atom asocaţ fecăre pozţ, procedeul devne efcent. Pozţle atomlor sunt descrse de vector de bază B k, k =,,..., n, în raport cu pozţa nedeformată a reţele. Pozţle dn latcea nedeformată sunt daţ de R+ B, k =,,..., n. Pozţle atomlor în reţeaua deformată se scru sub forma k Energa potenţală W ( FX ( )) devne rk = la + ma + na3 + b k, k = k unde Ω este volumul une celule untare ş b FB, k =,,..., n. (7.3.6) Ea ( ( )) ( F W = ( X FX )), (7.3.7) Ω E a = E este energa totală atomcă, cu E energa atomulu. Legea Cauchy-Born este smlară cu poteza dn FEM, prn care gradele de lbertate atomce nterne ale une celule untare sunt legate cnematc de pozţle dn reţeaua Bravas. Prn urmare, pentru deformaţ mc energa se poate calcula conform leg Cauchy-Born. Pentru a obţne rezultate realstce, se aplcă această lege pentru atom pentru care k =, ş se mnmzează energa în raport cu gradele nterne de lbertate b k, k =,..., n. Observăm că propretatea de localtate a funcţe W ( X ) permte construrea metodelor cuplate, deoarece energa atomcă reală are un caracter nelocal. Dacă F este mare, caracterul nelocal joacă un rol mportant. Într-un model contnuu, W ( X) nclude nteracţunle atomce nelocale, datortă presupuner că deformaţa este omogenă în orce element, ş nu pentru că s-a luat în consderare deformaţa neomogenă (Curtn ş Mller 3). Pentru a obţne echlbrul mecanc, energa se mnmzează în raport cu gradele de lbertate. Este utl să dentfcăm consecnţele aproxmăr funcţe W ( X ) asupra forţelor dn nodur. Forţa c E dn nodul se calculează cu formula, ş corespunde energe care rezultă dn varaţa U deplasăr U nodulu, după ce nodul s-a deplasat cu o canttate nfntezmală. În FEM, varaţa deplasăr nodulu produce o varaţe a gradentulu de deformaţe F pentru toate elementele care conţn nodul. Dacă n e este numărul elementelor conectate cu nodul, varaţa energe totale este E U c n c e Eµ =. (7.3.8) U µ= Energa asocată elementelor care nu sunt conectate la nodul rămâne neschmbată. În contrast, când un atom este deplasat sau mutat (într-o smulare atomcă), toţ atom care se află în vecnătatea sa, să zcem regunea R, suferă o modfcare a energe. c
231 98 Într-o formulare atomstcă, forţa dn nodul este E r a = E ne j. (7.3.9) jr, j < R r c În metodele cuplate, se face o descrere atomstcă pentru anumte regun dn materal ş o descrere contnuă pentru alte regun dn materal. Regunea de tranzţe sau frontera dntre regunea atomcă ş regunea contnuă (nterfaţa tampon, sau pad) necestă o atenţe deosebtă. Această nterfaţă este modelată în aşa fel încât nteracţunle nelocale dntre atom să fe luate în consderaţe. O altă metodă de a descre nterfaţa dntre domenul contnuu ş domenul atomstc este tranzţa prn scara mezoscopcă de la mcron la mlmetr. Această metodă este utlă în modelarea propagăr fsurlor macroscopce. Se presupune că fsura are o mşcare în dervă cu vârful fsur executând o mşcare de dfuze, pentru a reflecta efectul vteze de osclaţe a fsur observată la nvel atomc, în traectora fsur observată macroscopc. Componenta de dfuze este caracterzată de un process stocastc Wener. Se utlzează modelul Ensten al dnamc Browane (Raf-Tabar ) D= r t r () (), (7.3.) st t unde t este tmpul de întârzere, s dmensunea spaţulu dfuzv ( s = în cazul prezent), ar r este coordonata atomulu dn vârful fsur. În acest model, propagarea fsur se modelează în tre scăr metrce dferte. Ma întâ se realzează o tranzţe de la scara macro la scara nanometrcă prn ntermedul scăr mezoscopce. Se calculează deplasărle atomlor la scară macro, ş apo cu dnamca moleculară se calculează forţele ş tensunle la vârful fsur. Se calculează vteza crtcă a fsur V m, adcă vteza de la care apar osclaţle, ş constanta de dfuze D a atomulu dn vârful fsur. Pe urmă se realzează o tranzţe reversă, de la scara nanometrcă la scara contnuă, tot prn ntermedul scăr mezoscopce. Se deplasează atomul dn vârful fsur, în noua pozţe calculată anteror, ş se calculează traectora fsur, cu metoda stocastcă Ito d X () t = X( t+ d) t X() t = A[ X(),]d t t t+ DdW() t, (7.3.) unde Xt () este traectora stocastcă a fsur în spaţul real, A[ Xt (),] t este vteza de mşcare a fsur, ş Wt () este Gaussanul stocastc al procesulu Wener Metoda de rezolvare a ecuatlor nelnare (metoda cnodala) Functle cnodale sunt ma bogate decat functle snus s cosnus, deoarece modulul m al functe cnodale ( m ) poate vara pentru a obtne o functe snusodalã ( m ), o vbrate Stokes ( m.5) sau o vbrate de tp solton ( m ). Osborne a rezolvat ecuata nelnara KdV cu metoda cnodala, cunoscuta în lteraturã s sub numele de metoda împraster înverse prn reprezentar cnodale sau reprezentar theta ( functa theta). S-a dovedt ca nu numa ecuata KdV poate f rezolvata cu aceasta metoda, ecuat nelnare celebre cum ar f ecuata sne-gordon s ecuata nelnara a lu Schrödnger, precum s alte ecuat nelnare au fost rezolvate cu reprezentarea theta (Munteanu s Donescu, 4) Consderam functa () t ntrodusa de Weerstrass (85-897) n 85 care verfca ecuata 4 g g, (7.4.) 3 = 3
232 99 unde punctul noteaza dervata n raport cu t. Daca e, e, e 3 sunt radacnle reale ale ecuate = cu e > e > e 3, atunc (7.4.) se poate scre sub forma 3 4y gy g3 cu 4( )( )( ), (7.4.) = e e e3 g = ( e + e + e3), g3 = 4eee 3, e + e + e 3 =. Introducem determnantul = g 7g. (7.4.3) 3 3 Pentru >, ecuata (7.4.) admte ca solute partculara functa elptca Weerstrass care se reduce, în acest caz, la functa cosnus elptc jacoban cn (functe cnodala) unde δ este o constanta reala arbtrara. Daca atasam ecuate (7.4.) condtle ntale ( t+δ ; g, g ) = e ( e e )cn ( e e t+δ ), (7.4.4) () =θ, () =θ p, (7.4.5) atunc o suprapunere lneara (suma) de funct cnodale de forma (7.4.4) este de asemenea o solute a ecuate (7.4.) n ln kcn [ kt; mk ] k= θ = α ω, (7.4.6) unde m k, frecventele ω k s ampltudnle αk depnd de θ, θ p. Pentru < soluta ecuate (7.4.) este data de + cn( t H +δ ) = e + H cn( t H +δ ), n care avem 3e g m =, H = 3e. 4H 4 Daca = avem e = e = c, e3 = c s soluta ecuate ( 7.4.) este data de = c + 3c ct +δ. snh ( 3 ) Consderam acum o ecuate de tp Weerstrass cu polnom de ordnul 5 s ne propunem sa- determnam solutle. Aceasta ecuate apare n analza dnamca a pendululu smpatc s se scre sub forma θ = A θ + A θ + A θ + A θ + A θ, (7.4.7) unde,,...5 A = se exprma cu ajutorul a doua constante R s S care pot f reale sau pur magnare
233 Atasam condtle ntale A 6 4 = S, A A = RS, 3 4 = R S, A A 3 3 = RS, (7.4.8a) 4 5 = R. (7.4.8b) θ () =θ, θ () =θp. (7.4.9) Vom arata ca soluta ecuate (7.4.7) admte pe langa o solute de tpul (7.4.6) s o solute de nteractune nelnara (o suprapunere nelnara de funct cnodale). Pentru a arata aceasta, presupunem ca aceasta solute este de forma λ ( t) θ nt () t =, (7.4.) +µ ( t) unde () t este functa elptc Weerstrass care satsface ecuata dferentala (7.4.), cu nvarant g s g3 real ce satsfac >, s λ s µ constante arbtrare. Inlocund (7.4.) în (7.4.7) se obtne un set de 4 ecuat pentru necunoscutele λ, µ, g s g 3 Dn ecuatle (7.4.a), (7.4.b) obtnem Tnand seama de (7.4.8) ecuata (7.4.) se reduce la Astfel, µ s λ se pot exprma sub forma λµ = A µ + Aλµ + Aλ µ + A λ µ + Aλ, (7.4.a) λµ = 4A µ + 3Aλµ + Aλ µ + Aλ, (7.4.b) λ+ λµ g = 6Aµ + 3Aλµ + A3λ, (7.4.c) λµ g + λµ g = Aµ + A λ. (7.4.d) 3 6Aµ + 5A λµ + 4Aλ µ + 3Aλ µ + Aλ =. (7.4.) ( R S ) λ+ µ =. (7.4.3) A 3A /4 5 µ = λ, (7.4.4) Dn (7.4.c) s (7.4.d) putem calcula necunoscutele g s g 3 g 3 3/ λ= 3(3 AA 5}. (7.4.5) A A λa = λ µ 3 µ µ, A g3 = + A g. (7.4.6) λµ µ µ
234 Pentru parametr care ntervn n aceasta analza exsta întotdeauna solut reale pentru λ, µ, g s g 3. Termenul de nteractune nelnara al solute ecuate (7.4.7) devne λ ( t+ δ ; g, g3) θ () t =, (7.4.7) +µ ( t +δ ; g, g ) unde λ s µ sunt date de (7.4.4) s (7.4.5) s δ este o constanta de ntegrare. Inlocund functa elptca Weerstrass cu functa elptca cn unde e, e, e 3 sunt r d cnle 3 reale ale ecuate 4y gy g3 =, cu e > e > e 3 obtnem 3 λ[ e ( e e )cn ( e e t+δ )] θ = + µ [ e ( e e )cn ( e e t+δ )] 3 3 nt () t 3 3. (7.4.8) Modulul m al functe elptce jacobene este dat de e e3 m =. (7.4.9) e e Vbrata soltara este o vbrate perodca cu peroada nfnta s acest lucru se întâmpla atunc când m = sau e = e. Deoarece e, e, e 3 sunt radacnle ecuate cubce 3 4y gy g3 =, soluta de tp vbrate soltara poate f posbla pentru anumte valor ale parametrlor λ, µ, g, g 3, s în acest caz ea se scre sub forma 3 λ[ e ( e e )sech ( e e t+δ )] θ = + µ [ e ( e e )sech ( e e t+δ )] 3 3 nt () t 3 3. (7.4.9) Pentru condt ntale arbtrare (7.4.9) termenul de nteractune nelnara se poate scre sub forma generalzata θ ( xt, ) = nt n βkcn [ ωktm ; k] k = n + γkcn [ ωkt; mk] k =, (7.4.) unde m k, ω k,β s γk depnd de θ, θ p s A k. Prn urmare, în cazul ecuate (7.4.7) s-a obtnut o solute formata dn do termen. Prmul termen repreznta o suprapunere lneara de funct cnodale (7.4.6) s cel de al dolea un termen nelnar de nteractune de funct cnodale (7.4.). Ecuaţle dferentale care guverneaza mscarea unu sstem dnamc se scru de obce sub forma dx F( x, x,..., xn),,..., n, n 3 dt = =, (7.4.) t T, T R, unde F poate avea dverse forme polnomale x R n, [, ]
235 d dt n n n θ = ap θ p + bpq θ p θ q + cpqr θ p θ q θ r + p= pq, = pqr,, = n + d θ θ θ θ + e θ θ θ θθ +... pqrl p q r l pqrlm p q r l m pqrl,,, = pqrlm,,,, = n (7.4.) =,,... n. Sstemul de ecuat (7.4.) sau (7.4.) are propretatea remarcabla de a se reduce la ecuat polnomale Weerstrass. In contnuare prezentam metoda cnodala n forma generala aplcabla sstemelor de ecuat (7.4.) sau (7.4.). Pentru smpltatea screr omtem ndcele s notam soluta sstemulu de ecuay θ.introducem urmatoarea transformare de functe unde functa Θ este dezvoltata n sere unde Presupunem ca Pentru n = obtnem Pentru un n arbtrar avem d θ= log Θ ( ) n dt t, (7.4.3) Θ = +εθ +ε Θ + (7.4.4) () () n n n... n () Θ n = exp( ωt). (7.4.5) = Θ = + exp( ω t + B ), Θ = + exp( ω t + B ) + exp( ω t+ B) + exp( ω +ω + B), Θ 3 = + exp( ω t+ B) + exp( ω t+ B) + + exp( ω 3t+ B33) + exp( ω +ω + B) + + exp( ω +ω 3 + B3) + exp( ω +ω 3 + B3) + + exp( ω +ω +ω + B + B + B ) Θ = exp( ω + ) n n n M t B jmm j M (, ) = < j, (7.4.6) exp B ω ω j j = ω+ω j, exp B =ω. (7.4.7) Matrcea de nteractune B se poate descompune într-o matrce dagonala D s o matrce fara componente pe dagonala, adca B = D + O. M = [ MM... M n ] este un vector de numere Τntreg, ω= [ ωω... ω n ] este vectorul frecventa, s n este un numar fnt care repreznta numa rul gradelor de lbertate ale une solut partculare. Screm soluta (7.4.3) sub forma.
236 3 θ ( t) = log Θ ( ) ( ) n η =θln η +θnt ( η), (7.4.8) t unde η= [ ηη... η n]. Prmul termen θln repreznta o suprapunere lneara de funct cnodale s este dat de θln ( η ) = log G ( η), (7.4.9) t T G( η ) = exp( Mη+ M DM ), (7.4.3) M ar dolea termen dat de θ nt repreznta o suprapunere (nteractune) nelnara de funct cnodale s este F ( η, C) θnt ( η ) = log( + ), (7.4.3) t G ( η) T F ( η, C) = Cexp( Mη+ M DM), (7.4.3) α T C = exp( M OM), (7.4.33) Descompunerea (7.4.8) se obtne usor dn (7.4.3) s (7.4.3). Vom dscuta pe scurt de ce prmul termen θ ln poate f nterpretat ca o suprapunere lnara de funct cnodale. Vectorul η are forma Notam Fazele constante sunt de asemenea vector M η = ω t +Λ. (7.4.34) Mη = Ω t+λ, Ω= M ω, Λ= Mβ. (7.4.35) β = [ ββ... β ]. (7.4.36) Consderam acum cazul când nu avem nteractune nelnara. In acest caz termen care nu se afla pe dagonala prncpala dn matrcea O sunt nul. Dn (7.4.33) rezulta C =. Functa G( η ) se poate scre sub forma unu produs n unde n G( η ) = Gm ( Mmηm) (7.4.37) m= G M M D. (7.4.38) m ( η m) = exp( mη m + m mm) M m = Termenul lnar (7.4.9) devne π q θ = α + πω t n k + / l l ln l[ [ cos(k ) ] ] k+ l= K k ql K l ml = + l. (7.4.39)
237 4 cu In (7.4.39) recunoastem espresa q = exp( π K / K), n ln lcn [ lt; ml ] l = θ = α ω, (7.4.4) π / du K = K( m) +, -msn u K ( m ) = K( m), m+ m =. Acestea sunt solut cnodale. Modul m l s vtezele de faza ale functe elptce depnd de coefcent care apar n sstemul de ecuat. Relata (7.4.4) justfca nterpretarea prmulu termen dn solute ca o suprapunere lnara de funct cnodale. Cel de al dolea termen θ nt ntroduce o perturbate în solute datorta nteractun nelnare ale functlor cnodale. Avem dn (7.4.3) d F() t βkcn ( ωtm ; k) log[ + ] =. (7.4.4) 3 dt G( t) +γ cn ( ω t; m ) Daca modul mk au valor sau, relata (7.4.4) se verfca drect. Pentru alte 7 valor ale modullor m k relata se verfca cu o eroare maxma de e 5. Astfel ncat obtnem θ ( xt, ) = nt n βkcn [ ωktm ; k] k= n + λkcn [ ωkt; mk] k= k k. (7.4.4) In reprezentarea solute sub forma functe Θ, ampltudnea osclate cnodale pentru fecare frecventa consttue un spectru Fourer nelnar. Fecare frecventa se asocaza cu un ndce j, j n. Aceste ampltudn sunt legate de termen de pe dagonala în matrcea B prn B jj relata q = exp ar termen dn B care nu se afla pe dagonala determna nteractunea j nelnara dntre componentele θ nt. Functa Θ se poate scre sub forma vectorala Θ ( t) = CM exp( Mη), M CM T = exp( M BM). (7.4.43) Combnata cu (7.4.35) ultma exprese seamana cu sera Fourer ordnara. Fecare termen dn sere corespunde une aleger partculare a vectorulu l un parametru de ordne. Fecare M l genereazã valor partculare pentru coefcent Fourer frecventele Ω M a fazele β M. Condtle ntale atasate functe Θ sunt Θ () = CM. M M, unde l este C M, Astfel, coefcent C M s spectrul de putere Pθ ( f l ) a functe Θ este dat de T CM = Pθ ( fl) f, Pθ ( fl ) = exp( M BM). (7.4.44)
238 5 Frecventele Ω l sunt multpl ntreg I l de ω unde s Ω = l Il ω, I l n = mm, (7.4.45) m= πm ω m = m ω= = πm f, (7.4.46) T l m n l l l l M l M l [ M, M,..., M][,,... n] mmm m= Ω Ω = ω= ω= ω, (7.4.47) cu l nmax. n Numãrul de frecvente în spectru este dat de nmax = [(M + ) ]. Sumele partale corespunzãtoare unu ndce M m sunt luate n lmtele ( M, M ), astfel încât ( J ) Il J pentru n J = M m= Mn( n+ ). m= Testele numerce analzate au consderat M s n = 3. Pentru aceste valor avem 3 5 = 4 frecvente n spectru s dec 4 termen n functa theta. Pentru n = 5 numarul de 3 termen se rdca la 34. Pentru M = s n = acest numar devne. 7 O state moderna de calcul realzeaza aproxmatv operat pe secunda, dec numarul de termen poate f calculat ntr-un nterval de tmp egal cu vata estmata a unversulu (aprox. 8 s). In concluze, soluta sstemulu de ecuat (3.) se scre, asa cum am specfcat, ca o suma dntre o suprapunere lneara de vbrat cnodale s un termen de nteractune nelnar a vbratlor cnodale. cu θ ln s θ nt dat de (3.4) s respectv (7.4.4). Parametr ω j, β j s B j de determna dn condtle ntale atasate θ ( t) =θ ( t) +θ ( t), (7.4.48) ln nt θ =θ, =,,... n, (7.4.49) s dn sstemul de ecuat obtnut prn echlbrarea termenlor care nmultesc aceeas exponentala. 8. Integrare s desgn tehnologc a nanonstrumentate vrtuale pentru masurarea propretatlor elastce s vasco-elastce ale materalelor Prn termenul de Instrumentaţe Vrtuală se înţelege utlzarea unu computer, dotat cu echpamente perferce de ntrare ş eşre specalzate, pentru a smula caracterstcle ş funcţonarea unu nstrument sau sstem de măsurare, de testare sau de a înregstrare a datelor. Instrumentele vrtuale fac uz de traductoare ş senzor pentru a ntra în contact cu mărmea fzcă măsurată, de eventuale ssteme de condţonare a semnalelor, precum ş de crcute pentru conversa analog-dgtal. Dferenţa în raport cu sstemele de măsurare clasce este aceea că de această dată toate funcţunle de prelucrare ş analză a valorlor măsurate, de stocare a acestor
239 6 nformaţ ş de transmtere a lor către utlzatorul uman sunt realzate de către computer ş nu de către aparatura dedcată. Aplcaţle software înlocuesc astfel componente estmate a reprezenta 8% dn crcutele unu aparat de măsurare sau testare specalzat clasc. Software-ul care realzează aceste funcţun posedă în majortatea cazurlor o nterfaţă grafcă având acelaş aspect ca ş al panoulu frontal al unu aparat de măsurare. Acesta este motvul pentru care aplcaţle repectve sunt numte Instrumente Vrtuale. În urmă cu 5 de an, NI a ntrodus conceptul de nstrumentaţe vrtuală care a revoluţonat măsurătorle ş automatzărle în domenul ndustral, ş nu numa, dezvoltând pentru nstrumentaţa vrtuală. In ceeace prveste software, medle de dezvoltare LabVIEW, LabWndows/CVI, precum ş produsele add-on sunt recunoscute pentru flexbltate ş uşurnţă în utlzare. De peste de an, medul de programare grafcă NI LabVIEW a revoluţonat dezvoltarea aplcaţlor de testare scalable, măsurare, ş aplcaţle pentru control de proces. Fără a dspune de o experenţă deosebtă, ngner ş oamen de ştnţă pot realza în mod rapd ş efcent nterfeţe cu dspoztvele hardware de măsurare ş control, pot realza analza datelor, dstrbuţa rezultatelor, ş construrea de ssteme dstrbute. Integrarea s desgn-ul tehnologc a nanonstrumentate vrtuale pentru masurarea propretatlor elastce s vasco-elastce ale materalelor formeaza contnutul unu brevet de nvente (probabl va f fnalzat la sfarstul anulu ). Se urmareste realzarea unu sstem în care se pot obţne nformaţ, în condţ de efcenţă maxmă ş preţ de cost mnm. Acest mod de ntegrare poate f folost atât de utlzator de ssteme prepress, care doresc să îş realzeze sngur lucrărle color necesare desfăşurăr actvtăţlor lor, cât ş de producător sau furnzor de ssteme prepress la chee. Sstemul va putea f utlzat ş de organsmele complexe de tp nanotehnologc, de tp reţea, pentru crearea ş nterogarea bazelor de date specfce domenulu lor de actvtate de către specalşt reţele, sstem care elmnă barerele geografce prn utlzarea nfrastructur dgtale, a reţelelor ultrarapde ş a tehnologlor de comuncaţe moderne- nternet. 8.. O problema nversa de dentfcare a propretatlor vasco-elastce s de amortzare a unu materal nanostructurat Consderam un nanocrstal monoclnc de grosme h, lungme l s latme d, n raport cu un sstem de coordonate Cartezan x, x, x3. Sstemul de refernta este orentat n drecta axelor crstalografce a, b, c (fg.8..). Axele a s c sunt perpendculare pe axa b. Orgnea este localzata la ntersecta dagonalelor, ar margnle crstalulu sunt x = ± l / s x = ± d /. Fe Ξ suprafata lbera de tensun a crstalulu. Legea consttutva este data de T kl = C E + η E (8..) klmn mn unde T este tensorul tensune, H = grad u( x, t) gradentul deplasar, u ( x, t) vectorul T deplasare, x = ( x, x, x3 ), E = ( H + H ) tensorul de deformate lnar Lagrangan, C klmn constantele elastce de ordnal do s η klmn constantele vscoase. klmn mn
240 7. Ecuatle de mscare sunt date de Utlzam conventa Vogt de sumare Conform cu aceasta convente, Fg Nanocrstal monoclnc T = ρ u,, k, l =,, 3. (8..) kl l l (, j) δj + (9 j)( δj ) C klmn =C αβ, η klmn =ηαβ,,3, n tmp ce ndc grec, valorle,,,6. Componentele T kl, E α, conform leg, unde ndc latn au valorle E kl se nlocuesc cu T α, T kl = T α, Ekl ( + δ kl ) = Eα, k, l =,, 3, α =,,... 6 Condtle pe frontera sunt ux (, t) = u( t) pentru x =, t (8..3) unde u ( ) este deplasarea data n orgne t u = U sn ωt (8..4) Ecuatle de mscare (8..) admt solut de forma u = Re{ aexp[(k N x ωt)]} (8..5) unde a este ampltudnea complexa a vectorulu u, k este numarul de unda complex k = k + k, N este vectorul untary al drecte de propagare a unde u, k = k N, s ω > este frecventa unghulara. Canttatea complexa k este vectorul complex de unda de cosnus drector ( m, n, l). Drecta de propagare N ( m, n, l) se presupune cunoscuta. Vteza complexa a ω ωk ωk ω unde este data de v = = +, cu partea reala V =. Se observa ca k k + k k + k k + k
241 8 atenuarea nfluenteaza propagarea undelor n crystal, prn aparta undelor omogene, evanescente s heterogene. Inlocund (8..5) n (8..) avem k D ~ ( N )a = ρω (8..6) k k a unde D ~ ( N k ) este D ~ C ~ k ( N ) mkn N m N n (8..7) este matrcea characterstc corespunzatoare drecte de propagare N. Canttatle D ~ ( N k ) se defnesc usor, utlzand conventa Vogt pentru C ~ mkn ~ ~ ~ ~ ~ D = Cm + C66n + C55l + C6mn ~ ~ ~ ~ ~ ~ ~ D = D = C6m + C6n + C45l + ( C + C66 ) mn ~ ~ ~ ~ ~ ~ D = D = ( C + C ) ml + ( C + C ) nl ~ D ~ D ~ D ~ = C ~ = D ~ = C ~ ~ ~ m + Cn + C44l + C6mn ~ ~ ~ ~ = ( C36 + C45 ) ml + ( C3 + C44 ) nl ~ ~ ~ ~ m + C n + C l + C mn + ( C ~ + C 45 ) nl (8..8) ~ In (.7) s (.8), Cklmn = Cklmn + ωη klmn ( C ~ αβ = Cαβ + ωη αβ repreznta matrcea rgdtatlor complexe, cu 3 constante ndependente complexe de ordnal do ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ C jkl = C αβ = C, C, C, C, C, C, C, C, C, C, C, C, C, ( ) 3 l 6 cu α = β =, Screm (8..6) sub forma ~ ρ v δ a = D a (8..9) nul l Pentru ca (8..9) sa admta solut nenule, determnatul complex Chrstoffel trebue sa fe l 3 l 6 33 ~ det( ρv δ D ) = (8..) l Partea reala a acestu detremnant nu este dentca cu determnantul Chrstoffel pentru un medu fara atenuare. Dn (8..) se obtn relat ntre k s matrcea complexa a rgdtatlor C ~, s ne asgura 3 radacn complexe v pentru orce drecte ( m, n, l). Cunoscand v, se pot determna ampltudnle A. In nanostructura nu exsta numa unde pure longtudnale ( P ) sau transversale ( S ). Exsta unde care se propaga n vecnatatea drecte ( m, n, l), cum ar f unde cvas-longtudnal ( qp ), cvas-transversal ( qs ). Daca P este o unda pura, atunc S s S sunt de asemenea pure. Daca numa S este pura, atunc undele P s S nu sunt pure, dare se propaga ntr-un plan perpendcular pe S. l
242 9 Pentru a determna cele 3 constante complexe, se utlzeaza date expermentale de ndentare, dn care se evalueaza vteza de faza. Se alege o functe obectv I ca masura a dstante dntre teore s experment I( C) = m = e {[ v v ( C)] + δ }, (8..) unde v e sunt vtezele masurate, v, evaluar teoretce ale vtezelor, s m numarul masuratorlor n dferte drect m > n, cu n numarul parametrlor necunoscut ( 3+3=6). In (8..), δ estmeaza verfcarea condtlor (8..4) cu u ( ) dat de (8..),.e. δ = ( u (, t ) u ( t )). Vectorul C~ contne 6 necunoscute ~ ~ t T T C = ( C αβ`, ) = ( C, C,... C6 ). (8..) Problema de optmzare se rezolva cu un algortm genetc. Rezultate sunt prezentate n tabelele Dmensunle structur sunt h = 35nm, lungme l = 5nm s latme d = 4nm. Vtezele se admensonalzeaza prn mpartre la o vteza lumn n vacuum. Tabel 8... Unde longtudnals s cvas-longtudnale n nanostructura. No. Drecta de propagare Drecte aproxmatva a deplasar Voteza teoretca admensonala Vteza admensonala expermantala v l v l v l 3 v l 4 v l 5 v.698,.588, ,.588, l 6 v l 7.698,, ,, v.5,, ,, l8 v.5,.588, ,.588, l9 v.95,, ,, l v.5,, ,, l v.75,.788, ,.788, l v.698,.588, ,.588, l3 v.5,, ,, l4 v.5,.788, ,.788, l5 v.95,.588, ,.588, l6 v.5,,.395.5,, l7 v.655,.588, ,.588, l8
243 v.5,, ,, l9 v.55,.588, ,.588, l v.555,.788, ,.588, l v.95,, ,, l Tabel 8... Unde transversals s cvas-transversale. No. Drecta de propagare Drecte aproxmatva a deplasar Voteza teoretca admensonala Vteza admensonala expermantala v t v t v t 3 v t 4 v t 5 v t 6 v t v t8 v t9 v t v.95,, t v.95,, ,, t v.698,, ,, t3 v.698,, t4 v.5,, ,, t5 v.5,.588, transversal t6 v.5,.588, transversal t7 v.698,, ,, t8 v.5,, ,, t9 v.5,, t v.95,.588,.395 transversal.45 - t v.95,.588,.395 transversal.4 - t v.698,.588, transversal t 3 v.698,.588, transversal.57 - t 4 v.5,.588,.395 transversal.43 - t 5 v.5,.588,.395 transversal t 6 v.395,.588, transversal.89 - t 7
244 v.395,.588, transversal.69 - t 8 v.75,, ,, t 9 v.75,.588,.695 transversal t3 v.75,.588,.695 transversal t3 v.5,.788, transversal t3 v.5,.788, transversal t33 v.595,.788, transversal t34 v.595,.788, transversal.7 - t35 C C ~ αβ αβ = + ωη αβ Tabel Valorle constantelor complexe. Valor masurate [GPa] Prawer et al. Valor calculate dn algortm genetc [GPa] Valor utlzate n problema drecta ~ C ω 8.83 ± ω ~ C ω.4 ± ω ~ C ω 4.87 ± ω 3 ~ C ω 5.3 ± ω 6 ~ C ω 6.67 ± ω ~ C ω 4.5 ± ω 3 ~ C ω 8.4 ± ω 6 ~ C ω ± ω 33 ~ C ω 7.5 ± ω 36 ~ C ω 8. ± ω 44 ~ C ω -.5 ± ω 45 ~ C ω 5. ± ω 55 ~ C ω 9.7 ± ω Expermente de nanondentare smulate realst pe computer (I. Model). Teste nr. s. Prezentăm ma jos două teste (T ş T), plecând de la două nţalzăr arbtrare dferte. Testul de ndentare unaxală constă în apăsarea vertcală a unu ndentor rgd pe semspaţul materalulu ce se doreşte a f caracterzat (fg s fg. 8..). Nanondeterul înregstrează atât forţa de apăsare P cât ş adâncmea de pătrundere h varf a capulu sferc al ndenterulu în semspaţul materalulu studat. Capul sferc al ndenterulu nu este complet rgd, fnd alcătut dntr-un materal hpoelastc având modulul Young E varf = 6 GPa ş coefcentul Posson ν varf =.7.
245 Fg Modelare axsmetrcă cu elemente fnte a testulu de ndentare. Modelarea axsmetrcă cu elemente fnte a capulu sferc al ndenterulu ş a semspaţulu ce consttue materalul este prezentată în fg. 8..b, fnd foloste elemente fnte patrulatere pentru a modela jumătate dn semspaţul materalulu ndentat ş 47 elemente fnte patrulatere pentru a modela un sfert dn capul sferc al ndenterulu. În prvnţa contactulu dntre capul sferc al ndenterulu ş materalul ndentat, modelarea acestua se face împedcând întrepătrunderea geometrcă dntre cele două corpur în contact, fapt ce se realzează prn aplcarea unor tracţun pe suprafaţa de contact. Aceste tracţun ntroduse de modelarea contactulu se calculează pe baza dstanţe locale dntre nodurle semspaţulu materalulu ş proecţa acestor nodur pe suprafaţa ndenterulu (Rauchs 6). Ecuaţle consttutve ale materalulu supus ndentăr sunt defnte ma jos. Comportarea plastcă a materalulu ndentat este defntă de teora fluxulu J zotropc (Rauchs 6), curgerea plastcă fnd determnată de funcţa de curgere f f = P :( σ α) K y f < pentru comportare elastca, f = pentru comportare plastca, f > exclus, (8..) y unde K este lmta de curgere, α este aşa-numtul back-stress, o varablă nternă de răspuns a materalulu, σ este tensorul Cauchy al tensunlor, ar P este operatorul devatorc de proecţe S P = I I I, (8..) 3 unde I S y este tensorul untate smetrc de ordnul 4. Varaţa lmte de curgere K este descrsă consderând ecrusarea sotropcă:
246 3 t p ( )d j K, { s β } = σ + [ exp( β )], 3 (8..3) y y R y, unde s = ε τ τ 3 este lungmea deformaţe plastce, σ este tensunea nţală unaxală la curgere, ar R ş β sunt parametr zotropc de ecrusare. Pentru ecrusarea cnematcă, am folost formula nelnară Armstrong-Frederck: p α = H knε Hnls α, (8..4) 3 unde H kn ş H nl sunt parametr de ecrusare cnematcă. Comportarea hpoelastcă a materalulu ndentat este descrsă folosnd legea lu Hooke, exprmând tensorul Cauchy al tensunlor σ în funcţe de deformaţle elastce ε el prn ntermedulu constantelor Lamé G ş λ: S el el σ = ( G I +λi I): ε = C : ε, (8..5) unde C este tensorul de ordnul 4 respectv. Pentru a putea caracterza evoluţa dnamcă a procesulu de ndentare, ecuaţle consttutve (8..)-(8..5) sunt formulate ncremental în cele ce urmează. Varablele de stare la începutul pasulu ncremental de tmp sunt notate cu ndcele superor, varablele de stare la sfârştul pasulu ncremental sunt notate cu ndcele, în tmp ce pentru varablele de stare la jumătatea pasulu ncremental se foloseşte ndcele /. Având de-a face cu deformaţ fnte în dferte puncte ale materalulu ndentat, este necesar să exprmăm toate varablele de stare tensorale în acelaş sstem de coordonate global care să nu depndă de rotaţa unu element fnt sau a altua. În acest sstem de coordonate global, evoluţle ncrementale ale lungm deformaţe plastce s, tensorulu deformaţlor plastce ε p, tensorulu Cauchy al tensunlor ş tensorulu α sunt (Rauchs 6): s = s + g, (8..6) 3 ˆ ˆ g ˆ p, p, ε = ε + N, (8..7) ˆ ˆ ˆ ˆ σ = σ + C : ε G g N, (8..8) αˆ = exp( H g) αˆ + [ exp( H g)] H N ˆ, (8..9) kn nl nl H nl unde tensorul normalzat ˆN este dat de: ˆ ˆ ˆ P :( σˆ α) ˆ P :( σˆ α) ˆ N = =. ˆ y P :(ˆ σ α) ˆ K Parametrul de vâscoztate plastcă (8..): g se obţne egalând cu zero funcţa de curgere f dată de
247 4 H y f = P: σˆ + GP: εˆ exp( H g) α ˆ G g [ exp( H g)] K =. kn nl H nl Această ecuaţe algebrcă nelnară se rezolvă folosnd o schemă teratvă Newton-Raphson, determnându-se astfel parametrul g. Programul de elemente fnte SPPRc mplementează ecuaţle consttutve sub formă ncrementală (8..5)-(8..9) pentru a descre comportarea elasto-plastcă a materalulu ndentat. În practcă, parametr de ecrusare lnar H kn ş R au fost înlocuţ cu parametr de ecrusare * * H kn ş R ce au semnfcaţa fzcă a unor tensun: * H kn * R H kn = ş R =. H β nl În cadrul aceste probleme nverse, ce şapte parametr elasto-plastc de dentfcat pe baza testelor de nanondentare sunt: modulul lu Young E ş coefcentul Posson ν pentru comportarea elastcă, respectv tensunea nţală unaxală la curgere σ y,, parametr zotropc de * * ecrusare R, β ş parametr de ecrusare cnematcă H kn, H nl pentru comportarea plastcă nelnară. Notăm cu x vectorul ce regrupează aceşt şapte parametr de dentfcat: x y, * * = E ν σ R β Hkn H nl. Ideea dentfcăr parametrlor elasto-plastc de materal pe baza testelor de ndentare este reprezentată în fg.. Pentru un cclu încărcare-descărcare-reîncărcare-încărcare-descărcare, curba expermentală forţă-adâncme de pătrundere este reprezentată punctat. Necunoscând apror ce şapte parametr de dentfcat, se dau valor arbtrare acestor parametr (în absenţa une tehnc de estmare), după care se smulează cu ajutorul programulu SPPRc, obţnându-se curba smulată forţă-adâncme de pătrundere, reprezentată cu lne contnuă în fg T nl Fg Curba forţă-adâncme de pătrundere (curba expermentală versus cea smulată) pentru un cclu încărcare-descărcare-reîncărcare-încărcare-descărcare.
248 5 După cum se observă, cele două curbe (cea expermentală ş cea smulată consderând valor nţale arbtrare ale parametrlor de dentfcat) dferă între ele. Se aplcă o procedură de corectare teratvă a acestor parametr, cu scopul de a mnmza (a aduce cât ma aproape de zero) următoarea funcţe obectv ce exprmă dferenţa dntre curba expermentală ş cea smulată: N sm k exp k hvarf ( P ) hvarf ( P ), (8..) k= Ξ= sm unde N este numărul de puncte de comparaţe, ( k h ) varf P este valoarea smulată a adâncm de k pătrundere a capulu ndenterulu în materal pentru o apăsare cu forţa P, la tmpul t k, ar exp ( k ) k hvarf P este valoarea expermentală a adâncm de pătrundere pentru forţa de apăsare P. De menţonat că, pe lângă adâncmea de pătrundere, ma pot f comparate ş valorle smulate ş expermentale ale amprente radale rezultate în urma ndentăr. Am ales să mnmzăm funcţa obectv Ξ prn metode de tp gradent, ce necestă calculul gradentulu funcţe obectv în raport cu vectorul x al varablelor probleme de optmzare : T Ξ Ξ Ξ Ξ Ξ Ξ Ξ Ξ Ξ Ξ = = y, * *, x x7 E ν σ R β Hkn Hnl unde dervata funcţe obectv Ξ în raport cu parametrul de materal x ( =,,7) se deduce dn (8..): N k Ξ h ( P ) = h ( P ) h ( P ) x. (8..) k = sm sm k exp k varf varf varf x sm k hvarf ( P ) În prvnţa dervatelor, deş pot f calculate numerc, s-a preferat calculul lor analtc x (Rauchs 6), cu scopul reducer semnfcatve a tmpulu computaţonal. Elementele H j ale matrce Hessene H se calculează dervând încă o dată (8..): N sm k sm k sm k Ξ hvarf ( P ) hvarf ( P ) sm k exp k hvarf ( P ) Hj = = + hvarf ( P ) hvarf ( P ) x xj k= x x. j x xj Procedura de mnmzare folostă constă în aplcarea succesvă a două metode de tp gradent, ş anume ma întă metoda Gauss-Newton ş apo metoda Levenberg-Marquardt (Nocedal ş Wrght 999, Ponthot ş Klenermann 6). Au fost foloste subrutnele Gauss- Newton ş Levenberg-Marquardt ale lbrăre Fortran IMSL (Vsual Numercs Inc. 997). Metoda Gauss-Newton constă în următoarea corectare teratvă: [ ] ( ) p p p p x + = x µ H Ξ p, (8..) p p unde p este numărul teraţe, H este matrcea Hessană ar µ este un parametru de căutare a p p cele ma mc valor a funcţe obectv Ξ de-a lungul drecţe de căutare [ H ] ( Ξ). Metoda Levenberg-Marquardt constă în următoarea corectare teratvă a vectorulu x: [( ) ] ( ) p p p T p p p T x + = x J J +ξ I J Ξ p, (8..3) T
249 6 p, ar ξ este un parametru de căutare a cele ma mc valor a funcţe p obectv de-a lungul drecţe de căutare. De remarcat faptul că matrcele H ş T T [( J p ) J p +ξ p I] ( J p ) trebue să fe poztv defnte pentru ca drecţa de căutare să fe o drecţe descendentă, de dmnuare a funcţe obectv. Plecând de la dverse nţalzăr ale parametrlor de dentfcat, procedura de corectare teratvă a parametrlor trebue să conveargă către mnmzarea (char anularea, dacă este posbl) funcţe obectv. Prezentăm ma jos două teste (T ş T), plecând de la două nţalzăr arbtrare dferte. Tabelul 8.. prezntă valorle nţale arbtrar alese în cadrul testulu T, valorle nţale arbtrar alese în cadrul testulu T, valorle căutate (soluţa probleme), lmtele nferoare ş cele superoare ale parametrlor. unde Jacobanul J = ( Ξ) T Tabel 8... Dferte valor ale celor 7 parametr: valorle nţale arbtrar alese în cadrul testulu T, valorle nţale arbtrar alese în cadrul testulu T, valorle căutate (soluţa probleme), lmtele nferoare ş cele superoare ale parametrlor Inţalzar e test T Inţalzar e test T Soluţa probleme Lmte nferoare Lmte superoar e E [MPa] ν σ y, [MPa] * R [MPa] β [-] * H kn [MPa] H nl [-] Procedura de mnmzare folostă este compusă dn următoarele patru etape: metoda Gauss-Newton (8..) aplcată varablelor E ş σ y,, celelalte varable fnd blocate (denumtă G-N, maxmum 8 teraţ admse); metoda Gauss-Newton (8..) aplcată pentru toate cele şapte varable (denumtă G-N, maxmum teraţ admse); metoda Levenberg-Marquardt (8..3) aplcată pentru tre varable, alese după ordnea de prortate: ) varablele temporar blocate pe lmta nferoară sau superoară, ) varablele x Ξ corespunzătoare cele ma mc pante ), restul de patru varable fnd blocate (denumtă L- x M, maxmum 5 teraţ admse); metoda Levenberg-Marquardt (8..3) aplcată pentru toate cele şapte varable (denumtă L-M, maxmum 3 teraţ admse).
250 7 Aplcând procedura de mnmzare de ma sus probleme nverse de dentfcare a celor şapte parametr elasto-plastc de materal, s-a obţnut convergenţa procedur de mnmzare în cazul celor două teste efectuate. Identfcarea parametrlor s-a efectuat dec cu succes, astfel fg. 8..3a prezntă dmnuarea funcţe obectv cu creşterea numărulu de teraţ, pentru prmul test T, de la Ξ ntal, T =.8 [µm - ] până la valoarea mnmzată de Ξ mn,t =.8 [µm ]. Fg Dmnuarea funcţe obectv log Ξ cu numărul de teraţ: a) prmul test T; b) al dolea test T. Fg. 8..3b prezntă dmnuarea funcţe obectv în cazul celu de-al dolea test T, de la Ξ ntal, T =.36 [µm -9 ] până la valoarea mnmzată de Ξ mn,t = 7.6 [µm ]. Lnle punctate
251 8 vertcale ndcă trecerea de la o metodă la alta (G-N, G-N, L-M, L-M) în cadrul procedur de mnmzare. Rezultatele obţnute sunt satsfăcătoare. Funcţa obectv descreşte permanent în cazul ambelor teste, fără a dverge sau a se bloca în mnme locale. Ea descreşte până la valor apropate de zero, ceea ce înseamnă că datele smulate ş cele expermentale au fost practc suprapuse. Procedura de mnmzare propusă, bazată pe metodele Gauss-Newton ş Levenberg- Marquardt, este dec funcţonală. Totuş, metodele de tp gradent precum Gauss-Newton ş Levenberg-Marquardt sunt metode de mnmzare locală, fnd necesară o bună nţalzare a parametrlor probleme nverse pentru a converge către mnmul global dort ş nu către un mnm local. Astfel, pentru a evta nţalzărle arbtrare ale celor şapte parametr de dentfcat, vom încerca găsrea une metode de nţalzare/estmare ma elaborate. De asemenea, în combnaţe cu metodele de tp gradent s-ar putea folos ş metode evoluate de căutare, cum ar f algortm genetc. Test nr.3. Testul consta n determnarea prn nanondentare dnamca a propretatlor vscoelastce a tre probe: o proba de epoxna, o proba dn polymethyl mrthacrylate (PMMA) s o proba dn polydmethyl sloxane (PDMS) (Ferry 98). Nanondentarea a fost realzata cu un Indenter DCM (MTS Systems, Inc.) (Gdansk Unversty of Technology s Brtsh Unversty of Caro). Schema modelulu dnamc (aparat Brnbom) este reprezentata n fg.8..4, ar n fg. 8..5, se repreznta schema sstemulu de ndentare (stanga) pentru modelul dnamc corespunzator (dreapta). Domenul fortelor aplcate este de la to. la 5 mn, frecventele varaza de la la 3 Hz. Ampltudnea osclatlor se mentne n jur de 5. ±.5 nm pentru proba PMMA s epoxna, s de aprox. 5 nm pentru PDMS. Indenterul este de tp Berkovch cu varf pramdal. S-au efectuat pentru fecare proba, cate masurator prn ndentare. Modulul redus de elastctate E r s modulul perdut E r se calculeaza pentru fecare frecventa dn S π ωcs π E r =, E r =, (8..4) A A unde S este rgdtatea de contact, C s este coefcentul de amortzare a ndenterulu, A este ara de contact, s ω este frecventa unghulara. Pentru modulul redus E avem s formula r ( νs) ( ν ) E r = +, (8..5) E E s unde E modulul de elastctate al ndenterulu, ν coefcentul Posson al ndenterulu, E s modulul de elastctate al probe, ν s coefcentul Posson al probe. Pentru polmer ν =.33 s ν =.5 pentru elastomer.
252 9 Fg Schema modelulu dynamc (aparat Brnbom). Fg Schema sstemulu de ndentare (stanga) pentru pentru modelul dnmac corespunzator (dreapta). In fg este reprezentata dependenta modululu de elastctate redus E r pentru proba de epoxna, la o temperature de refernta de C. Sunt reprezentate s date de nanondentare, precum s datele obtnute dn analza dnamca (DMA) mecance. Pentru DMA se folosesc formulele π P π P E r = cosδ, E r = sn δ, (8..6) A h A h unde P este forta aplcata, h este ampltudnea deplasar, δ este unghul de faza ntre forta s deplasare. Comparam rezultatele obtnute orn ndentare cu rezultatele DMA. Dn fg se observa ca valorle modululu redus de elastctate obtnute prn nanondentare sunt ma reduse decat cele obtnute prn DMA.
7 ECUAŢII ALGEBRICE ŞI TRANSCENDENTE
 7 ECUAŢII ALGEBRICE ŞI TRANSCENDENTE 7 Separarea rădăcnlor Ecuaţe algebrcă dacă ( este polnom Ecuaţa transcendentă în caz contrar ( = Rădăcnă apromatvă valoare ξ apropată de valoarea eactă ξ Denţ neechvalente:
7 ECUAŢII ALGEBRICE ŞI TRANSCENDENTE 7 Separarea rădăcnlor Ecuaţe algebrcă dacă ( este polnom Ecuaţa transcendentă în caz contrar ( = Rădăcnă apromatvă valoare ξ apropată de valoarea eactă ξ Denţ neechvalente:
2. Lema chinezească a resturilor. Fie,,..., mai mari decât 1 astfel încât pentru. Atunci, oricare ar fi ϵ există unic determinat astfel încât,, unde.
 Lea chneză a resturlor Aplcaț COLUMNA, nr 4, 2015 Ion MUNTEANU unteanuon74@galco ABSTRACT: Ths paper presents soe applcatons of Lea chnezească a resturlor The an dea of Modular arthetc s the study of ssues
Lea chneză a resturlor Aplcaț COLUMNA, nr 4, 2015 Ion MUNTEANU unteanuon74@galco ABSTRACT: Ths paper presents soe applcatons of Lea chnezească a resturlor The an dea of Modular arthetc s the study of ssues
Fig. 2 a) Secventele de impulsuri RMN specifice membranelor PFSA/SiO 2 hidratate pentru corelatiile 2D de tipul a) T 2 T 2 si b) T 1 T 2.
 Raport stntfc prvnd mplementarea proectulu: Relatle structura-dnamca-propretat s efectele mbatranr elastomerlor nanocompozt s membranelor de schmb protonce n peroada anuare decembre 04 Obectvele anulu
Raport stntfc prvnd mplementarea proectulu: Relatle structura-dnamca-propretat s efectele mbatranr elastomerlor nanocompozt s membranelor de schmb protonce n peroada anuare decembre 04 Obectvele anulu
CONVEIOARE DE CURENT: TIPURI SI APLICATII
 CONVEOARE DE CURENT: TPUR S APLCAT Conf. un. dr. ng. Octaan BOGDAN. ntroducere Anul de nastere al coneorulu de curent este anul 966 când A.S. Sedra a realzat un prm crcut analogc cu comanda n curent s
CONVEOARE DE CURENT: TPUR S APLCAT Conf. un. dr. ng. Octaan BOGDAN. ntroducere Anul de nastere al coneorulu de curent este anul 966 când A.S. Sedra a realzat un prm crcut analogc cu comanda n curent s
Revista Informatica Economica, nr. 1 (21)/2002. Program pentru utilizarea functiilor spline în probleme de interpolare neliniara
 84 Revsta Inormatca Economca, nr. ()/00 Program pentru utlzarea unctlor splne în probleme de nterpolare nelnara Con.dr. Maela MUNTEAN Catedra de Inormatca Economca, Facultatea de Stnte Economce Unverstatea
84 Revsta Inormatca Economca, nr. ()/00 Program pentru utlzarea unctlor splne în probleme de nterpolare nelnara Con.dr. Maela MUNTEAN Catedra de Inormatca Economca, Facultatea de Stnte Economce Unverstatea
FD. FIZICĂ STATISTICĂ
 FD. FIZICĂ STATISTICĂ C u p r n s Introucere... 4 Captolul FD.0. Obect ş metoă. Prncple ş postulatele fzc statstce 5 FD.0.. Obectul fzc statstce... 5 FD.0.. Metoa statstcă... 7 FD.0.3. Prncple fzc statstce...
FD. FIZICĂ STATISTICĂ C u p r n s Introucere... 4 Captolul FD.0. Obect ş metoă. Prncple ş postulatele fzc statstce 5 FD.0.. Obectul fzc statstce... 5 FD.0.. Metoa statstcă... 7 FD.0.3. Prncple fzc statstce...
O V E R V I E W. This study suggests grouping of numbers that do not divide the number
 MSCN(2010) : 11A99 Author : Barar Stelian Liviu Adress : Israel e-mail : stelibarar@yahoo.com O V E R V I E W This study suggests grouping of numbers that do not divide the number 3 and/or 5 in eight collumns.
MSCN(2010) : 11A99 Author : Barar Stelian Liviu Adress : Israel e-mail : stelibarar@yahoo.com O V E R V I E W This study suggests grouping of numbers that do not divide the number 3 and/or 5 in eight collumns.
1.3. OPERAŢII CU NUMERE NEZECIMALE
 1.3. OPERAŢII CU NUMERE NEZECIMALE 1.3.1 OPERAŢII CU NUMERE BINARE A. ADUNAREA NUMERELOR BINARE Reguli de bază: 0 + 0 = 0 transport 0 0 + 1 = 1 transport 0 1 + 0 = 1 transport 0 1 + 1 = 0 transport 1 Pentru
1.3. OPERAŢII CU NUMERE NEZECIMALE 1.3.1 OPERAŢII CU NUMERE BINARE A. ADUNAREA NUMERELOR BINARE Reguli de bază: 0 + 0 = 0 transport 0 0 + 1 = 1 transport 0 1 + 0 = 1 transport 0 1 + 1 = 0 transport 1 Pentru
REZOLVAREA PROBLEMELOR DE TRANSPORT SPECIFICE DOMENIULUI MILITAR
 REZOLVAREA PROBLEMELOR E TRANSPORT SPECIFICE OMENILI MILITAR Slt. Pal TORACHE Teora grafrlor, care este n captol dstnct al cercetăr operaţonale, s-a dezvoltat recent, având aplcaţ mltple în actvtatea de
REZOLVAREA PROBLEMELOR E TRANSPORT SPECIFICE OMENILI MILITAR Slt. Pal TORACHE Teora grafrlor, care este n captol dstnct al cercetăr operaţonale, s-a dezvoltat recent, având aplcaţ mltple în actvtatea de
ON THE QUATERNARY QUADRATIC DIOPHANTINE EQUATIONS (II) NICOLAE BRATU 1 ADINA CRETAN 2
 ON THE QUATERNARY QUADRATIC DIOPHANTINE EQUATIONS (II) NICOLAE BRATU 1 ADINA CRETAN ABSTRACT This paper has been updated and completed thanks to suggestions and critics coming from Dr. Mike Hirschhorn,
ON THE QUATERNARY QUADRATIC DIOPHANTINE EQUATIONS (II) NICOLAE BRATU 1 ADINA CRETAN ABSTRACT This paper has been updated and completed thanks to suggestions and critics coming from Dr. Mike Hirschhorn,
Sisteme cu logica fuzzy
 Sisteme cu logica fuzzy 1/15 Sisteme cu logica fuzzy Mamdani Fie un sistem cu logică fuzzy Mamdani două intrări x şi y ieşire z x y SLF Structura z 2/15 Sisteme cu logica fuzzy Mamdani Baza de reguli R
Sisteme cu logica fuzzy 1/15 Sisteme cu logica fuzzy Mamdani Fie un sistem cu logică fuzzy Mamdani două intrări x şi y ieşire z x y SLF Structura z 2/15 Sisteme cu logica fuzzy Mamdani Baza de reguli R
DESPRE COMPLEMENTAREA METODELOR JEFFERSON, ADAMS, WEBSTER ŞI HUNTINGTON-HILL
 DESPRE COMPLEMENTAREA METODELOR JEFFERSON ADAMS WEBSTER ŞI HUNTINGTON-HILL Dr hab prof unv Ion BOLUN ASEM Sunt propuse compementăr de depăşre a stuaţor în care foosrea metodeor Jefferson Adams Webster
DESPRE COMPLEMENTAREA METODELOR JEFFERSON ADAMS WEBSTER ŞI HUNTINGTON-HILL Dr hab prof unv Ion BOLUN ASEM Sunt propuse compementăr de depăşre a stuaţor în care foosrea metodeor Jefferson Adams Webster
Soluţii juniori., unde 1, 2
 Soluţii juniori Problema 1 Se consideră suma S x1x x3x4... x015 x016 Este posibil să avem S 016? Răspuns: Da., unde 1,,..., 016 3, 3 Termenii sumei sunt de forma 3 3 1, x x x. 3 5 6 sau Cristian Lazăr
Soluţii juniori Problema 1 Se consideră suma S x1x x3x4... x015 x016 Este posibil să avem S 016? Răspuns: Da., unde 1,,..., 016 3, 3 Termenii sumei sunt de forma 3 3 1, x x x. 3 5 6 sau Cristian Lazăr
Cristalul cu N atomi = un sistem de N oscilatori de amplitudini mici;
 Curs 8 Caldura specifica a retelei Cristalul cu N atomi = un sistem de N oscilatori de amplitudini mici; pentru tratarea cuantica, se inlocuieste tratamentul clasic al oscilatorilor cuplati, cu cel cuantic
Curs 8 Caldura specifica a retelei Cristalul cu N atomi = un sistem de N oscilatori de amplitudini mici; pentru tratarea cuantica, se inlocuieste tratamentul clasic al oscilatorilor cuplati, cu cel cuantic
FINITE ELEMENT ANALYSIS OF FRICTIONAL CONTACTS
 BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LIV (LVIII), Fasc. 3, 2011 Secţia CONSTRUCŢII. ARHITECTURĂ FINITE ELEMENT ANALYSIS OF FRICTIONAL
BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LIV (LVIII), Fasc. 3, 2011 Secţia CONSTRUCŢII. ARHITECTURĂ FINITE ELEMENT ANALYSIS OF FRICTIONAL
Lucrarea de laborator nr. 11
 Metode Nuerce - Lucrarea de laborator 11 Lucrarea de laborator r. 11 I. Scopul lucrăr Aproxarea î ede pr etoda celor a c pătrate II. Coţutul lucrăr 1. Metoda celor a c pătrate. Procedur MAPLE ş exeple
Metode Nuerce - Lucrarea de laborator 11 Lucrarea de laborator r. 11 I. Scopul lucrăr Aproxarea î ede pr etoda celor a c pătrate II. Coţutul lucrăr 1. Metoda celor a c pătrate. Procedur MAPLE ş exeple
Rezolvarea ecuaţiilor şi sistemelor de ecuaţii diferenţiale ordinare (II)
 Rezolvarea ecuaţiilor şi sistemelor de ecuaţii diferenţiale ordinare (II) Metode multipas Prof.dr.ing. Universitatea "Politehnica" Bucureşti, Facultatea de Inginerie Electrică Suport didactic pentru disciplina
Rezolvarea ecuaţiilor şi sistemelor de ecuaţii diferenţiale ordinare (II) Metode multipas Prof.dr.ing. Universitatea "Politehnica" Bucureşti, Facultatea de Inginerie Electrică Suport didactic pentru disciplina
 lectures accompanying the book: Solid State Physics: An Introduction, by Philip ofmann (2nd edition 2015, ISBN-10: 3527412824, ISBN-13: 978-3527412822, Wiley-VC Berlin. www.philiphofmann.net 1 Bonds between
lectures accompanying the book: Solid State Physics: An Introduction, by Philip ofmann (2nd edition 2015, ISBN-10: 3527412824, ISBN-13: 978-3527412822, Wiley-VC Berlin. www.philiphofmann.net 1 Bonds between
Ecuatii si inecuatii de gradul al doilea si reductibile la gradul al doilea. Ecuatii de gradul al doilea
 Ecuatii si inecuatii de gradul al doilea si reductibile la gradul al doilea Ecuatia de forma Ecuatii de gradul al doilea a + b + c = 0, (1) unde a, b, c R, a 0, - variabila, se numeste ecuatie de gradul
Ecuatii si inecuatii de gradul al doilea si reductibile la gradul al doilea Ecuatia de forma Ecuatii de gradul al doilea a + b + c = 0, (1) unde a, b, c R, a 0, - variabila, se numeste ecuatie de gradul
Universitatea din Bucureşti Facultatea de Matematică şi Informatică. Matematică (Varianta 1)
 Uverstatea d Bucureşt 9.07.05 Facultatea de Matematcă ş Iformatcă Cocursul de admtere ule 05 Domeul de lceţă Calculatoare ş Tehologa Iformaţe Matematcă (Varata ). Toate valorle parametrulu real a petru
Uverstatea d Bucureşt 9.07.05 Facultatea de Matematcă ş Iformatcă Cocursul de admtere ule 05 Domeul de lceţă Calculatoare ş Tehologa Iformaţe Matematcă (Varata ). Toate valorle parametrulu real a petru
Teorema Reziduurilor şi Bucuria Integralelor Reale Prezentare de Alexandru Negrescu
 Teorema Reiduurilor şi Bucuria Integralelor Reale Preentare de Alexandru Negrescu Integrale cu funcţii raţionale ce depind de sint şi cost u notaţia e it, avem: cost sint i ( + ( dt d i, iar integrarea
Teorema Reiduurilor şi Bucuria Integralelor Reale Preentare de Alexandru Negrescu Integrale cu funcţii raţionale ce depind de sint şi cost u notaţia e it, avem: cost sint i ( + ( dt d i, iar integrarea
Reactoare chimice cu curgere piston (ideala) cu amestecare completa de tip batch (autoclava)
 Reactoare chimice cu curgere piston (ideala) cu amestecare completa de tip batch (autoclava) Reactorul cu curgere ideala Toate particulele se deplaseaza intr-o directie de-a lungul reactorului, precum
Reactoare chimice cu curgere piston (ideala) cu amestecare completa de tip batch (autoclava) Reactorul cu curgere ideala Toate particulele se deplaseaza intr-o directie de-a lungul reactorului, precum
Speed of light c = m/s. x n e a x d x = 1. 2 n+1 a n π a. He Li Ne Na Ar K Ni 58.
 Physical Chemistry II Test Name: KEY CHEM 464 Spring 18 Chapters 7-11 Average = 1. / 16 6 questions worth a total of 16 points Planck's constant h = 6.63 1-34 J s Speed of light c = 3. 1 8 m/s ħ = h π
Physical Chemistry II Test Name: KEY CHEM 464 Spring 18 Chapters 7-11 Average = 1. / 16 6 questions worth a total of 16 points Planck's constant h = 6.63 1-34 J s Speed of light c = 3. 1 8 m/s ħ = h π
UNITATEA DE ÎNVĂȚARE 3 Analiza algoritmilor
 UNITATEA DE ÎNVĂȚARE 3 Analiza algoritmilor Obiective urmărite: La sfârşitul parcurgerii acestei UI, studenţii vor 1.1 cunoaște conceptul de eficienta a unui algoritm vor cunoaste si inţelege modalitatile
UNITATEA DE ÎNVĂȚARE 3 Analiza algoritmilor Obiective urmărite: La sfârşitul parcurgerii acestei UI, studenţii vor 1.1 cunoaște conceptul de eficienta a unui algoritm vor cunoaste si inţelege modalitatile
COMPARATIVE DISCUSSION ABOUT THE DETERMINING METHODS OF THE STRESSES IN PLANE SLABS
 74 COMPARATIVE DISCUSSION ABOUT THE DETERMINING METHODS OF THE STRESSES IN PLANE SLABS Codrin PRECUPANU 3, Dan PRECUPANU,, Ștefan OPREA Correspondent Member of Technical Sciences Academy Gh. Asachi Technical
74 COMPARATIVE DISCUSSION ABOUT THE DETERMINING METHODS OF THE STRESSES IN PLANE SLABS Codrin PRECUPANU 3, Dan PRECUPANU,, Ștefan OPREA Correspondent Member of Technical Sciences Academy Gh. Asachi Technical
THE EXERGY ANALYSIS OF THE INDUSTRIAL SYSTEMS
 THE EXERGY ANALYSIS OF THE INUSTRIAL SYSTEMS 75 THE EXERGY ANALYSIS OF THE INUSTRIAL SYSTEMS Ile SIMINICEANU, Correspondg Member of the Romanan Academy of Techncal Scences, Gh. Asach Techncal Unversty
THE EXERGY ANALYSIS OF THE INUSTRIAL SYSTEMS 75 THE EXERGY ANALYSIS OF THE INUSTRIAL SYSTEMS Ile SIMINICEANU, Correspondg Member of the Romanan Academy of Techncal Scences, Gh. Asach Techncal Unversty
Divizibilitate în mulțimea numerelor naturale/întregi
 Divizibilitate în mulțimea numerelor naturale/întregi Teorema îmărţirii cu rest în mulțimea numerelor naturale Fie a, b, b 0. Atunci există q, r astfel încât a=bq+r, cu 0 r < b. În lus, q şi r sunt unic
Divizibilitate în mulțimea numerelor naturale/întregi Teorema îmărţirii cu rest în mulțimea numerelor naturale Fie a, b, b 0. Atunci există q, r astfel încât a=bq+r, cu 0 r < b. În lus, q şi r sunt unic
THE BEHAVIOUR OF ELASTOMERIC BEARINGS UNDER LOAD COMBINATIONS
 BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LX (LXIV), Fasc. 3, 2014 Secţia CONSTRUCŢII. ARHITECTURĂ THE BEHAVIOUR OF ELASTOMERIC BEARINGS
BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LX (LXIV), Fasc. 3, 2014 Secţia CONSTRUCŢII. ARHITECTURĂ THE BEHAVIOUR OF ELASTOMERIC BEARINGS
ELECTRONIC TECHNIQUES IN TIMING MEASUREMENTS FOR NUCLEAR STRUCTURE
 U.P.B. Sci. Bull., Series A, Vol. 70, Iss. 4, 2008 ISSN 1223-7027 ELECTRONIC TECHNIQUES IN TIMING MEASUREMENTS FOR NUCLEAR STRUCTURE Dan Gabriel GHIŢĂ 1 Prezenta lucrare descrie în detaliu două metode
U.P.B. Sci. Bull., Series A, Vol. 70, Iss. 4, 2008 ISSN 1223-7027 ELECTRONIC TECHNIQUES IN TIMING MEASUREMENTS FOR NUCLEAR STRUCTURE Dan Gabriel GHIŢĂ 1 Prezenta lucrare descrie în detaliu două metode
Barem de notare clasa a V-a
 Barem de notare clasa a V-a Problema1. Determinați mulțimile A și B, formate din numere naturale, știind că îndeplinesc simultan condițiile: a) A B,5,6 ; b) B A 0,7 ; c) card AB 3; d) suma elementelor
Barem de notare clasa a V-a Problema1. Determinați mulțimile A și B, formate din numere naturale, știind că îndeplinesc simultan condițiile: a) A B,5,6 ; b) B A 0,7 ; c) card AB 3; d) suma elementelor
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
Probleme de numărare: combinări, aranjamente, permutări de Manuela Prajea 1)
 Probleme de umărare: combăr, arajamete, permutăr de Mauela Prajea 1) Lecța se adresează î prmul râd elevlor de gmazu care focuseaza cocursurle de matematcă hgh-level ș d acest motv se îcepe expuerea de
Probleme de umărare: combăr, arajamete, permutăr de Mauela Prajea 1) Lecța se adresează î prmul râd elevlor de gmazu care focuseaza cocursurle de matematcă hgh-level ș d acest motv se îcepe expuerea de
Legi de distribuţie (principalele distribuţii de probabilitate) Tudor Drugan
 Legi de distribuţie (principalele distribuţii de probabilitate) Tudor Drugan Introducere In general distribuţiile variabilelor aleatoare definite pe o populaţie, care face obiectul unui studiu, nu se cunosc.
Legi de distribuţie (principalele distribuţii de probabilitate) Tudor Drugan Introducere In general distribuţiile variabilelor aleatoare definite pe o populaţie, care face obiectul unui studiu, nu se cunosc.
Programarea Dinamica. (si alte chestii adiacente) Andrei Olariu
 Programarea Dinamica (si alte chestii adiacente) Andrei Olariu andrei@olariu.org Despre mine - Absolvent FMI UniBuc - Doctorand in prelucrarea limbajului natural, in special in mediul online (Twitter)
Programarea Dinamica (si alte chestii adiacente) Andrei Olariu andrei@olariu.org Despre mine - Absolvent FMI UniBuc - Doctorand in prelucrarea limbajului natural, in special in mediul online (Twitter)
PETROLOGIE MAGMATICĂ
 presunea ICHID MAGMAIC + SOUŢIE HIDROERMAĂ UNIVERSIAEA DIN BUCUREŞI FACUAEA DE GEOOGIE ŞI GEOFIZICĂ Marn Şeclăman Sorn Constantn Bărzo Anca uca PEROOGIE MAGMAICĂ SISEME ŞI PROCESE MAGMAICE (P 1 ) RM (P
presunea ICHID MAGMAIC + SOUŢIE HIDROERMAĂ UNIVERSIAEA DIN BUCUREŞI FACUAEA DE GEOOGIE ŞI GEOFIZICĂ Marn Şeclăman Sorn Constantn Bărzo Anca uca PEROOGIE MAGMAICĂ SISEME ŞI PROCESE MAGMAICE (P 1 ) RM (P
All chemical bonding is based on the following relationships of electrostatics: 2. Each period on the periodic table
 UNIT VIII ATOMS AND THE PERIODIC TABLE 25 E. Chemical Bonding 1. An ELECTROSTATIC FORCE is All chemical bonding is based on the following relationships of electrostatics: The greater the distance between
UNIT VIII ATOMS AND THE PERIODIC TABLE 25 E. Chemical Bonding 1. An ELECTROSTATIC FORCE is All chemical bonding is based on the following relationships of electrostatics: The greater the distance between
Lecture 6 - Bonding in Crystals
 Lecture 6 onding in Crystals inding in Crystals (Kittel Ch. 3) inding of atoms to form crystals A crystal is a repeated array of atoms Why do they form? What are characteristic bonding mechanisms? How
Lecture 6 onding in Crystals inding in Crystals (Kittel Ch. 3) inding of atoms to form crystals A crystal is a repeated array of atoms Why do they form? What are characteristic bonding mechanisms? How
Physical Chemistry I CHEM 4641 Final Exam 13 questions, 30 points
 Physical Chemistry I CHEM 4641 Final Exam 13 questions, 30 points Name: KEY Gas constant: R = 8.314 J mol -1 K -1 = 0.008314 kj mol -1 K -1. Boltzmann constant k = 1.381 10-23 J/K = 0.6950 cm -1 /K h =
Physical Chemistry I CHEM 4641 Final Exam 13 questions, 30 points Name: KEY Gas constant: R = 8.314 J mol -1 K -1 = 0.008314 kj mol -1 K -1. Boltzmann constant k = 1.381 10-23 J/K = 0.6950 cm -1 /K h =
5 questions, 3 points each, 15 points total possible. 26 Fe Cu Ni Co Pd Ag Ru 101.
 Physical Chemistry II Lab CHEM 4644 spring 2017 final exam KEY 5 questions, 3 points each, 15 points total possible h = 6.626 10-34 J s c = 3.00 10 8 m/s 1 GHz = 10 9 s -1. B= h 8π 2 I ν= 1 2 π k μ 6 P
Physical Chemistry II Lab CHEM 4644 spring 2017 final exam KEY 5 questions, 3 points each, 15 points total possible h = 6.626 10-34 J s c = 3.00 10 8 m/s 1 GHz = 10 9 s -1. B= h 8π 2 I ν= 1 2 π k μ 6 P
SOI prin smart-cut. Caracterizarea TEM-HRTEM a defectelor structuale induse in Si prin hidrogenare in plasma.
 SOI prin smart-cut. Caracterizarea TEM-HRTEM a defectelor structuale induse in Si prin hidrogenare in plasma. Dr. Corneliu GHICA, Dr. Leona NISTOR Proiect IDEI, Contract Nr. 233/2007 1. C. Ghica, L. C.
SOI prin smart-cut. Caracterizarea TEM-HRTEM a defectelor structuale induse in Si prin hidrogenare in plasma. Dr. Corneliu GHICA, Dr. Leona NISTOR Proiect IDEI, Contract Nr. 233/2007 1. C. Ghica, L. C.
From Atoms to Materials: Predictive Theory and Simulations
 From Atoms to Materials: Predictive Theory and Simulations Week 3 Lecture 4 Potentials for metals and semiconductors Ale Strachan strachan@purdue.edu School of Materials Engineering & Birck anotechnology
From Atoms to Materials: Predictive Theory and Simulations Week 3 Lecture 4 Potentials for metals and semiconductors Ale Strachan strachan@purdue.edu School of Materials Engineering & Birck anotechnology
CHEMICAL COMPOUNDS MOLECULAR COMPOUNDS
 48 CHEMICAL COMPOUNDS - Dalton's theory does not mention this, but there is more than one way for atoms to come together to make chemical compounds! - There are TWO common kinds of chemical compound, classified
48 CHEMICAL COMPOUNDS - Dalton's theory does not mention this, but there is more than one way for atoms to come together to make chemical compounds! - There are TWO common kinds of chemical compound, classified
REGARDING THE OPTICAL TRAPPING FORCES ON MICROPARTICLES
 U.P.B. Sci. Bull., Series B, Vol. 68, No. 2, 2006 REGARDING THE OPTICAL TRAPPING FORCES ON MICROPARTICLES Monica NĂDĂŞAN, T. VIŞAN Cu un fascicul laser bine focalizat se pot capta şi manipula particule
U.P.B. Sci. Bull., Series B, Vol. 68, No. 2, 2006 REGARDING THE OPTICAL TRAPPING FORCES ON MICROPARTICLES Monica NĂDĂŞAN, T. VIŞAN Cu un fascicul laser bine focalizat se pot capta şi manipula particule
FORMULELE LUI STIRLING, WALLIS, GAUSS ŞI APLICAŢII
 DIDACTICA MATHEMATICA, Vol. 34), pp. 53 67 FORMULELE LUI STIRLING, WALLIS, GAUSS ŞI APLICAŢII Eugenia Duca, Emilia Copaciu şi Dorel I. Duca Abstract. In this paper are presented the Wallis, Stirling, Gauss
DIDACTICA MATHEMATICA, Vol. 34), pp. 53 67 FORMULELE LUI STIRLING, WALLIS, GAUSS ŞI APLICAŢII Eugenia Duca, Emilia Copaciu şi Dorel I. Duca Abstract. In this paper are presented the Wallis, Stirling, Gauss
CHEM 10113, Quiz 5 October 26, 2011
 CHEM 10113, Quiz 5 October 26, 2011 Name (please print) All equations must be balanced and show phases for full credit. Significant figures count, show charges as appropriate, and please box your answers!
CHEM 10113, Quiz 5 October 26, 2011 Name (please print) All equations must be balanced and show phases for full credit. Significant figures count, show charges as appropriate, and please box your answers!
Acta Technica Napocensis: Civil Engineering & Architecture Vol. 54 No.1 (2011)
 1 Technical University of Cluj-Napoca, Faculty of Civil Engineering. 15 C Daicoviciu Str., 400020, Cluj-Napoca, Romania Received 25 July 2011; Accepted 1 September 2011 The Generalised Beam Theory (GBT)
1 Technical University of Cluj-Napoca, Faculty of Civil Engineering. 15 C Daicoviciu Str., 400020, Cluj-Napoca, Romania Received 25 July 2011; Accepted 1 September 2011 The Generalised Beam Theory (GBT)
APPENDIX Z. USEFUL FORMULAS 1. Appendix Z. Useful Formulas. DRAFT 13:41 June 30, 2006 c J.D Callen, Fundamentals of Plasma Physics
 APPENDIX Z. USEFUL FORMULAS 1 Appendix Z Useful Formulas APPENDIX Z. USEFUL FORMULAS 2 Key Vector Relations A B = B A, A B = B A, A A = 0, A B C) = A B) C A B C) = B A C) C A B), bac-cab rule A B) C D)
APPENDIX Z. USEFUL FORMULAS 1 Appendix Z Useful Formulas APPENDIX Z. USEFUL FORMULAS 2 Key Vector Relations A B = B A, A B = B A, A A = 0, A B C) = A B) C A B C) = B A C) C A B), bac-cab rule A B) C D)
CLASS TEST GRADE 11. PHYSICAL SCIENCES: CHEMISTRY Test 4: Matter and materials 1
 CLASS TEST GRADE PHYSICAL SCIENCES: CHEMISTRY Test 4: Matter and materials MARKS: 45 TIME: hour INSTRUCTIONS AND INFORMATION. Answer ALL the questions. 2. You may use non-programmable calculators. 3. You
CLASS TEST GRADE PHYSICAL SCIENCES: CHEMISTRY Test 4: Matter and materials MARKS: 45 TIME: hour INSTRUCTIONS AND INFORMATION. Answer ALL the questions. 2. You may use non-programmable calculators. 3. You
Proiect PNII IDEI contract nr. 106/1 octombrie 2007
 INSTITUTUL DE MECANICA SOLIDELOR ACADEMIA ROMANA Str. Ctin Mille nr. 15, C.P. 1-863, 010141 Bucuresti Programul: I IDEI Tipul Proiecte de cercetare exploratorie proiectului: Cod proiect: ID_247/2007 Proiect
INSTITUTUL DE MECANICA SOLIDELOR ACADEMIA ROMANA Str. Ctin Mille nr. 15, C.P. 1-863, 010141 Bucuresti Programul: I IDEI Tipul Proiecte de cercetare exploratorie proiectului: Cod proiect: ID_247/2007 Proiect
THE METROLOGY OF OPTICAL FIBRE LOSSES
 U. P. B. Sci. Bull., Series A, Vol. 7, Iss. 3, 009 ISSN 3-707 THE METROLOGY OF OPTICAL FIBRE LOSSES Sorin GHINOIU, Niculae N. PUŞCAŞ În aceastǎ lucrare sunt prezentate şi analizate din punct de vedere
U. P. B. Sci. Bull., Series A, Vol. 7, Iss. 3, 009 ISSN 3-707 THE METROLOGY OF OPTICAL FIBRE LOSSES Sorin GHINOIU, Niculae N. PUŞCAŞ În aceastǎ lucrare sunt prezentate şi analizate din punct de vedere
A GENERALIZATION OF A CLASSICAL MONTE CARLO ALGORITHM TO ESTIMATE π
 U.P.B. Sci. Bull., Series A, Vol. 68, No., 6 A GENERALIZATION OF A CLASSICAL MONTE CARLO ALGORITHM TO ESTIMATE π S.C. ŞTEFĂNESCU Algoritmul Monte Carlo clasic A1 estimeazează valoarea numărului π bazându-se
U.P.B. Sci. Bull., Series A, Vol. 68, No., 6 A GENERALIZATION OF A CLASSICAL MONTE CARLO ALGORITHM TO ESTIMATE π S.C. ŞTEFĂNESCU Algoritmul Monte Carlo clasic A1 estimeazează valoarea numărului π bazându-se
AN APPROACH TO THE NONLINEAR LOCAL PROBLEMS IN MECHANICAL STRUCTURES
 U.P.B. Sci. Bull., Series D, Vol. 74, Iss. 3, 2012 ISSN 1454-2358 AN APPROACH TO THE NONLINEAR LOCAL PROBLEMS IN MECHANICAL STRUCTURES Marius-Alexandru GROZEA 1, Anton HADĂR 2 Acest articol prezintă o
U.P.B. Sci. Bull., Series D, Vol. 74, Iss. 3, 2012 ISSN 1454-2358 AN APPROACH TO THE NONLINEAR LOCAL PROBLEMS IN MECHANICAL STRUCTURES Marius-Alexandru GROZEA 1, Anton HADĂR 2 Acest articol prezintă o
Parts Manual. EPIC II Critical Care Bed REF 2031
 EPIC II Critical Care Bed REF 2031 Parts Manual For parts or technical assistance call: USA: 1-800-327-0770 2013/05 B.0 2031-109-006 REV B www.stryker.com Table of Contents English Product Labels... 4
EPIC II Critical Care Bed REF 2031 Parts Manual For parts or technical assistance call: USA: 1-800-327-0770 2013/05 B.0 2031-109-006 REV B www.stryker.com Table of Contents English Product Labels... 4
MANY ELECTRON ATOMS Chapter 15
 MANY ELECTRON ATOMS Chapter 15 Electron-Electron Repulsions (15.5-15.9) The hydrogen atom Schrödinger equation is exactly solvable yielding the wavefunctions and orbitals of chemistry. Howev er, the Schrödinger
MANY ELECTRON ATOMS Chapter 15 Electron-Electron Repulsions (15.5-15.9) The hydrogen atom Schrödinger equation is exactly solvable yielding the wavefunctions and orbitals of chemistry. Howev er, the Schrödinger
8. Relax and do well.
 CHEM 1515 Exam II John II. Gelder October 14, 1993 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 8 different pages. The last two pages include a periodic table, a
CHEM 1515 Exam II John II. Gelder October 14, 1993 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 8 different pages. The last two pages include a periodic table, a
Atoms and the Periodic Table
 Atoms and the Periodic Table Parts of the Atom Proton Found in the nucleus Number of protons defines the element Charge +1, mass 1 Parts of the Atom Neutron Found in the nucleus Stabilizes the nucleus
Atoms and the Periodic Table Parts of the Atom Proton Found in the nucleus Number of protons defines the element Charge +1, mass 1 Parts of the Atom Neutron Found in the nucleus Stabilizes the nucleus
STRUCTURAL INTENSITY METHOD APPLIED TO STUDY OF VIBRATIONS DAMPING / METODA INTENSIMETRIEI STUCTURALE APLICATĂ LA STUDIUL AMORTIZĂRII VIBRAŢIILOR
 Vol.48, No. / 06 STRUCTURAL INTENSITY METHOD APPLIED TO STUDY OF VIBRATIONS DAMPING / METODA INTENSIMETRIEI STUCTURALE APLICATĂ LA STUDIUL AMORTIZĂRII VIBRAŢIILOR Assoc. Prof. Ph.D. Eng. Carp-Ciocârdia
Vol.48, No. / 06 STRUCTURAL INTENSITY METHOD APPLIED TO STUDY OF VIBRATIONS DAMPING / METODA INTENSIMETRIEI STUCTURALE APLICATĂ LA STUDIUL AMORTIZĂRII VIBRAŢIILOR Assoc. Prof. Ph.D. Eng. Carp-Ciocârdia
VEHICLE DYNAMICS MODELING DURING MOVING ALONG A CURVED PATH. MATHEMATICAL MODEL USAGE ON STUDYING THE ROBUST STABILITY
 U.P.B. Sc. Bull., Seres C, Vol. 4, Iss. 70, 008 ISSN 1454-34x VHICL DYNAMICS MODLING DURING MOVING ALONG A CURVD PATH. MATHMATICAL MODL USAG ON STUDYING TH ROBUST STABILITY Oana-Carmen NICULSCU-FAIDA 1,
U.P.B. Sc. Bull., Seres C, Vol. 4, Iss. 70, 008 ISSN 1454-34x VHICL DYNAMICS MODLING DURING MOVING ALONG A CURVD PATH. MATHMATICAL MODL USAG ON STUDYING TH ROBUST STABILITY Oana-Carmen NICULSCU-FAIDA 1,
Solutions and Ions. Pure Substances
 Class #4 Solutions and Ions CHEM 107 L.S. Brown Texas A&M University Pure Substances Pure substance: described completely by a single chemical formula Fixed composition 1 Mixtures Combination of 2 or more
Class #4 Solutions and Ions CHEM 107 L.S. Brown Texas A&M University Pure Substances Pure substance: described completely by a single chemical formula Fixed composition 1 Mixtures Combination of 2 or more
CHEMICAL COMPOUNDS MOLECULAR COMPOUNDS
 48 CHEMICAL COMPOUNDS - Dalton's theory does not mention this, but there is more than one way for atoms to come together to make chemical compounds! - There are TWO common kinds of chemical compound, classified
48 CHEMICAL COMPOUNDS - Dalton's theory does not mention this, but there is more than one way for atoms to come together to make chemical compounds! - There are TWO common kinds of chemical compound, classified
STRESS AND STRAIN ANALYSIS IN CONTINUUM MECHANICS WITH APPLICABILITY IN SOIL MECHANICS
 BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Volumul 63 (67), Numărul 3, 2017 Secţia CONSTRUCŢII. ARHITECTURĂ STRESS AND STRAIN ANALYSIS IN CONTINUUM
BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Volumul 63 (67), Numărul 3, 2017 Secţia CONSTRUCŢII. ARHITECTURĂ STRESS AND STRAIN ANALYSIS IN CONTINUUM
Chemistry Standard level Paper 1
 Chemistry Standard level Paper 1 Thursday 12 May 2016 (morning) 45 minutes Instructions to candidates Do not open this examination paper until instructed to do so. Answer all the questions. For each question,
Chemistry Standard level Paper 1 Thursday 12 May 2016 (morning) 45 minutes Instructions to candidates Do not open this examination paper until instructed to do so. Answer all the questions. For each question,
Spin Cut-off Parameter of Nuclear Level Density and Effective Moment of Inertia
 Commun. Theor. Phys. (Beijing, China) 43 (005) pp. 709 718 c International Academic Publishers Vol. 43, No. 4, April 15, 005 Spin Cut-off Parameter of Nuclear Level Density and Effective Moment of Inertia
Commun. Theor. Phys. (Beijing, China) 43 (005) pp. 709 718 c International Academic Publishers Vol. 43, No. 4, April 15, 005 Spin Cut-off Parameter of Nuclear Level Density and Effective Moment of Inertia
BROOKLYN COLLEGE Department of Chemistry. Chemistry 1 Second Lecture Exam Nov. 27, Name Page 1 of 5
 BROOKLYN COLLEGE Department of Chemistry Chemistry 1 Second Lecture Exam Nov. 27, 2002 Name Page 1 of 5 Circle the name of your lab instructor Kobrak, Zhou, Girotto, Hussey, Du Before you begin the exam,
BROOKLYN COLLEGE Department of Chemistry Chemistry 1 Second Lecture Exam Nov. 27, 2002 Name Page 1 of 5 Circle the name of your lab instructor Kobrak, Zhou, Girotto, Hussey, Du Before you begin the exam,
Lab Day and Time: Instructions. 1. Do not open the exam until you are told to start.
 Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
CHEM 107 (Spring-2005) Exam 3 (100 pts)
 CHEM 107 (Spring-2005) Exam 3 (100 pts) Name: ------------------------------------------------------------------------, Clid # ------------------------------ LAST NAME, First (Circle the alphabet segment
CHEM 107 (Spring-2005) Exam 3 (100 pts) Name: ------------------------------------------------------------------------, Clid # ------------------------------ LAST NAME, First (Circle the alphabet segment
STRUCTURAL PARASITIC CAPACITANCE REDUCTION TECHNIQUES IN PLANAR MAGNETIC INTEGRATED STRUCTURES
 STRUCTURAL PARASITIC CAPACITANCE REDUCTION TECHNIQUES IN PLANAR MAGNETIC INTEGRATED STRUCTURES STRUCTURAL PARASITIC CAPACITANCE REDUCTION TECHNIQUES IN PLANAR MAGNETIC INTEGRATED STRUCTURES Lecturer Eng.
STRUCTURAL PARASITIC CAPACITANCE REDUCTION TECHNIQUES IN PLANAR MAGNETIC INTEGRATED STRUCTURES STRUCTURAL PARASITIC CAPACITANCE REDUCTION TECHNIQUES IN PLANAR MAGNETIC INTEGRATED STRUCTURES Lecturer Eng.
Lab Day and Time: Instructions. 1. Do not open the exam until you are told to start.
 Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
Last 4 Digits of USC ID:
 Chemistry 05 B Practice Exam Dr. Jessica Parr First Letter of last Name PLEASE PRINT YOUR NAME IN BLOCK LETTERS Name: Last 4 Digits of USC ID: Lab TA s Name: Question Points Score Grader 8 2 4 3 9 4 0
Chemistry 05 B Practice Exam Dr. Jessica Parr First Letter of last Name PLEASE PRINT YOUR NAME IN BLOCK LETTERS Name: Last 4 Digits of USC ID: Lab TA s Name: Question Points Score Grader 8 2 4 3 9 4 0
PART 1 Introduction to Theory of Solids
 Elsevier UK Job code: MIOC Ch01-I044647 9-3-2007 3:03p.m. Page:1 Trim:165 240MM TS: Integra, India PART 1 Introduction to Theory of Solids Elsevier UK Job code: MIOC Ch01-I044647 9-3-2007 3:03p.m. Page:2
Elsevier UK Job code: MIOC Ch01-I044647 9-3-2007 3:03p.m. Page:1 Trim:165 240MM TS: Integra, India PART 1 Introduction to Theory of Solids Elsevier UK Job code: MIOC Ch01-I044647 9-3-2007 3:03p.m. Page:2
The Periodic Table. Periodic Properties. Can you explain this graph? Valence Electrons. Valence Electrons. Paramagnetism
 Periodic Properties Atomic & Ionic Radius Energy Electron Affinity We want to understand the variations in these properties in terms of electron configurations. The Periodic Table Elements in a column
Periodic Properties Atomic & Ionic Radius Energy Electron Affinity We want to understand the variations in these properties in terms of electron configurations. The Periodic Table Elements in a column
(C) Pavel Sedach and Prep101 1
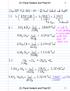 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach
(C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach
02/05/09 Last 4 Digits of USC ID: Dr. Jessica Parr
 Chemistry 05 B First Letter of PLEASE PRINT YOUR NAME IN BLOCK LETTERS Exam last Name Name: 02/05/09 Last 4 Digits of USC ID: Dr. Jessica Parr Lab TA s Name: Question Points Score Grader 2 2 9 3 9 4 2
Chemistry 05 B First Letter of PLEASE PRINT YOUR NAME IN BLOCK LETTERS Exam last Name Name: 02/05/09 Last 4 Digits of USC ID: Dr. Jessica Parr Lab TA s Name: Question Points Score Grader 2 2 9 3 9 4 2
Pentru clasa a X-a Ştiinţele naturii-sem II
 Pentru clasa a X-a Ştiinţele naturii-sem II Reprezentarea algoritmilor. Pseudocod. Principiile programării structurate. Structuri de bază: structura liniară structura alternativă structura repetitivă Algoritmi
Pentru clasa a X-a Ştiinţele naturii-sem II Reprezentarea algoritmilor. Pseudocod. Principiile programării structurate. Structuri de bază: structura liniară structura alternativă structura repetitivă Algoritmi
Essential Chemistry for Biology
 1 Chapter 2 Essential Chemistry for Biology Biology and Society: More Precious than Gold A drought is a period of abnormally dry weather that changes the environment and one of the most devastating disasters.
1 Chapter 2 Essential Chemistry for Biology Biology and Society: More Precious than Gold A drought is a period of abnormally dry weather that changes the environment and one of the most devastating disasters.
Chem Exam 1. September 26, Dr. Susan E. Bates. Name 9:00 OR 10:00
 Chem 1711 Exam 1 September 26, 2013 Dr. Susan E. Bates Name 9:00 OR 10:00 N A = 6.022 x 10 23 mol 1 I A II A III B IV B V B VI B VII B VIII I B II B III A IV A V A VI A VII A inert gases 1 H 1.008 3 Li
Chem 1711 Exam 1 September 26, 2013 Dr. Susan E. Bates Name 9:00 OR 10:00 N A = 6.022 x 10 23 mol 1 I A II A III B IV B V B VI B VII B VIII I B II B III A IV A V A VI A VII A inert gases 1 H 1.008 3 Li
1. Following Dalton s Atomic Theory, 2. In 1869 Russian chemist published a method. of organizing the elements. Mendeleev showed that
 20 CHEMISTRY 11 D. Organizing the Elements The Periodic Table 1. Following Dalton s Atomic Theory, By 1817, chemists had discovered 52 elements and by 1863 that number had risen to 62. 2. In 1869 Russian
20 CHEMISTRY 11 D. Organizing the Elements The Periodic Table 1. Following Dalton s Atomic Theory, By 1817, chemists had discovered 52 elements and by 1863 that number had risen to 62. 2. In 1869 Russian
Modelling the Steady State Characteristic of ph Neutralization Process: a Neuro-Fuzzy Approach
 BULETINUL Universităţii Petrol Gaze din Ploieşti Vol. LXVII No. 2/2015 79 84 Seria Tehnică Modelling the Steady State Characteristic of ph Neutralization Process: a Neuro-Fuzzy Approach Gabriel Rădulescu
BULETINUL Universităţii Petrol Gaze din Ploieşti Vol. LXVII No. 2/2015 79 84 Seria Tehnică Modelling the Steady State Characteristic of ph Neutralization Process: a Neuro-Fuzzy Approach Gabriel Rădulescu
Radiometric Dating (tap anywhere)
 Radiometric Dating (tap anywhere) Protons Neutrons Electrons Elements on the periodic table are STABLE Elements can have radioactive versions of itself called ISOTOPES!! Page 1 in your ESRT has your list!
Radiometric Dating (tap anywhere) Protons Neutrons Electrons Elements on the periodic table are STABLE Elements can have radioactive versions of itself called ISOTOPES!! Page 1 in your ESRT has your list!
Universitatea Politehnica Bucureşti Facultatea de Automatică şi Calculatoare Departamentul de Automatică şi Ingineria Sistemelor
 Universitatea Politehnica Bucureşti Facultatea de Automatică şi Calculatoare Departamentul de Automatică şi Ingineria Sistemelor TEZĂ DE ABILITARE Metode de Descreştere pe Coordonate pentru Optimizare
Universitatea Politehnica Bucureşti Facultatea de Automatică şi Calculatoare Departamentul de Automatică şi Ingineria Sistemelor TEZĂ DE ABILITARE Metode de Descreştere pe Coordonate pentru Optimizare
EXCESS PROPERTIES IN DIMETHYL SULFOXIDE + 1- BUTANOL AND 1,4-DIOXANE+1-BUTANOL BINARY MIXTURES AT K
 U.P.B. Sc. Bull., Seres B, Vol. 7, Iss. 4, 009 ISSN 454- ECESS PROPERTIES IN DIMETHYL SULFOIDE + - BUTANOL AND,4-DIOANE+-BUTANOL BINARY MITURES AT 98.5 K Anca FEDELEŞ, Oana CIOCÎRLAN, Olga IULIAN În lucrare
U.P.B. Sc. Bull., Seres B, Vol. 7, Iss. 4, 009 ISSN 454- ECESS PROPERTIES IN DIMETHYL SULFOIDE + - BUTANOL AND,4-DIOANE+-BUTANOL BINARY MITURES AT 98.5 K Anca FEDELEŞ, Oana CIOCÎRLAN, Olga IULIAN În lucrare
Rădăcina pătrată a unei matrici reale de ordinul 2
 Rădăcina pătrată a unei matrici reale de ordinul Mircea Crasmareanu Mai 19, 017 ( a c Actorii acestei poveşti: matricile A = M b d (R. PROBLEMA STUDIATĂ: Există B M (R aşa încât: B = A? O astfel de matrice
Rădăcina pătrată a unei matrici reale de ordinul Mircea Crasmareanu Mai 19, 017 ( a c Actorii acestei poveşti: matricile A = M b d (R. PROBLEMA STUDIATĂ: Există B M (R aşa încât: B = A? O astfel de matrice
CHEM 172 EXAMINATION 1. January 15, 2009
 CHEM 17 EXAMINATION 1 January 15, 009 Dr. Kimberly M. Broekemeier NAME: Circle lecture time: 9:00 11:00 Constants: c = 3.00 X 10 8 m/s h = 6.63 X 10-34 J x s J = kg x m /s Rydberg Constant = 1.096776 x
CHEM 17 EXAMINATION 1 January 15, 009 Dr. Kimberly M. Broekemeier NAME: Circle lecture time: 9:00 11:00 Constants: c = 3.00 X 10 8 m/s h = 6.63 X 10-34 J x s J = kg x m /s Rydberg Constant = 1.096776 x
Advanced Placement. Chemistry. Integrated Rates
 Advanced Placement Chemistry Integrated Rates 204 47.90 9.22 78.49 (26) 50.94 92.9 80.95 (262) 52.00 93.94 83.85 (263) 54.938 (98) 86.2 (262) 55.85 0. 90.2 (265) 58.93 02.9 92.2 (266) H Li Na K Rb Cs Fr
Advanced Placement Chemistry Integrated Rates 204 47.90 9.22 78.49 (26) 50.94 92.9 80.95 (262) 52.00 93.94 83.85 (263) 54.938 (98) 86.2 (262) 55.85 0. 90.2 (265) 58.93 02.9 92.2 (266) H Li Na K Rb Cs Fr
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A. Ήχος Πα. to os se e e na aș te e e slă ă ă vi i i i i
 CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
Electronic supplementary information
 Electronic Supplementary Material (ESI) for Journal of Materials Chemistry A. This journal is The Royal Society of Chemistry 2018 Electronic supplementary information Computational screening of hydrophobic
Electronic Supplementary Material (ESI) for Journal of Materials Chemistry A. This journal is The Royal Society of Chemistry 2018 Electronic supplementary information Computational screening of hydrophobic
Lab Day and Time: Instructions. 1. Do not open the exam until you are told to start.
 Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
CHEM 130 Exp. 8: Molecular Models
 CHEM 130 Exp. 8: Molecular Models In this lab, we will learn and practice predicting molecular structures from molecular formulas. The Periodic Table of the Elements IA 1 H IIA IIIA IVA VA VIA VIIA 3 5
CHEM 130 Exp. 8: Molecular Models In this lab, we will learn and practice predicting molecular structures from molecular formulas. The Periodic Table of the Elements IA 1 H IIA IIIA IVA VA VIA VIIA 3 5
CURS 6: APROXIMAREA FUNCTIILOR PRIN REGRESIE
 CURS 6: APROXIMAREA FUNCTIILOR PRIN REGRESIE Metoda celor ma mc pătrate. Formularea probleme. Notaț Metoda celor ma mc pătrate (ale eror) este cea ma uzuală metodă de aproxmare a ue depedeţe y=y(x), date
CURS 6: APROXIMAREA FUNCTIILOR PRIN REGRESIE Metoda celor ma mc pătrate. Formularea probleme. Notaț Metoda celor ma mc pătrate (ale eror) este cea ma uzuală metodă de aproxmare a ue depedeţe y=y(x), date
Despre AGC cuasigrupuri V. Izbaș
 Despre AGC cuasigrupuri V Izbaș 1 Introducere Se ştie că grupurile au apărut în matematică ca grupuri de automorfisme Rolul automorfismelor este remarcabil şi bine cunoscut La studierea diverselor structuri
Despre AGC cuasigrupuri V Izbaș 1 Introducere Se ştie că grupurile au apărut în matematică ca grupuri de automorfisme Rolul automorfismelor este remarcabil şi bine cunoscut La studierea diverselor structuri
2D AND 3D PROCESSING OF THE INTERDEPENDENCE BETWEEN THE COMFORT MAIN INDICATORS
 BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LVII (LXI), Fasc. 1, 2011 SecŃia TEXTILE. PIELĂRIE 2D AND 3D PROCESSING OF THE INTERDEPENDENCE
BULETINUL INSTITUTULUI POLITEHNIC DIN IAŞI Publicat de Universitatea Tehnică Gheorghe Asachi din Iaşi Tomul LVII (LXI), Fasc. 1, 2011 SecŃia TEXTILE. PIELĂRIE 2D AND 3D PROCESSING OF THE INTERDEPENDENCE
Chemistry 431 Practice Final Exam Fall Hours
 Chemistry 431 Practice Final Exam Fall 2018 3 Hours R =8.3144 J mol 1 K 1 R=.0821 L atm mol 1 K 1 R=.08314 L bar mol 1 K 1 k=1.381 10 23 J molecule 1 K 1 h=6.626 10 34 Js N A = 6.022 10 23 molecules mol
Chemistry 431 Practice Final Exam Fall 2018 3 Hours R =8.3144 J mol 1 K 1 R=.0821 L atm mol 1 K 1 R=.08314 L bar mol 1 K 1 k=1.381 10 23 J molecule 1 K 1 h=6.626 10 34 Js N A = 6.022 10 23 molecules mol
Clasa a 10-a. Review of preview
 1 of 12 2/1/2016 11:10 AM PHI 2016 You are logged in as Admin User (Logout) edesc PHI2016 Quizzes Clasa a 10-a Review of preview Info Results Preview Edit Clasa a 10-a Review of preview Started on Monday,
1 of 12 2/1/2016 11:10 AM PHI 2016 You are logged in as Admin User (Logout) edesc PHI2016 Quizzes Clasa a 10-a Review of preview Info Results Preview Edit Clasa a 10-a Review of preview Started on Monday,
CHEMICAL COMPOUNDS MOLECULAR COMPOUNDS
 48 CHEMICAL COMPOUNDS - Dalton's theory does not mention this, but there is more than one way for atoms to come together to make chemical compounds! - There are TWO common kinds of chemical compound, classified
48 CHEMICAL COMPOUNDS - Dalton's theory does not mention this, but there is more than one way for atoms to come together to make chemical compounds! - There are TWO common kinds of chemical compound, classified
Ch. 9 NOTES ~ Chemical Bonding NOTE: Vocabulary terms are in boldface and underlined. Supporting details are in italics.
 Ch. 9 NOTES ~ Chemical Bonding NOTE: Vocabulary terms are in boldface and underlined. Supporting details are in italics. I. Review: Comparison of ionic and molecular compounds Molecular compounds Ionic
Ch. 9 NOTES ~ Chemical Bonding NOTE: Vocabulary terms are in boldface and underlined. Supporting details are in italics. I. Review: Comparison of ionic and molecular compounds Molecular compounds Ionic
INSTRUCTIONS: Exam III. November 10, 1999 Lab Section
 CHEM 1215 Exam III John III. Gelder November 10, 1999 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last page includes a periodic table and
CHEM 1215 Exam III John III. Gelder November 10, 1999 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last page includes a periodic table and
What is the periodic table?
 The periodic table of the elements represents one of the greatest discoveries in the history of science that certain elements, the basic chemical substances from which all matter is made, resemble each
The periodic table of the elements represents one of the greatest discoveries in the history of science that certain elements, the basic chemical substances from which all matter is made, resemble each
Atomic Structure & Interatomic Bonding
 Atomic Structure & Interatomic Bonding Chapter Outline Review of Atomic Structure Atomic Bonding Atomic Structure Atoms are the smallest structural units of all solids, liquids & gases. Atom: The smallest
Atomic Structure & Interatomic Bonding Chapter Outline Review of Atomic Structure Atomic Bonding Atomic Structure Atoms are the smallest structural units of all solids, liquids & gases. Atom: The smallest
Inteligenta Artificiala
 Inteligenta Artificiala Universitatea Politehnica Bucuresti Anul universitar 2010-2011 Adina Magda Florea http://turing.cs.pub.ro/ia_10 si curs.cs.pub.ro 1 Curs nr. 4 Cautare cu actiuni nedeterministe
Inteligenta Artificiala Universitatea Politehnica Bucuresti Anul universitar 2010-2011 Adina Magda Florea http://turing.cs.pub.ro/ia_10 si curs.cs.pub.ro 1 Curs nr. 4 Cautare cu actiuni nedeterministe
single-layer transition metal dichalcogenides MC2
 single-layer transition metal dichalcogenides MC2 Period 1 1 H 18 He 2 Group 1 2 Li Be Group 13 14 15 16 17 18 B C N O F Ne 3 4 Na K Mg Ca Group 3 4 5 6 7 8 9 10 11 12 Sc Ti V Cr Mn Fe Co Ni Cu Zn Al Ga
single-layer transition metal dichalcogenides MC2 Period 1 1 H 18 He 2 Group 1 2 Li Be Group 13 14 15 16 17 18 B C N O F Ne 3 4 Na K Mg Ca Group 3 4 5 6 7 8 9 10 11 12 Sc Ti V Cr Mn Fe Co Ni Cu Zn Al Ga
