Barycentric Coordinates
|
|
|
- Rudolf Briggs
- 5 years ago
- Views:
Transcription
1 rentri oordintes,, re the distnes from the verties to the ontt points of the eires with the sides. + = + = + from whih = s - = s - The three rs in this pitures re Gergonne r, medin, nd Ngel r. This piture n e used to show tht the Gergonne nd Ngel points re isotomes. ontents rentri oordintes The inenter fmil of points onw on rentris onw ompres vrious oordinte sstems
2 Two oordintes to desrie point in the plne. For severl resons it is etter to desrie points in two dimensionl tringle geometr three oordintes. Tringles re the fundmentl shpe nd tend to see things in threes. rentri oordintes (,, ) re suh oordinte sstem. Sine three numers re used when onl two re needed, we dd one other ondition to these oordintes. If + + = 1, we s tht the oordintes re normlied. lterntel onl rtios re used with (,, ) = (k, k, k) nd k > 0. In this se we write the oordintes s ( ). oordintes vlid up to rtio re lled homogeneous oordintes. Mn properties of tringles re independent of sle so rtio independene n e n dvntge. rentri oordintes P The rentri oordintes ( ) of point P n e red from the evin rtios of P or the res used P (see piture). It is surprisingl es to find the oordintes this w. If,, nd re the vetors representing the verties of the tringle then the rentri oordintes re used to write P s P = + + where + + = 1. + The verties re (1, 0, 0), (0, 1, 0), nd + + (0, 0, 1). + + The signs of the oordintes re shown in the digrm to the right. The oordinte's sign (0,1,0) depends on its position reltive to side. It is + (1,0,0) = 0 on side + not possile for ll three oordintes to e + + negtive. omputtions in homogeneous oordintes re it unusul sine we re free to multipl the oordintes n ftor. s n emple ( ) = (1/ 1/ 1/) sine we n divide eh oordinte the ftor. Often oordintes re smmetrill epressed in terms of the sides or ngles of the tringle. For emple the oordintes of the Ngel point re ( ). In this se shorthnd nottion n e used ( +- ), showing onl the middle oordinte. The importne of smmetri forms smmetri epressions in the ngles or sides of tringle hve speil importne. The re, the semiperimeter, nd the rdii of the insried nd irumirles re ll smmetri in the sides of the tringle. Using the rtio independene of the oordintes the inenter ( ) n e written in seond form s follows ( ) = ( /2R ) = ( sin ), where R is the irumrdius. = 0 on side (0,0,1) = 0 on side The entroid s n emple of the use of rentri oordintes, we n see tht the oordintes of G, the entroid, re (111). This is seen sine the entroid is the onurrene of the medins, whih divide eh side equll in 11 rtio.
3 rentris of the Inenter fmil of points The Inenter n ngle isetor stisfies the formul / = /. ppling this reltionship to ll three isetors we otin these rtios. We red the rentri oordintes from the evin rtios. Inenter oordintes ( ) = ( ) This finl form is onw's shorthnd nottion. For points where the oordintes hve the sme form onl the middle oordinte is shown. The Gergonne Point The Gergonne point Go is the onurrene of the evins to the ontt points of the inirle with the sides. We first find some properties of the tringle with its inirle. Let,, nd e the distnes from the verties of to the ontt points of the inirle with the tringle. The Ngel Point The Ngel point No is the onurrene of the evins to the ontt points of the eirle with. Ngel point oordintes ( s ) nd re the distnes from the verties to the ontt points of the eires with the sides = perimeter + + = s = s ( + ) = s We use the shorthnd s = s -. s - s - s - G o Gergonne point oordintes ( s s s s s s ) = ( 1/s 1/s 1/s ) = ( 1/s ) Divide ll oordintes s s s to get this form. The three rs in this pitures re Gergonne r, medin, nd Ngel r. This piture n e used to show tht the Gergonne nd Ngel points re isotomes. s - + = + = + from whih = s - = s - s - s - We djust the evin rtios so we n see the rentri oordintes. (s - )(s - ) (s - )(s - ) (s - )(s - ) G o (s - )(s - ) (s - )(s - ) (s - )(s-) How to red the rentri rtios from mesurements on the tringle. oordinte orresponds to verte. Notie the position of the 's ompred to their verte. The nd oordintes re equivlentl pled. Rememering tht we re free to djust rtios multipling oth elements the sme numer, we dnust the rtios so tht the rentri oordintes n e red. P
4 Dte From To 12/2/ PM John onw, Steve Sigur, Unfortuntel I red few introdutor ooks mself, nd the onl ones I know tht use rentris re ver old nd in n se, s ver little. ut there is in ft ver little tht needs to e sid! The NORMLIZED rentris of P with respet to,, re the unique numers (X,Y,Z) dding up to 1 for whih the vetor eqution P = X + Y + Z holds - UNNORMLIZED ones re n triple proportionl to these. For the ltter I write (XYZ) with olons to indite tht onl their rtios mtter. Sine ou re fmilir with orthogonl triliners, whih I write [,,] or [], ou'll need to know the onversion rules [] onverts to (XYZ) onverts to () [X/Y/Z/]. So there's ver little differene, ut the differene is vlule! If ou drw our tringles the w round I do, XYZ re esil red off from the evin rtios or re-rtios Z / \ X / \ / \ / \ * * / \ Y / P \ Y / X P Z \ / \ / Y \ -----* *----- X Z (sorr I n't drw the seprting lines P,P). So plinl G = (111), or, when normlied (1/3,1/3,1/3), mening tht G = (++)/3 in vetor terms. The suordinte nd superior of P re 3G/2 - P/2 nd 3G-2P (normlied) or (Y+ZZ+XX+Y) nd (-X+Y+ZX-Y+ZX+Y-Z) (unnormlied) s we see using G = (X+Y+ZX+Y+ZX+Y+Z). nd The isotomi nd isogonl onjugtes of P re (/X/Y/Z) (onjugl) (1/X1/Y1/Z) (isotome).
5 Sometimes, of ourse, the OT formul is the simpler one. For instne the onjugl of [] = () is (///) = (///) = [1/1/1/], simpler thn the rentri formul, while its isotome is [1/1/1/] (more omple). ut THIS simpliit osures the sitution. The isotomi onjugte is n ffinel invrint onept (in other words, if ou linerl streth the tringle, this reltion remins the sme) - we n see this euse the rentri formul (1/X1/Y1/Z) mentions no speil onstnts like,,. The isogonl onjugl isn't ffinel invrint (it depends on ngles); so its rentri formul SHOULD mention the shpe of the tringle. If ou look upstirs, ou'll see tht the formule for suordintes nd superiors re lso onstnt-free in rentris, gin euse these re ffinel invrint - gin tht is osured in OTs. nother instne of the sme phenomenon is tht G = (111) in rentris, ut [1/1/1/] in OTs, while I = () in rentris, ut [111] in OTs. gin, the simpliit of G in rentris tells us something - tht the entroid is n ffinel invrint onept - while tht of I in OTs tells us nothing. The swith to rentris should e quite pinless if t first ou just get into the hit of lling the tpil point [X/Y/Z/] rther thn [,,] - in other words, regrd the rentris just s renmed triliners. s I sid, the're ver muh the sme, ut the slight differene is importnt. The numers,, re mere nuisneftors tht lutter up most of the OT theor nd often osure the sitution. John onw I'm sending this to severl people interested in tringles, nd hope the'll onfirm reeipt (eept for rkg, who might e out of emil touh), nd send n further sustntil messges out tringles to everone else on the list. There re three stndrd sstems tht use three oordintes to represent point in the plne of give tringle, nmel RYENTRIS (), RELS (), nd ORTHOGONL TRILINERS (OT). Often the lst is shortened to "TRILINERS", ut I prefer the longer nme sine in ft ll three sstems re triliner. Eh m or m not e normlied. For the not-neessril normlied versions I'll use (XYZ) for nd, nd [] for OT nd for the normlied ones (X,Y,Z) for, nd [,,] for OT. ll three (unnormlied) sstems re ver similr - indeed the oinide for rentris nd rels, so I'll usull ll these jointl, nd the onversion from TO to these is ver simple [] eomes (). So for mn purposes it hrdl mtters whih sstem one uses. However, there RE ws in whih one or other of the sstems is etter thn nother, nd it is the purpose of this note to point out tht when one tkes ll these into ount the rentri sstem emerges s the ler winner. The letters,,,ot efore eh numered point elow show how this deision ws rehed. letter N indites tht normlied oordintes re involved.
6 OT 0N. The distnes of P from the sides re 2X.Delt/, 2Y.Delt/, 2Z.Delt/ [,, ]. 1N. The res of P, P, P re the normlised rel oordintes X.Delt, Y.Delt, Z.Delt [ /2, /2, /2 ] 2N. If V, V, V re vetors to,,, then P = X.V + Y.V + Z.V [Of ourse these re just the definitions of the three sstems.] 3. The evin rtios re YZ, ZX, XY [,, ]. 4. The Menelen rtios of the lines PX + QY + RZ = 0 nd p + q + r = 0 re -QR -RP -PQ nd -qr -rp -pq 5. The normliing ondition is X + Y + Z = 1 () or Delt (), [ + + = 2Delt ] OT 6. The isogonl onjugte (or "onjugl") is o-p = ( ^2/X ^2/Y ^2/Z ) [ 1/X 1/Y 1/Z ] 7. The isotomi onjugte (or "isotome") is iso-p = ( 1/X 1/Y 1/Z ) [ 1/(.^2) 1/(.^2) 1/(.^2) ] 8. FFINE INVRINE. If n ffine trnsformtion tkes,,, nd P = (X,Y,Z) to 1, 1, 1 nd P1, then the rentri oordintes of P1 with respet to he new tringle re still (X,Y,Z). (It is euse isotomi onjugtion is n ffinel invrint onept tht its epression (see #7) in rentris nnot involve the edge lengths of the tringle.) 9. The onepts of suordinte nd superior points These points re the imges of P in the suordinte (or "medil") tringle, whose verties re the midpoints of the edges of, nd the superior (or "ntiomplementr") tringle, the midpoints of whose edges re,,. We hve su-p = ( Y+Z Z+X X+Y ) [ (+)/ (+)/ (+)/ ] super-p = (Y+Z-XZ+X-YX+Y-Z) [(+-)/(+-)/(+-)/] (gin the simpliit of the oordintes is due to ffine invrine.) 10. RTIONLITY. X,Y,Z re rtionl funtions of the Euliden oordintes of the points,,,p. If P is point tht's rtionll defined from,,, then its rentri oordintes re rtionl funtions of ^2, ^2, ^2. This is true, for instne, of the entroid, orthoenter, irumenter, smmedin point, rord points, nd so on. (This is n etremel importnt point, nd etends to give the ver useful propert elow.)
7 11. LGERI ONJUGTES. Mn points (suh s the inenter) n e otined solving lgeri equtions tht hve other (lgerill onjugte) solutions. Pssing to these other solutions then ields further points tht hve essentill the sme geometri properties (in this w, we get from the inenter to the eenters). We n get the rentri oordintes of suh "ompnions" s the pproprite lgeri onjugtes of those of the originl. The simplest se of this is when the oordintes re rtionl funtions of,, ut not of ^2, ^2, ^2. So for emple if point tht's rtionll onstruted from the inenter hs rentri oordintes ( X(,,), Y(,,), Z(,,) ) then the orresponding point otined from the -eenter is simpl otined "hnging the sign of ", thus ( X(-,,), Y(,-,), Z(,,-) ). For emple the Ngel point is the "super-inenter" ( ), nd so its -ompnion is ( ). The OT oordintes of these points re muh hrder to understnd [ / + / - 1 / + / - 1 / + / - 1] nd [ / + / + 1 / - / - 1 -/ + / - 1]. Well, tht will do for now. I'll just surve the "winners" OT OT In onl two ses is OT the winner, nd in ll other ses ut one (the definition of!) is t lest joint winner. I hve deliertel preferred oneptul resons for preferring one sstem to nother, rther thn mere omprisons of the simpliit of the oordintes for prtiulr points. Some points re simpler under one sstem rther thn nother, nd often it's OT tht would give the simpler ones. ut this differene n never e gret, sine[,,] trnsltes to [,,]; nd in rentris the simpliit often hs useful oneptul mening. For emple (111) = [ 1/ 1/ 1/ ] is the entroid, nd its simpliit in rentris omes from its ffine invrine. On the other hnd () = [111] is the inenter, more omplited in rentris sine it hs lgeri onjugtes (-) (-) (-). The pprent simpliit in triliners disppers when we pss to the su-inenter (Spieker point) (+++) = ( (+)/ (+)/ (+)/ ). The "Morle perspetors" look simpler in OT [ os(/3) os(/3) os(/3) ] nd [ se(/3) se(/3) se(/3) ] ut gin this pprent simpliit disppers when we wnt it more the rentri versions (.os(/3)... ) nd (.se(/3)... ) n e onjugted to get ll the "ompnion Morle perspetors" just s esil. In summr, the simpliit of oordintes for prtiulr points n go either w, nd in n se is not strong rgument. It's their theoretil properties tht mke rentris the ler winner. John onw
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
m m m m m m m m P m P m ( ) m m P( ) ( ). The o-ordinte of the point P( ) dividing the line segment joining the two points ( ) nd ( ) eternll in the r
 CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
y z A left-handed system can be rotated to look like the following. z
 Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
Green s Theorem. (2x e y ) da. (2x e y ) dx dy. x 2 xe y. (1 e y ) dy. y=1. = y e y. y=0. = 2 e
 Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
8.3 THE HYPERBOLA OBJECTIVES
 8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
Exercise sheet 6: Solutions
 Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
m A 1 1 A ! and AC 6
 REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
H (2a, a) (u 2a) 2 (E) Show that u v 4a. Explain why this implies that u v 4a, with equality if and only u a if u v 2a.
 Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
THREE DIMENSIONAL GEOMETRY
 MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
SIMPLE NONLINEAR GRAPHS
 S i m p l e N o n l i n e r G r p h s SIMPLE NONLINEAR GRAPHS www.mthletis.om.u Simple SIMPLE Nonliner NONLINEAR Grphs GRAPHS Liner equtions hve the form = m+ where the power of (n ) is lws. The re lle
S i m p l e N o n l i n e r G r p h s SIMPLE NONLINEAR GRAPHS www.mthletis.om.u Simple SIMPLE Nonliner NONLINEAR Grphs GRAPHS Liner equtions hve the form = m+ where the power of (n ) is lws. The re lle
Lesson 2: The Pythagorean Theorem and Similar Triangles. A Brief Review of the Pythagorean Theorem.
 27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
Ellipses. The second type of conic is called an ellipse.
 Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Two Triads of Congruent Circles from Reflections
 Forum Geometriorum Volume 8 (2008) 7 12. FRUM GEM SSN 1534-1178 Two Trids of ongruent irles from Refletions Qung Tun ui strt. Given tringle, we onstrut two trids of ongruent irles through the verties,
Forum Geometriorum Volume 8 (2008) 7 12. FRUM GEM SSN 1534-1178 Two Trids of ongruent irles from Refletions Qung Tun ui strt. Given tringle, we onstrut two trids of ongruent irles through the verties,
Logarithms LOGARITHMS.
 Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
Numbers and indices. 1.1 Fractions. GCSE C Example 1. Handy hint. Key point
 GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
HS Pre-Algebra Notes Unit 9: Roots, Real Numbers and The Pythagorean Theorem
 HS Pre-Alger Notes Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Roots nd Cue Roots Syllus Ojetive 5.4: The student will find or pproximte squre roots of numers to 4. CCSS 8.EE.-: Evlute squre roots
HS Pre-Alger Notes Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Roots nd Cue Roots Syllus Ojetive 5.4: The student will find or pproximte squre roots of numers to 4. CCSS 8.EE.-: Evlute squre roots
1.3 SCALARS AND VECTORS
 Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Lesson 4.1 Triangle Sum Conjecture
 Lesson 4.1 ringle um onjeture me eriod te n erises 1 9, determine the ngle mesures. 1. p, q 2., 3., 31 82 p 98 q 28 53 17 79 23 50 4. r, s, 5., 6. t t s r 100 85 100 30 4 7 31 7. s 8. m 9. m s 76 35 m
Lesson 4.1 ringle um onjeture me eriod te n erises 1 9, determine the ngle mesures. 1. p, q 2., 3., 31 82 p 98 q 28 53 17 79 23 50 4. r, s, 5., 6. t t s r 100 85 100 30 4 7 31 7. s 8. m 9. m s 76 35 m
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
 PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
Reflection Property of a Hyperbola
 Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
] dx (3) = [15x] 2 0
![] dx (3) = [15x] 2 0 ] dx (3) = [15x] 2 0](/thumbs/80/81916477.jpg) Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
Trigonometry and Constructive Geometry
 Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Factorising FACTORISING.
 Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Electromagnetism Notes, NYU Spring 2018
 Eletromgnetism Notes, NYU Spring 208 April 2, 208 Ation formultion of EM. Free field desription Let us first onsider the free EM field, i.e. in the bsene of ny hrges or urrents. To tret this s mehnil system
Eletromgnetism Notes, NYU Spring 208 April 2, 208 Ation formultion of EM. Free field desription Let us first onsider the free EM field, i.e. in the bsene of ny hrges or urrents. To tret this s mehnil system
Core 2 Logarithms and exponentials. Section 1: Introduction to logarithms
 Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Mathematics 10 Page 1 of 5 Properties of Triangle s and Quadrilaterals. Isosceles Triangle. - 2 sides and 2 corresponding.
 Mthemtis 10 Pge 1 of 5 Properties of s Pthgoren Theorem 2 2 2 used to find the length of sides of right tringle Tpe of s nd Some s Theorems ngles s Slene Isoseles Equilterl ute - ll ngles re less thn 90
Mthemtis 10 Pge 1 of 5 Properties of s Pthgoren Theorem 2 2 2 used to find the length of sides of right tringle Tpe of s nd Some s Theorems ngles s Slene Isoseles Equilterl ute - ll ngles re less thn 90
Tutorial Worksheet. 1. Find all solutions to the linear system by following the given steps. x + 2y + 3z = 2 2x + 3y + z = 4.
 Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
3 Angle Geometry. 3.1 Measuring Angles. 1. Using a protractor, measure the marked angles.
 3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
PROPERTIES OF TRIANGLES
 PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
Calculus Module C21. Areas by Integration. Copyright This publication The Northern Alberta Institute of Technology All Rights Reserved.
 Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
Vectors. a Write down the vector AB as a column vector ( x y ). A (3, 2) x point C such that BC = 3. . Go to a OA = a
 Streth lesson: Vetors Streth ojetives efore you strt this hpter, mrk how onfident you feel out eh of the sttements elow: I n lulte using olumn vetors nd represent the sum nd differene of two vetors grphilly.
Streth lesson: Vetors Streth ojetives efore you strt this hpter, mrk how onfident you feel out eh of the sttements elow: I n lulte using olumn vetors nd represent the sum nd differene of two vetors grphilly.
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
Vectors. Chapter14. Syllabus reference: 4.1, 4.2, 4.5 Contents:
 hpter Vetors Syllus referene:.,.,.5 ontents: D E F G H I J K Vetors nd slrs Geometri opertions with vetors Vetors in the plne The mgnitude of vetor Opertions with plne vetors The vetor etween two points
hpter Vetors Syllus referene:.,.,.5 ontents: D E F G H I J K Vetors nd slrs Geometri opertions with vetors Vetors in the plne The mgnitude of vetor Opertions with plne vetors The vetor etween two points
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
5. Every rational number have either terminating or repeating (recurring) decimal representation.
 CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
This enables us to also express rational numbers other than natural numbers, for example:
 Overview Study Mteril Business Mthemtis 05-06 Alger The Rel Numers The si numers re,,3,4, these numers re nturl numers nd lso lled positive integers. The positive integers, together with the negtive integers
Overview Study Mteril Business Mthemtis 05-06 Alger The Rel Numers The si numers re,,3,4, these numers re nturl numers nd lso lled positive integers. The positive integers, together with the negtive integers
GRAND PLAN. Visualizing Quaternions. I: Fundamentals of Quaternions. Andrew J. Hanson. II: Visualizing Quaternion Geometry. III: Quaternion Frames
 Visuliing Quternions Andrew J. Hnson Computer Siene Deprtment Indin Universit Siggrph Tutoril GRAND PLAN I: Fundmentls of Quternions II: Visuliing Quternion Geometr III: Quternion Frmes IV: Clifford Algers
Visuliing Quternions Andrew J. Hnson Computer Siene Deprtment Indin Universit Siggrph Tutoril GRAND PLAN I: Fundmentls of Quternions II: Visuliing Quternion Geometr III: Quternion Frmes IV: Clifford Algers
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Integration. antidifferentiation
 9 Integrtion 9A Antidifferentition 9B Integrtion of e, sin ( ) nd os ( ) 9C Integrtion reognition 9D Approimting res enlosed funtions 9E The fundmentl theorem of integrl lulus 9F Signed res 9G Further
9 Integrtion 9A Antidifferentition 9B Integrtion of e, sin ( ) nd os ( ) 9C Integrtion reognition 9D Approimting res enlosed funtions 9E The fundmentl theorem of integrl lulus 9F Signed res 9G Further
50 AMC Lectures Problem Book 2 (36) Substitution Method
 0 AMC Letures Prolem Book Sustitution Metho PROBLEMS Prolem : Solve for rel : 9 + 99 + 9 = Prolem : Solve for rel : 0 9 8 8 Prolem : Show tht if 8 Prolem : Show tht + + if rel numers,, n stisf + + = Prolem
0 AMC Letures Prolem Book Sustitution Metho PROBLEMS Prolem : Solve for rel : 9 + 99 + 9 = Prolem : Solve for rel : 0 9 8 8 Prolem : Show tht if 8 Prolem : Show tht + + if rel numers,, n stisf + + = Prolem
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
The Ellipse. is larger than the other.
 The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
 Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
( ) { } [ ] { } [ ) { } ( ] { }
![( ) { } [ ] { } [ ) { } ( ] { } ( ) { } [ ] { } [ ) { } ( ] { }](/thumbs/96/129291861.jpg) Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
2.1 ANGLES AND THEIR MEASURE. y I
 .1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
.1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
INTEGRATION. 1 Integrals of Complex Valued functions of a REAL variable
 INTEGRATION NOTE: These notes re supposed to supplement Chpter 4 of the online textbook. 1 Integrls of Complex Vlued funtions of REAL vrible If I is n intervl in R (for exmple I = [, b] or I = (, b)) nd
INTEGRATION NOTE: These notes re supposed to supplement Chpter 4 of the online textbook. 1 Integrls of Complex Vlued funtions of REAL vrible If I is n intervl in R (for exmple I = [, b] or I = (, b)) nd
Vibration with more (than one) degrees of freedom (DOF) a) longitudinal vibration with 3 DOF. b) rotational (torsional) vibration with 3 DOF
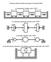 irtion with ore (thn one) degrees of freedo (DOF) ) longitudinl irtion with DOF ) rottionl (torsionl) irtion with DOF ) ending irtion with DOF d) the D (plnr) irtion of the fleil supported rigid od with
irtion with ore (thn one) degrees of freedo (DOF) ) longitudinl irtion with DOF ) rottionl (torsionl) irtion with DOF ) ending irtion with DOF d) the D (plnr) irtion of the fleil supported rigid od with
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
STRAND J: TRANSFORMATIONS, VECTORS and MATRICES
 Mthemtics SKE: STRN J STRN J: TRNSFORMTIONS, VETORS nd MTRIES J3 Vectors Text ontents Section J3.1 Vectors nd Sclrs * J3. Vectors nd Geometry Mthemtics SKE: STRN J J3 Vectors J3.1 Vectors nd Sclrs Vectors
Mthemtics SKE: STRN J STRN J: TRNSFORMTIONS, VETORS nd MTRIES J3 Vectors Text ontents Section J3.1 Vectors nd Sclrs * J3. Vectors nd Geometry Mthemtics SKE: STRN J J3 Vectors J3.1 Vectors nd Sclrs Vectors
Triangles The following examples explore aspects of triangles:
 Tringles The following exmples explore spects of tringles: xmple 1: ltitude of right ngled tringle + xmple : tringle ltitude of the symmetricl ltitude of n isosceles x x - 4 +x xmple 3: ltitude of the
Tringles The following exmples explore spects of tringles: xmple 1: ltitude of right ngled tringle + xmple : tringle ltitude of the symmetricl ltitude of n isosceles x x - 4 +x xmple 3: ltitude of the
Symmetrical Components 1
 Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
LINEAR ALGEBRA APPLIED
 5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
Matrices SCHOOL OF ENGINEERING & BUILT ENVIRONMENT. Mathematics (c) 1. Definition of a Matrix
 tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
Discrete Structures Lecture 11
 Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
VECTOR ALGEBRA. Syllabus :
 MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
Reference : Croft & Davison, Chapter 12, Blocks 1,2. A matrix ti is a rectangular array or block of numbers usually enclosed in brackets.
 I MATRIX ALGEBRA INTRODUCTION TO MATRICES Referene : Croft & Dvison, Chpter, Blos, A mtri ti is retngulr rr or lo of numers usull enlosed in rets. A m n mtri hs m rows nd n olumns. Mtri Alger Pge If the
I MATRIX ALGEBRA INTRODUCTION TO MATRICES Referene : Croft & Dvison, Chpter, Blos, A mtri ti is retngulr rr or lo of numers usull enlosed in rets. A m n mtri hs m rows nd n olumns. Mtri Alger Pge If the
Lecture 6: Coding theory
 Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Introduction to Algebra - Part 2
 Alger Module A Introduction to Alger - Prt Copright This puliction The Northern Alert Institute of Technolog 00. All Rights Reserved. LAST REVISED Oct., 008 Introduction to Alger - Prt Sttement of Prerequisite
Alger Module A Introduction to Alger - Prt Copright This puliction The Northern Alert Institute of Technolog 00. All Rights Reserved. LAST REVISED Oct., 008 Introduction to Alger - Prt Sttement of Prerequisite
( ) 1. 1) Let f( x ) = 10 5x. Find and simplify f( 2) and then state the domain of f(x).
 Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
PROPERTIES OF AREAS In general, and for an irregular shape, the definition of the centroid at position ( x, y) is given by
 PROPERTES OF RES Centroid The concept of the centroid is prol lred fmilir to ou For plne shpe with n ovious geometric centre, (rectngle, circle) the centroid is t the centre f n re hs n is of smmetr, the
PROPERTES OF RES Centroid The concept of the centroid is prol lred fmilir to ou For plne shpe with n ovious geometric centre, (rectngle, circle) the centroid is t the centre f n re hs n is of smmetr, the
Chapter 4 Contravariance, Covariance, and Spacetime Diagrams
 Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
Pythagorean Theorem and Trigonometry
 Ptgoren Teorem nd Trigonometr Te Ptgoren Teorem is nient, well-known, nd importnt. It s lrge numer of different proofs, inluding one disovered merin President Jmes. Grfield. Te we site ttp://www.ut-te-knot.org/ptgors/inde.stml
Ptgoren Teorem nd Trigonometr Te Ptgoren Teorem is nient, well-known, nd importnt. It s lrge numer of different proofs, inluding one disovered merin President Jmes. Grfield. Te we site ttp://www.ut-te-knot.org/ptgors/inde.stml
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
The Inspherical Gergonne Center of a Tetrahedron
 Journl for Geometry nd Grphis Volume 8 (2004), No. 1, 23 32. The Inspheril Gergonne Center of Tetrhedron Mowffq Hjj 1, Peter Wlker 2 1 Deprtment of Mthemtis, Yrmouk University Irbid, Jordn emil: mhjj@yu.edu.jo
Journl for Geometry nd Grphis Volume 8 (2004), No. 1, 23 32. The Inspheril Gergonne Center of Tetrhedron Mowffq Hjj 1, Peter Wlker 2 1 Deprtment of Mthemtis, Yrmouk University Irbid, Jordn emil: mhjj@yu.edu.jo
Instructions. An 8.5 x 11 Cheat Sheet may also be used as an aid for this test. MUST be original handwriting.
 ID: B CSE 2021 Computer Orgniztion Midterm Test (Fll 2009) Instrutions This is losed ook, 80 minutes exm. The MIPS referene sheet my e used s n id for this test. An 8.5 x 11 Chet Sheet my lso e used s
ID: B CSE 2021 Computer Orgniztion Midterm Test (Fll 2009) Instrutions This is losed ook, 80 minutes exm. The MIPS referene sheet my e used s n id for this test. An 8.5 x 11 Chet Sheet my lso e used s
Math 32B Discussion Session Week 8 Notes February 28 and March 2, f(b) f(a) = f (t)dt (1)
 Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
Something found at a salad bar
 Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
set is not closed under matrix [ multiplication, ] and does not form a group.
![set is not closed under matrix [ multiplication, ] and does not form a group. set is not closed under matrix [ multiplication, ] and does not form a group.](/thumbs/78/78412113.jpg) Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Linear Algebra Introduction
 Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Non Right Angled Triangles
 Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
M344 - ADVANCED ENGINEERING MATHEMATICS
 M3 - ADVANCED ENGINEERING MATHEMATICS Lecture 18: Lplce s Eqution, Anltic nd Numericl Solution Our emple of n elliptic prtil differentil eqution is Lplce s eqution, lso clled the Diffusion Eqution. If
M3 - ADVANCED ENGINEERING MATHEMATICS Lecture 18: Lplce s Eqution, Anltic nd Numericl Solution Our emple of n elliptic prtil differentil eqution is Lplce s eqution, lso clled the Diffusion Eqution. If
Using technology to teach and solve challenging math problems
 Using tehnology to teh nd solve hllenging mth prolems Ellin Grigoriev, PhD Astrt Dr. Ellin Grigoriev is Professor of Mthemtis t Tes Womn's University (TWU). he grduted from Mosow tte University first in
Using tehnology to teh nd solve hllenging mth prolems Ellin Grigoriev, PhD Astrt Dr. Ellin Grigoriev is Professor of Mthemtis t Tes Womn's University (TWU). he grduted from Mosow tte University first in
Solutions to Assignment 1
 MTHE 237 Fll 2015 Solutions to Assignment 1 Problem 1 Find the order of the differentil eqution: t d3 y dt 3 +t2 y = os(t. Is the differentil eqution liner? Is the eqution homogeneous? b Repet the bove
MTHE 237 Fll 2015 Solutions to Assignment 1 Problem 1 Find the order of the differentil eqution: t d3 y dt 3 +t2 y = os(t. Is the differentil eqution liner? Is the eqution homogeneous? b Repet the bove
The Relationship between the Nine-Point Circle, the Circumscribed Circle and the Inscribed Circle of Archimedes Triangle Yuporn Rimcholakarn
 Nresun Universit Journl: Siene nd Tehnolog 08; 63 The Reltionship between the Nine-Point irle, the irusribed irle nd the Insribed irle of rhiedes Tringle Yuporn Riholkrn Fult of Siene nd Tehnolog, Pibulsongkr
Nresun Universit Journl: Siene nd Tehnolog 08; 63 The Reltionship between the Nine-Point irle, the irusribed irle nd the Insribed irle of rhiedes Tringle Yuporn Riholkrn Fult of Siene nd Tehnolog, Pibulsongkr
CONIC SECTIONS. Chapter 11
 CONIC SECTIONS Chpter. Overview.. Sections of cone Let l e fied verticl line nd m e nother line intersecting it t fied point V nd inclined to it t n ngle α (Fig..). Fig.. Suppose we rotte the line m round
CONIC SECTIONS Chpter. Overview.. Sections of cone Let l e fied verticl line nd m e nother line intersecting it t fied point V nd inclined to it t n ngle α (Fig..). Fig.. Suppose we rotte the line m round
Part 4. Integration (with Proofs)
 Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
Forces on curved surfaces Buoyant force Stability of floating and submerged bodies
 Stti Surfe ores Stti Surfe ores 8m wter hinge? 4 m ores on plne res ores on urved surfes Buont fore Stbilit of floting nd submerged bodies ores on Plne res Two tpes of problems Horizontl surfes (pressure
Stti Surfe ores Stti Surfe ores 8m wter hinge? 4 m ores on plne res ores on urved surfes Buont fore Stbilit of floting nd submerged bodies ores on Plne res Two tpes of problems Horizontl surfes (pressure
Section - 2 MORE PROPERTIES
 LOCUS Section - MORE PROPERTES n section -, we delt with some sic properties tht definite integrls stisf. This section continues with the development of some more properties tht re not so trivil, nd, when
LOCUS Section - MORE PROPERTES n section -, we delt with some sic properties tht definite integrls stisf. This section continues with the development of some more properties tht re not so trivil, nd, when
