Project 6: Minigoals Towards Simplifying and Rewriting Expressions
|
|
|
- Tracey Davis
- 6 years ago
- Views:
Transcription
1 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy tht we often think out like terms is tht it isn t lwys ler wht is ment y like. Relly, omining like terms is relly just pplying the distriutive property in reverse: + = ( + ) Or, more generlly (for ny numer of terms, where njust denotes the numer of terms) we ould write: n = ( n ) Any time we hve sequene of terms, eh of whih is produt (two things eing multiplied together), nd the seond ftor in eh produt is the SAME, then we n used the distriutive property to rewrite the expression. So, now let s work on prtiing when we n pply the distriutive property. Exmples: Whih of these hve the form of the left side of one of the distriutive properties ove? For eh one, CIRCLE, nd identify,, or 1,, n, : 5x 3x 5x 3y 8p 2 q 2 12p 2 q The distriutive property n e pplied if we rewrite the sutrtion s dding negtive first: 5x 3x = 5x + 3x So 5 x + 3 x And = 5, = 3, = x Or we ould write 1 = 5, 2 = 3, = x The distriutive property n NOT e pplied here euse these two terms don t hve nything in ommon. I nnot find nything of the form +, even if I rewrite the sutrtion s dding negtive first. The distriutive property n e pplied if we rewrite the sutrtion s dding negtive first: 8p 2 q 2 12p 2 q 2 = 8p 2 q p 2 q 2 So 8 p 2 q p 2 q 2 And = 8, = 12, = p 2 q 2 Or we ould write 1 = 8, 2 = 12, = p 2 q 2 The distriutive property n e pplied if we rewrite the sutrtion s dding negtive first: = So And 1 = 8, 2 = 5, 3 = 2, = 5 Note: here we hve to use the formul with 1,, n in it, euse here we hve more thn two terms. The distriutive property n NOT e pplied here euse these two terms don t hve nything in ommon. I nnot find nything of the form +, even if I use the ommuttive property = to reorder the ftors in eh term first. Note: 2 is NOT the sme s 2, nd 3 is NOT the sme s 2. The distriutive property n e pplied if we think out how to group ll the ftors in the first term, nd then group the 5 together nd tret it s one unit: = (5) + 4 So (5) + 4
2 3x(x 1) + 2(x 1) 5x 3x 2 Here I hve s nd s in my expression nd in the distriutive property identity, so I m going to hnge the letters in the first distriutive property like this: + = ( + ) pp + qq = (p + q)r Then p = 5, q = 4, r = Or we ould write 1 = 5, 2 = 4, = The distriutive property n e pplied: So 3x (x 1) + 2 (x 1) And = 3x, = 2, = (x 1) Or we ould write 1 = 3x, 2 = 2, = (x 1) The distriutive property n e pplied if we 1) rewrite the sutrtion s dding negtive, nd think out how to group ll the ftors in the seond term, fter rememering tht x 2 n e repled with x x: 5x 3x 2 = 5x + 3 x x = 5x + ( 3x) x So 5 x + ( 3x) x And = 5, = 3x, = x Or we ould write 1 = 5, 2 = 3x, = x Do we lwys wnt to use the distriute property in exmples like this? For eh of these exmples, we ould see how we n pply the distriutive property in mny ses to omine terms, even in mny ses tht you proly didn t previously think of s like terms. In more omplex ses like these, we my or my not wnt to pply the distriutive property in reverse it will depend on our gols with the prtiulr expression. But it is importnt to understnd tht the distriutive property CAN e used in ll of these ses. Now you try! Whih of these hve the form of the left side of one of the distriutive properties ove? For eh one: ) Stte whether or not one of the distriutive properties n e pplied; ) If it n, explin whih identities, if ny, need to e pplied first; if it n NOT, explin WHY not; ) CIRCLE ; nd d) identify,, (or 1,, n,, depending on the distriutive property tht you re using) from one of the two given distriutive properties: 1. Two terms: + = ( + ) 2. Any numer of terms: n = ( n ) Use the exmples ove s model
3 4. 4x 3 y 2 + 5x 3 y xx 3y 8. 2x(2x + 1) + 3(2x + 1)
4 Rewriting expressions with speifi gol in mind Typilly when we rewrite expressions, it is with speifi gol in mind. We my wnt to simplify them, or we my wnt to put them into prtiulr form tht llows us to see reltionships (for exmple, when we ome to equtions, we often put them in prtiulr form in order to e le to solve them or grph them). When we hve gol in mind for rewriting n expression (or eqution), we then hve to put together mny of the things tht we hve lredy een doing so tht we pply identities to the expressions one fter nother. This requires severl steps: 1) We hve to identify our end gol (e.g. Why re we rewriting the expression/eqution? Wht does it need to look like when we re done?). 2) We hve to selet prtiulr identities tht ould e pplied to the urrent expression (either in its urrent form, or with little rewriting), nd we need to onsider eh of these possile identities s wy of rewriting the expression. If the rewriting is somewht omplex, this my require us to set some smller gols tht we need to meet long the wy to meet our lrger gol. 3) Eh time we pply n identity to the expression, we hve to sk ourselves if this hs rought us loser to our gol or not.. If not, we my need to put tht work side nd to strt over y pplying different identity to the originl eqution.. If it hs gotten us loser, then we need to think out wht identity we should pply to this new rewritten funtion in order to get even loser to our gol. 4) We keep repeting this proess until we reh our gol. As prolems grow more omplex, we might hve to pply mny, mny identities sequentilly to get to our finl result. Let s just jump in nd strt trying to simplify expressions y using the identities we hve een using so fr. To keep things simple, we will only need to use the identities on the list elow s we work to simplify the next set of prolems. x = 1x = + + = + ( + ) + = ( + ) = + + = () = () = ( + ) = + ( + ) = + x n = x x n mmmm ttttt x = 1 x (wheeeeee x 0) (wheeeeee 0) d (wheeeeee, d 0) + = + (wheeeeee 0) = x 2 = x (wheeeeee x 0)
5
6 Exmples: A) Rewrite the following expression, with the im of simplifying it s muh s possile: (6x 2 + 5) (2x 2 + 6) If our gol is to simplify this, we will likely wnt to rewrite this without the prentheses so tht we n try to omine wht is in eh set of prentheses with eh other. If tht is possile, it will very likely mke the expression simpler. So, our first mini-gol is: Rewrite the expression without prentheses. If the expression ws of this form: ( + ) +, then we ould use the identity ( + ) + = + + to rewrite this expression without the first set of prentheses. But we need to rewrite ll of the sutrtion in this expression s ddition first. So this leds us to nother mini-gol, whih must ome BEFORE our gol of rewriting the expression without prentheses: Rewrite ll sutrtion in the expression s ddition. Let s put these two gols in the order tht we need to do them, nd list the identities needed to omplish eh gol: Mini-gol Identities needed 1) Rewrite ll sutrtion in the expression s ddition. = + 2) Rewrite the expression without prentheses. We will ( + ) + = + + strt with the first set of prentheses nd then fous on the seond set. Now let s try to do these two steps, nd see wht hppens: Step 1: Rewrite the sutrtion in the expression s ddition, using the identity = + = (6x 2 + 5), = (2x 2 + 6) = + ( ) (6x 2 + 5) (2x 2 + 6) = (6x 2 + 5) + (2x 2 + 6) So (6x 2 + 5) (2x 2 + 6) = (6x 2 + 5) + (2x 2 + 6) ( ) = ( ) + ( ) Step 2: Rewrite the expression without (the first set of) prentheses, using the identity ( + ) + = + +. Fousing on rewriting without the first set of prentheses: = 6x 2, = 5, = (2x 2 + 6) ( + ) + = + + ( ) (6x 2 ) = ( ) + (5) + (2x 2 + 6) = (6x 2 ) So (6x 2 + 5) + (2x 2 + 6) = 6x (2x 2 + 6) + (5) + (2x 2 + 6) Now we need to fous on rewriting the expression without the seond set of prentheses. The su-expression (2x 2 + 6) lmost looks like the left side of the identity ( + ) = +, exept tht the vrile n t stnd in for negtive sign lone the negtive sign hs to elong to numer or n expression. So now we form some new mini-gols, on our wy to the gol of rewriting the expression without prentheses: Mini-gol: Put 2x into the form ( + ). We n do this if we notie tht we n pply the identity x = 1x to the expression (2x 2 + 6). So, let s do tht: First let s rewrite the identity x = 1x with nother vrile to void onfusion: q = 1q. q = (2x 2 + 6), q = 1q ( ) q q = 1 ( ) So 6x (2x 2 + 6) = 6x (2x 2 + 6) q (2x 2 + 6) q = 1 (2x 2 + 6)
7 Now, k to our first mini gol: Mini-gol: Rewrite the expression without the seond set of prentheses. We see tht we n now use the identity ( + ) = + to rewrite the seond hlf of the expression without prentheses: = 1, = 2x 2, = 6 ( + ) = + ( ) ( 1) (2x 2 ) + (6) = ( 1) (2x 2 ) + ( 1) (6) ( ) So 6x (2x 2 + 6) = 6x ( 1)(2x 2 ) + ( 1)(6) + ( ) = ( ) ( ) So now we hve simplified the originl expression to this equivlent expression: 6x ( 1)(2x 2 ) + ( 1)(6) How n we simplify this expression further? The most ovious step is for us to perform the multiplition in the lst few terms: 6x ( 1)(2x 2 ) + ( 1)(6) = 6x ( 1)(2x 2 ) + 6 euse ( 1)(6) = 6 6x ( 1)(2x 2 ) + 6 = 6x x euse ( 1)(2x 2 ) = 1 2 x 2 = 2x 2 So now we hve simplified the originl expression to this equivlent expression: 6x x Wht might help to mke this simpler? It would e good for us to look to see if we n omine ny of these terms together. For exmple, if 5 nd 6 were next to eh other, we ould dd them. Similrly, if 6x 2 nd 2x 2 were next to eh other, we ould use the identity ( + ) = + to omine them. So, our next mini-gol is: ( ) Mini-gol: Reorder the terms so tht like terms re next to eh other. I n use the identity + = + to do this: = 5, = 2x 2 + = + ( ) = ( ) (5) + ( 2x 2 ) = ( 2x 2 ) + (5) So 6x x = 6x 2 + 2x Now we n simply dd the finl two like terms: 6x 2 + 2x = 6x 2 + 2x euse = 1 And now our finl mini-gol is: Mini-gol: Used the identity ( + ) = + to omine the first two terms. We noted tht the first two terms hve the form of the right side of the identity. = 6, = 2, = x 2 ( + ) = + ( ) (6) + ( 2) (x 2 ) = (6) (x 2 ) + ( 2) (x 2 ) ( ) = ( ) So, 6x 2 + 2x = (6 + 2)x euse (6 + 2)x 2 = 6x 2 + 2x 2 ( ) And finlly, we n dd the 6 nd the 2 inside the prentheses, so we go hed nd do tht: (6 + 2) x = 4 x euse = 4 So now we hve repled the originl expression with the equivlent expression 4x This is out s simple s it gets, lthough, we ould do one finl step nd rewrite the ddition of negtive s sutrtion, if we wnt: = 4x 2, = 1 = + ( ) ( ) = ( ) + ( ) (4x 2 ) (1) ( ) = (4x 2 ) + (1)
8 So, 4x = 4x 2 1. This is definitely s simple s we ould mke this expression, so our finl expression is 4x 2 1 nd: (6x 2 + 5) (2x 2 + 6) = 4x 2 1 Now you try! We re going to strt trying to rewrite expressions with speifi gol in mind. However, first you re going to strt y working on prolems where you will e given severl minigols in order. You should try to omplete eh minigol, nd tht will help led you to the overll gol. Be sure to do the minigols in order, nd e sure to work sequentilly, pplying identities to the results of the previous step, NOT to the originl expression. In mny sts, you will first hve to use severl identities to rewrite the expression efore you n omplish the minigol. Use the previous exmple s guide to help you work through these prolems. 1. Rewrite the following expression, with the im of simplifying it s muh s possile: (2x + 3) (3x + 1) Minigol 1: Apply the identity ( + ) = + in order to rewrite the expression without prentheses. Minigol 2: Apply the identity + = ( + ) in order to omine like terms. 2. Rewrite the following expression, with the im of simplifying it s muh s possile: (2x + 3)(3x + 1) Minigol 1: Apply the identity ( + ) = + in order to rewrite the expression without prentheses. Minigol 2: Apply the identity ( + ) = + in order to rewrite the expression without prentheses. Minigol 3: Apply the identity + = ( + ) in order to omine like terms.
9 3. Rewrite the following expression, with the im of simplifying it s muh s possile: 3x 2 2x + 5x 2 5 Minigol 1: Apply the identity + = ( + ) in order to omine like terms. 4. Rewrite the following expression, with the im of simplifying it s muh s possile: 2xy 3 2xx (x, y 0) Minigol 1: Apply the identity = to rewrite the expression so tht the whole expression is under single rdil. Minigol 2: Rewrite ll multiplition under the rdil s produt of squres, insofr s possile. Prt A: Rewrite ll the multiplition under the rdil sign so tht numers re next to numers, nd the sme letters re next to eh other, y using the identity = s mny times s neessry.
10 Prt B: Use the identity = n to rewrite ll exponents s multiplition. n ttttt Prt C: Use the identity = 2 to rewrite ll multiplition s multiplition of squres (inluding numers nd vriles), wherever possile. Minigol 3: Use the identity 2 = to rewrite the expression without rdils, where possile. 5. Rewrite the following expression, with the im of simplifying it s muh s possile: 6x 2 3x 3x (x 0) Minigol 1: Use the identity + = + to rewrite this expression s two frtions, so tht you n fous on one frtion t time. Minigol 2: Use the identity = to rewrite the expression so tht something of the form p is isolted y itself. d d p
11 6. Rewrite the following expression, with the im of simplifying it s muh s possile: 2x 2 y 3 Minigol 1: Use the identity = d to rewrite the expression so tht something of the form p p x 4 is isolted y itself. 7. Put the following expression into x form, where,, re rel numers: 2x(3x 6) + 5 Minigol 1: Apply the identity ( + ) = + in order to rewrite the expression without prentheses. Minigol 2: Apply the identity + = ( + ) in order to omine like terms.
12
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
Factorising FACTORISING.
 Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Chapter 8 Roots and Radicals
 Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
Polynomials. Polynomials. Curriculum Ready ACMNA:
 Polynomils Polynomils Curriulum Redy ACMNA: 66 www.mthletis.om Polynomils POLYNOMIALS A polynomil is mthemtil expression with one vrile whose powers re neither negtive nor frtions. The power in eh expression
Polynomils Polynomils Curriulum Redy ACMNA: 66 www.mthletis.om Polynomils POLYNOMIALS A polynomil is mthemtil expression with one vrile whose powers re neither negtive nor frtions. The power in eh expression
2.4 Linear Inequalities and Interval Notation
 .4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
.4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
Surds and Indices. Surds and Indices. Curriculum Ready ACMNA: 233,
 Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Project 3: Using Identities to Rewrite Expressions
 MAT 5 Projet 3: Usig Idetities to Rewrite Expressios Wldis I lger, equtios tht desrie properties or ptters re ofte lled idetities. Idetities desrie expressio e repled with equl or equivlet expressio tht
MAT 5 Projet 3: Usig Idetities to Rewrite Expressios Wldis I lger, equtios tht desrie properties or ptters re ofte lled idetities. Idetities desrie expressio e repled with equl or equivlet expressio tht
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Logarithms LOGARITHMS.
 Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Improper Integrals. The First Fundamental Theorem of Calculus, as we ve discussed in class, goes as follows:
 Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
NON-DETERMINISTIC FSA
 Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Intermediate Math Circles Wednesday, November 14, 2018 Finite Automata II. Nickolas Rollick a b b. a b 4
 Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
Improper Integrals, and Differential Equations
 Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Homework 3 Solutions
 CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 3 Solutions 1. Give NFAs with the specified numer of sttes recognizing ech of the following lnguges. In ll cses, the lphet is Σ = {,1}.
CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 3 Solutions 1. Give NFAs with the specified numer of sttes recognizing ech of the following lnguges. In ll cses, the lphet is Σ = {,1}.
Chapter 8.2: The Integral
 Chpter 8.: The Integrl You cn think of Clculus s doule-wide triler. In one width of it lives differentil clculus. In the other hlf lives wht is clled integrl clculus. We hve lredy eplored few rooms in
Chpter 8.: The Integrl You cn think of Clculus s doule-wide triler. In one width of it lives differentil clculus. In the other hlf lives wht is clled integrl clculus. We hve lredy eplored few rooms in
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Bases for Vector Spaces
 Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
The University of Nottingham SCHOOL OF COMPUTER SCIENCE A LEVEL 2 MODULE, SPRING SEMESTER MACHINES AND THEIR LANGUAGES ANSWERS
 The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
Chapters Five Notes SN AA U1C5
 Chpters Five Notes SN AA U1C5 Nme Period Section 5-: Fctoring Qudrtic Epressions When you took lger, you lerned tht the first thing involved in fctoring is to mke sure to fctor out ny numers or vriles
Chpters Five Notes SN AA U1C5 Nme Period Section 5-: Fctoring Qudrtic Epressions When you took lger, you lerned tht the first thing involved in fctoring is to mke sure to fctor out ny numers or vriles
CS311 Computational Structures Regular Languages and Regular Grammars. Lecture 6
 CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
10. AREAS BETWEEN CURVES
 . AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
. AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
Linear Algebra Introduction
 Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Tutorial Worksheet. 1. Find all solutions to the linear system by following the given steps. x + 2y + 3z = 2 2x + 3y + z = 4.
 Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Vectors , (0,0). 5. A vector is commonly denoted by putting an arrow above its symbol, as in the picture above. Here are some 3-dimensional vectors:
 Vectors 1-23-2018 I ll look t vectors from n lgeric point of view nd geometric point of view. Algericlly, vector is n ordered list of (usully) rel numers. Here re some 2-dimensionl vectors: (2, 3), ( )
Vectors 1-23-2018 I ll look t vectors from n lgeric point of view nd geometric point of view. Algericlly, vector is n ordered list of (usully) rel numers. Here re some 2-dimensionl vectors: (2, 3), ( )
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
Numbers and indices. 1.1 Fractions. GCSE C Example 1. Handy hint. Key point
 GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
Algebra Basics. Algebra Basics. Curriculum Ready ACMNA: 133, 175, 176, 177, 179.
 Curriulum Redy ACMNA: 33 75 76 77 79 www.mthletis.om Fill in the spes with nything you lredy know out Alger Creer Opportunities: Arhitets eletriins plumers et. use it to do importnt lultions. Give this
Curriulum Redy ACMNA: 33 75 76 77 79 www.mthletis.om Fill in the spes with nything you lredy know out Alger Creer Opportunities: Arhitets eletriins plumers et. use it to do importnt lultions. Give this
Bridging the gap: GCSE AS Level
 Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
5. (±±) Λ = fw j w is string of even lengthg [ 00 = f11,00g 7. (11 [ 00)± Λ = fw j w egins with either 11 or 00g 8. (0 [ ffl)1 Λ = 01 Λ [ 1 Λ 9.
 Regulr Expressions, Pumping Lemm, Right Liner Grmmrs Ling 106 Mrch 25, 2002 1 Regulr Expressions A regulr expression descries or genertes lnguge: it is kind of shorthnd for listing the memers of lnguge.
Regulr Expressions, Pumping Lemm, Right Liner Grmmrs Ling 106 Mrch 25, 2002 1 Regulr Expressions A regulr expression descries or genertes lnguge: it is kind of shorthnd for listing the memers of lnguge.
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
I1 = I2 I1 = I2 + I3 I1 + I2 = I3 + I4 I 3
 2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
Mathematics Number: Logarithms
 plce of mind F A C U L T Y O F E D U C A T I O N Deprtment of Curriculum nd Pedgogy Mthemtics Numer: Logrithms Science nd Mthemtics Eduction Reserch Group Supported y UBC Teching nd Lerning Enhncement
plce of mind F A C U L T Y O F E D U C A T I O N Deprtment of Curriculum nd Pedgogy Mthemtics Numer: Logrithms Science nd Mthemtics Eduction Reserch Group Supported y UBC Teching nd Lerning Enhncement
= x x 2 = 25 2
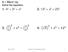 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Linear Inequalities. Work Sheet 1
 Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
Non Right Angled Triangles
 Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
CH 9 INTRO TO EQUATIONS
 CH 9 INTRO TO EQUATIONS INTRODUCTION I m thinking of number. If I dd 10 to the number, the result is 5. Wht number ws I thinking of? R emember this question from Chpter 1? Now we re redy to formlize the
CH 9 INTRO TO EQUATIONS INTRODUCTION I m thinking of number. If I dd 10 to the number, the result is 5. Wht number ws I thinking of? R emember this question from Chpter 1? Now we re redy to formlize the
Symmetrical Components 1
 Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
Lecture 2e Orthogonal Complement (pages )
 Lecture 2e Orthogonl Complement (pges -) We hve now seen tht n orthonorml sis is nice wy to descrie suspce, ut knowing tht we wnt n orthonorml sis doesn t mke one fll into our lp. In theory, the process
Lecture 2e Orthogonl Complement (pges -) We hve now seen tht n orthonorml sis is nice wy to descrie suspce, ut knowing tht we wnt n orthonorml sis doesn t mke one fll into our lp. In theory, the process
Parse trees, ambiguity, and Chomsky normal form
 Prse trees, miguity, nd Chomsky norml form In this lecture we will discuss few importnt notions connected with contextfree grmmrs, including prse trees, miguity, nd specil form for context-free grmmrs
Prse trees, miguity, nd Chomsky norml form In this lecture we will discuss few importnt notions connected with contextfree grmmrs, including prse trees, miguity, nd specil form for context-free grmmrs
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
1 ELEMENTARY ALGEBRA and GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE
 ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
The graphs of Rational Functions
 Lecture 4 5A: The its of Rtionl Functions s x nd s x + The grphs of Rtionl Functions The grphs of rtionl functions hve severl differences compred to power functions. One of the differences is the behvior
Lecture 4 5A: The its of Rtionl Functions s x nd s x + The grphs of Rtionl Functions The grphs of rtionl functions hve severl differences compred to power functions. One of the differences is the behvior
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Exam Review. John Knight Electronics Department, Carleton University March 2, 2009 ELEC 2607 A MIDTERM
 riting Exms: Exm Review riting Exms += riting Exms synhronous iruits Res, yles n Stte ssignment Synhronous iruits Stte-Grph onstrution n Smll Prolems lso Multiple Outputs, n Hrer omintionl Prolem riting
riting Exms: Exm Review riting Exms += riting Exms synhronous iruits Res, yles n Stte ssignment Synhronous iruits Stte-Grph onstrution n Smll Prolems lso Multiple Outputs, n Hrer omintionl Prolem riting
Lecture 08: Feb. 08, 2019
 4CS4-6:Theory of Computtion(Closure on Reg. Lngs., regex to NDFA, DFA to regex) Prof. K.R. Chowdhry Lecture 08: Fe. 08, 2019 : Professor of CS Disclimer: These notes hve not een sujected to the usul scrutiny
4CS4-6:Theory of Computtion(Closure on Reg. Lngs., regex to NDFA, DFA to regex) Prof. K.R. Chowdhry Lecture 08: Fe. 08, 2019 : Professor of CS Disclimer: These notes hve not een sujected to the usul scrutiny
Farey Fractions. Rickard Fernström. U.U.D.M. Project Report 2017:24. Department of Mathematics Uppsala University
 U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
Generalization of 2-Corner Frequency Source Models Used in SMSIM
 Generliztion o 2-Corner Frequeny Soure Models Used in SMSIM Dvid M. Boore 26 Mrh 213, orreted Figure 1 nd 2 legends on 5 April 213, dditionl smll orretions on 29 My 213 Mny o the soure spetr models ville
Generliztion o 2-Corner Frequeny Soure Models Used in SMSIM Dvid M. Boore 26 Mrh 213, orreted Figure 1 nd 2 legends on 5 April 213, dditionl smll orretions on 29 My 213 Mny o the soure spetr models ville
Chapter 4 State-Space Planning
 Leture slides for Automted Plnning: Theory nd Prtie Chpter 4 Stte-Spe Plnning Dn S. Nu CMSC 722, AI Plnning University of Mrylnd, Spring 2008 1 Motivtion Nerly ll plnning proedures re serh proedures Different
Leture slides for Automted Plnning: Theory nd Prtie Chpter 4 Stte-Spe Plnning Dn S. Nu CMSC 722, AI Plnning University of Mrylnd, Spring 2008 1 Motivtion Nerly ll plnning proedures re serh proedures Different
Lecture 6: Coding theory
 Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
Probability. b a b. a b 32.
 Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
System Validation (IN4387) November 2, 2012, 14:00-17:00
 System Vlidtion (IN4387) Novemer 2, 2012, 14:00-17:00 Importnt Notes. The exmintion omprises 5 question in 4 pges. Give omplete explntion nd do not onfine yourself to giving the finl nswer. Good luk! Exerise
System Vlidtion (IN4387) Novemer 2, 2012, 14:00-17:00 Importnt Notes. The exmintion omprises 5 question in 4 pges. Give omplete explntion nd do not onfine yourself to giving the finl nswer. Good luk! Exerise
Section 6: Area, Volume, and Average Value
 Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
TOPIC: LINEAR ALGEBRA MATRICES
 Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
5.2 Exponent Properties Involving Quotients
 5. Eponent Properties Involving Quotients Lerning Objectives Use the quotient of powers property. Use the power of quotient property. Simplify epressions involving quotient properties of eponents. Use
5. Eponent Properties Involving Quotients Lerning Objectives Use the quotient of powers property. Use the power of quotient property. Simplify epressions involving quotient properties of eponents. Use
UNIT 5 QUADRATIC FUNCTIONS Lesson 3: Creating Quadratic Equations in Two or More Variables Instruction
 Lesson 3: Creting Qudrtic Equtions in Two or More Vriles Prerequisite Skills This lesson requires the use of the following skill: solving equtions with degree of Introduction 1 The formul for finding the
Lesson 3: Creting Qudrtic Equtions in Two or More Vriles Prerequisite Skills This lesson requires the use of the following skill: solving equtions with degree of Introduction 1 The formul for finding the
CARLETON UNIVERSITY. 1.0 Problems and Most Solutions, Sect B, 2005
 RLETON UNIVERSIT eprtment of Eletronis ELE 2607 Swithing iruits erury 28, 05; 0 pm.0 Prolems n Most Solutions, Set, 2005 Jn. 2, #8 n #0; Simplify, Prove Prolem. #8 Simplify + + + Reue to four letters (literls).
RLETON UNIVERSIT eprtment of Eletronis ELE 2607 Swithing iruits erury 28, 05; 0 pm.0 Prolems n Most Solutions, Set, 2005 Jn. 2, #8 n #0; Simplify, Prove Prolem. #8 Simplify + + + Reue to four letters (literls).
HS Pre-Algebra Notes Unit 9: Roots, Real Numbers and The Pythagorean Theorem
 HS Pre-Alger Notes Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Roots nd Cue Roots Syllus Ojetive 5.4: The student will find or pproximte squre roots of numers to 4. CCSS 8.EE.-: Evlute squre roots
HS Pre-Alger Notes Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Roots nd Cue Roots Syllus Ojetive 5.4: The student will find or pproximte squre roots of numers to 4. CCSS 8.EE.-: Evlute squre roots
Section 7.1 Area of a Region Between Two Curves
 Section 7.1 Are of Region Between Two Curves White Bord Chllenge The circle elow is inscried into squre: Clcultor 0 cm Wht is the shded re? 400 100 85.841cm White Bord Chllenge Find the re of the region
Section 7.1 Are of Region Between Two Curves White Bord Chllenge The circle elow is inscried into squre: Clcultor 0 cm Wht is the shded re? 400 100 85.841cm White Bord Chllenge Find the re of the region
Week 10: Line Integrals
 Week 10: Line Integrls Introduction In this finl week we return to prmetrised curves nd consider integrtion long such curves. We lredy sw this in Week 2 when we integrted long curve to find its length.
Week 10: Line Integrls Introduction In this finl week we return to prmetrised curves nd consider integrtion long such curves. We lredy sw this in Week 2 when we integrted long curve to find its length.
MA123, Chapter 10: Formulas for integrals: integrals, antiderivatives, and the Fundamental Theorem of Calculus (pp.
 MA123, Chpter 1: Formuls for integrls: integrls, ntiderivtives, nd the Fundmentl Theorem of Clculus (pp. 27-233, Gootmn) Chpter Gols: Assignments: Understnd the sttement of the Fundmentl Theorem of Clculus.
MA123, Chpter 1: Formuls for integrls: integrls, ntiderivtives, nd the Fundmentl Theorem of Clculus (pp. 27-233, Gootmn) Chpter Gols: Assignments: Understnd the sttement of the Fundmentl Theorem of Clculus.
CSCI 340: Computational Models. Kleene s Theorem. Department of Computer Science
 CSCI 340: Computtionl Models Kleene s Theorem Chpter 7 Deprtment of Computer Science Unifiction In 1954, Kleene presented (nd proved) theorem which (in our version) sttes tht if lnguge cn e defined y ny
CSCI 340: Computtionl Models Kleene s Theorem Chpter 7 Deprtment of Computer Science Unifiction In 1954, Kleene presented (nd proved) theorem which (in our version) sttes tht if lnguge cn e defined y ny
7.1 Integral as Net Change and 7.2 Areas in the Plane Calculus
 7.1 Integrl s Net Chnge nd 7. Ares in the Plne Clculus 7.1 INTEGRAL AS NET CHANGE Notecrds from 7.1: Displcement vs Totl Distnce, Integrl s Net Chnge We hve lredy seen how the position of n oject cn e
7.1 Integrl s Net Chnge nd 7. Ares in the Plne Clculus 7.1 INTEGRAL AS NET CHANGE Notecrds from 7.1: Displcement vs Totl Distnce, Integrl s Net Chnge We hve lredy seen how the position of n oject cn e
expression simply by forming an OR of the ANDs of all input variables for which the output is
 2.4 Logic Minimiztion nd Krnugh Mps As we found ove, given truth tle, it is lwys possile to write down correct logic expression simply y forming n OR of the ANDs of ll input vriles for which the output
2.4 Logic Minimiztion nd Krnugh Mps As we found ove, given truth tle, it is lwys possile to write down correct logic expression simply y forming n OR of the ANDs of ll input vriles for which the output
Designing Information Devices and Systems I Discussion 8B
 Lst Updted: 2018-10-17 19:40 1 EECS 16A Fll 2018 Designing Informtion Devices nd Systems I Discussion 8B 1. Why Bother With Thévenin Anywy? () Find Thévenin eqiuvlent for the circuit shown elow. 2kΩ 5V
Lst Updted: 2018-10-17 19:40 1 EECS 16A Fll 2018 Designing Informtion Devices nd Systems I Discussion 8B 1. Why Bother With Thévenin Anywy? () Find Thévenin eqiuvlent for the circuit shown elow. 2kΩ 5V
CS103B Handout 18 Winter 2007 February 28, 2007 Finite Automata
 CS103B ndout 18 Winter 2007 Ferury 28, 2007 Finite Automt Initil text y Mggie Johnson. Introduction Severl childrens gmes fit the following description: Pieces re set up on plying ord; dice re thrown or
CS103B ndout 18 Winter 2007 Ferury 28, 2007 Finite Automt Initil text y Mggie Johnson. Introduction Severl childrens gmes fit the following description: Pieces re set up on plying ord; dice re thrown or
1. For each of the following theorems, give a two or three sentence sketch of how the proof goes or why it is not true.
 York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
Chapter 0. What is the Lebesgue integral about?
 Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Lecture 3: Equivalence Relations
 Mthcmp Crsh Course Instructor: Pdric Brtlett Lecture 3: Equivlence Reltions Week 1 Mthcmp 2014 In our lst three tlks of this clss, we shift the focus of our tlks from proof techniques to proof concepts
Mthcmp Crsh Course Instructor: Pdric Brtlett Lecture 3: Equivlence Reltions Week 1 Mthcmp 2014 In our lst three tlks of this clss, we shift the focus of our tlks from proof techniques to proof concepts
Nondeterministic Automata vs Deterministic Automata
 Nondeterministi Automt vs Deterministi Automt We lerned tht NFA is onvenient model for showing the reltionships mong regulr grmmrs, FA, nd regulr expressions, nd designing them. However, we know tht n
Nondeterministi Automt vs Deterministi Automt We lerned tht NFA is onvenient model for showing the reltionships mong regulr grmmrs, FA, nd regulr expressions, nd designing them. However, we know tht n
Arrow s Impossibility Theorem
 Rep Voting Prdoxes Properties Arrow s Theorem Arrow s Impossiility Theorem Leture 12 Arrow s Impossiility Theorem Leture 12, Slide 1 Rep Voting Prdoxes Properties Arrow s Theorem Leture Overview 1 Rep
Rep Voting Prdoxes Properties Arrow s Theorem Arrow s Impossiility Theorem Leture 12 Arrow s Impossiility Theorem Leture 12, Slide 1 Rep Voting Prdoxes Properties Arrow s Theorem Leture Overview 1 Rep
Formal languages, automata, and theory of computation
 Mälrdlen University TEN1 DVA337 2015 School of Innovtion, Design nd Engineering Forml lnguges, utomt, nd theory of computtion Thursdy, Novemer 5, 14:10-18:30 Techer: Dniel Hedin, phone 021-107052 The exm
Mälrdlen University TEN1 DVA337 2015 School of Innovtion, Design nd Engineering Forml lnguges, utomt, nd theory of computtion Thursdy, Novemer 5, 14:10-18:30 Techer: Dniel Hedin, phone 021-107052 The exm
Chapter 3. Vector Spaces. 3.1 Images and Image Arithmetic
 Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
Exponentials - Grade 10 [CAPS] *
![Exponentials - Grade 10 [CAPS] * Exponentials - Grade 10 [CAPS] *](/thumbs/88/115984632.jpg) OpenStx-CNX module: m859 Exponentils - Grde 0 [CAPS] * Free High School Science Texts Project Bsed on Exponentils by Rory Adms Free High School Science Texts Project Mrk Horner Hether Willims This work
OpenStx-CNX module: m859 Exponentils - Grde 0 [CAPS] * Free High School Science Texts Project Bsed on Exponentils by Rory Adms Free High School Science Texts Project Mrk Horner Hether Willims This work
For a, b, c, d positive if a b and. ac bd. Reciprocal relations for a and b positive. If a > b then a ab > b. then
 Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
Review of Gaussian Quadrature method
 Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
A study of Pythagoras Theorem
 CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins
CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins
1B40 Practical Skills
 B40 Prcticl Skills Comining uncertinties from severl quntities error propgtion We usully encounter situtions where the result of n experiment is given in terms of two (or more) quntities. We then need
B40 Prcticl Skills Comining uncertinties from severl quntities error propgtion We usully encounter situtions where the result of n experiment is given in terms of two (or more) quntities. We then need
Introduction to Algebra - Part 2
 Alger Module A Introduction to Alger - Prt Copright This puliction The Northern Alert Institute of Technolog 00. All Rights Reserved. LAST REVISED Oct., 008 Introduction to Alger - Prt Sttement of Prerequisite
Alger Module A Introduction to Alger - Prt Copright This puliction The Northern Alert Institute of Technolog 00. All Rights Reserved. LAST REVISED Oct., 008 Introduction to Alger - Prt Sttement of Prerequisite
Math 154B Elementary Algebra-2 nd Half Spring 2015
 Mth 154B Elementry Alger- nd Hlf Spring 015 Study Guide for Exm 4, Chpter 9 Exm 4 is scheduled for Thursdy, April rd. You my use " x 5" note crd (oth sides) nd scientific clcultor. You re expected to know
Mth 154B Elementry Alger- nd Hlf Spring 015 Study Guide for Exm 4, Chpter 9 Exm 4 is scheduled for Thursdy, April rd. You my use " x 5" note crd (oth sides) nd scientific clcultor. You re expected to know
Simplifying Algebra. Simplifying Algebra. Curriculum Ready.
 Simplifying Alger Curriculum Redy www.mthletics.com This ooklet is ll out turning complex prolems into something simple. You will e le to do something like this! ( 9- # + 4 ' ) ' ( 9- + 7-) ' ' Give this
Simplifying Alger Curriculum Redy www.mthletics.com This ooklet is ll out turning complex prolems into something simple. You will e le to do something like this! ( 9- # + 4 ' ) ' ( 9- + 7-) ' ' Give this
Minimal DFA. minimal DFA for L starting from any other
 Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Designing Information Devices and Systems I Spring 2018 Homework 7
 EECS 16A Designing Informtion Devices nd Systems I Spring 2018 omework 7 This homework is due Mrch 12, 2018, t 23:59. Self-grdes re due Mrch 15, 2018, t 23:59. Sumission Formt Your homework sumission should
EECS 16A Designing Informtion Devices nd Systems I Spring 2018 omework 7 This homework is due Mrch 12, 2018, t 23:59. Self-grdes re due Mrch 15, 2018, t 23:59. Sumission Formt Your homework sumission should
Infinite Geometric Series
 Infinite Geometric Series Finite Geometric Series ( finite SUM) Let 0 < r < 1, nd let n be positive integer. Consider the finite sum It turns out there is simple lgebric expression tht is equivlent to
Infinite Geometric Series Finite Geometric Series ( finite SUM) Let 0 < r < 1, nd let n be positive integer. Consider the finite sum It turns out there is simple lgebric expression tht is equivlent to
Ellipses. The second type of conic is called an ellipse.
 Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
MAT 403 NOTES 4. f + f =
 MAT 403 NOTES 4 1. Fundmentl Theorem o Clulus We will proo more generl version o the FTC thn the textook. But just like the textook, we strt with the ollowing proposition. Let R[, ] e the set o Riemnn
MAT 403 NOTES 4 1. Fundmentl Theorem o Clulus We will proo more generl version o the FTC thn the textook. But just like the textook, we strt with the ollowing proposition. Let R[, ] e the set o Riemnn
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
set is not closed under matrix [ multiplication, ] and does not form a group.
![set is not closed under matrix [ multiplication, ] and does not form a group. set is not closed under matrix [ multiplication, ] and does not form a group.](/thumbs/78/78412113.jpg) Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
University of Sioux Falls. MAT204/205 Calculus I/II
 University of Sioux Flls MAT204/205 Clulus I/II Conepts ddressed: Clulus Textook: Thoms Clulus, 11 th ed., Weir, Hss, Giordno 1. Use stndrd differentition nd integrtion tehniques. Differentition tehniques
University of Sioux Flls MAT204/205 Clulus I/II Conepts ddressed: Clulus Textook: Thoms Clulus, 11 th ed., Weir, Hss, Giordno 1. Use stndrd differentition nd integrtion tehniques. Differentition tehniques
Fast Boolean Algebra
 Fst Boolen Alger ELEC 267 notes with the overurden removed A fst wy to lern enough to get the prel done honorly Printed; 3//5 Slide Modified; Jnury 3, 25 John Knight Digitl Circuits p. Fst Boolen Alger
Fst Boolen Alger ELEC 267 notes with the overurden removed A fst wy to lern enough to get the prel done honorly Printed; 3//5 Slide Modified; Jnury 3, 25 John Knight Digitl Circuits p. Fst Boolen Alger
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
 Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Chapter 1: Fundamentals
 Chpter 1: Fundmentls 1.1 Rel Numbers Types of Rel Numbers: Nturl Numbers: {1, 2, 3,...}; These re the counting numbers. Integers: {... 3, 2, 1, 0, 1, 2, 3,...}; These re ll the nturl numbers, their negtives,
Chpter 1: Fundmentls 1.1 Rel Numbers Types of Rel Numbers: Nturl Numbers: {1, 2, 3,...}; These re the counting numbers. Integers: {... 3, 2, 1, 0, 1, 2, 3,...}; These re ll the nturl numbers, their negtives,
Lecture 3. In this lecture, we will discuss algorithms for solving systems of linear equations.
 Lecture 3 3 Solving liner equtions In this lecture we will discuss lgorithms for solving systems of liner equtions Multiplictive identity Let us restrict ourselves to considering squre mtrices since one
Lecture 3 3 Solving liner equtions In this lecture we will discuss lgorithms for solving systems of liner equtions Multiplictive identity Let us restrict ourselves to considering squre mtrices since one
Lesson 25: Adding and Subtracting Rational Expressions
 Lesson 2: Adding nd Subtrcting Rtionl Expressions Student Outcomes Students perform ddition nd subtrction of rtionl expressions. Lesson Notes This lesson reviews ddition nd subtrction of frctions using
Lesson 2: Adding nd Subtrcting Rtionl Expressions Student Outcomes Students perform ddition nd subtrction of rtionl expressions. Lesson Notes This lesson reviews ddition nd subtrction of frctions using
