Forces on curved surfaces Buoyant force Stability of floating and submerged bodies
|
|
|
- Victor McCarthy
- 6 years ago
- Views:
Transcription
1 Stti Surfe ores Stti Surfe ores 8m wter hinge? 4 m ores on plne res ores on urved surfes Buont fore Stbilit of floting nd submerged bodies ores on Plne res Two tpes of problems Horizontl surfes (pressure is ) onstnt nlined surfes dp Two unknowns Totl fore Line of tion dz Two tehniques to find the line of tion of the resultnt fore Moments Pressure prism ores on Plne res: Horizontl surfes Wht is the fore on the bottom of this tnk of wter? h pd p d p =weight g of overling fluid! p = h is norml to the surfe nd towrds the surfe if p is positive. entroid psses through the of the re. h Side view h = Vertil distne to free surfe Top view
2 ores on Plne res: nlined Surfes Diretion of fore Norml to the plne Mgnitude of fore integrte the pressure over the re pressure is no longer onstnt! Line of tion Moment of the resultnt fore must equl the moment of the distributed pressure fore HW#.89,.,.6,.7,.9,.0,.8,.4,.44,.47 ores on Plne res: nlined Surfes ree surfe h entroid h O B O Mgnitude of ore on nlined Plne re pd sin d sin p h sin d enter of pressure The origin of the is is on the free surfe h h p h is the vertil distne between free surfe nd entroid p is the pressure t the entroid of the re
3 irst Moments Seond Moments d Moment of n re bout the is lso lled moment of inerti of the re d d Lotion of entroidl is h d is the nd moment with respet to n is pssing through its entroid nd prllel to the is. Prllel lis theorem or plte of uniform thikness the intersetion of the entroidl es is lso the enter of grvit Produt of nerti mesure of the smmetr of the re d Produt of inerti = 0 = 0 f = or = is n is of smmetr then the produt of inerti is zero. b b b d Properties of res b 0 b b d b b bd
4 Properties of res ores on Plne res: Center of Pressure: b b b The enter of pressure is not t the entroid (beuse pressure is inresing with depth) oordinte of enter of pressure: pd Moment of resultnt fore = sum of moment of distributed fores pd sin p sin sind sin d Center of Pressure: Center of Pressure: d d Produt of inerti Prllel is theorem pd pd sin d Sum of the moments sin sind d p sin Prllel is theorem
5 nlined Surfe indings The horizontl enter of pressure nd the horizontl entroid oinide id when the surfe hs either horizontl or vertil is of smmetr The enter of pressure is lws below the entroid The vertil distne between the entroid nd the enter of pressure dereses s the surfe is lowered deeper into the liquid ( inreses) Wht do ou do if there isn t free surfe? 0 >0 Emple using Moments n elliptil gte overs the end of pipe 4 m in dimeter. f the gte is hinged t the top, wht norml fore pplied t the bottom of the gte is required to open the gte when wter is 8 m deep bove the top of the pipe nd the pipe is open to the tmosphere on the other side? Neglet the weight of the gte. Solution Sheme Mgnitude of the fore pplied b the wter Lotion of the resultnt fore 8 m ind using moments bout hinge wter hinge 4 m Mgnitude of the ore Lotion of esultnt ore p b 8 m h = 0 m Depth to the entroid p = h hb N m π.5 m m = 54MN.54 m wter =.5 m b = m hinge 4 m h 8 m Slnt distne.5 m to surfe b b bb 4b 4 5m m 0.5 m r wter =.5 m b = m hinge 4 m p
6 ore equired to Open Gte ores on Plne Surfes eview How do we find the required fore? Moments bout the hinge M hinge 0 =l tot - l p l l p tot N.65 m 5 m 8 m l p =.65 m r wter.5 m hinge 4 m p l tot The verge mgnitude of the pressure fore is the pressure t the entroid The horizontl lotion of the pressure fore ws t (WHY?) The gte ws smmetril bout t lest one of the entroidl es. The vertil lotion of the pressure fore is below the entroid. (WHY?) Pressure inreses with depth. = 809 kn b = m ores on Plne res: Pressure Prism simpler pproh tht works well for res of onstnt width ( ) retngles f the lotion of the resultnt fore is required nd the re doesn t interset the free surfe, then the moment of inerti method is bout s es ores on Plne res: Pressure Prism ree surfe h h h O h ore = Volume of pressure prism p h pd d Center of pressure is t entroid of d pressure prism
7 Emple : Pressure Prism Emple : Pressure Prism O h/os 8 m wter h=0 m 4º Dm hinge h = Volume = (h/os)(h)(w)/ = (0 m/0.95)(9800 N/m *0 m)(50 m)/ = 6 MN m 5m 8 m 4 m 5 m (retngulr onduit) 4 m Solution : Pressure Prism ores on Curved Surfes Mgnitude of fore (9800 N/m =.96 MN Lotion of resultnt fore h h )(0 m)(5 m)(4 m) h mesured from hinge 5m h Horizontl omponent Vertil omponent w h w h h 5 m 8 m m 0 m 6 w h h w0 m 6 =.667 m
8 ores on Curved Surfes: Horizontl Component Wht is the horizontl omponent of pressure fore on urved surfe equl to? The enter of pressure is loted using the moment of inerti or pressure prism tehnique. The horizontl omponent of pressure fore on losed bod is. zero ores on Curved Surfes: Vertil Component Wht is the mgnitude of the vertil omponent of fore on the up? = p p = h =hr =W! r h ores on Curved Surfes: Vertil Component The vertil omponent of pressure fore on urved surfe is equl to the weight of liquid vertill bove the urved surfe nd etending up to the (virtul or rel) free surfe. Streeter, et. l Wht if the up hd sloping sides?
9 Emple: ores on Curved Surfes ind the resultnt fore (mgnitude nd lotion) on m wide setion of the irulr r. V = W + W m W = ( m)( m)( m) +/4( m) ( m) wter = 58.9 kn kn = 89.7 kn H = p p h = (4 m)( m)( m) = 78.5 kn m m W Emple: ores on Curved Surfes The vertil omponent line of tion goes through the entroid of the volume of wter bove the surfe. Tke moments bout vertil is through. 4 m W 4( m) wter V ( m) W W 4( m) m W ( m)(58.9 kn) (0.8 kn) (89.7 kn) m = m (mesured from ) with mgnitude of 89.7 kn Emple: ores on Curved Surfes Emple: ores on Curved Surfes The lotion of the line of tion of the horizontl omponent is given b b b ( m)( m) / = m 4 wter m W m m W 4.08 m m 78.5 kn 89.7 kn horizontl vertil 4 m m m 4.08 m 4 m m m 9. kn resultnt
10 Clindril Surfe ore Chek Curved Surfe Trik m C 89.7kN ll pressure fores pss C through h point C. The pressure fore.08 m pplies no moment bout point C. The resultnt t must pss through point C. 78.5kN (78.5kN)(.08m) - (89.7kN)(0.948m) = 0 ind fore required to open the gte. ll the horizontl fore is rried b the hinge m W The pressure fores nd fore wter O pss through O. Thus the hinge W fore must pss through O! Hinge rries onl horizontl fores! ( = ) W + W m Curved Surfe Trik Solution Sheme Trditionl w: M hinge 0 : (89.7)( 0.948) (78.5)(.08) () 89.7 (kn) Sme s v = W +W.08 m 78.5kN C m 89.7kN Determine pressure dtum nd lotion in fluid where pressure is zero ( origin) i Determine totl elertion vetor () inluding elertion of grvit Define h tngent to elertion vetor (ll this vertil!) Determine if surfe is norml to, inlined, or urved
11 Stti Surfe ores Summr Buont ore ores used b grvit (or ) totl elertion on submerged surfes horizontl surfes (norml to totl elertion) h Lotion where p = p ref inlined surfes ( oordinte hs origin t free surfe) h urved surfes h Horizontl omponent Vertil omponent ( ) weight of fluid bove surfe Virtul surfes The resultnt fore eerted on bod b stti fluid in whih it is full or prtill submerged The projetion of the bod on vertil plne is lws. zero The vertil omponents of pressure on the top nd bottom surfes re different Buont ore: Thought Eperiment Ple thin wll blloon filled with wter in tnk of wter. Wht is the net fore on the B blloon? zero Does the shpe of the blloon mtter? no Wht is the buont fore on the blloon? Wi Weight of wter displed Where is the line of tion of B =V the buont fore? Thru entroid of blloon Buont ore: Line of tion The buont fore ts through the entroid of fth the displed d volume of ffl fluid id( (enter of buon) = volume d = distributed fore = entroid of volume V dv V V V dv
12 Buont ore: pplitions Buont ore: pplitions > Using buon it is > possible to determine: Weight of n objet Volume of n objet Speifi grvit of n objet W W ore blne V W V W (With,,, nd given) V W V W (fore blne) Equte weights Equte volumes V V W W V V W W V W V W Suppose the speifi weight of the first fluid is zero Buont ore (Just for fun) ottionl Stbilit of Submerged Bodies silbot is siling on Lke Brn. The ptin is in hurr to get to shore nd deides to ut the nhor off nd toss it overbord to lighten the bot. Does the wter level of Lke Brn inrese or derese? Wh? The nhor disples less wter when it is ling on the bottom of the lke thn it did when in the bot. ompletel submerged bod is stble when its enter of grvit is below the enter of buon B G B G
13 End of Chpter Question End of Chpter Write n eqution for the pressure ting on the bottom of onil tnk of wter. Write n eqution for the totl fore ting on the bottom of the tnk. L d Wht didn t ou understnd so fr bout sttis? sk the person net to ou Cirle n questions tht still need nswers d Grnd Coulee Dm Gtes
14 Gtes
Static Surface Forces. Forces on Plane Areas: Horizontal surfaces. Forces on Plane Areas. Hydrostatic Forces on Plane Surfaces
Hdrostti ores on Plne Surfes Stti Surfe ores ores on lne res ores on urved surfes Buont fore Stbilit of floting nd submerged bodies ores on Plne res Two tes of roblems Horizontl surfes (ressure is ) onstnt
Static Surface Forces. Forces on Curved Surfaces: Horizontal Component. Forces on Curved Surfaces. Hydrostatic Forces on Curved Surfaces
Hdrostati Fores on Curved Surfaes Stati Surfae Fores Fores on plane areas Fores on urved surfaes Buoant fore Stabilit of floating and submerged bodies Fores on Curved Surfaes Horizontal omponent Vertial
H (2a, a) (u 2a) 2 (E) Show that u v 4a. Explain why this implies that u v 4a, with equality if and only u a if u v 2a.
Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
The Ellipse. is larger than the other.
The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
m m m m m m m m P m P m ( ) m m P( ) ( ). The o-ordinte of the point P( ) dividing the line segment joining the two points ( ) nd ( ) eternll in the r
CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
8.3 THE HYPERBOLA OBJECTIVES
8.3 THE HYPERBOLA OBJECTIVES 1. Define Hperol. Find the Stndrd Form of the Eqution of Hperol 3. Find the Trnsverse Ais 4. Find the Eentriit of Hperol 5. Find the Asmptotes of Hperol 6. Grph Hperol HPERBOLAS
Applications of Definite Integral
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
] dx (3) = [15x] 2 0
![] dx (3) = [15x] 2 0](/thumbs/80/81916477.jpg "] dx (3) = [15x] 2 0")
Leture 6. Double Integrls nd Volume on etngle Welome to Cl IV!!!! These notes re designed to be redble nd desribe the w I will eplin the mteril in lss. Hopefull the re thorough, but it s good ide to hve
m A 1 1 A ! and AC 6
REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
Instructions to students: Use your Text Book and attempt these questions.
Instrutions to students: Use your Text Book nd ttempt these questions. Due Dte: 16-09-2018 Unit 2 Chpter 8 Test Slrs nd vetors Totl mrks 50 Nme: Clss: Dte: Setion A Selet the est nswer for eh question.
Standard Trigonometric Functions
CRASH KINEMATICS For ngle A: opposite sine A = = hypotenuse djent osine A = = hypotenuse opposite tngent A = = djent For ngle B: opposite sine B = = hypotenuse djent osine B = = hypotenuse opposite tngent
Applications of Definite Integral
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Green s Theorem. (2x e y ) da. (2x e y ) dx dy. x 2 xe y. (1 e y ) dy. y=1. = y e y. y=0. = 2 e
Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
( ) 1. 1) Let f( x ) = 10 5x. Find and simplify f( 2) and then state the domain of f(x).
Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
Math 32B Discussion Session Week 8 Notes February 28 and March 2, f(b) f(a) = f (t)dt (1)
Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
Type 2: Improper Integrals with Infinite Discontinuities
mth imroer integrls: tye 6 Tye : Imroer Integrls with Infinite Disontinuities A seond wy tht funtion n fil to be integrble in the ordinry sense is tht it my hve n infinite disontinuity (vertil symtote)
y z A left-handed system can be rotated to look like the following. z
Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
VECTOR ALGEBRA. Syllabus :
MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
THREE DIMENSIONAL GEOMETRY
MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
2. Topic: Summation of Series (Mathematical Induction) When n = 1, L.H.S. = S 1 = u 1 = 3 R.H.S. = 1 (1)(1+1)(4+5) = 3
GCE A Level Otober/November 008 Suggested Solutions Mthemtis H (970/0) version. MATHEMATICS (H) Pper Suggested Solutions. Topi: Definite Integrls From the digrm: Are A = y dx = x Are B = x dy = y dy dx
The Double Integral. The Riemann sum of a function f (x; y) over this partition of [a; b] [c; d] is. f (r j ; t k ) x j y k
![The Double Integral. The Riemann sum of a function f (x; y) over this partition of [a; b] [c; d] is. f (r j ; t k ) x j y k](/thumbs/86/94790710.jpg "The Double Integral. The Riemann sum of a function f (x; y) over this partition of [a; b] [c; d] is. f (r j ; t k ) x j y k")
The Double Integrl De nition of the Integrl Iterted integrls re used primrily s tool for omputing double integrls, where double integrl is n integrl of f (; y) over region : In this setion, we de ne double
First, we will find the components of the force of gravity: Perpendicular Forces (using away from the ramp as positive) ma F
1.. In Clss or Homework Eercise 1. An 18.0 kg bo is relesed on 33.0 o incline nd ccelertes t 0.300 m/s. Wht is the coeicient o riction? m 18.0kg 33.0? 0 0.300 m / s irst, we will ind the components o the
1.3 SCALARS AND VECTORS
Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Due to gravity and wind load, the post supporting the sign shown is subjected simultaneously to compression, bending, and torsion.
ue to grvit nd wind lod, the post supporting the sign shown is sujeted simultneousl to ompression, ending, nd torsion. In this hpter ou will lern to determine the stresses reted suh omined lodings in strutures
for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx
![for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx](/thumbs/74/70408252.jpg "for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx")
Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
Applications of Bernoulli s theorem. Lecture - 7
Applictions of Bernoulli s theorem Lecture - 7 Prcticl Applictions of Bernoulli s Theorem The Bernoulli eqution cn be pplied to gret mny situtions not just the pipe flow we hve been considering up to now.
Ellipses. The second type of conic is called an ellipse.
Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
SIMPLE NONLINEAR GRAPHS
S i m p l e N o n l i n e r G r p h s SIMPLE NONLINEAR GRAPHS www.mthletis.om.u Simple SIMPLE Nonliner NONLINEAR Grphs GRAPHS Liner equtions hve the form = m+ where the power of (n ) is lws. The re lle
3 Angle Geometry. 3.1 Measuring Angles. 1. Using a protractor, measure the marked angles.
3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
Logarithms LOGARITHMS.
Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
PROPERTIES OF AREAS In general, and for an irregular shape, the definition of the centroid at position ( x, y) is given by
PROPERTES OF RES Centroid The concept of the centroid is prol lred fmilir to ou For plne shpe with n ovious geometric centre, (rectngle, circle) the centroid is t the centre f n re hs n is of smmetr, the
( ) as a fraction. Determine location of the highest
AB/ Clulus Exm Review Sheet Solutions A Prelulus Type prolems A1 A A3 A4 A5 A6 A7 This is wht you think of doing Find the zeros of f( x) Set funtion equl to Ftor or use qudrti eqution if qudrti Grph to
Distributed Forces: Centroids and Centers of Gravity
Distriuted Forces: Centroids nd Centers of Grvit Introduction Center of Grvit of D Bod Centroids nd First Moments of Ares nd Lines Centroids of Common Shpes of Ares Centroids of Common Shpes of Lines Composite
Reflection Property of a Hyperbola
Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
[ ( ) ( )] Section 6.1 Area of Regions between two Curves. Goals: 1. To find the area between two curves
![[ ( ) ( )] Section 6.1 Area of Regions between two Curves. Goals: 1. To find the area between two curves](/thumbs/74/70299306.jpg "[ ( ) ( )] Section 6.1 Area of Regions between two Curves. Goals: 1. To find the area between two curves")
Gols: 1. To find the re etween two curves Section 6.1 Are of Regions etween two Curves I. Are of Region Between Two Curves A. Grphicl Represention = _ B. Integrl Represention [ ( ) ( )] f x g x dx = C.
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
Problems set # 3 Physics 169 February 24, 2015
Prof. Anhordoqui Problems set # 3 Physis 169 Februry 4, 015 1. A point hrge q is loted t the enter of uniform ring hving liner hrge density λ nd rdius, s shown in Fig. 1. Determine the totl eletri flux
Comparing the Pre-image and Image of a Dilation
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
are coplanar. ˆ ˆ ˆ and iˆ
SML QUSTION Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor ii The question pper onsists of 6 questions divided into three Setions, B nd C iii Question No
Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx
![Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx](/thumbs/79/79316452.jpg "Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx")
Fill in the Blnks for the Big Topis in Chpter 5: The Definite Integrl Estimting n integrl using Riemnn sum:. The Left rule uses the left endpoint of eh suintervl.. The Right rule uses the right endpoint
HOMEWORK FOR CLASS XII ( )
HOMEWORK FOR CLASS XII 8-9 Show tht the reltion R on the set Z of ll integers defined R,, Z,, is, divisile,, is n equivlene reltion on Z Let f: R R e defined if f if Is f one-one nd onto if If f, g : R
Chapter 5 Bending Moments and Shear Force Diagrams for Beams
Chpter 5 ending Moments nd Sher Force Digrms for ems n ddition to illy loded brs/rods (e.g. truss) nd torsionl shfts, the structurl members my eperience some lods perpendiculr to the is of the bem nd will
Solutions to Assignment 1
MTHE 237 Fll 2015 Solutions to Assignment 1 Problem 1 Find the order of the differentil eqution: t d3 y dt 3 +t2 y = os(t. Is the differentil eqution liner? Is the eqution homogeneous? b Repet the bove
(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.
![(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.](/thumbs/72/66745617.jpg "(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.")
Chpter 7: The Riemnn Integrl When the derivtive is introdued, it is not hrd to see tht the it of the differene quotient should be equl to the slope of the tngent line, or when the horizontl xis is time
Core 2 Logarithms and exponentials. Section 1: Introduction to logarithms
Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
f (x)dx = f(b) f(a). a b f (x)dx is the limit of sums
Green s Theorem If f is funtion of one vrible x with derivtive f x) or df dx to the Fundmentl Theorem of lulus, nd [, b] is given intervl then, ording This is not trivil result, onsidering tht b b f x)dx
Vector Integration. Line integral: Let F ( x y,
Vetor Integrtion Thi hpter tret integrtion in vetor field. It i the mthemti tht engineer nd phiit ue to deribe fluid flow, deign underwter trnmiion ble, eplin the flow of het in tr, nd put tellite in orbit.
VTU NOTES QUESTION PAPERS NEWS RESULTS FORUMS Vector Integration
www.boopr.om VTU NOTES QUESTION PAPERS NEWS RESULTS FORUMS Vetor Integrtion Thi hpter tret integrtion in vetor field. It i the mthemti tht engineer nd phiit ue to deribe fluid flow, deign underwter trnmiion
Structural Systems. Structural Engineering
101-305 Theor of Strutures 1-1 Instrutor: ST, P, J nd TPS Struturl Engineering 101-305 Theor of Strutures 1 - Instrutor: ST, P, J nd TPS Struturl Sstems Struture the tion of building: ONSTUTION Struturl
GRAND PLAN. Visualizing Quaternions. I: Fundamentals of Quaternions. Andrew J. Hanson. II: Visualizing Quaternion Geometry. III: Quaternion Frames
Visuliing Quternions Andrew J. Hnson Computer Siene Deprtment Indin Universit Siggrph Tutoril GRAND PLAN I: Fundmentls of Quternions II: Visuliing Quternion Geometr III: Quternion Frmes IV: Clifford Algers
Multiple Integrals. Review of Single Integrals. Planar Area. Volume of Solid of Revolution
Multiple Integrls eview of Single Integrls eding Trim 7.1 eview Appliction of Integrls: Are 7. eview Appliction of Integrls: olumes 7.3 eview Appliction of Integrls: Lengths of Curves Assignment web pge
MATH Final Review
MATH 1591 - Finl Review November 20, 2005 1 Evlution of Limits 1. the ε δ definition of limit. 2. properties of limits. 3. how to use the diret substitution to find limit. 4. how to use the dividing out
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
In Mathematics for Construction, we learnt that
III DOUBLE INTEGATION THE ANTIDEIVATIVE OF FUNCTIONS OF VAIABLES In Mthemtics or Construction, we lernt tht the indeinite integrl is the ntiderivtive o ( d ( Double Integrtion Pge Hence d d ( d ( The ntiderivtive
Section 3.6. Definite Integrals
The Clulus of Funtions of Severl Vribles Setion.6 efinite Integrls We will first define the definite integrl for funtion f : R R nd lter indite how the definition my be extended to funtions of three or
MEP Practice Book ES3. 1. Calculate the size of the angles marked with a letter in each diagram. None to scale
ME rctice ook ES3 3 ngle Geometr 3.3 ngle Geometr 1. lculte the size of the ngles mrked with letter in ech digrm. None to scle () 70 () 20 54 65 25 c 36 (d) (e) (f) 56 62 d e 60 40 70 70 f 30 g (g) (h)
Linear Algebra Introduction
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
STATICS VECTOR MECHANICS FOR ENGINEERS: and Centers of Gravity. Eighth Edition CHAPTER. Ferdinand P. Beer E. Russell Johnston, Jr.
007 The McGrw-Hill Compnies, Inc. All rights reserved. Eighth E CHAPTER 5 Distriuted VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinnd P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Wlt Oler Tes Tech
STATICS. Vector Mechanics for Engineers: Statics VECTOR MECHANICS FOR ENGINEERS: Centroids and Centers of Gravity.
5 Distributed CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinnd P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Wlt Oler Texs Tech Universit Forces: Centroids nd Centers of Grvit Contents Introduction
GM1 Consolidation Worksheet
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Perimeter, area and volume
6 Perimeter, re nd volume Syllus topi M. Perimeter, re nd volume This topi will develop your skills to ompetently solve prolems involving perimeter, re, volume nd pity. Outomes Clulte the re of irles nd
Calculating Tank Wetted Area Saving time, increasing accuracy
Clulting Tnk Wetted Are ving time, inresing ur B n Jones, P.., P.E. C lulting wetted re in rtillfilled orizontl or vertil lindril or ellitil tnk n e omlited, deending on fluid eigt nd te se of te eds (ends)
Lecture Summaries for Multivariable Integral Calculus M52B
These leture summries my lso be viewed online by liking the L ion t the top right of ny leture sreen. Leture Summries for Multivrible Integrl Clulus M52B Chpter nd setion numbers refer to the 6th edition.
AP Calculus AB Unit 4 Assessment
Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
Solutions to Supplementary Problems
Solutions to Supplementry Problems Chpter 8 Solution 8.1 Step 1: Clculte the line of ction ( x ) of the totl weight ( W ).67 m W = 5 kn W 1 = 16 kn 3.5 m m W 3 = 144 kn Q 4m Figure 8.10 Tking moments bout
6.5 Improper integrals
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Integration. antidifferentiation
9 Integrtion 9A Antidifferentition 9B Integrtion of e, sin ( ) nd os ( ) 9C Integrtion reognition 9D Approimting res enlosed funtions 9E The fundmentl theorem of integrl lulus 9F Signed res 9G Further
Time : 3 hours 03 - Mathematics - March 2007 Marks : 100 Pg - 1 S E CT I O N - A
Time : hours 0 - Mthemtics - Mrch 007 Mrks : 100 Pg - 1 Instructions : 1. Answer ll questions.. Write your nswers ccording to the instructions given below with the questions.. Begin ech section on new
X Fx = F A. If applied force is small, book does not move (static), a x =0, then f=f s
A Appl ewton s nd Lw X 0 X A I pplied orce is sll, boo does not ove sttic, 0, then s A Increse pplied orce, boo still does not ove Increse A ore, now boo oves, 0 > A A here is soe iu sttic rictionl orce,
UNCORRECTED SAMPLE PAGES. Australian curriculum NUMBER AND ALGEBRA
7A 7B 7C 7D 7E 7F 7G 7H 7I 7J 7K Chpter Wht ou will lern 7Prols nd other grphs Eploring prols Skething prols with trnsformtions Skething prols using ftoristion Skething ompleting the squre Skething using
For the flux through a surface: Ch.24 Gauss s Law In last chapter, to calculate electric filede at a give location: q For point charges: K i r 2 ˆr
Ch.24 Guss s Lw In lst hpter, to lulte eletri filed t give lotion: q For point hrges: K i e r 2 ˆr i dq For ontinuous hrge distributions: K e r 2 ˆr However, for mny situtions with symmetri hrge distribution,
Precalculus Notes: Unit 6 Law of Sines & Cosines, Vectors, & Complex Numbers. A can be rewritten as
Dte: 6.1 Lw of Sines Syllus Ojetie: 3.5 Te student will sole pplition prolems inoling tringles (Lw of Sines). Deriing te Lw of Sines: Consider te two tringles. C C In te ute tringle, sin In te otuse tringle,
Learning Objectives of Module 2 (Algebra and Calculus) Notes:
67 Lerning Ojetives of Module (Alger nd Clulus) Notes:. Lerning units re grouped under three res ( Foundtion Knowledge, Alger nd Clulus ) nd Further Lerning Unit.. Relted lerning ojetives re grouped under
Calculus Module C21. Areas by Integration. Copyright This publication The Northern Alberta Institute of Technology All Rights Reserved.
Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
are coplanar. ˆ ˆ ˆ and iˆ
SMLE QUESTION ER Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor. ii The question pper onsists of 6 questions divided into three Setions, B nd C. iii Question
Vibration with more (than one) degrees of freedom (DOF) a) longitudinal vibration with 3 DOF. b) rotational (torsional) vibration with 3 DOF
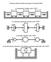irtion with ore (thn one) degrees of freedo (DOF) ) longitudinl irtion with DOF ) rottionl (torsionl) irtion with DOF ) ending irtion with DOF d) the D (plnr) irtion of the fleil supported rigid od with
Version 001 HW#6 - Circular & Rotational Motion arts (00223) 1
Version 001 HW#6 - Circulr & ottionl Motion rts (00223) 1 This print-out should hve 14 questions. Multiple-choice questions my continue on the next column or pge find ll choices before nswering. Circling
Calculus Cheat Sheet. Integrals Definitions. where F( x ) is an anti-derivative of f ( x ). Fundamental Theorem of Calculus. dx = f x dx g x dx
Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,
![MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,](/thumbs/89/98261542.jpg "MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,")
MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
QUADRATIC EQUATION. Contents
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
VECTORS VECTORS VECTORS VECTORS. 2. Vector Representation. 1. Definition. 3. Types of Vectors. 5. Vector Operations I. 4. Equal and Opposite Vectors
1. Defnton A vetor s n entt tht m represent phsl quntt tht hs mgntude nd dreton s opposed to slr tht ls dreton.. Vetor Representton A vetor n e represented grphll n rrow. The length of the rrow s the mgntude
Unit-VII: Linear Algebra-I. To show what are the matrices, why they are useful, how they are classified as various types and how they are solved.
Unit-VII: Liner lger-i Purpose of lession : To show wht re the mtries, wh the re useful, how the re lssified s vrious tpes nd how the re solved. Introdution: Mtries is powerful tool of modern Mthemtis
fractions Let s Learn to
5 simple lgebric frctions corne lens pupil retin Norml vision light focused on the retin concve lens Shortsightedness (myopi) light focused in front of the retin Corrected myopi light focused on the retin
Lecture 1 - Introduction and Basic Facts about PDEs
* 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
PhysicsAndMathsTutor.com
1. A uniform circulr disc hs mss m, centre O nd rdius. It is free to rotte bout fixed smooth horizontl xis L which lies in the sme plne s the disc nd which is tngentil to the disc t the point A. The disc
Final Exam Review. [Top Bottom]dx =
![Final Exam Review. [Top Bottom]dx =](/thumbs/90/103300886.jpg "Final Exam Review. [Top Bottom]dx =")
Finl Exm Review Are Between Curves See 7.1 exmples 1, 2, 4, 5 nd exerises 1-33 (odd) The re of the region bounded by the urves y = f(x), y = g(x), nd the lines x = nd x = b, where f nd g re ontinuous nd
Review: The Riemann Integral Review: The definition of R b
eview: The iemnn Integrl eview: The definition of b f (x)dx. For ontinuous funtion f on the intervl [, b], Z b f (x) dx lim mx x i!0 nx i1 f (x i ) x i. This limit omputes the net (signed) re under the
Chapter Gauss Quadrature Rule of Integration
Chpter 7. Guss Qudrture Rule o Integrtion Ater reding this hpter, you should e le to:. derive the Guss qudrture method or integrtion nd e le to use it to solve prolems, nd. use Guss qudrture method to
( ) { } [ ] { } [ ) { } ( ] { }
![( ) { } [ ] { } [ ) { } ( ] { }](/thumbs/96/129291861.jpg "( ) { } [ ] { } [ ) { } ( ] { }")
Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Multiple Integrals. Review of Single Integrals. Planar Area. Volume of Solid of Revolution
Multiple Integrls eview of Single Integrls eding Trim 7.1 eview Appliction of Integrls: Are 7. eview Appliction of Integrls: Volumes 7.3 eview Appliction of Integrls: Lengths of Curves Assignment web pge
, MATHS H.O.D.: SUHAG R.KARIYA, BHOPAL, CONIC SECTION PART 8 OF
DOWNLOAD FREE FROM www.tekoclsses.com, PH.: 0 903 903 7779, 98930 5888 Some questions (Assertion Reson tpe) re given elow. Ech question contins Sttement (Assertion) nd Sttement (Reson). Ech question hs
EXPECTED ANSWERS/VALUE POINTS SECTION - A
6 QUESTION PPE ODE 65// EXPETED NSWES/VLUE POINTS SETION - -.... 6. / 5. 5 6. 5 7. 5. ( ) { } ( ) kˆ ĵ î kˆ ĵ î r 9. or ( ) kˆ ĵ î r. kˆ ĵ î m SETION - B.,, m,,, m O Mrks m 9 5 os θ 9, θ eing ngle etween
SPH3UW Unit 7.5 Snell s Law Page 1 of Total Internal Reflection occurs when the incoming refraction angle is
SPH3UW Uit 7.5 Sell s Lw Pge 1 of 7 Notes Physis Tool ox Refrtio is the hge i diretio of wve due to hge i its speed. This is most ommoly see whe wve psses from oe medium to other. Idex of refrtio lso lled
Chapter 2. Vectors. 2.1 Vectors Scalars and Vectors
Chpter 2 Vectors 2.1 Vectors 2.1.1 Sclrs nd Vectors A vector is quntity hving both mgnitude nd direction. Emples of vector quntities re velocity, force nd position. One cn represent vector in n-dimensionl
Tutorial Worksheet. 1. Find all solutions to the linear system by following the given steps. x + 2y + 3z = 2 2x + 3y + z = 4.
Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
AP CALCULUS Test #6: Unit #6 Basic Integration and Applications
AP CALCULUS Test #6: Unit #6 Bsi Integrtion nd Applitions A GRAPHING CALCULATOR IS REQUIRED FOR SOME PROBLEMS OR PARTS OF PROBLEMS IN THIS PART OF THE EXAMINATION. () The ext numeril vlue of the orret