Factorising FACTORISING.
|
|
|
- Ruby Stanley
- 5 years ago
- Views:
Transcription
1 Ftorising FACTORISING
2
3 Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will lern how ifferent kins of expressions re ftorise in their own wy. Answer these questions, efore working through the hpter. I use to think: Wht ftors 0 n 1 hve in ommon? Wht ftors o 0 n 1 hve in ommon? ( x- )( x+ ) x - 4. Complete the following: x - 16 ( x-?)( x +?) How mny ftors is qurti trinomil ftorise into? Answer these questions, fter working through the hpter. But now I think: Wht ftors 0 n 1 hve in ommon? Wht ftors o 0 n 1 hve in ommon? ( x- )( x+ ) x - 4. Complete the following: x - 16 ( x-?)( x +?) How mny ftors is qurti polynomil ftorise into? Wht o I know now tht I in t know efore? 100% Ftorising Mthletis 100% 3P Lerning 1
4 Ftorising Bsis Common Ftors Whole numers tht multiply together to give prtiulr numer re lle the ftors of tht numer. For exmple, the numer 6 n e expresse s the prout of two whole numers in two wys: 6 6# 1 n 6 # 3. So the ftors of 6 re: 1,, 3, 6. A ommon ftor of two numers is numer tht is ftor of oth numers. Here is n exmple of fining the highest ommon ftor. Wht is the highest ommon ftor (HCF) of 1 n 18? To get the highest ommon ftor, first get the ftors of eh numer. Then pik the highest one. 1 1 # 1 1 6# # # 1 4# # 3 Ftors of 1 re 1,, 3, 4, 6, 1. Ftors of 18 re 1,, 3, 4, 9, 18. ` The highest ommon ftor (HCF) of 1 n 8 is 6. Ftors our in lger too. In lger the expression mens #. So n re ftors of. Here re some exmples of ommon ftors in lger. Wht is the ommon ftor of eh of these: n. The ommon ftor is, sine it is ftor of oth terms. xy n xz. The ommon ftor is x. A ommon ftor of n is. But lso ours in oth terms, so is lso ommon ftor. The highest ommon ftor of n is. Here is nother exmple. Wht is the highest ommon ftor of xy 4 n xz? 4 xy x # x y # xz x z 4 Rememer tht x x # x. x is the highest power of x whih ours in oth 4 xy n xz. 4 ` The highest ommon ftor of xy n xz is x. In term suh s 10xy, the numer 10 is lle the oeffiient. The oeffiient is the numer in front. Here is n exmple. Wht is the highest ommon ftor of 0xyz 4 n 1x 3 z? The highest ommon ftor of the oeffiients, 0 n 1, is The highest ommon ftor of xyzn xzis xz 3. Therefore putting these together, the HCF is 4xz 3. x 3 is the highest power of x whih ours in oth terms. z is ommon to oth. 100% Ftorising Mthletis 100% 3P Lerning
5 Ftorising Bsis Ftorising Ftorising is the opposite of expning. The gol of expning is to remove rkets from expressions, like this exmple: ( + ) + The gol of ftorising is to put expressions into rkets, like this exmple: + ( + ) Using Common Ftors Common ftors re si to e ftorise out of expressions. In the expression +, the vrile is ommon in oth terms. So is ommon ftor of oth terms. This mens n e ftorise out of the expression s ove. Here re some exmples: Ftorise these expressions: 5xy + 5y 5yx ( + 1) xy-4xy xy( x-y) 5 y is ommon in oth terms xy is ommon in oth terms In ove, oth 5 n y re ommon ftors on their own, ut 5 y is the highest ommon ftor (HCF). In, xy is the highest ommon ftor. To fin the HCF, fin the highest ommon numeril ftor of the oeffiients n then the lowest ommon power of eh vrile. Ftorise these expressions: ( + 3 ) 1xy-4xy xy( 3y -x) is the HCF 4x y 3 is the HCF 3 is the HCF of the oeffiients 3 is the lowest power of 3 is the lowest power of 4 is the HCF of the oeffiients x is the lowest power of x y 3 is the lowest power of y Sometimes there will e more thn two terms. Then the HCF must e foun for ll the terms! Ftorise this expression: ( ) 4 is the HCF of the oeffiients is the lowest power of 3 is the lowest power of 100% Ftorising Mthletis 100% 3P Lerning 3
6 Ftorising Bsis Brkets s Common Ftors Sometimes rket is ommon ftor. If this hppens then the whole rket is ftorise out. Look t this exmple: Ftorise the following: xx ( + 3) + 5yx ( + 3) ( x + 3) is ommon in oth terms ( x+ 3)( x+ 5y) Ftorising using Grouping n Brkets The ove exmple my not hve een groupe into rkets, n my hve een in expne form Ftorise the following (y grouping in pirs): x + 6x+ 5xy + 15y Mny expressions, like in the ove line, oul hve 4 (or more) terms without ommon ftor ross ll terms x -9xy- 4x+ 6y is ommon 4 is ommon 3 x is ommon - is ommon ( + ) + 4 ( + ) 3 x(x-3 y) -(x-3) y ( + ) is ommon rket ( x - 3y ) is ommon rket ( + )( + 4 ) ( x-3y)( 3x - ) Sometimes the expression nees to e reorere efore it n e groupe to fin ommon rket. Here is n exmple: Ftorise the following into two rkets: Step 1: Reorer. Step : Fin ommon ftors. Step 3: Ftorise out the ommon rket ( - ) + 3( - ) ( - )( + 3) Chek this y expning the rkets to see if you get the originl expression % Ftorising Mthletis 100% 3P Lerning
7 Ftorising Questions Bsis 1. Fin the HCF of these terms: 6x n x 5 8x n 6x y 1 n ef, 10 ef n 16ef. Ftorise the HCF out of the following: 6x+ y 4-8pq 10q - - 3pq+ 1pq 4 4 e 10xy-40xy 4 4 f g 6pq+ 3p -15pq h 7mn - 14mn+ 1mn % Ftorising Mthletis 100% 3P Lerning 5
8 Ftorising Questions Bsis 3. Ftorise the ommon rket out of the following: 3x ( x- 1) + 5y( x- 1) 4xxy ( 3 - y ) + ( xy 3 - y ) 4. Ftorise these expressions into two rkets using grouping: xy + y+ x x + 3x + 4xy + 6y mn 3 m 3 m + + n % Ftorising Mthletis 100% 3P Lerning
9 Ftorising Questions Bsis e 3 8xy + 4x -4y - xy f p + 3p q+ 4p+ 6pq g 4mn + 3mn -4m- 3mn 4 h 4 3 y+ xy + y + xy i 18pq+ 1pq + 6pq+ 4pq 3 4 j % Ftorising Mthletis 100% 3P Lerning 7
10 Ftorising Knowing More Expning rkets proues wht is lle qurti trinomil. Look t this exmple: ( x+ )( x+ 3) x + 5x+ 6 The expression on the right is qurti trinomil euse it hs three terms n the highest power is. In generl, qurti trinomil looks like this: x x + + Leing Coeffiient (in front of x ) Coeffiient of x onstnt (no x ) Rememer, ftorising is the opposite of expning. So ftorising qurti trinomil mens hnging it k to rkets. Ftorising these trinomils is one ifferently epening on the vlue of (the leing oeffiient). Ftorising Qurti Trinomils if 1 If 1then the qurti trinomil looks like this: x x + + To ftorise these expressions, two numers re neee suh tht: 1. Their prout is (the onstnt). Their sum is (the oeffiient of x) n These two numers re written in the rkets. Here re some exmples: Ftorise these qurti trinomils into two rkets: x + 5x+ 6 Step 1: Fin two numers with prout of 6 (the onstnt) n sum of 5 (the oeffiient of x). # 3 6 n Prout Sum So the numers re + n +3. Step : Ftorise y writing these two numers in rkets with x. x + 5x+ 6 ( x+ )( x+ 3) x -5x-6 Step 1: Fin two numers with prout of -6 (the onstnt) n sum of -5 (the oeffiient of x). 1 # (- 6) - 6 n 1 + (- 6) -5 Prout Sum So the numers re +1 n -6. Step : Ftorise y writing these two numers in rkets with x. x -5x- 6 ( x+ 1)( x- 6) The orer of these numers is not importnt 8 100% Ftorising Mthletis 100% 3P Lerning
11 Ftorising Questions Knowing More 1. Fin vlues for m n n if they hve these sums n prouts: m+ n 3 n mn m+ n 7 n mn 1 m+ n 0 n mn -4 m+ n - 3 n mn e m+ n 3 n mn -10 f m+ n - 3 n mn -18. Answer these questions out the trinomil x + 9x+ 0: Write own the vlue of the leing oeffiient (), the oeffiient of x () n the onstnt (). Fin two numers whose prout is () onstnt n whose sum is (). Ftorise the trinomil into two rkets. 3. Answer these questions out the trinomil x -4x- 1: Write own the vlue of the leing oeffiient (), the oeffiient of x () n the onstnt (). Fin two numers whose prout is () onstnt n whose sum is (). Ftorise the trinomil into two rkets. 100% Ftorising Mthletis 100% 3P Lerning 9
12 Ftorising Questions Knowing More 4. Ftorise these trinomils into rkets: x + 4x + 3 x + x- 6 x - 6x + 5 x + x- 4 e x - 6x - 16 f x - 14 x+ 40 g x - 5x - 14 h x - 1 x % Ftorising Mthletis 100% 3P Lerning
13 Ftorising Knowing More Ftorising Qurti Trinomils if! 1 Ftorising x + x + when is not 1 is slightly more omplite. This will e shown with n exmple. Ftorise 1x + x- 4 into two rkets Step 1: Fin the vlue of # # # - - Step : Fin the two numer whih hve prout of # (-48) n sum of (). 8 # (- 6) - 48 n 8 + (- 6) So the two numers re 8 n -6 Step 3: Rewrite the originl (oeffiient of x) in terms of the two numers in Step. 1x + x -4 1x + 8x-6x -4 The 'x' is reple y 8x- 6x Step 4: Use grouping to ftorise. 4 x(3x+ ) - (3x + ) ( 3x+ )( 4x- ) Here is nother exmple: Ftorise 1y + 10y - 1 into two rkets Step 1: Fin the vlue of # # # - - Step : Fin the two numer whih hve prout of # (-4) n sum of (-10). # (- 1) - 4 n + (- 1) -10 So the two numers re n -1 Step 3: Rewrite the originl (oeffiient of y) in terms of the two numers in Step. 4y - 10y -1 4y + y-1y -1 Step 4: Use grouping to ftorise. 4y - 1y+ y -1 1 y(y- 1) + (y -1) ( y- 1)( 1y+ 1) 100% Ftorising Mthletis 100% 3P Lerning 11
14 Ftorising Questions Knowing More 5. Look t 16x + 1x+. Ientify, n. Fin the vlue of #. Fin two numers whih hve prout equl to # n sum equl to. Ftorise 16x + 1x+ into two rkets. 6. Look t 6x -x-. Ientify, n. Fin the vlue of #. Fin two numers whih hve prout equl to # n sum equl to. Ftorise 16x -x- into two rkets % Ftorising Mthletis 100% 3P Lerning
15 Ftorising Questions Knowing More 7. Ftorise these qurti trinomils: x + 5x+ 1m + 5m p + 3p + 3 5t + 37t + 14 e 8k - k + 5 f % Ftorising Mthletis 100% 3P Lerning 13
16 Ftorising Knowing More Differene of Squres Rememer when expning rkets tht iffer in sign only ^x+ yh^x- yh x -y. This mens tht if qurti expression is in the form x - y then it n e ftorise esily into ^x+ yh^x-yh. Herer re some exmples. Ftorise the following into two rkets using the ifferene of squres: x m - 5n x -4 ( m) -( 5n) ( x+ 4)( x- 4) ( m- 5n)( m+ 5n) Don t get onfuse: x this wy. + y n t e ftorise into two rkets. Only ifferene of squres n e ftorise Perfet Squres Rememer, for perfet squres ( x+ y) ^x+ yh^x+ yh x + xy+ y. This mens tht if qurti expression is in the form x + xy+ y then it n esily e ftorise into ( x+ y). Here re some exmples. Ftorise the following: m + 6m+ 9 x - 4x+ 4 m + ( m)( 3) + 3 x + ()( x - ) + (-) ( m + 3) ( x -) p - 6pq+ q ( 3) + ( 3)( ) + ( ) ( 3p) + ( 3p)( - q) + (-q) ( 3+ ) ( 3p-q) Whenever you ftorise nything, you n lwys hek y expning the rkets to see if you get the originl expression % Ftorising Mthletis 100% 3P Lerning
17 Ftorising Questions Knowing More 8. Ftorise these expressions: x + 14x + 49 y - 9 4y + 8y+ 4 16q - 36p e 81p - 11q f 64m + 3mn+ 4n g 49t - 56tu+ 16u h 9xy+ 1pqxy+ 4p q 100% Ftorising Mthletis 100% 3P Lerning 15
18 Ftorising Using Our Knowlege Using more thn one Metho to Ftorise The methos lerne up until nee to e omine sometimes to ftorise ertin expressions. Ftorise 4y -1y-16 Metho 1 Metho 4y 1y 16 4 y -1 y -16 Step 1: Ftor out ommon ftor Step 1: Ftorise the trinomil 4( y -3y- 4) 4y 16y 4y # 4-64( # ) 4yy ( - 4) + 4( y -4) () ( y- 4)( 4y+ 4) Step : Ftorise the qurti trinomil Step : Ftorise the ommon ftor out from the seon rket 4( y- 4)( y+ 1) 4( y- 4)( y+ 1) Sometimes the ifferene of squres metho nees to e use more thn one, or omine with ftorising out ommon ftor. Here re some exmples. Ftorise the following: m - n 4 4 3x 108x 3 - ( m ) -^n h ^m + n h^m - m h ^m + n h^m+ nh^m-nh Rememer: only ifferene of squres n e ftorise this wy 3xx ^ -36h 3xx ^ + 6h^x - 6h Differene of squres Common ftor If there re four terms or more, then grouping my hve to e use with other methos. Here is n exmple. Ftorise p + 4p- q + 4q p + 4p- q + 4q p - q + 4p+ 4q ^p+ qh^p- qh+ 4( p+ q) Differene of squres Common ftor ^p+ qh6 ^p- qh+ 4@ ^p+ qh^p- q+ 4h % Ftorising Mthletis 100% 3P Lerning
19 Ftorising Using Our Knowlege Ftorising Trinomils with more thn one Vrile. Wht hppens if qurti trinomil like x -xy- 6y or x + 7xy- 15y nees to e ftorise? If the first n lst terms re oth squre, then the sme is proess for ftorising trinomils is followe. Ftorise x -xy-6y Step 1: Fin two numers with prout of - 6y (oeffiient of en term) n sum of - 1y (oeffiient of mile term). - 3y# y 6y n - 3y+ y -1y Prout Sum So the numers re - 3y n + y. Step : Ftorise y writing these two numers in rkets with x n y. x -xy- 6y ^x- 3yh^x+ yh Ftorise x + 7xy- 15y Step 1: Step : Fin the prout of the first oeffiient n the lst oeffiient. # Fin the two numers with prout of the ove numer n sum of the mile oeffiient. 10 # (- 3) - 30 n 10+ ^- 3h 7 So the two numers re 10 n -3 Step 3: Rewrite the originl mile oeffiient in terms of the two numers in Step. x + 10xy-3xy- 15y x - 3xy+ 10xy-15y Step 4: Use grouping to ftorise. x^x- 3yh+ 5y^x-3yh ^x- 3yh^x+ 5yh Sometimes, of ourse, this metho of ftorising will e omine with nother. Ftorise 3pq+ pq-4pq pq+ pq- 4pq pq^3p + pq- 4q h pq^3p - 3pq+ pq-4q h pq6 3p^p- qh+ 4q^p-qh@ - 3# 4-1 ( # ) () pq^p- qh^3p+ 4qh 100% Ftorising Mthletis 100% 3P Lerning 17
20 Ftorising Questions Using Our Knowlege 1. Ftorise the following: 10m + 5m x + 6 x+ 40 x - y 8x -xy-y 8 8 e 3 8t -6t -10t f 3x + 5xy-y % Ftorising Mthletis 100% 3P Lerning
21 Ftorising Questions Using Our Knowlege g 10x x h i -4x - xy+ 1y j ( y-3) -( y- 5) k m 4n 4n m l - 1t + 7u -1t-18u 100% Ftorising Mthletis 100% 3P Lerning 19
22 Ftorising Thinking More Algeri Frtions Numeril frtions n e simplifie y fining ommon ftors in the numertor n enomintor. For exmple 1 18 # 6 3# 6 Algeri frtions hve lgeri expressions in the numertor n the enomintor. They n lso e simplifie y nelling ommon ftors. To o this, oth the numertor n enomintor nee to e ftorise. Here re some exmples: Simplify these lgeri frtions: 3 x - 8 x + 4 y -y-15 3y ( y- 5) + ( y - 5) ( x - 4) ( x + ) Common ftor ( y+ 3)( y-5) 3y ( y- 5) + ( y - 5) ( x+ )( x-) ( x + ) Differene of squres ( y+ 3)( y-5) ( y - 5)( 3y + ) ( x+ ) ( x-) ( x + ) Cnel ommon rkets ( y+ 3)( y-5) ( y - 5)( 3y + ) x - y + 3 3y + To simplify ny lgeri frtion, ftorise the numertor n enomintor n remove the ommon rkets n ftors. Simplify these lgeri frtions s muh s possile: 3 x -3x - 8x + 1 x + x-6 ( m-n) -( m+ 3n) m + 10mn+ 5n x ( x-3) -4 ( x - 3) ( x- 3)( x+ ) 6( m-n) -( m+ 6( m- n) + ( m+ ( m+ 5n) ( x-3)( x -4) ( x- 3)( x+ ) (-m- 5n)( 3m+ n) ( m+ 5n)( m+ 5n) (x- 3)( x+ )( x - ) (x- 3)( x+ ) -( m+ 5 n)( 3m+ n) ( m+ 5 n)( m+ 5n) x - -( 3m+ n) m+ 5n -3m-n m+ 5n 0 100% Ftorising Mthletis 100% 3P Lerning
23 Ftorising Questions Thinking More 1. Simplify these frtions s muh s possile: m + 14m+ 4 m + 3 9x - 4y 9x + 10xy+ 4y 3 4t - t + 4t - 1 4t % Ftorising Mthletis 100% 3P Lerning 1
24 Ftorising Thinking More Multiplying n Diviing Frtions Algeri frtions re multiplie n ivie the sme wy s numeril frtions. Before multiplying or iviing, ftorise eh frtion s muh s possile. Then rkets n e nelle to mke lultions esier. Here is n exmple multiplying two lgeri frtions Multiply these two lgeri frtions 4-1 # Ftorise the numertor n enomintor in oth frtions. ( + )( -) ( + 3)( -4) # ( - 4)( + 5) ( + )( -3) Cnel the ommon rkets. ( + )( -) ( + 3)( -4) # ( - 4)( + 5) ( + )( -3) ( - )( + 3) ( + 5)( - 3) Here is n exmple iviing two lgeri frtions Fin the following quotient 8x -6x-5 ' x + 7x+ 3 x 4x x+ 9 Ftorise the numertor n enomintor in oth frtions. ( x+ 1)( 4x-5) 4x - 5 ' ( x+ 3)( x+ 1) ( x + ) 3 Flip the seon frtion to rete prout of frtions. Cnel the ommon rkets. ( x+ 1)( 4x-5) ( x + 3) # ( x+ 3)( x+ 1) 4x - 5 ( x+ 1)( 4x-5) ( x + 3) # ( x+ 3)( x+ 1) 4x - 5 x % Ftorising Mthletis 100% 3P Lerning
25 Ftorising Thinking More Aing n Sutrting Frtions When ing n sutrting lgeri frtions, ommon enomintor must e foun. Simplify the following (y omining the frtions): 4-3 x x 10 3y y y 8-3 x x 4 4# 8 x x# x 10y 3y y y # y 10y y y# y y x 10y+ 3y+ 1 y 5 x 13y + 1 y Here re two exmples where the enomintors hve ifferent letters. Simplify the following (y omining the frtions): x x 1# + 1# # # ^5x- 1h # x + # 7 7 # x x # 7 + ^5x- 1hx+ 14 7x + + Rememer tht s the orer of multiplying oesn't mtter. 5x - x+ 14 7x Here re two more exmples where ifferent numers or letters our in the enomintor. Simplify the following (y omining the frtions): x 3x m 5n 3 # x + 5# 8 8x # 3 3x # 8 5# 5n + 3# 7m 7m# 5n 5n# 7m x 5n + 1m 35mn 35mn 49 4x 5n+ 1m 35mn 100% Ftorising Mthletis 100% 3P Lerning 3
26 Ftorising Thinking More The next two exmples involve enomintors with two or more terms. Simplify the following (y omining the frtions): 3 4 x+ + 5x+ 1 3# ^5x + 1h 4# ^x + h + ^x + h# ^5x + 1h ^5x+ 1h# ^x+ h 35 ^ x+ 1h+ 4^x+ h ^x+ h^5x+ 1h 15x+ 3+ 4x+ 8 ^x+ h^5x+ 1h 19x + 11 ^x + h^5x + 1h 3 p - 5p 3 + p -3p-10 p + Hint: Ftorise the enomintor 3 p - 5p + 3 ( p + )( p - 5) p + 3 p - 5p 3 ( p - 5) + ( p + )( p - 5) ( p + )( p - 5) Ftorise enomintor Common enomintor 3 p - 5p + 3 ( p - 5) ( p+ )( p-5) 3 p - 5p + 6p - 15 ( p+ )( p-5) p ( p- 5) + 3 ( p - 5) ( p+ )( p-5) Grouping in pirs ( p- 5)( p + 3) ( p+ )( p-5) (p- 5) ( p + 3) ( p+ )(p-5) Cnel ommon rkets p + 3 p % Ftorising Mthletis 100% 3P Lerning
27 Ftorising Questions Thinking More. Simplify the following prouts n quotients: y - 3x - 3xy # 3x- 3y y - y m + 13m-7 m 14m # - m - 49 m - 1 p + 5 ' p - p + 10p+ 5 p - 4p x 6+ 11x+ 4x ' - x 6-11x+ 4x 100% Ftorising Mthletis 100% 3P Lerning 5
28 Ftorising Questions Thinking More e # f 4x- 3y 8x + 10xy-3y ' x+ y 4x - 9y 6 100% Ftorising Mthletis 100% 3P Lerning
29 Ftorising Questions Thinking More 3. Simplify these expressions: x x+ 1 6x 4 100% Ftorising Mthletis 100% 3P Lerning 7
30 Ftorising Questions Thinking More 4x + + x - 4 x + 1 x + y 3y y y % Ftorising Mthletis 100% 3P Lerning
31 Ftorising Questions Thinking More e 3 3 x+ - x+ 1 f 1 ( y+ 3)( y+ 4) - ( y+ 3)( y-4) 100% Ftorising Mthletis 100% 3P Lerning 9
32 Ftorising Questions Thinking More g p p 3p + 5p+ - p + 1 h m m m m+ 30 m % Ftorising Mthletis 100% 3P Lerning
33 Ftorising Questions Thinking More i x+ 1 + x+ + x - 1 j 4- ' % Ftorising Mthletis 100% 3P Lerning 31
34 Ftorising Answers Bsis: Knowing More: 1. x n ef + 3 n + 4. (3 x+ y) - ( ) q(4pq - 5) 4 3 pq( - q + 4 p ) e f - n + - n n n + 3 e 10 xy( y - 4 x ). 1, 9, 0 f ( + 3 ) + 5 n + 4 g p(pq + p -5 q ) ( x+ 5)( x+ 4) h mn (1- mn+ 3 m) 3. 1, - 4, 1 3. (x- 1)(3x + 5) y + 3 n -7 3 ( xy- y )(4x+ ) ( x+ 3)( x-7) 4. ( x+ 1)( y+ ) 4. ( x+ 3)( x+ 1) ( - )( + 4) ( x+ 3)( x-) ( x+ 3)( y+ x) ( x-5)( x-1) ( mn+ 1)( 3+ m) ( x+ 6)( x-4) e ( 4x- y)( y + x) e ( x- 8)( x+ ) f ( p+ 3pq)( p+ ) f ( x-4)( x-10) g ( 4m+ 3mn )( n -1) g ( x+ )( x-7) h yxy ( + 1)( y + 1) h ( x-8)( x-4) i pq( 3p + q)( 3+ p) j -( - )( + 1) % Ftorising Mthletis 100% 3P Lerning
35 Ftorising Answers Knowing More: Using Our Knowlege: 5. 16, 1, 1. 5 ( m- 1)( m+ 1) 3 -( x- 10)( x+ 4) + 8 n ( x + y )( x + y )( x+ y)( x-y) ( 8x+ )( x+ 1) ( 4x+ y)( x-y) 6. 6, - 1, n -4 ( 3x- )( x+ 1) e f g h i t( 7t- 5)( t + 1) ( 3x- y)( x+ y) 10xx ( - 10)( x + 10) ( + )( + )( - ) -(( x+ y)( 4x- 6y)) 7. ( x+ )( x+ 1) j ( y - 8) ( 3m- 1)( 4m+ 3) k ( m+ n)( m-n- ) ( 7p+ 1)( p+ 3) l - 3 ( t+ 3u)( t- 3u+ ) 8. ( 5t+ )( t+ 7) ( 4k-1)( k-5) ( 3-5)( -3) ( x + 7) ( y+ 3)( y-3) ( y + ) 1. Thinking More: ( m + 4) ( 3x) - ( y) 9x + 10xy+ 4y t + 1 ( - + 4) ( - ) e ( 4q- 6p)( 4q+ 6p) ( 9p- 11q)( 9p+ 11q). x y f ( 8m+ n) m g h ( 7t- 4u) ( 3xy + pq) ( p - ) ( p + 5) 1 ( 4x-3)( x-) # ( 4x + 3) 1 100% Ftorising Mthletis 100% 3P Lerning 33
36 Ftorising Answers Thinking More:. e f ( + ) ( - ) ( 4x-3y)( x-3y) ( x+ y)( 4x-y) e f g h i j x - 3x 6 1x - 9x ( x + 1) 3y ( y + 1) 3( x - 1) ( x+ )( x+ 1) ( y - 8) ( y+ 3)( y+ 4)( y - 4) - p ( 3p+ )( p+ 1) 3 m - 1 ( m + 3) 3x + 4x-1 ( x+ 1)( x+ )( x - 1) ( - ) % Ftorising Mthletis 100% 3P Lerning
37
38
Surds and Indices. Surds and Indices. Curriculum Ready ACMNA: 233,
 Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Polynomials. Polynomials. Curriculum Ready ACMNA:
 Polynomils Polynomils Curriulum Redy ACMNA: 66 www.mthletis.om Polynomils POLYNOMIALS A polynomil is mthemtil expression with one vrile whose powers re neither negtive nor frtions. The power in eh expression
Polynomils Polynomils Curriulum Redy ACMNA: 66 www.mthletis.om Polynomils POLYNOMIALS A polynomil is mthemtil expression with one vrile whose powers re neither negtive nor frtions. The power in eh expression
Numbers and indices. 1.1 Fractions. GCSE C Example 1. Handy hint. Key point
 GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
K 7. Quadratic Equations. 1. Rewrite these polynomials in the form ax 2 + bx + c = 0. Identify the values of a, b and c:
 Qudrti Equtions The Null Ftor Lw Let's sy there re two numers nd. If # = then = or = (or oth re ) This mens tht if the produt of two epressions is zero, then t lest one of the epressions must e equl to
Qudrti Equtions The Null Ftor Lw Let's sy there re two numers nd. If # = then = or = (or oth re ) This mens tht if the produt of two epressions is zero, then t lest one of the epressions must e equl to
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
SIMPLE NONLINEAR GRAPHS
 S i m p l e N o n l i n e r G r p h s SIMPLE NONLINEAR GRAPHS www.mthletis.om.u Simple SIMPLE Nonliner NONLINEAR Grphs GRAPHS Liner equtions hve the form = m+ where the power of (n ) is lws. The re lle
S i m p l e N o n l i n e r G r p h s SIMPLE NONLINEAR GRAPHS www.mthletis.om.u Simple SIMPLE Nonliner NONLINEAR Grphs GRAPHS Liner equtions hve the form = m+ where the power of (n ) is lws. The re lle
Section 2.3. Matrix Inverses
 Mtri lger Mtri nverses Setion.. Mtri nverses hree si opertions on mtries, ition, multiplition, n sutrtion, re nlogues for mtries of the sme opertions for numers. n this setion we introue the mtri nlogue
Mtri lger Mtri nverses Setion.. Mtri nverses hree si opertions on mtries, ition, multiplition, n sutrtion, re nlogues for mtries of the sme opertions for numers. n this setion we introue the mtri nlogue
Logarithms LOGARITHMS.
 Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Chapter 8 Roots and Radicals
 Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
Algebraic fractions. This unit will help you to work with algebraic fractions and solve equations. rs r s 2. x x.
 Get strted 25 Algeri frtions This unit will help you to work with lgeri frtions nd solve equtions. AO1 Flueny hek 1 Ftorise 2 2 5 2 25 2 6 5 d 2 2 6 2 Simplify 2 6 3 rs r s 2 d 8 2 y 3 6 y 2 3 Write s
Get strted 25 Algeri frtions This unit will help you to work with lgeri frtions nd solve equtions. AO1 Flueny hek 1 Ftorise 2 2 5 2 25 2 6 5 d 2 2 6 2 Simplify 2 6 3 rs r s 2 d 8 2 y 3 6 y 2 3 Write s
Algebra 2 Semester 1 Practice Final
 Alger 2 Semester Prtie Finl Multiple Choie Ientify the hoie tht est ompletes the sttement or nswers the question. To whih set of numers oes the numer elong?. 2 5 integers rtionl numers irrtionl numers
Alger 2 Semester Prtie Finl Multiple Choie Ientify the hoie tht est ompletes the sttement or nswers the question. To whih set of numers oes the numer elong?. 2 5 integers rtionl numers irrtionl numers
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Simplifying Algebra. Simplifying Algebra. Curriculum Ready.
 Simplifying Alger Curriculum Redy www.mthletics.com This ooklet is ll out turning complex prolems into something simple. You will e le to do something like this! ( 9- # + 4 ' ) ' ( 9- + 7-) ' ' Give this
Simplifying Alger Curriculum Redy www.mthletics.com This ooklet is ll out turning complex prolems into something simple. You will e le to do something like this! ( 9- # + 4 ' ) ' ( 9- + 7-) ' ' Give this
Algebra Basics. Algebra Basics. Curriculum Ready ACMNA: 133, 175, 176, 177, 179.
 Curriulum Redy ACMNA: 33 75 76 77 79 www.mthletis.om Fill in the spes with nything you lredy know out Alger Creer Opportunities: Arhitets eletriins plumers et. use it to do importnt lultions. Give this
Curriulum Redy ACMNA: 33 75 76 77 79 www.mthletis.om Fill in the spes with nything you lredy know out Alger Creer Opportunities: Arhitets eletriins plumers et. use it to do importnt lultions. Give this
Non Right Angled Triangles
 Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
Equivalent fractions have the same value but they have different denominators. This means they have been divided into a different number of parts.
 Frtions equivlent frtions Equivlent frtions hve the sme vlue ut they hve ifferent enomintors. This mens they hve een ivie into ifferent numer of prts. Use the wll to fin the equivlent frtions: Wht frtions
Frtions equivlent frtions Equivlent frtions hve the sme vlue ut they hve ifferent enomintors. This mens they hve een ivie into ifferent numer of prts. Use the wll to fin the equivlent frtions: Wht frtions
Bridging the gap: GCSE AS Level
 Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
H SERIES. Algebra Basics. Algebra Basics. Curriculum Ready.
 H SERIES Curriulum Rey www.mthletis.om Copyright 009 P Lerning. All rights reserve. First eition printe 009 in Austrli. A tlogue reor for this ook is ville from P Lerning Lt. ISBN 978--986-4-6 Ownership
H SERIES Curriulum Rey www.mthletis.om Copyright 009 P Lerning. All rights reserve. First eition printe 009 in Austrli. A tlogue reor for this ook is ville from P Lerning Lt. ISBN 978--986-4-6 Ownership
QUADRATIC EQUATION EXERCISE - 01 CHECK YOUR GRASP
 QUADRATIC EQUATION EXERCISE - 0 CHECK YOUR GRASP. Sine sum of oeffiients 0. Hint : It's one root is nd other root is 8 nd 5 5. tn other root 9. q 4p 0 q p q p, q 4 p,,, 4 Hene 7 vlues of (p, q) 7 equtions
QUADRATIC EQUATION EXERCISE - 0 CHECK YOUR GRASP. Sine sum of oeffiients 0. Hint : It's one root is nd other root is 8 nd 5 5. tn other root 9. q 4p 0 q p q p, q 4 p,,, 4 Hene 7 vlues of (p, q) 7 equtions
Eigenvectors and Eigenvalues
 MTB 050 1 ORIGIN 1 Eigenvets n Eigenvlues This wksheet esries the lger use to lulte "prinipl" "hrteristi" iretions lle Eigenvets n the "prinipl" "hrteristi" vlues lle Eigenvlues ssoite with these iretions.
MTB 050 1 ORIGIN 1 Eigenvets n Eigenvlues This wksheet esries the lger use to lulte "prinipl" "hrteristi" iretions lle Eigenvets n the "prinipl" "hrteristi" vlues lle Eigenvlues ssoite with these iretions.
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Lecture 6: Coding theory
 Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx
![for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx](/thumbs/74/70408252.jpg) Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Now we must transform the original model so we can use the new parameters. = S max. Recruits
 MODEL FOR VARIABLE RECRUITMENT (ontinue) Alterntive Prmeteriztions of the pwner-reruit Moels We n write ny moel in numerous ifferent ut equivlent forms. Uner ertin irumstnes it is onvenient to work with
MODEL FOR VARIABLE RECRUITMENT (ontinue) Alterntive Prmeteriztions of the pwner-reruit Moels We n write ny moel in numerous ifferent ut equivlent forms. Uner ertin irumstnes it is onvenient to work with
MULTIPLE CHOICE QUESTIONS
 . Qurti Equtions C h p t e r t G l n e The generl form of qurti polynomil is + + = 0 where,, re rel numers n. Zeroes of qurti polynomil n e otine y equtions given eqution equl to zero n solution it. Methos
. Qurti Equtions C h p t e r t G l n e The generl form of qurti polynomil is + + = 0 where,, re rel numers n. Zeroes of qurti polynomil n e otine y equtions given eqution equl to zero n solution it. Methos
Probability. b a b. a b 32.
 Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
50 AMC Lectures Problem Book 2 (36) Substitution Method
 0 AMC Letures Prolem Book Sustitution Metho PROBLEMS Prolem : Solve for rel : 9 + 99 + 9 = Prolem : Solve for rel : 0 9 8 8 Prolem : Show tht if 8 Prolem : Show tht + + if rel numers,, n stisf + + = Prolem
0 AMC Letures Prolem Book Sustitution Metho PROBLEMS Prolem : Solve for rel : 9 + 99 + 9 = Prolem : Solve for rel : 0 9 8 8 Prolem : Show tht if 8 Prolem : Show tht + + if rel numers,, n stisf + + = Prolem
18.06 Problem Set 4 Due Wednesday, Oct. 11, 2006 at 4:00 p.m. in 2-106
 8. Problem Set Due Wenesy, Ot., t : p.m. in - Problem Mony / Consier the eight vetors 5, 5, 5,..., () List ll of the one-element, linerly epenent sets forme from these. (b) Wht re the two-element, linerly
8. Problem Set Due Wenesy, Ot., t : p.m. in - Problem Mony / Consier the eight vetors 5, 5, 5,..., () List ll of the one-element, linerly epenent sets forme from these. (b) Wht re the two-element, linerly
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
UNCORRECTED SAMPLE PAGES. surds NUMBER AND ALGEBRA
 Chpter Wht you will lern A Irrtionl numers n surs (0A) B Aing n sutrting surs (0A) C Multiplying n iviing surs (0A) D Binomil prouts (0A) E Rtionlising the enomintor (0A) F Review of inex lws (Consoliting)
Chpter Wht you will lern A Irrtionl numers n surs (0A) B Aing n sutrting surs (0A) C Multiplying n iviing surs (0A) D Binomil prouts (0A) E Rtionlising the enomintor (0A) F Review of inex lws (Consoliting)
5. Every rational number have either terminating or repeating (recurring) decimal representation.
 CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
S i m p l i f y i n g A l g e b r a SIMPLIFYING ALGEBRA.
 S i m p l i y i n g A l g r SIMPLIFYING ALGEBRA www.mthltis.o.nz Simpliying SIMPLIFYING Algr ALGEBRA Algr is mthmtis with mor thn just numrs. Numrs hv ix vlu, ut lgr introus vrils whos vlus n hng. Ths
S i m p l i y i n g A l g r SIMPLIFYING ALGEBRA www.mthltis.o.nz Simpliying SIMPLIFYING Algr ALGEBRA Algr is mthmtis with mor thn just numrs. Numrs hv ix vlu, ut lgr introus vrils whos vlus n hng. Ths
CARLETON UNIVERSITY. 1.0 Problems and Most Solutions, Sect B, 2005
 RLETON UNIVERSIT eprtment of Eletronis ELE 2607 Swithing iruits erury 28, 05; 0 pm.0 Prolems n Most Solutions, Set, 2005 Jn. 2, #8 n #0; Simplify, Prove Prolem. #8 Simplify + + + Reue to four letters (literls).
RLETON UNIVERSIT eprtment of Eletronis ELE 2607 Swithing iruits erury 28, 05; 0 pm.0 Prolems n Most Solutions, Set, 2005 Jn. 2, #8 n #0; Simplify, Prove Prolem. #8 Simplify + + + Reue to four letters (literls).
Tutorial Worksheet. 1. Find all solutions to the linear system by following the given steps. x + 2y + 3z = 2 2x + 3y + z = 4.
 Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Project 3: Using Identities to Rewrite Expressions
 MAT 5 Projet 3: Usig Idetities to Rewrite Expressios Wldis I lger, equtios tht desrie properties or ptters re ofte lled idetities. Idetities desrie expressio e repled with equl or equivlet expressio tht
MAT 5 Projet 3: Usig Idetities to Rewrite Expressios Wldis I lger, equtios tht desrie properties or ptters re ofte lled idetities. Idetities desrie expressio e repled with equl or equivlet expressio tht
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
Section 2.1 Special Right Triangles
 Se..1 Speil Rigt Tringles 49 Te --90 Tringle Setion.1 Speil Rigt Tringles Te --90 tringle (or just 0-60-90) is so nme euse of its ngle mesures. Te lengts of te sies, toug, ve very speifi pttern to tem
Se..1 Speil Rigt Tringles 49 Te --90 Tringle Setion.1 Speil Rigt Tringles Te --90 tringle (or just 0-60-90) is so nme euse of its ngle mesures. Te lengts of te sies, toug, ve very speifi pttern to tem
Matrix- System of rows and columns each position in a matrix has a purpose. 5 Ex: 5. Ex:
 Mtries Prelulus Mtri- Sstem of rows n olumns eh position in mtri hs purpose. Element- Eh vlue in the mtri mens the element in the n row, r olumn Dimensions- How mn rows b number of olumns Ientif the element:
Mtries Prelulus Mtri- Sstem of rows n olumns eh position in mtri hs purpose. Element- Eh vlue in the mtri mens the element in the n row, r olumn Dimensions- How mn rows b number of olumns Ientif the element:
Bases for Vector Spaces
 Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
Chapters Five Notes SN AA U1C5
 Chpters Five Notes SN AA U1C5 Nme Period Section 5-: Fctoring Qudrtic Epressions When you took lger, you lerned tht the first thing involved in fctoring is to mke sure to fctor out ny numers or vriles
Chpters Five Notes SN AA U1C5 Nme Period Section 5-: Fctoring Qudrtic Epressions When you took lger, you lerned tht the first thing involved in fctoring is to mke sure to fctor out ny numers or vriles
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
I 3 2 = I I 4 = 2A
 ECE 210 Eletril Ciruit Anlysis University of llinois t Chigo 2.13 We re ske to use KCL to fin urrents 1 4. The key point in pplying KCL in this prolem is to strt with noe where only one of the urrents
ECE 210 Eletril Ciruit Anlysis University of llinois t Chigo 2.13 We re ske to use KCL to fin urrents 1 4. The key point in pplying KCL in this prolem is to strt with noe where only one of the urrents
Counting Paths Between Vertices. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs
 Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
Math Lesson 4-5 The Law of Cosines
 Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
CS 491G Combinatorial Optimization Lecture Notes
 CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
Introduction to Differentiation
 Introution to Differentition Introution to Differentition Curriulum Rey www.mtletis.om Copyrigt 009 P Lerning. All rigts reserve. First eition printe 009 in Austrli. A tlogue reor for tis ook is ville
Introution to Differentition Introution to Differentition Curriulum Rey www.mtletis.om Copyrigt 009 P Lerning. All rigts reserve. First eition printe 009 in Austrli. A tlogue reor for tis ook is ville
Mathematical Proofs Table of Contents
 Mthemtil Proofs Tle of Contents Proof Stnr Pge(s) Are of Trpezoi 7MG. Geometry 8.0 Are of Cirle 6MG., 9 6MG. 7MG. Geometry 8.0 Volume of Right Cirulr Cyliner 6MG. 4 7MG. Geometry 8.0 Volume of Sphere Geometry
Mthemtil Proofs Tle of Contents Proof Stnr Pge(s) Are of Trpezoi 7MG. Geometry 8.0 Are of Cirle 6MG., 9 6MG. 7MG. Geometry 8.0 Volume of Right Cirulr Cyliner 6MG. 4 7MG. Geometry 8.0 Volume of Sphere Geometry
For a, b, c, d positive if a b and. ac bd. Reciprocal relations for a and b positive. If a > b then a ab > b. then
 Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
CS311 Computational Structures Regular Languages and Regular Grammars. Lecture 6
 CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
Linear Algebra Introduction
 Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
= x x 2 = 25 2
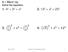 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
Pythagoras Theorem PYTHAGORAS THEOREM.
 Pthgors Theorem PYTHAGORAS THEOREM www.mthletis.om.u How oes it work? Solutions Pthgors Theorem Pge 3 questions Right-ngle tringles D E x z Hotenuse is sie: F Hotenuse is sie: DF Q k j l Hotenuse is sie:
Pthgors Theorem PYTHAGORAS THEOREM www.mthletis.om.u How oes it work? Solutions Pthgors Theorem Pge 3 questions Right-ngle tringles D E x z Hotenuse is sie: F Hotenuse is sie: DF Q k j l Hotenuse is sie:
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
1 ELEMENTARY ALGEBRA and GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE
 ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
Lesson 55 - Inverse of Matrices & Determinants
 // () Review Lesson - nverse of Mtries & Determinnts Mth Honors - Sntowski - t this stge of stuying mtries, we know how to, subtrt n multiply mtries i.e. if Then evlute: () + B (b) - () B () B (e) B n
// () Review Lesson - nverse of Mtries & Determinnts Mth Honors - Sntowski - t this stge of stuying mtries, we know how to, subtrt n multiply mtries i.e. if Then evlute: () + B (b) - () B () B (e) B n
Directed Numbers. Directed Numbers. Curriculum Ready.
 Direte Numers Curriulum Rey www.mthletis.om Numers ome in ll sizes n forms. They n e positive or negtive, whole numers, frtions or eimls n rtionl or irrtionl. Before you strt, investigte these terms n
Direte Numers Curriulum Rey www.mthletis.om Numers ome in ll sizes n forms. They n e positive or negtive, whole numers, frtions or eimls n rtionl or irrtionl. Before you strt, investigte these terms n
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
TOPIC: LINEAR ALGEBRA MATRICES
 Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
Pythagoras Theorem. The area of the square on the hypotenuse is equal to the sum of the squares on the other two sides
 Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
y = c 2 MULTIPLE CHOICE QUESTIONS (MCQ's) (Each question carries one mark) is...
 . Liner Equtions in Two Vriles C h p t e r t G l n e. Generl form of liner eqution in two vriles is x + y + 0, where 0. When we onsier system of two liner equtions in two vriles, then suh equtions re lle
. Liner Equtions in Two Vriles C h p t e r t G l n e. Generl form of liner eqution in two vriles is x + y + 0, where 0. When we onsier system of two liner equtions in two vriles, then suh equtions re lle
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Total score: /100 points
 Points misse: Stuent's Nme: Totl sore: /100 points Est Tennessee Stte University Deprtment of Computer n Informtion Sienes CSCI 2710 (Trnoff) Disrete Strutures TEST 2 for Fll Semester, 2004 Re this efore
Points misse: Stuent's Nme: Totl sore: /100 points Est Tennessee Stte University Deprtment of Computer n Informtion Sienes CSCI 2710 (Trnoff) Disrete Strutures TEST 2 for Fll Semester, 2004 Re this efore
Linear Inequalities. Work Sheet 1
 Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
Equations and Inequalities
 Equtions nd Inequlities Equtions nd Inequlities Curriculum Redy ACMNA: 4, 5, 6, 7, 40 www.mthletics.com Equtions EQUATIONS & Inequlities & INEQUALITIES Sometimes just writing vribles or pronumerls in
Equtions nd Inequlities Equtions nd Inequlities Curriculum Redy ACMNA: 4, 5, 6, 7, 40 www.mthletics.com Equtions EQUATIONS & Inequlities & INEQUALITIES Sometimes just writing vribles or pronumerls in
Solutions to Problem Set #1
 CSE 233 Spring, 2016 Solutions to Prolem Set #1 1. The movie tse onsists of the following two reltions movie: title, iretor, tor sheule: theter, title The first reltion provies titles, iretors, n tors
CSE 233 Spring, 2016 Solutions to Prolem Set #1 1. The movie tse onsists of the following two reltions movie: title, iretor, tor sheule: theter, title The first reltion provies titles, iretors, n tors
Lecture 2: Cayley Graphs
 Mth 137B Professor: Pri Brtlett Leture 2: Cyley Grphs Week 3 UCSB 2014 (Relevnt soure mteril: Setion VIII.1 of Bollos s Moern Grph Theory; 3.7 of Gosil n Royle s Algeri Grph Theory; vrious ppers I ve re
Mth 137B Professor: Pri Brtlett Leture 2: Cyley Grphs Week 3 UCSB 2014 (Relevnt soure mteril: Setion VIII.1 of Bollos s Moern Grph Theory; 3.7 of Gosil n Royle s Algeri Grph Theory; vrious ppers I ve re
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
Chapter Gauss Quadrature Rule of Integration
 Chpter 7. Guss Qudrture Rule o Integrtion Ater reding this hpter, you should e le to:. derive the Guss qudrture method or integrtion nd e le to use it to solve prolems, nd. use Guss qudrture method to
Chpter 7. Guss Qudrture Rule o Integrtion Ater reding this hpter, you should e le to:. derive the Guss qudrture method or integrtion nd e le to use it to solve prolems, nd. use Guss qudrture method to
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Identifying and Classifying 2-D Shapes
 Ientifying n Clssifying -D Shpes Wht is your sign? The shpe n olour of trffi signs let motorists know importnt informtion suh s: when to stop onstrution res. Some si shpes use in trffi signs re illustrte
Ientifying n Clssifying -D Shpes Wht is your sign? The shpe n olour of trffi signs let motorists know importnt informtion suh s: when to stop onstrution res. Some si shpes use in trffi signs re illustrte
( ) { } [ ] { } [ ) { } ( ] { }
![( ) { } [ ] { } [ ) { } ( ] { } ( ) { } [ ] { } [ ) { } ( ] { }](/thumbs/96/129291861.jpg) Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Preliminary preparation
 Preliminry preprtion Syllus prerequisite: Preliminry preprtion This topi provies the si knowlege, skills n unerstnings require in Yer. Outomes Simplify n lgeri expression. Estlish n pply inex lws in lgeri
Preliminry preprtion Syllus prerequisite: Preliminry preprtion This topi provies the si knowlege, skills n unerstnings require in Yer. Outomes Simplify n lgeri expression. Estlish n pply inex lws in lgeri
Review of Gaussian Quadrature method
 Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
MA123, Chapter 10: Formulas for integrals: integrals, antiderivatives, and the Fundamental Theorem of Calculus (pp.
 MA123, Chpter 1: Formuls for integrls: integrls, ntiderivtives, nd the Fundmentl Theorem of Clculus (pp. 27-233, Gootmn) Chpter Gols: Assignments: Understnd the sttement of the Fundmentl Theorem of Clculus.
MA123, Chpter 1: Formuls for integrls: integrls, ntiderivtives, nd the Fundmentl Theorem of Clculus (pp. 27-233, Gootmn) Chpter Gols: Assignments: Understnd the sttement of the Fundmentl Theorem of Clculus.
Solutions for HW9. Bipartite: put the red vertices in V 1 and the black in V 2. Not bipartite!
 Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
Area and Perimeter. Area and Perimeter. Solutions. Curriculum Ready.
 Are n Perimeter Are n Perimeter Solutions Curriulum Rey www.mthletis.om How oes it work? Solutions Are n Perimeter Pge questions Are using unit squres Are = whole squres Are = 6 whole squres = units =
Are n Perimeter Are n Perimeter Solutions Curriulum Rey www.mthletis.om How oes it work? Solutions Are n Perimeter Pge questions Are using unit squres Are = whole squres Are = 6 whole squres = units =
MCH T 111 Handout Triangle Review Page 1 of 3
 Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
The graphs of Rational Functions
 Lecture 4 5A: The its of Rtionl Functions s x nd s x + The grphs of Rtionl Functions The grphs of rtionl functions hve severl differences compred to power functions. One of the differences is the behvior
Lecture 4 5A: The its of Rtionl Functions s x nd s x + The grphs of Rtionl Functions The grphs of rtionl functions hve severl differences compred to power functions. One of the differences is the behvior
Lecture 1 - Introduction and Basic Facts about PDEs
 * 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
* 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
Improper Integrals. The First Fundamental Theorem of Calculus, as we ve discussed in class, goes as follows:
 Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
2Linear and UNCORRECTED SAMPLE PAGES. simultaneous equations. Australian curriculum. What you will learn. Chapter 2A 2B 2C 2D 2E 2F 2G 2H 2I
 A B C D E F G H I J K Chpter Wht you will lern Liner n simultneous equtions Algeri epressions (Consoliting) Simplifying lgeri epressions (Consoliting) Epning lgeri epressions Solving liner equtions Equtions
A B C D E F G H I J K Chpter Wht you will lern Liner n simultneous equtions Algeri epressions (Consoliting) Simplifying lgeri epressions (Consoliting) Epning lgeri epressions Solving liner equtions Equtions
Exam Review. John Knight Electronics Department, Carleton University March 2, 2009 ELEC 2607 A MIDTERM
 riting Exms: Exm Review riting Exms += riting Exms synhronous iruits Res, yles n Stte ssignment Synhronous iruits Stte-Grph onstrution n Smll Prolems lso Multiple Outputs, n Hrer omintionl Prolem riting
riting Exms: Exm Review riting Exms += riting Exms synhronous iruits Res, yles n Stte ssignment Synhronous iruits Stte-Grph onstrution n Smll Prolems lso Multiple Outputs, n Hrer omintionl Prolem riting
NON-DETERMINISTIC FSA
 Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Discrete Structures Lecture 11
 Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
Vectors. a Write down the vector AB as a column vector ( x y ). A (3, 2) x point C such that BC = 3. . Go to a OA = a
 Streth lesson: Vetors Streth ojetives efore you strt this hpter, mrk how onfident you feel out eh of the sttements elow: I n lulte using olumn vetors nd represent the sum nd differene of two vetors grphilly.
Streth lesson: Vetors Streth ojetives efore you strt this hpter, mrk how onfident you feel out eh of the sttements elow: I n lulte using olumn vetors nd represent the sum nd differene of two vetors grphilly.
A Primer on Continuous-time Economic Dynamics
 Eonomis 205A Fll 2008 K Kletzer A Primer on Continuous-time Eonomi Dnmis A Liner Differentil Eqution Sstems (i) Simplest se We egin with the simple liner first-orer ifferentil eqution The generl solution
Eonomis 205A Fll 2008 K Kletzer A Primer on Continuous-time Eonomi Dnmis A Liner Differentil Eqution Sstems (i) Simplest se We egin with the simple liner first-orer ifferentil eqution The generl solution
Farey Fractions. Rickard Fernström. U.U.D.M. Project Report 2017:24. Department of Mathematics Uppsala University
 U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
Necessary and sucient conditions for some two. Abstract. Further we show that the necessary conditions for the existence of an OD(44 s 1 s 2 )
 Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
Mathematics Number: Logarithms
 plce of mind F A C U L T Y O F E D U C A T I O N Deprtment of Curriculum nd Pedgogy Mthemtics Numer: Logrithms Science nd Mthemtics Eduction Reserch Group Supported y UBC Teching nd Lerning Enhncement
plce of mind F A C U L T Y O F E D U C A T I O N Deprtment of Curriculum nd Pedgogy Mthemtics Numer: Logrithms Science nd Mthemtics Eduction Reserch Group Supported y UBC Teching nd Lerning Enhncement
Matrices SCHOOL OF ENGINEERING & BUILT ENVIRONMENT. Mathematics (c) 1. Definition of a Matrix
 tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
