2.1 ANGLES AND THEIR MEASURE. y I
|
|
|
- Erik Jones
- 6 years ago
- Views:
Transcription
1 .1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the ngle etween them. Angles re usully mesured in degrees (denoted ), rdins (denoted rd, or without unit), or sometimes grdins (denoted grd). II y I β nd re oterminl ngles euse they hve the sme initil nd sme terminl side. - β Vertex Terminl side + Initil side Rys re hlf-lines, tht is, portion of line tht strts vertex point nd extends indefinitely in one diretion. x III IV In retngulr oordinte system, ngles re defined s the rottion from one ry to nother. The ry t the strting position is lled the initil side nd the ry t then ending position is the terminl side. Rottion in ounterlokwise diretion is positive nd rottion in lokwise diretion is negtive. An ngle is in stndrd position if its vertex is t the origin nd its initil side oinides with the positive x-xis.
2 II Qudrntl Angles One full rottion in these three mesures orresponds to 360, π rdins, or 400 grdins. Hlf full rottion is 180 nd is lled stright ngle, nd qurter of full rottion is 90 nd is lled right ngle. An ngle less thn right ngle is lled n ute ngle, nd n ngle greter thn right ngle is lled n otuse ngle. y α 90, 40, 810, -70, et. I β 180, 40,900, et. β φ α δ 0, 360,70, et. III δ IV 360 is one full revolution. A right ngle, 90, is 90/360 1/4 revolution. Φ 70, 40, 810, - 90, et. Converting from Degrees, Minutes, Seonds (D, M,S ) to Deiml Form The use of degrees to mesure ngles hrks k to the Bylonins, whose sexgesiml numer system ws sed on the numer 60. likely rises from the Bylonin yer, whih ws omposed of 360 dys (1 months of 30 dys eh). The degree is further divided into 60 r minutes (denoted ), nd n r minute into 60 r seonds(denoted ). A more nturl mesure of n ngle is the rdin. It hs the property tht the r length round irle is simply given y the rdin ngle mesure times the irle rdius. The rdin is lso the most useful ngle mesure in lulus. Grdins re sometimes used in surveying (they hve the nie property tht right ngle is extly 100 grdins), ut re enountered infrequently, if t ll, in mthemtis. 1 ounterlokwise revolution minutes 1 minute seonds Exmple on p.101 Convert to deiml in degrees whih mens 1 1 / so 1 1 /60 (1 /60)/60 1 / *1 / *1 / Convert 1.6 to (D, M,S ) in degrees. Strt with the deiml prt, *60 / Tke the deiml prt of 1.36 nd onvert to seonds..36 * 60 /1 1.6 Thus,
3 Converting from Degrees, Minutes, Seonds (D, M,S ) to Deiml Form Using TI-83 or TI-83 plus Convert to deiml in degrees. 0 nd [ANGLE] 1 6 nd [ANGLE] 1 ALPHA ENTER Selets Degree nottion Selets Minute nottion Selets Seond nottion To onvert from deiml to DMS, just type the numer in deiml form, then press nd [ANGLE] 4 to see it in DMS form.
4 Centrl Angles nd Ar Length A entrl ngle is n ngle whose vertex is t the enter of irle. The rys of entrl ngle sutend (interset) n r on the irle. [The entrl ngle is etween 0 nd 360 degrees]. 1 rdin is defined s entrl ngle of irle with rdius r tht hs n r length of r. If the irumferene of irle is πr, how mny rdins re there in 1 full revolution of the irle? Terminl Side Vertex r 3 r r 1 1 Ar length r 1 1 Ar length r 3 1 rdin Initil side r Ar length s 1 1 r Ar length s From geometry, we know tht the rtio of the mesures of the ngles equls the rtio of the orresponding lengths of the rs sutended y these ngles. s 1 s 1 s 1 r If 1 1 rdin, then the r length s 1 r, so nd ross-multiplying givess r for ny in theirle ARC LENGTH For irle of rdius r, entrl ngle of rdins sutends n r whose length s is s r Now try #37 on p.109
5 How do you find r length if the ngle is given in degrees? Rell tht the irumferene of irle is πr. The r length of full revolution ( full ) is πr r full Therefore full π rdins 1 full revolution 360 π rdins ½ revolution 180 π rdins ¼ revolution 90 π/ rdins Exmple 4 () on p. 104 Convert 60 to rdins. 60 * π rdins/ π /180 rdins π/3 rdins Now you do #13 on p.109 Exmple () on p.10 Convert -3π/4 rdins to degrees. (-3π/4)*180 / π -13 Now you do # on p.109 Ltitude is G N s AG is the r length of the entrl ngle, AG, t point G. sutended y the ry from Erth s enter to Glsgow nd the ry from Erth s enter to Aluquerque. Tht is the distne from Glsgow to Aluquerque. G s AG Step 1: A AG G A Step : Ltitude is 0 Convert from DMS to deiml degreest Equtor /(1 /60 ) Step 3: Convert from deiml degrees to rdins *(π rdins/180) 0.8 rdins. Step 4: Clulte r length s AG. s AG R Erth * AG rdins 3960* miles G We use this ft to onvert from degrees to rdins. 1 rdin 180 / π 1 degree π rdins/180 Exmple 6 on p.10 Ltitude of lotion is the ngle formed y ry drwn from the enter of Erth to the Equtor nd ry drwn from the enter of Erth to the lotion. Glsgow, Montn is due north Aluquerque, New Mexio. Glsgow s ltitude is 48 9 N nd Aluquerque s ltitude is 3 N. Find the distne etween these ities. A Rdius 3960 miles Now do #91 on p.110
6 Common Degree to Rdin Conversions Degrees Rdins 0 π/6 π/4 π/3 π/ π/3 3π/4 π/6 π 7π/6 π/4 4π/3 3π/ π/3 7π/4 11π/6 π * * * * * Memorize these
7 Are of Setor From geometry, we know tht the rtio of the mesures of the ngles equls the rtio of the orresponding res of the setors formed y these ngles. Tht is, A 1 A 1 If 1 π rdins, then A 1 re of irle. A π πr A A π πr r r Multiply oth sides y to solve for A. Are of setor formed y entrl ngle of rdins is A 1 r Now you do #4 on p.109
8 Liner nd Angulr Speed Liner speed distne trveled round irle (s) divided y the elpsed time of trvel (t). veloity v s/t Angulr speed the entrl ngle swept out in time (), divided y the elpsed time, (t). Angulr speed ω /t where ngulr speed is in rdins per unit time. Exmple: An engine is revving t 900 RPM. If you re given RPM insted of ngulr speed, you n onvert to ngulr speed y using tht ft tht 1 revolution π rdins revolutions revolutions π rdins rdins π minute minute 1 revolution minute Liner speed v s/t (r)/t r(/t) rω where ω is mesured in rdins per unit time. Exmple 8 on p.108 A hild is spinning rok t the end of -foot rope t rte of 180 revolutions per minute. Find the lier speed of the rok when it releses. revolutions revolutions π rdins rdins π minute minute 1 revolution minute Liner speed v rw (ft) * (360π rdins/minute) 70π feet/min 6 feet/min feet 1mile 60 min 6 * *.7 mph min 80 feet 1hour Now you do # 87 on p.110
9 Right Tringle Trigonometry is n ute ngle euse it is less thn 90 degrees. Hypotenuse Adjent to 90 - Opposite to From geometry, we know tht the rtios of the sides of similr tringles re equl so: ', ' ', ' ', ' ', ' These rtios re the sme for ny right tringle with ute ngle. They re lled the trigonometri funtions of ute ngles. ' ' ' ' FUNCTION NAME ABBREV. VALUE Notie these funtions re the reiprols of sine, osine, & tngent, respetively. Sine of Cosine of Tngent of Cosent of Sent of Cotngent of sin() /opposite/hypotenuse os() /djent/hypotenuse tn() /opposite/djent s() /hypotenuse/opposite se() /hypotenuse/djent ot() /djent/opposite Rememer SOH-CAH-TOA! In other words: s()1/sin(), se()1/os(), ot()1/tn()
10 Finding Trig Funtions Exmple on p.114 Finding the Vlue of the Remining Trig Funtions, given sin nd os. Given sin( ), nd os( ), find the remining trig funtions of tn( ) sin( ) os( ) se( ) 1/ os( ) s( ) 1/ sin( ) 1 NOW YOU DO #11 on p11
11 Fundmentl Identities of Trigonometry We n use the Pythgoren Theorem to derive the fundmentl identities of trigonometry. We know +, right? Let s rerrnge some terms nd divide eh side y ( sin( )) + ( os( )) whih n lso e written s follows: sin Now we n get nother identity y dividing oth sides of this eqution y os sin ( ) os + os ( ) os tn sin sin + 1+ ot ( ) + os ( ) + 1 se ( ) os + ( ) sin 1 1 ( ) 1 ( ) ( ) ( ) Similrly, you hd divided eh side of + + ( ) s ( ) 1 1 os ( ) ( ) 1 ( ) sin ( ) Exmple 3 on p.11 tht eqution y sin Fundmentl Identities ( ) : ( ) tn() sin()/ os() ot() os()/ sin() s() 1/sin() se() 1/ os() ot() os()/ sin() sin () + os () 1 tn () + 1 se () 1 + ot () s ()
12 Finding the ext vlue of the trig funtions, given one. Exmple 4 Given tht sin() 1/3 nd is n ute ngle, find the ext vlue of eh of the remining five trigonometri funtions of. Rememer sin() 1/3 opposite/hypotenuse so let s mke right tringle with the opposite of to e 1 nd the hypotenuse to e 3. We n use the Pythgoren Theorem to find the djent side,. 3? Now tht you know ll three sides of the tringle, just use the definitions to find the ext vlues of the trig funtions. Trig Funtion sin() os() tn() s() se() ot() Definition /opposite/hypotenuse /djent/hypotenuse /opposite/djent /hypotenuse/opposite /hypotenuse/djent /djent/opposite Ext Vlue /1/3 / 3 / 1 /3/1 3 / 3 /
13 Complementry Angles; Cofuntions α 90- β Hypotenuse β α Opposite to β Adjent to α α nd β re omplementry ngle euse their sum is right ngle, 90. Adjent to β Opposite to α Complementry Angle Theorem Cofuntions of omplementry ngles re equl. Cofuntions re trigonometri funtions tht shre the sme ngles of right tringle. sin(β)opposite to β / hypotenuse djent to α/hypotenuse os(α)os(90- β) os(β)djent to β / hypotenuse opposite to α/hypotenuse sin(α)sin(90- β) tn(β)opposite to β / djent to α djent to α/ opposite to β ot(α) ot(90- β) Likewise, the reiprol of these properties is true. s(β) hypotenuse / opposite to β / hypotenuse /djent to α se(α)se(90- β) se(β) hypotenuse /djent to β hypotenuse/opposite to α s(α) s(90- β) ot(β) djent to α /opposite to β opposite to β / djent to α tn(90- β)
14 HOMEWORK Homework p #1, 3, 7, 39, 41, 47, 1, 3, 7, 69,7,81,8,91 p. 11 #3, 13,17, 3,37, 47, 3, 7
at its center, then the measure of this angle in radians (abbreviated rad) is the length of the arc that subtends the angle.
 Notes 6 ngle Mesure Definition of Rdin If circle of rdius is drwn with the vertex of n ngle Mesure: t its center, then the mesure of this ngle in rdins (revited rd) is the length of the rc tht sutends
Notes 6 ngle Mesure Definition of Rdin If circle of rdius is drwn with the vertex of n ngle Mesure: t its center, then the mesure of this ngle in rdins (revited rd) is the length of the rc tht sutends
( ) { } [ ] { } [ ) { } ( ] { }
![( ) { } [ ] { } [ ) { } ( ] { } ( ) { } [ ] { } [ ) { } ( ] { }](/thumbs/96/129291861.jpg) Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Similar Right Triangles
 Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Trigonometric Functions
 Exercise. Degrees nd Rdins Chpter Trigonometric Functions EXERCISE. Degrees nd Rdins 4. Since 45 corresponds to rdin mesure of π/4 rd, we hve: 90 = 45 corresponds to π/4 or π/ rd. 5 = 7 45 corresponds
Exercise. Degrees nd Rdins Chpter Trigonometric Functions EXERCISE. Degrees nd Rdins 4. Since 45 corresponds to rdin mesure of π/4 rd, we hve: 90 = 45 corresponds to π/4 or π/ rd. 5 = 7 45 corresponds
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
 PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
Trigonometry and Constructive Geometry
 Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
Sect 10.2 Trigonometric Ratios
 86 Sect 0. Trigonometric Rtios Objective : Understnding djcent, Hypotenuse, nd Opposite sides of n cute ngle in right tringle. In right tringle, the otenuse is lwys the longest side; it is the side opposite
86 Sect 0. Trigonometric Rtios Objective : Understnding djcent, Hypotenuse, nd Opposite sides of n cute ngle in right tringle. In right tringle, the otenuse is lwys the longest side; it is the side opposite
MATHEMATICS AND STATISTICS 1.6
 MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
Something found at a salad bar
 Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Calculus Cheat Sheet. Integrals Definitions. where F( x ) is an anti-derivative of f ( x ). Fundamental Theorem of Calculus. dx = f x dx g x dx
 Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
3.1 Review of Sine, Cosine and Tangent for Right Angles
 Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
Topics Covered: Pythagoras Theorem Definition of sin, cos and tan Solving right-angle triangles Sine and cosine rule
 Trigonometry Topis overed: Pythgors Theorem Definition of sin, os nd tn Solving right-ngle tringles Sine nd osine rule Lelling right-ngle tringle Opposite (Side opposite the ngle θ) Hypotenuse (Side opposite
Trigonometry Topis overed: Pythgors Theorem Definition of sin, os nd tn Solving right-ngle tringles Sine nd osine rule Lelling right-ngle tringle Opposite (Side opposite the ngle θ) Hypotenuse (Side opposite
PROPERTIES OF TRIANGLES
 PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
Pythagoras Theorem. The area of the square on the hypotenuse is equal to the sum of the squares on the other two sides
 Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
= x x 2 = 25 2
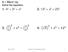 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Non Right Angled Triangles
 Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Green s Theorem. (2x e y ) da. (2x e y ) dx dy. x 2 xe y. (1 e y ) dy. y=1. = y e y. y=0. = 2 e
 Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
 Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Standard Trigonometric Functions
 CRASH KINEMATICS For ngle A: opposite sine A = = hypotenuse djent osine A = = hypotenuse opposite tngent A = = djent For ngle B: opposite sine B = = hypotenuse djent osine B = = hypotenuse opposite tngent
CRASH KINEMATICS For ngle A: opposite sine A = = hypotenuse djent osine A = = hypotenuse opposite tngent A = = djent For ngle B: opposite sine B = = hypotenuse djent osine B = = hypotenuse opposite tngent
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx
![Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx](/thumbs/79/79316452.jpg) Fill in the Blnks for the Big Topis in Chpter 5: The Definite Integrl Estimting n integrl using Riemnn sum:. The Left rule uses the left endpoint of eh suintervl.. The Right rule uses the right endpoint
Fill in the Blnks for the Big Topis in Chpter 5: The Definite Integrl Estimting n integrl using Riemnn sum:. The Left rule uses the left endpoint of eh suintervl.. The Right rule uses the right endpoint
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Naming the sides of a right-angled triangle
 6.2 Wht is trigonometry? The word trigonometry is derived from the Greek words trigonon (tringle) nd metron (mesurement). Thus, it literlly mens to mesure tringle. Trigonometry dels with the reltionship
6.2 Wht is trigonometry? The word trigonometry is derived from the Greek words trigonon (tringle) nd metron (mesurement). Thus, it literlly mens to mesure tringle. Trigonometry dels with the reltionship
MCH T 111 Handout Triangle Review Page 1 of 3
 Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
THE KENNESAW STATE UNIVERSITY HIGH SCHOOL MATHEMATICS COMPETITION PART I MULTIPLE CHOICE NO CALCULATORS 90 MINUTES
 THE 08 09 KENNESW STTE UNIVERSITY HIGH SHOOL MTHEMTIS OMPETITION PRT I MULTIPLE HOIE For ech of the following questions, crefully blcken the pproprite box on the nswer sheet with # pencil. o not fold,
THE 08 09 KENNESW STTE UNIVERSITY HIGH SHOOL MTHEMTIS OMPETITION PRT I MULTIPLE HOIE For ech of the following questions, crefully blcken the pproprite box on the nswer sheet with # pencil. o not fold,
Section 13.1 Right Triangles
 Section 13.1 Right Tringles Ojectives: 1. To find vlues of trigonometric functions for cute ngles. 2. To solve tringles involving right ngles. Review - - 1. SOH sin = Reciprocl csc = 2. H cos = Reciprocl
Section 13.1 Right Tringles Ojectives: 1. To find vlues of trigonometric functions for cute ngles. 2. To solve tringles involving right ngles. Review - - 1. SOH sin = Reciprocl csc = 2. H cos = Reciprocl
Objective: Use the Pythagorean Theorem and its converse to solve right triangle problems. CA Geometry Standard: 12, 14, 15
 Geometry CP Lesson 8.2 Pythgoren Theorem nd its Converse Pge 1 of 2 Ojective: Use the Pythgoren Theorem nd its converse to solve right tringle prolems. CA Geometry Stndrd: 12, 14, 15 Historicl Bckground
Geometry CP Lesson 8.2 Pythgoren Theorem nd its Converse Pge 1 of 2 Ojective: Use the Pythgoren Theorem nd its converse to solve right tringle prolems. CA Geometry Stndrd: 12, 14, 15 Historicl Bckground
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
1.3 SCALARS AND VECTORS
 Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
m A 1 1 A ! and AC 6
 REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
Perimeter and Area. Mathletics Instant Workbooks. Copyright
 Perimeter nd Are Student Book - Series J- L B Mthletis Instnt Workooks Copyright Student Book - Series J Contents Topis Topi - Plne shpes Topi 2 - Perimeter of regulr shpes Topi 3 - Perimeter of irregulr
Perimeter nd Are Student Book - Series J- L B Mthletis Instnt Workooks Copyright Student Book - Series J Contents Topis Topi - Plne shpes Topi 2 - Perimeter of regulr shpes Topi 3 - Perimeter of irregulr
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
Date Lesson Text TOPIC Homework. Solving for Obtuse Angles QUIZ ( ) More Trig Word Problems QUIZ ( )
 UNIT 5 TRIGONOMETRI RTIOS Dte Lesson Text TOPI Homework pr. 4 5.1 (48) Trigonometry Review WS 5.1 # 3 5, 9 11, (1, 13)doso pr. 6 5. (49) Relted ngles omplete lesson shell & WS 5. pr. 30 5.3 (50) 5.3 5.4
UNIT 5 TRIGONOMETRI RTIOS Dte Lesson Text TOPI Homework pr. 4 5.1 (48) Trigonometry Review WS 5.1 # 3 5, 9 11, (1, 13)doso pr. 6 5. (49) Relted ngles omplete lesson shell & WS 5. pr. 30 5.3 (50) 5.3 5.4
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
I1 = I2 I1 = I2 + I3 I1 + I2 = I3 + I4 I 3
 2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
Polynomials and Division Theory
 Higher Checklist (Unit ) Higher Checklist (Unit ) Polynomils nd Division Theory Skill Achieved? Know tht polynomil (expression) is of the form: n x + n x n + n x n + + n x + x + 0 where the i R re the
Higher Checklist (Unit ) Higher Checklist (Unit ) Polynomils nd Division Theory Skill Achieved? Know tht polynomil (expression) is of the form: n x + n x n + n x n + + n x + x + 0 where the i R re the
Math Lesson 4-5 The Law of Cosines
 Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Mathematics 10 Page 1 of 5 Properties of Triangle s and Quadrilaterals. Isosceles Triangle. - 2 sides and 2 corresponding.
 Mthemtis 10 Pge 1 of 5 Properties of s Pthgoren Theorem 2 2 2 used to find the length of sides of right tringle Tpe of s nd Some s Theorems ngles s Slene Isoseles Equilterl ute - ll ngles re less thn 90
Mthemtis 10 Pge 1 of 5 Properties of s Pthgoren Theorem 2 2 2 used to find the length of sides of right tringle Tpe of s nd Some s Theorems ngles s Slene Isoseles Equilterl ute - ll ngles re less thn 90
GEOMETRY OF THE CIRCLE TANGENTS & SECANTS
 Geometry Of The ircle Tngents & Secnts GEOMETRY OF THE IRLE TNGENTS & SENTS www.mthletics.com.u Tngents TNGENTS nd N Secnts SENTS Tngents nd secnts re lines tht strt outside circle. Tngent touches the
Geometry Of The ircle Tngents & Secnts GEOMETRY OF THE IRLE TNGENTS & SENTS www.mthletics.com.u Tngents TNGENTS nd N Secnts SENTS Tngents nd secnts re lines tht strt outside circle. Tngent touches the
Ellipses. The second type of conic is called an ellipse.
 Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
03 Qudrtic Functions Completing the squre: Generl Form f ( x) x + x + c f ( x) ( x + p) + q where,, nd c re constnts nd 0. (i) (ii) (iii) (iv) *Note t
 A-PDF Wtermrk DEMO: Purchse from www.a-pdf.com to remove the wtermrk Add Mths Formule List: Form 4 (Updte 8/9/08) 0 Functions Asolute Vlue Function Inverse Function If f ( x ), if f ( x ) 0 f ( x) y f
A-PDF Wtermrk DEMO: Purchse from www.a-pdf.com to remove the wtermrk Add Mths Formule List: Form 4 (Updte 8/9/08) 0 Functions Asolute Vlue Function Inverse Function If f ( x ), if f ( x ) 0 f ( x) y f
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
VECTOR ALGEBRA. Syllabus :
 MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
THREE DIMENSIONAL GEOMETRY
 MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
m m m m m m m m P m P m ( ) m m P( ) ( ). The o-ordinte of the point P( ) dividing the line segment joining the two points ( ) nd ( ) eternll in the r
 CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
Lesson 2: The Pythagorean Theorem and Similar Triangles. A Brief Review of the Pythagorean Theorem.
 27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
Edexcel GCE Core Mathematics (C2) Required Knowledge Information Sheet. Daniel Hammocks
 Edexcel GCE Core Mthemtics (C) Required Knowledge Informtion Sheet C Formule Given in Mthemticl Formule nd Sttisticl Tles Booklet Cosine Rule o = + c c cosine (A) Binomil Series o ( + ) n = n + n 1 n 1
Edexcel GCE Core Mthemtics (C) Required Knowledge Informtion Sheet C Formule Given in Mthemticl Formule nd Sttisticl Tles Booklet Cosine Rule o = + c c cosine (A) Binomil Series o ( + ) n = n + n 1 n 1
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Precalculus Notes: Unit 6 Law of Sines & Cosines, Vectors, & Complex Numbers. A can be rewritten as
 Dte: 6.1 Lw of Sines Syllus Ojetie: 3.5 Te student will sole pplition prolems inoling tringles (Lw of Sines). Deriing te Lw of Sines: Consider te two tringles. C C In te ute tringle, sin In te otuse tringle,
Dte: 6.1 Lw of Sines Syllus Ojetie: 3.5 Te student will sole pplition prolems inoling tringles (Lw of Sines). Deriing te Lw of Sines: Consider te two tringles. C C In te ute tringle, sin In te otuse tringle,
Basic Angle Rules 5. A Short Hand Geometric Reasons. B Two Reasons. 1 Write in full the meaning of these short hand geometric reasons.
 si ngle Rules 5 6 Short Hnd Geometri Resons 1 Write in full the mening of these short hnd geometri resons. Short Hnd Reson Full Mening ) se s isos Δ re =. ) orr s // lines re =. ) sum s t pt = 360. d)
si ngle Rules 5 6 Short Hnd Geometri Resons 1 Write in full the mening of these short hnd geometri resons. Short Hnd Reson Full Mening ) se s isos Δ re =. ) orr s // lines re =. ) sum s t pt = 360. d)
Mathematics. Area under Curve.
 Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Applications of Definite Integral
 Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
NOT TO SCALE. We can make use of the small angle approximations: if θ á 1 (and is expressed in RADIANS), then
 3. Stellr Prllx y terrestril stndrds, the strs re extremely distnt: the nerest, Proxim Centuri, is 4.24 light yers (~ 10 13 km) wy. This mens tht their prllx is extremely smll. Prllx is the pprent shifting
3. Stellr Prllx y terrestril stndrds, the strs re extremely distnt: the nerest, Proxim Centuri, is 4.24 light yers (~ 10 13 km) wy. This mens tht their prllx is extremely smll. Prllx is the pprent shifting
Section 4.4. Green s Theorem
 The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
15 - TRIGONOMETRY Page 1 ( Answers at the end of all questions )
 - TRIGONOMETRY Pge P ( ) In tringle PQR, R =. If tn b c = 0, 0, then Q nd tn re the roots of the eqution = b c c = b b = c b = c [ AIEEE 00 ] ( ) In tringle ABC, let C =. If r is the inrdius nd R is the
- TRIGONOMETRY Pge P ( ) In tringle PQR, R =. If tn b c = 0, 0, then Q nd tn re the roots of the eqution = b c c = b b = c b = c [ AIEEE 00 ] ( ) In tringle ABC, let C =. If r is the inrdius nd R is the
Chapter 4 Trigonometric Functions
 Chter Trigonometric Functions Chter Trigonometric Functions Section. Angles nd Their Mesures Exlortion. r. rdins ( lengths of ted). No, not quite, since the distnce r would require iece of ted times s
Chter Trigonometric Functions Chter Trigonometric Functions Section. Angles nd Their Mesures Exlortion. r. rdins ( lengths of ted). No, not quite, since the distnce r would require iece of ted times s
AP Calculus AB Unit 4 Assessment
 Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
Clss: Dte: 0-04 AP Clulus AB Unit 4 Assessment Multiple Choie Identify the hoie tht best ompletes the sttement or nswers the question. A lultor my NOT be used on this prt of the exm. (6 minutes). The slope
What else can you do?
 Wht else cn you do? ngle sums The size of specil ngle types lernt erlier cn e used to find unknown ngles. tht form stright line dd to 180c. lculte the size of + M, if L is stright line M + L = 180c( stright
Wht else cn you do? ngle sums The size of specil ngle types lernt erlier cn e used to find unknown ngles. tht form stright line dd to 180c. lculte the size of + M, if L is stright line M + L = 180c( stright
Triangles The following examples explore aspects of triangles:
 Tringles The following exmples explore spects of tringles: xmple 1: ltitude of right ngled tringle + xmple : tringle ltitude of the symmetricl ltitude of n isosceles x x - 4 +x xmple 3: ltitude of the
Tringles The following exmples explore spects of tringles: xmple 1: ltitude of right ngled tringle + xmple : tringle ltitude of the symmetricl ltitude of n isosceles x x - 4 +x xmple 3: ltitude of the
Chapter 6 Techniques of Integration
 MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
Exploring parametric representation with the TI-84 Plus CE graphing calculator
 Exploring prmetric representtion with the TI-84 Plus CE grphing clcultor Richrd Prr Executive Director Rice University School Mthemtics Project rprr@rice.edu Alice Fisher Director of Director of Technology
Exploring prmetric representtion with the TI-84 Plus CE grphing clcultor Richrd Prr Executive Director Rice University School Mthemtics Project rprr@rice.edu Alice Fisher Director of Director of Technology
The unit circle and radian measure
 hter 8 The unit irle nd rdin mesure Sllus referene:.,.,. ontents: Rdin mesure r length nd setor re The unit irle nd the trigonometri rtios D litions of the unit irle E Multiles of ¼ 6 nd ¼ F The eqution
hter 8 The unit irle nd rdin mesure Sllus referene:.,.,. ontents: Rdin mesure r length nd setor re The unit irle nd the trigonometri rtios D litions of the unit irle E Multiles of ¼ 6 nd ¼ F The eqution
Math 32B Discussion Session Week 8 Notes February 28 and March 2, f(b) f(a) = f (t)dt (1)
 Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
BEGINNING ALGEBRA (ALGEBRA I)
 /0 BEGINNING ALGEBRA (ALGEBRA I) SAMPLE TEST PLACEMENT EXAMINATION Downlod the omplete Study Pket: http://www.glendle.edu/studypkets Students who hve tken yer of high shool lger or its equivlent with grdes
/0 BEGINNING ALGEBRA (ALGEBRA I) SAMPLE TEST PLACEMENT EXAMINATION Downlod the omplete Study Pket: http://www.glendle.edu/studypkets Students who hve tken yer of high shool lger or its equivlent with grdes
7.1 Integral as Net Change and 7.2 Areas in the Plane Calculus
 7.1 Integrl s Net Chnge nd 7. Ares in the Plne Clculus 7.1 INTEGRAL AS NET CHANGE Notecrds from 7.1: Displcement vs Totl Distnce, Integrl s Net Chnge We hve lredy seen how the position of n oject cn e
7.1 Integrl s Net Chnge nd 7. Ares in the Plne Clculus 7.1 INTEGRAL AS NET CHANGE Notecrds from 7.1: Displcement vs Totl Distnce, Integrl s Net Chnge We hve lredy seen how the position of n oject cn e
MATH Final Review
 MATH 1591 - Finl Review November 20, 2005 1 Evlution of Limits 1. the ε δ definition of limit. 2. properties of limits. 3. how to use the diret substitution to find limit. 4. how to use the dividing out
MATH 1591 - Finl Review November 20, 2005 1 Evlution of Limits 1. the ε δ definition of limit. 2. properties of limits. 3. how to use the diret substitution to find limit. 4. how to use the dividing out
( ) 1. 1) Let f( x ) = 10 5x. Find and simplify f( 2) and then state the domain of f(x).
 Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
2. VECTORS AND MATRICES IN 3 DIMENSIONS
 2 VECTORS AND MATRICES IN 3 DIMENSIONS 21 Extending the Theory of 2-dimensionl Vectors x A point in 3-dimensionl spce cn e represented y column vector of the form y z z-xis y-xis z x y x-xis Most of the
2 VECTORS AND MATRICES IN 3 DIMENSIONS 21 Extending the Theory of 2-dimensionl Vectors x A point in 3-dimensionl spce cn e represented y column vector of the form y z z-xis y-xis z x y x-xis Most of the
Interpreting Integrals and the Fundamental Theorem
 Interpreting Integrls nd the Fundmentl Theorem Tody, we go further in interpreting the mening of the definite integrl. Using Units to Aid Interprettion We lredy know tht if f(t) is the rte of chnge of
Interpreting Integrls nd the Fundmentl Theorem Tody, we go further in interpreting the mening of the definite integrl. Using Units to Aid Interprettion We lredy know tht if f(t) is the rte of chnge of
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
MATH SPEAK - TO BE UNDERSTOOD AND MEMORIZED
 FOM 11 T20 RIGHT TRINGLE TRIGONOMETRY 1 MTH SPEK - TO E UNDERSTOOD ND MEMIZED 1) TRINGLE = 2-dimentionl she hving 3 sides nd 3 ngles. HRTERISTI OF TRINGLES I) Every tringle is n enclosed she tht hs these
FOM 11 T20 RIGHT TRINGLE TRIGONOMETRY 1 MTH SPEK - TO E UNDERSTOOD ND MEMIZED 1) TRINGLE = 2-dimentionl she hving 3 sides nd 3 ngles. HRTERISTI OF TRINGLES I) Every tringle is n enclosed she tht hs these
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Reflection Property of a Hyperbola
 Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
5. Every rational number have either terminating or repeating (recurring) decimal representation.
 CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
03. Early Greeks & Aristotle
 03. Erly Greeks & Aristotle I. Erly Greeks Topis I. Erly Greeks II. The Method of Exhustion III. Aristotle. Anximnder (. 60 B.C.) to peiron - the unlimited, unounded - fundmentl sustne of relity - underlying
03. Erly Greeks & Aristotle I. Erly Greeks Topis I. Erly Greeks II. The Method of Exhustion III. Aristotle. Anximnder (. 60 B.C.) to peiron - the unlimited, unounded - fundmentl sustne of relity - underlying
MAT 1275: Introduction to Mathematical Analysis
 MAT 75: Intrdutin t Mthemtil Anlysis Dr. A. Rzenlyum Trignmetri Funtins fr Aute Angles Definitin f six trignmetri funtins Cnsider the fllwing girffe prlem: A girffe s shdw is 8 meters. Hw tll is the girffe
MAT 75: Intrdutin t Mthemtil Anlysis Dr. A. Rzenlyum Trignmetri Funtins fr Aute Angles Definitin f six trignmetri funtins Cnsider the fllwing girffe prlem: A girffe s shdw is 8 meters. Hw tll is the girffe
Sample Problems for the Final of Math 121, Fall, 2005
 Smple Problems for the Finl of Mth, Fll, 5 The following is collection of vrious types of smple problems covering sections.8,.,.5, nd.8 6.5 of the text which constitute only prt of the common Mth Finl.
Smple Problems for the Finl of Mth, Fll, 5 The following is collection of vrious types of smple problems covering sections.8,.,.5, nd.8 6.5 of the text which constitute only prt of the common Mth Finl.
Trigonometry. Trigonometry. labelling conventions. Evaluation of areas of non-right-angled triangles using the formulas A = 1 ab sin (C )
 8 8 Pythgors theorem 8 Pythgoren trids 8 Three-dimensionl Pythgors theorem 8D Trigonometri rtios 8E The sine rule 8F miguous se of the sine rule 8G The osine rule 8H Speil tringles 8I re of tringles res
8 8 Pythgors theorem 8 Pythgoren trids 8 Three-dimensionl Pythgors theorem 8D Trigonometri rtios 8E The sine rule 8F miguous se of the sine rule 8G The osine rule 8H Speil tringles 8I re of tringles res
= = 6 radians 15. θ = s 30 feet (2π) = 13 radians. rad θ R, we have: 180 = 60
 SECTION - 7 CHAPTER Section. A positive ngle is produced y counterclockwise rottion from the initil side to the terminl side, negtive ngle y clockwise rottion.. Answers will vry. 5. Answers will vry. 7.
SECTION - 7 CHAPTER Section. A positive ngle is produced y counterclockwise rottion from the initil side to the terminl side, negtive ngle y clockwise rottion.. Answers will vry. 5. Answers will vry. 7.
= = 6 radians 15. θ = s 30 feet (2π) = 13 radians. rad θ R, we have: 180 = 60
 SECTION - 7 CHAPTER Section. A positive ngle is produced y counterclockwise rottion from the initil side to the terminl side, negtive ngle y clockwise rottion.. Answers will vry. 5. Answers will vry. 7.
SECTION - 7 CHAPTER Section. A positive ngle is produced y counterclockwise rottion from the initil side to the terminl side, negtive ngle y clockwise rottion.. Answers will vry. 5. Answers will vry. 7.
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
H (2a, a) (u 2a) 2 (E) Show that u v 4a. Explain why this implies that u v 4a, with equality if and only u a if u v 2a.
 Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
2.4 Linear Inequalities and Interval Notation
 .4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
.4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
Applications of Definite Integral
 Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
5Trigonometric UNCORRECTED PAGE PROOFS. ratios and their applications
 5Trigonometri rtios nd their pplitions 5.1 Kik off with CS 5.2 Trigonometry of right-ngled tringles 5.3 Elevtion, depression nd erings 5.4 The sine rule 5.5 The osine rule 5.6 rs, setors nd segments 5.7
5Trigonometri rtios nd their pplitions 5.1 Kik off with CS 5.2 Trigonometry of right-ngled tringles 5.3 Elevtion, depression nd erings 5.4 The sine rule 5.5 The osine rule 5.6 rs, setors nd segments 5.7
Section 11.2: The Law of Sines, from College Trigonometry: Corrected Edition by Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a
 Setion 11.: The Lw of Sines, from College Trigonometry: Correted Edition y Crl Stitz, Ph.D. nd Jeff Zeger, Ph.D. is ville under Cretive Commons Attriution-NonCommeril-ShreAlike 3.0 liense. 013, Crl Stitz.
Setion 11.: The Lw of Sines, from College Trigonometry: Correted Edition y Crl Stitz, Ph.D. nd Jeff Zeger, Ph.D. is ville under Cretive Commons Attriution-NonCommeril-ShreAlike 3.0 liense. 013, Crl Stitz.
