Lesson 2: The Pythagorean Theorem and Similar Triangles. A Brief Review of the Pythagorean Theorem.
|
|
|
- Noah Thornton
- 6 years ago
- Views:
Transcription
1 27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we ll the tringle right tringle. In right tringle, the two sides of the tringle tht form the right ngle re lled the legs of the right tringle, nd the side of the tringle whih is opposite to the right ngle is lled the hypotenuse of the tringle. leg hypotenuse right ngle leg Right Tringle We re now redy to stte: The Pythgoren Theorem. In tringle whih hs sides of lengths, nd, if the sides of length nd form right ngle, then side lengths stisfy the following eqution: = 2. In words, the Pythgoren Theorem sys The squre of the hypotenuse is equl to the sum of the squres of the other two sides.
2 28 There re mny different explntions of why the Pythgoren Theorem is true. These explntions re lled proofs of the Pythgoren Theorem nd we will give them more ttention lter in this lesson. 1 Here we fous on pplitions of the Pythgoren Theorem. We now present three smple pplitions of the Pythgoren Theorem. In eh pplition, we will use the Pythgoren Theorem to find the unknown side length. When performing these lultions, we will py reful ttention to the units in whih the given dt is presented, nd we will oey the two Clultion Rules stted in Lesson 1. Applition m =? 3.3 m In the tringle shown ove, the lengths of two sides re given to the nerest tenth of meter. In this sitution Clultion Rule 2 tells us tht our finl nswer for side length should e expressed to the nerest tenth of meter. Aording to the Pythgoren Theorem: Hene, Using poket lultor, we find tht 2 = (3.3) 2 + (4.4) 2. = (3.3) 2 + (4.4) 2. (3.3) 2 + (4.4) 2 = 5.5 meters. In this lultion, we re fortunte. The nswer produed y the lultor requires no rounding. Hene, the solution to this prolem is: 1 Here re four wesites tht present vriety of proofs of the Pythgoren Theorem: The first site displys n esily understood nimted proof. The seond site ontins 43 different proofs. The third site views the proof in the first site from more sophistited perspetive tht revels the proof to e one of fmily of similr proofs. The fourth site gives rief history of the Theorem, speultion out how it ws disovered, nd referenes to other interesting sites.
3 29 = 5.5 m to the nerest tenth of meter. Applition 2. =? 19 in 8 in In the tringle shown ove, the lengths of two sides re given to the nerest inh. Thus, ording to Clultion Rule 2, our finl nswer for side length should e expressed to the nerest inh. Here, the Pythgoren Theorem implies tht Hene, Therefore, Using poket lultor, we find tht = = = 19 2 " " 8 2 = We round to the nerest inh, to otin the solution to this prolem: = 17 in to the nerest inh. Applition 3. =? = 1342 miles = 1980 miles to the nerest 10 miles In the tringle pitured ove, the lest urte mesurement is in units of 10 miles. Therefore, Clultion Rule 2 stipultes tht our finl nswer should e in units of 10 miles (even though one of the lengths is given in 1 mile units). The Pythgoren Theorem implies tht =
4 30 Notie tht we do not round the numer 1342 to 1340 even though our finl nswer must e in units of 10 miles. Here we re oeying Clultion Rule 1 whih tells us tht to preserve ury we should not do ny rounding until the end of the lultion. Hene, Using poket lultor, we find tht = " " = We round to the nerest 10 miles to otin the solution to this prolem: = 1460 miles to the nerest 10 miles. Ativity 1. Different groups should work on prolems ) nd ) elow nd report their solutions to the lss. The lss should disuss ny disrepnies in the solutions. In eh prolem, find the unknown side length. Be sure to oey the two Clultion Rules. ) ) m =? =? 14 in 8.6 m 9.2 in Next we present n illustrtion of how the Clultion Rules sve us from error. Suppose we re given right tringle in whih oth legs mesure.1 m to the nerest tenth of entimeter. Let us lulte the length of the hypotenuse of this right tringle. Clultion Rule 2 instruts us to ompute the length of the hypotenuse in units of tenths of entimeter. Aording to the Pythgoren Theorem the length of the hypotenuse is (.1) 2 + (.1) 2 = =.02 =.1414? 0.1 m 0.1 m
5 31 Hene, rounded to the nerest tenth of entimeter, the length of the hypotenuse of this right tringle is.1 m. During this omputtion, we oeyed oth Clultions Rules 1 nd 2. We didn t round during the lultion, ut we rounded t the end of the lultion to mke our nswer hve the sme degree of ury s the dt given t the eginning of the prolem. Suppose we hd disoeyed Clultion Rule 1 y rounding the quntity.02 to the nerest tenth of entimeter efore we ompleted the lultion y tking squre root. This would hnge.02 to.0. Then the lultion would eome: (.1) 2 + (.1) 2 = =.02.0 = 0. We would thus rrive t the onlusion tht the length of the hypotenuse of this right tringle is 0 m to the nerest tenth of entimeter. Sine the legs of this tringle re.1 m eh nd sine the hypotenuse of right tringle is lwys longer thn its legs, this is n surd onlusion. Morl: Don t rek the two Clultion Rules. Notie tht we hve not used the onept of signifint figures in the preeding pplitions of the Pythgoren Theorem. In Lesson 1 we hd dvised the use of signifint figures in lultions involving multiplition or division prtiulrly when input dt is expressed in different units. Pythgoren Theorem lultions involve squring whih is form of multiplition. So it is not unresonle to think tht it would e pproprite to use signifint figures in these lultions. However, the method of signifint figures is only rule of thum to void inury whih doesn t lwys produe optimlly urte results. It turns out tht Pythgoren Theorem pplitions re lultions in whih the method of signifint figures sometimes retes inury. So we dvise not using signifint figures in these kinds of lultions. We illustrte how the use of signifint figures n introdue inury y reexmining Applition 2 ove. In pplition 2 we onsider right tringle in whih the hypotenuse hs length 19 inhes nd one leg hs length 8 inhes, oth to the nerest inh. We wnt to estimte the length of the other leg. Clultion yields = =? 19 in 8 in , figure whih must e rounded ppropritely. Beuse the input dt for this prolem ws given to the nerest inh, we rounded to the nerest inh to get =
6 32 17 inhes. However, if we were to use the method of signifint figures, then euse one of the input dt 8 inhes hs only one signifint figure, we would onsequently round to one signifint figure, otining = 20 inhes. This estimte is oviously inorret euse the length of leg must lwys e less thn the length of the hypotenuse whih is 19 inhes. To get more preise ide out the inury of the estimte = 20 inhes, we perform n intervl nlysis on this prolem. Let represent the length of the leg whih is 8 inhes to the nerest inh, nd let represent the length of the hypotenuse 19 inhes to the nerest inh. Then nd tully lie in the following rnges: nd Sine = 2 " 2, then the smllest possile vlue of is nd the lrgest possile vlue of is Thus, lies in the rnge = " = = " = This rnge omfortly ontins our originl estimte, = 17. However, the estimte = 20 otin y using signifint figures lies well outside this rnge. The length of this rnge is = Hene, the estimte = 20 lies frther ove the upper end, 18, of the rnge thn the entire length of the rnge! Thus, the use of signifint figures in this lultion introdues signifint mount of inury. Morl: Don t use signifint figures in Pythgoren Theorem lultions. A Brief Review of Similr Tringles Two tringles T nd T re similr if there is orrespondene etween the sides of T nd the sides of T nd there is rel numer r > 0 lled sle ftor suh tht the length of eh side of T is equl to r times the length of the orresponding side of T. In the figure on the next pge, suppose tht tringle T with side lengths, nd is similr to tringle T with side lengths, nd so tht the side of T of length orresponds to the side of T of length, the side of T of length orresponds to the side of T of length nd the side of T of length orresponds to the side of T of length. Then there is sle ftor r > 0 suh tht = r, = r nd = r.
7 33 T T We oserve tht in this sitution, the similrity of tringles T nd T n e expressed without expliitly mentioning the sle ftor r. This is euse the rtios ", " nd re ll equl to the sle ftor r. Hene the three equtions " = r, = r nd = r n e expressed without mentioning the sle ftor r y writing the equtions " = " = ". Furthermore, y ross-multiplying these equtions n e trnsformed into the equtions = ", = " nd = ". Thus, the similrity of tringles T nd T n e expressed y ny one of the following three different fmilies of similrity equtions: 1) = r, = r nd = r. 2) " = " = ". 3) = ", = " nd = ". In two of these fmilies of similrity equtions, the sle ftor doesn t pper. The importnt lesson for student onfronted with prolem involving similr tringles is: the student should use the fmily of similrity equtions tht provides the most help with the solving the prolem t hnd. The knk of hoosing the most helpful fmily of similrity equtions to solve prtiulr similr tringles prolem is prt of the rt of prolem solving. We mke seond oservtion out this sitution. The lengths, nd of the sides of tringle T must ll e expressed in the sme units. Similrly, the lengths, nd of the sides of tringle T must ll e expressed in the sme units. However,
8 34, nd n e expressed in different units from, nd! The three fmilies of similrity equtions will vlidly express the similrity of tringles T nd T even if the side lengths of T re mesured in different units thn the side lengths of T. There is no need to onvert the side lengths of T nd T to ommon units of mesure to use the similrity equtions. We will solve prolem elow whih illustrtes this oservtion; in this prolem the side lengths of T re expressed in inhes, the side lengths of T re expressed in entimeters, nd the prolem is solved without ever onverting to ommon unit of mesure. Aording to our definition, the similrity of two tringles depends on the rtios of side lengths of the two tringles. There is surprising nd useful geometri ft (or theorem) tht whih llows us to detet the similrity of two tringles, not from the lengths of their sides, ut insted from the mesures of their ngles. This theorem, whih we ll the Angle Theorem for Similr Tringles sys tht if two ngles in tringle T hve the sme mesure (i.e. size) s two ngles in tringle T, then tringles T nd T re similr. We stte this theorem more preisely: The Angle Theorem for Similr Tringles. Suppose T is tringle with side lengths, nd nd T is tringle with side lengths, nd. If the ngle in tringle T tht is opposite the side of length hs the sme mesure s the ngle in tringle T tht is opposite the side of length, nd the ngle in tringle T tht is opposite the side of length hs the sme mesure s the ngle in tringle T tht is opposite the side of length, then tringles T nd T re similr, nd, in prtiulr, there is sle ftor r > 0 suh tht = r, = r nd = r. (Then, of ourse, the other two fmilies of similrity equtions lso hold: " = " = " nd = ", = " nd = ".) T T We will now show how pply this theorem together with the two Clultion Rules to solve prolem. In the figure on the next pge, suppose two ngles in the tringle T on the left hve the sme mesures s two ngles in the tringle T on the
9 35 right (s indited). The lengths of two sides of T nd one side of T re given. Find the side length leled in tringle T in entimeters. =? 13 inhes T T 18 inhes 6.89 m Beuse two ngles in T hve the sme mesures s two ngles in T, the Angle Theorem for Similr Tringles implies tht T nd T re similr in suh wy tht the following eqution holds. Solving this eqution for, we get " 6.89 = = 6.89 x Using lultor, we evlute the expression on the right side of this eqution. Following Clultion Rule 1, we don t round t ny point during this lultion. For exmple, we don t lulte the frtion 13/18 nd round it efore multiplying y This lultion gives us: = Hving ompleted this lultion, we round the finl nswer following Clultion Rule 2. This lultion is n pproprite ple to use signifint figures, euse the input dt is expressed in different units (inhes nd entimeters) nd the lultion involves division. Our vlue for n e no more urte thn the lest urte input. Sine the two inputs 13 inhes nd 18 inhes hve only two signifint figures, then we should round our vlue for to hve only two signifint figures. This gives us: = 5.0 entimeters (to the nerest tenth of entimeter). Oserve tht the side lengths of T re expressed in inhes, the side lengths of T re expressed in entimeters, nd the prolem is solved without onverting the lengths to ommon unit of mesure.
10 36 Ativity 2. Eh group should work on the prolem stted elow nd report its solution to the lss. The lss should disuss ny disrepnies in the solutions. Be sure to oey the two Clultion Rules. As indited in the figure elow, two ngles in the tringle T on the left hve the sme mesures s two ngles in the tringle T on the right. The lengths of one side of T nd two sides of T re given. Find the side length leled in tringle T in inhes. 1.3 feet 1.83 feet 6.45 inhes =? T T
11 37 A Proof of the Pythgoren Theorem Ativity 3. Groups should work on the following prolem. This tivity is designed to led you to proof of the Pythgoren Theorem. Suppose you re given the tringle shown here whih hs sides of length, nd suh tht the sides of length nd form right ngle. The following tivity is designed to led you to proof of the eqution = 2. Below re two squres of the sme re, eh with sides of length +. We ll the squre on the left Big Squre 1 nd the squre on the right Big Squre 2. Big Squre 1 Big Squre 2 On the next pge re 11 figures: 8 opies of the ove tringle together with 3 squres, one of whih hs sides of length, nother of whih hs sides of length, nd the third of whih hs sides of length. Photoopy this pge onto stiffer pper if possile. Cut out the 11 figures in the photoopy nd rrnge them so tht they extly over the Big Squres 1 nd 2 without overlpping. Furthermore, over Big Squre 1
12 38 with 4 tringles nd the two squres of side lengths nd, nd over Big Squre 2 with 4 tringles nd the squre of side length. Compre the sum of the res of the figures overing Big Squre 1 to the sum of the res of the figures overing Big Squre 2. From this omprison, prove the eqution = 2.
13 39 Homework Prolem 1. This prolem hs prts ) through k). In prts ) through h), find the unknown side lengths. Be sure to oey the two Clultion Rules in ll prts of the prolem. ) ) 15.0 m =? =? 5.05 in 8.0 m 3.03 in ) d).01 km.02 km =? =? = 25 m = 60 m to the nerest 10m e) f) 3.5 ft 3.70 ft m x =? z =? m g) h) =?.5 m mi =?.16 m mi
14 40 i) The distne from the enter of the Erth to the enter of the Sun is 93,000,000 miles to the nerest 100,000 miles. The rdius of the Erth is 4000 miles to the nerest 100 miles. P is point on the surfe of the Erth with the property tht the line joining the enter of the Erth to P is perpendiulr to the line joining the enters of the Erth nd the Sun. How fr is P from the enter of the Sun? P 4000 mi? Sun Erth 93,000,000 mi j) A ldder lens ginst wll. The foot of the ldder is 3 feet 5 1 / 4 inhes from the ottom of the wll to the nerest qurter of n inh. The ldder is 12 feet long to the nerest inh. How high ove the ground is the top of the ldder? k) On piee of grph pper drw the x nd y xes nd lel units on these xes so tht you n plot the points A = (17,2), B = (2,19) nd C = (3,11) on the piee of pper. Clulte the perimeter of the tringle with verties A, B nd C to the nerest tenth of unit. Homework Prolem 2. In prts ) nd ) of this prolem, two ngles in the tringle on the left hve the sme mesures s two ngles in the tringle on the right (s indited). Find the unknown side lengths. Be sure to oey the two Clultion Rules. ) 2.7 in 237 mi =? 320 mi
15 41 ) 75 feet =? 98 feet.0583 m Homework Prolem 3. ) Refer to Ativity 3. Write out nd hnd in detiled nd reful explntion (i.e., proof) of why = 2. You my use fts out res of squres nd tringles in your proof. ) Adpt this rgument to the tringle with sides of length x, y nd z shown elow. In other words, drw two squres of side x + y nd sudivide them into squres nd tringles so tht the proof desried ove for the tringle with side lengths, nd n e modified to yield proof tht x 2 + y 2 = z 2. z y x Homework Prolem 4. The gol of this prolem is lso to led you to proof of the Pythgoren Theorem. This proof is different from the one presented in Ativity 3. Agin suppose you re given the tringle shown here whih hs sides of length, nd suh tht the sides of length nd form right ngle.
16 42 ) In the figure elow, we eret three squres on the sides of this tringle. One squre hs side length, the seond hs side length, nd the third hs side length. The squre of side length is sudivided y dotted lines. Photoopy this digrm onto stiffer pper if possile. Cut out the squre of side length nd ut it prt long the dotted lines to otin five piees. Show tht the five piees n e rrnged to over the two squres of side lengths nd with no overlp. Argue tht this proves = 2. ) Adpt this rgument to the tringle with sides of length x, y nd z shown elow. In other words, eret 3 squres on the sides of this tringle nd show how to sudivide the squre of side length z into five piees tht will extly over the two squres of side lengths x nd y. z y x
17 43 Homework Prolem 5. This prolem leds to yet nother proof of the Pythgoren Theorem. This proof is similr to the previous one. Agin strt with the tringle shown here with side lengths, nd nd right ngle etween the sides of length nd. ) Agin, in the figure elow, we eret three squres on the sides of this tringle. This time the ig squre with side length is sudivided y four dotted line segments. These dotted line segments re determined y the rule tht they re either horizontl or vertil nd one endpoint of eh dotted line segment is the midpoint of side of the ig squre. Agin, photoopy this digrm onto stiffer pper if possile, nd ut the ig squre prt long the dotted line segments to otin five piees, nd show tht the five piees n e rrnged to over the two smller squres with no overlp. Argue tht this proves = 2.
18 44 ) Adpt this rgument to the tringle with sides of length x, y nd z shown elow. z y x Homework Prolem 6. The gol of this prolem is to led you to proof of the Pythgoren Theorem tht ws known to the nient Chinese out 1000 BC. (Pythgors lived out 500 BC.) Suppose you re given the tringle T shown here whih hs sides of length, nd suh tht the sides of length nd form right ngle. T ) Consider the following two figures. The figure on the left is squre whih hs sides of length. The figure on the right is the union of two squres, one of whih hs sides of length nd the other of whih hs sides of length. Eh figure is sudivided y dotted lines into 5 piees: 4 opies of the originl tringle T nd squre. Compre the sum of the res of the piees mking up the squre on the left one with the sum of the res of the piees mking up the figure on the right. Try to derive the eqution = 2. (Hint: Eh figure ontins 4 tringles nd squre. How long re the sides of these squres?) T T T T T T T T
19 45 ) Adpt this rgument to the tringle with sides of length x, y nd z shown elow. z y x
20 46
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Part I: Study the theorem statement.
 Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
HS Pre-Algebra Notes Unit 9: Roots, Real Numbers and The Pythagorean Theorem
 HS Pre-Alger Notes Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Roots nd Cue Roots Syllus Ojetive 5.4: The student will find or pproximte squre roots of numers to 4. CCSS 8.EE.-: Evlute squre roots
HS Pre-Alger Notes Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Roots nd Cue Roots Syllus Ojetive 5.4: The student will find or pproximte squre roots of numers to 4. CCSS 8.EE.-: Evlute squre roots
Numbers and indices. 1.1 Fractions. GCSE C Example 1. Handy hint. Key point
 GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
Math Lesson 4-5 The Law of Cosines
 Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
Ellipses. The second type of conic is called an ellipse.
 Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
= x x 2 = 25 2
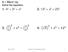 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
Pythagoras Theorem. Pythagoras Theorem. Curriculum Ready ACMMG: 222, 245.
 Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
 PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Non Right Angled Triangles
 Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Logarithms LOGARITHMS.
 Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
3 Angle Geometry. 3.1 Measuring Angles. 1. Using a protractor, measure the marked angles.
 3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
Trigonometry and Constructive Geometry
 Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
Pythagoras theorem and surds
 HPTER Mesurement nd Geometry Pythgors theorem nd surds In IE-EM Mthemtis Yer 8, you lernt out the remrkle reltionship etween the lengths of the sides of right-ngled tringle. This result is known s Pythgors
HPTER Mesurement nd Geometry Pythgors theorem nd surds In IE-EM Mthemtis Yer 8, you lernt out the remrkle reltionship etween the lengths of the sides of right-ngled tringle. This result is known s Pythgors
Green s Theorem. (2x e y ) da. (2x e y ) dx dy. x 2 xe y. (1 e y ) dy. y=1. = y e y. y=0. = 2 e
 Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
5. Every rational number have either terminating or repeating (recurring) decimal representation.
 CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
Lesson 8.1 Graphing Parametric Equations
 Lesson 8.1 Grphing Prmetric Equtions 1. rete tle for ech pir of prmetric equtions with the given vlues of t.. x t 5. x t 3 c. x t 1 y t 1 y t 3 y t t t {, 1, 0, 1, } t {4,, 0,, 4} t {4, 0,, 4, 8}. Find
Lesson 8.1 Grphing Prmetric Equtions 1. rete tle for ech pir of prmetric equtions with the given vlues of t.. x t 5. x t 3 c. x t 1 y t 1 y t 3 y t t t {, 1, 0, 1, } t {4,, 0,, 4} t {4, 0,, 4, 8}. Find
The Ellipse. is larger than the other.
 The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
1 ELEMENTARY ALGEBRA and GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE
 ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
10. AREAS BETWEEN CURVES
 . AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
. AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Pythagoras Theorem. The area of the square on the hypotenuse is equal to the sum of the squares on the other two sides
 Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Something found at a salad bar
 Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Section 2.1 Special Right Triangles
 Se..1 Speil Rigt Tringles 49 Te --90 Tringle Setion.1 Speil Rigt Tringles Te --90 tringle (or just 0-60-90) is so nme euse of its ngle mesures. Te lengts of te sies, toug, ve very speifi pttern to tem
Se..1 Speil Rigt Tringles 49 Te --90 Tringle Setion.1 Speil Rigt Tringles Te --90 tringle (or just 0-60-90) is so nme euse of its ngle mesures. Te lengts of te sies, toug, ve very speifi pttern to tem
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Plotting Ordered Pairs Using Integers
 SAMPLE Plotting Ordered Pirs Using Integers Ple two elsti nds on geoord to form oordinte xes shown on the right to help you solve these prolems.. Wht letter of the lphet does eh set of pirs nme?. (, )
SAMPLE Plotting Ordered Pirs Using Integers Ple two elsti nds on geoord to form oordinte xes shown on the right to help you solve these prolems.. Wht letter of the lphet does eh set of pirs nme?. (, )
Improper Integrals. The First Fundamental Theorem of Calculus, as we ve discussed in class, goes as follows:
 Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
Computing data with spreadsheets. Enter the following into the corresponding cells: A1: n B1: triangle C1: sqrt
 Computing dt with spredsheets Exmple: Computing tringulr numers nd their squre roots. Rell, we showed 1 ` 2 ` `n npn ` 1q{2. Enter the following into the orresponding ells: A1: n B1: tringle C1: sqrt A2:
Computing dt with spredsheets Exmple: Computing tringulr numers nd their squre roots. Rell, we showed 1 ` 2 ` `n npn ` 1q{2. Enter the following into the orresponding ells: A1: n B1: tringle C1: sqrt A2:
2.1 ANGLES AND THEIR MEASURE. y I
 .1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
.1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
Discrete Structures Lecture 11
 Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
Bridging the gap: GCSE AS Level
 Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Review Topic 14: Relationships between two numerical variables
 Review Topi 14: Reltionships etween two numeril vriles Multiple hoie 1. Whih of the following stterplots est demonstrtes line of est fit? A B C D E 2. The regression line eqution for the following grph
Review Topi 14: Reltionships etween two numeril vriles Multiple hoie 1. Whih of the following stterplots est demonstrtes line of est fit? A B C D E 2. The regression line eqution for the following grph
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
NON-DETERMINISTIC FSA
 Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Similar Right Triangles
 Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Matrices SCHOOL OF ENGINEERING & BUILT ENVIRONMENT. Mathematics (c) 1. Definition of a Matrix
 tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
Chapter 8 Roots and Radicals
 Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
3.1 Review of Sine, Cosine and Tangent for Right Angles
 Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
m m m m m m m m P m P m ( ) m m P( ) ( ). The o-ordinte of the point P( ) dividing the line segment joining the two points ( ) nd ( ) eternll in the r
 CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
Chapter 9 Definite Integrals
 Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
Naming the sides of a right-angled triangle
 6.2 Wht is trigonometry? The word trigonometry is derived from the Greek words trigonon (tringle) nd metron (mesurement). Thus, it literlly mens to mesure tringle. Trigonometry dels with the reltionship
6.2 Wht is trigonometry? The word trigonometry is derived from the Greek words trigonon (tringle) nd metron (mesurement). Thus, it literlly mens to mesure tringle. Trigonometry dels with the reltionship
Calculus Cheat Sheet. Integrals Definitions. where F( x ) is an anti-derivative of f ( x ). Fundamental Theorem of Calculus. dx = f x dx g x dx
 Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Section 4.4. Green s Theorem
 The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
The Clulus of Funtions of Severl Vriles Setion 4.4 Green s Theorem Green s theorem is n exmple from fmily of theorems whih onnet line integrls (nd their higher-dimensionl nlogues) with the definite integrls
Review of Gaussian Quadrature method
 Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Exercise sheet 6: Solutions
 Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Interpreting Integrals and the Fundamental Theorem
 Interpreting Integrls nd the Fundmentl Theorem Tody, we go further in interpreting the mening of the definite integrl. Using Units to Aid Interprettion We lredy know tht if f(t) is the rte of chnge of
Interpreting Integrls nd the Fundmentl Theorem Tody, we go further in interpreting the mening of the definite integrl. Using Units to Aid Interprettion We lredy know tht if f(t) is the rte of chnge of
Reflection Property of a Hyperbola
 Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
Refletion Propert of Hperol Prefe The purpose of this pper is to prove nltill nd to illustrte geometrill the propert of hperol wherein r whih emntes outside the onvit of the hperol, tht is, etween the
Date Lesson Text TOPIC Homework. Solving for Obtuse Angles QUIZ ( ) More Trig Word Problems QUIZ ( )
 UNIT 5 TRIGONOMETRI RTIOS Dte Lesson Text TOPI Homework pr. 4 5.1 (48) Trigonometry Review WS 5.1 # 3 5, 9 11, (1, 13)doso pr. 6 5. (49) Relted ngles omplete lesson shell & WS 5. pr. 30 5.3 (50) 5.3 5.4
UNIT 5 TRIGONOMETRI RTIOS Dte Lesson Text TOPI Homework pr. 4 5.1 (48) Trigonometry Review WS 5.1 # 3 5, 9 11, (1, 13)doso pr. 6 5. (49) Relted ngles omplete lesson shell & WS 5. pr. 30 5.3 (50) 5.3 5.4
Trigonometric Functions
 Exercise. Degrees nd Rdins Chpter Trigonometric Functions EXERCISE. Degrees nd Rdins 4. Since 45 corresponds to rdin mesure of π/4 rd, we hve: 90 = 45 corresponds to π/4 or π/ rd. 5 = 7 45 corresponds
Exercise. Degrees nd Rdins Chpter Trigonometric Functions EXERCISE. Degrees nd Rdins 4. Since 45 corresponds to rdin mesure of π/4 rd, we hve: 90 = 45 corresponds to π/4 or π/ rd. 5 = 7 45 corresponds
( ) 1. 1) Let f( x ) = 10 5x. Find and simplify f( 2) and then state the domain of f(x).
 Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx
![Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx Formula for Trapezoid estimate using Left and Right estimates: Trap( n) If the graph of f is decreasing on [a, b], then f ( x ) dx](/thumbs/79/79316452.jpg) Fill in the Blnks for the Big Topis in Chpter 5: The Definite Integrl Estimting n integrl using Riemnn sum:. The Left rule uses the left endpoint of eh suintervl.. The Right rule uses the right endpoint
Fill in the Blnks for the Big Topis in Chpter 5: The Definite Integrl Estimting n integrl using Riemnn sum:. The Left rule uses the left endpoint of eh suintervl.. The Right rule uses the right endpoint
ILLUSTRATING THE EXTENSION OF A SPECIAL PROPERTY OF CUBIC POLYNOMIALS TO NTH DEGREE POLYNOMIALS
 ILLUSTRATING THE EXTENSION OF A SPECIAL PROPERTY OF CUBIC POLYNOMIALS TO NTH DEGREE POLYNOMIALS Dvid Miller West Virgini University P.O. BOX 6310 30 Armstrong Hll Morgntown, WV 6506 millerd@mth.wvu.edu
ILLUSTRATING THE EXTENSION OF A SPECIAL PROPERTY OF CUBIC POLYNOMIALS TO NTH DEGREE POLYNOMIALS Dvid Miller West Virgini University P.O. BOX 6310 30 Armstrong Hll Morgntown, WV 6506 millerd@mth.wvu.edu
MCH T 111 Handout Triangle Review Page 1 of 3
 Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
2.4 Linear Inequalities and Interval Notation
 .4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
.4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
Section 4: Integration ECO4112F 2011
 Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
List all of the possible rational roots of each equation. Then find all solutions (both real and imaginary) of the equation. 1.
 Mth Anlysis CP WS 4.X- Section 4.-4.4 Review Complete ech question without the use of grphing clcultor.. Compre the mening of the words: roots, zeros nd fctors.. Determine whether - is root of 0. Show
Mth Anlysis CP WS 4.X- Section 4.-4.4 Review Complete ech question without the use of grphing clcultor.. Compre the mening of the words: roots, zeros nd fctors.. Determine whether - is root of 0. Show
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
I1 = I2 I1 = I2 + I3 I1 + I2 = I3 + I4 I 3
 2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
1.3 SCALARS AND VECTORS
 Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Trigonometry. Trigonometry. labelling conventions. Evaluation of areas of non-right-angled triangles using the formulas A = 1 ab sin (C )
 8 8 Pythgors theorem 8 Pythgoren trids 8 Three-dimensionl Pythgors theorem 8D Trigonometri rtios 8E The sine rule 8F miguous se of the sine rule 8G The osine rule 8H Speil tringles 8I re of tringles res
8 8 Pythgors theorem 8 Pythgoren trids 8 Three-dimensionl Pythgors theorem 8D Trigonometri rtios 8E The sine rule 8F miguous se of the sine rule 8G The osine rule 8H Speil tringles 8I re of tringles res
INTEGRATION. 1 Integrals of Complex Valued functions of a REAL variable
 INTEGRATION NOTE: These notes re supposed to supplement Chpter 4 of the online textbook. 1 Integrls of Complex Vlued funtions of REAL vrible If I is n intervl in R (for exmple I = [, b] or I = (, b)) nd
INTEGRATION NOTE: These notes re supposed to supplement Chpter 4 of the online textbook. 1 Integrls of Complex Vlued funtions of REAL vrible If I is n intervl in R (for exmple I = [, b] or I = (, b)) nd
The University of Nottingham SCHOOL OF COMPUTER SCIENCE A LEVEL 2 MODULE, SPRING SEMESTER MACHINES AND THEIR LANGUAGES ANSWERS
 The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
Chapter Gauss Quadrature Rule of Integration
 Chpter 7. Guss Qudrture Rule o Integrtion Ater reding this hpter, you should e le to:. derive the Guss qudrture method or integrtion nd e le to use it to solve prolems, nd. use Guss qudrture method to
Chpter 7. Guss Qudrture Rule o Integrtion Ater reding this hpter, you should e le to:. derive the Guss qudrture method or integrtion nd e le to use it to solve prolems, nd. use Guss qudrture method to
Section 6: Area, Volume, and Average Value
 Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Symmetrical Components 1
 Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
Symmetril Components. Introdution These notes should e red together with Setion. of your text. When performing stedy-stte nlysis of high voltge trnsmission systems, we mke use of the per-phse equivlent
Polynomials. Polynomials. Curriculum Ready ACMNA:
 Polynomils Polynomils Curriulum Redy ACMNA: 66 www.mthletis.om Polynomils POLYNOMIALS A polynomil is mthemtil expression with one vrile whose powers re neither negtive nor frtions. The power in eh expression
Polynomils Polynomils Curriulum Redy ACMNA: 66 www.mthletis.om Polynomils POLYNOMIALS A polynomil is mthemtil expression with one vrile whose powers re neither negtive nor frtions. The power in eh expression
Part 4. Integration (with Proofs)
 Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
A study of Pythagoras Theorem
 CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins
CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins
STRAND J: TRANSFORMATIONS, VECTORS and MATRICES
 Mthemtics SKE: STRN J STRN J: TRNSFORMTIONS, VETORS nd MTRIES J3 Vectors Text ontents Section J3.1 Vectors nd Sclrs * J3. Vectors nd Geometry Mthemtics SKE: STRN J J3 Vectors J3.1 Vectors nd Sclrs Vectors
Mthemtics SKE: STRN J STRN J: TRNSFORMTIONS, VETORS nd MTRIES J3 Vectors Text ontents Section J3.1 Vectors nd Sclrs * J3. Vectors nd Geometry Mthemtics SKE: STRN J J3 Vectors J3.1 Vectors nd Sclrs Vectors
CS 491G Combinatorial Optimization Lecture Notes
 CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
Surds and Indices. Surds and Indices. Curriculum Ready ACMNA: 233,
 Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
5Trigonometric UNCORRECTED PAGE PROOFS. ratios and their applications
 5Trigonometri rtios nd their pplitions 5.1 Kik off with CS 5.2 Trigonometry of right-ngled tringles 5.3 Elevtion, depression nd erings 5.4 The sine rule 5.5 The osine rule 5.6 rs, setors nd segments 5.7
5Trigonometri rtios nd their pplitions 5.1 Kik off with CS 5.2 Trigonometry of right-ngled tringles 5.3 Elevtion, depression nd erings 5.4 The sine rule 5.5 The osine rule 5.6 rs, setors nd segments 5.7
Sect 10.2 Trigonometric Ratios
 86 Sect 0. Trigonometric Rtios Objective : Understnding djcent, Hypotenuse, nd Opposite sides of n cute ngle in right tringle. In right tringle, the otenuse is lwys the longest side; it is the side opposite
86 Sect 0. Trigonometric Rtios Objective : Understnding djcent, Hypotenuse, nd Opposite sides of n cute ngle in right tringle. In right tringle, the otenuse is lwys the longest side; it is the side opposite
Lecture 3. In this lecture, we will discuss algorithms for solving systems of linear equations.
 Lecture 3 3 Solving liner equtions In this lecture we will discuss lgorithms for solving systems of liner equtions Multiplictive identity Let us restrict ourselves to considering squre mtrices since one
Lecture 3 3 Solving liner equtions In this lecture we will discuss lgorithms for solving systems of liner equtions Multiplictive identity Let us restrict ourselves to considering squre mtrices since one
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
 Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Precalculus Notes: Unit 6 Law of Sines & Cosines, Vectors, & Complex Numbers. A can be rewritten as
 Dte: 6.1 Lw of Sines Syllus Ojetie: 3.5 Te student will sole pplition prolems inoling tringles (Lw of Sines). Deriing te Lw of Sines: Consider te two tringles. C C In te ute tringle, sin In te otuse tringle,
Dte: 6.1 Lw of Sines Syllus Ojetie: 3.5 Te student will sole pplition prolems inoling tringles (Lw of Sines). Deriing te Lw of Sines: Consider te two tringles. C C In te ute tringle, sin In te otuse tringle,
Math 32B Discussion Session Week 8 Notes February 28 and March 2, f(b) f(a) = f (t)dt (1)
 Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
Green s Theorem Mth 3B isussion Session Week 8 Notes Februry 8 nd Mrh, 7 Very shortly fter you lerned how to integrte single-vrible funtions, you lerned the Fundmentl Theorem of lulus the wy most integrtion
