HS Pre-Algebra Notes Unit 9: Roots, Real Numbers and The Pythagorean Theorem
|
|
|
- Gertrude Hunter
- 6 years ago
- Views:
Transcription
1 HS Pre-Alger Notes Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Roots nd Cue Roots Syllus Ojetive 5.4: The student will find or pproximte squre roots of numers to 4. CCSS 8.EE.-: Evlute squre roots of smll perfet squres nd ue roots of smll perfet ues. The squre root of numer n is numer m suh tht m n. The rdil sign,, represents the nonnegtive squre root. The symol ±, red plus or minus, refers to oth the positive nd negtive squre root. Therefore, the squre roots of 6 re 6 nd 6, euse 6 6 nd ( 6) 6. Also, 6 6, 6 6, nd ± 6 ± 6. We understnd tht will e the positive vlue. We refer to this s the prinipl squre root. Students should memorize the vlues of the squres for 1 through. These perfet squres (squres of integers) re listed elow: Perfet s: Simplifying expressions suh s the 5 nd 64 re pretty stright forwrd. 5 5 nd Even expressions like re esy to simplify one we see n exmple But wht if the expression is lrge, like 576? We will onsider method for determining this nswer whih extends eyond wht is required y the CCSS. Consider the perfet squres of few multiples of 1: nd so on... MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 1 of 19 Revised 1 - CCSS
2 Now to find 576 : 4 < 576 < 9 Identify perfet squres losest to < 576 < 9 Tke positive squre root of eh numer. < 576 < Evlute squre root of eh perfe t squre tht I know. Vlues we now need to onsider re 1,,, 4, 5, 6, 7, 8, nd 9. But wit! Sine we know n even even even, our nswer must e even. So now our nswer hoies re redued to, 4, 6, nd 8. We now need to sk ourselves whih of those nswer hoies will give us 6 in the one s ple ( 576 ). There re only two: 4 (sine 4 16 ) nd 6 (sine 6 6). Sine 576 is loser to 4 thn it is to 9, we quikly know tht the nswer is 4. A quik hek will identify 4 s the nswer: Let s look t nother exmple, finding < 15 < 16 Identify perfet squres losest to < 15 < 16 Tke positive squre root of eh numer. < 15 < 4 Evlute squre root of e h perfet squre tht I know. The vlues we need to onsider re 1,,, 4, 5, 6, 7, 8, nd 9. Sine our rdind is odd, we ondense those onsidertions to 1,, 5, 7, nd 9. However, if we look t the rdind 15, we n quikly reognize tht the only numer whose squre will give us 5 is 5. We hve our nswer very quikly! In review, evlute the following: 16, 16, ± denotes the prinipl (positive) squre root, so the nswer is 4 euse 16 denotes the negtive squre root, so the nswer is 4 euse ± 16 denotes the positive nd negtive squre roots. It is red plus or minus the squre root of 16. The nswer is ± 4 euse (4)(4) 16 nd ( 4)( 4) 16. Speil Cses: root of :. Sine is neither positive nor negtive, only hs one squre root. There should e mention of the squre root of negtive numer: negtive numers hve no rel squre roots, euse the squre of every rel numer is nonnegtive. Emphsize tht negtive numers hve no REAL squre roots (they hve imginry roots) not tht negtive numers hve no squre roots. MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge of 19 Revised 1 - CCSS ( )
3 The ue root of numer n is numer m suh tht m n. The rdil sign,, represents the ue root. Therefore, the ue root of 8 is, euse 8. Students should memorize the vlues of the ues for 1 through 5. These perfet ues (ues of integers) re listed elow: Perfet Cues: Therefore, 64 4 (sine 4 64). NOTE: Whenever there is n even numer of identil ftors, the produt will positive euse every pir of identil ftors hs positive produt positive positive positive ( 5)( 5) 5 negtive negtive positive However, when there is n odd numer of n identil ftor, the produt will hve the sme sign s the ftors. So, while negtive squre root is imginry, negtive ue root is possile positive positive positive positive ( 5)( 5)( 5) 15 negtive negtive negtive negtive So 8 nd 7. (Note: onsidertion of negtive numers is not inluded in the CCSS for this grde level.) Simplifying Roots To simplify squre root, you rewrite the rdind s produt of the lrgest perfet squre tht is ftor nd some other numer. You then tke the squre root of the perfet squre. Exmple: Simplify 5. Now 5 n e written s produt of 5 nd 1. Should I use those ftors? Hopefully, you sid no. We wnt to rewrite the rdind s produt of the lrgest perfet squre, nd neither 5 nor 1 re perfet squres. So, looking t my list of perfet squres, whih, if ny, re ftors of 5? MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge of 19 Revised 1 - CCSS
4 Tht s right, 5 is ftor of 5 nd it is perfet squre. Simplifying, I now hve Exmple: Simplify 98x y xy x y 7 x y 7x y Exmple: Simplify Solving Equtions using Root nd Cue Root CCSS 8.EE.-1: Use squre root nd ue root symols to represent solutions to equtions of the form x p nd x p, where p is positive rtionl numer. We re now redy to solve equtions in the form x. Exmple: Solve x 9. Solve 5 p x x 9 9 x ± 5 5 ± 15 p p p MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 4 of 19 Revised 1 - CCSS
5 Exmple: Solve x 8 Solve 15 r x x 8 x 8 15 r 15 5 r r Rel Numers CCSS 8.NS.1-1: Know tht numers tht re not rtionl re lled irrtionl. CCSS 8.EE.-: Know tht is irrtionl. The set of rel numers onsists of ll rtionl nd irrtionl numers. This reltionship n e shown in Venn digrm. Rel Numers Counting/Nturl Numers {1,, } Integers Whole Numers {, 1,, } Rtionl Numers {, 1,,1,, } Irrtionl Numers π A rtionl numer is numer tht n e written s quotient of two integers. The deiml form repets or termintes. An irrtionl numer is numer tht nnot e written s quotient of two integers. The deiml form neither termintes nor repets. You n illustrte n irrtionl numer y hving students try to "Think of numer, when multiplied y itself, equls. Perhps we re finding the length of the side of squre when we know the re is. Or for more visul representtion, use tngrms s disussed elow. MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 5 of 19 Revised 1 - CCSS
6 The tsk is to ompre the three squres nd try to estimte the side length of the middle squre. side 1 unit side? side units re 1 squre unit re squre units re 4 squre units You n tell tht the smll squre is 1 y 1, so its re is 1 squre unit. The iggest squre hs units on side, so its re is 4 squre units euse it is y. But the middle squre is mde from 4 hlf-squres, so it must hve n re of squre units. Wht is its side length? nd 4. But? By mthing the sides to eh other, students n see tht the unknown side is etween 1 nd, perhps 1 nd hlf. Hve students get out lultors nd try 1.5 times 1.5 nd mke tle, with lrge gp etween 1 nd. side length re Students will find 1.5 to e too lrge (.5) nd 1.4 to e too smll (1.96). Wht numer squred will mke? It must e etween 1.4 nd 1.5. MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 6 of 19 Revised 1 - CCSS
7 Further investigtion: side length re This is n exellent form of interpoltion tht tehers n uild upon to lrify ple vlue in the deimls. Let students go for s long s they wnt within reson, getting ever loser y never rehing extly. Review some repeting deimls. By now students re redy to her tht there re some speil numers tht will never repet s deimls, silly rtios tht go on to infinity with no repeting pttern. We were looking for one of them ( ) nd it does not repet. In ft, these deiml ples will only round to when squred rised to the seond power. Insted of rememering the deiml nd sying it is when squred, we hve etter wy to del with this. The side length, tht when squred is, we ll the squre root of nd write it. It n never e expressed s repeting deiml euse it is not the rtio of two numers, like 1/6 or /8. Therefore it is lled irrtionl. (You might hve students explore the squre root key on the lultor to see how mny deiml ples they get.) Another wy to model is to wit until you hve introdued the Pythgoren Theorem. Drw right tringle with eh leg mesuring 1 unit. Find the length of the hypotenuse of the right tringle y using the Pythgoren Theorem MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 7 of 19 Revised 1 - CCSS
8 Approximting Roots CCSS 8.NS.-: Estimte the vlue of irrtionl expressions (e.g., π ) You n use perfet squres to pproximte the squre root of numer. Exmple: Approximte 5 to the nerest integer. First, find the perfet squre tht is losest ut less thn 5. Tht would e 49. The perfet squre losest to 5 ut greter thn 5 is 64. So, 5 is etween 49 nd < 5 < 64 Identify perfet squres losest to < 5 < 64 Tke positive squre root of eh numer. 7 < 5 < 8 Evlute squre root of eh perfet squre. Beuse 5 is loser to 49, 5 is loser to 7. Therefore, 5 7. Students n pproximte squre roots y itertive proesses. Exmple: Approximte the vlue of 5 to the nerest hundredth. Solution: Students strt with rough estimte sed upon perfet squres. 5 flls etween nd euse 5 flls etween 4 nd 9. The vlue will e loser to thn to. Students ontinue the itertive proess with the tenths ple vlue. 5 flls etween. nd. euse 5 flls etween nd The vlue is loser to.. Further itertion shows tht the vlue of 5 is etween. nd.4 sine. is nd.4 is Another wy to mke the estimte is shown elow: Exmple: Approximte 5. Strt s we did with the previous exmple. 49 < 5 < Determine the differene etween 49 (smller perfet squre) nd 5 (the rdind). The differene is 4. Then find the differene etween 49 (smller perfet squre) nd 64 (the lrger perfet squre). The differene is 15. We know tht 5 flls etween 7 nd 8. To pproximte the deiml, tke We would estimte Using lultor, we find 5 7.8, whih is very lose to our estimte! MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 8 of 19 Revised 1 - CCSS
9 CCSS 8.NS.-: Lote irrtionl numers pproximtely on numer line digrm. Exmple: Compre nd y estimting their vlues, plotting them on numer line, nd mking omprtive sttements. Solution: Sttements for the omprison ould inlude: is pproximtely 1.4 is etween the whole numers 1 nd is etween 1.7 nd 1.8 Ordering Rel Numers Syllus Ojetive 5.7: The student will ompre nd order rel numers. CCSS 8.NS.-1: Use rtionl pproximtions of irrtionl numers to ompre the size of irrtionl numers. Now is good time to return to the onept of ordering rel numers, inluding irrtionl numers. Exmple: Order the numers from lest to gretest: 4,, 4.1, 5 One wy to solve this would e to onvert ll terms into deiml form (or pproximte deiml form). 4 6 < 4 < 49 Identify perfet squres losest to 4. 6 < 4 < 49 Tke the positive squre root of ll terms. 6 < 4 < 7 Simplify the perfet squres tht I know. 5 4 will fll etween 6 nd 7, loser to < < 5 Identify perfet squres losest to. 16 < < 5 Tke the positive squre root of ll terms. 4 < < 5 Simplify the perfet squres tht I know. will fll etween 4 nd 5, loser to 5. Thus will fll loser to 5 thn 4. So I would order these numers from lest to gretest: loser to 5, 4.1, 4.4, loser to 6. Tht trnsltes to, 4.1,, 4. 5 MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 9 of 19 Revised 1 - CCSS
10 The Pythgoren Theorem Syllus Ojetive 5.6: The student will explin the Pythgoren Theorem. CCSS 8.G.6-1: Explin proof of the Pythgoren Theorem nd its onverse. In right tringle, the side opposite the right ngle is lled the hypotenuse. The legs re the sides tht form the right ngle. We typilly lel the legs nd, while the hypotenuse is. hypotenuse legs If we look t enough right tringles nd experiment little, we will notie reltionship developing. Drw right tringle on piee of grph pper, with leg mesurements of units nd 4 units. Drw squre on eh side of the tringle s shown. Cut out squres A nd B nd ple them side y side. A B Tpe the repositioned tringles. Compre your new squre with squre C. A C Drw two tringles s shown; ut long the hypotenuses nd slide s shown. A B B A B It ppers tht the sum of the res of the squres formed y the legs is equl to the re of the squre formed y the hypotenuse. There is nother wy to look t this reltionship. MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 1 of 19 Revised 1 - CCSS
11 Begin with right tringle, legs nd with hypotenuse. Crete squre tht hs mesure + on side, using 4 ongruent tringles s shown. The re of this new squre n e expressed two wys: 1) A ( + ) (length of side is +, so multiply sides to get re) 1 ) A 4 + (4 tringles, eh with re of 1 ; dd to the re of the squre with side ) Setting these two vlues equl to eh other, we get ( ) This is n importnt reltionship in mthemtis. Sine it is importnt, we will give this reltionship nme, the Pythgoren Theorem. MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 11 of 19 Revised 1 - CCSS
12 And yet nother wy to model the theorem: Drw right tringle on piee of grph pper, with leg mesurements of units nd 4 units. Drw squre on eh side of the tringle s shown. Cut out squres eh, ongruent to A nd B, in two different olors Glue one A nd one B on the originl grph. Lel with the re. B A B A C Are 16 units B A Are 9 units C Hve students ut nd pste the remining squres (9 + 16) to form third squre C, whih represents the re of 5. Hve students ut nd pste the remining squres (9 + 16) to form third squre C, whih represents the re of 5. Are 16 units Are 9 units Are 5 units Finlly, hve students lel the legs of the originl right tringle with nd, hypotenuse. (This represents one possile solution.) It ppers tht the sum of the res of the squres formed y the legs is equl to the re of the squre formed y the hypotenuse, or +. Pythgoren Theorem: If tringle is right tringle, then +. MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 1 of 19 Revised 1 - CCSS
13 The onverse of the Pythgoren Theorem sys If tringle. Let s see if this seems to e true. +, then the tringle is right Fill in the first empty olumn in the hrt elow. Then, use grid strips ut to one squre width to rete the tringle with the side lengths given (see exmple elow the hrt). Does it pper to e right tringle? Is + true? Does this pper to e right tringle? true Yes, see elow Looks like right tringle. To model the onverse, use the exmple of the Egyptin rope-strethers. Some nient toms depit sries rrying ropes tied with 1 eqully sped knots. It turns out tht if the rope ws pegged to the ground in the dimensions of -4-5, right tringle would emerge. This enled the Anient Egyptin uilders to ly the foundtions for their uildings urtely. To model this, deide on unit length nd mke 1 knots (representing this unit s mesure) in piee of rope or twine. This wy you n hold the first nd lst knot together. Using people you n streth the rope into -4-5 tringle nd model where/how the right ngle ourred. Syllus Ojetive 5.5: The student will use the Pythgoren Theorem to solve prolems. CCSS 8.G.7-1: Apply the Pythgoren Theorem to determine unknown side lengths in right tringles in rel-world nd mthemtil prolems in two dimensions. Exmple: Find the unknown length in simplest form MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 1 of 19 Revised 1 - CCSS
14 Plese note tht this is one of our Pythgoren triples. A Pythgoren triple is set of three positive integers,,, nd suh tht +. Another triple worth noting is You n rete other Pythgoren triples y multiplying the originl triple y ftor. For instne, -4-5 eomes y multiplying ll the sides y. One might rete nother, 1-4-6, y multiplying the y. This skill is very vlule when working with prolems on the Nevd CRT nd NV High Shool Profiieny Exm. It n sve the student time nd frustrtion! Exmple: Find the unknown length If we reognize the ommon ftor of 5, we n think: This is leg nd the hypotenuse of the So the missing side would e 5 4, whih is. We hd -4-5 tht ws multiplied y ftor of 5 to produe So. Exmple: A 1-foot ldder is pled ginst uilding. The foot of the ldder is 5 feet from the se of the uilding. How high up the side of the uilding does the ldder reh? Give your nswer to the nerest foot < 119 < 11 1 < 119 < 11 1 < 119 < 11 Sine 119 is loser to 11, 119 is loser to 11. Therefore, the ldder rehes pproximtely 11 feet up the side of the uilding. 1 ft 5 ft MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 14 of 19 Revised 1 - CCSS
15 Exmple: You use four stkes nd string to mrk the foundtion of house. You wnt to mke sure the foundtion is retngulr. The four sides mesure ft, 7 ft, ft nd 7 ft. You then mesure digonl to e 78 ft. Is your foundtion retngulr? The digonl divides the foundtion into tringles. If the tringles re right tringles, + will e true sttement. Beuse ( ), you n onlude tht the tringles re right nd your foundtion is retngulr. CCSS 8.G.7-: Apply the Pythgoren Theorem to determine unknown side lengths in right tringles in rel-world nd mthemtil prolems in three dimensions. Exmple: Find the length of the longest line segment (lled the min digonl) in the retngulr prism shown on the piture elow. Solution: We will pply the Pythgoren Theorem twie. First, lel the points nd sides tht will used on the piture. We will find x using the Pythgoren Theorem in tringle ABC. Then we n find y using the Pythgoren Theorem in tringle ACD. For ABC, x x 41 x We do not hve to simplify x s we need it in tht form in the Pythgoren Theorem: MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 15 of 19 Revised 1 - CCSS
16 For ACD, y 45 y 45 y 45 y The length of the min digonl would e 45 feet (or pproximtely 6.7 feet). Note: Our result is tully Indeed, we n see tht the length of the min digonl in retngulr prism with sides x, y, nd z is L x + y + z. This is sometimes lled the -dimensionl Pythgoren Theorem. Another Retngulr Box prolem: You hve huge retngulr ox with dimensions1ft 15ft 9ft. Wht is the length of the longest rod you ould fit in your ox? 9 ft 15 ft 1 ft Solution: We will pply the Pythgoren Theorem twie. First, lel the points nd sides tht will used on the piture. We will find AC using the Pythgoren Theorem in tringle ABC. n find AD using the Pythgoren Theorem in tringle ACD. Then we For ABC, x D x 69 x For ACD, y 9 ft A 1 ft B 15 ft C 45 y 45 y 45 y The length of the longest rod would e 45 feet (or pproximtely 1. feet). MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 16 of 19 Revised 1 - CCSS
17 The Distne nd Midpoint Formuls Syllus Ojetive 5.8: The student will use distne nd midpoint formuls. CCSS 8.G.8: Apply the Pythgoren Theorem to find the distne etween two points in oordinte system. Tke the time to link the distne formul with the Pythgoren Theorem. Here s wy to show it. You re given two points, (, 1) nd (6, 5). You re sked to find the distne etween them. Plot the points You n drw right tringle, using these points s two of the verties, s shown Find the lengths of the horizontl nd vertil sides of the right tringle y sutrting the x- nd y- vlues. or You ould simply ount the units from one point to the next. 6 4 (, 1) 4 6 (6, 5) We now will use the Pythgoren Theorem to find the missing length, whih is the hypotenuse. + ( 6 ) ( 5 1) ± 5; however, sine we re looking t mesurement, only the positive vlue will e onsidered. 6 MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 17 of 19 Revised 1 - CCSS
18 Now, insted of using the ordered pirs (, 1) nd (6, 5), we use pir of points, x, y nd x, y. Sustituting into the Pythgoren Theorem one gin: ( ) ( ) ( ) ( ) x x1 + y + y1 ( ) ( ) 1 1 x x + y + y Sine we re determining distne, we reple the with d, nd we will only onsider the positive vlue. So we now hve the distne formul: ( ) ( ) d x x + y y 1 1 Exmple: Find the distne etween the points A(, 1 ) nd B(, 5) ( ) ( ) d x x + y y 1 1 ( ) 5 ( 1) d + ( ) 4 6 d +. d d ( 5 is etween 7 nd 8, ut loser to 7) d 4 1 d 1 The distne etween the points A(, 1 ) nd B(, 5) is 5 or 1 units. Sine 49 < 5 < 64 7 < 5 < 8 nd. then 5 7. units 15 Students need to know the midpoint formul lso. Consider the line segment with endpoints (, 1 ) nd ( 6, 5 ) MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 18 of 19 Revised 1 - CCSS
19 The midpoint is the point on the segment tht is equidistnt from the endpoints. We re looking for the middle! If we think of this s finding the verge, we ould dd the two x vlues nd divide y. We ould likewise verge the y vlues. Finding the verge for our exmple, it ppers the midpoint is t (4, ). x1 y1 x y, we n rrive t the formul for finding the midpoint: x 1+ x 1, y + M y If we use endpoints (, ) nd (, ) Exmple: Find the midpoint of the segment with endpoints ( 5, 7 ) nd ( 1, 5). x1+ x y1+ y M, 5+ ( 1) 7+ ( 5) M, 5+ 1 M (, 6) The midpoint of the segment with endpoints ( 5, 7 ) nd ( 1, 5) is (, 6) MDougl Littell, Chpter 9, Setions 1-5 HS Pre-Alger, Unit 9: Roots, Rel Numers nd The Pythgoren Theorem Pge 19 of 19 Revised 1 - CCSS
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
Chapter 8 Roots and Radicals
 Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
= x x 2 = 25 2
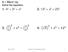 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Plotting Ordered Pairs Using Integers
 SAMPLE Plotting Ordered Pirs Using Integers Ple two elsti nds on geoord to form oordinte xes shown on the right to help you solve these prolems.. Wht letter of the lphet does eh set of pirs nme?. (, )
SAMPLE Plotting Ordered Pirs Using Integers Ple two elsti nds on geoord to form oordinte xes shown on the right to help you solve these prolems.. Wht letter of the lphet does eh set of pirs nme?. (, )
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
Lesson 2: The Pythagorean Theorem and Similar Triangles. A Brief Review of the Pythagorean Theorem.
 27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Pythagoras Theorem. Pythagoras Theorem. Curriculum Ready ACMMG: 222, 245.
 Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
Math 7, Unit 9: Measurement: Two-Dimensional Figures Notes
 Mth 7, Unit 9: Mesurement: Two-Dimensionl Figures Notes Precision nd Accurcy Syllus Ojective: (6.) The student will red the pproprite mesurement tool to the required degree of ccurcy. We often use numers
Mth 7, Unit 9: Mesurement: Two-Dimensionl Figures Notes Precision nd Accurcy Syllus Ojective: (6.) The student will red the pproprite mesurement tool to the required degree of ccurcy. We often use numers
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
5. Every rational number have either terminating or repeating (recurring) decimal representation.
 CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
Similar Right Triangles
 Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Ellipses. The second type of conic is called an ellipse.
 Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Part I: Study the theorem statement.
 Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Something found at a salad bar
 Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Pythagoras theorem and surds
 HPTER Mesurement nd Geometry Pythgors theorem nd surds In IE-EM Mthemtis Yer 8, you lernt out the remrkle reltionship etween the lengths of the sides of right-ngled tringle. This result is known s Pythgors
HPTER Mesurement nd Geometry Pythgors theorem nd surds In IE-EM Mthemtis Yer 8, you lernt out the remrkle reltionship etween the lengths of the sides of right-ngled tringle. This result is known s Pythgors
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
1 ELEMENTARY ALGEBRA and GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE
 ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
 PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
Math 154B Elementary Algebra-2 nd Half Spring 2015
 Mth 154B Elementry Alger- nd Hlf Spring 015 Study Guide for Exm 4, Chpter 9 Exm 4 is scheduled for Thursdy, April rd. You my use " x 5" note crd (oth sides) nd scientific clcultor. You re expected to know
Mth 154B Elementry Alger- nd Hlf Spring 015 Study Guide for Exm 4, Chpter 9 Exm 4 is scheduled for Thursdy, April rd. You my use " x 5" note crd (oth sides) nd scientific clcultor. You re expected to know
Linear Algebra Introduction
 Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
( ) 1. 1) Let f( x ) = 10 5x. Find and simplify f( 2) and then state the domain of f(x).
 Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Pythagoras Theorem. The area of the square on the hypotenuse is equal to the sum of the squares on the other two sides
 Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Non Right Angled Triangles
 Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
THE KENNESAW STATE UNIVERSITY HIGH SCHOOL MATHEMATICS COMPETITION PART I MULTIPLE CHOICE NO CALCULATORS 90 MINUTES
 THE 08 09 KENNESW STTE UNIVERSITY HIGH SHOOL MTHEMTIS OMPETITION PRT I MULTIPLE HOIE For ech of the following questions, crefully blcken the pproprite box on the nswer sheet with # pencil. o not fold,
THE 08 09 KENNESW STTE UNIVERSITY HIGH SHOOL MTHEMTIS OMPETITION PRT I MULTIPLE HOIE For ech of the following questions, crefully blcken the pproprite box on the nswer sheet with # pencil. o not fold,
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Numbers and indices. 1.1 Fractions. GCSE C Example 1. Handy hint. Key point
 GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
List all of the possible rational roots of each equation. Then find all solutions (both real and imaginary) of the equation. 1.
 Mth Anlysis CP WS 4.X- Section 4.-4.4 Review Complete ech question without the use of grphing clcultor.. Compre the mening of the words: roots, zeros nd fctors.. Determine whether - is root of 0. Show
Mth Anlysis CP WS 4.X- Section 4.-4.4 Review Complete ech question without the use of grphing clcultor.. Compre the mening of the words: roots, zeros nd fctors.. Determine whether - is root of 0. Show
Bridging the gap: GCSE AS Level
 Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Naming the sides of a right-angled triangle
 6.2 Wht is trigonometry? The word trigonometry is derived from the Greek words trigonon (tringle) nd metron (mesurement). Thus, it literlly mens to mesure tringle. Trigonometry dels with the reltionship
6.2 Wht is trigonometry? The word trigonometry is derived from the Greek words trigonon (tringle) nd metron (mesurement). Thus, it literlly mens to mesure tringle. Trigonometry dels with the reltionship
10. AREAS BETWEEN CURVES
 . AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
. AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Math Lesson 4-5 The Law of Cosines
 Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
 Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Probability. b a b. a b 32.
 Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
Discrete Structures Lecture 11
 Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
BEGINNING ALGEBRA (ALGEBRA I)
 /0 BEGINNING ALGEBRA (ALGEBRA I) SAMPLE TEST PLACEMENT EXAMINATION Downlod the omplete Study Pket: http://www.glendle.edu/studypkets Students who hve tken yer of high shool lger or its equivlent with grdes
/0 BEGINNING ALGEBRA (ALGEBRA I) SAMPLE TEST PLACEMENT EXAMINATION Downlod the omplete Study Pket: http://www.glendle.edu/studypkets Students who hve tken yer of high shool lger or its equivlent with grdes
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
8Similarity UNCORRECTED PAGE PROOFS. 8.1 Kick off with CAS 8.2 Similar objects 8.3 Linear scale factors. 8.4 Area and volume scale factors 8.
 8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8. re nd volume scle fctors 8. Review U N O R R E TE D P G E PR O O FS 8.1 Kick off with S Plese refer to the Resources t in the Prelims
8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8. re nd volume scle fctors 8. Review U N O R R E TE D P G E PR O O FS 8.1 Kick off with S Plese refer to the Resources t in the Prelims
Green s Theorem. (2x e y ) da. (2x e y ) dx dy. x 2 xe y. (1 e y ) dy. y=1. = y e y. y=0. = 2 e
 Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Polynomials. Polynomials. Curriculum Ready ACMNA:
 Polynomils Polynomils Curriulum Redy ACMNA: 66 www.mthletis.om Polynomils POLYNOMIALS A polynomil is mthemtil expression with one vrile whose powers re neither negtive nor frtions. The power in eh expression
Polynomils Polynomils Curriulum Redy ACMNA: 66 www.mthletis.om Polynomils POLYNOMIALS A polynomil is mthemtil expression with one vrile whose powers re neither negtive nor frtions. The power in eh expression
I1 = I2 I1 = I2 + I3 I1 + I2 = I3 + I4 I 3
 2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
We use metres to measure length. There are 100 centimetres in a metre. a 6 m = cm b 3 m = cm c 9 m = cm
 Units of length metres We use metres to mesure length. There re 00 entimetres in metre. 00 m = m Convert these metres to entimetres: 6 m = m 3 m = m 9 m = m 600 300 900 Estimte nd then mesure the length
Units of length metres We use metres to mesure length. There re 00 entimetres in metre. 00 m = m Convert these metres to entimetres: 6 m = m 3 m = m 9 m = m 600 300 900 Estimte nd then mesure the length
Surds and Indices. Surds and Indices. Curriculum Ready ACMNA: 233,
 Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Before we can begin Ch. 3 on Radicals, we need to be familiar with perfect squares, cubes, etc. Try and do as many as you can without a calculator!!!
 Nme: Algebr II Honors Pre-Chpter Homework Before we cn begin Ch on Rdicls, we need to be fmilir with perfect squres, cubes, etc Try nd do s mny s you cn without clcultor!!! n The nth root of n n Be ble
Nme: Algebr II Honors Pre-Chpter Homework Before we cn begin Ch on Rdicls, we need to be fmilir with perfect squres, cubes, etc Try nd do s mny s you cn without clcultor!!! n The nth root of n n Be ble
The Ellipse. is larger than the other.
 The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
Computing data with spreadsheets. Enter the following into the corresponding cells: A1: n B1: triangle C1: sqrt
 Computing dt with spredsheets Exmple: Computing tringulr numers nd their squre roots. Rell, we showed 1 ` 2 ` `n npn ` 1q{2. Enter the following into the orresponding ells: A1: n B1: tringle C1: sqrt A2:
Computing dt with spredsheets Exmple: Computing tringulr numers nd their squre roots. Rell, we showed 1 ` 2 ` `n npn ` 1q{2. Enter the following into the orresponding ells: A1: n B1: tringle C1: sqrt A2:
(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.
![(a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P. (a) A partition P of [a, b] is a finite subset of [a, b] containing a and b. If Q is another partition and P Q, then Q is a refinement of P.](/thumbs/72/66745617.jpg) Chpter 7: The Riemnn Integrl When the derivtive is introdued, it is not hrd to see tht the it of the differene quotient should be equl to the slope of the tngent line, or when the horizontl xis is time
Chpter 7: The Riemnn Integrl When the derivtive is introdued, it is not hrd to see tht the it of the differene quotient should be equl to the slope of the tngent line, or when the horizontl xis is time
Section 2.1 Special Right Triangles
 Se..1 Speil Rigt Tringles 49 Te --90 Tringle Setion.1 Speil Rigt Tringles Te --90 tringle (or just 0-60-90) is so nme euse of its ngle mesures. Te lengts of te sies, toug, ve very speifi pttern to tem
Se..1 Speil Rigt Tringles 49 Te --90 Tringle Setion.1 Speil Rigt Tringles Te --90 tringle (or just 0-60-90) is so nme euse of its ngle mesures. Te lengts of te sies, toug, ve very speifi pttern to tem
Proving the Pythagorean Theorem. Proving the Pythagorean Theorem and the Converse of the Pythagorean Theorem
 .5 Proving the Pythgoren Theorem Proving the Pythgoren Theorem nd the Converse of the Pythgoren Theorem Lerning Gols In this lesson, you will: Prove the Pythgoren Theorem using similr tringles. Prove the
.5 Proving the Pythgoren Theorem Proving the Pythgoren Theorem nd the Converse of the Pythgoren Theorem Lerning Gols In this lesson, you will: Prove the Pythgoren Theorem using similr tringles. Prove the
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Review Topic 14: Relationships between two numerical variables
 Review Topi 14: Reltionships etween two numeril vriles Multiple hoie 1. Whih of the following stterplots est demonstrtes line of est fit? A B C D E 2. The regression line eqution for the following grph
Review Topi 14: Reltionships etween two numeril vriles Multiple hoie 1. Whih of the following stterplots est demonstrtes line of est fit? A B C D E 2. The regression line eqution for the following grph
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
Trigonometry and Constructive Geometry
 Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
8Similarity ONLINE PAGE PROOFS. 8.1 Kick off with CAS 8.2 Similar objects 8.3 Linear scale factors. 8.4 Area and volume scale factors 8.
 8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8.4 re nd volume scle fctors 8. Review Plese refer to the Resources t in the Prelims section of your eookplus for comprehensive step-y-step
8.1 Kick off with S 8. Similr ojects 8. Liner scle fctors 8Similrity 8.4 re nd volume scle fctors 8. Review Plese refer to the Resources t in the Prelims section of your eookplus for comprehensive step-y-step
Special Numbers, Factors and Multiples
 Specil s, nd Student Book - Series H- + 3 + 5 = 9 = 3 Mthletics Instnt Workooks Copyright Student Book - Series H Contents Topics Topic - Odd, even, prime nd composite numers Topic - Divisiility tests
Specil s, nd Student Book - Series H- + 3 + 5 = 9 = 3 Mthletics Instnt Workooks Copyright Student Book - Series H Contents Topics Topic - Odd, even, prime nd composite numers Topic - Divisiility tests
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
Intermediate Math Circles Wednesday, November 14, 2018 Finite Automata II. Nickolas Rollick a b b. a b 4
 Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
Shape and measurement
 C H A P T E R 5 Shpe nd mesurement Wht is Pythgors theorem? How do we use Pythgors theorem? How do we find the perimeter of shpe? How do we find the re of shpe? How do we find the volume of shpe? How do
C H A P T E R 5 Shpe nd mesurement Wht is Pythgors theorem? How do we use Pythgors theorem? How do we find the perimeter of shpe? How do we find the re of shpe? How do we find the volume of shpe? How do
Algebra Basics. Algebra Basics. Curriculum Ready ACMNA: 133, 175, 176, 177, 179.
 Curriulum Redy ACMNA: 33 75 76 77 79 www.mthletis.om Fill in the spes with nything you lredy know out Alger Creer Opportunities: Arhitets eletriins plumers et. use it to do importnt lultions. Give this
Curriulum Redy ACMNA: 33 75 76 77 79 www.mthletis.om Fill in the spes with nything you lredy know out Alger Creer Opportunities: Arhitets eletriins plumers et. use it to do importnt lultions. Give this
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
1 ELEMENTARY ALGEBRA and GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE
 ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
For a, b, c, d positive if a b and. ac bd. Reciprocal relations for a and b positive. If a > b then a ab > b. then
 Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
TOPIC: LINEAR ALGEBRA MATRICES
 Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
( ) { } [ ] { } [ ) { } ( ] { }
![( ) { } [ ] { } [ ) { } ( ] { } ( ) { } [ ] { } [ ) { } ( ] { }](/thumbs/96/129291861.jpg) Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
2.1 ANGLES AND THEIR MEASURE. y I
 .1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
.1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
Logarithms LOGARITHMS.
 Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Minnesota State University, Mankato 44 th Annual High School Mathematics Contest April 12, 2017
 Minnesot Stte University, Mnkto 44 th Annul High School Mthemtics Contest April, 07. A 5 ft. ldder is plced ginst verticl wll of uilding. The foot of the ldder rests on the floor nd is 7 ft. from the wll.
Minnesot Stte University, Mnkto 44 th Annul High School Mthemtics Contest April, 07. A 5 ft. ldder is plced ginst verticl wll of uilding. The foot of the ldder rests on the floor nd is 7 ft. from the wll.
03. Early Greeks & Aristotle
 03. Erly Greeks & Aristotle I. Erly Greeks Topis I. Erly Greeks II. The Method of Exhustion III. Aristotle. Anximnder (. 60 B.C.) to peiron - the unlimited, unounded - fundmentl sustne of relity - underlying
03. Erly Greeks & Aristotle I. Erly Greeks Topis I. Erly Greeks II. The Method of Exhustion III. Aristotle. Anximnder (. 60 B.C.) to peiron - the unlimited, unounded - fundmentl sustne of relity - underlying
Section 6: Area, Volume, and Average Value
 Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Counting Paths Between Vertices. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs
 Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
The graphs of Rational Functions
 Lecture 4 5A: The its of Rtionl Functions s x nd s x + The grphs of Rtionl Functions The grphs of rtionl functions hve severl differences compred to power functions. One of the differences is the behvior
Lecture 4 5A: The its of Rtionl Functions s x nd s x + The grphs of Rtionl Functions The grphs of rtionl functions hve severl differences compred to power functions. One of the differences is the behvior
A study of Pythagoras Theorem
 CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins
CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins
Chapter 9 Definite Integrals
 Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Part 4. Integration (with Proofs)
 Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
Prt 4. Integrtion (with Proofs) 4.1 Definition Definition A prtition P of [, b] is finite set of points {x 0, x 1,..., x n } with = x 0 < x 1
Linear Inequalities. Work Sheet 1
 Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
8 Measurement. How is measurement used in your home? 8E Area of a circle 8B Circumference of a circle. 8A Length and perimeter
 8A Length nd perimeter 8E Are of irle 8B Cirumferene of irle 8F Surfe re 8C Are of retngles nd tringles 8G Volume of prisms 8D Are of other qudrilterls 8H Are nd volume onversions SA M PL E Mesurement
8A Length nd perimeter 8E Are of irle 8B Cirumferene of irle 8F Surfe re 8C Are of retngles nd tringles 8G Volume of prisms 8D Are of other qudrilterls 8H Are nd volume onversions SA M PL E Mesurement
ONLINE PAGE PROOFS. Trigonometry Kick off with CAS 12.2 Trigonometry 12.3 Pythagorean triads
 12 12.1 Kik off with S 12.2 Trigonometry 12.3 Pythgoren trids Trigonometry 12.4 Three-dimensionl Pythgors theorem 12.5 Trigonometri rtios 12.6 The sine rule 12.7 miguous se of the sine rule 12.8 The osine
12 12.1 Kik off with S 12.2 Trigonometry 12.3 Pythgoren trids Trigonometry 12.4 Three-dimensionl Pythgors theorem 12.5 Trigonometri rtios 12.6 The sine rule 12.7 miguous se of the sine rule 12.8 The osine
CS 491G Combinatorial Optimization Lecture Notes
 CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
What else can you do?
 Wht else cn you do? ngle sums The size of specil ngle types lernt erlier cn e used to find unknown ngles. tht form stright line dd to 180c. lculte the size of + M, if L is stright line M + L = 180c( stright
Wht else cn you do? ngle sums The size of specil ngle types lernt erlier cn e used to find unknown ngles. tht form stright line dd to 180c. lculte the size of + M, if L is stright line M + L = 180c( stright
