Non Right Angled Triangles
|
|
|
- Julie Porter
- 6 years ago
- Views:
Transcription
1 Non Right ngled Tringles Non Right ngled Tringles urriulum Redy
2
3 Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit will show you how to use these trigonometri rtios to find the sizes of ngles nd length of sides. Try to nswer these questions now, efore working through the hpter. I used to think: How re sides leled in reltion to the leling ngles of non right ngled tringle? Drw nd lel tringle. The "osine rule" is used when two sides of the tringle nd the ngle etween them is given Wht is this rule? nswer these questions fter you hve worked through the hpter. ut now I think: How re sides leled in reltion to the leling ngles of non right ngled tringle? Drw nd lel tringle. The "osine rule" is used when two sides of the tringle nd the ngle etween them is given Wht is this rule? Wht do I know now tht I didn t know efore? 00% Non Right ngled Tringles Mthletis 00% 3P Lerning K 8 TOPI
4 Non Right ngled Tringles sis Leling Tringles Everyone lels tringles the sme wy. Eh ngle is leled with pitl letter, nd their opposite sides re leled with the sme letter, ut non-pitl. For T Opposite to Opposite to Opposite to For TLMN Opposite to m Opposite to n M l N n m L Opposite to l K 8 00% Non Right ngled Tringles TOPI Mthletis 00% 3P Lerning
5 Non Right ngled Tringles Questions sis. Lel the sides in the following tringles. X Y J H K W. Lel the ngles in the following the tringles. m q p g f r 3. omplete the leling of the following tringles. T u M k s L 00% Non Right ngled Tringles Mthletis 00% 3P Lerning K 8 3 TOPI
6 Non Right ngled Tringles Knowing More So fr we've used trigonometry in right-ngled tringles, ut we n tully use it to find sides nd ngles in ny tringle! The re Rule T is not right-ngled. The perpendiulr height, h, is drwn in. ` re # se # height re # # h We nsee: h sin ` h sin re # # sin h ` re sin So the re is hlf the produt of two sides nd the sine of their interior ngle. ny two sides nd their interior ngle will work: re sin or re sin or re sin Find the re of T DEF to deiml ple D 0 m 00 E F 4 m d nd f re given, so we will use re df sin E re TDEF dfsin E ^ 4 h^ 0 hsin f. 9. 7m ^deimlpleh Find the re of T to deiml ple nd re given, so we will use re re T sin sin (write this in T ) ^ h^ 8 hsin m ( deiml ple) 4 K 8 00% Non Right ngled Tringles TOPI Mthletis 00% 3P Lerning
7 Non Right ngled Tringles Questions Knowing More. Find the re of the following tringles to deiml ple. 7 m m 0 m 6.4 m 78. T hs , ,. 4mnd. m. Drw the tringle. Find + to nerest degree. Find the re of the tringle to deiml ple. 00% Non Right ngled Tringles Mthletis 00% 3P Lerning K 8 5 TOPI
8 Non Right ngled Tringles Questions Knowing More 3. n you find the res of the following shpes to the nerest squre m? E 0 m 3 6 m D 3 m Hint: Drw in Digonl D m 9.5 m m 0 m 93 6 K 8 00% Non Right ngled Tringles TOPI Mthletis 00% 3P Lerning
9 Non Right ngled Tringles Questions Knowing More 4. Luke wnts to mke kite in the shpe elow. How mny squre m of mteril will he need? m m 44 D 5. The re of the tringle T PQR is 38.6 m. Find + Q. (Hint: Find+ P first) Q 0 m P m R 00% Non Right ngled Tringles K 8 7 Mthletis 00% 3P Lerning TOPI
10 Non Right ngled Tringles Using Our Knowledge The Sine Rule In ny tringle T we hve the formuls: sin sin sin or sin sin sin The proof is different depending on whether the tringle is ute or otuse. If T is n ute tringle If T is n otuse tringle h h D 80 - D In TD: h sin ` h sin In TD: h sin ` h sin In TD: ` sin sin h sin ` h sin (oth equl h) In TD: h sin^80 -h ` h sin^80 -h ` h sin Rememer sin^80 - θh sin θ ` sin sin ` sin sin (oth equl h) If we drew the ltitude from to then we ould show ` sin sin sin sin If we drew the ltitude from to then we ould show sin sin 8 K 8 00% Non Right ngled Tringles TOPI Mthletis 00% 3P Lerning
11 Non Right ngled Tringles Using Our Knowledge Find the vlue of in T to deiml ples 0 m 8 7 m 8 Using the Sine Rule: ` sin sin 0 sin8 sin 8 ` 0 sin 8 sin 8 0^0469. fh f m f ( deiml ples) Find the vlue of + E in T DEF to the nerest degree D 36 E Using the Sine Rule: m F 3 m sine sin D e d ` sine sin 36 3 ` sin E 3 sin f - ` E sin ^0. 694fh f. 44 (nerest degree) Use the digrm elow to nswer these questions L Find + LPN to the nerest degree. N 55 0 m 3 9 m P 7 m M sin+ LPN sin + LNP LN LP ` sin+ LPN sin ` sin + LPN 0 sin ` + LPN sin ( ) ( nerest degree) Find the length of LM to the nerest m. First, find + LPM + LPM LPN Now, use the sine rule LM PM sin+ LPM sin + PLM ` LM 7 sin4 sin 3 ` LM 7sin m (nerest m) sin 3 00% Non Right ngled Tringles Mthletis 00% 3P Lerning K 8 9 TOPI
12 Non Right ngled Tringles Questions Using Our Knowledge The Sine Rule. Find the length y in the tringles elow to deiml ple. m y 6 37 y 9 m 4 0. Find the size of ngle in the following tringles: 9 m m 0 6 m 46 m 0 K 8 00% Non Right ngled Tringles TOPI Mthletis 00% 3P Lerning
13 Non Right ngled Tringles Questions Using Our Knowledge 3. ship hs sils s drwn in the digrm elow: D 5 0 m 85 Find the length of. Find the lengths of D nd D. 00% Non Right ngled Tringles Mthletis 00% 3P Lerning K 8 TOPI
14 Non Right ngled Tringles Using Our Knowledge The osine Rule In ny tringle T we hve the formuls + - os or + - os or + - os The proof is different depending on if the tringle is ute or otuse. If T is n ute tringle If T is n otuse tringle h h x D (-x) D (x- ) x In T D: h + ^- xh h + x + -x (Pythgors) In T D: h + ^x- h h + x + -x (Pythgors) Susitute Susitute Susitute Susitute In T D: h + x (Pythgors) In T D: h + x (Pythgors) nd os x ` x os nd os x ` x os + - os + - os If the h is drwn from other orners we n show + - os or + - os If the h is drwn from other orners we n show + - os or + - os K 8 00% Non Right ngled Tringles TOPI Mthletis 00% 3P Lerning
15 Non Right ngled Tringles Using Our Knowledge Find the vlue of in T to deiml ples 8 m 30 5 m Using the osine Rule: ` ` + - os ^ h^8hos ^0. 866fh ` 9. 77f ` m ( deiml ples) Find the vlue of + Q to the nerest degree P 6 m 5 m Using the osine Rule: q p + r - pros Q ` ^0h^5hos Q R 0 m Q Mke os Q the sujet 0 ^ h^5hos Q os Q ` os Q f 300 Solve for + Q - + Q os ^ h 5. 56f. 6 (nerest degree) Find + in the following to deiml ple D 49. D + D - # D # D # os D ^ h^hos 49. This is the osine rule 5 m m f 9. 49fm Write this in the digrm + - # # # os 6 m 8 m ^9. 49fh ^6h^8 hos ^9. 49fh ` os 6 ^ h^8h f ` + os - ^0347. fh f ( deiml ple) 00% Non Right ngled Tringles Mthletis 00% 3P Lerning K 8 3 TOPI
16 Non Right ngled Tringles Questions Using Our Knowledge The osine Rule 4. Find the length of the missing side x in eh of the following to deiml ple. D P 9 m x 5 m 73 x E m F Q 5 m 56 R 5. Find the vlue of the ngle in eh of the following to the nerest degree. 50 m 47 m 55 m 39 m W 6 m Y X 3 m 4 K 8 00% Non Right ngled Tringles TOPI Mthletis 00% 3P Lerning
17 Non Right ngled Tringles Questions Using Our Knowledge 6. nyon hs the following dimensions: N 46 m L m M 50 m P To wlk round this nyon, would it e shorter to wlk long LNM or LPM? Use working to support your nswer. 00% Non Right ngled Tringles Mthletis 00% 3P Lerning K 8 5 TOPI
18 Non Right ngled Tringles Questions Using Our Knowledge oth Rules 7. Use the sine nd osine rules to find the missing sides nd ngles in these tringles to deiml ples m 67 Q 38 m 55 m P 4 R 6 K 8 00% Non Right ngled Tringles TOPI Mthletis 00% 3P Lerning
19 Non Right ngled Tringles Thinking More n miguous se For The Sine Rule Rememer tht sini sin(80-i). So when the sine rule is used to find n ngle (using sin - ) two nswers re possile. For exmple if sini 0.5 then i 30 or 50 (80-30). It is our jo to determine whether one or oth nswers re vlid. This depends on whether third ngle exists or not. Find + (to deiml ple) in T if + 50, 4m nd 7. m ording to the sine rule sin sin ` sin sin ` sin 7. # sin ` + sin ^094. h - ` or dd eh nswer to the given ngle. If this sum is less thn 80 then the nswer is vlid euse the third ngle exists. The given ngle in the question is + 50 ` ` vlid or ` vlid oth sums re less thn 80, nd so oth nswers for + re vlid. So T my look like either of these tringles: 4 m m 50 or 4 m m 50 se where oth nswers re vlid (like ove) is sid to e "miguous." 00% Non Right ngled Tringles Mthletis 00% 3P Lerning K 8 7 TOPI
20 Non Right ngled Tringles Thinking More Determining if nswers re Vlid Of the two possile nswers, one will lwys e otuse So if you know the tringle is ute, then the otuse ngle is invlid. If you know the missing ngle is otuse, then the ute ngle is invlid. (90to80 ) nd the other will lwys e ute ^0to 90h. The sum of ngles in tringle is 80. So if the sum of possile nswer nd the given ngle is 80 or more it mens tht the third ngle in the tringle is 0 or negtive. This is impossile, so the nswer would e invlid. Find + L (to deiml ple) in T LMN if + N 80, n m nd l m ording to the sine rule sinl sin N l n ` sinl sin ` sin L 40. 5# sin f ` + L sin ^0806. fh ` + L 55. 5f. 55. or +L dd eh nswer to the given ngle ^+ N 80h. ` + L+ + N ` vlid or + L+ + N ` invlid So only the first nswer is vlid nd + L 55.. This is not n miguous se. + L 55. nd T LMN looks like this M 40.5m 48.6m N L 8 K 8 00% Non Right ngled Tringles TOPI Mthletis 00% 3P Lerning
21 Non Right ngled Tringles Questions Thinking More. In tringle T 9m, 5m nd + 0. Find two possile vlues for + to the nerest degree. hek if these nswers re vlid. Is this n miguous se? Drw rough sketh of the tringle(s). d Find the third ngle in the tringle(s) nd dd them to the digrm in. 00% Non Right ngled Tringles Mthletis 00% 3P Lerning K 8 9 TOPI
22 Non Right ngled Tringles Questions Thinking More. In T PQR, + R 40, p 0.3m nd r Find the two possile vlues for + P to the nerest degree. Is this n miguous se (re oth ngles vlid)? Whih nswer is vlid if T PQR is ute? Whih nswer is invlid? d Whih nswer is vlid if + P is otuse? Whih nswer is invlid? 0 K 8 00% Non Right ngled Tringles TOPI Mthletis 00% 3P Lerning
23 Non Right ngled Tringles Questions Thinking More 3. In tringle T JKL, + K 70, k 5. 4m nd l 4m. Find the vlid size(s) of + L. Find + J. Find the length of j. d Drw T JKL. 00% Non Right ngled Tringles Mthletis 00% 3P Lerning K 8 TOPI
24 Non Right ngled Tringles nswers sis: sis:. 3. X w Y T u y x s S t W H k j K h J U l M m k L. K Knowing More:. re T 8. 5m R re T 74. m q p. P F m r Q G m.m g f re T 89. 0m M K 8 00% Non Right ngled Tringles TOPI Mthletis 00% 3P Lerning
25 Non Right ngled Tringles nswers Knowing More: Thinking More: 3. Totl re m. + 6 or + 54 Totl re 3m oth nswers re vlid; therefore this is n miguous se. 4. Totl re 99m Q m 5m Using Our Knowledge: 0 6. y 9. m y. 7m 5m m 0 40 d + 34 or m(to d.p.) or + 0 D. 0.0m nd D. 6.0m oth nswers re vlid; therefore this is n miguous se. 4. x 9.6m (to d.p.) x.5m (tod.p.) If PQR is ute, the ngles re in the rnge 0-90, +P 70 is the vlid nswer nd + P 0 is invlid (tonerest degree) (tonerest degree) d If PQR is otuse, the ngles re in the rnge 90-80, +P 0 is the vlid nswer nd +P 70 is invlid. 6. It would e shorter to wlk long LPM thn LNM 3. + L 50 +J m (tod.p.) 9.89m (tod.p.) q 7.0m (tod.p.) d j 47. 3m K 70 4m 47.3m + Q (tod.p.) + R (tod.p.) J m 50 L 00% Non Right ngled Tringles Mthletis 00% 3P Lerning K 8 3 TOPI
26 Non Right ngled Tringles Notes 4 K 8 00% Non Right ngled Tringles TOPI Mthletis 00% 3P Lerning
27
28 Non Right ngled Tringles
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Pythagoras Theorem. The area of the square on the hypotenuse is equal to the sum of the squares on the other two sides
 Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Topics Covered: Pythagoras Theorem Definition of sin, cos and tan Solving right-angle triangles Sine and cosine rule
 Trigonometry Topis overed: Pythgors Theorem Definition of sin, os nd tn Solving right-ngle tringles Sine nd osine rule Lelling right-ngle tringle Opposite (Side opposite the ngle θ) Hypotenuse (Side opposite
Trigonometry Topis overed: Pythgors Theorem Definition of sin, os nd tn Solving right-ngle tringles Sine nd osine rule Lelling right-ngle tringle Opposite (Side opposite the ngle θ) Hypotenuse (Side opposite
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
Similarity and Congruence
 Similrity nd ongruence urriculum Redy MMG: 201, 220, 221, 243, 244 www.mthletics.com SIMILRITY N ONGRUN If two shpes re congruent, it mens thy re equl in every wy ll their corresponding sides nd ngles
Similrity nd ongruence urriculum Redy MMG: 201, 220, 221, 243, 244 www.mthletics.com SIMILRITY N ONGRUN If two shpes re congruent, it mens thy re equl in every wy ll their corresponding sides nd ngles
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Math Lesson 4-5 The Law of Cosines
 Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Trigonometry and Constructive Geometry
 Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
 PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Date Lesson Text TOPIC Homework. Solving for Obtuse Angles QUIZ ( ) More Trig Word Problems QUIZ ( )
 UNIT 5 TRIGONOMETRI RTIOS Dte Lesson Text TOPI Homework pr. 4 5.1 (48) Trigonometry Review WS 5.1 # 3 5, 9 11, (1, 13)doso pr. 6 5. (49) Relted ngles omplete lesson shell & WS 5. pr. 30 5.3 (50) 5.3 5.4
UNIT 5 TRIGONOMETRI RTIOS Dte Lesson Text TOPI Homework pr. 4 5.1 (48) Trigonometry Review WS 5.1 # 3 5, 9 11, (1, 13)doso pr. 6 5. (49) Relted ngles omplete lesson shell & WS 5. pr. 30 5.3 (50) 5.3 5.4
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
Polynomials. Polynomials. Curriculum Ready ACMNA:
 Polynomils Polynomils Curriulum Redy ACMNA: 66 www.mthletis.om Polynomils POLYNOMIALS A polynomil is mthemtil expression with one vrile whose powers re neither negtive nor frtions. The power in eh expression
Polynomils Polynomils Curriulum Redy ACMNA: 66 www.mthletis.om Polynomils POLYNOMIALS A polynomil is mthemtil expression with one vrile whose powers re neither negtive nor frtions. The power in eh expression
Logarithms LOGARITHMS.
 Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
Logrithms LOGARITHMS www.mthletis.om.u Logrithms LOGARITHMS Logrithms re nother method to lulte nd work with eponents. Answer these questions, efore working through this unit. I used to think: In the
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
Pythagoras Theorem. Pythagoras Theorem. Curriculum Ready ACMMG: 222, 245.
 Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
Area and Perimeter. Area and Perimeter. Solutions. Curriculum Ready.
 Are n Perimeter Are n Perimeter Solutions Curriulum Rey www.mthletis.om How oes it work? Solutions Are n Perimeter Pge questions Are using unit squres Are = whole squres Are = 6 whole squres = units =
Are n Perimeter Are n Perimeter Solutions Curriulum Rey www.mthletis.om How oes it work? Solutions Are n Perimeter Pge questions Are using unit squres Are = whole squres Are = 6 whole squres = units =
PROPERTIES OF TRIANGLES
 PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
Naming the sides of a right-angled triangle
 6.2 Wht is trigonometry? The word trigonometry is derived from the Greek words trigonon (tringle) nd metron (mesurement). Thus, it literlly mens to mesure tringle. Trigonometry dels with the reltionship
6.2 Wht is trigonometry? The word trigonometry is derived from the Greek words trigonon (tringle) nd metron (mesurement). Thus, it literlly mens to mesure tringle. Trigonometry dels with the reltionship
Similar Right Triangles
 Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Shape and measurement
 C H A P T E R 5 Shpe nd mesurement Wht is Pythgors theorem? How do we use Pythgors theorem? How do we find the perimeter of shpe? How do we find the re of shpe? How do we find the volume of shpe? How do
C H A P T E R 5 Shpe nd mesurement Wht is Pythgors theorem? How do we use Pythgors theorem? How do we find the perimeter of shpe? How do we find the re of shpe? How do we find the volume of shpe? How do
Surds and Indices. Surds and Indices. Curriculum Ready ACMNA: 233,
 Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
3 Angle Geometry. 3.1 Measuring Angles. 1. Using a protractor, measure the marked angles.
 3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
MTH 4-16a Trigonometry
 MTH 4-16 Trigonometry Level 4 [UNIT 5 REVISION SECTION ] I cn identify the opposite, djcent nd hypotenuse sides on right-ngled tringle. Identify the opposite, djcent nd hypotenuse in the following right-ngled
MTH 4-16 Trigonometry Level 4 [UNIT 5 REVISION SECTION ] I cn identify the opposite, djcent nd hypotenuse sides on right-ngled tringle. Identify the opposite, djcent nd hypotenuse in the following right-ngled
Factorising FACTORISING.
 Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Trigonometry. Trigonometry. labelling conventions. Evaluation of areas of non-right-angled triangles using the formulas A = 1 ab sin (C )
 8 8 Pythgors theorem 8 Pythgoren trids 8 Three-dimensionl Pythgors theorem 8D Trigonometri rtios 8E The sine rule 8F miguous se of the sine rule 8G The osine rule 8H Speil tringles 8I re of tringles res
8 8 Pythgors theorem 8 Pythgoren trids 8 Three-dimensionl Pythgors theorem 8D Trigonometri rtios 8E The sine rule 8F miguous se of the sine rule 8G The osine rule 8H Speil tringles 8I re of tringles res
3.1 Review of Sine, Cosine and Tangent for Right Angles
 Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
Foundtions of Mth 11 Section 3.1 Review of Sine, osine nd Tngent for Right Tringles 125 3.1 Review of Sine, osine nd Tngent for Right ngles The word trigonometry is derived from the Greek words trigon,
ONLINE PAGE PROOFS. Trigonometry Kick off with CAS 12.2 Trigonometry 12.3 Pythagorean triads
 12 12.1 Kik off with S 12.2 Trigonometry 12.3 Pythgoren trids Trigonometry 12.4 Three-dimensionl Pythgors theorem 12.5 Trigonometri rtios 12.6 The sine rule 12.7 miguous se of the sine rule 12.8 The osine
12 12.1 Kik off with S 12.2 Trigonometry 12.3 Pythgoren trids Trigonometry 12.4 Three-dimensionl Pythgors theorem 12.5 Trigonometri rtios 12.6 The sine rule 12.7 miguous se of the sine rule 12.8 The osine
2 Calculate the size of each angle marked by a letter in these triangles.
 Cmridge Essentils Mthemtics Support 8 GM1.1 GM1.1 1 Clculte the size of ech ngle mrked y letter. c 2 Clculte the size of ech ngle mrked y letter in these tringles. c d 3 Clculte the size of ech ngle mrked
Cmridge Essentils Mthemtics Support 8 GM1.1 GM1.1 1 Clculte the size of ech ngle mrked y letter. c 2 Clculte the size of ech ngle mrked y letter in these tringles. c d 3 Clculte the size of ech ngle mrked
GEOMETRY OF THE CIRCLE TANGENTS & SECANTS
 Geometry Of The ircle Tngents & Secnts GEOMETRY OF THE IRLE TNGENTS & SENTS www.mthletics.com.u Tngents TNGENTS nd N Secnts SENTS Tngents nd secnts re lines tht strt outside circle. Tngent touches the
Geometry Of The ircle Tngents & Secnts GEOMETRY OF THE IRLE TNGENTS & SENTS www.mthletics.com.u Tngents TNGENTS nd N Secnts SENTS Tngents nd secnts re lines tht strt outside circle. Tngent touches the
MATHEMATICS AND STATISTICS 1.6
 MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
Triangles The following examples explore aspects of triangles:
 Tringles The following exmples explore spects of tringles: xmple 1: ltitude of right ngled tringle + xmple : tringle ltitude of the symmetricl ltitude of n isosceles x x - 4 +x xmple 3: ltitude of the
Tringles The following exmples explore spects of tringles: xmple 1: ltitude of right ngled tringle + xmple : tringle ltitude of the symmetricl ltitude of n isosceles x x - 4 +x xmple 3: ltitude of the
S56 (5.3) Vectors.notebook January 29, 2016
 Dily Prctice 15.1.16 Q1. The roots of the eqution (x 1)(x + k) = 4 re equl. Find the vlues of k. Q2. Find the rte of chnge of 剹 x when x = 1 / 8 Tody we will e lerning out vectors. Q3. Find the eqution
Dily Prctice 15.1.16 Q1. The roots of the eqution (x 1)(x + k) = 4 re equl. Find the vlues of k. Q2. Find the rte of chnge of 剹 x when x = 1 / 8 Tody we will e lerning out vectors. Q3. Find the eqution
Trigonometry. cosθ. sinθ tanθ. Mathletics Instant Workbooks. Copyright
 Student Book - Series K- sinθ tnθ osθ Mtletis Instnt Workooks Copyrigt Student Book - Series K Contents Topis Topi - Nming te sides of rigt-ngled tringle Topi 2 - Te trigonometri rtios Topi 3 - Using lultor
Student Book - Series K- sinθ tnθ osθ Mtletis Instnt Workooks Copyrigt Student Book - Series K Contents Topis Topi - Nming te sides of rigt-ngled tringle Topi 2 - Te trigonometri rtios Topi 3 - Using lultor
Trigonometry. Trigonometry. Solutions. Curriculum Ready ACMMG: 223, 224, 245.
 Trgonometry Trgonometry Solutons Currulum Redy CMMG:, 4, 4 www.mthlets.om Trgonometry Solutons Bss Pge questons. Identfy f the followng trngles re rght ngled or not. Trngles,, d, e re rght ngled ndted
Trgonometry Trgonometry Solutons Currulum Redy CMMG:, 4, 4 www.mthlets.om Trgonometry Solutons Bss Pge questons. Identfy f the followng trngles re rght ngled or not. Trngles,, d, e re rght ngled ndted
m A 1 1 A ! and AC 6
 REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
UNIT 31 Angles and Symmetry: Data Sheets
 UNIT 31 Angles nd Symmetry Dt Sheets Dt Sheets 31.1 Line nd Rottionl Symmetry 31.2 Angle Properties 31.3 Angles in Tringles 31.4 Angles nd Prllel Lines: Results 31.5 Angles nd Prllel Lines: Exmple 31.6
UNIT 31 Angles nd Symmetry Dt Sheets Dt Sheets 31.1 Line nd Rottionl Symmetry 31.2 Angle Properties 31.3 Angles in Tringles 31.4 Angles nd Prllel Lines: Results 31.5 Angles nd Prllel Lines: Exmple 31.6
Something found at a salad bar
 Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Section 13.1 Right Triangles
 Section 13.1 Right Tringles Ojectives: 1. To find vlues of trigonometric functions for cute ngles. 2. To solve tringles involving right ngles. Review - - 1. SOH sin = Reciprocl csc = 2. H cos = Reciprocl
Section 13.1 Right Tringles Ojectives: 1. To find vlues of trigonometric functions for cute ngles. 2. To solve tringles involving right ngles. Review - - 1. SOH sin = Reciprocl csc = 2. H cos = Reciprocl
Lesson 8.1 Graphing Parametric Equations
 Lesson 8.1 Grphing Prmetric Equtions 1. rete tle for ech pir of prmetric equtions with the given vlues of t.. x t 5. x t 3 c. x t 1 y t 1 y t 3 y t t t {, 1, 0, 1, } t {4,, 0,, 4} t {4, 0,, 4, 8}. Find
Lesson 8.1 Grphing Prmetric Equtions 1. rete tle for ech pir of prmetric equtions with the given vlues of t.. x t 5. x t 3 c. x t 1 y t 1 y t 3 y t t t {, 1, 0, 1, } t {4,, 0,, 4} t {4, 0,, 4, 8}. Find
Part I: Study the theorem statement.
 Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
Precalculus Notes: Unit 6 Law of Sines & Cosines, Vectors, & Complex Numbers. A can be rewritten as
 Dte: 6.1 Lw of Sines Syllus Ojetie: 3.5 Te student will sole pplition prolems inoling tringles (Lw of Sines). Deriing te Lw of Sines: Consider te two tringles. C C In te ute tringle, sin In te otuse tringle,
Dte: 6.1 Lw of Sines Syllus Ojetie: 3.5 Te student will sole pplition prolems inoling tringles (Lw of Sines). Deriing te Lw of Sines: Consider te two tringles. C C In te ute tringle, sin In te otuse tringle,
m m m m m m m m P m P m ( ) m m P( ) ( ). The o-ordinte of the point P( ) dividing the line segment joining the two points ( ) nd ( ) eternll in the r
 CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
On the diagram below the displacement is represented by the directed line segment OA.
 Vectors Sclrs nd Vectors A vector is quntity tht hs mgnitude nd direction. One exmple of vector is velocity. The velocity of n oject is determined y the mgnitude(speed) nd direction of trvel. Other exmples
Vectors Sclrs nd Vectors A vector is quntity tht hs mgnitude nd direction. One exmple of vector is velocity. The velocity of n oject is determined y the mgnitude(speed) nd direction of trvel. Other exmples
STRAND J: TRANSFORMATIONS, VECTORS and MATRICES
 Mthemtics SKE: STRN J STRN J: TRNSFORMTIONS, VETORS nd MTRIES J3 Vectors Text ontents Section J3.1 Vectors nd Sclrs * J3. Vectors nd Geometry Mthemtics SKE: STRN J J3 Vectors J3.1 Vectors nd Sclrs Vectors
Mthemtics SKE: STRN J STRN J: TRNSFORMTIONS, VETORS nd MTRIES J3 Vectors Text ontents Section J3.1 Vectors nd Sclrs * J3. Vectors nd Geometry Mthemtics SKE: STRN J J3 Vectors J3.1 Vectors nd Sclrs Vectors
Area and Perimeter. Area and Perimeter. Curriculum Ready.
 Are nd Perimeter Curriculum Redy www.mthletics.com This ooklet shows how to clculte the re nd perimeter of common plne shpes. Footll fields use rectngles, circles, qudrnts nd minor segments with specific
Are nd Perimeter Curriculum Redy www.mthletics.com This ooklet shows how to clculte the re nd perimeter of common plne shpes. Footll fields use rectngles, circles, qudrnts nd minor segments with specific
Perimeter and Area. Mathletics Instant Workbooks. Copyright
 Perimeter nd Are Student Book - Series J- L B Mthletis Instnt Workooks Copyright Student Book - Series J Contents Topis Topi - Plne shpes Topi 2 - Perimeter of regulr shpes Topi 3 - Perimeter of irregulr
Perimeter nd Are Student Book - Series J- L B Mthletis Instnt Workooks Copyright Student Book - Series J Contents Topis Topi - Plne shpes Topi 2 - Perimeter of regulr shpes Topi 3 - Perimeter of irregulr
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
10. AREAS BETWEEN CURVES
 . AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
. AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
R(3, 8) P( 3, 0) Q( 2, 2) S(5, 3) Q(2, 32) P(0, 8) Higher Mathematics Objective Test Practice Book. 1 The diagram shows a sketch of part of
 Higher Mthemtics Ojective Test Prctice ook The digrm shows sketch of prt of the grph of f ( ). The digrm shows sketch of the cuic f ( ). R(, 8) f ( ) f ( ) P(, ) Q(, ) S(, ) Wht re the domin nd rnge of
Higher Mthemtics Ojective Test Prctice ook The digrm shows sketch of prt of the grph of f ( ). The digrm shows sketch of the cuic f ( ). R(, 8) f ( ) f ( ) P(, ) Q(, ) S(, ) Wht re the domin nd rnge of
S2 (2.2) Pythagoras.notebook March 04, 2016
 S2 (2.2) Pythgors.noteook Mrh 04, 2016 Dily Prtie 16.12.2015 Q1. Multiply out nd simplify 9x 3(2x + 1) Q2. Solve the eqution 3(2x + 4) = 18 Q3. If 1 = $1.30, how muh is 50 in dollrs? Tody we will e lerning
S2 (2.2) Pythgors.noteook Mrh 04, 2016 Dily Prtie 16.12.2015 Q1. Multiply out nd simplify 9x 3(2x + 1) Q2. Solve the eqution 3(2x + 4) = 18 Q3. If 1 = $1.30, how muh is 50 in dollrs? Tody we will e lerning
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
 Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
MCH T 111 Handout Triangle Review Page 1 of 3
 Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Algebra & Functions (Maths ) opposite side
 Instructor: Dr. R.A.G. Seel Trigonometr Algebr & Functions (Mths 0 0) 0th Prctice Assignment hpotenuse hpotenuse side opposite side sin = opposite hpotenuse tn = opposite. Find sin, cos nd tn in 9 sin
Instructor: Dr. R.A.G. Seel Trigonometr Algebr & Functions (Mths 0 0) 0th Prctice Assignment hpotenuse hpotenuse side opposite side sin = opposite hpotenuse tn = opposite. Find sin, cos nd tn in 9 sin
Pythagoras Theorem PYTHAGORAS THEOREM.
 Pthgors Theorem PYTHAGORAS THEOREM www.mthletis.om.u How oes it work? Solutions Pthgors Theorem Pge 3 questions Right-ngle tringles D E x z Hotenuse is sie: F Hotenuse is sie: DF Q k j l Hotenuse is sie:
Pthgors Theorem PYTHAGORAS THEOREM www.mthletis.om.u How oes it work? Solutions Pthgors Theorem Pge 3 questions Right-ngle tringles D E x z Hotenuse is sie: F Hotenuse is sie: DF Q k j l Hotenuse is sie:
2.1 ANGLES AND THEIR MEASURE. y I
 .1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
.1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
Things to Memorize: A Partial List. January 27, 2017
 Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
Basic Angle Rules 5. A Short Hand Geometric Reasons. B Two Reasons. 1 Write in full the meaning of these short hand geometric reasons.
 si ngle Rules 5 6 Short Hnd Geometri Resons 1 Write in full the mening of these short hnd geometri resons. Short Hnd Reson Full Mening ) se s isos Δ re =. ) orr s // lines re =. ) sum s t pt = 360. d)
si ngle Rules 5 6 Short Hnd Geometri Resons 1 Write in full the mening of these short hnd geometri resons. Short Hnd Reson Full Mening ) se s isos Δ re =. ) orr s // lines re =. ) sum s t pt = 360. d)
Special Numbers, Factors and Multiples
 Specil s, nd Student Book - Series H- + 3 + 5 = 9 = 3 Mthletics Instnt Workooks Copyright Student Book - Series H Contents Topics Topic - Odd, even, prime nd composite numers Topic - Divisiility tests
Specil s, nd Student Book - Series H- + 3 + 5 = 9 = 3 Mthletics Instnt Workooks Copyright Student Book - Series H Contents Topics Topic - Odd, even, prime nd composite numers Topic - Divisiility tests
K 7. Quadratic Equations. 1. Rewrite these polynomials in the form ax 2 + bx + c = 0. Identify the values of a, b and c:
 Qudrti Equtions The Null Ftor Lw Let's sy there re two numers nd. If # = then = or = (or oth re ) This mens tht if the produt of two epressions is zero, then t lest one of the epressions must e equl to
Qudrti Equtions The Null Ftor Lw Let's sy there re two numers nd. If # = then = or = (or oth re ) This mens tht if the produt of two epressions is zero, then t lest one of the epressions must e equl to
Probability. b a b. a b 32.
 Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
9.5 Start Thinking. 9.5 Warm Up. 9.5 Cumulative Review Warm Up
 9.5 Strt Thinking In Lesson 9.4, we discussed the tngent rtio which involves the two legs of right tringle. In this lesson, we will discuss the sine nd cosine rtios, which re trigonometric rtios for cute
9.5 Strt Thinking In Lesson 9.4, we discussed the tngent rtio which involves the two legs of right tringle. In this lesson, we will discuss the sine nd cosine rtios, which re trigonometric rtios for cute
青藜苑教育 The digrm shows the position of ferry siling between Folkestone nd lis. The ferry is t X. X 4km The pos
 青藜苑教育 www.thetopedu.com 010-6895997 1301951457 Revision Topic 9: Pythgors Theorem Pythgors Theorem Pythgors Theorem llows you to work out the length of sides in right-ngled tringle. c The side opposite
青藜苑教育 www.thetopedu.com 010-6895997 1301951457 Revision Topic 9: Pythgors Theorem Pythgors Theorem Pythgors Theorem llows you to work out the length of sides in right-ngled tringle. c The side opposite
MTH 505: Number Theory Spring 2017
 MTH 505: Numer Theory Spring 207 Homework 2 Drew Armstrong The Froenius Coin Prolem. Consider the eqution x ` y c where,, c, x, y re nturl numers. We cn think of $ nd $ s two denomintions of coins nd $c
MTH 505: Numer Theory Spring 207 Homework 2 Drew Armstrong The Froenius Coin Prolem. Consider the eqution x ` y c where,, c, x, y re nturl numers. We cn think of $ nd $ s two denomintions of coins nd $c
Polynomials and Division Theory
 Higher Checklist (Unit ) Higher Checklist (Unit ) Polynomils nd Division Theory Skill Achieved? Know tht polynomil (expression) is of the form: n x + n x n + n x n + + n x + x + 0 where the i R re the
Higher Checklist (Unit ) Higher Checklist (Unit ) Polynomils nd Division Theory Skill Achieved? Know tht polynomil (expression) is of the form: n x + n x n + n x n + + n x + x + 0 where the i R re the
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
I1.1 Pythagoras' Theorem. I1.2 Further Work With Pythagoras' Theorem. I1.3 Sine, Cosine and Tangent. I1.4 Finding Lengths in Right Angled Triangles
 UNIT I1 Pythgors' Theorem nd Trigonometric Rtios: Tet STRAND I: Geometry nd Trigonometry I1 Pythgors' Theorem nd Trigonometric Rtios Tet Contents Section I1.1 Pythgors' Theorem I1. Further Work With Pythgors'
UNIT I1 Pythgors' Theorem nd Trigonometric Rtios: Tet STRAND I: Geometry nd Trigonometry I1 Pythgors' Theorem nd Trigonometric Rtios Tet Contents Section I1.1 Pythgors' Theorem I1. Further Work With Pythgors'
= x x 2 = 25 2
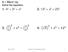 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
Section 6: Area, Volume, and Average Value
 Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
For a, b, c, d positive if a b and. ac bd. Reciprocal relations for a and b positive. If a > b then a ab > b. then
 Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
Slrs-7.2-ADV-.7 Improper Definite Integrls 27.. D.dox Pge of Improper Definite Integrls Before we strt the min topi we present relevnt lger nd it review. See Appendix J for more lger review. Inequlities:
QUADRATIC EQUATIONS OBJECTIVE PROBLEMS
 QUADRATIC EQUATIONS OBJECTIVE PROBLEMS +. The solution of the eqution will e (), () 0,, 5, 5. The roots of the given eqution ( p q) ( q r) ( r p) 0 + + re p q r p (), r p p q, q r p q (), (d), q r p q.
QUADRATIC EQUATIONS OBJECTIVE PROBLEMS +. The solution of the eqution will e (), () 0,, 5, 5. The roots of the given eqution ( p q) ( q r) ( r p) 0 + + re p q r p (), r p p q, q r p q (), (d), q r p q.
Geometry. Trigonometry of Right Triangles. Slide 2 / 240. Slide 1 / 240. Slide 3 / 240. Slide 4 / 240. Slide 6 / 240.
 Slide 1 / 240 Slide 2 / 240 New Jerse enter for Tehing nd Lerning Progressive Mthemtis Inititive This mteril is mde freel ville t www.njtl.org nd is intended for the non-ommeril use of students nd tehers.
Slide 1 / 240 Slide 2 / 240 New Jerse enter for Tehing nd Lerning Progressive Mthemtis Inititive This mteril is mde freel ville t www.njtl.org nd is intended for the non-ommeril use of students nd tehers.
Applications of trigonometry
 3 3 3 3 3D 3E 3F 3G 3H Review of right-ngled tringles erings Using the sine rule to find side lengths Using the sine rule to find ngles re of tringle Using the osine rule to find side lengths Using the
3 3 3 3 3D 3E 3F 3G 3H Review of right-ngled tringles erings Using the sine rule to find side lengths Using the sine rule to find ngles re of tringle Using the osine rule to find side lengths Using the
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
Numbers and indices. 1.1 Fractions. GCSE C Example 1. Handy hint. Key point
 GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GEOMETRICAL PROPERTIES OF ANGLES AND CIRCLES, ANGLES PROPERTIES OF TRIANGLES, QUADRILATERALS AND POLYGONS:
 GEOMETRICL PROPERTIES OF NGLES ND CIRCLES, NGLES PROPERTIES OF TRINGLES, QUDRILTERLS ND POLYGONS: 1.1 TYPES OF NGLES: CUTE NGLE RIGHT NGLE OTUSE NGLE STRIGHT NGLE REFLEX NGLE 40 0 4 0 90 0 156 0 180 0
GEOMETRICL PROPERTIES OF NGLES ND CIRCLES, NGLES PROPERTIES OF TRINGLES, QUDRILTERLS ND POLYGONS: 1.1 TYPES OF NGLES: CUTE NGLE RIGHT NGLE OTUSE NGLE STRIGHT NGLE REFLEX NGLE 40 0 4 0 90 0 156 0 180 0
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
Sect 10.2 Trigonometric Ratios
 86 Sect 0. Trigonometric Rtios Objective : Understnding djcent, Hypotenuse, nd Opposite sides of n cute ngle in right tringle. In right tringle, the otenuse is lwys the longest side; it is the side opposite
86 Sect 0. Trigonometric Rtios Objective : Understnding djcent, Hypotenuse, nd Opposite sides of n cute ngle in right tringle. In right tringle, the otenuse is lwys the longest side; it is the side opposite
5Trigonometric UNCORRECTED PAGE PROOFS. ratios and their applications
 5Trigonometri rtios nd their pplitions 5.1 Kik off with CS 5.2 Trigonometry of right-ngled tringles 5.3 Elevtion, depression nd erings 5.4 The sine rule 5.5 The osine rule 5.6 rs, setors nd segments 5.7
5Trigonometri rtios nd their pplitions 5.1 Kik off with CS 5.2 Trigonometry of right-ngled tringles 5.3 Elevtion, depression nd erings 5.4 The sine rule 5.5 The osine rule 5.6 rs, setors nd segments 5.7
Vectors. a Write down the vector AB as a column vector ( x y ). A (3, 2) x point C such that BC = 3. . Go to a OA = a
 Streth lesson: Vetors Streth ojetives efore you strt this hpter, mrk how onfident you feel out eh of the sttements elow: I n lulte using olumn vetors nd represent the sum nd differene of two vetors grphilly.
Streth lesson: Vetors Streth ojetives efore you strt this hpter, mrk how onfident you feel out eh of the sttements elow: I n lulte using olumn vetors nd represent the sum nd differene of two vetors grphilly.
QUADRATIC EQUATION EXERCISE - 01 CHECK YOUR GRASP
 QUADRATIC EQUATION EXERCISE - 0 CHECK YOUR GRASP. Sine sum of oeffiients 0. Hint : It's one root is nd other root is 8 nd 5 5. tn other root 9. q 4p 0 q p q p, q 4 p,,, 4 Hene 7 vlues of (p, q) 7 equtions
QUADRATIC EQUATION EXERCISE - 0 CHECK YOUR GRASP. Sine sum of oeffiients 0. Hint : It's one root is nd other root is 8 nd 5 5. tn other root 9. q 4p 0 q p q p, q 4 p,,, 4 Hene 7 vlues of (p, q) 7 equtions
5. Every rational number have either terminating or repeating (recurring) decimal representation.
 CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
CHAPTER NUMBER SYSTEMS Points to Rememer :. Numer used for ounting,,,,... re known s Nturl numers.. All nturl numers together with zero i.e. 0,,,,,... re known s whole numers.. All nturl numers, zero nd
A B= ( ) because from A to B is 3 right, 2 down.
 8. Vectors nd vector nottion Questions re trgeted t the grdes indicted Remember: mgnitude mens size. The vector ( ) mens move left nd up. On Resource sheet 8. drw ccurtely nd lbel the following vectors.
8. Vectors nd vector nottion Questions re trgeted t the grdes indicted Remember: mgnitude mens size. The vector ( ) mens move left nd up. On Resource sheet 8. drw ccurtely nd lbel the following vectors.
Green s Theorem. (2x e y ) da. (2x e y ) dx dy. x 2 xe y. (1 e y ) dy. y=1. = y e y. y=0. = 2 e
 Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Algebra Basics. Algebra Basics. Curriculum Ready ACMNA: 133, 175, 176, 177, 179.
 Curriulum Redy ACMNA: 33 75 76 77 79 www.mthletis.om Fill in the spes with nything you lredy know out Alger Creer Opportunities: Arhitets eletriins plumers et. use it to do importnt lultions. Give this
Curriulum Redy ACMNA: 33 75 76 77 79 www.mthletis.om Fill in the spes with nything you lredy know out Alger Creer Opportunities: Arhitets eletriins plumers et. use it to do importnt lultions. Give this
Definition :- A shape has a line of symmetry if, when folded over the line. 1 line of symmetry 2 lines of symmetry
 Symmetry Lines of Symmetry Definition :- A shpe hs line of symmetry if, when folded over the line the hlves of the shpe mtch up exctly. Some shpes hve more thn one line of symmetry : line of symmetry lines
Symmetry Lines of Symmetry Definition :- A shpe hs line of symmetry if, when folded over the line the hlves of the shpe mtch up exctly. Some shpes hve more thn one line of symmetry : line of symmetry lines
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
This chapter will show you What you should already know Quick check 111
 1 Pythgors theorem 2 Finding shorter side 3 Solving prolems using Pythgors theorem This chpter will show you how to use Pythgors theorem in right-ngled tringles how to solve prolems using Pythgors theorem
1 Pythgors theorem 2 Finding shorter side 3 Solving prolems using Pythgors theorem This chpter will show you how to use Pythgors theorem in right-ngled tringles how to solve prolems using Pythgors theorem
