Basic Angle Rules 5. A Short Hand Geometric Reasons. B Two Reasons. 1 Write in full the meaning of these short hand geometric reasons.
|
|
|
- Georgiana Dawson
- 6 years ago
- Views:
Transcription
1 si ngle Rules 5 6 Short Hnd Geometri Resons 1 Write in full the mening of these short hnd geometri resons. Short Hnd Reson Full Mening ) se s isos Δ re =. ) orr s // lines re =. ) sum s t pt = 360. d) vert opp s re =. e) o-in s // lines dd to180. f) sum s in Δ = 180. g) dj s on str line dd to 180. h) lt s // lines re =. Two Resons 1 If there is no rule linking the wnted ngle diretly to one of the given ngles, then the lultion is done in two (or more) steps, This mens you lso hve to give two (or more) geometri resons in your justifition. lulte the size of the lelled ngles. Give geometri reson (in short hnd) for eh step in your solution. ) ) 65 ) d) d Sigm Mths Workook S Geometri Resoning Sigm ulitions Ltd ISN opyright Liensing Ltd liene is required to opy ny prt of this resoure.
2 ngles in irles 4 16 ngles t the irumferene Smll Steps Rule : 1 omplete the 3 steps tken to lulte the size of ngle. Two ngles, oth on the irumferene nd stnding on the sme r, re equl. Short : s sme r = 1 lulte ngles nd y y ) Δ is right-ngled. Reson : = y = ) = 66. Reson :.. 2 lulte ngles to f. Give geometri resons. ) ngle = Reson :... =. reson : 2 =. reson : =. reson : d =. reson : 27 d D ) Δ is right-ngled. Reson : ) = Reson :.. ) ngle = Reson :... e =. reson : e f =. reson : f Sigm Mths Workook S Geometri Resoning Sigm ulitions Ltd ISN opyright Liensing Ltd liene is required to opy ny prt of this resoure.
3 31 The Rule of ythgors 2 Not the Hypotenuse ythgors Rule n e written in three different wys. 1. Strting with : 2 = Strting with : = 2 3. Strting with : = 2 1 Write down ythgors rule for this tringle in three different wys. strting with p : strting with q : strting with r : r p q Lots of rtie 1 lulte the length of the lelled sides. ) ) Write down ythgors s rule just one for eh tringle, ) the rule must strt with 2. If it is not the hypotenuse ut one of the other sides tht must e lulted, more diffiult eqution needs to e solved. lwys strt the rule with the side whih must e lulted. 9 Emple : lulte side. Working : Rule : = = = = 7.5 (2 sf) ) p q 5 2 In this question it my e the hypotenuse or one of the other sides for you to lulte. lwys write ythgors rule down, strting with the side to e lulted. Then solve the eqution nd round sensily. ) ) v w 3 omplete these lultions of side. ) 2 + = =... = ) ) = (2 sf) ) d) 0.52 y = 2 =. = 2 + = 2 =. = e) 3.4 z = (3 sf) =. 2.4 Sigm Mths Workook S Geometri Resoning Sigm ulitions Ltd ISN opyright Liensing Ltd liene is required to opy ny prt of this resoure.
4 43 pplitions of Trigonometry 4 Shpes with Stright Lines 1 Tringle is not right-ngled tringle. Show how the length of n e lulted y utting the tringle in two. Show your working m m Working with irles 1 setor hs n ngle of 75 nd hord of 5.0 m. lulte the rdius. Show your working. 5.0 m For prllellogrm re = se height. Show how you work out the re of this prllelogrm. Justify eh step. 2 Three rolls of lnk newspper re stked s shown. Eh roll hs rdius of 50 m. lulte the totl height of the stk. Show your resoning lerly. D h 6.4 m 10.2 m 125 Sigm Mths Workook S Geometri Resoning Sigm ulitions Ltd ISN opyright Liensing Ltd liene is required to opy ny prt of this resoure.
5 Geometri Resoning 4 52 Steel Frme 1 tringulr steel frme is reinfored with em, where is hlfwy side nd. Given tht = 2.0 m nd = 4.0 m, lulte... ) the distne () ) ngle ttery omprtment 1 The digrm shows ttery fitting snugly in omprtment. The ttery touhes the sides t,, R nd S. ) SR = 40. lulte SR. Give resons for your nswer. 40 S R ) Suppose SR =. Write n epression for SR in terms of. ) If SR = nd the rdius of the ttery is r mm, write n epression for the depth of the omprtment ()..... Sigm Mths Workook S Geometri Resoning Sigm ulitions Ltd ISN opyright Liensing Ltd liene is required to opy ny prt of this resoure.
MATHEMATICS AND STATISTICS 1.6
 MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
MTHMTIS N STTISTIS 1.6 pply geometri resoning in solving prolems ternlly ssessed 4 redits S 91031 inding unknown ngles When finding the size of unknown ngles in figure, t lest two steps of resoning will
LESSON 11: TRIANGLE FORMULAE
 . THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
. THE SEMIPERIMETER OF TRINGLE LESSON : TRINGLE FORMULE In wht follows, will hve sides, nd, nd these will e opposite ngles, nd respetively. y the tringle inequlity, nd..() So ll of, & re positive rel numers.
Geometry of the Circle - Chords and Angles. Geometry of the Circle. Chord and Angles. Curriculum Ready ACMMG: 272.
 Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Geometry of the irle - hords nd ngles Geometry of the irle hord nd ngles urriulum Redy MMG: 272 www.mthletis.om hords nd ngles HRS N NGLES The irle is si shpe nd so it n e found lmost nywhere. This setion
Trigonometry Revision Sheet Q5 of Paper 2
 Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
Trigonometry Revision Sheet Q of Pper The Bsis - The Trigonometry setion is ll out tringles. We will normlly e given some of the sides or ngles of tringle nd we use formule nd rules to find the others.
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
Trigonometry and Constructive Geometry
 Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Trigonometry nd Construtive Geometry Trining prolems for M2 2018 term 1 Ted Szylowie tedszy@gmil.om 1 Leling geometril figures 1. Prtie writing Greek letters. αβγδɛθλµπψ 2. Lel the sides, ngles nd verties
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MCH T 111 Handout Triangle Review Page 1 of 3
 Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Hnout Tringle Review Pge of 3 In the stuy of sttis, it is importnt tht you e le to solve lgeri equtions n tringle prolems using trigonometry. The following is review of trigonometry sis. Right Tringle:
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
UNIT 31 Angles and Symmetry: Data Sheets
 UNIT 31 Angles nd Symmetry Dt Sheets Dt Sheets 31.1 Line nd Rottionl Symmetry 31.2 Angle Properties 31.3 Angles in Tringles 31.4 Angles nd Prllel Lines: Results 31.5 Angles nd Prllel Lines: Exmple 31.6
UNIT 31 Angles nd Symmetry Dt Sheets Dt Sheets 31.1 Line nd Rottionl Symmetry 31.2 Angle Properties 31.3 Angles in Tringles 31.4 Angles nd Prllel Lines: Results 31.5 Angles nd Prllel Lines: Exmple 31.6
Pythagoras Theorem. The area of the square on the hypotenuse is equal to the sum of the squares on the other two sides
 Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
Pythgors theorem nd trigonometry Pythgors Theorem The hypotenuse of right-ngled tringle is the longest side The hypotenuse is lwys opposite the right-ngle 2 = 2 + 2 or 2 = 2-2 or 2 = 2-2 The re of the
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
MTH 4-16a Trigonometry
 MTH 4-16 Trigonometry Level 4 [UNIT 5 REVISION SECTION ] I cn identify the opposite, djcent nd hypotenuse sides on right-ngled tringle. Identify the opposite, djcent nd hypotenuse in the following right-ngled
MTH 4-16 Trigonometry Level 4 [UNIT 5 REVISION SECTION ] I cn identify the opposite, djcent nd hypotenuse sides on right-ngled tringle. Identify the opposite, djcent nd hypotenuse in the following right-ngled
Non Right Angled Triangles
 Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Non Right ngled Tringles Non Right ngled Tringles urriulum Redy www.mthletis.om Non Right ngled Tringles NON RIGHT NGLED TRINGLES sin i, os i nd tn i re lso useful in non-right ngled tringles. This unit
Topics Covered: Pythagoras Theorem Definition of sin, cos and tan Solving right-angle triangles Sine and cosine rule
 Trigonometry Topis overed: Pythgors Theorem Definition of sin, os nd tn Solving right-ngle tringles Sine nd osine rule Lelling right-ngle tringle Opposite (Side opposite the ngle θ) Hypotenuse (Side opposite
Trigonometry Topis overed: Pythgors Theorem Definition of sin, os nd tn Solving right-ngle tringles Sine nd osine rule Lelling right-ngle tringle Opposite (Side opposite the ngle θ) Hypotenuse (Side opposite
Proving the Pythagorean Theorem
 Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
Proving the Pythgoren Theorem W. Bline Dowler June 30, 2010 Astrt Most people re fmilir with the formul 2 + 2 = 2. However, in most ses, this ws presented in lssroom s n solute with no ttempt t proof or
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Vectors. a Write down the vector AB as a column vector ( x y ). A (3, 2) x point C such that BC = 3. . Go to a OA = a
 Streth lesson: Vetors Streth ojetives efore you strt this hpter, mrk how onfident you feel out eh of the sttements elow: I n lulte using olumn vetors nd represent the sum nd differene of two vetors grphilly.
Streth lesson: Vetors Streth ojetives efore you strt this hpter, mrk how onfident you feel out eh of the sttements elow: I n lulte using olumn vetors nd represent the sum nd differene of two vetors grphilly.
Mathematics. Area under Curve.
 Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Numbers and indices. 1.1 Fractions. GCSE C Example 1. Handy hint. Key point
 GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
Math Lesson 4-5 The Law of Cosines
 Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
Mth-1060 Lesson 4-5 The Lw of osines Solve using Lw of Sines. 1 17 11 5 15 13 SS SSS Every pir of loops will hve unknowns. Every pir of loops will hve unknowns. We need nother eqution. h Drop nd ltitude
3 Angle Geometry. 3.1 Measuring Angles. 1. Using a protractor, measure the marked angles.
 3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
3 ngle Geometry MEP Prtie ook S3 3.1 Mesuring ngles 1. Using protrtor, mesure the mrked ngles. () () (d) (e) (f) 2. Drw ngles with the following sizes. () 22 () 75 120 (d) 90 (e) 153 (f) 45 (g) 180 (h)
Proportions: A ratio is the quotient of two numbers. For example, 2 3
 Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Proportions: rtio is the quotient of two numers. For exmple, 2 3 is rtio of 2 n 3. n equlity of two rtios is proportion. For exmple, 3 7 = 15 is proportion. 45 If two sets of numers (none of whih is 0)
Something found at a salad bar
 Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
CHENG Chun Chor Litwin The Hong Kong Institute of Education
 PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
PE-hing Mi terntionl onferene IV: novtion of Mthemtis Tehing nd Lerning through Lesson Study- onnetion etween ssessment nd Sujet Mtter HENG hun hor Litwin The Hong Kong stitute of Edution Report on using
Comparing the Pre-image and Image of a Dilation
 hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
hpter Summry Key Terms Postultes nd Theorems similr tringles (.1) inluded ngle (.2) inluded side (.2) geometri men (.) indiret mesurement (.6) ngle-ngle Similrity Theorem (.2) Side-Side-Side Similrity
Perimeter and Area. Mathletics Instant Workbooks. Copyright
 Perimeter nd Are Student Book - Series J- L B Mthletis Instnt Workooks Copyright Student Book - Series J Contents Topis Topi - Plne shpes Topi 2 - Perimeter of regulr shpes Topi 3 - Perimeter of irregulr
Perimeter nd Are Student Book - Series J- L B Mthletis Instnt Workooks Copyright Student Book - Series J Contents Topis Topi - Plne shpes Topi 2 - Perimeter of regulr shpes Topi 3 - Perimeter of irregulr
Maintaining Mathematical Proficiency
 Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
Nme Dte hpter 9 Mintining Mthemtil Profiieny Simplify the epression. 1. 500. 189 3. 5 4. 4 3 5. 11 5 6. 8 Solve the proportion. 9 3 14 7. = 8. = 9. 1 7 5 4 = 4 10. 0 6 = 11. 7 4 10 = 1. 5 9 15 3 = 5 +
PYTHAGORAS THEOREM,TRIGONOMETRY,BEARINGS AND THREE DIMENSIONAL PROBLEMS
 PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
PYTHGORS THEOREM,TRIGONOMETRY,ERINGS ND THREE DIMENSIONL PROLEMS 1.1 PYTHGORS THEOREM: 1. The Pythgors Theorem sttes tht the squre of the hypotenuse is equl to the sum of the squres of the other two sides
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
 Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
Mth 3329-Uniform Geometries Leture 06 1. Review of trigonometry While we re looking t Eulid s Elements, I d like to look t some si trigonometry. Figure 1. The Pythgoren theorem sttes tht if = 90, then
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
GEOMETRY OF THE CIRCLE TANGENTS & SECANTS
 Geometry Of The ircle Tngents & Secnts GEOMETRY OF THE IRLE TNGENTS & SENTS www.mthletics.com.u Tngents TNGENTS nd N Secnts SENTS Tngents nd secnts re lines tht strt outside circle. Tngent touches the
Geometry Of The ircle Tngents & Secnts GEOMETRY OF THE IRLE TNGENTS & SENTS www.mthletics.com.u Tngents TNGENTS nd N Secnts SENTS Tngents nd secnts re lines tht strt outside circle. Tngent touches the
Naming the sides of a right-angled triangle
 6.2 Wht is trigonometry? The word trigonometry is derived from the Greek words trigonon (tringle) nd metron (mesurement). Thus, it literlly mens to mesure tringle. Trigonometry dels with the reltionship
6.2 Wht is trigonometry? The word trigonometry is derived from the Greek words trigonon (tringle) nd metron (mesurement). Thus, it literlly mens to mesure tringle. Trigonometry dels with the reltionship
I1.1 Pythagoras' Theorem. I1.2 Further Work With Pythagoras' Theorem. I1.3 Sine, Cosine and Tangent. I1.4 Finding Lengths in Right Angled Triangles
 UNIT I1 Pythgors' Theorem nd Trigonometric Rtios: Tet STRAND I: Geometry nd Trigonometry I1 Pythgors' Theorem nd Trigonometric Rtios Tet Contents Section I1.1 Pythgors' Theorem I1. Further Work With Pythgors'
UNIT I1 Pythgors' Theorem nd Trigonometric Rtios: Tet STRAND I: Geometry nd Trigonometry I1 Pythgors' Theorem nd Trigonometric Rtios Tet Contents Section I1.1 Pythgors' Theorem I1. Further Work With Pythgors'
2.1 ANGLES AND THEIR MEASURE. y I
 .1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
.1 ANGLES AND THEIR MEASURE Given two interseting lines or line segments, the mount of rottion out the point of intersetion (the vertex) required to ring one into orrespondene with the other is lled the
STRAND J: TRANSFORMATIONS, VECTORS and MATRICES
 Mthemtics SKE: STRN J STRN J: TRNSFORMTIONS, VETORS nd MTRIES J3 Vectors Text ontents Section J3.1 Vectors nd Sclrs * J3. Vectors nd Geometry Mthemtics SKE: STRN J J3 Vectors J3.1 Vectors nd Sclrs Vectors
Mthemtics SKE: STRN J STRN J: TRNSFORMTIONS, VETORS nd MTRIES J3 Vectors Text ontents Section J3.1 Vectors nd Sclrs * J3. Vectors nd Geometry Mthemtics SKE: STRN J J3 Vectors J3.1 Vectors nd Sclrs Vectors
Similar Right Triangles
 Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Geometry V1.noteook Ferury 09, 2012 Similr Right Tringles Cn I identify similr tringles in right tringle with the ltitude? Cn I identify the proportions in right tringles? Cn I use the geometri mens theorems
Problem Set 9. Figure 1: Diagram. This picture is a rough sketch of the 4 parabolas that give us the area that we need to find. The equations are:
 (x + y ) = y + (x + y ) = x + Problem Set 9 Discussion: Nov., Nov. 8, Nov. (on probbility nd binomil coefficients) The nme fter the problem is the designted writer of the solution of tht problem. (No one
(x + y ) = y + (x + y ) = x + Problem Set 9 Discussion: Nov., Nov. 8, Nov. (on probbility nd binomil coefficients) The nme fter the problem is the designted writer of the solution of tht problem. (No one
Identifying and Classifying 2-D Shapes
 Ientifying n Clssifying -D Shpes Wht is your sign? The shpe n olour of trffi signs let motorists know importnt informtion suh s: when to stop onstrution res. Some si shpes use in trffi signs re illustrte
Ientifying n Clssifying -D Shpes Wht is your sign? The shpe n olour of trffi signs let motorists know importnt informtion suh s: when to stop onstrution res. Some si shpes use in trffi signs re illustrte
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Sect 10.2 Trigonometric Ratios
 86 Sect 0. Trigonometric Rtios Objective : Understnding djcent, Hypotenuse, nd Opposite sides of n cute ngle in right tringle. In right tringle, the otenuse is lwys the longest side; it is the side opposite
86 Sect 0. Trigonometric Rtios Objective : Understnding djcent, Hypotenuse, nd Opposite sides of n cute ngle in right tringle. In right tringle, the otenuse is lwys the longest side; it is the side opposite
and that at t = 0 the object is at position 5. Find the position of the object at t = 2.
 7.2 The Fundmentl Theorem of Clculus 49 re mny, mny problems tht pper much different on the surfce but tht turn out to be the sme s these problems, in the sense tht when we try to pproimte solutions we
7.2 The Fundmentl Theorem of Clculus 49 re mny, mny problems tht pper much different on the surfce but tht turn out to be the sme s these problems, in the sense tht when we try to pproimte solutions we
Green s Theorem. (2x e y ) da. (2x e y ) dx dy. x 2 xe y. (1 e y ) dy. y=1. = y e y. y=0. = 2 e
 Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Higher Maths. Self Check Booklet. visit for a wealth of free online maths resources at all levels from S1 to S6
 Higher Mths Self Check Booklet visit www.ntionl5mths.co.uk for welth of free online mths resources t ll levels from S to S6 How To Use This Booklet You could use this booklet on your own, but it my be
Higher Mths Self Check Booklet visit www.ntionl5mths.co.uk for welth of free online mths resources t ll levels from S to S6 How To Use This Booklet You could use this booklet on your own, but it my be
Pythagoras Theorem. Pythagoras Theorem. Curriculum Ready ACMMG: 222, 245.
 Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
Pythgors Theorem Pythgors Theorem Curriulum Redy ACMMG:, 45 www.mthletis.om Fill in these spes with ny other interesting fts you n find out Pythgors. In the world of Mthemtis, Pythgors is legend. He lived
Chapter 1: Logarithmic functions and indices
 Chpter : Logrithmic functions nd indices. You cn simplify epressions y using rules of indices m n m n m n m n ( m ) n mn m m m m n m m n Emple Simplify these epressions: 5 r r c 4 4 d 6 5 e ( ) f ( ) 4
Chpter : Logrithmic functions nd indices. You cn simplify epressions y using rules of indices m n m n m n m n ( m ) n mn m m m m n m m n Emple Simplify these epressions: 5 r r c 4 4 d 6 5 e ( ) f ( ) 4
THE PYTHAGOREAN THEOREM
 THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
THE PYTHAGOREAN THEOREM The Pythgoren Theorem is one of the most well-known nd widely used theorems in mthemtis. We will first look t n informl investigtion of the Pythgoren Theorem, nd then pply this
PROPERTIES OF TRIANGLES
 PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
PROPERTIES OF TRINGLES. RELTION RETWEEN SIDES ND NGLES OF TRINGLE:. tringle onsists of three sides nd three ngles lled elements of the tringle. In ny tringle,,, denotes the ngles of the tringle t the verties.
ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 1 - Thurs 28th Sept 17 Review of trigonometry and basic calculus
 ES 111 Mthemticl Methods in the Erth Sciences Lecture Outline 1 - Thurs 28th Sept 17 Review of trigonometry nd bsic clculus Trigonometry When is it useful? Everywhere! Anything involving coordinte systems
ES 111 Mthemticl Methods in the Erth Sciences Lecture Outline 1 - Thurs 28th Sept 17 Review of trigonometry nd bsic clculus Trigonometry When is it useful? Everywhere! Anything involving coordinte systems
STRAND I: Geometry and Trigonometry. UNIT 32 Angles, Circles and Tangents: Student Text Contents. Section Compass Bearings
 ME Jmi: STR I UIT 32 ngles, irles n Tngents: Stuent Tet ontents STR I: Geometry n Trigonometry Unit 32 ngles, irles n Tngents Stuent Tet ontents Setion 32.1 ompss erings 32.2 ngles n irles 1 32.3 ngles
ME Jmi: STR I UIT 32 ngles, irles n Tngents: Stuent Tet ontents STR I: Geometry n Trigonometry Unit 32 ngles, irles n Tngents Stuent Tet ontents Setion 32.1 ompss erings 32.2 ngles n irles 1 32.3 ngles
m A 1 1 A ! and AC 6
 REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
Pythagoras theorem and surds
 HPTER Mesurement nd Geometry Pythgors theorem nd surds In IE-EM Mthemtis Yer 8, you lernt out the remrkle reltionship etween the lengths of the sides of right-ngled tringle. This result is known s Pythgors
HPTER Mesurement nd Geometry Pythgors theorem nd surds In IE-EM Mthemtis Yer 8, you lernt out the remrkle reltionship etween the lengths of the sides of right-ngled tringle. This result is known s Pythgors
ONLINE PAGE PROOFS. Trigonometry Kick off with CAS 12.2 Trigonometry 12.3 Pythagorean triads
 12 12.1 Kik off with S 12.2 Trigonometry 12.3 Pythgoren trids Trigonometry 12.4 Three-dimensionl Pythgors theorem 12.5 Trigonometri rtios 12.6 The sine rule 12.7 miguous se of the sine rule 12.8 The osine
12 12.1 Kik off with S 12.2 Trigonometry 12.3 Pythgoren trids Trigonometry 12.4 Three-dimensionl Pythgors theorem 12.5 Trigonometri rtios 12.6 The sine rule 12.7 miguous se of the sine rule 12.8 The osine
5Trigonometric UNCORRECTED PAGE PROOFS. ratios and their applications
 5Trigonometri rtios nd their pplitions 5.1 Kik off with CS 5.2 Trigonometry of right-ngled tringles 5.3 Elevtion, depression nd erings 5.4 The sine rule 5.5 The osine rule 5.6 rs, setors nd segments 5.7
5Trigonometri rtios nd their pplitions 5.1 Kik off with CS 5.2 Trigonometry of right-ngled tringles 5.3 Elevtion, depression nd erings 5.4 The sine rule 5.5 The osine rule 5.6 rs, setors nd segments 5.7
MEP Practice Book ES3. 1. Calculate the size of the angles marked with a letter in each diagram. None to scale
 ME rctice ook ES3 3 ngle Geometr 3.3 ngle Geometr 1. lculte the size of the ngles mrked with letter in ech digrm. None to scle () 70 () 20 54 65 25 c 36 (d) (e) (f) 56 62 d e 60 40 70 70 f 30 g (g) (h)
ME rctice ook ES3 3 ngle Geometr 3.3 ngle Geometr 1. lculte the size of the ngles mrked with letter in ech digrm. None to scle () 70 () 20 54 65 25 c 36 (d) (e) (f) 56 62 d e 60 40 70 70 f 30 g (g) (h)
Level I MAML Olympiad 2001 Page 1 of 6 (A) 90 (B) 92 (C) 94 (D) 96 (E) 98 (A) 48 (B) 54 (C) 60 (D) 66 (E) 72 (A) 9 (B) 13 (C) 17 (D) 25 (E) 38
 Level I MAML Olympid 00 Pge of 6. Si students in smll clss took n em on the scheduled dte. The verge of their grdes ws 75. The seventh student in the clss ws ill tht dy nd took the em lte. When her score
Level I MAML Olympid 00 Pge of 6. Si students in smll clss took n em on the scheduled dte. The verge of their grdes ws 75. The seventh student in the clss ws ill tht dy nd took the em lte. When her score
MEP Practice Book ES19
 19 Vectors M rctice ook S19 19.1 Vectors nd Sclrs 1. Which of the following re vectors nd which re sclrs? Speed ccelertion Mss Velocity (e) Weight (f) Time 2. Use the points in the grid elow to find the
19 Vectors M rctice ook S19 19.1 Vectors nd Sclrs 1. Which of the following re vectors nd which re sclrs? Speed ccelertion Mss Velocity (e) Weight (f) Time 2. Use the points in the grid elow to find the
Stage 11 Prompt Sheet
 Stge 11 rompt Sheet 11/1 Simplify surds is NOT surd ecuse it is exctly is surd ecuse the nswer is not exct surd is n irrtionl numer To simplify surds look for squre numer fctors 7 = = 11/ Mnipulte expressions
Stge 11 rompt Sheet 11/1 Simplify surds is NOT surd ecuse it is exctly is surd ecuse the nswer is not exct surd is n irrtionl numer To simplify surds look for squre numer fctors 7 = = 11/ Mnipulte expressions
Equations, expressions and formulae
 Get strted 2 Equtions, epressions nd formule This unit will help you to work with equtions, epressions nd formule. AO1 Fluency check 1 Work out 2 b 2 c 7 2 d 7 2 2 Simplify by collecting like terms. b
Get strted 2 Equtions, epressions nd formule This unit will help you to work with equtions, epressions nd formule. AO1 Fluency check 1 Work out 2 b 2 c 7 2 d 7 2 2 Simplify by collecting like terms. b
Ellipses. The second type of conic is called an ellipse.
 Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Ellipses The seond type of oni is lled n ellipse. Definition of Ellipse An ellipse is the set of ll points (, y) in plne, the sum of whose distnes from two distint fied points (foi) is onstnt. (, y) d
Similarity and Congruence
 Similrity nd ongruence urriculum Redy MMG: 201, 220, 221, 243, 244 www.mthletics.com SIMILRITY N ONGRUN If two shpes re congruent, it mens thy re equl in every wy ll their corresponding sides nd ngles
Similrity nd ongruence urriculum Redy MMG: 201, 220, 221, 243, 244 www.mthletics.com SIMILRITY N ONGRUN If two shpes re congruent, it mens thy re equl in every wy ll their corresponding sides nd ngles
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
Alg. Sheet (1) Department : Math Form : 3 rd prep. Sheet
 Ciro Governorte Nozh Directorte of Eduction Nozh Lnguge Schools Ismili Rod Deprtment : Mth Form : rd prep. Sheet Alg. Sheet () [] Find the vlues of nd in ech of the following if : ) (, ) ( -5, 9 ) ) (,
Ciro Governorte Nozh Directorte of Eduction Nozh Lnguge Schools Ismili Rod Deprtment : Mth Form : rd prep. Sheet Alg. Sheet () [] Find the vlues of nd in ech of the following if : ) (, ) ( -5, 9 ) ) (,
21.1 Using Formulae Construct and Use Simple Formulae Revision of Negative Numbers Substitution into Formulae
 MEP Jmi: STRAND G UNIT 1 Formule: Student Tet Contents STRAND G: Alger Unit 1 Formule Student Tet Contents Setion 1.1 Using Formule 1. Construt nd Use Simple Formule 1.3 Revision of Negtive Numers 1.4
MEP Jmi: STRAND G UNIT 1 Formule: Student Tet Contents STRAND G: Alger Unit 1 Formule Student Tet Contents Setion 1.1 Using Formule 1. Construt nd Use Simple Formule 1.3 Revision of Negtive Numers 1.4
1 ELEMENTARY ALGEBRA and GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE
 ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
Mathematics SKE: STRAND F. F1.1 Using Formulae. F1.2 Construct and Use Simple Formulae. F1.3 Revision of Negative Numbers
 Mthemtis SKE: STRAND F UNIT F1 Formule: Tet STRAND F: Alger F1 Formule Tet Contents Setion F1.1 Using Formule F1. Construt nd Use Simple Formule F1.3 Revision of Negtive Numers F1.4 Sustitution into Formule
Mthemtis SKE: STRAND F UNIT F1 Formule: Tet STRAND F: Alger F1 Formule Tet Contents Setion F1.1 Using Formule F1. Construt nd Use Simple Formule F1.3 Revision of Negtive Numers F1.4 Sustitution into Formule
= x x 2 = 25 2
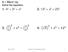 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
Area and Perimeter. Area and Perimeter. Solutions. Curriculum Ready.
 Are n Perimeter Are n Perimeter Solutions Curriulum Rey www.mthletis.om How oes it work? Solutions Are n Perimeter Pge questions Are using unit squres Are = whole squres Are = 6 whole squres = units =
Are n Perimeter Are n Perimeter Solutions Curriulum Rey www.mthletis.om How oes it work? Solutions Are n Perimeter Pge questions Are using unit squres Are = whole squres Are = 6 whole squres = units =
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Algebraic fractions. This unit will help you to work with algebraic fractions and solve equations. rs r s 2. x x.
 Get strted 25 Algeri frtions This unit will help you to work with lgeri frtions nd solve equtions. AO1 Flueny hek 1 Ftorise 2 2 5 2 25 2 6 5 d 2 2 6 2 Simplify 2 6 3 rs r s 2 d 8 2 y 3 6 y 2 3 Write s
Get strted 25 Algeri frtions This unit will help you to work with lgeri frtions nd solve equtions. AO1 Flueny hek 1 Ftorise 2 2 5 2 25 2 6 5 d 2 2 6 2 Simplify 2 6 3 rs r s 2 d 8 2 y 3 6 y 2 3 Write s
Part I: Study the theorem statement.
 Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Nme 1 Nme 2 Nme 3 A STUDY OF PYTHAGORAS THEOREM Instrutions: Together in groups of 2 or 3, fill out the following worksheet. You my lift nswers from the reding, or nswer on your own. Turn in one pket for
Shape and measurement
 C H A P T E R 5 Shpe nd mesurement Wht is Pythgors theorem? How do we use Pythgors theorem? How do we find the perimeter of shpe? How do we find the re of shpe? How do we find the volume of shpe? How do
C H A P T E R 5 Shpe nd mesurement Wht is Pythgors theorem? How do we use Pythgors theorem? How do we find the perimeter of shpe? How do we find the re of shpe? How do we find the volume of shpe? How do
Lesson 2.1 Inductive Reasoning
 Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Lesson 2.1 Inutive Resoning Nme Perio Dte For Eerises 1 7, use inutive resoning to fin the net two terms in eh sequene. 1. 4, 8, 12, 16,, 2. 400, 200, 100, 50, 25,, 3. 1 8, 2 7, 1 2, 4, 5, 4. 5, 3, 2,
Trigonometry. Trigonometry. labelling conventions. Evaluation of areas of non-right-angled triangles using the formulas A = 1 ab sin (C )
 8 8 Pythgors theorem 8 Pythgoren trids 8 Three-dimensionl Pythgors theorem 8D Trigonometri rtios 8E The sine rule 8F miguous se of the sine rule 8G The osine rule 8H Speil tringles 8I re of tringles res
8 8 Pythgors theorem 8 Pythgoren trids 8 Three-dimensionl Pythgors theorem 8D Trigonometri rtios 8E The sine rule 8F miguous se of the sine rule 8G The osine rule 8H Speil tringles 8I re of tringles res
Lesson 2: The Pythagorean Theorem and Similar Triangles. A Brief Review of the Pythagorean Theorem.
 27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
27 Lesson 2: The Pythgoren Theorem nd Similr Tringles A Brief Review of the Pythgoren Theorem. Rell tht n ngle whih mesures 90º is lled right ngle. If one of the ngles of tringle is right ngle, then we
Algebra & Functions (Maths ) opposite side
 Instructor: Dr. R.A.G. Seel Trigonometr Algebr & Functions (Mths 0 0) 0th Prctice Assignment hpotenuse hpotenuse side opposite side sin = opposite hpotenuse tn = opposite. Find sin, cos nd tn in 9 sin
Instructor: Dr. R.A.G. Seel Trigonometr Algebr & Functions (Mths 0 0) 0th Prctice Assignment hpotenuse hpotenuse side opposite side sin = opposite hpotenuse tn = opposite. Find sin, cos nd tn in 9 sin
Integration. antidifferentiation
 9 Integrtion 9A Antidifferentition 9B Integrtion of e, sin ( ) nd os ( ) 9C Integrtion reognition 9D Approimting res enlosed funtions 9E The fundmentl theorem of integrl lulus 9F Signed res 9G Further
9 Integrtion 9A Antidifferentition 9B Integrtion of e, sin ( ) nd os ( ) 9C Integrtion reognition 9D Approimting res enlosed funtions 9E The fundmentl theorem of integrl lulus 9F Signed res 9G Further
along the vector 5 a) Find the plane s coordinate after 1 hour. b) Find the plane s coordinate after 2 hours. c) Find the plane s coordinate
 L8 VECTOR EQUATIONS OF LINES HL Mth - Sntowski Vector eqution of line 1 A plne strts journey t the point (4,1) moves ech hour long the vector. ) Find the plne s coordinte fter 1 hour. b) Find the plne
L8 VECTOR EQUATIONS OF LINES HL Mth - Sntowski Vector eqution of line 1 A plne strts journey t the point (4,1) moves ech hour long the vector. ) Find the plne s coordinte fter 1 hour. b) Find the plne
A study of Pythagoras Theorem
 CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins
CHAPTER 19 A study of Pythgors Theorem Reson is immortl, ll else mortl. Pythgors, Diogenes Lertius (Lives of Eminent Philosophers) Pythgors Theorem is proly the est-known mthemticl theorem. Even most nonmthemticins
15 - TRIGONOMETRY Page 1 ( Answers at the end of all questions )
 - TRIGONOMETRY Pge P ( ) In tringle PQR, R =. If tn b c = 0, 0, then Q nd tn re the roots of the eqution = b c c = b b = c b = c [ AIEEE 00 ] ( ) In tringle ABC, let C =. If r is the inrdius nd R is the
- TRIGONOMETRY Pge P ( ) In tringle PQR, R =. If tn b c = 0, 0, then Q nd tn re the roots of the eqution = b c c = b b = c b = c [ AIEEE 00 ] ( ) In tringle ABC, let C =. If r is the inrdius nd R is the
Calculus Module C21. Areas by Integration. Copyright This publication The Northern Alberta Institute of Technology All Rights Reserved.
 Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
What else can you do?
 Wht else cn you do? ngle sums The size of specil ngle types lernt erlier cn e used to find unknown ngles. tht form stright line dd to 180c. lculte the size of + M, if L is stright line M + L = 180c( stright
Wht else cn you do? ngle sums The size of specil ngle types lernt erlier cn e used to find unknown ngles. tht form stright line dd to 180c. lculte the size of + M, if L is stright line M + L = 180c( stright
MATHEMATICS PART A. 1. ABC is a triangle, right angled at A. The resultant of the forces acting along AB, AC
 FIITJEE Solutions to AIEEE MATHEMATICS PART A. ABC is tringle, right ngled t A. The resultnt of the forces cting long AB, AC with mgnitudes AB nd respectively is the force long AD, where D is the AC foot
FIITJEE Solutions to AIEEE MATHEMATICS PART A. ABC is tringle, right ngled t A. The resultnt of the forces cting long AB, AC with mgnitudes AB nd respectively is the force long AD, where D is the AC foot
Algebra Basics. Algebra Basics. Curriculum Ready ACMNA: 133, 175, 176, 177, 179.
 Curriulum Redy ACMNA: 33 75 76 77 79 www.mthletis.om Fill in the spes with nything you lredy know out Alger Creer Opportunities: Arhitets eletriins plumers et. use it to do importnt lultions. Give this
Curriulum Redy ACMNA: 33 75 76 77 79 www.mthletis.om Fill in the spes with nything you lredy know out Alger Creer Opportunities: Arhitets eletriins plumers et. use it to do importnt lultions. Give this
Continuous Random Variables Class 5, Jeremy Orloff and Jonathan Bloom
 Lerning Gols Continuous Rndom Vriles Clss 5, 8.05 Jeremy Orloff nd Jonthn Bloom. Know the definition of continuous rndom vrile. 2. Know the definition of the proility density function (pdf) nd cumultive
Lerning Gols Continuous Rndom Vriles Clss 5, 8.05 Jeremy Orloff nd Jonthn Bloom. Know the definition of continuous rndom vrile. 2. Know the definition of the proility density function (pdf) nd cumultive
On the diagram below the displacement is represented by the directed line segment OA.
 Vectors Sclrs nd Vectors A vector is quntity tht hs mgnitude nd direction. One exmple of vector is velocity. The velocity of n oject is determined y the mgnitude(speed) nd direction of trvel. Other exmples
Vectors Sclrs nd Vectors A vector is quntity tht hs mgnitude nd direction. One exmple of vector is velocity. The velocity of n oject is determined y the mgnitude(speed) nd direction of trvel. Other exmples
Exercise sheet 6: Solutions
 Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Eerise sheet 6: Solutions Cvet emptor: These re merel etended hints, rther thn omplete solutions. 1. If grph G hs hromti numer k > 1, prove tht its verte set n e prtitioned into two nonempt sets V 1 nd
Date Lesson Text TOPIC Homework. Solving for Obtuse Angles QUIZ ( ) More Trig Word Problems QUIZ ( )
 UNIT 5 TRIGONOMETRI RTIOS Dte Lesson Text TOPI Homework pr. 4 5.1 (48) Trigonometry Review WS 5.1 # 3 5, 9 11, (1, 13)doso pr. 6 5. (49) Relted ngles omplete lesson shell & WS 5. pr. 30 5.3 (50) 5.3 5.4
UNIT 5 TRIGONOMETRI RTIOS Dte Lesson Text TOPI Homework pr. 4 5.1 (48) Trigonometry Review WS 5.1 # 3 5, 9 11, (1, 13)doso pr. 6 5. (49) Relted ngles omplete lesson shell & WS 5. pr. 30 5.3 (50) 5.3 5.4
BEGINNING ALGEBRA (ALGEBRA I)
 /0 BEGINNING ALGEBRA (ALGEBRA I) SAMPLE TEST PLACEMENT EXAMINATION Downlod the omplete Study Pket: http://www.glendle.edu/studypkets Students who hve tken yer of high shool lger or its equivlent with grdes
/0 BEGINNING ALGEBRA (ALGEBRA I) SAMPLE TEST PLACEMENT EXAMINATION Downlod the omplete Study Pket: http://www.glendle.edu/studypkets Students who hve tken yer of high shool lger or its equivlent with grdes
Study Guide and Intervention
 - Stud Guide nd Intervention with the Sme Sign The quotient of two integers with the sme sign is positive. Emple. 7 The dividend nd the divisor hve the sme sign. b. () The dividend nd divisor hve the sme
- Stud Guide nd Intervention with the Sme Sign The quotient of two integers with the sme sign is positive. Emple. 7 The dividend nd the divisor hve the sme sign. b. () The dividend nd divisor hve the sme
A B= ( ) because from A to B is 3 right, 2 down.
 8. Vectors nd vector nottion Questions re trgeted t the grdes indicted Remember: mgnitude mens size. The vector ( ) mens move left nd up. On Resource sheet 8. drw ccurtely nd lbel the following vectors.
8. Vectors nd vector nottion Questions re trgeted t the grdes indicted Remember: mgnitude mens size. The vector ( ) mens move left nd up. On Resource sheet 8. drw ccurtely nd lbel the following vectors.
HW3, Math 307. CSUF. Spring 2007.
 HW, Mth 7. CSUF. Spring 7. Nsser M. Abbsi Spring 7 Compiled on November 5, 8 t 8:8m public Contents Section.6, problem Section.6, problem Section.6, problem 5 Section.6, problem 7 6 5 Section.6, problem
HW, Mth 7. CSUF. Spring 7. Nsser M. Abbsi Spring 7 Compiled on November 5, 8 t 8:8m public Contents Section.6, problem Section.6, problem Section.6, problem 5 Section.6, problem 7 6 5 Section.6, problem
5: The Definite Integral
 5: The Definite Integrl 5.: Estimting with Finite Sums Consider moving oject its velocity (meters per second) t ny time (seconds) is given y v t = t+. Cn we use this informtion to determine the distnce
5: The Definite Integrl 5.: Estimting with Finite Sums Consider moving oject its velocity (meters per second) t ny time (seconds) is given y v t = t+. Cn we use this informtion to determine the distnce
PROPERTIES OF AREAS In general, and for an irregular shape, the definition of the centroid at position ( x, y) is given by
 PROPERTES OF RES Centroid The concept of the centroid is prol lred fmilir to ou For plne shpe with n ovious geometric centre, (rectngle, circle) the centroid is t the centre f n re hs n is of smmetr, the
PROPERTES OF RES Centroid The concept of the centroid is prol lred fmilir to ou For plne shpe with n ovious geometric centre, (rectngle, circle) the centroid is t the centre f n re hs n is of smmetr, the
Triangles The following examples explore aspects of triangles:
 Tringles The following exmples explore spects of tringles: xmple 1: ltitude of right ngled tringle + xmple : tringle ltitude of the symmetricl ltitude of n isosceles x x - 4 +x xmple 3: ltitude of the
Tringles The following exmples explore spects of tringles: xmple 1: ltitude of right ngled tringle + xmple : tringle ltitude of the symmetricl ltitude of n isosceles x x - 4 +x xmple 3: ltitude of the
青藜苑教育 The digrm shows the position of ferry siling between Folkestone nd lis. The ferry is t X. X 4km The pos
 青藜苑教育 www.thetopedu.com 010-6895997 1301951457 Revision Topic 9: Pythgors Theorem Pythgors Theorem Pythgors Theorem llows you to work out the length of sides in right-ngled tringle. c The side opposite
青藜苑教育 www.thetopedu.com 010-6895997 1301951457 Revision Topic 9: Pythgors Theorem Pythgors Theorem Pythgors Theorem llows you to work out the length of sides in right-ngled tringle. c The side opposite
ART LESSONS & EXERCISES
 RT LESSONS & EXERISES Rmón Gllego. www.diujormon.wordpress.com www.diujormon.wordpress.com English - Pge 1 www.diujormon.wordpress.com English - Pge 2 STRTING UP WITH GEOMETRY. DEFINITION OF GEOMETRY Geometry
RT LESSONS & EXERISES Rmón Gllego. www.diujormon.wordpress.com www.diujormon.wordpress.com English - Pge 1 www.diujormon.wordpress.com English - Pge 2 STRTING UP WITH GEOMETRY. DEFINITION OF GEOMETRY Geometry
Individual Events I3 a 10 I4. d 90 angle 57 d Group Events. d 220 Probability
 Answers: (98-8 HKMO Finl Events) Creted by: Mr. Frncis Hung Lst updted: 8 Jnury 08 I 800 I Individul Events I 0 I4 no. of routes 6 I5 + + b b 0 b b c *8 missing c 0 c c See the remrk 600 d d 90 ngle 57
Answers: (98-8 HKMO Finl Events) Creted by: Mr. Frncis Hung Lst updted: 8 Jnury 08 I 800 I Individul Events I 0 I4 no. of routes 6 I5 + + b b 0 b b c *8 missing c 0 c c See the remrk 600 d d 90 ngle 57
