Robot Modeling and Kinematics Errata R. Manseur. List of errors and typos reported as of 4/1/2007:
|
|
|
- Esmond Shaw
- 5 years ago
- Views:
Transcription
1 Robot Modelng and Knematcs Errata R. Manseur. Lst of errors and typos reported as of 4//7:. Fle CF4.wrl mentoned on page 45 s not on the CD. Fle ZYZ_Sm.wrl mentoned on page 67 s not on the CD. 3. Pg. 43. End of frst paragraph below Eq..3, correct v = [4.767,.] T. 4. Pg. 46. Example., Use F = {O, x, y, z }. 5. Pg. 5. Lne below Eq..33. Z coordnate of Q s Page 57. Equatons.57 to.59 are wrong. Correct equatons are: R ( α) R ( β) R ( γ) F F F F. (.57) z y z 3 R= R = R R R = Rz Ry Rz 3 3 ( α) ( β) ( γ) cα sα c s β β cγ sγ = s c α α sγ cγ sβ c β (.58) c c c s s c c s s c c s R = s c c + c s s c s + c c s s sβ cγ sβ sγ cβ α β γ α γ α β γ α γ α β α β γ α γ α β γ α γ α β. (.59) 7. Page 59. Lne above Fgure.9. Correct φ = angle( x, ) and ψ = angle( z, u) r + r + r33 8. Page 6. Bottom of page: c θ =, u xy 9. Page 6: r + r + r33 θ = cos ( ). (.74). Page 69. Example.5. nd lne. Refer to Fgure.5.. Page 74. Exercse 7. Refer to Example.5.. Page 78. Last lne should be See fle: CHAPTERS\CHAPTER3\VRML3\C3F.wrl 3. Page 87. Second lne below Fgure 3.8. CHAPTERS\CHAPTER3\VRML3\C3F8.wrl 4. Page 9. Last paragraph, nd and thrd lnes. Correct (d, a, α, θ) = (,, -45, 6 ) for consstency wth Fg Page 9. Fgure 3.. Boxes 4 and 5 and ther captons should be swtched. 6. Page 9. Pont A s mssng n Fgure 3.. It should located at the center base of the robot.
2 Last part of tem. Correct α = 9. Table at the bottom of the page, d should be r3. 7. Page 93. In Fgure 3.3, Frames F and F 3 should have ther z-axs pontng down. 8. Page 95. End of top paragraph. θ 3 = -9. Second CD reference. Should be CHAPTERS\CHAPTER3\VRML3\C3F6.wrl. 9. Page 96. CD reference should be CHAPTERS\CHAPTER3\VRML3\C3F7.wrl. Page 97. Table 3.4. Should be θ = -θ 3 and θ 4 = π-θ.. Page 99. Table 3.6 has several errors. It should be: Table 3.6 DH Parameters of Converse Manpulator for Example 3.4 Lnk d a α θ Page. Sentence above Table 3.7. Should state d and d 3 are arbtrary, d must be zero. Parameters α and α must be 9 but α 3 s arbtrary. In Table 3.7. the value of α 3 may be set to zero. 3. Page. Fgure 3.3. Frame F should be moved up to the same orgn as F. 4. page 9. Change PUMAMod.exe to PUMAsm.exe. (Top of page and capton of Fg. 3.3) 5. Page 3. Exercse. Part b. Delete s drawn n ts home poston and ts 6. Pg.. Eq. 4.. Matrx A 3, Elements (,) = +c 3 and (,) = -s 3. Parameter d 3 s zero. c3 s3 a3c3 s3 c3 a3s 3 Matrx A3 should be A3 = Equatons 4. should be corrected to be ccc 3+ ss 3 cc s3+ sc 3 cs a3( ccc 3+ ss 3) + acc + ac + ds scc 3cs 3 sc s3cc 3 ss a3( scc 3 cs 3) + asc + as dc P= T3 = AAA3 = sc 3 ss 3 c asc as + d 7. Pg.. Equatons 4. to 4.4. Delete the term before last. Eqs. should be: p = a ( cc c + ss ) + a cc + ac + d s ; (4.) x p = a ( sc c cs ) + a sc + as d c ; (4.3) y z p = asc + as + d. (4.4) 3 3 a+ a + a3 Equaton 4.6 should be p = d. (4.6) d
3 8. Pg. 3. Eq. 4.9 needs mnus sgns n last column of matrx. Should be: c s a R R p γ s γc σ dσ A j = A = = σ s σc γ dγ Thrd lne above Eq Should refer to R -. (4.9) 9. Pg. 5. Eq. 4.4 should be p= R(...( Rn( Rn pn + pn ) + pn)...) + p Eq. 4.4: correct subscrpts and 3 on the poston vectors. Correct equaton s: p= R( R( R3( R4( R5p6 + p5) + p4) + p3) + p) + p 3. Pg. 6. Add parentheses n Eqs to In Eq. 4.5, replace x by z rght before closng paren. In Eq change t x to t z. 3. Pg. 3. Lne after Eq change end-effector frame to frame F Pg. 3. Eqs and Element (,3) should be s 4 s 5 n all relevant matrces. 8. Pg. 34. Secton 4.9, lne 4, Refer to Fgure Pg. 36. Eq A 4 (,) = s Pg. 43. nd lne above Eq Correct typo on product 3. Pg. 43. Eq Matrx has three sgn errors. Correct matrx s: cc + ss + γ+ cs + γ+ sc + σ+ cs + + σ+ sc + a+ cc + a+ ss + + ac sc + + cs + γ+ cc + γ+ ss + σ+ ss + σ+ cc + a+ sc + + a+ cs + + ac AA + = σ+ γ+ d+ + d 3. Pg. 48. Exercse 6. Part b. Should be Four A-matrces Part d: Second lne. Fourth jont value s mssng. It s -6 Next lne. Fourth jont value s 9. Exercse 7. Insert descrbed after the fourth word....robot s descrbed by Page 57. Md page. Left bracket s mssng for matrx R. 34. Pg. 59. Frst lne, mssng sgn: θ 3 = Pg. 67, Eq. 5.49, Frst element of vector should be σ 6 s 6. Second lne of secton , Refer to Fgure 5.7, not Fg Lne before last, bold vector p. 36. Pg. 68. Thrd lne below Eq. 5.58, bold vector t. 37. Pg. 7. Eq should be θ = atan( ± a + b d, d) atan( b, a). Eq Should be: = d =± d d θ = ± s c ( s ) atan[ (, ] b b b 38. pg. 73. Lne followng Eq Refer to Eq. D.36
4 Lne followng Eq. 5.75: ( p a a3 d3 d4) c = a 36. Pg. 74. Lne after Eq Refer to D.36, not D.35. Thrd lne after Eq. 5.78b, change 4.73j to 4.73g. Second lne after Eq change θ 4 + θ 5 to θ 4 + θ Pg. 75. Lne above Eq Correct b=d 4. Lne after Eq value of e must be changed to e = c 3 t x + c s 3 t z. 38. Pg. 76. Ffth lne below Eq refer to Example Pg. 8. Exercse. Matrx P element (,) should be s c Pg 87. Eq. 6.. Should be: Rp 3 z+ p z= Rp z-rp z Eq Should be Rzp R zp = R p z+ p z 3 4. Pg. 88. Eq. 6. Should be c γs σs ac ac R p z+ p z = s γc σc as as + = dγ+ d σ γ d d 4. Pg. 89. Eq Sgn error. Should be σ t x s - σ t y c + σ σ 3 c 3 = e Eq Change t z to p z n term between parentheses. 43. Pg. 9. Eq. 6.36: Sgn error. Should be: ( a+ a3c3) s ( σ d3 γa3s3) c= γpx s+ γpyc+ σ( pz d) 44. Pg. 9. Table 6. s ncorrect. The values of the a parameter are lsted under column d and vce versa. 45. Pg. 93. Eqs and 6.46 are ncomplete. The last w 4 n Eq dd not prnt and the second lne n Eq s mssng. Correct equatons are: d = σσ a[ a ( a w + σ w ) + σσ a d w ] + σ a [ σ ( a + σ d ) + σ a ] w (6.45) H or n expanded form: d = σσ aa a w + σσσ aa w + σσ σaa d w + σ σ a a w H σ3a3σσ d w4 + σ3σaa3 w4 46. Pg. 94. Table 6.. Entres 5 and 7 are ncomplete. A w 4 s mssng at the very end. 47. Pg. 96. Fgure 6.. Cases 4 and 6 are wrongly numbered 3 and 5 respectvely. 48. Pg. 97. Eq Second term of equaton starts wth e 4. Correct Equaton s: y x 3 4 y x 3 (6.46) {[ e ( at s + at c )]/ a σ } + {[ e ( a p s + a p c )]/ a a } =. (6.55) Eq should be: t y = σ 3 c 3 ; (6.57) 49. Pg. 98. Lne below Equaton 6.6. Should refer to Eq. D.43. (not D.39) 5. Pg.. Second lne after Eq Msprnt. Should be θ =-4.
5 Eqs and 6.74 : Second mnus sgn must be replaced by an arrow. Eqs. are: θ = and θ = 4 θ 3 = = (6.73) θ = 35 and θ = 4 θ 3 = = (6.74) 5. Pg.. Lne above Eq Should refer to D.4 (not D.39) 5. Pg. 3. Frst lne. Should be (θ, θ 3 ) Second lne below Equaton 6.89 should be: form of Equaton D.39 wth a = a, b = σ d 3, c = p x s + p y c, and d = p x c + p y s a. 5. Pg. 7. Exercse 5. Part b. Second lne. Change. m to. m 5. Pg.. Eq. 7.5 should be: Q= A P. (7.5) 5. Pg. 3. Secton 7., second lne. Refer to Eq. 7. or 7.4 (not 7.4 or 7.8). 53. Pg. 4. Eq Mssng mnus sgn n top rght expresson of matrx, should be: -R - p Eq. 7.9 should be q R p R p R = (p p ) = (Replace q by p ) 5. Pg. 5. Eq Frst and fourth terms n equaton need to be corrected. Correct equaton s ul ql= γ 4d4 + a3σ4 s4 d3σ3σ4c4 + d3γ3γ4 + σ4 s4( ac3+ σd s3) σ4c4( σdγ3c3 aγ3s3+ γdσ3) + γ4( aσ3s3 σdσ3c3+ γdγ3). Eq. 7.7: Bold vector t. 53. Pg. 6. Eq top vector value should be p x c +p y s -a. Eq Add +t z p z to the rght sde. Eq. s: u q= tx( px ac) + ty( py as) + tz pz Eq. 7.3 should be changed to q q= p p + a ( pxa c + pyas ). Eq Element (,3) of matrx should be a 3 σ 4 Element (3,3) should be -σ 3 a Pg. 7. Eq Second vector element should be γ 3 γ 4 -γ u z Item 3. Second lne. Refer to Equatons 6.35 and 6.36 (not 6.4 and 6.35) Equaton Rght vector. Second element. Sgn error. Change to γ q s + γ q c + σ ( q d ) x y z 55. Pg. 3. Eq has a sgn error. It should be e = ( σtx) s+ ( σty) c γtz + γ4 = 56. Pg. 8 Exercse 5, Part b. Change matrx P values to
6 P = Pg. 3. Lne below Eq. 8.. Insert be between can and manpulated. 58. Pg. 35. Eq. 8.8 has a sgn error. It should be: ( a4+ a5c5) s4 ( σ 4d5 γ4a5s5) c4= γ3qx s3+ γ3qyc3+ σ3( qz d3) 59. Pg. 37. Eq. 8.6 and Eq Second term s ncorrect. Eq. 8.6 should be ux = ( cc γss ) tx + ( sc + γcs ) ty + σstz Eq. 8.9 should be: qx = ( cc γss ) px + ( sc + γcs ) py + σspz ac a 6. Pg. 38. Eq Thrd lne, second mnus sgn s wrong. Change to +. Eq Frst lne. Fourth term on the rght. Insert γ 4 between d 4 and γ 5. Thrd lne, mddle term should be -σ 3 d 3 σ 4 c 4 6. Pg. 4. Eq Matrx has wrong ndexes. Correct Equaton s f f θ θ θ θ f ( θ, θ ) θ = θ new f f f ( θ, θ ) θ θ Second lne after Eq. 8.47, same matrx correcton s needed. Eq Rght sde numerator. Mssng ndex. Change θ to θ 6. Pg. 43. Eq Top element of vector, mddle term should be +s c t x Eq Top element of vector, second term should be +s c p y 63. Pg. 44. Eq Sgn error. Equaton should be ( a4+ a5c5) s4 d5 c4= qz d3 Eq Second lne, second term, delete σ Pg. 56. Bottom lne. Refer to equatons D.8 and D.9 (not D7 and D.8). 65. Pg. 6. Exercse 4. Change Matrx 3 P 6 to P6 = Exercse 6. Part b. Change matrx P to:
7 P = Exercse 7. Part a. Change pose matrx element. to. 66. Pg 66. Frst lne angles should be noted (α, β, γ). 67. Pg 67. Eqs., 9.6 and 9.8. Dots are mssng on q. 68. Pg. 7. Fgure 9.. Vector ω should have a subscrpt: ω Equaton 9.8. Last vector should be p -,n. Eq dot s mssng on θ. 69. Pg. 7. Eq. 9.. subscrpt on last vector element should be n (not 3). 7. Pg. 7. Second lne above Eq Refer to Fgure 9.3. Eqs. 9.7 and 9.8. A dot s needed on all the θ varables. 7. Pg. 77. Eq dot are mssng on all θ. 7. Pg. 78. Eq Decmal pont s mssng on second element of vector V (-.5) Mnus sgn s mssng on thrd element of vector ω. (-.4) Eqs. 9.5 and Dots are mssng on all q vectors and elements. 73. Pg. 8. Eq end of equaton s mssng 5 ω 6. Eq Dots are mssng on all θ. Eq Refer to Eq (not 4.35). 6. Pg. 8. Eq J vl (3,3) = a 3 c 3 +d 4 s Pg. 8. Eq Dots mssng on q vector 6. Pg. 87. Eq In second matrx, R x T (,) =. not. 63. Pg. 88. Eq Matrx elements Q(,) and Q(,) are ncorrect; They should be: ( s & βα & γ) ( s c & γ βα + c & γβ) ωz ω y Q = ( s & βα & γ) ( cγc & βα + s & γβ) = ωz ωx ( sc γ βα + cγβ) ( cc γ βα + sγβ) ωy ωx & & & & Eqs and Elements of vector ω should not be bold. Example 9.5. Second lne, The RPY angles should be (6, -3, ). 64. Pg. 89. Lne above Eq. 9.. Mssng dot on θ. 65. Pg. 9. Eq Element (,) of matrx should be s. Eq Last two vectors n cross product are duplcated and must be deleted. 66. Pg. 94. Exercse. Frst paragraph. Replace the two lnes rght before the matrx J by jonts are all movng at the same rate of.3 rd/s. Replace the lne mmedately after matrx J (last lne of exercse) by Compute the end-effector twst vector V. 67. Pg. 96. Exercse 7. Part a. θ, θ, θ3 must be dotted. Exercse 8. Part b. Begnnng of second lne. Mssng closng bracket.
8 Part e. Change the word speeds to rates. 68. Pg. 33. Lne before Eq..7. Refer to Example 9.4 (not 9.5). 69. Pg. 3. Eq..3. J(,) = (not -.7) 7. Pg. 3. Eq..3. Matrx has wrong numercal values. Should be: J + = Pg. 35. Exercse 7-d, nd lne, change ω to dq/dt 7. Pg. 34. Eq. D.4. Should be tan(α) = a / b and cot(α) = b / a. 73. Pg. 34. Eq. D.7 should be sn(α + β) = sn(α) cos(β) + cos(α) sn(β). 74. Pg Eq. D.37. Mddle value of α should be atan(-b, -a) f sn β < Eq. D.38. Result should be β (not α) Eq. D.4. Left sde of equaton should be a cos(α + β) + b cos(α) = c a sn(α + β) + b sn(α) = d
Corrections to Weak Scale Supersymmetry
 Correctons to Weak Scale Supersymmetry Paper Back Edton, 0 Howard Baer and Xerxes Tata, Cambrdge Unversty Press Chapter 8 page 63, unnumbered equaton at the top of the page: The SU3 couplng matrces n the
Correctons to Weak Scale Supersymmetry Paper Back Edton, 0 Howard Baer and Xerxes Tata, Cambrdge Unversty Press Chapter 8 page 63, unnumbered equaton at the top of the page: The SU3 couplng matrces n the
ERRATA. COMPUTER-AIDED ANALYSIS OF MECHANICAL SYSTEMS Parviz E. Nikravesh Prentice-Hall, (Corrections as of November 2014)
 ERRATA COMPUTER-AIDED ANALYSIS OF MECHANICAL SYSTEMS Parvz E. Nkravesh Prentce-Hall, 1988 (Correctons as of November 2014 Address to an error s gven n the frst column by the page number and n the second
ERRATA COMPUTER-AIDED ANALYSIS OF MECHANICAL SYSTEMS Parvz E. Nkravesh Prentce-Hall, 1988 (Correctons as of November 2014 Address to an error s gven n the frst column by the page number and n the second
NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING. Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582
 NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582 4. Moton Knematcs 4.2 Angular Velocty Knematcs Summary From the last lecture we concluded that: If the jonts
NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582 4. Moton Knematcs 4.2 Angular Velocty Knematcs Summary From the last lecture we concluded that: If the jonts
ERRATA For the book A farewell to Entropy, Statistical Thermodynamics Based on Information
 ERRAA For the book A farewell to Entropy, Statstcal hermodynamcs Based on Informaton Chapter : Page, lnes 4-6 of paragraph should be revsed to: hs defnton s vald wthout any reference to the atomc consttuency
ERRAA For the book A farewell to Entropy, Statstcal hermodynamcs Based on Informaton Chapter : Page, lnes 4-6 of paragraph should be revsed to: hs defnton s vald wthout any reference to the atomc consttuency
APPENDIX 2 FITTING A STRAIGHT LINE TO OBSERVATIONS
 Unversty of Oulu Student Laboratory n Physcs Laboratory Exercses n Physcs 1 1 APPEDIX FITTIG A STRAIGHT LIE TO OBSERVATIOS In the physcal measurements we often make a seres of measurements of the dependent
Unversty of Oulu Student Laboratory n Physcs Laboratory Exercses n Physcs 1 1 APPEDIX FITTIG A STRAIGHT LIE TO OBSERVATIOS In the physcal measurements we often make a seres of measurements of the dependent
Iterative General Dynamic Model for Serial-Link Manipulators
 EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
ERRATUM Joseph John Bevelacqua Contemporary Health Physics 2nd, updated and enlarged edition
 ERRATUM Joseph John Bevelacqua Contemporary Health Physcs 2nd, updated and enlarged edton Page XXIII, Contents, Solutons for Chapter 7 Add the entry: Scenaro 7.4 504 Page 14, 2 nd Lne, Scenaro 1.14, Item
ERRATUM Joseph John Bevelacqua Contemporary Health Physcs 2nd, updated and enlarged edton Page XXIII, Contents, Solutons for Chapter 7 Add the entry: Scenaro 7.4 504 Page 14, 2 nd Lne, Scenaro 1.14, Item
Formulas for the Determinant
 page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
 COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
= = = (a) Use the MATLAB command rref to solve the system. (b) Let A be the coefficient matrix and B be the right-hand side of the system.
 Chapter Matlab Exercses Chapter Matlab Exercses. Consder the lnear system of Example n Secton.. x x x y z y y z (a) Use the MATLAB command rref to solve the system. (b) Let A be the coeffcent matrx and
Chapter Matlab Exercses Chapter Matlab Exercses. Consder the lnear system of Example n Secton.. x x x y z y y z (a) Use the MATLAB command rref to solve the system. (b) Let A be the coeffcent matrx and
An Algorithm to Solve the Inverse Kinematics Problem of a Robotic Manipulator Based on Rotation Vectors
 An Algorthm to Solve the Inverse Knematcs Problem of a Robotc Manpulator Based on Rotaton Vectors Mohamad Z. Al-az*, Mazn Z. Othman**, and Baker B. Al-Bahr* *AL-Nahran Unversty, Computer Eng. Dep., Baghdad,
An Algorthm to Solve the Inverse Knematcs Problem of a Robotc Manpulator Based on Rotaton Vectors Mohamad Z. Al-az*, Mazn Z. Othman**, and Baker B. Al-Bahr* *AL-Nahran Unversty, Computer Eng. Dep., Baghdad,
Chapter 11 Angular Momentum
 Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
11. Dynamics in Rotating Frames of Reference
 Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
C/CS/Phy191 Problem Set 3 Solutions Out: Oct 1, 2008., where ( 00. ), so the overall state of the system is ) ( ( ( ( 00 ± 11 ), Φ ± = 1
 C/CS/Phy9 Problem Set 3 Solutons Out: Oct, 8 Suppose you have two qubts n some arbtrary entangled state ψ You apply the teleportaton protocol to each of the qubts separately What s the resultng state obtaned
C/CS/Phy9 Problem Set 3 Solutons Out: Oct, 8 Suppose you have two qubts n some arbtrary entangled state ψ You apply the teleportaton protocol to each of the qubts separately What s the resultng state obtaned
Effects of Ignoring Correlations When Computing Sample Chi-Square. John W. Fowler February 26, 2012
 Effects of Ignorng Correlatons When Computng Sample Ch-Square John W. Fowler February 6, 0 It can happen that ch-square must be computed for a sample whose elements are correlated to an unknown extent.
Effects of Ignorng Correlatons When Computng Sample Ch-Square John W. Fowler February 6, 0 It can happen that ch-square must be computed for a sample whose elements are correlated to an unknown extent.
1. Estimation, Approximation and Errors Percentages Polynomials and Formulas Identities and Factorization 52
 ontents ommonly Used Formulas. Estmaton, pproxmaton and Errors. Percentages. Polynomals and Formulas 8. Identtes and Factorzaton. Equatons and Inequaltes 66 6. Rate and Rato 8 7. Laws of Integral Indces
ontents ommonly Used Formulas. Estmaton, pproxmaton and Errors. Percentages. Polynomals and Formulas 8. Identtes and Factorzaton. Equatons and Inequaltes 66 6. Rate and Rato 8 7. Laws of Integral Indces
Module 1 : The equation of continuity. Lecture 1: Equation of Continuity
 1 Module 1 : The equaton of contnuty Lecture 1: Equaton of Contnuty 2 Advanced Heat and Mass Transfer: Modules 1. THE EQUATION OF CONTINUITY : Lectures 1-6 () () () (v) (v) Overall Mass Balance Momentum
1 Module 1 : The equaton of contnuty Lecture 1: Equaton of Contnuty 2 Advanced Heat and Mass Transfer: Modules 1. THE EQUATION OF CONTINUITY : Lectures 1-6 () () () (v) (v) Overall Mass Balance Momentum
(c) (cos θ + i sin θ) 5 = cos 5 θ + 5 cos 4 θ (i sin θ) + 10 cos 3 θ(i sin θ) cos 2 θ(i sin θ) 3 + 5cos θ (i sin θ) 4 + (i sin θ) 5 (A1)
 . (a) (cos θ + sn θ) = cos θ + cos θ( sn θ) + cos θ(sn θ) + (sn θ) = cos θ cos θ sn θ + ( cos θ sn θ sn θ) (b) from De Movre s theorem (cos θ + sn θ) = cos θ + sn θ cos θ + sn θ = (cos θ cos θ sn θ) +
. (a) (cos θ + sn θ) = cos θ + cos θ( sn θ) + cos θ(sn θ) + (sn θ) = cos θ cos θ sn θ + ( cos θ sn θ sn θ) (b) from De Movre s theorem (cos θ + sn θ) = cos θ + sn θ cos θ + sn θ = (cos θ cos θ sn θ) +
From Biot-Savart Law to Divergence of B (1)
 From Bot-Savart Law to Dvergence of B (1) Let s prove that Bot-Savart gves us B (r ) = 0 for an arbtrary current densty. Frst take the dvergence of both sdes of Bot-Savart. The dervatve s wth respect to
From Bot-Savart Law to Dvergence of B (1) Let s prove that Bot-Savart gves us B (r ) = 0 for an arbtrary current densty. Frst take the dvergence of both sdes of Bot-Savart. The dervatve s wth respect to
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Errata to Invariant Theory with Applications January 28, 2017
 Invarant Theory wth Applcatons Jan Drasma and Don Gjswjt http: //www.wn.tue.nl/~jdrasma/teachng/nvtheory0910/lecturenotes12.pdf verson of 7 December 2009 Errata and addenda by Darj Grnberg The followng
Invarant Theory wth Applcatons Jan Drasma and Don Gjswjt http: //www.wn.tue.nl/~jdrasma/teachng/nvtheory0910/lecturenotes12.pdf verson of 7 December 2009 Errata and addenda by Darj Grnberg The followng
Canonical transformations
 Canoncal transformatons November 23, 2014 Recall that we have defned a symplectc transformaton to be any lnear transformaton M A B leavng the symplectc form nvarant, Ω AB M A CM B DΩ CD Coordnate transformatons,
Canoncal transformatons November 23, 2014 Recall that we have defned a symplectc transformaton to be any lnear transformaton M A B leavng the symplectc form nvarant, Ω AB M A CM B DΩ CD Coordnate transformatons,
Lecture 2: Numerical Methods for Differentiations and Integrations
 Numercal Smulaton of Space Plasmas (I [AP-4036] Lecture 2 by Lng-Hsao Lyu March, 2018 Lecture 2: Numercal Methods for Dfferentatons and Integratons As we have dscussed n Lecture 1 that numercal smulaton
Numercal Smulaton of Space Plasmas (I [AP-4036] Lecture 2 by Lng-Hsao Lyu March, 2018 Lecture 2: Numercal Methods for Dfferentatons and Integratons As we have dscussed n Lecture 1 that numercal smulaton
AP Physics 1 & 2 Summer Assignment
 AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Module 14: THE INTEGRAL Exploring Calculus
 Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
This model contains two bonds per unit cell (one along the x-direction and the other along y). So we can rewrite the Hamiltonian as:
 1 Problem set #1 1.1. A one-band model on a square lattce Fg. 1 Consder a square lattce wth only nearest-neghbor hoppngs (as shown n the fgure above): H t, j a a j (1.1) where,j stands for nearest neghbors
1 Problem set #1 1.1. A one-band model on a square lattce Fg. 1 Consder a square lattce wth only nearest-neghbor hoppngs (as shown n the fgure above): H t, j a a j (1.1) where,j stands for nearest neghbors
DARWIN-OP HUMANOID ROBOT KINEMATICS. Robert L. Williams II, Ph.D., Mechanical Engineering, Ohio University, Athens, Ohio, USA
 Proceedngs of the ASME 1 Internatonal Desgn Engneerng Techncal onferences & omputers and Informaton n Engneerng onference IDET/IE 1 August 1-15, 1, hcago, IL, USA DET1-765 DARWIN-OP HUMANOID ROBOT KINEMATIS
Proceedngs of the ASME 1 Internatonal Desgn Engneerng Techncal onferences & omputers and Informaton n Engneerng onference IDET/IE 1 August 1-15, 1, hcago, IL, USA DET1-765 DARWIN-OP HUMANOID ROBOT KINEMATIS
Srednicki Chapter 34
 Srednck Chapter 3 QFT Problems & Solutons A. George January 0, 203 Srednck 3.. Verfy that equaton 3.6 follows from equaton 3.. We take Λ = + δω: U + δω ψu + δω = + δωψ[ + δω] x Next we use equaton 3.3,
Srednck Chapter 3 QFT Problems & Solutons A. George January 0, 203 Srednck 3.. Verfy that equaton 3.6 follows from equaton 3.. We take Λ = + δω: U + δω ψu + δω = + δωψ[ + δω] x Next we use equaton 3.3,
PARALLEL MECHANISMS WITH VARIABLE COMPLIANCE
 PRLLEL MECHNISMS WIH VRIBLE COMPLINCE By HYUN KWON JUNG DISSERION PRESENED O HE GRDUE SCHOOL OF HE UNIVERSIY OF FLORID IN PRIL FULFILLMEN OF HE REQUIREMENS FOR HE DEGREE OF DOCOR OF PHILOSOPHY UNIVERSIY
PRLLEL MECHNISMS WIH VRIBLE COMPLINCE By HYUN KWON JUNG DISSERION PRESENED O HE GRDUE SCHOOL OF HE UNIVERSIY OF FLORID IN PRIL FULFILLMEN OF HE REQUIREMENS FOR HE DEGREE OF DOCOR OF PHILOSOPHY UNIVERSIY
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
DIFFERENTIAL KINEMATICS OF CONTEMPORARY INDUSTRIAL ROBOTS
 Int. J. of Appled Mechancs and Engneerng 0 vol.9 No. pp.-9 DOI: 0.78/jame-0-00 DIFFERENTIAL KINEMATICS OF CONTEMPORARY INDUSTRIAL ROBOTS T. SZKODNY Insttute of Automatc Control Slesan Unversty of Technology
Int. J. of Appled Mechancs and Engneerng 0 vol.9 No. pp.-9 DOI: 0.78/jame-0-00 DIFFERENTIAL KINEMATICS OF CONTEMPORARY INDUSTRIAL ROBOTS T. SZKODNY Insttute of Automatc Control Slesan Unversty of Technology
Problem Do any of the following determine homomorphisms from GL n (C) to GL n (C)?
 Homework 8 solutons. Problem 16.1. Whch of the followng defne homomomorphsms from C\{0} to C\{0}? Answer. a) f 1 : z z Yes, f 1 s a homomorphsm. We have that z s the complex conjugate of z. If z 1,z 2
Homework 8 solutons. Problem 16.1. Whch of the followng defne homomomorphsms from C\{0} to C\{0}? Answer. a) f 1 : z z Yes, f 1 s a homomorphsm. We have that z s the complex conjugate of z. If z 1,z 2
Complex Numbers. x = B B 2 4AC 2A. or x = x = 2 ± 4 4 (1) (5) 2 (1)
 Complex Numbers If you have not yet encountered complex numbers, you wll soon do so n the process of solvng quadratc equatons. The general quadratc equaton Ax + Bx + C 0 has solutons x B + B 4AC A For
Complex Numbers If you have not yet encountered complex numbers, you wll soon do so n the process of solvng quadratc equatons. The general quadratc equaton Ax + Bx + C 0 has solutons x B + B 4AC A For
1 Derivation of Point-to-Plane Minimization
 1 Dervaton of Pont-to-Plane Mnmzaton Consder the Chen-Medon (pont-to-plane) framework for ICP. Assume we have a collecton of ponts (p, q ) wth normals n. We want to determne the optmal rotaton and translaton
1 Dervaton of Pont-to-Plane Mnmzaton Consder the Chen-Medon (pont-to-plane) framework for ICP. Assume we have a collecton of ponts (p, q ) wth normals n. We want to determne the optmal rotaton and translaton
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
Lecture Torsion Properties for Line Segments and Computational Scheme for Piecewise Straight Section Calculations
 Lecture - 003 Torson Propertes for Lne Segments and Computatonal Scheme for Pecewse Straght Secton Calculatons ths conssts of four parts (and how we wll treat each) A - dervaton of geometrc algorthms for
Lecture - 003 Torson Propertes for Lne Segments and Computatonal Scheme for Pecewse Straght Secton Calculatons ths conssts of four parts (and how we wll treat each) A - dervaton of geometrc algorthms for
AERODYNAMICS I LECTURE 6 AERODYNAMICS OF A WING FUNDAMENTALS OF THE LIFTING-LINE THEORY
 LECTURE 6 AERODYNAMICS OF A WING FUNDAMENTALS OF THE LIFTING-LINE THEORY The Bot-Savart Law The velocty nduced by the sngular vortex lne wth the crculaton can be determned by means of the Bot- Savart formula
LECTURE 6 AERODYNAMICS OF A WING FUNDAMENTALS OF THE LIFTING-LINE THEORY The Bot-Savart Law The velocty nduced by the sngular vortex lne wth the crculaton can be determned by means of the Bot- Savart formula
EXAM INFORMATION. Harmonic Oscillator. Anharmonic Oscillator 1 ~ 1. Rigid Rotor
 EXAM INFORMATION Harmonc Oscllator Hamltonan: H d dx 1 kx Energy Levels: 1 k mm 1 En n n 0,1,, c m m 1 Anharmonc Oscllator Energy Levels: E n 1 ~ 1 n hc n hcx ~ e n 0,1,,... Rgd Rotor Quantum Numbers:
EXAM INFORMATION Harmonc Oscllator Hamltonan: H d dx 1 kx Energy Levels: 1 k mm 1 En n n 0,1,, c m m 1 Anharmonc Oscllator Energy Levels: E n 1 ~ 1 n hc n hcx ~ e n 0,1,,... Rgd Rotor Quantum Numbers:
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Important Instructions to the Examiners:
 Summer 0 Examnaton Subject & Code: asc Maths (70) Model Answer Page No: / Important Instructons to the Examners: ) The Answers should be examned by key words and not as word-to-word as gven n the model
Summer 0 Examnaton Subject & Code: asc Maths (70) Model Answer Page No: / Important Instructons to the Examners: ) The Answers should be examned by key words and not as word-to-word as gven n the model
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Homework Notes Week 7
 Homework Notes Week 7 Math 4 Sprng 4 #4 (a Complete the proof n example 5 that s an nner product (the Frobenus nner product on M n n (F In the example propertes (a and (d have already been verfed so we
Homework Notes Week 7 Math 4 Sprng 4 #4 (a Complete the proof n example 5 that s an nner product (the Frobenus nner product on M n n (F In the example propertes (a and (d have already been verfed so we
NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING. Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582
 NMT EE 589 & UNM ME 48/58 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 48/58 7. Robot Dynamcs 7.5 The Equatons of Moton Gven that we wsh to fnd the path q(t (n jont space) whch mnmzes the energy
NMT EE 589 & UNM ME 48/58 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 48/58 7. Robot Dynamcs 7.5 The Equatons of Moton Gven that we wsh to fnd the path q(t (n jont space) whch mnmzes the energy
Physics 181. Particle Systems
 Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
PhysicsAndMathsTutor.com
 PhscsAndMathsTutor.com phscsandmathstutor.com June 005 5. The random varable X has probablt functon k, = 1,, 3, P( X = ) = k ( + 1), = 4, 5, where k s a constant. (a) Fnd the value of k. (b) Fnd the eact
PhscsAndMathsTutor.com phscsandmathstutor.com June 005 5. The random varable X has probablt functon k, = 1,, 3, P( X = ) = k ( + 1), = 4, 5, where k s a constant. (a) Fnd the value of k. (b) Fnd the eact
Programming Project 1: Molecular Geometry and Rotational Constants
 Programmng Project 1: Molecular Geometry and Rotatonal Constants Center for Computatonal Chemstry Unversty of Georga Athens, Georga 30602 Summer 2012 1 Introducton Ths programmng project s desgned to provde
Programmng Project 1: Molecular Geometry and Rotatonal Constants Center for Computatonal Chemstry Unversty of Georga Athens, Georga 30602 Summer 2012 1 Introducton Ths programmng project s desgned to provde
Field and Wave Electromagnetic. Chapter.4
 Fel an Wave Electromagnetc Chapter.4 Soluton of electrostatc Problems Posson s s an Laplace s Equatons D = ρ E = E = V D = ε E : Two funamental equatons for electrostatc problem Where, V s scalar electrc
Fel an Wave Electromagnetc Chapter.4 Soluton of electrostatc Problems Posson s s an Laplace s Equatons D = ρ E = E = V D = ε E : Two funamental equatons for electrostatc problem Where, V s scalar electrc
Section 8.1 Exercises
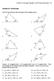 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: Instructor s Name and Secton: (Crcle Your Secton) Sectons:
Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: Instructor s Name and Secton: (Crcle Your Secton) Sectons:
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space
NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space
Chapter 3. r r. Position, Velocity, and Acceleration Revisited
 Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Linear Momentum. Center of Mass.
 Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
The path of ants Dragos Crisan, Andrei Petridean, 11 th grade. Colegiul National "Emil Racovita", Cluj-Napoca
 Ths artcle s wrtten by students. It may nclude omssons and mperfectons, whch were dentfed and reported as mnutely as possble by our revewers n the edtoral notes. The path of ants 07-08 Students names and
Ths artcle s wrtten by students. It may nclude omssons and mperfectons, whch were dentfed and reported as mnutely as possble by our revewers n the edtoral notes. The path of ants 07-08 Students names and
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
Supporting Information Part 1. DFTB3: Extension of the self-consistent-charge. density-functional tight-binding method (SCC-DFTB)
 Supportng Informaton Part 1 DFTB3: Extenson of the self-consstent-charge densty-functonal tght-ndng method SCC-DFTB Mchael Gaus, Qang Cu, and Marcus Elstner, Insttute of Physcal Chemstry, Karlsruhe Insttute
Supportng Informaton Part 1 DFTB3: Extenson of the self-consstent-charge densty-functonal tght-ndng method SCC-DFTB Mchael Gaus, Qang Cu, and Marcus Elstner, Insttute of Physcal Chemstry, Karlsruhe Insttute
COMPOSITE BEAM WITH WEAK SHEAR CONNECTION SUBJECTED TO THERMAL LOAD
 COMPOSITE BEAM WITH WEAK SHEAR CONNECTION SUBJECTED TO THERMAL LOAD Ákos Jósef Lengyel, István Ecsed Assstant Lecturer, Professor of Mechancs, Insttute of Appled Mechancs, Unversty of Mskolc, Mskolc-Egyetemváros,
COMPOSITE BEAM WITH WEAK SHEAR CONNECTION SUBJECTED TO THERMAL LOAD Ákos Jósef Lengyel, István Ecsed Assstant Lecturer, Professor of Mechancs, Insttute of Appled Mechancs, Unversty of Mskolc, Mskolc-Egyetemváros,
Physics 2A Chapter 3 HW Solutions
 Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
T f. Geometry. R f. R i. Homogeneous transformation. y x. P f. f 000. Homogeneous transformation matrix. R (A): Orientation P : Position
 Homogeneous transformaton Geometr T f R f R T f Homogeneous transformaton matr Unverst of Genova T f Phlppe Martnet = R f 000 P f 1 R (A): Orentaton P : Poston 123 Modelng and Control of Manpulator robots
Homogeneous transformaton Geometr T f R f R T f Homogeneous transformaton matr Unverst of Genova T f Phlppe Martnet = R f 000 P f 1 R (A): Orentaton P : Poston 123 Modelng and Control of Manpulator robots
I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 ME 270 Fall 2012 Fnal Exam Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem
ME 270 Fall 2012 Fnal Exam Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem
Week 11: Differential Amplifiers
 ELE 0A Electronc rcuts Week : Dfferental Amplfers Lecture - Large sgnal analyss Topcs to coer A analyss Half-crcut analyss eadng Assgnment: hap 5.-5.8 of Jaeger and Blalock or hap 7. - 7.3, of Sedra and
ELE 0A Electronc rcuts Week : Dfferental Amplfers Lecture - Large sgnal analyss Topcs to coer A analyss Half-crcut analyss eadng Assgnment: hap 5.-5.8 of Jaeger and Blalock or hap 7. - 7.3, of Sedra and
Measurement Indices of Positional Uncertainty for Plane Line Segments Based on the ε
 Proceedngs of the 8th Internatonal Smposum on Spatal ccurac ssessment n Natural Resources and Envronmental Scences Shangha, P R Chna, June 5-7, 008, pp 9-5 Measurement Indces of Postonal Uncertant for
Proceedngs of the 8th Internatonal Smposum on Spatal ccurac ssessment n Natural Resources and Envronmental Scences Shangha, P R Chna, June 5-7, 008, pp 9-5 Measurement Indces of Postonal Uncertant for
Affine transformations and convexity
 Affne transformatons and convexty The purpose of ths document s to prove some basc propertes of affne transformatons nvolvng convex sets. Here are a few onlne references for background nformaton: http://math.ucr.edu/
Affne transformatons and convexty The purpose of ths document s to prove some basc propertes of affne transformatons nvolvng convex sets. Here are a few onlne references for background nformaton: http://math.ucr.edu/
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM
 ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
9 Characteristic classes
 THEODORE VORONOV DIFFERENTIAL GEOMETRY. Sprng 2009 [under constructon] 9 Characterstc classes 9.1 The frst Chern class of a lne bundle Consder a complex vector bundle E B of rank p. We shall construct
THEODORE VORONOV DIFFERENTIAL GEOMETRY. Sprng 2009 [under constructon] 9 Characterstc classes 9.1 The frst Chern class of a lne bundle Consder a complex vector bundle E B of rank p. We shall construct
CHAPTER 14 GENERAL PERTURBATION THEORY
 CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
Inner Product. Euclidean Space. Orthonormal Basis. Orthogonal
 Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
ERRATA THERMAL RADIATION HEAT TRANSFER, 5 TH Edition, 1 st Printing John R. Howell, Robert Siegel, M. Pinar Mengüç
 //05 ERRATA THERMAL RADIATION HEAT TRANSFER, 5 TH Edto, st Prt Joh R. Howell, Robert Seel, M. Par Meüç Pae 5 Three les before Eq. (.7), I b should be I b, 7 I Eq.., ( ) should be ( ). I last equato o pae,
//05 ERRATA THERMAL RADIATION HEAT TRANSFER, 5 TH Edto, st Prt Joh R. Howell, Robert Seel, M. Par Meüç Pae 5 Three les before Eq. (.7), I b should be I b, 7 I Eq.., ( ) should be ( ). I last equato o pae,
The Jacobsthal and Jacobsthal-Lucas Numbers via Square Roots of Matrices
 Internatonal Mathematcal Forum, Vol 11, 2016, no 11, 513-520 HIKARI Ltd, wwwm-hkarcom http://dxdoorg/1012988/mf20166442 The Jacobsthal and Jacobsthal-Lucas Numbers va Square Roots of Matrces Saadet Arslan
Internatonal Mathematcal Forum, Vol 11, 2016, no 11, 513-520 HIKARI Ltd, wwwm-hkarcom http://dxdoorg/1012988/mf20166442 The Jacobsthal and Jacobsthal-Lucas Numbers va Square Roots of Matrces Saadet Arslan
χ x B E (c) Figure 2.1.1: (a) a material particle in a body, (b) a place in space, (c) a configuration of the body
 Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
G = G 1 + G 2 + G 3 G 2 +G 3 G1 G2 G3. Network (a) Network (b) Network (c) Network (d)
 Massachusetts Insttute of Technology Department of Electrcal Engneerng and Computer Scence 6.002 í Electronc Crcuts Homework 2 Soluton Handout F98023 Exercse 21: Determne the conductance of each network
Massachusetts Insttute of Technology Department of Electrcal Engneerng and Computer Scence 6.002 í Electronc Crcuts Homework 2 Soluton Handout F98023 Exercse 21: Determne the conductance of each network
THE SUMMATION NOTATION Ʃ
 Sngle Subscrpt otaton THE SUMMATIO OTATIO Ʃ Most of the calculatons we perform n statstcs are repettve operatons on lsts of numbers. For example, we compute the sum of a set of numbers, or the sum of the
Sngle Subscrpt otaton THE SUMMATIO OTATIO Ʃ Most of the calculatons we perform n statstcs are repettve operatons on lsts of numbers. For example, we compute the sum of a set of numbers, or the sum of the
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 ME 270 Sprng 2017 Exam 1 NAME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: Instructor s Name
ME 270 Sprng 2017 Exam 1 NAME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: Instructor s Name
Chapter 8. Potential Energy and Conservation of Energy
 Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Inductance Calculation for Conductors of Arbitrary Shape
 CRYO/02/028 Aprl 5, 2002 Inductance Calculaton for Conductors of Arbtrary Shape L. Bottura Dstrbuton: Internal Summary In ths note we descrbe a method for the numercal calculaton of nductances among conductors
CRYO/02/028 Aprl 5, 2002 Inductance Calculaton for Conductors of Arbtrary Shape L. Bottura Dstrbuton: Internal Summary In ths note we descrbe a method for the numercal calculaton of nductances among conductors
Complex Numbers Alpha, Round 1 Test #123
 Complex Numbers Alpha, Round Test #3. Wrte your 6-dgt ID# n the I.D. NUMBER grd, left-justfed, and bubble. Check that each column has only one number darkened.. In the EXAM NO. grd, wrte the 3-dgt Test
Complex Numbers Alpha, Round Test #3. Wrte your 6-dgt ID# n the I.D. NUMBER grd, left-justfed, and bubble. Check that each column has only one number darkened.. In the EXAM NO. grd, wrte the 3-dgt Test
2 Finite difference basics
 Numersche Methoden 1, WS 11/12 B.J.P. Kaus 2 Fnte dfference bascs Consder the one- The bascs of the fnte dfference method are best understood wth an example. dmensonal transent heat conducton equaton T
Numersche Methoden 1, WS 11/12 B.J.P. Kaus 2 Fnte dfference bascs Consder the one- The bascs of the fnte dfference method are best understood wth an example. dmensonal transent heat conducton equaton T
From the Euclidean Algorithm for Solving a Key Equation for Dual Reed Solomon Codes to the Berlekamp-Massey Algorithm
 1 / 32 From the Eucldean Algorthm for Solvng a Key Equaton for Dual Reed Solomon Codes to the Berlekamp-Massey Algorthm Mara Bras-Amorós, Mchael E O Sullvan The Claude Shannon Insttute Workshop on Codng
1 / 32 From the Eucldean Algorthm for Solvng a Key Equaton for Dual Reed Solomon Codes to the Berlekamp-Massey Algorthm Mara Bras-Amorós, Mchael E O Sullvan The Claude Shannon Insttute Workshop on Codng
ln 2 = 1 + max{c m,n/2 2 t 1, t + C m 1,n/2 1} + m 107
 Errata to The Analyss of Algorthms, Second Prntng. 8 7 006 Usually just the corrected segment of text s gven. Negatve lne numbers ndcate the number of lnes from the bottom. p, l 3. (Only for n > 5 10 17
Errata to The Analyss of Algorthms, Second Prntng. 8 7 006 Usually just the corrected segment of text s gven. Negatve lne numbers ndcate the number of lnes from the bottom. p, l 3. (Only for n > 5 10 17
Min Cut, Fast Cut, Polynomial Identities
 Randomzed Algorthms, Summer 016 Mn Cut, Fast Cut, Polynomal Identtes Instructor: Thomas Kesselhem and Kurt Mehlhorn 1 Mn Cuts n Graphs Lecture (5 pages) Throughout ths secton, G = (V, E) s a mult-graph.
Randomzed Algorthms, Summer 016 Mn Cut, Fast Cut, Polynomal Identtes Instructor: Thomas Kesselhem and Kurt Mehlhorn 1 Mn Cuts n Graphs Lecture (5 pages) Throughout ths secton, G = (V, E) s a mult-graph.
Lecture 5 Decoding Binary BCH Codes
 Lecture 5 Decodng Bnary BCH Codes In ths class, we wll ntroduce dfferent methods for decodng BCH codes 51 Decodng the [15, 7, 5] 2 -BCH Code Consder the [15, 7, 5] 2 -code C we ntroduced n the last lecture
Lecture 5 Decodng Bnary BCH Codes In ths class, we wll ntroduce dfferent methods for decodng BCH codes 51 Decodng the [15, 7, 5] 2 -BCH Code Consder the [15, 7, 5] 2 -code C we ntroduced n the last lecture
CALCULUS CLASSROOM CAPSULES
 CALCULUS CLASSROOM CAPSULES SESSION S86 Dr. Sham Alfred Rartan Valley Communty College salfred@rartanval.edu 38th AMATYC Annual Conference Jacksonvlle, Florda November 8-, 202 2 Calculus Classroom Capsules
CALCULUS CLASSROOM CAPSULES SESSION S86 Dr. Sham Alfred Rartan Valley Communty College salfred@rartanval.edu 38th AMATYC Annual Conference Jacksonvlle, Florda November 8-, 202 2 Calculus Classroom Capsules
Four Bar Linkages in Two Dimensions. A link has fixed length and is joined to other links and also possibly to a fixed point.
 Four bar lnkages 1 Four Bar Lnkages n Two Dmensons lnk has fed length and s oned to other lnks and also possbly to a fed pont. The relatve velocty of end B wth regard to s gven by V B = ω r y v B B = +y
Four bar lnkages 1 Four Bar Lnkages n Two Dmensons lnk has fed length and s oned to other lnks and also possbly to a fed pont. The relatve velocty of end B wth regard to s gven by V B = ω r y v B B = +y
Statistics MINITAB - Lab 2
 Statstcs 20080 MINITAB - Lab 2 1. Smple Lnear Regresson In smple lnear regresson we attempt to model a lnear relatonshp between two varables wth a straght lne and make statstcal nferences concernng that
Statstcs 20080 MINITAB - Lab 2 1. Smple Lnear Regresson In smple lnear regresson we attempt to model a lnear relatonshp between two varables wth a straght lne and make statstcal nferences concernng that
A NOTE OF DIFFERENTIAL GEOMETRY
 A NOTE OF DIFFERENTIAL GEOMETRY - APPLICATION OF THE METHOD OF THE REPÈRE MOBILE TO THE ELLIPSOID OF REFERENCE IN GEODESY - by ABDELMAJID BEN HADJ SALEM INGÉNIEUR GÉNÉRAL RETIRED FROM THE Offce de la Topographe
A NOTE OF DIFFERENTIAL GEOMETRY - APPLICATION OF THE METHOD OF THE REPÈRE MOBILE TO THE ELLIPSOID OF REFERENCE IN GEODESY - by ABDELMAJID BEN HADJ SALEM INGÉNIEUR GÉNÉRAL RETIRED FROM THE Offce de la Topographe
Class: Life-Science Subject: Physics
 Class: Lfe-Scence Subject: Physcs Frst year (6 pts): Graphc desgn of an energy exchange A partcle (B) of ass =g oves on an nclned plane of an nclned angle α = 3 relatve to the horzontal. We want to study
Class: Lfe-Scence Subject: Physcs Frst year (6 pts): Graphc desgn of an energy exchange A partcle (B) of ass =g oves on an nclned plane of an nclned angle α = 3 relatve to the horzontal. We want to study
Chapter 4 The Wave Equation
 Chapter 4 The Wave Equaton Another classcal example of a hyperbolc PDE s a wave equaton. The wave equaton s a second-order lnear hyperbolc PDE that descrbes the propagaton of a varety of waves, such as
Chapter 4 The Wave Equaton Another classcal example of a hyperbolc PDE s a wave equaton. The wave equaton s a second-order lnear hyperbolc PDE that descrbes the propagaton of a varety of waves, such as
Professor Terje Haukaas University of British Columbia, Vancouver The Q4 Element
 Professor Terje Haukaas Unversty of Brtsh Columba, ancouver www.nrsk.ubc.ca The Q Element Ths document consders fnte elements that carry load only n ther plane. These elements are sometmes referred to
Professor Terje Haukaas Unversty of Brtsh Columba, ancouver www.nrsk.ubc.ca The Q Element Ths document consders fnte elements that carry load only n ther plane. These elements are sometmes referred to
EPR Paradox and the Physical Meaning of an Experiment in Quantum Mechanics. Vesselin C. Noninski
 EPR Paradox and the Physcal Meanng of an Experment n Quantum Mechancs Vesseln C Nonnsk vesselnnonnsk@verzonnet Abstract It s shown that there s one purely determnstc outcome when measurement s made on
EPR Paradox and the Physcal Meanng of an Experment n Quantum Mechancs Vesseln C Nonnsk vesselnnonnsk@verzonnet Abstract It s shown that there s one purely determnstc outcome when measurement s made on
THEOREMS OF QUANTUM MECHANICS
 THEOREMS OF QUANTUM MECHANICS In order to develop methods to treat many-electron systems (atoms & molecules), many of the theorems of quantum mechancs are useful. Useful Notaton The matrx element A mn
THEOREMS OF QUANTUM MECHANICS In order to develop methods to treat many-electron systems (atoms & molecules), many of the theorems of quantum mechancs are useful. Useful Notaton The matrx element A mn
Chapter 3 Differentiation and Integration
 MEE07 Computer Modelng Technques n Engneerng Chapter Derentaton and Integraton Reerence: An Introducton to Numercal Computatons, nd edton, S. yakowtz and F. zdarovsky, Mawell/Macmllan, 990. Derentaton
MEE07 Computer Modelng Technques n Engneerng Chapter Derentaton and Integraton Reerence: An Introducton to Numercal Computatons, nd edton, S. yakowtz and F. zdarovsky, Mawell/Macmllan, 990. Derentaton
The equation of motion of a dynamical system is given by a set of differential equations. That is (1)
 Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
The Dirac Equation for a One-electron atom. In this section we will derive the Dirac equation for a one-electron atom.
 The Drac Equaton for a One-electron atom In ths secton we wll derve the Drac equaton for a one-electron atom. Accordng to Ensten the energy of a artcle wth rest mass m movng wth a velocty V s gven by E
The Drac Equaton for a One-electron atom In ths secton we wll derve the Drac equaton for a one-electron atom. Accordng to Ensten the energy of a artcle wth rest mass m movng wth a velocty V s gven by E
I have not received unauthorized aid in the completion of this exam.
 ME 270 Sprng 2013 Fnal Examnaton Please read and respond to the followng statement, I have not receved unauthorzed ad n the completon of ths exam. Agree Dsagree Sgnature INSTRUCTIONS Begn each problem
ME 270 Sprng 2013 Fnal Examnaton Please read and respond to the followng statement, I have not receved unauthorzed ad n the completon of ths exam. Agree Dsagree Sgnature INSTRUCTIONS Begn each problem
= 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W]
![= 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W] = 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W]](/thumbs/78/76802454.jpg) Secton 1.3: Acceleraton Tutoral 1 Practce, page 24 1. Gven: 0 m/s; 15.0 m/s [S]; t 12.5 s Requred: Analyss: a av v t v f v t a v av f v t 15.0 m/s [S] 0 m/s 12.5 s 15.0 m/s [S] 12.5 s 1.20 m/s 2 [S] Statement:
Secton 1.3: Acceleraton Tutoral 1 Practce, page 24 1. Gven: 0 m/s; 15.0 m/s [S]; t 12.5 s Requred: Analyss: a av v t v f v t a v av f v t 15.0 m/s [S] 0 m/s 12.5 s 15.0 m/s [S] 12.5 s 1.20 m/s 2 [S] Statement:
6 Supplementary Materials
 6 Supplementar Materals 61 Proof of Theorem 31 Proof Let m Xt z 1:T : l m Xt X,z 1:t Wethenhave mxt z1:t ˆm HX Xt z 1:T mxt z1:t m HX Xt z 1:T + mxt z 1:T HX We consder each of the two terms n equaton
6 Supplementar Materals 61 Proof of Theorem 31 Proof Let m Xt z 1:T : l m Xt X,z 1:t Wethenhave mxt z1:t ˆm HX Xt z 1:T mxt z1:t m HX Xt z 1:T + mxt z 1:T HX We consder each of the two terms n equaton
Quantum Mechanics I Problem set No.1
 Quantum Mechancs I Problem set No.1 Septembe0, 2017 1 The Least Acton Prncple The acton reads S = d t L(q, q) (1) accordng to the least (extremal) acton prncple, the varaton of acton s zero 0 = δs = t
Quantum Mechancs I Problem set No.1 Septembe0, 2017 1 The Least Acton Prncple The acton reads S = d t L(q, q) (1) accordng to the least (extremal) acton prncple, the varaton of acton s zero 0 = δs = t
