Section 8.3 Polar Form of Complex Numbers
|
|
|
- Damian Charles
- 6 years ago
- Views:
Transcription
1 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the sum of a real number and an magnary number Whle these are useful for expressng the solutons to quadratc equatons, they have much rcher applcatons n electrcal engneerng, sgnal analyss, and other felds Most of these more advanced applcatons rely on propertes that arse from lookng at complex numbers from the perspectve of polar coordnates We wll begn wth a revew of the defnton of complex numbers Imagnary Number The most basc complex number s, defned to be 1, commonly called an magnary number Any real multple of s also an magnary number Example 1 Smplfy 9 We can separate 9 as 9 1 We can take the square root of 9, and wrte the square root of -1 as A complex number s the sum of a real number and an magnary number Complex Number A complex number s a number z a + b, where a and b are real numbers a s the real part of the complex number b s the magnary part of the complex number 1 Plottng a complex number We can plot real numbers on a number lne For example, f we wanted to show the number, we plot a pont:
2 Secton 8 Polar Form of Complex Numbers 81 To plot a complex number lke, we need more than just a number lne snce there are two components to the number To plot ths number, we need two number lnes, crossed to form a complex plane Complex Plane In the complex plane, the horzontal axs s the real axs and the vertcal axs s the magnary axs magnary real Example Plot the number on the complex plane The real part of ths number s, and the magnary part s - To plot ths, we draw a pont unts to the rght of the orgn n the horzontal drecton and unts down n the vertcal drecton magnary real Because ths s analogous to the Cartesan coordnate system for plottng ponts, we can thnk about plottng our complex number z a + b as f we were plottng the pont (a, b) n Cartesan coordnates Sometmes people wrte complex numbers as z x + y to hghlght ths relaton Arthmetc on Complex Numbers Before we dve nto the more complcated uses of complex numbers, let s make sure we remember the basc arthmetc nvolved To add or subtract complex numbers, we smply add the lke terms, combnng the real parts and combnng the magnary parts Example Add and + 5 Addng ( ) + ( + 5), we add the real parts and the magnary parts Try t Now 1 Subtract + 5 from We can also multply and dvde complex numbers
3 8 Chapter 8 Example Multply: ( + 5) To multply the complex number by a real number, we smply dstrbute as we would when multplyng polynomals ( + 5) Example 5 Dvde ( + 5 ) ( ) To dvde two complex numbers, we have to devse a way to wrte ths as a complex number wth a real part and an magnary part We start ths process by elmnatng the complex number n the denomnator To do ths, we multply the numerator and denomnator by a specal complex number so that the result n the denomnator s a real number The number we need to multply by s called the complex conjugate, n whch the sgn of the magnary part s changed Here, + s the complex conjugate of Of course, obeyng our algebrac rules, we must multply by + on both the top and bottom ( + 5 ) ( + ) ( ) ( + ) To multply two complex numbers, we expand the product as we would wth polynomals (the process commonly called FOIL frst outer nner last ) In the numerator: ( + 5 )( + ) Expand Snce 1, ( 1) Smplfy + Followng the same process to multply the denomnator ( )( + ) Expand (1 + ) Snce 1, 1 (1 ( 1)) 17 Combnng ths we get
4 Secton 8 Polar Form of Complex Numbers 8 Try t Now Multply and + Wth the nterpretaton of complex numbers as ponts n a plane, whch can be related to the Cartesan coordnate system, you mght be startng to guess our next step to refer to ths pont not by ts horzontal and vertcal components, but usng ts polar locaton, gven by the dstance from the orgn and an angle Polar Form of Complex Numbers Remember, because the complex plane s analogous to the Cartesan plane that we can thnk of a complex number z x + y as analogous to the Cartesan pont (x, y) and recall how we converted from (x, y) to polar (r, θ) coordnates n the last secton Brngng n all of our old rules we remember the followng: x cos(θ ) r x r cos(θ ) y sn(θ ) r y r sn(θ ) y tan(θ ) x + y r x magnary r θ x x + y y real Wth ths n mnd, we can wrte z x + y r cos( θ) + r sn( θ) Example Express the complex number usng polar coordnates On the complex plane, the number s a dstance of from the orgn at an angle of, so cos + sn Note that the real part of ths complex number s 0 In the 18 th century, Leonhard Euler demonstrated a relatonshp between exponental and trgonometrc functons that allows the use of complex numbers to greatly smplfy some trgonometrc calculatons Whle the proof s beyond the scope of ths class, you wll lkely see t n a later calculus class
5 8 Chapter 8 Polar Form of a Complex Number and Euler s Formula θ The polar form of a complex number s z re, where Euler s Formula holds: θ re r cos( θ ) + r sn( θ ) Smlar to plottng a pont n the polar coordnate system we need r and θ to fnd the polar form of a complex number Example 7 Fnd the polar form of the complex number -7 Treatng ths s a complex number, we can consder the unsmplfed verson -7+0 Plotted n the complex plane, the number -7 s on the negatve horzontal axs, a dstance of 7 from the orgn at an angle of from the postve horzontal axs The polar form of the number -7 s 7 e Pluggng r 7 and θ back nto Euler s formula, we have: 7e 7cos( ) + 7 sn( ) as desred Example 8 Fnd the polar form of + On the complex plane, ths complex number would correspond to the pont (-, ) on a Cartesan plane We can fnd the dstance r and angle θ as we dd n the last secton r x + r y ( ) + r To fnd θ, we can use cos(θ ) cos( θ ) Ths s one of known cosne values, and snce the pont s n the second quadrant, we can conclude that θ The polar form of ths complex number s x r e -+
6 Secton 8 Polar Form of Complex Numbers 85 Note we could have used check the quadrant y tan(θ ) nstead to fnd the angle, so long as we remember to x Try t Now Wrte + n polar form Example 9 Wrte e n complex a + b form e cos + sn Evaluate the trg functons 1 + Smplfy + The polar form of a complex number provdes a powerful way to compute powers and roots of complex numbers by usng exponent rules you learned n algebra To compute a power of a complex number, we: 1) Convert to polar form ) Rase to the power, usng exponent rules to smplfy ) Convert back to a + b form, f needed Example 10 Evaluate ( + ) Whle we could multply ths number by tself fve tmes, that would be very tedous To compute ths more effcently, we can utlze the polar form of the complex number In an earler example, we found that ( + ) + e Usng ths, Wrte the complex number n polar form e ( ) e m Utlze the exponent rule ( ab ) a m n On the second factor, use the rule ( a ) a m b m mn
7 8 Chapter 8 ( ) 78 e 9 e Smplfy At ths pont, we have found the power as a complex number n polar form If we want the answer n standard a + b form, we can utlze Euler s formula 9 78e 9 78cos + 78sn 9 9 Snce s cotermnal wth, we can use our specal angle knowledge to evaluate the sne and cosne cos + 78sn 78 (0) + 78(1) 78 We have found that ( + ) 78 The result of the process can be summarzed by DeMovre s Theorem DeMovre s Theorem z r cos θ sn ( ) ( ) n n If ( ) + ( θ), then for any nteger n, z r cos( nθ) + sn ( nθ) We omt the proof, but note we can easly verfy t holds n one case usng Example 10: 9 9 ( + ) cos + sn 78 cos + sn 78 ( ) Example 11 Evaluate 9 To evaluate the square root of a complex number, we can frst note that the square root 1 s the same as havng an exponent of : 1/ 9 (9) To evaluate the power, we frst wrte the complex number n polar form Snce 9 has no real part, we know that ths value would be plotted along the vertcal axs, a dstance of 9 from the orgn at an angle of Ths gves the polar form: 9 9e
8 Secton 8 Polar Form of Complex Numbers e 1/ (9 ) Use the polar form 1/ 9 9 1/ e e 1/ 1 1/ Use exponent rules to smplfy Smplfy e Rewrte usng Euler s formula f desred cos + sn Evaluate the sne and cosne + Usng the polar form, we were able to fnd a square root of a complex number 9 + Alternatvely, usng DeMovre s Theorem we can wrte 9e 1/ cos + sn and smplfy Try t Now Wrte ( + ) n polar form You may remember that equatons lke x have two solutons, and - n ths case, though the square root only gves one of those solutons Lkewse, the square root we found n Example 11 s only one of two complex numbers whose square s 9 Smlarly, the equaton z 8 would have three solutons where only one s gven by the cube root In ths case, however, only one of those solutons, z, s a real value To fnd the others, we can use the fact that complex numbers have multple representatons n polar form Example 1 Fnd all complex solutons to z 8
9 88 Chapter 8 1/ Snce we are tryng to solve z 8, we can solve for x as z 8 Certanly one of these solutons s the basc cube root, gvng z To fnd others, we can turn to the polar representaton of 8 Snce 8 s a real number, s would st n the complex plane on the horzontal axs at an angle of 0, gvng the polar form 8 e 0 Takng the 1/ power of ths gves the real soluton: 0 ( 8 ) 1/ 8 1/ 0 0 e ( e ) 1/ e cos(0) + sn(0) However, snce the angle s cotermnal wth the angle of 0, we could also represent the number 8 as 8 e Takng the 1/ power of ths gves a frst complex soluton: 1/ 1/ 1 8e 8 1/ e e cos + sn + 1+ ( ) ( ) To fnd the thrd root, we use the angle of, whch s also cotermnal wth an angle of 0 1/ 1/ 1 8e 8 1/ e e cos + sn + 1 Altogether, we found all three complex solutons to z 8, 1+ z, 1+, 1 ( ) ( ) Graphed, these three numbers would be equally spaced on a crcle about the orgn at a radus of 1 Important Topcs of Ths Secton Complex numbers Imagnary numbers Plottng ponts n the complex coordnate system Basc operatons wth complex numbers Euler s Formula DeMovre s Theorem Fndng complex solutons to equatons Try t Now Answers 1 ( ) ( + 5 ) 1 9 ( )( + ) n polar form s e
10 Secton 8 Polar Form of Complex Numbers 89 Secton 8 Exercses Smplfy each expresson to a sngle complex number Smplfy each expresson to a sngle complex number (5 ) ( + ) + 8 ( ) ( ) 9 ( 5 + ) ( ) 10 ( ) 11 ( + ) ( ) 1 ( ) ( + ) 5 ( ) 1 ( ) (5) 1 ( + )( 8) 15 ( + ) ( ) 1 ( ) 1+ ( + ) 17 ( ) ( + ) 18 ( + )( ) Rewrte each complex number from polar form nto a + b form 9 e 0 e 1 e 8e e 5 5e 7 Rewrte each complex number nto polar 5 8 re θ form
11 90 Chapter 8 Compute each of the followng, leavng the result n polar 51 e e 5 5 e e re θ 5 form e e 5 e 55 e e 10 5 e 57 1 e 58 9e Compute each of the followng, smplfyng the result nto a + b form 59 ( + ) 8 0 ( + ) Solve each of the followng equatons for all complex solutons z z 7 z 1 8 z 1
Section 3.6 Complex Zeros
 04 Chapter Secton 6 Comple Zeros When fndng the zeros of polynomals, at some pont you're faced wth the problem Whle there are clearly no real numbers that are solutons to ths equaton, leavng thngs there
04 Chapter Secton 6 Comple Zeros When fndng the zeros of polynomals, at some pont you're faced wth the problem Whle there are clearly no real numbers that are solutons to ths equaton, leavng thngs there
8.6 The Complex Number System
 8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
Chapter 8: Further Applications of Trigonometry
 Secton 8. Polar Form of Complex Numbers 1 Chapter 8: Further Applcatons of Trgonometry In ths chapter, we wll explore addtonal applcatons of trgonometry. We wll begn wth an extenson of the rght trangle
Secton 8. Polar Form of Complex Numbers 1 Chapter 8: Further Applcatons of Trgonometry In ths chapter, we wll explore addtonal applcatons of trgonometry. We wll begn wth an extenson of the rght trangle
Unit 5: Quadratic Equations & Functions
 Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
Complex Numbers. x = B B 2 4AC 2A. or x = x = 2 ± 4 4 (1) (5) 2 (1)
 Complex Numbers If you have not yet encountered complex numbers, you wll soon do so n the process of solvng quadratc equatons. The general quadratc equaton Ax + Bx + C 0 has solutons x B + B 4AC A For
Complex Numbers If you have not yet encountered complex numbers, you wll soon do so n the process of solvng quadratc equatons. The general quadratc equaton Ax + Bx + C 0 has solutons x B + B 4AC A For
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
 COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
THE SUMMATION NOTATION Ʃ
 Sngle Subscrpt otaton THE SUMMATIO OTATIO Ʃ Most of the calculatons we perform n statstcs are repettve operatons on lsts of numbers. For example, we compute the sum of a set of numbers, or the sum of the
Sngle Subscrpt otaton THE SUMMATIO OTATIO Ʃ Most of the calculatons we perform n statstcs are repettve operatons on lsts of numbers. For example, we compute the sum of a set of numbers, or the sum of the
Advanced Circuits Topics - Part 1 by Dr. Colton (Fall 2017)
 Advanced rcuts Topcs - Part by Dr. olton (Fall 07) Part : Some thngs you should already know from Physcs 0 and 45 These are all thngs that you should have learned n Physcs 0 and/or 45. Ths secton s organzed
Advanced rcuts Topcs - Part by Dr. olton (Fall 07) Part : Some thngs you should already know from Physcs 0 and 45 These are all thngs that you should have learned n Physcs 0 and/or 45. Ths secton s organzed
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
C/CS/Phy191 Problem Set 3 Solutions Out: Oct 1, 2008., where ( 00. ), so the overall state of the system is ) ( ( ( ( 00 ± 11 ), Φ ± = 1
 C/CS/Phy9 Problem Set 3 Solutons Out: Oct, 8 Suppose you have two qubts n some arbtrary entangled state ψ You apply the teleportaton protocol to each of the qubts separately What s the resultng state obtaned
C/CS/Phy9 Problem Set 3 Solutons Out: Oct, 8 Suppose you have two qubts n some arbtrary entangled state ψ You apply the teleportaton protocol to each of the qubts separately What s the resultng state obtaned
Difference Equations
 Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
332600_08_1.qxp 4/17/08 11:29 AM Page 481
 336_8_.qxp 4/7/8 :9 AM Page 48 8 Complex Vector Spaces 8. Complex Numbers 8. Conjugates and Dvson of Complex Numbers 8.3 Polar Form and DeMovre s Theorem 8.4 Complex Vector Spaces and Inner Products 8.5
336_8_.qxp 4/7/8 :9 AM Page 48 8 Complex Vector Spaces 8. Complex Numbers 8. Conjugates and Dvson of Complex Numbers 8.3 Polar Form and DeMovre s Theorem 8.4 Complex Vector Spaces and Inner Products 8.5
of Nebraska - Lincoln
 Unversty of Nebraska - Lncoln DgtalCommons@Unversty of Nebraska - Lncoln MAT Exam Expostory Papers Math n the Mddle Insttute Partnershp 008 The Square Root of Tffany Lothrop Unversty of Nebraska-Lncoln
Unversty of Nebraska - Lncoln DgtalCommons@Unversty of Nebraska - Lncoln MAT Exam Expostory Papers Math n the Mddle Insttute Partnershp 008 The Square Root of Tffany Lothrop Unversty of Nebraska-Lncoln
Lectures - Week 4 Matrix norms, Conditioning, Vector Spaces, Linear Independence, Spanning sets and Basis, Null space and Range of a Matrix
 Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Solutions to Problem Set 6
 Solutons to Problem Set 6 Problem 6. (Resdue theory) a) Problem 4.7.7 Boas. n ths problem we wll solve ths ntegral: x sn x x + 4x + 5 dx: To solve ths usng the resdue theorem, we study ths complex ntegral:
Solutons to Problem Set 6 Problem 6. (Resdue theory) a) Problem 4.7.7 Boas. n ths problem we wll solve ths ntegral: x sn x x + 4x + 5 dx: To solve ths usng the resdue theorem, we study ths complex ntegral:
Chapter Twelve. Integration. We now turn our attention to the idea of an integral in dimensions higher than one. Consider a real-valued function f : D
 Chapter Twelve Integraton 12.1 Introducton We now turn our attenton to the dea of an ntegral n dmensons hgher than one. Consder a real-valued functon f : R, where the doman s a nce closed subset of Eucldean
Chapter Twelve Integraton 12.1 Introducton We now turn our attenton to the dea of an ntegral n dmensons hgher than one. Consder a real-valued functon f : R, where the doman s a nce closed subset of Eucldean
1. Estimation, Approximation and Errors Percentages Polynomials and Formulas Identities and Factorization 52
 ontents ommonly Used Formulas. Estmaton, pproxmaton and Errors. Percentages. Polynomals and Formulas 8. Identtes and Factorzaton. Equatons and Inequaltes 66 6. Rate and Rato 8 7. Laws of Integral Indces
ontents ommonly Used Formulas. Estmaton, pproxmaton and Errors. Percentages. Polynomals and Formulas 8. Identtes and Factorzaton. Equatons and Inequaltes 66 6. Rate and Rato 8 7. Laws of Integral Indces
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Digital Signal Processing
 Dgtal Sgnal Processng Dscrete-tme System Analyss Manar Mohasen Offce: F8 Emal: manar.subh@ut.ac.r School of IT Engneerng Revew of Precedent Class Contnuous Sgnal The value of the sgnal s avalable over
Dgtal Sgnal Processng Dscrete-tme System Analyss Manar Mohasen Offce: F8 Emal: manar.subh@ut.ac.r School of IT Engneerng Revew of Precedent Class Contnuous Sgnal The value of the sgnal s avalable over
P A = (P P + P )A = P (I P T (P P ))A = P (A P T (P P )A) Hence if we let E = P T (P P A), We have that
 Backward Error Analyss for House holder Reectors We want to show that multplcaton by householder reectors s backward stable. In partcular we wsh to show fl(p A) = P (A) = P (A + E where P = I 2vv T s the
Backward Error Analyss for House holder Reectors We want to show that multplcaton by householder reectors s backward stable. In partcular we wsh to show fl(p A) = P (A) = P (A + E where P = I 2vv T s the
The Number of Ways to Write n as a Sum of ` Regular Figurate Numbers
 Syracuse Unversty SURFACE Syracuse Unversty Honors Program Capstone Projects Syracuse Unversty Honors Program Capstone Projects Sprng 5-1-01 The Number of Ways to Wrte n as a Sum of ` Regular Fgurate Numbers
Syracuse Unversty SURFACE Syracuse Unversty Honors Program Capstone Projects Syracuse Unversty Honors Program Capstone Projects Sprng 5-1-01 The Number of Ways to Wrte n as a Sum of ` Regular Fgurate Numbers
9. Complex Numbers. 1. Numbers revisited. 2. Imaginary number i: General form of complex numbers. 3. Manipulation of complex numbers
 9. Comple Numbers. Numbers revsted. Imagnar number : General form of comple numbers 3. Manpulaton of comple numbers 4. The Argand dagram 5. The polar form for comple numbers 9.. Numbers revsted We saw
9. Comple Numbers. Numbers revsted. Imagnar number : General form of comple numbers 3. Manpulaton of comple numbers 4. The Argand dagram 5. The polar form for comple numbers 9.. Numbers revsted We saw
Complex Numbers, Signals, and Circuits
 Complex Numbers, Sgnals, and Crcuts 3 August, 009 Complex Numbers: a Revew Suppose we have a complex number z = x jy. To convert to polar form, we need to know the magntude of z and the phase of z. z =
Complex Numbers, Sgnals, and Crcuts 3 August, 009 Complex Numbers: a Revew Suppose we have a complex number z = x jy. To convert to polar form, we need to know the magntude of z and the phase of z. z =
(c) (cos θ + i sin θ) 5 = cos 5 θ + 5 cos 4 θ (i sin θ) + 10 cos 3 θ(i sin θ) cos 2 θ(i sin θ) 3 + 5cos θ (i sin θ) 4 + (i sin θ) 5 (A1)
 . (a) (cos θ + sn θ) = cos θ + cos θ( sn θ) + cos θ(sn θ) + (sn θ) = cos θ cos θ sn θ + ( cos θ sn θ sn θ) (b) from De Movre s theorem (cos θ + sn θ) = cos θ + sn θ cos θ + sn θ = (cos θ cos θ sn θ) +
. (a) (cos θ + sn θ) = cos θ + cos θ( sn θ) + cos θ(sn θ) + (sn θ) = cos θ cos θ sn θ + ( cos θ sn θ sn θ) (b) from De Movre s theorem (cos θ + sn θ) = cos θ + sn θ cos θ + sn θ = (cos θ cos θ sn θ) +
Exercises. 18 Algorithms
 18 Algorthms Exercses 0.1. In each of the followng stuatons, ndcate whether f = O(g), or f = Ω(g), or both (n whch case f = Θ(g)). f(n) g(n) (a) n 100 n 200 (b) n 1/2 n 2/3 (c) 100n + log n n + (log n)
18 Algorthms Exercses 0.1. In each of the followng stuatons, ndcate whether f = O(g), or f = Ω(g), or both (n whch case f = Θ(g)). f(n) g(n) (a) n 100 n 200 (b) n 1/2 n 2/3 (c) 100n + log n n + (log n)
The Schrödinger Equation
 Chapter 1 The Schrödnger Equaton 1.1 (a) F; () T; (c) T. 1. (a) Ephoton = hν = hc/ λ =(6.66 1 34 J s)(.998 1 8 m/s)/(164 1 9 m) = 1.867 1 19 J. () E = (5 1 6 J/s)( 1 8 s) =.1 J = n(1.867 1 19 J) and n
Chapter 1 The Schrödnger Equaton 1.1 (a) F; () T; (c) T. 1. (a) Ephoton = hν = hc/ λ =(6.66 1 34 J s)(.998 1 8 m/s)/(164 1 9 m) = 1.867 1 19 J. () E = (5 1 6 J/s)( 1 8 s) =.1 J = n(1.867 1 19 J) and n
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
For all questions, answer choice E) NOTA" means none of the above answers is correct.
 0 MA Natonal Conventon For all questons, answer choce " means none of the above answers s correct.. In calculus, one learns of functon representatons that are nfnte seres called power 3 4 5 seres. For
0 MA Natonal Conventon For all questons, answer choce " means none of the above answers s correct.. In calculus, one learns of functon representatons that are nfnte seres called power 3 4 5 seres. For
Formulas for the Determinant
 page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
Some basic inequalities. Definition. Let V be a vector space over the complex numbers. An inner product is given by a function, V V C
 Some basc nequaltes Defnton. Let V be a vector space over the complex numbers. An nner product s gven by a functon, V V C (x, y) x, y satsfyng the followng propertes (for all x V, y V and c C) (1) x +
Some basc nequaltes Defnton. Let V be a vector space over the complex numbers. An nner product s gven by a functon, V V C (x, y) x, y satsfyng the followng propertes (for all x V, y V and c C) (1) x +
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
CHAPTER 4. Vector Spaces
 man 2007/2/16 page 234 CHAPTER 4 Vector Spaces To crtcze mathematcs for ts abstracton s to mss the pont entrel. Abstracton s what makes mathematcs work. Ian Stewart The man am of ths tet s to stud lnear
man 2007/2/16 page 234 CHAPTER 4 Vector Spaces To crtcze mathematcs for ts abstracton s to mss the pont entrel. Abstracton s what makes mathematcs work. Ian Stewart The man am of ths tet s to stud lnear
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
One-sided finite-difference approximations suitable for use with Richardson extrapolation
 Journal of Computatonal Physcs 219 (2006) 13 20 Short note One-sded fnte-dfference approxmatons sutable for use wth Rchardson extrapolaton Kumar Rahul, S.N. Bhattacharyya * Department of Mechancal Engneerng,
Journal of Computatonal Physcs 219 (2006) 13 20 Short note One-sded fnte-dfference approxmatons sutable for use wth Rchardson extrapolaton Kumar Rahul, S.N. Bhattacharyya * Department of Mechancal Engneerng,
Math 261 Exercise sheet 2
 Math 261 Exercse sheet 2 http://staff.aub.edu.lb/~nm116/teachng/2017/math261/ndex.html Verson: September 25, 2017 Answers are due for Monday 25 September, 11AM. The use of calculators s allowed. Exercse
Math 261 Exercse sheet 2 http://staff.aub.edu.lb/~nm116/teachng/2017/math261/ndex.html Verson: September 25, 2017 Answers are due for Monday 25 September, 11AM. The use of calculators s allowed. Exercse
MTH 263 Practice Test #1 Spring 1999
 Pat Ross MTH 6 Practce Test # Sprng 999 Name. Fnd the area of the regon bounded by the graph r =acos (θ). Observe: Ths s a crcle of radus a, for r =acos (θ) r =a ³ x r r =ax x + y =ax x ax + y =0 x ax
Pat Ross MTH 6 Practce Test # Sprng 999 Name. Fnd the area of the regon bounded by the graph r =acos (θ). Observe: Ths s a crcle of radus a, for r =acos (θ) r =a ³ x r r =ax x + y =ax x ax + y =0 x ax
Section 8.1 Exercises
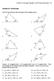 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Problem Solving in Math (Math 43900) Fall 2013
 Problem Solvng n Math (Math 43900) Fall 2013 Week four (September 17) solutons Instructor: Davd Galvn 1. Let a and b be two nteger for whch a b s dvsble by 3. Prove that a 3 b 3 s dvsble by 9. Soluton:
Problem Solvng n Math (Math 43900) Fall 2013 Week four (September 17) solutons Instructor: Davd Galvn 1. Let a and b be two nteger for whch a b s dvsble by 3. Prove that a 3 b 3 s dvsble by 9. Soluton:
The Order Relation and Trace Inequalities for. Hermitian Operators
 Internatonal Mathematcal Forum, Vol 3, 08, no, 507-57 HIKARI Ltd, wwwm-hkarcom https://doorg/0988/mf088055 The Order Relaton and Trace Inequaltes for Hermtan Operators Y Huang School of Informaton Scence
Internatonal Mathematcal Forum, Vol 3, 08, no, 507-57 HIKARI Ltd, wwwm-hkarcom https://doorg/0988/mf088055 The Order Relaton and Trace Inequaltes for Hermtan Operators Y Huang School of Informaton Scence
UNIT 4 EXTENDING THE NUMBER SYSTEM Lesson 3: Operating with Complex Numbers Instruction
 Prerequste Sklls Ths lesson requres the use of the followng sklls: understandng that multplyng the numerator and denomnator of a fracton by the same quantty produces an equvalent fracton multplyng complex
Prerequste Sklls Ths lesson requres the use of the followng sklls: understandng that multplyng the numerator and denomnator of a fracton by the same quantty produces an equvalent fracton multplyng complex
and problem sheet 2
 -8 and 5-5 problem sheet Solutons to the followng seven exercses and optonal bonus problem are to be submtted through gradescope by :0PM on Wednesday th September 08. There are also some practce problems,
-8 and 5-5 problem sheet Solutons to the followng seven exercses and optonal bonus problem are to be submtted through gradescope by :0PM on Wednesday th September 08. There are also some practce problems,
THE CHINESE REMAINDER THEOREM. We should thank the Chinese for their wonderful remainder theorem. Glenn Stevens
 THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chnese for ther wonderful remander theorem. Glenn Stevens 1. Introducton The Chnese remander theorem says we can unquely solve any par of
THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chnese for ther wonderful remander theorem. Glenn Stevens 1. Introducton The Chnese remander theorem says we can unquely solve any par of
Advanced Quantum Mechanics
 Advanced Quantum Mechancs Rajdeep Sensarma! sensarma@theory.tfr.res.n ecture #9 QM of Relatvstc Partcles Recap of ast Class Scalar Felds and orentz nvarant actons Complex Scalar Feld and Charge conjugaton
Advanced Quantum Mechancs Rajdeep Sensarma! sensarma@theory.tfr.res.n ecture #9 QM of Relatvstc Partcles Recap of ast Class Scalar Felds and orentz nvarant actons Complex Scalar Feld and Charge conjugaton
Linear Feature Engineering 11
 Lnear Feature Engneerng 11 2 Least-Squares 2.1 Smple least-squares Consder the followng dataset. We have a bunch of nputs x and correspondng outputs y. The partcular values n ths dataset are x y 0.23 0.19
Lnear Feature Engneerng 11 2 Least-Squares 2.1 Smple least-squares Consder the followng dataset. We have a bunch of nputs x and correspondng outputs y. The partcular values n ths dataset are x y 0.23 0.19
Chapter 3. r r. Position, Velocity, and Acceleration Revisited
 Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
8.1 Arc Length. What is the length of a curve? How can we approximate it? We could do it following the pattern we ve used before
 .1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments
.1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments
Integrals and Invariants of Euler-Lagrange Equations
 Lecture 16 Integrals and Invarants of Euler-Lagrange Equatons ME 256 at the Indan Insttute of Scence, Bengaluru Varatonal Methods and Structural Optmzaton G. K. Ananthasuresh Professor, Mechancal Engneerng,
Lecture 16 Integrals and Invarants of Euler-Lagrange Equatons ME 256 at the Indan Insttute of Scence, Bengaluru Varatonal Methods and Structural Optmzaton G. K. Ananthasuresh Professor, Mechancal Engneerng,
Gravitational Acceleration: A case of constant acceleration (approx. 2 hr.) (6/7/11)
 Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
MEM 255 Introduction to Control Systems Review: Basics of Linear Algebra
 MEM 255 Introducton to Control Systems Revew: Bascs of Lnear Algebra Harry G. Kwatny Department of Mechancal Engneerng & Mechancs Drexel Unversty Outlne Vectors Matrces MATLAB Advanced Topcs Vectors A
MEM 255 Introducton to Control Systems Revew: Bascs of Lnear Algebra Harry G. Kwatny Department of Mechancal Engneerng & Mechancs Drexel Unversty Outlne Vectors Matrces MATLAB Advanced Topcs Vectors A
princeton univ. F 17 cos 521: Advanced Algorithm Design Lecture 7: LP Duality Lecturer: Matt Weinberg
 prnceton unv. F 17 cos 521: Advanced Algorthm Desgn Lecture 7: LP Dualty Lecturer: Matt Wenberg Scrbe: LP Dualty s an extremely useful tool for analyzng structural propertes of lnear programs. Whle there
prnceton unv. F 17 cos 521: Advanced Algorthm Desgn Lecture 7: LP Dualty Lecturer: Matt Wenberg Scrbe: LP Dualty s an extremely useful tool for analyzng structural propertes of lnear programs. Whle there
Foundations of Arithmetic
 Foundatons of Arthmetc Notaton We shall denote the sum and product of numbers n the usual notaton as a 2 + a 2 + a 3 + + a = a, a 1 a 2 a 3 a = a The notaton a b means a dvdes b,.e. ac = b where c s an
Foundatons of Arthmetc Notaton We shall denote the sum and product of numbers n the usual notaton as a 2 + a 2 + a 3 + + a = a, a 1 a 2 a 3 a = a The notaton a b means a dvdes b,.e. ac = b where c s an
Spectral Graph Theory and its Applications September 16, Lecture 5
 Spectral Graph Theory and ts Applcatons September 16, 2004 Lecturer: Danel A. Spelman Lecture 5 5.1 Introducton In ths lecture, we wll prove the followng theorem: Theorem 5.1.1. Let G be a planar graph
Spectral Graph Theory and ts Applcatons September 16, 2004 Lecturer: Danel A. Spelman Lecture 5 5.1 Introducton In ths lecture, we wll prove the followng theorem: Theorem 5.1.1. Let G be a planar graph
Quantum Mechanics I - Session 4
 Quantum Mechancs I - Sesson 4 Aprl 3, 05 Contents Operators Change of Bass 4 3 Egenvectors and Egenvalues 5 3. Denton....................................... 5 3. Rotaton n D....................................
Quantum Mechancs I - Sesson 4 Aprl 3, 05 Contents Operators Change of Bass 4 3 Egenvectors and Egenvalues 5 3. Denton....................................... 5 3. Rotaton n D....................................
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
U.C. Berkeley CS294: Beyond Worst-Case Analysis Luca Trevisan September 5, 2017
 U.C. Berkeley CS94: Beyond Worst-Case Analyss Handout 4s Luca Trevsan September 5, 07 Summary of Lecture 4 In whch we ntroduce semdefnte programmng and apply t to Max Cut. Semdefnte Programmng Recall that
U.C. Berkeley CS94: Beyond Worst-Case Analyss Handout 4s Luca Trevsan September 5, 07 Summary of Lecture 4 In whch we ntroduce semdefnte programmng and apply t to Max Cut. Semdefnte Programmng Recall that
Quadratic Formula, Completing the Square, Systems Review Sheet
 Quadratc Formula Completng the Square Systems Revew Sheet 1. Factor the polynomal completely. 6. Use the graph to approxmate the real zeros of the functon. 2. Fnd the real-number solutons of the equaton.
Quadratc Formula Completng the Square Systems Revew Sheet 1. Factor the polynomal completely. 6. Use the graph to approxmate the real zeros of the functon. 2. Fnd the real-number solutons of the equaton.
Spin-rotation coupling of the angularly accelerated rigid body
 Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
= z 20 z n. (k 20) + 4 z k = 4
 Problem Set #7 solutons 7.2.. (a Fnd the coeffcent of z k n (z + z 5 + z 6 + z 7 + 5, k 20. We use the known seres expanson ( n+l ( z l l z n below: (z + z 5 + z 6 + z 7 + 5 (z 5 ( + z + z 2 + z + 5 5
Problem Set #7 solutons 7.2.. (a Fnd the coeffcent of z k n (z + z 5 + z 6 + z 7 + 5, k 20. We use the known seres expanson ( n+l ( z l l z n below: (z + z 5 + z 6 + z 7 + 5 (z 5 ( + z + z 2 + z + 5 5
= = = (a) Use the MATLAB command rref to solve the system. (b) Let A be the coefficient matrix and B be the right-hand side of the system.
 Chapter Matlab Exercses Chapter Matlab Exercses. Consder the lnear system of Example n Secton.. x x x y z y y z (a) Use the MATLAB command rref to solve the system. (b) Let A be the coeffcent matrx and
Chapter Matlab Exercses Chapter Matlab Exercses. Consder the lnear system of Example n Secton.. x x x y z y y z (a) Use the MATLAB command rref to solve the system. (b) Let A be the coeffcent matrx and
From Biot-Savart Law to Divergence of B (1)
 From Bot-Savart Law to Dvergence of B (1) Let s prove that Bot-Savart gves us B (r ) = 0 for an arbtrary current densty. Frst take the dvergence of both sdes of Bot-Savart. The dervatve s wth respect to
From Bot-Savart Law to Dvergence of B (1) Let s prove that Bot-Savart gves us B (r ) = 0 for an arbtrary current densty. Frst take the dvergence of both sdes of Bot-Savart. The dervatve s wth respect to
Lecture 10: Euler s Equations for Multivariable
 Lecture 0: Euler s Equatons for Multvarable Problems Let s say we re tryng to mnmze an ntegral of the form: {,,,,,, ; } J f y y y y y y d We can start by wrtng each of the y s as we dd before: y (, ) (
Lecture 0: Euler s Equatons for Multvarable Problems Let s say we re tryng to mnmze an ntegral of the form: {,,,,,, ; } J f y y y y y y d We can start by wrtng each of the y s as we dd before: y (, ) (
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM
 ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
Kernel Methods and SVMs Extension
 Kernel Methods and SVMs Extenson The purpose of ths document s to revew materal covered n Machne Learnng 1 Supervsed Learnng regardng support vector machnes (SVMs). Ths document also provdes a general
Kernel Methods and SVMs Extenson The purpose of ths document s to revew materal covered n Machne Learnng 1 Supervsed Learnng regardng support vector machnes (SVMs). Ths document also provdes a general
Polynomials. 1 More properties of polynomials
 Polynomals 1 More propertes of polynomals Recall that, for R a commutatve rng wth unty (as wth all rngs n ths course unless otherwse noted), we defne R[x] to be the set of expressons n =0 a x, where a
Polynomals 1 More propertes of polynomals Recall that, for R a commutatve rng wth unty (as wth all rngs n ths course unless otherwse noted), we defne R[x] to be the set of expressons n =0 a x, where a
The Ramanujan-Nagell Theorem: Understanding the Proof By Spencer De Chenne
 The Ramanujan-Nagell Theorem: Understandng the Proof By Spencer De Chenne 1 Introducton The Ramanujan-Nagell Theorem, frst proposed as a conjecture by Srnvasa Ramanujan n 1943 and later proven by Trygve
The Ramanujan-Nagell Theorem: Understandng the Proof By Spencer De Chenne 1 Introducton The Ramanujan-Nagell Theorem, frst proposed as a conjecture by Srnvasa Ramanujan n 1943 and later proven by Trygve
Bernoulli Numbers and Polynomials
 Bernoull Numbers and Polynomals T. Muthukumar tmk@tk.ac.n 17 Jun 2014 The sum of frst n natural numbers 1, 2, 3,..., n s n n(n + 1 S 1 (n := m = = n2 2 2 + n 2. Ths formula can be derved by notng that
Bernoull Numbers and Polynomals T. Muthukumar tmk@tk.ac.n 17 Jun 2014 The sum of frst n natural numbers 1, 2, 3,..., n s n n(n + 1 S 1 (n := m = = n2 2 2 + n 2. Ths formula can be derved by notng that
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Mathematics Intersection of Lines
 a place of mnd F A C U L T Y O F E D U C A T I O N Department of Currculum and Pedagog Mathematcs Intersecton of Lnes Scence and Mathematcs Educaton Research Group Supported b UBC Teachng and Learnng Enhancement
a place of mnd F A C U L T Y O F E D U C A T I O N Department of Currculum and Pedagog Mathematcs Intersecton of Lnes Scence and Mathematcs Educaton Research Group Supported b UBC Teachng and Learnng Enhancement
Outline and Reading. Dynamic Programming. Dynamic Programming revealed. Computing Fibonacci. The General Dynamic Programming Technique
 Outlne and Readng Dynamc Programmng The General Technque ( 5.3.2) -1 Knapsac Problem ( 5.3.3) Matrx Chan-Product ( 5.3.1) Dynamc Programmng verson 1.4 1 Dynamc Programmng verson 1.4 2 Dynamc Programmng
Outlne and Readng Dynamc Programmng The General Technque ( 5.3.2) -1 Knapsac Problem ( 5.3.3) Matrx Chan-Product ( 5.3.1) Dynamc Programmng verson 1.4 1 Dynamc Programmng verson 1.4 2 Dynamc Programmng
MAGNETISM MAGNETIC DIPOLES
 MAGNETISM We now turn to magnetsm. Ths has actually been used for longer than electrcty. People were usng compasses to sal around the Medterranean Sea several hundred years BC. However t was not understood
MAGNETISM We now turn to magnetsm. Ths has actually been used for longer than electrcty. People were usng compasses to sal around the Medterranean Sea several hundred years BC. However t was not understood
Complex Numbers Alpha, Round 1 Test #123
 Complex Numbers Alpha, Round Test #3. Wrte your 6-dgt ID# n the I.D. NUMBER grd, left-justfed, and bubble. Check that each column has only one number darkened.. In the EXAM NO. grd, wrte the 3-dgt Test
Complex Numbers Alpha, Round Test #3. Wrte your 6-dgt ID# n the I.D. NUMBER grd, left-justfed, and bubble. Check that each column has only one number darkened.. In the EXAM NO. grd, wrte the 3-dgt Test
Iterative General Dynamic Model for Serial-Link Manipulators
 EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
UNIT 3 EXPRESSIONS AND EQUATIONS Lesson 4: Fundamental Theorem of Algebra. Instruction. Guided Practice Example 1
 Guded Practce 3.4. Example 1 Instructon For each equaton, state the number and type of solutons by frst fndng the dscrmnant. x + 3x =.4x x = 3x = x 9x + 1 = 6x 1. Fnd the dscrmnant of x + 3x =. The equaton
Guded Practce 3.4. Example 1 Instructon For each equaton, state the number and type of solutons by frst fndng the dscrmnant. x + 3x =.4x x = 3x = x 9x + 1 = 6x 1. Fnd the dscrmnant of x + 3x =. The equaton
CHAPTER 10 ROTATIONAL MOTION
 CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
Stanford University CS359G: Graph Partitioning and Expanders Handout 4 Luca Trevisan January 13, 2011
 Stanford Unversty CS359G: Graph Parttonng and Expanders Handout 4 Luca Trevsan January 3, 0 Lecture 4 In whch we prove the dffcult drecton of Cheeger s nequalty. As n the past lectures, consder an undrected
Stanford Unversty CS359G: Graph Parttonng and Expanders Handout 4 Luca Trevsan January 3, 0 Lecture 4 In whch we prove the dffcult drecton of Cheeger s nequalty. As n the past lectures, consder an undrected
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Inner Product. Euclidean Space. Orthonormal Basis. Orthogonal
 Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
1 Generating functions, continued
 Generatng functons, contnued. Generatng functons and parttons We can make use of generatng functons to answer some questons a bt more restrctve than we ve done so far: Queston : Fnd a generatng functon
Generatng functons, contnued. Generatng functons and parttons We can make use of generatng functons to answer some questons a bt more restrctve than we ve done so far: Queston : Fnd a generatng functon
Indeterminate pin-jointed frames (trusses)
 Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
U.C. Berkeley CS294: Spectral Methods and Expanders Handout 8 Luca Trevisan February 17, 2016
 U.C. Berkeley CS94: Spectral Methods and Expanders Handout 8 Luca Trevsan February 7, 06 Lecture 8: Spectral Algorthms Wrap-up In whch we talk about even more generalzatons of Cheeger s nequaltes, and
U.C. Berkeley CS94: Spectral Methods and Expanders Handout 8 Luca Trevsan February 7, 06 Lecture 8: Spectral Algorthms Wrap-up In whch we talk about even more generalzatons of Cheeger s nequaltes, and
PHYS 705: Classical Mechanics. Newtonian Mechanics
 1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
Four Bar Linkages in Two Dimensions. A link has fixed length and is joined to other links and also possibly to a fixed point.
 Four bar lnkages 1 Four Bar Lnkages n Two Dmensons lnk has fed length and s oned to other lnks and also possbly to a fed pont. The relatve velocty of end B wth regard to s gven by V B = ω r y v B B = +y
Four bar lnkages 1 Four Bar Lnkages n Two Dmensons lnk has fed length and s oned to other lnks and also possbly to a fed pont. The relatve velocty of end B wth regard to s gven by V B = ω r y v B B = +y
Solutions to exam in SF1811 Optimization, Jan 14, 2015
 Solutons to exam n SF8 Optmzaton, Jan 4, 25 3 3 O------O -4 \ / \ / The network: \/ where all lnks go from left to rght. /\ / \ / \ 6 O------O -5 2 4.(a) Let x = ( x 3, x 4, x 23, x 24 ) T, where the varable
Solutons to exam n SF8 Optmzaton, Jan 4, 25 3 3 O------O -4 \ / \ / The network: \/ where all lnks go from left to rght. /\ / \ / \ 6 O------O -5 2 4.(a) Let x = ( x 3, x 4, x 23, x 24 ) T, where the varable
AGC Introduction
 . Introducton AGC 3 The prmary controller response to a load/generaton mbalance results n generaton adjustment so as to mantan load/generaton balance. However, due to droop, t also results n a non-zero
. Introducton AGC 3 The prmary controller response to a load/generaton mbalance results n generaton adjustment so as to mantan load/generaton balance. However, due to droop, t also results n a non-zero
The Fundamental Theorem of Algebra. Objective To use the Fundamental Theorem of Algebra to solve polynomial equations with complex solutions
 5-6 The Fundamental Theorem of Algebra Content Standards N.CN.7 Solve quadratc equatons wth real coeffcents that have comple solutons. N.CN.8 Etend polnomal denttes to the comple numbers. Also N.CN.9,
5-6 The Fundamental Theorem of Algebra Content Standards N.CN.7 Solve quadratc equatons wth real coeffcents that have comple solutons. N.CN.8 Etend polnomal denttes to the comple numbers. Also N.CN.9,
Fundamental loop-current method using virtual voltage sources technique for special cases
 Fundamental loop-current method usng vrtual voltage sources technque for specal cases George E. Chatzaraks, 1 Marna D. Tortorel 1 and Anastasos D. Tzolas 1 Electrcal and Electroncs Engneerng Departments,
Fundamental loop-current method usng vrtual voltage sources technque for specal cases George E. Chatzaraks, 1 Marna D. Tortorel 1 and Anastasos D. Tzolas 1 Electrcal and Electroncs Engneerng Departments,
Important Instructions to the Examiners:
 Summer 0 Examnaton Subject & Code: asc Maths (70) Model Answer Page No: / Important Instructons to the Examners: ) The Answers should be examned by key words and not as word-to-word as gven n the model
Summer 0 Examnaton Subject & Code: asc Maths (70) Model Answer Page No: / Important Instructons to the Examners: ) The Answers should be examned by key words and not as word-to-word as gven n the model
CALCULUS CLASSROOM CAPSULES
 CALCULUS CLASSROOM CAPSULES SESSION S86 Dr. Sham Alfred Rartan Valley Communty College salfred@rartanval.edu 38th AMATYC Annual Conference Jacksonvlle, Florda November 8-, 202 2 Calculus Classroom Capsules
CALCULUS CLASSROOM CAPSULES SESSION S86 Dr. Sham Alfred Rartan Valley Communty College salfred@rartanval.edu 38th AMATYC Annual Conference Jacksonvlle, Florda November 8-, 202 2 Calculus Classroom Capsules
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
3.1 Expectation of Functions of Several Random Variables. )' be a k-dimensional discrete or continuous random vector, with joint PMF p (, E X E X1 E X
 Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Structure and Drive Paul A. Jensen Copyright July 20, 2003
 Structure and Drve Paul A. Jensen Copyrght July 20, 2003 A system s made up of several operatons wth flow passng between them. The structure of the system descrbes the flow paths from nputs to outputs.
Structure and Drve Paul A. Jensen Copyrght July 20, 2003 A system s made up of several operatons wth flow passng between them. The structure of the system descrbes the flow paths from nputs to outputs.
Physics 53. Rotational Motion 3. Sir, I have found you an argument, but I am not obliged to find you an understanding.
 Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Bezier curves. Michael S. Floater. August 25, These notes provide an introduction to Bezier curves. i=0
 Bezer curves Mchael S. Floater August 25, 211 These notes provde an ntroducton to Bezer curves. 1 Bernsten polynomals Recall that a real polynomal of a real varable x R, wth degree n, s a functon of the
Bezer curves Mchael S. Floater August 25, 211 These notes provde an ntroducton to Bezer curves. 1 Bernsten polynomals Recall that a real polynomal of a real varable x R, wth degree n, s a functon of the
Physics 201, Lecture 4. Vectors and Scalars. Chapters Covered q Chapter 1: Physics and Measurement.
 Phscs 01, Lecture 4 Toda s Topcs n Vectors chap 3) n Scalars and Vectors n Vector ddton ule n Vector n a Coordnator Sstem n Decomposton of a Vector n Epected from prevew: n Scalars and Vectors, Vector
Phscs 01, Lecture 4 Toda s Topcs n Vectors chap 3) n Scalars and Vectors n Vector ddton ule n Vector n a Coordnator Sstem n Decomposton of a Vector n Epected from prevew: n Scalars and Vectors, Vector
Module 14: THE INTEGRAL Exploring Calculus
 Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
G = G 1 + G 2 + G 3 G 2 +G 3 G1 G2 G3. Network (a) Network (b) Network (c) Network (d)
 Massachusetts Insttute of Technology Department of Electrcal Engneerng and Computer Scence 6.002 í Electronc Crcuts Homework 2 Soluton Handout F98023 Exercse 21: Determne the conductance of each network
Massachusetts Insttute of Technology Department of Electrcal Engneerng and Computer Scence 6.002 í Electronc Crcuts Homework 2 Soluton Handout F98023 Exercse 21: Determne the conductance of each network
12. The Hamilton-Jacobi Equation Michael Fowler
 1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
Introduction to Complex Numbers
 Introducton to Complex Numbers Let s revew the varous classfcaton of number we have encountered Number Systems Natural Numbers (Postve Integers) {1,, 3, 4, } Whole Numbers (Postve Integers plus zero) {0,
Introducton to Complex Numbers Let s revew the varous classfcaton of number we have encountered Number Systems Natural Numbers (Postve Integers) {1,, 3, 4, } Whole Numbers (Postve Integers plus zero) {0,
Singular Value Decomposition: Theory and Applications
 Sngular Value Decomposton: Theory and Applcatons Danel Khashab Sprng 2015 Last Update: March 2, 2015 1 Introducton A = UDV where columns of U and V are orthonormal and matrx D s dagonal wth postve real
Sngular Value Decomposton: Theory and Applcatons Danel Khashab Sprng 2015 Last Update: March 2, 2015 1 Introducton A = UDV where columns of U and V are orthonormal and matrx D s dagonal wth postve real
Lecture 10 Support Vector Machines II
 Lecture 10 Support Vector Machnes II 22 February 2016 Taylor B. Arnold Yale Statstcs STAT 365/665 1/28 Notes: Problem 3 s posted and due ths upcomng Frday There was an early bug n the fake-test data; fxed
Lecture 10 Support Vector Machnes II 22 February 2016 Taylor B. Arnold Yale Statstcs STAT 365/665 1/28 Notes: Problem 3 s posted and due ths upcomng Frday There was an early bug n the fake-test data; fxed
