Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
|
|
|
- Florence Ward
- 5 years ago
- Views:
Transcription
1 ME 270 Sprng 2017 Exam 1 NAME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: Instructor s Name and Secton: (Crcle Your Secton) Sectons: J Jones 9:30-10:20AM A Buganza 1:30-2:20PM B L 3:30-4:20PM J Jones Dstance Learnng INSTRUCTIONS Begn each problem n the space provded on the examnaton sheets. If addtonal space s requred, use the whte lned paper provded to you. Work on one sde of each sheet only, wth only one problem on a sheet. Each problem s worth 20 ponts. Please remember that for you to obtan maxmum credt for a problem, t must be clearly presented,.e. The only authorzed exam calculator s the TI-30IIS The allowable exam tme for Exam 1 s 70 mnutes. The coordnate system must be clearly dentfed. Where approprate, free body dagrams must be drawn. These should be drawn separately from the gven fgures. Unts must be clearly stated as part of the answer. You must carefully delneate vector and scalar quanttes. If the soluton does not follow a logcal thought process, t wll be assumed n error. When handng n the test, please make sure that all sheets are n the correct sequental order and make sure that your name s at the top of every page that you wsh to have graded. Problem 1 Problem 2 Problem 3 Total ME 270 Exam 1 Sprng 2017 Page 1
2 ME 270 Sprng 2017 Exam 1 NAME (Last, Frst): PROBLEM 1 (20 ponts 1A. The tenson n rope AC s 100 lbs. Determne the angle (θ) between cables AB and AC and the magntude of the projecton of the tenson n cable AC tenson n the drecton of AB. θ θ = Proj = (3 pts) ME 270 Exam 1 Sprng 2017 Page 2
3 ME 270 Sprng 2017 Exam 1 1B. The tenson n cable AB s 10kN. Determne the force vector NAME (Last, Frst): z T AB and the moment vector M D due to the cable about pont D. y x T AB = M D = (3 pts) ME 270 Exam 1 Sprng 2017 Page 3
4 ME 270 Sprng 2017 Exam 1 NAME (Last, Frst): 1C. Three of these four systems are equvalent. Whch system s not equvalent? What couple must be added to ths system to make t equvalent? System (Crcle One) M = k kn-m (3 pts) 1D. Determne the x-centrod of the shaded area. If the 2-n radus hole was removed (.e., the block was sold), what qualtatve effect would ths have on the x-centrod? x = (3 pts) x-centrod would: Increase Reman Same Decrease (Crcle One) ME 270 Exam 1 Sprng 2017 Page 4
5 ME 270 Sprng 2017 Exam 1 NAME (Last, Frst): PROBLEM 2. (20 ponts) GIVEN: A tractor s lfted by three ndependent cables as shown n the fgure. Determne the tenson n the cables AB, AC, and AD f the tractor s weght s 80kN. FIND: a) Draw the free body dagram of the system of forces actng at pont A (3 pts) b) Lst the cable force vectors as an unknown magntude multpled by a known unt vector (6 pts): T AB = ( + j + k ) T AC = ( + j + k ) = ( + j + k ) T AD ME 270 Exam 1 Sprng 2017 Page 5
6 ME 270 Sprng 2017 Exam 1 NAME (Last, Frst): c) Formulate the equatons of equlbrum. (3 pts): ΣF 0 = ΣF y = 0 = (1 pt) (1 pt) ΣF z = 0 = (1 pt) d) Solve the equatons of statc equlbrum for the magntude of the tenson n each cable. (6 pts): T AB = T AC = T AD = ME 270 Exam 1 Sprng 2017 Page 6
7 ME 270 Sprng 2017 Exam 1 NAME (Last, Frst): e) What s the maxmum load ths cable system can hold f the largest allowable tenson n any sngle cable s 60kN? W ma ME 270 Exam 1 Sprng 2017 Page 7
8 ME 270 Sprng 2017 Exam 1 NAME (Last, Frst): PROBLEM 3. (20 ponts) GIVEN: Frame ABCD s loaded as shown and s held n statc equlbrum by a fxed support at A. FIND: a) For the dstrbuted load shown, determne the magntude of the sngle-force equvalent and ts locaton measured from the y-axs. F eq = b) Draw the free body dagram of the system, lst all appled and reacton forces and moments, replace the trangular dstrbuted load wth a sngle equvalent load and mark ts locaton. (3 pts) ME 270 Exam 1 Sprng 2017 Page 8
9 ME 270 Sprng 2017 Exam 1 NAME (Last, Frst): c) Fnd the reactons at pont A. Express the results n vector form. (10 pts) F j (4 pts) A M A (6 pts) d) Qualtatvely descrbe the change n the magntude of the reactons at pont A f the 500 lb force s slghtly decreased by crclng the approprate trend. (3 pts) (F A ) x Increases Remans Same Decreases (Crcle One) (1 pt) (F A ) y Increases Remans Same Decreases (Crcle One) (1 pt) (M A ) Increases Remans Same Decreases (Crcle One) (1 pt) ME 270 Exam 1 Sprng 2017 Page 9
10 ME 270 Sprng 2017 Exam 1 NAME (Last, Frst): SOLUTIONS 1A. θ = 42.8 degrees Proj = 73.3 lbs 1B. T AB = j 6.67 k kn M D = j 6.67 k kn m 1C. System s 3 s not equvalent M = 80 k kn m 1D. x = 6.98 n x-centrod - Decreases 2A. Free body dagram 2B. T AB = T AB ( ( 0.327)j + ( 0.786) k ) T AC = T AC ( j + ( 0.786) k ) T AD = T AD ( j + ( 0.948) k ) 2C. F x = 0 = T AB T AC T AD F y = 0 = T AB T AC F z = 0 = T AB T AC T AD + 80kN 2D. T AB = kn T AC = kn T AD = kn 2E. W ma 85.2 kn 3A. F eq = 300 lb 3 ft 3B. Free Body Dagram 3C. F A = ( j ) lb M A = ( 800k )lb ft 3D. (F A )x Decreases (F A )y Decreases (M A ) Decreases ME 270 Exam 1 Sprng 2017 Page 10
11 ME 270 Sprng 2017 Exam 1 NAME (Last, Frst): ME 270 Exam 1 Equatons Dstrbuted Loads F = eq eq xf = 0 L w x dx 0 L Centrods y = y = In 3D, x da c da y da c da x A c A c x w x dx y A A x V c V Centers of Mass y = y = xcmρda x ρda ycmρda ρda y Buoyancy FB gv Flud Statcs p gh cm ρa ρa cm ρa F p Lw eq avg ρa ME 270 Exam 1 Sprng 2017 Page 11
If the solution does not follow a logical thought process, it will be assumed in error.
 Group # Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space provded
Group # Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space provded
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space
NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: Instructor s Name and Secton: (Crcle Your Secton) Sectons:
Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: Instructor s Name and Secton: (Crcle Your Secton) Sectons:
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: Instructor s Name and Secton: (Crcle Your Secton) Sectons:
Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: Instructor s Name and Secton: (Crcle Your Secton) Sectons:
I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 ME 270 Fall 2012 Fnal Exam Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem
ME 270 Fall 2012 Fnal Exam Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 ME 270 Summer 2014 Fnal Exam NAME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS
ME 270 Summer 2014 Fnal Exam NAME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 ME 270 Sprng 2014 Fnal Exam NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS
ME 270 Sprng 2014 Fnal Exam NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS
I have not received unauthorized aid in the completion of this exam.
 ME 270 Sprng 2013 Fnal Examnaton Please read and respond to the followng statement, I have not receved unauthorzed ad n the completon of ths exam. Agree Dsagree Sgnature INSTRUCTIONS Begn each problem
ME 270 Sprng 2013 Fnal Examnaton Please read and respond to the followng statement, I have not receved unauthorzed ad n the completon of ths exam. Agree Dsagree Sgnature INSTRUCTIONS Begn each problem
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 ME 270 Fall 2013 Fnal Exam NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS
ME 270 Fall 2013 Fnal Exam NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS
Increase Decrease Remain the Same (Circle one) (2 pts)
 ME 270 Sample Fnal Eam PROBLEM 1 (25 ponts) Prob. 1 questons are all or nothng. PROBLEM 1A. (5 ponts) FIND: A 2000 N crate (D) s suspended usng ropes AB and AC and s n statc equlbrum. If θ = 53.13, determne
ME 270 Sample Fnal Eam PROBLEM 1 (25 ponts) Prob. 1 questons are all or nothng. PROBLEM 1A. (5 ponts) FIND: A 2000 N crate (D) s suspended usng ropes AB and AC and s n statc equlbrum. If θ = 53.13, determne
If the solution does not follow a logical thought process, it will be assumed in error.
 Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. If I detect cheating I will write a note on my exam and raise
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. If I detect cheating I will write a note on my exam and raise
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: INSTRUCTIONS Begin each problem in the space provided
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: INSTRUCTIONS Begin each problem in the space provided
I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 Examination No. 2 Please review the following statement: Group Number: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: INSTRUCTIONS Begin
Examination No. 2 Please review the following statement: Group Number: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: INSTRUCTIONS Begin
Please initial the statement below to show that you have read it
 EN0: Structural nalyss Exam I Wednesday, March 2, 2005 Dvson of Engneerng rown Unversty NME: General Instructons No collaboraton of any nd s permtted on ths examnaton. You may consult your own wrtten lecture
EN0: Structural nalyss Exam I Wednesday, March 2, 2005 Dvson of Engneerng rown Unversty NME: General Instructons No collaboraton of any nd s permtted on ths examnaton. You may consult your own wrtten lecture
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: INSTRUCTIONS Begin each problem in the space provided
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: INSTRUCTIONS Begin each problem in the space provided
AP Physics 1 & 2 Summer Assignment
 AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: Instructor s Name and Section: (Circle Your Section)
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: Instructor s Name and Section: (Circle Your Section)
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: Instructor s Name and Section: (Circle Your Section)
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: Instructor s Name and Section: (Circle Your Section)
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: INSTRUCTIONS Begin each problem in the space provided
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: INSTRUCTIONS Begin each problem in the space provided
MTH 263 Practice Test #1 Spring 1999
 Pat Ross MTH 6 Practce Test # Sprng 999 Name. Fnd the area of the regon bounded by the graph r =acos (θ). Observe: Ths s a crcle of radus a, for r =acos (θ) r =a ³ x r r =ax x + y =ax x ax + y =0 x ax
Pat Ross MTH 6 Practce Test # Sprng 999 Name. Fnd the area of the regon bounded by the graph r =acos (θ). Observe: Ths s a crcle of radus a, for r =acos (θ) r =a ³ x r r =ax x + y =ax x ax + y =0 x ax
FUZZY FINITE ELEMENT METHOD
 FUZZY FINITE ELEMENT METHOD RELIABILITY TRUCTURE ANALYI UING PROBABILITY 3.. Maxmum Normal tress Internal force s the shear force, V has a magntude equal to the load P and bendng moment, M. Bendng moments
FUZZY FINITE ELEMENT METHOD RELIABILITY TRUCTURE ANALYI UING PROBABILITY 3.. Maxmum Normal tress Internal force s the shear force, V has a magntude equal to the load P and bendng moment, M. Bendng moments
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
UNIVERSITY OF BOLTON RAK ACADEMIC CENTRE BENG(HONS) MECHANICAL ENGINEERING SEMESTER TWO EXAMINATION 2017/2018 FINITE ELEMENT AND DIFFERENCE SOLUTIONS
 OCD0 UNIVERSITY OF BOLTON RAK ACADEMIC CENTRE BENG(HONS) MECHANICAL ENGINEERING SEMESTER TWO EXAMINATION 07/08 FINITE ELEMENT AND DIFFERENCE SOLUTIONS MODULE NO. AME6006 Date: Wednesda 0 Ma 08 Tme: 0:00
OCD0 UNIVERSITY OF BOLTON RAK ACADEMIC CENTRE BENG(HONS) MECHANICAL ENGINEERING SEMESTER TWO EXAMINATION 07/08 FINITE ELEMENT AND DIFFERENCE SOLUTIONS MODULE NO. AME6006 Date: Wednesda 0 Ma 08 Tme: 0:00
Slide. King Saud University College of Science Physics & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART 2) LECTURE NO.
 Slde Kng Saud Unersty College of Scence Physcs & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART ) LECTURE NO. 6 THIS PRESENTATION HAS BEEN PREPARED BY: DR. NASSR S. ALZAYED Lecture
Slde Kng Saud Unersty College of Scence Physcs & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART ) LECTURE NO. 6 THIS PRESENTATION HAS BEEN PREPARED BY: DR. NASSR S. ALZAYED Lecture
TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES. PHYS 2211, Exam 2 Section 1 Version 1 October 18, 2013 Total Weight: 100 points
 TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES PHYS, Exam Secton Verson October 8, 03 Total Weght: 00 ponts. Check your examnaton or completeness pror to startng. There are a total o nne
TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES PHYS, Exam Secton Verson October 8, 03 Total Weght: 00 ponts. Check your examnaton or completeness pror to startng. There are a total o nne
EN40: Dynamics and Vibrations. Homework 4: Work, Energy and Linear Momentum Due Friday March 1 st
 EN40: Dynamcs and bratons Homework 4: Work, Energy and Lnear Momentum Due Frday March 1 st School of Engneerng Brown Unversty 1. The fgure (from ths publcaton) shows the energy per unt area requred to
EN40: Dynamcs and bratons Homework 4: Work, Energy and Lnear Momentum Due Frday March 1 st School of Engneerng Brown Unversty 1. The fgure (from ths publcaton) shows the energy per unt area requred to
Gravitational Acceleration: A case of constant acceleration (approx. 2 hr.) (6/7/11)
 Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
STAT 511 FINAL EXAM NAME Spring 2001
 STAT 5 FINAL EXAM NAME Sprng Instructons: Ths s a closed book exam. No notes or books are allowed. ou may use a calculator but you are not allowed to store notes or formulas n the calculator. Please wrte
STAT 5 FINAL EXAM NAME Sprng Instructons: Ths s a closed book exam. No notes or books are allowed. ou may use a calculator but you are not allowed to store notes or formulas n the calculator. Please wrte
Rao IIT Academy/ SSC - Board Exam 2018 / Mathematics Code-A / QP + Solutions JEE MEDICAL-UG BOARDS KVPY NTSE OLYMPIADS SSC - BOARD
 Rao IIT Academy/ SSC - Board Exam 08 / Mathematcs Code-A / QP + Solutons JEE MEDICAL-UG BOARDS KVPY NTSE OLYMPIADS SSC - BOARD - 08 Date: 0.03.08 MATHEMATICS - PAPER- - SOLUTIONS Q. Attempt any FIVE of
Rao IIT Academy/ SSC - Board Exam 08 / Mathematcs Code-A / QP + Solutons JEE MEDICAL-UG BOARDS KVPY NTSE OLYMPIADS SSC - BOARD - 08 Date: 0.03.08 MATHEMATICS - PAPER- - SOLUTIONS Q. Attempt any FIVE of
Module 11 Design of Joints for Special Loading. Version 2 ME, IIT Kharagpur
 Module 11 Desgn o Jonts or Specal Loadng Verson ME, IIT Kharagpur Lesson 1 Desgn o Eccentrcally Loaded Bolted/Rveted Jonts Verson ME, IIT Kharagpur Instructonal Objectves: At the end o ths lesson, the
Module 11 Desgn o Jonts or Specal Loadng Verson ME, IIT Kharagpur Lesson 1 Desgn o Eccentrcally Loaded Bolted/Rveted Jonts Verson ME, IIT Kharagpur Instructonal Objectves: At the end o ths lesson, the
If the solution does not follow a logical thought process, it will be assumed in error.
 Please indicate your group number (If applicable) Circle Your Instructor s Name and Section: MWF 8:30-9:20 AM Prof. Kai Ming Li MWF 2:30-3:20 PM Prof. Fabio Semperlotti MWF 9:30-10:20 AM Prof. Jim Jones
Please indicate your group number (If applicable) Circle Your Instructor s Name and Section: MWF 8:30-9:20 AM Prof. Kai Ming Li MWF 2:30-3:20 PM Prof. Fabio Semperlotti MWF 9:30-10:20 AM Prof. Jim Jones
ENGI 1313 Mechanics I
 ENGI 11 Mechancs I Lecture 40: Center of Gravty, Center of Mass and Geometrc Centrod Shan Kenny, Ph.D., P.Eng. ssstant Professor Faculty of Engneerng and ppled Scence Memoral Unversty of Nefoundland spkenny@engr.mun.ca
ENGI 11 Mechancs I Lecture 40: Center of Gravty, Center of Mass and Geometrc Centrod Shan Kenny, Ph.D., P.Eng. ssstant Professor Faculty of Engneerng and ppled Scence Memoral Unversty of Nefoundland spkenny@engr.mun.ca
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
ME 300 Exam 2 November 18, :30 p.m. to 7:30 p.m.
 CICLE YOU LECTUE BELOW: Frst Name Last Name 1:3 a.m. 1:3 p.m. Nak Gore ME 3 Exam November 18, 14 6:3 p.m. to 7:3 p.m. INSTUCTIONS 1. Ths s a closed book and closed notes examnaton. You are provded wth
CICLE YOU LECTUE BELOW: Frst Name Last Name 1:3 a.m. 1:3 p.m. Nak Gore ME 3 Exam November 18, 14 6:3 p.m. to 7:3 p.m. INSTUCTIONS 1. Ths s a closed book and closed notes examnaton. You are provded wth
EN40: Dynamics and Vibrations. Homework 7: Rigid Body Kinematics
 N40: ynamcs and Vbratons Homewor 7: Rgd Body Knematcs School of ngneerng Brown Unversty 1. In the fgure below, bar AB rotates counterclocwse at 4 rad/s. What are the angular veloctes of bars BC and C?.
N40: ynamcs and Vbratons Homewor 7: Rgd Body Knematcs School of ngneerng Brown Unversty 1. In the fgure below, bar AB rotates counterclocwse at 4 rad/s. What are the angular veloctes of bars BC and C?.
Physics 114 Exam 3 Spring Name:
 Physcs 114 Exam 3 Sprng 015 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem 4. Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse
Physcs 114 Exam 3 Sprng 015 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem 4. Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse
SCHOOL OF COMPUTING, ENGINEERING AND MATHEMATICS SEMESTER 2 EXAMINATIONS 2011/2012 DYNAMICS ME247 DR. N.D.D. MICHÉ
 s SCHOOL OF COMPUTING, ENGINEERING ND MTHEMTICS SEMESTER EXMINTIONS 011/01 DYNMICS ME47 DR. N.D.D. MICHÉ Tme allowed: THREE hours nswer: ny FOUR from SIX questons Each queston carres 5 marks Ths s a CLOSED-BOOK
s SCHOOL OF COMPUTING, ENGINEERING ND MTHEMTICS SEMESTER EXMINTIONS 011/01 DYNMICS ME47 DR. N.D.D. MICHÉ Tme allowed: THREE hours nswer: ny FOUR from SIX questons Each queston carres 5 marks Ths s a CLOSED-BOOK
GAUTENG DEPARTMENT OF EDUCATION SENIOR SECONDARY INTERVENTION PROGRAMME PHYSICAL SCIENCES GRADE 12 SESSION 1 (LEARNER NOTES)
 PHYSICAL SCIENCES GRADE 1 SESSION 1 (LEARNER NOTES) TOPIC 1: MECHANICS PROJECTILE MOTION Learner Note: Always draw a dagram of the stuaton and enter all the numercal alues onto your dagram. Remember to
PHYSICAL SCIENCES GRADE 1 SESSION 1 (LEARNER NOTES) TOPIC 1: MECHANICS PROJECTILE MOTION Learner Note: Always draw a dagram of the stuaton and enter all the numercal alues onto your dagram. Remember to
Physics 111: Mechanics Lecture 11
 Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
First Law: A body at rest remains at rest, a body in motion continues to move at constant velocity, unless acted upon by an external force.
 Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Formulas for the Determinant
 page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
ENGN 40 Dynamics and Vibrations Homework # 7 Due: Friday, April 15
 NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
Physics 607 Exam 1. ( ) = 1, Γ( z +1) = zγ( z) x n e x2 dx = 1. e x2
 Physcs 607 Exam 1 Please be well-organzed, and show all sgnfcant steps clearly n all problems. You are graded on your wor, so please do not just wrte down answers wth no explanaton! Do all your wor on
Physcs 607 Exam 1 Please be well-organzed, and show all sgnfcant steps clearly n all problems. You are graded on your wor, so please do not just wrte down answers wth no explanaton! Do all your wor on
I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 NAME: ME 270 Fall 2012 Examination No. 3 - Makeup Please review the following statement: Group No.: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
NAME: ME 270 Fall 2012 Examination No. 3 - Makeup Please review the following statement: Group No.: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
Chapter 3. r r. Position, Velocity, and Acceleration Revisited
 Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Newton s Laws of Motion
 Chapter 4 Newton s Laws of Moton 4.1 Forces and Interactons Fundamental forces. There are four types of fundamental forces: electromagnetc, weak, strong and gravtatonal. The frst two had been successfully
Chapter 4 Newton s Laws of Moton 4.1 Forces and Interactons Fundamental forces. There are four types of fundamental forces: electromagnetc, weak, strong and gravtatonal. The frst two had been successfully
Chapter 9: Statistical Inference and the Relationship between Two Variables
 Chapter 9: Statstcal Inference and the Relatonshp between Two Varables Key Words The Regresson Model The Sample Regresson Equaton The Pearson Correlaton Coeffcent Learnng Outcomes After studyng ths chapter,
Chapter 9: Statstcal Inference and the Relatonshp between Two Varables Key Words The Regresson Model The Sample Regresson Equaton The Pearson Correlaton Coeffcent Learnng Outcomes After studyng ths chapter,
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
COMPOSITE BEAM WITH WEAK SHEAR CONNECTION SUBJECTED TO THERMAL LOAD
 COMPOSITE BEAM WITH WEAK SHEAR CONNECTION SUBJECTED TO THERMAL LOAD Ákos Jósef Lengyel, István Ecsed Assstant Lecturer, Professor of Mechancs, Insttute of Appled Mechancs, Unversty of Mskolc, Mskolc-Egyetemváros,
COMPOSITE BEAM WITH WEAK SHEAR CONNECTION SUBJECTED TO THERMAL LOAD Ákos Jósef Lengyel, István Ecsed Assstant Lecturer, Professor of Mechancs, Insttute of Appled Mechancs, Unversty of Mskolc, Mskolc-Egyetemváros,
Physics 207: Lecture 20. Today s Agenda Homework for Monday
 Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
1. The tie-rod AB exerts the 250 N force on the steering knuckle AO as shown. Replace this force by an equivalent force-couple system at O.
 1. The terod AB exerts the 50 N force on the steerng knuckle AO as shown. Replace ths force by an equvalent forcecouple system at O. . The devce shown s part of an automoble seatbackrelease mechansm. The
1. The terod AB exerts the 50 N force on the steerng knuckle AO as shown. Replace ths force by an equvalent forcecouple system at O. . The devce shown s part of an automoble seatbackrelease mechansm. The
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 Group Number: Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: INSTRUCTIONS Begin each problem
Group Number: Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: INSTRUCTIONS Begin each problem
Rotational Dynamics. Physics 1425 Lecture 19. Michael Fowler, UVa
 Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Physics 53. Rotational Motion 3. Sir, I have found you an argument, but I am not obliged to find you an understanding.
 Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
% & 5.3 PRACTICAL APPLICATIONS. Given system, (49) , determine the Boolean Function, , in such a way that we always have expression: " Y1 = Y2
 5.3 PRACTICAL APPLICATIONS st EXAMPLE: Gven system, (49) & K K Y XvX 3 ( 2 & X ), determne the Boolean Functon, Y2 X2 & X 3 v X " X3 (X2,X)", n such a way that we always have expresson: " Y Y2 " (50).
5.3 PRACTICAL APPLICATIONS st EXAMPLE: Gven system, (49) & K K Y XvX 3 ( 2 & X ), determne the Boolean Functon, Y2 X2 & X 3 v X " X3 (X2,X)", n such a way that we always have expresson: " Y Y2 " (50).
One Dimensional Axial Deformations
 One Dmensonal al Deformatons In ths secton, a specfc smple geometr s consdered, that of a long and thn straght component loaded n such a wa that t deforms n the aal drecton onl. The -as s taken as the
One Dmensonal al Deformatons In ths secton, a specfc smple geometr s consdered, that of a long and thn straght component loaded n such a wa that t deforms n the aal drecton onl. The -as s taken as the
Problem Points Score Total 100
 Physcs 450 Solutons of Sample Exam I Problem Ponts Score 1 8 15 3 17 4 0 5 0 Total 100 All wor must be shown n order to receve full credt. Wor must be legble and comprehensble wth answers clearly ndcated.
Physcs 450 Solutons of Sample Exam I Problem Ponts Score 1 8 15 3 17 4 0 5 0 Total 100 All wor must be shown n order to receve full credt. Wor must be legble and comprehensble wth answers clearly ndcated.
Physics 114 Exam 2 Fall 2014 Solutions. Name:
 Physcs 114 Exam Fall 014 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse ndcated,
Physcs 114 Exam Fall 014 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse ndcated,
Physics 2113 Lecture 14: WED 18 FEB
 Physcs 2113 Jonathan Dowlng Physcs 2113 Lecture 14: WED 18 FEB Electrc Potental II Danger! Electrc Potental Energy, Unts : Electrc Potental Potental Energy = U = [J] = Joules Electrc Potental = V = U/q
Physcs 2113 Jonathan Dowlng Physcs 2113 Lecture 14: WED 18 FEB Electrc Potental II Danger! Electrc Potental Energy, Unts : Electrc Potental Potental Energy = U = [J] = Joules Electrc Potental = V = U/q
Last Name, First Name. I have not received unauthorized aid in the completion of this exam.
 ME 270 Spring 2013 Examination No. 2 Please read and respond to the following statement, I have not received unauthorized aid in the completion of this exam. Agree Disagree Signature INSTRUCTIONS Begin
ME 270 Spring 2013 Examination No. 2 Please read and respond to the following statement, I have not received unauthorized aid in the completion of this exam. Agree Disagree Signature INSTRUCTIONS Begin
. You need to do this for each force. Let s suppose that there are N forces, with components ( N) ( N) ( N) = i j k
 EN3: Introducton to Engneerng and Statcs Dvson of Engneerng Brown Unversty 3. Resultant of systems of forces Machnes and structures are usually subected to lots of forces. When we analyze force systems
EN3: Introducton to Engneerng and Statcs Dvson of Engneerng Brown Unversty 3. Resultant of systems of forces Machnes and structures are usually subected to lots of forces. When we analyze force systems
Please initial the statement below to show that you have read it
 EN40: Dynamcs and Vbratons Mdterm Examnaton Thursday March 5 009 Dvson of Engneerng rown Unversty NME: Isaac Newton General Instructons No collaboraton of any knd s permtted on ths examnaton. You may brng
EN40: Dynamcs and Vbratons Mdterm Examnaton Thursday March 5 009 Dvson of Engneerng rown Unversty NME: Isaac Newton General Instructons No collaboraton of any knd s permtted on ths examnaton. You may brng
Be true to your work, your word, and your friend.
 Chemstry 13 NT Be true to your work, your word, and your frend. Henry Davd Thoreau 1 Chem 13 NT Chemcal Equlbrum Module Usng the Equlbrum Constant Interpretng the Equlbrum Constant Predctng the Drecton
Chemstry 13 NT Be true to your work, your word, and your frend. Henry Davd Thoreau 1 Chem 13 NT Chemcal Equlbrum Module Usng the Equlbrum Constant Interpretng the Equlbrum Constant Predctng the Drecton
DUE: WEDS FEB 21ST 2018
 HOMEWORK # 1: FINITE DIFFERENCES IN ONE DIMENSION DUE: WEDS FEB 21ST 2018 1. Theory Beam bendng s a classcal engneerng analyss. The tradtonal soluton technque makes smplfyng assumptons such as a constant
HOMEWORK # 1: FINITE DIFFERENCES IN ONE DIMENSION DUE: WEDS FEB 21ST 2018 1. Theory Beam bendng s a classcal engneerng analyss. The tradtonal soluton technque makes smplfyng assumptons such as a constant
a) No books or notes are permitted. b) You may use a calculator.
 PHYS 050 Sprng 06 Name: Test 3 Aprl 7, 06 INSTRUCTIONS: a) No books or notes are permtted. b) You may use a calculator. c) You must solve all problems begnnng wth the equatons on the Inormaton Sheet provded
PHYS 050 Sprng 06 Name: Test 3 Aprl 7, 06 INSTRUCTIONS: a) No books or notes are permtted. b) You may use a calculator. c) You must solve all problems begnnng wth the equatons on the Inormaton Sheet provded
The optimal delay of the second test is therefore approximately 210 hours earlier than =2.
 THE IEC 61508 FORMULAS 223 The optmal delay of the second test s therefore approxmately 210 hours earler than =2. 8.4 The IEC 61508 Formulas IEC 61508-6 provdes approxmaton formulas for the PF for smple
THE IEC 61508 FORMULAS 223 The optmal delay of the second test s therefore approxmately 210 hours earler than =2. 8.4 The IEC 61508 Formulas IEC 61508-6 provdes approxmaton formulas for the PF for smple
Indeterminate pin-jointed frames (trusses)
 Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
 COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
MOUNT SAINT JOSEPH MILPERRA
 Student Name : MOUNT SAINT JOSEPH MILPERRA MOUNT SAINT JOSEPH I YEAR 8 MATHEMATICS 17th November 2006 70 MINUTES (plus 5 mnutes readng tme)... :... INSTRUCTIONS: > WRITE IN BLUE OR BLACK PEN ONLY > ALL
Student Name : MOUNT SAINT JOSEPH MILPERRA MOUNT SAINT JOSEPH I YEAR 8 MATHEMATICS 17th November 2006 70 MINUTES (plus 5 mnutes readng tme)... :... INSTRUCTIONS: > WRITE IN BLUE OR BLACK PEN ONLY > ALL
Second Order Analysis
 Second Order Analyss In the prevous classes we looked at a method that determnes the load correspondng to a state of bfurcaton equlbrum of a perfect frame by egenvalye analyss The system was assumed to
Second Order Analyss In the prevous classes we looked at a method that determnes the load correspondng to a state of bfurcaton equlbrum of a perfect frame by egenvalye analyss The system was assumed to
Lecture 5 Decoding Binary BCH Codes
 Lecture 5 Decodng Bnary BCH Codes In ths class, we wll ntroduce dfferent methods for decodng BCH codes 51 Decodng the [15, 7, 5] 2 -BCH Code Consder the [15, 7, 5] 2 -code C we ntroduced n the last lecture
Lecture 5 Decodng Bnary BCH Codes In ths class, we wll ntroduce dfferent methods for decodng BCH codes 51 Decodng the [15, 7, 5] 2 -BCH Code Consder the [15, 7, 5] 2 -code C we ntroduced n the last lecture
Physics 207 Lecture 6
 Physcs 207 Lecture 6 Agenda: Physcs 207, Lecture 6, Sept. 25 Chapter 4 Frames of reference Chapter 5 ewton s Law Mass Inerta s (contact and non-contact) Frcton (a external force that opposes moton) Free
Physcs 207 Lecture 6 Agenda: Physcs 207, Lecture 6, Sept. 25 Chapter 4 Frames of reference Chapter 5 ewton s Law Mass Inerta s (contact and non-contact) Frcton (a external force that opposes moton) Free
Section 8.1 Exercises
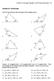 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
CHAPTER 6. LAGRANGE S EQUATIONS (Analytical Mechanics)
 CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
Error Bars in both X and Y
 Error Bars n both X and Y Wrong ways to ft a lne : 1. y(x) a x +b (σ x 0). x(y) c y + d (σ y 0) 3. splt dfference between 1 and. Example: Prmordal He abundance: Extrapolate ft lne to [ O / H ] 0. [ He
Error Bars n both X and Y Wrong ways to ft a lne : 1. y(x) a x +b (σ x 0). x(y) c y + d (σ y 0) 3. splt dfference between 1 and. Example: Prmordal He abundance: Extrapolate ft lne to [ O / H ] 0. [ He
Important Dates: Post Test: Dec during recitations. If you have taken the post test, don t come to recitation!
 Important Dates: Post Test: Dec. 8 0 durng rectatons. If you have taken the post test, don t come to rectaton! Post Test Make-Up Sessons n ARC 03: Sat Dec. 6, 0 AM noon, and Sun Dec. 7, 8 PM 0 PM. Post
Important Dates: Post Test: Dec. 8 0 durng rectatons. If you have taken the post test, don t come to rectaton! Post Test Make-Up Sessons n ARC 03: Sat Dec. 6, 0 AM noon, and Sun Dec. 7, 8 PM 0 PM. Post
Chapter Eight. Review and Summary. Two methods in solid mechanics ---- vectorial methods and energy methods or variational methods
 Chapter Eght Energy Method 8. Introducton 8. Stran energy expressons 8.3 Prncpal of statonary potental energy; several degrees of freedom ------ Castglano s frst theorem ---- Examples 8.4 Prncpal of statonary
Chapter Eght Energy Method 8. Introducton 8. Stran energy expressons 8.3 Prncpal of statonary potental energy; several degrees of freedom ------ Castglano s frst theorem ---- Examples 8.4 Prncpal of statonary
Application to Plane (rigid) frame structure
 Advanced Computatonal echancs 18 Chapter 4 Applcaton to Plane rgd frame structure 1. Dscusson on degrees of freedom In case of truss structures, t was enough that the element force equaton provdes onl
Advanced Computatonal echancs 18 Chapter 4 Applcaton to Plane rgd frame structure 1. Dscusson on degrees of freedom In case of truss structures, t was enough that the element force equaton provdes onl
SIMPLE LINEAR REGRESSION
 Smple Lnear Regresson and Correlaton Introducton Prevousl, our attenton has been focused on one varable whch we desgnated b x. Frequentl, t s desrable to learn somethng about the relatonshp between two
Smple Lnear Regresson and Correlaton Introducton Prevousl, our attenton has been focused on one varable whch we desgnated b x. Frequentl, t s desrable to learn somethng about the relatonshp between two
Modeling of Dynamic Systems
 Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: INSTRUCTIONS Begin each problem in the space provided
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam. Signature: INSTRUCTIONS Begin each problem in the space provided
UNIVERSITY OF TORONTO Faculty of Arts and Science. December 2005 Examinations STA437H1F/STA1005HF. Duration - 3 hours
 UNIVERSITY OF TORONTO Faculty of Arts and Scence December 005 Examnatons STA47HF/STA005HF Duraton - hours AIDS ALLOWED: (to be suppled by the student) Non-programmable calculator One handwrtten 8.5'' x
UNIVERSITY OF TORONTO Faculty of Arts and Scence December 005 Examnatons STA47HF/STA005HF Duraton - hours AIDS ALLOWED: (to be suppled by the student) Non-programmable calculator One handwrtten 8.5'' x
Study Guide For Exam Two
 Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
NAME and Section No. it is found that 0.6 mol of O
 NAME and Secton No. Chemstry 391 Fall 7 Exam III KEY 1. (3 Ponts) ***Do 5 out of 6***(If 6 are done only the frst 5 wll be graded)*** a). In the reacton 3O O3 t s found that.6 mol of O are consumed. Fnd
NAME and Secton No. Chemstry 391 Fall 7 Exam III KEY 1. (3 Ponts) ***Do 5 out of 6***(If 6 are done only the frst 5 wll be graded)*** a). In the reacton 3O O3 t s found that.6 mol of O are consumed. Fnd
Chapter 11: Angular Momentum
 Chapter 11: ngular Momentum Statc Equlbrum In Chap. 4 we studed the equlbrum of pontobjects (mass m) wth the applcaton of Newton s aws F 0 F x y, 0 Therefore, no lnear (translatonal) acceleraton, a0 For
Chapter 11: ngular Momentum Statc Equlbrum In Chap. 4 we studed the equlbrum of pontobjects (mass m) wth the applcaton of Newton s aws F 0 F x y, 0 Therefore, no lnear (translatonal) acceleraton, a0 For
PES 1120 Spring 2014, Spendier Lecture 6/Page 1
 PES 110 Sprng 014, Spender Lecture 6/Page 1 Lecture today: Chapter 1) Electrc feld due to charge dstrbutons -> charged rod -> charged rng We ntroduced the electrc feld, E. I defned t as an nvsble aura
PES 110 Sprng 014, Spender Lecture 6/Page 1 Lecture today: Chapter 1) Electrc feld due to charge dstrbutons -> charged rod -> charged rng We ntroduced the electrc feld, E. I defned t as an nvsble aura
Finite Element Modelling of truss/cable structures
 Pet Schreurs Endhoven Unversty of echnology Department of Mechancal Engneerng Materals echnology November 3, 214 Fnte Element Modellng of truss/cable structures 1 Fnte Element Analyss of prestressed structures
Pet Schreurs Endhoven Unversty of echnology Department of Mechancal Engneerng Materals echnology November 3, 214 Fnte Element Modellng of truss/cable structures 1 Fnte Element Analyss of prestressed structures
First Year Examination Department of Statistics, University of Florida
 Frst Year Examnaton Department of Statstcs, Unversty of Florda May 7, 010, 8:00 am - 1:00 noon Instructons: 1. You have four hours to answer questons n ths examnaton.. You must show your work to receve
Frst Year Examnaton Department of Statstcs, Unversty of Florda May 7, 010, 8:00 am - 1:00 noon Instructons: 1. You have four hours to answer questons n ths examnaton.. You must show your work to receve
Chapter 8. Potential Energy and Conservation of Energy
 Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Numerical Transient Heat Conduction Experiment
 Numercal ransent Heat Conducton Experment OBJECIVE 1. o demonstrate the basc prncples of conducton heat transfer.. o show how the thermal conductvty of a sold can be measured. 3. o demonstrate the use
Numercal ransent Heat Conducton Experment OBJECIVE 1. o demonstrate the basc prncples of conducton heat transfer.. o show how the thermal conductvty of a sold can be measured. 3. o demonstrate the use
Physics 207: Lecture 27. Announcements
 Physcs 07: ecture 7 Announcements ake-up labs are ths week Fnal hwk assgned ths week, fnal quz next week Revew sesson on Thursday ay 9, :30 4:00pm, Here Today s Agenda Statcs recap Beam & Strngs» What
Physcs 07: ecture 7 Announcements ake-up labs are ths week Fnal hwk assgned ths week, fnal quz next week Revew sesson on Thursday ay 9, :30 4:00pm, Here Today s Agenda Statcs recap Beam & Strngs» What
So far: simple (planar) geometries
 Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physics 141. Lecture 14. Frank L. H. Wolfs Department of Physics and Astronomy, University of Rochester, Lecture 14, Page 1
 Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
The equation of motion of a dynamical system is given by a set of differential equations. That is (1)
 Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
: 5: ) A
 Revew 1 004.11.11 Chapter 1: 1. Elements, Varable, and Observatons:. Type o Data: Qualtatve Data and Quanttatve Data (a) Qualtatve data may be nonnumerc or numerc. (b) Quanttatve data are always numerc.
Revew 1 004.11.11 Chapter 1: 1. Elements, Varable, and Observatons:. Type o Data: Qualtatve Data and Quanttatve Data (a) Qualtatve data may be nonnumerc or numerc. (b) Quanttatve data are always numerc.
FREQUENCY DISTRIBUTIONS Page 1 of The idea of a frequency distribution for sets of observations will be introduced,
 FREQUENCY DISTRIBUTIONS Page 1 of 6 I. Introducton 1. The dea of a frequency dstrbuton for sets of observatons wll be ntroduced, together wth some of the mechancs for constructng dstrbutons of data. Then
FREQUENCY DISTRIBUTIONS Page 1 of 6 I. Introducton 1. The dea of a frequency dstrbuton for sets of observatons wll be ntroduced, together wth some of the mechancs for constructng dstrbutons of data. Then
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
Linear Momentum. Center of Mass.
 Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
