Physics 2A Chapter 3 HW Solutions
|
|
|
- Camron Andrews
- 6 years ago
- Views:
Transcription
1 Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C = A B A and B are n the opposte drecton to each other. Sze matters onl n that A > B because C as a magntude can onl be postve. Assess: Vsualze the stuaton wth arrows. Q3.6. Reason: The acceleraton o the ball s due to gravt, so the acceleraton the ball eperences s alwas straght downward. (a) The veloct vector o the ball alwas has a component n the horzontal drecton snce t was thrown at an angle o 40. The horzontal component o the ball s veloct s constant throughout ts trajector. Snce the veloct vector alwas has a component n the horzontal drecton, t s never pontng entrel straght up or down. So there s no pont on the trajector where the acceleraton and veloct are parallel. Note that the ball were thrown straght up or down nstead o at 40, the ball s veloct and acceleraton would be parallel. (b) The acceleraton o the ball s alwas straght downward. For the veloct vector to be perpendcular to the acceleraton vector, the veloct must pont entrel n the horzontal drecton. The veloct vector alwas has a component n the horzontal drecton, as reasoned n part (a). It has a component n the vertcal drecton durng most o ts moton also snce the ball travels upward and downward n the vertcal drecton. There s one pont where the ball s not travelng up or down, and that s at the top o ts trajector. Ths s the onl pont where the veloct and acceleraton are perpendcular. Assess: The acceleraton due to gravt alwas ponts straght downward. See Fgure 3.30, whch shows the average veloct vectors and acceleraton along the trajector o a tossed ball. Q3.8. Reason: Runnng whle throwng a ball ncreases the dstance o the throw because t ncreases the horzontal component o the ball s veloct wthout changng the tme o lght. Relatve to the ground, the ball s horzontal veloct component s ncreased b an amount equal to the speed o the runner. Snce the veloct o the runner s purel horzontal, the vertcal veloct component o the ball s unchanged and so the tme o lght o the ball s unchanged. It s nterestng to note that snce, relatve to the ground, the ball has a greater horzontal component o veloct, the angle o the ball s veloct s hgher relatve to the person throwng the ball than relatve to the ground. However, nether relatve to the ground, nor relatve to the person throwng the ball wll a launch angle o 45 gve the mamum range. The angle 45 gves the mamum range or a ball launched b someone not movng because t gves the best compromse between havng a hgh tme o lght and a large horzontal component o veloct. But when the person s runnng, the horzontal component o veloct gets an advantage so the tme o lght can be greater at the epense o the horzontal component o veloct. Thus the best angle relatve to the person s greater than 45. Assess: Whle the best launch angle s no longer 45, t s stll true that runnng ncreases the range o the ball.
2 Q3.. Reason: The tme or an object to ht the ground does not depend on ts horzontal speed, but onl on ts heght and ntal vertcal speed. When the plot goes twce as ast, all that changes s the horzontal speed o the projectle. Thereore the tme o lght wll be the same n both cases,.0 s. However the dstance travelled horzontall wll be doubled snce the horzontal speed s doubled and the tme o lght s the same. At the doubled speed, the weght wll travel twce as ar, or 00 m. Assess: The above answer assumed no ar resstance. Actuall the greater speed o the aster projectle wll slghtl ncrease the tme o lght snce a aster object eperences more ar resstance. P3.5. Prepare: Acceleraton s ound b the method o Tactcs Bo 3.. Solve: The acceleraton vector at each locaton ponts drectl toward the center o the Ferrs wheel s crcular moton. Assess: As we wll learn later, ths acceleraton that s drected toward the center s called centrpetal acceleraton. P3.. Prepare: We wll ollow rules gven n the Tactcs Bo 3.3. Solve: (a) Vector d ponts to the rght and down, so the components d and d are postve and negatve, respectvel: d = d cos θ = (00 m) cos 45 = 70.7 m d = d sn θ = (00 m) sn 45 =7m (b) Vector v ponts to the rght and up, so the components v and v are both postve:
3 (c) Vector v = v cos θ = (300 m/s) cos 0 = 80 m/s v = v sn θ = (300 m/s) sn 0 = 00 m/s a has the ollowng components: a = a cos θ = (5.0 m/s ) cos 90 = 0 m/s a = a sn θ = (5.0 m/s ) sn 90 =5.0 m/s Assess: The components have same unts as the vectors. Note the mnus sgns we have manuall nserted accordng to the Tactcs Bo 3.3. P3.8. Prepare: We can nd the acceleraton on the ramp and then use the acceleraton to nd the nal veloct o the car. Solve: (a) The mamum possble acceleraton s gven b the ormula a = g sn θ. Pluggng n the values o g and θ, we get a =. m/s. (b) The nal veloct can be obtaned rom the ormula ( v ) ( v ) = a Δ, usng ( v ) = 0 m/s and Δ = 6.8 m, the m m latter beng obtaned b convertng 55 t: 55 t = 55 t. 3.8 t 55 t = 55 t The soluton to the rst equaton 3.8 t s ( v ) = 8.6 m/s. Assess: As wth most ramp problems, ths one was best solved b usng a rotated coordnate sstem wth the -as along the ramp. P3.7. Prepare: We wll assume the ball s n ree all (.e., we neglect ar resstance). The trajector o a projectle s a parabola because t s a combnaton o constant horzontal veloct (a = 0.0 m/s ) combned wth constant vertcal acceleraton (a = g). In ths case we see onl hal o the parabola. The ntal speed gven s all n the horzontal drecton, that s, (v ) = 5.0 m/s and (v ) = 0.0 m/s. Solve: (a) (b) (c) (d) Ths s a two-step problem. We rst use the vertcal drecton to determne the tme t takes, then plug that result nto the equaton or the horzontal drecton. Δ = a ( Δ t ) Δ ( 0 m) Δ t = = =.0 s a 9.8 m/s
4 We we use the.0 s n the equaton or the horzontal moton. Δ = v Δ t = (5.0 m/s)(.0 s) = 0 m Assess: The answers seem reasonable, and we would get the same answers to two sgncant gures n a quck mental calculaton usng g 0m/s. In act, I dd ths beore computng the algebra so I would know how to scale the graphs. P3.3. Prepare: We wll appl the constant-acceleraton knematc equatons to the horzontal and vertcal motons as descrbed b Equatons 3.5. The eect o ar resstance on the moton o the bullet s neglected. Solve: (a) Usng (b) Usng v t t a t t = + ( ) ( ) + ( ), we obtan (.0 0 m) = 0 m + 0 m + ( 9.8 m/s )( t 0 s) v t t a t t = + ( ) ( ) + ( ), (50 m) = 0 m + ( v ) ( s 0 s) + 0 m v t = s ( ) = 78 m/s Assess: The bullet alls cm durng a horzontal dsplacement o 50 m. Ths mples a large ntal veloct, and a value o 78 m/s s not surprsng. P3.44. Prepare: Because A= A + A, and B = B + B, so the components o the resultant vector are E = A + 3B and E = A + 3B. The vectors A, B, and E = A+ 3B are shown. Solve: (a) Wth A = 5, A =, B = 3, and B = 5, we have E = and E =. (b) Vectors A, B, and E are shown n the above gure. (c) From the E vector, E = and E =. Thereore, the magntude and drecton o E are
5 Assess: E = () + ( ) = E φ = tan = tan = 5. E Note that φ s the angle made wth the -as, and that s wh φ = tan ( E / E ) rather than whch would be the case φ were the angle made wth the -as. tan ( E / E) P3.46. Prepare: The vectors then obtan the magntude and the drecton o the vector D. A, B, and C are shown. We wll rst calculate the - and -components o each vector and Solve: (a) The vectors A, B, and C are drawn above. (b) The components o the vectors A, B, and C are A = (3 m) cos 0 =.8 m and A = (3 m) sn 0 =.03 m; B = 0m and B = m; C = (5 m) cos 70 =.7m and C = (5 m) sn 70 =4. 70 m. (c) We have D= A+ B+ C = D + D, whch means D =. and D = D = (.m) + (3.73 m) = 3.9 m θ = tan = tan 3.36 = 73. The drecton o D s south o east, 73 below the postve -as. P3.69. Prepare: We wll appl the constant-acceleraton knematcs equatons to the horzontal and vertcal motons o the tenns ball as descrbed b Equatons 3.5. A vsual overvew s shown as ollows. To nd whether the ball clears the net, we wll determne the vertcal all o the ball as t travels to the net. Solve: The ntal veloct s ( v ) = v cos 5 = (0 m/s) cos 5 = 9.9 m/s ( v ) = v sn 5 = (0m/s)sn 5 =.743m/s The tme t takes or the ball to reach the net s = + ( v) ( t t) 7.0 m = 0 m + (9.9 m/s)( t 0 s) t = 0.35s
6 The vertcal poston at t = 0.35 s s = + ( v) ( t t) + a ( t t) = + + = (.0 m) (.743 m/s)(0.35 s 0 s) ( 9.8 m/s )(0.35s 0 s).0 m Thus the ball clears the net b.0 m. Assess: The vertcal ree all o the ball, wth zero ntal veloct, n 0.35 s s 0.6 m. The ball wll clear b appromatel 0.4 m the ball s thrown horzontall. The ntal launch angle o 5 provdes some ntal vertcal veloct and the ball clears b a larger dstance. The above result s reasonable. P3.70. Prepare: We can use the equaton or vertcal moton at constant acceleraton to nd the tme o all and then use the tme to nd the nal veloct. Solve: Snce the water s launched horzontall, ts tme o lght and vertcal dsplacement are related b the equaton: Δ = gδ t. Solvng or the tme, we have Δ t = Δ g = = / (53 m) / 9.8 m/s 3.9 s The horzontal component o the veloct, v, s constant, but the vertcal component s gven b the equaton: ( v ) = ( v ) + a Δt. At the moment the water strkes the pool, the vertcal component s ( ) ( v ) = 0 m/s 9.8 m/s (3.9 s) = 3. m/s At the moment o mpact the veloct o the water s: (9.0 m/s, 3. m/s). The angle that the water makes wth the vertcal s gven b The water s allng at an angle o 6 wth the vertcal. φ = = tan ((9.0 m/s)/(3. m/s)) 6 Assess: Even though the water s launched at a arl hgh speed ( 9.0 m/s s about 0 m/hr ), t s close to the vertcal when t lands because t spends such a long tme n the ar durng whch tme the absolute value o v ncreases steadl.
7 P3.73. Prepare: Frst draw a pcture. In part (a) use tlted aes so the -as runs down the slde. The acceleraton wll be a = g sn θ. Part (b) s a amlar two-step projectle moton problem where we use the vertcal drecton to determne the tme o lght and then plug t nto then equaton or constant horzontal veloct. Use aes that are not tlted or part (b). Solve: (a) We use Equaton.3 wth ( ) = 0.0 m/s. v v g θ Δ ( v ) =a Δ o ( ) = ( sn ) = (9.8 m/s )(sn40 )(3.0 m) = 6.m/s (b) We use Equaton.4 to nd the tme or an object to all 0.4 m rom rest: Δ = 0.4m. Δ = a ( Δ t) Δ ( 0.4m) Δ t = = = 0.86 s g 9.8 m/s At last we combne ths normaton nto the equaton or constant horzontal veloct. Δ= v Δ t = (6.5 m/s)(0.86 s) =.8 m Assess: We reported the speed at the bottom o the slde to two sgncant gures, but kept track o a thrd to use as a guard dgt because ths result s also an ntermedate result or the nal answer. We also kept a thrd sgncant gure on the Δt as a guard dgt. The result o landng.8 m rom the end o the rctonless slde seems just a bt large because ths slde was rctonless and real sldes aren t, but t doesn t seem to be too ar out o epectaton, so our result s probabl correct.
Physics 2A Chapter 9 HW Solutions
 Phscs A Chapter 9 HW Solutons Chapter 9 Conceptual Queston:, 4, 8, 13 Problems: 3, 8, 1, 15, 3, 40, 51, 6 Q9.. Reason: We can nd the change n momentum o the objects b computng the mpulse on them and usng
Phscs A Chapter 9 HW Solutons Chapter 9 Conceptual Queston:, 4, 8, 13 Problems: 3, 8, 1, 15, 3, 40, 51, 6 Q9.. Reason: We can nd the change n momentum o the objects b computng the mpulse on them and usng
Physics 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn in the following problems from Chapter 4 Knight
 Physcs 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn n the ollowng problems rom Chapter 4 Knght Conceptual Questons: 8, 0, ; 4.8. Anta s approachng ball and movng away rom where ball was
Physcs 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn n the ollowng problems rom Chapter 4 Knght Conceptual Questons: 8, 0, ; 4.8. Anta s approachng ball and movng away rom where ball was
Chapter 3. r r. Position, Velocity, and Acceleration Revisited
 Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Name: PHYS 110 Dr. McGovern Spring 2018 Exam 1. Multiple Choice: Circle the answer that best evaluates the statement or completes the statement.
 Name: PHYS 110 Dr. McGoern Sprng 018 Exam 1 Multple Choce: Crcle the answer that best ealuates the statement or completes the statement. #1 - I the acceleraton o an object s negate, the object must be
Name: PHYS 110 Dr. McGoern Sprng 018 Exam 1 Multple Choce: Crcle the answer that best ealuates the statement or completes the statement. #1 - I the acceleraton o an object s negate, the object must be
PHYSICS 203-NYA-05 MECHANICS
 PHYSICS 03-NYA-05 MECHANICS PROF. S.D. MANOLI PHYSICS & CHEMISTRY CHAMPLAIN - ST. LAWRENCE 790 NÉRÉE-TREMBLAY QUÉBEC, QC GV 4K TELEPHONE: 48.656.69 EXT. 449 EMAIL: smanol@slc.qc.ca WEBPAGE: http:/web.slc.qc.ca/smanol/
PHYSICS 03-NYA-05 MECHANICS PROF. S.D. MANOLI PHYSICS & CHEMISTRY CHAMPLAIN - ST. LAWRENCE 790 NÉRÉE-TREMBLAY QUÉBEC, QC GV 4K TELEPHONE: 48.656.69 EXT. 449 EMAIL: smanol@slc.qc.ca WEBPAGE: http:/web.slc.qc.ca/smanol/
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Supplemental Instruction sessions next week
 Homework #4 Wrtten homework due now Onlne homework due on Tue Mar 3 by 8 am Exam 1 Answer keys and scores wll be posted by end of the week Supplemental Instructon sessons next week Wednesday 8:45 10:00
Homework #4 Wrtten homework due now Onlne homework due on Tue Mar 3 by 8 am Exam 1 Answer keys and scores wll be posted by end of the week Supplemental Instructon sessons next week Wednesday 8:45 10:00
TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES. PHYS 2211, Exam 2 Section 1 Version 1 October 18, 2013 Total Weight: 100 points
 TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES PHYS, Exam Secton Verson October 8, 03 Total Weght: 00 ponts. Check your examnaton or completeness pror to startng. There are a total o nne
TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES PHYS, Exam Secton Verson October 8, 03 Total Weght: 00 ponts. Check your examnaton or completeness pror to startng. There are a total o nne
= 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W]
![= 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W] = 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W]](/thumbs/78/76802454.jpg) Secton 1.3: Acceleraton Tutoral 1 Practce, page 24 1. Gven: 0 m/s; 15.0 m/s [S]; t 12.5 s Requred: Analyss: a av v t v f v t a v av f v t 15.0 m/s [S] 0 m/s 12.5 s 15.0 m/s [S] 12.5 s 1.20 m/s 2 [S] Statement:
Secton 1.3: Acceleraton Tutoral 1 Practce, page 24 1. Gven: 0 m/s; 15.0 m/s [S]; t 12.5 s Requred: Analyss: a av v t v f v t a v av f v t 15.0 m/s [S] 0 m/s 12.5 s 15.0 m/s [S] 12.5 s 1.20 m/s 2 [S] Statement:
Spring Force and Power
 Lecture 13 Chapter 9 Sprng Force and Power Yeah, energy s better than orces. What s net? Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi IN THIS CHAPTER, you wll learn how to solve problems
Lecture 13 Chapter 9 Sprng Force and Power Yeah, energy s better than orces. What s net? Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi IN THIS CHAPTER, you wll learn how to solve problems
GAUTENG DEPARTMENT OF EDUCATION SENIOR SECONDARY INTERVENTION PROGRAMME PHYSICAL SCIENCES GRADE 12 SESSION 1 (LEARNER NOTES)
 PHYSICAL SCIENCES GRADE 1 SESSION 1 (LEARNER NOTES) TOPIC 1: MECHANICS PROJECTILE MOTION Learner Note: Always draw a dagram of the stuaton and enter all the numercal alues onto your dagram. Remember to
PHYSICAL SCIENCES GRADE 1 SESSION 1 (LEARNER NOTES) TOPIC 1: MECHANICS PROJECTILE MOTION Learner Note: Always draw a dagram of the stuaton and enter all the numercal alues onto your dagram. Remember to
Kinematics in 2-Dimensions. Projectile Motion
 Knematcs n -Dmensons Projectle Moton A medeval trebuchet b Kolderer, c1507 http://members.net.net.au/~rmne/ht/ht0.html#5 Readng Assgnment: Chapter 4, Sectons -6 Introducton: In medeval das, people had
Knematcs n -Dmensons Projectle Moton A medeval trebuchet b Kolderer, c1507 http://members.net.net.au/~rmne/ht/ht0.html#5 Readng Assgnment: Chapter 4, Sectons -6 Introducton: In medeval das, people had
Work is the change in energy of a system (neglecting heat transfer). To examine what could
 Work Work s the change n energy o a system (neglectng heat transer). To eamne what could cause work, let s look at the dmensons o energy: L ML E M L F L so T T dmensonally energy s equal to a orce tmes
Work Work s the change n energy o a system (neglectng heat transer). To eamne what could cause work, let s look at the dmensons o energy: L ML E M L F L so T T dmensonally energy s equal to a orce tmes
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
AP Physics 1 & 2 Summer Assignment
 AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
Chapter 8 Potential Energy and Conservation of Energy Important Terms (For chapters 7 and 8)
 Pro. Dr. I. Nasser Chapter8_I November 3, 07 Chapter 8 Potental Energy and Conservaton o Energy Important Terms (For chapters 7 and 8) conservatve orce: a orce whch does wor on an object whch s ndependent
Pro. Dr. I. Nasser Chapter8_I November 3, 07 Chapter 8 Potental Energy and Conservaton o Energy Important Terms (For chapters 7 and 8) conservatve orce: a orce whch does wor on an object whch s ndependent
Problem While being compressed, A) What is the work done on it by gravity? B) What is the work done on it by the spring force?
 Problem 07-50 A 0.25 kg block s dropped on a relaed sprng that has a sprng constant o k 250.0 N/m (2.5 N/cm). The block becomes attached to the sprng and compresses t 0.12 m beore momentarl stoppng. Whle
Problem 07-50 A 0.25 kg block s dropped on a relaed sprng that has a sprng constant o k 250.0 N/m (2.5 N/cm). The block becomes attached to the sprng and compresses t 0.12 m beore momentarl stoppng. Whle
Physics 2A Chapters 6 - Work & Energy Fall 2017
 Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
Physics for Scientists and Engineers. Chapter 9 Impulse and Momentum
 Physcs or Scentsts and Engneers Chapter 9 Impulse and Momentum Sprng, 008 Ho Jung Pak Lnear Momentum Lnear momentum o an object o mass m movng wth a velocty v s dened to be p mv Momentum and lnear momentum
Physcs or Scentsts and Engneers Chapter 9 Impulse and Momentum Sprng, 008 Ho Jung Pak Lnear Momentum Lnear momentum o an object o mass m movng wth a velocty v s dened to be p mv Momentum and lnear momentum
Chapter 2. Pythagorean Theorem. Right Hand Rule. Position. Distance Formula
 Chapter Moton n One Dmenson Cartesan Coordnate System The most common coordnate system or representng postons n space s one based on three perpendcular spatal axes generally desgnated x, y, and z. Any
Chapter Moton n One Dmenson Cartesan Coordnate System The most common coordnate system or representng postons n space s one based on three perpendcular spatal axes generally desgnated x, y, and z. Any
where v means the change in velocity, and t is the
 1 PHYS:100 LECTURE 4 MECHANICS (3) Ths lecture covers the eneral case of moton wth constant acceleraton and free fall (whch s one of the more mportant examples of moton wth constant acceleraton) n a more
1 PHYS:100 LECTURE 4 MECHANICS (3) Ths lecture covers the eneral case of moton wth constant acceleraton and free fall (whch s one of the more mportant examples of moton wth constant acceleraton) n a more
1. The number of significant figures in the number is a. 4 b. 5 c. 6 d. 7
 Name: ID: Anwer Key There a heet o ueul ormulae and ome converon actor at the end. Crcle your anwer clearly. All problem are pont ecept a ew marked wth ther own core. Mamum core 100. There are a total
Name: ID: Anwer Key There a heet o ueul ormulae and ome converon actor at the end. Crcle your anwer clearly. All problem are pont ecept a ew marked wth ther own core. Mamum core 100. There are a total
Chapter 7: Conservation of Energy
 Lecture 7: Conservaton o nergy Chapter 7: Conservaton o nergy Introucton I the quantty o a subject oes not change wth tme, t means that the quantty s conserve. The quantty o that subject remans constant
Lecture 7: Conservaton o nergy Chapter 7: Conservaton o nergy Introucton I the quantty o a subject oes not change wth tme, t means that the quantty s conserve. The quantty o that subject remans constant
Slide. King Saud University College of Science Physics & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART 2) LECTURE NO.
 Slde Kng Saud Unersty College of Scence Physcs & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART ) LECTURE NO. 6 THIS PRESENTATION HAS BEEN PREPARED BY: DR. NASSR S. ALZAYED Lecture
Slde Kng Saud Unersty College of Scence Physcs & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART ) LECTURE NO. 6 THIS PRESENTATION HAS BEEN PREPARED BY: DR. NASSR S. ALZAYED Lecture
You will analyze the motion of the block at different moments using the law of conservation of energy.
 Physcs 00A Homework 7 Chapter 8 Where s the Energy? In ths problem, we wll consder the ollowng stuaton as depcted n the dagram: A block o mass m sldes at a speed v along a horzontal smooth table. It next
Physcs 00A Homework 7 Chapter 8 Where s the Energy? In ths problem, we wll consder the ollowng stuaton as depcted n the dagram: A block o mass m sldes at a speed v along a horzontal smooth table. It next
11. Dynamics in Rotating Frames of Reference
 Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
SCALARS AND VECTORS All physical quantities in engineering mechanics are measured using either scalars or vectors.
 SCALARS AND ECTORS All phscal uanttes n engneerng mechancs are measured usng ether scalars or vectors. Scalar. A scalar s an postve or negatve phscal uantt that can be completel specfed b ts magntude.
SCALARS AND ECTORS All phscal uanttes n engneerng mechancs are measured usng ether scalars or vectors. Scalar. A scalar s an postve or negatve phscal uantt that can be completel specfed b ts magntude.
PHYS 1441 Section 002 Lecture #16
 PHYS 1441 Secton 00 Lecture #16 Monday, Mar. 4, 008 Potental Energy Conservatve and Non-conservatve Forces Conservaton o Mechancal Energy Power Today s homework s homework #8, due 9pm, Monday, Mar. 31!!
PHYS 1441 Secton 00 Lecture #16 Monday, Mar. 4, 008 Potental Energy Conservatve and Non-conservatve Forces Conservaton o Mechancal Energy Power Today s homework s homework #8, due 9pm, Monday, Mar. 31!!
PHYS 1101 Practice problem set 12, Chapter 32: 21, 22, 24, 57, 61, 83 Chapter 33: 7, 12, 32, 38, 44, 49, 76
 PHYS 1101 Practce problem set 1, Chapter 3: 1,, 4, 57, 61, 83 Chapter 33: 7, 1, 3, 38, 44, 49, 76 3.1. Vsualze: Please reer to Fgure Ex3.1. Solve: Because B s n the same drecton as the ntegraton path s
PHYS 1101 Practce problem set 1, Chapter 3: 1,, 4, 57, 61, 83 Chapter 33: 7, 1, 3, 38, 44, 49, 76 3.1. Vsualze: Please reer to Fgure Ex3.1. Solve: Because B s n the same drecton as the ntegraton path s
PHYS 1441 Section 002 Lecture #15
 PHYS 1441 Secton 00 Lecture #15 Monday, March 18, 013 Work wth rcton Potental Energy Gravtatonal Potental Energy Elastc Potental Energy Mechancal Energy Conservaton Announcements Mdterm comprehensve exam
PHYS 1441 Secton 00 Lecture #15 Monday, March 18, 013 Work wth rcton Potental Energy Gravtatonal Potental Energy Elastc Potental Energy Mechancal Energy Conservaton Announcements Mdterm comprehensve exam
Section 8.1 Exercises
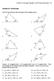 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Prof. Dr. I. Nasser T /16/2017
 Pro. Dr. I. Nasser T-171 10/16/017 Chapter Part 1 Moton n one dmenson Sectons -,, 3, 4, 5 - Moton n 1 dmenson We le n a 3-dmensonal world, so why bother analyzng 1-dmensonal stuatons? Bascally, because
Pro. Dr. I. Nasser T-171 10/16/017 Chapter Part 1 Moton n one dmenson Sectons -,, 3, 4, 5 - Moton n 1 dmenson We le n a 3-dmensonal world, so why bother analyzng 1-dmensonal stuatons? Bascally, because
Motion in One Dimension
 Moton n One Dmenson Speed ds tan ce traeled Aerage Speed tme of trael Mr. Wolf dres hs car on a long trp to a physcs store. Gen the dstance and tme data for hs trp, plot a graph of hs dstance ersus tme.
Moton n One Dmenson Speed ds tan ce traeled Aerage Speed tme of trael Mr. Wolf dres hs car on a long trp to a physcs store. Gen the dstance and tme data for hs trp, plot a graph of hs dstance ersus tme.
Physics 201, Lecture 4. Vectors and Scalars. Chapters Covered q Chapter 1: Physics and Measurement.
 Phscs 01, Lecture 4 Toda s Topcs n Vectors chap 3) n Scalars and Vectors n Vector ddton ule n Vector n a Coordnator Sstem n Decomposton of a Vector n Epected from prevew: n Scalars and Vectors, Vector
Phscs 01, Lecture 4 Toda s Topcs n Vectors chap 3) n Scalars and Vectors n Vector ddton ule n Vector n a Coordnator Sstem n Decomposton of a Vector n Epected from prevew: n Scalars and Vectors, Vector
Week 6, Chapter 7 Sect 1-5
 Week 6, Chapter 7 Sect 1-5 Work and Knetc Energy Lecture Quz The frctonal force of the floor on a large sutcase s least when the sutcase s A.pushed by a force parallel to the floor. B.dragged by a force
Week 6, Chapter 7 Sect 1-5 Work and Knetc Energy Lecture Quz The frctonal force of the floor on a large sutcase s least when the sutcase s A.pushed by a force parallel to the floor. B.dragged by a force
PHYS 1443 Section 004 Lecture #12 Thursday, Oct. 2, 2014
 PHYS 1443 Secton 004 Lecture #1 Thursday, Oct., 014 Work-Knetc Energy Theorem Work under rcton Potental Energy and the Conservatve Force Gravtatonal Potental Energy Elastc Potental Energy Conservaton o
PHYS 1443 Secton 004 Lecture #1 Thursday, Oct., 014 Work-Knetc Energy Theorem Work under rcton Potental Energy and the Conservatve Force Gravtatonal Potental Energy Elastc Potental Energy Conservaton o
Displacement at any time. Velocity at any displacement in the x-direction u 2 = v ] + 2 a x ( )
![Displacement at any time. Velocity at any displacement in the x-direction u 2 = v ] + 2 a x ( ) Displacement at any time. Velocity at any displacement in the x-direction u 2 = v ] + 2 a x ( )](/thumbs/89/97691613.jpg) The Language of Physcs Knematcs The branch of mechancs that descrbes the moton of a body wthout regard to the cause of that moton (p. 39). Average velocty The average rate at whch the dsplacement vector
The Language of Physcs Knematcs The branch of mechancs that descrbes the moton of a body wthout regard to the cause of that moton (p. 39). Average velocty The average rate at whch the dsplacement vector
Period & Frequency. Work and Energy. Methods of Energy Transfer: Energy. Work-KE Theorem 3/4/16. Ranking: Which has the greatest kinetic energy?
 Perod & Frequency Perod (T): Tme to complete one ull rotaton Frequency (): Number o rotatons completed per second. = 1/T, T = 1/ v = πr/t Work and Energy Work: W = F!d (pcks out parallel components) F
Perod & Frequency Perod (T): Tme to complete one ull rotaton Frequency (): Number o rotatons completed per second. = 1/T, T = 1/ v = πr/t Work and Energy Work: W = F!d (pcks out parallel components) F
Conservation of Energy
 Lecture 3 Chapter 8 Physcs I 0.3.03 Conservaton o Energy Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcsall.html 95.4, Fall 03,
Lecture 3 Chapter 8 Physcs I 0.3.03 Conservaton o Energy Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcsall.html 95.4, Fall 03,
Chapter 5. Answers to Even Numbered Problems m kj. 6. (a) 900 J (b) (a) 31.9 J (b) 0 (c) 0 (d) 31.9 J. 10.
 Answers to Even Numbered Problems Chapter 5. 3.6 m 4..6 J 6. (a) 9 J (b).383 8. (a) 3.9 J (b) (c) (d) 3.9 J. 6 m s. (a) 68 J (b) 84 J (c) 5 J (d) 48 J (e) 5.64 m s 4. 9. J 6. (a). J (b) 5. m s (c) 6.3
Answers to Even Numbered Problems Chapter 5. 3.6 m 4..6 J 6. (a) 9 J (b).383 8. (a) 3.9 J (b) (c) (d) 3.9 J. 6 m s. (a) 68 J (b) 84 J (c) 5 J (d) 48 J (e) 5.64 m s 4. 9. J 6. (a). J (b) 5. m s (c) 6.3
Week 11: Chapter 11. The Vector Product. The Vector Product Defined. The Vector Product and Torque. More About the Vector Product
 The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
General Tips on How to Do Well in Physics Exams. 1. Establish a good habit in keeping track of your steps. For example, when you use the equation
 General Tps on How to Do Well n Physcs Exams 1. Establsh a good habt n keepng track o your steps. For example when you use the equaton 1 1 1 + = d d to solve or d o you should rst rewrte t as 1 1 1 = d
General Tps on How to Do Well n Physcs Exams 1. Establsh a good habt n keepng track o your steps. For example when you use the equaton 1 1 1 + = d d to solve or d o you should rst rewrte t as 1 1 1 = d
One Dimensional Axial Deformations
 One Dmensonal al Deformatons In ths secton, a specfc smple geometr s consdered, that of a long and thn straght component loaded n such a wa that t deforms n the aal drecton onl. The -as s taken as the
One Dmensonal al Deformatons In ths secton, a specfc smple geometr s consdered, that of a long and thn straght component loaded n such a wa that t deforms n the aal drecton onl. The -as s taken as the
Mathematics Intersection of Lines
 a place of mnd F A C U L T Y O F E D U C A T I O N Department of Currculum and Pedagog Mathematcs Intersecton of Lnes Scence and Mathematcs Educaton Research Group Supported b UBC Teachng and Learnng Enhancement
a place of mnd F A C U L T Y O F E D U C A T I O N Department of Currculum and Pedagog Mathematcs Intersecton of Lnes Scence and Mathematcs Educaton Research Group Supported b UBC Teachng and Learnng Enhancement
Gravitational Acceleration: A case of constant acceleration (approx. 2 hr.) (6/7/11)
 Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
PHYS 1443 Section 002
 PHYS 443 Secton 00 Lecture #6 Wednesday, Nov. 5, 008 Dr. Jae Yu Collsons Elastc and Inelastc Collsons Two Dmensonal Collsons Center o ass Fundamentals o Rotatonal otons Wednesday, Nov. 5, 008 PHYS PHYS
PHYS 443 Secton 00 Lecture #6 Wednesday, Nov. 5, 008 Dr. Jae Yu Collsons Elastc and Inelastc Collsons Two Dmensonal Collsons Center o ass Fundamentals o Rotatonal otons Wednesday, Nov. 5, 008 PHYS PHYS
Linear Momentum. Center of Mass.
 Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
Lecture 16. Chapter 11. Energy Dissipation Linear Momentum. Physics I. Department of Physics and Applied Physics
 Lecture 16 Chapter 11 Physcs I Energy Dsspaton Lnear Momentum Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi Department o Physcs and Appled Physcs IN IN THIS CHAPTER, you wll learn
Lecture 16 Chapter 11 Physcs I Energy Dsspaton Lnear Momentum Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi Department o Physcs and Appled Physcs IN IN THIS CHAPTER, you wll learn
Page 1. Clicker Question 9: Physics 131: Lecture 15. Today s Agenda. Clicker Question 9: Energy. Energy is Conserved.
 Physcs 3: Lecture 5 Today s Agenda Intro to Conseraton o Energy Intro to some derent knds o energy Knetc Potental Denton o Mechancal Energy Conseraton o Mechancal Energy Conserate orces Examples Pendulum
Physcs 3: Lecture 5 Today s Agenda Intro to Conseraton o Energy Intro to some derent knds o energy Knetc Potental Denton o Mechancal Energy Conseraton o Mechancal Energy Conserate orces Examples Pendulum
Chapter 07: Kinetic Energy and Work
 Chapter 07: Knetc Energy and Work Conservaton o Energy s one o Nature s undamental laws that s not volated. Energy can take on derent orms n a gven system. Ths chapter we wll dscuss work and knetc energy.
Chapter 07: Knetc Energy and Work Conservaton o Energy s one o Nature s undamental laws that s not volated. Energy can take on derent orms n a gven system. Ths chapter we wll dscuss work and knetc energy.
So far: simple (planar) geometries
 Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
EMU Physics Department
 Physcs 0 Lecture 8 Potental Energy and Conservaton Assst. Pro. Dr. Al ÖVGÜN EMU Physcs Department www.aovgun.com Denton o Work W q The work, W, done by a constant orce on an object s dened as the product
Physcs 0 Lecture 8 Potental Energy and Conservaton Assst. Pro. Dr. Al ÖVGÜN EMU Physcs Department www.aovgun.com Denton o Work W q The work, W, done by a constant orce on an object s dened as the product
First Law: A body at rest remains at rest, a body in motion continues to move at constant velocity, unless acted upon by an external force.
 Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Rotational and Translational Comparison. Conservation of Angular Momentum. Angular Momentum for a System of Particles
 Conservaton o Angular Momentum 8.0 WD Rotatonal and Translatonal Comparson Quantty Momentum Ang Momentum Force Torque Knetc Energy Work Power Rotaton L cm = I cm ω = dl / cm cm K = (/ ) rot P rot θ W =
Conservaton o Angular Momentum 8.0 WD Rotatonal and Translatonal Comparson Quantty Momentum Ang Momentum Force Torque Knetc Energy Work Power Rotaton L cm = I cm ω = dl / cm cm K = (/ ) rot P rot θ W =
Chapter 8. Potential Energy and Conservation of Energy
 Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Use these variables to select a formula. x = t Average speed = 100 m/s = distance / time t = x/v = ~2 m / 100 m/s = 0.02 s or 20 milliseconds
 The speed o a nere mpulse n the human body s about 100 m/s. I you accdentally stub your toe n the dark, estmatethe tme t takes the nere mpulse to trael to your bran. Tps: pcture, poste drecton, and lst
The speed o a nere mpulse n the human body s about 100 m/s. I you accdentally stub your toe n the dark, estmatethe tme t takes the nere mpulse to trael to your bran. Tps: pcture, poste drecton, and lst
A Tale of Friction Basic Rollercoaster Physics. Fahrenheit Rollercoaster, Hershey, PA max height = 121 ft max speed = 58 mph
 A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
Chapter Seven - Potential Energy and Conservation of Energy
 Chapter Seven - Potental Energy and Conservaton o Energy 7 1 Potental Energy Potental energy. e wll nd that the potental energy o a system can only be assocated wth specc types o orces actng between members
Chapter Seven - Potental Energy and Conservaton o Energy 7 1 Potental Energy Potental energy. e wll nd that the potental energy o a system can only be assocated wth specc types o orces actng between members
EN40: Dynamics and Vibrations. Homework 4: Work, Energy and Linear Momentum Due Friday March 1 st
 EN40: Dynamcs and bratons Homework 4: Work, Energy and Lnear Momentum Due Frday March 1 st School of Engneerng Brown Unversty 1. The fgure (from ths publcaton) shows the energy per unt area requred to
EN40: Dynamcs and bratons Homework 4: Work, Energy and Lnear Momentum Due Frday March 1 st School of Engneerng Brown Unversty 1. The fgure (from ths publcaton) shows the energy per unt area requred to
ONE-DIMENSIONAL COLLISIONS
 Purpose Theory ONE-DIMENSIONAL COLLISIONS a. To very the law o conservaton o lnear momentum n one-dmensonal collsons. b. To study conservaton o energy and lnear momentum n both elastc and nelastc onedmensonal
Purpose Theory ONE-DIMENSIONAL COLLISIONS a. To very the law o conservaton o lnear momentum n one-dmensonal collsons. b. To study conservaton o energy and lnear momentum n both elastc and nelastc onedmensonal
Chapter 3 and Chapter 4
 Chapter 3 and Chapter 4 Chapter 3 Energy 3. Introducton:Work Work W s energy transerred to or rom an object by means o a orce actng on the object. Energy transerred to the object s postve work, and energy
Chapter 3 and Chapter 4 Chapter 3 Energy 3. Introducton:Work Work W s energy transerred to or rom an object by means o a orce actng on the object. Energy transerred to the object s postve work, and energy
OPTIMISATION. Introduction Single Variable Unconstrained Optimisation Multivariable Unconstrained Optimisation Linear Programming
 OPTIMIATION Introducton ngle Varable Unconstraned Optmsaton Multvarable Unconstraned Optmsaton Lnear Programmng Chapter Optmsaton /. Introducton In an engneerng analss, sometmes etremtes, ether mnmum or
OPTIMIATION Introducton ngle Varable Unconstraned Optmsaton Multvarable Unconstraned Optmsaton Lnear Programmng Chapter Optmsaton /. Introducton In an engneerng analss, sometmes etremtes, ether mnmum or
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Physics 207 Lecture 6
 Physcs 207 Lecture 6 Agenda: Physcs 207, Lecture 6, Sept. 25 Chapter 4 Frames of reference Chapter 5 ewton s Law Mass Inerta s (contact and non-contact) Frcton (a external force that opposes moton) Free
Physcs 207 Lecture 6 Agenda: Physcs 207, Lecture 6, Sept. 25 Chapter 4 Frames of reference Chapter 5 ewton s Law Mass Inerta s (contact and non-contact) Frcton (a external force that opposes moton) Free
Force = F Piston area = A
 CHAPTER III Ths chapter s an mportant transton between the propertes o pure substances and the most mportant chapter whch s: the rst law o thermodynamcs In ths chapter, we wll ntroduce the notons o heat,
CHAPTER III Ths chapter s an mportant transton between the propertes o pure substances and the most mportant chapter whch s: the rst law o thermodynamcs In ths chapter, we wll ntroduce the notons o heat,
Page 1. SPH4U: Lecture 7. New Topic: Friction. Today s Agenda. Surface Friction... Surface Friction...
 SPH4U: Lecture 7 Today s Agenda rcton What s t? Systeatc catagores of forces How do we characterze t? Model of frcton Statc & Knetc frcton (knetc = dynac n soe languages) Soe probles nvolvng frcton ew
SPH4U: Lecture 7 Today s Agenda rcton What s t? Systeatc catagores of forces How do we characterze t? Model of frcton Statc & Knetc frcton (knetc = dynac n soe languages) Soe probles nvolvng frcton ew
Please initial the statement below to show that you have read it
 EN40: Dynamcs and Vbratons Mdterm Examnaton Thursday March 5 009 Dvson of Engneerng rown Unversty NME: Isaac Newton General Instructons No collaboraton of any knd s permtted on ths examnaton. You may brng
EN40: Dynamcs and Vbratons Mdterm Examnaton Thursday March 5 009 Dvson of Engneerng rown Unversty NME: Isaac Newton General Instructons No collaboraton of any knd s permtted on ths examnaton. You may brng
Page 1. Physics 131: Lecture 14. Today s Agenda. Things that stay the same. Impulse and Momentum Non-constant forces
 Physcs 131: Lecture 14 Today s Agenda Imulse and Momentum Non-constant forces Imulse-momentum momentum thm Conservaton of Lnear momentum Eternal/Internal forces Eamles Physcs 201: Lecture 1, Pg 1 Physcs
Physcs 131: Lecture 14 Today s Agenda Imulse and Momentum Non-constant forces Imulse-momentum momentum thm Conservaton of Lnear momentum Eternal/Internal forces Eamles Physcs 201: Lecture 1, Pg 1 Physcs
Week 8: Chapter 9. Linear Momentum. Newton Law and Momentum. Linear Momentum, cont. Conservation of Linear Momentum. Conservation of Momentum, 2
 Lnear omentum Week 8: Chapter 9 Lnear omentum and Collsons The lnear momentum of a partcle, or an object that can be modeled as a partcle, of mass m movng wth a velocty v s defned to be the product of
Lnear omentum Week 8: Chapter 9 Lnear omentum and Collsons The lnear momentum of a partcle, or an object that can be modeled as a partcle, of mass m movng wth a velocty v s defned to be the product of
Conservation of Angular Momentum = "Spin"
 Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
CHAPTER 10 ROTATIONAL MOTION
 CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
Summary with Examples for Root finding Methods -Bisection -Newton Raphson -Secant
 Summary wth Eamples or Root ndng Methods -Bsecton -Newton Raphson -Secant Nonlnear Equaton Solvers Bracketng Graphcal Open Methods Bsecton False Poston (Regula-Fals) Newton Raphson Secant All Iteratve
Summary wth Eamples or Root ndng Methods -Bsecton -Newton Raphson -Secant Nonlnear Equaton Solvers Bracketng Graphcal Open Methods Bsecton False Poston (Regula-Fals) Newton Raphson Secant All Iteratve
Physics 4B. A positive value is obtained, so the current is counterclockwise around the circuit.
 Physcs 4B Solutons to Chapter 7 HW Chapter 7: Questons:, 8, 0 Problems:,,, 45, 48,,, 7, 9 Queston 7- (a) no (b) yes (c) all te Queston 7-8 0 μc Queston 7-0, c;, a;, d; 4, b Problem 7- (a) Let be the current
Physcs 4B Solutons to Chapter 7 HW Chapter 7: Questons:, 8, 0 Problems:,,, 45, 48,,, 7, 9 Queston 7- (a) no (b) yes (c) all te Queston 7-8 0 μc Queston 7-0, c;, a;, d; 4, b Problem 7- (a) Let be the current
Chapter 8: Potential Energy and The Conservation of Total Energy
 Chapter 8: Potental Energy and The Conservaton o Total Energy Work and knetc energy are energes o moton. K K K mv r v v F dr Potental energy s an energy that depends on locaton. -Dmenson F x d U( x) dx
Chapter 8: Potental Energy and The Conservaton o Total Energy Work and knetc energy are energes o moton. K K K mv r v v F dr Potental energy s an energy that depends on locaton. -Dmenson F x d U( x) dx
Recitation: Energy, Phys Energies. 1.2 Three stones. 1. Energy. 1. An acorn falling from an oak tree onto the sidewalk.
 Rectaton: Energy, Phys 207. Energy. Energes. An acorn fallng from an oak tree onto the sdewalk. The acorn ntal has gravtatonal potental energy. As t falls, t converts ths energy to knetc. When t hts the
Rectaton: Energy, Phys 207. Energy. Energes. An acorn fallng from an oak tree onto the sdewalk. The acorn ntal has gravtatonal potental energy. As t falls, t converts ths energy to knetc. When t hts the
Physics 141. Lecture 14. Frank L. H. Wolfs Department of Physics and Astronomy, University of Rochester, Lecture 14, Page 1
 Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
v c motion is neither created nor destroyed, but transferred via interactions. Fri. Wed (.18,.19) Introducing Potential Energy RE 6.
 r. 6.5-.7 (.) Rest Mass,ork by Changng orces Columba Rep 3pm, here RE 6.b (last day to drop) ed. 6.8-.9(.8,.9) Introducng Potental Energy RE 6.c Tues. H6: Ch 6 Pr s 58,59, 99(a-c), 05(a-c) moton s nether
r. 6.5-.7 (.) Rest Mass,ork by Changng orces Columba Rep 3pm, here RE 6.b (last day to drop) ed. 6.8-.9(.8,.9) Introducng Potental Energy RE 6.c Tues. H6: Ch 6 Pr s 58,59, 99(a-c), 05(a-c) moton s nether
1 cos. where v v sin. Range Equations: for an object that lands at the same height at which it starts. v sin 2 i. t g. and. sin g
 SPH3UW Unt.5 Projectle Moton Pae 1 of 10 Note Phc Inventor Parabolc Moton curved oton n the hape of a parabola. In the drecton, the equaton of oton ha a t ter Projectle Moton the parabolc oton of an object,
SPH3UW Unt.5 Projectle Moton Pae 1 of 10 Note Phc Inventor Parabolc Moton curved oton n the hape of a parabola. In the drecton, the equaton of oton ha a t ter Projectle Moton the parabolc oton of an object,
Modeling motion with VPython Every program that models the motion of physical objects has two main parts:
 1 Modelng moton wth VPython Eery program that models the moton o physcal objects has two man parts: 1. Beore the loop: The rst part o the program tells the computer to: a. Create numercal alues or constants
1 Modelng moton wth VPython Eery program that models the moton o physcal objects has two man parts: 1. Beore the loop: The rst part o the program tells the computer to: a. Create numercal alues or constants
Chapter 11 Angular Momentum
 Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
Physics 207: Lecture 20. Today s Agenda Homework for Monday
 Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
Spring 2002 Lecture #13
 44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
Unit 5: Quadratic Equations & Functions
 Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
Important Dates: Post Test: Dec during recitations. If you have taken the post test, don t come to recitation!
 Important Dates: Post Test: Dec. 8 0 durng rectatons. If you have taken the post test, don t come to rectaton! Post Test Make-Up Sessons n ARC 03: Sat Dec. 6, 0 AM noon, and Sun Dec. 7, 8 PM 0 PM. Post
Important Dates: Post Test: Dec. 8 0 durng rectatons. If you have taken the post test, don t come to rectaton! Post Test Make-Up Sessons n ARC 03: Sat Dec. 6, 0 AM noon, and Sun Dec. 7, 8 PM 0 PM. Post
Chapter 6. Operational Amplifier. inputs can be defined as the average of the sum of the two signals.
 6 Operatonal mpler Chapter 6 Operatonal mpler CC Symbol: nput nput Output EE () Non-nvertng termnal, () nvertng termnal nput mpedance : Few mega (ery hgh), Output mpedance : Less than (ery low) Derental
6 Operatonal mpler Chapter 6 Operatonal mpler CC Symbol: nput nput Output EE () Non-nvertng termnal, () nvertng termnal nput mpedance : Few mega (ery hgh), Output mpedance : Less than (ery low) Derental
Module 14: THE INTEGRAL Exploring Calculus
 Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Part C Dynamics and Statics of Rigid Body. Chapter 5 Rotation of a Rigid Body About a Fixed Axis
 Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Physics 101 Lecture 9 Linear Momentum and Collisions
 Physcs 0 Lecture 9 Lnear Momentum and Collsons Dr. Al ÖVGÜN EMU Physcs Department www.aogun.com Lnear Momentum and Collsons q q q q q q q Conseraton o Energy Momentum Impulse Conseraton o Momentum -D Collsons
Physcs 0 Lecture 9 Lnear Momentum and Collsons Dr. Al ÖVGÜN EMU Physcs Department www.aogun.com Lnear Momentum and Collsons q q q q q q q Conseraton o Energy Momentum Impulse Conseraton o Momentum -D Collsons
PHYS 1443 Section 003 Lecture #17
 PHYS 144 Secton 00 ecture #17 Wednesda, Oct. 9, 00 1. Rollng oton of a Rgd od. Torque. oment of Inerta 4. Rotatonal Knetc Energ 5. Torque and Vector Products Remember the nd term eam (ch 6 11), onda, Nov.!
PHYS 144 Secton 00 ecture #17 Wednesda, Oct. 9, 00 1. Rollng oton of a Rgd od. Torque. oment of Inerta 4. Rotatonal Knetc Energ 5. Torque and Vector Products Remember the nd term eam (ch 6 11), onda, Nov.!
Linear Momentum. Center of Mass.
 Lecture 16 Chapter 9 Physcs I 11.06.2013 Lnear oentu. Center of ass. Course webste: http://faculty.ul.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.ul.edu/danylov2013/physcs1fall.htl
Lecture 16 Chapter 9 Physcs I 11.06.2013 Lnear oentu. Center of ass. Course webste: http://faculty.ul.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.ul.edu/danylov2013/physcs1fall.htl
Chapter 3 Differentiation and Integration
 MEE07 Computer Modelng Technques n Engneerng Chapter Derentaton and Integraton Reerence: An Introducton to Numercal Computatons, nd edton, S. yakowtz and F. zdarovsky, Mawell/Macmllan, 990. Derentaton
MEE07 Computer Modelng Technques n Engneerng Chapter Derentaton and Integraton Reerence: An Introducton to Numercal Computatons, nd edton, S. yakowtz and F. zdarovsky, Mawell/Macmllan, 990. Derentaton
Angular Momentum and Fixed Axis Rotation. 8.01t Nov 10, 2004
 Angular Momentum and Fxed Axs Rotaton 8.01t Nov 10, 2004 Dynamcs: Translatonal and Rotatonal Moton Translatonal Dynamcs Total Force Torque Angular Momentum about Dynamcs of Rotaton F ext Momentum of a
Angular Momentum and Fxed Axs Rotaton 8.01t Nov 10, 2004 Dynamcs: Translatonal and Rotatonal Moton Translatonal Dynamcs Total Force Torque Angular Momentum about Dynamcs of Rotaton F ext Momentum of a
Linear Momentum and Collisions
 Lnear Momentum and Collsons Chater 9 Lnear Momentum [kg m/s] x y mv x mv y Newton s nd Law n terms o momentum: Imulse I - [kg m/s] I t t Fdt I = area under curve bounded by t axs Imulse-Momentum Theorem
Lnear Momentum and Collsons Chater 9 Lnear Momentum [kg m/s] x y mv x mv y Newton s nd Law n terms o momentum: Imulse I - [kg m/s] I t t Fdt I = area under curve bounded by t axs Imulse-Momentum Theorem
Physics 114 Exam 3 Spring Name:
 Physcs 114 Exam 3 Sprng 015 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem 4. Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse
Physcs 114 Exam 3 Sprng 015 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem 4. Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse
Spin-rotation coupling of the angularly accelerated rigid body
 Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Ground Rules. PC1221 Fundamentals of Physics I. Linear Momentum, cont. Linear Momentum. Lectures 17 and 18. Linear Momentum and Collisions
 PC Fundamentals of Physcs I Lectures 7 and 8 Lnear omentum and Collsons Dr Tay Seng Chuan Ground Rules Swtch off your handphone and pager Swtch off your laptop computer and keep t No talkng whle lecture
PC Fundamentals of Physcs I Lectures 7 and 8 Lnear omentum and Collsons Dr Tay Seng Chuan Ground Rules Swtch off your handphone and pager Swtch off your laptop computer and keep t No talkng whle lecture
