= 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W]
|
|
|
- Berenice Charleen Matthews
- 6 years ago
- Views:
Transcription
1 Secton 1.3: Acceleraton Tutoral 1 Practce, page Gven: 0 m/s; 15.0 m/s [S]; t 12.5 s Requred: Analyss: a av v t v f v t a v av f v t 15.0 m/s [S] 0 m/s 12.5 s 15.0 m/s [S] 12.5 s 1.20 m/s 2 [S] Statement: The rock s average acceleraton s 1.20 m/s 2 [S]. 2. Gven: 17 m/s [N]; 25 m/s [N]; t 12 s Requred: Analyss: v t v t 25 m/s [N] 17 m/s [N] 12 s 8 m/s [N] 12 s 0.67 m/s 2 [N] Statement: The car s average acceleraton s 0.67 m/s 2 [N]. 3. Gven: 25 m/s [W]; 29 m/s [E]; t 0.25 s Requred: Analyss: v t v t 29 m/s [E] 25 m/s [W] 0.25 s 29 m/s [E] + 25 m/s [E] 0.25 s 54 m/s [E] 0.25 s 220 m/s 2 [E] Statement: The squash ball s average acceleraton s 220 m/s 2 [E] or m/s 2 [E]. Tutoral 2 Practce, page Gven: 3.2 m/s [W]; 5.8 m/s [W]; 1.23 m/s 2 [W] Requred: t Analyss: a av t v t f v t v 5.8 m/s [W] 3.2 m/s [W] 1.23 m/s 2 [W] 2.6 m [W] s 1.23 m s [W] 2 t 2.1 s Statement: The rado-controlled car s acceleraton wll take 2.1 s. 2. Gven: 17 m/s [W]; 2.4 m/s 2 [W]; t 6.2 s Requred: Analyss: t t t v f v v f a av t 17 m/s [W] 2.4 m s [W] 2 ' 6.2 s ( ) 17 m/s [W] m/s [W] (two extra dgts carred) 2.1 m/s [W] Statement: The ntal velocty of the speedboat was 2.1 m/s [W]. Tutoral 3 Practce, page (a) Gven: b 4.0 s; h 8.0 m/s [S] Requred: d Analyss: d A trangle Copyrght 2011 Nelson Educaton Ltd. Chapter 1: Moton n a Straght Lne 1.3-1
2 d A trangle B. Postve velocty value: 1 2 bh ( ) 8.0 m s [S] s d 16 m [S] Statement: The object has travelled 16 m [S] after 4.0 s. (b) Gven: b 5.0 s; h 10.0 m/s [S]; l 2.5 s; w 10.0 m/s [S] Requred: d Analyss: d A trangle d A trangle 1 bh + lw 2 ( ) 10.0 m s [S] s 25.0 m [S] m [S] s ( ) 10.0 m s [S] d 50 m [S] Statement: The object has travelled 50 m [S] after 7.5 s. Negatve velocty value: Mn Investgaton: Moton Smulatons, page 27 A. Postve velocty value: The poston tme graph wll be a straght lne startng at the orgn wth a postve slope. The velocty tme graph wll be a horzontal lne wth postve value. Negatve velocty value: The poston tme graph wll be a straght lne startng at the orgn wth a negatve slope. The velocty tme graph wll be a horzontal lne wth negatve value. Negatve ntal poston, postve velocty value: The poston tme graph wll be a straght lne startng below the x-axs wth a postve slope. The velocty tme graph wll be a horzontal lne wth postve value. Negatve ntal poston, negatve velocty value: The poston tme graph wll be a straght lne startng below the x-axs wth a negatve slope. The velocty tme graph wll be a horzontal lne wth negatve value. Copyrght 2011 Nelson Educaton Ltd. Chapter 1: Moton n a Straght Lne 1.3-2
3 Negatve ntal poston, postve velocty value: Negatve ntal poston, negatve velocty value: C. Dfferences are due to the dffculty n usng the mouse to mmc constant velocty. Tutoral 4 Practce, page (a) Gven: t 1.0 s; poston tme graph Requred: nst Analyss: nst tangent to the curve at t 1.0 s, so m d t. By placng a ruler along the curve n Fgure 6 at t 1.0 s, I can pcture the tangent. The tangent has a rse of 4.0 m [E] over a run of 2.0 s. m d t 4.0 m [E] m 2.0 s nst 2.0 m/s [E] object at 1.0 s s 2.0 m/s [E]. (b) Gven: t 3.0 s; poston tme graph Requred: nst Analyss: nst tangent to the curve at t 3.0 s, so m d t. By placng a ruler along the curve n Fgure 6 at t 3.0 s, I can pcture the tangent. The tangent has a rse of 12.0 m [E] over a run of 2.0 s. m d t 12.0 m [E] m 2.0 s nst 6.0 m/s [E] object at 3.0 s s 6.0 m/s [E]. (c) At t 1.0 s, nst s 2.0 m/s [E], at t 2.0 s, nst s 4.0 m/s [E], and at t 3.0 s, nst s 6.0 m/s [E]. Snce the ncrease n the nstantaneous velocty s constant (2.0 m/s [E] every second), t s possble that the object s movng wth constant acceleraton. 2. (a) Gven: t 5.0 s; poston tme graph Requred: nst Analyss: nst tangent to the curve at t 5.0 s, so m d t. By placng a ruler along the curve n Fgure 7 at t 5.0 s, I can pcture the tangent. The tangent has a rse of 150 m [E] over a run of 5.0 s. m d t 150 m [E] 5.0 s nst 30 m/s [E] object at 5.0 s s 30 m/s [E]. Copyrght 2011 Nelson Educaton Ltd. Chapter 1: Moton n a Straght Lne 1.3-3
4 (b) Gven: d m [E]; m [E]; t s; 10.0 s Requred: Analyss: v av d t d 1 t 1 d 1 v av t m [E] 0.0 m [E] 10.0 s 0.0 s 30 m/s [E] Statement: The average velocty of the object over the tme nterval from 0.0 s to 10.0 s s 30 m/s [E]. (c) When an object s acceleratng unformly (constant acceleraton), the average velocty over an nterval of tme equals the nstantaneous velocty of the mdpont n that nterval of tme. Secton 1.3 Questons, page Answers may vary. Sample answer: An acceleratng object may exhbt ncreasng velocty, such as a horse acceleratng from a slow trot to a gallop. An acceleratng object may exhbt decreasng velocty, such as a cyclst who slows down whle rdng up a steep road. An acceleratng object may come to a complete stop, such as a car travellng east that accelerates west untl t stops. 2. Answers may vary. Sample answer: To determne the acceleraton of an object from a velocty-tme graph, dvde the velocty by the tme at a gven pont. 3. Answers may vary. Sample answer: To determne the dsplacement of an object from a velocty tme graph, calculate the area under the graph from the ntal tme to the fnal tme. The area s equal to the dsplacement between those two tmes. 4. (a) Gven: v 28 m/s [E]; t 7.0 s Requred: Analyss: a av v t a av v t 28 m/s [E] 7.0 s 4.0 m/s 2 [E] Statement: The average acceleraton descrbed by the graph s 4.0 m/s 2 [E]. (b) Gven: v 24.5 m/s [E]; t 7.0 s Requred: Analyss: a av v t a av v t 24.5 m/s [E] 7.0 s 3.5 m/s 2 [E] Statement: The average acceleraton descrbed by the graph s 3.5 m/s 2 [E]. (c) Gven: v 2.1 m/s [E]; t 7.0 s Requred: Analyss: a av v t a av v t 2.1 m/s [E] 7.0 s 0.30 m/s 2 [E] Statement: The average acceleraton descrbed by the graph s 0.30 m/s 2 [E]. 5. Answers may vary. Sample answer: What you sad about the constant speed of the object sn t rght. Even though the speed s stll the same, the drecton has changed from north to south. That means that the velocty has changed, so there must have been an acceleraton n the drecton of south. 6. (a) In the frst segment, the object accelerates from 0.0 m/s to 6.0 m/s [W] n the frst 4.0 s. In the second segment, the object contnues at a constant velocty of 6.0 m/s [W] for 3.0 s. In the thrd segment, the object accelerates east so the velocty changes from 60.0 m/s [W] to 0.0 m/s n the fnal 3.0 s. Copyrght 2011 Nelson Educaton Ltd. Chapter 1: Moton n a Straght Lne 1.3-4
5 (b) For the frst segment: Gven: v 6.0 m/s [W]; t 4.0 s Requred: Analyss: a av v t a av v t 6.0 m/s [W] 4.0 s 1.5 m/s 2 [W] Statement: The average acceleraton n the frst segment of the graph s 1.5 m/s 2 [W]. For the second segment: Gven: v 0.0 m/s; t 3.0 s Requred: Analyss: a av v t a av v t 0.0 m/s 4.0 s 0.0 m/s 2 Statement: The average acceleraton n the second segment of the graph s 0.0 m/s 2. For the thrd segment: Gven: v 6.0 m/s [W]; t 3.0 s Requred: Analyss: a av v t a av v t 6.0 m/s [W] 3.0 s 6.0 m/s [E] 3.0 s 2.0 m/s 2 [E] Statement: The average acceleraton n the thrd segment of the graph s 2.0 m/s 2 [E]. (c) Gven: b s; b s; h 6.0 m/s [W]; l 3.0 s Requred: d Analyss: d A trangle 1 + A trangle 2 d A trangle 1 + A trangle b 1 h + lh b 2 h ( ) 6.0 m s [W] s s s ( ) 6.0 m s [W] ( ) 6.0 m s [W] 12 m [W] + 18 m [W] + 9 m [W] d 39 m [W] Statement: The object has travelled 39 m [W] after 10.0 s. 7. Gven: 2.0 m/s [W]; 4.5 m/s [W]; t 1.9 s Requred: Analyss: v t v t 4.5 m/s [W] 2.0 m/s [W] 1.9 s 2.5 m/s [W] 1.9 s 1.3 m/s 2 [W] Statement: The average acceleraton of the car s 1.3 m/s 2 [W]. 8. Gven: 0.68 m/s [N]; 0.89 m/s [N]; 0.53 m/s 2 [N] Requred: t Analyss: a av t v t f v t v 0.89 m/s [N] 0.68 m/s [N] 0.21 m [N] s 0.53 m s [N] m/s 2 [N] t 0.40 s Statement: It wll take 0.40 s to ncrease the bcycle s velocty. Copyrght 2011 Nelson Educaton Ltd. Chapter 1: Moton n a Straght Lne 1.3-5
6 9. (a) Gven: 0.0 m/s; 2.90 m/s 2 [S]; t 5.72 s Requred: Analyss: t t v f v v f a av t t 0.0 m/s 2.90 m s [S] 2 ' 5.72 s 0.0 m/s 16.6 m/s [S] 16.6 m/s [N] ( ) Statement: The ntal velocty of the car was 16.6 m/s [N]. (b) To decrease the velocty, the drver must accelerate n the opposte drecton. In ths example, to stop gong north, the drver accelerated south. 10. Gven: 6.0 m/s [E]; 7.3 m/s [W]; t s Requred: Analyss: v t v t 7.3 m/s [W] 6.0 m/s [E] s 7.3 m/s [W] m/s [W] s 13.3 m/s [W] s 140 m/s 2 [W] Statement: The average acceleraton of the tenns ball s 140 m/s 2 [W] or m/s 2 [W]. 11. (a) Gven: t 6.0 s; poston tme graph Requred: nst Analyss: nst tangent to the curve at t 6.0 s, so m d t. By placng a ruler along the curve n Fgure 9 at t 6.0 s, I can pcture the tangent. The tangent has a rse of 120 m [E] over a run of 5.0 s. m d t 120 m [E] m 5.0 s nst 24 m/s [E] object at 6.0 s s 24 m/s [E]. (b) Gven: d m; 200 m; t s; 10.0 s Requred: Analyss: v av d t d 1 t 1 d 1 v av t m [W] 0.0 m [W] 10.0 s 0.0 s 20 m/s [W] Statement: The average velocty of the object over the tme nterval from 0.0 s to 10.0 s s 20 m/s [W]. Copyrght 2011 Nelson Educaton Ltd. Chapter 1: Moton n a Straght Lne 1.3-6
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Physics 2A Chapter 3 HW Solutions
 Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
AP Physics 1 & 2 Summer Assignment
 AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
Chapter 3. r r. Position, Velocity, and Acceleration Revisited
 Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Name: PHYS 110 Dr. McGovern Spring 2018 Exam 1. Multiple Choice: Circle the answer that best evaluates the statement or completes the statement.
 Name: PHYS 110 Dr. McGoern Sprng 018 Exam 1 Multple Choce: Crcle the answer that best ealuates the statement or completes the statement. #1 - I the acceleraton o an object s negate, the object must be
Name: PHYS 110 Dr. McGoern Sprng 018 Exam 1 Multple Choce: Crcle the answer that best ealuates the statement or completes the statement. #1 - I the acceleraton o an object s negate, the object must be
Mathematics Intersection of Lines
 a place of mnd F A C U L T Y O F E D U C A T I O N Department of Currculum and Pedagog Mathematcs Intersecton of Lnes Scence and Mathematcs Educaton Research Group Supported b UBC Teachng and Learnng Enhancement
a place of mnd F A C U L T Y O F E D U C A T I O N Department of Currculum and Pedagog Mathematcs Intersecton of Lnes Scence and Mathematcs Educaton Research Group Supported b UBC Teachng and Learnng Enhancement
PHYSICS 203-NYA-05 MECHANICS
 PHYSICS 03-NYA-05 MECHANICS PROF. S.D. MANOLI PHYSICS & CHEMISTRY CHAMPLAIN - ST. LAWRENCE 790 NÉRÉE-TREMBLAY QUÉBEC, QC GV 4K TELEPHONE: 48.656.69 EXT. 449 EMAIL: smanol@slc.qc.ca WEBPAGE: http:/web.slc.qc.ca/smanol/
PHYSICS 03-NYA-05 MECHANICS PROF. S.D. MANOLI PHYSICS & CHEMISTRY CHAMPLAIN - ST. LAWRENCE 790 NÉRÉE-TREMBLAY QUÉBEC, QC GV 4K TELEPHONE: 48.656.69 EXT. 449 EMAIL: smanol@slc.qc.ca WEBPAGE: http:/web.slc.qc.ca/smanol/
Section 8.1 Exercises
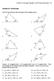 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Supplemental Instruction sessions next week
 Homework #4 Wrtten homework due now Onlne homework due on Tue Mar 3 by 8 am Exam 1 Answer keys and scores wll be posted by end of the week Supplemental Instructon sessons next week Wednesday 8:45 10:00
Homework #4 Wrtten homework due now Onlne homework due on Tue Mar 3 by 8 am Exam 1 Answer keys and scores wll be posted by end of the week Supplemental Instructon sessons next week Wednesday 8:45 10:00
Gravitational Acceleration: A case of constant acceleration (approx. 2 hr.) (6/7/11)
 Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Chapter 2. Pythagorean Theorem. Right Hand Rule. Position. Distance Formula
 Chapter Moton n One Dmenson Cartesan Coordnate System The most common coordnate system or representng postons n space s one based on three perpendcular spatal axes generally desgnated x, y, and z. Any
Chapter Moton n One Dmenson Cartesan Coordnate System The most common coordnate system or representng postons n space s one based on three perpendcular spatal axes generally desgnated x, y, and z. Any
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Week 11: Chapter 11. The Vector Product. The Vector Product Defined. The Vector Product and Torque. More About the Vector Product
 The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
Chapter 8. Potential Energy and Conservation of Energy
 Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
PHYS 1101 Practice problem set 12, Chapter 32: 21, 22, 24, 57, 61, 83 Chapter 33: 7, 12, 32, 38, 44, 49, 76
 PHYS 1101 Practce problem set 1, Chapter 3: 1,, 4, 57, 61, 83 Chapter 33: 7, 1, 3, 38, 44, 49, 76 3.1. Vsualze: Please reer to Fgure Ex3.1. Solve: Because B s n the same drecton as the ntegraton path s
PHYS 1101 Practce problem set 1, Chapter 3: 1,, 4, 57, 61, 83 Chapter 33: 7, 1, 3, 38, 44, 49, 76 3.1. Vsualze: Please reer to Fgure Ex3.1. Solve: Because B s n the same drecton as the ntegraton path s
where v means the change in velocity, and t is the
 1 PHYS:100 LECTURE 4 MECHANICS (3) Ths lecture covers the eneral case of moton wth constant acceleraton and free fall (whch s one of the more mportant examples of moton wth constant acceleraton) n a more
1 PHYS:100 LECTURE 4 MECHANICS (3) Ths lecture covers the eneral case of moton wth constant acceleraton and free fall (whch s one of the more mportant examples of moton wth constant acceleraton) n a more
Displacement at any time. Velocity at any displacement in the x-direction u 2 = v ] + 2 a x ( )
![Displacement at any time. Velocity at any displacement in the x-direction u 2 = v ] + 2 a x ( ) Displacement at any time. Velocity at any displacement in the x-direction u 2 = v ] + 2 a x ( )](/thumbs/89/97691613.jpg) The Language of Physcs Knematcs The branch of mechancs that descrbes the moton of a body wthout regard to the cause of that moton (p. 39). Average velocty The average rate at whch the dsplacement vector
The Language of Physcs Knematcs The branch of mechancs that descrbes the moton of a body wthout regard to the cause of that moton (p. 39). Average velocty The average rate at whch the dsplacement vector
Please initial the statement below to show that you have read it
 EN40: Dynamcs and Vbratons Mdterm Examnaton Thursday March 5 009 Dvson of Engneerng rown Unversty NME: Isaac Newton General Instructons No collaboraton of any knd s permtted on ths examnaton. You may brng
EN40: Dynamcs and Vbratons Mdterm Examnaton Thursday March 5 009 Dvson of Engneerng rown Unversty NME: Isaac Newton General Instructons No collaboraton of any knd s permtted on ths examnaton. You may brng
Physics 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn in the following problems from Chapter 4 Knight
 Physcs 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn n the ollowng problems rom Chapter 4 Knght Conceptual Questons: 8, 0, ; 4.8. Anta s approachng ball and movng away rom where ball was
Physcs 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn n the ollowng problems rom Chapter 4 Knght Conceptual Questons: 8, 0, ; 4.8. Anta s approachng ball and movng away rom where ball was
Motion in One Dimension
 Moton n One Dmenson Speed ds tan ce traeled Aerage Speed tme of trael Mr. Wolf dres hs car on a long trp to a physcs store. Gen the dstance and tme data for hs trp, plot a graph of hs dstance ersus tme.
Moton n One Dmenson Speed ds tan ce traeled Aerage Speed tme of trael Mr. Wolf dres hs car on a long trp to a physcs store. Gen the dstance and tme data for hs trp, plot a graph of hs dstance ersus tme.
So far: simple (planar) geometries
 Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
First Law: A body at rest remains at rest, a body in motion continues to move at constant velocity, unless acted upon by an external force.
 Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
ONE-DIMENSIONAL COLLISIONS
 Purpose Theory ONE-DIMENSIONAL COLLISIONS a. To very the law o conservaton o lnear momentum n one-dmensonal collsons. b. To study conservaton o energy and lnear momentum n both elastc and nelastc onedmensonal
Purpose Theory ONE-DIMENSIONAL COLLISIONS a. To very the law o conservaton o lnear momentum n one-dmensonal collsons. b. To study conservaton o energy and lnear momentum n both elastc and nelastc onedmensonal
The equation of motion of a dynamical system is given by a set of differential equations. That is (1)
 Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Linear Momentum. Center of Mass.
 Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
A Tale of Friction Basic Rollercoaster Physics. Fahrenheit Rollercoaster, Hershey, PA max height = 121 ft max speed = 58 mph
 A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
Lecture 16. Chapter 11. Energy Dissipation Linear Momentum. Physics I. Department of Physics and Applied Physics
 Lecture 16 Chapter 11 Physcs I Energy Dsspaton Lnear Momentum Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi Department o Physcs and Appled Physcs IN IN THIS CHAPTER, you wll learn
Lecture 16 Chapter 11 Physcs I Energy Dsspaton Lnear Momentum Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi Department o Physcs and Appled Physcs IN IN THIS CHAPTER, you wll learn
Recitation: Energy, Phys Energies. 1.2 Three stones. 1. Energy. 1. An acorn falling from an oak tree onto the sidewalk.
 Rectaton: Energy, Phys 207. Energy. Energes. An acorn fallng from an oak tree onto the sdewalk. The acorn ntal has gravtatonal potental energy. As t falls, t converts ths energy to knetc. When t hts the
Rectaton: Energy, Phys 207. Energy. Energes. An acorn fallng from an oak tree onto the sdewalk. The acorn ntal has gravtatonal potental energy. As t falls, t converts ths energy to knetc. When t hts the
Physics 207: Lecture 27. Announcements
 Physcs 07: ecture 7 Announcements ake-up labs are ths week Fnal hwk assgned ths week, fnal quz next week Revew sesson on Thursday ay 9, :30 4:00pm, Here Today s Agenda Statcs recap Beam & Strngs» What
Physcs 07: ecture 7 Announcements ake-up labs are ths week Fnal hwk assgned ths week, fnal quz next week Revew sesson on Thursday ay 9, :30 4:00pm, Here Today s Agenda Statcs recap Beam & Strngs» What
Chapter 11 Angular Momentum
 Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
Physics 111: Mechanics Lecture 11
 Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Week 8: Chapter 9. Linear Momentum. Newton Law and Momentum. Linear Momentum, cont. Conservation of Linear Momentum. Conservation of Momentum, 2
 Lnear omentum Week 8: Chapter 9 Lnear omentum and Collsons The lnear momentum of a partcle, or an object that can be modeled as a partcle, of mass m movng wth a velocty v s defned to be the product of
Lnear omentum Week 8: Chapter 9 Lnear omentum and Collsons The lnear momentum of a partcle, or an object that can be modeled as a partcle, of mass m movng wth a velocty v s defned to be the product of
Prof. Dr. I. Nasser T /16/2017
 Pro. Dr. I. Nasser T-171 10/16/017 Chapter Part 1 Moton n one dmenson Sectons -,, 3, 4, 5 - Moton n 1 dmenson We le n a 3-dmensonal world, so why bother analyzng 1-dmensonal stuatons? Bascally, because
Pro. Dr. I. Nasser T-171 10/16/017 Chapter Part 1 Moton n one dmenson Sectons -,, 3, 4, 5 - Moton n 1 dmenson We le n a 3-dmensonal world, so why bother analyzng 1-dmensonal stuatons? Bascally, because
CHAPTER 10 ROTATIONAL MOTION
 CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
Spring Force and Power
 Lecture 13 Chapter 9 Sprng Force and Power Yeah, energy s better than orces. What s net? Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi IN THIS CHAPTER, you wll learn how to solve problems
Lecture 13 Chapter 9 Sprng Force and Power Yeah, energy s better than orces. What s net? Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi IN THIS CHAPTER, you wll learn how to solve problems
ENGN 40 Dynamics and Vibrations Homework # 7 Due: Friday, April 15
 NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
Page 1. Physics 131: Lecture 14. Today s Agenda. Things that stay the same. Impulse and Momentum Non-constant forces
 Physcs 131: Lecture 14 Today s Agenda Imulse and Momentum Non-constant forces Imulse-momentum momentum thm Conservaton of Lnear momentum Eternal/Internal forces Eamles Physcs 201: Lecture 1, Pg 1 Physcs
Physcs 131: Lecture 14 Today s Agenda Imulse and Momentum Non-constant forces Imulse-momentum momentum thm Conservaton of Lnear momentum Eternal/Internal forces Eamles Physcs 201: Lecture 1, Pg 1 Physcs
Work is the change in energy of a system (neglecting heat transfer). To examine what could
 Work Work s the change n energy o a system (neglectng heat transer). To eamne what could cause work, let s look at the dmensons o energy: L ML E M L F L so T T dmensonally energy s equal to a orce tmes
Work Work s the change n energy o a system (neglectng heat transer). To eamne what could cause work, let s look at the dmensons o energy: L ML E M L F L so T T dmensonally energy s equal to a orce tmes
MATH 5630: Discrete Time-Space Model Hung Phan, UMass Lowell March 1, 2018
 MATH 5630: Dscrete Tme-Space Model Hung Phan, UMass Lowell March, 08 Newton s Law of Coolng Consder the coolng of a well strred coffee so that the temperature does not depend on space Newton s law of collng
MATH 5630: Dscrete Tme-Space Model Hung Phan, UMass Lowell March, 08 Newton s Law of Coolng Consder the coolng of a well strred coffee so that the temperature does not depend on space Newton s law of collng
International Mathematical Olympiad. Preliminary Selection Contest 2012 Hong Kong. Outline of Solutions
 Internatonal Mathematcal Olympad Prelmnary Selecton ontest Hong Kong Outlne of Solutons nswers: 7 4 7 4 6 5 9 6 99 7 6 6 9 5544 49 5 7 4 6765 5 6 6 7 6 944 9 Solutons: Snce n s a two-dgt number, we have
Internatonal Mathematcal Olympad Prelmnary Selecton ontest Hong Kong Outlne of Solutons nswers: 7 4 7 4 6 5 9 6 99 7 6 6 9 5544 49 5 7 4 6765 5 6 6 7 6 944 9 Solutons: Snce n s a two-dgt number, we have
Review of Taylor Series. Read Section 1.2
 Revew of Taylor Seres Read Secton 1.2 1 Power Seres A power seres about c s an nfnte seres of the form k = 0 k a ( x c) = a + a ( x c) + a ( x c) + a ( x c) k 2 3 0 1 2 3 + In many cases, c = 0, and the
Revew of Taylor Seres Read Secton 1.2 1 Power Seres A power seres about c s an nfnte seres of the form k = 0 k a ( x c) = a + a ( x c) + a ( x c) + a ( x c) k 2 3 0 1 2 3 + In many cases, c = 0, and the
PHYS 1441 Section 002 Lecture #15
 PHYS 1441 Secton 00 Lecture #15 Monday, March 18, 013 Work wth rcton Potental Energy Gravtatonal Potental Energy Elastc Potental Energy Mechancal Energy Conservaton Announcements Mdterm comprehensve exam
PHYS 1441 Secton 00 Lecture #15 Monday, March 18, 013 Work wth rcton Potental Energy Gravtatonal Potental Energy Elastc Potental Energy Mechancal Energy Conservaton Announcements Mdterm comprehensve exam
Spin-rotation coupling of the angularly accelerated rigid body
 Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Electric Potential Energy & Potential. Electric Potential Energy. Potential Energy. Potential Energy. Example: Charge launcher
 Electrc & Electrc Gravtatonal Increases as you move farther from Earth mgh Sprng Increases as you ncrease sprng extenson/comp resson Δ Increases or decreases as you move farther from the charge U ncreases
Electrc & Electrc Gravtatonal Increases as you move farther from Earth mgh Sprng Increases as you ncrease sprng extenson/comp resson Δ Increases or decreases as you move farther from the charge U ncreases
Linear Momentum. Center of Mass.
 Lecture 16 Chapter 9 Physcs I 11.06.2013 Lnear oentu. Center of ass. Course webste: http://faculty.ul.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.ul.edu/danylov2013/physcs1fall.htl
Lecture 16 Chapter 9 Physcs I 11.06.2013 Lnear oentu. Center of ass. Course webste: http://faculty.ul.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.ul.edu/danylov2013/physcs1fall.htl
PHYS 1443 Section 004 Lecture #12 Thursday, Oct. 2, 2014
 PHYS 1443 Secton 004 Lecture #1 Thursday, Oct., 014 Work-Knetc Energy Theorem Work under rcton Potental Energy and the Conservatve Force Gravtatonal Potental Energy Elastc Potental Energy Conservaton o
PHYS 1443 Secton 004 Lecture #1 Thursday, Oct., 014 Work-Knetc Energy Theorem Work under rcton Potental Energy and the Conservatve Force Gravtatonal Potental Energy Elastc Potental Energy Conservaton o
Physics 2A Chapter 9 HW Solutions
 Phscs A Chapter 9 HW Solutons Chapter 9 Conceptual Queston:, 4, 8, 13 Problems: 3, 8, 1, 15, 3, 40, 51, 6 Q9.. Reason: We can nd the change n momentum o the objects b computng the mpulse on them and usng
Phscs A Chapter 9 HW Solutons Chapter 9 Conceptual Queston:, 4, 8, 13 Problems: 3, 8, 1, 15, 3, 40, 51, 6 Q9.. Reason: We can nd the change n momentum o the objects b computng the mpulse on them and usng
Physics 114 Exam 3 Spring Name:
 Physcs 114 Exam 3 Sprng 015 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem 4. Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse
Physcs 114 Exam 3 Sprng 015 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem 4. Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse
GAUTENG DEPARTMENT OF EDUCATION SENIOR SECONDARY INTERVENTION PROGRAMME PHYSICAL SCIENCES GRADE 12 SESSION 1 (LEARNER NOTES)
 PHYSICAL SCIENCES GRADE 1 SESSION 1 (LEARNER NOTES) TOPIC 1: MECHANICS PROJECTILE MOTION Learner Note: Always draw a dagram of the stuaton and enter all the numercal alues onto your dagram. Remember to
PHYSICAL SCIENCES GRADE 1 SESSION 1 (LEARNER NOTES) TOPIC 1: MECHANICS PROJECTILE MOTION Learner Note: Always draw a dagram of the stuaton and enter all the numercal alues onto your dagram. Remember to
Physics 114 Exam 2 Fall 2014 Solutions. Name:
 Physcs 114 Exam Fall 014 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse ndcated,
Physcs 114 Exam Fall 014 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse ndcated,
Part C Dynamics and Statics of Rigid Body. Chapter 5 Rotation of a Rigid Body About a Fixed Axis
 Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
χ x B E (c) Figure 2.1.1: (a) a material particle in a body, (b) a place in space, (c) a configuration of the body
 Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
You will analyze the motion of the block at different moments using the law of conservation of energy.
 Physcs 00A Homework 7 Chapter 8 Where s the Energy? In ths problem, we wll consder the ollowng stuaton as depcted n the dagram: A block o mass m sldes at a speed v along a horzontal smooth table. It next
Physcs 00A Homework 7 Chapter 8 Where s the Energy? In ths problem, we wll consder the ollowng stuaton as depcted n the dagram: A block o mass m sldes at a speed v along a horzontal smooth table. It next
Rotational and Translational Comparison. Conservation of Angular Momentum. Angular Momentum for a System of Particles
 Conservaton o Angular Momentum 8.0 WD Rotatonal and Translatonal Comparson Quantty Momentum Ang Momentum Force Torque Knetc Energy Work Power Rotaton L cm = I cm ω = dl / cm cm K = (/ ) rot P rot θ W =
Conservaton o Angular Momentum 8.0 WD Rotatonal and Translatonal Comparson Quantty Momentum Ang Momentum Force Torque Knetc Energy Work Power Rotaton L cm = I cm ω = dl / cm cm K = (/ ) rot P rot θ W =
Module 14: THE INTEGRAL Exploring Calculus
 Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Newton s Laws of Motion
 Chapter 4 Newton s Laws of Moton 4.1 Forces and Interactons Fundamental forces. There are four types of fundamental forces: electromagnetc, weak, strong and gravtatonal. The frst two had been successfully
Chapter 4 Newton s Laws of Moton 4.1 Forces and Interactons Fundamental forces. There are four types of fundamental forces: electromagnetc, weak, strong and gravtatonal. The frst two had been successfully
Rotational Dynamics. Physics 1425 Lecture 19. Michael Fowler, UVa
 Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
11. Dynamics in Rotating Frames of Reference
 Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
PY2101 Classical Mechanics Dr. Síle Nic Chormaic, Room 215 D Kane Bldg
 PY2101 Classcal Mechancs Dr. Síle Nc Chormac, Room 215 D Kane Bldg s.ncchormac@ucc.e Lectures stll some ssues to resolve. Slots shared between PY2101 and PY2104. Hope to have t fnalsed by tomorrow. Mondays
PY2101 Classcal Mechancs Dr. Síle Nc Chormac, Room 215 D Kane Bldg s.ncchormac@ucc.e Lectures stll some ssues to resolve. Slots shared between PY2101 and PY2104. Hope to have t fnalsed by tomorrow. Mondays
Angular Momentum and Fixed Axis Rotation. 8.01t Nov 10, 2004
 Angular Momentum and Fxed Axs Rotaton 8.01t Nov 10, 2004 Dynamcs: Translatonal and Rotatonal Moton Translatonal Dynamcs Total Force Torque Angular Momentum about Dynamcs of Rotaton F ext Momentum of a
Angular Momentum and Fxed Axs Rotaton 8.01t Nov 10, 2004 Dynamcs: Translatonal and Rotatonal Moton Translatonal Dynamcs Total Force Torque Angular Momentum about Dynamcs of Rotaton F ext Momentum of a
Conservation of Angular Momentum = "Spin"
 Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
measurement and the charge the electric field will be calculated using E =. The direction of the field will be the . But, so
 THE ELECTRIC FIELD 6 Conceptual Questons 6.. A tny, postve test charge wll be placed at the pont n space and the force wll be measured. From the force F measurement and the charge the electrc feld wll
THE ELECTRIC FIELD 6 Conceptual Questons 6.. A tny, postve test charge wll be placed at the pont n space and the force wll be measured. From the force F measurement and the charge the electrc feld wll
Chapter 7: Conservation of Energy
 Lecture 7: Conservaton o nergy Chapter 7: Conservaton o nergy Introucton I the quantty o a subject oes not change wth tme, t means that the quantty s conserve. The quantty o that subject remans constant
Lecture 7: Conservaton o nergy Chapter 7: Conservaton o nergy Introucton I the quantty o a subject oes not change wth tme, t means that the quantty s conserve. The quantty o that subject remans constant
Page 1. SPH4U: Lecture 7. New Topic: Friction. Today s Agenda. Surface Friction... Surface Friction...
 SPH4U: Lecture 7 Today s Agenda rcton What s t? Systeatc catagores of forces How do we characterze t? Model of frcton Statc & Knetc frcton (knetc = dynac n soe languages) Soe probles nvolvng frcton ew
SPH4U: Lecture 7 Today s Agenda rcton What s t? Systeatc catagores of forces How do we characterze t? Model of frcton Statc & Knetc frcton (knetc = dynac n soe languages) Soe probles nvolvng frcton ew
Chapter 8: Further Applications of Trigonometry
 Secton 8. Polar Form of Complex Numbers 1 Chapter 8: Further Applcatons of Trgonometry In ths chapter, we wll explore addtonal applcatons of trgonometry. We wll begn wth an extenson of the rght trangle
Secton 8. Polar Form of Complex Numbers 1 Chapter 8: Further Applcatons of Trgonometry In ths chapter, we wll explore addtonal applcatons of trgonometry. We wll begn wth an extenson of the rght trangle
Physics 4B. Question and 3 tie (clockwise), then 2 and 5 tie (zero), then 4 and 6 tie (counterclockwise) B i. ( T / s) = 1.74 V.
 Physcs 4 Solutons to Chapter 3 HW Chapter 3: Questons:, 4, 1 Problems:, 15, 19, 7, 33, 41, 45, 54, 65 Queston 3-1 and 3 te (clockwse), then and 5 te (zero), then 4 and 6 te (counterclockwse) Queston 3-4
Physcs 4 Solutons to Chapter 3 HW Chapter 3: Questons:, 4, 1 Problems:, 15, 19, 7, 33, 41, 45, 54, 65 Queston 3-1 and 3 te (clockwse), then and 5 te (zero), then 4 and 6 te (counterclockwse) Queston 3-4
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
PHYS 1441 Section 002 Lecture #16
 PHYS 1441 Secton 00 Lecture #16 Monday, Mar. 4, 008 Potental Energy Conservatve and Non-conservatve Forces Conservaton o Mechancal Energy Power Today s homework s homework #8, due 9pm, Monday, Mar. 31!!
PHYS 1441 Secton 00 Lecture #16 Monday, Mar. 4, 008 Potental Energy Conservatve and Non-conservatve Forces Conservaton o Mechancal Energy Power Today s homework s homework #8, due 9pm, Monday, Mar. 31!!
Ground Rules. PC1221 Fundamentals of Physics I. Linear Momentum, cont. Linear Momentum. Lectures 17 and 18. Linear Momentum and Collisions
 PC Fundamentals of Physcs I Lectures 7 and 8 Lnear omentum and Collsons Dr Tay Seng Chuan Ground Rules Swtch off your handphone and pager Swtch off your laptop computer and keep t No talkng whle lecture
PC Fundamentals of Physcs I Lectures 7 and 8 Lnear omentum and Collsons Dr Tay Seng Chuan Ground Rules Swtch off your handphone and pager Swtch off your laptop computer and keep t No talkng whle lecture
Four Bar Linkages in Two Dimensions. A link has fixed length and is joined to other links and also possibly to a fixed point.
 Four bar lnkages 1 Four Bar Lnkages n Two Dmensons lnk has fed length and s oned to other lnks and also possbly to a fed pont. The relatve velocty of end B wth regard to s gven by V B = ω r y v B B = +y
Four bar lnkages 1 Four Bar Lnkages n Two Dmensons lnk has fed length and s oned to other lnks and also possbly to a fed pont. The relatve velocty of end B wth regard to s gven by V B = ω r y v B B = +y
Structure and Drive Paul A. Jensen Copyright July 20, 2003
 Structure and Drve Paul A. Jensen Copyrght July 20, 2003 A system s made up of several operatons wth flow passng between them. The structure of the system descrbes the flow paths from nputs to outputs.
Structure and Drve Paul A. Jensen Copyrght July 20, 2003 A system s made up of several operatons wth flow passng between them. The structure of the system descrbes the flow paths from nputs to outputs.
Use these variables to select a formula. x = t Average speed = 100 m/s = distance / time t = x/v = ~2 m / 100 m/s = 0.02 s or 20 milliseconds
 The speed o a nere mpulse n the human body s about 100 m/s. I you accdentally stub your toe n the dark, estmatethe tme t takes the nere mpulse to trael to your bran. Tps: pcture, poste drecton, and lst
The speed o a nere mpulse n the human body s about 100 m/s. I you accdentally stub your toe n the dark, estmatethe tme t takes the nere mpulse to trael to your bran. Tps: pcture, poste drecton, and lst
Physics for Scientists and Engineers. Chapter 9 Impulse and Momentum
 Physcs or Scentsts and Engneers Chapter 9 Impulse and Momentum Sprng, 008 Ho Jung Pak Lnear Momentum Lnear momentum o an object o mass m movng wth a velocty v s dened to be p mv Momentum and lnear momentum
Physcs or Scentsts and Engneers Chapter 9 Impulse and Momentum Sprng, 008 Ho Jung Pak Lnear Momentum Lnear momentum o an object o mass m movng wth a velocty v s dened to be p mv Momentum and lnear momentum
Chapter 5. Answers to Even Numbered Problems m kj. 6. (a) 900 J (b) (a) 31.9 J (b) 0 (c) 0 (d) 31.9 J. 10.
 Answers to Even Numbered Problems Chapter 5. 3.6 m 4..6 J 6. (a) 9 J (b).383 8. (a) 3.9 J (b) (c) (d) 3.9 J. 6 m s. (a) 68 J (b) 84 J (c) 5 J (d) 48 J (e) 5.64 m s 4. 9. J 6. (a). J (b) 5. m s (c) 6.3
Answers to Even Numbered Problems Chapter 5. 3.6 m 4..6 J 6. (a) 9 J (b).383 8. (a) 3.9 J (b) (c) (d) 3.9 J. 6 m s. (a) 68 J (b) 84 J (c) 5 J (d) 48 J (e) 5.64 m s 4. 9. J 6. (a). J (b) 5. m s (c) 6.3
EN40: Dynamics and Vibrations. Homework 7: Rigid Body Kinematics
 N40: ynamcs and Vbratons Homewor 7: Rgd Body Knematcs School of ngneerng Brown Unversty 1. In the fgure below, bar AB rotates counterclocwse at 4 rad/s. What are the angular veloctes of bars BC and C?.
N40: ynamcs and Vbratons Homewor 7: Rgd Body Knematcs School of ngneerng Brown Unversty 1. In the fgure below, bar AB rotates counterclocwse at 4 rad/s. What are the angular veloctes of bars BC and C?.
Adiabatic Sorption of Ammonia-Water System and Depicting in p-t-x Diagram
 Adabatc Sorpton of Ammona-Water System and Depctng n p-t-x Dagram J. POSPISIL, Z. SKALA Faculty of Mechancal Engneerng Brno Unversty of Technology Techncka 2, Brno 61669 CZECH REPUBLIC Abstract: - Absorpton
Adabatc Sorpton of Ammona-Water System and Depctng n p-t-x Dagram J. POSPISIL, Z. SKALA Faculty of Mechancal Engneerng Brno Unversty of Technology Techncka 2, Brno 61669 CZECH REPUBLIC Abstract: - Absorpton
Single Variable Optimization
 8/4/07 Course Instructor Dr. Raymond C. Rump Oce: A 337 Phone: (95) 747 6958 E Mal: rcrump@utep.edu Topc 8b Sngle Varable Optmzaton EE 4386/530 Computatonal Methods n EE Outlne Mathematcal Prelmnares Sngle
8/4/07 Course Instructor Dr. Raymond C. Rump Oce: A 337 Phone: (95) 747 6958 E Mal: rcrump@utep.edu Topc 8b Sngle Varable Optmzaton EE 4386/530 Computatonal Methods n EE Outlne Mathematcal Prelmnares Sngle
Physics 207 Lecture 6
 Physcs 207 Lecture 6 Agenda: Physcs 207, Lecture 6, Sept. 25 Chapter 4 Frames of reference Chapter 5 ewton s Law Mass Inerta s (contact and non-contact) Frcton (a external force that opposes moton) Free
Physcs 207 Lecture 6 Agenda: Physcs 207, Lecture 6, Sept. 25 Chapter 4 Frames of reference Chapter 5 ewton s Law Mass Inerta s (contact and non-contact) Frcton (a external force that opposes moton) Free
Physics 111 Final Exam, Fall 2013, Version A
 Physcs 111 Fnal Exam, Fall 013, Verson A Name (Prnt): 4 Dgt ID: Secton: Honors Code Pledge: For ethcal and farness reasons all students are pledged to comply wth the provsons of the NJIT Academc Honor
Physcs 111 Fnal Exam, Fall 013, Verson A Name (Prnt): 4 Dgt ID: Secton: Honors Code Pledge: For ethcal and farness reasons all students are pledged to comply wth the provsons of the NJIT Academc Honor
The classical spin-rotation coupling
 LOUAI H. ELZEIN 2018 All Rghts Reserved The classcal spn-rotaton couplng Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 louaelzen@gmal.com Abstract Ths paper s prepared to show that a rgd
LOUAI H. ELZEIN 2018 All Rghts Reserved The classcal spn-rotaton couplng Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 louaelzen@gmal.com Abstract Ths paper s prepared to show that a rgd
Week 6, Chapter 7 Sect 1-5
 Week 6, Chapter 7 Sect 1-5 Work and Knetc Energy Lecture Quz The frctonal force of the floor on a large sutcase s least when the sutcase s A.pushed by a force parallel to the floor. B.dragged by a force
Week 6, Chapter 7 Sect 1-5 Work and Knetc Energy Lecture Quz The frctonal force of the floor on a large sutcase s least when the sutcase s A.pushed by a force parallel to the floor. B.dragged by a force
Axial Turbine Analysis
 Axal Turbne Analyss From Euler turbomachnery (conservaton) equatons need to Nole understand change n tangental velocty to relate to forces on blades and power m W m rc e rc uc uc e Analye flow n a plane
Axal Turbne Analyss From Euler turbomachnery (conservaton) equatons need to Nole understand change n tangental velocty to relate to forces on blades and power m W m rc e rc uc uc e Analye flow n a plane
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
 COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
The path of ants Dragos Crisan, Andrei Petridean, 11 th grade. Colegiul National "Emil Racovita", Cluj-Napoca
 Ths artcle s wrtten by students. It may nclude omssons and mperfectons, whch were dentfed and reported as mnutely as possble by our revewers n the edtoral notes. The path of ants 07-08 Students names and
Ths artcle s wrtten by students. It may nclude omssons and mperfectons, whch were dentfed and reported as mnutely as possble by our revewers n the edtoral notes. The path of ants 07-08 Students names and
THE CURRENT BALANCE Physics 258/259
 DSH 1988, 005 THE CURRENT BALANCE Physcs 58/59 The tme average force between two parallel conductors carryng an alternatng current s measured by balancng ths force aganst the gravtatonal force on a set
DSH 1988, 005 THE CURRENT BALANCE Physcs 58/59 The tme average force between two parallel conductors carryng an alternatng current s measured by balancng ths force aganst the gravtatonal force on a set
CHAPTER 4d. ROOTS OF EQUATIONS
 CHAPTER 4d. ROOTS OF EQUATIONS A. J. Clark School o Engneerng Department o Cvl and Envronmental Engneerng by Dr. Ibrahm A. Assakka Sprng 00 ENCE 03 - Computaton Methods n Cvl Engneerng II Department o
CHAPTER 4d. ROOTS OF EQUATIONS A. J. Clark School o Engneerng Department o Cvl and Envronmental Engneerng by Dr. Ibrahm A. Assakka Sprng 00 ENCE 03 - Computaton Methods n Cvl Engneerng II Department o
Mechanics Cycle 3 Chapter 9++ Chapter 9++
 Chapter 9++ More on Knetc Energy and Potental Energy BACK TO THE FUTURE I++ More Predctons wth Energy Conservaton Revst: Knetc energy for rotaton Potental energy M total g y CM for a body n constant gravty
Chapter 9++ More on Knetc Energy and Potental Energy BACK TO THE FUTURE I++ More Predctons wth Energy Conservaton Revst: Knetc energy for rotaton Potental energy M total g y CM for a body n constant gravty
An Algorithm to Solve the Inverse Kinematics Problem of a Robotic Manipulator Based on Rotation Vectors
 An Algorthm to Solve the Inverse Knematcs Problem of a Robotc Manpulator Based on Rotaton Vectors Mohamad Z. Al-az*, Mazn Z. Othman**, and Baker B. Al-Bahr* *AL-Nahran Unversty, Computer Eng. Dep., Baghdad,
An Algorthm to Solve the Inverse Knematcs Problem of a Robotc Manpulator Based on Rotaton Vectors Mohamad Z. Al-az*, Mazn Z. Othman**, and Baker B. Al-Bahr* *AL-Nahran Unversty, Computer Eng. Dep., Baghdad,
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
Name (print neatly): Section #: First, write your name on this sheet and on the Scantron Card. The Physics faculty would like to help you do well:
 Name (prnt neatly): Secton #: Physcs 111 Exam Frst, wrte your name on ths sheet and on the Scantron Card. The Physcs faculty would lke to help you do well: 1. Budget your tme: 80 mnutes/0 questons=4 mn
Name (prnt neatly): Secton #: Physcs 111 Exam Frst, wrte your name on ths sheet and on the Scantron Card. The Physcs faculty would lke to help you do well: 1. Budget your tme: 80 mnutes/0 questons=4 mn
How Differential Equations Arise. Newton s Second Law of Motion
 page 1 CHAPTER 1 Frst-Order Dfferental Equatons Among all of the mathematcal dscplnes the theory of dfferental equatons s the most mportant. It furnshes the explanaton of all those elementary manfestatons
page 1 CHAPTER 1 Frst-Order Dfferental Equatons Among all of the mathematcal dscplnes the theory of dfferental equatons s the most mportant. It furnshes the explanaton of all those elementary manfestatons
Physics 2A Chapters 6 - Work & Energy Fall 2017
 Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
(T > w) F R = T - w. Going up. T - w = ma
 ANSES Suspended Acceleratng-Objects A resultant orce causes a syste to accelerate. he drecton o the acceleraton s n the drecton o the resultant orce. As llustrated belo, hen suspended objects accelerate,
ANSES Suspended Acceleratng-Objects A resultant orce causes a syste to accelerate. he drecton o the acceleraton s n the drecton o the resultant orce. As llustrated belo, hen suspended objects accelerate,
Chapter 07: Kinetic Energy and Work
 Chapter 07: Knetc Energy and Work Conservaton o Energy s one o Nature s undamental laws that s not volated. Energy can take on derent orms n a gven system. Ths chapter we wll dscuss work and knetc energy.
Chapter 07: Knetc Energy and Work Conservaton o Energy s one o Nature s undamental laws that s not volated. Energy can take on derent orms n a gven system. Ths chapter we wll dscuss work and knetc energy.
Linear Momentum. Equation 1
 Lnear Momentum OBJECTIVE Obsere collsons between two carts, testng or the conseraton o momentum. Measure energy changes durng derent types o collsons. Classy collsons as elastc, nelastc, or completely
Lnear Momentum OBJECTIVE Obsere collsons between two carts, testng or the conseraton o momentum. Measure energy changes durng derent types o collsons. Classy collsons as elastc, nelastc, or completely
Physics 181. Particle Systems
 Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Chapter Newton s Method
 Chapter 9. Newton s Method After readng ths chapter, you should be able to:. Understand how Newton s method s dfferent from the Golden Secton Search method. Understand how Newton s method works 3. Solve
Chapter 9. Newton s Method After readng ths chapter, you should be able to:. Understand how Newton s method s dfferent from the Golden Secton Search method. Understand how Newton s method works 3. Solve
