Math1110 (Spring 2009) Prelim 3 - Solutions
|
|
|
- Eugene Watkins
- 5 years ago
- Views:
Transcription
1 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers. x 1 x b 1 sn(x) (b) (4 ponts) Please evaluate lm x π 1 cos(x). (c) (4 ponts) Please evaluate lm x x2 e x. (d) (4 ponts) Please wrte the sum (n 1) n n sgma notaton and fnd a closed form expresson for t. What s the value of the sum when n = 10? Soluton to Queston 1. (a) usng l Hoptal s rule, we get (b) lm x π (c) Usng l Hoptal s rule twce we get (d) x a 1 lm x 1 x b 1 = lm ax a 1 h 1 bx = a b 1 b. sn(x) 1 cos(x) = sn π 1 cos π = 0 1 ( 1) = 0. lm x x2 e x = lm x x 2 = lm e x x 3x = lm e x x 2e x (n 1) n = (7 + ) When n = 10, then the sum equals = 7 + = 7n + (n (n 1))/2. 10 (10 1) 2 = = 115.
2 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 2 Queston 2. (20 ponts) True/False. Determne whether the followng statements are true or false, and crcle your response. Please gve a bref explanaton (n a complete sentence!). (a) (4 ponts) If a dfferentable functon f s defned at c, and c s a crtcal pont of f, then f has ether a local mnmum or a local maxmum at c. TRUE FALSE (b) (4 ponts) The functon f(x) = sn(cos(x)) + x3 + 7 e x s ntegrable on the nterval [a, b] for any real numbers a and b. TRUE FALSE (c) (4 ponts) Let f(x) be a functon, and P n (x) ts order n Maclaurn polynomal. Suppose that P n (0.1) = and E n (0.1) Then we know for certan that f(0.1), rounded to two decmal places, s TRUE FALSE (d) (4 ponts) The area of the regon bounded by sn x and the x-axs, between x = π and x = π s computed by π π sn x dx. TRUE FALSE (e) (4 ponts) To estmate the area below the functon y = x between x = 0 and x = 2, we may wrte a Remann sum ( ( ) 2 2 S n = + 4) 2 n n. Ths sum S n s less than the actual area for all n. TRUE FALSE Soluton to Queston 2. (a) FALSE. The functon y = x 3 has a crtcal pont at x = 0, but nether a local max nor a local mn there. (b) TRUE. Ths functon s contnuous at all real numbers x : each of the functons sn(x), cos(x), x 3 + 7, e x s contnuous, and composton, sums, and quotents are contnuous (snce e x 0, there are no ssues when we have t n the denomnator). A theorem from 5.3 says that f f(x) s contnuous on [a, b], t s ntegrable on [a, b]. (c) FALSE. If E n (0.1) = 0.005, then f(0.1) = P n (0.1) + E n (0.1) = = whch s 3.72 when rounded to two decmal places. (d) FALSE. Because from π to 0, n the above ntegral, the area between π to 0 has a mnus sgn (below the x-axs. (The ntegral becomes actually 0 because of the symmetry of sn x around the orgn). (e) TRUE. The functon s decreasng on [0, 2] but stays postve.
3 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 3 Queston 3. (20 ponts) Consder the functon f(x) = 1 x2 x 2 4. We wll get you started by computng the frst two dervatves: f (x) = (a) Fnd all crtcal and sngular ponts of f. (b) Fnd all asymptotes of f. (c) Where s f ncreasng and decreasng? (d) Where s f concave up and concave down? 6x (x 2 4) 2 and f (x) = 18x (x 2 4) 3. (e) Usng what you have calculated n the frst four parts of ths problem, please graph the functon f(x) = 1 x2 x 2 4 on the axes gven below. There s a practce sheet of graph paper on the last sheet of ths exam that you may wsh to use to make a frst attempt at the graph. Soluton to Queston 3. (a) Set f (x) = 0 to get 6x = 0, so we have crtcal ponts when x = 0. We have sngular ponts when f (x) s undefned but f(x) = 0 s defned. Note that f (x) s undefned f (x 2 4) 2 = 0,.e x = ±2. But f(2), f( 2) are undefned, so there are no sngular ponts. (b) To fnd vertcal asymptotes, we look for 0 n the denomnator, so x = ±2. To fnd horzontal asymptotes, observe that the lm x ± f(x) = 1, so we have a horzontal asymptote y = 1. We only get oblque asymptotes f the degree of the numerator s equal to the degree of the denomnator plus 1, so there are no oblque asymptotes. (c) f s decreasng n (, 2) and ( 2, 0), and ncreasng n (0, 2) and (2, ). (d) f s concave up when 2 < x < 2, and concave down when x > 0 or x < 2.
4 Math LL10 (Sprng 2009) Prelm 3 (A4/21/2009) (e) Usng what you have calculated n the frst four parts of ths problem, please graph the functon 1-x2 f(x) : x2-4 on the axes gven below. There s a practce sheet of graph paper on the last sheet of ths exam that you may wsh to use to make a frst attempt at the graph. Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 4 FINAL ANSWER:... ' "...,... l II y=l J- -r- --. t -..: : :: -.-:- ".. (e) Queston 4. (9 ponts) Suppose that a functon f satsfes f(1) = 3 and ts DERIVATIVE s d ( (Keep ) gong!!) f(x) = e x2. dx Please show your work when you answer the questons below. (a) Fnd the lnear approxmaton to f about x = 1. (b) Use the lnear approxmaton to estmate the value of f(1.5). (c) Is you answer n (b) an under- or over-estmate? Please gve an argument supportng your answer. (Hnt: you do not need to compute the exact value of the error.) Soluton to Queston 4. (a) L(x) = f(1) + f (1)(x 1), so L(x) = 3 + (x 1)/e. (b) f(1.5) L(1.5) = /e = 6e 1 2e. (c) The formula for the error s E 1 (x) = f (s) 2 (x 1)2, wth 1 s x. We have x = 1.5, and an easy calculaton shows that f (x) = 2xe x2. Snce s s postve, we have f (s) < 0, whch means that the error s negatve. Ths means that the answer n part b s an overestmate.
5 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 5 Queston 5. (15 ponts) A clown s fllng a sphercal balloon wth helum from a tank that emts helum at a rate of 250 cm 3 /s. Please answer the followng questons, showng your work and specfyng the unts of your answers. You may wsh to refer to the formulæ at the end of ths exam. (a) How fast s the radus of the balloon changng when the radus s 5 cm? (Hnt: your answer should have a π n t.) (b) How fast s the surface area of the balloon changng when the radus of the balloon s 5 cm? (c) After 20 seconds, the balloon escapes the clown s grp. Helum blows out of the balloon at a rate of 350 cm 3 /s. How fast s the radus changng when the radus of the balloon s 10 cm?
6 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 6 Soluton to Queston 5. (a) The formula for the volume fo a sphere s V = 4 3 πr3, so dv dt and substtutng for r and dv dr, we get dt dt = 1 dv 4πr 2 dt = π cm/sec. (b) The formula for the surface area of a sphere s S = 4πr 2, so ds dt = 8πrdr dt 100cm 2 /sec. (c) Usng the formula dv dr = 4πr2 dt dt ( 350) = 400π 400π cm/sec. = 4πr2 dr dt. Rearrangng = 40π π cm/sec = we derved before, we get dr dt = 1 4πr 2 ( 350) = Queston 6. (20 ponts) You are n the woods 4 km due north of the nearest pont P on a straght east-west road. You need to get to the bus stop on the road that s 10 km west of the pont P. You can walk 3 km/h n the wood and 5 km/h on the road. Please answer the followng questons. (a) Draw a fgure ndcatng your poston, the pont P, and the bus stop. Suppose that you walk to a pont on the road, x km west of P. Wrte the travel tme T (hours) as a functon of x (km). (b) Suppose that the doman of T(x) s all real numbers. Lst the sngular ponts and crtcal ponts of T(x), and determne all local maxmum and local mnmum of T(x). (c) To what pont on the road between P and the bus stop should you head n order to mnmze the travel tme to the bus stop? Justfy your answer. (d) The last bus of the day leaves the stop n three hours. Can you make t, or wll you be sleepng under the stars? Please gve evdence to support your answer. Soluton to Queston 6. Let x be the dstance on the road beween P and the pont A you head. (a) The travel tme s wrtten as T(x) = 10 x 5 x (b) To fnd sngular and crtcal ponts on the doman, compute T T (x) = x 3 x
7 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 7 We don t have sngular ponts. The crtcal ponts are computed by settng T (x) = x 3 x = 0 5x = 3 x x > 0, x 2 = 9 x = 3. Here note that the rght hand sde of 5x = 3 x s postve, so x must be postve. We should compute T(3) = 7/5 + 5/3 = ( )/15 = 46/15 = 3 + 1/15. T (x) < 0 on x < 3. (you can plug n 0 nto T (x)) T (x) > 0 on x > 3. (you can take lmt x or plug n some number > 3, lke 10, and see that t s greater than 3 + 1/15.) Therefore x = 3 gves a local mnmum and there s no local maxmum. (c) x = 3 gves a mnmum of T(x) snce the functon s ncreasng on x > 3 and decreasng on x < 3. Therefore we should head to the pont 3 km west of the pont P. (d) Snce 3 + 1/15 s greater than 3, we can not make t to the bus.
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
ACTM State Calculus Competition Saturday April 30, 2011
 ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
Chapter 3. r r. Position, Velocity, and Acceleration Revisited
 Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
PES 1120 Spring 2014, Spendier Lecture 6/Page 1
 PES 110 Sprng 014, Spender Lecture 6/Page 1 Lecture today: Chapter 1) Electrc feld due to charge dstrbutons -> charged rod -> charged rng We ntroduced the electrc feld, E. I defned t as an nvsble aura
PES 110 Sprng 014, Spender Lecture 6/Page 1 Lecture today: Chapter 1) Electrc feld due to charge dstrbutons -> charged rod -> charged rng We ntroduced the electrc feld, E. I defned t as an nvsble aura
Solutions to Homework 7, Mathematics 1. 1 x. (arccos x) (arccos x) 1
 Solutons to Homework 7, Mathematcs 1 Problem 1: a Prove that arccos 1 1 for 1, 1. b* Startng from the defnton of the dervatve, prove that arccos + 1, arccos 1. Hnt: For arccos arccos π + 1, the defnton
Solutons to Homework 7, Mathematcs 1 Problem 1: a Prove that arccos 1 1 for 1, 1. b* Startng from the defnton of the dervatve, prove that arccos + 1, arccos 1. Hnt: For arccos arccos π + 1, the defnton
Chapter Newton s Method
 Chapter 9. Newton s Method After readng ths chapter, you should be able to:. Understand how Newton s method s dfferent from the Golden Secton Search method. Understand how Newton s method works 3. Solve
Chapter 9. Newton s Method After readng ths chapter, you should be able to:. Understand how Newton s method s dfferent from the Golden Secton Search method. Understand how Newton s method works 3. Solve
Module 14: THE INTEGRAL Exploring Calculus
 Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
= 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W]
![= 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W] = 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W]](/thumbs/78/76802454.jpg) Secton 1.3: Acceleraton Tutoral 1 Practce, page 24 1. Gven: 0 m/s; 15.0 m/s [S]; t 12.5 s Requred: Analyss: a av v t v f v t a v av f v t 15.0 m/s [S] 0 m/s 12.5 s 15.0 m/s [S] 12.5 s 1.20 m/s 2 [S] Statement:
Secton 1.3: Acceleraton Tutoral 1 Practce, page 24 1. Gven: 0 m/s; 15.0 m/s [S]; t 12.5 s Requred: Analyss: a av v t v f v t a v av f v t 15.0 m/s [S] 0 m/s 12.5 s 15.0 m/s [S] 12.5 s 1.20 m/s 2 [S] Statement:
For all questions, answer choice E) NOTA" means none of the above answers is correct.
 0 MA Natonal Conventon For all questons, answer choce " means none of the above answers s correct.. In calculus, one learns of functon representatons that are nfnte seres called power 3 4 5 seres. For
0 MA Natonal Conventon For all questons, answer choce " means none of the above answers s correct.. In calculus, one learns of functon representatons that are nfnte seres called power 3 4 5 seres. For
Module 2. Random Processes. Version 2 ECE IIT, Kharagpur
 Module Random Processes Lesson 6 Functons of Random Varables After readng ths lesson, ou wll learn about cdf of functon of a random varable. Formula for determnng the pdf of a random varable. Let, X be
Module Random Processes Lesson 6 Functons of Random Varables After readng ths lesson, ou wll learn about cdf of functon of a random varable. Formula for determnng the pdf of a random varable. Let, X be
Solutions to Problem Set 6
 Solutons to Problem Set 6 Problem 6. (Resdue theory) a) Problem 4.7.7 Boas. n ths problem we wll solve ths ntegral: x sn x x + 4x + 5 dx: To solve ths usng the resdue theorem, we study ths complex ntegral:
Solutons to Problem Set 6 Problem 6. (Resdue theory) a) Problem 4.7.7 Boas. n ths problem we wll solve ths ntegral: x sn x x + 4x + 5 dx: To solve ths usng the resdue theorem, we study ths complex ntegral:
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
Complex Numbers Alpha, Round 1 Test #123
 Complex Numbers Alpha, Round Test #3. Wrte your 6-dgt ID# n the I.D. NUMBER grd, left-justfed, and bubble. Check that each column has only one number darkened.. In the EXAM NO. grd, wrte the 3-dgt Test
Complex Numbers Alpha, Round Test #3. Wrte your 6-dgt ID# n the I.D. NUMBER grd, left-justfed, and bubble. Check that each column has only one number darkened.. In the EXAM NO. grd, wrte the 3-dgt Test
U.C. Berkeley CS294: Beyond Worst-Case Analysis Luca Trevisan September 5, 2017
 U.C. Berkeley CS94: Beyond Worst-Case Analyss Handout 4s Luca Trevsan September 5, 07 Summary of Lecture 4 In whch we ntroduce semdefnte programmng and apply t to Max Cut. Semdefnte Programmng Recall that
U.C. Berkeley CS94: Beyond Worst-Case Analyss Handout 4s Luca Trevsan September 5, 07 Summary of Lecture 4 In whch we ntroduce semdefnte programmng and apply t to Max Cut. Semdefnte Programmng Recall that
Complex Numbers. x = B B 2 4AC 2A. or x = x = 2 ± 4 4 (1) (5) 2 (1)
 Complex Numbers If you have not yet encountered complex numbers, you wll soon do so n the process of solvng quadratc equatons. The general quadratc equaton Ax + Bx + C 0 has solutons x B + B 4AC A For
Complex Numbers If you have not yet encountered complex numbers, you wll soon do so n the process of solvng quadratc equatons. The general quadratc equaton Ax + Bx + C 0 has solutons x B + B 4AC A For
Lectures - Week 4 Matrix norms, Conditioning, Vector Spaces, Linear Independence, Spanning sets and Basis, Null space and Range of a Matrix
 Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Singular Value Decomposition: Theory and Applications
 Sngular Value Decomposton: Theory and Applcatons Danel Khashab Sprng 2015 Last Update: March 2, 2015 1 Introducton A = UDV where columns of U and V are orthonormal and matrx D s dagonal wth postve real
Sngular Value Decomposton: Theory and Applcatons Danel Khashab Sprng 2015 Last Update: March 2, 2015 1 Introducton A = UDV where columns of U and V are orthonormal and matrx D s dagonal wth postve real
n α j x j = 0 j=1 has a nontrivial solution. Here A is the n k matrix whose jth column is the vector for all t j=0
 MODULE 2 Topcs: Lnear ndependence, bass and dmenson We have seen that f n a set of vectors one vector s a lnear combnaton of the remanng vectors n the set then the span of the set s unchanged f that vector
MODULE 2 Topcs: Lnear ndependence, bass and dmenson We have seen that f n a set of vectors one vector s a lnear combnaton of the remanng vectors n the set then the span of the set s unchanged f that vector
Section 3.6 Complex Zeros
 04 Chapter Secton 6 Comple Zeros When fndng the zeros of polynomals, at some pont you're faced wth the problem Whle there are clearly no real numbers that are solutons to ths equaton, leavng thngs there
04 Chapter Secton 6 Comple Zeros When fndng the zeros of polynomals, at some pont you're faced wth the problem Whle there are clearly no real numbers that are solutons to ths equaton, leavng thngs there
Transfer Functions. Convenient representation of a linear, dynamic model. A transfer function (TF) relates one input and one output: ( ) system
 Transfer Functons Convenent representaton of a lnear, dynamc model. A transfer functon (TF) relates one nput and one output: x t X s y t system Y s The followng termnology s used: x y nput output forcng
Transfer Functons Convenent representaton of a lnear, dynamc model. A transfer functon (TF) relates one nput and one output: x t X s y t system Y s The followng termnology s used: x y nput output forcng
Causal Diamonds. M. Aghili, L. Bombelli, B. Pilgrim
 Causal Damonds M. Aghl, L. Bombell, B. Plgrm Introducton The correcton to volume of a causal nterval due to curvature of spacetme has been done by Myrhem [] and recently by Gbbons & Solodukhn [] and later
Causal Damonds M. Aghl, L. Bombell, B. Plgrm Introducton The correcton to volume of a causal nterval due to curvature of spacetme has been done by Myrhem [] and recently by Gbbons & Solodukhn [] and later
Solutions to Selected Exercises
 6 Solutons to Selected Eercses Chapter Secton.. a. f ( 0) b. Tons of garbage per week s produced by a cty wth a populaton of,000.. a. In 99 there are 0 ducks n the lake b. In 000 there are 0 ducks n the
6 Solutons to Selected Eercses Chapter Secton.. a. f ( 0) b. Tons of garbage per week s produced by a cty wth a populaton of,000.. a. In 99 there are 0 ducks n the lake b. In 000 there are 0 ducks n the
8.1 Arc Length. What is the length of a curve? How can we approximate it? We could do it following the pattern we ve used before
 .1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments
.1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments
2 Finite difference basics
 Numersche Methoden 1, WS 11/12 B.J.P. Kaus 2 Fnte dfference bascs Consder the one- The bascs of the fnte dfference method are best understood wth an example. dmensonal transent heat conducton equaton T
Numersche Methoden 1, WS 11/12 B.J.P. Kaus 2 Fnte dfference bascs Consder the one- The bascs of the fnte dfference method are best understood wth an example. dmensonal transent heat conducton equaton T
Physics 114 Exam 3 Spring Name:
 Physcs 114 Exam 3 Sprng 015 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem 4. Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse
Physcs 114 Exam 3 Sprng 015 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem 4. Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse
Unit 5: Quadratic Equations & Functions
 Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
CALCULUS CLASSROOM CAPSULES
 CALCULUS CLASSROOM CAPSULES SESSION S86 Dr. Sham Alfred Rartan Valley Communty College salfred@rartanval.edu 38th AMATYC Annual Conference Jacksonvlle, Florda November 8-, 202 2 Calculus Classroom Capsules
CALCULUS CLASSROOM CAPSULES SESSION S86 Dr. Sham Alfred Rartan Valley Communty College salfred@rartanval.edu 38th AMATYC Annual Conference Jacksonvlle, Florda November 8-, 202 2 Calculus Classroom Capsules
Bezier curves. Michael S. Floater. August 25, These notes provide an introduction to Bezier curves. i=0
 Bezer curves Mchael S. Floater August 25, 211 These notes provde an ntroducton to Bezer curves. 1 Bernsten polynomals Recall that a real polynomal of a real varable x R, wth degree n, s a functon of the
Bezer curves Mchael S. Floater August 25, 211 These notes provde an ntroducton to Bezer curves. 1 Bernsten polynomals Recall that a real polynomal of a real varable x R, wth degree n, s a functon of the
Problem Solving in Math (Math 43900) Fall 2013
 Problem Solvng n Math (Math 43900) Fall 2013 Week four (September 17) solutons Instructor: Davd Galvn 1. Let a and b be two nteger for whch a b s dvsble by 3. Prove that a 3 b 3 s dvsble by 9. Soluton:
Problem Solvng n Math (Math 43900) Fall 2013 Week four (September 17) solutons Instructor: Davd Galvn 1. Let a and b be two nteger for whch a b s dvsble by 3. Prove that a 3 b 3 s dvsble by 9. Soluton:
C/CS/Phy191 Problem Set 3 Solutions Out: Oct 1, 2008., where ( 00. ), so the overall state of the system is ) ( ( ( ( 00 ± 11 ), Φ ± = 1
 C/CS/Phy9 Problem Set 3 Solutons Out: Oct, 8 Suppose you have two qubts n some arbtrary entangled state ψ You apply the teleportaton protocol to each of the qubts separately What s the resultng state obtaned
C/CS/Phy9 Problem Set 3 Solutons Out: Oct, 8 Suppose you have two qubts n some arbtrary entangled state ψ You apply the teleportaton protocol to each of the qubts separately What s the resultng state obtaned
Physics 2A Chapter 3 HW Solutions
 Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Mathematics Intersection of Lines
 a place of mnd F A C U L T Y O F E D U C A T I O N Department of Currculum and Pedagog Mathematcs Intersecton of Lnes Scence and Mathematcs Educaton Research Group Supported b UBC Teachng and Learnng Enhancement
a place of mnd F A C U L T Y O F E D U C A T I O N Department of Currculum and Pedagog Mathematcs Intersecton of Lnes Scence and Mathematcs Educaton Research Group Supported b UBC Teachng and Learnng Enhancement
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
Solutions to exam in SF1811 Optimization, Jan 14, 2015
 Solutons to exam n SF8 Optmzaton, Jan 4, 25 3 3 O------O -4 \ / \ / The network: \/ where all lnks go from left to rght. /\ / \ / \ 6 O------O -5 2 4.(a) Let x = ( x 3, x 4, x 23, x 24 ) T, where the varable
Solutons to exam n SF8 Optmzaton, Jan 4, 25 3 3 O------O -4 \ / \ / The network: \/ where all lnks go from left to rght. /\ / \ / \ 6 O------O -5 2 4.(a) Let x = ( x 3, x 4, x 23, x 24 ) T, where the varable
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space
NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space
MTH 263 Practice Test #1 Spring 1999
 Pat Ross MTH 6 Practce Test # Sprng 999 Name. Fnd the area of the regon bounded by the graph r =acos (θ). Observe: Ths s a crcle of radus a, for r =acos (θ) r =a ³ x r r =ax x + y =ax x ax + y =0 x ax
Pat Ross MTH 6 Practce Test # Sprng 999 Name. Fnd the area of the regon bounded by the graph r =acos (θ). Observe: Ths s a crcle of radus a, for r =acos (θ) r =a ³ x r r =ax x + y =ax x ax + y =0 x ax
CHALMERS, GÖTEBORGS UNIVERSITET. SOLUTIONS to RE-EXAM for ARTIFICIAL NEURAL NETWORKS. COURSE CODES: FFR 135, FIM 720 GU, PhD
 CHALMERS, GÖTEBORGS UNIVERSITET SOLUTIONS to RE-EXAM for ARTIFICIAL NEURAL NETWORKS COURSE CODES: FFR 35, FIM 72 GU, PhD Tme: Place: Teachers: Allowed materal: Not allowed: January 2, 28, at 8 3 2 3 SB
CHALMERS, GÖTEBORGS UNIVERSITET SOLUTIONS to RE-EXAM for ARTIFICIAL NEURAL NETWORKS COURSE CODES: FFR 35, FIM 72 GU, PhD Tme: Place: Teachers: Allowed materal: Not allowed: January 2, 28, at 8 3 2 3 SB
Math 217 Fall 2013 Homework 2 Solutions
 Math 17 Fall 013 Homework Solutons Due Thursday Sept. 6, 013 5pm Ths homework conssts of 6 problems of 5 ponts each. The total s 30. You need to fully justfy your answer prove that your functon ndeed has
Math 17 Fall 013 Homework Solutons Due Thursday Sept. 6, 013 5pm Ths homework conssts of 6 problems of 5 ponts each. The total s 30. You need to fully justfy your answer prove that your functon ndeed has
Math 702 Midterm Exam Solutions
 Math 702 Mdterm xam Solutons The terms measurable, measure, ntegrable, and almost everywhere (a.e.) n a ucldean space always refer to Lebesgue measure m. Problem. [6 pts] In each case, prove the statement
Math 702 Mdterm xam Solutons The terms measurable, measure, ntegrable, and almost everywhere (a.e.) n a ucldean space always refer to Lebesgue measure m. Problem. [6 pts] In each case, prove the statement
One Dimension Again. Chapter Fourteen
 hapter Fourteen One Dmenson Agan 4 Scalar Lne Integrals Now we agan consder the dea of the ntegral n one dmenson When we were ntroduced to the ntegral back n elementary school, we consdered only functons
hapter Fourteen One Dmenson Agan 4 Scalar Lne Integrals Now we agan consder the dea of the ntegral n one dmenson When we were ntroduced to the ntegral back n elementary school, we consdered only functons
Review of Taylor Series. Read Section 1.2
 Revew of Taylor Seres Read Secton 1.2 1 Power Seres A power seres about c s an nfnte seres of the form k = 0 k a ( x c) = a + a ( x c) + a ( x c) + a ( x c) k 2 3 0 1 2 3 + In many cases, c = 0, and the
Revew of Taylor Seres Read Secton 1.2 1 Power Seres A power seres about c s an nfnte seres of the form k = 0 k a ( x c) = a + a ( x c) + a ( x c) + a ( x c) k 2 3 0 1 2 3 + In many cases, c = 0, and the
Conservation of Angular Momentum = "Spin"
 Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Section 8.1 Exercises
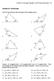 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Modelli Clamfim Equazione del Calore Lezione ottobre 2014
 CLAMFIM Bologna Modell 1 @ Clamfm Equazone del Calore Lezone 17 15 ottobre 2014 professor Danele Rtell danele.rtell@unbo.t 1/24? Convoluton The convoluton of two functons g(t) and f(t) s the functon (g
CLAMFIM Bologna Modell 1 @ Clamfm Equazone del Calore Lezone 17 15 ottobre 2014 professor Danele Rtell danele.rtell@unbo.t 1/24? Convoluton The convoluton of two functons g(t) and f(t) s the functon (g
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
PHY2049 Exam 2 solutions Fall 2016 Solution:
 PHY2049 Exam 2 solutons Fall 2016 General strategy: Fnd two resstors, one par at a tme, that are connected ether n SERIES or n PARALLEL; replace these two resstors wth one of an equvalent resstance. Now
PHY2049 Exam 2 solutons Fall 2016 General strategy: Fnd two resstors, one par at a tme, that are connected ether n SERIES or n PARALLEL; replace these two resstors wth one of an equvalent resstance. Now
From Biot-Savart Law to Divergence of B (1)
 From Bot-Savart Law to Dvergence of B (1) Let s prove that Bot-Savart gves us B (r ) = 0 for an arbtrary current densty. Frst take the dvergence of both sdes of Bot-Savart. The dervatve s wth respect to
From Bot-Savart Law to Dvergence of B (1) Let s prove that Bot-Savart gves us B (r ) = 0 for an arbtrary current densty. Frst take the dvergence of both sdes of Bot-Savart. The dervatve s wth respect to
Please initial the statement below to show that you have read it
 EN40: Dynamcs and Vbratons Mdterm Examnaton Thursday March 5 009 Dvson of Engneerng rown Unversty NME: Isaac Newton General Instructons No collaboraton of any knd s permtted on ths examnaton. You may brng
EN40: Dynamcs and Vbratons Mdterm Examnaton Thursday March 5 009 Dvson of Engneerng rown Unversty NME: Isaac Newton General Instructons No collaboraton of any knd s permtted on ths examnaton. You may brng
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
UNIT 3 EXPRESSIONS AND EQUATIONS Lesson 4: Fundamental Theorem of Algebra. Instruction. Guided Practice Example 1
 Guded Practce 3.4. Example 1 Instructon For each equaton, state the number and type of solutons by frst fndng the dscrmnant. x + 3x =.4x x = 3x = x 9x + 1 = 6x 1. Fnd the dscrmnant of x + 3x =. The equaton
Guded Practce 3.4. Example 1 Instructon For each equaton, state the number and type of solutons by frst fndng the dscrmnant. x + 3x =.4x x = 3x = x 9x + 1 = 6x 1. Fnd the dscrmnant of x + 3x =. The equaton
The Schrödinger Equation
 Chapter 1 The Schrödnger Equaton 1.1 (a) F; () T; (c) T. 1. (a) Ephoton = hν = hc/ λ =(6.66 1 34 J s)(.998 1 8 m/s)/(164 1 9 m) = 1.867 1 19 J. () E = (5 1 6 J/s)( 1 8 s) =.1 J = n(1.867 1 19 J) and n
Chapter 1 The Schrödnger Equaton 1.1 (a) F; () T; (c) T. 1. (a) Ephoton = hν = hc/ λ =(6.66 1 34 J s)(.998 1 8 m/s)/(164 1 9 m) = 1.867 1 19 J. () E = (5 1 6 J/s)( 1 8 s) =.1 J = n(1.867 1 19 J) and n
18.781: Solution to Practice Questions for Final Exam
 18.781: Soluton to Practce Questons for Fnal Exam 1. Fnd three solutons n postve ntegers of x 6y = 1 by frst calculatng the contnued fracton expanson of 6. Soluton: We have 1 6=[, ] 6 6+ =[, ] 1 =[,, ]=[,,
18.781: Soluton to Practce Questons for Fnal Exam 1. Fnd three solutons n postve ntegers of x 6y = 1 by frst calculatng the contnued fracton expanson of 6. Soluton: We have 1 6=[, ] 6 6+ =[, ] 1 =[,, ]=[,,
Physics 4B. Question and 3 tie (clockwise), then 2 and 5 tie (zero), then 4 and 6 tie (counterclockwise) B i. ( T / s) = 1.74 V.
 Physcs 4 Solutons to Chapter 3 HW Chapter 3: Questons:, 4, 1 Problems:, 15, 19, 7, 33, 41, 45, 54, 65 Queston 3-1 and 3 te (clockwse), then and 5 te (zero), then 4 and 6 te (counterclockwse) Queston 3-4
Physcs 4 Solutons to Chapter 3 HW Chapter 3: Questons:, 4, 1 Problems:, 15, 19, 7, 33, 41, 45, 54, 65 Queston 3-1 and 3 te (clockwse), then and 5 te (zero), then 4 and 6 te (counterclockwse) Queston 3-4
Stanford University CS359G: Graph Partitioning and Expanders Handout 4 Luca Trevisan January 13, 2011
 Stanford Unversty CS359G: Graph Parttonng and Expanders Handout 4 Luca Trevsan January 3, 0 Lecture 4 In whch we prove the dffcult drecton of Cheeger s nequalty. As n the past lectures, consder an undrected
Stanford Unversty CS359G: Graph Parttonng and Expanders Handout 4 Luca Trevsan January 3, 0 Lecture 4 In whch we prove the dffcult drecton of Cheeger s nequalty. As n the past lectures, consder an undrected
Introduction to Vapor/Liquid Equilibrium, part 2. Raoult s Law:
 CE304, Sprng 2004 Lecture 4 Introducton to Vapor/Lqud Equlbrum, part 2 Raoult s Law: The smplest model that allows us do VLE calculatons s obtaned when we assume that the vapor phase s an deal gas, and
CE304, Sprng 2004 Lecture 4 Introducton to Vapor/Lqud Equlbrum, part 2 Raoult s Law: The smplest model that allows us do VLE calculatons s obtaned when we assume that the vapor phase s an deal gas, and
Problem Set 9 Solutions
 Desgn and Analyss of Algorthms May 4, 2015 Massachusetts Insttute of Technology 6.046J/18.410J Profs. Erk Demane, Srn Devadas, and Nancy Lynch Problem Set 9 Solutons Problem Set 9 Solutons Ths problem
Desgn and Analyss of Algorthms May 4, 2015 Massachusetts Insttute of Technology 6.046J/18.410J Profs. Erk Demane, Srn Devadas, and Nancy Lynch Problem Set 9 Solutons Problem Set 9 Solutons Ths problem
Georgia Tech PHYS 6124 Mathematical Methods of Physics I
 Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
EEE 241: Linear Systems
 EEE : Lnear Systems Summary #: Backpropagaton BACKPROPAGATION The perceptron rule as well as the Wdrow Hoff learnng were desgned to tran sngle layer networks. They suffer from the same dsadvantage: they
EEE : Lnear Systems Summary #: Backpropagaton BACKPROPAGATION The perceptron rule as well as the Wdrow Hoff learnng were desgned to tran sngle layer networks. They suffer from the same dsadvantage: they
APPENDIX 2 FITTING A STRAIGHT LINE TO OBSERVATIONS
 Unversty of Oulu Student Laboratory n Physcs Laboratory Exercses n Physcs 1 1 APPEDIX FITTIG A STRAIGHT LIE TO OBSERVATIOS In the physcal measurements we often make a seres of measurements of the dependent
Unversty of Oulu Student Laboratory n Physcs Laboratory Exercses n Physcs 1 1 APPEDIX FITTIG A STRAIGHT LIE TO OBSERVATIOS In the physcal measurements we often make a seres of measurements of the dependent
REAL ANALYSIS I HOMEWORK 1
 REAL ANALYSIS I HOMEWORK CİHAN BAHRAN The questons are from Tao s text. Exercse 0.0.. If (x α ) α A s a collecton of numbers x α [0, + ] such that x α
REAL ANALYSIS I HOMEWORK CİHAN BAHRAN The questons are from Tao s text. Exercse 0.0.. If (x α ) α A s a collecton of numbers x α [0, + ] such that x α
THE CHINESE REMAINDER THEOREM. We should thank the Chinese for their wonderful remainder theorem. Glenn Stevens
 THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chnese for ther wonderful remander theorem. Glenn Stevens 1. Introducton The Chnese remander theorem says we can unquely solve any par of
THE CHINESE REMAINDER THEOREM KEITH CONRAD We should thank the Chnese for ther wonderful remander theorem. Glenn Stevens 1. Introducton The Chnese remander theorem says we can unquely solve any par of
Linear Approximation with Regularization and Moving Least Squares
 Lnear Approxmaton wth Regularzaton and Movng Least Squares Igor Grešovn May 007 Revson 4.6 (Revson : March 004). 5 4 3 0.5 3 3.5 4 Contents: Lnear Fttng...4. Weghted Least Squares n Functon Approxmaton...
Lnear Approxmaton wth Regularzaton and Movng Least Squares Igor Grešovn May 007 Revson 4.6 (Revson : March 004). 5 4 3 0.5 3 3.5 4 Contents: Lnear Fttng...4. Weghted Least Squares n Functon Approxmaton...
1. Estimation, Approximation and Errors Percentages Polynomials and Formulas Identities and Factorization 52
 ontents ommonly Used Formulas. Estmaton, pproxmaton and Errors. Percentages. Polynomals and Formulas 8. Identtes and Factorzaton. Equatons and Inequaltes 66 6. Rate and Rato 8 7. Laws of Integral Indces
ontents ommonly Used Formulas. Estmaton, pproxmaton and Errors. Percentages. Polynomals and Formulas 8. Identtes and Factorzaton. Equatons and Inequaltes 66 6. Rate and Rato 8 7. Laws of Integral Indces
Complex Variables. Chapter 18 Integration in the Complex Plane. March 12, 2013 Lecturer: Shih-Yuan Chen
 omplex Varables hapter 8 Integraton n the omplex Plane March, Lecturer: Shh-Yuan hen Except where otherwse noted, content s lcensed under a BY-N-SA. TW Lcense. ontents ontour ntegrals auchy-goursat theorem
omplex Varables hapter 8 Integraton n the omplex Plane March, Lecturer: Shh-Yuan hen Except where otherwse noted, content s lcensed under a BY-N-SA. TW Lcense. ontents ontour ntegrals auchy-goursat theorem
Chapter 5. Solution of System of Linear Equations. Module No. 6. Solution of Inconsistent and Ill Conditioned Systems
 Numercal Analyss by Dr. Anta Pal Assstant Professor Department of Mathematcs Natonal Insttute of Technology Durgapur Durgapur-713209 emal: anta.bue@gmal.com 1 . Chapter 5 Soluton of System of Lnear Equatons
Numercal Analyss by Dr. Anta Pal Assstant Professor Department of Mathematcs Natonal Insttute of Technology Durgapur Durgapur-713209 emal: anta.bue@gmal.com 1 . Chapter 5 Soluton of System of Lnear Equatons
Chapter 12. Ordinary Differential Equation Boundary Value (BV) Problems
 Chapter. Ordnar Dfferental Equaton Boundar Value (BV) Problems In ths chapter we wll learn how to solve ODE boundar value problem. BV ODE s usuall gven wth x beng the ndependent space varable. p( x) q(
Chapter. Ordnar Dfferental Equaton Boundar Value (BV) Problems In ths chapter we wll learn how to solve ODE boundar value problem. BV ODE s usuall gven wth x beng the ndependent space varable. p( x) q(
Chapter Twelve. Integration. We now turn our attention to the idea of an integral in dimensions higher than one. Consider a real-valued function f : D
 Chapter Twelve Integraton 12.1 Introducton We now turn our attenton to the dea of an ntegral n dmensons hgher than one. Consder a real-valued functon f : R, where the doman s a nce closed subset of Eucldean
Chapter Twelve Integraton 12.1 Introducton We now turn our attenton to the dea of an ntegral n dmensons hgher than one. Consder a real-valued functon f : R, where the doman s a nce closed subset of Eucldean
find (x): given element x, return the canonical element of the set containing x;
 COS 43 Sprng, 009 Dsjont Set Unon Problem: Mantan a collecton of dsjont sets. Two operatons: fnd the set contanng a gven element; unte two sets nto one (destructvely). Approach: Canoncal element method:
COS 43 Sprng, 009 Dsjont Set Unon Problem: Mantan a collecton of dsjont sets. Two operatons: fnd the set contanng a gven element; unte two sets nto one (destructvely). Approach: Canoncal element method:
ANSWERS. Problem 1. and the moment generating function (mgf) by. defined for any real t. Use this to show that E( U) var( U)
 Econ 413 Exam 13 H ANSWERS Settet er nndelt 9 deloppgaver, A,B,C, som alle anbefales å telle lkt for å gøre det ltt lettere å stå. Svar er gtt . Unfortunately, there s a prntng error n the hnt of
Econ 413 Exam 13 H ANSWERS Settet er nndelt 9 deloppgaver, A,B,C, som alle anbefales å telle lkt for å gøre det ltt lettere å stå. Svar er gtt . Unfortunately, there s a prntng error n the hnt of
STAT 3340 Assignment 1 solutions. 1. Find the equation of the line which passes through the points (1,1) and (4,5).
 (out of 15 ponts) STAT 3340 Assgnment 1 solutons (10) (10) 1. Fnd the equaton of the lne whch passes through the ponts (1,1) and (4,5). β 1 = (5 1)/(4 1) = 4/3 equaton for the lne s y y 0 = β 1 (x x 0
(out of 15 ponts) STAT 3340 Assgnment 1 solutons (10) (10) 1. Fnd the equaton of the lne whch passes through the ponts (1,1) and (4,5). β 1 = (5 1)/(4 1) = 4/3 equaton for the lne s y y 0 = β 1 (x x 0
The equation of motion of a dynamical system is given by a set of differential equations. That is (1)
 Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Prof. Dr. I. Nasser Phys 630, T Aug-15 One_dimensional_Ising_Model
 EXACT OE-DIMESIOAL ISIG MODEL The one-dmensonal Isng model conssts of a chan of spns, each spn nteractng only wth ts two nearest neghbors. The smple Isng problem n one dmenson can be solved drectly n several
EXACT OE-DIMESIOAL ISIG MODEL The one-dmensonal Isng model conssts of a chan of spns, each spn nteractng only wth ts two nearest neghbors. The smple Isng problem n one dmenson can be solved drectly n several
Exercise Solutions to Real Analysis
 xercse Solutons to Real Analyss Note: References refer to H. L. Royden, Real Analyss xersze 1. Gven any set A any ɛ > 0, there s an open set O such that A O m O m A + ɛ. Soluton 1. If m A =, then there
xercse Solutons to Real Analyss Note: References refer to H. L. Royden, Real Analyss xersze 1. Gven any set A any ɛ > 0, there s an open set O such that A O m O m A + ɛ. Soluton 1. If m A =, then there
Math 261 Exercise sheet 2
 Math 261 Exercse sheet 2 http://staff.aub.edu.lb/~nm116/teachng/2017/math261/ndex.html Verson: September 25, 2017 Answers are due for Monday 25 September, 11AM. The use of calculators s allowed. Exercse
Math 261 Exercse sheet 2 http://staff.aub.edu.lb/~nm116/teachng/2017/math261/ndex.html Verson: September 25, 2017 Answers are due for Monday 25 September, 11AM. The use of calculators s allowed. Exercse
Summary with Examples for Root finding Methods -Bisection -Newton Raphson -Secant
 Summary wth Eamples or Root ndng Methods -Bsecton -Newton Raphson -Secant Nonlnear Equaton Solvers Bracketng Graphcal Open Methods Bsecton False Poston (Regula-Fals) Newton Raphson Secant All Iteratve
Summary wth Eamples or Root ndng Methods -Bsecton -Newton Raphson -Secant Nonlnear Equaton Solvers Bracketng Graphcal Open Methods Bsecton False Poston (Regula-Fals) Newton Raphson Secant All Iteratve
Linear Feature Engineering 11
 Lnear Feature Engneerng 11 2 Least-Squares 2.1 Smple least-squares Consder the followng dataset. We have a bunch of nputs x and correspondng outputs y. The partcular values n ths dataset are x y 0.23 0.19
Lnear Feature Engneerng 11 2 Least-Squares 2.1 Smple least-squares Consder the followng dataset. We have a bunch of nputs x and correspondng outputs y. The partcular values n ths dataset are x y 0.23 0.19
Physics 4B. A positive value is obtained, so the current is counterclockwise around the circuit.
 Physcs 4B Solutons to Chapter 7 HW Chapter 7: Questons:, 8, 0 Problems:,,, 45, 48,,, 7, 9 Queston 7- (a) no (b) yes (c) all te Queston 7-8 0 μc Queston 7-0, c;, a;, d; 4, b Problem 7- (a) Let be the current
Physcs 4B Solutons to Chapter 7 HW Chapter 7: Questons:, 8, 0 Problems:,,, 45, 48,,, 7, 9 Queston 7- (a) no (b) yes (c) all te Queston 7-8 0 μc Queston 7-0, c;, a;, d; 4, b Problem 7- (a) Let be the current
Applied Stochastic Processes
 STAT455/855 Fall 23 Appled Stochastc Processes Fnal Exam, Bref Solutons 1. (15 marks) (a) (7 marks) The dstrbuton of Y s gven by ( ) ( ) y 2 1 5 P (Y y) for y 2, 3,... The above follows because each of
STAT455/855 Fall 23 Appled Stochastc Processes Fnal Exam, Bref Solutons 1. (15 marks) (a) (7 marks) The dstrbuton of Y s gven by ( ) ( ) y 2 1 5 P (Y y) for y 2, 3,... The above follows because each of
Dynamic Systems on Graphs
 Prepared by F.L. Lews Updated: Saturday, February 06, 200 Dynamc Systems on Graphs Control Graphs and Consensus A network s a set of nodes that collaborates to acheve what each cannot acheve alone. A network,
Prepared by F.L. Lews Updated: Saturday, February 06, 200 Dynamc Systems on Graphs Control Graphs and Consensus A network s a set of nodes that collaborates to acheve what each cannot acheve alone. A network,
Appendix B. Criterion of Riemann-Stieltjes Integrability
 Appendx B. Crteron of Remann-Steltes Integrablty Ths note s complementary to [R, Ch. 6] and [T, Sec. 3.5]. The man result of ths note s Theorem B.3, whch provdes the necessary and suffcent condtons for
Appendx B. Crteron of Remann-Steltes Integrablty Ths note s complementary to [R, Ch. 6] and [T, Sec. 3.5]. The man result of ths note s Theorem B.3, whch provdes the necessary and suffcent condtons for
THE SUMMATION NOTATION Ʃ
 Sngle Subscrpt otaton THE SUMMATIO OTATIO Ʃ Most of the calculatons we perform n statstcs are repettve operatons on lsts of numbers. For example, we compute the sum of a set of numbers, or the sum of the
Sngle Subscrpt otaton THE SUMMATIO OTATIO Ʃ Most of the calculatons we perform n statstcs are repettve operatons on lsts of numbers. For example, we compute the sum of a set of numbers, or the sum of the
If the solution does not follow a logical thought process, it will be assumed in error.
 Group # Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space provded
Group # Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space provded
DUE: WEDS FEB 21ST 2018
 HOMEWORK # 1: FINITE DIFFERENCES IN ONE DIMENSION DUE: WEDS FEB 21ST 2018 1. Theory Beam bendng s a classcal engneerng analyss. The tradtonal soluton technque makes smplfyng assumptons such as a constant
HOMEWORK # 1: FINITE DIFFERENCES IN ONE DIMENSION DUE: WEDS FEB 21ST 2018 1. Theory Beam bendng s a classcal engneerng analyss. The tradtonal soluton technque makes smplfyng assumptons such as a constant
PHYS 705: Classical Mechanics. Calculus of Variations II
 1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
Curvature and isoperimetric inequality
 urvature and sopermetrc nequalty Julà ufí, Agustí Reventós, arlos J Rodríguez Abstract We prove an nequalty nvolvng the length of a plane curve and the ntegral of ts radus of curvature, that has as a consequence
urvature and sopermetrc nequalty Julà ufí, Agustí Reventós, arlos J Rodríguez Abstract We prove an nequalty nvolvng the length of a plane curve and the ntegral of ts radus of curvature, that has as a consequence
Bernoulli Numbers and Polynomials
 Bernoull Numbers and Polynomals T. Muthukumar tmk@tk.ac.n 17 Jun 2014 The sum of frst n natural numbers 1, 2, 3,..., n s n n(n + 1 S 1 (n := m = = n2 2 2 + n 2. Ths formula can be derved by notng that
Bernoull Numbers and Polynomals T. Muthukumar tmk@tk.ac.n 17 Jun 2014 The sum of frst n natural numbers 1, 2, 3,..., n s n n(n + 1 S 1 (n := m = = n2 2 2 + n 2. Ths formula can be derved by notng that
Chapter 8. Potential Energy and Conservation of Energy
 Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
A NOTE ON CES FUNCTIONS Drago Bergholt, BI Norwegian Business School 2011
 A NOTE ON CES FUNCTIONS Drago Bergholt, BI Norwegan Busness School 2011 Functons featurng constant elastcty of substtuton CES are wdely used n appled economcs and fnance. In ths note, I do two thngs. Frst,
A NOTE ON CES FUNCTIONS Drago Bergholt, BI Norwegan Busness School 2011 Functons featurng constant elastcty of substtuton CES are wdely used n appled economcs and fnance. In ths note, I do two thngs. Frst,
Bézier curves. Michael S. Floater. September 10, These notes provide an introduction to Bézier curves. i=0
 Bézer curves Mchael S. Floater September 1, 215 These notes provde an ntroducton to Bézer curves. 1 Bernsten polynomals Recall that a real polynomal of a real varable x R, wth degree n, s a functon of
Bézer curves Mchael S. Floater September 1, 215 These notes provde an ntroducton to Bézer curves. 1 Bernsten polynomals Recall that a real polynomal of a real varable x R, wth degree n, s a functon of
a. (All your answers should be in the letter!
 Econ 301 Blkent Unversty Taskn Econometrcs Department of Economcs Md Term Exam I November 8, 015 Name For each hypothess testng n the exam complete the followng steps: Indcate the test statstc, ts crtcal
Econ 301 Blkent Unversty Taskn Econometrcs Department of Economcs Md Term Exam I November 8, 015 Name For each hypothess testng n the exam complete the followng steps: Indcate the test statstc, ts crtcal
Gravitational Acceleration: A case of constant acceleration (approx. 2 hr.) (6/7/11)
 Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
8.6 The Complex Number System
 8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
Robert Eisberg Second edition CH 09 Multielectron atoms ground states and x-ray excitations
 Quantum Physcs 量 理 Robert Esberg Second edton CH 09 Multelectron atoms ground states and x-ray exctatons 9-01 By gong through the procedure ndcated n the text, develop the tme-ndependent Schroednger equaton
Quantum Physcs 量 理 Robert Esberg Second edton CH 09 Multelectron atoms ground states and x-ray exctatons 9-01 By gong through the procedure ndcated n the text, develop the tme-ndependent Schroednger equaton
Lecture Note 3. Eshelby s Inclusion II
 ME340B Elastcty of Mcroscopc Structures Stanford Unversty Wnter 004 Lecture Note 3. Eshelby s Incluson II Chrs Wenberger and We Ca c All rghts reserved January 6, 004 Contents 1 Incluson energy n an nfnte
ME340B Elastcty of Mcroscopc Structures Stanford Unversty Wnter 004 Lecture Note 3. Eshelby s Incluson II Chrs Wenberger and We Ca c All rghts reserved January 6, 004 Contents 1 Incluson energy n an nfnte
12. The Hamilton-Jacobi Equation Michael Fowler
 1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
Celestial Mechanics. Basic Orbits. Why circles? Tycho Brahe. PHY celestial-mechanics - J. Hedberg
 PHY 454 - celestal-mechancs - J. Hedberg - 207 Celestal Mechancs. Basc Orbts. Why crcles? 2. Tycho Brahe 3. Kepler 4. 3 laws of orbtng bodes 2. Newtonan Mechancs 3. Newton's Laws. Law of Gravtaton 2. The
PHY 454 - celestal-mechancs - J. Hedberg - 207 Celestal Mechancs. Basc Orbts. Why crcles? 2. Tycho Brahe 3. Kepler 4. 3 laws of orbtng bodes 2. Newtonan Mechancs 3. Newton's Laws. Law of Gravtaton 2. The
