Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
|
|
|
- Ashlie Gaines
- 6 years ago
- Views:
Transcription
1 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle at x =.0 m s.0 m/s. What s the acceleraton durng ths tme nterval? A. 4.0 m/s B. 3. m/s C. 6.4 m/s D. 8.0 m/s E. 5.7 m/s Moton n Two Dmensons In two- or three-dmensonal knematcs, everythng s the same as n one-dmensonal moton except that we must now use full vector notaton Postve and negatve sgns are no longer suffcent to determne the drecton Poston and Dsplacement The poston of an object s descrbed by ts poston vector, r The dsplacement of the object s defned as the change n ts poston r r r f Average Velocty The average velocty s the rato of the dsplacement to the tme nterval for the dsplacement r vavg t The drecton of the average velocty s the drecton of the dsplacement vector The average velocty between ponts s ndependent of the path taken Ths s because t s dependent on the dsplacement, also ndependent of the path Instantaneous Velocty The nstantaneous velocty s the lmt of the average velocty as Δt approaches zero r dr v lm t 0 t dt As the tme nterval becomes smaller, the drecton of the dsplacement approaches that of the lne tangent to the curve 1
2 Instantaneous Velocty, cont The drecton of the nstantaneous velocty vector at any pont n a partcle s path s along a lne tangent to the path at that pont and n the drecton of moton The magntude of the nstantaneous velocty vector s the speed The speed s a scalar quantty Average Acceleraton The average acceleraton of a partcle as t moves s defned as the change n the nstantaneous velocty vector dvded by the tme nterval durng whch that change occurs. vf v v aavg t t t f Average Acceleraton, cont As a partcle moves, the drecton of the change n velocty s found by vector subtracton v vf v The average acceleraton s a vector quantty drected along v Instantaneous Acceleraton The nstantaneous acceleraton s the lmtng value of the rato v t as Δt approaches zero lm v dv a t 0 t dt The nstantaneous equals the dervatve of the velocty vector wth respect to tme Producng An Acceleraton Varous changes n a partcle s moton may produce an acceleraton The magntude of the velocty vector may change The drecton of the velocty vector may change Even f the magntude remans constant Both may change smultaneously Knematc Equatons for Two- Dmensonal Moton When the two-dmensonal moton has a constant acceleraton, a seres of equatons can be developed that descrbe the moton These equatons wll be smlar to those of onedmensonal knematcs Moton n two dmensons can be modeled as two ndependent motons n each of the two perpendcular drectons assocated wth the x and y axes Any nfluence n the y drecton does not affect the moton n the x drecton
3 Knematc Equatons, Poston vector for a partcle movng n the xy plane r xˆy ˆj The velocty vector can be found from the poston vector dr v v ˆ ˆ x vyj dt Snce acceleraton s constant, we can also fnd an expresson for the velocty as a functon of tme: v v a f t Knematc Equatons, 3 The poston vector can also be expressed as a functon of tme: r r vt 1 at f Ths ndcates that the poston vector s the sum of three other vectors: The ntal poston vector The dsplacement resultng from the ntal velocty The dsplacement resultng from the acceleraton Knematc Equatons, Graphcal Representaton of Fnal Velocty The velocty vector can be represented by ts components v f s generally not along the drecton of ether v or a Knematc Equatons, Graphcal Representaton of Fnal Poston The vector representaton of the poston vector r s generally not along f the same drecton as v or as a v f and r f are generally not n the same drecton Graphcal Representaton Summary Varous startng postons and ntal veloctes can be chosen Note the relatonshps between changes made n ether the poston or velocty and the resultng effect on the other Lecture Quz A boy on a skate board skates off a horzontal bench at a velocty of 10 m/s. One tenth of a second after he leaves the bench, to two sgnfcant fgures, the magntudes of hs velocty and acceleraton are: A. 10 m/s; 9.8 m/s. B. 9.0 m/s; 9.8 m/s. C. 9.0 m/s; 9.0 m/s. D. 1.0 m/s; 9.0 m/s. E. 1.0 m/s; 9.8 m/s. 3
4 Projectle Moton An object may move n both the x and y drectons smultaneously The form of two-dmensonal moton we wll deal wth s called projectle moton Assumptons of Projectle Moton The free-fall acceleraton s constant over the range of moton It s drected downward Ths s the same as assumng a flat Earth over the range of the moton It s reasonable as long as the range s small compared to the radus of the Earth The effect of ar frcton s neglgble Wth these assumptons, an object n projectle moton wll follow a parabolc path Ths path s called the trajectory Projectle Moton Dagram Clcker Queston If a baseball player throws a ball wth a fxed ntal speed, but wth varable angles, the ball wll move furthest f the angle from horzontal drecton s: A: 0 degrees B: 30 degrees C: 45 degrees D: 60 degrees E: 90 degrees Analyzng Projectle Moton Consder the moton as the superposton of the motons n the x- and y-drectons The actual poston at any tme s gven by: r r v t 1 g t f The ntal velocty can be expressed n terms of ts components v x = v cos and v y = v sn The x-drecton has constant velocty a x = 0 The y-drecton s free fall a y = -g Effects of Changng Intal Condtons The velocty vector components depend on the value of the ntal velocty Change the angle and note the effect Change the magntude and note the effect 4
5 Analyss Model The analyss model s the superposton of two motons Moton of a partcle under constant velocty n the horzontal drecton Moton of a partcle under constant acceleraton n the vertcal drecton Specfcally, free fall Projectle Moton Vectors r r v t 1 g t f The fnal poston s the vector sum of the ntal poston, the poston resultng from the ntal velocty and the poston resultng from the acceleraton Projectle Moton Implcatons The y-component of the velocty s zero at the maxmum heght of the trajectory The acceleraton stays the same throughout the trajectory Range and Maxmum Heght of a Projectle When analyzng projectle moton, two characterstcs are of specal nterest The range, R, s the horzontal dstance of the projectle The maxmum heght the projectle reaches s h Heght of a Projectle, equaton The maxmum heght of the projectle can be found n terms of the ntal velocty vector: v sn h g Ths equaton s vald only for symmetrc moton Range of a Projectle, equaton The range of a projectle can be expressed n terms of the ntal velocty vector: v sn R g Ths s vald only for symmetrc trajectory 5
6 More About the Range of a Projectle Range of a Projectle, fnal The maxmum range occurs at = 45 o Complementary angles wll produce the same range The maxmum heght wll be dfferent for the two angles The tmes of the flght wll be dfferent for the two angles Non-Symmetrc Projectle Moton Follow the general rules for projectle moton Break the y-drecton nto parts up and down or symmetrcal back to ntal heght and then the rest of the heght Apply the problem solvng process to determne and solve the necessary equatons May be non-symmetrc n other ways Unform Crcular Moton Unform crcular moton occurs when an object moves n a crcular path wth a constant speed The assocated analyss moton s a partcle n unform crcular moton An acceleraton exsts snce the drecton of the moton s changng Ths change n velocty s related to an acceleraton The velocty vector s always tangent to the path of the object Clcker Queston A partcle s undergong constant-speed crcular moton, whch of the followng statements s correct? A. The moton velocty s a constant. B. The velocty s perpendcular to acceleraton. C. The velocty s parallel to the dsplacement. D. The acceleraton s perpendcular to dsplacement. E. The acceleraton s perpendcular to the plane of moton. Changng Velocty n Unform Crcular Moton The change n the velocty vector s due to the change n drecton The vector dagram shows v f v v 6
7 Centrpetal Acceleraton The acceleraton s always perpendcular to the path of the moton The acceleraton always ponts toward the center of the crcle of moton Ths acceleraton s called the centrpetal acceleraton Centrpetal Acceleraton, cont The magntude of the centrpetal acceleraton vector s gven by v ac r The drecton of the centrpetal acceleraton vector s always changng, to stay drected toward the center of the crcle of moton Perod The perod, T, s the tme requred for one complete revoluton The speed of the partcle would be the crcumference of the crcle of moton dvded by the perod Therefore, the perod s defned as r T v Tangental Acceleraton The magntude of the velocty could also be changng In ths case, there would be a tangental acceleraton The moton would be under the nfluence of both tangental and centrpetal acceleratons Note the changng acceleraton vectors Total Acceleraton The tangental acceleraton causes the change n the speed of the partcle The radal acceleraton comes from a change n the drecton of the velocty vector Total Acceleraton, equatons dv The tangental acceleraton: at dt v The radal acceleraton: ar ac r The total acceleraton: Magntude a a a r t Drecton Same as velocty vector f v s ncreasng, opposte f v s decreasng 7
8 Relatve Velocty Two observers movng relatve to each other generally do not agree on the outcome of an experment However, the observatons seen by each are related to one another A frame of reference can descrbed by a Cartesan coordnate system for whch an observer s at rest wth respect to the orgn Dfferent Measurements, example Observer A measures pont P at +5 m from the orgn Observer B measures pont P at +10 m from the orgn The dfference s due to the dfferent frames of reference beng used Dfferent Measurements, another example The man s walkng on the movng beltway The woman on the beltway sees the man walkng at hs normal walkng speed The statonary woman sees the man walkng at a much hgher speed The combnaton of the speed of the beltway and the walkng The dfference s due to the relatve velocty of ther frames of reference Relatve Velocty, generalzed Reference frame S A s statonary Reference frame S B s movng to the rght relatve to S A at v AB Ths also means that S A moves at v relatve to BA S B Defne tme t = 0 as that tme when the orgns concde Relatve Velocty, equatons The postons as seen from the two reference frames are related through the velocty r r v t PA PB BA The dervatve of the poston equaton wll gve the velocty equaton u PA u u PB v BA s the velocty of the partcle P measured by observer A PA u s the velocty of the partcle P measured by observer B PB These are called the Gallean transformaton equatons Acceleraton n Dfferent Frames of Reference The dervatve of the velocty equaton wll gve the acceleraton equaton The acceleraton of the partcle measured by an observer n one frame of reference s the same as that measured by any other observer movng at a constant velocty relatve to the frst frame. 8
Chapter 3. r r. Position, Velocity, and Acceleration Revisited
 Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Slide. King Saud University College of Science Physics & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART 2) LECTURE NO.
 Slde Kng Saud Unersty College of Scence Physcs & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART ) LECTURE NO. 6 THIS PRESENTATION HAS BEEN PREPARED BY: DR. NASSR S. ALZAYED Lecture
Slde Kng Saud Unersty College of Scence Physcs & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART ) LECTURE NO. 6 THIS PRESENTATION HAS BEEN PREPARED BY: DR. NASSR S. ALZAYED Lecture
Week 11: Chapter 11. The Vector Product. The Vector Product Defined. The Vector Product and Torque. More About the Vector Product
 The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
Physics 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn in the following problems from Chapter 4 Knight
 Physcs 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn n the ollowng problems rom Chapter 4 Knght Conceptual Questons: 8, 0, ; 4.8. Anta s approachng ball and movng away rom where ball was
Physcs 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn n the ollowng problems rom Chapter 4 Knght Conceptual Questons: 8, 0, ; 4.8. Anta s approachng ball and movng away rom where ball was
11. Dynamics in Rotating Frames of Reference
 Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
Week 8: Chapter 9. Linear Momentum. Newton Law and Momentum. Linear Momentum, cont. Conservation of Linear Momentum. Conservation of Momentum, 2
 Lnear omentum Week 8: Chapter 9 Lnear omentum and Collsons The lnear momentum of a partcle, or an object that can be modeled as a partcle, of mass m movng wth a velocty v s defned to be the product of
Lnear omentum Week 8: Chapter 9 Lnear omentum and Collsons The lnear momentum of a partcle, or an object that can be modeled as a partcle, of mass m movng wth a velocty v s defned to be the product of
Physics 2A Chapter 3 HW Solutions
 Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Week 6, Chapter 7 Sect 1-5
 Week 6, Chapter 7 Sect 1-5 Work and Knetc Energy Lecture Quz The frctonal force of the floor on a large sutcase s least when the sutcase s A.pushed by a force parallel to the floor. B.dragged by a force
Week 6, Chapter 7 Sect 1-5 Work and Knetc Energy Lecture Quz The frctonal force of the floor on a large sutcase s least when the sutcase s A.pushed by a force parallel to the floor. B.dragged by a force
= 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W]
![= 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W] = 1.23 m/s 2 [W] Required: t. Solution:!t = = 17 m/s [W]! m/s [W] (two extra digits carried) = 2.1 m/s [W]](/thumbs/78/76802454.jpg) Secton 1.3: Acceleraton Tutoral 1 Practce, page 24 1. Gven: 0 m/s; 15.0 m/s [S]; t 12.5 s Requred: Analyss: a av v t v f v t a v av f v t 15.0 m/s [S] 0 m/s 12.5 s 15.0 m/s [S] 12.5 s 1.20 m/s 2 [S] Statement:
Secton 1.3: Acceleraton Tutoral 1 Practce, page 24 1. Gven: 0 m/s; 15.0 m/s [S]; t 12.5 s Requred: Analyss: a av v t v f v t a v av f v t 15.0 m/s [S] 0 m/s 12.5 s 15.0 m/s [S] 12.5 s 1.20 m/s 2 [S] Statement:
Chapter 2. Pythagorean Theorem. Right Hand Rule. Position. Distance Formula
 Chapter Moton n One Dmenson Cartesan Coordnate System The most common coordnate system or representng postons n space s one based on three perpendcular spatal axes generally desgnated x, y, and z. Any
Chapter Moton n One Dmenson Cartesan Coordnate System The most common coordnate system or representng postons n space s one based on three perpendcular spatal axes generally desgnated x, y, and z. Any
Physics 111: Mechanics Lecture 11
 Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Chapter 11 Angular Momentum
 Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
Name: PHYS 110 Dr. McGovern Spring 2018 Exam 1. Multiple Choice: Circle the answer that best evaluates the statement or completes the statement.
 Name: PHYS 110 Dr. McGoern Sprng 018 Exam 1 Multple Choce: Crcle the answer that best ealuates the statement or completes the statement. #1 - I the acceleraton o an object s negate, the object must be
Name: PHYS 110 Dr. McGoern Sprng 018 Exam 1 Multple Choce: Crcle the answer that best ealuates the statement or completes the statement. #1 - I the acceleraton o an object s negate, the object must be
coordinates. Then, the position vectors are described by
 Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
Work is the change in energy of a system (neglecting heat transfer). To examine what could
 Work Work s the change n energy o a system (neglectng heat transer). To eamne what could cause work, let s look at the dmensons o energy: L ML E M L F L so T T dmensonally energy s equal to a orce tmes
Work Work s the change n energy o a system (neglectng heat transer). To eamne what could cause work, let s look at the dmensons o energy: L ML E M L F L so T T dmensonally energy s equal to a orce tmes
So far: simple (planar) geometries
 Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Part C Dynamics and Statics of Rigid Body. Chapter 5 Rotation of a Rigid Body About a Fixed Axis
 Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Mathematical Preparations
 1 Introducton Mathematcal Preparatons The theory of relatvty was developed to explan experments whch studed the propagaton of electromagnetc radaton n movng coordnate systems. Wthn expermental error the
1 Introducton Mathematcal Preparatons The theory of relatvty was developed to explan experments whch studed the propagaton of electromagnetc radaton n movng coordnate systems. Wthn expermental error the
Spring 2002 Lecture #13
 44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
First Law: A body at rest remains at rest, a body in motion continues to move at constant velocity, unless acted upon by an external force.
 Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
PHYSICS 203-NYA-05 MECHANICS
 PHYSICS 03-NYA-05 MECHANICS PROF. S.D. MANOLI PHYSICS & CHEMISTRY CHAMPLAIN - ST. LAWRENCE 790 NÉRÉE-TREMBLAY QUÉBEC, QC GV 4K TELEPHONE: 48.656.69 EXT. 449 EMAIL: smanol@slc.qc.ca WEBPAGE: http:/web.slc.qc.ca/smanol/
PHYSICS 03-NYA-05 MECHANICS PROF. S.D. MANOLI PHYSICS & CHEMISTRY CHAMPLAIN - ST. LAWRENCE 790 NÉRÉE-TREMBLAY QUÉBEC, QC GV 4K TELEPHONE: 48.656.69 EXT. 449 EMAIL: smanol@slc.qc.ca WEBPAGE: http:/web.slc.qc.ca/smanol/
ENGN 40 Dynamics and Vibrations Homework # 7 Due: Friday, April 15
 NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
Physics 207 Lecture 6
 Physcs 207 Lecture 6 Agenda: Physcs 207, Lecture 6, Sept. 25 Chapter 4 Frames of reference Chapter 5 ewton s Law Mass Inerta s (contact and non-contact) Frcton (a external force that opposes moton) Free
Physcs 207 Lecture 6 Agenda: Physcs 207, Lecture 6, Sept. 25 Chapter 4 Frames of reference Chapter 5 ewton s Law Mass Inerta s (contact and non-contact) Frcton (a external force that opposes moton) Free
Physics 207 Lecture 13. Lecture 13
 Physcs 07 Lecture 3 Goals: Lecture 3 Chapter 0 Understand the relatonshp between moton and energy Defne Potental Energy n a Hooke s Law sprng Develop and explot conservaton of energy prncple n problem
Physcs 07 Lecture 3 Goals: Lecture 3 Chapter 0 Understand the relatonshp between moton and energy Defne Potental Energy n a Hooke s Law sprng Develop and explot conservaton of energy prncple n problem
Displacement at any time. Velocity at any displacement in the x-direction u 2 = v ] + 2 a x ( )
![Displacement at any time. Velocity at any displacement in the x-direction u 2 = v ] + 2 a x ( ) Displacement at any time. Velocity at any displacement in the x-direction u 2 = v ] + 2 a x ( )](/thumbs/89/97691613.jpg) The Language of Physcs Knematcs The branch of mechancs that descrbes the moton of a body wthout regard to the cause of that moton (p. 39). Average velocty The average rate at whch the dsplacement vector
The Language of Physcs Knematcs The branch of mechancs that descrbes the moton of a body wthout regard to the cause of that moton (p. 39). Average velocty The average rate at whch the dsplacement vector
Physics 114 Exam 3 Spring Name:
 Physcs 114 Exam 3 Sprng 015 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem 4. Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse
Physcs 114 Exam 3 Sprng 015 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem 4. Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse
Physics 207: Lecture 20. Today s Agenda Homework for Monday
 Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
CHAPTER 10 ROTATIONAL MOTION
 CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
Chapter 8. Potential Energy and Conservation of Energy
 Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Linear Momentum. Center of Mass.
 Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
EN40: Dynamics and Vibrations. Homework 7: Rigid Body Kinematics
 N40: ynamcs and Vbratons Homewor 7: Rgd Body Knematcs School of ngneerng Brown Unversty 1. In the fgure below, bar AB rotates counterclocwse at 4 rad/s. What are the angular veloctes of bars BC and C?.
N40: ynamcs and Vbratons Homewor 7: Rgd Body Knematcs School of ngneerng Brown Unversty 1. In the fgure below, bar AB rotates counterclocwse at 4 rad/s. What are the angular veloctes of bars BC and C?.
CHAPTER 6. LAGRANGE S EQUATIONS (Analytical Mechanics)
 CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
Gravitational Acceleration: A case of constant acceleration (approx. 2 hr.) (6/7/11)
 Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Gravtatonal Acceleraton: A case of constant acceleraton (approx. hr.) (6/7/11) Introducton The gravtatonal force s one of the fundamental forces of nature. Under the nfluence of ths force all objects havng
Kinematics of Fluids. Lecture 16. (Refer the text book CONTINUUM MECHANICS by GEORGE E. MASE, Schaum s Outlines) 17/02/2017
 17/0/017 Lecture 16 (Refer the text boo CONTINUUM MECHANICS by GEORGE E. MASE, Schaum s Outlnes) Knematcs of Fluds Last class, we started dscussng about the nematcs of fluds. Recall the Lagrangan and Euleran
17/0/017 Lecture 16 (Refer the text boo CONTINUUM MECHANICS by GEORGE E. MASE, Schaum s Outlnes) Knematcs of Fluds Last class, we started dscussng about the nematcs of fluds. Recall the Lagrangan and Euleran
Physics 5153 Classical Mechanics. D Alembert s Principle and The Lagrangian-1
 P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
Conservation of Angular Momentum = "Spin"
 Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
PY2101 Classical Mechanics Dr. Síle Nic Chormaic, Room 215 D Kane Bldg
 PY2101 Classcal Mechancs Dr. Síle Nc Chormac, Room 215 D Kane Bldg s.ncchormac@ucc.e Lectures stll some ssues to resolve. Slots shared between PY2101 and PY2104. Hope to have t fnalsed by tomorrow. Mondays
PY2101 Classcal Mechancs Dr. Síle Nc Chormac, Room 215 D Kane Bldg s.ncchormac@ucc.e Lectures stll some ssues to resolve. Slots shared between PY2101 and PY2104. Hope to have t fnalsed by tomorrow. Mondays
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM
 ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
Physics for Scientists & Engineers 2
 Equpotental Surfaces and Lnes Physcs for Scentsts & Engneers 2 Sprng Semester 2005 Lecture 9 January 25, 2005 Physcs for Scentsts&Engneers 2 1 When an electrc feld s present, the electrc potental has a
Equpotental Surfaces and Lnes Physcs for Scentsts & Engneers 2 Sprng Semester 2005 Lecture 9 January 25, 2005 Physcs for Scentsts&Engneers 2 1 When an electrc feld s present, the electrc potental has a
Study Guide For Exam Two
 Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
Physics 181. Particle Systems
 Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Rotational Dynamics. Physics 1425 Lecture 19. Michael Fowler, UVa
 Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Supplemental Instruction sessions next week
 Homework #4 Wrtten homework due now Onlne homework due on Tue Mar 3 by 8 am Exam 1 Answer keys and scores wll be posted by end of the week Supplemental Instructon sessons next week Wednesday 8:45 10:00
Homework #4 Wrtten homework due now Onlne homework due on Tue Mar 3 by 8 am Exam 1 Answer keys and scores wll be posted by end of the week Supplemental Instructon sessons next week Wednesday 8:45 10:00
Chapter 20 Rigid Body: Translation and Rotational Motion Kinematics for Fixed Axis Rotation
 Chapter 20 Rgd Body: Translaton and Rotatonal Moton Knematcs for Fxed Axs Rotaton 20.1 Introducton... 1 20.2 Constraned Moton: Translaton and Rotaton... 1 20.2.1 Rollng wthout slppng... 5 Example 20.1
Chapter 20 Rgd Body: Translaton and Rotatonal Moton Knematcs for Fxed Axs Rotaton 20.1 Introducton... 1 20.2 Constraned Moton: Translaton and Rotaton... 1 20.2.1 Rollng wthout slppng... 5 Example 20.1
Motion in One Dimension
 Moton n One Dmenson Speed ds tan ce traeled Aerage Speed tme of trael Mr. Wolf dres hs car on a long trp to a physcs store. Gen the dstance and tme data for hs trp, plot a graph of hs dstance ersus tme.
Moton n One Dmenson Speed ds tan ce traeled Aerage Speed tme of trael Mr. Wolf dres hs car on a long trp to a physcs store. Gen the dstance and tme data for hs trp, plot a graph of hs dstance ersus tme.
Physics 53. Rotational Motion 3. Sir, I have found you an argument, but I am not obliged to find you an understanding.
 Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Celestial Mechanics. Basic Orbits. Why circles? Tycho Brahe. PHY celestial-mechanics - J. Hedberg
 PHY 454 - celestal-mechancs - J. Hedberg - 207 Celestal Mechancs. Basc Orbts. Why crcles? 2. Tycho Brahe 3. Kepler 4. 3 laws of orbtng bodes 2. Newtonan Mechancs 3. Newton's Laws. Law of Gravtaton 2. The
PHY 454 - celestal-mechancs - J. Hedberg - 207 Celestal Mechancs. Basc Orbts. Why crcles? 2. Tycho Brahe 3. Kepler 4. 3 laws of orbtng bodes 2. Newtonan Mechancs 3. Newton's Laws. Law of Gravtaton 2. The
Physics 141. Lecture 14. Frank L. H. Wolfs Department of Physics and Astronomy, University of Rochester, Lecture 14, Page 1
 Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
A Tale of Friction Basic Rollercoaster Physics. Fahrenheit Rollercoaster, Hershey, PA max height = 121 ft max speed = 58 mph
 A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
Chapter 10 Rotational motion
 Prof. Dr. I. Nasser Chapter0_I November 6, 07 Important Terms Chapter 0 Rotatonal moton Angular Dsplacement s, r n radans where s s the length of arc and r s the radus. Angular Velocty The rate at whch
Prof. Dr. I. Nasser Chapter0_I November 6, 07 Important Terms Chapter 0 Rotatonal moton Angular Dsplacement s, r n radans where s s the length of arc and r s the radus. Angular Velocty The rate at whch
χ x B E (c) Figure 2.1.1: (a) a material particle in a body, (b) a place in space, (c) a configuration of the body
 Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
GAUTENG DEPARTMENT OF EDUCATION SENIOR SECONDARY INTERVENTION PROGRAMME PHYSICAL SCIENCES GRADE 12 SESSION 1 (LEARNER NOTES)
 PHYSICAL SCIENCES GRADE 1 SESSION 1 (LEARNER NOTES) TOPIC 1: MECHANICS PROJECTILE MOTION Learner Note: Always draw a dagram of the stuaton and enter all the numercal alues onto your dagram. Remember to
PHYSICAL SCIENCES GRADE 1 SESSION 1 (LEARNER NOTES) TOPIC 1: MECHANICS PROJECTILE MOTION Learner Note: Always draw a dagram of the stuaton and enter all the numercal alues onto your dagram. Remember to
PHYS 1443 Section 003 Lecture #17
 PHYS 144 Secton 00 ecture #17 Wednesda, Oct. 9, 00 1. Rollng oton of a Rgd od. Torque. oment of Inerta 4. Rotatonal Knetc Energ 5. Torque and Vector Products Remember the nd term eam (ch 6 11), onda, Nov.!
PHYS 144 Secton 00 ecture #17 Wednesda, Oct. 9, 00 1. Rollng oton of a Rgd od. Torque. oment of Inerta 4. Rotatonal Knetc Energ 5. Torque and Vector Products Remember the nd term eam (ch 6 11), onda, Nov.!
Spin-rotation coupling of the angularly accelerated rigid body
 Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
PHYSICS - CLUTCH CH 28: INDUCTION AND INDUCTANCE.
 !! www.clutchprep.com CONCEPT: ELECTROMAGNETIC INDUCTION A col of wre wth a VOLTAGE across each end wll have a current n t - Wre doesn t HAVE to have voltage source, voltage can be INDUCED V Common ways
!! www.clutchprep.com CONCEPT: ELECTROMAGNETIC INDUCTION A col of wre wth a VOLTAGE across each end wll have a current n t - Wre doesn t HAVE to have voltage source, voltage can be INDUCED V Common ways
Angular Momentum and Fixed Axis Rotation. 8.01t Nov 10, 2004
 Angular Momentum and Fxed Axs Rotaton 8.01t Nov 10, 2004 Dynamcs: Translatonal and Rotatonal Moton Translatonal Dynamcs Total Force Torque Angular Momentum about Dynamcs of Rotaton F ext Momentum of a
Angular Momentum and Fxed Axs Rotaton 8.01t Nov 10, 2004 Dynamcs: Translatonal and Rotatonal Moton Translatonal Dynamcs Total Force Torque Angular Momentum about Dynamcs of Rotaton F ext Momentum of a
Problem While being compressed, A) What is the work done on it by gravity? B) What is the work done on it by the spring force?
 Problem 07-50 A 0.25 kg block s dropped on a relaed sprng that has a sprng constant o k 250.0 N/m (2.5 N/cm). The block becomes attached to the sprng and compresses t 0.12 m beore momentarl stoppng. Whle
Problem 07-50 A 0.25 kg block s dropped on a relaed sprng that has a sprng constant o k 250.0 N/m (2.5 N/cm). The block becomes attached to the sprng and compresses t 0.12 m beore momentarl stoppng. Whle
Physics for Scientists and Engineers. Chapter 9 Impulse and Momentum
 Physcs or Scentsts and Engneers Chapter 9 Impulse and Momentum Sprng, 008 Ho Jung Pak Lnear Momentum Lnear momentum o an object o mass m movng wth a velocty v s dened to be p mv Momentum and lnear momentum
Physcs or Scentsts and Engneers Chapter 9 Impulse and Momentum Sprng, 008 Ho Jung Pak Lnear Momentum Lnear momentum o an object o mass m movng wth a velocty v s dened to be p mv Momentum and lnear momentum
10/9/2003 PHY Lecture 11 1
 Announcements 1. Physc Colloquum today --The Physcs and Analyss of Non-nvasve Optcal Imagng. Today s lecture Bref revew of momentum & collsons Example HW problems Introducton to rotatons Defnton of angular
Announcements 1. Physc Colloquum today --The Physcs and Analyss of Non-nvasve Optcal Imagng. Today s lecture Bref revew of momentum & collsons Example HW problems Introducton to rotatons Defnton of angular
AP Physics 1 & 2 Summer Assignment
 AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
Section 8.1 Exercises
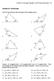 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
The equation of motion of a dynamical system is given by a set of differential equations. That is (1)
 Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Mechanics Physics 151
 Mechancs Physcs 151 Lecture 3 Lagrange s Equatons (Goldsten Chapter 1) Hamlton s Prncple (Chapter 2) What We Dd Last Tme! Dscussed mult-partcle systems! Internal and external forces! Laws of acton and
Mechancs Physcs 151 Lecture 3 Lagrange s Equatons (Goldsten Chapter 1) Hamlton s Prncple (Chapter 2) What We Dd Last Tme! Dscussed mult-partcle systems! Internal and external forces! Laws of acton and
Spring Force and Power
 Lecture 13 Chapter 9 Sprng Force and Power Yeah, energy s better than orces. What s net? Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi IN THIS CHAPTER, you wll learn how to solve problems
Lecture 13 Chapter 9 Sprng Force and Power Yeah, energy s better than orces. What s net? Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi IN THIS CHAPTER, you wll learn how to solve problems
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
Kinematics in 2-Dimensions. Projectile Motion
 Knematcs n -Dmensons Projectle Moton A medeval trebuchet b Kolderer, c1507 http://members.net.net.au/~rmne/ht/ht0.html#5 Readng Assgnment: Chapter 4, Sectons -6 Introducton: In medeval das, people had
Knematcs n -Dmensons Projectle Moton A medeval trebuchet b Kolderer, c1507 http://members.net.net.au/~rmne/ht/ht0.html#5 Readng Assgnment: Chapter 4, Sectons -6 Introducton: In medeval das, people had
Classical Mechanics Virtual Work & d Alembert s Principle
 Classcal Mechancs Vrtual Work & d Alembert s Prncple Dpan Kumar Ghosh UM-DAE Centre for Excellence n Basc Scences Kalna, Mumba 400098 August 15, 2016 1 Constrants Moton of a system of partcles s often
Classcal Mechancs Vrtual Work & d Alembert s Prncple Dpan Kumar Ghosh UM-DAE Centre for Excellence n Basc Scences Kalna, Mumba 400098 August 15, 2016 1 Constrants Moton of a system of partcles s often
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Important Dates: Post Test: Dec during recitations. If you have taken the post test, don t come to recitation!
 Important Dates: Post Test: Dec. 8 0 durng rectatons. If you have taken the post test, don t come to rectaton! Post Test Make-Up Sessons n ARC 03: Sat Dec. 6, 0 AM noon, and Sun Dec. 7, 8 PM 0 PM. Post
Important Dates: Post Test: Dec. 8 0 durng rectatons. If you have taken the post test, don t come to rectaton! Post Test Make-Up Sessons n ARC 03: Sat Dec. 6, 0 AM noon, and Sun Dec. 7, 8 PM 0 PM. Post
EN40: Dynamics and Vibrations. Homework 4: Work, Energy and Linear Momentum Due Friday March 1 st
 EN40: Dynamcs and bratons Homework 4: Work, Energy and Lnear Momentum Due Frday March 1 st School of Engneerng Brown Unversty 1. The fgure (from ths publcaton) shows the energy per unt area requred to
EN40: Dynamcs and bratons Homework 4: Work, Energy and Lnear Momentum Due Frday March 1 st School of Engneerng Brown Unversty 1. The fgure (from ths publcaton) shows the energy per unt area requred to
Physics 114 Exam 2 Fall 2014 Solutions. Name:
 Physcs 114 Exam Fall 014 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse ndcated,
Physcs 114 Exam Fall 014 Name: For gradng purposes (do not wrte here): Queston 1. 1... 3. 3. Problem Answer each of the followng questons. Ponts for each queston are ndcated n red. Unless otherwse ndcated,
LAB # 4 - Torque. d (1)
 LAB # 4 - Torque. Introducton Through the use of Newton's three laws of moton, t s possble (n prncple, f not n fact) to predct the moton of any set of partcles. That s, n order to descrbe the moton of
LAB # 4 - Torque. Introducton Through the use of Newton's three laws of moton, t s possble (n prncple, f not n fact) to predct the moton of any set of partcles. That s, n order to descrbe the moton of
SCALARS AND VECTORS All physical quantities in engineering mechanics are measured using either scalars or vectors.
 SCALARS AND ECTORS All phscal uanttes n engneerng mechancs are measured usng ether scalars or vectors. Scalar. A scalar s an postve or negatve phscal uantt that can be completel specfed b ts magntude.
SCALARS AND ECTORS All phscal uanttes n engneerng mechancs are measured usng ether scalars or vectors. Scalar. A scalar s an postve or negatve phscal uantt that can be completel specfed b ts magntude.
Modeling of Dynamic Systems
 Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
ACTM State Calculus Competition Saturday April 30, 2011
 ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
12. The Hamilton-Jacobi Equation Michael Fowler
 1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
The classical spin-rotation coupling
 LOUAI H. ELZEIN 2018 All Rghts Reserved The classcal spn-rotaton couplng Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 louaelzen@gmal.com Abstract Ths paper s prepared to show that a rgd
LOUAI H. ELZEIN 2018 All Rghts Reserved The classcal spn-rotaton couplng Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 louaelzen@gmal.com Abstract Ths paper s prepared to show that a rgd
where v means the change in velocity, and t is the
 1 PHYS:100 LECTURE 4 MECHANICS (3) Ths lecture covers the eneral case of moton wth constant acceleraton and free fall (whch s one of the more mportant examples of moton wth constant acceleraton) n a more
1 PHYS:100 LECTURE 4 MECHANICS (3) Ths lecture covers the eneral case of moton wth constant acceleraton and free fall (whch s one of the more mportant examples of moton wth constant acceleraton) n a more
Georgia Tech PHYS 6124 Mathematical Methods of Physics I
 Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
N S. 4/4/2006 Magnetic Fields ( F.Robilliard) 1
 y F N +q + θ S v x z 4/4/6 Magnetc Felds ( F.obllard) 1 4/4/6 Magnetc Felds ( F.obllard) Introducton: It has been known, snce antquty, that when certan peces of rock are hung by a thread, from ther centre
y F N +q + θ S v x z 4/4/6 Magnetc Felds ( F.obllard) 1 4/4/6 Magnetc Felds ( F.obllard) Introducton: It has been known, snce antquty, that when certan peces of rock are hung by a thread, from ther centre
Physics 2A Chapters 6 - Work & Energy Fall 2017
 Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
measurement and the charge the electric field will be calculated using E =. The direction of the field will be the . But, so
 THE ELECTRIC FIELD 6 Conceptual Questons 6.. A tny, postve test charge wll be placed at the pont n space and the force wll be measured. From the force F measurement and the charge the electrc feld wll
THE ELECTRIC FIELD 6 Conceptual Questons 6.. A tny, postve test charge wll be placed at the pont n space and the force wll be measured. From the force F measurement and the charge the electrc feld wll
PHYSICS - CLUTCH 1E CH 28: INDUCTION AND INDUCTANCE.
 !! www.clutchprep.com CONCEPT: ELECTROMAGNETIC INDUCTION A col of wre wth a VOLTAGE across each end wll have a current n t - Wre doesn t HAVE to have voltage source, voltage can be INDUCED V Common ways
!! www.clutchprep.com CONCEPT: ELECTROMAGNETIC INDUCTION A col of wre wth a VOLTAGE across each end wll have a current n t - Wre doesn t HAVE to have voltage source, voltage can be INDUCED V Common ways
Inner Product. Euclidean Space. Orthonormal Basis. Orthogonal
 Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
An Algorithm to Solve the Inverse Kinematics Problem of a Robotic Manipulator Based on Rotation Vectors
 An Algorthm to Solve the Inverse Knematcs Problem of a Robotc Manpulator Based on Rotaton Vectors Mohamad Z. Al-az*, Mazn Z. Othman**, and Baker B. Al-Bahr* *AL-Nahran Unversty, Computer Eng. Dep., Baghdad,
An Algorthm to Solve the Inverse Knematcs Problem of a Robotc Manpulator Based on Rotaton Vectors Mohamad Z. Al-az*, Mazn Z. Othman**, and Baker B. Al-Bahr* *AL-Nahran Unversty, Computer Eng. Dep., Baghdad,
Module 1 : The equation of continuity. Lecture 1: Equation of Continuity
 1 Module 1 : The equaton of contnuty Lecture 1: Equaton of Contnuty 2 Advanced Heat and Mass Transfer: Modules 1. THE EQUATION OF CONTINUITY : Lectures 1-6 () () () (v) (v) Overall Mass Balance Momentum
1 Module 1 : The equaton of contnuty Lecture 1: Equaton of Contnuty 2 Advanced Heat and Mass Transfer: Modules 1. THE EQUATION OF CONTINUITY : Lectures 1-6 () () () (v) (v) Overall Mass Balance Momentum
From Biot-Savart Law to Divergence of B (1)
 From Bot-Savart Law to Dvergence of B (1) Let s prove that Bot-Savart gves us B (r ) = 0 for an arbtrary current densty. Frst take the dvergence of both sdes of Bot-Savart. The dervatve s wth respect to
From Bot-Savart Law to Dvergence of B (1) Let s prove that Bot-Savart gves us B (r ) = 0 for an arbtrary current densty. Frst take the dvergence of both sdes of Bot-Savart. The dervatve s wth respect to
Indeterminate pin-jointed frames (trusses)
 Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
3.1 Expectation of Functions of Several Random Variables. )' be a k-dimensional discrete or continuous random vector, with joint PMF p (, E X E X1 E X
 Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
PHYS 705: Classical Mechanics. Calculus of Variations II
 1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
MEV442 Introduction to Robotics Module 2. Dr. Santhakumar Mohan Assistant Professor Mechanical Engineering National Institute of Technology Calicut
 MEV442 Introducton to Robotcs Module 2 Dr. Santhakumar Mohan Assstant Professor Mechancal Engneerng Natonal Insttute of Technology Calcut Jacobans: Veloctes and statc forces Introducton Notaton for tme-varyng
MEV442 Introducton to Robotcs Module 2 Dr. Santhakumar Mohan Assstant Professor Mechancal Engneerng Natonal Insttute of Technology Calcut Jacobans: Veloctes and statc forces Introducton Notaton for tme-varyng
PHYS 1441 Section 001 Lecture #15 Wednesday, July 8, 2015
 PHYS 1441 Secton 001 Lecture #15 Wednesday, July 8, 2015 Concept of the Center of Mass Center of Mass & Center of Gravty Fundamentals of the Rotatonal Moton Rotatonal Knematcs Equatons of Rotatonal Knematcs
PHYS 1441 Secton 001 Lecture #15 Wednesday, July 8, 2015 Concept of the Center of Mass Center of Mass & Center of Gravty Fundamentals of the Rotatonal Moton Rotatonal Knematcs Equatons of Rotatonal Knematcs
Page 1. Physics 131: Lecture 14. Today s Agenda. Things that stay the same. Impulse and Momentum Non-constant forces
 Physcs 131: Lecture 14 Today s Agenda Imulse and Momentum Non-constant forces Imulse-momentum momentum thm Conservaton of Lnear momentum Eternal/Internal forces Eamles Physcs 201: Lecture 1, Pg 1 Physcs
Physcs 131: Lecture 14 Today s Agenda Imulse and Momentum Non-constant forces Imulse-momentum momentum thm Conservaton of Lnear momentum Eternal/Internal forces Eamles Physcs 201: Lecture 1, Pg 1 Physcs
Physics 106a, Caltech 11 October, Lecture 4: Constraints, Virtual Work, etc. Constraints
 Physcs 106a, Caltech 11 October, 2018 Lecture 4: Constrants, Vrtual Work, etc. Many, f not all, dynamcal problems we want to solve are constraned: not all of the possble 3 coordnates for M partcles (or
Physcs 106a, Caltech 11 October, 2018 Lecture 4: Constrants, Vrtual Work, etc. Many, f not all, dynamcal problems we want to solve are constraned: not all of the possble 3 coordnates for M partcles (or
CHAPTER 14 GENERAL PERTURBATION THEORY
 CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
CONDUCTORS AND INSULATORS
 CONDUCTORS AND INSULATORS We defne a conductor as a materal n whch charges are free to move over macroscopc dstances.e., they can leave ther nucle and move around the materal. An nsulator s anythng else.
CONDUCTORS AND INSULATORS We defne a conductor as a materal n whch charges are free to move over macroscopc dstances.e., they can leave ther nucle and move around the materal. An nsulator s anythng else.
