T f. Geometry. R f. R i. Homogeneous transformation. y x. P f. f 000. Homogeneous transformation matrix. R (A): Orientation P : Position
|
|
|
- Shana Harmon
- 5 years ago
- Views:
Transcription
1 Homogeneous transformaton Geometr T f R f R T f Homogeneous transformaton matr Unverst of Genova T f Phlppe Martnet = R f 000 P f 1 R (A): Orentaton P : Poston 123 Modelng and Control of Manpulator robots
2 124 Modelng and Control of Manpulator robots Phlppe Martnet Unverst of Genova Homogeneous transformaton Geometr Consder a 3D pont n space R f R 1 f T 1 = R f 1 Then f P f R R f R + =
3 Homogeneous transformaton Geometr T f Homogeneous transformaton matr Dfferent representatons R : Orentaton s, n, a Cosnus drectors RPY angles (Roll (), Ptch(), Yaw()) Brant angles (,,) Euler angles (,,) u.θ, u.sn(θ), u.sn(θ/2 θ/2), P : Poston Cartesan coordnates Clndrcal coordnates Sphercal coordnates Quaternon λ 1, λ 2, λ 3, λ 4 Unverst of Genova Phlppe Martnet 125 Modelng and Control of Manpulator robots
4 Homogeneous transformaton Geometr T f Homogeneous transformaton matr Dfferent representatons (.e) R : Orentaton s, n, a Drector Cosnus P : Poston Cartesan coordnates R s = s s n n n a a a P = P P P No rotaton No translaton P=(0,0,0) T Unverst of Genova Phlppe Martnet 126 Modelng and Control of Manpulator robots
5 Homogeneous transformaton Geometr T f Homogeneous transformaton matr Man propertes of the rotaton matr R : Orentaton s, n, a Drector Cosnus s = n = a = s n = 0 s 1 n = a s R= s s n n n a a a s a a n 1 T R = R = = 0 0 n a a s = = s n Unverst of Genova Phlppe Martnet 127 Modelng and Control of Manpulator robots
6 Geometr Homogeneous transformaton: Rotaton matr R f Rotaton matr Rot(,θ ) Matr to change the frame for one vector Unverst of Genova Phlppe Martnet 128 Modelng and Control of Manpulator robots
7 Geometr Homogeneous transformaton: Rotaton matr R f Rotaton matr Rot(,θ ) Unverst of Genova Phlppe Martnet 129 Modelng and Control of Manpulator robots
8 Geometr Homogeneous transformaton: Rotaton matr R f Rotaton matr Rot(,θ ) Unverst of Genova Phlppe Martnet 130 Modelng and Control of Manpulator robots
9 Homogeneous transformaton propertes Geometr T f Homogeneous transformaton matr Prop. 1) Prop. 2) Unverst of Genova Phlppe Martnet 131 Modelng and Control of Manpulator robots
10 Homogeneous transformaton propertes Geometr T f Homogeneous transformaton matr Prop. 3) Prop. 4) Unverst of Genova Phlppe Martnet 132 Modelng and Control of Manpulator robots
11 Homogeneous transformaton propertes Geometr T f Homogeneous transformaton matr Prop. 5) Prop. 6) Unverst of Genova Phlppe Martnet 133 Modelng and Control of Manpulator robots
12 Homogeneous transformaton propertes Geometr T f Homogeneous transformaton matr T s defned n R Prop. 7) T s defned n R j Unverst of Genova Phlppe Martnet 134 Modelng and Control of Manpulator robots
13 Homogeneous transformaton propertes Geometr T f Homogeneous transformaton matr Unverst of Genova Phlppe Martnet 135 Modelng and Control of Manpulator robots
14 Homogeneous transformaton propertes Geometr T f Homogeneous transformaton matr Prop. 8) Unverst of Genova Phlppe Martnet 136 Modelng and Control of Manpulator robots
15 Rgd bod pose parameteraton: poston Cartesan coordnates Unverst of Genova Phlppe Martnet 137 Modelng and Control of Manpulator robots
16 Rgd bod pose parameteraton: poston Clndrcal coordnates Sngulart : P=P=0 Unverst of Genova Phlppe Martnet 138 Modelng and Control of Manpulator robots
17 Rgd bod pose parameteraton: poston Sphercal coordnates f or f f or f Unverst of Genova Phlppe Martnet 139 Modelng and Control of Manpulator robots
18 Rgd bod pose parameteraton: orentaton Euler angles or Remarks: Euler angles can be defned also b (,,) Unverst of Genova Phlppe Martnet 140 Modelng and Control of Manpulator robots
19 Rgd bod pose parameteraton: orentaton RPY angles (,,) A RPY or Unverst of Genova Phlppe Martnet 141 Modelng and Control of Manpulator robots
20 Rgd bod pose parameteraton: orentaton Brant angles (,,) or Unverst of Genova Phlppe Martnet 142 Modelng and Control of Manpulator robots
21 Rgd bod pose parameteraton: orentaton Orentaton (u,θ) Rodrgues formula Unverst of Genova Phlppe Martnet 143 Modelng and Control of Manpulator robots
22 Rgd bod pose parameteraton: orentaton Orentaton (u.θ) Rodrgues formula, Unverst of Genova Phlppe Martnet 144 Modelng and Control of Manpulator robots
23 Orentaton (u.θ) T 2 (, θ ) = I u sθ + uˆ 3 ˆ..( 1 cθ ) T (, θ ) A( u, θ ) = 2.ˆ. u sθ A u A u 2 ( A( u, θ )) = Trace I + u sθ + uˆ 3 ˆ..( 1 cθ ) 2 ( A( u, θ )) = 3+ ( 1 cθ ). Trace( uˆ ) ( A( u, θ )) = 3 + ( 1 cθ )(. 2) ( A( u, θ )) = 1+ 2 cθ Trace Trace Trace Trace. Rgd bod pose parameteraton: orentaton ( ) [ u. sθ ] = [ u. sθ ] = (, θ ) A( u, θ ) A u 2 ( A( u, θ )) = 1+ 2 cθ Tr( A( u, θ )) 1 Tr. cosθ = 2 T s s s n n n a a a s n a n a Unverst of Genova s s n = s a s snθ = ± n a n n s 0 a Phlppe Martnet a a s n 0 s - n a - s n - a ( s n ) 2 + ( a s ) 2 + ( n a ) 2 = 2 u sθ = 2 u sθ = 2 u sθ n 1 a 2.snθ s a s n 145 Modelng and Control of Manpulator robots u =
24 Rgd bod pose parameteraton: orentaton Quaternon (λ 1,λ 2,λ 3,λ 4 ) Unverst of Genova Phlppe Martnet 146 Modelng and Control of Manpulator robots
25 Case of seral manpulator robot R 0 R 1 C 0 C 1 C 2 Mult-Rgd bodes R k R k+1 C k C n Consder a robot wth n+1 rgd bodes C k We assocate n+1 frames C 0 s the base of the robot (fed) R e Unverst of Genova Phlppe Martnet 147 Modelng and Control of Manpulator robots
26 Case of seral manpulator robot Mult-Rgd bodes The problem to solve s to obtan the poston and orentaton of the end effector frame R e n the fed frame R 0 k k k Rk + 1 Pk + 1 Tk + 1 = Elementar frame transform 0 T e = 0 T 1 1 T 2 2 T 3 L n 1 T n n T e Unverst of Genova Phlppe Martnet 148 Modelng and Control of Manpulator robots
27 Rgd bod knematcs Crcular moton v: tangental velct ω: angular veloct Unverst of Genova Phlppe Martnet 149 Modelng and Control of Manpulator robots
28 Rgd bod knematcs Rotatng frame R f : fed frame (orgn O fed) R m : moble frame just n rotaton w.r.t R f ω: angular veloct Unverst of Genova Phlppe Martnet 150 Modelng and Control of Manpulator robots
29 R f D Rgd bod knematcs R m d O m P O f R f : fed frame R m : Moble frame P : one pont n R m V ( P) d dt R f = V ( O ) + V ( P) + ω m d ( d) = D& + ( d) + ω dt R R f R m f R m d O m P ω : angular veloct of R m relatve to R f Unverst of Genova Phlppe Martnet 151 Modelng and Control of Manpulator robots
30 Knematc Rgd bod knematcs Usng ths relaton we can establshed The knematc evoluton of a mult-rgdbod robot See net slde Remarks : V ( P) R f = V ( O ) + V ( P) + ω m R f R m O m P If D=0 then V ( P) R f = V ( P) + ω R m O m P If D=0 and V ( P ) 0 then Unverst of Genova R = m = Om P ω 0 ω = ~ ~ ω ω d ω = ω 0 ω = [ ω] = [ ω] = [ ˆ ω AS ] ω ω 0 Phlppe Martnet V ( P) R f = ω O m 152 Modelng and Control of Manpulator robots P
31 Mult-Rgd bodes knematcs Angular veloct of R w.r.t R 0 epressed n R Veloct of O +1 w.r.t R epressed n R Veloct of O w.r.t R 0 epressed n R Veloct of O +1 w.r.t R 0 epressed n R Unverst of Genova Phlppe Martnet 153 Modelng and Control of Manpulator robots
32 Mult-Rgd bodes knematcs C -1 C C +1 = Angular veloct of R w.r.t R -1 epressed n R Angular veloct of R w.r.t R 0 epressed n R Angular veloct of R -1 w.r.t R 0 epressed n R -1 Unverst of Genova Phlppe Martnet 154 Modelng and Control of Manpulator robots
33 Mult-Rgd bodes knematcs C -1 C C +1 = Angular veloct of R w.r.t R -1 epressed n R Angular veloct of R w.r.t R 0 epressed n R Angular veloct of R -1 w.r.t R 0 epressed n R -1 Unverst of Genova Phlppe Martnet 155 Modelng and Control of Manpulator robots
34 Mult-Rgd bodes knematcs Consderng two frames R a and R b rgdl lnked (case for R n and R E ) twst Unverst of Genova Phlppe Martnet 156 Modelng and Control of Manpulator robots
35 Mult-Rgd bodes knematcs Consderng two frames R and R j and a twst V =(v,ω ) T epressed n O We wsh to compute the correspondng twst V j =(v j,ω j ) T epressed n O j Projecton wth Unverst of Genova Phlppe Martnet 157 Modelng and Control of Manpulator robots
36 Dfferental translaton and rotaton of frames Consder a dfferental translaton vector dp epressng the translaton of the orgn of frame R, and of a dfferental rotaton vector δ, equal to u.dθ, representng the rotaton of an angle dθ about an as, wth unt vector u, passng through the orgn O. The dfferental transformaton matr s defned as [Paul 81] Unverst of Genova Phlppe Martnet 158 Modelng and Control of Manpulator robots
37 Ra a T b = a R b Unverst of Genova a t b R b Phlppe Martnet =a Ṙ b. a R T b R= a R b R.R T =I3 Ω b/a a T Ṙ.R T +R.Ṙ T =0 Ṙ.R T = R.ṘT = Ṙ.R T Ṙ.R T =S(t) Ṙ=S(t).R p a (t)=r(t).p b (t) ṗ a (t)=ṙ(t).p b (t) ṗ a (t)=s(t).r.p b (t) ṗ a (t)=ω p a (t) ṗ a (t)=[ω] ṗ a (t)=ω (R.p b (t)).r.p b (t) S(t)=[Ω] Ωb/a a Consderp b (t)constant Angular veloct propertes 159 Modelng and Control of Manpulator robots
38 b T a = b R a Angular veloct propertes b t a b R a representstheorentaton b t a representstheposton Ra R b Ω b/a a a t b a T b = a R b Ω a/b b Ω b/a a Ω b/a a = Ω a/b a Ω b/a a = a R b.ω b/a b Ωb/a a Ω a/b b Ω a/b b = Ω b/a b Ω a/b b = b R a.ω a/b a Ωa/b b =a Ṙ b. a Rb T =b Ṙ a. b Ra T Unverst of Genova Phlppe Martnet 160 Modelng and Control of Manpulator robots
39 Representaton of forces (wrench) A collecton of forces and moments actng on a bod can be reduced to a wrench F at pont O, whch s composed of a force f at O and a moment m about O: Note that the vector feld of the moments consttutes a screw where the vector of the screw s f. Thus, the wrench forms a screw. Consder a gven wrench F, epressed n frame R. For calculatng the equvalent wrench j F j, we use the transformaton matr between screws such that: Unverst of Genova Phlppe Martnet 161 Modelng and Control of Manpulator robots
Rigid body simulation
 Rgd bod smulaton Rgd bod smulaton Once we consder an object wth spacal etent, partcle sstem smulaton s no longer suffcent Problems Problems Unconstraned sstem rotatonal moton torques and angular momentum
Rgd bod smulaton Rgd bod smulaton Once we consder an object wth spacal etent, partcle sstem smulaton s no longer suffcent Problems Problems Unconstraned sstem rotatonal moton torques and angular momentum
So far: simple (planar) geometries
 Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING. Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582
 NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582 4. Moton Knematcs 4.2 Angular Velocty Knematcs Summary From the last lecture we concluded that: If the jonts
NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582 4. Moton Knematcs 4.2 Angular Velocty Knematcs Summary From the last lecture we concluded that: If the jonts
An Algorithm to Solve the Inverse Kinematics Problem of a Robotic Manipulator Based on Rotation Vectors
 An Algorthm to Solve the Inverse Knematcs Problem of a Robotc Manpulator Based on Rotaton Vectors Mohamad Z. Al-az*, Mazn Z. Othman**, and Baker B. Al-Bahr* *AL-Nahran Unversty, Computer Eng. Dep., Baghdad,
An Algorthm to Solve the Inverse Knematcs Problem of a Robotc Manpulator Based on Rotaton Vectors Mohamad Z. Al-az*, Mazn Z. Othman**, and Baker B. Al-Bahr* *AL-Nahran Unversty, Computer Eng. Dep., Baghdad,
Iterative General Dynamic Model for Serial-Link Manipulators
 EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
Week 11: Chapter 11. The Vector Product. The Vector Product Defined. The Vector Product and Torque. More About the Vector Product
 The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
Geometry and Screw Theory for Robotics
 Tutoral (T9) Geometry and Screw Theory for Robotcs Stefano Stramgol and Herman Bruynnckx March 15, 2001 2 Contents 1 Moton of a Rgd Body 5 1.1 Introducton... 5 1.2 The Eucldean Space... 6 1.2.1 Ponts versus
Tutoral (T9) Geometry and Screw Theory for Robotcs Stefano Stramgol and Herman Bruynnckx March 15, 2001 2 Contents 1 Moton of a Rgd Body 5 1.1 Introducton... 5 1.2 The Eucldean Space... 6 1.2.1 Ponts versus
MEV442 Introduction to Robotics Module 2. Dr. Santhakumar Mohan Assistant Professor Mechanical Engineering National Institute of Technology Calicut
 MEV442 Introducton to Robotcs Module 2 Dr. Santhakumar Mohan Assstant Professor Mechancal Engneerng Natonal Insttute of Technology Calcut Jacobans: Veloctes and statc forces Introducton Notaton for tme-varyng
MEV442 Introducton to Robotcs Module 2 Dr. Santhakumar Mohan Assstant Professor Mechancal Engneerng Natonal Insttute of Technology Calcut Jacobans: Veloctes and statc forces Introducton Notaton for tme-varyng
Torsten Mayer-Gürr Institute of Geodesy, NAWI Graz Technische Universität Graz
 Insttute of Geodes GGOS and Reference Sstems Euler-ouvlle equaton 16-1-31 Torsten Maer-Gürr Insttute of Geodes, NWI Gra Technsche Unverstät Gra Torsten Maer-Gürr 1 Insttute of Geodes Reference sstem Need
Insttute of Geodes GGOS and Reference Sstems Euler-ouvlle equaton 16-1-31 Torsten Maer-Gürr Insttute of Geodes, NWI Gra Technsche Unverstät Gra Torsten Maer-Gürr 1 Insttute of Geodes Reference sstem Need
Chapter 11 Angular Momentum
 Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
5.76 Lecture #21 2/28/94 Page 1. Lecture #21: Rotation of Polyatomic Molecules I
 5.76 Lecture # /8/94 Page Lecture #: Rotaton of Polatomc Molecules I A datomc molecule s ver lmted n how t can rotate and vbrate. * R s to nternuclear as * onl one knd of vbraton A polatomc molecule can
5.76 Lecture # /8/94 Page Lecture #: Rotaton of Polatomc Molecules I A datomc molecule s ver lmted n how t can rotate and vbrate. * R s to nternuclear as * onl one knd of vbraton A polatomc molecule can
Spin-rotation coupling of the angularly accelerated rigid body
 Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
2010 vds-3d. Professor Kyongsu Yi. Vehicle Dynamics and Control Laboratory
 3D Dnamcs 2010 vds-3d Professor Kongsu Y 2010 VDCL Vehcle Dnamcs and Control Laborator 1 Knetcs of Rgd Bodes n Three Dmensons ma G Translatonal Dnamc Equaton of Rgd Bod (Newton Equaton F ma G Rotatonal
3D Dnamcs 2010 vds-3d Professor Kongsu Y 2010 VDCL Vehcle Dnamcs and Control Laborator 1 Knetcs of Rgd Bodes n Three Dmensons ma G Translatonal Dnamc Equaton of Rgd Bod (Newton Equaton F ma G Rotatonal
Classical Mechanics ( Particles and Biparticles )
 Classcal Mechancs ( Partcles and Bpartcles ) Alejandro A. Torassa Creatve Commons Attrbuton 3.0 Lcense (0) Buenos Ares, Argentna atorassa@gmal.com Abstract Ths paper consders the exstence of bpartcles
Classcal Mechancs ( Partcles and Bpartcles ) Alejandro A. Torassa Creatve Commons Attrbuton 3.0 Lcense (0) Buenos Ares, Argentna atorassa@gmal.com Abstract Ths paper consders the exstence of bpartcles
Modeling of Dynamic Systems
 Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING. Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582
 NMT EE 589 & UNM ME 48/58 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 48/58 7. Robot Dynamcs 7.5 The Equatons of Moton Gven that we wsh to fnd the path q(t (n jont space) whch mnmzes the energy
NMT EE 589 & UNM ME 48/58 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 48/58 7. Robot Dynamcs 7.5 The Equatons of Moton Gven that we wsh to fnd the path q(t (n jont space) whch mnmzes the energy
PHYS 1443 Section 003 Lecture #17
 PHYS 144 Secton 00 ecture #17 Wednesda, Oct. 9, 00 1. Rollng oton of a Rgd od. Torque. oment of Inerta 4. Rotatonal Knetc Energ 5. Torque and Vector Products Remember the nd term eam (ch 6 11), onda, Nov.!
PHYS 144 Secton 00 ecture #17 Wednesda, Oct. 9, 00 1. Rollng oton of a Rgd od. Torque. oment of Inerta 4. Rotatonal Knetc Energ 5. Torque and Vector Products Remember the nd term eam (ch 6 11), onda, Nov.!
Mathematical Preparations
 1 Introducton Mathematcal Preparatons The theory of relatvty was developed to explan experments whch studed the propagaton of electromagnetc radaton n movng coordnate systems. Wthn expermental error the
1 Introducton Mathematcal Preparatons The theory of relatvty was developed to explan experments whch studed the propagaton of electromagnetc radaton n movng coordnate systems. Wthn expermental error the
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Geometric Registration for Deformable Shapes. 2.1 ICP + Tangent Space optimization for Rigid Motions
 Geometrc Regstraton for Deformable Shapes 2.1 ICP + Tangent Space optmzaton for Rgd Motons Regstraton Problem Gven Two pont cloud data sets P (model) and Q (data) sampled from surfaces Φ P and Φ Q respectvely.
Geometrc Regstraton for Deformable Shapes 2.1 ICP + Tangent Space optmzaton for Rgd Motons Regstraton Problem Gven Two pont cloud data sets P (model) and Q (data) sampled from surfaces Φ P and Φ Q respectvely.
NEWTON S LAWS. These laws only apply when viewed from an inertial coordinate system (unaccelerated system).
 EWTO S LAWS Consder two partcles. 1 1. If 1 0 then 0 wth p 1 m1v. 1 1 2. 1.. 3. 11 These laws only apply when vewed from an nertal coordnate system (unaccelerated system). consder a collecton of partcles
EWTO S LAWS Consder two partcles. 1 1. If 1 0 then 0 wth p 1 m1v. 1 1 2. 1.. 3. 11 These laws only apply when vewed from an nertal coordnate system (unaccelerated system). consder a collecton of partcles
CHAPTER 10 ROTATIONAL MOTION
 CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
Part C Dynamics and Statics of Rigid Body. Chapter 5 Rotation of a Rigid Body About a Fixed Axis
 Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Chapter 11: Angular Momentum
 Chapter 11: ngular Momentum Statc Equlbrum In Chap. 4 we studed the equlbrum of pontobjects (mass m) wth the applcaton of Newton s aws F 0 F x y, 0 Therefore, no lnear (translatonal) acceleraton, a0 For
Chapter 11: ngular Momentum Statc Equlbrum In Chap. 4 we studed the equlbrum of pontobjects (mass m) wth the applcaton of Newton s aws F 0 F x y, 0 Therefore, no lnear (translatonal) acceleraton, a0 For
Chapter 3. r r. Position, Velocity, and Acceleration Revisited
 Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Quantum Mechanics I Problem set No.1
 Quantum Mechancs I Problem set No.1 Septembe0, 2017 1 The Least Acton Prncple The acton reads S = d t L(q, q) (1) accordng to the least (extremal) acton prncple, the varaton of acton s zero 0 = δs = t
Quantum Mechancs I Problem set No.1 Septembe0, 2017 1 The Least Acton Prncple The acton reads S = d t L(q, q) (1) accordng to the least (extremal) acton prncple, the varaton of acton s zero 0 = δs = t
Study Guide For Exam Two
 Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
EN40: Dynamics and Vibrations. Homework 7: Rigid Body Kinematics
 N40: ynamcs and Vbratons Homewor 7: Rgd Body Knematcs School of ngneerng Brown Unversty 1. In the fgure below, bar AB rotates counterclocwse at 4 rad/s. What are the angular veloctes of bars BC and C?.
N40: ynamcs and Vbratons Homewor 7: Rgd Body Knematcs School of ngneerng Brown Unversty 1. In the fgure below, bar AB rotates counterclocwse at 4 rad/s. What are the angular veloctes of bars BC and C?.
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
The classical spin-rotation coupling
 LOUAI H. ELZEIN 2018 All Rghts Reserved The classcal spn-rotaton couplng Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 louaelzen@gmal.com Abstract Ths paper s prepared to show that a rgd
LOUAI H. ELZEIN 2018 All Rghts Reserved The classcal spn-rotaton couplng Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 louaelzen@gmal.com Abstract Ths paper s prepared to show that a rgd
Teaching Spatial Kinematics for Engineers
 845 Teachng Spatal Knematcs for Engneers Author: Hellmuth Stachel, Insttute of Dscrete Mathematcs and Geometry, Venna Unversty of Technology, stachel@dmgtuwenacat Abstract Spatal knematcs s a challengng
845 Teachng Spatal Knematcs for Engneers Author: Hellmuth Stachel, Insttute of Dscrete Mathematcs and Geometry, Venna Unversty of Technology, stachel@dmgtuwenacat Abstract Spatal knematcs s a challengng
Important Dates: Post Test: Dec during recitations. If you have taken the post test, don t come to recitation!
 Important Dates: Post Test: Dec. 8 0 durng rectatons. If you have taken the post test, don t come to rectaton! Post Test Make-Up Sessons n ARC 03: Sat Dec. 6, 0 AM noon, and Sun Dec. 7, 8 PM 0 PM. Post
Important Dates: Post Test: Dec. 8 0 durng rectatons. If you have taken the post test, don t come to rectaton! Post Test Make-Up Sessons n ARC 03: Sat Dec. 6, 0 AM noon, and Sun Dec. 7, 8 PM 0 PM. Post
Elshaboury SM et al.; Sch. J. Phys. Math. Stat., 2015; Vol-2; Issue-2B (Mar-May); pp
 Elshabour SM et al.; Sch. J. Phs. Math. Stat. 5; Vol-; Issue-B (Mar-Ma); pp-69-75 Scholars Journal of Phscs Mathematcs Statstcs Sch. J. Phs. Math. Stat. 5; (B):69-75 Scholars Academc Scentfc Publshers
Elshabour SM et al.; Sch. J. Phs. Math. Stat. 5; Vol-; Issue-B (Mar-Ma); pp-69-75 Scholars Journal of Phscs Mathematcs Statstcs Sch. J. Phs. Math. Stat. 5; (B):69-75 Scholars Academc Scentfc Publshers
Lie Group Formulation of Articulated Rigid Body Dynamics
 Le Group Formulaton of Artculated Rgd Body Dynamcs Junggon Km 11/9/2012, Ver 1.01 Abstract It has been usual n most old-style text books for dynamcs to treat the formulas descrbng lnearor translatonal
Le Group Formulaton of Artculated Rgd Body Dynamcs Junggon Km 11/9/2012, Ver 1.01 Abstract It has been usual n most old-style text books for dynamcs to treat the formulas descrbng lnearor translatonal
10/9/2003 PHY Lecture 11 1
 Announcements 1. Physc Colloquum today --The Physcs and Analyss of Non-nvasve Optcal Imagng. Today s lecture Bref revew of momentum & collsons Example HW problems Introducton to rotatons Defnton of angular
Announcements 1. Physc Colloquum today --The Physcs and Analyss of Non-nvasve Optcal Imagng. Today s lecture Bref revew of momentum & collsons Example HW problems Introducton to rotatons Defnton of angular
Dynamics of a Spatial Multibody System using Equimomental System of Point-masses
 Dynamcs of a Spatal Multbody System usng Equmomental System of Pont-masses Vnay Gupta Dept. of Mechancal Engg. Indan Insttute of echnology Delh New Delh, Inda vnayguptaec@gmal.com Hmanshu Chaudhary Dept.
Dynamcs of a Spatal Multbody System usng Equmomental System of Pont-masses Vnay Gupta Dept. of Mechancal Engg. Indan Insttute of echnology Delh New Delh, Inda vnayguptaec@gmal.com Hmanshu Chaudhary Dept.
Chapter 20 Rigid Body: Translation and Rotational Motion Kinematics for Fixed Axis Rotation
 Chapter 20 Rgd Body: Translaton and Rotatonal Moton Knematcs for Fxed Axs Rotaton 20.1 Introducton... 1 20.2 Constraned Moton: Translaton and Rotaton... 1 20.2.1 Rollng wthout slppng... 5 Example 20.1
Chapter 20 Rgd Body: Translaton and Rotatonal Moton Knematcs for Fxed Axs Rotaton 20.1 Introducton... 1 20.2 Constraned Moton: Translaton and Rotaton... 1 20.2.1 Rollng wthout slppng... 5 Example 20.1
Georgia Tech PHYS 6124 Mathematical Methods of Physics I
 Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
10/23/2003 PHY Lecture 14R 1
 Announcements. Remember -- Tuesday, Oct. 8 th, 9:30 AM Second exam (coverng Chapters 9-4 of HRW) Brng the followng: a) equaton sheet b) Calculator c) Pencl d) Clear head e) Note: If you have kept up wth
Announcements. Remember -- Tuesday, Oct. 8 th, 9:30 AM Second exam (coverng Chapters 9-4 of HRW) Brng the followng: a) equaton sheet b) Calculator c) Pencl d) Clear head e) Note: If you have kept up wth
Spring 2002 Lecture #13
 44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
Physics 181. Particle Systems
 Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
SCALARS AND VECTORS All physical quantities in engineering mechanics are measured using either scalars or vectors.
 SCALARS AND ECTORS All phscal uanttes n engneerng mechancs are measured usng ether scalars or vectors. Scalar. A scalar s an postve or negatve phscal uantt that can be completel specfed b ts magntude.
SCALARS AND ECTORS All phscal uanttes n engneerng mechancs are measured usng ether scalars or vectors. Scalar. A scalar s an postve or negatve phscal uantt that can be completel specfed b ts magntude.
LAGRANGIAN MECHANICS
 LAGRANGIAN MECHANICS Generalzed Coordnates State of system of N partcles (Newtonan vew): PE, KE, Momentum, L calculated from m, r, ṙ Subscrpt covers: 1) partcles N 2) dmensons 2, 3, etc. PE U r = U x 1,
LAGRANGIAN MECHANICS Generalzed Coordnates State of system of N partcles (Newtonan vew): PE, KE, Momentum, L calculated from m, r, ṙ Subscrpt covers: 1) partcles N 2) dmensons 2, 3, etc. PE U r = U x 1,
Conservation of Angular Momentum = "Spin"
 Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
RIGID BODY MOTION. Next, we rotate counterclockwise about ξ by angle. Next we rotate counterclockwise about γ by angle to get the final set (x,y z ).
 RGD BODY MOTON We now consder the moton of rgd bodes. The frst queston s what coordnates are needed to specf the locaton and orentaton of such an object. Clearl 6 are needed 3 to locate a partcular pont
RGD BODY MOTON We now consder the moton of rgd bodes. The frst queston s what coordnates are needed to specf the locaton and orentaton of such an object. Clearl 6 are needed 3 to locate a partcular pont
Angular Momentum and Fixed Axis Rotation. 8.01t Nov 10, 2004
 Angular Momentum and Fxed Axs Rotaton 8.01t Nov 10, 2004 Dynamcs: Translatonal and Rotatonal Moton Translatonal Dynamcs Total Force Torque Angular Momentum about Dynamcs of Rotaton F ext Momentum of a
Angular Momentum and Fxed Axs Rotaton 8.01t Nov 10, 2004 Dynamcs: Translatonal and Rotatonal Moton Translatonal Dynamcs Total Force Torque Angular Momentum about Dynamcs of Rotaton F ext Momentum of a
12. The Hamilton-Jacobi Equation Michael Fowler
 1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
ENGN 40 Dynamics and Vibrations Homework # 7 Due: Friday, April 15
 NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
Minimal representations of orientation
 Robotics 1 Minimal representations of orientation (Euler and roll-pitch-yaw angles) Homogeneous transformations Prof. lessandro De Luca Robotics 1 1 Minimal representations rotation matrices: 9 elements
Robotics 1 Minimal representations of orientation (Euler and roll-pitch-yaw angles) Homogeneous transformations Prof. lessandro De Luca Robotics 1 1 Minimal representations rotation matrices: 9 elements
Physics 111: Mechanics Lecture 11
 Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
VEKTORANALYS GAUSS THEOREM STOKES THEOREM. and. Kursvecka 3. Kapitel 6 7 Sidor 51 82
 VEKTORANAY Kursvecka 3 GAU THEOREM and TOKE THEOREM Kaptel 6 7 dor 51 82 TARGET PROBEM Do magnetc monopoles est? EECTRIC FIED MAGNETIC FIED N +? 1 TARGET PROBEM et s consder some EECTRIC CHARGE 2 - + +
VEKTORANAY Kursvecka 3 GAU THEOREM and TOKE THEOREM Kaptel 6 7 dor 51 82 TARGET PROBEM Do magnetc monopoles est? EECTRIC FIED MAGNETIC FIED N +? 1 TARGET PROBEM et s consder some EECTRIC CHARGE 2 - + +
Dynamics 12e. Copyright 2010 Pearson Education South Asia Pte Ltd. Chapter 20 3D Kinematics of a Rigid Body
 Engineering Mechanics: Dynamics 12e Chapter 20 3D Kinematics of a Rigid Body Chapter Objectives Kinematics of a body subjected to rotation about a fixed axis and general plane motion. Relative-motion analysis
Engineering Mechanics: Dynamics 12e Chapter 20 3D Kinematics of a Rigid Body Chapter Objectives Kinematics of a body subjected to rotation about a fixed axis and general plane motion. Relative-motion analysis
PHYS 705: Classical Mechanics. Newtonian Mechanics
 1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
(δr i ) 2. V i. r i 2,
 Cartesan coordnates r, = 1, 2,... D for Eucldean space. Dstance by Pythagoras: (δs 2 = (δr 2. Unt vectors ê, dsplacement r = r ê Felds are functons of poston, or of r or of {r }. Scalar felds Φ( r, Vector
Cartesan coordnates r, = 1, 2,... D for Eucldean space. Dstance by Pythagoras: (δs 2 = (δr 2. Unt vectors ê, dsplacement r = r ê Felds are functons of poston, or of r or of {r }. Scalar felds Φ( r, Vector
χ x B E (c) Figure 2.1.1: (a) a material particle in a body, (b) a place in space, (c) a configuration of the body
 Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Solution 1 for USTC class Physics of Quantum Information
 Soluton 1 for 018 019 USTC class Physcs of Quantum Informaton Shua Zhao, Xn-Yu Xu and Ka Chen Natonal Laboratory for Physcal Scences at Mcroscale and Department of Modern Physcs, Unversty of Scence and
Soluton 1 for 018 019 USTC class Physcs of Quantum Informaton Shua Zhao, Xn-Yu Xu and Ka Chen Natonal Laboratory for Physcal Scences at Mcroscale and Department of Modern Physcs, Unversty of Scence and
Lecture 23: Newton-Euler Formulation. Vaibhav Srivastava
 Lecture 23: Newton-Euler Formulaton Based on Chapter 7, Spong, Hutchnson, and Vdyasagar Vabhav Srvastava Department of Electrcal & Computer Engneerng Mchgan State Unversty Aprl 10, 2017 ECE 818: Robotcs
Lecture 23: Newton-Euler Formulaton Based on Chapter 7, Spong, Hutchnson, and Vdyasagar Vabhav Srvastava Department of Electrcal & Computer Engneerng Mchgan State Unversty Aprl 10, 2017 ECE 818: Robotcs
Dynamics of Rotational Motion
 Dynamcs of Rotatonal Moton Torque: the rotatonal analogue of force Torque = force x moment arm = Fl moment arm = perpendcular dstance through whch the force acts a.k.a. leer arm l F l F l F l F = Fl =
Dynamcs of Rotatonal Moton Torque: the rotatonal analogue of force Torque = force x moment arm = Fl moment arm = perpendcular dstance through whch the force acts a.k.a. leer arm l F l F l F l F = Fl =
Screw and Lie group theory in multibody kinematics
 Multbody Syst Dyn DOI 10.1007/s11044-017-9582-7 Screw and Le group theory n multbody knematcs Moton representaton and recursve knematcs of tree-topology systems Andreas Müller 1 Receved: 10 Aprl 2016 /
Multbody Syst Dyn DOI 10.1007/s11044-017-9582-7 Screw and Le group theory n multbody knematcs Moton representaton and recursve knematcs of tree-topology systems Andreas Müller 1 Receved: 10 Aprl 2016 /
A particle in a state of uniform motion remain in that state of motion unless acted upon by external force.
 The fundamental prncples of classcal mechancs were lad down by Galleo and Newton n the 16th and 17th centures. In 1686, Newton wrote the Prncpa where he gave us three laws of moton, one law of gravty,
The fundamental prncples of classcal mechancs were lad down by Galleo and Newton n the 16th and 17th centures. In 1686, Newton wrote the Prncpa where he gave us three laws of moton, one law of gravty,
Stereo 3D Simulation of Rigid Body Inertia Ellipsoid for The Purpose of Unmanned Helicopter Autopilot Tuning
 nternatonal Journal of Engneerng Scence nventon SSN (Onlne): 319 6734, SSN (Prnt): 319 676 www.jes.org Volume 3 ssue 8 ǁ August 14 ǁ PP.8-35 Stereo 3D Smulaton of Rgd Bod nerta Ellpsod for The Purpose
nternatonal Journal of Engneerng Scence nventon SSN (Onlne): 319 6734, SSN (Prnt): 319 676 www.jes.org Volume 3 ssue 8 ǁ August 14 ǁ PP.8-35 Stereo 3D Smulaton of Rgd Bod nerta Ellpsod for The Purpose
τ rf = Iα I point = mr 2 L35 F 11/14/14 a*er lecture 1
 A mass s attached to a long, massless rod. The mass s close to one end of the rod. Is t easer to balance the rod on end wth the mass near the top or near the bottom? Hnt: Small α means sluggsh behavor
A mass s attached to a long, massless rod. The mass s close to one end of the rod. Is t easer to balance the rod on end wth the mass near the top or near the bottom? Hnt: Small α means sluggsh behavor
Tensor Analysis. For orthogonal curvilinear coordinates, ˆ ˆ (98) Expanding the derivative, we have, ˆ. h q. . h q h q
 For orthogonal curvlnear coordnates, eˆ grad a a= ( aˆ ˆ e). h q (98) Expandng the dervatve, we have, eˆ aˆ ˆ e a= ˆ ˆ a h e + q q 1 aˆ ˆ ˆ a e = ee ˆˆ ˆ + e. h q h q Now expandng eˆ / q (some of the detals
For orthogonal curvlnear coordnates, eˆ grad a a= ( aˆ ˆ e). h q (98) Expandng the dervatve, we have, eˆ aˆ ˆ e a= ˆ ˆ a h e + q q 1 aˆ ˆ ˆ a e = ee ˆˆ ˆ + e. h q h q Now expandng eˆ / q (some of the detals
coordinates. Then, the position vectors are described by
 Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
VEKTORANALYS. GAUSS s THEOREM and STOKES s THEOREM. Kursvecka 3. Kapitel 6-7 Sidor 51-82
 VEKTORANAY Kursvecka 3 GAU s THEOREM and TOKE s THEOREM Kaptel 6-7 dor 51-82 TARGET PROBEM EECTRIC FIED MAGNETIC FIED N + Magnetc monopoles do not est n nature. How can we epress ths nformaton for E and
VEKTORANAY Kursvecka 3 GAU s THEOREM and TOKE s THEOREM Kaptel 6-7 dor 51-82 TARGET PROBEM EECTRIC FIED MAGNETIC FIED N + Magnetc monopoles do not est n nature. How can we epress ths nformaton for E and
1. Review of Mechanics Newton s Laws
 . Revew of Mechancs.. Newton s Laws Moton of partcles. Let the poston of the partcle be gven by r. We can always express ths n Cartesan coordnates: r = xˆx + yŷ + zẑ, () where we wll always use ˆ (crcumflex)
. Revew of Mechancs.. Newton s Laws Moton of partcles. Let the poston of the partcle be gven by r. We can always express ths n Cartesan coordnates: r = xˆx + yŷ + zẑ, () where we wll always use ˆ (crcumflex)
Rotational Dynamics. Physics 1425 Lecture 19. Michael Fowler, UVa
 Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Physics 5153 Classical Mechanics. D Alembert s Principle and The Lagrangian-1
 P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
EML 5223 Structural Dynamics HW 10. Gun Lee(UFID )
 E 5 Structural Dynamcs HW Gun ee(ufid895-47) Problem 9. ubular shaft of radus r ( ) r[ + ( )/ ], thcknesst, mass per unt volume ρ and shear modulus G. t r( ). Shaft s symmetrc wth respect to /. ass moment
E 5 Structural Dynamcs HW Gun ee(ufid895-47) Problem 9. ubular shaft of radus r ( ) r[ + ( )/ ], thcknesst, mass per unt volume ρ and shear modulus G. t r( ). Shaft s symmetrc wth respect to /. ass moment
CHAPTER 6. LAGRANGE S EQUATIONS (Analytical Mechanics)
 CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
Anglo-Chinese Junior College H2 Mathematics JC 2 PRELIM PAPER 1 Solutions
 Anglo-Chnese Junor College H Mathematcs 97 8 JC PRELIM PAPER Solutons ( ( + + + + + 8 range of valdty: > or < but snce number, reject < wll result n the sq rt of a negatve . no. of
Anglo-Chnese Junor College H Mathematcs 97 8 JC PRELIM PAPER Solutons ( ( + + + + + 8 range of valdty: > or < but snce number, reject < wll result n the sq rt of a negatve . no. of
Chapter 2 Math Fundamentals
 Chapter 2 Math Fundamentals Part 4 2.7 Transform Graphs and Pose Networks 1 Moble Robotcs - Prof Alonzo Kelly, CMU RI Outlne 2.7.1 Transforms as Relatonshps 2.7.2 Solvng Pose Networks 2.7.3 Overconstraned
Chapter 2 Math Fundamentals Part 4 2.7 Transform Graphs and Pose Networks 1 Moble Robotcs - Prof Alonzo Kelly, CMU RI Outlne 2.7.1 Transforms as Relatonshps 2.7.2 Solvng Pose Networks 2.7.3 Overconstraned
6.3.4 Modified Euler s method of integration
 6.3.4 Modfed Euler s method of ntegraton Before dscussng the applcaton of Euler s method for solvng the swng equatons, let us frst revew the basc Euler s method of numercal ntegraton. Let the general from
6.3.4 Modfed Euler s method of ntegraton Before dscussng the applcaton of Euler s method for solvng the swng equatons, let us frst revew the basc Euler s method of numercal ntegraton. Let the general from
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 What is a conservation law?
 MATHEMATICS 7302 (Analytcal Dynamcs) YEAR 2016 2017, TERM 2 HANDOUT #6: MOMENTUM, ANGULAR MOMENTUM, AND ENERGY; CONSERVATION LAWS In ths handout we wll develop the concepts of momentum, angular momentum,
MATHEMATICS 7302 (Analytcal Dynamcs) YEAR 2016 2017, TERM 2 HANDOUT #6: MOMENTUM, ANGULAR MOMENTUM, AND ENERGY; CONSERVATION LAWS In ths handout we wll develop the concepts of momentum, angular momentum,
First Law: A body at rest remains at rest, a body in motion continues to move at constant velocity, unless acted upon by an external force.
 Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Kinematics and geometry review. Based on figures from J Xiao
 Knematcs and geometr ree Based on fgres from J Xao Otlne ee obot Manlators obot onfgraton obot ecfcaton Nmber of Aes DOF recson eeatablt Knematcs relmnar World frame ont frame end-effector frame otaton
Knematcs and geometr ree Based on fgres from J Xao Otlne ee obot Manlators obot onfgraton obot ecfcaton Nmber of Aes DOF recson eeatablt Knematcs relmnar World frame ont frame end-effector frame otaton
Lesson 5: Kinematics and Dynamics of Particles
 Lesson 5: Knematcs and Dynamcs of Partcles hs set of notes descrbes the basc methodology for formulatng the knematc and knetc equatons for multbody dynamcs. In order to concentrate on the methodology and
Lesson 5: Knematcs and Dynamcs of Partcles hs set of notes descrbes the basc methodology for formulatng the knematc and knetc equatons for multbody dynamcs. In order to concentrate on the methodology and
Linear Momentum. Center of Mass.
 Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
SCHOOL OF COMPUTING, ENGINEERING AND MATHEMATICS SEMESTER 2 EXAMINATIONS 2011/2012 DYNAMICS ME247 DR. N.D.D. MICHÉ
 s SCHOOL OF COMPUTING, ENGINEERING ND MTHEMTICS SEMESTER EXMINTIONS 011/01 DYNMICS ME47 DR. N.D.D. MICHÉ Tme allowed: THREE hours nswer: ny FOUR from SIX questons Each queston carres 5 marks Ths s a CLOSED-BOOK
s SCHOOL OF COMPUTING, ENGINEERING ND MTHEMTICS SEMESTER EXMINTIONS 011/01 DYNMICS ME47 DR. N.D.D. MICHÉ Tme allowed: THREE hours nswer: ny FOUR from SIX questons Each queston carres 5 marks Ths s a CLOSED-BOOK
11. Dynamics in Rotating Frames of Reference
 Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
Physics 607 Exam 1. ( ) = 1, Γ( z +1) = zγ( z) x n e x2 dx = 1. e x2
 Physcs 607 Exam 1 Please be well-organzed, and show all sgnfcant steps clearly n all problems. You are graded on your wor, so please do not just wrte down answers wth no explanaton! Do all your wor on
Physcs 607 Exam 1 Please be well-organzed, and show all sgnfcant steps clearly n all problems. You are graded on your wor, so please do not just wrte down answers wth no explanaton! Do all your wor on
16 Reflection and transmission, TE mode
 16 Reflecton transmsson TE mode Last lecture we learned how to represent plane-tem waves propagatng n a drecton ˆ n terms of feld phasors such that η = Ẽ = E o e j r H = ˆ Ẽ η µ ɛ = ˆ = ω µɛ E o =0. Such
16 Reflecton transmsson TE mode Last lecture we learned how to represent plane-tem waves propagatng n a drecton ˆ n terms of feld phasors such that η = Ẽ = E o e j r H = ˆ Ẽ η µ ɛ = ˆ = ω µɛ E o =0. Such
In this section is given an overview of the common elasticity models.
 Secton 4.1 4.1 Elastc Solds In ths secton s gven an overvew of the common elastcty models. 4.1.1 The Lnear Elastc Sold The classcal Lnear Elastc model, or Hooean model, has the followng lnear relatonshp
Secton 4.1 4.1 Elastc Solds In ths secton s gven an overvew of the common elastcty models. 4.1.1 The Lnear Elastc Sold The classcal Lnear Elastc model, or Hooean model, has the followng lnear relatonshp
C. J. PAPACHRISTOU INTRODUCTION TO
 C. J. PAPACHRISTOU INTRODUCTION TO MECHANICS OF PARTICLES AND SYSTEMS HELLENIC NAVAL ACADEMY Introducton to MECHANICS of Partcles and Systems Costas J. Papachrstou Department of Physcal Scences Hellenc
C. J. PAPACHRISTOU INTRODUCTION TO MECHANICS OF PARTICLES AND SYSTEMS HELLENIC NAVAL ACADEMY Introducton to MECHANICS of Partcles and Systems Costas J. Papachrstou Department of Physcal Scences Hellenc
Port-Hamiltonian Modeling for Soft-Finger Manipulation
 The 2010 IEEE/RSJ Internatonal Conference on Intellgent Robots and Systems October 18-22, 2010, Tape, Tawan Port-Hamltonan Modelng for Soft-Fnger Manpulaton F. Fcucello, R. Carlon, L.C. Vsser and S. Stramgol
The 2010 IEEE/RSJ Internatonal Conference on Intellgent Robots and Systems October 18-22, 2010, Tape, Tawan Port-Hamltonan Modelng for Soft-Fnger Manpulaton F. Fcucello, R. Carlon, L.C. Vsser and S. Stramgol
MTH 263 Practice Test #1 Spring 1999
 Pat Ross MTH 6 Practce Test # Sprng 999 Name. Fnd the area of the regon bounded by the graph r =acos (θ). Observe: Ths s a crcle of radus a, for r =acos (θ) r =a ³ x r r =ax x + y =ax x ax + y =0 x ax
Pat Ross MTH 6 Practce Test # Sprng 999 Name. Fnd the area of the regon bounded by the graph r =acos (θ). Observe: Ths s a crcle of radus a, for r =acos (θ) r =a ³ x r r =ax x + y =ax x ax + y =0 x ax
A Hamiltonian formulation of the dynamics of spatial mechanisms using Lie Groups and Screw Theory
 A Hamltonan formulaton of the dynamcs of spatal mechansms usng Le Groups and Screw Theory Stefano Stramgol Delft Unversty of Technology Dept. of Informaton Tech. and Systems, P.O. Box 5031, NL-2600 GA
A Hamltonan formulaton of the dynamcs of spatal mechansms usng Le Groups and Screw Theory Stefano Stramgol Delft Unversty of Technology Dept. of Informaton Tech. and Systems, P.O. Box 5031, NL-2600 GA
PY2101 Classical Mechanics Dr. Síle Nic Chormaic, Room 215 D Kane Bldg
 PY2101 Classcal Mechancs Dr. Síle Nc Chormac, Room 215 D Kane Bldg s.ncchormac@ucc.e Lectures stll some ssues to resolve. Slots shared between PY2101 and PY2104. Hope to have t fnalsed by tomorrow. Mondays
PY2101 Classcal Mechancs Dr. Síle Nc Chormac, Room 215 D Kane Bldg s.ncchormac@ucc.e Lectures stll some ssues to resolve. Slots shared between PY2101 and PY2104. Hope to have t fnalsed by tomorrow. Mondays
Spring Force and Power
 Lecture 13 Chapter 9 Sprng Force and Power Yeah, energy s better than orces. What s net? Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi IN THIS CHAPTER, you wll learn how to solve problems
Lecture 13 Chapter 9 Sprng Force and Power Yeah, energy s better than orces. What s net? Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi IN THIS CHAPTER, you wll learn how to solve problems
2D Motion of Rigid Bodies: Falling Stick Example, Work-Energy Principle
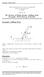 Example: Fallng Stck 1.003J/1.053J Dynamcs and Control I, Sprng 007 Professor Thomas Peacock 3/1/007 ecture 10 D Moton of Rgd Bodes: Fallng Stck Example, Work-Energy Prncple Example: Fallng Stck Fgure
Example: Fallng Stck 1.003J/1.053J Dynamcs and Control I, Sprng 007 Professor Thomas Peacock 3/1/007 ecture 10 D Moton of Rgd Bodes: Fallng Stck Example, Work-Energy Prncple Example: Fallng Stck Fgure
ENGI9496 Lecture Notes Multiport Models in Mechanics
 ENGI9496 Moellng an Smulaton of Dynamc Systems Mechancs an Mechansms ENGI9496 Lecture Notes Multport Moels n Mechancs (New text Secton 4..3; Secton 9.1 generalzes to 3D moton) Defntons Generalze coornates
ENGI9496 Moellng an Smulaton of Dynamc Systems Mechancs an Mechansms ENGI9496 Lecture Notes Multport Moels n Mechancs (New text Secton 4..3; Secton 9.1 generalzes to 3D moton) Defntons Generalze coornates
Classical Mechanics Virtual Work & d Alembert s Principle
 Classcal Mechancs Vrtual Work & d Alembert s Prncple Dpan Kumar Ghosh UM-DAE Centre for Excellence n Basc Scences Kalna, Mumba 400098 August 15, 2016 1 Constrants Moton of a system of partcles s often
Classcal Mechancs Vrtual Work & d Alembert s Prncple Dpan Kumar Ghosh UM-DAE Centre for Excellence n Basc Scences Kalna, Mumba 400098 August 15, 2016 1 Constrants Moton of a system of partcles s often
MEASUREMENT OF MOMENT OF INERTIA
 1. measurement MESUREMENT OF MOMENT OF INERTI The am of ths measurement s to determne the moment of nerta of the rotor of an electrc motor. 1. General relatons Rotatng moton and moment of nerta Let us
1. measurement MESUREMENT OF MOMENT OF INERTI The am of ths measurement s to determne the moment of nerta of the rotor of an electrc motor. 1. General relatons Rotatng moton and moment of nerta Let us
A Tale of Friction Basic Rollercoaster Physics. Fahrenheit Rollercoaster, Hershey, PA max height = 121 ft max speed = 58 mph
 A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
Symmetric Lie Groups and Conservation Laws in Physics
 Symmetrc Le Groups and Conservaton Laws n Physcs Audrey Kvam May 1, 1 Abstract Ths paper eamnes how conservaton laws n physcs can be found from analyzng the symmetrc Le groups of certan physcal systems.
Symmetrc Le Groups and Conservaton Laws n Physcs Audrey Kvam May 1, 1 Abstract Ths paper eamnes how conservaton laws n physcs can be found from analyzng the symmetrc Le groups of certan physcal systems.
EE 570: Location and Navigation: Theory & Practice
 EE 570: Locaton and Navgaton: Theory & Practce Navgaton Sensors and INS Mechanzaton Tuesday 26 Fe 2013 NMT EE 570: Locaton and Navgaton: Theory & Practce Slde 1 of 14 Navgaton Sensors and INS Mechanzaton
EE 570: Locaton and Navgaton: Theory & Practce Navgaton Sensors and INS Mechanzaton Tuesday 26 Fe 2013 NMT EE 570: Locaton and Navgaton: Theory & Practce Slde 1 of 14 Navgaton Sensors and INS Mechanzaton
Introductory Optomechanical Engineering. 2) First order optics
 Introductory Optomechancal Engneerng 2) Frst order optcs Moton of optcal elements affects the optcal performance? 1. by movng the mage 2. hgher order thngs (aberratons) The frst order effects are most
Introductory Optomechancal Engneerng 2) Frst order optcs Moton of optcal elements affects the optcal performance? 1. by movng the mage 2. hgher order thngs (aberratons) The frst order effects are most
