Chapter 2. Stellar Dynamics in Galaxies. 2.1 Introduction. 2.2 The Virial Theorem The basic result
|
|
|
- Godwin Bell
- 6 years ago
- Views:
Transcription
1 Chapter 2 Stellar Dynamcs n Galaxes 2.1 Introducton A system of stars behaves lke a flud, but one wth unusual propertes. In a normal flud two-body nteractons are crucal n the dynamcs, but n contrast star-star encounters are very rare. Instead stellar dynamcs s mostly governed by the nteracton of ndvdual stars wth the mean gravtatonal feld of all the other stars combned. Ths has profound consequences for how the dynamcs of the stars wthn galaxes are descrbed mathematcally, allowng for some consderable smplfcatons. Ths chapter establshes some basc results relatng to the motons of stars wthn galaxes. The vral theorem provdes a very smple relaton between the total potental and knetc energes of stars wthn a galaxy, or other system of stars, that has settled down nto a steady state. The vral theorem s derved formally here. The tmescale for stars to cross a system of stars, known as the crossng tme, s a smple but mportant measure of the motons of stars. The relaxaton tme measures how long t takes for two-body encounters to nfluence the dynamcs of a galaxy, or other system of stars. An expresson for the relaxaton tme s derved here, whch s then used to show that encounters between stars are so rare wthn galaxes that they have had lttle effect over the lfetme of the Unverse. The motons of stars wthn galaxes can be descrbed by the collsonless Boltzmann equaton, whch allows the numbers of stars to be calculated as a functon of poston and velocty n the galaxy. The equaton s derved from frst prncples here. Smlarly, the Jeans Equatons relate the denstes of stars to poston, velocty, velocty dsperson and gravtatonal potental. 2.2 The Vral Theorem The basc result Before gong nto the man materal on stellar dynamcs, t s worth statng and dervng a basc prncple known as the vral theorem. It states that for any system of partcles bound by an nverse-square force law, the tme-averaged knetc energy T and the tme-averaged potental energy U satsfy 2 T + U = 0,
2 for a steady equlbrum state. T wll be a very large postve quantty and U a very large negatve quantty. Of course, for a galaxy to hold together, the total energy T + U < 0 ; the vral theorem provdes a much tghter constrant than ths alone. Typcally, T and U to J for galaxes. In practce, many systems of stars are not n a perfect fnal steady state and the vral theorem does not apply exactly. Despte ths, t does gve mportant, approxmate results for many astronomcal systems. The vral theorem was frst devsed by Rudolf Clausus to descrbe motons of partcles n thermodynamcs. The term vral comes from the Latn word for force, vs Dervng the vral theorem from frst prncples To prove the vral theorem, consder a system of N stars. Let the th star have a mass m and a poston vector x. The poston vector wll be measured from the centre of mass of the system, and we shall assume that ths centre of mass moves wth unform moton. The velocty of the th star s ẋ dx /, where t s the tme. Consder the moment of nerta I of ths system of stars defned here as I N m x.x = =1 N m x Note that ths s a dfferent defnton of moment of nerta to the moment of nerta about a partcular axs that s used to study the rotaton of bodes about an axs. Dfferentatng wth respect to tme t, di = d m x.x = d m x.x = d m x.x assumng that the masses m do not change = m ẋ.x + x.ẋ from the product rule =1 = 2 m ẋ.x Dfferentatng agan, d 2 I = 2 d m 2 ẋ.x = 2 = 2 m ẍ.x + ẋ.ẋ d m ẋ.x = 2 d m ẋ.x = 2 m ẍ.x + 2 m 2 x 2.3 The knetc energy of the th partcle s 1m 2 x 2. Therefore the total knetc energy of the entre system of stars s T = 1 2 m ẋ 2 m ẋ 2 = 2 T 16
3 Substtutng ths nto Equaton 2.3, d 2 I 2 = 4 T + 2 m ẍ.x, 2.4 at any tme t. We now need to remember that the average of any parameter yt over tme t = 0 to τ s y = 1 τ τ 0 yt Consder the average value of d 2 I/ 2 over a tme nterval t = 0 to τ. d 2 I = 1 τ 4 T + 2 m 2 ẍ.x τ 0 = 4 τ T + 2 τ m ẍ.x τ τ 0 = 4 T + 2 = 4 T m τ τ 0 ẍ.x assumng m s constant over tme m ẍ.x 2.5 When the system of stars eventually reaches equlbrum, the moment of nerta I wll be constant. So, d 2 I/ 2 = 0. An alternatve way of vsualsng ths s by consderng that I wll be bounded n any physcal system and d 2 I/ 2 wll also be fnte. Therefore the long-tme average d2 I wll vansh as τ becomes large,.e. 2 lm τ d2 I = lm 2 τ 1 τ d 2 I 0 because d 2 I/ 2 remans fnte. τ 0 2 Substtutng for d 2 I/ 2 = 0 nto Equaton 2.5, 4 T + 2 m ẍ.x = 0. 2 T + m ẍ.x = The term m ẍ.x s related to the gravtatonal potental. We next need to show how. Newton s Second Law of Moton gves for the th star, m ẍ = j j where F j s the force exerted on the th star by the jth star. Usng the law of unversal gravtaton, m ẍ = G m m j x x j 3 j x x j. j Takng the scalar product dot product wth x, m ẍ.x = j j F j G m m j x x j 3 x x j 17.x
4 Summng over all, m ẍ.x = j j Swtchng and j, we have Addng Equatons 2.7 and 2.8, m ẍ.x + j But 2 j G m m j x x j 3 x x j.x =,j j m j ẍ j.x j = j, j m j ẍ j.x j =,j j m ẍ.x =,j j G m m j x x j 3 x x j.x 2.7 G m j m x j x 3 x j x.x j 2.8 G m m j x x j 3 x x j.x,j j G m m j x x j 3 G m j m x j x 3 x j x.x j x x j.x + x j x.x j x x j.x + x j x.x j = x x j.x x x j.x j = x x j.x x j factorsng = x x j 2 2 m ẍ.x =,j j m ẍ.x = 1 2 G m m j x x j 3 x x j 2,j j G m m j x x j We now need to fnd the total potental energy of the system. The gravtatonal potental at star due to star j s 2.9 Φ j = G m j x x j Therefore the gravtatonal potental at star due to all other stars s Φ = j j Φ j = j j G m j x x j Therefore the gravtatonal potental energy of star due to all the other stars s U = m Φ = m j j G m j x x j 18
5 The total potental energy of the system s therefore U = U = 1 2 m j j G m j x x j The factor 1 ensures that we only count each par of stars once otherwse we would 2 count each par twce and would get a result twce as large as we should. Therefore, U = 1 2,j j G m m j x x j Substtutng for the total potental energy nto Equaton 2.9, m ẍ.x = U Equaton 2.6 uses tme-averaged quanttes. So, averagng over tme t = 0 to τ, 1 τ τ 0 Substtutng ths nto Equaton 2.6, m ẍ.x = U τ 1 m ẍ.x = U τ 0 m ẍ.x = U 2 T + U = 0 Ths s Equaton 2.1, the Vral Theorem. It s also possble to rederve the vral theorem usng tensors. Ths tensor vral theorem uses a tensor moment of nerta and tensor representatons of the knetc and potental energes. Ths s beyond the scope of ths course Usng the Vral Theorem The vral theorem apples to systems of stars that have reached a steady equlbrum state. It can be used for many galaxes, but can also be used for other systems such as some star clusters. However, we need to be careful that we use the theorem only for equlbrum systems. The theorem can be appled, for example, to: ellptcal galaxes evolved star clusters, e.g. globular clusters evolved clusters of galaxes wth the galaxes actng as the partcles, not the ndvdual stars Examples of places where the vral theorem cannot be used are: 19
6 mergng galaxes newly formed star clusters clusters of galaxes that are stll formng/stll have nfallng galaxes Note that the vral theorem does also apply to stars or planets n crcular orbts, but we do not normally use t for these smple cases because a drect analyss based on the acceleraton s more straghtforward. The vral theorem provdes an easy way to make rough estmates of masses, because velocty measurements can gve T. To do ths we need to measure the observed velocty dsperson of stars the dsperson along the lne of sght usng radal veloctes obtaned from spectroscopy. The theorem then gves the total gravtatonal potental energy, whch can provde the total mass. Ths mass, of course, s mportant because t ncludes dark matter. Vral masses are partcularly mportant for some galaxy clusters usng galaxes, or atoms n X-ray emttng gas, as the partcles. But t s prudent to consder vral mass estmates as order-of-magntude only, because generally one can measure only lne-of-sght veloctes, and gettng T = m ẋ 2 1 from these requres more assumptons e.g. sotropy of the velocty dstrbuton; and the systems nvolved may not be n a steady state, n whch case of 2 course the vral theorem does not apply some clusters of galaxes are may be qute far from a steady state. Note that for galaxes beyond our own, we cannot measure three-dmensonal veloctes of stars drectly although some projects are now achevng ths for some Local Group galaxes. We have to use radal veloctes the component of the velocty along the lne of sght to the galaxy only, obtaned from spectroscopy through the Doppler shft of spectral lnes. Beyond nearby galaxes, radal veloctes of ndvdual stars become dffcult to obtan. It becomes necessary to measure velocty dspersons along the lne of sght from the observed whs of spectral lnes n the combned lght of mllons of stars Dervng masses from the Vral Theorem: a nave example Consder a sphercal ellptcal galaxy of radus R that has unform densty and whch conssts of N stars each of mass m havng typcal veloctes v. From the vral theorem, 2 T + U = 0 where T s the tme-averaged total knetc energy and U s the average total potental energy. We have N 1 T = 2 mv2 = 1 2 Nmv2 =1 and averagng over tme, T = 1 2 Nmv2 also. Note that strctly speakng we are takng the typcal velocty to mean the root mean square velocty. The total gravtatonal potental energy of a unform sphere of mass M and radus R a standard result s U = 3 GM 2 5 R 20
7 where G s the unversal gravtatonal constant. So the tme-averaged potental energy of the galaxy s U = 3 GM 2 5 R where M s the total mass. Substtutng ths nto the vral theorem equaton, Nmv2 3 GM 2 = 0 5 R But the total mass s M = Nm. v 2 = 3 5 NGm R = 3 5 The calculaton s only approxmate, so we shall use Ths gves the mass to be v 2 NGm R GM R GM R M v2 R G So an ellptcal galaxy havng a typcal velocty v = 350 km s 1 = m s 1, and a radus R = 10 kpc = m, wll have a mass M kg M Example: the fundamental plane for ellptcal galaxes We can derve a relatonshp between scale sze, central surface brghtness and central velocty dsperson for ellptcal galaxes that s rather smlar to the fundamental plane, usng only assumptons about a constant mass-to-lght rato and a constant functonal form for the surface brghtness profle. We shall assume here that: the mass-to-lght rato s constant for ellptcals all E galaxes have the same M/L regardless of ther sze or mass, and ellptcal galaxes have the same functonal form for the mass dstrbuton, only scalable. Let I 0 be the central surface brghtness and R 0 be a scale sze of a galaxy n ths case, dfferent galaxes wll have dfferent values of I 0 and R 0. The total lumnosty wll be L I 0 R 2 0, because I 0 s the lght per unt projected area. Snce the mass-to-lght rato s a constant for all galaxes, the mass of the galaxy s M L. M I 0 R 2 0. From the vral theorem, f v s a typcal velocty of the stars n the galaxy v 2 GM R 0. 21
8 The observed velocty dsperson along the lne sght, σ 0, wll be related to the typcal velocty v by σ 0 v because v s a three-dmensonal space velocty. So σ 2 0 M R 0. M σ 2 0 R 0. Equatng ths wth M I 0 R 2 0 from above, σ 2 0 R 0 I 0 R 2 0. R 0 I 0 σ 2 0 constant. Ths s close to, but not the same, as the observed fundamental plane result R 0 I0 0.8 σ0 1.3 constant. The devaton from ths vral predcton probably has somethng to do wth a varyng mass-to-lght rato, and may be caused by dfferences n ages between galaxes causng dfferences n lumnosty. 2.3 The Crossng Tme, T cross The crossng tme s a smple, but mportant, parameter that measures the tmescale for stars to move sgnfcantly wthn a system of stars. It s sometmes called the dynamcal tmescale. It s defned as T cross R v, 2.12 where R s the sze of the system and v s a typcal velocty of the stars. As a smple example, consder a stellar system of radus R and therefore an overall sze 2R, havng N stars each of mass m; the stars are dstrbuted roughly homogeneously, wth v beng a typcal velocty, and the system s n dynamcal equlbrum. Then from the vral theorem, v 2 NGm. R The crossng tme s then T cross 2R v 2R NGm R 2 R 3 NGm But the mass densty s So approxmately, ρ = Nm 4 = 3Nm 3 πr3 4πR. 3 R3 Nm = 3 4πρ. 3 T cross = 2 4πGρ T cross 1 Gρ Although ths equaton has been derved for a partcular case, that of a homogeneous sphere, t s an mportant result and can be used for order of magntude estmates n other stuatons. Note that ρ here s the mass densty of the system, averaged over a 22
9 volume of space, and not the densty of ndvdual stars. Example: an ellptcal galaxy of stars, radus 10 kpc. R 10 kpc m N = m 1 M kg R 3 T cross 2 NGm gves T cross s 10 8 yr. The Unverse s 14 Gyr old. So f a galaxy s 14 Gyr old, there are few 100 crossng tmes n a galaxy s lfetme so far. 2.4 The Relaxaton Tme, T relax The relaxaton tme s the tme taken for a star s velocty v to be changed sgnfcantly by two-body nteractons. It s defned as the tme needed for a change v 2 n v 2 to be the same as v 2,.e. the tme for v 2 = v To estmate the relaxaton tme we need to consder the nature of encounters between stars n some detal. 2.5 Star-Star Encounters Types of encounters We mght expect that stars, as they move around nsde a galaxy or other system of stars, wll experence close encounters wth other stars. The gravtatonal effects of one star on another would change ther veloctes and these velocty perturbatons would have a profound effect on the overall dynamcs of the galaxy. The dynamcs of the galaxy mght evolve wth tme, as a result only of the nternal encounters between stars. The truth, however, s rather dfferent. Close star-star encounters are extremely rare and even the effects of dstant encounters are so slght that t takes an extremely long tme for the dynamcs of galaxes to change substantally. We can consder two dfferent types of star-star encounters: strong encounters a close encounter that strongly changes a star s velocty these are very rare n practce weak encounters occur at a dstance they produce only very small changes n a star s velocty, but are much more common 23
10 2.5.2 Strong encounters A strong encounter between two stars s defned so that we have a strong encounter f, at the closest approach, the change n the potental energy s larger than or equal to the ntal knetc energy. For two stars of mass m that approach to a dstance r 0, f the change n potental energy s larger than than ntal knetc energy, Gm 2 r mv2, where v s the ntal velocty of one star relatve to the other. So we defne a strong encounter radus r 0 2Gm v 2. r S 2Gm v A strong encounter occurs f two stars approach to wthn a dstance r S 2Gm/v 2. For an ellptcal galaxy, v 300 kms 1. Usng m = 1M, we fnd that r S m 0.02 AU. Ths s a very small fgure on the scale of a galaxy. The typcal separaton between stars s 1 pc AU. For stars n the Galactc dsc n the solar neghbourhood, we can use a velocty dsperson of v = 30 kms 1 and m = 1M. Ths gves r S m 2 AU. Ths agan s very small on the scale of the Galaxy. So strong encounters are very rare. The mean tme between them n the Galactc dsc s yr, whle the age of the Galaxy s yr. In practce, we can gnore ther effect on the dynamcs of stars Dstant weak encounters between stars A star experences a weak encounter f t approaches another to a mnmum dstance r 0 when r 0 > r S 2Gm v where v s the relatve velocty before the encounter and m s the mass of the perturbng star. Weak encounters n general provde only a tny perturbaton to the motons of stars n a stellar system, but they are so much more numerous than strong encounters that they are more mportant than strong encounters n practce. We shall now derve a formula that expresses the change δv n the velocty v durng a weak encounter Equaton 2.19 below. Ths result wll later be used to derve an expresson for the square of the velocty change caused by a large number of weak encounters, whch wll then be used to obtan an estmate of the relaxaton tme n a system of stars. Consder a star of mass m s approachng a perturbng star of mass m wth an mpact parameter b. Because the encounter s weak, the change n the drecton of moton wll be small and the change n velocty wll be perpendcular to the ntal drecton 24
11 of moton. At any tme t when the separaton s r, the component of the gravtatonal force perpendcular to the drecton of moton wll be F perp = Gm sm r 2 cos φ, where φ s the angle at the perturbng mass between the pont of closest approach and the perturbed star. Let the component of velocty perpendcular to the ntal drecton of moton be v perp and let the fnal value be v perp f. Makng the approxmaton that the speed along the trajectory s constant, r b2 + v 2 t 2 at tme t f t = 0 at the pont of closest approach. Usng cos φ = b/r b/ b 2 + v 2 t 2 and applyng F = ma perpendcular to the drecton of moton we obtan dv perp = G m b b 2 + v 2 t 2 3/2, where v perp s the component at tme t of the velocty perpendcular to the ntal drecton of moton. Integratng from tme t = to, [ ] vperp f v perp = G m b. 0 b 2 + v 2 t 2 3/2 We have the standard ntegral 1 + s2 3/2 ds = 2 whch can be shown usng the substtuton s = tan x. Usng ths standard ntegral, the fnal component of the velocty perpendcular to the ntal drecton of moton s v perp f = 2Gm bv Because the deflecton s small, the change of velocty s δv δv = v perp f. Therefore the change n the velocty v s gven by δv = 2Gm bv, 2.19 where G s the constant of gravtaton, b s the mpact parameter and m s the mass of the perturbng star. 25
12 As a star moves through space, t wll experence a number of perturbatons caused by weak encounters. Many of these velocty changes wll cancel, but some net change wll occur over tme. As a result, the sum over all δv wll reman small, but the sum of the squares δv 2 wll buld up wth tme. It s ths change n v 2 that we need to consder n the defnton of the relaxaton tme Equaton Because the change n velocty δv s perpendcular to the ntal velocty v n a weak encounter, the change n v 2 s therefore δv 2 vf 2 v2 = v + δv 2 v 2 = v + δv.v + δv v 2 = v.v + 2v.δv + δv.δv v 2 = 2v.δv + δv 2 = δv 2, where v f s the fnal velocty of the star. The change n v 2 resultng from a sngle encounter that we need to consder s 2 2Gm δv 2 = bv Consder all weak encounters occurrng n a tme perod t that have mpact parameters n the range b to b + db wthn a unform sphercal system of N stars and radus R. The volume swept out by mpact parameters b to b + db n tme t s 2 π b db v t. Therefore the number of stars encountered wth mpact parameters between b and b + db n tme t s volume swept out number densty of stars = 2 π b db v t N 4 = 3 b v t N db 3 πr3 2R 3 The total change n v 2 caused by all encounters n tme t wth mpact parameters n the range b to b + db wll be 2 2Gm 3 b v t N db v 2 = bv 2 R 3 Integratng over b, the total change n a tme t from all mpact parameters from b mn to b max s bmax 2 2Gm 3 b v t N db v 2 t = = 3 2 2Gm v t N bmax db bv 2 R 3 2 v R 3 b b mn 26 b mn
13 2 Gm v 2 v t N t = 6 v R 3 ln bmax b mn It s sometmes useful to have an expresson for the change n v 2 that occurs n one crossng tme. In one crossng tme T cross = 2R/v, the change n v 2 s 2 Gm v 2 v 2R bmax T cross = 6 N ln v R 3 v b mn 2 Gm bmax = 12 N ln Rv The maxmum scale over whch weak encounters wll occur corresponds to the sze of the system of stars. So we shall use b max R. v 2 T cross = 12 N b mn 2 Gm R ln Rv b mn We are more nterested here n the relaxaton tme T relax. The relaxaton tme s defned as the tme taken for v 2 = v 2. Substtutng for v 2 from Equaton 2.21 we get, 2 Gm v T relax N bmax 6 ln = v 2. v R 3 or puttng b max R, T relax = 6N ln 1 b mn bmax b mn Rv 3 Gm 2, 2.24 T relax = 1 6N ln R b mn Rv 3 Gm Equaton 2.25 enables us to estmate the relaxaton tme for a system of stars, such as a galaxy or a globular cluster. Dfferent dervatons can have slghtly dfferent numercal constants because of the dfferent assumptons made. In practce, b mn s often set to the scale on whch strong encounters begn to operate, so b mn 1 AU. The precse values of b max and b mn have relatvely lttle effect on the estmaton of the relaxaton tme because of the log dependence. As an example of the calculaton of the relaxaton tme, consder an ellptcal galaxy. Ths has: v 300 kms 1 = ms 1, N 10 11, R 10 kpc m and m 1 M kg. So, lnr/b mn 21 and T relax s yr. The Unverse s yr old, whch means that the relaxaton tme s 10 8 tmes the age of the Unverse. So star-star encounters are of no sgnfcance for galaxes. For a large globular cluster, we have: v 10 kms 1 = 10 4 ms 1, N , R 5 pc m and m 1 M kg. So, lnr/b mn 15 and T relax s 10 7 yr. Ths s a small fracton 10 3 of the age of the Galaxy. Two body nteractons are therefore sgnfcant n globular clusters. The mportance of the relaxaton tme calculaton s that t enables us to decde whether we need to allow for star-star nteractons when modellng the dynamcs of a system of stars. Ths s dscussed further n Secton 2.7 below. 27
14 2.6 The Rato of the Relaxaton Tme to the Crossng Tme An approxmate expresson for the rato of the relaxaton tme to the crossng tme can be calculated easly. Dvdng the expressons for the relaxaton and crossng tmes Equatons 2.25 and 2.12, T relax T cross = 1 12N ln R b mn R 2 v 4 Gm 2. For a unform sphere, from the vral theorem Equaton 2.10, v 2 NGm R and settng b mn equal to the strong encounter radus r S = 2GM/v 2 Equaton 2.16, we get, T relax 1 = T cross 12N ln R 2 v 4 N 2 Rv 2 Gm 2 12N lnn 2GM T relax T cross N 12 ln N For a galaxy, N Therefore T relax /T cross For a globular cluster, N 10 5 and T relax /T cross Collsonal and Collsonless Systems It s possble to classfy the dynamcs of systems of matter accordng to whether the nteractons of ndvdual partcles n those systems are mportant or not. Such systems are sad to be ether collsonal or collsonless. The dynamcs are of these systems are: collsonal f nteractons between ndvdual partcles substantally affect ther motons; collsonless f nteractons between ndvdual partcles do not substantally affect ther motons. Note that ths defnton was encountered n Chapter 1 relatng to the encounters between dfferent systems. Here t apples wthn a sngle system of mass: the effects are all nternal to the system. The relaxaton tme calculatons showed that galaxes are n general collsonless systems. But an excepton to ths mght be the regon around the central nucle of galaxes where the densty of stars s very large. Globular clusters are collsonal over the lfetme of the Unverse. Gas, whether n galaxes or n the laboratory, s collsonal. Modellng becomes much easer f two-body encounters can be gnored. Fortunately, we can gnore these star-star nteractons when modellng galaxes and ths makes possble the use of a result called the collsonless Boltzmann equaton later. 28
15 2.8 Volent Relaxaton Stars n galaxes are collsonless systems, as we have seen. Therefore, the stars n a steady state galaxy wll contnue n steady state orbts wthout perturbng each other. The average dstrbuton of stars wll not change wth tme. However, the stuaton can be very dfferent n a system that s not n equlbrum. A changng gravtatonal potental wll cause the orbts of the stars to change. Because the stars determne the overall potental, the change n ther orbts wll change the potental. Ths process of changes n the dynamcs of stars caused by changes n ther net potental s called volent relaxaton. Galaxes experenced volent relaxaton durng ther formaton, and ths was a process that brought them to the equlbrum state that we see many of them n today. Interactons between galaxes can also brng about volent relaxaton. The process takes place relatvely quckly 10 8 yr and redstrbutes the motons of stars. 2.9 The Nature of the Gravtatonal Potental n a Galaxy The gravtatonal potental n a galaxy can be represented as essentally havng two components. The frst of these s the broad, smooth, underlyng potental due to the entre galaxy. Ths s the sum of the potentals of all the stars, and also of the dark matter and the nterstellar medum. The second component s the localsed deeper potentals due to ndvdual stars. We can effectvely regard the potental as beng made of a smooth component wth very localsed deep potentals supermposed on t. Ths s llustrated fguratvely n Fgure 2.1. Fgure 2.1: A sketch of the gravtatonal potental of a galaxy, showng the broad potental of the galaxy as a whole, and the deeper, localsed potentals of ndvdual stars. Interactons between ndvdual stars are rare, as we have seen, and therefore t s the broad dstrbuton that determnes the motons of stars. Therefore, we can represent the dynamcs of a system of stars usng only the smooth underlyng component of the gravtatonal potental Φx, t, where x s the poston vector of a pont and t s the tme. If the galaxy has reached a steady state, Φ s Φx only. We shall 29
16 neglect the effect of the localsed potentals of stars n the followng sectons, whch s an acceptable approxmaton as we have shown Gravtatonal potentals, densty dstrbutons and masses General prncples The dstrbuton of mass n a galaxy ncludng both the vsble and dark matter determnes the gravtatonal potental. The potental Φ at any pont s related to the local densty ρ by Posson s Equaton, 2 Φ. Φ = 4π Gρ Ths means that f we know the densty ρx as a functon of poston across a galaxy, we can calculate the potental Φ, ether analytcally or numercally, by ntegraton. Alternatvely, f we know Φx, we can calculate the densty profle ρx by dfferentaton. In addton, because the acceleraton due to gravty g s related to the potental by g = Φ, we can compute gx from Φx and vce-versa. Smlarly, substtutng for g = Φ n the Posson Equaton gves.g = 4πGρ. These computatons are often done for some example theoretcal representatons of the potental or densty. A number of convenent analytcal functons are encountered n the lterature, dependng on the type of galaxy beng modelled and partcular crcumstances. The ssue of determnng actual densty profles and potentals from observatons of galaxes s much more challengng, however. Observatons readly gve the projected densty dstrbutons of stars on the sky, and we can attempt to derve the threedmensonal dstrbuton of stars from ths; ths n turn can gve the densty of vsble matter ρ V IS x across the galaxy. However, t s the total densty ρx, ncludng dark matter ρ DM x, that s relevant gravtatonally, wth ρx = ρ DM x + ρ V IS x. The dark matter dstrbuton can only be nferred from the dynamcs of vsble matter or to a lmted extent from gravtatonal lensng of background objects. In practce, therefore, the three-dmenson densty dstrbuton ρx and the gravtatonal potental Φx are poorly known, partcularly where dark matter domnates far from the central regons Sphercal symmetry Calculatng the relatonshp between densty and potental s much smpler f we are dealng wth sphercally symmetrc dstrbutons, whch are approprate n some crcumstances such as sphercal ellptcal galaxes. Under sphercal symmetry, ρ and Φ are functons only of the radal dstance r from the centre of the dstrbuton. Therefore, 2 Φ = 1 r 2 d dr r 2 dφ dr = 4 π G ρ 2.28 because Φ s ndependent of the angles θ and φ n a sphercal coordnate system see Appendx C. 30
17 Another useful parameter for sphercally symmetrc dstrbutons s the mass Mr that les nsde a radus r. We can relate ths to the densty ρr by consderng a thn sphercal shell of radus r and thckness dr centred on the dstrbuton. The mass of ths shell s dmr = ρr surface area thckness = 4πr 2 ρr dr. Ths gves us the dfferental equaton dm = 4π r 2 ρ, 2.29 dr often known as the equaton of contnuty of mass. The total mass s M tot = lm r Mr. The gravtatonal acceleraton g n a sphercal dstrbuton has an absolute value g of g = GMr, 2.30 r 2 at a dstance r from the centre, where G s the constant of gravtaton derved n Appendx B, and s drected towards the centre of the dstrbuton. If we know how one of these functons ρ, Φ or Mr depends on radal dstance r, we can calculate the others relatvely easly when we have sphercal symmetry. For example, f know the potental Φr as a functon of r, we can dfferentate t to get the mass Mr nteror to r, and by dfferentatng t agan we can get the densty ρr. On the other hand, f we know ρr as a functon of r, we can ntegrate t to get Mr, and ntegratng t agan gves Φr. Comparng equatons 2.28 and 2.29, we fnd that Mr = r2 G dφ dr, 2.31 when we have sphercal symmetry. Ths allows us to convert between Mr and Φr drectly for ths sphercally symmetrc case Two examples of sphercal potentals The Plummer Potental A functon that s often used for the theoretcal modellng of sphercally-symmetrc galaxes s the Plummer potental. Ths has a gravtatonal potental Φ at a radal dstance r from the centre that s gven by Φr = GM tot r2 + a 2, 2.32 where M tot s the total mass of the galaxy and a s a constant. The constant a serves to flatten the potental n the core. For ths potental the densty ρ at a radal dstance r s ρr = 3M tot 4π a 2 r 2 + a 2 5/2, 2.33 whch can be derved from the expresson for Φ usng the Posson equaton 2 Φ = 4πGρ. Ths densty scales wth radus as ρ r 5 at large rad. The mass nteror to a pont Mr can be computed from the densty ρ usng dm/dr = 4πr 2 ρ, or from the potental Φ usng Gauss s Law n the form S Φ.dS = 4πGMr for a sphercal surface of radus r. The result s Mr = M tot r 3 r 2 + a 2 3/
18 The Plummer potental was frst used n 1911 by H. C. K. Plummer to descrbe globular clusters. Because of the smple functonal forms, the Plummer model s sometmes useful for approxmate analytcal modellng of galaxes, but the r 5 densty profle s much steeper than ellptcal galaxes are observed to have. The Dark Matter Profle A densty dstrbuton that s often used n modellng galaxes s one that s sometmes called the dark matter profle. The total densty s gven by ρr = ρ r/a 2 = ρ 0 a 2 r 2 + a 2, 2.35 where ρ 0 s the central densty ρr at r = 0 and a s a constant. The mass nteror to a radus r s Mr = 4πρ 0 r 0 r r 2 /a 2 dr = 4πρ 0 a 2 r a tan 1 r/a. Spral galaxes wth ths profle would have rotaton curves that are flat for r a, whch s exactly what s observed. Ths profle therefore represents successfully the large amount of dark matter that s observed at large dstances r from the centres of galaxes. One weakness s that the mass nteror to a radus tends to nfnty as r ncreases: lm r Mr. In practce, therefore, the densty profles of real galaxes must fall below the dark matter profle at some very large dstances. These ssues are dscussed further n Chapter 5. The Isothermal Sphere The densty dstrbuton known as the sothermal sphere s a sphercal model of a galaxy that s dentcal to the dstrbuton that would be followed by a stable cloud of gas havng the same temperature everywhere. A sphercally-symmetrc cloud of gas havng a sngle temperature T throughout would have a gas pressure P r at a radus r from ts centre that s related to T by the deal gas law as P r = n p k B T, where n p r s the number densty of gas partcles atoms or molecules at radus r and k B s the Boltzmann constant. Ths can also be expressed n terms of the densty ρ as P r = k B ρrt/m p, where m p s the mean mass of each partcle n the gas. The cloud wll be supported by hydrostatc equlbrum, so therefore dp dr where Mr s the mass enclosed wthn a radus r. dm/dr = 4πr 2 ρr. These equatons have a soluton = GMr r 2 ρr, 2.36 The gradent n the mass s ρr = σ 2 2σ2, and Mr = 2πG r2 G r, where σ2 k BT, 2.37 m p where m p s the mass of each gas partcle. The parameter σ s the root-mean-square velocty n any drecton. Ths s only one of a number of solutons and t s called the sngular sothermal sphere. 32
19 The sothermal sphere model for a system of stars s defned to be a model that has the same densty dstrbuton as the sothermal gas cloud. Therefore, an sothermal galaxy would also have a densty ρr and mass Mr nteror to a radus r gven by ρr = σ 2 2σ2, and Mr = 2πG r2 G r, 2.38 for a sngular sothermal sphere, where σ s root-mean-square velocty of the stars along any drecton. The sngular sothermal sphere model s sometmes used for the analytcal modellng of galaxes. Whle t has some advantages of smplcty, t does suffer from the dsadvantage of beng unrealstc n some mportant respects. Most sgnfcantly, the model fals totally at large rad: formally the lmt of Mr as r s nfnte Phase Space and the Dstrbuton Functon fx, v, t To descrbe the dynamcs of a galaxy, we could use: the postons of each star, x the veloctes of each star, v where = 1 to N, wth N 10 6 to However, ths would be mpractcal numercally. If we tred to store these data on a computer as 4-byte numbers for every star n a galaxy havng N stars, we would need bytes bytes Gbyte. Ths s such a large data sze that the storage requrements are prohbtve. If we needed to smulate a galaxy theoretcally, we would need to follow the galaxy over tme usng a large number of tme steps. Storng the complete set of data for, say, tme steps would be mpossble. Observatonally, meanwhle, t s mpossble to determne the postons and motons of every star n any galaxy, even our own. In practce, therefore, people represent the stars n a galaxy usng the dstrbuton functon fx, v, t over poston x and velocty v, at a tme t. Ths s the probablty densty n the 6-dmensonal phase space of poston and velocty at a gven tme. It s also known as the phase space densty. It requres only modest data resources to store the functon numercally for a model of a galaxy, whle f can also be modelled analytcally. The number of stars n a rectangular box between x and x + dx, y and y + dy, z and z + dz, wth velocty components between v x and v x + dv x, v y and v y + dv y, v z and v z + dv z, s fx, v, t dx dy dz dv x dv y dv z fx, v, t d 3 x d 3 v. The number densty nx, v, t of stars n space can be obtaned from the dstrbuton functon f by ntegratng over the velocty components, nx, v, t = fx, v, t dv x dv y dv z = fx, v, t d 3 v
20 2.12 The Contnuty Equaton We shall assume here that stars are conserved: for the purpose of modellng galaxes we shall assume that the number of stars does not change. Ths means gnorng star formaton and the deaths of stars, but t s acceptable for the present purposes. The assumpton that stars are conserved results n the contnuty equaton. Ths expresses the rate of change n the dstrbuton functon f as a functon of tme to the rates of change wth poston and velocty. The equaton becomes an mportant startng pont n dervng other equatons that relate f to the gravtatonal potental and to observatonal quanttes. Consder the x v x plane wthn the 6-dmensonal phase space x, y, z, v x, v y, v z n Cartesan coordnates. Consder a rectangular box n the plane extendng from x to x + x and v x to v x + v x. But the velocty v x means that stars move n x v x dx/. So there s a flow of stars through the box n both the x and the v x drectons. We can represent the flow of stars by the contnuty equaton: + f dx + f dy + f dz + f dv x + x y z v x f dv y + f dv z = v y v z 34
21 Ths can be abbrevated as + =1 f dx + f dv v = 0, 2.41 where x 1 x, x 2 y, x 3 z, v 1 v x, v 2 v y, and v 3 v z. It s sometmes also abbrevated as +. f dx +. f dv = 0, 2.42 x v where, n ths notaton, for any vectors a and b wth components a 1, a 2, a 3 and b 1, b 2, b 3, a.b =1 b a Note that t does not mean a drect dfferentaton by a vector. It s also possble to smplfy the notaton further by ntroducng a combned phase space coordnate system w = x, v wth components w 1, w 2, w 3, w 4, w 5, w 6 = x, y, z, v x, v y, v z. In ths case the contnuty equaton becomes + 6 =1 w fẇ = The equaton of contnuty can also be expressed n terms of the momentum p = mv, where m s mass of an element of gas, as +. f dx +. f dp = x p 2.13 The Collsonless Boltzmann Equaton The mportance of the Collsonless Boltzmann Equaton Equaton 2.25 showed that the relaxaton tme for galaxes s very long, sgnfcantly longer than the age of the Unverse: galaxes are collsonless systems. Ths, fortunately, smplfes the analyss of the dynamcs of stars n galaxes. It s possble to derve an equaton from the contnuty equaton that more explctly states the relaton between the dstrbuton functon f, poston x, velocty v and tme t. Ths s the collsonless Boltzmann equaton C.B.E., whch takes ts name from a smlar equaton n statstcal physcs derved by Boltzmann to descrbe partcles n a gas. It states that + =1 dx + dv v df = The collsonless Boltzmann equaton therefore provdes a relatonshp between the densty of stars n phase space for a galaxy wth poston x, stellar velocty v and tme t. 35
22 A dervaton of the Collsonless Boltzmann Equaton The contnuty equaton 2.41 states that + =1 f dx + f dv v = 0, where f s the dstrbuton functon n the Cartesan phase space x 1, x 2, x 3, v 1, v 2, v 3. But the acceleraton of a star s gven by the gradent of the gravtatonal potental Φ: dv = Φ n each drecton.e. for each value of for = 1, 2, 3. Ths s smply dv/ = g = Φ resolved nto each dmenson. We also have dx = v, so, + =1 fv + v f Φ = 0. But v s a coordnate, not a value assocated wth a partcular star: we are usng the contnuous functon f rather than consderng ndvdual stars. Therefore v s ndependent of x. So, fv = v. The potental Φ Φx, t does not depend on v : Φ s ndependent of velocty. f dφ = Φ v dx v But dv = Φ, so, + + =1 =1 v v Φ + dv v v = 0. Ths s the collsonless Boltzmann equaton. It can also be wrtten as = =1 dx + dv v = Alternatvely t can expressed as, + 6 w =1 36 w = 0, 2.48
23 where w = x, v s a 6-dmensonal coordnate system, and also as and as Note the use here of the notaton + dx. x + dv. v = 0, dx. x + dp. p = dx. x dx =1, etc Dervng the Collsonless Boltzmann Equaton usng Hamltonan Mechancs [Ths secton s not examnable.] The collsonless Boltzmann equaton can also be derved from the contnuty equaton usng Hamltonan mechancs. Ths dervaton s gven here. It has the advantage of beng neat. However, do not worry f you are not famlar wth Hamltonan mechancs: ths s gven as an alternatve to Secton Hamlton s Equatons relate the dfferentals of the poston vector x and of the generalsed momentum p to the dfferental of the Hamltonan H: dx In ths notaton ths means = H p, dp = H x dx = H and dp p = H for = 1 to 3, 2.53 where x and p are the components of x and p. Substtutng for dx/ and dp/ nto the contnuty equaton, +. f H +. f H = 0. x p p x For a star movng n a gravtatonal potental Φ, the Hamltonan s H = p2 2m + m Φx = p.p 2m + m Φx
24 where p s ts momentum and m s ts mass. Dfferentatng, and H p H x = d dp p.p 2m p = m + 0 p = m p 2 = x 2m = 0 + m Φ x = m Φ x. Substtutng for H/p and H/x, +. f p x m + d dp mφ because Φx, t s ndependent of p + m Φ x because p 2 = p.p s ndependent of x. fm Φ p x = 0 + p m. x m Φ x. p = 0 because p s ndependent of x, and because Φ/s ndependent of p snce Φ Φx, t. But the momentum p = m dx/ and the acceleraton s 1 dp/ = Φ/x the m gradent of the potental. Φ x = 1 dp. m So, + m m dx. x m The left-hand sde s the dfferental df/. So, 1 m + dx. x + dp. p = 0. dp. p = 0 + dx. x + dp. p df = the collsonless Boltzmann equaton. Whle ths equaton s called the collsonless Boltzmann equaton or CBE n stellar dynamcs, n Hamltonan dynamcs t s known as Louvlle s theorem The mplcatons of the Collsonless Boltzmann Equaton The collsonless Boltzmann equaton tells us that df/ = 0. Ths means that the densty n phase space, f, does not change wth tme for a test partcle. Therefore f 38
25 we follow a star n orbt, the densty f n 6-dmensonal phase space around the star s constant. Ths smple result has mportant mplcatons. If a star moves nwards n a galaxy as t follows ts orbt, the densty of stars n space ncreases because the densty of stars n the galaxy s greater closer to the centre. df/ = 0 then tells us that the spread of stellar veloctes around the star wll ncrease to keep f constant. Therefore the velocty dsperson around the star ncreases as the star moves nwards. The velocty dsperson s therefore larger n regons of the galaxy where the densty of stars s greater. Conversely, f a star moves out from the centre, the densty of stars around t wll decrease and the velocty dsperson wll decrease to keep f constant. The collsonless Boltzmann equaton, and the Posson equaton whch s the gravtatonal analogue of Gauss s law n electrostatcs together consttute the basc equatons of stellar dynamcs: df = 0, 2 Φx = 4πGρx, 2.56 where f s the dstrbuton functon, t s tme, Φx, t s the gravtatonal potental at pont x, ρx, t s the mass densty at pont x, and G s the constant of gravtaton. The collsonless Boltzmann equaton apples because star-star encounters do not change the motons of stars sgnfcantly over the lfetme of a galaxy, as was shown n Secton 2.5. Were ths not the case and the system were collsonal, the CBE would have to be modfed by addng a collsonal term on the rght-hand sde. Though f s a densty n phase space, the full form of the collsonless Boltzmann equaton does not necessarly have to be wrtten n terms of x and p. We can express df = 0 n any set of sx varables n phase space. You should remember that f s always taken to be a densty n sx-dmensonal phase space, even n stuatons where t s a functon of fewer varables. For example, f f happens to be a functon of energy alone, t s not the same as the densty n energy space The Collsonless Boltzmann Equaton n Cylndrcal Coordnates [Ths secton s not examnable.] So far we have consdered Cartesan coordnates x, y, z, v x, v y, v z. However, the form dx + + dv = 0, v =1 for the collsonless Boltzmann equaton of Equaton 2.46 apples to any coordnate system. For a galaxy, t s often more convenent to use cylndrcal coordnates wth the centre of the galaxy as the orgn. 39
26 The coordnates of a star are R, φ, z. A cylndrcal system s partcularly useful for spral galaxes lke our own where the z = 0 plane s set to be the Galactc plane. Note the use of a lower-case φ as a coordnate angle, whereas elsewhere we have used a captal Φ to denote the gravtatonal potental. The collsonless Boltzmann equaton n ths system s df = + dr R + dφ φ + dz z + dv R v R + dv φ v φ + dv z v z = 0, 2.57 where v R, v φ, and v z are the components of the velocty n the R, φ, z drectons. We need to replace the dfferentals of the velocty components wth more convenent terms. dv R /, dv φ / and dv z / are related to the acceleraton a but are not actually the components of the acceleraton for the R and φ drectons. The velocty and acceleraton n terms of these dfferentals n a cylndrcal coordnate system are v = dr a = dv = dr = êr d 2 R 2 + R dφ êφ + dz R dφ 2 êz ê R + 2 dr dφ + R d2 φ ê 2 φ + d2 z 2 êz 2.58 where ê R, ê φ and ê z are unt vectors n the R, φ and z drectons a standard result for any cylndrcal coordnate system, and for any velocty, acceleraton or force, gravtatonal or any other knd: see Appendx C5. Representng the velocty as v = v R ê R + v φ ê φ + v z ê z and equatng coeffcents of the unt vectors, dr = v R, dφ = v φ R, dz = v z The acceleraton can be related to the gravtatonal potental Φ wth a = Φ because the only forces actng on the star are those of gravty. In a cylndrcal coordnate system, ê R R + ê φ 1 R φ + ê z z
27 Usng ths result and equatng coeffcents, we obtan, d 2 R 2 R 2 dφ = Φ R, 2 dr dφ + R d2 φ 2 = 1 R Φ φ, d 2 z 2 = dφ dz Rearrangng these and substtutng for dr/, dφ/ and dz/ from 2.59, we obtan, dv R and wth some more manpulaton, dv φ = d = v R v φ R = Φ R + v2 φ R, and dv z R dφ 1 R = dr dφ + R d2 φ 2 Φ φ 2 v v φ R R = 1 R Substtutng these nto Equaton 2.57, we obtan, = Φ z, = v R v φ R + 1 R Φ φ 2 dr dφ Φ φ v R v φ R df = + v R R + v φ R φ 1 R + v z z v R v φ + Φ φ + v 2 φ R Φ R v R Φ v φ z v z = 0, 2.62 Ths s the collsonless Boltzmann equaton n cylndrcal coordnates. Ths form relates f to observable parameters R, φ, z, v R, v φ, v z and the potental Φ. In many practcal cases, partcularly spral galaxes, Φ wll be ndependent of φ, so Φ/φ = 0 but not f we nclude spral arms where the potental wll be slghtly deeper Orbts of Stars n Galaxes The character of orbts The term orbt s used to descrbe the trajectores of stars wthn galaxes, even though they are very dfferent to Kepleran orbts such as those of planets n the Solar System. The orbts of stars n a galaxy are usually not closed paths and n general they are three dmensonal they do not le n a plane. They are often complex. In general they are hghly chaotc, even f the galaxy s n equlbrum. The orbt of a star n a sphercal potental, to consder the smplest example, s confned to a plane perpendcular to the angular momentum vector of the star. It s, however, not a closed path and has an appearance that s usually descrbed as a rosette. In axsymmetrc potentals e.g. an oblate ellptcal galaxy the orbt s confned to a plane that precesses. Ths plane s nclned to the axs of symmetry and rotates about the axs. The orbt wthn the plane s smlar to that n a sphercal potental. Traxal potentals can have orbts that are much more complex. Traxal potentals often have the tendency to tumble about one axs, whch leads to chaotc star orbts. 41
28 Fgure 2.2: An example of the orbt of a star n a sphercal potental. An example star has been put nto an orbt n the x y plane. Its orbt follows a rosette pattern, but t remans n the x y plane. [These dagrams were plotted usng data generated assumng a Plummer potental: the potental lacks a deep central cusp.] Fgure 2.3: The orbt of a star n a flattened oblate potental. An example star has been put nto an orbt nclned to the x y plane. The galaxy s flattened n the z drecton wth an axs rato of 0.7. The orbt follows a rosette pattern, but the plane of the orbt precesses. Ths llustrates the trajectory of a star n an oblate ellptcal galaxy, for example The chaotc nature of many orbts In chaotc systems, stars that ntally move along smlar paths wll dverge, eventually movng along very dfferent orbts. The dvergence n ther paths s exponental n tme, whch s the techncal defnton of chaos n dynamcal systems. Ther moton shows 42
29 Fgure 2.4: The orbt of a star n a traxal potental. An example star has been put nto an orbt nclned to the x y plane. The galaxy has dfferent dmensons dfferent scale szes n each of the x, y and z drectons. The orbt s complex and t maps out a regon of space. Ths llustrates the trajectory of a star n a traxal ellptcal galaxy, for example. Ths smulaton extends over a longer tme perod than those of Fgures 2.2 and 2.3. a stretchng and foldng n phase space. Ths can be so even f there s no collectve moton of stars at all f n equlbrum. Ths stretchng and foldng n phase space can be apprecated usng an analogy. When makng bread, a baker s dough behaves essentally as a flud. Dough s ncompressble, but that does not prevent the baker stretchng t n one drecton and shrnkng t n others, and then foldng t back. So whle the dough keeps much the same overall shape, partcles ntally nearby wthn t can be dspersed to wdely dfferent parts of t, through the repeated stretchng and foldng. The same stretchng and foldng operaton can take place for stars n phase space. In fact t appears that phase space s typcally rddled wth regons where f gets stretched n one drecton whle beng shrunk n others. Thus nearby orbts tend to dverge, and the dvergence s exponental n tme. Smulatons show that the tmescale for dvergence the e-foldng tme s T dverge T cross, the crossng tme, and gets shorter for hgher star denstes. However, n some specal cases, there s no chaos. These systems are sad to be ntegrable. If the dynamcs s confned to one real-space dmenson hence two phase-space dmensons then no stretchng-and-foldng can happen, and orbts are regular. So n a sphercal system all orbts are regular. In addton, there are certan potentals usually referred to as Stäckel potentals where the dynamcs decouples nto three effectvely one-dmensonal systems; so f some equlbrum f generates a Stäckel potental, the orbts wll stay chaos-free. Also, small perturbatons of non-chaotc systems tend to produce only small regons of chaos, 1 and orbts may be well descrbed through 1 If you ever come across the KAM theorem, that s bascally t. 43
30 perturbaton theory Integrals of the moton To solve the collsonless Boltzmann equaton for stars n a galaxy, we need further constrants on the poston and velocty. Ths can be done usng ntegrals of the moton. These are smply functons of the star s poston x and velocty v that are constant along ts orbt. They are useful n potentals Φx that are constant over tme. The dstrbuton functon f s also constant along the orbt and can be wrtten as a functon of ntegrals of the moton. Examples of ntegrals of the moton are: The total energy. The mechancal energy E of a partcular star n a potental s constant over tme, so Ex, v = 1 2 mv2 + mφx. Because ths s dependent on the mass of the star, t s more normal to work wth the energy per unt mass, whch wll be wrtten as E m here. So E m = 1 2 v2 + Φ s a constant. In an axsymmetrc potental e.g. our Galaxy, the z-component of the angular momentum, L z, s conserved. Therefore L z s an ntegral of the moton n such a potental. In a sphercal potental, the total angular momentum L s constant. Therefore L s an ntegral of the moton n ths potental, and the x, y and z components of L are each ntegrals of the moton. An orbt s sad to be regular f t has as many solatng ntegrals that can defne the orbt unambguously as there are spatal dmensons Isolatng ntegrals and ntegrable systems The collsonless Boltzmann equaton tells us that df/ = 0 Secton As was dscussed earler, f we move wth a star n ts orbt, f s constant locally as the star passes through phase space at that nstant n tme. But f the system s n a steady state the potental s constant over tme, f s constant along the star s path at all tmes. Ths means that the orbts of stars map out constant values of f. An ntegral of the moton for a star e.g. energy per unt mass, E m s constant by defnton. They therefore defne a 5-dmensonal hypersurface n 6-dmensonal phase space. The moton of a star s confned to that 5-dmensonal surface n phase space. Therefore f s constant over that hypersurface. A dfferent value of the solatng ntegral e.g. a dfferent value of E m wll defne a dfferent hypersurface. In turn, f wll be dfferent on ths surface. So f s a functon of the solatng ntegral,.e. fx, y, z, v x, v y, v z = fni 1 where I 1 s an ntegral of the moton. I 1 here solates a hypersurface. Therefore the ntegral of the moton s known as an solatng ntegral. Integrals that fal to confne orbts are called non-solatng ntegrals. A system s ntegrable f we can defne solatng ntegrals that enable the orbt to be determned. In ntegrable systems there are sgnfcant smplfcatons. Each orbt s confned to a three-dmensonal torodal subspace of sx-dmensonal phase space, and flls 44
Physics 181. Particle Systems
 Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
CHAPTER 14 GENERAL PERTURBATION THEORY
 CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
r i r j 3. (2) Gm j m i r i (r i r j ) r i r j 3. (3)
 N-body problem There s a lot of nterestng physcs related to the nteractons of a few bodes, but there are also many systems that can be well-approxmated by a large number of bodes that nteract exclusvely
N-body problem There s a lot of nterestng physcs related to the nteractons of a few bodes, but there are also many systems that can be well-approxmated by a large number of bodes that nteract exclusvely
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM
 ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
Celestial Mechanics. Basic Orbits. Why circles? Tycho Brahe. PHY celestial-mechanics - J. Hedberg
 PHY 454 - celestal-mechancs - J. Hedberg - 207 Celestal Mechancs. Basc Orbts. Why crcles? 2. Tycho Brahe 3. Kepler 4. 3 laws of orbtng bodes 2. Newtonan Mechancs 3. Newton's Laws. Law of Gravtaton 2. The
PHY 454 - celestal-mechancs - J. Hedberg - 207 Celestal Mechancs. Basc Orbts. Why crcles? 2. Tycho Brahe 3. Kepler 4. 3 laws of orbtng bodes 2. Newtonan Mechancs 3. Newton's Laws. Law of Gravtaton 2. The
PHYS 705: Classical Mechanics. Newtonian Mechanics
 1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Physics 53. Rotational Motion 3. Sir, I have found you an argument, but I am not obliged to find you an understanding.
 Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Physics 5153 Classical Mechanics. D Alembert s Principle and The Lagrangian-1
 P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
Physics 607 Exam 1. ( ) = 1, Γ( z +1) = zγ( z) x n e x2 dx = 1. e x2
 Physcs 607 Exam 1 Please be well-organzed, and show all sgnfcant steps clearly n all problems. You are graded on your wor, so please do not just wrte down answers wth no explanaton! Do all your wor on
Physcs 607 Exam 1 Please be well-organzed, and show all sgnfcant steps clearly n all problems. You are graded on your wor, so please do not just wrte down answers wth no explanaton! Do all your wor on
Physics 207: Lecture 20. Today s Agenda Homework for Monday
 Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
PY2101 Classical Mechanics Dr. Síle Nic Chormaic, Room 215 D Kane Bldg
 PY2101 Classcal Mechancs Dr. Síle Nc Chormac, Room 215 D Kane Bldg s.ncchormac@ucc.e Lectures stll some ssues to resolve. Slots shared between PY2101 and PY2104. Hope to have t fnalsed by tomorrow. Mondays
PY2101 Classcal Mechancs Dr. Síle Nc Chormac, Room 215 D Kane Bldg s.ncchormac@ucc.e Lectures stll some ssues to resolve. Slots shared between PY2101 and PY2104. Hope to have t fnalsed by tomorrow. Mondays
CHAPTER 5 NUMERICAL EVALUATION OF DYNAMIC RESPONSE
 CHAPTER 5 NUMERICAL EVALUATION OF DYNAMIC RESPONSE Analytcal soluton s usually not possble when exctaton vares arbtrarly wth tme or f the system s nonlnear. Such problems can be solved by numercal tmesteppng
CHAPTER 5 NUMERICAL EVALUATION OF DYNAMIC RESPONSE Analytcal soluton s usually not possble when exctaton vares arbtrarly wth tme or f the system s nonlnear. Such problems can be solved by numercal tmesteppng
Physics 111: Mechanics Lecture 11
 Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
12. The Hamilton-Jacobi Equation Michael Fowler
 1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
Spring 2002 Lecture #13
 44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
Week 11: Chapter 11. The Vector Product. The Vector Product Defined. The Vector Product and Torque. More About the Vector Product
 The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
Week 8: Chapter 9. Linear Momentum. Newton Law and Momentum. Linear Momentum, cont. Conservation of Linear Momentum. Conservation of Momentum, 2
 Lnear omentum Week 8: Chapter 9 Lnear omentum and Collsons The lnear momentum of a partcle, or an object that can be modeled as a partcle, of mass m movng wth a velocty v s defned to be the product of
Lnear omentum Week 8: Chapter 9 Lnear omentum and Collsons The lnear momentum of a partcle, or an object that can be modeled as a partcle, of mass m movng wth a velocty v s defned to be the product of
3.1 Expectation of Functions of Several Random Variables. )' be a k-dimensional discrete or continuous random vector, with joint PMF p (, E X E X1 E X
 Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
So far: simple (planar) geometries
 Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Chapter 8. Potential Energy and Conservation of Energy
 Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
NUMERICAL DIFFERENTIATION
 NUMERICAL DIFFERENTIATION 1 Introducton Dfferentaton s a method to compute the rate at whch a dependent output y changes wth respect to the change n the ndependent nput x. Ths rate of change s called the
NUMERICAL DIFFERENTIATION 1 Introducton Dfferentaton s a method to compute the rate at whch a dependent output y changes wth respect to the change n the ndependent nput x. Ths rate of change s called the
First Law: A body at rest remains at rest, a body in motion continues to move at constant velocity, unless acted upon by an external force.
 Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Open Systems: Chemical Potential and Partial Molar Quantities Chemical Potential
 Open Systems: Chemcal Potental and Partal Molar Quanttes Chemcal Potental For closed systems, we have derved the followng relatonshps: du = TdS pdv dh = TdS + Vdp da = SdT pdv dg = VdP SdT For open systems,
Open Systems: Chemcal Potental and Partal Molar Quanttes Chemcal Potental For closed systems, we have derved the followng relatonshps: du = TdS pdv dh = TdS + Vdp da = SdT pdv dg = VdP SdT For open systems,
Mathematical Preparations
 1 Introducton Mathematcal Preparatons The theory of relatvty was developed to explan experments whch studed the propagaton of electromagnetc radaton n movng coordnate systems. Wthn expermental error the
1 Introducton Mathematcal Preparatons The theory of relatvty was developed to explan experments whch studed the propagaton of electromagnetc radaton n movng coordnate systems. Wthn expermental error the
Inductance Calculation for Conductors of Arbitrary Shape
 CRYO/02/028 Aprl 5, 2002 Inductance Calculaton for Conductors of Arbtrary Shape L. Bottura Dstrbuton: Internal Summary In ths note we descrbe a method for the numercal calculaton of nductances among conductors
CRYO/02/028 Aprl 5, 2002 Inductance Calculaton for Conductors of Arbtrary Shape L. Bottura Dstrbuton: Internal Summary In ths note we descrbe a method for the numercal calculaton of nductances among conductors
University of Washington Department of Chemistry Chemistry 453 Winter Quarter 2015
 Lecture 2. 1/07/15-1/09/15 Unversty of Washngton Department of Chemstry Chemstry 453 Wnter Quarter 2015 We are not talkng about truth. We are talkng about somethng that seems lke truth. The truth we want
Lecture 2. 1/07/15-1/09/15 Unversty of Washngton Department of Chemstry Chemstry 453 Wnter Quarter 2015 We are not talkng about truth. We are talkng about somethng that seems lke truth. The truth we want
10. Canonical Transformations Michael Fowler
 10. Canoncal Transformatons Mchael Fowler Pont Transformatons It s clear that Lagrange s equatons are correct for any reasonable choce of parameters labelng the system confguraton. Let s call our frst
10. Canoncal Transformatons Mchael Fowler Pont Transformatons It s clear that Lagrange s equatons are correct for any reasonable choce of parameters labelng the system confguraton. Let s call our frst
Module 1 : The equation of continuity. Lecture 1: Equation of Continuity
 1 Module 1 : The equaton of contnuty Lecture 1: Equaton of Contnuty 2 Advanced Heat and Mass Transfer: Modules 1. THE EQUATION OF CONTINUITY : Lectures 1-6 () () () (v) (v) Overall Mass Balance Momentum
1 Module 1 : The equaton of contnuty Lecture 1: Equaton of Contnuty 2 Advanced Heat and Mass Transfer: Modules 1. THE EQUATION OF CONTINUITY : Lectures 1-6 () () () (v) (v) Overall Mass Balance Momentum
CONDUCTORS AND INSULATORS
 CONDUCTORS AND INSULATORS We defne a conductor as a materal n whch charges are free to move over macroscopc dstances.e., they can leave ther nucle and move around the materal. An nsulator s anythng else.
CONDUCTORS AND INSULATORS We defne a conductor as a materal n whch charges are free to move over macroscopc dstances.e., they can leave ther nucle and move around the materal. An nsulator s anythng else.
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
Supplementary Notes for Chapter 9 Mixture Thermodynamics
 Supplementary Notes for Chapter 9 Mxture Thermodynamcs Key ponts Nne major topcs of Chapter 9 are revewed below: 1. Notaton and operatonal equatons for mxtures 2. PVTN EOSs for mxtures 3. General effects
Supplementary Notes for Chapter 9 Mxture Thermodynamcs Key ponts Nne major topcs of Chapter 9 are revewed below: 1. Notaton and operatonal equatons for mxtures 2. PVTN EOSs for mxtures 3. General effects
Implicit Integration Henyey Method
 Implct Integraton Henyey Method In realstc stellar evoluton codes nstead of a drect ntegraton usng for example the Runge-Kutta method one employs an teratve mplct technque. Ths s because the structure
Implct Integraton Henyey Method In realstc stellar evoluton codes nstead of a drect ntegraton usng for example the Runge-Kutta method one employs an teratve mplct technque. Ths s because the structure
Module 3 LOSSY IMAGE COMPRESSION SYSTEMS. Version 2 ECE IIT, Kharagpur
 Module 3 LOSSY IMAGE COMPRESSION SYSTEMS Verson ECE IIT, Kharagpur Lesson 6 Theory of Quantzaton Verson ECE IIT, Kharagpur Instructonal Objectves At the end of ths lesson, the students should be able to:
Module 3 LOSSY IMAGE COMPRESSION SYSTEMS Verson ECE IIT, Kharagpur Lesson 6 Theory of Quantzaton Verson ECE IIT, Kharagpur Instructonal Objectves At the end of ths lesson, the students should be able to:
STATISTICAL MECHANICS
 STATISTICAL MECHANICS Thermal Energy Recall that KE can always be separated nto 2 terms: KE system = 1 2 M 2 total v CM KE nternal Rgd-body rotaton and elastc / sound waves Use smplfyng assumptons KE of
STATISTICAL MECHANICS Thermal Energy Recall that KE can always be separated nto 2 terms: KE system = 1 2 M 2 total v CM KE nternal Rgd-body rotaton and elastc / sound waves Use smplfyng assumptons KE of
The Feynman path integral
 The Feynman path ntegral Aprl 3, 205 Hesenberg and Schrödnger pctures The Schrödnger wave functon places the tme dependence of a physcal system n the state, ψ, t, where the state s a vector n Hlbert space
The Feynman path ntegral Aprl 3, 205 Hesenberg and Schrödnger pctures The Schrödnger wave functon places the tme dependence of a physcal system n the state, ψ, t, where the state s a vector n Hlbert space
CHAPTER 6. LAGRANGE S EQUATIONS (Analytical Mechanics)
 CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
χ x B E (c) Figure 2.1.1: (a) a material particle in a body, (b) a place in space, (c) a configuration of the body
 Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Introduction to Vapor/Liquid Equilibrium, part 2. Raoult s Law:
 CE304, Sprng 2004 Lecture 4 Introducton to Vapor/Lqud Equlbrum, part 2 Raoult s Law: The smplest model that allows us do VLE calculatons s obtaned when we assume that the vapor phase s an deal gas, and
CE304, Sprng 2004 Lecture 4 Introducton to Vapor/Lqud Equlbrum, part 2 Raoult s Law: The smplest model that allows us do VLE calculatons s obtaned when we assume that the vapor phase s an deal gas, and
Chapter 5. Solution of System of Linear Equations. Module No. 6. Solution of Inconsistent and Ill Conditioned Systems
 Numercal Analyss by Dr. Anta Pal Assstant Professor Department of Mathematcs Natonal Insttute of Technology Durgapur Durgapur-713209 emal: anta.bue@gmal.com 1 . Chapter 5 Soluton of System of Lnear Equatons
Numercal Analyss by Dr. Anta Pal Assstant Professor Department of Mathematcs Natonal Insttute of Technology Durgapur Durgapur-713209 emal: anta.bue@gmal.com 1 . Chapter 5 Soluton of System of Lnear Equatons
A particle in a state of uniform motion remain in that state of motion unless acted upon by external force.
 The fundamental prncples of classcal mechancs were lad down by Galleo and Newton n the 16th and 17th centures. In 1686, Newton wrote the Prncpa where he gave us three laws of moton, one law of gravty,
The fundamental prncples of classcal mechancs were lad down by Galleo and Newton n the 16th and 17th centures. In 1686, Newton wrote the Prncpa where he gave us three laws of moton, one law of gravty,
Transfer Functions. Convenient representation of a linear, dynamic model. A transfer function (TF) relates one input and one output: ( ) system
 Transfer Functons Convenent representaton of a lnear, dynamc model. A transfer functon (TF) relates one nput and one output: x t X s y t system Y s The followng termnology s used: x y nput output forcng
Transfer Functons Convenent representaton of a lnear, dynamc model. A transfer functon (TF) relates one nput and one output: x t X s y t system Y s The followng termnology s used: x y nput output forcng
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
Lecture Note 3. Eshelby s Inclusion II
 ME340B Elastcty of Mcroscopc Structures Stanford Unversty Wnter 004 Lecture Note 3. Eshelby s Incluson II Chrs Wenberger and We Ca c All rghts reserved January 6, 004 Contents 1 Incluson energy n an nfnte
ME340B Elastcty of Mcroscopc Structures Stanford Unversty Wnter 004 Lecture Note 3. Eshelby s Incluson II Chrs Wenberger and We Ca c All rghts reserved January 6, 004 Contents 1 Incluson energy n an nfnte
Robert Eisberg Second edition CH 09 Multielectron atoms ground states and x-ray excitations
 Quantum Physcs 量 理 Robert Esberg Second edton CH 09 Multelectron atoms ground states and x-ray exctatons 9-01 By gong through the procedure ndcated n the text, develop the tme-ndependent Schroednger equaton
Quantum Physcs 量 理 Robert Esberg Second edton CH 09 Multelectron atoms ground states and x-ray exctatons 9-01 By gong through the procedure ndcated n the text, develop the tme-ndependent Schroednger equaton
CHAPTER 10 ROTATIONAL MOTION
 CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
Lagrange Multipliers. A Somewhat Silly Example. Monday, 25 September 2013
 Lagrange Multplers Monday, 5 September 013 Sometmes t s convenent to use redundant coordnates, and to effect the varaton of the acton consstent wth the constrants va the method of Lagrange undetermned
Lagrange Multplers Monday, 5 September 013 Sometmes t s convenent to use redundant coordnates, and to effect the varaton of the acton consstent wth the constrants va the method of Lagrange undetermned
Physics 141. Lecture 14. Frank L. H. Wolfs Department of Physics and Astronomy, University of Rochester, Lecture 14, Page 1
 Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
Physics 2A Chapters 6 - Work & Energy Fall 2017
 Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
PES 1120 Spring 2014, Spendier Lecture 6/Page 1
 PES 110 Sprng 014, Spender Lecture 6/Page 1 Lecture today: Chapter 1) Electrc feld due to charge dstrbutons -> charged rod -> charged rng We ntroduced the electrc feld, E. I defned t as an nvsble aura
PES 110 Sprng 014, Spender Lecture 6/Page 1 Lecture today: Chapter 1) Electrc feld due to charge dstrbutons -> charged rod -> charged rng We ntroduced the electrc feld, E. I defned t as an nvsble aura
Lectures - Week 4 Matrix norms, Conditioning, Vector Spaces, Linear Independence, Spanning sets and Basis, Null space and Range of a Matrix
 Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Linear Momentum. Center of Mass.
 Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
EPR Paradox and the Physical Meaning of an Experiment in Quantum Mechanics. Vesselin C. Noninski
 EPR Paradox and the Physcal Meanng of an Experment n Quantum Mechancs Vesseln C Nonnsk vesselnnonnsk@verzonnet Abstract It s shown that there s one purely determnstc outcome when measurement s made on
EPR Paradox and the Physcal Meanng of an Experment n Quantum Mechancs Vesseln C Nonnsk vesselnnonnsk@verzonnet Abstract It s shown that there s one purely determnstc outcome when measurement s made on
Lecture 7: Boltzmann distribution & Thermodynamics of mixing
 Prof. Tbbtt Lecture 7 etworks & Gels Lecture 7: Boltzmann dstrbuton & Thermodynamcs of mxng 1 Suggested readng Prof. Mark W. Tbbtt ETH Zürch 13 März 018 Molecular Drvng Forces Dll and Bromberg: Chapters
Prof. Tbbtt Lecture 7 etworks & Gels Lecture 7: Boltzmann dstrbuton & Thermodynamcs of mxng 1 Suggested readng Prof. Mark W. Tbbtt ETH Zürch 13 März 018 Molecular Drvng Forces Dll and Bromberg: Chapters
Electricity and Magnetism - Physics 121 Lecture 10 - Sources of Magnetic Fields (Currents) Y&F Chapter 28, Sec. 1-7
 Electrcty and Magnetsm - Physcs 11 Lecture 10 - Sources of Magnetc Felds (Currents) Y&F Chapter 8, Sec. 1-7 Magnetc felds are due to currents The Bot-Savart Law Calculatng feld at the centers of current
Electrcty and Magnetsm - Physcs 11 Lecture 10 - Sources of Magnetc Felds (Currents) Y&F Chapter 8, Sec. 1-7 Magnetc felds are due to currents The Bot-Savart Law Calculatng feld at the centers of current
Physics 207 Lecture 13. Lecture 13
 Physcs 07 Lecture 3 Goals: Lecture 3 Chapter 0 Understand the relatonshp between moton and energy Defne Potental Energy n a Hooke s Law sprng Develop and explot conservaton of energy prncple n problem
Physcs 07 Lecture 3 Goals: Lecture 3 Chapter 0 Understand the relatonshp between moton and energy Defne Potental Energy n a Hooke s Law sprng Develop and explot conservaton of energy prncple n problem
Work is the change in energy of a system (neglecting heat transfer). To examine what could
 Work Work s the change n energy o a system (neglectng heat transer). To eamne what could cause work, let s look at the dmensons o energy: L ML E M L F L so T T dmensonally energy s equal to a orce tmes
Work Work s the change n energy o a system (neglectng heat transer). To eamne what could cause work, let s look at the dmensons o energy: L ML E M L F L so T T dmensonally energy s equal to a orce tmes
Spin-rotation coupling of the angularly accelerated rigid body
 Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
(Online First)A Lattice Boltzmann Scheme for Diffusion Equation in Spherical Coordinate
 Internatonal Journal of Mathematcs and Systems Scence (018) Volume 1 do:10.494/jmss.v1.815 (Onlne Frst)A Lattce Boltzmann Scheme for Dffuson Equaton n Sphercal Coordnate Debabrata Datta 1 *, T K Pal 1
Internatonal Journal of Mathematcs and Systems Scence (018) Volume 1 do:10.494/jmss.v1.815 (Onlne Frst)A Lattce Boltzmann Scheme for Dffuson Equaton n Sphercal Coordnate Debabrata Datta 1 *, T K Pal 1
Week 6, Chapter 7 Sect 1-5
 Week 6, Chapter 7 Sect 1-5 Work and Knetc Energy Lecture Quz The frctonal force of the floor on a large sutcase s least when the sutcase s A.pushed by a force parallel to the floor. B.dragged by a force
Week 6, Chapter 7 Sect 1-5 Work and Knetc Energy Lecture Quz The frctonal force of the floor on a large sutcase s least when the sutcase s A.pushed by a force parallel to the floor. B.dragged by a force
1 Derivation of Rate Equations from Single-Cell Conductance (Hodgkin-Huxley-like) Equations
 Physcs 171/271 -Davd Klenfeld - Fall 2005 (revsed Wnter 2011) 1 Dervaton of Rate Equatons from Sngle-Cell Conductance (Hodgkn-Huxley-lke) Equatons We consder a network of many neurons, each of whch obeys
Physcs 171/271 -Davd Klenfeld - Fall 2005 (revsed Wnter 2011) 1 Dervaton of Rate Equatons from Sngle-Cell Conductance (Hodgkn-Huxley-lke) Equatons We consder a network of many neurons, each of whch obeys
Integrals and Invariants of Euler-Lagrange Equations
 Lecture 16 Integrals and Invarants of Euler-Lagrange Equatons ME 256 at the Indan Insttute of Scence, Bengaluru Varatonal Methods and Structural Optmzaton G. K. Ananthasuresh Professor, Mechancal Engneerng,
Lecture 16 Integrals and Invarants of Euler-Lagrange Equatons ME 256 at the Indan Insttute of Scence, Bengaluru Varatonal Methods and Structural Optmzaton G. K. Ananthasuresh Professor, Mechancal Engneerng,
9 Derivation of Rate Equations from Single-Cell Conductance (Hodgkin-Huxley-like) Equations
 Physcs 171/271 - Chapter 9R -Davd Klenfeld - Fall 2005 9 Dervaton of Rate Equatons from Sngle-Cell Conductance (Hodgkn-Huxley-lke) Equatons We consder a network of many neurons, each of whch obeys a set
Physcs 171/271 - Chapter 9R -Davd Klenfeld - Fall 2005 9 Dervaton of Rate Equatons from Sngle-Cell Conductance (Hodgkn-Huxley-lke) Equatons We consder a network of many neurons, each of whch obeys a set
Econ107 Applied Econometrics Topic 3: Classical Model (Studenmund, Chapter 4)
 I. Classcal Assumptons Econ7 Appled Econometrcs Topc 3: Classcal Model (Studenmund, Chapter 4) We have defned OLS and studed some algebrac propertes of OLS. In ths topc we wll study statstcal propertes
I. Classcal Assumptons Econ7 Appled Econometrcs Topc 3: Classcal Model (Studenmund, Chapter 4) We have defned OLS and studed some algebrac propertes of OLS. In ths topc we wll study statstcal propertes
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
σ τ τ τ σ τ τ τ σ Review Chapter Four States of Stress Part Three Review Review
 Chapter Four States of Stress Part Three When makng your choce n lfe, do not neglect to lve. Samuel Johnson Revew When we use matrx notaton to show the stresses on an element The rows represent the axs
Chapter Four States of Stress Part Three When makng your choce n lfe, do not neglect to lve. Samuel Johnson Revew When we use matrx notaton to show the stresses on an element The rows represent the axs
j) = 1 (note sigma notation) ii. Continuous random variable (e.g. Normal distribution) 1. density function: f ( x) 0 and f ( x) dx = 1
 Random varables Measure of central tendences and varablty (means and varances) Jont densty functons and ndependence Measures of assocaton (covarance and correlaton) Interestng result Condtonal dstrbutons
Random varables Measure of central tendences and varablty (means and varances) Jont densty functons and ndependence Measures of assocaton (covarance and correlaton) Interestng result Condtonal dstrbutons
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Numerical Heat and Mass Transfer
 Master degree n Mechancal Engneerng Numercal Heat and Mass Transfer 06-Fnte-Dfference Method (One-dmensonal, steady state heat conducton) Fausto Arpno f.arpno@uncas.t Introducton Why we use models and
Master degree n Mechancal Engneerng Numercal Heat and Mass Transfer 06-Fnte-Dfference Method (One-dmensonal, steady state heat conducton) Fausto Arpno f.arpno@uncas.t Introducton Why we use models and
Rotational Dynamics. Physics 1425 Lecture 19. Michael Fowler, UVa
 Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Study Guide For Exam Two
 Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
Difference Equations
 Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
coordinates. Then, the position vectors are described by
 Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
Georgia Tech PHYS 6124 Mathematical Methods of Physics I
 Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
Title: Radiative transitions and spectral broadening
 Lecture 6 Ttle: Radatve transtons and spectral broadenng Objectves The spectral lnes emtted by atomc vapors at moderate temperature and pressure show the wavelength spread around the central frequency.
Lecture 6 Ttle: Radatve transtons and spectral broadenng Objectves The spectral lnes emtted by atomc vapors at moderate temperature and pressure show the wavelength spread around the central frequency.
Part C Dynamics and Statics of Rigid Body. Chapter 5 Rotation of a Rigid Body About a Fixed Axis
 Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Global Sensitivity. Tuesday 20 th February, 2018
 Global Senstvty Tuesday 2 th February, 28 ) Local Senstvty Most senstvty analyses [] are based on local estmates of senstvty, typcally by expandng the response n a Taylor seres about some specfc values
Global Senstvty Tuesday 2 th February, 28 ) Local Senstvty Most senstvty analyses [] are based on local estmates of senstvty, typcally by expandng the response n a Taylor seres about some specfc values
Temperature. Chapter Heat Engine
 Chapter 3 Temperature In prevous chapters of these notes we ntroduced the Prncple of Maxmum ntropy as a technque for estmatng probablty dstrbutons consstent wth constrants. In Chapter 9 we dscussed the
Chapter 3 Temperature In prevous chapters of these notes we ntroduced the Prncple of Maxmum ntropy as a technque for estmatng probablty dstrbutons consstent wth constrants. In Chapter 9 we dscussed the
10/23/2003 PHY Lecture 14R 1
 Announcements. Remember -- Tuesday, Oct. 8 th, 9:30 AM Second exam (coverng Chapters 9-4 of HRW) Brng the followng: a) equaton sheet b) Calculator c) Pencl d) Clear head e) Note: If you have kept up wth
Announcements. Remember -- Tuesday, Oct. 8 th, 9:30 AM Second exam (coverng Chapters 9-4 of HRW) Brng the followng: a) equaton sheet b) Calculator c) Pencl d) Clear head e) Note: If you have kept up wth
Uncertainty and auto-correlation in. Measurement
 Uncertanty and auto-correlaton n arxv:1707.03276v2 [physcs.data-an] 30 Dec 2017 Measurement Markus Schebl Federal Offce of Metrology and Surveyng (BEV), 1160 Venna, Austra E-mal: markus.schebl@bev.gv.at
Uncertanty and auto-correlaton n arxv:1707.03276v2 [physcs.data-an] 30 Dec 2017 Measurement Markus Schebl Federal Offce of Metrology and Surveyng (BEV), 1160 Venna, Austra E-mal: markus.schebl@bev.gv.at
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
Snce h( q^; q) = hq ~ and h( p^ ; p) = hp, one can wrte ~ h hq hp = hq ~hp ~ (7) the uncertanty relaton for an arbtrary state. The states that mnmze t
 8.5: Many-body phenomena n condensed matter and atomc physcs Last moded: September, 003 Lecture. Squeezed States In ths lecture we shall contnue the dscusson of coherent states, focusng on ther propertes
8.5: Many-body phenomena n condensed matter and atomc physcs Last moded: September, 003 Lecture. Squeezed States In ths lecture we shall contnue the dscusson of coherent states, focusng on ther propertes
Solution Thermodynamics
 Soluton hermodynamcs usng Wagner Notaton by Stanley. Howard Department of aterals and etallurgcal Engneerng South Dakota School of nes and echnology Rapd Cty, SD 57701 January 7, 001 Soluton hermodynamcs
Soluton hermodynamcs usng Wagner Notaton by Stanley. Howard Department of aterals and etallurgcal Engneerng South Dakota School of nes and echnology Rapd Cty, SD 57701 January 7, 001 Soluton hermodynamcs
Lecture 3: Probability Distributions
 Lecture 3: Probablty Dstrbutons Random Varables Let us begn by defnng a sample space as a set of outcomes from an experment. We denote ths by S. A random varable s a functon whch maps outcomes nto the
Lecture 3: Probablty Dstrbutons Random Varables Let us begn by defnng a sample space as a set of outcomes from an experment. We denote ths by S. A random varable s a functon whch maps outcomes nto the
11. Dynamics in Rotating Frames of Reference
 Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
A Tale of Friction Basic Rollercoaster Physics. Fahrenheit Rollercoaster, Hershey, PA max height = 121 ft max speed = 58 mph
 A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
Chapter 13: Multiple Regression
 Chapter 13: Multple Regresson 13.1 Developng the multple-regresson Model The general model can be descrbed as: It smplfes for two ndependent varables: The sample ft parameter b 0, b 1, and b are used to
Chapter 13: Multple Regresson 13.1 Developng the multple-regresson Model The general model can be descrbed as: It smplfes for two ndependent varables: The sample ft parameter b 0, b 1, and b are used to
Lecture 4. Instructor: Haipeng Luo
 Lecture 4 Instructor: Hapeng Luo In the followng lectures, we focus on the expert problem and study more adaptve algorthms. Although Hedge s proven to be worst-case optmal, one may wonder how well t would
Lecture 4 Instructor: Hapeng Luo In the followng lectures, we focus on the expert problem and study more adaptve algorthms. Although Hedge s proven to be worst-case optmal, one may wonder how well t would
Electrical double layer: revisit based on boundary conditions
 Electrcal double layer: revst based on boundary condtons Jong U. Km Department of Electrcal and Computer Engneerng, Texas A&M Unversty College Staton, TX 77843-318, USA Abstract The electrcal double layer
Electrcal double layer: revst based on boundary condtons Jong U. Km Department of Electrcal and Computer Engneerng, Texas A&M Unversty College Staton, TX 77843-318, USA Abstract The electrcal double layer
Rate of Absorption and Stimulated Emission
 MIT Department of Chemstry 5.74, Sprng 005: Introductory Quantum Mechancs II Instructor: Professor Andre Tokmakoff p. 81 Rate of Absorpton and Stmulated Emsson The rate of absorpton nduced by the feld
MIT Department of Chemstry 5.74, Sprng 005: Introductory Quantum Mechancs II Instructor: Professor Andre Tokmakoff p. 81 Rate of Absorpton and Stmulated Emsson The rate of absorpton nduced by the feld
Chapter 11: Angular Momentum
 Chapter 11: ngular Momentum Statc Equlbrum In Chap. 4 we studed the equlbrum of pontobjects (mass m) wth the applcaton of Newton s aws F 0 F x y, 0 Therefore, no lnear (translatonal) acceleraton, a0 For
Chapter 11: ngular Momentum Statc Equlbrum In Chap. 4 we studed the equlbrum of pontobjects (mass m) wth the applcaton of Newton s aws F 0 F x y, 0 Therefore, no lnear (translatonal) acceleraton, a0 For
ANSWERS. Problem 1. and the moment generating function (mgf) by. defined for any real t. Use this to show that E( U) var( U)
 Econ 413 Exam 13 H ANSWERS Settet er nndelt 9 deloppgaver, A,B,C, som alle anbefales å telle lkt for å gøre det ltt lettere å stå. Svar er gtt . Unfortunately, there s a prntng error n the hnt of
Econ 413 Exam 13 H ANSWERS Settet er nndelt 9 deloppgaver, A,B,C, som alle anbefales å telle lkt for å gøre det ltt lettere å stå. Svar er gtt . Unfortunately, there s a prntng error n the hnt of
N-Body Simulation. Typical uncertainty: π = 4 Acircle/Asquare! 4 ncircle/n. πest π = O(n
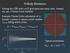 N-Body Smulaton Solvng the CBE wth a 6-D grd takes too many cells. Instead, we use a Monte-Carlo method. Example: Monte-Carlo calculaton of π. Scatter n ponts n square; count number ncrcle fallng wthn
N-Body Smulaton Solvng the CBE wth a 6-D grd takes too many cells. Instead, we use a Monte-Carlo method. Example: Monte-Carlo calculaton of π. Scatter n ponts n square; count number ncrcle fallng wthn
PHYS 705: Classical Mechanics. Calculus of Variations II
 1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
Conservation of Angular Momentum = "Spin"
 Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
1. Review of Mechanics Newton s Laws
 . Revew of Mechancs.. Newton s Laws Moton of partcles. Let the poston of the partcle be gven by r. We can always express ths n Cartesan coordnates: r = xˆx + yŷ + zẑ, () where we wll always use ˆ (crcumflex)
. Revew of Mechancs.. Newton s Laws Moton of partcles. Let the poston of the partcle be gven by r. We can always express ths n Cartesan coordnates: r = xˆx + yŷ + zẑ, () where we wll always use ˆ (crcumflex)
