r B -r A EN40: Dynamics and Vibrations Homework 7: Rigid Body Kinematics, Inertial properties of rigid bodies Due Friday April 20, 2018
|
|
|
- Charleen Parrish
- 6 years ago
- Views:
Transcription
1 EN40: Dynamcs and Vbratons Homewor 7: Rgd Body Knematcs, Inertal propertes of rgd bodes Due Frday Aprl 20, 2018 School of Engneerng Brown Unversty 1. The rgd body shown n the fgure s at rest at tme t=0, and rotates counterclocwse wth constant angular acceleraton vector 2α Fnd 1.1 The angular velocty vector as a functon of tme 2L r B -r A B θ L We can ust ntegrate the angular acceleraton ω= 2α t A 1.2 The spn tensor W (as a 2x2 matrx, also a functon of tme) Usng the formula 0 2α t W = 2α t The rotaton tensor (a 2x2 matrx for a 2D problem) R that rotates the rectangle from ts ntal to ts fnal poston shown n the fgure. Chec your answer by computng dr R T dt R cosαt snαt snαt = cosαt dr T 2αtsnαt 2αtcosαt cosαt snαt R dt = 2α t cosα t 2α t snα t snα t cosα t 0 2α t = 2α t 0 Ths reduces to W as expected. 1.4 Hence, express the rotated vector rb r A n (,) components. r r can be found usng the mappng r r = Rp ( p ) B A B A B A cosαt snαt 2L 2Lcosαt Lsnαt snαt cosαt L = 2 Lsnαt + Lcosαt
2 2. The rectangular prsm shown n the fgure s subected to two sequental rotatons: (1) A 45 degree rotaton about the axs (2) A -90 degree rotaton about the axs 2.1 Wrte down the rotaton tensor (matrx) for each rotaton We can use the general formula 2 cos θ + (1 cos θ) n (1 cos θ) nn sn θn (1 cos θ) nn + snθn 2 R = (1 cos θ) nn + snθn cos θ + (1 cos θ) n (1 cos θ) nn snθn 2 (1 cos θ) nn x z sn θny (1 cos θ) nn y z + snθnx cos θ + (1 cos θ) n z For the frst rotaton θ = 45, n = n = 0 n = 1 R (1) x x y z x z y x y z y y z x x z y cos 45 0 sn 45 1/ 2 0 1/ 2 = 0 cos 45 (1 cos 45) 0 + = sn 45 0 cos 45 1/ 2 0 1/ 2 For the second rotaton θ = (2) R = [3 POINTS] (2) (1) 2.2 Fnd the rotaton matrx R = R R that descrbes the combned effects of both rotatons (you can use matlab to do the matrx multplcaton, but there s no need to submt the code or scrpt). Matlab gves R = 1/ 2 0 1/ 2 1/ 2 0 1/ 2
3 2.3 Fnd the axs n and rotaton angle θ that wll complete the rotaton R drectly. We can use the formula 1+ 2cosθ = R + R + R xx yy zz ( Rzy Ryz ) ( Rxz Rzx ) ( Ryx Rxy ) n 1 = + + 2snθ 1 2 Ths gves cosθ = 1 θ = rad n= (1 ) sn( ) = + 2 [3 POINTS] Optonal: You can chec your answer by downloadng a matlab scrpt from the homewor page of the course webste that wll anmate a rgd rotaton through an angle θ about an axs parallel to a unt vector n. You can use the code by navgatng to the drectory storng the fle n the Matlab command wndow, and then typng Anmate_rotaton(angle,[ nx, ny, n z ]) Where angle s your soluton for the rotaton angle θ (n radans), and nx, ny, n z are the components of your soluton for the unt vector n. 3. The fgure shows a four-bar chan mechansm that appears nsde both natural and artfcal nee onts. Member OB rotates counterclocwse at constant angular speed ω. Calculate the angular veloctes and angular acceleratons of members CB and AC. At the nstant shown, calculate the angular velocty and acceleraton of lns AB and BC. The rgd body formulas for the three members gve vb vo = ω ( rb ro) = ω ( L+ L) = Lω( + ) vc vb = ωbc ( rc rb ) = ωbc ( L) = LωBC va vc = ωac ( ra rc ) = ωac L( ) = LωAC ( + ) ω C O L B A L We now that vo = vc = 0 so f we add all the equatons lsted above we get Lω( + ) Lω + Lω ( + ) = 0 BC + = The component of ths equaton gves ω ω AC 0 The component gves ω ω + ω = 0 BC AC AC Solve these to get ω = ω ω = 2ω AC BC [3 POINTS]
4 For acceleratons, use αb αo = ω ( rb ro) = Lω ( + ) αc αb = αbc ( rc rb ) ωbc ( rc rb ) = LαBC + L4ω αa αc = αac ( ra rc ) ωac ( ra rc ) = αac L( + ) + Lω ( + ) At the statonary ponts ao = ac = 0, and add everythng: 2 Lω ( + ) LαBC + L4 ω + LαAC ( + ) + Lω ( + ) = 0 2 The component gves LαAC + 2Lω = 0. The component gves αbc + αac = 0 ThusαAC = 2ω αbc = 2ω [3 POINTS] 4. Ths publcaton descrbes a varable speed transmsson for a wnd turbne 1. The transmsson has 6 possble gear ratos, whch are acheved by connectng one of 6 possble (blue) gears to the output shaft (connected to the generator). The numbers of teeth on each gear or pnon are shown n the table (n each case the red gear drves a blue pnon. Calculate the 6 possble transmsson ratos ω / ω generator gearbox Let NA, N B be the numbers of teeth on the man gearbox and gearset 1. Let NC, N D be the numbers of teeth on Gearset 2 and the generator gear. Then use the gear formula 1 In practce most modern turbnes are drect drve: t s very dffcult to desgn a gearbox capable of transmttng the necessary power for 20 years wthout falure.
5 N / A NC generator gearbox NB ND ω ω = The resultng numbers (from matlab) are lsted below
6 5. The fgure (from ths publcaton) shows a schematc of the splt-power transmsson system for the second generaton Chevy Volt. The transmsson contans two epcyclc gears: the wheels are always connected to the planet carrers through the fnal drve gearng. The sun gears are drven by two electrc tracton motor, whle the rng gear can ether be loced (close clutch C1 and open C2), to mae the car an electrc vehcle, or connected to the nternal combuston engne (open C1 and close C2,C3) to mae the car a hybrd. We can fnd the followng specfcatons for the vehcle: Tre dameter 16.5 nches The gear rato between the planet carrers and wheels s ωpc / ω W = 2.64 Planetary gear 1 has 60 teeth on the sun and 112 teeth on the rng gear Planetary gear 2 has 52 teeth on the sun and 108 on the rng gear. 5.1 In EV mode the car drves wth the nternal combuston engne off, and rng gears of both planetary gearsets statonary (clutch 2 s closed). For a vehcle drvng at 30mph n EV mode, calculate the angular speeds of the two sun gears. The angular speed of the wheel s ω = v / r = 13.4 / = rad / s The planet carrers spn at ω PC = = rad / s
7 The general expresson relatng angular speeds n an epcyclc gear s ωr ωpc N = S ω ω N S PC R The rng gear s loced n EV mode so ω R = 0 gvng N 1 R ωpc + = ωs NS Substtutng numbers gves ω = 484 rad / s (4622rpm) for PG1 ω = 519 rad / s (4956rpm) for PG2 [3 POINTS] 5.2 Another mode used at hgher speeds s Fxed Rato Extended Range mode, n whch the IC engne s runnng; both clutches are closed (so the sun gear on PG1 s statonary and the rng gear n PG2 s statonary). For a vehcle drvng at 35mph n ths mode, calculate the angular speeds of MGB and the nternal combuston engne. The angular speed of the wheel s ω = v / r = / = rad / s The planet carrers spn at ω PC = = rad / s Wth the clutches closed the sun gear of PG1 s statonary, the rng gear of PG2 s statonary. For PG1 the general formula gves N 1 S ωr = + ωpc = rad / s NR (2891 rpm) For PG2 we have ω PC N 1 R + = ωs = rad / s NS (5793 rpm) 5.3 At hgh speeds the car drves n Hgh Extended Range Mode wth clutch 1 closed, clutch 2 open, and the IC engne runnng. In ths mode the sun gear of PG1 has the same speed as the rng gear of PG2, and MGB s run slowly or bacwards. For a car runnng at 53 mph, calculate the speeds of the IC engne and MGA n ths mode, assumng MGB s statonary. The angular speed of the wheel s ω = v / r = / = rad / s The planet carrers spn at ω PC = = rad / s The sun gear of PG2 s statonary, so ts rng gear has speed N 1 S ωr = + ωpc = rad / s NR
8 The sun on PG1 spns at the same speed. The general epcyclc gear formula can be rearranged to gve Substtutng numbers gves ω N (1 S N ) S R = ω PC + S NR N ω R ω R = rad / s 6. The fgure shows three partcles wth equal mass m connected by rgd massless lns. 6.1 Calculate the poston of the center of mass of the assembly 1 1 L rg = m r ( ml ml ) ( ) M = 3m + = Calculate the 2D mass moment of nerta of the system about the center of mass ( ) IGzz = m dx + dy where = dx + dy = G [3 POINTS] d r r s the poston vector of the th partcle wth respect to the center of mass. L L L 2L 4 2 I m d d m 2m = + = = ml Use the formula Gzz ( x y ) 6.3 Suppose that the assembly rotates about ts center of mass wth angular velocty ω (the center of mass s statonary). What are the speeds of the partcles A,B and C? Use the crcular moton formula. Partcles B and C are dstances 5 L /3 from the COM, and partcle A s a dstance 2 L /3 from the COM. Therefore VB = VC = 5 Lω /3 VA = 2 Lω /3 6.4 Calculate the total netc energy of the system (a) usng your answer to 6.2; and (b) usng your answer to (a) The netc energy formula n terms of mass moment of nerta s T = I ω = 2 ml ω /3 2 Gzz z (b) Summng the netc energes of the masses drectly gves 1 ( ) 2 5 /3 ( 2 /3) 3 T = m Lω + m L = ml ω /3 2 C A m m L m B L
9 7. The fgure shows a pyramd wth heght h and base axa and unform mass densty ρ Usng a Matlab Lve Scrpt, calculate h θ O a a a/2 a/2 7.1 The total mass M h a(1 zh / ) a(1 zh / )/2 1 2 M = ρ COM = ρdxdydz = ρa h /3 M (see below for Lve Scrpt) 0 0 a(1 zh / )/2 7.2 The poston vector of the center of mass (wth respect to the orgn shown n the fgure) h a(1 zh / ) a(1 zh / )/2 1 ρcom = ( x y z ) dxdydz M ρ a(1 zh / )/2 3a h = + 8h 4 (see below for Lve Scrpt) 7.3 The nerta tensor (matrx) about the center of mass, n the bass shown The nerta matrx s (see below for Lve Scrpt) I dy + dz dxdy dxdz h a(1 zh / ) a(1 zh / )/2 ρ x y x z y z x y z 0 0 a(1 zh / )/2 dxdz dydz dx + d y = d d d + d d d dxdydz d = x d = y 3 a /8 d = z h / a + h = M 0 h ah ah a [ 3 POINTS] Graders equvalent solutons that nclude the densty should get credt too
10 8.4 Usng the parallel axs theorem, calculate the mass moment of nerta about the tp O. The general formula s dy + dz dxdy dxd z IO = I G + M dxdy dx + dz dyd z dxdz dydz dx + d y In the problem here d = d = 0 d = 3 h/4 so x y z a + h = M 0 h ah ah a Equvalent solutons that nclude the densty should get credt (see below for numbers) The Lve Scrpt for ths problem s shown.
11
12
ENGN 40 Dynamics and Vibrations Homework # 7 Due: Friday, April 15
 NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
NGN 40 ynamcs and Vbratons Homework # 7 ue: Frday, Aprl 15 1. Consder a concal hostng drum used n the mnng ndustry to host a mass up/down. A cable of dameter d has the mass connected at one end and s wound/unwound
EN40: Dynamics and Vibrations. Homework 7: Rigid Body Kinematics
 N40: ynamcs and Vbratons Homewor 7: Rgd Body Knematcs School of ngneerng Brown Unversty 1. In the fgure below, bar AB rotates counterclocwse at 4 rad/s. What are the angular veloctes of bars BC and C?.
N40: ynamcs and Vbratons Homewor 7: Rgd Body Knematcs School of ngneerng Brown Unversty 1. In the fgure below, bar AB rotates counterclocwse at 4 rad/s. What are the angular veloctes of bars BC and C?.
Chapter 6 Rigid Body Dynamics
 Chapter 6 Rgd Body Dynamcs 6. Introducton In practce, t s often not possble to dealze a system as a partcle. In ths secton, we construct a more sophstcated descrpton of the world, n whch obects rotate,
Chapter 6 Rgd Body Dynamcs 6. Introducton In practce, t s often not possble to dealze a system as a partcle. In ths secton, we construct a more sophstcated descrpton of the world, n whch obects rotate,
EN40: Dynamics and Vibrations. Homework 4: Work, Energy and Linear Momentum Due Friday March 1 st
 EN40: Dynamcs and bratons Homework 4: Work, Energy and Lnear Momentum Due Frday March 1 st School of Engneerng Brown Unversty 1. The fgure (from ths publcaton) shows the energy per unt area requred to
EN40: Dynamcs and bratons Homework 4: Work, Energy and Lnear Momentum Due Frday March 1 st School of Engneerng Brown Unversty 1. The fgure (from ths publcaton) shows the energy per unt area requred to
Homework 2: Kinematics and Dynamics of Particles Due Friday Feb 7, 2014 Max Score 45 Points + 8 Extra Credit
 EN40: Dynamcs and Vbratons School of Engneerng Brown Unversty Homework : Knematcs and Dynamcs of Partcles Due Frday Feb 7, 014 Max Score 45 Ponts + 8 Extra Credt 1. An expermental mcro-robot (see a descrpton
EN40: Dynamcs and Vbratons School of Engneerng Brown Unversty Homework : Knematcs and Dynamcs of Partcles Due Frday Feb 7, 014 Max Score 45 Ponts + 8 Extra Credt 1. An expermental mcro-robot (see a descrpton
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Please initial the statement below to show that you have read it
 EN40: Dynamcs and Vbratons Mdterm Examnaton Thursday March 5 009 Dvson of Engneerng rown Unversty NME: Isaac Newton General Instructons No collaboraton of any knd s permtted on ths examnaton. You may brng
EN40: Dynamcs and Vbratons Mdterm Examnaton Thursday March 5 009 Dvson of Engneerng rown Unversty NME: Isaac Newton General Instructons No collaboraton of any knd s permtted on ths examnaton. You may brng
CHAPTER 10 ROTATIONAL MOTION
 CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
1.3 Hence, calculate a formula for the force required to break the bond (i.e. the maximum value of F)
 EN40: Dynacs and Vbratons Hoework 4: Work, Energy and Lnear Moentu Due Frday March 6 th School of Engneerng Brown Unversty 1. The Rydberg potental s a sple odel of atoc nteractons. It specfes the potental
EN40: Dynacs and Vbratons Hoework 4: Work, Energy and Lnear Moentu Due Frday March 6 th School of Engneerng Brown Unversty 1. The Rydberg potental s a sple odel of atoc nteractons. It specfes the potental
10/9/2003 PHY Lecture 11 1
 Announcements 1. Physc Colloquum today --The Physcs and Analyss of Non-nvasve Optcal Imagng. Today s lecture Bref revew of momentum & collsons Example HW problems Introducton to rotatons Defnton of angular
Announcements 1. Physc Colloquum today --The Physcs and Analyss of Non-nvasve Optcal Imagng. Today s lecture Bref revew of momentum & collsons Example HW problems Introducton to rotatons Defnton of angular
Chapter 3. r r. Position, Velocity, and Acceleration Revisited
 Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
Chapter 3 Poston, Velocty, and Acceleraton Revsted The poston vector of a partcle s a vector drawn from the orgn to the locaton of the partcle. In two dmensons: r = x ˆ+ yj ˆ (1) The dsplacement vector
EN40: Dynamics and Vibrations. Final Examination Wed May : 2pm-5pm
 EN4: Dynacs and Vbratons Fnal Exanaton Wed May 1 17: p-5p School of Engneerng Brown Unversty NAME: General Instructons No collaboraton of any knd s pertted on ths exanaton. You ay brng double sded pages
EN4: Dynacs and Vbratons Fnal Exanaton Wed May 1 17: p-5p School of Engneerng Brown Unversty NAME: General Instructons No collaboraton of any knd s pertted on ths exanaton. You ay brng double sded pages
Physics 111: Mechanics Lecture 11
 Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING. Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582
 NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582 4. Moton Knematcs 4.2 Angular Velocty Knematcs Summary From the last lecture we concluded that: If the jonts
NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582 4. Moton Knematcs 4.2 Angular Velocty Knematcs Summary From the last lecture we concluded that: If the jonts
Rotational Dynamics. Physics 1425 Lecture 19. Michael Fowler, UVa
 Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Spin-rotation coupling of the angularly accelerated rigid body
 Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Chapter 11 Angular Momentum
 Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
CHAPTER 14 GENERAL PERTURBATION THEORY
 CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
DO NOT DO HOMEWORK UNTIL IT IS ASSIGNED. THE ASSIGNMENTS MAY CHANGE UNTIL ANNOUNCED.
 EE 539 Homeworks Sprng 08 Updated: Tuesday, Aprl 7, 08 DO NOT DO HOMEWORK UNTIL IT IS ASSIGNED. THE ASSIGNMENTS MAY CHANGE UNTIL ANNOUNCED. For full credt, show all work. Some problems requre hand calculatons.
EE 539 Homeworks Sprng 08 Updated: Tuesday, Aprl 7, 08 DO NOT DO HOMEWORK UNTIL IT IS ASSIGNED. THE ASSIGNMENTS MAY CHANGE UNTIL ANNOUNCED. For full credt, show all work. Some problems requre hand calculatons.
10/23/2003 PHY Lecture 14R 1
 Announcements. Remember -- Tuesday, Oct. 8 th, 9:30 AM Second exam (coverng Chapters 9-4 of HRW) Brng the followng: a) equaton sheet b) Calculator c) Pencl d) Clear head e) Note: If you have kept up wth
Announcements. Remember -- Tuesday, Oct. 8 th, 9:30 AM Second exam (coverng Chapters 9-4 of HRW) Brng the followng: a) equaton sheet b) Calculator c) Pencl d) Clear head e) Note: If you have kept up wth
Modeling of Dynamic Systems
 Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
Chapter 11: Angular Momentum
 Chapter 11: ngular Momentum Statc Equlbrum In Chap. 4 we studed the equlbrum of pontobjects (mass m) wth the applcaton of Newton s aws F 0 F x y, 0 Therefore, no lnear (translatonal) acceleraton, a0 For
Chapter 11: ngular Momentum Statc Equlbrum In Chap. 4 we studed the equlbrum of pontobjects (mass m) wth the applcaton of Newton s aws F 0 F x y, 0 Therefore, no lnear (translatonal) acceleraton, a0 For
Physics 607 Exam 1. ( ) = 1, Γ( z +1) = zγ( z) x n e x2 dx = 1. e x2
 Physcs 607 Exam 1 Please be well-organzed, and show all sgnfcant steps clearly n all problems. You are graded on your wor, so please do not just wrte down answers wth no explanaton! Do all your wor on
Physcs 607 Exam 1 Please be well-organzed, and show all sgnfcant steps clearly n all problems. You are graded on your wor, so please do not just wrte down answers wth no explanaton! Do all your wor on
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
Study on Active Micro-vibration Isolation System with Linear Motor Actuator. Gong-yu PAN, Wen-yan GU and Dong LI
 2017 2nd Internatonal Conference on Electrcal and Electroncs: echnques and Applcatons (EEA 2017) ISBN: 978-1-60595-416-5 Study on Actve Mcro-vbraton Isolaton System wth Lnear Motor Actuator Gong-yu PAN,
2017 2nd Internatonal Conference on Electrcal and Electroncs: echnques and Applcatons (EEA 2017) ISBN: 978-1-60595-416-5 Study on Actve Mcro-vbraton Isolaton System wth Lnear Motor Actuator Gong-yu PAN,
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM
 ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
Georgia Tech PHYS 6124 Mathematical Methods of Physics I
 Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
Georga Tech PHYS 624 Mathematcal Methods of Physcs I Instructor: Predrag Cvtanovć Fall semester 202 Homework Set #7 due October 30 202 == show all your work for maxmum credt == put labels ttle legends
Part C Dynamics and Statics of Rigid Body. Chapter 5 Rotation of a Rigid Body About a Fixed Axis
 Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Conservation of Angular Momentum = "Spin"
 Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Section 8.1 Exercises
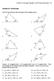 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Linear Momentum. Center of Mass.
 Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
MEASUREMENT OF MOMENT OF INERTIA
 1. measurement MESUREMENT OF MOMENT OF INERTI The am of ths measurement s to determne the moment of nerta of the rotor of an electrc motor. 1. General relatons Rotatng moton and moment of nerta Let us
1. measurement MESUREMENT OF MOMENT OF INERTI The am of ths measurement s to determne the moment of nerta of the rotor of an electrc motor. 1. General relatons Rotatng moton and moment of nerta Let us
The classical spin-rotation coupling
 LOUAI H. ELZEIN 2018 All Rghts Reserved The classcal spn-rotaton couplng Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 louaelzen@gmal.com Abstract Ths paper s prepared to show that a rgd
LOUAI H. ELZEIN 2018 All Rghts Reserved The classcal spn-rotaton couplng Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 louaelzen@gmal.com Abstract Ths paper s prepared to show that a rgd
Angular Momentum and Fixed Axis Rotation. 8.01t Nov 10, 2004
 Angular Momentum and Fxed Axs Rotaton 8.01t Nov 10, 2004 Dynamcs: Translatonal and Rotatonal Moton Translatonal Dynamcs Total Force Torque Angular Momentum about Dynamcs of Rotaton F ext Momentum of a
Angular Momentum and Fxed Axs Rotaton 8.01t Nov 10, 2004 Dynamcs: Translatonal and Rotatonal Moton Translatonal Dynamcs Total Force Torque Angular Momentum about Dynamcs of Rotaton F ext Momentum of a
11. Dynamics in Rotating Frames of Reference
 Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
Physics 141. Lecture 14. Frank L. H. Wolfs Department of Physics and Astronomy, University of Rochester, Lecture 14, Page 1
 Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
Iterative General Dynamic Model for Serial-Link Manipulators
 EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
PERFORMANCE OF HEAVY-DUTY PLANETARY GEARS
 THE INTERNATIONAL CONFERENCE OF THE CARPATHIAN EURO-REGION SPECIALISTS IN INDUSTRIAL SYSTEMS 6 th edton PERFORMANCE OF HEAVY-DUTY PLANETARY GEARS Attla Csobán, Mhály Kozma 1, 1 Professor PhD., Eng. Budapest
THE INTERNATIONAL CONFERENCE OF THE CARPATHIAN EURO-REGION SPECIALISTS IN INDUSTRIAL SYSTEMS 6 th edton PERFORMANCE OF HEAVY-DUTY PLANETARY GEARS Attla Csobán, Mhály Kozma 1, 1 Professor PhD., Eng. Budapest
Physics 2A Chapter 3 HW Solutions
 Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Spring 2002 Lecture #13
 44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
Solutions for Homework #9
 Solutons for Hoewor #9 PROBEM. (P. 3 on page 379 n the note) Consder a sprng ounted rgd bar of total ass and length, to whch an addtonal ass s luped at the rghtost end. he syste has no dapng. Fnd the natural
Solutons for Hoewor #9 PROBEM. (P. 3 on page 379 n the note) Consder a sprng ounted rgd bar of total ass and length, to whch an addtonal ass s luped at the rghtost end. he syste has no dapng. Fnd the natural
Rigid body simulation
 Rgd bod smulaton Rgd bod smulaton Once we consder an object wth spacal etent, partcle sstem smulaton s no longer suffcent Problems Problems Unconstraned sstem rotatonal moton torques and angular momentum
Rgd bod smulaton Rgd bod smulaton Once we consder an object wth spacal etent, partcle sstem smulaton s no longer suffcent Problems Problems Unconstraned sstem rotatonal moton torques and angular momentum
NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING. Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582
 NMT EE 589 & UNM ME 48/58 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 48/58 7. Robot Dynamcs 7.5 The Equatons of Moton Gven that we wsh to fnd the path q(t (n jont space) whch mnmzes the energy
NMT EE 589 & UNM ME 48/58 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 48/58 7. Robot Dynamcs 7.5 The Equatons of Moton Gven that we wsh to fnd the path q(t (n jont space) whch mnmzes the energy
Important Dates: Post Test: Dec during recitations. If you have taken the post test, don t come to recitation!
 Important Dates: Post Test: Dec. 8 0 durng rectatons. If you have taken the post test, don t come to rectaton! Post Test Make-Up Sessons n ARC 03: Sat Dec. 6, 0 AM noon, and Sun Dec. 7, 8 PM 0 PM. Post
Important Dates: Post Test: Dec. 8 0 durng rectatons. If you have taken the post test, don t come to rectaton! Post Test Make-Up Sessons n ARC 03: Sat Dec. 6, 0 AM noon, and Sun Dec. 7, 8 PM 0 PM. Post
AP Physics 1 & 2 Summer Assignment
 AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
AP Physcs 1 & 2 Summer Assgnment AP Physcs 1 requres an exceptonal profcency n algebra, trgonometry, and geometry. It was desgned by a select group of college professors and hgh school scence teachers
SCHOOL OF COMPUTING, ENGINEERING AND MATHEMATICS SEMESTER 2 EXAMINATIONS 2011/2012 DYNAMICS ME247 DR. N.D.D. MICHÉ
 s SCHOOL OF COMPUTING, ENGINEERING ND MTHEMTICS SEMESTER EXMINTIONS 011/01 DYNMICS ME47 DR. N.D.D. MICHÉ Tme allowed: THREE hours nswer: ny FOUR from SIX questons Each queston carres 5 marks Ths s a CLOSED-BOOK
s SCHOOL OF COMPUTING, ENGINEERING ND MTHEMTICS SEMESTER EXMINTIONS 011/01 DYNMICS ME47 DR. N.D.D. MICHÉ Tme allowed: THREE hours nswer: ny FOUR from SIX questons Each queston carres 5 marks Ths s a CLOSED-BOOK
π e ax2 dx = x 2 e ax2 dx or x 3 e ax2 dx = 1 x 4 e ax2 dx = 3 π 8a 5/2 (a) We are considering the Maxwell velocity distribution function: 2πτ/m
 Homework Solutons Problem In solvng ths problem, we wll need to calculate some moments of the Gaussan dstrbuton. The brute-force method s to ntegrate by parts but there s a nce trck. The followng ntegrals
Homework Solutons Problem In solvng ths problem, we wll need to calculate some moments of the Gaussan dstrbuton. The brute-force method s to ntegrate by parts but there s a nce trck. The followng ntegrals
Week 11: Chapter 11. The Vector Product. The Vector Product Defined. The Vector Product and Torque. More About the Vector Product
 The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
Four Bar Linkages in Two Dimensions. A link has fixed length and is joined to other links and also possibly to a fixed point.
 Four bar lnkages 1 Four Bar Lnkages n Two Dmensons lnk has fed length and s oned to other lnks and also possbly to a fed pont. The relatve velocty of end B wth regard to s gven by V B = ω r y v B B = +y
Four bar lnkages 1 Four Bar Lnkages n Two Dmensons lnk has fed length and s oned to other lnks and also possbly to a fed pont. The relatve velocty of end B wth regard to s gven by V B = ω r y v B B = +y
An Algorithm to Solve the Inverse Kinematics Problem of a Robotic Manipulator Based on Rotation Vectors
 An Algorthm to Solve the Inverse Knematcs Problem of a Robotc Manpulator Based on Rotaton Vectors Mohamad Z. Al-az*, Mazn Z. Othman**, and Baker B. Al-Bahr* *AL-Nahran Unversty, Computer Eng. Dep., Baghdad,
An Algorthm to Solve the Inverse Knematcs Problem of a Robotc Manpulator Based on Rotaton Vectors Mohamad Z. Al-az*, Mazn Z. Othman**, and Baker B. Al-Bahr* *AL-Nahran Unversty, Computer Eng. Dep., Baghdad,
Physics 1202: Lecture 11 Today s Agenda
 Physcs 122: Lecture 11 Today s Agenda Announcements: Team problems start ths Thursday Team 1: Hend Ouda, Mke Glnsk, Stephane Auger Team 2: Analese Bruder, Krsten Dean, Alson Smth Offce hours: Monday 2:3-3:3
Physcs 122: Lecture 11 Today s Agenda Announcements: Team problems start ths Thursday Team 1: Hend Ouda, Mke Glnsk, Stephane Auger Team 2: Analese Bruder, Krsten Dean, Alson Smth Offce hours: Monday 2:3-3:3
Programming Project 1: Molecular Geometry and Rotational Constants
 Programmng Project 1: Molecular Geometry and Rotatonal Constants Center for Computatonal Chemstry Unversty of Georga Athens, Georga 30602 Summer 2012 1 Introducton Ths programmng project s desgned to provde
Programmng Project 1: Molecular Geometry and Rotatonal Constants Center for Computatonal Chemstry Unversty of Georga Athens, Georga 30602 Summer 2012 1 Introducton Ths programmng project s desgned to provde
First Law: A body at rest remains at rest, a body in motion continues to move at constant velocity, unless acted upon by an external force.
 Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Physics 106 Lecture 6 Conservation of Angular Momentum SJ 7 th Ed.: Chap 11.4
 Physcs 6 ecture 6 Conservaton o Angular Momentum SJ 7 th Ed.: Chap.4 Comparson: dentons o sngle partcle torque and angular momentum Angular momentum o a system o partcles o a rgd body rotatng about a xed
Physcs 6 ecture 6 Conservaton o Angular Momentum SJ 7 th Ed.: Chap.4 Comparson: dentons o sngle partcle torque and angular momentum Angular momentum o a system o partcles o a rgd body rotatng about a xed
PHYS 705: Classical Mechanics. Newtonian Mechanics
 1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
2 Finite difference basics
 Numersche Methoden 1, WS 11/12 B.J.P. Kaus 2 Fnte dfference bascs Consder the one- The bascs of the fnte dfference method are best understood wth an example. dmensonal transent heat conducton equaton T
Numersche Methoden 1, WS 11/12 B.J.P. Kaus 2 Fnte dfference bascs Consder the one- The bascs of the fnte dfference method are best understood wth an example. dmensonal transent heat conducton equaton T
2010 vds-3d. Professor Kyongsu Yi. Vehicle Dynamics and Control Laboratory
 3D Dnamcs 2010 vds-3d Professor Kongsu Y 2010 VDCL Vehcle Dnamcs and Control Laborator 1 Knetcs of Rgd Bodes n Three Dmensons ma G Translatonal Dnamc Equaton of Rgd Bod (Newton Equaton F ma G Rotatonal
3D Dnamcs 2010 vds-3d Professor Kongsu Y 2010 VDCL Vehcle Dnamcs and Control Laborator 1 Knetcs of Rgd Bodes n Three Dmensons ma G Translatonal Dnamc Equaton of Rgd Bod (Newton Equaton F ma G Rotatonal
#64. ΔS for Isothermal Mixing of Ideal Gases
 #64 Carnot Heat Engne ΔS for Isothermal Mxng of Ideal Gases ds = S dt + S T V V S = P V T T V PV = nrt, P T ds = v T = nr V dv V nr V V = nrln V V = - nrln V V ΔS ΔS ΔS for Isothermal Mxng for Ideal Gases
#64 Carnot Heat Engne ΔS for Isothermal Mxng of Ideal Gases ds = S dt + S T V V S = P V T T V PV = nrt, P T ds = v T = nr V dv V nr V V = nrln V V = - nrln V V ΔS ΔS ΔS for Isothermal Mxng for Ideal Gases
Lesson 5: Kinematics and Dynamics of Particles
 Lesson 5: Knematcs and Dynamcs of Partcles hs set of notes descrbes the basc methodology for formulatng the knematc and knetc equatons for multbody dynamcs. In order to concentrate on the methodology and
Lesson 5: Knematcs and Dynamcs of Partcles hs set of notes descrbes the basc methodology for formulatng the knematc and knetc equatons for multbody dynamcs. In order to concentrate on the methodology and
Dynamics of Rotational Motion
 Dynamcs of Rotatonal Moton Torque: the rotatonal analogue of force Torque = force x moment arm = Fl moment arm = perpendcular dstance through whch the force acts a.k.a. leer arm l F l F l F l F = Fl =
Dynamcs of Rotatonal Moton Torque: the rotatonal analogue of force Torque = force x moment arm = Fl moment arm = perpendcular dstance through whch the force acts a.k.a. leer arm l F l F l F l F = Fl =
Supplemental Material: Causal Entropic Forces
 Supplemental Materal: Causal Entropc Forces A. D. Wssner-Gross 1, 2, and C. E. Freer 3 1 Insttute for Appled Computatonal Scence, Harvard Unversty, Cambrdge, Massachusetts 02138, USA 2 The Meda Laboratory,
Supplemental Materal: Causal Entropc Forces A. D. Wssner-Gross 1, 2, and C. E. Freer 3 1 Insttute for Appled Computatonal Scence, Harvard Unversty, Cambrdge, Massachusetts 02138, USA 2 The Meda Laboratory,
Please initial the statement below to show that you have read it
 EN0: Structural nalyss Exam I Wednesday, March 2, 2005 Dvson of Engneerng rown Unversty NME: General Instructons No collaboraton of any nd s permtted on ths examnaton. You may consult your own wrtten lecture
EN0: Structural nalyss Exam I Wednesday, March 2, 2005 Dvson of Engneerng rown Unversty NME: General Instructons No collaboraton of any nd s permtted on ths examnaton. You may consult your own wrtten lecture
A Tale of Friction Basic Rollercoaster Physics. Fahrenheit Rollercoaster, Hershey, PA max height = 121 ft max speed = 58 mph
 A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
Notes on Analytical Dynamics
 Notes on Analytcal Dynamcs Jan Peters & Mchael Mstry October 7, 004 Newtonan Mechancs Basc Asssumptons and Newtons Laws Lonely pontmasses wth postve mass Newtons st: Constant velocty v n an nertal frame
Notes on Analytcal Dynamcs Jan Peters & Mchael Mstry October 7, 004 Newtonan Mechancs Basc Asssumptons and Newtons Laws Lonely pontmasses wth postve mass Newtons st: Constant velocty v n an nertal frame
Linear Momentum. Center of Mass.
 Lecture 16 Chapter 9 Physcs I 11.06.2013 Lnear oentu. Center of ass. Course webste: http://faculty.ul.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.ul.edu/danylov2013/physcs1fall.htl
Lecture 16 Chapter 9 Physcs I 11.06.2013 Lnear oentu. Center of ass. Course webste: http://faculty.ul.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.ul.edu/danylov2013/physcs1fall.htl
coordinates. Then, the position vectors are described by
 Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
Supplemental Instruction sessions next week
 Homework #4 Wrtten homework due now Onlne homework due on Tue Mar 3 by 8 am Exam 1 Answer keys and scores wll be posted by end of the week Supplemental Instructon sessons next week Wednesday 8:45 10:00
Homework #4 Wrtten homework due now Onlne homework due on Tue Mar 3 by 8 am Exam 1 Answer keys and scores wll be posted by end of the week Supplemental Instructon sessons next week Wednesday 8:45 10:00
Chapter 11 Torque and Angular Momentum
 Chapter Torque and Angular Momentum I. Torque II. Angular momentum - Defnton III. Newton s second law n angular form IV. Angular momentum - System of partcles - Rgd body - Conservaton I. Torque - Vector
Chapter Torque and Angular Momentum I. Torque II. Angular momentum - Defnton III. Newton s second law n angular form IV. Angular momentum - System of partcles - Rgd body - Conservaton I. Torque - Vector
Physics 207: Lecture 20. Today s Agenda Homework for Monday
 Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
Physcs 207: Lecture 20 Today s Agenda Homework for Monday Recap: Systems of Partcles Center of mass Velocty and acceleraton of the center of mass Dynamcs of the center of mass Lnear Momentum Example problems
So far: simple (planar) geometries
 Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Study Guide For Exam Two
 Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
Physics 181. Particle Systems
 Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Slide. King Saud University College of Science Physics & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART 2) LECTURE NO.
 Slde Kng Saud Unersty College of Scence Physcs & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART ) LECTURE NO. 6 THIS PRESENTATION HAS BEEN PREPARED BY: DR. NASSR S. ALZAYED Lecture
Slde Kng Saud Unersty College of Scence Physcs & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART ) LECTURE NO. 6 THIS PRESENTATION HAS BEEN PREPARED BY: DR. NASSR S. ALZAYED Lecture
STATISTICAL MECHANICS
 STATISTICAL MECHANICS Thermal Energy Recall that KE can always be separated nto 2 terms: KE system = 1 2 M 2 total v CM KE nternal Rgd-body rotaton and elastc / sound waves Use smplfyng assumptons KE of
STATISTICAL MECHANICS Thermal Energy Recall that KE can always be separated nto 2 terms: KE system = 1 2 M 2 total v CM KE nternal Rgd-body rotaton and elastc / sound waves Use smplfyng assumptons KE of
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
A particle in a state of uniform motion remain in that state of motion unless acted upon by external force.
 The fundamental prncples of classcal mechancs were lad down by Galleo and Newton n the 16th and 17th centures. In 1686, Newton wrote the Prncpa where he gave us three laws of moton, one law of gravty,
The fundamental prncples of classcal mechancs were lad down by Galleo and Newton n the 16th and 17th centures. In 1686, Newton wrote the Prncpa where he gave us three laws of moton, one law of gravty,
Physics 207: Lecture 27. Announcements
 Physcs 07: ecture 7 Announcements ake-up labs are ths week Fnal hwk assgned ths week, fnal quz next week Revew sesson on Thursday ay 9, :30 4:00pm, Here Today s Agenda Statcs recap Beam & Strngs» What
Physcs 07: ecture 7 Announcements ake-up labs are ths week Fnal hwk assgned ths week, fnal quz next week Revew sesson on Thursday ay 9, :30 4:00pm, Here Today s Agenda Statcs recap Beam & Strngs» What
THERMAL DISTRIBUTION IN THE HCL SPECTRUM OBJECTIVE
 ame: THERMAL DISTRIBUTIO I THE HCL SPECTRUM OBJECTIVE To nvestgate a system s thermal dstrbuton n dscrete states; specfcally, determne HCl gas temperature from the relatve occupatons of ts rotatonal states.
ame: THERMAL DISTRIBUTIO I THE HCL SPECTRUM OBJECTIVE To nvestgate a system s thermal dstrbuton n dscrete states; specfcally, determne HCl gas temperature from the relatve occupatons of ts rotatonal states.
CHAPTER 6. LAGRANGE S EQUATIONS (Analytical Mechanics)
 CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 ME 270 Fall 2013 Fnal Exam NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS
ME 270 Fall 2013 Fnal Exam NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS
Physics 5153 Classical Mechanics. D Alembert s Principle and The Lagrangian-1
 P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
Important Instructions to the Examiners:
 Summer 0 Examnaton Subject & Code: asc Maths (70) Model Answer Page No: / Important Instructons to the Examners: ) The Answers should be examned by key words and not as word-to-word as gven n the model
Summer 0 Examnaton Subject & Code: asc Maths (70) Model Answer Page No: / Important Instructons to the Examners: ) The Answers should be examned by key words and not as word-to-word as gven n the model
Physics 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn in the following problems from Chapter 4 Knight
 Physcs 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn n the ollowng problems rom Chapter 4 Knght Conceptual Questons: 8, 0, ; 4.8. Anta s approachng ball and movng away rom where ball was
Physcs 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn n the ollowng problems rom Chapter 4 Knght Conceptual Questons: 8, 0, ; 4.8. Anta s approachng ball and movng away rom where ball was
Finite Element Modelling of truss/cable structures
 Pet Schreurs Endhoven Unversty of echnology Department of Mechancal Engneerng Materals echnology November 3, 214 Fnte Element Modellng of truss/cable structures 1 Fnte Element Analyss of prestressed structures
Pet Schreurs Endhoven Unversty of echnology Department of Mechancal Engneerng Materals echnology November 3, 214 Fnte Element Modellng of truss/cable structures 1 Fnte Element Analyss of prestressed structures
The Schrödinger Equation
 Chapter 1 The Schrödnger Equaton 1.1 (a) F; () T; (c) T. 1. (a) Ephoton = hν = hc/ λ =(6.66 1 34 J s)(.998 1 8 m/s)/(164 1 9 m) = 1.867 1 19 J. () E = (5 1 6 J/s)( 1 8 s) =.1 J = n(1.867 1 19 J) and n
Chapter 1 The Schrödnger Equaton 1.1 (a) F; () T; (c) T. 1. (a) Ephoton = hν = hc/ λ =(6.66 1 34 J s)(.998 1 8 m/s)/(164 1 9 m) = 1.867 1 19 J. () E = (5 1 6 J/s)( 1 8 s) =.1 J = n(1.867 1 19 J) and n
Amplification and Relaxation of Electron Spin Polarization in Semiconductor Devices
 Amplfcaton and Relaxaton of Electron Spn Polarzaton n Semconductor Devces Yury V. Pershn and Vladmr Prvman Center for Quantum Devce Technology, Clarkson Unversty, Potsdam, New York 13699-570, USA Spn Relaxaton
Amplfcaton and Relaxaton of Electron Spn Polarzaton n Semconductor Devces Yury V. Pershn and Vladmr Prvman Center for Quantum Devce Technology, Clarkson Unversty, Potsdam, New York 13699-570, USA Spn Relaxaton
Irregular vibrations in multi-mass discrete-continuous systems torsionally deformed
 (2) 4 48 Irregular vbratons n mult-mass dscrete-contnuous systems torsonally deformed Abstract In the paper rregular vbratons of dscrete-contnuous systems consstng of an arbtrary number rgd bodes connected
(2) 4 48 Irregular vbratons n mult-mass dscrete-contnuous systems torsonally deformed Abstract In the paper rregular vbratons of dscrete-contnuous systems consstng of an arbtrary number rgd bodes connected
Recitation: Energy, Phys Energies. 1.2 Three stones. 1. Energy. 1. An acorn falling from an oak tree onto the sidewalk.
 Rectaton: Energy, Phys 207. Energy. Energes. An acorn fallng from an oak tree onto the sdewalk. The acorn ntal has gravtatonal potental energy. As t falls, t converts ths energy to knetc. When t hts the
Rectaton: Energy, Phys 207. Energy. Energes. An acorn fallng from an oak tree onto the sdewalk. The acorn ntal has gravtatonal potental energy. As t falls, t converts ths energy to knetc. When t hts the
Lecture 23: Newton-Euler Formulation. Vaibhav Srivastava
 Lecture 23: Newton-Euler Formulaton Based on Chapter 7, Spong, Hutchnson, and Vdyasagar Vabhav Srvastava Department of Electrcal & Computer Engneerng Mchgan State Unversty Aprl 10, 2017 ECE 818: Robotcs
Lecture 23: Newton-Euler Formulaton Based on Chapter 7, Spong, Hutchnson, and Vdyasagar Vabhav Srvastava Department of Electrcal & Computer Engneerng Mchgan State Unversty Aprl 10, 2017 ECE 818: Robotcs
PY2101 Classical Mechanics Dr. Síle Nic Chormaic, Room 215 D Kane Bldg
 PY2101 Classcal Mechancs Dr. Síle Nc Chormac, Room 215 D Kane Bldg s.ncchormac@ucc.e Lectures stll some ssues to resolve. Slots shared between PY2101 and PY2104. Hope to have t fnalsed by tomorrow. Mondays
PY2101 Classcal Mechancs Dr. Síle Nc Chormac, Room 215 D Kane Bldg s.ncchormac@ucc.e Lectures stll some ssues to resolve. Slots shared between PY2101 and PY2104. Hope to have t fnalsed by tomorrow. Mondays
Kinematics in 2-Dimensions. Projectile Motion
 Knematcs n -Dmensons Projectle Moton A medeval trebuchet b Kolderer, c1507 http://members.net.net.au/~rmne/ht/ht0.html#5 Readng Assgnment: Chapter 4, Sectons -6 Introducton: In medeval das, people had
Knematcs n -Dmensons Projectle Moton A medeval trebuchet b Kolderer, c1507 http://members.net.net.au/~rmne/ht/ht0.html#5 Readng Assgnment: Chapter 4, Sectons -6 Introducton: In medeval das, people had
PHYS 1441 Section 001 Lecture #15 Wednesday, July 8, 2015
 PHYS 1441 Secton 001 Lecture #15 Wednesday, July 8, 2015 Concept of the Center of Mass Center of Mass & Center of Gravty Fundamentals of the Rotatonal Moton Rotatonal Knematcs Equatons of Rotatonal Knematcs
PHYS 1441 Secton 001 Lecture #15 Wednesday, July 8, 2015 Concept of the Center of Mass Center of Mass & Center of Gravty Fundamentals of the Rotatonal Moton Rotatonal Knematcs Equatons of Rotatonal Knematcs
Inductance Calculation for Conductors of Arbitrary Shape
 CRYO/02/028 Aprl 5, 2002 Inductance Calculaton for Conductors of Arbtrary Shape L. Bottura Dstrbuton: Internal Summary In ths note we descrbe a method for the numercal calculaton of nductances among conductors
CRYO/02/028 Aprl 5, 2002 Inductance Calculaton for Conductors of Arbtrary Shape L. Bottura Dstrbuton: Internal Summary In ths note we descrbe a method for the numercal calculaton of nductances among conductors
Physics 111 Final Exam, Fall 2013, Version A
 Physcs 111 Fnal Exam, Fall 013, Verson A Name (Prnt): 4 Dgt ID: Secton: Honors Code Pledge: For ethcal and farness reasons all students are pledged to comply wth the provsons of the NJIT Academc Honor
Physcs 111 Fnal Exam, Fall 013, Verson A Name (Prnt): 4 Dgt ID: Secton: Honors Code Pledge: For ethcal and farness reasons all students are pledged to comply wth the provsons of the NJIT Academc Honor
DUE: WEDS FEB 21ST 2018
 HOMEWORK # 1: FINITE DIFFERENCES IN ONE DIMENSION DUE: WEDS FEB 21ST 2018 1. Theory Beam bendng s a classcal engneerng analyss. The tradtonal soluton technque makes smplfyng assumptons such as a constant
HOMEWORK # 1: FINITE DIFFERENCES IN ONE DIMENSION DUE: WEDS FEB 21ST 2018 1. Theory Beam bendng s a classcal engneerng analyss. The tradtonal soluton technque makes smplfyng assumptons such as a constant
Chapter 3. Estimation of Earthquake Load Effects
 Chapter 3. Estmaton of Earthquake Load Effects 3.1 Introducton Sesmc acton on chmneys forms an addtonal source of natural loads on the chmney. Sesmc acton or the earthquake s a short and strong upheaval
Chapter 3. Estmaton of Earthquake Load Effects 3.1 Introducton Sesmc acton on chmneys forms an addtonal source of natural loads on the chmney. Sesmc acton or the earthquake s a short and strong upheaval
Δ x. u(x,t) Fig. Schematic view of elastic bar undergoing axial motions
 ME67 - Handout 4 Vbratons of Contnuous Systems Axal vbratons of elastc bars The fgure shows a unform elastc bar of length and cross secton A. The bar materal propertes are ts densty ρ and elastc modulus
ME67 - Handout 4 Vbratons of Contnuous Systems Axal vbratons of elastc bars The fgure shows a unform elastc bar of length and cross secton A. The bar materal propertes are ts densty ρ and elastc modulus
Chapter 12. Ordinary Differential Equation Boundary Value (BV) Problems
 Chapter. Ordnar Dfferental Equaton Boundar Value (BV) Problems In ths chapter we wll learn how to solve ODE boundar value problem. BV ODE s usuall gven wth x beng the ndependent space varable. p( x) q(
Chapter. Ordnar Dfferental Equaton Boundar Value (BV) Problems In ths chapter we wll learn how to solve ODE boundar value problem. BV ODE s usuall gven wth x beng the ndependent space varable. p( x) q(
