SPECTRAL APPROXIMATION OF TIME-HARMONIC MAXWELL EQUATIONS IN THREE-DIMENSIONAL EXTERIOR DOMAINS. 1. Introduction
|
|
|
- Mervin Wilkins
- 5 years ago
- Views:
Transcription
1 PECTRAL APPROXIMATION OF TIME-HARMONIC MAXWELL EQUATION IN THREE-DIMENIONAL EXTERIOR DOMAIN LINA MA 1, JIE HEN 1 AND LI-LIAN WANG 2 Abstrct. We deveop in this pper n efficient nd robust spectr-gerkin method to sove the three-dimension time-hrmonic Mxwe equtions in exterior domins. We first reduce the probem to bounded domin by using the cpcity opertor which chrcterizes the nonrefecting boundry condition. Then, we dpt the trnsformed fied expnsion TFE pproch to reduce the probem to sequence of Mxwe equtions in seprbe spheric she. Finy, we deveop n efficient spectr gorithm by using Legendre pproximtion in the rdi direction nd vector spheric hrmonic expnsion in the tngenti directions. 1. Introduction We consider in this pper the pproximtion of the time-hrmonic Mxwe equtions in three-dimension exterior domin: iωµh + cur E = 0, iωεe cur H = 0, in R 3 \ D; E n D = g; im r r µ/ε H e r E = 0, 1.1 where D is three-dimension, simpy connected, bounded sctterer, i = 1 is the compex unit, g is resuted from given incident fied, µ is the mgnetic permebiity, ε is the eectric permittivity, ω is the frequency of the hrmonic wve, n is the unit outwrd norm of D nd e r = x/r with r = x. The boundry condition t infinity in 1.1 is known s the iver-müer rdition condition. The Mxwe equtions 1.1 py n importnt roe in mny scientific nd engineering ppictions, nd re so of fundment mthemtic interest see e.g., [13, 4, 11]. Despite its seemingy simpicity, the system 1.1 is notoriousy difficut to sove numericy. ome of the min chenges incude: i the indefiniteness when ω is not sm; ii highy oscitory soutions when ω is rge; iii the incompressibiity i.e., 1991 Mthemtics ubject Cssifiction. 65N35, 65N22, 65F05, 35J05. Key words nd phrses. Mthieu. 1 Deprtment of Mthemtics, Purdue University, West Lfyette, IN, 47907, UA. The work of this uthor is prtiy supported by NF grnt DM nd AFOR FA Division of Mthemtic ciences, choo of Physic nd Mthemtic ciences, Nnyng Technoogic University, , ingpore. The reserch of this uthor is prtiy supported by ingpore MOE AcRF Tier 1 Grnt RG 15/12, MOE AcRF Tier 2 Grnt MOE 2013-T , ARC 44/13 nd ingpore A TAR-ERC-PF Grnt 122-PF
2 2 L.N. MA, J. HEN & L.L. WANG divµh = divεe = 0, which is impicity impied by 1.1; nd iv the unboundedness of the domin. On the one hnd, one needs to construct pproximtion spces such tht the discrete probems re we posed nd ed to good pproximtions for wide rnge of wve number. On the other hnd, perhps more difficut probem is to deveop efficient gorithms for soving the indefinite iner system, prticury for rge wve numbers, from the given discretiztion. We refer to [11] nd the references therein, for vrious contributions with respect to numeric pproximtions of the time-hrmonic Mxwe equtions. Most notby, very popur nd effective method for deing with the unboundedness of the domin is to introduce perfecty mtched yer PML, initiy proposed in [3]. In this pper, we propose spectr pproximtion bsed on the tensor-product of vector spheric hrmonics VH, which forms compete orthogon bsis for L 2 -vector-vued functions on the spheric surfce, nd Legendre poynomis in the rdi direction. It is we-known tht the Mxwe equtions with constnt mgnetic permebiity nd eectric permittivity re seprbe if D is b, nd its soution cn be expicity expressed in terms of the VH nd the spheric Hnke functions [13]. Whie the expicit soution is very usefu for some theoretic considertions, it hs much ess vue in prctice, since most prctic probems woud hve one or more of the foowing situtions: non-spheric domins, non-constnt mgnetic permebiity nd eectric permittivity, non-homogeneous source etc., where n expicit soution woud not be vibe. In order to de with more gener sctterers D nd non-homogeneous source functions, we dpt the so-ced trnsformed fied expnsion TFE [15], which hs proven to be effective for vriety of situtions cf. [14, 5, 6, 9]. The TFE pproch consists of four steps: i reduce the probem in n unbounded domin to bounded domin with trnsprent boundry conditions; ii trnsform the reduced bounded domin to seprbe domin, consider the reduced domin s perturbtion of the seprbe domin, nd expnd the soution in term of the perturbtion prmeter ε; iii sove for ech expnsion coefficient in the seprbe domin; nd iv sum up the expnsion terms using robust Pdé pproximtion. The essenti step in the bove TFE pproch is the step iii, i.e., sove the Mxwe equtions in the seprbe domin which is spheric she in this cse with non-homogeneous source term nd non-oc boundry conditions t the outer spheric surfce. In this pper, we sh deveop n efficient nd robust spectr sover for the nonhomogeneous Mxwe equtions in spheric she. More precisey, we sh use VH to decoupe the probem into sequence of one-dimension probems tht cn be efficienty soved using direct spectr-gerkin method. Therefore, the entire TFE pproch does
3 MAXWELL EQUATION 3 not invove ny itertive sover, nd it is robust for ow to modertey high wve numbers nd to sctterers which hve sufficienty smooth boundries. The rest of the pper is orgnized s foows. In the next section, we introduce the VH nd present the formution of the cpcity opertor chrcterizing the exct nonrefecting boundry condition. In ection 3, we present the TFE gorithm, nd nd formue in Appendix B. In ection 4, we describe the Legendre spectr-gerkin method for the reduced one-dimension probems, nd give the numeric resuts in ection 5. In Appendix A, we provide some usefu formue for the VH, whie in Appendix B, we derive the Mxwe eqution in the trnsformed coordintes, nd the recursion formue in the TFE pproch. 2. Vector spheric hrmonics nd the cpcity opertor In this section, we rec some essenti properties of VH, nd derive the expicit formu for the cpcity opertor expressed in terms of VH, which chrcterizes the exct DtN boundry condition t the outer spheric surfce Vector spheric hrmonics. ever versions of VH with different nottion nd properties hve been used in prctice see e.g., [12, 10, 2, 13, 8, 7]. In wht foows, we dopt the fmiy of VH in [10, 13], nd remrk its retion with sever other fmiies documented in the bove iterture see Remrk 2.1 beow. Rec tht the spheric coordintes r, θ, φ re reted to the Crtesin coordintes x = x 1, x 2, x 3 by cf. [13]: x 1 = r sin θ cos φ, x 2 = r sin θ sin φ, x 3 = r cos θ, 2.1 with the moving right-hnded orthonorm coordinte bsis {e r, e θ, e φ } : e r = x/r, e θ = cos θ cos φ, cos θ sin φ, sin θ, e φ = sin φ, cos φ, For ny v = v 1, v 2, v 3, we denote by v r, v θ nd v φ the projections of v onto e r, e θ nd e φ, respectivey, tht is, v = v r e r + v θ e θ + v φ e φ with v r = v e r, v θ = v e θ, v φ = v e φ. 2.3 Herefter, et be the unit spheric surfce, nd denote by nd the Lpce- Betrmi nd tngent grdient opertors on. Rec tht u = 1 sin θ u u sin θ θ θ sin 2 θ φ 2, u = u θ e θ + 1 u sin θ φ e φ. 2.4 The spheric hrmonics {Y m } s normized in [13] re eigenfunctions of, nmey, Y m = + 1Y m, 0, m ; 2.5
4 4 L.N. MA, J. HEN & L.L. WANG nd form n orthonorm bsis for L 2 : Y m Y m d = δ δ mm. 2.6 The fmiy of VH is defined by T m V m W m = Y m e r = 1 sin θ = + 1Y m e r Y m Y m φ e θ Y m θ e φ, for 1, 0 m, 2.7, for 0, 0 m, 2.8 = Y m e r + Y m, for 1, 0 m. 2.9 Notice tht V 0 0 = e r / 4π. With the understnding of T 0 0 = W 0 0 = 0, the indexes {, m} run over {, m : 0, 0 m }. We coect in Appendix A the properties of VH to be used throughout the pper. Remrk 2.1. The VH in Hi [10] were denoted by {V m, X m, W m }. In fct, we hve the retion V m V m =, X m = it m, + 1 W m W m = Nédéec [13] empoyed the nottion {I m Y m e r = W m + V m 2 + 1, T m, N m }, nd there hod N+1 m = V m, = T m, I 1 m = W m The pherepck [18] used the nottion { Y m e r, Y m, } cur Y m in Morse nd Feshbch [12] so see [13, Thm ]. Noting tht cur Y m = Y m e r cf. [13, ], we hve, cur Y m = T m T m, Y m = + 1W m V m In the numeric experiments in ection 5, we sh use the VH in the pherepck. Define the vector L 2 -spce nd its tngenti vector spce: L 2 = L 2 3, TL 2 = { u L 2 : u e r = 0 } The fmiy of VH, {T m, V m, W m }, forms compete, orthogon bsis of L 2, whie the fmiy {T m, Y m } forms n orthogon bsis for TL 2 cf. 2.4 nd A.1-A The cpcity opertor. As the probem 1.1 is set in n unbounded domin, we first truncte the unbounded domin t n rtifici spheric surfce r = b. ince the exct soution for the homogeneous Mxwe equtions 1.1 exterior to the b r b with µ nd ε being constnt cn be obtined by using the seprtion of vribes [13], we cn set up the exct DtN nonrefecting boundry condition: H n T b E = 0, t r = b, 2.14 where for simpicity, we ssume herefter µ = ε = 1 so the wve number k = ω εµ = ω, nd the cpcity opertor T b, cting on the tngenti component of E i.e., E = E
5 MAXWELL EQUATION 5 n n, cn be determined s in [13] see 2.22 beow. Here, for the reders reference, we sketch the derivtion. Given the tngenti component of E on the rtifici surfce note tht E TL 2, we write Then the exterior probem: E r=b = =1 m =0 cur E e = ikh e, cur H e = ike e, r > b; E e e r = E, t r = b; [ c m T m + d m Y m ] im r r H e e r E e = 0, 2.16 cn be soved nyticy by using seprtion of vribes. The soution {H e, E e } cn be expressed in VH series in terms of {c m, d m } see [13, Thm ]. Then, the cpcity opertor T b, which ssocites E to H e e r on the rtifici spheric surfce, is given by see [13, ] with kb in pce of k: where T b E = H e e r r=b = =1 m =0 [ c m ikb Θ kbt m + ikb ] dm Θ kb Y m, 2.17 d dr h1 r Θ kb = z kb + 1 with z r = r h 1 r, 2.18 nd h 1 r is the spheric Hnke function of the first kind cf. [1]. By imposing H e r = H e e r t r = b, we obtin the exct boundry condition t r = b with T b E given by , but it is expressed by the expnsion coefficients {c m, d m } of E. Thus, it is necessry to represent it in terms of the expnsion coefficients of the fied E with r b. For this purpose, we write [ ] Er, θ, φ = v m rv m θ, φ + t m rt m θ, φ + w m rw m θ, φ, 2.19 =0 m =0 where we rec tht T 0 0 = W 0 0 = 0. Using 2.19 nd the identities: V m e r = T m, T m e r = Y m, W m e r = T m, Y m e r = T m, 2.20 we find E r=b = E e r er r=b = =1 m =0 =1 m =0 [ t m bt m + w m v m Compring the coefficients in 2.17 nd 2.21 eds to [ T b E r=b t m = b ikb Θ kbt m + ikb w m v m b Θ kb where Θ is defined by ] b Y m ] Y m, 2.22
6 6 L.N. MA, J. HEN & L.L. WANG 3. Trnsformed fied expnsion nd dimension reduction Eiminting H nd using the cpcity opertor, we reduce the probem 1.1 with µ = ε = 1 to cur cur E k 2 E = 0, in Ω b \ D; E n D = g; cure e r ikt b E = 0, t r = b, where Ω b is the b of rdius b, nd T b is defined in We now ppy the TFE pproch to Chnge of vribes. Assume tht the sctterer is given by D = { r < + hθ, φ : θ [0, π, φ [0, 2π }, 3.1 for some > 0. Let us choose b such tht b > mx θ,φ { + hθ, φ}, nd then mp the domin: Ω b \ D = { + hθ, φ < r < b} to the spheric she: Ω = { < r < b} with the chnge of vribes: where d = b. r = dr bhθ, φ d hθ, φ, θ = θ, φ = φ, 3.2 Let E = E r, E, where E r nd E re the xi component nd tngenti component of E, respectivey. We first notice tht we cn rewrite the Mxwe eqution fter mutipying both sides by r 2, s cur cur E k 2 E = 0, E r + r re r 2 k 2 E r = 0, 3.3 E e r e r + r r E r r 2 r re r 2 k 2 E = Let us denote the trnsformed fied by F r, θ, φ := Er, θ, φ = E r + Ar, θ, φ, θ, φ := F r, F, 3.5 d with Ar, θ, φ = hθ, φ b r. After some tedious mniputions see Appendix B, we find tht the system is trnsformed into: F r + r r F r 2 k 2 F r = f r, F e r e r + r r F r r 2 r r F r 2 k 2 F = f tp, F e r + F r h = g, t r =, cur F e r ikt b F = J, t r = b, where f r, f tp, g nd J re given in B.5-B.8 in Appendix B. 3.6
7 MAXWELL EQUATION Recursion by boundry perturbtion. Now we ssume h = εq, nd expnd F r, θ, φ ; ε = F n r, θ, φ ε n. 3.7 n=0 Writing F n = Fr n, F n, pugging the bove expnsion into 3.6, nd coecting the terms in powers of ε, we rrive t the foowing recursion for n 0: F n r + r r F n r 2 k 2 F n r = f n r F n e r e r + r r F n r r 2 r r F n r 2 k 2 F n = f n tp F n e r = g n, t r = cur F n e r ikt b F n = J n, t r = b, 3.8 where f n r, f n tp, g n nd J n re given in B.9-B.12 in Appendix B. We note in prticur tht f n r, f n tp nd J n ony depend on the previous four expnsion terms, nmey {F n i, i = 1, 2, 3, 4}. We cn rewrite the bove system in the more compct form: cur cur F n k 2 F n = 1 r 2 f n, in Ω, 3.9 F n e r r= = g n ; cur F n e r ikt b F n = J n, t r = b, 3.10 where f n = f n r, f n tp. Hence, using the TFE pproch, it bois down to soving sequence of non-homogeneous Mxwe equtions in the spheric she Ω. We re therefore concerned with deveoping n efficient, robust sover for this prototype system Dimension reduction. We now consider the foowing probem: cur cur E k 2 E = F, in Ω, 3.11 E e r r= = g; cure e r ikt b E = h, t r = b, 3.12 which hs to be soved for ech expnsion order n with given F, g nd h. It foows from [13, Thm ] tht the probem dmits unique soution, provided tht F L 2 Ω with F = 0 nd g, h TL 2. We refer the interested reders to [4, 13] for deicte regurity nysis of the bove probem. We first expnd, in terms of VH, the unknown function E s in 2.19, nd the source function F s: F r, θ, φ = =0 m =0 [ ] f,mrv v m θ, φ + f,mrt t m θ, φ + f,mrw w m θ, φ. 3.13
8 8 L.N. MA, J. HEN & L.L. WANG Then, we expnd the given dt g nd h in terms of VH bsis of TL 2 : [ ] gθ, φ = ĝ m T m θ, φ + g m Y m θ, φ ; hθ, φ = =1 m =0 =1 m =0 [ĥm T m θ, φ + h ] m Y m θ, φ. For simpicity of presenttion, we define the hndy differentition opertors: 3.14 d + = d dr + r, d = d dr r Inserting the expnsion 2.19 nd into 3.11, we find from the property A.9 tht 3.11 reduces to sequence of one-dimension probems in {v m, t m, w m }. More precisey, we hve v0 0 = 0, nd for 1 nd m, [ d d 1 wm d + ] +2 vm k 2 v m = f,m, v r, b, [ d+ +1 d + +2 vm d ] 1 wm k 2 w m = f,m, t r, b, d r 2 r 2 dtm dr dr r 2 t m k 2 t m = f,m, w r, b imiry, Inserting the expnsion 2.19 nd 3.14 into 3.12, nd using 2.20, 2.22 nd A.9, the boundry conditions 3.12 become Note tht the modes t m nd w m. w m v m = ĝ m, t m = g m ; 3.19 [ d 1 wm d + +2 vm ] b + k 2 b wm v m b Θ kb = ĥm, 3.20 r t m b b 1 z kbt m b = h m coefficients of T m re competey decouped from the modes v m In summry, we ony hve to sove the foowing sequence 1 nd m of onedimension probems with unknowns: v = v m, w = w m, u = t m, nd with given dt f v = f v,m, f w = f w,m, ĝ = ĝm, ĥ = ĥm, g = g m, h = h m : nd β d [ d 1 w d+ +2 v] k 2 v = f v, r, b, β d + [ +1 d + +2 v d 1 w] k 2 w = f w, r, b, 3.23 [ w v = ĝ, d 1 w d+ +2 v] b + k 2 w vb b = ĥ; 3.24 Θ kb 1 d r 2 r 2 du dr dr r 2 u k 2 u = f t, r, b, 3.25 u = g, u b b 1 z kbub = h, 3.26 where β = /2 + 1 nd z is defined in 2.18.
9 MAXWELL EQUATION 9 Remrk 3.1. We derive immeditey from the sovbiity of the 3D probem tht there exists unique tripe {v, w, u} for ech, m tht soves Remrk 3.2. Observe tht the probem is excty the eqution reduced from the time-hrmonic Hemhotz eqution with exct DtN boundry condition in spheric she cf. [17, 3.6]. ince efficient gorithms nd wve number-expicit priori estimtes for this probem hve redy presented in [17], we sh concentrte beow on pectr-gerkin method for the one-dimension systems We now construct the spectr-gerkin method for the couped system First, we mke simpe vribe trnsform, e.g., w ĝ w, to homogenize the Dirichet boundry condition in t r =. Hence, it suffices to consider β d [d 1 w d+ +2 v] k2 v = f 1, r, b, β d + +1 [d+ +2 v d 1 w] k2 w = f 2, r, b, 4.2 w v = 0, [d 1 w d+ +2 v]b + w vb k2 b = h b. 4.3 Θ kb Define the compex vector-vued functions v = v, w t, f = f 1, f 2 t, φ = φ 1, φ 2 t, nd the differenti opertors: = d + +2, d 1, v = d + +2 v d 1w Wek formution nd we-posedness. Let I =, b, nd P N be the set of re gebric poynomis of degree t most N. Define the pproximtion spce X N = { φ = φ 1, φ 2 t P N + ip N 2 : φ 1 φ 2 = 0 }, 4.5 nd the weighted inner product by u, v ω = I ur vrωrdr with ωr = r2, where v is the compex conjugte of v. Then, the spectr-gerkin pproximtion of is to find v N = v N, w N t X N such tht Bv N, φ := v N, φ ω k 2 Lv N, φ ω + k2 b 3 = I N Lf, φ ω + b 2 h b φ 1 φ 2 b, φ X N, Θ kb v N w N bφ 1 φ 2 b 4.6 where L is 2-by-2 digon mtrix: L = dig 2 + 1/, 2 + 1/ + 1,
10 10 L.N. MA, J. HEN & L.L. WANG nd I N is the Legendre-Guss-Lobtto interpotion opertor. In the derivtion of 4.6, we used the identities obtined from integrtion by prts nd the buit-in boundry condition in X N : b b d d 1 w N d + +2 v N φ 1 r 2 dr = d + +1 d+ +2 v N d 1 w N φ 2 r 2 dr = b d 1 w N d + +2 v Nd + +2 φ 1r 2 dr + d 1 w N d + +2 v N φ 1 r 2 b ; b d + +2 v N d 1 w Nd 1 φ 2r 2 dr + d + +2 v N d 1 w N φ 2 r 2 b. Proposition 4.1. For ny fixed, k, b, N, the probem 4.6 dmits unique soution v N X N. Proof. Rec tht cf. [11, Lemm 9.20]: c 1 Θ kb c 2, 1, 4.7 where c 1, c 2 re positive constnts depending on kb. Thus, tking φ = v N in 4.6, nd tking the re prt of the resuted eqution, eds to Re Bv N, v N v N 2 ω k 2 Lv N, v N ω k2 b 3 c 1 v N w N b 2, 4.8 where u 2 ω = u, u ω. In view of v N w N = 0, we derive from [16, Thm. 3.33] tht v N w N b = b r v N w N dr b r v N w N cn 2 v N w N, 4.9 where c is positive constnt independent of N. Notice tht v N 2 ω = r v N w N v N 1 2 w N r r ω 2 r v N w N v N 2 + w N 2 ; Lv N, v N ω v N 2 + w N 2. We find from the bove nd tht for > 0, Re Bv N, v N 2 r v N w N 2 C v N 2 + w N 2, 4.10 where C is positive constnt depending on, b, k, N. ince X N is finite dimension nd v N w N = 0, it is esy to check tht v N := r v N w N is norm on X N. Hence, 4.10 is indeed Gårding type inequity which impies the unique sovbiity of the probem 4.6.
11 MAXWELL EQUATION 11 We remrk tht since Re 1/Θ kb < 0 which cn be derived from [13, ], the corresponding term cn not contribute to the energy norm. Consequenty, we hve to use the trce inequity 4.9 to derive the Gårding type inequity Note so tht the bove proof does not provide wve-number expicit priori estimte on the energy norm. Hence, it is not possibe to derive, from the bove resut, wvenumber expicit error estimte for 4.6, s ws done for the decouped eqution in [17]. In forthcoming pper, we sh consider different pproch, which is more suitbe for nysis but ess convenient for impementtion, nd derive wve-number expicit error estimtes Impementtion. We now describe n efficient impementtion of the scheme 4.6. The efficiency of the gorithm essentiy reies on the choice of bsis functions for X N defined in 4.5. Let L n r be the re-vued Legendre poynomis of degree n, trnsformed from [ 1, 1] to [, b] vi iner mpping, which stisfies L n = 1 n nd L n b = 1. Define φ 0 = 1 + i 2 x + 1; φ j = 1 + il j 1 L j+1, 1 j N 1; φ N = 1 + i x 1. 2 et φj 0 φn ψ j =, ψ 0 N+j =, 0 j N 1; ψ φ 2N = j One verifies rediy tht ψ j X N for 0 j 2N nd tht they re inery independent. ince dimx N = 2N + 1, we hve X N = spn { ψ 0, ψ 1,, ψ 2N } Hence, the pproximte soution v N cn be written s 2N N 1 j=0 v N = α j ψ j = α jφ j + α 2N φ N N 1 j=0 j=0 α = N+jφ j + α 2N φ N etting ψ j = ψ 1,j, ψ 2,j t, 0 j 2N; α = α 0, α 1,, α 2N t ; s ij = b vn d + +2 ψ 1,j d 1 ψ 2,jd + +2 ψ 1,i d 1 ψ 2,ir 2 dr, 0 i, j 2N; w N φ N b ij = k 2 ψ 1,j ψ 1,i ψ 2,jψ 2,i r 2 dr, 0 i, j 2N; b ij = k2 b 3 Θ kb ψ 1,j ψ 2,j bψ 1,i ψ 2,i b, 0 i, j 2N; b f i = I N f 1 ψ 1,i I Nf 2 ψ 2,i r 2 dr b 2 g b ψ 1,i ψ 2,i b, f = f 0, f 1,, f 2N t ; = s ij, A = ij, B = b ij,
12 12 L.N. MA, J. HEN & L.L. WANG nz = 1085 Figure 4.1. Nonzero entries of the system mtrix in we find tht the iner system 4.6 reduces to the mtrix form: + A + B α = f We note tht the coefficient mtrices, A nd B re sprse, see Figure 4.1, nd Hermitin, i.e., = t, nd ikewise for A nd B. To compute their non-zero entries, we ony need to compute b φ jrφ i rr2 dr, b φ jrφ i rr 2 dr, b φ j rφ i rr 2 dr, which cn be evuted excty by using the properties of Legendre poynomis.
13 MAXWELL EQUATION 13 It is worthwhie to point out tht the bsis functions in 4.11 re constructed to minimize the couping of v N nd w N. Indeed, they re couped through the singe bsis function ψ 0. Hence, the system 4.14 cn be soved efficienty by using bock Gussin eimintion process to sove for α 2N first, foowed by soving two decouped systems of size N ech for α 0,, α N 1 t nd α N,, α 2N 1 t. 5. Numeric resuts In this section, we provide some numeric resuts to show the ccurcy nd efficiency of the proposed method. We use the exct mutipe soutions of cf. [13] s the reference soution. In the first exmpe, we tke the exct soution of to be M 0 { E = =1 m h 1 krt m θ, φ + cur h 1 krt m θ, φ }, 5.1 which is iner combintion of the trnsverse eectric nd mgnetic mutipoe soutions. By using 2.12, we find cur h 1 krt m θ, φ = k d dz h1 k d dz h1 Hence, the exct soution {v, w, u} of is v := v m = k d dz h1 w := w m = + 1 k d dz h1 u := t m = h 1 kr. We ook for the pproximte fied: E M0 N M0 r, θ, φ = =1 m =0 kr r h1 kr V m kr r kr r h1 kr kr r h 1 kr W m., h 1 kr, [ ] v,n m rv m θ, φ + t m,n rt m θ, φ + w,n m rw m θ, φ, 5.4 where {v m,n, wm,n } re computed from 4.6, i.e., spectr-gerkin pproximtion of {vm, w m }, nd {t m,n } re the spectr-gerkin pproximtion of {tm }. Using the orthogonity A.1, we hve the expression: E E M 0 2 M 0 N L 2 Ω = t m t m,n 2 L 2 I + 1 =1 m + vm v m,n 2 L 2 I wm w,n m 2 L 2 I In the computtion, we tke = 2, b = 4 nd M 0 = 10. In Figure 5.1, we pot the retive discrete L 2 -error: E E M0 N / E, 2 Ω 2 Ω
14 14 L.N. MA, J. HEN & L.L. WANG ginst vrious N for k = 10 eft nd k = 40 right. We observe tht the error decys exponentiy, s soon s N enters the symptotic rnge, which is for this cse roughy N > k k=40 k=60 k=100 discrete retive L 2 error Figure 5.1. Retive discrete 2 -errors ginst N for k = 10, 40, 100. In the second exmpe, we consider n exct soution generted by the boundry dt g t the sctterer s surfce. More precisey, the exct eectric fied E is given by where E = M 1 =1 m =0 { g1,h m 1 krt m θ, φ + g2, m 1 cur h krt m θ, φ }, g m 1, = g m 2, = 1 + 1h 1 k + 1h 1 kz k + 1 g Y m dσ; g cur Y m dσ. For given g, we cn compute g1, m nd gm 2, using pherepck [18]. Consider the incident wve: e ikx so tht g = e ikx. We tke = 2, b = 4 nd M 1 = 20, nd pot in Figure 5.2, the discrete retive L 2 -errors ginst N for k = 10, 20, 40 We observe tht the error behves very simiry s in the first exmpe. 6. Concuding remrks We deveoped in this pper n efficient nd robust spectr-gerkin method to sove the three-dimension time-hrmonic Mxwe equtions in exterior domins. The method is bsed on the trnsformed fied expnsion TFE pproch which reduces the origin probem in gener exterior domin to sequence of Mxwe equtions in seprbe spheric she. By using proper set of vector spheric hrmonic functions, we re
15 MAXWELL EQUATION k=10 k=20 k=30 discrete retive L 2 error N Figure 5.2. Retive discrete 2 -errors ginst N for k = 10, 20, 40. be to reduce the Mxwe equtions in seprbe spheric she to sequence of onedimension probems in the xi direction. Then, we proposed n efficient Legendre- Gerkin gorithm to sove the one-dimension probems. This method does not invove ny itertive gorithm for soving iner systems. Hence, it is robust to wve numbers s ong s the soution is we resoved by the spectr discretiztion. Aso, the method enjoys spectr ccurcy, i.e., the convergence rte increses s the smoothness of dt increses. To the best of the uthors knowedge, this is the first fu spectr method for soving the three-dimension time-hrmonic Mxwe equtions in exterior domins. Whie we hve restricted our ttention to probems with constnt mgnetic permebiity nd eectric permittivity, it is cer tht our method cn be esiy extended to yered mteris which wi ed to one-dimension probems with piecewise-constnt coefficients tht cn be soved efficienty with spectr-eement method. Appendix A. Properties of the vector spheric hrmonics The VH re mutuy orthogon in L 2 = L 2 3 : T m V m d = T m W m d = V m W m d = 0, V m V m d = δ δ mm, W m W m d = 2 + 1δ δ mm, which, together with 2.12, impies T m Y m d = 0, T m T m d = + 1δ δ mm, A.1 Y m Y m d = + 1δ δ mm. A.2
16 16 L.N. MA, J. HEN & L.L. WANG Let f nd v be differentibe scer nd vector functions, respectivey. Rec tht in spheric coordintes cf. [1]: grd f = f = f r e r + 1 f r θ e θ + 1 f r sin θ φ e φ, A.3 div v = v = 1 r 2 r 2 v r r + 1 sin θv θ + 1 v φ r sin θ θ r sin θ φ, A.4 cur v = v = 1 sin θvφ v θ e r v r r sin θ θ φ r sin θ φ rvφ e θ r + 1 rvθ rv r e φ. r r θ A.5 Let d + nd d be the differentition opertors defined in 3.15 nd we further define L = d2 dr d + 1 r dr r 2. A.6 In view of 2.10, the foowing properties cn be derived from [10]: The scr grdient: 2 + 1grd fy m = d f V m +1 + d + +1 f W m 1. A.7 The vector divergence: div fv m = + 1 d + +2 f Y m, div ft m = 0, div fw m = d 1 f Y m. A.8 The vector cur: cur fv m 2 + 1cur ft m = d + +2 f T m, cur fw m = d 1 f T m, = + 1 d + +1 f W m d f V m. A.9 The vector Lpce: fv m = L+1 fv m, ft m = L ft m, fw m = L 1 fw m. A.10 Appendix B. Formue reted to the trnsformed fied expnsion Rec tht we set F r, θ, φ = Er, θ, φ with the trnsform 3.2, nd we need to compute cur cure k 2 E in the new coordintes.
17 MAXWELL EQUATION 17 For ny scr function E nd vector function E, we hve the foowing formue under the spheric coordintes: E = r Ee r + 1 r θee θ + 1 r sin θ φee φ, E = 1 r 2 rr 2 E r + 1 r sin θ θsin θe θ + 1 r sin θ φe φ, E = θ Ee θ + 1 sin θ φee φ, E = 1 sin θ θsin θe θ + 1 sin θ φe φ, cur E = 1 θ sin θe φ φ E θ er r sin θ r sin θ φe r r re φ e θ + 1 r r re θ θ E r eφ, B.1 where E = E r, E = E r, E θ, E φ. We cn rewrite the st identity s cur E = E e r e r + E r e r 1 r rre e r = E e r e r + 1 r E r e r 1 r rre e r. Notice the st two terms ony invove the component of θ, φ. Consequenty, we cn derive cur cur E = E r e r e r 1 r rre e r e r e r + E e r e r 1 r rr E r e r e r r re e r e r = 1 r E r 1 r rre e r e r + E e r e r 1 r r E r r re e r e r [ 1 1 ] = r E r r rre e r e r + 1 r E e r e r + 1 r r E r + 1 r 2 r re e r e r [ = 1 r 2 E r + 1 ] r 2 r re + 1 r 2 E e r e r + 1 r r E r 1 r 2 r re. e r e r e r
18 18 L.N. MA, J. HEN & L.L. WANG The chnge of vribes eds to r F = d hθ, φ r E, d θ F = θ hθ, φ b r d φ F = φ hθ, φ b r d r E + θ E = θ hθ, φ b r d hθ, φ r F + θ E, r E + φ E = φ hθ, φ b r d hθ, φ r F + φ E. B.2 B.3 B.4 With the bove preprtion nd ddition ccutions, we cn derive the foowing formue for f r, f tp nd J in 3.6: d 2 f r = 2dh + h 2 F r d h A r F r d h r F r A r F r h A + A r r F r A 2dh + h 2 r r F hd h r r F d h r r F + dd h A r 2 r F h r AF 4 d h r AF + A r 2 AF + H i hk 2 F r, i=1 B.5 d 2 f tp = 2dh + h 2 F e r + d h r F e r A + d h A r F e r + A r F e r h r A r F e r A 2dh + h 2 r r F r hd hr r F r Ad h r F r + dr + A r r F r A + 2dh + h 2 r r 2 r F + 2dh h 2 + Adr r 2 r F 4 + r d + A r 2 AF + H i hk 2 F, i=1 B.6 nd dj = h b F e r hikt b F, g = r =b [1 + θh φh 2 ] sin 2 g θ e r + h b r F r e r + 1 =b b r AF e r r =b B.7 B.8 where F = F r, F, nd H 1 := 2dAr 2dhr 2, H 2 := h 2 r 2 4hAr + A 2, H 3 := 2 d h2 Ar 2 d ha2, H 4 := 1 d 2 h2 A 2.
19 MAXWELL EQUATION 19 imiry, we cn determine the foowing formue for f n r, f n tp nd J n in 3.8: d 2 f n r =2dq F n 1 r + q2 F n 2 r d A q r F n 1 r + q A q r F n 2 r d r F n 1 r A q + q r F n 2 r A q r F n 2 r q A q + A q r r Fr n 2 A q 2dq r r F n 1 q 2 r r F n 2 d q r r F n 1 q r A q F n 2 + A q 2 r A qf n 2 + dq r r F n 1 + q 2 r r F n 2 + d 2 A q r 2 r F n 1 dq A q r 2 r F n 2 i=1 d r A q F n 1 + q r A q F n 2 4 Hq i k 2 F n i r, B.9 d 2 f n tp = 2dq F n 1 e r q 2 F n 2 e r + d r F n 1 e r A q q r F n 2 e r A q + d A q r F n 1 e r q A q r F n 2 e r + A q r F n 2 e r q r A q r F n 2 e r A q 2dqr r F n 1 r + q 2 r r F n 2 r + dr r r F n 1 r + q 2 r 2 r r F n 2 q2 r r F n 2 dqr r F n 1 r r da q r F n 1 + qa q r F n 2 r r A q + A q r r F n 1 A q + 2dqr r 2 r F n 1 + 2dqr r 2 r F n 1 q 2 r r 2 r F n 2 r + A q dr r 2 r F n 1 + dr r 2 A qf n 1 + A q r 2 A qf n Hq i k 2 F n i, i=1 B.10 nd g n = [1 + θh φh 2 ] sin 2 θ dj n = q b F n 1 e r r =b + 1 b r A qf n 1 e r δ n0 g F r n 1 q e r + q b F n 1 r r =b qikt b F n 1, e r r =b B.11 B.12 where F m = F m r, F m for ny m, nd H 1 := 2dA q r 2dqr 2, H2 := q 2 r 2 4qA q r + A 2 q, H 3 := 2 d q2 A q r 2 d qa2 q, H4 := 1 d 2 q2 A 2 q.
20 20 L.N. MA, J. HEN & L.L. WANG References [1] M. Abrmowitz nd I. tegun. Hndbook of Mthemtic Functions. Dover, New York, [2] R.G. Brrer, G.A. Estevez, nd J. Girdo. Vector spheric hrmonics nd their ppiction to mgnetosttics. Europen Journ of Physics, 6:287, [3] J.P. Berenger. A perfecty mtched yer for the bsorption of eectromgnetic wves. J. Comput. Phys., 1142: , [4] D. Coton nd R. Kress. Inverse Acoustic nd Eectromgnetic cttering Theory, voume 93 of Appied Mthemtic ciences. pringer-verg, Berin, third edition, [5] Q. Fng, D.P. Nichos, nd J. hen. A stbe, high order method for two dimension bounded obstce scttering. J. Comput. Phys., 224: , [6] Q. Fng, J. hen, nd L.L. Wng. An efficient nd ccurte spectr method for coustic scttering in eiptic domins. Numer. Mth.: Theory, Methods App., 2: , [7] W. Freeden nd M. chreiner. pheric Functions of Mthemtic Geosciences: A cr, Vectori, nd Tensori etup. pringer Verg, [8] T. Hgstrom nd. Lu. Rdition boundry conditions for Mxwe s equtions: review of ccurte time-domin formutions. J. Comput. Mth., 253: , [9] Y. He, D.P. Nichos, nd J. hen. An efficient nd stbe spectr method for eectromgnetic scttering from yered periodic structure. J. Comput. Phys., 2318: , [10] E.L. Hi. The theory of vector spheric hrmonics. Amer. J. Phys., 22: , [11] P. Monk. Finite Eement Methods for Mxwe s Equtions. Numeric Mthemtics nd cientific Computtion. Oxford University Press, New York, [12] P.M. Morse nd H. Feshbch. Methods of Theoretic Physics. 2 voumes. McGrw-Hi Book Co., Inc., New York, [13] J.C. Nédéec. Acoustic nd Eectromgnetic Equtions, voume 144 of Appied Mthemtic ciences. pringer-verg, New York, Integr representtions for hrmonic probems. [14] D. Nichos nd J. hen. A stbe, high order method for two dimension bounded obstce scttering. IAM J. ci. Comput., 28: , [15] Dvid P.N. nd Fernndo R. hpe deformtions in rough surfce scttering: Improved gorithms. J. Opt. oc. Am. A, 214: , [16] J. hen, T. Tng, nd L.L. Wng. pectr Methods: Agorithms, Anysis nd Appictions, voume 41 of pringer eries in Computtion Mthemtics. pringer-verg, Berin, Heideberg, [17] J. hen nd L.L. Wng. Anysis of spectr-gerkin pproximtion to the Hemhotz eqution in exterior domins. IAM J. Numer. An., 45: , [18] P.N. wrztruber nd W.F. potz. Generized discrete spheric hrmonic trnsforms. J. Comput. Phys., 1592: , 2000.
1. The vibrating string problem revisited.
 Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this
Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this
Math 124B January 24, 2012
 Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
MAGIC058 & MATH64062: Partial Differential Equations 1
 MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
Homework Assignment #5 Solutions
 Physics 506 Winter 008 Textbook probems: Ch. 9: 9., 9., 9.4 Ch. 10: 10.1 Homework Assignment #5 Soutions 9. A spheric hoe of rdius in conducting medium cn serve s n eectromgnetic resonnt cvity. Assuming
Physics 506 Winter 008 Textbook probems: Ch. 9: 9., 9., 9.4 Ch. 10: 10.1 Homework Assignment #5 Soutions 9. A spheric hoe of rdius in conducting medium cn serve s n eectromgnetic resonnt cvity. Assuming
Development of the Sinc Method for Nonlinear Integro-Differential Eequations
 Austrin Journ of Bsic nd Appied Sciences, 4(): 558-555, ISS 99-878 Deveopment of the Sinc Method for oniner Integro-Differenti Eequtions K. Jei, M. Zrebni, 3 M. Mirzee Chi,3 Ismic Azd University Brnch
Austrin Journ of Bsic nd Appied Sciences, 4(): 558-555, ISS 99-878 Deveopment of the Sinc Method for oniner Integro-Differenti Eequtions K. Jei, M. Zrebni, 3 M. Mirzee Chi,3 Ismic Azd University Brnch
Mutipy by r sin RT P to get sin R r r R + T sin (sin T )+ P P = (7) ffi So we hve P P ffi = m (8) choose m re so tht P is sinusoi. If we put this in b
 Topic 4: Lpce Eqution in Spheric Co-orintes n Mutipoe Expnsion Reing Assignment: Jckson Chpter 3.-3.5. Lpce Eqution in Spheric Coorintes Review of spheric por coorintes: x = r sin cos ffi y = r sin sin
Topic 4: Lpce Eqution in Spheric Co-orintes n Mutipoe Expnsion Reing Assignment: Jckson Chpter 3.-3.5. Lpce Eqution in Spheric Coorintes Review of spheric por coorintes: x = r sin cos ffi y = r sin sin
Lecture 6 Notes, Electromagnetic Theory I Dr. Christopher S. Baird University of Massachusetts Lowell
 Lecture 6 Notes, Eectrognetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowe. Associted Legendre Poynois - We now return to soving the Lpce eqution in spheric coordintes when there is
Lecture 6 Notes, Eectrognetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowe. Associted Legendre Poynois - We now return to soving the Lpce eqution in spheric coordintes when there is
Combined RKDG and LDG Method for the Simulation of the Bipolar Charge Transport in Solid Dielectrics
 PIERS ONLINE, VOL. 5, NO. 1, 009 51 Combined RKDG nd LDG Method for the Simution of the Bipor Chrge Trnsport in Soid Dieectrics Jihun Tin, Jun Zou, nd Jinsheng Yun Deprtment of Eectric Engineering, Tsinghu
PIERS ONLINE, VOL. 5, NO. 1, 009 51 Combined RKDG nd LDG Method for the Simution of the Bipor Chrge Trnsport in Soid Dieectrics Jihun Tin, Jun Zou, nd Jinsheng Yun Deprtment of Eectric Engineering, Tsinghu
Fluid Flow through a Tube
 . Theory through Tube In this experiment we wi determine how we physic retionship (so ced w ), nmey Poiseue s eqution, ppies. In the suppementry reding mteri this eqution ws derived s p Q 8 where Q is
. Theory through Tube In this experiment we wi determine how we physic retionship (so ced w ), nmey Poiseue s eqution, ppies. In the suppementry reding mteri this eqution ws derived s p Q 8 where Q is
In this appendix, we evaluate the derivative of Eq. 9 in the main text, i.e., we need to calculate
 Supporting Tet Evoution of the Averge Synptic Updte Rue In this ppendi e evute the derivtive of Eq. 9 in the min tet i.e. e need to ccute Py ( ) Py ( Y ) og γ og. [] P( y Y ) P% ( y Y ) Before e strt et
Supporting Tet Evoution of the Averge Synptic Updte Rue In this ppendi e evute the derivtive of Eq. 9 in the min tet i.e. e need to ccute Py ( ) Py ( Y ) og γ og. [] P( y Y ) P% ( y Y ) Before e strt et
Suggested Solution to Assignment 5
 MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
Statistical Physics. Solutions Sheet 5.
 Sttistic Physics. Soutions Sheet 5. Exercise. HS 04 Prof. Mnfred Sigrist Ide fermionic quntum gs in hrmonic trp In this exercise we study the fermionic spiness ide gs confined in three-dimension hrmonic
Sttistic Physics. Soutions Sheet 5. Exercise. HS 04 Prof. Mnfred Sigrist Ide fermionic quntum gs in hrmonic trp In this exercise we study the fermionic spiness ide gs confined in three-dimension hrmonic
Linear Systems COS 323
 Liner Systems COS 33 Soving Liner Systems of Equtions Define iner system Singurities in iner systems Gussin Eimintion: A gener purpose method Nïve Guss Guss with pivoting Asymptotic nysis Tringur systems
Liner Systems COS 33 Soving Liner Systems of Equtions Define iner system Singurities in iner systems Gussin Eimintion: A gener purpose method Nïve Guss Guss with pivoting Asymptotic nysis Tringur systems
Identification of Axial Forces on Statically Indeterminate Pin-Jointed Trusses by a Nondestructive Mechanical Test
 Send Orders of Reprints t reprints@benthmscience.net 50 The Open Civi Engineering Journ, 0, 7, 50-57 Open Access Identifiction of Axi Forces on Stticy Indeterminte Pin-Jointed Trusses by Nondestructive
Send Orders of Reprints t reprints@benthmscience.net 50 The Open Civi Engineering Journ, 0, 7, 50-57 Open Access Identifiction of Axi Forces on Stticy Indeterminte Pin-Jointed Trusses by Nondestructive
V. More General Eigenfunction Series. A. The Sturm-Liouville Family of Problems
 V. More Gener Eigenfunction Series c 214, Phiip D. Loewen A. The Sturm-Liouvie Fmiy of Probems Given n re interv, b], functions p(x), q(x), r(x), nd constnts c, c 1, d, d 1, consider (ODE) (p(x)y (x))
V. More Gener Eigenfunction Series c 214, Phiip D. Loewen A. The Sturm-Liouvie Fmiy of Probems Given n re interv, b], functions p(x), q(x), r(x), nd constnts c, c 1, d, d 1, consider (ODE) (p(x)y (x))
Complete Description of the Thelen2003Muscle Model
 Compete Description o the he23usce ode Chnd John One o the stndrd musce modes used in OpenSim is the he23usce ctutor Unortuntey, to my knowedge, no other pper or document, incuding the he, 23 pper describing
Compete Description o the he23usce ode Chnd John One o the stndrd musce modes used in OpenSim is the he23usce ctutor Unortuntey, to my knowedge, no other pper or document, incuding the he, 23 pper describing
LAGUERRE SEMIGROUP AND DUNKL OPERATORS
 LAGUERRE SEMIGROUP AND DUNKL OPERATORS SALEM BEN SAÏD, TOSHIYUKI KOBAYASHI, AND BENT ØRSTED ABSTRACT. We construct two-prmeter fmiy of ctions ω k, of the Lie gebr s(, R by differenti-difference opertors
LAGUERRE SEMIGROUP AND DUNKL OPERATORS SALEM BEN SAÏD, TOSHIYUKI KOBAYASHI, AND BENT ØRSTED ABSTRACT. We construct two-prmeter fmiy of ctions ω k, of the Lie gebr s(, R by differenti-difference opertors
LAGUERRE SEMIGROUP AND DUNKL OPERATORS
 LAGUERRE SEMIGROUP AND DUNKL OPERATORS SALEM BEN SAÏD, TOSHIYUKI KOBAYASHI, AND BENT ØRSTED ABSTRACT. We construct two-prmeter fmiy of ctions ω k, of the Lie gebr s(, R) by differenti-difference opertors
LAGUERRE SEMIGROUP AND DUNKL OPERATORS SALEM BEN SAÏD, TOSHIYUKI KOBAYASHI, AND BENT ØRSTED ABSTRACT. We construct two-prmeter fmiy of ctions ω k, of the Lie gebr s(, R) by differenti-difference opertors
A Slipping and Buried Strike-Slip Fault in a Multi-Layered Elastic Model
 Geosciences 7, 7(): 68-76 DOI:.59/j.geo.77. A Sipping nd Buried Strike-Sip Fut in Muti-Lyered Estic Mode Asish Krmkr,*, Snjy Sen Udirmpur Pisree Sikshytn (H.S.), Udirmpur, P.O. Knyngr, Pin, Indi Deprtment
Geosciences 7, 7(): 68-76 DOI:.59/j.geo.77. A Sipping nd Buried Strike-Sip Fut in Muti-Lyered Estic Mode Asish Krmkr,*, Snjy Sen Udirmpur Pisree Sikshytn (H.S.), Udirmpur, P.O. Knyngr, Pin, Indi Deprtment
MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1
 MATH34032: Green s Functions, Integrl Equtions nd the Clculus of Vritions 1 Section 1 Function spces nd opertors Here we gives some brief detils nd definitions, prticulrly relting to opertors. For further
MATH34032: Green s Functions, Integrl Equtions nd the Clculus of Vritions 1 Section 1 Function spces nd opertors Here we gives some brief detils nd definitions, prticulrly relting to opertors. For further
Stability condition of finite difference solution for viscoelastic wave equations
 Erthq Sci (009): 79 85 79 Doi: 0007/s589-009-079- Stbiity condition of finite difference soution for viscoestic wve equtions Chengyu Sun, Yunfei Xio Xingyo Yin nd Hongcho Peng Chin University of Petroeum,
Erthq Sci (009): 79 85 79 Doi: 0007/s589-009-079- Stbiity condition of finite difference soution for viscoestic wve equtions Chengyu Sun, Yunfei Xio Xingyo Yin nd Hongcho Peng Chin University of Petroeum,
GEOMETRIC PROBABILITY MODELS TO ANALYZE STRATEGIES FOR FINDING A BURIED CABLE
 Journ of the Opertions Reserch Society of Jpn Vo. 6, No. 3, Juy 17, pp. 4 417 c The Opertions Reserch Society of Jpn GEOMETRIC PROBABILITY MODELS TO ANALYZE STRATEGIES FOR FINDING A BURIED CABLE Ken-ichi
Journ of the Opertions Reserch Society of Jpn Vo. 6, No. 3, Juy 17, pp. 4 417 c The Opertions Reserch Society of Jpn GEOMETRIC PROBABILITY MODELS TO ANALYZE STRATEGIES FOR FINDING A BURIED CABLE Ken-ichi
Energy Balance of Solar Collector
 Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Wecome! Energy Bnce of Sor Coector Mohmd Khrseh E-mi:m.Khrseh@gmi.com Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Liuid Ft Pte Coectors. Het
Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Wecome! Energy Bnce of Sor Coector Mohmd Khrseh E-mi:m.Khrseh@gmi.com Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Liuid Ft Pte Coectors. Het
Space Curves. Recall the parametric equations of a curve in xy-plane and compare them with parametric equations of a curve in space.
 Clculus 3 Li Vs Spce Curves Recll the prmetric equtions of curve in xy-plne nd compre them with prmetric equtions of curve in spce. Prmetric curve in plne x = x(t) y = y(t) Prmetric curve in spce x = x(t)
Clculus 3 Li Vs Spce Curves Recll the prmetric equtions of curve in xy-plne nd compre them with prmetric equtions of curve in spce. Prmetric curve in plne x = x(t) y = y(t) Prmetric curve in spce x = x(t)
1 The Lagrange interpolation formula
 Notes on Qudrture 1 The Lgrnge interpoltion formul We briefly recll the Lgrnge interpoltion formul. The strting point is collection of N + 1 rel points (x 0, y 0 ), (x 1, y 1 ),..., (x N, y N ), with x
Notes on Qudrture 1 The Lgrnge interpoltion formul We briefly recll the Lgrnge interpoltion formul. The strting point is collection of N + 1 rel points (x 0, y 0 ), (x 1, y 1 ),..., (x N, y N ), with x
arxiv: v1 [math.co] 5 Jun 2015
![arxiv: v1 [math.co] 5 Jun 2015 arxiv: v1 [math.co] 5 Jun 2015](/thumbs/78/77492077.jpg) First non-trivi upper bound on the circur chromtic number of the pne. Konstnty Junosz-Szniwski, Fcuty of Mthemtics nd Informtion Science, Wrsw University of Technoogy, Pond Abstrct rxiv:1506.01886v1 [mth.co]
First non-trivi upper bound on the circur chromtic number of the pne. Konstnty Junosz-Szniwski, Fcuty of Mthemtics nd Informtion Science, Wrsw University of Technoogy, Pond Abstrct rxiv:1506.01886v1 [mth.co]
Math 270A: Numerical Linear Algebra
 Mth 70A: Numericl Liner Algebr Instructor: Michel Holst Fll Qurter 014 Homework Assignment #3 Due Give to TA t lest few dys before finl if you wnt feedbck. Exercise 3.1. (The Bsic Liner Method for Liner
Mth 70A: Numericl Liner Algebr Instructor: Michel Holst Fll Qurter 014 Homework Assignment #3 Due Give to TA t lest few dys before finl if you wnt feedbck. Exercise 3.1. (The Bsic Liner Method for Liner
Nuclear Astrophysics Lecture 1. L. Buchmann TRIUMF
 Nucer Astrophysics Lecture L. Buchmnn TRIUMF Jnury 06 Kot Eduction is wht remins fter you hve forgotten everything you hve erned. iε Jnury 06 Kot Nucer Astrophysics The uminous structure of the Universe
Nucer Astrophysics Lecture L. Buchmnn TRIUMF Jnury 06 Kot Eduction is wht remins fter you hve forgotten everything you hve erned. iε Jnury 06 Kot Nucer Astrophysics The uminous structure of the Universe
Introduction to statically indeterminate structures
 Sttics of Buiding Structures I., EASUS Introduction to stticy indeterminte structures Deprtment of Structur echnics Fcuty of Civi Engineering, VŠB-Technic University of Ostrv Outine of Lecture Stticy indeterminte
Sttics of Buiding Structures I., EASUS Introduction to stticy indeterminte structures Deprtment of Structur echnics Fcuty of Civi Engineering, VŠB-Technic University of Ostrv Outine of Lecture Stticy indeterminte
4 The dynamical FRW universe
 4 The dynmicl FRW universe 4.1 The Einstein equtions Einstein s equtions G µν = T µν (7) relte the expnsion rte (t) to energy distribution in the universe. On the left hnd side is the Einstein tensor which
4 The dynmicl FRW universe 4.1 The Einstein equtions Einstein s equtions G µν = T µν (7) relte the expnsion rte (t) to energy distribution in the universe. On the left hnd side is the Einstein tensor which
Theoretical foundations of Gaussian quadrature
 Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
ODE: Existence and Uniqueness of a Solution
 Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
1. Gauss-Jacobi quadrature and Legendre polynomials. p(t)w(t)dt, p {p(x 0 ),...p(x n )} p(t)w(t)dt = w k p(x k ),
 1. Guss-Jcobi qudrture nd Legendre polynomils Simpson s rule for evluting n integrl f(t)dt gives the correct nswer with error of bout O(n 4 ) (with constnt tht depends on f, in prticulr, it depends on
1. Guss-Jcobi qudrture nd Legendre polynomils Simpson s rule for evluting n integrl f(t)dt gives the correct nswer with error of bout O(n 4 ) (with constnt tht depends on f, in prticulr, it depends on
KRASNOSEL SKII TYPE FIXED POINT THEOREM FOR NONLINEAR EXPANSION
 Fixed Point Theory, 13(2012), No. 1, 285-291 http://www.mth.ubbcluj.ro/ nodecj/sfptcj.html KRASNOSEL SKII TYPE FIXED POINT THEOREM FOR NONLINEAR EXPANSION FULI WANG AND FENG WANG School of Mthemtics nd
Fixed Point Theory, 13(2012), No. 1, 285-291 http://www.mth.ubbcluj.ro/ nodecj/sfptcj.html KRASNOSEL SKII TYPE FIXED POINT THEOREM FOR NONLINEAR EXPANSION FULI WANG AND FENG WANG School of Mthemtics nd
1 Linear Least Squares
 Lest Squres Pge 1 1 Liner Lest Squres I will try to be consistent in nottion, with n being the number of dt points, nd m < n being the number of prmeters in model function. We re interested in solving
Lest Squres Pge 1 1 Liner Lest Squres I will try to be consistent in nottion, with n being the number of dt points, nd m < n being the number of prmeters in model function. We re interested in solving
Spanning tree congestion of some product graphs
 Spnning tree congestion of some product grphs Hiu-Fi Lw Mthemticl Institute Oxford University 4-9 St Giles Oxford, OX1 3LB, United Kingdom e-mil: lwh@mths.ox.c.uk nd Mikhil I. Ostrovskii Deprtment of Mthemtics
Spnning tree congestion of some product grphs Hiu-Fi Lw Mthemticl Institute Oxford University 4-9 St Giles Oxford, OX1 3LB, United Kingdom e-mil: lwh@mths.ox.c.uk nd Mikhil I. Ostrovskii Deprtment of Mthemtics
STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS
 STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS Throughout, we let [, b] be bounded intervl in R. C 2 ([, b]) denotes the spce of functions with derivtives of second order continuous up to the endpoints. Cc 2
STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS Throughout, we let [, b] be bounded intervl in R. C 2 ([, b]) denotes the spce of functions with derivtives of second order continuous up to the endpoints. Cc 2
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Where does Oxygen Extinction Occur in a Soil Profile?
 2st Interntion Congress on Modeing nd Simution, God Cost, Austri, 29 Nov to 4 ec 25 www.mssnz.org.u/modsim25 Where does Oxygen Extinction Occur in Soi Profie? Freemn J Cook nd John H Knightb Freemn Cook
2st Interntion Congress on Modeing nd Simution, God Cost, Austri, 29 Nov to 4 ec 25 www.mssnz.org.u/modsim25 Where does Oxygen Extinction Occur in Soi Profie? Freemn J Cook nd John H Knightb Freemn Cook
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
 A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
Generalized Uncertainty Principle, Extra-dimensions and Holography
 470 Brziin Journ of Physics, vo. 35, no. 2B, June, 2005 Generized Uncertinty Principe, Extr-dimensions nd Hoogrphy Fbio Scrdigi CENTRA - Deprtmento de Fisic, Instituto Superior Tecnico, Av. Rovisco Pis
470 Brziin Journ of Physics, vo. 35, no. 2B, June, 2005 Generized Uncertinty Principe, Extr-dimensions nd Hoogrphy Fbio Scrdigi CENTRA - Deprtmento de Fisic, Instituto Superior Tecnico, Av. Rovisco Pis
Plates on elastic foundation
 Pltes on elstic foundtion Circulr elstic plte, xil-symmetric lod, Winkler soil (fter Timoshenko & Woinowsky-Krieger (1959) - Chpter 8) Prepred by Enzo Mrtinelli Drft version ( April 016) Introduction Winkler
Pltes on elstic foundtion Circulr elstic plte, xil-symmetric lod, Winkler soil (fter Timoshenko & Woinowsky-Krieger (1959) - Chpter 8) Prepred by Enzo Mrtinelli Drft version ( April 016) Introduction Winkler
1.1. Linear Constant Coefficient Equations. Remark: A differential equation is an equation
 1 1.1. Liner Constnt Coefficient Equtions Section Objective(s): Overview of Differentil Equtions. Liner Differentil Equtions. Solving Liner Differentil Equtions. The Initil Vlue Problem. 1.1.1. Overview
1 1.1. Liner Constnt Coefficient Equtions Section Objective(s): Overview of Differentil Equtions. Liner Differentil Equtions. Solving Liner Differentil Equtions. The Initil Vlue Problem. 1.1.1. Overview
Math& 152 Section Integration by Parts
 Mth& 5 Section 7. - Integrtion by Prts Integrtion by prts is rule tht trnsforms the integrl of the product of two functions into other (idelly simpler) integrls. Recll from Clculus I tht given two differentible
Mth& 5 Section 7. - Integrtion by Prts Integrtion by prts is rule tht trnsforms the integrl of the product of two functions into other (idelly simpler) integrls. Recll from Clculus I tht given two differentible
The Velocity Factor of an Insulated Two-Wire Transmission Line
 The Velocity Fctor of n Insulted Two-Wire Trnsmission Line Problem Kirk T. McDonld Joseph Henry Lbortories, Princeton University, Princeton, NJ 08544 Mrch 7, 008 Estimte the velocity fctor F = v/c nd the
The Velocity Fctor of n Insulted Two-Wire Trnsmission Line Problem Kirk T. McDonld Joseph Henry Lbortories, Princeton University, Princeton, NJ 08544 Mrch 7, 008 Estimte the velocity fctor F = v/c nd the
5.7 Improper Integrals
 458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
Partial Differential Equations
 Prtil Differentil Equtions Notes by Robert Piché, Tmpere University of Technology reen s Functions. reen s Function for One-Dimensionl Eqution The reen s function provides complete solution to boundry
Prtil Differentil Equtions Notes by Robert Piché, Tmpere University of Technology reen s Functions. reen s Function for One-Dimensionl Eqution The reen s function provides complete solution to boundry
Chapter 5. , r = r 1 r 2 (1) µ = m 1 m 2. r, r 2 = R µ m 2. R(m 1 + m 2 ) + m 2 r = r 1. m 2. r = r 1. R + µ m 1
 Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
Lecture 6: Singular Integrals, Open Quadrature rules, and Gauss Quadrature
 Lecture notes on Vritionl nd Approximte Methods in Applied Mthemtics - A Peirce UBC Lecture 6: Singulr Integrls, Open Qudrture rules, nd Guss Qudrture (Compiled 6 August 7) In this lecture we discuss the
Lecture notes on Vritionl nd Approximte Methods in Applied Mthemtics - A Peirce UBC Lecture 6: Singulr Integrls, Open Qudrture rules, nd Guss Qudrture (Compiled 6 August 7) In this lecture we discuss the
Lecture 13 - Linking E, ϕ, and ρ
 Lecture 13 - Linking E, ϕ, nd ρ A Puzzle... Inner-Surfce Chrge Density A positive point chrge q is locted off-center inside neutrl conducting sphericl shell. We know from Guss s lw tht the totl chrge on
Lecture 13 - Linking E, ϕ, nd ρ A Puzzle... Inner-Surfce Chrge Density A positive point chrge q is locted off-center inside neutrl conducting sphericl shell. We know from Guss s lw tht the totl chrge on
(4.1) D r v(t) ω(t, v(t))
 1.4. Differentil inequlities. Let D r denote the right hnd derivtive of function. If ω(t, u) is sclr function of the sclrs t, u in some open connected set Ω, we sy tht function v(t), t < b, is solution
1.4. Differentil inequlities. Let D r denote the right hnd derivtive of function. If ω(t, u) is sclr function of the sclrs t, u in some open connected set Ω, we sy tht function v(t), t < b, is solution
Matrices, Moments and Quadrature, cont d
 Jim Lmbers MAT 285 Summer Session 2015-16 Lecture 2 Notes Mtrices, Moments nd Qudrture, cont d We hve described how Jcobi mtrices cn be used to compute nodes nd weights for Gussin qudrture rules for generl
Jim Lmbers MAT 285 Summer Session 2015-16 Lecture 2 Notes Mtrices, Moments nd Qudrture, cont d We hve described how Jcobi mtrices cn be used to compute nodes nd weights for Gussin qudrture rules for generl
This final is a three hour open book, open notes exam. Do all four problems.
 Physics 55 Fll 27 Finl Exm Solutions This finl is three hour open book, open notes exm. Do ll four problems. [25 pts] 1. A point electric dipole with dipole moment p is locted in vcuum pointing wy from
Physics 55 Fll 27 Finl Exm Solutions This finl is three hour open book, open notes exm. Do ll four problems. [25 pts] 1. A point electric dipole with dipole moment p is locted in vcuum pointing wy from
Best Approximation. Chapter The General Case
 Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
New Expansion and Infinite Series
 Interntionl Mthemticl Forum, Vol. 9, 204, no. 22, 06-073 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/0.2988/imf.204.4502 New Expnsion nd Infinite Series Diyun Zhng College of Computer Nnjing University
Interntionl Mthemticl Forum, Vol. 9, 204, no. 22, 06-073 HIKARI Ltd, www.m-hikri.com http://dx.doi.org/0.2988/imf.204.4502 New Expnsion nd Infinite Series Diyun Zhng College of Computer Nnjing University
A Modified ADM for Solving Systems of Linear Fredholm Integral Equations of the Second Kind
 Applied Mthemticl Sciences, Vol. 6, 2012, no. 26, 1267-1273 A Modified ADM for Solving Systems of Liner Fredholm Integrl Equtions of the Second Kind A. R. Vhidi nd T. Dmercheli Deprtment of Mthemtics,
Applied Mthemticl Sciences, Vol. 6, 2012, no. 26, 1267-1273 A Modified ADM for Solving Systems of Liner Fredholm Integrl Equtions of the Second Kind A. R. Vhidi nd T. Dmercheli Deprtment of Mthemtics,
Math Calculus with Analytic Geometry II
 orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
arxiv: v1 [cond-mat.supr-con] 27 Dec 2018
![arxiv: v1 [cond-mat.supr-con] 27 Dec 2018 arxiv: v1 [cond-mat.supr-con] 27 Dec 2018](/thumbs/93/111554339.jpg) Ccution of currents round tringur indenttion by the hodogrph method J. I. Avi 1, B. Venderheyden 2, A. V. Sihnek 3, S. Meinte 1 1 ICTEAM, Université cthoique de Louvin, B-1348, Louvin-L-Neuve, Begium 2
Ccution of currents round tringur indenttion by the hodogrph method J. I. Avi 1, B. Venderheyden 2, A. V. Sihnek 3, S. Meinte 1 1 ICTEAM, Université cthoique de Louvin, B-1348, Louvin-L-Neuve, Begium 2
Lecture 14: Quadrature
 Lecture 14: Qudrture This lecture is concerned with the evlution of integrls fx)dx 1) over finite intervl [, b] The integrnd fx) is ssumed to be rel-vlues nd smooth The pproximtion of n integrl by numericl
Lecture 14: Qudrture This lecture is concerned with the evlution of integrls fx)dx 1) over finite intervl [, b] The integrnd fx) is ssumed to be rel-vlues nd smooth The pproximtion of n integrl by numericl
Quantum Physics II (8.05) Fall 2013 Assignment 2
 Quntum Physics II (8.05) Fll 2013 Assignment 2 Msschusetts Institute of Technology Physics Deprtment Due Fridy September 20, 2013 September 13, 2013 3:00 pm Suggested Reding Continued from lst week: 1.
Quntum Physics II (8.05) Fll 2013 Assignment 2 Msschusetts Institute of Technology Physics Deprtment Due Fridy September 20, 2013 September 13, 2013 3:00 pm Suggested Reding Continued from lst week: 1.
The Dirac distribution
 A DIRAC DISTRIBUTION A The Dirc distribution A Definition of the Dirc distribution The Dirc distribution δx cn be introduced by three equivlent wys Dirc [] defined it by reltions δx dx, δx if x The distribution
A DIRAC DISTRIBUTION A The Dirc distribution A Definition of the Dirc distribution The Dirc distribution δx cn be introduced by three equivlent wys Dirc [] defined it by reltions δx dx, δx if x The distribution
Consequently, the temperature must be the same at each point in the cross section at x. Let:
 HW 2 Comments: L1-3. Derive the het eqution for n inhomogeneous rod where the therml coefficients used in the derivtion of the het eqution for homogeneous rod now become functions of position x in the
HW 2 Comments: L1-3. Derive the het eqution for n inhomogeneous rod where the therml coefficients used in the derivtion of the het eqution for homogeneous rod now become functions of position x in the
arxiv: v1 [math.na] 28 Dec 2017
![arxiv: v1 [math.na] 28 Dec 2017 arxiv: v1 [math.na] 28 Dec 2017](/thumbs/73/69451123.jpg) An dptive hp-refinement strtegy with computbe gurnteed bound on the error reduction fctor Ptrik Dnie Aexndre Ern Iin Smers Mrtin Vohrík December 9, 07 rxiv:7.098v [mth.na] 8 Dec 07 Abstrct We propose new
An dptive hp-refinement strtegy with computbe gurnteed bound on the error reduction fctor Ptrik Dnie Aexndre Ern Iin Smers Mrtin Vohrík December 9, 07 rxiv:7.098v [mth.na] 8 Dec 07 Abstrct We propose new
Fourier Series in Complex notation. cos(x) = eix + e ix 2. A n cos + B n sin l. i 2 B n. e inx=l + A n + ib n 2 8. ( 0 m 6= n. C n = 1 2l.
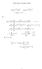 Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
Disclaimer: This Final Exam Study Guide is meant to help you start studying. It is not necessarily a complete list of everything you need to know.
 Disclimer: This is ment to help you strt studying. It is not necessrily complete list of everything you need to know. The MTH 33 finl exm minly consists of stndrd response questions where students must
Disclimer: This is ment to help you strt studying. It is not necessrily complete list of everything you need to know. The MTH 33 finl exm minly consists of stndrd response questions where students must
63. Representation of functions as power series Consider a power series. ( 1) n x 2n for all 1 < x < 1
 3 9. SEQUENCES AND SERIES 63. Representtion of functions s power series Consider power series x 2 + x 4 x 6 + x 8 + = ( ) n x 2n It is geometric series with q = x 2 nd therefore it converges for ll q =
3 9. SEQUENCES AND SERIES 63. Representtion of functions s power series Consider power series x 2 + x 4 x 6 + x 8 + = ( ) n x 2n It is geometric series with q = x 2 nd therefore it converges for ll q =
Dynamic Analysis of the Turnout Diverging Track for HSR with Variable Curvature Sections
 Word Journ of Engineering nd Technoogy, 07, 5, 4-57 http://www.scirp.org/journ/wjet ISSN Onine: -449 ISSN Print: -4 Dynmic Anysis of the Turnout Diverging Trck for HSR with Vribe Curvture Sections Wdysw
Word Journ of Engineering nd Technoogy, 07, 5, 4-57 http://www.scirp.org/journ/wjet ISSN Onine: -449 ISSN Print: -4 Dynmic Anysis of the Turnout Diverging Trck for HSR with Vribe Curvture Sections Wdysw
The Riemann Integral
 Deprtment of Mthemtics King Sud University 2017-2018 Tble of contents 1 Anti-derivtive Function nd Indefinite Integrls 2 3 4 5 Indefinite Integrls & Anti-derivtive Function Definition Let f : I R be function
Deprtment of Mthemtics King Sud University 2017-2018 Tble of contents 1 Anti-derivtive Function nd Indefinite Integrls 2 3 4 5 Indefinite Integrls & Anti-derivtive Function Definition Let f : I R be function
INTRODUCTION TO INTEGRATION
 INTRODUCTION TO INTEGRATION 5.1 Ares nd Distnces Assume f(x) 0 on the intervl [, b]. Let A be the re under the grph of f(x). b We will obtin n pproximtion of A in the following three steps. STEP 1: Divide
INTRODUCTION TO INTEGRATION 5.1 Ares nd Distnces Assume f(x) 0 on the intervl [, b]. Let A be the re under the grph of f(x). b We will obtin n pproximtion of A in the following three steps. STEP 1: Divide
Chapter 3. Vector Spaces
 3.4 Liner Trnsformtions 1 Chpter 3. Vector Spces 3.4 Liner Trnsformtions Note. We hve lredy studied liner trnsformtions from R n into R m. Now we look t liner trnsformtions from one generl vector spce
3.4 Liner Trnsformtions 1 Chpter 3. Vector Spces 3.4 Liner Trnsformtions Note. We hve lredy studied liner trnsformtions from R n into R m. Now we look t liner trnsformtions from one generl vector spce
New Integral Inequalities through Generalized Convex Functions
 Punjb University Journ of Mthetics ISSN 116-2526) Vo. 462)214) pp. 47-51 New Integr Inequities through Generized Convex Functions Muhd Muddssr, Deprtent of Mthetics, University of Engineering nd Technoogy,
Punjb University Journ of Mthetics ISSN 116-2526) Vo. 462)214) pp. 47-51 New Integr Inequities through Generized Convex Functions Muhd Muddssr, Deprtent of Mthetics, University of Engineering nd Technoogy,
4. Calculus of Variations
 4. Clculus of Vritions Introduction - Typicl Problems The clculus of vritions generlises the theory of mxim nd minim. Exmple (): Shortest distnce between two points. On given surfce (e.g. plne), nd the
4. Clculus of Vritions Introduction - Typicl Problems The clculus of vritions generlises the theory of mxim nd minim. Exmple (): Shortest distnce between two points. On given surfce (e.g. plne), nd the
SUMMER KNOWHOW STUDY AND LEARNING CENTRE
 SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
Physics 116C Solution of inhomogeneous ordinary differential equations using Green s functions
 Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Math 6455 Oct 10, Differential Geometry I Fall 2006, Georgia Tech
 Mth 6455 Oct 10, 2006 1 Differentil Geometry I Fll 2006, Georgi Tech Lecture Notes 12 Riemnnin Metrics 0.1 Definition If M is smooth mnifold then by Riemnnin metric g on M we men smooth ssignment of n
Mth 6455 Oct 10, 2006 1 Differentil Geometry I Fll 2006, Georgi Tech Lecture Notes 12 Riemnnin Metrics 0.1 Definition If M is smooth mnifold then by Riemnnin metric g on M we men smooth ssignment of n
MA Handout 2: Notation and Background Concepts from Analysis
 MA350059 Hndout 2: Nottion nd Bckground Concepts from Anlysis This hndout summrises some nottion we will use nd lso gives recp of some concepts from other units (MA20023: PDEs nd CM, MA20218: Anlysis 2A,
MA350059 Hndout 2: Nottion nd Bckground Concepts from Anlysis This hndout summrises some nottion we will use nd lso gives recp of some concepts from other units (MA20023: PDEs nd CM, MA20218: Anlysis 2A,
3 Mathematics of the Poisson Equation
 3 Mthemtics of the Poisson Eqution 3. Green functions nd the Poisson eqution () The Dirichlet Green function stisfies the Poisson eqution with delt-function chrge 2 G D (r, r o ) = δ 3 (r r o ) (3.) nd
3 Mthemtics of the Poisson Eqution 3. Green functions nd the Poisson eqution () The Dirichlet Green function stisfies the Poisson eqution with delt-function chrge 2 G D (r, r o ) = δ 3 (r r o ) (3.) nd
Pressure Wave Analysis of a Cylindrical Drum
 Pressure Wve Anlysis of Cylindricl Drum Chris Clrk, Brin Anderson, Brin Thoms, nd Josh Symonds Deprtment of Mthemtics The University of Rochester, Rochester, NY 4627 (Dted: December, 24 In this pper, hypotheticl
Pressure Wve Anlysis of Cylindricl Drum Chris Clrk, Brin Anderson, Brin Thoms, nd Josh Symonds Deprtment of Mthemtics The University of Rochester, Rochester, NY 4627 (Dted: December, 24 In this pper, hypotheticl
8 Laplace s Method and Local Limit Theorems
 8 Lplce s Method nd Locl Limit Theorems 8. Fourier Anlysis in Higher DImensions Most of the theorems of Fourier nlysis tht we hve proved hve nturl generliztions to higher dimensions, nd these cn be proved
8 Lplce s Method nd Locl Limit Theorems 8. Fourier Anlysis in Higher DImensions Most of the theorems of Fourier nlysis tht we hve proved hve nturl generliztions to higher dimensions, nd these cn be proved
Quantum Physics I (8.04) Spring 2016 Assignment 8
 Quntum Physics I (8.04) Spring 206 Assignment 8 MIT Physics Deprtment Due Fridy, April 22, 206 April 3, 206 2:00 noon Problem Set 8 Reding: Griffiths, pges 73-76, 8-82 (on scttering sttes). Ohnin, Chpter
Quntum Physics I (8.04) Spring 206 Assignment 8 MIT Physics Deprtment Due Fridy, April 22, 206 April 3, 206 2:00 noon Problem Set 8 Reding: Griffiths, pges 73-76, 8-82 (on scttering sttes). Ohnin, Chpter
Math 220A Homework 2 Solutions
 Mth 22A Homework 2 Solutions Jim Agler. Let G be n open set in C. ()Show tht the product rule for nd holds for products of C z z functions on G. (b) Show tht if f is nlytic on G, then 2 z z f(z) 2 f (z)
Mth 22A Homework 2 Solutions Jim Agler. Let G be n open set in C. ()Show tht the product rule for nd holds for products of C z z functions on G. (b) Show tht if f is nlytic on G, then 2 z z f(z) 2 f (z)
ANALYZING EFFECT OF TEMPERATURE VARIATION ON SKIN SUB-LAYERS USING FINITE ELEMENT APPROACH
 Origin Reserch Artice Aied sciences Interntion Journ of Phrm nd Bio Sciences ISSN 0975-699 ANALYZING EFFECT OF TEMPERATURE VARIATION ON SKIN SUB-LAYERS USING FINITE ELEMENT APPROACH MONA DWIVEDI 1 * AND
Origin Reserch Artice Aied sciences Interntion Journ of Phrm nd Bio Sciences ISSN 0975-699 ANALYZING EFFECT OF TEMPERATURE VARIATION ON SKIN SUB-LAYERS USING FINITE ELEMENT APPROACH MONA DWIVEDI 1 * AND
An iterative method for solving nonlinear functional equations
 J. Mth. Anl. Appl. 316 (26) 753 763 www.elsevier.com/locte/jm An itertive method for solving nonliner functionl equtions Vrsh Dftrdr-Gejji, Hossein Jfri Deprtment of Mthemtics, University of Pune, Gneshkhind,
J. Mth. Anl. Appl. 316 (26) 753 763 www.elsevier.com/locte/jm An itertive method for solving nonliner functionl equtions Vrsh Dftrdr-Gejji, Hossein Jfri Deprtment of Mthemtics, University of Pune, Gneshkhind,
PENALIZED LEAST SQUARES FITTING. Manfred von Golitschek and Larry L. Schumaker
 Serdic Mth. J. 28 2002), 329-348 PENALIZED LEAST SQUARES FITTING Mnfred von Golitschek nd Lrry L. Schumker Communicted by P. P. Petrushev Dedicted to the memory of our collegue Vsil Popov Jnury 4, 942
Serdic Mth. J. 28 2002), 329-348 PENALIZED LEAST SQUARES FITTING Mnfred von Golitschek nd Lrry L. Schumker Communicted by P. P. Petrushev Dedicted to the memory of our collegue Vsil Popov Jnury 4, 942
AN INTEGRAL INEQUALITY FOR CONVEX FUNCTIONS AND APPLICATIONS IN NUMERICAL INTEGRATION
 Applied Mthemtics E-Notes, 5(005), 53-60 c ISSN 1607-510 Avilble free t mirror sites of http://www.mth.nthu.edu.tw/ men/ AN INTEGRAL INEQUALITY FOR CONVEX FUNCTIONS AND APPLICATIONS IN NUMERICAL INTEGRATION
Applied Mthemtics E-Notes, 5(005), 53-60 c ISSN 1607-510 Avilble free t mirror sites of http://www.mth.nthu.edu.tw/ men/ AN INTEGRAL INEQUALITY FOR CONVEX FUNCTIONS AND APPLICATIONS IN NUMERICAL INTEGRATION
Improper Integrals, and Differential Equations
 Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Z b. f(x)dx. Yet in the above two cases we know what f(x) is. Sometimes, engineers want to calculate an area by computing I, but...
 Chpter 7 Numericl Methods 7. Introduction In mny cses the integrl f(x)dx cn be found by finding function F (x) such tht F 0 (x) =f(x), nd using f(x)dx = F (b) F () which is known s the nlyticl (exct) solution.
Chpter 7 Numericl Methods 7. Introduction In mny cses the integrl f(x)dx cn be found by finding function F (x) such tht F 0 (x) =f(x), nd using f(x)dx = F (b) F () which is known s the nlyticl (exct) solution.
RFID Technologies HF Part I
 RFID Technoogies HF Prt I Diprtimento di Ingegneri de Informzione e Scienze Mtemtiche Ampere s w h(r,t) ĉ d = j(r,t) ˆnds t C brt (, ) = µ hrt (, ) S S d(r,t) ˆnds j(r,t) d(r,t) ds ˆn Ø Biot-Svrt (sttic
RFID Technoogies HF Prt I Diprtimento di Ingegneri de Informzione e Scienze Mtemtiche Ampere s w h(r,t) ĉ d = j(r,t) ˆnds t C brt (, ) = µ hrt (, ) S S d(r,t) ˆnds j(r,t) d(r,t) ds ˆn Ø Biot-Svrt (sttic
Math Theory of Partial Differential Equations Lecture 2-9: Sturm-Liouville eigenvalue problems (continued).
 Mth 412-501 Theory of Prtil Differentil Equtions Lecture 2-9: Sturm-Liouville eigenvlue problems (continued). Regulr Sturm-Liouville eigenvlue problem: d ( p dφ ) + qφ + λσφ = 0 ( < x < b), dx dx β 1 φ()
Mth 412-501 Theory of Prtil Differentil Equtions Lecture 2-9: Sturm-Liouville eigenvlue problems (continued). Regulr Sturm-Liouville eigenvlue problem: d ( p dφ ) + qφ + λσφ = 0 ( < x < b), dx dx β 1 φ()
APPROXIMATE LIMIT CYCLES FOR THE RAYLEIGH MODEL
 ROMAI J, 4, 228, 73 8 APPROXIMATE LIMIT CYCLES FOR THE RAYLEIGH MODEL Adelin Georgescu, Petre Băzăvn, Mihel Sterpu Acdemy of Romnin Scientists, Buchrest Deprtment of Mthemtics nd Computer Science, University
ROMAI J, 4, 228, 73 8 APPROXIMATE LIMIT CYCLES FOR THE RAYLEIGH MODEL Adelin Georgescu, Petre Băzăvn, Mihel Sterpu Acdemy of Romnin Scientists, Buchrest Deprtment of Mthemtics nd Computer Science, University
Advanced Calculus: MATH 410 Notes on Integrals and Integrability Professor David Levermore 17 October 2004
 Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
VI. The Heat Equation. A. The Diffusion Equation Conservation in Action
 VI. The Het Eqution c 214, Phiip D. Loewen A. The Diffusion Eqution Conservtion in Action The simpest PDE describing diffusion (of het, perfume, poutnt) ong the x-xis is u t = α 2 u xx. ( ) Theme: Concvity
VI. The Het Eqution c 214, Phiip D. Loewen A. The Diffusion Eqution Conservtion in Action The simpest PDE describing diffusion (of het, perfume, poutnt) ong the x-xis is u t = α 2 u xx. ( ) Theme: Concvity
1.9 C 2 inner variations
 46 CHAPTER 1. INDIRECT METHODS 1.9 C 2 inner vritions So fr, we hve restricted ttention to liner vritions. These re vritions of the form vx; ǫ = ux + ǫφx where φ is in some liner perturbtion clss P, for
46 CHAPTER 1. INDIRECT METHODS 1.9 C 2 inner vritions So fr, we hve restricted ttention to liner vritions. These re vritions of the form vx; ǫ = ux + ǫφx where φ is in some liner perturbtion clss P, for
Partial Derivatives. Limits. For a single variable function f (x), the limit lim
 Limits Prtil Derivtives For single vrible function f (x), the limit lim x f (x) exists only if the right-hnd side limit equls to the left-hnd side limit, i.e., lim f (x) = lim f (x). x x + For two vribles
Limits Prtil Derivtives For single vrible function f (x), the limit lim x f (x) exists only if the right-hnd side limit equls to the left-hnd side limit, i.e., lim f (x) = lim f (x). x x + For two vribles
Section 6.1 INTRO to LAPLACE TRANSFORMS
 Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Review of Calculus, cont d
 Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Best Approximation in the 2-norm
 Jim Lmbers MAT 77 Fll Semester 1-11 Lecture 1 Notes These notes correspond to Sections 9. nd 9.3 in the text. Best Approximtion in the -norm Suppose tht we wish to obtin function f n (x) tht is liner combintion
Jim Lmbers MAT 77 Fll Semester 1-11 Lecture 1 Notes These notes correspond to Sections 9. nd 9.3 in the text. Best Approximtion in the -norm Suppose tht we wish to obtin function f n (x) tht is liner combintion
221B Lecture Notes WKB Method
 Clssicl Limit B Lecture Notes WKB Method Hmilton Jcobi Eqution We strt from the Schrödinger eqution for single prticle in potentil i h t ψ x, t = [ ] h m + V x ψ x, t. We cn rewrite this eqution by using
Clssicl Limit B Lecture Notes WKB Method Hmilton Jcobi Eqution We strt from the Schrödinger eqution for single prticle in potentil i h t ψ x, t = [ ] h m + V x ψ x, t. We cn rewrite this eqution by using
The Wave Equation I. MA 436 Kurt Bryan
 1 Introduction The Wve Eqution I MA 436 Kurt Bryn Consider string stretching long the x xis, of indeterminte (or even infinite!) length. We wnt to derive n eqution which models the motion of the string
1 Introduction The Wve Eqution I MA 436 Kurt Bryn Consider string stretching long the x xis, of indeterminte (or even infinite!) length. We wnt to derive n eqution which models the motion of the string
Chapters 4 & 5 Integrals & Applications
 Contents Chpters 4 & 5 Integrls & Applictions Motivtion to Chpters 4 & 5 2 Chpter 4 3 Ares nd Distnces 3. VIDEO - Ares Under Functions............................................ 3.2 VIDEO - Applictions
Contents Chpters 4 & 5 Integrls & Applictions Motivtion to Chpters 4 & 5 2 Chpter 4 3 Ares nd Distnces 3. VIDEO - Ares Under Functions............................................ 3.2 VIDEO - Applictions
