VI. The Heat Equation. A. The Diffusion Equation Conservation in Action
|
|
|
- Amie Strickland
- 5 years ago
- Views:
Transcription
1 VI. The Het Eqution c 214, Phiip D. Loewen A. The Diffusion Eqution Conservtion in Action The simpest PDE describing diffusion (of het, perfume, poutnt) ong the x-xis is u t = α 2 u xx. ( ) Theme: Concvity drives Rte of Chnge. (Concvity is u xx ; rte of chnge is u t.) Here α > is given constnt; t is time; x is position; u = u(x, t) is some kind of concentrtion t (x, t). Often u is the concentrtion of het, i.e., temperture: this ppiction eds to the nicknme het eqution for ( ). Derivtion. Consider ong stright eve pipe of sty wter ong the x-xis. Let the st concentrtion t oction x nd time t be u(x, t), in units of kg/m 3. If the cross-section of wter in the pipe is A (with units of m 2 ), the tot mss of st between points x = nd x = b is m [,b] (t) = u(x, t)a dx. Fick s Lw expins how concentrtion tends to equize: t ny test oction, ike x =, the mss fow rte (kg/s) is proportion to the concentrtion grdient nd the re invoved. Thus st diffuses from eft to right t x = t rte of κau x (, t). The sme thing hppens t x = b. Now focus on m [,b] (t), the mss of st in [, b]. If diffusion is the ony process ctive here, then conservtion of mss requires dm [,b] dt = (rte in) (rte out) [ ] = κau x (, t) κau x (b, t) But, proceeding directy, ṁ [,b] (t) = i.e., = κa u xx (x, t) dx. u t (x, t) dx = u t (x, t) dx. So for every re interv [, b], κau xx (x, t) dx [u t (x, t) κau xx (x, t)] dx =. Since the interv [, b] is rbitrry here, the function in brckets cn never hve positive vue. (If it did, we coud zoom in on tiny region where tht function is Fie 214notes, version of 24 Juy 214, pge 1. Typeset t 16:32 Juy 24, 214.
2 2 PHILIP D. LOEWEN wys positive, nd get positive resut for the integr.) Likewise it cn never be negtive. The ony terntive is tht the brcketed expression is zero for x, nd this is the diffusion eqution: u t = α 2 u xx [α 2 = κa]. This ine of resoning ppies to the concentrtion of nything tht stisfies Fick s Lw. Temperture (pproximtey the concentrtion of het per unit mss) is fmous exmpe. Units. Rec the nottion [z] for the units of z. Suppose [t] =s, [x] =m. Then [ ] [ ] u = α 2 2 u t x 2 [u] ( ) s = [u] m 2 [α]2 m 2 [α]2 =. s B. Boundry Vue Probems A we-formed probem for diffusion in < x < hs 3 ingredients: (PDE) concvity drives rte of chnge Fick s Lw pus conservtion: [More gener forms possibe here.] u t = α 2 u xx < x <, t >. (BC) concentrtion nd/or fow-rte info t ech end of the physic interv. In het probems, choices incude (i) u(, t) = = u(, t)... both ends fixed t temperture, (ii) u x (, t) = = u x (, t)... both ends insuted (fow rte is ), (iii) u x (, t) + u(, t) = = u x (, t) bu(, t)... het ost or gined through rdition, (iv) u(, t) = L(t), u(, t) = R(t)... end tempertures decreed by some given fcns of time [e.g., diy temp of ground surfce], not both identicy zero. Cdx (i) (iii) re homogeneous; (iv) is not. Aow different conditions t different ends. For sty wter in stright pipe occupying < x <, Fick s Lw supports option (ii). (IC) initi conditions. One is enough: u(x, ) = f(x), < x <... initi concentrtion or temperture. Function f must be given in probem sttement. Story Probems. A typic physic interprettion of the boundry-vue probem bove invoves temperture in met br tht hs been wrpped in insution so tht het cn fow ong its ength (the x-xis) but not through its sides. The insution my or my not cover the ends of the br: this depends on the boundry condition. The BC u(, t) =, t >, indictes tht the eft end of the br is connected to some Fie 214notes, version of 22 Juy 214, pge 2. Typeset t 16:32 Juy 24, 214.
3 VI. The Het Eqution 3 constnt-temperture energy reservoir ike bucket of ice-wter. If the br is hot to strt with, het wi fow into the bucket nd met some of the ice, but we ssume there is enough ice in there (or somebody shoveing more in t good rte) so tht the temperture does not rise. If the br is very cod t first, het wi fow from the bucket into the br: more wter wi freeze. But we ssume tht there is enough iquid wter (or more running in from hose) tht the reservoir never freezes soid nd strts to chnge temperture. Trnsting Engish text into boundry conditions is ski students shoud be prepred to demonstrte on homework nd tests. C. Four Stndrd Homogeneous Probems The simpest het probem in < x < ooks ike this. (PDE) u t = α 2 u xx, < x <,t >, (BC) x = : Choose frozen (u = ) or insuted (u x = ), t >, x = : Choose frozen (u = ) or insuted (u x = ), t >, (IC) u(x, ) = f(x), < x <. Guessing u(x, t) = X(x)T(t) in (PDE)/(BC) eds s usu to pir of ODE probems, inked by seprtion constnt λ: (i) X (x) + λx(x) =, < x < ; some (BC) inherited from (PDE), (ii) T (t) + α 2 λt(t) =, t >. Depending on origin (BC), (i) wi be n eigenvue probem we recognize, giving sequence of eigenfunctions X n (x) nd eigenvues λ n. E.g., for n insuted end t x = nd frozen (zero-temp) end t x =, we hve u x (, t) = = u(, t) in the origin probem, so X () = = X() in (i), so HPCS eigenfunctions: ( 2n 1 X n (x) = cos 2 ) ( πx 2n 1, λ n = 2 ) 2 π, n = 1, 2, 3,.... Use eigenfunctions from (i) to postute soution in form u(x, t) = [ 1 2 T (t)+ ] Tn (t)x n (x), where eigenfcns X n re known nd time-vrying coeffs T n (t) remin to be found. (Tke T (t) = in FSS, HPSS, HPCS cses.) Initiize T n. IC: f(x) = u(x, ) = [ 1 2 T ()+ ] Tn ()X n (x) gives Propgte T n forwrd in time. T n () = 2 f(x)x n (x) dx. Fie 214notes, version of 21 Juy 214, pge 3. Typeset t 16:32 Juy 24, 214.
4 4 PHILIP D. LOEWEN = u t α 2 u xx = [ 1 2 T (t)+] ( T n (t)x n (x) α 2 T n (t)x n (x)) = [ 1 2 T (t)+] ( T n (t)x n (x) α 2 T n (t)( λ n ) ) X n (x). (Here we used X n = λ nx n. The vues of λ n come out utomticy when we ( ) 2 nπ differentite X n for known choice. We hve λ n = in FSS nd FCS cses, nd λ n = ((2n 1)π/(2)) 2 in the HPSS nd HPCS cses. Notice tht λ n > whenever n 1; the number λ = is n eigenvue ony for the FCS cse, which we wi discuss seprtey beow.) This gives, for ech n, T n(t) + α 2 λ n T n (t) =, t >. The gener soution (for n 1) is T n (t) = A n e α2 λ n t. Note tht A n = T n () = (integr formu bove). [For cse n =, T (t) = A constnt, nd sme integr formu works.] We concude tht in four cses, u(x, t) = [ 1 2 A + ] An e α2 λ n t X n (x), A n = 2 f(x)x n (x) dx. Both Ends Frozen. If u(, t) = = u(, t) in the origin BVP, then X() = = X() in (i), nd we hve eigenfunctions ssocited with FSS. Soution u(x, t) = ( ) b n e α2 n 2 π 2 t/ 2 nπx sin, b n = 2 ( ) nπx f(x) sin dx. Left End Frozen, Right End Insuted. If u(, t) = = u x (, t) in the origin BVP, then X() = = X () in (i), nd we hve eigenfunctions ssocited with HPSS. Soution u(x, t) = ( ) p n e α2 (2n 1) 2 π 2 t/4 2 (2n 1)πx sin, 2 p n = 2 ( ) (2n 1)πx f(x) sin dx. 2 Left End Insuted, Right End Frozen. (Try t home.) u(x, t) = ( ) q n e α2 (2n 1) 2 π 2 t/4 2 (2n 1)πx cos, 2 q n = 2 ( ) (2n 1)πx f(x) cos dx. 2 Fie 214notes, version of 21 Juy 214, pge 4. Typeset t 16:32 Juy 24, 214.
5 VI. The Het Eqution 5 Both Ends Insuted. See Section E beow for some more discussion of this cse. u(x, t) = 2 + ) n e α 2 n 2 π 2 t/ cos( 2 nπx, n = 2 ( ) nπx f(x) cos dx. Consider cse = π to sve gebr. D. Modes For both ends frozen, our series soution is combintion of bsic products u n (x, t) = e α2 n 2t sin(nx). Mode shpes X n (x) = sin(nx) sme s for guitr string, but now they don t oscite s t dvnces. They just decy exponentiy. Lrger n more curvture, fster decy rte. Even for sm t >, decy of high modes is so fst tht 1 3 terms in the series soutions cn give resonbe nswers. Simir remrks ppy to other BC s chosen from either frozen or insuted. E. Long-Term Behviour (1) In cses FSS, HPSS, HPCS, every term in every sum hs the form e α2 λ n t X n (x) for some λ n >. The time-dependent exponenti fctor therefore represents exponenti decy: ech term converges to s t. It foows tht u(x, t) s t. This mkes physic sense, becuse the boundry conditions for these three cses invove t est one end of the br hed t temperture forever. Het wi fow out this end if the br is wrmer thn, nd wi fow in this end if the br is coder. Hence the br wi eventuy come into therm equiibrium t temperture. The series soution found bove ets us ccute excty how the pproch to equiibrium tkes pce. (2) In cse FCS, the story is itte different, becuse when X n (x) = cos(nπx/), subscript n = is owed. Here u(x, t) = e α2 n 2 π 2 t/ 2 cos(nπx/). As t, terms except the first tend to zero. Hence u(x, t) 1 2. This, too, mkes physic sense: the FCS soution comes up when both ends of the br re insuted. Conservtion of het energy impies tht the tot het content of the br cn never chnge. And by the Fourier coefficient formu, the imiting vue cn be expressed s 1 2 = f(x) dx = 1 f(x) dx. Fie 214notes, version of 21 Juy 214, pge 5. Typeset t 16:32 Juy 24, 214.
6 6 PHILIP D. LOEWEN This is precisey the verge vue of the initi temperture u(x, ) = f(x). As expected, het diffuses unti therm equiibrium is reched. (3) Cse FCS is so nice one for conservtion of het energy. Any function u(x, t) stisfying both (PDE) nd (BC) in cse FCS mkes the foowing function constnt in the interv t : F(t) = u(x, t) dx. To see this, ccuute F (t): ccording to the PDE nd BC s, F (t) = for ech t >. See homework probem hetcte for detis. (4) The spti frequency is inked directy to the tempor decy rte. Higher spti modes hve higher temperture grdients, hence higher het fow rtes, nd hence fster neutriztion of bumpy temperture profies. (5) The exponenti decy ssocited with higher modes is so rpid tht keeping ony sm number of ow modes is enough to get resonby ccurte pproximte soutions. We iustrted this on HPSS exmpe in css (Mpe V nimtions re vibe on the Web site). F. Nonhomogeneity: Spitting or Fncy ODE s Probem 1 [mid]. Seprtion of vribes does not work on nonhomogeneous PDE s. E.g., consider the effect of the nonhomogeneous term f(x, t) in the generic form A(t)u tt + B(t)u t + C(t)u = α(x)u xx + β(x)u x + γ(x)u + f(x, t). Trying for u(x, t) = X(x)T(t) eds to A(t)T (t) + B(t)T (t) + C(t)T(t) T(t) = α(x)x (x) + β(x)x (x) + γ(x)x(x) X(x) + f(x, t) X(x)T(t). For nonzero function f, no nice rerrngement wi seprte the vribes t nd x. (Of course, if f(x, t) =, then the PDE is homogeneous nd both sides bove must equ some constnt.) Remedy 1. Use ony the homogeneous prt of whtever PDE is given when buiding n eigenvue probem nd postuting soution form. But use the fu origin PDE for propgtion. The term f(x, t) wi infuence the ODE s for the coefficients T n (t). We hve redy seen some exmpes. Probem 2 [severe]. Seprtion of vribes does not work on nonhomogeneous BC s. E.g., suppose the interv of interest is < x < π, with u(x, ) = 257, u(x, π) = 316. Fie 214notes, version of 24 Juy 214, pge 6. Typeset t 16:32 Juy 24, 214.
7 VI. The Het Eqution 7 If functions u 1 nd u 2 both obey these, the combintion u 1 + u 2 wi not... so superposition of bsic pieces cn t work. Just ignoring the nonhomogeneity nd hoping to compenste ter might suggest FSS postute, T n (t) sin(nx), but this evutes to t x = nd t x = π no mtter wht we do with T n (t). A more fundment cure wi be required. Remedy 2. Revisit the big-picture frmework used for inhomogeneous ODE s: 1. Find one soution. Invent v(x, t) to stisfy BC s. Mny choices exist: it s nice if v cn so stisfy PDE. 2. Buid the rest. Using v(x, t) from bove, spit u(x, t) = v(x, t) + w(x, t) ( ) nd now pursue w. Recommendtion: Write down expicity the fu BVP for w. 3. Seect the nswer of interest. Recipe steps 3 5 for w, then reporting (step 6) for u = v + w. Physic Interprettion. In diffusion probems with Big Four eigenfunctions, the w-probem wi hve soutions converging to constnt (often ) s t. Thus u(x, t) v(x, t) s t, nd w(x, t) = u(x, t) v(x, t) precisey quntifies the discrepncy from the ong-term behviour. Especiy when v = v(x) is independent of t, spitting u = v + w presents the desired soution into two components: the stedy-stte v nd some trnsient w. Usuy the stedystte is pretty esy to find: see the Trench textbook, Section 12.1, for further for discussion, exmpes, nd prctice probems. (Aterntivey, ook into the cssic text on Differenti Equtions nd Boundry Vue Probems by Boyce nd DiPrim. There section ced Seprtion of Vribes; Het Conduction in Rod outines the homogeneous cse, nd ter section ced Other Het Conduction Probems extends this to nonhomogeneous situtions.) Exmpe 1. This one is competey routine: (PDE) u t = α 2 u xx, < x < π, t >, (BC) u(, t) =, u(π, t) = 1, t >, (IC) u(x, ) =, < x < π. Here the BC s re not homogeneous, so spit u(x, t) = v(x, t) + w(x, t), where v is chosen to stisfy (BC): v(, t) =, v(π, t) = 1. ( ) One fesibe (but unwise) choice is v(x, t) = sin(x/2)+x(x π)e t, nd there re mny more. For guidnce bout how to choose v wisey, pug the spit-form u = v +w into (PDE): Fie 214notes, version of 24 Juy 214, pge 7. Typeset t 16:32 Juy 24, 214.
8 8 PHILIP D. LOEWEN (PDE) w t = α 2 w xx + [ α 2 v xx v t ], < x < π, t >. The new PDE for w wi be simpe nd stndrd if the brcketed term invoving v goes wy. Try to rrnge tht s we s ( ): ook for v = v(x) independent of t, so PDE wi hod iff v (x) =. So v(x) = mx + b for some m, b nd the choices b =, m = 1/π give cndidte v(x) = x/π. With this choice, we ook for soution in the form u(x, t) = x + w(x, t). π Pugging this into (PDE)/(BC)/(IC) bove produces some usefu cncetions, nd reduces the given sitution to new probem for the function w: (PDE) w t = α 2 w xx, < x < π, t >, (BC) w(, t) =, w(π, t) =, t >, (IC) w(x, ) = x/π, < x < π. The usu methods bove give the resut for w, so our fin report for u is u(x, t) = x π + w(x, t) = x π + b n e n2 α 2t sin(nx), b n = 2 π π [ x ] sin(nx) dx = 2 π nπ ( 1)n. Exmpe 2. Here the PDE is modified by n extr term on the right-hnd side. The expression x 2 πx is negtive when < x < π, so this represents some kind of het-extrctor operting t different rtes t different points ong the met br in our stndrd interprettion. (PDE) u t = u xx + x 2 πx, < x < π, t >, (BC) u(, t) = 1π, u(π, t) = π4 12, t >, (IC) u(x, ) = 2π x x 3, < x < π. 12 Agin spitting is required, but this time there is choice. Choice 1: Choosing v = v(x) to obey PDE/BC is ide: v (x) = πx x 2 = v (x) = π 2 x2 1 3 x3 + C = v(x) = π 6 x x4 + Cx + E. Now 1π = v() = E nd we get C = 1 from the other end, eving v(x) = π 6 x x4 1x + 1π. ( ) Pugging u(x, t) = v(x) + w(x, t) into the origin probem produces new BVP for w tht is quite mngebe. (This refects crefu dvnce pnning by the probem designer... something sedom vibe in bortory situtions!) (PDE) w t = w xx, < x < π, t >, (BC) w(, t) =, w(π, t) =, t >, Fie 214notes, version of 24 Juy 214, pge 8. Typeset t 16:32 Juy 24, 214.
9 VI. The Het Eqution 9 (IC) w(x, ) = 1(x π), < x < π. The soution wi be u(x, t) = v(x) + w(x, t) with v s in ( ) nd w(x, t) = b n e n2t sin(nx), b n = 2 π π 1[x π] sin(nx) dx = 2 n. Choice 2: There re infinitey mny functions v = v(x) tht mtch the given BC s, nd iner one wi so do the job. Ccution gives ( ) v = 1(π x) + π3 x π 3 12 = 12 1 x + 1π. Spitting u(x, t) = v(x) + w(x, t) for this choice of v eves ess-ttrctive probem for w. (The PDE remins nonhomogeneous, nd the IC s sty ugy.) Substitution produces (PDE) w t = w xx + x 2 πx, < x < π, t >, (BC) w(, t) =, w(π, t) =, t >, (IC) w(x, ) = 2π x x 3 1(π x) π3 x 12 12, < x < π. Stndrd methods wi work on this one; detis in person on request. //// Exmpe 3. Sti ess routine re cses where it s not so esy to find v tht obeys the PDE in ddition to the BC s. Here is sitution tht fits this description: (PDE) u t = u xx + e t sin(4x), < x < π, t >, (BC) u(, t) =, u(π, t) = π, t >, (IC) u(x, ) = x, < x < π. It s cer tht no choice of v = v(x) independent of t cn possiby stisfy the PDE. An inspired guess t some v depending on both t nd x my be possibe (the soution beow suggests one), but sometimes inspirtion is scrce. At such times, remember this: it is impertive to stisfy the BC s. With this in mind, et s work with the simpe choice v(x) = x. This does stisfy the BC s, nd the function u(x, t) = x + w(x, t) soves the stted probem if nd ony if the new unknown w stisfies (PDE) w t = w xx + e t sin(4x), < x < π, t >, (BC) w(, t) =, w(π, t) =, t >, (IC) w(x, ) =, < x < π. This is not so pretty, but not terrifying either. The homogeneous prt of the PDE is w t = w xx, which eds by seprtion of vribes to the eigenvue probem X (x) + λx(x) =, < x < π; X() = = X(π) nd the FSS eigenfunctions. So we postute soution of the form w(x, t) = T n (t) sin(nx). ( ) Fie 214notes, version of 24 Juy 214, pge 9. Typeset t 16:32 Juy 24, 214.
10 1 PHILIP D. LOEWEN The initi condition sys = w(x, ) = T n () sin(nx), so T n () = for ech n by FSS coefficient-extrction. Menwhie, pugging the series ( ) into the fu nonhomogeneous PDE for w gives e t [ sin(4x) = w t w xx = T n (t) + n 2 T n (t) ] sin(nx). How convenient: both sides invove FSS with respect to x hving t-dependent coefficients. Mtching gives { T n e (t) + n2 T n (t) = t, if n = 4,, if n 4. When n 4, this gives T n (t) = T n ()e n2t. But T n () = so in fct T n (t) = for every n 4. When n = 4, we must sove T 4 (t) + 16T 4(t) = e t, T 4 () =. One prticur soution of the ODE here wi hve the form T p 4 (t) = Ce t for some constnt C: substitution gives C + 16C = 1, so C = 1/15. The gener soution of the homogeneous eqution y +16y = is y = Ae 16t, A R, so the gener soution for T 4 is given by T 4 (t) = (1/15)e t + Ae 16t, A R. From this infinite set of possibiities, we seect the function for which = T 4 () = (1/15) + A, i.e., A = 1/15. Now we know bout T 4, nd the other T n, we see tht the sum ( ) hs ony one nonzero term: w(x, t) = T 4 (t) sin(4x) = 1 15 [ e t e 16t] sin(4x). Report: The soution to the origin probem concerning u is u(x, t) = x + w(x, t) = x + 1 [ e t e 16t] sin(4x). 15 //// Fie 214notes, version of 24 Juy 214, pge 1. Typeset t 16:32 Juy 24, 214.
MAGIC058 & MATH64062: Partial Differential Equations 1
 MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
Math 124B January 24, 2012
 Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
1. The vibrating string problem revisited.
 Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this
Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this
V. More General Eigenfunction Series. A. The Sturm-Liouville Family of Problems
 V. More Gener Eigenfunction Series c 214, Phiip D. Loewen A. The Sturm-Liouvie Fmiy of Probems Given n re interv, b], functions p(x), q(x), r(x), nd constnts c, c 1, d, d 1, consider (ODE) (p(x)y (x))
V. More Gener Eigenfunction Series c 214, Phiip D. Loewen A. The Sturm-Liouvie Fmiy of Probems Given n re interv, b], functions p(x), q(x), r(x), nd constnts c, c 1, d, d 1, consider (ODE) (p(x)y (x))
Suggested Solution to Assignment 5
 MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
Consequently, the temperature must be the same at each point in the cross section at x. Let:
 HW 2 Comments: L1-3. Derive the het eqution for n inhomogeneous rod where the therml coefficients used in the derivtion of the het eqution for homogeneous rod now become functions of position x in the
HW 2 Comments: L1-3. Derive the het eqution for n inhomogeneous rod where the therml coefficients used in the derivtion of the het eqution for homogeneous rod now become functions of position x in the
PDE Notes. Paul Carnig. January ODE s vs PDE s 1
 PDE Notes Pul Crnig Jnury 2014 Contents 1 ODE s vs PDE s 1 2 Section 1.2 Het diffusion Eqution 1 2.1 Fourier s w of Het Conduction............................. 2 2.2 Energy Conservtion.....................................
PDE Notes Pul Crnig Jnury 2014 Contents 1 ODE s vs PDE s 1 2 Section 1.2 Het diffusion Eqution 1 2.1 Fourier s w of Het Conduction............................. 2 2.2 Energy Conservtion.....................................
Fluid Flow through a Tube
 . Theory through Tube In this experiment we wi determine how we physic retionship (so ced w ), nmey Poiseue s eqution, ppies. In the suppementry reding mteri this eqution ws derived s p Q 8 where Q is
. Theory through Tube In this experiment we wi determine how we physic retionship (so ced w ), nmey Poiseue s eqution, ppies. In the suppementry reding mteri this eqution ws derived s p Q 8 where Q is
Mutipy by r sin RT P to get sin R r r R + T sin (sin T )+ P P = (7) ffi So we hve P P ffi = m (8) choose m re so tht P is sinusoi. If we put this in b
 Topic 4: Lpce Eqution in Spheric Co-orintes n Mutipoe Expnsion Reing Assignment: Jckson Chpter 3.-3.5. Lpce Eqution in Spheric Coorintes Review of spheric por coorintes: x = r sin cos ffi y = r sin sin
Topic 4: Lpce Eqution in Spheric Co-orintes n Mutipoe Expnsion Reing Assignment: Jckson Chpter 3.-3.5. Lpce Eqution in Spheric Coorintes Review of spheric por coorintes: x = r sin cos ffi y = r sin sin
The Wave Equation I. MA 436 Kurt Bryan
 1 Introduction The Wve Eqution I MA 436 Kurt Bryn Consider string stretching long the x xis, of indeterminte (or even infinite!) length. We wnt to derive n eqution which models the motion of the string
1 Introduction The Wve Eqution I MA 436 Kurt Bryn Consider string stretching long the x xis, of indeterminte (or even infinite!) length. We wnt to derive n eqution which models the motion of the string
Separation of Variables. A. Three Famous PDE s
 Separation of Variables c 14, Philip D. Loewen A. Three Famous PDE s 1. Wave Equation. Displacement u depends on position and time: u = u(x, t. Concavity drives acceleration: u tt = c u xx.. Heat Equation.
Separation of Variables c 14, Philip D. Loewen A. Three Famous PDE s 1. Wave Equation. Displacement u depends on position and time: u = u(x, t. Concavity drives acceleration: u tt = c u xx.. Heat Equation.
Energy Balance of Solar Collector
 Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Wecome! Energy Bnce of Sor Coector Mohmd Khrseh E-mi:m.Khrseh@gmi.com Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Liuid Ft Pte Coectors. Het
Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Wecome! Energy Bnce of Sor Coector Mohmd Khrseh E-mi:m.Khrseh@gmi.com Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Liuid Ft Pte Coectors. Het
Heat flux and total heat
 Het flux nd totl het John McCun Mrch 14, 2017 1 Introduction Yesterdy (if I remember correctly) Ms. Prsd sked me question bout the condition of insulted boundry for the 1D het eqution, nd (bsed on glnce
Het flux nd totl het John McCun Mrch 14, 2017 1 Introduction Yesterdy (if I remember correctly) Ms. Prsd sked me question bout the condition of insulted boundry for the 1D het eqution, nd (bsed on glnce
Math 113 Exam 1-Review
 Mth 113 Exm 1-Review September 26, 2016 Exm 1 covers 6.1-7.3 in the textbook. It is dvisble to lso review the mteril from 5.3 nd 5.5 s this will be helpful in solving some of the problems. 6.1 Are Between
Mth 113 Exm 1-Review September 26, 2016 Exm 1 covers 6.1-7.3 in the textbook. It is dvisble to lso review the mteril from 5.3 nd 5.5 s this will be helpful in solving some of the problems. 6.1 Are Between
Introduction to statically indeterminate structures
 Sttics of Buiding Structures I., EASUS Introduction to stticy indeterminte structures Deprtment of Structur echnics Fcuty of Civi Engineering, VŠB-Technic University of Ostrv Outine of Lecture Stticy indeterminte
Sttics of Buiding Structures I., EASUS Introduction to stticy indeterminte structures Deprtment of Structur echnics Fcuty of Civi Engineering, VŠB-Technic University of Ostrv Outine of Lecture Stticy indeterminte
PhysicsAndMathsTutor.com
 M Dynmics - Dmped nd forced hrmonic motion. A P α B A ight estic spring hs ntur ength nd moduus of esticity mg. One end of the spring is ttched to point A on pne tht is incined to the horizont t n nge
M Dynmics - Dmped nd forced hrmonic motion. A P α B A ight estic spring hs ntur ength nd moduus of esticity mg. One end of the spring is ttched to point A on pne tht is incined to the horizont t n nge
Math 5440 Problem Set 3 Solutions
 Mth 544 Mth 544 Problem Set 3 Solutions Aron Fogelson Fll, 213 1: (Logn, 1.5 # 2) Repet the derivtion for the eqution of motion of vibrting string when, in ddition, the verticl motion is retrded by dmping
Mth 544 Mth 544 Problem Set 3 Solutions Aron Fogelson Fll, 213 1: (Logn, 1.5 # 2) Repet the derivtion for the eqution of motion of vibrting string when, in ddition, the verticl motion is retrded by dmping
Math 5440 Problem Set 3 Solutions
 Mth 544 Mth 544 Problem Set 3 Solutions Aron Fogelson Fll, 25 1: Logn, 1.5 # 2) Repet the derivtion for the eqution of motion of vibrting string when, in ddition, the verticl motion is retrded by dmping
Mth 544 Mth 544 Problem Set 3 Solutions Aron Fogelson Fll, 25 1: Logn, 1.5 # 2) Repet the derivtion for the eqution of motion of vibrting string when, in ddition, the verticl motion is retrded by dmping
1 E3102: a study guide and review, Version 1.0
 1 E3102: study guide nd review, Version 1.0 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in very
1 E3102: study guide nd review, Version 1.0 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in very
SUMMER KNOWHOW STUDY AND LEARNING CENTRE
 SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
Improper Integrals, and Differential Equations
 Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Conservation Law. Chapter Goal. 5.2 Theory
 Chpter 5 Conservtion Lw 5.1 Gol Our long term gol is to understnd how mny mthemticl models re derived. We study how certin quntity chnges with time in given region (sptil domin). We first derive the very
Chpter 5 Conservtion Lw 5.1 Gol Our long term gol is to understnd how mny mthemticl models re derived. We study how certin quntity chnges with time in given region (sptil domin). We first derive the very
Physics 116C Solution of inhomogeneous ordinary differential equations using Green s functions
 Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
Statistical Physics. Solutions Sheet 5.
 Sttistic Physics. Soutions Sheet 5. Exercise. HS 04 Prof. Mnfred Sigrist Ide fermionic quntum gs in hrmonic trp In this exercise we study the fermionic spiness ide gs confined in three-dimension hrmonic
Sttistic Physics. Soutions Sheet 5. Exercise. HS 04 Prof. Mnfred Sigrist Ide fermionic quntum gs in hrmonic trp In this exercise we study the fermionic spiness ide gs confined in three-dimension hrmonic
In this appendix, we evaluate the derivative of Eq. 9 in the main text, i.e., we need to calculate
 Supporting Tet Evoution of the Averge Synptic Updte Rue In this ppendi e evute the derivtive of Eq. 9 in the min tet i.e. e need to ccute Py ( ) Py ( Y ) og γ og. [] P( y Y ) P% ( y Y ) Before e strt et
Supporting Tet Evoution of the Averge Synptic Updte Rue In this ppendi e evute the derivtive of Eq. 9 in the min tet i.e. e need to ccute Py ( ) Py ( Y ) og γ og. [] P( y Y ) P% ( y Y ) Before e strt et
1.1. Linear Constant Coefficient Equations. Remark: A differential equation is an equation
 1 1.1. Liner Constnt Coefficient Equtions Section Objective(s): Overview of Differentil Equtions. Liner Differentil Equtions. Solving Liner Differentil Equtions. The Initil Vlue Problem. 1.1.1. Overview
1 1.1. Liner Constnt Coefficient Equtions Section Objective(s): Overview of Differentil Equtions. Liner Differentil Equtions. Solving Liner Differentil Equtions. The Initil Vlue Problem. 1.1.1. Overview
Math 8 Winter 2015 Applications of Integration
 Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
Coordinate Geometry. Coordinate Geometry. Curriculum Ready ACMNA: 178, 214, 294.
 Coordinte Geometr Coordinte Geometr Curricuum Red ACMNA: 78, 4, 94 www.mthetics.com Coordinte COORDINATE Geometr GEOMETRY Shpes ou ve seen in geometr re put onto es nd nsed using gebr. Epect bit of both
Coordinte Geometr Coordinte Geometr Curricuum Red ACMNA: 78, 4, 94 www.mthetics.com Coordinte COORDINATE Geometr GEOMETRY Shpes ou ve seen in geometr re put onto es nd nsed using gebr. Epect bit of both
Summary: Method of Separation of Variables
 Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
Physics 246 Electricity nd Mgnetism I, Fll 26, Lecture 22 1 Summry: Method of Seprtion of Vribles 1. Seprtion of Vribles in Crtesin Coordintes 2. Fourier Series Suggested Reding: Griffiths: Chpter 3, Section
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER /2019
 ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS MATH00030 SEMESTER 208/209 DR. ANTHONY BROWN 7.. Introduction to Integrtion. 7. Integrl Clculus As ws the cse with the chpter on differentil
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS MATH00030 SEMESTER 208/209 DR. ANTHONY BROWN 7.. Introduction to Integrtion. 7. Integrl Clculus As ws the cse with the chpter on differentil
MA 124 January 18, Derivatives are. Integrals are.
 MA 124 Jnury 18, 2018 Prof PB s one-minute introduction to clculus Derivtives re. Integrls re. In Clculus 1, we lern limits, derivtives, some pplictions of derivtives, indefinite integrls, definite integrls,
MA 124 Jnury 18, 2018 Prof PB s one-minute introduction to clculus Derivtives re. Integrls re. In Clculus 1, we lern limits, derivtives, some pplictions of derivtives, indefinite integrls, definite integrls,
Lecture 6 Notes, Electromagnetic Theory I Dr. Christopher S. Baird University of Massachusetts Lowell
 Lecture 6 Notes, Eectrognetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowe. Associted Legendre Poynois - We now return to soving the Lpce eqution in spheric coordintes when there is
Lecture 6 Notes, Eectrognetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowe. Associted Legendre Poynois - We now return to soving the Lpce eqution in spheric coordintes when there is
Chapter 5. , r = r 1 r 2 (1) µ = m 1 m 2. r, r 2 = R µ m 2. R(m 1 + m 2 ) + m 2 r = r 1. m 2. r = r 1. R + µ m 1
 Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
Math Calculus with Analytic Geometry II
 orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
Review SOLUTIONS: Exam 2
 Review SOUTIONS: Exm. True or Flse? (And give short nswer ( If f(x is piecewise smooth on [, ], we cn find series representtion using either sine or cosine series. SOUTION: TRUE. If we use sine series,
Review SOUTIONS: Exm. True or Flse? (And give short nswer ( If f(x is piecewise smooth on [, ], we cn find series representtion using either sine or cosine series. SOUTION: TRUE. If we use sine series,
7.2 The Definite Integral
 7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Review of Calculus, cont d
 Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Name Solutions to Test 3 November 8, 2017
 Nme Solutions to Test 3 November 8, 07 This test consists of three prts. Plese note tht in prts II nd III, you cn skip one question of those offered. Some possibly useful formuls cn be found below. Brrier
Nme Solutions to Test 3 November 8, 07 This test consists of three prts. Plese note tht in prts II nd III, you cn skip one question of those offered. Some possibly useful formuls cn be found below. Brrier
Chapter 0. What is the Lebesgue integral about?
 Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Method of Separation of Variables
 MODUE 5: HEAT EQUATION 11 ecture 3 Method of Separation of Variables Separation of variables is one of the oldest technique for solving initial-boundary value problems (IBVP) and applies to problems, where
MODUE 5: HEAT EQUATION 11 ecture 3 Method of Separation of Variables Separation of variables is one of the oldest technique for solving initial-boundary value problems (IBVP) and applies to problems, where
1 2-D Second Order Equations: Separation of Variables
 Chpter 12 PDEs in Rectngles 1 2-D Second Order Equtions: Seprtion of Vribles 1. A second order liner prtil differentil eqution in two vribles x nd y is A 2 u x + B 2 u 2 x y + C 2 u y + D u 2 x + E u +
Chpter 12 PDEs in Rectngles 1 2-D Second Order Equtions: Seprtion of Vribles 1. A second order liner prtil differentil eqution in two vribles x nd y is A 2 u x + B 2 u 2 x y + C 2 u y + D u 2 x + E u +
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
 A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
Overview of Calculus I
 Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
When a force f(t) is applied to a mass in a system, we recall that Newton s law says that. f(t) = ma = m d dt v,
 Impulse Functions In mny ppliction problems, n externl force f(t) is pplied over very short period of time. For exmple, if mss in spring nd dshpot system is struck by hmmer, the ppliction of the force
Impulse Functions In mny ppliction problems, n externl force f(t) is pplied over very short period of time. For exmple, if mss in spring nd dshpot system is struck by hmmer, the ppliction of the force
Chapters 4 & 5 Integrals & Applications
 Contents Chpters 4 & 5 Integrls & Applictions Motivtion to Chpters 4 & 5 2 Chpter 4 3 Ares nd Distnces 3. VIDEO - Ares Under Functions............................................ 3.2 VIDEO - Applictions
Contents Chpters 4 & 5 Integrls & Applictions Motivtion to Chpters 4 & 5 2 Chpter 4 3 Ares nd Distnces 3. VIDEO - Ares Under Functions............................................ 3.2 VIDEO - Applictions
1 E3102: A study guide and review, Version 1.2
 1 E3102: A study guide nd review, Version 1.2 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in
1 E3102: A study guide nd review, Version 1.2 Here is list of subjects tht I think we ve covered in clss (your milege my vry). If you understnd nd cn do the bsic problems in this guide you should be in
6 Wave Equation on an Interval: Separation of Variables
 6 Wave Equation on an Interva: Separation of Variabes 6.1 Dirichet Boundary Conditions Ref: Strauss, Chapter 4 We now use the separation of variabes technique to study the wave equation on a finite interva.
6 Wave Equation on an Interva: Separation of Variabes 6.1 Dirichet Boundary Conditions Ref: Strauss, Chapter 4 We now use the separation of variabes technique to study the wave equation on a finite interva.
ODE: Existence and Uniqueness of a Solution
 Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
arxiv: v1 [math.co] 5 Jun 2015
![arxiv: v1 [math.co] 5 Jun 2015 arxiv: v1 [math.co] 5 Jun 2015](/thumbs/78/77492077.jpg) First non-trivi upper bound on the circur chromtic number of the pne. Konstnty Junosz-Szniwski, Fcuty of Mthemtics nd Informtion Science, Wrsw University of Technoogy, Pond Abstrct rxiv:1506.01886v1 [mth.co]
First non-trivi upper bound on the circur chromtic number of the pne. Konstnty Junosz-Szniwski, Fcuty of Mthemtics nd Informtion Science, Wrsw University of Technoogy, Pond Abstrct rxiv:1506.01886v1 [mth.co]
Math 231E, Lecture 33. Parametric Calculus
 Mth 31E, Lecture 33. Prmetric Clculus 1 Derivtives 1.1 First derivtive Now, let us sy tht we wnt the slope t point on prmetric curve. Recll the chin rule: which exists s long s /. = / / Exmple 1.1. Reconsider
Mth 31E, Lecture 33. Prmetric Clculus 1 Derivtives 1.1 First derivtive Now, let us sy tht we wnt the slope t point on prmetric curve. Recll the chin rule: which exists s long s /. = / / Exmple 1.1. Reconsider
Best Approximation. Chapter The General Case
 Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
Math 124B January 31, 2012
 Math 124B January 31, 212 Viktor Grigoryan 7 Inhomogeneous boundary vaue probems Having studied the theory of Fourier series, with which we successfuy soved boundary vaue probems for the homogeneous heat
Math 124B January 31, 212 Viktor Grigoryan 7 Inhomogeneous boundary vaue probems Having studied the theory of Fourier series, with which we successfuy soved boundary vaue probems for the homogeneous heat
Section 10.2 Angles and Triangles
 117 Ojective #1: Section 10.2 nges n Tringes Unerstning efinitions of ifferent types of nges. In the intersection of two ines, the nges tht re cttycorner fro ech other re vertic nges. Vertic nges wi hve
117 Ojective #1: Section 10.2 nges n Tringes Unerstning efinitions of ifferent types of nges. In the intersection of two ines, the nges tht re cttycorner fro ech other re vertic nges. Vertic nges wi hve
and that at t = 0 the object is at position 5. Find the position of the object at t = 2.
 7.2 The Fundmentl Theorem of Clculus 49 re mny, mny problems tht pper much different on the surfce but tht turn out to be the sme s these problems, in the sense tht when we try to pproimte solutions we
7.2 The Fundmentl Theorem of Clculus 49 re mny, mny problems tht pper much different on the surfce but tht turn out to be the sme s these problems, in the sense tht when we try to pproimte solutions we
1 1D heat and wave equations on a finite interval
 1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
UNIFORM CONVERGENCE. Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3
 UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
Convergence of Fourier Series and Fejer s Theorem. Lee Ricketson
 Convergence of Fourier Series nd Fejer s Theorem Lee Ricketson My, 006 Abstrct This pper will ddress the Fourier Series of functions with rbitrry period. We will derive forms of the Dirichlet nd Fejer
Convergence of Fourier Series nd Fejer s Theorem Lee Ricketson My, 006 Abstrct This pper will ddress the Fourier Series of functions with rbitrry period. We will derive forms of the Dirichlet nd Fejer
4 1-D Boundary Value Problems Heat Equation
 4 -D Boundary Vaue Probems Heat Equation The main purpose of this chapter is to study boundary vaue probems for the heat equation on a finite rod a x b. u t (x, t = ku xx (x, t, a < x < b, t > u(x, = ϕ(x
4 -D Boundary Vaue Probems Heat Equation The main purpose of this chapter is to study boundary vaue probems for the heat equation on a finite rod a x b. u t (x, t = ku xx (x, t, a < x < b, t > u(x, = ϕ(x
Reversing the Chain Rule. As we have seen from the Second Fundamental Theorem ( 4.3), the easiest way to evaluate an integral b
 Mth 32 Substitution Method Stewrt 4.5 Reversing the Chin Rule. As we hve seen from the Second Fundmentl Theorem ( 4.3), the esiest wy to evlute n integrl b f(x) dx is to find n ntiderivtive, the indefinite
Mth 32 Substitution Method Stewrt 4.5 Reversing the Chin Rule. As we hve seen from the Second Fundmentl Theorem ( 4.3), the esiest wy to evlute n integrl b f(x) dx is to find n ntiderivtive, the indefinite
Problems for HW X. C. Gwinn. November 30, 2009
 Problems for HW X C. Gwinn November 30, 2009 These problems will not be grded. 1 HWX Problem 1 Suppose thn n object is composed of liner dielectric mteril, with constnt reltive permittivity ɛ r. The object
Problems for HW X C. Gwinn November 30, 2009 These problems will not be grded. 1 HWX Problem 1 Suppose thn n object is composed of liner dielectric mteril, with constnt reltive permittivity ɛ r. The object
MATH 144: Business Calculus Final Review
 MATH 144: Business Clculus Finl Review 1 Skills 1. Clculte severl limits. 2. Find verticl nd horizontl symptotes for given rtionl function. 3. Clculte derivtive by definition. 4. Clculte severl derivtives
MATH 144: Business Clculus Finl Review 1 Skills 1. Clculte severl limits. 2. Find verticl nd horizontl symptotes for given rtionl function. 3. Clculte derivtive by definition. 4. Clculte severl derivtives
Linear Systems COS 323
 Liner Systems COS 33 Soving Liner Systems of Equtions Define iner system Singurities in iner systems Gussin Eimintion: A gener purpose method Nïve Guss Guss with pivoting Asymptotic nysis Tringur systems
Liner Systems COS 33 Soving Liner Systems of Equtions Define iner system Singurities in iner systems Gussin Eimintion: A gener purpose method Nïve Guss Guss with pivoting Asymptotic nysis Tringur systems
Review of basic calculus
 Review of bsic clculus This brief review reclls some of the most importnt concepts, definitions, nd theorems from bsic clculus. It is not intended to tech bsic clculus from scrtch. If ny of the items below
Review of bsic clculus This brief review reclls some of the most importnt concepts, definitions, nd theorems from bsic clculus. It is not intended to tech bsic clculus from scrtch. If ny of the items below
CBE 291b - Computation And Optimization For Engineers
 The University of Western Ontrio Fculty of Engineering Science Deprtment of Chemicl nd Biochemicl Engineering CBE 9b - Computtion And Optimiztion For Engineers Mtlb Project Introduction Prof. A. Jutn Jn
The University of Western Ontrio Fculty of Engineering Science Deprtment of Chemicl nd Biochemicl Engineering CBE 9b - Computtion And Optimiztion For Engineers Mtlb Project Introduction Prof. A. Jutn Jn
We will see what is meant by standard form very shortly
 THEOREM: For fesible liner progrm in its stndrd form, the optimum vlue of the objective over its nonempty fesible region is () either unbounded or (b) is chievble t lest t one extreme point of the fesible
THEOREM: For fesible liner progrm in its stndrd form, the optimum vlue of the objective over its nonempty fesible region is () either unbounded or (b) is chievble t lest t one extreme point of the fesible
Math 1B, lecture 4: Error bounds for numerical methods
 Mth B, lecture 4: Error bounds for numericl methods Nthn Pflueger 4 September 0 Introduction The five numericl methods descried in the previous lecture ll operte by the sme principle: they pproximte the
Mth B, lecture 4: Error bounds for numericl methods Nthn Pflueger 4 September 0 Introduction The five numericl methods descried in the previous lecture ll operte by the sme principle: they pproximte the
Math 3B Final Review
 Mth 3B Finl Review Written by Victori Kl vtkl@mth.ucsb.edu SH 6432u Office Hours: R 9:45-10:45m SH 1607 Mth Lb Hours: TR 1-2pm Lst updted: 12/06/14 This is continution of the midterm review. Prctice problems
Mth 3B Finl Review Written by Victori Kl vtkl@mth.ucsb.edu SH 6432u Office Hours: R 9:45-10:45m SH 1607 Mth Lb Hours: TR 1-2pm Lst updted: 12/06/14 This is continution of the midterm review. Prctice problems
Section 5.1 #7, 10, 16, 21, 25; Section 5.2 #8, 9, 15, 20, 27, 30; Section 5.3 #4, 6, 9, 13, 16, 28, 31; Section 5.4 #7, 18, 21, 23, 25, 29, 40
 Mth B Prof. Audrey Terrs HW # Solutions by Alex Eustis Due Tuesdy, Oct. 9 Section 5. #7,, 6,, 5; Section 5. #8, 9, 5,, 7, 3; Section 5.3 #4, 6, 9, 3, 6, 8, 3; Section 5.4 #7, 8,, 3, 5, 9, 4 5..7 Since
Mth B Prof. Audrey Terrs HW # Solutions by Alex Eustis Due Tuesdy, Oct. 9 Section 5. #7,, 6,, 5; Section 5. #8, 9, 5,, 7, 3; Section 5.3 #4, 6, 9, 3, 6, 8, 3; Section 5.4 #7, 8,, 3, 5, 9, 4 5..7 Since
(PDE) u t k(u xx + u yy ) = 0 (x, y) in Ω, t > 0, (BC) u(x, y, t) = 0 (x, y) on Γ, t > 0, (IC) u(x, y, 0) = f(x, y) (x, y) in Ω.
 Seprtion of Vriles for Higher Dimensionl Het Eqution 1. Het Eqution nd Eigenfunctions of the Lplcin: An 2-D Exmple Ojective: Let Ω e plnr region with oundry curve Γ. Consider het conduction in Ω with fixed
Seprtion of Vriles for Higher Dimensionl Het Eqution 1. Het Eqution nd Eigenfunctions of the Lplcin: An 2-D Exmple Ojective: Let Ω e plnr region with oundry curve Γ. Consider het conduction in Ω with fixed
14 Separation of Variables Method
 14 Separation of Variabes Method Consider, for exampe, the Dirichet probem u t = Du xx < x u(x, ) = f(x) < x < u(, t) = = u(, t) t > Let u(x, t) = T (t)φ(x); now substitute into the equation: dt
14 Separation of Variabes Method Consider, for exampe, the Dirichet probem u t = Du xx < x u(x, ) = f(x) < x < u(, t) = = u(, t) t > Let u(x, t) = T (t)φ(x); now substitute into the equation: dt
Read section 3.3, 3.4 Announcements:
 Dte: 3/1/13 Objective: SWBAT pply properties of exponentil functions nd will pply properties of rithms. Bell Ringer: 1. f x = 3x 6, find the inverse, f 1 x., Using your grphing clcultor, Grph 1. f x,f
Dte: 3/1/13 Objective: SWBAT pply properties of exponentil functions nd will pply properties of rithms. Bell Ringer: 1. f x = 3x 6, find the inverse, f 1 x., Using your grphing clcultor, Grph 1. f x,f
1 Probability Density Functions
 Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Lecture 1. Functional series. Pointwise and uniform convergence.
 1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
Math 1102: Calculus I (Math/Sci majors) MWF 3pm, Fulton Hall 230 Homework 2 solutions
 Mth 1102: Clculus I (Mth/Sci mjors) MWF 3pm, Fulton Hll 230 Homework 2 solutions Plese write netly, nd show ll work. Cution: An nswer with no work is wrong! Do the following problems from Chpter III: 6,
Mth 1102: Clculus I (Mth/Sci mjors) MWF 3pm, Fulton Hll 230 Homework 2 solutions Plese write netly, nd show ll work. Cution: An nswer with no work is wrong! Do the following problems from Chpter III: 6,
Definition of Continuity: The function f(x) is continuous at x = a if f(a) exists and lim
 Mth 9 Course Summry/Study Guide Fll, 2005 [1] Limits Definition of Limit: We sy tht L is the limit of f(x) s x pproches if f(x) gets closer nd closer to L s x gets closer nd closer to. We write lim f(x)
Mth 9 Course Summry/Study Guide Fll, 2005 [1] Limits Definition of Limit: We sy tht L is the limit of f(x) s x pproches if f(x) gets closer nd closer to L s x gets closer nd closer to. We write lim f(x)
Fourier Series in Complex notation. cos(x) = eix + e ix 2. A n cos + B n sin l. i 2 B n. e inx=l + A n + ib n 2 8. ( 0 m 6= n. C n = 1 2l.
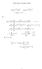 Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
W. We shall do so one by one, starting with I 1, and we shall do it greedily, trying
 Vitli covers 1 Definition. A Vitli cover of set E R is set V of closed intervls with positive length so tht, for every δ > 0 nd every x E, there is some I V with λ(i ) < δ nd x I. 2 Lemm (Vitli covering)
Vitli covers 1 Definition. A Vitli cover of set E R is set V of closed intervls with positive length so tht, for every δ > 0 nd every x E, there is some I V with λ(i ) < δ nd x I. 2 Lemm (Vitli covering)
Math 42 Chapter 7 Practice Problems Set B
 Mth 42 Chpter 7 Prctice Problems Set B 1. Which of the following functions is solution of the differentil eqution dy dx = 4xy? () y = e 4x (c) y = e 2x2 (e) y = e 2x (g) y = 4e2x2 (b) y = 4x (d) y = 4x
Mth 42 Chpter 7 Prctice Problems Set B 1. Which of the following functions is solution of the differentil eqution dy dx = 4xy? () y = e 4x (c) y = e 2x2 (e) y = e 2x (g) y = 4e2x2 (b) y = 4x (d) y = 4x
4 7x =250; 5 3x =500; Read section 3.3, 3.4 Announcements: Bell Ringer: Use your calculator to solve
 Dte: 3/14/13 Objective: SWBAT pply properties of exponentil functions nd will pply properties of rithms. Bell Ringer: Use your clcultor to solve 4 7x =250; 5 3x =500; HW Requests: Properties of Log Equtions
Dte: 3/14/13 Objective: SWBAT pply properties of exponentil functions nd will pply properties of rithms. Bell Ringer: Use your clcultor to solve 4 7x =250; 5 3x =500; HW Requests: Properties of Log Equtions
ARITHMETIC OPERATIONS. The real numbers have the following properties: a b c ab ac
 REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
Homework #04 Answers and Hints (MATH4052 Partial Differential Equations)
 Homework #4 Answers and Hints (MATH452 Partia Differentia Equations) Probem 1 (Page 89, Q2) Consider a meta rod ( < x < ), insuated aong its sides but not at its ends, which is initiay at temperature =
Homework #4 Answers and Hints (MATH452 Partia Differentia Equations) Probem 1 (Page 89, Q2) Consider a meta rod ( < x < ), insuated aong its sides but not at its ends, which is initiay at temperature =
Complete Description of the Thelen2003Muscle Model
 Compete Description o the he23usce ode Chnd John One o the stndrd musce modes used in OpenSim is the he23usce ctutor Unortuntey, to my knowedge, no other pper or document, incuding the he, 23 pper describing
Compete Description o the he23usce ode Chnd John One o the stndrd musce modes used in OpenSim is the he23usce ctutor Unortuntey, to my knowedge, no other pper or document, incuding the he, 23 pper describing
Lecture Notes for Math 251: ODE and PDE. Lecture 34: 10.7 Wave Equation and Vibrations of an Elastic String
 ecture Notes for Math 251: ODE and PDE. ecture 3: 1.7 Wave Equation and Vibrations of an Eastic String Shawn D. Ryan Spring 212 ast Time: We studied other Heat Equation probems with various other boundary
ecture Notes for Math 251: ODE and PDE. ecture 3: 1.7 Wave Equation and Vibrations of an Eastic String Shawn D. Ryan Spring 212 ast Time: We studied other Heat Equation probems with various other boundary
Improper Integrals. Type I Improper Integrals How do we evaluate an integral such as
 Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
f(a+h) f(a) x a h 0. This is the rate at which
 M408S Concept Inventory smple nswers These questions re open-ended, nd re intended to cover the min topics tht we lerned in M408S. These re not crnk-out-n-nswer problems! (There re plenty of those in the
M408S Concept Inventory smple nswers These questions re open-ended, nd re intended to cover the min topics tht we lerned in M408S. These re not crnk-out-n-nswer problems! (There re plenty of those in the
u t = k 2 u x 2 (1) a n sin nπx sin 2 L e k(nπ/l) t f(x) = sin nπx f(x) sin nπx dx (6) 2 L f(x 0 ) sin nπx 0 2 L sin nπx 0 nπx
 Chpter 9: Green s functions for time-independent problems Introductory emples One-dimensionl het eqution Consider the one-dimensionl het eqution with boundry conditions nd initil condition We lredy know
Chpter 9: Green s functions for time-independent problems Introductory emples One-dimensionl het eqution Consider the one-dimensionl het eqution with boundry conditions nd initil condition We lredy know
MA 201: Partial Differential Equations Lecture - 10
 MA 201: Partia Differentia Equations Lecture - 10 Separation of Variabes, One dimensiona Wave Equation Initia Boundary Vaue Probem (IBVP) Reca: A physica probem governed by a PDE may contain both boundary
MA 201: Partia Differentia Equations Lecture - 10 Separation of Variabes, One dimensiona Wave Equation Initia Boundary Vaue Probem (IBVP) Reca: A physica probem governed by a PDE may contain both boundary
Section 6: Area, Volume, and Average Value
 Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Theoretical foundations of Gaussian quadrature
 Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
4 Separation of Variables
 4 Separation of Variabes In this chapter we describe a cassica technique for constructing forma soutions to inear boundary vaue probems. The soution of three cassica (paraboic, hyperboic and eiptic) PDE
4 Separation of Variabes In this chapter we describe a cassica technique for constructing forma soutions to inear boundary vaue probems. The soution of three cassica (paraboic, hyperboic and eiptic) PDE
Distance And Velocity
 Unit #8 - The Integrl Some problems nd solutions selected or dpted from Hughes-Hllett Clculus. Distnce And Velocity. The grph below shows the velocity, v, of n object (in meters/sec). Estimte the totl
Unit #8 - The Integrl Some problems nd solutions selected or dpted from Hughes-Hllett Clculus. Distnce And Velocity. The grph below shows the velocity, v, of n object (in meters/sec). Estimte the totl
f(x) dx, If one of these two conditions is not met, we call the integral improper. Our usual definition for the value for the definite integral
 Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
2.4 Linear Inequalities and Interval Notation
 .4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
.4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
AP Calculus Multiple Choice: BC Edition Solutions
 AP Clculus Multiple Choice: BC Edition Solutions J. Slon Mrch 8, 04 ) 0 dx ( x) is A) B) C) D) E) Divergent This function inside the integrl hs verticl symptotes t x =, nd the integrl bounds contin this
AP Clculus Multiple Choice: BC Edition Solutions J. Slon Mrch 8, 04 ) 0 dx ( x) is A) B) C) D) E) Divergent This function inside the integrl hs verticl symptotes t x =, nd the integrl bounds contin this
Math 31S. Rumbos Fall Solutions to Assignment #16
 Mth 31S. Rumbos Fll 2016 1 Solutions to Assignment #16 1. Logistic Growth 1. Suppose tht the growth of certin niml popultion is governed by the differentil eqution 1000 dn N dt = 100 N, (1) where N(t)
Mth 31S. Rumbos Fll 2016 1 Solutions to Assignment #16 1. Logistic Growth 1. Suppose tht the growth of certin niml popultion is governed by the differentil eqution 1000 dn N dt = 100 N, (1) where N(t)
