arxiv: v1 [math.na] 28 Dec 2017
|
|
|
- Charlotte Quinn
- 6 years ago
- Views:
Transcription
1 An dptive hp-refinement strtegy with computbe gurnteed bound on the error reduction fctor Ptrik Dnie Aexndre Ern Iin Smers Mrtin Vohrík December 9, 07 rxiv:7.098v [mth.na] 8 Dec 07 Abstrct We propose new prctic dptive refinement strtegy for hp-finite eement pproximtions of eiptic probems. Foowing recent theoretic deveopments in poynomi-degree-robust posteriori error nysis, we sove two types of discrete oc probems on vertex-bsed ptches. The first type invoves the soution on ech ptch of mixed finite eement probem with homogeneous Neumnn boundry conditions, which eds to n H(div, Ω)-conforming equiibrted fux. This, in turn, yieds gurnteed upper bound on the error nd serves to mrk mesh vertices for refinement vi Dörfer s buk-chsing criterion. The second type of oc probems invoves the soution, on ptches ssocited with mrked vertices ony, of two seprte prim finite eement probems with homogeneous Dirichet boundry conditions, which serve to decide between h-, p-, or hp-refinement. Atogether, we show tht these ingredients ed to computbe gurnteed bound on the rtio of the errors between successive refinements (error reduction fctor). In series of numeric experiments feturing smooth nd singur soutions, we study the performnce of the proposed hp-dptive strtegy nd observe exponenti convergence rtes. We so investigte the ccurcy of our bound on the reduction fctor by evuting the rtio of the predicted reduction fctor retive to the true error reduction, nd we find tht this rtio is in gener quite cose to the optim vue of one. Key words: posteriori error estimte, dptivity, hp-refinement, finite eement method, error reduction, equiibrted fux, residu ifting Introduction Adptive discretiztion methods constitute n importnt too in computtion science nd engineering. Since the pioneering works on the hp-finite eement method by Gui nd Bbušk [, ] nd Bbušk nd Guo [, ] in the 980s, where it ws shown tht for one-dimension probems hp-refinement eds to exponenti convergence with respect to the number of degrees of freedom on priori dpted meshes, there hs been gret mount of work devoted to deveoping dptive hp-refinement strtegies bsed on posteriori error estimtes. Convergence of hp-dptive finite eement pproximtions for eiptic probems, hs, though, been ddressed ony very recenty in Dörfer nd Heuveine [7], Bürg nd Dörfer [7], nd Bnk, Prsni, nd Suter [3]. The first optimity resut we re wre of is by Cnuto et. [8], where n importnt ingredient is the hp-corsening routine by Binev [, 5]. These works extend to the hp-context the previous h-convergence nd optimity resuts by Dörfer [6], Morin, Nochetto, nd Siebert [6, 7], Stevenson [30], Cscón et. [], Crstensen et. [0], see so Nochetto et. [8] nd the references therein. It is worth mentioning tht most of the vibe convergence resuts re formuted for dptive This project hs received funding from the Europen Reserch Counci (ERC) under the Europen Union s Horizon 00 reserch nd innovtion progrm (grnt greement No 673 GATIPOR). Inri Pris, rue Simone Iff, Pris, Frnce & Université Pris-Est, CERMICS (ENPC) (ptrik.dnie@inri.fr, mrtin.vohrik@inri.fr). Université Pris-Est, CERMICS (ENPC), 7755 Mrne--Vée cedex, Frnce & Inri Pris, Pris, Frnce (exndre.ern@enpc.fr). Deprtment of Mthemtics, University Coege London, Gower Street, WCE 6BT London, United Kingdom (i.smers@uc.c.uk).
2 methods driven by residu-type posteriori error estimtors; other estimtors hve in prticur been ddressed in Cscón nd Nochetto [] nd Kreuzer nd Siebert []. A key ingredient for dptive hp-refinement is oc criterion in ech mesh ce mrked for refinement tht ows one to decide whether h-, p-, or hp-refinement shoud be performed. There is substnti mount of such criteri proposed in the iterture; computtion overview cn be found in Mitche nd McCin [5]. Some of the mthemticy motivted hp-decision criteri incude, mong others, those proposed by Eibner nd Meenk [8], Houston nd Süi [3] which both estimte the oc regurity of the exct wek soution. Our proposed strtegy fits into the group of gorithms bsed on soving oc boundry vue probems owing us to forecst the benefits of performing h- or p-refinement, s recenty considered in, e.g., [7, 7]. Simiry to [7], we use the oc finite eement spces ssocited with specific type of refinement to perform the bove forecst nd to tke the oc hp-refinement decision. We so mention the work of Demkowicz et. [3] for n erier, yet more expensive, version of the ook-hed ide, where it is proposed to sove n uxiiry probem on gob finite eement spce corresponding to mesh refined uniformy either in h or in p. In the present work, we focus on the Poisson mode probem with (homogeneous) Dirichet boundry conditions. In wek form, the mode probem reds s foows: Find u H0 (Ω) such tht ( u, v) = (f, v) v H 0 (Ω), (.) where Ω R d, d =, 3, is poygon/poyhedr domin (open, bounded, nd connected set) with Lipschitz boundry, f L (Ω), H 0 (Ω) denotes the Soboev spce of functions in L (Ω) which hve their first-order wek derivtives in L (Ω) nd zero trce on Ω, nd (, ) stnds for the L (Ω) or [L (Ω)] d inner product. Our first go is to propose reibe nd computtiony-efficient hp-dptive strtegy to pproximte the mode probem (.) tht hinges on the recent theoretic deveopments on poynomi-degree-robust posteriori error estimtes due to Bress et. [6] nd Ern nd Vohrík [9, 0]. The present hp-dptive gorithm foows the we-estbished prdigm bsed on n itertive oop where ech step consists of the foowing four modues: SOLVE ESTIMATE MARK REFINE. (.) Here, SOLVE stnds for ppiction of the conforming finite eement method on mtching (no hnging nodes) simpici mesh to pproximte the mode probem (.); sptiy-vrying poynomi degree is owed. The modue ESTIMATE is bsed on n equiibrted fux posteriori error estimte, obtined by soving, for ech mesh vertex, oc mixed finite eement probem with (homogeneous) Neumnn boundry condition on the ptch of ces shring the given vertex. The modue MARK is bsed on buk-chsing criterion inspired by the we-known Dörfer s mrking [6]; here we mrk mesh vertices nd not simpices since we observe smoother performnce in prctice nd since we ter work with some vertex-bsed uxiiry quntities. The modue REFINE, where we incude our hp-decision criterion, is orgnized into three steps. First, we sove two oc finite eement probems on ech ptch of simpices ttched to mesh vertex mrked for refinement, with either the mesh refined or the poynomi degree incresed. This is inspired by the key observtion from [9, Lemm 3.3] tht gurnteed oc efficiency cn be mteriized by some oc conforming finite eement soves. These conforming residu iftings ow us, in prticur, to estimte the effect of ppying h- or p-refinement, nd ed to prtition of the set of mrked vertices into two disjoint subsets, one coecting the mesh vertices fgged for h-refinement nd the other coecting the mesh vertices fgged for p-refinement. The second step of the modue REFINE uses these two subsets to fg the simpices for h-, p, or hp-refinement. Finy, the third step of the modue REFINE uses the bove sets of fgged simpices to buid the next simpici mesh nd the next poynomi-degree distribution. Let us mention tht recenty, Doejší et. [5] so devised n hp-dptive gorithm driven by poynomi-degree-robust posteriori error estimtes bsed on the equiibrted fuxes from [6, 9, 0]. The differences with the present work re tht the interior penty discontinuous Gerkin method is considered in [5], nd more importnty, tht the present hp-decision criterion hinges on oc prim soves on ptches round mrked vertices. The second go of the present work is to show tht the proposed hp-dptive strtegy utomticy eds to computbe gurnteed bound on the error reduction fctor between two consecutive steps of the
3 dptive oop (.). More precisey, we show how to compute expicity re number C red [0, ] so tht (u u + ) C red (u u ), (.3) where u denotes the discrete soution on -th itertion of the dptive oop, see Theorem 5. beow. Thus the number C red gives gurnteed (constnt-free) bound on the rtio of the errors between successive refinements. This must not be confused with sying tht the error is gurnteed to be reduced, since the cse C red = cnnot be rued out in gener without ddition ssumptions (e.g. n interior node property, see [6] for further detis). The computtion of C red cruciy reies on combined use of the equiibrted fuxes nd of the conforming residu iftings, which were redy used for the error estimtion nd hprefinement decision criterion respectivey. It is worth noting tht we consider homogeneous Dirichet boundry condition for the oc residu iftings in order to obtin n estimte on the error reduction fctor tht is s shrp s possibe. The rest of this mnuscript is orgnized s foows. Section describes the discrete setting nd introduces some usefu nottion. Section 3 presents the modues SOLVE, ESTIMATE, nd MARK, wheres Section presents the modue REFINE. Section 5 contins our min resut on gurnteed bound on the error reduction fctor. Finy, numeric experiments on two-dimension test cses feturing smooth nd singur soutions re discussed in Section 6, nd concusions re drwn in Section 7. Discrete setting The min purpose of the dptive oop (.) is to generte sequence of finite-dimension H 0 -conforming finite eement spces (V ) 0, where the integer 0 stnds for the itertion counter in (.). H 0 -conformity mens tht V H 0 (Ω) for 0. In this work, we sh mke the foowing nestedness ssumption: V V +, 0. (.) The spce V is buit from two ingredients: (i) mtching simpici mesh T of the computtion domin Ω, tht is, finite coection of (cosed) non-overpping simpices K T covering Ω excty nd such tht the intersection of two different simpices is either empty, common vertex, common edge, or common fce; (ii) poynomi-degree distribution described by the vector p := (p,k ) K T tht ssigns poynomi degree to ech simpex K T. The conforming finite eement spce V is then defined s V := P p (T ) H 0 (Ω), 0, where P p (T ) denotes the spce of piecewise poynomis of tot degree p,k on ech simpex K T. In other words, ny function v V stisfies v H0 (Ω) nd v K P p,k (K) for K T, where for n integer p, P p (K) stnds for the spce of poynomis of tot degree t most p on the simpex K. The initi mesh T 0 nd the initi poynomi-degree distribution p 0 re given, nd the purpose of ech step 0 of the dptive oop (.) is to produce the next mesh T + nd the next poynomi-degree distribution p +. In order to ensure the nestedness property (.), the foowing two properties re to be stisfied: (i) The sequence (T ) 0 is hierrchic, i.e., for 0 nd K T+, there is unique simpex K T, ced the prent of K so tht K K; (ii) The oc poynomi degree is ocy incresing, i.e., for 0 nd K T+, p +, K p,k where K T is the prent of K. Moreover, we ssume the foowing shpe-regurity property: There exists constnt κ T > 0 such tht mx K T h K /ρ K κ T for 0, where h K is the dimeter of K nd ρ K is the dimeter of the rgest b inscribed in K. Before cosing this section, we introduce some further usefu nottion. The set of vertices V of ech mesh T is decomposed into V int nd V ext, the set of inner nd boundry vertices, respectivey. For ech vertex V, the so-ced ht function ψ is the continuous, piecewise ffine function tht tkes the vue t the vertex nd the vue 0 t the other vertices of V ; the function ψ is in V for V int. Moreover, we consider the simpex ptch T T which is the coection of the simpices in T shring the vertex V, nd we denote by ω the corresponding open subdomin. Finy, for ech simpex K T, V K denotes the set of vertices of K. 3
4 3 The modues SOLVE, ESTIMATE, nd MARK In this section we present the modues SOLVE, ESTIMATE, nd MARK from the dptive oop (.). Let 0 denote the current itertion number. 3. The modue SOLVE The modue SOLVE tkes s input the H 0 -conforming finite eement spce V nd outputs the discrete function u V which is the unique soution of 3. The modue ESTIMATE ( u, v ) = (f, v ) v V. (3.) Foowing [, 6, 9, 5, 0], see so the references therein, the modue ESTIMATE reies on n equiibrted fux posteriori error estimte on the energy error (u u ). The modue ESTIMATE tkes s input the finite eement soution u nd outputs coection of oc error indictors {η K } K T. The equiibrted fux is constructed ocy from mixed finite eement soves on the simpex ptches T ttched to ech vertex V. For this construction, we consider s in [5] the oc poynomi degree p est := mx K T p,k (ny other choice so tht p est mx K T p,k cn so be empoyed). We consider the oc Rvirt Thoms Nédéec mixed finite eement spces (V, Q ) which re defined for Vint by nd, for V ext, where RTN p est V := {v H(div, ω ); v K RTN p est Q := {q P p est (T ); (q, ) ω = 0}, (K), K T, v n ω = 0 on ω }, V :={v H(div, ω ); v K RTN p est(k), K T, v n ω = 0 on ω \ Ω}, Q :=P p est (T ), (K) := [P p est(k)]d + P p est (K)x, nd n ω denotes the unit outwrd-pointing norm to ω. Definition 3. (Fux reconstruction σ ). Let u sove (3.). The gob equiibrted fux σ is constructed s σ := V σ, where, for ech vertex V, (σ, γ ) V Q soves or, equiventy, (σ, v ) ω (γ, v ) ω = (ψ u, v ) ω v V, (3.) nd where σ is extended by zero outside ω. ( σ, q ) ω = (fψ u ψ, q ) ω q Q ; (3.b) σ := rg min v V, v =Π Q (fψ u ψ ) ψ u + v ω, Note tht the Neumnn comptibiity condition for the probem (3.) is stisfied for V int (tke v = ψ s test function in (3.)). Moreover, Definition 3. yieds goby H(div, Ω)-conforming fux reconstruction σ such tht, for K T, ( σ, v ) K = (f, v ) K for v P min VK p est (K), see [5, Lemm 3.6]. Using the current nottion, [5, Theorem 3.3] sttes the foowing resut. Theorem 3. (Gurnteed upper bound on the error). Let u sove (.) nd u sove (3.). Let σ be the equiibrted fux reconstruction of Definition 3.. Then { } (u u ) η(t ) :=, η K := u + σ K + h K π f σ K. (3.3) K T η K As discussed in, e.g., [9, Remrk 3.6], the term h K π f σ K represents, for K T, oc oscition in the source dtum f tht, under suitbe smoothness ssumptions, converges to zero two orders fster thn the error. To cover the whoe computtion rnge in our numeric experiments, this term is kept in the error indictor η K.
5 3.3 The modue MARK The modue MARK tkes s input the oc error estimtors {η K } K T from Theorem 3. nd outputs set of mrked vertices Ṽ V using buk-chsing criterion inspired by the we-known Dörfer s mrking criterion [6]. The reson why we mrk vertices nd not simpices is tht our hp-decision criterion in the modue REFINE (see Section beow) hinges on the soution of oc prim soves posed on the ptches T ssocited with the mrked vertices Ṽ; we so observe in prctice smoother performnce of the over hp-dptive procedure when mrking vertices thn when mrking eements. Vertex-mrking strtegies re so considered, mong others, in [6, 9]. For subset S T, we use the nottion η(s) := { K S η K }/. In the modue MARK, the set of mrked vertices Ṽ is seected in such wy tht ( ) η T θ η(t ), (3.) Ṽ where θ (0, ] is fixed threshod. Letting M := T T (3.5) Ṽ be the coection of the simpices tht beong to ptch ssocited with mrked vertex, we observe tht (3.) mens tht η(m ) θ η(t ). To seect set Ṽ of minim crdinity, the mesh vertices in V re sorted by compring the vertex-bsed error estimtors η(t ) for V, nd greedy gorithm is empoyed to buid the set Ṽ. The modue MARK is summrized in Agorithm. A possiby sighty rger set Ṽ cn be constructed with iner cost in terms of the number of mesh vertices by using the gorithm proposed in [6, Section 5.]. Agorithm (modue MARK) : procedure MARK({η K } K T, θ) : Input: error indictors {η K } K T, mrking prmeter θ (0, ] 3: Output: set of mrked vertices Ṽ : for V do 5: Compute the vertex-bsed error estimtor η(t ) 6: end for 7: Sort the vertices ccording to η(t ) 8: Set Ṽ := 9: whie η( Ṽ T ) < θ η(t ) do 0: Add to Ṽ the next sorted vertex V \ Ṽ : end whie : end procedure The modue REFINE The modue REFINE tkes s input the set of mrked vertices Ṽ nd outputs the mesh T + nd the poynomi-degree distribution p + to be used t the next step of the dptive oop (.); the integer 0 is the current itertion number therein. This modue is orgnized into three steps. First, n hp-decision is mde on the mrked vertices so tht ech mrked vertex Ṽ is fgged either for h-refinement or for p-refinement. This mens tht the set Ṽ is spit into two disjoint subsets Ṽ = Ṽh Ṽp with obvious nottion. Then, in the second step, the subsets Ṽh nd Ṽp re used to define subsets Mh nd Mp of the set of mrked simpices M (see (3.5)). The subsets M h nd Mp re not necessriy disjoint which mens tht some simpices cn be fgged for hp-refinement. Finy, the two subsets M h nd Mp re used to construct T + nd p +. 5
6 . hp-decision on vertices Our hp-decision on mrked vertices is mde on the bsis of two oc prim soves on the ptch T ttched to ech mrked vertex Ṽ. The ide is to construct two distinct oc ptch-bsed spces in order to emute seprtey the effects of h- nd p-refinement. Let us denote the poynomi-degree distribution in the ptch T by the vector p := (p,k) K T. Figure : An exmpe of ptch T together with its poynomi-degree distribution p (center) nd p-refined versions (right) from Definitions. nd. respectivey. (eft) nd its h-refined Definition. (h-refinement residu). Let Ṽ be mrked vertex with ssocited ptch T poynomi-degree distribution p. We set nd where T,h V,h is obtined s mtching simpici refinement of T est two chidren simpices, nd the poynomi-degree distribution p,h := P p,h(t,h ) H0 (ω ), (.) by dividing ech simpex K T is obtined from p ech newy-creted simpex the sme poynomi degree s its prent. Then, we et r,h V,h ( r,h, v,h ) ω = (f, v,h ) ω ( u, v,h ) ω v,h V,h. into t by ssigning to sove Definition. (p-refinement residu). Let Ṽ be mrked vertex with ssocited ptch T poynomi-degree distribution p. We set nd V,p := P p,p(t,p ) H0 (ω ), (.) where T,p := T, nd the poynomi-degree distribution p,p is obtined from p by ssigning to ech simpex K T,p = T the poynomi degree p,k + δk where { δk if p,k = min K T := p,k, (.3) 0 otherwise. Then, we et r,p V,p sove ( r,p, v,p ) ω = (f, v,p ) ω ( u, v,p ) ω v,p V,p. The oc residu iftings r,h nd r,p from Definitions. nd., respectivey, re used to define the foowing two disjoint subsets of the set of mrked vertices Ṽ: Ṽ h := { Ṽ r,h ω r,p ω }, (.) Ṽ p := { Ṽ r,h ω < r,p ω }, (.b) 6
7 in such wy tht Ṽ = Ṽh Ṽp, Ṽh Ṽp =. The bove hp-decision criterion on vertices mens tht mrked vertex is fgged for h-refinement if the oc residu norm r,h ω is rger thn r,p ω ; otherwise, this vertex is fgged for p-refinement. Further motivtion for this choice is discussed in Remrk 5.3 beow. Remrk.3 (p-refinement). Other choices re possibe for the poynomi-degree increment defined in (.3). One possibiity is to set δk = for K T. However, in our numeric experiments, we observe tht this choice eds to rther scttered poynomi-degree distributions over the whoe computtion domin. The choice (.3) is more conservtive nd eds to smoother over poynomi-degree distribution. We beieve tht this choice is preferbe, t est s ong s poynomi-degree corsening procedure is not incuded in the dptive oop. Another possibiity is to use αp,k with α > insted of p,k + δk, which corresponds to the theoretic deveopments in [9].. hp-decision on simpices The second step in the modue REFINE is to use the subsets Ṽh nd Ṽp to decide whether h-, p-, or hp-refinement shoud be performed on ech simpex hving t est one fgged vertex. To this purpose, we define the foowing subsets: M h := {K T V K Ṽh } M, (.5) M p := {K T V K Ṽp } M. (.5b) In other words, simpex K T is fgged for h-refinement (resp., p-refinement) if it hs t est one vertex fgged for h-refinement (resp., p-refinement). Note tht the subsets M h nd Mp re not necessriy disjoint since simpex cn hve some vertices fgged for h-refinement nd others fgged for p-refinement; such simpices re then fgged for hp-refinement. Note so tht M h Mp = T Ṽ = M is indeed the set of mrked simpices considered in the modue MARK..3 hp-refinement In this st nd fin step, the subsets M h nd Mp re used to produce first the next mesh T + nd then the next poynomi-degree distribution p + on the mesh T +. The next mesh T + is mtching simpici refinement of T obtined by dividing ech fgged simpex K M h into t est two simpices in wy tht is consistent with the mtching simpici refinement of T considered in Definition. to buid T,h, i.e., such tht T,h T + for Ṽh. Note tht to preserve the conformity of the mesh, ddition refinements beyond the set of fgged simpices M h my be crried out when buiding T +. Sever gorithms cn be considered to refine the mesh. In our numeric experiments, we used the newest vertex bisection gorithm [9]. After hving constructed the next mesh T +, we ssign the next poynomi-degree distribution p + s foows. For K T+, et K denote its prent simpex in T. We then set p +, K := p,k if K M p, (.6) tht is, we ssign the sme poynomi degree to the chidren of simpex tht is not fgged for p-refinement, wheres we set ( p +, K := mx p,k + δk) if K M p, (.7) V K Ṽp tht is, we ssign to the chidren of simpex K M p fgged for p-refinement the rgest of the poynomi degrees considered in Definition. to buid the oc residu iftings ssocited with the vertices of K fgged for p-refinement. 7
8 Agorithm (modue REFINE) : modue REFINE(Ṽ) : Input: set of mrked vertices Ṽ 3: Output: next eve mesh T + nd poynomi-degree distribution p + : for Ṽ do 5: Compute the h-refinement residu ifting r,h from Definition. 6: Compute the p-refinement residu ifting r,p from Definition. 7: end for 8: hp-decision on vertices: buid the subsets Ṽh nd Ṽp from (.) 9: hp-decision on simpices: buid the subsets M h nd Mp from (.5) 0: Buid T + from T nd M h : Buid p + on T + from p, {δk } Ṽp,K T : end modue, nd M p using (.6) nd (.7). Summry of the modue REFINE The modue REFINE is summrized in Agorithm. To iustrte Agorithm, we exmine in deti prticur sitution with three mrked vertices s encountered on the 0th itertion ( = 0) of the dptive oop ppied to the L-shpe probem described in Section 6. beow. In Figure (eft pne), we dispy the mesh T 0 nd the poynomi-degree distribution p 0. There re three mrked vertices in Ṽ0. In Figure 3, for the three mrked vertices, we visuize the norms r,h ω 0 nd r,p ω 0 which re the key ingredients for the hp-decision on vertices. The resuting simpices fgged for h- nd p-refinement re shown in the centr pne of Figure, wheres the right pne of Figure dispys the next mesh T nd the next poynomi-degree distribution p. (T 0; p 0) P5 M p (T ; p ) P5 P P P3 M h P3 P P P no ref. P Figure : [L-shpe probem from Section 6.] The mesh nd the poynomi degree distribution on the 0th itertion of the dptive procedure (eft). Resut of the hp-decision: simpices in M h 0 re shown in bue nd simpices in M p 0 re shown in red, the two subsets Mh 0 nd M p 0 being here disjoint (center). The resuting mesh T nd poynomi-degree distribution p (right). 5 Gurnteed bound on the error reduction fctor In this section we show tht it is possibe to compute, t mrgin ddition costs, gurnteed bound on the energy error reduction fctor C red from (.3) on ech itertion of the dptive oop (.). This bound cn be computed right fter the end of modue REFINE t the modest price of one ddition prim sove in ech ptch T ssocited with ech mrked vertex Ṽ. Rec the set of mrked simpices M = Ṽ T. Let us denote by ω := Ṽ ω the corresponding open subdomin; notice tht point x is in ω if nd ony if there is K M so tht x K. We strt with the foowing discrete ower bound resut: 8
9 r,h ω r,p ω Figure 3: [L-shpe probem from Section 6.] For the three mrked vertices in Ṽ0, we dispy the piecewise P functions which tke the vue r,h ω 0 in the vertex nd 0 esewhere (eft) nd the vue r,p ω 0 in the vertex nd 0 esewhere (right). Lemm 5. (Gurnteed ower bound on the increment error on mrked simpices). Let the mesh T + nd the poynomi-degree distribution p + resut from Agorithm, nd rec tht V + = P p+ (T + ) H 0 (Ω) is the finite eement spce to be used on itertion ( + ) of the dptive oop (.). For the mrked vertices Ṽ, et us set, in extension of (.), (.), V,hp := V + ω H 0 (ω ), nd construct the residu ifting r,hp V,hp by soving ( r,hp, v,hp ) ω = (f, v,hp ) ω ( u, v,hp ) ω v,hp V,hp. (5.) Then, extending r,hp by zero outside ω, the foowing hods true: Ṽ r,hp ω ( (u + u ) ω η M, η M := ) if r,hp 0, Ṽ Ṽ r,hp ω 0 otherwise. (5.) Proof. Let V + (ω ) stnd for the restriction of the spce V + to the subdomin ω nd et V 0 + (ω ) := V + (ω ) H 0 (ω ) stnd for the corresponding homogeneous Dirichet subspce. Note tht (u + u ) is member of V + (ω ), but not necessriy of V 0 + (ω ). Then, the foowing hods true: ( (u + u ), v + ) ω (u + u ) ω = sup v + V + (ω ) v + ω ( (u + u ), v + ) ω sup v + V+ 0 (ω ) v + ω (f, v + ) ω ( u, v + ) ω = sup, v + V+ 0 (ω ) v + ω where we hve used the definition (3.) of u + on the mesh T +, since v + extended by zero outside of ω beongs to the spce V + whenever v + V 0 + (ω ). Now, choosing v + = Ṽ r,hp (note tht this 9
10 function indeed beongs to V+ 0 (ω )), we infer tht ( f, ( ( )) r,hp u, r Ṽ )ω,hp Ṽ = {( f, r,hp ) ( u ω, r,hp) ω Ṽ ω } = r,hp, ω Ṽ where we hve empoyed r,hp s test function in (5.). This finishes the proof. Our min resut is summrized in the foowing contrction property in the spirit of [, Theorem 5.], [9, Proposition.], nd the references therein. The specificity of the present work is tht we obtin gurnteed nd computbe bound on the error reduction fctor. In contrst to these references, however, we do not prove here tht C red is stricty smer thn one, though we observe it numericy in Section 6 beow. It ctuy becomes possibe to show tht C red < under ddition ssumptions on the refinements, such s the interior node property [6], but we wi not pursue this considertion further here. Theorem 5. (Gurnteed bound on the energy error reduction fctor). Let the mesh T + nd the poynomi-degree distribution p + resut from Agorithm, nd et V + = P p+ (T + ) H0 (Ω) be the finite eement spce to be used on itertion ( + ) of the dptive oop (.). Let η M be defined by (5.). Then, uness η(m ) = 0 in which cse u = u nd the dptive oop termintes, the new numeric soution u + V + stisfies (u u + ) C red (u u ) with 0 C red := η θ M η. (5.3) (M ) Proof. We first observe tht η(m ) = 0 impies using (3.) nd (3.3) tht the error is zero on itertion, i.e., u = u, so tht the dptive oop (.) termintes. Let us now ssume tht η(m ) 0. Since the spces {V } 0 re nested, cf. (.), Gerkin s orthogonity impies the foowing Pythgoren identity: Moreover, owing to Lemm 5., we infer tht (u u + ) = (u u ) (u + u ). (u + u ) (u + u ) ω η M = η M η(m ) η(m ). Using the mrking criterion (3.) nd the definition of M, we next see tht (u u + ) (u u ) η M η (M ) η (M ) η M (u u ) θ η (M ) η (T ). The ssertion (5.3) foows from the error estimte (3.3) nd tking the squre root. Remrk 5.3 (Loc residu optimiztion). The use of the oc residu iftings r,h nd r,p from Definitions. nd. respectivey in the hp-decision criterion (.) on mrked vertices is motivted by the resut of Theorem 5.. Indeed, suppose tht r,h is rger thn r,p in norm, nd tht ony h-refinement is performed in the subdomin ω t the end of Agorithm. Then, the oc residu r,hp from Lemm 5. coincides with r,h which mens tht by fgging the mrked vertex for h-refinement, one mximizes the contribution r,hp ω in the numertor of (5.) defining η M. It is so possibe to design more compex hp-refinement strtegy expoiting directy (5.3). Here we simpy stick to Agorithm which in our numeric experiments reported in Section 6 beow eds to exponenti convergence rtes. Remrk 5. (A shrper bound). Theorem 5. obviousy so hods true with the sighty shrper constnt C red = η M η (T ). This is equivent to considering in (5.3) θ such tht η(m ) = θ η(t ) in pce of θ, strtegy dopted in the numeric experiments in Section 6 beow. 0
11 6 Numeric experiments In this section, we present our numeric resuts. We consider two test cses for the mode probem (.), both in two spce dimensions, one with (retivey) smooth wek soution nd one with singur wek soution. Our min go with the numeric experiments is to verify tht the hp-refinement strtegy of Agorithm eds to n exponenti rte of convergence with respect to the number of degrees of freedom DoF of the finite eement spces V in the form ) (u u ) C exp ( C DoF 3, with positive constnts C, C independent of DoF. In ddition, we ssess the shrpness of the gurnteed bound on the reduction fctor C red from Theorem 5. by mens of the effectivity index defined s I eff red = C red (u u + ) (u u ). (6.) We wys consider the (we-estbished) choice θ = 0.5 for the mrking prmeter, fine-tuning it on ech step to θ s described in Remrk 5.. As mentioned bove, we ppy the newest vertex bisection gorithm [9] to perform h-refinement nd we use the poynomi-degree increment (.3) to perform p- refinement. We compre the performnce of our hp-refinement gorithm to two other gorithms bsed on different hp-decision criterion, nmey the PARAM nd PRIOR criteri from the survey pper [5] which re both bsed on oc smoothness estimtion. Both criteri hinge on the oc L -orthogon projection u p of the numeric soution u onto the oc ower-poynomi-degree spce P p,k (K) for the mrked simpices K M. This eds to the oc quntity η p K := (u u p ) K ; in cse of p,k =, when the quntity η p K is not vibe, for both criteri the mrked simpex K is p-refined. The criterion PARAM [] reies on the oc smoothness indictor g K := η K /η p K nd user-defined prmeter γ > 0; the mrked simpex K is h-refined if g K > γ, nd otherwise it is p-refined. The presence of the prmeter γ is drwbck of this criterion; in our experiments we use the vues γ = 0.3 nd γ = 0.6, s suggested in [5]. The criterion PRIOR, which is simpified version of the one proposed in [3], reies on the quntity s K := og(η K /η p K )/ og(p,k/(p,k )); the mrked simpex K is h-refined if p,k > s K, nd otherwise it is p-refined. To mke the comprison with our pproch more objective, we ppy for both criteri the suggested p-refinement ony to those simpices such tht p,k = min K T p,k. 6. Smooth soution (shrp Gussin) We consider squre domin Ω = (, ) (, ) nd wek soution tht is smooth but hs rther shrp pek u(x, y) = (x )(y ) exp ( 00(x + y )). We strt from criss-cross initi mesh T 0 with mx K T0 h K = 0.5 nd uniform poynomi-degree distribution equ to on simpices. Figure presents the fin mesh nd poynomi-degree distribution obtined fter 30 steps of the hpdptive procedure (.) (eft pne) ong with the obtined numeric soution (right pne). Figure 5 dispys the retive error (u u ) / u nd the retive estimtor η(t )/ u s function of DoF 3 in ogrithmic-iner sce to iustrte tht the present hp-dptive procedure eds to n symptotic exponenti rte of convergence. For comprison, we so pot the retive estimtor obtined when using the hp-decision criteri PRIOR nd PARAM described bove nd so for the pure h-version of the dptive oop. The quity of the posteriori error estimtors of Theorem 3. cn be pprecited in Figure 6, where we compre the ctu nd estimted error distributions on itertion = 0 of the dptive oop, showing exceent greement. Figure 7 (eft pne) presents the effectivity index for the reduction fctor C red, see (6.), throughout the dptive process. Over, vues quite cose to one re obtined, except t some of the first itertions where the vues re rger but do not exceed.5. Moreover, the vues re rger thn one, confirming tht the bound on the reduction fctor C red is indeed gurnteed. Figure 7 (right pne) exmines the quity of the ower bound η M from Lemm 5. by potting the rtio of the eft-hnd
12 side to the right-hnd side of the ower bound in (5.). Except for one itertion where this rtio tkes rger vue cose to.5, we observe tht this rtio tkes wys vues quite cose to, nd rger thn, one, indicting tht η M deivers shrp nd gurnteed ower bound on the energy error decrese. To give some further insight into the proposed hp-dptive process, we present in Tbes nd some detis on the hp-refinement decisions throughout the first 0 nd the st 0 itertions of the dptive oop. Finy, Tbe 5 (top) compres the different strtegies nmey in terms of the number of itertions of the dptive oop (.); here our strtegy is cer winner. P5 P P3 P P Figure : [Shrp-Gussin of Section 6.] The fin mesh nd poynomi-degree distribution obtined fter 30 itertions of the hp-dptive procedure (eft) nd the obtined numeric soution u 30 (right). retive errors nd estimte in energy norm 0 0 error (hp version) estimte (hp version) error (PRIOR) error (PARAM γ = 0.3) error (PARAM γ = 0.6) error (h version) DoF /3 Figure 5: [Shrp-Gussin of Section 6.] Retive energy error (u u ) / u nd retive estimtor η(t )/ u s function of DoF 3, obtined using the present hp-decision criterion, the criteri PRIOR nd PARAM (γ = 0.3, γ = 0.6), nd using ony h-refinement.
13 Discretiztion error on eements #0 - effectivity index Estimted discretiztion error on eements # Figure 6: [Shrp-Gussin of Section 6.] The distribution of the energy error (u u ) K (eft) nd of the error estimtors η K from Theorem 3. (right), = 0. The effectivity index of the estimte defined s η(t 0 )/ (u u 0 ) is effectivity index of C red DoF / DoF /3 Figure 7: [Shrp-Gussin of Section 6.] Effectivity indices (6.) for the error reduction fctor C red from Theorem 5. (eft) nd effectivity indices for the ower bound η M from Lemm 5. defined s the rtio (u + u ) ω /η M (right). Itertion Simpices Mxim poynomi degree 3 Mrked vertices Simpices fgged for h-refinement Simpices fgged for p-refinement Simpices fgged for hp-refinement Tbe : [Shrp-Gussin of Section 6.] Refinement decisions in Agorithm during the first 0 itertions of the dptive oop (.). 3
14 Itertion Simpices Mxim poynomi degree Mrked vertices Simpices fgged for h-refinement Simpices fgged for p-refinement Simpices fgged for hp-refinement Tbe : [Shrp-Gussin of Section 6.] Refinement decisions in Agorithm during the st 0 itertions of the dptive oop (.).
15 6. Singur soution (L-shpe domin) In our second test cse, we consider the L-shpe domin Ω = (, ) (, ) \ [0, ] [, 0] with f = 0 nd the exct soution (in por coordintes) ( ) u(r, ϕ) = r ϕ 3 sin. 3 We negect here the error from the pproximtion of the inhomogeneous Dirichet boundry condition prescribed by the exct soution on Ω; it coud be tken into ccount foowing [5, Theorem 3.3], see so the references therein. We strt the computtion on criss-cross grid with the poynomi degrees set uniformy to. Figure 8 presents the fin mesh nd poynomi-degree distribution fter 65 steps of the hp-dptive procedure (.) (eft pne) ong with zoom in the window [ 0 6, 0 6 ] [ 0 6, 0 6 ] ner the reentrnt corner (right pne). Figure 9 (eft pne) dispys the retive error (u u ) / u nd the retive estimtor η(t )/ u s function of DoF /3 in ogrithmic-iner sce to iustrte tht, s in the previous test cse, the present hp-dptive procedure eds to n symptotic exponenti rte of convergence. A detied view when the error tkes ower vues is provided in the right pne of Figure 9. For comprison, we so pot the retive errors obtined when using the hp-decision criteri PRIOR nd PARAM, s we s those obtined when expoiting the priori knowedge of the exct soution (mrked simpices re h-refined ony if they touch the corner singurity, otherwise they re p-refined). Figure 0 compres the ctu nd estimted error distributions on itertion = 5 of the dptive oop, showing exceent greement. Figure (eft pne) presents the effectivity index for the reduction fctor C red, see (6.), throughout the dptive process, wheres the right pne of Figure exmines the quity of the ower bound η M from Lemm 5. by potting the rtio of the eft-hnd side to the right-hnd side of the ower bound in (5.). For both quntities, we cn drw simir concusions to the previous test cse, thereby confirming tht shrp estimtes on the error reduction fctor re vibe. Addition numeric experiments (not shown here) indicte tht the ower bound estimte cn be mde even shrper by performing h-refinement so s to stisfy the interior node property. Finy, to give some further insight into the hp-dptive process, we present in Tbes 3 nd some detis on the hp-refinement decisions mde by the proposed hp-refinement criterion during the first 0 nd the st 0 itertions of the dptive oop. We observe tht in the initi itertions where the underying mesh is sti rther corse, the poynomi degree is incresed so on those simpices touching the re-entrnt corner. Nevertheess, this decision does not occur nymore ter when the mesh round the singurity is redy more strongy refined thn in the rest of the domin. Therefore, n improvement of our pproch is expected, s suggested in [8], in conjunction with n pproprite corsening strtegy correcting the excessive p-refinement in the ery stges. Tbe 5 (bottom) gin brings some fin ddition comprisons. P5 P5 P P P3 P3 Figure 8: [L-shpe domin of Section 6.] The fin mesh nd poynomi-degree distribution obtined fter 65 itertions of the hp-dptive procedure (eft) nd zoom in [ 0 6, 0 6 ] [ 0 6, 0 6 ] ner the re-entrnt corner (right). 5
16 retive errors nd estimte in energy norm retive errors nd estimte in energy norm - 0 error (hp version) estimte (hp version) error ( priori) error (PRIOR) 0 - error (PARAM γ = 0.3) error (PARAM γ = 0.6) error (hp version) estimte (hp version) error ( priori) error (PRIOR) error (PARAM. = 0.3) error (PARAM. = 0.6) DoF / DoF /3 Figure 9: [L-shpe domin of Section 6.] The retive energy error (u u ) / u nd the estimtor η(t )/ u s function of DoF 3, obtined using the present hp-decision criterion, the criteri PRIOR nd PARAM (γ = 0.3 nd γ = 0.6), nd the priori hp-strtegy (eft) nd detied view (right). Discretiztion error on eements #0-5 6 Estimted discretiztion error on eements # Figure 0: [L-shpe domin of Section 6.] The distribution of the energy error (u u ) K (eft) nd of the oc error estimtors η K from Theorem 3. (right), = 5. The effectivity index of the estimte defined s η(t 5 )/ (u u 5 ) is.077. Itertion Simpices Mxim poynomi degree Mrked vertices 3 3 Simpices fgged for h-refinement Simpices fgged for p-refinement Simpices fgged for hp-refinement Tbe 3: [L-shpe domin of Section 6.] Refinement decisions in Agorithm during the first 0 itertions of the dptive oop (.). 6
17 effectivity index of.5.5 effectivity index of C red DoF / DoF /3 Figure : [L-shpe domin of Section 6.] Effectivity indices (6.) for the error reduction fctor C red from Theorem 5. (eft) nd effectivity indices for the ower bound η M from Lemm 5. defined s the rtio (u + u ) ω / η M (right). Itertion Simpices Mxim poynomi degree Mrked vertices Simpices fgged for h-refinement Simpices fgged for p-refinement Simpices fgged for hp-refinement Tbe : [L-shpe domin of Section 6.] Refinement decisions in Agorithm during the st 0 itertions of the dptive oop (.). our priori PRIOR PARAM 0.3 PARAM 0.6 Shrp Gussin iter (retive error 0 3 ) DoF / L-shpe domin iter (retive error 0 5 ) DoF / Tbe 5: Comprison of the different hp-strtegies in terms of the number of itertions of the dptive oop (.) nd of the number of degrees of freedom necessry to rech the given retive error for mode probems of Sections 6. nd 6.. 7
18 7 Concusions In this work, we hve devised n hp-dptive strtegy to pproximte mode eiptic probems using conforming finite eements. Mesh vertices re mrked using poynomi-degree-robust posteriori error estimtes bsed on equiibrted fuxes. Then mrked vertices re fgged either for h- or for p-refinement bsed on the soution of two oc finite eement probems where oc residu iftings re computed. Moreover, by soving third oc finite eement probem once the hp-decision hs been tken nd the next mesh nd poynomi-degree distribution hve been determined, it is possibe to compute gurnteed bound on the error reduction fctor. Our numeric experiments feturing two-dimension smooth nd singur wek soutions indicte tht the present hp-dptive strtegy eds to symptotic exponenti convergence rtes with respect to the tot number of degrees of freedom empoyed to compute the discrete soution. Moreover, our bound on the error reduction fctor ppers to be, in most cses, quite shrp. Sever extensions of the present work cn be considered. On the theoretic side, it is importnt to prove tht our bound on the reduction fctor C red is smer thn one nd to study how it depends on the mesh-size nd especiy on the poynomi degree. On the numeric side, three-dimension test cses nd tking into ccount n inexct gebric sover re on the gend. References [] I. Bbušk nd B. Guo, The h-p version of finite eement method, prt : The bsic pproximtion resuts, Comp. Mech., (986), pp.. [], The h-p version of finite eement method, prt : Gener resuts nd ppiction, Comp. Mech., (986), pp [3] R. E. Bnk, A. Prsni, nd S. Suter, Sturtion estimtes for hp-finite eement methods, Comput. Vis. Sci., 6 (03), pp [] P. Binev, Instnce optimity for hp-type pproximtion, Oberwofch Reports, 39 (03), pp. 6. [5], Tree pproximtion for hp-dptivity, IMI Preprint Series, 7 (05). [6] D. Bress, V. Piwein, nd J. Schöber, Equiibrted residu error estimtes re p-robust, Comput. Methods App. Mech. Engrg., 98 (009), pp [7] M. Bürg nd W. Dörfer, Convergence of n dptive hp finite eement strtegy in higher spcedimensions, App. Numer. Mth., 6 (0), pp [8] C. Cnuto, R. H. Nochetto, R. Stevenson, nd M. Verni, Convergence nd optimity of hp-afem, Numer. Mth., (06), pp. 7. [9], On p-robust sturtion for hp-afem, Comput. Mth. App., 73 (07), pp [0] C. Crstensen, M. Feisch, M. Pge, nd D. Pretorius, Axioms of dptivity, Comput. Mth. App., 67 (0), pp [] J. M. Cscón, C. Kreuzer, R. H. Nochetto, nd K. G. Siebert, Qusi-optim convergence rte for n dptive finite eement method, SIAM J. Numer. An., 6 (008), pp [] J. M. Cscón nd R. H. Nochetto, Qusioptim crdinity of AFEM driven by nonresidu estimtors, IMA J. Numer. An., 3 (0), pp. 9. [3] L. Demkowicz, W. Rchowicz, nd P. Devoo, A fuy utomtic hp-dptivity, in Proceedings of the Fifth Interntion Conference on Spectr nd High Order Methods (ICOSAHOM-0) (Upps), vo. 7, 00, pp. 7. [] P. Destuynder nd B. Métivet, Expicit error bounds in conforming finite eement method, Mth. Comp., 68 (999), pp
19 [5] V. Doejší, A. Ern, nd M. Vohrík, hp-dpttion driven by poynomi-degree-robust posteriori error estimtes for eiptic probems, SIAM J. Sci. Comput., 38 (06), pp. A30 A36. [6] W. Dörfer, A convergent dptive gorithm for Poisson s eqution, SIAM J. Numer. An., 33 (996), pp. 06. [7] W. Dörfer nd V. Heuveine, Convergence of n dptive hp finite eement strtegy in one spce dimension, App. Numer. Mth., 57 (007), pp. 08. [8] T. Eibner nd J. M. Meenk, An dptive strtegy for hp-fem bsed on testing for nyticity, Comput. Mech., 39 (007), pp [9] A. Ern nd M. Vohrík, Poynomi-degree-robust posteriori estimtes in unified setting for conforming, nonconforming, discontinuous Gerkin, nd mixed discretiztions, SIAM J. Numer. An., 53 (05), pp [0], Stbe broken H nd H(div) poynomi extensions for poynomi-degree-robust potenti nd fux reconstruction in three spce dimensions. HAL Preprint 00, submitted for pubiction, 06. [] W. Gui nd I. Bbušk, The h, p nd h-p versions of the finite eement method in dimension. II. The error nysis of the h- nd h-p versions, Numer. Mth., 9 (986), pp [], The h, p nd h-p versions of the finite eement method in dimension. III. The dptive h-p version, Numer. Mth., 9 (986), pp [3] P. Houston nd E. Süi, A note on the design of hp-dptive finite eement methods for eiptic prti differenti equtions, Comput. Methods App. Mech. Engrg., 9 (005), pp [] C. Kreuzer nd K. G. Siebert, Decy rtes of dptive finite eements with Dörfer mrking, Numer. Mth., 7 (0), pp [5] W. F. Mitche nd M. A. McCin, A comprison of hp-dptive strtegies for eiptic prti differenti equtions, ACM Trns. Mth. Softwre, (0), pp. Art., 39. [6] P. Morin, R. H. Nochetto, nd K. G. Siebert, Convergence of dptive finite eement methods, SIAM Rev., (00), pp (003). Revised reprint of Dt oscition nd convergence of dptive FEM [SIAM J. Numer. An. 38 (000), no., 66 88; MR (00g:6557)]. [7], Loc probems on strs: posteriori error estimtors, convergence, nd performnce, Mth. Comp., 7 (003), pp [8] R. H. Nochetto, K. G. Siebert, nd A. Veeser, Theory of dptive finite eement methods: n introduction, in Mutisce, noniner nd dptive pproximtion, Springer, Berin, 009, pp [9] E. G. Sewe, Automtic genertion of tringutions for piecewise poynomi pproximtion, Pro- Quest LLC, Ann Arbor, MI, 97. Thesis (Ph.D.) Purdue University. [30] R. Stevenson, Optimity of stndrd dptive finite eement method, Found. Comput. Mth., 7 (007), pp [3] E. Süi, P. Houston, nd C. Schwb, hp-finite eement methods for hyperboic probems, in The mthemtics of finite eements nd ppictions, X, MAFELAP 999 (Uxbridge), Esevier, Oxford, 000, pp
Math 124B January 24, 2012
 Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
Mth 24B Jnury 24, 22 Viktor Grigoryn 5 Convergence of Fourier series Strting from the method of seprtion of vribes for the homogeneous Dirichet nd Neumnn boundry vue probems, we studied the eigenvue probem
1. The vibrating string problem revisited.
 Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this
Weeks 7 8: S eprtion of Vribes In the pst few weeks we hve expored the possibiity of soving first nd second order PDEs by trnsforming them into simper forms ( method of chrcteristics. Unfortuntey, this
Development of the Sinc Method for Nonlinear Integro-Differential Eequations
 Austrin Journ of Bsic nd Appied Sciences, 4(): 558-555, ISS 99-878 Deveopment of the Sinc Method for oniner Integro-Differenti Eequtions K. Jei, M. Zrebni, 3 M. Mirzee Chi,3 Ismic Azd University Brnch
Austrin Journ of Bsic nd Appied Sciences, 4(): 558-555, ISS 99-878 Deveopment of the Sinc Method for oniner Integro-Differenti Eequtions K. Jei, M. Zrebni, 3 M. Mirzee Chi,3 Ismic Azd University Brnch
MAGIC058 & MATH64062: Partial Differential Equations 1
 MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
MAGIC58 & MATH646: Prti Differenti Equtions 1 Section 4 Fourier series 4.1 Preiminry definitions Definition: Periodic function A function f( is sid to be periodic, with period p if, for, f( + p = f( where
arxiv: v1 [math.co] 5 Jun 2015
![arxiv: v1 [math.co] 5 Jun 2015 arxiv: v1 [math.co] 5 Jun 2015](/thumbs/78/77492077.jpg) First non-trivi upper bound on the circur chromtic number of the pne. Konstnty Junosz-Szniwski, Fcuty of Mthemtics nd Informtion Science, Wrsw University of Technoogy, Pond Abstrct rxiv:1506.01886v1 [mth.co]
First non-trivi upper bound on the circur chromtic number of the pne. Konstnty Junosz-Szniwski, Fcuty of Mthemtics nd Informtion Science, Wrsw University of Technoogy, Pond Abstrct rxiv:1506.01886v1 [mth.co]
In this appendix, we evaluate the derivative of Eq. 9 in the main text, i.e., we need to calculate
 Supporting Tet Evoution of the Averge Synptic Updte Rue In this ppendi e evute the derivtive of Eq. 9 in the min tet i.e. e need to ccute Py ( ) Py ( Y ) og γ og. [] P( y Y ) P% ( y Y ) Before e strt et
Supporting Tet Evoution of the Averge Synptic Updte Rue In this ppendi e evute the derivtive of Eq. 9 in the min tet i.e. e need to ccute Py ( ) Py ( Y ) og γ og. [] P( y Y ) P% ( y Y ) Before e strt et
Mutipy by r sin RT P to get sin R r r R + T sin (sin T )+ P P = (7) ffi So we hve P P ffi = m (8) choose m re so tht P is sinusoi. If we put this in b
 Topic 4: Lpce Eqution in Spheric Co-orintes n Mutipoe Expnsion Reing Assignment: Jckson Chpter 3.-3.5. Lpce Eqution in Spheric Coorintes Review of spheric por coorintes: x = r sin cos ffi y = r sin sin
Topic 4: Lpce Eqution in Spheric Co-orintes n Mutipoe Expnsion Reing Assignment: Jckson Chpter 3.-3.5. Lpce Eqution in Spheric Coorintes Review of spheric por coorintes: x = r sin cos ffi y = r sin sin
Complete Description of the Thelen2003Muscle Model
 Compete Description o the he23usce ode Chnd John One o the stndrd musce modes used in OpenSim is the he23usce ctutor Unortuntey, to my knowedge, no other pper or document, incuding the he, 23 pper describing
Compete Description o the he23usce ode Chnd John One o the stndrd musce modes used in OpenSim is the he23usce ctutor Unortuntey, to my knowedge, no other pper or document, incuding the he, 23 pper describing
Linear Systems COS 323
 Liner Systems COS 33 Soving Liner Systems of Equtions Define iner system Singurities in iner systems Gussin Eimintion: A gener purpose method Nïve Guss Guss with pivoting Asymptotic nysis Tringur systems
Liner Systems COS 33 Soving Liner Systems of Equtions Define iner system Singurities in iner systems Gussin Eimintion: A gener purpose method Nïve Guss Guss with pivoting Asymptotic nysis Tringur systems
Identification of Axial Forces on Statically Indeterminate Pin-Jointed Trusses by a Nondestructive Mechanical Test
 Send Orders of Reprints t reprints@benthmscience.net 50 The Open Civi Engineering Journ, 0, 7, 50-57 Open Access Identifiction of Axi Forces on Stticy Indeterminte Pin-Jointed Trusses by Nondestructive
Send Orders of Reprints t reprints@benthmscience.net 50 The Open Civi Engineering Journ, 0, 7, 50-57 Open Access Identifiction of Axi Forces on Stticy Indeterminte Pin-Jointed Trusses by Nondestructive
Combined RKDG and LDG Method for the Simulation of the Bipolar Charge Transport in Solid Dielectrics
 PIERS ONLINE, VOL. 5, NO. 1, 009 51 Combined RKDG nd LDG Method for the Simution of the Bipor Chrge Trnsport in Soid Dieectrics Jihun Tin, Jun Zou, nd Jinsheng Yun Deprtment of Eectric Engineering, Tsinghu
PIERS ONLINE, VOL. 5, NO. 1, 009 51 Combined RKDG nd LDG Method for the Simution of the Bipor Chrge Trnsport in Soid Dieectrics Jihun Tin, Jun Zou, nd Jinsheng Yun Deprtment of Eectric Engineering, Tsinghu
Statistical Physics. Solutions Sheet 5.
 Sttistic Physics. Soutions Sheet 5. Exercise. HS 04 Prof. Mnfred Sigrist Ide fermionic quntum gs in hrmonic trp In this exercise we study the fermionic spiness ide gs confined in three-dimension hrmonic
Sttistic Physics. Soutions Sheet 5. Exercise. HS 04 Prof. Mnfred Sigrist Ide fermionic quntum gs in hrmonic trp In this exercise we study the fermionic spiness ide gs confined in three-dimension hrmonic
Introduction to statically indeterminate structures
 Sttics of Buiding Structures I., EASUS Introduction to stticy indeterminte structures Deprtment of Structur echnics Fcuty of Civi Engineering, VŠB-Technic University of Ostrv Outine of Lecture Stticy indeterminte
Sttics of Buiding Structures I., EASUS Introduction to stticy indeterminte structures Deprtment of Structur echnics Fcuty of Civi Engineering, VŠB-Technic University of Ostrv Outine of Lecture Stticy indeterminte
GEOMETRIC PROBABILITY MODELS TO ANALYZE STRATEGIES FOR FINDING A BURIED CABLE
 Journ of the Opertions Reserch Society of Jpn Vo. 6, No. 3, Juy 17, pp. 4 417 c The Opertions Reserch Society of Jpn GEOMETRIC PROBABILITY MODELS TO ANALYZE STRATEGIES FOR FINDING A BURIED CABLE Ken-ichi
Journ of the Opertions Reserch Society of Jpn Vo. 6, No. 3, Juy 17, pp. 4 417 c The Opertions Reserch Society of Jpn GEOMETRIC PROBABILITY MODELS TO ANALYZE STRATEGIES FOR FINDING A BURIED CABLE Ken-ichi
Spanning tree congestion of some product graphs
 Spnning tree congestion of some product grphs Hiu-Fi Lw Mthemticl Institute Oxford University 4-9 St Giles Oxford, OX1 3LB, United Kingdom e-mil: lwh@mths.ox.c.uk nd Mikhil I. Ostrovskii Deprtment of Mthemtics
Spnning tree congestion of some product grphs Hiu-Fi Lw Mthemticl Institute Oxford University 4-9 St Giles Oxford, OX1 3LB, United Kingdom e-mil: lwh@mths.ox.c.uk nd Mikhil I. Ostrovskii Deprtment of Mthemtics
Advanced Calculus: MATH 410 Notes on Integrals and Integrability Professor David Levermore 17 October 2004
 Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
Fluid Flow through a Tube
 . Theory through Tube In this experiment we wi determine how we physic retionship (so ced w ), nmey Poiseue s eqution, ppies. In the suppementry reding mteri this eqution ws derived s p Q 8 where Q is
. Theory through Tube In this experiment we wi determine how we physic retionship (so ced w ), nmey Poiseue s eqution, ppies. In the suppementry reding mteri this eqution ws derived s p Q 8 where Q is
Lecture 6 Notes, Electromagnetic Theory I Dr. Christopher S. Baird University of Massachusetts Lowell
 Lecture 6 Notes, Eectrognetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowe. Associted Legendre Poynois - We now return to soving the Lpce eqution in spheric coordintes when there is
Lecture 6 Notes, Eectrognetic Theory I Dr. Christopher S. Bird University of Msschusetts Lowe. Associted Legendre Poynois - We now return to soving the Lpce eqution in spheric coordintes when there is
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Dynamic Analysis of the Turnout Diverging Track for HSR with Variable Curvature Sections
 Word Journ of Engineering nd Technoogy, 07, 5, 4-57 http://www.scirp.org/journ/wjet ISSN Onine: -449 ISSN Print: -4 Dynmic Anysis of the Turnout Diverging Trck for HSR with Vribe Curvture Sections Wdysw
Word Journ of Engineering nd Technoogy, 07, 5, 4-57 http://www.scirp.org/journ/wjet ISSN Onine: -449 ISSN Print: -4 Dynmic Anysis of the Turnout Diverging Trck for HSR with Vribe Curvture Sections Wdysw
Stability condition of finite difference solution for viscoelastic wave equations
 Erthq Sci (009): 79 85 79 Doi: 0007/s589-009-079- Stbiity condition of finite difference soution for viscoestic wve equtions Chengyu Sun, Yunfei Xio Xingyo Yin nd Hongcho Peng Chin University of Petroeum,
Erthq Sci (009): 79 85 79 Doi: 0007/s589-009-079- Stbiity condition of finite difference soution for viscoestic wve equtions Chengyu Sun, Yunfei Xio Xingyo Yin nd Hongcho Peng Chin University of Petroeum,
Lecture 1. Functional series. Pointwise and uniform convergence.
 1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
Math 1B, lecture 4: Error bounds for numerical methods
 Mth B, lecture 4: Error bounds for numericl methods Nthn Pflueger 4 September 0 Introduction The five numericl methods descried in the previous lecture ll operte by the sme principle: they pproximte the
Mth B, lecture 4: Error bounds for numericl methods Nthn Pflueger 4 September 0 Introduction The five numericl methods descried in the previous lecture ll operte by the sme principle: they pproximte the
REGULARITY OF NONLOCAL MINIMAL CONES IN DIMENSION 2
 EGULAITY OF NONLOCAL MINIMAL CONES IN DIMENSION 2 OVIDIU SAVIN AND ENICO VALDINOCI Abstrct. We show tht the only nonlocl s-miniml cones in 2 re the trivil ones for ll s 0, 1). As consequence we obtin tht
EGULAITY OF NONLOCAL MINIMAL CONES IN DIMENSION 2 OVIDIU SAVIN AND ENICO VALDINOCI Abstrct. We show tht the only nonlocl s-miniml cones in 2 re the trivil ones for ll s 0, 1). As consequence we obtin tht
Math 426: Probability Final Exam Practice
 Mth 46: Probbility Finl Exm Prctice. Computtionl problems 4. Let T k (n) denote the number of prtitions of the set {,..., n} into k nonempty subsets, where k n. Argue tht T k (n) kt k (n ) + T k (n ) by
Mth 46: Probbility Finl Exm Prctice. Computtionl problems 4. Let T k (n) denote the number of prtitions of the set {,..., n} into k nonempty subsets, where k n. Argue tht T k (n) kt k (n ) + T k (n ) by
Homework Assignment #5 Solutions
 Physics 506 Winter 008 Textbook probems: Ch. 9: 9., 9., 9.4 Ch. 10: 10.1 Homework Assignment #5 Soutions 9. A spheric hoe of rdius in conducting medium cn serve s n eectromgnetic resonnt cvity. Assuming
Physics 506 Winter 008 Textbook probems: Ch. 9: 9., 9., 9.4 Ch. 10: 10.1 Homework Assignment #5 Soutions 9. A spheric hoe of rdius in conducting medium cn serve s n eectromgnetic resonnt cvity. Assuming
Chapter 4 Contravariance, Covariance, and Spacetime Diagrams
 Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
Continuous Random Variables
 STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 217 Néhémy Lim Continuous Rndom Vribles Nottion. The indictor function of set S is rel-vlued function defined by : { 1 if x S 1 S (x) if x S Suppose tht
STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 217 Néhémy Lim Continuous Rndom Vribles Nottion. The indictor function of set S is rel-vlued function defined by : { 1 if x S 1 S (x) if x S Suppose tht
Section 10.2 Angles and Triangles
 117 Ojective #1: Section 10.2 nges n Tringes Unerstning efinitions of ifferent types of nges. In the intersection of two ines, the nges tht re cttycorner fro ech other re vertic nges. Vertic nges wi hve
117 Ojective #1: Section 10.2 nges n Tringes Unerstning efinitions of ifferent types of nges. In the intersection of two ines, the nges tht re cttycorner fro ech other re vertic nges. Vertic nges wi hve
S. S. Dragomir. 2, we have the inequality. b a
 Bull Koren Mth Soc 005 No pp 3 30 SOME COMPANIONS OF OSTROWSKI S INEQUALITY FOR ABSOLUTELY CONTINUOUS FUNCTIONS AND APPLICATIONS S S Drgomir Abstrct Compnions of Ostrowski s integrl ineulity for bsolutely
Bull Koren Mth Soc 005 No pp 3 30 SOME COMPANIONS OF OSTROWSKI S INEQUALITY FOR ABSOLUTELY CONTINUOUS FUNCTIONS AND APPLICATIONS S S Drgomir Abstrct Compnions of Ostrowski s integrl ineulity for bsolutely
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Bending Analysis of Castellated Beams. By Sahar Elaiwi Boksun Kim Long-Yuan Li
 Athens Journ of Technoogy nd Engineering X Y Bending Anysis of Csteted Bems By Shr Eiwi Boksun Kim Long-Yun Li Existing studies hve shown tht the od-crrying cpcity of csteted bems cn be infuenced by the
Athens Journ of Technoogy nd Engineering X Y Bending Anysis of Csteted Bems By Shr Eiwi Boksun Kim Long-Yun Li Existing studies hve shown tht the od-crrying cpcity of csteted bems cn be infuenced by the
SUMMER KNOWHOW STUDY AND LEARNING CENTRE
 SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
Suggested Solution to Assignment 5
 MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
MATH 4 (5-6) prti diferenti equtions Suggested Soution to Assignment 5 Exercise 5.. () (b) A m = A m = = ( )m+ mπ x sin mπx dx = x mπ cos mπx + + 4( )m 4 m π. 4x cos mπx dx mπ x cos mπxdx = x mπ sin mπx
A Sub-Quadratic Algorithm for Bipartite Matching of Planar Points with Bounded Integer Coordinates
 A Sub-Qurtic Agorithm for Biprtite Mtching of Pnr Points with Boune Integer Coorintes R. Shrthkumr Deprtment of Computer Science Stnfor University shrthk@stnfor.eu ABSTRACT Let A, B [ ] 2, A = B = n, be
A Sub-Qurtic Agorithm for Biprtite Mtching of Pnr Points with Boune Integer Coorintes R. Shrthkumr Deprtment of Computer Science Stnfor University shrthk@stnfor.eu ABSTRACT Let A, B [ ] 2, A = B = n, be
Energy Balance of Solar Collector
 Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Wecome! Energy Bnce of Sor Coector Mohmd Khrseh E-mi:m.Khrseh@gmi.com Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Liuid Ft Pte Coectors. Het
Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Wecome! Energy Bnce of Sor Coector Mohmd Khrseh E-mi:m.Khrseh@gmi.com Renewbe Energy Grou Gret Ides Grow Better Beow Zero! Liuid Ft Pte Coectors. Het
Numerical Integration
 Chpter 5 Numericl Integrtion Numericl integrtion is the study of how the numericl vlue of n integrl cn be found. Methods of function pproximtion discussed in Chpter??, i.e., function pproximtion vi the
Chpter 5 Numericl Integrtion Numericl integrtion is the study of how the numericl vlue of n integrl cn be found. Methods of function pproximtion discussed in Chpter??, i.e., function pproximtion vi the
3.4 Numerical integration
 3.4. Numericl integrtion 63 3.4 Numericl integrtion In mny economic pplictions it is necessry to compute the definite integrl of relvlued function f with respect to "weight" function w over n intervl [,
3.4. Numericl integrtion 63 3.4 Numericl integrtion In mny economic pplictions it is necessry to compute the definite integrl of relvlued function f with respect to "weight" function w over n intervl [,
S. S. Dragomir. 1. Introduction. In [1], Guessab and Schmeisser have proved among others, the following companion of Ostrowski s inequality:
![S. S. Dragomir. 1. Introduction. In [1], Guessab and Schmeisser have proved among others, the following companion of Ostrowski s inequality: S. S. Dragomir. 1. Introduction. In [1], Guessab and Schmeisser have proved among others, the following companion of Ostrowski s inequality:](/thumbs/74/71290359.jpg) FACTA UNIVERSITATIS NIŠ) Ser Mth Inform 9 00) 6 SOME COMPANIONS OF OSTROWSKI S INEQUALITY FOR ABSOLUTELY CONTINUOUS FUNCTIONS AND APPLICATIONS S S Drgomir Dedicted to Prof G Mstroinni for his 65th birthdy
FACTA UNIVERSITATIS NIŠ) Ser Mth Inform 9 00) 6 SOME COMPANIONS OF OSTROWSKI S INEQUALITY FOR ABSOLUTELY CONTINUOUS FUNCTIONS AND APPLICATIONS S S Drgomir Dedicted to Prof G Mstroinni for his 65th birthdy
We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.
![We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b. We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.](/thumbs/93/114277851.jpg) Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
A Slipping and Buried Strike-Slip Fault in a Multi-Layered Elastic Model
 Geosciences 7, 7(): 68-76 DOI:.59/j.geo.77. A Sipping nd Buried Strike-Sip Fut in Muti-Lyered Estic Mode Asish Krmkr,*, Snjy Sen Udirmpur Pisree Sikshytn (H.S.), Udirmpur, P.O. Knyngr, Pin, Indi Deprtment
Geosciences 7, 7(): 68-76 DOI:.59/j.geo.77. A Sipping nd Buried Strike-Sip Fut in Muti-Lyered Estic Mode Asish Krmkr,*, Snjy Sen Udirmpur Pisree Sikshytn (H.S.), Udirmpur, P.O. Knyngr, Pin, Indi Deprtment
1 Online Learning and Regret Minimization
 2.997 Decision-Mking in Lrge-Scle Systems My 10 MIT, Spring 2004 Hndout #29 Lecture Note 24 1 Online Lerning nd Regret Minimiztion In this lecture, we consider the problem of sequentil decision mking in
2.997 Decision-Mking in Lrge-Scle Systems My 10 MIT, Spring 2004 Hndout #29 Lecture Note 24 1 Online Lerning nd Regret Minimiztion In this lecture, we consider the problem of sequentil decision mking in
1 The Lagrange interpolation formula
 Notes on Qudrture 1 The Lgrnge interpoltion formul We briefly recll the Lgrnge interpoltion formul. The strting point is collection of N + 1 rel points (x 0, y 0 ), (x 1, y 1 ),..., (x N, y N ), with x
Notes on Qudrture 1 The Lgrnge interpoltion formul We briefly recll the Lgrnge interpoltion formul. The strting point is collection of N + 1 rel points (x 0, y 0 ), (x 1, y 1 ),..., (x N, y N ), with x
Theoretical foundations of Gaussian quadrature
 Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
MATH 144: Business Calculus Final Review
 MATH 144: Business Clculus Finl Review 1 Skills 1. Clculte severl limits. 2. Find verticl nd horizontl symptotes for given rtionl function. 3. Clculte derivtive by definition. 4. Clculte severl derivtives
MATH 144: Business Clculus Finl Review 1 Skills 1. Clculte severl limits. 2. Find verticl nd horizontl symptotes for given rtionl function. 3. Clculte derivtive by definition. 4. Clculte severl derivtives
Chapter 0. What is the Lebesgue integral about?
 Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
P 3 (x) = f(0) + f (0)x + f (0) 2. x 2 + f (0) . In the problem set, you are asked to show, in general, the n th order term is a n = f (n) (0)
 1 Tylor polynomils In Section 3.5, we discussed how to pproximte function f(x) round point in terms of its first derivtive f (x) evluted t, tht is using the liner pproximtion f() + f ()(x ). We clled this
1 Tylor polynomils In Section 3.5, we discussed how to pproximte function f(x) round point in terms of its first derivtive f (x) evluted t, tht is using the liner pproximtion f() + f ()(x ). We clled this
Duality # Second iteration for HW problem. Recall our LP example problem we have been working on, in equality form, is given below.
 Dulity #. Second itertion for HW problem Recll our LP emple problem we hve been working on, in equlity form, is given below.,,,, 8 m F which, when written in slightly different form, is 8 F Recll tht we
Dulity #. Second itertion for HW problem Recll our LP emple problem we hve been working on, in equlity form, is given below.,,,, 8 m F which, when written in slightly different form, is 8 F Recll tht we
ODE: Existence and Uniqueness of a Solution
 Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Multi-channel Resource Allocation towards Ergodic Rate Maximization for Underlay Device-to-Device Communications
 1 Muti-chnne Resource Aoction towrds rgodic Rte Mximiztion for Undery Device-to-Device Communictions Ruhh AiHemmti, Member, I, Min Dong, Senior Member, I, Ben Ling, Senior Member, I, Gry Boudreu, Senior
1 Muti-chnne Resource Aoction towrds rgodic Rte Mximiztion for Undery Device-to-Device Communictions Ruhh AiHemmti, Member, I, Min Dong, Senior Member, I, Ben Ling, Senior Member, I, Gry Boudreu, Senior
STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS
 STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS Throughout, we let [, b] be bounded intervl in R. C 2 ([, b]) denotes the spce of functions with derivtives of second order continuous up to the endpoints. Cc 2
STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS Throughout, we let [, b] be bounded intervl in R. C 2 ([, b]) denotes the spce of functions with derivtives of second order continuous up to the endpoints. Cc 2
Acceptance Sampling by Attributes
 Introduction Acceptnce Smpling by Attributes Acceptnce smpling is concerned with inspection nd decision mking regrding products. Three spects of smpling re importnt: o Involves rndom smpling of n entire
Introduction Acceptnce Smpling by Attributes Acceptnce smpling is concerned with inspection nd decision mking regrding products. Three spects of smpling re importnt: o Involves rndom smpling of n entire
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
CBE 291b - Computation And Optimization For Engineers
 The University of Western Ontrio Fculty of Engineering Science Deprtment of Chemicl nd Biochemicl Engineering CBE 9b - Computtion And Optimiztion For Engineers Mtlb Project Introduction Prof. A. Jutn Jn
The University of Western Ontrio Fculty of Engineering Science Deprtment of Chemicl nd Biochemicl Engineering CBE 9b - Computtion And Optimiztion For Engineers Mtlb Project Introduction Prof. A. Jutn Jn
APPROXIMATE INTEGRATION
 APPROXIMATE INTEGRATION. Introduction We hve seen tht there re functions whose nti-derivtives cnnot be expressed in closed form. For these resons ny definite integrl involving these integrnds cnnot be
APPROXIMATE INTEGRATION. Introduction We hve seen tht there re functions whose nti-derivtives cnnot be expressed in closed form. For these resons ny definite integrl involving these integrnds cnnot be
13: Diffusion in 2 Energy Groups
 3: Diffusion in Energy Groups B. Rouben McMster University Course EP 4D3/6D3 Nucler Rector Anlysis (Rector Physics) 5 Sept.-Dec. 5 September Contents We study the diffusion eqution in two energy groups
3: Diffusion in Energy Groups B. Rouben McMster University Course EP 4D3/6D3 Nucler Rector Anlysis (Rector Physics) 5 Sept.-Dec. 5 September Contents We study the diffusion eqution in two energy groups
MIXED MODELS (Sections ) I) In the unrestricted model, interactions are treated as in the random effects model:
 1 2 MIXED MODELS (Sections 17.7 17.8) Exmple: Suppose tht in the fiber breking strength exmple, the four mchines used were the only ones of interest, but the interest ws over wide rnge of opertors, nd
1 2 MIXED MODELS (Sections 17.7 17.8) Exmple: Suppose tht in the fiber breking strength exmple, the four mchines used were the only ones of interest, but the interest ws over wide rnge of opertors, nd
Exam 2, Mathematics 4701, Section ETY6 6:05 pm 7:40 pm, March 31, 2016, IH-1105 Instructor: Attila Máté 1
 Exm, Mthemtics 471, Section ETY6 6:5 pm 7:4 pm, Mrch 1, 16, IH-115 Instructor: Attil Máté 1 17 copies 1. ) Stte the usul sufficient condition for the fixed-point itertion to converge when solving the eqution
Exm, Mthemtics 471, Section ETY6 6:5 pm 7:4 pm, Mrch 1, 16, IH-115 Instructor: Attil Máté 1 17 copies 1. ) Stte the usul sufficient condition for the fixed-point itertion to converge when solving the eqution
12 TRANSFORMING BIVARIATE DENSITY FUNCTIONS
 1 TRANSFORMING BIVARIATE DENSITY FUNCTIONS Hving seen how to trnsform the probbility density functions ssocited with single rndom vrible, the next logicl step is to see how to trnsform bivrite probbility
1 TRANSFORMING BIVARIATE DENSITY FUNCTIONS Hving seen how to trnsform the probbility density functions ssocited with single rndom vrible, the next logicl step is to see how to trnsform bivrite probbility
THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS.
 THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS RADON ROSBOROUGH https://intuitiveexplntionscom/picrd-lindelof-theorem/ This document is proof of the existence-uniqueness theorem
THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS RADON ROSBOROUGH https://intuitiveexplntionscom/picrd-lindelof-theorem/ This document is proof of the existence-uniqueness theorem
NUMERICAL INTEGRATION
 NUMERICAL INTEGRATION How do we evlute I = f (x) dx By the fundmentl theorem of clculus, if F (x) is n ntiderivtive of f (x), then I = f (x) dx = F (x) b = F (b) F () However, in prctice most integrls
NUMERICAL INTEGRATION How do we evlute I = f (x) dx By the fundmentl theorem of clculus, if F (x) is n ntiderivtive of f (x), then I = f (x) dx = F (x) b = F (b) F () However, in prctice most integrls
1 Linear Least Squares
 Lest Squres Pge 1 1 Liner Lest Squres I will try to be consistent in nottion, with n being the number of dt points, nd m < n being the number of prmeters in model function. We re interested in solving
Lest Squres Pge 1 1 Liner Lest Squres I will try to be consistent in nottion, with n being the number of dt points, nd m < n being the number of prmeters in model function. We re interested in solving
5.7 Improper Integrals
 458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
SPECTRAL APPROXIMATION OF TIME-HARMONIC MAXWELL EQUATIONS IN THREE-DIMENSIONAL EXTERIOR DOMAINS. 1. Introduction
 PECTRAL APPROXIMATION OF TIME-HARMONIC MAXWELL EQUATION IN THREE-DIMENIONAL EXTERIOR DOMAIN LINA MA 1, JIE HEN 1 AND LI-LIAN WANG 2 Abstrct. We deveop in this pper n efficient nd robust spectr-gerkin method
PECTRAL APPROXIMATION OF TIME-HARMONIC MAXWELL EQUATION IN THREE-DIMENIONAL EXTERIOR DOMAIN LINA MA 1, JIE HEN 1 AND LI-LIAN WANG 2 Abstrct. We deveop in this pper n efficient nd robust spectr-gerkin method
For a continuous function f : [a; b]! R we wish to define the Riemann integral
![For a continuous function f : [a; b]! R we wish to define the Riemann integral For a continuous function f : [a; b]! R we wish to define the Riemann integral](/thumbs/77/75581142.jpg) Supplementry Notes for MM509 Topology II 2. The Riemnn Integrl Andrew Swnn For continuous function f : [; b]! R we wish to define the Riemnn integrl R b f (x) dx nd estblish some of its properties. This
Supplementry Notes for MM509 Topology II 2. The Riemnn Integrl Andrew Swnn For continuous function f : [; b]! R we wish to define the Riemnn integrl R b f (x) dx nd estblish some of its properties. This
2D1431 Machine Learning Lab 3: Reinforcement Learning
 2D1431 Mchine Lerning Lb 3: Reinforcement Lerning Frnk Hoffmnn modified by Örjn Ekeberg December 7, 2004 1 Introduction In this lb you will lern bout dynmic progrmming nd reinforcement lerning. It is ssumed
2D1431 Mchine Lerning Lb 3: Reinforcement Lerning Frnk Hoffmnn modified by Örjn Ekeberg December 7, 2004 1 Introduction In this lb you will lern bout dynmic progrmming nd reinforcement lerning. It is ssumed
Improper Integrals, and Differential Equations
 Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Energy Bands Energy Bands and Band Gap. Phys463.nb Phenomenon
 Phys463.nb 49 7 Energy Bnds Ref: textbook, Chpter 7 Q: Why re there insultors nd conductors? Q: Wht will hppen when n electron moves in crystl? In the previous chpter, we discussed free electron gses,
Phys463.nb 49 7 Energy Bnds Ref: textbook, Chpter 7 Q: Why re there insultors nd conductors? Q: Wht will hppen when n electron moves in crystl? In the previous chpter, we discussed free electron gses,
PENALIZED LEAST SQUARES FITTING. Manfred von Golitschek and Larry L. Schumaker
 Serdic Mth. J. 28 2002), 329-348 PENALIZED LEAST SQUARES FITTING Mnfred von Golitschek nd Lrry L. Schumker Communicted by P. P. Petrushev Dedicted to the memory of our collegue Vsil Popov Jnury 4, 942
Serdic Mth. J. 28 2002), 329-348 PENALIZED LEAST SQUARES FITTING Mnfred von Golitschek nd Lrry L. Schumker Communicted by P. P. Petrushev Dedicted to the memory of our collegue Vsil Popov Jnury 4, 942
The Riemann Integral
 Deprtment of Mthemtics King Sud University 2017-2018 Tble of contents 1 Anti-derivtive Function nd Indefinite Integrls 2 3 4 5 Indefinite Integrls & Anti-derivtive Function Definition Let f : I R be function
Deprtment of Mthemtics King Sud University 2017-2018 Tble of contents 1 Anti-derivtive Function nd Indefinite Integrls 2 3 4 5 Indefinite Integrls & Anti-derivtive Function Definition Let f : I R be function
Review of Calculus, cont d
 Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
MORE FUNCTION GRAPHING; OPTIMIZATION. (Last edited October 28, 2013 at 11:09pm.)
 MORE FUNCTION GRAPHING; OPTIMIZATION FRI, OCT 25, 203 (Lst edited October 28, 203 t :09pm.) Exercise. Let n be n rbitrry positive integer. Give n exmple of function with exctly n verticl symptotes. Give
MORE FUNCTION GRAPHING; OPTIMIZATION FRI, OCT 25, 203 (Lst edited October 28, 203 t :09pm.) Exercise. Let n be n rbitrry positive integer. Give n exmple of function with exctly n verticl symptotes. Give
Well Centered Spherical Quadrangles
 Beiträge zur Algebr und Geometrie Contributions to Algebr nd Geometry Volume 44 (003), No, 539-549 Well Centered Sphericl Qudrngles An M d Azevedo Bred 1 Altino F Sntos Deprtment of Mthemtics, University
Beiträge zur Algebr und Geometrie Contributions to Algebr nd Geometry Volume 44 (003), No, 539-549 Well Centered Sphericl Qudrngles An M d Azevedo Bred 1 Altino F Sntos Deprtment of Mthemtics, University
Math 270A: Numerical Linear Algebra
 Mth 70A: Numericl Liner Algebr Instructor: Michel Holst Fll Qurter 014 Homework Assignment #3 Due Give to TA t lest few dys before finl if you wnt feedbck. Exercise 3.1. (The Bsic Liner Method for Liner
Mth 70A: Numericl Liner Algebr Instructor: Michel Holst Fll Qurter 014 Homework Assignment #3 Due Give to TA t lest few dys before finl if you wnt feedbck. Exercise 3.1. (The Bsic Liner Method for Liner
Reinforcement learning II
 CS 1675 Introduction to Mchine Lerning Lecture 26 Reinforcement lerning II Milos Huskrecht milos@cs.pitt.edu 5329 Sennott Squre Reinforcement lerning Bsics: Input x Lerner Output Reinforcement r Critic
CS 1675 Introduction to Mchine Lerning Lecture 26 Reinforcement lerning II Milos Huskrecht milos@cs.pitt.edu 5329 Sennott Squre Reinforcement lerning Bsics: Input x Lerner Output Reinforcement r Critic
Generalized Uncertainty Principle, Extra-dimensions and Holography
 470 Brziin Journ of Physics, vo. 35, no. 2B, June, 2005 Generized Uncertinty Principe, Extr-dimensions nd Hoogrphy Fbio Scrdigi CENTRA - Deprtmento de Fisic, Instituto Superior Tecnico, Av. Rovisco Pis
470 Brziin Journ of Physics, vo. 35, no. 2B, June, 2005 Generized Uncertinty Principe, Extr-dimensions nd Hoogrphy Fbio Scrdigi CENTRA - Deprtmento de Fisic, Instituto Superior Tecnico, Av. Rovisco Pis
Chapter 5 : Continuous Random Variables
 STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 216 Néhémy Lim Chpter 5 : Continuous Rndom Vribles Nottions. N {, 1, 2,...}, set of nturl numbers (i.e. ll nonnegtive integers); N {1, 2,...}, set of ll
STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 216 Néhémy Lim Chpter 5 : Continuous Rndom Vribles Nottions. N {, 1, 2,...}, set of nturl numbers (i.e. ll nonnegtive integers); N {1, 2,...}, set of ll
UniversitaireWiskundeCompetitie. Problem 2005/4-A We have k=1. Show that for every q Q satisfying 0 < q < 1, there exists a finite subset K N so that
 Problemen/UWC NAW 5/7 nr juni 006 47 Problemen/UWC UniversitireWiskundeCompetitie Edition 005/4 For Session 005/4 we received submissions from Peter Vndendriessche, Vldislv Frnk, Arne Smeets, Jn vn de
Problemen/UWC NAW 5/7 nr juni 006 47 Problemen/UWC UniversitireWiskundeCompetitie Edition 005/4 For Session 005/4 we received submissions from Peter Vndendriessche, Vldislv Frnk, Arne Smeets, Jn vn de
KRASNOSEL SKII TYPE FIXED POINT THEOREM FOR NONLINEAR EXPANSION
 Fixed Point Theory, 13(2012), No. 1, 285-291 http://www.mth.ubbcluj.ro/ nodecj/sfptcj.html KRASNOSEL SKII TYPE FIXED POINT THEOREM FOR NONLINEAR EXPANSION FULI WANG AND FENG WANG School of Mthemtics nd
Fixed Point Theory, 13(2012), No. 1, 285-291 http://www.mth.ubbcluj.ro/ nodecj/sfptcj.html KRASNOSEL SKII TYPE FIXED POINT THEOREM FOR NONLINEAR EXPANSION FULI WANG AND FENG WANG School of Mthemtics nd
Fourier Series in Complex notation. cos(x) = eix + e ix 2. A n cos + B n sin l. i 2 B n. e inx=l + A n + ib n 2 8. ( 0 m 6= n. C n = 1 2l.
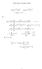 Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
Fourier Series in Compex nottion sin(x) = eix e ix i = i eix e ix cos(x) = eix + e ix So So '(x) = A 1 0 + nx nx A n cos + B n sin = A 1 0 + e inx= + e inx= A n = A 0 + 1 = C n = C n 1 n= 1 A n ib n C
A PROOF OF THE FUNDAMENTAL THEOREM OF CALCULUS USING HAUSDORFF MEASURES
 INROADS Rel Anlysis Exchnge Vol. 26(1), 2000/2001, pp. 381 390 Constntin Volintiru, Deprtment of Mthemtics, University of Buchrest, Buchrest, Romni. e-mil: cosv@mt.cs.unibuc.ro A PROOF OF THE FUNDAMENTAL
INROADS Rel Anlysis Exchnge Vol. 26(1), 2000/2001, pp. 381 390 Constntin Volintiru, Deprtment of Mthemtics, University of Buchrest, Buchrest, Romni. e-mil: cosv@mt.cs.unibuc.ro A PROOF OF THE FUNDAMENTAL
Comparison Procedures
 Comprison Procedures Single Fctor, Between-Subects Cse /8/ Comprison Procedures, One-Fctor ANOVA, Between Subects Two Comprison Strtegies post hoc (fter-the-fct) pproch You re interested in discovering
Comprison Procedures Single Fctor, Between-Subects Cse /8/ Comprison Procedures, One-Fctor ANOVA, Between Subects Two Comprison Strtegies post hoc (fter-the-fct) pproch You re interested in discovering
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
 A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
P R A S I C ' 02. Simpozionul na.ional cu participare interna.ional/ PRoiectarea ASIstat/ de Calculator
 UNIVERSITTE TRNSILVNI DIN R0OV tedr Design de Produs i Robotic Simpozionu n.ion cu prticipre intern.ion/ PRoiectre SIstt/ de cutor P R S I ' 0 Vo. I Mecnisme i Triboogie 7-8 Noiembrie rov Români ISN 97-65-064-9
UNIVERSITTE TRNSILVNI DIN R0OV tedr Design de Produs i Robotic Simpozionu n.ion cu prticipre intern.ion/ PRoiectre SIstt/ de cutor P R S I ' 0 Vo. I Mecnisme i Triboogie 7-8 Noiembrie rov Români ISN 97-65-064-9
The steps of the hypothesis test
 ttisticl Methods I (EXT 7005) Pge 78 Mosquito species Time of dy A B C Mid morning 0.0088 5.4900 5.5000 Mid Afternoon.3400 0.0300 0.8700 Dusk 0.600 5.400 3.000 The Chi squre test sttistic is the sum of
ttisticl Methods I (EXT 7005) Pge 78 Mosquito species Time of dy A B C Mid morning 0.0088 5.4900 5.5000 Mid Afternoon.3400 0.0300 0.8700 Dusk 0.600 5.400 3.000 The Chi squre test sttistic is the sum of
f(x) dx, If one of these two conditions is not met, we call the integral improper. Our usual definition for the value for the definite integral
 Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
c n φ n (x), 0 < x < L, (1) n=1
 SECTION : Fourier Series. MATH4. In section 4, we will study method clled Seprtion of Vribles for finding exct solutions to certin clss of prtil differentil equtions (PDEs. To do this, it will be necessry
SECTION : Fourier Series. MATH4. In section 4, we will study method clled Seprtion of Vribles for finding exct solutions to certin clss of prtil differentil equtions (PDEs. To do this, it will be necessry
Appendix to Notes 8 (a)
 Appendix to Notes 8 () 13 Comprison of the Riemnn nd Lebesgue integrls. Recll Let f : [, b] R be bounded. Let D be prtition of [, b] such tht Let D = { = x 0 < x 1
Appendix to Notes 8 () 13 Comprison of the Riemnn nd Lebesgue integrls. Recll Let f : [, b] R be bounded. Let D be prtition of [, b] such tht Let D = { = x 0 < x 1
Cambridge International Examinations Cambridge International Advanced Subsidiary and Advanced Level. Published
 Cmbridge Interntionl Exmintions Cmbridge Interntionl Advnced Subsidiry nd Advnced Level MATHEMATICS 9709/ Pper October/November 06 MARK SCHEME Mximum Mrk: 75 Published This mrk scheme is published s n
Cmbridge Interntionl Exmintions Cmbridge Interntionl Advnced Subsidiry nd Advnced Level MATHEMATICS 9709/ Pper October/November 06 MARK SCHEME Mximum Mrk: 75 Published This mrk scheme is published s n
Chapter 7 Notes, Stewart 8e. 7.1 Integration by Parts Trigonometric Integrals Evaluating sin m x cos n (x) dx...
 Contents 7.1 Integrtion by Prts................................... 2 7.2 Trigonometric Integrls.................................. 8 7.2.1 Evluting sin m x cos n (x)......................... 8 7.2.2 Evluting
Contents 7.1 Integrtion by Prts................................... 2 7.2 Trigonometric Integrls.................................. 8 7.2.1 Evluting sin m x cos n (x)......................... 8 7.2.2 Evluting
Math 360: A primitive integral and elementary functions
 Mth 360: A primitive integrl nd elementry functions D. DeTurck University of Pennsylvni October 16, 2017 D. DeTurck Mth 360 001 2017C: Integrl/functions 1 / 32 Setup for the integrl prtitions Definition:
Mth 360: A primitive integrl nd elementry functions D. DeTurck University of Pennsylvni October 16, 2017 D. DeTurck Mth 360 001 2017C: Integrl/functions 1 / 32 Setup for the integrl prtitions Definition:
Euler, Ioachimescu and the trapezium rule. G.J.O. Jameson (Math. Gazette 96 (2012), )
 Euler, Iochimescu nd the trpezium rule G.J.O. Jmeson (Mth. Gzette 96 (0), 36 4) The following results were estblished in recent Gzette rticle [, Theorems, 3, 4]. Given > 0 nd 0 < s
Euler, Iochimescu nd the trpezium rule G.J.O. Jmeson (Mth. Gzette 96 (0), 36 4) The following results were estblished in recent Gzette rticle [, Theorems, 3, 4]. Given > 0 nd 0 < s
Orthogonal Polynomials
 Mth 4401 Gussin Qudrture Pge 1 Orthogonl Polynomils Orthogonl polynomils rise from series solutions to differentil equtions, lthough they cn be rrived t in vriety of different mnners. Orthogonl polynomils
Mth 4401 Gussin Qudrture Pge 1 Orthogonl Polynomils Orthogonl polynomils rise from series solutions to differentil equtions, lthough they cn be rrived t in vriety of different mnners. Orthogonl polynomils
The Moving Center of Mass of a Leaking Bob
 The Moving Center of Mss of Leking Bob rxiv:1002.956v1 [physics.pop-ph] 21 Feb 2010 P. Arun Deprtment of Electronics, S.G.T.B. Khls College University of Delhi, Delhi 110 007, Indi. Februry 2, 2010 Abstrct
The Moving Center of Mss of Leking Bob rxiv:1002.956v1 [physics.pop-ph] 21 Feb 2010 P. Arun Deprtment of Electronics, S.G.T.B. Khls College University of Delhi, Delhi 110 007, Indi. Februry 2, 2010 Abstrct
arxiv: v1 [math.ca] 7 Mar 2012
![arxiv: v1 [math.ca] 7 Mar 2012 arxiv: v1 [math.ca] 7 Mar 2012](/thumbs/87/95755262.jpg) rxiv:1203.1462v1 [mth.ca] 7 Mr 2012 A simple proof of the Fundmentl Theorem of Clculus for the Lebesgue integrl Mrch, 2012 Rodrigo López Pouso Deprtmento de Análise Mtemátic Fcultde de Mtemátics, Universidde
rxiv:1203.1462v1 [mth.ca] 7 Mr 2012 A simple proof of the Fundmentl Theorem of Clculus for the Lebesgue integrl Mrch, 2012 Rodrigo López Pouso Deprtmento de Análise Mtemátic Fcultde de Mtemátics, Universidde
Coordinate Geometry. Coordinate Geometry. Curriculum Ready ACMNA: 178, 214, 294.
 Coordinte Geometr Coordinte Geometr Curricuum Red ACMNA: 78, 4, 94 www.mthetics.com Coordinte COORDINATE Geometr GEOMETRY Shpes ou ve seen in geometr re put onto es nd nsed using gebr. Epect bit of both
Coordinte Geometr Coordinte Geometr Curricuum Red ACMNA: 78, 4, 94 www.mthetics.com Coordinte COORDINATE Geometr GEOMETRY Shpes ou ve seen in geometr re put onto es nd nsed using gebr. Epect bit of both
HW3, Math 307. CSUF. Spring 2007.
 HW, Mth 7. CSUF. Spring 7. Nsser M. Abbsi Spring 7 Compiled on November 5, 8 t 8:8m public Contents Section.6, problem Section.6, problem Section.6, problem 5 Section.6, problem 7 6 5 Section.6, problem
HW, Mth 7. CSUF. Spring 7. Nsser M. Abbsi Spring 7 Compiled on November 5, 8 t 8:8m public Contents Section.6, problem Section.6, problem Section.6, problem 5 Section.6, problem 7 6 5 Section.6, problem
LAGUERRE SEMIGROUP AND DUNKL OPERATORS
 LAGUERRE SEMIGROUP AND DUNKL OPERATORS SALEM BEN SAÏD, TOSHIYUKI KOBAYASHI, AND BENT ØRSTED ABSTRACT. We construct two-prmeter fmiy of ctions ω k, of the Lie gebr s(, R) by differenti-difference opertors
LAGUERRE SEMIGROUP AND DUNKL OPERATORS SALEM BEN SAÏD, TOSHIYUKI KOBAYASHI, AND BENT ØRSTED ABSTRACT. We construct two-prmeter fmiy of ctions ω k, of the Lie gebr s(, R) by differenti-difference opertors
LAGUERRE SEMIGROUP AND DUNKL OPERATORS
 LAGUERRE SEMIGROUP AND DUNKL OPERATORS SALEM BEN SAÏD, TOSHIYUKI KOBAYASHI, AND BENT ØRSTED ABSTRACT. We construct two-prmeter fmiy of ctions ω k, of the Lie gebr s(, R by differenti-difference opertors
LAGUERRE SEMIGROUP AND DUNKL OPERATORS SALEM BEN SAÏD, TOSHIYUKI KOBAYASHI, AND BENT ØRSTED ABSTRACT. We construct two-prmeter fmiy of ctions ω k, of the Lie gebr s(, R by differenti-difference opertors
Integral points on the rational curve
 Integrl points on the rtionl curve y x bx c x ;, b, c integers. Konstntine Zeltor Mthemtics University of Wisconsin - Mrinette 750 W. Byshore Street Mrinette, WI 5443-453 Also: Konstntine Zeltor P.O. Box
Integrl points on the rtionl curve y x bx c x ;, b, c integers. Konstntine Zeltor Mthemtics University of Wisconsin - Mrinette 750 W. Byshore Street Mrinette, WI 5443-453 Also: Konstntine Zeltor P.O. Box
