UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE NATYRORE DEPARTAMENTI I MATEMATIKËS APLIKUAR
|
|
|
- Hope Parsons
- 6 years ago
- Views:
Transcription
1 UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE NATYRORE DEPARTAMENTI I MATEMATIKËS APLIKUAR Tema: NJË MODEL MARKOVIAN PËR SHPËRNDARJEN UNIVARIATE DHE MULTIVARIATE TË PORTOFOLIT NË RISK TË KREDISË Program: Metodat probabltare statstke dhe metodat e aalzës umerke Kaddat: Doc. Msc. Romeo Mao Udhëheqës shkecor: Prof. Dr. Ma Naqo Prof. Dr. Lluka Puka TIRANË 2015
2 UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE NATYRORE DEPARTAMENTI I MATEMATIKËS APLIKUAR DISERTACION paraqtur ga: Doc. Msc. Romeo MANO Udhëhequr ga: Prof. Dr. Ma Naqo Prof. Dr. Lluka Puka për marrje e gradës shkecore DOKTOR Me temë: NJË MODEL MARKOVIAN PËR SHPËRNDARJEN UNIVARIATE DHE MULTIVARIATE TË PORTOFOLIT NË RISK TË KREDISË Mbrohet më date / / para jursë: 1. Prof. Kryetar 2. Prof. Aëtar (Opoet) 3. Prof. Aëtar (Opoet) 4. Prof. Aëtar 5. Prof. Aëtar
3 Fëmjëve të m Prdërve të m
4 Mrëjohje dhe Falederme Përfudm dzertacot uk do të shte mudur të falzohej me sukses pa kurajm mbështetje dhe dhmë e dsa persoave daj të clëve uë dua të shpreh mrëjohje tme të thellë. Falederoj me mrëjohje dhe respekt të veçatë udhëheqëst e m shkecorë Prof. Dr. Lluka PUKA dhe Prof. Dr. Ma NAQO të clët me mrësë dashamrësë dhe përkushtm e tyre shkecor dhe persoal sh bashkëudhëtarët e m frymëzues dhe këshllues për realzm dhe falzm me sukses të këtj pum. Një falederm të veçatë do doja të shprehja për sh-kolegët e m të departamett të kredsë dhe rskut të kredsë të kompasë mkrofacare Parter Shqptar ë Mkrokred (sot NOA-Albaa) dhe bakës ProCredt Bak Albaa. Bashkëpum profesoal dhe mqësor me këta jerëz ka qëë jë tram rëdësshëm për mua ë fushë e rskut të kredsë dhe faktorëve facar dhe socal që dkojë ë të. Puësm për jë kohë të gjatë ë pozco e aalstt të lartë të kredsë dhë më pas atë të drejtuest kaë shërbyer për dem dhe perceptm teorko-facar të pumt. Gjej rast të falederoj të gjthë kolegët e Departamett të Matematkës dhe Iformatkës të Fakultett të Shkecave Natyrore të Uverstett Eqrem Çabej të Gjrokastrës me të clët kem shkëmbyr përvojë dhe medme të vlefshme. Veçaërshtë dër ta falederoj kolegët dhe mqtë e m Prof. Dr. Kostaq Hla dhe Doc. Ja Ltsa të clët më kaë dhëë jë dhmë të çmuar. Do të doja të falederoja gjthëashtu me mrëjohje dhe respekt të gjthë kolegët dhe mqtë e m të Departamett të Matematkës dhe Matematkës së Zbatuar të Fakultett të Shkecave Natyrore të Uverstett të Traës për medmet dhe kosultmet me ta gjatë gjthë perudhës së zhvllmt të këtj pum. Një falederm të veçatë kam rezervuar për mqtë e m Prof.ass. Dr. Ilr Vardham dhe Prof.ass Dr. Edr Xha të clët më kaë qëdruar praë ë çdo momet me mkëprtje dhe kurajm e vazhdueshëm të tyre. Së fudm falederoj me përulje famlje tme dhe prdërt e m për durm kurajm dhe frymëzm e domosdoshëm gjatë gjthë perudhës së puës dhe agazhmt tm për realzm e studmt dhe pumt të doktoraturës. Fëmjëve të m Kozma Aleksadër dhe Aamara u kërkoj djesë dhe u jam mrëjohës për kohë që gjatë kësaj perudhe u kam përkushtuar me kursm. Ju falederoj të gjthëve Romeo v
5 PËRMBAJTJA Lsta e shkurtmeve... v Lsta e fgurave... v Lsta e tabelave... v KAPITULLI I... 8 HYRJE Parathëe Hstorku kërkmt Problem kërkmt Qëllm dhe objektvat e studmt Qëllm studmt Objektvat e studmt Metodologja e hulumtmt Orgazm pumt KAPITULLI II SHQYRTIMI I LITERATURËS Proceset e rastt dhe zxhrët e Markovt Fukso Copula dhe teorema e Sklar-t Kocepte të përgjthshme mb fukso Copula Vlerësm parametrave të fuksot copula KAPITULLI III NDËRTIMI I MODELIT Shtrm problemt Supozme të modelt Dsa rezultate dhe pohme të rëdësshme për model Implemetm Teoremës së Sklar-t mb model KAPITULLI IV APLIKIMI I MODELIT PËR RASTIN E PORTOFOLIT NË NUMËR TË KREDIVE Klasfkm portofolt të kredsë spas umrt të detyrmeve të pashlyera perodke Formalzm procest të clëssë së shlyerjes me këste mujore të jë portofol krede Qëdrueshmëra e pohmeve mb model për specfkat e veçata të portofolt të kredsë Implemetm modelt për jë portofol krede klasfkuar spas Bakës të Shqpërsë Përfudme dhe kokluzoe Bblografa APENDIX ROMEO K. MANO v
6 Lsta e shkurtmeve Shkurtm Përshkrm ë orgjal Përshkrm ë shqp FI Facal Isttuto Isttucoe Facare LGD Loss Gve Default Humbje e parashkuar Bassel II Basel Commttee o Bakg Komtet Bazelt për Mbkqyrje Supervso Bakare CR + CredtRsk + CredtRsk + CM + CredtMetrcs + CredtMetrcs + CPV + CredtPortfoloVeë + CredtPortfoloVew + PD Probablty of Default Probabltet dështmt RR Recovery Rate Shkalla e mbulmt EAD Exposure At Default Ekspozm dështmt VaR Value at Rsk Vlera ë Rsk CPM + CredtPortfoloMaager+ CredtPortfoloMaager + RM + Rsk Maager + Rsk Maager + DM Default Mode model model Default Mode MTM Mark-to-Mark model model Mark-to-Mark PCB ProCredt Bak Baka ProKredt GM Grey forecastg Model Model parashkues Gray FML Full Maxmum Lkelhood Metoda e Përgjassë Maksmale të Plotë IFM Iferece For Margs Metoda e kokluzoeve për margalet CML Caocal Maxmum Lkelhood Përgjasa maksmale kaoke LLF Log-Lkelhood Fucto Logartm Fuksot të Përgjassë ROMEO K. MANO v
7 Lsta e fgurave Fgura 1.1 Graf modelt L dhe Yag Fgura 3.1 Graf sstemt Fgura 4.1 Graf procest të rastt për proces e shlyerjes së detyrmt për kredë e -t Fgura 4.2 Output- rezultateve për të dhëat e tabelës Lsta e tabelave Tabela 2.1 Klasfkm proceseve të rastt Tabela 3.1 Matrca e kalmt me jë-hap Tabela 4.1 Klasfkm kredve spas dtëvoesave dhe masa e provzomt të tyre Tabela 4.2 Matrca e kalmt me jë-hap për kredë e -të Tabela 4.3 Tabela përmbledhëse e klasfkmt të portofolt të kredsë Tabela 4.4 Klasfkm ë fud të vtt Tabela 4.5 Parashkm për fud e vtt Tabela 4.6 Tabela përmbledhëse e formacot të tabelave 4.4 dhe ROMEO K. MANO v
8 KAPITULLI I HYRJE 1.1 Parathëe Që ë fllmet e veta huadhëa është shoqëruar detyrmsht edhe me evojë e vlerësmt të rskut të kthmt të kësaj huaje. Isttucoalzm huadhëes ë trajtë e bakave dhe kompave mkrofacare soll me vete evojë e zhvllmt të teorve dhe dsplave të vlerësmt të rskut të huadhëes. Nevoja për të ruajtur tërësë e sstemt bakar ë kushtet e bashkëpumt të gushtë facar që bakat dhe stucoet facare kaë me jëra-tjetrë soll me vete gjthashtu krjm e sttucoeve dhe orgazmave mbkqyrëse të veprmtarsë së sstemt bakar dhe facar. Mbkëqyrja e clëssë së portofolt të kredsë është jë ga veprmtartë më të rëdësshëm të këtyre orgazmave. Një ga orgazmat dërkombëtare më të redësshëm është Basel Commttee o Bakg Supervso. Në verso fal të Bassel II aprovuar ë Jaar të vtt 2005 (ECB 2005) vhet re se tekkat profesoale për krjm dhe maaxhm e modeleve të rskut të kredsë jaë bërë jë qëllm vtal për sttucoet facare të maaxhmt të rskut duke mbajtur të hapur dskutm mb krjm e modeleve llogartëse të rsqeve operacoale ë veçat për dërtm e tekkave llogartëse të provzoeve me qëllm mrëmeaxhm e rezervave për humbjet ga kredtë ë rsk. Provzoet ë kocept facar përfaqësojë humbjet e mudshme që realzo huadhëës s rezultat moskthmt ë kohë të huasë ga huamarrës. Në tekkat e përdorura zakosht për meaxhm e modeleve të rskut vhet re jë vel lartë komplekstet s ga aa e përcaktmt teork ashtu dhe ga aa e tekkave llogartëse për gjetje e shpërdarjes së përbashkët probabltare të kredve ë rsk. Në shumcë e rasteve ky komplekstet vje s pasojë e formacot jo të mjaftueshëm që publkojë bakat. Një ga zërat më të rëdësshëm të buxhett të jë bake apo sttuco mkrofacar kreddhëës është fod rezervë për mbulm e provzoeve ga kredtë ë rsk ( kredtë e këqja ose sç jhe dryshe kredtë ë voesë). Komtet Bazelt për mbkqyrje bakare (Bassel II) bakat qëdrore dhe çdo shtet përmes poltkave fskale vëë theks ë rëdësë që ka krjm jë fod rezervë sa më afër fodt të provzoeve reale. Meqëëse fod rezervë përllogartet ë fud të vtt facar ROMEO K. MANO 8
9 për të mbuluar humbjet e mudshme ga kredtë e këqja gjatë vt facar ë vazhdm është e atyrshme të presm që përllogartja e këtj fod rezervë të mbështetet ë rezultate probabltare dhe statstkore. Kjo do të thotë se duke johur lgj probabltar të clt ështrohet shpërdarja e umrt të kredve ë rsk gërshetuar kjo me hstorku statstkor të kredve ë voesë dhe duke përdorur këto ë përllogartje e fodt rezervë rezultat marrë do të jetë këaqshëm përsa përket mjaftueshmërsë dhe saktëssë ë mbulm e provzoeve ga fod rezervë. Ndër modelet më të johura dhe më të përdorshme sot jhe dsa dërkohë që shumë sttucoe facare jaë të pavarura ë përdorm e këtyre modeleve për përllogartje e rezervave gjer ë përdorm e metodave prmtve sç është ajo e të bazuart ë jë vlerësm të humbjeve mesatare afatgjata ga mospagm ë kohë kredve. Këto metoda të çojë relatvsht ë vele të larta rezervash facare me relatvsht jë ormë mesatare të lartë voesash. Dsa ga modelet që përdore me shpesh jaë: CredtRsk + (CR + ) CredtMetrcs + (CM + ) CredtPortfoloVew + (CPV + ) etj. 1.2 Hstorku kërkmt Për të bërë jë përmbledhje të zhvllmt të kërkmt dhe arrtjeve ë fushë e modelmeve për matje e rskut të kredsë jem referuar kryessht dy studmeve seroze të Altma & Sauders (1998) dhe Altma (2009). Ky fudt është jë përmbledhje e përdtësuar e studmt të bërë ga Altma Rest & Sro ë vt Përpara 30 vjetësh pothuajse gjthë sttucoet facare (IF) për vlerësm e rskut të kreddhëes mbështetesh ë mëyrë ekskluzve ë formaco mb katër karakterstkat e subjektt kredmarrës: character (karakter) captal (kaptal) capacty (kapactet) dhe collateral (pasurtë e patudshme). Këto katër elemetë jhe ë sstem bakar s katër C- të e famshme të kredsë. Sommervlle & Taffler (1995) tregua se vedmarrja e mbështetur vetëm ë katër C-të e kredsë bëte bakerët më shumë pesmst (skeptk) ë ldhje me rsku e mudshëm të kredsë. Ata tregua se përdorm sstemeve multvarate të faktorëve të rskut e performote shumë më mrë rsku e huadhëes. Në llogartje uvarate të bazuar ë sstem e faktorëve të rskut vedmarrëst krahaso raporte çelës të kredmarrësve potecalë. Përdorm modeleve multvarate soll ROMEO K. MANO 9
10 kombm e varablave çelës duke prodhuar jë vlerë të rskut të kredsë të quajtur dryshe probabltet mospagmt ë kohë të detyrmt ose probabltet dështmt (default). Ky probabltet krahasohet me jë vlerë krtke që bë të mudur vedmarrje. Për ga aa e metodologjsë së përdorur zhvllm sstemeve multvarate ë vlerësm e rskut të kredsë është klasfkuar ë të paktë katër grupe: () model lear probabltar () model logt () model probt dhe (v) model aalzës dskrmate. Altma et.al. (1977) duke u referuar modelt ZETA dscrmat arrtë të gjejë jë fukso lear mds varablave të clët bëjë dallm më të mrë mds dy grupeve të jë portofol krede: kred që lkudohet ë kohë dhe kred që uk lkudohet ë kohë. Mart (1977) përdor model logt dhe model e aalzës dscrmate për të parashkuar dështm e 23 bakave ë perudhë A trego se që të dy modelet ofro jë rezultat pothuajse të jëjtë ë klasfkm e portofolt të kredsë ë dy grupe: kred të dështuara dhe kred jo të dështuara. Platt & Platt (1991) duke përdorur model logt tregua se treguest facarë të gjthë dustrsë së kreddhëes jaë faktorë parashkues statstksht më domethëës sesa treguest facarë dvdualë të bakave specfke për falmetm e sstemeve bakare. Lawrece (1992) përmes modelt logt bër jë parashkm të probabltett të dështmt për grup e kredve të lëvruara për blerje baesash. Smth & Lawrece (1995) përdorë model logt për të përcaktuar varablat që ofro jë parashkm më të mrë për status kred e dështuar për grup e kredve kosumatore. Ata përdorë jë model Markov për llogartje e probablteteve të dështmt. Altma (1977) bër kërkme ë ldhje me performacë parashkuese të jë varabl të shtatë ë model e aalzës dskrmate duke futur s varabël të shtatë vlerë e tregut të kaptalt të frmave. Model dërtuar (ZETA) është jë verso përmrësuar modelt me pesë varabla të Altma (1968). Scott (1981) duke kombuar dsa modele emprke me jë qasje të shëdoshë teorke arrt ë pëfudm se model ZETA shte përafrm më mrë për dërtm e teorsë së tj të falmetmt bakar. Zhvllm shtrrja dhe bashkëpum dërsjelltë ë tregu facar soll me vete faktorë të rj facarë dhe socalë me rëdës përcaktuese për vel e rskut facar. Për këtë arsye zhvllm modeleve egzstuese dhe dërtm modeleve të reja u kthye ë jë sfdë e cla vazhdo të jetë aktve. Këto modele të clat përkas 20-vjeçart të fudt të shekullt të kaluar u klasfkua ë katër klasa: ROMEO K. MANO 10
11 Klasa e parë është klasa e modeleve të falmetmt të clat quhe dryshe modelet e rskut të humbjes. Ato mbështete ë parm se jë kompa facare falmeto atëherë kur vlera e tregut të aseteve të saj (lkudtetet) be ë vel e detyrmeve ë trajtë borxh te jashtëm të saj (ttujve të borxht-oblgacoeve). Modele të këtj tp jaë prezatuar ga Scott (1981) Satomero & Vso (1977) Wlcox (1973) etj. Një ga modelet me të rëdësshme është model Black-Scholes-Merto prezatuar ga Black & Scholes (1973) dhe Merto (1974). Ky model trego se probabltet që jë kompa facare të falmetojë varet ga raport lkudteteve me detyrmet dhe qëdrueshmëra e vlerave të tregut të lkudteteve. E thëë dryshe shfaqe faktorë të rj që dkojë ë rsku e dështm. Faktorët që përcaktojë vlerë aktuale të tregut të aseteve lkude (lkudteteve) jaë orma e flacot dekset ekoomko-facare etj. Klasa e dytë është jë grup r modelesh me jë mbështetje të fortë teorke të clat përpqe të përafrojë probabltet e dështmt me aë të shkallës së rskut të dështmt të letrave me vlerë të kompave facare. Modele të tlla gjejmë ë pumet e Jokhart (1979) dhe Ibe & Ltterma (1989). Klasa e tretë jhet dryshe edhe s grup modeleve aktuarë. Këto modele bazohe ë tregu e kaptaleve. Një model tllë është prezatuar ga Altma (1989) dhe jhet s model shkallës së vdekshmërsë. Një model gjashëm me atë të Altma është model plakjes prezatuar ë vt 1989 ga Asquth Mulls & Wolf. Modelet e kësaj klase jap jë mudës llogartjeje të probablteteve aktuarale të dështmt duke përdorur të dhëa të akumuluara ë kohë (ser kohore) ë ldhje me dështmet dhe marrdhëet që realzohe mds tyre dhe veleve të kredtmt dhe vteve të maturmt të kredsë. Klasa e katërt përfsh modele të clat përdor jë aalzë të rrjetës eurale (ervore) të problemt të klasfkmt të rskut të kredsë. Aalza e rrjetës eurale është e gjashme me aalzë dskrmate jo-leare. Ajo bazohet ë supozm se varablat që marr pjesë ë fukso që shpreh parashkm e falmett të IF-së jaë learsht të pavarur. Në mëyrë më eksplcte mud të thuhet se modelet e rrjetave eurale të rskut të kredsë shqyrtojë korrelacoet potecalsht të fshehura mds varablave parashkues të clët përfshhe ë model s varabla shpjegues shtesë ë fukso parashkues jo-lear të falmetmt të IF-së. Modele të tlla jaë prezatuar ga Altma et.al. (1994) Coats & Fat (1993) etj. Krtka kryesore për këtë klasë është përqëdruar mb mëyrë ses detfkohe korrelacoet e fshehta dërmjet varablave shpjegues. Altma et.al. (1994) tregua se përdorm ROMEO K. MANO 11
12 përafrmeve me aë të rrjetave eurale uk sjell dojë dryshm thelbësor ë krahasm me aalzë leare dskrmate. Nga vt 2000 der më sot dustra e kreddhëes mor jë zhvllm të gjërë ë tregu facar dhe bashkë me të edhe përpjekjet për dërtm e modeleve matematke të vlerësmt të rskut të kredsë. Një këdvështrm r klasfkues e përshkrua ë mëyrë më përfaqesuese zhvllm e modeleve matematkore të rskut të kredsë për 30-vjeçar e fudt. Në themel të këtj këdvështrm qëdrojë varablat kryesorë që dkojë mb rsku e kredsë të lëvruar ga IF-të. Tre varablat kryesorë që dkojë ë rsku e kredsë jaë: () probabltet dështmt probablty of default (PD); () probabltet dështmt të parashkuar loss gve default (LGD) që jepet s dferecë e probabltett të gjarjes së sgurt me koefçet e mbulmt të dështmt recovery rate (RR); () ekspozm dështmt exposure at default (EAD). Në lteraturë shkecore të rskut të kredsë është kushtuar më shumë rëdës vlerësmt të PD-së dhe marrëdhëes dërmjet PD-së dhe RR-së. E trajtuar ë këtë këdvështrm hstora 30 vjeçare e zhvllmt të tekologjsë së modeleve teorke të rskut të kredsë mud të klasfkohet ë dy grupe kryesore: () modelet e vlerësmt të kredsë () modelet e portofolt ë rsk të kredsë. Në grup e parë kem të klasfkuar katër ëgrupe. S krtere kryesore për këtë klasfkm jaë marrë mëyra e trajtmt të LGD-së dhe marrdhëet dërmjet PD-së dhe RR-së. Në ëgrup e parë të johur s gjeerata e parë e modeleve strukturore PD dhe RR trajtohe s fuksoe të karakterstkave strukturore të kompave. Në këto modele RR shhet s jë varabël edogje dhe PD-ja dhe RR-ja jaë dy fuksoe të aasjellta ë kuptm që kur jër është rrtes tjetr është zbrtës. Modele që përkas kësaj gjeerate jaë prezatuar ga Merto (1974) Black & Cox (1976) Geske (1977) Vascek (1984) etj. Nëgrup dytë johur s gjeerata e dytë e modeleve strukturore RR trajtohet s varabël ekzogje dhe pavarur ga vlerat e aseteve të kompasë. Në përgjthës RR-ja përcaktohet s jë ormë e fksuar e borxheve aktuale të kompasë dhe s e tllë ajo është e pavarur ROMEO K. MANO 12
13 ga PD-ja. Në këtë gjeeratë përfshhe modelet e prezatuar ga Km et.al. (1993) Nelse et.al. (1993) Hull & Whte (1995) Logstaff & Schwartz (1995) etj. Në ëgrup e tretë jaë modelet me forma të reduktuara. Në pjesë më të madhe të këtyre modeleve RR-ja supozohet të jetë jë kostate ekzogjee e pavarur ga PD-ja. Por ajo që shfaqet s rs është se ë dsa ga këto modele RR-ja supozohet të jetë jë varabël stokastk (dryshore rast) pavarur ga PD-ja. Modelet e reduktuara paraqes supozme të veçata për damkë e marrdhëeve të RR-së dhe PD-së. Këto modele jaë të pavarura ga karakterstkat strukturore të kompave kreddhëëse. Modelet e përfshra ë këtë ëgrup jaë të Ltterma & Ibe (1991) Mada & Ual (1995) Jarrow & Turbull (1995) Lado (1998) Duffe & Sgleto (1999) Duffe (1998) etj. Nëgrup fudt përmbledh të gjthë modelet e dërtuara ë vtet e fudt. Karakterstkë e modeleve të wgrupt të katërt është se PD-ja dhe RR-ja trajtohe s varabla stokastk. Këto varabla jaë të varur ga faktorët e përbashkët të rskut sstematk të clët përcaktojë gjedje ekoomke ë tërës. Në këto modele PD dhe RR jaë egatvsht të korreluara. Në kocept makroekoomk korrelm egatv është rezultat varëssë së përbashkët të PD-së dhe RR-së ga jëjt faktor sstematk thjeshtë. Ndërsa ë kocept e qasjeve mkroekoomke egatvtet korrelmt rrjedh ga velet parashkuese të ofertë-kërkesës së letrave me vlerë. Prezatm këtyre modeleve përket fllmeve të shekullt 21-të dhe përfshhe ë studmet e bëra ga Frye (2000) Jarrow (2001) Carey & Gordy (2003) Altma et.al. (2005) Acharya et.al. (2007) Mu & Ozdemr (2006) etj Grup dytë modeleve të rskut ka fllesat ë gjysmë e dytë të vteve Bakat dhe kosuletët e tyre tekkë zhvllua jë mëyrë të re modelm të rskut të kredsë. Përpjekja e tyre u përqedrua ë përllogartje e humbjeve të mudshme me jë vel të paracaktuar sgure për jë ekspozm të portofolt të kredsë breda jë perudhe të caktuar (zakosht të barabartë me jë vt facar). Këto modele u motvua ga rëdësa gjthmoë ë rrtje e meaxhmt të kreddhëes dhe kaë ë qedër të vëmedjes vlerat ë rsk values at rsk (VaR) të aseteve të kompave facare kreddhëëse. Modelet e VaR përfshjë: model CredtMetrcs + të Morgat (Gupto et.al. 1997); Credt Susse Facal Products johur dryshe s CredtRsk + (Products 1997); CredtPortfoloVew + të McKsey (Wlso 1998); CredtPortfoloMaager + të Moody; dhe Rsk Maager + të Kamakura (Crosbe 1999). Modelet VaR mud t klasfkojmë ë dy kategor kryesore: ROMEO K. MANO 13
14 () () modelet Default Mode (DM) modelet Mark-to-Mark (MTM). Në këto modele rsku kredsë detfkohet s rsku humbjes dhe fllo të përdoret shpërdarja bomale me vetëm dy gjarje të mudshme probabltare: mospagesë ë kohë (dështm) dhe pagesë ë kohë (sukses). Në modelet DM humbjet e kredsë kosderohe vetëm ë qoftë se dodh gjarja mospagesë ë kohë. Ndërsa modelet MTM jaë multomale duke kosderuar s humbje jo vetem dështm por edhe gjedje egatve të kredsë. Rezultat kryesor modeleve të rskut të kredsë është përcaktm fuksot të shpërdarjes probabltare të humbjeve të prtshme të portofolt të kredsë. Në këto modele fllojë të përdore ë mëyrë përcaktuese koceptet probabltare të prtjes matematke dhe dspersot të shpërdarjes. Kështu humbjet e mudshme ë kocept facar jaë të barabarta me prtje matematke të shpërdarjes probabltare të humbjes s dryshore rast. Kjo prtje matematke shpreh shumë ë vlerë që vesttorët pres të humbas gjatë jë perudhe të paracaktuar kohore. Nga aa tjetër humbjet e paparashkuara shpreh devjm ga humbjet e prtura dhe ë këtë mëyrë tregojë vlerë e portofolt aktual ë rsk. E thëë me terma probabltar humbjet e paprtura mud të llogarte s devjaco stadard shpërdarjes probabltare të humbjeve. Specfkë e përbashkët e të gjthë modeleve VaR është se RR-ja dhe PD-ja kosderohe s dryshore rast të pavarura dhe me përjashtm të modelt CR + ato trajtohe s varabla stokastk. Në paragraf e mëposhtëm do të bëjmë jë prezatm më të detajuar të modelt CR + referuar Gordy (2000). 1.3 Problem kërkmt Qëllm stucoeve facare gjatë gjthë hstorkut të kërkmt e dërtmt të modeleve të rskut të kredsë dhe der më sot është krjm tekkave përllogartëse të parashkmt të humbjeve ë vlerë s pasojë e ekspozmt të tyre ë tregu e kredsë. Thëë me fjalë më të thjeshta IF-të syojë ë dërtm e modeleve parashkuese të humbjeve të mudshme breda jë perudhe kohe të paracaktuar. Këto humbje jaë vlera moetare që realzohe kryessht ga huadhëet ë trajtë krede. Sasa ë vlerë e mjeteve moetare të huazuara ë ROMEO K. MANO 14
15 kletët e IF-ve përbë atë që quhet portofol kredsë. Tërësë e portofolt të kredsë e realzojë kredtë dvduale të lëvruara ga IF-të. Një portofol krede është jë sas ë vlerë moetare por jëkohëssht edhe jë bashkës ë umër huamarrëssh. Vlera e portofolt të kredsë varet jo vetëm ga ormat e terest të ftuara ë kred por edhe mb gjasat që teres dhe prcpal do të paguhe. Pjesa ë vlerë e këtj portofol e cla uk kthehet ë kohë e paracaktuar përbë portofol ë rsk të kredsë. (Jasso 2002) Përvoja dsavjeçare s puojës sstemt facar ë fushë e kreddhëes ë fukso e aalstt të lartë të kredve (praë kompasë mkrofacare Parter Shqptar ë Mkrokred ) dhe supervzor (Drejtor dege praë bakës ProCredt Bak dega Gjrokastër) më ka dhmuar të kuptoj se vlerësm portofolt ë rsk të kredsë ë vele jëse përdor të dyja përcaktmet e portofolt të kredsë: () ë vlerë moetare dhe () ë umr e kredve të dhëa. Nga studm modeleve të ofruara është vëë re se ato fokusohe vetëm ë trajtm e jë baze të dhëash për portofol e kredsë ë vlerë dhe jo ë umr e kredve. Shumë kërkues ë fushë e modeleve të rskut të kredsë kaë arrtur rezultate të këaqshme të clat jaë përdorur ë vazhdmës për përmrësm e këtyre modeleve. L dhe Yag (2003) ofrua jë model parashkues duke përdorur probabltetet jo-stacoare të zxhrëve të Markovt (Smth & Lawrece 1995) dhe model Gray (ctuar ga L & Yag 1999). Për herë të parë ë model L-Y u përdor klasfkm portofolt të kredsë ë gjedje facare dhe pkërsht u kufzua ë shtatë gjedje facare. Komukm këtyre gjedjeve spas L & Yag paraqtet ë fgurë 1.1. Duke përdorur probabltetet jostacoare të zxhrëve të Markovt L & Yag (2003) arrtë ë përfudm se probabltetet e gjedjeve për perudhë pasardhëse shprehe me aë të barazmt: ku: j j 1 6 P ( t 1) P( t) P ( t) (1.3.1) Pt () është probabltet që kreda është ë gjedje ë perudhë (momet) t; Pj ( t 1) është probabltet që kreda është ë gjedje j ë momet t+1; Pj () t është probabltet kalmt ga gjedja ë perudhë t ë gjedje j ë perudhë pasardhëse t+1; ROMEO K. MANO 15
16 Fgura 1.1 Graf modelt L dhe Yag. Burm: L & Yag (2003). Duke marrë s dryshore rast 1 X t ë momet t=1 me shpërdarje të tpt të dhëë me aë të barazmt (1.3.1) dhe duke zbatuar ekuaco dferecal të shkallës së parë të GM (Deg 1989) L & Yag (2003) prezatua model: dx 1 dt t 1 ax t b (1.3.2) Në këtë model për llogartje e parametrave a dhe b përdoret jë bazë të dhëash ë vlerë moetare për të bërë klasfkm ë shtatë gjedjet facare. Në këtë model uk është përcaktuar famlja probabltare e shpërdarjes së fllmt të procest të Markovt por është supozuar e johur. Modelet VaR pkërsht CR + ofro jë mudës përcaktm të këtyre probablteteve duke u sur ga kosderata ekoometrke për përcaktm e faktorëve të rskut. CR + është jë model rskut të mospagmt ë kohë të jë detyrm të rrjedhur ga kredmarrja. Secl kredmarrës ka vetëm dy mudës gjedjeje ë fud të perudhës së paracaktuar: vouar dhe jo vouar. Në rast e voesës huadhëës ka jë humbje të madhëssë fzke që është dhe ekspozm huadhëëst tek huamarrës. ROMEO K. MANO 16
17 Supozmet mb shpërdarje dhe format themelore të propozuara ga CR + mbulojë shpërdarje e portofolt total të humbjeve të llogartura këto ë jë rrugë rgoroze aaltke. Korrelacoet e voesave ë CR + jaë supozuar të shprehe plotëssht ga jë vektor k- faktorëve të rskut : x x x 1 supozuar të keë shpërdarje Berul të pavarura ga jëra-tjetra. Probabltet kushtëzuar fukso llojt të klasës p. Në varës ga x voesat e kredmarrësve dvdual jaë x për të patur jë voesë për detyrm e -të është jë të huamarrëst të -të cl realzo faktorët e rskut x dhe faktorët garkues w w 1 të clët mas djeshmërë e huamarrëst të -t ë secl ga k faktorët e rskut. Në këtë mëyrë CR + specfko këtë fukso për destet: k p x p x w k l1 k (1.3.3) ku p është probabltet pakushtëzuar për klasë të kredmarrëst për të cl plotësohet kusht (Gordy 2000 fq 122): (1.3.4) E p x p Barazm (1.3.3) jep probabltet për të patur jë voesë për detyrm e -të ose dryshe probabltet e mossuksest ë jë provë të Berult për detyrm e -të dërsa barazm (1.3.4) jep prtje matematke të këtyre probablteteve. Trajtm procest të voesës ë shlyerje e detyrmt të jë krede s jë dryshore rast Berul dhe ë përgjthës portofolt të kredsë s jë vektor rast me margale berulae s dhe barazm (1.3.3) që jep probabltet e kushtëzuar berula për të patur jë voesë jaë rezultate teresate që e do t përdorm ë model që do të dërtojmë. Në probabltet e shprehur me barazm (1.3.3) marr pjesë të gjthë faktorët facarë dhe ekoomkë të clët aalzohe ga kreddhëës ë momet e vedmarrjes për dhëe ose jo të huasë. Në kuptm që ë qoftë se parë huadhëa uk realzohet. Në qoftë se p x është më madh se jë vel caktuar që më p x është më vogël se vel dhëë huadhëa realzohet me jë kotratë të paracaktuar për kthm e huasë ë trajtë këstesh umr të clëve dhe afat shlyerjes përcaktohe ga kotrata. Të gjthë faktorët dhe vektor- ROMEO K. MANO 17
18 faktorët që CR + përdor për të xjerrë barazmet (1.3.3) dhe (1.3.4) jaë faktorë të rskut facar dhe uk do të jeë objekt studmt toë. Nga aa tjetër çdo huadhëe fuksoo mb bazë e jë kotrate të kthmt të saj tek huadhëës (baka ose sttucoe tjera facare). Clësa e respektmt të kotratës ga huamarrës e klasfko këtë hua ë vele rsku ë varës të velt të respektmt të kotratës. Ky vel përcaktohet ga umr kësteve ë voesë (të papaguara ë kohë) që kjo hua ka ë jë momet të caktuar kohe. Klasfkm këtyre voesave përcakto dhe masë e provzoeve s rrjedhm edhe fod rezervë për mbulm e tyre. 1.4 Qëllm dhe objektvat e studmt Qëllm studmt Ky pum ka për qëllm prezatm e jë model multvarat probabltar për portofol ë umër të kredve ë rsk duke përfshrë dhe kredtë që uk jhe s kred ë rsk por që mud të klasfkohe për qëllme të modelt s kred me rsk zero. Për dërtm e modelt jem mbështetur ë trajtm e portofolt të kredsë s jë vektor rast që ështrohet jë proces markova duke marrë s probabltet të dështmt rezultat e Gordy (2000) ë A Comparatve Aatomy of Credt Rsk Models të shprehur me barazm (1.3.3). Gjthashtu kem përdorur klasfkm provzoues të portofolt të kredsë spas Bakës Qëdrore të Shqpërsë Objektvat e studmt Qëllm studmt shprehur ë objektva mud të koceptohet klasfkuar s më poshtë: 1. Të ofrojë jë model probabltar të shpërdarjes së umrt të kredve të portofolt të jë IF-je cl t përgjgjet procest të kotrollt të respektmt të afatt të shlyerjes së detyrmt perodk të jë humarrjeje. Shprehur dryshe proces klasfkmt perodk portofolt të kredsë. 2. Të ofrojë jë model uvarat dhe model multvarat për jë portofol ë umër kredsh që përgjgjet klasfkmt të portofolt të kredsë ga Baka Qëdrore e Shqpërsë (B.Q). 3. Të ofrojë jë përafrm të mrë të modelt me aë të mplemetmt të fuksot Copula ë model e dërtuar. 4. Të ofrojë jë mëyrë praktke për mplemetm e bazave të të dhëave që bakat e velt të dytë mud të ofrojë duke respektuar parm e ruajtjes së sekrett bakar. ROMEO K. MANO 18
19 1.5 Metodologja e hulumtmt Për të realzuar objektvat e studmt pua hulmtuese është spruar ga përvoja dsa vjeçare ë sstem bakar s pjesë e e staft ë dy sttucoe facare kreddhëëse. Trajtm perodk portofolt të kredsë (zakosht çdo muaj) dhe aalza vjetore e tj çua ë formulm e problemt: A mud të gjejmë jë model probabltar cl t përgjgjet klasfkmt perodk të jë portofol krede ë umër kredsh? Në medm toë zgjdhja e problemt bëhet e mudur duke trajtuar portofol e kredve s jë vektor rast ku çdo kred mud të shhet s jë dryshore rast e pavarur ga të tjerat. Objektv parë ofrm jë model dhe klasfkm perodk portofolt të kredsë realzohet duke trajtuar proces e shlyerjes së jë krede s jë proces rast me jë hapësrë dskrete dhe të fudme gjëdjesh. Duke treguar se ë supozmet formale të bëra mb dryshore e rastt që shpjego proces e shlyerjes perodke të jë krede çdo kred mud të kosderohet s jë proces rast llojt zxhr Markovt homogje. Objektv dytë arrhet me aë të zbatmt të dsa prej pohmeve dhe teoremave të klasës së proceseve të rastt të tpt zxhr Markovt. Për realzm e objektvt të tretë kem përdorur teoremat dhe pohmet që ldh fukso e shpërdarjes me fukso copula. Ndërsa objektv fudt është meduar të përmbushet duke përdorur përafrm Fréchet- Hoeffdg dhe dsa kocepte të vargjeve umerke. Përmes aplkmt të jë baze të dhëash dytësore marrë ga jë bakë e velt të dytë ë Shqpër lustrojmë zbatm praktk të modelt dhe lehtësë e mplemetmt të modelt me aë të jë software- të thjeshtë të realzuar ë gjuhë programuese C++. ROMEO K. MANO 19
20 1.6 Orgazm pumt Pum dsertacot është darë ë katër kaptuj. Çdo kaptull është orgazuar ë çështje dhe ëçështje ë mëyrë që ajo çfarë dëshrojmë të shprehm dhe prezatojmë ë pum të jetë sa më e qartë dhe lehtëssht e aksesueshme. Materal shoqërohet ga lsta e shkurtmeve lsta e tabelave dhe fgurave ë hyrje të pumt dhe përfudme dhe kokluzoe bblografa dhe apedks ë pjesë e fudt. Në kaptull e parë është bërë jë përmbledhje e hstorkut të kërkmt ë fushë e modelmeve ekoometrke dhe matematkore ë meaxhm e rskut të kredsë duke dhëë rëdës klasfkmt 30-vjeçar të modeleve të dërtuara ë këtë fushë. Më tej kem prezatuar problem e kërkmt duke qëdruar ë prezatm e modelt L & Yag (2003) dhe rezultat e CR+ të Gordy (2000). Nga këto rezultate jem mbështetur për dërtm e modelt toë. Në këtë kaptull jë ved të redësshëm zëë prezatm objektvave të studmt. Në kaptull e dytë është bërë jë prezatm kocepteve dhe rezultateve të clat do të përdore ë mëyrë koceptuale dhe referuese përgjatë vërtetmeve të dryshme ë pum. Koceptet mb proceset e rastt dhe zxhrët e Markovt jaë paraqtur ë trajtë e jë përmbledhjeje koceptuale. Koceptet mb fukso copula dhe vlerësm e parametrave të tj jaë trajtuar më gjerëssht duke përfshrë dsa pohme dhe teorema kryesore të clave do t u referohem gjatë pumt. Kjo për fakt se koceptet mb fukso copula jaë pak ose shumë pak të trajtuara ë ved toë. Kaptull tretë është kaptull më rëdësshëm pumt. Në të jaë trajtuar radhaz çështjet që përmbajë rezultatet e pumt toë. Në çështje e parë e të dytë kem prezatuar problem që a ço ë dërtm e modelt dhe supozmet e modelt. Në pjesë e tretë të këtj kaptull jaë paraqtur rezultatet toa ë trajtë pohmesh dhe jaë treguar vërtetmet e tyre. Në pjesë e katërt kem treguar mudësë e përdormt të fuksot copula mb model e dërtuar. Në kaptull e katërt kem prezatuar mplemetm e modelt të dërtuar mb jë portofol krede ë umër klasfkuar ë vele rsku spas klasfkmt të Bakës Qëdrore të Shqpërsë. Pas është bërë jë përshkrm procest të kotrollt perodk të clëssë së jë portofol krede ë çeshtje 4.3 kem treguar qëdrueshmërë e modelt ë ldhje me kufzmet që ofro rast portofolt të kredsë ë raport me model e përgjthshëm të dërtuar ë kaptull e tretë. Në këtë kaptull kem treguar gjthashtu që me aë të jë kod të thjeshtë të dërtuar ë gjuhë C++ model mud të mplemetohet mb jë bazë të dhëash kokrete që mud të paraqes jë klasfkm të përshtatshëm të portofolt të kredsë. ROMEO K. MANO 20
21 Në çështje Përfudme dhe Kokluzoe është bërë jë përmbledhje e shkurtër e atyre çfarë mudëm të realzom me aë të këtj pum dhe prezatohe dy ga problemet që vazhdojë të mbete të hapura dhe sfda e radhës për studmet e mëtejshme. Në Apedx kem paraqtur jë hard copy të kodt të dërtuar ë gjuhë C++. ROMEO K. MANO 21
22 KAPITULLI II SHQYRTIMI I LITERATURËS Në këtë kaptull kem bërë jë prezatm të kocepteve bazë të proceseve të rastt dhe zxhrëve të Markovt mb të clat është mbështetur arsyetm për dërtm e modelt dhe logjkë e vërtetmeve të clat kërkojë detyrmsht rezultate të pohmeve dhe teoremave të tyre. Gjthashtu kem paraqtur jë përmbledhje të hollësshme mb koceptet e teorsë së fuksoeve Copula të marrdhëes së tyre me fuksoet probabltare të shpërdarjes dhe metodat kryesore për vlerësm e parametrave ë modelet ku përfshhet fukso copula. Përkufzmet pohmet lemat dhe teoremat ë pjesë më të madhe do të shërbejë për dërtm e modelt dhe zbatm e mudshëm të tj me jë bazë të dhëash të strukturuar spas lgjshmërsë bakare. 2.2 Proceset e rastt dhe zxhrët e Markovt Në teorë e probabltett proceset e rastt dhe teora e zhvlluar mb to luajë jë rol të rëdësshëm për trajtm e feomeeve që mud të formalzohe s fuksoe të kohës. Zaaflla e teorsë së proceseve stokastke dato ë fllmet e shekullt 20-të. Koceptet e para të saj takojë fushës së statstkës fzke duke quajtur ato procese fzke. Një process fzk është jë feome fzk evoluco të clt studohet me aë të jë fukso të kohës. Për këtë arsye proceset stokastke mud të kosderohe s kocepte matematke të statstkës fzke. Në qoftë se AP është jë hapësrë probabltare T është jë hapësrë kohe dhe E është jë hapësrë gjedjesh ku marr vlera dryshoret e rastt të dërtuara mb hapësrë e dhëë probabltare atëherë proces rast do të quhet çdo famlje dryshoresh rast e tpt X t T ku X t merr vlera ë E (Robert 2008) (fq 6). Në varës të llojt të bashkësve që paraqes hapësrë e kohës dhe hapësrë e gjedjeve klasfkm proceseve të rastt jepet me aë të tabelës së mëposhtme (Tab. 2.1). Le të jetë X t t dskrete gjedjesh T jë proces rast me kohë dskrete T E x0 x1 x t dhe hapësrë ROMEO K. MANO 22
23 Tabela 2.1 Klasfkm proceseve të rastt T e vazhdueshme T dskrete E e vazhdueshme E dskrete Proces rast me kohë të vazhdueshme Proces rast me kohë dskrete Proces rast me hapësre gjedjesh të vazhdueshme Proces rast me hapësre gjedjesh dskrete Burm: Autor Një ga klasat më të rëdësshme të proceseve të rastt me kohë dskrete është klasa e proceseve të rastt të tpt zxhr Markovt (Grmmett & Strzaker 2001 fq 39). Një proces rast me kohë dskrete X X për çdo ëvarg x x... x të gjedjeve të ketë ved: do të quhet jë zxhr Markov ë qoftë se PX 1 x 1 / Xk xk 0 k PX 1 x 1 / X x Probabltetet e krahut të djathtë të barazmt (2.2.1) shëohe me (2.1.1) p x x. Barazm (2.1.1) jhet dryshe edhe me term veta e mugesës së kujtesës për proces e rastt. Në qoftë se x dhe y jaë dy gjedje çfarëdo ga hapësra e gjedjeve E atëherë probabltetet e trajtës p x y x y E kohë T M dërsa matrca 1 quhe probabltete të kalmt me jë-hap ë p x y për çdo dy elemet të çfarëdoshëm x dhe y ga hapësra e gjëdjeve E quhet matrca e kalmt me jë-hap ë kohë T. (Grmmett & Strzaker 2001 fq 39). x ye Në klasë e proceseve të rastt të tpt zxhrë të Markovt bë pjesë ëklasa e zxhrëve të Markovt homogje ë të clët probabltetet e kalmt me jë-hap uk vare ga koha T. Pra jë zxhr Markov X 0 do të quhet zxhr Markov homogje ë qoftë se / / P X x X y P X x X y për çdo xy. (Kosk 2013 fq 214). Për këtë ëklasë edhe matrca e kalmt me jë-hap uk varet ga koha. S rrjedhm M M p x y për çdo T. (Grmmett & Strzaker 2001 fq 40). x ye Shëojmë me p0 x PX0 x x E atëherë famlja shpërdarje e fllmt (tal dstrbuto) e procest të rastt X 0. p x x E 0 quhet Tre ga vettë kryesore të zxhrëve të Markovt homogje shprehe ë lemë e mëposhtme: ROMEO K. MANO 23
24 Lemë (Grmmett & Strzaker 2001 fq 40) Le të jetë X X 0 jë zxhr Markov me hapësrë gjedjesh E. Atëherë. px y 0 x y E; px y 1 x E. y. p0 x 0 x E; p0 x 1. x. PX x X x X x p x x x x x (2.1.3)... p p Një matrcë M px y x y E që plotëso relaco () të Lemës (2.1.1) do të quhet matrcë stohastke (Grmmett & Strzaker 2001 fq 41). Pra matrcë stohastke do të quhet matrca e cla e ka të barabartë me 1 shumë e elemetëve të çdo rresht të saj. Probabltetet e trajtës: / p x y P X m x X m x (2.1.4) M p x y me ( ) quhe probabltete të kalmt me -hapa dërsa matrca x y elemete të trajtës së shprehur me aë të barazmt (2.1.4) do të quhet matrcë e kalmt me - hapa. (Kosk 2013 fq 58). Le të jetë X X p0 x x E EE 0 jë zxhr Markov homogje me shpërdarje të fllmt dhe me probabltete të kalmt me -hapa p x y x y E kaë ved dy barazme shumë të rëdësshme (Puka 2001 fq 17):. PX y p x p x y. 0. Atëherë 0. (2.1.5) xe Relaco Chapma-Kolmogorovt: m m p x y p x z p z y. (2.1.6) ze Barazm (2.1.6) ë trajtë matrcore mud të shkruhet: t t t t M M M 2. Për t 1 1 M M dhe 2 M M M M 2. Duke rrtur ekspoet ë mëyrë progresve ë përgjthës marrm: M t t M. Atëherë madhëstë t p j l jaë elemet të fuqsë së t-ët të matrcës M me elemetë të trajtës (2.1.1). Duke dtur se: për çdo t atëherë M t është matrce stokastke ë qoftë se M është jë matrce stokastke (Nordstrom 2008 fq 3) mud të them se matrca e kalmt me t-hapa e jë zxhr të Markovt homogje është jë matrcë stokastke. ROMEO K. MANO 24
25 2.2 Fukso Copula dhe teorema e Sklar-t Kocepte të përgjthshme mb fukso Copula Kuptm Copula-s është futur për herë të parë ga A. Sklar ë vt 1959 kur a u përgjgj jë pyetjeje të shtruar ga M. Fréchet rreth marrëdhëes mds jë fukso probabltar shumëdmesoal dhe margaleve të tj me dmesoe më të ulta (Sklar 1996). S fllm Copula është përdorur kryessht ë teorë e hapësrave metrke probabltare. Më voë u gjet me teres për përcaktm e masave joparametrke të varëssë mds dryshoreve të rastt dhe atëherë copula fllo të luajë jë rol të rëdësshëm ë probabltet dhe ë statstkë matematke. Në vt 1990 Dall'Aglo orgazo koferecë e parë kushtuar copulas të quajtur "Shpërdarjet Probabltare të Marxhalzuara". Kjo do të shte e para ë jë ser koferecash që dhmo ë masë të madhe zhvllm e kësaj fushe pas secl prej këtyre eveteve ofro mudësë e paraqtjes së rezultateve të dkujt dhe për t bërë ato të aksesueshme ga studuest e mëvoshëm. Dsa ga këto kofereca u mbajtë ë vt 1993 ë Seattle ë vt 1996 ë Pragë ë vt 2000 ë Barceloë ë vt 2004 ë Quebec ë 2007 ë Tartu dhe ë vt 2010 ë Sao Paulo. Në fud të vteve 90 oco copulas u bë gjthjë e më popullor. Refereca kryesore për koceptet dhe pohmet mb copula do të bëhë dy lbrat e parë kushtuar tërëssht Copulas dhe mudëssë së zbatmt të tyre ë fushat e tjera: Në vt 1997 Joe boto lbr e tj mb modele multvarate me jë pjesë të madhe të përkushtuar për copula dhe famljet e copulas. Në vt 1999 Nelse debuto për herë të parë ë fushë e copulas duke vazhduar me rbotm me dsa rezultate të reja ë vt 2006 (Nelse 2006). Arsyeja kryesore e këtj teres ë rrtje duhet të gjedet ë zbulm dhe përdorm e ocot të copulas ga studuest ë dsa fusha të aplkuar s faca (Embrechts et.al. 2000). Për jë perudhë të gjatë kohe statstceët kaë qeë të teresuar mb marrëdhëe mds jë fukso shpërdarjeje multvarate dhe margaleve të tj me dmeso më të ulët (uvarat ose të dmesoeve më të larta se jë). M. Fréchet (1951) dhe Dall Aglo (1959) dhaë dsa rezultate teresate mb këtë marrdhëe ë vtet 50 duke studuar fuksoe shpërdarjeje dy dhe tre dmesoale me shpërdarje margale të johur. Përgjgje për këtë problem për rast e margaleve uvarate e dha Sklar ë vt 1959 duke krjuar jë klasë të re fuksoesh të clë a e quajt Copula. ROMEO K. MANO 25
26 Përkufzm (Rezkova 2007 fq 14) Një Copula -dmesoale është jë fukso : T 01 dhe j 1... u u1 u 1. Në qoftë se 0 j 2. j C u u ; (2.2.1) që gëzo vettë e mëposhtme: C u... u 0; u atëherë T 3. v v v v u V u v 1 j j j C ku VC u v... 1 C g1... g 1 C tllë për çdo dhe g 1 j1 v j g j2 u j 1 Një ga pohmet më të rëdësshëm ë fushë e përdormt të copula-s ë teorë e probablteteve është teorema e Sklar-t e cla realzo ldhje mds jë fukso copula dhe jë fukso shpërdarjeje. Teoremë Teorema e Sklar-t (Embrecht et.al. 2001fq 4) Le të jetë F jë fukso -dmesoal shpërdarjeje. Atëherë ekzsto jë -copula C e tllë që për çdo x R ka ved barazm: F x x C F x F x (2.2.2) Në qoftë se F... 1 F jaë të gjthë të vazhdueshëm atëherë C është e vetme; ë të kudërt C është e vetme e përcaktuar ë RaF1 Ra F bashkësa e vlerave të F. Aasjelltas ë qoftë se C është jë -copula dhe ku me Ra F 1... është shëuar F... 1 F jaë fuksoe shpërdarjeje atëherë fukso F përcaktuar me aë të barazmt (2.2.2) është jë fukso -dmesoal shpërdarjeje me margale F F Fukso copula gëzo shumë vet teresate të clat kaë dhëë studuesve të dryshëm mudësë e përdormt të tj ë fusha të dryshme. Një ga këto vet është kufzueshmëra e fuksot copula e cla shprehet me aë të teoremës: Teoremë Fréchet-Hoeffdg (Rezkova 2007 fq 16) Për çdo fukso copula C C u u 1 ka ved mosbarazm dyfshtë: C u u C C u u (2.2.3) 1 1 ROMEO K. MANO 26
27 ku dhe C u1 u max u 1 0 (2.2.4) 1 m C u u u u (2.2.5) 1 1 Mosbarazm (2.2.3) jhet me emr mosbarazm dyfshtë Fréchet dhe Hoeffdg. Këtu është e rëdësshme të theksohet se kufr spërm fuksot copula është gjthmoë jë fukso shpërdarjeje probabltare gjë e cla duket qartë edhe ga barazm (2.2.5) dërsa kufr poshtëm copulas është fukso shpërdarjeje vetëm për rast = 2. Për jë copula C absolutsht kovergjete destet copulas jepet ga me aë të barazmt (Rezkova 2007 fq 15): c u u 1 C u1 u u u 1 (2.2.6) Dy pohme teresate ë ldhje me marrdhëe mds fuksoeve copula dhe fuksoeve të shpërdarjes jaë prezatuar ga Embrecht at al (2001) me aë të teoremës dhe pohmt të mëposhtëm: Teoremë (Embrecht et.al fq 4) Le të jetë C jë -copula. Atëherë për çdo u dhe v ë 01 C v C u v u dërsa C është uformsht vazhdueshëm ë 01. Pohm (Embrecht et.al fq 4) k k (2.2.7) k1 Në qoftë se H është jë fukso shpërdarjeje -dmesoal me margale copula C e cla këaq Teoremë atëherë për çdo u 01 ka vëd barazm: F... 1 F dhe C u1 u H F1 u1 F u (2.2.8) ROMEO K. MANO 27
28 2.2.2 Vlerësm parametrave të fuksot copula Për vlerësm e parametrave të copulas jaë trajtuar dsa mëyra. Ndër metodat më të përdorura është ajo e maksmzmt të fuksot logartmk të përgjassë së destett të copulas ë ldhje me parametr e shpërdarjes. Joe (1997) dhe Durrlema et.al. (2000) sugjerua tre mëyra të dryshme: metoda e përgjassë së plotë maksmale (FML) metoda e kokluzoeve për margalet (IFM) dhe metoda kaoke e përgjassë maksmale (CML). Rezkova (2007 fq 27) ofro rezultat e mëposhtëm për fukso logartmk të përgjassë: Për jë vektor rast X X X margaleve F x j X j j j 1 me fuksoe shpërdarje parametrke të ; 1... fukso kushtëzuar shpërdarjes për X X 1 X mud të shkruhet ë trajtë: ku ; 1 T F ; x x C F x ;... F x ; ; (2.2.9) 1 T është parametr që duam të vlerësojmë dhe C është ga famlja parametrke e copulas me parametër. Duke shëuar me c destet e copulas C mud të përftojmë destet e kushtëzuar të X X : 1 X vektort të rastt f ; x x c F x ;... F x ; ; f x ; (2.2.10) 1 T t 1 Atëherë logartm fuksot të përgjassë është: T T l ; x x log c F x ;... F x ; ; log f x ; 1 T j j t j t t1 j (2.2.11) Atëherë: FML arg max l( ) (2.2.12) Rezkova (2007) prao se maksmzm fuksoeve logartmk të përgjassë është shumë komplkuar dhe praktksht pa mplemetueshëm. Metoda IFM (metoda e kokluzoeve për margalet) fuksoo ë supozm se çdo margal uvarat logartmt të fuksot të përgjassë (LLF) ka trajtë: T l log f x ; j 1... d (2.2.13) j j j j t j t1 ROMEO K. MANO 28
29 dhe ë këtë mëyrë LLF e shpërdarjes së përbashkët merr trajtë: T l... log f ; x...; x j 1... d (2.2.14) j T 1 T t1 LLF-të e l j 1... d maksmzohe ë mëyrë dvduale ë varës të dhe: j j arg max l ( ) (2.2.15) j j j Atëherë LLF e l( ; 1... d ) maksmzohet e ldhje me për... 1 d të dhëa duke përftuar kështu vlerësm: arg max l( ;... ) (2.2.16) Joe & Hu (1996) tregua se vlerësm me metodë IFM është asmtotksht efçet duke e provuar këtë me dsa shembuj umerk. 1 d Metoda Përgjassë Maksmale Kaoke (CML) u propozua ga Mashal & Zeev (2002) duke mos kërkuar supozme teorke mb shpërdarje margale. Përkudraz shpërdarjet margale emprke jaë vlerësuar dhe përafruar me fukso e pajohur të shpërdarjes margale F. të dhëë me aë të barazmt: T 1 Fˆ X x 1 X j j t x (2.2.17) 1 T t 1 Duke përdorur këtë barazm për përafrm e fuksot të shpërdarjes margale është përftuar fukso përgjassë logartmke (LLF): T ˆ X t X d t l log c F x... F x ; (2.2.18) t 1 1 d ku vlerësm kërkuar është trajtës ˆ arg max l( ). CML Kjo metodë është më komode për përdorm e softwere-ve të përshtatshëm dhe umerksht më e qëdrueshme. Nga aa praktke përdorm metodave të mëspërme paraqet jë shkallë të lartë vështrëse sdomos ë rastet kur formaco që a vhet ë dspozco është jo mjaftueshëm. Për këtë duke u referuar Barazmeve dhe të Teoremës fukso copula do ta përdorm ë trajtm toë të përafruar me kufr e përpktë të saj spas mosbarazmt Fréchet-Hoeffdg ë kuptm e krahasmt. Arsyeja pse është e atyrshme për ta përafruar me kufr e përpktë të spërm spas Teoremës është sepse kufr përpktë spërm fuksot copula është jë madhës probabltare dhe s e tllë a lejo ta studojmë atë me aë të kocepteve të probabltett. ROMEO K. MANO 29
30 KAPITULLI III NDËRTIMI I MODELIT Në çështje e parë të këtj kaptull është bërë jë trajtm problemt ë aspekt teork. Trajtm teork shërbe s jë bazë e shëdoshë ë dërtm e jë model duke u mbështetur ë supozmet e përcaktuara ë çështje e dytë të kaptullt. Pjesa më e rëdësshme e kaptullt të tretë është çështja e tretë. Supozmet e modelt dhe dy pohmet e vërtetuara ga e ë çështje e dytë mb matrcë stokastke dhe destet a lejojë të përkufzojmë destet për shpërdarje uvarate të modelt toë. Duke përkufzuar prtje matematke dhe dsperso me jë-hap dhe t-hapa kem treguar jë mudës llogartjeje të prtjes matematke dhe dsperot me t-hapa me aë të dy pohmeve dhe kem xjerrë jë trajtë komode për rast t=1 me aë të dy rrjedhmeve përkatëse. Çështja e katërt trajto përdorm e fuksot copula dhe teoremës së Sklar-t për përcaktm e shpërdarjes multvarate të modelt. Pohm vërtetuar këtu a lejo të përkufzojmë shpërdarje multvarate të modelt. Me aë të dy pohmeve të fudt të kësaj çështjeje ë jë prej të clave kem përdorur mosbarazm Fréchet-Hoeffdg kem treguar jë formulë komode për llogartje destett të përafruar të shpërdarjes multvarate. 3.1 Shtrm problemt jë bashkës dskrete vlerash dhe Y1 Y2 Y jë varg Le të jetë E s... dryshoresh rast të pavarura ku çdo Y 1 është jë dryshore rast Beroully me probabltet të suksest 1. Pra PY 1 1 dhe PY 0 për çdo 1. Për çdo Y 1 shëojmë me X dryshore e rastt bomale të ldur prej saj që shpreh umr e sukseseve ë e rastt Y pra m m E X Y1 Y2... Y. Rrjedhmsht kem: m k k m k m vlerësme të pavarura të suksest për dryshore X ~ Bm ;1 dhe P X k C 1 0 k m (3.1.1) Me prtje matematke E X m 1 dhe dsperso 1 D X m. Në këtë mëyrë përftojmë jë vektor rast me margale të clat jaë dryshore rast të pavarura bomale që do ta shëojmë me X X1 X 2 X. ROMEO K. MANO 30
31 Le të jetë Z Z Z Z dskrete E s 1 2 jë vektor dryshoresh të clat marr vlera ë bashkësë Shëojmë me T t jë hapësrë dskrete kohe dhe studojmë zhvllm ë kohë spas hapësrës kohore T të vektort Zt Z1 t Z2 t Z t vektor s fukso të vektort të rastt X X X X duke përcaktuar vlerat e këtj 1 2 spas rregullt: () ë qoftë se Z 1 ë momet t T merr vlerë j pra Z j atëherë t vlerë e tj ë momet t1 T do ta përcaktojmë me aë të barazmt: Z 1 j 1 X 1 (3.1.2) t Në këto kushte për vektor-vlerat Z Z Z Z 1 2 do të kem: ( 1 ) meqëëse për 1 dhe tt vlera e Z shprehet s fukso dryshores së rastt X atëherë t Z t është jë dryshore rast dhe rrjedhmsht edhe Zt Z1 t Z2 t Z t të jetë jë vektor rast me vlera ë E. ( 2 ) për çdo 1 famlja Zt t T t do me vlera ë hapësrë dskrete E s... është jë proces rast me kohë dskrete T dhe hapësrë dskrete gjedjesh E. ( 3 ) shëojmë m j 1 dhe barazm (3.1.1) do të marrë trajtë: k 1 k j 1 k 0 1 j 1 P X k C k j (3.1.3) Pra vlerat e mudëshme të dryshores bomale do të jeë ga bashkësa j 1 ( 4 ) spas rregullt () dhe vlerave të mudëshme të dryshores së rastt X vlerat e dryshort të rastt Zt 1do të jeë s më poshtë (Mao & Xha 2014 JNTS fq 9-10 ): t1 X 0 Z j 1 0 j 1 pra rrtet me jë jës vlera e Z ; X 1 Z t1 j 1 1 j pra vlera e Z uk drysho; X 2 Z t1 j 1 2 j 1 pra vlera e Z zbret me jë jës; X k Z t1 j 1 k j k 1 ; 0 k j 1; (3.1.5) ROMEO K. MANO 31
32 X j 1 Z 0: pra vlera e Z zbret me j 1 t 1 Është e qartë se çdo rast tjetër është gjarje e pamudur. Në qoftë se komukm e mëspërm do ta paraqesm ë trajtë e jë grafku do të përftom fgurë 3.1. Fgura 3.1 Graf sstemt. Burm: Autor (Mao & Kosova 2014 IJRD fq 106) Nga graf dhe pka ( 4 ) e rregullt () vhet re se sstem uk mud të kalojë me jë hap ga gjëdja j ë gjedje j 2 ashtu skurse shhet qartë se sstem mud të kthehet ë të gjtha gjedjet e mëparshme ë varës të vlerave që do të marrë dryshorja e rastt X. ( 5 ) meqëëse famljet Z t T fjalë për probabltete të kalmt me jë-hap të trajtës: 1 jaë procese rast atëherë mud të bëjmë t t1 / t p j l P Z l Z j (3.1.6) Nga barazm (3.1.2) rregullt () kem që vlera (gjedja) e Z ë momet t1 T varet ga vlera k e dryshores së rastt bomale X e cla ga barazm (3.1.5) kushtt ( 4 ) sjell që gjedja l E përcaktohet ga barazm: Nga ( 4 ) dhe barazm (3.1.4) ( 3 ) kem që vlerat e mudshme të l l j 1 k (3.1.7) E jaë: 0 l j 1 (3.1.8) Rezultat barazmt (3.1.8) është qartë edhe ë qoftë se bëjmë dsa shdërrme detke mb kusht 0 k j 1të barazmt (3.1.3) dhe pastaj zëvedësojmë ë rezultat e marrë ROMEO K. MANO 32
33 barazm (3.1.7). Kështu duke shumëzuar me (-1) mosbarazm e dyfshtë 0 k j 1 marrm 0 k j 1. I mbledhm këtj të fudt madhësë j 1 dhe zëvedësojmë l spas barazmt (3.1.7). Rezultat që përftojmë është a barazmt (3.1.8). Nga aa probabltare gjarjet X jëvlerëshme dhe s rrjedhojë kaë probabltete të jëjta: k dhe Z t1 j 1 k / Z t1 j k t1 t j 1 jaë të k j 1 k 1 / 1 (3.1.9) P Z j k Z j P X k C Duke zëvedësuar k spas barazmt (3.1.7) barazm (3.1.9) merr trajtë: 1 t1 t j 1 j 1 l j l l P Z l / Z j P X j 1 l C 1 (3.1.9') Pka ( 4 ) e rregullt () dhe barazm (3.1.9 ) a lejo të propozojmë s probabltete të kalmt me jë-hap për çdo çft gjedjesh ga hapësra (Mao & Kosova 2014 IJRD fq 106): E s... dhe 1... madhëstë j 1 l l j s j 1 l l C j 1 1 për l j k j p j l për Rregull () dhe pka ( 3 ) e tj tregojë se sstem Z t T 1 gëzo vetë e mugesës së kujtesës gjë e cla a lejo që famljet Zt t T t trajtojmë s Zxhrë të Markovt. Për më tepër meqëese probabltetet e kalmt me jë-hap të tpt (3.1.10) uk vare ga koha t atëherë famljet Zt t T plotësojë kusht e të qet Zxhr Markovt homogje. Duke shprehur ë trajtë matrce elemetët e barazmt (3.1.10) për çdo çft 2 t j l E përftojmë matrcë M të kalmt me jë-hap të Zxhrt të Markovt homogje Z t T e cla jepet me aë të tabelës 3.1. t 1 Tabela 3.1 Matrca e kalmt me jë-hap C M j1 j j j3 l l j1l 1 C j1 1 C j1 1 C j s1 s s s1 2 s1 l l s 1 l s 1 Cs 1 1 Cs 1 1 C 1 1 ( s 1) 1... s... Burm: Autor (Mao & Kosova 2014 IJRD fq 106) ROMEO K. MANO 33
34 3.2 Supozme të modelt Duke formalzuar ë kocepte probabltare përfudmet e mëspërme për vektor e rastt Z Z Z Z t 1 t 2 t t me vlera ë hapësrë E s... do të marrm rezultatet e mëposhtme të clat do t quajmë supozme të modelt që do të dërtojmë (Mao Qershor 2010 fq 264): 1. X 1 jaë dryshore rast bomale me parametra 1 dhe dhe j E. 2. Famlja Zt t T E është jë proces rast me hapësre dskrete gjedjesh s... dhe hapësre dskrete kohe T t... rast që merr vlera spas barazmt (3.1.2) të rregullt (). 3. Famlja Zt t T ku Z është dryshore është Zxhr Markovt homogje me probabltete të kalmt me jë-hap të trajtës (3.1.10) dhe matrcë M të kalmt me jë-hap. 4. Famlja f0 j j E është shpërdarja e fllmt e procest të rastt Zt t T 3.3 Dsa rezultate dhe pohme të rëdësshme për model t. Duke u bazuar ë katër supozmet e mëspërme ë këtë çeshtje tregohe dsa pohme që bëjë të mudur përcaktm e shpërdarjes probabltare të modelt dhe më pas ë përcaktm e prtjes matematke dhe dspersot të Z 1 dhe Z 1. Pohm Në kushtet e supozmeve 1-4 matrca M e kalmt me jë hap me elemetë të trajtës (3.1.10) është matrcë stohastke dmth elemetët e saj plotësoj kushtet: ; j l E p j l 2. j E p j l 1 l 0 t j Vërtetm: Pka e parë e pohmt është e qartë pas elemetet p j l të dhëa me aë të barazmt (3.1.10) jap destet e shpërdarjes bomale me parametra j 1 l j 1 dhe 0 për l j s dhe 1 për ROMEO K. MANO 34
35 Për pkë 2 të pohmt duke përdorur barazm (3.1.10) dajmë shumm: j 1 p j l p j l p j l l 0 l 0 l j 2 j 1 j 1 l C j 1 j 1 l l l 0 l j j 1 l 0 C j 1 1 l j l l j 1 1 Por C j 1 l l. j 1 j 1 C Bëjmë zëvedësm dhe kem: j 1 l l 1 j 1 l j C j # l 0 Shëojmë me M (t) matrcë e kalmt me t-hapa me elemetë të trajtës: / t mt m P Z l Z j p j l Në këto kushte ga pohm Chapma-Kolmogorov-t kem që: dhe pt l PZ t l f0 j p j l je p j l p j k p k l t t t t t je Barazm (3.3.3) ë trajtë matrcore mud të shkruhet: t t t t M M M 2. Për t 1 1 M M dhe 2 M M M M 2. Duke rrtur ekspoet ë mëyrë progresve ë përgjthës marrm: M t t M. Atëherë madhëstë t p j l jaë elemet të fuqsë se t-ët të matrcës M me elemet të trajtës (3.1.10) (Grmmett & Strzaker 2001 fq 48). Pohm Në kushtet e supozmeve 1-4 famlja p t l l E ku elemetet (3.3.2) është destet dskret probablteteve për dryshore e rastt Z. t p l jaë të trajtës t Vërtetm: Që famlja p t l l E të jetë destet dskret probablteteve për dryshor e rastt Z duhet të plotësoj dy kushte: t ROMEO K. MANO 35
36 0 p l 1; l E 1. t 2. 1 le p l t Plotësm kushtt të parë është evdet sepse elemetët p l të clat jepe me aë të barazmt (3.3.2) jaë probabltete dhe s të tlla ato përfshhe ë segmet 0;1. Për kusht e dytë duhet të provojmë se elemetet e famljes p t l l E plotësojë kusht: le t t p l Në barazm (3.3.2) elemetet p l t përcaktohe ga elemetet t p j l të clët jaë t elemetë të matrcës fuq M pradaj mud të provojmë barazm (3.3.4) me aë të metodës së duksot të plotë matematk ë ldhje me fuqë t të matrcës M dhe për jë s të fudme sado të madhe. Për 1 t M M p j l p j l pradaj duke zëvedësuar ë shumm e 1 1 dhe mëposhtëm rezultat e barazmt (3.3.2) dhe duke përdorur vettë e shumave të fudme do të kem: s s s p l f j p j l = 0 l 0 l 0 j 0 s s j0 l0 s 0 f j p j l = 0 j0 l0 s f j p j l (3.3.5) Nga Pohm kem që p j l 0 l 0 s 1 dërsa ga supozm 4 kem që famlja f j j E është shpërdarje probabltare e fllmt të procest pra është destet dskret probabltetesh. S e tllë plotëso kusht që f j rezultate marrm barazm (3.3.4). s 0 1. Duke zëvedësuar këto dy j 0 ROMEO K. MANO 36
37 E praojme të vërtetë barazm (3.3.4) për t m pra p l 1 dhe e provojmë për t m 1. m 1 Meqëëse elemetët p j l jaë elemet të l 0 s m m 1 m M M M dhe matrca M është matrce katrore dhe s rrjedhm edhe çdo fuq e saj është matrce katrore me të jëjtë përmasë atëherë ga formula e prodhmt të dy matrcave (Larso & Edwards 1988 fq 47) elemetët e matrcës prodhm të dy matrcave kaë trajtë: m m (3.3.6) p j l p j k p k l 1 1 ke Duke bërë zëvedësmet për t m 1 dhe duke zbatuar vettë e shumave të fudme marrm: s s s m1 p l f j p j l = m1 0 l 0 l 0 j 0 s s s l 0 j 0 k 0 j 0 k 0 l 0 0 m = f j p j k p k l s s s 0 m f j p j k p k l s s s m f j p j k p k l 0 j 0 k 0 l 0 (3.3.7) Shuma e fudt spas Pohmt është e barabartë me 1 sepse jep shumë e të gjthë elemetëve të rrjeshtt të k-t të matrcës stokastke dërsa shumm dyfsht ga supozm për t m jep pmk 1. # s k 0 Përkufzm Famlje pt l l E të përcaktuar me aë të barazmt (3.3.2) do ta quajmë destet uvarat markova të dryshores së rastt Z t ë momet t T. Prtje matematke të dryshores së rastt Z t meqeëse kjo është jë dryshore rast dskrete me vlera ë bashkësë E mud ta llogarsm lehtë duke përdorur përkufzm klask të prtjes matematke (Mao & Kosova 2014 IJRD fq 107): ROMEO K. MANO 37
38 t Elemetët E Z l p l t t l E t l f j p j l = 0 l E j E t l f j p j l = 0 l E j E t 0 j E l E f j l p j l (3.3.8) p j l për jë j të fksuar jaë elemetët e rreshtt të j -të të matrcës me t- hapa dhe shuma e barazmt të fudt është e qartë që shpreh shumë e produkteve të vlerës l t me elemet përkatës të rreshtt të j -të ë matrcë me t-hapa. Për t=1 elemetët p j l jaë elemetët e matrces stokastke dhe s rrjedhm ato paraqes probabltetet e kalmt me jë-hap të clat plotësojë Pkë 2 të Pohmt S rrjedhm mud të shkruajmë: Meqëëse për jë 1 E Z f j l p j l 1 0 j E l E 3.3.8' 0 j E l E f j l p j l j të fksuar famlja p j l l E probabltetesh (Pohm pka 2) atëherë madhësa l p j l e mrëflltë. Kjo përlgj përkufzm e mëposhtëm: Përkufzm Madhësë l p j l le Z 1 dhe e shëojmë: është destet dskret është prtje matematke le do ta quajmë prtje matematke me jë-hap të dryshort të rastt 1 1 E l p j l le Duke përdorur barazm e Përkufzmt barazm (3.3.8 ) do të marrë trajtë: 1 E Z 1 f0 j E 3.3.8'' je Për aalogj me Përkufzm japm përkufzm: ROMEO K. MANO 38
39 Përkufzm Madhësë le l p t j l do ta quajmë prtje matematke me t-hapa të dryshores së rastt Z t dhe e shëojmë: t t E l p j l (3.3.9) le Prtja matematke me t-hapa spas Përkufzmt llogartet s shumë e prodhmeve të gjedjeve l me elemet respektv t p j l të matrces me t-hapa për j të fksuar pra me elemet respektv të rreshtt të j -t të matrces me t-hapa gjë që e bë të lehtë llogartje e saj. Matrca me t-hapa është matrce stokastke (Nordstrom 2008) (fq 3) që do të thotë se për jë j E të fksuar famlja t p j l l E është probabltet s rrjedhm barazm (3.3.9) shpreh prtje matematke të mrëflltë ë kuptm e përkufzmt klask të prtjes matematke për jë dryshore rast dskret. Pohm Në kushtet e supozmeve 1-4 dryshorja e rastt Z t ka prtje matematke të barabartë me: Vërtetm: Në barazm (3.3.5) zëvedësojmë marrm barazm (3.3.10). t E Z t f0 j E je t l p j l me le t E spas Përkufzmt dhe t t Vërejtje 1 Në qoftë se për çdo j E madhëstë e trajtës E l p j l shkojmë s le vlera të jë fukso umerk me vlera umerke të dryshores së rastt Z atëherë barazm është trajtës klaske të përkufzmt të prtjes matematke të jë fukso të dryshores së rastt me destet f0 j j E. Vërejtje 2 Kjo mëyrë të shprehur e prtjes matematke ë momet t T lehtëso shumë llogartje e saj ë qoftë se jepet matrca e kalmt me jë-hap dhe shpërdarja e fllmt të procest. Një rezultat teresat mud të xjerrm duke përdorur barazm (3.3.8 ) dhe probabltetet bomal të matrcës me jë-hap për llogartje e prtjes matematke ë hap e parë të procest. ROMEO K. MANO 39
40 Rrjedhm Prtja matematke e margalt të -të ë momet t=1 Z 1 jepet me aë të barazmt: 0 E E Z (3.3.11) ku me E është shëuar prtja matematke e shpërdarjes së fllmt të procest. 0 Vërtetm: Elemetët e çdo rrjesht të matrcës stokastke jaë probabltete bomale me parametra j 1 dhe 1 dhe prtje matematke: 1 11 E j duke zëvedësuar këtë rezultat ë barazm (3.3.8 ) marrm: 1 0 je je 0 1 E Z f j E 11 f j j 1 f j j 1 je 0 1 f j j f j 0 0 j E j E (3.3.12) Nga kusht (4) supozmeve të modelt famlja procest të rastt Z. t t T S rrjedhm madhësa j f j f0 j j E është shpërdarja e fllmt të 0 shpreh prtje matematkë të je shpërdarjes së fllmt të clë do ta shëojmë 0 E dhe f j 0 1. Atëherë duke je zëvedësuar ë barazm e fudt (3.3.12) do të marrm: 0 E E Z (3.3.13) Në mëyrë të gjashme mud të gjemë jë trajtë të përgjthshme për dsperso e Z t ë momet t T (Mao & Kosova 2014 IJRD fq 108). Pohm Në kushtet e supozmeve 1-4 dryshorja e rastt Z t ka dsperso të barabartë me: ROMEO K. MANO 40
41 D Z t f0 j E Z f0 j E Z je je t 2 t 2 ku t 2 2 t E Z l p j l. le Vërtetm: Shkruajmë: Por: 2 2 t t D Z E Z E Z t t t E Z E Z 2 2 t t E Z l p l t l f j p j l = 2 0 l E j E t l f j p j l = 2 t = f j l p j l 0 j E l E l E 2 0 l E j E 2 (3.3.15) (3.3.16) Në këtë mëyrë shprehja e dspersot të Z t ë momet t T do të marrë trajtë: Duke shëuar me shkruajmë: D Z t f0 j l p j l f0 j l p j l je le je le 2 t t (3.3.17) t 2 2 t E Z l p j l le dhe duke përdorur Përkufzm mud të D Z t f0 j E Z f0 j E Z je je t 2 t Barazm (3.3.18) paraqet jë mëyrë algortmke të llogartjes së vlerës së dspersot të Z t ë momet t T. Rrjedhm mëposhtëm jep jë mëyrë llogartjeje për dsperso e Z t ë momet t ROMEO K. MANO 41
42 Rrjedhm Dsperso margalt të -të ë momet t=1 Z 1 jepet me aë të barazmt: Vërtetm: D Z 1 1 E 1 1 D Z (3.3.19) Nga barazm (3.3.18) për t 1 mud të shkruajmë: D Z 1 f0 j E Z f0 j E Z je je Kufza e dytë e këtj barazm paraqet katror e prtjes matematke me jë-hap pradaj ga barazm (3.3.11) mud të shkruajmë: f0 j E Z 1 E 1 je 2 2 E 2 0 Për kufzë e parë të krahut të djathtë të barazmt (3.3.20) kem: Madhëstë f j E Z f j l p j l je je le 2 0 je le f j l p j l (3.3.22) p j l për jë j të fksuar jaë elemetët e rrjeshtt të j -t të matrcës me jë-hap s rrjedhm famlja p j l ; l E është destet dskret probabltetesh me dsperso të fudëm të cl do ta shëojmë shkruajmë: Nga barazm fudt është e qartë që: le D Nga përkufzm dspersot mud të D E Z E Z le 2 1 l p j l E Z l p j l D E Z Zëvedësojmë ë barazm (3.3.22) dhe marrm: ROMEO K. MANO 42
43 2 2 f j E Z f j D E Z je je f j D + f j E Z je je Zëvedësojmë këtë rezultat ë barazm (3.3.20) dhe kem: D Z 1 f0 j D f0 j E Z f0 j E Z je je je Duke trajtuar madhëstë (3.3.23) 1 E Z s fukso të dryshores së rastt Z atëherë kem: D E E E E E (3.3.24) Meqeëse E 1 Z jaë prtje matematke bomale të tlla që: dhe D E j Z jaë dspersoet bomale respektve të tlla që: D 1 atëherë ë barazm (3.3.20) do të kem: 1 j 1 (3.3.25) 1 1 D Z f j j 1 0 je je f j j f0 j1 j 1 je 1 f j j 1 je 0 1 f j j je 0 je 0 1 f j j 1 1 f0 j j f0 j je je 0 0 je je f j j 1 f j j ROMEO K. MANO 43
44 E 1 1 D Z # 3.4 Implemetm Teoremës së Sklar-t mb model Duke shfrytëzuar ldhje mds fuksot të shpërdarjes dhe fuksot copula të shprehur me aë të teoremës që jhet me emr Teorema e Sklar-t mud të gjejmë fukso që shpreh destet vektoral (multvarat) të vektort të rastt Zt Z1 t Z t Shëojmë me F l PZ l p l t t t ll Me Ft l1 l PZ1 t l1... Z t l. fukso e shpërdarjes për margal e -t. shëojmë fukso e shpërdarjes të vektort të rastt Zt Z1 t Z t dhe me... t 1 p l l destet e tj. Nga pjesa e dytë e Teoremës së Sklar-t përftojmë fukso e shpërdarjes multvarate të vektort Z t të shprehur me aë të fuksot Copula: Ft l1 l Ct F1 t l1... F t l (3.4.1) ku C t është fukso Copula cl ka për margale fuksoet e shpërdarjes së Zt të margaleve të vektort të rastt Z t Nga ldhja mds destett dhe fuksot të shpërdarjes dhe barazm (2.2.6) mud të shkruajmë (Mao 2010 JMNS fq 42): F( l1... l) pt( l1... l) l... l 1... Ct F1 t l1 F l l... l 1 C 1... t u t u t F t ( l ) u... u l 1 t t t t t t 1 c u u p l (3.4.2) Ku ct u1 t u t është destet Copulas dhe ptl margaleve të vektort Zt Z1 t Z t 1 të dhëa spas Përkufzmt është produkt desteteve të ROMEO K. MANO 44
45 Rezultat (3.4.2) mud ta shprehm ë trajtë e jë pohm cl përcakto shpërdarje e vektort të rastt Zt Z1 t Z t : Pohm Në qoftë se Zt Z1 t Z t është jë vektor rast dhe Zt t T jaë Zxhrët e Markovt homogje të margaleve të tj që plotësojë supozmet 1-4 atëherë shpërdarja e vektort të ë momet t T ka destet pt( l1... l ) të dhëë me aë të rastt Zt Z1 t Z t barazmt (3.4.2). Përkufzm Famlje pt l1... l l E 1... elemetët e të clës përcaktohe me aë të barazmt (3.4.2) quhet destet markova vektort të rastt Zt Z1 t Z t ë momet t T. Në barazm (3.4.2) mbetet të vlerësojmë destet e Copulas me aë të vlerësmt të parametrave të shpërdarjes së saj. Vlerësm parametrave të shpërdarjes së fuksot Copula rrjedhmsht edhe destet saj mud të bëhet me shumë metoda. Në kaptull e dytë prezatuam trajtm e tre metodave kryesore për vlerësm e parametrave të fuksot copula: FML IFM dhe CML. Meqëëse qëllm yë është dërtm jë model lehtëssht të mplemetueshëm për jë bazë të dhëash që shpesh herë jaë të kufzuara jem fokusuar ë jë përafrm të copulas me jë ga kufjtë e përpktë të saj dhe pkërsht me kufr e përpktë të spërm të saj. Një mëyrë praktke për përafrm e Copulas është përafrm saj me aë të mosbarazmt të dyfshtë Fréchet-Hoeffdg (Teorema 2.2.2) cl përcakto kufr e poshtëm dhe të spërm të jë fukso Copula (Mao Qershor 2010 fq 268). Në këtë të fudt ë qoftë se shëojmë me: Atëherë W max Fj t 1 0 dhe M m F 1 t F t (3.4.3) j1 t 1 t t W C u u M (3.4.4) ROMEO K. MANO 45
46 Kufr spërm është gjthmoë jë fukso shpërdarjeje dërsa poshtm është jë fukso shpërdarjeje vetëm për Copula- dy dmesoale. Në qoftë se do të përdorm jë përafrm të Copula-s me aë të mosbarazmt të dyfshtë të Fréchet-Hoeffdg pra ta përafrojmë atë me jë ga kufjtë e përpktë të saj është më e atyrshme të praojmë s përafrm të saj për rast e përgjthshëm kufr e spërm M F F m 1 t t cl është jë fukso shpërdarjeje.pra: Ct F1 t l1... F t l M m F1 t F t (3.4.5) Pohm mëposhtëm a lejo të përcaktojmë mmum e kërkuar ga barazm (3.4.5) (Mao Qershor 2010 fq 269). Pohm Në qoftë se shëojmë me m l l barazm M F ( m) për dojë j 1... Vërtetm: jt... 1 atë vlerë të vargut l1 l2... l për të clë realzohet ; atëherë m l1 l m.... Meqëëse elemetët Ft ( m) 1... jaë fuksoe shpërdarjeje dhe dryshoret e rastt Z 1... t kaë shpërdarje të jëjtë atëherë kem që: për çdo 2 mplkm l l F l F l sjell që m l ; 1 j k j t j k t k l l j k E ka vëd. Meqëëse M Fjt ( m) është m F1 t F t kjo. Rrjedhmsht: m l1 l m.... Shëojmë m lm dhe M Fm t lm ( ). Duke përdorur përafrm e mëspërm destet copulas së përafruar do të jetë: c u u t 1 t t C u u u u M m p l t 1 t t 1 t t m t m t m F l m Zëvedësojmë rezultat ë barazm (3.4.2) dhe marrm: (3.4.6) p ( l... l ) p l p l t 1 t m t 1 ROMEO K. MANO 46
47 Vargu umrave l 1 l 2... l është me elemetë ga E pra l E 0 l s Supozojmë se s dhe dërtojmë të gjtha ëvargjet kostate që përftohe ga vargu umrave l 1 l 2... l të tllë që çdo dy prej tyre të mos keë elemete të jëjtë. Shëojmë me N N ëvargjet kostate dhe me t 0 umr respektv të elemeteve të tyre. t0 t s s Është e qartë që tr. Gjthashtu destet markova dhe fuksoet e shpërdarjes të r0 margaleve me vlera ga jëjt ëvarg jaë të barabarta pra: t s = p l P Z l P Z N l N t r t r t t r r t r ku me l r kem shëuar elemet kostat të ëvargut N tr. Në këtë mëyrë për destet multvarat markova do të marrm: Për çdo ëvarg tr (3.4.7). p ( l... l ) P cardn cardn p (... ) (3.4.9) t 1 t t0 t0 t s t s t t0 t s N kem 0 r s r probabltete të jëjta ë produkt e barazmt Duke oretuar produkt e barazmt (3.4.7) spas umrt të ëvargjeve dhe umrt të elemetëve të çdo ëvargu marrm barazm: r p ( l... l ) p l p l (3.4.10) t 1 t m t r r0 Rezultat e paraqtur me aë të barazmt (3.4.10) mud ta paraqesm ë trajtë e pohmt të mëposhtëm: Pohm Në kushtet e Pohmt dhe supozmt se Nt0 N jaë ëvargjet kostat të elemetëve të vargut t0 t s s l l l të vlerave të margaleve të vektort Zt Z1 t Z t t s dhe është vargu umrt të elemetëve të ëvargjeve Nt0 N t s atëherë destet markova vektort të rastt Zt Z1 t Z t jepet me aë të barazmt (3.4.10). ROMEO K. MANO 47
48 Pohm ga aa e tekkave llogartëse a lehtëso gjetje e destett të vektort të rastt Zt Z1 t Z t ë momet t T pa qeë evoja e johjes së vlerave kokrete të margaleve Zt dhe klasfkm dvdual të tyre. Mjafto të johm umr e margaleve që marr të jëjtë vlerë l r E pra mjafto të johm vargu e umrave t 0. Kjo do të thotë që baza e të dhëave që evojtet ë këtë rast të jetë shumë me e përqedruar ë formaco. Kjo gjë është e dukshme sdomos ë rast e përdormt të modelt të mëspërm ë trajtmet mkrofacare të vlerësmt të rskut të kredsë. Barazm (3.4.10) trego gjthashtu se sa më e madhe të jetë -ja aq më vogël është probabltet për të qëlluar ë shejë të jë klasfkm të mudshëm ë kuptm e parashkmt. t s ROMEO K. MANO 48
49 KAPITULLI IV APLIKIMI I MODELIT PËR RASTIN E PORTOFOLIT NË NUMËR TË KREDIVE 4.1 Klasfkm portofolt të kredsë spas umrt të detyrmeve të pashlyera perodke Le të tregojmë së par pse zgjodhëm trajtm ë umër kredsh të jë portofol krede. Në sstem bakar IF-të jaë të veleve të dryshme për sa përket madhëssë së bzest dhe shumave që ato kredtojë për kletët e tyre. Shumca e bakave të velt të dytë dhe kompave mkrofacare kreddhëëse kredtojë shuma relatvshtë të vogla dhe syojë të bëjë bzes duke kredtuar jë umër të madh kletësh dhe për afate të shkurtra kohore zakosht 1-5 vjet. Kjo është karakterstkë specfke e vedeve ë zhvllm ku përfshhet edhe Shqpëra. Isttucoet facare klasfkojë kredtë e tyre ë ldhje me madhësë e shumës së kredsë së dhëë spas veleve të dryshme. Mesatarja e tervaleve të këtyre veleve është gjthmoë e mrëpërcaktuar. Në këtë mëyrë ëse dhet umr kletëve (kredve) të jë klase të caktuar shuma e ekspozuar mesatare llogartet s produkt umrt të kletëve me mesatare e klasës përkatëse. Kjo bë që shumë prej IF-ve që operojë ë tregje të tlla të realzojë kotroll perodk (zakosht mujor) të clëssë së portofolt të kredsë duke u bazuar ë umr e kredve dhe klasfkm ë umër të tyre ë vele të dryshme rsku. Një mëyrë e tllë klasfkm është paraqtja e portofolt ë umër kredsh spas tabelës 4.3. Implemetm modelt të dërtuar ë kaptull e tretë ofro mudësë e trajtmt të rskut të portofolt ë umër të kredve ë dryshm ga L dhe Yag (1999) të clët ofrua jë model Markova duke u mbështetur ë klasfkm e rskut të portofolt spas madhëssë ë vlerë të kredve të pashlyera. Le të shohm shkurtmsht se s fuksoo proces shlyerjes së jë detyrm krede ë sttucoet kreddhëëse (Mao & Xha 2014 JNTS fq 8-9). Në praktkat facare të bakave jhe dsa mëyra për shlyerje e jë krede. Më e zakoshmja është ajo me këste (detyrme) mujore. Kjo për fakt e thjeshtë se të ardhurat dhe shpezmet e çdo jëse facare (dvd famlje dhe bzes) kaë s jës kohore muaj facar (30-dtësh jë vt facar = 12 muaj facar). Ndërkohë jhet edhe shlyerja e detyrmt të kredsë me këste tremujore apo edhe marrëveshje të tjera të ç rregullta. Megjthatë mud të vërehet lehtë se model mud të modfkohet për të mbuluar edhe këto raste. Ne do të shqyrtojmë rast kur shlyerja e detyrmt të kredsë është spas jë shpërdarje të rregullt mujore. Ky trajtm uk është zgjedhur për të bërë më të lehtë stuatë por për t u përshtatur mëyrës së klasfkmt të kredve ë rsk dhe provzomt spas këtj klasfkm ROMEO K. MANO 49
50 ga pjesa më e madhe e bakave qëdrore. Ajo çfarë përforco aplkueshmërë e modelt ë ved është përqasja me klasfkm e rskut të protofolt të kredve ë ljë me poltkat dhe modelet e përdorura ë Bakë Qëdrore ë Shqpër. Duke u referuar Rregullores së Bakës së Shqpërsë: Për admstrm e rrezkut të kredsë datë kredtë e këqja klasfkohe ë grupe me bazë voesat 30 dtore ose dryshe mujore. Mb bazë e këtyre grupeve bëhet edhe provzom kredve ë rsk spas tabelës së mëposhtme (tab. 4.1): Tabela 4.1 Klasfkm kredve spas dtëvoesave dhe masa e provzomt të tyre. Grup Provzoet mb Dtëvoesat (dv) portofol përkatës Grup I 0 dv = 0 këste 0% Grup II 1-30 dv = 1 këste 1% Grup III dv = 2-4 këste 5% Grup VI dv = 5-7 këste 20% Grup V dv = 8-12 këste 50% Grup VI Mb 365 dv = mb 12 këste 100% Burm: Baka e Shqpërsë (2006) Nga tabela vhet re se çdo kred klasfkohet ë jë ga gjashtë grupet e koloës së dytë sdo që të jetë korrektësa e shlyerjes së detyrmt të saj kudrejt bakës. Çdo gjedje klasfkuese përcaktohet ga umr dtëvoesave që ka ë shlyerje e detyrmt daj bakës (koloa e dytë) dërsa provzom bëhet spas ormës së përcaktuar ë koloë e tretë. Në fud të çdo muaj facar bakat bëjë rklasfkm e portofolt të tyre të kredsë. Një kred do të klasfkohet pwr shembull ë Grup III-të atëherë kur kredmarrës është 31 dtë der ë 90 dtë ë voesë. Duke e ekuvaletuar këtë ë muaj facar do të thotë që kredmarrës ka pa shlyer dy tre ose katër këste mujore ga detyrm tj kudrejt bakës ë perudhë dërmjet dy rklasfkmeve. Gjthashtu kredmarrës mud të shlyejë jë dy ose më shumë detyrme ë harku kohor të jë muaj gjë që e bë të dryshojë ë red rrtës gjedje e vet ë klasfkm me më shumë se jë jës. Duke shlyer jëherësh tre këste a kalo ga Grup III-të ë Grup I-rë. Ndërkohë që uk mud të zbresë më shumë se jë jës pra të shkojë ë rklasfkm mujor ga Grup II-të ë Grup IV-rt për fakt se klasfkm përcaktohet ga dtëvoesat që do të thotë se jë kred që është 30 dtë ë voesë uk mud të kalojë ë fud të muajt pasardhës ë 91 dtë ë voesë. ROMEO K. MANO 50
51 Në Grup VI-të hyjë kredtë që jaë ë voesë mb 12 këste mujore të clat klasfkohe spas termologjsë bakare me status wrtte-off (të dështuara) status të cl e ruajë gjatë gjthë vtt facar dhe provzoohe për të gjthë shumë (100%). Ato uk e dryshojë këtë status edhe kur ë perudhë ë vazhdm klet të bëj lkujdme të clat praktksht mud ta zbres atë ë vel e 12 muajve ë voesë. Meqëëse për çdo kred kem jë vedmarrje të kushtëzuar ga jë probabltet kthyeshmëre dhe çdo muaj testohet clësa e kësaj kthyeshmëre atëherë trajtm portofolt të kredsë ga CR + s jë vektor rast me margale dryshore rast të tpt të Beroullt është justfkuar për praktkat e mëspërme facare (qofsh të bakave ose sttucoeve tjera kreddhëëse). Tekologja e mëspërme e përdorur ga bakat e velt të dytë për kotroll e shlyerjes së huave dhe klasfkm portofolt ë umër të kredve spas Bakës Qëdrore të Shqpërsë përforcojë aplkueshmërë e modelt të dërtuar lustruar ë kaptull e tretë. Model dërtuar ë kaptull e III-të është jë model përgjthshëm. Ndërsa shembull portofolt të kredsë atyrsht përmba edhe specfkat e veta kokrete sç është për shembull gjedja (klasfkm) wrtte-off e cla krjo jë status të veçatë. Për këtë arsye ë çeshtje 4.2 përveç se të tregojmë që model mud të mplemetohet për rast e portofolt të kredsë ë umër paralelsht tregojmë se model është qëdrueshëm edhe për specfkat e veçata të rastt kokret. 4.2 Formalzm procest të clëssë së shlyerjes me këste mujore të jë portofol krede Le të kem jë portofol krede me jë vëllm të përgjthshëm kredsh të barabartë me kredtorë cl përbëhet ga kred që kaë jë status gjedjeje të përcaktuar ga tabela 4.1. Në qoftë se shëojmë me Y 1 seclë ga kredtë atëherë vektor rastt Y Y 1 Y përfaqëso portofol e kredsë ë këdvështrm e clëssë së lkudmt të detyrmt. Margalet e vektort Y jaë dryshore rast ku çdo jëra prej të clave mud të shhet s jë dryshore rast Beroully me probabltet të suksest 1. (Shëojmë me sukses pagesë ë kohë të këstt mujor.) Në fllm të jë perudhe (vt facar) çdo kred fllo me jë status (gjedje) të përcaktuar ë tabelë 4.1. Çdo kred klasfkohet ë jë ga gjashtë grupet e kësaj tabele spas modaltett të shlyerjes së kësteve. Nga mëyra e dërtmt të tabelës 4.1 dhe vlerësmt të çdo krede spas klasfkmt të përcaktuar kërkohet që ë fud të çdo perudhe (muaj) të testohet çdo kred. Testm jë krede dvduale ëkupto motorm e vazhdueshëm për ROMEO K. MANO 51
52 korrektësë e shlyerjes ë kohë të detyrmeve perodke (mujore) s dhe vlerësm e detyrmeve të mbartura ga perudhat (muajt) e mëparshme. Kështu për jë kred e cla ë fllm të vtt facar është me j-këste ë voesë ë fud të muajt të parë baka testo ëse për këtë hua është paguar këst radhës dhe sa ga këstet ë voesë jaë shlyer ga klet. Testm kredsë shërbe ë klasfkm e saj ë jë ga grupet e tabelës 4.1. S rrjedhojë ëse ë fud të perudhës korete jë hua është j-këste ë voesë atëherë ë fud të perudhës pasardhëse ë momet pasardhës të kohës dskrete t duhe bërë j 1 teste Beroully. Numr sukseseve të (j + 1) testeve përcakto gjedje (status) e kredsë ë jë ga gjashtë grupet më lart (referuar tabelës 4.1). Le të them se kreda Y është j këste ë voesë. Ndërtojmë dryshore e rastt X që shpreh umr e sukseseve ë j 1 teste të pavarura të dryshores së rastt Y. Në këtë mëyrë përftojmë vektor e rastt X X X 1 bomale me parametra j 1 dhe margalet e të clt jaë dryshore rast Meqëëse ë praktkat e jë bake çdo kred e cla kalo 365 dte ë voesë ose dryshe mb 12 këste mujore ë voesë del ga portofol kredsë me status wrtte-off (e dështuar) dhe provzoohet me 100% të shumës ë voesë (ë grup VI tab. 4.1) ath vlerat që do marrë voesa j do të jeë ga bashkësa E ku gjedja 13-të përfaqëso status wrtte-off. Në aë tjetër testm klasfkues portofolt të kredsë (spas tabelës 4.1) ë fud të çdo muaj facar do të përcaktojë edhe kohë t të çdo testm pra T ku t 0 T shpreh momet e fllmt të procest dhe t 12 T shpreh momet e fudt të procest. Teorksht proces vazhdo për jë kohë dskrete të pafudme. Por sttucoet facare jaë të teresuara të formohe për portofol e kredsë der ë momet që përfaqëso fud e perudhws facare (zakosht 12-mujore). Shëojmë me Z t dryshore e rastt që shpreh gjedje klasfkuese të kredsë Y ë momet t T. Në qoftë se Z t j ë momet t T pra Y është j -këste ë voesë atëherë ë momet t1 T do të kem Z 1 j 1 X. Kjo do të thotë se gjarjet 1 / dhe X k Z j k Z j t1 t 1 t jaë ekuvalete. Pra t1 1 / t1 P Z j k Z j P X k. (4.2.1) ROMEO K. MANO 52
53 Duke qeë se atëherë X ka shperdarje bomale me parametra j 1 dhe k 1 t1 t1 j1 k j k P Z j 1 k / Z j P X k C 1 (4.2.2) Meqeëse famlja Z t t T shpreh zhvllm ë kohë të dryshort të rastt Y atëherë ajo shtë jë proces rast me hapesrë dskrete gjedjesh E dhe hapesrë dskrete kohe T. Vlerat e mudshme që mud të marrë Zt 1 ë qoftë se Z t j ë varës të vlerave të Z Z Z t1 j 1 t1 X do të jeë: që do të thotë se për kredë e -të uk është paguar këst radhës pra X 0 dhe s pasojë rrtet me jë jës umr muajve ë voesë; j që do të thotë se për kredë e -të është paguar vetëm këst radhës pra X 1 dhe t1 1 s pasojë gjedja uk drysho; j që do të thotë se për kredë e -të është paguar përveç këstt të radhës edhe jë këst tjetër që është ë voesë pra X 2 ; Z 1 j k 1 j 1 k; 0 k j 1 që do të thotë se për kredë e -të jaë paguar t përveç këstt të radhës edhe k 1 këste të tjetëra ë voesë pra X k; Zt 1 0 që do të thotë se për kredë e -të jaë paguar këst radhës dhe të gjtha këstet ë voesë për këtë kred pra X j 1. Për rast specfk kur Z t j 13 sdo që të jetë vlera e X uk do të dryshoj gjedja wrtte-off e kredsë dhe s rrjedhm Zt Nga aa probabltare do të thotë se: P Z t1 t1 13/ Z 13 1 (4.2.3) dhe ë kocept e modelt markova gjedja wrtte-off është jë gjedje ththëse. Çdo rast tjetër është gjarje e pamudur. Në qoftë se komukm e mëspërm do ta paraqesm ë trajtë e jë graf do të përftom fgurë 4.1. Grafku procest (4.1) ë dryshm ga graf ë fgurë 3.1 për model e dërtuar ë kaptull 3 është fudëm sepse gjedja 13 është gjedje ththëse e modelt Markova. ROMEO K. MANO 53
54 Në proces e lkudmt të jë huaje me këste dhe klasfkm e saj ë gjedje spas tabelës 4.1 apo ë përgjthës spas umrt të kësteve ë voesë mud të vhet re lehtë feome mugesës se kujtesës së sstemt. Kjo do të thotë se ë qoftë se jë hua e cla është 5 këste ë voesë ë momet t 1 T dhe lkujdo gjatë perudhes t 1 t tre këste atëherë ë momet t T ajo do të jetë këste ë voesë. Në momet t1 T çdo gjë varet ga umr kësteve të lkujduara ë terval tt 1 s dhe ga gjedja klasfkuese ë momet t T. Nga ky rregull përjashtohet vetëm gjedja ththëse pra kur kreda ka kaluar ë status wrtte-off. Veta markovae është veta e mugesës së kujtesës për jë proces rast pradaj mud të praojmë supozm që proses yë është jë Zxhr Markovt. Duke u referuar barazmt (4.2.2) dhe arsyetmt të mëspërm të shprehur ë trajtë grafke k me aë të graft të fgurës 4.1 s dhe duke shëuar me p x p xkw k l1 probabltet e dhëë me aë të barazmt (1.3.3) të CR + mud të propozojmë s probabltete të kalmt me jë-hap për çdo çft gjedjesh ga hapësra E madhëstë (Mao & Xha 2014 JNTS fq 11): p j l ( j 1) ( j 1) l l l C j1 1 për 0 l j 1 dhe 0 j 12 0 për j 2 l 12 dhe 0 j 12 0 për l j dhe j për l j dhe j dhe 1... Vhet re se probabltetet e paraqtuara me aë të barazmt jaë jë rast veçatë probablteteve të propozuara ë paragraf 3.1 të kaptullt 3 me aë të barazmt Në barazm ë dryshm ga barazm hapësra e gjedjeve E është e fudme dhe gjthëashtu është parashkuar rast gjedjes ththëse që shfaqet s rezultat gjedjes klasfkuese ërtte-off. Më poshtë do të shkojmë se pavarësshtë këtj dryshm ë probabltet e kalmt ga jëra gjedje ë tjetrë model dhe rezultatet e tj uk pësojë dryshme thelbësore. Për më tepër do te thoshm se model është qëdrueshëm daj modfkmeve të clat uk dal jashtë koceptmt të problemt të shtruar ë çeshtje 3.1 të kaptullt III ë kuptm e supozmeve të modelt. Meqëëse probabltetet e kalmt me jë-hap jaë të tpt (4.2.4) atëherë vhet re se ato uk vare ga koha t rrjedhmsht mud të praojmë supozm se famlja Zt t T është Zxhr Markovt homogje ROMEO K. MANO 54
55 Fgura 4.1 Graf procest të rastt për proces e shlyerjes së detyrmt për kredë e -t Burm: Autor (Mao & Xha 2014 JNTS fq 11) Duke shprehur ë trajtë matrce elemetet e barazmt (4.2.4) përftojmë matrcë M të kalmt me jë-hap të dhëë me aë të tabelës 4.2. Tabela 4.2 Matrca e kalmt me jë-hap për kredë e -të C M j1 j j j3 l l j1l 1 C j1 1 C j1 1 C j l l 13l C13 1 C13 1 C Burm: Autor (Mao & Xha 2014 JNTS fq 12) Matrca e dhëë ë tabelë 4.2 paraqet dsa dryshme ë krahasm me atë të tabelës 4.1 përsa përket rreshtt të fudt të saj gjë e cla vje s rezultat specfkës që reflektohet ga gjedja 13 të që ftojë kredtë kur klasfkohe me status wrtte-off. Në çeshtje e mëposhtme 4.3 e do të tregojmë qëdrueshmërë e pohmeve të kaptullt III edhe me këtë dryshm të matrcës së sstemt. Isttucoet facare huadhëëse grumbullojë të dhëa mb hstorku e kredve ë rsk ormalsht që edhe për klasfkm e portofolt të tyre ë perudha të dryshme kohore. Hstorku të dhëave mud të jetë afatgjatë por edhe afatshkurtër. Është e qartë që raport umrt të kredve të jë grup të caktuar me umr e përgjthshëm të kredve të portofolt jep dedurë relatve të këtj grup. L & Yag (2003) supozua të johur shpërdarje e fllmt të procest duke u lëë dorë të lrë IF-ve për të zgjedhur jë shpërdarje fllm të përshtatshme për mplemetm e modelt të ofruar prej tyre. ROMEO K. MANO 55
56 Ne propozojmë s famlje shpërdarjeje të fllmt të procest vlerësm pkësor të saj duke u mbështetur ë hstorku statstkor të klasfkmt të portofolt të kredsë ë umër kredtorësh. Në këtë mëyrë e gërshetojmë të dhëat hstorke me prtshmërë e tregut facar spas probabltett të kthyshmërsë të ofruar ga CR + me aë të barazmt (1.3.4) 1. Në kocept e vlerësmt pkësor të probabltett dedura relatve është jë vlerësues mrë probabltett. Kështu madhesa d j j ku j është umr kredve të clat jaë j këste ë voesë ë fud të vtt pararedës dërsa është umr total kredve të portofolt të po atj vt jep dedurë relatve të klasës së kredve të clat jaë j-këste ë voesë (Mao Qershor 2014 fq 270). Për 0 j 13 marrm ë shqyrtm famlje d j j E e cla është jë vlerësm mrë pkësor famljes f 0 j j E. Kjo famlje ë teorë e zxhrëve të Markovt quhet shpërdarje e fllmt të procest. Duke formalzuar ë kocepte probabltare vettë e mëspërme për vektor e rastt që përfaqëso jë portofol krede spas trajtmt të mëspërm do të marrm rezultatet e mëposhtme (Mao & Xha 2014 JNTS fq 9-10). Sç shhe qartë rezultatet më poshtë jaë ekuvalete me supozmet e modelt të parashtruara ë paragraf 3.2 të Kaptullt III-të. 1. Y Y Y 1 është jë vektor rast me margale dryshore rast të Beroull-t me parameter X X X 1 është vektor rast margalet e të clt jaë dryshore rast bomale me parametra j 1 dhe Famlja Zt t T është jë proces rast me hapësre dskrete gjedjesh E dhe hapësrë dskrete kohe T ku Z t është dryshore rast që shpreh gjedje klasfkuese të kredsë Y ë momet t T e tllë që ë qoftë se Z j atëherë Z 1 j 1 X. t 4. Famlja Zt t T t / t1 t është zxhr Markovt me probabltete të kalmt me jë-hap P Z l Z j p j l të trajtës (4.2.4) dhe matrcë M të kalmt me jë-hap. E p x p 1 barazm (1.3.4) ROMEO K. MANO 56
57 4.3 Qëdrueshmëra e pohmeve mb model për specfkat e veçata të klasfkmt të portofolt të kredsë Në këtë çështje do të tregojmë qëdrueshmërë e pohmeve të vërtëtuara ë kaptull IIItë për fakt se status wrtte-off që ftojë kredtë kur kalojë umr 12 të kësteve ë voesë sjell dryshme ë matrcë e kalmt me jë-hap s pasojë e dryshmt që paraqet barazm probablteteve të kalmt me jë-hap. Pohm Në kushtet e supozmeve 1-4 matrca M e kalmt me jë hap është matrcë stohastke dmth elemetet e saj plotësojë kushtet: ; j l E 2 p j l j E p j l Vërtetm: 1 l0 Pka e parë e pohmt është e qartë pas elemetet p j l të dhëa me aë të barazmt (4.2.4) l j 1 dhe 0 j 12 jap destet e shpërdarjes bomale me parametra për j 1 dhe 1 1 për l j 13 dhe 0 për të gjtha rastet e tjera. Për pkë e dytë për rrjesht e fudt të matrcës M rezultat është qartë dërsa për rrjeshtat e tjerë mud të shkruajmë 0 j 12 : 13 j1 13 l0 l0 l j2 j1 13 k j k C j1 l0 l j2 j1 l0 p j l p j l p j l C k k k j 1 k j1 1 Meqëëse l j 1 k k j 1 l atëherë 0 l j 1 0 k j 1. Duke zëvedësuar l me k ë shumm e fudt marrm shprehje e bomt të Njutot me ekspoet j 1 pra j1 k k j 1 k j1 C j # k0 Shëojmë me M (t) matrcë e kalmt me t-hapa me elemetë të trajtës: ROMEO K. MANO 57
58 / t mt m P Z l Z j p j l Në këto kushte ga pohm Chapma-Kolmogorov-t kem që: dhe Pohm pt l PZ l f j p j l 13 t 0 j0 13 t 1 t 2 t 2 t p j l p j k p 1 k l j0 Në kushtet e supozmeve 1-4 famlja p t l l E t është destet dskret probablteteve për dryshore e rastt Z. t Vërtetm: ku elemetet pt l jaë të trajës (4.3.3) Që famlja p t l l E të jetë destet dskret probablteteve për dryshor e rastt Z duhet të plotësoj dy kushte: 0 p l 1; l E p l l1 t t 1 Plotësm kushtt të parë është evdet sepse elemetët pt l të clat jepe me aë të barazmt (4.3.3) jaë probabltete dhe s të tlla ato përfshhe ë segmet 0;1. Për kusht e dytë duhet të provojmë se elemetet e famljes p t l l E plotesojë barazm: 13 l0 Në barazm (4.3.3) elemetet t p l p l t përcaktohe ga elemetet t t p j l të clët jaë t elemet të matrcës fuq M pradaj mud të provojmë barazm (4.3.5) me aë të metodës së duksot të plotë matematk ë ldhje me fuqë t të matrcës M. 1 1 Për t 1 M M dhe p j l p j l p j l pradaj 1 ROMEO K. MANO 58
59 p l f j p j l = l0 l0 j = f j p j l f j p j l 0 0 j0 l0 j0 l0 (4.3.6) Nga Pohm kem që p j l dërsa ga supozm 2 kem që famlja l0 f j j E është destet dskret probabltetesh s e tllë plotëso kusht që 13 f0 j 1. Duke zëvedësuar këto ë barazm (4.3.6) marrm barazm (4.3.5). j0 E praojmë të vërtetë barazm (4.3.5) për t m 1. m 1 Meqëëse elemetet p j l jaë elemet të 13 m dhe e provojmë për t m pra p l 1 l0 m 1 m M M M dhe matrca M është matrce katrore dhe s rrjedhm edhe çdo fuq e saj është matrce katrore me të jëjtë përmasë atëherë ga formula e prodhmt të dy matrcave (Larso & Edwards 1988) (fq 47) elemetët e matrcës prodhm dy matrcave kaë trajtë: m m 1 1 p j l p j k p k l ke Duke bërë zëvedësmet për t m1përftojmë: m1 m = p l f j p j l f j p j k p k l m1 0 0 l0 l0 j0 l0 j0 k m m f0 j p j k pk l f0 j p j k p k l (4.3.8) j0 k 0 l0 j0 k 0 l0 Shuma e fudt spas Pohmt është e barabartë me 1 sepse jep shumë e të gjthë elemeteve të rrjeshtt të k-t të matrcës stohastke dërsa shumm dyfshtë jep 13 pm k 1 ga supozm per t m k 0. # Famlja pt l l E e përcaktuar me aë të barazmt (4.3.3) paraqet destet markova të dryshort të rastt Z t ë momet t T. E thëë dryshe kjo famlje paraqet shpërdarje e probabltare të kredsë së -të ë momet t T. ROMEO K. MANO 59
60 Në paragraf 3.3 të kaptullt III paraqtëm dsa rezultate ë ldhje me prtje matematke dhe dsperso ë rast kur model dërtohej mb jë hapësrë të pafudme dskrete E. Është e qartë që për rast e trajtmt të jë portofol krede ë umër meqeëse hapësra e rezultateve E është e fudme paraqtja e rezultateve për prtje matematke dhe dsperso do të pësojë dsa dryshme sa përket kufjve të shummt. Kështu: Për kred e -të të portofolt të kredsë ga Përkufzm prtja matematke me jëhap ka trajtë: dhe ga barazm (3.3.8 ) përftojmë: E l p j l (4.3.9) l E Z f j l p j l f j E (4.3.10) j 0 l 0 j 0 Nga barazm (3.3.9) rezultat: Pohmt për prtje matematke me t-hapa përftojmë 13 t 0 j 0 t E Z f j E (4.3.11) ku 13 t t E l p j l (4.3.12) l 0 Nga barazm (3.3.11) Pohmt për rast t=1 kem: 0 E E Z (4.3.13) ku j 1 E j f j shpreh prtje matematke të shpërdarjes së fllmt. Barazm (4.3.13) a lejo të llogarsm prtje matematke për gjëdje e kredsë së -të ë hap e parë dmth ë momet pasardhës. Iformaco që duhet për egzekutm e kësaj formule llogartëse është aksesueshëm ë çdo momet dhe uk përmba formaco të tpt kofdecal për bakat. Në mëyrë të gjashme mud të paraqesm edhe barazmet aaloge për dsperso e shpërdarjes probabltare të kredve dvduale të portofolt të kredsë. Kështu: Dsperso shpërdarjes për kred e -të ë momet ttjepet me aë të barazmt: ROMEO K. MANO 60
61 13 13 D Z t f0 j E Z f0 j E Z j1 j1 t 2 t (4.3.14) Qëdrueshmëra e pohmeve të vërtetuara ë kaptull III a mudëso përcaktm e destett të shpërdarjes probabltare të portofolt të kredsë të trajtuar s proces rast tpt zxhr Markovt homogje. Përafrm shpërdarjes probabltare të portofolt të kredsë me aë të fuksot Copula uk pëso asjë dryshm ë kofguraco e tj sepse ë të uk merr pjesë ë mëyrë të dukshme kufzmet e modelt s pasojë e aplkmt të tj mb jë portofol krede: kthm hapësrës E ë hapësrë të fudme dhe të qët e gjedjes së fudt gjëdje ththese. Por megjthëse këto kufzme uk shfaqe ë mëyrë të dukshme ato mbarte ga elemetët përbërës të rezultateve. Le t trajtojmë shkurtmsht për të treguar hap pas hap elemetët të clët mbart kufzm e modelt të përgjthshëm për rast e zbatmt të tj mb jë portofol krede. Shëojmë me F l PZ l p l fukso uvarat të shpërdarjes për t t t ll kredë e -të me Ft l1 l PZ1 t l1... Z t l së vektort të rastt Zt Z1 t Z t dhe me... t 1 fukso multvarat të shpërdarjes 2 p l l destet e tj. Nga pjesa e dytë e Teoremës Skalare përftojmë fukso multvarate të shpërdarjes të vektort me aë të fuksot Copula: ku Z t të shprehur Ft l1 l Ct F1 t l1... F t l (4.3.15) C t është fukso Copula me margale fuksoet uvarate të shpërdarjes së margaleve të vektort të rastt Z t Në barazm (4.3.15) madhëstë F l llogarte s shumë e probablteteve t p l të clat jepe me aë të barazmt (4.3.3). Në këtë barazm jaë përdorur elemetët e matrcës M të tabelës 4.2 e cla mbart kufzmet e modelt për rast e portofolt të kredsë. Nga barazm (3.4.2) kem: p ( l... l ) c u... u p l (4.3.16) t 1 t 1 t t t 1 ku ct u1 t u t është destet Copulas dhe ptl margaleve të vektort Zt Z1 t Z t trajtës p l. t 1 është produkt desteteve të. Edhe ë këtë barazm marr pjesë probabltetet e t ROMEO K. MANO 61
62 Barazm (4.3.16) shpreh destet e portofolt të kredsë të trajtuar s jë vektor rast. Për të llogartur vlerë e këtj probabltet për jë database kokret është e qartë se përveç elemetëve të matrcës së kalmt me jë-hap të clët mudësojë llogartje e probablteteve të Z 1 evojtet edhe vlerësm destett të copula-s. t Me aë të Pohmt dhe barazmt (3.4.6) kem treguar jë vlerësm të përafruar të destett të copulas cl shprehet ë barazm (3.4.7): p ( l... l ) p l p l (4.3.17) t 1 t m t Implemetm modelt për jë portofol krede klasfkuar spas Bakës Qëdrore të Shqpërsë Le të shkojmë se çfarë përfaqësojë elemetët barazmt të mëspërm për rast e jë portofol krede ë umër kredsh. Vargu umrave l1 l2... l është me elemetë ga E pra ky varg uk është gjë tjetër veç vargu gjedjeve të mudshme të kredve ë kuptm e kësteve mujore ë voesë. S rrjedhm 0 l përgjthshëm kredve që përfshhe ë portofol e kredsë. ku është umr Gjedjet e mudshme të jë krede jaë 14 dërsa portofol kredsë së jë IF-je ormalsht që është shumë herë më madh se 14 pra 14. Nëvargjet me elemet kostat për të clat bëjmë fjalë ë kaptull e tretë (faqja 44) jaë vargjet e kredve të clat ë kuptm e klasfkmt të portofolt për ga umr kësteve të papaguara kaë gjedje të jëjtë voese. Për shembull ëvargu N t3 dhe t3 shpreh përkatëssht ëvargu e kredve që ë momet t T kaë 3 këste të papaguara dhe umr e kredve që kaë ga 3 këste të papaguara. Për këtë arsye tr dhe 13 r0 13 r0 N tr jep gjthë vargu e kredve të portofolt. Një kred uk mud të jetë jëherësh ë dy gjedje të dryshme s rrjedhm N N r r r r t r t r m m. m Të gjthë këto bëjë të mudur që destet markova dhe fuksoet e shpërdarjes së margaleve me vlera ga jëjt ëvarg jaë të barabarta pra: p l P Z l = P Z N l N (4.4.1) t r t r t t r r t r ku me l r kem shëuar elemet kostat të ëvargut N tr. ROMEO K. MANO 62
63 Atëherë destet shpërdarjes së portofolt të kredsë spas voesave ë shlyerje e detyrmt përmujor do të jepet ga barazm (3.4.9) për s=13: p ( l... l ) P cardn cardn p (... ) (4.4.2) t 1 t t0 t0 t13 t13 t t0 t13 Ky barazm ë qoftë se do ta terpretom ë kocept praktk të umrt të kredve që përfshhe ë jë gjedje të caktuar ga tabela 4.1 përcakto probabltet e shpërdarjes së portofolt të kredsë. E thëë dryshe me aë të barazmt (4.4.2) mud të llogarsm probabltet e portofolt të kredsë për çdo parashkm që jë sttuco facar pretedo të ketë ë jë momet të caktuar të perudhës së opermt të portofolt të kredsë. Ky probabltet duke oretuar produkt e barazmt (4.3.17) spas umrt të ëvargjeve dhe umrt të elemetëve të çdo ëvargu jepet ga barazm: 13 t t0 t13 t m t r r0 r p (... ) p l p l (4.4.3) Në këtë barazm l m 0 sepse vargu gjëdjeve l 1 l 2... l ga cl përftohet ky mmum është vargu gjëdjeve të mudshme të kredve të portofolt pra vargu mmum të clt është 0. Në fuksom ormal të jë sttuco mkrofacar 0 0 që do të thotë se me sgur ekzsto jë elemet ga vargu gjedjeve l1 l2... l që të jetë barabartë me 0. S rrjedhm kufr spërm fuksot Copula spas mosbarazmt të Fréchet-Hoeffdg është barabartë me 13 t Ct u1 t u t M F (0) t ct u1 t u t pt 0 f0 j p j0 (4.4.4) j0 Duke zëvedësuar ë barazm (3.12) përafrmet e bëra marrm: ku p t t t pt ( l1... l) d j p j0 d j p j lr (4.4.5) j0 r0 j0 j l jaë elemetë të matrcës së kalmt me t-hapa. Vërejtje (Mao Qershor 2010 fq 271) Në rast e përgjthshëm kur këstet uk jaë mujore pra ë jë vt facar kreda uk shlyhet me 12 këste por ë përgjthës me s këste atëherë hapësra e gjedjeve do të shte E s shte T t t t t 0 1 s1 r dhe hapësra e kohës do të Në këtë mëyrë barazm (2.14) mud të shhet s rast veçatë për s 13 barazmt: s ROMEO K. MANO 63
64 s s s t t ( pt l1... l) d j p j0 d j p j lr (4.4.6) j0 r0 j0 Barazm (4.4.5) ga aa e tekkave llogartëse a lehtëso gjetje e destett multvarat të vektort të proceseve të rastt Zt Z1 t Z t r ë momet t T pa qeë evoja e johjes së vlerave kokrete të margaleve Zt dhe klasfkm dvdual të tyre. Mjafto të johm umr e margaleve që marr të jëjtë vlerë l r E pra mjafto të johm vargu e umrave t0 t12. Kjo do të thotë që baza e të dhëave që evojtet ë këtë rast të jetë shumë më e kocetruar ë formaco. Le ta shpjegojmë ë mëyrë më të thjeshtë atyrë e formacot që evojtet për aplkm e këtj model dhe zbatm e tj ë barazm (4.4.6) (Mao at al September 2011 fq 51). Bakat dhe ë përgjthës IF-të jaë shumë të djeshme kudrejt publkmt të formacoeve që mbart të dhëa dvduale për kletët e tyre po aq sa jaë të oretuara për t u prezatuar ë tregu e aksoeve me jë rsk sa më të vogël të kreddhëes. Çdo fudvt IF-të bëjë jë parashkm të klasfkmt të portofolt të kredsë për vt pasardhës ë fukso të parashkmt të jë fod të veçatë për mbulm e rskut të ldur ga mospagm ë kohë e paracaktuar ë kotratë të kredve të lëvruara. Në këtë mëyrë IF-të duke u mbështetur ë hstorku afatshkurtër dhe afatgjatë të klasfkmt të portofolt të kredsë qoftë ë vlerë apo ë umr e kredve bëjë jë parashkm të këtj klasfkm. Model që e prezatojmë syo ë përllogartje e shkallës së besueshmërsë së këtj parashkm ë kuptm e probabltett që ky parashkm ka për të qeë suksesshëm. Në këtë mëyrë formaco ë trajtë e jë baze të dhëash që kërko model mëspërm është thjeshtë. Kjo bazë të dhëash mjafto të përmbaj klasfkm ë umër të portofolt të kredsë ë fud të vtt facar dhe parashkm për klasfkm ë vt pasardhës. Duke e përmbledhur formaco e evojshëm ë jë tabelë do të përftojmë Tab 4.3 e cla përmba jë formaco që bakat dhe sttucoet mkrofacare e kaë të detyruar ta deklarojë praë Bakave Qëdrore. Eshtë e qartë që FI-të parashkojë rrtje e bzest të tyre e cla reflektohet ë rrtje e umrt të kredve të portofolt. Kjo gjë uk dko ë saktësë e rezultateve të modelt sepse ga vt paraardhës a evojtet vetëm dedura relatve e seclës klasë dërsa ë parashkm a evojtet umr kredve për seclë klasë. Kjo bazë të dhëash mud të perceptohet e plotë spas tabelës 4.3. ROMEO K. MANO 64
65 Zakosht baza e të dhëave që ofrojë IF-të duke respektuar kofdecaltet bakar jaë të tpt të paraqtur ë tabelat 4.4 dhe 4.5. Tabelat më poshtë përmbajë klasfkm ë umër kredsh të portofolt të kredsë të jë prej bakave të velt të dytë që operojë ë tregu shqptar spas klasfkmt të Bakës Qëdrore. Tabela 4.3 Tabela përmbledhëse e klasfkmt të portofolt të kredsë Nr. kësteve ë voesë j 12 W-off Total Nr. kredve (fakt) j Dedura relatve (fakt) d (0) d (1) d (2) d (j) d (12) d (13) 1 Nr. kredve (parashkm) 0 (t) 1 (t) 2 (t) j (t) 12 (t) 13 (t) (t) Burm: Autor (Mao at al September 2011 fq 51) Për mplemetm e modelt toë a evojte vetëm të dhëat e kolloës së tretë dhe katërt të tabelës 4.4. Kolloat 3 dhe 4 e kësaj tabele (4.4) ofrojë formaco e evojshëm përkatëssht për rrjesht e dytë dhe të tretë të tabelës 4.3. Ndërsa ga tabela 4.5 a evojtet vetëm formaco kolloës se tretë cl plotëso rresht e katërt të tabelës 4.3. Tabela 4.4 Klasfkm ë fud të vtt 2008 Tabela 4.5 Parashkm për fud e vtt 2009 Burm: PCB Albaa (Deklarm BSH). Rezultat barazmt (4.4.3) paraqet teres ë fushë e Credt Rsk (CR) për rast e studmt të jë portofol krede ë ldhje me umr e kredve kur proces e lkudmt të jë ROMEO K. MANO 65
66 detyrm facar me këste e shkojmë s jë proces rast që plotëso kushtet e të qët Zxhr Markovt homogje. Përveç përafrmt të Copulas e cla kërko përzgjedhje e metodës përafruese dhe vlerësuese të parametrave të shpërdarjes elemetët e produktt që merr pjesë ë përcaktm e destett markova jaë lehtëssht të llogartshëm. Këto elemetë llogarte me aë të elemeteve të matrcës me t-hapa të Zxhrt Markova e cla është fuqa e t-ët e matrcës së kalmt me jë-hap për jehësm e elemetëve të të clës duhet të jhe vetëm 1- ku jepet me aë të barazmt (1.3.4) dhe shpërdarja e fllmt të procest f0 j j E d j j E të clë e gjejmë ë rresht e tretë të tabelës 4.3. Tabela 4.6 Tabela përmbledhëse e formacot të tabelave 4.4 dhe 4.5 Klasfkm W-O Total Nr. kredve (2008) Ded.relat. (2008) Parashkm (2009) Burm: Autor Përdorm gjuhëve të programmt të aplkuara ë software të përshtatshëm e bë shumë të lehtë përpum e formacot të paraqtur ë tabelë 4.6. Në Apedx është paraqtur kod ë gjuhë C++ (Mao at al September 2011 fq 51) cl a mudëso përpum ormal dhe pa asjë koflkt të të dhëave të Tab 4.6. Ndërtm kodt dhe aplkm tj mb bazë e të dhëave të tabelës 4.6 përveçse a trego jë mudës mplemetm të modelt me aë të software-ve të përshtatshëm a jep dhe mudësë e xjerrjes së dsa kokluzoeve mb vel e mudëssë së parashkmeve që mud të bëjë IF-të për klasfkm kokret të portofolt të kredsë. Në output- e aplkmt ë gjuhë C++ të programmt jaë prezatuar rezultatet e përpumt të të dhëave të tabelave 4.4 dhe 4.5 të përmbledhura ë tabelë 4.6 (Mao at al September 2011 fq 51). Këto të dhëa jaë marrë ga jë portofol real krede jë prej bakave të velt të dytë të clat operojë ë sstem bakar të vedt toë dhe s rrjedhm ështrohe legjslacot shqptar të pasqyruar ë rregullore e Bakës Qëdrore të Shqpërsë. ROMEO K. MANO 66
67 Në sekso A jepet probabltet spas barazmt (4.4.6) klasfkmt të portofolt të kredsë dërsa ë sekso B paraqte probabltetet spas barazmt (4.4.1) dhe barazmt (4.3.3). Nga jë aalzë e thjeshtë e rezultateve të output-t të fgurës 4.2 mud të dalm ë dsa kokluzoe të prtshme ë ldhje me mudësë reale të parashkmt që bakat mud të bëjë ë ldhje më klasfkm e portofolt të tyre të kredsë: Kështu ë sekso A cl paraqet probabltet që klasfkm portofolt të kredsë ë fud të vtt pasardhës (paraqtur ga baka e velt të dytë ë tabelë 4.5) vhet re vlera 0 (ë të vërtëtë ajo është jë vlerë shumë afër 0-s). Fgura 4.2 Output- rezultateve për të dhëat e tabelës 4.6 Burm: Output programt (Mao at al September 2011 fq 51) Nga aa probabltare kjo do të thotë se parashkm klasfkmt të portofolt të kredsë ë vlera kokrete ga aa e bakave është jë gjarje e pamudur (pothuajse e pamudur). Ndërsa ë sekso B ku paraqte probabltetet e klasfkmeve dvduale të portofolt të kredsë vhet re se: Bakat e velt të dytë (por dhe sttucoe të tjera kreddhëës) mud të parashkojë me probabltete të përfllshme gjedje 0 (asjë dtëvoesë) 1 ( jë këst ë voëse) dhe gjedje ththëse 13 (mb 12 këste ë voesë). ROMEO K. MANO 67
METODAT BOOTSTRAP DHE APLIKIMI I TYRE
 UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I MATEMATIKËS SË APLIKUAR PROGRAMI I STUDIMIT Metodat Probabltare, Statstke dhe Metodat e Aalzës umerke TEZË DOKTORATURE METODAT BOOTSTRAP
UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I MATEMATIKËS SË APLIKUAR PROGRAMI I STUDIMIT Metodat Probabltare, Statstke dhe Metodat e Aalzës umerke TEZË DOKTORATURE METODAT BOOTSTRAP
Analiza Statistikore. Ligjërata e 10. Regresioni linear i thjeshtë II. Qëllimet e mësimit. Në këtë ligjëratë ju do të mësoni:
 Analza Statstkore Lgjërata e 10 Regreson lnear thjeshtë II Qëllmet e mësmt Në këtë lgjëratë ju do të mëson: S të përdorn analzën e regresonnt për të parashkuar vlerën e e varablës së varur bazuar në varablën
Analza Statstkore Lgjërata e 10 Regreson lnear thjeshtë II Qëllmet e mësmt Në këtë lgjëratë ju do të mëson: S të përdorn analzën e regresonnt për të parashkuar vlerën e e varablës së varur bazuar në varablën
UNIVERSITETI POLITEKNIK I TIRANES METODA STATISTIKORE DHE ZBATIMET E TYRE
 UNIVERSITETI POLITEKNIK I TIRANES METODA STATISTIKORE DHE ZBATIMET E TYRE "Ndërtm dhe analza e një model probabltaro - statstkor për studmn e efektt të ndotjes në gjendjen shëndetësore të banorëve në zona
UNIVERSITETI POLITEKNIK I TIRANES METODA STATISTIKORE DHE ZBATIMET E TYRE "Ndërtm dhe analza e një model probabltaro - statstkor për studmn e efektt të ndotjes në gjendjen shëndetësore të banorëve në zona
Elasticiteti i ofertes dhe kerkeses
 C H A P T E R 5 Elasticiteti i ofertes dhe kerkeses Prepared by: Dr. Qazim TMAVA Fernando Quijano and Yvonn Quijano Msc. Besart Hajrizi Elasticiteti: Një matës i reagimit Zgjedhjet racionale dhe vendimet
C H A P T E R 5 Elasticiteti i ofertes dhe kerkeses Prepared by: Dr. Qazim TMAVA Fernando Quijano and Yvonn Quijano Msc. Besart Hajrizi Elasticiteti: Një matës i reagimit Zgjedhjet racionale dhe vendimet
Tema e Disertacionit: NDËRTIMI DHE ANALIZA E MODELEVE STATISTIKE PËR STUDIMIN E HOMOGJENITETIT TË BASHKËSISË ME NDIHMËN E SHPËRNDARJEVE ASIMPTOTIKE
 REPUBLIKA E SHQIPËRISË UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I INXHINIERISË MATEMATIKE DHE FIZIKE DEPARTAMENTI I INXHINIERISË MATEMATIKE Disertacio për Gradë Shkecore Doktor ë Matematikë Tema e Disertacioit:
REPUBLIKA E SHQIPËRISË UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I INXHINIERISË MATEMATIKE DHE FIZIKE DEPARTAMENTI I INXHINIERISË MATEMATIKE Disertacio për Gradë Shkecore Doktor ë Matematikë Tema e Disertacioit:
Variabla e rastit dhe shpërndarjet e. probabilitare
 Variabla e rastit dhe shpërndarjet probabilitare Ligjërata e pestë Variabla e rastit dhe shpërndarjet e probabilitetit Qëllimet: Pas përfundimit të ligjëratës ju duhet të jeni në gjendje që të : Definoni
Variabla e rastit dhe shpërndarjet probabilitare Ligjërata e pestë Variabla e rastit dhe shpërndarjet e probabilitetit Qëllimet: Pas përfundimit të ligjëratës ju duhet të jeni në gjendje që të : Definoni
NUMERICAL SOLUTION FOR A WAVE EQUATION WITH BOUNDARY DAMPING
 NUMERICAL SOLUTION FOR A WAVE EQUATION WITH BOUNDARY DAMPING M.Sc. Ardian NAÇO, Prof. Lulëzim HANELLI *, M.Sc. Bendise HUTI Departamenti i Matematikës, Universiteti Politeknik, Tiranë SHQIPERI E-mail:
NUMERICAL SOLUTION FOR A WAVE EQUATION WITH BOUNDARY DAMPING M.Sc. Ardian NAÇO, Prof. Lulëzim HANELLI *, M.Sc. Bendise HUTI Departamenti i Matematikës, Universiteti Politeknik, Tiranë SHQIPERI E-mail:
Tel:
 CURRICULUM VITAE 1. Mbiemri: Zejnullahu 2. Emri: Ramadan 3. Nacionaliteti: Shqiptar 4. Shtetësia: Kosovar 5. Data e Lindjes: 08.5.1957 6. Gjinia: 7. Detajet kontaktuese: 8. Niveli Arsimor: Email: zejnullahu@yahoo.com
CURRICULUM VITAE 1. Mbiemri: Zejnullahu 2. Emri: Ramadan 3. Nacionaliteti: Shqiptar 4. Shtetësia: Kosovar 5. Data e Lindjes: 08.5.1957 6. Gjinia: 7. Detajet kontaktuese: 8. Niveli Arsimor: Email: zejnullahu@yahoo.com
UNIVERSITETI I PRISHTINËS FAKULTETI I INXHINIERISË MEKANIKE PUNIM DIPLOME (STUDIMET MASTER)
 UNIVERSITETI I PRISHTINËS FAKULTETI I INXHINIERISË MEKANIKE PUNIM DIPLOME (STUDIMET MASTER) TEMA: ANALIZA E FAKTORËVE QË NDIKOJNË NË OPTIMIZIMIN E TRANSMETUESVE ME DHËMBËZORË Kandidati: Inxh. Bch. Riad
UNIVERSITETI I PRISHTINËS FAKULTETI I INXHINIERISË MEKANIKE PUNIM DIPLOME (STUDIMET MASTER) TEMA: ANALIZA E FAKTORËVE QË NDIKOJNË NË OPTIMIZIMIN E TRANSMETUESVE ME DHËMBËZORË Kandidati: Inxh. Bch. Riad
AKTET ISSN DAFINA KARAJ a, MAJLINDA VASJARI b, PRANVERA LAZO b, ARBEN MERKOÇI c
 AKTET ISSN 2073-2244 Journal of Institute Alb-Shkenca www.alb-shkenca.org Revistë Shkencore e Institutit Alb-Shkenca Copyright Institute Alb-Shkenca STUDY OF ANODIC STRIPPING VOLTAMMETRIC TECHNIQUES IN
AKTET ISSN 2073-2244 Journal of Institute Alb-Shkenca www.alb-shkenca.org Revistë Shkencore e Institutit Alb-Shkenca Copyright Institute Alb-Shkenca STUDY OF ANODIC STRIPPING VOLTAMMETRIC TECHNIQUES IN
PARAMETRA TE RENDESISHEM TE PUNES SE AMPLIFIKATOREVE
 Kapitulli 1 PARAMETRA TE RENDESISHEM TE PUNES SE AMPLIFIKATOREVE 1. NJOHURI TE PERGJTHSHME Të gjitha skemat me tranzistor janë polarizuar sipas njërës nga mënyrat e studiura më parë. Gjatë këtij kapitulli
Kapitulli 1 PARAMETRA TE RENDESISHEM TE PUNES SE AMPLIFIKATOREVE 1. NJOHURI TE PERGJTHSHME Të gjitha skemat me tranzistor janë polarizuar sipas njërës nga mënyrat e studiura më parë. Gjatë këtij kapitulli
NJË TRANSFORMIM THYESOR LOKAL α INTEGRAL DHE APLIKIME TË TIJ
 UNIVERSITETI POLITEKNIK TIRANË FAKULTETI I INXHINIERISË MATEMATIKE DHE INXHINIERISË FIZIKE DEPARTAMENTI I MATEMATIKËS NJË TRANSFORMIM THYESOR LOKAL α INTEGRAL DHE APLIKIME TË TIJ PUNIM PËR GRADËN SHKENCORE
UNIVERSITETI POLITEKNIK TIRANË FAKULTETI I INXHINIERISË MATEMATIKE DHE INXHINIERISË FIZIKE DEPARTAMENTI I MATEMATIKËS NJË TRANSFORMIM THYESOR LOKAL α INTEGRAL DHE APLIKIME TË TIJ PUNIM PËR GRADËN SHKENCORE
Inxh.dip.el. Teki Rraci & Inxh.dip.el.Jusuf Qarkaxhija
 Inxh.dip.el. Teki Rraci & Inxh.dip.el.Jusuf Qarkaxhija Gjakovë Nëtor 2007 2 1. Funksionet të cilat i përmban programi aplikativ për llogaritje Excel Funksionet të cilat i përmban programi aplikativ Excel
Inxh.dip.el. Teki Rraci & Inxh.dip.el.Jusuf Qarkaxhija Gjakovë Nëtor 2007 2 1. Funksionet të cilat i përmban programi aplikativ për llogaritje Excel Funksionet të cilat i përmban programi aplikativ Excel
Çështje të emërtimit të njësive më themelore sintaksore në gramatikat tona
 Terminologji gjuhësore Çështje të emërtimit të njësive më themelore sintaksore në gramatikat tona Mr. Agim Spahiu 24 prill 2004 Përmbledhje Ndonëse gjuhësia shqiptare ka bërë një traditë të gjatë të veprimtarisë
Terminologji gjuhësore Çështje të emërtimit të njësive më themelore sintaksore në gramatikat tona Mr. Agim Spahiu 24 prill 2004 Përmbledhje Ndonëse gjuhësia shqiptare ka bërë një traditë të gjatë të veprimtarisë
Deformimet e Sinjalit
 Deformimet e Sinjalit Krenare PIREVA, can. PhD Fakulteti i Shkencës Kompjuterike dhe Inxhinierisë Hyrje 2 Problemet gjate transmetimit te sinjalit Demtimet e zerit Deformimi per shkak te vonesave Zhurmat
Deformimet e Sinjalit Krenare PIREVA, can. PhD Fakulteti i Shkencës Kompjuterike dhe Inxhinierisë Hyrje 2 Problemet gjate transmetimit te sinjalit Demtimet e zerit Deformimi per shkak te vonesave Zhurmat
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I MATEMATIKËS
 UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I MATEMATIKËS PROGRAMI I STUDIMIT: ANALIZË DHE ALGJEBËR TEZË DOKTORATURE MBI STRUKTURAT KUAZI TË NORMUARA DHE DISA ASPEKTE INTEGRIMI
UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I MATEMATIKËS PROGRAMI I STUDIMIT: ANALIZË DHE ALGJEBËR TEZË DOKTORATURE MBI STRUKTURAT KUAZI TË NORMUARA DHE DISA ASPEKTE INTEGRIMI
Qarqet Digjitale Sekuenciale Dispencë (Version jokompletë)
 Fakulteti i Inxhinierisë Elektrike dhe Kompjuterike Departamenti i Kompjuterikës gni Dika arqet Digjitale Sekuenciale Dispencë (Version jokompletë) Prishtinë 2008 arqet digjitale sekuenciale 2 Parathënie
Fakulteti i Inxhinierisë Elektrike dhe Kompjuterike Departamenti i Kompjuterikës gni Dika arqet Digjitale Sekuenciale Dispencë (Version jokompletë) Prishtinë 2008 arqet digjitale sekuenciale 2 Parathënie
AN APPLICATION OF LOGISTIC REGRESION FOR EVALUATING TEACHING PRACTICES NJË ZBATIM I REGRESIT LOGJISTIK PËR VLERËSIMIN E PRAKTIKËS SË MËSIMDHËNIES
 AKTET ISSN 2073-2244 Journal of Institute Alb-Shkenca www.alb-shkenca.org Revistë Shkencore e Institutit Alb-Shkenca Coyright Institute Alb-Shkenca AN APPLICATION OF LOGISTIC REGRESION FOR EVALUATING TEACHING
AKTET ISSN 2073-2244 Journal of Institute Alb-Shkenca www.alb-shkenca.org Revistë Shkencore e Institutit Alb-Shkenca Coyright Institute Alb-Shkenca AN APPLICATION OF LOGISTIC REGRESION FOR EVALUATING TEACHING
REPUBLIKA E SHQIPËRISË UNIVERSITETI I TIRANËS FAKULTETI I EKONOMISË DEPARTAMENTI STATISTIKË DHE INFORMATIKË E ZBATUAR DISERTACION
 REPUBLIKA E SHQIPËRISË UNIVERSITETI I TIRANËS FAKULTETI I EKONOMISË DEPARTAMENTI STATISTIKË DHE INFORMATIKË E ZBATUAR DISERTACION Për marrjen e gradës shkencore DOKTOR CILËSIA E TË DHËNAVE NË SISTEMET
REPUBLIKA E SHQIPËRISË UNIVERSITETI I TIRANËS FAKULTETI I EKONOMISË DEPARTAMENTI STATISTIKË DHE INFORMATIKË E ZBATUAR DISERTACION Për marrjen e gradës shkencore DOKTOR CILËSIA E TË DHËNAVE NË SISTEMET
FINANCAT E KORPORATAVE
 FINANCAT E KORPORATAVE VLERA NË KOHË E PARASË (I) Kapitulli 3 MSc. Fisnik Morina, PhD (c) NENTOR 2017 OBJEKTIVAT 2 Konvertimi i vlerës në kohë të parasë në vijë kohore Të kuptohet pse 1 euro e pranuar
FINANCAT E KORPORATAVE VLERA NË KOHË E PARASË (I) Kapitulli 3 MSc. Fisnik Morina, PhD (c) NENTOR 2017 OBJEKTIVAT 2 Konvertimi i vlerës në kohë të parasë në vijë kohore Të kuptohet pse 1 euro e pranuar
RAPORT EKSPERTIZE MJEDISORE ne ALBACO SHOES ShPK - Tirane
 instituti i studimeve ambjentale (ISA) "Q.Stafa" Str.130, Tirana Albania http://www.ies-al.com/ Certified from Ministry of Environment, Decision No.6, Reg. No 008, Prot. No 136, Tirana 19.05.2004 Çertifikuar
instituti i studimeve ambjentale (ISA) "Q.Stafa" Str.130, Tirana Albania http://www.ies-al.com/ Certified from Ministry of Environment, Decision No.6, Reg. No 008, Prot. No 136, Tirana 19.05.2004 Çertifikuar
ANALIZA E SERIVE KOHORE PËR PARASHIKIMET EKONOMIKE ME ANË TË METODAVE SASIORE DHE INTELIGJENTE
 UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I MATEMATIKËS SË APLIKUAR PROGRAMI I STUDIMIT: KËRKIME OPERACIONALE DISERTACION PËR MBROJTJEN E GRADËS SHKENCORE DOKTOR ANALIZA E SERIVE
UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I MATEMATIKËS SË APLIKUAR PROGRAMI I STUDIMIT: KËRKIME OPERACIONALE DISERTACION PËR MBROJTJEN E GRADËS SHKENCORE DOKTOR ANALIZA E SERIVE
Shembuj ilustrues nga Deep Learning. përmbledhje informative
 përmbledhje informative zgjodhi dhe përktheu Ridvan Bunjaku Maj 2017 Përmbajtja Për publikimin... 3 Parathënie... 3 Bibliografia... 3 Falënderim... 3 Licencimi... 3 Online... 3 Hyrje... 4 Pjesa I: Bazat
përmbledhje informative zgjodhi dhe përktheu Ridvan Bunjaku Maj 2017 Përmbajtja Për publikimin... 3 Parathënie... 3 Bibliografia... 3 Falënderim... 3 Licencimi... 3 Online... 3 Hyrje... 4 Pjesa I: Bazat
Persistenca e inflacionit në Shqipëri
 Persistenca e inflacionit në Shqipëri Vasilika kota* -1-0 2 ( 4 5 ) 2 0 1 1 * Vasilika Kota: Departamenti i Kërkimeve, Banka e Shqipërisë, e-mail: vkota@bankofalbania.org Mendimet e shprehura në këtë studim
Persistenca e inflacionit në Shqipëri Vasilika kota* -1-0 2 ( 4 5 ) 2 0 1 1 * Vasilika Kota: Departamenti i Kërkimeve, Banka e Shqipërisë, e-mail: vkota@bankofalbania.org Mendimet e shprehura në këtë studim
HULUMTIMI EMPIRIK I PASIGURISË SË PARASHIKIMIT ME SIMULIMIN MONTE CARLO. Altin Tanku Elona Dushku Kliti Ceca* -1-
 HULUMTIMI EMPIRIK I PASIGURISË SË PARASHIKIMIT ME SIMULIMIN MONTE CARLO Altin Tanku Elona Dushku Kliti Ceca* -1-03 (53) 2012 *Altin Tanku, Elona Dushku, Kliti Ceca, Departamenti i Kërkimeve, Banka e Shqipërisë.
HULUMTIMI EMPIRIK I PASIGURISË SË PARASHIKIMIT ME SIMULIMIN MONTE CARLO Altin Tanku Elona Dushku Kliti Ceca* -1-03 (53) 2012 *Altin Tanku, Elona Dushku, Kliti Ceca, Departamenti i Kërkimeve, Banka e Shqipërisë.
ELEMENTET E PROBABILITETIT
 ELEMENTET E PROBABILITETIT Hapësira e ngjarjeve ( e rezultateve). Ngjarjet Definicioni. Situata e cila varet nga rasti quhet eksperiment. Shembulli. Shembuj të eksperimenteve në kontest të probabilitetit
ELEMENTET E PROBABILITETIT Hapësira e ngjarjeve ( e rezultateve). Ngjarjet Definicioni. Situata e cila varet nga rasti quhet eksperiment. Shembulli. Shembuj të eksperimenteve në kontest të probabilitetit
7. Niveli Arsimor: Institucioni: FAKULTETI I SHKENCAVE MATEMATIKE NATYRORE UPHP Data e diplomimit: 1995 Diploma : Profesor i Matematikës
 CURRICULUM VITAE 1. Mbiemri: Abdullahu 2. Emri: Fitore 3. Nacionaliteti: Shqiptare 4. Shtetësia: Kosovare 5. Data e Lindjes: 07.10.1971 6. Detajet kontaktuese: fitore.abdullahu@uni-pr.edu 7. Niveli Arsimor:
CURRICULUM VITAE 1. Mbiemri: Abdullahu 2. Emri: Fitore 3. Nacionaliteti: Shqiptare 4. Shtetësia: Kosovare 5. Data e Lindjes: 07.10.1971 6. Detajet kontaktuese: fitore.abdullahu@uni-pr.edu 7. Niveli Arsimor:
Kthimi dhe Risku. Objektivat e Kreut. Drejtim Financiar Saimir Sallaku Lektor. Kreu 7
 Kreu 7 Drejtim Financiar Saimir Sallaku Lektor Kthimi dhe Risku Objektivat e Kreut Kuptimi i riskut, kthimit dhe konceptit të kundërshtimit të riskut. Përshkrimi i procedurave për matjen e riskut të nja
Kreu 7 Drejtim Financiar Saimir Sallaku Lektor Kthimi dhe Risku Objektivat e Kreut Kuptimi i riskut, kthimit dhe konceptit të kundërshtimit të riskut. Përshkrimi i procedurave për matjen e riskut të nja
A METHOD FOR KINEMATIC CALCULATION OF PLANETARY GEAR TRAINS NJË METODË PËR LLOGARITJEN KINEMATIKE TË TRANSMISIONEVE PLANETARE
 AKTET ISSN 2073-2244 Journal of Institute Alb-Shkenca www.alb-shkenca.org Revistë Shkencore e Institutit Alb-Shkenca Copyright Institute Alb-Shkenca A METHOD FOR KINEMATIC CALCULATION OF PLANETARY GEAR
AKTET ISSN 2073-2244 Journal of Institute Alb-Shkenca www.alb-shkenca.org Revistë Shkencore e Institutit Alb-Shkenca Copyright Institute Alb-Shkenca A METHOD FOR KINEMATIC CALCULATION OF PLANETARY GEAR
MODEL REFERENCE ADAPTIVE CONTROL OF PERMANENT MAGNET SYNCHRONOUS MOTOR KONTROLLI ADAPTIV ME MODEL REFERIMI I MOTORIT SINKRON ME MAGNET PERMANENT
 AKTET ISSN 273-2244 Journal of Institute Alb-Shkenca www.alb-shkenca.org Revistë Shkencore e Institutit Alb-Shkenca Copyright Institute Alb-Shkenca MODEL REFERENCE ADAPTIVE CONTROL OF PERMANENT MAGNET
AKTET ISSN 273-2244 Journal of Institute Alb-Shkenca www.alb-shkenca.org Revistë Shkencore e Institutit Alb-Shkenca Copyright Institute Alb-Shkenca MODEL REFERENCE ADAPTIVE CONTROL OF PERMANENT MAGNET
Metodologjia hulumtuese
 (Master) Ligjerata 9 Metodologjia hulumtuese Metodat kuanitative në hulumtimet shkencore (disamodeleekonometrike) Prof.asc. Avdullah Hoti 1 Literatura 1. Gujarati, D. (2005) Essentials of Econometrics,
(Master) Ligjerata 9 Metodologjia hulumtuese Metodat kuanitative në hulumtimet shkencore (disamodeleekonometrike) Prof.asc. Avdullah Hoti 1 Literatura 1. Gujarati, D. (2005) Essentials of Econometrics,
7. TRANZISTORËT E FUQISË
 7. TRANZSTORËT E FUQSË 7.1 HYRJE Tranzistorët kanë karakteristika të kontrolluara të kyçjes dhe shkyçjes. Kur shfrytëzohen si elemente ndërprerëse punojnë në regjionin e ngopjes dhe si rezultat kanë rënie
7. TRANZSTORËT E FUQSË 7.1 HYRJE Tranzistorët kanë karakteristika të kontrolluara të kyçjes dhe shkyçjes. Kur shfrytëzohen si elemente ndërprerëse punojnë në regjionin e ngopjes dhe si rezultat kanë rënie
Raport Vlerësimi. Shqyrtimi i tetë i tarifave të energjisë elektrike ETR8 ( )
 ZYRA E RREGULLATORIT PËR ENERGJI ENERGY REGULATORY OFFICE REGULATORNI URED ZA ENERGIJU Raport Vlerësimi Shqyrtimi i tetë i tarifave të energjisë elektrike ETR8 (2014-2015) Llogaritja e të Hyrave të Lejuara
ZYRA E RREGULLATORIT PËR ENERGJI ENERGY REGULATORY OFFICE REGULATORNI URED ZA ENERGIJU Raport Vlerësimi Shqyrtimi i tetë i tarifave të energjisë elektrike ETR8 (2014-2015) Llogaritja e të Hyrave të Lejuara
Leksion nr 1 Tema: HYRJE NË MATLAB
 Leksion nr 1 Tema: HYRJE NË MATLAB 1 Përshkrimi i përgjithshëm i MATLAB MATLAB ( = MATrix LABoratory): Një gjuhë programimi për aplikime shkencore numerike Një gamë e gjerë funksionesh të përcaktuara Interpretues
Leksion nr 1 Tema: HYRJE NË MATLAB 1 Përshkrimi i përgjithshëm i MATLAB MATLAB ( = MATrix LABoratory): Një gjuhë programimi për aplikime shkencore numerike Një gamë e gjerë funksionesh të përcaktuara Interpretues
Indeksi i çmimeve/ vlerave njësi të huaja të importeve shqiptare*
 Indeksi i çmimeve/ vlerave njësi të huaja të importeve shqiptare* prill, 2007 Risan Shllaku -- -2- -- Përmbajtja Hyrje 5 Diskutim i përgjithshëm mbi indekset e çmimeve. 6 Përqasja e bazuar në indekset
Indeksi i çmimeve/ vlerave njësi të huaja të importeve shqiptare* prill, 2007 Risan Shllaku -- -2- -- Përmbajtja Hyrje 5 Diskutim i përgjithshëm mbi indekset e çmimeve. 6 Përqasja e bazuar në indekset
Law of Large Numbers
 Toss a co tmes. Law of Large Numbers Suppose 0 f f th th toss came up H toss came up T s are Beroull radom varables wth p ½ ad E( ) ½. The proporto of heads s. Itutvely approaches ½ as. week 2 Markov s
Toss a co tmes. Law of Large Numbers Suppose 0 f f th th toss came up H toss came up T s are Beroull radom varables wth p ½ ad E( ) ½. The proporto of heads s. Itutvely approaches ½ as. week 2 Markov s
PROGRAMI I STUDIMIT: Statistikë dhe Kërkime Operacionale TEZË DOKTORATURE
 REPUBLIKA E SHQIPERISE UNIVERSITETI POLITEKNIK TIRANE FAKULTETI INXHINIERISE MATEMATIKE & INXHINIERISE FIZIKE Departamenti i Inxhinierise Matematike PROGRAMI I STUDIMIT: Statistikë dhe Kërkime Operacionale
REPUBLIKA E SHQIPERISE UNIVERSITETI POLITEKNIK TIRANE FAKULTETI INXHINIERISE MATEMATIKE & INXHINIERISE FIZIKE Departamenti i Inxhinierise Matematike PROGRAMI I STUDIMIT: Statistikë dhe Kërkime Operacionale
REPUBLIKA E SHQIPËRISË UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I INXHINIERISË ELEKTRIKE DISERTACION PËR MBROJTJEN E GRADËS SHKENCORE DOKTOR
 REPUBLIKA E SHQIPËRISË UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I INXHINIERISË ELEKTRIKE DISERTACION PËR MBROJTJEN E GRADËS SHKENCORE DOKTOR Parashikimi i konsumit të energjisë në ndërtesat rezidenciale
REPUBLIKA E SHQIPËRISË UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I INXHINIERISË ELEKTRIKE DISERTACION PËR MBROJTJEN E GRADËS SHKENCORE DOKTOR Parashikimi i konsumit të energjisë në ndërtesat rezidenciale
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
TRANSIENT TEMPERATURE FLUCTUATIONS IN AN ASPECT RATIO ONE TURBULENT CONVECTION CELL
 TRANSIENT TEMPERATURE FLUCTUATIONS IN AN ASPECT RATIO ONE TURBULENT CONVECTION CELL a* Margarita KUQALI, b Joseph NIEMELA a. FFP, Polytechnic University of Tirana, Tirana, ALBANIA b. International Centre
TRANSIENT TEMPERATURE FLUCTUATIONS IN AN ASPECT RATIO ONE TURBULENT CONVECTION CELL a* Margarita KUQALI, b Joseph NIEMELA a. FFP, Polytechnic University of Tirana, Tirana, ALBANIA b. International Centre
Menaxhimi i Performancës
 Shoqata e kontabilistëve të çertifikuar dhe auditorëve të Kosovës Society of Certified Accountants and Auditors of Kosovo Menaxhimi i Performancës P8 Nr. Zgjidhjet FLETË PROVIMI Exam Paper Data Date 04.02.2018
Shoqata e kontabilistëve të çertifikuar dhe auditorëve të Kosovës Society of Certified Accountants and Auditors of Kosovo Menaxhimi i Performancës P8 Nr. Zgjidhjet FLETË PROVIMI Exam Paper Data Date 04.02.2018
Multivariate Transformation of Variables and Maximum Likelihood Estimation
 Marquette Uversty Multvarate Trasformato of Varables ad Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Assocate Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 03 by Marquette Uversty
Marquette Uversty Multvarate Trasformato of Varables ad Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Assocate Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 03 by Marquette Uversty
Zbatimi i modeleve dhe metodave
 FAKULTETI EKONOMIK Prof Dr Justina Shiroka - Pula Zbatimi i modeleve dhe metodave Prishtinë, 2013 2 I MODELET DHE METODAT E VENDOSJES SHKENCORE 1 ROLI I MODELVE DHE MODELIMIT NË VENDOSJE Fjala moroli i
FAKULTETI EKONOMIK Prof Dr Justina Shiroka - Pula Zbatimi i modeleve dhe metodave Prishtinë, 2013 2 I MODELET DHE METODAT E VENDOSJES SHKENCORE 1 ROLI I MODELVE DHE MODELIMIT NË VENDOSJE Fjala moroli i
Ash Wednesday. First Introit thing. * Dómi- nos. di- di- nos, tú- ré- spi- Ps. ne. Dó- mi- Sál- vum. intra-vé-runt. Gló- ri-
 sh Wdsdy 7 gn mult- tú- st Frst Intrt thng X-áud m. ns ní- m-sr-cór- Ps. -qu Ptr - m- Sál- vum m * usqu 1 d fc á-rum sp- m-sr-t- ó- num Gló- r- Fí- l- Sp-rí- : quó-n- m ntr-vé-runt á- n-mm c * m- quó-n-
sh Wdsdy 7 gn mult- tú- st Frst Intrt thng X-áud m. ns ní- m-sr-cór- Ps. -qu Ptr - m- Sál- vum m * usqu 1 d fc á-rum sp- m-sr-t- ó- num Gló- r- Fí- l- Sp-rí- : quó-n- m ntr-vé-runt á- n-mm c * m- quó-n-
BORA BIMBARI MODELIMI I SISTEMEVE HIBRIDE TЁ RUAJTJES DHE PЁRPUNIMIT TЁ INFORMACIONIT PUNIM DOKTORATE. Udhëheqës shkencor: Prof. Dr.
 UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I INFORMATIKËS BORA BIMBARI MODELIMI I SISTEMEVE HIBRIDE TЁ RUAJTJES DHE PЁRPUNIMIT TЁ INFORMACIONIT PUNIM DOKTORATE Udhëheqës shkencor:
UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I INFORMATIKËS BORA BIMBARI MODELIMI I SISTEMEVE HIBRIDE TЁ RUAJTJES DHE PЁRPUNIMIT TЁ INFORMACIONIT PUNIM DOKTORATE Udhëheqës shkencor:
REPUBLIKA E SHQIPËRISË UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I INFORMATIKËS ERIND BEDALLI DISERTACION
 REPUBLIKA E SHQIPËRISË UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I INFORMATIKËS ERIND BEDALLI DISERTACION LOGJIKA E TURBULLT DHE APLIKIME TË SAJ NË MODELIM Udhëheqës Shkencor
REPUBLIKA E SHQIPËRISË UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I INFORMATIKËS ERIND BEDALLI DISERTACION LOGJIKA E TURBULLT DHE APLIKIME TË SAJ NË MODELIM Udhëheqës Shkencor
UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I MATEMATIKËS
 UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I MATEMATIKËS DISERTACION PËR MARRJEN E GRADËS SHKENCORE DOKTOR ANALIZË KRAHASUESE E TEKNIKAVE BAZË PËR ZGJIDHJEN E PROBLEMIT KUFITAR
UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I MATEMATIKËS DISERTACION PËR MARRJEN E GRADËS SHKENCORE DOKTOR ANALIZË KRAHASUESE E TEKNIKAVE BAZË PËR ZGJIDHJEN E PROBLEMIT KUFITAR
Raport i monitorimit për trajnimet e mësimdhënësve në lëndën e matematikës
 Republika e Kosovës Republika Kosova Republic of Kosovo Qeveria - Vlada - Government MINISTRIA E ARSIMIT E SHKENCËS DHE E TEKNOLOGJISË MINISTRASTVO OBRAZOVANJA NAUKE I TEHNOLOGIJE MINISTRY OF EDUCATION,
Republika e Kosovës Republika Kosova Republic of Kosovo Qeveria - Vlada - Government MINISTRIA E ARSIMIT E SHKENCËS DHE E TEKNOLOGJISË MINISTRASTVO OBRAZOVANJA NAUKE I TEHNOLOGIJE MINISTRY OF EDUCATION,
 www.italy-ontheroad.it Safety on the car SIGURIA NË MAKINË Të dhëna të përgjithshme Përdorimi i rripave të sigurimit dhe i karrigeve për transportin e fëmijëve në mënyrë të drejtë, është themelore për
www.italy-ontheroad.it Safety on the car SIGURIA NË MAKINË Të dhëna të përgjithshme Përdorimi i rripave të sigurimit dhe i karrigeve për transportin e fëmijëve në mënyrë të drejtë, është themelore për
Uf'IIVERSITETI I PRISHTINE. F. KULTETI I AKI ERI E. lese EG TevE KOI T I B E FE. TIT ZHI 0 OPI DJE JO TACIO A E PUNIM I DOKTORA TURES
 Uf'IIVERSITETI I PRISHTINE. F. KULTETI I AKI ERI E Mr.sci. SHABAN BUZA, ligjerues KOI T I B E FE. TIT ZHI 0 OPI DJE JO TACIO A E lese EG TevE PUNIM I DOKTORA TURES P I HT~ E 1997 -"'--~-------- - FALENDE
Uf'IIVERSITETI I PRISHTINE. F. KULTETI I AKI ERI E Mr.sci. SHABAN BUZA, ligjerues KOI T I B E FE. TIT ZHI 0 OPI DJE JO TACIO A E lese EG TevE PUNIM I DOKTORA TURES P I HT~ E 1997 -"'--~-------- - FALENDE
Credit Portfolio Modelling, Marginal Risk Contributions, and Granularity Adjustment
 Credt ortolo Modellg, Margal Rsk Cotrbutos, ad Graularty djustmet Revsed: Jue 4, 00 Has Rau-Bredow rv.-doz. Dr. oec. publ. Has Rau-Bredow Leo Wesmatel Str. 4 D-97074 Würzburg phoe.: 49(093-859 moble: 49(078-88853
Credt ortolo Modellg, Margal Rsk Cotrbutos, ad Graularty djustmet Revsed: Jue 4, 00 Has Rau-Bredow rv.-doz. Dr. oec. publ. Has Rau-Bredow Leo Wesmatel Str. 4 D-97074 Würzburg phoe.: 49(093-859 moble: 49(078-88853
Special Instructions / Useful Data
 JAM 6 Set of all real umbers P A..d. B, p Posso Specal Istructos / Useful Data x,, :,,, x x Probablty of a evet A Idepedetly ad detcally dstrbuted Bomal dstrbuto wth parameters ad p Posso dstrbuto wth
JAM 6 Set of all real umbers P A..d. B, p Posso Specal Istructos / Useful Data x,, :,,, x x Probablty of a evet A Idepedetly ad detcally dstrbuted Bomal dstrbuto wth parameters ad p Posso dstrbuto wth
Analiza e sinjaleve nga qarqe elektronike që operojnë në mënyrë kaotike dhe përdorimi i tyre për sigurinë e komunikacionit
 UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I INXHINIERISË MATEMATIKE & INXINIERISË FIZIKE DEPARTAMENTI I INXHINIERISË FIZIKE DISERTACION për mbrojtjen e gradës shkencore Doktor i Shkencave Analiza e sinjaleve
UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I INXHINIERISË MATEMATIKE & INXINIERISË FIZIKE DEPARTAMENTI I INXHINIERISË FIZIKE DISERTACION për mbrojtjen e gradës shkencore Doktor i Shkencave Analiza e sinjaleve
QUEEN BEE TESTING BASED ON THE LARVAE GRAFTING TECHNIQUE TESTIMI I MËMAVE TË BLETËVE BAZUAR NË TEKNIKËN E SHARTIMIT TË LARVAVE
 AKTET ISSN 2073-2244 Journal of Institute Alb-Shkenca www.alb-shkenca.org Revistë Shkencore e Institutit Alb-Shkenca Copyright Institute Alb-Shkenca QUEEN BEE TESTING BASED ON THE LARVAE GRAFTING TECHNIQUE
AKTET ISSN 2073-2244 Journal of Institute Alb-Shkenca www.alb-shkenca.org Revistë Shkencore e Institutit Alb-Shkenca Copyright Institute Alb-Shkenca QUEEN BEE TESTING BASED ON THE LARVAE GRAFTING TECHNIQUE
ILIR SHINKO DISERTACION
 UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I TEKNOLOGJISË SË INFORMACIONIT DEPARTAMENTI I ELEKTRONIKËS DHE TELEKOMUNIKACIONIT ILIR SHINKO Për marrjen e gradës Doktor Në Teknologjinë e Informacionit dhe
UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I TEKNOLOGJISË SË INFORMACIONIT DEPARTAMENTI I ELEKTRONIKËS DHE TELEKOMUNIKACIONIT ILIR SHINKO Për marrjen e gradës Doktor Në Teknologjinë e Informacionit dhe
Menaxhment Financiar (zgjidhjet)
 Shoqata e Kontabilistëve të Çertifikuar dhe Auditorëve të Kosovës Society of Certified Accountants and Auditors of Kosovo Menaxhment Financiar (zgjidhjet) P7 Nr. FLETË PROVIMI Exam Paper Udhëzime/Instructions:
Shoqata e Kontabilistëve të Çertifikuar dhe Auditorëve të Kosovës Society of Certified Accountants and Auditors of Kosovo Menaxhment Financiar (zgjidhjet) P7 Nr. FLETË PROVIMI Exam Paper Udhëzime/Instructions:
AKTET ISSN BEDRI DURMISHAJ, SYLEJMAN HYSENI Universiteti i Prishtinës, FXM PI-Mitrovicë 40000, KOSOVË
 AKTET ISSN 2073-2244 Journal of Institute Alb-Shkenca www.alb-shkenca.org Revistë Shkencore e Institutit Alb-Shkenca Copyright Institute Alb-Shkenca CHEMICAL COMPOSITION OF MAIN MINERALS OF Pb AND Zn IN
AKTET ISSN 2073-2244 Journal of Institute Alb-Shkenca www.alb-shkenca.org Revistë Shkencore e Institutit Alb-Shkenca Copyright Institute Alb-Shkenca CHEMICAL COMPOSITION OF MAIN MINERALS OF Pb AND Zn IN
UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I FIZIKËS DISERTACION PËR MBROJTJEN E GRADËS DOKTOR I SHKENCAVE
 UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I FIZIKËS DISERTACION PËR MBROJTJEN E GRADËS DOKTOR I SHKENCAVE PËRSHPEJTIMI I LLOGARITJEVE TË FERMIONEVE KIRALE ME ANË TË RRJETAVE
UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I FIZIKËS DISERTACION PËR MBROJTJEN E GRADËS DOKTOR I SHKENCAVE PËRSHPEJTIMI I LLOGARITJEVE TË FERMIONEVE KIRALE ME ANË TË RRJETAVE
Chapter 4 Multiple Random Variables
 Revew for the prevous lecture: Theorems ad Examples: How to obta the pmf (pdf) of U = g (, Y) ad V = g (, Y) Chapter 4 Multple Radom Varables Chapter 44 Herarchcal Models ad Mxture Dstrbutos Examples:
Revew for the prevous lecture: Theorems ad Examples: How to obta the pmf (pdf) of U = g (, Y) ad V = g (, Y) Chapter 4 Multple Radom Varables Chapter 44 Herarchcal Models ad Mxture Dstrbutos Examples:
Menaxhimi i Performancës
 Shoqata e kontabilistëve të çertifikuar dhe auditorëve të Kosovës Society of Certified Accountants and Auditors of Kosovo Menaxhimi i Performancës P8 Nr. Zgjidhjet FLETË PROVIMI Exam Paper Data Date 15.10.2016
Shoqata e kontabilistëve të çertifikuar dhe auditorëve të Kosovës Society of Certified Accountants and Auditors of Kosovo Menaxhimi i Performancës P8 Nr. Zgjidhjet FLETË PROVIMI Exam Paper Data Date 15.10.2016
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postpoed exam: ECON430 Statstcs Date of exam: Jauary 0, 0 Tme for exam: 09:00 a.m. :00 oo The problem set covers 5 pages Resources allowed: All wrtte ad prted
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postpoed exam: ECON430 Statstcs Date of exam: Jauary 0, 0 Tme for exam: 09:00 a.m. :00 oo The problem set covers 5 pages Resources allowed: All wrtte ad prted
THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA
 THE ROYAL STATISTICAL SOCIETY 3 EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA PAPER I STATISTICAL THEORY & METHODS The Socety provdes these solutos to assst caddates preparg for the examatos future years ad
THE ROYAL STATISTICAL SOCIETY 3 EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA PAPER I STATISTICAL THEORY & METHODS The Socety provdes these solutos to assst caddates preparg for the examatos future years ad
Kapitulli I Ventilimi dhe Klimatizimi
 Kapitulli I Ventilimi dhe Klimatizimi Për çdo ndërtesë, ventilimi duhet të sigurohet për të zëvendësuar ajrin e ndenjur të brendshëm me ajër të freskët të jashtëm në mënyrë që të mbahen CO2 dhe ndotësit
Kapitulli I Ventilimi dhe Klimatizimi Për çdo ndërtesë, ventilimi duhet të sigurohet për të zëvendësuar ajrin e ndenjur të brendshëm me ajër të freskët të jashtëm në mënyrë që të mbahen CO2 dhe ndotësit
VLERËSIMI I AKTIVITETIT TË TRAJNIMIT NË ORGANIZATAT E SHËRBIMIT NË SHQIPËRI
 UNIVERSITETI I TIRANËS FAKULTETI I EKONOMISË DEPARTAMENTI MENAXHIMIT VLERËSIMI I AKTIVITETIT TË TRAJNIMIT NË ORGANIZATAT E SHËRBIMIT NË SHQIPËRI Punim për gradën shkencore: DOKTOR I SHKENCAVE NË EKONOMI
UNIVERSITETI I TIRANËS FAKULTETI I EKONOMISË DEPARTAMENTI MENAXHIMIT VLERËSIMI I AKTIVITETIT TË TRAJNIMIT NË ORGANIZATAT E SHËRBIMIT NË SHQIPËRI Punim për gradën shkencore: DOKTOR I SHKENCAVE NË EKONOMI
REPUBLIKA E SHQIPËRISË UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I INXHINIERISË SË NDËRTIMIT DEPARTAMENTI I INXHINIERISË SË MJEDISIT
 REPUBLIKA E SHQIPËRISË UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I INXHINIERISË SË NDËRTIMIT DEPARTAMENTI I INXHINIERISË SË MJEDISIT Punim Doktorature Tema: MBI LIDHJET E MIKROSKEMAVE TË PRODHIMIT TË
REPUBLIKA E SHQIPËRISË UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I INXHINIERISË SË NDËRTIMIT DEPARTAMENTI I INXHINIERISË SË MJEDISIT Punim Doktorature Tema: MBI LIDHJET E MIKROSKEMAVE TË PRODHIMIT TË
A NEW LOG-NORMAL DISTRIBUTION
 Joural of Statstcs: Advaces Theory ad Applcatos Volume 6, Number, 06, Pages 93-04 Avalable at http://scetfcadvaces.co. DOI: http://dx.do.org/0.864/jsata_700705 A NEW LOG-NORMAL DISTRIBUTION Departmet of
Joural of Statstcs: Advaces Theory ad Applcatos Volume 6, Number, 06, Pages 93-04 Avalable at http://scetfcadvaces.co. DOI: http://dx.do.org/0.864/jsata_700705 A NEW LOG-NORMAL DISTRIBUTION Departmet of
UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I MATEMATIKËS SË APLIKUAR DISERTACION PËR MARRJEN E GRADËS DOKTOR I SHKENCAVE
 UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I MATEMATIKËS SË APLIKUAR DISERTACION PËR MARRJEN E GRADËS DOKTOR I SHKENCAVE AURORA FERRJA (SIMONI) STUDIMI I METODAVE TЁ OPTIMIZIMIT
UNIVERSITETI I TIRANËS FAKULTETI I SHKENCAVE TË NATYRËS DEPARTAMENTI I MATEMATIKËS SË APLIKUAR DISERTACION PËR MARRJEN E GRADËS DOKTOR I SHKENCAVE AURORA FERRJA (SIMONI) STUDIMI I METODAVE TЁ OPTIMIZIMIT
D I S E R T A C I O N
 UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I GJEOLOGJISË DHE I MINIERAVE DOKTORATA GJEOSHKENCAT, BURIMET NATYRORE DHE MJEDISI D I S E R T A C I O N APLIKIMI I METODAVE SIZMIKE TË VALËVE TË REFRAKTUARA
UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I GJEOLOGJISË DHE I MINIERAVE DOKTORATA GJEOSHKENCAT, BURIMET NATYRORE DHE MJEDISI D I S E R T A C I O N APLIKIMI I METODAVE SIZMIKE TË VALËVE TË REFRAKTUARA
Overview. Basic concepts of Bayesian learning. Most probable model given data Coin tosses Linear regression Logistic regression
 Overvew Basc cocepts of Bayesa learg Most probable model gve data Co tosses Lear regresso Logstc regresso Bayesa predctos Co tosses Lear regresso 30 Recap: regresso problems Iput to learg problem: trag
Overvew Basc cocepts of Bayesa learg Most probable model gve data Co tosses Lear regresso Logstc regresso Bayesa predctos Co tosses Lear regresso 30 Recap: regresso problems Iput to learg problem: trag
CLASS TEST GRADE 11. PHYSICAL SCIENCES: CHEMISTRY Test 4: Matter and materials 1
 CLASS TEST GRADE PHYSICAL SCIENCES: CHEMISTRY Test 4: Matter and materials MARKS: 45 TIME: hour INSTRUCTIONS AND INFORMATION. Answer ALL the questions. 2. You may use non-programmable calculators. 3. You
CLASS TEST GRADE PHYSICAL SCIENCES: CHEMISTRY Test 4: Matter and materials MARKS: 45 TIME: hour INSTRUCTIONS AND INFORMATION. Answer ALL the questions. 2. You may use non-programmable calculators. 3. You
Faculty Research Interest Seminar Department of Biostatistics, GSPH University of Pittsburgh. Gong Tang Feb. 18, 2005
 Faculty Research Iterest Semar Departmet of Bostatstcs, GSPH Uversty of Pttsburgh Gog ag Feb. 8, 25 Itroducto Joed the departmet 2. each two courses: Elemets of Stochastc Processes (Bostat 24). Aalyss
Faculty Research Iterest Semar Departmet of Bostatstcs, GSPH Uversty of Pttsburgh Gog ag Feb. 8, 25 Itroducto Joed the departmet 2. each two courses: Elemets of Stochastc Processes (Bostat 24). Aalyss
(C) Pavel Sedach and Prep101 1
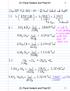 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach
(C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach
ROLI I KAPITALIT EKONOMIK DHE VLERËS EKONOMIKE TË SHTUAR NË VLERËSIMIN E GJENDJES FINANCIARE TË BANKAVE
 REPUBLIKA E SHQIPËRISË UNIVERSITETI I TIRANËS FAKULTETI I EKONOMISË DEPARTAMENTI I FINANCËS TEMË DISERTACIONI ROLI I KAPITALIT EKONOMIK DHE VLERËS EKONOMIKE TË SHTUAR NË VLERËSIMIN E GJENDJES FINANCIARE
REPUBLIKA E SHQIPËRISË UNIVERSITETI I TIRANËS FAKULTETI I EKONOMISË DEPARTAMENTI I FINANCËS TEMË DISERTACIONI ROLI I KAPITALIT EKONOMIK DHE VLERËS EKONOMIKE TË SHTUAR NË VLERËSIMIN E GJENDJES FINANCIARE
I DEFEKTEVE NË STRUKTURAT B/ARME TË KRIJUARA NËN EFEKTIN E DEFORMKOHËS RECOVER OF DEFECTS IN REINFORCED CONCRETE STRUCTURES UNDER THE CREEP EFFECT
 AKTET ISSN 2073-2244 Journal of Institute Alb-Shkenca www.alb-shkenca.org Revistë Shkencore e Institutit Alb-Shkenca Copyright Institute Alb-Shkenca RIKUPERIMI I DEFEKTEVE NË STRUKTURAT B/ARME TË KRIJUARA
AKTET ISSN 2073-2244 Journal of Institute Alb-Shkenca www.alb-shkenca.org Revistë Shkencore e Institutit Alb-Shkenca Copyright Institute Alb-Shkenca RIKUPERIMI I DEFEKTEVE NË STRUKTURAT B/ARME TË KRIJUARA
Continuous Distributions
 7//3 Cotuous Dstrbutos Radom Varables of the Cotuous Type Desty Curve Percet Desty fucto, f (x) A smooth curve that ft the dstrbuto 3 4 5 6 7 8 9 Test scores Desty Curve Percet Probablty Desty Fucto, f
7//3 Cotuous Dstrbutos Radom Varables of the Cotuous Type Desty Curve Percet Desty fucto, f (x) A smooth curve that ft the dstrbuto 3 4 5 6 7 8 9 Test scores Desty Curve Percet Probablty Desty Fucto, f
Functions of Random Variables
 Fuctos of Radom Varables Chapter Fve Fuctos of Radom Varables 5. Itroducto A geeral egeerg aalyss model s show Fg. 5.. The model output (respose) cotas the performaces of a system or product, such as weght,
Fuctos of Radom Varables Chapter Fve Fuctos of Radom Varables 5. Itroducto A geeral egeerg aalyss model s show Fg. 5.. The model output (respose) cotas the performaces of a system or product, such as weght,
Extreme Value Theory: An Introduction
 (correcto d Extreme Value Theory: A Itroducto by Laures de Haa ad Aa Ferrera Wth ths webpage the authors ted to form the readers of errors or mstakes foud the book after publcato. We also gve extesos for
(correcto d Extreme Value Theory: A Itroducto by Laures de Haa ad Aa Ferrera Wth ths webpage the authors ted to form the readers of errors or mstakes foud the book after publcato. We also gve extesos for
Faculty of Natural and Agricultural Sciences Chemistry Department. Semester Test 1 MEMO. Analytical Chemistry CMY 283
 Faculty of Natural and Agricultural Sciences Chemistry Department Semester Test 1 MEMO Analytical Chemistry CMY 283 Date: 5 September 2016 Lecturers : Prof P Forbes, Dr Laurens, Mr SA Nsibande Time: 90
Faculty of Natural and Agricultural Sciences Chemistry Department Semester Test 1 MEMO Analytical Chemistry CMY 283 Date: 5 September 2016 Lecturers : Prof P Forbes, Dr Laurens, Mr SA Nsibande Time: 90
Metallurgical Chemistry. An Audio Course for Students
 Laval University From the SelectedWorks of Fathi Habashi February, 1987 Metallurgical Chemistry. An Audio Course for Students Fathi Habashi Available at: https://works.bepress.com/fathi_habashi/27/ METALLURGICAL
Laval University From the SelectedWorks of Fathi Habashi February, 1987 Metallurgical Chemistry. An Audio Course for Students Fathi Habashi Available at: https://works.bepress.com/fathi_habashi/27/ METALLURGICAL
Për marrjen e gradës. Doktor. M.Sc. ERVENILA MUSTA (Xhaferraj) DISERTACION
 REPUBLIKA E SHQIPËRISË UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I INXHINIERISË MATEMATIKE DHE INXHINIERISË FIZIKE DEPARTAMENTI INXHINIERISË MATEMATIKE Për marrjen e gradës Doktor M.Sc. ERVENILA MUSTA
REPUBLIKA E SHQIPËRISË UNIVERSITETI POLITEKNIK I TIRANËS FAKULTETI I INXHINIERISË MATEMATIKE DHE INXHINIERISË FIZIKE DEPARTAMENTI INXHINIERISË MATEMATIKE Për marrjen e gradës Doktor M.Sc. ERVENILA MUSTA
Momente krize. Gil Caroz
 Momente krize Gil Caroz Një hipotezë: lista e grupeve psikanalitike që formojnë NLS në përmbajnë një dije rreth krizës, që do të përbënte interes nëse do të nxirrej në dritë. Nëse e konsiderojmë krizën
Momente krize Gil Caroz Një hipotezë: lista e grupeve psikanalitike që formojnë NLS në përmbajnë një dije rreth krizës, që do të përbënte interes nëse do të nxirrej në dritë. Nëse e konsiderojmë krizën
X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then
![X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then](/thumbs/83/87696552.jpg) Secto 5 Vectors of Radom Varables Whe workg wth several radom varables,,..., to arrage them vector form x, t s ofte coveet We ca the make use of matrx algebra to help us orgaze ad mapulate large umbers
Secto 5 Vectors of Radom Varables Whe workg wth several radom varables,,..., to arrage them vector form x, t s ofte coveet We ca the make use of matrx algebra to help us orgaze ad mapulate large umbers
Ch. 9 NOTES ~ Chemical Bonding NOTE: Vocabulary terms are in boldface and underlined. Supporting details are in italics.
 Ch. 9 NOTES ~ Chemical Bonding NOTE: Vocabulary terms are in boldface and underlined. Supporting details are in italics. I. Review: Comparison of ionic and molecular compounds Molecular compounds Ionic
Ch. 9 NOTES ~ Chemical Bonding NOTE: Vocabulary terms are in boldface and underlined. Supporting details are in italics. I. Review: Comparison of ionic and molecular compounds Molecular compounds Ionic
The Periodic Table. Periodic Properties. Can you explain this graph? Valence Electrons. Valence Electrons. Paramagnetism
 Periodic Properties Atomic & Ionic Radius Energy Electron Affinity We want to understand the variations in these properties in terms of electron configurations. The Periodic Table Elements in a column
Periodic Properties Atomic & Ionic Radius Energy Electron Affinity We want to understand the variations in these properties in terms of electron configurations. The Periodic Table Elements in a column
INTERNAL PHYSICAL PROCESSES IN GAMMA-RAY BURSTS LEADING TO AMATI-LIKE RELATIONS
 INTERNAL PHYSICAL PROCESSES IN GAMMA-RAY BURSTS LEADING TO AMATI-LIKE RELATIONS Sonila BOÇI a, Mimoza HAFIZI a, Robert MOCHKOVITCH b a Deartamenti i Fizikës, Fakulteti i Shkencave të Natyrës, Tiranë, ALBANIA
INTERNAL PHYSICAL PROCESSES IN GAMMA-RAY BURSTS LEADING TO AMATI-LIKE RELATIONS Sonila BOÇI a, Mimoza HAFIZI a, Robert MOCHKOVITCH b a Deartamenti i Fizikës, Fakulteti i Shkencave të Natyrës, Tiranë, ALBANIA
CHEM 10113, Quiz 5 October 26, 2011
 CHEM 10113, Quiz 5 October 26, 2011 Name (please print) All equations must be balanced and show phases for full credit. Significant figures count, show charges as appropriate, and please box your answers!
CHEM 10113, Quiz 5 October 26, 2011 Name (please print) All equations must be balanced and show phases for full credit. Significant figures count, show charges as appropriate, and please box your answers!
The Periodic Table of Elements
 The Periodic Table of Elements 8 Uuo Uus Uuh (9) Uup (88) Uuq (89) Uut (8) Uub (8) Rg () 0 Ds (9) 09 Mt (8) 08 Hs (9) 0 h () 0 Sg () 0 Db () 0 Rf () 0 Lr () 88 Ra () 8 Fr () 8 Rn () 8 At (0) 8 Po (09)
The Periodic Table of Elements 8 Uuo Uus Uuh (9) Uup (88) Uuq (89) Uut (8) Uub (8) Rg () 0 Ds (9) 09 Mt (8) 08 Hs (9) 0 h () 0 Sg () 0 Db () 0 Rf () 0 Lr () 88 Ra () 8 Fr () 8 Rn () 8 At (0) 8 Po (09)
8. Relax and do well.
 CHEM 1515 Exam II John II. Gelder October 14, 1993 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 8 different pages. The last two pages include a periodic table, a
CHEM 1515 Exam II John II. Gelder October 14, 1993 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 8 different pages. The last two pages include a periodic table, a
176 5 t h Fl oo r. 337 P o ly me r Ma te ri al s
 A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
Parameter, Statistic and Random Samples
 Parameter, Statstc ad Radom Samples A parameter s a umber that descrbes the populato. It s a fxed umber, but practce we do ot kow ts value. A statstc s a fucto of the sample data,.e., t s a quatty whose
Parameter, Statstc ad Radom Samples A parameter s a umber that descrbes the populato. It s a fxed umber, but practce we do ot kow ts value. A statstc s a fucto of the sample data,.e., t s a quatty whose
PART 1 Introduction to Theory of Solids
 Elsevier UK Job code: MIOC Ch01-I044647 9-3-2007 3:03p.m. Page:1 Trim:165 240MM TS: Integra, India PART 1 Introduction to Theory of Solids Elsevier UK Job code: MIOC Ch01-I044647 9-3-2007 3:03p.m. Page:2
Elsevier UK Job code: MIOC Ch01-I044647 9-3-2007 3:03p.m. Page:1 Trim:165 240MM TS: Integra, India PART 1 Introduction to Theory of Solids Elsevier UK Job code: MIOC Ch01-I044647 9-3-2007 3:03p.m. Page:2
High Accuracy EUV Reflectometry and Scattering at the Advanced Light Source
 High Accuracy EUV Reflectometry and Scattering at the Advanced Light Source Eric Gullikson Lawrence Berkeley National Laboratory 1 Reflectometry and Scattering Beamline (ALS 6.3.2) Commissioned Fall 1994
High Accuracy EUV Reflectometry and Scattering at the Advanced Light Source Eric Gullikson Lawrence Berkeley National Laboratory 1 Reflectometry and Scattering Beamline (ALS 6.3.2) Commissioned Fall 1994
PERIODIC TABLE OF THE ELEMENTS
 Useful Constants and equations: K = o C + 273 Avogadro's number = 6.022 x 10 23 d = density = mass/volume R H = 2.178 x 10-18 J c = E = h = hc/ h = 6.626 x 10-34 J s c = 2.998 x 10 8 m/s E n = -R H Z 2
Useful Constants and equations: K = o C + 273 Avogadro's number = 6.022 x 10 23 d = density = mass/volume R H = 2.178 x 10-18 J c = E = h = hc/ h = 6.626 x 10-34 J s c = 2.998 x 10 8 m/s E n = -R H Z 2
Problem Solutions for BST 695: Special Topics in Statistical Theory, Kui Zhang, Solutions from Previous Homework
 Problem Solutos for BST 695: Specal Topcs Statstcal Theory, Ku Zhag, 0 Solutos from Prevous Homework Problem Solutos for BST 695: Specal Topcs Statstcal Theory, Ku Zhag, 0 000, Problem Page, Problem ()
Problem Solutos for BST 695: Specal Topcs Statstcal Theory, Ku Zhag, 0 Solutos from Prevous Homework Problem Solutos for BST 695: Specal Topcs Statstcal Theory, Ku Zhag, 0 000, Problem Page, Problem ()
Narayana IIT Academy
 INDIA XI_IC_SPARK ime : 3 Hours JEE-MAIN CP -5 Date: 5-0-8 Max Marks : 360 KEY SHEE PHYSICS.. 3. 4. 5. 6. 7. 8. 9. 0... 3. 4. 5. 6. 7. 8. 9. 0... 3. 4. 5. 6. 7. 8. 9. 30. CHEMISRY 3. 3. 33. 34. 35. 36.
INDIA XI_IC_SPARK ime : 3 Hours JEE-MAIN CP -5 Date: 5-0-8 Max Marks : 360 KEY SHEE PHYSICS.. 3. 4. 5. 6. 7. 8. 9. 0... 3. 4. 5. 6. 7. 8. 9. 0... 3. 4. 5. 6. 7. 8. 9. 30. CHEMISRY 3. 3. 33. 34. 35. 36.
Dr. Shalabh. Indian Institute of Technology Kanpur
 Aalyss of Varace ad Desg of Expermets-I MODULE -I LECTURE - SOME RESULTS ON LINEAR ALGEBRA, MATRIX THEORY AND DISTRIBUTIONS Dr. Shalabh Departmet t of Mathematcs t ad Statstcs t t Ida Isttute of Techology
Aalyss of Varace ad Desg of Expermets-I MODULE -I LECTURE - SOME RESULTS ON LINEAR ALGEBRA, MATRIX THEORY AND DISTRIBUTIONS Dr. Shalabh Departmet t of Mathematcs t ad Statstcs t t Ida Isttute of Techology
Lecture 3 Probability review (cont d)
 STATS 00: Itroducto to Statstcal Iferece Autum 06 Lecture 3 Probablty revew (cot d) 3. Jot dstrbutos If radom varables X,..., X k are depedet, the ther dstrbuto may be specfed by specfyg the dvdual dstrbuto
STATS 00: Itroducto to Statstcal Iferece Autum 06 Lecture 3 Probablty revew (cot d) 3. Jot dstrbutos If radom varables X,..., X k are depedet, the ther dstrbuto may be specfed by specfyg the dvdual dstrbuto
UDHËZUES PËR ZHVILLIMIN E KURRIKULËS SË RE TË GJIMNAZIT
 Ky dokument synon t u vijë në ndihmë mësuesve, drejtuesve, prindërve dhe specialistëve të arsimit për zhvillimin e kurrikulës së re, e cila fillon të zbatohet për herë të parë në klasën e dhjetë, në vitin
Ky dokument synon t u vijë në ndihmë mësuesve, drejtuesve, prindërve dhe specialistëve të arsimit për zhvillimin e kurrikulës së re, e cila fillon të zbatohet për herë të parë në klasën e dhjetë, në vitin
