Statistical mechanics canonical ensemble
|
|
|
- Jessica Green
- 5 years ago
- Views:
Transcription
1 canoncal ensemble system n thermal equlbrum wth bath of system probablty of mcro state T = k/ bath system p = 1 Z e E Z = e E average energy of system he = p E = what about? P E E e P e E ln
2 replcate many tme ensemble of N replcas
3 replcate many tme ensemble of N replcas number of replcas n mcro-state n = Np p =1
4 replcate many tme ensemble of N replcas number of replcas n mcro-state n = Np total number of mcro-states N = N! n 1!n 2!...n!... p =1
5 replcate many tme ensemble of N replcas number of replcas n mcro-state n = Np total number of mcro-states N = N! n 1!n 2!...n!... of ensemble p =1 apple N! S N = k ln N = k ln n 1!n 2!...n!...
6 replcate many tme ensemble of N replcas number of replcas n mcro-state n = Np total number of mcro-states N = N! n 1!n 2!...n!... of ensemble apple N! S N = k ln N = k ln n 1!n 2!...n!... Strlng approxmaton: lm ln x! =x ln x x x!1 p =1
7 replcate many tme ensemble of N replcas number of replcas n mcro-state n = Np of ensemble p =1 apple N! S N = k ln N = k ln n 1!n 2!...n!...
8 replcate many tme ensemble of N replcas number of replcas n mcro-state n = Np of ensemble p =1 apple N! S N = k ln N = k ln n 1!n 2!...n!... S N = k " N ln N N (n ln n n ) #
9 replcate many tme ensemble of N replcas number of replcas n mcro-state n = Np of ensemble p =1 apple N! S N = k ln N = k ln n 1!n 2!...n!... S N = k " N ln N N (n ln n n ) # S N = k " N ln N N N (p ln[np ] p ) #
10 replcate many tme ensemble of N replcas number of replcas n mcro-state n = Np of ensemble S N = k " p =1 N ln N N N (p ln[np ] p ) #
11 replcate many tme ensemble of N replcas number of replcas n mcro-state n = Np of ensemble S N = k " p =1 N ln N N N (p ln[np ] p ) # " # S N = k N ln N N N ln N N p ln p N
12 replcate many tme ensemble of N replcas number of replcas n mcro-state n = Np of ensemble S N = k " p =1 N ln N N N (p ln[np ] p ) # " # S N = k N ln N N N ln N N p ln p N S N = Nk p ln p
13 replcate many tme ensemble of N replcas number of replcas n mcro-state n = Np of ensemble p =1 S N = Nk p ln p
14 replcate many tme ensemble of N replcas number of replcas n mcro-state n = Np of ensemble p =1 S N = Nk p ln p of replca S = k p ln p
15 canoncal ensemble system n thermal equlbrum wth bath of system T = k/ bath system S = k p ln p
16 canoncal ensemble system n thermal equlbrum wth bath of system T = k/ bath system S = k p ln p Boltzmann dstrbuton p = 1 Z e E Z = e E 1 kt
17 canoncal ensemble system n thermal equlbrum wth bath of system T = k/ bath system S = k p ln p Boltzmann dstrbuton p = 1 Z e E Z = e E 1 kt substtutng and rearrangng S = k Z e E E + k Z e E ln Z
18 canoncal ensemble system n thermal equlbrum wth bath of system T = k/ bath system S = k p ln p Boltzmann dstrbuton p = 1 Z e E Z = e E 1 kt substtutng and rearrangng S = k Z e E E + k Z e E ln Z an almost famlar expresson S = 1 T he + k ln Z
19 canoncal ensemble system n thermal equlbrum wth bath free energy of system mcroscopc T = k/ bath system S = 1 T he + k ln Z
20 canoncal ensemble system n thermal equlbrum wth bath free energy of system mcroscopc T = k/ bath system S = 1 T he + k ln Z mcroscopc free energy kt ln Z = he TS
21 canoncal ensemble system n thermal equlbrum wth bath free energy of system mcroscopc T = k/ bath system S = 1 T he + k ln Z mcroscopc free energy kt ln Z = he TS A = kt ln Z
22 canoncal ensemble system n thermal equlbrum wth bath free energy of system mcroscopc T = k/ bath system S = 1 T he + k ln Z mcroscopc free energy kt ln Z = he TS A = kt ln Z macroscopc free energy A = U TS
23 canoncal ensemble system n thermal equlbrum wth bath free energy of system mcroscopc T = k/ bath system S = 1 T he + k ln Z mcroscopc free energy kt ln Z = he TS A = kt ln Z macroscopc free energy A = U TS from mcro to macro: generate partton functon Monte Carlo molecular dynamcs smulatons
24 p z A =4 p 2 p x p y dp p x = hn x 2L p y = hn y 2L p z = hn z 2L n x,n y,n z =1, 2, 3,... V (p + p) =4 p 2 dp
University of Washington Department of Chemistry Chemistry 453 Winter Quarter 2015
 Lecture 2. 1/07/15-1/09/15 Unversty of Washngton Department of Chemstry Chemstry 453 Wnter Quarter 2015 We are not talkng about truth. We are talkng about somethng that seems lke truth. The truth we want
Lecture 2. 1/07/15-1/09/15 Unversty of Washngton Department of Chemstry Chemstry 453 Wnter Quarter 2015 We are not talkng about truth. We are talkng about somethng that seems lke truth. The truth we want
10.40 Appendix Connection to Thermodynamics and Derivation of Boltzmann Distribution
 10.40 Appendx Connecton to Thermodynamcs Dervaton of Boltzmann Dstrbuton Bernhardt L. Trout Outlne Cannoncal ensemble Maxmumtermmethod Most probable dstrbuton Ensembles contnued: Canoncal, Mcrocanoncal,
10.40 Appendx Connecton to Thermodynamcs Dervaton of Boltzmann Dstrbuton Bernhardt L. Trout Outlne Cannoncal ensemble Maxmumtermmethod Most probable dstrbuton Ensembles contnued: Canoncal, Mcrocanoncal,
Lecture 3: Boltzmann distribution
 Lecture 3: Boltzmann dstrbuton Statstcal mechancs: concepts Ams: Dervaton of Boltzmann dstrbuton: Basc postulate of statstcal mechancs. All states equally lkely. Equal a-pror probablty: Statstcal vew of
Lecture 3: Boltzmann dstrbuton Statstcal mechancs: concepts Ams: Dervaton of Boltzmann dstrbuton: Basc postulate of statstcal mechancs. All states equally lkely. Equal a-pror probablty: Statstcal vew of
Thermodynamics and statistical mechanics in materials modelling II
 Course MP3 Lecture 8/11/006 (JAE) Course MP3 Lecture 8/11/006 Thermodynamcs and statstcal mechancs n materals modellng II A bref résumé of the physcal concepts used n materals modellng Dr James Ellott.1
Course MP3 Lecture 8/11/006 (JAE) Course MP3 Lecture 8/11/006 Thermodynamcs and statstcal mechancs n materals modellng II A bref résumé of the physcal concepts used n materals modellng Dr James Ellott.1
STATISTICAL MECHANICAL ENSEMBLES 1 MICROSCOPIC AND MACROSCOPIC VARIABLES PHASE SPACE ENSEMBLES. CHE 524 A. Panagiotopoulos 1
 CHE 54 A. Panagotopoulos STATSTCAL MECHACAL ESEMBLES MCROSCOPC AD MACROSCOPC ARABLES The central queston n Statstcal Mechancs can be phrased as follows: f partcles (atoms, molecules, electrons, nucle,
CHE 54 A. Panagotopoulos STATSTCAL MECHACAL ESEMBLES MCROSCOPC AD MACROSCOPC ARABLES The central queston n Statstcal Mechancs can be phrased as follows: f partcles (atoms, molecules, electrons, nucle,
and Statistical Mechanics Material Properties
 Statstcal Mechancs and Materal Propertes By Kuno TAKAHASHI Tokyo Insttute of Technology, Tokyo 15-855, JAPA Phone/Fax +81-3-5734-3915 takahak@de.ttech.ac.jp http://www.de.ttech.ac.jp/~kt-lab/ Only for
Statstcal Mechancs and Materal Propertes By Kuno TAKAHASHI Tokyo Insttute of Technology, Tokyo 15-855, JAPA Phone/Fax +81-3-5734-3915 takahak@de.ttech.ac.jp http://www.de.ttech.ac.jp/~kt-lab/ Only for
Lecture 7: Boltzmann distribution & Thermodynamics of mixing
 Prof. Tbbtt Lecture 7 etworks & Gels Lecture 7: Boltzmann dstrbuton & Thermodynamcs of mxng 1 Suggested readng Prof. Mark W. Tbbtt ETH Zürch 13 März 018 Molecular Drvng Forces Dll and Bromberg: Chapters
Prof. Tbbtt Lecture 7 etworks & Gels Lecture 7: Boltzmann dstrbuton & Thermodynamcs of mxng 1 Suggested readng Prof. Mark W. Tbbtt ETH Zürch 13 März 018 Molecular Drvng Forces Dll and Bromberg: Chapters
STATISTICAL MECHANICS
 STATISTICAL MECHANICS Thermal Energy Recall that KE can always be separated nto 2 terms: KE system = 1 2 M 2 total v CM KE nternal Rgd-body rotaton and elastc / sound waves Use smplfyng assumptons KE of
STATISTICAL MECHANICS Thermal Energy Recall that KE can always be separated nto 2 terms: KE system = 1 2 M 2 total v CM KE nternal Rgd-body rotaton and elastc / sound waves Use smplfyng assumptons KE of
ESCI 341 Atmospheric Thermodynamics Lesson 10 The Physical Meaning of Entropy
 ESCI 341 Atmospherc Thermodynamcs Lesson 10 The Physcal Meanng of Entropy References: An Introducton to Statstcal Thermodynamcs, T.L. Hll An Introducton to Thermodynamcs and Thermostatstcs, H.B. Callen
ESCI 341 Atmospherc Thermodynamcs Lesson 10 The Physcal Meanng of Entropy References: An Introducton to Statstcal Thermodynamcs, T.L. Hll An Introducton to Thermodynamcs and Thermostatstcs, H.B. Callen
Physics 115. Molecular motion and temperature Phase equilibrium, evaporation
 Physcs 115 General Physcs II Sesson 9 Molecular moton and temperature Phase equlbrum, evaporaton R. J. Wlkes Emal: phy115a@u.washngton.edu Home page: http://courses.washngton.edu/phy115a/ 4/14/14 Physcs
Physcs 115 General Physcs II Sesson 9 Molecular moton and temperature Phase equlbrum, evaporaton R. J. Wlkes Emal: phy115a@u.washngton.edu Home page: http://courses.washngton.edu/phy115a/ 4/14/14 Physcs
Markov Chain Monte Carlo (MCMC), Gibbs Sampling, Metropolis Algorithms, and Simulated Annealing Bioinformatics Course Supplement
 Markov Chan Monte Carlo MCMC, Gbbs Samplng, Metropols Algorthms, and Smulated Annealng 2001 Bonformatcs Course Supplement SNU Bontellgence Lab http://bsnuackr/ Outlne! Markov Chan Monte Carlo MCMC! Metropols-Hastngs
Markov Chan Monte Carlo MCMC, Gbbs Samplng, Metropols Algorthms, and Smulated Annealng 2001 Bonformatcs Course Supplement SNU Bontellgence Lab http://bsnuackr/ Outlne! Markov Chan Monte Carlo MCMC! Metropols-Hastngs
10.34 Fall 2015 Metropolis Monte Carlo Algorithm
 10.34 Fall 2015 Metropols Monte Carlo Algorthm The Metropols Monte Carlo method s very useful for calculatng manydmensonal ntegraton. For e.g. n statstcal mechancs n order to calculate the prospertes of
10.34 Fall 2015 Metropols Monte Carlo Algorthm The Metropols Monte Carlo method s very useful for calculatng manydmensonal ntegraton. For e.g. n statstcal mechancs n order to calculate the prospertes of
Thermodynamics Second Law Entropy
 Thermodynamcs Second Law Entropy Lana Sherdan De Anza College May 8, 2018 Last tme the Boltzmann dstrbuton (dstrbuton of energes) the Maxwell-Boltzmann dstrbuton (dstrbuton of speeds) the Second Law of
Thermodynamcs Second Law Entropy Lana Sherdan De Anza College May 8, 2018 Last tme the Boltzmann dstrbuton (dstrbuton of energes) the Maxwell-Boltzmann dstrbuton (dstrbuton of speeds) the Second Law of
Lecture 2 Grand Canonical Ensemble GCE
 Lecture 2 Grand Canoncal Ensemble GCE 2.1 hermodynamc Functons Contnung on from last day we also note that thus, dω = df dµ µd = Sd P dv dµ (2.1) P = V = S = From the expresson for the entropy, we therefore
Lecture 2 Grand Canoncal Ensemble GCE 2.1 hermodynamc Functons Contnung on from last day we also note that thus, dω = df dµ µd = Sd P dv dµ (2.1) P = V = S = From the expresson for the entropy, we therefore
Lecture 4. Macrostates and Microstates (Ch. 2 )
 Lecture 4. Macrostates and Mcrostates (Ch. ) The past three lectures: we have learned about thermal energy, how t s stored at the mcroscopc level, and how t can be transferred from one system to another.
Lecture 4. Macrostates and Mcrostates (Ch. ) The past three lectures: we have learned about thermal energy, how t s stored at the mcroscopc level, and how t can be transferred from one system to another.
TP A SOLUTION. For an ideal monatomic gas U=3/2nRT, Since the process is at constant pressure Q = C. giving ) =1000/(5/2*8.31*10)
 T A SOLUTION For an deal monatomc gas U/nRT, Snce the process s at constant pressure Q C pn T gvng a: n Q /( 5 / R T ) /(5/*8.*) C V / R and C / R + R 5 / R. U U / nr T (/ ) R T ( Q / 5 / R T ) Q / 5 Q
T A SOLUTION For an deal monatomc gas U/nRT, Snce the process s at constant pressure Q C pn T gvng a: n Q /( 5 / R T ) /(5/*8.*) C V / R and C / R + R 5 / R. U U / nr T (/ ) R T ( Q / 5 / R T ) Q / 5 Q
Introduction to Statistical Methods
 Introducton to Statstcal Methods Physcs 4362, Lecture #3 hermodynamcs Classcal Statstcal Knetc heory Classcal hermodynamcs Macroscopc approach General propertes of the system Macroscopc varables 1 hermodynamc
Introducton to Statstcal Methods Physcs 4362, Lecture #3 hermodynamcs Classcal Statstcal Knetc heory Classcal hermodynamcs Macroscopc approach General propertes of the system Macroscopc varables 1 hermodynamc
π e ax2 dx = x 2 e ax2 dx or x 3 e ax2 dx = 1 x 4 e ax2 dx = 3 π 8a 5/2 (a) We are considering the Maxwell velocity distribution function: 2πτ/m
 Homework Solutons Problem In solvng ths problem, we wll need to calculate some moments of the Gaussan dstrbuton. The brute-force method s to ntegrate by parts but there s a nce trck. The followng ntegrals
Homework Solutons Problem In solvng ths problem, we wll need to calculate some moments of the Gaussan dstrbuton. The brute-force method s to ntegrate by parts but there s a nce trck. The followng ntegrals
Phase Space N p t 2 2 t 1 Phase space p, p, p,..., p, r, r, r,..., r N N 1 N r
 Phase Space p t 2 2 t1 1 Phase space p,..., 1, p2, p3,..., p, r1, r1, r3 r r Phase Orbt If thehamltonan of the system s denoted by H(q,p), the moton of phase pont can be along the phase orbt and s determned
Phase Space p t 2 2 t1 1 Phase space p,..., 1, p2, p3,..., p, r1, r1, r3 r r Phase Orbt If thehamltonan of the system s denoted by H(q,p), the moton of phase pont can be along the phase orbt and s determned
Property calculation I
 .0, 3.0, 0.333,.00 Introducton to Modelng and Smulaton Sprng 0 Part I Contnuum and partcle methods Property calculaton I Lecture 3 Markus J. Buehler Laboratory for Atomstc and Molecular Mechancs Department
.0, 3.0, 0.333,.00 Introducton to Modelng and Smulaton Sprng 0 Part I Contnuum and partcle methods Property calculaton I Lecture 3 Markus J. Buehler Laboratory for Atomstc and Molecular Mechancs Department
Quantum Statistical Mechanics
 Chapter 8 Quantum Statstcal Mechancs 8.1 Mcrostates For a collecton of N partcles the classcal mcrostate of the system s unquely specfed by a vector (q, p) (q 1...q N, p 1...p 3N )(q 1...q 3N,p 1...p 3N
Chapter 8 Quantum Statstcal Mechancs 8.1 Mcrostates For a collecton of N partcles the classcal mcrostate of the system s unquely specfed by a vector (q, p) (q 1...q N, p 1...p 3N )(q 1...q 3N,p 1...p 3N
Amplification and Relaxation of Electron Spin Polarization in Semiconductor Devices
 Amplfcaton and Relaxaton of Electron Spn Polarzaton n Semconductor Devces Yury V. Pershn and Vladmr Prvman Center for Quantum Devce Technology, Clarkson Unversty, Potsdam, New York 13699-570, USA Spn Relaxaton
Amplfcaton and Relaxaton of Electron Spn Polarzaton n Semconductor Devces Yury V. Pershn and Vladmr Prvman Center for Quantum Devce Technology, Clarkson Unversty, Potsdam, New York 13699-570, USA Spn Relaxaton
Chapter 1. Probability
 Chapter. Probablty Mcroscopc propertes of matter: quantum mechancs, atomc and molecular propertes Macroscopc propertes of matter: thermodynamcs, E, H, C V, C p, S, A, G How do we relate these two propertes?
Chapter. Probablty Mcroscopc propertes of matter: quantum mechancs, atomc and molecular propertes Macroscopc propertes of matter: thermodynamcs, E, H, C V, C p, S, A, G How do we relate these two propertes?
PHY688, Statistical Mechanics
 Department of Physcs & Astronomy 449 ESS Bldg. Stony Brook Unversty January 31, 2017 Nuclear Astrophyscs James.Lattmer@Stonybrook.edu Thermodynamcs Internal Energy Densty and Frst Law: ε = E V = Ts P +
Department of Physcs & Astronomy 449 ESS Bldg. Stony Brook Unversty January 31, 2017 Nuclear Astrophyscs James.Lattmer@Stonybrook.edu Thermodynamcs Internal Energy Densty and Frst Law: ε = E V = Ts P +
MOLECULAR DYNAMICS ,..., What is it? 2 = i i
 MOLECULAR DYNAMICS What s t? d d x t 2 m 2 = F ( x 1,..., x N ) =1,,N r ( x1 ( t),..., x ( t)) = v = ( x& 1 ( t ),..., x& ( t )) N N What are some uses of molecular smulatons and modelng? Conformatonal
MOLECULAR DYNAMICS What s t? d d x t 2 m 2 = F ( x 1,..., x N ) =1,,N r ( x1 ( t),..., x ( t)) = v = ( x& 1 ( t ),..., x& ( t )) N N What are some uses of molecular smulatons and modelng? Conformatonal
Chap.5 Statistical Thermodynamics
 Chap5 Statstcal Thermodynamcs () Free expanson & adabatc from macroscopc: Δ S dq T R adabatc Q, free expanson W rrev rrev ΔU, deal gas ΔT If reversble & sothermal QR + WR ΔU 因 Uf(T) RT QR WR ( Pd ) Pd
Chap5 Statstcal Thermodynamcs () Free expanson & adabatc from macroscopc: Δ S dq T R adabatc Q, free expanson W rrev rrev ΔU, deal gas ΔT If reversble & sothermal QR + WR ΔU 因 Uf(T) RT QR WR ( Pd ) Pd
Chapter 02: Numerical methods for microfluidics. Xiangyu Hu Technical University of Munich
 Chapter 02: Numercal methods for mcrofludcs Xangyu Hu Techncal Unversty of Munch Possble numercal approaches Macroscopc approaches Fnte volume/element method Thn flm method Mcroscopc approaches Molecular
Chapter 02: Numercal methods for mcrofludcs Xangyu Hu Techncal Unversty of Munch Possble numercal approaches Macroscopc approaches Fnte volume/element method Thn flm method Mcroscopc approaches Molecular
Introduction to the lattice Boltzmann method
 Introducton to LB Introducton to the lattce Boltzmann method Burkhard Dünweg Max Planck Insttute for Polymer Research Ackermannweg 10, D-55128 Manz, Germany duenweg@mpp-manz.mpg.de Introducton Naver-Stokes
Introducton to LB Introducton to the lattce Boltzmann method Burkhard Dünweg Max Planck Insttute for Polymer Research Ackermannweg 10, D-55128 Manz, Germany duenweg@mpp-manz.mpg.de Introducton Naver-Stokes
 HEAT CONDUCTION MODELING WITH ENERGY CONSERVATION DISSIPATIVE PARTICLE DYNAMICS Marsol Rpoll, Pep Espa~nol Departamento de Fsca Fundamental, UNED, C/ Senda del Rey 9, 84 Madrd, Span, E-mals: mrpoll@sfun.uned.es,
HEAT CONDUCTION MODELING WITH ENERGY CONSERVATION DISSIPATIVE PARTICLE DYNAMICS Marsol Rpoll, Pep Espa~nol Departamento de Fsca Fundamental, UNED, C/ Senda del Rey 9, 84 Madrd, Span, E-mals: mrpoll@sfun.uned.es,
Hopfield networks and Boltzmann machines. Geoffrey Hinton et al. Presented by Tambet Matiisen
 Hopfeld networks and Boltzmann machnes Geoffrey Hnton et al. Presented by Tambet Matsen 18.11.2014 Hopfeld network Bnary unts Symmetrcal connectons http://www.nnwj.de/hopfeld-net.html Energy functon The
Hopfeld networks and Boltzmann machnes Geoffrey Hnton et al. Presented by Tambet Matsen 18.11.2014 Hopfeld network Bnary unts Symmetrcal connectons http://www.nnwj.de/hopfeld-net.html Energy functon The
Grand Canonical Ensemble
 Th nsmbl of systms mmrsd n a partcl-hat rsrvor at constant tmpratur T, prssur P, and chmcal potntal. Consdr an nsmbl of M dntcal systms (M =,, 3,...M).. Thy ar mutually sharng th total numbr of partcls
Th nsmbl of systms mmrsd n a partcl-hat rsrvor at constant tmpratur T, prssur P, and chmcal potntal. Consdr an nsmbl of M dntcal systms (M =,, 3,...M).. Thy ar mutually sharng th total numbr of partcls
0.1 Required Classical Mechanics
 0.1 Requred Classcal Mechancs The subject of statstcal mechancs deals wth macroscopc (large szed systems consstng of 10 23 partcles) systems. As a result, they have a huge number of degrees of freedom.
0.1 Requred Classcal Mechancs The subject of statstcal mechancs deals wth macroscopc (large szed systems consstng of 10 23 partcles) systems. As a result, they have a huge number of degrees of freedom.
Randomness and Computation
 Randomness and Computaton or, Randomzed Algorthms Mary Cryan School of Informatcs Unversty of Ednburgh RC 208/9) Lecture 0 slde Balls n Bns m balls, n bns, and balls thrown unformly at random nto bns usually
Randomness and Computaton or, Randomzed Algorthms Mary Cryan School of Informatcs Unversty of Ednburgh RC 208/9) Lecture 0 slde Balls n Bns m balls, n bns, and balls thrown unformly at random nto bns usually
Equilibrium Statistical Mechanics
 Equlbrum Statstcal Mechancs Ref. Davdson, Statstcal Mechancs McGraw-Hll, 96 We wsh to study plasmas n equlbrum for at least two reasons: (a) Many tmes real plasmas are near true equlbrum, at least locally
Equlbrum Statstcal Mechancs Ref. Davdson, Statstcal Mechancs McGraw-Hll, 96 We wsh to study plasmas n equlbrum for at least two reasons: (a) Many tmes real plasmas are near true equlbrum, at least locally
Molecular Dynamics Simulations: from Basics to Applications.
 Molecular Dynamcs Smulatons: from ascs to Applcatons. Lecture 7 04.06.01 1 Content of the Lecture 7: 1. Smple thermodynamc averages. Fluctuatons Specfc heat capactes Thermal expanson coeffcent Isothermal
Molecular Dynamcs Smulatons: from ascs to Applcatons. Lecture 7 04.06.01 1 Content of the Lecture 7: 1. Smple thermodynamc averages. Fluctuatons Specfc heat capactes Thermal expanson coeffcent Isothermal
Physics 607 Exam 1. ( ) = 1, Γ( z +1) = zγ( z) x n e x2 dx = 1. e x2
 Physcs 607 Exam 1 Please be well-organzed, and show all sgnfcant steps clearly n all problems. You are graded on your wor, so please do not just wrte down answers wth no explanaton! Do all your wor on
Physcs 607 Exam 1 Please be well-organzed, and show all sgnfcant steps clearly n all problems. You are graded on your wor, so please do not just wrte down answers wth no explanaton! Do all your wor on
Q e E i /k B. i i i i
 Water and Aqueous Solutons 3. Lattce Model of a Flud Lattce Models Lattce models provde a mnmalst, or coarse-graned, framework for descrbng the translatonal, rotatonal, and conformatonal degrees of freedom
Water and Aqueous Solutons 3. Lattce Model of a Flud Lattce Models Lattce models provde a mnmalst, or coarse-graned, framework for descrbng the translatonal, rotatonal, and conformatonal degrees of freedom
6. Stochastic processes (2)
 Contents Markov processes Brth-death processes Lect6.ppt S-38.45 - Introducton to Teletraffc Theory Sprng 5 Markov process Consder a contnuous-tme and dscrete-state stochastc process X(t) wth state space
Contents Markov processes Brth-death processes Lect6.ppt S-38.45 - Introducton to Teletraffc Theory Sprng 5 Markov process Consder a contnuous-tme and dscrete-state stochastc process X(t) wth state space
Artificial Intelligence Bayesian Networks
 Artfcal Intellgence Bayesan Networks Adapted from sldes by Tm Fnn and Mare desjardns. Some materal borrowed from Lse Getoor. 1 Outlne Bayesan networks Network structure Condtonal probablty tables Condtonal
Artfcal Intellgence Bayesan Networks Adapted from sldes by Tm Fnn and Mare desjardns. Some materal borrowed from Lse Getoor. 1 Outlne Bayesan networks Network structure Condtonal probablty tables Condtonal
II.D Many Random Variables
 II.D Many Random Varables Wth more than one random varable, the set of outcomes s an -dmensonal space, S x = { < x 1, x 2,, x < }. For example, descrbng the locaton and velocty of a gas partcle requres
II.D Many Random Varables Wth more than one random varable, the set of outcomes s an -dmensonal space, S x = { < x 1, x 2,, x < }. For example, descrbng the locaton and velocty of a gas partcle requres
PES 2130 Fall 2014, Spendier Lecture 7/Page 1
 PES 2130 Fall 2014, Spender Lecture 7/Page 1 Lecture today: Chapter 20 (ncluded n exam 1) 1) Entropy 2) Second Law o hermodynamcs 3) Statstcal Vew o Entropy Announcements: Next week Wednesday Exam 1! -
PES 2130 Fall 2014, Spender Lecture 7/Page 1 Lecture today: Chapter 20 (ncluded n exam 1) 1) Entropy 2) Second Law o hermodynamcs 3) Statstcal Vew o Entropy Announcements: Next week Wednesday Exam 1! -
6. Stochastic processes (2)
 6. Stochastc processes () Lect6.ppt S-38.45 - Introducton to Teletraffc Theory Sprng 5 6. Stochastc processes () Contents Markov processes Brth-death processes 6. Stochastc processes () Markov process
6. Stochastc processes () Lect6.ppt S-38.45 - Introducton to Teletraffc Theory Sprng 5 6. Stochastc processes () Contents Markov processes Brth-death processes 6. Stochastc processes () Markov process
10. Canonical Transformations Michael Fowler
 10. Canoncal Transformatons Mchael Fowler Pont Transformatons It s clear that Lagrange s equatons are correct for any reasonable choce of parameters labelng the system confguraton. Let s call our frst
10. Canoncal Transformatons Mchael Fowler Pont Transformatons It s clear that Lagrange s equatons are correct for any reasonable choce of parameters labelng the system confguraton. Let s call our frst
CSC321 Tutorial 9: Review of Boltzmann machines and simulated annealing
 CSC321 Tutoral 9: Revew of Boltzmann machnes and smulated annealng (Sldes based on Lecture 16-18 and selected readngs) Yue L Emal: yuel@cs.toronto.edu Wed 11-12 March 19 Fr 10-11 March 21 Outlne Boltzmann
CSC321 Tutoral 9: Revew of Boltzmann machnes and smulated annealng (Sldes based on Lecture 16-18 and selected readngs) Yue L Emal: yuel@cs.toronto.edu Wed 11-12 March 19 Fr 10-11 March 21 Outlne Boltzmann
Macroscopic Momentum Balances
 Lecture 13 F. Morrson CM3110 2013 10/22/2013 CM3110 Transport I Part I: Flud Mechancs Macroscopc Momentum Balances Professor Fath Morrson Department of Chemcal Engneerng Mchgan Technologcal Unersty 1 Macroscopc
Lecture 13 F. Morrson CM3110 2013 10/22/2013 CM3110 Transport I Part I: Flud Mechancs Macroscopc Momentum Balances Professor Fath Morrson Department of Chemcal Engneerng Mchgan Technologcal Unersty 1 Macroscopc
Homework 9 for BST 631: Statistical Theory I Problems, 11/02/2006
 Due Tme: 5:00PM Thursda, on /09/006 Problem (8 ponts) Book problem 45 Let U = X + and V = X, then the jont pmf of ( UV, ) s θ λ θ e λ e f( u, ) = ( = 0, ; u =, +, )! ( u )! Then f( u, ) u θ λ f ( x x+
Due Tme: 5:00PM Thursda, on /09/006 Problem (8 ponts) Book problem 45 Let U = X + and V = X, then the jont pmf of ( UV, ) s θ λ θ e λ e f( u, ) = ( = 0, ; u =, +, )! ( u )! Then f( u, ) u θ λ f ( x x+
5.60 Thermodynamics & Kinetics Spring 2008
 MIT OpenCourseWare http://ocw.mt.edu 5.60 Thermodynamcs & Knetcs Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocw.mt.edu/terms. 5.60 Sprng 2008 Lecture #29 page 1
MIT OpenCourseWare http://ocw.mt.edu 5.60 Thermodynamcs & Knetcs Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocw.mt.edu/terms. 5.60 Sprng 2008 Lecture #29 page 1
Online Appendix to The Allocation of Talent and U.S. Economic Growth
 Onlne Appendx to The Allocaton of Talent and U.S. Economc Growth Not for publcaton) Chang-Ta Hseh, Erk Hurst, Charles I. Jones, Peter J. Klenow February 22, 23 A Dervatons and Proofs The propostons n the
Onlne Appendx to The Allocaton of Talent and U.S. Economc Growth Not for publcaton) Chang-Ta Hseh, Erk Hurst, Charles I. Jones, Peter J. Klenow February 22, 23 A Dervatons and Proofs The propostons n the
...Thermodynamics. If Clausius Clapeyron fails. l T (v 2 v 1 ) = 0/0 Second order phase transition ( S, v = 0)
 If Clausus Clapeyron fals ( ) dp dt pb =...Thermodynamcs l T (v 2 v 1 ) = 0/0 Second order phase transton ( S, v = 0) ( ) dp = c P,1 c P,2 dt Tv(β 1 β 2 ) Two phases ntermngled Ferromagnet (Excess spn-up
If Clausus Clapeyron fals ( ) dp dt pb =...Thermodynamcs l T (v 2 v 1 ) = 0/0 Second order phase transton ( S, v = 0) ( ) dp = c P,1 c P,2 dt Tv(β 1 β 2 ) Two phases ntermngled Ferromagnet (Excess spn-up
Econ107 Applied Econometrics Topic 3: Classical Model (Studenmund, Chapter 4)
 I. Classcal Assumptons Econ7 Appled Econometrcs Topc 3: Classcal Model (Studenmund, Chapter 4) We have defned OLS and studed some algebrac propertes of OLS. In ths topc we wll study statstcal propertes
I. Classcal Assumptons Econ7 Appled Econometrcs Topc 3: Classcal Model (Studenmund, Chapter 4) We have defned OLS and studed some algebrac propertes of OLS. In ths topc we wll study statstcal propertes
Let s treat the problem of the response of a system to an applied external force. Again,
 Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Chapters 18 & 19: Themodynamics review. All macroscopic (i.e., human scale) quantities must ultimately be explained on the microscopic scale.
 Chapters 18 & 19: Themodynamcs revew ll macroscopc (.e., human scale) quanttes must ultmately be explaned on the mcroscopc scale. Chapter 18: Thermodynamcs Thermodynamcs s the study o the thermal energy
Chapters 18 & 19: Themodynamcs revew ll macroscopc (.e., human scale) quanttes must ultmately be explaned on the mcroscopc scale. Chapter 18: Thermodynamcs Thermodynamcs s the study o the thermal energy
An (almost) unbiased estimator for the S-Gini index
 An (almost unbased estmator for the S-Gn ndex Thomas Demuynck February 25, 2009 Abstract Ths note provdes an unbased estmator for the absolute S-Gn and an almost unbased estmator for the relatve S-Gn for
An (almost unbased estmator for the S-Gn ndex Thomas Demuynck February 25, 2009 Abstract Ths note provdes an unbased estmator for the absolute S-Gn and an almost unbased estmator for the relatve S-Gn for
Assignment 5. Simulation for Logistics. Monti, N.E. Yunita, T.
 Assgnment 5 Smulaton for Logstcs Mont, N.E. Yunta, T. November 26, 2007 1. Smulaton Desgn The frst objectve of ths assgnment s to derve a 90% two-sded Confdence Interval (CI) for the average watng tme
Assgnment 5 Smulaton for Logstcs Mont, N.E. Yunta, T. November 26, 2007 1. Smulaton Desgn The frst objectve of ths assgnment s to derve a 90% two-sded Confdence Interval (CI) for the average watng tme
Why Monte Carlo Integration? Introduction to Monte Carlo Method. Continuous Probability. Continuous Probability
 Introducton to Monte Carlo Method Kad Bouatouch IRISA Emal: kad@rsa.fr Wh Monte Carlo Integraton? To generate realstc lookng mages, we need to solve ntegrals of or hgher dmenson Pel flterng and lens smulaton
Introducton to Monte Carlo Method Kad Bouatouch IRISA Emal: kad@rsa.fr Wh Monte Carlo Integraton? To generate realstc lookng mages, we need to solve ntegrals of or hgher dmenson Pel flterng and lens smulaton
Monte Carlo method II
 Course MP3 Lecture 5 14/11/2006 Monte Carlo method II How to put some real physcs nto the Monte Carlo method Dr James Ellott 5.1 Monte Carlo method revsted In lecture 4, we ntroduced the Monte Carlo (MC)
Course MP3 Lecture 5 14/11/2006 Monte Carlo method II How to put some real physcs nto the Monte Carlo method Dr James Ellott 5.1 Monte Carlo method revsted In lecture 4, we ntroduced the Monte Carlo (MC)
Fluctuation Theorem for Pure Quantum States
 Fluctuaton Theorem for Pure Quantum States Takahro Sagawa Department of Appled Physcs, The Unversty of Tokyo 7-9 January 2017 Quantum ntanglement 2017, Tape, Tawan Kazuya Kaneko arxv:1603.07857 k Iyoda
Fluctuaton Theorem for Pure Quantum States Takahro Sagawa Department of Appled Physcs, The Unversty of Tokyo 7-9 January 2017 Quantum ntanglement 2017, Tape, Tawan Kazuya Kaneko arxv:1603.07857 k Iyoda
CHAPTER 5 NUMERICAL EVALUATION OF DYNAMIC RESPONSE
 CHAPTER 5 NUMERICAL EVALUATION OF DYNAMIC RESPONSE Analytcal soluton s usually not possble when exctaton vares arbtrarly wth tme or f the system s nonlnear. Such problems can be solved by numercal tmesteppng
CHAPTER 5 NUMERICAL EVALUATION OF DYNAMIC RESPONSE Analytcal soluton s usually not possble when exctaton vares arbtrarly wth tme or f the system s nonlnear. Such problems can be solved by numercal tmesteppng
Simulation and Probability Distribution
 CHAPTER Probablty, Statstcs, and Relablty for Engneers and Scentsts Second Edton PROBABILIT DISTRIBUTION FOR CONTINUOUS RANDOM VARIABLES A. J. Clark School of Engneerng Department of Cvl and Envronmental
CHAPTER Probablty, Statstcs, and Relablty for Engneers and Scentsts Second Edton PROBABILIT DISTRIBUTION FOR CONTINUOUS RANDOM VARIABLES A. J. Clark School of Engneerng Department of Cvl and Envronmental
(Online First)A Lattice Boltzmann Scheme for Diffusion Equation in Spherical Coordinate
 Internatonal Journal of Mathematcs and Systems Scence (018) Volume 1 do:10.494/jmss.v1.815 (Onlne Frst)A Lattce Boltzmann Scheme for Dffuson Equaton n Sphercal Coordnate Debabrata Datta 1 *, T K Pal 1
Internatonal Journal of Mathematcs and Systems Scence (018) Volume 1 do:10.494/jmss.v1.815 (Onlne Frst)A Lattce Boltzmann Scheme for Dffuson Equaton n Sphercal Coordnate Debabrata Datta 1 *, T K Pal 1
Analysis of Discrete Time Queues (Section 4.6)
 Analyss of Dscrete Tme Queues (Secton 4.6) Copyrght 2002, Sanjay K. Bose Tme axs dvded nto slots slot slot boundares Arrvals can only occur at slot boundares Servce to a job can only start at a slot boundary
Analyss of Dscrete Tme Queues (Secton 4.6) Copyrght 2002, Sanjay K. Bose Tme axs dvded nto slots slot slot boundares Arrvals can only occur at slot boundares Servce to a job can only start at a slot boundary
Lecture 3. Interaction of radiation with surfaces. Upcoming classes
 Radaton transfer n envronmental scences Lecture 3. Interacton of radaton wth surfaces Upcomng classes When a ray of lght nteracts wth a surface several nteractons are possble: 1. It s absorbed. 2. It s
Radaton transfer n envronmental scences Lecture 3. Interacton of radaton wth surfaces Upcomng classes When a ray of lght nteracts wth a surface several nteractons are possble: 1. It s absorbed. 2. It s
Supplemental Material: Causal Entropic Forces
 Supplemental Materal: Causal Entropc Forces A. D. Wssner-Gross 1, 2, and C. E. Freer 3 1 Insttute for Appled Computatonal Scence, Harvard Unversty, Cambrdge, Massachusetts 02138, USA 2 The Meda Laboratory,
Supplemental Materal: Causal Entropc Forces A. D. Wssner-Gross 1, 2, and C. E. Freer 3 1 Insttute for Appled Computatonal Scence, Harvard Unversty, Cambrdge, Massachusetts 02138, USA 2 The Meda Laboratory,
Computing Correlated Equilibria in Multi-Player Games
 Computng Correlated Equlbra n Mult-Player Games Chrstos H. Papadmtrou Presented by Zhanxang Huang December 7th, 2005 1 The Author Dr. Chrstos H. Papadmtrou CS professor at UC Berkley (taught at Harvard,
Computng Correlated Equlbra n Mult-Player Games Chrstos H. Papadmtrou Presented by Zhanxang Huang December 7th, 2005 1 The Author Dr. Chrstos H. Papadmtrou CS professor at UC Berkley (taught at Harvard,
Lecture 5: Ideal monatomic gas
 Lecture 5: Ideal monatomc gas Statstcal mechancs of the perfect gas Ams: Key new concepts and methods: Countng states Waves n a box. Demonstraton that β / kt Heat, work and Entropy n statstcal mechancs
Lecture 5: Ideal monatomc gas Statstcal mechancs of the perfect gas Ams: Key new concepts and methods: Countng states Waves n a box. Demonstraton that β / kt Heat, work and Entropy n statstcal mechancs
Chapter 2 Transformations and Expectations. , and define f
 Revew for the prevous lecture Defnton: support set of a ranom varable, the monotone functon; Theorem: How to obtan a cf, pf (or pmf) of functons of a ranom varable; Eamples: several eamples Chapter Transformatons
Revew for the prevous lecture Defnton: support set of a ranom varable, the monotone functon; Theorem: How to obtan a cf, pf (or pmf) of functons of a ranom varable; Eamples: several eamples Chapter Transformatons
(# = %(& )(* +,(- Closed system, well-defined energy (or e.g. E± E/2): Microcanonical ensemble
 Recall from before: Internal energy (or Entropy): &, *, - (# = %(& )(* +,(- Closed system, well-defined energy (or e.g. E± E/2): Microcanonical ensemble & = /01Ω maximized Ω: fundamental statistical quantity
Recall from before: Internal energy (or Entropy): &, *, - (# = %(& )(* +,(- Closed system, well-defined energy (or e.g. E± E/2): Microcanonical ensemble & = /01Ω maximized Ω: fundamental statistical quantity
Fermi-Dirac statistics
 UCC/Physcs/MK/EM/October 8, 205 Fer-Drac statstcs Fer-Drac dstrbuton Matter partcles that are eleentary ostly have a type of angular oentu called spn. hese partcles are known to have a agnetc oent whch
UCC/Physcs/MK/EM/October 8, 205 Fer-Drac statstcs Fer-Drac dstrbuton Matter partcles that are eleentary ostly have a type of angular oentu called spn. hese partcles are known to have a agnetc oent whch
A stochastic framework for modeling the population dynamics of convective clouds
 A stochastc framework for modelng the populaton dynamcs of convectve clouds SAMSON HAGOS, ZHE FENG, BOB PLANT, ROBERT HOUZE, HENG XIAO Acknowledgement: Alan Protat and hs team at the Australan BOM 1 Introducton
A stochastc framework for modelng the populaton dynamcs of convectve clouds SAMSON HAGOS, ZHE FENG, BOB PLANT, ROBERT HOUZE, HENG XIAO Acknowledgement: Alan Protat and hs team at the Australan BOM 1 Introducton
Wilbur and Ague 4 WILBUR AND AGUE; APPENDIX DR1. Two-dimensional chemical maps as well as chemical profiles were done at 15 kv using
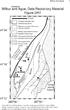 DR2006139 Wlbur and Ague 4 WILBUR AND AGUE; APPENDIX DR1 MINERAL ANALYSES Two-dmensonal chemcal maps as well as chemcal profles were done at 15 kv usng the JEOL JXA-8600 electron mcroprobe at Yale Unversty
DR2006139 Wlbur and Ague 4 WILBUR AND AGUE; APPENDIX DR1 MINERAL ANALYSES Two-dmensonal chemcal maps as well as chemcal profles were done at 15 kv usng the JEOL JXA-8600 electron mcroprobe at Yale Unversty
Transfer Functions. Convenient representation of a linear, dynamic model. A transfer function (TF) relates one input and one output: ( ) system
 Transfer Functons Convenent representaton of a lnear, dynamc model. A transfer functon (TF) relates one nput and one output: x t X s y t system Y s The followng termnology s used: x y nput output forcng
Transfer Functons Convenent representaton of a lnear, dynamc model. A transfer functon (TF) relates one nput and one output: x t X s y t system Y s The followng termnology s used: x y nput output forcng
Topics on Statistical Mechanics TCMM Lecture Notes
 Topcs on Statstcal Mechancs TCMM Lecture otes Fernando Fernandes Department of Chemstry and Bochemstry, Faculty of Scences, Unversty of Lsbon, Portugal Emal: fslva@fc.ul.pt A short revew of basc concepts
Topcs on Statstcal Mechancs TCMM Lecture otes Fernando Fernandes Department of Chemstry and Bochemstry, Faculty of Scences, Unversty of Lsbon, Portugal Emal: fslva@fc.ul.pt A short revew of basc concepts
DETAILED DERIVATION OF THE GENERAL MASTER EQUATION IN QUANTUM OPTICS
 DETAILED DERIVATION OF THE GENERAL MASTER EQUATION IN QUANTUM OPTICS TIMOTHY JONES Abstract. An unorgnal but more detaled dervaton that typcal s presented of the master equaton. 1. Assumptons We begn by
DETAILED DERIVATION OF THE GENERAL MASTER EQUATION IN QUANTUM OPTICS TIMOTHY JONES Abstract. An unorgnal but more detaled dervaton that typcal s presented of the master equaton. 1. Assumptons We begn by
Calculus of Variations Basics
 Chapter 1 Calculus of Varatons Bascs 1.1 Varaton of a General Functonal In ths chapter, we derve the general formula for the varaton of a functonal of the form J [y 1,y 2,,y n ] F x,y 1,y 2,,y n,y 1,y
Chapter 1 Calculus of Varatons Bascs 1.1 Varaton of a General Functonal In ths chapter, we derve the general formula for the varaton of a functonal of the form J [y 1,y 2,,y n ] F x,y 1,y 2,,y n,y 1,y
Stanford University CS359G: Graph Partitioning and Expanders Handout 4 Luca Trevisan January 13, 2011
 Stanford Unversty CS359G: Graph Parttonng and Expanders Handout 4 Luca Trevsan January 3, 0 Lecture 4 In whch we prove the dffcult drecton of Cheeger s nequalty. As n the past lectures, consder an undrected
Stanford Unversty CS359G: Graph Parttonng and Expanders Handout 4 Luca Trevsan January 3, 0 Lecture 4 In whch we prove the dffcult drecton of Cheeger s nequalty. As n the past lectures, consder an undrected
Why BP Works STAT 232B
 Why BP Works STAT 232B Free Energes Helmholz & Gbbs Free Energes 1 Dstance between Probablstc Models - K-L dvergence b{ KL b{ p{ = b{ ln { } p{ Here, p{ s the eact ont prob. b{ s the appromaton, called
Why BP Works STAT 232B Free Energes Helmholz & Gbbs Free Energes 1 Dstance between Probablstc Models - K-L dvergence b{ KL b{ p{ = b{ ln { } p{ Here, p{ s the eact ont prob. b{ s the appromaton, called
Physics 181. Particle Systems
 Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
5.62 Physical Chemistry II Spring 2008
 MIT OpenCourseWare http://ocw.mt.edu 5.62 Physcal Chemstry II Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocw.mt.edu/terms. 5.62 Lecture #8: Boltzmann, Ferm-Drac,
MIT OpenCourseWare http://ocw.mt.edu 5.62 Physcal Chemstry II Sprng 2008 For nformaton about ctng these materals or our Terms of Use, vst: http://ocw.mt.edu/terms. 5.62 Lecture #8: Boltzmann, Ferm-Drac,
Lecture 4 Hypothesis Testing
 Lecture 4 Hypothess Testng We may wsh to test pror hypotheses about the coeffcents we estmate. We can use the estmates to test whether the data rejects our hypothess. An example mght be that we wsh to
Lecture 4 Hypothess Testng We may wsh to test pror hypotheses about the coeffcents we estmate. We can use the estmates to test whether the data rejects our hypothess. An example mght be that we wsh to
Thermodynamics and Kinetics of Solids 33. III. Statistical Thermodynamics. Â N i = N (5.3) N i. i =0. Â e i = E (5.4) has a maximum.
 hermodynamcs and Knetcs of Solds 33 III. Statstcal hermodynamcs 5. Statstcal reatment of hermodynamcs 5.1. Statstcs and Phenomenologcal hermodynamcs. Calculaton of the energetc state of each atomc or molecular
hermodynamcs and Knetcs of Solds 33 III. Statstcal hermodynamcs 5. Statstcal reatment of hermodynamcs 5.1. Statstcs and Phenomenologcal hermodynamcs. Calculaton of the energetc state of each atomc or molecular
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Problem Points Score Total 100
 Physcs 450 Solutons of Sample Exam I Problem Ponts Score 1 8 15 3 17 4 0 5 0 Total 100 All wor must be shown n order to receve full credt. Wor must be legble and comprehensble wth answers clearly ndcated.
Physcs 450 Solutons of Sample Exam I Problem Ponts Score 1 8 15 3 17 4 0 5 0 Total 100 All wor must be shown n order to receve full credt. Wor must be legble and comprehensble wth answers clearly ndcated.
EPR Paradox and the Physical Meaning of an Experiment in Quantum Mechanics. Vesselin C. Noninski
 EPR Paradox and the Physcal Meanng of an Experment n Quantum Mechancs Vesseln C Nonnsk vesselnnonnsk@verzonnet Abstract It s shown that there s one purely determnstc outcome when measurement s made on
EPR Paradox and the Physcal Meanng of an Experment n Quantum Mechancs Vesseln C Nonnsk vesselnnonnsk@verzonnet Abstract It s shown that there s one purely determnstc outcome when measurement s made on
Physics 212: Statistical mechanics II Lecture I
 Physcs 212: Statstcal mechancs II Lecture I A theory s the more mpressve the greater the smplcty of ts premses, the more dfferent knds of thngs t relates, and the more extended ts area of applcablty. Therefore
Physcs 212: Statstcal mechancs II Lecture I A theory s the more mpressve the greater the smplcty of ts premses, the more dfferent knds of thngs t relates, and the more extended ts area of applcablty. Therefore
Minimum Bias Events at ATLAS
 Camille Bélanger-Champagne Lehman McGill College University City University of New York Thermodynamics Charged Particle and Correlations Statistical Mechanics in Minimum Bias Events at ATLAS Statistical
Camille Bélanger-Champagne Lehman McGill College University City University of New York Thermodynamics Charged Particle and Correlations Statistical Mechanics in Minimum Bias Events at ATLAS Statistical
Title: Radiative transitions and spectral broadening
 Lecture 6 Ttle: Radatve transtons and spectral broadenng Objectves The spectral lnes emtted by atomc vapors at moderate temperature and pressure show the wavelength spread around the central frequency.
Lecture 6 Ttle: Radatve transtons and spectral broadenng Objectves The spectral lnes emtted by atomc vapors at moderate temperature and pressure show the wavelength spread around the central frequency.
Introduction Statistical Thermodynamics. Monday, January 6, 14
 Introduction Statistical Thermodynamics 1 Molecular Simulations Molecular dynamics: solve equations of motion Monte Carlo: importance sampling r 1 r 2 r n MD MC r 1 r 2 2 r n 2 3 3 4 4 Questions How can
Introduction Statistical Thermodynamics 1 Molecular Simulations Molecular dynamics: solve equations of motion Monte Carlo: importance sampling r 1 r 2 r n MD MC r 1 r 2 2 r n 2 3 3 4 4 Questions How can
CE 530 Molecular Simulation
 CE 530 Molecular Smulaton Lecture 3 Molecular Dynamcs n Other Ensembles Davd A. Kofke Department of Chemcal Engneerng SUY Buffalo kofke@eng.buffalo.edu Revew Molecular dynamcs s a numercal ntegraton of
CE 530 Molecular Smulaton Lecture 3 Molecular Dynamcs n Other Ensembles Davd A. Kofke Department of Chemcal Engneerng SUY Buffalo kofke@eng.buffalo.edu Revew Molecular dynamcs s a numercal ntegraton of
y i x P vap 10 A T SOLUTION TO HOMEWORK #7 #Problem
 SOLUTION TO HOMEWORK #7 #roblem 1 10.1-1 a. In order to solve ths problem, we need to know what happens at the bubble pont; at ths pont, the frst bubble s formed, so we can assume that all of the number
SOLUTION TO HOMEWORK #7 #roblem 1 10.1-1 a. In order to solve ths problem, we need to know what happens at the bubble pont; at ths pont, the frst bubble s formed, so we can assume that all of the number
KINECTIC THEORY AND STATISTICAL MECHANICS COURSE GUIDE NATIONAL OPEN UNIVERSITY OF NIGERIA
 PHY 311 KINECTIC THEORY AND STATISTICAL MECHANICS COURSE GUIDE NATIONAL OPEN UNIVERSITY OF NIGERIA Course Code PHY 311 Course Ttle Wrter KINECTIC THEORY AND STATISTICAL MECHANICS Mr. A. Adeleke Aderem
PHY 311 KINECTIC THEORY AND STATISTICAL MECHANICS COURSE GUIDE NATIONAL OPEN UNIVERSITY OF NIGERIA Course Code PHY 311 Course Ttle Wrter KINECTIC THEORY AND STATISTICAL MECHANICS Mr. A. Adeleke Aderem
Hydrological statistics. Hydrological statistics and extremes
 5--0 Stochastc Hydrology Hydrologcal statstcs and extremes Marc F.P. Berkens Professor of Hydrology Faculty of Geoscences Hydrologcal statstcs Mostly concernes wth the statstcal analyss of hydrologcal
5--0 Stochastc Hydrology Hydrologcal statstcs and extremes Marc F.P. Berkens Professor of Hydrology Faculty of Geoscences Hydrologcal statstcs Mostly concernes wth the statstcal analyss of hydrologcal
Engineering Risk Benefit Analysis
 Engneerng Rsk Beneft Analyss.55, 2.943, 3.577, 6.938, 0.86, 3.62, 6.862, 22.82, ESD.72, ESD.72 RPRA 2. Elements of Probablty Theory George E. Apostolaks Massachusetts Insttute of Technology Sprng 2007
Engneerng Rsk Beneft Analyss.55, 2.943, 3.577, 6.938, 0.86, 3.62, 6.862, 22.82, ESD.72, ESD.72 RPRA 2. Elements of Probablty Theory George E. Apostolaks Massachusetts Insttute of Technology Sprng 2007
Part II Statistical Mechanics, Lent 2005
 Part II Statstcal Mechancs, Lent 25 Prof. R.R. Horgan February 14, 25 1 Statstcal Mechancs 1.1 Introducton The classcal and quantum dynamcs of smple systems wth few degrees of freedom s well understood
Part II Statstcal Mechancs, Lent 25 Prof. R.R. Horgan February 14, 25 1 Statstcal Mechancs 1.1 Introducton The classcal and quantum dynamcs of smple systems wth few degrees of freedom s well understood
Continuous Time Markov Chain
 Contnuous Tme Markov Chan Hu Jn Department of Electroncs and Communcaton Engneerng Hanyang Unversty ERICA Campus Contents Contnuous tme Markov Chan (CTMC) Propertes of sojourn tme Relatons Transton probablty
Contnuous Tme Markov Chan Hu Jn Department of Electroncs and Communcaton Engneerng Hanyang Unversty ERICA Campus Contents Contnuous tme Markov Chan (CTMC) Propertes of sojourn tme Relatons Transton probablty
Lecture 9: Converse of Shannon s Capacity Theorem
 Error Correctng Codes: Combnatorcs, Algorthms and Alcatons (Fall 2007) Lecture 9: Converse of Shannon s Caacty Theorem Setember 17, 2007 Lecturer: Atr Rudra Scrbe: Thanh-Nhan Nguyen & Atr Rudra In the
Error Correctng Codes: Combnatorcs, Algorthms and Alcatons (Fall 2007) Lecture 9: Converse of Shannon s Caacty Theorem Setember 17, 2007 Lecturer: Atr Rudra Scrbe: Thanh-Nhan Nguyen & Atr Rudra In the
A Solution of the Harry-Dym Equation Using Lattice-Boltzmannn and a Solitary Wave Methods
 Appled Mathematcal Scences, Vol. 11, 2017, no. 52, 2579-2586 HIKARI Ltd, www.m-hkar.com https://do.org/10.12988/ams.2017.79280 A Soluton of the Harry-Dym Equaton Usng Lattce-Boltzmannn and a Soltary Wave
Appled Mathematcal Scences, Vol. 11, 2017, no. 52, 2579-2586 HIKARI Ltd, www.m-hkar.com https://do.org/10.12988/ams.2017.79280 A Soluton of the Harry-Dym Equaton Usng Lattce-Boltzmannn and a Soltary Wave
Entropic Dynamics: an Inference Approach to Time and Quantum Theory
 Entropc Dynamcs: an Inference Approach to Tme and Quantum Theory Arel Catcha Department of hyscs Unversty at Albany - SUNY EmQM-13 Venna, 10/013 Queston: Do the laws of hyscs reflect Laws of Nature? Or...
Entropc Dynamcs: an Inference Approach to Tme and Quantum Theory Arel Catcha Department of hyscs Unversty at Albany - SUNY EmQM-13 Venna, 10/013 Queston: Do the laws of hyscs reflect Laws of Nature? Or...
APPROXIMATE PRICES OF BASKET AND ASIAN OPTIONS DUPONT OLIVIER. Premia 14
 APPROXIMAE PRICES OF BASKE AND ASIAN OPIONS DUPON OLIVIER Prema 14 Contents Introducton 1 1. Framewor 1 1.1. Baset optons 1.. Asan optons. Computng the prce 3. Lower bound 3.1. Closed formula for the prce
APPROXIMAE PRICES OF BASKE AND ASIAN OPIONS DUPON OLIVIER Prema 14 Contents Introducton 1 1. Framewor 1 1.1. Baset optons 1.. Asan optons. Computng the prce 3. Lower bound 3.1. Closed formula for the prce
Mass Transfer Processes
 Mass Transfer Processes S. Majd Hassanzadeh Department of Earth Scences Faculty of Geoscences Utrecht Unversty Outlne: 1. Measures of Concentraton 2. Volatlzaton and Dssoluton 3. Adsorpton Processes 4.
Mass Transfer Processes S. Majd Hassanzadeh Department of Earth Scences Faculty of Geoscences Utrecht Unversty Outlne: 1. Measures of Concentraton 2. Volatlzaton and Dssoluton 3. Adsorpton Processes 4.
SUPPLEMENTARY INFORMATION
 do: 0.08/nature09 I. Resonant absorpton of XUV pulses n Kr + usng the reduced densty matrx approach The quantum beats nvestgated n ths paper are the result of nterference between two exctaton paths of
do: 0.08/nature09 I. Resonant absorpton of XUV pulses n Kr + usng the reduced densty matrx approach The quantum beats nvestgated n ths paper are the result of nterference between two exctaton paths of
