SIMETRIČNI BICIRKULANTI
|
|
|
- Aldous Page
- 5 years ago
- Views:
Transcription
1 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA GORAZD VASILJEVIĆ SIMETRIČNI BICIRKULANTI DIPLOMSKO DELO Ljubljana, 2014
2
3 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika - računalništvo GORAZD VASILJEVIĆ Mentor: doc. dr. PRIMOŽ ŠPARL SIMETRIČNI BICIRKULANTI DIPLOMSKO DELO Ljubljana, 2014
4
5 Mentorju doc. dr. Primožu Šparlu se zahvaljujem za vso pomoč, koristne nasvete in za trud, ki ga je prispeval pri nastajanju mojega diplomskega dela. Zahvaljujem se tudi vsem svojim najbližjim, ki so mi ob nastajanju tega diplomskega dela in tudi ob celotnem študiju stali ob strani, me spodbujali in podpirali.
6
7 Povzetek Diplomsko delo sodi na področje teorije grafov. Ko govorimo o preučevanju grafov, s tem največkrat mislimo na preučevanje njihove strukture in z njo povezanih lastnosti. Pri tem nas največkrat zanimajo avtomorfizmi grafa (simetrije). Gre za permutacije množice vozlišč grafa, ki ohranjajo sosednost. Pri nekateri grafih, ki so dovolj lepi, grupa vseh avtomorfizmov na vozlišča tega grafa deluje tranzitivno, kar pomeni, da za poljuben par vozlišč obstaja avtomorfizem, ki eno vozlišče preslika v drugo. Taki grafi so vozliščno tranzitivni grafi. Podobno je graf povezavno tranzitiven, če grupa avtomorfizmov deluje tranzitivno na množico njegovih povezav in je ločno tranzitiven, če grupa avtomorfizmov deluje tranzitivno na množico njegovih lokov. Bicirkulant je graf, ki dopušča avtomorfizem z dvema orbitama iste dolžine. Pri preučevanju bicirkulantov je en izmed ciljev klasifikacija oziroma vsaj identifikacija neskočnih družin vozliščno, povezavno ali pa ločno tranzitivnih bicirkulantov pri kakšnih dodatnih omejitvah kot je na primer stopnja vozlišč. V diplomskem delu si ogledamo rezultate Fruchta, Graverja in Watkinsa, ki so preučili tako imenovanje Posplošene Petersenove grafe (kubične bicirkulante), ter izmed njih identificiramo vozliščno in povezavno tranzitivne. Naslednji naravni korak je študij posplošitve Posplošenih Petersenovih grafov, tako imenovanih Rozetnih grafov. Prvi, ki se je z njimi ukvarjal je bil Wilson ki je tudi identificiral štiri družine povezavno tranzitivnih Rozetnih grafov. Prav Wilsonovemu delu je v diplomskem delu namenjene največ pozornosti, ker predstavimo identificirane družine in pokažemo, da so njihovi člani res povezavno tranzitivni bicirkulanti. Ključne besede: teorija grafov, bicirkulant, avtomorfizem, Rozetni graf, povezavno tranzitiven graf Klasifikacija MSC (2010): 05C25, 05C99, 20B25
8
9 Title: Symmetric bicirculants Abstract This BSc thesis deals with certain topics from graph theory. When we talk about studying graphs, we usually mean studying their structure and their structural properties. By doing that, we are often interested in automorphisms of a graph (symmetries), which are permutations of its vertex set, preserving adjacency. There exist graphs, which are symmetric enough, so that automorhism group acts transitively on their vertex set. This means that for any pair of vertices of the graph, there is an automorphism, mapping one vertex to the other. Such graphs are called vertex-transitive. Similarly, a graph is edge-transitive, if its automorphism group acts transitively on its edge set and is arc-transitive, if its automorphism group acts transitively on its arc set. A bicirculant is a graph, which admits an automorhpism with two orbits of the same length. When studying bicirculants, one of the goals is to classify or at least identify infinite families of vertex-, edge- or arc-transitive bicirculants, given additional restrictions, such as the degree of vertices. In this thesis, we will examine the results of Frucht, Graver and Watkins, who studied the so-called Generalised Petersen graphs (cubic bicirculants) and classified the vertexand edge-transitive ones. The next natural step is to study the natural generalizations of Generalised Petersen graphs, the so-called Rose-window graphs. The first to study them was Wilson, who also identified four families of edge-transitive Rose-window graphs. The main focus of this thesis is on Wilson s work. We present four families of Rose-Window graphs from Wilson s paper and show, that their members are in fact edge-transitive bicirculants. Keywords: graph theory, bicirculant, automorphism, Rose-Window graph, edge-transitive graph MSC (2010) classification: 05C25, 05C99, 20B25
10
11 Kazalo 1 Uvod 1 2 Osnovne definicije, trditve in izreki Teorija grup Nekatere znane družine grup Teorija grafov Nekatere standardne družine grafov Cirkulanti in bicirkulanti Posplošeni Petersenovi grafi GP (n, k) 17 4 Rozetni grafi R n (a, k) Osnovne definicije in dejstva, povezana z R n (a, k) Povezavna tranzitivnost grafov R n (a, k) Družina R n (2, 1) Družina R 2m (m + 2, m + 1) Družina R 12m (3m + 2, 3m 1) in R 12m (3m 2, 3m + 1) Družina R 2m (2b, r) Zaključek 37 Literatura 39
12
13 Poglavje 1 Uvod Diplomsko delo, ki ga bralec drži v rokah sodi na področje mlade veje matematike, imenovane teorija grafov. Ta je sestavljena iz več podpodročij, od katerih se vsako ukvarja z drugačnimi pogledi na grafe. Tako na primer poznamo kombinatorično, topološko, algoritmično in algebraično vejo teorije grafov. Prav v zadnjo lahko umestimo diplomsko delo, saj se bomo naslonili na številne postopke, rezultate in pristope s področja algebre. Pri preučevanju grafov nas najbolj zanima njihova struktura in z njo povezane lastnosti. Z algebraičnega vidika nas pri tem najpogosteje zanimajo simetrije oziroma avtomorfizmi grafov, to je permutacije vozlišč danega grafa, ki ohranjajo sosednosti. Z vidika njihovega preučevanja obstajajo dovolj lepi grafi, ki dopuščajo tolikšno mero simetrije, da za poljuben par vozlišč obstaja avtomorfizem grafa, ki eno vozlišče preslika v drugo (grupa avtomorfizmov na množico vozlišč deluje tranzitivno). Taki grafi so vozliščno tranzitivni grafi. Podobno je graf povezavno tranzitiven, če grupa avtomorfizmov na njegovo množico povezav deluje tranzitivno in ločno tranzitiven, če grupa avtomorfizmov na množico njegovih lokov deluje tranzitivno. Preučevanje simetrij je morda najbolj smiselno začeti pri družini grafov, imenovani cirkulanti (grafi, ki dovoljujejo avtomorfizem, ki ciklično permutira vsa njihova vozlišča), naslednji naraven korak pa je študij bicirkulantov. Takšni grafi dopuščajo avtomorfizem z dvema orbitama iste dolžine, začetek njihovega preučevanja pa sega v sedemdeseta leta prejšnjega stoletja, ko so Graver, Frucht in Watkins klasificirali vozliščno in povezavno tranzitivne Posplošene Petersenove grafe. Če je mogoča, je naš cilj pri tovrstnem študiju navadno prav klasifikacija, v nasprotnem primeru pa vsaj konstrukcija neskončnih družin grafov s študiranimi lastnostmi. V splošnem je klasifikacija simetričnih bicirkulantov, ki ohranjajo strukturo Posplošenih Petersenovih grafov, precej zahtevna naloga. O tem priča tudi klasifikacija povezavno tranzitivnih t. i. Rozetnih grafov, ki so posplošitev Posplošenih Petersenovih grafov na valenco (stopnjo) 4. To je začel Wilson, ki je identificiral štiri družine takih grafov, nadaljevali pa so jo Kovács, Kutnar in Marušič s svojim dokazom, da gre resnično za edine družine povezavno tranzitivnih Rozetnih grafov. Podobna situacije je tudi pri posplošitvi Posplošenih Petersenovih grafov na valenco 5, t. i. Tabačjn grafih. Njihovo 1
14 klasifikacijo so naredili Arroyo, Hubard, Kutnar, O Reilly in Šparl. V diplomskem delu bomo največ pozornosti namenili Wilsonovi identifikaciji povezavno tranzitivnih Rozetnih grafov. V diplomskem delu bomo v drugem poglavju najprej obnovili potrebno predznanje s področja algebre, natančneje teorije grup, in predznanje s področja teorije grafov. V tretjem poglavju si bomo ogledali pomembnejše rezultate dela Graverja, Fruchta in Watkinsa. V četrtem poglavju se bomo natančneje posvetili Rozetnim grafom in s pomočjo Wilsonovega dela identificirali štiri povezavno tranzitivne družine s pripadajočimi avtomorfizmi. Dokazu, da gre res za edine povezavno tranzitivne Rozetne grafe se bomo v diplomskem delu izognili, ker presega njegove okvirje. 2
15 Poglavje 2 Osnovne definicije, trditve in izreki V prvem poglavju bomo podali osnovne definicije in rezultate, ki jih bo bralec potreboval pri prebiranju tega diplomskega dela, pri tem pa bomo navedli le nekaj dokazov. Za rezultate, ki na tem mestu niso dokazani, bralca spodbujamo, da jih skuša dokazati sam ali pa jih poišče v literaturi. Pri obravnavi razdelka 2.1 izhajamo iz [6] in [9], razdelek 2.2 pa je (skupaj s svojima podrazdelkoma) povzet po [4] in [10]. 2.1 Teorija grup Osnovni pojem in glavna struktura pri obravnavi teorije grup je grupa, zato si najprej oglejmo njeno definicijo: Definicija. Neprazna množica G skupaj z dvočleno operacijo : G G G tvori grupo (zapišemo (G, )), če velja: 1. Operacija je asociativna: 2. V G obstaja element 1 G, da velja: g 1, g 2, g 3 G: (g 1 g 2 ) g 3 = g 1 (g 2 g 3 ). g G: 1 G g = g 1 G = g. Element 1 G imenujemo nevtralni element (enica) grupe G Za vsak element g G obstaja element g 1 G, da velja: g g 1 = g 1 g = 1 G. Element g 1 imenujemo inverz elementa g v grupi G. 2 1 V različnih virih zasledimo različne oznake za nevtralni element. Navadno ga označimo s simbolom 1, ki mu v indeks dodamo oznako grupe, zelo pogosta pa je tudi oznaka e. 2 Tudi za inverze se v različnih virih pojavljajo različne oznake. Najpogosteje se za inverz elementa g uporablja g 1, če vemo, da je operacija množenje, in g, če vemo, da je operacija seštevanje, lahko pa tudi g, itd. 3
16 Opomba. Bralca spomnimo, da dejstvo, da je dvočlena operacija na dani množici pomeni, da produkt poljubnih dveh elementov iz te množice leži v tej isti množici. Za grupo (G, ) torej velja: g 1, g 2 G: g 1 g 2 G. Ta pogoj navadno imenujemo zaprtost grupe za operacijo. Omeniti velja tudi dejstvo, da je nevtralni element 1 G v grupi (G, ) en sam, prav tako pa je inverzi g 1 elementa g G enolično določen, zato je tak zapis smiseln. Če poleg zgoraj naštetih lastnosti velja tudi, da je operacija komutativna ( g 1, g 2 G: g 1 g 2 = g 2 g 1 ), pravimo, da je grupa G abelska oz. komutativna. Dogovor. V nadaljevanju oklepaje in operacijo navadno izpuščamo, torej namesto grupa (G, ) pišemo grupa G, namesto g 1 g 2 pa kar g 1 g 2. Definicija. Neprazna podmnožica H G je podgrupa grupe G (označimo H G), če je H grupa za podedovano operacijo. Izkaže se, da je zgornja definicija ekvivalentna naslednji trditvi, ki pa je na tem mestu ne bomo dokazovali. Trditev 2.1. Neprazna podmnožica H G grupe G je njena podgrupa, če velja: 1. H je za operacijo zaprta množica. 2. H vsebuje nevtralni element 1 G. 3. H vsebuje inverze vseh svojih elementov. Opomba. Očitno je, da lahko preverjanje asociativnosti operacije spustimo, ker gre za podedovano operacijo iz G. Vsaka grupa G ima vsaj dve podgrupi: {1 G } G. To podgrupo imenujemo trivialna podgrupa. G G. To podgrupo imenujemo neprava podgrupa. Vse druge podgrupe v grupi G so prave, netrivialne podgrupe. Če je množica G končna, pravimo, da je G končna grupa. V nasprotnem primeru je G neskočna grupa. V nadaljevanju se bomo srečevali s končnimi grupami, zato je smiselno uvesti tudi pojem red grupe (označimo G ), ki nam pove, koliko elementov premore grupa G. Gre pravzaprav za moč (kardinalnost) množice G. Za poljuben g G je red elementa g (označimo g ) enak najmanjšemu naravnemu številu n, za katerega je g n = 1 G, če obstaja. V nasprotnem primeru ima g neskončen red, bralcu pa ne bo težko razmisliti, da se to lahko zgodi le v neskončnih grupah. 4
17 Definicija. Naj bo (G, ) grupa in naj bo M G, M. Podgrupa, generirana z M (oznaka M ) je najmanjša podgrupa grupe G, ki vsebuje M. Elemente množice M imenujemo generatorji grupe M. Zelo pomemben pojem, s katerim se bo bralec pri obravnavi tega diplomskega dela srečal, je tudi preslikava. Čeprav gre za dobro poznane pojme, pa na tem mestu vendarle spomnimo, da je preslikava α : A B: surjektivna, če ustreza vsakemu elementu iz B vsaj en element iz A ( b B a A: α(a) = b), injektivna, če ustreza vsakemu elementu iz B največ en element iz A ( a 1, a 2 A: (a 1 a 2 α(a 1 ) α(a 2 ))), in bijektivna, če ustreza vsakemu elementu iz B natančno en element iz A (torej če je preslikava injektivna in surjektivna hkrati). Bralca spomnimo, da ima bijektivna preslikava α: A B enolično inverzno preslikavo α 1 : B A. Gre za preslikavo, ki deluje ravno obratno kot α, in je tudi sama bijektivna. Definicija. Naj bo A množica. Bijektivni preslikavi α: A A pravimo permutacija množice A. Opomba. Naj bo α: A B preslikava. Če želimo preveriti, ali je α bijektivna, moramo v splošnem preveriti njeno injektivnost in surjektivnost. Naj bo zdaj β : C C, kjer je C končna množica. Očitno je, da je za preverjanje bijektivnosti β dovolj preveriti le njeno injektivnost. Spomnimo, da preslikave lahko komponiramo. Bralec se bo na tem mestu spomnil, da je komponiranje preslikav asociativna operacija. Definicija. Naj bosta (G 1, ) in (G 2, ) grupi. Preslikava ϕ: G 1 G 2 je homomorfizem grup, če velja: g, h G 1 : ϕ(g h) = ϕ(g) ϕ(h) Bijektivnemu homomorfizmu ϕ: G 1 G 2 rečemo izomorfizem. Trditev 2.2. Kompozitum dveh homomorfizmov grup je homomorfizem. Dokaz. Imejmo homomorfizma ϕ 1 : G 1 G 2 in ϕ 2 : G 2 G 3, kjer so (G 1, ), (G 2, ) in (G 3, ) grupe. Če želimo pokazati, da je ϕ 2 ϕ 1 : G 1 G 3 homomorfizem, moramo po definiciji pokazati: g, h G 1 : (ϕ 2 ϕ 1 )(g h) = (ϕ 2 ϕ 1 )(g) (ϕ 2 ϕ 1 )(h) 3 Ker je ϕ 2 homomorfizem. (ϕ 2 ϕ 1 )(g h) = ϕ 2 (ϕ 1 (g h)) = 3 5
18 = ϕ 2 (ϕ 1 (g) ϕ 1 (h)) = 4 = ϕ 2 (ϕ 1 (g)) ϕ 2 (ϕ 1 (h)) = = (ϕ 2 ϕ 1 )(g) (ϕ 2 ϕ 1 )(h) Opomba. Ker velja, da je kompozitum dveh bijektivnih preslikav bijektivna preslikava in ker smo v trditvi 2.2 pokazali, da je kompozitum dveh homomorfizmov spet homomorfizem, iz tega sledi, da je kompozitum dveh izomorfizmov tudi izomorfizem. Bijektivnemu homomorfizmu grup ϕ: G G rečemo avtomorfizem. Zelo pomemben pojem, s katerim se bo bralec srečal v nadaljevanju diplomskega dela, je delovanje grup in z njim povezani izreki, predvsem pa izrek o orbiti in stabilizatorju. Definicija. Naj bo X neprazna množica in G poljubna grupa. (Levo) delovanje grupe G na množico X je vsaka preslikava : G X X, za katero velja: (a) x X : (1 G, x) = x, (b) x X, g 1, g 2 G: (g 1 g 2, x) = (g 1, (g 2, x)). Dogovor. Navadno znak za delovanje opuščamo in namesto (g, x) pišemo kar gx. Definicija. Naj bo G grupa, ki deluje na množico X in naj bo x X. Tedaj je orbita točke x pri delovanju G množica O G (x) = {gx: g G} vseh točk v katere lahko z elementi grupe G preslikamo x. Stabilizator G x točke x je množica vseh g G, ki fiksirajo (pustijo na miru) x, to je G x = {g G: gx = x}. Izrek 2.3. Naj bo G grupa, ki deluje na neprazni množici X in naj bo x X. Tedaj je stabilizator G x podgrupa v grupi G, to je: G x G. Izrek 2.4. (Izrek o orbiti in stabilizatorju). Naj bo G končna grupa, ki deluje na množici X. Tedaj za vsak x X velja: G = O G (x) G x Opomba. Naj bo G grupa, ki deluje na množico X in naj bodo x 1, x 2,...x k X. Stabilizator G x1,x 2,...,x k točk x 1, x 2,...x k je množica {g G: gx i = x i i: 1 i k} vseh g G, ki fiksirajo (pustijo na miru) vsakega izmed elementov x 1, x 2,..., x k X. Ker očitno velja G x1,x 2,...,x k = G x1 G x2... G xk, je tudi G x1,x 2,...,x k podgrupa grupe G, to je G x1,x 2,...,x k G. Definicija. Naj bo G grupa, ki deluje na množico X in naj bo x 1, x 2 X. Če obstaja g G, da velja gx = y, grupa G na množico X deluje tranzitivno. Drugače: Če ima grupa G pri delovanju na množico X eno samo orbito, tako delovanje imenujemo tranzitivno delovanje. 4 Ker je ϕ 1 homomorfizem. 6
19 2.1.1 Nekatere znane družine grup Na tem mestu bralca spomnimo še na nekatere znane družine grup. Ciklična grupa Z n : V resnici gre za komutativno grupo (Z n, +) = 1, pri čemer je Z n množica ostankov pri deljenju z n, seštevamo pa po modulu n. Velja Z n = n. Diedrska grupa D n : Gre za množico simetrij pravilnega n-kotnika, operacija pa je komponiranje preslikav. Velja D n = r, z : r = n, z = 2, zrz = r 1. Grupa D n je reda 2n. Obstaja še veliko znanih družin grup, kot so simetrične grupe S n, alternirajoče grupe A n (za katere velja A n S n ), več vrst matričnih in funkcijskih grup itn., ki pa jih v tem diplomskem delu ne bomo potrebovali. Kot zanimivost lahko dodamo le, da velja D n S n, o čemer lahko bralec premisli sam. 2.2 Teorija grafov Definicija. (Enostaven neusmerjen) graf Γ = (V (Γ), E(Γ)) je urejen par množic, od katerih je V (Γ) neprazna množica vozlišč, E(Γ) {{u, v} : u, v V (Γ), u v} pa množica povezav, ki je torej podmnožica množice vseh neurejenih parov različnih elementov iz V (Γ). Kardinalonsti (moči) množice V (Γ) rečemo tudi red grafa Γ. Opomba. Obstajajo tudi posplošitve enostavnih neusmerjenih grafov, pri katerih dopuščamo usmeritve povezav, večkratne povezave in zanke 5. Zainteresirani bralec si lahko več o tem prebere v literaturi, v tem diplomskem delu pa se bomo od tukaj naprej ukvarjali le z enostavnimi neusmerjenimi grafi. Bralca na tem mestu opomnimo, da nam bo beseda graf v nadaljevanju dela torej predstavljala enostaven neusmerjen graf, vsako povezavo {u, v} pa bomo, kjer bo to potrebno, opazovali kot par usmerjenih lokov (u, v) in (v, u). Definicija. Naj bo Γ graf in u, v V (Γ) poljubni vozlišči. Če velja {u, v} E(Γ), imenujemo u in v krajišči povezave {u, v} in rečemo, da sta vozlišči u in v povezani oziroma sosednji, kar označimo z u v. Definicija. Naj bo Γ graf. Če za poljuben par vozlišč u, v V (Γ) obstaja zaporedje vozlišč, katerega prvi in zadnji element sta vozlišči u in v in je v njem vsak par zaporednih vozlišč povezava danega grafa, je Γ povezan graf. Definicija. Naj bo Γ graf in v V (Γ) poljubno vozlišče. Stopnja vozlišča v (označimo deg(v)) je število povezav v grafu Γ, ki imajo v za krajišče. Če velja deg(v) = k za vsak v V (Γ), pravimo, da je graf Γ k regularen. Število k imenujemo stopnja (tudi valenca) grafa Γ. 5 Zanka je povezava, ki ima začetek in konec v istem vozlišču. 7
20 Definicija. Naj bosta Γ 1 in Γ 2 grafa. Γ 2 je podgraf grafa Γ 1, če velja: V (Γ 2 ) V (Γ 1 ), E(Γ 2 ) E(Γ 1 ). Če velja V (Γ 2 ) = V (Γ 1 ), je graf Γ 2 vpeti podgraf grafa Γ 1. Definicija. Naj bosta Γ 1 in Γ 2 grafa. Preslikava ϕ: V (Γ 1 ) V (Γ 2 ) je izomorfizem grafov, če je bijektivna in ohranja sosednost, to je, če velja u, v V (Γ 1 ): u v ϕ(u) ϕ(v). Grafa Γ 1 in Γ 2 sta izomorfna, če med njima obstaja izomorfizem grafov (označimo Γ 1 = Γ2 ). Opomba. Na tem mestu bralca opomnimo, da je treba graf obravnavati kot abstrakten objekt. Za lažjo predstavo pa lahko graf Γ predstavimo oziroma upodobimo tako, da elemente množice vozlišč V (Γ) narišemo kot točke, različni točki u in v pa povežemo natanko tedaj, ko velja {u, v} E(Γ) (v ravnini, ali pa na kakšni drugi ploskvi). S tem je graf pravzaprav do izomorfizma natančno določen. Zaradi tega običajno grafe študiramo le do izomorfizma natančno. Definicija. Naj bo Γ graf. Preslikava ϕ: V (Γ) V (Γ) je avtomorfizem grafa Γ, če je bijektivna in za poljubna u, v V (Γ) velja: u v ϕ(u) ϕ(v) Drugače: Avtomorfizmi grafa so permutacije množice vozlišč tega grafa, ki ohranjajo sosednost. Gre torej za izomorfizem grafa nase. Opomba. V definiciji izomorfizma (ter tako posledično tudi avtomorfizma) je treba zahtevati, da gre za bijektivno preslikavo, ki povezave preslika v povezave in nepovezave v nepovezave. Kljub temu je pri preverjanju ali je neka permutacija vozlišč končnega grafa res avtomorfizem grafa, dovolj preveriti samo ali ta permutacija preslika povezave v povezave. Bralcu ne bo težko razmisliti, da zaradi bijektivnosti preslikave od tod avtomatsko sledi, da se nepovezave preslikajo v povezave. Prav tako je v primeru, ko dokazujemo, da je neka bijekcija med dvema grafoma istega reda in z istim številom povezav res izomorfizem grafov, dovolj preveriti le, da se vse povezave preslikajo v povezave. Trditev 2.5. Množica avtomorfizmov grafa Aut(Γ) skupaj z operacijo komponiranja preslikav tvori grupo. Dokaz. Recimo, da sta α in β avtomorfizma grafa Γ, torej α, β Aut(Γ). Preverimo vse lastnosti, ki morajo za grupo veljati: Zaprtost za operacijo: Za α, β Aut(Γ) želimo pokazati, da je njun kompozitum β α avtomorfizem grafa Γ, torej da je izomorfizem, ki ohranja sosednosti. Ker α, β Aut(Γ), velja, da sta α in β bijekciji. Ker je kompozitum bijektivnih preslikav prav tako bijektivna preslikava, sledi, da je β α bijektivna preslikava. 8
21 Oglejmo si zdaj, kako kompozitum β α ohranja sosednosti. Naj bosta u, v V (Γ) poljubni vozlišči grafa Γ in naj velja u v. Ker je α Aut(Γ), je α(u) α(v). Ker je β Aut(Γ), je β(α(u)) β(α(v)), kar pa je ravno (β α)(v) (β α)(v). Kompozitum avtomorfizmov torej res ohranja sosednost. Asociativnost: Bralec se bo spomnil, da smo že v prejšnjem razdelku omenili, da je komponiranje preslikav asociativno. Vsebovanost nevtralnega elementa: Ker je avtomorfizem permutacija, se bo bralec spomnil, da je edina možnost za nevtralni element id (identiteta). Da je identiteta avtomorfizem in vsebovana v Aut(Γ) je očitno, saj množico vozlišč preslika samo nase, pri tem pa ohrani sosednosti. Obstoj inverzov: Ker je α Aut(Γ), je bijektivna preslikava. Bralec se bo spomnil, da smo že v prejšnjem razdelku omenili, da za bijektivne preslikave obstaja inverzna preslikava. Sledi torej, da za α obstaja α 1. Oglejmo si, kako α 1 ohranja sosednosti. Naj bosta x, y V (Γ) poljubni vozlišči grafa Γ in naj velja x y. Ker je α bijektivna preslikava, je tudi surjektivna. Iz tega sledi, da gotovo obstajata neki vozlišči u in v, za kateri velja α(u) = x in α(v) = y oziroma u = α 1 (x) in v = α 1 (y). Ker je α avtomorfizem grafa Γ in je α(u) α(v), mora torej veljati tudi u v. Po prejšnjem zapisu sledi α 1 (x) α 1 (y), kar pomeni, da inverzna preslikava ohranja sosednosti. Sledi (Aut(Γ), ) je grupa. Definicija. Naj bo Γ graf in Aut(Γ) njegova grupa avtomorfizmov. Γ je točkovno tranzitiven, če Aut(Γ) na množico V (Γ) deluje tranzitvno, to je, če za poljubni vozlišči u, v V (Γ) obstaja ϕ Aut(Γ), da je ϕ(u) = v. Γ je povezavno tranzitiven, če Aut(Γ) na množico E(Γ) deluje tranzitvno, to je, če za poljubni povezavi {u 1, v 1 }, {u 2, v 2 } E(Γ) obstaja ϕ Aut(Γ), da je ϕ({u 1, v 2 }) = {u 2, v 2 }. Γ je simetričen oz. ločno tranzitiven, če Aut(Γ) na množico lokov grafa Γ deluje tranzitivno, to je, če za poljubna para povezanih vozlišč {u 1, v 1 } in {u 2, v 2 } obstajata ϕ, ψ Aut(Γ), tako da je ϕ(u 1 ) = u 2, ϕ(v 1 ) = v 2, ψ(u 1 ) = v 2 in ψ(v 1 ) = u 2. Drugače: Graf Γ je točkovno tranzitiven, če za poljuben par vozlišče u, v V (Γ) obstaja avtomorfizem, ki prvo vozlišče preslika v drugo. Graf Γ je povezavno tranzitiven, če za poljuben par povezav iz E(Γ) obstaja avtomorfizem, ki prvo povezavo preslika v drugo. Graf Γ je simetričen (ločno tranztiven), če za poljuben par lokov obstaja avtomorfizem, ki prvi lok preslika v drugi lok. Na tem mestu si bolj natančno oglejmo razliko med povezavno in ločno tranzitivnostjo. Pri preverjanju prve nas pravzaprav ne zanima, kako izbrani avtomorfizem ϕ Aut(Γ) povezavo {u 1, v 1 } E(Γ) preslika v povezavo {u 2, v 2 } E(Γ). Velja lahko ϕ(u 1 ) = u 2 9
22 in ϕ(v 1 ) = v 2 ali pa ϕ(u 1 ) = v 2 in ϕ(v 1 ) = u 2, pomembno je le, da se vsaka povezava lahko preslika na vsako drugo povezavo. Pri preverjanju ločne tranzitivnosti smo precej zahtevnejši. Pri njenem preverjanju si želimo, da se lahko povezava {u 1, v 1 } E(Γ) z izbranima avtomorfizmoma ϕ, ψ Aut(Γ) preslika v povezavo {u 2, v 2 } E(Γ) tako, da velja ϕ(u 1 ) = u 2, ϕ(v 1 ) = v 2 in tudi ψ(u 1 ) = v 2, ψ(v 1 ) = u 2. Zelo zanimivo je dejstvo, da povezavno tranzitivni grafi niso nujno tudi vozliščno tranzitivni. Lep primer je družina grafov K n1,n 2, imenovana polni dvodelni, oziroma bipartitni grafi (o njih si lahko zainteresirani bralec več prebere v literaturi), kjer n 1 n 2. Če velja ta pogoj, gre za neregularne grafe, kar avtomatsko pomeni, da graf ni vozliščno tranzitiven, pa vendar obstajajo avtomorfizmi, ki poskrbijo, da je graf povezavno tranzitiven. Njihovo iskanje prepuščamo bralcu, primer takega grafa pa je prikazan na sliki 2.1. Slika 2.1: Graf K 2,3. Naslednja trditev še dodatno utrjuje, da je med povezavno in ločno tranzitivnostjo bistvena razlika. Povezavna tranzitivnost namreč ni zadosten pogoj za ločno tranzitivnost, medtem ko ločna za povezavno je. Trditev 2.6. Naj bo Γ povezan graf, ki je ločno tranizitiven. Potem je Γ tudi vozliščno in povezavno tranizitiven. Dokaz. Naj bosta u in v poljubni vozlišči ločno tranzitivnega grafa Γ. Ker gre za povezan graf, imata u in v vsaj po enega soseda. Označimo ju z u in v, kjer je u u in v v. Ker je Γ ločno tranzitiven, obstaja avtomorfizem ϕ Aut(Γ), ki lok (u, u ) preslika v lok (v, v ), posledično pa u v v. Iz tega sledi, da je Γ vozliščno tranzitiven. Že zgoraj smo ugotovili, da je ločna tranzitivnost strožji pogoj kot povezavna tranzitivnost zato je očitno, da je vsak ločno tranzitiven graf tudi povezavno tranzitiven. Omeniti velja, da obrat trditve 2.6 ne velja. Obstajajo namreč velike družine grafov, ki so vozliščno in povezavno tranzitivni, pa vendar niso ločno tranzitivni. Takšne grafe imenujemo pol-ločno tranzitivni grafi, zainteresirani bralec pa si lahko več o njih prebere v literaturi ([7]). Omenimo lahko še, da je najmanjši pol-ločno tranzitiven graf Holtov oziroma Doylov graf na 27 vozliščih Nekatere standardne družine grafov Poln graf K n je graf z množico vozlišč V (K n ) = {u 0, u 1,..., u n 1 } in množico povezav E(K n ) = {{u i, u j }: u i, u j V (K n ), i j}. Primer polnega grafa je prikazan na sliki
23 Slika 2.2: Graf K 5. Slika 2.3: Graf C 7. Cikel C n je graf z množico vozlišč V (C n ) = {u 0, u 1,..., u n 1 } in množico povezav E(C n ) = {{u i, u i+1 }: i Z n }. Primer cikla je prikazan na sliki 2.3. Naj bo G grupa, S pa taka podmnožica S G, da velja S = S 1 in 1 G S. Tedaj je Cayleyev graf Cay(G, S) grupe G glede na podmnožico S graf z množico vozlišč V (Cay(G, S)) = G in množico povezav E(Cay(G, S)) = {{g, gs} : g G, s S}. Primer Cayleyevega grafa je prikazan na sliki 2.4. Slika 2.4: Graf Cay(D 4 = r, z r 4 = z 2 = 1, zrz = r 1, {r, z, z 3 }). Obstaja še veliko dobro znanih družin grafov, kot so poti (P n ), Hammingovi grafi (H(d, q)), hiperkocke (Q n ) itn., vendar jih na tem mestu ne bomo posebej obravnavali Cirkulanti in bicirkulanti Zdaj, ko smo spoznali osnovne pojme, se lahko posvetimo družini grafov, s katero se bomo ukvarjali v nadaljevanju diplomskega dela, družini bicirkulantov. Bralec bo opazil, da je beseda bicirkulant sestavljena iz besede cirkulant in predpone bi, zato je naravno, da najprej spoznamo družino cirkulantov. Definicija. Imejmo ciklično grupo Z n in poljubno podmnožico S Z n \{0}, za katero velja S = S. Tedaj Cayleyjev graf Cay(Z n, S) označimo s Circ(n, S) in ga imenujemo cirkulant (reda n). Vozlišča cirkulanta Circ(n, S) torej lahko označimo z u i, kjer i Z n, 11
24 povezave pa so tedaj neurejeni pari {u i, u j }, za katere je j i S, i j (povezave lahko drugače zapišemo tudi {u i, u i+s }). Primer cirkulanta je prikazan na sliki 2.5. Slika 2.5: Circ(14, {±2, ±7}). Trditev 2.7. Naj bo n 3 naravno število in S Z n taka množica, da S = S in 0 S. Tedaj grupa avtomorfizmov Aut(Circ(n, S)) vsebuje podgrupo reda 2n, ki je izomorfna diedrski grupi D n. Dokaz. Definirajmo permutaciji r in z vozlišč cirkulanta Γ = Circ(n, S), za kateri velja: i Z n : r(u i ) = u i+1, i Z n : z(u i ) = u i. Pokažimo, da ti dve permutaciji ohranjata sosednosti v Γ. Sosednosti cirkulanta so oblike u i u i+s, zato si poglejmo, kaj se s krajiščema povezave dogaja, če jih preslikamo z r in z: r(u i ) = u i+1, r(u i+s ) = u i+s+1 = u i+1+s, z(u i ) = u i, z(u i+s ) = u i s. Bralec lahko opazi, da r in z ohranjata sosednosti, saj r povezavo {u i, u i+s } preslika v {u i+1, u i+1+s }, z pa v {u i, u i s } (zadnja je res povezava, saj velja S = S). Sledi, da sta r in z avtomorfizma grafa Γ. Ni težko opaziti, da velja r = n in z = 2, saj r pravzaprav predstavlja rotacijo za en korak (torej moramo graf n-krat zavrteti, da dobimo začetno situacijo), z pa zrcaljanje (graf moramo dvakrat prezrcaliti, da se vrnemo v izhodiščno situacijo). 12
25 Označimo H = r, z. Da bo veljalo H = D n, moramo preveriti še pogoj, ki velja v diedrskih grupah, namreč zrz = r 1 : r 1 (u i ) = u i 1, zrz(u i ) = zr(u i ) = z(u i+1 ) = u i 1. Sledi H = r, z = D n Aut(Circ(n, S)). Trditev 2.8. Naj bo Γ graf reda n. Tedaj je Γ = Circ(n, S) za neki S natanko tedaj, ko Γ dopušča avtomorfizem reda n, ki ciklično permutira njegova vozlišča. Dokaz. ( ) Da Γ dopušča ustrezen avtomorfizem r, če velja Γ = Circ(n, S), smo pokazali že v dokazu trditve 2.7. ( ) Predpostavimo zdaj, da Γ dopušča avtomorfizem reda n, ki ciklično permutira njegova vozlišča in ga označimo z r. Avtomorfizem r ima eno orbito dolžine n. Izberimo u V (Γ) in definirajmo u i = r i (u) za vsak i Z n. Naj bo S = {s Z n : u 0 u s } (torej množica vseh indeksov vozlišč, s katerimi je povezano vozlišče u 0 ). Oglejmo si poljubno povezavo u 0 u s in kaj se z njo zgodi po delovanju z r i : u 0 u s r i (u 0 ) r i (u s ) u i u i+s Dobimo ravno znano obliko povezav, ki jih imajo cirkulanti Circ(n, S). Sedaj, ko smo spoznali družino cirkulantov, lahko definiramo družino grafov, imenovano bicirkulanti ([1]). Oglejmo si definicijo. Definicija. Bicirkulant je graf sodega reda 2n za neki n 3, ki dovoljuje avtomorfizem z dvema orbitama dolžine n. Vpeljimo zdaj naslednjo družino grafov. Naj bo n 3 in L, M in R take pomnožice Z n, da velja L = L, R = R in 0 L R. Tedaj je BC n [L, M, R] družina grafov, za katere velja, da imajo množico vozlišč V (BC n [L, M, R]) = {u i, v i : i Z n } in množico povezav E(BC n [L, M, R]), ki jo lahko predstavimo s tremi množicami: L = i Z n {{u i, u i+l }: l L}, M = {{u i, v i+m }: m M}, i Z n R = {{v i, v i+r }: r R}. i Z n Oglejmo si množice povezav L, M in R. Bralec lahko opazi, da sta množici L in R pravzaprav enake oblike kot množica E(Circ(n, S)), torej skupaj z množicama vozlišč, ki ju lahko izluščimo iz njune formulacije (pri L je to {u i : i Z n }, pri R pa {v i : i Z n }) predstavljata dva cirkulanta. Množica M je množica povezav, ki ta dva cirkulanta povezujejo. 13
26 Izrek 2.9. Družina grafov BC n [L, M, R] je natanko družina bicirkulantov. Dokaz. ( ) Naj bo n 3 in Γ = BC n [L, M, R] za neke podmnožice L, M in R, za katere velja L = L, R = R in 0 L R. Graf Γ je torej reda 2n. Pokažimo, da dopušča avtomorfizem z dvema orbitama dolžine n. V trditvi 2.8 smo pokazali, da cirkulanti dopuščajo avtomorfizem r, ki ima eno orbito dolžine n, zgoraj pa smo ugotovili, da je pravzaprav družina grafov BC n [L, M, R] takšna, da je posamezen graf sestavljen iz dveh cirkulantov, ki imata vmesne povezave, ki ju povezujejo. Poiskati želeni avtomorfizem grafa Γ, ki ima dve orbiti dolžine n, torej ni težko. Definirajmo permutacijo ϕ, za katero velja: i Z n : ϕ(u i ) = u i+1 i Z n : ϕ(v i ) = v i+1 Po zgornjem komentarju je dovolj preveriti, da ϕ ohranja povezave iz množice M, kar je jasno razvidno že iz same defincije ϕ. Bralec zdaj lahko opazi, da ima avtomorfizem ϕ pri delovanju na množico V (Γ) dve orbiti: O ϕ (u 0 ) = {u i : i Z n } O ϕ (v 0 ) = {v i : i Z n } Po definiciji je torej Γ bicirkulant. ( ) Imejmo graf Γ, ki spada v družino bicirkulantov in tako dopušča avtomorfizem ϕ Aut(Γ) z dvema orbitama dolžine n. Izberimo u, v V (Γ), pri čemer iz vsake orbite vzamemo po eno vozlišče, in definirajmo u i = ϕ i (u) ter v i = ϕ i (v) za vsak i Z n. Naj bo L = {l Z n : u 0 u l }, R = {r Z n : v 0 v r } in M = {m Z n : u 0 v m }. Oglejmo si povezave u 0 u l, v 0 v r in u 0 v m in kaj se z njimi dogaja ob permutiranju vozlišč s pomočjo ϕ i : u 0 u l ϕ i (u 0 ) ϕ i (u l ) v 0 v r ϕ i (v 0 ) ϕ i (v r ) u 0 v m ϕ i (u 0 ) ϕ i (v m ) u i u i+l v i v i+r u i v i+m Dobimo ravno znano obliko povezav, ki jih imajo grafi BC n [L, M, R]. Primer bicirkulanta je prikazan na sliki 2.6. Druga formulacija družine bicirkulantov nam omogoča naslednjo upodobitev takih grafov v ravnini: Narišemo dve koncentrični orbiti vozlišč, od katerih zunanja označimo z u i, i Z n, notranja pa z v i, i Z n. Množica L nam pove, kako med seboj povezati vozlišča u i, i Z n. 14
27 Slika 2.6: BC 10 [{±2}, {±4, ±5}, {±3}]. Množica M nam pove, kako moramo povezati vozlišča u i, i Z n z vozlišči v i, i Z n. Množica R nam pove, kako med seboj povezati vozlišča v i, i Z n. Bralec lahko razmisli, da je bicirkulant BC n [L, M, R] regularen natanko tedaj, ko velja L = R. V nadaljevanju diplomskega dela se bomo ukvarjali s simetrijami bicirkulantov. Pri tem nas bo predvsem zanimalo, kateri bicirkulanti so ločno tranzitivni, največ pozornosti pa bomo namenili določeni družini bicirkulantov, imenovani Rozetni grafi. 15
28 16
29 Poglavje 3 Posplošeni Petersenovi grafi GP (n, k) Prvi pomemben korak v preučevanju simetričnih bicirkulantov so naredili Frucht, Graver in Watkins v svojem članku [3], po katerem je povzeto naslednje poglavje. V omenjenem članku so avtorji prvi klasificirali vozliščno in povezavno tranzitivne Posplošene Petersenove grafe, kar so uspeli tudi dokazati s pomočjo posebne podgrupe avtomorfizmov. V diplomskem delu se v podrobnosti ne bomo spuščali, zainteresirani bralec pa lahko v članku najde vse trditve, izreke in leme ter njihove podrobne dokaze, pri čemer mu bo v pomoč tudi diplomsko delo [11], ki je posvečeno obravnavi omenjenega članka. Oglejmo si definicijo Posplošenih Petersenovih grafov: Definicija. Za naravni števili n in k, za kateri velja 2 2k < n je Posplošeni Petersenov graf GP (n, k) graf, ki ima množico vozlišč V (GP (n, k)) = {u i, v i : i Z n } in množico povezav E(GP (n, k)) = {{u i, u i+1 }, {u i, v i }, {v i, v i+k }: i Z n }. Če si pomagamo z definicijo bicirkulantov iz podrazdelka 2.2.2, lahko torej GP (n, k) zapišemo tudi kot BC n [{±1}, {0}, {±k}]. Ti grafi predstavljajo začeten korak v preučevanju povezanih bicirkulantov na splošno, saj gre za kubične grafe (torej regularne grafe stopnje 3), pri katerih ima vsako vozlišče le po enega soseda v drugi orbiti ustreznega avtomorfizma z dvema orbitama enake dolžine. Najbolj znan primer Posplošenega Petersenovega grafa je graf GP (5, 2), ki ga imenujemo kar Petersenov graf, po katerem so ti grafi dobili tudi svoje ime. Povezave v grafu GP (n, k), ki so oblike {u i, u i+1 }, imenujemo zunanje povezave, povezave, ki so oblike {v i, v i+k }, imenujemo notranje povezave, povezave, ki pa so oblike {u i, v i } imenujemo špice. Naj bo Aut(GP (n, k)) grupa avtomorfizmov grafa GP (n, k). Zelo pomembno vlogo pri obravnavi simetričnosti Posplošenih Petersenovih grafov ima podgrupa grupe Aut(GP (n, k)), ki so jo avtorji v [3] poimenovali B(n, k) in sestoji iz vseh avtomorfizmov, ki pri delovanju na GP (n, k) ohranjajo množico špic. Izkaže se, da velja D n Aut(GP (n, k)) in tudi D n B(n, k), bralcu pa prepuščamo razmislek, zakaj je to tako. 17
30 Slika 3.1: Petersenov graf GP (5, 2). Definirajmo preslikavo α na množici V (GP (n, k)), da velja: i Z n : α(u i ) = v ki, i Z n : α(v i ) = u ki. Jasno je, da je α bijekcija (in torej permutacija) natanko tedaj, ko je D(n, k) = 1. Da je α avtomorfizem grafa GP (n, k), mora veljati še nekaj več. Trditev 3.1. Naj bo α permutacija množice vozlišč grafa GP (n, k), definirana kot v predhodem odstavku. Tedaj je α Aut(GP (n, k)) če in samo če k 2 ±1(mod n). Dokaz. Oglejmo si delovanje permutacije α na množico E(GP (n, k)): Zunanje povezave {u i, u i+1 } se preslikajo v notranje povezave {v ki, v k(i+1) } = {v ki, v ki+k }. Špice {u i, v i } se preslikajo v špice {v ki, u ki }. Notranje povezave {v i, v i+k } se preslikajo v {u ki, u (i+k)k } = {u ki, u ki+k 2}, ki pa so zunanje povezave natanko tedaj, ko velja k 2 ±1(mod n). Preslikava α je tako avtomorfizem grafa GP (n, k) natanko tedaj, ko velja k 2 ±1(mod n). Rezultat, ki so ga avtorji članka [3] dosegli prek formuliranja in dokazovanja številnih lem, trditev in izrekov, lahko strnemo v nekaj rezultatov, ki sledijo. Izrek 3.2. Graf GP (n, k) je vozliščno tranzitiven, če in samo če velja k 2 ±1(mod n) ali pa n = 10 in k = 2. Izrek 3.3. Graf GP (n, k) je povezavno tranzitiven natanko tedaj, ko je (n, k) en izmed naslednjih parov: (4, 1), (5, 2), (8, 3), (10, 2), (10, 3), (12, 5), (24, 5). 18
31 Posledica 3.4. Vsak graf GP (n, k), ki je povezavno tranzitiven, je tudi vozliščno tranzitiven. V [3] je poglavitno vlogo pri dokazu izreka 3.3 igrala naslednja lema. Lema 3.5. Naslednje trditve so si ekvivalentne: (a) Graf GP (n, k) je povezavno tranzitiven. (b) Obstaja ϕ Aut(GP (n, k)), ki neko špico preslika v povezavo, ki ni špica. (c) B(n, k) je prava podgrupa Aut(GP (n, k)). Lema nam torej pove, da je pri preverjanju povezavne tranzitivnosti grafov GP (n, k) dovolj najti tak avtomorfizem, ki neko špico preslika v povezavo, ki ni špica. Kot bomo videli v naslednjem poglavju, bo analogen rezultat veljal tudi za Rozetne grafe. Vsi povezavno (in vozliščno) tranzitivni grafi GP (n, k) so prikazani na slikah Slika 3.2: GP (4, 1). Slika 3.3: GP (8, 3). Slika 3.4: GP (10, 2). Slika 3.5: GP (10, 3). 19
32 Slika 3.6: GP (12, 5). Slika 3.7: GP (24, 5). Na tem mestu v diplomskem delu končujemo pregled Posplošenih Petersenovih grafov in se pomikamo na naslednjo družino bicirkulantov. Zaradi standardne upodobitve grafov GP (n, k), iz katere je jasno razvidna njihova struktura (vozlišča znotraj vsake orbite so povezana v enega ali več disjunktnih ciklov, obstajajo pa tudi povezave med tema orbitama, ki vsako vozlišče iz prve orbite poveže z natanko enim vozliščem v drugi orbiti), bi se lahko bralcu zazdelo, da je naslednji logičen korak povečanje števila vmesnih povezav oziroma špic. To je dejansko tudi smer, ki jo uberemo v tem diplomskem delu. Opozoriti pa velja, da ta korak vendarle ni tako očiten. GP (n, k) niso edini kubični bicirkulanti, ampak obstaja še nekaj takih družin. Tako na primer poznamo tudi družino, v kateri vozlišča znotraj ene izmed orbit niso povezana in to pomeni povečano število špic pa tudi druge. V zvezi s temi družinami kubičnih bicirkulantov omenimo samo to, da je klasifikacijo vseh povzavno tranzitivnih kubičnih bicirkulantov dokončal Pisanski leta 2007 ([8]). Kot že omenjeno, v tem diplomskem delu preučujemo bicirkulante, ki ohranjajo strukturo Posplošenih Petersenovih grafov, zato pri tem povečujemo valenco tako, da dodajamo vmesne povezave med orbitama vozlišč. 20
33 Poglavje 4 Rozetni grafi R n (a, k) Družina tako imenovanih Rozetnih grafov je družina bicirkulantov, ki se od Posplošenih Petersenovih grafov razlikuje v tem, da ima med zunanjimi vozlišči u i in notranjimi vozlišči v i po dve povezavi, torej eno več, kot v GP (n, k). Grafe iz obravnavane družine, ki v izvirniku nosijo ime Rose-Window graphs, mi pa smo ga v tem diplomskem delu podomačili, je uvedel S. Wilson, ki je v svojem članku [12] tudi prvi identificiral štiri poddružine povezavno tranzitivnih Rozetnih grafov. Po omenjenem članku je povzeto poglavje 4. Ime Rozetni graf najverjetneje izhaja iz dejstva, da grafi, ki spadajo v to družino, z uporabo nekaj domišljije, spominjajo na t. i. rozete (Rose windows). To so okrogla okna, ki se pojavljajo predvsem v gotskih cerkvah in so razdeljena na segmente s kamnitimi križi in krogovičjem. Rozetne grafe označimo z R n (a, k), več o pomenih parametrov pa bomo povedali v razdelku, ki sledi. Kovács, Kutnar in Marušič so v svojem članku [5] iz leta 2010 uspeli pokazati, da so grafi iz štirih družin, ki jih je identificiral Wilson, pravzaprav edini povezavno tranzitivni Rozetni grafi. Dokaz njihovega rezultata presega okvire tega diplomskega dela, zato ga ne bomo navajali. 4.1 Osnovne definicije in dejstva, povezana z R n (a, k) Definicija. Naj bo n 3, n N in naj bosta a in k taki naravni števili, da velja 1 a, k n 1. Tedaj je Rozetni graf R n (a, k) graf z množico vozlišč V (R n (a, k)) = {u i, v i : i Z n } in množico povezav E(R n (a, k)), ki sestoji iz štirih disjunktnih podmnožic: Podmnožica vseh zunanjih povezav oblike {u i, u i+1 }, i Z n. Podmnožica vseh ravnih špic oblike {u i, v i }, i Z n. Podmnožica vseh poševnih špic oblike {v i, u i+a }, i Z n. Podmnožica vseh notranjih povezav oblike {v i, v i+k }, i Z n. Primer Rozetnega grafa je prikazan na sliki
34 Slika 4.1: R 12 (2, 4). Rozetne grafe R n (a, k) lahko, ob pomoči druge formulacije bicirkulantov iz podrazdelka zapišemo tudi kot BC n [{±1}, {0, a}, {±k}]. Gre za tetravalentne (včasih rečemo tudi 4-valentne) grafe, kar pomeni, da velja deg(v) = 4 za vsak v V (R n (a, k)). Izjema je primer, ko je n sodo število in je k = n 2. Oglejmo si nekaj dejstev v povezavi z grafi R n (a, k), od katerih so nekatera očitnejša, zato bomo razmislek o njih prepustili bralcu, druga pa bomo dokazali. Trditev 4.1. Graf GP (n, k) je vedno vpeti podgraf grafa R n (a, k). Trditev 4.2. Naj bo n 3, n N in naj bosta a in k taki naravni števili, da velja 1 a, k n 1. Tedaj velja R n (a, k) = R n ( a, k). Dokaz. Označimo vozlišča grafa Γ 1 = R n (a, k) z u i in v i za i Z n in vozlišča grafa Γ 2 = R n ( a, k) z u i in v i za i Z n kot običajno. Definirajmo preslikavo ϕ: V (Γ 1 ) V (Γ 2 ), ki je podana s predpisom: u i u i, v i v i. Oglejmo si delovanje preslikave ϕ: Zunanje povezave {u i, u i+1 } grafa Γ 1 se preslikajo v zunanje povezave {u i, u i 1} grafa Γ 2. Ravne špice {u i, v i } grafa Γ 1 se preslikajo v ravne špice {u i, v i} grafa Γ 2. Poševne špice {v i, u i+a } grafa Γ 1 se preslikajo v poševne špice {v i, u i a} grafa Γ 2. Notranje povezave {v i, v i+k } grafa Γ 1 se preslikajo v notranje povezave {v i, v i k } grafa Γ 2. 22
35 S tem smo dokazali, da je preslikava ϕ izomorfizem grafov in tako res velja R n (a, k) = R n ( a, k). Trditev 4.3. Naj bo n 3, n N in naj bosta a in k taki naravni števili, da velja 1 a, k n 1. Tedaj velja R n (a, k) = R n (a, k). Opomba. Bralec naj opazi, da v prejšnjem primeru govorimo o izomorfnosti, v tem pa celo o enakosti, gre v tem primeru kar za isti graf, ne samo izomorfen. Trditev 4.4. Naj bo n 3, n N in naj bosta a in k taki naravni števili, da velja 1 a, k n 1. Če velja D(n, k) = 1, potem R n (a, k) = R n (ak 1, k 1 ), kjer je k 1 multiplikativni inverz elementa k v kolobarju Z n. Dokaz. Ker velja D(n, k) = 1, vemo, da ima k multiplikativni inverz v kolobarju Z n. Označimo ga s k 1. Označimo vozlišča grafa Γ 1 = R n (a, k) z u i in v i za i Z n in vozlišča grafa Γ 2 = R n (ak 1, k 1 ) z u i in v i za i Z n. Definirajmo preslikavo ϕ: V (Γ 1 ) V (Γ 2 ), ki je podana s predpisom: u i v ik 1, v i u ik 1. Ker velja D(n, k) = 1, gre očitno za bijektivno preslikavo. Oglejmo si njeno delovanje na povezavah grafa Γ 1 : Zunanje povezave {u i, u i+1 } se preslikajo v notranje povezave {v ik 1, v ik 1 k 1 }. Ravne špice {u i, v i } se preslikajo v ravne špice {v ik 1, u ik 1 }. Poševne špice {v i, u i+a } se preslikajo v poševne povezave {u ik 1, v ik 1 ak 1 }. Notranje povezave {v i, v i+k } se preslikajo v zunanje povezave {u ik 1, u ik 1 kk 1 } = 1 {u ik 1, u ik 1 1 }. Bijektivna preslikava ϕ torej ohranja sosednosti in je zato izomorfizem grafov. Ker je D(7, 3) = 1, je R 7 (5, 3) (prikaz levo) = R 7 (4, 5) (po trditvi prikaz desno in drugače na naslednji strani levo) = R 7 (4, 2) (po trditvi 4.3) = R 7 (3, 2) (po trditvi prikaz na naslednji strani desno). 1 Ker je k 1 inverz k v Z n. 23
36 4.2 Povezavna tranzitivnost grafov R n (a, k) V naslednjem razdelku se bomo posvetili klasifikaciji povezavno tranzitivnih Rozetnih grafov. Ta sestoji iz dveh korakov. V prvem se identificira štiri takšne družine grafov, medtem ko se v drugem pokaže, da drugih povezavno tranzitivnih Rozetnih grafov ni. Kot že omenjeno, se bomo v tem diplomskem delu omejili le na prvi korak. Za začetek obravnave povezavne tranzitivnosti grafov R n (a, k) si oglejmo trditev, ki nam bo v nadaljevanju obravnave precej olajšala delo. Trditev 4.5. Naj bo n 3, n N in naj bosta a in k taki naravni števili, da velja 1 a, k n 1. Tedaj grupa avtomorfizmov Aut(R n (a, k)) vsebuje podgrupo reda 2n, ki je izomorfna diedrski grupi D n. Dokaz. Definirajmo permutaciji vozlišč r in z grafa R n (a, k), da velja: i Z n : r(u i ) = u i+1, r(v i ) = v i+1 i Z n : z(u i ) = u i, z(v i ) = v a i Zaradi dejstva, da so Rozetni grafi bicirkulanti, iz dokaza izreka 2.9 sledi, da je r avtomorfizem. Permutacija z preslika zunanjo povezavo {u i, u i+1 } v zunanjo povezavo {u i, u i 1 }, ravno špico {u i, v i } v poševno špico {u i, v a i } = {v i a, u i a+a }, poševno špico {v i, u i+a } v ravno špico {v i a, u i a } ter notranjo povezavo {v i, v i+k } v notranjo povezavo {v i a, v i k a }. Tako sta permutaciji r in z avtomorfizma grafa R n (a, k). Poleg tega velja r = n in z = 2. Označimo K = r, z. Da bo veljalo K = D n, moramo preveriti še pogoj, ki velja v diedrskih grupah, namreč zrz = r 1 : r 1 (u i ) = u i 1, zrz(u i ) = zr(u i ) = z(u i+1 ) = u i 1 in 24
37 r 1 (v i ) = v i 1, zrz(v i ) = zr(v i a ) = z(v i a+1 ) = v ( i a+1) a = v i+a a 1 = v i 1. Sledi zrz = r 1 in zato K = r, z = D n Aut(R n (a, k)). Označimo zdaj s H(R n (a, k)) podgrupo Aut(R n (a, k)), ki ohranja množico zunanjih povezav, in naj bosta r in z kot v zgornjem dokazu. Ker r preslika zunanjo povezavo {u i, u i+1 } v zunanjo povezavo {u i+1, u i+2 }, z pa v zunanjo povezavo {u i, u i 1 }, lahko bralec opazi, da velja r, z = D n H(R n (a, k)). Wilson je v svojem članku na začetku obravnave povezavno tranzitivnih grafov R n (a, k) zmotno zapisal, da je grupa H(R n (a, k)) kar izomorfna grupi D n. To v splošnem ni res, saj velja naslednje trditev. Trditev 4.6. Naj bo n 3, n N in naj bosta a in k taki naravni števili, da velja 1 a, k n 1. Označimo s H(R n (a, k)) podgrupo Aut(R n (a, k)), ki ohranja množico zunanjih povezav, kot zgoraj. Tedaj velja H(R n (a, k)) > 2n n 0 (mod 2) in a = n. 2 Dokaz. ( ) Naj bosta r in z kot v dokazu trditve 4.5. Ker podgrupa K = r, z na množici {u i : i Z n } deluje tranzitivno, poleg tega pa v K u0 obstaja avtomorfizem (namreč z), ki fiksira u 0 in u 1 preslika v u 1, iz H(R n (a, k)) > r, z po izreku o orbiti in stabilizatorju (2.4) sledi, da obstaja avtomorfizem α H(R n (a, k)), ki fiksira tako u 0, kot u 1. Ker mora α ohranjati množico zunanjih povezav, od tod očitno sledi α(u i ) = u i i Z n. Ker α ni trivialen, obstaja nek v i, ki ga α ne fiksira, ker pa je v i eden od dveh sosedov vozlišča u i, od tod sledi, da α zamenja v i in v i a. Brez škode za splošnost lahko privzamemo, da je i = 0 in tako velja α(v 0 ) = v a in α(v a ) = v 0. Ker za soseda vozlišča v a velja α(u a ) = u a in α(u 0 ) = u 0, se poševna špica {v a, u 0 } preslika v ravno špico {v 0, u 0 }, ravna špica {v a, u a } pa v povezavo {v 0, u a }. Od tod sledi, da je n sod in a = n. 2 ( ) Predpostavimo, da velja n 0 (mod 2) in a = n. Oglejmo si permutacijo α 2 vozlišč grafa R n (a, k), ki je podana s predpisom: α(u i ) = u i, i Z n, α(v i ) = v i+ n, i Z n. 2 Permutacija α povezavo {u i, v i } preslika v {u i, v i+ n } = {u i, v 2 i+a } = {u i, v i a }, povezavo {u i, u i+1 } preslika v povezavo {u i, u i+1 }, povezavo {u i, v i a } = {u i, v i+ n } 2 preslika v {u i, v (i+ n 2 )+ n } = {u i, v 2 i }, povezavo {v i, v i+k } pa preslika v {v i+ n, v i+ n 2 2 +k }. Očitno je, da α ohranja sosednosti in je zato avtomorfizem grafa R n (a, k). Še več, α ohranja množico zunanjih povezav in zato α H(R n (a, k)). Ker pa α ne moremo dobiti kot kompozitum znanih avtomorfizmov z in r (oziroma potence r-ja), torej velja α r, z in zato gotovo velja H(R n (a, k)) > r, z in tako H(R n (a, k)) > 2n. 25
38 Kot konkreten protiprimer Wilsonove trditve lahko bralec preuči graf R 8 (4, 3), za katerega velja H(R 8 (4, 3)) = 32, vendar pa naj ga to ne zavede, saj v splošnem ne velja, da je α kot v zgornjem dokazu le en sam, zato tudi v splošnem ne velja H(R n (a, k)) = 4n, ko je a = n 2. Delovanje grupe r, z na množico povezav E(R n (a, k)) ima tri orbite. Kot smo omenili že zgoraj, r in z ohranjata zunanje povezave, bralcu pa ne bo težko razmisliti, da ohranjata tudi notranje. Tretja orbita delovanja r, z na množico povezav Rozetnega grafa je množica vseh špic. Dejstvo, da so ravne in poševne špice v isti orbiti pri delovanju r, z, sledi iz tega, da z preslika ravno špico {u i, v i } v poševno {u i, v a i } = {v i a, u i a+a } (medtem ko r ciklično permutira ravne in poševne špice). Naravna interpretacija povezavne tranzitivnosti je, da ima grupa Aut(Γ) pri delovanju na množico E(Γ) le eno samo orbito. S pomočjo grupe r, z smo za zdaj pokazali, da imamo pri grafih R n (a, k) največ tri orbite. Kot pokaže naslednja trditev je dokazati, da je nek Rozetni graf povezavno tranzitiven, vsaj načeloma, precej lahko. Trditev 4.7. Naj bo n 3, n N in naj bosta a in k taki naravni števili, da velja 1 a, k n 1. Graf R n (a, k) je povezavno tranzitiven natanko tedaj, ko obstaja avtomorfizem, ki neko špico preslika v povezavo, ki ni špica. Dokaz. ( ) Imejmo graf R n (a, k), ki je povezavno tranzitiven. To po definiciji pomeni, da lahko vsako povezavo preslikamo v vsako drugo, iz česar pa sledi, da lahko tudi neko špico preslikamo v povezavo, ki ni špica. ( ) Imejmo graf R n (a, k) in avtomorfizem α, ki neko špico preslika v povezavo, ki ni špica. Vemo, da ima α pri delovanju na množico E(R n (a, k)) največ tri orbite, pri čemer sta orbita množice zunanjih povezav in orbita množice notranjih povezav dolžine n, orbita množice vseh špic pa dolžine 2n. Po predpostavki torej α neko špico (recimo {u i, v j }, kjer j {i, i a}) preslika v povezavo, ki ni špica, recimo v neko zunanjo povezavo. To pomeni, da špice in zunanje povezave pripadajo isti orbiti O delovanja grupe avtomorfizmov R n (a, k) na množici vseh povezav. Ker pa α v j preslika v neko vozlišče oblike u l, se notranja povezava {v j, v j+k } preslika bodisi v špico, bodisi v zunanjo povezavo in tako so tudi vse zunanje povezave v orbiti O. Ni težko premisliti, da povsem analogen premislek velja, če bi avtomorfizem α neko špico preslikal v notranjo povezavo. Sledi, da lahko vsako povezavo preslikamo v vsako drugo, kar po definiciji pomeni, da je graf R n (a, k) povezavno tranzitiven. Kot smo že omenili, je Wilson identificiral štiri družine povezavno tranzitivnih Rozetnih grafov, Kovács, Kutnar in Marušič pa so dokazali, da drugih povezavno tranzitivnih Rozetnih grafov ni. Njihov rezultat je naslednji izrek. Izrek 4.8. Naj bo n 3, n N in naj bosta a in k taki naravni števili, da velja 1 a, k n 1. Tedaj vsak povezavno tranzitiven graf R n (a, k) pripada eni izmed štirih družin: 26
39 Družina R n (2, 1), kjer je n 3. Družina R 2m (m + 2, m + 1), kjer je m 3. Družina R 12m (3m + 2, 3m 1) in R 12m (3m 2, 3m + 1), kjer je m 1. Družina R 2m (2b, r), kjer je m 2, b 2 {1, m 1}, 2 k ±1(mod m), 2 2b m in k V nadaljevanju bomo v ločenih podrazdelkih pokazali, da gre res za družine povezavno tranzitivnih grafov. To bomo storili s pomočjo zgornje trditve 4.7. Kot smo že omenili, dokaza da drugih povezavno tranzitivnih Rozetnih grafov ni, ne bomo navajali Družina R n (2, 1) Družina grafov R n (2, 1) je tako imenovani leksikografski produkt cikla in dveh točk. Zainteresirani bralec si lahko več o takem produktu prebere v [4]. Zanimiva je tudi naslednja trditev: Trditev 4.9. Naj bo n 3. Tedaj velja R n (2, 1) = Circ(2n, {±1, ±(n 1)}). Dokaz. Označimo vozlišča grafa Γ 1 = R n (2, 1) z u i in v i za i Z n kot običajno in vozlišča grafa Γ 2 = Circ(2n, {±1, ±(n 1)}) z u i za i Z 2n. Definirajmo preslikavo γ : V (Γ 1 ) V (Γ 2 ), ki je podana s predpisom: { γ(u i ) = u i, γ(v i ) = u n : i = n 1. u i+n+1 : drugače Oglejmo si delovanje preslikave γ: Zunanje povezave {u i, u i+1 } grafa Γ 1 se preslikajo v povezave grafa Γ 2, ki so oblike {u i, u i+1}, razen povezave {u 0, u n 1 }, ki pa se preslika v povezavo {u 0, u n 1} (saj je (n + 1) = n 1 v Z 2n ). Ravne špice {u i, v i } grafa Γ 1 se preslikajo v povezave grafa Γ 2, ki so oblike {u i, u i+(n+1) }, razen povezave {u n 1, v n 1 }, ki se preslika v povezavo {u n 1, u n}. Poševne špice {v i, u i+2 } grafa Γ 1 se preslikajo v povezave grafa Γ 2, ki so oblike {u i+(n+1), u i+2}, razen povezave {v n 1, u 1 }, ki se preslika v povezavo{u n, u 1}. Notranje povezave {v i, v i+1 } grafa Γ 1 se preslikajo v povezave grafa Γ 2, ki so oblike {u i+(n+1), u i+1+(n+1) }, razen povezave {v n 2, v n 1 }, ki se preslikav v povezavo {u (n 2)+n+1, u n} = {u 2n 1, u n}. Opazimo torej, da preslikava γ ohranja sosednosti in je zato izomorfizem grafov, zato sledi, da velja R n (2, 1) = Circ(2n, {±1, ±(n 1)}). Primer grafa iz obravnavane družine je prikazan na sliki 4.2, njegova upodobitev kot cirkulant pa na sliki
40 Slika 4.2: R 7 (2, 1). Slika 4.3: R 7 (2, 1) kot Circ(14, {±1, ±6}). Pri obravnavi te poddružine Rozetnih grafov je precej ugodno, da graf upodobimo na drugačen način (kot na sliki 4.4), pri tem pa vpeljemo tudi nove oznake, kot na sliki 4.5: i Z n : t i = v i 1 Povezave v novem grafu so torej: zunanje povezave: {u i, u i+1 }, ravne špice: {u i, t i+1 }, poševne špice: {t i, u i+1 } in notranje povezave: {t i, t i+1 }. Slika 4.4: R 7 (2, 1) drugače. Slika 4.5: R 7 (2, 1) še drugače. Bralec bo opazil, da imata vozlišči u i in t i natanko iste sosede: u i+1, u i 1, t i 1, t i+1. Opomba. Zgornje velja v vseh primerih, kjer n 4. Če velja, da je n = 4, potem t i ni edino vozlišče, ki ima natanko iste sosede kot u i, bralec pa bo o tem premislil sam. Za grafe s tako lastnostjo velja naslednja očitna, a precej uporabna trditev. 28
41 Trditev Naj bo Γ graf, ki premore vozlišči u in v, ki imata natanko iste sosede. Tedaj obstaja avtomorfizem grafa Γ, ki ti dve vozlišči zamenja, vse druge pa fiksira. Na tem mestu je vse pripravljeno, da pokažemo povezavno tranzitivnost obravnavane poddružine Rozetnih grafov. Trditev Naj bo n 3. Graf Γ = R n (2, 1) je povezavno tranzitiven. Dokaz. Upodobimo graf R n (2, 1) kot na sliki 4.5, označimo in si oglejmo lokalno situacijo kot na sliki 4.6. Slika 4.6: Lokalna situacija v grafu R n (2, 1). Slika 4.7: Lokalna situacija v grafu R n (2, 1) po delovanju avtomorfizma δ. Po trditvi 4.7 je graf Γ povezavno tranzitiven natanko tedaj, ko obstaja avtomorfizem, ki neko špico preslika v povezavo, ki ni špica. Ker vemo, da imata vozlišči u i in t i grafa Γ natanko iste sosede, po trditvi 4.10 obstaja avtomorfizem δ, ki ti dve vozlišči zamenja, ostale pa fiksira. Oglejmo si lokalno delovanje avtomorfizma δ na povezave grafa Γ (slika 4.7): {u i, u i+1 } {t i, u i+1 } {u i, t i+1 } {t i, t i+1 } {t i, u i+1 } {u i, u i+1 } {t i, t i+1 } {u i, t i+1 } Avtomorfizem δ torej preslika špico v povezavo, ki ni špica, iz česar sledi, da je Γ = R n (2, 1) povezavno tranzitiven. Bralca na tem mestu opomnimo, da oznaka δ v zgornjem dokazu predstavlja avtomorfizem, ki zamenja vozlišči u i in t i za nek i Z n, ostala vozlišča pa fiksira. Pri tem moramo biti pozorni na očitno dejstvo, da je za vsak par vozlišč u i, t i, i Z n avtomorfizem, ki ju zamenja, ostale pa fiksira, drugačen. Zato je smiselno (in tega se bomo do konca podrazdelka tudi držali), da označujemo avtomorfizem, ki zamenja par vozlišč u i, t i, ostale pa fiksira, z δ i Naš osnovni cilj, to je dokazati, da so grafi v obravnavani družini povezavno tranzitivni, smo na tem mestu dosegli, vendar bomo storili še korak dlje. Določili bomo red celotne grupe avtomorfizmov Aut(R n (2, 1)), vendar le za to družino. Pri ostalih treh obravnavanih družinah je to precej težje, zato se tam s tem ne bomo ukvarjali. 29
42 Trditev Naj bo n 3, n 4. Velja Aut(R n (2, 1)) = 2n 2 n. Dokaz. Imejmo graf Γ = R n (2, 1), kjer n 3, n 4 in označimo G = Aut(Γ). Vzemimo vozlišče u 0 V (Γ). Po izreku o orbiti in stabilizatorju (2.4) velja G = O G (u 0 ) G u0. Ker vemo, da Γ premore vozlišči z istimi sosedi, po trditvi 4.10 poznamo obstoj avtomorfizma δ 0, ki zamenja vozlišči u 0 in t 0, druge pa fiksira, poznamo pa tudi obstoj avtomorfizma r, ki ciklično permutira vozlišča u i, hkrati pa tudi t i, grafa Γ. Ker ta dva avtomorfizma omogočita, da lahko vozlišče u 0 preslikamo v katerokoli drugo vozlišče grafa Γ, iz tega sledi O G (u 0 ) = 2n (ker je Γ reda 2n). Oglejmo si zdaj red stabilizatorja vozlišča u 0. Ker po izreku 2.3 vemo, da G u0 G, po izreku o orbiti in stabilizatorju spet velja G u0 = O Gu0 (u 1 ) G u0,u 1, kjer zdaj opazujemo situacijo, ko je vozlišče u 0 fiksirano. Prav zaradi tega je O Gu0 (u 1 ) = 4, saj se lahko vozlišče u 1 preslika le samo vase, v u 1 (z avtomorfizmom z, obstoj katerega poznamo), v vozlišče t 1 (z avtomorfizmom δ 1 ) in v vozlišče t 1 (s kompozitumom avtomorfizmov zδ 1 ). Na tem mestu nadaljujemo podoben premislek in po izreku o orbiti in stabilizatorju zapišemo G u0,u 1 = O Gu0,u 1 (u 2 ) G u0,u 1,u 2. Ker sta v tej situaciji fiksirani vozlišči u 0 in u 1, je O Gu0,u 1 (u 2 ) = 2, saj se vozlišče u 2 lahko preslika le samo vase ali pa v t 2 (z avtomorfizmom δ 2 ). Ker je namreč n 4, je t 0 edino vozlišče, ki ima natanko iste sosede kot u 0, zato mora biti zaradi fiksnosti u 0 fiksirano tudi vozlišče t 0. Ni težko opaziti, da za vsa naslednja vozlišča u i, i Z n \ {0, 1}, velja O Gu0,u 1,...,u i 1 (u i ) = 2, stabilizator G u0,u 1,...,u i pa lahko razbijemo ( G u0,u 1,...,u i = O Gu0,u 1,...,u i (u i+1 ) G u0,u 1,...,u i,u i+1 ) tako, da fiksiramo trenutno vozlišče u i. Za nazadnje izbrano vozlišče očitno velja G u0,u 1,...,u n 1 = 1, saj so vsa druga vozlišča že fiksirana. Tako dobimo enakost: Aut(R n (2, 1)) = 2n 4 2 } 2 {{... 2} = 2n 2 n n 2 Opomba. Bralec lahko opazi, da smo v trditvi zahtevali n 4. Izkaže se namreč, da v primeru, ko je n = 4, obstajajo še neki dodatni avtomorfizmi, o katerih pa lahko bralec premisli sam, saj jih v tem diplomskem delu ne bomo obravnavali Družina R 2m (m + 2, m + 1) Tudi pri študiju povezavne tranzitivnosti družine Rozetnih grafov R 2m (m + 2, m + 1) je ugodno, da grafe upodobimo drugače ter tako dobimo bolj simetrično upodobitev. Primer grafa, ki spada v obravnavano družino (m = 5) je prikazan na sliki 4.8, njegova drugačna upodobitev pa je podana na sliki 4.9. Avtomorfizma r in z, katerih obstoj poznamo že od prej, sedaj slikata takole: r(u i ) = u i+1, r(v i ) = v i+1 z(u i ) = u i, z(v i ) = v m 2 i 30
43 Slika 4.8: R 10 (7, 6). Slika 4.9: R 10 (7, 6) drugače. Trditev Naj bo m 3. Graf Γ = R 2m (m + 2, m + 1) je povezavno tranzitiven. Dokaz. Imejmo graf Γ = R 2m (m + 2, m + 1), kjer je m 3. Upodobimo Γ kot na sliki 4.9 in del grafa Γ upodobimo kot na sliki Slika 4.10: Del grafa R 2m (m + 2, m + 1), upodobljen drugače. Po trditvi 4.7 je graf Γ povezavno tranzitiven natanko tedaj, ko obstaja avtomorfizem, ki neko špico preslika v povezavo, ki ni špica. Oglejmo si permutacijo τ = (u 0, v 1 )(u m, v m 1 )(u 1, v m )(u m+1, v 0 ) (slika 4.10). τ torej premakne le teh osem vozlišč, preostala vozlišča v grafu Γ pa fiskira. Precej preprosto je preveriti, da je τ res avtomorfizem, saj je potrebno le preučiti delovanje permutacije na delu grafa, ki je prikazan na sliki Velja torej τ Aut(Γ). Ker τ preslika špico {u 1, v 1 } v zunanjo povezavo {u 1, u 0 }, je Γ po trditvi 4.7 povezavno tranzitiven. 31
44 4.2.3 Družina R 12m (3m + 2, 3m 1) in R 12m (3m 2, 3m + 1) V tretji družini Rozetnih grafov so vsi tisti grafi R n (a, k), ki so oblike (3a) R 12m (3m + 2, 9m + 1) = R 12m (3m + 2, 3m 1) ali pa (3b) R 12m (9m + 2, 3m + 1) = R 12m (3m 2, 3m + 1). Pri obravnavi te družine je precej priročno, da poddružini (3a) in (3b) združimo pod enotnim zapisom R 12m (3d+2, 9d+1), kjer je d lahko m (mod 12m) ali pa d m (mod 12m). Primera grafov za m = 2 sta prikazana na slikah 4.11 (poddružina (3a)) in 4.12 (poddružina (3b)). Slika 4.11: R 24 (8, 5). Slika 4.12: R 24 (4, 7). Trditev Naj bo m 2. Graf Γ = R 12m (3d+2, 9d+1), kjer je d lahko m (mod n) ali pa d m (mod 12m), je povezavno tranzitiven. Dokaz. Imejmo graf Γ = R 12m (3d+2, 9d+1), kjer m 2, d pa je lahko m (mod 12m) ali pa d = m (mod 12m). Po trditvi 4.7 je graf Γ povezavno tranzitiven natanko tedaj, ko obstaja avtomorfizem, ki neko špico preslika v povezavo, ki ni špica. Označimo a = 3d + 2 in k = 9d + 1. Oglejmo si permutacijo ε, podano z naslednjim predpisom: i Z 12m : u i : i 0 (mod 3) ε(u i ) = v i 1 : i 1 (mod 3) v i a+1 = v i 3d 1 : i 2 (mod 3) u i+1 : i 0 (mod 3) ε(v i ) = u i+a 1 = u i+3d+1 : i 1 (mod 3) v i+6d : i 2 (mod 3) 32
45 V nasprotju s prejšnjim podrazdelkom, v tem primeru ni tako očitno, da ε ohranja sosednosti. Oglejmo si, kako permutacija ε slika povezave iz E(Γ) za i {0, 1, 2} (mod 3) (oziroma, kako ohranja sosednosti): i 0 (mod 3): {u i, u i+1 } {u i, v (i+1) 1 } = {u i, v i } {u i, v i } {u i, u i+1 } {v i, v i+k } = {v i, v i+9d+1 } {u i+1, u (i+9d+1)+3d+1 } = {u i+1, u i+12d+2 } = {u i+1, u i+2 } {v i, u i+a } = {v i, u i+3d+2 } {u i+1, v (i+3d+2) 3d 1 } = {u i+1, v i+1 } i 1 (mod 3): {u i, u i+1 } {v i 1, v (i+1) 3d 1 } = {v i 1, v i 3d } = {v i 1, v i+9d } = {v i 1, v (i 1)+9d+1 } = {v i 1, v (i 1)+k } {u i, v i } {v i 1, u i+3d+1 } = {v i 1, u (i+3d+2) 1 } = {v i 1, u (i+a) 1 } {v i, v i+k } = {v i, v i+9d+1 } {u i+3d+1, v (i+9d+1)+6d } = {u (i+a) 1, v i+3d+1 } = {u (i+a) 1, v (i+a) 1 } {v i, u i+a } = {v i, u i+3d+2 } {u i+3d+1, u i+3d+2 } = {u (i+a) 1, u i+a } i 2 (mod 3): {u i, u i+1 } {v i 3d 1, u i+1 } = {v i+1 (3d+2), u i+1 } = {v (i+1) a, u i+1 } {u i, v i } {v i 3d 1, v i+6d } = {v (i+1) (3d+2), v i 6d } = {v (i+1) a, v (i+1) (3d+2) 3d 1 } = {v (i+1) a, v (i+1) a+9d+1 } = {v (i+1) a, v (i+1) a+k } {v i, v i+k } = {v i, v i+9d+1 } {v i+6d, u (i+9d+1)+1 } = {v i 6d, u i+6d+3d+2 } = {v i 3d 3d+2 2, u (i+6d)+a } = {v (i+1) (3d+2)(9d+1),u(i+6d)+a } = {v (i+1) a+k, u (i+1)+k } {v i, u i+a } = {v i, u i+3d+2 } {v i+6d, u (i+3d+2)+3d+1 } = {v i+6d, u i+6d } = {v (i+1) a+k,u(i+1) a+k } S tem smo pokazali, da permutacija ε za vsak i Z 12m ohranja sosednosti, zato sledi ε Aut(Γ). Ker ε preslika špico {u 0, v 0 } v nešpico {u 0, v 1 }, je po trditvi 4.7 Γ povezavno tranzitiven Družina R 2m (2b, r) V zadnji, četrti družini Rozetnih grafov so vsi grafi oblike R 2m (2b, k), kjer m 2, b 2 ±1 (mod m), k 1 (mod 2) (torej k je lih) in k 1 (mod m). Bralec lahko razmisli, da obstajajo tudi grafi, ki pripadajo družini R 2m (2b, k) in tudi eni izmed družin R n (2, 1) (za vsak sod n, b = 1, k = 1) ali pa R 2m (m + 2, m + 1) (npr. R 8 (6, 5)), vendar bomo pri trenutno obravnavani družini izvzeli vse grafe, ki pripadajo 33
46 že obravnavanima družinama. Pri sami obravnavi družine R 2m (2b, k) je ugodno, da grafe, ki ji pripadajo, razdelimo na dve poddružini: (4a) R 2m (2b, k), kjer b 2 1 (mod m) (4b) R 2m (2b, k), kjer b 2 1 (mod m) Primera grafov sta prikazana na slikah 4.13 (poddružina (4a)) in 4.14 (poddružina (4b)). Slika 4.13: R 6 (4, 1). Slika 4.14: R 10 (4, 1). Trditev Naj bo m 2. Grafi, ki pripadajo družini Rozetnih grafov R 2m (2b, k), kjer je b 2 ±1 (mod m), k 1 (mod 2) in k 1 (mod m), so povezavno tranzitivni. Dokaz. Pri dokazu zgornje trditve nam bo v veliko pomoč razdelitev trenutno obravnavane družine na poddružini (4a) in (4b). Imejmo torej graf Γ 1, ki pripada poddružini (4a) (torej Γ 1 = R 2m (2b, k), kjer je b 2 1 (mod m)) in graf Γ 2, ki pripada družini (4b) (torej Γ 2 = R 2m (2b, k), kjer je b 2 1 (mod m)). Po trditvi 4.7 sta grafa Γ 1 in Γ 2 povezavno tranzitivna natanko tedaj, ko obstaja avtomorfizem, ki neko špico preslika v povezavo, ki ni špica. Oglejmo si permutacijo ρ, podano z naslednjim predpisom: Za graf Γ 1 (torej za družino (4a)): i Z 2m : { u bi : i 0 (mod 2) ρ(u i ) = v bi b : i 1 (mod 2) ρ(v i ) = { u 1+bi : i 0 (mod 2) v bi b+k : i 1 (mod 2) 34
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Simetrije cirkulantnih grafov
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Magistrsko delo Simetrije cirkulantnih grafov (Symmetry of circulant graphs) Ime in priimek: Maruša Saksida Študijski
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Magistrsko delo Simetrije cirkulantnih grafov (Symmetry of circulant graphs) Ime in priimek: Maruša Saksida Študijski
POLDIREKTNI PRODUKT GRUP
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUCIJA ŽNIDARIČ POLDIREKTNI PRODUKT GRUP DIPLOMSKO DELO LJUBLJANA 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Univerzitetni študijski program 1. stopnje: Dvopredmetni
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUCIJA ŽNIDARIČ POLDIREKTNI PRODUKT GRUP DIPLOMSKO DELO LJUBLJANA 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Univerzitetni študijski program 1. stopnje: Dvopredmetni
NIKJER-NIČELNI PRETOKI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA ALJA ŠUBIC NIKJER-NIČELNI PRETOKI DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika - računalništvo ALJA
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA ALJA ŠUBIC NIKJER-NIČELNI PRETOKI DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika - računalništvo ALJA
Matej Mislej HOMOMORFIZMI RAVNINSKIH GRAFOV Z VELIKIM NOTRANJIM OBSEGOM
 UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO Matematika - uporabna smer (UNI) Matej Mislej HOMOMORFIZMI RAVNINSKIH GRAFOV Z VELIKIM NOTRANJIM OBSEGOM Diplomsko delo Ljubljana, 2006 Zahvala Zahvaljujem
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO Matematika - uporabna smer (UNI) Matej Mislej HOMOMORFIZMI RAVNINSKIH GRAFOV Z VELIKIM NOTRANJIM OBSEGOM Diplomsko delo Ljubljana, 2006 Zahvala Zahvaljujem
DELOVANJA GRUP IN BLOKI NEPRIMITIVNOSTI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DEJAN KREJIĆ DELOVANJA GRUP IN BLOKI NEPRIMITIVNOSTI DIPLOMSKO DELO Ljubljana, 2015 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika -
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DEJAN KREJIĆ DELOVANJA GRUP IN BLOKI NEPRIMITIVNOSTI DIPLOMSKO DELO Ljubljana, 2015 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika -
Hipohamiltonovi grafi
 Hipohamiltonovi grafi Marko Čmrlec, Bor Grošelj Simić Mentor(ica): Vesna Iršič Matematično raziskovalno srečanje 1. avgust 016 1 Uvod V marsovskem klubu je želel predsednik prirediti večerjo za svoje člane.
Hipohamiltonovi grafi Marko Čmrlec, Bor Grošelj Simić Mentor(ica): Vesna Iršič Matematično raziskovalno srečanje 1. avgust 016 1 Uvod V marsovskem klubu je želel predsednik prirediti večerjo za svoje člane.
AKSIOMATSKA KONSTRUKCIJA NARAVNIH
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Poučevanje: Predmetno poučevanje ŠPELA ZOBAVNIK AKSIOMATSKA KONSTRUKCIJA NARAVNIH ŠTEVIL MAGISTRSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Poučevanje: Predmetno poučevanje ŠPELA ZOBAVNIK AKSIOMATSKA KONSTRUKCIJA NARAVNIH ŠTEVIL MAGISTRSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO. Oddelek za matematiko in računalništvo DIPLOMSKO DELO.
 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo DIPLOMSKO DELO Sabina Skornšek Maribor, 2012 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo DIPLOMSKO DELO Sabina Skornšek Maribor, 2012 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
Eulerjevi in Hamiltonovi grafi
 Eulerjevi in Hamiltonovi grafi Bojan Možina 30. december 006 1 Eulerjevi grafi Štirje deli mesta Königsberg v Prusiji so bili povezani s sedmimi mostovi (glej levi del slike 1). Zdaj se Königsberg imenuje
Eulerjevi in Hamiltonovi grafi Bojan Možina 30. december 006 1 Eulerjevi grafi Štirje deli mesta Königsberg v Prusiji so bili povezani s sedmimi mostovi (glej levi del slike 1). Zdaj se Königsberg imenuje
Problem umetnostne galerije
 Problem umetnostne galerije Marko Kandič 17. september 2006 Za začetek si oglejmo naslednji primer. Recimo, da imamo v galeriji polno vrednih slik in nočemo, da bi jih kdo ukradel. Seveda si želimo, da
Problem umetnostne galerije Marko Kandič 17. september 2006 Za začetek si oglejmo naslednji primer. Recimo, da imamo v galeriji polno vrednih slik in nočemo, da bi jih kdo ukradel. Seveda si želimo, da
Ana Mlinar Fulereni. Delo diplomskega seminarja. Mentor: izred. prof. dr. Riste Škrekovski
 UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO Matematika 1. stopnja Ana Mlinar Fulereni Delo diplomskega seminarja Mentor: izred. prof. dr. Riste Škrekovski Ljubljana, 2011 Kazalo 1. Uvod 4 2.
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO Matematika 1. stopnja Ana Mlinar Fulereni Delo diplomskega seminarja Mentor: izred. prof. dr. Riste Škrekovski Ljubljana, 2011 Kazalo 1. Uvod 4 2.
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Kvadratne forme nad končnimi obsegi
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Kvadratne forme nad končnimi obsegi (Quadratic Forms over Finite Fields) Ime in priimek: Borut
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Kvadratne forme nad končnimi obsegi (Quadratic Forms over Finite Fields) Ime in priimek: Borut
SLIKE CANTORJEVE PAHLJAµCE
 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in raµcunalništvo Diplomsko delo SLIKE CANTORJEVE PAHLJAµCE Mentor: dr. Iztok Baniµc docent Kandidatka: Anja Belošević
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in raµcunalništvo Diplomsko delo SLIKE CANTORJEVE PAHLJAµCE Mentor: dr. Iztok Baniµc docent Kandidatka: Anja Belošević
Diskretna matematika 1 / Teorija grafov
 Diskretna matematika 1 / Teorija grafov 1. Osnovni pojmi Vladimir Batagelj Univerza v Ljubljani FMF, matematika Finančna matematika Ljubljana, december 2013 / februar 2008 1 / 31 Kazalo 1 2 3 4 5 6 Pajek
Diskretna matematika 1 / Teorija grafov 1. Osnovni pojmi Vladimir Batagelj Univerza v Ljubljani FMF, matematika Finančna matematika Ljubljana, december 2013 / februar 2008 1 / 31 Kazalo 1 2 3 4 5 6 Pajek
Jernej Azarija. Štetje vpetih dreves v grafih
 UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO FAKULTETA ZA MATEMATIKO IN FIZIKO Jernej Azarija Štetje vpetih dreves v grafih DIPLOMSKO DELO NA INTERDISCIPLINARNEM UNIVERZITETNEM ŠTUDIJU
UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO FAKULTETA ZA MATEMATIKO IN FIZIKO Jernej Azarija Štetje vpetih dreves v grafih DIPLOMSKO DELO NA INTERDISCIPLINARNEM UNIVERZITETNEM ŠTUDIJU
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO. Oddelek za matematiko in računalništvo MAGISTRSKA NALOGA. Tina Lešnik
 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo MAGISTRSKA NALOGA Tina Lešnik Maribor, 2014 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo MAGISTRSKA NALOGA Tina Lešnik Maribor, 2014 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Kromatično število in kromatični indeks grafa
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Magistrsko delo Kromatično število in kromatični indeks grafa (The chromatic number and the chromatic index of
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Magistrsko delo Kromatično število in kromatični indeks grafa (The chromatic number and the chromatic index of
Arc-transitive Bicirculants
 1 / 27 Arc-transitive Bicirculants Klavdija Kutnar University of Primorska, Slovenia This is a joint work with Iva Antončič, Aubin Arroyo, Isabel Hubard, Ademir Hujdurović, Eugenia O Reilly and Primož
1 / 27 Arc-transitive Bicirculants Klavdija Kutnar University of Primorska, Slovenia This is a joint work with Iva Antončič, Aubin Arroyo, Isabel Hubard, Ademir Hujdurović, Eugenia O Reilly and Primož
DOMINACIJSKO TEVILO GRAFA
 UNIVERZA V LJUBLJANI PEDAGO KA FAKULTETA tudijski program: MATEMATIKA in RAƒUNALNI TVO DOMINACIJSKO TEVILO GRAFA DIPLOMSKO DELO Mentor: doc. dr. Primoº parl Kandidatka: Neja Zub i Ljubljana, maj, 2011
UNIVERZA V LJUBLJANI PEDAGO KA FAKULTETA tudijski program: MATEMATIKA in RAƒUNALNI TVO DOMINACIJSKO TEVILO GRAFA DIPLOMSKO DELO Mentor: doc. dr. Primoº parl Kandidatka: Neja Zub i Ljubljana, maj, 2011
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SAŠO ZUPANEC MAX-PLUS ALGEBRA DIPLOMSKO DELO
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SAŠO ZUPANEC MAX-PLUS ALGEBRA DIPLOMSKO DELO Ljubljana, 2013 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA ODDELEK ZA MATEMATIKO IN RAČUNALNIŠTVO SAŠO ZUPANEC Mentor:
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SAŠO ZUPANEC MAX-PLUS ALGEBRA DIPLOMSKO DELO Ljubljana, 2013 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA ODDELEK ZA MATEMATIKO IN RAČUNALNIŠTVO SAŠO ZUPANEC Mentor:
Mary Agnes SERVATIUS Izomorfni Cayleyevi grafi nad neizomorfnimi grupami (Isomorphic Cayley Graphs on Non-Isomorphic Groups)
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Matematične znanosti Študijski program 2. stopnje Mary Agnes SERVATIUS Izomorfni Cayleyevi grafi nad neizomorfnimi
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Matematične znanosti Študijski program 2. stopnje Mary Agnes SERVATIUS Izomorfni Cayleyevi grafi nad neizomorfnimi
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Verjetnostni algoritmi za testiranje praštevilskosti
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Verjetnostni algoritmi za testiranje praštevilskosti (Algorithms for testing primality) Ime in
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Verjetnostni algoritmi za testiranje praštevilskosti (Algorithms for testing primality) Ime in
APLIKACIJA ZA DELO Z GRAFI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Študijski program: MATEMATIKA IN RAČUNALNIŠTVO APLIKACIJA ZA DELO Z GRAFI DIPLOMSKO DELO Mentor: doc. dr. Primož Šparl Kandidat: Luka Jurković Somentor: asist.
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Študijski program: MATEMATIKA IN RAČUNALNIŠTVO APLIKACIJA ZA DELO Z GRAFI DIPLOMSKO DELO Mentor: doc. dr. Primož Šparl Kandidat: Luka Jurković Somentor: asist.
Iskanje najcenejše poti v grafih preko polkolobarjev
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Veronika Horvat Iskanje najcenejše poti v grafih preko polkolobarjev DIPLOMSKO DELO VISOKOŠOLSKI STROKOVNI ŠTUDIJSKI PROGRAM PRVE STOPNJE
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Veronika Horvat Iskanje najcenejše poti v grafih preko polkolobarjev DIPLOMSKO DELO VISOKOŠOLSKI STROKOVNI ŠTUDIJSKI PROGRAM PRVE STOPNJE
TEORIJA GRAFOV IN LOGISTIKA
 TEORIJA GRAFOV IN LOGISTIKA Maja Fošner in Tomaž Kramberger Univerza v Mariboru Fakulteta za logistiko Mariborska cesta 2 3000 Celje Slovenija maja.fosner@uni-mb.si tomaz.kramberger@uni-mb.si Povzetek
TEORIJA GRAFOV IN LOGISTIKA Maja Fošner in Tomaž Kramberger Univerza v Mariboru Fakulteta za logistiko Mariborska cesta 2 3000 Celje Slovenija maja.fosner@uni-mb.si tomaz.kramberger@uni-mb.si Povzetek
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO ODDELEK ZA MATEMATIKO
 UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO ODDELEK ZA MATEMATIKO Rok Erman BARVANJA RAVNINSKIH IN SORODNIH DRUŽIN GRAFOV Doktorska disertacija MENTOR: prof. dr. Riste Škrekovski Ljubljana,
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO ODDELEK ZA MATEMATIKO Rok Erman BARVANJA RAVNINSKIH IN SORODNIH DRUŽIN GRAFOV Doktorska disertacija MENTOR: prof. dr. Riste Škrekovski Ljubljana,
Hadamardove matrike in misija Mariner 9
 Hadamardove matrike in misija Mariner 9 Aleksandar Jurišić, 25. avgust, 2009 J. Hadamard (1865-1963) je bil eden izmed pomembnejših matematikov na prehodu iz 19. v 20. stoletje. Njegova najpomembnejša
Hadamardove matrike in misija Mariner 9 Aleksandar Jurišić, 25. avgust, 2009 J. Hadamard (1865-1963) je bil eden izmed pomembnejših matematikov na prehodu iz 19. v 20. stoletje. Njegova najpomembnejša
Grafi, igre in še kaj
 Grafi, igre in še kaj Martin Milanič martin.milanic@upr.si Inštitut Andrej Marušič Fakulteta za matematiko, naravoslovje in informacijske tehnologije Univerza na Primorskem, Koper Matematika je kul 2016,
Grafi, igre in še kaj Martin Milanič martin.milanic@upr.si Inštitut Andrej Marušič Fakulteta za matematiko, naravoslovje in informacijske tehnologije Univerza na Primorskem, Koper Matematika je kul 2016,
JERNEJ TONEJC. Fakulteta za matematiko in fiziko
 . ARITMETIKA DVOJIŠKIH KONČNIH OBSEGOV JERNEJ TONEJC Fakulteta za matematiko in fiziko Math. Subj. Class. (2010): 11T{06, 22, 55, 71}, 12E{05, 20, 30}, 68R05 V članku predstavimo končne obsege in aritmetiko
. ARITMETIKA DVOJIŠKIH KONČNIH OBSEGOV JERNEJ TONEJC Fakulteta za matematiko in fiziko Math. Subj. Class. (2010): 11T{06, 22, 55, 71}, 12E{05, 20, 30}, 68R05 V članku predstavimo končne obsege in aritmetiko
Matematika 1. Gabrijel Tomšič Bojan Orel Neža Mramor Kosta
 Matematika 1 Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 15. december 2010 Poglavje 3 Funkcije 3.1 Osnovni pojmi Preslikavam v množico R ali C običajno pravimo funkcije v prvem primeru realne, v drugem
Matematika 1 Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 15. december 2010 Poglavje 3 Funkcije 3.1 Osnovni pojmi Preslikavam v množico R ali C običajno pravimo funkcije v prvem primeru realne, v drugem
TOPLJENEC ASOCIIRA LE V VODNI FAZI
 TOPLJENEC ASOCIIRA LE V VODNI FAZI V primeru asociacij molekul topljenca v vodni ali organski fazi eksperimentalno določeni navidezni porazdelitveni koeficient (P n ) v odvisnosti od koncentracije ni konstanten.
TOPLJENEC ASOCIIRA LE V VODNI FAZI V primeru asociacij molekul topljenca v vodni ali organski fazi eksperimentalno določeni navidezni porazdelitveni koeficient (P n ) v odvisnosti od koncentracije ni konstanten.
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SARA BREZEC HAUSDORFFOV PARADOKS DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ MATEMATIKA-FIZIKA SARA BREZEC mentor:
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SARA BREZEC HAUSDORFFOV PARADOKS DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ MATEMATIKA-FIZIKA SARA BREZEC mentor:
Kode za popravljanje napak
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE KOPER MATEMATIČNE ZNANOSTI MAGISTRSKI ŠTUDIJSKI PROGRAM 2. STOPNJE Aljaž Slivnik Kode za popravljanje napak Magistrska
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE KOPER MATEMATIČNE ZNANOSTI MAGISTRSKI ŠTUDIJSKI PROGRAM 2. STOPNJE Aljaž Slivnik Kode za popravljanje napak Magistrska
Analiza omrežij Zgradba omrežij:
 Univerza v Ljubljani podiplomski študij statistike Analiza omrežij Zgradba omrežij: podomrežja in povezanosti Vladimir Batagelj Anuška Ferligoj Univerza v Ljubljani Ljubljana, 0. in 7. november 2003 izpisano:
Univerza v Ljubljani podiplomski študij statistike Analiza omrežij Zgradba omrežij: podomrežja in povezanosti Vladimir Batagelj Anuška Ferligoj Univerza v Ljubljani Ljubljana, 0. in 7. november 2003 izpisano:
Reševanje problemov in algoritmi
 Reševanje problemov in algoritmi Vhod Algoritem Izhod Kaj bomo spoznali Zgodovina algoritmov. Primeri algoritmov. Algoritmi in programi. Kaj je algoritem? Algoritem je postopek, kako korak za korakom rešimo
Reševanje problemov in algoritmi Vhod Algoritem Izhod Kaj bomo spoznali Zgodovina algoritmov. Primeri algoritmov. Algoritmi in programi. Kaj je algoritem? Algoritem je postopek, kako korak za korakom rešimo
Izbrana poglavja iz algebrai ne teorije grafov. Zbornik seminarskih nalog iz algebrai ne teorije grafov
 Izbrana poglavja iz algebrai ne teorije grafov Zbornik seminarskih nalog iz algebrai ne teorije grafov Ljubljana, 2015 CIP Kataloºni zapis o publikaciji Narodna in univerzitetna knjiºnica, Ljubljana 519.24(082)(0.034.2)
Izbrana poglavja iz algebrai ne teorije grafov Zbornik seminarskih nalog iz algebrai ne teorije grafov Ljubljana, 2015 CIP Kataloºni zapis o publikaciji Narodna in univerzitetna knjiºnica, Ljubljana 519.24(082)(0.034.2)
Izbrana poglavja iz velikih omreºij 1. Zbornik seminarskih nalog iz velikih omreºij
 Izbrana poglavja iz velikih omreºij 1 Zbornik seminarskih nalog iz velikih omreºij Ljubljana, 2015 CIP Kataloºni zapis o publikaciji Narodna in univerzitetna knjiºnica, Ljubljana 123.45(678)(9.012.3) Izbrana
Izbrana poglavja iz velikih omreºij 1 Zbornik seminarskih nalog iz velikih omreºij Ljubljana, 2015 CIP Kataloºni zapis o publikaciji Narodna in univerzitetna knjiºnica, Ljubljana 123.45(678)(9.012.3) Izbrana
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POLONA ŠENKINC REŠEVANJE LINEARNIH DIFERENCIALNIH ENAČB DRUGEGA REDA S POMOČJO POTENČNIH VRST DIPLOMSKO DELO
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POLONA ŠENKINC REŠEVANJE LINEARNIH DIFERENCIALNIH ENAČB DRUGEGA REDA S POMOČJO POTENČNIH VRST DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POLONA ŠENKINC REŠEVANJE LINEARNIH DIFERENCIALNIH ENAČB DRUGEGA REDA S POMOČJO POTENČNIH VRST DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO. Oddelek za matematiko in računalništvo DIPLOMSKO DELO. Gregor Ambrož
 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo DIPLOMSKO DELO Gregor Ambrož Maribor, 2010 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo DIPLOMSKO DELO Gregor Ambrož Maribor, 2010 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA FAKULTETA ZA MATEMATIKO IN FIZIKO DIPLOMSKO DELO MIHAELA REMIC
 UNIVERZ V LJULJNI PEDGOŠK FKULTET FKULTET Z MTEMTIKO IN FIZIKO DIPLOMSKO DELO MIHEL REMI UNIVERZ V LJULJNI PEDGOŠK FKULTET FKULTET Z MTEMTIKO IN FIZIKO Študijski program: Matematika in fizika ROUTHOV
UNIVERZ V LJULJNI PEDGOŠK FKULTET FKULTET Z MTEMTIKO IN FIZIKO DIPLOMSKO DELO MIHEL REMI UNIVERZ V LJULJNI PEDGOŠK FKULTET FKULTET Z MTEMTIKO IN FIZIKO Študijski program: Matematika in fizika ROUTHOV
OPTIMIZACIJSKE METODE skripta v pripravi
 OPTIMIZACIJSKE METODE skripta v pripravi Vladimir Batagelj Ljubljana 17. december 2003 2 Kazalo Predgovor 5 1 Optimizacijske naloge 7 1.1 Osnovni pojmi........................... 7 1.2 Primeri optimizacijskih
OPTIMIZACIJSKE METODE skripta v pripravi Vladimir Batagelj Ljubljana 17. december 2003 2 Kazalo Predgovor 5 1 Optimizacijske naloge 7 1.1 Osnovni pojmi........................... 7 1.2 Primeri optimizacijskih
NEODLOČLJIVI PROBLEMI V TEORIJI IZRAČUNLJIVOSTI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUKA VIKTOR ROGAČ NEODLOČLJIVI PROBLEMI V TEORIJI IZRAČUNLJIVOSTI MAGISTRSKO DELO LJUBLJANA, 2017 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POUČEVANJE, PREDMETNO
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUKA VIKTOR ROGAČ NEODLOČLJIVI PROBLEMI V TEORIJI IZRAČUNLJIVOSTI MAGISTRSKO DELO LJUBLJANA, 2017 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POUČEVANJE, PREDMETNO
Neli Blagus. Iterativni funkcijski sistemi in konstrukcija fraktalov
 UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Neli Blagus Iterativni funkcijski sistemi in konstrukcija fraktalov DIPLOMSKO DELO NA INTERDISCIPLINARNEM UNIVERZITETNEM ŠTUDIJU Mentorica:
UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Neli Blagus Iterativni funkcijski sistemi in konstrukcija fraktalov DIPLOMSKO DELO NA INTERDISCIPLINARNEM UNIVERZITETNEM ŠTUDIJU Mentorica:
DIOFANTSKE ČETVERICE
 Fakulteta za aravoslovje i matematiko Oddelek za matematiko i račualištvo Diplomsko delo DIOFANTSKE ČETVERICE Metor: Doc. dr. Daiel Eremita Kadidatka: Jožica Špec Maribor 009 II ZAHVALA Zahvaljujem se
Fakulteta za aravoslovje i matematiko Oddelek za matematiko i račualištvo Diplomsko delo DIOFANTSKE ČETVERICE Metor: Doc. dr. Daiel Eremita Kadidatka: Jožica Špec Maribor 009 II ZAHVALA Zahvaljujem se
Katastrofalno zaporedje okvar v medsebojno odvisnih omrežjih
 Katastrofalno zaporedje okvar v medsebojno odvisnih omrežjih Daniel Grošelj Mentor: Prof. Dr. Rudi Podgornik 2. marec 2011 Kazalo 1 Uvod 2 2 Nekaj osnovnih pojmov pri teoriji omrežij 3 2.1 Matrika sosednosti.......................................
Katastrofalno zaporedje okvar v medsebojno odvisnih omrežjih Daniel Grošelj Mentor: Prof. Dr. Rudi Podgornik 2. marec 2011 Kazalo 1 Uvod 2 2 Nekaj osnovnih pojmov pri teoriji omrežij 3 2.1 Matrika sosednosti.......................................
UČNI NAČRT PREDMETA / COURSE SYLLABUS. Študijska smer Study field. Samost. delo Individ. work Klinične vaje work
 Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS Teorija grafov Graph theory Študijski program in stopnja Study programme and level Magistrski študijski program Matematika Master's study
Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS Teorija grafov Graph theory Študijski program in stopnja Study programme and level Magistrski študijski program Matematika Master's study
FRAKTALNA DIMENZIJA. Fakulteta za matematiko in fiziko Univerza v Ljubljani
 FRAKTALNA DIMENZIJA VESNA IRŠIČ Fakulteta za matematiko in fiziko Univerza v Ljubljani PACS: 07.50.Hp, 01.65.+g V članku je predstavljen zgodovinski razvoj teorije fraktalov in natančen opis primerov,
FRAKTALNA DIMENZIJA VESNA IRŠIČ Fakulteta za matematiko in fiziko Univerza v Ljubljani PACS: 07.50.Hp, 01.65.+g V članku je predstavljen zgodovinski razvoj teorije fraktalov in natančen opis primerov,
Naloge iz LA T EXa : 3. del
 Naloge iz LA T EXa : 3. del 1. V besedilo vklju ite naslednjo tabelo skupaj z napisom Kontrolna naloga Dijak 1 2 Povpre je Janko 67 72 70.5 Metka 72 67 70.5 Povpre je 70.5 70.5 Tabela 1: Rezultati kontrolnih
Naloge iz LA T EXa : 3. del 1. V besedilo vklju ite naslednjo tabelo skupaj z napisom Kontrolna naloga Dijak 1 2 Povpre je Janko 67 72 70.5 Metka 72 67 70.5 Povpre je 70.5 70.5 Tabela 1: Rezultati kontrolnih
Miha Drole. Sintaksna analiza rahlo kontekstno odvisnih jezikov
 UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Miha Drole Sintaksna analiza rahlo kontekstno odvisnih jezikov DIPLOMSKO DELO NA UNIVERZITETNEM ŠTUDIJU Mentor: prof. dr. Igor Kononenko Ljubljana,
UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Miha Drole Sintaksna analiza rahlo kontekstno odvisnih jezikov DIPLOMSKO DELO NA UNIVERZITETNEM ŠTUDIJU Mentor: prof. dr. Igor Kononenko Ljubljana,
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga (Final project paper) Grafi struktur proteinov: Uporaba teorije grafov za analizo makromolekulskih
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga (Final project paper) Grafi struktur proteinov: Uporaba teorije grafov za analizo makromolekulskih
Attempt to prepare seasonal weather outlook for Slovenia
 Attempt to prepare seasonal weather outlook for Slovenia Main available sources (ECMWF, EUROSIP, IRI, CPC.NCEP.NOAA,..) Two parameters (T and RR anomally) Textual information ( Met Office like ) Issued
Attempt to prepare seasonal weather outlook for Slovenia Main available sources (ECMWF, EUROSIP, IRI, CPC.NCEP.NOAA,..) Two parameters (T and RR anomally) Textual information ( Met Office like ) Issued
SIMETRIČNE KOMPONENTE
 Univerza v Ljubljani Fakulteta za elektrotehniko SIMETRIČNE KOMPONENTE Seminarska naloga pri predmetu Razdelilna in industrijska omrežja Poročilo izdelala: ELIZABETA STOJCHEVA Mentor: prof. dr. Grega Bizjak,
Univerza v Ljubljani Fakulteta za elektrotehniko SIMETRIČNE KOMPONENTE Seminarska naloga pri predmetu Razdelilna in industrijska omrežja Poročilo izdelala: ELIZABETA STOJCHEVA Mentor: prof. dr. Grega Bizjak,
Linearna regresija. Poglavje 4
 Poglavje 4 Linearna regresija Vinkove rezultate iz kemije so založili. Enostavno, komisija je izgubila izpitne pole. Rešitev: Vinko bo kemijo pisal še enkrat. Ampak, ne more, je ravno odšel na trening
Poglavje 4 Linearna regresija Vinkove rezultate iz kemije so založili. Enostavno, komisija je izgubila izpitne pole. Rešitev: Vinko bo kemijo pisal še enkrat. Ampak, ne more, je ravno odšel na trening
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
ENERGY AND MASS SPECTROSCOPY OF IONS AND NEUTRALS IN COLD PLASMA
 UDK621.3:(53+54+621 +66), ISSN0352-9045 Informaclje MIDEM 3~(~UU8)4, Ljubljana ENERGY AND MASS SPECTROSCOPY OF IONS AND NEUTRALS IN COLD PLASMA Marijan Macek 1,2* Miha Cekada 2 1 University of Ljubljana,
UDK621.3:(53+54+621 +66), ISSN0352-9045 Informaclje MIDEM 3~(~UU8)4, Ljubljana ENERGY AND MASS SPECTROSCOPY OF IONS AND NEUTRALS IN COLD PLASMA Marijan Macek 1,2* Miha Cekada 2 1 University of Ljubljana,
Particija grafa, odkrivanje skupnosti in maksimalen prerez
 Univerza na Primorskem Fakulteta za matematiko, naravoslovje in informacijske tehnologije Matemati ne znanosti - 2. stopnja Peter Mur²i Particija grafa, odkrivanje skupnosti in maksimalen prerez Magistrsko
Univerza na Primorskem Fakulteta za matematiko, naravoslovje in informacijske tehnologije Matemati ne znanosti - 2. stopnja Peter Mur²i Particija grafa, odkrivanje skupnosti in maksimalen prerez Magistrsko
Topološki model za brezžična senzorska omrežja
 UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Jan Terzer Topološki model za brezžična senzorska omrežja DIPLOMSKO DELO UNIVERZITETNI ŠTUDIJSKI PROGRAM PRVE STOPNJE RAČUNALNIŠTVO IN INFORMATIKA
UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Jan Terzer Topološki model za brezžična senzorska omrežja DIPLOMSKO DELO UNIVERZITETNI ŠTUDIJSKI PROGRAM PRVE STOPNJE RAČUNALNIŠTVO IN INFORMATIKA
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DIPLOMSKO DELO MAJA OSTERMAN
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DIPLOMSKO DELO MAJA OSTERMAN UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Študijski program: Matematika in računalništvo Fibonaccijevo zaporedje in krožna konstanta
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DIPLOMSKO DELO MAJA OSTERMAN UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Študijski program: Matematika in računalništvo Fibonaccijevo zaporedje in krožna konstanta
Călugăreanu-White-Fullerjev teorem in topologija DNA
 Univerza v Ljubljani Fakulteta za matematiko in fiziko Oddelek za fiziko Călugăreanu-White-Fullerjev teorem in topologija DNA Seminar Jure Aplinc, dipl. fiz. (UN) Mentor: prof. dr. Rudolf Podgornik 26.
Univerza v Ljubljani Fakulteta za matematiko in fiziko Oddelek za fiziko Călugăreanu-White-Fullerjev teorem in topologija DNA Seminar Jure Aplinc, dipl. fiz. (UN) Mentor: prof. dr. Rudolf Podgornik 26.
Interpolacija s parametričnimi polinomskimikrivuljami 1
 Interpolacija s parametričnimi polinomskimikrivuljami Emil Žagar 22. november 200 Skriptajevnastajanju,zatojegotovopolnanapak. Hvaleˇzenbomzavse pripombe. Iskanje napak je obenem del učnega procesa pri
Interpolacija s parametričnimi polinomskimikrivuljami Emil Žagar 22. november 200 Skriptajevnastajanju,zatojegotovopolnanapak. Hvaleˇzenbomzavse pripombe. Iskanje napak je obenem del učnega procesa pri
Linearne enačbe. Matrična algebra. Linearne enačbe. Linearne enačbe. Linearne enačbe. Linearne enačbe
 Sistem linearnih enačb Matrična algebra Oseba X X X3 B A.A. 3 B.B. 7 C.C. Doc. dr. Anja Podlesek Oddelek za psihologijo, Filozofska fakulteta, Univerza v Ljubljani Študijski program prve stopnje Psihologija
Sistem linearnih enačb Matrična algebra Oseba X X X3 B A.A. 3 B.B. 7 C.C. Doc. dr. Anja Podlesek Oddelek za psihologijo, Filozofska fakulteta, Univerza v Ljubljani Študijski program prve stopnje Psihologija
ZVEZDASTI MNOGOKOTNIKI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA BLAŽKA RIOSA ZVEZDASTI MNOGOKOTNIKI DIPLOMSKO DELO Ljubljana, 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ BLAŽKA RIOSA Mentor: dr. Matija
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA BLAŽKA RIOSA ZVEZDASTI MNOGOKOTNIKI DIPLOMSKO DELO Ljubljana, 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ BLAŽKA RIOSA Mentor: dr. Matija
Topološka obdelava slik
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Matjaž Cerar Topološka obdelava slik DIPLOMSKO DELO UNIVERZITETNI INTERDISCIPLINARNI ŠTUDIJ RAČUNALNIŠTVA
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Matjaž Cerar Topološka obdelava slik DIPLOMSKO DELO UNIVERZITETNI INTERDISCIPLINARNI ŠTUDIJ RAČUNALNIŠTVA
SVM = Support Vector Machine = Metoda podpornih vektorjev
 Uvod 2/60 SVM = Support Vector Machine = Metoda podpornih vektorjev Vapnik in Lerner 1963 (generalized portrait) jedra: Aronszajn 1950; Aizerman 1964; Wahba 1990, Poggio in Girosi 1990 Boser, Guyon in
Uvod 2/60 SVM = Support Vector Machine = Metoda podpornih vektorjev Vapnik in Lerner 1963 (generalized portrait) jedra: Aronszajn 1950; Aizerman 1964; Wahba 1990, Poggio in Girosi 1990 Boser, Guyon in
Računalnik iz domin. Škafar, Maja Šafarič, Nina Sangawa Hmeljak Mentor: Vid Kocijan
 Računalnik iz domin Primož Škafar, Maja Šafarič, Nina Sangawa Hmeljak Mentor: Vid Kocijan Povzetek Naša naloga je bila ugotoviti kako sestaviti računalnik (Turingov stroj) iz domin in logičnih izrazov.
Računalnik iz domin Primož Škafar, Maja Šafarič, Nina Sangawa Hmeljak Mentor: Vid Kocijan Povzetek Naša naloga je bila ugotoviti kako sestaviti računalnik (Turingov stroj) iz domin in logičnih izrazov.
Multipla korelacija in regresija. Multipla regresija, multipla korelacija, statistično zaključevanje o multiplem R
 Multipla koelacia in egesia Multipla egesia, multipla koelacia, statistično zaklučevane o multiplem Multipla egesia osnovni model in ačunane paametov Z multiplo egesio napoveduemo vednost kiteia (odvisne
Multipla koelacia in egesia Multipla egesia, multipla koelacia, statistično zaklučevane o multiplem Multipla egesia osnovni model in ačunane paametov Z multiplo egesio napoveduemo vednost kiteia (odvisne
Cveto Trampuž PRIMERJAVA ANALIZE VEČRAZSEŽNIH TABEL Z RAZLIČNIMI MODELI REGRESIJSKE ANALIZE DIHOTOMNIH SPREMENLJIVK
 Cveto Trampuž PRIMERJAVA ANALIZE VEČRAZSEŽNIH TABEL Z RAZLIČNIMI MODELI REGRESIJSKE ANALIZE DIHOTOMNIH SPREMENLJIVK POVZETEK. Namen tega dela je prikazati osnove razlik, ki lahko nastanejo pri interpretaciji
Cveto Trampuž PRIMERJAVA ANALIZE VEČRAZSEŽNIH TABEL Z RAZLIČNIMI MODELI REGRESIJSKE ANALIZE DIHOTOMNIH SPREMENLJIVK POVZETEK. Namen tega dela je prikazati osnove razlik, ki lahko nastanejo pri interpretaciji
Multiply transitive permutation groups via the small Mathieu groups
 UNIVERSITY OF PRIMORSKA FACULTY OF MATHEMATICS, NATURAL SCIENCES AND INFORMATION TECHNOLOGIES Master s Study Programme Mathematical Sciences Second Bologna cycle Anna Klymenko Multiply transitive permutation
UNIVERSITY OF PRIMORSKA FACULTY OF MATHEMATICS, NATURAL SCIENCES AND INFORMATION TECHNOLOGIES Master s Study Programme Mathematical Sciences Second Bologna cycle Anna Klymenko Multiply transitive permutation
Solutions. Name and surname: Instructions
 Uiversity of Ljubljaa, Faculty of Ecoomics Quatitative fiace ad actuarial sciece Probability ad statistics Writte examiatio September 4 th, 217 Name ad surame: Istructios Read the problems carefull before
Uiversity of Ljubljaa, Faculty of Ecoomics Quatitative fiace ad actuarial sciece Probability ad statistics Writte examiatio September 4 th, 217 Name ad surame: Istructios Read the problems carefull before
Luka Taras Korošec ANALIZA IN NADGRADNJA APLIKACIJE ZA DELO Z GRAFI
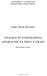 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Luka Taras Korošec ANALIZA IN NADGRADNJA APLIKACIJE ZA DELO Z GRAFI DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA UNIVERZITETNI ŠTUDIJSKI
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Luka Taras Korošec ANALIZA IN NADGRADNJA APLIKACIJE ZA DELO Z GRAFI DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA UNIVERZITETNI ŠTUDIJSKI
Univerza v Ljubljani Fakulteta za matematiko in fiziko. Oddelek za fiziko. Seminar - 3. letnik, I. stopnja. Kvantni računalniki. Avtor: Tomaž Čegovnik
 Univerza v Ljubljani Fakulteta za matematiko in fiziko Oddelek za fiziko Seminar - 3. letnik, I. stopnja Kvantni računalniki Avtor: Tomaž Čegovnik Mentor: prof. dr. Anton Ramšak Ljubljana, marec 01 Povzetek
Univerza v Ljubljani Fakulteta za matematiko in fiziko Oddelek za fiziko Seminar - 3. letnik, I. stopnja Kvantni računalniki Avtor: Tomaž Čegovnik Mentor: prof. dr. Anton Ramšak Ljubljana, marec 01 Povzetek
UNIVERSITY OF LJUBLJANA FACULTY OF MATHEMATICS AND PHYSICS DEPARTMENT OF MATHEMATICS. Nino Bašić
 UNIVERSITY OF LJUBLJANA FACULTY OF MATHEMATICS AND PHYSICS DEPARTMENT OF MATHEMATICS Nino Bašić ALGEBRAIC APPROACH TO SEVERAL FAMILIES OF CHEMICAL GRAPHS Doctoral thesis Adviser: Prof. Dr. Tomaž Pisanski
UNIVERSITY OF LJUBLJANA FACULTY OF MATHEMATICS AND PHYSICS DEPARTMENT OF MATHEMATICS Nino Bašić ALGEBRAIC APPROACH TO SEVERAL FAMILIES OF CHEMICAL GRAPHS Doctoral thesis Adviser: Prof. Dr. Tomaž Pisanski
Intervalske Bézierove krivulje in ploskve
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Tadej Borovšak Intervalske Bézierove krivulje in ploskve DIPLOMSKO DELO UNIVERZITETNI ŠTUDIJSKI PROGRAM
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Tadej Borovšak Intervalske Bézierove krivulje in ploskve DIPLOMSKO DELO UNIVERZITETNI ŠTUDIJSKI PROGRAM
Simulation of multilayer coating growth in an industrial magnetron sputtering system
 RMZ Materials and Geoenvironment, Vol. 57, No. 3, pp. 317 330, 2010 317 Simulation of multilayer coating growth in an industrial magnetron sputtering system Simulacija rasti večplastnih prevlek v industrijski
RMZ Materials and Geoenvironment, Vol. 57, No. 3, pp. 317 330, 2010 317 Simulation of multilayer coating growth in an industrial magnetron sputtering system Simulacija rasti večplastnih prevlek v industrijski
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA VERONIKA MIHELAK PRAVILNI IKOZAEDER DIPLOMSKO DELO
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA VERONIKA MIHELAK PRAVILNI IKOZAEDER DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ VERONIKA MIHELAK MENTOR: izr. prof.
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA VERONIKA MIHELAK PRAVILNI IKOZAEDER DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ VERONIKA MIHELAK MENTOR: izr. prof.
Linearna algebra. Bojan Orel. Univerza v Ljubljani
 Linearna algebra Bojan Orel 07 Univerza v Ljubljani Fakulteta za računalništvo in informatiko CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana 5.64(075.8) OREL, Bojan Linearna
Linearna algebra Bojan Orel 07 Univerza v Ljubljani Fakulteta za računalništvo in informatiko CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana 5.64(075.8) OREL, Bojan Linearna
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. O neeksaknotsti eksaktnega binomskega intervala zaupanja
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga (Final project paper) O neeksaknotsti eksaktnega binomskega intervala zaupanja (On the inexactness
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga (Final project paper) O neeksaknotsti eksaktnega binomskega intervala zaupanja (On the inexactness
Zgoščevanje podatkov
 Zgoščevanje podatkov Pojem zgoščevanje podatkov vključuje tehnike kodiranja, ki omogočajo skrajšan zapis neke datoteke. Poznan program za zgoščevanje datotek je WinZip. Podatke je smiselno zgostiti v primeru
Zgoščevanje podatkov Pojem zgoščevanje podatkov vključuje tehnike kodiranja, ki omogočajo skrajšan zapis neke datoteke. Poznan program za zgoščevanje datotek je WinZip. Podatke je smiselno zgostiti v primeru
Obisk iz rezultatov iskanj na iskalniku Google
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Uroš Okorn Obisk iz rezultatov iskanj na iskalniku Google DIPLOMSKO DELO VISOKOŠOLSKI STROKOVNI ŠTUDIJSKI PROGRAM PRVE STOPNJE RAČUNALNIŠTVO
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Uroš Okorn Obisk iz rezultatov iskanj na iskalniku Google DIPLOMSKO DELO VISOKOŠOLSKI STROKOVNI ŠTUDIJSKI PROGRAM PRVE STOPNJE RAČUNALNIŠTVO
Gradnja Vietoris-Ripsovega simplicialnega kompleksa
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Leonard Štefančič Gradnja Vietoris-Ripsovega simplicialnega kompleksa DIPLOMSKO DELO NA INTERDISCIPLINARNEM
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Leonard Štefančič Gradnja Vietoris-Ripsovega simplicialnega kompleksa DIPLOMSKO DELO NA INTERDISCIPLINARNEM
arxiv: v1 [cs.dm] 21 Dec 2016
![arxiv: v1 [cs.dm] 21 Dec 2016 arxiv: v1 [cs.dm] 21 Dec 2016](/thumbs/74/69772342.jpg) UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE arxiv:1612.07113v1 [cs.dm] 21 Dec 2016 Zaključna naloga (Final project paper) Odčitljivost digrafov in dvodelnih
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE arxiv:1612.07113v1 [cs.dm] 21 Dec 2016 Zaključna naloga (Final project paper) Odčitljivost digrafov in dvodelnih
Distance reduction with the use of UDF and Mathematica. Redukcija dolžin z uporabo MS Excel ovih lastnih funkcij in programa Mathematica
 RMZ Materials and Geoenvironment, Vol. 54, No. 2, pp. 265-286, 2007 265 Distance reduction with the use of UDF and Mathematica Redukcija dolžin z uporabo MS Excel ovih lastnih funkcij in programa Mathematica
RMZ Materials and Geoenvironment, Vol. 54, No. 2, pp. 265-286, 2007 265 Distance reduction with the use of UDF and Mathematica Redukcija dolžin z uporabo MS Excel ovih lastnih funkcij in programa Mathematica
JEDRSKA URA JAN JURKOVIČ. Fakulteta za matematiko in fiziko Univerza v Ljubljani
 JEDRSKA URA JAN JURKOVIČ Fakulteta za matematiko in fiziko Univerza v Ljubljani Natančnost časa postaja vse bolj uporabna in pomembna, zato se rojevajo novi načini merjenja časa. Do danes najbolj natančnih
JEDRSKA URA JAN JURKOVIČ Fakulteta za matematiko in fiziko Univerza v Ljubljani Natančnost časa postaja vse bolj uporabna in pomembna, zato se rojevajo novi načini merjenja časa. Do danes najbolj natančnih
Univerza na Primorskem. Fakulteta za matematiko, naravoslovje in informacijske tehnologije. Zaznavanje gibov. Zaključna naloga
 Univerza na Primorskem Fakulteta za matematiko, naravoslovje in informacijske tehnologije Boštjan Markežič Zaznavanje gibov Zaključna naloga Koper, september 2011 Mentor: doc. dr. Peter Rogelj Kazalo Slovarček
Univerza na Primorskem Fakulteta za matematiko, naravoslovje in informacijske tehnologije Boštjan Markežič Zaznavanje gibov Zaključna naloga Koper, september 2011 Mentor: doc. dr. Peter Rogelj Kazalo Slovarček
Introduction of Branching Degrees of Octane Isomers
 DOI: 10.17344/acsi.2016.2361 Acta Chim. Slov. 2016, 63, 411 415 411 Short communication Introduction of Branching Degrees of Octane Isomers Anton Perdih Faculty of Chemistry and Chemical Technology, University
DOI: 10.17344/acsi.2016.2361 Acta Chim. Slov. 2016, 63, 411 415 411 Short communication Introduction of Branching Degrees of Octane Isomers Anton Perdih Faculty of Chemistry and Chemical Technology, University
Verifikacija napovedi padavin
 Oddelek za Meteorologijo Seminar: 4. letnik - univerzitetni program Verifikacija napovedi padavin Avtor: Matic Šavli Mentor: doc. dr. Nedjeljka Žagar 26. februar 2012 Povzetek Pojem verifikacije je v meteorologiji
Oddelek za Meteorologijo Seminar: 4. letnik - univerzitetni program Verifikacija napovedi padavin Avtor: Matic Šavli Mentor: doc. dr. Nedjeljka Žagar 26. februar 2012 Povzetek Pojem verifikacije je v meteorologiji
DOKTORSKA DISERTACIJA (DOCTORAL THESIS)
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE DOKTORSKA DISERTACIJA (DOCTORAL THESIS) O PROBLEMU IZOMORFNOSTI BI-CAYLEYJEVIH GRAFOV (ON THE ISOMORPHISM PROBLEM
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE DOKTORSKA DISERTACIJA (DOCTORAL THESIS) O PROBLEMU IZOMORFNOSTI BI-CAYLEYJEVIH GRAFOV (ON THE ISOMORPHISM PROBLEM
OPTIMIRANJE IZDELOVALNIH PROCESOV
 OPTIMIRANJE IZDELOVALNIH PROCESOV asist. Damir GRGURAŠ, mag. inž. str izr. prof. dr. Davorin KRAMAR damir.grguras@fs.uni-lj.si Namen vaje: Ugotoviti/določiti optimalne parametre pri struženju za dosego
OPTIMIRANJE IZDELOVALNIH PROCESOV asist. Damir GRGURAŠ, mag. inž. str izr. prof. dr. Davorin KRAMAR damir.grguras@fs.uni-lj.si Namen vaje: Ugotoviti/določiti optimalne parametre pri struženju za dosego
D I P L O M S K A N A L O G A
 FAKULTETA ZA INFORMACIJSKE ŠTUDIJE V NOVEM MESTU D I P L O M S K A N A L O G A UNIVERZITETNEGA ŠTUDIJSKEGA PROGRAMA PRVE STOPNJE ALEŠ HOČEVAR FAKULTETA ZA INFORMACIJSKE ŠTUDIJE V NOVEM MESTU DIPLOMSKA
FAKULTETA ZA INFORMACIJSKE ŠTUDIJE V NOVEM MESTU D I P L O M S K A N A L O G A UNIVERZITETNEGA ŠTUDIJSKEGA PROGRAMA PRVE STOPNJE ALEŠ HOČEVAR FAKULTETA ZA INFORMACIJSKE ŠTUDIJE V NOVEM MESTU DIPLOMSKA
USING THE DIRECTION OF THE SHOULDER S ROTATION ANGLE AS AN ABSCISSA AXIS IN COMPARATIVE SHOT PUT ANALYSIS. Matej Supej* Milan Čoh
 Kinesiologia Slovenica, 14, 3, 5 14 (28) Faculty of Sport, University of Ljubljana, ISSN 1318-2269 5 Matej Supej* Milan Čoh USING THE DIRECTION OF THE SHOULDER S ROTATION ANGLE AS AN ABSCISSA AXIS IN COMPARATIVE
Kinesiologia Slovenica, 14, 3, 5 14 (28) Faculty of Sport, University of Ljubljana, ISSN 1318-2269 5 Matej Supej* Milan Čoh USING THE DIRECTION OF THE SHOULDER S ROTATION ANGLE AS AN ABSCISSA AXIS IN COMPARATIVE
OFF-LINE NALOGA NAJKRAJŠI SKUPNI NADNIZ
 1 OFF-LINE NALOGA NAJKRAJŠI SKUPNI NADNIZ Opis problema. Danih je k vhodnih nizov, ki jih označimo s t 1,..., t k. Množico vseh znakov, ki se pojavijo v vsaj enem vhodnem nizu, imenujmo abeceda in jo označimo
1 OFF-LINE NALOGA NAJKRAJŠI SKUPNI NADNIZ Opis problema. Danih je k vhodnih nizov, ki jih označimo s t 1,..., t k. Množico vseh znakov, ki se pojavijo v vsaj enem vhodnem nizu, imenujmo abeceda in jo označimo
Modelska Analiza 1. University of Ljubljana Faculty of Mathematics and Physics. 3. naloga - Numeri na minimizacija
 University of Ljubljana Faculty of Mathematics and Physics Modelska Analiza 1 3. naloga - Numeri na minimizacija Avtor: Matic Lubej Asistent: dr. Simon ƒopar Predavatelj: prof. dr. Alojz Kodre Ljubljana,
University of Ljubljana Faculty of Mathematics and Physics Modelska Analiza 1 3. naloga - Numeri na minimizacija Avtor: Matic Lubej Asistent: dr. Simon ƒopar Predavatelj: prof. dr. Alojz Kodre Ljubljana,
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUKA VIKTOR ROGAČ KONČNI AVTOMATI DIPLOMSKO DELO
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUKA VIKTOR ROGAČ KONČNI AVTOMATI DIPLOMSKO DELO LJUBLJANA, 2015 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Univerzitetni študijski program 1. stopnje: Dvopredmetni
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUKA VIKTOR ROGAČ KONČNI AVTOMATI DIPLOMSKO DELO LJUBLJANA, 2015 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Univerzitetni študijski program 1. stopnje: Dvopredmetni
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Uporaba logistične regresije za napovedovanje razreda, ko je število enot v preučevanih razredih
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Uporaba logistične regresije za napovedovanje razreda, ko je število enot v preučevanih razredih
MICROWAVE PLASMAS AT ATMOSPHERIC PRESSURE: NEW THEORETICAL DEVELOPMENTS AND APPLICATIONS IN SURFACE SCIENCE
 UDK621.3:(53+54+621 +66), ISSN0352-9045 Informacije MIDEM 38(2008)4, Ljubljana MICROWAVE PLASMAS AT ATMOSPHERIC PRESSURE: NEW THEORETICAL DEVELOPMENTS AND APPLICATIONS IN SURFACE SCIENCE T. 8elmonte*,
UDK621.3:(53+54+621 +66), ISSN0352-9045 Informacije MIDEM 38(2008)4, Ljubljana MICROWAVE PLASMAS AT ATMOSPHERIC PRESSURE: NEW THEORETICAL DEVELOPMENTS AND APPLICATIONS IN SURFACE SCIENCE T. 8elmonte*,
Hiperbolične funkcije DIPLOMSKO DELO
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA FAKULTETA ZA MATEMATIKO IN FIZIKO Študijski program: Matematika in fizika Hiperbolične funkcije DIPLOMSKO DELO Mentor: dr. Marko Razpet Kandidatka: Teja Bergant
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA FAKULTETA ZA MATEMATIKO IN FIZIKO Študijski program: Matematika in fizika Hiperbolične funkcije DIPLOMSKO DELO Mentor: dr. Marko Razpet Kandidatka: Teja Bergant
INTELLIGENTNI SISTEMI Mehka Logika
 INTELLIGENTNI SISTEMI Mehka Logika MEHKA LOGIKA (FUZZY LOGIC) 2011/12 Jurij F. Tasič Emil Plesnik 2011/12 1 Splošna definicija Mehka logika - Fuzzy Logic; 1965 Lotfi Zadeh, Berkely Nadgradnja konvencionalne
INTELLIGENTNI SISTEMI Mehka Logika MEHKA LOGIKA (FUZZY LOGIC) 2011/12 Jurij F. Tasič Emil Plesnik 2011/12 1 Splošna definicija Mehka logika - Fuzzy Logic; 1965 Lotfi Zadeh, Berkely Nadgradnja konvencionalne
Semiregular automorphisms of vertex-transitive graphs
 Semiregular automorphisms of vertex-transitive graphs Michael Giudici http://www.maths.uwa.edu.au/ giudici/research.html Semiregular automorphisms A semiregular automorphism of a graph is a nontrivial
Semiregular automorphisms of vertex-transitive graphs Michael Giudici http://www.maths.uwa.edu.au/ giudici/research.html Semiregular automorphisms A semiregular automorphism of a graph is a nontrivial
Preprečevanje neizvedljivosti urnikov pri metahevrističnem razvrščanju proizvodnih procesov
 Univerza v Ljubljani Fakulteta za elektrotehniko Boštjan Murovec Preprečevanje neizvedljivosti urnikov pri metahevrističnem razvrščanju proizvodnih procesov Doktorska disertacija Mentor: prof. dr. Peter
Univerza v Ljubljani Fakulteta za elektrotehniko Boštjan Murovec Preprečevanje neizvedljivosti urnikov pri metahevrističnem razvrščanju proizvodnih procesov Doktorska disertacija Mentor: prof. dr. Peter
TEORIJA SKUPOVA Zadaci
 TEORIJA SKUPOVA Zadai LOGIKA 1 I. godina 1. Zapišite simbolima: ( x nije element skupa S (b) d je član skupa S () F je podskup slupa S (d) Skup S sadrži skup R 2. Neka je S { x;2x 6} = = i neka je b =
TEORIJA SKUPOVA Zadai LOGIKA 1 I. godina 1. Zapišite simbolima: ( x nije element skupa S (b) d je član skupa S () F je podskup slupa S (d) Skup S sadrži skup R 2. Neka je S { x;2x 6} = = i neka je b =
