UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Kromatično število in kromatični indeks grafa
|
|
|
- Malcolm Wilkins
- 5 years ago
- Views:
Transcription
1 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Magistrsko delo Kromatično število in kromatični indeks grafa (The chromatic number and the chromatic index of a graph) Ime in priimek: Angelina Ćirković Študijski program: Matematične znanosti, 2. stopnja Mentor: izr. prof. dr. Martin Milanič Koper, september 2017
2 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, 2017 II Ključna dokumentacijska informacija Ime in PRIIMEK: Angelina ĆIRKOVIĆ Naslov magistrskega dela: Kromatično število in kromatični indeks grafa Kraj: Koper Leto: 2017 Število listov: 53 Število slik: 18 Število referenc: 38 Mentor: izr. prof. dr. Martin Milanič UDK: (043.2) Ključne besede: barvanje točk, barvanje povezav, kromatično število, kromatični indeks, popoln graf. Math. Subj. Class. (2010): 05C15, 05C17, 05C70 Izvleček: V magistrskem delu so najprej opisani osnovni pojmi teorije grafov, nato pa se osredotočimo na najpomembnejša koncepta s področja kromatične teorije grafov, kromatično število in kromatični indeks grafa. Izraz barvanje grafov se namreč lahko nanaša na (vsaj) dve različni vrsti barvanj: barvanje točk in barvanje povezav, pri čemer je cilj določitev najmanjšega števila barv, potrebnega v takem barvanju točk oziroma povezav, da sta sosednji točki oziroma povezavi obarvani različno. V magistrskem delu so podane številne trditve, vezane na obravnavane teme, vključno z dokazi, in številni zgledi. Obravnavane teme med drugim zajemajo zgornje in spodnje meje za kromatično število in kromatični indeks grafa, lastnosti barvno kritičnih grafov, različne konstrukcije grafov brez trikotnikov s poljubno velikim kromatičnim številom, vključno z Erdősevim pristopom na osnovi verjetnostne metode, popolne grafe in Galvinov izrek o seznamskih povezavnih barvanjih dvodelnih grafov. V nekaterih trditvah in dokazih so uporabljeni tudi usmerjeni grafi.
3 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, 2017 III Key words documentation Name and SURNAME: Angelina ĆIRKOVIĆ Title of the thesis: The chromatic number and the chromatic index of a graph Place: Koper Year: 2017 Number of pages: 53 Number of figures: 18 Number of references: 38 Mentor: Assoc. Prof. Martin Milanič, PhD UDC: (043.2) Keywords: vertex coloring, edge coloring, chromatic number, chromatic index, perfect graph. Math. Subj. Class. (2010): 05C15, 05C17, 05C70 Abstract: In the master s thesis we first describe the basic concepts of graph theory and then focus on two fundamental concepts studied by chromatic graph theory, the chromatic number and the chromatic index of a graph. Namely, the term graph colouring can refer to (at least) two different types of colouring: vertex colouring and edge colouring, where the goal is to determine the smallest number of colours, either in a vertex colouring or in an edge colouring of the graph, considering that neighbouring vertices or adjacent edges have to be coloured differently. Numerous theorems and propositions will be given, with proofs, as well as various examples. Considered topics include, among others, upper and lower bounds for the chromatic number and the chromatic index of a graph, properties of colour-critical graphs, various constructions of triangle-free graphs of large chromatic number, including the approach due to Erdős based on the probabilistic method, perfect graphs, and Galvin s theorem on list edge colourings of bipartite graphs. In some of the propositions directed graphs are also used.
4 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, 2017 IV Kazalo vsebine 1 Uvod 1 2 Osnovne definicije 3 3 Kromatično število grafa Osnovne definicije in zgledi Osnovni rezultati o kromatičnem številu grafa Barvanje digrafov Kritični grafi Grafi velike ožine in velikega kromatičnega števila Popolni grafi Kromatični indeks grafa Povezavno barvanje dvodelnih grafov Vizingov izrek Seznamska barvanja povezav Zaključek 49 6 Literatura in viri 51
5 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, 2017 V Kazalo slik 1 Graf na šestih točkah Cikel na petih točkah, C Pot na štirih točkah, P Cikel na sedmih točkah, C Cikel na osmih točkah, C Barvanje točk polnega dvodelnega grafa z točkami, K 1, Barvanje točk cikla na petih točkah, C Barvanje točk polnega grafa na šestih točkah, K Barvanje točk grafa (kolesa) na petih točkah, W Graf G = C 7 s točkama u in v Graf G Graf G Graf na osmih točkah Barvanje povezav polnega dvodelnega grafa z točkami, K 1, Barvanje povezav cikla na petih točkah, C Barvanje povezav polnega grafa na šestih točkah, K Barvanje povezav grafa (kolesa) na petih točkah, W Barvanje povezav Petersenovega grafa
6 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, 2017 VI Zahvala Zahvaljujem se mentorju izr. prof. dr. Martinu Milaniču, za vso strokovno pomoč, čas in trud, ki ga je vložil v času pisanja magistrskega dela. Posebno se zahvaljujem staršem in sestri za neizmerno podporo v teku mojega študija.
7 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, 2017 VII Seznam kratic idr. in drugi itd. in tako dalje oz. oziroma npr. na primer t.i. tako imenovani tj. to je
8 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Uvod Predvsem zaradi znamenitega problema štirih barv iz leta 1852 se je področje barvanja grafov razvilo v eno najbolj priljubljenih podpodročij teorije grafov. Tako imenovana kromatična teorija grafov raziskuje povezave med klasičnimi koncepti teorije grafov in številnimi različicami barvanj grafov. Na tem področju je bilo narejenega že veliko. Osrednji probem, ki ga študira kromatična teorija grafov, je določitev najmanjšega števila barv točkam grafa, tako da bodo sosednje točke imele različno barvo. Skozi leta so se razvile različne vrste barvanj grafov: poleg barvanja točk tudi seznamska barvanja in barvanja povezav. Pri točkovnem barvanju barvamo točke tako, da poljubni dve sosednji točki ne dobita enake barve. Pri seznamskem barvanju vsaki točki priredimo seznam razpoložljivih barv namesto univerzalnega seznama barv, ki so na voljo za vse točke. Pri barvanju povezav barvamo povezave grafa, tako da poljubni dve sosednji povezavi dobita različno barvo. Magistrsko delo je teoretične narave. Najprej bomo opisali osnovne pojme iz teorije grafov, nato pa se bomo osredotočili na najpomembnejša koncepta s področja kromatične teorije grafov: kromatično število grafa in kromatični indeks grafa. Namen magistrskega dela je torej poglobiti se v analizo teoretičnih vsebin dveh vrst barvanj grafov, točkovnih in povezavnih. Podan bo pregled temeljnih rezultatov s področij točkovnih in povezavnih barvanj grafov. Rešitve samostojno rešenih nalog iz knjige Bondyja in Murtyja [3] bomo prikazali v obliki trditev z dokazi. Poleg tega bomo predstavili še nekaj zgledov, ki se navezujejo na osnovne pojme obravnavanih tem. Na začetku magistrske naloge bomo predstavili nekaj osnovnih definicij in pojmov s področja teorije grafov. Nato bomo nadaljevali s poglavjem o kromatičnem številu. Opisali bomo požrešno metodo barvanja grafov ter barvanje digrafov. Obravnavali bomo kritične grafe, grafe velike ožine in velikega kromatičega števila ter popolne grafe. Nato bomo nadaljevali s poglavjem o kromatičnem indeksu grafa. Nazadnje bomo opisali povezavno barvanje dvodelnih grafov, Vizingov izrek in zaključili s seznamskim barvanjem povezav. Metode raziskovanja, ki smo jih uporabili pri pisanju magistrskega dela, so: analiza strokovne literature (vključno s sintezo rezultatov in poenotenjem oznak in strokovnih
9 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, izrazov), deskriptivna metoda (opisovali smo ter razlagali s pomočjo uporabe strokovne literature), pri samostojnem reševanju nalog pa smo uporabili standardne metode dokazovanja v teoriji grafov, torej metodo indukcije, metodo dokazovanja s protislovjem, ekstremalnost. Cilj magistrskega dela je, da po analizi literature o točkovnih in povezavnih barvanjih grafov prikažemo pregled izbranih, ključnih rezultatov s področja. Pri tem bomo pokazali poznavanje temeljnih konceptov in rezultatov iz teorije grafov, s posebnim poudarkom na kromatični teoriji grafov.
10 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Osnovne definicije Preden preidemo na glavno temo magistrske naloge, moramo najprej definirati nekaj osnovnih pojmov. Glavni vir za to poglavje so knjige [3, 36, 37]. Graf G je urejen par (V, E), sestavljen iz množice točk, V = V (G) in množice povezav, E = E(G). Povezave so definirane kot (neurejeni) pari točk. Povezavo e = {u, v} lahko skrajšano zapišemo tudi kot uv, kjer u in v imenujemo krajišči povezave e. Rečemo, da sta točki u, v V (G) grafa G sosednji, če je (neurejen) par {u, v} element množice povezav E(G). Število povezav, ki imajo točko v za krajišče, imenujemo stopnja točke v in označimo z d G (v). Največjo stopnjo točke grafa G označimo z (G), najmanjšo pa z δ(g). Množico vseh sosedov točke v označimo z N(v) in jo imenujemo soseščina točk e v. Množico vseh povezav, incidenčnih s točko v, pa označimo z (v). Zanka je povezava, ki ima obe krajišči v isti točki. Večkratne povezave so take povezave (dve ali več), ki povezujejo isti par točk. Multigrafi so grafi, kjer so dovoljene tudi večkratne povezave in zanke. V multigrafu G označimo z µ(g) večkratnost povezav, tj. največje število večkratnih povezav med poljubnima dvema točkama multigrafa. V literaturi so grafi pogosto imenovani enostavni grafi, multigrafi pa kot grafi. V magistrskem delu so obravnavani le grafi, razen poglavja 5, kjer so obravnavani multigrafi brez zank. Graf G = (V, E) tako lahko označuje tudi multigraf brez zank, pri tem je E multimnožica, posamezne povezave se lahko pojavijo več kot enkrat. Graf H = (V (H), E(H)) je podgraf grafa G = (V (G), E(G)) natanko tedaj, ko je V (H) V (G) in E(H) E(G). Graf H je induciran podgraf grafa G, če ima na svojih točkah vse iste povezave kot graf G. Rečemo, da sta grafa G in H izomorfna, če obstaja taka bijektivna preslikava f : V (G) V (H), da velja: xy E(G), če in samo če f(x)f(y) E(H). Naj bosta x 0, x n V (G) točki grafa G. Potem imenujemo zaporedje povezav x 0 x 1, x 1 x 2,..., x n 1 x n grafa G sprehod med točkama x 0 in x n. Pot P v grafu je sprehod, v katerem so vse točke različne. Poleg tega dopuščamo tudi trivialno pot, tj. pot, ki sestoji iz ene same točke. Dolžina poti je število povezav v poti. Dolžino najkrajše poti med točkama u in v imenujemo razdalja med točkama in jo označimo z d G (u, v) ali d(u, v), če je razvidno, za kateri graf gre. Sklenjen sprehod je sprehod, v katerem sta prva in zadnja točka enaki. Cikel v grafu pa je sklenjen sprehod, v katerem so vse točke, razen prve in zadnje, različne. Graf G je povezan, če za poljubni dve točki iz
11 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, grafa G obstaja pot iz ene točke v drugo, sicer je nepovezan. Komponente grafa G so njegovi maksimalni povezani podgrafi. Komplement grafa G je graf G, ki ga dobimo iz G tako, da ohranimo točke V (G) = V (G), dve različni točki pa sta povezani v grafu G natanko tedaj, ko nista povezani v grafu G. Unija grafov G 1 in G 2 je graf G (G = G 1 G 2 ), za katerega velja V (G) = V (G 1 ) V (G 2 ) in E(G) = E(G 1 ) E(G 2 ). cikla. Ožina grafa G je najmanjše število točk v ciklu v grafu G, oz.velikost najmanjšega Prirejanje M je množica povezav grafa G, ki nimajo skupnih krajišč oz. noben par povezav množice M nima skupnega krajišča. Prirejanje M je popolno, če je vsaka točka grafa G krajišče povezave množice M. K n je poln graf na n točkah, tj. graf, v katerem je vsak par različnih točk povezan z natanko eno povezavo. Število povezav v polnem grafu K n je enako ( n 2). P n je pot na n točkah, tj. graf, ki ima množico točk V (P n ) = {v i ; i = 1,..., n} in množico povezav E(P n ) = {v i v i+1 ; i = 1,..., n 1}. Z oznako C n označimo cikel na n točkah, tj. graf, ki ima množico točk V (C n ) = V (P n ) in množico povezav E(C n ) = E(P n ) {v 1 v n }. Dolžina cikla je enaka številu točk v ciklu. Če je število točk v ciklu liho (oz. sodo), bomo govorili o lihih (oz. sodih) ciklih. Cikel, ki gre skozi vse točke grafa, imenujemo Hamiltonov cikel. Pot, ki gre skozi vse točke grafa, imenujemo Hamiltonova pot. Graf brez ciklov se imenuje gozd. Če je gozd povezan graf, mu bomo rekli drevo. Graf G je dvodelen, če lahko njegovo množico točk razdelimo na dve podmnožici X in Y, tako, da ima vsaka povezava eno krajišče v X in eno v Y. Dvodelen graf označimo z G[X, Y ]. Poln dvodelen graf K m,n je graf definiran na m točkah iz ene množice in n točkah iz druge množice, pri čemer velja, da so točke iz prve povezane s točkami iz druge množice. Kolo imenujemo graf W n, ki je spoj cikla C n in točke brez povezav, K 1, torej W n = C n K 1. Graf W n ima n + 1 točk. Rečemo, da je graf G n-delen, kjer je n 2, če lahko množico točk V (G) razdelimo na n disjunktnih podmnožic V 1, V 2,..., V n, kjer je V (G) = n i=1 V i, tako da velja: če je uv E(G) in u V i, v V j, potem je i j. Particija množice X je družina paroma disjunktnih (običajno nepraznih) množic, katerih unija je X. Neodvisna množica točk grafa G je taka množica S G, za katero velja, da noben par točk iz množice S ni soseden v grafu G. Neodvisnostno število grafa G, α(g), je velikost največje neodvisne množice grafa G. Klika v grafu G je množica paroma povezanih točk. število grafa G. Število točk v največji kliki označimo z ω(g) in ga imenujemo klično Točkoven prerez grafa G je taka množica točk, da z odstranitvijo
12 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, teh točk postane graf nepovezan. Prerezna klika je točkoven prerez, ki je tudi klika. Prerezna točka je prerezna klika z eno samo točko. Graf je neločljiv, če je povezan in nima prereznih točk. Za nenegativno število k pravimo, da je graf G k-regularen, če je d G (u) = k za vse u V (G). Regularen graf je graf, ki je k-regularen za neko število k. Kubičen graf je graf, kjer imajo vse točke stopnjo 3. Graf je sebi-komplementaren, če je izomorfen svojemu komplementu. Naj bo M prirejanje grafa G. M-alternirajoča pot G je taka pot, kjer se povezave alternirajo (izmenjujejo) v M in E \ M. Če niti začetna niti končna točka nista pokriti z M, imenujemo pot M-naraščajoča pot. Naj bo G = (V, E) graf. Njegov presečni graf je tak graf, za katerega velja, da je E množica točk, dve točki v E pa sta sosednji, če je njun presek neprazen; z drugimi besedami, dve povezavi sta sosednji, če imata skupno krajišče. Tak graf imenujemo tudi povezavni graf grafa G in ga označimo z L(G). Usmerjen graf D (ali digraf) je definiran kot urejen par (V, A), sestavljen iz množice točk V = V (G) in množice (usmerjenih) povezav A = A(D). Velja naslednje: če za točki u, v V (D) urejen par (u, v) A(D), potem rečemo, da je povezava uv usmerjena od točke u k točki v (oz. da gre iz točke u v točko v). Če v digrafu D zamenjamo vse usmerjene povezave z ustreznimi neusmerjenimi povezavami, dobimo graf, ki ga imenujemo temeljni graf digrafa D. Zaporedje k usmerjenih povezav iz množice usmerjenih povezav A(D) oblike v 0 v 1, v 1 v 2,..., v k 1 v k imenujemo usmerjen sprehod dolžine k v digrafu D oziroma sprehod od točke v 0 do točke v k. Če so vse usmerjene povezave in vse točke sprehoda različne, sprehod imenujemo usmerjena pot od točke v 0 do točke v k. Rečemo, da je digraf D povezan, če je njegov temeljni graf povezan, sicer pa je nepovezan. Če v digrafu D obstaja usmerjena pot med poljubnim urejenim parom točk, rečemo, da je digraf D krepko povezan. Usmeritev neusmerjenega grafa je digraf, ki ga dobimo z dodelitvijo smeri vsaki povezavi. Na ta način lahko poljuben neusmerjen graf pretvorimo v usmerjen graf. Turnir je poljubna usmeritev polnega grafa, t.j. digraf, da za poljubni različni točki u, v velja, da je natanko ena izmed uv in vu usmerjena povezava. Če za poljubne točke u, v in w velja, da je uw usmerjena povezava, kadarkoli sta tako uv kot vw usmerjeni povezavi, rečemo, da je turnir tranzitiven. V usmerjenem grafu je treba ločiti med izhodno stopnjo točke x (število povezav, ki se pričnejo v točki x), ki jo označujemo z d + (x) in njeno vhodno stopnjo (število povezav, ki se končajo v točki x), ki jo označujemo z d (x). Izvirna točka (izvor) je točka z vhodno stopnjo 0 (d (v) = 0), ponor pa je točka z izhodno stopnjo 0 (d + (v) = 0). Največjo vhodno stopnjo označimo z, največjo izhodno stopnjo pa z +. Jedro digrafa D je taka neodvisna množica S, da ima vsaka točka digrafa D S
13 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, povezavo do neke točke v množici S. Dirichletov princip pravi, če n predmetov razporedimo v r škatel, pri čemer je n > r, potem vsaj ena od škatel vsebuje več kot en predmet (glej npr. [12]). Lema 2.1 (Lema o rokovanju). Vsota stopenj vseh točk poljubnega multigrafa brez zank je enaka dvakratniku števila vseh povezav v multigrafu. Učinkovitost algoritma oz. njegovo časovno zahtevnost lahko izrazimo s številom korakov, ki jih algoritem potrebuje za reševanje problema. Če za odločitveni problem obstaja polinomski algoritem, ki za dano rešitev preveri, ali je rešitev ustrezna, se odločitveni problem nahaja v razredu NP. V razredu NP obstaja posebna podmnožica problemov, NP-polni problemi. Za NP-polne probleme velja, da če bi obstajal polinomski algoritem za reševanje enega od njih, potem bi lahko v polinomskem času rešili katerikoli problem iz množice NP. Preden preidemo na pojem barvanja grafov, si oglejmo nekaj zgledov, vezanih na nekatere zgoraj definirane pojme. Zgledi 1. Naj bo graf G = (V, E) definiran na množici točk V = {v 1, v 2, v 3, v 4, v 5, v 6 } z množico povezav E = {{v 1, v 2 }, {v 1, v 5 }, {v 2, v 3 }, {v 2, v 5 }, {v 3, v 4 }, {v 4, v 5 }, {v 4, v 6 }} (glej sliko 1). Analizirajmo soseščino točk, največjo stopnjo točke in najmanjšo stopnjo točke. Slika 1: Graf na šestih točkah.
14 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Soseščina točk N(v 1 ) = {v 2, v 5 } N(v 2 ) = {v 1, v 3, v 5 } N(v 3 ) = {v 2, v 4 } N(v 4 ) = {v 3, v 5, v 6 } N(v 5 ) = {v 1, v 2, v 4 } N(v 6 ) = {v 4 } Največja stopnja točke Točke največje stopnje so v 2, v 4 in v 5. (G) = 3. Najmanjša stopnja točke Točka v 6 ima najmanjšo stopnjo. d G (v 6 ) = Naj bo graf G definiran na množici točk V (G) = {v 1, v 2, v 3, v 4, v 5 } z množico povezav E(G) = {{v 1, v 2 }, {v 2, v 3 }, {v 3, v 4 }, {v 4, v 5 }, {v 5, v 1 }}. Očitno je graf G cikel C 5. Naj bo podgraf H definiran na množici točk V (H) = {v 1, v 2, v 3, v 4 } z množico povezav E(H) = {{v 1, v 2 }, {v 2, v 3 }, {v 3, v 4 }}. Opazimo, da je H pot P 4. Slika 2: Cikel na petih točkah, C 5. Slika 3: Pot na štirih točkah, P 4.
15 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Podgraf H je induciran podgraf grafa G, ki ga dobimo z odstranitvijo ene točke v grafu G. 3. Oglejmo si zgleda za neodvisnostno število in klično število dveh grafov, in sicer ciklov, na sedmih in osmih točkah. (a) Cikel na sedmih točkah, C 7, ima neodvisnostno število enako 3, saj je velikost največje neodvisne množice enaka 3. Njegovo klično število pa je enako 2, saj je velikost največje klike enaka 2. S simboli zapisano: α(c 7 ) = 3 in ω(c 7 ) = 2. Klike: klike velikosti 0: {} (prazna množica) klike velikosti 1: {v 1 },..., {v 7 }; klike velikosti 2: {v 1, v 2 }, {v 2, v 3 },..., {v 7, v 1 }. Največje neodvisne množice: {v 1, v 3, v 5 }, {v 2, v 4, v 6 }, {v 3, v 5, v 7 }, {v 4, v 6, v 1 }, {v 5, v 7, v 2 }, {v 6, v 1, v 3 }, {v 7, v 2, v 4 }. Slika 4: Cikel na sedmih točkah, C 7.
16 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, (b) Cikel na osmih točkah, C 8, ima neodvisnostno število enako 4, saj je velikost največje neodvisne množice enaka 4. Njegovo klično število pa je enako 2, saj je velikost največje klike enaka 2. S simboli zapisano: α(c 8 ) = 4 in ω(c 8 ) = 2. Klike: klike velikosti 0: {} (prazna množica) klike velikosti 1: {v 1 },..., {v 8 }; klike velikosti 2: {v 1, v 2 }, {v 2, v 3 },..., {v 8, v 1 }. Največji neodvisni množici sta dve: {v 1, v 3, v 5, v 7 } in {v 2, v 4, v 6, v 8 }. Slika 5: Cikel na osmih točkah, C 8.
17 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Kromatično število grafa V tem poglavju bomo obravnavali koncept barvanja točk grafa. poglavje so knjige [3, 33, 36, 37]. Glavni viri za to 3.1 Osnovne definicije in zgledi Naj bo G = (V, E) graf in k N, kjer N = {1, 2, 3,...}. Rečemo, da je k-barvanje grafa G preslikava c : V (G) S, kjer je S množica k barv, {1, 2,..., k}. k-barvanje je dodelitev k barv točkam grafa G. Barvanje c je pravo, če dvema sosednjima točkama ni dodeljena ista barva. Po drugi strani lahko na k-barvanje gledamo tudi kot na particijo {V 1, V 2,..., V k } množice V, kjer V i označuje (morda prazno) množico točk, katerim je dodeljena barva i. Množice V i imenujemo barvni razredi. Pravo k-barvanje je torej k-barvanje, v katerem je vsak razred neodvisna množica. V tem poglavju se bomo osredotočili samo na prava barvanja. V nadaljevanju bomo uporabili namesto izraza pravo barvanje izraz barvanje in namesto izraza pravo k-barvanje izraz k-barvanje. Graf G je k-obarvljiv, če ima k-barvanje. Graf je 1- obarvljiv natanko takrat ko je brez povezav. 2-obarvljivi grafi pa so natanko dvodelni grafi. Najmanjše število k, za katerega je graf G k-obarvljiv, imenujemo kromatično število grafa G in ga označimo s χ(g). Če je χ(g) = k, je graf G k-kromatičen. Pravo k- barvanje k-kromatičnega grafa je optimalno barvanje. Na primer, trikotnik (cikel na treh točkah, C 3 ) in vsi lihi cikli so 3-obarvljivi in niso 2-obarvljivi, ker niso dvodelni. Njihovo kromatično število je enako 3, torej so 3-kromatični. Poln graf K n ima kromatično število n, saj ne obstajata dve točki, ki bi lahko imeli enako barvo. Splošneje, vsak graf G zadošča neenakosti: χ(g) V (G) α(g), (3.1) saj je vsak razred barv neodvisna množica in ima torej največ α(g) točk. Problem barvanja grafov se pojavi v številnih praktičnih problemih, v katerih je potrebna razdelitev množice objektov v skupine, tako da so člani vsake skupine med
18 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, seboj usklajeni po nekem kriteriju. Podali bomo dva tovrstna primera [3]. Primer 3.1. Razporejanje izpitov. Študenti neke univerze imajo v študijskem letu izpite pri vseh predmetih, ki jih poslušajo. Izpiti iz različnih predmetov ne morejo biti istočasno, če so pri teh predmetih skupine istih študentov. Kako lahko razporedimo izpite v čim manj možnih vzporednih sej? Da bi uskladili datume oz.ustvarili takšen razpored, konstruiramo graf G, katerega množica točk je množica vseh predmetov; povezavo dodamo, če imata dva predmeta skupnega študenta (saj v tem primeru izpita ne moreta potekati sočasno). Neodvisne množice grafa G tedaj predstavljajo skupine predmetov brez konfliktov. Tako je iskano najmanjše število vzporednih sej ravno kromatično število grafa G. Primer 3.2. Skladiščenje kemikalij. Podjetje proizvaja n kemikalij, ki jih označimo s C 1, C 2,..., C n. Nekateri pari teh kemikalij so nezdružljivi in povzročijo eksplozijo, če kemikaliji v paru prideta v stik druga z drugo. Kot previdnostni ukrep želi podjetje razdeliti svoje skladišče v oddelke in shraniti nezdružljive (nekompatibilne) kemikalije v različne oddelke. Kolikšno je najmanjše število oddelkov, na katere bo skladišče razdeljeno? Dobimo graf G na množici točk {v 1, v 2,..., v n }, kjer sta točki v i in v j povezani, če in samo če sta kemikaliji C i in C j nekompatibilni. Najmanjše število oddelkov, na katere bo skladišče razdeljeno, je enako kromatičnemu številu grafa G. Če je H podgraf grafa G in je graf G k-obarvljiv, potem je tak tudi H. Velja χ(h) χ(g). Če graf G vsebuje kopijo polnega grafa K r, potem je χ(g) r. Sklepamo, da za vsak graf G velja naslednja spodnja meja za kromatično število: χ(g) ω(g), (3.2) saj morajo biti točke klike obarvane z različnimi barvami. Lihi cikli dolžine pet ali več za katere velja, da je ω(g) = 2 in χ(g) = 3 nam dajo videti, da meja (3.2) za kromatično število ni vselej dosežena z enakostjo. Ta meja je lahko celo poljubno slaba. Kot bo vidno v nadaljevanju, obstajajo grafi s poljubno veliko ožino in kromatičnim številom. Oglejmo si nekaj zgledov za kromatično število grafa. Zgled 3.3. Naj bo N = {1, 2, 3,...} množica barv, ki jih bomo uporabili za barvanje grafov. Podano bo kromatično število za naslednje grafe:
19 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Poln dvodelen graf z točkami: G = K 1,5. Najmanjše število barv, potrebnih za barvanje tega grafa, je enako 2. Slika 6: Barvanje točk polnega dvodelnega grafa z točkami, K 1,5. Opazimo, da graf vsebuje kliko velikosti 2, od koder po (3.2) sledi χ(k 1,5 ) 2. Barvanje grafa z 2 barvama je podano na sliki 6; od tod sledi χ(k 1,5 ) 2. Cikel na petih točkah: G = C 5 Najmanjše število barv, potrebnih za barvanje tega grafa, je enako 3. Slika 7: Barvanje točk cikla na petih točkah, C 5. Ker cikel C 5 ni dvodelen, je χ(c 5 ) 3. Barvanje grafa s 3 barvami je podano na sliki 7; od tod sledi χ(c 5 ) 3.
20 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Poln graf na šestih točkah: G = K 6 Najmanjše število barv, potrebnih za barvanje tega grafa, je enako 6. Slika 8: Barvanje točk polnega grafa na šestih točkah, K 6. Opazimo, da graf vsebuje kliko velikosti 6, od koder po (3.2) sledi χ(k 6 ) 6. Barvanje grafa s 6 barvami je podano na sliki 8; od tod sledi χ(k 6 ) 6. Graf - kolo na petih točkah: G = W 4 Najmanjše število barv, potrebnih za barvanje tega grafa, je enako 3. Slika 9: Barvanje točk grafa (kolesa) na petih točkah, W 4. Opazimo, da graf vsebuje kliko velikosti 3, od koder po (3.2) sledi χ(w 4 ) 3. Barvanje grafa s 3 barvami je podano na sliki 9; od tod sledi χ(w 4 ) 3.
21 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Osnovni rezultati o kromatičnem številu grafa Ker je graf 2-obarvljiv, če in samo če je dvodelen, obstaja algoritem polinomske časovne zahtevnosti za odločanje, ali je dani graf 2-obarvljiv. Nasprotno pa je že problem 3- obarvljivosti NP-poln. Iz tega sledi, da je problem iskanja kromatičnega števila grafa NP-težek. Pri praktičnih primerih moramo biti zato zadovoljni z učinkoviti hevrističnimi postopki, ki izračunajo razmeroma dobre rešitve. Najbolj naraven pristop je barvanje točk s požrešno metodo, kot sledi v nadaljevanju. Hevristika: Požrešno (hevristično) barvanje Vhodni podatki: graf G Izhodni podatki: barvanje grafa G 1. Razvrsti točke grafa G v linearno zaporedje: v 1, v 2,..., v n. 2. Pobarvaj točke eno za drugo v tem vrstnem redu in dodeli točki v i najmanjše naravno število, ki še ni dodeljeno eni od sosednjih točk, ki so že obarvane. Treba je poudariti, da je število barv, ki je uporabljeno pri tem požrešnem hevrističnem barvanju, zelo odvisno od vrstnega reda, ki smo ga izbrali za točke. Na primer, če je graf K n,n poln dvodelen graf z množicama X := {x 1, x 2,..., x n } in Y := {y 1, y 2,..., y n }, potem bi dvodelen graf G[X, Y ], ki ga dobimo iz tega grafa z brisanjem popolnega prirejanja {x i y i : 1 i n} potreboval n barv, če bi bile točke razporejene v vrstnem redu x 1, y 1, x 2, y 2,..., x n, y n. Po drugi strani pa bi bili potrebni le dve barvi, če bi bile točke razporejene v vrstnem redu x 1, x 2,..., x n, y 1, y 2,..., y n ; dejansko vedno obstaja vrstni red, ki določa optimalno barvanje. Problem je, da je težko vedeti vnaprej, katera zaporedja bodo vodila do optimalnih barvanj. Kljub temu pa število barv, ki je uporabljeno pri požrešnem hevrističnem barvanju, ni nikoli večje od (G) + 1, ne glede na vrstni red, po katerem so razporejene točke. Kadar je točka v ravno pred barvanjem, število njenih sosednjih točk, ki so že obarvane, ni večje od njene stopnje d G (v), in to ni večje od največje stopnje, (G). Tako bo ena izmed barv 1, 2,..., (G) + 1 vsekakor na voljo za točko v. Sklepamo torej, da za vsak graf G velja naslednja zgornja meja za kromatično število: χ(g) (G) + 1. (3.3) Vsak k-kromatičen graf ima torej točko stopnje vsaj k 1. k-kromatičen graf ima vsaj k točk stopnje vsaj k 1. Velja še več: vsak Trditev 3.4 (Bondy in Murty [3], naloga a). Naj bo G k-kromatičen graf in naj bo c poljubno k-barvanje grafa G. Tedaj za vsako barvo i obstaja točka barve i, ki je sosednja točkam vseh drugih barv.
22 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Dokaz. Dokazujemo s protislovjem. Naj bo (G, c) protiprimer trditve, torej, c je k- barvanje k-kromatičnega grafa G, za katerega ni res, da za vsako barvo i obstaja točka barve i, ki je sosednja točkam vseh drugih barv. Obstaja torej taka barva i, da za vsako točko v barve i obstaja taka barva j(v) i, da nobena točka sosednja s točko v ni barve j. Naj bo c : V (G) {1,..., k} \ {i} preslikava, definirana s predpisom c(v); c (v) = j(v); c(v) i sicer Opazimo, da je c (v) barvanje grafa G s k 1 barvami, kar je protislovje z dejstvom, da je graf G k-kromatičen. Posledica 3.5 (Bondy in Murty [3], naloga b). Vsak k-kromatičen graf ima vsaj k točk stopnje vsaj k 1. Dokaz. Po trditvi 3.4 vemo, da za poljubno k-barvanje k-kromatičnega grafa G za vsako barvo i obstaja točka barve i, ki je sosednja točkam vseh drugih barv. Vzemimo vsako tako točko. Skupno imamo k takih točk in vsaka od njih ima stopnjo vsaj k 1. Meja (3.3) za kromatično število ne poda nobene informacije o tem, koliko točk vsake barve obstaja v ( (G) + 1) barvanjih. Hajnal in Szemerédi [19] sta podkrepila neenakost χ(g) (G) + 1 in sta pokazala, da vsak graf G dopušča uravnoteženo ( (G) + 1) barvanje, tj., barvanje, v katerem se velikosti barvnih razredov razlikujejo za kvečjemu ena. Brooks [4] je pokazal, da v primeru povezanih grafov neenakost χ(g) (G) + 1 velja z enakostjo samo za polne grafe in lihe cikle. Zgled 3.6. Oglejmo si zgled za polne grafe in lihe cikle. 1. Za polne grafe velja: χ(k n ) = n in (K n ) = n 1. Torej χ(k n ) > (K n ). 2. Za lihe cikle velja: χ(c 2n+1 ) = 3 in (C 2n+1 ) = 2. Torej χ(c 2n+1 ) > (C 2n+1 ). Naslednjo lemo bomo uporabili v dokazu Brooksovega izreka (izreka 3.8). Lema 3.7 (Chartrand in Kronk [6]). Če je vsako DFS drevo grafa G Hamiltonova pot s korenom v enem od njenih krajišč, potem je graf G cikel, poln graf ali poln dvodelen graf K n,n. Izrek 3.8 (Brooksov izrek [4]). Naj bo G povezan graf, ki ni ne lih cikel ne poln graf. Potem je χ(g) (G).
23 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Dokaz, povzet po Bondyju in Murtyju [3]. Predpostavimo najprej, da graf G ni regularen. Naj bo x točka stopnje δ in T vpeto drevo grafa G, ki ima koren v točki x. Pobarvamo točke z barvami 1, 2,...,, v skladu z metodo požrešnega hevrističnega barvanja, tako da na vsakem koraku izberemo list poddrevesa T, ki ga inducirajo točke, ki še niso obarvane, in dodelimo tem listom najmanjšo možno barvo, dokler ne pridemo do konca, do korena x drevesa T. Ko je točka v x tik pred barvanjem, je sosednja v T vsaj eni nepobarvani točki, in je torej sosednja v grafu G kvečjemu d G (v) 1 1 obarvanim točkam. Dodeljena ji je torej ena od barv 1, 2,...,. Na koncu, ko je točka x pobarvana, ji je tudi dodeljena ena od barv 1, 2,...,, ker d G (x) = δ 1. Požrešno hevristično barvanje tako proizvede -barvanje grafa G. Predpostavimo sedaj, da je G regularen graf. Če ima graf G prererezno točko x, potem je G = G 1 G 2, kjer sta G 1 in G 2 povezana in V (G 1 ) V (G 2 ) = {x}. Ker je stopnja točke x v grafu G i manjša od (G), nobeden od podgrafov G i ni regularen, torej χ(g i ) (G i ) = (G), i = 1, 2, in χ(g) = max{χ(g 1 ), χ(g 2 )} (G). Lahko torej privzamemo, da je graf G neločljiv. Če je vsako DFS drevo grafa G Hamiltonova pot s korenom v enem od njenih krajišč, potem iz leme 3.7 in predpostavke izreka zaključimo, da je G bodisi sod cikel bodisi poln dvodelen graf, sledi torej χ(g) = 2 (G). Predpostavimo sedaj, da je T DFS drevo grafa G, ki ni pot. Naj bo x točka drevesa T z vsaj dvema otrokoma, y in z. Ker je G neločljiv, sta tako G y kot G z povezana. Tako sta y in z bodisi lista drevesa T ali pa imata ustrezne potomce, ki so povezani s predniki točke x. Iz tega sledi, da je G := G {y, z} povezan. Oglejmo si DFS drevo T s korenom x v grafu G. Z barvanjem točk y in z z barvo 1 in točk drevesa T z upoštevanjem požrešnega hevrističnega barvanja, kot zgoraj, ki se konča s korenom x, dobimo -barvanje grafa G. Trditev 3.9 (S.A. Burr [5]; Bondy in Murty [3], naloga ). Naj bo graf G = G 1 G 2. Tedaj velja χ(g) k 1 k 2 natanko tedaj, ko je χ(g i ) k i, i = 1, 2. Dokaz. Naj bo C = {(i, j) N 2 : 1 i k 1, 1 j k 2 } množica barv. Očitno je C = k 1 k 2. Naj bo c : V (G) C barvanje grafa G. Naj bo G i graf, kjer za i = 1, 2 velja: V (G i ) = V (G) in E(G i ) = {uv E(G) : (c(u)) i (c(v)) i }. Tedaj je: (a) G = G 1 G 2, saj za vsako povezavo uv E(G) obstaja i {1, 2}, da velja uv E(G i ). Ker je c pravo barvanje grafa G, namreč velja c(u) c(v). Tedaj velja (c(u)) i (c(v)) i ) za nek i {1, 2}, kar je ekvivalentno pogoju, da je uv E(G i ) za nek i {1, 2}.
24 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, (b) χ(g i ) k i za i = 1, 2: za vsak j {1,..., k i } je množica {u V (G) : (c(u)) i = j} neodvisna v grafu G i. Sledi χ(g i ) k i. Pokažimo še implikacijo v drugo smer. Naj bo {I1, i..., Ik i i } particija množice V (G i ) na k i neodvisnih množic v G i, i = 1, 2. Za vse (i, j) {1,..., k 1 } {1,..., k 2 } naj bo I ij = Ii 1 Ij 2. Tedaj je {I ij : i = 1,..., k 1, j = 1,..., k 2 } particija množice V (G) na k 1 k 2 neodvisnih množic grafa G: (i) Vsaka točka v V (G) se pojavi v natanko eni od množic Ii 1 in v natanko eni od množic Ij 2, torej se pojavi tudi v natanko eni od množic Ii 1 Ij 2 = I ij. (ii) Vsaka od množic I ij je neodvisna v grafu G. Denimo, da množica I ij vsebuje par povezanih točk, recimo uv E(G). Potem bi imeli uv E(G k ) za nek k {1, 2} (ker je G = G 1 G 2 ). Brez škode za splošnost lahko predpostavimo k = 1. Opazimo, da je {u, v} Ii 1, kar pa je v protislovju z dejstvom, da je Ii 1 neodvisna množica v G 1. Dokazali smo torej, da obstaja particija množice točk grafa G na k 1 k 2 neodvisnih množic. Graf G je torej k 1 k 2 -obarvljiv, kar smo želeli dokazati. Graf je k-degeneriran, če obstaja taka linearna razvrstitev množice točk, V (G) = {v 1,..., v n }, da velja: za vsak i {1,..., n} je d Gi (v i ) k, kjer je G i = G[{v 1,..., v i }] [30]. Trditev 3.10 (Bondy in Murty [3], naloga a). Graf G je k-degeneriran, če in samo če ima vsak podgraf točko stopnje največ k. Dokaz. Naj bo G k-degeneriran graf. Dokazujemo s protislovjem. Predpostavimo, da obstaja podgraf H, za katerega velja, da nima točke stopnje največ k. Ker je G k- degeneriran graf, obstaja taka razvrstitev točk od v 1 do v n, da je za vsak i {1,..., n}, stopnja točke v i v grafu G i omejena z d Gi (v i ) k, kjer je G i = G[{v 1,..., v i }]. Naj bo j = max{i : 1 i n, v i V (H)}. Definicija indeksa j implicira, da je H G j, kar nadalje implicira, da je točka v j točka podgrafa H stopnje največ k. Dobimo torej: d H (v j ) d Gj (v j ) k, kar pa ni možno, saj je v protislovju s predpostavko. Pokažimo še implikacijo v drugo smer. Dokazujemo z indukcijo po n = V (G). Za n = 1 je trditev očitna. Naj bo sedaj n > 1. Predpostavimo, da ima vsak podgraf grafa G točko stopnje največ k. Ker je G podgraf samega sebe, bo tudi v grafu G
25 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, obstajala točka stopnje največ k. Recimo, da je to točka v n. Naj bo G = G v n. Naj bo H poljuben podgraf grafa G. Ker je H G, obstaja v grafu H točka stopnje največ k. Po indukcijski predpostavki je G k-degeneriran, torej imamo tako zaporedje v 1,..., v n 1 točk grafa G, da za vsak i {1,..., n 1} velja d G i (v i ) k, kjer je G i = G [{v 1,..., v i }]. Ker je G i = G i, iz tega izhaja, da je graf G k-degeneriran. Trditev 3.11 (Bondy in Murty [3], naloga b). Graf G je 1-degeneriran natanko tedaj, ko je gozd. Dokaz. Naj bo G 1-degeneriran graf, za katerega velja, da ni gozd (je cikličen). Torej v grafu G obstaja 2-regularen podgraf (ima točke stopnje 2), kar je v protislovju s trditvijo Pokažimo še implikacijo v drugo smer. Vsak gozd vsebuje točko stopnje največ 1. Ker je vsak podgraf gozda tudi gozd, je po trditvi 3.10 vsak gozd 1-degeneriran. Trditev 3.12 (Bondy in Murty [3], naloga c). Vsak k-degeneriran graf je (k +1)- obarvljiv. Dokaz. Točke lahko tako razvrstimo, da bo imela vsaka točka največ k povezav do točk z manjšim indeksom. Vzemimo točko z najmanjšo stopnjo v grafu, odstranimo iz grafa točko in njene povezave z ostalimi točkami in jo uvrstimo na začetek zaporedja predhodno odstranjenih točk. Ko bomo točke barvali po vrsti, bomo pri posamezni točki dobili največ k različno obarvanih sosedov, ki že imajo določeno barvo. Torej bo vsaj ena izmed k + 1 barv na voljo za barvanje trenutne točke. Torej χ(g) k + 1. Posledica 3.13 (Bondy in Murty [3], naloga d). Unija k-degeneriranega grafa in l-degeneriranega grafa je (k + 1)(l + 1)-obarvljiva. Dokaz. Iz trditve 3.9 sledi: Za k-degeneriran graf G 1 velja χ(g 1 ) k + 1 in za l- degeneriran graf G 2 bo veljalo χ(g 2 ) l + 1. Iz dejstva, da je χ(g) k 1 k 2, če in samo če je G = G 1 G 2, za χ(g i ) k i, za i = 1, 2, izhaja, da je unija k-degeneriranega in l-degeneriranega grafa (k + 1)(l + 1)-obarvljiva. Trditev 3.14 (Bondy in Murty [3], naloga a). Naj bo G graf, v katerem se katerakoli dva liha cikla sekata. Potem je χ(g) 5.
26 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Dokaz. Naj bo G = (V, E) graf, v katerem se katerakoli dva cikla sekata. Če G ne bi imel lihega cikla, bi G bil dvodelen graf, torej 2-obarvljiv in bi dobili χ(g) 2 5. Predpostavimo, da ima G vsaj en lih cikel. Naj bo C najkrajši lih cikel grafa G. Naj bo G = G V (C). Ker se lihi cikli paroma sekajo, bomo z odstranitvijo V (C) iz grafa G izbrisali vsaj eno točko vsakega lihega cikla iz grafa G. Sledi, da graf G nima lihih ciklov; je torej dvodelen. Katerikoli dvodelen graf je 2-obarvljiv, torej velja χ(g ) 2. Ker je C najkrajši lih cikel, je induciran podgraf G[V (C)] izomorfen lihemu ciklu. Posledično je χ(g[v (C)]) = χ(c) = 3. Točke grafa G lahko torej pobarvamo z 2 barvama in točke cikla C s 3 barvami, ki bodo različne od tistih dveh, uporabljenih v grafu G. Torej χ(g) χ(g V (C)) + χ(g[v (C)]) = χ(g ) + χ(c) = 5. Kneserjev graf K a:b je graf, katerega točke predstavljajo b-elementne podmnožice množice a elementov {1, 2,..., a}, dve točki Kneserjevega grafa pa sta sosednji natanko tedaj, ko sta pripadajoči množici disjunktni. Petersenov graf je K 5:2. Za G = K a:b velja: ω(g) = a. Pokažimo sedaj, da kromatično število ne more b biti večje od a 2b + 2. Trditev 3.15 (Scheinerman in Ullman [33], naloga 3.7). χ(k a:b ) a 2b + 2, če a 2b. Dokaz. Pobarvajmo točke Kneserjevega grafa na naslednji način: za vse F V (K a:b ) naj bo: c(f ) := min{min(f ), a 2b + 2}. Na ta način bomo dodelili barvo c(f ) {1, 2,..., a 2b + 2} vsaki podmnožici F ( ) [a] b (družina vseh b-elementnih podmnožic množice [a] := {1, 2,..., a}; Ka:b = K ( ) [a] b ). Če dve množici F in F pobarvamo z enako barvo, c(f ) = c(f ) = i < a 2b+2, potem ne moreta biti disjunktni, saj obe množici vsebujeta element i. Če obe množici velikosti b pobarvamo z barvo a 2b + 2, bosta tako F kot F vsebovani v množici {a 2b+2,..., a}, saj je tako minimum množice F kot F vsebovan v mnnožici {a + 2b + 2,..., a}, min(f ) a 2b + 2 in podobno za F. Ker ta množica vsebuje le 2b 1 elementov, množici ne bosta disjunktni, saj bi v nasprotnem primeru njuna unija vsebovala 2b elementov. Zgornji argument pokaže: χ(k a:b ) a 2b+2. Lovász [25] je podal globok rezultat o tem, da je zgornja meja iz trditve 3.15 dosežena z enakostjo.
27 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Barvanje digrafov Pravo barvanje točk digrafa D je definirano kot barvanje točk njegovega temeljnega grafa G, njegovo kromatično število χ(d) pa je definirano kot kromatično število χ(g) grafa G. Zakaj torej študirati barvanja digrafov? Izkaže se, da kromatično število digrafa poda zanimive informacije o njegovih poddigrafih. Naslednji izrek Gallaia [15] in Roya [32] nam pove, da imajo digrafi z visokim kromatičnim številom vedno dolge usmerjene poti. Digraf je acikličen, če nima usmerjenega cikla. Maksimalen acikličen poddigraf digrafa D = (V, A) je tak njegov vpet acikličen poddigraf D = (V, A ), da za vse a A \ A digraf D + a, definiran kot (V, A {a}) ni acikličen. Izrek 3.16 (Gallai [15] in Roy [32]). Vsak digraf D vsebuje usmerjeno pot s χ(d) točkami. Dokaz. Naj bo k število točk v najdaljši usmerjeni poti digrafa D. Naj bo D maksimalen acikličen poddigraf digrafa D. Ker je D poddigraf digrafa D, ima vsaka usmerjena pot v D največ k točk. Obarvajmo digraf D s k barvami tako, da dodelimo točki v barvo c(v), kjer je c(v) število točk najdaljše usmerjene poti v poddigrafu D s pričetkom v točki v. Pokažimo, da je to barvanje pravo. Naj bo (u, v) poljubna povezava digrafa D. Če je (u, v) povezava poddigrafa D, naj bo vp w najdaljša usmerjena pot v D s pričetkom v točki v. Potem u / V (P ), v nasprotnem primeru bi bil namreč vp uv usmerjen cikel v poddigrafu D. Tako je uvp w usmerjena u-pot v poddigrafu D, kar pomeni, da c(u) > c(v). Če (u, v) ni povezava poddigrafa D, potem D + (u, v) vsebuje usmerjen cikel, saj je poddigraf D maksimalno acikličen, torej D vsebuje usmerjeno v, u-pot P. Naj bo Q najdaljša usmerjena pot v D s pričetkom v točki u. Ker je D acikličen je V (P ) V (Q) = {u}. Torej je P Q usmerjena pot v poddigrafu D s pričetkom v točki v in posledično c(v) > c(u). V obeh primerih c(u) c(v). 3.4 Kritični grafi Ko govorimo o barvanju, je koristno preučiti lastnosti posebnega razreda grafov, ki se imenujejo barvno kritični grafi. Pravimo, da je graf G barvno kritičen, če je χ(h) < χ(g) za vsak pravi podgraf H grafa G. Tovrstne grafe je najprej raziskoval Dirac [11]. Izraz barvno kritičen bomo poenostavili s kritičen. k-kritičen graf je graf, ki je k-kromatičen in kritičen. Podgraf H grafa G je minimalno k-kromatičen, če je
28 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, k-kromatičen, noben njegov pravi podgraf pa ni k-kromatičen. Vsak minimalno k- kromatičen podgraf k-kromatičnega grafa je k-kritičen. Torej ima vsak k-kromatičen graf vsaj en k-kritičen podgraf. Oglejmo si nekaj zgledov za kritične grafe. Zgled ) Naj bo graf G = K 2. χ(g) = 2 in χ(h) 1 za vse prave podgrafe H grafa K 2. Sledi: graf K 2 je 2-kritičen. 2) Naj bo n 1 in graf G = C 2n+1. χ(g) = 3 in χ(h) 2 za vse prave podgrafe H grafa C 2n+1. Sledi: graf C 2n+1 je 3-kritičen za vse n 1. 3) Naj bo graf G = W 2n+1. χ(g) = 4 in χ(h) 3 za vse prave podgrafe H grafa W 2n+1. Sledi: graf W 2n+1 je 4-kritičen za vse n 1. Podani zgledi so k-kritični, ker je χ(h) < χ(g) = k za vsak pravi podgraf H grafa G. Če odstranimo poljubno povezavo, se kromatično število zmanjša: χ(g) = k in χ(g e) = k 1. Izrek Če je graf G k-kritičen, potem δ(g) k 1. Dokaz. S protislovjem. Recimo, da je najmanjša stopnja grafa G strogo manjša od k 1, torej δ(g) < k 1. Naj bo v V (G) točka stopnje δ(g). Ker je graf G k-kritičen, velja χ(g v) < χ(g) = k. Torej obstaja particija grafa G v na k 1 neodvisnih množic V 1, V 2,..., V k 1 (barvnih razredov). Če bi točka v imela soseda v vsaki izmed neodvisnih množic V 1, V 2,..., V k 1, bi veljalo d G (v) k 1 > δ(g), kar je protislovje. Naj bo i {1,..., k 1} tak indeks, da točka v ni sosednja nobeni točki v množici V i. Tedaj je V i {v} neodvisna množica v grafu G in je χ(g) k 1, kar je protislovje.
29 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Izrek 3.18 implicira, da ima vsak k-kromatičen graf vsaj k točk stopnje vsaj k 1, kot smo opazili že v posledici 3.5. Naj bo S točkovni prerez povezanega grafa G in naj imajo komponente grafa G S množice točk V 1, V 2,..., V t. Podgrafi G i := G[V i S] se imenujejo S-komponente grafa G. Pravimo, da se barvanja grafov G 1, G 2,..., G t ujemajo na prerezni kliki S, če je za vsak v S točki v dodeljena enaka barva v vsakem od teh barvanj. Izrek Noben kritičen graf nima prerezne klike. Dokaz. S protislovjem. Naj bo G k-kritičen graf. Predpostavimo, da ima graf G prerezno kliko S. Poimenujmo S-komponente grafa G z G 1, G 2,..., G t. Ker je G k- kritičen, je vsak G i (k 1)-obarvljiv. Poleg tega, ker je S klika, dobijo točke v S različne barve v vsakem (k 1)-barvanju grafa G i. Iz tega sledi, da obstajajo taka (k 1)- barvanja grafov G 1, G 2,..., G t, ki se ujemajo na S. Ta barvanja lahko združimo, da dobimo (k 1)-barvanje grafa G, kar je protislovje. Posledica Vsak kritičen graf je neločljiv. Po izreku 3.19, če ima k-kritičen graf 2-točkovni prerez {u, v}, potem točki u in v ne moreta biti sosednji. Rečemo, da je {u, v}-komponenta G i grafa G tipa 1, če vsako (k 1)-barvanje grafa G i dodeli enako barvo točkama u in v, in tipa 2, če vsako (k 1)-barvanje grafa G i dodeli različni barvi točkama u in v. Naj bo G graf in S V (G). Graf, dobljen s krčenjem množice S, označimo z G/S in definiramo na naslednji način: V (G S) = V (G S) {w}, kjer je w nova točka, E(G S) = E(G S) {wx : x N G (S)}. Izrek Naj bo G k-kritičen graf z 2-točkovnim prerezom {u, v} in naj bo e nova povezava, ki povezuje točki u in v. Potem: 1. G = G 1 G 2, kjer je G i neka {u, v}-komponenta grafa G tipa i, i = 1, 2, 2. Tako H 1 := G 1 + e kot H 2 := G 2 {u, v} sta k-kritična.
30 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Dokaz. 1. Ker je graf G kritičen, je vsaka {u, v}-komponenta grafa G (k 1) obarvljiva. Ne morejo obstajati (k 1)-barvanja teh {u, v}-komponent, za katere velja, da se vsa ujemajo na množici {u, v}, saj bi taka barvanja skupaj dala (k 1) barvanje grafa G. Obstajata torej dve taki {u, v}-komponenti G 1 in G 2, da se nobeno (k 1) barvanje od G 1 ne ujema z nobenim (k 1) barvanjem grafa G 2. Lahko torej predpostavimo, da je graf G 1 tipa 1 in graf G 2 tipa 2. Ker sta G 1 in G 2 različnega tipa, podgraf G 1 G 2 grafa G ni (k 1) obarvljiv. Ker je graf G kritičen, sklepamo, da G = G 1 G Ker je graf G 1 tipa 1, je H 1 k-kromatičen. Da je H 1 kritičen, lahko dokažemo tako, da pokažemo, da je za vsako povezavo f grafa H 1 podgraf H 1 f (k 1)- obarvljiv. Očitno je, da če je f = e, bo v tem primeru H 1 e = G 1. Naj bo f neka druga povezava grafa H 1. V vsakem (k 1) barvanju grafa G f dobita točki u in v različni barvi, ker je G 2 podgraf grafa G f. Zožitev takega barvanja točk na V (G 1 ) je (k 1) barvanje grafa H 1 f. Torej je H 1 k-kritičen. Na podoben način pokažemo, da je H 2 k-kritičen. Oglejmo si zgled, ki temelji na izreku Zgled Naj bo k = 3 in graf G = C 7. Naj bosta u in v poljubni točki na razdalji 3 (glej sliko 10). Tedaj je G 3-kritičen graf in {u, v} 2-točkovni prerez v G. Slika 10: Graf G = C 7 s točkama u in v. Če označimo z G 1 in G 2 {u, v}-komponenti grafa G, kjer je G 1 izomorfen poti P 5, G 2 pa poti P 4, tedaj opazimo, da je graf G i tipa i (glej sliki 11 in 12).
31 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Slika 11: Graf G 1. Slika 12: Graf G 2. Če sta H 1 in H 2 definirana kot v izreku 3.21, potem je H 1 izomorfen grafu C 5 in H 2 je izomorfen grafu C 3. Dobljena grafa H 1 in H 2 sta res 3-kritična. Trditev 3.23 (Bondy in Murty [3], naloga a). Naj bosta u in v dve točki kritičnega grafa G. Potem velja N(u) N(v). Dokaz. Dokažimo trditev s protislovjem. Naj bo G k kritičen graf. Predpostavimo, da obstajata dve točki u, v V (G), kjer u v in N(u) N(v). Ker je G k-kritičen graf (χ(g) = k), bo χ(g u) = k 1. Privzemimo, da imamo pravo barvanje grafa G u s k 1 barvami. Ker velja N(u) N(v), lahko to barvanje razširimo do pravega barvanja grafa G s k 1 barvami, in sicer tako, da obarvamo točko u z enako barvo kot točko v. Iz tega izhaja, da χ(g) = χ(g u), kar je v nasprotju z lastnostjo, da je G kritičen graf.
32 Univerza na Primorskem, Fakulteta za matematiko, naravoslovje in informacijske tehnologije, Trditev 3.24 (Bondy in Murty [3], naloga b). Ne obstaja k-kritičen graf, ki bi imel natanko k + 1 točk. Dokaz. Dokažimo trditev s protislovjem. Predpostavimo, da obstaja k-kritičen graf G, ki ima natanko k + 1 točk. Če obstaja točka stopnje, manjše od k 1, recimo ji v, jo zbrišemo. Po predpostavki bi lahko namreč pobarvali s k 1 barvami preostanek grafa, saj χ(g v) = k 1. Če vrnemo nazaj odstranjeno točko, bo ta lahko sosednja točkam, obarvanim s kvečjemu k 2 barvami. Če je stopnja točke v kvečjemu k 2, potem lahko (k 1)-barvanje grafa G v razširimo do (k 1)-barvanja grafa G. To je v protislovju s predpostavko, da je G k-kritičen. Lahko torej privzamemo, da je vsaka točka stopnje k 1 ali k. Ker ima graf G k + 1 točk in so vse točke stopnje k 1 ali k, iz tega sledi, da so v grafu G, komplementu grafa G, vse točke stopnje 0 ali 1. Torej graf G sestoji iz izoliranih točk in/ali izoliranih povezav. Po trditvi 3.23 velja da ne sme biti izoliranih povezav. Če bi namreč obstajala izolirana povezava v grafu G, med točkama u in v, bi veljalo N G (u) = N G (v), kar je v protislovju s trditvijo Torej so vse točke grafa G izolirane, kar pomeni, da je G poln graf na k + 1 točkah in posledično je χ(g) = k + 1, protislovje. 3.5 Grafi velike ožine in velikega kromatičnega števila Graf, ki vsebuje veliko kliko, ima nujno visoko kromatično število. Po drugi strani pa obstajajo grafi brez trikotnikov s poljubno visokim kromatičnim številom. Erdős [13] je uporabil verjetnostno metodo, da bi pokazal obstoj grafov s poljubno visoko ožino in kromatičnim številom. Izrek Za vsako pozitivno celo število k obstaja graf z ožino vsaj k in kromatičnim številom vsaj k. Definirajmo verjetnostni prostor slučajnih grafov G n,p, uporabljen v izreku Končen verjetnostni prostor (Ω, P) sestoji iz končne množice Ω, ki se imenuje vzorčni prostor in iz verjetnostne funkcije P : Ω [0, 1], tako da je ω Ω P(ω) = 1. Množico grafov na n točkah, G n, lahko obravnavamo kot vzorčni prostor končnega verjetnostnega prostora (G n, P). Rezultat izbire elementa G tega vzorčnega prostora glede na verjetnostno funkcijo P imenujemo naključni graf. V grafu G n,p je n število točk, p pa predstavlja verjetnost, da je poljubna povezava vsebovana v grafu G. Graf G zgradimo z naključnim povezovanjem točk, oz. tako da se za vsako povezavo naključno odločimo,
Matej Mislej HOMOMORFIZMI RAVNINSKIH GRAFOV Z VELIKIM NOTRANJIM OBSEGOM
 UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO Matematika - uporabna smer (UNI) Matej Mislej HOMOMORFIZMI RAVNINSKIH GRAFOV Z VELIKIM NOTRANJIM OBSEGOM Diplomsko delo Ljubljana, 2006 Zahvala Zahvaljujem
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO Matematika - uporabna smer (UNI) Matej Mislej HOMOMORFIZMI RAVNINSKIH GRAFOV Z VELIKIM NOTRANJIM OBSEGOM Diplomsko delo Ljubljana, 2006 Zahvala Zahvaljujem
Hipohamiltonovi grafi
 Hipohamiltonovi grafi Marko Čmrlec, Bor Grošelj Simić Mentor(ica): Vesna Iršič Matematično raziskovalno srečanje 1. avgust 016 1 Uvod V marsovskem klubu je želel predsednik prirediti večerjo za svoje člane.
Hipohamiltonovi grafi Marko Čmrlec, Bor Grošelj Simić Mentor(ica): Vesna Iršič Matematično raziskovalno srečanje 1. avgust 016 1 Uvod V marsovskem klubu je želel predsednik prirediti večerjo za svoje člane.
Problem umetnostne galerije
 Problem umetnostne galerije Marko Kandič 17. september 2006 Za začetek si oglejmo naslednji primer. Recimo, da imamo v galeriji polno vrednih slik in nočemo, da bi jih kdo ukradel. Seveda si želimo, da
Problem umetnostne galerije Marko Kandič 17. september 2006 Za začetek si oglejmo naslednji primer. Recimo, da imamo v galeriji polno vrednih slik in nočemo, da bi jih kdo ukradel. Seveda si želimo, da
Eulerjevi in Hamiltonovi grafi
 Eulerjevi in Hamiltonovi grafi Bojan Možina 30. december 006 1 Eulerjevi grafi Štirje deli mesta Königsberg v Prusiji so bili povezani s sedmimi mostovi (glej levi del slike 1). Zdaj se Königsberg imenuje
Eulerjevi in Hamiltonovi grafi Bojan Možina 30. december 006 1 Eulerjevi grafi Štirje deli mesta Königsberg v Prusiji so bili povezani s sedmimi mostovi (glej levi del slike 1). Zdaj se Königsberg imenuje
Ana Mlinar Fulereni. Delo diplomskega seminarja. Mentor: izred. prof. dr. Riste Škrekovski
 UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO Matematika 1. stopnja Ana Mlinar Fulereni Delo diplomskega seminarja Mentor: izred. prof. dr. Riste Škrekovski Ljubljana, 2011 Kazalo 1. Uvod 4 2.
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO Matematika 1. stopnja Ana Mlinar Fulereni Delo diplomskega seminarja Mentor: izred. prof. dr. Riste Škrekovski Ljubljana, 2011 Kazalo 1. Uvod 4 2.
NIKJER-NIČELNI PRETOKI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA ALJA ŠUBIC NIKJER-NIČELNI PRETOKI DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika - računalništvo ALJA
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA ALJA ŠUBIC NIKJER-NIČELNI PRETOKI DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika - računalništvo ALJA
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO. Oddelek za matematiko in računalništvo DIPLOMSKO DELO.
 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo DIPLOMSKO DELO Sabina Skornšek Maribor, 2012 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo DIPLOMSKO DELO Sabina Skornšek Maribor, 2012 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
Grafi, igre in še kaj
 Grafi, igre in še kaj Martin Milanič martin.milanic@upr.si Inštitut Andrej Marušič Fakulteta za matematiko, naravoslovje in informacijske tehnologije Univerza na Primorskem, Koper Matematika je kul 2016,
Grafi, igre in še kaj Martin Milanič martin.milanic@upr.si Inštitut Andrej Marušič Fakulteta za matematiko, naravoslovje in informacijske tehnologije Univerza na Primorskem, Koper Matematika je kul 2016,
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Simetrije cirkulantnih grafov
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Magistrsko delo Simetrije cirkulantnih grafov (Symmetry of circulant graphs) Ime in priimek: Maruša Saksida Študijski
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Magistrsko delo Simetrije cirkulantnih grafov (Symmetry of circulant graphs) Ime in priimek: Maruša Saksida Študijski
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO ODDELEK ZA MATEMATIKO
 UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO ODDELEK ZA MATEMATIKO Rok Erman BARVANJA RAVNINSKIH IN SORODNIH DRUŽIN GRAFOV Doktorska disertacija MENTOR: prof. dr. Riste Škrekovski Ljubljana,
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO ODDELEK ZA MATEMATIKO Rok Erman BARVANJA RAVNINSKIH IN SORODNIH DRUŽIN GRAFOV Doktorska disertacija MENTOR: prof. dr. Riste Škrekovski Ljubljana,
arxiv: v1 [cs.dm] 21 Dec 2016
![arxiv: v1 [cs.dm] 21 Dec 2016 arxiv: v1 [cs.dm] 21 Dec 2016](/thumbs/74/69772342.jpg) UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE arxiv:1612.07113v1 [cs.dm] 21 Dec 2016 Zaključna naloga (Final project paper) Odčitljivost digrafov in dvodelnih
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE arxiv:1612.07113v1 [cs.dm] 21 Dec 2016 Zaključna naloga (Final project paper) Odčitljivost digrafov in dvodelnih
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Kvadratne forme nad končnimi obsegi
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Kvadratne forme nad končnimi obsegi (Quadratic Forms over Finite Fields) Ime in priimek: Borut
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Kvadratne forme nad končnimi obsegi (Quadratic Forms over Finite Fields) Ime in priimek: Borut
Mary Agnes SERVATIUS Izomorfni Cayleyevi grafi nad neizomorfnimi grupami (Isomorphic Cayley Graphs on Non-Isomorphic Groups)
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Matematične znanosti Študijski program 2. stopnje Mary Agnes SERVATIUS Izomorfni Cayleyevi grafi nad neizomorfnimi
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Matematične znanosti Študijski program 2. stopnje Mary Agnes SERVATIUS Izomorfni Cayleyevi grafi nad neizomorfnimi
DOMINACIJSKO TEVILO GRAFA
 UNIVERZA V LJUBLJANI PEDAGO KA FAKULTETA tudijski program: MATEMATIKA in RAƒUNALNI TVO DOMINACIJSKO TEVILO GRAFA DIPLOMSKO DELO Mentor: doc. dr. Primoº parl Kandidatka: Neja Zub i Ljubljana, maj, 2011
UNIVERZA V LJUBLJANI PEDAGO KA FAKULTETA tudijski program: MATEMATIKA in RAƒUNALNI TVO DOMINACIJSKO TEVILO GRAFA DIPLOMSKO DELO Mentor: doc. dr. Primoº parl Kandidatka: Neja Zub i Ljubljana, maj, 2011
Analiza omrežij Zgradba omrežij:
 Univerza v Ljubljani podiplomski študij statistike Analiza omrežij Zgradba omrežij: podomrežja in povezanosti Vladimir Batagelj Anuška Ferligoj Univerza v Ljubljani Ljubljana, 0. in 7. november 2003 izpisano:
Univerza v Ljubljani podiplomski študij statistike Analiza omrežij Zgradba omrežij: podomrežja in povezanosti Vladimir Batagelj Anuška Ferligoj Univerza v Ljubljani Ljubljana, 0. in 7. november 2003 izpisano:
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Verjetnostni algoritmi za testiranje praštevilskosti
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Verjetnostni algoritmi za testiranje praštevilskosti (Algorithms for testing primality) Ime in
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Verjetnostni algoritmi za testiranje praštevilskosti (Algorithms for testing primality) Ime in
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. O neeksaknotsti eksaktnega binomskega intervala zaupanja
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga (Final project paper) O neeksaknotsti eksaktnega binomskega intervala zaupanja (On the inexactness
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga (Final project paper) O neeksaknotsti eksaktnega binomskega intervala zaupanja (On the inexactness
Reševanje problemov in algoritmi
 Reševanje problemov in algoritmi Vhod Algoritem Izhod Kaj bomo spoznali Zgodovina algoritmov. Primeri algoritmov. Algoritmi in programi. Kaj je algoritem? Algoritem je postopek, kako korak za korakom rešimo
Reševanje problemov in algoritmi Vhod Algoritem Izhod Kaj bomo spoznali Zgodovina algoritmov. Primeri algoritmov. Algoritmi in programi. Kaj je algoritem? Algoritem je postopek, kako korak za korakom rešimo
AKSIOMATSKA KONSTRUKCIJA NARAVNIH
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Poučevanje: Predmetno poučevanje ŠPELA ZOBAVNIK AKSIOMATSKA KONSTRUKCIJA NARAVNIH ŠTEVIL MAGISTRSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Poučevanje: Predmetno poučevanje ŠPELA ZOBAVNIK AKSIOMATSKA KONSTRUKCIJA NARAVNIH ŠTEVIL MAGISTRSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
Izbrana poglavja iz velikih omreºij 1. Zbornik seminarskih nalog iz velikih omreºij
 Izbrana poglavja iz velikih omreºij 1 Zbornik seminarskih nalog iz velikih omreºij Ljubljana, 2015 CIP Kataloºni zapis o publikaciji Narodna in univerzitetna knjiºnica, Ljubljana 123.45(678)(9.012.3) Izbrana
Izbrana poglavja iz velikih omreºij 1 Zbornik seminarskih nalog iz velikih omreºij Ljubljana, 2015 CIP Kataloºni zapis o publikaciji Narodna in univerzitetna knjiºnica, Ljubljana 123.45(678)(9.012.3) Izbrana
TEORIJA GRAFOV IN LOGISTIKA
 TEORIJA GRAFOV IN LOGISTIKA Maja Fošner in Tomaž Kramberger Univerza v Mariboru Fakulteta za logistiko Mariborska cesta 2 3000 Celje Slovenija maja.fosner@uni-mb.si tomaz.kramberger@uni-mb.si Povzetek
TEORIJA GRAFOV IN LOGISTIKA Maja Fošner in Tomaž Kramberger Univerza v Mariboru Fakulteta za logistiko Mariborska cesta 2 3000 Celje Slovenija maja.fosner@uni-mb.si tomaz.kramberger@uni-mb.si Povzetek
Jernej Azarija. Štetje vpetih dreves v grafih
 UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO FAKULTETA ZA MATEMATIKO IN FIZIKO Jernej Azarija Štetje vpetih dreves v grafih DIPLOMSKO DELO NA INTERDISCIPLINARNEM UNIVERZITETNEM ŠTUDIJU
UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO FAKULTETA ZA MATEMATIKO IN FIZIKO Jernej Azarija Štetje vpetih dreves v grafih DIPLOMSKO DELO NA INTERDISCIPLINARNEM UNIVERZITETNEM ŠTUDIJU
POLDIREKTNI PRODUKT GRUP
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUCIJA ŽNIDARIČ POLDIREKTNI PRODUKT GRUP DIPLOMSKO DELO LJUBLJANA 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Univerzitetni študijski program 1. stopnje: Dvopredmetni
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUCIJA ŽNIDARIČ POLDIREKTNI PRODUKT GRUP DIPLOMSKO DELO LJUBLJANA 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Univerzitetni študijski program 1. stopnje: Dvopredmetni
SLIKE CANTORJEVE PAHLJAµCE
 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in raµcunalništvo Diplomsko delo SLIKE CANTORJEVE PAHLJAµCE Mentor: dr. Iztok Baniµc docent Kandidatka: Anja Belošević
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in raµcunalništvo Diplomsko delo SLIKE CANTORJEVE PAHLJAµCE Mentor: dr. Iztok Baniµc docent Kandidatka: Anja Belošević
Matematika 1. Gabrijel Tomšič Bojan Orel Neža Mramor Kosta
 Matematika 1 Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 15. december 2010 Poglavje 3 Funkcije 3.1 Osnovni pojmi Preslikavam v množico R ali C običajno pravimo funkcije v prvem primeru realne, v drugem
Matematika 1 Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 15. december 2010 Poglavje 3 Funkcije 3.1 Osnovni pojmi Preslikavam v množico R ali C običajno pravimo funkcije v prvem primeru realne, v drugem
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO. Oddelek za matematiko in računalništvo MAGISTRSKA NALOGA. Tina Lešnik
 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo MAGISTRSKA NALOGA Tina Lešnik Maribor, 2014 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo MAGISTRSKA NALOGA Tina Lešnik Maribor, 2014 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
UČNI NAČRT PREDMETA / COURSE SYLLABUS. Študijska smer Study field. Samost. delo Individ. work Klinične vaje work
 Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS Teorija grafov Graph theory Študijski program in stopnja Study programme and level Magistrski študijski program Matematika Master's study
Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS Teorija grafov Graph theory Študijski program in stopnja Study programme and level Magistrski študijski program Matematika Master's study
DELOVANJA GRUP IN BLOKI NEPRIMITIVNOSTI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DEJAN KREJIĆ DELOVANJA GRUP IN BLOKI NEPRIMITIVNOSTI DIPLOMSKO DELO Ljubljana, 2015 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika -
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DEJAN KREJIĆ DELOVANJA GRUP IN BLOKI NEPRIMITIVNOSTI DIPLOMSKO DELO Ljubljana, 2015 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika -
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SAŠO ZUPANEC MAX-PLUS ALGEBRA DIPLOMSKO DELO
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SAŠO ZUPANEC MAX-PLUS ALGEBRA DIPLOMSKO DELO Ljubljana, 2013 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA ODDELEK ZA MATEMATIKO IN RAČUNALNIŠTVO SAŠO ZUPANEC Mentor:
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SAŠO ZUPANEC MAX-PLUS ALGEBRA DIPLOMSKO DELO Ljubljana, 2013 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA ODDELEK ZA MATEMATIKO IN RAČUNALNIŠTVO SAŠO ZUPANEC Mentor:
Particija grafa, odkrivanje skupnosti in maksimalen prerez
 Univerza na Primorskem Fakulteta za matematiko, naravoslovje in informacijske tehnologije Matemati ne znanosti - 2. stopnja Peter Mur²i Particija grafa, odkrivanje skupnosti in maksimalen prerez Magistrsko
Univerza na Primorskem Fakulteta za matematiko, naravoslovje in informacijske tehnologije Matemati ne znanosti - 2. stopnja Peter Mur²i Particija grafa, odkrivanje skupnosti in maksimalen prerez Magistrsko
Izbrana poglavja iz algebrai ne teorije grafov. Zbornik seminarskih nalog iz algebrai ne teorije grafov
 Izbrana poglavja iz algebrai ne teorije grafov Zbornik seminarskih nalog iz algebrai ne teorije grafov Ljubljana, 2015 CIP Kataloºni zapis o publikaciji Narodna in univerzitetna knjiºnica, Ljubljana 519.24(082)(0.034.2)
Izbrana poglavja iz algebrai ne teorije grafov Zbornik seminarskih nalog iz algebrai ne teorije grafov Ljubljana, 2015 CIP Kataloºni zapis o publikaciji Narodna in univerzitetna knjiºnica, Ljubljana 519.24(082)(0.034.2)
Hadamardove matrike in misija Mariner 9
 Hadamardove matrike in misija Mariner 9 Aleksandar Jurišić, 25. avgust, 2009 J. Hadamard (1865-1963) je bil eden izmed pomembnejših matematikov na prehodu iz 19. v 20. stoletje. Njegova najpomembnejša
Hadamardove matrike in misija Mariner 9 Aleksandar Jurišić, 25. avgust, 2009 J. Hadamard (1865-1963) je bil eden izmed pomembnejših matematikov na prehodu iz 19. v 20. stoletje. Njegova najpomembnejša
Iskanje najcenejše poti v grafih preko polkolobarjev
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Veronika Horvat Iskanje najcenejše poti v grafih preko polkolobarjev DIPLOMSKO DELO VISOKOŠOLSKI STROKOVNI ŠTUDIJSKI PROGRAM PRVE STOPNJE
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Veronika Horvat Iskanje najcenejše poti v grafih preko polkolobarjev DIPLOMSKO DELO VISOKOŠOLSKI STROKOVNI ŠTUDIJSKI PROGRAM PRVE STOPNJE
SIMETRIČNI BICIRKULANTI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA GORAZD VASILJEVIĆ SIMETRIČNI BICIRKULANTI DIPLOMSKO DELO Ljubljana, 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika - računalništvo
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA GORAZD VASILJEVIĆ SIMETRIČNI BICIRKULANTI DIPLOMSKO DELO Ljubljana, 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika - računalništvo
Diskretna matematika 1 / Teorija grafov
 Diskretna matematika 1 / Teorija grafov 1. Osnovni pojmi Vladimir Batagelj Univerza v Ljubljani FMF, matematika Finančna matematika Ljubljana, december 2013 / februar 2008 1 / 31 Kazalo 1 2 3 4 5 6 Pajek
Diskretna matematika 1 / Teorija grafov 1. Osnovni pojmi Vladimir Batagelj Univerza v Ljubljani FMF, matematika Finančna matematika Ljubljana, december 2013 / februar 2008 1 / 31 Kazalo 1 2 3 4 5 6 Pajek
UČNI NAČRT PREDMETA / COURSE SYLLABUS. Študijska smer Study field. Samost. delo Individ. work Klinične vaje work
 Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS Statistika Statistics Študijski program in stopnja Study programme and level Univerzitetni študijski program Matematika First cycle academic
Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS Statistika Statistics Študijski program in stopnja Study programme and level Univerzitetni študijski program Matematika First cycle academic
Kode za popravljanje napak
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE KOPER MATEMATIČNE ZNANOSTI MAGISTRSKI ŠTUDIJSKI PROGRAM 2. STOPNJE Aljaž Slivnik Kode za popravljanje napak Magistrska
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE KOPER MATEMATIČNE ZNANOSTI MAGISTRSKI ŠTUDIJSKI PROGRAM 2. STOPNJE Aljaž Slivnik Kode za popravljanje napak Magistrska
Multipla korelacija in regresija. Multipla regresija, multipla korelacija, statistično zaključevanje o multiplem R
 Multipla koelacia in egesia Multipla egesia, multipla koelacia, statistično zaklučevane o multiplem Multipla egesia osnovni model in ačunane paametov Z multiplo egesio napoveduemo vednost kiteia (odvisne
Multipla koelacia in egesia Multipla egesia, multipla koelacia, statistično zaklučevane o multiplem Multipla egesia osnovni model in ačunane paametov Z multiplo egesio napoveduemo vednost kiteia (odvisne
Neli Blagus. Iterativni funkcijski sistemi in konstrukcija fraktalov
 UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Neli Blagus Iterativni funkcijski sistemi in konstrukcija fraktalov DIPLOMSKO DELO NA INTERDISCIPLINARNEM UNIVERZITETNEM ŠTUDIJU Mentorica:
UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Neli Blagus Iterativni funkcijski sistemi in konstrukcija fraktalov DIPLOMSKO DELO NA INTERDISCIPLINARNEM UNIVERZITETNEM ŠTUDIJU Mentorica:
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POLONA ŠENKINC REŠEVANJE LINEARNIH DIFERENCIALNIH ENAČB DRUGEGA REDA S POMOČJO POTENČNIH VRST DIPLOMSKO DELO
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POLONA ŠENKINC REŠEVANJE LINEARNIH DIFERENCIALNIH ENAČB DRUGEGA REDA S POMOČJO POTENČNIH VRST DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POLONA ŠENKINC REŠEVANJE LINEARNIH DIFERENCIALNIH ENAČB DRUGEGA REDA S POMOČJO POTENČNIH VRST DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA FAKULTETA ZA MATEMATIKO IN FIZIKO DIPLOMSKO DELO MIHAELA REMIC
 UNIVERZ V LJULJNI PEDGOŠK FKULTET FKULTET Z MTEMTIKO IN FIZIKO DIPLOMSKO DELO MIHEL REMI UNIVERZ V LJULJNI PEDGOŠK FKULTET FKULTET Z MTEMTIKO IN FIZIKO Študijski program: Matematika in fizika ROUTHOV
UNIVERZ V LJULJNI PEDGOŠK FKULTET FKULTET Z MTEMTIKO IN FIZIKO DIPLOMSKO DELO MIHEL REMI UNIVERZ V LJULJNI PEDGOŠK FKULTET FKULTET Z MTEMTIKO IN FIZIKO Študijski program: Matematika in fizika ROUTHOV
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Računalniške metode za načrtovanje polipeptidnega origamija
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga (Final project paper) Računalniške metode za načrtovanje polipeptidnega origamija (Computational
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga (Final project paper) Računalniške metode za načrtovanje polipeptidnega origamija (Computational
TOPLJENEC ASOCIIRA LE V VODNI FAZI
 TOPLJENEC ASOCIIRA LE V VODNI FAZI V primeru asociacij molekul topljenca v vodni ali organski fazi eksperimentalno določeni navidezni porazdelitveni koeficient (P n ) v odvisnosti od koncentracije ni konstanten.
TOPLJENEC ASOCIIRA LE V VODNI FAZI V primeru asociacij molekul topljenca v vodni ali organski fazi eksperimentalno določeni navidezni porazdelitveni koeficient (P n ) v odvisnosti od koncentracije ni konstanten.
UČNI NAČRT PREDMETA / COURSE SYLLABUS Predmet: Analiza 1 Course title: Analysis 1. Študijska smer Study field. Samost. delo Individ.
 UČNI NAČRT PREDMETA / COURSE SYLLABUS Predmet: Analiza 1 Course title: Analysis 1 Študijski program in stopnja Study programme and level Univerzitetni študijski program Finančna matematika First cycle
UČNI NAČRT PREDMETA / COURSE SYLLABUS Predmet: Analiza 1 Course title: Analysis 1 Študijski program in stopnja Study programme and level Univerzitetni študijski program Finančna matematika First cycle
APLIKACIJA ZA DELO Z GRAFI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Študijski program: MATEMATIKA IN RAČUNALNIŠTVO APLIKACIJA ZA DELO Z GRAFI DIPLOMSKO DELO Mentor: doc. dr. Primož Šparl Kandidat: Luka Jurković Somentor: asist.
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Študijski program: MATEMATIKA IN RAČUNALNIŠTVO APLIKACIJA ZA DELO Z GRAFI DIPLOMSKO DELO Mentor: doc. dr. Primož Šparl Kandidat: Luka Jurković Somentor: asist.
OPTIMIZACIJSKE METODE skripta v pripravi
 OPTIMIZACIJSKE METODE skripta v pripravi Vladimir Batagelj Ljubljana 17. december 2003 2 Kazalo Predgovor 5 1 Optimizacijske naloge 7 1.1 Osnovni pojmi........................... 7 1.2 Primeri optimizacijskih
OPTIMIZACIJSKE METODE skripta v pripravi Vladimir Batagelj Ljubljana 17. december 2003 2 Kazalo Predgovor 5 1 Optimizacijske naloge 7 1.1 Osnovni pojmi........................... 7 1.2 Primeri optimizacijskih
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga (Final project paper) Grafi struktur proteinov: Uporaba teorije grafov za analizo makromolekulskih
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga (Final project paper) Grafi struktur proteinov: Uporaba teorije grafov za analizo makromolekulskih
UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Predmet: Optimizacija 1 Course title: Optimization 1. Študijska smer Study field
 UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Predmet: Optimizacija 1 Course title: Optimization 1 Študijski program in stopnja Study programme and level Univerzitetni študijski program Matematika
UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Predmet: Optimizacija 1 Course title: Optimization 1 Študijski program in stopnja Study programme and level Univerzitetni študijski program Matematika
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Uporaba logistične regresije za napovedovanje razreda, ko je število enot v preučevanih razredih
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Uporaba logistične regresije za napovedovanje razreda, ko je število enot v preučevanih razredih
FRAKTALNA DIMENZIJA. Fakulteta za matematiko in fiziko Univerza v Ljubljani
 FRAKTALNA DIMENZIJA VESNA IRŠIČ Fakulteta za matematiko in fiziko Univerza v Ljubljani PACS: 07.50.Hp, 01.65.+g V članku je predstavljen zgodovinski razvoj teorije fraktalov in natančen opis primerov,
FRAKTALNA DIMENZIJA VESNA IRŠIČ Fakulteta za matematiko in fiziko Univerza v Ljubljani PACS: 07.50.Hp, 01.65.+g V članku je predstavljen zgodovinski razvoj teorije fraktalov in natančen opis primerov,
JERNEJ TONEJC. Fakulteta za matematiko in fiziko
 . ARITMETIKA DVOJIŠKIH KONČNIH OBSEGOV JERNEJ TONEJC Fakulteta za matematiko in fiziko Math. Subj. Class. (2010): 11T{06, 22, 55, 71}, 12E{05, 20, 30}, 68R05 V članku predstavimo končne obsege in aritmetiko
. ARITMETIKA DVOJIŠKIH KONČNIH OBSEGOV JERNEJ TONEJC Fakulteta za matematiko in fiziko Math. Subj. Class. (2010): 11T{06, 22, 55, 71}, 12E{05, 20, 30}, 68R05 V članku predstavimo končne obsege in aritmetiko
OPTIMIRANJE IZDELOVALNIH PROCESOV
 OPTIMIRANJE IZDELOVALNIH PROCESOV asist. Damir GRGURAŠ, mag. inž. str izr. prof. dr. Davorin KRAMAR damir.grguras@fs.uni-lj.si Namen vaje: Ugotoviti/določiti optimalne parametre pri struženju za dosego
OPTIMIRANJE IZDELOVALNIH PROCESOV asist. Damir GRGURAŠ, mag. inž. str izr. prof. dr. Davorin KRAMAR damir.grguras@fs.uni-lj.si Namen vaje: Ugotoviti/določiti optimalne parametre pri struženju za dosego
UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Predmet: Analiza 3 Course title: Analysis 3. Študijska smer Study field ECTS
 UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Predmet: Analiza 3 Course title: Analysis 3 Študijski program in stopnja Study programme and level Univerzitetni študijski program Matematika
UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Predmet: Analiza 3 Course title: Analysis 3 Študijski program in stopnja Study programme and level Univerzitetni študijski program Matematika
NEODLOČLJIVI PROBLEMI V TEORIJI IZRAČUNLJIVOSTI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUKA VIKTOR ROGAČ NEODLOČLJIVI PROBLEMI V TEORIJI IZRAČUNLJIVOSTI MAGISTRSKO DELO LJUBLJANA, 2017 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POUČEVANJE, PREDMETNO
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUKA VIKTOR ROGAČ NEODLOČLJIVI PROBLEMI V TEORIJI IZRAČUNLJIVOSTI MAGISTRSKO DELO LJUBLJANA, 2017 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POUČEVANJE, PREDMETNO
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SARA BREZEC HAUSDORFFOV PARADOKS DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ MATEMATIKA-FIZIKA SARA BREZEC mentor:
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SARA BREZEC HAUSDORFFOV PARADOKS DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ MATEMATIKA-FIZIKA SARA BREZEC mentor:
Topološka obdelava slik
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Matjaž Cerar Topološka obdelava slik DIPLOMSKO DELO UNIVERZITETNI INTERDISCIPLINARNI ŠTUDIJ RAČUNALNIŠTVA
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Matjaž Cerar Topološka obdelava slik DIPLOMSKO DELO UNIVERZITETNI INTERDISCIPLINARNI ŠTUDIJ RAČUNALNIŠTVA
Minimizacija učne množice pri učenju odločitvenih dreves
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Ivan Štajduhar Minimizacija učne množice pri učenju odločitvenih dreves Diplomska naloga Mentor: prof. dr. Ivan Bratko Ljubljana, 2001 Izjava
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Ivan Štajduhar Minimizacija učne množice pri učenju odločitvenih dreves Diplomska naloga Mentor: prof. dr. Ivan Bratko Ljubljana, 2001 Izjava
UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Parcialne diferencialne enačbe Partial differential equations. Študijska smer Study field
 Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Parcialne diferencialne enačbe Partial differential equations Študijski program in stopnja Study programme and level Magistrski
Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Parcialne diferencialne enačbe Partial differential equations Študijski program in stopnja Study programme and level Magistrski
Katastrofalno zaporedje okvar v medsebojno odvisnih omrežjih
 Katastrofalno zaporedje okvar v medsebojno odvisnih omrežjih Daniel Grošelj Mentor: Prof. Dr. Rudi Podgornik 2. marec 2011 Kazalo 1 Uvod 2 2 Nekaj osnovnih pojmov pri teoriji omrežij 3 2.1 Matrika sosednosti.......................................
Katastrofalno zaporedje okvar v medsebojno odvisnih omrežjih Daniel Grošelj Mentor: Prof. Dr. Rudi Podgornik 2. marec 2011 Kazalo 1 Uvod 2 2 Nekaj osnovnih pojmov pri teoriji omrežij 3 2.1 Matrika sosednosti.......................................
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO. Oddelek za matematiko in računalništvo DIPLOMSKO DELO. Gregor Ambrož
 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo DIPLOMSKO DELO Gregor Ambrož Maribor, 2010 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo DIPLOMSKO DELO Gregor Ambrož Maribor, 2010 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
UČNI NAČRT PREDMETA / COURSE SYLLABUS Numerical linear algebra. Študijska smer Study field. Samost. delo Individ. work Klinične vaje work
 Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS Numerična linearna algebra Numerical linear algebra Študijski program in stopnja Study programme and level Univerzitetni študijski program Matematika
Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS Numerična linearna algebra Numerical linear algebra Študijski program in stopnja Study programme and level Univerzitetni študijski program Matematika
OFF-LINE NALOGA NAJKRAJŠI SKUPNI NADNIZ
 1 OFF-LINE NALOGA NAJKRAJŠI SKUPNI NADNIZ Opis problema. Danih je k vhodnih nizov, ki jih označimo s t 1,..., t k. Množico vseh znakov, ki se pojavijo v vsaj enem vhodnem nizu, imenujmo abeceda in jo označimo
1 OFF-LINE NALOGA NAJKRAJŠI SKUPNI NADNIZ Opis problema. Danih je k vhodnih nizov, ki jih označimo s t 1,..., t k. Množico vseh znakov, ki se pojavijo v vsaj enem vhodnem nizu, imenujmo abeceda in jo označimo
Mill Hill East. Finchley Central Bounds Green. East Finchley Wood Green. Highgate Turnpike Lane. Archway. Manor House. Gospel. Tufnell Park.
 h Special fares apply for printed single and return North White Holland Notting Lancaster Bond Oxford Chancery Acton City Park Hill Gate Gate Street Circus Holborn Lane West East Shepherd's Queensway Marble
h Special fares apply for printed single and return North White Holland Notting Lancaster Bond Oxford Chancery Acton City Park Hill Gate Gate Street Circus Holborn Lane West East Shepherd's Queensway Marble
UČNI NAČRT PREDMETA / COURSE SYLLABUS. Študijska smer Study field. Samost. delo Individ. work Klinične vaje work
 Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS Optimizacija Optimization Študijski program in stopnja Study programme and level Visokošolski strokovni študijski program Praktična matematika
Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS Optimizacija Optimization Študijski program in stopnja Study programme and level Visokošolski strokovni študijski program Praktična matematika
Upper Bounds of Dynamic Chromatic Number
 Upper Bounds of Dynamic Chromatic Number Hong-Jian Lai, Bruce Montgomery and Hoifung Poon Department of Mathematics West Virginia University, Morgantown, WV 26506-6310 June 22, 2000 Abstract A proper vertex
Upper Bounds of Dynamic Chromatic Number Hong-Jian Lai, Bruce Montgomery and Hoifung Poon Department of Mathematics West Virginia University, Morgantown, WV 26506-6310 June 22, 2000 Abstract A proper vertex
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Ekstremne porazdelitve za odvisne spremenljivke
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Ekstremne porazdelitve za odvisne spremenljivke (Extremal Distributions for Dependent Variables)
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Ekstremne porazdelitve za odvisne spremenljivke (Extremal Distributions for Dependent Variables)
Luka Taras Korošec ANALIZA IN NADGRADNJA APLIKACIJE ZA DELO Z GRAFI
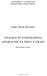 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Luka Taras Korošec ANALIZA IN NADGRADNJA APLIKACIJE ZA DELO Z GRAFI DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA UNIVERZITETNI ŠTUDIJSKI
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Luka Taras Korošec ANALIZA IN NADGRADNJA APLIKACIJE ZA DELO Z GRAFI DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA UNIVERZITETNI ŠTUDIJSKI
Gradnja Vietoris-Ripsovega simplicialnega kompleksa
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Leonard Štefančič Gradnja Vietoris-Ripsovega simplicialnega kompleksa DIPLOMSKO DELO NA INTERDISCIPLINARNEM
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Leonard Štefančič Gradnja Vietoris-Ripsovega simplicialnega kompleksa DIPLOMSKO DELO NA INTERDISCIPLINARNEM
UČNI NAČRT PREDMETA / COURSE SYLLABUS
 UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Predmet: Izbrana poglavja iz diskretne matematike 1 Course title: Topics in discrete mathematics 1 Študijski program in stopnja Study programme
UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Predmet: Izbrana poglavja iz diskretne matematike 1 Course title: Topics in discrete mathematics 1 Študijski program in stopnja Study programme
UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Diferencialne enačbe. Študijska smer Study field ECTS
 Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Diferencialne enačbe Differential equations Študijski program in stopnja Study programme and level Visokošolski strokovni
Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Diferencialne enačbe Differential equations Študijski program in stopnja Study programme and level Visokošolski strokovni
Naloge iz LA T EXa : 3. del
 Naloge iz LA T EXa : 3. del 1. V besedilo vklju ite naslednjo tabelo skupaj z napisom Kontrolna naloga Dijak 1 2 Povpre je Janko 67 72 70.5 Metka 72 67 70.5 Povpre je 70.5 70.5 Tabela 1: Rezultati kontrolnih
Naloge iz LA T EXa : 3. del 1. V besedilo vklju ite naslednjo tabelo skupaj z napisom Kontrolna naloga Dijak 1 2 Povpre je Janko 67 72 70.5 Metka 72 67 70.5 Povpre je 70.5 70.5 Tabela 1: Rezultati kontrolnih
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA VERONIKA MIHELAK PRAVILNI IKOZAEDER DIPLOMSKO DELO
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA VERONIKA MIHELAK PRAVILNI IKOZAEDER DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ VERONIKA MIHELAK MENTOR: izr. prof.
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA VERONIKA MIHELAK PRAVILNI IKOZAEDER DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ VERONIKA MIHELAK MENTOR: izr. prof.
Coloring. Basics. A k-coloring of a loopless graph G is a function f : V (G) S where S = k (often S = [k]).
![Coloring. Basics. A k-coloring of a loopless graph G is a function f : V (G) S where S = k (often S = [k]). Coloring. Basics. A k-coloring of a loopless graph G is a function f : V (G) S where S = k (often S = [k]).](/thumbs/83/87488957.jpg) Coloring Basics A k-coloring of a loopless graph G is a function f : V (G) S where S = k (often S = [k]). For an i S, the set f 1 (i) is called a color class. A k-coloring is called proper if adjacent
Coloring Basics A k-coloring of a loopless graph G is a function f : V (G) S where S = k (often S = [k]). For an i S, the set f 1 (i) is called a color class. A k-coloring is called proper if adjacent
Študijska smer Study field. Samost. delo Individ. work Klinične vaje work. Vaje / Tutorial: Slovensko/Slovene
 UČNI NAČRT PREDMETA / COURSE SYLLABUS Predmet: Matematika 2 Course title: Mathematics 2 Študijski program in stopnja Study programme and level Univerzitetni študijski program 1.stopnje Fizika First cycle
UČNI NAČRT PREDMETA / COURSE SYLLABUS Predmet: Matematika 2 Course title: Mathematics 2 Študijski program in stopnja Study programme and level Univerzitetni študijski program 1.stopnje Fizika First cycle
Iterativne metode podprostorov 2010/2011 Domače naloge
 Iterativne metode podprostorov 2010/2011 Domače naloge Naloge so razdeljene v 6 skupin. Za pozitivno oceno morate rešiti toliko nalog, da bo končna vsota za pozitivno oceno vsaj 8 točk oz. vsaj 10 točk
Iterativne metode podprostorov 2010/2011 Domače naloge Naloge so razdeljene v 6 skupin. Za pozitivno oceno morate rešiti toliko nalog, da bo končna vsota za pozitivno oceno vsaj 8 točk oz. vsaj 10 točk
On the Local Colorings of Graphs
 On the Local Colorings of Graphs Behnaz Omoomi and Ali Pourmiri Department of Mathematical Sciences Isfahan University of Technology 84154, Isfahan, Iran Abstract A local coloring of a graph G is a function
On the Local Colorings of Graphs Behnaz Omoomi and Ali Pourmiri Department of Mathematical Sciences Isfahan University of Technology 84154, Isfahan, Iran Abstract A local coloring of a graph G is a function
Călugăreanu-White-Fullerjev teorem in topologija DNA
 Univerza v Ljubljani Fakulteta za matematiko in fiziko Oddelek za fiziko Călugăreanu-White-Fullerjev teorem in topologija DNA Seminar Jure Aplinc, dipl. fiz. (UN) Mentor: prof. dr. Rudolf Podgornik 26.
Univerza v Ljubljani Fakulteta za matematiko in fiziko Oddelek za fiziko Călugăreanu-White-Fullerjev teorem in topologija DNA Seminar Jure Aplinc, dipl. fiz. (UN) Mentor: prof. dr. Rudolf Podgornik 26.
Linearne enačbe. Matrična algebra. Linearne enačbe. Linearne enačbe. Linearne enačbe. Linearne enačbe
 Sistem linearnih enačb Matrična algebra Oseba X X X3 B A.A. 3 B.B. 7 C.C. Doc. dr. Anja Podlesek Oddelek za psihologijo, Filozofska fakulteta, Univerza v Ljubljani Študijski program prve stopnje Psihologija
Sistem linearnih enačb Matrična algebra Oseba X X X3 B A.A. 3 B.B. 7 C.C. Doc. dr. Anja Podlesek Oddelek za psihologijo, Filozofska fakulteta, Univerza v Ljubljani Študijski program prve stopnje Psihologija
5. Zgradba omrežij povezanosti. Vladimir Batagelj. Interdisciplinarni doktorski študijski program Statistika Ljubljana, april 2014
 5. Zgradba povezanosti Vladimir Batagelj Univerza v Ljubljani, FMF, matematika Interdisciplinarni doktorski študijski program Statistika Ljubljana, april 204 Textphone Website Transport for London Grid
5. Zgradba povezanosti Vladimir Batagelj Univerza v Ljubljani, FMF, matematika Interdisciplinarni doktorski študijski program Statistika Ljubljana, april 204 Textphone Website Transport for London Grid
Linearna algebra. Bojan Orel. Univerza v Ljubljani
 Linearna algebra Bojan Orel 07 Univerza v Ljubljani Fakulteta za računalništvo in informatiko CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana 5.64(075.8) OREL, Bojan Linearna
Linearna algebra Bojan Orel 07 Univerza v Ljubljani Fakulteta za računalništvo in informatiko CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana 5.64(075.8) OREL, Bojan Linearna
Cveto Trampuž PRIMERJAVA ANALIZE VEČRAZSEŽNIH TABEL Z RAZLIČNIMI MODELI REGRESIJSKE ANALIZE DIHOTOMNIH SPREMENLJIVK
 Cveto Trampuž PRIMERJAVA ANALIZE VEČRAZSEŽNIH TABEL Z RAZLIČNIMI MODELI REGRESIJSKE ANALIZE DIHOTOMNIH SPREMENLJIVK POVZETEK. Namen tega dela je prikazati osnove razlik, ki lahko nastanejo pri interpretaciji
Cveto Trampuž PRIMERJAVA ANALIZE VEČRAZSEŽNIH TABEL Z RAZLIČNIMI MODELI REGRESIJSKE ANALIZE DIHOTOMNIH SPREMENLJIVK POVZETEK. Namen tega dela je prikazati osnove razlik, ki lahko nastanejo pri interpretaciji
Računalnik iz domin. Škafar, Maja Šafarič, Nina Sangawa Hmeljak Mentor: Vid Kocijan
 Računalnik iz domin Primož Škafar, Maja Šafarič, Nina Sangawa Hmeljak Mentor: Vid Kocijan Povzetek Naša naloga je bila ugotoviti kako sestaviti računalnik (Turingov stroj) iz domin in logičnih izrazov.
Računalnik iz domin Primož Škafar, Maja Šafarič, Nina Sangawa Hmeljak Mentor: Vid Kocijan Povzetek Naša naloga je bila ugotoviti kako sestaviti računalnik (Turingov stroj) iz domin in logičnih izrazov.
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Primerjava modernih pristopov za identifikacijo pomembno izraženih genov za dve skupini (Comparison
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Primerjava modernih pristopov za identifikacijo pomembno izraženih genov za dve skupini (Comparison
ZVEZDASTI MNOGOKOTNIKI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA BLAŽKA RIOSA ZVEZDASTI MNOGOKOTNIKI DIPLOMSKO DELO Ljubljana, 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ BLAŽKA RIOSA Mentor: dr. Matija
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA BLAŽKA RIOSA ZVEZDASTI MNOGOKOTNIKI DIPLOMSKO DELO Ljubljana, 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ BLAŽKA RIOSA Mentor: dr. Matija
Topics on Computing and Mathematical Sciences I Graph Theory (6) Coloring I
 Topics on Computing and Mathematical Sciences I Graph Theory (6) Coloring I Yoshio Okamoto Tokyo Institute of Technology May, 008 Last updated: Wed May 6: 008 Y. Okamoto (Tokyo Tech) TCMSI Graph Theory
Topics on Computing and Mathematical Sciences I Graph Theory (6) Coloring I Yoshio Okamoto Tokyo Institute of Technology May, 008 Last updated: Wed May 6: 008 Y. Okamoto (Tokyo Tech) TCMSI Graph Theory
DIOFANTSKE ČETVERICE
 Fakulteta za aravoslovje i matematiko Oddelek za matematiko i račualištvo Diplomsko delo DIOFANTSKE ČETVERICE Metor: Doc. dr. Daiel Eremita Kadidatka: Jožica Špec Maribor 009 II ZAHVALA Zahvaljujem se
Fakulteta za aravoslovje i matematiko Oddelek za matematiko i račualištvo Diplomsko delo DIOFANTSKE ČETVERICE Metor: Doc. dr. Daiel Eremita Kadidatka: Jožica Špec Maribor 009 II ZAHVALA Zahvaljujem se
D I P L O M S K A N A L O G A
 FAKULTETA ZA INFORMACIJSKE ŠTUDIJE V NOVEM MESTU D I P L O M S K A N A L O G A UNIVERZITETNEGA ŠTUDIJSKEGA PROGRAMA PRVE STOPNJE ALEŠ HOČEVAR FAKULTETA ZA INFORMACIJSKE ŠTUDIJE V NOVEM MESTU DIPLOMSKA
FAKULTETA ZA INFORMACIJSKE ŠTUDIJE V NOVEM MESTU D I P L O M S K A N A L O G A UNIVERZITETNEGA ŠTUDIJSKEGA PROGRAMA PRVE STOPNJE ALEŠ HOČEVAR FAKULTETA ZA INFORMACIJSKE ŠTUDIJE V NOVEM MESTU DIPLOMSKA
UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2016/17) Diferencialne enačbe. Študijska smer Study field ECTS
 Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2016/17) Diferencialne enačbe Differential equations Študijski program in stopnja Study programme and level Visokošolski strokovni
Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2016/17) Diferencialne enačbe Differential equations Študijski program in stopnja Study programme and level Visokošolski strokovni
Group Colorability of Graphs
 Group Colorability of Graphs Hong-Jian Lai, Xiankun Zhang Department of Mathematics West Virginia University, Morgantown, WV26505 July 10, 2004 Abstract Let G = (V, E) be a graph and A a non-trivial Abelian
Group Colorability of Graphs Hong-Jian Lai, Xiankun Zhang Department of Mathematics West Virginia University, Morgantown, WV26505 July 10, 2004 Abstract Let G = (V, E) be a graph and A a non-trivial Abelian
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DIPLOMSKO DELO MAJA OSTERMAN
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DIPLOMSKO DELO MAJA OSTERMAN UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Študijski program: Matematika in računalništvo Fibonaccijevo zaporedje in krožna konstanta
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DIPLOMSKO DELO MAJA OSTERMAN UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Študijski program: Matematika in računalništvo Fibonaccijevo zaporedje in krožna konstanta
Domen Perc. Implementacija in eksperimentalna analiza tehnike razvrščanja podatkov s konsenzom
 UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Domen Perc Implementacija in eksperimentalna analiza tehnike razvrščanja podatkov s konsenzom DIPLOMSKO DELO NA UNIVERZITETNEM ŠTUDIJU Mentor:
UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Domen Perc Implementacija in eksperimentalna analiza tehnike razvrščanja podatkov s konsenzom DIPLOMSKO DELO NA UNIVERZITETNEM ŠTUDIJU Mentor:
Interpolacija s parametričnimi polinomskimikrivuljami 1
 Interpolacija s parametričnimi polinomskimikrivuljami Emil Žagar 22. november 200 Skriptajevnastajanju,zatojegotovopolnanapak. Hvaleˇzenbomzavse pripombe. Iskanje napak je obenem del učnega procesa pri
Interpolacija s parametričnimi polinomskimikrivuljami Emil Žagar 22. november 200 Skriptajevnastajanju,zatojegotovopolnanapak. Hvaleˇzenbomzavse pripombe. Iskanje napak je obenem del učnega procesa pri
Statistika 2 z računalniško analizo podatkov. Neizpolnjevanje predpostavk regresijskega modela
 Statistika 2 z računalniško analizo podatkov Neizpolnjevanje predpostavk regresijskega modela 1 Predpostavke regresijskega modela (ponovitev) V regresijskem modelu navadno privzamemo naslednje pogoje:
Statistika 2 z računalniško analizo podatkov Neizpolnjevanje predpostavk regresijskega modela 1 Predpostavke regresijskega modela (ponovitev) V regresijskem modelu navadno privzamemo naslednje pogoje:
SVM = Support Vector Machine = Metoda podpornih vektorjev
 Uvod 2/60 SVM = Support Vector Machine = Metoda podpornih vektorjev Vapnik in Lerner 1963 (generalized portrait) jedra: Aronszajn 1950; Aizerman 1964; Wahba 1990, Poggio in Girosi 1990 Boser, Guyon in
Uvod 2/60 SVM = Support Vector Machine = Metoda podpornih vektorjev Vapnik in Lerner 1963 (generalized portrait) jedra: Aronszajn 1950; Aizerman 1964; Wahba 1990, Poggio in Girosi 1990 Boser, Guyon in
Zbornik seminarjev iz hevristik
 Zbornik seminarjev iz hevristik Izbrana poglavja iz optimizacijskih metod (2010-11) 2. marec 2012 Ljubljana, 2011 Zbornik seminarskih nalog sta po knjigi [3] izbrala in uredila R. Škrekovski (FMF) in Vida
Zbornik seminarjev iz hevristik Izbrana poglavja iz optimizacijskih metod (2010-11) 2. marec 2012 Ljubljana, 2011 Zbornik seminarskih nalog sta po knjigi [3] izbrala in uredila R. Škrekovski (FMF) in Vida
Hibridizacija požrešnih algoritmov in hitrega urejanja
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Nina Vehovec Hibridizacija požrešnih algoritmov in hitrega urejanja DIPLOMSKO DELO INTERDISCIPLINARNI UNIVERZITETNI ŠTUDIJSKI PROGRAM PRVE
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Nina Vehovec Hibridizacija požrešnih algoritmov in hitrega urejanja DIPLOMSKO DELO INTERDISCIPLINARNI UNIVERZITETNI ŠTUDIJSKI PROGRAM PRVE
A taste of perfect graphs
 A taste of perfect graphs Remark Determining the chromatic number of a graph is a hard problem, in general, and it is even hard to get good lower bounds on χ(g). An obvious lower bound we have seen before
A taste of perfect graphs Remark Determining the chromatic number of a graph is a hard problem, in general, and it is even hard to get good lower bounds on χ(g). An obvious lower bound we have seen before
MICROWAVE PLASMAS AT ATMOSPHERIC PRESSURE: NEW THEORETICAL DEVELOPMENTS AND APPLICATIONS IN SURFACE SCIENCE
 UDK621.3:(53+54+621 +66), ISSN0352-9045 Informacije MIDEM 38(2008)4, Ljubljana MICROWAVE PLASMAS AT ATMOSPHERIC PRESSURE: NEW THEORETICAL DEVELOPMENTS AND APPLICATIONS IN SURFACE SCIENCE T. 8elmonte*,
UDK621.3:(53+54+621 +66), ISSN0352-9045 Informacije MIDEM 38(2008)4, Ljubljana MICROWAVE PLASMAS AT ATMOSPHERIC PRESSURE: NEW THEORETICAL DEVELOPMENTS AND APPLICATIONS IN SURFACE SCIENCE T. 8elmonte*,
Topološki model za brezžična senzorska omrežja
 UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Jan Terzer Topološki model za brezžična senzorska omrežja DIPLOMSKO DELO UNIVERZITETNI ŠTUDIJSKI PROGRAM PRVE STOPNJE RAČUNALNIŠTVO IN INFORMATIKA
UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Jan Terzer Topološki model za brezžična senzorska omrežja DIPLOMSKO DELO UNIVERZITETNI ŠTUDIJSKI PROGRAM PRVE STOPNJE RAČUNALNIŠTVO IN INFORMATIKA
Destroying non-complete regular components in graph partitions
 Destroying non-complete regular components in graph partitions Landon Rabern landon.rabern@gmail.com June 27, 2011 Abstract We prove that if G is a graph and r 1,..., r k Z 0 such that k i=1 r i (G) +
Destroying non-complete regular components in graph partitions Landon Rabern landon.rabern@gmail.com June 27, 2011 Abstract We prove that if G is a graph and r 1,..., r k Z 0 such that k i=1 r i (G) +
