UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO. Oddelek za matematiko in računalništvo DIPLOMSKO DELO. Gregor Ambrož
|
|
|
- Marcus Tate
- 5 years ago
- Views:
Transcription
1 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo DIPLOMSKO DELO Gregor Ambrož Maribor, 2010
2
3 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo Diplomsko delo ANTISIMETRIČNE MATRIKE Mentorica: doc. dr. Ajda Fošner Kandidat: Gregor Ambrož Somentor: doc. dr. Dominik Benkovič Maribor, 2010
4 ZAHVALA Pot ne bi bila ista brez vas, vas, ki me napolnjujete z modrostjo, upanjem in življenjem. Hvala vam! Posebna zahvala velja moji mentorici, spoštovani doc. dr. Ajdi Fošner, in somentorju, spoštovanemu doc. dr. Dominiku Benkoviču, za strokovno pomoč in vodenje pri izdelavi diplomskega dela.
5 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO IZJAVA Podpisani Gregor Ambrož, rojen 8. maja 1984, študent Fakultete za naravoslovje in matematiko Univerze v Mariboru, študijskega programa matematika in računalništvo, izjavljam, da je diplomsko delo z naslovom ANTISIMETRIČNE MATRIKE pri mentorici doc. dr. Ajdi Fošner in somentorju doc. dr. Dominiku Benkoviču avtorsko delo. V diplomskem delu so uporabljeni viri in literatura korektno navedeni; teksti niso uporabljeni brez navedbe avtorjev. Maribor, 19. maj 2010
6 Antisimetrične matrike program diplomskega dela Diplomsko delo naj obravnava osnovne lastnosti antisimetričnih matrik. Predstavljeni naj bodo osnovni izreki, ki vključujejo antisimetrične matrike, ter njihovi dokazi. Prav tako naj bo vključena primerjava med simetričnimi in antisimetričnimi matrikami. Osnovna literatura: 1. R. A. Horn, C. R. Johnson, Matrix analysis, Cambridge University Press, Cambridge (1985). 2. D. Kurepa, Viša algebra, Školska knjiga, Zagreb (1965). 3. E. M. Landesman, M. R. Hestens, Linear algebra for mathematics, science and engineering, Practice-Hall International (1992). doc. dr. Ajda Fošner
7 AMBROŽ, G.: ANTISIMETRIČNE MATRIKE. Diplomsko delo, Univerza v Mariboru, Fakulteta za naravoslovje in matematiko, Oddelek za matematiko in računalništvo, IZVLEČEK Diplomsko delo je sestavljeno iz treh poglavij. V prvem poglavju predstavimo osnovne pojme matrik in njihove definicije. Nato podrobneje opišemo računske operacije med njimi in jih ponazorimo z zgledi. Nazadnje predstavimo tudi determinanto matrike in njene lastnosti, lastne vrednosti in Jordanovo kanonično formo matrike. V naslednjem poglavju se posvetimo simetričnim matrikam. Najprej opišemo definicijo simetrične matrike, nato spoznamo njene osnovne lastnosti. Vsako lastnost ponazorimo z zgledom. Na koncu drugega poglavja se usmerimo tudi k definitnosti in semidefinitnosti simetričnih matrik. V uvodu tretjega poglavja predstavimo antisimetrične matrike. Nadaljujemo z osnovnimi izreki, ki jih dokažemo in ponazorimo z zgledi. V tem poglavju vpeljemo tudi ostale izreke in definicije, ki so povezane z antisimetričnimi matrikami. Poglavje zaključimo s primerjavo simetričnih in antisimetričnih matrik, ki smo jih zasledili skozi celotno drugo in tretje poglavje diplomskega dela. Ključne besede: simetrične matrike, antisimetrične matrike, definitnost, semidefinitnost. Math. Subj. Class. (2010): 15A18,15B48.
8 AMBROŽ, G.: Antisymmetric matrices. Graduation Thesis, University of Maribor, Faculty of Natural Scicences and Mathematics, Department of Mathematics and Computer Science, ABSTRACT The thesis consist of three chapters. In the first chapter the basics of matrices and their definitions are presented. Arithmetic operations between them are described furthermore in greater detail and are illustrated by examples. Finally matrix s determinant and its characteristics, eigenvalues and Jordan canonical form are presented. Next chapter deals with symmetrical matrices. First the definition of symmetrical matrix is described and then its basic characteristics are recognized. Each characteristic is illustrated by an example. The end of the second chapter is directed to definite and semidefinite of the symmetrical matrices. In the introduction of the third chapter antisymmetrical matrices are presented. Basic theorems are preceded, which are proved and illustrated by examples. This chapter also introduces other theorems and definitions that are connected with antisymmetrical matrices. The chapter ends with comparisons of symmetrical and antisymmetrical matrices that were presented throughout the entire second and third chapter of the thesis. Keywords: symmetrical matrices, antisymmetrical matrices, definite, semidefinite. Math. Subj. Class. (2010): 15A18,15B48.
9 Kazalo Uvod 1 1 Matrike Definicija matrike Računske operacije z matrikami Determinanta matrike Lastne vrednosti Jordanova kanonična forma matrike Simetrične matrike Definicija in osnovne lastnosti Definitnost in semidefinitnost simetričnih matrik Antisimetrične matrike Uvod v antisimetrične matrike Osnovni izreki za antisimetrične matrike Primerjava simetričnih in antisimetričnih matrik Literatura 53 ix
10 Uvod Raziskovanje matrik je dokaj staro. Latinske kvadrate in magične kvadrate so raziskovali že v prazgodovinskih časih. Nemški matematik Gottfried Wilhelm Leibniz ( ) je razvil teorijo determinant leta Švicarski matematik Gabriel Cramer ( ) je teorijo razvil naprej in leta 1750 vpeljal Cramerjevo pravilo. Izraz matrika pa je prvi skoval, leta 1848, angleški matematik James Joseph Sylvester ( ). V začetku 19. stoletja sta nemški matematik Carl Friedrich Gauss ( ) in nemški geodet Wilhelm Jordan ( ) razvila Gauss-Jordanovo eliminacijsko metodo. Matematiki, kot so Cayley, Hamilton, Hermann Günther Grassmann, so kasneje še veliko raziskovali matrike in njihove teorije. Matrike že dolgo uporabljamo pri reševanju linearnih enačb. Matrika je v matematiki pravokotna tabela števil. V diplomskem delu bodo elementi matrik realna ali kompleksna števila. Matrike uporabljamo za zapis podatkov, ki so odvisni od dveh kategorij, saj je vsaka matrika sestavljena iz vrstic in stolpcev. Uporabne pa so tudi za proučevanje koeficientov sistemov linearnih enačb in linearnih transformacij. Začetek diplomskega dela bomo posvetili matrikam. Najprej bomo povedali kaj so matrike, kako jih označimo in kako so sestavljene. Prvo poglavje bomo nadaljevali z vrstami matrik, katere bomo tudi opisali in jih prikazali na konkretnih primerih. Predstavili bomo ničelno, spodnje in zgornje trikotno, diagonalno, skalarno, identično, unitarno in ortogonalno matriko. V drugem delu prvega poglavja si bomo pogledali računske operacije med matrikami. Najprej bomo opisali kdaj sta dve matriki enaki in podali lastnosti, ki veljajo za enakost matrik. Nato pa se bomo osredotočili na računske operacije. Kot prvo računsko operacijo bomo predstavili seštevanje dveh matrik, naslednja bo množenje matrike s skalarjem in kot zadnja bo produkt dveh matrik. Za vsako operacijo bomo opisali njene lastnosti ter kdaj je operacijo sploh izvedljiva in jo na koncu tudi prikazali na konkretnem primeru. V tem delu bomo tudi opisali kako dobimo nasprotno matriko poljubne matrike. V tretjem delu prvega poglavja se bomo osredotočili na determinanto matrike. Najprej bomo vpeljali determinanto poljubne n n matrike, nato pa si bomo podrobneje pogledali kako izračunamo determinanto matrike, ki ima dimenzijo 2 2 ter nato kako izračunamo determinanto matrike 1
11 2 dimenzije 3 3. Nadaljevali bomo z lastnostmi determinant in sicer, da je determinanta transponirane matrike enaka determinanti matrike same, kdaj je vrednost determinante enaka 0, kaj se zgodi če v determinanti zamenjamo dve vrstici ali stolpca in še nekaj osnovnih lastnosti. Tukaj bomo proučili pomen poddeterminante ali minorja ter kdaj je minor vogalen in kdaj glaven. Prav tako bomo opisali razvoj determinante po vrstici in stolpcu. Povedali bomo kdaj je matrika inverzna ter kako jo izračunamo in kdaj je matrika obrnljiva in kdaj ne. V naslednjem delu poglavja se bomo posvetili lastni vrednosti. Pojasnili bomo pomen lastne vrednosti in lastnega vektorja ter opisali osnovne lastnosti. Tukaj bomo tudi podali karakteristični in minimalni polinom. Povedali bomo kdaj sta si matriki podobni in prav tako kdaj sta ortogonalno oziroma unitarno podobni. Zadnji del prvega poglavja pa bomo namenili Jordanovi kanonični formi matrike. V uvodu bomo predstavili kdaj je matrika diagonalizabilna, ter s pomočjo diagonalizabilnosti, izpeljali Jordanovo formo, Nadalje bomo pojasnili njen pomen in sestavo. Drugo poglavje bomo namenili simetričnim matrikam. Najprej bomo predstavili nekaj zgledov, kje vse se srečujemo s simetričnimi matrikami in s pozitivno definitnostjo, nato bomo opisali osnovne definicije in lastnosti simetričnih matrik. Pogledali si bomo, da so lastne vrednosti realne simetrične matrike realne. V nadaljevanju poglavja bomo proučevali pozitivno in negativno definitnost in semidefinitnost. Najprej bomo navedeno dokazovali s pomočjo minorjev, kasneje pa še s pomočjo lastnih vrednosti. Na koncu poglavja bomo ugotovili, da je simetrična matrika ortogonalno podobna diagonalni matriki. V tretjem poglavju pa se bomo posvetili antisimetričnim matrikam. V uvodu v antisimetrične matrike bomo spoznali osnovno definicijo antisimetrične matrike. Nadalje bomo analizirali izreke, ki vključujejo antisimetrične matrike, jih dokazali in ponazorili z zgledi. Pogledali si bomo tudi lastne vrednosti antisimetričnih matrik, ki so 0 ali imaginarno število. Nato si bomo pogledali ali lahko vsako kvadratno matriko zapišemo na enoličen način kot vsoto simetrične in antisimetrične. Ter ugotovili, da navedeno drži. V zaključku podpoglavja si bomo pogledali Jordanovo formo antisimetrične matrike in ugotovili, da je antisimetrična matrika unitarno podobna diagonalni matriki. V zadnjem podpoglavju bomo analizirali simetrične in antisimetrične matrike ter povzeli njihove podobnosti in razlike.
12 Poglavje 1 Matrike V tem poglavju bomo predstavili nekaj osnovnih definicij o matrikah ter vrste matrik, ki jih bomo potrebovali za razumevanje naslednjih poglavij. Definicije in vrste matrik bomo ponazorili z zgledi. 1.1 Definicija matrike Matrika je pravokotna shema m n realnih ali kompleksnih števil, razvrščenih v m vrstic in n stolpcev. Označujemo jih z velikimi tiskanimi črkami: A,B,C,D... Matriko m n zapišemo takole: a 11 a a 1n a 21 a a 2n a m1 a m2... a mn Matriko, ki ima enako število vrstic kot stolpcev, m = n, imenujemo kvadratna matrika. Kvadratna matrika je reda n. V kvadratni matriki poznamo tudi pojem glavne diagonale, ki jo tvorijo vsi elementi a ij, kjer je i = j. To so elementi: a 11, a 22,..., a nn. Matriko, ki ima število vrstic, m, različno od število stolpcev, n, imenujemo pravokotna matrika. Matriko A, dimenzije m n, lahko zapišemo tudi v naslednji obliki [a ij ] m n. Zgled 1 Primer kvadratne matrike B in pravokotne matrike C. a 11 a a 1n a 21 a a 2n B =. C =..... a n1 a n2... a nn a 11 a a 1n a 21 a a 2n a m1 a m2... a mn 3
13 1.1 Definicija matrike 4 Zgled 2 Diagonalni elementi v matriki so 8, 4, 1. D = Število a ij imenujemo element matrike A, podatka i in j pa indeksa. Z njima točno določimo položaj elementa v matriki. Element a ij leži v i-ti vrstici in j-tem stolpcu. Zgled 3 Naj bo Glede na matriko A ugotovimo, da je v našem primeru a 13 = 31 element, kjer se sekata prva vrstica in tretji stolpec. Torej, vsi elementi, ki imajo enak prvi indeks, ležijo v isti vrstici, elementi pri katerih se ujemajo drugi indeksi, pa spadajo v isti stolpec. Torej bo prva vrstica, glede na našo matriko A, enaka: [a 11 a 12 a 13 a 14 ] = [ ]. Prvi stolpec pa bo enak: a 11 a 21 a 31 = Matrika A je dimenzije m n. Prvi podatek (m) nam pove število vrstic, drugi (n) pa število stolpcev. Oba podatka skupaj določata razsežnost, dimenzijo ali red matrike A. Operacijo, pri kateri v dani matriki zamenjamo vrstice s stolpci, imenujemo transponiranje matrike. Transponirano matriko, ki jo dobimo iz prvotne matrike A, označimo z A T. Zgled 4 Poglejmo si transponirano matriko A T, ki jo dobimo iz prvotne matrike A AT = Opazimo, da ima matrika A, dimenzijo 3 4, matrika A T pa ima dimenzijo 4 3.
14 1.1 Definicija matrike 5 Neposredno iz definicije transponiranja matrik sledi (A T ) T = A. Opazimo torej, da nam dvakratno transponiranje vrne prvotno matriko. Zgled 5 Poglejmo si primer dvakratnega transponiranja matrike A A T = (AT ) T = = A Če velja A T oziroma, da je a ij = a ji, za vse i,j, pravimo, da je matrika A simetrična. Opazimo, da je za simetrične matrike značilno, da zamenjava obeh indeksov ne spremeni elementa, posledično se s tem ne spremeni niti dimenzija matrike, zato lahko simetrične matrike najdemo le med kvadratnimi matrikami. Simetrične matrike si bomo podrobneje pogledali v nadaljevanju diplomskega dela. Sedaj pa si poglejmo še nekaj tipov matrik s posebnimi lastnostmi: Matrični stolpec ali stolpčni vektor je matrika dimenzije m 1 : a 1 a 2. a m. Matrična vrstica ali vrstični vektor je matrika dimenzije 1 n : [ a 1 a 2... a n ]. Ničelna matrika je matrika dane dimenzije, ki ima vse elemente enake 0 : [0] m n : O =. = [O]..... m n Matriki rečemo, da je zgornje trikotna, če so vsi elementi v kvadratni matriki pod glavno diagonalo enaki 0: to pomeni, da je a ij = 0, za vse i > j. Zgornje trikotno matriko označimo z A z. A z =
15 1.1 Definicija matrike 6 S transponiranjem zgornje trikotne matrike pa dobimo spodnje trikotno matriko, za katero velja, da so vsi elementi nad glavno diagonalo enaki 0: to pomeni, da je a ij = 0, za vse i < j. Spodnje trikotno matriko označimo z A s. A s = Opazimo, da obema družinama skupaj (zgornjim in spodnjim trikotnim matrikam) rečemo trikotne matrike. Diagonalna matrika je posebni primer trikotne matrike, pri kateri so vsi elementi izven glavne diagonale enaki 0. D = Če so si vsi elementi na diagonali diagonalne matrike enaki, a ii = a, imenujemo to matriko skalarna matrika in jo lahko identificiramo s tem realnim številom (a). Posebni primer skalarne matrike so matrike reda 1, ki jih poistovetimo s števili. D = a a a Identična matrika (matrična enota) reda n (I n ) je skalarna matrika, ki ima na diagonali same enice, vsi preostali elementi pa so enaki 0. I 3 = Za identično matriko velja naslednje pravilo: AI = I A. Opazimo, da ima identična matrika, pri množenju matrik, vlogo nevtralnega elementa, ki je enaka vlogi, ki jo ima število 1, pri množenju realnih števil, (a 1 = 1 a = a). Za matrike, za katere velja A 2 = A, pravimo, da so idempotentne. KvadratnamatrikaP jeunitarna matrika,čejep H = P 1,kjerP H predstavljahermitsko matriko (konjugirano transponirano matriko) in P 1 inverzno matriko. Potem velja: P H P = PP H = I.
16 1.2 Računske operacije z matrikami 7 P = ( i) ( i) i ; P je unitarna matrika. Kvadratna matrika A je ortogonalna matrika, če je A T = A 1, kjer A T predstavlja transponirano matriko. Potem velja: AA T = A T I ; A je ortogonalna matrika. 1.2 Računske operacije z matrikami V tem podpoglavju si bomo pogledali računske operacije med matrikami in njihove lastnosti terjihprikazalinakonkretnihprimerih. Čeimamomatrikeistedimenzijelahko, napodoben način kot pri realnih številih, definiramo različne relacije in operacije. Dve matriki sta enaki, če imata isto dimenzijo in če se ujemata v vseh istoležnih elementih: A m n = B m n a ij = b ij,( i,j)(i = 1,...,m,j = 1,...,n). Zgled 6 Enakost dveh matrik , B = B Za tako definirano enakost matrik veljajo naslednje lastnosti: refleksivnost: A, za vse A, simetričnost: B B = A, za vse A,B, tranzitivnost: B B = C C, za vse A,B,C. Na primerjavi istoležnih elementov lahko definiramo, za matrike enake dimenzije, tudi druge relacije: >,<,,... Matriki enakih dimenzij lahko tudi seštejemo. To naredimo tako, da seštejemo istoležne elemente:
17 1.2 Računske operacije z matrikami 8 A m n +B m n = C m n c ij = a ij +b ij,( i,j)(i = 1,...,m,j = 1,...,n). Zgled 7 Seštevanje dveh matrik , B = A+B = = Iz definicije vsote matrik in iz veljavnosti zakonov komutativnosti in asociativnosti, pri seštevanju realnih števil, oziroma iz definicije transponirane matrike, sledijo za seštevanje matrik naslednje lastnosti: kumutativnost: A+B = B +A, za vse A,B, asociativnost: A+(B +C) = (A+B)+C, za vse A,B,C, za transponiranje vsote matrik velja pravilo: (A+B) T = A T +B T, za vse A,B, inverz za seštevanje matrik: A+ 0 za vse A. Matriko lahko pomnožimo s skalarjem, ki je neko poljubno število. To naredimo tako, da z njim pomnožimo vse elemente v matriki: c A m n = c [a ij ] m n = [c a ij ] m n. Zgled 8 Množenje matrike A s skalarjem c. c = Pri množenju matrike s skalarjem veljajo naslednje lastnosti: asociativnost: a(ba) = (ab)a, za vse a,b R in vse A, distributivnost seštevanja matrik in množenja s skalarjem: a(a+b) = aa+ab, za vse a R in za vse A,B,
18 1.2 Računske operacije z matrikami 9 distributivnost seštevanja skalarjev in množenja matrike s skalarjem: (a+b) aa+ba, za vse a,b R in za vse A,B, (aa) T = aa T, za vse a R in za vse A, množenje s skalarjem 1: 1 A 1 = A, za vse A. Nasprotno matriko, A, dobimo tako, da nasprotno predznačimo vse elemente matrike A, torej [ a ij ]. Nasprotno matriko matrike A torej dobimo tako, da prvotno matriko A pomnožimo s skalarjem (-1). Zgled 9 Primer seštevanja matrike A z njeno nasprotno matriko (-A) , A+( A) = = 0 Naslednja matrična operacija, ki si jo bomo pogledali, je množenje dveh matrik. Vendar bomo pred tem pogledali še, kaj je skalarni produkt. Podana imamo vrstični vektor a 1 n in stolpčni vektor b n 1 : b 2 a = [a 1 a 2... a n ], b =. Njun skalarni produkt je definiran z naslednjim predpisom: b 2 a b = [a 1 a 2... a n ]. b 1 b n = b 1 b n. n a i b j. i=1 Skalarni produkt smo si pogledali, sedaj pa bomo definirali produkt dveh matrik.
19 1.2 Računske operacije z matrikami 10 Produkt matrike A z matriko B je taka matrika C (A B = C), da je vsak njen element c ij skalarni produkt i-te vrstice matrike A z j-tim stolpcem matrike B: c ij = a i1 b 1j +...+a in b nj = n a ik b kj = [a i1... a in ] k=1 Opazimo, da lahko skalarni produkt izračunamo le za vektorja enake dolžine, tako od tod dobimo pogoj za izvedljivost tako definiranega množenja. Produkt dveh matrik obstaja natanko takrat, ko se število stolpcev prve matrike A ujema s številom vrstic druge matrike B: A m p B p n = C m n, c ij = p a ik b kj. k=1 b 1j. b nj. Rezultat množenja A B je matrika C, ki ima toliko vrstic, kot jih ima prva matrika (A), in toliko stolpcev, kot jih ima druga matrika (B). Zgled 10 Produkt dveh matrik. A 4 2 B 2 3 = [ ] = = = = = C 4 3 Za matrični produkt veljajo naslednje lastnosti: množenje matrik v splošnem ni komutativno: AB BA, množenje matrik je asociativno: (AB)C = A(BC), za vse A,B,C,
20 1.3 Determinanta matrike 11 množenje matrik je distributivno: A(B +C) = AB +AC, (A+B)C = AC +BC, za vse A,B,C, za matrični produkt velja formula: (AB) T = B T A T, za vse A,B, enota za množenje je identična matrika I. Produkt ničelne matrike z dano matriko A je enak ničelni matriki, (A 0 = 0 0). Vendar obstajajo primeri, kjer je produkt dveh neničelnih matrik enak ničelni matriki. Zgled 11 Primer, kjer je produkt dveh neničelnih matrik ničelna matrika ,B = A B = = Ugotovili smo, da lahko matriko pomnožimo samo s seboj le v primeru, ko je matrika kvadratna, saj v nasprotnem primeru množenje ni izvedljivo, ker nimamo izpolnjenega pogoja glede dimenzij matrik. Za kvadratno matriko poljubne dimenzije pa lahko, na enak način kot v skalarnem primeru, definiramo potence na naslednji način: A n = A A... A }{{}, n N. n Za produkt potenc velja naslednji obrazec: A n A m = A n+m, potenciranje potenc pa poteka po pravilu: (A n ) m = A nm. 1.3 Determinanta matrike V tem podpoglavju bomo vpeljali pojem determinante matrike, spoznali njene lastnosti in nekaj metod za računanje determinant.
21 1.3 Determinanta matrike 12 Kvadratni matriki dimenzije n: a 11 a a 1n a 21 a a 2n a n1 a n2... a nn = [a ij ] n n priredimo njeno determinanto: det A = a 11 a a 1n a 21 a a 2n a n1 a n2... a nn R. To naredimo tako, da tvorimo vse možne produkte po n elementov matrike A, v katerih je iz vsake vrstice in iz vsakega stolpca natanko po en element. Vsak produkt pomnožimo s faktorjem ( 1) i(v)+i(s), kjer je v permutacija indeksov vrstic in s permutacija indeksov stolpcev. Kadar je permutacija stolpčnih indeksov soda, temu produktu ohranimo predznak, ko pa gre za liho permutacijo, pa mu predznak spremenimo. Na koncu ustrezno predznačene produkte seštejemo: det R ( 1) i(i 1,..., i n)+i(j 1,..., j n) a i1 j 1...a inj n, kjer R pomeni množico vseh možnih permutacij, katerih je n!. Opazimo torej, da je determinanta preslikava iz množice kvadratnih matrik v množico realnih števil, saj vsaki kvadratni matriki (in sicer samo kvadratni) priredi natanko določeno realno število. Torej, če je A M n (F) in i N n velja: n det(a) = ( 1) i+j a ij det(a ij ). j=1 Determinanto že poznamo, zato si bomo v nadaljevanju pogledali še kako jo izračunamo. Računanje determinante matrike dimenzije 2 2. Determinanto drugega reda izračunamo tako, da od produkta elementov na glavni diagonali odštejemo produkt elementov na stranski diagonali, det a 11 a 22 a 12 a 21. Zgled 12 Računanje determinante matrike dimenzije 2 2. det 8 5 = = =
22 1.3 Determinanta matrike 13 Računanje determinante matrike dimenzije 3 3. a 11 a 12 a 13 det A = a 21 a 22 a 23 a 31 a 32 a 33 Pri dimenziji n = 3 imamo šest različnih produktov pomnoženih z ustreznimi faktorji. Da imamo šest produktov smo ugotovili s pomočjo permutacije: P 3 = 3! = 6. Determinanto tretjega reda izračunamo s pomočjo Sarrusega pravila. Ta postopek poteka tako, da najprej k prvotni determinanti na desni strani pripišemo 1. in 2. stolpec. Nato seštejemo produkte elementov na glavni diagonali in njenih vzporednicah ter na koncu še odštejemo produkte elementov na stranski diagonali in njenih vzporednicah. a 11 a 12 a 13 a 11 a 12 a 21 a 22 a 23 a 21 a 22 a 31 a 31 a 32 a 33 a Zato je vrednost determinante takšne matrike določena z naslednjim izrazom: det A = a 11 a 22 a 33 a 11 a 23 a 32 a 12 a 21 a 33 +a 12 a 23 a 31 +a 13 a 21 a 32 a 13 a 22 a 31 Zgled 13 Računanje determinante matrike dimenzije 3 3 s pomočjo Sarrusega pravila , det det = 176 Determinante četrtega ali višjega reda računamo s pomočjo determinant nižjega reda (poddeterminant), tako da uporabimo izrek o razvoju determinante po vrstici oziroma stolpcu. Ta izrek bomo opisali nekoliko kasneje. Lastnosti determinant Vrednost determinante se ne spremeni, če vrstice zamenjamo s stolpci oziroma če matriko transponiramo: det deta T. Zaradi te lastnosti veljajo vse nadaljnje lastnosti tako za vrstice kot tudi za stolpce.
23 1.3 Determinanta matrike 14 Izrek 1.1 Determinanta transponirane matrike A T je enaka determinanti matrike A same. Dokaz. det ε Π a 1,Π(1) a 2,Π(2)...a n,π(n) Π S n Po dogovoru sledi: = ε Π a k1,π(k 1 )a k2,π(k 2 )...a kn,π(k n) Π S n Nato vzamemo, da je k j = Π 1 (j) = ε Π a Π 1 (1),1a Π 1 (2),2...a Π 1 (n),n = deta T Π S n Zgled 14 [ ] [ 8 31,A T = 5 10 ] det = = = 75 deta T = = = = 75 Če so v dani matriki vsi elementi neke vrstice enaki 0, je vrednost determinante enaka 0. Če v determinanti matrike A med seboj zamenjamo dve vrstici ali stolpca, se spremeni le predznak determinante. a 11 a 12 det a 21 a 22 = a 21 a 22 a 11 a 12 det a 11 a 12 a 21 a 22 = a 12 a 11 a 22 a 21 Zgled 15 det = = = 75
24 1.3 Determinanta matrike 15 Če pomnožimo vse elemente v neki vrstici s poljubnim številom k R, je dobljena determinanta enaka prvotni determinanti, pomnoženi s številom k. Zgled 16 [ ],k = = = = 150 = 2 deta Determinanta z dvema identičnima ali proporcionalnima vrsticama je enaka 0. Proporcionalni vrstici i in l sta tisti vrstici, kjer je i-ta vrstica mnogokotnik l-te, zato za vsak stolpčni indeks j velja a ij = k a lj. Zgled 17 [ 8 8k 5 5k ], det 8 8k 5 5k = 40k ( 40k) = 0 Če so vsi elementi, ki ležijo na eni strani glavne diagonale enaki 0, je determinanta enaka produktu diagonalnih elementov. Taki determinanti pravimo trikotna determinanta. Zgled , det = 32 Determinanto poljubne matrike lahko zapišemo kot vsoto determinant dveh matrik, ki se v vseh vrsticah razen v eni ujemata s prvotno matriko. Za to vrstico velja, da je vsota istoležnih elementov novih matrik enaka ustreznemu elementu v prvotni matriki. Zgled 19 [ ] det = = = 75
25 1.3 Determinanta matrike 16 Determinanta se ne spremeni, če h katerikoli vrstici prištejemo s poljubnim faktorjem pomnoženo neko drugo vrstico. Zgled 20 [ ],k = = = = = 75 Če matriko pomnožimo s skalarjem, potem velja: det(ka) = k n A. Poddeterminanto ali minor ij elementa a ij dobimo, če v determinanti izpustimo i-to vrstico in j-ti stolpec. Če tako dobljeno determinanto pomnožimo z ( 1) i+j, dobimo kofaktor-algeberski koeficient elementa a ij. Kofaktor označimo z A ij. a a 1n a ij i-ta vrstica (jo črtamo) a n a nn j-ti stolpec (ga črtamo) Med poddeterminanto ij in kofaktorjem A ij velja torej naslednja zveza: A ij = ( 1) i+j ij Zgled 21 Iskanje poddeterminante 33 in kofaktorja A 23 za dano matriko A = = = = 18
26 1.3 Determinanta matrike 17 A 23 = ( 1) = = (24 35) = 11 i-vrsten minor matrike je vogalen, če ga sestavimo iz prvih i vrstic in stolpcev matrike. Minor matrike je glaven, če ga sestavimo iz vrstic in stolpcev z enakimi indeksi. Poznamo enovrstne, dvovrstne,..., n-vrstne glavne minorje. Zgled 22 Podano imamo poljubno matriko A Za matriko A so vogalni minorji: 8, , Za matriko A so glavni minorji: - enovrstni: 8, 4, 1 ; - dvovrstni: , , ; - trivrstni: Razvoj determinante po vrstici oziroma stolpcu. Če je v zadnji vrstici determinante A od nič različen le zadnji element a nn, je determinanta A enaka produktu elementa a nn s poddeterminanto nn : A = a nn nn.
27 1.3 Determinanta matrike 18 Zgled 23 det = = 2 (32 50) = 36 Če pa je v i-ti vrstici dane determinante le element a ij različen od 0, je determinanta enaka produktu tega elementa z njegovim kofaktorjem: A = a ij A ij. Po prvi lastnosti, ki smo jo prejle napisali, ugotovimo, da ta izrek velja tudi za stolpce. In sicer, če je v j-tem stolpcu determinante le element a ij različen od 0, je determinanta enaka produktu tega elementa z njegovim kofaktorjem. Zgled 24 det = 2 ( 1) = 2 ( 1)(32 50) = 36 Determinanta dane kvadratne matrike je enaka skalarnemu produktu poljubne vrstice (ali stolpca) z naborom pripadajočih kofaktorjev. Zgled det ( 2) = = 4 ( 1) = = 4 ( ) = 640 Razvoj determinante po i-ti vrstici: n A = a i1 A i1 +a i2 A i a in A in = a ik A ik. k=1
28 1.3 Determinanta matrike 19 Zgled 26 det = 0 ( 1) ( 1) ( 1) = = 640 Razvoj determinante po j-tem stolpcu: n A = a 1j A 1j +a 2j A 2j +...+a nj A nj = a kj A kj. k=1 Zgled 27 det = 4 ( 1) ( 1) ( 1) = = 640 Skalarni produkt poljubne vrstice z naborom kofaktorjev, ki pripadajo kaki drugi vrstici, je vedno enak 0. Zgled 28 Za determinanto matrike A, A, bomo izračunali skalarni produkt druge vrstice s kofaktorji tretje vrstice , det j=1 a 2j A 3j = 0 ( 1) ( 1) ( 1) = = 0
29 1.3 Determinanta matrike 20 Izrek 1.2 Za poljubni kvadratni matriki A in B iste velikosti velja: det(ab) = det(a) det(b). Dokaz. det(ab) = n j 1 =1 a 1,j 1 b j1,1. n j 1 =1 a n,j 1 b j1,1 n j 2 =1 a 1,j 2 b j2,2... n j a n=1 1,j n b jn,n..... n j 2 =1 a n,j 2 b j2,2... n j a n=1 n,j n b jn,n = n = b j1,1 j 1 =1 j 2 =1 n b j2,2... n j n=1 b jn,n a 1,j1 a 1,j2... a 1,jn a n,j1 a n,j2... a n,jn = detb T { }}{ = b j1,1 b j2,2... b jn,n ε Π det deta detb Π= n j 1 j 2... j n Inverzna ali obratna matrika A 1 Zanima nas ali obstaja za vsako neničelno matriko A takšna matrika A 1, da velja: A A 1 = A 1 I. Iz te zahteve lahko s pomočjo pravila o množenju matrik razberemo, da morata biti tako matrika A kot tudi njena inverzna matrika A 1 kvadratni matriki enakih dimenzij. Kvadratnim matrikam, ki premorejo inverzno matriko, pravimo obrnljive (neizrojene, nesingularne) matrike. Njihove pripadajoče inverzne matrike bomo izračunali s pomočjo determinant in kofaktorjev. Iz tega sledi, da ima vsaka obrnljiva matrika enolično določeno pripadajočo inverzno ali obratno matriko A 1. Vendar smo ugotovili, da so tudi med neničelnimi kvadratnimi matrikami take izrojene (singularne) matrike, ki ne premorejo inverzne matrike A 1. Izrek 1.3 Naj bo A kvadratna matrika z dimenzijo n n, za katero velja, da ima homogeni sistem AX = 0 samo trivialno rešitev. Potem velja, da je matrika A nesingularna. Enakovredno lahko trdimo, da če je matrika A singularna, potem ima homogeni sistem AX = 0 netrivialno rešitev.
30 1.3 Determinanta matrike 21 Dokaz. Če je A kvadratna matrika dimenzije n n, homogeni sistem AX = 0 pa ima samo eno trivialno rešitev, potem sledi, da stopničasta matrika B, ki je vrstično ekvivalentna matriki A, ne more imeti neničelnih vrstic in je enaka I n (enotski matriki dimenzije n). Matriki A in B sta vrstično ekvivalentni, če obstajajo take elementarne matrike E 1,E 2,...,E n, da velja, da je E 1 E 2...E n B. Zato je A nesingularna. Če je matrika A nesingularna in AX = 0, potem je X = A 1 0 = 0. Posledica 1.4 Če je matrika A obrnljiva, potem je deta 1 = 1 deta. Dokaz. Ker velja AA 1 = I in deti = 1, sledi iz izreka 1.2 (deta)(deta 1 ) = 1. Torej je deta 1 = 1 deta. Zgled 29 Primer neničelne kvadratne matrike, ki nima inverzne matrike. [ ] det = = 0 Ugotovimo, da A 1 ne obstaja, saj je det 0 in ni izpolnjen pogoj za računanje inverzne matrike. Izrek 1.5 Inverzna matrika A 1 obstaja natanko tedaj, ko je deta 0 in velja: A 1 = 1 deta [A ij] T. Dokaz. Vemo, da velja: AA 1 = I in deti = 1. A [A ij] T det 1 deta a 1,1 a 1,2... a 1,n a n,1 a n,2... a n,n A 1,1 A 2,1... A n, A 1,n A 2,n... A n,n =
31 1.3 Determinanta matrike 22 = 1 deta n j=1 a n 1,jA 1,j j=1 a 1,jA 2,j... n j=1 a 1,jA n,j n j=1 a n n,ja 1,j j=1 a n,ja 2,j... n j=1 a n,ja n,j = 1. i = k n n a ij A ij = a ij ( 1) i+j det(a ij ) = deta j=1 j=1 2. i k n a ij A kj = j=1 a 1,1 a 1,2... a 1,n a i,1 a i,1. a i,2... a i,n a i,2... a i,n..... a n,1 a n,2... a n,n = 0 A [A] T = deta deta deta Če je to res, potem je 1 deta [A ij] T inverz matrike A. Torej je: A 1 = 1 deta [A ij] T. (A[A] T ) ij = n a ij [A T ] jk = j=1 n a ij [A] kj = j=1 n a ij ( 1) k+j det(a kj ) j=1 = { deta; i = j 0; sicer Inverzno matriko dane kvadratne matrike A izračunamo tako, da z recipročno vrednostjo determinante matrike A pomnožimo transponirano matriko kofaktorjev: A 1 = 1 A [A ij] T.
32 1.3 Determinanta matrike 23 Zgled 30 Računanje inverzne matrike Najprej preverimo, če je determinanta A različna od 0 (poglej zgled 13): A = = (!A 1 ) Ker je determinanta različna 0, nadaljujemo z računanjem. Po formuli A ij = ( 1) i+j ij izračunamo kofaktorje A ij : A 11 = ( 1) = 4 36 = 32 A 12 = ( 1) = (10 84) = 74 A 13 = ( 1) 1+3 A 21 = ( 1) 2+1 A 22 = ( 1) = = 2 = (5 93) = 88 = = 209 A 23 = ( 1) = (24 35) = 11 A 31 = ( 1) = = 64 A 32 = ( 1) = (96 310) = 214
33 1.4 Lastne vrednosti 24 A 33 = ( 1) = = 18 Dobili smo matriko kofaktorjev [A ij ] = , ki jo moramo transponirati in dobimo: [A ij ] T = , katero pomnožimo z recipročno vrednostjo A A 1 = Lastne vrednosti V nadaljevanju si bomo pogledali, kaj je lastna vrednost in kaj lastni vektor. Nato bomo opisali karakteristični in minimalni polinom. Prav tako si bomo pogledali podobnost matrik in ortogonalno podobnost matrik. Definicija 1.6 Naj bo A : V V endomorfizem. Tedaj je λ F lastna vrednost preslikave A, če obstaja tak neničelni vektor v V, da velja A(v) = λv. Vektor v pa imenujemo lastni vektor za lastno vrednost λ. Podobno velja za matrike. Naj bo A kvadratna matrika s kompleksnimi koeficienti: A C n n. Potem je število λ lastna vrednost matrike A, če obstaja tak neničelni vektor v, da velja: Av = λv. Trditev 1.7 Kompleksno število λ je lastna vrednost za A C n n natanko tedaj, ko je ker(a λi) 0.
34 1.4 Lastne vrednosti 25 Dokaz. Število λ je lastna vrednost matrike A natanko tedaj, ko je Av = λv in v 0. To lahko zapišemo v obliki (A λi)v = 0, kjer je v 0. To je ekvivalentno zahtevi, da ker(a λi) 0, saj je 0 v ker(a λi). Izrek 1.8 Množica vseh lastnih vektorjev preslikave A : V V, za isto pripadajočo lastno vrednost λ, tvori skupaj z ničelnim vektorjem tako imenovani lastni podprostor U λ prostora V. Dokaz. Naj bo U λ = {v V; Av = λv} V lastni podprostor prostora V za preslikavo A : V V. Če so vsi α,β F in vsi u,v U λ, potem je Au = λu in Av = λv, ter velja αu+βv U λ. Od tod sledi, da je: A(αu+βv) = αau+βav = α(λu)+β(λv) = (αλ)u+(βλ)v = λ(αu+βv) Definicija 1.9 Veččlenik p A (λ) = det(a λi), kjer je A matrika linearnega operatorja A : V V glede na neko bazo prostora V in I identična matrika, imenujemo karakteristični polinom matrike A (oziroma preslikave A). a 1,1 λ a 1,2... a 1,n. a 2,1 a 2,2 λ... p A (λ) = an 1,n a n,1... a n,n 1 a n,n λ Izrek 1.10 Število λ F je lastna vrednost linearne preslikave A : V V (oziroma matrike A) natanko tedaj, če je ničla karakterističnega polinoma p A : p A (λ) = 0. Dokaz. Število λ je lastna vrednost preslikave A natanko tedaj, če obstaja tak neničelni vektor v, da velja Av = λv. Kar lahko zapišemo v obliki (A λi) = 0, kjer je v 0. To je ekvivalentno homogenemu sistemu linearnih enačb (A λi) = 0, za katerega velja, da je det(a λi) = 0. To pa je ekvivalentno p A (λ) = 0, ko upoštevamo definicijo Definicija 1.11 Polinom imenujemo moničen, če ima vodilni koeficient enak 1. Definicija 1.12 Naj bo A : V V. Tedaj je minimalni polinom preslikave A moničen polinom najmanjše stopnje p(v), tako, da je p(a) = 0. Analogno lahko definiramo tudi minimalni polinom matrike A.
35 1.4 Lastne vrednosti 26 Izrek 1.13 Naj bo A : V V. Tedaj je λ F lastna vrednost za A natanko tedaj, ko je λ ničla minimalnega polinoma preslikave A: m A (λ) = 0. Dokaz. Število λ je lastna vrednost preslikave A natanko tedaj, če obstaja tak neničelni vektor v, da velja Av = λv. Naj bo m A (v) = v k +a k 1 v k a 0 minimalni polinom preslikave A in naj bo lastna vrednost λ ničla minimalnega polinoma preslikave A, m A (λ) = 0 (preslika vse v 0, med drugim tudi vektor v). Če je 0 = m A (A)(v) = = (A k +a k 1 A k a 0 I)(v) = = A k v +a k 1 A k 1 v +...+a 0 Iv = = λ k v +a k 1 λ k 1 v +...+a 0 v = = (λ k +a k 1 λ k a 0 ) v = 0; v 0, }{{} skalar potem je λ k +a k 1 λ k a 0 = 0. Od tod sledi, da je m A (λ) = 0. Opomba k dokazu izreka Naj bo Av = λv, potem velja A 2 = A(A(v)) = A(λv) = λav = λ 2 v. = A n v = λ n v. Definicija 1.14 Dve kvadratni matriki enake velikosti, A, B, sta podobni, če obstaja obrnljiva matrika P, za katero velja P 1 BP. Trditev 1.15 polinoma. Če sta matriki A in B podobni matriki, potem imata enaka karakteristična Dokaz. S P označimo obrnljivo matriko, za katero je PBP 1. Od tod, z uporabo lastnosti determinante, sledi: p A (λ) = det(a λi) = det(pbp 1 λi) = det(p(b λi)p 1 ) =
36 1.5 Jordanova kanonična forma matrike 27 = detpdet(b λi)detp 1 = detpdetp 1 det(b λi) = = det(b λi) = p B (λ). Definicija 1.16 Matriki A in B sta ortogonalno podobni, če obstaja ortogonalna (v R) matrika P, za katero je P T BP. Če je P ortogonalna, je PP T = P T P = I, od koder sledi, da je P T = P 1. Torej je P prehodna matrika v smislu običajne podobnosti. Definicija 1.17 Matriki A in B sta unitarno podobni, če obstaja unitarna matrika P, za katero je P H BP. Če je P unitarna, je PP H = P H P = I, od koder sledi, da je P H = P 1. Torej je P prehodna matrika v smislu običajne podobnosti. 1.5 Jordanova kanonična forma matrike Definicija 1.18 Matrika A je diagonalizabilna, če obstaja taka matrika P, da je P 1 AP diagonalna matrika. Primer diagonalizabilne matrike: Trditev 1.19 Matrika A je diagonalizabilna natanko tedaj, ko obstaja baza prostora sestavljena iz lastnih vektorjev. Dokaz. Recimo, da je A : U U diagonalizabilna. Torej obstaja urejena baza B = {u 1,u 2,...,u n }, tako da je matrika λ λ.. 2. A[B,B] = λ n
37 1.5 Jordanova kanonična forma matrike 28 Nato matriko A[B, B] zapišemo v bazi: Au 1 = λ 1 u 1 +0u u n ; u 1 0 Au 2 = 0u 1 +λ 2 u u n ; u 2 0. Au n = 0u 1 +0u λ n u n ; u n 0 Ker je matrika diagonalizabilna, imamo bazo iz lastnih vektorjev. Če imamo neko matriko A, želimo poiskati tako bazo oziroma matriko P, da je P 1 AP preprosta. Jordanova kanonična forma je posplošitev diagonalizacije, kar pomeni, da bodo po diagonali šle samo lastne vrednosti. Dokaz naslednjega izreka najde bralec v [16, str. 130]. Izrek 1.20 (primarna dekompozicija) Naj bo A : V V endomorfizem in m (X λ 1 ) e 1 (X λ 2 ) e 2...(X λ r ) er. W 1,W 2,...,W r naj bodo posplošeni podprostori, torej W i = ker((a λ i I) e i ); 1 i r. Tedaj velja: U = W 1 W 2... W r. (U je direktna vsota A i.) Posledica 1.21 Ohranimo oznake iz prejšnjega izreka. Naj bodo B 1,B 2,...,B r baze za W 1,W 2,...,W r. Potem je B = B 1 B 2... B r baza za V in A A.. 2. A[B,B] = A r bločno diagonalna matrika, kjer je blok A i dimenzije e i e i. Naj bo A : V V endomorfizem in m A (X) = (X λ 1 ) n 1 (X λ 2 ) n 2...(X λ r ) nr ter p A (X) = ( 1) e 1+e e r (x λ 1 ) e 1 (x λ 2 ) e 2...(x λ r ) er. Potem obstaja baza B za V, da velja: J J.. 2. A[B,B] =....., J r
38 1.5 Jordanova kanonična forma matrike 29 kjer so J i Jordanovi bloki. Torej je λ i edina lastna vrednost za J i. Število Jordanovih blokov je r, kar je število različnih lastnih vrednosti. Blok J i je dimenzije e i e i. Posamični blok J i pa je bločno diagonalno sestavljen iz Jordanovih kletk. Te kletke predstavljajo matrike oblike: λ i λ..... i λi λ i Pri tem je število kletk, ki nastopajo v J i enako dimenziji lastnega podprostora za lastno vrednost λ i. Največja kletka je dimenzije n i n i (prva kletka). Zgled 31 Naj bo matrika M 5 (C). Karakteristični polinom matrike A je p (2 λ) 5. Izračunajmo (A 2I) 2 = , (A 2I) 3 = Iz tega sledi, da je m A (λ) = (λ 2I) 3 minimalni polinom preslikave A (matrike A). Opazimo, da bo Jordanova kanonična forma matrike A imela prvo kletko dimenzije 3. Ker imamo dva lastna vektorja, bomo imeli dve kletki in druga kletka bo dimenzije 2. In tako dobimo: J =
39 Poglavje 2 Simetrične matrike V prvem delu tega poglavja bomo proučili nekaj zgledov, v katerih se srečamo s simetričnimi matrikami. Nato bomo s pomočjo Hessejeve matrike odvodov drugega reda določili, kdaj ima funkcija lokalne ekstreme. Poglavje bomo nadaljevali z zgledoma o nenegativni definitnosti. Nato se bomo posvetili definiciji simetrične matrike in zapisali osnovne lastnosti simetričnih matrik. V drugem delu pa se bomo osredotočili na definitnost in semidefinitnost simetrične matrike. Simetrične matrike srečamo na različnih področjih matematike. Nekaj osnovnejših si bomo pogledali in jih prikazali z zgledi. Zgled 32 Če je f : D R dvakrat zvezno odvedljiva funkcija na isti domeni D Rn, potem je realna matrika, [ ] f(x) H(x) = [h ij (x)] M n (R), x i x j znana kot Hessejeva matrika drugih parcialnih odvodov funkcije f. Za naše namene je H = H(x) v tem primeru edina lastnost, ki nas zanima. Ta izhaja iz pomembnega dejstva in sicer, da so mešani parcialni odvodi enaki 2 f = 2 f, za vse i,j = 1,2,...,n. x i x j x j x i Če imamo Hessejevo matriko H = [h ij ] vemo, da je h ij = h ji, za vse i,j = 1,2,...,n. Tako je H = H T. Matriko A M n, kjer je A T, imenujemo simetrična matrika. Hessejeva matrika realnih vrednosti, ki je dvakrat zvezno odvedljiva je vedno simetrična matrika. Zgled 33 Naj bo [a ij ] n n realna ali kompleksna matrika. Kvadratno formo za R n 30
40 31 ali C n generiramo z matriko A na naslednji način: Q(x) x T Ax = n a ij x i x j i,j=1 n 1 = 2 (a ij +a ji )x i x j i,j=1 [ ] 1 = x T 2 (A+AT ) x Tako matriki A in 1 2 (A + AT ) generirata enako kvadratno formo, kjer je zadnja matrika simetrična matrika. Zgled 34 Linearni parcialni diferencialni operator L drugega reda definiramo z Lf(x) n i,j=1 a ij (x) 2 f(x) x i x j. Koeficientia ij (x) infunkcijaf(x) sodefinirani visti domeni D R n infunkcijaf jedvakrat zvezno odvedljiva na D. Operator L je povezan na naravni način z matriko. Matrika [a ij (x)] ne rabi biti simetrična, ampak, ker so mešani parcialni odvodi funkcije f enaki, imamo Lf = = n 2 f a ij (x) = x i x j i,j=1 n i,j=1 n [ 1 2 f 2 ] f a ij (x) +a ji (x) 2 x i x j x j x i i,j=1 1 2 [a 2 f ij(x)+a ji (x)]. x i x j Tako simetrična matrika 1 2 (A+AT ) predstavlja isti operator kot matrika A. Zgled 35 NajboΓneusmerjengraf. GrafΓjesestavljenizmnožicenvozlišč{P 1,P 2,...,P n } inmnožicee neurejenihparovvozlišč,kijihimenujemopovezavee = {{P i1 P j1 },{P i2,p j2 },...}. GrafΓlahkoopišemozelonakratko, znjegovotakoimenovanomatrikososednosti [a ij ]. Kjer je { 1; {Pi,P j } E a ij = 0; sicer Ker je Γ neusmerjen graf, je matrika A realno simetrična matrika. Tako je A T = A. Nadalje si bomo ogledali trditev iz katere je razvidno, da so simetrično bilinearne forme naravno povezane s simetričnimi matrikami.
41 32 Trditev 2.1 Bilinearna forma Q(x,y) = x T Ay na vektorskem prostoru F n je simetrična natanko tedaj, ko je matrika A simetrična. Dokaz. Predpostavimo, da je matrika A simetrična, to pomeni A T = A. Ker je skalar matrika velikosti 1 1 in je enak svoji transponirani vrednosti, lahko sedaj izračunamo Q(y,x) = y T Ax = (y T Ax) T = x T A T y = x T Ay = Q(x,y). Torej je Q simetrična bilinearna forma. Drugo implikacijo dobimo, ko vstavimo, da je x = e i in y = e j in ugotovimo, da je Q(e i,e j ) = e i Ae j = a ij Q(e j,e i ) = e j Ae i = a ji. Ker je sama bilinearna forma simetrična, iz tega sledi, da je a ij = a ji in zato je matrika A simetrična. Sedaj si bomo pogledali še dva zgleda, ki prikazujeta pozitivno definitnost matrik. Zgled 36 Naj bo f(x) gladka realna funkcija iz množice D R n. Če je y = [y i ] notranja točka množice D, potem, glede na Taylorjev izrek, velja: f(x) = f(y)+ n (x i y i ) f x i + y i=1 n 2 f (x i y i )(x j y j ) x i x j +..., y i,j=1 za vse točke x D, ki so blizu y. Če je y stacionarna točka funkcije f, potem vsi parcialni odvodi prvega reda v y izginejo in dobimo izraz: f(x) f(y) = n 2 f (x i y i )(x j y j ) x i x j +... y i,j=1 = (x y) T H(f;y)(x y)+..., ki opredeljuje obnašanje funkcije f v bližini točke y. Naj bo [ 2 ] f H(f;y) x i x j y Hessejeva matrika funkcije f v točki y; gre za simetrično matriko zaradi enakosti mešanih parcialnih odvodov funkcije f. Če je kvadratna forma, z T H(f;y)z, z 0, z R n,
42 33 vedno pozitivna, potem je y relativni (lokalni) minimum za funkcijo f. Če pa je kvadratna forma vedno negativna, potem pa je y relativni (lokalni) maksimum za funkcijo f. Če je kvadratna forma nenegativna v vseh točkah množice D (ne samo v kritičnih točkah funkcije f), potem je funkcija f konveksna funkcija v množici D. Zgled 37 NajbodoX 1,X 2,...,X n realnealikompleksnenaključnespremenljivkeskončnimi drugimi momenti na nekem verjetnostnem prostoru z matematičnim upanjem in predpostavimo, da µ i = E(X i ) predstavlja ustrezne srednje vrednosti. Kovariančna matrika naključnega vektorja X = (X 1,X 2,...,X n ) T je matrika [a ij ], za katero velja: a ij = E[(X i µ i )(X j µ j )], i,j = 1,2,...,n. Iz enačbe je razvidno, da je A hermitska matrika. Če je z = [z i ] C n, potem lahko enostavno izračunamo, da je: [ n z Az = E = E i,j=1 ] z i (X i µ i )z j (X j µ j ) n z i (X i µ i ) i,j= Edine lastnosti za funkcional pričakovane vrednosti, ki nastopajo v tem primeru, so linearnost, homogenost in nenegativnost, kar pomeni, da je E[Y] 0, kadar je Y nenegativna naključna spremenljivka. Podobnolahkoopazimotudibrezuporabejezikaizpodročjaverjetnosti. Čeobstajadružina kompleksnih funkcij f 1,f 2,...,f n na realni osi, če je g realna funkcija in če so vsi integrali a ij = f i (x)f j (x)g(x)dx, i,j = 1,2,...,n definirani in konvergentni, potem je matrika [a ij ] očitno hermitska. Enostavno lahko izračunamo, da z Az = = n i,j=1 i=1 z i f i (x)z j f j (x)g(x)dx n 2 z i f i (x) g(x)dx potem bo podana kvadratna forma vedno nenegativna, če je g(x) nenegativna funkcija.
43 2.1 Definicija in osnovne lastnosti Definicija in osnovne lastnosti Kvadratno matriko A imenujemo simetrična matrika, če velja, da je A T. Iz tega sledi, da so simetrične matrike tiste kvadratne matrike, pri katerih so elementi simetrični glede na glavno diagonalo enaki: za vsak i in j velja, da je a ij = a ji. Za simetrične matrike je značilno, da zamenjava obeh indeksov ne spremeni elementa. Torej lahko rečemu tudi, da je matrika simetrična, kadar je i-ta vrstica enaka i-temu stolpcu. Splošen zapis simetrične matrike: a 11 a a 1n a 12 a a 2n a 1n a 2n... a nn Zgled 38 Podano imamo matriko A: nato transponiramo matriko A in dobimo: A T = Ugotovimo, da je A T oziroma A T = A, kar pomeni, da je matrika A simetrična. Izrek 2.2 Za poljubno matriko A sta matriki AA T in A T A vedno simetrični. Dokaz. Za dokaz bomo uporabili lastnost transponiranja (AB) T = B T A T in preveriti moramo, ali je A T = A: (A T A) T = A T (A T ) T = A T A (AA T ) T = (A T ) T A T = AA T.,. Zgled 39 Poglejmo ali je produkt AA T simetrična matrika , AT =
44 2.1 Definicija in osnovne lastnosti 35 AA T = = Ugotovimo, da je produkt AA T simetrična matrika. Posledica 2.3 Če je X matrični stolpec reda n, potem je X XT simetrična matrika reda n. Zgled 40 Podan imamo matrični stolpec X: X = [ XT = ] X X T = [ ] = Opazimo, da je produkt simetrična matrika. Izrek 2.4 Za vsako kvadratno matriko A je matrika A+A T simetrična. Dokaz. Za dokaz bomo uporabili lastnost transponiranja (A+B) T = A T +B T : (A+A T ) T = A T +(A T ) T = A T + A+A T. Zgled 41 Poglejmo, ali je vsota A+A T, kjer je A kvadratna matrika, simetrična matrika. A+A T = , AT = = Ugotovimo, da je vsota A+A T, kjer je A kvadratna matrika, simetrična matrika.
45 2.1 Definicija in osnovne lastnosti 36 Opomba 2.5 Vsaka diagonalna, skalarna, identična matrika in matrika nič je simetrična matrika. Trditev 2.6 Če je matrika A simetrična, potem je tudi A 1 simetrična matrika. Dokaz. Zgornjo trditev bomo dokazali enako kot lastnost inverzne matrike: (A T ) 1 = (A 1 ) T. Vemo, da velja: AA 1 = A 1 I. Nato transponiramo enakost AA 1 = I in dobimo: (AA 1 ) T = I T, nato upoštevamo pravilo za množenje produkta pri transponiranju ter dobimo: (A 1 ) T A T = I T = I. Ekvivalentno naredimo tudi z drugo enakostjo A 1 I in dobimo: A T (A 1 ) T = I T = I. Nato primerjamo oba rezultata transponiranja: (A 1 ) T A T = I T = I in A T (A 1 ) T = I T = I ter ugotovimo, da je matrika (A 1 ) T obratna oziroma inverzna matrika matrike A T. Zato je (A T ) 1 = (A 1 ) T. Zgled 42 Preverimo ali je inverzna matrika A 1 simetrične matrike A simetrična Najprej moramo izračunati inverzno matriko A 1. Izkaže se, da je inverzna matrika matrike A enaka: A 1 = Ugotovili smo, da je inverzna matrika A 1, simetrične matrike A prav tako simetrična matrika..
46 2.2 Definitnost in semidefinitnost simetričnih matrik 37 Izrek 2.7 Lastne vrednosti realne simetrične matrike so realne. Dokaz. Izrek bomo dokazali kot posebni primer. Za dokaz izreka bomo uporabili kompleksno število. Kompleksno število označimo z z, kje je z = a+ib. Konjugacijo kompleksnega števila označimo z a+ib, ki je podana s formulo a+ib = a ib. Torej konjugacijo kompleksnega števila označimo z z = a ib. Oznaka x bo označevala vektor, ki ima vsak element zamenjan z njegovim kompleksnim konjugiranim. Recimo, da je A realno simetrična matrika in Ax = λx. Potem velja: λx T x = (Ax) T x = x T A T x = x T Ax = λx T x. Obe strani enačbe delimo z x T x in dobimo, da je λ = λ, kar nam pove, da je λ realno. Zgled 43 Naj bo A simetrična matrika, kateri bomo poiskali lastno vrednost. [ ] Lastno vrednost dobimo s pomočjo determinante: 1 λ 5 det = 5 3 λ = 3 4λ+λ2 = 0. Rešitvi dane enačbe sta λ 1 = 2+ 5 in λ 2 = Definitnost in semidefinitnost simetričnih matrik V tem delu diplomskega dela bomo spoznali, kdaj je matrika pozitivno ali negativno definitna oziroma semidefinitna. Naj bo SR n n = {A R n n A T = A} množica vseh simetričnih matrik. Potem je A SR n n pozitivno semidefinitna, če je x T Ax 0, za vse x R n. Če je A še obrnljiva, potem ji rečemo pozitivno definitna in velja x T Ax > 0, za vse x R n. V primeru, da pa je x T Ax 0, potem je A SR n n negativno semidefinitna, za vse x R n in če je še A obrnljiva, potem ji rečemo negativno definitna in velja x T Ax < 0, za vse x R n. Trditev 2.8 Simetrična matrika A je pozitivno definitna natančno takrat, kadar so vsi njeni vogalni minorji pozitivni.
Linearne enačbe. Matrična algebra. Linearne enačbe. Linearne enačbe. Linearne enačbe. Linearne enačbe
 Sistem linearnih enačb Matrična algebra Oseba X X X3 B A.A. 3 B.B. 7 C.C. Doc. dr. Anja Podlesek Oddelek za psihologijo, Filozofska fakulteta, Univerza v Ljubljani Študijski program prve stopnje Psihologija
Sistem linearnih enačb Matrična algebra Oseba X X X3 B A.A. 3 B.B. 7 C.C. Doc. dr. Anja Podlesek Oddelek za psihologijo, Filozofska fakulteta, Univerza v Ljubljani Študijski program prve stopnje Psihologija
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO. Oddelek za matematiko in računalništvo MAGISTRSKA NALOGA. Tina Lešnik
 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo MAGISTRSKA NALOGA Tina Lešnik Maribor, 2014 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo MAGISTRSKA NALOGA Tina Lešnik Maribor, 2014 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
Linearna algebra. Bojan Orel. Univerza v Ljubljani
 Linearna algebra Bojan Orel 07 Univerza v Ljubljani Fakulteta za računalništvo in informatiko CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana 5.64(075.8) OREL, Bojan Linearna
Linearna algebra Bojan Orel 07 Univerza v Ljubljani Fakulteta za računalništvo in informatiko CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana 5.64(075.8) OREL, Bojan Linearna
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Kvadratne forme nad končnimi obsegi
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Kvadratne forme nad končnimi obsegi (Quadratic Forms over Finite Fields) Ime in priimek: Borut
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Kvadratne forme nad končnimi obsegi (Quadratic Forms over Finite Fields) Ime in priimek: Borut
AKSIOMATSKA KONSTRUKCIJA NARAVNIH
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Poučevanje: Predmetno poučevanje ŠPELA ZOBAVNIK AKSIOMATSKA KONSTRUKCIJA NARAVNIH ŠTEVIL MAGISTRSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Poučevanje: Predmetno poučevanje ŠPELA ZOBAVNIK AKSIOMATSKA KONSTRUKCIJA NARAVNIH ŠTEVIL MAGISTRSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SAŠO ZUPANEC MAX-PLUS ALGEBRA DIPLOMSKO DELO
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SAŠO ZUPANEC MAX-PLUS ALGEBRA DIPLOMSKO DELO Ljubljana, 2013 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA ODDELEK ZA MATEMATIKO IN RAČUNALNIŠTVO SAŠO ZUPANEC Mentor:
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SAŠO ZUPANEC MAX-PLUS ALGEBRA DIPLOMSKO DELO Ljubljana, 2013 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA ODDELEK ZA MATEMATIKO IN RAČUNALNIŠTVO SAŠO ZUPANEC Mentor:
Kode za popravljanje napak
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE KOPER MATEMATIČNE ZNANOSTI MAGISTRSKI ŠTUDIJSKI PROGRAM 2. STOPNJE Aljaž Slivnik Kode za popravljanje napak Magistrska
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE KOPER MATEMATIČNE ZNANOSTI MAGISTRSKI ŠTUDIJSKI PROGRAM 2. STOPNJE Aljaž Slivnik Kode za popravljanje napak Magistrska
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POLONA ŠENKINC REŠEVANJE LINEARNIH DIFERENCIALNIH ENAČB DRUGEGA REDA S POMOČJO POTENČNIH VRST DIPLOMSKO DELO
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POLONA ŠENKINC REŠEVANJE LINEARNIH DIFERENCIALNIH ENAČB DRUGEGA REDA S POMOČJO POTENČNIH VRST DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POLONA ŠENKINC REŠEVANJE LINEARNIH DIFERENCIALNIH ENAČB DRUGEGA REDA S POMOČJO POTENČNIH VRST DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
Iskanje najcenejše poti v grafih preko polkolobarjev
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Veronika Horvat Iskanje najcenejše poti v grafih preko polkolobarjev DIPLOMSKO DELO VISOKOŠOLSKI STROKOVNI ŠTUDIJSKI PROGRAM PRVE STOPNJE
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Veronika Horvat Iskanje najcenejše poti v grafih preko polkolobarjev DIPLOMSKO DELO VISOKOŠOLSKI STROKOVNI ŠTUDIJSKI PROGRAM PRVE STOPNJE
Reševanje problemov in algoritmi
 Reševanje problemov in algoritmi Vhod Algoritem Izhod Kaj bomo spoznali Zgodovina algoritmov. Primeri algoritmov. Algoritmi in programi. Kaj je algoritem? Algoritem je postopek, kako korak za korakom rešimo
Reševanje problemov in algoritmi Vhod Algoritem Izhod Kaj bomo spoznali Zgodovina algoritmov. Primeri algoritmov. Algoritmi in programi. Kaj je algoritem? Algoritem je postopek, kako korak za korakom rešimo
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO. Oddelek za matematiko in računalništvo DIPLOMSKO DELO.
 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo DIPLOMSKO DELO Sabina Skornšek Maribor, 2012 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in računalništvo DIPLOMSKO DELO Sabina Skornšek Maribor, 2012 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO
POLDIREKTNI PRODUKT GRUP
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUCIJA ŽNIDARIČ POLDIREKTNI PRODUKT GRUP DIPLOMSKO DELO LJUBLJANA 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Univerzitetni študijski program 1. stopnje: Dvopredmetni
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUCIJA ŽNIDARIČ POLDIREKTNI PRODUKT GRUP DIPLOMSKO DELO LJUBLJANA 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Univerzitetni študijski program 1. stopnje: Dvopredmetni
Študijska smer Study field. Samost. delo Individ. work Klinične vaje work. Vaje / Tutorial: Slovensko/Slovene
 UČNI NAČRT PREDMETA / COURSE SYLLABUS Predmet: Matematika 2 Course title: Mathematics 2 Študijski program in stopnja Study programme and level Univerzitetni študijski program 1.stopnje Fizika First cycle
UČNI NAČRT PREDMETA / COURSE SYLLABUS Predmet: Matematika 2 Course title: Mathematics 2 Študijski program in stopnja Study programme and level Univerzitetni študijski program 1.stopnje Fizika First cycle
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Verjetnostni algoritmi za testiranje praštevilskosti
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Verjetnostni algoritmi za testiranje praštevilskosti (Algorithms for testing primality) Ime in
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Verjetnostni algoritmi za testiranje praštevilskosti (Algorithms for testing primality) Ime in
Jernej Azarija. Štetje vpetih dreves v grafih
 UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO FAKULTETA ZA MATEMATIKO IN FIZIKO Jernej Azarija Štetje vpetih dreves v grafih DIPLOMSKO DELO NA INTERDISCIPLINARNEM UNIVERZITETNEM ŠTUDIJU
UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO FAKULTETA ZA MATEMATIKO IN FIZIKO Jernej Azarija Štetje vpetih dreves v grafih DIPLOMSKO DELO NA INTERDISCIPLINARNEM UNIVERZITETNEM ŠTUDIJU
NIKJER-NIČELNI PRETOKI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA ALJA ŠUBIC NIKJER-NIČELNI PRETOKI DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika - računalništvo ALJA
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA ALJA ŠUBIC NIKJER-NIČELNI PRETOKI DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika - računalništvo ALJA
Cveto Trampuž PRIMERJAVA ANALIZE VEČRAZSEŽNIH TABEL Z RAZLIČNIMI MODELI REGRESIJSKE ANALIZE DIHOTOMNIH SPREMENLJIVK
 Cveto Trampuž PRIMERJAVA ANALIZE VEČRAZSEŽNIH TABEL Z RAZLIČNIMI MODELI REGRESIJSKE ANALIZE DIHOTOMNIH SPREMENLJIVK POVZETEK. Namen tega dela je prikazati osnove razlik, ki lahko nastanejo pri interpretaciji
Cveto Trampuž PRIMERJAVA ANALIZE VEČRAZSEŽNIH TABEL Z RAZLIČNIMI MODELI REGRESIJSKE ANALIZE DIHOTOMNIH SPREMENLJIVK POVZETEK. Namen tega dela je prikazati osnove razlik, ki lahko nastanejo pri interpretaciji
Hadamardove matrike in misija Mariner 9
 Hadamardove matrike in misija Mariner 9 Aleksandar Jurišić, 25. avgust, 2009 J. Hadamard (1865-1963) je bil eden izmed pomembnejših matematikov na prehodu iz 19. v 20. stoletje. Njegova najpomembnejša
Hadamardove matrike in misija Mariner 9 Aleksandar Jurišić, 25. avgust, 2009 J. Hadamard (1865-1963) je bil eden izmed pomembnejših matematikov na prehodu iz 19. v 20. stoletje. Njegova najpomembnejša
Matematika 1. Gabrijel Tomšič Bojan Orel Neža Mramor Kosta
 Matematika 1 Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 15. december 2010 Poglavje 3 Funkcije 3.1 Osnovni pojmi Preslikavam v množico R ali C običajno pravimo funkcije v prvem primeru realne, v drugem
Matematika 1 Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 15. december 2010 Poglavje 3 Funkcije 3.1 Osnovni pojmi Preslikavam v množico R ali C običajno pravimo funkcije v prvem primeru realne, v drugem
Problem umetnostne galerije
 Problem umetnostne galerije Marko Kandič 17. september 2006 Za začetek si oglejmo naslednji primer. Recimo, da imamo v galeriji polno vrednih slik in nočemo, da bi jih kdo ukradel. Seveda si želimo, da
Problem umetnostne galerije Marko Kandič 17. september 2006 Za začetek si oglejmo naslednji primer. Recimo, da imamo v galeriji polno vrednih slik in nočemo, da bi jih kdo ukradel. Seveda si želimo, da
TOPLJENEC ASOCIIRA LE V VODNI FAZI
 TOPLJENEC ASOCIIRA LE V VODNI FAZI V primeru asociacij molekul topljenca v vodni ali organski fazi eksperimentalno določeni navidezni porazdelitveni koeficient (P n ) v odvisnosti od koncentracije ni konstanten.
TOPLJENEC ASOCIIRA LE V VODNI FAZI V primeru asociacij molekul topljenca v vodni ali organski fazi eksperimentalno določeni navidezni porazdelitveni koeficient (P n ) v odvisnosti od koncentracije ni konstanten.
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Simetrije cirkulantnih grafov
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Magistrsko delo Simetrije cirkulantnih grafov (Symmetry of circulant graphs) Ime in priimek: Maruša Saksida Študijski
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Magistrsko delo Simetrije cirkulantnih grafov (Symmetry of circulant graphs) Ime in priimek: Maruša Saksida Študijski
SIMETRIČNE KOMPONENTE
 Univerza v Ljubljani Fakulteta za elektrotehniko SIMETRIČNE KOMPONENTE Seminarska naloga pri predmetu Razdelilna in industrijska omrežja Poročilo izdelala: ELIZABETA STOJCHEVA Mentor: prof. dr. Grega Bizjak,
Univerza v Ljubljani Fakulteta za elektrotehniko SIMETRIČNE KOMPONENTE Seminarska naloga pri predmetu Razdelilna in industrijska omrežja Poročilo izdelala: ELIZABETA STOJCHEVA Mentor: prof. dr. Grega Bizjak,
DELOVANJA GRUP IN BLOKI NEPRIMITIVNOSTI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DEJAN KREJIĆ DELOVANJA GRUP IN BLOKI NEPRIMITIVNOSTI DIPLOMSKO DELO Ljubljana, 2015 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika -
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DEJAN KREJIĆ DELOVANJA GRUP IN BLOKI NEPRIMITIVNOSTI DIPLOMSKO DELO Ljubljana, 2015 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika -
JERNEJ TONEJC. Fakulteta za matematiko in fiziko
 . ARITMETIKA DVOJIŠKIH KONČNIH OBSEGOV JERNEJ TONEJC Fakulteta za matematiko in fiziko Math. Subj. Class. (2010): 11T{06, 22, 55, 71}, 12E{05, 20, 30}, 68R05 V članku predstavimo končne obsege in aritmetiko
. ARITMETIKA DVOJIŠKIH KONČNIH OBSEGOV JERNEJ TONEJC Fakulteta za matematiko in fiziko Math. Subj. Class. (2010): 11T{06, 22, 55, 71}, 12E{05, 20, 30}, 68R05 V članku predstavimo končne obsege in aritmetiko
Izbrana poglavja iz algebrai ne teorije grafov. Zbornik seminarskih nalog iz algebrai ne teorije grafov
 Izbrana poglavja iz algebrai ne teorije grafov Zbornik seminarskih nalog iz algebrai ne teorije grafov Ljubljana, 2015 CIP Kataloºni zapis o publikaciji Narodna in univerzitetna knjiºnica, Ljubljana 519.24(082)(0.034.2)
Izbrana poglavja iz algebrai ne teorije grafov Zbornik seminarskih nalog iz algebrai ne teorije grafov Ljubljana, 2015 CIP Kataloºni zapis o publikaciji Narodna in univerzitetna knjiºnica, Ljubljana 519.24(082)(0.034.2)
SLIKE CANTORJEVE PAHLJAµCE
 UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in raµcunalništvo Diplomsko delo SLIKE CANTORJEVE PAHLJAµCE Mentor: dr. Iztok Baniµc docent Kandidatka: Anja Belošević
UNIVERZA V MARIBORU FAKULTETA ZA NARAVOSLOVJE IN MATEMATIKO Oddelek za matematiko in raµcunalništvo Diplomsko delo SLIKE CANTORJEVE PAHLJAµCE Mentor: dr. Iztok Baniµc docent Kandidatka: Anja Belošević
Iterativne metode podprostorov 2010/2011 Domače naloge
 Iterativne metode podprostorov 2010/2011 Domače naloge Naloge so razdeljene v 6 skupin. Za pozitivno oceno morate rešiti toliko nalog, da bo končna vsota za pozitivno oceno vsaj 8 točk oz. vsaj 10 točk
Iterativne metode podprostorov 2010/2011 Domače naloge Naloge so razdeljene v 6 skupin. Za pozitivno oceno morate rešiti toliko nalog, da bo končna vsota za pozitivno oceno vsaj 8 točk oz. vsaj 10 točk
OPTIMIZACIJSKE METODE skripta v pripravi
 OPTIMIZACIJSKE METODE skripta v pripravi Vladimir Batagelj Ljubljana 17. december 2003 2 Kazalo Predgovor 5 1 Optimizacijske naloge 7 1.1 Osnovni pojmi........................... 7 1.2 Primeri optimizacijskih
OPTIMIZACIJSKE METODE skripta v pripravi Vladimir Batagelj Ljubljana 17. december 2003 2 Kazalo Predgovor 5 1 Optimizacijske naloge 7 1.1 Osnovni pojmi........................... 7 1.2 Primeri optimizacijskih
SIMETRIČNI BICIRKULANTI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA GORAZD VASILJEVIĆ SIMETRIČNI BICIRKULANTI DIPLOMSKO DELO Ljubljana, 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika - računalništvo
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA GORAZD VASILJEVIĆ SIMETRIČNI BICIRKULANTI DIPLOMSKO DELO Ljubljana, 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Dvopredmetni učitelj: matematika - računalništvo
Matrices and Linear Algebra
 Contents Quantitative methods for Economics and Business University of Ferrara Academic year 2017-2018 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2
Contents Quantitative methods for Economics and Business University of Ferrara Academic year 2017-2018 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2
Multipla korelacija in regresija. Multipla regresija, multipla korelacija, statistično zaključevanje o multiplem R
 Multipla koelacia in egesia Multipla egesia, multipla koelacia, statistično zaklučevane o multiplem Multipla egesia osnovni model in ačunane paametov Z multiplo egesio napoveduemo vednost kiteia (odvisne
Multipla koelacia in egesia Multipla egesia, multipla koelacia, statistično zaklučevane o multiplem Multipla egesia osnovni model in ačunane paametov Z multiplo egesio napoveduemo vednost kiteia (odvisne
UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Predmet: Algebra 1 Course title: Algebra 1. Študijska smer Study field ECTS
 UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Predmet: Algebra 1 Course title: Algebra 1 Študijski program in stopnja Study programme and level Univerzitetni študijski program Matematika
UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Predmet: Algebra 1 Course title: Algebra 1 Študijski program in stopnja Study programme and level Univerzitetni študijski program Matematika
Linear Algebra. Matrices Operations. Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0.
 Matrices Operations Linear Algebra Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0 The rectangular array 1 2 1 4 3 4 2 6 1 3 2 1 in which the
Matrices Operations Linear Algebra Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0 The rectangular array 1 2 1 4 3 4 2 6 1 3 2 1 in which the
Formula for the inverse matrix. Cramer s rule. Review: 3 3 determinants can be computed expanding by any row or column
 Math 20F Linear Algebra Lecture 18 1 Determinants, n n Review: The 3 3 case Slide 1 Determinants n n (Expansions by rows and columns Relation with Gauss elimination matrices: Properties) Formula for the
Math 20F Linear Algebra Lecture 18 1 Determinants, n n Review: The 3 3 case Slide 1 Determinants n n (Expansions by rows and columns Relation with Gauss elimination matrices: Properties) Formula for the
Matej Mislej HOMOMORFIZMI RAVNINSKIH GRAFOV Z VELIKIM NOTRANJIM OBSEGOM
 UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO Matematika - uporabna smer (UNI) Matej Mislej HOMOMORFIZMI RAVNINSKIH GRAFOV Z VELIKIM NOTRANJIM OBSEGOM Diplomsko delo Ljubljana, 2006 Zahvala Zahvaljujem
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO Matematika - uporabna smer (UNI) Matej Mislej HOMOMORFIZMI RAVNINSKIH GRAFOV Z VELIKIM NOTRANJIM OBSEGOM Diplomsko delo Ljubljana, 2006 Zahvala Zahvaljujem
UČNI NAČRT PREDMETA / COURSE SYLLABUS. Študijska smer Study field. Samost. delo Individ. work Klinične vaje work
 Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS Linearna algebra Linear algebra Študijski program in stopnja Study programme and level Visokošolski strokovni študijski program Praktična matematika
Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS Linearna algebra Linear algebra Študijski program in stopnja Study programme and level Visokošolski strokovni študijski program Praktična matematika
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Kromatično število in kromatični indeks grafa
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Magistrsko delo Kromatično število in kromatični indeks grafa (The chromatic number and the chromatic index of
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Magistrsko delo Kromatično število in kromatični indeks grafa (The chromatic number and the chromatic index of
UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Študijska smer Study field ECTS Vaje / Tutorial: slovenski / Slovene
 Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Linearna algebra Linear algebra Študijski program in stopnja Study programme and level Visokošolski strokovni študijski
Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Linearna algebra Linear algebra Študijski program in stopnja Study programme and level Visokošolski strokovni študijski
FRAKTALNA DIMENZIJA. Fakulteta za matematiko in fiziko Univerza v Ljubljani
 FRAKTALNA DIMENZIJA VESNA IRŠIČ Fakulteta za matematiko in fiziko Univerza v Ljubljani PACS: 07.50.Hp, 01.65.+g V članku je predstavljen zgodovinski razvoj teorije fraktalov in natančen opis primerov,
FRAKTALNA DIMENZIJA VESNA IRŠIČ Fakulteta za matematiko in fiziko Univerza v Ljubljani PACS: 07.50.Hp, 01.65.+g V članku je predstavljen zgodovinski razvoj teorije fraktalov in natančen opis primerov,
Hipohamiltonovi grafi
 Hipohamiltonovi grafi Marko Čmrlec, Bor Grošelj Simić Mentor(ica): Vesna Iršič Matematično raziskovalno srečanje 1. avgust 016 1 Uvod V marsovskem klubu je želel predsednik prirediti večerjo za svoje člane.
Hipohamiltonovi grafi Marko Čmrlec, Bor Grošelj Simić Mentor(ica): Vesna Iršič Matematično raziskovalno srečanje 1. avgust 016 1 Uvod V marsovskem klubu je želel predsednik prirediti večerjo za svoje člane.
Linear Systems and Matrices
 Department of Mathematics The Chinese University of Hong Kong 1 System of m linear equations in n unknowns (linear system) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2.......
Department of Mathematics The Chinese University of Hong Kong 1 System of m linear equations in n unknowns (linear system) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2.......
Ivan Pucelj: RIMSKE ŠTEVILKE IN RAČUNANJE Z NJIMI. List za mlade matematike, fizike, astronome in računalnikarje
 List za mlade matematike, fizike, astronome in računalnikarje ISSN 0351-6652 Letnik 12 (1984/1985) Številka 3 Strani 110 119 Ivan Pucelj: RIMSKE ŠTEVILKE IN RAČUNANJE Z NJIMI Ključne besede: matematika.
List za mlade matematike, fizike, astronome in računalnikarje ISSN 0351-6652 Letnik 12 (1984/1985) Številka 3 Strani 110 119 Ivan Pucelj: RIMSKE ŠTEVILKE IN RAČUNANJE Z NJIMI Ključne besede: matematika.
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DIPLOMSKO DELO MAJA OSTERMAN
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DIPLOMSKO DELO MAJA OSTERMAN UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Študijski program: Matematika in računalništvo Fibonaccijevo zaporedje in krožna konstanta
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DIPLOMSKO DELO MAJA OSTERMAN UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA Študijski program: Matematika in računalništvo Fibonaccijevo zaporedje in krožna konstanta
Intervalske Bézierove krivulje in ploskve
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Tadej Borovšak Intervalske Bézierove krivulje in ploskve DIPLOMSKO DELO UNIVERZITETNI ŠTUDIJSKI PROGRAM
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Tadej Borovšak Intervalske Bézierove krivulje in ploskve DIPLOMSKO DELO UNIVERZITETNI ŠTUDIJSKI PROGRAM
Particija grafa, odkrivanje skupnosti in maksimalen prerez
 Univerza na Primorskem Fakulteta za matematiko, naravoslovje in informacijske tehnologije Matemati ne znanosti - 2. stopnja Peter Mur²i Particija grafa, odkrivanje skupnosti in maksimalen prerez Magistrsko
Univerza na Primorskem Fakulteta za matematiko, naravoslovje in informacijske tehnologije Matemati ne znanosti - 2. stopnja Peter Mur²i Particija grafa, odkrivanje skupnosti in maksimalen prerez Magistrsko
Excel. Matjaž Željko
 Excel Matjaž Željko Elektronska preglednica Excel Excel je zmogljiv kalkulator. Omogoča izdelavo grafikonov statistično analizo podatkov lepo oblikovanje poročila za natis Podatke predstavljamo tabelarično,
Excel Matjaž Željko Elektronska preglednica Excel Excel je zmogljiv kalkulator. Omogoča izdelavo grafikonov statistično analizo podatkov lepo oblikovanje poročila za natis Podatke predstavljamo tabelarično,
ENAČBA STANJA VODE IN VODNE PARE
 ENAČBA STANJA VODE IN VODNE PARE SEMINARSKA NALOGA PRI PREDMETU JEDRSKA TEHNIKA IN ENERGETIKA TAMARA STOJANOV MENTOR: IZRED. PROF. DR. IZTOK TISELJ NOVEMBER 2011 Enačba stanja idealni plin: pv = RT p tlak,
ENAČBA STANJA VODE IN VODNE PARE SEMINARSKA NALOGA PRI PREDMETU JEDRSKA TEHNIKA IN ENERGETIKA TAMARA STOJANOV MENTOR: IZRED. PROF. DR. IZTOK TISELJ NOVEMBER 2011 Enačba stanja idealni plin: pv = RT p tlak,
Math 4377/6308 Advanced Linear Algebra
 2.3 Composition Math 4377/6308 Advanced Linear Algebra 2.3 Composition of Linear Transformations Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu math.uh.edu/ jiwenhe/math4377
2.3 Composition Math 4377/6308 Advanced Linear Algebra 2.3 Composition of Linear Transformations Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu math.uh.edu/ jiwenhe/math4377
Eulerjevi in Hamiltonovi grafi
 Eulerjevi in Hamiltonovi grafi Bojan Možina 30. december 006 1 Eulerjevi grafi Štirje deli mesta Königsberg v Prusiji so bili povezani s sedmimi mostovi (glej levi del slike 1). Zdaj se Königsberg imenuje
Eulerjevi in Hamiltonovi grafi Bojan Možina 30. december 006 1 Eulerjevi grafi Štirje deli mesta Königsberg v Prusiji so bili povezani s sedmimi mostovi (glej levi del slike 1). Zdaj se Königsberg imenuje
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO ODDELEK ZA MATEMATIKO
 UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO ODDELEK ZA MATEMATIKO Rok Erman BARVANJA RAVNINSKIH IN SORODNIH DRUŽIN GRAFOV Doktorska disertacija MENTOR: prof. dr. Riste Škrekovski Ljubljana,
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO ODDELEK ZA MATEMATIKO Rok Erman BARVANJA RAVNINSKIH IN SORODNIH DRUŽIN GRAFOV Doktorska disertacija MENTOR: prof. dr. Riste Škrekovski Ljubljana,
Hiperbolične funkcije DIPLOMSKO DELO
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA FAKULTETA ZA MATEMATIKO IN FIZIKO Študijski program: Matematika in fizika Hiperbolične funkcije DIPLOMSKO DELO Mentor: dr. Marko Razpet Kandidatka: Teja Bergant
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA FAKULTETA ZA MATEMATIKO IN FIZIKO Študijski program: Matematika in fizika Hiperbolične funkcije DIPLOMSKO DELO Mentor: dr. Marko Razpet Kandidatka: Teja Bergant
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA FAKULTETA ZA MATEMATIKO IN FIZIKO DIPLOMSKO DELO MIHAELA REMIC
 UNIVERZ V LJULJNI PEDGOŠK FKULTET FKULTET Z MTEMTIKO IN FIZIKO DIPLOMSKO DELO MIHEL REMI UNIVERZ V LJULJNI PEDGOŠK FKULTET FKULTET Z MTEMTIKO IN FIZIKO Študijski program: Matematika in fizika ROUTHOV
UNIVERZ V LJULJNI PEDGOŠK FKULTET FKULTET Z MTEMTIKO IN FIZIKO DIPLOMSKO DELO MIHEL REMI UNIVERZ V LJULJNI PEDGOŠK FKULTET FKULTET Z MTEMTIKO IN FIZIKO Študijski program: Matematika in fizika ROUTHOV
Equality: Two matrices A and B are equal, i.e., A = B if A and B have the same order and the entries of A and B are the same.
 Introduction Matrix Operations Matrix: An m n matrix A is an m-by-n array of scalars from a field (for example real numbers) of the form a a a n a a a n A a m a m a mn The order (or size) of A is m n (read
Introduction Matrix Operations Matrix: An m n matrix A is an m-by-n array of scalars from a field (for example real numbers) of the form a a a n a a a n A a m a m a mn The order (or size) of A is m n (read
Symmetric and anti symmetric matrices
 Symmetric and anti symmetric matrices In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if. A = A Because equal matrices have equal
Symmetric and anti symmetric matrices In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if. A = A Because equal matrices have equal
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Uporaba logistične regresije za napovedovanje razreda, ko je število enot v preučevanih razredih
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Uporaba logistične regresije za napovedovanje razreda, ko je število enot v preučevanih razredih
MATRIČNI POPULACIJSKI MODELI
 TURK ZAKLJUČNA NALOGA 2014 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE ZAKLJUČNA NALOGA MATRIČNI POPULACIJSKI MODELI LEV TURK UNIVERZA NA PRIMORSKEM FAKULTETA
TURK ZAKLJUČNA NALOGA 2014 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE ZAKLJUČNA NALOGA MATRIČNI POPULACIJSKI MODELI LEV TURK UNIVERZA NA PRIMORSKEM FAKULTETA
SVM = Support Vector Machine = Metoda podpornih vektorjev
 Uvod 2/60 SVM = Support Vector Machine = Metoda podpornih vektorjev Vapnik in Lerner 1963 (generalized portrait) jedra: Aronszajn 1950; Aizerman 1964; Wahba 1990, Poggio in Girosi 1990 Boser, Guyon in
Uvod 2/60 SVM = Support Vector Machine = Metoda podpornih vektorjev Vapnik in Lerner 1963 (generalized portrait) jedra: Aronszajn 1950; Aizerman 1964; Wahba 1990, Poggio in Girosi 1990 Boser, Guyon in
Topološka obdelava slik
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Matjaž Cerar Topološka obdelava slik DIPLOMSKO DELO UNIVERZITETNI INTERDISCIPLINARNI ŠTUDIJ RAČUNALNIŠTVA
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Matjaž Cerar Topološka obdelava slik DIPLOMSKO DELO UNIVERZITETNI INTERDISCIPLINARNI ŠTUDIJ RAČUNALNIŠTVA
UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Parcialne diferencialne enačbe Partial differential equations. Študijska smer Study field
 Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Parcialne diferencialne enačbe Partial differential equations Študijski program in stopnja Study programme and level Magistrski
Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS (leto / year 2017/18) Parcialne diferencialne enačbe Partial differential equations Študijski program in stopnja Study programme and level Magistrski
Linearna regresija. Poglavje 4
 Poglavje 4 Linearna regresija Vinkove rezultate iz kemije so založili. Enostavno, komisija je izgubila izpitne pole. Rešitev: Vinko bo kemijo pisal še enkrat. Ampak, ne more, je ravno odšel na trening
Poglavje 4 Linearna regresija Vinkove rezultate iz kemije so založili. Enostavno, komisija je izgubila izpitne pole. Rešitev: Vinko bo kemijo pisal še enkrat. Ampak, ne more, je ravno odšel na trening
Klemen Kregar, Mitja Lakner, Dušan Kogoj KEY WORDS
 G 2014 V ROTACIJA Z ENOTSKIM KVATERNIONOM GEODETSKI VESTNIK letn. / Vol. 58 št. / No. 2 ROTATION WITH UNIT QUATERNION 58/2 Klemen Kregar, Mitja Lakner, Dušan Kogoj UDK: 512.626.824:528 Klasifikacija prispevka
G 2014 V ROTACIJA Z ENOTSKIM KVATERNIONOM GEODETSKI VESTNIK letn. / Vol. 58 št. / No. 2 ROTATION WITH UNIT QUATERNION 58/2 Klemen Kregar, Mitja Lakner, Dušan Kogoj UDK: 512.626.824:528 Klasifikacija prispevka
UČNI NAČRT PREDMETA / COURSE SYLLABUS Numerical linear algebra. Študijska smer Study field. Samost. delo Individ. work Klinične vaje work
 Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS Numerična linearna algebra Numerical linear algebra Študijski program in stopnja Study programme and level Univerzitetni študijski program Matematika
Predmet: Course title: UČNI NAČRT PREDMETA / COURSE SYLLABUS Numerična linearna algebra Numerical linear algebra Študijski program in stopnja Study programme and level Univerzitetni študijski program Matematika
Ana Mlinar Fulereni. Delo diplomskega seminarja. Mentor: izred. prof. dr. Riste Škrekovski
 UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO Matematika 1. stopnja Ana Mlinar Fulereni Delo diplomskega seminarja Mentor: izred. prof. dr. Riste Škrekovski Ljubljana, 2011 Kazalo 1. Uvod 4 2.
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO Matematika 1. stopnja Ana Mlinar Fulereni Delo diplomskega seminarja Mentor: izred. prof. dr. Riste Škrekovski Ljubljana, 2011 Kazalo 1. Uvod 4 2.
Topološki model za brezžična senzorska omrežja
 UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Jan Terzer Topološki model za brezžična senzorska omrežja DIPLOMSKO DELO UNIVERZITETNI ŠTUDIJSKI PROGRAM PRVE STOPNJE RAČUNALNIŠTVO IN INFORMATIKA
UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Jan Terzer Topološki model za brezžična senzorska omrežja DIPLOMSKO DELO UNIVERZITETNI ŠTUDIJSKI PROGRAM PRVE STOPNJE RAČUNALNIŠTVO IN INFORMATIKA
Math113: Linear Algebra. Beifang Chen
 Math3: Linear Algebra Beifang Chen Spring 26 Contents Systems of Linear Equations 3 Systems of Linear Equations 3 Linear Systems 3 2 Geometric Interpretation 3 3 Matrices of Linear Systems 4 4 Elementary
Math3: Linear Algebra Beifang Chen Spring 26 Contents Systems of Linear Equations 3 Systems of Linear Equations 3 Linear Systems 3 2 Geometric Interpretation 3 3 Matrices of Linear Systems 4 4 Elementary
Attempt to prepare seasonal weather outlook for Slovenia
 Attempt to prepare seasonal weather outlook for Slovenia Main available sources (ECMWF, EUROSIP, IRI, CPC.NCEP.NOAA,..) Two parameters (T and RR anomally) Textual information ( Met Office like ) Issued
Attempt to prepare seasonal weather outlook for Slovenia Main available sources (ECMWF, EUROSIP, IRI, CPC.NCEP.NOAA,..) Two parameters (T and RR anomally) Textual information ( Met Office like ) Issued
DIOFANTSKE ČETVERICE
 Fakulteta za aravoslovje i matematiko Oddelek za matematiko i račualištvo Diplomsko delo DIOFANTSKE ČETVERICE Metor: Doc. dr. Daiel Eremita Kadidatka: Jožica Špec Maribor 009 II ZAHVALA Zahvaljujem se
Fakulteta za aravoslovje i matematiko Oddelek za matematiko i račualištvo Diplomsko delo DIOFANTSKE ČETVERICE Metor: Doc. dr. Daiel Eremita Kadidatka: Jožica Špec Maribor 009 II ZAHVALA Zahvaljujem se
II. Determinant Functions
 Supplemental Materials for EE203001 Students II Determinant Functions Chung-Chin Lu Department of Electrical Engineering National Tsing Hua University May 22, 2003 1 Three Axioms for a Determinant Function
Supplemental Materials for EE203001 Students II Determinant Functions Chung-Chin Lu Department of Electrical Engineering National Tsing Hua University May 22, 2003 1 Three Axioms for a Determinant Function
OPTIMIZACIJA Z ROJEM DELCEV
 UNIVERZA V MARIBORU FAKULTETA ZA ORGANIZACIJSKE VEDE Smer: organizacijska informatika OPTIMIZACIJA Z ROJEM DELCEV Mentor: doc. dr. Igor Bernik Kandidat: Matjaž Lipovšek Kranj, december 2005 Izjava: "Študent
UNIVERZA V MARIBORU FAKULTETA ZA ORGANIZACIJSKE VEDE Smer: organizacijska informatika OPTIMIZACIJA Z ROJEM DELCEV Mentor: doc. dr. Igor Bernik Kandidat: Matjaž Lipovšek Kranj, december 2005 Izjava: "Študent
Naloge iz LA T EXa : 3. del
 Naloge iz LA T EXa : 3. del 1. V besedilo vklju ite naslednjo tabelo skupaj z napisom Kontrolna naloga Dijak 1 2 Povpre je Janko 67 72 70.5 Metka 72 67 70.5 Povpre je 70.5 70.5 Tabela 1: Rezultati kontrolnih
Naloge iz LA T EXa : 3. del 1. V besedilo vklju ite naslednjo tabelo skupaj z napisom Kontrolna naloga Dijak 1 2 Povpre je Janko 67 72 70.5 Metka 72 67 70.5 Povpre je 70.5 70.5 Tabela 1: Rezultati kontrolnih
DOMINACIJSKO TEVILO GRAFA
 UNIVERZA V LJUBLJANI PEDAGO KA FAKULTETA tudijski program: MATEMATIKA in RAƒUNALNI TVO DOMINACIJSKO TEVILO GRAFA DIPLOMSKO DELO Mentor: doc. dr. Primoº parl Kandidatka: Neja Zub i Ljubljana, maj, 2011
UNIVERZA V LJUBLJANI PEDAGO KA FAKULTETA tudijski program: MATEMATIKA in RAƒUNALNI TVO DOMINACIJSKO TEVILO GRAFA DIPLOMSKO DELO Mentor: doc. dr. Primoº parl Kandidatka: Neja Zub i Ljubljana, maj, 2011
Linear Algebra Primer
 Introduction Linear Algebra Primer Daniel S. Stutts, Ph.D. Original Edition: 2/99 Current Edition: 4//4 This primer was written to provide a brief overview of the main concepts and methods in elementary
Introduction Linear Algebra Primer Daniel S. Stutts, Ph.D. Original Edition: 2/99 Current Edition: 4//4 This primer was written to provide a brief overview of the main concepts and methods in elementary
MATH 2030: EIGENVALUES AND EIGENVECTORS
 MATH 2030: EIGENVALUES AND EIGENVECTORS Determinants Although we are introducing determinants in the context of matrices, the theory of determinants predates matrices by at least two hundred years Their
MATH 2030: EIGENVALUES AND EIGENVECTORS Determinants Although we are introducing determinants in the context of matrices, the theory of determinants predates matrices by at least two hundred years Their
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SARA BREZEC HAUSDORFFOV PARADOKS DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ MATEMATIKA-FIZIKA SARA BREZEC mentor:
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA SARA BREZEC HAUSDORFFOV PARADOKS DIPLOMSKO DELO LJUBLJANA, 2016 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ MATEMATIKA-FIZIKA SARA BREZEC mentor:
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE. Ekstremne porazdelitve za odvisne spremenljivke
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Ekstremne porazdelitve za odvisne spremenljivke (Extremal Distributions for Dependent Variables)
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Zaključna naloga Ekstremne porazdelitve za odvisne spremenljivke (Extremal Distributions for Dependent Variables)
Călugăreanu-White-Fullerjev teorem in topologija DNA
 Univerza v Ljubljani Fakulteta za matematiko in fiziko Oddelek za fiziko Călugăreanu-White-Fullerjev teorem in topologija DNA Seminar Jure Aplinc, dipl. fiz. (UN) Mentor: prof. dr. Rudolf Podgornik 26.
Univerza v Ljubljani Fakulteta za matematiko in fiziko Oddelek za fiziko Călugăreanu-White-Fullerjev teorem in topologija DNA Seminar Jure Aplinc, dipl. fiz. (UN) Mentor: prof. dr. Rudolf Podgornik 26.
Mary Agnes SERVATIUS Izomorfni Cayleyevi grafi nad neizomorfnimi grupami (Isomorphic Cayley Graphs on Non-Isomorphic Groups)
 UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Matematične znanosti Študijski program 2. stopnje Mary Agnes SERVATIUS Izomorfni Cayleyevi grafi nad neizomorfnimi
UNIVERZA NA PRIMORSKEM FAKULTETA ZA MATEMATIKO, NARAVOSLOVJE IN INFORMACIJSKE TEHNOLOGIJE Matematične znanosti Študijski program 2. stopnje Mary Agnes SERVATIUS Izomorfni Cayleyevi grafi nad neizomorfnimi
Linear Algebra Primer
 Linear Algebra Primer D.S. Stutts November 8, 995 Introduction This primer was written to provide a brief overview of the main concepts and methods in elementary linear algebra. It was not intended to
Linear Algebra Primer D.S. Stutts November 8, 995 Introduction This primer was written to provide a brief overview of the main concepts and methods in elementary linear algebra. It was not intended to
TOPIC III LINEAR ALGEBRA
 [1] Linear Equations TOPIC III LINEAR ALGEBRA (1) Case of Two Endogenous Variables 1) Linear vs. Nonlinear Equations Linear equation: ax + by = c, where a, b and c are constants. 2 Nonlinear equation:
[1] Linear Equations TOPIC III LINEAR ALGEBRA (1) Case of Two Endogenous Variables 1) Linear vs. Nonlinear Equations Linear equation: ax + by = c, where a, b and c are constants. 2 Nonlinear equation:
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Matrix Algebra Determinant, Inverse matrix. Matrices. A. Fabretti. Mathematics 2 A.Y. 2015/2016. A. Fabretti Matrices
 Matrices A. Fabretti Mathematics 2 A.Y. 2015/2016 Table of contents Matrix Algebra Determinant Inverse Matrix Introduction A matrix is a rectangular array of numbers. The size of a matrix is indicated
Matrices A. Fabretti Mathematics 2 A.Y. 2015/2016 Table of contents Matrix Algebra Determinant Inverse Matrix Introduction A matrix is a rectangular array of numbers. The size of a matrix is indicated
MATH 213 Linear Algebra and ODEs Spring 2015 Study Sheet for Midterm Exam. Topics
 MATH 213 Linear Algebra and ODEs Spring 2015 Study Sheet for Midterm Exam This study sheet will not be allowed during the test Books and notes will not be allowed during the test Calculators and cell phones
MATH 213 Linear Algebra and ODEs Spring 2015 Study Sheet for Midterm Exam This study sheet will not be allowed during the test Books and notes will not be allowed during the test Calculators and cell phones
NEODLOČLJIVI PROBLEMI V TEORIJI IZRAČUNLJIVOSTI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUKA VIKTOR ROGAČ NEODLOČLJIVI PROBLEMI V TEORIJI IZRAČUNLJIVOSTI MAGISTRSKO DELO LJUBLJANA, 2017 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POUČEVANJE, PREDMETNO
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA LUKA VIKTOR ROGAČ NEODLOČLJIVI PROBLEMI V TEORIJI IZRAČUNLJIVOSTI MAGISTRSKO DELO LJUBLJANA, 2017 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA POUČEVANJE, PREDMETNO
A = 3 B = A 1 1 matrix is the same as a number or scalar, 3 = [3].
![A = 3 B = A 1 1 matrix is the same as a number or scalar, 3 = [3]. A = 3 B = A 1 1 matrix is the same as a number or scalar, 3 = [3].](/thumbs/78/77913594.jpg) Appendix : A Very Brief Linear ALgebra Review Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics Very often in this course we study the shapes
Appendix : A Very Brief Linear ALgebra Review Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics Very often in this course we study the shapes
ZVEZDASTI MNOGOKOTNIKI
 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA BLAŽKA RIOSA ZVEZDASTI MNOGOKOTNIKI DIPLOMSKO DELO Ljubljana, 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ BLAŽKA RIOSA Mentor: dr. Matija
UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA BLAŽKA RIOSA ZVEZDASTI MNOGOKOTNIKI DIPLOMSKO DELO Ljubljana, 2014 UNIVERZA V LJUBLJANI PEDAGOŠKA FAKULTETA DVOPREDMETNI UČITELJ BLAŽKA RIOSA Mentor: dr. Matija
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
A VERY BRIEF LINEAR ALGEBRA REVIEW for MAP 5485 Introduction to Mathematical Biophysics Fall 2010
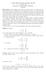 A VERY BRIEF LINEAR ALGEBRA REVIEW for MAP 5485 Introduction to Mathematical Biophysics Fall 00 Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics
A VERY BRIEF LINEAR ALGEBRA REVIEW for MAP 5485 Introduction to Mathematical Biophysics Fall 00 Introduction Linear Algebra, also known as matrix theory, is an important element of all branches of mathematics
Neli Blagus. Iterativni funkcijski sistemi in konstrukcija fraktalov
 UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Neli Blagus Iterativni funkcijski sistemi in konstrukcija fraktalov DIPLOMSKO DELO NA INTERDISCIPLINARNEM UNIVERZITETNEM ŠTUDIJU Mentorica:
UNIVERZA V LJUBLJANI FAKULTETA ZA RAČUNALNIŠTVO IN INFORMATIKO Neli Blagus Iterativni funkcijski sistemi in konstrukcija fraktalov DIPLOMSKO DELO NA INTERDISCIPLINARNEM UNIVERZITETNEM ŠTUDIJU Mentorica:
A matrix over a field F is a rectangular array of elements from F. The symbol
 Chapter MATRICES Matrix arithmetic A matrix over a field F is a rectangular array of elements from F The symbol M m n (F ) denotes the collection of all m n matrices over F Matrices will usually be denoted
Chapter MATRICES Matrix arithmetic A matrix over a field F is a rectangular array of elements from F The symbol M m n (F ) denotes the collection of all m n matrices over F Matrices will usually be denoted
Univerza v Ljubljani Fakulteta za matematiko in fiziko. Oddelek za fiziko. Seminar - 3. letnik, I. stopnja. Kvantni računalniki. Avtor: Tomaž Čegovnik
 Univerza v Ljubljani Fakulteta za matematiko in fiziko Oddelek za fiziko Seminar - 3. letnik, I. stopnja Kvantni računalniki Avtor: Tomaž Čegovnik Mentor: prof. dr. Anton Ramšak Ljubljana, marec 01 Povzetek
Univerza v Ljubljani Fakulteta za matematiko in fiziko Oddelek za fiziko Seminar - 3. letnik, I. stopnja Kvantni računalniki Avtor: Tomaž Čegovnik Mentor: prof. dr. Anton Ramšak Ljubljana, marec 01 Povzetek
MATH 1210 Assignment 4 Solutions 16R-T1
 MATH 1210 Assignment 4 Solutions 16R-T1 Attempt all questions and show all your work. Due November 13, 2015. 1. Prove using mathematical induction that for any n 2, and collection of n m m matrices A 1,
MATH 1210 Assignment 4 Solutions 16R-T1 Attempt all questions and show all your work. Due November 13, 2015. 1. Prove using mathematical induction that for any n 2, and collection of n m m matrices A 1,
MATH 106 LINEAR ALGEBRA LECTURE NOTES
 MATH 6 LINEAR ALGEBRA LECTURE NOTES FALL - These Lecture Notes are not in a final form being still subject of improvement Contents Systems of linear equations and matrices 5 Introduction to systems of
MATH 6 LINEAR ALGEBRA LECTURE NOTES FALL - These Lecture Notes are not in a final form being still subject of improvement Contents Systems of linear equations and matrices 5 Introduction to systems of
MATH 423 Linear Algebra II Lecture 20: Geometry of linear transformations. Eigenvalues and eigenvectors. Characteristic polynomial.
 MATH 423 Linear Algebra II Lecture 20: Geometry of linear transformations. Eigenvalues and eigenvectors. Characteristic polynomial. Geometric properties of determinants 2 2 determinants and plane geometry
MATH 423 Linear Algebra II Lecture 20: Geometry of linear transformations. Eigenvalues and eigenvectors. Characteristic polynomial. Geometric properties of determinants 2 2 determinants and plane geometry
POGLAVJE V: Matrično-produkni nastavki in učinkovite simulacije mnogo-delčnih problemov v eni dimenziji (aka metode DMRG)
 POGLAVJE V: Matrično-produkni nastavki in učinkovite simulacije mnogo-delčnih problemov v eni dimenziji (aka metode DMRG) V tem poglavju se bomo posvetili glavnim idejam učunkovite simulacije kvantne in
POGLAVJE V: Matrično-produkni nastavki in učinkovite simulacije mnogo-delčnih problemov v eni dimenziji (aka metode DMRG) V tem poglavju se bomo posvetili glavnim idejam učunkovite simulacije kvantne in
A matrix is a rectangular array of. objects arranged in rows and columns. The objects are called the entries. is called the size of the matrix, and
 Section 5.5. Matrices and Vectors A matrix is a rectangular array of objects arranged in rows and columns. The objects are called the entries. A matrix with m rows and n columns is called an m n matrix.
Section 5.5. Matrices and Vectors A matrix is a rectangular array of objects arranged in rows and columns. The objects are called the entries. A matrix with m rows and n columns is called an m n matrix.
a 11 a 12 a 11 a 12 a 13 a 21 a 22 a 23 . a 31 a 32 a 33 a 12 a 21 a 23 a 31 a = = = = 12
 24 8 Matrices Determinant of 2 2 matrix Given a 2 2 matrix [ ] a a A = 2 a 2 a 22 the real number a a 22 a 2 a 2 is determinant and denoted by det(a) = a a 2 a 2 a 22 Example 8 Find determinant of 2 2
24 8 Matrices Determinant of 2 2 matrix Given a 2 2 matrix [ ] a a A = 2 a 2 a 22 the real number a a 22 a 2 a 2 is determinant and denoted by det(a) = a a 2 a 2 a 22 Example 8 Find determinant of 2 2
UČNI NAČRT PREDMETA / COURSE SYLLABUS Predmet: Analiza 1 Course title: Analysis 1. Študijska smer Study field. Samost. delo Individ.
 UČNI NAČRT PREDMETA / COURSE SYLLABUS Predmet: Analiza 1 Course title: Analysis 1 Študijski program in stopnja Study programme and level Univerzitetni študijski program Finančna matematika First cycle
UČNI NAČRT PREDMETA / COURSE SYLLABUS Predmet: Analiza 1 Course title: Analysis 1 Študijski program in stopnja Study programme and level Univerzitetni študijski program Finančna matematika First cycle
A matrix is a rectangular array of. objects arranged in rows and columns. The objects are called the entries. is called the size of the matrix, and
 Section 5.5. Matrices and Vectors A matrix is a rectangular array of objects arranged in rows and columns. The objects are called the entries. A matrix with m rows and n columns is called an m n matrix.
Section 5.5. Matrices and Vectors A matrix is a rectangular array of objects arranged in rows and columns. The objects are called the entries. A matrix with m rows and n columns is called an m n matrix.
1. In this problem, if the statement is always true, circle T; otherwise, circle F.
 Math 1553, Extra Practice for Midterm 3 (sections 45-65) Solutions 1 In this problem, if the statement is always true, circle T; otherwise, circle F a) T F If A is a square matrix and the homogeneous equation
Math 1553, Extra Practice for Midterm 3 (sections 45-65) Solutions 1 In this problem, if the statement is always true, circle T; otherwise, circle F a) T F If A is a square matrix and the homogeneous equation
