A Simple Model for Axial Displacement in a Cylindrical Pipe With Internal Shock Loading
|
|
|
- Augustus Watts
- 5 years ago
- Views:
Transcription
1 A Simple Model for Axil Displcemen in Cylindricl Pipe Wih Inernl Shock Loding Nel P. Bier e-mil: Joseph E. Shepherd Grdue Aerospce Lborories, Cliforni Insiue of Technology, Psden, CA This pper describes simplified model for predicing he xil displcemen, sress, nd srin in pipes subjeced o inernl shock wves. This model involves he neglec of rdil nd rory ineri of he pipe, so is predicions represen he spilly verged or low-pss filered response of he ube. The simplified model is developed firs by pplicion of he physicl principles of conservion of mss nd momenum on ech side of he shock wve. This model is hen reproduced using he mhemicl heory of he Green s funcion, which llows oher lod nd boundry condiions o be more esily incorpored. Comprisons wih finie elemen simulions demonsre h he simple model dequely cpures he ube s xil moion, excep p ffiffiffiffiffiffiffiffi ner he criicl velociy corresponding o he br wve speed E=q. Ner his poin, he simplified model, despie being n unsedy model, predics ime-independen resonnce, while he finie elemen model predics resonnce h grows wih ime. [DOI: / ] Inroducion Exensive experimenl observions of he srucurl response of pipes nd ubes o inernl shock nd deonion wve loding hve been crried ou over he ls decde he Explosion Dynmics Lborory, s documened in Refs. [1] nd [2]. These observions consis primrily of poin mesuremens of srin, which hve been exremely useful for quniive chrcerizion of srucurl loding s well s poin vlidion of simulions. However, due o he lrge number of poenil vibrion modes nd he siffness of ypicl piping sysems, i is ofen difficul o infer he globl response, due o he confounding presence of high-frequency oscillions in srin signls. Finie-elemen simulions nd reduced order models re priculrly useful ools o use in conjuncion wih experimens o gin insigh ino lrgescle, lower frequency response modes. This noe presens n nlysis of he xil displcemen induced by shock loding nd proposes simplified bu quniively predicive model. Numericl Simulion Resuls One exmple for which we hve crried ou n nlysis is finie-elemen simulion (LS-Dyn) of shock wve wih pressure rise of 2.52 MP rveling 20 m/s in 2-m long secion of 2-in dimeer, schedule 40 sinless seel pipe (see Tble 1). This exmple is relevn o he evluion of he srucurl response of piping in he Hydrogen in Pipes nd Ancillry Vessels evluion crried ou for he wse remen pln he Hnford Sie [3,4]. Typicl resuls re shown in Figs. 1 nd 2 for ime of 225 ls, before ny wve reflecions occur from he RHS end of he pipe. The shock wve propges wih consn speed, sring from he Mnuscrip received April 22, 2013; finl mnuscrip received July 30, 2013; cceped mnuscrip posed Ocober 16, 2013; published online Ocober 16, Assoc. Edior: Weinong Chen. origin he LHS nd propging owrd he righ. The fluid dynmics ssocied wih he shock wve re no considered, s we re only ineresed in he srucurl response of he pipe o n idelized rveling lod. The boundry condiions re zero xil nd rdil displcemen ech end of he pipe. The pipe is modeled s liner elsic solid wih Young s modulus E ¼ P, densiy q ¼ 040 kg/m 3, nd Poisson s rio ¼ The inner rdius of he pipe is mm, nd he wll hickness is 3.91 mm. For he membrne model of moion discussed subsequenly, he effecive membrne rdius ¼ 2.2 mm nd he rio /h ¼ 7.2. The rdil displcemen w nd xil displcemen u propge s progressive wve sysems, s shown in Fig. 3. The leding edgepof ffiffiffiffiffiffiffiffi he wve is moving pproximely he br wve speed b ¼ E=q ¼ 4900 m/s, nd he wveform is n pproximely biliner displcemen field u(x, ) wih mximum mpliude u p moving he speed of he shock wve fron. The enire srucure is self-similr if he shock speed is consn nd pressure is uniform behind he shock. The mximum mpliude of he displcemen increses in mgniude pproximely linerly in ime u p ¼ _u p, where _u p < 0. Smll oscillions in xil displcemen re superposed on he min biliner profile. These re primrily consequence of he lrge oscillions in rdil displcemen shown in Fig. 1 nd he Poisson coupling beween rdil nd xil srin. Addiionl conribuions re due o he exciion of sher wves in he region jus hed of he shock fron nd propgion of xil disurbnces hed of he fron creed by he periodic moion behind he fron. The rdil displcemen w nd hoop srin e h ¼ w/ show very subsnil oscillions behind he shock fron nd much smller oscillions hed. The response behind he shock fron is periodic in spce nd lso in ime, wih n oscillion frequency of pproximely sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi f h ¼ 1 E 2p qð1 2 Þ nd spil wvelengh of k h ¼ /f h. The oscillory moion is deermined by he ube ineri nd he symmeric rdil moion being opposed primrily by he hoop sress ssocied wih rdil displcemen, s discussed in Ref. [5]. Numericlly, his frequency is 29 khz nd he ssocied spil wvelengh behind he fron is 72 mm. The xil displcemen oscillions re much more ppren in xil srin (Fig. 2), due o he mplifying effecs of differeniion used o obin srin from displcemen, e x ¼ =@x. The evoluion of he xil displcemen wve wih ime cn be more clerly visulized if he profiles differen imes re overlid, shown in Fig. 4. This mehod of presenion shows h, for he cse of zero displcemen he pipe LHS, he displcemen field o he lef of he pressure wve fron is in sedy se. Tble 1 Dimensions, meril properies, nd lod condiions of schedule 40 sinless seel pipe Densiy q kg/m Young s modulus E GP 193 Poisson s rio 0.3 Br wve speed b m/s 4900 Shell dilionl wve speed d m/s 5190 Pressure wve speed m/s 20 Pressure lod P MP 2.52 Pipe inner rdius R i mm Pipe wll hickness R o mm 3.91 Men rdius mm 2.2 (1) Journl of Applied Mechnics Copyrigh VC 2014 by ASME MARCH 2014, Vol. 1 /
2 Fig. 1 Simulion resuls for rdil nd xil displcemen on he ouer surfce of he pipe 225 ls; he shock wve fron is loced 0.47 m nd he br wve fron is 1.1 m Membrne Model Moived by he simple form of he xil displcemen wves shown in Fig. 3, we seek model of he xil displcemen h focuses on xil wve moion nd simplifies or elimines he high-frequency oscillions h re prominen in he xil srin resuls. The firs sep is o pproxime he pipe s shell wihou ny sher deformion or rory ineri. This will elimine he high-frequency oscillions observed in he xil srin jus hed Fig. 3 Simulion resuls for rdil nd xil displcemen wve sysems shown incremens of 100 ls. For clriy, successive rces hve he zero vlues offse by n moun proporionl o he ime incremen. of he pressure fron in Fig. 2. The second sep is o consider he shell s membrne wihou ny bending siffness or rdil ineri o elimine rdil displcemen oscillions (i.e., he rdil moion is qusisedy in chrcer). This will elimine he hoop mode oscillions observed in he rdil displcemen bu will cree disconinuiies in rdil displcemen he shock fron s well s he shell end poins. Including bending siffness would smer hese disconinuiies over he chrcerisic bending lengh of he shell, so his needs o be kep in mind when inerpreing he model resuls. Fig. 2 Simulion resuls for hoop nd xil srins on he ouer surfce of he pipe 225 ls Fig. 4 Seleced xil displcemens from Fig. 3 shown wihou offseing he zero srin / Vol. 1, MARCH 2014 Trnscions of he ASME
3 In doping qusisedy membrne model of rdil moion, we re effecively ime-verging he rdil displcemen oscillions behind he fron, replcing hese by men response. This is resonble pproximion, s long s he ime scles of he rdil oscillion re much smller hn he xil wve propgion imes. In he exmple discussed bove, he period of rdil oscillion is 34 ls nd he ime for pressure wve o rvel he lengh of he pipe (2 m) is 95 ls. So pproximely 2 hoop oscillion cycles will occur in he ime i kes he pressure wve o rverse he lengh of he pipe. The xil moion of he ube is modeled using he following xil force blnce: 2 x where N x is he xil sress resuln, defined s he inegrl of xil sress hrough he wll hickness. Since we re neglecing he rdil dynmics nd xil bending of he pipe nd blncing he hoop sress gins he pressure lod, he Lme soluion [6] for hick-wlled pressure vessel cn be used o model he vriion of hoop nd rdil sresses hrough he wll hickness. This model is vlid only in regions of he pipe where he xil srin is uniform in boh he xil nd rdil direcions, bu due o our neglec of xil bending nd rory ineri, hese condiions re me everywhere excep ner he lod fron nd he boundries of he pipe. As resul, he use of he Lme soluion is consisen wih he ssumpions lredy mde in developing his simplified model. Noe h, for hin ubes, one cn lernively use he hin shell pproximions r r r h nd r h ¼ P=h, bu in he presen formulion, he hick-wll effecs cn be included wihou ddiionl difficuly. The Lme soluions for he hoop nd rdil sresses in long cylinder re he following: r h ðrþ ¼ PR2 i R 2 1 þ R2 o i R 2 o r 2 (3) r r ðrþ ¼ PR2 i R 2 1 R2 o i R 2 o r 2 (3b) where R i nd R o re he inner nd ouer rdii of he ube. From Hooke s lw, he xil sress is hen r x ¼ Ee x þ ðr r þ r h Þ ¼ Ee x þ 2PR2 (4) i R 2 o R2 i The xil sress resuln N x is found by inegring r x hrough he wll hickness. Since, in his cse, r x is uniform hrough he hickness, he resul is Upon insering Eq. (6) ino Eq. (2) nd replcing e x ¼ =@x, we obin p ffiffiffiffiffiffiffiffi where b is he br wve speed E=q. This resul is wve equion for he xil displcemen u, which is forced by he grdien of pressure. For hin ube, he correcion fcor C ends o 1.0 nd he quniy P= is he qusisic rdil displcemen of he ube from clssicl hin shell heory. Thus, he forcing erm cn lso be inerpreed s he grdien of he qusisic rdil displcemen. In he conex of rveling shock wves, he pressure disribuion is modeled s Pðx; Þ ¼P o Hð xþ () where H is he Heviside sep funcion nd is he speed of he shock wve. Under his lod, Eq. (7) becomes 2 2 ¼ C (7) P o dð xþ (9) where d(x) is he Dirc d funcion. In his cse, he source erm vnishes everywhere excep he shock fron x ¼ nd he xil wve moion of he ube is driven solely by he disconinuiy in pressure (which resuls in jump in hoop, xil, nd rdil sresses) he wvefron. Observions on he Numericl Simulion Resuls The numericl soluion exhibis liner growh in ime for boh he spil exen nd mpliude of he xil displcemen u. The poin of mximum displcemen mpliude u p moves wih he speed of he pressure wve nd s shown in Fig. 5 nd grows linerly wih ime wih speed of _u p ¼ 0:035m=s. The xil displcemen lso shows nerly liner vriion wih disnce (Fig. 4) in he segmens of he wve hed nd behind he pressure wve fron. We will herefore idelize he srin in hese segmens s ime-independen, wih disinc vlues hed of, e x,1, nd behind, e x,2, he wve fron. From he coninuiy of he xil displcemen he pressure wve fron, we cn inegre he srin hrough he wve o rele he wo srin mgniudes o he wve speeds nd obin he following relionship: e x;1 ¼ b e x;2 (10) In erms of _u p, he idelized srins cn be compued o be e x;1 ¼ _u p b (11) N x ¼ e x þ 2PhR2 i R 2 o R2 i (5) I my be noed h he wll hickness is h ¼ R o R i nd he men rdius is ¼ 0:5ðR o þ R i Þ. Using hese definiions, he xil sress resuln cn be expressed in he form N x ¼ e x þ P R2 i 2 (6) The quniy in prenheses is he correcion due o hick-wll effecs, which will herefer be denoed C. As he wll hickness is reduced, his fcor pproches 1.0 nd he expression h remins is he resul from clssicl hin shell heory. In his pper, he correcion erm mus be reined, since we re nlyzing ube wih inner rdius R i ¼ mm nd men rdius ¼ 2.2 mm, which gives correcion fcor of C ¼ Fig. 5 Exremum xil displcemen ( x 5 ) s funcion of ime showing he liner relionship Journl of Applied Mechnics MARCH 2014, Vol. 1 /
4 e x;2 ¼ _u p (12) Using Eq. (12), we cn wrie he displcemen field s uðx; Þ ¼ _u p x for 0 x (24) Soluion of he Model Equions Bsed on he resuls of he numericl simulions, we cn divide he soluion domin ino hree segmens: Region 0. b x L. Ahed of he br wve fron, here is no disurbnce nd he xil displcemen vnishes. Once he wve reches he RHS of he pipe, x ¼ L, refleced wve propging he lef is creed in order o sisfy he boundry condiion. This wve cn be redily compued using he mehod of chrcerisics [7] bu, in he ineres of breviy, will no be considered in his noe. Wih his limiion, he soluion is simply uðx; Þ ¼0 for b x L (13) Region 1. x b. Beween he pressure wve fron nd he br wve fron, he xil displcemen propges s righ fcing wve wih consn xil srin e x,1 nd sress resuln N x,1. The mgniude of he srin ws given bove by Eq. (11). Since he pressure is zero in his region, he xil sress resuln in Eq. (6) reduces o N x ¼ e x (14) which is consisen wih he se of unixil srin hed of he pressure wve fron. From he heory of chrcerisics for wve equions [7], he xil displcemen in his region hs he generl form u ¼ f ðx b Þ (15) From he ssumpion of consn xil srin in his region, we conclude h uðx; Þ ¼e x;1 ðx b Þ (16) which is consisen wih our previous observions. This implies ¼ e x;1 b ¼ e x;1 (1) Using Eq. (11), we cn wrie he displcemen field s uðx; Þ ¼ _u p ð b x bþ for x b (19) Region 2. 0 x. Beween he LHS (x ¼ 0) of he pipe nd he pressure wve fron x ¼, he displcemen is sedy (independen of ime) nd linerly proporionl o he disnce from he LHS of he ¼ 0 ¼ e x;2 (21) This cn be inegred o yield he complee soluion uðx; Þ ¼e x;2 x (22) The xil sress resuln in his region is N x;2 ¼ e x;2 þ PC (23) In order o complee he soluion, we need one more relionship o deermine he vlue of he srin in eiher region 1 or 2 or else he mgniude of _u p. An ddiionl relionship cn be obined by considering he xil force blnce in he shell on ech side of he pressure fron. In generl, he xil sress resulns on ech side will be differen in order o hve blnce of momenum he fron h correcly ccouns for he jump in meril velociy V ¼ =@ hrough he fron. The simples wy o consruc he blnce of momenum is o consider fixed conrol volume h encloses he shell. A ime, he lef boundry of he conrol volume is in region 2, jus behind he pressure fron, nd he righ boundry is well in fron of he br wve, compleely enclosing region 1. Recognizing h he velociy in region 2 is zero, he chnge in momenum in ime D will be he sum of he loss of momenum in he shell meril h is brough o res by he moion of he fron nd he gin of momenum due o he moion of he br wve. This hs o be blnced by he impulse pplied o he conrol volume by he sress resuln in region 2, since he sress resuln hed of region 1 vnishes. The resuling momenum blnce is N x;2 D ¼ qhð b ÞV 1 D (25) Subsiuing for he xil sress resuln nd he velociy, we hve e x;2 þ PC ¼ qhð b Þð e x;1 b Þ (26) Subsiuions of expressions for xil srins in Eqs. (11) nd (12) led o _u p ¼ b P b þ h E C (27) b P e x;2 ¼ b þ h E C (2) b P e x;1 ¼þ h E C (29) From Hooke s lw, he hoop srin is given by e h ¼ 1 ½ E r h ðr x þ r r ÞŠ (30) A he ouer surfce of he ube, r r is zero, nd in region 2, r h nd r x re evlued using Eqs. (3) nd (4). Using hese equions, he hoop srin he ouer surfce in region 2 is found o be e h;2 ¼ 1 2 P b þ C (31) In region 1, boh r r nd r h re zero, so he pplicion of Eq. (30) gives e h;1 ¼ 2 b P C (32) As expeced, e h,2 is inermedie beween he limiing cses of zero xil srin, e x,2 ¼ 0, nd zero xil sress, N x,2 ¼ 0, which give he limis P 1 2 C e h;2 P C (33) Subsiuing he prmeers lised in Tble 1, we obin he numericl vlues given in Tble 2. The corresponding LS-Dyn simulion resuls were nlyzed o exrc men vlues for / Vol. 1, MARCH 2014 Trnscions of he ASME
5 Tble 2 Comprison of model resuls wih he LS-Dyn soluion Propery LS-Dyn Model _u p (m/s) e x,1 (lsrin) e x,2 (lsrin) e h,1 (lsrin) e h,2 (lsrin) comprison o he model. Given he simplificions of he model, he resuls compre fvorbly wih he vlues compued by he rnsien finie-elemen soluion. Green s Funcion Soluion The exc soluion for he xil displcemens cn lso be found using he mhemicl echnique of he Green s funcion. To do so, Eq. (7) will be solved on semi-infinie inervl [0, 1] wih he boundry condiion u(0, ) ¼ 0 he origin. The Green s funcion gðx; x o ; ; o Þ is found by replcing he inhomogeneous erm in Eq. (7) by spil nd emporl Dirc d funcions, 2 2 ¼ dðx x oþdð o Þ (34) The Green s funcion sisfying his equion is given by [] gðx; x o ; ; o Þ¼ b 2 H ð bð o Þ jx x o jþ ( b jx x o j < b ð o Þ ¼ 2 0 jx x o j > b ð o Þ (35) where H is he Heviside funcion. Soluions o he inhomogeneous wve Eq. (7) re found by inegring he Green s funcion gins he source erm, ð ð uðx; Þ ¼ gðx; x o ; ; o ÞC Pðx o ; o Þdx o d o o 0 1 We re only ineresed in soluions on he inervl [0, 1], bu in order o evlue his inegrl, i is necessry o specify he pressure P(x o, o ) for x o < 0. To sisfy he boundry condiion u(0, ) ¼ 0, he pressure disribuion is mirrored symmericlly bou he origin, i.e., Pð x o ; o Þ¼Pðx o ; o Þ (37) Equion (39) cn be inerpreed s he inegrl of he pplied pressure P long he C þ nd C chrcerisics, where inegrion long hese phs is prmeerized by o. This siuion is shown schemiclly on n x digrm in Fig. 6. The righ hlf of he digrm depics he domin of ineres, while he lef hlf is he mirror imge used o sisfy he zero displcemen boundry condiion. There re wo wves in he region of ineres. The fser wve, rveling speed b, is he leding chrcerisic, nd in fron of his wve (region 0), no moion of he ube occurs. The slower wve, rveling speed, is he pplied pressure lod. Wihin he shded region on his plo, he pplied pressure is consn nd equl o P o, while ouside his region, he pressure is zero. In his digrm, we re seeking he soluion u pir of coordines (x, ). As represened in Eq. (39), he soluion his poin is found by inegring he pressure long he C þ nd C chrcerisics, shown s dshed lines in he figure. If he poin of ineres lies in region 2, s depiced by poin (x, ), hen boh he C þ nd C chrcerisics pss hrough he shded region, where he pressure is nonzero. On he oher hnd, for poin such s (x b, b ), lying in region 1, only he C þ chrcerisic psses hrough he shded region. As resul, he form of he soluion is differen in ech of hese regions. Region 2 To evlue Eq. (39) in region 2, we need only o inegre from 1 < o < long he C þ chrcerisic nd from 2 < o < long he C chrcerisic, where 1 nd 2 re he imes which he chrcerisics inersec he pressure wve fron. Thus, Eq. (39) becomes ð b ð P o d o P o d o (41) b ¼ C 2 P oð 1 2 Þ From he geomery of he problem, he imes 1 nd 2 re found o be 1 ¼ b x (42) þ b 2 ¼ x þ b þ b Thus, he displcemen in region 2 is given by (42b) Since he Green s funcion is only nonzero when jx x o j < b ð o Þ, he limis of he spil inegrl in Eq. (36) re replced by finie vlues nd he soluion cn be wrien s b 2 ð ð xþbð oþ 0 x bð Pðx o ; o Þdx o d o o which is redily inegred o obin b 2 ð 0 Pxþ ð b ð o Þ; o Þ (39) Px ð b ð o Þ; o Þd o The bove resul is vlid for n rbirry pressure disribuion. We now specilize o he cse of shock wve rveling velociy, for which he pressure is sep funcion of mpliude P o, Pðx o ; o Þ¼P o Hð o x o Þ (40) Fig. 6 Wve digrm for shock wve rveling long ube speed Journl of Applied Mechnics MARCH 2014, Vol. 1 /
6 uðx; Þ ¼ C P b o x ðx < Þ (43) þ b Region 1 The soluion in Region 1 is found using he sme pproch; however, only he C þ chrcerisic psses hrough he shded region in Fig. 6. As resul, Eq. (39) becomes b 2 P oð 4 3 Þ (44) Referring o Fig. 6, 3 is excly he sme s 1 bove nd 4 is given by 4 ¼ x b (45) b Hence, he displcemen in region 1 becomes P b o ðx b Þ ðx > Þ (46) A plo compring he xil displcemen prediced by his simple model wih finie elemen simulions (using condiions from Tble 1) is shown in Fig. 7. The simplified model cpures he xil moion remrkbly well, given he level of simplificion involved. Srins nd Sresses By differeniing he displcemens, he srins re found o be C P b o x < þ e x ¼ b (47) þc P b o x > These expressions re excly he sme s hose deermined in Eqs. (2) nd (29) using mss nd momenum blnces. Mking use of he definiion in Eq. (6), he xil sress resuln is found o be N x < x þ ¼ b (4) P o C b x > A similr nlysis cn be performed for he cse of pressure lod h is supersonic relive o he br wve velociy ( > b ), nd expressions for he xil displcemen u under hese condiions re provided in Tble 3. We hve lso reproduced hese resuls by king he semiinfinie Fourier sine rnsform of Eq. (7) nd solving he resuling emporl ordinry differenil equion. Upon invering he rnsform, he following form of soluion is obined: P 1 b o 2 2 ½ðjx þ b j jx b jþ b (49) b ðjx þ j jx jþš This resul is equivlen o Eqs. (43) nd (46) bu convenienly encpsules he displcemens for regions 0, 1, nd 2 s well s he subsonic ( < b ) nd supersonic ( > b ) cses in single expression. Zero-Sress Boundry Condiions In ddiion o he boundry condiion u(0, ) ¼ 0 used in he preceding secions, second prcicl boundry condiion is one of zero xil sress: N x (0, ) ¼ 0. This will occur if he pipe end is no fixed bu free o slide long he xil direcion. An exmple is when glnd sels re used o connec pipe secions. Referring o Ref. [6], his boundry condiion is equivlen o ¼ P x¼0 C (50) Since ny liner funcion of x nd sisfies he wve Eq. (7), iis possible o dd such funcion y(x, ) o he bove soluion u(x, ) in order o sisfy zero-sress boundry condiions rher hn zero-displcemen. The funcion h sisfies his propery is yðx; Þ ¼ C P b þ ðx b Þ (51) Afer dding his funcion o u(x, ) from Eqs. (43) nd (46), he resuling displcemen field for condiions of zero xil sress is he following: x b P o x < þ b uðx; Þ ¼ C 2 (52) ðx bþ x > The corresponding srin is e x ¼ C P o < 1 x < : 2 x > nd he xil sress resuln is N < 0 x < x ¼ 2 P o C : x > (53) (54) Once gin, similr expressions cn be obined for he cse of supersonic lod ( > b ), which re given in Tble 3. The xil displcemen profile for he sress-free boundry condiion is compred wih finie elemen resuls in Fig.. Once gin, excellen greemen beween he simple heory nd he finie elemen mehod (FEM) is observed. Fig. 7 Comprison of xil displcemens from finie elemen simulions nd he presen simple model. Boundry condiion is u(0, ) 5 0. Simulion condiions re hose summrized in Tble 1. Comprison Wih Finie Elemen Simulions Figure 9 compres he xil srin prediced by he simplified model wih he resuls of finie elemen simulions over wide rnge of lod speeds. The condiions oher hn lod speed re hose lised in Tble 1. As his figure shows, he simplified model / Vol. 1, MARCH 2014 Trnscions of he ASME
7 Tble 3 Lis of expressions for he xil displcemen for severl differen boundry condiions nd lod condiions. The displcemen is zero if x/ > mx(, b ). Lod cse Boundry condiion Displcemen b u(0) ¼ 0 bx P x < þ uðx; Þ ¼C b b ðx bþ x > b u(0) ¼ 0 bx P x < b þ b 2 2 ðx Þ x > b b b N x (0) ¼ 0 x þ b P x < þ b 2 ðx bþ x > b N x (0) ¼ 0 x þ 2 P x < b þ uðx; Þ ¼C b b ðx Þ x > b b cpures he spilly verged xil srins quie well. The srins in his plo re normlized by he men hoop srin e h ¼ P o C =, which is he sme for ll lod speeds. This scling demonsres he subsnil mplificion h occurs s he br velociy b is pproched. I is ineresing o noe h he simplified model, despie being n unsedy model, predics pek srins h do no vry wih ime. In conrs, he finie elemen model predics pek xil srins h grow wih ime re very close o 2/3 (which is in good greemen wih he heoreicl predicions of Ref. [9]). The simplified model does no cpure his emporl growh, since his effec involves he coupling beween rdil, rory, nd xil modes of moion, which re negleced in he simple heory. To enble more quniive comprison beween he predicions of he simplified model nd he finie elemen simulions, he simuled srin rces were verged on he inervls [0, ] nd [, b ], corresponding o he primry nd precursor wves. These verge srins re compred wih he predicions of he simple model in Fig. 10. In boh he precursor wve nd he primry wve, he xil srin predicions of he simplified model re in very good greemen wih he finie elemen simulions. Only ner he resonn poin / b ¼ 1 re significn differences observed. One reson for hese differences is he fc h he pek Fig. 9 Comprison of xil srin profiles for severl speeds of pressure lod. For he cse of / b 5 1.0, he model predics funcion of infinie heigh nd zero widh. The boundry condiion is N x (0, ) 5 0, nd srins re normlized by he sic hoop srin P o /. Fig. Comprison of xil displcemen from finie elemen simulions nd he presen simple model. Boundry condiion is N x (0, ) 5 0. Simulion condiions re summrized in Tble 1. Fig. 10 Averge xil srins in precursor nd primry wve regions. Symbols correspond o finie elemen simulions nd solid lines o he simple model. Boundry condiion is N x (0, ) 5 0. Journl of Applied Mechnics MARCH 2014, Vol. 1 /
8 srin prediced by he finie elemen model grows wih ime. The pek srin observed in he simulions is herefore limied by he finie lengh of he pipe, nd closer greemen wih he simplified model would probbly be obined if longer pipe were simuled. Conclusions A simplified model ws proposed for predicing he xil displcemen, sress, nd srin in pipes subjeced o inernl shock wves. This model ws derived using boh physicl rgumens from mss nd momenum conservion s well s direc soluion of he governing pril differenil equion of moion. Comprisons wih finie elemen simulions show h his model dequely cpures he low-frequency behvior over wide rnge of lod speeds, p wih speeds vrying from zero o greer hn he br speed b ¼ ffiffiffiffiffiffiffiffi E=q. When he lod speed pproches he br speed, he simple model predics ime-independen resonnce wih unbounded sresses nd srins. In conrs, he finie elemen model predics pek srins h grow wih 2/3. However, for lod speeds differing by more hn bou 10% from b, he predicions of he simple model re quie deque. Nomenclure ¼ men rdius of pipe 0:5ðR i þ R o Þ C ¼ correcion fcor ðr i =Þ 2 due o hick-wll effecs E ¼ elsic modulus of pipe g ¼ Green s funcion for he wve equion h ¼ pipe wll hickness N x ¼ xil sress resuln N h ¼ hoop sress resuln P ¼ pressure of shock wve R i ¼ inner rdius of pipe R o ¼ ouer rdius of pipe u ¼ xil displcemen of pipe u p ¼ mximum xil displcemen long pipe V ¼ xil velociy of pipe meril =@ w ¼ rdil displcemen of pipe e x ¼ xil membrne srin e h ¼ hoop srin H ¼ Heviside sep funcion ¼ Poisson s rio q ¼ pipe densiy ¼ speed of shock wve pffiffiffiffiffiffiffiffi b ¼ br wve speed E=q pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi d ¼ dilionl shell wve speed E=qð1 2 Þ References [1] Belmn, W., Burscu, E., Shepherd, J., nd Zuhl, L., 1999, The Srucurl Response of Cylindricl Shells o Inernl Shock Loding, ASME J. Pressure Vessel Technol., 121(3), pp [2] Belmn, W., nd Shepherd, J., 2002, Liner Elsic Response of Tubes o Inernl Deonion Loding, J. Sound Vib., 252(4), pp [3] Shepherd, J. E., nd Akbr, R., 2009, Forces Due o Deonion Propgion in Bend, Grdue Aeronuicl Lborories Cliforni Insiue of Technology, Psden, CA, Technicl Repor No. FM [4] Shepherd, J. E., nd Akbr, R., 2009, Piping Sysem Response o Deonions. Resuls of ES1, TS1 nd SS1 Tesing, Grdue Aeronuicl Lborories Cliforni Insiue of Technology, Psden, CA, Technicl Repor No. FM [5] Krnesky, J., Dmzo, J. S., Chow-Yee, K., Rusinek, A., nd Shepherd, J. E., 2013, Plsic Deformion Due o Refleced Deonion, In. J. Solids Sruc., 50(1), pp [6] Timoshenko, S. P., 1934, Theory of Elsiciy, 1s ed., McGrw-Hill, New York. [7] Kolsky, H., 1963, Sress Wves in Solids, Dover, New York. [] Hbermn, R., 2004, Applied Pril Differenil Equions, 4h ed., Person Educion, Upper Sddle River, NJ. [9] Schiffner, K., nd Seele, C. R., 1971, Cylindricl Shell Wih n Axisymmeric Moving Lod, AIAA J., 9(1), pp / Vol. 1, MARCH 2014 Trnscions of he ASME
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Physics 2A HW #3 Solutions
 Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Magnetostatics Bar Magnet. Magnetostatics Oersted s Experiment
 Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
The Finite Element Method for the Analysis of Non-Linear and Dynamic Systems
 Swiss Federl Insiue of Pge 1 The Finie Elemen Mehod for he Anlysis of Non-Liner nd Dynmic Sysems Prof. Dr. Michel Hvbro Fber Dr. Nebojs Mojsilovic Swiss Federl Insiue of ETH Zurich, Swizerlnd Mehod of
Swiss Federl Insiue of Pge 1 The Finie Elemen Mehod for he Anlysis of Non-Liner nd Dynmic Sysems Prof. Dr. Michel Hvbro Fber Dr. Nebojs Mojsilovic Swiss Federl Insiue of ETH Zurich, Swizerlnd Mehod of
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
RESPONSE UNDER A GENERAL PERIODIC FORCE. When the external force F(t) is periodic with periodτ = 2π
 RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
M r. d 2. R t a M. Structural Mechanics Section. Exam CT5141 Theory of Elasticity Friday 31 October 2003, 9:00 12:00 hours. Problem 1 (3 points)
 Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
MATH 124 AND 125 FINAL EXAM REVIEW PACKET (Revised spring 2008)
 MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 9: The High Beta Tokamak
 .65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
.65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
A 1.3 m 2.5 m 2.8 m. x = m m = 8400 m. y = 4900 m 3200 m = 1700 m
 PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
6. Gas dynamics. Ideal gases Speed of infinitesimal disturbances in still gas
 6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
( ) ( ) ( ) ( ) ( ) ( y )
 8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
S Radio transmission and network access Exercise 1-2
 S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
A new model for limit order book dynamics
 Anewmodelforlimiorderbookdynmics JeffreyR.Russell UniversiyofChicgo,GrdueSchoolofBusiness TejinKim UniversiyofChicgo,DeprmenofSisics Absrc:Thispperproposesnewmodelforlimiorderbookdynmics.Thelimiorderbookconsiss
Anewmodelforlimiorderbookdynmics JeffreyR.Russell UniversiyofChicgo,GrdueSchoolofBusiness TejinKim UniversiyofChicgo,DeprmenofSisics Absrc:Thispperproposesnewmodelforlimiorderbookdynmics.Thelimiorderbookconsiss
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q). INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg) INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples.
 Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Probability, Estimators, and Stationarity
 Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
Chapter Direct Method of Interpolation
 Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
IX.2 THE FOURIER TRANSFORM
 Chper IX The Inegrl Trnsform Mehods IX. The Fourier Trnsform November, 7 7 IX. THE FOURIER TRANSFORM IX.. The Fourier Trnsform Definiion 7 IX.. Properies 73 IX..3 Emples 74 IX..4 Soluion of ODE 76 IX..5
Chper IX The Inegrl Trnsform Mehods IX. The Fourier Trnsform November, 7 7 IX. THE FOURIER TRANSFORM IX.. The Fourier Trnsform Definiion 7 IX.. Properies 73 IX..3 Emples 74 IX..4 Soluion of ODE 76 IX..5
FM Applications of Integration 1.Centroid of Area
 FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
1 jordan.mcd Eigenvalue-eigenvector approach to solving first order ODEs. -- Jordan normal (canonical) form. Instructor: Nam Sun Wang
 jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
Soliton Scattering on the External Potential in Weakly Nonlocal Nonlinear Media
 Mlysin Journl of Mhemicl Sciences 1(S) Februry: 219 226 (216) Specil Issue: The 3 rd Inernionl Conference on Mhemicl Applicions in Engineering 214 (ICMAE 14) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES
Mlysin Journl of Mhemicl Sciences 1(S) Februry: 219 226 (216) Specil Issue: The 3 rd Inernionl Conference on Mhemicl Applicions in Engineering 214 (ICMAE 14) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES
Think of the Relationship Between Time and Space Again
 Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
 PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
A NUMERICAL STUDY ON MULTI-CHAMBER OSCILLATING WATER COLUMNS
 Journl of JSCE, Vol. 3, 93-4, 5 A UMERICAL STUDY O MULTI-CAMBER OSCILLATIG WATER COLUMS Pllv KOIRALA, Shuichi AGATA, Ysuk IMAI 3, Tengen MURAKAMI 4 nd Toshiki SETOGUCI 5 Posdocorl Resercher, Insiue of
Journl of JSCE, Vol. 3, 93-4, 5 A UMERICAL STUDY O MULTI-CAMBER OSCILLATIG WATER COLUMS Pllv KOIRALA, Shuichi AGATA, Ysuk IMAI 3, Tengen MURAKAMI 4 nd Toshiki SETOGUCI 5 Posdocorl Resercher, Insiue of
EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE BOUNDARY-VALUE PROBLEM
 Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Chapter 2. Motion along a straight line. 9/9/2015 Physics 218
 Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Solutions for Nonlinear Partial Differential Equations By Tan-Cot Method
 IOSR Journl of Mhemics (IOSR-JM) e-issn: 78-578. Volume 5, Issue 3 (Jn. - Feb. 13), PP 6-11 Soluions for Nonliner Pril Differenil Equions By Tn-Co Mehod Mhmood Jwd Abdul Rsool Abu Al-Sheer Al -Rfidin Universiy
IOSR Journl of Mhemics (IOSR-JM) e-issn: 78-578. Volume 5, Issue 3 (Jn. - Feb. 13), PP 6-11 Soluions for Nonliner Pril Differenil Equions By Tn-Co Mehod Mhmood Jwd Abdul Rsool Abu Al-Sheer Al -Rfidin Universiy
Solutions to Problems from Chapter 2
 Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Composite Reinforcement of Cylindrical Pressure Vessels
 Comosie einorcemen o Cylindricl Pressure Vessels Cylindricl Pressure Vessels Cylindricl ressure vessels re in idesred use or vriey o licions SCBA nd SCUBA nks Prone nks Comressed Nurl Gs (CNG) nd ydrogen
Comosie einorcemen o Cylindricl Pressure Vessels Cylindricl Pressure Vessels Cylindricl ressure vessels re in idesred use or vriey o licions SCBA nd SCUBA nks Prone nks Comressed Nurl Gs (CNG) nd ydrogen
Thermal neutron self-shielding factor in foils: a universal curve
 Proceedings of he Inernionl Conference on Reserch Recor Uilizion, Sfey, Decommissioning, Fuel nd Wse Mngemen (Snigo, Chile, -4 Nov.3) Pper IAEA-CN-/, IAEA Proceedings Series, Vienn, 5 Therml neuron self-shielding
Proceedings of he Inernionl Conference on Reserch Recor Uilizion, Sfey, Decommissioning, Fuel nd Wse Mngemen (Snigo, Chile, -4 Nov.3) Pper IAEA-CN-/, IAEA Proceedings Series, Vienn, 5 Therml neuron self-shielding
Soil-Pile Dynamic Interaction in the Viscous Damping Layered Soils
 1 The Open Civil Engineering Journl, 11, 5, 1-18 Soil-Pile Dynmic Inercion in he Viscous Dmping Lyered Soils Open Access Yinhui Wng 1, Kuihu Wng, Zhixing Zh 1, * nd Reno Que 1 Deprmen of Civil Engineering
1 The Open Civil Engineering Journl, 11, 5, 1-18 Soil-Pile Dynmic Inercion in he Viscous Dmping Lyered Soils Open Access Yinhui Wng 1, Kuihu Wng, Zhixing Zh 1, * nd Reno Que 1 Deprmen of Civil Engineering
LAPLACE TRANSFORM OVERCOMING PRINCIPLE DRAWBACKS IN APPLICATION OF THE VARIATIONAL ITERATION METHOD TO FRACTIONAL HEAT EQUATIONS
 Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
Wu, G.-.: Lplce Trnsform Overcoming Principle Drwbcks in Applicion... THERMAL SIENE: Yer 22, Vol. 6, No. 4, pp. 257-26 257 Open forum LAPLAE TRANSFORM OVEROMING PRINIPLE DRAWBAKS IN APPLIATION OF THE VARIATIONAL
Phys 110. Answers to even numbered problems on Midterm Map
 Phys Answers o een numbered problems on Miderm Mp. REASONING The word per indices rio, so.35 mm per dy mens.35 mm/d, which is o be epressed s re in f/cenury. These unis differ from he gien unis in boh
Phys Answers o een numbered problems on Miderm Mp. REASONING The word per indices rio, so.35 mm per dy mens.35 mm/d, which is o be epressed s re in f/cenury. These unis differ from he gien unis in boh
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
Mathematics 805 Final Examination Answers
 . 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
. 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR IAN KNOWLES
 A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
Physics 235 Chapter 2. Chapter 2 Newtonian Mechanics Single Particle
 Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Version 001 test-1 swinney (57010) 1. is constant at m/s.
 Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
T-Match: Matching Techniques For Driving Yagi-Uda Antennas: T-Match. 2a s. Z in. (Sections 9.5 & 9.7 of Balanis)
 3/0/018 _mch.doc Pge 1 of 6 T-Mch: Mching Techniques For Driving Ygi-Ud Anenns: T-Mch (Secions 9.5 & 9.7 of Blnis) l s l / l / in The T-Mch is shun-mching echnique h cn be used o feed he driven elemen
3/0/018 _mch.doc Pge 1 of 6 T-Mch: Mching Techniques For Driving Ygi-Ud Anenns: T-Mch (Secions 9.5 & 9.7 of Blnis) l s l / l / in The T-Mch is shun-mching echnique h cn be used o feed he driven elemen
NEW FRACTIONAL DERIVATIVES WITH NON-LOCAL AND NON-SINGULAR KERNEL Theory and Application to Heat Transfer Model
 Angn, A., e l.: New Frcionl Derivives wih Non-Locl nd THERMAL SCIENCE, Yer 216, Vol. 2, No. 2, pp. 763-769 763 NEW FRACTIONAL DERIVATIVES WITH NON-LOCAL AND NON-SINGULAR KERNEL Theory nd Applicion o He
Angn, A., e l.: New Frcionl Derivives wih Non-Locl nd THERMAL SCIENCE, Yer 216, Vol. 2, No. 2, pp. 763-769 763 NEW FRACTIONAL DERIVATIVES WITH NON-LOCAL AND NON-SINGULAR KERNEL Theory nd Applicion o He
Procedia Computer Science
 Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
Procedi Compuer Science 00 (0) 000 000 Procedi Compuer Science www.elsevier.com/loce/procedi The Third Informion Sysems Inernionl Conference The Exisence of Polynomil Soluion of he Nonliner Dynmicl Sysems
(b) 10 yr. (b) 13 m. 1.6 m s, m s m s (c) 13.1 s. 32. (a) 20.0 s (b) No, the minimum distance to stop = 1.00 km. 1.
 Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
1. Introduction. 1 b b
 Journl of Mhemicl Inequliies Volume, Number 3 (007), 45 436 SOME IMPROVEMENTS OF GRÜSS TYPE INEQUALITY N. ELEZOVIĆ, LJ. MARANGUNIĆ AND J. PEČARIĆ (communiced b A. Čižmešij) Absrc. In his pper some inequliies
Journl of Mhemicl Inequliies Volume, Number 3 (007), 45 436 SOME IMPROVEMENTS OF GRÜSS TYPE INEQUALITY N. ELEZOVIĆ, LJ. MARANGUNIĆ AND J. PEČARIĆ (communiced b A. Čižmešij) Absrc. In his pper some inequliies
P441 Analytical Mechanics - I. Coupled Oscillators. c Alex R. Dzierba
 Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Neural assembly binding in linguistic representation
 Neurl ssembly binding in linguisic represenion Frnk vn der Velde & Mrc de Kmps Cogniive Psychology Uni, Universiy of Leiden, Wssenrseweg 52, 2333 AK Leiden, The Neherlnds, vdvelde@fsw.leidenuniv.nl Absrc.
Neurl ssembly binding in linguisic represenion Frnk vn der Velde & Mrc de Kmps Cogniive Psychology Uni, Universiy of Leiden, Wssenrseweg 52, 2333 AK Leiden, The Neherlnds, vdvelde@fsw.leidenuniv.nl Absrc.
ECE Microwave Engineering
 EE 537-635 Microwve Engineering Adped from noes y Prof. Jeffery T. Willims Fll 8 Prof. Dvid R. Jcson Dep. of EE Noes Wveguiding Srucures Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model
EE 537-635 Microwve Engineering Adped from noes y Prof. Jeffery T. Willims Fll 8 Prof. Dvid R. Jcson Dep. of EE Noes Wveguiding Srucures Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model
1. Consider a PSA initially at rest in the beginning of the left-hand end of a long ISS corridor. Assume xo = 0 on the left end of the ISS corridor.
 In Eercise 1, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 1. Consider PSA iniilly res in he beginning of he lef-hnd
In Eercise 1, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 1. Consider PSA iniilly res in he beginning of he lef-hnd
Average & instantaneous velocity and acceleration Motion with constant acceleration
 Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Convergence of Singular Integral Operators in Weighted Lebesgue Spaces
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
2D Motion WS. A horizontally launched projectile s initial vertical velocity is zero. Solve the following problems with this information.
 Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
Nonlinear System Modelling: How to Estimate the. Highest Significant Order
 IEEE Insrumenion nd Mesuremen Technology Conference nchorge,, US, - My Nonliner Sysem Modelling: ow o Esime he ighes Significn Order Neophyos Chirs, Ceri Evns nd Dvid Rees, Michel Solomou School of Elecronics,
IEEE Insrumenion nd Mesuremen Technology Conference nchorge,, US, - My Nonliner Sysem Modelling: ow o Esime he ighes Significn Order Neophyos Chirs, Ceri Evns nd Dvid Rees, Michel Solomou School of Elecronics,
This UR does not apply to CSR Bulk Carriers and Oil Tankers or to container ships to which UR S11A is applicable.
 (1989) (Rev.1 199) (Rev. Nov 001) (Rev. June 00) (Rev.4 July 004) (Rev.5 Jn 006) (Rev.6 My 0) (Rev.7 Nov 0) (Rev.8 June 015) Longiudinl Srengh Sndrd.1 Applicion This requiremen pplies only o seel ships
(1989) (Rev.1 199) (Rev. Nov 001) (Rev. June 00) (Rev.4 July 004) (Rev.5 Jn 006) (Rev.6 My 0) (Rev.7 Nov 0) (Rev.8 June 015) Longiudinl Srengh Sndrd.1 Applicion This requiremen pplies only o seel ships
ECE Microwave Engineering. Fall Prof. David R. Jackson Dept. of ECE. Notes 10. Waveguides Part 7: Transverse Equivalent Network (TEN)
 EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
SOME USEFUL MATHEMATICS
 SOME USEFU MAHEMAICS SOME USEFU MAHEMAICS I is esy o mesure n preic he behvior of n elecricl circui h conins only c volges n currens. However, mos useful elecricl signls h crry informion vry wih ime. Since
SOME USEFU MAHEMAICS SOME USEFU MAHEMAICS I is esy o mesure n preic he behvior of n elecricl circui h conins only c volges n currens. However, mos useful elecricl signls h crry informion vry wih ime. Since
Mathematical Modeling
 ME pplie Engineering nlsis Chper Mhemicl Moeling Professor Ti-Rn Hsu, Ph.D. Deprmen of Mechnicl n erospce Engineering Sn Jose Se Universi Sn Jose, Cliforni, US Jnur Chper Lerning Ojecives Mhemicl moeling
ME pplie Engineering nlsis Chper Mhemicl Moeling Professor Ti-Rn Hsu, Ph.D. Deprmen of Mechnicl n erospce Engineering Sn Jose Se Universi Sn Jose, Cliforni, US Jnur Chper Lerning Ojecives Mhemicl moeling
EXERCISE - 01 CHECK YOUR GRASP
 UNIT # 09 PARABOLA, ELLIPSE & HYPERBOLA PARABOLA EXERCISE - 0 CHECK YOUR GRASP. Hin : Disnce beween direcri nd focus is 5. Given (, be one end of focl chord hen oher end be, lengh of focl chord 6. Focus
UNIT # 09 PARABOLA, ELLIPSE & HYPERBOLA PARABOLA EXERCISE - 0 CHECK YOUR GRASP. Hin : Disnce beween direcri nd focus is 5. Given (, be one end of focl chord hen oher end be, lengh of focl chord 6. Focus
Errors Due to Transverse Sensitivity in Strain Gages
 Micro-Mesuremens Srin Gges nd Insrumens Errors Due o Trnsverse Sensiivi in Srin Gges Tech Noe TN-509 Trnsverse Sensiivi Trnsverse sensiivi in srin gge refers o he behvior of he gge in responding o srins
Micro-Mesuremens Srin Gges nd Insrumens Errors Due o Trnsverse Sensiivi in Srin Gges Tech Noe TN-509 Trnsverse Sensiivi Trnsverse sensiivi in srin gge refers o he behvior of he gge in responding o srins
Tax Audit and Vertical Externalities
 T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
T Audi nd Vericl Eernliies Hidey Ko Misuyoshi Yngihr Ngoy Keizi Universiy Ngoy Universiy 1. Inroducion The vericl fiscl eernliies rise when he differen levels of governmens, such s he federl nd se governmens,
Longitudinal Strength Standard. S11 (cont) S11
 (1989) (Rev.1 199) (Rev. Nov 001) (Rev. June 00) (Rev.4 July 004) (Rev.5 Jn 006) (Rev.6 My 0) Longiudinl Srengh Sndrd.1 Applicion This requiremen pplies only o seel ships of lengh 90 m nd greer in unresriced
(1989) (Rev.1 199) (Rev. Nov 001) (Rev. June 00) (Rev.4 July 004) (Rev.5 Jn 006) (Rev.6 My 0) Longiudinl Srengh Sndrd.1 Applicion This requiremen pplies only o seel ships of lengh 90 m nd greer in unresriced
14. The fundamental theorem of the calculus
 4. The funmenl heorem of he clculus V 20 00 80 60 40 20 0 0 0.2 0.4 0.6 0.8 v 400 200 0 0 0.2 0.5 0.8 200 400 Figure : () Venriculr volume for subjecs wih cpciies C = 24 ml, C = 20 ml, C = 2 ml n (b) he
4. The funmenl heorem of he clculus V 20 00 80 60 40 20 0 0 0.2 0.4 0.6 0.8 v 400 200 0 0 0.2 0.5 0.8 200 400 Figure : () Venriculr volume for subjecs wih cpciies C = 24 ml, C = 20 ml, C = 2 ml n (b) he
How to Prove the Riemann Hypothesis Author: Fayez Fok Al Adeh.
 How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
Physic 231 Lecture 4. Mi it ftd l t. Main points of today s lecture: Example: addition of velocities Trajectories of objects in 2 = =
 Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
Some basic notation and terminology. Deterministic Finite Automata. COMP218: Decision, Computation and Language Note 1
 COMP28: Decision, Compuion nd Lnguge Noe These noes re inended minly s supplemen o he lecures nd exooks; hey will e useful for reminders ou noion nd erminology. Some sic noion nd erminology An lphe is
COMP28: Decision, Compuion nd Lnguge Noe These noes re inended minly s supplemen o he lecures nd exooks; hey will e useful for reminders ou noion nd erminology. Some sic noion nd erminology An lphe is
Vibrations of a Parametrically and Self-Excited System with Ideal and Non-Ideal Energy Sources
 Vibrions of Prmericlly nd Self-Excied Sysem wih J. Wrminski Deprmen of Applied Mechnics, Technicl Universiy of Lublin Ndbysrzyck 36, -68 Lublin. Polnd jwr@rchimedes.pol.lublin.pl J. M. Blhzr Deprmen of
Vibrions of Prmericlly nd Self-Excied Sysem wih J. Wrminski Deprmen of Applied Mechnics, Technicl Universiy of Lublin Ndbysrzyck 36, -68 Lublin. Polnd jwr@rchimedes.pol.lublin.pl J. M. Blhzr Deprmen of
3 Motion with constant acceleration: Linear and projectile motion
 3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
IDENTIFICATION OF NONLINEAR DAMPING AND STIFFNESS OF SPRING-SUSPENDED SECTIONAL MODEL
 The Eighh Asi-Pcific Conference on Wind Engineering, December 1 14, 13, Chenni, Indi IDENTIFICATION OF NONLINEAR DAMPING AND STIFFNESS OF SPRING-SUSPENDED SECTIONAL MODEL Gung-Zhong Go 1, Le-Dong Zhu,
The Eighh Asi-Pcific Conference on Wind Engineering, December 1 14, 13, Chenni, Indi IDENTIFICATION OF NONLINEAR DAMPING AND STIFFNESS OF SPRING-SUSPENDED SECTIONAL MODEL Gung-Zhong Go 1, Le-Dong Zhu,
3D Transformations. Computer Graphics COMP 770 (236) Spring Instructor: Brandon Lloyd 1/26/07 1
 D Trnsformions Compuer Grphics COMP 770 (6) Spring 007 Insrucor: Brndon Lloyd /6/07 Geomery Geomeric eniies, such s poins in spce, exis wihou numers. Coordines re nming scheme. The sme poin cn e descried
D Trnsformions Compuer Grphics COMP 770 (6) Spring 007 Insrucor: Brndon Lloyd /6/07 Geomery Geomeric eniies, such s poins in spce, exis wihou numers. Coordines re nming scheme. The sme poin cn e descried
IX.1.1 The Laplace Transform Definition 700. IX.1.2 Properties 701. IX.1.3 Examples 702. IX.1.4 Solution of IVP for ODEs 704
 Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
15. Vector Valued Functions
 1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
Physics Worksheet Lesson 4: Linear Motion Section: Name:
 Physics Workshee Lesson 4: Liner Moion Secion: Nme: 1. Relie Moion:. All moion is. b. is n rbirry coorine sysem wih reference o which he posiion or moion of somehing is escribe or physicl lws re formule.
Physics Workshee Lesson 4: Liner Moion Secion: Nme: 1. Relie Moion:. All moion is. b. is n rbirry coorine sysem wih reference o which he posiion or moion of somehing is escribe or physicl lws re formule.
Deposition of Submicron Charged Spherical Particles in the Trachea of the Human Airways.
 eposiion of Submicron Chrged Sphericl Pricles in he Trche of he Humn Airwys. eprmen of Engineering Sciences nd Mhemics ivision of Fluid nd Experimenl Mechnics Luleå Universiy of Technology Corresponding
eposiion of Submicron Chrged Sphericl Pricles in he Trche of he Humn Airwys. eprmen of Engineering Sciences nd Mhemics ivision of Fluid nd Experimenl Mechnics Luleå Universiy of Technology Corresponding
Honours Introductory Maths Course 2011 Integration, Differential and Difference Equations
 Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
Collision Detection and Bouncing
 Collision Deecion nd Bouncing Collisions re Hndled in Two Prs. Deecing he collision Mike Biley mj@cs.oregonse.edu. Hndling he physics of he collision collision-ouncing.ppx If You re Lucky, You Cn Deec
Collision Deecion nd Bouncing Collisions re Hndled in Two Prs. Deecing he collision Mike Biley mj@cs.oregonse.edu. Hndling he physics of he collision collision-ouncing.ppx If You re Lucky, You Cn Deec
2. Nonlinear Conservation Law Equations
 . Nonlinear Conservaion Law Equaions One of he clear lessons learned over recen years in sudying nonlinear parial differenial equaions is ha i is generally no wise o ry o aack a general class of nonlinear
. Nonlinear Conservaion Law Equaions One of he clear lessons learned over recen years in sudying nonlinear parial differenial equaions is ha i is generally no wise o ry o aack a general class of nonlinear
GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS
 - TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
- TAMKANG JOURNAL OF MATHEMATICS Volume 5, Number, 7-5, June doi:5556/jkjm555 Avilble online hp://journlsmhkueduw/ - - - GENERALIZATION OF SOME INEQUALITIES VIA RIEMANN-LIOUVILLE FRACTIONAL CALCULUS MARCELA
FRACTIONAL-order differential equations (FDEs) are
 Proceedings of he Inernionl MuliConference of Engineers nd Compuer Scieniss 218 Vol I IMECS 218 Mrch 14-16 218 Hong Kong Comprison of Anlyicl nd Numericl Soluions of Frcionl-Order Bloch Equions using Relible
Proceedings of he Inernionl MuliConference of Engineers nd Compuer Scieniss 218 Vol I IMECS 218 Mrch 14-16 218 Hong Kong Comprison of Anlyicl nd Numericl Soluions of Frcionl-Order Bloch Equions using Relible
Properties of Logarithms. Solving Exponential and Logarithmic Equations. Properties of Logarithms. Properties of Logarithms. ( x)
 Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Analytic solution of linear fractional differential equation with Jumarie derivative in term of Mittag-Leffler function
 Anlyic soluion of liner frcionl differenil equion wih Jumrie derivive in erm of Mig-Leffler funcion Um Ghosh (), Srijn Sengup (2), Susmi Srkr (2b), Shnnu Ds (3) (): Deprmen of Mhemics, Nbdwip Vidysgr College,
Anlyic soluion of liner frcionl differenil equion wih Jumrie derivive in erm of Mig-Leffler funcion Um Ghosh (), Srijn Sengup (2), Susmi Srkr (2b), Shnnu Ds (3) (): Deprmen of Mhemics, Nbdwip Vidysgr College,
23.2. Representing Periodic Functions by Fourier Series. Introduction. Prerequisites. Learning Outcomes
 Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
IX.1.1 The Laplace Transform Definition 700. IX.1.2 Properties 701. IX.1.3 Examples 702. IX.1.4 Solution of IVP for ODEs 704
 Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 6, 8 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 6, 8 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
A Time Truncated Improved Group Sampling Plans for Rayleigh and Log - Logistic Distributions
 ISSNOnline : 39-8753 ISSN Prin : 347-67 An ISO 397: 7 Cerified Orgnizion Vol. 5, Issue 5, My 6 A Time Trunced Improved Group Smpling Plns for Ryleigh nd og - ogisic Disribuions P.Kvipriy, A.R. Sudmni Rmswmy
ISSNOnline : 39-8753 ISSN Prin : 347-67 An ISO 397: 7 Cerified Orgnizion Vol. 5, Issue 5, My 6 A Time Trunced Improved Group Smpling Plns for Ryleigh nd og - ogisic Disribuions P.Kvipriy, A.R. Sudmni Rmswmy
Reduction of Cross-Field Plasma Transport in Tokamaks due to Power Input Redistribution and Sheared Flow Profile Modification
 TH/P8-6 Reducion of Cross-Field Plsm Trnspor in Tokmks due o Power Inpu Redisribuion nd Shered Flow Profile Modificion V.P. Psukhov, N.V. Chudin RRC «Kurchov Insiue», 8 Moscow, Russin Federion e-mil conc
TH/P8-6 Reducion of Cross-Field Plsm Trnspor in Tokmks due o Power Inpu Redisribuion nd Shered Flow Profile Modificion V.P. Psukhov, N.V. Chudin RRC «Kurchov Insiue», 8 Moscow, Russin Federion e-mil conc
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
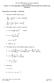 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
At the end of this lesson, the students should be able to understand
 Insrucional Objecives A he end of his lesson, he sudens should be able o undersand Sress concenraion and he facors responsible. Deerminaion of sress concenraion facor; experimenal and heoreical mehods.
Insrucional Objecives A he end of his lesson, he sudens should be able o undersand Sress concenraion and he facors responsible. Deerminaion of sress concenraion facor; experimenal and heoreical mehods.
Two Coupled Oscillators / Normal Modes
 Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
