1. Consider a PSA initially at rest in the beginning of the left-hand end of a long ISS corridor. Assume xo = 0 on the left end of the ISS corridor.
|
|
|
- Tamsyn Cooper
- 6 years ago
- Views:
Transcription
1 In Eercise 1, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 1. Consider PSA iniilly res in he beginning of he lef-hnd end of long ISS corridor. Assume o = 0 on he lef end of he ISS corridor. A 0 n sronu requess n emergency ideo conference wih ground conrol nd he PSA uniformly cceleres o he righ for seerl seconds > 3. A. For he PSA s moion described boe, In he firs digrm, skech he grph of ccelerion s. ime. In he second digrm, skech he grph of elociy s. ime, nd In he hird digrm skech of displcemen s. ime. B. For he PSA s moion described boe, drw ecors represening Accelerion, Velociy nd Displcemen he four imes lised below. o o o C. In ech cse, circle he nswer h bes describes he siuion. When 1 < < 3 Accelerion is: consn chnging zero posiie negie When 1 < < 3 Velociy is: consn chnging zero posiie negie When 1 < < 3 Displcemen is: consn chnging zero posiie negie
2 In Eercise 2, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 2. Ground conrol is using PSA s ideo cmer o surey he progress of seerl dozen biology eperimens. A o he PSA is iniilly moing consn speed in srigh line from lef o righ. A 2 ground conrol direcs he PSA o ccelere o greer speed in he sme direcion for seerl seconds > 3. A. For he PSA s moion described boe, In he firs digrm, skech he grph of ccelerion s. ime. In he second digrm, skech he grph of elociy s. ime, nd In he hird digrm skech of displcemen s. ime. B. For he PSA s moion described boe, drw ecors represening Accelerion, Velociy nd Displcemen he four imes lised below. o o o C. In ech cse, circle he nswer h bes describes he siuion. When o < < 2 Accelerion is: consn chnging zero posiie negie When o < < 2 Velociy is: consn chnging zero posiie negie When 2 < < 3 Displcemen is: consn chnging zero posiie negie In Eercise 3, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is.
3 Assume ll ccelerions nd decelerions re consn. 3. Consider PSA iniilly moing consn elociy from lef o righ in long ISS corridor. A o n sronu commnds he PSA o decelere. A 1.5 he PSA sops moing o he righ nd begins ccelering o he lef. A 3 he PSA hs reched he sme consn speed i sred wih, only now moing from righ o lef. A. For he PSA s moion described boe, In he firs digrm, skech he grph of ccelerion s. ime. In he second digrm, skech he grph of elociy s. ime, nd In he hird digrm skech of displcemen s. ime. B. For he PSA s moion described boe, drw ecors represening Accelerion, Velociy nd Displcemen he four imes lised below. o o o C. In ech cse, circle he nswer h bes describes he siuion. When 0 < < 1.5 ccelerion is: consn chnging zero posiie negie When 1.5 < < 3 elociy is: consn chnging zero posiie negie When 0 < < 1.5 displcemen is: consn chnging zero posiie negie
4 In Eercise 4, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 4. Consider PSA moing op speed in srigh line from lef o righ. Suddenly, n sronu flos down nd sops direcly in fron of he PSA. Beween 0 nd 1 he PSA quickly deceleres o res in order o oid hiing he sronu. Beween 1 nd 2 he PSA sops nd remins res s he sronu moes ou of he wy. A 2 he PSA begins o ccelere from lef o righ unil reching i s op speed. A. For he PSA s moion described boe, In he firs digrm, skech he grph of ccelerion s. ime. In he second digrm, skech he grph of elociy s. ime, nd In he hird digrm skech of displcemen s. ime. B. For he PSA s moion described boe, drw ecors represening Accelerion, Velociy nd Displcemen he four imes lised below. o o o C. In ech cse, circle he nswer h bes describes he siuion. When 0 < < 1 ccelerion is: consn chnging zero posiie negie When 1 < < 2 elociy is: consn chnging zero posiie negie When 2 < < 3 displcemen is: consn chnging zero posiie negie
5 In Eercise 5, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 5. Consider PSA iniilly res. A 0 he PSA cceleres from lef o righ owrds he cener of long ISS corridor. A 1 he PSA sops ccelering nd coninues moing consn speed unil 2. A 2 he PSA deceleres nd comes o res 3. A. For he PSA s moion described boe, In he firs digrm, skech he grph of ccelerion s. ime. In he second digrm, skech he grph of elociy s. ime, nd In he hird digrm skech of displcemen s. ime. B. For he PSA s moion described boe, drw ecors represening Accelerion, Velociy nd Displcemen he four imes lised below. o o o C. In ech cse, circle he nswer h bes describes he siuion. When 1 < < 2 ccelerion is: consn chnging zero posiie negie When 2 < < 3 elociy is: consn chnging zero posiie negie When 0 < < 3 displcemen is: consn chnging zero posiie negie
6 Vericl Posiion s. Time of P O S I T I O N (m) Time (s) Consider he boe Displcemen s. Time grph boe. I represens he ericl displcemen of squirrel s i climbs up nd down ree. The squirrel srs Y = 0 m which represens he lowes brnch on he ree. 1. During which imes is he Squirrel moing: ) owrds he op of he ree? (0s < < 2s), (4s < < 6s), (13s < < 16s), (18s < < 20s) b) wy from he op of he ree? (6s < < 12s), (16s < < 18s) c) no moing ericlly? (2s < < 4s), (12s < < 13s), (20s < < 22s) 2. Find he erge elociy for: ) he ime inerl beween 3 5 seconds. 3-5s = + 3 m/s b) he ime inerl beween seconds s = - 8/3 m/s c) he ime inerl beween 0 20 seconds. V 0-20s = 0 m/s
7 3. How mny imes does he squirrel reurn o he lowes brnch on he ree? Four Times 4. Find he erge elociy beween =18 o =20 seconds. V g = + 5 m/s 5. Predic he squirrel s elociy = 12.5 s. V 12.5 = 0 m/s 6. When he displcemen is negie, wh does h men in erms of he squirrels posiion on he ree wih respec o he lowes brnch? The squirrel is below he lowes brnch. 7. A wh ime(s) does he Squirrel chnge direcion? = 6s, = 13s, = 16s, = 18s 8. Wh is he Squirrel s mimum displcemen from he lowes brnch? + 12 m 9. When is he Squirrel speeding up? = 4s, = 6s, = 10s, = 16s, = 18s 10. When is he Squirrel slowing down? = 2s, (4s < < 6s), (10s < < 13s), (14s < < 16s), = 18s 11. Wh is he Squirrel s ccelerion beween =6 nd =10 seconds? 0 m/s 2
8 Kinemics Grphs Gien eiher n ccelerion, elociy or displcemen grph, skech grphs of he missing wo. Emple: Gien consn posiie elociy skech grphs of ccelerion nd displcemen.. b. c.
9 d. e. f. g.
10 In-Clss Problems 1 Dimensionl Kinemics Neglec ir resisnce unless oherwise specified. 1. The posiion of model rdio conrolled cr rcing down srigh rck ws obsered rious imes nd he resuls re summrized in he ble below. (m) (s) Find he erge elociy of he cr for he 1s second. b. Find he erge elociy of he cr for he ls 3 seconds. c. Find he erge elociy of he cr for enire period of ime. d. Find he erge speed of he cr for he enire period of ime.
11 2. A LAHS swimmer swims he lengh of 50.0m pool in 20.0s nd mkes he reurn rip o he sring posiion in 22.5s. A. Predic he erge elociy in he firs hlf of he swim. B. Predic he erge elociy in he ls hlf of he swim. C. Predic he erge elociy in he round rip. D. Predic he erge speed in he round rip.
12 3. A ery ligh cheerleder is hrown srigh up in he ir by her collegues. Her iniil elociy upon losing conc wih he hrowers is 14.7 m/s =0. A =1.50 s she reches he pe of her ericl rjecory where her elociy 0 m/s. A. Predic he cheerleder s erge ccelerion during his 1.50 s inerl? Wh is he significnce of he negie sign of your nswer? B. If he cheerleder coninues o ccelere he sme re, predic he cheerleder s finl elociy jus before she s cugh he sme leel she ws hrown? C. Grph he cheerleder s displcemen, elociy nd ccelerion s. ime.
13 4. Consider cliff dier flling from res from he op of 125 m ll cliff edge. A. Predic he ime i kes he dier o rech he wer 125 m below he cliff s edge. B. Predic he elociy of he cliff dier jus before she reches he wer. C. Predic he erge elociy of he cliff dier during her freefll. D. Grph he cliff dier s displcemen, elociy nd ccelerion s. ime.
14 5. Consider furniure moer rying o se ime by lunching boes upwrd from he ground leel o noher moer lening ou 3 rd sory window. If he second moer s hnds re 11.5 m boe he ground A. Predic he iniil elociy bo mus he such h he 2 nd moer cn rech ou nd grb he bo when i s is pe. B. Predic he ime for he bo o rech is pe. C. If he 2 nd moer doesn cch he bo, predic is elociy jus before i his he ground. D. Grph he bo s displcemen, elociy nd ccelerion s. ime.
15 7. Consider Sprin cr drier rcing consn speed round circulr rck wih rdius of 85.0 m. A. Clcule her erge speed if she complees one qurer of lp in 8.0 s. B. Clcule her erge elociy for he sme 8.0 s qurer urn. C. Clcule her erge elociy for complee reoluion.
16 8. Consider Crl driing long srigh srech of rodwy consn elociy of 35 m/s. A he ec sme ime she psses police cr i begins o uniformly ccelere fer her, from res, 4.5 m/s 2. A. How much ime psses before he police cr cches up o Crl? B. How fr hs Crl drien before he police cr psses her? C. How fr hs he police cr drien before pssing Crl? D. Grph Crl s nd he police officer s displcemen s. ime on he sme grph. Wh does he inersecion poin represen? E. Grph Crl s nd he police officer s elociy s. ime on he sme grph. Wh does he inersecion poin represen? How is he re under Crl s elociy s. ime grph reled o he re under he officer s elociy s. ime grph?
Name: Per: L o s A l t o s H i g h S c h o o l. Physics Unit 1 Workbook. 1D Kinematics. Mr. Randall Room 705
Nme: Per: L o s A l o s H i g h S c h o o l Physics Uni 1 Workbook 1D Kinemics Mr. Rndll Room 705 Adm.Rndll@ml.ne www.laphysics.com Uni 1 - Objecies Te: Physics 6 h Ediion Cunel & Johnson The objecies
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
A 1.3 m 2.5 m 2.8 m. x = m m = 8400 m. y = 4900 m 3200 m = 1700 m
PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
Motion in a Straight Line
Moion in Srigh Line. Preei reched he mero sion nd found h he esclor ws no working. She wlked up he sionry esclor in ime. On oher dys, if she remins sionry on he moing esclor, hen he esclor kes her up in
2D Motion WS. A horizontally launched projectile s initial vertical velocity is zero. Solve the following problems with this information.
Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
Physics 101 Lecture 4 Motion in 2D and 3D
Phsics 11 Lecure 4 Moion in D nd 3D Dr. Ali ÖVGÜN EMU Phsics Deprmen www.ogun.com Vecor nd is componens The componens re he legs of he righ ringle whose hpoenuse is A A A A A n ( θ ) A Acos( θ) A A A nd
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
Average & instantaneous velocity and acceleration Motion with constant acceleration
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
(b) 10 yr. (b) 13 m. 1.6 m s, m s m s (c) 13.1 s. 32. (a) 20.0 s (b) No, the minimum distance to stop = 1.00 km. 1.
Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Physics Worksheet Lesson 4: Linear Motion Section: Name:
Physics Workshee Lesson 4: Liner Moion Secion: Nme: 1. Relie Moion:. All moion is. b. is n rbirry coorine sysem wih reference o which he posiion or moion of somehing is escribe or physicl lws re formule.
Physics 2A HW #3 Solutions
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Chapter 2. Motion along a straight line. 9/9/2015 Physics 218
Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
A Kalman filtering simulation
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
Chapter 2 PROBLEM SOLUTIONS
Chper PROBLEM SOLUTIONS. We ssume h you re pproximely m ll nd h he nere impulse rels uniform speed. The elpsed ime is hen Δ x m Δ = m s s. s.3 Disnces reled beween pirs of ciies re ( ) Δx = Δ = 8. km h.5
Physic 231 Lecture 4. Mi it ftd l t. Main points of today s lecture: Example: addition of velocities Trajectories of objects in 2 = =
Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
Introduction to LoggerPro
Inroducion o LoggerPro Sr/Sop collecion Define zero Se d collecion prmeers Auoscle D Browser Open file Sensor seup window To sr d collecion, click he green Collec buon on he ool br. There is dely of second
Lecture 3: 1-D Kinematics. This Week s Announcements: Class Webpage: visit regularly
Lecure 3: 1-D Kinemics This Week s Announcemens: Clss Webpge: hp://kesrel.nm.edu/~dmeier/phys121/phys121.hml isi regulrly Our TA is Lorrine Bowmn Week 2 Reding: Chper 2 - Gincoli Week 2 Assignmens: Due:
CHAPTER 2 KINEMATICS IN ONE DIMENSION ANSWERS TO FOCUS ON CONCEPTS QUESTIONS
Physics h Ediion Cunell Johnson Young Sdler Soluions Mnul Soluions Mnul, Answer keys, Insrucor's Resource Mnul for ll chpers re included. Compleed downlod links: hps://esbnkre.com/downlod/physics-h-ediion-soluions-mnulcunell-johnson-young-sdler/
3 Motion with constant acceleration: Linear and projectile motion
3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
Phys 110. Answers to even numbered problems on Midterm Map
Phys Answers o een numbered problems on Miderm Mp. REASONING The word per indices rio, so.35 mm per dy mens.35 mm/d, which is o be epressed s re in f/cenury. These unis differ from he gien unis in boh
PHY2048 Exam 1 Formula Sheet Vectors. Motion. v ave (3 dim) ( (1 dim) dt. ( (3 dim) Equations of Motion (Constant Acceleration)
Insrucors: Field/Mche PHYSICS DEPATMENT PHY 48 Em Ferur, 5 Nme prin, ls firs: Signure: On m honor, I he neiher gien nor receied unuhoried id on his eminion. YOU TEST NUMBE IS THE 5-DIGIT NUMBE AT THE TOP
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
MATH 124 AND 125 FINAL EXAM REVIEW PACKET (Revised spring 2008)
MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
t s (half of the total time in the air) d?
.. In Cl or Homework Eercie. An Olmpic long jumper i cpble of jumping 8.0 m. Auming hi horizonl peed i 9.0 m/ he lee he ground, how long w he in he ir nd how high did he go? horizonl? 8.0m 9.0 m / 8.0
What distance must an airliner travel down a runway before reaching
2 LEARNING GALS By sudying his chper, you will lern: How o describe srigh-line moion in erms of erge elociy, insnneous elociy, erge ccelerion, nd insnneous ccelerion. How o inerpre grphs of posiion ersus
Physics for Scientists and Engineers I
Physics for Scieniss nd Engineers I PHY 48, Secion 4 Dr. Beriz Roldán Cueny Uniersiy of Cenrl Florid, Physics Deprmen, Orlndo, FL Chper - Inroducion I. Generl II. Inernionl Sysem of Unis III. Conersion
Physics 100: Lecture 1
Physics : Lecure Agen for Toy Aice Scope of his course Mesuremen n Unis Funmenl unis Sysems of unis Conering beween sysems of unis Dimensionl Anlysis -D Kinemics (reiew) Aerge & insnneous elociy n ccelerion
CHAPTER 2: Describing Motion: Kinematics in One Dimension
CHAPTER : Describing Moion: Kinemics in One Dimension Answers o Quesions A cr speeomeer mesures only spee I oes no gie ny informion bou he irecion, n so oes no mesure elociy By efiniion, if n objec hs
An object moving with speed v around a point at distance r, has an angular velocity. m/s m
Roion The mosphere roes wih he erh n moions wihin he mosphere clerly follow cure phs (cyclones, nicyclones, hurricnes, ornoes ec.) We nee o epress roion quniiely. For soli objec or ny mss h oes no isor
when t = 2 s. Sketch the path for the first 2 seconds of motion and show the velocity and acceleration vectors for t = 2 s.(2/63)
. The -coordine of pricle in curiliner oion i gien b where i in eer nd i in econd. The -coponen of ccelerion in eer per econd ured i gien b =. If he pricle h -coponen = nd when = find he gniude of he eloci
Physics Notes - Ch. 2 Motion in One Dimension
Physics Noes - Ch. Moion in One Dimension I. The naure o physical quaniies: scalars and ecors A. Scalar quaniy ha describes only magniude (how much), NOT including direcion; e. mass, emperaure, ime, olume,
Chapter Direct Method of Interpolation
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Version 001 test-1 swinney (57010) 1. is constant at m/s.
Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
2/5/2012 9:01 AM. Chapter 11. Kinematics of Particles. Dr. Mohammad Abuhaiba, P.E.
/5/1 9:1 AM Chper 11 Kinemic of Pricle 1 /5/1 9:1 AM Inroducion Mechnic Mechnic i Th cience which decribe nd predic he condiion of re or moion of bodie under he cion of force I i diided ino hree pr 1.
MTH 146 Class 11 Notes
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
September 20 Homework Solutions
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
Brock University Physics 1P21/1P91 Fall 2013 Dr. D Agostino. Solutions for Tutorial 3: Chapter 2, Motion in One Dimension
Brock Uniersiy Physics 1P21/1P91 Fall 2013 Dr. D Agosino Soluions for Tuorial 3: Chaper 2, Moion in One Dimension The goals of his uorial are: undersand posiion-ime graphs, elociy-ime graphs, and heir
UNIT # 01 (PART II) JEE-Physics KINEMATICS EXERCISE I. 2h g. 8. t 1 = (4 1)i ˆ (2 2) ˆj (3 3)kˆ 1. ˆv = 2 2h g. t 2 = 2 3h g
J-Physics UNI # (PR II) KINMICS XRCIS I ( )i ˆ ( ) ˆj ( )kˆ i. ˆ ˆ ˆ j i ˆ ˆ j ˆ 6i ˆ 8ˆj 8. h h h C h h.. elociy m/s h D. ˆ i i cos6ˆi sin 6ˆj f ˆ i ˆj i ˆ ˆj i ˆ ˆj i ˆ ˆj f i ˆj ˆj m/s. For,, nd d d
Chapter 3: Motion in One Dimension
Lecure : Moion in One Dimension Chper : Moion in One Dimension In his lesson we will iscuss moion in one imension. The oles one o he Phsics subjecs is he Mechnics h inesiges he moion o bo. I els no onl
Sph3u Practice Unit Test: Kinematics (Solutions) LoRusso
Sph3u Prcice Uni Te: Kinemic (Soluion) LoRuo Nme: Tuey, Ocober 3, 07 Ku: /45 pp: /0 T&I: / Com: Thi i copy of uni e from 008. Thi will be imilr o he uni e you will be wriing nex Mony. you cn ee here re
Unit 1 Test Review Physics Basics, Movement, and Vectors Chapters 1-3
A.P. Physics B Uni 1 Tes Reiew Physics Basics, Moemen, and Vecors Chapers 1-3 * In sudying for your es, make sure o sudy his reiew shee along wih your quizzes and homework assignmens. Muliple Choice Reiew:
Chapter 10. Simple Harmonic Motion and Elasticity. Goals for Chapter 10
Chper 0 Siple Hronic Moion nd Elsiciy Gols or Chper 0 o ollow periodic oion o sudy o siple hronic oion. o sole equions o siple hronic oion. o use he pendulu s prooypicl syse undergoing siple hronic oion.
Ch.4 Motion in 2D. Ch.4 Motion in 2D
Moion in plne, such s in he sceen, is clled 2-dimensionl (2D) moion. 1. Posiion, displcemen nd eloci ecos If he picle s posiion is ( 1, 1 ) 1, nd ( 2, 2 ) 2, he posiions ecos e 1 = 1 1 2 = 2 2 Aege eloci
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Phys 221 Fall Chapter 2. Motion in One Dimension. 2014, 2005 A. Dzyubenko Brooks/Cole
Phys 221 Fall 2014 Chaper 2 Moion in One Dimension 2014, 2005 A. Dzyubenko 2004 Brooks/Cole 1 Kinemaics Kinemaics, a par of classical mechanics: Describes moion in erms of space and ime Ignores he agen
Chapter 3 Kinematics in Two Dimensions
Chaper 3 KINEMATICS IN TWO DIMENSIONS PREVIEW Two-dimensional moion includes objecs which are moing in wo direcions a he same ime, such as a projecile, which has boh horizonal and erical moion. These wo
a 10.0 (m/s 2 ) 5.0 Name: Date: 1. The graph below describes the motion of a fly that starts out going right V(m/s)
Name: Dae: Kinemaics Review (Honors. Physics) Complee he following on a separae shee of paper o be urned in on he day of he es. ALL WORK MUST BE SHOWN TO RECEIVE CREDIT. 1. The graph below describes he
Science Advertisement Intergovernmental Panel on Climate Change: The Physical Science Basis 2/3/2007 Physics 253
Science Adeisemen Inegoenmenl Pnel on Clime Chnge: The Phsicl Science Bsis hp://www.ipcc.ch/spmfeb7.pdf /3/7 Phsics 53 hp://www.fonews.com/pojecs/pdf/spmfeb7.pdf /3/7 Phsics 53 3 Sus: Uni, Chpe 3 Vecos
PHYSICS 211 MIDTERM I 21 April 2004
PHYSICS MIDERM I April 004 Exm is closed book, closed notes. Use only your formul sheet. Write ll work nd nswers in exm booklets. he bcks of pges will not be grded unless you so request on the front of
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
1. Six acceleration vectors are shown for the car whose velocity vector is directed forward. For each acceleration vector describe in words the
Si ccelerio ecors re show for he cr whose eloci ecor is direced forwrd For ech ccelerio ecor describe i words he iseous moio of he cr A ri eers cured horizol secio of rck speed of 00 km/h d slows dow wih
Motion in One Dimension 2
The curren bsolue lnd speed record holder is he Briish designed ThrusSSC, win urbofn-powered cr which chieved 763 miles per hour (1,8 km/h) for he mile (1.6 km), breking he sound brrier. The cr ws driven
CHAPTER 11 PARAMETRIC EQUATIONS AND POLAR COORDINATES
CHAPTER PARAMETRIC EQUATIONS AND POLAR COORDINATES. PARAMETRIZATIONS OF PLANE CURVES., 9, _ _ Ê.,, Ê or, Ÿ. 5, 7, _ _.,, Ÿ Ÿ Ê Ê 5 Ê ( 5) Ê ˆ Ê 6 Ê ( 5) 7 Ê Ê, Ÿ Ÿ $ 5. cos, sin, Ÿ Ÿ 6. cos ( ), sin (
Displacement ( x) x x x
Kinemaics Kinemaics is he branch of mechanics ha describes he moion of objecs wihou necessarily discussing wha causes he moion. 1-Dimensional Kinemaics (or 1- Dimensional moion) refers o moion in a sraigh
NEWTON S SECOND LAW OF MOTION
Course and Secion Dae Names NEWTON S SECOND LAW OF MOTION The acceleraion of an objec is defined as he rae of change of elociy. If he elociy changes by an amoun in a ime, hen he aerage acceleraion during
Position, Velocity, and Acceleration
rev 06/2017 Posiion, Velociy, and Acceleraion Equipmen Qy Equipmen Par Number 1 Dynamic Track ME-9493 1 Car ME-9454 1 Fan Accessory ME-9491 1 Moion Sensor II CI-6742A 1 Track Barrier Purpose The purpose
1. Kinematics I: Position and Velocity
1. Kinemaics I: Posiion and Velociy Inroducion The purpose of his eperimen is o undersand and describe moion. We describe he moion of an objec by specifying is posiion, velociy, and acceleraion. In his
Introduction to Mechanics Practice using the Kinematics Equations
Introduction to Mechnics Prctice using the Kinemtics Equtions Ln Sheridn De Anz College Jn 24, 2018 Lst time finished deriing the kinemtics equtions some problem soling prctice Oeriew using kinemtics equtions
Physics 101: Lecture 03 Kinematics Today s lecture will cover Textbook Sections (and some Ch. 4)
Physics 101: Lecure 03 Kinemaics Today s lecure will coer Texbook Secions 3.1-3.3 (and some Ch. 4) Physics 101: Lecure 3, Pg 1 A Refresher: Deermine he force exered by he hand o suspend he 45 kg mass as
KINEMATICS IN ONE DIMENSION
KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
2.1: What is physics? Ch02: Motion along a straight line. 2.2: Motion. 2.3: Position, Displacement, Distance
Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Chapter 12: Velocity, acceleration, and forces
To Feel a Force Chaper Spring, Chaper : A. Saes of moion For moion on or near he surface of he earh, i is naural o measure moion wih respec o objecs fixed o he earh. The 4 hr. roaion of he earh has a measurable
1. The graph below shows the variation with time t of the acceleration a of an object from t = 0 to t = T. a
Kinemaics Paper 1 1. The graph below shows he ariaion wih ime of he acceleraion a of an objec from = o = T. a T The shaded area under he graph represens change in A. displacemen. B. elociy. C. momenum.
0 for t < 0 1 for t > 0
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
Suggested Practice Problems (set #2) for the Physics Placement Test
Deparmen of Physics College of Ars and Sciences American Universiy of Sharjah (AUS) Fall 014 Suggesed Pracice Problems (se #) for he Physics Placemen Tes This documen conains 5 suggesed problems ha are
PARABOLA. moves such that PM. = e (constant > 0) (eccentricity) then locus of P is called a conic. or conic section.
wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
FM Applications of Integration 1.Centroid of Area
FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
A B C D September 25 Exam I Physics 105. Circle the letter of the single best answer. Each question is worth 1 point
2012 Sepember 25 Eam I Physics 105 Circle he leer of he single bes answer. Each uesion is worh 1 poin Physical Consans: Earh s free-fall acceleraion = g = 9.80 m/s 2 3. (Mark wo leers!) The below graph
Equations of motion for constant acceleration
Lecure 3 Chaper 2 Physics I 01.29.2014 Equaions of moion for consan acceleraion Course websie: hp://faculy.uml.edu/andriy_danylo/teaching/physicsi Lecure Capure: hp://echo360.uml.edu/danylo2013/physics1spring.hml
2.1 Position. 2.2 Rest and Motion.
Moion In ne Dimenion. Poiion. ny objec i ied poin nd hree oberer from hree differen plce re looking for me objec, hen ll hree oberer will he differen oberion bo he poiion of poin nd no one will be wrong.
Physics 201, Lecture 5
Phsics 1 Lecue 5 Tod s Topics n Moion in D (Chp 4.1-4.3): n D Kinemicl Quniies (sec. 4.1) n D Kinemics wih Consn Acceleion (sec. 4.) n D Pojecile (Sec 4.3) n Epeced fom Peiew: n Displcemen eloci cceleion
Page 1 o 13 1. The brighes sar in he nigh sky is α Canis Majoris, also known as Sirius. I lies 8.8 ligh-years away. Express his disance in meers. ( ligh-year is he disance coered by ligh in one year. Ligh
Forms of Energy. Mass = Energy. Page 1. SPH4U: Introduction to Work. Work & Energy. Particle Physics:
SPH4U: Inroducion o ork ork & Energy ork & Energy Discussion Definiion Do Produc ork of consn force ork/kineic energy heore ork of uliple consn forces Coens One of he os iporn conceps in physics Alernive
Of all of the intellectual hurdles which the human mind has confronted and has overcome in the last fifteen hundred years, the one which seems to me
Of all of he inellecual hurdles which he human mind has confroned and has overcome in he las fifeen hundred years, he one which seems o me o have been he mos amazing in characer and he mos supendous in
Course II. Lesson 7 Applications to Physics. 7A Velocity and Acceleration of a Particle
Course II Lesson 7 Applicaions o Physics 7A Velociy and Acceleraion of a Paricle Moion in a Sraigh Line : Velociy O Aerage elociy Moion in he -ais + Δ + Δ 0 0 Δ Δ Insananeous elociy d d Δ Δ Δ 0 lim [ m/s
Motion. Acceleration. Part 2: Constant Acceleration. October Lab Phyiscs. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
Motion ccelertion Prt : Constnt ccelertion ccelertion ccelertion ccelertion is the rte of chnge of elocity. = - o t = Δ Δt ccelertion = = - o t chnge of elocity elpsed time ccelertion is ector, lthough
The order of reaction is defined as the number of atoms or molecules whose concentration change during the chemical reaction.
www.hechemisryguru.com Re Lw Expression Order of Recion The order of recion is defined s he number of oms or molecules whose concenrion chnge during he chemicl recion. Or The ol number of molecules or
K The slowest step in a mechanism has this
CM 6 Generl Chemisry II Nme SLUTINS Exm, Spring 009 Dr. Seel. (0 pins) Selec he nswer frm he clumn n he righ h bes mches ech descripin frm he clumn n he lef. Ech nswer cn be used, ms, nly nce. E G This
IB Physics Kinematics Worksheet
IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
3.6 Derivatives as Rates of Change
3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
In this chapter the model of free motion under gravity is extended to objects projected at an angle. When you have completed it, you should
Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
1.0 Electrical Systems
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
One-Dimensional Kinematics
One-Dimensional Kinemaics One dimensional kinemaics refers o moion along a sraigh line. Een hough we lie in a 3-dimension world, moion can ofen be absraced o a single dimension. We can also describe moion
0 time. 2 Which graph represents the motion of a car that is travelling along a straight road with a uniformly increasing speed?
1 1 The graph relaes o he moion of a falling body. y Which is a correc descripion of he graph? y is disance and air resisance is negligible y is disance and air resisance is no negligible y is speed and
e t dt e t dt = lim e t dt T (1 e T ) = 1
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
x(m) t(sec ) Homework #2. Ph 231 Introductory Physics, Sp-03 Page 1 of 4
Homework #2. Ph 231 Inroducory Physics, Sp-03 Page 1 of 4 2-1A. A person walks 2 miles Eas (E) in 40 minues and hen back 1 mile Wes (W) in 20 minues. Wha are her average speed and average velociy (in ha
Motion along a Straight Line
chaper 2 Moion along a Sraigh Line verage speed and average velociy (Secion 2.2) 1. Velociy versus speed Cone in he ebook: fer Eample 2. Insananeous velociy and insananeous acceleraion (Secions 2.3, 2.4)
AP Calculus BC Chapter 10 Part 1 AP Exam Problems
AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
(3.2.3) r x x x y y y. 2. Average Velocity and Instantaneous Velocity 2 1, (3.2.2)
Lecture 3- Kinemtics in Two Dimensions Durin our preious discussions we he been tlkin bout objects moin lon the striht line. In relity, howeer, it rrely hppens when somethin moes lon the striht pth. For
Two Dimensional Dynamics
Physics 11: Lecure 6 Two Dimensional Dynamics Today s lecure will coer Chaper 4 Saring Wed Sep 15, W-F oice hours will be in 3 Loomis. Exam I M oice hours will coninue in 36 Loomis Physics 11: Lecure 6,
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
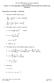.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
Solutions to Problems from Chapter 2
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Collision Detection and Bouncing
Collision Deecion nd Bouncing Collisions re Hndled in Two Prs. Deecing he collision Mike Biley mj@cs.oregonse.edu. Hndling he physics of he collision collision-ouncing.ppx If You re Lucky, You Cn Deec
!!"#"$%&#'()!"#&'(*%)+,&',-)./0)1-*23)
"#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
Think of the Relationship Between Time and Space Again
Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
A. Using Newton s second law in one dimension, F net. , write down the differential equation that governs the motion of the block.
Simple SIMPLE harmonic HARMONIC moion MOTION I. Differenial equaion of moion A block is conneced o a spring, one end of which is aached o a wall. (Neglec he mass of he spring, and assume he surface is
Two Dimensional Dynamics
Physics 11: Lecure 6 Two Dimensional Dynamics Today s lecure will coer Chaper 4 Exam I Physics 11: Lecure 6, Pg 1 Brie Reiew Thus Far Newon s Laws o moion: SF=ma Kinemaics: x = x + + ½ a Dynamics Today
LAB # 2 - Equilibrium (static)
AB # - Equilibrium (saic) Inroducion Isaac Newon's conribuion o physics was o recognize ha despie he seeming compleiy of he Unierse, he moion of is pars is guided by surprisingly simple aws. Newon's inspiraion
4.8 Improper Integrals
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
Physics for Scientists and Engineers I
Physics for Scieniss and Engineers I PHY 48, Secion 4 Dr. Beariz Roldán Cuenya Universiy of Cenral Florida, Physics Deparmen, Orlando, FL Chaper - Inroducion I. General II. Inernaional Sysem of Unis III.