0 for t < 0 1 for t > 0
|
|
|
- Sylvia Holmes
- 6 years ago
- Views:
Transcription
1 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside funcion. The grph of u() is simple. u() Inegrls of u () From clculus we know u () d = u() For exmple: 5 2 u () d = u(5) u( 2) =, nd b u () d = u(b) u(). u () d = u() u() = 0, 5 u () d = u( ) u( 5) = 0. In fc, he inegrl over ny inervl [, b] conining 0 equls nd over for ny inervl no conining 0 i equls 0. Le 0 + be infiniesimlly o he lef of 0 nd 0 + infiniesimlly o he righ of 0. Th is, 0 < 0 < 0 +. We hve more exmples of inegrls of u : u () d =, 0 u () d = 0, 0 u () d =. Generlized funcions nd derivives Of course u() is no coninuous funcion, so in he 8.0 sense is derivive doesn exis. Noneheless we sw h we could mke sense of is inegrls. We cll u () he generlized derivive of u(). You cn do everyhing wih u () you cn do wih n ordinry funcion, bu i cn go nywhere we hve n inpu funcion in 8.0. Le s delve lile deeper ino u (). I s cler u () = 0 if 0. A = 0 he slope is infinie so u (0) =. We define δ() = u ()
2 8.0 Sep nd Del Funcions 2 nd cll i he del funcion or he uni impulse funcion. We hve seen he following properies of δ(). 0 if 0. δ() = if = δ() d = u(), δ() d = δ() d =. 0 We cn grph δ() s n infinie spike he origin. The inegrls show h he re under his grph equls nd i is ll concenred he origin. δ() δ( ) We lso show δ( ) which is jus δ() shifed o he righ. Del funcions re your friend Recll how pinful inegrion could be. In conrs, inegrls wih del funcions re lwys esy nd involve no echniques of inegrion. Suppose we scle δ(): he inegrls re jus scled. 5 5 δ() d =, The inegrl b 5 δ() d = 0, f()δ() d is lso esy. We hve b f() d = This jus mouns o evluing f. 0 δ() d =, f(0) if [, b] conins 0 0 if [, b] does no conin δ() d = 0. Reson: δ() is 0 everywhere excep = 0 so f()δ() is 0 everywhere excep = 0 nd scles he del funcion by f(0) 0. Technicliy: We mus hve f() coninuous = 0. If we shif by we hve, e.g., Prcice wih δ δ()2e 42 d = 2, δ( 2)2e 42 d = 2e 6, δ()2e 42 d = 0, 5 0 δ( 2)2e n2 () d = 2e n2 (8). δ( ) = f(). δ( 2)2e 42 d = 0, δ()2e 42 d = 2, 0 0 δ()2e n2 () d =. δ( 2)2e 42 d = 2e 6 0
3 8.0 Sep nd Del Funcions Tol inpu s he inegrl of inpu re Consider he re equion dx + k f(). To be specific, ssume x is in unis of d kilogrms. The derivive x nd he inpu f() re in unis of kg/ime. So, he ol moun inpu from ime 0 o ime is 4 Exmple : If f() = /4 0 f(u) du. or f() = /8 hen (in eiher cse) he ol inpu over ll ime is kg. Suppose we coninue o shoren he ime inervl in which we inpu ol of kg. In he limiing cse we dump kg in ll once. This is n insnneous jump in he moun x, clled n impulse. In generl, for firs order sysem n impulse is n insnneous jump in he moun. Now consider he second order sysem mx + bx + k F (). Here, F () is force i chnges momemum over ime. The ol momemum dded in he inervl [0, ] is 0 F (u) du. Similr o he firs order cse, n impulse is when we dd ll he momemum once. In his cse, we ge jump in he momemum. For our ypicl fixed mss sysem his is he sme s jump in he momenum. Th is, jump in mx. Pre nd pos-iniil condiions. Becuse n impulse cuses n insnneous jump in some vlue we hve o consider he condiions jus before nd jus fer he impulse. Assume he impulse occures = 0 hen A = 0 : A = 0 + : he condiions re pre-iniil condiions he condiions re pos-iniil condiions Del funcion s uni impulse An impulse o sysem cuses n insnneous jump. To hrmonic oscillor kick cuses jump in momenum. To firs order sysem, e.g. dumping lemmings in wildlife refuge, n impulse is sudden ddiion of lod of lemmings. A uni impulse cuses uni chnge. I is modeled by he δ funcion: For exmple, consider he equion x + k δ() wih inpu δ.. The ol inpu (inegrl of δ()) is. 2. All he inpu occurs = 0. Exmple 2: Solve x + k δ; res IC. nswer: This is firs order exponenil decy sysem. The uni impulse he = 0 cuses n insnneous jump of in he vlue of x. The pre-iniil condiion is x(0 ) = 0, so he pos-ic is x(0 + ) =. Afer h he sysem is homogeneous. So, 8
4 8.0 Sep nd Del Funcions 4 for > 0 we hve x + k 0, x(0 + ) =. The soluion for > 0 is x() = e k (check he vlue 0 + ). The full soluion is 0 for < 0 e k for > 0. x Response from res o inpu = δ Exmple : Solve mx + bx + k δ; res IC. nswer: Res IC mens h x() = 0 for < 0. So our pre-ic re x(0 ) = x (0 ) = 0. The uni impulse cuses uni jump in momenum so he pos-ic re x(0 + ) = 0, mx(0 + ) = x(0 + ) = /m. For > 0 we hve he homogeneous equion mx + bx + k 0. We won grind hrough he symbolic lgebr. Insed le s work our sndrd exmple Exmple 4: Solve x + 8x + 7 δ; res IC. nswer: Here m = so for > 0 we hve o solve x + 8x + 7 0, x(0 + ) = 0, x (zp) =. We know c e + c 2 e 7. The pos-ic deermine he coefficiens nd we ge 0 for < 0 6 e 6 e 7 for > 0 δ s limi of owers We define uni box of widh h funcion by u h () = h for 0 < < h 0 for h < (See grphs below.) The ol re under he grph of u h () is lwys. So, if we use u h () s inpu he ol inpu is. As h 0 he grph ges ller nd hinner nd looks more like spike. Also s h 0 he inpu is pplied over shorer nd shorer ime nd cs more like uni impulse. Th is, δ = lim h 0 u h 2 2
5 8.0 Sep nd Del Funcions 5 The funcions u, u /2, u / limiing o δ(). Exmple 5: Le s compre uni box (u h ()) inpu wih uni impulse (δ()) inpu: Solve x + k u h wih res IC. (physicl resoning:) This models rdiocive dumping. u h = re mer dded over ime ol moun dded = h 0 u h =. The grph shows he inpu u h s blck box. The response is grphed in red. If here were no decy we would see x increse linerly from 0 o over he inervl [0, h]. Since here is decy, he end of he inervl we hve x <. Afer ime = h here is no more inpu nd he response shows exponenil decy. As h 0 he inpu becomes he uni impulse δ(). The ol moun dded = 0 δ() d = nd i is dumped in ll once. The response curve shows jump of = 0. I is wrong o pu he re nd moun on he sme xes since hey hve differen unis. A he very les we should use lef vericl xis wih unis of x nd righ vericl xis wih unis of x. / 2 /2 / Inpu nd response o sequence of box funcions limiing o δ(). For compleeness we give he exc soluion o he IVP x + k u h, res IC. ( hk e k ) hk (ekh )e k for 0 < < h for h < Jus s expeced, s h 0 he inpu becomes δ nd he oupu becomes e k e kh (i.e. lim = ) h 0 hk Exmple 6: Solve x + δ() wih res IC. nswer: Pre-inil condiions re 0. The pos-iniil condiions ( = 0 + ) re x(0 + ) = 0, x (0 + ) =. For > 0 he DE becomes x + 0. This DE is esy o solve: For > 0 : x() = c cos() + c 2 sin(). We find c nd c 2 using he pos-iniil condiions: c = 0, c 2 =. The complee soluion is 0 for < 0 x() = sin() for > 0.
6 8.0 Sep nd Del Funcions 6 Physicl explnion: = 0 n impulse kicks he simple hrmonic oscillor ino moion. Afer h inpu is 0 nd he sysem is in simple hrmonic moion. The jump in momenum = corner in grph 0. x Exmple 7: Solve x + δ( ) wih res IC. The physicl explnion nd grph re he sme s in he previous exmple shifed by. x Exmple 8: (Resonnce) Solve x + f; res IC. Where f = blow every 2π seconds, mgniude 2 in he posiive direcion. nswer: We hve f = 2δ() + 2δ( 2π) + 2δ( 4π) +... Using he previous exmple nd superposiion we ge 2 sin for 0 < < 2π 4 sin for 2π < < 4π 6 sin for 4π < < 6π The deils showing his re no hrd. Keep in mind h he response o δ( 2nπ) is 0 before = 2nπ nd 2 sin( 2nπ) = 2 sin() fer = 2nπ. This mens h every 2π seconds we dd noher copy of 2 sin() o he oupu. This is resonnce he blows come he nurl frequence (every 2π seconds) of he sysem. Derivive of squre wve The grphs below re of funcion sq() (clled squre wve) nd is derivive. sq() lernes every π seconds beween ±. The derivive sq () is clerly 0 everywhere excep he jumps. A jump of +2 gives (generlized) derivive of 2δ nd jump of 2 gives (generlized) derivive of 2δ. Thus we hve sq () = δ( + 2π) 2δ( + π) + 2δ() 2δ( π) + 2δ( 2π) 2δ( π) +...
7 8.0 Sep nd Del Funcions π 2π π π 2π π 4π Grph of sq() = squre wve π π π π 2π 2π 4π Grph of sq () = impulse rin End opic sep nd del noes
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
F (u) du. or f(t) = t
 8.3 Topic 9: Impulses and dela funcions. Auor: Jeremy Orloff Reading: EP 4.6 SN CG.3-4 pp.2-5. Warmup discussion abou inpu Consider e rae equaion d + k = f(). To be specific, assume is in unis of d kilograms.
8.3 Topic 9: Impulses and dela funcions. Auor: Jeremy Orloff Reading: EP 4.6 SN CG.3-4 pp.2-5. Warmup discussion abou inpu Consider e rae equaion d + k = f(). To be specific, assume is in unis of d kilograms.
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
Solutions to Problems from Chapter 2
 Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
( ) ( ) ( ) ( ) ( ) ( y )
 8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
graph of unit step function t
 .5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
.5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
Physics 2A HW #3 Solutions
 Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples.
 Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Mathematics 805 Final Examination Answers
 . 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
. 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
RESPONSE UNDER A GENERAL PERIODIC FORCE. When the external force F(t) is periodic with periodτ = 2π
 RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q). INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg) INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
Chapter 2. Motion along a straight line. 9/9/2015 Physics 218
 Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
MATH 124 AND 125 FINAL EXAM REVIEW PACKET (Revised spring 2008)
 MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
Average & instantaneous velocity and acceleration Motion with constant acceleration
 Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
14. The fundamental theorem of the calculus
 4. The funmenl heorem of he clculus V 20 00 80 60 40 20 0 0 0.2 0.4 0.6 0.8 v 400 200 0 0 0.2 0.5 0.8 200 400 Figure : () Venriculr volume for subjecs wih cpciies C = 24 ml, C = 20 ml, C = 2 ml n (b) he
4. The funmenl heorem of he clculus V 20 00 80 60 40 20 0 0 0.2 0.4 0.6 0.8 v 400 200 0 0 0.2 0.5 0.8 200 400 Figure : () Venriculr volume for subjecs wih cpciies C = 24 ml, C = 20 ml, C = 2 ml n (b) he
A LOG IS AN EXPONENT.
 Ojeives: n nlze nd inerpre he ehvior of rihmi funions, inluding end ehvior nd smpoes. n solve rihmi equions nlill nd grphill. n grph rihmi funions. n deermine he domin nd rnge of rihmi funions. n deermine
Ojeives: n nlze nd inerpre he ehvior of rihmi funions, inluding end ehvior nd smpoes. n solve rihmi equions nlill nd grphill. n grph rihmi funions. n deermine he domin nd rnge of rihmi funions. n deermine
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
How to Prove the Riemann Hypothesis Author: Fayez Fok Al Adeh.
 How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
How o Prove he Riemnn Hohesis Auhor: Fez Fok Al Adeh. Presiden of he Srin Cosmologicl Socie P.O.Bo,387,Dmscus,Sri Tels:963--77679,735 Emil:hf@scs-ne.org Commens: 3 ges Subj-Clss: Funcionl nlsis, comle
Properties of Logarithms. Solving Exponential and Logarithmic Equations. Properties of Logarithms. Properties of Logarithms. ( x)
 Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
EECE 301 Signals & Systems Prof. Mark Fowler
 EECE 3 Signals & Sysems Prof. Mark Fowler Noe Se # Wha are Coninuous-Time Signals??? /6 Coninuous-Time Signal Coninuous Time (C-T) Signal: A C-T signal is defined on he coninuum of ime values. Tha is:
EECE 3 Signals & Sysems Prof. Mark Fowler Noe Se # Wha are Coninuous-Time Signals??? /6 Coninuous-Time Signal Coninuous Time (C-T) Signal: A C-T signal is defined on he coninuum of ime values. Tha is:
can be viewed as a generalized product, and one for which the product of f and g. That is, does
 Boyce/DiPrim 9 h e, Ch 6.6: The Convoluion Inegrl Elemenry Differenil Equion n Bounry Vlue Problem, 9 h eiion, by Willim E. Boyce n Richr C. DiPrim, 9 by John Wiley & Son, Inc. Someime i i poible o wrie
Boyce/DiPrim 9 h e, Ch 6.6: The Convoluion Inegrl Elemenry Differenil Equion n Bounry Vlue Problem, 9 h eiion, by Willim E. Boyce n Richr C. DiPrim, 9 by John Wiley & Son, Inc. Someime i i poible o wrie
Chapter Direct Method of Interpolation
 Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
( ) ( ) if t = t. It must satisfy the identity. So, bulkiness of the unit impulse (hyper)function is equal to 1. The defining characteristic is
 UNIT IMPULSE RESPONSE, UNIT STEP RESPONSE, STABILITY. Uni impulse funcion (Dirac dela funcion, dela funcion) rigorously defined is no sricly a funcion, bu disribuion (or measure), precise reamen requires
UNIT IMPULSE RESPONSE, UNIT STEP RESPONSE, STABILITY. Uni impulse funcion (Dirac dela funcion, dela funcion) rigorously defined is no sricly a funcion, bu disribuion (or measure), precise reamen requires
dt = C exp (3 ln t 4 ). t 4 W = C exp ( ln(4 t) 3) = C(4 t) 3.
 Mah Rahman Exam Review Soluions () Consider he IVP: ( 4)y 3y + 4y = ; y(3) = 0, y (3) =. (a) Please deermine he longes inerval for which he IVP is guaraneed o have a unique soluion. Soluion: The disconinuiies
Mah Rahman Exam Review Soluions () Consider he IVP: ( 4)y 3y + 4y = ; y(3) = 0, y (3) =. (a) Please deermine he longes inerval for which he IVP is guaraneed o have a unique soluion. Soluion: The disconinuiies
Laplace transfom: t-translation rule , Haynes Miller and Jeremy Orloff
 Laplace ransfom: -ranslaion rule 8.03, Haynes Miller and Jeremy Orloff Inroducory example Consider he sysem ẋ + 3x = f(, where f is he inpu and x he response. We know is uni impulse response is 0 for
Laplace ransfom: -ranslaion rule 8.03, Haynes Miller and Jeremy Orloff Inroducory example Consider he sysem ẋ + 3x = f(, where f is he inpu and x he response. We know is uni impulse response is 0 for
The order of reaction is defined as the number of atoms or molecules whose concentration change during the chemical reaction.
 www.hechemisryguru.com Re Lw Expression Order of Recion The order of recion is defined s he number of oms or molecules whose concenrion chnge during he chemicl recion. Or The ol number of molecules or
www.hechemisryguru.com Re Lw Expression Order of Recion The order of recion is defined s he number of oms or molecules whose concenrion chnge during he chemicl recion. Or The ol number of molecules or
How to prove the Riemann Hypothesis
 Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Scholrs Journl of Phsics, Mhemics nd Sisics Sch. J. Phs. Mh. S. 5; (B:5-6 Scholrs Acdemic nd Scienific Publishers (SAS Publishers (An Inernionl Publisher for Acdemic nd Scienific Resources *Corresonding
Honours Introductory Maths Course 2011 Integration, Differential and Difference Equations
 Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
IX.1.1 The Laplace Transform Definition 700. IX.1.2 Properties 701. IX.1.3 Examples 702. IX.1.4 Solution of IVP for ODEs 704
 Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chapter 2: Evaluative Feedback
 Chper 2: Evluive Feedbck Evluing cions vs. insrucing by giving correc cions Pure evluive feedbck depends olly on he cion ken. Pure insrucive feedbck depends no ll on he cion ken. Supervised lerning is
Chper 2: Evluive Feedbck Evluing cions vs. insrucing by giving correc cions Pure evluive feedbck depends olly on he cion ken. Pure insrucive feedbck depends no ll on he cion ken. Supervised lerning is
LAPLACE TRANSFORMS. 1. Basic transforms
 LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
LAPLACE TRANSFORMS. Bic rnform In hi coure, Lplce Trnform will be inroduced nd heir properie exmined; ble of common rnform will be buil up; nd rnform will be ued o olve ome dierenil equion by rnforming
Section 3.5 Nonhomogeneous Equations; Method of Undetermined Coefficients
 Secion 3.5 Nonhomogeneous Equaions; Mehod of Undeermined Coefficiens Key Terms/Ideas: Linear Differenial operaor Nonlinear operaor Second order homogeneous DE Second order nonhomogeneous DE Soluion o homogeneous
Secion 3.5 Nonhomogeneous Equaions; Mehod of Undeermined Coefficiens Key Terms/Ideas: Linear Differenial operaor Nonlinear operaor Second order homogeneous DE Second order nonhomogeneous DE Soluion o homogeneous
IX.1.1 The Laplace Transform Definition 700. IX.1.2 Properties 701. IX.1.3 Examples 702. IX.1.4 Solution of IVP for ODEs 704
 Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 6, 8 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 6, 8 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Lecture 3: 1-D Kinematics. This Week s Announcements: Class Webpage: visit regularly
 Lecure 3: 1-D Kinemics This Week s Announcemens: Clss Webpge: hp://kesrel.nm.edu/~dmeier/phys121/phys121.hml isi regulrly Our TA is Lorrine Bowmn Week 2 Reding: Chper 2 - Gincoli Week 2 Assignmens: Due:
Lecure 3: 1-D Kinemics This Week s Announcemens: Clss Webpge: hp://kesrel.nm.edu/~dmeier/phys121/phys121.hml isi regulrly Our TA is Lorrine Bowmn Week 2 Reding: Chper 2 - Gincoli Week 2 Assignmens: Due:
Question Details Int Vocab 1 [ ] Question Details Int Vocab 2 [ ]
![Question Details Int Vocab 1 [ ] Question Details Int Vocab 2 [ ] Question Details Int Vocab 1 [ ] Question Details Int Vocab 2 [ ]](/thumbs/92/109283538.jpg) /3/5 Assignmen Previewer 3 Bsic: Definie Inegrls (67795) Due: Wed Apr 5 5 9: AM MDT Quesion 3 5 6 7 8 9 3 5 6 7 8 9 3 5 6 Insrucions Red ody's Noes nd Lerning Gols. Quesion Deils In Vocb [37897] The chnge
/3/5 Assignmen Previewer 3 Bsic: Definie Inegrls (67795) Due: Wed Apr 5 5 9: AM MDT Quesion 3 5 6 7 8 9 3 5 6 7 8 9 3 5 6 Insrucions Red ody's Noes nd Lerning Gols. Quesion Deils In Vocb [37897] The chnge
MAT 266 Calculus for Engineers II Notes on Chapter 6 Professor: John Quigg Semester: spring 2017
 MAT 66 Clculus for Engineers II Noes on Chper 6 Professor: John Quigg Semeser: spring 7 Secion 6.: Inegrion by prs The Produc Rule is d d f()g() = f()g () + f ()g() Tking indefinie inegrls gives [f()g
MAT 66 Clculus for Engineers II Noes on Chper 6 Professor: John Quigg Semeser: spring 7 Secion 6.: Inegrion by prs The Produc Rule is d d f()g() = f()g () + f ()g() Tking indefinie inegrls gives [f()g
Collision Detection and Bouncing
 Collision Deecion nd Bouncing Collisions re Hndled in Two Prs. Deecing he collision Mike Biley mj@cs.oregonse.edu. Hndling he physics of he collision collision-ouncing.ppx If You re Lucky, You Cn Deec
Collision Deecion nd Bouncing Collisions re Hndled in Two Prs. Deecing he collision Mike Biley mj@cs.oregonse.edu. Hndling he physics of he collision collision-ouncing.ppx If You re Lucky, You Cn Deec
Solutions to Assignment 1
 MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
FM Applications of Integration 1.Centroid of Area
 FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
A 1.3 m 2.5 m 2.8 m. x = m m = 8400 m. y = 4900 m 3200 m = 1700 m
 PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
Some Inequalities variations on a common theme Lecture I, UL 2007
 Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
S Radio transmission and network access Exercise 1-2
 S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
 PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
Think of the Relationship Between Time and Space Again
 Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
SOME USEFUL MATHEMATICS
 SOME USEFU MAHEMAICS SOME USEFU MAHEMAICS I is esy o mesure n preic he behvior of n elecricl circui h conins only c volges n currens. However, mos useful elecricl signls h crry informion vry wih ime. Since
SOME USEFU MAHEMAICS SOME USEFU MAHEMAICS I is esy o mesure n preic he behvior of n elecricl circui h conins only c volges n currens. However, mos useful elecricl signls h crry informion vry wih ime. Since
Guest Lectures for Dr. MacFarlane s EE3350 Part Deux
 Gues Lecures for Dr. MacFarlane s EE3350 Par Deux Michael Plane Mon., 08-30-2010 Wrie name in corner. Poin ou his is a review, so I will go faser. Remind hem o go lisen o online lecure abou geing an A
Gues Lecures for Dr. MacFarlane s EE3350 Par Deux Michael Plane Mon., 08-30-2010 Wrie name in corner. Poin ou his is a review, so I will go faser. Remind hem o go lisen o online lecure abou geing an A
EECE 301 Signals & Systems Prof. Mark Fowler
 EECE 3 Signals & Sysems Prof. Mark Fowler Noe Se #2 Wha are Coninuous-Time Signals??? Reading Assignmen: Secion. of Kamen and Heck /22 Course Flow Diagram The arrows here show concepual flow beween ideas.
EECE 3 Signals & Sysems Prof. Mark Fowler Noe Se #2 Wha are Coninuous-Time Signals??? Reading Assignmen: Secion. of Kamen and Heck /22 Course Flow Diagram The arrows here show concepual flow beween ideas.
3 Motion with constant acceleration: Linear and projectile motion
 3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
Chapter 2. First Order Scalar Equations
 Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
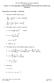 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
Green s Functions and Comparison Theorems for Differential Equations on Measure Chains
 Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
Green s Funcions nd Comprison Theorems for Differenil Equions on Mesure Chins Lynn Erbe nd Alln Peerson Deprmen of Mhemics nd Sisics, Universiy of Nebrsk-Lincoln Lincoln,NE 68588-0323 lerbe@@mh.unl.edu
IX.2 THE FOURIER TRANSFORM
 Chper IX The Inegrl Trnsform Mehods IX. The Fourier Trnsform November, 7 7 IX. THE FOURIER TRANSFORM IX.. The Fourier Trnsform Definiion 7 IX.. Properies 73 IX..3 Emples 74 IX..4 Soluion of ODE 76 IX..5
Chper IX The Inegrl Trnsform Mehods IX. The Fourier Trnsform November, 7 7 IX. THE FOURIER TRANSFORM IX.. The Fourier Trnsform Definiion 7 IX.. Properies 73 IX..3 Emples 74 IX..4 Soluion of ODE 76 IX..5
Overview of Calculus I
 Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
ES.1803 Topic 22 Notes Jeremy Orloff
 ES.83 Topic Noes Jeremy Orloff Fourier series inroducion: coninued. Goals. Be able o compue he Fourier coefficiens of even or odd periodic funcion using he simplified formulas.. Be able o wrie and graph
ES.83 Topic Noes Jeremy Orloff Fourier series inroducion: coninued. Goals. Be able o compue he Fourier coefficiens of even or odd periodic funcion using he simplified formulas.. Be able o wrie and graph
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
a < a+ x < a+2 x < < a+n x = b, n A i n f(x i ) x. i=1 i=1
 Mth 33 Volume Stewrt 5.2 Geometry of integrls. In this section, we will lern how to compute volumes using integrls defined by slice nlysis. First, we recll from Clculus I how to compute res. Given the
Mth 33 Volume Stewrt 5.2 Geometry of integrls. In this section, we will lern how to compute volumes using integrls defined by slice nlysis. First, we recll from Clculus I how to compute res. Given the
ECE Microwave Engineering
 EE 537-635 Microwve Engineering Adped from noes y Prof. Jeffery T. Willims Fll 8 Prof. Dvid R. Jcson Dep. of EE Noes Wveguiding Srucures Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model
EE 537-635 Microwve Engineering Adped from noes y Prof. Jeffery T. Willims Fll 8 Prof. Dvid R. Jcson Dep. of EE Noes Wveguiding Srucures Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model
Chapter 7: Solving Trig Equations
 Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
4/9/2012. Signals and Systems KX5BQY EE235. Today s menu. System properties
 Signals and Sysems hp://www.youube.com/v/iv6fo KX5BQY EE35 oday s menu Good weeend? Sysem properies iy Superposiion! Sysem properies iy: A Sysem is if i mees he following wo crieria: If { x( )} y( ) and
Signals and Sysems hp://www.youube.com/v/iv6fo KX5BQY EE35 oday s menu Good weeend? Sysem properies iy Superposiion! Sysem properies iy: A Sysem is if i mees he following wo crieria: If { x( )} y( ) and
f(x) dx with An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples dx x x 2
 Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
Convex Sets and Functions
 B Convex Sets nd Functions Definition B1 Let L, +, ) be rel liner spce nd let C be subset of L The set C is convex if, for ll x,y C nd ll [, 1], we hve 1 )x+y C In other words, every point on the line
B Convex Sets nd Functions Definition B1 Let L, +, ) be rel liner spce nd let C be subset of L The set C is convex if, for ll x,y C nd ll [, 1], we hve 1 )x+y C In other words, every point on the line
Integral Transform. Definitions. Function Space. Linear Mapping. Integral Transform
 Inegrl Trnsform Definiions Funcion Spce funcion spce A funcion spce is liner spce of funcions defined on he sme domins & rnges. Liner Mpping liner mpping Le VF, WF e liner spces over he field F. A mpping
Inegrl Trnsform Definiions Funcion Spce funcion spce A funcion spce is liner spce of funcions defined on he sme domins & rnges. Liner Mpping liner mpping Le VF, WF e liner spces over he field F. A mpping
Magnetostatics Bar Magnet. Magnetostatics Oersted s Experiment
 Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
PARABOLA. moves such that PM. = e (constant > 0) (eccentricity) then locus of P is called a conic. or conic section.
 wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
Linear Time-invariant systems, Convolution, and Cross-correlation
 Linear Time-invarian sysems, Convoluion, and Cross-correlaion (1) Linear Time-invarian (LTI) sysem A sysem akes in an inpu funcion and reurns an oupu funcion. x() T y() Inpu Sysem Oupu y() = T[x()] An
Linear Time-invarian sysems, Convoluion, and Cross-correlaion (1) Linear Time-invarian (LTI) sysem A sysem akes in an inpu funcion and reurns an oupu funcion. x() T y() Inpu Sysem Oupu y() = T[x()] An
Quadratic Forms. Quadratic Forms
 Qudrtic Forms Recll the Simon & Blume excerpt from n erlier lecture which sid tht the min tsk of clculus is to pproximte nonliner functions with liner functions. It s ctully more ccurte to sy tht we pproximte
Qudrtic Forms Recll the Simon & Blume excerpt from n erlier lecture which sid tht the min tsk of clculus is to pproximte nonliner functions with liner functions. It s ctully more ccurte to sy tht we pproximte
Probability, Estimators, and Stationarity
 Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE BOUNDARY-VALUE PROBLEM
 Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
d 1 = c 1 b 2 - b 1 c 2 d 2 = c 1 b 3 - b 1 c 3
 and d = c b - b c c d = c b - b c c This process is coninued unil he nh row has been compleed. The complee array of coefficiens is riangular. Noe ha in developing he array an enire row may be divided or
and d = c b - b c c d = c b - b c c This process is coninued unil he nh row has been compleed. The complee array of coefficiens is riangular. Noe ha in developing he array an enire row may be divided or
Available Online :
 fo/u fopjr Hh# u] ugh vjehs de] foifr ns[ NsMs rqjr e/;e eu dj ';ea iq#" flg ldyi dj] lgrs foifr vusd] ^cu^ u NsMs /;s; ds] j?qcj j[s VsdAA jfpr% euo /ez iz.sr ln~xq# Jh j.nsmnlh egj STUDY PACKAGE Subjec
fo/u fopjr Hh# u] ugh vjehs de] foifr ns[ NsMs rqjr e/;e eu dj ';ea iq#" flg ldyi dj] lgrs foifr vusd] ^cu^ u NsMs /;s; ds] j?qcj j[s VsdAA jfpr% euo /ez iz.sr ln~xq# Jh j.nsmnlh egj STUDY PACKAGE Subjec
MORE FUNCTION GRAPHING; OPTIMIZATION. (Last edited October 28, 2013 at 11:09pm.)
 MORE FUNCTION GRAPHING; OPTIMIZATION FRI, OCT 25, 203 (Lst edited October 28, 203 t :09pm.) Exercise. Let n be n rbitrry positive integer. Give n exmple of function with exctly n verticl symptotes. Give
MORE FUNCTION GRAPHING; OPTIMIZATION FRI, OCT 25, 203 (Lst edited October 28, 203 t :09pm.) Exercise. Let n be n rbitrry positive integer. Give n exmple of function with exctly n verticl symptotes. Give
a n = 1 58 a n+1 1 = 57a n + 1 a n = 56(a n 1) 57 so 0 a n+1 1, and the required result is true, by induction.
 MAS221(216-17) Exm Solutions 1. (i) A is () bounded bove if there exists K R so tht K for ll A ; (b) it is bounded below if there exists L R so tht L for ll A. e.g. the set { n; n N} is bounded bove (by
MAS221(216-17) Exm Solutions 1. (i) A is () bounded bove if there exists K R so tht K for ll A ; (b) it is bounded below if there exists L R so tht L for ll A. e.g. the set { n; n N} is bounded bove (by
38 Riemann sums and existence of the definite integral.
 38 Riemnn sums nd existence of the definite integrl. In the clcultion of the re of the region X bounded by the grph of g(x) = x 2, the x-xis nd 0 x b, two sums ppered: ( n (k 1) 2) b 3 n 3 re(x) ( n These
38 Riemnn sums nd existence of the definite integrl. In the clcultion of the re of the region X bounded by the grph of g(x) = x 2, the x-xis nd 0 x b, two sums ppered: ( n (k 1) 2) b 3 n 3 re(x) ( n These
The area under the graph of f and above the x-axis between a and b is denoted by. f(x) dx. π O
 1 Section 5. The Definite Integrl Suppose tht function f is continuous nd positive over n intervl [, ]. y = f(x) x The re under the grph of f nd ove the x-xis etween nd is denoted y f(x) dx nd clled the
1 Section 5. The Definite Integrl Suppose tht function f is continuous nd positive over n intervl [, ]. y = f(x) x The re under the grph of f nd ove the x-xis etween nd is denoted y f(x) dx nd clled the
Math Week 14 April 16-20: sections first order systems of linear differential equations; 7.4 mass-spring systems.
 Mah 2250-004 Week 4 April 6-20 secions 7.-7.3 firs order sysems of linear differenial equaions; 7.4 mass-spring sysems. Mon Apr 6 7.-7.2 Sysems of differenial equaions (7.), and he vecor Calculus we need
Mah 2250-004 Week 4 April 6-20 secions 7.-7.3 firs order sysems of linear differenial equaions; 7.4 mass-spring sysems. Mon Apr 6 7.-7.2 Sysems of differenial equaions (7.), and he vecor Calculus we need
Integrals - Motivation
 Integrls - Motivtion When we looked t function s rte of chnge If f(x) is liner, the nswer is esy slope If f(x) is non-liner, we hd to work hrd limits derivtive A relted question is the re under f(x) (but
Integrls - Motivtion When we looked t function s rte of chnge If f(x) is liner, the nswer is esy slope If f(x) is non-liner, we hd to work hrd limits derivtive A relted question is the re under f(x) (but
STEP FUNCTIONS, DELTA FUNCTIONS, AND THE VARIATION OF PARAMETERS FORMULA. 0 if t < 0, 1 if t > 0.
 STEP FUNCTIONS, DELTA FUNCTIONS, AND THE VARIATION OF PARAMETERS FORMULA STEPHEN SCHECTER. The unit step function nd piecewise continuous functions The Heviside unit step function u(t) is given by if t
STEP FUNCTIONS, DELTA FUNCTIONS, AND THE VARIATION OF PARAMETERS FORMULA STEPHEN SCHECTER. The unit step function nd piecewise continuous functions The Heviside unit step function u(t) is given by if t
The Fundamental Theorem of Calculus
 The Fundmentl Theorem of Clculus Professor Richrd Blecksmith richrd@mth.niu.edu Dept. of Mthemticl Sciences Northern Illinois University http://mth.niu.edu/ richrd/mth229. The Definite Integrl We define
The Fundmentl Theorem of Clculus Professor Richrd Blecksmith richrd@mth.niu.edu Dept. of Mthemticl Sciences Northern Illinois University http://mth.niu.edu/ richrd/mth229. The Definite Integrl We define
Chapter 1: Fundamentals
 Chpter 1: Fundmentls 1.1 Rel Numbers Types of Rel Numbers: Nturl Numbers: {1, 2, 3,...}; These re the counting numbers. Integers: {... 3, 2, 1, 0, 1, 2, 3,...}; These re ll the nturl numbers, their negtives,
Chpter 1: Fundmentls 1.1 Rel Numbers Types of Rel Numbers: Nturl Numbers: {1, 2, 3,...}; These re the counting numbers. Integers: {... 3, 2, 1, 0, 1, 2, 3,...}; These re ll the nturl numbers, their negtives,
Math 2142 Exam 1 Review Problems. x 2 + f (0) 3! for the 3rd Taylor polynomial at x = 0. To calculate the various quantities:
 Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 9: The High Beta Tokamak
 .65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
.65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Linear Response Theory: The connection between QFT and experiments
 Phys540.nb 39 3 Linear Response Theory: The connecion beween QFT and experimens 3.1. Basic conceps and ideas Q: How do we measure he conduciviy of a meal? A: we firs inroduce a weak elecric field E, and
Phys540.nb 39 3 Linear Response Theory: The connecion beween QFT and experimens 3.1. Basic conceps and ideas Q: How do we measure he conduciviy of a meal? A: we firs inroduce a weak elecric field E, and
1 jordan.mcd Eigenvalue-eigenvector approach to solving first order ODEs. -- Jordan normal (canonical) form. Instructor: Nam Sun Wang
 jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
Review of Calculus, cont d
 Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER /2019
 ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS MATH00030 SEMESTER 208/209 DR. ANTHONY BROWN 7.. Introduction to Integrtion. 7. Integrl Clculus As ws the cse with the chpter on differentil
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS MATH00030 SEMESTER 208/209 DR. ANTHONY BROWN 7.. Introduction to Integrtion. 7. Integrl Clculus As ws the cse with the chpter on differentil
Convergence of Fourier Series and Fejer s Theorem. Lee Ricketson
 Convergence of Fourier Series nd Fejer s Theorem Lee Ricketson My, 006 Abstrct This pper will ddress the Fourier Series of functions with rbitrry period. We will derive forms of the Dirichlet nd Fejer
Convergence of Fourier Series nd Fejer s Theorem Lee Ricketson My, 006 Abstrct This pper will ddress the Fourier Series of functions with rbitrry period. We will derive forms of the Dirichlet nd Fejer
Topic 1 Notes Jeremy Orloff
 Topic 1 Notes Jerem Orloff 1 Introduction to differentil equtions 1.1 Gols 1. Know the definition of differentil eqution. 2. Know our first nd second most importnt equtions nd their solutions. 3. Be ble
Topic 1 Notes Jerem Orloff 1 Introduction to differentil equtions 1.1 Gols 1. Know the definition of differentil eqution. 2. Know our first nd second most importnt equtions nd their solutions. 3. Be ble
