M r. d 2. R t a M. Structural Mechanics Section. Exam CT5141 Theory of Elasticity Friday 31 October 2003, 9:00 12:00 hours. Problem 1 (3 points)
|
|
|
- Darlene Ramsey
- 5 years ago
- Views:
Transcription
1 Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00 hours Prolem ( poins) Consider curved em of recngulr cross-secion (Figure ). The em is loded y momen. The norml sress σ θθ in cross-secion cn e derived s. where σ θθ Eε i fθθ, r r f θθ ln ln l r + n The momen in he cross-secion cn e derived s r R + R Figure. Curved em.0 d where E i εc, C ( ) + ln Derive he formul for he elsic secion modulus W (Duch: weersndsmomen). σ θθmx W W d d 6 d R Figure. Funcions W nd Derive he formul for he momen of ineri (Duch: rgheidsmomen). E κ (Noe h curvure κ is he chnge of roion of he cross-secions per rch lengh.). c The derived formuls W nd hve een ploed in Figure. Boh W nd cn e pproximed y he formuls for srigh ems. s his pproximion sfe or unsfe? Consider for his oh he serviceiliy limi se nd he ulime limi se of he srucurl componen. d The hypohesis of Bernoulli ses h plne cross-secions remin plne during ending. s his hypohesis correc for curved ems?
2 Prolem ( poins) Trdiionl imer floors consis of ems nd floorords (Duch: vloerdelen). n his prolem he deflecion of such floor is clculed. One of he ems crries line lod q [kn/m] (Figure ). The floorords rnsfer pr of his lod o he djcen ems. The conriuion of oher ems is negleced, so only hree ems re included in he srucurl model. The Young s modulus is E nd he momen of ineri of he ems is. The ords hve hickness. w q w w w floorord y em Figure. Cross-secion of imer floor We ssume deflecion funcion for he middle em, w deflecion funcion w for oh djcen ems nd deflecion funcion w for he ords. x x w wˆ + C + C l l x x w wˆ + C + C l l y y w w+ C5 + C 6 Figure. Srucurl model of imer floor Wh is he inerpreion of vriles w nd w ˆ. Formule he kinemic oundry ˆ condiions of he deflecion funcions. Which of hese oundry condiions re lredy sisfied? Show h he oundry condiions cn e used o solve he following coefficiens. C wˆ C C wˆ C C5 w w C6 Kinemic Equions d w d w κ κ dx dx d w κ dy Formule he poenil energy of he floor. Wrie i such h i cn e evlued y mhemicl compuer progrm. Consiuive Equions E κ E κ m E κ
3 c The resul of he compuer evluion is lrge funcion of he following vriles. Epo Epo(, l,, E,, q, wˆ, wˆ, C, C, C6 ) Wih respec o which vriles needs he poenil energy e miniml? How re he equions derived from which he deflecion cn e solved? d The compuer solves he deflecion s where 5 ql β+ 75β wˆ 8 E β+ 5β l β 000 The formul cn e simplified wih very lile loss of ccurcy o 5 ql 0 + 8β wˆ 8 E 0 + 8β Cn his resul e improved y using eer pproximions of he deflecion funcions? Prolem ( poins) A concree offshore plform hs cenrl shf wih five-cell cross-secion (Figure 5). The hickness of ech wll is, which is much smller hn he rdius R of he cells. The memrne nlogy will e used o deermine he orsion properies. Due o roion symmery jus wo cells need o e considered in he clculions. A nd A re he crosssecion res of hese cells. O nd O re he circumferences of hese cells. The following relions pply A A A R A A A A πr A ( π) R O πr O πr. Figure 5. Cross-secion of offshore plform shf Formule he equions from which he displcemens w nd w of he floing ples cn e solved. You do no need o solve hese equions.
4 The soluion of he equions is pr π+ w S 6π p R 8 w S π. Clcule he orsion siffness of he cross-secion. c Clcule he sher sresses in he wlls. ke simple wing of he cross-secion nd w he sher sresses in he correc direcions. Prolem ( poins) Consider n xil symmericl ple loded in ending. Derive he following equilirium equion. d ( r m rr ) dm + θθ rp
5 Exm CT5, Ocoer 00 Answers o Prolem Secion odulus n he lecure ook f θθ hs een ploed. From his we oserve h he exreme vlue occurs r. f θθ mx ln ln l + n ln 0 ln + ln 0+ ln ln 0 ln ln ( ) + ln Eε ic C W σ θθmx Eε ifθθmx fθθmx ln ( ) + ln W ln omen of neri Curvure is chnge of roion over rch lengh. ϕi ε κ i ( + ) ϕ + Eε ic C( + ) ( ) + ln ( E i + κ ε E + ( )( ) + ln ) c Approximion n he serviceiliy limi se he deformion is imporn. Since he pproximed is oo lrge he displcemens will e oo smll. Therefore he pproximion of is unsfe. n he ulime limi se he sresses re imporn. Since he pproximed W is oo lrge he clculed sresses will e oo smll. Therefore he pproximion of W is unsfe. 5
6 d Hypohesis The iniil srin ε i produces plne roions of he cross-secions. Therefore, he hypohesis is correc for curved ems. Encore (no n exm quesion) The firs wo non zero erms of he Tylor expnsion of W o d re W d 6 d 8. R The firs wo non zero erms of he Tylor expnsion of o d re 5 d d 65 R. These pproximions hve n error less hn % for d < R (Figure 6) W W d 6 d R + 5 d d 65 R d d d Figure 6. Funcions W, nd heir pproximions 6 d d R Answers o Prolem Kinemic Boundry Condiions The vriles w nd w ˆ re he mximum deflecions h occur in he middle of em nd ˆ respecively. The oundry condiions re x l w 0 x l w 0 x l w 0 This prolem hs een proposed y Dr. Linh Co Hong, COW Consul Denmrk 6
7 x l w 0 5 y 0 w w 6 y w w w 7 y 0 0 y The deflecion funcions re such h he oundry condiions,, 5 nd 7 re lredy sisfied. x l 0 wˆ + C + C C wˆ C Poenil Energy 6 x l 0 wˆ + C + C C 6 wˆ C 6 y w w+ C5 + C6 C5 w w C6 l l l l po κ + κ + κ x l x l x l y 0 x l E dx dx m dydx qw dx c iniml The poenil energy needs o e miniml wih respec o he prmeers h descrie he deformion,wˆ, w ˆ, C, C, C6. The equions re derived from Epo Epo Epo Epo Epo 0, 0, 0, 0, 0. ŵ ŵ C C C6 d mproved De inercion eween floorords nd em is no consn force over he em lengh. Therefore, fourh order polynomils re no sufficien o descrie he exc deflecion of he ems. So, he soluion is no exc nd in heory i cn e improved. Encore (no n exm prolem) The deflecion funcions cn e exended 6 x x x w wˆ + C + C + C 7 6 l l l 6 x x x w wˆ + C + C + C 8 6 l l l y y w w+ C5 + C 6 The clculed mximum deflecion is now 5 ql β β β wˆ 8 E β β β The pproximed formul 7
8 5 ql 0 + 8β wˆ 8 E 0 + 8β shows deviion eween 0. % nd 0. % for ll vlues of β. Answers o Prolem Consiuive Equions We ssume h ple hs higher liude hn ple. w w w Vericl equilirium of ple. pa S O + S O 0 w w Vericl equilirium of ple. pa S O 0 This cn e evlued o w w w pπr S π R + S π R 0 w w p( π) R S π R 0 The soluion of hese equions hs een provided. pr π+ w S 6π pr 8 w S π Torsion Siffness From he memrne he φ -ule is oined using he following susiuions w φ p θ S. G π+ φ θgr 6π 8 φ θgr π The orsion momen is wo imes he volume of he φ -ule. ( φ A+φA ) π+ 8 θgr π R + θgr ( π) R π π 6 8 GR θ 8π+ π For wire frme model of he shf we wrie G θ. 8
9 Therefore he orsion siffness is 8 G GR 8π+ π. c Sher Sresses The sher sress is he slope of he φ ule. Firs we rewrie he formul for he orsion momen π GRθ π + 8 R nd express φ nd φ in he orsion momen. π π+ π+ φ 6 π + 8 R π π + 8 R π 8 6 φ π + 8 R π π + 8 R The sher sresses re φ σ π+ σ π + 8 R 6 π+ φ φ π + 8 R π + 8 R π σ σ π + 8 R. 9
10 Answer o Prolem Vericl equilirium p ϕ r qr ϕr ( qr + dqr )( r + ) ϕ p r qr r qr( r + ) dqr( r + ) p r qr r qr r qr dqr r dqr p r qr dqr r dqr dq p r q r r r dqr dq pr q r r r d pr ( r q r ) () omen equilirium ϕ 0 ( mrr + dmrr ) ϕ ( r + ) mrr ϕ r + p ϕr qr ϕr mθθ 0 ( mrr + dmrr )( r + ) mrr r + p r qr r mθθ 0 mrr ( r + ) + dmrr ( r + ) mrr r + p r qr r mθθ 0 mrr r + mrr + dmrr r + dmrr mrr r + p r qr r mθθ 0 mrr + dmrr r + dmrr + p r qr r mθθ dm 0 rr mrr + r + dmrr + p r qr r mθθ dm 0 m rr rr + r qr r mθθ m ( ) 0 rr qr r mθθ () Susiuion of () in () gives pr d ( r mrr ) d + m θθ. Q. E. D. 0
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
Physics 2A HW #3 Solutions
 Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
FM Applications of Integration 1.Centroid of Area
 FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
A 1.3 m 2.5 m 2.8 m. x = m m = 8400 m. y = 4900 m 3200 m = 1700 m
 PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
Mathematical Modeling
 ME pplie Engineering nlsis Chper Mhemicl Moeling Professor Ti-Rn Hsu, Ph.D. Deprmen of Mechnicl n erospce Engineering Sn Jose Se Universi Sn Jose, Cliforni, US Jnur Chper Lerning Ojecives Mhemicl moeling
ME pplie Engineering nlsis Chper Mhemicl Moeling Professor Ti-Rn Hsu, Ph.D. Deprmen of Mechnicl n erospce Engineering Sn Jose Se Universi Sn Jose, Cliforni, US Jnur Chper Lerning Ojecives Mhemicl moeling
( ) ( ) ( ) ( ) ( ) ( y )
 8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
 PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
(b) 10 yr. (b) 13 m. 1.6 m s, m s m s (c) 13.1 s. 32. (a) 20.0 s (b) No, the minimum distance to stop = 1.00 km. 1.
 Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Version 001 test-1 swinney (57010) 1. is constant at m/s.
 Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
Properties of Logarithms. Solving Exponential and Logarithmic Equations. Properties of Logarithms. Properties of Logarithms. ( x)
 Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 9: The High Beta Tokamak
 .65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
.65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
Average & instantaneous velocity and acceleration Motion with constant acceleration
 Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
The Finite Element Method for the Analysis of Non-Linear and Dynamic Systems
 Swiss Federl Insiue of Pge 1 The Finie Elemen Mehod for he Anlysis of Non-Liner nd Dynmic Sysems Prof. Dr. Michel Hvbro Fber Dr. Nebojs Mojsilovic Swiss Federl Insiue of ETH Zurich, Swizerlnd Mehod of
Swiss Federl Insiue of Pge 1 The Finie Elemen Mehod for he Anlysis of Non-Liner nd Dynmic Sysems Prof. Dr. Michel Hvbro Fber Dr. Nebojs Mojsilovic Swiss Federl Insiue of ETH Zurich, Swizerlnd Mehod of
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Magnetostatics Bar Magnet. Magnetostatics Oersted s Experiment
 Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Physics 101 Lecture 4 Motion in 2D and 3D
 Phsics 11 Lecure 4 Moion in D nd 3D Dr. Ali ÖVGÜN EMU Phsics Deprmen www.ogun.com Vecor nd is componens The componens re he legs of he righ ringle whose hpoenuse is A A A A A n ( θ ) A Acos( θ) A A A nd
Phsics 11 Lecure 4 Moion in D nd 3D Dr. Ali ÖVGÜN EMU Phsics Deprmen www.ogun.com Vecor nd is componens The componens re he legs of he righ ringle whose hpoenuse is A A A A A n ( θ ) A Acos( θ) A A A nd
RESPONSE UNDER A GENERAL PERIODIC FORCE. When the external force F(t) is periodic with periodτ = 2π
 RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
MATH 124 AND 125 FINAL EXAM REVIEW PACKET (Revised spring 2008)
 MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
1. Consider a PSA initially at rest in the beginning of the left-hand end of a long ISS corridor. Assume xo = 0 on the left end of the ISS corridor.
 In Eercise 1, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 1. Consider PSA iniilly res in he beginning of he lef-hnd
In Eercise 1, use sndrd recngulr Cresin coordine sysem. Le ime be represened long he horizonl is. Assume ll ccelerions nd decelerions re consn. 1. Consider PSA iniilly res in he beginning of he lef-hnd
AN ANALYTICAL TOOL TO PREDICT LOAD DISTRIBUTION OF MULTI-BOLT SINGLE-LAP THICK LAMINATE JOINTS
 8 TH INTERNATIONAL CONERENCE ON COMOITE MATERIAL AN ANALYTICAL TOOL TO REDICT LOAD DITRIBUTION O MULTI-BOLT INGLE-LA THIC LAMINATE JOINT Longqun Liu*, Ying Mo, Rn Wei chool of Aeronuics nd Asronuics, hnghi
8 TH INTERNATIONAL CONERENCE ON COMOITE MATERIAL AN ANALYTICAL TOOL TO REDICT LOAD DITRIBUTION O MULTI-BOLT INGLE-LA THIC LAMINATE JOINT Longqun Liu*, Ying Mo, Rn Wei chool of Aeronuics nd Asronuics, hnghi
Phys 110. Answers to even numbered problems on Midterm Map
 Phys Answers o een numbered problems on Miderm Mp. REASONING The word per indices rio, so.35 mm per dy mens.35 mm/d, which is o be epressed s re in f/cenury. These unis differ from he gien unis in boh
Phys Answers o een numbered problems on Miderm Mp. REASONING The word per indices rio, so.35 mm per dy mens.35 mm/d, which is o be epressed s re in f/cenury. These unis differ from he gien unis in boh
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
3 Motion with constant acceleration: Linear and projectile motion
 3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
CHAPTER 11 PARAMETRIC EQUATIONS AND POLAR COORDINATES
 CHAPTER PARAMETRIC EQUATIONS AND POLAR COORDINATES. PARAMETRIZATIONS OF PLANE CURVES., 9, _ _ Ê.,, Ê or, Ÿ. 5, 7, _ _.,, Ÿ Ÿ Ê Ê 5 Ê ( 5) Ê ˆ Ê 6 Ê ( 5) 7 Ê Ê, Ÿ Ÿ $ 5. cos, sin, Ÿ Ÿ 6. cos ( ), sin (
CHAPTER PARAMETRIC EQUATIONS AND POLAR COORDINATES. PARAMETRIZATIONS OF PLANE CURVES., 9, _ _ Ê.,, Ê or, Ÿ. 5, 7, _ _.,, Ÿ Ÿ Ê Ê 5 Ê ( 5) Ê ˆ Ê 6 Ê ( 5) 7 Ê Ê, Ÿ Ÿ $ 5. cos, sin, Ÿ Ÿ 6. cos ( ), sin (
Think of the Relationship Between Time and Space Again
 Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
Longitudinal Strength Standard. S11 (cont) S11
 (1989) (Rev.1 199) (Rev. Nov 001) (Rev. June 00) (Rev.4 July 004) (Rev.5 Jn 006) (Rev.6 My 0) Longiudinl Srengh Sndrd.1 Applicion This requiremen pplies only o seel ships of lengh 90 m nd greer in unresriced
(1989) (Rev.1 199) (Rev. Nov 001) (Rev. June 00) (Rev.4 July 004) (Rev.5 Jn 006) (Rev.6 My 0) Longiudinl Srengh Sndrd.1 Applicion This requiremen pplies only o seel ships of lengh 90 m nd greer in unresriced
EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE BOUNDARY-VALUE PROBLEM
 Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
This UR does not apply to CSR Bulk Carriers and Oil Tankers or to container ships to which UR S11A is applicable.
 (1989) (Rev.1 199) (Rev. Nov 001) (Rev. June 00) (Rev.4 July 004) (Rev.5 Jn 006) (Rev.6 My 0) (Rev.7 Nov 0) (Rev.8 June 015) Longiudinl Srengh Sndrd.1 Applicion This requiremen pplies only o seel ships
(1989) (Rev.1 199) (Rev. Nov 001) (Rev. June 00) (Rev.4 July 004) (Rev.5 Jn 006) (Rev.6 My 0) (Rev.7 Nov 0) (Rev.8 June 015) Longiudinl Srengh Sndrd.1 Applicion This requiremen pplies only o seel ships
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
Combined Bending with Induced or Applied Torsion of FRP I-Section Beams
 Combined Bending wih Induced or Applied Torsion of FRP I-Secion Beams MOJTABA B. SIRJANI School of Science and Technology Norfolk Sae Universiy Norfolk, Virginia 34504 USA sirjani@nsu.edu STEA B. BONDI
Combined Bending wih Induced or Applied Torsion of FRP I-Secion Beams MOJTABA B. SIRJANI School of Science and Technology Norfolk Sae Universiy Norfolk, Virginia 34504 USA sirjani@nsu.edu STEA B. BONDI
On the reduction of the interfacial stresses in a repaired beam with an adhesively FRP plate
 On he reducion of he inerfcil sresses in reired em wih n dhesively FRP le Kernou ssim, Khlil Belkhdr D éremen de génie civil e hydrulique, Universié de Sid (Algérie) : nssimkernougeniecivil@yhoo.fr Déremen
On he reducion of he inerfcil sresses in reired em wih n dhesively FRP le Kernou ssim, Khlil Belkhdr D éremen de génie civil e hydrulique, Universié de Sid (Algérie) : nssimkernougeniecivil@yhoo.fr Déremen
EXERCISE - 01 CHECK YOUR GRASP
 UNIT # 09 PARABOLA, ELLIPSE & HYPERBOLA PARABOLA EXERCISE - 0 CHECK YOUR GRASP. Hin : Disnce beween direcri nd focus is 5. Given (, be one end of focl chord hen oher end be, lengh of focl chord 6. Focus
UNIT # 09 PARABOLA, ELLIPSE & HYPERBOLA PARABOLA EXERCISE - 0 CHECK YOUR GRASP. Hin : Disnce beween direcri nd focus is 5. Given (, be one end of focl chord hen oher end be, lengh of focl chord 6. Focus
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q). INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg) INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
Honours Introductory Maths Course 2011 Integration, Differential and Difference Equations
 Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
Soil-Pile Dynamic Interaction in the Viscous Damping Layered Soils
 1 The Open Civil Engineering Journl, 11, 5, 1-18 Soil-Pile Dynmic Inercion in he Viscous Dmping Lyered Soils Open Access Yinhui Wng 1, Kuihu Wng, Zhixing Zh 1, * nd Reno Que 1 Deprmen of Civil Engineering
1 The Open Civil Engineering Journl, 11, 5, 1-18 Soil-Pile Dynmic Inercion in he Viscous Dmping Lyered Soils Open Access Yinhui Wng 1, Kuihu Wng, Zhixing Zh 1, * nd Reno Que 1 Deprmen of Civil Engineering
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
v A Since the axial rigidity k ij is defined by P/v A, we obtain Pa 3
 The The rd rd Inernaional Conference on on Design Engineering and Science, ICDES 14 Pilsen, Czech Pilsen, Republic, Czech Augus Republic, 1 Sepember 1-, 14 In-plane and Ou-of-plane Deflecion of J-shaped
The The rd rd Inernaional Conference on on Design Engineering and Science, ICDES 14 Pilsen, Czech Pilsen, Republic, Czech Augus Republic, 1 Sepember 1-, 14 In-plane and Ou-of-plane Deflecion of J-shaped
Two Coupled Oscillators / Normal Modes
 Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
1. Find a basis for the row space of each of the following matrices. Your basis should consist of rows of the original matrix.
 Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
ECE Microwave Engineering
 EE 537-635 Microwve Engineering Adped from noes y Prof. Jeffery T. Willims Fll 8 Prof. Dvid R. Jcson Dep. of EE Noes Wveguiding Srucures Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model
EE 537-635 Microwve Engineering Adped from noes y Prof. Jeffery T. Willims Fll 8 Prof. Dvid R. Jcson Dep. of EE Noes Wveguiding Srucures Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model
Convergence of Singular Integral Operators in Weighted Lebesgue Spaces
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
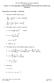 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
Shells with membrane behavior
 Chaper 3 Shells wih membrane behavior In he presen Chaper he sress saic response of membrane shells will be addressed. In Secion 3.1 an inroducory example emphasizing he difference beween bending and membrane
Chaper 3 Shells wih membrane behavior In he presen Chaper he sress saic response of membrane shells will be addressed. In Secion 3.1 an inroducory example emphasizing he difference beween bending and membrane
2D Motion WS. A horizontally launched projectile s initial vertical velocity is zero. Solve the following problems with this information.
 Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
Let us start with a two dimensional case. We consider a vector ( x,
 Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
Solutions to Problems from Chapter 2
 Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
PARABOLA. moves such that PM. = e (constant > 0) (eccentricity) then locus of P is called a conic. or conic section.
 wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
NMR Spectroscopy: Principles and Applications. Nagarajan Murali Advanced Tools Lecture 4
 NMR Specroscop: Principles nd Applicions Ngrjn Murli Advnced Tools Lecure 4 Advnced Tools Qunum Approch We know now h NMR is rnch of Specroscop nd he MNR specrum is n oucome of nucler spin inercion wih
NMR Specroscop: Principles nd Applicions Ngrjn Murli Advnced Tools Lecure 4 Advnced Tools Qunum Approch We know now h NMR is rnch of Specroscop nd he MNR specrum is n oucome of nucler spin inercion wih
Predator - Prey Model Trajectories and the nonlinear conservation law
 Predaor - Prey Model Trajecories and he nonlinear conservaion law James K. Peerson Deparmen of Biological Sciences and Deparmen of Mahemaical Sciences Clemson Universiy Ocober 28, 213 Ouline Drawing Trajecories
Predaor - Prey Model Trajecories and he nonlinear conservaion law James K. Peerson Deparmen of Biological Sciences and Deparmen of Mahemaical Sciences Clemson Universiy Ocober 28, 213 Ouline Drawing Trajecories
Probability, Estimators, and Stationarity
 Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
Chper Probbiliy, Esimors, nd Sionriy Consider signl genered by dynmicl process, R, R. Considering s funcion of ime, we re opering in he ime domin. A fundmenl wy o chrcerize he dynmics using he ime domin
DEFORMATION OF ACTIVE FLEXIBLE RODS WITH MEMORY SHAPE ALLOY FIBERS
 DEFORMTION OF CTIVE FLEXIBLE RODS WITH MEMORY SHPE LLOY FIBERS Sefni DONESCU Technicl Universiy of Civil Engineering, Dep. of Mhemics, Bdul Lcul Tei 4, Buchres 7 In his pper we consider hin rod of luminum
DEFORMTION OF CTIVE FLEXIBLE RODS WITH MEMORY SHPE LLOY FIBERS Sefni DONESCU Technicl Universiy of Civil Engineering, Dep. of Mhemics, Bdul Lcul Tei 4, Buchres 7 In his pper we consider hin rod of luminum
Abstract. W.W. Memudu 1 and O.A. Taiwo, 2
 Theoreicl Mhemics & Applicions, vol. 6, no., 06, 3-50 ISS: 79-9687 prin, 79-9709 online Scienpress d, 06 Eponenilly fied collocion pproimion mehod for he numericl soluions of Higher Order iner Fredholm
Theoreicl Mhemics & Applicions, vol. 6, no., 06, 3-50 ISS: 79-9687 prin, 79-9709 online Scienpress d, 06 Eponenilly fied collocion pproimion mehod for he numericl soluions of Higher Order iner Fredholm
Seismic history analysis of asymmetrical adjacent buildings with soil-structure interaction consideration
 Universiy of Wollongong Reserch Online Fculy of Engineering - Ppers (Archive) Fculy of Engineering nd Informion Sciences 2011 Seismic hisory nlysis of symmericl djcen buildings wih soil-srucure inercion
Universiy of Wollongong Reserch Online Fculy of Engineering - Ppers (Archive) Fculy of Engineering nd Informion Sciences 2011 Seismic hisory nlysis of symmericl djcen buildings wih soil-srucure inercion
ECE Microwave Engineering. Fall Prof. David R. Jackson Dept. of ECE. Notes 10. Waveguides Part 7: Transverse Equivalent Network (TEN)
 EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
Some basic notation and terminology. Deterministic Finite Automata. COMP218: Decision, Computation and Language Note 1
 COMP28: Decision, Compuion nd Lnguge Noe These noes re inended minly s supplemen o he lecures nd exooks; hey will e useful for reminders ou noion nd erminology. Some sic noion nd erminology An lphe is
COMP28: Decision, Compuion nd Lnguge Noe These noes re inended minly s supplemen o he lecures nd exooks; hey will e useful for reminders ou noion nd erminology. Some sic noion nd erminology An lphe is
Chapter Direct Method of Interpolation
 Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Y 0.4Y 0.45Y Y to a proper ARMA specification.
 HG Jan 04 ECON 50 Exercises II - 0 Feb 04 (wih answers Exercise. Read secion 8 in lecure noes 3 (LN3 on he common facor problem in ARMA-processes. Consider he following process Y 0.4Y 0.45Y 0.5 ( where
HG Jan 04 ECON 50 Exercises II - 0 Feb 04 (wih answers Exercise. Read secion 8 in lecure noes 3 (LN3 on he common facor problem in ARMA-processes. Consider he following process Y 0.4Y 0.45Y 0.5 ( where
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
Section 4.4 Logarithmic Properties
 Secion. Logarihmic Properies 59 Secion. Logarihmic Properies In he previous secion, we derived wo imporan properies of arihms, which allowed us o solve some asic eponenial and arihmic equaions. Properies
Secion. Logarihmic Properies 59 Secion. Logarihmic Properies In he previous secion, we derived wo imporan properies of arihms, which allowed us o solve some asic eponenial and arihmic equaions. Properies
S Radio transmission and network access Exercise 1-2
 S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
Math 2142 Exam 1 Review Problems. x 2 + f (0) 3! for the 3rd Taylor polynomial at x = 0. To calculate the various quantities:
 Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
23.5. Half-Range Series. Introduction. Prerequisites. Learning Outcomes
 Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
IX.1.1 The Laplace Transform Definition 700. IX.1.2 Properties 701. IX.1.3 Examples 702. IX.1.4 Solution of IVP for ODEs 704
 Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
A LOG IS AN EXPONENT.
 Ojeives: n nlze nd inerpre he ehvior of rihmi funions, inluding end ehvior nd smpoes. n solve rihmi equions nlill nd grphill. n grph rihmi funions. n deermine he domin nd rnge of rihmi funions. n deermine
Ojeives: n nlze nd inerpre he ehvior of rihmi funions, inluding end ehvior nd smpoes. n solve rihmi equions nlill nd grphill. n grph rihmi funions. n deermine he domin nd rnge of rihmi funions. n deermine
Chapter 2. First Order Scalar Equations
 Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
T-Match: Matching Techniques For Driving Yagi-Uda Antennas: T-Match. 2a s. Z in. (Sections 9.5 & 9.7 of Balanis)
 3/0/018 _mch.doc Pge 1 of 6 T-Mch: Mching Techniques For Driving Ygi-Ud Anenns: T-Mch (Secions 9.5 & 9.7 of Blnis) l s l / l / in The T-Mch is shun-mching echnique h cn be used o feed he driven elemen
3/0/018 _mch.doc Pge 1 of 6 T-Mch: Mching Techniques For Driving Ygi-Ud Anenns: T-Mch (Secions 9.5 & 9.7 of Blnis) l s l / l / in The T-Mch is shun-mching echnique h cn be used o feed he driven elemen
BME 207 Introduction to Biomechanics Spring 2018
 April 6, 28 UNIVERSITY O RHODE ISAND Deprtment of Electricl, Computer nd Biomedicl Engineering BME 27 Introduction to Biomechnics Spring 28 Homework 8 Prolem 14.6 in the textook. In ddition to prts -e,
April 6, 28 UNIVERSITY O RHODE ISAND Deprtment of Electricl, Computer nd Biomedicl Engineering BME 27 Introduction to Biomechnics Spring 28 Homework 8 Prolem 14.6 in the textook. In ddition to prts -e,
Navneet Saini, Mayank Goyal, Vishal Bansal (2013); Term Project AML310; Indian Institute of Technology Delhi
 Creep in Viscoelasic Subsances Numerical mehods o calculae he coefficiens of he Prony equaion using creep es daa and Herediary Inegrals Mehod Navnee Saini, Mayank Goyal, Vishal Bansal (23); Term Projec
Creep in Viscoelasic Subsances Numerical mehods o calculae he coefficiens of he Prony equaion using creep es daa and Herediary Inegrals Mehod Navnee Saini, Mayank Goyal, Vishal Bansal (23); Term Projec
An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples.
 Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Some Inequalities variations on a common theme Lecture I, UL 2007
 Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
6. Gas dynamics. Ideal gases Speed of infinitesimal disturbances in still gas
 6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
A Structural Approach to the Enforcement of Language and Disjunctive Constraints
 A Srucurl Aroch o he Enforcemen of Lnguge nd Disjuncive Consrins Mrin V. Iordche School of Engineering nd Eng. Tech. LeTourneu Universiy Longview, TX 7607-700 Pnos J. Ansklis Dermen of Elecricl Engineering
A Srucurl Aroch o he Enforcemen of Lnguge nd Disjuncive Consrins Mrin V. Iordche School of Engineering nd Eng. Tech. LeTourneu Universiy Longview, TX 7607-700 Pnos J. Ansklis Dermen of Elecricl Engineering
Systems Variables and Structural Controllability: An Inverted Pendulum Case
 Reserch Journl of Applied Sciences, Engineering nd echnology 6(: 46-4, 3 ISSN: 4-7459; e-issn: 4-7467 Mxwell Scienific Orgniion, 3 Submied: Jnury 5, 3 Acceped: Mrch 7, 3 Published: November, 3 Sysems Vribles
Reserch Journl of Applied Sciences, Engineering nd echnology 6(: 46-4, 3 ISSN: 4-7459; e-issn: 4-7467 Mxwell Scienific Orgniion, 3 Submied: Jnury 5, 3 Acceped: Mrch 7, 3 Published: November, 3 Sysems Vribles
P441 Analytical Mechanics - I. Coupled Oscillators. c Alex R. Dzierba
 Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddharth Nagar, Narayanavanam Road QUESTION BANK (DESCRIPTIVE)
 QUESTION BANK 6 SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddhrh Ngr, Nrynvnm Rod 5758 QUESTION BANK (DESCRIPTIVE) Subjec wih Code :Engineering Mhemic-I (6HS6) Coure & Brnch: B.Tech Com o ll Yer & Sem:
QUESTION BANK 6 SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddhrh Ngr, Nrynvnm Rod 5758 QUESTION BANK (DESCRIPTIVE) Subjec wih Code :Engineering Mhemic-I (6HS6) Coure & Brnch: B.Tech Com o ll Yer & Sem:
Homework 5 for BST 631: Statistical Theory I Solutions, 09/21/2006
 Homewok 5 fo BST 63: Sisicl Theoy I Soluions, 9//6 Due Time: 5:PM Thusy, on 9/8/6. Polem ( oins). Book olem.8. Soluion: E = x f ( x) = ( x) f ( x) + ( x ) f ( x) = xf ( x) + xf ( x) + f ( x) f ( x) Accoing
Homewok 5 fo BST 63: Sisicl Theoy I Soluions, 9//6 Due Time: 5:PM Thusy, on 9/8/6. Polem ( oins). Book olem.8. Soluion: E = x f ( x) = ( x) f ( x) + ( x ) f ( x) = xf ( x) + xf ( x) + f ( x) f ( x) Accoing
Collision Detection and Bouncing
 Collision Deecion nd Bouncing Collisions re Hndled in Two Prs. Deecing he collision Mike Biley mj@cs.oregonse.edu. Hndling he physics of he collision collision-ouncing.ppx If You re Lucky, You Cn Deec
Collision Deecion nd Bouncing Collisions re Hndled in Two Prs. Deecing he collision Mike Biley mj@cs.oregonse.edu. Hndling he physics of he collision collision-ouncing.ppx If You re Lucky, You Cn Deec
Week 1 Lecture 2 Problems 2, 5. What if something oscillates with no obvious spring? What is ω? (problem set problem)
 Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
Chapter 10. Simple Harmonic Motion and Elasticity. Goals for Chapter 10
 Chper 0 Siple Hronic Moion nd Elsiciy Gols or Chper 0 o ollow periodic oion o sudy o siple hronic oion. o sole equions o siple hronic oion. o use he pendulu s prooypicl syse undergoing siple hronic oion.
Chper 0 Siple Hronic Moion nd Elsiciy Gols or Chper 0 o ollow periodic oion o sudy o siple hronic oion. o sole equions o siple hronic oion. o use he pendulu s prooypicl syse undergoing siple hronic oion.
dy dx = xey (a) y(0) = 2 (b) y(1) = 2.5 SOLUTION: See next page
 Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
HW #1 Solutions. Lewis Structures: Using the above rules, determine the molecular structure for Cl2CO. Hint: C is at the center.
 HW # Soluions Cron Mss Prolem: ssuming n erge surfce pressure of m, n erge ropospheric emperure of 55 K, n glol CO mixing rio of 385 ppm, wh is he curren mospheric Cron reseroir (in unis of g m -? Compre
HW # Soluions Cron Mss Prolem: ssuming n erge surfce pressure of m, n erge ropospheric emperure of 55 K, n glol CO mixing rio of 385 ppm, wh is he curren mospheric Cron reseroir (in unis of g m -? Compre
Chapter 2. Motion along a straight line. 9/9/2015 Physics 218
 Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
23.2. Representing Periodic Functions by Fourier Series. Introduction. Prerequisites. Learning Outcomes
 Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
graph of unit step function t
 .5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
.5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
A Simple Method to Solve Quartic Equations. Key words: Polynomials, Quartics, Equations of the Fourth Degree INTRODUCTION
 Ausrlin Journl of Bsic nd Applied Sciences, 6(6): -6, 0 ISSN 99-878 A Simple Mehod o Solve Quric Equions Amir Fhi, Poo Mobdersn, Rhim Fhi Deprmen of Elecricl Engineering, Urmi brnch, Islmic Ad Universi,
Ausrlin Journl of Bsic nd Applied Sciences, 6(6): -6, 0 ISSN 99-878 A Simple Mehod o Solve Quric Equions Amir Fhi, Poo Mobdersn, Rhim Fhi Deprmen of Elecricl Engineering, Urmi brnch, Islmic Ad Universi,
Robust estimation based on the first- and third-moment restrictions of the power transformation model
 h Inernaional Congress on Modelling and Simulaion, Adelaide, Ausralia, 6 December 3 www.mssanz.org.au/modsim3 Robus esimaion based on he firs- and hird-momen resricions of he power ransformaion Nawaa,
h Inernaional Congress on Modelling and Simulaion, Adelaide, Ausralia, 6 December 3 www.mssanz.org.au/modsim3 Robus esimaion based on he firs- and hird-momen resricions of he power ransformaion Nawaa,
Physics 235 Chapter 2. Chapter 2 Newtonian Mechanics Single Particle
 Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Explain shortly the meaning of the following eight words in relation to shells structures.
 Delft University of Technology Fculty of Civil Engineering nd Geosciences Structurl Mechnics Section Write your nme nd study number t the top right-hnd of your work. Exm CIE4143 Shell Anlysis Tuesdy 15
Delft University of Technology Fculty of Civil Engineering nd Geosciences Structurl Mechnics Section Write your nme nd study number t the top right-hnd of your work. Exm CIE4143 Shell Anlysis Tuesdy 15
Positive and negative solutions of a boundary value problem for a
 Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
Invenion Journl of Reerch Technology in Engineering & Mngemen (IJRTEM) ISSN: 2455-3689 www.ijrem.com Volume 2 Iue 9 ǁ Sepemer 28 ǁ PP 73-83 Poiive nd negive oluion of oundry vlue prolem for frcionl, -difference
Physics 201, Lecture 5
 Phsics 1 Lecue 5 Tod s Topics n Moion in D (Chp 4.1-4.3): n D Kinemicl Quniies (sec. 4.1) n D Kinemics wih Consn Acceleion (sec. 4.) n D Pojecile (Sec 4.3) n Epeced fom Peiew: n Displcemen eloci cceleion
Phsics 1 Lecue 5 Tod s Topics n Moion in D (Chp 4.1-4.3): n D Kinemicl Quniies (sec. 4.1) n D Kinemics wih Consn Acceleion (sec. 4.) n D Pojecile (Sec 4.3) n Epeced fom Peiew: n Displcemen eloci cceleion
