Minimum Squared Error
|
|
|
- Bathsheba George
- 5 years ago
- Views:
Transcription
1 Minimum Squred Error
2 LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples y i solve sysem of liner equions Choose posiive consns,,, n ry o find weigh vecor s.. y i i for ll smples y i If we cn find weigh vecor such h y i i for ll smples y i, hen is soluion ecuse i s re posiive consider ll he smples (no jus he misclssified ones)
3 LDF: MSE Mrgins g(y) 0 y i y k Since we wn y i i, we expec smple y i o e disnce i from he sepring hyperplne (normlized y ) Thus,,, n give relive expeced disnces or mrgins of smples from he hyperplne Should mke i smll if smple i is expeced o e ner sepring hyperplne, nd mke i lrger oherwise In he sence of ny ddiionl informion, here re good resons o se n
4 LDF: MSE Mrix Noion Need o solve n equions Inroduce mrix noion: y y n M n ( 0) ( ) ( d) y y L y ( ) ( ) ( d) 0 0 y y L y ( ) ( ) ( ) M M M M M M d M 0 d y n n y n L y n Y Thus need o solve liner sysem Y
5 LDF: Exc Soluion is Rre Thus need o solve liner sysem Y Y is n n y (d +) mrix Exc soluion cn e found only if Y is nonsingulr nd squre, in which cse he inverse Y - exiss Y - (numer of smples) (numer of feures + ) lmos never hppens in prcice in his cse, gurneed o find he sepring hyperplne y y
6 LDF: Approxime Soluion Typiclly Y is overdeermined, h is i hs more rows (exmples) hn columns (feures) If i hs more feures hn exmples, should reduce dimensionliy Y Need Y, u no exc soluion exiss for n overdeermined sysem of equion More equions hn unknowns Find n pproxime soluion, h is Y Noe h pproxime soluion does no necessrily give he sepring hyperplne in he seprle cse Bu hyperplne corresponding o my sill e good soluion, especilly if here is no sepring hyperplne
7 LDF: MSE Crierion Funcion Minimum squred error pproch: find which minimizes he lengh of he error vecor e e Y e Thus minimize he minimum squred error crierion funcion: n ( ) Y y J s ( ) i i Unlike he percepron crierion funcion, we cn opimize he minimum squred error crierion funcion nlyiclly y seing he grdien o 0 i Y
8 LDF: Opimizing J s () J s ( ) Le s compue he grdien: J s n Y ( ) y i i i J ( ) M 0 Y ( Y ) s J Seing he grdien o 0: Y s d ( ) Y 0 Y Y Y
9 LDF: Pseudo Inverse Soluion Mrix Y Y is squre (i hs d + rows nd columns) nd i is ofen non-singulr If Y Y is non-singulr, is inverse exiss nd we cn solve for uniquely: ( ) Y Y Y pseudo inverse of Y ( ) ) Y Y Y Y ( Y Y) ( Y Y) I
10 LDF: Minimum Squred-Error Procedures If n, MSE procedure is equivlen o finding hyperplne of es fi hrough he smples y,,y n J ( ) Y s n n M n Then we shif his line o he origin, if his line ws good fi, ll smples will e clssified correcly
11 LDF: Minimum Squred-Error Procedures Only gurneed he sepring hyperplne if Y > 0 y h is if ll elemens of vecor Y M re posiive y n We hve Y + ε n + ε n Th is Y M where ε my e negive If ε,, ε n re smll relive o,, n, hen ech elemen of Y is posiive, nd gives sepring hyperplne If pproximion is no good, ε i my e lrge nd negive, for some i, hus i + ε i will e negive nd is no sepring hyperplne Thus in linerly seprle cse, les squres soluion does no necessrily gives sepring hyperplne Bu i will give resonle hyperplne
12 LDF: Minimum Squred-Error Procedures We re free o choose. My e emped o mke lrge s wy o insure Y > 0 Does no work Le β e sclr, le s ry β insed of if * is les squres soluion o Y, hen for ny sclr β, les squres soluion o Y β is β* rg min Y β rg minβ Y( / β) ( / ) rg min Y β β * hus if for some i h elemen of Y is less hn 0, h is y i < 0, hen y i (β) < 0, Relive difference eween componens of mers, u no he size of ech individul componen
13 LDF: Exmple Clss : (6 9), (5 7) Clss : (5 9), (0 4) Se vecors y, y, y 3, y 4 y dding exr feure nd normlizing 6 y 9 5 y 7 5 y 3 9 y Mrix Y is hen Y
14 LDF: Exmple Choose In ml, Y\ solves he les squres prolem Noe is n pproximion o Y, since no exc soluion exiss Y This soluion does give sepring hyperplne since Y > 0
15 LDF: Exmple Clss : (6 9), (5 7) Clss : (5 9), (0 0) The ls smple is very fr compred o ohers from he sepring hyperplne y Mrix y 7 5 y 3 9 y Y
16 LDF: Exmple Choose In ml, Y\ solves he les squres prolem Noe is n pproximion o Y, since no exc soluion exiss Y This soluion does no give sepring hyperplne since y 3 < 0
17 LDF: Exmple MSE pys o much enion o isoled noisy exmples (such exmples re clled ouliers) oulier MSE soluion desired soluion No prolems wih convergence hough, nd soluion i gives rnges from resonle o good
18 LDF: Exmple we know h 4 h poin is fr fr from sepring hyperplne In prcice we don know his Thus pproprie 0 In Ml, solve Y\ Noe is n pproximion o Y, This soluion does give he sepring hyperplne since Y > 0 Y 0
19 LDF: Grdien Descen for MSE soluion J s ( ) Y My wish o find MSE soluion y grdien descen:. Compuing he inverse of Y Y my e oo cosly. Y Y my e close o singulr if smples re highly correled (rows of Y re lmos liner cominions of ech oher) compuing he inverse of Y Y is no numericlly sle In he eginning of he lecure, compued he grdien: ( ) J Y ( Y ) s
20 LDF: Widrow-Hoff Procedure Thus he upde rule for grdien descen: ( ) ( ) ( ) ( ) J Y ( Y ) ( k+ ) ( k) ( k) ( k) η Y k If η η / k weigh vecor (k) converges o he MSE Y soluion, h is Y (Y-)0 s Widrow-Hoff procedure reduces sorge requiremens y considering single smples sequenilly: ( y ) ( k+ ) ( k) ( k) ( k) η y i i i
21 LDF: Ho-Kshyp Procedure In he MSE procedure, if is chosen rirrily, finding sepring hyperplne is no gurneed Suppose rining smples re linerly seprle. Then here is s nd posiive s s.. Y s s > 0 If we knew s could pply MSE procedure o find he sepring hyperplne Ide: find oh s nd s Minimize he following crierion funcion, resricing o posiive : ( ), Y J HK
22 LDF: Ho-Kshyp Procedure J HK ( ), Y As usul, ke pril derivives w.r.. nd J HK J HK ( Y ) 0 Y ( Y ) 0 Use modified grdien descen procedure o find minimum of J HK (,) Alerne he wo seps elow unil convergence: ) Fix nd minimize J HK (,) wih respec o ) Fix nd minimize J HK (,) wih respec o
23 LDF: Ho-Kshyp Procedure J HK ( Y ) 0 Y J HK ( Y ) 0 Alerne he wo seps elow unil convergence: ) Fix nd minimize J HK (,) wih respec o ) Fix nd minimize J HK (,) wih respec o Sep () cn e performed wih pseudoinverse For fixed minimum of J HK (,) wih respec o is found y solving Thus ( Y ) 0 Y ( ) Y Y Y
24 LDF: Ho-Kshyp Procedure Sep : fix nd minimize J HK (,) wih respec o We cn use Y ecuse hs o e posiive Soluion: use modified grdien descen sr wih posiive, follow negive grdien u refuse o decrese ny componens of This cn e chieved y seing ll he posiive componens of J o 0 No doing seepes descen nymore, u we re sill doing descen nd ensure h is posiive
25 LDF: Ho-Kshyp Procedure The Ho-Kshyp procedure: 0) Sr wih rirry () nd () > 0, le k repe seps () hrough (4) ( k) ( k) ( k) ) e Y ) Solve for (k+) using (k) nd (k) [ e e ] ( k+ ) ( k) ( k) ( k) + η + 3) Solve for (k+) using (k+) 4) k k + ( k+ ) ( ) ( k+ ) unil e (k) > 0 or k > k mx or (k+) (k) Y Y For convergence, lerning re should e fixed eween 0 < η < Y
26 LDF: Ho-Kshyp Procedure In he linerly seprle cse, e (k) 0, found soluion, sop one of componens of e (k) is posiive, lgorihm coninues In non seprle cse, e (k) will hve only negive componens evenully, hus found proof of nonsepriliy No ound on how mny ierion need for he proof of nonsepriliy
27 LDF: Ho-Kshyp Procedure Exmple Clss : (6 9), (5 7) Clss : (5 9), (0 0) Mrix Y ( ) Sr wih nd Use fixed lerning η ( ) A he sr Y ( )
28 LDF: Ho-Kshyp Procedure Exmple Ierion : e ( ) ( ) ( ) Y solve for () using () nd () [ e + e ] ( ) ( ) ( ) ( ) solve for () using () ( ) ( ) ( ) Y Y Y *
29 LDF: Ho-Kshyp Procedure Exmple Coninue ierions unil Y > 0 In prcice, coninue unil minimum componen of Y is less hen 0.0 Afer 04 ierions converged o soluion does gives sepring hyperplne Y
30 LDF: MSE for Muliple Clsses Suppose we hve m clsses Define m liner discriminn funcions g i ( x) w x+ w 0 i i i,...,m Given x, ssign clss c i if g i ( x ) g ( x ) j j i Such clssifier is clled liner mchine A liner mchine divides he feure spce ino c decision regions, wih g i (x) eing he lrges discriminn if x is in he region R i
31 LDF: MSE for Muliple Clsses For ech clss i, find weigh vecor i, s.. i i y y 0 y y clss clss Le Y i e mrix whose rows re smples from clss i, so i hs d + columns nd n i rows i i Le s pile ll smples in n y d + mrix Y: Y Y Y M Y m smple from smple from M smple from smple from clss clss clss m clss m
32 LDF: MSE for Muliple Clsses Le i e column vecor of lengh n which is 0 everywhere excep rows corresponding o smples from clss i, where i is : i 0 M M 0 M rows corresponding o smples from clss i
33 LDF: MSE for Muliple Clsses Le s pile ll i s columns in n y c mrix B B [ L ] n Le s pile ll i s columns in d + y m mrix A A [ L ] m m LSE prolems cn e represened in YA B: smple from clss smple from clss smple from clss smple from clss 3 smple from clss 3 smple from clss Y A B
34 LDF: MSE for Muliple Clsses Our ojecive funcion is: J m ( A) i Y i i J(A) is minimized wih he use of pseudoinverse A ( Y Y) YB
35 LDF: Summry Percepron procedures find sepring hyperplne in he linerly seprle cse, do no converge in he non-seprle cse cn force convergence y using decresing lerning re, u re no gurneed resonle sopping poin MSE procedures converge in seprle nd no seprle cse my no find sepring hyperplne if clsses re linerly seprle use pseudoinverse if Y Y is no singulr nd no oo lrge use grdien descen (Widrow-Hoff procedure) oherwise Ho-Kshyp procedures lwys converge find sepring hyperplne in he linerly seprle cse more cosly
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
( ) ( ) ( ) ( ) ( ) ( y )
 8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
1. Find a basis for the row space of each of the following matrices. Your basis should consist of rows of the original matrix.
 Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
Mh 7 Exm - Prcice Prolem Solions. Find sis for he row spce of ech of he following mrices. Yor sis shold consis of rows of he originl mrix. 4 () 7 7 8 () Since we wn sis for he row spce consising of rows
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Some Inequalities variations on a common theme Lecture I, UL 2007
 Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Chapter 2: Evaluative Feedback
 Chper 2: Evluive Feedbck Evluing cions vs. insrucing by giving correc cions Pure evluive feedbck depends olly on he cion ken. Pure insrucive feedbck depends no ll on he cion ken. Supervised lerning is
Chper 2: Evluive Feedbck Evluing cions vs. insrucing by giving correc cions Pure evluive feedbck depends olly on he cion ken. Pure insrucive feedbck depends no ll on he cion ken. Supervised lerning is
1 jordan.mcd Eigenvalue-eigenvector approach to solving first order ODEs. -- Jordan normal (canonical) form. Instructor: Nam Sun Wang
 jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples.
 Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
Chapter Direct Method of Interpolation
 Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
3D Transformations. Computer Graphics COMP 770 (236) Spring Instructor: Brandon Lloyd 1/26/07 1
 D Trnsformions Compuer Grphics COMP 770 (6) Spring 007 Insrucor: Brndon Lloyd /6/07 Geomery Geomeric eniies, such s poins in spce, exis wihou numers. Coordines re nming scheme. The sme poin cn e descried
D Trnsformions Compuer Grphics COMP 770 (6) Spring 007 Insrucor: Brndon Lloyd /6/07 Geomery Geomeric eniies, such s poins in spce, exis wihou numers. Coordines re nming scheme. The sme poin cn e descried
MATH 124 AND 125 FINAL EXAM REVIEW PACKET (Revised spring 2008)
 MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
P441 Analytical Mechanics - I. Coupled Oscillators. c Alex R. Dzierba
 Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q). INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg) INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
S Radio transmission and network access Exercise 1-2
 S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
S-7.330 Rdio rnsmission nd nework ccess Exercise 1 - P1 In four-symbol digil sysem wih eqully probble symbols he pulses in he figure re used in rnsmission over AWGN-chnnel. s () s () s () s () 1 3 4 )
Magnetostatics Bar Magnet. Magnetostatics Oersted s Experiment
 Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were
Collision Detection and Bouncing
 Collision Deecion nd Bouncing Collisions re Hndled in Two Prs. Deecing he collision Mike Biley mj@cs.oregonse.edu. Hndling he physics of he collision collision-ouncing.ppx If You re Lucky, You Cn Deec
Collision Deecion nd Bouncing Collisions re Hndled in Two Prs. Deecing he collision Mike Biley mj@cs.oregonse.edu. Hndling he physics of he collision collision-ouncing.ppx If You re Lucky, You Cn Deec
More on Magnetically C Coupled Coils and Ideal Transformers
 Appenix ore on gneiclly C Couple Coils Iel Trnsformers C. Equivlen Circuis for gneiclly Couple Coils A imes, i is convenien o moel mgneiclly couple coils wih n equivlen circui h oes no involve mgneic coupling.
Appenix ore on gneiclly C Couple Coils Iel Trnsformers C. Equivlen Circuis for gneiclly Couple Coils A imes, i is convenien o moel mgneiclly couple coils wih n equivlen circui h oes no involve mgneic coupling.
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
f(x) dx with An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples dx x x 2
 Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
Lecture 2: Network Flow. c 14
 Comp 260: Avne Algorihms Tufs Universiy, Spring 2016 Prof. Lenore Cowen Srie: Alexner LeNil Leure 2: Nework Flow 1 Flow Neworks s 16 12 13 10 4 20 14 4 Imgine some nework of pipes whih rry wer, represene
Comp 260: Avne Algorihms Tufs Universiy, Spring 2016 Prof. Lenore Cowen Srie: Alexner LeNil Leure 2: Nework Flow 1 Flow Neworks s 16 12 13 10 4 20 14 4 Imgine some nework of pipes whih rry wer, represene
3 Motion with constant acceleration: Linear and projectile motion
 3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
ECE Microwave Engineering. Fall Prof. David R. Jackson Dept. of ECE. Notes 10. Waveguides Part 7: Transverse Equivalent Network (TEN)
 EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
The Rosenblatt s LMS algorithm for Perceptron (1958) is built around a linear neuron (a neuron with a linear
 In The name of God Lecure4: Percepron and AALIE r. Majid MjidGhoshunih Inroducion The Rosenbla s LMS algorihm for Percepron 958 is buil around a linear neuron a neuron ih a linear acivaion funcion. Hoever,
In The name of God Lecure4: Percepron and AALIE r. Majid MjidGhoshunih Inroducion The Rosenbla s LMS algorihm for Percepron 958 is buil around a linear neuron a neuron ih a linear acivaion funcion. Hoever,
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
 PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
Honours Introductory Maths Course 2011 Integration, Differential and Difference Equations
 Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
Honours Inroducory Mhs Course 0 Inegrion, Differenil nd Difference Equions Reding: Ching Chper 4 Noe: These noes do no fully cover he meril in Ching, u re men o supplemen your reding in Ching. Thus fr
Some basic notation and terminology. Deterministic Finite Automata. COMP218: Decision, Computation and Language Note 1
 COMP28: Decision, Compuion nd Lnguge Noe These noes re inended minly s supplemen o he lecures nd exooks; hey will e useful for reminders ou noion nd erminology. Some sic noion nd erminology An lphe is
COMP28: Decision, Compuion nd Lnguge Noe These noes re inended minly s supplemen o he lecures nd exooks; hey will e useful for reminders ou noion nd erminology. Some sic noion nd erminology An lphe is
Mathematics 805 Final Examination Answers
 . 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
. 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
Introduction to Determinants. Remarks. Remarks. The determinant applies in the case of square matrices
 Introduction to Determinnts Remrks The determinnt pplies in the cse of squre mtrices squre mtrix is nonsingulr if nd only if its determinnt not zero, hence the term determinnt Nonsingulr mtrices re sometimes
Introduction to Determinnts Remrks The determinnt pplies in the cse of squre mtrices squre mtrix is nonsingulr if nd only if its determinnt not zero, hence the term determinnt Nonsingulr mtrices re sometimes
Location is relative. Coordinate Systems. Which of the following can be described with vectors??
 Locion is relive Coordine Sysems The posiion o hing is sed relive o noher hing (rel or virul) review o he physicl sis h governs mhemicl represenions Reerence oec mus e deined Disnce mus e nown Direcion
Locion is relive Coordine Sysems The posiion o hing is sed relive o noher hing (rel or virul) review o he physicl sis h governs mhemicl represenions Reerence oec mus e deined Disnce mus e nown Direcion
Average & instantaneous velocity and acceleration Motion with constant acceleration
 Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
EE 315 Notes. Gürdal Arslan CLASS 1. (Sections ) What is a signal?
 EE 35 Noes Gürdal Arslan CLASS (Secions.-.2) Wha is a signal? In his class, a signal is some funcion of ime and i represens how some physical quaniy changes over some window of ime. Examples: velociy of
EE 35 Noes Gürdal Arslan CLASS (Secions.-.2) Wha is a signal? In his class, a signal is some funcion of ime and i represens how some physical quaniy changes over some window of ime. Examples: velociy of
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
Convergence of Singular Integral Operators in Weighted Lebesgue Spaces
 EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
EUROPEAN JOURNAL OF PURE AND APPLIED MATHEMATICS Vol. 10, No. 2, 2017, 335-347 ISSN 1307-5543 www.ejpm.com Published by New York Business Globl Convergence of Singulr Inegrl Operors in Weighed Lebesgue
T-Match: Matching Techniques For Driving Yagi-Uda Antennas: T-Match. 2a s. Z in. (Sections 9.5 & 9.7 of Balanis)
 3/0/018 _mch.doc Pge 1 of 6 T-Mch: Mching Techniques For Driving Ygi-Ud Anenns: T-Mch (Secions 9.5 & 9.7 of Blnis) l s l / l / in The T-Mch is shun-mching echnique h cn be used o feed he driven elemen
3/0/018 _mch.doc Pge 1 of 6 T-Mch: Mching Techniques For Driving Ygi-Ud Anenns: T-Mch (Secions 9.5 & 9.7 of Blnis) l s l / l / in The T-Mch is shun-mching echnique h cn be used o feed he driven elemen
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Lecture 2e Orthogonal Complement (pages )
 Lecture 2e Orthogonl Complement (pges -) We hve now seen tht n orthonorml sis is nice wy to descrie suspce, ut knowing tht we wnt n orthonorml sis doesn t mke one fll into our lp. In theory, the process
Lecture 2e Orthogonl Complement (pges -) We hve now seen tht n orthonorml sis is nice wy to descrie suspce, ut knowing tht we wnt n orthonorml sis doesn t mke one fll into our lp. In theory, the process
rank Additionally system of equation only independent atfect Gawp (A) possible ( Alb ) easily process form rang A. Proposition with Definition
 Defiion nexivnol numer ler dependen rows mrix sid row Gwp elimion mehod does no fec h numer end process i possile esily red rng fc for mrix form der zz rn rnk wih m dcussion i holds rr o Proposiion ler
Defiion nexivnol numer ler dependen rows mrix sid row Gwp elimion mehod does no fec h numer end process i possile esily red rng fc for mrix form der zz rn rnk wih m dcussion i holds rr o Proposiion ler
FM Applications of Integration 1.Centroid of Area
 FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR IAN KNOWLES
 A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
Bases for Vector Spaces
 Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
(b) 10 yr. (b) 13 m. 1.6 m s, m s m s (c) 13.1 s. 32. (a) 20.0 s (b) No, the minimum distance to stop = 1.00 km. 1.
 Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Properties of Logarithms. Solving Exponential and Logarithmic Equations. Properties of Logarithms. Properties of Logarithms. ( x)
 Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Hamilton- J acobi Equation: Weak S olution We continue the study of the Hamilton-Jacobi equation:
 M ah 5 7 Fall 9 L ecure O c. 4, 9 ) Hamilon- J acobi Equaion: Weak S oluion We coninue he sudy of he Hamilon-Jacobi equaion: We have shown ha u + H D u) = R n, ) ; u = g R n { = }. ). In general we canno
M ah 5 7 Fall 9 L ecure O c. 4, 9 ) Hamilon- J acobi Equaion: Weak S oluion We coninue he sudy of he Hamilon-Jacobi equaion: We have shown ha u + H D u) = R n, ) ; u = g R n { = }. ). In general we canno
graph of unit step function t
 .5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
.5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
A LOG IS AN EXPONENT.
 Ojeives: n nlze nd inerpre he ehvior of rihmi funions, inluding end ehvior nd smpoes. n solve rihmi equions nlill nd grphill. n grph rihmi funions. n deermine he domin nd rnge of rihmi funions. n deermine
Ojeives: n nlze nd inerpre he ehvior of rihmi funions, inluding end ehvior nd smpoes. n solve rihmi equions nlill nd grphill. n grph rihmi funions. n deermine he domin nd rnge of rihmi funions. n deermine
MAT 266 Calculus for Engineers II Notes on Chapter 6 Professor: John Quigg Semester: spring 2017
 MAT 66 Clculus for Engineers II Noes on Chper 6 Professor: John Quigg Semeser: spring 7 Secion 6.: Inegrion by prs The Produc Rule is d d f()g() = f()g () + f ()g() Tking indefinie inegrls gives [f()g
MAT 66 Clculus for Engineers II Noes on Chper 6 Professor: John Quigg Semeser: spring 7 Secion 6.: Inegrion by prs The Produc Rule is d d f()g() = f()g () + f ()g() Tking indefinie inegrls gives [f()g
PARABOLA. moves such that PM. = e (constant > 0) (eccentricity) then locus of P is called a conic. or conic section.
 wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
Graduate Algorithms CS F-18 Flow Networks
 Grue Algorihm CS673-2016F-18 Flow Nework Dvi Glle Deprmen of Compuer Siene Univeriy of Sn Frnio 18-0: Flow Nework Diree Grph G Eh ege weigh i piy Amoun of wer/eon h n flow hrough pipe, for inne Single
Grue Algorihm CS673-2016F-18 Flow Nework Dvi Glle Deprmen of Compuer Siene Univeriy of Sn Frnio 18-0: Flow Nework Diree Grph G Eh ege weigh i piy Amoun of wer/eon h n flow hrough pipe, for inne Single
Online Convex Optimization Example And Follow-The-Leader
 CSE599s, Spring 2014, Online Learning Lecure 2-04/03/2014 Online Convex Opimizaion Example And Follow-The-Leader Lecurer: Brendan McMahan Scribe: Sephen Joe Jonany 1 Review of Online Convex Opimizaion
CSE599s, Spring 2014, Online Learning Lecure 2-04/03/2014 Online Convex Opimizaion Example And Follow-The-Leader Lecurer: Brendan McMahan Scribe: Sephen Joe Jonany 1 Review of Online Convex Opimizaion
Forms of Energy. Mass = Energy. Page 1. SPH4U: Introduction to Work. Work & Energy. Particle Physics:
 SPH4U: Inroducion o ork ork & Energy ork & Energy Discussion Definiion Do Produc ork of consn force ork/kineic energy heore ork of uliple consn forces Coens One of he os iporn conceps in physics Alernive
SPH4U: Inroducion o ork ork & Energy ork & Energy Discussion Definiion Do Produc ork of consn force ork/kineic energy heore ork of uliple consn forces Coens One of he os iporn conceps in physics Alernive
Solutions to assignment 3
 D Sruure n Algorihm FR 6. Informik Sner, Telikeplli WS 03/04 hp://www.mpi-.mpg.e/~ner/oure/lg03/inex.hml Soluion o ignmen 3 Exerie Arirge i he ue of irepnie in urreny exhnge re o rnform one uni of urreny
D Sruure n Algorihm FR 6. Informik Sner, Telikeplli WS 03/04 hp://www.mpi-.mpg.e/~ner/oure/lg03/inex.hml Soluion o ignmen 3 Exerie Arirge i he ue of irepnie in urreny exhnge re o rnform one uni of urreny
ECE Microwave Engineering
 EE 537-635 Microwve Engineering Adped from noes y Prof. Jeffery T. Willims Fll 8 Prof. Dvid R. Jcson Dep. of EE Noes Wveguiding Srucures Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model
EE 537-635 Microwve Engineering Adped from noes y Prof. Jeffery T. Willims Fll 8 Prof. Dvid R. Jcson Dep. of EE Noes Wveguiding Srucures Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 9: The High Beta Tokamak
 .65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
.65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
Lecture Solution of a System of Linear Equation
 ChE Lecture Notes, Dept. of Chemicl Engineering, Univ. of TN, Knoville - D. Keffer, 5/9/98 (updted /) Lecture 8- - Solution of System of Liner Eqution 8. Why is it importnt to e le to solve system of liner
ChE Lecture Notes, Dept. of Chemicl Engineering, Univ. of TN, Knoville - D. Keffer, 5/9/98 (updted /) Lecture 8- - Solution of System of Liner Eqution 8. Why is it importnt to e le to solve system of liner
Chapter 7: Solving Trig Equations
 Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
Continuous Random Variables Class 5, Jeremy Orloff and Jonathan Bloom
 Lerning Gols Continuous Rndom Vriles Clss 5, 8.05 Jeremy Orloff nd Jonthn Bloom. Know the definition of continuous rndom vrile. 2. Know the definition of the proility density function (pdf) nd cumultive
Lerning Gols Continuous Rndom Vriles Clss 5, 8.05 Jeremy Orloff nd Jonthn Bloom. Know the definition of continuous rndom vrile. 2. Know the definition of the proility density function (pdf) nd cumultive
Physics 2A HW #3 Solutions
 Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
Lecture 21: Order statistics
 Lecture : Order sttistics Suppose we hve N mesurements of sclr, x i =, N Tke ll mesurements nd sort them into scending order x x x 3 x N Define the mesured running integrl S N (x) = 0 for x < x = i/n for
Lecture : Order sttistics Suppose we hve N mesurements of sclr, x i =, N Tke ll mesurements nd sort them into scending order x x x 3 x N Define the mesured running integrl S N (x) = 0 for x < x = i/n for
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
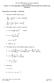 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
1B40 Practical Skills
 B40 Prcticl Skills Comining uncertinties from severl quntities error propgtion We usully encounter situtions where the result of n experiment is given in terms of two (or more) quntities. We then need
B40 Prcticl Skills Comining uncertinties from severl quntities error propgtion We usully encounter situtions where the result of n experiment is given in terms of two (or more) quntities. We then need
The Finite Element Method for the Analysis of Non-Linear and Dynamic Systems
 Swiss Federl Insiue of Pge 1 The Finie Elemen Mehod for he Anlysis of Non-Liner nd Dynmic Sysems Prof. Dr. Michel Hvbro Fber Dr. Nebojs Mojsilovic Swiss Federl Insiue of ETH Zurich, Swizerlnd Mehod of
Swiss Federl Insiue of Pge 1 The Finie Elemen Mehod for he Anlysis of Non-Liner nd Dynmic Sysems Prof. Dr. Michel Hvbro Fber Dr. Nebojs Mojsilovic Swiss Federl Insiue of ETH Zurich, Swizerlnd Mehod of
A 1.3 m 2.5 m 2.8 m. x = m m = 8400 m. y = 4900 m 3200 m = 1700 m
 PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
defines eigenvectors and associated eigenvalues whenever there are nonzero solutions ( 0
 Chper 7. Inroduion In his hper we ll explore eigeneors nd eigenlues from geomeri perspeies, lern how o use MATLAB o lgerilly idenify hem, nd ulimely see how hese noions re fmously pplied o he digonlizion
Chper 7. Inroduion In his hper we ll explore eigeneors nd eigenlues from geomeri perspeies, lern how o use MATLAB o lgerilly idenify hem, nd ulimely see how hese noions re fmously pplied o he digonlizion
Math 315: Linear Algebra Solutions to Assignment 6
 Mah 35: Linear Algebra s o Assignmen 6 # Which of he following ses of vecors are bases for R 2? {2,, 3, }, {4,, 7, 8}, {,,, 3}, {3, 9, 4, 2}. Explain your answer. To generae he whole R 2, wo linearly independen
Mah 35: Linear Algebra s o Assignmen 6 # Which of he following ses of vecors are bases for R 2? {2,, 3, }, {4,, 7, 8}, {,,, 3}, {3, 9, 4, 2}. Explain your answer. To generae he whole R 2, wo linearly independen
Let us start with a two dimensional case. We consider a vector ( x,
 Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
Lecture 2-1 Kinematics in One Dimension Displacement, Velocity and Acceleration Everything in the world is moving. Nothing stays still.
 Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
2.4 Linear Inequalities and Interval Notation
 .4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
.4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Lecture 10: Wave equation, solution by spherical means
 Lecure : Wave equaion, soluion by spherical means Physical modeling eample: Elasodynamics u (; ) displacemen vecor in elasic body occupying a domain U R n, U, The posiion of he maerial poin siing a U in
Lecure : Wave equaion, soluion by spherical means Physical modeling eample: Elasodynamics u (; ) displacemen vecor in elasic body occupying a domain U R n, U, The posiion of he maerial poin siing a U in
Transforms II - Wavelets Preliminary version please report errors, typos, and suggestions for improvements
 EECS 3 Digil Signl Processing Universiy of Cliforni, Berkeley: Fll 007 Gspr November 4, 007 Trnsforms II - Wveles Preliminry version plese repor errors, ypos, nd suggesions for improvemens We follow n
EECS 3 Digil Signl Processing Universiy of Cliforni, Berkeley: Fll 007 Gspr November 4, 007 Trnsforms II - Wveles Preliminry version plese repor errors, ypos, nd suggesions for improvemens We follow n
Definite Integrals. The area under a curve can be approximated by adding up the areas of rectangles = 1 1 +
 Definite Integrls --5 The re under curve cn e pproximted y dding up the res of rectngles. Exmple. Approximte the re under y = from x = to x = using equl suintervls nd + x evluting the function t the left-hnd
Definite Integrls --5 The re under curve cn e pproximted y dding up the res of rectngles. Exmple. Approximte the re under y = from x = to x = using equl suintervls nd + x evluting the function t the left-hnd
Matrix Algebra. Matrix Addition, Scalar Multiplication and Transposition. Linear Algebra I 24
 Mtrix lger Mtrix ddition, Sclr Multipliction nd rnsposition Mtrix lger Section.. Mtrix ddition, Sclr Multipliction nd rnsposition rectngulr rry of numers is clled mtrix ( the plurl is mtrices ) nd the
Mtrix lger Mtrix ddition, Sclr Multipliction nd rnsposition Mtrix lger Section.. Mtrix ddition, Sclr Multipliction nd rnsposition rectngulr rry of numers is clled mtrix ( the plurl is mtrices ) nd the
Bridging the gap: GCSE AS Level
 Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Numerical Analysis: Trapezoidal and Simpson s Rule
 nd Simpson s Mthemticl question we re interested in numericlly nswering How to we evlute I = f (x) dx? Clculus tells us tht if F(x) is the ntiderivtive of function f (x) on the intervl [, b], then I =
nd Simpson s Mthemticl question we re interested in numericlly nswering How to we evlute I = f (x) dx? Clculus tells us tht if F(x) is the ntiderivtive of function f (x) on the intervl [, b], then I =
Reinforcement learning
 CS 75 Mchine Lening Lecue b einfocemen lening Milos Huskech milos@cs.pi.edu 539 Senno Sque einfocemen lening We wn o len conol policy: : X A We see emples of bu oupus e no given Insed of we ge feedbck
CS 75 Mchine Lening Lecue b einfocemen lening Milos Huskech milos@cs.pi.edu 539 Senno Sque einfocemen lening We wn o len conol policy: : X A We see emples of bu oupus e no given Insed of we ge feedbck
1 Linear Least Squares
 Lest Squres Pge 1 1 Liner Lest Squres I will try to be consistent in nottion, with n being the number of dt points, nd m < n being the number of prmeters in model function. We re interested in solving
Lest Squres Pge 1 1 Liner Lest Squres I will try to be consistent in nottion, with n being the number of dt points, nd m < n being the number of prmeters in model function. We re interested in solving
() t. () t r () t or v. ( t) () () ( ) = ( ) or ( ) () () () t or dv () () Section 10.4 Motion in Space: Velocity and Acceleration
 Secion 1.4 Moion in Spce: Velociy nd Acceleion We e going o dive lile deepe ino somehing we ve ledy inoduced, nmely () nd (). Discuss wih you neighbo he elionships beween posiion, velociy nd cceleion you
Secion 1.4 Moion in Spce: Velociy nd Acceleion We e going o dive lile deepe ino somehing we ve ledy inoduced, nmely () nd (). Discuss wih you neighbo he elionships beween posiion, velociy nd cceleion you
Inventory Analysis and Management. Multi-Period Stochastic Models: Optimality of (s, S) Policy for K-Convex Objective Functions
 Muli-Period Sochasic Models: Opimali of (s, S) Polic for -Convex Objecive Funcions Consider a seing similar o he N-sage newsvendor problem excep ha now here is a fixed re-ordering cos (> 0) for each (re-)order.
Muli-Period Sochasic Models: Opimali of (s, S) Polic for -Convex Objecive Funcions Consider a seing similar o he N-sage newsvendor problem excep ha now here is a fixed re-ordering cos (> 0) for each (re-)order.
Version 001 test-1 swinney (57010) 1. is constant at m/s.
 Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
The order of reaction is defined as the number of atoms or molecules whose concentration change during the chemical reaction.
 www.hechemisryguru.com Re Lw Expression Order of Recion The order of recion is defined s he number of oms or molecules whose concenrion chnge during he chemicl recion. Or The ol number of molecules or
www.hechemisryguru.com Re Lw Expression Order of Recion The order of recion is defined s he number of oms or molecules whose concenrion chnge during he chemicl recion. Or The ol number of molecules or
Chapter 2. Motion along a straight line. 9/9/2015 Physics 218
 Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
378 Relations Solutions for Chapter 16. Section 16.1 Exercises. 3. Let A = {0,1,2,3,4,5}. Write out the relation R that expresses on A.
 378 Reltions 16.7 Solutions for Chpter 16 Section 16.1 Exercises 1. Let A = {0,1,2,3,4,5}. Write out the reltion R tht expresses > on A. Then illustrte it with digrm. 2 1 R = { (5,4),(5,3),(5,2),(5,1),(5,0),(4,3),(4,2),(4,1),
378 Reltions 16.7 Solutions for Chpter 16 Section 16.1 Exercises 1. Let A = {0,1,2,3,4,5}. Write out the reltion R tht expresses > on A. Then illustrte it with digrm. 2 1 R = { (5,4),(5,3),(5,2),(5,1),(5,0),(4,3),(4,2),(4,1),
Observability of flow dependent structure functions and their use in data assimilation
 Oserviliy of flow dependen srucure funcions nd heir use in d ssimilion Pierre Guhier nd Crisin Lupu Collorion wih Séphne Lroche, Mrk Buehner nd Ahmed Mhidji (Env. Cnd) 3rd meeing of he HORPEX DAOS-WG Monrél
Oserviliy of flow dependen srucure funcions nd heir use in d ssimilion Pierre Guhier nd Crisin Lupu Collorion wih Séphne Lroche, Mrk Buehner nd Ahmed Mhidji (Env. Cnd) 3rd meeing of he HORPEX DAOS-WG Monrél
Physic 231 Lecture 4. Mi it ftd l t. Main points of today s lecture: Example: addition of velocities Trajectories of objects in 2 = =
 Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
Review of Gaussian Quadrature method
 Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
Math 1B, lecture 4: Error bounds for numerical methods
 Mth B, lecture 4: Error bounds for numericl methods Nthn Pflueger 4 September 0 Introduction The five numericl methods descried in the previous lecture ll operte by the sme principle: they pproximte the
Mth B, lecture 4: Error bounds for numericl methods Nthn Pflueger 4 September 0 Introduction The five numericl methods descried in the previous lecture ll operte by the sme principle: they pproximte the
SCHOOL OF ENGINEERING & BUILT ENVIRONMENT. Mathematics
 SCHOOL OF ENGINEERING & BUIL ENVIRONMEN Mthemtics An Introduction to Mtrices Definition of Mtri Size of Mtri Rows nd Columns of Mtri Mtri Addition Sclr Multipliction of Mtri Mtri Multipliction 7 rnspose
SCHOOL OF ENGINEERING & BUIL ENVIRONMEN Mthemtics An Introduction to Mtrices Definition of Mtri Size of Mtri Rows nd Columns of Mtri Mtri Addition Sclr Multipliction of Mtri Mtri Multipliction 7 rnspose
Flow Networks Alon Efrat Slides courtesy of Charles Leiserson with small changes by Carola Wenk. Flow networks. Flow networks CS 445
 CS 445 Flow Nework lon Efr Slide corey of Chrle Leieron wih mll chnge by Crol Wenk Flow nework Definiion. flow nework i direced grph G = (V, E) wih wo diingihed erice: orce nd ink. Ech edge (, ) E h nonnegie
CS 445 Flow Nework lon Efr Slide corey of Chrle Leieron wih mll chnge by Crol Wenk Flow nework Definiion. flow nework i direced grph G = (V, E) wih wo diingihed erice: orce nd ink. Ech edge (, ) E h nonnegie
