Magnetostatics Bar Magnet. Magnetostatics Oersted s Experiment
|
|
|
- Caroline Williams
- 6 years ago
- Views:
Transcription
1 Mgneosics Br Mgne As fr bck s 4500 yers go, he Chinese discovered h cerin ypes of iron ore could rc ech oher nd cerin mels. Iron filings "mp" of br mgne s field Crefully suspended slivers of his mel were found o lwys poin in he sme direcion, nd s such could be used s compsses for nvigion. The firs compss is hough o hve been used by he Chinese in bou 76 B.C Greeks found his iron ore ner Mgnesi, in wh is presen dy Turkey. I conined mgneie (Fe O 4 ), nd cme o be known s mgneic lodesone. Mgneic field in br mgne Mgneosics Oersed s Experimen A compss is n exremely simple device. A mgneic compss consiss of smll, lighweigh mgne blnced on nerly fricionless pivo poin. Mgneic Compss The mgne is generlly clled needle. One end of he needle is ofen mrked "N," for norh, or colored in some wy o indice h i poins owrd norh. On he surfce, h's ll here is o compss In 1600, Willim Gilber of Englnd posuled h mgneic lodesones, or compsses, work becuse he erh is one big mgne. The mgneic field is genered by he spin of he molen inner core. The norh end of compss needle poins o he geogrphic norh pole, which corresponds o he erh s souh mgneic pole. Mgneic Compss The Erh cn be hough of gignic br mgne buried inside. In order for he norh end of he compss o poin owrd he Norh Pole, you hve o ssume h he buried br mgne hs is souh end he Norh Pole. 1
2 Mgneosics Oersed s Experimen In 180, Hns Chrisin Oersed ( ) used compss o show h curren produces mgneic fields h loop round he conducor Oersed s experimen Mgneism nd elecriciy were considered disinc phenomen unil 180 when Hns Chrisin Oersed conduced n experimen h showed compss needle deflecing when in proximiy o curren crrying wire. I ws observed h moving wy from he source of curren, he field grows weker. Oersed s discovery relesed flood of sudy h culmined in Mxwell s equions in Mgneosics Bio-Svr s Lw Shorly following Oersed s discovery h currens produce mgneic fields, Jen Bpise Bio ( ) nd Felix Svr ( ) rrived mhemicl relion beween he field nd curren. The Lw of Bio-Svr is dh IdL (A/m) To ge he ol field resuling from curren, you cn sum he conribuions from ech segmen by inegring IdL H Noe: The Bio-Svr lw is nlogous o he Coulomb s lw equion for he elecric field resuling from differenil chrge de dq 1 1 ε 1.. (A/m)
3 Mgneosics An Infinie Line curren Exmple.: Consider n infinie lengh line long he -xis conducing curren I in he + direcion. We wn o find he mgneic field everywhere. We firs inspec he symmery nd see h he field will be independen of nd φ nd only dependen on ρ. So we consider poin disnce r from he line long he ρ xis. The Bio-Svr Lw IdL H An infinie lengh line of curren IdL is simply Id, nd he vecor from he source o he es poin is +ρ ρ The Bio-Svr Lw becomes H ( + ρ ρ ) + ρ Id. Mgneosics An Infinie Line curren Pulling he consns o he lef of he inegrl nd reliing h x 0 nd x ρ φ, we hve I ρφ d H + ρ The inegrl cn be evlued using he formul given in Appendix D dx x + x + I + ρ ρ ρ ρ + + ρ ρ + When he limi d I ρ + ρ ρ ρ ρ + 1 ρ + 1 x d I ρ ρ ρ ρ ρ ρ ρ + ρ ρ +
4 Mgneosics An Infinie Line curren I ρφ d H + ρ d Using I ρ + ρ An infinie lengh line of curren We find he mgneic field inensiy resuling from n infinie lengh line of curren is I φ H πρ H 1 ρ φ Direcion: The direcion of he mgneic field cn be found using he righ hnd rule. Mgniude: The mgniude of he mgneic field is inversely proporionl o rdil disnce. Mgneosics A ing of Curren Exmple.: Le us now consider ring of curren wih rdius lying in he x-y plne wih curren I in he + direcion. The objecive is o find n expression for he field n rbirry poin heigh h on he -xis. The Bio-Svr Lw IdL H H The differenil segmen dl dφ φ The vecor drwn from he source o he es poin is h Mgniude: ρ h + Uni Vecor: ( h ) ρ The bio-svr Lw cn be wrien s ( ) ( ) Idφ h I dφ h π π φ ρ φ ρ φ 0 φ 0 h + h + 4
5 Mgneosics A ing of Curren We cn furher simplify his expression by considering he symmery of he problem ( ) ( ) π π I dφ h I dφ h + φ ρ ρ H 4 φ 0 h π + φ 0 h + A priculr differenil curren elemen will give field wih n ρ componen (from φ x ) nd n componen (from φ x ρ ). Tking he field from differenil curren elemen on he opposie side of he ring, i is ppren h he rdil componens cncel while he componens dd. componens dd ρ Componens Cncel I H π 0 ( h + ) I H dφ H I ( h + ) A h 0, he cener of he loop, his equion reduces o H Mgneosics A Solenoid Solenoids re mny urns of insuled wire coiled in he shpe of cylinder. Suppose he solenoid hs lengh h, rdius, nd is mde up of N urns of curren crrying wire. For igh wrpping, we cn consider he solenoid o be mde up of N loops of curren. A solenoid To find he mgneic field inensiy from single loop poin P long he xis of he solenoid, from we hve The differenil moun of field resuling from differenil moun of curren is given by dh P di ' ( + ) The differenil moun of curren cn be considered funcion of he number of loops nd he lengh of he solenoid s N di Id ' h 5
6 Mgneosics A Solenoid Fixing he poin P where he field is desired, will rnge from o h-, or h NI d ' H h ' + h NI d ' h ' ( + ). This inegrl is found from Appendix D, leding o he soluion NI h H + h h + + A he very cener of he solenoid ( h/), wih he ssumpion h he lengh is considerbly bigger hn he loop rdius (h >> ), he equion reduces o NI H h 6
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
MATH 124 AND 125 FINAL EXAM REVIEW PACKET (Revised spring 2008)
 MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
Phys 110. Answers to even numbered problems on Midterm Map
 Phys Answers o een numbered problems on Miderm Mp. REASONING The word per indices rio, so.35 mm per dy mens.35 mm/d, which is o be epressed s re in f/cenury. These unis differ from he gien unis in boh
Phys Answers o een numbered problems on Miderm Mp. REASONING The word per indices rio, so.35 mm per dy mens.35 mm/d, which is o be epressed s re in f/cenury. These unis differ from he gien unis in boh
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
 PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
FM Applications of Integration 1.Centroid of Area
 FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 9: The High Beta Tokamak
 .65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
.65, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 9: The High e Tokmk Summry of he Properies of n Ohmic Tokmk. Advnges:. good euilibrium (smll shif) b. good sbiliy ( ) c. good confinemen ( τ nr )
ECE Microwave Engineering
 EE 537-635 Microwve Engineering Adped from noes y Prof. Jeffery T. Willims Fll 8 Prof. Dvid R. Jcson Dep. of EE Noes Wveguiding Srucures Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model
EE 537-635 Microwve Engineering Adped from noes y Prof. Jeffery T. Willims Fll 8 Prof. Dvid R. Jcson Dep. of EE Noes Wveguiding Srucures Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
Version 001 test-1 swinney (57010) 1. is constant at m/s.
 Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
3 Motion with constant acceleration: Linear and projectile motion
 3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
September 20 Homework Solutions
 College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
Mathematics 805 Final Examination Answers
 . 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
. 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
Physics 2A HW #3 Solutions
 Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
Physics for Scientists & Engineers 2
 Direc Curren Physics for Scieniss & Engineers 2 Spring Semeser 2005 Lecure 16 This week we will sudy charges in moion Elecric charge moving from one region o anoher is called elecric curren Curren is all
Direc Curren Physics for Scieniss & Engineers 2 Spring Semeser 2005 Lecure 16 This week we will sudy charges in moion Elecric charge moving from one region o anoher is called elecric curren Curren is all
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q). INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg) INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
ECE Microwave Engineering. Fall Prof. David R. Jackson Dept. of ECE. Notes 10. Waveguides Part 7: Transverse Equivalent Network (TEN)
 EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
EE 537-635 Microwve Engineering Fll 7 Prof. Dvid R. Jcson Dep. of EE Noes Wveguides Pr 7: Trnsverse Equivlen Newor (N) Wveguide Trnsmission Line Model Our gol is o come up wih rnsmission line model for
Minimum Squared Error
 Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
A 1.3 m 2.5 m 2.8 m. x = m m = 8400 m. y = 4900 m 3200 m = 1700 m
 PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
REAL ANALYSIS I HOMEWORK 3. Chapter 1
 REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
REAL ANALYSIS I HOMEWORK 3 CİHAN BAHRAN The quesions re from Sein nd Shkrchi s e. Chper 1 18. Prove he following sserion: Every mesurble funcion is he limi.e. of sequence of coninuous funcions. We firs
graph of unit step function t
 .5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
.5 Piecewie coninuou forcing funcion...e.g. urning he forcing on nd off. The following Lplce rnform meril i ueful in yem where we urn forcing funcion on nd off, nd when we hve righ hnd ide "forcing funcion"
4. Electric field lines with respect to equipotential surfaces are
 Pre-es Quasi-saic elecromagneism. The field produced by primary charge Q and by an uncharged conducing plane disanced from Q by disance d is equal o he field produced wihou conducing plane by wo following
Pre-es Quasi-saic elecromagneism. The field produced by primary charge Q and by an uncharged conducing plane disanced from Q by disance d is equal o he field produced wihou conducing plane by wo following
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
Chapter Direct Method of Interpolation
 Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
PHY2048 Exam 1 Formula Sheet Vectors. Motion. v ave (3 dim) ( (1 dim) dt. ( (3 dim) Equations of Motion (Constant Acceleration)
 Insrucors: Field/Mche PHYSICS DEPATMENT PHY 48 Em Ferur, 5 Nme prin, ls firs: Signure: On m honor, I he neiher gien nor receied unuhoried id on his eminion. YOU TEST NUMBE IS THE 5-DIGIT NUMBE AT THE TOP
Insrucors: Field/Mche PHYSICS DEPATMENT PHY 48 Em Ferur, 5 Nme prin, ls firs: Signure: On m honor, I he neiher gien nor receied unuhoried id on his eminion. YOU TEST NUMBE IS THE 5-DIGIT NUMBE AT THE TOP
Physics 101 Lecture 4 Motion in 2D and 3D
 Phsics 11 Lecure 4 Moion in D nd 3D Dr. Ali ÖVGÜN EMU Phsics Deprmen www.ogun.com Vecor nd is componens The componens re he legs of he righ ringle whose hpoenuse is A A A A A n ( θ ) A Acos( θ) A A A nd
Phsics 11 Lecure 4 Moion in D nd 3D Dr. Ali ÖVGÜN EMU Phsics Deprmen www.ogun.com Vecor nd is componens The componens re he legs of he righ ringle whose hpoenuse is A A A A A n ( θ ) A Acos( θ) A A A nd
( ) ( ) ( ) ( ) ( ) ( y )
 8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
8. Lengh of Plne Curve The mos fmous heorem in ll of mhemics is he Pyhgoren Theorem. I s formulion s he disnce formul is used o find he lenghs of line segmens in he coordine plne. In his secion you ll
The solution is often represented as a vector: 2xI + 4X2 + 2X3 + 4X4 + 2X5 = 4 2xI + 4X2 + 3X3 + 3X4 + 3X5 = 4. 3xI + 6X2 + 6X3 + 3X4 + 6X5 = 6.
 [~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
[~ o o :- o o ill] i 1. Mrices, Vecors, nd Guss-Jordn Eliminion 1 x y = = - z= The soluion is ofen represened s vecor: n his exmple, he process of eliminion works very smoohly. We cn elimine ll enries
- If one knows that a magnetic field has a symmetry, one may calculate the magnitude of B by use of Ampere s law: The integral of scalar product
 11.1 APPCATON OF AMPEE S AW N SYMMETC MAGNETC FEDS - f one knows ha a magneic field has a symmery, one may calculae he magniude of by use of Ampere s law: The inegral of scalar produc Closed _ pah * d
11.1 APPCATON OF AMPEE S AW N SYMMETC MAGNETC FEDS - f one knows ha a magneic field has a symmery, one may calculae he magniude of by use of Ampere s law: The inegral of scalar produc Closed _ pah * d
CBSE 2014 ANNUAL EXAMINATION ALL INDIA
 CBSE ANNUAL EXAMINATION ALL INDIA SET Wih Complee Eplnions M Mrks : SECTION A Q If R = {(, y) : + y = 8} is relion on N, wrie he rnge of R Sol Since + y = 8 h implies, y = (8 ) R = {(, ), (, ), (6, )}
CBSE ANNUAL EXAMINATION ALL INDIA SET Wih Complee Eplnions M Mrks : SECTION A Q If R = {(, y) : + y = 8} is relion on N, wrie he rnge of R Sol Since + y = 8 h implies, y = (8 ) R = {(, ), (, ), (6, )}
2D Motion WS. A horizontally launched projectile s initial vertical velocity is zero. Solve the following problems with this information.
 Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
Physic 231 Lecture 4. Mi it ftd l t. Main points of today s lecture: Example: addition of velocities Trajectories of objects in 2 = =
 Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
Mi i fd l Phsic 3 Lecure 4 Min poins of od s lecure: Emple: ddiion of elociies Trjecories of objecs in dimensions: dimensions: g 9.8m/s downwrds ( ) g o g g Emple: A foobll pler runs he pern gien in he
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR IAN KNOWLES
 A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
A LIMIT-POINT CRITERION FOR A SECOND-ORDER LINEAR DIFFERENTIAL OPERATOR j IAN KNOWLES 1. Inroducion Consider he forml differenil operor T defined by el, (1) where he funcion q{) is rel-vlued nd loclly
Some Inequalities variations on a common theme Lecture I, UL 2007
 Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
Some Inequliies vriions on common heme Lecure I, UL 2007 Finbrr Hollnd, Deprmen of Mhemics, Universiy College Cork, fhollnd@uccie; July 2, 2007 Three Problems Problem Assume i, b i, c i, i =, 2, 3 re rel
An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples.
 Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Improper Inegrls To his poin we hve only considered inegrls f(x) wih he is of inegrion nd b finie nd he inegrnd f(x) bounded (nd in fc coninuous excep possibly for finiely mny jump disconinuiies) An inegrl
Motion in a Straight Line
 Moion in Srigh Line. Preei reched he mero sion nd found h he esclor ws no working. She wlked up he sionry esclor in ime. On oher dys, if she remins sionry on he moing esclor, hen he esclor kes her up in
Moion in Srigh Line. Preei reched he mero sion nd found h he esclor ws no working. She wlked up he sionry esclor in ime. On oher dys, if she remins sionry on he moing esclor, hen he esclor kes her up in
CHAPTER 2 KINEMATICS IN ONE DIMENSION ANSWERS TO FOCUS ON CONCEPTS QUESTIONS
 Physics h Ediion Cunell Johnson Young Sdler Soluions Mnul Soluions Mnul, Answer keys, Insrucor's Resource Mnul for ll chpers re included. Compleed downlod links: hps://esbnkre.com/downlod/physics-h-ediion-soluions-mnulcunell-johnson-young-sdler/
Physics h Ediion Cunell Johnson Young Sdler Soluions Mnul Soluions Mnul, Answer keys, Insrucor's Resource Mnul for ll chpers re included. Compleed downlod links: hps://esbnkre.com/downlod/physics-h-ediion-soluions-mnulcunell-johnson-young-sdler/
Chapter 2. Motion along a straight line. 9/9/2015 Physics 218
 Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Chapter 4 AC Network Analysis
 haper 4 A Nework Analysis Jaesung Jang apaciance Inducance and Inducion Time-Varying Signals Sinusoidal Signals Reference: David K. heng, Field and Wave Elecromagneics. Energy Sorage ircui Elemens Energy
haper 4 A Nework Analysis Jaesung Jang apaciance Inducance and Inducion Time-Varying Signals Sinusoidal Signals Reference: David K. heng, Field and Wave Elecromagneics. Energy Sorage ircui Elemens Energy
Unique Solutions R. All about Electromagnetism. C h a p t e r. G l a n c e
 5. C h p t e r t G l n c e When electric current is pssed through conductor, it produces mgnetic field round it. The first discovery of the connection between electricity nd mgnetism ws mde by H. C. Oersted.
5. C h p t e r t G l n c e When electric current is pssed through conductor, it produces mgnetic field round it. The first discovery of the connection between electricity nd mgnetism ws mde by H. C. Oersted.
copper ring magnetic field
 IB PHYSICS: Magneic Fields, lecromagneic Inducion, Alernaing Curren 1. This quesion is abou elecromagneic inducion. In 1831 Michael Faraday demonsraed hree ways of inducing an elecric curren in a ring
IB PHYSICS: Magneic Fields, lecromagneic Inducion, Alernaing Curren 1. This quesion is abou elecromagneic inducion. In 1831 Michael Faraday demonsraed hree ways of inducing an elecric curren in a ring
Solutions to Problems from Chapter 2
 Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Soluions o Problems rom Chper Problem. The signls u() :5sgn(), u () :5sgn(), nd u h () :5sgn() re ploed respecively in Figures.,b,c. Noe h u h () :5sgn() :5; 8 including, bu u () :5sgn() is undeined..5
Average & instantaneous velocity and acceleration Motion with constant acceleration
 Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
More on Magnetically C Coupled Coils and Ideal Transformers
 Appenix ore on gneiclly C Couple Coils Iel Trnsformers C. Equivlen Circuis for gneiclly Couple Coils A imes, i is convenien o moel mgneiclly couple coils wih n equivlen circui h oes no involve mgneic coupling.
Appenix ore on gneiclly C Couple Coils Iel Trnsformers C. Equivlen Circuis for gneiclly Couple Coils A imes, i is convenien o moel mgneiclly couple coils wih n equivlen circui h oes no involve mgneic coupling.
ME 141. Engineering Mechanics
 ME 141 Engineeing Mechnics Lecue 13: Kinemics of igid bodies hmd Shhedi Shkil Lecue, ep. of Mechnicl Engg, UET E-mil: sshkil@me.bue.c.bd, shkil6791@gmil.com Websie: eche.bue.c.bd/sshkil Couesy: Veco Mechnics
ME 141 Engineeing Mechnics Lecue 13: Kinemics of igid bodies hmd Shhedi Shkil Lecue, ep. of Mechnicl Engg, UET E-mil: sshkil@me.bue.c.bd, shkil6791@gmil.com Websie: eche.bue.c.bd/sshkil Couesy: Veco Mechnics
Hall effect. Formulae :- 1) Hall coefficient RH = cm / Coulumb. 2) Magnetic induction BY 2
 Page of 6 all effec Aim :- ) To deermine he all coefficien (R ) ) To measure he unknown magneic field (B ) and o compare i wih ha measured by he Gaussmeer (B ). Apparaus :- ) Gauss meer wih probe ) Elecromagne
Page of 6 all effec Aim :- ) To deermine he all coefficien (R ) ) To measure he unknown magneic field (B ) and o compare i wih ha measured by he Gaussmeer (B ). Apparaus :- ) Gauss meer wih probe ) Elecromagne
Circuits 24/08/2010. Question. Question. Practice Questions QV CV. Review Formula s RC R R R V IR ... Charging P IV I R ... E Pt.
 4/08/00 eview Fomul s icuis cice s BL B A B I I I I E...... s n n hging Q Q 0 e... n... Q Q n 0 e Q I I0e Dischging Q U Q A wie mde of bss nd nohe wie mde of silve hve he sme lengh, bu he dimee of he bss
4/08/00 eview Fomul s icuis cice s BL B A B I I I I E...... s n n hging Q Q 0 e... n... Q Q n 0 e Q I I0e Dischging Q U Q A wie mde of bss nd nohe wie mde of silve hve he sme lengh, bu he dimee of he bss
3. Renewal Limit Theorems
 Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Virul Lborories > 14. Renewl Processes > 1 2 3 3. Renewl Limi Theorems In he inroducion o renewl processes, we noed h he rrivl ime process nd he couning process re inverses, in sens The rrivl ime process
Chapter 7 Steady Magnetic Field. september 2016 Microwave Laboratory Sogang University
 Chpter 7 Stedy Mgnetic Field september 2016 Microwve Lbortory Sogng University Teching point Wht is the mgnetic field? Biot-Svrt s lw: Coulomb s lw of Mgnetic field Stedy current: current flow is independent
Chpter 7 Stedy Mgnetic Field september 2016 Microwve Lbortory Sogng University Teching point Wht is the mgnetic field? Biot-Svrt s lw: Coulomb s lw of Mgnetic field Stedy current: current flow is independent
Chapter 10. Simple Harmonic Motion and Elasticity. Goals for Chapter 10
 Chper 0 Siple Hronic Moion nd Elsiciy Gols or Chper 0 o ollow periodic oion o sudy o siple hronic oion. o sole equions o siple hronic oion. o use he pendulu s prooypicl syse undergoing siple hronic oion.
Chper 0 Siple Hronic Moion nd Elsiciy Gols or Chper 0 o ollow periodic oion o sudy o siple hronic oion. o sole equions o siple hronic oion. o use he pendulu s prooypicl syse undergoing siple hronic oion.
15. Vector Valued Functions
 1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
1 jordan.mcd Eigenvalue-eigenvector approach to solving first order ODEs. -- Jordan normal (canonical) form. Instructor: Nam Sun Wang
 jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
jordnmcd Eigenvlue-eigenvecor pproch o solving firs order ODEs -- ordn norml (cnonicl) form Insrucor: Nm Sun Wng Consider he following se of coupled firs order ODEs d d x x 5 x x d d x d d x x x 5 x x
() t. () t r () t or v. ( t) () () ( ) = ( ) or ( ) () () () t or dv () () Section 10.4 Motion in Space: Velocity and Acceleration
 Secion 1.4 Moion in Spce: Velociy nd Acceleion We e going o dive lile deepe ino somehing we ve ledy inoduced, nmely () nd (). Discuss wih you neighbo he elionships beween posiion, velociy nd cceleion you
Secion 1.4 Moion in Spce: Velociy nd Acceleion We e going o dive lile deepe ino somehing we ve ledy inoduced, nmely () nd (). Discuss wih you neighbo he elionships beween posiion, velociy nd cceleion you
An object moving with speed v around a point at distance r, has an angular velocity. m/s m
 Roion The mosphere roes wih he erh n moions wihin he mosphere clerly follow cure phs (cyclones, nicyclones, hurricnes, ornoes ec.) We nee o epress roion quniiely. For soli objec or ny mss h oes no isor
Roion The mosphere roes wih he erh n moions wihin he mosphere clerly follow cure phs (cyclones, nicyclones, hurricnes, ornoes ec.) We nee o epress roion quniiely. For soli objec or ny mss h oes no isor
Name: Total Points: Multiple choice questions [120 points]
![Name: Total Points: Multiple choice questions [120 points] Name: Total Points: Multiple choice questions [120 points]](/thumbs/88/115221528.jpg) Name: Toal Poins: (Las) (Firs) Muliple choice quesions [1 poins] Answer all of he following quesions. Read each quesion carefully. Fill he correc bubble on your scanron shee. Each correc answer is worh
Name: Toal Poins: (Las) (Firs) Muliple choice quesions [1 poins] Answer all of he following quesions. Read each quesion carefully. Fill he correc bubble on your scanron shee. Each correc answer is worh
in a uniform magnetic flux density B = Boa z. (a) Show that the electron moves in a circular path. (b) Find the radius r o
 6. THE TATC MAGNETC FELD 6- LOENTZ FOCE EQUATON Lorent force eqution F = Fe + Fm = q ( E + v B ) Exmple 6- An electron hs n initil velocity vo = vo y in uniform mgnetic flux density B = Bo. () how tht
6. THE TATC MAGNETC FELD 6- LOENTZ FOCE EQUATON Lorent force eqution F = Fe + Fm = q ( E + v B ) Exmple 6- An electron hs n initil velocity vo = vo y in uniform mgnetic flux density B = Bo. () how tht
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
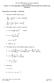 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
M r. d 2. R t a M. Structural Mechanics Section. Exam CT5141 Theory of Elasticity Friday 31 October 2003, 9:00 12:00 hours. Problem 1 (3 points)
 Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
Problem Set #1. i z. the complex propagation constant. For the characteristic impedance:
 Problem Se # Problem : a) Using phasor noaion, calculae he volage and curren waves on a ransmission line by solving he wave equaion Assume ha R, L,, G are all non-zero and independen of frequency From
Problem Se # Problem : a) Using phasor noaion, calculae he volage and curren waves on a ransmission line by solving he wave equaion Assume ha R, L,, G are all non-zero and independen of frequency From
Physics Jonathan Dowling. Lecture 9 FIRST MIDTERM REVIEW
 Physics 10 Jonthn Dowling Physics 10 ecture 9 FIRST MIDTERM REVIEW A few concepts: electric force, field nd potentil Electric force: Wht is the force on chrge produced by other chrges? Wht is the force
Physics 10 Jonthn Dowling Physics 10 ecture 9 FIRST MIDTERM REVIEW A few concepts: electric force, field nd potentil Electric force: Wht is the force on chrge produced by other chrges? Wht is the force
CHAPTER 12 DIRECT CURRENT CIRCUITS
 CHAPTER 12 DIRECT CURRENT CIUITS DIRECT CURRENT CIUITS 257 12.1 RESISTORS IN SERIES AND IN PARALLEL When wo resisors are conneced ogeher as shown in Figure 12.1 we said ha hey are conneced in series. As
CHAPTER 12 DIRECT CURRENT CIUITS DIRECT CURRENT CIUITS 257 12.1 RESISTORS IN SERIES AND IN PARALLEL When wo resisors are conneced ogeher as shown in Figure 12.1 we said ha hey are conneced in series. As
Think of the Relationship Between Time and Space Again
 Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
Repor nd Opinion, 1(3),009 hp://wwwsciencepubne sciencepub@gmilcom Think of he Relionship Beween Time nd Spce Agin Yng F-cheng Compny of Ruid Cenre in Xinjing 15 Hongxing Sree, Klmyi, Xingjing 834000,
Reinforcement learning
 CS 75 Mchine Lening Lecue b einfocemen lening Milos Huskech milos@cs.pi.edu 539 Senno Sque einfocemen lening We wn o len conol policy: : X A We see emples of bu oupus e no given Insed of we ge feedbck
CS 75 Mchine Lening Lecue b einfocemen lening Milos Huskech milos@cs.pi.edu 539 Senno Sque einfocemen lening We wn o len conol policy: : X A We see emples of bu oupus e no given Insed of we ge feedbck
Location is relative. Coordinate Systems. Which of the following can be described with vectors??
 Locion is relive Coordine Sysems The posiion o hing is sed relive o noher hing (rel or virul) review o he physicl sis h governs mhemicl represenions Reerence oec mus e deined Disnce mus e nown Direcion
Locion is relive Coordine Sysems The posiion o hing is sed relive o noher hing (rel or virul) review o he physicl sis h governs mhemicl represenions Reerence oec mus e deined Disnce mus e nown Direcion
Homework Assignment 3 Solution Set
 Homework Assignment 3 Solution Set PHYCS 44 6 Ferury, 4 Prolem 1 (Griffiths.5(c The potentil due to ny continuous chrge distriution is the sum of the contriutions from ech infinitesiml chrge in the distriution.
Homework Assignment 3 Solution Set PHYCS 44 6 Ferury, 4 Prolem 1 (Griffiths.5(c The potentil due to ny continuous chrge distriution is the sum of the contriutions from ech infinitesiml chrge in the distriution.
Ch.4 Motion in 2D. Ch.4 Motion in 2D
 Moion in plne, such s in he sceen, is clled 2-dimensionl (2D) moion. 1. Posiion, displcemen nd eloci ecos If he picle s posiion is ( 1, 1 ) 1, nd ( 2, 2 ) 2, he posiions ecos e 1 = 1 1 2 = 2 2 Aege eloci
Moion in plne, such s in he sceen, is clled 2-dimensionl (2D) moion. 1. Posiion, displcemen nd eloci ecos If he picle s posiion is ( 1, 1 ) 1, nd ( 2, 2 ) 2, he posiions ecos e 1 = 1 1 2 = 2 2 Aege eloci
200 points 5 Problems on 4 Pages and 20 Multiple Choice/Short Answer Questions on 5 pages 1 hour, 48 minutes
 PHYSICS 132 Smple Finl 200 points 5 Problems on 4 Pges nd 20 Multiple Choice/Short Answer Questions on 5 pges 1 hour, 48 minutes Student Nme: Recittion Instructor (circle one): nme1 nme2 nme3 nme4 Write
PHYSICS 132 Smple Finl 200 points 5 Problems on 4 Pges nd 20 Multiple Choice/Short Answer Questions on 5 pges 1 hour, 48 minutes Student Nme: Recittion Instructor (circle one): nme1 nme2 nme3 nme4 Write
Physics 202, Lecture 13. Today s Topics
 Physics 202, Lecture 13 Tody s Topics Sources of the Mgnetic Field (Ch. 30) Clculting the B field due to currents Biot-Svrt Lw Emples: ring, stright wire Force between prllel wires Ampere s Lw: infinite
Physics 202, Lecture 13 Tody s Topics Sources of the Mgnetic Field (Ch. 30) Clculting the B field due to currents Biot-Svrt Lw Emples: ring, stright wire Force between prllel wires Ampere s Lw: infinite
Motion on a Curve and Curvature
 Moion on Cue nd Cuue his uni is bsed on Secions 9. & 9.3, Chpe 9. All ssigned edings nd execises e fom he exbook Objecies: Mke cein h you cn define, nd use in conex, he ems, conceps nd fomuls lised below:
Moion on Cue nd Cuue his uni is bsed on Secions 9. & 9.3, Chpe 9. All ssigned edings nd execises e fom he exbook Objecies: Mke cein h you cn define, nd use in conex, he ems, conceps nd fomuls lised below:
EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE BOUNDARY-VALUE PROBLEM
 Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Elecronic Journl of Differenil Equions, Vol. 208 (208), No. 50, pp. 6. ISSN: 072-669. URL: hp://ejde.mh.xse.edu or hp://ejde.mh.un.edu EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR A SECOND-ORDER ITERATIVE
Available Online :
 fo/u fopjr Hh# u] ugh vjehs de] foifr ns[ NsMs rqjr e/;e eu dj ';ea iq#" flg ldyi dj] lgrs foifr vusd] ^cu^ u NsMs /;s; ds] j?qcj j[s VsdAA jfpr% euo /ez iz.sr ln~xq# Jh j.nsmnlh egj STUDY PACKAGE Subjec
fo/u fopjr Hh# u] ugh vjehs de] foifr ns[ NsMs rqjr e/;e eu dj ';ea iq#" flg ldyi dj] lgrs foifr vusd] ^cu^ u NsMs /;s; ds] j?qcj j[s VsdAA jfpr% euo /ez iz.sr ln~xq# Jh j.nsmnlh egj STUDY PACKAGE Subjec
(b) 10 yr. (b) 13 m. 1.6 m s, m s m s (c) 13.1 s. 32. (a) 20.0 s (b) No, the minimum distance to stop = 1.00 km. 1.
 Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
ECE 3318 Applied Electricity and Magnetism. Spring Prof. David R. Jackson Dept. of ECE. Notes 31 Inductance
 ECE 3318 Applied Electricity nd Mgnetism Spring 018 Prof. Dvid R. Jckson Dept. of ECE Notes 31 nductnce 1 nductnce ˆn S Single turn coil The current produces flux though the loop. Definition of inductnce:
ECE 3318 Applied Electricity nd Mgnetism Spring 018 Prof. Dvid R. Jckson Dept. of ECE Notes 31 nductnce 1 nductnce ˆn S Single turn coil The current produces flux though the loop. Definition of inductnce:
F is on a moving charged particle. F = 0, if B v. (sin " = 0)
 F is on moving chrged prticle. Chpter 29 Mgnetic Fields Ech mgnet hs two poles, north pole nd south pole, regrdless the size nd shpe of the mgnet. Like poles repel ech other, unlike poles ttrct ech other.
F is on moving chrged prticle. Chpter 29 Mgnetic Fields Ech mgnet hs two poles, north pole nd south pole, regrdless the size nd shpe of the mgnet. Like poles repel ech other, unlike poles ttrct ech other.
Two Coupled Oscillators / Normal Modes
 Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
D zone schemes
 Ch. 5. Enegy Bnds in Cysls 5.. -D zone schemes Fee elecons E k m h Fee elecons in cysl sinα P + cosα cosk α cos α cos k cos( k + π n α k + πn mv ob P 0 h cos α cos k n α k + π m h k E Enegy is peiodic
Ch. 5. Enegy Bnds in Cysls 5.. -D zone schemes Fee elecons E k m h Fee elecons in cysl sinα P + cosα cosk α cos α cos k cos( k + π n α k + πn mv ob P 0 h cos α cos k n α k + π m h k E Enegy is peiodic
!!"#"$%&#'()!"#&'(*%)+,&',-)./0)1-*23)
 "#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
"#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
14. The fundamental theorem of the calculus
 4. The funmenl heorem of he clculus V 20 00 80 60 40 20 0 0 0.2 0.4 0.6 0.8 v 400 200 0 0 0.2 0.5 0.8 200 400 Figure : () Venriculr volume for subjecs wih cpciies C = 24 ml, C = 20 ml, C = 2 ml n (b) he
4. The funmenl heorem of he clculus V 20 00 80 60 40 20 0 0 0.2 0.4 0.6 0.8 v 400 200 0 0 0.2 0.5 0.8 200 400 Figure : () Venriculr volume for subjecs wih cpciies C = 24 ml, C = 20 ml, C = 2 ml n (b) he
CHAPTER 11 PARAMETRIC EQUATIONS AND POLAR COORDINATES
 CHAPTER PARAMETRIC EQUATIONS AND POLAR COORDINATES. PARAMETRIZATIONS OF PLANE CURVES., 9, _ _ Ê.,, Ê or, Ÿ. 5, 7, _ _.,, Ÿ Ÿ Ê Ê 5 Ê ( 5) Ê ˆ Ê 6 Ê ( 5) 7 Ê Ê, Ÿ Ÿ $ 5. cos, sin, Ÿ Ÿ 6. cos ( ), sin (
CHAPTER PARAMETRIC EQUATIONS AND POLAR COORDINATES. PARAMETRIZATIONS OF PLANE CURVES., 9, _ _ Ê.,, Ê or, Ÿ. 5, 7, _ _.,, Ÿ Ÿ Ê Ê 5 Ê ( 5) Ê ˆ Ê 6 Ê ( 5) 7 Ê Ê, Ÿ Ÿ $ 5. cos, sin, Ÿ Ÿ 6. cos ( ), sin (
Application on Inner Product Space with. Fixed Point Theorem in Probabilistic
 Journl of Applied Mhemics & Bioinformics, vol.2, no.2, 2012, 1-10 ISSN: 1792-6602 prin, 1792-6939 online Scienpress Ld, 2012 Applicion on Inner Produc Spce wih Fixed Poin Theorem in Probbilisic Rjesh Shrivsv
Journl of Applied Mhemics & Bioinformics, vol.2, no.2, 2012, 1-10 ISSN: 1792-6602 prin, 1792-6939 online Scienpress Ld, 2012 Applicion on Inner Produc Spce wih Fixed Poin Theorem in Probbilisic Rjesh Shrivsv
Physics 1402: Lecture 22 Today s Agenda
 Physics 142: ecure 22 Today s Agenda Announcemens: R - RV - R circuis Homework 6: due nex Wednesday Inducion / A curren Inducion Self-Inducance, R ircuis X X X X X X X X X long solenoid Energy and energy
Physics 142: ecure 22 Today s Agenda Announcemens: R - RV - R circuis Homework 6: due nex Wednesday Inducion / A curren Inducion Self-Inducance, R ircuis X X X X X X X X X long solenoid Energy and energy
EXERCISE - 01 CHECK YOUR GRASP
 UNIT # 09 PARABOLA, ELLIPSE & HYPERBOLA PARABOLA EXERCISE - 0 CHECK YOUR GRASP. Hin : Disnce beween direcri nd focus is 5. Given (, be one end of focl chord hen oher end be, lengh of focl chord 6. Focus
UNIT # 09 PARABOLA, ELLIPSE & HYPERBOLA PARABOLA EXERCISE - 0 CHECK YOUR GRASP. Hin : Disnce beween direcri nd focus is 5. Given (, be one end of focl chord hen oher end be, lengh of focl chord 6. Focus
Physics 202, Lecture 14
 Physics 202, Lecture 14 Tody s Topics Sources of the Mgnetic Field (Ch. 28) Biot-Svrt Lw Ampere s Lw Mgnetism in Mtter Mxwell s Equtions Homework #7: due Tues 3/11 t 11 PM (4th problem optionl) Mgnetic
Physics 202, Lecture 14 Tody s Topics Sources of the Mgnetic Field (Ch. 28) Biot-Svrt Lw Ampere s Lw Mgnetism in Mtter Mxwell s Equtions Homework #7: due Tues 3/11 t 11 PM (4th problem optionl) Mgnetic
Integral Transform. Definitions. Function Space. Linear Mapping. Integral Transform
 Inegrl Trnsform Definiions Funcion Spce funcion spce A funcion spce is liner spce of funcions defined on he sme domins & rnges. Liner Mpping liner mpping Le VF, WF e liner spces over he field F. A mpping
Inegrl Trnsform Definiions Funcion Spce funcion spce A funcion spce is liner spce of funcions defined on he sme domins & rnges. Liner Mpping liner mpping Le VF, WF e liner spces over he field F. A mpping
PARABOLA. moves such that PM. = e (constant > 0) (eccentricity) then locus of P is called a conic. or conic section.
 wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
A Prelude to EE 4301
 A Prelude o EE 401 b Duncn L. McFrlne The Erik onsson School of Engineering nd Compuer Science The Universi of Tes Dlls Richrdson Tes 7508 dlm@udlls.edu Foreword This rher focused nd unfinished documen
A Prelude o EE 401 b Duncn L. McFrlne The Erik onsson School of Engineering nd Compuer Science The Universi of Tes Dlls Richrdson Tes 7508 dlm@udlls.edu Foreword This rher focused nd unfinished documen
Transformations. Ordered set of numbers: (1,2,3,4) Example: (x,y,z) coordinates of pt in space. Vectors
 Trnformion Ordered e of number:,,,4 Emple:,,z coordine of p in pce. Vecor If, n i i, K, n, i uni ecor Vecor ddiion +w, +, +, + V+w w Sclr roduc,, Inner do roduc α w. w +,.,. The inner produc i SCLR!. w,.,
Trnformion Ordered e of number:,,,4 Emple:,,z coordine of p in pce. Vecor If, n i i, K, n, i uni ecor Vecor ddiion +w, +, +, + V+w w Sclr roduc,, Inner do roduc α w. w +,.,. The inner produc i SCLR!. w,.,
We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.
![We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b. We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.](/thumbs/93/114277851.jpg) Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
Homework Assignment 9 Solution Set
 Homework Assignment 9 Solution Set PHYCS 44 3 Mrch, 4 Problem (Griffiths 77) The mgnitude of the current in the loop is loop = ε induced = Φ B = A B = π = π µ n (µ n) = π µ nk According to Lense s Lw this
Homework Assignment 9 Solution Set PHYCS 44 3 Mrch, 4 Problem (Griffiths 77) The mgnitude of the current in the loop is loop = ε induced = Φ B = A B = π = π µ n (µ n) = π µ nk According to Lense s Lw this
Physics 3323, Fall 2016 Problem Set 7 due Oct 14, 2016
 Physics 333, Fll 16 Problem Set 7 due Oct 14, 16 Reding: Griffiths 4.1 through 4.4.1 1. Electric dipole An electric dipole with p = p ẑ is locted t the origin nd is sitting in n otherwise uniform electric
Physics 333, Fll 16 Problem Set 7 due Oct 14, 16 Reding: Griffiths 4.1 through 4.4.1 1. Electric dipole An electric dipole with p = p ẑ is locted t the origin nd is sitting in n otherwise uniform electric
FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m)
![FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m) FURTHER GENERALIZATIONS. QI Feng. The value of the integral of f(x) over [a; b] can be estimated in a variety ofways. b a. 2(M m)](/thumbs/75/72845579.jpg) Univ. Beogrd. Pul. Elekroehn. Fk. Ser. M. 8 (997), 79{83 FUTHE GENEALIZATIONS OF INEQUALITIES FO AN INTEGAL QI Feng Using he Tylor's formul we prove wo inegrl inequliies, h generlize K. S. K. Iyengr's
Univ. Beogrd. Pul. Elekroehn. Fk. Ser. M. 8 (997), 79{83 FUTHE GENEALIZATIONS OF INEQUALITIES FO AN INTEGAL QI Feng Using he Tylor's formul we prove wo inegrl inequliies, h generlize K. S. K. Iyengr's
Homework Assignment 6 Solution Set
 Homework Assignment 6 Solution Set PHYCS 440 Mrch, 004 Prolem (Griffiths 4.6 One wy to find the energy is to find the E nd D fields everywhere nd then integrte the energy density for those fields. We know
Homework Assignment 6 Solution Set PHYCS 440 Mrch, 004 Prolem (Griffiths 4.6 One wy to find the energy is to find the E nd D fields everywhere nd then integrte the energy density for those fields. We know
