!!"#"$%&#'()!"#&'(*%)+,&',-)./0)1-*23)
|
|
|
- Ethan Gaines
- 5 years ago
- Views:
Transcription
1 "#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%<'9*-/= $&&'+*: %*,('&5 A'B&"-(%)C#"?%*%8)D%&E%%-)) )"-8) 5 "#"$%&#'()A%>'-'&',-),>)6*,7%5) ) "#"$%&#'()F-&%#7#%&"&',-B),>)"#&'(*%)+,&',-5) >1*.$%&'()*'+,9'-<)*7& >1*.$%&'()*'+,9'-<%'<1& >1*.$%&'()*'+,9'-<?,@- >1*.$%&'()*'+,9'-<. $-? >1*.$%&'()*'-,&+,9'-< "
2 AP#Calculus#BC# CHAPTER(11(WORKSHEET( PARAMETRIC)EQUATIONS)AND)POLAR)COORDINATES) Name Sea# Dae Moion(Problems(in(Parameric(Equaions( 1. on he coordinae plane xy is given by he vecor sec, an. a) Find he velociy vecor a any ime. Use your expression o find he velociy vecor for he paricle a. 6 b) Find he acceleraion vecor a any ime. Use your expression o find he acceleraion vecor for he paricle a. 6 c). 6 d) Find he equaion of he line angen o he moion of he paricle a. 6 e) Se up an inegral expression o find he oal disance raveled by he paricle in he ime inerval,. Use your calculaor o evaluae your expression.. on he coordinae plane xy is given by he vecor, 1. a) Find he velociy vecor of he paricle a ime =. b) Find he acceleraion vecor of he paricle a ime =. c) =. d) Find he equaion of he line angen o he moion of he paricle a. e) Se up an inegral expression o find he oal disance raveled by he paricle in he ime inerval,. Use your calculaor o evaluae your expression. (You)may)use)your)calculaor)o)answer)his)quesion.)). The posiion of a paricle moving on a plane is given by he parameric equaions x sin y cos, for. (. The acceleraion of an objec is he derivaive of is speed. 5. The velociy vecor poins in he direcion of moion. and a) Find an equaion for he normal line o he pah described by he paricle a =. The normal line is perpendicular o he angen line o he curve. b) Find he iniial and final posiion of he paricle for. Find he disance beween hese wo poins. c) Find he oal disance raveled by he paricle for. d) Are your answers o pars (b) and (c) equal? Explain. SEE(OTHER(SIDE(
3 6. The velociy of a moving paricle a ime is given by he vecor,. A ime 1, he 1 posiion vecor of he paricle was,. a) Find he posiion vecor of he paricle a any ime ime. To do so, solve he iniial value dr problem v. d b) Find he velociy vecor a =. Inerpre he values found for boh he horizonal and verical velociy of he paricle a ime =. c) Find he paric 1. d) Find he acceleraion vecor of he paricle a any ime ime. 7. The posiion of a paricle is given by he equaions x sin and y cos, for. a) Find he velociy vecor for he paricle a any ime ime. dr b) For wha value(s) of is d? c) While describing he moion of he paricle, wha is he significance of he value(s) you found in par (b)? Explain. #CALCULUS#BC#(no$calculaor$allowed)# 8. A moving paricle has posiion y x, a ime. The posiion of he paricle a ime = 1 is 1 1 (, 6), and he velociy vecor a any ime > is given by 1,. a) Find he acceleraion vecor a ime =. b) Find he posiion of he paricle a any ime. Use your formula o find he posiion of he paricle a ime =. c) For wha ime > does he line angen o he pah of he paricle a x, y have a slope of 8? d) The paricle approaches a line as. Find he slope of his line. Show he work ha leads o your conclusion.
4 AP Calculus BC Review Chaper 11 (Parameric Equaions and Polar Coordinaes) Things o Know and Be Able o Do Undersand he meaning of equaions given in parameric and polar forms, and develop a skech of he appropriae graph Find he slope of a angen line o a paramerically-given curve a a paricular poin using he equaion d =, and undersand how his is derived using he Chain Rule d Find he second derivaive of a paramerically-given curve a a paricular poin using he equaion d d ( ) =, and undersand how his is derived using he Chain Rule d Find he area enclosed by a paramerically-given curve Find he arc lengh of a paramerically-given curve and he area of he surface generaed by revolving a paramerically-given curve Find he area enclosed by a polar curve using he equaion A 1 = r dθ (undersanding ha r f ( θ )) undersand how his is derived. Be very careful wih finding he endpoins for evaluaing he inegral Find he arc lengh of a polar curve = and Pracice Problems These problems should be done wihou a calculaor, wih he excepion of 1, as explained below. The original es, of course, required ha you show relevan work for free-response problems. x = cos 1 For 1, an objec ravels along an ellipical pah given paramerically by. A he poin a which y = sin = 1, he objec leaves he pah and ravels along he line angen o he pah a ha poin. Wha is he slope of he line on which he objec ravels? an1 a b c d e an1 an1 x= The posiion of a paricle moving in he xy-plane is given by he parameric equaions. y = 1 values of is he paricle a res? a 1 only b only c only d 1 and only e 1,, and For wha A curve C is defined by he parameric equaions angen o he graph of C a he poin (,8 )? x= + y = a x = b x = c 8 1. Which of he following is an equaion of he line y = 7 d y= ( x+ ) + e y ( x ) 1 8 =
5 x= A paricle moves so ha is posiion a ime is given by. y = sin cos1 a 8sin1 b 6 5 Which of he following inegrals represens he area shaded in he graph shown a righ? The curve is given by r = sin θ. a sin ( θ ) dθ b 8sin ( θ ) dθ c sin θ dθ d sin ( θ ) dθ e sin θ dθ 6 Which of he following inegrals represens he arc lengh of he polar funcion r = 1+ cosθ from θ? a b 1+ cosθ + sinθ dθ 1+ sin θ dθ c ( + θ ) 1 cos dθ d Wha is he speed of he paricle when =? c ( cos1) + 6 d ( sin1) + 81 e ( cos1) θ 1 cos dθ e ( 1 + cos θ ) sin θ ( 1 + cos θ ) + ( sin θ ) d θ 7 Consider he graph of he vecor funcion r () = 1 +,+. Wha is he value of where x =? a b 8 A paricle moves so ha a ime c 8 d ln,. > is posiion vecor is 8 e 9 a he poin on he graph A ime =, is velociy vecor is a,8 b, c 1,8 d 1, e Consider he curves r 1 = cosθ and r =. a Skech he curves on he axes provided a righ. b Show use of calculus o find he area of he region common o boh graphs. x = 1 Consider he curve given paramerically by. y = 1 a In erms of, find. b Wrie an equaion for he line angen o he curve a he poin a which = 1. c Find he x- and y-coordinaes for each criical poin on he curve and idenify each poin as having a verical or horizonal angen. 16,
6 11 A projecile is launched from he edge of a cliff 19 fee above he ground below. The projecile has an iniial velociy of 18 fee per second and is launched a an angle of o he horizonal. A horizonal wind is also blowing agains he projecile a a velociy of 18 fee per second. The acceleraion of graviy is fee per second per second. a Skech he siuaion and he pah of he projecile. b Wrie a vecor equaion ha represens he pah of he projec ile, using in seconds as he parameer. c When does he projecile reach is maximum heigh, and wha is his maximum heigh? Jusify your answer. d How far, horizonally, does he projecile ravel before landing on he ground? When his es was originally adminisered, he following quesion was o be aken home and compleed wih he use of a calculaor bu wih no oher resources permied o be used, such as oher people, books, compuers, or anyhing else. Sudens had one weekend o complee his. 1 An objec moving along a curve in he xy-plane has posiion ( x, y( )) a ime wih 1 d = and = ln( 1 + ( ) ). A ime =, he objec is a posiion ( ) d 1,5. A ime =, he objec is a poin P wih x- coordinae. a Find he acceleraion vecor and he speed a ime =. b Find he y-coordinae of poin P. c Wrie an equaion for he line angen o he curve a poin P. d For wha value(s) of, if any, is he objec a res? Jusify your answer.
7 AP#Calculus#BC# CHAPTER(11(WORKSHEET( PARAMETRIC)EQUATIONS)AND)POLAR)COORDINATES) ANSWER(KEY( 1. a) v sec an, sec. A v b) a sec an sec, sec an. A a, 1.95, ,.. 5 c) Speed: ; a d d 6 d) A d. Poin: 6, y d e) sec an sec d.8. x. a) v 9, 8 b) a, c) Speed: d) 1 d 1. Poin: 6, 7 y 7 x d e) 1 d a) d sin Slope normal line:. 57. cos 1.97 d.599,.597 y x.599 Poin: b) Iniial:, 1, 1. Final: c) cos sin d Disance: d) No. One is he arc lengh he oher one is a chord (line segmen).
8 . False. The acceleraion is he derivaive of he velociy. 5. True. 6. a) Doing aniderivaives: r C1, C. Using he iniial condiion: 7 r, b) v,. The paricle horizonal velociy is zero: i is no moving horizonally. The paricle verical velociy is : i is moving upwards. c) Speed: 1 1 d) a, 1 7. a) v cos, sin b) d r cos d and sin. Tha happens when and. c) Those are he imes when he #CALCULUS#BC#(no$calculaor$allowed)# 8. a) a,. A a, r C1, C 5 1 r,, d d b) Doing aniderivaives: 1 1 r,. A = : 1 1 c) 1, 1 Since 8 d 1 1 d 1 d) lim lim. The slope of he line is Using he iniial condiion:
9 Answers 1 d c a c 5 b 6 a 7 d 8 a 9a see soluions 9b a = y 11 = x ,16, 16 ; 1b 1c horizonal a ( ) and verical a ( 1, 11) and (, ) 11a see soluions 11b r () = 6 18, c 56 f a = s 11d 8 18 f 1a a =, ; v = 1+ ( ln17) ln17 1b c y = ( x ) 1 1d = only Soluions 1 We find = sin and cos. d d = Then (by he Chain Rule) d cos = = =, d sin an. = an1 This is choice d. so a = 1, We wan a ime a which boh = and ; d d = ha is, boh 6= and 6 6 1=. The firs equaion is = 6 or =, and he second equaion is he same as =, which facors o ( )( + 1) =. Therefore, 1 ; he inersecion of he wo soluion ses is = only, choice c. d = for { } Firsly, find ha ( xy, ) = (,8) occurs a. = Now find d = and, d = so d = =. Then d 1 = =. This is undefined, so he angen line mus be verical. Since he poin has an x-value of =, he relevan angen line is x =, choice a. d d The paricle s velociy is given by v () =, =,cos. We are ineresed in v = 6 + cos1 = cos1 + 6, choice c. which is 6,cos 1, 1 5 Recall ha he area enclosed by a polar graph is given by r dθ. Therefore he inegrand mus be 1 1 ( sinθ ) = ( 16) sin θ = 8sin θ. Wihou even having o consider he limis, we alrea know ha he correc choice mus be b. dr r + dθ. Since 6 Recall ha he arc lengh of a curve represened in polar coordinaes is given by dθ dr = sin θ, he inegral mus ake he form ( 1 cos ) ( sin ) d. dθ + θ + θ θ We are given he limis, and he correc answer is a.
10 d d d 7 Recall ha when a curve is given paramerically, =. Therefore we mus find. = d This is. Therefore choice d. d 8 d 8 = = = 5. The poin a which x = is he poin a which = 1, so The velociy vecor is v () =, =,. A =, we have v ( ) =,8, choice a. d d + 9a The firs equaion is a circle of diameer angen o he y-axis and shifed along he posiive x-axis; he second is a circle of diameer cenered a he origin. The circles along wih he region referred o in par b are shown a righ. 9b As shown in he diagram, he circles inersec a he poins ( r θ ) d = = 1, =, 6 and,. Noe ha he region is symmeric abou he line θ =, so we 6 θ = 6 have he luxury of considering only he porion of i wih θ, and hen doubling is area. For θ,, he ouer limi of he region is r =, so ha par s area is dθ =. For θ,, he ouer limi of he region is r1 = cos θ, so ha par s area is 6 1 ( cos θ ) d θ = cos θ d θ. To evaluae his, recall he ideniy 6 6 cos θ = + cos θ. Therefore he ine- 1 gral may also be wrien as ( 1+ cosθ ) dθ θ ] θ , 9 = + sin = + =. The union of hese 6 wo regions is hen + = 7, which is half of he area of he enire region. Therefore he area of 1 he whole region is 7. 6 d 1a The Chain Rule gives =. This is d 6 6 If you are so inclined, you may facor ou a from he numeraor and a 6 from he denominaor, yielding 1., bu such simplificaion is enirely opional. θ = 6 ( 1) 1 9 1b We need = = =. We also mus find x and y values: x( 1) = ( 1) ( 1) = 1 6( 1) 6( 1) 1 = 5 and y( 1) = ( 1) 1( 1) = 11. Therefore an equaion for he angen line is given by, in poin-slope form, y 11 = ( x+ 5 ). 1c Criical poins are hose a which he curve s derivaive is eiher undefined (verical angen line) or zero (horizonal angen line). The derivaive will be undefined iff (if and only if) is denominaor is zero; ha is, =, so we d
11 solve ; = his gives { },1. A, has verical angen lines a ( 1, 11) and so we solve 1= o ge =±. A, he curve has horizonal angen lines a ( 8,16) = xy, =, ; a 1, = xy, = 1, 11. Therefore he curve,. The derivaive is zero iff is numeraor is zero; ha is,, d = xy, = 8,16, and a, xy, =, 16. Therefore = and (, 16 ). = 11a An annoaed hand-skech is presened below. I is very much no o scale, and he pah should be symmeric and parabolic. θ = wind = 18 f s a g = f s 11b The componen of he iniial velociy in he horizonal direcion is 18cos, and he wind slows he projecile x = 18cos 18= In he verical direcion, he down by 18 fee every second. Therefore () iniial velociy s componen is 18sin, he paricle has an iniial heigh of 19 f, and graviy s conribuion is 1 given by a = 1 = 16. The oal is y= 18sin = Therefore he g vecor equaion is r () = 6 18, c We wan o maximize y(), so we find = 6 and se i equal o zero, finding. d gives = 56 f. 11d To begin, find he ime a which he paricle lands by seing y= ; ha is, {,6 }, from which we can immediaely discard = Evaluaing y = This gives = because i is nonsensical o have negaive ime given he siuaion. Therefore he paricle his he ground a = 6 s; we find is horizonal displacemen by finding x ( 6) = ( 6 18)( 6) = 8 18 f. 1a The acceleraion vecor () h = 19 f a is given by a () =, = 1 6,. Evaluaing his a = gives d d 1+ a =, 17. The speed a = is given by he magniude of he velociy vecor a = ; since he velociy vecor is v () =, = 1,ln( 1+ ( ) ), we have v = 1,ln17, so v = 1 + ( ln17) d d 1.. 1b The change in he objec s y-coordinae is given by inegraing wih respec o ime over he ime inerval in d quesion; his is ln ( 1 + ( ) ) d. The inegrand canno be anidiffereniaed wihou he echniques of com-
12 plex analysis, bu he calculaor will (afer raher a while) give he approximaion However, noe ha his is he change in he objec s y-coordinae; o ge he acual y-coordinae, we mus add is iniial y-coordinae of 5, giving ( + ( ) ) ( ) d ln 1 ln 1 + ln17 1c We find he slope a P by = = ; a =, = =. Since we know d he x-coordinae of P (i is given) and he y-coordinae (from par b), we can wrie he equaion for he line in ln17 poin-slope form as y = ( x ). 1 1d The objec is saionary in he x-direcion when ; d = ha is, 1 =, or {, }. The objec is saionary in he y-direcion when = ; ha is, ln( 1 + ( ) ) =, or =. The objec is wholly saionary a he in- d ersecion of he soluion ses, which is =.
AP Calculus BC Chapter 10 Part 1 AP Exam Problems
 AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
Parametrics and Vectors (BC Only)
 Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
AP Calculus BC - Parametric equations and vectors Chapter 9- AP Exam Problems solutions
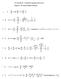 AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
15. Vector Valued Functions
 1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
Answers to 1 Homework
 Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
AP CALCULUS BC 2016 SCORING GUIDELINES
 6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
IB Physics Kinematics Worksheet
 IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
3.6 Derivatives as Rates of Change
 3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
2.1: What is physics? Ch02: Motion along a straight line. 2.2: Motion. 2.3: Position, Displacement, Distance
 Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
In this chapter the model of free motion under gravity is extended to objects projected at an angle. When you have completed it, you should
 Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
Solution: b All the terms must have the dimension of acceleration. We see that, indeed, each term has the units of acceleration
 PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
SMT 2014 Calculus Test Solutions February 15, 2014 = 3 5 = 15.
 SMT Calculus Tes Soluions February 5,. Le f() = and le g() =. Compue f ()g (). Answer: 5 Soluion: We noe ha f () = and g () = 6. Then f ()g () =. Plugging in = we ge f ()g () = 6 = 3 5 = 5.. There is a
SMT Calculus Tes Soluions February 5,. Le f() = and le g() =. Compue f ()g (). Answer: 5 Soluion: We noe ha f () = and g () = 6. Then f ()g () =. Plugging in = we ge f ()g () = 6 = 3 5 = 5.. There is a
KINEMATICS IN ONE DIMENSION
 KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
Things to Know and Be Able to Do Understand the meaning of equations given in parametric and polar forms, and develop a sketch of the appropriate
 AP Calculus BC Review Chapter (Parametric Equations and Polar Coordinates) Things to Know and Be Able to Do Understand the meaning of equations given in parametric and polar forms, and develop a sketch
AP Calculus BC Review Chapter (Parametric Equations and Polar Coordinates) Things to Know and Be Able to Do Understand the meaning of equations given in parametric and polar forms, and develop a sketch
AP CALCULUS AB 2003 SCORING GUIDELINES (Form B)
 SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
10.1 EXERCISES. y 2 t 2. y 1 t y t 3. y e
 66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
Lecture 2-1 Kinematics in One Dimension Displacement, Velocity and Acceleration Everything in the world is moving. Nothing stays still.
 Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
WEEK-3 Recitation PHYS 131. of the projectile s velocity remains constant throughout the motion, since the acceleration a x
 WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
Displacement ( x) x x x
 Kinemaics Kinemaics is he branch of mechanics ha describes he moion of objecs wihou necessarily discussing wha causes he moion. 1-Dimensional Kinemaics (or 1- Dimensional moion) refers o moion in a sraigh
Kinemaics Kinemaics is he branch of mechanics ha describes he moion of objecs wihou necessarily discussing wha causes he moion. 1-Dimensional Kinemaics (or 1- Dimensional moion) refers o moion in a sraigh
MEI Mechanics 1 General motion. Section 1: Using calculus
 Soluions o Exercise MEI Mechanics General moion Secion : Using calculus. s 4 v a 6 4 4 When =, v 4 a 6 4 6. (i) When = 0, s = -, so he iniial displacemen = - m. s v 4 When = 0, v = so he iniial velociy
Soluions o Exercise MEI Mechanics General moion Secion : Using calculus. s 4 v a 6 4 4 When =, v 4 a 6 4 6. (i) When = 0, s = -, so he iniial displacemen = - m. s v 4 When = 0, v = so he iniial velociy
Ground Rules. PC1221 Fundamentals of Physics I. Kinematics. Position. Lectures 3 and 4 Motion in One Dimension. A/Prof Tay Seng Chuan
 Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.
![1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx. 1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.](/thumbs/71/65799522.jpg) . Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
. Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
Kinematics Vocabulary. Kinematics and One Dimensional Motion. Position. Coordinate System in One Dimension. Kinema means movement 8.
 Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
1. VELOCITY AND ACCELERATION
 1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
Physics 180A Fall 2008 Test points. Provide the best answer to the following questions and problems. Watch your sig figs.
 Physics 180A Fall 2008 Tes 1-120 poins Name Provide he bes answer o he following quesions and problems. Wach your sig figs. 1) The number of meaningful digis in a number is called he number of. When numbers
Physics 180A Fall 2008 Tes 1-120 poins Name Provide he bes answer o he following quesions and problems. Wach your sig figs. 1) The number of meaningful digis in a number is called he number of. When numbers
Welcome Back to Physics 215!
 Welcome Back o Physics 215! (General Physics I) Thurs. Jan 19 h, 2017 Lecure01-2 1 Las ime: Syllabus Unis and dimensional analysis Today: Displacemen, velociy, acceleraion graphs Nex ime: More acceleraion
Welcome Back o Physics 215! (General Physics I) Thurs. Jan 19 h, 2017 Lecure01-2 1 Las ime: Syllabus Unis and dimensional analysis Today: Displacemen, velociy, acceleraion graphs Nex ime: More acceleraion
Math 116 Second Midterm March 21, 2016
 Mah 6 Second Miderm March, 06 UMID: EXAM SOLUTIONS Iniials: Insrucor: Secion:. Do no open his exam unil you are old o do so.. Do no wrie your name anywhere on his exam. 3. This exam has pages including
Mah 6 Second Miderm March, 06 UMID: EXAM SOLUTIONS Iniials: Insrucor: Secion:. Do no open his exam unil you are old o do so.. Do no wrie your name anywhere on his exam. 3. This exam has pages including
Guest Lecturer Friday! Symbolic reasoning. Symbolic reasoning. Practice Problem day A. 2 B. 3 C. 4 D. 8 E. 16 Q25. Will Armentrout.
 Pracice Problem day Gues Lecurer Friday! Will Armenrou. He d welcome your feedback! Anonymously: wrie somehing and pu i in my mailbox a 111 Whie Hall. Email me: sarah.spolaor@mail.wvu.edu Symbolic reasoning
Pracice Problem day Gues Lecurer Friday! Will Armenrou. He d welcome your feedback! Anonymously: wrie somehing and pu i in my mailbox a 111 Whie Hall. Email me: sarah.spolaor@mail.wvu.edu Symbolic reasoning
4.5 Constant Acceleration
 4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
Math 116 Practice for Exam 2
 Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
Phys 221 Fall Chapter 2. Motion in One Dimension. 2014, 2005 A. Dzyubenko Brooks/Cole
 Phys 221 Fall 2014 Chaper 2 Moion in One Dimension 2014, 2005 A. Dzyubenko 2004 Brooks/Cole 1 Kinemaics Kinemaics, a par of classical mechanics: Describes moion in erms of space and ime Ignores he agen
Phys 221 Fall 2014 Chaper 2 Moion in One Dimension 2014, 2005 A. Dzyubenko 2004 Brooks/Cole 1 Kinemaics Kinemaics, a par of classical mechanics: Describes moion in erms of space and ime Ignores he agen
4.6 One Dimensional Kinematics and Integration
 4.6 One Dimensional Kinemaics and Inegraion When he acceleraion a( of an objec is a non-consan funcion of ime, we would like o deermine he ime dependence of he posiion funcion x( and he x -componen of
4.6 One Dimensional Kinemaics and Inegraion When he acceleraion a( of an objec is a non-consan funcion of ime, we would like o deermine he ime dependence of he posiion funcion x( and he x -componen of
AP CALCULUS AB 2003 SCORING GUIDELINES (Form B)
 SCING GUIDELINES (Form B) Quesion 4 A paricle moves along he x-axis wih velociy a ime given by v( ) = 1 + e1. (a) Find he acceleraion of he paricle a ime =. (b) Is he speed of he paricle increasing a ime
SCING GUIDELINES (Form B) Quesion 4 A paricle moves along he x-axis wih velociy a ime given by v( ) = 1 + e1. (a) Find he acceleraion of he paricle a ime =. (b) Is he speed of he paricle increasing a ime
Chapter Let. 1) k be a vector-valued function. (a) Evaluate f (0). (b) What is the domain of f () t? (c) Is f () t continuous at t = 1?
 Chaper. Le f() = sin i+ ( 3+ ) j ln( + ) k be a vecor-valued funcion. (a) Evaluae f (). (b) Wha is he domain of f ()? (c) Is f () coninuous a =? Chaper. Le f() = sin i+ ( 3+ ) j ln( + ) k be a vecor-valued
Chaper. Le f() = sin i+ ( 3+ ) j ln( + ) k be a vecor-valued funcion. (a) Evaluae f (). (b) Wha is he domain of f ()? (c) Is f () coninuous a =? Chaper. Le f() = sin i+ ( 3+ ) j ln( + ) k be a vecor-valued
PHYSICS 220 Lecture 02 Motion, Forces, and Newton s Laws Textbook Sections
 PHYSICS 220 Lecure 02 Moion, Forces, and Newon s Laws Texbook Secions 2.2-2.4 Lecure 2 Purdue Universiy, Physics 220 1 Overview Las Lecure Unis Scienific Noaion Significan Figures Moion Displacemen: Δx
PHYSICS 220 Lecure 02 Moion, Forces, and Newon s Laws Texbook Secions 2.2-2.4 Lecure 2 Purdue Universiy, Physics 220 1 Overview Las Lecure Unis Scienific Noaion Significan Figures Moion Displacemen: Δx
3, so θ = arccos
 Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
10.6 Parametric Equations
 0_006.qd /8/05 9:05 AM Page 77 Secion 0.6 77 Parameric Equaions 0.6 Parameric Equaions Wha ou should learn Evaluae ses of parameric equaions for given values of he parameer. Skech curves ha are represened
0_006.qd /8/05 9:05 AM Page 77 Secion 0.6 77 Parameric Equaions 0.6 Parameric Equaions Wha ou should learn Evaluae ses of parameric equaions for given values of he parameer. Skech curves ha are represened
AP CALCULUS AB 2017 SCORING GUIDELINES
 AP CALCULUS AB 17 SCORING GUIDELINES 16 SCORING GUIDELINES Quesion For, a paricle moves along he x-axis. The velociy of he paricle a ime is given by v ( ) = 1 + sin. The paricle is a posiion x = a ime.
AP CALCULUS AB 17 SCORING GUIDELINES 16 SCORING GUIDELINES Quesion For, a paricle moves along he x-axis. The velociy of he paricle a ime is given by v ( ) = 1 + sin. The paricle is a posiion x = a ime.
SPH3U: Projectiles. Recorder: Manager: Speaker:
 SPH3U: Projeciles Now i s ime o use our new skills o analyze he moion of a golf ball ha was ossed hrough he air. Le s find ou wha is special abou he moion of a projecile. Recorder: Manager: Speaker: 0
SPH3U: Projeciles Now i s ime o use our new skills o analyze he moion of a golf ball ha was ossed hrough he air. Le s find ou wha is special abou he moion of a projecile. Recorder: Manager: Speaker: 0
Some Basic Information about M-S-D Systems
 Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
k 1 k 2 x (1) x 2 = k 1 x 1 = k 2 k 1 +k 2 x (2) x k series x (3) k 2 x 2 = k 1 k 2 = k 1+k 2 = 1 k k 2 k series
 Final Review A Puzzle... Consider wo massless springs wih spring consans k 1 and k and he same equilibrium lengh. 1. If hese springs ac on a mass m in parallel, hey would be equivalen o a single spring
Final Review A Puzzle... Consider wo massless springs wih spring consans k 1 and k and he same equilibrium lengh. 1. If hese springs ac on a mass m in parallel, hey would be equivalen o a single spring
Chapters 6 & 7: Trigonometric Functions of Angles and Real Numbers. Divide both Sides by 180
 Algebra Chapers & : Trigonomeric Funcions of Angles and Real Numbers Chapers & : Trigonomeric Funcions of Angles and Real Numbers - Angle Measures Radians: - a uni (rad o measure he size of an angle. rad
Algebra Chapers & : Trigonomeric Funcions of Angles and Real Numbers Chapers & : Trigonomeric Funcions of Angles and Real Numbers - Angle Measures Radians: - a uni (rad o measure he size of an angle. rad
a. Show that these lines intersect by finding the point of intersection. b. Find an equation for the plane containing these lines.
 Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
AP Calculus BC 2004 Free-Response Questions Form B
 AP Calculus BC 200 Free-Response Quesions Form B The maerials included in hese files are inended for noncommercial use by AP eachers for course and exam preparaion; permission for any oher use mus be sough
AP Calculus BC 200 Free-Response Quesions Form B The maerials included in hese files are inended for noncommercial use by AP eachers for course and exam preparaion; permission for any oher use mus be sough
AP CALCULUS AB 2004 SCORING GUIDELINES (Form B)
 4 SCORING GUIDELINES (Form B) Quesion A es plane flies in a sraigh line wih (min) 5 1 15 5 5 4 posiive velociy v (), in miles per v ()(mpm) 7. 9. 9.5 7. 4.5.4.4 4. 7. minue a ime minues, where v is a differeniable
4 SCORING GUIDELINES (Form B) Quesion A es plane flies in a sraigh line wih (min) 5 1 15 5 5 4 posiive velociy v (), in miles per v ()(mpm) 7. 9. 9.5 7. 4.5.4.4 4. 7. minue a ime minues, where v is a differeniable
Non-uniform circular motion *
 OpenSax-CNX module: m14020 1 Non-uniform circular moion * Sunil Kumar Singh This work is produced by OpenSax-CNX and licensed under he Creaive Commons Aribuion License 2.0 Wha do we mean by non-uniform
OpenSax-CNX module: m14020 1 Non-uniform circular moion * Sunil Kumar Singh This work is produced by OpenSax-CNX and licensed under he Creaive Commons Aribuion License 2.0 Wha do we mean by non-uniform
Physics 221 Fall 2008 Homework #2 Solutions Ch. 2 Due Tues, Sept 9, 2008
 Physics 221 Fall 28 Homework #2 Soluions Ch. 2 Due Tues, Sep 9, 28 2.1 A paricle moving along he x-axis moves direcly from posiion x =. m a ime =. s o posiion x = 1. m by ime = 1. s, and hen moves direcly
Physics 221 Fall 28 Homework #2 Soluions Ch. 2 Due Tues, Sep 9, 28 2.1 A paricle moving along he x-axis moves direcly from posiion x =. m a ime =. s o posiion x = 1. m by ime = 1. s, and hen moves direcly
Practicing Problem Solving and Graphing
 Pracicing Problem Solving and Graphing Tes 1: Jan 30, 7pm, Ming Hsieh G20 The Bes Ways To Pracice for Tes Bes If need more, ry suggesed problems from each new opic: Suden Response Examples A pas opic ha
Pracicing Problem Solving and Graphing Tes 1: Jan 30, 7pm, Ming Hsieh G20 The Bes Ways To Pracice for Tes Bes If need more, ry suggesed problems from each new opic: Suden Response Examples A pas opic ha
Solutions from Chapter 9.1 and 9.2
 Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Multiple Choice Solutions 1. E (2003 AB25) () xt t t t 2. A (2008 AB21/BC21) 3. B (2008 AB7) Using Fundamental Theorem of Calculus: 1
 Paricle Moion Soluions We have inenionally included more maerial han can be covered in mos Suden Sudy Sessions o accoun for groups ha are able o answer he quesions a a faser rae. Use your own judgmen,
Paricle Moion Soluions We have inenionally included more maerial han can be covered in mos Suden Sudy Sessions o accoun for groups ha are able o answer he quesions a a faser rae. Use your own judgmen,
x i v x t a dx dt t x
 Physics 3A: Basic Physics I Shoup - Miderm Useful Equaions A y A sin A A A y an A y A A = A i + A y j + A z k A * B = A B cos(θ) A B = A B sin(θ) A * B = A B + A y B y + A z B z A B = (A y B z A z B y
Physics 3A: Basic Physics I Shoup - Miderm Useful Equaions A y A sin A A A y an A y A A = A i + A y j + A z k A * B = A B cos(θ) A B = A B sin(θ) A * B = A B + A y B y + A z B z A B = (A y B z A z B y
AP CALCULUS AB/CALCULUS BC 2016 SCORING GUIDELINES. Question 1. 1 : estimate = = 120 liters/hr
 AP CALCULUS AB/CALCULUS BC 16 SCORING GUIDELINES Quesion 1 (hours) R ( ) (liers / hour) 1 3 6 8 134 119 95 74 7 Waer is pumped ino a ank a a rae modeled by W( ) = e liers per hour for 8, where is measured
AP CALCULUS AB/CALCULUS BC 16 SCORING GUIDELINES Quesion 1 (hours) R ( ) (liers / hour) 1 3 6 8 134 119 95 74 7 Waer is pumped ino a ank a a rae modeled by W( ) = e liers per hour for 8, where is measured
MEI STRUCTURED MATHEMATICS 4758
 OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
Motion along a Straight Line
 chaper 2 Moion along a Sraigh Line verage speed and average velociy (Secion 2.2) 1. Velociy versus speed Cone in he ebook: fer Eample 2. Insananeous velociy and insananeous acceleraion (Secions 2.3, 2.4)
chaper 2 Moion along a Sraigh Line verage speed and average velociy (Secion 2.2) 1. Velociy versus speed Cone in he ebook: fer Eample 2. Insananeous velociy and insananeous acceleraion (Secions 2.3, 2.4)
HOMEWORK # 2: MATH 211, SPRING Note: This is the last solution set where I will describe the MATLAB I used to make my pictures.
 HOMEWORK # 2: MATH 2, SPRING 25 TJ HITCHMAN Noe: This is he las soluion se where I will describe he MATLAB I used o make my picures.. Exercises from he ex.. Chaper 2.. Problem 6. We are o show ha y() =
HOMEWORK # 2: MATH 2, SPRING 25 TJ HITCHMAN Noe: This is he las soluion se where I will describe he MATLAB I used o make my picures.. Exercises from he ex.. Chaper 2.. Problem 6. We are o show ha y() =
Chapter 2. Motion in One-Dimension I
 Chaper 2. Moion in One-Dimension I Level : AP Physics Insrucor : Kim 1. Average Rae of Change and Insananeous Velociy To find he average velociy(v ) of a paricle, we need o find he paricle s displacemen
Chaper 2. Moion in One-Dimension I Level : AP Physics Insrucor : Kim 1. Average Rae of Change and Insananeous Velociy To find he average velociy(v ) of a paricle, we need o find he paricle s displacemen
and v y . The changes occur, respectively, because of the acceleration components a x and a y
 Week 3 Reciaion: Chaper3 : Problems: 1, 16, 9, 37, 41, 71. 1. A spacecraf is raveling wih a veloci of v0 = 5480 m/s along he + direcion. Two engines are urned on for a ime of 84 s. One engine gives he
Week 3 Reciaion: Chaper3 : Problems: 1, 16, 9, 37, 41, 71. 1. A spacecraf is raveling wih a veloci of v0 = 5480 m/s along he + direcion. Two engines are urned on for a ime of 84 s. One engine gives he
Roller-Coaster Coordinate System
 Winer 200 MECH 220: Mechanics 2 Roller-Coaser Coordinae Sysem Imagine you are riding on a roller-coaer in which he rack goes up and down, wiss and urns. Your velociy and acceleraion will change (quie abruply),
Winer 200 MECH 220: Mechanics 2 Roller-Coaser Coordinae Sysem Imagine you are riding on a roller-coaer in which he rack goes up and down, wiss and urns. Your velociy and acceleraion will change (quie abruply),
Applications of the Basic Equations Chapter 3. Paul A. Ullrich
 Applicaions of he Basic Equaions Chaper 3 Paul A. Ullrich paullrich@ucdavis.edu Par 1: Naural Coordinaes Naural Coordinaes Quesion: Why do we need anoher coordinae sysem? Our goal is o simplify he equaions
Applicaions of he Basic Equaions Chaper 3 Paul A. Ullrich paullrich@ucdavis.edu Par 1: Naural Coordinaes Naural Coordinaes Quesion: Why do we need anoher coordinae sysem? Our goal is o simplify he equaions
Check in: 1 If m = 2(x + 1) and n = find y when. b y = 2m n 2
 7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
1998 Calculus AB Scoring Guidelines
 AB{ / BC{ 1999. The rae a which waer ows ou of a pipe, in gallons per hour, is given by a diereniable funcion R of ime. The able above shows he rae as measured every hours for a {hour period. (a) Use a
AB{ / BC{ 1999. The rae a which waer ows ou of a pipe, in gallons per hour, is given by a diereniable funcion R of ime. The able above shows he rae as measured every hours for a {hour period. (a) Use a
a 10.0 (m/s 2 ) 5.0 Name: Date: 1. The graph below describes the motion of a fly that starts out going right V(m/s)
 Name: Dae: Kinemaics Review (Honors. Physics) Complee he following on a separae shee of paper o be urned in on he day of he es. ALL WORK MUST BE SHOWN TO RECEIVE CREDIT. 1. The graph below describes he
Name: Dae: Kinemaics Review (Honors. Physics) Complee he following on a separae shee of paper o be urned in on he day of he es. ALL WORK MUST BE SHOWN TO RECEIVE CREDIT. 1. The graph below describes he
Physics 3A: Basic Physics I Shoup Sample Midterm. Useful Equations. x f. x i v x. a x. x i. v xi v xf. 2a x f x i. y f. a r.
 Physics 3A: Basic Physics I Shoup Sample Miderm Useful Equaions A y Asin A A x A y an A y A x A = A x i + A y j + A z k A * B = A B cos(θ) A x B = A B sin(θ) A * B = A x B x + A y B y + A z B z A x B =
Physics 3A: Basic Physics I Shoup Sample Miderm Useful Equaions A y Asin A A x A y an A y A x A = A x i + A y j + A z k A * B = A B cos(θ) A x B = A B sin(θ) A * B = A x B x + A y B y + A z B z A x B =
INSTANTANEOUS VELOCITY
 INSTANTANEOUS VELOCITY I claim ha ha if acceleraion is consan, hen he elociy is a linear funcion of ime and he posiion a quadraic funcion of ime. We wan o inesigae hose claims, and a he same ime, work
INSTANTANEOUS VELOCITY I claim ha ha if acceleraion is consan, hen he elociy is a linear funcion of ime and he posiion a quadraic funcion of ime. We wan o inesigae hose claims, and a he same ime, work
Physics 101 Fall 2006: Exam #1- PROBLEM #1
 Physics 101 Fall 2006: Exam #1- PROBLEM #1 1. Problem 1. (+20 ps) (a) (+10 ps) i. +5 ps graph for x of he rain vs. ime. The graph needs o be parabolic and concave upward. ii. +3 ps graph for x of he person
Physics 101 Fall 2006: Exam #1- PROBLEM #1 1. Problem 1. (+20 ps) (a) (+10 ps) i. +5 ps graph for x of he rain vs. ime. The graph needs o be parabolic and concave upward. ii. +3 ps graph for x of he person
2. What is the displacement of the bug between t = 0.00 s and t = 20.0 s? A) cm B) 39.9 cm C) cm D) 16.1 cm E) +16.
 1. For which one of he following siuaions will he pah lengh equal he magniude of he displacemen? A) A jogger is running around a circular pah. B) A ball is rolling down an inclined plane. C) A rain ravels
1. For which one of he following siuaions will he pah lengh equal he magniude of he displacemen? A) A jogger is running around a circular pah. B) A ball is rolling down an inclined plane. C) A rain ravels
Physics 235 Chapter 2. Chapter 2 Newtonian Mechanics Single Particle
 Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Physics 20 Lesson 5 Graphical Analysis Acceleration
 Physics 2 Lesson 5 Graphical Analysis Acceleraion I. Insananeous Velociy From our previous work wih consan speed and consan velociy, we know ha he slope of a posiion-ime graph is equal o he velociy of
Physics 2 Lesson 5 Graphical Analysis Acceleraion I. Insananeous Velociy From our previous work wih consan speed and consan velociy, we know ha he slope of a posiion-ime graph is equal o he velociy of
Math 2142 Exam 1 Review Problems. x 2 + f (0) 3! for the 3rd Taylor polynomial at x = 0. To calculate the various quantities:
 Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
PROBLEMS FOR MATH 162 If a problem is starred, all subproblems are due. If only subproblems are starred, only those are due. SLOPES OF TANGENT LINES
 PROBLEMS FOR MATH 6 If a problem is sarred, all subproblems are due. If onl subproblems are sarred, onl hose are due. 00. Shor answer quesions. SLOPES OF TANGENT LINES (a) A ball is hrown ino he air. Is
PROBLEMS FOR MATH 6 If a problem is sarred, all subproblems are due. If onl subproblems are sarred, onl hose are due. 00. Shor answer quesions. SLOPES OF TANGENT LINES (a) A ball is hrown ino he air. Is
Math 2214 Solution Test 1A Spring 2016
 Mah 14 Soluion Tes 1A Spring 016 sec Problem 1: Wha is he larges -inerval for which ( 4) = has a guaraneed + unique soluion for iniial value (-1) = 3 according o he Exisence Uniqueness Theorem? Soluion
Mah 14 Soluion Tes 1A Spring 016 sec Problem 1: Wha is he larges -inerval for which ( 4) = has a guaraneed + unique soluion for iniial value (-1) = 3 according o he Exisence Uniqueness Theorem? Soluion
Midterm Exam Review Questions Free Response Non Calculator
 Name: Dae: Block: Miderm Eam Review Quesions Free Response Non Calculaor Direcions: Solve each of he following problems. Choose he BEST answer choice from hose given. A calculaor may no be used. Do no
Name: Dae: Block: Miderm Eam Review Quesions Free Response Non Calculaor Direcions: Solve each of he following problems. Choose he BEST answer choice from hose given. A calculaor may no be used. Do no
dy dx = xey (a) y(0) = 2 (b) y(1) = 2.5 SOLUTION: See next page
 Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Mechanics Acceleration The Kinematics Equations
 Mechanics Acceleraion The Kinemaics Equaions Lana Sheridan De Anza College Sep 27, 2018 Las ime kinemaic quaniies graphs of kinemaic quaniies Overview acceleraion he kinemaics equaions (consan acceleraion)
Mechanics Acceleraion The Kinemaics Equaions Lana Sheridan De Anza College Sep 27, 2018 Las ime kinemaic quaniies graphs of kinemaic quaniies Overview acceleraion he kinemaics equaions (consan acceleraion)
1. The graph below shows the variation with time t of the acceleration a of an object from t = 0 to t = T. a
 Kinemaics Paper 1 1. The graph below shows he ariaion wih ime of he acceleraion a of an objec from = o = T. a T The shaded area under he graph represens change in A. displacemen. B. elociy. C. momenum.
Kinemaics Paper 1 1. The graph below shows he ariaion wih ime of he acceleraion a of an objec from = o = T. a T The shaded area under he graph represens change in A. displacemen. B. elociy. C. momenum.
Chapter 3 Kinematics in Two Dimensions
 Chaper 3 KINEMATICS IN TWO DIMENSIONS PREVIEW Two-dimensional moion includes objecs which are moing in wo direcions a he same ime, such as a projecile, which has boh horizonal and erical moion. These wo
Chaper 3 KINEMATICS IN TWO DIMENSIONS PREVIEW Two-dimensional moion includes objecs which are moing in wo direcions a he same ime, such as a projecile, which has boh horizonal and erical moion. These wo
Section 3.8, Mechanical and Electrical Vibrations
 Secion 3.8, Mechanical and Elecrical Vibraions Mechanical Unis in he U.S. Cusomary and Meric Sysems Disance Mass Time Force g (Earh) Uni U.S. Cusomary MKS Sysem CGS Sysem fee f slugs seconds sec pounds
Secion 3.8, Mechanical and Elecrical Vibraions Mechanical Unis in he U.S. Cusomary and Meric Sysems Disance Mass Time Force g (Earh) Uni U.S. Cusomary MKS Sysem CGS Sysem fee f slugs seconds sec pounds
Math 115 Final Exam December 14, 2017
 On my honor, as a suden, I have neiher given nor received unauhorized aid on his academic work. Your Iniials Only: Iniials: Do no wrie in his area Mah 5 Final Exam December, 07 Your U-M ID # (no uniqname):
On my honor, as a suden, I have neiher given nor received unauhorized aid on his academic work. Your Iniials Only: Iniials: Do no wrie in his area Mah 5 Final Exam December, 07 Your U-M ID # (no uniqname):
x(m) t(sec ) Homework #2. Ph 231 Introductory Physics, Sp-03 Page 1 of 4
 Homework #2. Ph 231 Inroducory Physics, Sp-03 Page 1 of 4 2-1A. A person walks 2 miles Eas (E) in 40 minues and hen back 1 mile Wes (W) in 20 minues. Wha are her average speed and average velociy (in ha
Homework #2. Ph 231 Inroducory Physics, Sp-03 Page 1 of 4 2-1A. A person walks 2 miles Eas (E) in 40 minues and hen back 1 mile Wes (W) in 20 minues. Wha are her average speed and average velociy (in ha
Dynamics. Option topic: Dynamics
 Dynamics 11 syllabusref Opion opic: Dynamics eferenceence In his cha chaper 11A Differeniaion and displacemen, velociy and acceleraion 11B Inerpreing graphs 11C Algebraic links beween displacemen, velociy
Dynamics 11 syllabusref Opion opic: Dynamics eferenceence In his cha chaper 11A Differeniaion and displacemen, velociy and acceleraion 11B Inerpreing graphs 11C Algebraic links beween displacemen, velociy
Unit 1 Test Review Physics Basics, Movement, and Vectors Chapters 1-3
 A.P. Physics B Uni 1 Tes Reiew Physics Basics, Moemen, and Vecors Chapers 1-3 * In sudying for your es, make sure o sudy his reiew shee along wih your quizzes and homework assignmens. Muliple Choice Reiew:
A.P. Physics B Uni 1 Tes Reiew Physics Basics, Moemen, and Vecors Chapers 1-3 * In sudying for your es, make sure o sudy his reiew shee along wih your quizzes and homework assignmens. Muliple Choice Reiew:
15. Bicycle Wheel. Graph of height y (cm) above the axle against time t (s) over a 6-second interval. 15 bike wheel
 15. Biccle Wheel The graph We moun a biccle wheel so ha i is free o roae in a verical plane. In fac, wha works easil is o pu an exension on one of he axles, and ge a suden o sand on one side and hold he
15. Biccle Wheel The graph We moun a biccle wheel so ha i is free o roae in a verical plane. In fac, wha works easil is o pu an exension on one of he axles, and ge a suden o sand on one side and hold he
1. Kinematics I: Position and Velocity
 1. Kinemaics I: Posiion and Velociy Inroducion The purpose of his eperimen is o undersand and describe moion. We describe he moion of an objec by specifying is posiion, velociy, and acceleraion. In his
1. Kinemaics I: Posiion and Velociy Inroducion The purpose of his eperimen is o undersand and describe moion. We describe he moion of an objec by specifying is posiion, velociy, and acceleraion. In his
d = ½(v o + v f) t distance = ½ (initial velocity + final velocity) time
 BULLSEYE Lab Name: ANSWER KEY Dae: Pre-AP Physics Lab Projecile Moion Weigh = 1 DIRECTIONS: Follow he insrucions below, build he ramp, ake your measuremens, and use your measuremens o make he calculaions
BULLSEYE Lab Name: ANSWER KEY Dae: Pre-AP Physics Lab Projecile Moion Weigh = 1 DIRECTIONS: Follow he insrucions below, build he ramp, ake your measuremens, and use your measuremens o make he calculaions
Kinematics in One Dimension
 Kinemaics in One Dimension PHY 7 - d-kinemaics - J. Hedberg - 7. Inroducion. Differen Types of Moion We'll look a:. Dimensionaliy in physics 3. One dimensional kinemaics 4. Paricle model. Displacemen Vecor.
Kinemaics in One Dimension PHY 7 - d-kinemaics - J. Hedberg - 7. Inroducion. Differen Types of Moion We'll look a:. Dimensionaliy in physics 3. One dimensional kinemaics 4. Paricle model. Displacemen Vecor.
Matlab and Python programming: how to get started
 Malab and Pyhon programming: how o ge sared Equipping readers he skills o wrie programs o explore complex sysems and discover ineresing paerns from big daa is one of he main goals of his book. In his chaper,
Malab and Pyhon programming: how o ge sared Equipping readers he skills o wrie programs o explore complex sysems and discover ineresing paerns from big daa is one of he main goals of his book. In his chaper,
v x + v 0 x v y + a y + v 0 y + 2a y + v y Today: Projectile motion Soccer problem Firefighter example
 Thurs Sep 10 Assign 2 Friday SI Sessions: Moron 227 Mon 8:10-9:10 PM Tues 8:10-9:10 PM Thur 7:05-8:05 PM Read Read Draw/Image lay ou coordinae sysem Wha know? Don' know? Wan o know? Physical Processes?
Thurs Sep 10 Assign 2 Friday SI Sessions: Moron 227 Mon 8:10-9:10 PM Tues 8:10-9:10 PM Thur 7:05-8:05 PM Read Read Draw/Image lay ou coordinae sysem Wha know? Don' know? Wan o know? Physical Processes?
2.7. Some common engineering functions. Introduction. Prerequisites. Learning Outcomes
 Some common engineering funcions 2.7 Inroducion This secion provides a caalogue of some common funcions ofen used in Science and Engineering. These include polynomials, raional funcions, he modulus funcion
Some common engineering funcions 2.7 Inroducion This secion provides a caalogue of some common funcions ofen used in Science and Engineering. These include polynomials, raional funcions, he modulus funcion
Kinematics Motion in 1 Dimension and Graphs
 Kinemaics Moion in 1 Dimension and Graphs Lana Sheridan De Anza College Sep 27, 2017 Las ime moion in 1-dimension some kinemaic quaniies graphs Overview velociy and speed acceleraion more graphs Kinemaics
Kinemaics Moion in 1 Dimension and Graphs Lana Sheridan De Anza College Sep 27, 2017 Las ime moion in 1-dimension some kinemaic quaniies graphs Overview velociy and speed acceleraion more graphs Kinemaics
Robotics I. April 11, The kinematics of a 3R spatial robot is specified by the Denavit-Hartenberg parameters in Tab. 1.
 Roboics I April 11, 017 Exercise 1 he kinemaics of a 3R spaial robo is specified by he Denavi-Harenberg parameers in ab 1 i α i d i a i θ i 1 π/ L 1 0 1 0 0 L 3 0 0 L 3 3 able 1: able of DH parameers of
Roboics I April 11, 017 Exercise 1 he kinemaics of a 3R spaial robo is specified by he Denavi-Harenberg parameers in ab 1 i α i d i a i θ i 1 π/ L 1 0 1 0 0 L 3 0 0 L 3 3 able 1: able of DH parameers of
Be able to sketch a function defined parametrically. (by hand and by calculator)
 Pre Calculus Uni : Parameric and Polar Equaions (7) Te References: Pre Calculus wih Limis; Larson, Hoseler, Edwards. B he end of he uni, ou should be able o complee he problems below. The eacher ma provide
Pre Calculus Uni : Parameric and Polar Equaions (7) Te References: Pre Calculus wih Limis; Larson, Hoseler, Edwards. B he end of he uni, ou should be able o complee he problems below. The eacher ma provide
2017 AP CALCULUS AB FREE-RESPONSE QUESTIONS
 17 FREE-RESPONSE QUESTIONS 5. Two paricles move along he x-axis. For 8, he posiion of paricle P a ime is given by xp () ln ( 1 ), while he velociy of paricle Q a ime is given by vq () 8 15. Paricle Q is
17 FREE-RESPONSE QUESTIONS 5. Two paricles move along he x-axis. For 8, he posiion of paricle P a ime is given by xp () ln ( 1 ), while he velociy of paricle Q a ime is given by vq () 8 15. Paricle Q is
1.6. Slopes of Tangents and Instantaneous Rate of Change
 1.6 Slopes of Tangens and Insananeous Rae of Change When you hi or kick a ball, he heigh, h, in meres, of he ball can be modelled by he equaion h() 4.9 2 v c. In his equaion, is he ime, in seconds; c represens
1.6 Slopes of Tangens and Insananeous Rae of Change When you hi or kick a ball, he heigh, h, in meres, of he ball can be modelled by he equaion h() 4.9 2 v c. In his equaion, is he ime, in seconds; c represens
CALCULUS EXPLORATION OF THE SECOND FUNDAMENTAL THEOREM OF CALCULUS. Second Fundamental Theorem of Calculus (Chain Rule Version):
 CALCULUS EXPLORATION OF THE SECOND FUNDAMENTAL THEOREM OF CALCULUS 6 cos Secon Funamenal Theorem of Calculus: f a 4 a f 6 cos Secon Funamenal Theorem of Calculus (Chain Rule Version): g f a E. Use he Secon
CALCULUS EXPLORATION OF THE SECOND FUNDAMENTAL THEOREM OF CALCULUS 6 cos Secon Funamenal Theorem of Calculus: f a 4 a f 6 cos Secon Funamenal Theorem of Calculus (Chain Rule Version): g f a E. Use he Secon
72 Calculus and Structures
 72 Calculus and Srucures CHAPTER 5 DISTANCE AND ACCUMULATED CHANGE Calculus and Srucures 73 Copyrigh Chaper 5 DISTANCE AND ACCUMULATED CHANGE 5. DISTANCE a. Consan velociy Le s ake anoher look a Mary s
72 Calculus and Srucures CHAPTER 5 DISTANCE AND ACCUMULATED CHANGE Calculus and Srucures 73 Copyrigh Chaper 5 DISTANCE AND ACCUMULATED CHANGE 5. DISTANCE a. Consan velociy Le s ake anoher look a Mary s
Q2.1 This is the x t graph of the motion of a particle. Of the four points P, Q, R, and S, the velocity v x is greatest (most positive) at
 Q2.1 This is he x graph of he moion of a paricle. Of he four poins P, Q, R, and S, he velociy is greaes (mos posiive) a A. poin P. B. poin Q. C. poin R. D. poin S. E. no enough informaion in he graph o
Q2.1 This is he x graph of he moion of a paricle. Of he four poins P, Q, R, and S, he velociy is greaes (mos posiive) a A. poin P. B. poin Q. C. poin R. D. poin S. E. no enough informaion in he graph o
University Physics with Modern Physics 14th Edition Young TEST BANK
 Universi Phsics wih Modern Phsics 14h Ediion Young SOLUTIONS MANUAL Full clear download (no formaing errors) a: hps://esbankreal.com/download/universi-phsics-modern-phsics- 14h-ediion-oung-soluions-manual-/
Universi Phsics wih Modern Phsics 14h Ediion Young SOLUTIONS MANUAL Full clear download (no formaing errors) a: hps://esbankreal.com/download/universi-phsics-modern-phsics- 14h-ediion-oung-soluions-manual-/
Suggested Practice Problems (set #2) for the Physics Placement Test
 Deparmen of Physics College of Ars and Sciences American Universiy of Sharjah (AUS) Fall 014 Suggesed Pracice Problems (se #) for he Physics Placemen Tes This documen conains 5 suggesed problems ha are
Deparmen of Physics College of Ars and Sciences American Universiy of Sharjah (AUS) Fall 014 Suggesed Pracice Problems (se #) for he Physics Placemen Tes This documen conains 5 suggesed problems ha are
Challenge Problems. DIS 203 and 210. March 6, (e 2) k. k(k + 2). k=1. f(x) = k(k + 2) = 1 x k
 Challenge Problems DIS 03 and 0 March 6, 05 Choose one of he following problems, and work on i in your group. Your goal is o convince me ha your answer is correc. Even if your answer isn compleely correc,
Challenge Problems DIS 03 and 0 March 6, 05 Choose one of he following problems, and work on i in your group. Your goal is o convince me ha your answer is correc. Even if your answer isn compleely correc,
