15. Vector Valued Functions
|
|
|
- Kathlyn Gillian Banks
- 6 years ago
- Views:
Transcription
1 1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example, r() = + 1, + 3 presens a funcion whose inpu is a scalar, and whose oupu is a vecor in R. Such a funcion is called a vecor-valued funcion and is called a parameer variable. The common noaion is o wrie r() = x(), y() for vecor-valued funcions in R, and r() = x(), y(), z() for vecor-valued funcions in R 3. The number of parameer variables can be greaer han one. Example 1.1: Skech r() = + 1, + 3 for 1. Soluion: Le s build an inpu-oupu able: r() = + 1, r( 1) = ( 1) + 1, ( 1) + 3 = 1,4. r(.) = (.) + 1, (.) + 3 =, 3. r() = () + 1, () + 3 = 1,3. r(.) = (.) + 1, (.) + 3 =, 3. 1 r(1) = (1) + 1, (1) + 3 = 3,4 1. r(1.) = (1.) + 1, (1.) + 3 = 4,. r() = () + 1, () + 3 =,7 We hen skech vecors for each such ha is foo is a he origin: This looks like a mess, bu i is a ruhful and lieral represenaion of r() = + 1, + 3 for cerain values of in he inerval 1. However, when represening he graph of a vecor valued funcion, i is common o only show he posiion a he head of he vecor, and he curve ha resuls. 76
2 This image is much cleaner and we see ha he pah raced ou by he heads of he vecors given by r() = + 1, + 3 for 1 form a parabola. Noe ha some of he values are saed a cerain poins. I is common o place an arrow on his pah o show he direcion of increasing value of he variable. Example 1.: Skech r() = a cos, a sin, for π, and describe he curve ha is raced ou by he vecors. Soluion: We build an inpu-oupu able: r() = a cos, a sin r() = a cos, a sin = a, π 4 r(π 4) = a cos(π 4), a sin(π 4) = a, a π r(π ) = a cos(π ), a sin(π ) =, a 3π 4 r(3 π 4) = a cos(3 π 4), a sin(3π 4) = a, a π r(π) = a cos(π), a sin(π) = a, π 4 r(π 4) = a cos(π 4), a sin(π 4) = a, a 3π r(3π ) = a cos(3π ), a sin(3π ) =, a 7π 4 r(7π 4) = a cos(7π 4), a sin(7 π 4) = a, a π r(π) = a cos(π), a sin(π) = a, The curve is on he following page. The vecors are no acually drawn. Insead, he curve formed by he placemen of each vecor s head is drawn. 77
3 The curve is a circle of radius a, cenered a he origin. The bounds π ensure ha exacly one revoluion of he circle is skeched. Noe ha cerain poins on he pah are given by ordered pairs. Remember ha hese are he heads of he vecors, which are no drawn. Thus, he poin (, a) represens he head of he vecor, a when = π. The arrow shows he direcion of increasing, and he circle sars a he poin (a, ) and ends a his same poin, one revoluion laer. There is more han one way o define a circle of radius a. For example, r() = a sin, a cos, for π races he same circle, bu his ime saring a (, a) and in he clockwise direcion. Example 1.3: Rewrie he funcion y = f(x) = x 3 from (,) o (3,7) as a vecor-valued funcion. Soluion: Any funcion of he form y = f(x) can be rewrien as a vecor-valued funcion by leing x() = and y() = f(). Thus, he funcion y = f(x) = x 3 from (,) o (3,7) can be re-wrien as r() =, 3 for 3. Noe ha r() =, and ha r(3) = 3,7. These are vecors whose heads lie a he poins (,) and (3,7) respecively. Example 1.4: Find he domain of r() =,, 1. 3 Soluion: The domain is he larges subse of he real numbers for which all hree componen funcions are defined simulaneously. Noe ha x() = and y() = are defined for all real numbers, bu ha z() = 1 is no defined when = 3. Thus, he domain of r is given by 3 { (, 3) (3, )}. 78
4 Example 1.: Find he domain of r() =, 4 3, e. Soluion: The firs componen x() = requires ha, and he second componen y() = 4 3 requires ha 4 3, or 4. There are no resricions on implied by z() = 3 e. Thus, he domain of r is given by { (, ) (, 4 3 ]}. Example 1.6: Find a vecor valued funcion ha describes he line segmen in R 3 from (1,,) o (3,1, 4). Soluion: Find he direcion vecor: v = 3 1,1 ( ), 4 =,3, 9. Using (1,,) as he iniial poin, we have 1,, +,3, 9 as he line segmen using vecor noaion. As a vecor-valued funcion, we have r() = 1 +, + 3, 9 for 1. Noe ha r() = 1,,, a vecor whose head lies a he poin (1,,), and ha r(1) = 3,1, 4, a vecor whose head lies a he poin (3,1, 4). Example 1.7: Describe r() = cos, sin, for. Soluion: This is a curve in R 3. Look a wo of he componens a a ime: The componens x() = cos and y() = sin race a circle of radius repeaedly since increases wihou bound. The componens x() = cos and z() = race a cosine wave upward, e.g. assuming ha x is he horizonal axis and z he verical axis. The componens y() = sin and z() = race a sine wave upward. The curve is a helix, which looks like a coiled spring. This helix has a radius of cenered around he posiive z-axis, wrapping around he z-axis (bu never ouching i) as increases in value. 79
5 Example 1.8: In R 3, he circular cylinder x + y = is inerseced by he plane y + z = 4. Find a vecor-valued funcion r() = x(), y(), z() ha describes he curve formed by he inersecion of hese wo surfaces. Soluion: There are many possible vecor-valued funcions ha describe his curve. One possible way is o noe ha we can wrie x() = cos and y() = sin for π. Then, since y + z = 4, we have z = 4 y, so ha z() = 4 sin. The curve of inersecion is given by r() = cos, sin, 4 sin, for π. The number of parameer variables of a vecor-valued funcion describe he ype of graph ha will resul. For example, a vecor-valued funcion of one parameer variable will resul in a curve, as demonsraed in he previous examples. A vecor-valued funcion of wo variables resuls in a surface, as he nex wo examples show. Example 1.9: A circular cylinder of radius is cenered a he origin such ha he x-axis is he axis of symmery of he cylinder. Describe his surface paramerically, using u and v as he parameer variables. Soluion: Since he x-axis is he axis of symmery, we infer ha he circular cross secions lie on planes parallel o he yz-plane. For example, a circle of radius on he yz-plane (x = ) is described by y + z = 4. Using parameer variable u, we can describe he circle by leing y = cos u and z = sin u, where he represens he circle s radius. Noe ha he circular cross-secions depend only on variable u. Thus, we can le x = v, represening he exension of he circle ino he posiive and negaive x direcion, wih no resricions on v. The cylinder is described paramerically as r(u, v) = v, cos u, sin u, u π, < v <. Example 1.1: Describe he cone z = x + y paramerically using variables u and v. Soluion: Observe ha cross secions of his surface wih a plane z = k resuls in a circle of radius k. Thus, if we le z = u, we can hen define x = u cos v and y = u sin v, which resul in circles of radius u. Thus, we have r(u, v) = u cos v, u sin v, u, where v π and u. 8
6 16. Vecor Valued Funcions: Limis & Coninuiy The same noions of limis and coninuiy hold rue for vecor-valued funcions. For example, he limi of r() = x(), y(), z() as a is given by assuming ha all hree limis exis. lim r() = lim x(), lim y(), lim z(), a a a a Similarly, a vecor-valued funcion r() = x(), y(), z() is coninuous a = a if The limi as a exiss, The vecor r(a) exiss (ha is, a is in he domain of r), and lim r() = r(a). a Example 16.1: Given r() =, e, 1 +3, find lim r(). Is r coninuous a =? Soluion: The limi is lim r() = lim, lim e, lim ( 1 ) = 4, +3 e, 1. Noe ha r() = 4, e, 1. Since all hree condiions of coninuiy are me, he curve raced ou by r() =, e, 1 +3 is coninuous a =. In his example, he limi of r as 3 does no exis since he limi fails o exis for he expression 1. This curve is no coninuous when = 3. I is coninuous everywhere else. +3 Example 16.: Given r() = + 1, 9 3,, find lim 3 r(). Is r coninuous a = 3? Soluion: Noe ha he domain of r excludes he value = 3. However, he limi does exis as 3, since lim r() = lim ( + 1), lim ( 9 ), lim = 7,6,9. The middle expression simplifies as 9 = (+3)( 3) = + 3, hen he limi is aken. However, 3 3 he value = 3 is sill excluded from he domain, so r is no coninuous a = 3. There is a deleed poin in he curve when = 3. 81
7 17. Vecor Valued Funcions: Differeniaion Given a vecor-valued funcion r() = x(), y(), z(), he derivaive of r wih respec o is given by r () = d d r() = d x(), y(), z() d = d d x(), d d y(), d d z() = x (), y (), z (), assuming ha he derivaives exis. Noe ha r () = x (), y (), z () is iself a vecor-valued funcion. Visually, he vecors given by r () can be shifed in such a way so ha hey are angen o he curve raced ou by r() = x(), y(), z(). In a physical seing, if r() = x(), y(), z() represens he displacemen of an objec, hen v() = r () = x (), y (), z () represens he objec s velociy and he magniude, r (), is he objec s speed. Acceleraion is a() = v () = r () = x (), y (), z (). Example 17.1: An objec moves hrough R 3 along a pah defined by r() = 3, +, where all dimensions are in meers. Find he objec s velociy and is speed when = 4 seconds. Soluion: The derivaive of r() = 3, +, is r () = 3, 4 + 1,. Thus, when = 4 seconds, he objec has a velociy of r (4) = 3(4), 4(4) + 1, = 48,17,. The objec s speed a = 4 seconds is r (4) = meers per second. Example 17.: An objec moves hrough R along a pah defined by r() =, , where he firs componen is he horizonal displacemen in meers, and he second componen is verical displacemen in meers, and where is in seconds. Find he maximum heigh ha his objec achieves. Soluion: Noe ha he objec races a downward-opening parabolic arc in R. The objec will achieve is maximum heigh when he verical componen of velociy of he objec is emporarily. Thus, we differeniae: v() = r () = 1,
8 We hen se he verical componen of velociy o, and solve: = gives = seconds. 9.8 This is he ime a which he objec achieves is maximum heigh. When we subsiue =.449 ino r, we have r(.449) =.449, 4.9(.449) + 4(.449) =.449, The objec achieves a maximum heigh of abou meers above he ground afer.449 seconds in fligh. The objec has moved.449 meers horizonally in his same period of ime. Example 17.3: An objec moves hrough R along a pah defined by r() = 3, +, where he componens are in meers and is in seconds. Wha is he minimum speed of he objec? Soluion: The derivaive is r () = 3, +, so ha he speed can be now saed as a funcion in variable : s() = r () = (3 ) + ( + ) = We now minimize s(): d d s() = d d = This expression is when he numeraor is. Using a calculaor, we find ha = when =.48 seconds. This can be verified o be a minimum by using eiher he firs or second derivaive es. Thus, he objec s minimum speed occurs when =.48 seconds and is s(.48) = 9(.48) 4 + 4(.48) + 8(.48) meers per second. Example 17.4: An objec moves hrough R along a pah defined by r() = + 1, 4. Find he equaion of he angen line in vecor form when =. Soluion. The derivaive is r () = 4, 4 3. Thus, when =, he objec is moving (insananeously) in he direcion of r () = 4(), 4() 3 =,. This is he objec s direcion vecor. Furhermore, a =, he objec s locaion is r() = () + 1, () 4 = 1, 6. Thus, he objec s angen line in vecor form when = is 1, 6 +,, or equivalenly, 1 +,
9 Example 17.: An objec moves hrough R 3 along a pah defined by r() = + 3, +,. Find he equaion of he angen line o his pah when he objec is a (7,,). Soluion. As in he previous example, we need boh a direcion vecor and a posiion vecor. The locaion (7,,) corresponds o a posiion vecor 7,,, and seing his equal o r() = + 3, +,, we can deduce ha = 4. The derivaive is r () = 1, + 1,, so he direcion vecor is r (4) = 1, (4) + 1, = 1,9,. Thus, he objec s angen line in vecor form a his insan is 7,, + 1, 9,, or equivalenly, 7 +, + 9, +. Example 17.6: An objec revolves around he origin in a circular orbi. The circle is of radius meers and he objec complees a revoluion every 1 seconds. Assume he objec moves counerclockwise and ha is sared on he posiive x-axis. Find his objec s posiion (displacemen), velociy, speed and acceleraion a ime. Soluion: Le s assume ha 1 seconds represens one revoluion of he objec. Then, he objec s displacemen is given by r() = cos ( π ), sin (π) = cos (π), sin (π). The leading coefficien represens he radius, and noe ha when = 1, he argumens wihin he sine and cosine operaors are boh π (1) = π, he usual period of he sine and cosine funcions. 1 1 The velociy is v() = r () = sin ( π ) (π ), cos (π ) (π ) = π sin (π), π cos (π ), where he chain rule was used followed by simplificaion. Noe ha r() v() =. This is always rue for objecs moving in a circular pah: he (angenial) velociy vecor is orhogonal o he displacemen vecor. The objec s speed is v() = r () = ( π sin ( π )) + (π cos ( π )) = π meers per second. This makes sense: he circumference of he objec s pah is π() = 1π meers. If i akes he objec 1 seconds o complee one revoluion a π meers per second, hen i will have ravelled a disance of 1π meers in ha revoluion. The acceleraion is a() = v () = r () = π cos (π ), π sin (π). Noe ha he acceleraion vecor is always opposie he displacemen vecor for an objec in circular moion. 84
10 18. Vecor Valued Funcions: Inegraion Given a vecor-valued funcion r() = x(), y(), z(), he indefinie inegral of r wih respec o is given by r() d = x() d, y() d, z() d + a, b, c, where a, b, c is a vecor composed of he consans of inegraion of he componens of r. Example 18.1: Find r() d, where r() = 3, 1, sin(3), where >. Soluion: We have r() d = 3 d, ( 1 ) d, sin(3) d = 3, ln, 1 cos(3) + a, b, c. 3 Example 18.: Find r() = r () d, where r () = e,, sin, and r() =,,. Soluion: Noe ha r() = r () d + k, where k = a, b, c is a consan vecor. We have r() = r () d = e d, d, sin() d + k = 1 e, 3 3, cos + a, b, c. Since r() =,,, we have,, = 1 e(), 3 ()3, cos() + a, b, c,, = 1,, 1 + a, b, c. This forces a = 1, b = and c = 1. Thus, r() = 1 e, 3 3, cos + 1,,1, or simplified as r() = 1 (e 1), 3 3, 1 cos. Don confuse r() =,, as being he consan vecor a, b, c. 8
11 Example 18.3: An objec s acceleraion is given by a() =,, where is in seconds and he componens are meers per seconds-squared. Find v() and r() such ha v(1) =, and r(1) = 1,3. Soluion: Inegraing acceleraion, we obain velociy: v() = a() d =, d = k 1, 1 + k. To find k = k 1, k, noe ha v(1) =, :, = k 1, 1 (1) + k. This forces k 1 = and k = 9, so ha v() =, Nex, we have r() = v() d =, d = + m 1, m. To find m = m 1, m, we noe ha r(1) = 1,3 : 1,3 = (1) + m 1, 1 6 (1)3 + 9 (1) + m. This forces m 1 = 3 and m = 3. Therefore, r() = 3, Example 18.4: Find r() d, where r() =, e,. +1 Soluion: Inegrae. Noe ha u-du subsiuion is used for he laer wo componens. r() d = d = [ ], e d, [ 1 e ] = 8 3, e4 1, 1 ln., ( + 1 ) d, [ 1 ln( + 1)] 86
12 19. Arc Lengh Suppose he vecor-valued funcion r() = x(), y(), z() is defined over he closed inerval a b and differeniable over he open inerval a < < b. Visually, his means ha r is a smooh curve, wih no disconinuiies or corners. The arc lengh s of he curve r over he inerval a b is given by he definie inegral b s = (x ()) + (y ()) + (z ()) d. a Noe ha he inegrand (x ()) + (y ()) + (z ()) is he same as r (). Thus, we can wrie he inegral as b s = r () d. a Example 19.1: Find he lengh of he curve raced by r() = cos, sin for π. Soluion: Find he derivaive: r () = sin, cos. Then, using he arc lengh formula, we have π s = ( sin ) + ( cos ) d π = 4 sin + 4 cos d π = 4(sin + cos ) d π = d = π. The arc lengh is π unis. This can be verified using geomery: r races a semicircle of radius. The circumference of a circle of radius is π() = 4π, and half of his figure is π. 87
13 Example 19.: Find he arc lengh of he curve raced by r() = 4,, ln beween he poins (8,8, ln ) and (,, ln ). Soluion: The derivaive is r () = 4,4,. Furhermore, he bounds of can be inferred from he poins. The poin (8,8, ln ) suggess ha = and he poin (,, ln ) suggess ha =. We have s = 4 + (4) + ( ) d = d = d = (4 + ) d = ( 4 + ) d = (4 + ) d = [ + ln ] = ( + ln ) (8 + ln ) = 4 + ln ( ) unis. Example 19.3: Find he arc lengh of he curve raced by r() =, 3, 4 3 for 1 3. Soluion. The derivaive is r () =, 3,1. Thus, he arc lengh is given by 3 s = () (1 ) d 1 3 = d. 1 Using a calculaor or any numerical mehod of inegraing, we find ha he arc lengh is d unis. 88
14 Example 19.4: Find he lengh of he helix raced by r() = cos, sin, for π. Soluion: The derivaive is r () = sin, cos, 1. We have π s = ( sin ) + ( cos ) + 1 d π = 4 sin + 4 cos + 1 d π = 4(sin + cos ) + 1 d π = d = π unis. Arc Lengh as a Funcion b Consider he arc lengh formula, s = r () d, and allow he upper bound o be a variable a raher han a fixed value. If we allow he upper bound o be, and use a dummy variable wihin he inegral, we have arc lengh s as a funcion of : s() = r (u) du. a Differeniaing boh sides wih respec o, we have d d s() = d d r (u) du. Using he Fundamenal Theorem of Calculus, we have Thus, we have d d r (u) du = r (). a ds d = r (), or equivalenly, ds = r () d. This formula is exremely useful! Do no forge i! a 89
15 . Uni Tangen and Uni Normal Vecors Consider an objec ha moves along a differeniable (smooh, no disconinuiies) curve raced by r() = x(), y(), z(). A each poin on he curve, he angen vecor is given by r () = x (), y (), z (). The magniude of he angen vecor, r (), can be inerpreed as he objec s speed. For mos curves, no surprisingly, he speed of an objec can vary. In a rough sense, he speed of an objec dicaes he segmenaion of he curve. Example.1: Skech he curve raced by r() =, for 4. Soluion: The curve is shown below. I is a parabola y = x from (,) o (4,16). The values for ineger values of are shown on he graph. The segmens of he curve beween consecuive ineger values of vary in lengh. If is a uni of ime, hen he objec raverses each segmen in he same amoun of ime. Thus, he objec mus move faser in order o raverse longer segmens. The segmenaion of he curve in erms of a uni ime inerval is no consisen. The able below shows he objec s posiion, velociy and speed for ineger values of : r() =, r () = 1, r () = 1 + 4, 1, 1 1 1,1 1,,4 1, ,9 1, ,16 1,8 6 9
16 To conrol he speed of he objec, we can force all angen vecors o have a lengh of 1 uni. This is called he uni angen vecor, and is given by This means ha T() = 1. Example.: Find T(), where r() =,. T() = r () r (). Soluion: From he previous example, we have r () = 1, and r () = Thus, T() = r () r () = 1, = , You should verify ha T() = 1. If he objec moves along his curve a a consan speed of 1 uni of disance per uni of ime, hen his will force he segmenaion of he curve ino equal-sized segmens, so ha i can raverse he same lengh each ime, per uni of ime. This is ofen called he ds segmenaion. Example.3: Find T(), where r() = 3 cos, 3 sin,. Soluion: We have T() = r () 3 sin, 3 cos, 1 3 sin r = = () cos, 1, 1 1. Noe ha in his case, he speed of he objec is always 1 unis of disance per uni of ime. The uni normal vecor is given by N() = T () T (). The vecor N has a lengh of 1 uni. I is orhogonal o T (ha is, N T = ). For an objec moving along a differeniable curve, T will poin in he objec s (angenial) direcion of ravel, and N will poin orhogonal o T, represening one componen of acceleraion. I generally poins inward o concave side of he curve. 91
17 Example.4: Find N(), where r() =,. Soluion: From Example., we have 1 T() = 1 + 4, We now find T (): T 4 () = (1 + 4 ) 3, (1 + 4 ) 3. Now, we need T () : This simplifies afer many seps o Thus, he uni normal N is given by T 4 () = ( (1 + 4 ) 3 ) + ( (1 + 4 ) 3 T () = ) N() = T () T () = 1 4 ( ) (1 + 4 ) 3, (1 + 4 ) 3 = 1 + 4, Noe he similariies in T and N, and noe also ha N T =. Example.: Find N(), where r() = 3 cos, 3 sin,. Soluion: From Example.3, we have We find T (): 3 sin T() = 1 3 cos T () = 1, 3 cos 1, 1 1., 3 sin 1,.. 9
18 Noe ha T 3 cos () = ( 1 ) 3 sin + ( 1 ) = 3 1. Thus, 3 cos 3 sin N() = T (), T () = 1 1, 3 1 Observe ha N() = 1 and ha N T =. = cos, sin,. See an error? Have a suggesion? Please see 93
!!"#"$%&#'()!"#&'(*%)+,&',-)./0)1-*23)
 "#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
"#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
AP Calculus BC Chapter 10 Part 1 AP Exam Problems
 AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
Ground Rules. PC1221 Fundamentals of Physics I. Kinematics. Position. Lectures 3 and 4 Motion in One Dimension. A/Prof Tay Seng Chuan
 Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
Answers to 1 Homework
 Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
Parametrics and Vectors (BC Only)
 Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
KINEMATICS IN ONE DIMENSION
 KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
4.6 One Dimensional Kinematics and Integration
 4.6 One Dimensional Kinemaics and Inegraion When he acceleraion a( of an objec is a non-consan funcion of ime, we would like o deermine he ime dependence of he posiion funcion x( and he x -componen of
4.6 One Dimensional Kinemaics and Inegraion When he acceleraion a( of an objec is a non-consan funcion of ime, we would like o deermine he ime dependence of he posiion funcion x( and he x -componen of
23.2. Representing Periodic Functions by Fourier Series. Introduction. Prerequisites. Learning Outcomes
 Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
MEI Mechanics 1 General motion. Section 1: Using calculus
 Soluions o Exercise MEI Mechanics General moion Secion : Using calculus. s 4 v a 6 4 4 When =, v 4 a 6 4 6. (i) When = 0, s = -, so he iniial displacemen = - m. s v 4 When = 0, v = so he iniial velociy
Soluions o Exercise MEI Mechanics General moion Secion : Using calculus. s 4 v a 6 4 4 When =, v 4 a 6 4 6. (i) When = 0, s = -, so he iniial displacemen = - m. s v 4 When = 0, v = so he iniial velociy
PHYSICS 220 Lecture 02 Motion, Forces, and Newton s Laws Textbook Sections
 PHYSICS 220 Lecure 02 Moion, Forces, and Newon s Laws Texbook Secions 2.2-2.4 Lecure 2 Purdue Universiy, Physics 220 1 Overview Las Lecure Unis Scienific Noaion Significan Figures Moion Displacemen: Δx
PHYSICS 220 Lecure 02 Moion, Forces, and Newon s Laws Texbook Secions 2.2-2.4 Lecure 2 Purdue Universiy, Physics 220 1 Overview Las Lecure Unis Scienific Noaion Significan Figures Moion Displacemen: Δx
4.5 Constant Acceleration
 4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
3, so θ = arccos
 Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
AP Calculus BC - Parametric equations and vectors Chapter 9- AP Exam Problems solutions
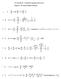 AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
AP CALCULUS BC 2016 SCORING GUIDELINES
 6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
IB Physics Kinematics Worksheet
 IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
1. VELOCITY AND ACCELERATION
 1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
Lecture 2-1 Kinematics in One Dimension Displacement, Velocity and Acceleration Everything in the world is moving. Nothing stays still.
 Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
PROBLEMS FOR MATH 162 If a problem is starred, all subproblems are due. If only subproblems are starred, only those are due. SLOPES OF TANGENT LINES
 PROBLEMS FOR MATH 6 If a problem is sarred, all subproblems are due. If onl subproblems are sarred, onl hose are due. 00. Shor answer quesions. SLOPES OF TANGENT LINES (a) A ball is hrown ino he air. Is
PROBLEMS FOR MATH 6 If a problem is sarred, all subproblems are due. If onl subproblems are sarred, onl hose are due. 00. Shor answer quesions. SLOPES OF TANGENT LINES (a) A ball is hrown ino he air. Is
Motion along a Straight Line
 chaper 2 Moion along a Sraigh Line verage speed and average velociy (Secion 2.2) 1. Velociy versus speed Cone in he ebook: fer Eample 2. Insananeous velociy and insananeous acceleraion (Secions 2.3, 2.4)
chaper 2 Moion along a Sraigh Line verage speed and average velociy (Secion 2.2) 1. Velociy versus speed Cone in he ebook: fer Eample 2. Insananeous velociy and insananeous acceleraion (Secions 2.3, 2.4)
2.1: What is physics? Ch02: Motion along a straight line. 2.2: Motion. 2.3: Position, Displacement, Distance
 Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
In this chapter the model of free motion under gravity is extended to objects projected at an angle. When you have completed it, you should
 Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
Displacement ( x) x x x
 Kinemaics Kinemaics is he branch of mechanics ha describes he moion of objecs wihou necessarily discussing wha causes he moion. 1-Dimensional Kinemaics (or 1- Dimensional moion) refers o moion in a sraigh
Kinemaics Kinemaics is he branch of mechanics ha describes he moion of objecs wihou necessarily discussing wha causes he moion. 1-Dimensional Kinemaics (or 1- Dimensional moion) refers o moion in a sraigh
Solution: b All the terms must have the dimension of acceleration. We see that, indeed, each term has the units of acceleration
 PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
Some Basic Information about M-S-D Systems
 Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Phys 221 Fall Chapter 2. Motion in One Dimension. 2014, 2005 A. Dzyubenko Brooks/Cole
 Phys 221 Fall 2014 Chaper 2 Moion in One Dimension 2014, 2005 A. Dzyubenko 2004 Brooks/Cole 1 Kinemaics Kinemaics, a par of classical mechanics: Describes moion in erms of space and ime Ignores he agen
Phys 221 Fall 2014 Chaper 2 Moion in One Dimension 2014, 2005 A. Dzyubenko 2004 Brooks/Cole 1 Kinemaics Kinemaics, a par of classical mechanics: Describes moion in erms of space and ime Ignores he agen
Kinematics Vocabulary. Kinematics and One Dimensional Motion. Position. Coordinate System in One Dimension. Kinema means movement 8.
 Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Physics 180A Fall 2008 Test points. Provide the best answer to the following questions and problems. Watch your sig figs.
 Physics 180A Fall 2008 Tes 1-120 poins Name Provide he bes answer o he following quesions and problems. Wach your sig figs. 1) The number of meaningful digis in a number is called he number of. When numbers
Physics 180A Fall 2008 Tes 1-120 poins Name Provide he bes answer o he following quesions and problems. Wach your sig figs. 1) The number of meaningful digis in a number is called he number of. When numbers
10.1 EXERCISES. y 2 t 2. y 1 t y t 3. y e
 66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
Chapter Let. 1) k be a vector-valued function. (a) Evaluate f (0). (b) What is the domain of f () t? (c) Is f () t continuous at t = 1?
 Chaper. Le f() = sin i+ ( 3+ ) j ln( + ) k be a vecor-valued funcion. (a) Evaluae f (). (b) Wha is he domain of f ()? (c) Is f () coninuous a =? Chaper. Le f() = sin i+ ( 3+ ) j ln( + ) k be a vecor-valued
Chaper. Le f() = sin i+ ( 3+ ) j ln( + ) k be a vecor-valued funcion. (a) Evaluae f (). (b) Wha is he domain of f ()? (c) Is f () coninuous a =? Chaper. Le f() = sin i+ ( 3+ ) j ln( + ) k be a vecor-valued
x(m) t(sec ) Homework #2. Ph 231 Introductory Physics, Sp-03 Page 1 of 4
 Homework #2. Ph 231 Inroducory Physics, Sp-03 Page 1 of 4 2-1A. A person walks 2 miles Eas (E) in 40 minues and hen back 1 mile Wes (W) in 20 minues. Wha are her average speed and average velociy (in ha
Homework #2. Ph 231 Inroducory Physics, Sp-03 Page 1 of 4 2-1A. A person walks 2 miles Eas (E) in 40 minues and hen back 1 mile Wes (W) in 20 minues. Wha are her average speed and average velociy (in ha
WEEK-3 Recitation PHYS 131. of the projectile s velocity remains constant throughout the motion, since the acceleration a x
 WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
Math Week 14 April 16-20: sections first order systems of linear differential equations; 7.4 mass-spring systems.
 Mah 2250-004 Week 4 April 6-20 secions 7.-7.3 firs order sysems of linear differenial equaions; 7.4 mass-spring sysems. Mon Apr 6 7.-7.2 Sysems of differenial equaions (7.), and he vecor Calculus we need
Mah 2250-004 Week 4 April 6-20 secions 7.-7.3 firs order sysems of linear differenial equaions; 7.4 mass-spring sysems. Mon Apr 6 7.-7.2 Sysems of differenial equaions (7.), and he vecor Calculus we need
Check in: 1 If m = 2(x + 1) and n = find y when. b y = 2m n 2
 7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
Kinematics Motion in 1 Dimension and Graphs
 Kinemaics Moion in 1 Dimension and Graphs Lana Sheridan De Anza College Sep 27, 2017 Las ime moion in 1-dimension some kinemaic quaniies graphs Overview velociy and speed acceleraion more graphs Kinemaics
Kinemaics Moion in 1 Dimension and Graphs Lana Sheridan De Anza College Sep 27, 2017 Las ime moion in 1-dimension some kinemaic quaniies graphs Overview velociy and speed acceleraion more graphs Kinemaics
2. Nonlinear Conservation Law Equations
 . Nonlinear Conservaion Law Equaions One of he clear lessons learned over recen years in sudying nonlinear parial differenial equaions is ha i is generally no wise o ry o aack a general class of nonlinear
. Nonlinear Conservaion Law Equaions One of he clear lessons learned over recen years in sudying nonlinear parial differenial equaions is ha i is generally no wise o ry o aack a general class of nonlinear
Today: Graphing. Note: I hope this joke will be funnier (or at least make you roll your eyes and say ugh ) after class. v (miles per hour ) Time
 +v Today: Graphing v (miles per hour ) 9 8 7 6 5 4 - - Time Noe: I hope his joke will be funnier (or a leas make you roll your eyes and say ugh ) afer class. Do yourself a favor! Prof Sarah s fail-safe
+v Today: Graphing v (miles per hour ) 9 8 7 6 5 4 - - Time Noe: I hope his joke will be funnier (or a leas make you roll your eyes and say ugh ) afer class. Do yourself a favor! Prof Sarah s fail-safe
3.6 Derivatives as Rates of Change
 3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
Physics 101 Fall 2006: Exam #1- PROBLEM #1
 Physics 101 Fall 2006: Exam #1- PROBLEM #1 1. Problem 1. (+20 ps) (a) (+10 ps) i. +5 ps graph for x of he rain vs. ime. The graph needs o be parabolic and concave upward. ii. +3 ps graph for x of he person
Physics 101 Fall 2006: Exam #1- PROBLEM #1 1. Problem 1. (+20 ps) (a) (+10 ps) i. +5 ps graph for x of he rain vs. ime. The graph needs o be parabolic and concave upward. ii. +3 ps graph for x of he person
Practicing Problem Solving and Graphing
 Pracicing Problem Solving and Graphing Tes 1: Jan 30, 7pm, Ming Hsieh G20 The Bes Ways To Pracice for Tes Bes If need more, ry suggesed problems from each new opic: Suden Response Examples A pas opic ha
Pracicing Problem Solving and Graphing Tes 1: Jan 30, 7pm, Ming Hsieh G20 The Bes Ways To Pracice for Tes Bes If need more, ry suggesed problems from each new opic: Suden Response Examples A pas opic ha
Chapter 7: Solving Trig Equations
 Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
Math 334 Test 1 KEY Spring 2010 Section: 001. Instructor: Scott Glasgow Dates: May 10 and 11.
 1 Mah 334 Tes 1 KEY Spring 21 Secion: 1 Insrucor: Sco Glasgow Daes: Ma 1 and 11. Do NOT wrie on his problem saemen bookle, excep for our indicaion of following he honor code jus below. No credi will be
1 Mah 334 Tes 1 KEY Spring 21 Secion: 1 Insrucor: Sco Glasgow Daes: Ma 1 and 11. Do NOT wrie on his problem saemen bookle, excep for our indicaion of following he honor code jus below. No credi will be
The equation to any straight line can be expressed in the form:
 Sring Graphs Par 1 Answers 1 TI-Nspire Invesigaion Suden min Aims Deermine a series of equaions of sraigh lines o form a paern similar o ha formed by he cables on he Jerusalem Chords Bridge. Deermine he
Sring Graphs Par 1 Answers 1 TI-Nspire Invesigaion Suden min Aims Deermine a series of equaions of sraigh lines o form a paern similar o ha formed by he cables on he Jerusalem Chords Bridge. Deermine he
Math 116 Practice for Exam 2
 Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
Topics covered in tutorial 01: 1. Review of definite integrals 2. Physical Application 3. Area between curves. 1. Review of definite integrals
 MATH4 Calculus II (8 Spring) MATH 4 Tuorial Noes Tuorial Noes (Phyllis LIANG) IA: Phyllis LIANG Email: masliang@us.hk Homepage: hps://masliang.people.us.hk Office: Room 3 (Lif/Lif 3) Phone number: 3587453
MATH4 Calculus II (8 Spring) MATH 4 Tuorial Noes Tuorial Noes (Phyllis LIANG) IA: Phyllis LIANG Email: masliang@us.hk Homepage: hps://masliang.people.us.hk Office: Room 3 (Lif/Lif 3) Phone number: 3587453
Chapters 6 & 7: Trigonometric Functions of Angles and Real Numbers. Divide both Sides by 180
 Algebra Chapers & : Trigonomeric Funcions of Angles and Real Numbers Chapers & : Trigonomeric Funcions of Angles and Real Numbers - Angle Measures Radians: - a uni (rad o measure he size of an angle. rad
Algebra Chapers & : Trigonomeric Funcions of Angles and Real Numbers Chapers & : Trigonomeric Funcions of Angles and Real Numbers - Angle Measures Radians: - a uni (rad o measure he size of an angle. rad
23.5. Half-Range Series. Introduction. Prerequisites. Learning Outcomes
 Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
Physics 221 Fall 2008 Homework #2 Solutions Ch. 2 Due Tues, Sept 9, 2008
 Physics 221 Fall 28 Homework #2 Soluions Ch. 2 Due Tues, Sep 9, 28 2.1 A paricle moving along he x-axis moves direcly from posiion x =. m a ime =. s o posiion x = 1. m by ime = 1. s, and hen moves direcly
Physics 221 Fall 28 Homework #2 Soluions Ch. 2 Due Tues, Sep 9, 28 2.1 A paricle moving along he x-axis moves direcly from posiion x =. m a ime =. s o posiion x = 1. m by ime = 1. s, and hen moves direcly
Chapter 2. Motion in One-Dimension I
 Chaper 2. Moion in One-Dimension I Level : AP Physics Insrucor : Kim 1. Average Rae of Change and Insananeous Velociy To find he average velociy(v ) of a paricle, we need o find he paricle s displacemen
Chaper 2. Moion in One-Dimension I Level : AP Physics Insrucor : Kim 1. Average Rae of Change and Insananeous Velociy To find he average velociy(v ) of a paricle, we need o find he paricle s displacemen
1998 Calculus AB Scoring Guidelines
 AB{ / BC{ 1999. The rae a which waer ows ou of a pipe, in gallons per hour, is given by a diereniable funcion R of ime. The able above shows he rae as measured every hours for a {hour period. (a) Use a
AB{ / BC{ 1999. The rae a which waer ows ou of a pipe, in gallons per hour, is given by a diereniable funcion R of ime. The able above shows he rae as measured every hours for a {hour period. (a) Use a
Announcements: Warm-up Exercise:
 Fri Apr 13 7.1 Sysems of differenial equaions - o model muli-componen sysems via comparmenal analysis hp//en.wikipedia.org/wiki/muli-comparmen_model Announcemens Warm-up Exercise Here's a relaively simple
Fri Apr 13 7.1 Sysems of differenial equaions - o model muli-componen sysems via comparmenal analysis hp//en.wikipedia.org/wiki/muli-comparmen_model Announcemens Warm-up Exercise Here's a relaively simple
AP CALCULUS AB 2003 SCORING GUIDELINES (Form B)
 SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
a. Show that these lines intersect by finding the point of intersection. b. Find an equation for the plane containing these lines.
 Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
MATH 4330/5330, Fourier Analysis Section 6, Proof of Fourier s Theorem for Pointwise Convergence
 MATH 433/533, Fourier Analysis Secion 6, Proof of Fourier s Theorem for Poinwise Convergence Firs, some commens abou inegraing periodic funcions. If g is a periodic funcion, g(x + ) g(x) for all real x,
MATH 433/533, Fourier Analysis Secion 6, Proof of Fourier s Theorem for Poinwise Convergence Firs, some commens abou inegraing periodic funcions. If g is a periodic funcion, g(x + ) g(x) for all real x,
MEI STRUCTURED MATHEMATICS 4758
 OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
d 1 = c 1 b 2 - b 1 c 2 d 2 = c 1 b 3 - b 1 c 3
 and d = c b - b c c d = c b - b c c This process is coninued unil he nh row has been compleed. The complee array of coefficiens is riangular. Noe ha in developing he array an enire row may be divided or
and d = c b - b c c d = c b - b c c This process is coninued unil he nh row has been compleed. The complee array of coefficiens is riangular. Noe ha in developing he array an enire row may be divided or
EXERCISES FOR SECTION 1.5
 1.5 Exisence and Uniqueness of Soluions 43 20. 1 v c 21. 1 v c 1 2 4 6 8 10 1 2 2 4 6 8 10 Graph of approximae soluion obained using Euler s mehod wih = 0.1. Graph of approximae soluion obained using Euler
1.5 Exisence and Uniqueness of Soluions 43 20. 1 v c 21. 1 v c 1 2 4 6 8 10 1 2 2 4 6 8 10 Graph of approximae soluion obained using Euler s mehod wih = 0.1. Graph of approximae soluion obained using Euler
k 1 k 2 x (1) x 2 = k 1 x 1 = k 2 k 1 +k 2 x (2) x k series x (3) k 2 x 2 = k 1 k 2 = k 1+k 2 = 1 k k 2 k series
 Final Review A Puzzle... Consider wo massless springs wih spring consans k 1 and k and he same equilibrium lengh. 1. If hese springs ac on a mass m in parallel, hey would be equivalen o a single spring
Final Review A Puzzle... Consider wo massless springs wih spring consans k 1 and k and he same equilibrium lengh. 1. If hese springs ac on a mass m in parallel, hey would be equivalen o a single spring
Solutions from Chapter 9.1 and 9.2
 Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
2.7. Some common engineering functions. Introduction. Prerequisites. Learning Outcomes
 Some common engineering funcions 2.7 Inroducion This secion provides a caalogue of some common funcions ofen used in Science and Engineering. These include polynomials, raional funcions, he modulus funcion
Some common engineering funcions 2.7 Inroducion This secion provides a caalogue of some common funcions ofen used in Science and Engineering. These include polynomials, raional funcions, he modulus funcion
Two Coupled Oscillators / Normal Modes
 Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Solutions to Assignment 1
 MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
Mechanics Acceleration The Kinematics Equations
 Mechanics Acceleraion The Kinemaics Equaions Lana Sheridan De Anza College Sep 27, 2018 Las ime kinemaic quaniies graphs of kinemaic quaniies Overview acceleraion he kinemaics equaions (consan acceleraion)
Mechanics Acceleraion The Kinemaics Equaions Lana Sheridan De Anza College Sep 27, 2018 Las ime kinemaic quaniies graphs of kinemaic quaniies Overview acceleraion he kinemaics equaions (consan acceleraion)
Math 2142 Exam 1 Review Problems. x 2 + f (0) 3! for the 3rd Taylor polynomial at x = 0. To calculate the various quantities:
 Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Of all of the intellectual hurdles which the human mind has confronted and has overcome in the last fifteen hundred years, the one which seems to me
 Of all of he inellecual hurdles which he human mind has confroned and has overcome in he las fifeen hundred years, he one which seems o me o have been he mos amazing in characer and he mos supendous in
Of all of he inellecual hurdles which he human mind has confroned and has overcome in he las fifeen hundred years, he one which seems o me o have been he mos amazing in characer and he mos supendous in
Physics 235 Chapter 2. Chapter 2 Newtonian Mechanics Single Particle
 Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Let us start with a two dimensional case. We consider a vector ( x,
 Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
Applications of the Basic Equations Chapter 3. Paul A. Ullrich
 Applicaions of he Basic Equaions Chaper 3 Paul A. Ullrich paullrich@ucdavis.edu Par 1: Naural Coordinaes Naural Coordinaes Quesion: Why do we need anoher coordinae sysem? Our goal is o simplify he equaions
Applicaions of he Basic Equaions Chaper 3 Paul A. Ullrich paullrich@ucdavis.edu Par 1: Naural Coordinaes Naural Coordinaes Quesion: Why do we need anoher coordinae sysem? Our goal is o simplify he equaions
Unit 1 Test Review Physics Basics, Movement, and Vectors Chapters 1-3
 A.P. Physics B Uni 1 Tes Reiew Physics Basics, Moemen, and Vecors Chapers 1-3 * In sudying for your es, make sure o sudy his reiew shee along wih your quizzes and homework assignmens. Muliple Choice Reiew:
A.P. Physics B Uni 1 Tes Reiew Physics Basics, Moemen, and Vecors Chapers 1-3 * In sudying for your es, make sure o sudy his reiew shee along wih your quizzes and homework assignmens. Muliple Choice Reiew:
AP CALCULUS AB/CALCULUS BC 2016 SCORING GUIDELINES. Question 1. 1 : estimate = = 120 liters/hr
 AP CALCULUS AB/CALCULUS BC 16 SCORING GUIDELINES Quesion 1 (hours) R ( ) (liers / hour) 1 3 6 8 134 119 95 74 7 Waer is pumped ino a ank a a rae modeled by W( ) = e liers per hour for 8, where is measured
AP CALCULUS AB/CALCULUS BC 16 SCORING GUIDELINES Quesion 1 (hours) R ( ) (liers / hour) 1 3 6 8 134 119 95 74 7 Waer is pumped ino a ank a a rae modeled by W( ) = e liers per hour for 8, where is measured
MATH 31B: MIDTERM 2 REVIEW. x 2 e x2 2x dx = 1. ue u du 2. x 2 e x2 e x2] + C 2. dx = x ln(x) 2 2. ln x dx = x ln x x + C. 2, or dx = 2u du.
![MATH 31B: MIDTERM 2 REVIEW. x 2 e x2 2x dx = 1. ue u du 2. x 2 e x2 e x2] + C 2. dx = x ln(x) 2 2. ln x dx = x ln x x + C. 2, or dx = 2u du. MATH 31B: MIDTERM 2 REVIEW. x 2 e x2 2x dx = 1. ue u du 2. x 2 e x2 e x2] + C 2. dx = x ln(x) 2 2. ln x dx = x ln x x + C. 2, or dx = 2u du.](/thumbs/86/93221008.jpg) MATH 3B: MIDTERM REVIEW JOE HUGHES. Inegraion by Pars. Evaluae 3 e. Soluion: Firs make he subsiuion u =. Then =, hence 3 e = e = ue u Now inegrae by pars o ge ue u = ue u e u + C and subsiue he definiion
MATH 3B: MIDTERM REVIEW JOE HUGHES. Inegraion by Pars. Evaluae 3 e. Soluion: Firs make he subsiuion u =. Then =, hence 3 e = e = ue u Now inegrae by pars o ge ue u = ue u e u + C and subsiue he definiion
Welcome Back to Physics 215!
 Welcome Back o Physics 215! (General Physics I) Thurs. Jan 19 h, 2017 Lecure01-2 1 Las ime: Syllabus Unis and dimensional analysis Today: Displacemen, velociy, acceleraion graphs Nex ime: More acceleraion
Welcome Back o Physics 215! (General Physics I) Thurs. Jan 19 h, 2017 Lecure01-2 1 Las ime: Syllabus Unis and dimensional analysis Today: Displacemen, velociy, acceleraion graphs Nex ime: More acceleraion
Midterm Exam Review Questions Free Response Non Calculator
 Name: Dae: Block: Miderm Eam Review Quesions Free Response Non Calculaor Direcions: Solve each of he following problems. Choose he BEST answer choice from hose given. A calculaor may no be used. Do no
Name: Dae: Block: Miderm Eam Review Quesions Free Response Non Calculaor Direcions: Solve each of he following problems. Choose he BEST answer choice from hose given. A calculaor may no be used. Do no
x i v x t a dx dt t x
 Physics 3A: Basic Physics I Shoup - Miderm Useful Equaions A y A sin A A A y an A y A A = A i + A y j + A z k A * B = A B cos(θ) A B = A B sin(θ) A * B = A B + A y B y + A z B z A B = (A y B z A z B y
Physics 3A: Basic Physics I Shoup - Miderm Useful Equaions A y A sin A A A y an A y A A = A i + A y j + A z k A * B = A B cos(θ) A B = A B sin(θ) A * B = A B + A y B y + A z B z A B = (A y B z A z B y
Guest Lectures for Dr. MacFarlane s EE3350 Part Deux
 Gues Lecures for Dr. MacFarlane s EE3350 Par Deux Michael Plane Mon., 08-30-2010 Wrie name in corner. Poin ou his is a review, so I will go faser. Remind hem o go lisen o online lecure abou geing an A
Gues Lecures for Dr. MacFarlane s EE3350 Par Deux Michael Plane Mon., 08-30-2010 Wrie name in corner. Poin ou his is a review, so I will go faser. Remind hem o go lisen o online lecure abou geing an A
Robotics I. April 11, The kinematics of a 3R spatial robot is specified by the Denavit-Hartenberg parameters in Tab. 1.
 Roboics I April 11, 017 Exercise 1 he kinemaics of a 3R spaial robo is specified by he Denavi-Harenberg parameers in ab 1 i α i d i a i θ i 1 π/ L 1 0 1 0 0 L 3 0 0 L 3 3 able 1: able of DH parameers of
Roboics I April 11, 017 Exercise 1 he kinemaics of a 3R spaial robo is specified by he Denavi-Harenberg parameers in ab 1 i α i d i a i θ i 1 π/ L 1 0 1 0 0 L 3 0 0 L 3 3 able 1: able of DH parameers of
10.6 Parametric Equations
 0_006.qd /8/05 9:05 AM Page 77 Secion 0.6 77 Parameric Equaions 0.6 Parameric Equaions Wha ou should learn Evaluae ses of parameric equaions for given values of he parameer. Skech curves ha are represened
0_006.qd /8/05 9:05 AM Page 77 Secion 0.6 77 Parameric Equaions 0.6 Parameric Equaions Wha ou should learn Evaluae ses of parameric equaions for given values of he parameer. Skech curves ha are represened
Physics 20 Lesson 5 Graphical Analysis Acceleration
 Physics 2 Lesson 5 Graphical Analysis Acceleraion I. Insananeous Velociy From our previous work wih consan speed and consan velociy, we know ha he slope of a posiion-ime graph is equal o he velociy of
Physics 2 Lesson 5 Graphical Analysis Acceleraion I. Insananeous Velociy From our previous work wih consan speed and consan velociy, we know ha he slope of a posiion-ime graph is equal o he velociy of
1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.
![1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx. 1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.](/thumbs/71/65799522.jpg) . Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
. Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
Second-Order Differential Equations
 WWW Problems and Soluions 3.1 Chaper 3 Second-Order Differenial Equaions Secion 3.1 Springs: Linear and Nonlinear Models www m Problem 3. (NonlinearSprings). A bod of mass m is aached o a wall b means
WWW Problems and Soluions 3.1 Chaper 3 Second-Order Differenial Equaions Secion 3.1 Springs: Linear and Nonlinear Models www m Problem 3. (NonlinearSprings). A bod of mass m is aached o a wall b means
Week 1 Lecture 2 Problems 2, 5. What if something oscillates with no obvious spring? What is ω? (problem set problem)
 Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
Today: Falling. v, a
 Today: Falling. v, a Did you ge my es email? If no, make sure i s no in your junk box, and add sbs0016@mix.wvu.edu o your address book! Also please email me o le me know. I will be emailing ou pracice
Today: Falling. v, a Did you ge my es email? If no, make sure i s no in your junk box, and add sbs0016@mix.wvu.edu o your address book! Also please email me o le me know. I will be emailing ou pracice
Math 116 Second Midterm March 21, 2016
 Mah 6 Second Miderm March, 06 UMID: EXAM SOLUTIONS Iniials: Insrucor: Secion:. Do no open his exam unil you are old o do so.. Do no wrie your name anywhere on his exam. 3. This exam has pages including
Mah 6 Second Miderm March, 06 UMID: EXAM SOLUTIONS Iniials: Insrucor: Secion:. Do no open his exam unil you are old o do so.. Do no wrie your name anywhere on his exam. 3. This exam has pages including
Chapter 2. First Order Scalar Equations
 Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Starting from a familiar curve
 In[]:= NoebookDirecory Ou[]= C:\Dropbox\Work\myweb\Courses\Mah_pages\Mah_5\ You can evaluae he enire noebook by using he keyboard shorcu Al+v o, or he menu iem Evaluaion Evaluae Noebook. Saring from a
In[]:= NoebookDirecory Ou[]= C:\Dropbox\Work\myweb\Courses\Mah_pages\Mah_5\ You can evaluae he enire noebook by using he keyboard shorcu Al+v o, or he menu iem Evaluaion Evaluae Noebook. Saring from a
KEY. Math 334 Midterm I Fall 2008 sections 001 and 003 Instructor: Scott Glasgow
 1 KEY Mah 4 Miderm I Fall 8 secions 1 and Insrucor: Sco Glasgow Please do NOT wrie on his eam. No credi will be given for such work. Raher wrie in a blue book, or on our own paper, preferabl engineering
1 KEY Mah 4 Miderm I Fall 8 secions 1 and Insrucor: Sco Glasgow Please do NOT wrie on his eam. No credi will be given for such work. Raher wrie in a blue book, or on our own paper, preferabl engineering
Multiple Choice Solutions 1. E (2003 AB25) () xt t t t 2. A (2008 AB21/BC21) 3. B (2008 AB7) Using Fundamental Theorem of Calculus: 1
 Paricle Moion Soluions We have inenionally included more maerial han can be covered in mos Suden Sudy Sessions o accoun for groups ha are able o answer he quesions a a faser rae. Use your own judgmen,
Paricle Moion Soluions We have inenionally included more maerial han can be covered in mos Suden Sudy Sessions o accoun for groups ha are able o answer he quesions a a faser rae. Use your own judgmen,
2. What is the displacement of the bug between t = 0.00 s and t = 20.0 s? A) cm B) 39.9 cm C) cm D) 16.1 cm E) +16.
 1. For which one of he following siuaions will he pah lengh equal he magniude of he displacemen? A) A jogger is running around a circular pah. B) A ball is rolling down an inclined plane. C) A rain ravels
1. For which one of he following siuaions will he pah lengh equal he magniude of he displacemen? A) A jogger is running around a circular pah. B) A ball is rolling down an inclined plane. C) A rain ravels
Challenge Problems. DIS 203 and 210. March 6, (e 2) k. k(k + 2). k=1. f(x) = k(k + 2) = 1 x k
 Challenge Problems DIS 03 and 0 March 6, 05 Choose one of he following problems, and work on i in your group. Your goal is o convince me ha your answer is correc. Even if your answer isn compleely correc,
Challenge Problems DIS 03 and 0 March 6, 05 Choose one of he following problems, and work on i in your group. Your goal is o convince me ha your answer is correc. Even if your answer isn compleely correc,
THE 2-BODY PROBLEM. FIGURE 1. A pair of ellipses sharing a common focus. (c,b) c+a ROBERT J. VANDERBEI
 THE 2-BODY PROBLEM ROBERT J. VANDERBEI ABSTRACT. In his shor noe, we show ha a pair of ellipses wih a common focus is a soluion o he 2-body problem. INTRODUCTION. Solving he 2-body problem from scrach
THE 2-BODY PROBLEM ROBERT J. VANDERBEI ABSTRACT. In his shor noe, we show ha a pair of ellipses wih a common focus is a soluion o he 2-body problem. INTRODUCTION. Solving he 2-body problem from scrach
Dynamics. Option topic: Dynamics
 Dynamics 11 syllabusref Opion opic: Dynamics eferenceence In his cha chaper 11A Differeniaion and displacemen, velociy and acceleraion 11B Inerpreing graphs 11C Algebraic links beween displacemen, velociy
Dynamics 11 syllabusref Opion opic: Dynamics eferenceence In his cha chaper 11A Differeniaion and displacemen, velociy and acceleraion 11B Inerpreing graphs 11C Algebraic links beween displacemen, velociy
Trajectory planning in Cartesian space
 Roboics 1 Trajecory planning in Caresian space Prof. Alessandro De Luca Roboics 1 1 Trajecories in Caresian space in general, he rajecory planning mehods proposed in he join space can be applied also in
Roboics 1 Trajecory planning in Caresian space Prof. Alessandro De Luca Roboics 1 1 Trajecories in Caresian space in general, he rajecory planning mehods proposed in he join space can be applied also in
Non-uniform circular motion *
 OpenSax-CNX module: m14020 1 Non-uniform circular moion * Sunil Kumar Singh This work is produced by OpenSax-CNX and licensed under he Creaive Commons Aribuion License 2.0 Wha do we mean by non-uniform
OpenSax-CNX module: m14020 1 Non-uniform circular moion * Sunil Kumar Singh This work is produced by OpenSax-CNX and licensed under he Creaive Commons Aribuion License 2.0 Wha do we mean by non-uniform
Roller-Coaster Coordinate System
 Winer 200 MECH 220: Mechanics 2 Roller-Coaser Coordinae Sysem Imagine you are riding on a roller-coaer in which he rack goes up and down, wiss and urns. Your velociy and acceleraion will change (quie abruply),
Winer 200 MECH 220: Mechanics 2 Roller-Coaser Coordinae Sysem Imagine you are riding on a roller-coaer in which he rack goes up and down, wiss and urns. Your velociy and acceleraion will change (quie abruply),
The Contradiction within Equations of Motion with Constant Acceleration
 The Conradicion wihin Equaions of Moion wih Consan Acceleraion Louai Hassan Elzein Basheir (Daed: July 7, 0 This paper is prepared o demonsrae he violaion of rules of mahemaics in he algebraic derivaion
The Conradicion wihin Equaions of Moion wih Consan Acceleraion Louai Hassan Elzein Basheir (Daed: July 7, 0 This paper is prepared o demonsrae he violaion of rules of mahemaics in he algebraic derivaion
One-Dimensional Kinematics
 One-Dimensional Kinemaics One dimensional kinemaics refers o moion along a sraigh line. Een hough we lie in a 3-dimension world, moion can ofen be absraced o a single dimension. We can also describe moion
One-Dimensional Kinemaics One dimensional kinemaics refers o moion along a sraigh line. Een hough we lie in a 3-dimension world, moion can ofen be absraced o a single dimension. We can also describe moion
ACCUMULATION. Section 7.5 Calculus AP/Dual, Revised /26/2018 7:27 PM 7.5A: Accumulation 1
 ACCUMULATION Secion 7.5 Calculus AP/Dual, Revised 2019 vie.dang@humbleisd.ne 12/26/2018 7:27 PM 7.5A: Accumulaion 1 APPLICATION PROBLEMS A. Undersand he quesion. I is ofen no necessary o as much compuaion
ACCUMULATION Secion 7.5 Calculus AP/Dual, Revised 2019 vie.dang@humbleisd.ne 12/26/2018 7:27 PM 7.5A: Accumulaion 1 APPLICATION PROBLEMS A. Undersand he quesion. I is ofen no necessary o as much compuaion
SOLUTIONS TO ECE 3084
 SOLUTIONS TO ECE 384 PROBLEM 2.. For each sysem below, specify wheher or no i is: (i) memoryless; (ii) causal; (iii) inverible; (iv) linear; (v) ime invarian; Explain your reasoning. If he propery is no
SOLUTIONS TO ECE 384 PROBLEM 2.. For each sysem below, specify wheher or no i is: (i) memoryless; (ii) causal; (iii) inverible; (iv) linear; (v) ime invarian; Explain your reasoning. If he propery is no
Suggested Practice Problems (set #2) for the Physics Placement Test
 Deparmen of Physics College of Ars and Sciences American Universiy of Sharjah (AUS) Fall 014 Suggesed Pracice Problems (se #) for he Physics Placemen Tes This documen conains 5 suggesed problems ha are
Deparmen of Physics College of Ars and Sciences American Universiy of Sharjah (AUS) Fall 014 Suggesed Pracice Problems (se #) for he Physics Placemen Tes This documen conains 5 suggesed problems ha are
dy dx = xey (a) y(0) = 2 (b) y(1) = 2.5 SOLUTION: See next page
 Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
