Technical Vibration - text 2 - forced vibration, rotational vibration
|
|
|
- Elizabeth Riley
- 6 years ago
- Views:
Transcription
1 Technicl Viion - e - foced viion, oionl viion 4. oced viion, viion unde he consn eenl foce The viion unde he eenl foce. eenl The quesion is if he eenl foce e is consn o vying. If vying, wh is he foce funcion. The consn foce nd he honiclly vying foce will e nlyzed. The viion unde he consn eenl foce he fee lengh undefoed sping he equiliiu posiion s v e = cons The equion of oion : i e s e
2 Technicl Viion - e - foced viion, oionl viion The heicl ppoch : ho Ce hoogenous picul sin p p p consn inlly : consn consn e s e whee Ce sin s s is so clled sic defoion (he defoion of he sping unde he consn foce ). e [] s Ce sin s [s]
3 Technicl Viion - e - foced viion, oionl viion The echnicl ppoch : Le us define he sic defoion s : e s Le us hen ove he oigin of he coodine syse y s (see figue). ol = s + () he fee lengh undefoed sping he equiliiu posiion s s v e = cons In he equiliiu posiion he sping foce, coesponding o he sic defoion (so clled sic pe-sess), is in he equiliiu wih he eenl consn foce e. s _ s s e The equion of oion is : e i e ol s v The ol defoion ol cn e epessed s he su of sic defoion s nd vying displceen () : The equion of oion is hen : nd : Becuse (see ove) : ol s e v s v e e s s 3
4 Technicl Viion - e - foced viion, oionl viion he igh side of he equion is hen equl o zeo : v In he end he equion of oion is he se s his fo fee (nul) viion. The soluion is lso he se : Ce sin The conclusion :. The viion unde consn eenl foce is nlyzed he se s fee (nul) viion. Bu :. The equiliiu posiion - he oigin of he coodine syse, is deeined no y he sping fee lengh u y he sic defoion s. 3. The ol loding of he sping is given y wo coniuions, sic nd dynic : s _ ol s _ s s _ dyn s 4
5 Technicl Viion - e - foced viion, oionl viion 5. The viion unde he honiclly vying eenl foce The honiclly vying eenl foce (eciing foce) ens foce, vying ccoding o he sinus funcion : sin hee - he pliude of he eciing foce (iu vlue) [N], - he cicul fequency of he eciing foce [s - ], f - he fequency of he eciing foce [Hz], T - he peiod of he eciing foce [s]. f s sin () The equion of oion is : v sin The soluion hs wo ps - hoogenous soluion nd picul soluion. hoogenous picul T f The hoogenous soluion is he soluion fo zeo igh side of he equion of oion, epesens fee (nul) viion (ed line see dig elow) : ho Ce sin T ho Ce sin o he pees see fee (nul) viion. 5
6 Technicl Viion - e - foced viion, oionl viion The picul soluion eflecs non-zeo igh side, epesens foced viion (lue line see dig elow) : p sin hee - he pliude of he picul soluion [, ], - he cicul fequency of he eciing foce [s - ], - phse shif [d]. T sin p The soluion of he equion of oion is he supeposiion of oh hoogenous nd picul soluion : hoogenous picul Ce sin sin Ce sin sin ho Ce sin sin p coplee soluion hoogenous soluion picul soluion nsien pocess sedy se The coplee soluion cn e spli ino wo phses.. phse - nsien pocess The soluion is deeined s supeposiion of oh hoogenous soluion (fee viion) nd picul soluion (foced viion). The ie ehvio is he copliced ecuse of he coinion of wo diffeen fequencies. Tes liied ie.. phse - sedy se Ss he oen he fee viion disppes (due o dping). Sedy se is epesened y he only picul soluion. Tes infinie ie. 6
7 Technicl Viion - e - foced viion, oionl viion The pliude nd phse shif clculion The picul soluion nd is deivives : p p p us sisfy he equion of oion : sin cos sin sin sin cos sin sin Using he igonoeic fouls : sin cos he equion cn e epessed s : sin cos cos sin cos cos sin sin cos sin cos sin sin cos sin cos sin Coping of he ces wih sin nd cos ee leds o : o he second equion diecly : o n cos sin The noe :, 8º o, d. sin cos sin n cos cn cos sin o he fis equion, if sin n nd n cos n hen : 7
8 Technicl Viion - e - foced viion, oionl viion o susequen nlysis i is useful o define he diensionless pees : he uning coefficien, he dping io (he elive dping). Hee is he nul cicul fequency of he fee undped viion. The cicul fequency of he eciing foce cn e epessed s : he decy consn cn e epessed s : Puing hese epessions ino he foul fo pliude of he foced viion : fcoizing : if hen siilly : s cn cn The io (pliude of he eciing foce) nd (siffness) is so clled sic defoion. This epesens he sic defoion of he sping unde he consn foce. s The physicl ening of he pliude is siply iu displceen. 8
9 Technicl Viion - e - foced viion, oionl viion The physicl ening of he phse shif is he ie dely of he displceen esponse () fe he foce ()., sin sin The iu vlue of displceen (lue cuve on he dig ove) ppes cein ie dely le hn he iu vlue of he eciing foce (ed cuve). This ie dely is deeined s whee - phse shif [d], - cicul fequency of he eciing foce [s - ]. The noe : Be ceful,, 8º o, d. If <, he clculo euns he vlue -9º,. Bu he coec esul is 9º, 8º. The eseche is esponsile o dd 8 º. The pliude nd phse shif soluion fo undped viion -,. s s s, cn cn cn = º if o <, = 8º if o >. 9
10 Technicl Viion - e - foced viion, oionl viion The pliude chceisic nd he phse chceisic These wo e he pliude s funcion of (cicul fequency of he eciing foce) nd phse shif s funcion of. The pliude chceisic s pliude ) = =, =, - dping io s ) - uning coefficien 3) es = = = On he dig he ed cuve efes o he undped foced viion, while lue nd geen cuves efe o he dped foced viion. Poin ) coesponds o he consn foce (zeo fequency, infinie long peiod), pliude is equl o he sic displceen = s. Poin ) coesponds o so clled esonnce. The esonnce ppes if o. In esonnce he pliude inceses o high vlues. Poin 3) coesponds o he eeely high fequency of he eciing foce. In his cse he sque oo in denoino of he epession fo inceses infiniely, he whole fcion nd lso he pliude deceses o zeo.
11 Technicl Viion - e - foced viion, oionl viion The phse chceisic cn cn phse shif = = / =, =, - uning coefficien 3 Wih incesing fequency of he eciing foce nd incesing uning coefficien he phse shif inceses fo = o = 8º ( d). o lge dping (ed cuve on dig) he cuve is sooh, fo slle dping (lue cuve) he funcion ends o sep chnge. In esonnce (see ove) he phse shif hs he vlue close o = 9º (/ d).
12 Technicl Viion - e - foced viion, oionl viion 6. The foced viion due o cenifugl foce The viing syse is epesened y he ss, siffness nd coefficien of dping. The p of he viing ody is oing ss o. y cen = o e,, e = cen sin( ) v o e - he oing ss [g], - he ngul velociy of he oing ss [d/s], - ecceniciy, he disnce of he cene of ss fo he is of oion []. The oing poduces he consn cenifugl foce : cen o e The cenifugl foce oes wih he oing ss wih he ngul velociy. The ngle eween he cenifugl foce nd y is (pependicul o he is, he diecion of viion) inceses s : The coponen of he cenifugl foce (he coponen pesen in he equion of oion) is : cen sin cen sin The equion of oion is hen : cen sin nd he picul soluion (see ove) is : p sin
13 Technicl Viion - e - foced viion, oionl viion The susequen soluion hs wo levels. Level A, he soluion fo given oionl speed. If he ngul velociy is defined s consn, he coesponding cenifugl foce cn e clculed : cen o e The pliude of foced viion is : cen cen 3
14 Technicl Viion - e - foced viion, oionl viion Level B, he pliude chceisic If we suppose vying oionl speed, hen he cenifugl foce depends on he ngul velociy nd he pliude of foced viion is : cen o e e o e o The funcion is diffeen fo he one if he pliude of he eciing foce is supposed o e consn. ) = =, - dping io =,35 e ) 3) 3 4 es = = = 3 - uning coefficien Poin ) coesponds o he zeo oionl speed, zeo cenifugl foce nd susequenly zeo displceen. Poin ) coesponds o so clled esonnce (see ove). Poin 3) coesponds o he eeely high oionl speed. Then he lii gives he pliude. o li e e o 4
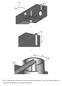
15 Technicl Viion - e - foced viion, oionl viion 7. The oionl viion, fee nd foced, osionl siffness The fee undped oionl viion Suppose he igid ody suppoed y he pin join nd fleile sping. In he equiliiu posiion he ody - he hin od is in he hoizonl posiion, he sping is in he veicl posiion, pependicul o he od. The ody will oe., I oion y = p sin p S p I - he ss oen of inei of he ody [g ], p - he sping siffness [N/], - he, he pependicul disnce of he pin-join o he sping is [], - he oionl ngle, he ngul coodine [d], - he ngul velociy [d/s], - he ngul cceleion [d/s ]. The echnicl unis : - he oionl ngle [º, evolue], d = (8/)º 57,3º, evolue = 36º = d 6,8 d. n - he oionl speed [ev/in], n 3, ev/in = /3 d/s,5 d/s. 5
16 Technicl Viion - e - foced viion, oionl viion Duing oion he sping is lenghened nd he sping foce S ppes. If he oionl ngle is he sll, he soluion cn e lineized. The equion of oion : I M i p S The sping foce is : he sping lenghening is : S p p sin p The noe : The siplificion sin is used. The eo depends on he vlue of he ngle sin eo sin sin [ ] [d] [-] [%],7453,745,5 % 5,877,876,3 %,7453,7365,5 % 5,6,59, %,349,34 % 3,54,5 5 % 6,47,866 % 9,57 57 % The siplificion sin is used usully if <5º. The equion of oion hen is : The susiuion = p oligoy). The equion of oion is hen : I p I p (oionl siffness [N /d]) cn e used (voluny, no I I The equion of oion cn e coped wih he equion of oion of he nslionl viion of he ss picle. 6
17 Technicl Viion - e - foced viion, oionl viion The pllel (nlogy) eween oh cn e seen. he nslionl viion of he ss picle equion of oion he ss he siffness he coodine nd i s second deivive he soluion C sin he nul cicul fequency he iniil condiions =... =, v=v - iniil displceen v - iniil velociy C pliude v phse shif cn v he oionl viion of he ss ody equion of oion I insed of he ss he ss oen of inei I is used insed of he siffness he oionl siffness = p is used insed of he coodine oionl coodine nd i s second deivive is used he soluion C sin he nul cicul fequency I p I he iniil condiions =... =, = - iniil oionl ngle - iniil ngul velociy pliude C phse shif cn 7
18 Technicl Viion - e - foced viion, oionl viion The fee dped oionl viion Suppose he igid ody suppoed y he pin join, fleile sping nd dpe. In he equiliiu posiion he ody - he hin od is in he hoizonl posiion, oh sping nd dpe e in he veicl posiion, pependicul o he od. I, oion y p v = q S q p Ecep of I,, p,, nd (see ove) : - he coefficien of dping [N - s], q - he, he pependicul disnce of he pin-join o he dpe is [], Duing oion he sping is lenghened nd he sping foce S ppes. The dpe pison oves nd he dping foce ppes. The sping foce is : The dping foce is : S p v q q The cicufeenil velociy is : whee is he ngul velociy. The equion of oion : v q I M i p q p p q q S I q I q p p Afe he susiuion = p s he oionl siffness [N /d] nd = q s he oionl coefficien of dping [N s] : I I The equion of oion is nlogous o he one of nslionl viion of he ss picle : 8
19 Technicl Viion - e - foced viion, oionl viion The pllel (nlogy) eween oh cn e seen. he nslionl viion of he ss picle equion of oion ecep of he ss, he siffness nd coodine nd i s deivives, he oionl viion of he ss ody equion of oion I ecep of he ss oen of inei I, he oionl siffness = p nd he oionl coodine nd i s deivives, he coefficien of dping Ce he soluion sin he nul cicul fequency of undped viion he decy consn he nul cicul fequency of dped viion insed of he coefficien of dping he oionl coefficien of dping Ce = q is used he soluion sin he nul cicul fequency of undped viion I p I he decy consn q I I he nul cicul fequency of dped viion he iniil condiions =... =, v=v - iniil displceen v - iniil velociy pliude C v phse shif cn v he iniil condiions =... =, = - iniil oionl ngle - iniil ngul velociy C pliude phse shif cn 9
20 Technicl Viion - e - foced viion, oionl viion The foced oionl viion Suppose he igid ody suppoed y he pin join, fleile sping nd dpe. In he equiliiu posiion he ody - he hin od is in he hoizonl posiion, oh sping nd dpe e in he veicl posiion, pependicul o he od. The honiclly vying eenl foce () ipcs on he ody.,, I oion S () = sin( ) q p Ecep of I,,, p, q,, nd (see ove) : () = sin( ) - he honiclly vying eenl foce [N], - he pliude of he foce [N], = f - he cicul fequency of he foce [s - ], f - he fequency of he foce [Hz], - he, he pependicul disnce of he pin-join o he foce []. Noe : The suden us PERECTELY diffeenie eween - he cicul fequency of he eenl foce nd - he ngul velociy of oion. The equion of oion is : I q I q p p sin sin Afe he susiuion = p s he oionl siffness [N /d] nd = q s he oionl coefficien of dping [N s] nd M = s he pliude of he eenl oen [N ] : I M sin
21 Technicl Viion - e - foced viion, oionl viion The equion of oion is nlogous o he one of nslionl viion of he ss picle : sin The pllel (nlogy) eween oh cn e seen. he nslionl viion he oionl viion of he ss ody of he ss picle equion of oion equion of oion sin I M sin ecep of he ss, he coefficien of dping, he siffness nd coodine nd i s deivives, ecep of he ss oen of inei I, he oionl coefficien of dping = q, he oionl siffness = p nd he oionl coodine nd i s deivives, he picul soluion sin s pliude phse shif cn cn whee : s - he sic defoion - he uning coefficien - he dping io M I I he picul soluion sin s pliude phse shif cn M cn whee : s - he sic p defoion - he uning coefficien - he dping io
22 Technicl Viion - e - foced viion, oionl viion The osionl siffness Suppose he long, hin od, fied on one end (op end on figue), eposed o he osionl oen (he oque). This esuls o he osionl defoion of he od, he osionl ngle. G, J p T - he lengh of he od [, ], G - he she elsic odulus (Young odulus) of he od eil [P, MP], J p - he coss secion pol qudic oen of inei [ 4, 4 ], e.g. fo cicul coss secion of he diee d, he pol oen of inei is : M T J p 3 d 4 M T - osionl oen (he oque) [N ], - he osionl ngle [d]. The osionl defoion of he od, epessed s he osionl ngle, is : M T G J The io of he osionl oen nd he osionl ngle cn e epessed s osionl siffness [N /d] : T M T P G J P Once, when he osionl defoion ppes, he ecion oen M R cs gins defoion. M T is he eenl oen s he cuse of defoion, M R is he secondy ecion oen s he esisnce gins defoion (nlogous o he sping foce). M T M R T
23 Technicl Viion - e - foced viion, oionl viion Suppose fhe he syeicl dis on he fee end of he osionl od. T I M R I - ss oen of inei of he dis [g ], T M R = T f - he osionl siffness of he od [N /d] - he ecion oen [N ], - he osionl ngle [d], - he ngul velociy [d/s], - he ngul cceleion [d/s ], The noe : Suppose he fee end of he od is suppoed y he eing o void he ending defoion. The equion of oion of fee undped osionl viion is : o including dping : I I T M i I T M R T T o fo foced viion : I T T M sin The soluion see ove.... 3
ME 141. Engineering Mechanics
ME 141 Engineeing Mechnics Lecue 13: Kinemics of igid bodies hmd Shhedi Shkil Lecue, ep. of Mechnicl Engg, UET E-mil: sshkil@me.bue.c.bd, shkil6791@gmil.com Websie: eche.bue.c.bd/sshkil Couesy: Veco Mechnics
() t. () t r () t or v. ( t) () () ( ) = ( ) or ( ) () () () t or dv () () Section 10.4 Motion in Space: Velocity and Acceleration
Secion 1.4 Moion in Spce: Velociy nd Acceleion We e going o dive lile deepe ino somehing we ve ledy inoduced, nmely () nd (). Discuss wih you neighbo he elionships beween posiion, velociy nd cceleion you
LECTURE 5. is defined by the position vectors r, 1. and. The displacement vector (from P 1 to P 2 ) is defined through r and 1.
LECTURE 5 ] DESCRIPTION OF PARTICLE MOTION IN SPACE -The displcemen, veloci nd cceleion in -D moion evel hei veco nue (diecion) houh he cuion h one mus p o hei sin. Thei full veco menin ppes when he picle
Motion on a Curve and Curvature
Moion on Cue nd Cuue his uni is bsed on Secions 9. & 9.3, Chpe 9. All ssigned edings nd execises e fom he exbook Objecies: Mke cein h you cn define, nd use in conex, he ems, conceps nd fomuls lised below:
USING LOWER CLASS WEIGHTS TO CORRECT AND CHECK THE NONLINEARITY OF BALANCES
USING OWER CSS WEIGHTS TO CORRECT ND CHECK THE NONINERITY OF BNCES Tiohy Chnglin Wng, Qiho Yun, hu Reichuh Mele-Toledo Insuens Shnghi Co. d, Shnghi, P R Chin Mele-Toledo GH, Geifensee, Swizelnd BSTRCT
1. Kinematics of Particles
1. Kinemics o Picles 1.1 Inoducion o Dnmics Dnmics - Kinemics: he sud o he geome o moion; ele displcemen, eloci, cceleion, nd ime, wihou eeence o he cuse o he moion. - Kineics: he sud o he elion eising
Ans: In the rectangular loop with the assigned direction for i2: di L dt , (1) where (2) a) At t = 0, i1(t) = I1U(t) is applied and (1) becomes
omewok # P7-3 ecngul loop of widh w nd heigh h is siued ne ve long wie cing cuen i s in Fig 7- ssume i o e ecngul pulse s shown in Fig 7- Find he induced cuen i in he ecngul loop whose self-inducnce is
Physics 201, Lecture 5
Phsics 1 Lecue 5 Tod s Topics n Moion in D (Chp 4.1-4.3): n D Kinemicl Quniies (sec. 4.1) n D Kinemics wih Consn Acceleion (sec. 4.) n D Pojecile (Sec 4.3) n Epeced fom Peiew: n Displcemen eloci cceleion
Science Advertisement Intergovernmental Panel on Climate Change: The Physical Science Basis 2/3/2007 Physics 253
Science Adeisemen Inegoenmenl Pnel on Clime Chnge: The Phsicl Science Bsis hp://www.ipcc.ch/spmfeb7.pdf /3/7 Phsics 53 hp://www.fonews.com/pojecs/pdf/spmfeb7.pdf /3/7 Phsics 53 3 Sus: Uni, Chpe 3 Vecos
v T Pressure Extra Molecular Stresses Constitutive equations for Stress v t Observation: the stress tensor is symmetric
Momenum Blnce (coninued Momenum Blnce (coninued Now, wh o do wih Π? Pessue is p of i. bck o ou quesion, Now, wh o do wih? Π Pessue is p of i. Thee e ohe, nonisoopic sesses Pessue E Molecul Sesses definiion:
Ch.4 Motion in 2D. Ch.4 Motion in 2D
Moion in plne, such s in he sceen, is clled 2-dimensionl (2D) moion. 1. Posiion, displcemen nd eloci ecos If he picle s posiion is ( 1, 1 ) 1, nd ( 2, 2 ) 2, he posiions ecos e 1 = 1 1 2 = 2 2 Aege eloci
Introduction to Mechanical Vibrations and Structural Dynamics
Inroducion o Mechanical Viraions and Srucural Dynaics The one seeser schedule :. Viraion - classificaion. ree undaped single DO iraion, equaion of oion, soluion, inegraional consans, iniial condiions..
Chapter 10. Simple Harmonic Motion and Elasticity. Goals for Chapter 10
Chper 0 Siple Hronic Moion nd Elsiciy Gols or Chper 0 o ollow periodic oion o sudy o siple hronic oion. o sole equions o siple hronic oion. o use he pendulu s prooypicl syse undergoing siple hronic oion.
Axis. Axis. Axis. Solid cylinder (or disk) about. Hoop about. Annular cylinder (or ring) about central axis. central axis.
Insucos: Fiel/che/Deweile PYSICS DEPATENT PY 48 Em ch 5, 5 Nme pin, ls fis: Signue: On m hono, I he neihe gien no eceie unuhoie i on his eminion. YOU TEST NUBE IS TE 5-DIGIT NUBE AT TE TOP OF EAC PAGE.
Motion. ( (3 dim) ( (1 dim) dt. Equations of Motion (Constant Acceleration) Newton s Law and Weight. Magnitude of the Frictional Force
Insucos: ield/mche PHYSICS DEPARTMENT PHY 48 Em Sepeme 6, 4 Nme pin, ls fis: Signue: On m hono, I he neihe gien no eceied unuhoied id on his eminion. YOUR TEST NUMBER IS THE 5-DIGIT NUMBER AT THE TOP O
D zone schemes
Ch. 5. Enegy Bnds in Cysls 5.. -D zone schemes Fee elecons E k m h Fee elecons in cysl sinα P + cosα cosk α cos α cos k cos( k + π n α k + πn mv ob P 0 h cos α cos k n α k + π m h k E Enegy is peiodic
Derivation of the differential equation of motion
Divion of h iffnil quion of oion Fis h noions fin h will us fo h ivion of h iffnil quion of oion. Rollo is hough o -insionl isk. xnl ius of h ll isnc cn of ll (O) - IDU s cn of gviy (M) θ ngl of inclinion
f(x) dx with An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples dx x x 2
Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
ÖRNEK 1: THE LINEAR IMPULSE-MOMENTUM RELATION Calculate the linear momentum of a particle of mass m=10 kg which has a. kg m s
MÜHENDİSLİK MEKANİĞİ. HAFTA İMPULS- MMENTUM-ÇARPIŞMA Linea oenu of a paicle: The sybol L denoes he linea oenu and is defined as he ass ies he elociy of a paicle. L ÖRNEK : THE LINEAR IMPULSE-MMENTUM RELATIN
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
Circuits 24/08/2010. Question. Question. Practice Questions QV CV. Review Formula s RC R R R V IR ... Charging P IV I R ... E Pt.
4/08/00 eview Fomul s icuis cice s BL B A B I I I I E...... s n n hging Q Q 0 e... n... Q Q n 0 e Q I I0e Dischging Q U Q A wie mde of bss nd nohe wie mde of silve hve he sme lengh, bu he dimee of he bss
ANALYSIS OF KINEMATICS AND KINETOSTATICS OF FOUR-BAR LINKAGE MECHANISM BASED ON GIVEN PROGRAM
SINTII POINGS IV INTNTIONL ONGSS "MINS. TNOLОGIS. MTILS." 7 - SUMM SSSION NLSIS O KINMTIS N KINTOSTTIS O OU- LINKG MNISM S ON GIVN POGM W ISSN - PINT ISSN - Pof.soc.. Shl Pof.soc.. Likj. * Pof.ss.. ji.
FM Applications of Integration 1.Centroid of Area
FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
Reinforcement learning
CS 75 Mchine Lening Lecue b einfocemen lening Milos Huskech milos@cs.pi.edu 539 Senno Sque einfocemen lening We wn o len conol policy: : X A We see emples of bu oupus e no given Insed of we ge feedbck
MEEN 617 Handout #11 MODAL ANALYSIS OF MDOF Systems with VISCOUS DAMPING
MEEN 67 Handou # MODAL ANALYSIS OF MDOF Sysems wih VISCOS DAMPING ^ Symmeic Moion of a n-dof linea sysem is descibed by he second ode diffeenial equaions M+C+K=F whee () and F () ae n ows vecos of displacemens
0 for t < 0 1 for t > 0
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
5.1-The Initial-Value Problems For Ordinary Differential Equations
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
Physics 232 Exam I Feb. 13, 2006
Phsics I Fe. 6 oc. ec # Ne..5 g ss is ched o hoizol spig d is eecuig siple hoic oio. The oio hs peiod o.59 secods. iiil ie i is oud o e 8.66 c o he igh o he equiliiu posiio d oig o he le wih eloci o sec.
P441 Analytical Mechanics - I. Coupled Oscillators. c Alex R. Dzierba
Lecure 3 Mondy - Deceber 5, 005 Wrien or ls upded: Deceber 3, 005 P44 Anlyicl Mechnics - I oupled Oscillors c Alex R. Dzierb oupled oscillors - rix echnique In Figure we show n exple of wo coupled oscillors,
Computer Aided Geometric Design
Copue Aided Geoei Design Geshon Ele, Tehnion sed on ook Cohen, Riesenfeld, & Ele Geshon Ele, Tehnion Definiion 3. The Cile Given poin C in plne nd nue R 0, he ile ih ene C nd dius R is defined s he se
Today - Lecture 13. Today s lecture continue with rotations, torque, Note that chapters 11, 12, 13 all involve rotations
Today - Lecue 13 Today s lecue coninue wih oaions, oque, Noe ha chapes 11, 1, 13 all inole oaions slide 1 eiew Roaions Chapes 11 & 1 Viewed fom aboe (+z) Roaional, o angula elociy, gies angenial elociy
Faraday s Law. To be able to find. motional emf transformer and motional emf. Motional emf
Objecie F s w Tnsfome Moionl To be ble o fin nsfome. moionl nsfome n moionl. 331 1 331 Mwell s quion: ic Fiel D: Guss lw :KV : Guss lw H: Ampee s w Poin Fom Inegl Fom D D Q sufce loop H sufce H I enclose
e t dt e t dt = lim e t dt T (1 e T ) = 1
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Sections 3.1 and 3.4 Exponential Functions (Growth and Decay)
Secions 3.1 and 3.4 Eponenial Funcions (Gowh and Decay) Chape 3. Secions 1 and 4 Page 1 of 5 Wha Would You Rahe Have... $1million, o double you money evey day fo 31 days saing wih 1cen? Day Cens Day Cens
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Chapter 4 Circular and Curvilinear Motions
Chp 4 Cicul n Cuilin Moions H w consi picls moing no long sigh lin h cuilin moion. W fis su h cicul moion, spcil cs of cuilin moion. Anoh mpl w h l sui li is h pojcil..1 Cicul Moion Unifom Cicul Moion
Fig. 1S. The antenna construction: (a) main geometrical parameters, (b) the wire support pillar and (c) the console link between wire and coaxial
a b c Fig. S. The anenna consucion: (a) ain geoeical paaees, (b) he wie suppo pilla and (c) he console link beween wie and coaial pobe. Fig. S. The anenna coss-secion in he y-z plane. Accoding o [], he
M r. d 2. R t a M. Structural Mechanics Section. Exam CT5141 Theory of Elasticity Friday 31 October 2003, 9:00 12:00 hours. Problem 1 (3 points)
Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
Forms of Energy. Mass = Energy. Page 1. SPH4U: Introduction to Work. Work & Energy. Particle Physics:
SPH4U: Inroducion o ork ork & Energy ork & Energy Discussion Definiion Do Produc ork of consn force ork/kineic energy heore ork of uliple consn forces Coens One of he os iporn conceps in physics Alernive
6. Gas dynamics. Ideal gases Speed of infinitesimal disturbances in still gas
6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
Physics Mechanics. Rule #2: LABEL/LIST YOUR KNOWN VALUES AND THOSE DESIRED (Include units!!)
Phic Mechnic Rule #1: DRAW A PICTURE (Picoil Repeenion, Moion Dim, ee-bod Dim) Dw picue o wh he queion i decibin. Ue moion dim nd ee-bod dim o i ou in eein wh i oin on in he queion. Moion Dim: + ee-bod
π,π is the angle FROM a! TO b
Mth 151: 1.2 The Dot Poduct We hve scled vectos (o, multiplied vectos y el nume clled scl) nd dded vectos (in ectngul component fom). Cn we multiply vectos togethe? The nswe is YES! In fct, thee e two
Average & instantaneous velocity and acceleration Motion with constant acceleration
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
1.0 Electrical Systems
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
Chapter Direct Method of Interpolation
Chper 5. Direc Mehod of Inerpolion Afer reding his chper, you should be ble o:. pply he direc mehod of inerpolion,. sole problems using he direc mehod of inerpolion, nd. use he direc mehod inerpolns o
Molecular Dynamics Simulations (Leach )
Molecul Dynmics Simulions Lech 7.-7.5 compue hemlly eged popeies by smpling epesenie phse-spce jecoy i numeicl soluion of he clssicl equions of moion fo sysem of N inecing picles he coupled e.o.m. e: d
Section 35 SHM and Circular Motion
Section 35 SHM nd Cicul Motion Phsics 204A Clss Notes Wht do objects do? nd Wh do the do it? Objects sometimes oscillte in simple hmonic motion. In the lst section we looed t mss ibting t the end of sping.
WORK POWER AND ENERGY Consevaive foce a) A foce is said o be consevaive if he wok done by i is independen of pah followed by he body b) Wok done by a consevaive foce fo a closed pah is zeo c) Wok done
Available online Journal of Scientific and Engineering Research, 2018, 5(10): Research Article
vilble online www.jse.com Jounl of Scienific n Engineeing Resech, 8, 5():5-58 Resech icle ISSN: 94-6 CODEN(US): JSERBR Soluion of he Poblem of Sess-Sin Se of Physiclly Non-Line Heeiily Plsic Infinie Ple
3 Motion with constant acceleration: Linear and projectile motion
3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
Perturbation Analysis of the LMI-Based Continuous-time Linear Quadratic Regulator Problem for Descriptor Systems
Pin SS: 3-6; Online SS: 367-5357 DO: 55/ic-6-7 Peuion nlsis of he -sed Coninuous-ime ine udic egulo Polem fo Desco Ssems onchev Ke Wods: Coninuous-ime desco ssems; peuion nlsis; line qudic egulo sed conol
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
Contraction Mapping Principle Approach to Differential Equations
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
MTH 146 Class 11 Notes
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
EXERCISE - 01 CHECK YOUR GRASP
UNIT # 09 PARABOLA, ELLIPSE & HYPERBOLA PARABOLA EXERCISE - 0 CHECK YOUR GRASP. Hin : Disnce beween direcri nd focus is 5. Given (, be one end of focl chord hen oher end be, lengh of focl chord 6. Focus
TEST - 4 (Paper-I) ANSWERS PHYSICS CHEMISTRY MATHEMATICS
TEST - 4 (Pper-I) NSWERS PHYSICS CHEMISTRY MTHEMTICS. (4). (). () 4. () 5. () 6. (4) 7. () 8. () 9. (). (). (). (). () 4. () 5. () 6. (4) 7. () 8. (4) 9. (). (). (). (). () 4. (4) 5. (4) 6. () 7. () 8.
PARABOLA. moves such that PM. = e (constant > 0) (eccentricity) then locus of P is called a conic. or conic section.
wwwskshieducioncom PARABOLA Le S be given fixed poin (focus) nd le l be given fixed line (Direcrix) Le SP nd PM be he disnce of vrible poin P o he focus nd direcrix respecively nd P SP moves such h PM
Physics 2A HW #3 Solutions
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
4.8 Improper Integrals
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
Axis Thin spherical shell about any diameter
Insucos: Fiel/che/Deweile PYSICS DEPATET PY 48 Finl Em Apil 5, 5 me pin, ls fis: Signue: On m hono, I he neihe gien no eceie unuhoie i on his eminion. YOU TEST UBE IS TE 5-DIGIT UBE AT TE TOP OF EAC PAGE.
The order of reaction is defined as the number of atoms or molecules whose concentration change during the chemical reaction.
www.hechemisryguru.com Re Lw Expression Order of Recion The order of recion is defined s he number of oms or molecules whose concenrion chnge during he chemicl recion. Or The ol number of molecules or
A 1.3 m 2.5 m 2.8 m. x = m m = 8400 m. y = 4900 m 3200 m = 1700 m
PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
Homework 5 for BST 631: Statistical Theory I Solutions, 09/21/2006
Homewok 5 fo BST 63: Sisicl Theoy I Soluions, 9//6 Due Time: 5:PM Thusy, on 9/8/6. Polem ( oins). Book olem.8. Soluion: E = x f ( x) = ( x) f ( x) + ( x ) f ( x) = xf ( x) + xf ( x) + f ( x) f ( x) Accoing
Minimum Squared Error
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > for ll smples y i solve sysem of liner inequliies MSE procedure y i = i for ll smples
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Minimum Squared Error
Minimum Squred Error LDF: Minimum Squred-Error Procedures Ide: conver o esier nd eer undersood prolem Percepron y i > 0 for ll smples y i solve sysem of liner inequliies MSE procedure y i i for ll smples
when t = 2 s. Sketch the path for the first 2 seconds of motion and show the velocity and acceleration vectors for t = 2 s.(2/63)
. The -coordine of pricle in curiliner oion i gien b where i in eer nd i in econd. The -coponen of ccelerion in eer per econd ured i gien b =. If he pricle h -coponen = nd when = find he gniude of he eloci
Combinatorial Approach to M/M/1 Queues. Using Hypergeometric Functions
Inenaional Mahemaical Foum, Vol 8, 03, no 0, 463-47 HIKARI Ld, wwwm-hikaicom Combinaoial Appoach o M/M/ Queues Using Hypegeomeic Funcions Jagdish Saan and Kamal Nain Depamen of Saisics, Univesiy of Delhi,
Lecture 23 Damped Motion
Differenial Equaions (MTH40) Lecure Daped Moion In he previous lecure, we discussed he free haronic oion ha assues no rearding forces acing on he oving ass. However No rearding forces acing on he oving
Classification of Equations Characteristics
Clssiiion o Eqions Cheisis Consie n elemen o li moing in wo imensionl spe enoe s poin P elow. The ph o P is inie he line. The posiion ile is s so h n inemenl isne long is s. Le he goening eqions e epesene
Physics 232 Exam I Feb. 14, 2005
Phsics I Fe., 5 oc. ec # Ne..5 g ss is ched o hoizol spig d is eecuig siple hoic oio wih gul eloci o dissec. gie is i ie i is oud o e 8 c o he igh o he equiliiu posiio d oig o he le wih eloci o.5 sec..
Modeling of the thermodilution curve for coronary flow assessment. Carel Stasse TU/e BMTE07.22
Eindhoven Univeiy of echnology Depen of Bioedicl Engineeing Meil echnology Modeling of he heodiluion cuve fo coony flow een Cel Se U/e 9-6-7 BME7. pof.d.i. F.N. vn de Voe Conen H Inoducion 3 H Mehod 5.
Electric Potential. and Equipotentials
Electic Potentil nd Euipotentils U Electicl Potentil Review: W wok done y foce in going fom to long pth. l d E dl F W dl F θ Δ l d E W U U U Δ Δ l d E W U U U U potentil enegy electic potentil Potentil
[5] Solving Multiple Linear Equations A system of m linear equations and n unknown variables:
![[5] Solving Multiple Linear Equations A system of m linear equations and n unknown variables:](/thumbs/78/77852027.jpg "[5] Solving Multiple Linear Equations A system of m linear equations and n unknown variables:")
[5] Solving Muliple Liner Equions A syse of liner equions nd n unknown vribles: + + + nn = b + + + = b n n : + + + nn = b n n A= b, where A =, : : : n : : : : n = : n A = = = ( ) where, n j = ( ); = :
Solvability of nonlinear Klein-Gordon equation by Laplace Decomposition Method
Vol. 84 pp. 37-4 Jly 5 DOI:.5897/JMCSR4.57 icle Nbe: 63F95459 ISSN 6-973 Copyigh 5 hos ein he copyigh of his icle hp://www.cdeicjonls.og/jmcsr ficn Jonl of Mheics nd Cope Science Resech Fll Lengh Resech
One of the common descriptions of curvilinear motion uses path variables, which are measurements made along the tangent t and normal n to the path of
Oe of he commo descipios of cuilie moio uses ph ibles, which e mesuemes mde log he ge d oml o he ph of he picles. d e wo ohogol xes cosideed sepely fo eey is of moio. These coodies poide ul descipio fo
PHYSICS 102. Intro PHYSICS-ELECTROMAGNETISM
PHYS 0 Suen Nme: Suen Numbe: FAUTY OF SIENE Viul Miem EXAMINATION PHYSIS 0 Ino PHYSIS-EETROMAGNETISM Emines: D. Yoichi Miyh INSTRUTIONS: Aemp ll 4 quesions. All quesions hve equl weighs 0 poins ech. Answes
September 20 Homework Solutions
College of Engineering nd Compuer Science Mechnicl Engineering Deprmen Mechnicl Engineering A Seminr in Engineering Anlysis Fll 7 Number 66 Insrucor: Lrry Creo Sepember Homework Soluions Find he specrum
KINEMATICS OF RIGID BODIES
KINEMTICS OF RIGID ODIES In igid body kinemaics, we use he elaionships govening he displacemen, velociy and acceleaion, bu mus also accoun fo he oaional moion of he body. Descipion of he moion of igid
PHYS PRACTICE EXAM 2
PHYS 1800 PRACTICE EXAM Pa I Muliple Choice Quesions [ ps each] Diecions: Cicle he one alenaive ha bes complees he saemen o answes he quesion. Unless ohewise saed, assume ideal condiions (no ai esisance,
THE FUNDAMENTAL CRITERION FOR ESTIMATION OF THE REFERENCE ELLIPSOID ACCURACY UDC (045)=111. Bogoljub Marjanović
FACTA UNIVERSITATIS Seies: Mechnics, Auomic Conol nd Rooics Vol. 6, N o 1, 007, pp. 179-187 THE FUNDAMENTAL CRITERION FOR ESTIMATION OF THE REFERENCE ELLIPSOID ACCURACY UDC 537.51+531.(045)=111 Boolju
QUESTION PAPER PHYSICS-PH
GATE-PH 7 Q. Q.5 : Cy ONE mk ech.. In he nucle ecion 6 e 7 PHYSICS-PH C v N X, he picle X is () n elecon n ni-elecon (c) muon (d) pion. Two idenicl msses of gm ech e conneced by mssless sping of sping
CHAPTER 11 PARAMETRIC EQUATIONS AND POLAR COORDINATES
CHAPTER PARAMETRIC EQUATIONS AND POLAR COORDINATES. PARAMETRIZATIONS OF PLANE CURVES., 9, _ _ Ê.,, Ê or, Ÿ. 5, 7, _ _.,, Ÿ Ÿ Ê Ê 5 Ê ( 5) Ê ˆ Ê 6 Ê ( 5) 7 Ê Ê, Ÿ Ÿ $ 5. cos, sin, Ÿ Ÿ 6. cos ( ), sin (
Mathematics 805 Final Examination Answers
. 5 poins Se he Weiersrss M-es. Mhemics 85 Finl Eminion Answers Answer: Suppose h A R, nd f n : A R. Suppose furher h f n M n for ll A, nd h Mn converges. Then f n converges uniformly on A.. 5 poins Se
IX.1.1 The Laplace Transform Definition 700. IX.1.2 Properties 701. IX.1.3 Examples 702. IX.1.4 Solution of IVP for ODEs 704
Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 4, 7 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
ME 391 Mechanical Engineering Analysis
Fall 04 ME 39 Mechanical Engineering Analsis Eam # Soluions Direcions: Open noes (including course web posings). No books, compuers, or phones. An calculaor is fair game. Problem Deermine he posiion of
1. The sphere P travels in a straight line with speed
1. The sphee P tels in stight line with speed = 10 m/s. Fo the instnt depicted, detemine the coesponding lues of,,,,, s mesued eltie to the fixed Oxy coodinte system. (/134) + 38.66 1.34 51.34 10sin 3.639
Valuation, Linear Information Dynamic, and Stochastic Discount rates. Dan Gode Stern School of Business New York University
Vluion, Line Infomion Dynmic, nd Sochsic Discoun es Dn Gode Sen School of Business New Yo Univesiy dgode@sen.nyu.edu Jmes Ohlson Sen School of Business New Yo Univesiy Johlson@sen.nyu.edu Mch 22, 2000
INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).
![INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).](/thumbs/78/77677920.jpg "INTEGRALS. Exercise 1. Let f : [a, b] R be bounded, and let P and Q be partitions of [a, b]. Prove that if P Q then U(P ) U(Q) and L(P ) L(Q).")
INTEGRALS JOHN QUIGG Eercise. Le f : [, b] R be bounded, nd le P nd Q be priions of [, b]. Prove h if P Q hen U(P ) U(Q) nd L(P ) L(Q). Soluion: Le P = {,..., n }. Since Q is obined from P by dding finiely
P a g e 5 1 of R e p o r t P B 4 / 0 9
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
BINOMIAL THEOREM OBJECTIVE PROBLEMS in the expansion of ( 3 +kx ) are equal. Then k =
wwwskshieduciocom BINOMIAL HEOREM OBJEIVE PROBLEMS he coefficies of, i e esio of k e equl he k /7 If e coefficie of, d ems i e i AP, e e vlue of is he coefficies i e,, 7 ems i e esio of e i AP he 7 7 em
RESPONSE OF A RECTANGULAR PLATE TO BASE EXCITATION Revision E W( )
RESPONSE OF A RECTANGULAR PLATE TO BASE EXCITATION Revisio E B To Ivie Eil: o@viiod.co Apil, 3 Viles A pliude coefficie E k leg id ple siffess fco elsic odulus ple ickess veue ple ss edig oe,, u, v ode
IX.1.1 The Laplace Transform Definition 700. IX.1.2 Properties 701. IX.1.3 Examples 702. IX.1.4 Solution of IVP for ODEs 704
Chper IX The Inegrl Trnform Mehod IX. The plce Trnform November 6, 8 699 IX. THE APACE TRANSFORM IX.. The plce Trnform Definiion 7 IX.. Properie 7 IX..3 Emple 7 IX..4 Soluion of IVP for ODE 74 IX..5 Soluion
Chapter 2. Motion along a straight line. 9/9/2015 Physics 218
Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
General Non-Arbitrage Model. I. Partial Differential Equation for Pricing A. Traded Underlying Security
1 Geneal Non-Abiage Model I. Paial Diffeenial Equaion fo Picing A. aded Undelying Secuiy 1. Dynamics of he Asse Given by: a. ds = µ (S, )d + σ (S, )dz b. he asse can be eihe a sock, o a cuency, an index,
Rotations.
oons j.lbb@phscs.o.c.uk To s summ Fmes of efeence Invnce une nsfomons oon of wve funcon: -funcons Eule s ngles Emple: e e - - Angul momenum s oon geneo Genec nslons n Noehe s heoem Fmes of efeence Conse
DEPARTMENT OF CIVIL AND ENVIRONMENTAL ENGINEERING FLUID MECHANICS III Solutions to Problem Sheet 3
DEPATMENT OF CIVIL AND ENVIONMENTAL ENGINEEING FLID MECHANICS III Solutions to Poblem Sheet 3 1. An tmospheic vote is moelle s combintion of viscous coe otting s soli boy with ngul velocity Ω n n iottionl
Narrow-band Receiver Radio Architectures
Now-bnd Receive Rdio chiecues l l l l l Double-convesion single-qud Supeheodyne Diec-convesion Single-convesion singlequd, hoodyne, Zeo- Double-convesion double-qud Low- Refeences Down-convesion; The ige
P h y s i c s F a c t s h e e t
P h y s i c s F a c s h e e Sepembe 2001 Numbe 20 Simple Hamonic Moion Basic Conceps This Facshee will:! eplain wha is mean by simple hamonic moion! eplain how o use he equaions fo simple hamonic moion!
RESPONSE UNDER A GENERAL PERIODIC FORCE. When the external force F(t) is periodic with periodτ = 2π
RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)