THE FUNDAMENTAL CRITERION FOR ESTIMATION OF THE REFERENCE ELLIPSOID ACCURACY UDC (045)=111. Bogoljub Marjanović
|
|
|
- Naomi Ross
- 5 years ago
- Views:
Transcription
1 FACTA UNIVERSITATIS Seies: Mechnics, Auomic Conol nd Rooics Vol. 6, N o 1, 007, pp THE FUNDAMENTAL CRITERION FOR ESTIMATION OF THE REFERENCE ELLIPSOID ACCURACY UDC (045)=111 Boolju Mjnović Hihe Technicl School, Sei, Kujevc, Kosovsk 8 E-mil: oc@k.c.yu Asc. The vlue of he semi-mjo xis, nd he vlue of he semi-mino xis e he eomeicl chceisics of he efeence ellipsoid. The ohe impon chceisic is he noml viy, which epesens he mniude of he dien of he viy poenil wih he ellipsoid s n equipoenil sufce. This ppe pesens he fundmenl cieion fo esimion of ccucy of he efeence ellipsoid, which sems fom he Newon's second lw. I hs een poved, y he nlysis of he moion of picle lon meidin of he efeence ellipsoid, h he leic sum of woks of viionl cion foce nd ceniful foce, excied y oionl ellipsoid ound is xis, equls o zeo. This is n indispensle em h he diecion of viy veco is eveywhee pependicul o he ellipsoid sufce s n equipoenil sufce. This is wh mkes his cieion elile nd enles he oinin of he quniive evluion of he ellipsoid's ccucy. Applyin his cieion fo esimion of ccucy of he ellipsoid, defined ccodin o he Geodeic Refeence Sysem 1980 (GRS80), i cn e concluded h he ellipsoid's semi-mino xis conins n eo of ou 599 m. Key wods: he efeence ellipsoid, semi-mino xis, viionl cion, GRS80 1. INTRODUCTION The efeence ellipsoid is n ellipsoid of evoluion, which would e oined y oionl n ellipse ound is mino xis. I is deemined y fou consns (Moiz, 1980), nd he IUGG hs chosen he followin ones - equoil dius, semi-mjo xis, GM - eocenic viionl consn, J - dynmic fom fco nd ω - nul velociy of he Eh The ohe eomeic consn, semi-mino xis, is oined y he followin fomul = 1 e, (1) Received Mch 15, 006
2 180 B. MARJANOVIĆ whee is e fis ecceniciy. Theefoe, he efeence ellipsoid is defined s pue eomeicl fiue. The coespondin efeence poenil (he Somilin-Pizzei efeence poenil) hs een deemined fom he condiion h efeence ellipsoid should e n equipoenil sufce of he efeence viy poenil (Heisknen nd Moiz, 1967). The quesion of he ellipsoid's ccucy is ised, nd pimily of he ccucy of he vlue of is semi-mino xis. I cn' e veified y suvey lon meidin, since i is hd o esime fo evey eodesic c, o wh exen i epesens he Eh s whole (Jeffeys, 1976). The elile cieion fo esimion of he efeence ellipsoid ccucy should e oined y physics. In his ppe i hs done y Newon's second lw.. THE DEFINITION OF THE FUNDAMENTAL CRITERION Le he picle of he uni mss move in he nonesisn medium lon ficionl idel smooh oove PQE (Fi. 1) lon he meidin of he efeence ellipsoid, wih he se iniil elive velociy v 0. Applyin he Newon's second lw, he moion of he picle is descied y he equion = + () whee is he veco of viionl cion, nd F w is he oove ecion. F w P z ψ ε F d 0 Q F d c 0 d T O N Fi. 1. Relive moion of he picle lon meidin Asolue cceleion is equl o veco sum of he nsfe cceleion, elive cceleion nd he Coiolis cceleion c, so he followin equion is oined E x nd his cn e wien in he fom + + = + F c w (3) o in he fom = + F (4) w c = + F + F + F (5) w c
3 The Fundmenl Cieion fo Esimion of he Refeence Ellipsoid Accucy 181 whee F is he nsfe ineil foce (ceniful foce) nd F c is he Coiolis ineil foce. Thee scl equions coespond o vecoil Eq. (5); one of hem defines he elive moion of he picle in he nenil diecion, whose uni veco is T. Considein h vecos F w nd F c, nd he veco sum of vecos nd F, e ll pependicul o he nenil diecion, y pojecin Eq. (5) ono h diecion, one oins h he elive nenil cceleion T equls o zeo, h is dv = 0. (6) d whee v is he elive velociy inensiy. Tkin he do poduc of Eq. (5), y he veco of he picle's elemeny elive displcemen d, one oins he equion v d = da + da + da + da ( ) ( Fw ) ( F ) ( Fc ) whee is, on he lef-hnd-side of Eq. (7), he kineic eney of he picle's elive moion, E k = v /, nd on he ih-hnd-side e he woks of he foces, F w, F nd F c, lon he picle's elemeny displcemen. Since he elive velociy of picle is of he consn inensiy, hen hee is no chne of he elive kineic eney, nd woks of he consin ecion F w nd he Coiolis foce F c e hen equl o zeo, since hose foces e pependicul o he diecion of he picle's elemeny displcemen. Thus, usin Eq. (7), he followin equion is oined da ( ) ( ) F, (7) + da = 0. (8) The wok of he ceniful foce cn e wien in he nlyicl fom if he foce F nd elemeny elive displcemen d e expessed in ems of pojecion ono he dil diecion 0 nd he diecion c 0 which is pependicul o 0 (Fi. 1), nmely in he fom F = ω sin 0 + ω sin cos c 0 (9) nd d = d + d c (10) 0 0, whee 0 nd c 0 e he uni vecos, nd ω is he nul velociy of he Eh's oion. By he do poduc of hese vecos, he followin equion is oined (F ) da = F d = ω sin d + ω sin cos d. (11) The wok of he ceniful foce, Eq. (11), cn e wien s ol diffeenil, nd he wok of he viionl cion s diffeenil of he viionl poenil du, so h he Eq. (8) ecomes d ω sin + du = 0. (1)
4 18 B. MARJANOVIĆ The Eq. (1) consiss of only cul pefomed woks, so h i expesses he fc h he sum of ceniful nd viionl poenil is consn. Fom he definiion of wok s do poduc of he foce veco nd he veco of he elemeny displcemen, he wok cn e undesood s poduc of foce inensiy nd he pojecion of elemeny displcemen ds = d ono foce diecion (Fi. ), so he cul wok of he viionl cion cn e wien in he fom ( ) da = sin ε ds = dh (13) 1 dh 1 Q M K N 0 χ ψ ε ψ ε c 0 d S χ Fi.. Incemens of meidin The flux of he foce (Rskovic, 1956) lon QN + NS phs, is equl o he sum of cul wok lon QK ph nd woks lon KN + NS phs ( ) da = cos ψ QK cosψ KN + sin ψ NS. (14) Since he wok of he foce expessed y lon KS ph is equl o zeo, hen i cn e 0 0 (KN + NS c ) = cosψ KN + sin ψ NS = 0. (15) The ol wok of he foce lon incemen d = QN is equl o he sum of cul wok lon QK ph nd ficiious wok lon KN ph, so h he Eq. (14) cn e wien in he fom ( ) da = cos ψ d + sin ψ d (16) Incemen QN is ou doule s le s incemen QK ecuse he sme io exiss eween nles χ nd ε. Bsed on he Eq. (15), i cn e concluded h he ficiious wok occus in wo foms wih he diffeen sins u he sme vlues. The equion of n ellipse in he Cesin coodine sysem ses
5 The Fundmenl Cieion fo Esimion of he Refeence Ellipsoid Accucy 183 x z + = 1, (17) nd usin spheicl coodines (x = sin nd z = cos), he equion of he ellipse is oined in he fom =. (18) 1+ cos 1 Eq. (11) expesses flux of he foce F lon QN + NS phs. I cn e poved h is he second em, on he ih-hnd-side of Eq. (11), he ficiious wok. The Eq. (18) cn e wien in he fom sin = 1 + nd y susiuin Eq. (19) ino Eq. (11), he followin equion is oined ( F ) ω ω d da = d + ω sin cos d. By diffeeniion of Eq. (18) one oins he equion d 1 sin cos d =, 1+ 1 cos nd y susiuin Eq. (1) ino Eq. (0), he followin equion is oined (19) (0) (1) ( F ) ω da = d ω sin cos d+ ω sin cos d. () The fis em in Eq. () is he cul wok, nd nohe wo ems e ficiious woks of he foce F. The ol wok of his foce is equl o he sum of cul wok nd he ficiious wok. Considein h he Eq. (8) ives he elion eween cul woks, s well s ficiious woks, of he foces F nd, nd usin he Eqs. (16) nd (), one oins he followin wo equions nd ω sin cos d+ sin ψ d = 0 (3) ω d d + ω ψ = sin cos d cos 0. (4)
6 184 B. MARJANOVIĆ The Eq. (4) epesens he sum of cul woks nd ficiious woks of ceniful foce nd viionl cion foce lon incemens of meidin. By ineion of Eq. (4) wihin limis fom posiion P o posiion Q (Fi. 1) whee nle chnes fom zeo o, nd dius chnes fom o, one oins he equion ( Q) ( Q) ω +ω sin cos d cosψ d = 0. (5) ( P) ( P) The fis inel in Eq. (5) cn e solved usin Eq. (18), o oin ( Q) cos d(cos ) 1 sin cos d ln = = ( P) cos cos nd usin Eq. (19), hen Eq. (5) cn e wien in he fom (6) ( Q) ω 1 ω ( P) sin + ln cosψ d = 0. (7) cos The fis em in Eq. (7) epesens he ceniful poenil in posiion Q. I could e ken h is cos ψ 1 ecuse he hihes vlue of he nle ψ is less hn If he picle is movin fom he poin P he pole o he poin E he equo, hen in Eq. (7) he susiuion should e mde = π / nd =, o ive ( E) ω 1 ω + ln d 0. (8) ( P) 1 The Eq. (8) should e sisfied if he efeence ellipsoid is ccue. If i is no, hen he sum of he ol woks of he ceniful foce nd he viionl cion foce shll no e equl o zeo nd shll epesen he eo of he ellipsoid A, h is ( E) ω 1 ω A = + ln d (9) ( P) 1 The Eq. (9) epesens he fundmenl cieion fo esimion of he efeence ellipsoid ccucy.
7 The Fundmenl Cieion fo Esimion of he Refeence Ellipsoid Accucy THE APPLICATION OF THE FUNDAMENTAL CRITERION The fundmenl cieion will e pplied fo he esimion of he ccucy of GRS80 ellipsoid whose semi-xes e = m, = m nd he viy is deemined ccodin o he Gviy Fomul 1980, which eds ( ) = [ sin φ sin φ ] m/ s, (30) whee φ is he eodeic liude. The vlue of inel in Eq. (9) will e compued usin he elionship eween viionl cion nd heih h. In h sense, he nle POE = π / will e divided o n equl ps, whee one will oin n ppoximely equl semens on he poion PQE of he ellipse (Fi. 3). The posiions of hese semens deemine y he (n+1) poins hei ends. Fo ech poin he mniude of he dius veco cn e compued sed on Eq. (18), nd hen he heih of he picle's ise duin he elive moion, s he diffeence of nd of he semi-mino xis h. (31) P Q χ F T O φ χ N φ E Fi. 3. Relevn viles fo deeminion of viionl cion The nle χ (Fi.) eween he veco nd dil diecion cn e compued y he equion 1 d χ=, (3) d nd hen sed on Eq. (1), he equion is oined sin cos cos χ= Fo ech of he poins whose posiion is deemined y nle, he eodeic liude cn e oined ccodin o fomul (33) φ =π +χ (34)
8 186 B. MARJANOVIĆ The mniude of viy cn e compued ccodin o Eq. (30), nd of ceniful foce ccodin o fomul F = sin ω (35) whee is Eh's nul velociy ω = d / s. The mniude of viionl cion is deemined ccodin o he cosine heoem = + F + F cos φ. (36) The ph of viionl cion ins heih h hs he shpe shown in Fiue 4. p e. dh O dh h Fi. 4. Gviionl cion vesus heih The vlue of inel in Eq. (9) is popoionl o he e unde he ph, which mouns Nm. I is ppoxime equl o he e of peze, nmely ( E) p + e dh ( ) = Nm, (37) ( P) whee p is he viionl cion he pole, nd e he equo. These vlues e compued ccodin o Eq. (36) nd hey moun o p = N nd e = N. The eminin p he ih-hnd-side of Eq. (9) epesens he ceniful foce wok nd i mouns o Nm. The leic sum of hese woks ccodin o Eq. (9) epesens he eo of he ellipsoid which is Nm. The ellipsoid eo wouldn' e sinificnly less even unde he consideion of he viionl cion o e unchnele wih he mximum vlue p = N, in which cse i would e 5697 Nm. The ceniful foce wok wekly depends on he possile eo in he vlue of semi-mino xis, considein he Eq. (9), so i cn e ken h he clculed vlue of his wok cn e consideed s ppoximely ccue, while he vlue of he viionl cion foce wok is diecly dependen on ccucy of he semi-xis. In ode fo ellipsoid o e ccue, vlues of hese woks mus e equl, nmely
9 The Fundmenl Cieion fo Esimion of he Refeence Ellipsoid Accucy 187 p + e ( ) Nm. (38) If one ssumes h vlues of, p nd e e ccue, hen fom Eq. (38) one oins h vlue of semi-mino xis should moun o m, wh is smlle hn he vlue oined ccodin o he model GRS80 of ou 599 m. 4. CONCLUSION The fundmenl cieion fo he esimion of ccucy of he efeence ellipsoid is elile cieion ecuse i ppes fom Newon's second lw. This is n indispensle em h he diecion of viy is eveywhee pependicul o he ellipsoid sufce s n equipoenil sufce. Applyin his cieion fo esimion of ccucy of he ellipsoid defined ccodin o he Geodeic Refeence Sysem 1980, i cn e concluded h he ellipsoid's semi-mino xis conins n eo of ou 599 m. REFERENCES 1. Moiz, H., (1980). Geodeic Refeence Sysem 1980, Bull Geod 54: [hp://eodesy.en.ohiose.edu/couse/efppes/ pdf]. Heisknen, W.A. nd Moiz, H., (1967). Physicl Geodesy, Feemn, Sn Fncisco, pp Jeffeys, S.H., (1976). The Eh is oiin hisoy nd physicl consiuion, 6 h ediion, Univesiy pess Cmide, Cmide, pp Rsković, D., (1956). Mechnics III Dynmics, he second ediion, scienific ook, Belde, pp. 389 (in Sein). OSNOVNI KRITERIJUM ZA OCENU TAČNOSTI REFERENTNOG ELIPSOIDA Boolju Mjnović Veličin veće poluose, i veličin mnje poluose su eomeijske kkeisike efeenno elipsoid. Du in kkeisik je nomln vicij, koj pesvlj inenzie dijen viciono poencijl n ekvipoencijlnoj povšini elipsoid. U ovom du je pesvljen osnovni kieijum z odedjivnje čnosi efeenno elipsoid koji poisiče is duo Njunovo zkon. Anlizom kenj meijlne čke, duž meidijn efeenno elipsoid, je dokzno d je leski zi dov sile viciono pivlčenj i cenifulne sile, nsle onjem elipsoid oko njeove ose, jednk nuli. Ovo je neophodn uslov d pvc veko vicije ude svud upvn n povšinu elipsoid ko ekvipoencijlnu povšinu. Zo je ovj kieijum pouzdn i omoućv d se doije kvniivn ocen čnosi elipsoid. Pimenjujući ovj kieijum z ocenu čnosi elipsoid definisno pem he Geodeic Refeence Sysem 1980 (GRS80), može se zključii d mnj poluos elipsoid sdži ešku od oko 599 m. Ključne eči: efeenni elipsoid, mnj poluos, viciono pivlčenje, GRS80
LECTURE 5. is defined by the position vectors r, 1. and. The displacement vector (from P 1 to P 2 ) is defined through r and 1.
 LECTURE 5 ] DESCRIPTION OF PARTICLE MOTION IN SPACE -The displcemen, veloci nd cceleion in -D moion evel hei veco nue (diecion) houh he cuion h one mus p o hei sin. Thei full veco menin ppes when he picle
LECTURE 5 ] DESCRIPTION OF PARTICLE MOTION IN SPACE -The displcemen, veloci nd cceleion in -D moion evel hei veco nue (diecion) houh he cuion h one mus p o hei sin. Thei full veco menin ppes when he picle
ME 141. Engineering Mechanics
 ME 141 Engineeing Mechnics Lecue 13: Kinemics of igid bodies hmd Shhedi Shkil Lecue, ep. of Mechnicl Engg, UET E-mil: sshkil@me.bue.c.bd, shkil6791@gmil.com Websie: eche.bue.c.bd/sshkil Couesy: Veco Mechnics
ME 141 Engineeing Mechnics Lecue 13: Kinemics of igid bodies hmd Shhedi Shkil Lecue, ep. of Mechnicl Engg, UET E-mil: sshkil@me.bue.c.bd, shkil6791@gmil.com Websie: eche.bue.c.bd/sshkil Couesy: Veco Mechnics
Technical Vibration - text 2 - forced vibration, rotational vibration
 Technicl Viion - e - foced viion, oionl viion 4. oced viion, viion unde he consn eenl foce The viion unde he eenl foce. eenl The quesion is if he eenl foce e is consn o vying. If vying, wh is he foce funcion.
Technicl Viion - e - foced viion, oionl viion 4. oced viion, viion unde he consn eenl foce The viion unde he eenl foce. eenl The quesion is if he eenl foce e is consn o vying. If vying, wh is he foce funcion.
() t. () t r () t or v. ( t) () () ( ) = ( ) or ( ) () () () t or dv () () Section 10.4 Motion in Space: Velocity and Acceleration
 Secion 1.4 Moion in Spce: Velociy nd Acceleion We e going o dive lile deepe ino somehing we ve ledy inoduced, nmely () nd (). Discuss wih you neighbo he elionships beween posiion, velociy nd cceleion you
Secion 1.4 Moion in Spce: Velociy nd Acceleion We e going o dive lile deepe ino somehing we ve ledy inoduced, nmely () nd (). Discuss wih you neighbo he elionships beween posiion, velociy nd cceleion you
Circuits 24/08/2010. Question. Question. Practice Questions QV CV. Review Formula s RC R R R V IR ... Charging P IV I R ... E Pt.
 4/08/00 eview Fomul s icuis cice s BL B A B I I I I E...... s n n hging Q Q 0 e... n... Q Q n 0 e Q I I0e Dischging Q U Q A wie mde of bss nd nohe wie mde of silve hve he sme lengh, bu he dimee of he bss
4/08/00 eview Fomul s icuis cice s BL B A B I I I I E...... s n n hging Q Q 0 e... n... Q Q n 0 e Q I I0e Dischging Q U Q A wie mde of bss nd nohe wie mde of silve hve he sme lengh, bu he dimee of he bss
Motion on a Curve and Curvature
 Moion on Cue nd Cuue his uni is bsed on Secions 9. & 9.3, Chpe 9. All ssigned edings nd execises e fom he exbook Objecies: Mke cein h you cn define, nd use in conex, he ems, conceps nd fomuls lised below:
Moion on Cue nd Cuue his uni is bsed on Secions 9. & 9.3, Chpe 9. All ssigned edings nd execises e fom he exbook Objecies: Mke cein h you cn define, nd use in conex, he ems, conceps nd fomuls lised below:
Ans: In the rectangular loop with the assigned direction for i2: di L dt , (1) where (2) a) At t = 0, i1(t) = I1U(t) is applied and (1) becomes
 omewok # P7-3 ecngul loop of widh w nd heigh h is siued ne ve long wie cing cuen i s in Fig 7- ssume i o e ecngul pulse s shown in Fig 7- Find he induced cuen i in he ecngul loop whose self-inducnce is
omewok # P7-3 ecngul loop of widh w nd heigh h is siued ne ve long wie cing cuen i s in Fig 7- ssume i o e ecngul pulse s shown in Fig 7- Find he induced cuen i in he ecngul loop whose self-inducnce is
Physics 201, Lecture 5
 Phsics 1 Lecue 5 Tod s Topics n Moion in D (Chp 4.1-4.3): n D Kinemicl Quniies (sec. 4.1) n D Kinemics wih Consn Acceleion (sec. 4.) n D Pojecile (Sec 4.3) n Epeced fom Peiew: n Displcemen eloci cceleion
Phsics 1 Lecue 5 Tod s Topics n Moion in D (Chp 4.1-4.3): n D Kinemicl Quniies (sec. 4.1) n D Kinemics wih Consn Acceleion (sec. 4.) n D Pojecile (Sec 4.3) n Epeced fom Peiew: n Displcemen eloci cceleion
D zone schemes
 Ch. 5. Enegy Bnds in Cysls 5.. -D zone schemes Fee elecons E k m h Fee elecons in cysl sinα P + cosα cosk α cos α cos k cos( k + π n α k + πn mv ob P 0 h cos α cos k n α k + π m h k E Enegy is peiodic
Ch. 5. Enegy Bnds in Cysls 5.. -D zone schemes Fee elecons E k m h Fee elecons in cysl sinα P + cosα cosk α cos α cos k cos( k + π n α k + πn mv ob P 0 h cos α cos k n α k + π m h k E Enegy is peiodic
Science Advertisement Intergovernmental Panel on Climate Change: The Physical Science Basis 2/3/2007 Physics 253
 Science Adeisemen Inegoenmenl Pnel on Clime Chnge: The Phsicl Science Bsis hp://www.ipcc.ch/spmfeb7.pdf /3/7 Phsics 53 hp://www.fonews.com/pojecs/pdf/spmfeb7.pdf /3/7 Phsics 53 3 Sus: Uni, Chpe 3 Vecos
Science Adeisemen Inegoenmenl Pnel on Clime Chnge: The Phsicl Science Bsis hp://www.ipcc.ch/spmfeb7.pdf /3/7 Phsics 53 hp://www.fonews.com/pojecs/pdf/spmfeb7.pdf /3/7 Phsics 53 3 Sus: Uni, Chpe 3 Vecos
1. Kinematics of Particles
 1. Kinemics o Picles 1.1 Inoducion o Dnmics Dnmics - Kinemics: he sud o he geome o moion; ele displcemen, eloci, cceleion, nd ime, wihou eeence o he cuse o he moion. - Kineics: he sud o he elion eising
1. Kinemics o Picles 1.1 Inoducion o Dnmics Dnmics - Kinemics: he sud o he geome o moion; ele displcemen, eloci, cceleion, nd ime, wihou eeence o he cuse o he moion. - Kineics: he sud o he elion eising
Molecular Dynamics Simulations (Leach )
 Molecul Dynmics Simulions Lech 7.-7.5 compue hemlly eged popeies by smpling epesenie phse-spce jecoy i numeicl soluion of he clssicl equions of moion fo sysem of N inecing picles he coupled e.o.m. e: d
Molecul Dynmics Simulions Lech 7.-7.5 compue hemlly eged popeies by smpling epesenie phse-spce jecoy i numeicl soluion of he clssicl equions of moion fo sysem of N inecing picles he coupled e.o.m. e: d
Ch.4 Motion in 2D. Ch.4 Motion in 2D
 Moion in plne, such s in he sceen, is clled 2-dimensionl (2D) moion. 1. Posiion, displcemen nd eloci ecos If he picle s posiion is ( 1, 1 ) 1, nd ( 2, 2 ) 2, he posiions ecos e 1 = 1 1 2 = 2 2 Aege eloci
Moion in plne, such s in he sceen, is clled 2-dimensionl (2D) moion. 1. Posiion, displcemen nd eloci ecos If he picle s posiion is ( 1, 1 ) 1, nd ( 2, 2 ) 2, he posiions ecos e 1 = 1 1 2 = 2 2 Aege eloci
ENGR 1990 Engineering Mathematics The Integral of a Function as a Function
 ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
ENGR 1990 Engineering Mhemics The Inegrl of Funcion s Funcion Previously, we lerned how o esime he inegrl of funcion f( ) over some inervl y dding he res of finie se of rpezoids h represen he re under
Electric Potential. and Equipotentials
 Electic Potentil nd Euipotentils U Electicl Potentil Review: W wok done y foce in going fom to long pth. l d E dl F W dl F θ Δ l d E W U U U Δ Δ l d E W U U U U potentil enegy electic potentil Potentil
Electic Potentil nd Euipotentils U Electicl Potentil Review: W wok done y foce in going fom to long pth. l d E dl F W dl F θ Δ l d E W U U U Δ Δ l d E W U U U U potentil enegy electic potentil Potentil
Faraday s Law. To be able to find. motional emf transformer and motional emf. Motional emf
 Objecie F s w Tnsfome Moionl To be ble o fin nsfome. moionl nsfome n moionl. 331 1 331 Mwell s quion: ic Fiel D: Guss lw :KV : Guss lw H: Ampee s w Poin Fom Inegl Fom D D Q sufce loop H sufce H I enclose
Objecie F s w Tnsfome Moionl To be ble o fin nsfome. moionl nsfome n moionl. 331 1 331 Mwell s quion: ic Fiel D: Guss lw :KV : Guss lw H: Ampee s w Poin Fom Inegl Fom D D Q sufce loop H sufce H I enclose
Motion. ( (3 dim) ( (1 dim) dt. Equations of Motion (Constant Acceleration) Newton s Law and Weight. Magnitude of the Frictional Force
 Insucos: ield/mche PHYSICS DEPARTMENT PHY 48 Em Sepeme 6, 4 Nme pin, ls fis: Signue: On m hono, I he neihe gien no eceied unuhoied id on his eminion. YOUR TEST NUMBER IS THE 5-DIGIT NUMBER AT THE TOP O
Insucos: ield/mche PHYSICS DEPARTMENT PHY 48 Em Sepeme 6, 4 Nme pin, ls fis: Signue: On m hono, I he neihe gien no eceied unuhoied id on his eminion. YOUR TEST NUMBER IS THE 5-DIGIT NUMBER AT THE TOP O
v T Pressure Extra Molecular Stresses Constitutive equations for Stress v t Observation: the stress tensor is symmetric
 Momenum Blnce (coninued Momenum Blnce (coninued Now, wh o do wih Π? Pessue is p of i. bck o ou quesion, Now, wh o do wih? Π Pessue is p of i. Thee e ohe, nonisoopic sesses Pessue E Molecul Sesses definiion:
Momenum Blnce (coninued Momenum Blnce (coninued Now, wh o do wih Π? Pessue is p of i. bck o ou quesion, Now, wh o do wih? Π Pessue is p of i. Thee e ohe, nonisoopic sesses Pessue E Molecul Sesses definiion:
 WORK POWER AND ENERGY Consevaive foce a) A foce is said o be consevaive if he wok done by i is independen of pah followed by he body b) Wok done by a consevaive foce fo a closed pah is zeo c) Wok done
WORK POWER AND ENERGY Consevaive foce a) A foce is said o be consevaive if he wok done by i is independen of pah followed by he body b) Wok done by a consevaive foce fo a closed pah is zeo c) Wok done
USING LOWER CLASS WEIGHTS TO CORRECT AND CHECK THE NONLINEARITY OF BALANCES
 USING OWER CSS WEIGHTS TO CORRECT ND CHECK THE NONINERITY OF BNCES Tiohy Chnglin Wng, Qiho Yun, hu Reichuh Mele-Toledo Insuens Shnghi Co. d, Shnghi, P R Chin Mele-Toledo GH, Geifensee, Swizelnd BSTRCT
USING OWER CSS WEIGHTS TO CORRECT ND CHECK THE NONINERITY OF BNCES Tiohy Chnglin Wng, Qiho Yun, hu Reichuh Mele-Toledo Insuens Shnghi Co. d, Shnghi, P R Chin Mele-Toledo GH, Geifensee, Swizelnd BSTRCT
f(x) dx with An integral having either an infinite limit of integration or an unbounded integrand is called improper. Here are two examples dx x x 2
 Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
Impope Inegls To his poin we hve only consideed inegls f() wih he is of inegion nd b finie nd he inegnd f() bounded (nd in fc coninuous ecep possibly fo finiely mny jump disconinuiies) An inegl hving eihe
Available online Journal of Scientific and Engineering Research, 2018, 5(10): Research Article
 vilble online www.jse.com Jounl of Scienific n Engineeing Resech, 8, 5():5-58 Resech icle ISSN: 94-6 CODEN(US): JSERBR Soluion of he Poblem of Sess-Sin Se of Physiclly Non-Line Heeiily Plsic Infinie Ple
vilble online www.jse.com Jounl of Scienific n Engineeing Resech, 8, 5():5-58 Resech icle ISSN: 94-6 CODEN(US): JSERBR Soluion of he Poblem of Sess-Sin Se of Physiclly Non-Line Heeiily Plsic Infinie Ple
FM Applications of Integration 1.Centroid of Area
 FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
FM Applicions of Inegrion.Cenroid of Are The cenroid of ody is is geomeric cenre. For n ojec mde of uniform meril, he cenroid coincides wih he poin which he ody cn e suppored in perfecly lnced se ie, is
PHYSICS 102. Intro PHYSICS-ELECTROMAGNETISM
 PHYS 0 Suen Nme: Suen Numbe: FAUTY OF SIENE Viul Miem EXAMINATION PHYSIS 0 Ino PHYSIS-EETROMAGNETISM Emines: D. Yoichi Miyh INSTRUTIONS: Aemp ll 4 quesions. All quesions hve equl weighs 0 poins ech. Answes
PHYS 0 Suen Nme: Suen Numbe: FAUTY OF SIENE Viul Miem EXAMINATION PHYSIS 0 Ino PHYSIS-EETROMAGNETISM Emines: D. Yoichi Miyh INSTRUTIONS: Aemp ll 4 quesions. All quesions hve equl weighs 0 poins ech. Answes
Physics 2A HW #3 Solutions
 Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Chper 3 Focus on Conceps: 3, 4, 6, 9 Problems: 9, 9, 3, 41, 66, 7, 75, 77 Phsics A HW #3 Soluions Focus On Conceps 3-3 (c) The ccelerion due o grvi is he sme for boh blls, despie he fc h he hve differen
Lecture 18: Kinetics of Phase Growth in a Two-component System: general kinetics analysis based on the dilute-solution approximation
 Lecue 8: Kineics of Phase Gowh in a Two-componen Sysem: geneal kineics analysis based on he dilue-soluion appoximaion Today s opics: In he las Lecues, we leaned hee diffeen ways o descibe he diffusion
Lecue 8: Kineics of Phase Gowh in a Two-componen Sysem: geneal kineics analysis based on he dilue-soluion appoximaion Today s opics: In he las Lecues, we leaned hee diffeen ways o descibe he diffusion
Reinforcement learning
 CS 75 Mchine Lening Lecue b einfocemen lening Milos Huskech milos@cs.pi.edu 539 Senno Sque einfocemen lening We wn o len conol policy: : X A We see emples of bu oupus e no given Insed of we ge feedbck
CS 75 Mchine Lening Lecue b einfocemen lening Milos Huskech milos@cs.pi.edu 539 Senno Sque einfocemen lening We wn o len conol policy: : X A We see emples of bu oupus e no given Insed of we ge feedbck
Motion. Part 2: Constant Acceleration. Acceleration. October Lab Physics. Ms. Levine 1. Acceleration. Acceleration. Units for Acceleration.
 Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
Moion Accelerion Pr : Consn Accelerion Accelerion Accelerion Accelerion is he re of chnge of velociy. = v - vo = Δv Δ ccelerion = = v - vo chnge of velociy elpsed ime Accelerion is vecor, lhough in one-dimensionl
MTH 146 Class 11 Notes
 8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
8.- Are of Surfce of Revoluion MTH 6 Clss Noes Suppose we wish o revolve curve C round n is nd find he surfce re of he resuling solid. Suppose f( ) is nonnegive funcion wih coninuous firs derivive on he
MEEN 617 Handout #11 MODAL ANALYSIS OF MDOF Systems with VISCOUS DAMPING
 MEEN 67 Handou # MODAL ANALYSIS OF MDOF Sysems wih VISCOS DAMPING ^ Symmeic Moion of a n-dof linea sysem is descibed by he second ode diffeenial equaions M+C+K=F whee () and F () ae n ows vecos of displacemens
MEEN 67 Handou # MODAL ANALYSIS OF MDOF Sysems wih VISCOS DAMPING ^ Symmeic Moion of a n-dof linea sysem is descibed by he second ode diffeenial equaions M+C+K=F whee () and F () ae n ows vecos of displacemens
Equations from The Four Principal Kinetic States of Material Bodies. Copyright 2005 Joseph A. Rybczyk
 Equions fom he Fou Pinipl Kinei Ses of Meil Bodies Copyigh 005 Joseph A. Rybzyk Following is omplee lis of ll of he equions used in o deied in he Fou Pinipl Kinei Ses of Meil Bodies. Eh equion is idenified
Equions fom he Fou Pinipl Kinei Ses of Meil Bodies Copyigh 005 Joseph A. Rybzyk Following is omplee lis of ll of he equions used in o deied in he Fou Pinipl Kinei Ses of Meil Bodies. Eh equion is idenified
Computer Aided Geometric Design
 Copue Aided Geoei Design Geshon Ele, Tehnion sed on ook Cohen, Riesenfeld, & Ele Geshon Ele, Tehnion Definiion 3. The Cile Given poin C in plne nd nue R 0, he ile ih ene C nd dius R is defined s he se
Copue Aided Geoei Design Geshon Ele, Tehnion sed on ook Cohen, Riesenfeld, & Ele Geshon Ele, Tehnion Definiion 3. The Cile Given poin C in plne nd nue R 0, he ile ih ene C nd dius R is defined s he se
Circular Motion. Radians. One revolution is equivalent to which is also equivalent to 2π radians. Therefore we can.
 1 Cicula Moion Radians One evoluion is equivalen o 360 0 which is also equivalen o 2π adians. Theefoe we can say ha 360 = 2π adians, 180 = π adians, 90 = π 2 adians. Hence 1 adian = 360 2π Convesions Rule
1 Cicula Moion Radians One evoluion is equivalen o 360 0 which is also equivalen o 2π adians. Theefoe we can say ha 360 = 2π adians, 180 = π adians, 90 = π 2 adians. Hence 1 adian = 360 2π Convesions Rule
Today - Lecture 13. Today s lecture continue with rotations, torque, Note that chapters 11, 12, 13 all involve rotations
 Today - Lecue 13 Today s lecue coninue wih oaions, oque, Noe ha chapes 11, 1, 13 all inole oaions slide 1 eiew Roaions Chapes 11 & 1 Viewed fom aboe (+z) Roaional, o angula elociy, gies angenial elociy
Today - Lecue 13 Today s lecue coninue wih oaions, oque, Noe ha chapes 11, 1, 13 all inole oaions slide 1 eiew Roaions Chapes 11 & 1 Viewed fom aboe (+z) Roaional, o angula elociy, gies angenial elociy
One of the common descriptions of curvilinear motion uses path variables, which are measurements made along the tangent t and normal n to the path of
 Oe of he commo descipios of cuilie moio uses ph ibles, which e mesuemes mde log he ge d oml o he ph of he picles. d e wo ohogol xes cosideed sepely fo eey is of moio. These coodies poide ul descipio fo
Oe of he commo descipios of cuilie moio uses ph ibles, which e mesuemes mde log he ge d oml o he ph of he picles. d e wo ohogol xes cosideed sepely fo eey is of moio. These coodies poide ul descipio fo
(b) 10 yr. (b) 13 m. 1.6 m s, m s m s (c) 13.1 s. 32. (a) 20.0 s (b) No, the minimum distance to stop = 1.00 km. 1.
 Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Answers o Een Numbered Problems Chper. () 7 m s, 6 m s (b) 8 5 yr 4.. m ih 6. () 5. m s (b).5 m s (c).5 m s (d) 3.33 m s (e) 8. ().3 min (b) 64 mi..3 h. ().3 s (b) 3 m 4..8 mi wes of he flgpole 6. (b)
Addition & Subtraction of Polynomials
 Addiion & Sucion of Polynomil Addiion of Polynomil: Adding wo o moe olynomil i imly me of dding like em. The following ocedue hould e ued o dd olynomil 1. Remove enhee if hee e enhee. Add imil em. Wie
Addiion & Sucion of Polynomil Addiion of Polynomil: Adding wo o moe olynomil i imly me of dding like em. The following ocedue hould e ued o dd olynomil 1. Remove enhee if hee e enhee. Add imil em. Wie
Axis. Axis. Axis. Solid cylinder (or disk) about. Hoop about. Annular cylinder (or ring) about central axis. central axis.
 Insucos: Fiel/che/Deweile PYSICS DEPATENT PY 48 Em ch 5, 5 Nme pin, ls fis: Signue: On m hono, I he neihe gien no eceie unuhoie i on his eminion. YOU TEST NUBE IS TE 5-DIGIT NUBE AT TE TOP OF EAC PAGE.
Insucos: Fiel/che/Deweile PYSICS DEPATENT PY 48 Em ch 5, 5 Nme pin, ls fis: Signue: On m hono, I he neihe gien no eceie unuhoie i on his eminion. YOU TEST NUBE IS TE 5-DIGIT NUBE AT TE TOP OF EAC PAGE.
0 for t < 0 1 for t > 0
 8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
8.0 Sep nd del funcions Auhor: Jeremy Orloff The uni Sep Funcion We define he uni sep funcion by u() = 0 for < 0 for > 0 I is clled he uni sep funcion becuse i kes uni sep = 0. I is someimes clled he Heviside
Chapter 4 Circular and Curvilinear Motions
 Chp 4 Cicul n Cuilin Moions H w consi picls moing no long sigh lin h cuilin moion. W fis su h cicul moion, spcil cs of cuilin moion. Anoh mpl w h l sui li is h pojcil..1 Cicul Moion Unifom Cicul Moion
Chp 4 Cicul n Cuilin Moions H w consi picls moing no long sigh lin h cuilin moion. W fis su h cicul moion, spcil cs of cuilin moion. Anoh mpl w h l sui li is h pojcil..1 Cicul Moion Unifom Cicul Moion
PHYSICS 1210 Exam 1 University of Wyoming 14 February points
 PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
PHYSICS 1210 Em 1 Uniersiy of Wyoming 14 Februry 2013 150 poins This es is open-noe nd closed-book. Clculors re permied bu compuers re no. No collborion, consulion, or communicion wih oher people (oher
Homework 5 for BST 631: Statistical Theory I Solutions, 09/21/2006
 Homewok 5 fo BST 63: Sisicl Theoy I Soluions, 9//6 Due Time: 5:PM Thusy, on 9/8/6. Polem ( oins). Book olem.8. Soluion: E = x f ( x) = ( x) f ( x) + ( x ) f ( x) = xf ( x) + xf ( x) + f ( x) f ( x) Accoing
Homewok 5 fo BST 63: Sisicl Theoy I Soluions, 9//6 Due Time: 5:PM Thusy, on 9/8/6. Polem ( oins). Book olem.8. Soluion: E = x f ( x) = ( x) f ( x) + ( x ) f ( x) = xf ( x) + xf ( x) + f ( x) f ( x) Accoing
Lecture 11: Potential Gradient and Capacitor Review:
 Lectue 11: Potentil Gdient nd Cpcito Review: Two wys to find t ny point in spce: Sum o Integte ove chges: q 1 1 q 2 2 3 P i 1 q i i dq q 3 P 1 dq xmple of integting ove distiution: line of chge ing of
Lectue 11: Potentil Gdient nd Cpcito Review: Two wys to find t ny point in spce: Sum o Integte ove chges: q 1 1 q 2 2 3 P i 1 q i i dq q 3 P 1 dq xmple of integting ove distiution: line of chge ing of
Technical Appendix for Inventory Management for an Assembly System with Product or Component Returns, DeCroix and Zipkin, Management Science 2005.
 Techc Appedx fo Iveoy geme fo Assemy Sysem wh Poduc o Compoe eus ecox d Zp geme Scece 2005 Lemm µ µ s c Poof If J d µ > µ he ˆ 0 µ µ µ µ µ µ µ µ Sm gumes essh he esu f µ ˆ > µ > µ > µ o K ˆ If J he so
Techc Appedx fo Iveoy geme fo Assemy Sysem wh Poduc o Compoe eus ecox d Zp geme Scece 2005 Lemm µ µ s c Poof If J d µ > µ he ˆ 0 µ µ µ µ µ µ µ µ Sm gumes essh he esu f µ ˆ > µ > µ > µ o K ˆ If J he so
Lecture 22 Electromagnetic Waves
 Lecue Elecomagneic Waves Pogam: 1. Enegy caied by he wave (Poyning veco).. Maxwell s equaions and Bounday condiions a inefaces. 3. Maeials boundaies: eflecion and efacion. Snell s Law. Quesions you should
Lecue Elecomagneic Waves Pogam: 1. Enegy caied by he wave (Poyning veco).. Maxwell s equaions and Bounday condiions a inefaces. 3. Maeials boundaies: eflecion and efacion. Snell s Law. Quesions you should
Lecture-V Stochastic Processes and the Basic Term-Structure Equation 1 Stochastic Processes Any variable whose value changes over time in an uncertain
 Lecue-V Sochasic Pocesses and he Basic Tem-Sucue Equaion 1 Sochasic Pocesses Any vaiable whose value changes ove ime in an unceain way is called a Sochasic Pocess. Sochasic Pocesses can be classied as
Lecue-V Sochasic Pocesses and he Basic Tem-Sucue Equaion 1 Sochasic Pocesses Any vaiable whose value changes ove ime in an unceain way is called a Sochasic Pocess. Sochasic Pocesses can be classied as
General Physics II. number of field lines/area. for whole surface: for continuous surface is a whole surface
 Genel Physics II Chpte 3: Guss w We now wnt to quickly discuss one of the moe useful tools fo clculting the electic field, nmely Guss lw. In ode to undestnd Guss s lw, it seems we need to know the concept
Genel Physics II Chpte 3: Guss w We now wnt to quickly discuss one of the moe useful tools fo clculting the electic field, nmely Guss lw. In ode to undestnd Guss s lw, it seems we need to know the concept
f t f a f x dx By Lin McMullin f x dx= f b f a. 2
 Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
Accumulion: Thoughs On () By Lin McMullin f f f d = + The gols of he AP* Clculus progrm include he semen, Sudens should undersnd he definie inegrl s he ne ccumulion of chnge. 1 The Topicl Ouline includes
10 m, so the distance from the Sun to the Moon during a solar eclipse is. The mass of the Sun, Earth, and Moon are = =
 Chpte 1 nivesl Gvittion 11 *P1. () The un-th distnce is 1.4 nd the th-moon 8 distnce is.84, so the distnce fom the un to the Moon duing sol eclipse is 11 8 11 1.4.84 = 1.4 The mss of the un, th, nd Moon
Chpte 1 nivesl Gvittion 11 *P1. () The un-th distnce is 1.4 nd the th-moon 8 distnce is.84, so the distnce fom the un to the Moon duing sol eclipse is 11 8 11 1.4.84 = 1.4 The mss of the un, th, nd Moon
KINEMATICS OF RIGID BODIES
 KINEMTICS OF RIGID ODIES In igid body kinemaics, we use he elaionships govening he displacemen, velociy and acceleaion, bu mus also accoun fo he oaional moion of he body. Descipion of he moion of igid
KINEMTICS OF RIGID ODIES In igid body kinemaics, we use he elaionships govening he displacemen, velociy and acceleaion, bu mus also accoun fo he oaional moion of he body. Descipion of he moion of igid
On the Eötvös effect
 On the Eötvös effect Mugu B. Răuţ The im of this ppe is to popose new theoy bout the Eötvös effect. We develop mthemticl model which loud us bette undestnding of this effect. Fom the eqution of motion
On the Eötvös effect Mugu B. Răuţ The im of this ppe is to popose new theoy bout the Eötvös effect. We develop mthemticl model which loud us bette undestnding of this effect. Fom the eqution of motion
1.0 Electrical Systems
 . Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
. Elecricl Sysems The ypes of dynmicl sysems we will e sudying cn e modeled in erms of lgeric equions, differenil equions, or inegrl equions. We will egin y looking fmilir mhemicl models of idel resisors,
3 Motion with constant acceleration: Linear and projectile motion
 3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
3 Moion wih consn ccelerion: Liner nd projecile moion cons, In he precedin Lecure we he considered moion wih consn ccelerion lon he is: Noe h,, cn be posiie nd neie h leds o rie of behiors. Clerl similr
A 1.3 m 2.5 m 2.8 m. x = m m = 8400 m. y = 4900 m 3200 m = 1700 m
 PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
PHYS : Soluions o Chper 3 Home Work. SSM REASONING The displcemen is ecor drwn from he iniil posiion o he finl posiion. The mgniude of he displcemen is he shores disnce beween he posiions. Noe h i is onl
5.1-The Initial-Value Problems For Ordinary Differential Equations
 5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
5.-The Iniil-Vlue Problems For Ordinry Differenil Equions Consider solving iniil-vlue problems for ordinry differenil equions: (*) y f, y, b, y. If we know he generl soluion y of he ordinry differenil
e t dt e t dt = lim e t dt T (1 e T ) = 1
 Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Improper Inegrls There re wo ypes of improper inegrls - hose wih infinie limis of inegrion, nd hose wih inegrnds h pproch some poin wihin he limis of inegrion. Firs we will consider inegrls wih infinie
Physics 11b Lecture #11
 Physics 11b Lectue #11 Mgnetic Fields Souces of the Mgnetic Field S&J Chpte 9, 3 Wht We Did Lst Time Mgnetic fields e simil to electic fields Only diffeence: no single mgnetic pole Loentz foce Moving chge
Physics 11b Lectue #11 Mgnetic Fields Souces of the Mgnetic Field S&J Chpte 9, 3 Wht We Did Lst Time Mgnetic fields e simil to electic fields Only diffeence: no single mgnetic pole Loentz foce Moving chge
U>, and is negative. Electric Potential Energy
 Electic Potentil Enegy Think of gvittionl potentil enegy. When the lock is moved veticlly up ginst gvity, the gvittionl foce does negtive wok (you do positive wok), nd the potentil enegy (U) inceses. When
Electic Potentil Enegy Think of gvittionl potentil enegy. When the lock is moved veticlly up ginst gvity, the gvittionl foce does negtive wok (you do positive wok), nd the potentil enegy (U) inceses. When
A Kalman filtering simulation
 A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
A Klmn filering simulion The performnce of Klmn filering hs been esed on he bsis of wo differen dynmicl models, ssuming eiher moion wih consn elociy or wih consn ccelerion. The former is epeced o beer
π,π is the angle FROM a! TO b
 Mth 151: 1.2 The Dot Poduct We hve scled vectos (o, multiplied vectos y el nume clled scl) nd dded vectos (in ectngul component fom). Cn we multiply vectos togethe? The nswe is YES! In fct, thee e two
Mth 151: 1.2 The Dot Poduct We hve scled vectos (o, multiplied vectos y el nume clled scl) nd dded vectos (in ectngul component fom). Cn we multiply vectos togethe? The nswe is YES! In fct, thee e two
Perturbation Analysis of the LMI-Based Continuous-time Linear Quadratic Regulator Problem for Descriptor Systems
 Pin SS: 3-6; Online SS: 367-5357 DO: 55/ic-6-7 Peuion nlsis of he -sed Coninuous-ime ine udic egulo Polem fo Desco Ssems onchev Ke Wods: Coninuous-ime desco ssems; peuion nlsis; line qudic egulo sed conol
Pin SS: 3-6; Online SS: 367-5357 DO: 55/ic-6-7 Peuion nlsis of he -sed Coninuous-ime ine udic egulo Polem fo Desco Ssems onchev Ke Wods: Coninuous-ime desco ssems; peuion nlsis; line qudic egulo sed conol
Physics Mechanics. Rule #2: LABEL/LIST YOUR KNOWN VALUES AND THOSE DESIRED (Include units!!)
 Phic Mechnic Rule #1: DRAW A PICTURE (Picoil Repeenion, Moion Dim, ee-bod Dim) Dw picue o wh he queion i decibin. Ue moion dim nd ee-bod dim o i ou in eein wh i oin on in he queion. Moion Dim: + ee-bod
Phic Mechnic Rule #1: DRAW A PICTURE (Picoil Repeenion, Moion Dim, ee-bod Dim) Dw picue o wh he queion i decibin. Ue moion dim nd ee-bod dim o i ou in eein wh i oin on in he queion. Moion Dim: + ee-bod
Contraction Mapping Principle Approach to Differential Equations
 epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
epl Journl of Science echnology 0 (009) 49-53 Conrcion pping Principle pproch o Differenil Equions Bishnu P. Dhungn Deprmen of hemics, hendr Rn Cmpus ribhuvn Universiy, Khmu epl bsrc Using n eension of
Low-complexity Algorithms for MIMO Multiplexing Systems
 Low-complexiy Algoihms fo MIMO Muliplexing Sysems Ouline Inoducion QRD-M M algoihm Algoihm I: : o educe he numbe of suviving pahs. Algoihm II: : o educe he numbe of candidaes fo each ansmied signal. :
Low-complexiy Algoihms fo MIMO Muliplexing Sysems Ouline Inoducion QRD-M M algoihm Algoihm I: : o educe he numbe of suviving pahs. Algoihm II: : o educe he numbe of candidaes fo each ansmied signal. :
RESPONSE UNDER A GENERAL PERIODIC FORCE. When the external force F(t) is periodic with periodτ = 2π
 RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
RESPONSE UNDER A GENERAL PERIODIC FORCE When he exernl force F() is periodic wih periodτ / ω,i cn be expnded in Fourier series F( ) o α ω α b ω () where τ F( ) ω d, τ,,,... () nd b τ F( ) ω d, τ,,... (3)
Physics 604 Problem Set 1 Due Sept 16, 2010
 Physics 64 Polem et 1 Due ept 16 1 1) ) Inside good conducto the electic field is eo (electons in the conducto ecuse they e fee to move move in wy to cncel ny electic field impessed on the conducto inside
Physics 64 Polem et 1 Due ept 16 1 1) ) Inside good conducto the electic field is eo (electons in the conducto ecuse they e fee to move move in wy to cncel ny electic field impessed on the conducto inside
Answers to test yourself questions
 Answes to test youself questions opic Descibing fields Gm Gm Gm Gm he net field t is: g ( d / ) ( 4d / ) d d Gm Gm Gm Gm Gm Gm b he net potentil t is: V d / 4d / d 4d d d V e 4 7 9 49 J kg 7 7 Gm d b E
Answes to test youself questions opic Descibing fields Gm Gm Gm Gm he net field t is: g ( d / ) ( 4d / ) d d Gm Gm Gm Gm Gm Gm b he net potentil t is: V d / 4d / d 4d d d V e 4 7 9 49 J kg 7 7 Gm d b E
4.8 Improper Integrals
 4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
4.8 Improper Inegrls Well you ve mde i hrough ll he inegrion echniques. Congrs! Unforunely for us, we sill need o cover one more inegrl. They re clled Improper Inegrls. A his poin, we ve only del wih inegrls
Combinatorial Approach to M/M/1 Queues. Using Hypergeometric Functions
 Inenaional Mahemaical Foum, Vol 8, 03, no 0, 463-47 HIKARI Ld, wwwm-hikaicom Combinaoial Appoach o M/M/ Queues Using Hypegeomeic Funcions Jagdish Saan and Kamal Nain Depamen of Saisics, Univesiy of Delhi,
Inenaional Mahemaical Foum, Vol 8, 03, no 0, 463-47 HIKARI Ld, wwwm-hikaicom Combinaoial Appoach o M/M/ Queues Using Hypegeomeic Funcions Jagdish Saan and Kamal Nain Depamen of Saisics, Univesiy of Delhi,
M r. d 2. R t a M. Structural Mechanics Section. Exam CT5141 Theory of Elasticity Friday 31 October 2003, 9:00 12:00 hours. Problem 1 (3 points)
 Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
Delf Universiy of Technology Fculy of Civil Engineering nd Geosciences Srucurl echnics Secion Wrie your nme nd sudy numer he op righ-hnd of your work. Exm CT5 Theory of Elsiciy Fridy Ocoer 00, 9:00 :00
MATH 124 AND 125 FINAL EXAM REVIEW PACKET (Revised spring 2008)
 MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
MATH 14 AND 15 FINAL EXAM REVIEW PACKET (Revised spring 8) The following quesions cn be used s review for Mh 14/ 15 These quesions re no cul smples of quesions h will pper on he finl em, bu hey will provide
P h y s i c s F a c t s h e e t
 P h y s i c s F a c s h e e Sepembe 2001 Numbe 20 Simple Hamonic Moion Basic Conceps This Facshee will:! eplain wha is mean by simple hamonic moion! eplain how o use he equaions fo simple hamonic moion!
P h y s i c s F a c s h e e Sepembe 2001 Numbe 20 Simple Hamonic Moion Basic Conceps This Facshee will:! eplain wha is mean by simple hamonic moion! eplain how o use he equaions fo simple hamonic moion!
Average & instantaneous velocity and acceleration Motion with constant acceleration
 Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
Physics 7: Lecure Reminders Discussion nd Lb secions sr meeing ne week Fill ou Pink dd/drop form if you need o swich o differen secion h is FULL. Do i TODAY. Homework Ch. : 5, 7,, 3,, nd 6 Ch.: 6,, 3 Submission
3.1 Magnetic Fields. Oersted and Ampere
 3.1 Mgnetic Fields Oested nd Ampee The definition of mgnetic induction, B Fields of smll loop (dipole) Mgnetic fields in mtte: ) feomgnetism ) mgnetiztion, (M ) c) mgnetic susceptiility, m d) mgnetic field,
3.1 Mgnetic Fields Oested nd Ampee The definition of mgnetic induction, B Fields of smll loop (dipole) Mgnetic fields in mtte: ) feomgnetism ) mgnetiztion, (M ) c) mgnetic susceptiility, m d) mgnetic field,
ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 9 Solutions [Theorems of Gauss and Stokes]
![ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 9 Solutions [Theorems of Gauss and Stokes] ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 9 Solutions [Theorems of Gauss and Stokes]](/thumbs/91/106162145.jpg) ENGI 44 Avance alculus fo Engineeing Faculy of Engineeing an Applie cience Poblem e 9 oluions [Theoems of Gauss an okes]. A fla aea A is boune by he iangle whose veices ae he poins P(,, ), Q(,, ) an R(,,
ENGI 44 Avance alculus fo Engineeing Faculy of Engineeing an Applie cience Poblem e 9 oluions [Theoems of Gauss an okes]. A fla aea A is boune by he iangle whose veices ae he poins P(,, ), Q(,, ) an R(,,
PHYS PRACTICE EXAM 2
 PHYS 1800 PRACTICE EXAM Pa I Muliple Choice Quesions [ ps each] Diecions: Cicle he one alenaive ha bes complees he saemen o answes he quesion. Unless ohewise saed, assume ideal condiions (no ai esisance,
PHYS 1800 PRACTICE EXAM Pa I Muliple Choice Quesions [ ps each] Diecions: Cicle he one alenaive ha bes complees he saemen o answes he quesion. Unless ohewise saed, assume ideal condiions (no ai esisance,
Chapter 7. Kleene s Theorem. 7.1 Kleene s Theorem. The following theorem is the most important and fundamental result in the theory of FA s:
 Chpte 7 Kleene s Theoem 7.1 Kleene s Theoem The following theoem is the most impotnt nd fundmentl esult in the theoy of FA s: Theoem 6 Any lnguge tht cn e defined y eithe egul expession, o finite utomt,
Chpte 7 Kleene s Theoem 7.1 Kleene s Theoem The following theoem is the most impotnt nd fundmentl esult in the theoy of FA s: Theoem 6 Any lnguge tht cn e defined y eithe egul expession, o finite utomt,
Week 8. Topic 2 Properties of Logarithms
 Week 8 Topic 2 Popeties of Logithms 1 Week 8 Topic 2 Popeties of Logithms Intoduction Since the esult of ithm is n eponent, we hve mny popeties of ithms tht e elted to the popeties of eponents. They e
Week 8 Topic 2 Popeties of Logithms 1 Week 8 Topic 2 Popeties of Logithms Intoduction Since the esult of ithm is n eponent, we hve mny popeties of ithms tht e elted to the popeties of eponents. They e
Lecture 17: Kinetics of Phase Growth in a Two-component System:
 Lecue 17: Kineics of Phase Gowh in a Two-componen Sysem: descipion of diffusion flux acoss he α/ ineface Today s opics Majo asks of oday s Lecue: how o deive he diffusion flux of aoms. Once an incipien
Lecue 17: Kineics of Phase Gowh in a Two-componen Sysem: descipion of diffusion flux acoss he α/ ineface Today s opics Majo asks of oday s Lecue: how o deive he diffusion flux of aoms. Once an incipien
Classification of Equations Characteristics
 Clssiiion o Eqions Cheisis Consie n elemen o li moing in wo imensionl spe enoe s poin P elow. The ph o P is inie he line. The posiion ile is s so h n inemenl isne long is s. Le he goening eqions e epesene
Clssiiion o Eqions Cheisis Consie n elemen o li moing in wo imensionl spe enoe s poin P elow. The ph o P is inie he line. The posiion ile is s so h n inemenl isne long is s. Le he goening eqions e epesene
Relative and Circular Motion
 Relaie and Cicula Moion a) Relaie moion b) Cenipeal acceleaion Mechanics Lecue 3 Slide 1 Mechanics Lecue 3 Slide 2 Time on Video Pelecue Looks like mosly eeyone hee has iewed enie pelecue GOOD! Thank you
Relaie and Cicula Moion a) Relaie moion b) Cenipeal acceleaion Mechanics Lecue 3 Slide 1 Mechanics Lecue 3 Slide 2 Time on Video Pelecue Looks like mosly eeyone hee has iewed enie pelecue GOOD! Thank you
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 10: The High Beta Tokamak Con d and the High Flux Conserving Tokamak.
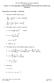 .615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
.615, MHD Theory of Fusion Sysems Prof. Freidberg Lecure 1: The High Be Tokmk Con d nd he High Flux Conserving Tokmk Proeries of he High Tokmk 1. Evlue he MHD sfey fcor: ψ B * ( ) 1 3 ρ 1+ ν ρ ρ cosθ *
Version 001 test-1 swinney (57010) 1. is constant at m/s.
 Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
Version 001 es-1 swinne (57010) 1 This prin-ou should hve 20 quesions. Muliple-choice quesions m coninue on he nex column or pge find ll choices before nswering. CubeUniVec1x76 001 10.0 poins Acubeis1.4fee
General Non-Arbitrage Model. I. Partial Differential Equation for Pricing A. Traded Underlying Security
 1 Geneal Non-Abiage Model I. Paial Diffeenial Equaion fo Picing A. aded Undelying Secuiy 1. Dynamics of he Asse Given by: a. ds = µ (S, )d + σ (S, )dz b. he asse can be eihe a sock, o a cuency, an index,
1 Geneal Non-Abiage Model I. Paial Diffeenial Equaion fo Picing A. aded Undelying Secuiy 1. Dynamics of he Asse Given by: a. ds = µ (S, )d + σ (S, )dz b. he asse can be eihe a sock, o a cuency, an index,
Derivation of the differential equation of motion
 Divion of h iffnil quion of oion Fis h noions fin h will us fo h ivion of h iffnil quion of oion. Rollo is hough o -insionl isk. xnl ius of h ll isnc cn of ll (O) - IDU s cn of gviy (M) θ ngl of inclinion
Divion of h iffnil quion of oion Fis h noions fin h will us fo h ivion of h iffnil quion of oion. Rollo is hough o -insionl isk. xnl ius of h ll isnc cn of ll (O) - IDU s cn of gviy (M) θ ngl of inclinion
Electric Field F E. q Q R Q. ˆ 4 r r - - Electric field intensity depends on the medium! origin
 1 1 Electic Field + + q F Q R oigin E 0 0 F E ˆ E 4 4 R q Q R Q - - Electic field intensity depends on the medium! Electic Flux Density We intoduce new vecto field D independent of medium. D E So, electic
1 1 Electic Field + + q F Q R oigin E 0 0 F E ˆ E 4 4 R q Q R Q - - Electic field intensity depends on the medium! Electic Flux Density We intoduce new vecto field D independent of medium. D E So, electic
2D Motion WS. A horizontally launched projectile s initial vertical velocity is zero. Solve the following problems with this information.
 Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
Nme D Moion WS The equions of moion h rele o projeciles were discussed in he Projecile Moion Anlsis Acii. ou found h projecile moes wih consn eloci in he horizonl direcion nd consn ccelerion in he ericl
Chapter 2. Motion along a straight line. 9/9/2015 Physics 218
 Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Chper Moion long srigh line 9/9/05 Physics 8 Gols for Chper How o describe srigh line moion in erms of displcemen nd erge elociy. The mening of insnneous elociy nd speed. Aerge elociy/insnneous elociy
Compressive modulus of adhesive bonded rubber block
 Songklnkin J. Sci. Tecnol. 0 (, -5, M. - Ap. 008 p://www.sjs.ps.c. Oiginl Aicle Compessive modls of desive bonded bbe block Coeny Decwykl nd Wiiy Tongng * Depmen of Mecnicl Engineeing, Fcly of Engineeing,
Songklnkin J. Sci. Tecnol. 0 (, -5, M. - Ap. 008 p://www.sjs.ps.c. Oiginl Aicle Compessive modls of desive bonded bbe block Coeny Decwykl nd Wiiy Tongng * Depmen of Mecnicl Engineeing, Fcly of Engineeing,
Particle Horizons in Cosmology
 Jounl of Moden Physics, 01, 4, 1194-1199 hp://dx.doi.og/10.46/jmp.01.4916 Published Online Sepembe 01 (hp://www.scip.og/jounl/jmp) Picle Hoizons in Cosmology K. Punchnd Ro School of Mhemicl nd Sisicl Sciences,
Jounl of Moden Physics, 01, 4, 1194-1199 hp://dx.doi.og/10.46/jmp.01.4916 Published Online Sepembe 01 (hp://www.scip.og/jounl/jmp) Picle Hoizons in Cosmology K. Punchnd Ro School of Mhemicl nd Sisicl Sciences,
Sharif University of Technology - CEDRA By: Professor Ali Meghdari
 Shaif Univesiy of echnology - CEDRA By: Pofesso Ali Meghai Pupose: o exen he Enegy appoach in eiving euaions of oion i.e. Lagange s Meho fo Mechanical Syses. opics: Genealize Cooinaes Lagangian Euaion
Shaif Univesiy of echnology - CEDRA By: Pofesso Ali Meghai Pupose: o exen he Enegy appoach in eiving euaions of oion i.e. Lagange s Meho fo Mechanical Syses. opics: Genealize Cooinaes Lagangian Euaion
MATHEMATICAL FOUNDATIONS FOR APPROXIMATING PARTICLE BEHAVIOUR AT RADIUS OF THE PLANCK LENGTH
 Fundamenal Jounal of Mahemaical Phsics Vol 3 Issue 013 Pages 55-6 Published online a hp://wwwfdincom/ MATHEMATICAL FOUNDATIONS FOR APPROXIMATING PARTICLE BEHAVIOUR AT RADIUS OF THE PLANCK LENGTH Univesias
Fundamenal Jounal of Mahemaical Phsics Vol 3 Issue 013 Pages 55-6 Published online a hp://wwwfdincom/ MATHEMATICAL FOUNDATIONS FOR APPROXIMATING PARTICLE BEHAVIOUR AT RADIUS OF THE PLANCK LENGTH Univesias
6. Gas dynamics. Ideal gases Speed of infinitesimal disturbances in still gas
 6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
6. Gs dynmics Dr. Gergely Krisóf De. of Fluid echnics, BE Februry, 009. Seed of infiniesiml disurbnces in sill gs dv d, dv d, Coninuiy: ( dv)( ) dv omenum r r heorem: ( ( dv) ) d 3443 4 q m dv d dv llievi
Chapter 10. Simple Harmonic Motion and Elasticity. Goals for Chapter 10
 Chper 0 Siple Hronic Moion nd Elsiciy Gols or Chper 0 o ollow periodic oion o sudy o siple hronic oion. o sole equions o siple hronic oion. o use he pendulu s prooypicl syse undergoing siple hronic oion.
Chper 0 Siple Hronic Moion nd Elsiciy Gols or Chper 0 o ollow periodic oion o sudy o siple hronic oion. o sole equions o siple hronic oion. o use he pendulu s prooypicl syse undergoing siple hronic oion.
The shortest path between two truths in the real domain passes through the complex domain. J. Hadamard
 Complex Analysis R.G. Halbud R.Halbud@ucl.ac.uk Depamen of Mahemaics Univesiy College London 202 The shoes pah beween wo uhs in he eal domain passes hough he complex domain. J. Hadamad Chape The fis fundamenal
Complex Analysis R.G. Halbud R.Halbud@ucl.ac.uk Depamen of Mahemaics Univesiy College London 202 The shoes pah beween wo uhs in he eal domain passes hough he complex domain. J. Hadamad Chape The fis fundamenal
ELECTROSTATICS. 4πε0. E dr. The electric field is along the direction where the potential decreases at the maximum rate. 5. Electric Potential Energy:
 LCTROSTATICS. Quntiztion of Chge: Any chged body, big o smll, hs totl chge which is n integl multile of e, i.e. = ± ne, whee n is n intege hving vlues,, etc, e is the chge of electon which is eul to.6
LCTROSTATICS. Quntiztion of Chge: Any chged body, big o smll, hs totl chge which is n integl multile of e, i.e. = ± ne, whee n is n intege hving vlues,, etc, e is the chge of electon which is eul to.6
Rotations.
 oons j.lbb@phscs.o.c.uk To s summ Fmes of efeence Invnce une nsfomons oon of wve funcon: -funcons Eule s ngles Emple: e e - - Angul momenum s oon geneo Genec nslons n Noehe s heoem Fmes of efeence Conse
oons j.lbb@phscs.o.c.uk To s summ Fmes of efeence Invnce une nsfomons oon of wve funcon: -funcons Eule s ngles Emple: e e - - Angul momenum s oon geneo Genec nslons n Noehe s heoem Fmes of efeence Conse
5-1. We apply Newton s second law (specifically, Eq. 5-2). F = ma = ma sin 20.0 = 1.0 kg 2.00 m/s sin 20.0 = 0.684N. ( ) ( )
 5-1. We apply Newon s second law (specfcally, Eq. 5-). (a) We fnd he componen of he foce s ( ) ( ) F = ma = ma cos 0.0 = 1.00kg.00m/s cos 0.0 = 1.88N. (b) The y componen of he foce s ( ) ( ) F = ma = ma
5-1. We apply Newon s second law (specfcally, Eq. 5-). (a) We fnd he componen of he foce s ( ) ( ) F = ma = ma cos 0.0 = 1.00kg.00m/s cos 0.0 = 1.88N. (b) The y componen of he foce s ( ) ( ) F = ma = ma
Properties of Logarithms. Solving Exponential and Logarithmic Equations. Properties of Logarithms. Properties of Logarithms. ( x)
 Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Properies of Logrihms Solving Eponenil nd Logrihmic Equions Properies of Logrihms Produc Rule ( ) log mn = log m + log n ( ) log = log + log Properies of Logrihms Quoien Rule log m = logm logn n log7 =
Outline. Part 1, Topic 3 Separation of Charge and Electric Fields. Dr. Sven Achenbach - based on a script by Dr. Eric Salt - Outline
 S. Achench: PHYS 55 (P, Topic 3) Hnous p. Ouline slie # Cunell & Johnson Univesiy of Sskchewn Unegue Couse Phys 55 Inoucion o leciciy n Mgneism conucos & insulos 6 8.3 pllel ple cpcios 68 8.9, 9.5 enegy
S. Achench: PHYS 55 (P, Topic 3) Hnous p. Ouline slie # Cunell & Johnson Univesiy of Sskchewn Unegue Couse Phys 55 Inoucion o leciciy n Mgneism conucos & insulos 6 8.3 pllel ple cpcios 68 8.9, 9.5 enegy
