AP Physics Enosburg Falls High School Mr. Bushey. Week 6: Work, Energy, Power
|
|
|
- Priscilla West
- 5 years ago
- Views:
Transcription
1 AP Physcs Enosburg Falls Hgh School Mr. Bushey ee 6: or, Energy, Power Homewor! Read Gancol Chapter AND/OR Read Saxon Lessons 1, 16, 9, 48! Read Topc Summary Handout! Answer Gancol p.174 Problems 1, 4, 7, 17, 18, 19, 0, 1, 3, 5! Answer Prnceton Reew p.79 AP Set multple choce, ree response questons Supplemental Reew / Study Group Focus! Reew Key Concepts Handout! Schaum s Outlnes, Chapter 6 Problems ! Schaum s Outlnes, Chapter 7 Problems ! Sole problems rom assocated Saxon lessons
2 or and or-energy Theorem or or s dened as the scalar product o orce and dsplacement. or s done when a non-zero net orce acts on a mong object. I a orce F moes an object oer a dstance d, wor can be ound by usng the ormula: F! " F! " d!!!! F " d I F and d are parallel, the wor s! F d cos".! Fd. I they are not parallel, then the wor s From ths ormula, one can conclude that or the wor to be done, the ollowng condtons must be met: # The object must moe (.e. d $ 0). A orce can be exerted on an object wth no wor done, e.g. pushng on a wall, holdng up 100 lb, etc. # I F and d are perpendcular, no wor s done (cos" = 0). For example, carryng somethng s not wor because the angle between the orce (upwards) and dsplacement (horzontal) s equal to 0. # The SI unt o wor s Joule (J), and 1 J = 1 N x 1 m. # I the angle between orce and dsplacement s less than 90 0, cos" >0, and the wor s poste. I 90 o <" < 180 o, cos" <0, and the wor s negate. Frcton always does negate wor because t always acts n the drecton opposte (180 o ) to the moton o the object. or ether changes the elocty o an object or counteracts the wor done by an opposng orce. For example, a car s mong at a constant speed, the engne does wor on the car to counteract the wor done by rcton n the opposte drecton. I an object s mong wth constant elocty, the net orce actng on t s zero. In ths case, the net amount o wor done on t must also be zero ( net =F net d).
3 Energy Energy s one o the most undamental concepts o Physcs. It s a ery abstract concept that does not hae a sngle denton. Energy s a characterstc o a system. Energy n a system ges t the capablty to perorm some operaton. hen wor s done on a system or by a system, the energy o the system changes. In other words, the system gans or loses energy through the process o wor. I poste wor s done, the system gans energy. I wor s negate, the system loses energy. I no wor s done, the total energy o the system does not change. There are many types o energy. Knetc energy (K or E ) s the energy o moton. It depends only upon the square o the speed and the mass o the object. K! 1 m or - Energy Theorem An object s mong wth an acceleraton a oer a dstance d. Then accordng to the ormula,! " a d : F! " ( ) d. m Solng or F d ges F! F! m F d! # ( ) d! The wor done on the object s gen by m 1 1! F d! ( # )! m # m! K # K Or, we can rewrte t as! K # K! $ K Ths s the netc energy wor theorem: The change o netc energy o a body s equal to the wor o all the orces actng upon t.
4 or and or-energy Theorem 1. A box, ntally at rest, s pulled a dstance o 5 m across a loor by a horzontal orce o 3 N. At the end o the 5 m, the netc energy o the box s 87 J. a. hat was the net wor done on the box? Accordng to the or-energy theorem, the net wor done on the box s equal to the change n the netc energy. net! " E! 87J b. How much wor was done by the 3 N orce? = F d = (3 N)(5 m) = 115 J c. How much wor was done by rcton? The net wor s equal to the sum o the wor done by the appled orce and the wor done by the rcton. net = A + = net A =87 J 115 J = 8 J d. How much wor was done by the gratatonal orce? The gratatonal orce s perpendcular to the dsplacement. Thus, the gratatonal orce does no wor. g = 0 J.. Bll carres a 35 N pacage rom the ground up to the th loor o a 15 m hgh oce buldng. How much wor s done by Bll on the pacage? The orce Bll s applyng to the pacage s drected up. He must be applyng a orce drected up to the pacage that s equal to the pacage s weght. He s also mong up. Thereore, # = 0. F = 35 N d = 15 m =? = F d cos# = F d = (35 N)(15 m)(cos 0º) = 55 J
5 3. A 4 g brc sldes a dstance (d) o 5m along an cy slope o nclnaton angle o 30 o. The coecent o netc rcton s! = 0.0. hat wll be the speed o the brc at the end o the slope? " There are three orces actng on the brc. The wor done by graty = m g d cos(90 - "), as the angle enclosed by G and the slope s 90 - ". Note that cos(90 - ") = sn" (trgonometry), thereore, g = m g d sn ". Note that d sn" = h where h s the heght o the slope. Thus, the wor s equal to m g h. The normal orce encloses 90 o wth the dsplacement, so n = F n d cos(90 o ) = 0. The wor o the rcton s r = -!#F n #d = -! m g d#cos("). The wor o all orces s = m g d (sn " -! cos ") and ths wll be equal to the netc energy K = 1/ m. m mgd(sn" $! cos ") % gd(sn" $! cos ") % % gd(sn" $! cos ") (9.81m/s )(5 m)(0.500 (0.0)(0.866)) % 5.7 m/s % $ 4. A g bloc s accelerated rom rest along a horzontal, smooth surace by a orce o 5 N oer a dstance o 6 m. a. Determne the acceleraton o the bloc and the nal elocty o the bloc. F 5 N a % % %.50 m/s m g $ % a # ( x o & ' & '& ' $ 0 m/s %.50m/s 6 m % 30 m /s % % 30 m /s 5.48 m/s
6 b. Calculate the wor done by the acceleratng orce. o! "! "! " $ F d Cos # $ 5 N 6 m Cos 0 $ 30 N % m $ 30.0 J c. Use the or-energy theorem to determne the nal elocty o the bloc. Compare your answer to the answer obtaned n part (a). $ & KE $ KE - KE KE $ ' KE $ 30 J ' 0 J $ 30 J 1! " g $ 30 J 30 J 1 g $ $ 30 m /s $ 5.48 m/s d. Fnd the nal elocty o the bloc t has an ntal elocty o + m/s. $ & KE $ KE - KE 1 1 $ m ( m J = g g m/s 30J = 1 g ( 4 J! " (! "! "! " 34 J $ $ $ 1 g 34 m /s 5.83 m/s e. I the bloc s mong wth a elocty o 8 m/s, what magntude retardng orce s needed to brng the bloc to rest oer a dstance o 5 m? & KE $ KE - KE F $ $ $ 1 1 m - m 1 1! g"! 0 m/s " -! g"! 8 m/s" -64 J & KE $ & x % Cos # -64 J $ (5 m)(1) $ -1.8 N
7 5. Hooe s law states that F!" x. a. Fnd the wor requred to compress the sprng through a dstance x. Because the orce s not constant throughout the dstance moed, we need to ntegrate the product o the dstance and the orce to determne the wor. Also the orce we exert s opposte n drecton to the orce exerted by the sprng, so the orce we exert s F! x. x x x x 1 1! # F dx! 0 0 # x dx!! x "! x 0 The wor requred s then 0 1! x. b. hat s the potental energy o a sprng whch was ntally at zero and was compressed to a pont x? hen the sprng has been compressed ts elocty s zero, so there s no netc energy, all o the energy s then potental energy. 1 or s equal to the change n the energy. Thus, Usprng! x.
8 Conserate Forces and Potental Energy Conserate Forces Denton: A orce s called conserate the wor t does on an object depends only on the ntal and nal postons o the object and s ndependent o the path taen between those postons. Graty s one such conserate orce. Near Earth s surace, the wor done by graty on an object o mass m depends only on the change n the object s heght h. In the case o conserate orces, we assgn a number--the potental energy, U--to each conguraton o the system. The zero leel o the potental energy s arbtrary; t can be assgned to any poston. I the place wth zero potental energy s chosen, the potental energy at any pont A s the wor done by the orce when the body moes rom the pont A to the pont 0 wth zero potental energy. So, U(A) = A0. The wor s addte. I the body moes rom A to B and then to pont 0, then! " B A0 AB 0, U ( A)! " U ( B) or! U ( A) # U ( B). AB AB Examples o Potental Energy The Gratatonal Potental Energy Graty s an example o a conserate orce. The wor done on an object o mass m when t s rased heght h at constant elocty by an external orce s mgh. U g = mgh s called the gratatonal potental energy o the object. The only physcally sgncant quantty s the change n potental energy, and not the absolute alue o the potental energy. For ths reason, n problem solng, we usually choose a conenent pont (table top leel, ground leel, sea leel, etc.) and set the potental energy at ths leel to be zero. All heghts are measured rom ths leel. Then, the object s below the zero leel, ts potental energy s negate. It s mportant to stress agan that only the change n potental energy s physcally sgncant. Gratatonal Potental Energy: U g = mgy Change n Gratatonal Potental Energy: $ U = U - U g g g o = mgh - mgh o
9 The Elastc Potental Energy Sprngs, rubber bands, and other sprngy objects also exert conserate orces. At relately small elongatons, the orce exerted by a sprng s proportonal to the amount x by whch the sprng has been stretched, Fspr! " x, (The - sgn ndcates that the orce s drected n the opposte drecton to the stretch.) s the constant o proportonalty and s called the sprng s sprng constant. Ths proportonalty between the orce F and the amount o stretchng (or compresson) x s nown as Hooe s Law. The wor done by a sprng wth a gen sprng constant depends only on x, so an assocated potental energy s U x x 1 spr ( )!. Note that x = 0 s at the equlbrum (unstretched) poston o the sprng. Nonconserate orces Unle conserate orces, the wor done by nonconserate orces depends on the path the object moes and not just on the ntal and nal ponts. Frcton s an example o a nonconserate orce. A nonconserate orce s oten called a dsspate orce.
10 Conserate Forces and Potental Energy 1. A 5 g bowlng ball s carred to the top o a tower that s 45 m hgh. The bowlng ball s released rom rest and allng reely to the ground. a. hat orce s requred to lt the bowlng ball to the top o the tower at constant elocty? F 0 N - Net!! FAppled F!! m g= (5g)(10 m/s)! 50 N Appled F App = 50 N t = 50 N b. How much wor s done by the ltng orce to lt the bowlng ball rom the ground to the top o the tower? " #" #! FNet d! 50 N 45 m! 50 J c. hat s the Gratatonal Potental Energy o the bowlng ball on the top o the tower? GPEtop!! $ 50 J d. How do the GPE and the KE o the bowlng ball change the bowlng ball alls rom the top o the tower to the ground? As the bowlng ball alls, t loses heght and ts GPE decreases. Because o the gratatonal orce, the bowlng ball accelerates (g = 10 m/s ), ts speed ncreases, and ts KE ncreases. e. Use the equatons o moton to nd the speed o the bowlng ball at the moment t hts the ground. hat s the KE o the bowlng ball at the nstant t stres the ground? Compare t wth the answer rom part (c). d! % 45 m ;! 0 m/s ; a! % 10 m/s %! a d o 0 " #" # % (0 m/s)! % 10 m/s % 45 m! 900 m /s E!! 900 m /s 30 m/s 1 1! m! " 5 g#" 30 m/s #! 50 J The answer s the same as n part (c).
11 . Use the equatons o moton or ree all to determne the heght aboe the ground and the potental energy o the bowlng ball at t = s ater t s released. 1 h # h0 $ 0t $ at 1 # 45m $ 0 m/s s $ % 10m/s s h # 5 m! "! "! "! " GPE! "! "! " # mgh # 5 g 10m/s 5 m # 150 J g. Calculate the elocty and the KE o the bowlng ball at tme t = s ater t s released. KE # $ a t 0! "! " # 0 m/s $ % 10 m/s s # % 0 m/s # 1 m 1 (5 g) 0 m/s 1000 J! " # % # h. Calculate the sum o the KE and GPE o the bowlng ball at ths tme and compare t wth ts ntal potental energy and wth ts nal netc energy at the moment t hts the ground. GPE + KE = 1000J + 150J = 50J = GPE top = KE. The bowlng ball hts the ground and compresses the ground a dstance o 0.00 m. hat s the magntude o the aerage orce exerted by the ground on the bowlng ball as t comes to rest? Ignorng the small change n GPE as the ground s compressed, the Change n KE s equal to the wor done by the orce exerted by the ground: & KE # KE % KE # 0 J - 50 J # -50 J o or Done # & KE F d = F( d % d ) # & KE F( % 0.00 m % 0 m) # % 50 J % 50 J F # # 113,000 N % 0.00 m
12 Accordng to the or-energy Theorem, All _ Forces!" K Conseraton o Energy and Power or o all orces can be separated nto two components, wor o conserate orces and wor o non-conserate orces.! # _ All _ Forces Consearate _ Forces Non _ Conserate Forces Further, Conserate _ Forces! $" U Then the wor energy theorem becomes Non _ Conserate _ Forces $ " U! " K Non _ Conserate _ Forces! " K # " U Ths leads to the concept o the conseraton o mechancal energy. I there s no non-conserate orce n the system, Non _ Conserate _ Forces! 0 and 0! " K # " U. In the absence o dsspate orces n a mechancal system, the mechancal energy E mech = K + U s a constant. For example, E mech n tme t = t ntal s the same as E mech at tme t = t nal. The wor energy theorem ges the result " Emech! " K # " U! 0 In an solated system where only conserate orces cause energy to be transormed, the mechancal energy o the system s constant. I no non-conserate orces are actng n a system, then 0! " K # " U. hen there are orces such as rcton present, we can stll nclude these orces and consere total energy tang nto account the heat generated as a result o wor o dsspate orces such as rcton.
13 !!"!" For Frcton, nc " # d " $! Nd Ths wor taes away mechancal energy and transers ths detracted amount nto heat. From the wor energy theorem, $! Nd " % K & % U 0 " % & % &! K U Nd 0 " % Emech & % Ethermal Thermal energy s one o the orms o non-mechancal nternal energy stored nsde o the bodes. Internal energy wll be coered n the ollowng unts o the course. The conseraton o energy wth ncluson o nternal energy becomes 0 Emech " % & % E nt I there are external orces appled to an solated system as a whole then, the wor energy theorem s or,!!!"!" F # d " % E & % E ext mech nt Fext "% E Total All o ths can by summed up n the ollowng equaton: Total nal mechancal energy = Total ntal + Any wor done mechancal energy - Any losses due to nonconserate orces or K & U " K & U & $ app loss
14 Power Power s the rate (how ast) at whch wor s done. or Done Power!. Tme Spent Perormng or P! t The unt o power s the "att," whch s equal to a Joule/second. The "horsepower" s the Englsh system unt o power; t s equal to 746.
15 Conseraton o Energy and Power 1. An electrcal motor lts a 575 N box 0 m straght up by a rope n 10 s. hat power s deeloped by the motor? F = 575 N the amount o orce the rope must apply to the object to lt t up at constant elocty s equal to the object s weght F = 575 N P! t d = 0 m! F d t = 10 s P =? Fd P! t (575 N)(0 m) 3 P!! 1.15" 10 10s. A bloc sldes down a rctonless nclned plane o heght h = 1 m, mang angle # wth the horzontal. At the bottom o the plane, the bloc contnues to moe on a lat surace wth a coecent o rcton $ = How ar does the mass moe on the lat surace? e apply the law o Conseraton o energy. The equaton s % E! % K & % U The elocty o the bloc s zero both n the begnnng and the end. Thus, % K! 0 e also hae % E!! ' $ m g d rcton The change n GPE s % U! ' mgh Puttng t all together % E! % K & % U ' $ m g d! ' mgh h 1m d!!! 3.3m $ A cyclst approaches the bottom o a hll at a speed o 11 m/s. The hll s 6 m hgh. Ignorng rcton, how ast s the cyclst mong at the top o the hll? Assume that he doesn t peddle and gnore ar resstance. Snce there s no rcton, the total mechancal energy s consered. Thus, % U & % K! % U! mgh ' 0! mgh and % K! m ' m, Substtute these nto the energy conseraton equaton 1 1 mgh & m ' m! 0! ' gh Thus,! ' gh! (11m/s) ' (9.81m/s )(6 m) = 3.8m /s! 1.81m/s.
16 4. A 100 g mass traelng wth a elocty o 15 m/s on a horzontal surace stres a sprng wth a sprng constant = 5 N/m. a. Fnd the compresson o the sprng requred to stop the mass the surace s rctonless. Snce there s no dsspate orce, we wll use the Law o Conseraton o Energy.! U "! K # ! U # x $ 0 # x! K # 0 $ m # $ m 1 1 x $ m # Sole or x: x # m 100 g x # (15m/s) # 67.1m 5 N/m b. Fnd the compresson o the sprng the surace s rough ( % # 0.4 0). The more general orm o the equaton ncludng nonconserate orces s! E # U "! K!!! E # F & d # $% m g x 1! U # x and! K # $ Puttng t all together we get: 1 m % $ m g x # x $ m 1 1 where and and $ # $ # $ % m g x 0.40(100 g)(9.81 m/s ) x ( 39.4 N) x x # (5 N/m) x # (.5 N/m) x 1 1 m # (100g)(15m/s) # 1150N 1 1 Smplyng (and leang o the unts to mae the quadratc equaton easer to read) $ 39.4x#.5x $ 1150 In standard orm ths quadratc equaton becomes.5x " 39.4x$ 1150 # 0 Solng by the quadratc ormula we obtan x# 4.8 m or x# $ 18 m The physcal soluton here s poste. Thus, x = 5 m.
17 5. An amusement par roller coaster car has a mass o 50 g. Durng the rde, t s towed to the top o a 30 m hll, where t s released rom rest and allowed to roll. The car plunges down the hll, then up a 10 m hll and through a loop wth a radus o 10 m. Assume that the tracs are rctonless. (Use g = 10 m/s.) a. hat s the Potental Energy o the car at the top o the 30 m hll? GPE # # Top o Hll #! 50 g"! 10 m/s "! 30 m" J m g h b. hat are the Knetc Energy and the speed o the car at the bottom o the 30 m hll? GPE # E # KE # KE Top o Hll Tot Bottom o Hll Bottom o Hll # 1 m J KE (75000 J) # # # # m 50 g 600 m /s 4 m/s c. hat are the Knetc Energy and the speed o the car at the top o the 10 m hll? GPE 10 m 10 m 10 m 10 m Tot 10 m Tot 10 m! "! "! " # m g h # 50 g 10 m/s 10 m # 5000 J GPE $ KE # E # J KE # E % GPE # J % 5000 J # J KE (50000 J) # # # # m 50 g 400 m /s 0 m/s d. I the hll maes an angle o 60 o wth the horzontal and the car taes 15 seconds to be towed up the hll, determne the length o the hll, the elocty o the car, the orce requred to tow the car up the hll, and the power o the motor pullng the car up the hll. o 30m # L(sn 60 ) 30m L # # o 34.64m sn 60 o F # t & sn 60 o (500 N)(sn 60 ) # 165 N = 00 N L 34.64m # # #.31m/s =.3m/s ' t 15s or Done 75000J P # # # 5000 J/s # 5000 ' t 15s or P # F!! = (m g)(sn 60 )( )=(50 g)(10 m/s )(sn 60 )(.31! " = (165 N).31m/s # 5001J/s # 5.0 m/s)
Page 1. Clicker Question 9: Physics 131: Lecture 15. Today s Agenda. Clicker Question 9: Energy. Energy is Conserved.
 Physcs 3: Lecture 5 Today s Agenda Intro to Conseraton o Energy Intro to some derent knds o energy Knetc Potental Denton o Mechancal Energy Conseraton o Mechancal Energy Conserate orces Examples Pendulum
Physcs 3: Lecture 5 Today s Agenda Intro to Conseraton o Energy Intro to some derent knds o energy Knetc Potental Denton o Mechancal Energy Conseraton o Mechancal Energy Conserate orces Examples Pendulum
PHYS 1443 Section 004 Lecture #12 Thursday, Oct. 2, 2014
 PHYS 1443 Secton 004 Lecture #1 Thursday, Oct., 014 Work-Knetc Energy Theorem Work under rcton Potental Energy and the Conservatve Force Gravtatonal Potental Energy Elastc Potental Energy Conservaton o
PHYS 1443 Secton 004 Lecture #1 Thursday, Oct., 014 Work-Knetc Energy Theorem Work under rcton Potental Energy and the Conservatve Force Gravtatonal Potental Energy Elastc Potental Energy Conservaton o
PHYS 1441 Section 002 Lecture #15
 PHYS 1441 Secton 00 Lecture #15 Monday, March 18, 013 Work wth rcton Potental Energy Gravtatonal Potental Energy Elastc Potental Energy Mechancal Energy Conservaton Announcements Mdterm comprehensve exam
PHYS 1441 Secton 00 Lecture #15 Monday, March 18, 013 Work wth rcton Potental Energy Gravtatonal Potental Energy Elastc Potental Energy Mechancal Energy Conservaton Announcements Mdterm comprehensve exam
EMU Physics Department
 Physcs 0 Lecture 8 Potental Energy and Conservaton Assst. Pro. Dr. Al ÖVGÜN EMU Physcs Department www.aovgun.com Denton o Work W q The work, W, done by a constant orce on an object s dened as the product
Physcs 0 Lecture 8 Potental Energy and Conservaton Assst. Pro. Dr. Al ÖVGÜN EMU Physcs Department www.aovgun.com Denton o Work W q The work, W, done by a constant orce on an object s dened as the product
Physics 207, Lecture 13, Oct. 15. Energy
 Physcs 07 Lecture 3 Physcs 07, Lecture 3, Oct. 5 Goals: Chapter 0 Understand the relatonshp between moton and energy Dene Potental Energy n a Hooke s Law sprng Deelop and explot conseraton o energy prncple
Physcs 07 Lecture 3 Physcs 07, Lecture 3, Oct. 5 Goals: Chapter 0 Understand the relatonshp between moton and energy Dene Potental Energy n a Hooke s Law sprng Deelop and explot conseraton o energy prncple
Chapter 3 and Chapter 4
 Chapter 3 and Chapter 4 Chapter 3 Energy 3. Introducton:Work Work W s energy transerred to or rom an object by means o a orce actng on the object. Energy transerred to the object s postve work, and energy
Chapter 3 and Chapter 4 Chapter 3 Energy 3. Introducton:Work Work W s energy transerred to or rom an object by means o a orce actng on the object. Energy transerred to the object s postve work, and energy
Chapter Seven - Potential Energy and Conservation of Energy
 Chapter Seven - Potental Energy and Conservaton o Energy 7 1 Potental Energy Potental energy. e wll nd that the potental energy o a system can only be assocated wth specc types o orces actng between members
Chapter Seven - Potental Energy and Conservaton o Energy 7 1 Potental Energy Potental energy. e wll nd that the potental energy o a system can only be assocated wth specc types o orces actng between members
TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES. PHYS 2211, Exam 2 Section 1 Version 1 October 18, 2013 Total Weight: 100 points
 TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES PHYS, Exam Secton Verson October 8, 03 Total Weght: 00 ponts. Check your examnaton or completeness pror to startng. There are a total o nne
TIME OF COMPLETION NAME SOLUTION DEPARTMENT OF NATURAL SCIENCES PHYS, Exam Secton Verson October 8, 03 Total Weght: 00 ponts. Check your examnaton or completeness pror to startng. There are a total o nne
Spring Force and Power
 Lecture 13 Chapter 9 Sprng Force and Power Yeah, energy s better than orces. What s net? Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi IN THIS CHAPTER, you wll learn how to solve problems
Lecture 13 Chapter 9 Sprng Force and Power Yeah, energy s better than orces. What s net? Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi IN THIS CHAPTER, you wll learn how to solve problems
Physics 131: Lecture 16. Today s Agenda
 Physcs 131: Lecture 16 Today s Agenda Intro to Conseraton o Energy Intro to some derent knds o energy Knetc Potental Denton t o Mechancal Energy Conseraton o Mechancal Energy Conserate orces Examples Pendulum
Physcs 131: Lecture 16 Today s Agenda Intro to Conseraton o Energy Intro to some derent knds o energy Knetc Potental Denton t o Mechancal Energy Conseraton o Mechancal Energy Conserate orces Examples Pendulum
Chapter 8: Potential Energy and The Conservation of Total Energy
 Chapter 8: Potental Energy and The Conservaton o Total Energy Work and knetc energy are energes o moton. K K K mv r v v F dr Potental energy s an energy that depends on locaton. -Dmenson F x d U( x) dx
Chapter 8: Potental Energy and The Conservaton o Total Energy Work and knetc energy are energes o moton. K K K mv r v v F dr Potental energy s an energy that depends on locaton. -Dmenson F x d U( x) dx
Chapter 8 Potential Energy and Conservation of Energy Important Terms (For chapters 7 and 8)
 Pro. Dr. I. Nasser Chapter8_I November 3, 07 Chapter 8 Potental Energy and Conservaton o Energy Important Terms (For chapters 7 and 8) conservatve orce: a orce whch does wor on an object whch s ndependent
Pro. Dr. I. Nasser Chapter8_I November 3, 07 Chapter 8 Potental Energy and Conservaton o Energy Important Terms (For chapters 7 and 8) conservatve orce: a orce whch does wor on an object whch s ndependent
Momentum. Momentum. Impulse. Momentum and Collisions
 Momentum Momentum and Collsons From Newton s laws: orce must be present to change an object s elocty (speed and/or drecton) Wsh to consder eects o collsons and correspondng change n elocty Gol ball ntally
Momentum Momentum and Collsons From Newton s laws: orce must be present to change an object s elocty (speed and/or drecton) Wsh to consder eects o collsons and correspondng change n elocty Gol ball ntally
Chapter 2. Pythagorean Theorem. Right Hand Rule. Position. Distance Formula
 Chapter Moton n One Dmenson Cartesan Coordnate System The most common coordnate system or representng postons n space s one based on three perpendcular spatal axes generally desgnated x, y, and z. Any
Chapter Moton n One Dmenson Cartesan Coordnate System The most common coordnate system or representng postons n space s one based on three perpendcular spatal axes generally desgnated x, y, and z. Any
Conservation of Energy
 Lecture 3 Chapter 8 Physcs I 0.3.03 Conservaton o Energy Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcsall.html 95.4, Fall 03,
Lecture 3 Chapter 8 Physcs I 0.3.03 Conservaton o Energy Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcsall.html 95.4, Fall 03,
Physics 105: Mechanics Lecture 13
 Physcs 05: Mechancs Lecture 3 Wenda Cao NJIT Physcs Department Momentum and Momentum Conseraton Momentum Impulse Conseraton o Momentum Collsons Lnear Momentum A new undamental quantty, lke orce, energy
Physcs 05: Mechancs Lecture 3 Wenda Cao NJIT Physcs Department Momentum and Momentum Conseraton Momentum Impulse Conseraton o Momentum Collsons Lnear Momentum A new undamental quantty, lke orce, energy
PHYS 1441 Section 002 Lecture #16
 PHYS 1441 Secton 00 Lecture #16 Monday, Mar. 4, 008 Potental Energy Conservatve and Non-conservatve Forces Conservaton o Mechancal Energy Power Today s homework s homework #8, due 9pm, Monday, Mar. 31!!
PHYS 1441 Secton 00 Lecture #16 Monday, Mar. 4, 008 Potental Energy Conservatve and Non-conservatve Forces Conservaton o Mechancal Energy Power Today s homework s homework #8, due 9pm, Monday, Mar. 31!!
You will analyze the motion of the block at different moments using the law of conservation of energy.
 Physcs 00A Homework 7 Chapter 8 Where s the Energy? In ths problem, we wll consder the ollowng stuaton as depcted n the dagram: A block o mass m sldes at a speed v along a horzontal smooth table. It next
Physcs 00A Homework 7 Chapter 8 Where s the Energy? In ths problem, we wll consder the ollowng stuaton as depcted n the dagram: A block o mass m sldes at a speed v along a horzontal smooth table. It next
Name: PHYS 110 Dr. McGovern Spring 2018 Exam 1. Multiple Choice: Circle the answer that best evaluates the statement or completes the statement.
 Name: PHYS 110 Dr. McGoern Sprng 018 Exam 1 Multple Choce: Crcle the answer that best ealuates the statement or completes the statement. #1 - I the acceleraton o an object s negate, the object must be
Name: PHYS 110 Dr. McGoern Sprng 018 Exam 1 Multple Choce: Crcle the answer that best ealuates the statement or completes the statement. #1 - I the acceleraton o an object s negate, the object must be
Force = F Piston area = A
 CHAPTER III Ths chapter s an mportant transton between the propertes o pure substances and the most mportant chapter whch s: the rst law o thermodynamcs In ths chapter, we wll ntroduce the notons o heat,
CHAPTER III Ths chapter s an mportant transton between the propertes o pure substances and the most mportant chapter whch s: the rst law o thermodynamcs In ths chapter, we wll ntroduce the notons o heat,
Physics 101 Lecture 9 Linear Momentum and Collisions
 Physcs 0 Lecture 9 Lnear Momentum and Collsons Dr. Al ÖVGÜN EMU Physcs Department www.aogun.com Lnear Momentum and Collsons q q q q q q q Conseraton o Energy Momentum Impulse Conseraton o Momentum -D Collsons
Physcs 0 Lecture 9 Lnear Momentum and Collsons Dr. Al ÖVGÜN EMU Physcs Department www.aogun.com Lnear Momentum and Collsons q q q q q q q Conseraton o Energy Momentum Impulse Conseraton o Momentum -D Collsons
Period & Frequency. Work and Energy. Methods of Energy Transfer: Energy. Work-KE Theorem 3/4/16. Ranking: Which has the greatest kinetic energy?
 Perod & Frequency Perod (T): Tme to complete one ull rotaton Frequency (): Number o rotatons completed per second. = 1/T, T = 1/ v = πr/t Work and Energy Work: W = F!d (pcks out parallel components) F
Perod & Frequency Perod (T): Tme to complete one ull rotaton Frequency (): Number o rotatons completed per second. = 1/T, T = 1/ v = πr/t Work and Energy Work: W = F!d (pcks out parallel components) F
CHAPTER 8 Potential Energy and Conservation of Energy
 CHAPTER 8 Potental Energy and Conservaton o Energy One orm o energy can be converted nto another orm o energy. Conservatve and non-conservatve orces Physcs 1 Knetc energy: Potental energy: Energy assocated
CHAPTER 8 Potental Energy and Conservaton o Energy One orm o energy can be converted nto another orm o energy. Conservatve and non-conservatve orces Physcs 1 Knetc energy: Potental energy: Energy assocated
Chapter 07: Kinetic Energy and Work
 Chapter 07: Knetc Energy and Work Conservaton o Energy s one o Nature s undamental laws that s not volated. Energy can take on derent orms n a gven system. Ths chapter we wll dscuss work and knetc energy.
Chapter 07: Knetc Energy and Work Conservaton o Energy s one o Nature s undamental laws that s not volated. Energy can take on derent orms n a gven system. Ths chapter we wll dscuss work and knetc energy.
Problem While being compressed, A) What is the work done on it by gravity? B) What is the work done on it by the spring force?
 Problem 07-50 A 0.25 kg block s dropped on a relaed sprng that has a sprng constant o k 250.0 N/m (2.5 N/cm). The block becomes attached to the sprng and compresses t 0.12 m beore momentarl stoppng. Whle
Problem 07-50 A 0.25 kg block s dropped on a relaed sprng that has a sprng constant o k 250.0 N/m (2.5 N/cm). The block becomes attached to the sprng and compresses t 0.12 m beore momentarl stoppng. Whle
GAUTENG DEPARTMENT OF EDUCATION SENIOR SECONDARY INTERVENTION PROGRAMME PHYSICAL SCIENCES GRADE 12 SESSION 1 (LEARNER NOTES)
 PHYSICAL SCIENCES GRADE 1 SESSION 1 (LEARNER NOTES) TOPIC 1: MECHANICS PROJECTILE MOTION Learner Note: Always draw a dagram of the stuaton and enter all the numercal alues onto your dagram. Remember to
PHYSICAL SCIENCES GRADE 1 SESSION 1 (LEARNER NOTES) TOPIC 1: MECHANICS PROJECTILE MOTION Learner Note: Always draw a dagram of the stuaton and enter all the numercal alues onto your dagram. Remember to
Physics 2A Chapter 3 HW Solutions
 Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
EMU Physics Department.
 Physcs 0 Lecture 9 Lnear Momentum and Collsons Assst. Pro. Dr. Al ÖVGÜN EMU Physcs Department www.aogun.com Lnear Momentum q Conseraton o Energy q Momentum q Impulse q Conseraton o Momentum q -D Collsons
Physcs 0 Lecture 9 Lnear Momentum and Collsons Assst. Pro. Dr. Al ÖVGÜN EMU Physcs Department www.aogun.com Lnear Momentum q Conseraton o Energy q Momentum q Impulse q Conseraton o Momentum q -D Collsons
Physics 2A Chapters 6 - Work & Energy Fall 2017
 Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
Physcs A Chapters 6 - Work & Energy Fall 017 These notes are eght pages. A quck summary: The work-energy theorem s a combnaton o Chap and Chap 4 equatons. Work s dened as the product o the orce actng on
Energy and Energy Transfer
 Energy and Energy Transer Chapter 7 Scalar Product (Dot) Work Done by a Constant Force F s constant over the dsplacement r 1 Denton o the scalar (dot) product o vectors Scalar product o unt vectors = 1
Energy and Energy Transer Chapter 7 Scalar Product (Dot) Work Done by a Constant Force F s constant over the dsplacement r 1 Denton o the scalar (dot) product o vectors Scalar product o unt vectors = 1
Motion in One Dimension
 Moton n One Dmenson Speed ds tan ce traeled Aerage Speed tme of trael Mr. Wolf dres hs car on a long trp to a physcs store. Gen the dstance and tme data for hs trp, plot a graph of hs dstance ersus tme.
Moton n One Dmenson Speed ds tan ce traeled Aerage Speed tme of trael Mr. Wolf dres hs car on a long trp to a physcs store. Gen the dstance and tme data for hs trp, plot a graph of hs dstance ersus tme.
Physics for Scientists and Engineers. Chapter 9 Impulse and Momentum
 Physcs or Scentsts and Engneers Chapter 9 Impulse and Momentum Sprng, 008 Ho Jung Pak Lnear Momentum Lnear momentum o an object o mass m movng wth a velocty v s dened to be p mv Momentum and lnear momentum
Physcs or Scentsts and Engneers Chapter 9 Impulse and Momentum Sprng, 008 Ho Jung Pak Lnear Momentum Lnear momentum o an object o mass m movng wth a velocty v s dened to be p mv Momentum and lnear momentum
Prof. Dr. I. Nasser T /16/2017
 Pro. Dr. I. Nasser T-171 10/16/017 Chapter Part 1 Moton n one dmenson Sectons -,, 3, 4, 5 - Moton n 1 dmenson We le n a 3-dmensonal world, so why bother analyzng 1-dmensonal stuatons? Bascally, because
Pro. Dr. I. Nasser T-171 10/16/017 Chapter Part 1 Moton n one dmenson Sectons -,, 3, 4, 5 - Moton n 1 dmenson We le n a 3-dmensonal world, so why bother analyzng 1-dmensonal stuatons? Bascally, because
A Tale of Friction Basic Rollercoaster Physics. Fahrenheit Rollercoaster, Hershey, PA max height = 121 ft max speed = 58 mph
 A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
total If no external forces act, the total linear momentum of the system is conserved. This occurs in collisions and explosions.
 Lesson 0: Collsons, Rotatonal netc Energy, Torque, Center o Graty (Sectons 7.8 Last te we used ewton s second law to deelop the pulse-oentu theore. In words, the theore states that the change n lnear oentu
Lesson 0: Collsons, Rotatonal netc Energy, Torque, Center o Graty (Sectons 7.8 Last te we used ewton s second law to deelop the pulse-oentu theore. In words, the theore states that the change n lnear oentu
Chapter 9 Linear Momentum and Collisions
 Chapter 9 Lnear Momentum and Collsons m = 3. kg r = ( ˆ ˆ j ) P9., r r (a) p m ( ˆ ˆj ) 3. 4. m s = = 9.. kg m s Thus, p x = 9. kg m s and p y =. kg m s (b) p px p y p y θ = tan = tan (.33) = 37 px = +
Chapter 9 Lnear Momentum and Collsons m = 3. kg r = ( ˆ ˆ j ) P9., r r (a) p m ( ˆ ˆj ) 3. 4. m s = = 9.. kg m s Thus, p x = 9. kg m s and p y =. kg m s (b) p px p y p y θ = tan = tan (.33) = 37 px = +
Chapter 5. Answers to Even Numbered Problems m kj. 6. (a) 900 J (b) (a) 31.9 J (b) 0 (c) 0 (d) 31.9 J. 10.
 Answers to Even Numbered Problems Chapter 5. 3.6 m 4..6 J 6. (a) 9 J (b).383 8. (a) 3.9 J (b) (c) (d) 3.9 J. 6 m s. (a) 68 J (b) 84 J (c) 5 J (d) 48 J (e) 5.64 m s 4. 9. J 6. (a). J (b) 5. m s (c) 6.3
Answers to Even Numbered Problems Chapter 5. 3.6 m 4..6 J 6. (a) 9 J (b).383 8. (a) 3.9 J (b) (c) (d) 3.9 J. 6 m s. (a) 68 J (b) 84 J (c) 5 J (d) 48 J (e) 5.64 m s 4. 9. J 6. (a). J (b) 5. m s (c) 6.3
How does the momentum before an elastic and an inelastic collision compare to the momentum after the collision?
 Experent 9 Conseraton o Lnear Moentu - Collsons In ths experent you wll be ntroduced to the denton o lnear oentu. You wll learn the derence between an elastc and an nelastc collson. You wll explore how
Experent 9 Conseraton o Lnear Moentu - Collsons In ths experent you wll be ntroduced to the denton o lnear oentu. You wll learn the derence between an elastc and an nelastc collson. You wll explore how
Lecture 16. Chapter 11. Energy Dissipation Linear Momentum. Physics I. Department of Physics and Applied Physics
 Lecture 16 Chapter 11 Physcs I Energy Dsspaton Lnear Momentum Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi Department o Physcs and Appled Physcs IN IN THIS CHAPTER, you wll learn
Lecture 16 Chapter 11 Physcs I Energy Dsspaton Lnear Momentum Course webste: http://aculty.uml.edu/andry_danylov/teachng/physcsi Department o Physcs and Appled Physcs IN IN THIS CHAPTER, you wll learn
Physics 106 Lecture 6 Conservation of Angular Momentum SJ 7 th Ed.: Chap 11.4
 Physcs 6 ecture 6 Conservaton o Angular Momentum SJ 7 th Ed.: Chap.4 Comparson: dentons o sngle partcle torque and angular momentum Angular momentum o a system o partcles o a rgd body rotatng about a xed
Physcs 6 ecture 6 Conservaton o Angular Momentum SJ 7 th Ed.: Chap.4 Comparson: dentons o sngle partcle torque and angular momentum Angular momentum o a system o partcles o a rgd body rotatng about a xed
K = 100 J. [kg (m/s) ] K = mv = (0.15)(36.5) !!! Lethal energies. m [kg ] J s (Joule) Kinetic Energy (energy of motion) E or KE.
![K = 100 J. [kg (m/s) ] K = mv = (0.15)(36.5) !!! Lethal energies. m [kg ] J s (Joule) Kinetic Energy (energy of motion) E or KE. K = 100 J. [kg (m/s) ] K = mv = (0.15)(36.5) !!! Lethal energies. m [kg ] J s (Joule) Kinetic Energy (energy of motion) E or KE.](/thumbs/80/81648220.jpg) Knetc Energy (energy of moton) E or KE K = m v = m(v + v y + v z ) eample baseball m=0.5 kg ptche at v = 69 mph = 36.5 m/s K = mv = (0.5)(36.5) [kg (m/s) ] Unts m [kg ] J s (Joule) v = 69 mph K = 00 J
Knetc Energy (energy of moton) E or KE K = m v = m(v + v y + v z ) eample baseball m=0.5 kg ptche at v = 69 mph = 36.5 m/s K = mv = (0.5)(36.5) [kg (m/s) ] Unts m [kg ] J s (Joule) v = 69 mph K = 00 J
Conservation of Energy
 Chapter 8 Conseraton o Ener 8.3 U + K = U + K mh + = m ( ) + m ( 3.5 ) = ( ) + F= m = 3. n+ m= m 3. n = m = m =.m 3 n =. 5. 9.8 m s =.98 N downward FIG. 8.3 (5. 3.) Δ A B 8.4 (a) K = W = W = m Δ h = m
Chapter 8 Conseraton o Ener 8.3 U + K = U + K mh + = m ( ) + m ( 3.5 ) = ( ) + F= m = 3. n+ m= m 3. n = m = m =.m 3 n =. 5. 9.8 m s =.98 N downward FIG. 8.3 (5. 3.) Δ A B 8.4 (a) K = W = W = m Δ h = m
Chapter 7. Potential Energy and Conservation of Energy
 Chapter 7 Potental Energy and Conservaton o Energy 1 Forms o Energy There are many orms o energy, but they can all be put nto two categores Knetc Knetc energy s energy o moton Potental Potental energy
Chapter 7 Potental Energy and Conservaton o Energy 1 Forms o Energy There are many orms o energy, but they can all be put nto two categores Knetc Knetc energy s energy o moton Potental Potental energy
Modeling motion with VPython Every program that models the motion of physical objects has two main parts:
 1 Modelng moton wth VPython Eery program that models the moton o physcal objects has two man parts: 1. Beore the loop: The rst part o the program tells the computer to: a. Create numercal alues or constants
1 Modelng moton wth VPython Eery program that models the moton o physcal objects has two man parts: 1. Beore the loop: The rst part o the program tells the computer to: a. Create numercal alues or constants
Linear Momentum. Equation 1
 Lnear Momentum OBJECTIVE Obsere collsons between two carts, testng or the conseraton o momentum. Measure energy changes durng derent types o collsons. Classy collsons as elastc, nelastc, or completely
Lnear Momentum OBJECTIVE Obsere collsons between two carts, testng or the conseraton o momentum. Measure energy changes durng derent types o collsons. Classy collsons as elastc, nelastc, or completely
Study Guide For Exam Two
 Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
PHYSICS 203-NYA-05 MECHANICS
 PHYSICS 03-NYA-05 MECHANICS PROF. S.D. MANOLI PHYSICS & CHEMISTRY CHAMPLAIN - ST. LAWRENCE 790 NÉRÉE-TREMBLAY QUÉBEC, QC GV 4K TELEPHONE: 48.656.69 EXT. 449 EMAIL: smanol@slc.qc.ca WEBPAGE: http:/web.slc.qc.ca/smanol/
PHYSICS 03-NYA-05 MECHANICS PROF. S.D. MANOLI PHYSICS & CHEMISTRY CHAMPLAIN - ST. LAWRENCE 790 NÉRÉE-TREMBLAY QUÉBEC, QC GV 4K TELEPHONE: 48.656.69 EXT. 449 EMAIL: smanol@slc.qc.ca WEBPAGE: http:/web.slc.qc.ca/smanol/
Chapter 8. Momentum Impulse and Collisions. Analysis of motion: 2 key ideas. Newton s laws of motion. Conservation of Energy
 Chapter 8 Moentu Ipulse and Collsons Analyss o oton: key deas Newton s laws o oton Conseraton o Energy Newton s Laws st Law: An object at rest or traelng n unor oton wll rean at rest or traelng n unor
Chapter 8 Moentu Ipulse and Collsons Analyss o oton: key deas Newton s laws o oton Conseraton o Energy Newton s Laws st Law: An object at rest or traelng n unor oton wll rean at rest or traelng n unor
Slide. King Saud University College of Science Physics & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART 2) LECTURE NO.
 Slde Kng Saud Unersty College of Scence Physcs & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART ) LECTURE NO. 6 THIS PRESENTATION HAS BEEN PREPARED BY: DR. NASSR S. ALZAYED Lecture
Slde Kng Saud Unersty College of Scence Physcs & Astronomy Dept. PHYS 103 (GENERAL PHYSICS) CHAPTER 5: MOTION IN 1-D (PART ) LECTURE NO. 6 THIS PRESENTATION HAS BEEN PREPARED BY: DR. NASSR S. ALZAYED Lecture
Momentum and Collisions. Rosendo Physics 12-B
 Moentu and Collsons Rosendo Physcs -B Conseraton o Energy Moentu Ipulse Conseraton o Moentu -D Collsons -D Collsons The Center o Mass Lnear Moentu and Collsons February 7, 08 Conseraton o Energy D E =
Moentu and Collsons Rosendo Physcs -B Conseraton o Energy Moentu Ipulse Conseraton o Moentu -D Collsons -D Collsons The Center o Mass Lnear Moentu and Collsons February 7, 08 Conseraton o Energy D E =
First Law: A body at rest remains at rest, a body in motion continues to move at constant velocity, unless acted upon by an external force.
 Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Dynamics of Rotational Motion
 Dynamcs of Rotatonal Moton Torque: the rotatonal analogue of force Torque = force x moment arm = Fl moment arm = perpendcular dstance through whch the force acts a.k.a. leer arm l F l F l F l F = Fl =
Dynamcs of Rotatonal Moton Torque: the rotatonal analogue of force Torque = force x moment arm = Fl moment arm = perpendcular dstance through whch the force acts a.k.a. leer arm l F l F l F l F = Fl =
Week 11: Chapter 11. The Vector Product. The Vector Product Defined. The Vector Product and Torque. More About the Vector Product
 The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
Angular momentum. Instructor: Dr. Hoi Lam TAM ( 譚海嵐 )
 Angular momentum Instructor: Dr. Ho Lam TAM ( 譚海嵐 ) Physcs Enhancement Programme or Gted Students The Hong Kong Academy or Gted Educaton and Department o Physcs, HKBU Department o Physcs Hong Kong Baptst
Angular momentum Instructor: Dr. Ho Lam TAM ( 譚海嵐 ) Physcs Enhancement Programme or Gted Students The Hong Kong Academy or Gted Educaton and Department o Physcs, HKBU Department o Physcs Hong Kong Baptst
Lecture 09 Systems of Particles and Conservation of Linear Momentum
 Lecture 09 Systes o Partcles and Conseraton o Lnear oentu 9. Lnear oentu and Its Conseraton 9. Isolated Syste lnear oentu: P F dp dt d( dt d dt a solated syste F ext 0 dp dp F, F dt dt dp dp d F F 0, 0
Lecture 09 Systes o Partcles and Conseraton o Lnear oentu 9. Lnear oentu and Its Conseraton 9. Isolated Syste lnear oentu: P F dp dt d( dt d dt a solated syste F ext 0 dp dp F, F dt dt dp dp d F F 0, 0
Use these variables to select a formula. x = t Average speed = 100 m/s = distance / time t = x/v = ~2 m / 100 m/s = 0.02 s or 20 milliseconds
 The speed o a nere mpulse n the human body s about 100 m/s. I you accdentally stub your toe n the dark, estmatethe tme t takes the nere mpulse to trael to your bran. Tps: pcture, poste drecton, and lst
The speed o a nere mpulse n the human body s about 100 m/s. I you accdentally stub your toe n the dark, estmatethe tme t takes the nere mpulse to trael to your bran. Tps: pcture, poste drecton, and lst
Physics 207 Lecture 13. Lecture 13
 Physcs 07 Lecture 3 Goals: Lecture 3 Chapter 0 Understand the relatonshp between moton and energy Defne Potental Energy n a Hooke s Law sprng Develop and explot conservaton of energy prncple n problem
Physcs 07 Lecture 3 Goals: Lecture 3 Chapter 0 Understand the relatonshp between moton and energy Defne Potental Energy n a Hooke s Law sprng Develop and explot conservaton of energy prncple n problem
Chapter 8. Potential Energy and Conservation of Energy
 Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
Chapter 8 Potental Energy and Conservaton of Energy In ths chapter we wll ntroduce the followng concepts: Potental Energy Conservatve and non-conservatve forces Mechancal Energy Conservaton of Mechancal
p p +... = p j + p Conservation Laws in Physics q Physical states, process, and state quantities: Physics 201, Lecture 14 Today s Topics
 Physcs 0, Lecture 4 Conseraton Laws n Physcs q Physcal states, process, and state quanttes: Today s Topcs Partcle Syste n state Process Partcle Syste n state q Lnear Moentu And Collsons (Chapter 9.-9.4)
Physcs 0, Lecture 4 Conseraton Laws n Physcs q Physcal states, process, and state quanttes: Today s Topcs Partcle Syste n state Process Partcle Syste n state q Lnear Moentu And Collsons (Chapter 9.-9.4)
10/24/2013. PHY 113 C General Physics I 11 AM 12:15 PM TR Olin 101. Plan for Lecture 17: Review of Chapters 9-13, 15-16
 0/4/03 PHY 3 C General Physcs I AM :5 PM T Oln 0 Plan or Lecture 7: evew o Chapters 9-3, 5-6. Comment on exam and advce or preparaton. evew 3. Example problems 0/4/03 PHY 3 C Fall 03 -- Lecture 7 0/4/03
0/4/03 PHY 3 C General Physcs I AM :5 PM T Oln 0 Plan or Lecture 7: evew o Chapters 9-3, 5-6. Comment on exam and advce or preparaton. evew 3. Example problems 0/4/03 PHY 3 C Fall 03 -- Lecture 7 0/4/03
v c motion is neither created nor destroyed, but transferred via interactions. Fri. Wed (.18,.19) Introducing Potential Energy RE 6.
 r. 6.5-.7 (.) Rest Mass,ork by Changng orces Columba Rep 3pm, here RE 6.b (last day to drop) ed. 6.8-.9(.8,.9) Introducng Potental Energy RE 6.c Tues. H6: Ch 6 Pr s 58,59, 99(a-c), 05(a-c) moton s nether
r. 6.5-.7 (.) Rest Mass,ork by Changng orces Columba Rep 3pm, here RE 6.b (last day to drop) ed. 6.8-.9(.8,.9) Introducng Potental Energy RE 6.c Tues. H6: Ch 6 Pr s 58,59, 99(a-c), 05(a-c) moton s nether
Physics for Scientists and Engineers. Chapter 10 Energy
 Physcs or Scentsts and Engneers Chapter 0 Energy Sprng, 008 Ho Jung Pak Introducton to Energy Energy s one o the ost portant concepts n scence although t s not easly dened Eery physcal process that occurs
Physcs or Scentsts and Engneers Chapter 0 Energy Sprng, 008 Ho Jung Pak Introducton to Energy Energy s one o the ost portant concepts n scence although t s not easly dened Eery physcal process that occurs
Chapter 7: Conservation of Energy
 Lecture 7: Conservaton o nergy Chapter 7: Conservaton o nergy Introucton I the quantty o a subject oes not change wth tme, t means that the quantty s conserve. The quantty o that subject remans constant
Lecture 7: Conservaton o nergy Chapter 7: Conservaton o nergy Introucton I the quantty o a subject oes not change wth tme, t means that the quantty s conserve. The quantty o that subject remans constant
Physics 207 Lecture 6
 Physcs 207 Lecture 6 Agenda: Physcs 207, Lecture 6, Sept. 25 Chapter 4 Frames of reference Chapter 5 ewton s Law Mass Inerta s (contact and non-contact) Frcton (a external force that opposes moton) Free
Physcs 207 Lecture 6 Agenda: Physcs 207, Lecture 6, Sept. 25 Chapter 4 Frames of reference Chapter 5 ewton s Law Mass Inerta s (contact and non-contact) Frcton (a external force that opposes moton) Free
Linear Momentum and Collisions
 Lnear Momentum and Collsons Chater 9 Lnear Momentum [kg m/s] x y mv x mv y Newton s nd Law n terms o momentum: Imulse I - [kg m/s] I t t Fdt I = area under curve bounded by t axs Imulse-Momentum Theorem
Lnear Momentum and Collsons Chater 9 Lnear Momentum [kg m/s] x y mv x mv y Newton s nd Law n terms o momentum: Imulse I - [kg m/s] I t t Fdt I = area under curve bounded by t axs Imulse-Momentum Theorem
Work is the change in energy of a system (neglecting heat transfer). To examine what could
 Work Work s the change n energy o a system (neglectng heat transer). To eamne what could cause work, let s look at the dmensons o energy: L ML E M L F L so T T dmensonally energy s equal to a orce tmes
Work Work s the change n energy o a system (neglectng heat transer). To eamne what could cause work, let s look at the dmensons o energy: L ML E M L F L so T T dmensonally energy s equal to a orce tmes
2.00 kg 4.00 kg 3.00 kg m. y com. (2.00 kg)(0.500 m) 4.00 kg m 3.00 kg m m m kg 4.00 kg 3.00 kg m.
 Chapter 9. We use Eq. 9-5 to sole or ( x, y ). (a) The x coordnate o the system s center o mass s: x com x m x m (.00 kg)(.0 m) 4.00 kg 0.600 m.00 kg x mx m m m.00 kg 4.00 kg.00 kg 0.500 m. Solng the equaton
Chapter 9. We use Eq. 9-5 to sole or ( x, y ). (a) The x coordnate o the system s center o mass s: x com x m x m (.00 kg)(.0 m) 4.00 kg 0.600 m.00 kg x mx m m m.00 kg 4.00 kg.00 kg 0.500 m. Solng the equaton
From Newton s 2 nd Law: v v. The time rate of change of the linear momentum of a particle is equal to the net force acting on the particle.
 From Newton s 2 nd Law: F ma d dm ( ) m dt dt F d dt The tme rate of change of the lnear momentum of a artcle s equal to the net force actng on the artcle. Conseraton of Momentum +x The toy rocket n dee
From Newton s 2 nd Law: F ma d dm ( ) m dt dt F d dt The tme rate of change of the lnear momentum of a artcle s equal to the net force actng on the artcle. Conseraton of Momentum +x The toy rocket n dee
Conservation of Energy
 Conservaton o nergy The total energy o a system can change only by amounts o energy that are transerred nto or out o the system W mec th nt Ths s one o the great conservaton laws n nature! Other conservaton
Conservaton o nergy The total energy o a system can change only by amounts o energy that are transerred nto or out o the system W mec th nt Ths s one o the great conservaton laws n nature! Other conservaton
WYSE Academic Challenge 2004 State Finals Physics Solution Set
 WYSE Acaemc Challenge 00 State nals Physcs Soluton Set. Answer: c. Ths s the enton o the quantty acceleraton.. Answer: b. Pressure s orce per area. J/m N m/m N/m, unts o orce per area.. Answer: e. Aerage
WYSE Acaemc Challenge 00 State nals Physcs Soluton Set. Answer: c. Ths s the enton o the quantty acceleraton.. Answer: b. Pressure s orce per area. J/m N m/m N/m, unts o orce per area.. Answer: e. Aerage
a) No books or notes are permitted. b) You may use a calculator.
 PHYS 050 Sprng 06 Name: Test 3 Aprl 7, 06 INSTRUCTIONS: a) No books or notes are permtted. b) You may use a calculator. c) You must solve all problems begnnng wth the equatons on the Inormaton Sheet provded
PHYS 050 Sprng 06 Name: Test 3 Aprl 7, 06 INSTRUCTIONS: a) No books or notes are permtted. b) You may use a calculator. c) You must solve all problems begnnng wth the equatons on the Inormaton Sheet provded
in state i at t i, Initial State E = E i
 Physcs 01, Lecture 1 Today s Topcs n More Energy and Work (chapters 7 & 8) n Conservatve Work and Potental Energy n Sprng Force and Sprng (Elastc) Potental Energy n Conservaton of Mechanc Energy n Exercse
Physcs 01, Lecture 1 Today s Topcs n More Energy and Work (chapters 7 & 8) n Conservatve Work and Potental Energy n Sprng Force and Sprng (Elastc) Potental Energy n Conservaton of Mechanc Energy n Exercse
Week 6, Chapter 7 Sect 1-5
 Week 6, Chapter 7 Sect 1-5 Work and Knetc Energy Lecture Quz The frctonal force of the floor on a large sutcase s least when the sutcase s A.pushed by a force parallel to the floor. B.dragged by a force
Week 6, Chapter 7 Sect 1-5 Work and Knetc Energy Lecture Quz The frctonal force of the floor on a large sutcase s least when the sutcase s A.pushed by a force parallel to the floor. B.dragged by a force
Rotational and Translational Comparison. Conservation of Angular Momentum. Angular Momentum for a System of Particles
 Conservaton o Angular Momentum 8.0 WD Rotatonal and Translatonal Comparson Quantty Momentum Ang Momentum Force Torque Knetc Energy Work Power Rotaton L cm = I cm ω = dl / cm cm K = (/ ) rot P rot θ W =
Conservaton o Angular Momentum 8.0 WD Rotatonal and Translatonal Comparson Quantty Momentum Ang Momentum Force Torque Knetc Energy Work Power Rotaton L cm = I cm ω = dl / cm cm K = (/ ) rot P rot θ W =
Physics 2A Chapter 9 HW Solutions
 Phscs A Chapter 9 HW Solutons Chapter 9 Conceptual Queston:, 4, 8, 13 Problems: 3, 8, 1, 15, 3, 40, 51, 6 Q9.. Reason: We can nd the change n momentum o the objects b computng the mpulse on them and usng
Phscs A Chapter 9 HW Solutons Chapter 9 Conceptual Queston:, 4, 8, 13 Problems: 3, 8, 1, 15, 3, 40, 51, 6 Q9.. Reason: We can nd the change n momentum o the objects b computng the mpulse on them and usng
PHYS 1101 Practice problem set 12, Chapter 32: 21, 22, 24, 57, 61, 83 Chapter 33: 7, 12, 32, 38, 44, 49, 76
 PHYS 1101 Practce problem set 1, Chapter 3: 1,, 4, 57, 61, 83 Chapter 33: 7, 1, 3, 38, 44, 49, 76 3.1. Vsualze: Please reer to Fgure Ex3.1. Solve: Because B s n the same drecton as the ntegraton path s
PHYS 1101 Practce problem set 1, Chapter 3: 1,, 4, 57, 61, 83 Chapter 33: 7, 1, 3, 38, 44, 49, 76 3.1. Vsualze: Please reer to Fgure Ex3.1. Solve: Because B s n the same drecton as the ntegraton path s
ONE-DIMENSIONAL COLLISIONS
 Purpose Theory ONE-DIMENSIONAL COLLISIONS a. To very the law o conservaton o lnear momentum n one-dmensonal collsons. b. To study conservaton o energy and lnear momentum n both elastc and nelastc onedmensonal
Purpose Theory ONE-DIMENSIONAL COLLISIONS a. To very the law o conservaton o lnear momentum n one-dmensonal collsons. b. To study conservaton o energy and lnear momentum n both elastc and nelastc onedmensonal
Physics 4C. Chapter 19: Conceptual Questions: 6, 8, 10 Problems: 3, 13, 24, 31, 35, 48, 53, 63, 65, 78, 87
 Physcs 4C Solutons to Chater 9 HW Chater 9: Concetual Questons: 6, 8, 0 Problems:,, 4,,, 48,, 6, 6, 78, 87 Queston 9-6 (a) 0 (b) 0 (c) negate (d) oste Queston 9-8 (a) 0 (b) 0 (c) negate (d) oste Queston
Physcs 4C Solutons to Chater 9 HW Chater 9: Concetual Questons: 6, 8, 0 Problems:,, 4,,, 48,, 6, 6, 78, 87 Queston 9-6 (a) 0 (b) 0 (c) negate (d) oste Queston 9-8 (a) 0 (b) 0 (c) negate (d) oste Queston
Physics 111: Mechanics Lecture 11
 Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Page 1. SPH4U: Lecture 7. New Topic: Friction. Today s Agenda. Surface Friction... Surface Friction...
 SPH4U: Lecture 7 Today s Agenda rcton What s t? Systeatc catagores of forces How do we characterze t? Model of frcton Statc & Knetc frcton (knetc = dynac n soe languages) Soe probles nvolvng frcton ew
SPH4U: Lecture 7 Today s Agenda rcton What s t? Systeatc catagores of forces How do we characterze t? Model of frcton Statc & Knetc frcton (knetc = dynac n soe languages) Soe probles nvolvng frcton ew
Physic 231 Lecture 14
 Physc 3 Lecture 4 Man ponts o last lecture: Ipulses: orces that last only a short te Moentu p Ipulse-Moentu theore F t p ( ) Ipulse-Moentu theore ptot, p, p, p, p, ptot, Moentu and external orces F p ext
Physc 3 Lecture 4 Man ponts o last lecture: Ipulses: orces that last only a short te Moentu p Ipulse-Moentu theore F t p ( ) Ipulse-Moentu theore ptot, p, p, p, p, ptot, Moentu and external orces F p ext
Recitation: Energy, Phys Energies. 1.2 Three stones. 1. Energy. 1. An acorn falling from an oak tree onto the sidewalk.
 Rectaton: Energy, Phys 207. Energy. Energes. An acorn fallng from an oak tree onto the sdewalk. The acorn ntal has gravtatonal potental energy. As t falls, t converts ths energy to knetc. When t hts the
Rectaton: Energy, Phys 207. Energy. Energes. An acorn fallng from an oak tree onto the sdewalk. The acorn ntal has gravtatonal potental energy. As t falls, t converts ths energy to knetc. When t hts the
KIRCHHOFF CURRENT LAW
 KRCHHOFF CURRENT LAW ONE OF THE FUNDAMENTAL CONSERATON PRNCPLES N ELECTRCAL ENGNEERNG CHARGE CANNOT BE CREATED NOR DESTROYED NODES, BRANCHES, LOOPS A NODE CONNECTS SEERAL COMPONENTS. BUT T DOES NOT HOLD
KRCHHOFF CURRENT LAW ONE OF THE FUNDAMENTAL CONSERATON PRNCPLES N ELECTRCAL ENGNEERNG CHARGE CANNOT BE CREATED NOR DESTROYED NODES, BRANCHES, LOOPS A NODE CONNECTS SEERAL COMPONENTS. BUT T DOES NOT HOLD
OPTIMISATION. Introduction Single Variable Unconstrained Optimisation Multivariable Unconstrained Optimisation Linear Programming
 OPTIMIATION Introducton ngle Varable Unconstraned Optmsaton Multvarable Unconstraned Optmsaton Lnear Programmng Chapter Optmsaton /. Introducton In an engneerng analss, sometmes etremtes, ether mnmum or
OPTIMIATION Introducton ngle Varable Unconstraned Optmsaton Multvarable Unconstraned Optmsaton Lnear Programmng Chapter Optmsaton /. Introducton In an engneerng analss, sometmes etremtes, ether mnmum or
Physics 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn in the following problems from Chapter 4 Knight
 Physcs 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn n the ollowng problems rom Chapter 4 Knght Conceptual Questons: 8, 0, ; 4.8. Anta s approachng ball and movng away rom where ball was
Physcs 40 HW #4 Chapter 4 Key NEATNESS COUNTS! Solve but do not turn n the ollowng problems rom Chapter 4 Knght Conceptual Questons: 8, 0, ; 4.8. Anta s approachng ball and movng away rom where ball was
Physics 141. Lecture 14. Frank L. H. Wolfs Department of Physics and Astronomy, University of Rochester, Lecture 14, Page 1
 Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
9/19/2013. PHY 113 C General Physics I 11 AM-12:15 PM MWF Olin 101
 PHY 3 C General Physcs I AM-:5 PM MF Oln 0 Plan or Lecture 8: Chapter 8 -- Conservaton o energy. Potental and knetc energy or conservatve orces. Energy and non-conservatve orces 3. Power PHY 3 C Fall 03--
PHY 3 C General Physcs I AM-:5 PM MF Oln 0 Plan or Lecture 8: Chapter 8 -- Conservaton o energy. Potental and knetc energy or conservatve orces. Energy and non-conservatve orces 3. Power PHY 3 C Fall 03--
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
Rotational Dynamics. Physics 1425 Lecture 19. Michael Fowler, UVa
 Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
EN40: Dynamics and Vibrations. Homework 4: Work, Energy and Linear Momentum Due Friday March 1 st
 EN40: Dynamcs and bratons Homework 4: Work, Energy and Lnear Momentum Due Frday March 1 st School of Engneerng Brown Unversty 1. The fgure (from ths publcaton) shows the energy per unt area requred to
EN40: Dynamcs and bratons Homework 4: Work, Energy and Lnear Momentum Due Frday March 1 st School of Engneerng Brown Unversty 1. The fgure (from ths publcaton) shows the energy per unt area requred to
Week 8: Chapter 9. Linear Momentum. Newton Law and Momentum. Linear Momentum, cont. Conservation of Linear Momentum. Conservation of Momentum, 2
 Lnear omentum Week 8: Chapter 9 Lnear omentum and Collsons The lnear momentum of a partcle, or an object that can be modeled as a partcle, of mass m movng wth a velocty v s defned to be the product of
Lnear omentum Week 8: Chapter 9 Lnear omentum and Collsons The lnear momentum of a partcle, or an object that can be modeled as a partcle, of mass m movng wth a velocty v s defned to be the product of
Lecture 22: Potential Energy
 Lecture : Potental Energy We have already studed the work-energy theorem, whch relates the total work done on an object to the change n knetc energy: Wtot = KE For a conservatve orce, the work done by
Lecture : Potental Energy We have already studed the work-energy theorem, whch relates the total work done on an object to the change n knetc energy: Wtot = KE For a conservatve orce, the work done by
Physics 53. Rotational Motion 3. Sir, I have found you an argument, but I am not obliged to find you an understanding.
 Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Collisions! Short, Sharp Shocks
 d b n, b d,, -4 Introducng Collsons Quz 9 L9 Mult-artcle Systes 6-8 Scatterng 9- Collson Colcatons L Collsons 5, Derent Reerence Fraes ranslatonal ngular Moentu Quz RE a RE b RE c EP9 RE a; HW: Pr s 3*,,
d b n, b d,, -4 Introducng Collsons Quz 9 L9 Mult-artcle Systes 6-8 Scatterng 9- Collson Colcatons L Collsons 5, Derent Reerence Fraes ranslatonal ngular Moentu Quz RE a RE b RE c EP9 RE a; HW: Pr s 3*,,
5/24/2007 Collisions ( F.Robilliard) 1
 5/4/007 Collsons ( F.Robllard) 1 Interactons: In our earler studes o orce and work, we saw, that both these quanttes arse n the context o an nteracton between two bodes. We wll now look ore closely at
5/4/007 Collsons ( F.Robllard) 1 Interactons: In our earler studes o orce and work, we saw, that both these quanttes arse n the context o an nteracton between two bodes. We wll now look ore closely at
86 Chapter 7 Energy 7-11 POWER. Answers to the Conceptual Questions
 86 Chater 7 Energy nented to make eerythng alrght. We eel t s mortant to show that the nenton o other orms o energy s not whmscal or a arce. A newly nented orm o energy would be alse the new orm was not
86 Chater 7 Energy nented to make eerythng alrght. We eel t s mortant to show that the nenton o other orms o energy s not whmscal or a arce. A newly nented orm o energy would be alse the new orm was not
Lecture 5: Operational Amplifiers and Op Amp Circuits
 Lecture 5: peratonal mplers and p mp Crcuts Gu-Yeon We Dson o Engneerng and ppled Scences Harard Unersty guyeon@eecs.harard.edu We erew eadng S&S: Chapter Supplemental eadng Background rmed wth our crcut
Lecture 5: peratonal mplers and p mp Crcuts Gu-Yeon We Dson o Engneerng and ppled Scences Harard Unersty guyeon@eecs.harard.edu We erew eadng S&S: Chapter Supplemental eadng Background rmed wth our crcut
RETURN ONLY THE SCANTRON SHEET!
 Andrzej Czajkowsk PHY/ exam Page out o Prncples o Physcs I PHY PHY Instructor: Dr. Andrzej Czajkowsk Fnal Exam December Closed book exam pages questons o equal value 5 correct answers pass the test! Duraton:
Andrzej Czajkowsk PHY/ exam Page out o Prncples o Physcs I PHY PHY Instructor: Dr. Andrzej Czajkowsk Fnal Exam December Closed book exam pages questons o equal value 5 correct answers pass the test! Duraton:
Section 8.1 Exercises
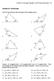 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
