Part I Formulation of convex optimization problems
|
|
|
- Ethan Newman
- 5 years ago
- Views:
Transcription
1 Nonlinear Optimization Part I Formulation of convex optimization problems Instituto Superior Técnico Carnegie Mellon University jxavier@isr.ist.utl.pt 1
2 Convex sets 2
3 Definition (Convex set) Let V be a vector space over R (usually, V = R n, V = R n m, V = S n ). A set S V is convex if x, y S [x, y] S y x 3
4 Convex sets: 4
5 Nonconvex sets: 5
6 How do we recognize convex sets? Vocabulary of simple ones + Apply convexity-preserving operations 6
7 Example (Hyperplanes): for s V {0} and r R H s,r := {x V : s, x = r} V = R 2 V = R 3 s s H s,r H s,r 7
8 Example (Closed half-spaces): for s V {0} and r R H s,r := {x V : s, x r} V = R 2 s H s,r 8
9 Example (Open half-spaces): for s V {0} and r R H s,r := {x V : s, x < r} V = R 2 s H s,r 9
10 Example (norm balls): where denotes a norm on V B(c, R) = {x V : x c R} 10
11 Special case: l p norms in V = R n ( n i=1 x p = x i p ) 1/p if 1 p < max i=1,...,n x i if p = V = R 2 p = p = 2 B 1 (0, 1) p = 1 11
12 Special case: σ max norm in V = R n m SVD: for A R n m (n m), there exist U : n m (U U = I m ), V : m m (V V = I m ) and σ σ..... Σ = : m m σ m with σ max = σ 1 σ 2 σ r > σ r+1 = = σ m = 0 (r = ranka) such that A = UΣV 12
13 We also have σ max = sup { u Av : u = 1, v = 1 } and Ax σ max (A) x for all x 13
14 Definition (Convex cone) Let V be a vector space. A set K V is a convex cone if K is convex and R + K = {αx : α 0, x K} K V = R 2 K 14
15 Example (Nonnegative orthant): with V = R n R n + = {x R n : x 0} V = R 2 R
16 Example (2nd order cone): with V = R n+1 L n+1 = {(x, t) R n R : x t} V = R 3 L 3 16
17 Example (Positive semidefinite cone): with V = S n S n + = {X S n : X 0} R n n S n S n + Note that X S n + iff λ(x) := (λ min (X), λ 2 (X),..., λ max (X)) R n + 17
18 Convexity is preserved by: intersections affine images or inverse-images affine map affine map before after after before 18
19 Proposition Let {S j : j J} be a collection of convex subsets of the vector space V. Then, S j is convex. j J Note: the index set J might be uncountable Proposition Let V, W be vector spaces and A : V W be affine. If S V is convex, then A(S) is convex. If S W is convex, then A 1 (S) is convex 19
20 More examples of convex sets: Polyhedrons Polynomial separators for pattern recognition Sets of pre-filter signals Ellipsoids Linear Matrix Inequalities (LMIs) V = S n and S = {X S n : λ max (X) 1} Contraction matrices 20
21 Example (Polyhedrons): P = {x V : s i, x r i : i = 1, 2,...,m} = m i=1 H s i,r i V = R 2 s i P 21
22 Example (Polynomials separators): consider two sets in R n X = {x 1, x 2,...,x K } Y = {y 1, y 2,...,y K } A separator is a function f : R n R such that f(x k ) > 0 for all x k X f(y l ) < 0 for all y l Y Some classes of separators: (linear) f s,r (x) = s, x + r (quadratic) f A,s,r (x) = Ax, x + s, x + r 22
23 R n y l R n x k y l x k 23
24 The set of linear separators is convex S = {(s, r) R n R : f s,r is a separator} The set of quadratic separators is convex S = {(A, s, r) S n R n R : f A,s,r is a separator} 24
25 Example (Pre-filter signals): a single-input multiple-output channel x[n] R H(z) y[n] R m with finite impulse-response (FIR) H(z) = h 0 + h 1 z 1 + h 2 z h d z d Input-output equation: y[n] = h 0 x[n] + h 1 x[n 1] + h 2 x[n 2] + + h d x[n d] 25
26 Stacking N output samples (zero initial conditions): y[1] h x[1] y[2]. h = 1 h x[2] y[n] 0 h 1 h 0 x[n] }{{}}{{}}{{} y R mn H R mn N x R N A desired output signal y des R mn and tolerance ǫ > 0 are given 26
27 Set of inputs fulfilling the specs is convex S = {x R N : Hx y des ǫ} R N H R mn S = H 1 (B (y des, ǫ)) 27
28 Example (Ellipsoids): E(A, c) = {x R n : (x c) A 1 (x c) 1} (A 0) A = QΛQ Q = [q 1 q 2 ] Λ = λ λ 2 R 2 q 2 q 1 λ2 c λ1 28
29 Special case A = R 2 I n correspond to the ball B(c, R) The function A 1 : R n R x x A 1 = x A 1 x is a norm (note that x A 1 = A 1/2 x ) The ellipsoid is convex (norm ball) E(A, c) = {x R n : x c A 1 1} 29
30 Example (Linear Matrix Inequalities): S = {(x 1, x 2,...,x n ) R n : A 0 + x 1 A 1 + x 2 A x n A n 0} where A 0, A 1,...,A n are given m m symmetric matrices 30
31 The set S is convex because where S = A 1 ( S n ) + A : R n S n x A(x) = A 0 + x 1 A 1 + x 2 A x n A n R n A S n R n n S = A 1 (S n +) S n + 31
32 Example: V = S n and S = {X S n : λ max (X) 1} The set S is convex: S = u R n : u =1 { X S n : u Xu 1 } }{{} S u : convex (closed half-space) 32
33 Example (Contraction matrices): S = {X R n m : σ max (X) 1} The set S is convex: S = u R n : u =1,v R m : v =1 { X R n m : u Xv 1 } }{{} S u,v : convex (closed half-space) 33
34 Definition (Convex hull) The convex hull of a set S, written co S, is the smallest convex set containing S: { k } k co S = α i x i : x i S, α i 0, α i = 1, k = 1, 2,... i=1 i=1 34
35 Example: S cos 35
36 Example: S cos 36
37 Example: S cos 37
38 Example (l p unit-sphere): S = {x R n : x p = 1} co S = {x R n : x p 1} Example (binary vectors): S = {(±1, ±1,...,±1)} R n co S = B (0, 1) Example (unit vectors): S = {(0,...,1,...,0)} R n co S = {x R n : x 0, 1 x = 1} cos is called the unit simplex 38
39 Example (Stiefel matrices): S = {X R m n : X X = I n } cos = {X : σ max (X) 1} Example (permutation matrices): S = {X : X ij {0, 1}, n X ij = 1} R n n i=1 X ij = 1, j=1 n cos = {X : X 0, X ij = 1, X ij = 1} i=1 j=1 cos is the set of doubly-stochastic matrices (this is Birkhoff s theorem) 39
40 Theorem (Projection onto closed convex sets) Let V be a vector space with inner-product, and induced norm x = x, x. Let S V be a non-empty closed convex set and x V. Then, (Existence and uniqueness) There is an unique x S such that x x x y for all y S x is called the projection of x onto S and is denoted by p S (x) (Characterization) A point x S is the projection p S (x) if and only if x x, y x 0 for all y S. 40
41 x x p S (x) y p S (x) p S (x) y 41
42 Inner-product induced norm is necessary: S = {(u, v) : v 0} x = (0, 1) = Convexity is necessary: S = [ 2, 1] [1, 2] x = 0 Closedness is necessary: S =]1, 2] x = 0 42
43 Examples of projections: V = R n, S = R n +, p S (x) = x + V = S n, S = S n +, p S (X) = X + 43
44 Corollary (Hyperplane separation) Let V be vector space with inner-product,. Let S V be a non-empty closed convex set and x S. Then, there exists an hyperplane H s,r (s V {0}, r R) that strictly separates x from S: S H s,r and x H s,r. That is, s, y r for all y S and s, x > r. 44
45 s x S H s,r 45
46 Proposition. Let A R n m. The set is closed AR m + = {Ax : x 0} R n Lemma (Farkas). Let A R m n and c R n. One and only one of the following sets is non-empty: S 1 = {x R n : Ax 0, c x > 0} S 2 = {y R m : c = A y, y 0} 46
47 Application: stationary distributions for Markov chains n states: S = {S 1, S 2,...,S n } X t S (t = 0, 1, 2,...) state at time t P j i = Prob(X t+1 = S j X t = S i ) S 1 P 1 i P n i S n S i P i i P 2 i S 2 p(t) := [ ] Prob(X t = S 1 ) Prob(X t = S 2 ) Prob(X t = S n ) 47
48 p(t) is a probability mass function (pmf): for all t p(t) 0 1 p(t) = 1 Dynamics of p(t): p(t + 1) = P 1 1 P 1 2 P 1 n P 2 1 P 2 2 P 2 n. p(t).. P n 1 P n 2 P n n }{{} P : Transition matrix 48
49 A pmf p is said to be stationary if p = Pp Result: any Markov chain has a stationary distribution 49
50 Definition (Proper cone) A convex cone K is proper if it is: closed solid (int K ) pointed (x, x K x = 0) Examples: non-negative orthant R n + = {x R n : x 0} 2nd order cone L n+1 = {(x, t) R n R : x t} positive semidefinite cone S n + = {X S n : X 0} 50
51 Definition (Dual cone) Let K be a convex cone in the vector space V with inner-product,. The dual cone of K is K = {s V : s, x 0 for all x K} K K 51
52 Dual cones are important for constructing dual programs Examples: K = L (linear subspace) K = L K = cone(a 1,...,a m ) = { m i=1 µ ia i : µ i 0} K = {s : s, a i 0} K = {x : a i, x 0 for i = 1,...,m} K = cone(a 1,...,a m ) K = {x R n : x 1 x n 0} K = {s R n : i j=1 s j 0, i } 52
53 Definition (Self-dual cones) A convex cone K is said to be self-dual if K = K Examples of self-dual cones: non-negative orthant R n + = {x R n : x 0} 2nd order cone L n+1 = {(x, t) R n R : x t} positive semidefinite cone S n + = {X S n : X 0} 53
54 Convex functions 54
55 Definition (Convex function) Let V be a vector space over R. f : S R is convex if S V is convex and f((1 α)x + αy) (1 α)f(x) + αf(y) for all x, y S and α [0, 1] f(y) (1 α)f(x) + αf(y) f(x) f((1 α)x + αy) x (1 α)x + αy y 55
56 Convex functions: 56
57 Nonconvex functions: 57
58 Proposition (Convexity is a 1D property) f : S V R is convex iff for all x S and d V φ x,d : I x,d := {t R : x + td S} R R φ(t) = f(x + td) is convex 58
59 How do we recognize convex functions? Vocabulary of simple ones (definition, differentiability, epigraph) + Apply convexity-preserving operations 59
60 Example (Affine functions): f(x) = s, x + r Example (norms): f(x) = x Special cases: l p norms, Frobenius norm, spectral norm,... 60
61 Proposition (Convexity through differentiability) Let V be a vector space over R and S V an open convex set. (1st order criterion) f : S R is convex iff f(y) f(x) + f(x), y x for all x, y S (2nd order criterion) f : S R is convex iff 2 f(x) 0 for all x S 61
62 Geometrical interpretation of 1st order criterion: f(y) f(x) + f(x), y x x y Local information f(x), f(x) yields a global bound 62
63 Geometrical interpretation of 2nd order criterion: f(y) x y The graph of f is pointing upwards 63
64 Examples: f : R ++ R f(x) = 1 x f : R ++ R f(x) = log(x) f : R + R f(x) = xlog(x) (0 log(0) := 0) 64
65 Examples: f : R n R (A symmetric) f(x) = x Ax + b x + c is convex iff A 0 f : R n R f(x 1,...,x n ) = 1 γ log (eγx 1 + e γx e γx n ) (γ > 0) smooth approximation for non-smooth function max{x 1, x 2,...,x n } f : R n ++ R f(x 1,...,x n ) = (x 1 x n ) 1/n is concave 65
66 Fact: for any A 0 and symmetric B, there exists S such that A = SS B = SΛS where Λ is diagonal (contains the eigenvalues of A 1/2 BA 1/2 ) f : S n ++ R f : S n ++ R f(x) = tr ( X 1) f(x) = log det(x) 66
67 Definition (Epigraph) Let V be a vector space. The epigraph of f : S V R is the set epi f = {(x, t) : f(x) t, x S} V R R epif f(x) x V S 67
68 Proposition (Convexity through epigraph) f is a convex function epif is a convex set Example: λ max : S n R 68
69 Operations that preserve convexity: f 1,...,f n are cvx f 1 + f f n is cvx f is cvx (f affine) is cvx f j (j J) are cvx sup j J f j is cvx 69
70 Proposition (Operations preserving convexity) Let V, W be vector spaces. if f j : S j V R is convex for j = 1,...,m and α j 0 then m α j f j : j=1 m j=1 S j V R is convex if A : V W is an affine map and f : S W R is convex, then f A : A 1 (W) R is convex if f j : S j V R is convex for j J then sup j J f j : S R is convex where S := {x j J S j : sup j J f j (x) < + } 70
71 Example (entropy): H : n R is concave H(p 1,...,p n ) = n p i log(p i ) i=1 71
72 Example (mutual information): a discrete memoryless channel (DMC) DMC x 1 y 1 x i x n P j i y j y m P j i := Prob(Y = y j X = x i ) Input X has a probability mass function (pmf) p X n 72
73 Output Y has a pmf p Y m given by p Y = Pp X P 1 1 P 1 2 P 1 n P 2 1 P 2 2 P 2 n P :=... P m 1 P m 2 P m n }{{} DMC transition matrix Mutual information between X and Y is I(X; Y ) = H(Y ) H(Y X) = H(Y ) n H(Y X = x i ) p X (i) i=1 I : n R is a concave function of p X 73
74 Example (log-barrier for polyhedrons): f : P R f(x) = m log(b i a i x) i=1 is convex where P = {x R n : a i x < b i for i = 1,...,m} Example (sum of k largest eigenvalues): f : S n R is convex f(x) = λ 1 (X) + λ 2 (X) + + λ k (X) 74
75 Convexity through composition rules: g : R n R m, g = (g 1,...,g m ) f : R m R f convex and ր in each variable g i convex f convex and ց in each variable g i concave (f g) convex (f g) convex Proof (smooth case): 2 (f g)(x) = Dg(x) 2 f(g(x))dg(x) + Dg(x) := [ g 1 (x) g 2 (x) g m (x) ] m i=1 f x i (g(x)) 2 g i (x) 75
76 Examples: f : R n R f(x) = log (e ) x e max{a 1 x+b 1,a 2 x+b 2} f : R n R f(x) = g [1] (x) + g [2] (x) + + g [k] (x) with g j : R n R convex 76
77 Proposition (Sublevel sets of convex functions are convex) Let V be a vector space and f : S V R be convex. For any r R the sublevel set is convex S r (f) = {x S : f(x) r} Example: the set {X S n ++ : tr ( X 1) 5} is convex 77
78 Definition (Convexity w.r.t a generalized inequality) Let V, W be a vector spaces, S V a convex set and K W a proper cone. The map F : S V W is said to be K-convex if F((1 α)x + αy) K (1 α)f(x) + αf(y) for all x, y S and α [0, 1] Examples: F : R n R m F = (F 1,...,F m ) is R m +-convex iff all F j are convex F : R n m S m F(X) = X AX with A 0 is S m +-convex 78
79 Convex optimization problems 79
80 General optimization problem: minimize f(x) subject to g j (x) 0 j = 1,...,m h i (x) = 0 i = 1,...,p f is the objective or cost function x is the optimization variable If m = p = 0 the problem is unconstrained A point x is feasible if g j (x) 0, h i (x) = 0, f(x) < + 80
81 The optimal value of the problem is f := inf{f(x) : g j (x) 0 for all j, h i (x) = 0 for all i} If f = we say the problem is unbounded If problem is infeasible we set f = + 81
82 Examples: f = 0 minimize x subject to x 0 f = (unbounded problem) minimize x subject to x 0 f = + (infeasible problem) minimize x subject to x 2 x 3 82
83 A (global) solution is a feasible point x satisfying f(x ) = f There might be no solutions (problem is unsolvable). Examples: f = minimize x subject to x 0 f = 0 is not achieved minimize e x 83
84 A local solution is a feasible point x which solves minimize f(x) subject to g j (x) 0 j = 1,...,m h i (x) = 0 i = 1,...,p x x R for some R > 0 84
85 Convex optimization problem: minimize f(x) subject to g j (x) 0 j = 1,...,m h i (x) = 0 i = 1,...,p f is convex g j are convex h i are affine The set of feasible points is convex Any local solution is a global solution 85
86 Linear optimization problem: minimize f(x) subject to g j (x) 0 j = 1,...,m h i (x) = 0 i = 1,...,p f is affine g j are affine h i are affine 86
87 Linear optimization problem (inequality form): minimize subject to c x Ax b Linear optimization problem (standard form): minimize subject to c x Ax = b x 0 87
88 Geometrical interpretation: c 88
89 Examples: Air traffic control Pattern separation: linear, quadratic,... separators Chebyshev center of a polyhedron Problems involving the l norm Problems involving the l 1 norm Testing sphericity of a constellation Boolean relaxation 89
90 Air traffic example: n airplanes must land in the order i = 1, 2,...,n t i =time of arrival of plane i ith airplane must land in given time interval [m i, M i ] Goal: design t 1, t 2,...,t n as to maximize min{t i+1 t i : i} 90
91 Initial formulation: maximize min{t 2 t 1, t 3 t 2,...,t n t n 1 } }{{} f(t 1,...,t n ) subject to t i t i+1 m i t i M i Optimization variable: (t 1, t 2,...,t n ) 91
92 Epigraph form: maximize s subject to s min{t 2 t 1, t 3 t 2,...,t n t n 1 } t i t i+1 m i t i M i Optimization variable: (t 1, t 2,...,t n, s) 92
93 maximize s subject to s t i+1 t i t i t i+1 m i t i M i Optimization variable: (t 1, t 2,...,t n, s) 93
94 Inequality form: minimize subject to c x Ax b x = (t 1,...,t n, s) c = (0,...,0, 1) A = D D I n I n 1 n 1 0 n 1 0 n 0 n b = 0 n 1 0 n 1 m M 94
95 where D = : n (n 1) m = m 1 m 2. m n M = M 1 M 2. M n 95
96 Pattern separation example: constellations X = {x 1,...,x K } and Y = {y 1,...,y L } in R n find a strict linear separator: (s, r, δ) R n R R ++ such that s x k r + δ for all k = 1,...,K s y l r δ for all l = 1,...,L 96
97 System is homogeneous in (s, r, δ): normalize δ = 1 Find (s, r) R n R such that s x k r + 1 s y l r 1 for all k = 1,...,K for all l = 1,...,L 97
98 Infeasible system if constellations overlap Way out: allow model violations but minimize them Problem formulation: find (s, r, u, v) R n R R K R L such that s x k r + 1 u k for all k = 1,...,K s y l r 1 + v l for all l = 1,...,L u k 0 for all k = 1,...,K v l 0 for all l = 1,...,L and the average of model violations u and v is minimized 98
99 Linear program: minimize 1 K 1 K u + 1 L 1 L v subject to s x k r + 1 u k s y l r 1 + v l u k 0 v l 0 k = 1,...,K l = 1,...,L k = 1,...,K l = 1,...,L Optimization variable: (s, r, u, v) R n R R K R L 99
100 Inequality form: minimize subject to c x Ax b x(:= (s, r, u, v)) R n+1+k+l c = (0 n, 0, 1 K 1 K, 1 L 1 L) A = X 1 K I K 0 K L Y 1 L 0 L K I L 0 K n 0 K I K 0 K L 0 L n 0 L 0 L K I L b = 1 K 1 L 0 K where X = [x 1 x 2 x K ] Y = 0 L [y 1 y 2 y L ] 100
101 Example: constellations do not overlap
102 Example: constellations overlap
103 K = 30; L = 20; margin = 2; % choose margin = -2 for overlap X = 4*rand(2,K); Y = 4+margin+4*rand(2,L); figure(1); clf; plot(x(1,:),x(2,:), bs ); grid on; axis( equal ); hold on; plot(y(1,:),y(2,:), ro ); f = [ zeros(2,1) ; 0 ; (1/K)*ones(K,1) ; (1/L)*ones(L,1) ]; A = [ -X ones(k,1) -eye(k) zeros(k,l) ; Y -ones(l,1) zeros(l,k) -eye(l) ; zeros(k,2) zeros(k,1) -eye(k) zeros(k,l) ; zeros(l,2) zeros(l,1) zeros(l,k) -eye(l) ]; b = [ -ones(k,1) ; -ones(l,1) ; zeros(k,1); zeros(l,1) ]; x = linprog(f,a,b); asol = x(1:2,:); bsol = x(3); t = 0:0.5:10; y = (bsol-asol(1)*t)/asol(2); plot(t,y, k.- ); 103
104 Chebyshev center example: find largest ball contained in a polyhedron R P = {x : Ex f} c application: largest robot arm that can operate in a polyhedral room 104
105 Initial formulation: maximize subject to R B(c, r) P Optimization variable: (c, R) R n R 105
106 Equivalent formulation: maximize R subject to B(c, R) H e 1,f 1. B(c, R) H e m,f m Optimization variable: (c, R) R n R 106
107 Key-fact: B(c, R) H e,f = {x : e x f} e c + R e f Linear program: maximize R subject to e 1 c + e 1 R f 1. e mc + e m R f m Optimization variable: (c, R) R n R 107
108 Example involving the l norm: SIMO channel is given x[n] R H(z) y[n] R m stacked data model: y = Hx (recall page 25) input constraints: Cx d e.g. x[n] P, x[n] x[n 1] S, x[n] x[m] V,... design input x such that Hx y des is minimized 108
109 Initial formulation: minimize subject to Hx y des Cx d Optimization variable: x R N 109
110 Epigraph form: minimize subject to t Hx y des t Cx d Optimization variable: (x, t) R N R 110
111 Linear program: minimize subject to t t1 Hx y des t1 Cx d Optimization variable: (x, t) R N R 111
112 Example involving the l 1 norm: dictionary A : m n (m n) and b are given find the sparsest solution of Ax = b Initial formulation: minimize subject to card(x) Ax = b Optimization variable: x R n 112
113 Convex approximation: minimize x 1 subject to Ax = b Optimization variable: x R n 113
114 Linear program: minimize subject to 1 y + 1 z A(y z) = b y 0, z 0 Optimization variable: (y, z) R n R n 114
115 Sphericity example: constellation X = {x 1, x 2,...,x K } is given how much spherical is the constellation? Spherical Non spherical 115
116 Initial formulation: minimize R 2 r 2 subject to r c x k R k = 1,...,K Optimization variable: (c, r, R) R n R R X is spherical value of the problem is 0 116
117 Linear program: minimize R r subject to r x k 2 2x k c R k = 1,...,K Optimization variable: (c, r, R) R n R R 117
118 Boolean relaxation example: difficult optimization problem minimize c x subject to Ax b x i {0, 1} i = 1,...,n relaxing x i {0, 1} to x i [0, 1] yields a linear program: minimize c x subject to Ax b 0 x i 1 i = 1,...,n 118
119 Convex quadratic optimization problem: minimize f(x) subject to g j (x) 0 j = 1,...,m h i (x) = 0 i = 1,...,p f is convex and quadratic g j are affine h i are affine 119
120 Geometrical interpretation: 120
121 Examples: ML estimation of constrained signals in additive Gaussian noise Portfolio optimization Basis pursuit denoising Support vector machines 121
122 ML estimation example: w[n] x[n] + y[n] w[n] is Gaussian noise 122
123 Collect N samples: y[1] y[2]. y[n] }{{} y = x[1] w[1] x[2] w[2] +.. x[n] }{{} x w[n] }{{} w Goal: estimate x given y 123
124 Signal x obeys polyhedral constraints Cx d Examples: known signal prefix x[1] = 1, x[2] = 0, x[3] = 1 power constraint equal boundary values x[n] P x[1] = x[n] mean value is between 5 and +5 rate constraint 5 1 N (x[1] + x[2] + + x[n]) 5 x[n] x[n 1] R 124
125 Letting w N(0, Σ) the pdf of y is p Y (y; x) = 1 exp (2π) N/2 det(σ) 1/2 ( 1 ) 2 (y x) Σ 1 (y x) The ML estimate of x corresponds to the solution of maximize p Y (y; x) subject to Cx d Optimization variable: x R N 125
126 Convex quadratic program: minimize (x y) Σ 1 (x y) subject to Cx d 126
127 Portfolio optimization example: T euros to invest among n assets r i is the random rate of return of ith asset first 2 moments of the random vector r = (r 1, r 2,...,r n ) are known: µ = E{r} Σ = E { (r µ)(r µ) } 127
128 The return of an investment x = (x 1, x 2,...,x n ) is the random variable: s(x) = r 1 x 1 + r 2 x r n x n First 2 moments of s(x) are: E{s(x)} = µ x var(s(x)) = E{(s(x) E{s(x)}) 2 } = x Σx 128
129 Goal: find the portfolio x with minimum variance guaranteeing a given mean return s 0 Optimization problem: minimize var(s(x)) subject to x 0 1 n x = T E{s(x)} = s 0 129
130 Convex quadratic program: minimize x Σx subject to x 0 1 n x = T µ x = s 0 130
131 Goal: find the portfolio maximizing the expected mean return with a risk penalization Optimization problem: maximize E{s(x)} β var(s(x)) subject to x 0 1 n x = T β 0 is the risk-aversion parameter 131
132 Convex quadratic program: minimize µ x + βx Σx subject to x 0 1 n x = T 132
133 Basis pursuit denoising example: dictionary A : m n (m n) and b R m are given find x such that Ax b and x is sparse Heuristic to find sparse solutions: minimize Ax b 2 + β x 1 β 0 trades off data fidelity and sparsity 133
134 Convex quadratic program: minimize A(y z) b 2 + β ( 1 n y + 1 n z ) subject to y 0 z 0 Optimization variable: (y, z) R n R n 134
135 Support vector machine example: constellations X = {x 1,...,x K } and Y = {y 1,...,y L } are given find the best linear separator 135
136 Optimization variable: (s, r, δ) R n R R ++ H(s, r δ) H(s, r + δ) H(s, r) = {x : s x = r} Constraints: X H(s, r + δ) + = {x : s x r + δ} Y H(s, r δ) = {x : s x r δ} 136
137 Initial formulation: maximize dist (H(s, r δ), H(s, r + δ)) subject to X H(s, r + δ) + Y H(s, r δ) δ > 0 Optimization variable: (s, r, δ) R n R R 137
138 Optimization problem: maximize 2 δ s subject to s x k r + δ s y l r δ k = 1,...,K l = 1,...,L δ > 0 138
139 If (s, r, δ) is feasible so is α(s, r, δ) (α > 0) with same cost value Normalize δ = 1: maximize 2 1 s subject to s x k r + 1 k = 1,...,K s y l r 1 l = 1,...,L Optimization variable: (s, r) R n R 139
140 Convex quadratic program: minimize s 2 subject to s x k r + 1 k = 1,...,K s y l r 1 l = 1,...,L 140
141 Convex conic optimization problem: minimize c x subject to A i (x) K i i = 1,...,p A i are affine maps K i are convex cones 141
142 Example: linear program minimize subject to c x Ax b is the conic optimization problem minimize subject to c x A(x) K A(x) = Ax b K = R m
143 Second-order cone program (SOCP): minimize c x subject to A i (x) K i i = 1,...,p A i are affine maps K i are second-order cones 143
144 Equivalently: minimize c x subject to A i x + b i c i x + d i i = 1,...,p 144
145 Examples: l approximation with complex data Geometric approximation Hyperbolic constraints Robust beamforming 145
146 Given A C m n and b C m minimize Az b Optimization variable: z C n For w = (w 1, w 2,...,w n ) C n, w = max{ w i : i} 146
147 Epigraph reformulation: minimize subject to t a i z b i t i = 1,...,m Optimization variable: (t, z) R C n 147
148 Writing z := x + jy, yields the SOCP minimize subject to t (Rea i) (Im a i ) (Im a i ) x (Rea i ) y Reb i Imb i t i = 1,...,m Optimization variable: (t, x, y) R R n R n 148
149 Find the smallest ball B(c, R) containing n given ones B(c i, R i ) R c 149
150 Initial formulation: minimize subject to R B(c i, R i ) B(c, R) i = 1,...,n Optimization variable: (c, R) R R n 150
151 SOCP: minimize R subject to c c i + R i R i = 1,...,n Optimization variable: (c, R) R R n 151
152 Fact: w 2 yz y 0 z 0 2w y z y + z 152
153 Application: Optimization variable: x R n minimize Ax b 4 + Cx d 2 153
154 Reformulation: minimize subject to s + t Ax b 4 s Cx d 2 t Optimization variable: (x, s, t) R n R R 154
155 minimize subject to s + t Ax b 4 s 2(Cx d) t 1 t + 1 Optimization variable: (x, s, t) R n R R 155
156 minimize subject to s + t Ax b 2 u u 2 s 2(Cx d) t 1 t + 1 Optimization variable: (x, s, t, u) R n R R 156
157 SOCP: minimize subject to s + t 2(Ax b) u 1 u + 1 2u s 1 s + 1 2(Cx d) t 1 t + 1 Optimization variable: (x, s, t, u) R n R R 157
158 Robust beamforming: N antennas at the base station P users s p [t] y n [t] 158
159 Baseband data model: y[t] = P h p s p [t] + n[t] p=1 y[t] C N is array snapshot at time t h p C N is pth channel vector s p [t] C is symbol transmitted by pth user at time t n[t] C N is additive noise Goal: given y[t] estimate s 1 [t] Assumption: h 1 is known and sources and noise are uncorrelated 159
160 Linear receiver: ŝ 1 [t] = w H y[t] Minimum variance distortionless receiver (MVDR): w MVDR = arg min w H Rw subject to w H h 1 = 1 R = E { y[t]y[t] H} 1 T T t=1 y[t]y[t]h 160
161 Robust formulation: minimize w H Rw subject to w H h 1 for all h B(h 1, ǫ) Optimization variable: w C N 161
162 Equivalent formulation: minimize w H Rw subject to w H h 1 ǫ w 1 If w is feasible, so is e jθ w with same cost 162
163 minimize w H Rw subject to w H h 1 ǫ w 1 Re { } w H h 1 0 Im { } w H h 1 = 0 163
164 Writing w = x + jy leads to SOCP: minimize subject to t A x y t ǫ x [(Reh y 1 ) (Imh 1 ) ] x 1 y [(Imh 1 ) (Reh 1 ) ] x = 0 y 164
165 A is the square-root of ReR (Im R) ImR ReR 165
166 Semi-definite program (SDP): minimize c x subject to A i (x) K i i = 1,...,p A i are affine maps K i are semi-definite matrix cones 166
167 Equivalently: minimize c x subject to A 0 + x 1 A 1 + x 2 A 2 + x n A n 0 167
168 Examples: Eigenvalue optimization Manifold learning MAXCUT 168
169 Eigenvalue optimization: minimize λ max (A 0 + x 1 A 1 + x 2 A x n A n ) where A i S m are given Equivalent SDP: minimize t subject to A 0 + x 1 A 1 + x 2 A x n A n ti m 169
170 Manifold learning: R N R n x k y k 170
171 Approach: open the manifold (maximum variance unfolding) maximize K k=1 y k 2 subject to 1 K K k=1 y k = 0 y k y l 2 = x k x l 2 for all (k, l) N Optimization variable: (y 1, y 2,...,y K ) R n R n R n 171
172 Equivalent formulation: maximize tr ( Y Y ) subject to 1 Y Y 1 = 0 e k Y Y e k + e l Y Y e l 2e k Y Y e l = x k x l 2 for all (k, l) N Optimization variable: Y R n K 172
173 maximize tr(g) subject to 1 G1 = 0 e k Ge k + e l Ge l 2e k Ge l = x k x l 2 G = Y Y for all (k, l) N Optimization variable: (G, Y ) R K K R n K 173
174 We can drop the variable Y maximize tr(g) subject to 1 G1 = 0 e k Ge k + e l Ge l 2e k Ge l = x k x l 2 G 0 rank(g) n for all (k, l) N Optimization variable: G R K K 174
175 Removing the rank constraint yields the SDP: maximize tr(g) subject to 1 G1 = 0 e k Ge k + e l Ge l 2e k Ge l = x k x l 2 G 0 for all (k, l) N 175
176 MAXCUT problem j i w ij w ij 0 is weight of edge (i, j) Value of a cut = sum of weights of broken edges Find the maximum cut 176
177 MAXCUT = max φ(x) subject to x 2 i = 1 i = 1, 2,...,n where φ(x) = 1 2 n i,j=1 w ij 1 x i x j 2 Optimization variable: x = (x 1, x 2,...,x n ) R n 177
178 MAXCUT = max 1 2 subject to X ii = 1 n i,j=1 w ij 1 X ij 2 i = 1, 2,...,n X = xx Optimization variable: (X, x) R n n R n 178
179 MAXCUT = max n W1 n 1 4 tr(wx) subject to X ii = 1 i = 1, 2,...,n X = xx Optimization variable: (X, x) R n n R n 179
180 We can drop the variable x MAXCUT = max n W1 n 1 4 tr(wx) subject to X ii = 1 i = 1, 2,...,n X 0 rank(x) = 1 Optimization variable: X R n n 180
181 Removing the rank constraint yields the SDP: SDP = max n W1 n 1 4 tr(wx) subject to X ii = 1 i = 1, 2,...,n X 0 181
182 Let X solve the SDP and z N(0, X ) There holds SDP MAXCUT E {φ(sgn(z))} 0.87 SDP 182
Definition of convex function in a vector space
 Convex functions Nonlinear optimization Instituto Superior Técnico and Carnegie Mellon University PhD course João Xavier TAs: Brian Swenson, Shanghang Zhang, Lucas Balthazar Convex functions Nonconvex
Convex functions Nonlinear optimization Instituto Superior Técnico and Carnegie Mellon University PhD course João Xavier TAs: Brian Swenson, Shanghang Zhang, Lucas Balthazar Convex functions Nonconvex
Lecture: Convex Optimization Problems
 1/36 Lecture: Convex Optimization Problems http://bicmr.pku.edu.cn/~wenzw/opt-2015-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/36 optimization
1/36 Lecture: Convex Optimization Problems http://bicmr.pku.edu.cn/~wenzw/opt-2015-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/36 optimization
4. Convex optimization problems
 Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
Convex optimization problems. Optimization problem in standard form
 Convex optimization problems optimization problem in standard form convex optimization problems linear optimization quadratic optimization geometric programming quasiconvex optimization generalized inequality
Convex optimization problems optimization problem in standard form convex optimization problems linear optimization quadratic optimization geometric programming quasiconvex optimization generalized inequality
4. Convex optimization problems
 Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
A Brief Review on Convex Optimization
 A Brief Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one convex, two nonconvex sets): A Brief Review
A Brief Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one convex, two nonconvex sets): A Brief Review
Chapter 2: Preliminaries and elements of convex analysis
 Chapter 2: Preliminaries and elements of convex analysis Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-14-15.shtml Academic year 2014-15
Chapter 2: Preliminaries and elements of convex analysis Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-14-15.shtml Academic year 2014-15
ELE539A: Optimization of Communication Systems Lecture 15: Semidefinite Programming, Detection and Estimation Applications
 ELE539A: Optimization of Communication Systems Lecture 15: Semidefinite Programming, Detection and Estimation Applications Professor M. Chiang Electrical Engineering Department, Princeton University March
ELE539A: Optimization of Communication Systems Lecture 15: Semidefinite Programming, Detection and Estimation Applications Professor M. Chiang Electrical Engineering Department, Princeton University March
HW1 solutions. 1. α Ef(x) β, where Ef(x) is the expected value of f(x), i.e., Ef(x) = n. i=1 p if(a i ). (The function f : R R is given.
 HW1 solutions Exercise 1 (Some sets of probability distributions.) Let x be a real-valued random variable with Prob(x = a i ) = p i, i = 1,..., n, where a 1 < a 2 < < a n. Of course p R n lies in the standard
HW1 solutions Exercise 1 (Some sets of probability distributions.) Let x be a real-valued random variable with Prob(x = a i ) = p i, i = 1,..., n, where a 1 < a 2 < < a n. Of course p R n lies in the standard
CSCI : Optimization and Control of Networks. Review on Convex Optimization
 CSCI7000-016: Optimization and Control of Networks Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one
CSCI7000-016: Optimization and Control of Networks Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one
Lecture Note 5: Semidefinite Programming for Stability Analysis
 ECE7850: Hybrid Systems:Theory and Applications Lecture Note 5: Semidefinite Programming for Stability Analysis Wei Zhang Assistant Professor Department of Electrical and Computer Engineering Ohio State
ECE7850: Hybrid Systems:Theory and Applications Lecture Note 5: Semidefinite Programming for Stability Analysis Wei Zhang Assistant Professor Department of Electrical and Computer Engineering Ohio State
Convex Optimization and Modeling
 Convex Optimization and Modeling Convex Optimization Fourth lecture, 05.05.2010 Jun.-Prof. Matthias Hein Reminder from last time Convex functions: first-order condition: f(y) f(x) + f x,y x, second-order
Convex Optimization and Modeling Convex Optimization Fourth lecture, 05.05.2010 Jun.-Prof. Matthias Hein Reminder from last time Convex functions: first-order condition: f(y) f(x) + f x,y x, second-order
Convex Optimization. (EE227A: UC Berkeley) Lecture 6. Suvrit Sra. (Conic optimization) 07 Feb, 2013
 Convex Optimization (EE227A: UC Berkeley) Lecture 6 (Conic optimization) 07 Feb, 2013 Suvrit Sra Organizational Info Quiz coming up on 19th Feb. Project teams by 19th Feb Good if you can mix your research
Convex Optimization (EE227A: UC Berkeley) Lecture 6 (Conic optimization) 07 Feb, 2013 Suvrit Sra Organizational Info Quiz coming up on 19th Feb. Project teams by 19th Feb Good if you can mix your research
EE/ACM Applications of Convex Optimization in Signal Processing and Communications Lecture 17
 EE/ACM 150 - Applications of Convex Optimization in Signal Processing and Communications Lecture 17 Andre Tkacenko Signal Processing Research Group Jet Propulsion Laboratory May 29, 2012 Andre Tkacenko
EE/ACM 150 - Applications of Convex Optimization in Signal Processing and Communications Lecture 17 Andre Tkacenko Signal Processing Research Group Jet Propulsion Laboratory May 29, 2012 Andre Tkacenko
Nonlinear Programming Models
 Nonlinear Programming Models Fabio Schoen 2008 http://gol.dsi.unifi.it/users/schoen Nonlinear Programming Models p. Introduction Nonlinear Programming Models p. NLP problems minf(x) x S R n Standard form:
Nonlinear Programming Models Fabio Schoen 2008 http://gol.dsi.unifi.it/users/schoen Nonlinear Programming Models p. Introduction Nonlinear Programming Models p. NLP problems minf(x) x S R n Standard form:
Lecture: Examples of LP, SOCP and SDP
 1/34 Lecture: Examples of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2018.html wenzw@pku.edu.cn Acknowledgement:
1/34 Lecture: Examples of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2018.html wenzw@pku.edu.cn Acknowledgement:
Introduction and Math Preliminaries
 Introduction and Math Preliminaries Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/ yyye Appendices A, B, and C, Chapter
Introduction and Math Preliminaries Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/ yyye Appendices A, B, and C, Chapter
Convex Optimization and l 1 -minimization
 Convex Optimization and l 1 -minimization Sangwoon Yun Computational Sciences Korea Institute for Advanced Study December 11, 2009 2009 NIMS Thematic Winter School Outline I. Convex Optimization II. l
Convex Optimization and l 1 -minimization Sangwoon Yun Computational Sciences Korea Institute for Advanced Study December 11, 2009 2009 NIMS Thematic Winter School Outline I. Convex Optimization II. l
Linear and non-linear programming
 Linear and non-linear programming Benjamin Recht March 11, 2005 The Gameplan Constrained Optimization Convexity Duality Applications/Taxonomy 1 Constrained Optimization minimize f(x) subject to g j (x)
Linear and non-linear programming Benjamin Recht March 11, 2005 The Gameplan Constrained Optimization Convexity Duality Applications/Taxonomy 1 Constrained Optimization minimize f(x) subject to g j (x)
Semidefinite Programming Basics and Applications
 Semidefinite Programming Basics and Applications Ray Pörn, principal lecturer Åbo Akademi University Novia University of Applied Sciences Content What is semidefinite programming (SDP)? How to represent
Semidefinite Programming Basics and Applications Ray Pörn, principal lecturer Åbo Akademi University Novia University of Applied Sciences Content What is semidefinite programming (SDP)? How to represent
Solution to EE 617 Mid-Term Exam, Fall November 2, 2017
 Solution to EE 67 Mid-erm Exam, Fall 207 November 2, 207 EE 67 Solution to Mid-erm Exam - Page 2 of 2 November 2, 207 (4 points) Convex sets (a) (2 points) Consider the set { } a R k p(0) =, p(t) for t
Solution to EE 67 Mid-erm Exam, Fall 207 November 2, 207 EE 67 Solution to Mid-erm Exam - Page 2 of 2 November 2, 207 (4 points) Convex sets (a) (2 points) Consider the set { } a R k p(0) =, p(t) for t
13. Convex programming
 CS/ISyE/ECE 524 Introduction to Optimization Spring 2015 16 13. Convex programming Convex sets and functions Convex programs Hierarchy of complexity Example: geometric programming Laurent Lessard (www.laurentlessard.com)
CS/ISyE/ECE 524 Introduction to Optimization Spring 2015 16 13. Convex programming Convex sets and functions Convex programs Hierarchy of complexity Example: geometric programming Laurent Lessard (www.laurentlessard.com)
Lecture 2: Convex Sets and Functions
 Lecture 2: Convex Sets and Functions Hyang-Won Lee Dept. of Internet & Multimedia Eng. Konkuk University Lecture 2 Network Optimization, Fall 2015 1 / 22 Optimization Problems Optimization problems are
Lecture 2: Convex Sets and Functions Hyang-Won Lee Dept. of Internet & Multimedia Eng. Konkuk University Lecture 2 Network Optimization, Fall 2015 1 / 22 Optimization Problems Optimization problems are
8. Geometric problems
 8. Geometric problems Convex Optimization Boyd & Vandenberghe extremal volume ellipsoids centering classification placement and facility location 8 Minimum volume ellipsoid around a set Löwner-John ellipsoid
8. Geometric problems Convex Optimization Boyd & Vandenberghe extremal volume ellipsoids centering classification placement and facility location 8 Minimum volume ellipsoid around a set Löwner-John ellipsoid
Geometric problems. Chapter Projection on a set. The distance of a point x 0 R n to a closed set C R n, in the norm, is defined as
 Chapter 8 Geometric problems 8.1 Projection on a set The distance of a point x 0 R n to a closed set C R n, in the norm, is defined as dist(x 0,C) = inf{ x 0 x x C}. The infimum here is always achieved.
Chapter 8 Geometric problems 8.1 Projection on a set The distance of a point x 0 R n to a closed set C R n, in the norm, is defined as dist(x 0,C) = inf{ x 0 x x C}. The infimum here is always achieved.
Interior Point Methods: Second-Order Cone Programming and Semidefinite Programming
 School of Mathematics T H E U N I V E R S I T Y O H F E D I N B U R G Interior Point Methods: Second-Order Cone Programming and Semidefinite Programming Jacek Gondzio Email: J.Gondzio@ed.ac.uk URL: http://www.maths.ed.ac.uk/~gondzio
School of Mathematics T H E U N I V E R S I T Y O H F E D I N B U R G Interior Point Methods: Second-Order Cone Programming and Semidefinite Programming Jacek Gondzio Email: J.Gondzio@ed.ac.uk URL: http://www.maths.ed.ac.uk/~gondzio
Exercises. Exercises. Basic terminology and optimality conditions. 4.2 Consider the optimization problem
 Exercises Basic terminology and optimality conditions 4.1 Consider the optimization problem f 0(x 1, x 2) 2x 1 + x 2 1 x 1 + 3x 2 1 x 1 0, x 2 0. Make a sketch of the feasible set. For each of the following
Exercises Basic terminology and optimality conditions 4.1 Consider the optimization problem f 0(x 1, x 2) 2x 1 + x 2 1 x 1 + 3x 2 1 x 1 0, x 2 0. Make a sketch of the feasible set. For each of the following
Module 04 Optimization Problems KKT Conditions & Solvers
 Module 04 Optimization Problems KKT Conditions & Solvers Ahmad F. Taha EE 5243: Introduction to Cyber-Physical Systems Email: ahmad.taha@utsa.edu Webpage: http://engineering.utsa.edu/ taha/index.html September
Module 04 Optimization Problems KKT Conditions & Solvers Ahmad F. Taha EE 5243: Introduction to Cyber-Physical Systems Email: ahmad.taha@utsa.edu Webpage: http://engineering.utsa.edu/ taha/index.html September
8. Geometric problems
 8. Geometric problems Convex Optimization Boyd & Vandenberghe extremal volume ellipsoids centering classification placement and facility location 8 1 Minimum volume ellipsoid around a set Löwner-John ellipsoid
8. Geometric problems Convex Optimization Boyd & Vandenberghe extremal volume ellipsoids centering classification placement and facility location 8 1 Minimum volume ellipsoid around a set Löwner-John ellipsoid
I.3. LMI DUALITY. Didier HENRION EECI Graduate School on Control Supélec - Spring 2010
 I.3. LMI DUALITY Didier HENRION henrion@laas.fr EECI Graduate School on Control Supélec - Spring 2010 Primal and dual For primal problem p = inf x g 0 (x) s.t. g i (x) 0 define Lagrangian L(x, z) = g 0
I.3. LMI DUALITY Didier HENRION henrion@laas.fr EECI Graduate School on Control Supélec - Spring 2010 Primal and dual For primal problem p = inf x g 0 (x) s.t. g i (x) 0 define Lagrangian L(x, z) = g 0
Matrix Rank Minimization with Applications
 Matrix Rank Minimization with Applications Maryam Fazel Haitham Hindi Stephen Boyd Information Systems Lab Electrical Engineering Department Stanford University 8/2001 ACC 01 Outline Rank Minimization
Matrix Rank Minimization with Applications Maryam Fazel Haitham Hindi Stephen Boyd Information Systems Lab Electrical Engineering Department Stanford University 8/2001 ACC 01 Outline Rank Minimization
Conic Linear Programming. Yinyu Ye
 Conic Linear Programming Yinyu Ye December 2004, revised October 2017 i ii Preface This monograph is developed for MS&E 314, Conic Linear Programming, which I am teaching at Stanford. Information, lecture
Conic Linear Programming Yinyu Ye December 2004, revised October 2017 i ii Preface This monograph is developed for MS&E 314, Conic Linear Programming, which I am teaching at Stanford. Information, lecture
12. Interior-point methods
 12. Interior-point methods Convex Optimization Boyd & Vandenberghe inequality constrained minimization logarithmic barrier function and central path barrier method feasibility and phase I methods complexity
12. Interior-point methods Convex Optimization Boyd & Vandenberghe inequality constrained minimization logarithmic barrier function and central path barrier method feasibility and phase I methods complexity
Lecture 2: Convex functions
 Lecture 2: Convex functions f : R n R is convex if dom f is convex and for all x, y dom f, θ [0, 1] f is concave if f is convex f(θx + (1 θ)y) θf(x) + (1 θ)f(y) x x convex concave neither x examples (on
Lecture 2: Convex functions f : R n R is convex if dom f is convex and for all x, y dom f, θ [0, 1] f is concave if f is convex f(θx + (1 θ)y) θf(x) + (1 θ)f(y) x x convex concave neither x examples (on
3. Convex functions. basic properties and examples. operations that preserve convexity. the conjugate function. quasiconvex functions
 3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
Agenda. 1 Cone programming. 2 Convex cones. 3 Generalized inequalities. 4 Linear programming (LP) 5 Second-order cone programming (SOCP)
 Agenda 1 Cone programming 2 Convex cones 3 Generalized inequalities 4 Linear programming (LP) 5 Second-order cone programming (SOCP) 6 Semidefinite programming (SDP) 7 Examples Optimization problem in
Agenda 1 Cone programming 2 Convex cones 3 Generalized inequalities 4 Linear programming (LP) 5 Second-order cone programming (SOCP) 6 Semidefinite programming (SDP) 7 Examples Optimization problem in
Convex Optimization M2
 Convex Optimization M2 Lecture 8 A. d Aspremont. Convex Optimization M2. 1/57 Applications A. d Aspremont. Convex Optimization M2. 2/57 Outline Geometrical problems Approximation problems Combinatorial
Convex Optimization M2 Lecture 8 A. d Aspremont. Convex Optimization M2. 1/57 Applications A. d Aspremont. Convex Optimization M2. 2/57 Outline Geometrical problems Approximation problems Combinatorial
Selected Examples of CONIC DUALITY AT WORK Robust Linear Optimization Synthesis of Linear Controllers Matrix Cube Theorem A.
 . Selected Examples of CONIC DUALITY AT WORK Robust Linear Optimization Synthesis of Linear Controllers Matrix Cube Theorem A. Nemirovski Arkadi.Nemirovski@isye.gatech.edu Linear Optimization Problem,
. Selected Examples of CONIC DUALITY AT WORK Robust Linear Optimization Synthesis of Linear Controllers Matrix Cube Theorem A. Nemirovski Arkadi.Nemirovski@isye.gatech.edu Linear Optimization Problem,
Mathematics 530. Practice Problems. n + 1 }
 Department of Mathematical Sciences University of Delaware Prof. T. Angell October 19, 2015 Mathematics 530 Practice Problems 1. Recall that an indifference relation on a partially ordered set is defined
Department of Mathematical Sciences University of Delaware Prof. T. Angell October 19, 2015 Mathematics 530 Practice Problems 1. Recall that an indifference relation on a partially ordered set is defined
Convex Optimization. 4. Convex Optimization Problems. Prof. Ying Cui. Department of Electrical Engineering Shanghai Jiao Tong University
 Conve Optimization 4. Conve Optimization Problems Prof. Ying Cui Department of Electrical Engineering Shanghai Jiao Tong University 2017 Autumn Semester SJTU Ying Cui 1 / 58 Outline Optimization problems
Conve Optimization 4. Conve Optimization Problems Prof. Ying Cui Department of Electrical Engineering Shanghai Jiao Tong University 2017 Autumn Semester SJTU Ying Cui 1 / 58 Outline Optimization problems
Convex Optimization M2
 Convex Optimization M2 Lecture 3 A. d Aspremont. Convex Optimization M2. 1/49 Duality A. d Aspremont. Convex Optimization M2. 2/49 DMs DM par email: dm.daspremont@gmail.com A. d Aspremont. Convex Optimization
Convex Optimization M2 Lecture 3 A. d Aspremont. Convex Optimization M2. 1/49 Duality A. d Aspremont. Convex Optimization M2. 2/49 DMs DM par email: dm.daspremont@gmail.com A. d Aspremont. Convex Optimization
5. Duality. Lagrangian
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
EE Applications of Convex Optimization in Signal Processing and Communications Dr. Andre Tkacenko, JPL Third Term
 EE 150 - Applications of Convex Optimization in Signal Processing and Communications Dr. Andre Tkacenko JPL Third Term 2011-2012 Due on Thursday May 3 in class. Homework Set #4 1. (10 points) (Adapted
EE 150 - Applications of Convex Optimization in Signal Processing and Communications Dr. Andre Tkacenko JPL Third Term 2011-2012 Due on Thursday May 3 in class. Homework Set #4 1. (10 points) (Adapted
Convex Optimization and Modeling
 Convex Optimization and Modeling Introduction and a quick repetition of analysis/linear algebra First lecture, 12.04.2010 Jun.-Prof. Matthias Hein Organization of the lecture Advanced course, 2+2 hours,
Convex Optimization and Modeling Introduction and a quick repetition of analysis/linear algebra First lecture, 12.04.2010 Jun.-Prof. Matthias Hein Organization of the lecture Advanced course, 2+2 hours,
Conic Linear Programming. Yinyu Ye
 Conic Linear Programming Yinyu Ye December 2004, revised January 2015 i ii Preface This monograph is developed for MS&E 314, Conic Linear Programming, which I am teaching at Stanford. Information, lecture
Conic Linear Programming Yinyu Ye December 2004, revised January 2015 i ii Preface This monograph is developed for MS&E 314, Conic Linear Programming, which I am teaching at Stanford. Information, lecture
LMI MODELLING 4. CONVEX LMI MODELLING. Didier HENRION. LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ. Universidad de Valladolid, SP March 2009
 LMI MODELLING 4. CONVEX LMI MODELLING Didier HENRION LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ Universidad de Valladolid, SP March 2009 Minors A minor of a matrix F is the determinant of a submatrix
LMI MODELLING 4. CONVEX LMI MODELLING Didier HENRION LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ Universidad de Valladolid, SP March 2009 Minors A minor of a matrix F is the determinant of a submatrix
What can be expressed via Conic Quadratic and Semidefinite Programming?
 What can be expressed via Conic Quadratic and Semidefinite Programming? A. Nemirovski Faculty of Industrial Engineering and Management Technion Israel Institute of Technology Abstract Tremendous recent
What can be expressed via Conic Quadratic and Semidefinite Programming? A. Nemirovski Faculty of Industrial Engineering and Management Technion Israel Institute of Technology Abstract Tremendous recent
Sparse Optimization Lecture: Basic Sparse Optimization Models
 Sparse Optimization Lecture: Basic Sparse Optimization Models Instructor: Wotao Yin July 2013 online discussions on piazza.com Those who complete this lecture will know basic l 1, l 2,1, and nuclear-norm
Sparse Optimization Lecture: Basic Sparse Optimization Models Instructor: Wotao Yin July 2013 online discussions on piazza.com Those who complete this lecture will know basic l 1, l 2,1, and nuclear-norm
Appendix PRELIMINARIES 1. THEOREMS OF ALTERNATIVES FOR SYSTEMS OF LINEAR CONSTRAINTS
 Appendix PRELIMINARIES 1. THEOREMS OF ALTERNATIVES FOR SYSTEMS OF LINEAR CONSTRAINTS Here we consider systems of linear constraints, consisting of equations or inequalities or both. A feasible solution
Appendix PRELIMINARIES 1. THEOREMS OF ALTERNATIVES FOR SYSTEMS OF LINEAR CONSTRAINTS Here we consider systems of linear constraints, consisting of equations or inequalities or both. A feasible solution
subject to (x 2)(x 4) u,
 Exercises Basic definitions 5.1 A simple example. Consider the optimization problem with variable x R. minimize x 2 + 1 subject to (x 2)(x 4) 0, (a) Analysis of primal problem. Give the feasible set, the
Exercises Basic definitions 5.1 A simple example. Consider the optimization problem with variable x R. minimize x 2 + 1 subject to (x 2)(x 4) 0, (a) Analysis of primal problem. Give the feasible set, the
Assignment 1: From the Definition of Convexity to Helley Theorem
 Assignment 1: From the Definition of Convexity to Helley Theorem Exercise 1 Mark in the following list the sets which are convex: 1. {x R 2 : x 1 + i 2 x 2 1, i = 1,..., 10} 2. {x R 2 : x 2 1 + 2ix 1x
Assignment 1: From the Definition of Convexity to Helley Theorem Exercise 1 Mark in the following list the sets which are convex: 1. {x R 2 : x 1 + i 2 x 2 1, i = 1,..., 10} 2. {x R 2 : x 2 1 + 2ix 1x
Convex Optimization in Classification Problems
 New Trends in Optimization and Computational Algorithms December 9 13, 2001 Convex Optimization in Classification Problems Laurent El Ghaoui Department of EECS, UC Berkeley elghaoui@eecs.berkeley.edu 1
New Trends in Optimization and Computational Algorithms December 9 13, 2001 Convex Optimization in Classification Problems Laurent El Ghaoui Department of EECS, UC Berkeley elghaoui@eecs.berkeley.edu 1
COURSE ON LMI PART I.2 GEOMETRY OF LMI SETS. Didier HENRION henrion
 COURSE ON LMI PART I.2 GEOMETRY OF LMI SETS Didier HENRION www.laas.fr/ henrion October 2006 Geometry of LMI sets Given symmetric matrices F i we want to characterize the shape in R n of the LMI set F
COURSE ON LMI PART I.2 GEOMETRY OF LMI SETS Didier HENRION www.laas.fr/ henrion October 2006 Geometry of LMI sets Given symmetric matrices F i we want to characterize the shape in R n of the LMI set F
12. Interior-point methods
 12. Interior-point methods Convex Optimization Boyd & Vandenberghe inequality constrained minimization logarithmic barrier function and central path barrier method feasibility and phase I methods complexity
12. Interior-point methods Convex Optimization Boyd & Vandenberghe inequality constrained minimization logarithmic barrier function and central path barrier method feasibility and phase I methods complexity
Convex Optimization in Communications and Signal Processing
 Convex Optimization in Communications and Signal Processing Prof. Dr.-Ing. Wolfgang Gerstacker 1 University of Erlangen-Nürnberg Institute for Digital Communications National Technical University of Ukraine,
Convex Optimization in Communications and Signal Processing Prof. Dr.-Ing. Wolfgang Gerstacker 1 University of Erlangen-Nürnberg Institute for Digital Communications National Technical University of Ukraine,
Optimization and Optimal Control in Banach Spaces
 Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
N. L. P. NONLINEAR PROGRAMMING (NLP) deals with optimization models with at least one nonlinear function. NLP. Optimization. Models of following form:
 0.1 N. L. P. Katta G. Murty, IOE 611 Lecture slides Introductory Lecture NONLINEAR PROGRAMMING (NLP) deals with optimization models with at least one nonlinear function. NLP does not include everything
0.1 N. L. P. Katta G. Murty, IOE 611 Lecture slides Introductory Lecture NONLINEAR PROGRAMMING (NLP) deals with optimization models with at least one nonlinear function. NLP does not include everything
Summer School: Semidefinite Optimization
 Summer School: Semidefinite Optimization Christine Bachoc Université Bordeaux I, IMB Research Training Group Experimental and Constructive Algebra Haus Karrenberg, Sept. 3 - Sept. 7, 2012 Duality Theory
Summer School: Semidefinite Optimization Christine Bachoc Université Bordeaux I, IMB Research Training Group Experimental and Constructive Algebra Haus Karrenberg, Sept. 3 - Sept. 7, 2012 Duality Theory
Convex Optimization and Modeling
 Convex Optimization and Modeling Duality Theory and Optimality Conditions 5th lecture, 12.05.2010 Jun.-Prof. Matthias Hein Program of today/next lecture Lagrangian and duality: the Lagrangian the dual
Convex Optimization and Modeling Duality Theory and Optimality Conditions 5th lecture, 12.05.2010 Jun.-Prof. Matthias Hein Program of today/next lecture Lagrangian and duality: the Lagrangian the dual
Lecture: Duality of LP, SOCP and SDP
 1/33 Lecture: Duality of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2017.html wenzw@pku.edu.cn Acknowledgement:
1/33 Lecture: Duality of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2017.html wenzw@pku.edu.cn Acknowledgement:
EE/ACM Applications of Convex Optimization in Signal Processing and Communications Lecture 18
 EE/ACM 150 - Applications of Convex Optimization in Signal Processing and Communications Lecture 18 Andre Tkacenko Signal Processing Research Group Jet Propulsion Laboratory May 31, 2012 Andre Tkacenko
EE/ACM 150 - Applications of Convex Optimization in Signal Processing and Communications Lecture 18 Andre Tkacenko Signal Processing Research Group Jet Propulsion Laboratory May 31, 2012 Andre Tkacenko
Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization
 Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization Compiled by David Rosenberg Abstract Boyd and Vandenberghe s Convex Optimization book is very well-written and a pleasure to read. The
Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization Compiled by David Rosenberg Abstract Boyd and Vandenberghe s Convex Optimization book is very well-written and a pleasure to read. The
Lagrangian Duality Theory
 Lagrangian Duality Theory Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/ yyye Chapter 14.1-4 1 Recall Primal and Dual
Lagrangian Duality Theory Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/ yyye Chapter 14.1-4 1 Recall Primal and Dual
LMI Methods in Optimal and Robust Control
 LMI Methods in Optimal and Robust Control Matthew M. Peet Arizona State University Lecture 02: Optimization (Convex and Otherwise) What is Optimization? An Optimization Problem has 3 parts. x F f(x) :
LMI Methods in Optimal and Robust Control Matthew M. Peet Arizona State University Lecture 02: Optimization (Convex and Otherwise) What is Optimization? An Optimization Problem has 3 parts. x F f(x) :
9. Geometric problems
 9. Geometric problems EE/AA 578, Univ of Washington, Fall 2016 projection on a set extremal volume ellipsoids centering classification 9 1 Projection on convex set projection of point x on set C defined
9. Geometric problems EE/AA 578, Univ of Washington, Fall 2016 projection on a set extremal volume ellipsoids centering classification 9 1 Projection on convex set projection of point x on set C defined
Convex Optimization Boyd & Vandenberghe. 5. Duality
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
Convex Optimization. (EE227A: UC Berkeley) Lecture 28. Suvrit Sra. (Algebra + Optimization) 02 May, 2013
 Convex Optimization (EE227A: UC Berkeley) Lecture 28 (Algebra + Optimization) 02 May, 2013 Suvrit Sra Admin Poster presentation on 10th May mandatory HW, Midterm, Quiz to be reweighted Project final report
Convex Optimization (EE227A: UC Berkeley) Lecture 28 (Algebra + Optimization) 02 May, 2013 Suvrit Sra Admin Poster presentation on 10th May mandatory HW, Midterm, Quiz to be reweighted Project final report
Lecture 3. Optimization Problems and Iterative Algorithms
 Lecture 3 Optimization Problems and Iterative Algorithms January 13, 2016 This material was jointly developed with Angelia Nedić at UIUC for IE 598ns Outline Special Functions: Linear, Quadratic, Convex
Lecture 3 Optimization Problems and Iterative Algorithms January 13, 2016 This material was jointly developed with Angelia Nedić at UIUC for IE 598ns Outline Special Functions: Linear, Quadratic, Convex
Advances in Convex Optimization: Theory, Algorithms, and Applications
 Advances in Convex Optimization: Theory, Algorithms, and Applications Stephen Boyd Electrical Engineering Department Stanford University (joint work with Lieven Vandenberghe, UCLA) ISIT 02 ISIT 02 Lausanne
Advances in Convex Optimization: Theory, Algorithms, and Applications Stephen Boyd Electrical Engineering Department Stanford University (joint work with Lieven Vandenberghe, UCLA) ISIT 02 ISIT 02 Lausanne
Course Outline. FRTN10 Multivariable Control, Lecture 13. General idea for Lectures Lecture 13 Outline. Example 1 (Doyle Stein, 1979)
 Course Outline FRTN Multivariable Control, Lecture Automatic Control LTH, 6 L-L Specifications, models and loop-shaping by hand L6-L8 Limitations on achievable performance L9-L Controller optimization:
Course Outline FRTN Multivariable Control, Lecture Automatic Control LTH, 6 L-L Specifications, models and loop-shaping by hand L6-L8 Limitations on achievable performance L9-L Controller optimization:
Chapter 14 Unconstrained and Constrained Optimization Problems
 main def 2011/9/26 15:22 page 480 #511 Chapter 14 Unconstrained and Constrained Optimization Problems Shuguang Cui, Man-Cho Anthony So, and Rui Zhang Texas A&M University, College Station, USA Chinese
main def 2011/9/26 15:22 page 480 #511 Chapter 14 Unconstrained and Constrained Optimization Problems Shuguang Cui, Man-Cho Anthony So, and Rui Zhang Texas A&M University, College Station, USA Chinese
The proximal mapping
 The proximal mapping http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes Outline 2/37 1 closed function 2 Conjugate function
The proximal mapping http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes Outline 2/37 1 closed function 2 Conjugate function
Convex Functions and Optimization
 Chapter 5 Convex Functions and Optimization 5.1 Convex Functions Our next topic is that of convex functions. Again, we will concentrate on the context of a map f : R n R although the situation can be generalized
Chapter 5 Convex Functions and Optimization 5.1 Convex Functions Our next topic is that of convex functions. Again, we will concentrate on the context of a map f : R n R although the situation can be generalized
The Q-parametrization (Youla) Lecture 13: Synthesis by Convex Optimization. Lecture 13: Synthesis by Convex Optimization. Example: Spring-mass System
 The Q-parametrization (Youla) Lecture 3: Synthesis by Convex Optimization controlled variables z Plant distubances w Example: Spring-mass system measurements y Controller control inputs u Idea for lecture
The Q-parametrization (Youla) Lecture 3: Synthesis by Convex Optimization controlled variables z Plant distubances w Example: Spring-mass system measurements y Controller control inputs u Idea for lecture
Characterizing Robust Solution Sets of Convex Programs under Data Uncertainty
 Characterizing Robust Solution Sets of Convex Programs under Data Uncertainty V. Jeyakumar, G. M. Lee and G. Li Communicated by Sándor Zoltán Németh Abstract This paper deals with convex optimization problems
Characterizing Robust Solution Sets of Convex Programs under Data Uncertainty V. Jeyakumar, G. M. Lee and G. Li Communicated by Sándor Zoltán Németh Abstract This paper deals with convex optimization problems
CSCI 1951-G Optimization Methods in Finance Part 10: Conic Optimization
 CSCI 1951-G Optimization Methods in Finance Part 10: Conic Optimization April 6, 2018 1 / 34 This material is covered in the textbook, Chapters 9 and 10. Some of the materials are taken from it. Some of
CSCI 1951-G Optimization Methods in Finance Part 10: Conic Optimization April 6, 2018 1 / 34 This material is covered in the textbook, Chapters 9 and 10. Some of the materials are taken from it. Some of
CO 250 Final Exam Guide
 Spring 2017 CO 250 Final Exam Guide TABLE OF CONTENTS richardwu.ca CO 250 Final Exam Guide Introduction to Optimization Kanstantsin Pashkovich Spring 2017 University of Waterloo Last Revision: March 4,
Spring 2017 CO 250 Final Exam Guide TABLE OF CONTENTS richardwu.ca CO 250 Final Exam Guide Introduction to Optimization Kanstantsin Pashkovich Spring 2017 University of Waterloo Last Revision: March 4,
Approximation Algorithms
 Approximation Algorithms Chapter 26 Semidefinite Programming Zacharias Pitouras 1 Introduction LP place a good lower bound on OPT for NP-hard problems Are there other ways of doing this? Vector programs
Approximation Algorithms Chapter 26 Semidefinite Programming Zacharias Pitouras 1 Introduction LP place a good lower bound on OPT for NP-hard problems Are there other ways of doing this? Vector programs
3. Convex functions. basic properties and examples. operations that preserve convexity. the conjugate function. quasiconvex functions
 3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
minimize x subject to (x 2)(x 4) u,
 Math 6366/6367: Optimization and Variational Methods Sample Preliminary Exam Questions 1. Suppose that f : [, L] R is a C 2 -function with f () on (, L) and that you have explicit formulae for
Math 6366/6367: Optimization and Variational Methods Sample Preliminary Exam Questions 1. Suppose that f : [, L] R is a C 2 -function with f () on (, L) and that you have explicit formulae for
Lecture 6: Conic Optimization September 8
 IE 598: Big Data Optimization Fall 2016 Lecture 6: Conic Optimization September 8 Lecturer: Niao He Scriber: Juan Xu Overview In this lecture, we finish up our previous discussion on optimality conditions
IE 598: Big Data Optimization Fall 2016 Lecture 6: Conic Optimization September 8 Lecturer: Niao He Scriber: Juan Xu Overview In this lecture, we finish up our previous discussion on optimality conditions
LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE
 LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE CONVEX ANALYSIS AND DUALITY Basic concepts of convex analysis Basic concepts of convex optimization Geometric duality framework - MC/MC Constrained optimization
LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE CONVEX ANALYSIS AND DUALITY Basic concepts of convex analysis Basic concepts of convex optimization Geometric duality framework - MC/MC Constrained optimization
COM Optimization for Communications 8. Semidefinite Programming
 COM524500 Optimization for Communications 8. Semidefinite Programming Institute Comm. Eng. & Dept. Elect. Eng., National Tsing Hua University 1 Semidefinite Programming () Inequality form: min c T x s.t.
COM524500 Optimization for Communications 8. Semidefinite Programming Institute Comm. Eng. & Dept. Elect. Eng., National Tsing Hua University 1 Semidefinite Programming () Inequality form: min c T x s.t.
Mathematical Optimization Models and Applications
 Mathematical Optimization Models and Applications Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/ yyye Chapters 1, 2.1-2,
Mathematical Optimization Models and Applications Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/ yyye Chapters 1, 2.1-2,
Convex Optimization. Convex Analysis - Functions
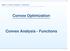 Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
10-725/36-725: Convex Optimization Prerequisite Topics
 10-725/36-725: Convex Optimization Prerequisite Topics February 3, 2015 This is meant to be a brief, informal refresher of some topics that will form building blocks in this course. The content of the
10-725/36-725: Convex Optimization Prerequisite Topics February 3, 2015 This is meant to be a brief, informal refresher of some topics that will form building blocks in this course. The content of the
Lecture: Introduction to LP, SDP and SOCP
 Lecture: Introduction to LP, SDP and SOCP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2015.html wenzw@pku.edu.cn Acknowledgement:
Lecture: Introduction to LP, SDP and SOCP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2015.html wenzw@pku.edu.cn Acknowledgement:
4. Convex optimization problems (part 1: general)
 EE/AA 578, Univ of Washington, Fall 2016 4. Convex optimization problems (part 1: general) optimization problem in standard form convex optimization problems quasiconvex optimization 4 1 Optimization problem
EE/AA 578, Univ of Washington, Fall 2016 4. Convex optimization problems (part 1: general) optimization problem in standard form convex optimization problems quasiconvex optimization 4 1 Optimization problem
Chapter 1. Preliminaries. The purpose of this chapter is to provide some basic background information. Linear Space. Hilbert Space.
 Chapter 1 Preliminaries The purpose of this chapter is to provide some basic background information. Linear Space Hilbert Space Basic Principles 1 2 Preliminaries Linear Space The notion of linear space
Chapter 1 Preliminaries The purpose of this chapter is to provide some basic background information. Linear Space Hilbert Space Basic Principles 1 2 Preliminaries Linear Space The notion of linear space
Semidefinite Programming
 Chapter 2 Semidefinite Programming 2.0.1 Semi-definite programming (SDP) Given C M n, A i M n, i = 1, 2,..., m, and b R m, the semi-definite programming problem is to find a matrix X M n for the optimization
Chapter 2 Semidefinite Programming 2.0.1 Semi-definite programming (SDP) Given C M n, A i M n, i = 1, 2,..., m, and b R m, the semi-definite programming problem is to find a matrix X M n for the optimization
FRTN10 Multivariable Control, Lecture 13. Course outline. The Q-parametrization (Youla) Example: Spring-mass System
 FRTN Multivariable Control, Lecture 3 Anders Robertsson Automatic Control LTH, Lund University Course outline The Q-parametrization (Youla) L-L5 Purpose, models and loop-shaping by hand L6-L8 Limitations
FRTN Multivariable Control, Lecture 3 Anders Robertsson Automatic Control LTH, Lund University Course outline The Q-parametrization (Youla) L-L5 Purpose, models and loop-shaping by hand L6-L8 Limitations
Gauge optimization and duality
 1 / 54 Gauge optimization and duality Junfeng Yang Department of Mathematics Nanjing University Joint with Shiqian Ma, CUHK September, 2015 2 / 54 Outline Introduction Duality Lagrange duality Fenchel
1 / 54 Gauge optimization and duality Junfeng Yang Department of Mathematics Nanjing University Joint with Shiqian Ma, CUHK September, 2015 2 / 54 Outline Introduction Duality Lagrange duality Fenchel
Chapter 2 Convex Analysis
 Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
Lecture: Duality.
 Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
Selected Methods for Modern Optimization in Data Analysis Department of Statistics and Operations Research UNC-Chapel Hill Fall 2018
 Selected Methods for Modern Optimization in Data Analysis Department of Statistics and Operations Research UNC-Chapel Hill Fall 208 Instructor: Quoc Tran-Dinh Scriber: Quoc Tran-Dinh Lecture : Introduction
Selected Methods for Modern Optimization in Data Analysis Department of Statistics and Operations Research UNC-Chapel Hill Fall 208 Instructor: Quoc Tran-Dinh Scriber: Quoc Tran-Dinh Lecture : Introduction
More First-Order Optimization Algorithms
 More First-Order Optimization Algorithms Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/ yyye Chapters 3, 8, 3 The SDM
More First-Order Optimization Algorithms Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/ yyye Chapters 3, 8, 3 The SDM
Math 273a: Optimization Subgradients of convex functions
 Math 273a: Optimization Subgradients of convex functions Made by: Damek Davis Edited by Wotao Yin Department of Mathematics, UCLA Fall 2015 online discussions on piazza.com 1 / 20 Subgradients Assumptions
Math 273a: Optimization Subgradients of convex functions Made by: Damek Davis Edited by Wotao Yin Department of Mathematics, UCLA Fall 2015 online discussions on piazza.com 1 / 20 Subgradients Assumptions
Primal-Dual Geometry of Level Sets and their Explanatory Value of the Practical Performance of Interior-Point Methods for Conic Optimization
 Primal-Dual Geometry of Level Sets and their Explanatory Value of the Practical Performance of Interior-Point Methods for Conic Optimization Robert M. Freund M.I.T. June, 2010 from papers in SIOPT, Mathematics
Primal-Dual Geometry of Level Sets and their Explanatory Value of the Practical Performance of Interior-Point Methods for Conic Optimization Robert M. Freund M.I.T. June, 2010 from papers in SIOPT, Mathematics
Static Problem Set 2 Solutions
 Static Problem Set Solutions Jonathan Kreamer July, 0 Question (i) Let g, h be two concave functions. Is f = g + h a concave function? Prove it. Yes. Proof: Consider any two points x, x and α [0, ]. Let
Static Problem Set Solutions Jonathan Kreamer July, 0 Question (i) Let g, h be two concave functions. Is f = g + h a concave function? Prove it. Yes. Proof: Consider any two points x, x and α [0, ]. Let
Lagrange Duality. Daniel P. Palomar. Hong Kong University of Science and Technology (HKUST)
 Lagrange Duality Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Lagrangian Dual function Dual
Lagrange Duality Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Lagrangian Dual function Dual
