13. Convex programming
|
|
|
- Rosa Anderson
- 6 years ago
- Views:
Transcription
1 CS/ISyE/ECE 524 Introduction to Optimization Spring Convex programming Convex sets and functions Convex programs Hierarchy of complexity Example: geometric programming Laurent Lessard (
2 Convex sets A set of points C R n is convex if for all points x, y C and any real number 0 α 1, we have αx + (1 α)y C. all points in C can see each other. can be closed or open (includes boundary or not), or some combination where only some boundary points are included. can be bounded or unbounded. x C y 13-2
3 Convex sets Intersections preserve convexity: If I is a collection of convex sets {C i } i I, then the intersection S = i I C i is convex. proof: Suppose x, y S and 0 α 1. By definition, x, y C i for each i I. By the convexity of C i, we must have αx + (1 α)y C i as well. Therefore αx + (1 α)y S, and we are done. note: The union of convex sets C 1 C 2 is need not be convex! 13-3
4 Convex sets Constraints can be characterized by sets! If we define C 1 := {x R n Ax b} then: Ax b x C 1 If we define C 2 := {x R n Fx = g} then: Ax b and Fx = g x C 1 C
5 Convex sets Example: SOCP Let C := { x R n Ax + b c T x + d }. To prove C is convex, suppose x, y C and let z := αx + (1 α)y. Then: Az + b = A(αx + (1 α)y) + b = α(ax + b) + (1 α)(ay + b) α Ax + b + (1 α) Ay + b α(c T x + d) + (1 α)(c T y + d) = c T z + d Therefore, Az + b c T z + d, i.e. C is convex. 13-5
6 Convex sets Example: spectrahedron { [ ] } 1 x1 x 2 Let C := x R 3 x 1 1 x 3 0. To prove C is x 2 x 3 1 convex, consider the set S := { X R 3 3 X = X T 0 } Note that S is the PSD cone. It is convex because if we define Z := αx + (1 α)y where X, Y S and 0 α 1, then w T Zw = w T (αx + (1 α)y ) w = αw T Xw + (1 α)w T Yw So if X 0 and Y 0, then Z 0. So S is convex. Now, C is convex because it s the intersection of two convex sets: the PSD cone S and the affine space {X R 3 3 X ii = 1}. 13-6
7 Convex functions If C R n, a function f : C R is convex if C is a convex set and for all x, y C and 0 α 1, we have: f (αx + (1 α)y) αf (x) + (1 α)f (y) f is concave if f is convex. f(x) 3 2 y 1 x x 13-7
8 Convex and concave functions Convex functions on R: Affine: ax + b. Absolute value: x. Quadratic: ax 2 for any a 0. Exponential: a x for any a > 0. Powers: x α for x > 0, α 1 or α 0. Negative entropy: x log x for x > 0. Concave functions on R: Affine: ax + b. Quadratic: ax 2 for any a 0. Powers: x α for x > 0, 0 α 1. Logarithm: log x for x >
9 Convex and concave functions Convex functions on R n : Affine: a T x + b. Norms: x 2, x 1, x Quadratic form: x T Qx for any Q
10 Building convex functions 1. Nonnegative weighted sum: If f (x) and g(x) are convex and α, β 0, then αf (x) + βg(x) is convex. 2. Composition with an affine function: If f (x) is convex, so is g(x) := f (Ax + b) 3. Pointwise maximum: If f 1 (x),..., f k (x) are convex, then g(x) := max {f 1 (x),..., f k (x)} is convex. proof: Let z := αx + (1 α)y as usual. g(z) = f (Az + b) = f (α(ax + b) + (1 α)(ay + b)) αf (Ax + b) + (1 α)f (Ay + b) = αg(x) + (1 α)g(y) 13-10
11 Convex functions vs sets Level set: If f is a convex function, then the set of points satisfying f (x) a is a convex set. If all level sets are convex, then f is not necessarily convex! 13-11
12 Convex functions vs sets Epigraph: f : R n R is a convex function if and only if the set {(x, t) R n+1 f (x) t} is convex. f(x) t x x plot of f (x) {(x, t) f (x) t} 13-12
13 Convex programs The standard form for a convex optimization problem: minimize x f 0 (x) subject to: f i (x) 0 for i = 1,..., k Ax = b x C f 0, f 1,..., f k are convex functions C is a convex set 13-13
14 Convex programs Can turn f 0 (x) into a linear constraint (use epigraph) Can characterize constraints using sets. Minimalist form: minimize x S c T x S is a convex set 13-14
15 Key properties and advantages 1. The set of optimal points x is itself a convex set. Proof: If x and y are optimal, then we must have f = f 0 (x ) = f 0 (y ). Also, f f 0 (z) for any z. Choose z := αx + (1 α)y with 0 α 1. By convexity of f 0, f f 0 (αx + (1 α)y ) αf 0 (x ) + (1 α)f 0 (y ) = f. Therefore, f 0 (z) = f, i.e. z is also an optimal point. 2. If x is a locally optimal point, then it is globally optimal. Follows from the result above. A very powerful fact! 3. Upper an lower bounds available via duality (more later!) 4. Often numerically tractable (not always!) 13-15
16 Hierarchy of programs From least general to most general model: 1. LP: linear cost and linear constraints 2. QP: convex quadratic cost and linear constraints 3. QCQP: convex quadratic cost and constraints 4. SOCP: linear cost, second order cone constraints 5. SDP: linear cost, semidefinite constraints 6. CVX: convex cost and constraints Less general (simpler) models are typically preferable! 13-16
17 Solving convex problems Simpler models are usually more efficient to solve Factors affecting solver speed: How difficult is it to verify that x C? How difficult is it to project onto C? How difficult is it to evaluate f (x)? How difficult is it to compute f (x)? Can the solver take advantage of sparsity? 13-17
18 Example: geometric programming The log-sum-exp function (shown left) is convex: ( n ) f (x) := log exp x k k=1 It s a smoothed version of max{x 1,..., x k } (shown right) 13-18
19 Example: geometric programming Suppose we have positive decision variables x i > 0, and constraints of the form (with each c j > 0 and α jk R): j=1 c j x α j1 1 x α j2 2 x α jn n 1 Then by using the substitution y i := log(x i ), we have: ( n ) log exp (a j0 + a j1 y a jn y n ) 0 j=1 (where a j0 := log c j ). This is a log-sum-exp function composed with an affine function (convex!) 13-19
20 Example: geometric programming Example: We want to design a box of height h, width w, and depth d with maximum volume (hwd) subject to the limits: total wall area: 2(hw + hd) A wall total floor area: wd A flr height-width aspect ratio: α h w β width-depth aspect ratio: γ d w δ We can make some of the constraints linear, but not all of them. This appears to be a nonconvex optimization problem
21 Example: geometric programming Example: We want to design a box of height h, width w, and depth d with maximum volume (hwd) subject to the limits: total wall area: 2(hw + hd) A wall total floor area: wd A flr height-width aspect ratio: α h w β width-depth aspect ratio: γ d w δ minimize h,w,d > 0 h 1 w 1 d 1 subject to: 2 A wall hw + 2 A wall hd 1, 1 A flr wd 1 αh 1 w 1, 1 β hw 1 1 γwd 1 1, 1 δ w 1 d
22 Example: geometric programming minimize h,w,d > 0 h 1 w 1 d 1 subject to: 2 A wall hw + 2 A wall hd 1, 1 A flr wd 1 αh 1 w 1, 1 β hw 1 1 γwd 1 1, 1 δ w 1 d 1 Define: x := log h, y := log w, and z := log d. Express the problem in terms of the new variables x, y, z. Note: h, w, d are positive but x, y, z are unconstrained
23 Example: geometric programming minimize x,y,z log(e x y z ) subject to: log(e log(2/a wall)+x+y + e log(2/a wall)+x+z ) 0 log(e log(1/a flr)+y+z ) 0 log(e log α x+y ) 0, log(e log β+x y ) 0 log(e log γ+y z ) 0, log(e log δ y+z ) 0 this is a convex model, but it can be simplified! most of the constraints are actually linear
24 Example: geometric programming minimize x,y,z x y z subject to: log(e log(2/a wall)+x+y + e log(2/a wall)+x+z ) 0 y + z log A flr log α x y log β log γ z y log δ This is a convex optimization problem
Lecture 2: Convex Sets and Functions
 Lecture 2: Convex Sets and Functions Hyang-Won Lee Dept. of Internet & Multimedia Eng. Konkuk University Lecture 2 Network Optimization, Fall 2015 1 / 22 Optimization Problems Optimization problems are
Lecture 2: Convex Sets and Functions Hyang-Won Lee Dept. of Internet & Multimedia Eng. Konkuk University Lecture 2 Network Optimization, Fall 2015 1 / 22 Optimization Problems Optimization problems are
14. Duality. ˆ Upper and lower bounds. ˆ General duality. ˆ Constraint qualifications. ˆ Counterexample. ˆ Complementary slackness.
 CS/ECE/ISyE 524 Introduction to Optimization Spring 2016 17 14. Duality ˆ Upper and lower bounds ˆ General duality ˆ Constraint qualifications ˆ Counterexample ˆ Complementary slackness ˆ Examples ˆ Sensitivity
CS/ECE/ISyE 524 Introduction to Optimization Spring 2016 17 14. Duality ˆ Upper and lower bounds ˆ General duality ˆ Constraint qualifications ˆ Counterexample ˆ Complementary slackness ˆ Examples ˆ Sensitivity
15. Conic optimization
 L. Vandenberghe EE236C (Spring 216) 15. Conic optimization conic linear program examples modeling duality 15-1 Generalized (conic) inequalities Conic inequality: a constraint x K where K is a convex cone
L. Vandenberghe EE236C (Spring 216) 15. Conic optimization conic linear program examples modeling duality 15-1 Generalized (conic) inequalities Conic inequality: a constraint x K where K is a convex cone
Linear and non-linear programming
 Linear and non-linear programming Benjamin Recht March 11, 2005 The Gameplan Constrained Optimization Convexity Duality Applications/Taxonomy 1 Constrained Optimization minimize f(x) subject to g j (x)
Linear and non-linear programming Benjamin Recht March 11, 2005 The Gameplan Constrained Optimization Convexity Duality Applications/Taxonomy 1 Constrained Optimization minimize f(x) subject to g j (x)
N. L. P. NONLINEAR PROGRAMMING (NLP) deals with optimization models with at least one nonlinear function. NLP. Optimization. Models of following form:
 0.1 N. L. P. Katta G. Murty, IOE 611 Lecture slides Introductory Lecture NONLINEAR PROGRAMMING (NLP) deals with optimization models with at least one nonlinear function. NLP does not include everything
0.1 N. L. P. Katta G. Murty, IOE 611 Lecture slides Introductory Lecture NONLINEAR PROGRAMMING (NLP) deals with optimization models with at least one nonlinear function. NLP does not include everything
4. Convex optimization problems
 Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
The Q-parametrization (Youla) Lecture 13: Synthesis by Convex Optimization. Lecture 13: Synthesis by Convex Optimization. Example: Spring-mass System
 The Q-parametrization (Youla) Lecture 3: Synthesis by Convex Optimization controlled variables z Plant distubances w Example: Spring-mass system measurements y Controller control inputs u Idea for lecture
The Q-parametrization (Youla) Lecture 3: Synthesis by Convex Optimization controlled variables z Plant distubances w Example: Spring-mass system measurements y Controller control inputs u Idea for lecture
5. Duality. Lagrangian
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
Convex Optimization M2
 Convex Optimization M2 Lecture 3 A. d Aspremont. Convex Optimization M2. 1/49 Duality A. d Aspremont. Convex Optimization M2. 2/49 DMs DM par email: dm.daspremont@gmail.com A. d Aspremont. Convex Optimization
Convex Optimization M2 Lecture 3 A. d Aspremont. Convex Optimization M2. 1/49 Duality A. d Aspremont. Convex Optimization M2. 2/49 DMs DM par email: dm.daspremont@gmail.com A. d Aspremont. Convex Optimization
Semidefinite Programming Basics and Applications
 Semidefinite Programming Basics and Applications Ray Pörn, principal lecturer Åbo Akademi University Novia University of Applied Sciences Content What is semidefinite programming (SDP)? How to represent
Semidefinite Programming Basics and Applications Ray Pörn, principal lecturer Åbo Akademi University Novia University of Applied Sciences Content What is semidefinite programming (SDP)? How to represent
FRTN10 Multivariable Control, Lecture 13. Course outline. The Q-parametrization (Youla) Example: Spring-mass System
 FRTN Multivariable Control, Lecture 3 Anders Robertsson Automatic Control LTH, Lund University Course outline The Q-parametrization (Youla) L-L5 Purpose, models and loop-shaping by hand L6-L8 Limitations
FRTN Multivariable Control, Lecture 3 Anders Robertsson Automatic Control LTH, Lund University Course outline The Q-parametrization (Youla) L-L5 Purpose, models and loop-shaping by hand L6-L8 Limitations
3. Convex functions. basic properties and examples. operations that preserve convexity. the conjugate function. quasiconvex functions
 3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
Lecture: Convex Optimization Problems
 1/36 Lecture: Convex Optimization Problems http://bicmr.pku.edu.cn/~wenzw/opt-2015-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/36 optimization
1/36 Lecture: Convex Optimization Problems http://bicmr.pku.edu.cn/~wenzw/opt-2015-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/36 optimization
Convex Optimization. (EE227A: UC Berkeley) Lecture 6. Suvrit Sra. (Conic optimization) 07 Feb, 2013
 Convex Optimization (EE227A: UC Berkeley) Lecture 6 (Conic optimization) 07 Feb, 2013 Suvrit Sra Organizational Info Quiz coming up on 19th Feb. Project teams by 19th Feb Good if you can mix your research
Convex Optimization (EE227A: UC Berkeley) Lecture 6 (Conic optimization) 07 Feb, 2013 Suvrit Sra Organizational Info Quiz coming up on 19th Feb. Project teams by 19th Feb Good if you can mix your research
minimize x x2 2 x 1x 2 x 1 subject to x 1 +2x 2 u 1 x 1 4x 2 u 2, 5x 1 +76x 2 1,
 4 Duality 4.1 Numerical perturbation analysis example. Consider the quadratic program with variables x 1, x 2, and parameters u 1, u 2. minimize x 2 1 +2x2 2 x 1x 2 x 1 subject to x 1 +2x 2 u 1 x 1 4x
4 Duality 4.1 Numerical perturbation analysis example. Consider the quadratic program with variables x 1, x 2, and parameters u 1, u 2. minimize x 2 1 +2x2 2 x 1x 2 x 1 subject to x 1 +2x 2 u 1 x 1 4x
Lecture: Duality.
 Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
Course Outline. FRTN10 Multivariable Control, Lecture 13. General idea for Lectures Lecture 13 Outline. Example 1 (Doyle Stein, 1979)
 Course Outline FRTN Multivariable Control, Lecture Automatic Control LTH, 6 L-L Specifications, models and loop-shaping by hand L6-L8 Limitations on achievable performance L9-L Controller optimization:
Course Outline FRTN Multivariable Control, Lecture Automatic Control LTH, 6 L-L Specifications, models and loop-shaping by hand L6-L8 Limitations on achievable performance L9-L Controller optimization:
Lecture: Duality of LP, SOCP and SDP
 1/33 Lecture: Duality of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2017.html wenzw@pku.edu.cn Acknowledgement:
1/33 Lecture: Duality of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2017.html wenzw@pku.edu.cn Acknowledgement:
Agenda. 1 Cone programming. 2 Convex cones. 3 Generalized inequalities. 4 Linear programming (LP) 5 Second-order cone programming (SOCP)
 Agenda 1 Cone programming 2 Convex cones 3 Generalized inequalities 4 Linear programming (LP) 5 Second-order cone programming (SOCP) 6 Semidefinite programming (SDP) 7 Examples Optimization problem in
Agenda 1 Cone programming 2 Convex cones 3 Generalized inequalities 4 Linear programming (LP) 5 Second-order cone programming (SOCP) 6 Semidefinite programming (SDP) 7 Examples Optimization problem in
Convex Optimization. (EE227A: UC Berkeley) Lecture 28. Suvrit Sra. (Algebra + Optimization) 02 May, 2013
 Convex Optimization (EE227A: UC Berkeley) Lecture 28 (Algebra + Optimization) 02 May, 2013 Suvrit Sra Admin Poster presentation on 10th May mandatory HW, Midterm, Quiz to be reweighted Project final report
Convex Optimization (EE227A: UC Berkeley) Lecture 28 (Algebra + Optimization) 02 May, 2013 Suvrit Sra Admin Poster presentation on 10th May mandatory HW, Midterm, Quiz to be reweighted Project final report
Convex Optimization Boyd & Vandenberghe. 5. Duality
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
Convex Optimization and l 1 -minimization
 Convex Optimization and l 1 -minimization Sangwoon Yun Computational Sciences Korea Institute for Advanced Study December 11, 2009 2009 NIMS Thematic Winter School Outline I. Convex Optimization II. l
Convex Optimization and l 1 -minimization Sangwoon Yun Computational Sciences Korea Institute for Advanced Study December 11, 2009 2009 NIMS Thematic Winter School Outline I. Convex Optimization II. l
Convex Functions. Daniel P. Palomar. Hong Kong University of Science and Technology (HKUST)
 Convex Functions Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Definition convex function Examples
Convex Functions Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Definition convex function Examples
Convex optimization problems. Optimization problem in standard form
 Convex optimization problems optimization problem in standard form convex optimization problems linear optimization quadratic optimization geometric programming quasiconvex optimization generalized inequality
Convex optimization problems optimization problem in standard form convex optimization problems linear optimization quadratic optimization geometric programming quasiconvex optimization generalized inequality
Interior Point Methods: Second-Order Cone Programming and Semidefinite Programming
 School of Mathematics T H E U N I V E R S I T Y O H F E D I N B U R G Interior Point Methods: Second-Order Cone Programming and Semidefinite Programming Jacek Gondzio Email: J.Gondzio@ed.ac.uk URL: http://www.maths.ed.ac.uk/~gondzio
School of Mathematics T H E U N I V E R S I T Y O H F E D I N B U R G Interior Point Methods: Second-Order Cone Programming and Semidefinite Programming Jacek Gondzio Email: J.Gondzio@ed.ac.uk URL: http://www.maths.ed.ac.uk/~gondzio
EE Applications of Convex Optimization in Signal Processing and Communications Dr. Andre Tkacenko, JPL Third Term
 EE 150 - Applications of Convex Optimization in Signal Processing and Communications Dr. Andre Tkacenko JPL Third Term 2011-2012 Due on Thursday May 3 in class. Homework Set #4 1. (10 points) (Adapted
EE 150 - Applications of Convex Optimization in Signal Processing and Communications Dr. Andre Tkacenko JPL Third Term 2011-2012 Due on Thursday May 3 in class. Homework Set #4 1. (10 points) (Adapted
3. Convex functions. basic properties and examples. operations that preserve convexity. the conjugate function. quasiconvex functions
 3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
8. Conjugate functions
 L. Vandenberghe EE236C (Spring 2013-14) 8. Conjugate functions closed functions conjugate function 8-1 Closed set a set C is closed if it contains its boundary: x k C, x k x = x C operations that preserve
L. Vandenberghe EE236C (Spring 2013-14) 8. Conjugate functions closed functions conjugate function 8-1 Closed set a set C is closed if it contains its boundary: x k C, x k x = x C operations that preserve
A : k n. Usually k > n otherwise easily the minimum is zero. Analytical solution:
 1-5: Least-squares I A : k n. Usually k > n otherwise easily the minimum is zero. Analytical solution: f (x) =(Ax b) T (Ax b) =x T A T Ax 2b T Ax + b T b f (x) = 2A T Ax 2A T b = 0 Chih-Jen Lin (National
1-5: Least-squares I A : k n. Usually k > n otherwise easily the minimum is zero. Analytical solution: f (x) =(Ax b) T (Ax b) =x T A T Ax 2b T Ax + b T b f (x) = 2A T Ax 2A T b = 0 Chih-Jen Lin (National
ORF 523 Lecture 9 Spring 2016, Princeton University Instructor: A.A. Ahmadi Scribe: G. Hall Thursday, March 10, 2016
 ORF 523 Lecture 9 Spring 2016, Princeton University Instructor: A.A. Ahmadi Scribe: G. Hall Thursday, March 10, 2016 When in doubt on the accuracy of these notes, please cross check with the instructor
ORF 523 Lecture 9 Spring 2016, Princeton University Instructor: A.A. Ahmadi Scribe: G. Hall Thursday, March 10, 2016 When in doubt on the accuracy of these notes, please cross check with the instructor
Lecture: Examples of LP, SOCP and SDP
 1/34 Lecture: Examples of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2018.html wenzw@pku.edu.cn Acknowledgement:
1/34 Lecture: Examples of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2018.html wenzw@pku.edu.cn Acknowledgement:
CS675: Convex and Combinatorial Optimization Fall 2016 Convex Optimization Problems. Instructor: Shaddin Dughmi
 CS675: Convex and Combinatorial Optimization Fall 2016 Convex Optimization Problems Instructor: Shaddin Dughmi Outline 1 Convex Optimization Basics 2 Common Classes 3 Interlude: Positive Semi-Definite
CS675: Convex and Combinatorial Optimization Fall 2016 Convex Optimization Problems Instructor: Shaddin Dughmi Outline 1 Convex Optimization Basics 2 Common Classes 3 Interlude: Positive Semi-Definite
A : k n. Usually k > n otherwise easily the minimum is zero. Analytical solution:
 1-5: Least-squares I A : k n. Usually k > n otherwise easily the minimum is zero. Analytical solution: f (x) =(Ax b) T (Ax b) =x T A T Ax 2b T Ax + b T b f (x) = 2A T Ax 2A T b = 0 Chih-Jen Lin (National
1-5: Least-squares I A : k n. Usually k > n otherwise easily the minimum is zero. Analytical solution: f (x) =(Ax b) T (Ax b) =x T A T Ax 2b T Ax + b T b f (x) = 2A T Ax 2A T b = 0 Chih-Jen Lin (National
Module 04 Optimization Problems KKT Conditions & Solvers
 Module 04 Optimization Problems KKT Conditions & Solvers Ahmad F. Taha EE 5243: Introduction to Cyber-Physical Systems Email: ahmad.taha@utsa.edu Webpage: http://engineering.utsa.edu/ taha/index.html September
Module 04 Optimization Problems KKT Conditions & Solvers Ahmad F. Taha EE 5243: Introduction to Cyber-Physical Systems Email: ahmad.taha@utsa.edu Webpage: http://engineering.utsa.edu/ taha/index.html September
Tutorial on Convex Optimization for Engineers Part II
 Tutorial on Convex Optimization for Engineers Part II M.Sc. Jens Steinwandt Communications Research Laboratory Ilmenau University of Technology PO Box 100565 D-98684 Ilmenau, Germany jens.steinwandt@tu-ilmenau.de
Tutorial on Convex Optimization for Engineers Part II M.Sc. Jens Steinwandt Communications Research Laboratory Ilmenau University of Technology PO Box 100565 D-98684 Ilmenau, Germany jens.steinwandt@tu-ilmenau.de
4. Convex optimization problems
 Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
I.3. LMI DUALITY. Didier HENRION EECI Graduate School on Control Supélec - Spring 2010
 I.3. LMI DUALITY Didier HENRION henrion@laas.fr EECI Graduate School on Control Supélec - Spring 2010 Primal and dual For primal problem p = inf x g 0 (x) s.t. g i (x) 0 define Lagrangian L(x, z) = g 0
I.3. LMI DUALITY Didier HENRION henrion@laas.fr EECI Graduate School on Control Supélec - Spring 2010 Primal and dual For primal problem p = inf x g 0 (x) s.t. g i (x) 0 define Lagrangian L(x, z) = g 0
Convex Optimization and Modeling
 Convex Optimization and Modeling Convex Optimization Fourth lecture, 05.05.2010 Jun.-Prof. Matthias Hein Reminder from last time Convex functions: first-order condition: f(y) f(x) + f x,y x, second-order
Convex Optimization and Modeling Convex Optimization Fourth lecture, 05.05.2010 Jun.-Prof. Matthias Hein Reminder from last time Convex functions: first-order condition: f(y) f(x) + f x,y x, second-order
Lecture Note 5: Semidefinite Programming for Stability Analysis
 ECE7850: Hybrid Systems:Theory and Applications Lecture Note 5: Semidefinite Programming for Stability Analysis Wei Zhang Assistant Professor Department of Electrical and Computer Engineering Ohio State
ECE7850: Hybrid Systems:Theory and Applications Lecture Note 5: Semidefinite Programming for Stability Analysis Wei Zhang Assistant Professor Department of Electrical and Computer Engineering Ohio State
14. Nonlinear equations
 L. Vandenberghe ECE133A (Winter 2018) 14. Nonlinear equations Newton method for nonlinear equations damped Newton method for unconstrained minimization Newton method for nonlinear least squares 14-1 Set
L. Vandenberghe ECE133A (Winter 2018) 14. Nonlinear equations Newton method for nonlinear equations damped Newton method for unconstrained minimization Newton method for nonlinear least squares 14-1 Set
CSCI : Optimization and Control of Networks. Review on Convex Optimization
 CSCI7000-016: Optimization and Control of Networks Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one
CSCI7000-016: Optimization and Control of Networks Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one
HW1 solutions. 1. α Ef(x) β, where Ef(x) is the expected value of f(x), i.e., Ef(x) = n. i=1 p if(a i ). (The function f : R R is given.
 HW1 solutions Exercise 1 (Some sets of probability distributions.) Let x be a real-valued random variable with Prob(x = a i ) = p i, i = 1,..., n, where a 1 < a 2 < < a n. Of course p R n lies in the standard
HW1 solutions Exercise 1 (Some sets of probability distributions.) Let x be a real-valued random variable with Prob(x = a i ) = p i, i = 1,..., n, where a 1 < a 2 < < a n. Of course p R n lies in the standard
Lecture 1: January 12
 10-725/36-725: Convex Optimization Fall 2015 Lecturer: Ryan Tibshirani Lecture 1: January 12 Scribes: Seo-Jin Bang, Prabhat KC, Josue Orellana 1.1 Review We begin by going through some examples and key
10-725/36-725: Convex Optimization Fall 2015 Lecturer: Ryan Tibshirani Lecture 1: January 12 Scribes: Seo-Jin Bang, Prabhat KC, Josue Orellana 1.1 Review We begin by going through some examples and key
Lecture 6: Conic Optimization September 8
 IE 598: Big Data Optimization Fall 2016 Lecture 6: Conic Optimization September 8 Lecturer: Niao He Scriber: Juan Xu Overview In this lecture, we finish up our previous discussion on optimality conditions
IE 598: Big Data Optimization Fall 2016 Lecture 6: Conic Optimization September 8 Lecturer: Niao He Scriber: Juan Xu Overview In this lecture, we finish up our previous discussion on optimality conditions
A Brief Review on Convex Optimization
 A Brief Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one convex, two nonconvex sets): A Brief Review
A Brief Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one convex, two nonconvex sets): A Brief Review
LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE
 LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE CONVEX ANALYSIS AND DUALITY Basic concepts of convex analysis Basic concepts of convex optimization Geometric duality framework - MC/MC Constrained optimization
LECTURE 25: REVIEW/EPILOGUE LECTURE OUTLINE CONVEX ANALYSIS AND DUALITY Basic concepts of convex analysis Basic concepts of convex optimization Geometric duality framework - MC/MC Constrained optimization
Solution to EE 617 Mid-Term Exam, Fall November 2, 2017
 Solution to EE 67 Mid-erm Exam, Fall 207 November 2, 207 EE 67 Solution to Mid-erm Exam - Page 2 of 2 November 2, 207 (4 points) Convex sets (a) (2 points) Consider the set { } a R k p(0) =, p(t) for t
Solution to EE 67 Mid-erm Exam, Fall 207 November 2, 207 EE 67 Solution to Mid-erm Exam - Page 2 of 2 November 2, 207 (4 points) Convex sets (a) (2 points) Consider the set { } a R k p(0) =, p(t) for t
Optimisation convexe: performance, complexité et applications.
 Optimisation convexe: performance, complexité et applications. Introduction, convexité, dualité. A. d Aspremont. M2 OJME: Optimisation convexe. 1/128 Today Convex optimization: introduction Course organization
Optimisation convexe: performance, complexité et applications. Introduction, convexité, dualité. A. d Aspremont. M2 OJME: Optimisation convexe. 1/128 Today Convex optimization: introduction Course organization
ELE539A: Optimization of Communication Systems Lecture 15: Semidefinite Programming, Detection and Estimation Applications
 ELE539A: Optimization of Communication Systems Lecture 15: Semidefinite Programming, Detection and Estimation Applications Professor M. Chiang Electrical Engineering Department, Princeton University March
ELE539A: Optimization of Communication Systems Lecture 15: Semidefinite Programming, Detection and Estimation Applications Professor M. Chiang Electrical Engineering Department, Princeton University March
Lecture 4: Convex Functions, Part I February 1
 IE 521: Convex Optimization Instructor: Niao He Lecture 4: Convex Functions, Part I February 1 Spring 2017, UIUC Scribe: Shuanglong Wang Courtesy warning: These notes do not necessarily cover everything
IE 521: Convex Optimization Instructor: Niao He Lecture 4: Convex Functions, Part I February 1 Spring 2017, UIUC Scribe: Shuanglong Wang Courtesy warning: These notes do not necessarily cover everything
EE5138R: Problem Set 5 Assigned: 16/02/15 Due: 06/03/15
 EE538R: Problem Set 5 Assigned: 6/0/5 Due: 06/03/5. BV Problem 4. The feasible set is the convex hull of (0, ), (0, ), (/5, /5), (, 0) and (, 0). (a) x = (/5, /5) (b) Unbounded below (c) X opt = {(0, x
EE538R: Problem Set 5 Assigned: 6/0/5 Due: 06/03/5. BV Problem 4. The feasible set is the convex hull of (0, ), (0, ), (/5, /5), (, 0) and (, 0). (a) x = (/5, /5) (b) Unbounded below (c) X opt = {(0, x
1 Strict local optimality in unconstrained optimization
 ORF 53 Lecture 14 Spring 016, Princeton University Instructor: A.A. Ahmadi Scribe: G. Hall Thursday, April 14, 016 When in doubt on the accuracy of these notes, please cross check with the instructor s
ORF 53 Lecture 14 Spring 016, Princeton University Instructor: A.A. Ahmadi Scribe: G. Hall Thursday, April 14, 016 When in doubt on the accuracy of these notes, please cross check with the instructor s
LMI MODELLING 4. CONVEX LMI MODELLING. Didier HENRION. LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ. Universidad de Valladolid, SP March 2009
 LMI MODELLING 4. CONVEX LMI MODELLING Didier HENRION LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ Universidad de Valladolid, SP March 2009 Minors A minor of a matrix F is the determinant of a submatrix
LMI MODELLING 4. CONVEX LMI MODELLING Didier HENRION LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ Universidad de Valladolid, SP March 2009 Minors A minor of a matrix F is the determinant of a submatrix
Lecture 2: Convex functions
 Lecture 2: Convex functions f : R n R is convex if dom f is convex and for all x, y dom f, θ [0, 1] f is concave if f is convex f(θx + (1 θ)y) θf(x) + (1 θ)f(y) x x convex concave neither x examples (on
Lecture 2: Convex functions f : R n R is convex if dom f is convex and for all x, y dom f, θ [0, 1] f is concave if f is convex f(θx + (1 θ)y) θf(x) + (1 θ)f(y) x x convex concave neither x examples (on
Static Problem Set 2 Solutions
 Static Problem Set Solutions Jonathan Kreamer July, 0 Question (i) Let g, h be two concave functions. Is f = g + h a concave function? Prove it. Yes. Proof: Consider any two points x, x and α [0, ]. Let
Static Problem Set Solutions Jonathan Kreamer July, 0 Question (i) Let g, h be two concave functions. Is f = g + h a concave function? Prove it. Yes. Proof: Consider any two points x, x and α [0, ]. Let
Appendix PRELIMINARIES 1. THEOREMS OF ALTERNATIVES FOR SYSTEMS OF LINEAR CONSTRAINTS
 Appendix PRELIMINARIES 1. THEOREMS OF ALTERNATIVES FOR SYSTEMS OF LINEAR CONSTRAINTS Here we consider systems of linear constraints, consisting of equations or inequalities or both. A feasible solution
Appendix PRELIMINARIES 1. THEOREMS OF ALTERNATIVES FOR SYSTEMS OF LINEAR CONSTRAINTS Here we consider systems of linear constraints, consisting of equations or inequalities or both. A feasible solution
Constrained Optimization and Lagrangian Duality
 CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
Geometric problems. Chapter Projection on a set. The distance of a point x 0 R n to a closed set C R n, in the norm, is defined as
 Chapter 8 Geometric problems 8.1 Projection on a set The distance of a point x 0 R n to a closed set C R n, in the norm, is defined as dist(x 0,C) = inf{ x 0 x x C}. The infimum here is always achieved.
Chapter 8 Geometric problems 8.1 Projection on a set The distance of a point x 0 R n to a closed set C R n, in the norm, is defined as dist(x 0,C) = inf{ x 0 x x C}. The infimum here is always achieved.
Tutorial on Convex Optimization: Part II
 Tutorial on Convex Optimization: Part II Dr. Khaled Ardah Communications Research Laboratory TU Ilmenau Dec. 18, 2018 Outline Convex Optimization Review Lagrangian Duality Applications Optimal Power Allocation
Tutorial on Convex Optimization: Part II Dr. Khaled Ardah Communications Research Laboratory TU Ilmenau Dec. 18, 2018 Outline Convex Optimization Review Lagrangian Duality Applications Optimal Power Allocation
L. Vandenberghe EE236C (Spring 2016) 18. Symmetric cones. definition. spectral decomposition. quadratic representation. log-det barrier 18-1
 L. Vandenberghe EE236C (Spring 2016) 18. Symmetric cones definition spectral decomposition quadratic representation log-det barrier 18-1 Introduction This lecture: theoretical properties of the following
L. Vandenberghe EE236C (Spring 2016) 18. Symmetric cones definition spectral decomposition quadratic representation log-det barrier 18-1 Introduction This lecture: theoretical properties of the following
1. Introduction. mathematical optimization. least-squares and linear programming. convex optimization. example. course goals and topics
 1. Introduction Convex Optimization Boyd & Vandenberghe mathematical optimization least-squares and linear programming convex optimization example course goals and topics nonlinear optimization brief history
1. Introduction Convex Optimization Boyd & Vandenberghe mathematical optimization least-squares and linear programming convex optimization example course goals and topics nonlinear optimization brief history
1. Introduction. mathematical optimization. least-squares and linear programming. convex optimization. example. course goals and topics
 1. Introduction Convex Optimization Boyd & Vandenberghe mathematical optimization least-squares and linear programming convex optimization example course goals and topics nonlinear optimization brief history
1. Introduction Convex Optimization Boyd & Vandenberghe mathematical optimization least-squares and linear programming convex optimization example course goals and topics nonlinear optimization brief history
Constrained optimization
 Constrained optimization DS-GA 1013 / MATH-GA 2824 Optimization-based Data Analysis http://www.cims.nyu.edu/~cfgranda/pages/obda_fall17/index.html Carlos Fernandez-Granda Compressed sensing Convex constrained
Constrained optimization DS-GA 1013 / MATH-GA 2824 Optimization-based Data Analysis http://www.cims.nyu.edu/~cfgranda/pages/obda_fall17/index.html Carlos Fernandez-Granda Compressed sensing Convex constrained
Convex Functions. Wing-Kin (Ken) Ma The Chinese University of Hong Kong (CUHK)
 Convex Functions Wing-Kin (Ken) Ma The Chinese University of Hong Kong (CUHK) Course on Convex Optimization for Wireless Comm. and Signal Proc. Jointly taught by Daniel P. Palomar and Wing-Kin (Ken) Ma
Convex Functions Wing-Kin (Ken) Ma The Chinese University of Hong Kong (CUHK) Course on Convex Optimization for Wireless Comm. and Signal Proc. Jointly taught by Daniel P. Palomar and Wing-Kin (Ken) Ma
Chapter 2: Preliminaries and elements of convex analysis
 Chapter 2: Preliminaries and elements of convex analysis Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-14-15.shtml Academic year 2014-15
Chapter 2: Preliminaries and elements of convex analysis Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-14-15.shtml Academic year 2014-15
Convex Optimization in Communications and Signal Processing
 Convex Optimization in Communications and Signal Processing Prof. Dr.-Ing. Wolfgang Gerstacker 1 University of Erlangen-Nürnberg Institute for Digital Communications National Technical University of Ukraine,
Convex Optimization in Communications and Signal Processing Prof. Dr.-Ing. Wolfgang Gerstacker 1 University of Erlangen-Nürnberg Institute for Digital Communications National Technical University of Ukraine,
12. Interior-point methods
 12. Interior-point methods Convex Optimization Boyd & Vandenberghe inequality constrained minimization logarithmic barrier function and central path barrier method feasibility and phase I methods complexity
12. Interior-point methods Convex Optimization Boyd & Vandenberghe inequality constrained minimization logarithmic barrier function and central path barrier method feasibility and phase I methods complexity
Part I Formulation of convex optimization problems
 Nonlinear Optimization Part I Formulation of convex optimization problems Instituto Superior Técnico Carnegie Mellon University jxavier@isr.ist.utl.pt 1 Convex sets 2 Definition (Convex set) Let V be a
Nonlinear Optimization Part I Formulation of convex optimization problems Instituto Superior Técnico Carnegie Mellon University jxavier@isr.ist.utl.pt 1 Convex sets 2 Definition (Convex set) Let V be a
minimize x subject to (x 2)(x 4) u,
 Math 6366/6367: Optimization and Variational Methods Sample Preliminary Exam Questions 1. Suppose that f : [, L] R is a C 2 -function with f () on (, L) and that you have explicit formulae for
Math 6366/6367: Optimization and Variational Methods Sample Preliminary Exam Questions 1. Suppose that f : [, L] R is a C 2 -function with f () on (, L) and that you have explicit formulae for
Lecture 1: Convex Sets January 23
 IE 521: Convex Optimization Instructor: Niao He Lecture 1: Convex Sets January 23 Spring 2017, UIUC Scribe: Niao He Courtesy warning: These notes do not necessarily cover everything discussed in the class.
IE 521: Convex Optimization Instructor: Niao He Lecture 1: Convex Sets January 23 Spring 2017, UIUC Scribe: Niao He Courtesy warning: These notes do not necessarily cover everything discussed in the class.
EE/AA 578, Univ of Washington, Fall Duality
 7. Duality EE/AA 578, Univ of Washington, Fall 2016 Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
7. Duality EE/AA 578, Univ of Washington, Fall 2016 Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
Lecture 3. Optimization Problems and Iterative Algorithms
 Lecture 3 Optimization Problems and Iterative Algorithms January 13, 2016 This material was jointly developed with Angelia Nedić at UIUC for IE 598ns Outline Special Functions: Linear, Quadratic, Convex
Lecture 3 Optimization Problems and Iterative Algorithms January 13, 2016 This material was jointly developed with Angelia Nedić at UIUC for IE 598ns Outline Special Functions: Linear, Quadratic, Convex
COURSE ON LMI PART I.2 GEOMETRY OF LMI SETS. Didier HENRION henrion
 COURSE ON LMI PART I.2 GEOMETRY OF LMI SETS Didier HENRION www.laas.fr/ henrion October 2006 Geometry of LMI sets Given symmetric matrices F i we want to characterize the shape in R n of the LMI set F
COURSE ON LMI PART I.2 GEOMETRY OF LMI SETS Didier HENRION www.laas.fr/ henrion October 2006 Geometry of LMI sets Given symmetric matrices F i we want to characterize the shape in R n of the LMI set F
Lecture 7: Convex Optimizations
 Lecture 7: Convex Optimizations Radu Balan, David Levermore March 29, 2018 Convex Sets. Convex Functions A set S R n is called a convex set if for any points x, y S the line segment [x, y] := {tx + (1
Lecture 7: Convex Optimizations Radu Balan, David Levermore March 29, 2018 Convex Sets. Convex Functions A set S R n is called a convex set if for any points x, y S the line segment [x, y] := {tx + (1
Convex Optimization. Convex Analysis - Functions
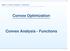 Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
A solution approach for linear optimization with completely positive matrices
 A solution approach for linear optimization with completely positive matrices Franz Rendl http://www.math.uni-klu.ac.at Alpen-Adria-Universität Klagenfurt Austria joint work with M. Bomze (Wien) and F.
A solution approach for linear optimization with completely positive matrices Franz Rendl http://www.math.uni-klu.ac.at Alpen-Adria-Universität Klagenfurt Austria joint work with M. Bomze (Wien) and F.
Convex functions. Definition. f : R n! R is convex if dom f is a convex set and. f ( x +(1 )y) < f (x)+(1 )f (y) f ( x +(1 )y) apple f (x)+(1 )f (y)
 Convex functions I basic properties and I operations that preserve convexity I quasiconvex functions I log-concave and log-convex functions IOE 611: Nonlinear Programming, Fall 2017 3. Convex functions
Convex functions I basic properties and I operations that preserve convexity I quasiconvex functions I log-concave and log-convex functions IOE 611: Nonlinear Programming, Fall 2017 3. Convex functions
Math 205b Homework 2 Solutions
 Math 5b Homework Solutions January 5, 5 Problem (R-S, II.) () For the R case, we just expand the right hand side and use the symmetry of the inner product: ( x y x y ) = = ((x, x) (y, y) (x, y) (y, x)
Math 5b Homework Solutions January 5, 5 Problem (R-S, II.) () For the R case, we just expand the right hand side and use the symmetry of the inner product: ( x y x y ) = = ((x, x) (y, y) (x, y) (y, x)
Lagrange duality. The Lagrangian. We consider an optimization program of the form
 Lagrange duality Another way to arrive at the KKT conditions, and one which gives us some insight on solving constrained optimization problems, is through the Lagrange dual. The dual is a maximization
Lagrange duality Another way to arrive at the KKT conditions, and one which gives us some insight on solving constrained optimization problems, is through the Lagrange dual. The dual is a maximization
Chapter 1. Preliminaries. The purpose of this chapter is to provide some basic background information. Linear Space. Hilbert Space.
 Chapter 1 Preliminaries The purpose of this chapter is to provide some basic background information. Linear Space Hilbert Space Basic Principles 1 2 Preliminaries Linear Space The notion of linear space
Chapter 1 Preliminaries The purpose of this chapter is to provide some basic background information. Linear Space Hilbert Space Basic Principles 1 2 Preliminaries Linear Space The notion of linear space
EE 546, Univ of Washington, Spring Proximal mapping. introduction. review of conjugate functions. proximal mapping. Proximal mapping 6 1
 EE 546, Univ of Washington, Spring 2012 6. Proximal mapping introduction review of conjugate functions proximal mapping Proximal mapping 6 1 Proximal mapping the proximal mapping (prox-operator) of a convex
EE 546, Univ of Washington, Spring 2012 6. Proximal mapping introduction review of conjugate functions proximal mapping Proximal mapping 6 1 Proximal mapping the proximal mapping (prox-operator) of a convex
Lecture 7: Weak Duality
 EE 227A: Conve Optimization and Applications February 7, 2012 Lecture 7: Weak Duality Lecturer: Laurent El Ghaoui 7.1 Lagrange Dual problem 7.1.1 Primal problem In this section, we consider a possibly
EE 227A: Conve Optimization and Applications February 7, 2012 Lecture 7: Weak Duality Lecturer: Laurent El Ghaoui 7.1 Lagrange Dual problem 7.1.1 Primal problem In this section, we consider a possibly
Lecture: Cone programming. Approximating the Lorentz cone.
 Strong relaxations for discrete optimization problems 10/05/16 Lecture: Cone programming. Approximating the Lorentz cone. Lecturer: Yuri Faenza Scribes: Igor Malinović 1 Introduction Cone programming is
Strong relaxations for discrete optimization problems 10/05/16 Lecture: Cone programming. Approximating the Lorentz cone. Lecturer: Yuri Faenza Scribes: Igor Malinović 1 Introduction Cone programming is
A Note on Representations of Linear Inequalities in Non-Convex Mixed-Integer Quadratic Programs
 A Note on Representations of Linear Inequalities in Non-Convex Mixed-Integer Quadratic Programs Adam N. Letchford Daniel J. Grainger To appear in Operations Research Letters Abstract In the literature
A Note on Representations of Linear Inequalities in Non-Convex Mixed-Integer Quadratic Programs Adam N. Letchford Daniel J. Grainger To appear in Operations Research Letters Abstract In the literature
Convex Optimization Problems. Prof. Daniel P. Palomar
 Conve Optimization Problems Prof. Daniel P. Palomar The Hong Kong University of Science and Technology (HKUST) MAFS6010R- Portfolio Optimization with R MSc in Financial Mathematics Fall 2018-19, HKUST,
Conve Optimization Problems Prof. Daniel P. Palomar The Hong Kong University of Science and Technology (HKUST) MAFS6010R- Portfolio Optimization with R MSc in Financial Mathematics Fall 2018-19, HKUST,
What can be expressed via Conic Quadratic and Semidefinite Programming?
 What can be expressed via Conic Quadratic and Semidefinite Programming? A. Nemirovski Faculty of Industrial Engineering and Management Technion Israel Institute of Technology Abstract Tremendous recent
What can be expressed via Conic Quadratic and Semidefinite Programming? A. Nemirovski Faculty of Industrial Engineering and Management Technion Israel Institute of Technology Abstract Tremendous recent
Gauge optimization and duality
 1 / 54 Gauge optimization and duality Junfeng Yang Department of Mathematics Nanjing University Joint with Shiqian Ma, CUHK September, 2015 2 / 54 Outline Introduction Duality Lagrange duality Fenchel
1 / 54 Gauge optimization and duality Junfeng Yang Department of Mathematics Nanjing University Joint with Shiqian Ma, CUHK September, 2015 2 / 54 Outline Introduction Duality Lagrange duality Fenchel
The proximal mapping
 The proximal mapping http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes Outline 2/37 1 closed function 2 Conjugate function
The proximal mapping http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghes lecture notes Outline 2/37 1 closed function 2 Conjugate function
E5295/5B5749 Convex optimization with engineering applications. Lecture 5. Convex programming and semidefinite programming
 E5295/5B5749 Convex optimization with engineering applications Lecture 5 Convex programming and semidefinite programming A. Forsgren, KTH 1 Lecture 5 Convex optimization 2006/2007 Convex quadratic program
E5295/5B5749 Convex optimization with engineering applications Lecture 5 Convex programming and semidefinite programming A. Forsgren, KTH 1 Lecture 5 Convex optimization 2006/2007 Convex quadratic program
EE/ACM Applications of Convex Optimization in Signal Processing and Communications Lecture 17
 EE/ACM 150 - Applications of Convex Optimization in Signal Processing and Communications Lecture 17 Andre Tkacenko Signal Processing Research Group Jet Propulsion Laboratory May 29, 2012 Andre Tkacenko
EE/ACM 150 - Applications of Convex Optimization in Signal Processing and Communications Lecture 17 Andre Tkacenko Signal Processing Research Group Jet Propulsion Laboratory May 29, 2012 Andre Tkacenko
Convex Optimization in Classification Problems
 New Trends in Optimization and Computational Algorithms December 9 13, 2001 Convex Optimization in Classification Problems Laurent El Ghaoui Department of EECS, UC Berkeley elghaoui@eecs.berkeley.edu 1
New Trends in Optimization and Computational Algorithms December 9 13, 2001 Convex Optimization in Classification Problems Laurent El Ghaoui Department of EECS, UC Berkeley elghaoui@eecs.berkeley.edu 1
Chapter 13. Convex and Concave. Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 1 / 44
 Chapter 13 Convex and Concave Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 1 / 44 Monotone Function Function f is called monotonically increasing, if x 1 x 2 f (x 1 ) f (x 2 ) It
Chapter 13 Convex and Concave Josef Leydold Mathematical Methods WS 2018/19 13 Convex and Concave 1 / 44 Monotone Function Function f is called monotonically increasing, if x 1 x 2 f (x 1 ) f (x 2 ) It
Convex Optimization and Modeling
 Convex Optimization and Modeling Duality Theory and Optimality Conditions 5th lecture, 12.05.2010 Jun.-Prof. Matthias Hein Program of today/next lecture Lagrangian and duality: the Lagrangian the dual
Convex Optimization and Modeling Duality Theory and Optimality Conditions 5th lecture, 12.05.2010 Jun.-Prof. Matthias Hein Program of today/next lecture Lagrangian and duality: the Lagrangian the dual
ELE539A: Optimization of Communication Systems Lecture 6: Quadratic Programming, Geometric Programming, and Applications
 ELE539A: Optimization of Communication Systems Lecture 6: Quadratic Programming, Geometric Programming, and Applications Professor M. Chiang Electrical Engineering Department, Princeton University February
ELE539A: Optimization of Communication Systems Lecture 6: Quadratic Programming, Geometric Programming, and Applications Professor M. Chiang Electrical Engineering Department, Princeton University February
LMI Methods in Optimal and Robust Control
 LMI Methods in Optimal and Robust Control Matthew M. Peet Arizona State University Lecture 02: Optimization (Convex and Otherwise) What is Optimization? An Optimization Problem has 3 parts. x F f(x) :
LMI Methods in Optimal and Robust Control Matthew M. Peet Arizona State University Lecture 02: Optimization (Convex and Otherwise) What is Optimization? An Optimization Problem has 3 parts. x F f(x) :
Selected Methods for Modern Optimization in Data Analysis Department of Statistics and Operations Research UNC-Chapel Hill Fall 2018
 Selected Methods for Modern Optimization in Data Analysis Department of Statistics and Operations Research UNC-Chapel Hill Fall 208 Instructor: Quoc Tran-Dinh Scriber: Quoc Tran-Dinh Lecture : Introduction
Selected Methods for Modern Optimization in Data Analysis Department of Statistics and Operations Research UNC-Chapel Hill Fall 208 Instructor: Quoc Tran-Dinh Scriber: Quoc Tran-Dinh Lecture : Introduction
Conic Linear Programming. Yinyu Ye
 Conic Linear Programming Yinyu Ye December 2004, revised October 2017 i ii Preface This monograph is developed for MS&E 314, Conic Linear Programming, which I am teaching at Stanford. Information, lecture
Conic Linear Programming Yinyu Ye December 2004, revised October 2017 i ii Preface This monograph is developed for MS&E 314, Conic Linear Programming, which I am teaching at Stanford. Information, lecture
Lecture 5: September 12
 10-725/36-725: Convex Optimization Fall 2015 Lecture 5: September 12 Lecturer: Lecturer: Ryan Tibshirani Scribes: Scribes: Barun Patra and Tyler Vuong Note: LaTeX template courtesy of UC Berkeley EECS
10-725/36-725: Convex Optimization Fall 2015 Lecture 5: September 12 Lecturer: Lecturer: Ryan Tibshirani Scribes: Scribes: Barun Patra and Tyler Vuong Note: LaTeX template courtesy of UC Berkeley EECS
On the interior of the simplex, we have the Hessian of d(x), Hd(x) is diagonal with ith. µd(w) + w T c. minimize. subject to w T 1 = 1,
 Math 30 Winter 05 Solution to Homework 3. Recognizing the convexity of g(x) := x log x, from Jensen s inequality we get d(x) n x + + x n n log x + + x n n where the equality is attained only at x = (/n,...,
Math 30 Winter 05 Solution to Homework 3. Recognizing the convexity of g(x) := x log x, from Jensen s inequality we get d(x) n x + + x n n log x + + x n n where the equality is attained only at x = (/n,...,
Convex Analysis and Optimization Chapter 2 Solutions
 Convex Analysis and Optimization Chapter 2 Solutions Dimitri P. Bertsekas with Angelia Nedić and Asuman E. Ozdaglar Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
Convex Analysis and Optimization Chapter 2 Solutions Dimitri P. Bertsekas with Angelia Nedić and Asuman E. Ozdaglar Massachusetts Institute of Technology Athena Scientific, Belmont, Massachusetts http://www.athenasc.com
