N. L. P. NONLINEAR PROGRAMMING (NLP) deals with optimization models with at least one nonlinear function. NLP. Optimization. Models of following form:
|
|
|
- Dwayne Ward
- 5 years ago
- Views:
Transcription
1 0.1 N. L. P. Katta G. Murty, IOE 611 Lecture slides Introductory Lecture NONLINEAR PROGRAMMING (NLP) deals with optimization models with at least one nonlinear function. NLP does not include everything other than linear. NLP does not include IP or Discrete Opt. Needs special Enumerative Techniques. NLP, also called Continuous Optimization or Smooth Optimization. Models of following form: Minimize θ(x) s. to h i (x) = 0, i =1tom g p (x) > = 0, p =1tot All functions θ(x),h i (x),g p (x) assumed Smooth Functions. Smooth Function = one with all derivatives. 1
2 Beyond 2nd derivatives, impractical particularly when many variables. So, for us smooth means: Continuously differentiable if using gradients only Twice continuously differentiable if using Hessians Inequality constraints include lower and upper bounds on decision variables: l < j = xj < = uj. f( x) denotes ( f(x) x j )atx = x written as row vector. Also called the gradient of f(x) at x. 2 xxf( x) denotes ( 2 f(x) x i x j ), n n Hessian matrix of f(x) at x, If g(x) =(g 1 (x),...,g m (x)) T is vector of functions, then g(x) = ( g i(x) x j : i =1tom, j =1ton), the m n Jacobian matrix of g(x) at x. Each row vector in g(x) is the gradient vector of one function in g(x). 2
3 QUADRATIC FUNCTIONS: Simplest nonlinear functions A Quadratic Form in x =(x 1,...,x n ) T is of form f(x) = n i=1 q ii x 2 i + n n i=1 j=i+1 q ij x i x j. Define Square symmetric matrix D =(d ij ) of order n where d ii = q ii d ij = d ji = 1 2 q ij for i =1ton for i j, j > i Then f(x) =x T Dx Example: h(x) =81x 2 1 7x2 2 +5x 1x 2 6x 1 x 3 +18x 2 x 3. A Quadratic Function is of form Q(x) =x T Dx + cx + c 0. A square matrix M of order n, whether symmetric or not, is: Positive semidefinite (PSD) if x T Mx > = 0 for all x R n Positive definite (PD) if x T Mx > 0 for all x 0 Convex, Concave Functions: A function f(x) defined over R n, or some convex subset of R n,isconvex Function iff for all x 1,x 2 in that set, and all 3
4 0 α 1, f(αx 1 +(1 α)x 2 ) αf(x 1 )+(1 α)f(x 2 ) Inequality called Jensen s Inequality after Danish mathematician who defined it in Geometric interpretation as function lying beneath every chord Function f(x) Concave if above inequality holds other way, i.e., f(x) is convex. 4
5 Some Properties of Convex Functions 1. Nonnegative Combinations of convex functions convex. 2. If f(x) is convex defined on convex set Γ, then for all x 1,...,x r Γ and α 1,...,α r 0 satisfying r i=1 α i =1, f( r i=1 α i x i ) r i=1 α i f(x i ) 3. f(x) convex iff its Epigraph is a convex set. 4. If f(x) convex, for all α, the set {x : f(x) α} is a convex set. Converse not true. 5. Pointwise supremum function of convex functions convex. 6. Differentiable function defined on real line convex iff its 1st derivative is a monotonic increasing function, i.e., iff its 2nd derivative is nonnegative function. 7. Quadratic function defined over R n covex over R n iff its Hessian is PSD. Quadratic function whose Hessian not PSD, may be convex 5
6 over a subspace of R n. 8. Twice continuously differentiable f(x) defined over R n is convex iff its Hessian PSD for all x. 9. Gradient Support Inequality: Differentiable function f(x) defined over R n is convex iff for all x f(x) l(x) =f( x)+ f( x)(x x), for all x Lower bound property of LINEARIZATION: Function l(x) defined above called linearization of f(x) at x. For convex functions, linearization at any point, lower bound for function at every point. So approximating convex function by linearization, leads to underestimating it at every point. 6
7 How to check if a given function is convex? One variable functions like x 2 1,x4 1,e x 1,e x 1, log(x 1 ) [over x 1 > 0] are convex. For many variables, checking convexity hard, as it involves checking PSD of Hessian at every point! Local Convexity: If Hessian of f(x) at x is PD, in small neighborhood of x, f(x) convex. In this case we say f(x) is locally convex at x. 7
8 Types of NLPs Unconstrained Minimization: No constraints. Real world problems have constraints. Unconstrained min. very imp. because constrained problems can be transformed into unconstrained ones by penalty function methods. LP: If all functions affine. QP: If objective function quadratic, all constraints affine. Linearly constrained NLP: Objective function nonlinear, all constraints affine. Equality constrained NLP: All constraints equations, and no bounds on variables. Convex Programming Problem: Of form Minimize θ(x) s. to h i (x) = 0, i =1tom g p (x) > = 0, p =1tot 8
9 where θ(x) convex, all h i (x) affine, all g p (x) concave. Nicest among NLPs. Useful necessary and sufficient optimality conditions for global minimum are only known for convex programming problems. Nonconvex Programming Problems: Violates some of the conditions for convex programming. 9
10 Types of Solutions For NLP Feasible solution x is Local Minimum For ɛ>0, θ(x) θ( x) for all feasible x satisfying x x <ɛ. Strong local min if θ(x) > θ( x) for all feasible x x satisfying x x < ɛ. Weak local min If not strong. Global min If θ(x) θ( x) for all feasible x. Stationary Point If it satisfies necessary condition for local minimum. Local (strong, weak) maxima, and global maxima similar. 10
11 Differences In Constructing LP Models & NLP Models Variety of functional forms: In LP all affine. In NLP unlimited variety of functional forms. Data: LP involving m constraints in n variables has (m + 1)(n + 1) 1 coefficients as data elements. Large scale LP refers to one with m>1000s, and n> 10,000s. Such models solved to global optimality, in reasonable time. To construct an NLP model need to determine functional forms for objective, constraint functions. Usually involves Curve Fitting and Parameter estimation. Usually by Least Squares Method using special unconstrained min algos. So even constructing NLP model, needs NLP algos. So, even 200 variable NLP model considered large scale. Expectation on solution: LP we don t even talk about local min, because we get global min. 11
12 In NLP, if model nonconvex, no efficient algos can guarantee finding global min. So, one compromises on type of solution expected. Convex Programs Are Nicest NLPs! Theorem: For convex program every local min is global min. For convex program, any method finding local min will find global min. Also, every stationary point is global min in convex programs. 12
13 Properties of PSD, PD matrices, Algos to check. Preserved under symmetrization: M PD, PSD, iff D = 1 2 (M + M T ) is. Signs of diagonal elements: M =(m ij ). If PD, all m ii > 0. If PSD all m ii 0. Skew-symmetry on a 0 diagonal element: If M =(m ij ) PSD and m ii = 0, then for all j, m ij + m ji =0. So in symmetric PSD matrix if diagonal element is 0, its row and col must be 0. Preservation in Principal submatrix after Gaussian Pivot step: Let D =(d ij ) be symmetric n n, and suppose d Perform Gaussian pivot step with d 11 as pivot element. After pivot step eliminate row 1 and column 1, resulting in matrix D 1 of order (n 1) (n 1). D is PD iff d 11 > 0 and D 1 is PD. D is PSD iff d 11 > 0 and D 1 is PSD. 13
14 Superdiagonalization Algorithm for checking if M PD: Symmetrize: Let D = 1 2 (M + M T ). Perform Gaussian Pivot Steps: Let D 0 = D Do for i =1ton 1. Let D i 1 be matrix from previous operation. If any diagonal entries in D i 1 0, terminate. Conclude M not PD. Otherwise, carry out Gaussian pivot step on D i 1 with its ith diagonal element as pivot element, resulting in matrix D i. If all Gaussian pivot steps carried out and all diagonal elements of final matrix D n 1 are > 0, M PD, terminate. Examples ,
15 Superdiagonalization Algo for checking M PSD Symmetrize: Let D = 1 2 (M + M T ). Perform Gaussian Pivot Steps: Let E 0 = D Do for i =1ton 1. Let E i 1 be current matrix after previous operation. If any diagonal entries in E i 1 are < 0, terminate. Conclude M not PSD. If top diagonal entry in E i 1 is=0 If top row or 1st col of E i 1 are nonzero, terminate. Conclude M not PSD. Otherwise strike off the zero top row and 1st col of E i 1 and let remaining matrix be new current matrix E i. If top diagonal entry in E i 1 is > 0 Perform Gaussian pivot step on E i 1 with the top diagonal element as pivot element. 15
16 After this pivot step, erase top row and 1st col of resulting matrix, and let remaining matrix be the new current matrix E i. If no termination in above steps, M PSD, terminate. Examples ,
17 Other Properties of PSD, PD Matrices Property preserved for Principal submatrices: If M PD (PSD) so are all the principal submatrices of M Sign of determinants: If M is PD (PSD), whether symmetric or not, all its principal subdeterminants are > 0( 0). A square symmetric matrix PD iff all its principal subdeterminants are > 0 A square symmetric matrix of order n PD iff all its n staircase or leading principal subdeterminants are > 0. P -matrix: A square matrix, whether symmetric or not, is P -matrix, iff all its principal subdeterminants are > 0. A symmetric P -matrix is PD. An assymetric P -matrix may not be PD, it may be PSD, or even indefinite. Linear Dependence Relation at Optimum: If M is PSD, and x minimizes x T Mx, then (M + M T ) x =0. 17
Appendix PRELIMINARIES 1. THEOREMS OF ALTERNATIVES FOR SYSTEMS OF LINEAR CONSTRAINTS
 Appendix PRELIMINARIES 1. THEOREMS OF ALTERNATIVES FOR SYSTEMS OF LINEAR CONSTRAINTS Here we consider systems of linear constraints, consisting of equations or inequalities or both. A feasible solution
Appendix PRELIMINARIES 1. THEOREMS OF ALTERNATIVES FOR SYSTEMS OF LINEAR CONSTRAINTS Here we consider systems of linear constraints, consisting of equations or inequalities or both. A feasible solution
Math (P)refresher Lecture 8: Unconstrained Optimization
 Math (P)refresher Lecture 8: Unconstrained Optimization September 2006 Today s Topics : Quadratic Forms Definiteness of Quadratic Forms Maxima and Minima in R n First Order Conditions Second Order Conditions
Math (P)refresher Lecture 8: Unconstrained Optimization September 2006 Today s Topics : Quadratic Forms Definiteness of Quadratic Forms Maxima and Minima in R n First Order Conditions Second Order Conditions
Lecture 3. Optimization Problems and Iterative Algorithms
 Lecture 3 Optimization Problems and Iterative Algorithms January 13, 2016 This material was jointly developed with Angelia Nedić at UIUC for IE 598ns Outline Special Functions: Linear, Quadratic, Convex
Lecture 3 Optimization Problems and Iterative Algorithms January 13, 2016 This material was jointly developed with Angelia Nedić at UIUC for IE 598ns Outline Special Functions: Linear, Quadratic, Convex
y Ray of Half-line or ray through in the direction of y
 Chapter LINEAR COMPLEMENTARITY PROBLEM, ITS GEOMETRY, AND APPLICATIONS. THE LINEAR COMPLEMENTARITY PROBLEM AND ITS GEOMETRY The Linear Complementarity Problem (abbreviated as LCP) is a general problem
Chapter LINEAR COMPLEMENTARITY PROBLEM, ITS GEOMETRY, AND APPLICATIONS. THE LINEAR COMPLEMENTARITY PROBLEM AND ITS GEOMETRY The Linear Complementarity Problem (abbreviated as LCP) is a general problem
Algorithm for QP thro LCP
 8.1 Algorithm for QP thro LCP Katta G. Murty, IOE 611 Lecture slides Linear Complementarity Problem (LCP) Input Data: M n n,q R n Desired output: A w R n,z R n satisfying w Mz = q w, z 0 w j z j = 0, j
8.1 Algorithm for QP thro LCP Katta G. Murty, IOE 611 Lecture slides Linear Complementarity Problem (LCP) Input Data: M n n,q R n Desired output: A w R n,z R n satisfying w Mz = q w, z 0 w j z j = 0, j
Constrained Optimization
 1 / 22 Constrained Optimization ME598/494 Lecture Max Yi Ren Department of Mechanical Engineering, Arizona State University March 30, 2015 2 / 22 1. Equality constraints only 1.1 Reduced gradient 1.2 Lagrange
1 / 22 Constrained Optimization ME598/494 Lecture Max Yi Ren Department of Mechanical Engineering, Arizona State University March 30, 2015 2 / 22 1. Equality constraints only 1.1 Reduced gradient 1.2 Lagrange
Lecture 2: Convex Sets and Functions
 Lecture 2: Convex Sets and Functions Hyang-Won Lee Dept. of Internet & Multimedia Eng. Konkuk University Lecture 2 Network Optimization, Fall 2015 1 / 22 Optimization Problems Optimization problems are
Lecture 2: Convex Sets and Functions Hyang-Won Lee Dept. of Internet & Multimedia Eng. Konkuk University Lecture 2 Network Optimization, Fall 2015 1 / 22 Optimization Problems Optimization problems are
Introduction to Machine Learning Lecture 7. Mehryar Mohri Courant Institute and Google Research
 Introduction to Machine Learning Lecture 7 Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu Convex Optimization Differentiation Definition: let f : X R N R be a differentiable function,
Introduction to Machine Learning Lecture 7 Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu Convex Optimization Differentiation Definition: let f : X R N R be a differentiable function,
Introduction and Math Preliminaries
 Introduction and Math Preliminaries Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/ yyye Appendices A, B, and C, Chapter
Introduction and Math Preliminaries Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/ yyye Appendices A, B, and C, Chapter
Semidefinite Programming Basics and Applications
 Semidefinite Programming Basics and Applications Ray Pörn, principal lecturer Åbo Akademi University Novia University of Applied Sciences Content What is semidefinite programming (SDP)? How to represent
Semidefinite Programming Basics and Applications Ray Pörn, principal lecturer Åbo Akademi University Novia University of Applied Sciences Content What is semidefinite programming (SDP)? How to represent
Lecture Note 5: Semidefinite Programming for Stability Analysis
 ECE7850: Hybrid Systems:Theory and Applications Lecture Note 5: Semidefinite Programming for Stability Analysis Wei Zhang Assistant Professor Department of Electrical and Computer Engineering Ohio State
ECE7850: Hybrid Systems:Theory and Applications Lecture Note 5: Semidefinite Programming for Stability Analysis Wei Zhang Assistant Professor Department of Electrical and Computer Engineering Ohio State
ISM206 Lecture Optimization of Nonlinear Objective with Linear Constraints
 ISM206 Lecture Optimization of Nonlinear Objective with Linear Constraints Instructor: Prof. Kevin Ross Scribe: Nitish John October 18, 2011 1 The Basic Goal The main idea is to transform a given constrained
ISM206 Lecture Optimization of Nonlinear Objective with Linear Constraints Instructor: Prof. Kevin Ross Scribe: Nitish John October 18, 2011 1 The Basic Goal The main idea is to transform a given constrained
1 Strict local optimality in unconstrained optimization
 ORF 53 Lecture 14 Spring 016, Princeton University Instructor: A.A. Ahmadi Scribe: G. Hall Thursday, April 14, 016 When in doubt on the accuracy of these notes, please cross check with the instructor s
ORF 53 Lecture 14 Spring 016, Princeton University Instructor: A.A. Ahmadi Scribe: G. Hall Thursday, April 14, 016 When in doubt on the accuracy of these notes, please cross check with the instructor s
Week 4: Calculus and Optimization (Jehle and Reny, Chapter A2)
 Week 4: Calculus and Optimization (Jehle and Reny, Chapter A2) Tsun-Feng Chiang *School of Economics, Henan University, Kaifeng, China September 27, 2015 Microeconomic Theory Week 4: Calculus and Optimization
Week 4: Calculus and Optimization (Jehle and Reny, Chapter A2) Tsun-Feng Chiang *School of Economics, Henan University, Kaifeng, China September 27, 2015 Microeconomic Theory Week 4: Calculus and Optimization
Module 04 Optimization Problems KKT Conditions & Solvers
 Module 04 Optimization Problems KKT Conditions & Solvers Ahmad F. Taha EE 5243: Introduction to Cyber-Physical Systems Email: ahmad.taha@utsa.edu Webpage: http://engineering.utsa.edu/ taha/index.html September
Module 04 Optimization Problems KKT Conditions & Solvers Ahmad F. Taha EE 5243: Introduction to Cyber-Physical Systems Email: ahmad.taha@utsa.edu Webpage: http://engineering.utsa.edu/ taha/index.html September
Applications of Linear Programming
 Applications of Linear Programming lecturer: András London University of Szeged Institute of Informatics Department of Computational Optimization Lecture 9 Non-linear programming In case of LP, the goal
Applications of Linear Programming lecturer: András London University of Szeged Institute of Informatics Department of Computational Optimization Lecture 9 Non-linear programming In case of LP, the goal
Written Examination
 Division of Scientific Computing Department of Information Technology Uppsala University Optimization Written Examination 202-2-20 Time: 4:00-9:00 Allowed Tools: Pocket Calculator, one A4 paper with notes
Division of Scientific Computing Department of Information Technology Uppsala University Optimization Written Examination 202-2-20 Time: 4:00-9:00 Allowed Tools: Pocket Calculator, one A4 paper with notes
The general programming problem is the nonlinear programming problem where a given function is maximized subject to a set of inequality constraints.
 1 Optimization Mathematical programming refers to the basic mathematical problem of finding a maximum to a function, f, subject to some constraints. 1 In other words, the objective is to find a point,
1 Optimization Mathematical programming refers to the basic mathematical problem of finding a maximum to a function, f, subject to some constraints. 1 In other words, the objective is to find a point,
CE 191: Civil and Environmental Engineering Systems Analysis. LEC 05 : Optimality Conditions
 CE 191: Civil and Environmental Engineering Systems Analysis LEC : Optimality Conditions Professor Scott Moura Civil & Environmental Engineering University of California, Berkeley Fall 214 Prof. Moura
CE 191: Civil and Environmental Engineering Systems Analysis LEC : Optimality Conditions Professor Scott Moura Civil & Environmental Engineering University of California, Berkeley Fall 214 Prof. Moura
Lecture 2: Convex functions
 Lecture 2: Convex functions f : R n R is convex if dom f is convex and for all x, y dom f, θ [0, 1] f is concave if f is convex f(θx + (1 θ)y) θf(x) + (1 θ)f(y) x x convex concave neither x examples (on
Lecture 2: Convex functions f : R n R is convex if dom f is convex and for all x, y dom f, θ [0, 1] f is concave if f is convex f(θx + (1 θ)y) θf(x) + (1 θ)f(y) x x convex concave neither x examples (on
Symmetric Matrices and Eigendecomposition
 Symmetric Matrices and Eigendecomposition Robert M. Freund January, 2014 c 2014 Massachusetts Institute of Technology. All rights reserved. 1 2 1 Symmetric Matrices and Convexity of Quadratic Functions
Symmetric Matrices and Eigendecomposition Robert M. Freund January, 2014 c 2014 Massachusetts Institute of Technology. All rights reserved. 1 2 1 Symmetric Matrices and Convexity of Quadratic Functions
Optimization: an Overview
 Optimization: an Overview Moritz Diehl University of Freiburg and University of Leuven (some slide material was provided by W. Bangerth and K. Mombaur) Overview of presentation Optimization: basic definitions
Optimization: an Overview Moritz Diehl University of Freiburg and University of Leuven (some slide material was provided by W. Bangerth and K. Mombaur) Overview of presentation Optimization: basic definitions
Convex Functions. Daniel P. Palomar. Hong Kong University of Science and Technology (HKUST)
 Convex Functions Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Definition convex function Examples
Convex Functions Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Definition convex function Examples
58 Appendix 1 fundamental inconsistent equation (1) can be obtained as a linear combination of the two equations in (2). This clearly implies that the
 Appendix PRELIMINARIES 1. THEOREMS OF ALTERNATIVES FOR SYSTEMS OF LINEAR CONSTRAINTS Here we consider systems of linear constraints, consisting of equations or inequalities or both. A feasible solution
Appendix PRELIMINARIES 1. THEOREMS OF ALTERNATIVES FOR SYSTEMS OF LINEAR CONSTRAINTS Here we consider systems of linear constraints, consisting of equations or inequalities or both. A feasible solution
I.3. LMI DUALITY. Didier HENRION EECI Graduate School on Control Supélec - Spring 2010
 I.3. LMI DUALITY Didier HENRION henrion@laas.fr EECI Graduate School on Control Supélec - Spring 2010 Primal and dual For primal problem p = inf x g 0 (x) s.t. g i (x) 0 define Lagrangian L(x, z) = g 0
I.3. LMI DUALITY Didier HENRION henrion@laas.fr EECI Graduate School on Control Supélec - Spring 2010 Primal and dual For primal problem p = inf x g 0 (x) s.t. g i (x) 0 define Lagrangian L(x, z) = g 0
Common-Knowledge / Cheat Sheet
 CSE 521: Design and Analysis of Algorithms I Fall 2018 Common-Knowledge / Cheat Sheet 1 Randomized Algorithm Expectation: For a random variable X with domain, the discrete set S, E [X] = s S P [X = s]
CSE 521: Design and Analysis of Algorithms I Fall 2018 Common-Knowledge / Cheat Sheet 1 Randomized Algorithm Expectation: For a random variable X with domain, the discrete set S, E [X] = s S P [X = s]
Chapter 2 BASIC PRINCIPLES. 2.1 Introduction. 2.2 Gradient Information
 Chapter 2 BASIC PRINCIPLES 2.1 Introduction Nonlinear programming is based on a collection of definitions, theorems, and principles that must be clearly understood if the available nonlinear programming
Chapter 2 BASIC PRINCIPLES 2.1 Introduction Nonlinear programming is based on a collection of definitions, theorems, and principles that must be clearly understood if the available nonlinear programming
Conic Linear Programming. Yinyu Ye
 Conic Linear Programming Yinyu Ye December 2004, revised January 2015 i ii Preface This monograph is developed for MS&E 314, Conic Linear Programming, which I am teaching at Stanford. Information, lecture
Conic Linear Programming Yinyu Ye December 2004, revised January 2015 i ii Preface This monograph is developed for MS&E 314, Conic Linear Programming, which I am teaching at Stanford. Information, lecture
Optimality Conditions
 Chapter 2 Optimality Conditions 2.1 Global and Local Minima for Unconstrained Problems When a minimization problem does not have any constraints, the problem is to find the minimum of the objective function.
Chapter 2 Optimality Conditions 2.1 Global and Local Minima for Unconstrained Problems When a minimization problem does not have any constraints, the problem is to find the minimum of the objective function.
3. Convex functions. basic properties and examples. operations that preserve convexity. the conjugate function. quasiconvex functions
 3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
13. Convex programming
 CS/ISyE/ECE 524 Introduction to Optimization Spring 2015 16 13. Convex programming Convex sets and functions Convex programs Hierarchy of complexity Example: geometric programming Laurent Lessard (www.laurentlessard.com)
CS/ISyE/ECE 524 Introduction to Optimization Spring 2015 16 13. Convex programming Convex sets and functions Convex programs Hierarchy of complexity Example: geometric programming Laurent Lessard (www.laurentlessard.com)
Linear and non-linear programming
 Linear and non-linear programming Benjamin Recht March 11, 2005 The Gameplan Constrained Optimization Convexity Duality Applications/Taxonomy 1 Constrained Optimization minimize f(x) subject to g j (x)
Linear and non-linear programming Benjamin Recht March 11, 2005 The Gameplan Constrained Optimization Convexity Duality Applications/Taxonomy 1 Constrained Optimization minimize f(x) subject to g j (x)
3. Vector spaces 3.1 Linear dependence and independence 3.2 Basis and dimension. 5. Extreme points and basic feasible solutions
 A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
A. LINEAR ALGEBRA. CONVEX SETS 1. Matrices and vectors 1.1 Matrix operations 1.2 The rank of a matrix 2. Systems of linear equations 2.1 Basic solutions 3. Vector spaces 3.1 Linear dependence and independence
Linear Algebra And Its Applications Chapter 6. Positive Definite Matrix
 Linear Algebra And Its Applications Chapter 6. Positive Definite Matrix KAIST wit Lab 2012. 07. 10 남성호 Introduction The signs of the eigenvalues can be important. The signs can also be related to the minima,
Linear Algebra And Its Applications Chapter 6. Positive Definite Matrix KAIST wit Lab 2012. 07. 10 남성호 Introduction The signs of the eigenvalues can be important. The signs can also be related to the minima,
Generalization to inequality constrained problem. Maximize
 Lecture 11. 26 September 2006 Review of Lecture #10: Second order optimality conditions necessary condition, sufficient condition. If the necessary condition is violated the point cannot be a local minimum
Lecture 11. 26 September 2006 Review of Lecture #10: Second order optimality conditions necessary condition, sufficient condition. If the necessary condition is violated the point cannot be a local minimum
3. Convex functions. basic properties and examples. operations that preserve convexity. the conjugate function. quasiconvex functions
 3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
3. Convex functions Convex Optimization Boyd & Vandenberghe basic properties and examples operations that preserve convexity the conjugate function quasiconvex functions log-concave and log-convex functions
NONLINEAR. (Hillier & Lieberman Introduction to Operations Research, 8 th edition)
 NONLINEAR PROGRAMMING (Hillier & Lieberman Introduction to Operations Research, 8 th edition) Nonlinear Programming g Linear programming has a fundamental role in OR. In linear programming all its functions
NONLINEAR PROGRAMMING (Hillier & Lieberman Introduction to Operations Research, 8 th edition) Nonlinear Programming g Linear programming has a fundamental role in OR. In linear programming all its functions
AM 205: lecture 18. Last time: optimization methods Today: conditions for optimality
 AM 205: lecture 18 Last time: optimization methods Today: conditions for optimality Existence of Global Minimum For example: f (x, y) = x 2 + y 2 is coercive on R 2 (global min. at (0, 0)) f (x) = x 3
AM 205: lecture 18 Last time: optimization methods Today: conditions for optimality Existence of Global Minimum For example: f (x, y) = x 2 + y 2 is coercive on R 2 (global min. at (0, 0)) f (x) = x 3
Mathematical Economics. Lecture Notes (in extracts)
 Prof. Dr. Frank Werner Faculty of Mathematics Institute of Mathematical Optimization (IMO) http://math.uni-magdeburg.de/ werner/math-ec-new.html Mathematical Economics Lecture Notes (in extracts) Winter
Prof. Dr. Frank Werner Faculty of Mathematics Institute of Mathematical Optimization (IMO) http://math.uni-magdeburg.de/ werner/math-ec-new.html Mathematical Economics Lecture Notes (in extracts) Winter
CS-E4830 Kernel Methods in Machine Learning
 CS-E4830 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 27. September, 2017 Juho Rousu 27. September, 2017 1 / 45 Convex optimization Convex optimisation This
CS-E4830 Kernel Methods in Machine Learning Lecture 3: Convex optimization and duality Juho Rousu 27. September, 2017 Juho Rousu 27. September, 2017 1 / 45 Convex optimization Convex optimisation This
4. Convex optimization problems (part 1: general)
 EE/AA 578, Univ of Washington, Fall 2016 4. Convex optimization problems (part 1: general) optimization problem in standard form convex optimization problems quasiconvex optimization 4 1 Optimization problem
EE/AA 578, Univ of Washington, Fall 2016 4. Convex optimization problems (part 1: general) optimization problem in standard form convex optimization problems quasiconvex optimization 4 1 Optimization problem
E5295/5B5749 Convex optimization with engineering applications. Lecture 5. Convex programming and semidefinite programming
 E5295/5B5749 Convex optimization with engineering applications Lecture 5 Convex programming and semidefinite programming A. Forsgren, KTH 1 Lecture 5 Convex optimization 2006/2007 Convex quadratic program
E5295/5B5749 Convex optimization with engineering applications Lecture 5 Convex programming and semidefinite programming A. Forsgren, KTH 1 Lecture 5 Convex optimization 2006/2007 Convex quadratic program
Lecture: Examples of LP, SOCP and SDP
 1/34 Lecture: Examples of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2018.html wenzw@pku.edu.cn Acknowledgement:
1/34 Lecture: Examples of LP, SOCP and SDP Zaiwen Wen Beijing International Center For Mathematical Research Peking University http://bicmr.pku.edu.cn/~wenzw/bigdata2018.html wenzw@pku.edu.cn Acknowledgement:
CSCI : Optimization and Control of Networks. Review on Convex Optimization
 CSCI7000-016: Optimization and Control of Networks Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one
CSCI7000-016: Optimization and Control of Networks Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one
MATH2070 Optimisation
 MATH2070 Optimisation Nonlinear optimisation with constraints Semester 2, 2012 Lecturer: I.W. Guo Lecture slides courtesy of J.R. Wishart Review The full nonlinear optimisation problem with equality constraints
MATH2070 Optimisation Nonlinear optimisation with constraints Semester 2, 2012 Lecturer: I.W. Guo Lecture slides courtesy of J.R. Wishart Review The full nonlinear optimisation problem with equality constraints
Convex Optimization & Lagrange Duality
 Convex Optimization & Lagrange Duality Chee Wei Tan CS 8292 : Advanced Topics in Convex Optimization and its Applications Fall 2010 Outline Convex optimization Optimality condition Lagrange duality KKT
Convex Optimization & Lagrange Duality Chee Wei Tan CS 8292 : Advanced Topics in Convex Optimization and its Applications Fall 2010 Outline Convex optimization Optimality condition Lagrange duality KKT
6.252 NONLINEAR PROGRAMMING LECTURE 10 ALTERNATIVES TO GRADIENT PROJECTION LECTURE OUTLINE. Three Alternatives/Remedies for Gradient Projection
 6.252 NONLINEAR PROGRAMMING LECTURE 10 ALTERNATIVES TO GRADIENT PROJECTION LECTURE OUTLINE Three Alternatives/Remedies for Gradient Projection Two-Metric Projection Methods Manifold Suboptimization Methods
6.252 NONLINEAR PROGRAMMING LECTURE 10 ALTERNATIVES TO GRADIENT PROJECTION LECTURE OUTLINE Three Alternatives/Remedies for Gradient Projection Two-Metric Projection Methods Manifold Suboptimization Methods
Computational Finance
 Department of Mathematics at University of California, San Diego Computational Finance Optimization Techniques [Lecture 2] Michael Holst January 9, 2017 Contents 1 Optimization Techniques 3 1.1 Examples
Department of Mathematics at University of California, San Diego Computational Finance Optimization Techniques [Lecture 2] Michael Holst January 9, 2017 Contents 1 Optimization Techniques 3 1.1 Examples
A Brief Review on Convex Optimization
 A Brief Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one convex, two nonconvex sets): A Brief Review
A Brief Review on Convex Optimization 1 Convex set S R n is convex if x,y S, λ,µ 0, λ+µ = 1 λx+µy S geometrically: x,y S line segment through x,y S examples (one convex, two nonconvex sets): A Brief Review
Numerisches Rechnen. (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang. Institut für Geometrie und Praktische Mathematik RWTH Aachen
 Numerisches Rechnen (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang Institut für Geometrie und Praktische Mathematik RWTH Aachen Wintersemester 2011/12 IGPM, RWTH Aachen Numerisches Rechnen
Numerisches Rechnen (für Informatiker) M. Grepl P. Esser & G. Welper & L. Zhang Institut für Geometrie und Praktische Mathematik RWTH Aachen Wintersemester 2011/12 IGPM, RWTH Aachen Numerisches Rechnen
Constrained Optimization Theory
 Constrained Optimization Theory Stephen J. Wright 1 2 Computer Sciences Department, University of Wisconsin-Madison. IMA, August 2016 Stephen Wright (UW-Madison) Constrained Optimization Theory IMA, August
Constrained Optimization Theory Stephen J. Wright 1 2 Computer Sciences Department, University of Wisconsin-Madison. IMA, August 2016 Stephen Wright (UW-Madison) Constrained Optimization Theory IMA, August
Lecture 18: The Rank of a Matrix and Consistency of Linear Systems
 Lecture 18: The Rank of a Matrix and Consistency of Linear Systems Winfried Just Department of Mathematics, Ohio University February 28, 218 Review: The linear span Definition Let { v 1, v 2,..., v n }
Lecture 18: The Rank of a Matrix and Consistency of Linear Systems Winfried Just Department of Mathematics, Ohio University February 28, 218 Review: The linear span Definition Let { v 1, v 2,..., v n }
Lecture 7: Positive Semidefinite Matrices
 Lecture 7: Positive Semidefinite Matrices Rajat Mittal IIT Kanpur The main aim of this lecture note is to prepare your background for semidefinite programming. We have already seen some linear algebra.
Lecture 7: Positive Semidefinite Matrices Rajat Mittal IIT Kanpur The main aim of this lecture note is to prepare your background for semidefinite programming. We have already seen some linear algebra.
SWFR ENG 4TE3 (6TE3) COMP SCI 4TE3 (6TE3) Continuous Optimization Algorithm. Convex Optimization. Computing and Software McMaster University
 SWFR ENG 4TE3 (6TE3) COMP SCI 4TE3 (6TE3) Continuous Optimization Algorithm Convex Optimization Computing and Software McMaster University General NLO problem (NLO : Non Linear Optimization) (N LO) min
SWFR ENG 4TE3 (6TE3) COMP SCI 4TE3 (6TE3) Continuous Optimization Algorithm Convex Optimization Computing and Software McMaster University General NLO problem (NLO : Non Linear Optimization) (N LO) min
OR MSc Maths Revision Course
 OR MSc Maths Revision Course Tom Byrne School of Mathematics University of Edinburgh t.m.byrne@sms.ed.ac.uk 15 September 2017 General Information Today JCMB Lecture Theatre A, 09:30-12:30 Mathematics revision
OR MSc Maths Revision Course Tom Byrne School of Mathematics University of Edinburgh t.m.byrne@sms.ed.ac.uk 15 September 2017 General Information Today JCMB Lecture Theatre A, 09:30-12:30 Mathematics revision
Sequential Convex Programming
 Sequential Convex Programming sequential convex programming alternating convex optimization convex-concave procedure Prof. S. Boyd, EE364b, Stanford University Methods for nonconvex optimization problems
Sequential Convex Programming sequential convex programming alternating convex optimization convex-concave procedure Prof. S. Boyd, EE364b, Stanford University Methods for nonconvex optimization problems
Functions of Several Variables
 Functions of Several Variables The Unconstrained Minimization Problem where In n dimensions the unconstrained problem is stated as f() x variables. minimize f()x x, is a scalar objective function of vector
Functions of Several Variables The Unconstrained Minimization Problem where In n dimensions the unconstrained problem is stated as f() x variables. minimize f()x x, is a scalar objective function of vector
Lecture: Convex Optimization Problems
 1/36 Lecture: Convex Optimization Problems http://bicmr.pku.edu.cn/~wenzw/opt-2015-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/36 optimization
1/36 Lecture: Convex Optimization Problems http://bicmr.pku.edu.cn/~wenzw/opt-2015-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/36 optimization
Copositive Plus Matrices
 Copositive Plus Matrices Willemieke van Vliet Master Thesis in Applied Mathematics October 2011 Copositive Plus Matrices Summary In this report we discuss the set of copositive plus matrices and their
Copositive Plus Matrices Willemieke van Vliet Master Thesis in Applied Mathematics October 2011 Copositive Plus Matrices Summary In this report we discuss the set of copositive plus matrices and their
MATH 5720: Unconstrained Optimization Hung Phan, UMass Lowell September 13, 2018
 MATH 57: Unconstrained Optimization Hung Phan, UMass Lowell September 13, 18 1 Global and Local Optima Let a function f : S R be defined on a set S R n Definition 1 (minimizers and maximizers) (i) x S
MATH 57: Unconstrained Optimization Hung Phan, UMass Lowell September 13, 18 1 Global and Local Optima Let a function f : S R be defined on a set S R n Definition 1 (minimizers and maximizers) (i) x S
Optimality Conditions for Constrained Optimization
 72 CHAPTER 7 Optimality Conditions for Constrained Optimization 1. First Order Conditions In this section we consider first order optimality conditions for the constrained problem P : minimize f 0 (x)
72 CHAPTER 7 Optimality Conditions for Constrained Optimization 1. First Order Conditions In this section we consider first order optimality conditions for the constrained problem P : minimize f 0 (x)
Convex Optimization. Convex Analysis - Functions
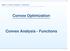 Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
minimize x subject to (x 2)(x 4) u,
 Math 6366/6367: Optimization and Variational Methods Sample Preliminary Exam Questions 1. Suppose that f : [, L] R is a C 2 -function with f () on (, L) and that you have explicit formulae for
Math 6366/6367: Optimization and Variational Methods Sample Preliminary Exam Questions 1. Suppose that f : [, L] R is a C 2 -function with f () on (, L) and that you have explicit formulae for
MATHEMATICAL ECONOMICS: OPTIMIZATION. Contents
 MATHEMATICAL ECONOMICS: OPTIMIZATION JOÃO LOPES DIAS Contents 1. Introduction 2 1.1. Preliminaries 2 1.2. Optimal points and values 2 1.3. The optimization problems 3 1.4. Existence of optimal points 4
MATHEMATICAL ECONOMICS: OPTIMIZATION JOÃO LOPES DIAS Contents 1. Introduction 2 1.1. Preliminaries 2 1.2. Optimal points and values 2 1.3. The optimization problems 3 1.4. Existence of optimal points 4
0.1 O. R. Katta G. Murty, IOE 510 Lecture slides Introductory Lecture. is any organization, large or small.
 0.1 O. R. Katta G. Murty, IOE 510 Lecture slides Introductory Lecture Operations Research is the branch of science dealing with techniques for optimizing the performance of systems. System is any organization,
0.1 O. R. Katta G. Murty, IOE 510 Lecture slides Introductory Lecture Operations Research is the branch of science dealing with techniques for optimizing the performance of systems. System is any organization,
4. Convex optimization problems
 Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
Convex Optimization Boyd & Vandenberghe 4. Convex optimization problems optimization problem in standard form convex optimization problems quasiconvex optimization linear optimization quadratic optimization
Constrained optimization
 Constrained optimization DS-GA 1013 / MATH-GA 2824 Optimization-based Data Analysis http://www.cims.nyu.edu/~cfgranda/pages/obda_fall17/index.html Carlos Fernandez-Granda Compressed sensing Convex constrained
Constrained optimization DS-GA 1013 / MATH-GA 2824 Optimization-based Data Analysis http://www.cims.nyu.edu/~cfgranda/pages/obda_fall17/index.html Carlos Fernandez-Granda Compressed sensing Convex constrained
Mathematical Economics (ECON 471) Lecture 3 Calculus of Several Variables & Implicit Functions
 Mathematical Economics (ECON 471) Lecture 3 Calculus of Several Variables & Implicit Functions Teng Wah Leo 1 Calculus of Several Variables 11 Functions Mapping between Euclidean Spaces Where as in univariate
Mathematical Economics (ECON 471) Lecture 3 Calculus of Several Variables & Implicit Functions Teng Wah Leo 1 Calculus of Several Variables 11 Functions Mapping between Euclidean Spaces Where as in univariate
Optimality, Duality, Complementarity for Constrained Optimization
 Optimality, Duality, Complementarity for Constrained Optimization Stephen Wright University of Wisconsin-Madison May 2014 Wright (UW-Madison) Optimality, Duality, Complementarity May 2014 1 / 41 Linear
Optimality, Duality, Complementarity for Constrained Optimization Stephen Wright University of Wisconsin-Madison May 2014 Wright (UW-Madison) Optimality, Duality, Complementarity May 2014 1 / 41 Linear
14. Nonlinear equations
 L. Vandenberghe ECE133A (Winter 2018) 14. Nonlinear equations Newton method for nonlinear equations damped Newton method for unconstrained minimization Newton method for nonlinear least squares 14-1 Set
L. Vandenberghe ECE133A (Winter 2018) 14. Nonlinear equations Newton method for nonlinear equations damped Newton method for unconstrained minimization Newton method for nonlinear least squares 14-1 Set
Solution Methods. Richard Lusby. Department of Management Engineering Technical University of Denmark
 Solution Methods Richard Lusby Department of Management Engineering Technical University of Denmark Lecture Overview (jg Unconstrained Several Variables Quadratic Programming Separable Programming SUMT
Solution Methods Richard Lusby Department of Management Engineering Technical University of Denmark Lecture Overview (jg Unconstrained Several Variables Quadratic Programming Separable Programming SUMT
Review of Optimization Methods
 Review of Optimization Methods Prof. Manuela Pedio 20550 Quantitative Methods for Finance August 2018 Outline of the Course Lectures 1 and 2 (3 hours, in class): Linear and non-linear functions on Limits,
Review of Optimization Methods Prof. Manuela Pedio 20550 Quantitative Methods for Finance August 2018 Outline of the Course Lectures 1 and 2 (3 hours, in class): Linear and non-linear functions on Limits,
1 Computing with constraints
 Notes for 2017-04-26 1 Computing with constraints Recall that our basic problem is minimize φ(x) s.t. x Ω where the feasible set Ω is defined by equality and inequality conditions Ω = {x R n : c i (x)
Notes for 2017-04-26 1 Computing with constraints Recall that our basic problem is minimize φ(x) s.t. x Ω where the feasible set Ω is defined by equality and inequality conditions Ω = {x R n : c i (x)
Lectures 9 and 10: Constrained optimization problems and their optimality conditions
 Lectures 9 and 10: Constrained optimization problems and their optimality conditions Coralia Cartis, Mathematical Institute, University of Oxford C6.2/B2: Continuous Optimization Lectures 9 and 10: Constrained
Lectures 9 and 10: Constrained optimization problems and their optimality conditions Coralia Cartis, Mathematical Institute, University of Oxford C6.2/B2: Continuous Optimization Lectures 9 and 10: Constrained
Interior Point Methods for Convex Quadratic and Convex Nonlinear Programming
 School of Mathematics T H E U N I V E R S I T Y O H F E D I N B U R G Interior Point Methods for Convex Quadratic and Convex Nonlinear Programming Jacek Gondzio Email: J.Gondzio@ed.ac.uk URL: http://www.maths.ed.ac.uk/~gondzio
School of Mathematics T H E U N I V E R S I T Y O H F E D I N B U R G Interior Point Methods for Convex Quadratic and Convex Nonlinear Programming Jacek Gondzio Email: J.Gondzio@ed.ac.uk URL: http://www.maths.ed.ac.uk/~gondzio
Convex Functions. Wing-Kin (Ken) Ma The Chinese University of Hong Kong (CUHK)
 Convex Functions Wing-Kin (Ken) Ma The Chinese University of Hong Kong (CUHK) Course on Convex Optimization for Wireless Comm. and Signal Proc. Jointly taught by Daniel P. Palomar and Wing-Kin (Ken) Ma
Convex Functions Wing-Kin (Ken) Ma The Chinese University of Hong Kong (CUHK) Course on Convex Optimization for Wireless Comm. and Signal Proc. Jointly taught by Daniel P. Palomar and Wing-Kin (Ken) Ma
Lecture 2 - Unconstrained Optimization Definition[Global Minimum and Maximum]Let f : S R be defined on a set S R n. Then
![Lecture 2 - Unconstrained Optimization Definition[Global Minimum and Maximum]Let f : S R be defined on a set S R n. Then Lecture 2 - Unconstrained Optimization Definition[Global Minimum and Maximum]Let f : S R be defined on a set S R n. Then](/thumbs/86/93291808.jpg) Lecture 2 - Unconstrained Optimization Definition[Global Minimum and Maximum]Let f : S R be defined on a set S R n. Then 1. x S is a global minimum point of f over S if f (x) f (x ) for any x S. 2. x S
Lecture 2 - Unconstrained Optimization Definition[Global Minimum and Maximum]Let f : S R be defined on a set S R n. Then 1. x S is a global minimum point of f over S if f (x) f (x ) for any x S. 2. x S
Conic Linear Programming. Yinyu Ye
 Conic Linear Programming Yinyu Ye December 2004, revised October 2017 i ii Preface This monograph is developed for MS&E 314, Conic Linear Programming, which I am teaching at Stanford. Information, lecture
Conic Linear Programming Yinyu Ye December 2004, revised October 2017 i ii Preface This monograph is developed for MS&E 314, Conic Linear Programming, which I am teaching at Stanford. Information, lecture
Chapter 2: Unconstrained Extrema
 Chapter 2: Unconstrained Extrema Math 368 c Copyright 2012, 2013 R Clark Robinson May 22, 2013 Chapter 2: Unconstrained Extrema 1 Types of Sets Definition For p R n and r > 0, the open ball about p of
Chapter 2: Unconstrained Extrema Math 368 c Copyright 2012, 2013 R Clark Robinson May 22, 2013 Chapter 2: Unconstrained Extrema 1 Types of Sets Definition For p R n and r > 0, the open ball about p of
1 Convexity, concavity and quasi-concavity. (SB )
 UNIVERSITY OF MARYLAND ECON 600 Summer 2010 Lecture Two: Unconstrained Optimization 1 Convexity, concavity and quasi-concavity. (SB 21.1-21.3.) For any two points, x, y R n, we can trace out the line of
UNIVERSITY OF MARYLAND ECON 600 Summer 2010 Lecture Two: Unconstrained Optimization 1 Convexity, concavity and quasi-concavity. (SB 21.1-21.3.) For any two points, x, y R n, we can trace out the line of
LMI MODELLING 4. CONVEX LMI MODELLING. Didier HENRION. LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ. Universidad de Valladolid, SP March 2009
 LMI MODELLING 4. CONVEX LMI MODELLING Didier HENRION LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ Universidad de Valladolid, SP March 2009 Minors A minor of a matrix F is the determinant of a submatrix
LMI MODELLING 4. CONVEX LMI MODELLING Didier HENRION LAAS-CNRS Toulouse, FR Czech Tech Univ Prague, CZ Universidad de Valladolid, SP March 2009 Minors A minor of a matrix F is the determinant of a submatrix
Nonlinear Optimization: What s important?
 Nonlinear Optimization: What s important? Julian Hall 10th May 2012 Convexity: convex problems A local minimizer is a global minimizer A solution of f (x) = 0 (stationary point) is a minimizer A global
Nonlinear Optimization: What s important? Julian Hall 10th May 2012 Convexity: convex problems A local minimizer is a global minimizer A solution of f (x) = 0 (stationary point) is a minimizer A global
Support Vector Machines
 Support Vector Machines Support vector machines (SVMs) are one of the central concepts in all of machine learning. They are simply a combination of two ideas: linear classification via maximum (or optimal
Support Vector Machines Support vector machines (SVMs) are one of the central concepts in all of machine learning. They are simply a combination of two ideas: linear classification via maximum (or optimal
Convex optimization problems. Optimization problem in standard form
 Convex optimization problems optimization problem in standard form convex optimization problems linear optimization quadratic optimization geometric programming quasiconvex optimization generalized inequality
Convex optimization problems optimization problem in standard form convex optimization problems linear optimization quadratic optimization geometric programming quasiconvex optimization generalized inequality
CHAPTER 2: QUADRATIC PROGRAMMING
 CHAPTER 2: QUADRATIC PROGRAMMING Overview Quadratic programming (QP) problems are characterized by objective functions that are quadratic in the design variables, and linear constraints. In this sense,
CHAPTER 2: QUADRATIC PROGRAMMING Overview Quadratic programming (QP) problems are characterized by objective functions that are quadratic in the design variables, and linear constraints. In this sense,
Chapter 2: Preliminaries and elements of convex analysis
 Chapter 2: Preliminaries and elements of convex analysis Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-14-15.shtml Academic year 2014-15
Chapter 2: Preliminaries and elements of convex analysis Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-14-15.shtml Academic year 2014-15
1. First and Second Order Conditions for A Local Min or Max.
 1 MATH CHAPTER 3: UNCONSTRAINED OPTIMIZATION W. Erwin Diewert 1. First and Second Order Conditions for A Local Min or Max. Consider the problem of maximizing or minimizing a function of N variables, f(x
1 MATH CHAPTER 3: UNCONSTRAINED OPTIMIZATION W. Erwin Diewert 1. First and Second Order Conditions for A Local Min or Max. Consider the problem of maximizing or minimizing a function of N variables, f(x
10 Numerical methods for constrained problems
 10 Numerical methods for constrained problems min s.t. f(x) h(x) = 0 (l), g(x) 0 (m), x X The algorithms can be roughly divided the following way: ˆ primal methods: find descent direction keeping inside
10 Numerical methods for constrained problems min s.t. f(x) h(x) = 0 (l), g(x) 0 (m), x X The algorithms can be roughly divided the following way: ˆ primal methods: find descent direction keeping inside
Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization
 Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization Compiled by David Rosenberg Abstract Boyd and Vandenberghe s Convex Optimization book is very well-written and a pleasure to read. The
Extreme Abridgment of Boyd and Vandenberghe s Convex Optimization Compiled by David Rosenberg Abstract Boyd and Vandenberghe s Convex Optimization book is very well-written and a pleasure to read. The
September Math Course: First Order Derivative
 September Math Course: First Order Derivative Arina Nikandrova Functions Function y = f (x), where x is either be a scalar or a vector of several variables (x,..., x n ), can be thought of as a rule which
September Math Course: First Order Derivative Arina Nikandrova Functions Function y = f (x), where x is either be a scalar or a vector of several variables (x,..., x n ), can be thought of as a rule which
Convex Optimization. Dani Yogatama. School of Computer Science, Carnegie Mellon University, Pittsburgh, PA, USA. February 12, 2014
 Convex Optimization Dani Yogatama School of Computer Science, Carnegie Mellon University, Pittsburgh, PA, USA February 12, 2014 Dani Yogatama (Carnegie Mellon University) Convex Optimization February 12,
Convex Optimization Dani Yogatama School of Computer Science, Carnegie Mellon University, Pittsburgh, PA, USA February 12, 2014 Dani Yogatama (Carnegie Mellon University) Convex Optimization February 12,
Lecture Unconstrained optimization. In this lecture we will study the unconstrained problem. minimize f(x), (2.1)
 Lecture 2 In this lecture we will study the unconstrained problem minimize f(x), (2.1) where x R n. Optimality conditions aim to identify properties that potential minimizers need to satisfy in relation
Lecture 2 In this lecture we will study the unconstrained problem minimize f(x), (2.1) where x R n. Optimality conditions aim to identify properties that potential minimizers need to satisfy in relation
Math Matrix Algebra
 Math 44 - Matrix Algebra Review notes - (Alberto Bressan, Spring 7) sec: Orthogonal diagonalization of symmetric matrices When we seek to diagonalize a general n n matrix A, two difficulties may arise:
Math 44 - Matrix Algebra Review notes - (Alberto Bressan, Spring 7) sec: Orthogonal diagonalization of symmetric matrices When we seek to diagonalize a general n n matrix A, two difficulties may arise:
5. Duality. Lagrangian
 5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
5. Duality Convex Optimization Boyd & Vandenberghe Lagrange dual problem weak and strong duality geometric interpretation optimality conditions perturbation and sensitivity analysis examples generalized
CE 191: Civil & Environmental Engineering Systems Analysis. LEC 17 : Final Review
 CE 191: Civil & Environmental Engineering Systems Analysis LEC 17 : Final Review Professor Scott Moura Civil & Environmental Engineering University of California, Berkeley Fall 2014 Prof. Moura UC Berkeley
CE 191: Civil & Environmental Engineering Systems Analysis LEC 17 : Final Review Professor Scott Moura Civil & Environmental Engineering University of California, Berkeley Fall 2014 Prof. Moura UC Berkeley
ARE211, Fall 2005 CONTENTS. 5. Characteristics of Functions Surjective, Injective and Bijective functions. 5.2.
 ARE211, Fall 2005 LECTURE #18: THU, NOV 3, 2005 PRINT DATE: NOVEMBER 22, 2005 (COMPSTAT2) CONTENTS 5. Characteristics of Functions. 1 5.1. Surjective, Injective and Bijective functions 1 5.2. Homotheticity
ARE211, Fall 2005 LECTURE #18: THU, NOV 3, 2005 PRINT DATE: NOVEMBER 22, 2005 (COMPSTAT2) CONTENTS 5. Characteristics of Functions. 1 5.1. Surjective, Injective and Bijective functions 1 5.2. Homotheticity
Constrained Optimization and Lagrangian Duality
 CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
CIS 520: Machine Learning Oct 02, 2017 Constrained Optimization and Lagrangian Duality Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may
Lecture: Duality.
 Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
Lecture: Duality http://bicmr.pku.edu.cn/~wenzw/opt-2016-fall.html Acknowledgement: this slides is based on Prof. Lieven Vandenberghe s lecture notes Introduction 2/35 Lagrange dual problem weak and strong
Constrained optimization: direct methods (cont.)
 Constrained optimization: direct methods (cont.) Jussi Hakanen Post-doctoral researcher jussi.hakanen@jyu.fi Direct methods Also known as methods of feasible directions Idea in a point x h, generate a
Constrained optimization: direct methods (cont.) Jussi Hakanen Post-doctoral researcher jussi.hakanen@jyu.fi Direct methods Also known as methods of feasible directions Idea in a point x h, generate a
Quiz Discussion. IE417: Nonlinear Programming: Lecture 12. Motivation. Why do we care? Jeff Linderoth. 16th March 2006
 Quiz Discussion IE417: Nonlinear Programming: Lecture 12 Jeff Linderoth Department of Industrial and Systems Engineering Lehigh University 16th March 2006 Motivation Why do we care? We are interested in
Quiz Discussion IE417: Nonlinear Programming: Lecture 12 Jeff Linderoth Department of Industrial and Systems Engineering Lehigh University 16th March 2006 Motivation Why do we care? We are interested in
