Virtual Library of Faculty of Mathematics - University of Belgrade
|
|
|
- Chloe Davis
- 5 years ago
- Views:
Transcription
1 BEOGRADSKI UNIVERZITET PRIRODNO MATEMATItKI FAKULTET Tetiair I. BRANIOVIC ORWIrVIPN717MW11:1AYAiMMMTNMA 34 NA -I-EP/VF, 110,(NY ACTPOHOCIJY 21 El 0 T k A p o j bat*. Ba 1 / AG. IQ 4-5 Z4*-- itatym:. STABILNOST KRETANJA HOLONOMNIH I NEMOLONOMMIll SISTEMA PROMENLJIVE RASE Disortacija xa tiaaxja naujnog tepana dakitora xushaxiokih xauka BEO GRAD 1985,
2 Ixraiavam zahvalnost Prof. dr VELJXU A. VUJICIGT za pomod u mom nauanom usavriavanju, a Prof. dr ALEXSAN- DRU na savetima i primedbama ko- jet su mi pomogle u izradi ovog rada. Posebnu zahvalnoat dugujem tlanu A!1SSSR V.V. Rumjaneoevu Ala prunenu pomod u izuaavanju teorije stabilnosti kretanja mehaninih aistema. OMBRA OPIAMAIMIA Yppy}xl r PAAA 3A MATEMATHKY, MEXAHHXY I ACTPOHOAIHJY 1514b 'EK A 6 p o j: Lary
3 RtAJ Strana. PPI Jee,!na x. dnann,:2 ljive rits kretrja slobodne take promen- masn kietanja neslobodne tai ke 2.1. Dlferencijelne jednadine kretanja staciona - nos sitemai afernsanl oblik diferencijalnih jeelnakretanja sistema tadaka promenljive sew.,... 96,000.weAV* 4.3. Difererci j..r. jednadine kretanja sistema diramanth pro enliivih taeaka u 17.:onfieura- CiOaeu prorenljivom. proctors... 2o ;redact nov eblik diferencilainlh jednadina kretamja sietema taesika premenljive masc ,. Diferemcijalne jednaeine kretanja hclonom nog si3tema promenljive ease t1 faznom proztoen L:ifereecijalne jednadine perepedeneq Tay-notelnoc etanja sistema taeaka promenljive ase.., Uolovi stabilnosti ravnotelnog stanja ;tabilnost disipativnth sistema... 56, 3.5 Stabil -east ravnotetnog stanja matemati6koe DiferencijaIne jednadine poremedenog kretanja mehanidkog holonomno-skleronomnog sistema promenljive mace Uslov stabilnosti kretanje sistema ta6aka promenljive masa o Jedna6ina kretanja neholonomnih sistema mehani6k111 tadaka promenljtve mase.,
4 6.1. jednaftne kretanja neholonomnog sistema promenijive mase sa kvazicikli6nim kordinatama Jednaaine poremedenog kretanja neholonomnog sistema ta6aka promenijive mase Stabilnost kretanja neholonomnih sistema promenijive mass Stabilnost ravnotegnog stanja holonomnog i neholonomnog sistema ta6aka promenijive mase Stabilnost ravnotegnog stanja neholonomnog stacionarnog sistema Stanje ravnotege neholonomnog sistema tada- ka promenijive mase Nestabilnest stanja ravnotege neholonomnog sistema ================ nelf ONO PPrI171R95tIJA SA MATEVIATE:1 1, S p o j: PAAA 11 ACIPOHOMMJY Ja Li T.4., A Strana loo. 1o
5 03/M7.1 ror.tinavvja PAAA 3A MATEMATOY, IlE;CAWINY r1 ACTPONOMiiiY B poj: tilarym: e REDGOVOR Teorija kretanja mehaniakih sistema promenljive vase i stabilnosti kretanja mehaniakih sistema nije izgubila ni danas na aktuelnosti. Jednaaine MeAaersokog [19] objavijene C10 - dine i Ljapunovljeva teorija objavljena godine nailaze i sada na teorijski interes i Alroku praktianu primenu u raketnoj dinamici, u teoriji automatske regulacije i optimalnog upravljanja, u biologiji, hemiji, fizici i drugim nauanim oblastima i praksi. Kao Ato je poznato, Metterski je, prvo, reaavao problem kretanja slobodne materijalne taake gde se masa menja usled odvajanja aestica od osnovne taake, a posle i kretanje materijalne taake kojoj se masa menja usled istovremenog pripajanja i odvajanja aestica od osnovne materijalne taake. Radovima I.V. MeAaerskog i drugih nauanika Oblast istrafivanja je proirena na kretanje neslobodne materijalne take mehaniakog sistema i tela, za sluaaj holonomnih i neholonomnih veza i na druge oblasti. Posebno su interesantna s obzirom na konkretnu primenu, istrativanja, kretanje tela za Aupljinama i njihova stabilnost. Problemi stabilnosti pojavili su se prvo u meha-
6 2. nici u izudavanju ravnotegnog pologaja sistema na kojeg deluje sila Zemljine tege. E. Terrideli je godine formulisao princip o stabilnosti ravnote1e tela, koje se nalazi pod dejstvom site zemljine tege godine I. Lograng je dao dosta tame uslove stabilnosti ravnotege proizvoljnih konzervativni. h sistema. Prva tehnologka revolucija i sa njom sve gira primena parnih magina podsticala je naudna istragivanja u oblasti stabilnosti kretanja. Istragivanja Di.K. Marksvela (1868 godine i I.A. Vigegradskoga ( godine) i drugih nokazala su potrebu pronalagenja opgteg principa stabilnosti kretanja sistema, da bi se daije mogla razvijati teorija regulacije rada parnih magina, odnosno regio problem stabilnog regima rada parnih manna. U godini objavijena je A. M. Ljapunova disertacija "Oplti zadaci o stabilnosti kretanja" koja je dala odgovor na tadagnje zahteve tehnidke prakse. A. M. Ljapunov je objavio dve osnovne metode ispitivanja stabilnosti kretanja, od kojih je drugi metod (direktni metod) giroko prihvaden. Posle I. V. Magedskog i A. M. Ljapunova teorija sistema promenljive mase, odnosno stabilnosti kretanja sistema razvijala se novim putevima, razvijena istraftvanjlma i ostvarenim rezultatima velikog broja naudnika. Smatrali smo da pitanja stabilnosti ravnotege i kretanje holonomnih i neholonomnih mehanidkih sisterna promenljive mase gto je predmet ovog rada nisu
7 dovoijno istraiena. Osnovne ideje istra'iene u radu temelje se na radovima V. Vuji6ida [36.1.-Paj, A. Bake 5 :1 i V. V. Rumnjanceva Z 303. U radu smo : izvrnli pokugaj gire interpretacije diferen- 71jalnih jednaftna datih u tenzorskom obliku za mate, rijalnu taftu i mehanifti sistem promenljive mase u konfiguracionom i 2n - dimenzionom faznom prostoru izveli smo transformisane oblike nekih diferencijaljedna6ina holonomnog i neholonomnog mehaniftog sistema ta6aka promenljive mase i diferencijalne jednaeine poremedenog kretanja holonomnog i neholonomnog sistema ta6aka promenljive mese; Drugo, odredili smo dovoljne uslove da ravnotetno stanje, odnosno kretanje meheniakog holonomnog i. neholonomnog sistema promenljive mase buds stabilno, odnosno nestabilno; Trede, uslovi stabilnosti stanja ravnoteleikretanja sistema su dati u smislu direktnog Ljapunovljevog metoda. Pomodp/ovih uslova olakgava se regavanje zadataka jer se smanjuje broj promenljivih u funkciji u poredjenju sa odgovarajudom Ljapunovom funkcijom iii time gto se iskljuftje potreba odredjivanja funkcije Ljapunova pri ispitivanju stabilnosti kretanja, odnosno stanja ravnotete mehaniakog sistema. IICHMINA OPrAMISAIT-IA irapymnior PA4A 3A MATEMATNNY, flaalinky Yd ACIP0110MHJY
8 1.1. JEDNA6INE KRETANJA SLOBODNE TAoKE PROMENLJIVE VASE Hipoteza kontaktnog medjudejstva odbaeenih 6estica omoguala je I.V. Me66erskom [21] da izvede u vektorskom obliku diferencijalnu jedna6inu kretanja take promenljive mase: 2/` A:74. : i112 t U i ) tit d m masa osnovne take, F rezultanta aktivnih spoljagnjih sila, u brzina osnovne take, apsolutna brzina odbe6ene ( ) MeMerski je ovu jedna6inu izveo smatrajuft s da postoji uzajamno delovanje izmedju materijalne take i 6estice koja se odvaja od take i da ovo delovanje ima karakter udara. Izvedena jedna6ina (1) van samo kada se 6estica odvaja od osnovne take iii se pripaja materijalnoj ta6ki. Kada je apsolutna brzina odba6enih aestica jednaka null s tj. u O s tads se jedna6ina svodi na oblik: de (7? ) = F (2)
9 Skalarni oblik jednacina (1) kretanja take promenljive mase je: /77 d Cf.x t2 X + d d a2 ( lie ) n) d ay y 422 u 2 - Y t 2 - a t z d t d t (le gde su x, y, z projekcije brzine take u Dekarto-, 2 3 vim artogonalnim kordinatama, a 4cii,Lt,projekcije apsolutne brzine odbacenih 6estica. Kao gto je ve6 re6eno diferencijalna jedna- Una (1) primenljiva je za kretanje take u slue /07 6aju odbacivanja Cestica iii, pripajanja CM, 6estica 4727 > 0, materijalnoj taeki, I,V. Meg6erski je u raduniodredio jedna6ine kretanja take promenljive mase kada se masa take u toku kretanja menja usled istovremenog pripajanja i odvajanja 6estica od osnovne take. Reaktivna sila koja je stvorena odvajanjem Cestica masa dm, od osnovne take jednaka je r = dt gde je, CI" vet d t g - apsolutna brzina odvojene Cestice l relativna brzina odvojene Cestice. Analogono prethodnom za slu6aj pripajanja 6estice masa dm, osnovnoj ta6ki sila je: --- clin e - brzina take promenljive masa, (3 )
10 Us - apsolutna brzina pripojene 6estice, V2 - relativna brzina pripojene Cestice. Sada diferencijalnu jednannu kretanja take promen- ijive mase, 6ija se masa menja usled istovremenog pripajanja i odvajanja aestica od osnovne take mo- 'iemo kako je pokazano u [22] dati u obliku: d17 rt." "" dins (1, -.- ) m = (a, --"" d t ct e Oft gde je, m masa posmatrane take u datom momentu vre- (Pp/ dm, mena. Kada je tada se jednadt di Gina (4) svodi na oblik: rn gde je jednaka je: m tion ta MI -I = M e 1 =0 Ore dt f 5-4-T 4 ti t - masa odvojenih 6estica za vreme (t-to) - masa ys ) d = A7 emdimu ( sit Masa take u ma kojem momentu vremena t pripojenih Cestica za vreme (t-to) n4 - masa take u trenutku t = to. (4 ) JednaCina Al x 4 X y (4) u skalarnom vidu je: 71-!77'til( 14- ) ) ') )( di d t di in; :-.Z*-4-n( 14: -- i)t 1174 ( i ) f. at
11 Kada se ta6ka promenl jive masa nalazi u miru, de o tada se jednanne (5) transformigu u jednanne relativne ravnoteze ( A di I) a' t Y 4- dint 112 it; yt,;:.' 1 Z1 13 y ;c tl a't -24pc zamenom ovih vrednosti u (7) i komponovanjem sa ay L dobieemo c fif?, Z -7` ; 1-4 ea22 iej (6) ei g/ = 0 di 6' de (-` ) = ( 6 ) 0p5te jednanne MeHerskog u Dekartovom kordinantnom sistemu me obliku: dyl ei in ( t Y ti y",y3j molemo napisati i u ovo- drn - komponente vektora spoljagnjih sila u Dekartovom sistemu, komponente vektora apsolutne brzine otpadajunh 6estica Jednanne CI ) iz Dekartovog sistema kordinata moemo transformisati u krivolinijski sistem kordinata xl. Prvi izvod vektora je brzine =ai y, $ a. kordinate vektora ubrzanja su M if a : acep ; = yr xl` de (7) brzina dinamicke promene di mase usled. otpadanja 6estica 14;.3; xe`- 01,11ka
12 5.- odnosno, - P m ( X r, X jc din X 44 + ( - gde je - kontravarijanta kordinata spoljagnjih si- la tj i 3C.t Jedna6inu (8) mcaemo pisati u obliku: D t D D u faznom prostoru op6te jednaaine su prema (491 jednake:.±* = QKn p,-. tp = a r p4 lot Oft 74 Pat ap Ovde su generalisane reaktivne sile 7.. ( ) a Oil IL 2, ) su kontravarijante kordinate veki ra brzine otpadajuaih Cestica. Qr. pi X Fri acp,c4)( = Q4, 4- Y.:1, Generalisane kordinate sila izazvanih otpadanjem Ce - am 14. ay, stica su jednake cte ak% generalisane aktivne spaljagne sile su 1") rn (8) (9) r- r- id a c,4 X UCHOOFIA 07FAErISAWIJI Y PTIKEHOT PAM 3A MATEMATHXY, MaAHNKY H ACTPOHOMHJY b IribJ1 ss OTEIKA 6 poj: AaTym:
13 JEDNA6INE KRETANJA NESLOBODNE TALKE PROMENLJIVE VASE TaCka promenljive mase m = m (t) gde se masa menja usled pripajanja Cestica osnovnoj tanci na koju doluje aktivna sila F, je vezana i kreee se po povrgini = 0, '10,y,z) =O. (10) PolcAaj take odredjen je vektorom poloaja Ako kretanje neslobodne take po povrgini (10) posmatramo u Dekartovim kordinatama tads su jednanne kretanja take jednake [22 ) a >c = dm (a y h ax 1?-1 m d 2-Y voj d ze 2 y el!...n (a2 -j) A e # A 2-1 di' ail az Ako posmatramo kretanje take po datoj kri- jednanne su (x) t) (x, y, 0 Ire -`.-2L-2x x (U, - x1. A v ax ax LYZ2 J ay m eal....1z 4:6172 (a3 # -3 1/4P # ) y/ de 6a/e- az az
14 7.- Radijus vektor r take koja je painjena vezama (10) mote se napisati i u parametarskom obliku: (z = ' % 2 ) Brzina posmatrane take sada se maze izraziti u obliku: Zr a.2 4 a2 2 Izvod brzine po vremenu sada je civr = AWISINFI wg dt ad ili u skalarnom tijcp,...y,' dt jer je (f,,21). -(5 2 ;:$1.. i Ji/I s l a. 1,2) obliku..6 5 to, ,4 &rap (i (s = = 1, 1, Dr is 2) 2) (11) Diferencijalna vektorska jednaoina kretanja neslobodne tacke promenljive mase za posmatrano kretanje je 4fin m = F t2'' ( '_ i -t. A gra a (19, dt ili u sklarnom obliku 1. 2 ) m..:ly6* (a i" i de ac odnosno ', 2 - arc' ag.s ZS z), (14 = I)
15 Komponovanjem prethodnog izraza sa cijalna jedna6ina dobija oblik:, diferen- D 4: ay: a 2 V.Jo... 1? i31!; f. &.1 aysagi.3,e # ay, Generalisane site u konfiguracionom prostoru kao gto je ooznato mogu se napisati 6? 74" Yi IA Sila uslovljena otpadanjem 6estica Ye i le kompozicije sa 16- svodi se na oblik: af/3 Yr ic ay, corn ayg: Z.Y4: afp de ar gde je 4e ay. ay` are api vit "aa cp of pos- j 444 a44 P ( a. Kona6no diferencijalna jednaana kretanja neslobodne take promenljive mass u konfiguracionom prostoru K 2 2 i t dobija ovaj oblik:?i" C.ft Q ~ Koja zajedno sa jedna6inama veza (10) odredjuju kreta- nje sistema M. OMBRA OPrAHMAIDIJA YAPYMENOr PAAA MATEMATHKY, MEXAMY N ACTPOHOMHJY H JIHOTEKA tpoj: 40.TY14:
16 2,1. DIFERENCIJALNE JEDNA6INE KRETANJA STACIONARNOG SISTEMA Posmatramo kretanje sistema M kojeg Cini N dinami6kih tacaka promenljive mase m,, = m,(t) (y = 1, 'aja N). Poloaj take Mi odredjen je vektorom polo- e'en je sa k holonomnih veza:. Kretanje sistema ograni- ( o (13) ( = <3w) kao i relacijom promene mass CIM My = - dt Sistem se kreee pod dejstvom aktivnih sila = /cm ( , EA( v.; 14) I a zatim sila izazvanih promenom mase d/22 = 11 i sila reakcija veza R,, EA c e ra.. Kr4:t6je stacionarnog sistema tacaka promenijive mase moguee je opisati vektorskim diferencijalnim jednannama F tt # Z A 6-1r 2.4 di zr-/
17 10.- 2'; dt koje zajedno dam, 4t/ sa jednacinama - 24t Ad 71^4141,4(15) veza definigu kretanja sistema. id; mnohoci veza koji podle't'u odredjivanju, apsolutna brzina odbacenih 6estica, brzina ta6aka sistema. Ukoliko se kretanje posmatra u odnosu na neki pravolinijski kordinatni Dekartov sistem y', yi L l y; ( sa vektorskom bazom ef,,, Una (15) su ovoga oblika: q: ( M Y )'0i,)-= di 1-q(-17'14, 41 01/ d, I e;1)=. 0 jedna- e=r a 31, (16) = 1,..., = 1,2,3) may =0723 _J -073,_2 tada se jedna6ine svode na oblik: I or/ = ( 14; s'to zajedno sa (!3) ' a' 1- A( 34.d I di- 6.4 aye- 37, 3y-1, 3y-2 ) (y = Jedna6inu (15) moemo dalje izraziti u obliku: CiY. Ci rli C v.ww. ay; (17 ) cirri 3N k skalarnih jedna6ina. Integraleel ovaj sistem jednacina dobijamo kona6ne jedna6ine kretanja sta cionarnog sistema dinamiaih taaka promenljive mass.
18 Kada Dekartovom sistemu kordinata korespondiramo neki sistem krivolinijskih kordinata x1 x 2 x tada su Dekartova kordinate y i povezane sa generalisanim krivolinijskim kordinatama uz uslov J w axi I = o Baza sistema x,= I X, I X * ; I je gde su --a a -- an, 3 r; gio axe ' awl / gi a x Kada se skalarno pomnoii jednacina (15) vektorom sledi an, d -a 6, F at etzn,, 4- (18) dt +A( ra.., are tf y, y = 1, 4, 9 N) 6-1 Izraz na levoj strani jednazine (18) transformisa6emo na sledea nacin: d a r r; a'x', two uy axi I - V" _ dt Kako je : n a dalje, acidaxo ak 3cd a a x e _ an, an. d.xf ctx 07, ( my ax ax' to dobijamo, ax'spdt a r; a i n7 A, a); a tr> a/at 4E -- ax j. a Xi X Af X' de dt At/ Metrinci tenzor posmatranog Il prostora mote se definisati izrazom _6411 rm, Zfriṟar7 -- ax' a xi odnosno t (12)
19 12.- pa se prethodni izraz svodi na oblik (19) Generalisani impulsi mogu se izraziti relacijama (20) Iz(20)se dobija kontravarijanta koordinata brzina u obliku 6-2 4/p, gde sual kontravarijante kordinate tenzora6v, to je: k 1 za i = k za i k. Masa V-Let414csistema i brzine dinami6ke promene usled otpadanja 6estica ostaju invarijantne u odnosu na sve ovde posmatrane transformacije kordinata l s obzirom da zavise samo od vremena t. Skup koordinata fdefini5e n-dimenzionu mnogostrukost koja je snabdevena metrikom s 2 ti d.x- dx, Kada u jednaanu (19) unesemo relacije (20) dobijamo diferencijalne jednaane kretanja sistema u obliku
20 13.- Na desnoj strani jedna6ine (18) imamo, prim, kordinate spoljagnjih sila -Ow )( i; ax, xi Y;, zatim, kordinate sila reakcija, ca Dr = d.r.4 na kraju kordinate sila izazvanih odvajanjem Cesti- Kona6no t 4, = ct42 eī - v a xi* dobijamo jednaane koje odredjuju kretanje sistema tacaka promenljive mase u E314 prostoru D. /2. d 1 k jednaana veza (13). W741"010 ViAlinAPIJA YOYEIEHOr PAM, MAT:W.T;;;Y, ME,H B poj: Aatym: 5li1JIHOTEriA ACIP011ati# _ ( 21)
21 TRANSFORMISANI OBLIK DIFERENCIJALNIH jednaoina KRETANJA SISTEMA TAaAKA U radu se nalaze diferencijaine jednacine kretanja sistema tacaka promenljive mase u ovome obliku[349] : d 2 in 1,27 2 P - re, glavni glavni vektor svih spoljnih sila koje deluju na sistem M vektor svih reaktivnih sila - vektor polaaja centra inercije sistema 27 znak sume odnosi se samo na one take koje menjaju masu Polazea od jednacine Me6Cerskog izveeemo ovaj oblik diferencijalnih jednacina kretanja sistema ta- 6aka promenljive mase u konfiguracionom promenljivom prostoru i pokazati da se ove jedna6ine sa Dekartovim sistemom kordinata svode opet na jednanne (22) Da bi ovo dokazali napigemo diferencijalne jednaine kretanja holonomnog skleronomnog sistema materijalnih ta6aka promenljive mase u Dekartovom sistemu koordinata:. =F O P 2 n') -7- r /- (22) CI 3.4«-= m; 411.e -* E di gde su Ad Langranevi mnaitelji veza, - - -; 4 2, 3 (45' )
22 ku: Ove jednacine se mogu napisati i u ovome obli- d y = (23) YL:ee rn ' 1 2- A '331 4:4 Ako mesto Dekartovih kordinata uvedemo generalisane kordinate, tada se brzine mogu izraziti u obliku: "ay,.: *.c a- ` ar< Posle zamene ovih kordinata u jednannu (23) jedna- Cana se svodi na oblik k r -;.1 1. i; a 3/4: 1, y'.; E( ( 24 ) / e crt ai" Sada maemo Levu stranu diferencijalnih j dnanna transformisati na izraz - a ty; 'so V. d I (In!' 1?" ) AV; f - In; az'ea F/3 odnosno qrd. e aly - art;')jea Posle izvrgenog diferenciranja lave strane jedna- nne l di na oblik: -C4 It [iv 7ft i sredjivanja desne strane, jednanna se svo- f Z 74' mi ati3,e of ay, 7,e,y,' -07; 17; m; 177; i ip".# mi. --- tr/341. ay.74 A4 a-ie a afaia oe
23 16. Drugi i poslednji clan sa lave strane u jednanni su istih velinna a razlintog znaka to se potiru pa je jedna6ina jednaka d a d. -DYt - ayt' a te t rn f 1=y Dr- di a re dfee -Dyt + /77 ; f 41 / a 0,49 fp E - ax. 1 _Acr 'D E oz. Da bismo izraz dalje uprostili diferencirali smo Clancve sa lave strane jednanne -DY: e,4 -a ly,. a4.73 Dyz. 2 -t- f 2 + /72, in,. 41(4. - DE P4 af ago( ey) a Y:. P ---a)/4 - (2.5) a of, r!.74 /91; f.17/- + ; gc zy; a.f"aly3 ay 4. a-fcc4 Ako komponujemo jednacinu (25) sa dobijamo a, aye -- ay; t. 'DY; ) /1 a DPI ; agei atiar a r" d.r r m 'Or D//; 2, -" 4. a Yi v.., 9:,07, m, ar'.74 = 7 y m A -ay; a li ilk m" ; ay-,3i,. ae De ti,r4i /ti l'a 'D4r 4 ' ay; ay; ni : at 14 a r ay; ail ar ' Vic.a7c ay' f I 10-2'1As-- ari as J.-GI ay; ay Kako je ar ---).--4 "a%.* upravo na grad I to 'Dr ' a r 1) p!. all.- je proizvod gradf. ---ozbog toga poslednji zbir u kr jednacini sa desne strane otpada. Drugi clan sa lave strane i poslednji sa desne strane se medjusobno desnoj strani di na oblik potiru, to posle dodavanja i oduzimanja -ay; a-xnana /77; jednanna se svo;...
24 17.- N v.-- ay, a Yi ay; -ay. ay" ay, 2_ /72 ; g 1- m l=f 4-1AI z:r1 N 1 df z 4 ar af19 a, G2.0,e 4. 2 apemjp et ef'1 af` arl - are 9.14/ af Imajuoi u vidu da je 34 zy; aye. nz. a et ar 4=, 2.10/ 4"/ -as 2y/ "ay; are?!p yr.4/3 S obzirom da je drugi I ac d.fy are of, 11 aixs, *9 ) to se konacno dobija traieni oblik jednacine -ay,. #C2.0/1.#/a:/;,40:141ft=r00444*, (. a* 4-2 Ciasip e* Q.,#. i zvod od axe yet t - metri6ki tenzor - generalisane sile....., = C2.g r fi- 2 c2.t.ks f aii- 421.,), 9 2itv; - koeficijent povezanosti generalisana promena muse, diferencijalne jednacine moiemo sada izraziti ovome oboliku: jednak ax. 0/ ce I.z (c2..( 2 414) 4 r.:6 a, feat P = 620 (4114.4)#242all gie de adnosno 4- Caddy! d 2 (C2ocp g ft) tr. a ocko j_ Posle razvijanja leve strane jednaeine. 14 of vra6anja pojedinacnih Clanova sa desne strane jedna,. dine na. levu, dobija se 8 K 424- f di,,j aceap-2 4,4"-iti teetz,,of Q014%, ig (28)
25 18. to posle sredjivanja ovoga izraza, jedngnna se svodi na poznati oblik diferencijalnih jednacina kretanja sistema materijalnih tacaka promenljive masa. a 0 r4;j3 E D4 di) /1,. a/ Za slucaj da se masa materijalnih tacaka sistema ne menja, tj. m i = const, jednanne (2e)su jednake ue 2 S obzirom da su tada izvodi Cj4V i accp jednaki nuli, pa se sistem diferencijalnih jednanna (26) svodi na poznati oblik diferencijalnih jednanna kretanja sistema ta6aka nepromenljive mase:.e.1%edoa 6/(40 z b/ Ako je masa materijalnih ta6aka linearna funkcirni - a m 34)4) ja vrementitswpaitacine (26) se svode na oblik CI -L't (a = d 12-6e t.0( 4. C2'4Y g /Si g U prethodnoj jedna6ini nije sadrean Kan u kojem fi drays: guricemzvod mase sistema jer je jednak nuli, tj. 24e d 2 r 6 ) A -ay; "ayi Promena mase u jednanni (27) zamenjena je izrazom: ron ( -0- k't -ll art rr a" ' a ( 2 )
26 19.- c/ za pravolinijske sisteme koordinata jednacine (26) svode se na oblik det (62.,), ft) = a,.,a,,,(,-c_f-y#2,2.yeeṛ, (28) jer su Kristofelovi simboli jednaki nuli, pogto metricki tenzor zavisi same od vremena U slucaju ovog sistema koordinata ako je masa sistema linearna funkcija od vremena tj. dine (26) su: 2 a ti ei 0,,, 62..x., (a.74.2 c2, Diferencijalnim jednacinama de o do, 41 1 eit =a0 #42«y v-e7 r a-144 ciectip-2.17 s- X # rn, (6e: - oc,_ 2m e.2". (z yi ).2' y c - trre:la-e).r ) , 4. m i Ali /72; )1," dt ili u vektorskom obliku dz v Ow " 7110 gto nalazimo u radu [3 43 air e F p 2 2 /71 - L., m: /7
27 2c DTTERENCIJAINE JEDNAoINE KRETALJA SISTEMA DINAMIoKIH PROMENLJIVIH TAOA A U KONFIGURACICNCM PROMENIJIVOM PROS'IOPU Posmatramo sistem N od N tacaka promenl jive mase, gde su mase my = my (t). roloaj ta6aka sistema odredjen je vektorima polo'zaja ry ^ y-,, ce 4 try (n 3 N - k). Sistem je vezan nestacionarnim vezama fc, rt.., 1, nog,. k nestacionarnih veza sistem ima 3 N - k nezavisnih kordinatajr Kordinatefi njihovi izvodi po vremenu erm 9 - de k) dr di ' su nezavisni od m x = f (t). Kretanje se '4" posmatra a pro6irenom bonfiguracionom prostoru R, =12', n",i,de /e 1; 14 f tada kordinate vektor a polaaja reprezentativne take sistema zavise kordinata Tako se dimenzida potprostora proiruje na podprostorima Rn+I. to kretanje posmatramo na :Gaza prostora je 1. an, (y) (0) Jr 7/.3.5r :Da bi odredili diferencijalne jednanne kretanja sistema u posmatranom prostoru pomnonmo skalarno diferencijalnu jednannu vektorima ; s a-4 er cmo 11;1 1 ) 1, jr;.. I. I A, - = cee aft 4, I A6 :rad, di Transformigemo sada levu stranu jednanne (3C,) teagda oblik: (30
28 dm rizv 24, gri9l) 2't 71;' a, ay 2 r: 7 an, an: Ito - - =- -Tre Prethodni izraz dalje molemo napisati: 2"; " 12 a.fp af" 10..; 1'; 44 -a rai h., (2,1.? c.ov aft agp "/ al i* MetriCki tenzor posmatranog prostora je de-/ a g a /7, == ay alp ' --b. Z /3 --,... cz / /77/a f,, /bgc 42 ft/3 e se izraz (Mk, ) y(by svodi na oblik: Ole 4eca 1b4.T42.4 'a,ia Ie " a.2' ay' Kona6no dobijamo jedna6ine kretanja sistema M u obliku: 422, de gde je P 1 a. C2.cp (.31 ) (04 = -.'?) koje zajedno sa jednacinama veza omogueuju odredjivanje kretanja posmatranog sistema M. (31) Za siu6aj da su veze skleronomne tj. ( 32) diferencijalne jedna6ine kretanja stacionarnog sistema ima-
29 22. a' (ce f Ako je masa sistema konstantna a veze skleronomne 4( (0 su jednanne jednake / (it. p gde su p.,/ impulsi 61.( 1/3/. (34) Ako je cistern pored holonomnih nestacionarnih veka (433 Moo, odnosno ( r r r 0, --- 0,4,- ki),,--,* vezan i sa neholonomnim reonomnim linearnim vezama (yo 4 g,..,w), 0 4: (35) 14, ) de C16,4, ) / i relacijom promene rase 14,9 = = 44,n2 0/./ (Jo ) tada su diferencijaine jednanne kretanja posmatranog sistema jednake: Dry = Xtoji. fyl dt s Ovde je reaktivna sila t -Zri/e* I Ai% L. -re c [r/ 6a a ra: 6 /d4=f Vete ta6ke. Ako usvojimo indek- se, tj. i ,. v.v e Ain onda ove diferencijatne jednanne svodimo na tra.zeni oblik: k& D ar t = X '4/4 4 1,- Y' -,, X Aim I a' e 6 Cr( 4. de r-, ark 6.../ gdesuaiti 434.( mnontelji veza. Ove jednanne zajedno sa vezama odredjuju kretanje pojedinacnih taeaka sistema M.
30 23, U radupp. monografiji[wizvedene su diferencijalne jednanne kretanja skleronomnog i reonomnog sistema mehani6kih taaka Cije se mase menjaju u toku vremena u smislu Me5Cerskog [191 Medjutim, izmedju diferencijalnih jednacina izvedenih u radovima Pfli j43jpostoji odredjena nejednakost, pa ovaj rad pokazuje otkuda to razlika. S obzirom da je monografski rad [43 pisan veoma koncizno nije moguee izvrati prosto po- redjenje ovih jednacina kretanja bez detaljnije analize, 6 -to se ovde i 6ini. Na prvi pogled veoma je uo6ljiva razlika. Za kretanja jednog to istog sistema diferencijalne jednezine kretanja prema radu[33 3su oblika, 4.41 za gkleronomni siatem: n f (39) gde je _ aake 1.:am; ax az&,fre - az 0-2 7e a T et #""atitat dildt (11.0) a za reonomni sistem: (k,1 = 1,2,...$) (41).or gde su kovarijantne kordinate Kk vektora K, date izrazom: dl / Z)4C 'd.17,c. - k = - AK -"*.a72-- (6,t it I i aft 49.17/c.2 4 pri emu su: so 31 ax OX C A k = ---, at U monografiji imaju prostiji oblik i to: diferencijalne jedna6ine po formi
31 U monografiiip]diferencijalne jednacine po formi imaju prodtiji oblik i to: a J D 13 " Di gd.e je 4.9ve dp, a.6 at. 9' i, kao 5to se vidi, postoji jedna relacija vise, i to: ( 43) (44) Langraneove jednacine kretanja sistema tacaka promenijive mase su: d DT _ 62 2.fk (45 ) - s ) Autori radad.9 J uzimajuel kao usnov ove jedna6ine, posmatrajua, prvo skleronomni sistem, izvode jedna6ine u obliku (39) polazea od kineticke energije oblika i e nalaze da je d d 7 cy e a 44e 2'4 2 # ap a/it -- Da.ee DT 7 are dv-i9;e (j,1 ' k 1,2,... s) arc Posle smene izvoda kineti6ke energije u (45),,jedna6ine se svode na oblik: - e 3a4- * 6 - Date -1_/ oakeireil:-.:42,4-14)- ake2 1- a vi f odnosno a z. ake De e Dy_ a # p 4 p A k
32 25. - pri emu je at Isti sistem jednacina za skleronomni sistem u radu [43J napisan je u obliku: Di e /) a di gde je (74-ic --a art e z (k, 1 = 1,2, s) (46) (47) iz Cega se mote zakljueiti da postoji odredjena nejednakost izmedju (46) i (39) jedino u interpretaci ji izraza (40). U radu f 5] to je ag eia ag2,- ax. ax : (48) at apa u radu je, kao 5to se vidi iz (41) A = a 4. E e a 2.-2c`449),a e. a a,ft ag e t a~kattafeat z- 06igledno da je ova relacija neodreiva za sistem sa skleronomnim vezama, jer je u tom slaaju 21 2'oc i _t_ ed aeoc 4.= C a fic arazs obzirom da su svi izvodi t = 0. Kada je kretanje ograniceno pomo6u s < 3n holonomnih reonomnih belateralnih idealno glatkih veza u radu uzima se ponovno kao polazna osnova jedna6ina (45), pri emu je tada kineticka energija: (50 )
33 26.- a odgovarajuei su tada izvodi SA 2 Zamenom a,te e -a aii e *1 ask u (45) sledi -e aee vi e a ke 2 4- a!, a46 e af* - -e -a Air e J?,f±F ;Parr (51) io.t 0,7 e 7.i7e co//6 Kada se zamene aetiri poslednja nano. sa Kk jedna6i- na se konaono svodi na oblik (3), ali za koordinate vektora Kk se dobija Tfi -342,ce.e e 9 -e al*e 0 /2;.641c e = A -- de a f* awe a ne kao u (42). Da bi doui do kona6ne ocene da li postoje su5tinske ratlike potrebno je pooi od iste osnove i istim postupkom dda do formalnih iii kvalitetnih razlika. U tom cilju ne gubeoi nigta od op5tosti l dovoljno je posm atrati mehani6ki sistem od n ta5aka My ( 1 = 1,2, n) promenljive mase My - m, (t) a smislu Megeerskog Hje je kretanje kao 5to je ve6 re6eno ograniceno sa s holonomnih reonomnih veza 4 eabk a c Pki Pk2_.2?rt. ( 52) - -, aei (53) gde su r; vektori polaaja ta6aka
34 27.- Kretanje posmatranog sistema tacaka odredjuju diferencijalne jednanne Megoerskog ei 24, dffiz". de 4142" zajedno sa jednannama veza (53). rn, k; -77 (al"' - 245) 4' r Za transformisanje vektorskih diferencijalnih jednanna kretanja (53) u koordinatni oblik nekog konfigu racionog prostora treba veze (53) napisati u ekvivalen - tnom obliku: ry r, t -, 2 i s) s = 3/2 A-e) gde su f= if', - te, Veze (53) zadovoljavaju uslov brzine 01,120 a /-; no Langrangeove nezavisne kooi.dina- ) r,, -3 /cf., odakle se vidi da se vektor brzine ti;razlaie na s + 1 koordinatni vektor gi(f/t/:= A 10.j. 665'" Vektor ubrzanja taaka My ti, 4,21..14: t, aw a ii- a ;.a2, a 2 r = ---,---. d r A (5k) de ai, 4 Op ti4 dt i 2 a 6-4..,. f (i4 = 1,2,...,S) treba takodje razlaiti u s + 1 komponentu s + 1 dimenzionog vektorskog prostora R S-04 koga generigu vektori i jedan vektor n, upravan na R. Da bi dalje izvodjenje bilo preglednije i kraoe mo'ie se vreme t uzeti kao s+1 kordinata i to q = t, gto simbo- O a:t li6no zadovoljava izraz za generalisanu brzinu pa uslovi brzine kraee se pigu u obliku 24-=2 4'4g,),,c, a vektori ubrzanja 4/t _ ( 5 34) o
35 --11 e; -Dlry 67) -Dr; 2).z (32/3 a.?.e f 28.- gde sad indeksice) n tj.(ct ii3. 0, 1, 2, J3 uzimaju vrednosti od nule, do Kao to je reseno u svakoj tacki na s+1 konfigun#1 racionoj kordinatnoj mnogostrukosti R moze se vektor ubrzanja y -te take razloziti na sumarnu komponentu u s+1 dimenzionoj tangentnoj hiper ravni R i vektor R a to zna6i da se i vektori azir razlaiu na taj nann, tj. -a/ ap 2 ry e (55) afa p gvy- r 'e 0 13 a0.9 gde su otrs p (5-) koeficijenti povezanosti, a betfrdrugi metricki tenzor prostora Rsti u nju geometrijsku strukturu sada nema potrebe da se zalazi. Ako se zameni (54) u jednaanu (53) I uzmu u obzir relacije povezanosti (55) sledeee msv..4alt- 1-'44 cep i7ji /c) Ci;44' '270' atep kii317 7-, al /14,. /, (56) -t- j-0-2-# frodf-7:77" de 141"i Pomno'Z'e li se sve ove diferencijalne vektorske jedna- sine skalarno odgovarajuam kordinatnim vektorima 4g,9 1, 2, s) i sabere po indeksup, dobi- ja se S diferencijalnih jednaana oblika jer je cepde oe (0.1 p op 2-0 = kao (57 )
36 ZAvy reid )lr f su ne site, i ac; 29.- to kovarijantne kordinate generalisane aktiv- 12. /27 de- j 7-4. =2_ " --x / 470,),t. f cs') ale 2 odgovarajuee kovarijantne kordinate vektora reaktivne site. Jedna- Cine (57) odgovaraju jednacinama (43). Skalarnim mnoienjem relacija (56) vektorom= depi' sumiranjem Po dobice se jo6 relacija ave c/1.14* roc131,i',:i3j--rao 6to je indenti6no jednaoinama (44).- -a a ( 58) Relacija (58) nije za poredjivanje sa diferencijalnim jednacinama kretanja (45) jer u njima to relacija ne postoji. 0 smislu relacije (58) mote se opgiruije videti u radu g Prvo treba primetiti da u jednacinama (39) svi indeksi uzimaju vrednosti od 1 do s a u jednacinama (57) latinski/ indeksi j, k, 1 od 1 do s, a grcki 2 /3, &I 0 do s. Ako se i jednaine (57) svedu na istu vrednost indeksa, sledeee / /3 Ciipu? ce s g s/ Aq'o do') 6 / ---Qc -IL y--is.14 's / 2 a 2 odnosno: a - Dil,e) kj de a: -.2 or oki
37 tj.: 30. kako je roc; ae2 "aa.0 aqo aa.,0 Ft 7,)e- 1 az = at 2 a)..c.2; 1 / a Qk ( di- mole se papisti zbog 06 1 A7? O.F4 Zamenom u (59) = a pc: ("2,0 / r;o ci, obijamo jednannu koja se svodi na formu jedvanne (46) u obliku: cab; Ar k4:ab,.2, A I de, --- t.2 a aft 02 = de -P4. az,.aat. rf a 7- - ae ail at - -D.gc (60) Dakle, bilo da se podje od Lagraieovih jednanna druge vrste (45) iii od jednanna (43) dolazimo do re lacije (60), koje se razlikuju od jednanna (41), s obzirom na (42), za skalar de.2. Ova omagka ongledno se potkrala autorima rada 133 u izrazu (51), jer u radu nalazimo da je d 3 T 'ae:zee e ate -4,/ e aiztaft, g -74 aice doo b..e `DC a c ep i Q e 1-2 a.f a to je nemoguoe s obzirom da od C. jk 1 ne zavisi z A- Prema tome kovarijantni oblik diferencijalnih jed-
38 31. nacina kretanja sistema tacaka promenljive mase u n dimenzionom konfiguracionom prostoru su e2ic x die iti njima ekvivalentne jednanne eke gde je QK `` -72, ek (k = 1 n ( oc = 0,1... E n (") , ) '?/2ic e -e aft-zco `De2e0,-ej ;62 U progirenom n+1 dimenzionom konfiguracionom prostoru kovarijante diferencijalne jednanne kretanja posmatranog sistema su oblika (43). porixttior PANA anfrig41 S3 "f 3A _MATEMATCY, MEXAHNNY A UTONOMY B146JIRTE IKA Spo I:
39 JEDAN NOV OBLIK DIFERENCIJALNIH JEDNAOINA KRETANJA SISTEMA TAeAKA PROMENLJIVE MASE TJ svome radu I:4S] V. Vuj616 je izveo sistem od - 1 diferencijalnih jednacina kretanja sistema taeaka konstantne mase u obliku -().2.r',,_ -c a Z L., 6.. 0, ' (61) opc.e" / (ck '. ), , dt ( e = 60e,. _._,, / gde je Z Gausova prinuda. Gaus naziva E4 ] prinudom zbir proizvoda mase svake ta6ke sistema i kva- 4* grata odstupanja stvarnog poloaja take od polaaja koji bi ona zauzela kao slobodna za beskonacno malo vreme 1st. Usvaja se za prinudu Gausov izraz n2; ( 2= ( /77; odnosno, u Dekartovim pravouglim tordinatama A:.7' "&) Kako se Gausov princip, ustvari, zasniva na varijaciji ubrzanja W, a kako "generalisano ubrzanje"ftne 4 izraiava prirodu ubrzanja W to invarijantnost sistema kordinata u nekom konfiguracijskom prostoru 14ostvarujemo izrazom 2 d. 4i2 vv,
40 , 33. 4fi-T an" 40.i`k I aft' Or de -Or are pa je sada Gausova prinuda u konfiguracionom n-dimenzionom prostoru jednaka: (ovde je n broj stepeni slobode kretanja holonomnog sistema tacaka promenljive mase): /=l 1724 VC 47: 1221 ac Pip> 177; Cele Lc~ s ' /77; ^ I^7 ta. ; P. DR 441Pli de tn; 0.4 TP 4a/707i at Ako sile izrazimo pomoeu njihove projekcije na kordinatal& ose i ako upotrebimo Hercov izraz za mase ta6aka sistema \ I Xx.Xx rn-4 Mx Ka/.m/Z7t2 tad.a se mole pisati: 4-1 Sada prinuda dpbija invarijantni izraz u konfiguracionom n-dimenzionom prostoru u obliku Dia( DiP e dzi ct dt ft une uzima se u obzir normalna komponenta ubrzanja na konfiguracionom prostoru,
41 34.- Sledeai ideju rada 1,51 mogude je diferencijalne jednanne kretanja (61) uopgtiti i za sistem ta6aka promenljive mase. Zaista, posmatramo li u tom cilju N ta- 6aka mase = 720(i), razlika u izrazu za prinudu Z sa sistem konstantne mase, je sada u strukturi sila 7,7 zavisnosti kordinate tenzora Ca re(p. Kao gto je ranije istaknuto u tensor 0 ulaze maseglp=r44wte je INA ovaj tensor zavisan od vremena bez obzira da 1i su veze skieronomne 11i reonomne. Takodje je pokazano da u diferencijalnim jednainama oblika D- P /) 4.4 ce P at kao gto se vidi, pored generalisanih sila O ct figuri u reaktivne generalisane silo NP- P ) a t Otuda Gausovu prinudu treba pisati sada u ovom obliku 4V36ii gde indeksi sabiranja.2(120,#y4)-4 a't (62) (att 4' We) ( 11- Y1ct) / usima0 vrednost od 1 do n broja stepena slobode kretanja holonomnog sistema. Aka prinuda u taaki.e, ima najmanju vrednost(4.53 u toj tal6ki je jednako nuli, tj. stp±)=0 &Z = DPI tdi a(-- (63) gto predswtavlja Gausov princip u konfiguracionom pro- storu Vn.
42 Odavde sledi kao i za sistem ta6aka konstantne mase da su diferencijalne jedna6ine kretanja holonomnog sistema ta6aka promenljive mase oblika a z = 0 / ct- (64) koji daje jednacine kretanja sistema ta6aka promenljive mase u ovome obliku: 231.2A a., 42-4t,aj i74 271i4s ; Y:=K. Dakle, ako je moguae sastaviti Gausovu printdu u konfiguracionom prostoru za neki holonomni sistem tacaka promenljive mase tada su diferencijalne jednanne kretanja oblika (64). Ako, medjutim, na sistem tacaka promenljive mase dejstvuju i neholonomne veze oblika ili `Pr koje zadovoljavaju uslove (64a) E grczei_. (P/1/4. v, i. ( ) prirodiko je o6ekivati da relacije (63) i (65) dovedu do broja diferencijalnih jednacina kretanja koji je
43 38.- jednak broju stepeni slobode neholonomnog sistema. Zaista l akot ide od 1 do 1 iz jedna6ina, za uslov lo/,, a,' I z-# ( 4 moguoe je 1 zavisnih varijacija s / ddif D 2 Pc) 06' az 74- c, 7 DEvi CG S ( (66) izraziti pomoou n 1 nezavisnih (6 = 4- // - ( Pl.. Relacija (63) deli se u tom slaaju odnosno, zamenom izraza (66) u predhodnu relaciju dobijamo:. e na dve sume i to: f Di zit Odavde siobzirom da su varijacije nezavisne, sledi n 7 cs a ez7i D.e Yie- diferencijalnih jednacina kreta- nja neholonomnog sistema taoaka promenljive mase 4- CG az = a (67) (a= #4, koje zajedno sa jednacinama veza (64a) obrazuju potpun
44 a -P a?., (67 a ) ccl df ft Df it I = a e -4 Y ± C d ( 6 1 oc i Yd i oe de /.(e...-1,/,_...) Ove jednaeine zajedno sa 1 jedna6ina veza (65) ocfre - djuju kretanj neholonomnog sistema ta6aka promenljive mase. Sao i u slu6aju Gausove prinude, energija Apelovog ubrzanja je invarijantna. Znamo da je energija ubrzanja sistema tacaka promenijive mase u nekom konfiguracionom promenljivom prostoru Vn je N I 2 S /22," kada je - odnosno, s n49 vi. - = 44, a. Ar- n4/ n41 a;;;17 zroag s r-/ Sada 6emo dobiti koordinantni invarijantan oblik energije ubrzanja u Vn prostoru 39.- sistem od n diferencijalnih jednacina kretanja za regenje mehani6kog sistema. Posle zamene vrednosti Z u sistem jednacina (67) i parcijalnog diferenciranja sistema se svodi na oblik: 2S-=-2. MA. a 0./1 de gele" I (68) Ako izraz (68) zamenimo u (62) dobijamo:
45 4o.- 2 S 2 [(a. IP& cii(r Y7 1 pa se sada jednacine wa holonomne sisteme a (5r) svode na oblik: Za neholonomni sistem koristimo sada jedna6inu (67) 0. posle zamene Gausove prinude oblika Di a( / = 2 s_ 2 (a. a, 4 90 (zr# 4,) 09/t jednaine se dobijaju ovaj oblik S (a, irso 7, 2 Cc 1 S (4,,..6) )(i" odnosno t et` D S + 9, C c) / cil k tit ) Diferencijalne jednaaine (67) i (68 a ) prestavljaju nov oblik diferencijalnih jednaaina kretanja sistema promenliive mase.
46 DIFERENCIJALNE JEDNAoINE KRETANJA HOLONOMNOG SISTEMA PROMENLJIVE MASE U FAZNOM PROSTORU Kretanje holonomnog sistema ta6aka promenljive mase mozemo posmatrati u faznom prostoru Vn faznih promenljivih umesto u konfiguracionom - prostoru u kojem kretanje odredjujemo regavanjem diferencijalnih jednaana (8) i (9) kojih ima ukupno n i sve su drugog reda. Diferencijalne jednanne MegCerskog za sistem od N materijalnih ta6aka promenljive mase jednak je - - abo ili 4 2 i (1-17>v ) a /VI,---, ai GP) (69) ci t e-v.s. A za sistem vezan skleronomnim holonomnim ideeino gletkim vezama jednanne se mogu pisati k Ar) drl/i titioy 4I 69 Sys 70) d OM Y.: ) Yi -# E 3-2 i de,9. do/ -4))V Posle mnoienja jednanna (70) sa i sabiranje a2a po indeksima 1 jednaane (70) se svode net oblik: (ix 'ay; y // 2-. k ale.ayt. afat aya ait ay; 32 4 Ako se izvrgi transformacija koordinata u jednannam mam t aprebace6lenovi -Yne levu stranu t prethodni izraz se tada svodi na oblik:
47 43. 30( odnosno 3N ( rn 1) 1Y I. t i=1 Kako je y age J11 ay!' 311 1) 2- j C7 dm; II 4. mroy*,(71) din ;:1 O 1 de. ay; --,,c i = a,.,) = a naeina mote dalje predstaviti u obliku: 311 3# aiy d,./ayi 4# 7 ax. ay; f?-a izt4 9afia _f6 eft f 4.1,. P3 1=1 er I /3 aptt.z Imajua u vidu da je 31 ay; ay, :Pt ale arl to se jed- a 2 alf ydm,. ay,- Z=t9 I a2p chi sr az, cza, a y; ay; = r ap a g- aye P.4, metri6ki tenzor d"v" ay; 41. dt at de koeficijenti povezanosti ax ay; dea ati cp dt are- a fif2 3s idm, at - generalisana sekundna promena mase diferencijalne jedna6ine moemo tads napisati u obliku:
48 42 4 ) la: (14/ r el= 4 A II erp r t a ktp tat S obzirom da je m; posle kompozicije sa ay' affi 20/,' a Y / 1p a.244 e 71:744.2 K; to se `1 izraz svodi na oblik: 5to je pc) definiciji jednako generalisanom impulsu: g Posle anoienja jednaane (72) sa d2:1 tenzorom, jednaana (72) se svodi na oblik: 42,p CV 2 =Aft a" Pi (24/3 Kako je kontravarijantni metrifti tenzor jednak: Jit a se' ars.4s cts /, ( 2, - mi. 2)0,- ay; Sada se diferencijalna jednaana (71a) i (72a) mogu na kraju napisati v y; (72) pp Tx. aft Pe + 1; `11 ili posle zamene 1.1 &Q IPS dobijamo:. 0( 1) --= ( 73 )
49 45. sistem od 2n diferencijalnih jednachna prvog recta. nacine JednaCina (73) predstavljaju diferencijaine jed- kretanja sistema mehani6kih tacaka promenljive mase u 2n dimenzionom faznom prostoru. Odavde se vidi da su dovoljni uslovi da sistem (73) ima ravnotezno stanje da bude ((I ts + materijalnih tacaka promenijive mase u 2n dimenzionom faznom prostoru. Na sistem mehani6lah tacaka promenljive mace der,v /7 luje n generalnih sila, gde su 4i = potencijalne - aqn site sa potencijalom /I a 4 su disipativne site i sile izazvane promenom mase P*, tada se diferencijalne jedna6ine (73) svode na oblik 0). Ova cistern algebarskih nezavisnih jednacina imaju resenja za koja Fez umnjivanja ootosti molemo smatrati da su odredjena vied.- nostima. 0, = 0, za svako JednaCine ( 73 ) su ujedno i diferencijalne jed- na6ine poreme6aja ravnoteznog stanja 2=0,A, = O sistema 3,a3 =c2.44/1 /av a pip, = e:2 I-- f,b4 l OpY 1.4p t rp 74" 6 I OCHWIA orratiwv4311 YAPYINEWIr PIRA 3A MAT:MATHNY, MEXATIKY N AtTPONOWIJY 6 po j: Awry
50 46.- Kao 5to se vidi pomoeu diferencijalnih jedna6ina (73a) molemo da odredimo kretanje sistema tacaka promenljive ease u 2n- dimenzionom faznom prostoru kada na sistem deluju potencijalne disipativne i reaktivne sile lac. OCHOBRII OPrAIMAPJA MYMERV MP 3A MATEMATIIKY, ME/CAMAY H ACTPOHOMHJY B 14B./1110TEN.A Epoj: Tykt:
51 3.2. DIFEREN CI JALNE JEDNA6INE POREMEOENOG RAVNOTE2NOG STANJA SISTEMA TA6AKA PROMENLJIVE MASE U prethodnoj glavi izvedene su diferencijalne jedna6ine kretanja sistema ta6aka promenijive mase za slucaj delovanja generalisanih potencijalnih, disipativnih i reaktivnih sila. Ako na materijalni sistem deluje n generalnih potencijalnih sila gde je 17 = /7 (Q i v 2I7 ) 2'0 potencijalna energi- ja sistema mehaniakih tacaka promenljive mase i reaktivnih sila tada se diferencijalne jednacine kretanja. sistema mehanickih ta6aka promenljive mase u faznom prostoru mogu Q'( 0/3/3. 62 P(i") 1.73 I s fl* kao gto je pokazano u (73) u obliku: s Clv, zz ( U okolini ravnoteliystanjag..0 PD= 0 metri6ki ten- / zor je jednak
52 48. Kada je konfiguracioni prostor odgovarajueeg di-, nami5kog sistema s konstantnom masom takav da'metri- ka promenljivog konfiguracionog prostora zavisi samo od vremena t, tada je Kristofelov simbol druge vrste jednak 1 P Prema tome diferencijalne jednaane poremeeenog stanja ravnote'ie (74) sada se svode u takvom prostoru na oblik /1 190 # P (75) Razvijajuel potencijale /7 u red po koordinatima u okolini poloaja ravnote'ie l potencijalne sile maemo svesti na oblik a: -a2/7 2p= y'" air I cap P tada generalisane (76) kako su reaktivne sile u okolini istog poloaja ravnoteie jednake (012' (77 ) to se jednaane poremeeenog stanja ravnoteie svode u faznom prostoru na 2n linearnih diferencijalnih jed- naa na sa promenljivim koeficijentima ( 47 C i f) al; C. i to Vz. C ''')(oPft (Of c 2 (t) (78 )
53 49, gde je,2" atp I = 2=0 JednaCine izvedene u obliku (78) predstavljaju diferencijalne jednacine poremecaja stanja ravnotee sistema tacaka promenijive mase u 2n dimen- - «zionom faznom prostoru u okolini j? 0. JednaCine smo izveli u ovome obliku da bismo :ih mogli kashije koristiti za izvodjenje uslova stabilnosti stanja ravnotee u 12 ravnote'ie = 0 sistema ta6aka promenljive mase za s1u6aj kada na sistem deluju generalisane potencijalne i reaktivne site. Kada na sistem ne dejstvuju same potencijalne site, zavisne od polcaaja i vremena l nekih drugih fizickih parametara t tada je generalisana sila jednaka Nju moemo razviti u stepeni red po koordinatima brzinama u okolini polaaja ravnotae, i dobiti posle odbacivanja Clanova vigeg od prvog reda da je sila jednaka a.,,3 (0 = nego i sile koje zavise od brzine, vremena i impulsa p c-,13 2 /3 (79) Posle zamene (79) i (71) jednazine poremeeenog ravnotenog stanja za ovaj slucaj se tada svode na 2n linearnih diferencijalnih jednaaina
54 5o. (80) (t1) 2/3 4/3 (7`) C:2 P4A,J t 7, a,(z1) Jedna6ine (80) imaju svoj smisao ako se kretanje sistema posmatra u okolini stanja ravnotee r /0.,= 0, a na sistem materijalnih tacaka promenijive mase deluju generalisane potencijalne, reaktivne i disipativne sile a stanje sistema posmatramo u 2 n dimenzionom faznom prostoru. 0C11914,1 yg?y -nalnr PVIA 3A MATEMAMY, ACTPNOWAY p o j: J'it C T A
55 USLOVI STABILNOSTI RAVNOTEtNOG STANJA Stabilnost neporemeoenog ravnotenog stanja sisterna promenljive mase ispitujemo u slucaju delovanja reaktivnih i generalisanih potencijalnih sila s1ueei se kao osnovom radom Ljnpunova i radom V. VujCiea. Da bismo do6li do uslova za stabilnost stanja ravnotee sistema promenljive mase uzimamo za funkciju V zbir dve pozitivne definitivne funkcije V = T 1- (81) pri emu je T fp kineti6ka energija sistema promenljive mase, a \A/..w(t / ff;..en) neka pozitivno definitna funkcija zavisna od generalisanih koordinata2i vremena. Kako je obicni izvod kineticke energije po vremenu sistema promenljive mase jednak apsolutnorn izvodu po istom parametru, t, tj. T D DT /3 A ) t '777 = a/z sledi da je /7- DT Dip /b/3 # a cz--7; /7 ' a/li clz' 2 at (82) Izvod funkcije V mote se sada izraziti u obliku &V Dp. --acfp 1-5,-. a Pv toi7.49/3-7`.2 0 CAI a2/3 e (83) konfiguracionom promenljivom prostoru apsolutni izvod impulsa je
56 de` P?'d 52.- B obzirom da je Kristofelov simbol druge vrste za posmatrani slu6aj (75) jednak S ( S. 0 to se izraz (83) svodi na oblik d -aa qp a a /3 /19/31b' 2 a z /:)-(/,0 ara 27j at Posle zamenei Psa Q `/'f, / /0,0 - u jedna6inu (84), dobija se 6?; 67 /b-/b,0. i1li 2RO j e 14/ / -a a of:' 4 P +a-52,3 2 f2 /:;V2/3 (84) 71" Ce ae at (8 5 ) < (86) Uslov (85) i (86) predstavlja analogan Liapunovu i Vuj6iou kriterij stabilnosti stanja ravnoteie za slu6aj delovanja na sistem reaktivnih i potencijalnih sila. u obliku a) Ako generalisanu potencijalnu silu izrazi.mo?/7 64( -,:r a funkciju W molemo izjedna6iti sa potencijalom 17 za taj slu6aj uslov stabilnosti (86) postoje jednak: ri a/7 adc 02/' 2 at ( 87)
57 53. Ako potencijalnu energiju posmatramo u okolini polozaja a prethodno smo je izrazili u najni- 'io0 aproksimaciji /TV cp _ega to je generalisana potencijalna sila jednaka v a reaktivna sila u istom poloaju bila.bi 3/f,v-fi /72,. z7/3 (.. ( Pty3 a2g ag rre_a - to se uslov (86) svodi na oblik: g a k) W2 c( d 4 x p p 1) (.3:A a( 6to posle zamene /0/3 sa it) =,(2,93 2 i )(/' s postaje: 0 " p az (88).7,-.62 (89) az / a cf / C fi 2 a f-p a zt 22 (90) i:li kako je prema 139] Cic2,.-*62,44,4 to se izraz svodi na oblik cxp y'qp
58 54.- b) Uvodjenjem proporcionalnosti izmedju br- zina Uslove (90) i (91) dalje moemo izraziti tako gto ako vrednost za/puvrstimo u (90) dobijamo 7) 1 as -s aap '2,,(P.2 "s/32 iii poste izvrgene transformacije, s obzirom da je prema Lg ciz s uslov (86) je jednak -..< (93) 2 1- ayls2 8:2Pilc:tp.f2/6 $'0. Uslovi stabilnosti (90), (91) i (92) omoguouju da se utvrdi stabilnost stanja ravnotee sistema tac aka promenijive mase u okolini ravnote'i- nog poloi',aja j?-co, pct. ---(7 Ispitivanje stabilnosti ravnote'inog stanja pomoeu ovih uslova stabilnosti olak5avamo problem time gto ceo postupak ispitivanja svodimo na odredjivanje funkcija koje figuriraju u uslovima, a koje mo- Zemo ne sa tako velikim tegkooama i odrediti. c) U slucaju da posmatramo sistem sa jednim stepenom siobodne metricki tenzor jednak je: a. ' _ a,, odnosno 42" = Q i to se (90) svodi na oblik - I / 2 / a, a 74 cap, - / -.2 a I.C,Q - C2.12f C2 2 (94)
59 STABILNOST DISIPATIVNIH SISTEMA Na sistem mehanickih tacaka promenljive mase pored reaktivnih sila, deluju generalisane potencijalne i generalisane disipativne site. Za ovaj slucaj stanje ravnotee bilo bi sta- bilno ako je izraz: a w manji ili jednak null. Za sluoaj da je pozitivno definitivna funkcija W jednaka a 62" are (96) VC/ =-1 Cae/3 a da je generalisana disipativna sila izraiena pomoou Relejeve funkcije, gde je)q-pgeneralisana disipativna sila tada je generalisanadisipativna sila jednaka 1.4c - p pa se uslov (96) svodi na oblik: - 1 <6,ya.11,i6 42.,A *", czar cz.v,. "1 fc F o. (97) 2 Ovaj uslov moemo koristiti za ispitivanje stabilnosti ravnotenog stanja sistema tacaka promenljive mase, ako na sistem deluju reaktivne, potencijalne disipativne site. Ako je sistem sa jednim stepenom slobodan, uslov (97) se svodi na oblik - 2 a 2 60 jf (98 )
60 57.- Obi6no matemati6ko klatno je sistem.sa jednim stepenom slobode kretanja, to eemo s toga na njemu izvriti primenu uslova stabilnosti ravnotenog sta- nza (95) 1 (98).
61 58.- 3,5. STABILNOST STANJA RAVNOTE2E MATEMATIoKOG KI1ATNA PROMENLJIVE MASE a) Ispitati stabilnost stanja ravno- tee matematickog klatna kojemu se usled zamrzavanja Cestica vode ravnomerno po povrgini kugle ma- sa kugle ravnomerno menja. Kugla je poluprecnika r, i prvobitne mase m Na kuglu deluje sila zemljine tee Kako je matematicko klatno sistem sa jednim stepenom slobode, to da bi stanje ravnotee matematickog klatna bilo stabilno l ea - / " G. treba da je zadovoljen uslov; (99) Apsolutna brzina Cestica vodene pare, koje se zamrzavaju ravnomerno po povrini kuglice jednaka je nuti tj. 12 =0 i time prvi Clan u uslovu (99) otpada i on se svodi na oblik -:2- C2,2 (100) -2 1 c,,e.<0, inercioni koeficijent a 1 je odnosno /71 Z 42,.../771 2 a izvod inercionog koeficijenta po vremenu je 2 a,= /271. Koeficijenti restitucije c (t) i njihov izvod bill bi Ci = rn Ye. Akc uvrstimo vrednosti izvoda u usiov (100) on se
62 71 C' ",. 2 (1 2,74;i_ gite d?) 59 - akakc je izvod mase fn, kordinatap, i duhne klatna veeaod nule, to je izraz (1o1) uvek manji od nule, akb je )4' e 'IP pa je ravnote'zno stanje =n V=0 posmatra- nog klatna stabilno. b) Kugla prvobitne mase m, i poluprenika r e paveeava maasu pripajanjem novih Cestica usled zamrzavarja revnomerno po-njenoj povrgini 6estica vole i pri tome na nju deluje pored zemijine tee, sila izrelena promenom mase i disipativne sile Cija je funkcija rasipanja if /0 ti7 2 gde je o. Stabilnost stanja ravnote.ze ovoga sistema ispitaeemo na osnovu uslova (98) (c, -fr hi) 1114 C', g s o Apsolutna brzina Cestica vodene pare je u = 0, take da se uslov uprogauje na oblik - 7, c, 2 2 o. (1o2) Generalisana koordinata je ugaoni otklon tj. inercioni koeficijent je a njegov izvod =ff7l 2" /? = Th6 za male oscilacije potencijalna sila je ("1(1 v - mg/ = ct
63 6o. a izvod po vreenu koeficijenta rastitucije matematickog klatna bio bi j amo Zamenom gornjih vrednosti u uslove (1o2), dobi- 1;9/(ZY2-p4'.2)] C O. Kako je u posmatranom slueaju izvod mase pa vremenu uvek veci ad nule tj./72>0,a isti je slu6aj i sa b, 1 i g, o6ig1edno da je tada izraz sa leve strane za svako t manji od nule ako je ( 6 tr; 2 "i" /2.;z 2 ; 21.) 2z pa je ray- noteno stanje matematil'..kog klatna u Polo s aju 4"= o stabilno. Ovde jasno proizilazi i poznati slucaj ponas'anja matematickog klatna konstantne mase u okolini poloaja ravnotee pri dejstvu otpornih sila. U tom slucsiaju je izvod mase ni,= 0 gativnu funkciju pa se uslov (/02) svodi na ne- to prema kriterijumu (96' ) dobijamo da je ravnoteeno stanje /. o stabilno. OCWIBIA epiatisatlia a7:10r PAAA 3A MATEIAT11:(Y, NEXA',4Yd.(Y dj ACTP01-10NMY j 11 El T A to E p o j: AaTym:
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
176 5 t h Fl oo r. 337 P o ly me r Ma te ri al s
 A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
I N A C O M P L E X W O R L D
 IS L A M I C E C O N O M I C S I N A C O M P L E X W O R L D E x p l o r a t i o n s i n A g-b eanste d S i m u l a t i o n S a m i A l-s u w a i l e m 1 4 2 9 H 2 0 0 8 I s l a m i c D e v e l o p m e
IS L A M I C E C O N O M I C S I N A C O M P L E X W O R L D E x p l o r a t i o n s i n A g-b eanste d S i m u l a t i o n S a m i A l-s u w a i l e m 1 4 2 9 H 2 0 0 8 I s l a m i c D e v e l o p m e
P a g e 3 6 of R e p o r t P B 4 / 0 9
 P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
Projektovanje paralelnih algoritama II
 Projektovanje paralelnih algoritama II Primeri paralelnih algoritama, I deo Paralelni algoritmi za množenje matrica 1 Algoritmi za množenje matrica Ovde su data tri paralelna algoritma: Direktan algoritam
Projektovanje paralelnih algoritama II Primeri paralelnih algoritama, I deo Paralelni algoritmi za množenje matrica 1 Algoritmi za množenje matrica Ovde su data tri paralelna algoritma: Direktan algoritam
ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA. Šefket Arslanagić, Sarajevo, BiH
 MAT-KOL (Banja Luka) XXIII ()(7), -7 http://wwwimviblorg/dmbl/dmblhtm DOI: 75/МК7A ISSN 5-6969 (o) ISSN 986-588 (o) ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA Šefket Arslanagić,
MAT-KOL (Banja Luka) XXIII ()(7), -7 http://wwwimviblorg/dmbl/dmblhtm DOI: 75/МК7A ISSN 5-6969 (o) ISSN 986-588 (o) ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA Šefket Arslanagić,
Executive Committee and Officers ( )
 Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o
 I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
Software Process Models there are many process model s in th e li t e ra t u re, s om e a r e prescriptions and some are descriptions you need to mode
 Unit 2 : Software Process O b j ec t i ve This unit introduces software systems engineering through a discussion of software processes and their principal characteristics. In order to achieve the desireable
Unit 2 : Software Process O b j ec t i ve This unit introduces software systems engineering through a discussion of software processes and their principal characteristics. In order to achieve the desireable
Parts Manual. EPIC II Critical Care Bed REF 2031
 EPIC II Critical Care Bed REF 2031 Parts Manual For parts or technical assistance call: USA: 1-800-327-0770 2013/05 B.0 2031-109-006 REV B www.stryker.com Table of Contents English Product Labels... 4
EPIC II Critical Care Bed REF 2031 Parts Manual For parts or technical assistance call: USA: 1-800-327-0770 2013/05 B.0 2031-109-006 REV B www.stryker.com Table of Contents English Product Labels... 4
THIS PAGE DECLASSIFIED IAW E
 THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
f;g,7k ;! / C+!< 8R+^1 ;0$ Z\ \ K S;4 i!;g + 5 ;* \ C! 1+M, /A+1+> 0 /A+>! 8 J 4! 9,7 )F C!.4 ;* )F /0 u+\ 30< #4 8 J C!
 393/09/0 393//07 :,F! ::!n> b]( a.q 5 O +D5 S ١ ; ;* :'!3Qi C+0;$ < "P 4 ; M V! M V! ; a 4 / ;0$ f;g,7k ;! / C+!< 8R+^ ;0$ Z\ \ K S;4 "* < 8c0 5 *
393/09/0 393//07 :,F! ::!n> b]( a.q 5 O +D5 S ١ ; ;* :'!3Qi C+0;$ < "P 4 ; M V! M V! ; a 4 / ;0$ f;g,7k ;! / C+!< 8R+^ ;0$ Z\ \ K S;4 "* < 8c0 5 *
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A. Ήχος Πα. to os se e e na aș te e e slă ă ă vi i i i i
 CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
Red veze za benzen. Slika 1.
 Red veze za benzen Benzen C 6 H 6 je aromatično ciklično jedinjenje. Njegove dve rezonantne forme (ili Kekuléove structure), prema teoriji valentne veze (VB) prikazuju se uobičajeno kao na slici 1 a),
Red veze za benzen Benzen C 6 H 6 je aromatično ciklično jedinjenje. Njegove dve rezonantne forme (ili Kekuléove structure), prema teoriji valentne veze (VB) prikazuju se uobičajeno kao na slici 1 a),
F l a s h-b a s e d S S D s i n E n t e r p r i s e F l a s h-b a s e d S S D s ( S o-s ltiad t e D r i v e s ) a r e b e c o m i n g a n a t t r a c
 L i f e t i m e M a n a g e m e n t o f F l a-b s ah s e d S S D s U s i n g R e c o v e r-a y w a r e D y n a m i c T h r o t t l i n g S u n g j i n L e, e T a e j i n K i m, K y u n g h o, Kainmd J
L i f e t i m e M a n a g e m e n t o f F l a-b s ah s e d S S D s U s i n g R e c o v e r-a y w a r e D y n a m i c T h r o t t l i n g S u n g j i n L e, e T a e j i n K i m, K y u n g h o, Kainmd J
Trade Patterns, Production networks, and Trade and employment in the Asia-US region
 Trade Patterns, Production networks, and Trade and employment in the Asia-U region atoshi Inomata Institute of Developing Economies ETRO Development of cross-national production linkages, 1985-2005 1985
Trade Patterns, Production networks, and Trade and employment in the Asia-U region atoshi Inomata Institute of Developing Economies ETRO Development of cross-national production linkages, 1985-2005 1985
Last 4 Digits of USC ID:
 Chemistry 05 B Practice Exam Dr. Jessica Parr First Letter of last Name PLEASE PRINT YOUR NAME IN BLOCK LETTERS Name: Last 4 Digits of USC ID: Lab TA s Name: Question Points Score Grader 8 2 4 3 9 4 0
Chemistry 05 B Practice Exam Dr. Jessica Parr First Letter of last Name PLEASE PRINT YOUR NAME IN BLOCK LETTERS Name: Last 4 Digits of USC ID: Lab TA s Name: Question Points Score Grader 8 2 4 3 9 4 0
TEORIJA SKUPOVA Zadaci
 TEORIJA SKUPOVA Zadai LOGIKA 1 I. godina 1. Zapišite simbolima: ( x nije element skupa S (b) d je član skupa S () F je podskup slupa S (d) Skup S sadrži skup R 2. Neka je S { x;2x 6} = = i neka je b =
TEORIJA SKUPOVA Zadai LOGIKA 1 I. godina 1. Zapišite simbolima: ( x nije element skupa S (b) d je član skupa S () F je podskup slupa S (d) Skup S sadrži skup R 2. Neka je S { x;2x 6} = = i neka je b =
Ranking accounting, banking and finance journals: A note
 MPRA Munich Personal RePEc Archive Ranking accounting, banking and finance ournals: A note George Halkos and Nickolaos Tzeremes University of Thessaly, Department of Economics January 2012 Online at https://mpra.ub.uni-muenchen.de/36166/
MPRA Munich Personal RePEc Archive Ranking accounting, banking and finance ournals: A note George Halkos and Nickolaos Tzeremes University of Thessaly, Department of Economics January 2012 Online at https://mpra.ub.uni-muenchen.de/36166/
H STO RY OF TH E SA NT
 O RY OF E N G L R R VER ritten for the entennial of th e Foundin g of t lair oun t y on ay 8 82 Y EEL N E JEN K RP O N! R ENJ F ] jun E 3 1 92! Ph in t ed b y h e t l a i r R ep u b l i c a n O 4 1922
O RY OF E N G L R R VER ritten for the entennial of th e Foundin g of t lair oun t y on ay 8 82 Y EEL N E JEN K RP O N! R ENJ F ] jun E 3 1 92! Ph in t ed b y h e t l a i r R ep u b l i c a n O 4 1922
:,,.. ;,..,.,. 90 :.. :, , «-»,, -. : -,,, -, -., ,, -, -. - «-»:,,, ,.,.
 .,.,. 2015 1 614.8 68.9 90 :,,.. ;,. 90.,.,. :.. :, 2015. 164. - - 280700, «-»,, -. : -,,, -, -.,. -. -. -,, -, -. - «-»:,,, -. 614.8 68.9.,.,., 2015, 2015 2 ... 5... 7 1.... 7 1.1.... 7 1.2.... 9 1.3....
.,.,. 2015 1 614.8 68.9 90 :,,.. ;,. 90.,.,. :.. :, 2015. 164. - - 280700, «-»,, -. : -,,, -, -.,. -. -. -,, -, -. - «-»:,,, -. 614.8 68.9.,.,., 2015, 2015 2 ... 5... 7 1.... 7 1.1.... 7 1.2.... 9 1.3....
 shhgs@wgqqh.com chinapub 2002 7 Bruc Eckl 1000 7 Bruc Eckl 1000 Th gnsis of th computr rvolution was in a machin. Th gnsis of our programming languags thus tnds to look lik that Bruc machin. 10 7 www.wgqqh.com/shhgs/tij.html
shhgs@wgqqh.com chinapub 2002 7 Bruc Eckl 1000 7 Bruc Eckl 1000 Th gnsis of th computr rvolution was in a machin. Th gnsis of our programming languags thus tnds to look lik that Bruc machin. 10 7 www.wgqqh.com/shhgs/tij.html
M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7; ;J zy U;K z< mj ]!.,,+7;
![M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7; ;J zy U;K z< mj ]!.,,+7; M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7; ;J zy U;K z< mj ]!.,,+7;](/thumbs/78/78216077.jpg) V 3U. T, SK I 1393/08/21 :,F! 1393/10/29 ::!n> 2 1 /M + - /E+4q; Z R :'!3Qi M $,7 8$ 4,!AK 4 4/ * /;K "FA ƒf\,7 /;G2 @;J\ M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7;
V 3U. T, SK I 1393/08/21 :,F! 1393/10/29 ::!n> 2 1 /M + - /E+4q; Z R :'!3Qi M $,7 8$ 4,!AK 4 4/ * /;K "FA ƒf\,7 /;G2 @;J\ M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7;
Table of C on t en t s Global Campus 21 in N umbe r s R e g ional Capac it y D e v e lopme nt in E-L e ar ning Structure a n d C o m p o n en ts R ea
 G Blended L ea r ni ng P r o g r a m R eg i o na l C a p a c i t y D ev elo p m ent i n E -L ea r ni ng H R K C r o s s o r d e r u c a t i o n a n d v e l o p m e n t C o p e r a t i o n 3 0 6 0 7 0 5
G Blended L ea r ni ng P r o g r a m R eg i o na l C a p a c i t y D ev elo p m ent i n E -L ea r ni ng H R K C r o s s o r d e r u c a t i o n a n d v e l o p m e n t C o p e r a t i o n 3 0 6 0 7 0 5
[ ]:543.4(075.8) 35.20: ,..,..,.., : /... ;. 2-. ISBN , - [ ]:543.4(075.8) 35.20:34.
![[ ]:543.4(075.8) 35.20: ,..,..,.., : /... ;. 2-. ISBN , - [ ]:543.4(075.8) 35.20:34. [ ]:543.4(075.8) 35.20: ,..,..,.., : /... ;. 2-. ISBN , - [ ]:543.4(075.8) 35.20:34.](/thumbs/74/69911105.jpg) .. - 2-2009 [661.87.+661.88]:543.4(075.8) 35.20:34.2373-60..,..,..,..,.. -60 : /... ;. 2-. : -, 2008. 134. ISBN 5-98298-299-7 -., -,,. - «,, -, -», - 550800,, 240600 «-», -. [661.87.+661.88]:543.4(075.8)
.. - 2-2009 [661.87.+661.88]:543.4(075.8) 35.20:34.2373-60..,..,..,..,.. -60 : /... ;. 2-. : -, 2008. 134. ISBN 5-98298-299-7 -., -,,. - «,, -, -», - 550800,, 240600 «-», -. [661.87.+661.88]:543.4(075.8)
Advanced Placement. Chemistry. Integrated Rates
 Advanced Placement Chemistry Integrated Rates 204 47.90 9.22 78.49 (26) 50.94 92.9 80.95 (262) 52.00 93.94 83.85 (263) 54.938 (98) 86.2 (262) 55.85 0. 90.2 (265) 58.93 02.9 92.2 (266) H Li Na K Rb Cs Fr
Advanced Placement Chemistry Integrated Rates 204 47.90 9.22 78.49 (26) 50.94 92.9 80.95 (262) 52.00 93.94 83.85 (263) 54.938 (98) 86.2 (262) 55.85 0. 90.2 (265) 58.93 02.9 92.2 (266) H Li Na K Rb Cs Fr
r(j) -::::.- --X U.;,..;...-h_D_Vl_5_ :;;2.. Name: ~s'~o--=-i Class; Date: ID: A
 Name: ~s'~o--=-i Class; Date: U.;,..;...-h_D_Vl_5 _ MAC 2233 Chapter 4 Review for the test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the derivative
Name: ~s'~o--=-i Class; Date: U.;,..;...-h_D_Vl_5 _ MAC 2233 Chapter 4 Review for the test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the derivative
~,. :'lr. H ~ j. l' ", ...,~l. 0 '" ~ bl '!; 1'1. :<! f'~.., I,," r: t,... r':l G. t r,. 1'1 [<, ."" f'" 1n. t.1 ~- n I'>' 1:1 , I. <1 ~'..
 ,, 'l t (.) :;,/.I I n ri' ' r l ' rt ( n :' (I : d! n t, :?rj I),.. fl.),. f!..,,., til, ID f-i... j I. 't' r' t II!:t () (l r El,, (fl lj J4 ([) f., () :. -,,.,.I :i l:'!, :I J.A.. t,.. p, - ' I I I
,, 'l t (.) :;,/.I I n ri' ' r l ' rt ( n :' (I : d! n t, :?rj I),.. fl.),. f!..,,., til, ID f-i... j I. 't' r' t II!:t () (l r El,, (fl lj J4 ([) f., () :. -,,.,.I :i l:'!, :I J.A.. t,.. p, - ' I I I
02/05/09 Last 4 Digits of USC ID: Dr. Jessica Parr
 Chemistry 05 B First Letter of PLEASE PRINT YOUR NAME IN BLOCK LETTERS Exam last Name Name: 02/05/09 Last 4 Digits of USC ID: Dr. Jessica Parr Lab TA s Name: Question Points Score Grader 2 2 9 3 9 4 2
Chemistry 05 B First Letter of PLEASE PRINT YOUR NAME IN BLOCK LETTERS Exam last Name Name: 02/05/09 Last 4 Digits of USC ID: Dr. Jessica Parr Lab TA s Name: Question Points Score Grader 2 2 9 3 9 4 2
35H MPa Hydraulic Cylinder 3.5 MPa Hydraulic Cylinder 35H-3
 - - - - ff ff - - - - - - B B BB f f f f f f f 6 96 f f f f f f f 6 f LF LZ f 6 MM f 9 P D RR DD M6 M6 M6 M. M. M. M. M. SL. E 6 6 9 ZB Z EE RC/ RC/ RC/ RC/ RC/ ZM 6 F FP 6 K KK M. M. M. M. M M M M f f
- - - - ff ff - - - - - - B B BB f f f f f f f 6 96 f f f f f f f 6 f LF LZ f 6 MM f 9 P D RR DD M6 M6 M6 M. M. M. M. M. SL. E 6 6 9 ZB Z EE RC/ RC/ RC/ RC/ RC/ ZM 6 F FP 6 K KK M. M. M. M. M M M M f f
S U E K E AY S S H A R O N T IM B E R W IN D M A R T Z -PA U L L IN. Carlisle Franklin Springboro. Clearcreek TWP. Middletown. Turtlecreek TWP.
 F R A N K L IN M A D IS O N S U E R O B E R T LE IC H T Y A LY C E C H A M B E R L A IN T W IN C R E E K M A R T Z -PA U L L IN C O R A O W E N M E A D O W L A R K W R E N N LA N T IS R E D R O B IN F
F R A N K L IN M A D IS O N S U E R O B E R T LE IC H T Y A LY C E C H A M B E R L A IN T W IN C R E E K M A R T Z -PA U L L IN C O R A O W E N M E A D O W L A R K W R E N N LA N T IS R E D R O B IN F
Solutions and Ions. Pure Substances
 Class #4 Solutions and Ions CHEM 107 L.S. Brown Texas A&M University Pure Substances Pure substance: described completely by a single chemical formula Fixed composition 1 Mixtures Combination of 2 or more
Class #4 Solutions and Ions CHEM 107 L.S. Brown Texas A&M University Pure Substances Pure substance: described completely by a single chemical formula Fixed composition 1 Mixtures Combination of 2 or more
,\ I. . <- c}. " C:-)' ) I- p od--- -;::: 'J.--- d, cl cr -- I. ( I) Cl c,\. c. 1\'0\ ~ '~O'-_. e ~.\~\S
 Math 3306 - Test 1 Name: An d {"0v\ ( _ roj ~ ed Date: l'( ~0 { 1\ Fall 2011 1. (to Pts) Let S == {I, 2, 3,4, 5,6,7,8,9, 10}. of each of the following types of mappings, provide justification for why the
Math 3306 - Test 1 Name: An d {"0v\ ( _ roj ~ ed Date: l'( ~0 { 1\ Fall 2011 1. (to Pts) Let S == {I, 2, 3,4, 5,6,7,8,9, 10}. of each of the following types of mappings, provide justification for why the
Future Self-Guides. E,.?, :0-..-.,0 Q., 5...q ',D5', 4,] 1-}., d-'.4.., _. ZoltAn Dbrnyei Introduction. u u rt 5,4) ,-,4, a. a aci,, u 4.
![Future Self-Guides. E,.?, :0-..-.,0 Q., 5...q ',D5', 4,] 1-}., d-'.4.., _. ZoltAn Dbrnyei Introduction. u u rt 5,4) ,-,4, a. a aci,, u 4. Future Self-Guides. E,.?, :0-..-.,0 Q., 5...q ',D5', 4,] 1-}., d-'.4.., _. ZoltAn Dbrnyei Introduction. u u rt 5,4) ,-,4, a. a aci,, u 4.](/thumbs/92/109036622.jpg) te SelfGi ZltAn Dbnyei Intdtin ; ) Q) 4 t? ) t _ 4 73 y S _ E _ p p 4 t t 4) 1_ ::_ J 1 `i () L VI O I4 " " 1 D 4 L e Q) 1 k) QJ 7 j ZS _Le t 1 ej!2 i1 L 77 7 G (4) 4 6 t (1 ;7 bb F) t f; n (i M Q) 7S
te SelfGi ZltAn Dbnyei Intdtin ; ) Q) 4 t? ) t _ 4 73 y S _ E _ p p 4 t t 4) 1_ ::_ J 1 `i () L VI O I4 " " 1 D 4 L e Q) 1 k) QJ 7 j ZS _Le t 1 ej!2 i1 L 77 7 G (4) 4 6 t (1 ;7 bb F) t f; n (i M Q) 7S
CLASS TEST GRADE 11. PHYSICAL SCIENCES: CHEMISTRY Test 4: Matter and materials 1
 CLASS TEST GRADE PHYSICAL SCIENCES: CHEMISTRY Test 4: Matter and materials MARKS: 45 TIME: hour INSTRUCTIONS AND INFORMATION. Answer ALL the questions. 2. You may use non-programmable calculators. 3. You
CLASS TEST GRADE PHYSICAL SCIENCES: CHEMISTRY Test 4: Matter and materials MARKS: 45 TIME: hour INSTRUCTIONS AND INFORMATION. Answer ALL the questions. 2. You may use non-programmable calculators. 3. You
Mathcad sa algoritmima
 P R I M J E R I P R I M J E R I Mathcad sa algoritmima NAREDBE - elementarne obrade - sekvence Primjer 1 Napraviti algoritam za sabiranje dva broja. NAREDBE - elementarne obrade - sekvence Primjer 1 POČETAK
P R I M J E R I P R I M J E R I Mathcad sa algoritmima NAREDBE - elementarne obrade - sekvence Primjer 1 Napraviti algoritam za sabiranje dva broja. NAREDBE - elementarne obrade - sekvence Primjer 1 POČETAK
The Periodic Table. Periodic Properties. Can you explain this graph? Valence Electrons. Valence Electrons. Paramagnetism
 Periodic Properties Atomic & Ionic Radius Energy Electron Affinity We want to understand the variations in these properties in terms of electron configurations. The Periodic Table Elements in a column
Periodic Properties Atomic & Ionic Radius Energy Electron Affinity We want to understand the variations in these properties in terms of electron configurations. The Periodic Table Elements in a column
Chemistry 185 Exam #2 - A November 5, Lab Day and Time: Instructions. 1. Do not open the exam until you are told to start.
 Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
8. Relax and do well.
 CHEM 1515 Exam II John II. Gelder October 14, 1993 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 8 different pages. The last two pages include a periodic table, a
CHEM 1515 Exam II John II. Gelder October 14, 1993 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 8 different pages. The last two pages include a periodic table, a
(tnaiaun uaejna) o il?smitfl?^ni7wwuiinuvitgviisyiititvi2a-a a imaviitjivi5a^ qw^ww^i fiaa!i-j?s'u'uil?g'ijimqwuwiijami.wti. a nmj 1,965,333.
 0 fltu77jjiimviu«7mi^ gi^"ijhm?'ijjw?flfi^ V m 1 /14 il?mitfl?^i7wwuiinuvitgviiyiititvi2- imviitvi^ qw^ww^i fi!i-j?'u'uil?g'iqwuwiijmi.wti twwrlf^ imii2^
0 fltu77jjiimviu«7mi^ gi^"ijhm?'ijjw?flfi^ V m 1 /14 il?mitfl?^i7wwuiinuvitgviiyiititvi2- imviitvi^ qw^ww^i fi!i-j?'u'uil?g'iqwuwiijmi.wti twwrlf^ imii2^
Virtual Library of Faculty of Mathematics - University of Belgrade
 Marko D. Leko BORNOVO RELLtTIVISTICKI 6VRSTO TELO (doktorska disertacija) OMBRA 07 3M4M1JA IWY44Err PAAA 3A MATEMATW, MEXAHW H AUPOHOMMY ii B J1 U u T i & A EPoi:,i1, a T ym: elnci-i...q) V SADRZAJ Gleva
Marko D. Leko BORNOVO RELLtTIVISTICKI 6VRSTO TELO (doktorska disertacija) OMBRA 07 3M4M1JA IWY44Err PAAA 3A MATEMATW, MEXAHW H AUPOHOMMY ii B J1 U u T i & A EPoi:,i1, a T ym: elnci-i...q) V SADRZAJ Gleva
e2- THE FRANKLIN INSTITUTE We" D4rL E; 77.e //SY" Laboratories for Research and Development ceizrrra L , Ps" /.7.5-evr ge)/+.
 ozr/-6-7-aw We" 0 Ze12, DrL E; 77.e //SY" ceizrrra L s, Ps" e2- j 1 /1/ -tv /.7.5-evr ge)/+.,v) c7-/er-vi 0, I tr9 1 If,t) e" '*? /:7010 1, 7!, re, /7 1' 8c / 771 ;.7..) t) - or, Tin E ei:e1licir '.e.
ozr/-6-7-aw We" 0 Ze12, DrL E; 77.e //SY" ceizrrra L s, Ps" e2- j 1 /1/ -tv /.7.5-evr ge)/+.,v) c7-/er-vi 0, I tr9 1 If,t) e" '*? /:7010 1, 7!, re, /7 1' 8c / 771 ;.7..) t) - or, Tin E ei:e1licir '.e.
Circle the letters only. NO ANSWERS in the Columns!
 Chemistry 1304.001 Name (please print) Exam 5 (100 points) April 18, 2018 On my honor, I have neither given nor received unauthorized aid on this exam. Signed Date Circle the letters only. NO ANSWERS in
Chemistry 1304.001 Name (please print) Exam 5 (100 points) April 18, 2018 On my honor, I have neither given nor received unauthorized aid on this exam. Signed Date Circle the letters only. NO ANSWERS in
Lab Day and Time: Instructions. 1. Do not open the exam until you are told to start.
 Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
 lectures accompanying the book: Solid State Physics: An Introduction, by Philip ofmann (2nd edition 2015, ISBN-10: 3527412824, ISBN-13: 978-3527412822, Wiley-VC Berlin. www.philiphofmann.net 1 Bonds between
lectures accompanying the book: Solid State Physics: An Introduction, by Philip ofmann (2nd edition 2015, ISBN-10: 3527412824, ISBN-13: 978-3527412822, Wiley-VC Berlin. www.philiphofmann.net 1 Bonds between
Chemistry 431 Practice Final Exam Fall Hours
 Chemistry 431 Practice Final Exam Fall 2018 3 Hours R =8.3144 J mol 1 K 1 R=.0821 L atm mol 1 K 1 R=.08314 L bar mol 1 K 1 k=1.381 10 23 J molecule 1 K 1 h=6.626 10 34 Js N A = 6.022 10 23 molecules mol
Chemistry 431 Practice Final Exam Fall 2018 3 Hours R =8.3144 J mol 1 K 1 R=.0821 L atm mol 1 K 1 R=.08314 L bar mol 1 K 1 k=1.381 10 23 J molecule 1 K 1 h=6.626 10 34 Js N A = 6.022 10 23 molecules mol
CHEM 10113, Quiz 5 October 26, 2011
 CHEM 10113, Quiz 5 October 26, 2011 Name (please print) All equations must be balanced and show phases for full credit. Significant figures count, show charges as appropriate, and please box your answers!
CHEM 10113, Quiz 5 October 26, 2011 Name (please print) All equations must be balanced and show phases for full credit. Significant figures count, show charges as appropriate, and please box your answers!
Visit to meet more individuals who benefit from your time
 NOURISHINGN G. Vlz S 2009 BR i y ii li i Cl. N i. J l l. Rl. A y l l i i ky. Vii.li.l. iiil i y i &. 71 y l Cl y, i iil k. 28 y, k My W i ily l i. Uil y, y k i i. T j il y. Ty il iy ly y - li G, y Cl.
NOURISHINGN G. Vlz S 2009 BR i y ii li i Cl. N i. J l l. Rl. A y l l i i ky. Vii.li.l. iiil i y i &. 71 y l Cl y, i iil k. 28 y, k My W i ily l i. Uil y, y k i i. T j il y. Ty il iy ly y - li G, y Cl.
Exhibit 2-9/30/15 Invoice Filing Page 1841 of Page 3660 Docket No
 xhibit 2-9/3/15 Invie Filing Pge 1841 f Pge 366 Dket. 44498 F u v 7? u ' 1 L ffi s xs L. s 91 S'.e q ; t w W yn S. s t = p '1 F? 5! 4 ` p V -', {} f6 3 j v > ; gl. li -. " F LL tfi = g us J 3 y 4 @" V)
xhibit 2-9/3/15 Invie Filing Pge 1841 f Pge 366 Dket. 44498 F u v 7? u ' 1 L ffi s xs L. s 91 S'.e q ; t w W yn S. s t = p '1 F? 5! 4 ` p V -', {} f6 3 j v > ; gl. li -. " F LL tfi = g us J 3 y 4 @" V)
Fall 2011 CHEM Test 4, Form A
 Fall 2011 CHEM 1110.40413 Test 4, Form A Part I. Multiple Choice: Clearly circle the best answer. (60 pts) Name: 1. The common constituent in all acid solutions is A) H 2 SO 4 B) H 2 C) H + D) OH 2. Which
Fall 2011 CHEM 1110.40413 Test 4, Form A Part I. Multiple Choice: Clearly circle the best answer. (60 pts) Name: 1. The common constituent in all acid solutions is A) H 2 SO 4 B) H 2 C) H + D) OH 2. Which
8. Relax and do well.
 CHEM 15 Exam II John II. Gelder March 4, 1999 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last two pages includes a periodic table, a solubility
CHEM 15 Exam II John II. Gelder March 4, 1999 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last two pages includes a periodic table, a solubility
Speed of light c = m/s. x n e a x d x = 1. 2 n+1 a n π a. He Li Ne Na Ar K Ni 58.
 Physical Chemistry II Test Name: KEY CHEM 464 Spring 18 Chapters 7-11 Average = 1. / 16 6 questions worth a total of 16 points Planck's constant h = 6.63 1-34 J s Speed of light c = 3. 1 8 m/s ħ = h π
Physical Chemistry II Test Name: KEY CHEM 464 Spring 18 Chapters 7-11 Average = 1. / 16 6 questions worth a total of 16 points Planck's constant h = 6.63 1-34 J s Speed of light c = 3. 1 8 m/s ħ = h π
Discovery Guide. Beautiful, mysterious woman pursued by gunmen. Sounds like a spy story...
 Dv G W C T Gp, A T Af Hk T 39 Sp. M Mx Hk p j p v, f M P v...(!) Af Hk T 39 Sp, B,,, UNMISSABLE! T - f 4 p v 150 f-p f x v. Bf, k 4 p v 150. H k f f x? D,,,, v? W k, pf p f p? W f f f? W k k p? T p xp
Dv G W C T Gp, A T Af Hk T 39 Sp. M Mx Hk p j p v, f M P v...(!) Af Hk T 39 Sp, B,,, UNMISSABLE! T - f 4 p v 150 f-p f x v. Bf, k 4 p v 150. H k f f x? D,,,, v? W k, pf p f p? W f f f? W k k p? T p xp
Nucleus. Electron Cloud
 Atomic Structure I. Picture of an Atom Nucleus Electron Cloud II. Subatomic particles Particle Symbol Charge Relative Mass (amu) protons p + +1 1.0073 neutrons n 0 1.0087 electrons e - -1 0.00054858 Compare
Atomic Structure I. Picture of an Atom Nucleus Electron Cloud II. Subatomic particles Particle Symbol Charge Relative Mass (amu) protons p + +1 1.0073 neutrons n 0 1.0087 electrons e - -1 0.00054858 Compare
MANY ELECTRON ATOMS Chapter 15
 MANY ELECTRON ATOMS Chapter 15 Electron-Electron Repulsions (15.5-15.9) The hydrogen atom Schrödinger equation is exactly solvable yielding the wavefunctions and orbitals of chemistry. Howev er, the Schrödinger
MANY ELECTRON ATOMS Chapter 15 Electron-Electron Repulsions (15.5-15.9) The hydrogen atom Schrödinger equation is exactly solvable yielding the wavefunctions and orbitals of chemistry. Howev er, the Schrödinger
K. 27 Co. 28 Ni. 29 Cu Rb. 46 Pd. 45 Rh. 47 Ag Cs Ir. 78 Pt.
 1 IA 1 ydrogen 1.01 Atomic number Element symbol Element name Atomic mass VIIIA 1 1.01 IIA IIIA IVA VA VIA VIIA 2 e 4.00 Metalloids 3 Li 6.94 4 Be 9.01 5 B 10.81 6 C 12.01 7 N 14.01 8 O 16.00 9 F 19.00
1 IA 1 ydrogen 1.01 Atomic number Element symbol Element name Atomic mass VIIIA 1 1.01 IIA IIIA IVA VA VIA VIIA 2 e 4.00 Metalloids 3 Li 6.94 4 Be 9.01 5 B 10.81 6 C 12.01 7 N 14.01 8 O 16.00 9 F 19.00
(C) Pavel Sedach and Prep101 1
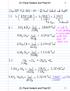 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach
(C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach
Helping Kids Prepare For Life (253)
 Hlpi Ki Pp F Lif.l.i. (253)-589-7489 Tilli it it L Livit iv f fiv CIS U H. Vip pt fll t Tilli Elt l tpi tff tt f vi t t CIS T Hll f i Cltt N Cli. - L ivi i CIS f Bill Milli CIS pit Dil Cili Ti l iz it
Hlpi Ki Pp F Lif.l.i. (253)-589-7489 Tilli it it L Livit iv f fiv CIS U H. Vip pt fll t Tilli Elt l tpi tff tt f vi t t CIS T Hll f i Cltt N Cli. - L ivi i CIS f Bill Milli CIS pit Dil Cili Ti l iz it
(please print) (1) (18) H IIA IIIA IVA VA VIA VIIA He (2) (13) (14) (15) (16) (17)
 CHEM 10113, Quiz 3 September 28, 2011 Name (please print) All equations must be balanced and show phases for full credit. Significant figures count, show charges as appropriate, and please box your answers!
CHEM 10113, Quiz 3 September 28, 2011 Name (please print) All equations must be balanced and show phases for full credit. Significant figures count, show charges as appropriate, and please box your answers!
PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU
 MAT KOL Banja Luka) ISSN 0354 6969 p) ISSN 1986 58 o) Vol. XXI )015) 105 115 http://www.imvibl.org/dmbl/dmbl.htm PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU Bernadin Ibrahimpašić 1 Senka Ibrahimpašić
MAT KOL Banja Luka) ISSN 0354 6969 p) ISSN 1986 58 o) Vol. XXI )015) 105 115 http://www.imvibl.org/dmbl/dmbl.htm PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU Bernadin Ibrahimpašić 1 Senka Ibrahimpašić
8. Relax and do well.
 CHEM 1314.03 Exam I John I. Gelder September 25, 1997 Name TA's Name Lab Section Please sign your name below to give permission to post, by the last 4 digits of your student I.D. number, your course scores
CHEM 1314.03 Exam I John I. Gelder September 25, 1997 Name TA's Name Lab Section Please sign your name below to give permission to post, by the last 4 digits of your student I.D. number, your course scores
Beginning and Ending Cash and Investment Balances for the month of January 2016
 ADIISTRATIVE STAFF REPRT T yr nd Tn uncil rch 15 216 SBJET Jnury 216 nth End Tresurer s Reprt BAKGRD The lifrni Gvernment de nd the Tn f Dnville s Investment Plicy require tht reprt specifying the investment
ADIISTRATIVE STAFF REPRT T yr nd Tn uncil rch 15 216 SBJET Jnury 216 nth End Tresurer s Reprt BAKGRD The lifrni Gvernment de nd the Tn f Dnville s Investment Plicy require tht reprt specifying the investment
Lab Day and Time: Instructions. 1. Do not open the exam until you are told to start.
 Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
ZANIMLJIVI ALGEBARSKI ZADACI SA BROJEM 2013 (Interesting algebraic problems with number 2013)
 MAT-KOL (Banja Luka) ISSN 0354-6969 (p), ISSN 1986-5228 (o) Vol. XIX (3)(2013), 35-44 ZANIMLJIVI ALGEBARSKI ZADACI SA BROJEM 2013 (Interesting algebraic problems with number 2013) Nenad O. Vesi 1 Du²an
MAT-KOL (Banja Luka) ISSN 0354-6969 (p), ISSN 1986-5228 (o) Vol. XIX (3)(2013), 35-44 ZANIMLJIVI ALGEBARSKI ZADACI SA BROJEM 2013 (Interesting algebraic problems with number 2013) Nenad O. Vesi 1 Du²an
CHEM 108 (Spring-2008) Exam. 3 (105 pts)
 CHEM 08 (Spring-008) Exam. (05 pts) Name: --------------------------------------------------------------------------, CLID # -------------------------------- LAST NAME, First (Circle the alphabet segment
CHEM 08 (Spring-008) Exam. (05 pts) Name: --------------------------------------------------------------------------, CLID # -------------------------------- LAST NAME, First (Circle the alphabet segment
Grilled it ems are prepared over real mesquit e wood CREATE A COMBO STEAKS. Onion Brewski Sirloin * Our signature USDA Choice 12 oz. Sirloin.
 TT & L Gl v l q T l q TK v i f i ' i i T K L G ' T G!? Ti 10 (Pik 3) -F- L P ki - ik T ffl i zzll ik Fi Pikl x i f l $3 (li 2) i f i i i - i f i jlñ i 84 6 - f ki i Fi 6 T i ffl i 10 -i i fi & i i ffl
TT & L Gl v l q T l q TK v i f i ' i i T K L G ' T G!? Ti 10 (Pik 3) -F- L P ki - ik T ffl i zzll ik Fi Pikl x i f l $3 (li 2) i f i i i - i f i jlñ i 84 6 - f ki i Fi 6 T i ffl i 10 -i i fi & i i ffl
 ,,,,..,,., {. (, ),, {,.,.,..,,.,.,,....... {.. : N {, Z {, Q {, Q p { p{ {. 3, R {, C {. : ord p {. 8, (k) {.42,!() { {. 24, () { {. 24, () { {. 25,., () { {. 26,. 9, () { {. 27,. 23, '() { ( ) {. 28,
,,,,..,,., {. (, ),, {,.,.,..,,.,.,,....... {.. : N {, Z {, Q {, Q p { p{ {. 3, R {, C {. : ord p {. 8, (k) {.42,!() { {. 24, () { {. 24, () { {. 25,., () { {. 26,. 9, () { {. 27,. 23, '() { ( ) {. 28,
Lab Day and Time: Instructions. 1. Do not open the exam until you are told to start.
 Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
rhtre PAID U.S. POSTAGE Can't attend? Pass this on to a friend. Cleveland, Ohio Permit No. 799 First Class
 rhtr irt Cl.S. POSTAG PAD Cllnd, Ohi Prmit. 799 Cn't ttnd? P thi n t frind. \ ; n l *di: >.8 >,5 G *' >(n n c. if9$9$.jj V G. r.t 0 H: u ) ' r x * H > x > i M
rhtr irt Cl.S. POSTAG PAD Cllnd, Ohi Prmit. 799 Cn't ttnd? P thi n t frind. \ ; n l *di: >.8 >,5 G *' >(n n c. if9$9$.jj V G. r.t 0 H: u ) ' r x * H > x > i M
INSTRUCTIONS: Exam III. November 10, 1999 Lab Section
 CHEM 1215 Exam III John III. Gelder November 10, 1999 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last page includes a periodic table and
CHEM 1215 Exam III John III. Gelder November 10, 1999 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last page includes a periodic table and
Instructions. 1. Do not open the exam until you are told to start.
 Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
Made the FIRST periodic table
 Made the FIRST periodic table 1869 Mendeleev organized the periodic table based on the similar properties and relativities of certain elements Later, Henri Moseley organized the elements by increasing
Made the FIRST periodic table 1869 Mendeleev organized the periodic table based on the similar properties and relativities of certain elements Later, Henri Moseley organized the elements by increasing
Atoms and the Periodic Table
 Atoms and the Periodic Table Parts of the Atom Proton Found in the nucleus Number of protons defines the element Charge +1, mass 1 Parts of the Atom Neutron Found in the nucleus Stabilizes the nucleus
Atoms and the Periodic Table Parts of the Atom Proton Found in the nucleus Number of protons defines the element Charge +1, mass 1 Parts of the Atom Neutron Found in the nucleus Stabilizes the nucleus
Radiometric Dating (tap anywhere)
 Radiometric Dating (tap anywhere) Protons Neutrons Electrons Elements on the periodic table are STABLE Elements can have radioactive versions of itself called ISOTOPES!! Page 1 in your ESRT has your list!
Radiometric Dating (tap anywhere) Protons Neutrons Electrons Elements on the periodic table are STABLE Elements can have radioactive versions of itself called ISOTOPES!! Page 1 in your ESRT has your list!
CHEM 107 (Spring-2005) Exam 3 (100 pts)
 CHEM 107 (Spring-2005) Exam 3 (100 pts) Name: ------------------------------------------------------------------------, Clid # ------------------------------ LAST NAME, First (Circle the alphabet segment
CHEM 107 (Spring-2005) Exam 3 (100 pts) Name: ------------------------------------------------------------------------, Clid # ------------------------------ LAST NAME, First (Circle the alphabet segment
Agenda Rationale for ETG S eek ing I d eas ETG fram ew ork and res u lts 2
 Internal Innovation @ C is c o 2 0 0 6 C i s c o S y s t e m s, I n c. A l l r i g h t s r e s e r v e d. C i s c o C o n f i d e n t i a l 1 Agenda Rationale for ETG S eek ing I d eas ETG fram ew ork
Internal Innovation @ C is c o 2 0 0 6 C i s c o S y s t e m s, I n c. A l l r i g h t s r e s e r v e d. C i s c o C o n f i d e n t i a l 1 Agenda Rationale for ETG S eek ing I d eas ETG fram ew ork
1 Genesis 1:1. Chapter 10 Matter. Lesson. Genesis 1:1 In the beginning God created the heavens and the earth. (NKJV)
 1 Genesis 1:1 Genesis 1:1 In the beginning God created the heavens and the earth. (NKJV) 1 Vocabulary Saturated having all the solute that can be dissolved at that temperature Neutron a particle with no
1 Genesis 1:1 Genesis 1:1 In the beginning God created the heavens and the earth. (NKJV) 1 Vocabulary Saturated having all the solute that can be dissolved at that temperature Neutron a particle with no
Element Cube Project (x2)
 Element Cube Project (x2) Background: As a class, we will construct a three dimensional periodic table by each student selecting two elements in which you will need to create an element cube. Helpful Links
Element Cube Project (x2) Background: As a class, we will construct a three dimensional periodic table by each student selecting two elements in which you will need to create an element cube. Helpful Links
9/20/2017. Elements are Pure Substances that cannot be broken down into simpler substances by chemical change (contain Only One Type of Atom)
 CAPTER 6: TE PERIODIC TABLE Elements are Pure Substances that cannot be broken down into simpler substances by chemical change (contain Only One Type of Atom) The Periodic Table (Mendeleev) In 1872, Dmitri
CAPTER 6: TE PERIODIC TABLE Elements are Pure Substances that cannot be broken down into simpler substances by chemical change (contain Only One Type of Atom) The Periodic Table (Mendeleev) In 1872, Dmitri
Chemistry 126 Final Examination, Prof. Hanson, May, Section B or D (circle one) Seat Coordinate Name
 Chemistry 126 Final Examination, Prof. Hanson, May, 2004 Section B or D (circle one) Seat Coordinate Name DO NOT OPEN THIS EXAM UNTIL INSTRUCTED TO DO SO Each asterisk () is 5 points. There are 40 s, for
Chemistry 126 Final Examination, Prof. Hanson, May, 2004 Section B or D (circle one) Seat Coordinate Name DO NOT OPEN THIS EXAM UNTIL INSTRUCTED TO DO SO Each asterisk () is 5 points. There are 40 s, for
c. What is the average rate of change of f on the interval [, ]? Answer: d. What is a local minimum value of f? Answer: 5 e. On what interval(s) is f
![c. What is the average rate of change of f on the interval [, ]? Answer: d. What is a local minimum value of f? Answer: 5 e. On what interval(s) is f c. What is the average rate of change of f on the interval [, ]? Answer: d. What is a local minimum value of f? Answer: 5 e. On what interval(s) is f](/thumbs/87/95703678.jpg) Essential Skills Chapter f ( x + h) f ( x ). Simplifying the difference quotient Section. h f ( x + h) f ( x ) Example: For f ( x) = 4x 4 x, find and simplify completely. h Answer: 4 8x 4 h. Finding the
Essential Skills Chapter f ( x + h) f ( x ). Simplifying the difference quotient Section. h f ( x + h) f ( x ) Example: For f ( x) = 4x 4 x, find and simplify completely. h Answer: 4 8x 4 h. Finding the
Use precise language and domain-specific vocabulary to inform about or explain the topic. CCSS.ELA-LITERACY.WHST D
 Lesson eight What are characteristics of chemical reactions? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading
Lesson eight What are characteristics of chemical reactions? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading
Fall / Winter Multi - Media Campaign
 Fall / Winter Multi - Media Campaign Bi g H or n R a di o N et w or k 1 B U B B A S B A R- B- Q U E R E ST A U R A N T 10% O F F B R E A K F A S T C o u p o n vali d M o n.- Fri. 7-11 a m Excl u des a
Fall / Winter Multi - Media Campaign Bi g H or n R a di o N et w or k 1 B U B B A S B A R- B- Q U E R E ST A U R A N T 10% O F F B R E A K F A S T C o u p o n vali d M o n.- Fri. 7-11 a m Excl u des a
COMPILATION OF AUTOMATA FROM MORPHOLOGICAL TWO-LEVEL RULES
 Kimmo Koskenniemi Re se ar ch Unit for Co mp ut at io na l Li ng ui st ic s University of Helsinki, Hallituskatu 11 SF-00100 Helsinki, Finland COMPILATION OF AUTOMATA FROM MORPHOLOGICAL TWO-LEVEL RULES
Kimmo Koskenniemi Re se ar ch Unit for Co mp ut at io na l Li ng ui st ic s University of Helsinki, Hallituskatu 11 SF-00100 Helsinki, Finland COMPILATION OF AUTOMATA FROM MORPHOLOGICAL TWO-LEVEL RULES
CMSC 313 Lecture 17 Postulates & Theorems of Boolean Algebra Semiconductors CMOS Logic Gates
 CMSC 313 Lecture 17 Postulates & Theorems of Boolean Algebra Semiconductors CMOS Logic Gates UMBC, CMSC313, Richard Chang Last Time Overview of second half of this course Logic gates &
CMSC 313 Lecture 17 Postulates & Theorems of Boolean Algebra Semiconductors CMOS Logic Gates UMBC, CMSC313, Richard Chang Last Time Overview of second half of this course Logic gates &
8. Relax and do well.
 CHEM 1215 Exam III John III. Gelder November 11, 1998 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last page includes a periodic table and
CHEM 1215 Exam III John III. Gelder November 11, 1998 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last page includes a periodic table and
M10/4/CHEMI/SPM/ENG/TZ2/XX+ CHEMISTRY. Wednesday 12 May 2010 (afternoon) 45 minutes INSTRUCTIONS TO CANDIDATES
 M10/4/CHEMI/SPM/ENG/TZ/XX+ 106116 CHEMISTRY standard level Paper 1 Wednesday 1 May 010 (afternoon) 45 minutes INSTRUCTIONS TO CANDIDATES Do not open this examination paper until instructed to do so. Answer
M10/4/CHEMI/SPM/ENG/TZ/XX+ 106116 CHEMISTRY standard level Paper 1 Wednesday 1 May 010 (afternoon) 45 minutes INSTRUCTIONS TO CANDIDATES Do not open this examination paper until instructed to do so. Answer
FINAL EXAM April 26, 2004
 CM 1045 (11:15 am Lecture) Dr. Light FINAL EXAM April 26, 2004 Name (please print) Check your recitation section: Sec. 21 5:30-6:20 pm (Popovic) Sec. 24 3:30-4:20 pm (Giunta) Sec. 22 6:30-7:20 pm (Popovic)
CM 1045 (11:15 am Lecture) Dr. Light FINAL EXAM April 26, 2004 Name (please print) Check your recitation section: Sec. 21 5:30-6:20 pm (Popovic) Sec. 24 3:30-4:20 pm (Giunta) Sec. 22 6:30-7:20 pm (Popovic)
`G 12 */" T A5&2/, ]&>b ; A%/=W, 62 S 35&.1?& S + ( A; 2 ]/0 ; 5 ; L) ( >>S.
![`G 12 */ T A5&2/, ]&>b ; A%/=W, 62 S 35&.1?& S + ( A; 2 ]/0 ; 5 ; L) ( >>S. `G 12 */ T A5&2/, ]&>b ; A%/=W, 62 S 35&.1?& S + ( A; 2 ]/0 ; 5 ; L) ( >>S.](/thumbs/76/73242945.jpg) 01(( +,-. ()*) $%&' "#! : : % $& - "#$ :, (!" -&. #0 12 + 34 2567 () *+ '!" #$%& ; 2 "1? + @)&2 A5&2 () 25& 89:2 *2 72, B97I J$K
01(( +,-. ()*) $%&' "#! : : % $& - "#$ :, (!" -&. #0 12 + 34 2567 () *+ '!" #$%& ; 2 "1? + @)&2 A5&2 () 25& 89:2 *2 72, B97I J$K
A/P Warrants. June 15, To Approve. To Ratify. Authorize the City Manager to approve such expenditures as are legally due and
 T. 7 TY LS ALATS A/P rrnts June 5, 5 Pges: To Approve - 5 89, 54.3 A/P rrnts 6/ 5/ 5 Subtotl $ 89, 54. 3 To Rtify Pges: 6-, 34. 98 Advnce rrnts 5/ 6/ 5-4 3, 659. 94 Advnce rrnts 6/ / 5 4, 7. 69 June Retirees
T. 7 TY LS ALATS A/P rrnts June 5, 5 Pges: To Approve - 5 89, 54.3 A/P rrnts 6/ 5/ 5 Subtotl $ 89, 54. 3 To Rtify Pges: 6-, 34. 98 Advnce rrnts 5/ 6/ 5-4 3, 659. 94 Advnce rrnts 6/ / 5 4, 7. 69 June Retirees
Physical Chemistry I CHEM 4641 Final Exam 13 questions, 30 points
 Physical Chemistry I CHEM 4641 Final Exam 13 questions, 30 points Name: KEY Gas constant: R = 8.314 J mol -1 K -1 = 0.008314 kj mol -1 K -1. Boltzmann constant k = 1.381 10-23 J/K = 0.6950 cm -1 /K h =
Physical Chemistry I CHEM 4641 Final Exam 13 questions, 30 points Name: KEY Gas constant: R = 8.314 J mol -1 K -1 = 0.008314 kj mol -1 K -1. Boltzmann constant k = 1.381 10-23 J/K = 0.6950 cm -1 /K h =
$%! & (, -3 / 0 4, 5 6/ 6 +7, 6 8 9/ 5 :/ 5 A BDC EF G H I EJ KL N G H I. ] ^ _ ` _ ^ a b=c o e f p a q i h f i a j k e i l _ ^ m=c n ^
![$%! & (, -3 / 0 4, 5 6/ 6 +7, 6 8 9/ 5 :/ 5 A BDC EF G H I EJ KL N G H I. ] ^ _ ` _ ^ a b=c o e f p a q i h f i a j k e i l _ ^ m=c n ^ $%! & (, -3 / 0 4, 5 6/ 6 +7, 6 8 9/ 5 :/ 5 A BDC EF G H I EJ KL N G H I. ] ^ _ ` _ ^ a b=c o e f p a q i h f i a j k e i l _ ^ m=c n ^](/thumbs/92/108125918.jpg) ! #" $%! & ' ( ) ) (, -. / ( 0 1#2 ' ( ) ) (, -3 / 0 4, 5 6/ 6 7, 6 8 9/ 5 :/ 5 ;=? @ A BDC EF G H I EJ KL M @C N G H I OPQ ;=R F L EI E G H A S T U S V@C N G H IDW G Q G XYU Z A [ H R C \ G ] ^ _ `
! #" $%! & ' ( ) ) (, -. / ( 0 1#2 ' ( ) ) (, -3 / 0 4, 5 6/ 6 7, 6 8 9/ 5 :/ 5 ;=? @ A BDC EF G H I EJ KL M @C N G H I OPQ ;=R F L EI E G H A S T U S V@C N G H IDW G Q G XYU Z A [ H R C \ G ] ^ _ `
POLYTECHNIC OF NAMIBIA
 POLYTECHNIC OF NAMIBIA DEPARTMENT OF HEALTH SCIENCES BACHELOR OF ENVIRONMENTAL HEALTH SCIENCES HEALTH SCIENCE CHEMISTRY (HSC 511S) NQF level 5 SECOND OPPORTUNITY EXAMINATION November 2014 TIME: MARKS:
POLYTECHNIC OF NAMIBIA DEPARTMENT OF HEALTH SCIENCES BACHELOR OF ENVIRONMENTAL HEALTH SCIENCES HEALTH SCIENCE CHEMISTRY (HSC 511S) NQF level 5 SECOND OPPORTUNITY EXAMINATION November 2014 TIME: MARKS:
Dangote Flour Mills Plc
 SUMMARY OF OFFER Opening Date 6 th September 27 Closing Date 27 th September 27 Shares on Offer 1.25bn Ord. Shares of 5k each Offer Price Offer Size Market Cap (Post Offer) Minimum Offer N15. per share
SUMMARY OF OFFER Opening Date 6 th September 27 Closing Date 27 th September 27 Shares on Offer 1.25bn Ord. Shares of 5k each Offer Price Offer Size Market Cap (Post Offer) Minimum Offer N15. per share
i;\-'i frz q > R>? >tr E*+ [S I z> N g> F 'x sa :r> >,9 T F >= = = I Y E H H>tr iir- g-i I * s I!,i --' - = a trx - H tnz rqx o >.F g< s Ire tr () -s
 5 C /? >9 T > ; '. ; J ' ' J. \ ;\' \.> ). L; c\ u ( (J ) \ 1 ) : C ) (... >\ > 9 e!) T C). '1!\ /_ \ '\ ' > 9 C > 9.' \( T Z > 9 > 5 P + 9 9 ) :> : + (. \ z : ) z cf C : u 9 ( :!z! Z c (! $ f 1 :.1 f.
5 C /? >9 T > ; '. ; J ' ' J. \ ;\' \.> ). L; c\ u ( (J ) \ 1 ) : C ) (... >\ > 9 e!) T C). '1!\ /_ \ '\ ' > 9 C > 9.' \( T Z > 9 > 5 P + 9 9 ) :> : + (. \ z : ) z cf C : u 9 ( :!z! Z c (! $ f 1 :.1 f.
I n t e r n a t i o n a l E l e c t r o n i c J o u r n a l o f E l e m e n t a r y E.7 d u, c ai ts is ou n e, 1 V3 1o-2 l6, I n t h i s a r t
 I n t e r n a t i o n a l E l e c t r o n i c J o ue rlne am l e not fa r y E d u c a t i o n, 2 0 1 4, 1 37-2 ( 16 ). H o w R e a d i n g V o l u m e A f f e c t s b o t h R e a d i n g F l u e n c y
I n t e r n a t i o n a l E l e c t r o n i c J o ue rlne am l e not fa r y E d u c a t i o n, 2 0 1 4, 1 37-2 ( 16 ). H o w R e a d i n g V o l u m e A f f e c t s b o t h R e a d i n g F l u e n c y
Faculty of Natural and Agricultural Sciences Chemistry Department. Semester Test 1. Analytical Chemistry CMY 283. Time: 120 min Marks: 100 Pages: 6
 Faculty of Natural and Agricultural Sciences Chemistry Department Semester Test 1 Analytical Chemistry CMY 283 Date: 5 September 2016 Lecturers : Prof P Forbes, Dr Laurens, Mr SA Nsibande Time: 120 min
Faculty of Natural and Agricultural Sciences Chemistry Department Semester Test 1 Analytical Chemistry CMY 283 Date: 5 September 2016 Lecturers : Prof P Forbes, Dr Laurens, Mr SA Nsibande Time: 120 min
