Analýza investi ného rozhodovania pri uplatnení reálnej opcie
|
|
|
- Gervais Francis
- 5 years ago
- Views:
Transcription
1 FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO V BRATISLAVE Katedra aplikovanej matematiky a ²tatistiky Analýza investi ného rozhodovania pri uplatnení reálnej opcie DIPLOMOVÁ PRÁCA BRATISLAVA 2008 Ingrid Michnová
2 Analýza investi ného rozhodovania pri uplatnení reálnej opcie DIPLOMOVÁ PRÁCA Diplomant: Ingrid Michnová FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO V BRATISLAVE Matematika Ekonomická a nan ná matematika Vedúci diplomovej práce: Dr. Zuzana Chladná BRATISLAVA 2008
3 ƒestné prehlásenie ƒestne prehlasujem, ºe som túto diplomovú prácu vypracovala samostatne, len s pomocou nadobudnutých teoretických vedomostí, konzultácií a uvedenej literatúry. V Bratislave, apríl Ingrid Michnová
4 Po akovanie Ve mi pekne akujem vedúcej diplomovej práce Dr. Zuzane Chladnej za jej odborné vedenie, pripomienky, návrhy a as, ktorý mi venovala pri vypracovávaní diplomovej práce.
5 Abstrakt V tejto diplomovej práci sa bliº²ie zaoberáme jednou z metód investi ného rozhodovania, tzv. metódou reálnej opcie, ktorá je zaloºená na vyuºití analógie investi nej príleºitosti s nan nou opciou. Uvedieme príklad projektu a taktieº jednu z moºností jeho rie²enia (vyuºitím parciálnych diferenciálnych rovníc a ich numerického rie²enia). Úlohu alej roz²írime o poh ad regulátora, ktorý optimalizuje as zásahu do stochastickej ceny aktíva (zavedenie dane) pri om sleduje daný cie. K ú ové slová: reálna opcia, NPV, investi ná analýza, vo ná hranica, stochastické diferenciálne rovnice Abstract This work demonstrates one of the methods of investment analysis real option approach that is based on analogy between investment opportunity and nancial option. We introduce a model of optimal realization of project and we provide a presentation of possible solution technique (transformation of stated problem into a sequence of partial dierential equations and its numerical solution). Moreover, we analyze optimal time of regulator's intervention on the stochastic price of underlying asset (put the tax) in order to achieve specied aim. Keywords: real option, NPV, investment analysis, free boundary problem, stochastic dierential equations
6 Obsah Zoznam skratiek a symbolov 3 Úvod 5 1 Metódy investi ného rozhodovania Porovnanie prístupu NPV a reálnej opcie Reálna opcia Typy reálnych opcií Stochastický kalkulus Brownov pohyb Itôva lema Model Predpoklady investovania Formulácia modelu Stochastické dynamické programovanie Odvodenie parciálnych diferenciálnych rovníc Problém vo nej hranice Matematická formulácia modelu Aplikácia modelu Motivácia Úloha Modelovanie ceny CO
7 5.4 Funkcie nákladov Numerické rie²enie Oblas rozhodovania Parametre a ich vplyv na oblas rozhodovania Vplyv regulátora Moºnosti roz²írenia modelu Modelovanie ceny Optimalizácia zásahu regulátora ako reálna opcia Záver 44 Literatúra 45 2
8 Zoznam skratiek a symbolov NPV Net present value ( istá sú asná hodnota nan ných tokov) W t S t Wienerov proces cena komodity t as x stav µ drift stochastického procesu σ volatilita stochastického procesu r úroková miera p.a. d hodnota dane alebo iného vplyvu regulátora na cenu komodity µ 1 drift stochastického procesu modelujúceho cenu komodity v období pred zásahom vlády µ 2 drift stochastického procesu modelujúceho cenu komodity v období po zásahu vlády σ 1 σ 2 t volatilita stochastického procesu modelujúceho cenu komodity v období pred zásahom vlády volatilita stochastického procesu modelujúceho cenu komodity v období po zásahu vlády as zásahu vlády 3
9 T maturita reálnej opcie I vý²ka investície (expira ná cena opcie) N (µ, σ 2 ) normálne rozdelenie so strednou hodnotou µ a disperziou σ 2 π 1 (S t, t) funkcia nákladov pred investíciou π 2 (S t, t) funkcia nákladov po realizácii investície V (S t, t) o akávaná istá sú asná hodnota budúcich pe aºných tokov od asu t do asu T za predpokladu, ºe sa rma rozhoduje optimálne vo v²etkých budúcich asových okamihoch V 2 (S t, t) o akávaná istá sú asná hodnota v²etkých budúcich pe aºných tokov od asu t do asu T za predpokladu, ºe spolo nos investovala v minulosti (do asu t) S f (t) funkcia (tzv. vo ná hranica) rozde ujúca rovinu (t, S t ) na oblas, kedy je optimálne investova a oblas, kedy je naopak výhodnej²ie neinvestova X produkcia CO 2 v tonách pred uskuto nením investície Y produkcia CO 2 v tonách po uskuto není investície A xné náklady pred uskuto nením investície B xné náklady po uskuto není investície G(ξ, t) Greenova funkcia 4
10 Úvod S rozvojom teoretických znalostí o nan ných opciách sa vedecká verejnos za ala zaobera my²lienkou aplikácie teórie opcií aj do iných odvetví. Podobnos denície americkej nan nej opcie s investi nou príleºitos ou spolo nosti viedlo k zavedeniu pojmu reálnej opcie. Tento koncept poskytuje iný poh ad na optimalitu rozhodovania sa o realizácii investície. Doteraz najviac pouºívaná metóda istej sú asnej hodnoty (NPV) platí iba za ur itých predpokladov (úplná návratnos vstupných nákladov v prípade odstúpenia od projektu, moºnos investova teraz alebo nikdy, deterministický vývoj vstupných parametrov), ktoré vä ²ina reálnych investi ných príleºitostí nesp a. Na druhej strane teória reálnych opcií priná²a do tejto problematiky vä ²iu exibilitu: zoh ad uje moºnos odloºi rozhodnutie na neskôr a dynamický ( asto stochastický) vývoj vstupných parametrov. Na rozdiel od nan ných opcií, kedy je primárnym cie om ur i ich hodnotu, v reálnych opciách sa vä ²í dôraz kladie na ur enie hranice, ktorá manaºérom poskytne presný návod za akých podmienok investova a za akých naopak vyuºi moºnos odloºi rozhodnutie na neskôr. Vzh adom na poºiadavku silného matematického zázemia pri práci s reálnymi opciami tento prístup zatia v praxi nie je ²tandardne vyuºívaný, o v²ak vedie k zvý²enej snahe sprístupni túto my²lienku verejnosti. V tejto diplomovej práci uvedieme pojem reálnej opcie, jej analógiu s nan nými opciami a zameriame sa odvodenie modelovej situácie investi nej príleºitosti, ktorá je riadená stochastickou cenou komodity. Následne tento model aplikujeme na konkrétnu situáciu z oblasti obchodovania s emisiami. Nakoniec ukáºeme, ako môºe by existencia v²eobecne známej dynamickej hranice rozhodovania vyuºitá autoritou, ktorej úsilím je za pomoci regulácie ceny komodity (zavedenia dane) 5
11 dosiahnu zvý²enie po tu spolo ností, ktoré realizujú projekt v ur enom asovom horizonte. Diplomová práca je rozdelená do ²iestich kapitol. V prvej sa venujeme rozdielom v prístupe analýzy investície pomocou NPV a reálnej opcie a demon²trujeme ich na príklade. Porovnanie nan nej a reálnej opcie je obsahom druhej kapitoly. Tretia kapitola poskytuje základné matematické poznatky z teórie stochastického kalkulu. V ²tvrtej kapitole v²eobecne denujeme model projektu. Tento model v piatej kapitole roz²írime predpokladom vstupu regulátora na trh a numericky vyrie²ime pre konkrétne parametre. iesta kapitola sa zaoberá moºnos ami roz²írenia modelu. Koncipovanie textu predpokladá dobrú matematická zru nos itate a a jeho skúsenos s oce ovaním nan ných opcií. 6
12 Kapitola 1 Metódy investi ného rozhodovania Investícia je v ekonómii asto denovaná ako akt obetovania sú asných nákladov v prospech o akávaných budúcich ziskov. Vä ²ina investi ných rozhodnutí má tri základné charakteristiky: Nenávratnos ak bola investícia úplne alebo iasto ne realizovaná, nie je moºné vrátenie nákladov v prípade odstúpenia od zámeru. Neistota príjmy (prípadne aj náklady) sú stochastické veli iny a ich budúci asový vývoj nie je známy v ase rozhodnutia. Na asovanie rozhodnutie je moºné oddiali za ú elom získania nových informácií. Klasická teória zjednodu²uje problematiku investi ného rozhodovania na ur enie znamienka istej sú asnej hodnoty budúcich pe aºných tokov (NPV = net present value): investova, ak do sú asnosti diskontované budúce príjmy prevy²ujú diskontované budúce náklady, v opa nom prípade neinvestova. V procese výpo tu istej sú asnej hodnoty budúcich pe aºných tokov sa v²ak vynárajú mnohé problémy, ako napríklad odhad o akávaného toku budúcich príjmov, inácie alebo diskontných faktorov. Veli iny stochastického charakteru sú v tomto prístupe nahrádzané ich strednými hodnotami. Táto metóda taktieº predpokladá iba jednu z dvoch moºností: úplnú návratnos nákladov v prípade odstúpenia od projektu alebo moºnos investova teraz alebo nikdy. Túto podmienku v²ak nesp a vä ²ina reálnych 7
13 investícií. Profesor Myers ako prvý vo svojom lánku s názvom Determinants of Corporate Borrowing 1 pouºil pojem reálna opcia a poukázal na vz ah medzi nan nými opciami a moºnos ami objavujúcimi sa v procese investi ného rozhodovania. Právo odloºi rozhodnutie o nenávratnej investícii na neskôr za ú elom získania novej informácie má na investorove správanie zásadný vplyv, a preto klasická teória vyuºívajúca analýzu pomocou NPV nevedie vºdy k optimálnej rozhodovacej stratégii. V nasledujúcej asti 1.1 porovnáme investi né rozhodnutia analyzované na základe prístupu NPV a reálnej opcie. 1.1 Porovnanie prístupu NPV a reálnej opcie Pre názornej²ie pochopenie rôzneho prístupu rozhodovania na základe istej sú asnej hodnoty (NPV) a tzv. reálnej opcie uvedieme jednoduchý príklad. Predstavme si, ºe pri kopaní studne v záhrade sme narazili na zlatú ºilu o objeme 1000 trójskych uncí (1 trójska unca = gramu). Predpokladáme, ºe cena zlata je výsledkom náhodného procesu: dnes je jeho hodnota 500$ za uncu, budúci rok vzrastie na hodnotu 600$/unca s pravdepodobnos ou 0.6 respektíve klesne na hodnotu 350 $/unca s pravdepodobnos ou 0.4 (v prípade, ºe pokusné vrty v západnej Ázii objavia nové zdroje zlata). Náklady na aºbu predstavujú 450 $/unca. Stojíme pred rozhodnutím, i zlato vytaºi dnes (stratégia I ) alebo aºbu odloºi o rok (stratégia II ), pri om predpokladáme, ºe v²etko zlato bude predané ihne za aktuálnu cenu. alej uvaºujeme, ºe cenové riziko je perfektne diferzikované, a teda budúce pe aºné toky diskontujeme bezrizikovou úrokovou mierou 5% per annum. Rozhodovanie na základe NPV Ako uº bolo spomenuté v úvode tejto kapitoly, istá sú asná hodnota investície je denovaná ako rozdiel sú asnej hodnoty príjmov a sú asnej hodnoty nákladov, 1 Uverejnený v Journal of Finance v roku 1977 [9]. 8
14 ktoré sú s touto investíciou spojené. V prípade, ºe hodnota NPV>0 (diskontované príjmy prevy²ujú diskontované náklady), manaºér odporu ní akceptova túto investíciu. Naopak pri zápornom znamienku investi nú príleºitos zamieta. Aplikujme teda túto metódu na uvedený príklad: Analyzovaním stratégie I dostávame Uvaºujme teraz stratégiu II : NP V n,i = 1000 ( ) = 50000$ > 0 Ak cena zlata v budúcom roku zaznamená pozitívny trend NP V n,ii up = Ak cena zlata v budúcom roku klesne 1000 ( ) 1.05 NP V n,ii 1000 ( ) down = = $. = 95240$ A teda NP V n,ii = 0.6 NP V n,ii up NP V n,ii down = 47620$ Ke ºe istá sú asná hodnota stratégie I je vä ²ia ako stratégie II (50000$ > 47620$), aºba okamºite sa javí ako výhodnej²ia. Rozhodovanie na základe prístupu reálnej opcie V prípade výpo tu zaloºenom na základe prístupu reálnej opcie sa taktieº rozhodujeme medzi stratégiou I a stratégiou II, av²ak zoh adníme fakt, ºe odloºenie rozhodnutia o rok (stratégia II) poskytne novú informáciu o cene zlata. ƒistá sú asná hodnota investície dnes sa vypo íta rovnako, ako bolo uvedené v predchádzajúcom prístupe (NP V o,i = NP V n,i = 50000$). Rozdiel nastáva pri stratégii II, kedy opciu investova uplatníme len v prípade, ºe cena zlata vzrastie, kým v prípade jej poklesu aºbu neuskuto níme (NP V o,ii up Potom dostávame NP V o,ii = 0.6 NP V o,ii up = , ale NP V o,ii down = 0) NP V o,ii down = 85716$ 9
15 Ke ºe NP V o,ii = > = NP V o,i, uvedená metóda rozhodovania povaºuje za optimálnu stratégiu po ka jeden rok a potom sa na základe trhovej ceny zlata prikloni k lep²iemu rie²eniu. Predchádzajúci príklad poukazuje na skuto nos, ºe nielenºe kaºdý z prístupov ohodnocuje projekt inak (pouºijúc klasický NPV prístup má investícia hodnotu 50000$, prístup reálnej opcie ohodnocuje túto príleºitos na 85716$), ale za optimálne povaºuje diametrálne odli²né stratégie. Doteraz asto vyuºívaný prístup NPV teda elí kritike najmä z dôvodu zanedbania moºnosti exibilného rozhodovania na základe novej informácie. alej si v²imnime, ºe rozdiel 85716$ 50000$ = 35716$ predstavuje hodnotu, o ktorú je príleºitos investova teraz alebo o rok cenne²ia oproti moºnosti investova teraz alebo nikdy. Ke ºe vä ²inu reálnych investi ných príleºitostí je moºné uskuto ni v nejakom asovom intervale a rozhodnutia sú prijímané na základe v²etkých v danom okamihu dostupných informácií, teória reálnych opcií oproti analýze pomocou NPV lep²ie popisuje realitu. 10
16 Kapitola 2 Reálna opcia Analógia medzi nan nými a reálnymi opciami je zrejmá z denícií oboch spomenutých nástrojov: Denícia 2.1 (Americká call (put) opcia) Predstavuje právo, nie v²ak povinnos, kúpi (preda ) podkladové aktívum (naj astej²ie akciu) za vopred stanovenú expira nú cenu kedyko vek do asu T (maturity). Denícia 2.2 (Reálna opcia) Poskytuje právo, nie v²ak povinnos, investova ur- itý nan ný obnos (kúpi dané podkladové aktívum za vopred stanovenú expira nú cenu) do stanoveného asu (maturity) a získa projekt (podkladové aktívum). 1 Investi ná príleºitos je teda analogická americkej call opcii, pri om vz ahy medzi vstupnými parametrami pre nan nú a reálnu opciu sú uvedené v tabu ke 2.1. Investícia sa povaºuje za nenávratnú. Ak rma investuje, vyuºije danú opciu, av²ak vzdáva sa moºnosti al²ieho odkladu rozhodnutia (náklady stratenej príleºitosti). Pripome me, ºe v oboch spomenutých deníciách predpokladáme stochastický vývoj ceny podkladového aktíva. 1 Dixit, Pindyck, 1994, str.30 [1]. 11
17 Reálna opcia Premenná Finan ná opcia Hodnota projektu S Cena akcie Náklady na investíciu I Expira ná cena opcie ƒas, dokedy je moºné investíciu uskuto ni T Maturita opcie Pe aºné toky plynúce z investície δ Dividendový výnos ƒasová hodnota pe azí r Bezrizik. úroková miera Rizikovos projektu σ 2 Volatilita akcie Tabu ka 2.1: Porovnanie reálnej a nan nej americkej call opcie na akciu vyplácajúcu dividendy. 2.1 Typy reálnych opcií V predchádzajúcej asti sme denovali reálnu opciu popisujúcu jednoduchú investi nú príleºitos. V praxi je takmer kaºdé rozhodovanie moºné popísa ur itým typom reálnej opcie. Dixit a Pindyck, 1994 [1] uvádzajú príklad manºelstva, kedy ² astie páru závisí od stochastických náhodných udalostí, ktoré sa v kaºdodennom ºivote vyskytnú. Expira ná cena tejto opcie rastie s rastúcimi nákladmi na rozvod alebo sociálnym odsúdením rozluky manºelov (náboºenské prekáºky). ƒím vä ²ie sú tieto prekáºky, tým cennej²ia je moºnos so sobá²om po ka a nájs o moºno najvyhovujúcej²ieho partnera. Iným príkladom je rozhodovanie o stupni dosiahnutého vzdelania. Reálnu opciu tu predstavuje moºnos al²ieho ²túdia, ktorým sa na nieko ko rokov vzdávame moºnosti zárobku (expira ná cena), av²ak o akávame vy²²iu mzdu v budúcnosti. Extrémnym prípadom nenávratného rozhodovania je samovraºda, pretoºe op ná hodnota odloºi rozhodnutie a po ka, i sa situácia zlep²í je v tomto prípade ve ká. Spomenuté príklady predstavujú len nieko ko názorných ukáºok reálnych opcií. Napriek ve kej rôznorodosti investi ných príleºitostí sa v literatúre uvádza istá kategorizácia. V nasledujúcom texte spomenieme v²eobecnú terminológiu základných 12
18 typov reálnych opcií zavedenú Copelandom a Antikarovom, option to wait predstavuje moºnos odloºi investi né rozhodnutie. Jej analógiou je americká call opcia na akciu vyplácajúcu dividendy, kde expira ná cena kore²ponduje s po iato nými nákladmi, vlastníctvo akcie s vlastníctvom projektu a dividendy s kladnými alebo zápornými nan nými tokmi plynúcimi z tejto investície. Moºnos oddiali rozhodovanie má ur itú nezápornú hodnotu (cenu opcie), pretoºe oproti príleºitosti teraz alebo nikdy umoº uje vyuºi dynamický systém rozhodovania v rôznych okamihoch na základe v²etkých vtedy dostupných informácií. option to abandon moºnos ukon i projekt pred predpokladaným termínom v prípade jeho nevýnosnosti a preda vybavenie (napríklad stroje alebo patent) za ur itú cenu (americká put opcia). Daný typ reálnej opcie chráni investora pred stratami v prípade, ºe situácia na trhu je hor²ia ako sa o akávalo. Treba pripomenú, ºe tento krok je nezvratný a opätovné spustenie projektu nákladné, preto v realite je investor ochotný akceptova do asné straty presved ený vierou v potenciálne budúce výnosy. option to switch reprezentuje exibilitu v prechode od jednej alternatívy k inej. Ide prevaºne o zmenu v technickom alebo softvérovom vybavení, pri om pôvodný model je optimálny v inej situácii ako model nový. Pre ilustráciu: kúrenie uhlím je výhodnej²ie v situácii, ked je jeho cena nízka, ale v prípade, ºe vzrastie, uprednostníme plynové kúrenie. compound option sú reálne opcie umoº ujúce viac realizácií (po uplatnení jednej opcie, môºe by realizovaná al²ia). Napríklad option to switch môºe by povaºovaná za compound option, ak je povolený prechod od jednej alternatívy k druhej a naopak neobmedzený po et krát. rainbow option reálne opcie obsahujúce nieko ko zdrojov náhodnosti. V²etky z vy²²ie spomínaných druhov opcií sa môºu správa ako rainbow v prípade, 2 Uvádza tieº Chladná, 2007, str.9 [5]. Vzh adom na fakt, ºe názvy nemajú slovenský ekvivalent, uvádzame pôvodné anglické názvy. 13
19 ºe rozhodnutie závisí od viacerých premenných (cien rôznych vstupov resp. výstupov), z ktorých kaºdá sleduje iný stochastický proces alebo sa tieto procesy lí²ia parametrami. V realite vä ²ina investi ných príleºitostí sp a deníciu posledných dvoch uvedených typov reálnych opcií. Spomínaný príklad manºelstva sa môºe správa ako compound option vychádzajúcu zo switch option, ke ºe vstupova do manºelstva a rozvádza sa je moºné neobmedzený po et krát. Rozhodovanie o samovraºde (option to abandon) zasa závisí na ve kom mnoºstve náhodných veli ín, teda ide o rainbow option. Vzh adom na ve ký po et moºných scenárov v mnohých prípadoch dochádza k zjednodu²ovaniu reálnych problémov (napríklad redukcia zdrojov náhodnosti, predpoklad jedného moºného vyuºitia opcie). Tieto komplikácie sú dôvodom pre preferenciu (zo strany manaºérov) síce statického, ale ah²ie dosiahnute ného výsledku vyuºijúc klasický prístup analýzy pomocou NPV a taktieº výzvou pre vedeckú obec sprístupni metódu reálnej opcie vyuºitiu v praxi. 14
20 Kapitola 3 Stochastický kalkulus Základným predpokladom pre oce ovanie opcií je fakt, ºe cena komodity (a teda aj od nej odvodené nan né toky) je riadená stochastickým procesom. Koncept Wienerovho a následne Brownovho pohybu má nieko ko dôleºitých vlastností, ktoré sú nevyhnutné pre al²ie matematické úvahy. 3.1 Brownov pohyb Denícia 3.1 (Wienerov proces) Wienerov proces je stochastický proces 1 s nasledujúcimi vlastnos ami: W 0 = 0 W t N (0, t) W t+s W s N (0, t) W t má nezávislé prírastky t.j. W t1, W t2 W t1,..., W tk W tk 1 v²etky 0 t 1 < t 2 <... < t k. 2 sú nezávislé pre 1 Stochastický proces je denovaný ako súbor náhodných premenných X = {X t ; t T } na pravdepodobnostnom priestore (Ω, F, P ) s hodnotami v R d. 2 Melicher ík, 2005, str.129 [3]. 15
21 Dôleºité charakteristiky Wienerovho procesu: Markovovskos procesu úplná informácia o minulom vývoji danej veli iny je obsiahnutá v poslednej hodnote. Teda táto je jediná potrebná na najlep²iu predpove budúcnosti. 3 Nezávislos prírastkov umoº uje limitný prechod od diskrétneho binárneho rozhodovacieho stromu (random walk) k jeho spojitej verzii. Normálne rozdelenie zmien Wienerovho procesu empirické pozorovania niektorých reálnych stochastických veli ín (alebo ich logaritmov) podporujú tento predpoklad. Formálny zápis Wienerovho pohybu (dw predstavuje diferenciál Wienerovho procesu, dt nekone ne malú asovú zmenu): dw = ɛ t dt (3.1) kde ɛ t N (0, 1) a E[ɛ t ɛ s ] = 0 pre t s. Denícia 3.2 (Brownov pohyb) Brownov pohyb je stochastický proces odvodený od Wienerovho procesu pridaním lineárneho trendu dx = αdt + σdw (3.2) kde α nazývame driftom a σ volatilitou daného procesu. Denícia 3.3 (Itôv proces) Zov²eobecnenie Brownovho pohybu, ktorého drift a volatilitu predstavujú nenáhodné funkcie asu a stavu nazývame Itôv proces, a teda: dx = a(x, t)dt + b(x, t)dw (3.3) Denícia 3.4 (Geometrický Brownov pohyb) peciálnym prípadom Itôvho procesu je geometrický Brownov pohyb, pre ktorý platí: dx = µxdt + σxdw (3.4) 3 Stochastický proces nazývame Markovovským, ak pre t T a pre t-ticu (x 1,..., x t ) X(Ω) platí P [X t = x t X 1 = x 1,..., X t 1 = x t 1 ] = P [X t = x t X t 1 = x t 1 ]. 16
22 resp. x t = x 0 e (µ 1 2 σ2 )t+σw t (3.5) kde x 0 predstavuje hodnotu procesu v ase 0 a µ resp. σ sú dané kon²tanty. Geometrický Brownov pohyb sa asto vyuºíva na modelovanie vývoja cien akcií (výnosy cien akcií sa modelujú ako nezávislé normálne rozdelené, vtedy µ predstavuje o akávaný výnos a σ neistotu tohto výnosu), úrokov, miezd a iných ekonomických a nan ných veli ín. Jeho výhody spo ívajú najmä v tom, ºe generuje iba kladné hodnoty, o je vhodné pri modelovaní veli ín, ktorých záporné hodnoty by nedávali praktický zmysel (napríklad cena alebo mnoºstvo) Itôva lema Jedným z pilierov analýz stochastických diferenciálnych rovníc sa stalo odvodenie Itôvej lemy (pomocou Taylorovho rozvoja). Táto lema denuje pravidlá pre derivovanie funkcií stochastických procesov. Lema 3.1 (Itôva lema) Nech x t je Itôv proces dx = a(x, t)dt + b(x, t)dw, nech f(x, t) C 2 (R < 0, )). Potom prvý diferenciál funkcie f(x t, t) je daný vz ahom df = f f dt + t x dx f 2 x 2 b2 (x, t)dt (3.6) dôsledkom oho funkcia f vyhovuje stochastickej diferenciálnej rovnici 5 df = ( f t + a(x, t) f x + 1 ) 2 b2 (x, t) 2 f dt + b(x, t) f dw (3.7) x 2 x 4 Niektoré ceny (napríklad ceny základných surovín) v²ak nevyhovujú exponenciálnemu trendu vývoja. Na ich modelovanie je moºné pouºi napríklad tzv.meanreverting proces (detailnej²ie v asti 6.1). 5 ev ovi, 2001, str.17 [4]. 17
23 Kapitola 4 Model Základom pre na²e úvahy o optimálnom procese rozhodovania je správna formulácia modelu popisujúceho realitu. Uvaºujme v²eobecnú úlohu zameriavajúcu sa na minimalizáciu nákladov (pre zjednodu²enie abstrahujeme od existencie príjmov), ktoré sú funkciou stochastickej ceny nejakej komodity. Túto úlohu neskôr bliº²ie ²pecikujeme (zvolením konkrétnych funkcií) a mierne modikujeme. 4.1 Predpoklady investovania Nech sa spolo nos rozhoduje optimálne (v zmysle minimalizácie nákladov) a jej rozhodnutie je riadené cenou S t nejakej komodity, ktorá sleduje geometrický Brownov pohyb (s parametrami ako v (3.4)). Uvaºujme investíciu vý²ky I. Náklady za jednotku asu pred investíciou nech denuje funkcia π 1 (S t, t), kým po nej funkcia π 2 (S t, t), pri om platí S t, t : π 1 (S t, t) π 2 (S t, t). Rozhodnutie investova je nenávratné, to znamená, ºe po uskuto není projektu sú náklady za jednotku asu vo v²etkých nasledovných asových okamihoch denované funkciou π 2 (S t, t). Uvaºujme spolo nos, ktorej ºivotnos je T rokov, po uplynutí ktorých spolo nos úplne zaniká a s jej innos ou nie sú spojené ºiadne al²ie výdavky. 18
24 Predpokladajme kon²tantnú, v ase nemennú ro nú úrokovú mieru r. 4.2 Formulácia modelu V nasledujúcej asti matematicky popí²eme skuto nosti uvedené v asti 4.1. Ozna me V 2 (S t, t) o akávanú istú sú asnú hodnotu v²etkých budúcich pe aºných tokov od asu t do asu T za predpokladu, ºe spolo nos investovala v minulosti (do asu t). Z h adiska al²ích úvah sa javí výhodné vyjadri hodnotu V 2 (S t, t) pomocou nasledujúcej Bellmanovej rovnice: V 2 (S t, t) = π 2 (S t, t) t + (1 + r t) 1 E[V 2 (S t+ t, t + t) S t ] (4.1) Kým prvý argument pravej strany vz ahu (4.1) predstavuje okamºité náklady v ase t, druhý popisuje diskontované budúce náklady, ktoré sú vyjadrené podmienenou strednou hodnotou na základe informácie o cene známej v ase t. Nech V (S t, t) predstavuje o akávanú istú sú asnú hodnotu budúcich pe aºných tokov od asu t do asu T ak predpokladáme, ºe sa rma rozhoduje optimálne vo v²etkých budúcich asových okamihoch. Úloha sa redukuje na Bellmanovu rovnicu pre úlohu optimálneho riadenia: V (S t, t) = min(π 1 (S t, t) t + (1 + r t) 1 E[V (S t+ t, t + t) S t ], V 2 (S t, t) + I) (4.2) s koncovou podmienkou V (S T, T ) = 0 (4.3) Prvý len prvého argumentu vz ahu (4.2) predstavuje pe aºný tok nákladov za as t, druhý len diskontovanú o akávanú hodnotu budúcich pe aºných tokov za predpokladu, ºe sa v kaºdom asovom okamihu rozhodujeme optimálne a v ase rozhodnutia je známa cena S t. Druhý argument vz ahu (4.2) interpretuje moºnos investície s jednorazovými nákladmi vo vý²ke I v ase t, al²ie pe aºné toky budú v tomto prípade dané funkciou V 2 (S t, t) (pretoºe investícia je nevratná). A teda v prípade, ºe sa minimum nadobúda v prvom argumente, investícia v ase t a pri danej cene S t nie je prijatá a naopak, jeho nadobudnutie v druhom argumente zodpovedá jej akceptovaniu. Koncová podmienka (4.3) zodpovedá ukon eniu prevádzky rmy v ase T. 19
25 4.3 Stochastické dynamické programovanie Úlohu sformulovanú vz ahom (4.2) je moºné prepísa do tvaru úlohy stochastického dynamického programovania s diskrétnym pevným asom a pevným koncom. Ozna me: j asový index prislúchajúci asu t j = j t, kde j {0, 1,..., m}, m = T t. Teda (t 0,..., t m ) je delenie asového intervalu. S j náhodná premenná prestavujúca cenu aktíva v ase t j sledujúca geometrický Brownov pohyb. Predpokladáme, ºe S(t 0 ) = S 0. u j riadiaca premenná, pri om 0 neinvestova u j = 1 investova Rovnica stochastického dynamického programovania teda v zmysle zavedeného ozna enia vyzerá nasledovne: V j (S j ) = min ((1 u j )(π 1j (S j ) t + (1 + r t) 1 E[V j+1 (S j+1 S j )]) + u j (V 2j (S j ) + I)) u j {0,1} s koncovou podmienkou V m (S j ) = 0 Táto úloha je zvy ajne rie²ená metódou programového riadenia alebo metódou optimálnej spätnej väzby, av²ak ako problematická sa ukazuje závislos náhodných premenných S j, S j+1. Preto zvolíme iný prístup zaloºený na numerickom rie²ení parciálnych diferenciálnych rovníc. 4.4 Odvodenie parciálnych diferenciálnych rovníc Ako bolo spomenuté, úloha optimálneho riadenia sa zvy ajne rie²i odzadu itera nou metódou, av²ak v tomto prípade je moºný jej prevod na h adanie minima 20
26 funkcií, ktoré vyhovujú parciálnym diferenciálnym rovniciam. 1 Pouºitím Taylorovho rozvoja, vz ahov (3.7) a (3.4) a faktu, ºe E[dW ] = 0 dostávame 2 E[V (S t+ t, t + t) S t ] = V (S t, t) + + [V t (S t, t) + µs t V S (S t, t) σ2 S 2 t V SS (S t, t)] t + + o( t) (4.4) kde o( t) sú leny vy²²ieho rádu. Ak sa vo vz ahu (4.2) nadobudne minimum v prvom argumente, potom platí: V (S t, t) = π 1 (S t, t) t + (1 + r t) 1 E[V (S t+ t, t + t)] (4.5) Prenásobením (1 + r t) a preusporiadaním dostávame r tv (S t, t) = π 1 (S t, t) t(1 + r t) + E[V (S t+ t, t + t) V (S t, t)] (4.6) Predelením t a limitným prechodom t 0 Vyuºijúc (4.4) vo vz ahu (4.7) rv (S t, t) = π 1 (S t, t) + 1 E[dV ] (4.7) dt rv (S t, t) = π 1 (S t, t) + V t (S t, t) + µs t V S (S t, t) σ2 S 2 t V SS (S t, t) (4.8) Nakoniec preusporiadaním dostávame parciálnu diferenciálnu rovnicu (PDR) V t (S, t) + µsv S (S, t) σ2 S 2 V SS (S, t) rv (S, t) + π 1 (S, t) = 0 (4.9) Analogickým postupom vychádzajúc zo vz ahu (4.1) dostávame PDR pre V 2 (S, t) V 2t (S, t) + µsv 2S (S, t) σ2 S 2 V 2SS (S, t) rv 2 (S, t) + π 2 (S, t) = 0 (4.10) 1 Detailnej²ie v Dixit, Pindyck, 1994, str [1]. 2 Dolný index ²tandardne ozna uje parciálnu deriváciu funkcie pod a indikovanej premennej. 21
27 4.5 Problém vo nej hranice Intuícia nám hovorí, ºe je optimálne investova pri vy²²ích hodnotách S a ºe celú oblas rozhodovania (rovinu (t, S(t))) môºeme krivkou S f (t) rozdeli na dva regióny, pri om v prvom je optimálne investova a v druhom naopak zotrva v sú asnom stave. Krivku S f nazývame vo nou hranicou. Poznamenajme, ºe táto krivka je analógiou vo nej hranice známej z teórie amerických nan ných opcií. Predpokladajme, ºe neinvestova je optimálne pre S < S f a investova pre S > S f. Detailnej²ie podmienky, za ktorých je tento prepoklad splnený uvádzajú Dixit, Pindyck, 1994, str [1]. Z formulácie vo nej hranice je zrejmé, ºe na hranici musí plati V (S f (t), t) = V 2 (S f (t), t) + I pre t. (4.11) Táto hranica je v²ak neznáma, preto potrebujeme al²iu podmienku, ktorá zvy ajne pochádza z ekonomického (fyzikálneho, biologického) pozadia daného problému. V na²om prípade predstavuje poºiadavku hladkého napojenia V (S, t) a V 2 (S, t) + I ako funkcií S v bodoch hranice S f (t) 3, teda V S (S f (t), t) = V 2S (S f (t), t) pre t (4.12) 4.6 Matematická formulácia modelu Vyuºijúc v²etky spomenuté fakty môºeme sformulova dve ekvivalentné denície uvedeného modelu: Denícia 4.1 Rie²ením úlohy (4.2) je dvojica (V (S, t), S f (t)) sp ajúca V t (S, t) + µsv S (S, t) σ2 S 2 V SS (S, t) rv (S, t) + π 1 (S, t) = 0 pre t (0, T ), S (0, S f (t)) V (S, T ) = 0 3 Podmienka je analogická podmienke vo nej hranice v teórii amerických opcií a je zaloºená na rovnakom ekonomickom základe. Pre bliº²ie matematické vysvetlenie pozri Dixit, Pindyck, 1994, str [1]. 22
28 V (0, t) = 0 V (S f (t), t) = V 2 (S f (t), t) + I kde V 2 (S, t) sp a rovnicu (4.10) V S (S f (t), t) = V 2S (S f (t), t) pre t (0, T ). Denícia 4.2 Rie²ením úlohy (4.2) je aspo C 1 hladká funkcia V (S, t) sp ajúca V (S, t) V 2 (S, t) + I pre t (0, T ), S > 0 ak V (S, t) < V 2 (S, t) + I, potom V (S, t) sp a parciálnu diferenciálnu rovnicu V t (S, t) + µsv S (S, t) σ2 S 2 V SS (S, t) rv (S, t) + π 1 (S, t) = 0, inak V (S, t) = V 2 (S, t) + I, kde V 2 (S, t) sp a rovnicu (4.10) Prvá uvedená denícia je vhodná na analytické úvahy o vlastnostiach rie²enia, kým druhá má vyuºitie najmä v numerických aproximáciách. 23
29 Kapitola 5 Aplikácia modelu Cie om nasledujúcej kapitoly je ukáza moºnosti roz²írenia úlohy (4.2) v prípade, ºe umoºníme regulátorovi (vláde, kartelu, inej autorite) ovplyvni cenu komodity S t zavedením jednorazového skoku d v ase t (kde t < T). Tento skok môºe by interpretovaný ako zavedenie dane, cla, alebo akáko vek zmena pomerov, ktorá má dopad na cenu komodity. 5.1 Motivácia Uvaºujme ²tát, ktorý chce zníºi výdavky na zdravotníctvo, respektíve dbá o zdravie obyvate stva, a preto uvaºuje o zavedení povinnosti preventívnych prehliadok pre svojich ob anov. Ideou je fakt, ºe náklady spolo nosti na pacienta, ktorého zdravie je pod doh adom lekára sú niº²ie (v dôsledku rýchlej diagnostiky ochorenia, a teda jeho men²ej závaºnosti). Pred zavedením tejto povinnosti ob an nenav²tevujúci lekára platí ur ité percento ceny lie by π 1 (S t ) = S t (kde S 1+d t je náhodná premenná predstavujúca náklady na lie bu danej choroby, d (0, 1)) a dobrovo ne nav²tevujúci platí ²tvrtinu ceny lie by, teda π 2 (S t ) = St 4. Naopak, ak ²tát túto my²lienku zrealizuje, ob an, ktorý sa rozhodne povinnos ignorova, hradí celú sumu π 1 (S t ) = S t, kým cena pre ob ana podstupujúceho prehliadku sa taktieº mierne zvý²i, povedzme na π 2 (S t ) = (1+d)S t 4. Jeho právo rozhodnú sa, 24
30 i podstúpi prehliadky alebo nie predstavuje opciu, ktorej expira nou cenou je cena stratenej príleºitosti, teda as strávený kaºdoro ne na vy²etreniach vyjadrený v peniazoch, ktoré by bol produktívny lovek schopný za túto dobu zarobi. Do expira nej ceny môºe by prípadne zahrnutý aj stres z akania na výsledky a podobne. Predpokladáme, ºe ak sa ob an rozhodne prehliadky absolvova, jeho rozhodnutie je nezvratné. Cie om ²tátu je v horizonte T rokov dosiahnu, aby sa ur ité stanovené percento jeho ob anov prehliadok zú ast ovalo. Z poh adu tohto regulátora je teda otázkou, kedy prija zákon o povinnosti prehliadok, aby boli naplnené jeho predstavy o nákladoch na lie bu pacientov. Vzh adom na fakt, ºe kvantikova jednotlivé veli iny v modeli popisujúcom náklady na lie bu a zdravie ako také, by bolo z dôvodu nedostatku dát náro né, nebudeme sa touto úlohou zaobera. Tento názorný príklad v²ak poukazuje na skuto nos, ºe schéma modelu, ktorým sa zaoberáme v tejto diplomovej práci, má opodstatnenie v mnoºstve aktuálnych problémov. 5.2 Úloha V nasledujúcom texte sa zaoberáme úlohou, ktorá je aplikovate ná na rozhodovanie v rôznych priemyselných odvetviach. Predpokladajme existenciu malých podnikate ov prevádzkujúcich spolo nosti, ktorých ved aj²ím produktom výroby sú splodiny vo forme CO 2. Reprezentujme v²etky spolo nosti jednou agregovanou spolo nos ou, ktorá predstavuje priemernú spolo nos (z h adiska prístupu k realizácii investície). Ke ºe ²tát má záujem na plnení kvót stanovených Kjótskym protokolom, za kaºdú tonu CO 2 vypustenú do ovzdu²ia nad povolené mnoºstvo je jej emitent povinný plati náklady, ktoré sa odvýjajú od aktuálnej ceny CO 2 a mnoºstva vyprodukovaných splodín. S touto splodinou je moºné reálne obchodovanie (v zmysle obchodu s emisiami) a jej cena je modelovaná ako geometrický Brownov pohyb. alej uvaºujme, ºe agregovaná spolo nos produkuje splodiny nad povolenú kvótu 25
31 a to v ase t 0 X ton CO 2 za as t. Táto spolo nos má moºnos nain²talova lter za cenu I, ktorý zníºi produkciu CO 2 nad limit na Y ton za as t (Y < X). Spolo nos má ºivotnos T rokov a rozhoduje sa optimálne (prioritou je minimalizova náklady spojené s produkciou CO 2 ). Je dôleºité si uvedomi, ºe úloha sp a predpoklady denované v asti 4.1. Regulátor uvaºuje o zavedení dane na CO 2 vo vý²ke d (detailnej²ie v asti 5.3) v ase t, s úmyslom zatraktívni zavedenie ltra, a teda zlep²i ºivotné prostredie. Toto rozhodnutie má moºnos urobi raz ro ne. Úlohou je ur i kedy (prípadne o ko ko, d < 0, 1 >) má regulátor k tomuto kroku pristúpi, aby postavenie ltra ur ité percento spolo ností po as zvoleného asového obdobia realizovalo. 5.3 Modelovanie ceny CO 2 Zavedením Kjótskeho protokolu, ktorý udáva jednotlivým krajinám kvóty na produkciu emisií zne is ujúcich ºivotné prostredie, sa vytvoril priestor na obchodovanie s týmito emisiami. Jednoducho povedané: ak ²tát stanovuje jednotlivým podnikom stropy na produkciu CO 2, potom tieto môºu rozdiel medzi stropom a ich skuto nou produkciou preda podniku, ktorý svoj limit prekra uje. Vyuºijúc predpoklad, ºe cena CO 2 (uvádzaná v prepo te na 1 tonu CO 2 ) sleduje geometrický Brownov pohyb, z historických dát cien za obdobie uverejnených na odhadneme parametre µ 1 = , σ 1 = (pre t = 1/250), S 0 = 0.95$. Vývoj ceny CO 2 za toto obdobie je znázornený na obrázku 5.1. Pod pojmom zavedenie dane v ase t rozumieme nasledovné: S 0 e (µ σ2 1 )t+σ 1W t pre t < t S t = (1 + d)s 0 e (µ σ2 1 )t +σ 1 W t e (µ σ2 2 )(t t )+σ 2 (W t W t ) pre t t Treba podotknú, ºe po zavedení dane cena opä sleduje geometrický Brownov pohyb, av²ak potenciálne s inými parametrami µ 2, σ Na obrázku 5.2 je zná-
32 zornená simulácia ceny za predpokladu zmeny týchto parametrov (0 < µ 2 µ 1, 0 < σ 2 σ 1 predpoklad niº²ích hodnôt rastu ceny a niº²ej volatility) Vyvoj ceny Co Cena Co2 [$/t] Dec Apr Sep Jan 2008 Datum Obrázok 5.1: Vývoj ceny CO 2 [$/t] v období od do Cena Cas v rokoch Obrázok 5.2: Simulácia ceny CO 2 pre parametre t = 1/250, S 0 = 0.95, µ 1 = , σ 1 = , µ 2 = 0.08, σ 2 = 0.2, t = 5 rokov, d = 0.5. alej je dôleºité si uvedomi, o sa deje s hodnotou V (S, t) v ase tejto intervencie. Kvôli jednoduchosti predpokladajme, ºe v ase uvalenia dane (t ) nie je moºná realizácia investície. 1 Potom môºe by vyuºitý vz ah: V (S t, t ) = lim t t + V ((1 + d)s t, t) (5.1) 1 Uvedený predpoklad je dôleºitý iba z technického h adiska pri numerickom rie²ení modelu, bliº²ie v asti
33 Vz ah (5.1) vyjadruje fakt, ºe istá sú asná hodnota budúcich nákladov od asu t do asu T pri cene S t je rovná týmto nákladom od asu t + dt do asu T pri cene (1 + d)s t. 5.4 Funkcie nákladov Pri rie²ení úlohy má na celkový tvar oblasti rozhodovania vplyv mnoºstvo faktorov. Jedným z nich je vo ba funkcií π 1 (S t, t), π 2 (S t, t), ktoré predstavujú mieru okamºitých nákladov rmy na produkciu splodín. V ekonomickej teórii sa stretávame s rôznymi typmi nákladových funkcií, vo v²eobecnosti v²ak rozli²ujeme: Fixné náklady náklady, ktoré musia by nevyhnutne vynaloºené na zabezpe- enie produkcie. Ich hodnota je kon²tatná a nezávisí od vyprodukovaného mnoºstva. Variabilné náklady zah ajú bezprostredné náklady na produkciu, závisia od po tu vyprodukovaných jednotiek. V kontexte problematiky produkcie CO 2 môºe by interpretáciou predpoklad, ºe kaºdý producent daného odvetvia prekra uje povolené mnoºstvá emisií. V dôsledku toho platí pokutu ²tátu alebo mestu za zhor²ené ºivotné prostredie (xné náklady). Nech je zavedená povinnos, ºe kaºdá al²ia tona nad limit, musí by odkúpená od spolo ností, ktoré limit nenap ajú. Teda emitent kupuje presne také mnoºstvo, aké vyprodukuje (variabilné náklady). Zaoberajme sa najjednoduch²ím typom nákladových funkcií: π 1 (S t, t) = XS t + A π 2 (S t, t) = Y S t + B X > Y 0, A B 0 V niektorých prípadoch je moºné parciálne diferneciálne rovnice (4.9) a (4.10) vyrie²i analyticky. V al²ej asti uvedieme koncept rie²enia rovnice (4.9) pre π 1 (S, t) kde A = 0. 28
34 Analytické rie²enie PDR V prípade, ºe budúce pe aºné toky (napr. náklady) sú lineárnou funkciou produkovaného mnoºstva X, teda π(s, t) = XS je rovnicu (4.9): V t (S, t) + µsv S (S, t) σ2 S 2 V SS (S, t) rv (S, t) + XS = 0 V (S, T ) = 0 moºné vyrie²i analyticky. Pouºitím transformácií x = lns, τ = T t a vz ahu V (S, t) = u(x, τ) dostávame u τ σ2 u 2 xx (µ σ2 )u 2 x + ru Xe x = 0 u(x, 0) = 0 Transformáciou v(x, τ) = e αx+βτ u(x, τ) a vhodným zvolením parametrov α = µ σ 2 1 2, β = µ2 1µ + σ2 + r sa rovnica redukuje na tvar: 2σ v τ σ2 2 v xx Xe (1+α)x+βτ = 0 v(x, 0) = 0 Následne aplikujeme vzorec na výpo et rie²enia nehomogénnej parabolickej parciálnej diferenciálnej rovnice v(x, τ) = G(x s, τ)v(s, 0)ds + τ G(x s, τ r)xe (1+α)s+βr dsdr (5.2) 0 kde G(ξ, t) = 1 ξ2 2σ 2 e 2σ 2 t πt je Greenova funkcia. v(x, τ) = X τ 1 (x s) 2 e 2σ 2 +(1+α)s+βr (τ r) dsdr (5.3) 2πσ2 (τ r) v(x, τ) = X τ 0 1 2πσ2 (τ r) (s (x+σ 2 (τ r)(1+α))) 2 e 2σ 2 (τ r) ds σ2 (1+α)x+ e 2 (τ r)(1+α)2 +βr dr 0 } {{ } 1 (5.4) Vyrie²ením integrálu dostávame v(x, τ) = Xe x(1+α) [ e σ2 ] τ 2 (τ r)(1+α)2 +βr β σ2 2 (1 + α2 ) 0 (5.5) 29
35 v(x, τ) = Xe x(1+α) eβτ e σ 2 2 τ(1+α)2 β σ2 (1 + (5.6) 2 α)2 Nakoniec spätnými transformáciami dostávame pri om α,β sú uvedené vy²²ie. V (S, t) = 2XSe β(t t) eβ(t t) e σ (T t)(1+α)2 2 (5.7) 2β σ 2 (1 + α) Numerické rie²enie V predchádzajúcej asti 5.4 sme sa zaoberali prípadom, kedy je moºné rovnice (4.9) a (4.10) pri ²peciálnej vo be nákladových funkcií vyrie²i analyticky. Nako ko v²ak existencia explicitného analytického rie²enia nie je vo v²eobecnosti zabezpe ená, model budeme rie²i numericky. Presnej²ie aplikujeme PSOR metódu 2 (s vyuºitím parametra ω = 1.8 ) postupujúc odzadu. Numerické rie²enie vyºaduje deníciu rozmerov siete a kroku. Vo v²etkých nasledujúcich výsledkoch (ak nie je uvedené inak) aplikujeme asový krok k = 1/250, priestorový krok (rozmer ceny) h = 0.05 a priestorové ohrani enie S max = 60$. Na v²etky neskôr analyzované úlohy sa alej vz ahujú nasledovné predpoklady o parametroch: T as ukon enia prevádzky spolo nosti a sú asne as maturity reálnej opcie. Zvy ajne volíme obdobie 10 rokov. t as intervencie regulátora (vlády) vo forme uvalenia dane na podkladové aktívum. Predpokladáme, ºe da môºe by uvalená raz ro ne vºdy na za iatku roka, teda v asoch rok 1, rok 2,..., rok T 1. µ 1 a σ 1 drift a volatilita stochastického procesu ceny CO 2 pred zásahom ²tátu, tieto sú pevne ur ené odhadnuté z realizácie ceny CO 2 (µ 1 = , σ 1 = ). 2 Projected super over relaxation method, jej algoritmus uvádza napríklad Seydel, 2002, str [2]. 30
36 Na obrázku 5.3 je znázornené numerické rie²enie V (S, t) pre uvedené parametre. Je zrejmé, ºe s plynúcim asom hodnota V (S, t) klesá, pretoºe sa skracuje ºivotnos spolo nosti (obdobie od asu t do asu T), a teda klesajú aj diskontované budúce náklady spojené s produkciou CO 2. Zlom je spôsobený zavedením dane v roku V Cas Cena Obrázok 5.3: Hodnota V (S t, t) pre parametre S 0 = 0.95, µ 1 = , σ 1 = , µ 2 = 0.08, σ 2 = 0.3, t = 6 rokov, d = 0.3, r = 0.05, I = 7$, T = 10 rokov, π 1 (S, t) = S + 1.2, π 2 (S, t) = 0.5S Oblas rozhodovania Tak ako pravidlo istej sú asnej hodnoty hovorí investova pre NP V > 0, aj pri teórii reálnej opcie existuje presná hranica medzi hodnotami S t kedy je výhodnej²ie investova a naopak, kedy nie. Na rozdiel od hodnoty NPV je táto hranica dynamická (závislá na ase) a je identická s vo nou hranicou uvedenou v asti 4.5. Obrázok 5.4 zobrazuje vo nú hranicu S f (t) v prípade zavedenia dane v roku 6. V²imnime si, ºe zásah ²tátu spôsobí posun vo nej hranice smerom dolu, o znamená, ºe sa investova oplatí uº pri niº²ej cene. Dôvod plynie z o akávaných vy²²ích hodnôt cien, a teda narastajúceho rozdielu medzi nákladmi na produkciu CO 2 bez ltra a po jeho zavedení. 31
37 Cena S INVESTOVAT 4 2 NEINVESTOVAT Cas Obrázok 5.4: Tvar oblasti rozhodovania resp. vo nej hranice S f (t) pre parametre S 0 = 0.95, µ 1 = , σ 1 = , µ 2 = 0.08, σ 2 = 0.3, t = 6 rokov, d = 0.3, r = 0.05, I = 7$, T = 10 rokov, π 1 (S, t) = S + 1.2, π 2 (S, t) = 0.5S Parametre a ich vplyv na oblas rozhodovania V nasledujúcom odseku sa budeme zaobera analýzou citlivosti krivky S f (t) na zmenu jedného z parametrov. V²etky nasledujúce zmeny parametrov a ich vplyvy budú aplikované na základnú úlohu denovanú parametrami S 0 = 0.95, µ 1 = , σ 1 = , µ 2 = 0.08, σ 2 = 0.25, t = 6 rokov, d = 0.35, r = 0.05, I = 11$, T = 10 rokov, π 1 (S, t) = S + 1, π 2 (S, t) = 0.5S Oblas rozhodovania tejto úlohy je na kaºdom z obrázkov 5.5 aº 5.12 znázornená plnou iarou. Preru²ovaná iara predstavuje zmenu tejto krivky pri zmene jedného z parametrov (²pecikácia parametera a na akú hodnotu je zmenený je uvedené pod kaºdým z obrázkov). d vý²ka dane. Uvaºujeme d (0, 1). Vplyv zvý²enia dane na krivku S f (t) je znázornený na obrázku 5.5. Je zrejmé, ºe ím je hodnota dane vä ²ia, tým je optimálnej²ie investova uº pri niº²ích hodnotách ceny CO 2. Dôvodom je fakt, ºe zavedenie dane má za následok vä ²í nárast nákladov na CO 2 pri jeho produkcii bez ltra ako s ním. I náklady na zavedenie ltra. Je zrejmé, ºe ím je cena in²talácie ltra vy²²ia, tým viac sa krivka S f (t) posúva smerom nahor (obrázok 5.6), pretoºe sa investova oplatí aº pri vy²²ích cenách CO 2. 32
38 r bezriziková úroková miera (% per annum). V dôsledku faktu, ºe cena reálnej opcie s rastúcim úrokom rastie, zvý²enie zvolenej úrokovej miery spôsobí posun S f (t) nahor (obrázok 5.7). 3 µ 2 drift stochastického procesu ceny CO 2 po zásahu ²tátu (uvaºujeme, ºe tento parameter sa potenciálne môºe lí²i od µ 1 ). Vy²²ie hodnoty µ 2 indikujú vy²²í rast ceny, a teda sa optimálnej²ie javí investova uº pri niº²ích hodnotách S (obrázok 5.8). σ 2 volatilita stochastického procesu ceny CO 2 po zásahu ²tátu (opä vo v²eobecnosti σ 2 σ 1 ). Vy²²ia volatilita posúva S f (t) nahor, pretoºe aj ke sa cena nachádza na vy²²ích hodnotách, investor v dôsledku vy²²ej volatility (a teda neistoty) aká, i cena neklesne (obrázok 5.9). alej uvaºujme aj o vplyve zmeny parametrov jednoduchých nákladových funkcií π 1 (S t, t) = XS t + A, π 2 (S t, t) = Y S t + B a zmene typu jednej z týchto funkcií na mocninový. X resp. Y je zrejmé, ºe nárast Y respektíve pokles X spôsobí men²iu atraktivitu moºnosti vyuºi reálnu opciu (obrázok 5.10). A resp. B vy²²ie xné náklady po realizácii projektu (B) alebo niº²ie xné náklady pred ou (A) majú opä za následok posun hranice oblasti rozhodovania k vy²²ím hodnotám (obrázok 5.11). π 1 mocninová funkcia π 1 v závislosti od ceny spôsobuje, ºe náklady pri vy²²ích cenách CO 2 prudko rastú. Z toho dôvodu je optimálnej²ia in²talácia ltra uº pri niº²ích hodnotách ceny (obrázok 5.12). 3 Výsledok je analogický ako pre americkú call opciu. 33
39 Cena 10 Cena S Cas Cas Obrázok 5.5: d = Obrázok 5.6: I = Cena S 10 Cena S Cas Cas Obrázok 5.7: r = 0.1. Obrázok 5.8: µ 2 = µ Cena S 10 Cena S Cas Cas Obrázok 5.9: σ 2 = σ 1. Obrázok 5.10: π 2 = 0.75S
40 Cena S 10 Cena S Cas Cas Obrázok 5.11: π 2 = 0.5S + 1. Obrázok 5.12: π 1 = S Vplyv regulátora Ako bolo uvedené v asti 5.2 záujmom ²tátu je vplyvom zavedenia dane dosiahnu, aby o najviac spolo ností in²taláciu ltra realizovalo. Pri rie²ení tohto problému predpokladajme, ºe spolo nos realizuje investíciu okamºite, ak simulácia ceny CO 2 prekro í hranicu S f (t). Ke ºe v²etky spolo nosti na trhu sú reprezentované jednou agregovanou, pravdepodobnos prijatia investície touto spolo nos ou môºe by interpretovaná ako relatívna po etnos realizácií opcie skuto nými spolo nos ami. V nasledujúcej analýze vºdy uvaºujme parametre S 0 = 0.95, µ 1 = , σ 1 = , µ 2 = 0.15, σ 2 = σ 1, r = 0.05, I = 10.2$, T = 10 rokov, π 1 (S, t) = 0.9S + 1.5, π 2 (S, t) = 0.5S a po et simulácií Pre vo bu d = 0.35 je z výsledkov prezentovaných v tabu ke 5.1 zrejmé, ºe je optimálne zavies da v roku 3, kedy je pravdepodobnos prijatia investície agregovanou spolo nos ou maximálna. Av²ak rozdiely najmä v prvých piatich rokoch sú minimálne a ve mi citlivé najmä na vo bu parametrov µ 2 a σ 2. V²imnime si, ºe takýmto zásahom do vývoja ceny CO 2 je moºné zvý²i po et spolo ností, ktoré investíciu prijmú o takmer 10% (oproti prípadu, kedy regulátor nezasahuje). Je dôleºité si uvedomi, ºe dôvodom pre o regulátor nezavedie da uº v roku 1 je 35
41 zmena driftu stochastického procesu po zásahu (µ 2 < µ 1 ), ktorú je moºné interpretova ako penalizáciu za zavedenie dane. Je tu teda riziko, ºe ak sa da zavedie príli² skoro, v dlhodobom horizonte bude cena niº²ia ako bez intervencie (pri zavedení dane totiº dochádza k protichodným javom: ím skôr sa zavednie da, tým sú v dôsledku skoku v cene pravdepodobnej²ie vy²²ie hodnoty ceny v budúcnosti; ím skôr sa zavedie da, tým pokles µ 2 spôsobí vä ²iu ²kodu v zmysle niº²ích hodnôt ceny). V prípade, ºe by sme uvaºovali o úlohe, v ktorej parameter µ 2 zostane nezmenený (µ 2 = µ 1 ), pre regulátora je najoptimálnej²ie zavies da okamºite v roku 1. Rok uvalenia dane (zásahu ²tátu) Pravdepodobnos realizácie investície % % % % % % % % % bez zásahu 72.5% Tabu ka 5.1: Vývoj percentuálneho po tu spolo ností, ktoré prijmú investíciu v závislosti od roku zásahu ²tátu. Taktieº je zaujímavé rozloºenie uplatnenií opcií na jednotlivé roky. Na obrázku 5.13 môºeme vidie, ºe v prípade zavedenia dane d = 0.35 v roku 6 sa na takmer 70% realizácia investície uskuto ní v prvom roku a na 20.2% sa neuskuto ní vôbec. Ostatné roky sú zastúpené iba nízkymi pravdepodobnos ami. Znamená to teda, ºe vä ²ina zo spolo ností uplat ujúcich opciu ju vyuºije uº v prvom roku. Hlavný vplyv na rozloºenie uplatnenia opcie na jednotlivé roky má tvar oblasti rozhodovania. Ak zvolíme mocninový typ funkcie nákladov π 1 (S, t) (tvar S f (t) je potom 36
42 napríklad uvedený iarkovanou iarou v obrázku 5.12) a dostato ne ve ké náklady na investíciu I, vä ²í po et spolo ností realizuje investíciu neskôr (obrázok 5.14). Obrázok 5.13: Rozloºenie precentuálneho po tu spolo ností, ktoré uplatnia opciu pod a roku uplatnenia pre základnú úlohu s t = 6 rokov. Obrázok 5.14: Rozloºenie precentuálneho po tu spolo ností, ktoré uplatnia opciu pod a roku uplatnenia pre úlohu s mocninovým typom nákladovej funkcie π 1 = S , σ 1 = σ 2 = 0.2, I = 55, t = 6 rokov (ostatné parametre ako v základnej úlohe). V tabu ke 5.2 sa zaoberáme rozdielmi v po te realizácií investície pri rôznej vý²ke dane uvalenej regulátorom. Z hodnôt vyplýva, ºe ím vy²²iu da autorita zavedie, tým vä ²ia je pravdepodobnos uplatnenia opcie agregovanou spolo nos ou. Taktieº je zaujímavý fakt, ºe ím vy²²iu da volíme, tým sa optimálny as jej zavedenia 37
43 blíºi k roku 1 (kým pre d = 0.25 je optimálnej²ie da zavies v rokoch 6-7, pre d = 0.55 je to rok 1). Tento fakt je moºné vysvetli tým, ºe pri vo be vy²²ích hodnôt d preváºi jeho pozitívny vplyv nad negatívnym ú inkom poklesu driftu µ 2, a preto je optimálne intervenova uº v roku 1. V²imnime si, ºe ak by pri vo be d = 0.1 regulátor zaviedol da v rokoch 1 aº 6, spôsobil by dokonca zníºenie po tu realizícií investície (negatívny vplyv poklesu µ 1 na µ 2 by preváºil nad skokom v cene). Rok zavedenia dane d=0.10 d=0.25 d=0.35 d=0.4 d=0.5 d=0.55 (zásahu ²tátu) % 73.4% 79.8% 82.8% 88.3% 91.9% % 73.9% 80.0% 82.6% 87.7% 90.8% % 75.3% 81.3% 82.8% 87.5% 89.6% % 76.0% 80.8% 82.4% 87.6% 88.3% % 77.3% 80.7% 82.6% 87.2% 87.7% % 77.8% 80.9% 82.0% 85.8% 87.3% % 77.5% 79.4% 81.0% 82.9% 84.5% % 76.5% 78.2% 78.6% 81.0% 82.0% % 75.1% 76.2% 76.7% 78.1% 78.2% bez zásahu 72.5% Tabu ka 5.2: Vývoj precentuálneho po tu spolo ností, ktoré prijmú investíciu v závislosti od roku zásahu ²tátu a hodnoty dane. 38
44 Kapitola 6 Moºnosti roz²írenia modelu V tejto kapitole uvedieme moºné alternatívy modikácie modelu, ktoré roz²íria aplikáciu modelu aj do iných odvetví. 6.1 Modelovanie ceny Pri v²etkých doteraj²ích úvahách bol vyuºitý predpoklad modelovania ceny geometrickým Brownovým pohybom. V tejto asti sa budeme zaobera al²ími procesmi, ktoré sa v realite vyºívajú na simuláciu cien. Meanreverting proces Ako uº bolo spomenuté, geometrický Brownov pohyb nie je vhodný na modelovanie cien niektorých komodít, pretoºe jeho asový vývoj sa vo ve kej miere vz a uje od svojej po iato nej hodnoty. Av²ak najmä ceny základných surovín ako elektrická energia alebo me sú v dlhodobom horizonte viazané na hrani né produk né náklady. Teda, kým krátkodobo napríklad cena elektrickej energie náhodne uktuuje (napríklad ako dôsledok zmien dopytu a ponuky), z dlhodobého h adiska sa vracia k hodnote hrani ných produk ných nákladov. Tejto poºiadavke správania sa vyhovuje tzv. meanreverting proces 1 denovaný 1 V slovenskom preklade proces vracajúci sa k priemeru. 39
Metódy vol nej optimalizácie
 Matematické programovanie Metódy vol nej optimalizácie p. 1/35 Informácie o predmete Informácie o predmete p. 2/35 Informácie o predmete METÓDY VOL NEJ OPTIMALIZÁCIE Prednášajúca: M. Trnovská (M 267) Cvičiaci:
Matematické programovanie Metódy vol nej optimalizácie p. 1/35 Informácie o predmete Informácie o predmete p. 2/35 Informácie o predmete METÓDY VOL NEJ OPTIMALIZÁCIE Prednášajúca: M. Trnovská (M 267) Cvičiaci:
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MOCNINOVÉ RADY A ICH VYUšITIE BAKALÁRSKA PRÁCA 04 Sára MINÁROVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MOCNINOVÉ RADY A ICH VYUšITIE BAKALÁRSKA PRÁCA 04 Sára MINÁROVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY. Kritéria nezápornosti Fourierových radov BAKALÁRSKA PRÁCA
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kritéria nezápornosti Fourierových radov BAKALÁRSKA PRÁCA Bratislava 2014 Andrej Iring UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kritéria nezápornosti Fourierových radov BAKALÁRSKA PRÁCA Bratislava 2014 Andrej Iring UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
Ing. Tomasz Kanik. doc. RNDr. Štefan Peško, CSc.
 Ing. Tomasz Kanik Školiteľ: doc. RNDr. Štefan Peško, CSc. Pracovisko: Študijný program: KMMOA, FRI, ŽU 9.2.9 Aplikovaná informatika 1 identifikácia problémovej skupiny pacientov, zlepšenie kvality rozhodovacích
Ing. Tomasz Kanik Školiteľ: doc. RNDr. Štefan Peško, CSc. Pracovisko: Študijný program: KMMOA, FRI, ŽU 9.2.9 Aplikovaná informatika 1 identifikácia problémovej skupiny pacientov, zlepšenie kvality rozhodovacích
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Vlastnosti spektrahedrálnych mnoºín a ich aplikácie v nelineárnej optimalizácii DIPLOMOVÁ PRÁCA 2016 Bc. Andrej Iring UNIVERZITA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Vlastnosti spektrahedrálnych mnoºín a ich aplikácie v nelineárnej optimalizácii DIPLOMOVÁ PRÁCA 2016 Bc. Andrej Iring UNIVERZITA
FILTRÁCIA GEODETICKÝCH DÁT NA POVRCHU ZEME POMOCOU NELINEÁRNYCH DIFÚZNYCH ROVNÍC
 Úvod FILTRÁCIA GEODETICKÝCH DÁT NA POVRCHU ZEME POMOCOU NELINEÁRNYCH DIFÚZNYCH ROVNÍC Martin Tunega, Róbert ƒunderlík, Karol Mikula V lánku vytvoríme metódu kone ných objemov na numerické rie²enie parabolických
Úvod FILTRÁCIA GEODETICKÝCH DÁT NA POVRCHU ZEME POMOCOU NELINEÁRNYCH DIFÚZNYCH ROVNÍC Martin Tunega, Róbert ƒunderlík, Karol Mikula V lánku vytvoríme metódu kone ných objemov na numerické rie²enie parabolických
The Golden Ratio and Signal Quantization
 The Golden Ratio and Signal Quantization Tom Hejda, tohecz@gmail.com based on the work of Ingrid Daubechies et al. Doppler Institute & Department of Mathematics, FNSPE, Czech Technical University in Prague
The Golden Ratio and Signal Quantization Tom Hejda, tohecz@gmail.com based on the work of Ingrid Daubechies et al. Doppler Institute & Department of Mathematics, FNSPE, Czech Technical University in Prague
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY DIPLOMOVÁ PRÁCA
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Vplyv zmien svetových cien komodít na vývoj inácie v SR DIPLOMOVÁ PRÁCA 2015 Bc. Vladimír HUDEC UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Vplyv zmien svetových cien komodít na vývoj inácie v SR DIPLOMOVÁ PRÁCA 2015 Bc. Vladimír HUDEC UNIVERZITA KOMENSKÉHO V BRATISLAVE
Technické rezervy v neºivotnom poistení
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Technické rezervy v neºivotnom poistení DIPLOMOVÁ PRÁCA 2012 Bc JAROSLAVA GATIALOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Technické rezervy v neºivotnom poistení DIPLOMOVÁ PRÁCA 2012 Bc JAROSLAVA GATIALOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
Short time oscillations of exchange rates
 Univerzita Komenského v Bratislave, Fakulta matematiky, fyziky a informatiky Short time oscillations of exchange rates Diploma Thesis Bratislava 2007 Tomáš Bokes Short time oscillations of exchange rates
Univerzita Komenského v Bratislave, Fakulta matematiky, fyziky a informatiky Short time oscillations of exchange rates Diploma Thesis Bratislava 2007 Tomáš Bokes Short time oscillations of exchange rates
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY DIPLOMOVÁ PRÁCA ZDENKA ZUBÁƒOVÁ
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY DIPLOMOVÁ PRÁCA 2011 ZDENKA ZUBÁƒOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Spracovanie
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY DIPLOMOVÁ PRÁCA 2011 ZDENKA ZUBÁƒOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Spracovanie
Jádrové odhady gradientu regresní funkce
 Monika Kroupová Ivana Horová Jan Koláček Ústav matematiky a statistiky, Masarykova univerzita, Brno ROBUST 2018 Osnova Regresní model a odhad gradientu Metody pro odhad vyhlazovací matice Simulace Závěr
Monika Kroupová Ivana Horová Jan Koláček Ústav matematiky a statistiky, Masarykova univerzita, Brno ROBUST 2018 Osnova Regresní model a odhad gradientu Metody pro odhad vyhlazovací matice Simulace Závěr
Kapitola S5. Skrutkovica na rotačnej ploche
 Kapitola S5 Skrutkovica na rotačnej ploche Nech je rotačná plocha určená osou rotácie o a meridiánom m. Skrutkový pohyb je pohyb zložený z rovnomerného rotačného pohybu okolo osi o a z rovnomerného translačného
Kapitola S5 Skrutkovica na rotačnej ploche Nech je rotačná plocha určená osou rotácie o a meridiánom m. Skrutkový pohyb je pohyb zložený z rovnomerného rotačného pohybu okolo osi o a z rovnomerného translačného
Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky
 Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Numerická analýza riešení nelineárnych parciálnych diferenciálnych rovníc vyskytujúcich sa vo finančnej matematike (Diplomová
Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Numerická analýza riešení nelineárnych parciálnych diferenciálnych rovníc vyskytujúcich sa vo finančnej matematike (Diplomová
ADM a logika. 4. prednáška. Výroková logika II, logický a sémantický dôsledok, teória a model, korektnosť a úplnosť
 ADM a logika 4. prednáška Výroková logika II, logický a sémantický dôsledok, teória a model, korektnosť a úplnosť 1 Odvodzovanie formúl výrokovej logiky, logický dôsledok, syntaktický prístup Logický dôsledok
ADM a logika 4. prednáška Výroková logika II, logický a sémantický dôsledok, teória a model, korektnosť a úplnosť 1 Odvodzovanie formúl výrokovej logiky, logický dôsledok, syntaktický prístup Logický dôsledok
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ZNÁME NEROVNOSTI V MATEMATIKE BAKALÁRSKA PRÁCA 014 Zuzana FRONCOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ZNÁME NEROVNOSTI V MATEMATIKE BAKALÁRSKA PRÁCA 014 Zuzana FRONCOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY
Kľúčové slová: SAR, šum spekl noise, evolučná PDR, lineárna difúzia, Perona-Malikova rovnica, štatistickéfiltre, Leeho filter
 Kľúčové slová: SAR, šum spekl noise, evolučná PDR, lineárna difúzia, Perona-Malikova rovnica, štatistickéfiltre, Leeho filter Tvorba šumu spekl radarový senzor vysiela elektromagneticlý pulz a meria odraz
Kľúčové slová: SAR, šum spekl noise, evolučná PDR, lineárna difúzia, Perona-Malikova rovnica, štatistickéfiltre, Leeho filter Tvorba šumu spekl radarový senzor vysiela elektromagneticlý pulz a meria odraz
Teória grafov. RNDr. Milan Stacho, PhD.
 Teória grafov RNDr. Milan Stacho, PhD. Literatúra Plesník: Grafové algoritmy, Veda Bratislava 1983 Sedláček: Úvod do teórie grafů, Academia Praha 1981 Bosák: Grafy a ich aplikácie, Alfa Bratislava 1980
Teória grafov RNDr. Milan Stacho, PhD. Literatúra Plesník: Grafové algoritmy, Veda Bratislava 1983 Sedláček: Úvod do teórie grafů, Academia Praha 1981 Bosák: Grafy a ich aplikácie, Alfa Bratislava 1980
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
Jádrové odhady regresní funkce pro korelovaná data
 Jádrové odhady regresní funkce pro korelovaná data Ústav matematiky a statistiky MÚ Brno Finanční matematika v praxi III., Podlesí 3.9.-4.9. 2013 Obsah Motivace Motivace Motivace Co se snažíme získat?
Jádrové odhady regresní funkce pro korelovaná data Ústav matematiky a statistiky MÚ Brno Finanční matematika v praxi III., Podlesí 3.9.-4.9. 2013 Obsah Motivace Motivace Motivace Co se snažíme získat?
DEA modely a meranie eko-efektívnosti
 Fakulta matematiky, fyziky a informatiky Univerzita Komenského v Bratislave DEA modely a meranie eko-efektívnosti 2008 Veronika Lennerová DEA modely a meranie eko-efektívnosti DIPLOMOVÁ PRÁCA Diplomant:
Fakulta matematiky, fyziky a informatiky Univerzita Komenského v Bratislave DEA modely a meranie eko-efektívnosti 2008 Veronika Lennerová DEA modely a meranie eko-efektívnosti DIPLOMOVÁ PRÁCA Diplomant:
Stochastické diferenciálne rovnice
 Slovenská technická univerzita v bratislave Stavebná fakulta Evidenčné číslo: SVF-5342-67660 Stochastické diferenciálne rovnice BAKALÁRSKA PRÁCA Štúdijný program: Matematicko-počítačové modelovanie Číslo
Slovenská technická univerzita v bratislave Stavebná fakulta Evidenčné číslo: SVF-5342-67660 Stochastické diferenciálne rovnice BAKALÁRSKA PRÁCA Štúdijný program: Matematicko-počítačové modelovanie Číslo
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY 80e687db-77df-4b93-992e-b291c6457462 Vyuºitie SATsolverov pri rie²ení aºkých úloh 2011 Matú² Kukan UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY 80e687db-77df-4b93-992e-b291c6457462 Vyuºitie SATsolverov pri rie²ení aºkých úloh 2011 Matú² Kukan UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Aplikácie matematiky v ekonómii a financiách BAKALÁRSKA PRÁCA 2012 Martin BUŠÍK UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Aplikácie matematiky v ekonómii a financiách BAKALÁRSKA PRÁCA 2012 Martin BUŠÍK UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
PRÍSPEVKOVO DEFINOVANÉ MODELY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY PRÍSPEVKOVO DEFINOVANÉ MODELY DÔCHODKOVÉHO SPORENIA DIPLOMOVÁ PRÁCA 2012 BC. ZUZANA MAŤOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY PRÍSPEVKOVO DEFINOVANÉ MODELY DÔCHODKOVÉHO SPORENIA DIPLOMOVÁ PRÁCA 2012 BC. ZUZANA MAŤOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MATEMATIKA NA POH ADNICIACH BAKALÁRSKA PRÁCA 2014 Katarína IVANOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MATEMATIKA NA POH ADNICIACH BAKALÁRSKA PRÁCA 2014 Katarína IVANOVÁ UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY
VYHLÁSENIE O PARAMETROCH. č SK
 VYHLÁSENIE O PARAMETROCH č. 0048 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: rá ová h oždi ka fischer SXR/SXRL 2. )a ýšľa é použitie/použitia: Produkt Plastové kotvy pre použitie v betóne a murive
VYHLÁSENIE O PARAMETROCH č. 0048 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: rá ová h oždi ka fischer SXR/SXRL 2. )a ýšľa é použitie/použitia: Produkt Plastové kotvy pre použitie v betóne a murive
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS A PRIORI ESTIMATES OF SOLUTIONS OF SUPERLINEAR ELLIPTIC AND PARABOLIC PROBLEMS Dissertation thesis 015 Július Pa uta COMENIUS
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS A PRIORI ESTIMATES OF SOLUTIONS OF SUPERLINEAR ELLIPTIC AND PARABOLIC PROBLEMS Dissertation thesis 015 Július Pa uta COMENIUS
Ekonomika a financie ako motivačný činitel rozvoja matematiky
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Ekonomika a financie ako motivačný činitel rozvoja matematiky BRATISLAVA 011 MAREK KABÁT UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Ekonomika a financie ako motivačný činitel rozvoja matematiky BRATISLAVA 011 MAREK KABÁT UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
Lucia Fuchsová Charakteristiky pravděpodobnostních
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Lucia Fuchsová Charakteristiky pravděpodobnostních předpovědí Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Lucia Fuchsová Charakteristiky pravděpodobnostních předpovědí Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské
Evolu né algoritmy. Martin Pelikan 1
 Martin Pelikan 1 Abstrakt. Evolu né algoritmy tvoria skupinu stochastick ch optimaliza n ch algoritmov, ktor ch základn princíp je in pirovan evolúciou a genetikou. Asi najvä ia v hoda evolu n ch algoritmov
Martin Pelikan 1 Abstrakt. Evolu né algoritmy tvoria skupinu stochastick ch optimaliza n ch algoritmov, ktor ch základn princíp je in pirovan evolúciou a genetikou. Asi najvä ia v hoda evolu n ch algoritmov
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VZ AHY SPEKTIER MATICE A JEJ PODMATÍC Bakalárska práca 2013 Viktor GREGOR UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VZ AHY SPEKTIER MATICE A JEJ PODMATÍC Bakalárska práca 2013 Viktor GREGOR UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
ANOTÁCIA ZHLUKOV GÉNOV
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY ANOTÁCIA ZHLUKOV GÉNOV 2011 Milan Mikula UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY ANOTÁCIA ZHLUKOV
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY ANOTÁCIA ZHLUKOV GÉNOV 2011 Milan Mikula UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY FYZIKY A INFORMATIKY ANOTÁCIA ZHLUKOV
Aplikácie subriemannovskej geometrie
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Aplikácie subriemannovskej geometrie Luká² Tomek 2011 Aplikácie subriemannovskej geometrie DIPLOMOVÁ PRÁCA (Eviden né íslo:
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Aplikácie subriemannovskej geometrie Luká² Tomek 2011 Aplikácie subriemannovskej geometrie DIPLOMOVÁ PRÁCA (Eviden né íslo:
Poisson Jumps in Credit Risk Modeling: a Partial Integro-differential Equation Formulation
 Poisson Jumps in Credit Risk Modeling: a Partial Integro-differential Equation Formulation Jingyi Zhu Department of Mathematics University of Utah zhu@math.utah.edu Collaborator: Marco Avellaneda (Courant
Poisson Jumps in Credit Risk Modeling: a Partial Integro-differential Equation Formulation Jingyi Zhu Department of Mathematics University of Utah zhu@math.utah.edu Collaborator: Marco Avellaneda (Courant
VYHLÁSENIE O PARAMETROCH. č SK. Predpoklada é použitie. stave ý h častí ako o kladov a stropov, pozri prílohu, najmä prílohy B 1 - B 8
 VYHLÁSENIE O PARAMETROCH č. 0007 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: i jektáž y systé FIS V 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v et e k upev e iu ťažký h systé
VYHLÁSENIE O PARAMETROCH č. 0007 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: i jektáž y systé FIS V 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v et e k upev e iu ťažký h systé
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A. Ήχος Πα. to os se e e na aș te e e slă ă ă vi i i i i
 CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
Matematika 17. a 18. storočia
 Matematika 17. a 18. storočia René Descartes Narodený : 31 Marec 1596 v La Haye (teraz Descartes),Touraine, France Zomrel : 11 Feb 1650 v Stockholm, Sweden Riešenie kvadratických rovníc podľa Descarta
Matematika 17. a 18. storočia René Descartes Narodený : 31 Marec 1596 v La Haye (teraz Descartes),Touraine, France Zomrel : 11 Feb 1650 v Stockholm, Sweden Riešenie kvadratických rovníc podľa Descarta
EXTREME SEVERAL-DAY PRECIPITATION TOTALS AT HURBANOVO DURING THE TWENTIETH CENTURY
 Rožnovský, J., Litschmann, T. (ed.): XIV. Česko-slovenská bioklimatologická konference, Lednice na Moravě 2.-4. září 2, ISBN -85813-99-8, s. 9-19 EXTREME SEVERAL-DAY PRECIPITATION TOTALS AT HURBANOVO DURING
Rožnovský, J., Litschmann, T. (ed.): XIV. Česko-slovenská bioklimatologická konference, Lednice na Moravě 2.-4. září 2, ISBN -85813-99-8, s. 9-19 EXTREME SEVERAL-DAY PRECIPITATION TOTALS AT HURBANOVO DURING
Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava. Multiparty Communication Complexity (Master thesis)
 Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Multiparty Communication Complexity (Master thesis) František Ďuriš Study programme: 921 Informatics Supervisor:
Katedra Informatiky Fakulta Matematiky, Fyziky a Informatiky Univerzita Komenského, Bratislava Multiparty Communication Complexity (Master thesis) František Ďuriš Study programme: 921 Informatics Supervisor:
ENVIRONMENTÁLNE FAKTORY V HODNOTENÍ EFEKTÍVNOSTI V POĽNOHOSPODÁRSTVE ENVIRONMENTAL FACTORS IN EFFICIENCY ASSESMENT IN AGRICULTURE.
 ENVIRONMENTÁLNE FAKTORY V HODNOTENÍ EFEKTÍVNOSTI V POĽNOHOSPODÁRSTVE ENVIRONMENTAL FACTORS IN EFFICIENCY ASSESMENT IN AGRICULTURE Peter FANDEL The paper focuses on the analysis of environmental factors
ENVIRONMENTÁLNE FAKTORY V HODNOTENÍ EFEKTÍVNOSTI V POĽNOHOSPODÁRSTVE ENVIRONMENTAL FACTORS IN EFFICIENCY ASSESMENT IN AGRICULTURE Peter FANDEL The paper focuses on the analysis of environmental factors
SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE FAKULTA CHEMICKEJ A POTRAVINÁRSKEJ TECHNOLÓGIE ÚSTAV INFORMATIZÁCIE, AUTOMATIZÁCIE A MATEMATIKY
 SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE FAKULTA CHEMICKEJ A POTRAVINÁRSKEJ TECHNOLÓGIE ÚSTAV INFORMATIZÁCIE, AUTOMATIZÁCIE A MATEMATIKY OPTIMÁLNE RIADENIE PROCESOV BAKALARÁSKA PRÁCA FCHPT-5415-17457
SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE FAKULTA CHEMICKEJ A POTRAVINÁRSKEJ TECHNOLÓGIE ÚSTAV INFORMATIZÁCIE, AUTOMATIZÁCIE A MATEMATIKY OPTIMÁLNE RIADENIE PROCESOV BAKALARÁSKA PRÁCA FCHPT-5415-17457
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
Optimálne riadenie. Viacetapové rozhodovacie procesy v ekonómii a financiách. Margaréta Halická Pavel Brunovský Pavol Jurča
 Optimálne riadenie Viacetapové rozhodovacie procesy v ekonómii a financiách Margaréta Halická Pavel Brunovský Pavol Jurča EPOS Bratislava 2009 Kniha predstavuje komplexný výklad teórie optimálneho rozhodovania
Optimálne riadenie Viacetapové rozhodovacie procesy v ekonómii a financiách Margaréta Halická Pavel Brunovský Pavol Jurča EPOS Bratislava 2009 Kniha predstavuje komplexný výklad teórie optimálneho rozhodovania
KRÁTKODOBÁ VERSUS DLHODOBÁ ROVNOVÁHA
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KRÁTKODOBÁ VERSUS DLHODOBÁ ROVNOVÁHA BAKALÁRSKA PRÁCA Bratislava 2013 Martin Čechvala UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KRÁTKODOBÁ VERSUS DLHODOBÁ ROVNOVÁHA BAKALÁRSKA PRÁCA Bratislava 2013 Martin Čechvala UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
Matematická analýza II.
 V. Diferenciálny počet (prezentácia k prednáške MANb/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prednáška 8 6. marca 2018 It has apparently not yet been observed, that...
V. Diferenciálny počet (prezentácia k prednáške MANb/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prednáška 8 6. marca 2018 It has apparently not yet been observed, that...
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA VZ AHOV MEDZI ƒasovými RADMI METÓDAMI SIE OVEJ ANALÝZY A ZHLUKOVANIA DIPLOMOVÁ PRÁCA 2018 Radka LITVAJOVÁ UNIVERZITA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA VZ AHOV MEDZI ƒasovými RADMI METÓDAMI SIE OVEJ ANALÝZY A ZHLUKOVANIA DIPLOMOVÁ PRÁCA 2018 Radka LITVAJOVÁ UNIVERZITA
Errors-in-variables models
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Ida Fürjesová Errors-in-variables models Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: RNDr. Michal
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Ida Fürjesová Errors-in-variables models Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: RNDr. Michal
VYHLÁSENIE O PARAMETROCH. č SK. Predpokladané použitie. stave ý h častí ako o kladov a stropov, pozri prílohu, najmä prílohy B 1 - B 4
 VYHLÁSENIE O PARAMETROCH č. 0009 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: o eľová kotva fis her FAZ II 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v betóne k upev e iu ťažký
VYHLÁSENIE O PARAMETROCH č. 0009 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: o eľová kotva fis her FAZ II 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v betóne k upev e iu ťažký
Samuel Flimmel. Univerzita Karlova v Praze Matematicko-fyzikální fakulta. Katedra pravděpodobnosti a matematické statistiky
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Samuel Flimmel Log-optimální investování Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: doc. RNDr.
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Samuel Flimmel Log-optimální investování Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: doc. RNDr.
HODNOTENIE KVALITY KOLY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY HODNOTENIE KVALITY KOLY DIPLOMOVÁ PRÁCA 2014 Luká² Ivica UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY HODNOTENIE KVALITY KOLY DIPLOMOVÁ PRÁCA 2014 Luká² Ivica UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
Solution Methods for Beam and Frames on Elastic Foundation Using the Finite Element Method
 Solution Methods for Beam and Frames on Elastic Foundation Using the Finite Element Method Spôsoby riešenie nosníkov a rámov na pružnom podklade pomocou metódy konečných prvkov Roland JANČO 1 Abstract:
Solution Methods for Beam and Frames on Elastic Foundation Using the Finite Element Method Spôsoby riešenie nosníkov a rámov na pružnom podklade pomocou metódy konečných prvkov Roland JANČO 1 Abstract:
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE
 FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE PÍSOMNÁ PRÁCA K DIZERTAČNEJ SKÚŠKE 2005 Zuzana Holeščáková FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE PÍSOMNÁ PRÁCA K DIZERTAČNEJ SKÚŠKE 2005 Zuzana Holeščáková FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE
Index Policies for Dynamic and Stochastic Problems
 Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Index Policies for Dynamic and Stochastic Problems 2011 Vladimír Novák Comenius University in Bratislava Faculty of Mathematics,
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Index Policies for Dynamic and Stochastic Problems 2011 Vladimír Novák Comenius University in Bratislava Faculty of Mathematics,
A new approach for investment performance measurement. 3rd WCMF, Santa Barbara November 2009
 A new approach for investment performance measurement 3rd WCMF, Santa Barbara November 2009 Thaleia Zariphopoulou University of Oxford, Oxford-Man Institute and The University of Texas at Austin 1 Performance
A new approach for investment performance measurement 3rd WCMF, Santa Barbara November 2009 Thaleia Zariphopoulou University of Oxford, Oxford-Man Institute and The University of Texas at Austin 1 Performance
Ur enie faktora kvality seizmických P-v n na základe analýzy seizmogramov
 Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Katedra astronómie, fyziky Zeme a meteorológie Oddelenie fyziky Zeme Ur enie faktora kvality seizmických P-v n na základe analýzy
Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Katedra astronómie, fyziky Zeme a meteorológie Oddelenie fyziky Zeme Ur enie faktora kvality seizmických P-v n na základe analýzy
JUDr. Eduard Szattler (NE) PATENTOVATEĽNOSŤ POČÍTAČOVÝCH PROGRAMOV
 JUDr. Eduard Szattler (NE) PATENTOVATEĽNOSŤ POČÍTAČOVÝCH PROGRAMOV ( č l á n o k p ô v o d n e p u b l i k o v a n ý v č a s o p i s e D u š e v n é v l a s t n í c t v o 3 / 2 0 0 5 ) V o d b o r n e
JUDr. Eduard Szattler (NE) PATENTOVATEĽNOSŤ POČÍTAČOVÝCH PROGRAMOV ( č l á n o k p ô v o d n e p u b l i k o v a n ý v č a s o p i s e D u š e v n é v l a s t n í c t v o 3 / 2 0 0 5 ) V o d b o r n e
Modely, metódy a algoritmy pre analýzu longitudinálnych dát
 Vedecká rada Fakulty matematiky, fyziky a informatiky Univerzity Komenského v Bratislave Mgr Gejza Wimmer Autoreferát dizertačnej práce Modely, metódy a algoritmy pre analýzu longitudinálnych dát pre získanie
Vedecká rada Fakulty matematiky, fyziky a informatiky Univerzity Komenského v Bratislave Mgr Gejza Wimmer Autoreferát dizertačnej práce Modely, metódy a algoritmy pre analýzu longitudinálnych dát pre získanie
ANALÝZA ZADLŽENOSTI PODNIKOV VO VYBRANÝCH ODVETVIACH SLOVENSKEJ REPUBLIKY ANALYSIS OF INDEBTEDNESS OF ENTERPRISES IN SELECTED SECTORS IN SLOVAKIA
 ANALÝZA ZADLŽENOSTI PODNIKOV VO VYBRANÝCH ODVETVIACH SLOVENSKEJ REPUBLIKY ANALYSIS OF INDEBTEDNESS OF ENTERPRISES IN SELECTED SECTORS IN SLOVAKIA Mária Taušová - Mária Muchová - Jaroslav Gonos ABSTRACT
ANALÝZA ZADLŽENOSTI PODNIKOV VO VYBRANÝCH ODVETVIACH SLOVENSKEJ REPUBLIKY ANALYSIS OF INDEBTEDNESS OF ENTERPRISES IN SELECTED SECTORS IN SLOVAKIA Mária Taušová - Mária Muchová - Jaroslav Gonos ABSTRACT
Prednáška 3. Optimalizačné metódy pre funkcie n-premenných. Študujme reálnu funkciu n-premenných. f: R R
 Prednáška 3 Optimalizačné metódy pre funkcie n-premenných Študujme reálnu funkciu n-premenných n f: R R Našou úlohou bude nájsť také x opt R n, pre ktoré má funkcia f minimum x opt = arg min ( f x) Túto
Prednáška 3 Optimalizačné metódy pre funkcie n-premenných Študujme reálnu funkciu n-premenných n f: R R Našou úlohou bude nájsť také x opt R n, pre ktoré má funkcia f minimum x opt = arg min ( f x) Túto
MAKROEKONÓMIA HETEROGÉNNYCH SUBJEKTOV
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MAKROEKONÓMIA HETEROGÉNNYCH SUBJEKTOV Diplomová práca Bratislava 2013 Bc. Barbora Mlynarčíková UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MAKROEKONÓMIA HETEROGÉNNYCH SUBJEKTOV Diplomová práca Bratislava 2013 Bc. Barbora Mlynarčíková UNIVERZITA KOMENSKÉHO V BRATISLAVE
DLHOVÉ PROBLÉMY NIEKTORÝCH KRAJÍN EUROZÓNY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY DLHOVÉ PROBLÉMY NIEKTORÝCH KRAJÍN EUROZÓNY BAKALÁRSKA PRÁCA 2012 Luká² Ivica UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY DLHOVÉ PROBLÉMY NIEKTORÝCH KRAJÍN EUROZÓNY BAKALÁRSKA PRÁCA 2012 Luká² Ivica UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
MASTER THESIS. Vlastnosti k-intervalových booleovských funkcí Properties of k-interval Boolean functions
 Charles University in Prague Faculty of Mathematics and Physics MASTER THESIS Pavol Gál Vlastnosti k-intervalových booleovských funkcí Properties of k-interval Boolean functions Department of Theoretical
Charles University in Prague Faculty of Mathematics and Physics MASTER THESIS Pavol Gál Vlastnosti k-intervalových booleovských funkcí Properties of k-interval Boolean functions Department of Theoretical
KAPITÁLOVÁ ŠTRUKTÚRA A ASYMETRICKÁ INFORMÁCIA
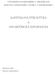 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KAPITÁLOVÁ ŠTRUKTÚRA A ASYMETRICKÁ INFORMÁCIA Bratislava 2011 Barbora Mlynarčíková UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KAPITÁLOVÁ ŠTRUKTÚRA A ASYMETRICKÁ INFORMÁCIA Bratislava 2011 Barbora Mlynarčíková UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
Štatisticky tolerančný interval nazýva ISO Statistics. Vocabulary and symbols. Part 1: Probability and general statistical terms ako štatistick
 Použitie štatistických tolerančných intervalov v riadení kvality Ivan Janiga Katedra matematiky SjF STU v Bratislave Štatisticky tolerančný interval nazýva ISO 3534-1 Statistics. Vocabulary and symbols.
Použitie štatistických tolerančných intervalov v riadení kvality Ivan Janiga Katedra matematiky SjF STU v Bratislave Štatisticky tolerančný interval nazýva ISO 3534-1 Statistics. Vocabulary and symbols.
Súťaž PALMA junior a programovanie v jazyku Python
 Súťaž PALMA junior a programovanie v jazyku Python Ján Guniš Ľubomír Šnajder Prírodovedecká fakulta Univerzity P. J. Šafárika v Košiciach DidInfo + DidactIG 2017, Banská Bystrica Obsah Súťaž PALMA junior
Súťaž PALMA junior a programovanie v jazyku Python Ján Guniš Ľubomír Šnajder Prírodovedecká fakulta Univerzity P. J. Šafárika v Košiciach DidInfo + DidactIG 2017, Banská Bystrica Obsah Súťaž PALMA junior
Matematický aparát modelu HGN na meranie výkonnosti nefinančného ziskového podniku
 Matematický aparát modelu HGN na meranie výkonnosti nefinančného ziskového podniku Mathematical Apparatus of HGN Model for Measuring Performance of Non-financial Profit Enterprise Michal Grell Abstract:
Matematický aparát modelu HGN na meranie výkonnosti nefinančného ziskového podniku Mathematical Apparatus of HGN Model for Measuring Performance of Non-financial Profit Enterprise Michal Grell Abstract:
VYHLÁSENIE O PARAMETROCH. č SK. Predpokladané použitie. stave ý h častí ako o kladov a stropov, pozri prílohu, najmä prílohy B 1 - B 3
 VYHLÁSENIE O PARAMETROCH č. 0017 SK 1. Jedi eč ý ide tifikač ý kód typu výro ku: fischer skrutka do betónu FBS, FBS A4 a FBS C 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v etó e
VYHLÁSENIE O PARAMETROCH č. 0017 SK 1. Jedi eč ý ide tifikač ý kód typu výro ku: fischer skrutka do betónu FBS, FBS A4 a FBS C 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v etó e
Computation of Information Value for Credit Scoring Models
 Jedovnice 20 Computation of Information Value for Credit Scoring Models Martin Řezáč, Jan Koláček Dept. of Mathematics and Statistics, Faculty of Science, Masaryk University Information value The special
Jedovnice 20 Computation of Information Value for Credit Scoring Models Martin Řezáč, Jan Koláček Dept. of Mathematics and Statistics, Faculty of Science, Masaryk University Information value The special
THIS PAGE DECLASSIFIED IAW E
 THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
DIPLOMOVÁ PRÁCE. Peter Baník Metody optimalizace ve financích
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Peter Baník Metody optimalizace ve financích Katedra pravděpodobnosti a matematické statistiky Vedoucí diplomové práce: Doc. RNDr.
Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Peter Baník Metody optimalizace ve financích Katedra pravděpodobnosti a matematické statistiky Vedoucí diplomové práce: Doc. RNDr.
Odhady veľkosti pokrytí náhodne indukovaných podgrafov n-rozmernej hyperkocky
 KATEDRA INFORMATIKY FAKULTA MATEMATIKY FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO Odhady veľkosti pokrytí náhodne indukovaných podgrafov nrozmernej hyperkocky Diplomová práca Bc. Ján Kliman študijný odbor:
KATEDRA INFORMATIKY FAKULTA MATEMATIKY FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO Odhady veľkosti pokrytí náhodne indukovaných podgrafov nrozmernej hyperkocky Diplomová práca Bc. Ján Kliman študijný odbor:
Ranking accounting, banking and finance journals: A note
 MPRA Munich Personal RePEc Archive Ranking accounting, banking and finance ournals: A note George Halkos and Nickolaos Tzeremes University of Thessaly, Department of Economics January 2012 Online at https://mpra.ub.uni-muenchen.de/36166/
MPRA Munich Personal RePEc Archive Ranking accounting, banking and finance ournals: A note George Halkos and Nickolaos Tzeremes University of Thessaly, Department of Economics January 2012 Online at https://mpra.ub.uni-muenchen.de/36166/
Use precise language and domain-specific vocabulary to inform about or explain the topic. CCSS.ELA-LITERACY.WHST D
 Lesson eight What are characteristics of chemical reactions? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading
Lesson eight What are characteristics of chemical reactions? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY. Robustné metódy vo faktorovej analýze
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Robustné metódy vo faktorovej analýze DIPLOMOVÁ PRÁCA Bratislava 2013 Bc. Zuzana Kuižová UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Robustné metódy vo faktorovej analýze DIPLOMOVÁ PRÁCA Bratislava 2013 Bc. Zuzana Kuižová UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA
Autoreferát dizerta nej práce. Jozef Rakovský. Od kvalitatívnej LIBS realizovanej prenosným zariadením po kvantitatívnu laboratórnu LIBS
 Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky a Université de Bourgogne à Dijon Laboratoire Interdisciplinaire Carnot de Bourgorne Jozef Rakovský Autoreferát dizerta nej práce
Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky a Université de Bourgogne à Dijon Laboratoire Interdisciplinaire Carnot de Bourgorne Jozef Rakovský Autoreferát dizerta nej práce
MASARYKOVA UNIVERZITA P írodov decká fakulta Ústav teoretické fyziky a astrofyziky. DIPLOMOVÁ PRÁCE 3D spektroskopie galaxií.
 MASARYKOVA UNIVERZITA P írodov decká fakulta Ústav teoretické fyziky a astrofyziky DIPLOMOVÁ PRÁCE 3D spektroskopie galaxií Lenka Janeková Vedoucí diplomové práce: RNDr. Bruno Jungwiert, Ph.D. Brno 2013
MASARYKOVA UNIVERZITA P írodov decká fakulta Ústav teoretické fyziky a astrofyziky DIPLOMOVÁ PRÁCE 3D spektroskopie galaxií Lenka Janeková Vedoucí diplomové práce: RNDr. Bruno Jungwiert, Ph.D. Brno 2013
ZIS OVANIE ANAEROBNÉHO PRAHU POMOCOU METÓDY IMPLEMENTOVANEJ DO MATLABU
 ZIS OVANIE ANAEROBNÉHO PRAHU POMOCOU METÓDY IMPLEMENTOVANEJ DO MATLABU Eva Jamrichová FMFI UK, Bratislava Abstrakt Pri výstavbe tréningového procesu je ve mi dôleºitým ukazovate om práve anaeróbny prah.
ZIS OVANIE ANAEROBNÉHO PRAHU POMOCOU METÓDY IMPLEMENTOVANEJ DO MATLABU Eva Jamrichová FMFI UK, Bratislava Abstrakt Pri výstavbe tréningového procesu je ve mi dôleºitým ukazovate om práve anaeróbny prah.
Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je spolufinancovaný zo zdrojov EÚ. Základné pojmy pravdepodobnosti
 Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je spolufinancovaný zo zdrojov EÚ Základné pojmy pravdepodobnosti Náhoda Pod náhodou možno rozumieť množstvo drobných faktorov, ktoré sa nedajú identifikovať.
Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je spolufinancovaný zo zdrojov EÚ Základné pojmy pravdepodobnosti Náhoda Pod náhodou možno rozumieť množstvo drobných faktorov, ktoré sa nedajú identifikovať.
Obsah. 2 Určenie objemu valčeka Teoretický úvod Postup merania a spracovanie výsledkov... 10
 Obsah 1 Chyby merania 1 1.1 áhodné a systematické chyby.................... 1 1.2 Aritmetický priemer a stredná kvadratická chyba......... 1 1.3 Rozdelenie nameraných dát..................... 3 1.4 Limitné
Obsah 1 Chyby merania 1 1.1 áhodné a systematické chyby.................... 1 1.2 Aritmetický priemer a stredná kvadratická chyba......... 1 1.3 Rozdelenie nameraných dát..................... 3 1.4 Limitné
MASARYKOVA UNIVERZITA ÚSTAV MATEMATIKY A STATISTIKY
 MASARYKOVA UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA ÚSTAV MATEMATIKY A STATISTIKY Diplomová práce BRNO 2014 MICHAL KOVÁČIK MASARYKOVA UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA ÚSTAV MATEMATIKY A STATISTIKY Metody testování
MASARYKOVA UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA ÚSTAV MATEMATIKY A STATISTIKY Diplomová práce BRNO 2014 MICHAL KOVÁČIK MASARYKOVA UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA ÚSTAV MATEMATIKY A STATISTIKY Metody testování
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY PREČO CHODÍ ČLOVEK V KRUHU JÁN DZÚRIK
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY PREČO CHODÍ ČLOVEK V KRUHU 2011 JÁN DZÚRIK UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY 45a87a64-1ec1-4718-a32f-6ba49c57d795
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY PREČO CHODÍ ČLOVEK V KRUHU 2011 JÁN DZÚRIK UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY 45a87a64-1ec1-4718-a32f-6ba49c57d795
Vplyv testosterónu na prežívanie lásky v romantických vzťahoch u mladých mužov
 Vplyv testosterónu na prežívanie lásky v romantických vzťahoch u mladých mužov RNDr. Jaroslava Durdiaková Školiteľka: prof. MUDr. Daniela Ostatníková, PhD. Fyziologický ústav, Lekárska fakulta, Univerzita
Vplyv testosterónu na prežívanie lásky v romantických vzťahoch u mladých mužov RNDr. Jaroslava Durdiaková Školiteľka: prof. MUDr. Daniela Ostatníková, PhD. Fyziologický ústav, Lekárska fakulta, Univerzita
METRICKÉ ÚLOHY V PRIESTORE
 1. ÚVOD METRICKÉ ÚLOHY V PRIESTORE Monika ĎURIKOVIČOVÁ 1 Katedra Matematiky, Strojnícka fakulta STU, Abstrakt: Popisujeme možnosti použitia programového systému Mathematica pri riešení špeciálnych metrických
1. ÚVOD METRICKÉ ÚLOHY V PRIESTORE Monika ĎURIKOVIČOVÁ 1 Katedra Matematiky, Strojnícka fakulta STU, Abstrakt: Popisujeme možnosti použitia programového systému Mathematica pri riešení špeciálnych metrických
NÁRODOHOSPODÁRSKY VÝZNAM
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a štatistiky NÁRODOHOSPODÁRSKY VÝZNAM ODVETVIA POL NOHOSPODÁRSTVO (SR) Diplomová práca Bc. Andrej
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a štatistiky NÁRODOHOSPODÁRSKY VÝZNAM ODVETVIA POL NOHOSPODÁRSTVO (SR) Diplomová práca Bc. Andrej
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY REKURENTNÉ POSTUPNOSTI
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Evidenčné číslo: 74b93af3-8dd5-43d9-b3f2-05523e0ba177 REKURENTNÉ POSTUPNOSTI 2011 András Varga UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Evidenčné číslo: 74b93af3-8dd5-43d9-b3f2-05523e0ba177 REKURENTNÉ POSTUPNOSTI 2011 András Varga UNIVERZITA KOMENSKÉHO V BRATISLAVE
Brownian Motion. An Undergraduate Introduction to Financial Mathematics. J. Robert Buchanan. J. Robert Buchanan Brownian Motion
 Brownian Motion An Undergraduate Introduction to Financial Mathematics J. Robert Buchanan 2010 Background We have already seen that the limiting behavior of a discrete random walk yields a derivation of
Brownian Motion An Undergraduate Introduction to Financial Mathematics J. Robert Buchanan 2010 Background We have already seen that the limiting behavior of a discrete random walk yields a derivation of
Errata for Stochastic Calculus for Finance II Continuous-Time Models September 2006
 1 Errata for Stochastic Calculus for Finance II Continuous-Time Models September 6 Page 6, lines 1, 3 and 7 from bottom. eplace A n,m by S n,m. Page 1, line 1. After Borel measurable. insert the sentence
1 Errata for Stochastic Calculus for Finance II Continuous-Time Models September 6 Page 6, lines 1, 3 and 7 from bottom. eplace A n,m by S n,m. Page 1, line 1. After Borel measurable. insert the sentence
Algoritmy metód vnútorného bodu v lineárnom programovaní
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Algoritmy metód vnútorného bodu v lineárnom programovaní RIGORÓZNA PRÁCA 14 Mgr. Marek KABÁT UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Algoritmy metód vnútorného bodu v lineárnom programovaní RIGORÓZNA PRÁCA 14 Mgr. Marek KABÁT UNIVERZITA KOMENSKÉHO V BRATISLAVE
3. Horninové prostredie / Rocks
 3.1 Základné charakteristiky geologickej a tektonickej stavby Basic features of geological and tectonic structure 3.2 Svahové pohyby Slope movements 3.3 Odvodená mapa radónového rizika Derived map of the
3.1 Základné charakteristiky geologickej a tektonickej stavby Basic features of geological and tectonic structure 3.2 Svahové pohyby Slope movements 3.3 Odvodená mapa radónového rizika Derived map of the
RESEARCH REPORT. ÚTIA AVČR, v.v.i., P.O.Box 18, Prague, Czech Republic Fax: (+420) ,
 Akademie věd České republiky Ústav teorie informace a automatizace, v.v.i. Academy of Sciences of the Czech Republic Institute of Information Theory and Automation RESEARCH REPORT Jan Šindelář, Václav
Akademie věd České republiky Ústav teorie informace a automatizace, v.v.i. Academy of Sciences of the Czech Republic Institute of Information Theory and Automation RESEARCH REPORT Jan Šindelář, Václav
TRHOVÉ ŠTRUKTÚRY: Monopol a Oligopol. Ing. Zuzana Staníková, PhD.
 TRHOVÉ ŠTRUKTÚRY: Monopol a Oligopol Rozdiely medzi dokonalou a nedokonalou konkurenciou Dokonalá konkurencia Nedokonalá konkurencia /Q 25 /Q 8 P=AR=MR 20 6 15 4 10 2 0 0 1 2 3 4 5 6 7 8 5 0 MR P=AR 0
TRHOVÉ ŠTRUKTÚRY: Monopol a Oligopol Rozdiely medzi dokonalou a nedokonalou konkurenciou Dokonalá konkurencia Nedokonalá konkurencia /Q 25 /Q 8 P=AR=MR 20 6 15 4 10 2 0 0 1 2 3 4 5 6 7 8 5 0 MR P=AR 0
Segmentace textury. Jan Kybic
 Segmentace textury Případová studie Jan Kybic Zadání Mikroskopický obrázek segmentujte do tříd: Příčná vlákna Podélná vlákna Matrice Trhliny Zvolená metoda Deskriptorový popis Učení s učitelem ML klasifikátor
Segmentace textury Případová studie Jan Kybic Zadání Mikroskopický obrázek segmentujte do tříd: Příčná vlákna Podélná vlákna Matrice Trhliny Zvolená metoda Deskriptorový popis Učení s učitelem ML klasifikátor
Modelovanie a simulácia logických systémov - proces návrhu íslicových systémov - CAD nástroje
 8 : Modelovanie a simulácia logických systémov - proces návrhu íslicových systémov - CAD nástroje Použitie MaS:. v procese návrhu a) špecifikácia správania sa overenie simuláciou b) modely funk ných prvkov
8 : Modelovanie a simulácia logických systémov - proces návrhu íslicových systémov - CAD nástroje Použitie MaS:. v procese návrhu a) špecifikácia správania sa overenie simuláciou b) modely funk ných prvkov
1 Matice a ich vlastnosti
 Pojem sústavy a jej riešenie 1 Matice a ich vlastnosti 11 Sústavy lineárnych rovníc a matice Príklad 11 V množine reálnych čísel riešte sústavu rovníc x - 2y + 4z + t = -6 2x + 3y - z + 2t = 13 2x + 5y
Pojem sústavy a jej riešenie 1 Matice a ich vlastnosti 11 Sústavy lineárnych rovníc a matice Príklad 11 V množine reálnych čísel riešte sústavu rovníc x - 2y + 4z + t = -6 2x + 3y - z + 2t = 13 2x + 5y
ŠTEFAN GUBO. Riešenie úloh nelineárnej regresie pomocou tabuľkového kalkulátora. Solution of nonlinear regression tasks using spredsheet application
 Wydawnictwo UR 2016 ISSN 2080-9069 ISSN 2450-9221 online Edukacja Technika Informatyka nr 1/15/2016 www.eti.rzeszow.pl DOI: 10.15584/eti.2016.1.27 ŠTEFAN GUBO Riešenie úloh nelineárnej regresie pomocou
Wydawnictwo UR 2016 ISSN 2080-9069 ISSN 2450-9221 online Edukacja Technika Informatyka nr 1/15/2016 www.eti.rzeszow.pl DOI: 10.15584/eti.2016.1.27 ŠTEFAN GUBO Riešenie úloh nelineárnej regresie pomocou
Ash Wednesday. First Introit thing. * Dómi- nos. di- di- nos, tú- ré- spi- Ps. ne. Dó- mi- Sál- vum. intra-vé-runt. Gló- ri-
 sh Wdsdy 7 gn mult- tú- st Frst Intrt thng X-áud m. ns ní- m-sr-cór- Ps. -qu Ptr - m- Sál- vum m * usqu 1 d fc á-rum sp- m-sr-t- ó- num Gló- r- Fí- l- Sp-rí- : quó-n- m ntr-vé-runt á- n-mm c * m- quó-n-
sh Wdsdy 7 gn mult- tú- st Frst Intrt thng X-áud m. ns ní- m-sr-cór- Ps. -qu Ptr - m- Sál- vum m * usqu 1 d fc á-rum sp- m-sr-t- ó- num Gló- r- Fí- l- Sp-rí- : quó-n- m ntr-vé-runt á- n-mm c * m- quó-n-
Le classeur à tampons
 Le classeur à tampons P a s à pa s Le matériel 1 gr a n d cla s s e u r 3 pa pi e r s co o r d o n n é s. P o u r le m o d è l e pr é s e n t é P a p i e r ble u D ai s y D s, pa pi e r bor d e a u x,
Le classeur à tampons P a s à pa s Le matériel 1 gr a n d cla s s e u r 3 pa pi e r s co o r d o n n é s. P o u r le m o d è l e pr é s e n t é P a p i e r ble u D ai s y D s, pa pi e r bor d e a u x,
Univerzita Komenského v Bratislave Fakulta Managementu Katedra stratégie a podnikania. Aplikácia nekooperatívnej teórie hier v
 Univerzita Komenského v Bratislave Fakulta Managementu Katedra stratégie a podnikania Aplikácia nekooperatívnej teórie hier v manažérskom rozhodovaní Diplomová práca Tomáš Kubiš Odbor: Manažment Špecializácia:
Univerzita Komenského v Bratislave Fakulta Managementu Katedra stratégie a podnikania Aplikácia nekooperatívnej teórie hier v manažérskom rozhodovaní Diplomová práca Tomáš Kubiš Odbor: Manažment Špecializácia:
